Preprint
Article
Leader-following Output Feedback H∞ Consensus of Fractional-order Multi-agent Systems with Input Saturation
This version is not peer-reviewed.
Submitted:
30 September 2024
Posted:
03 October 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
This paper investigates the leader-following H∞ consensus of fractional-order multi-agent systems (FOMASs) under input saturation via the output feedback. Based on the bounded real lemma for FOSs, the sufficient conditions of H∞ consensus for FOMASs are provided in α∈0,1 and 1,2, respectively. Furthermore, the iterative linear matrix inequalities (ILMIs) approaches are applied for solving quadratic matrix inequalities (QMIs). The ILMI algorithms show a method to derive initial values and transform QMIs into LMIs. Mathematical tools are employed to transform the input saturation issue into optimal solution of LMIs for estimating stable regions. The ILMI algorithms avoid the conditional constraints on matrix variables during the LMIs construction and reduce conservatism. The approach does not disassemble the entire MASs by transformations to the Laplacian matrix, instead adopting a holistic analytical perspective to obtain gain matrices. In the end, numerical examples are conducted to validate the efficiency of the approach.
Keywords:
fractional-order multi-agent systems
; H∞ control
; static output feedback
; iterative linear matrix inequality
1. Introduction
In recent decades, multi-agent systems (MASs) have been the subject of extensive research, resulting in substantial achievements on the field. MASs are utilized in many practical domains, including traffic management [1] and power systems [2,3]. These applications rely significantly on the consensus of MASs, which involves the states of agents converging to a desired state by the neighboring information [4]. Extensive studies are conducted on the consensus for MASs with integer-order differential models. However, integer-order models are inadequate for accurately representing some non-classical phenomena in various physical systems.
As the advancement of fractional calculus theory, fractional-order systems (FOSs) and fractional-order MASs (FOMASs) have emerged as a significant direction. Many achievements have been made in integer-order systems [5,6,7], but the utilization of fractional derivatives allows for a more comprehensive understanding of the characteristics of materials and systems exhibiting power-law, nonlocal, or long-term memory. FOSs offer enhanced capabilities for modelling and analysing complex systems, e.g., electrical systems [8,9], economic systems [10], motion models [11], and biological models [12,13]. The stability of control systems is fundamental problem, certainly including those involving FOSs. It is not possible to derive the stability criteria of FOSs directly from those of integer-order systems. Fortunately, in [14], authors establish the LMI-based stability criteria and design a method for robust feedback state stabilization control for commensurate FOSs with and . In [15], a necessary and sufficient condition in unified LMIs formulation is provided to ensure the stability of FOSs within . The aforementioned study makes a contribution to the consensus problem of FOMASs. In [16], the consensus of FOMASs with time delay is studied. Using the Lyapunov method, some consensus criteria are proposed to guarantee the consensus. Focusing on singular systems, the authors in [17] investigate the observer-based consensus problem of singular FOMASs. Then, the paper provides the corresponding control protocol and the calculation method of gain matrices. In [18], the distributed fixed-time consensus for FOMASs with a dynamic virtual leader under external disturbances is investigated, and a sliding-mode control protocol is designed. Meanwhile, the singular perturbation FOMASs are modeled and studied in [19], which provides a sufficient condition for consensus. Nevertheless, the consensus problem of FOMASs in these results is all based on state feedback. In most cases, only the measurement output of the agents is available, which indicates that the above method has certain limitations.
In comparison to the state feedback, the control via output feedback is a challenging problem, largely due to the affect of measurement matrices. Furthermore, the consensus of FOMASs via output feedback is a highly intricate issue. The stability criteria of FOSs with comprise two matrix variables, whereas in , the matrix variable is related to the order number. In [20,21,22,23], static output feedback control is employed for FOSs, and a matrix exchange condition is utilized to integrate matrix variable with gain matrices. This approach utilizes singular value decomposition (SVD) of the measurement matrices. Nevertheless, this approach imposes constraints on the form of matrix variables and tends to be conservative. Authors in [24] also adopt some strong assumptions to get a feasible solution, which brings conservatism. Similarly, in the output feedback consensus of FOMASs, the limitation often exist. In [20], sufficient conditions are provided for the leader-following consensus of singular FOMASs with . The authors in [25] also do the analogous study, and the SVD method is always indispensable. To complicate matters, disturbances persist in actual systems, and the output information transmitted between the agents contains the disturbances.
For FOMASs, the control method provides substantial benefits in addressing system uncertainty, robustness optimization, and other pertinent issues. The paper [26] derives the bounded real lemma for FOSs and establishes the foundation for control. In [27], a proposal is made to extend the application of control method from integer-order systems to FOSs. Robust fault-tolerant control for FOSs with actuator faults and uncertainties is addressed in [28] through the design of an output feedback controller. For singular FOSs, a state feedback control strategy is presented that guarantees the prescribed performance in [29]. These works form the foundation o the consensus of FOMASs. In [30], the admissible consensus of fuzzy singular FOMASs is considered, a sufficient condition for the system achieving admissible consensus while satisfying performance. The paper [31] investigates the consensus problem for discrete-time FOMASs. However, the relatively research is little. The output feedback consensus remains a challenging field. Meanwhile, the control input saturation is a common feature of practical engineering systems, due to physical limitations [32,33,34]. This renders the output feedback consensus for FOMASs a complex process.
The discussion provides the impetus for the ILMI algorithms towards the leader-following consensus of FOMASs with input saturation via output feedback. The contributions are as following:
(i) Based on the real bound lemma of FOSs, sufficient conditions for output feedback consensus of FOMASs in and are provided. The proposed method adopts a holistic analytical perspective to the entire system, which differs from the decomposition of the entire MASs.
(ii) For solving the QMIs, the ILMI algorithms are provided, which propose a calculation method for initial values. Based on the stability region of FOSs, the iterative condition are designed to guarantee the consensus condition of FOMASs. This paper delves deeper into the issue of the input saturation, which is reframed as an LMI-based optimisation problem. The ILMI algorithms circumvent the necessity for matrix exchange conditions from the SVD method. No strong assumptions are required for feasible solutions, and it reduces the conservatism.
Notations: Given a matrix A, sym denotes , where is the transpose of A, and her, where is conjugate transpose of matrix A. and represent that A is positive definite and negative definite, respectively. Then denotes that A is negative semi-definite and symbol ★ stands for the symmetric part. The Kronecker product is represented by ⊗. arg(·) denotes the argument of complex numbers, and spec(A) indicates the spectrum of matrix A. stands for sets of real matrices. diag(·) represents a diagonal matrix. With , denote , .
2. Problem Formulation and Preliminaries
An MAS consists of followers represented by the undirected graph , where presents a set of followers, and is the edge set. The adjacency matrix is , and if , , otherwise .
Furthermore, denote the communication graph between the leader and followers as . Define for representing the communication. If follower i receives the information from the leader, then , otherwise . The Laplacian matrix is defined as , where
Consider the FOMAS under actuator saturation, and the followers are described by
where , , , , and denote the state, control input, measured output, controlled output, and disturbances, respectively; A, B, , , , C, and are constant real matrices; represents the Caputo fractional derivative of as
and is the Euler Gamma function; the saturation function sat for is denoted as
The leader is described by
where is the state, and is the output.
For achieving consensus of the FOMAS in (1) and (2), a distributed consensus protocol is carried out by
The initial values are considered as . Denote the state trajectory as , and the domain of attraction is
For , let
where denotes the s-th row of the matrix F; denotes the region where does not saturate.
Lemma 1
.
Lemma 2
The system in (6) is stable if and only if
Remark 1.
Based on Lemma 2, if the eigenvalues of A are in the region of eigenvalues shown in Figure 1, it is obvious that the system in (6) is stable. Meanwhile, the system in (6) is also stable even if the eigenvalues of A are moved by unit in the positive direction of the x-axis, where . Thus, the presence of eigenvalues of A in a specific region of Figure 1 serves as a sufficient condition for the system stability.
Lemma 3
Definition 2
([39]). Define the norm of transfer function as where is the maximum singular value of a matrix.
3. Main Results
This section introduces the iterative algorithms for solving consensus of FOMASs via output feedback.
3.1. ILMI Algorithm for Output Feedback Consensus with
In this subsection , it is essential to reference the following lemmas, which form the basis of the ILMI algorithms. To facilitate the derivation process, the matrices are expressed as follows:
Lemma 6.
Proof.
In the case of of Lemma 4, consider matrices , such that
Then introduce a congruence transformation. Pre- and post- multiplying (13) by
and its transpose, one obtains
Meanwhile, there exist matrices and satisfy
To verify (14), only set X and Y as
which also satisfy and . It is easy to see , which proves (14). Then (13) is transformed into
And the positive definite property of is proved by pre- and post- multiplying it by .
Apply (15) in the consensus problem of the FOMAS in (4) via output feedback. Then, the consensus of the FOMAS in (4) without input saturation is achieved and is guaranteed with , if there exist X, Y, K, and F such that (8) and
where
Then, using basic matrix operations, one simplifies inequality (16) into (12). ;□
Lemma 7.
Proof.
Lemma 8.
Proof.
Lemma 9.
Proof.
Since , (22) holds, then (19) is guaranteed. Based on Lemma 8, if (19), (8), and (23) hold, the FOMAS in (4) achieves consensus without input saturation.
Then consider that input is limited. According to the statement in Lemma 3, the FOMAS achieves consensus for From (23), using Schur complement, one obtains
So holds, for , , and . Therefore, is estimated by . □
According to Lemma 9, the stable region is approximated by utilizing optimization theory:
It is evident that the LMIs from (22) display the nonlinear characteristics, particularly due to the incorporation of product terms. Nevertheless, if the matrix S is predetermined and holds constant, the QMIs (22) are simplied to into LMIs, which inherently possess the convexity. This transformation allows the LMIs to contain feasible solutions for the gain matrices K and F. Consequently, this paper presents an iterative algorithm aimed at solving (22) through the following steps.
Prior to commencing the ILMIs algorithm, it is essential to define the following notation:
Algorithm 1.
Step 1: Set and . Select and solve the Riccati equation:
Step 2: Set
Maximize subject to the following LMIs:
Step 3.
Denote as the maximum value of . If holds, go to Step 7.
Step 4.
Step 5.
Give a small tolerance . If holds, then go to Step 6, else set , , , and return to Step 2.
Step 6.
The leader-following consensus of the FOMAS in (4) may not be achieved by static output feedback, stop.
Step 7.
Remark 2.
Remark 3.
To verity the necessity of Step 1, one considers inequality (20), where equality holds with . S is closed to , then the solutions of (19) is also close to those of (18). For obtaining the appropriate initial value , consider the following equation based on (18):
where represents the product term . However, if is set to a certain positive definite matrix directly, the solution of is difficult to obtain and may not be formally consistent with that in . For convenient calculation, setting , it yields
where is the sub-block of . After setting and obtaining the solution of X, it is obvious that the results of other sub-blocks are obtained and is automatically generated. Therefore, it is only necessary to set in Algorithm 1.
Remark 4.
Considering (26) from Step 2, the system matrix is substituted with , whose eigenvalues are translated unit towards the x-axis relative to the eigenvalues of with .
Remark 5.
In Step 4, satisfy and its trace is 0. Thus, the minimization problem only involves the trace of .
3.2. ILMI Algorithm for Output Feedback Consensus with
In the section, the case of is considered. Complex numbers exist in (10) of Lemma 4 and bring difficulties to the solution. Thus, similar to the case in , the following lemmas are given for obtaining the gain matrices. Then the parameter matrices are set as
where , , and are shown in (11).
Lemma 10.
Proof.
Due to the similarity in the proof process with Lemma 7, 8, and 9, the following lemmas do not provide the relevant proof.
Lemma 11.
Lemma 12.
With and a given scalar , the leader-following consensus of the FOMAS in (4) without input saturation is achieved and is guaranteed, if there exist , , , and S with appropriate dimension such that
where , , , , and are shown in (28).
Lemma 13.
Similarly, as with the issue pertaining to , the domain of attraction is estimated by the following method:
In addition, (35) are not LMIs and difficult to solve with the LMI toolbox in MATLAB. Accordingly, the following iterative algorithm is provided for obtain matrices K and F. To simplify writing, one denotes
Algorithm 2.
Step 1: Set and select , then solve the Riccati equation:
Step 2: Set
Maximize subject to the following LMIs:
Step 3: Denote as the maximum value of , if , go to Step 7.
Step 4:
Minimize trace subject to the LMIs (39) and (38) with until the minimized trace is obtained.
Step 5:
Give a small tolerance , if , then go to Step 6, else set and , and go back to Step 2.
Step 6:
The leader-following consensus of the FOMAS in (4) may not be achieved by static output feedback, stop.
Remark 8.
In order to provide greater clarity, the inequalities are not presented in full detail. , , , and are shown in (28), and p is the iterative times. is from Lemma 13.
Remark 9.
The iterative process is similar to that in the Algorithm 1. Due to the difficulty in solving
is solved by (37), which is the sub-block in the first row and first column in the consolidation of the left matrices . In Step 2, is constructed and close to .
Remark 10.
After certain experiments, the initial value is related to the convergence of the algorithm. Then, the select of and in Step 1 indirectly influences the convergence property. In some cases, and are set as , where W is nonsingular. is also a choice, which leads to a convergent result.
Remark 11.
In most existing study, the consensus problem of MAS relies on transformation towards to , such as , where J is a diagonal matrix containing eigenvalues of . If each subsystem matrices satisfy the stability condition, i.e., , the consensus of the MAS is achieved. However, when an MAS contains disturbances or nonlinear terms, the analysis process becomes complex after multiplying the parameter matrix with the transformation matrix T. In contrast, ILMI algorithms contribute the holistic analysis of the MAS, which facilitates performance assessment under disturbances.
Remark 12.
From Algorithm 1 and 2, it is evident that no constraint is imposed on the matrix variables containing X and Y.
The existing main method involves SVD towards to , such as , where U and V are the unitary matrices. Then, the structure of X is restricted as
or a upper triangular matrix in special cases for satisfying exchange condition , where is another matrix variable. Note that, for satisfying exchange condition, the stability criterion used is similar to that of integer-order system, which is independent of the order . Thus, the method contains the conservatism.
Remark 13.
From Table 1, it is shown that this paper takes into account multiple scenarios in the study of FOMASs with or . In existing literature, there is relatively little research on consensus for FOMASs, e.g., [30]. With the further consideration of output feedback, the limitation to the matrix variables is a common feature of many articles and an essential condition. The ILMI algorithms presented in this article avoid this limitation and are used in cases where there are disturbances from the output information and the control input saturation. Then, the ILMI algorithms have a broad scope of applicability.
4. Numerical Examples
This section presents two numerical examples to verify the effectiveness of the proposed ILMI algorithms with and , respectively.
Example 1.
Based on Algorithm 1, select in Step 1. Solve the equation (25) and obtain
Then is obtained from Step 2.
Maximize subject to (39) and (27) and the result is . Go to Step 7 and maximize subject to (8), (37), and (23) with . The following feasible solutions are obtained:
Consider the case as . Calculating eig, one obtains j, j, j, j, j, j, j, j, , , , and , which satisfy the stability condition in Lemma 2.
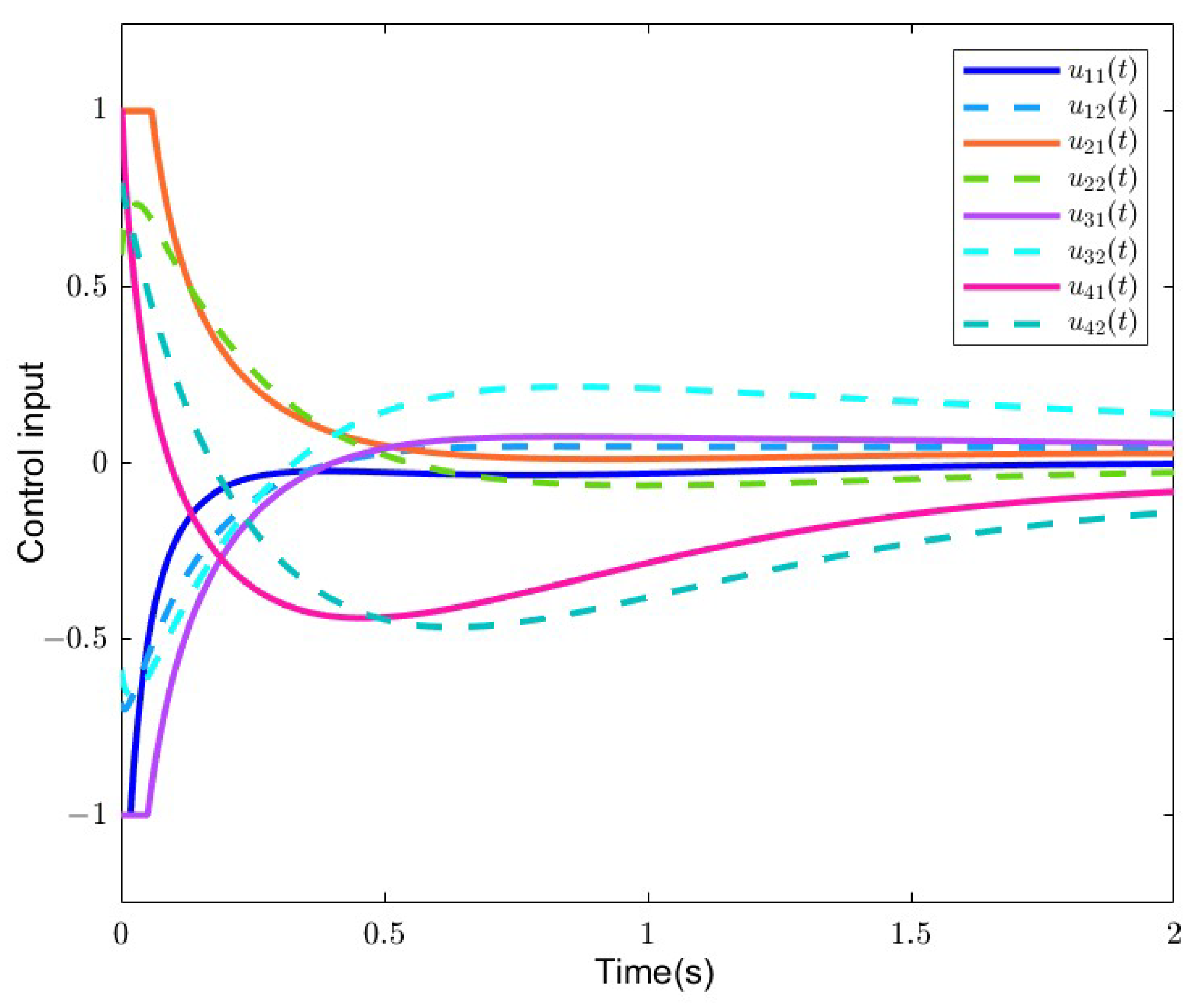
The state of each agent and the control input are shown as Figure 4. At the beginning, the input is saturated. From Figure 4, it is shown that the FOMAS has achieved consensus.
Figure 3.
The control input of each agent in Example 1
Remark 14.
From the eigenvalues in the results, it is obvious that j contain positive real parts. As mentioned in Remark 12, the stability criterion is not related to for the exchange condition . Thus, the eigenvalues of matrix must have negative real part. In other words, there exist gain matrices for the consensus of FOMASs, but they may not be obtained by using the SVD method. Thus, the ILMI algorithms in this paper are less conservative than the SVD method.
Example 2.
Consider the FOMAS in (4) with and set . The undirected graph is shown in Figure 5 and parameter matrices are as follow:
The eigenvalues of A are , j, and j, the latter two of which have positive real parts and satisfy
Then the consensus of FOMAS is not achieved. Given , the equation (37) has a feasible solution as
From Step 2, is set immediately.
Maximize subject to (39) and (38), then one obtains . Thus, go to Step 4 and minimize trace subject to the LMIs (39) and (38) with . The result is
Set and obtain . Then, maximize subject to (39) and (38), then one obtains . Jump to Step 7, and maximize subject to the LMIs (23), , and (35) with . The following feasible solutions are as
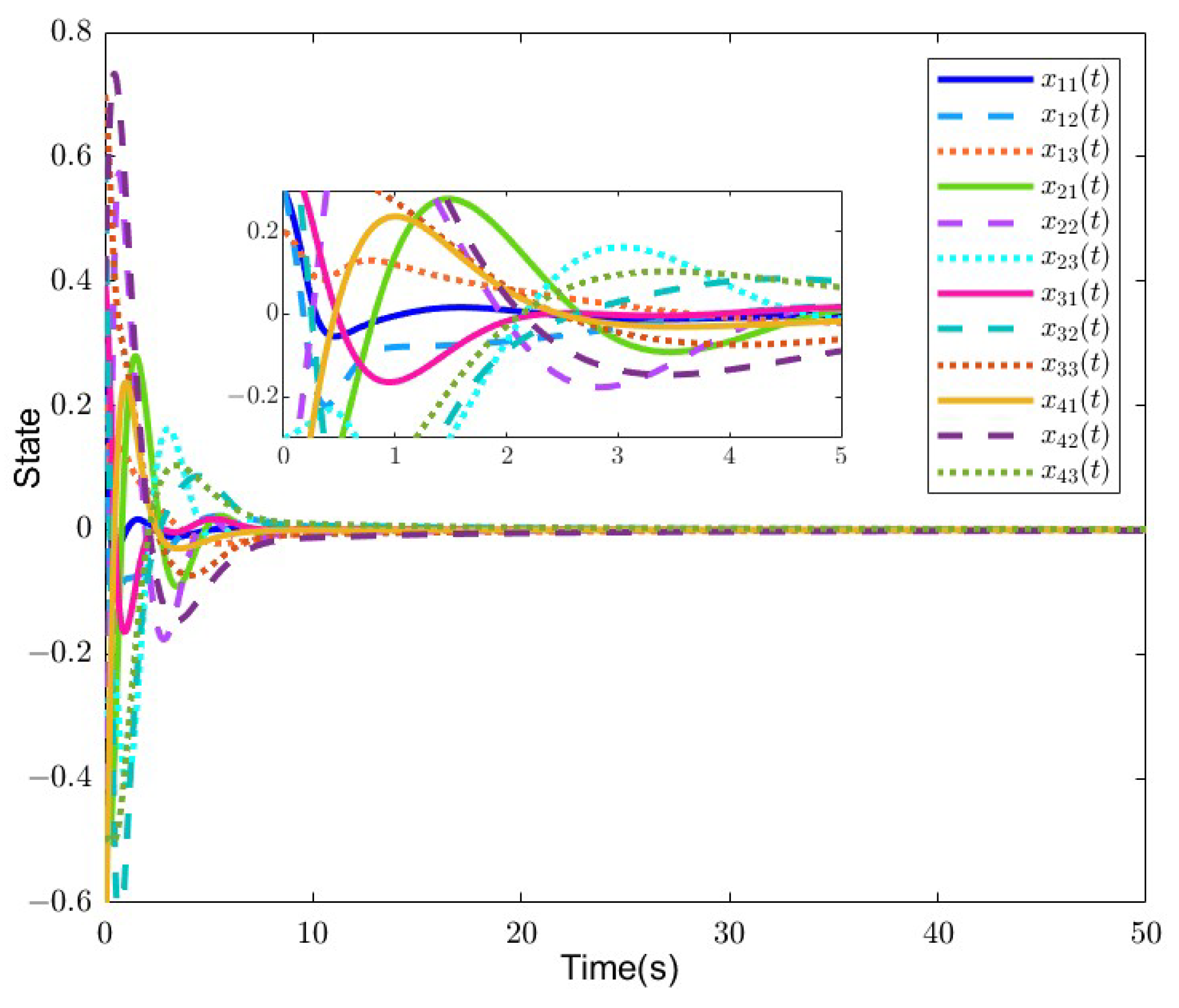
There exists the input saturation in FOMAS from Figure 6. The state of each agent is shown in Figure 7. It is shown that the FOMAS has achieved consensus.
One also chooses other for different initial values . In the start of algorithm, the positive definite matrix is selected as , where
Solve equation (37) and obtain
Then, maximize subject to (39) and (38), and the result is . Go to Step 7. The subsequent solving process is omitted.
Remark 15.
It is seen that the number of iterations in is less than that in . is convenient to set, but I is a diagonal matrix, which differs from the under general conditions. Thus, the choice of and affects the number of iterations. When the algorithm cannot converge, it may be considered to replace the initial value.
5. Conclusion
The leader-following consensus of FOMASs under input saturation via the output feedback has been investigated. Lemmas 8 and 12 have provided sufficient conditions of consensus for FOMAS in (4) with and , respectively. Additionally, based on the ILMI approach, the Algorithms 1 and 2 have been presented to compute the gain matrices. In both ILMI algorithms, the methods to derive initial values are also given and ILMI algorithms have solved the consensus problem for FOMASs under actuator saturation. The algorithms are effective and convergent, avoiding matrix exchange condition in the SVD method and strong assumption. The method also provides a holistic approach for calculating the gain matrices of MASs. Eventually, numerical examples have been conducted to validate the efficiency of the proposed approach.
Author Contributions
Conceptualization, methodology, software, and validation, H.-S.X. and D.B.; formal analysis, D.B.; data curation, H.-S.X.; writing—original draft, H.-S.X.; writing—review and editing, H.-S.X. and D.B.; visualization, H.-S.X. and Q.-G.W.; supervision, Q.-G.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 62103093, the National Key Research and Development Program of China under Grant 2022YFB3305905, the Fundamental Research Funds for the Central Universities under Grant N2224005-3, and the National Key Research and Development Program Topic under Grant 2020YFB1710003.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, J.; Zhang, J.; Wang, H. Urban traffic control in software defined internet of things via a multi-agent deep reinforcement learning approach. IEEE Transactions on Intelligent Transportation Systems 2020, 22, 3742–3754. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Transactions on Power Systems 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Xu, X.; Jia, Y.; Xu, Y.; Xu, Z.; Chai, S.; Lai, C.S. A multi-agent reinforcement learning-based data-driven method for home energy management. IEEE Transactions on Smart Grid 2020, 11, 3201–3211. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artificial Intelligence Review 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Zhang, J.X.; Ding, J.; Chai, T. Fault-tolerant prescribed performance control of wheeled mobile robots: A mixed-gain adaption approach. IEEE Transactions on Automatic Control 2024. [Google Scholar] [CrossRef]
- Zhang, J.X.; Wang, Q.G.; Ding, W. Global output-feedback prescribed performance control of nonlinear systems with unknown virtual control coefficients. IEEE Transactions on Automatic Control 2021, 67, 6904–6911. [Google Scholar] [CrossRef]
- Zhang, J.X.; Xu, K.D.; Wang, Q.G. Prescribed performance tracking control of time-delay nonlinear systems with output constraints. IEEE/CAA Journal of Automatica Sinica 2024, 11, 1557–1565. [Google Scholar] [CrossRef]
- Rana, M.; Pande, R.; Kukreti, K. Design of RF MEMS piezoelectric disk resonator for 5G communication. Materials Today: Proceedings 2023, 73, 13–17. [Google Scholar] [CrossRef]
- Radwan, A.G.; Emira, A.A.; AbdelAty, A.M.; Azar, A.T. Modeling and analysis of fractional order DC-DC converter. ISA Transactions 2018, 82, 184–199. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Khan, M.A. Fractional investigation of bank data with fractal-fractional Caputo derivative. Chaos, Solitons & Fractals 2020, 131, 109528. [Google Scholar]
- Yang, F.; Wang, P.; Wei, K.; Wang, F. Investigation on nonlinear and fractional derivative Zener model of coupled vehicle-track system. Vehicle System Dynamics 2020, 58, 864–889. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons & Fractals 2020, 135, 109811. [Google Scholar]
- Ghanbari, B. A fractional system of delay differential equation with nonsingular kernels in modeling hand-foot-mouth disease. Advances in Difference Equations 2020, 2020, 536. [Google Scholar] [CrossRef]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo state feedback stabilization of commensurate fractional order systems. In Proceedings of the 2009 European Control Conference (ECC). IEEE; 2009; pp. 3395–3400. [Google Scholar]
- Zhang, X.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0< α < 2. IEEE Transactions on Circuits and Systems II: Express Briefs 2020, 67, 3237–3241. [Google Scholar]
- Cheng, Y.; Hu, T.; Li, Y.; Zhang, X.; Zhong, S. Delay-dependent consensus criteria for fractional-order Takagi-Sugeno fuzzy multi-agent systems with time delay. Information Sciences 2021, 560, 456–475. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.X.; Zhang, X. Fuzzy control of singular fractional order multi-agent systems with actuator saturation. Information Sciences 2024, 665, 120397. [Google Scholar] [CrossRef]
- Zamani, H.; Khandani, K.; Majd, V.J. Fixed-time sliding-mode distributed consensus and formation control of disturbed fractional-order multi-agent systems. ISA Transactions 2023, 138, 37–48. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Pedrycz, W.; Yang, S.H.; Boutat, D. Consensus of TS fuzzy fractional-Order, singular perturbation, multi-agent systems. Fractal and Fractional 2024, 8, 523. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Wang, Y.; Zhang, K. Leader-following consensus conditions for fractional-order descriptor uncertain multi-agent systems with 0< α< 2 via output feedback control. Journal of the Franklin Institute 2020, 357, 2263–2281. [Google Scholar]
- Zhang, X.; Han, Z. Static and dynamic output feedback control for polytopic uncertain fractional order systems with 0< μ< 1. International Journal of Control, Automation and Systems 2023, 21, 52–60. [Google Scholar]
- N’doye, I.; Voos, H.; Darouach, M.; Schneider, J.G. Static output feedback H∞ control for a fractional-order glucose-insulin system. International Journal of Control, Automation and Systems 2015, 13, 798–807. [Google Scholar] [CrossRef]
- Sadabadi, M.S.; Peaucelle, D. From static output feedback to structured robust static output feedback: A survey. Annual reviews in control 2016, 42, 11–26. [Google Scholar] [CrossRef]
- Wei, Y.; Peter, W.T.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Transactions 2017, 69, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, D.; Pan, F. Output consensus for fuzzy singular multi-agent fractional order systems with actuator saturation. IEEE Transactions on Circuits and Systems II: Express Briefs 2022, 69, 3465–3469. [Google Scholar] [CrossRef]
- Liang, S.; Wei, Y.H.; Pan, J.W.; Gao, Q.; Wang, Y. Bounded real lemmas for fractional order systems. International Journal of Automation and Computing 2015, 12, 192–198. [Google Scholar] [CrossRef]
- Padula, F.; Alcántara, S.; Vilanova, R.; Visioli, A. H∞ control of fractional linear systems. Automatica 2013, 49, 2276–2280. [Google Scholar] [CrossRef]
- Li, H.; Yang, G.H. Dynamic output feedback H∞ control for fractional-order linear uncertain systems with actuator faults. Journal of the Franklin Institute 2019, 356, 4442–4466. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Basin, M.V. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica 2022, 135, 109962. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, D.; Pan, F. Admissible H∞ control of fuzzy singular fractional order multi-agent systems with external disturbances. IEEE Transactions on Automation Science and Engineering 2023. [Google Scholar] [CrossRef]
- An, C.; Su, H.; Chen, S. H∞ consensus for discrete-time fractional-order multi-agent systems with disturbance via Q-learning in zero-sum games. IEEE Transactions on Network Science and Engineering 2022, 9, 2803–2814. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, Z.; Yu, Y.; Guo, L.; Yang, H. Active disturbance rejection control for a pneumatic motion platform subject to actuator saturation: An extended state observer approach. Automatica 2019, 107, 353–361. [Google Scholar] [CrossRef]
- Selvaraj, P.; Sakthivel, R.; Ahn, C.K. Observer-based synchronization of complex dynamical networks under actuator saturation and probabilistic faults. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2018, 49, 1516–1526. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, H.; Mu, Y.; Sun, J. Fault-tolerant fuzzy-resilient control for fractional-order stochastic underactuated system with unmodeled dynamics and actuator saturation. IEEE Transactions on Cybernetics 2023, 54, 988–998. [Google Scholar] [CrossRef]
- Pan, H.; Yu, X.; Guo, L. Admissible leader-following consensus of fractional-order singular multiagent system via observer-based protocol. IEEE Transactions on Circuits and Systems II: Express Briefs 2018, 66, 1406–1410. [Google Scholar] [CrossRef]
- Fang, H.; Lin, Z.; Hu, T. Analysis of linear systems in the presence of actuator saturation and L2-disturbances. Automatica 2004, 40, 1229–1238. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational engineering in systems applications. Lille, France, 1996, Vol. 2, pp. 963–968.
- Lim, Y.H.; Oh, K.K.; Ahn, H.S. Stability and stabilization of fractional-order linear systems subject to input saturation. IEEE Transactions on Automatic Control 2013, 58, 1062–1067. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Basin, M.V. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica 2022, 135, 109962. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.X.; Zhang, X. Generalized criteria for admissibility of singular fractional order systems. Fractal and Fractional 2023, 7, 363. [Google Scholar] [CrossRef]
- Xiong, M.; Tan, Y.; Du, D.; Zhang, B.; Fei, S. Observer-based event-triggered output feedback control for fractional-order cyber–physical systems subject to stochastic network attacks. ISA Transactions 2020, 104, 15–25. [Google Scholar] [CrossRef]
- Jin, K.; Zhang, X. Output feedback stabilization of type 2 fuzzy singular fractional-order systems with mismatched membership functions. Soft Computing 2023, 27, 4917–4929. [Google Scholar] [CrossRef]
- Ji, Y.; Qiu, J. Stabilization of fractional-order singular uncertain systems. ISA Transactions 2015, 56, 53–64. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, W. Robust H∞ adaptive output feedback sliding mode control for interval type-2 fuzzy fractional-order systems with actuator faults. Nonlinear Dynamics 2021, 104, 537–550. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Chen, G. On H∞ and H2 performance regions of multi-agent systems. Automatica 2011, 47, 797–803. [Google Scholar] [CrossRef]
Figure 1.
Stability region of the system in (6) and region of spec (a) and (b) .
Figure 1.
Stability region of the system in (6) and region of spec (a) and (b) .
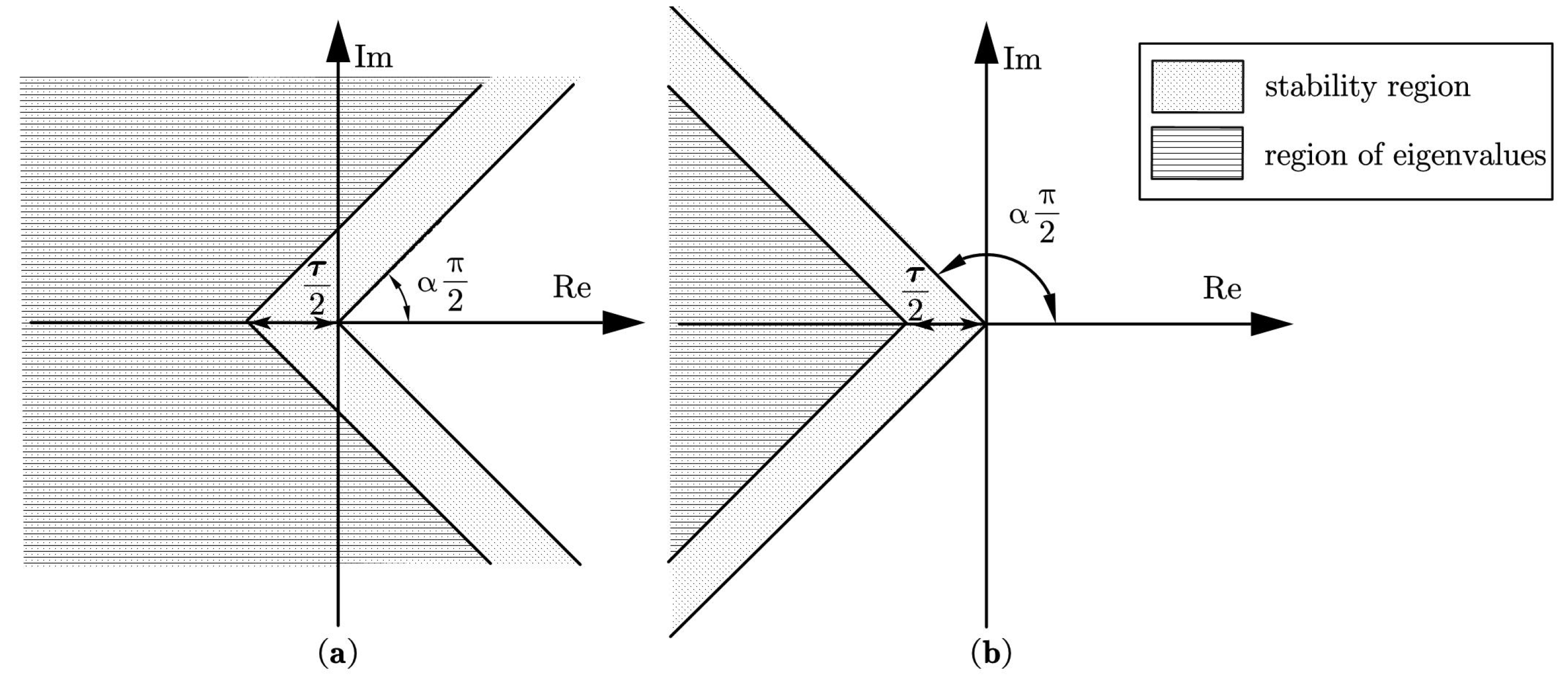
Figure 2.
The weighted undirected graph in Example 1.
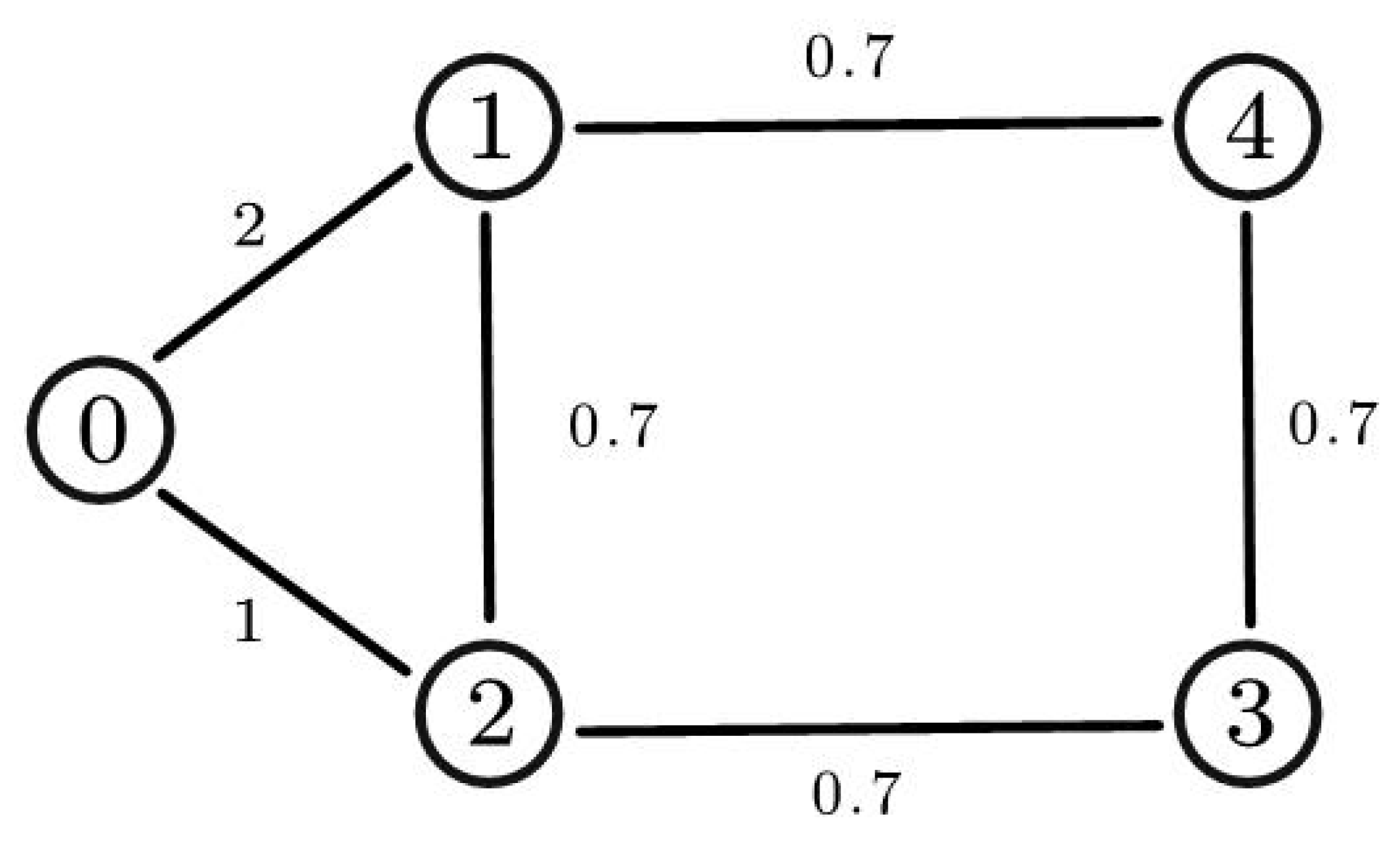
Figure 4.
The state of each agent in Example 1
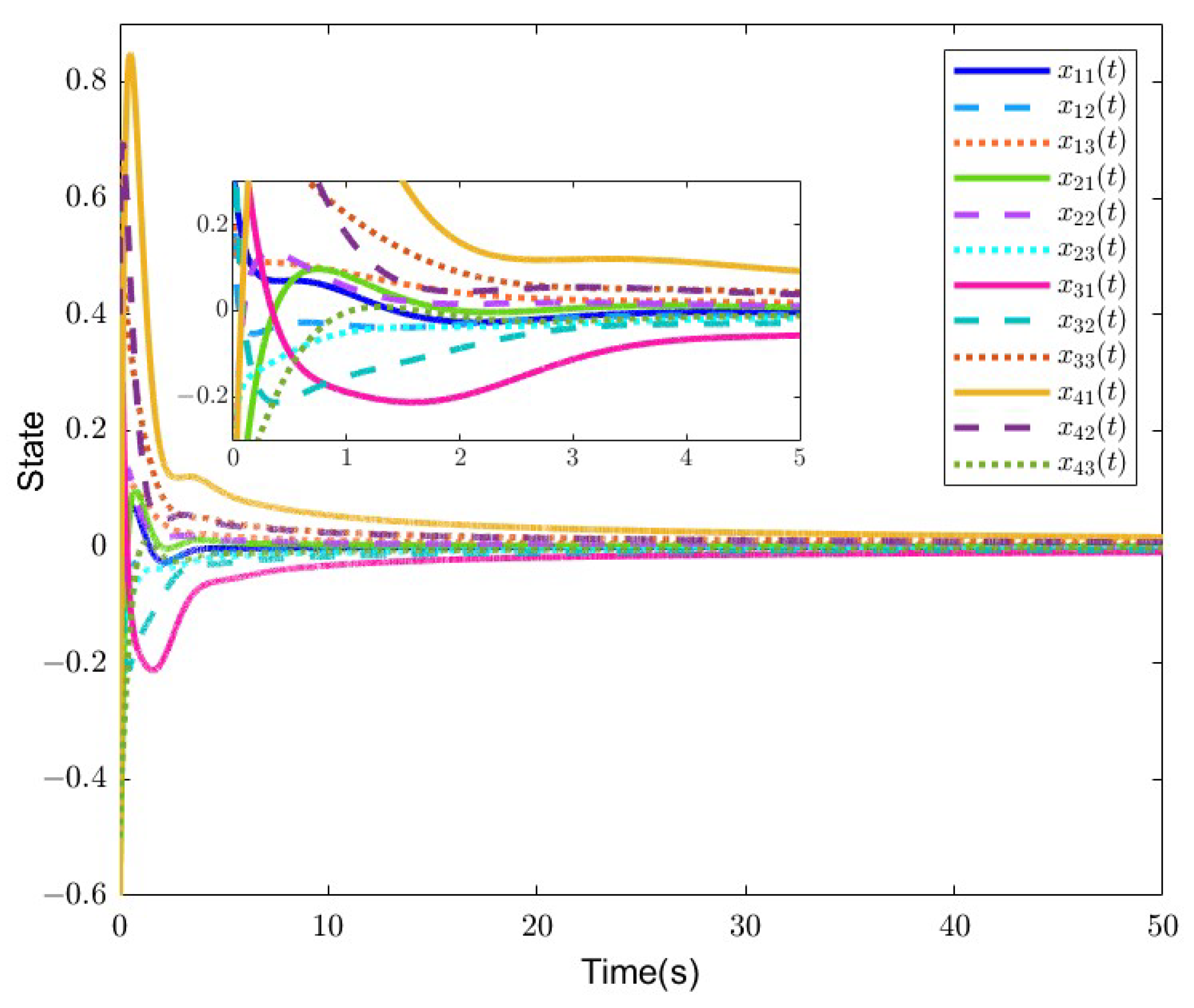
Figure 5.
The weighted undirected graph in Example 2.
Figure 6.
The control input of each agent in Example 2
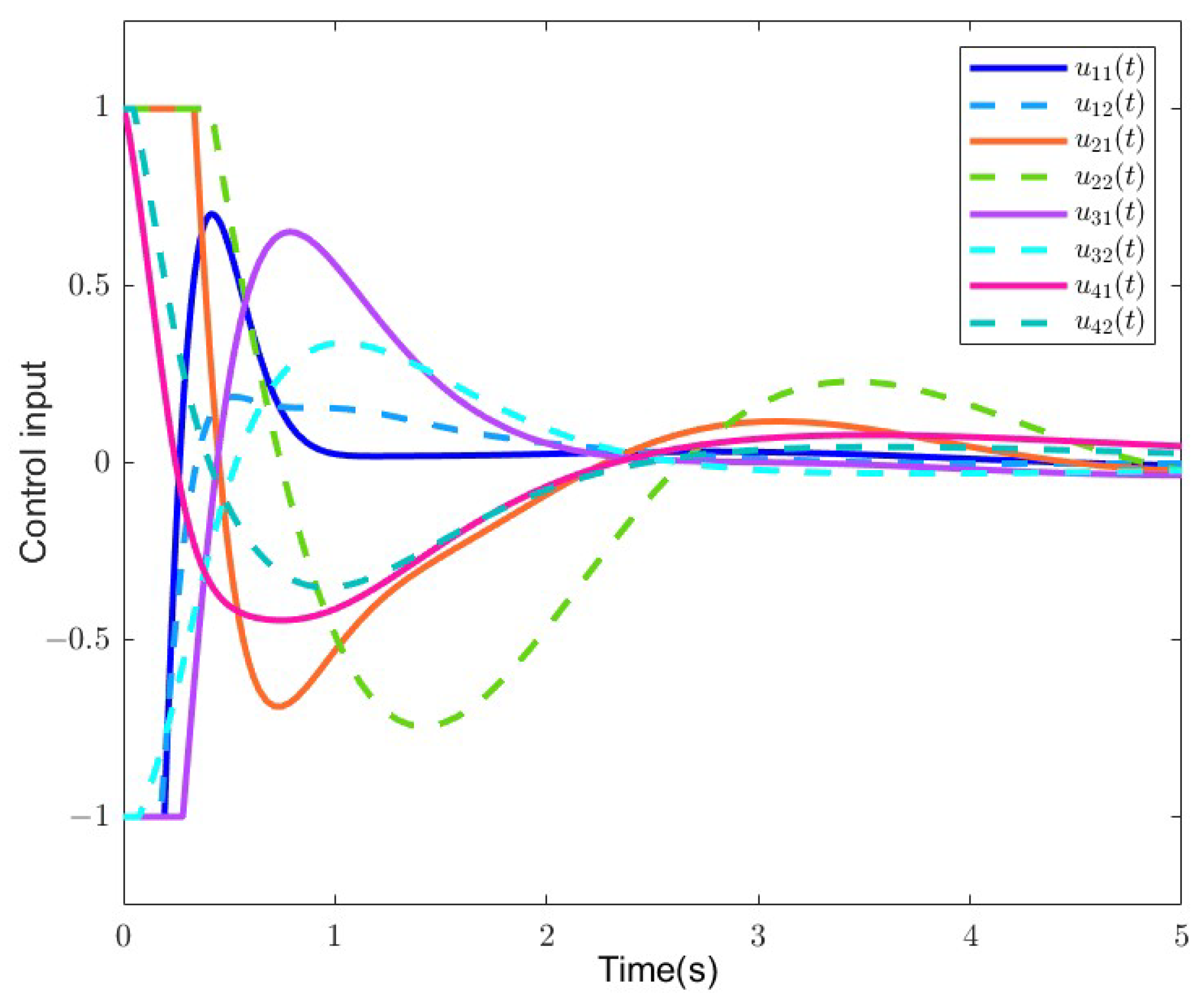
Figure 7.
The state of each agent in Example 2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Downloads
54
Views
31
Comments
0
Subscription
Notify me about updates to this article or when a peer-reviewed version is published.
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated







