Prerpints.org logo
Preprint
Article

Linguistic Secret Sharing via Ambiguous Token Selection for IoT Security

Altmetrics

Downloads

58

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 October 2024

Posted:

02 October 2024

You are already at the latest version

Alerts
Abstract
The proliferation of Internet of Things (IoT) devices has introduced significant security challenges, including weak authentication, insufficient data protection, and firmware vulnerabilities. To address these issues, we propose a linguistic secret sharing scheme tailored for IoT applications. This scheme leverages neural networks to embed private data within texts transmitted by IoT devices, using an ambiguous token selection algorithm that maintains the textual integrity of the cover messages. Our approach eliminates the need to share additional information for accurate data extraction, while also enhancing security through a secret sharing mechanism. Experimental results indicate that the generated steganographic text effectively preserves the sentiment and semantic information of the cover text.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

Steganography conceals the secret message in the cover media. A classic scenario illustrating linguistic steganography is the “Prisoner’s problem”. Consider that Alice and Bob were two inmates in a prison, planning to escape. To facilitate their plan, they decided to exchange secret messages via short notes. However, all message exchanges must be checked by Eve. If Eve successfully detects any concealed message, she retains the authority to terminate any further communication. In this scenario, Alice employed an embedding rule to conceal the secret message within the cover note, which was then sent to Bob under the surveillance of Eve. Upon receiving, Bob employed an extraction rule to retrieve the concealed message from the note.
In the rapidly evolving landscape of the Internet of Things (IoT), the surge of connected devices brings new security challenges. Ensuring secure and confidential data transmission is crucial in this context. Traditional encryption methods may be unsuitable due to the limited computational and storage capacities of IoT devices. Thus, steganography emerges as a potential alternative for protecting information.
As time has advanced, except for text, various cover media have been employed in steganography including images [1, 2], audio [3], 3D mesh models [4], and videos [5]. However, due to the development of deep neural networks, linguistic steganography attracts much attention again [6-8]. Linguistic steganography can be primarily categorized into two types based on whether the steganographic text maintains the semantics of the cover text: generation-based linguistic steganography [6-14] (GLS) and modification-based linguistic steganography [15-20] (MLS).
GLS primarily embeds secret bits during the generation of high-quality steganographic text, all accomplished via a neural network-based language model. This flexibility in word selection for each position based on secret data is especially beneficial in the IoT context, where devices generate large volumes of texts that can serve as cover messages. However, this mechanism results in significant differences in features between the cover text, generated through semantic predictions from the language model, and the steganographic text. To maintain the semantic expression of the generated steganographic text, some schemes [9-11] try to incorporate semantic constraints. Yang et al. [10] utilized context as the constraint, aiming to preserve strong semantic correlation between the steganographic text and the cover text. Wang et al. [11] enhanced the controllability of steganography generation by analyzing the discourse features of the cover, which serve as the inputs to the steganography generator. However, since these GLS schemes operate at the word level, they can still easily lead to significant distortion of the local semantics. Furthermore, state-of-the-art steganalysis models use deep neural networks to extract multidimensional statistical features, enhancing their ability to detect steganographic text. These models integrate temporal features derived from spatial features [21] or continuous text sequences [22], improving their effectiveness in detecting steganographic text. This significantly impacts the inherent embedding capacity of GLS.
MLS primarily embeds secret bits by modifying part of the cover text at the word [15, 16], phrase [17], and sentence levels [18-20]. Word or phrase-level MLS schemes generally utilize synonym substitutions to embed the secret. Sentence-level MLS tends to convert a sentence into another form maintaining the same meaning, such as through syntactic analysis [18] and sentence translation [19, 20]. In the context of IoT, where device-generated texts often follow specific structures or patterns, MLS can be used to subtly modify these texts to embed secret data. However, these MLS schemes suffer from low embedding capacity.
In summary, GLS schemes offer impressive embedding capacity but may introduce semantic ambiguity and increase suspicion by steganalysis. While MLS schemes successfully maintain the overall semantics, their limited embedding capacity poses a significant challenge. Moreover, previous linguistic steganography schemes typically involve encrypting the secret data, recording additional information for recovery, and managing the secret key, which is impractical in some applications.
In order to solve the above problems, we propose a novel linguistic secret sharing scheme for IoT security. In our scheme, only the most ambiguous word in each sentence is substituted to embed secret data, thereby preserving the semantic integrity of each sentence. Moreover, the receiver can also easily identify this specific word during the extracting process. Additionally, we employ a secret sharing mechanism to encrypt secret data. Instead of relying on a secret key, secret sharing distributes the secret into multiple shares, ensuring that a single share alone cannot restore the original secret. Our contributions are summarized as follows:
  • We propose a token-selection algorithm that enables both the sender and the receiver to identify the same most ambiguous word in each sentence.
  • Data embedding and extraction can be performed without the need to share any secret key.
  • The proposed scheme maintains the semantic coherence of the steganographic text.
  • Secret sharing over Galois field is first introduced to linguistic steganography.

2. Preliminary Work

We first review the concept of ( k ,   n ) -threshold secret sharing, which serves as the foundational framework of the proposed scheme for ensuring security. Then, a masked language model called “RoBERTa” is introduced, which will be modified to embed data in our scheme.

(𝑘,𝑛)-Threshold Secret Sharing over G F 2 m

In 1979, Shamir [12] proposed a cryptographic algorithm known as the (k, n)-threshold secret sharing, which improves security by distributing the secret to multiple participants. The concept of (k, n)-threshold secret sharing is to divide a secret into n shares and distribute to n participants. The original secret can only be reconstructed when at least k shares are available in recombination.
The fundamental operation of ( k ,   n ) -threshold secret sharing over G F ( 2 m ) involves the construction of a set of polynomial equations over Galois field. Provided x 1 , x 2 , … , x n ∈ G F ( 2 m ) denote n distinct binary polynomials. Given a secret s ∈ G F ( 2 m ) , we can construct a k − 1 degree polynomial as follows.
f x = [ s ⊕ ( a 1 ⊙ x ) ⊕ ( a 2 ⊙ x 2 ) ⊕ … ⊕ ( a k − 1 ⊙ x k − 1 ) ]   m o d   p ( x ) ,
where “ ⊕ ” and “ ⊙ ” represent the exclusive-or operation and the Galois field multiplication, respectively; { a 1 , a 2 , … , a k − 1 } ∈ G F ( 2 m ) and p ( x ) represent a group of random binary polynomials and an irreducible polynomial, respectively. After secret share generation, each participant holds a share ( x i , f ( x i ) ) , where x i is the owner’s private key and f ( x i ) is the corresponding secret share.
When at least k participants contribute their private keys and secret shares, the coefficients a 1 , a 2 , … a k − 1 and secret s can be restored via the Lagrange interpolating polynomial.
f ( x ) = ∑ q = 1 k { f ( x q ) ⊙ ∏ 1 ≤ w ≤ k w ≠ q ( x ⊕ x w ) ⊙ x q ⊕ x w − 1 }   m o d   p ( x ) .
s = ∑ q = 1 k { f ( x q ) ⊙ ∏ 1 ≤ w ≤ k w ≠ q x w ⊙ x q ⊕ x w − 1 }   m o d   p ( x )

2.2. RoBERTa-Masked Language Modeling

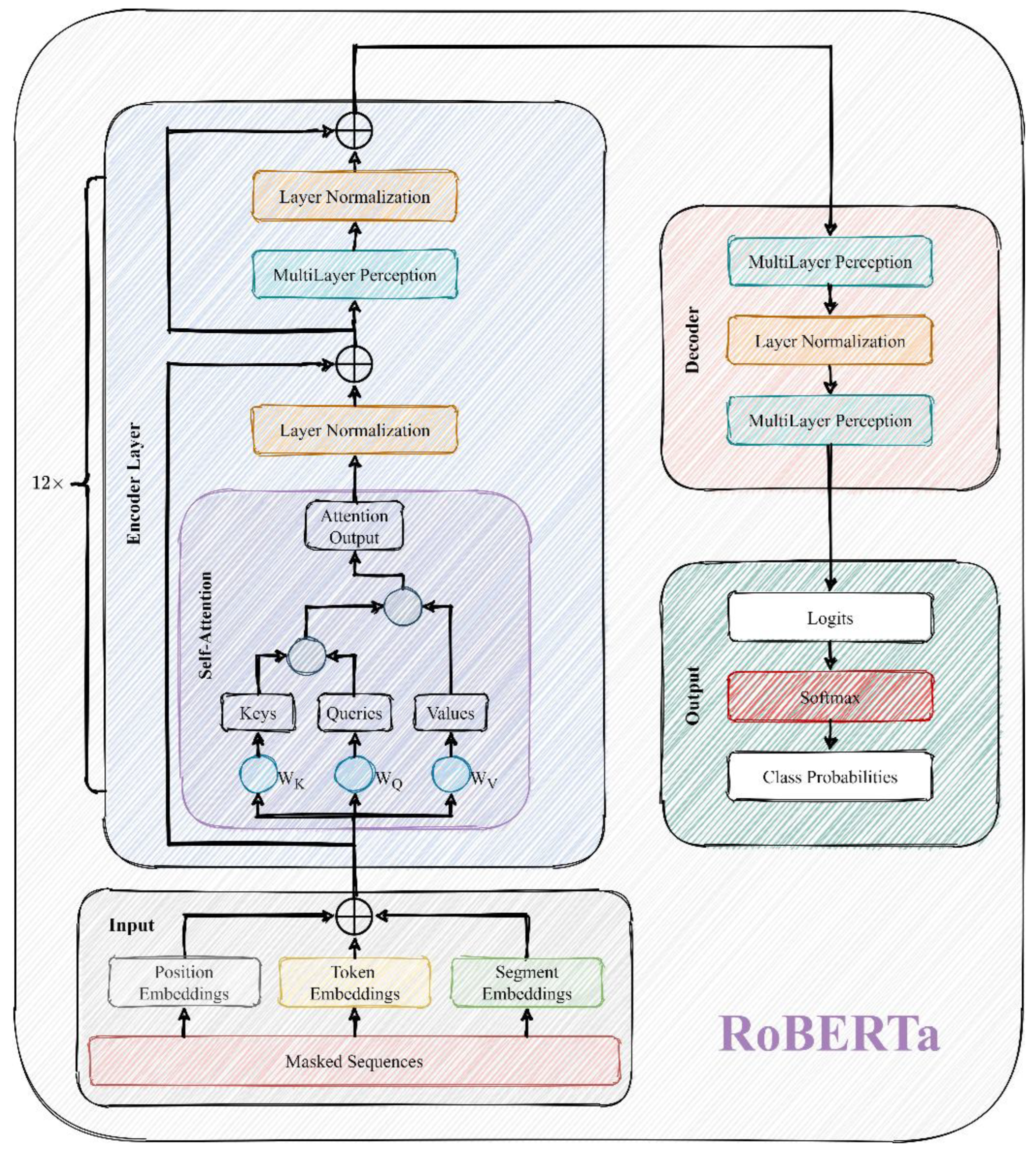
RoBERTa (Robustly Optimized Bidirectional Encoder Representations from Transformers Pretraining Approach) [24] is an NLP model that is built upon a variant of the Transformer architecture [25] and is specifically designed to handle language comprehension tasks. Its layout is depicted in Figure 1. The key objective of the RoBERTa model is to improve the pre-training process in order to effectively leverage large-scale unlabeled text data for model training. Compared to earlier BERT [26], RoBERTa incorporates a larger model size and a longer training time, while introducing several technical improvements such as dynamic masks, continuous text paragraph training, and larger batch sizes.
Masked language modeling is the fundamental task of RoBERTa, aiming to predict a masked word based on the context of surrounding words. Tokenization is an initial step, where a text sequence is split into tokens. An input sentence containing one or more mask tokens is fed into the model, which estimates the probability distribution of each mask token across the entire vocabulary. The predicted results can then be used to replace the masked tokens for data embedding.

3. Proposed Linguistic Secret Sharing

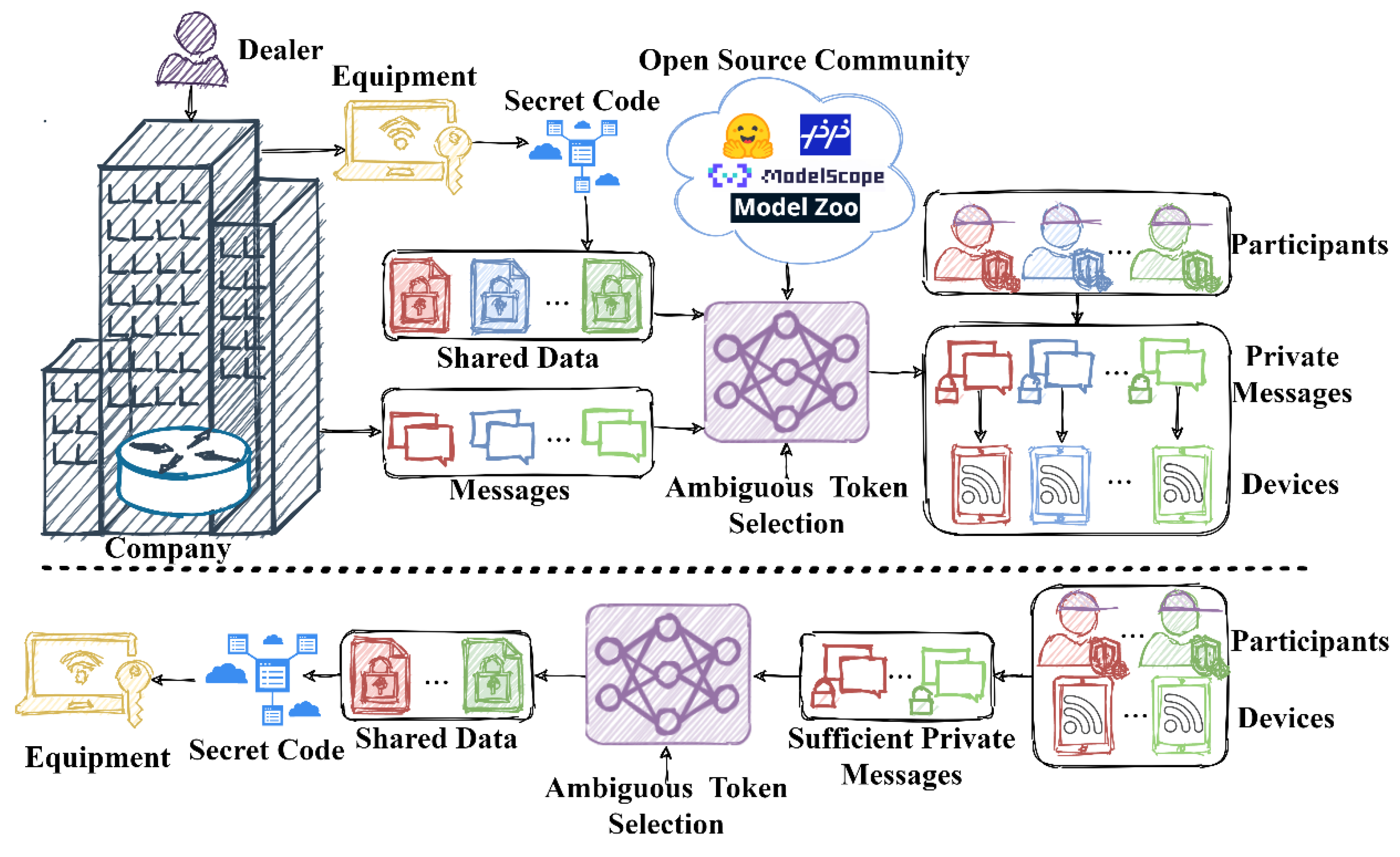
Consider a scenario in which a company produces advanced equipment that is restricted for use in certain areas or by specific companies. This equipment has an associated secret code to activate it. The equipment is delivered by a logistics company, while the secret code is distributed among multiple participants with a secret sharing scheme, to ensure authorized usage of the equipment.
As illustrated in Figure 2, during the share generation stage, the secret code is transformed into n distinct shares using a polynomial secret sharing technique. These shares are then concealed within the regular messages intended for the participants with an open-source pre-trained model. These steganographic messages are then transmitted over the IoT devices of the participants.
In the secret recovery stage, the system enables any k authorized personnel (where k < n ) to collaboratively extract the activation code of the equipment. By applying the same token-selection principle and data embedding rule, participants can extract the secret shares from the messages on their own IoT devices and combine them back into the activation code. This mechanism ensures authorized usage of the protected equipment by preventing unauthorized personnel or an insufficient number of participants from activating it.

3.1. Text Share Generation

Theoretically, the proposed scheme can employ any type of text as its carrier and the three carrier texts can be completely different in content. However, in our case, we choose to utilize texts generated by deep learning-based models. By utilizing generated texts, their uniqueness can prevent attackers from comparing the texts to existing content on social media or the Internet in order to decipher the secret. Additionally, the generated texts offer a greater control to tailor the contents according to the user’s requirements. Users can generate texts suitable for linguistic secret sharing by providing appropriate prompts. For implementing the text generation stage, GPT-4 [27] is applied as the text generator.

3.2. Token-Selection Algorithm and Data Embedding Rule

In the proposed scheme, an ambiguous token is selected and masked for each sentence first. The masked sentence is fed to a token predictor, which gives the prediction results for each masked token. Finally, the masked token is replaced with one of the prediction results according to the data embedding rule.
To select the target token, assume a sentence consists of l tokens denoted as T = ( t 1 , t 2 , … , t l ) . Each token can be masked and predicted by masked language modeling. For a token belonging to the vocabulary pool V , the initial candidate pool for prediction is denoted as [ c 1 , c 2 , … , c V ] with corresponding probabilities [ p 1 , p 2 , … , p V ] , where ∑ j = 1 | V | p j = 1 . Let us define probability difference indicator as
D t = ∑ j = 1 m − 1 ( p σ ( j ) − p σ ( j + 1 ) ) ,
where p σ ( j ) represents the j-th greatest prediction probability. If D t value of a token is low, it means the top-m prediction probabilities of candidates are very close and the predictor faces ambiguity to accurately predict this token. Altering this token does not significantly affect the overall semantics of the sentence. The algorithm for ambiguous token selection is given as follows.
Algorithm 1: Ambiguous Token Selection
Preprints 119931 i001
After selecting the ambiguous token t , log 2 ⁡ m bits of data can be embedded into T by replacing t with one of its top-m prediction candidates [ c 1 , c 2 , … , c m ] . To illustrate the token-selection algorithm and data embedding rule, an example is given in Figure 3. Suppose the cover text is “I am very happy.” and m is set to 4, the predictor can provide the top-4 prediction results with the highest probability for each masked token. In this case, “very” is selected as the ambiguous token because it has the lowest probability difference indicator compared to the other tokens. Then, log 2 ⁡ 4 = 2 bits of data can be embedded by replacing “very” with one of the top-4 candidates.
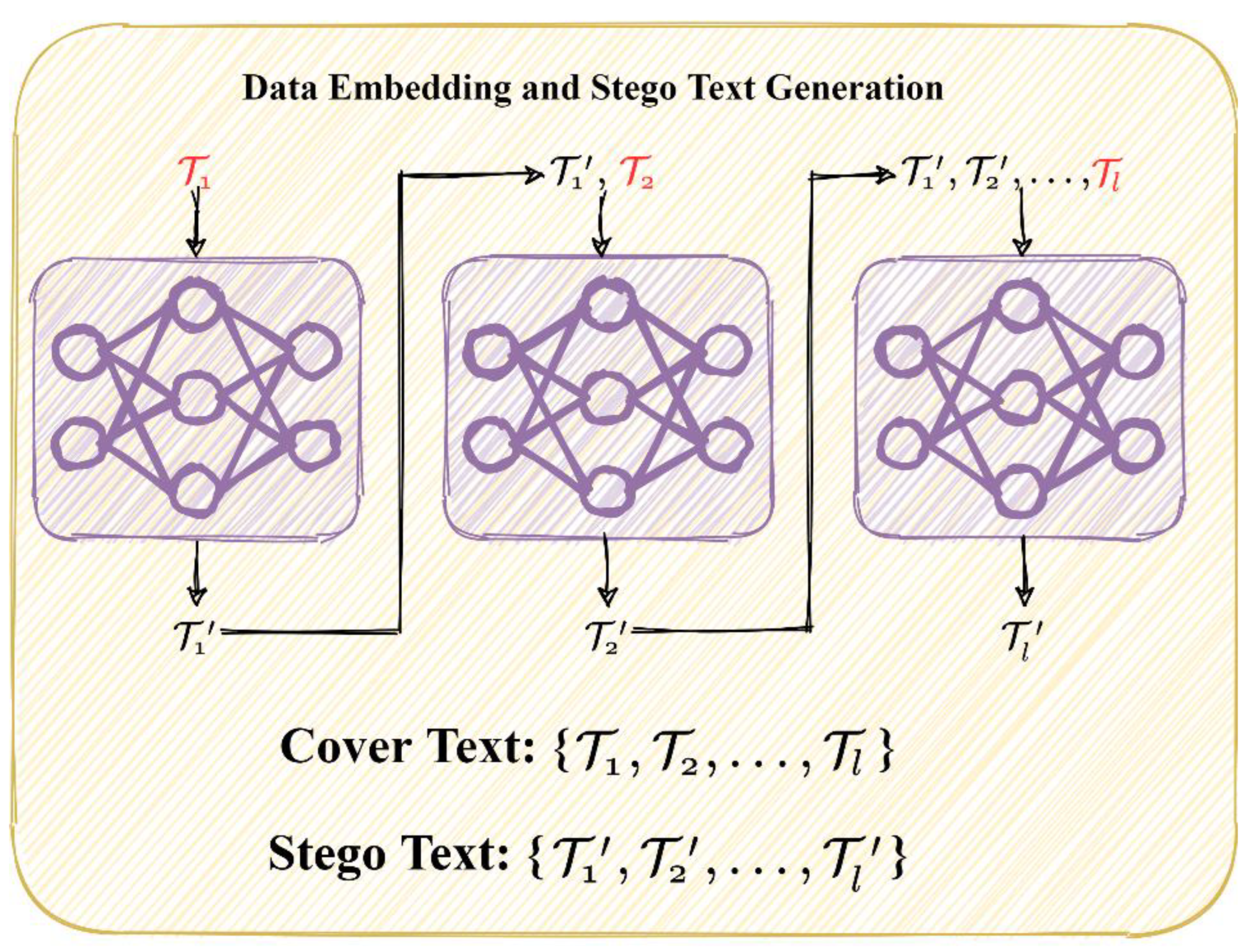
Note that when applying the token-selection and data embedding rule to a text, as shown in Figure 4, the modified sentence is considered as the preceding context for the current sentence. This ensures that the embedding process maintains coherence and consistency throughout the entire text.

3.3. Secret Share Generation

Refer to Figure 2 again, the dealer adopts the polynomial secret sharing over G F ( 2 m ) to distribute the secret data into secret shares and embeds the shares into distinct generated texts correspondingly using the token-selection algorithm and the data embedding rule. The procedures are given as follows.
Step 1: Convert the secret data into a sequence of binary segments S = { s 1 , s 2 , … , s k } , where s i is log 2 ⁡ m -bit in length.
Step 2: Generate n secret shares e i 1 , e i 2 , … , e i n using Eq. (1) by replacing s and the coefficients a 1 , a 2 , … a k − 1 with s 1 , s 2 , … , s k .
Step 3: Generate n texts T 1 , T 2 , … , T n using text generator with proper prompts.
Step 4: Embed the n secret shares into the n texts correspondingly using the token-selection algorithm and the data embedding rule to generate n text shares T 1 ' , T 2 ' , … , T n ' .

3.4. Secret Data Recovery

By collecting any k out of n text shares, a combiner can restore the secret data. The procedures are summarized as follows:
Step 1: Collect any k text shares.
Step 2: Split each text into sentences and identify a marked token for each sentence using the token-selection algorithm.
Step 3: Retrieve and collect the embedded secret bits from marked tokens according to the data embedding rule.
Step 4: Combine k secret shares to recover the original secret data using Eqs. (2) and (3).

4. Experimental Results

In this section, we introduce our experimental settings, give a demonstrative example, and evaluate the performance of our scheme in terms of sentiment and semantic analyses.

4.1. Experimental Setting

Model: Our experiments make use of the GPT-4 networks, a substantial language model developed by OpenAI for the purpose of generating cover texts. GPT-4 is a state-of-the-art model with a remarkable capacity for comprehending and producing both natural language and code. Furthermore, we employ RoBERTa as our token predictor in this study.
Implementation: Our experiments are implemented using Python 3.8 and rely on PyTorch 1.7.1 as the foundational framework. Acceleration is achieved through the utilization of Nvidia 3090 and CUDA 11.2. The secret messages applied are binary pseudo-random bitstreams.
Preprints 119931 g005
Figure 5. An example of (2, 3)- linguistic secret sharing.
Figure 5. An example of (2, 3)- linguistic secret sharing.
Preprints 119931 g005

4.2. Applicability Demonstration

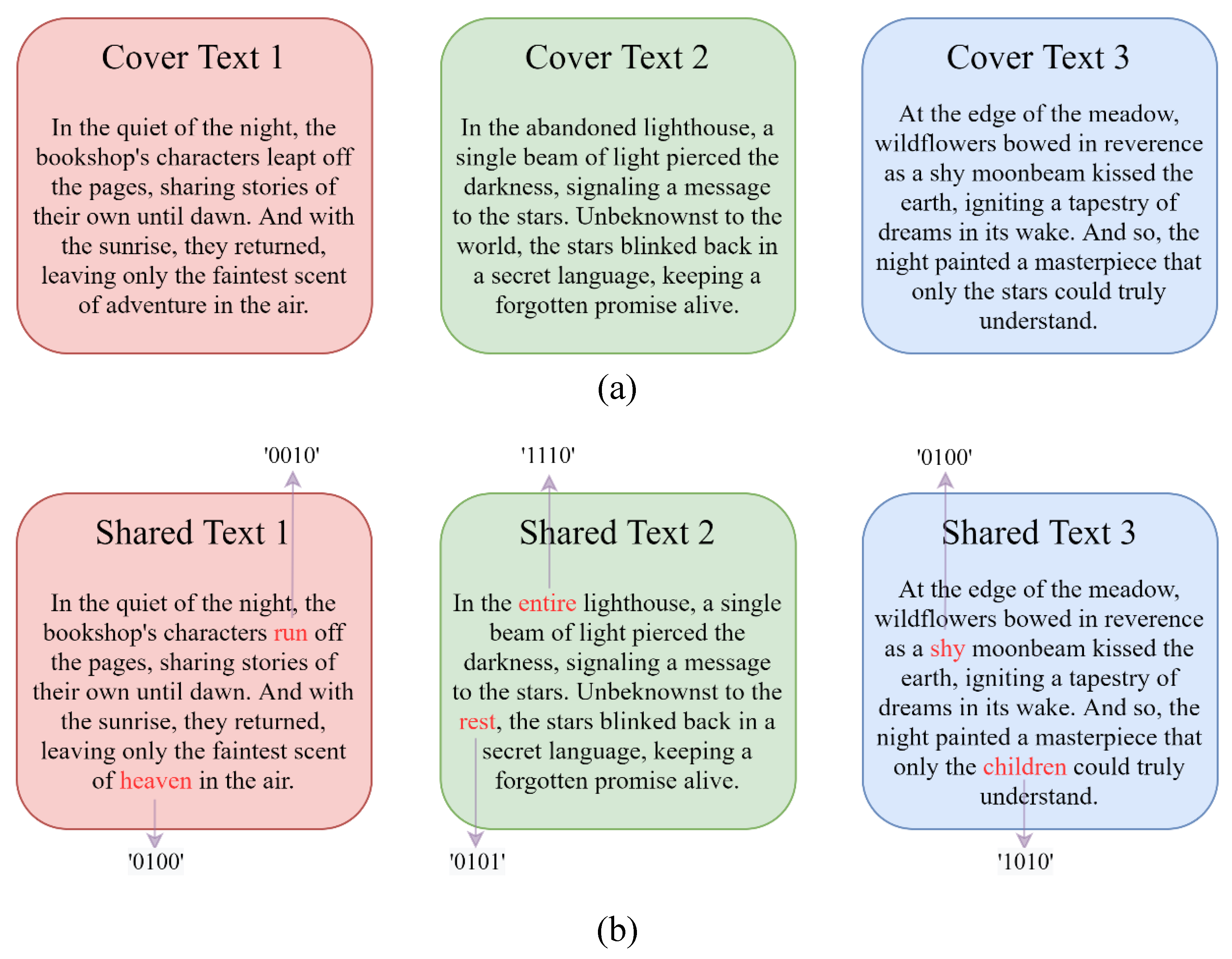
An example of (2, 3)-linguistic secret sharing is provided. Suppose the original secret data is an 8-bit binary random bitstream “11010011”, after secret sharing, three shared bitstreams “00100100”, “11100101”, and “01001010” are generated. Three cover texts and their corresponding text shares are shown in Figs. 5 (a) and (b), respectively. It is noteworthy that each sentence within the share text is capable to embed 4-bit shared data when the number of candidate pool of each selected token is set to 16. During the secret recovery process, the ambiguous token within each sentence can be easily identified through the proposed token-selection algorithm. Subsequently, the shared data can be extracted according to the order of selected tokens in the candidate pool. Following this step, any 2 out of 3 shared data can be combined to recover the original secret bitstream.

4.3. Performance Analysis

We evaluate the performance of steganographic text using sentiment and semantic analyses. The sentiment of a text is determined by its emotional nature: ‘positive’ refers to an optimistic or favorable emotion, while ‘negative’ refers to a pessimistic or unfavorable emotion. The sentiment of a text can be assessed using a pre-trained BERT-based sentiment classifier [26]. In our experiments, text share 1 (474 words) and text share 2 (248 words) are generated from texts classified with positive (P: 99.84%) and negative (N: 96.54%) emotions, respectively. Two strategies are used to segment the text into sentences: Strategy 1 segments the text with periods, while Strategy 2 segments the text with punctuation marks, including commas and periods. Thus, the number of resulting sentences for Strategy 1 is fewer than that for Strategy 2. Data embedding is executed by selecting only one word to replace within each sentence. As shown in Table 1, the steganographic texts generated with different m successfully preserve the sentiment classification results (CR) of the cover text.

4.4. Comparison

We further compare the characteristics of the proposed with two state-of-the-art schemes [18, 19]. Specifically, we use a testing set comprising 1,000 sentences, set m to 8, and employ Strategy 1 to execute (2, 3)-threshold linguistic secret sharing. As listed in Table 3, the average embedding capacities in bits per word (bpw) of Xiang et al.’s [18] and Yang et al.’s [19] schemes are higher than that of our scheme. However, in terms of security, the anti-steganalysis results show that the steganographic text generated by the proposed scheme is more difficult to detect by both steganalysis models [21, 22]. Additionally, our scheme is tolerant to data loss or user failure and requires no additional information or secret key management.

5. Conclusions

In this paper, we introduce a novel linguistic secret sharing scheme via ambiguous token selection algorithm for IoT security. Unlike previous schemes, the proposed scheme does not require to share additional information for correct data extraction. Besides, we employ a secret sharing mechanism to improve security. Experimental results show that the steganographic text generated by the proposed scheme can effectively preserve the sentiment and semantic information of the cover text. In the future, we will explore how to improve data embedding capacity of the proposed scheme.

Author Contributions

Conceptualization, Kai Gao; methodology, Kai Gao; software, Kai Gao; validation, Kai Gao, Ji-Hwei Horng, and Ching-Chun Chang; formal analysis, Kai Gao and Ji-Hwei Horng; investigation, Kai Gao, Ji-Hwei Horng, and Ching-Chun Chang; resources, Chin-Chen Chang; data curation, Kai Gao; writing—original draft preparation, Kai Gao; writing—review and editing, Ji-Hwei Horng; visualization, Kai Gao.; supervision, Chin-Chen Chang; project administration, Chin-Chen Chang. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data can be downloaded from https://huggingface.co.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. K. Gao, C.-C. Chang, J.-H. Horng, and I. Echizen, “Steganographic secret sharing via AI-generated photorealistic images,” EURASIP J Wirel. Commun. Netw., vol. 2022, no. 119, pp. 1 - 23, 2022. [CrossRef]
  2. L. Dong, J.T. Zhou, W. W. Sun, D. Q. Yan, and R. D. Wang, “First Steps Toward Concealing the Traces Left by Reversible Image Data Hiding,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 67, no. 5, pp. 951 - 955, 2020. [CrossRef]
  3. H. Dutta, R. K. Das, S. Nandi, and S. R. Mahadeva Prasanna, “An Overview of Digital Audio Steganography,” IETE Tech. Rev., vol. 97, no. 6, pp. 632 - 650, 2020. [CrossRef]
  4. K. Gao, J.-H. Horng, and C.-C. Chang, “Reversible Data Hiding for Encrypted 3D Mesh Models with Secret Sharing Over Galois Field,” IEEE Trans. Multimedia, vol. 26, pp. 5499 - 5510, 2023.
  5. J. Zhang, A. T. S. Ho, G. Qiu, and P. Marziliano, “Robust Video Watermarking of H.264/AVC,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 54, no. 2, pp. 205 - 209, 2007.
  6. J. P. Qiang, S. Y. Zhu, Y. Li, Y. Zhu, Y. H. Yuan, and X. D. Wu, “Natural Language Watermarking via Paraphraser-based Lexical Substitution,” Artif. Intell., vol. 317, pp. 103859, 2023. [CrossRef]
  7. R. Y. Yan, Y. T. Yang, and T. Song, “A Secure and Disambiguating Approach for Generative Linguistic Steganography,” IEEE Signal Process. Lett., vol. 30, pp. 1047-1051, 2023. [CrossRef]
  8. R. Wang, L. Y. Xiang, Y. F. Liu, and C. F. Yang, “PNG-Stega: Progressive Non-Autoregressive Generative Linguistic Steganography,” IEEE Signal Process. Lett., vol. 30, pp. 528-532, 2023. [CrossRef]
  9. S. Zhang, Z. Yang, J. Yang, and Y. Huang, “Provably Secure Generative Linguistic Steganography,” arXiv preprint arXiv:2106.02011, 2021. [CrossRef]
  10. Z. Yang, L. Xiang, S. Zhang, X. Sun, and Y. Huang, “Linguistic Generative Steganography with Enhanced Cognitive-imperceptibility,” IEEE Signal Process. Lett., vol. 28, pp. 409–413, 2021. [CrossRef]
  11. Y. Wang, R. Song, R. Zhang, J. Liu, and L. Li, “LLsM: Generative Linguistic Steganography with Large Language Model,” arXiv preprint arXiv:2401.15656, 2024.
  12. Z. Yang, N. Wei, Q. Liu, Y. Huang, and Y. Zhang, “GAN-TSTEGA: Text Steganography Based on Generative Adversarial Networks,” in Proc. 18th Int. Workshop Digit. Forensics Watermarking, 2019, pp. 18–31.
  13. T. Fang, M. Jaggi, and K. J. Argyraki, “Generating Steganographic Text with LSTMs,” in Proc. 55th Annu. Meeting Assoc. Comput. Linguistics, 2017, pp. 100–106.
  14. X. Zhou, W. Peng, B. Yang, J. Wen, Y. Xue, and P. Zhong, “Linguistic Steganography Based on Adaptive Probability Distribution,” IEEE Trans. Dependable Secure Comput., vol. 19, no. 5, pp. 2982–2997, 2022. [CrossRef]
  15. L. Xiang, Y. Li, W. Hao, P. Yang, and X. Shen, “Reversible Natural Language Watermarking Using Synonym Substitution and Arithmetic Coding,” Comput., Mater. Continua, vol. 55, no. 3, pp. 541–559, 2018. [CrossRef]
  16. C.-Y. Chang and S. Clark, “Practical Linguistic Steganography Using contextual synonym substitution and a novel vertex coding method,” Comput. Linguistics, vol. 40, no. 2, pp. 403–448, 2014. [CrossRef]
  17. A. Wilson and A. D. Ker, “Avoiding detection on twitter: Embedding strategies for linguistic steganography,” Electron. Imag., vol. 28, pp. 1–9, 2016. [CrossRef]
  18. L. Y. Xiang, C. F. Ou, and D. J. Zeng, “Linguistic Steganography: Hiding Information in Syntax Space,” IEEE Signal Process. Lett., vol. 31, pp. 261–265, 2023. [CrossRef]
  19. T. Yang, H. Wu, B. Yi, G. Feng, and X. Zhang, “Semantic-preserving Linguistic Steganography by Pivot Translation and Semantic-aware Bins Coding,” IEEE Trans. Dependable Secure Comput., vol. 21, no. 1, pp. 139-152 2024. [CrossRef]
  20. R. Stutsman, C. Grothoff, M. Atallah, and K. Grothoff, “Lost in Just the Translation,” in Proc. ACM Symp. Appl. Comput., 2006, pp. 338–345.
  21. J. Wen, X. Zhou, P. Zhong, and Y. Xue, “Convolutional Neural Network Based Text Steganalysis,” IEEE Signal Process. Lett., vol. 26, no. 3, pp. 460–464, 2019. [CrossRef]
  22. Z. Yang, K. Wang, J. Li, Y. Huang, and Y.-J. Zhang, “TS-RNN: Text Steganalysis Based on Recurrent Neural Networks,” IEEE Signal Process. Lett., vol. 26, no. 12, pp. 1743–1747, 2019. [CrossRef]
  23. A. Shamir, “How to Share a Secret,” Commun. ACM, vol. 22, no. 11, pp. 612-613, 1979. [CrossRef]
  24. Y. H. Liu, M. Ott, N. Goyal, J. F. Du, M. Joshi et al., “RoBERTa: A Robustly Optimized BERT Pretraining Approach,” arXiv preprint arXiv:1907.11692, 2019.
  25. V. Ashish, S. Noam, P. Niki, U. Jakob, J. Llion, et al., “Attention is All You Need,” Adv. Neural Inf. Process. Syst. 30, 2017.
  26. J. Devlin, M. W. Chang, K. Lee, and K. Toutanova, “Bert: Pre-training of Deep Bidirectional Transformers for Language Understanding,” arXiv preprint arXiv:1810.04805, 2018.
  27. OpenAI, “GPT-4 Technical Report,” arXiv preprint arXiv:2303.08774, Mar. 2023.
  28. A. Radford, J. W. Kim, C. Hallacy, A. Ramesh, G. Goh, et al., “Learning Transferable Visual Models From Natural Language Supervision,” in PMLR, vol. 139, pp. 8748-8763, 2021.
Preprints 119931 g001
Figure 1. Architecture of RoBERTa.
Figure 1. Architecture of RoBERTa.
Preprints 119931 g001
Preprints 119931 g002
Figure 2. Flowchart of proposed scheme.
Figure 2. Flowchart of proposed scheme.
Preprints 119931 g002
Preprints 119931 g003
Figure 3. An example of token-selection and data embedding.
Figure 3. An example of token-selection and data embedding.
Preprints 119931 g003
Preprints 119931 g004
Figure 4. Embedding rule.
Figure 4. Embedding rule.
Preprints 119931 g004
Table 1. Sentiment classification.
Table 1. Sentiment classification.
Top-m/CR Text share 1 (P: 99.84%) Text share 2 (N: 96.54%)
Strategy 1 Strategy 2 Strategy 1 Strategy 2
8 P: 99.76% P: 99.26% N: 95.52% N: 90.86%
16 P: 99.78% P: 99.54% N: 95.45% N: 87.41%
32 P: 99.71% P: 99.81% N: 97.35% N: 96.45%
64 P: 99.75% P: 99.59% N: 96.16% N: 96.39%
128 P: 99.85% P: 99.42% N: 96.76% N: 99.25%
Table 2. Semantic similarity.
Table 2. Semantic similarity.
Top-m/CS Text share 1 Text share 2
Strategy 1 Strategy 2 Strategy 1 Strategy 1
8 98.16% 94.98% 99.54% 95.61%
16 96.69% 91.13% 99.60% 94.54%
32 93.92% 90.95% 99.34% 93.69%
64 92.34% 89.20% 99.05% 95.39%
128 93.12% 87.97% 99.71% 95.73%
Table 3. Characteristics comparisons.
Table 3. Characteristics comparisons.
Schemes EC LSCNN [21] TSRNN [22] Tolerance Metadata
[18] 0.333 0.526 0.513 No Yes
[19] 0.333 0.594 0.559 No Yes
Proposed 0.162 0.514 0.504 Yes No
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated