Preprint
Article
Multi-Agent Reinforcement Learning for Smart Community Energy Management
Altmetrics
Downloads
67
Views
51
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.xlsx (143.19KB )
This version is not peer-reviewed
Submitted:
01 October 2024
Posted:
01 October 2024
You are already at the latest version
Alerts
Abstract
This paper investigates a Local Strategy-Driven Multi-Agent Deep Deterministic Policy Gradient (LSD-MADDPG) method for demand-side energy management systems (EMS) in smart communities. Addressing critical challenges in EMS solutions such as data overhead, single-point failures, nonstationary environments, and scalability, the proposed LSD-MADDPG effectively harmonizes individual building needs with entire community energy management goals. By leveraging and sharing only strategic information among agents, the proposed approach demonstrates to optimize the EMS decision-making processes, while enhancing training efficiency and safeguarding data privacy - a critical concern in the community setting. The proposed LSD-MADDPG has proven to be capable of reducing energy costs and flattening community demand curve by coordinating indoor temperature control and electric vehicle charging schedules across multiple buildings. Comparative case studies reveal that LSD-MADDPG excels in both cooperative and competitive settings, aligning individual buildings’ energy management actions with overall community goals in a fair manner, highlighting its potential for future smart community energy management advancements.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
The global push for adopting distributed and renewable energy resources alongside increased electrification and the gradual retirement of dispatchable fossil-fueled power plants is introducing new operational challenges to existing electric power grids [1]. As a result, there is a growing need for a new paradigm of energy management that shifts from supply-side to demand-side control [2]. Under this new paradigm, it becomes critical to comprehensively understand the evolving energy consumption patterns and controllability of diverse electric grid loads and their associated energy assets [3]. Failing to leverage energy consumption flexibility via strategically adapting consumer behaviors can significantly strain the power grids, potentially leading to unexpected generation capacity shortages during this energy transition. A notable example occurred in summer 2022 when a heatwave in California brought the state's power grid to the brink of rolling blackouts, impacting millions of residents. Authorities responded by urging residents to refrain from charging their electric vehicles (EVs) to conserve energy, challenging the feasibility of California's ambitious goal to eliminate all gas-powered vehicles by 2035 [4,5]. On the other hand, implementing effective demand-side energy management enabled by smart grid technologies can optimize energy consumption, assisting a stable and reliable power supply while improving consumer economic and comfort outcomes [6,7].
Conventional mathematical methods have been thoroughly studied for effective demand-side energy management systems (EMS), including rule-based methods often derived from expert knowledge of well-studied systems, which provide a static, definite, and easy-to-implement solution but lack the flexibility and adaptability for more complex dynamic environments [8]. Optimization-based techniques such as linear programming [9,10], mixed-integer linear programming [11,12,13,14,15], and quadratic programming [21,22,23], utilize mathematical formulations to model and manage objective systems over a fixed time horizon, but can be computationally intensive, hard to scale, and may struggle to adapt to changing conditions. Heuristic algorithms like Particle Swarm Optimization [16,17,18,19,20] and Genetic Algorithms [24,25,26] offer alternative approaches for non-linear optimization but, despite handling intricate systems, they often demand significant computational resources and are complex to implement and generalize. Model Predictive Control (MPC) complements these methods by incorporating system dynamics into the optimization process, predicting future states, and making real-time decisions over a moving horizon [27,28]. However, implementing MPC at the community level, which requires coordination among stakeholders, poses challenges due to the evolving conditions and the high costs of modeling large-scale energy assets [29]. Additionally, solution performances of all above-mentioned model-based methods highly depend on accurate system modeling, meaning that model inaccuracies and constrained data sharing can lead to suboptimal decisions, highlighting limitations of model-based methods in demand-side EMS where numerous independent energy consumers need to be modeled and coordinated.
Reinforcement Learning (RL) addresses many of these issues, including adaptation and generalization to dynamic environments, and reduced reliance on precise system models, making it well-suited to explore its potential for demand-side EMS [30]. Unlike traditional model-based methods, RL allows agents (representing heterogenous energy consumers) to learn optimal energy consumption control policies without explicit system dynamics modeling. By leveraging machine learning (ML) capabilities, RL-algorithm-equipped agents incrementally learn and understand complex systems through interactions with the environment, which reflects the energy system’s dynamics and external conditions, allowing RL agents to adapt their learned policies to evolving system conditions. The learning of RL agents can be implemented via either centralized methods, where a single entity coordinates the learning and decision-making for all agents, or decentralized methods, where multiple agents learn and make decisions for themselves.
Several centralized methods, including Q-learning [31,32,33], Deep Q-Network (DQN) [34,35], Double Deep Q-Network [36], Deep Deterministic Policy Gradient (DDPG) [37,38,39,40,41], and Proximal Policy Optimization [42], have been explored for both supply-side and demand-side EMSs. A centralized EMS provides a shared global perspective, enabling coordinated decision-making and comprehensive system understanding among RL agents for efficient energy management. However, a centralized controller managing an entire community’s energy consumption has widely recognized drawbacks: a) It imposes significant communication overhead due to large datasets shared among many energy consumers and the controller [43]. b) It faces scalability issues due to limited processing power and increasing computational complexity as the system grows. c) It represents a single point of failure, making the system vulnerable to outages and reliability issues. d) Centralized data storage raises concerns about data privacy and security, making the system a target for cyber-attacks.
In contrast, decentralized methods involve limited or no communication between multiple RL agents, relying primarily on local information for decision-making. This setting can improve problem-solving efficiency through parallel computations and enhance reliability by employing redundant agents [44,45]. However, when multiple decentralized RL agents are introduced for community energy management, individual agent’s access to the information of the entire community’s energy system as a whole could be limited due to physical and/or privacy constraints. Thus, a decentralized Multi-Agent Reinforcement Learning (MARL) design faces two major technical challenges: (i) interactions between agents give rise to a non-stationary environment, which inherently complicates learning convergence; and (ii) accurately attributing credit for an action to the responsible agent is difficult under the simultaneous actions of other agents [56]. Therefore, the main objective of a decentralized method is to help each RL agent build a belief system that aligns its decision-making with its teammates and thus achieve a consensus on the overall system energy management goals [47].
MARL approaches are typically categorized into three main strategies: Independent Learning, Centralized Critic, and Value Decomposition. Independent learning involves agents learning their policies without any data exchange, which simplifies the learning process but does not solve key challenges like non-stationarity and credit allocation. As a result, it often struggles with achieving objectives which require coordination and typically underperforms compared to centralized strategies. In a fully decentralized EMS, individual RL agents may improve the overall energy management performance through independent learning, but only if their actions are non-conflicting at all [48]. However, coordination among RL agents in a community EMS is often inevitable, as their actions inherently affect the shared environment, and thus are often conflicting. Centralized Training with Decentralized Execution (CTDE) is a framework in MARL that allows agents to utilize global information during training while ensuring that their execution remains decentralized, based only on local observations, effectively addressing non-stationarity and credit allocation issues. The Centralized Critic approach, as part of the CTDE framework, allows agents to share information during training, optimizing a centralized critic. While the Value Decomposition techniques follow another centralized training strategy, decomposing the global value function into individual components.
Various MARL algorithms have demonstrated significant improvements in energy trading, microgrid operation, building energy management, and other applications. Notable algorithms such as MA-DQN [49], MADDPG [50,51], MAAC [52], MAA2C [53], MAPPO [54,55,56], MATD3 [57], and MA-Q-learning [58,59,60,61] have been implemented in MARL, enabling RL agents to independently model, monitor, and control their respective environments. Such decentralization could naturally solve a complex system’s decentralized control problems, such as the community EMS we would like to study.
This paper explores a new decentralized MARL-based smart community EMS solution, targeting to address key challenges related to data overhead during execution, single-point failure risks, a nonstationary environment, solution scalability, and the interplay between cooperation and competition among distributed EMS controllers representing individual community energy consumers. Specifically, a Local Strategy-Driven MADDPG (LSD-MADDPG) is proposed to manage the energy consumption of individual smart buildings equipped with different energy assets in a community. The smart community EMS objective is to flatten the electricity demand curve of the entire community in a coordinated fashion while reducing energy costs of individual buildings, all within their respective levels of user satisfaction.
In the MADDPG framework, each RL agent is equipped with an actor responsible for executing actions and a critic that evaluates those actions to optimize the policy learning. Unlike conventional CTDE methods, in the proposed LSD-MADDPG, the critic of an agent does not have access to other agents’ observations; instead, RL agents only share their "strategies", which are specifically designed quantitative indicators representing each agent’s prioritized intent for energy consumption, i.e., the scheduling of HVAC usage and EV charging, based on the current state of its resources or needs. The critic of each agent leverages these shared “strategies” from other agents to improve its training while ensuring data privacy, whereas its actor’s execution remains locally decentralized, maintaining scalability and efficiency. For benchmarking purposes, this proposed demand-side community EMS, i.e., LSD-MADDPG, is then tested and compared against the common practice of a naïve controller (NC), a centralized single-agent controller, an independent learner or fully decentralized MADDPG controller with access to only local observations, and a conventional CTDE MADDPG with a centralized critic.
The major contributions of this work are summarized as follows:
1. A new LSD-MADDPG is proposed for smart community EMS, which modifies the conventional MADDPG framework to only share “strategies” instead of the global state for RL agent critic training, demonstrating enhanced control performance. Via an innovatively designed Markov game, LSD-MADDPG achieves superior solution scalability while offering more equitable reward distribution, emphasizing fairness in competition and coordination. Additionally, it maintains data privacy while achieving competitive results against conventional MADDPG in terms of reward, energy cost, EV charging and building comfort satisfaction, as well as community peak demand reduction.
2. Rigorously modeled a simulation environment for RL implementations, incorporating dedicated HVAC systems and EV charging stations to facilitate the development and testing of advanced control strategies in different community EMS scenarios.
This paper is organized as follows: Section 2 presents a detailed modeling of the smart community EMS problem, Section 3 discusses the Markov game formulation, encompassing the state-action space and reward design for the smart community EMS. Section 4 introduces the proposed MARL framework. Section 5 presents the case studies on different EMS controllers, as well as a comparison of their training and evaluation results, highlighting the performance of the proposed LSD-MADDPG. Finally, the paper concludes with Section 6, summarizing the key findings and outlining future work.
2. Smart Community EMS Modeling
The objective of the smart community EMS is to minimize , including the community’s building energy costs, penalties for EV charging deviations from the target state of charge (SoC, and community's peak demand costs, thereby encouraging energy demand shifting. This optimization problem can be expressed as in (1)
where and denote the average energy consumption of EV charging and the HVAC system, respectively, for building n during time period t. represents the electricity price during time t and the peak demand price is . The term λ1 is a weighting factor that emphasizes the importance of minimizing energy cost, while λ2 is a weighting factor penalizing deviations from the EVs’ charging targets . is defined as the final SoC of the EV in building n by the end of its charging period. Lastly, λ3 is a weighting factor for reducing community daily peak demand charge.
2.1. Building Electric Vehicle Charging Modeling
The building EV charging model focuses on optimally scheduling energy usage to ensure EVs are adequately charged before departure. Charging only occurs if an EV is present in building n within its charging periods , defined as the time interval during which the EV is available for charging (2), and within its charging capacity limits (3). represents the constrained energy available for charging, while and are the minimum and maximum charging capacities of the EV charger.
The average amount of energy consumed by the charging station is further constrained by the SoC of EVs plugged in, as modeled in (4). This limit is derived from the Tesla Model 3's charging behavior as it takes roughly 2 hours to charge from 0% to 80% and an additional 2 hours to charge from 80% to 100% using a 220V charger [62]. No losses are assumed, but there is a limit on power supply .
The energy losses during EV charging, primarily due to the onboard inverter's efficiency and the active cooling of the EV battery when charging at higher amps, for a longer time, or in hot climates, are modeled to fit the charging data published by Tesla Motors Club Forum [62]. The total energy charged to the EV battery, accounting for such charging efficiency, is calculated by (5), with SoC updated by (6) and constrained by (7) where is the EV battery capacity.
2.2. Building HVAC System Modeling
The building HVAC system modeling ensures temperature comfort levels, providing heating and cooling to the building occupants, every minute m, but the temperature settings could only be adjusted every hour. This modeling approach maintains a consistent optimal hourly scheduling for building EV charging and HVAC setting while accurately reflecting real-world thermodynamic conditions, where the HVAC system does not run continuously for an entire hour nor ramp up or down every second. Building resistance is used to quantify the building's ability to resist the flow of heat between the inside and outside environments, considering windows, insulations, and building size [63]. A higher value indicates better insulation and lower heat transfer.
The building temperature Tn,m is then updated via (8), accounting for thermal changes from the outdoor temperature and the heating gain Hg,n,m or cooling loss Cg,n,m from the building’s HVAC. In (8), is the mass of air and is the specific heat capacity of air. Indoor temperature of the building is constrained to the occupants’ comfort levels (9).
The control logic for heating and cooling is enabled by setting the thermostat temperature between the minimum and maximum thermostat setpoints (10-11). In this context, is a binary value indicating cooling, and is a binary value indicating heating.
The heating and cooling thermal energy inputs are calculated using (12) and (13), respectively. The HVAC’s heating output is a constant temperature Th,n and its cooling output is Tc,n, both supplied at air flow rate Mn.
The efficiency of the HVAC system, i.e., coefficient of performance (COP) , exhibits a reciprocal relationship with outdoor temperature, with 273.15 added to convert Celsius to Kelvin. The HVAC system’s COP and efficiency factor , determine the amount of thermal energy that can be supplied from electrical energy (14).
The constraints on heating (15) and cooling (16) are further restricted by the maximum HVAC power consumption and . The COP is constrained by the maximum COP, , as shown in (17).
The per minute (18) and per hour (19) electrical energy consumptions of a building HVAC system are then calculated as:
3. Markov Game Formulation of The Community EMS
A Markov Game could then be designed to reformulate the community EMS problem as elaborated in Section 2 into a model-free RL control framework including N agents (i.e., EMS controllers), a joint action set {A1:N}, a joint observation set {O1:N} representing the local information that each agent can perceive from the global state S, and a joint reward set {R1:N}, as well as a system global state transition function .
State Space Design: Each agent n receives a private observation at time t, which is influenced by the current state of the system environment S → , where state S is affected by the joint actions of all agents. The initial state S0 is sampled from a probability distribution p(S) over the range [Smin, Smax]. The observation for agent n at t is defined as:
Where represents the current date and time including month, day, hour. Since the charging period of an EV at the building charging station is assumed to be unknown to the agent, is a binary value indicating the presence of an EV. is the average temperature of Tn,m within the hour. Similarly, represents the total demand or "peak" for current time period t (hour in our study) of the community. It is not possible to predict the future precisely, so the daily peak cannot be optimized for a full 24-hour period in advance. Instead, provides an hourly "peak" that can be reduced and shifted through learning from historical measurements of the community electricity distribution system.
Action Space Design: The action taken by each agent n is defined as an hourly decision on EV charging and HVAC setting at time t to influence the system environment, i.e., = [, ]. Each agent n employs a deterministic policy πn: → , which maps its local observations to actions . Actions are normalized to the interval [ − 1, 1] to ensure consistent scaling and facilitate the neural network learning process. The relationship between designed agent actions and actual system control variables are:
The agent’s actions and are then transformed into EMS control variables and , representing the energy supplied to EV charging and the HVAC thermostat setting, respectively. The EV charging action is clipped and mapped to a value between the minimum and maximum charging capacities, naturally constraining power as per (3). Similarly, the HVAC action is mapped within the thermostat's operational range, ensuring compliance with (10).
Reward Design: The reward function is used to guide an RL agent’s learning process via mapping the immediate reward for each action, with the state-action-next state tuple (S, A, S`). In the community EMS, each agent's objective is to find the optimal control policy (π) that maximizes its cumulative reward, i.e., contribution to the EMS objective (1). Thus, the agent-level reward, , is designed to include the HVAC reward component , the EV charging reward component , the electricity cost reward component , and peak demand cost reward component as shown in (30).
Additionally, EV charging and SoC constraints (2) and (7) are soft-constrained, with penalties , applied to the reward components when constraints are violated (24).
The reward for EV charging is based on the energy supplied to vehicle, as shown in (25). If the EV is not present and the agent chooses not to charge, a small positive reward is given. This design provides feedback even during non-charging periods, reducing reward sparsity and ensuring appropriate rewards for inaction. Additionally, the agent is rewarded for charging during the designated charging period, independent of the time or EV SoC, encouraging completing charging within allowed time periods while penalizing charging outside, as described in (24). Decoupling the reward from specific time periods and SoC levels allows for flexible time-shifting, as each reward is independent of the charging status at any given time, with the electricity costs and peak demand cost being addressed in a later reward.
The HVAC reward component provides positive feedback when the temperature is maintained withing the comfort range and uses a soft-constraint to penalize the agent for deviations from this range, encouraging efficient HVAC management.
The electricity cost reward is designed as (27) to penalize the agent based on the cost of electric energy used for EV charging and HVAC operation, scaling them separately to prevent imbalances in different system capacities:
Peak demand calculated in (28) will be rewarded revolving around a predefined threshold D, which could be derived from historical data or based on distribution system operational experience. While D is set as a constant in our daily EMS model, it can be adjusted periodically to account for seasonal variations or system operation condition changes in peak demand. Each building agent is designed to be rewarded or penalized according to its contribution to reducing or increasing the peak demand, as expressed by (29). The reward design works by incentivizing agents to reduce peak demand by providing positive rewards when the total energy consumption is below D. If exceeds D, agents are penalized proportionally based on their contribution to the total demand, encouraging reducing energy usage during high demand periods.
Each reward component as designed above is then scaled between [-1,1], with weight parameters λ applied in (30) to distribute the importance of the reward components within each agent based on the building’s operation prioritizations.
State Transition Functions: After agent n executes an action at observation , the next observation is obtained according to the state transition function. The transition functions of the HVAC and EV are discussed in Section 2 through equations (8) and (6), but the transition function of EV presence and peak demand Kt are not fully observable by the agents, making this a Partially Observable Markov Decision Process (POMDP). Additionally, individual agents’ lack of comprehensive knowledge of the system's global state due to physical limitations realistically reflects real-world community EMS setting, with agents mainly relying on their own sensors and local information for operation.
Multi-Agent Decision Problem: Each agent n obtains rewards as a function of the system state and its own action, represented as : S × → ℝ. These rewards are influenced by other agents’ actions. The agent n aims to maximize its total expected reward Rn= over the time horizon T, where γ is a discount factor in time period t.
4. Proposed LSD-MADDPG Algorithm
This section presents the proposed LSD-MADDPG, tailored for the smart community EMS, towards a practical, scalable, and cost-effective approach. Since a specific building in a community cannot be assumed to be able to observe the operation parameters of other buildings, the community EMS problem as modeled in (1) – (19) cannot be solved directly without a central operator maintaining a global view. To mitigate major drawbacks introduced by a centralized solution, a model-free MARL algorithm is explored to guide individual building agents to learn optimal control policies from experience data to advise their actions that could maximize the cumulative reward Rn, which is designed to also reflect the community EMS objectives. Additionally, to preserve data privacy of each building while accelerating training speed, a centralized training and decentralized execution paradigm is adopted in the proposed MARL algorithm.
As each agent’s reward designed by (30) depends on cooperation to maximize collective reward while pursuing individual objectives, the interactions among agents in the community EMS form a mixed-cooperative-competitive dynamic. We propose the use of an MADDPG-based algorithm framework with additional enhancements, leading to the LSD-MADDPG to solve this problem.
In a conventional MADDPG framework, each agent is modeled using the DDPG configuration, including an actor network and a critic network. The critic network is configured to have full access to the observations and actions of other agents in the environment. During the training process, sharing these observations and actions allows each agent to evaluate its own actions in relation to the overall system state and the actions of others, building an understanding of the transition probabilities of the system environment and facilitating more informed decision-making based on the collective behaviors observed.
The proposed LSD-MADDPG differs in that each agent’s critic network is restricted to only have access to the “strategy” of other agents in addition to its own local observations and actions, reflecting the physical observability limitations in the community setting. The “strategy” of each building agent is defined as , which is further discretized to improve privacy protection as shown in (31-32). These agents’ operation strategies are proposed to introduce a simplified, quantifiable indication of each agent's energy demand priority at a given time, which could be derived from historical operation experiences. The HVAC operation strategy reflects the urgency for a building to bring temperature into the comfort range, while the EV charging strategy indicates the urgency of scheduling charging.
During training, the actor network maps RL agent's local observation to its optimal actions, employing a Tanh activation function in its output layer. Meanwhile, the output layer of the critic network produces a Q-value to evaluate the effectiveness of the actor’s actions. By incorporating other agents’ strategies into an agent’s critic network, the critic gains a comprehensive understanding of the global state, factoring in both the local observations and the energy consumption intentions of other agents. This expanded perspective allows the critic to more accurately calculate the Q-value, for evaluating the actor's performance. As a result, the critic can guide the actor toward more effective decision-making, improving policy optimization and coordination across the entire system.
During execution, the critic networks will not be used, and only the trained actor networks, which rely on agents’ local observations, are employed. Individual buildings’ energy consumptions are not directly shared; instead, the total community consumption, representing the global state, is provided as a reading to all buildings. The algorithm architecture of the LSD-MADDPG is illustrated in Figure. 1, with the training process detailed by Algorithm 1. Both the actor and critic networks of an agent are constructed as deep neural networks with dense layers, with ReLU activations in the hidden layers.
Figure 1.
Algorithm Architecture of LSD-MADDPG.
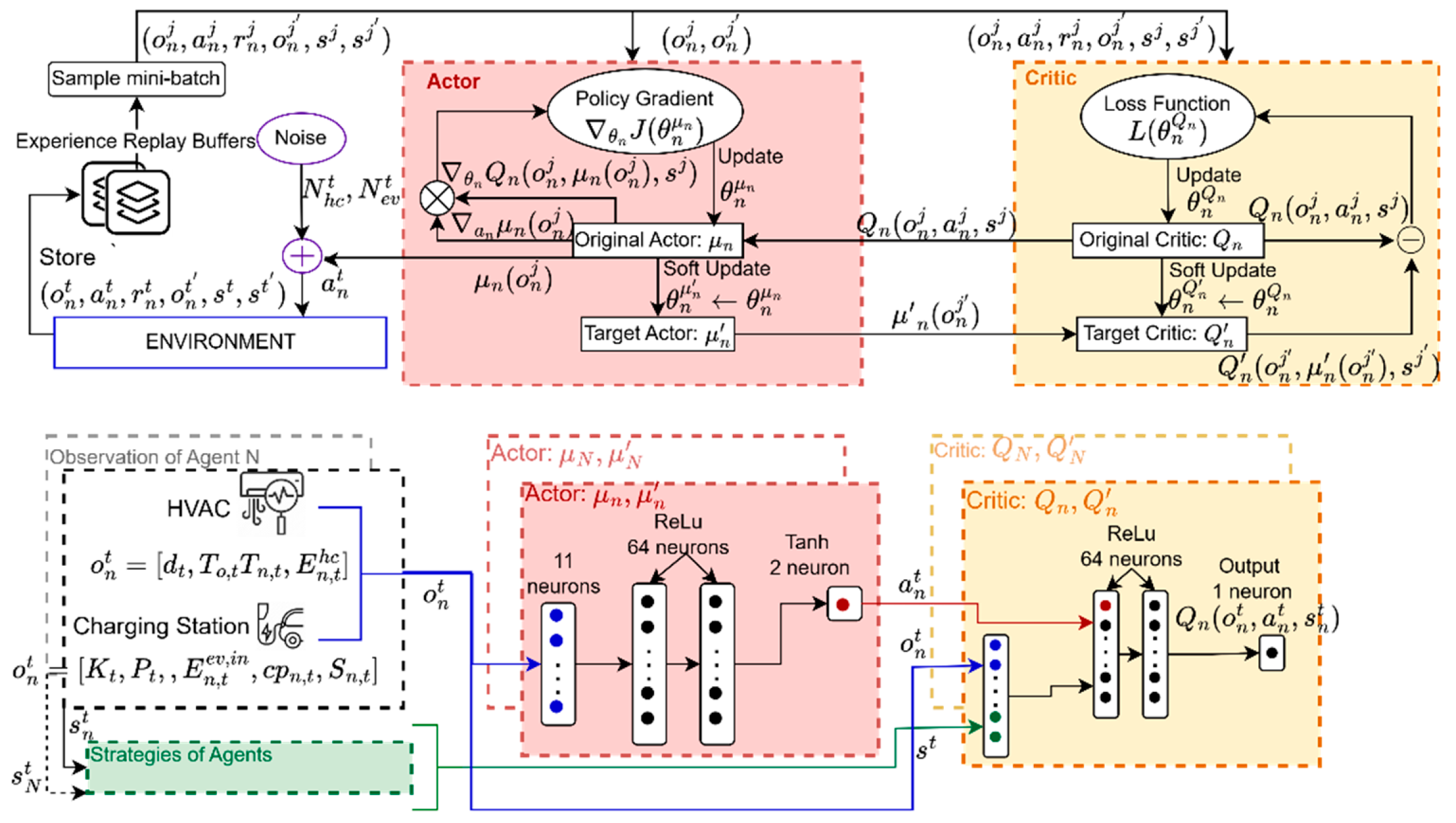
The designed actor and critic network of agent n is denoted as µn and Qn, and their associated weights are and . To enhance exploration in the deterministic MADDPG framework, noise is introduced to the action space. Two types of noise are used to tailor to the specific action: Orstein-Uhlenbeck noise [64], which generates temporally correlated noise mitigating large deviations in action exploration by selecting temperatures close to one another, and Arcsine noise [65] , characterized by a probability density function heavily weighted towards the minimum and maximum values, making it suitable for boundary decisions such as charging or not charging. Furthermore, to balance exploration and exploitation, ε-greedy is used, which gradually decreases exploration as training progresses, relying more on the learned policy. When not exploring, each agent takes action . During exploration, actions are adjusted by adding noise, resulting in or , where is the output action of the actor network .
| Algorithm 1 Offline training phase of LSD-MADDPG |
| 1. Initialize Networks and Replay Buffer: - Initialize actor network µn and critic network Qn for each agent, n - Initialize target networks and with weights: and . - Initialize experience replay buffer Ɗ 2. Training Loop - For each episode e - Initialize the environment and get - For each timestep t until terminal state: A. Observe current state and strategies B Select action using actor network C. Execute action bserve reward , next state and next strategies D. Store transition in Ɗ E. If episode e is divisible by δ: i. Sample minibatch of ρ transitions from Ɗ ii. Update Critic Network: - Compute target action using target actor network: - Compute target Q-value: - Compute current Q-value - Compute critic loss: . - Perform gradient descent on to update iii. Update Actor Network - Compute policy gradient: = . - Perform gradient ascent on to update iv. Update Target Networks - For each agent n 3. End Training |
Each agent’s actions , along with their observations at t, are applied to the simulated smart community to calculate building-level energy consumptions, resulting in an aggregated community demand on the distribution system. At the end of t, each agent calculates their reward given by (30), reads a new observation and shares its strategy values with the community. These shared strategies are then accessed by all agents, and the experience tuple is stored in the buffer Ɗ. After every δ number of episodes, all agents’ actor and critic networks are trained by randomly sampling ρ number of transitions from the buffer. The transitions j, j ρ are used to update the neural network weights for both the actor and critic networks.
After training completion, the critic network and buffer are removed and the actor network for each agent is retained, and its trained policy is used to act based on its local observations for online execution, .
5. Case Study
A smart community is simulated to evaluate the effectiveness of the proposed LSD-MADDPG demand-side EMS. Each building within the community is simulated to be equipped with an HVAC system and an EV charging station for ease of implementation, which could be expanded to multi-zone HVAC systems and multiple charging stations. The community EMS’s objectives are designed to minimize energy costs, ensure occupant comfort, and meet EV charging demands at the building level while reducing the peak energy demand at the community level.
The performance of the proposed LSD-MADDPG controller is further evaluated via a comprehensive comparison with four other controllers which are commonly seen in community EMS:
(1) Naïve controller (NC): Such EMS represents the common practice in building energy management, involving setting the thermostat at a constant 72℉ and using a simple plug in and charge at full capacity charger. This approach does not optimize the community objective or energy consumption, hence termed 'naïve'.
(2) DDPG controller: A centralized single-agent RL controller for the entire community EMS operating within the environment and state-action space described in Section 3.
(3) I-MADDPG controller: Independent Learning MADDPG with decentralized training and decentralized execution.
(4) CTDE-MADDPG controller: MADDPG with centralized critic training and decentralized execution, with the agent’s critic network accessing to the entire global state.
5.1. Simulation Parameters
Each episode was simulated for 48 hours, from 12 PM to 12 PM two days later, to capture extended peak demand periods, including both morning and evening peaks, and to accommodate realistic EV charging scenarios where vehicles may arrive, depart, and require multiple charging cycles. Episodes were randomly sampled from yearly data to account for temperature variations and introduce variability. Additionally, in our cases all weights in (30) are set equally for each reward component, and all other simulation parameters are summarized in Table 1.
5.2. Performance Analysis with Three Identical Buildings
To demonstrate the effectiveness of the proposed LSD-MADDPG in energy management via consumption shifting, all the EV schedules and building attributes, including HVAC system settings, were purposely set as identical across three buildings in the simulated community. This setting ensures that the observed charging patterns result from deliberate load-shifting rather than differences in EV availability. Hourly weather data and electricity prices, which featured two price points for peak ($0.54/kWh) and off-peak hours ($0.22/kWh), were sourced from CityLearn Challenge 2022 Phase 1 dataset [66]. EV presence were consistently maintained across each day, with the EV present during hours from 18 to 8 each day. Table 2 details the building, charging station, EV, and HVAC systems setting in the smart community EMS simulation.
Below Figure 2 illustrates the training results of the reward values of four RL based EMS controllers providing a comprehensive performance comparison. The results demonstrate that the LSD-MADDPG exhibits a robust performance in managing variability, consistently achieving higher cumulative rewards. Specifically, LSD-MADDPG outperforms all the other three RL controllers with the highest mean reward of 0.271 and minimal solution variability, indicated by a standard deviation of 0.0071. Meanwhile, the I-MADDPG and CTDE-MADDPG controllers also show robust performance with means of 0.270 and 0.269 and standard deviations of 0.0101 and 0.0122, respectively, while the DDPG controller lags with the lowest mean of 0.251 and highest variability of 0.047682.
The evaluation was conducted on the CityLearn Challenge 2022 Phase 2 dataset [66], spanning a 48-hour period from 12 PM on January 1st to 12PM on January 3rd. Table 3 presents the 2-day evaluation results of various EMS controllers, detailing their achieved community average daily peak demand, total energy consumption costs, community charging satisfaction, buildings’ peak contribution, total reward, and a Gini Coefficient [67]. Average peak reflects the highest community energy demand recorded within a day, averaged over two days of evaluation. Lower peak demand indicates better community energy load management, to reduce strain on the distribution system. Total cost refers to the total community electricity cost, where lower costs indicate more energy usage during low-price periods. Charge refers to the percentage of required power delivered for the entire community's EV charging, where a higher value indicates better fulfillment of EV charging needs. Peak contribution sums each building’s contribution to reducing community peak demand as described in (29), quantifying the communities’ hourly energy consumption shifting to reducing peak electricity demand. Total reward represents the controller's ability to optimize multiple objectives, including cost savings, temperature comfort, peak demand reduction, and efficient EV charging. Higher rewards indicate better overall system performance. Finally, the Gini Coefficient quantifies the equity of reward distribution among agents, where a lower Gini coefficient represents a more equitable allocation of rewards, indicating fairer distribution of energy cost savings, temperature comfort, and peak demand reduction contributions, and EV charging performance across all building agents. Throughout the simulation, building comfort is consistently maintained within predefined temperature requirements bounds, as a result, it is not tabulated.
The multi-objective problem in the demand-side EMS requires balancing various objectives included in (30). When full community information is shared among agents during training, CTDE-MADDPG demonstrates strong cooperation between building agents, achieving the highest community reward of 38.72. This is reflected in its superior ability to balance all objectives, especially peak contribution and community costs. However, LSD-MADDPG follows closely with a reward of 38.69, highlighting its comparable strong overall performance, without compromising data privacy. Both I-MADDPG and LSD-MADDPG, which promote more competitive environments for individual rewards, lead to higher total charge within the community and exhibit lower Gini Coefficients, resulting in a more equitable distribution of rewards. LSD-MADDPG achieves the lowest Gini Coefficient of 0.0125 and best peak contribution. I-MADDPG excels in charge management but lags in peak contribution and overall rewards, due to its lack of information sharing and thus coordination among RL agents. In contrast, DDPG, lacking competition, exploits individual buildings, resulting in the highest Gini coefficient and lowest community charging satisfaction, prioritizing reducing costs at the expense of other objectives.
Figure 3 further elaborates individual building agents’ performance across four metrics, i.e., building rewards, peak contribution, energy cost, charging satisfaction, with LSD-MADDPG showing the most balanced contribution, particularly in peak demand reduction, compared to other RL controllers. The LSD-MADDPG’s more even energy shifting (i.e., peak demand reduction) among buildings demonstrates that it secures a fair participation/coordination among agents, reducing the burden on any single building to manage the community energy demand. This balanced contribution enhances system reliability by lowering the risk of over-reliance on specific buildings and makes cost/benefit distribution more equitable. Additionally, it improves scalability, allowing the system to remain effective as more buildings are included in the community EMS.
Figure 4 compares the individual buildings’ 48-hour hourly energy consumptions achieved by CTDE-MADDPG and LSD-MADDPG, to illustrate how the two MADDPG algorithms manage the building HVAC and EV charging, in response to varying electricity prices. On the first price drop, coinciding with EV presence, buildings initiate charging, leading to the highest energy peaks observed throughout the day. This is a rational behavior as charging typically occurs when the SoC is low, benefiting from improved charging efficiencies. While both algorithms reduce energy consumption during high-price hours, CTDE-MADDPG exhibits steeper fluctuations, with only a few buildings responsible for most of the energy reduction. In contrast, LSD-MADDPG smooths out consumptions over a broader range of time, suggesting it prioritizes a more balanced distribution of energy shifting across all buildings, which explains the higher costs due to increased consumption during hour 19 of day 1. By involving more buildings in the energy management, LSD-MADDPG is expected to achieve a steadier and more evenly distributed electric load among the buildings, while CTDE-MADDPG tends to concentrate energy adjustments to fewer buildings. This feature of LSD-MADDPG will be better suited for achieving collective community energy management goals, such as peak reduction and load balancing across the entire community. Furthermore, LSD-MADDPG illustrates its advantages in achieving such collaboration while keeping data private. This proposed approach enables agents to both compete and cooperate effectively, striking a balance between equitable reward distribution and community collaboration.
5.3. Scalability Performance Analysis on the Proposed LSD-MADDPG
To evaluate the scalability of the proposed LSD-MADDPG, a smart community including nine buildings, with various EV charging and building HVAC configurations are simulated. Table 4 provides a detailed breakdown of building types and their respective thermal and EV charging station characteristics, capturing the diversity in energy requirements and capacities across various community buildings. These various buildings simulated in the community increase problem complexity and showcase the adaptability of the proposed EMS solution, from smaller residential homes to expansive commercial complexes and their interactions with one another.
Table 5 tabulates electricity prices based on the time of day and specific months, aligning with typical winter and summer peak energy consumption patterns. For instance, winter features morning and evening peaks due to high heating demands, while summer exhibits midday peaks driven by air conditioning usage. Transitional months typically experience more moderate weather conditions. Table 6 provides a detailed breakdown of the hourly presence patterns of EVs across various building types, segmented by day type—weekday, weekend, and holiday based upon [68]. For each building category, the table lists the probability of EV presence during specific hours, reflecting tailored energy management needs.
The four MARL controllers were trained using outdoor temperature data from [69] and the same number of timesteps, with average training rewards graphed in Figure 5. From Table 7. it is portrayed that LSD-MADDPG outperformed all other strategies, achieving the highest mean reward and the lowest variability during training. I-MADDPG and CTDE-MADDPG followed with comparable performance, while DDPG showed significantly lower rewards and higher variability, indicating challenges with scalability and in competitive environments where individual objectives must be balanced.
The main challenge in algorithm scalability lies in scheduling EV charging to balance peak demand reduction without overly sacrificing individual building needs or community objectives. The advantage of MADDPG, i.e., using separate actors and critics for each controller is that each building can learn its own objectives while still considering the community goal of reducing peak demand. Peak contribution is primarily influenced by EV schedules because buildings with more charging hours (i.e., EVs are present) can spread out their energy use, while those with fewer hours may have to concentrate their charging demands. As the system scales, managing such flexibilities becomes more complex, and varying schedules across buildings create fluctuations in community peak demand, making efficient coordination more challenging. This is reflected in Table 8’s evaluation results, which present the reward and total community charge, i.e., the total kWh provided to the EVs in the community. The naïve approach assumes all EVs are charged to their full target SoC whenever present, establishing the maximum possible charge demand for the community at the cost of all other objectives.
A 10-day evaluation period was chosen to capture the characteristics of different days and schedules, ensuring robustness in various scenarios. LSD-MADDPG outperforms all controllers, which struggle to identify optimal EV charging schedules, demonstrating LSD-MADDPG's adaptability and scalability in larger scale systems. It achieves the highest reward by meeting 83% of the total community’s EV charging demand, via evaluating the difference between the initial SoC and the target SoC of all EVs over the 10-day period. This indicates that LSD-MADDPG scales best, as its trained policy achieved superior results within the same number of timesteps as other algorithms, demonstrating more efficient adaptability in the complex environment, e.g., increasingly competitive settings with diverse buildings, varied equipment capacities, and schedules.
Ultimately, LSD-MADDPG's crucial strategic insights, allows agents to better plan and coordinate their energy usage to optimize community objectives, while satisfying their individual charging needs and maintaining thermal comfort. This proposed approach not only enhances scalability, privacy, and decision-making efficiency but also supports competition, a critical aspect as the complexity and variability of the community energy system increases.
5. Conclusions
This paper presents an enhanced MARL controller, i.e.: LSD-MADDPG, for demand-side energy management of smart communities. The proposed LSD-MADDPG emphasizes the equivalent priorities of pursuing community level energy management objective, as well as satisfying individual buildings’ operational requirements in maintaining indoor comfort and optimizing EV charging, two critical elements of energy consumption management in buildings of future smart communities. Through competitive and cooperative interactions among building agents, the proposed LSD-MADDPG EMS controller performs comparably to CTDE-MADDPG in small scale cases while preserving data privacy, but demonstrating better scalability in more complex system environments. This proposed approach, considering the physical limitation of practical EMS system in data access and privacy preserving, leverages the sharing of energy conservation strategies among agents, avoids the pitfalls of centralized systems, such as single points of failure, as well as reduces potential data leakage, and communication delay of conventional MADDPG. Future work aims to incorporate renewable energy sources into the building system, adding complexity but potentially increasing the sustainability and efficacy of demand-side energy management in communities dominated by distributed energy resources (DERs).
References
- Rathor, S., & Saxena, D. (2020). Energy management system for smart grid: An overview and key issues. International Journal of Energy Research, 44, 4067 - 4109. [CrossRef]
- Edstan Fernandez, M.J. Hossain, M.S.H. Nizami, Game-theoretic approach to demand-side energy management for a smart neighbourhood in Sydney incorporating renewable resources, Applied Energy, Volume 232, 2018, Pages 245-257, ISSN 0306-2619. [CrossRef]
- Benítez, I., & Díez, J. (2022). Automated Detection of Electric Energy Consumption Load Profile Patterns. Energies. [CrossRef]
- "California moves toward phasing out sale of gas-powered vehicles by 2035," in NewsHour: Nation, Aug 25, 2022, available: https://www.pbs.org/newshour/nation/california-moves-toward-phasing-out-sale-of-gas-powered-vehicles-by-2035.
- L. Albeck-Ripka, "Amid Heat Wave, California Asks Electric Vehicle Owners to Limit Charging," The New York Times, [Online]. Available: https://www.nytimes.com/2022/09/01/us/california-heat-wave-flex-alert-ac-ev-charging.html. [Accessed: 2-7-2023].
- Cecati, C., Citro, C., & Siano, P. (2011). Combined Operations of Renewable Energy Systems and Responsive Demand in a Smart Grid. IEEE Transactions on Sustainable Energy, 2, 468-476. [CrossRef]
- Khan, H., Usman, M., Hafeez, G., Albogamy, F., Khan, I., Shafiq, Z., Khan, M., & Alkhammash, H. (2021). Intelligent Optimization Framework for Efficient Demand-Side Management in Renewable Energy Integrated Smart Grid. IEEE Access, 9, 124235-124252. [CrossRef]
- Liu, H., Gegov, A., & Haig, E. (2017). Rule Based Networks: An Efficient and Interpretable Representation of Computational Models. Journal of Artificial Intelligence and Soft Computing Research, 7, 111 - 123. [CrossRef]
- Babonneau, F., Caramanis, M., & Haurie, A. (2016). A linear programming model for power distribution with demand response and variable renewable energy. Applied Energy, 181, 83-95. [CrossRef]
- Loganathan, N., & Lakshmi, K. (2015). Demand Side Energy Management for Linear Programming Method. Indonesian Journal of Electrical Engineering and Computer Science, 14, 72-79. [CrossRef]
- Nejad, B., Vahedi, M., Hoseina, M., & Moghaddam, M. (2022). Economic Mixed-Integer Model for Coordinating Large-Scale Energy Storage Power Plant with Demand Response Management Options in Smart Grid Energy Management. IEEE Access, PP, 1-1. [CrossRef]
- Omu, A., Choudhary, R., & Boies, A. (2013). Distributed energy resource system optimisation using mixed integer linear programming. Energy Policy, 61, 249-266. [CrossRef]
- Shakouri, G., & Kazemi, A. (2017). Multi-objective cost-load optimization for demand side management of a residential area in smart grids. Sustainable Cities and Society, 32, 171-180. [CrossRef]
- Wouters, C., Fraga, E., & James, A. (2015). An energy integrated, multi-microgrid, MILP (mixed-integer linear programming) approach for residential distributed energy system planning – A South Australian case-study. Energy, 85, 30-44. [CrossRef]
- Foroozandeh, Z., Ramos, S., Soares, J., Lezama, F., Vale, Z., Gomes, A., & Joench, R. (2020). A Mixed Binary Linear Programming Model for Optimal Energy Management of Smart Buildings. Energies. [CrossRef]
- Aghajani, G., Shayanfar, H., & Shayeghi, H. (2015). Presenting a multi-objective generation scheduling model for pricing demand response rate in micro-grid energy management. Energy Conversion and Management, 106, 308-321. [CrossRef]
- Viani, F., & Salucci, M. (2018). A User Perspective Optimization Scheme for Demand-Side Energy Management. IEEE Systems Journal, 12, 3857-3860. [CrossRef]
- Kumar, R., Raghav, L., Raju, D., & Singh, A. (2021). Intelligent demand side management for optimal energy scheduling of grid connected microgrids. Applied Energy, 285, 116435. [CrossRef]
- Aghajani, G., Shayanfar, H., & Shayeghi, H. (2015). Presenting a multi-objective generation scheduling model for pricing demand response rate in micro-grid energy management. Energy Conversion and Management, 106, 308-321. [CrossRef]
- Viani, F., & Salucci, M. (2018). A User Perspective Optimization Scheme for Demand-Side Energy Management. IEEE Systems Journal, 12, 3857-3860. [CrossRef]
- Saghezchi, F., Saghezchi, F., Nascimento, A., & Rodriguez, J. (2014). Quadratic Programming for Demand-Side Management in the Smart Grid. , 97-104. [CrossRef]
- Batista, A., & Batista, L. (2018). Demand Side Management using a multi-criteria ϵ-constraint based exact approach. Expert Syst. Appl., 99, 180-192. [CrossRef]
- Hosseini, S., Carli, R., & Dotoli, M. (2021). Robust Optimal Energy Management of a Residential Microgrid Under Uncertainties on Demand and Renewable Power Generation. IEEE Transactions on Automation Science and Engineering, 18, 618-637. [CrossRef]
- Rahim, S., Javaid, N., Ahmad, A., Khan, S., Khan, Z., Alrajeh, N., & Qasim, U. (2016). Exploiting heuristic algorithms to efficiently utilize energy management controllers with renewable energy sources. Energy and Buildings, 129, 452-470. [CrossRef]
- Jiang, X., & Xiao, C. (2019). Household Energy Demand Management Strategy Based on Operating Power by Genetic Algorithm. IEEE Access, 7, 96414-96423. [CrossRef]
- Eisenmann, A., Streubel, T., & Rudion, K. (2022). Power Quality Mitigation via Smart Demand-Side Management Based on a Genetic Algorithm. Energies. [CrossRef]
- A. Ouammi, "Optimal Power Scheduling for a Cooperative Network of Smart Residential Buildings," in IEEE Transactions on Sustainable Energy, vol. 7, no. 3, pp. 1317-1326, July 2016, . [CrossRef]
- Gbadega, P., & Saha, A. (2022). Predictive Control of Adaptive Micro-Grid Energy Management System Considering Electric Vehicles Integration. International Journal of Engineering Research in Africa, 59, 175 - 204. [CrossRef]
- J. Arroyo, C. Manna, F. Spiessens, and L. Helsen, "Reinforced model predictive control (RL-MPC) for building energy management," Applied Energy, vol. 309, pp. 118346, 2022. [CrossRef]
- D. Vamvakas, P. Michailidis, C. D. Korkas, and E. B. Kosmatopoulos, "Review and Evaluation of Reinforcement Learning Frameworks on Smart Grid Applications," Energies, 2023. [Online]. Available: https://api.semanticscholar.org/CorpusID:259862630.
- S. -J. Chen, W. -Y. Chiu and W. -J. Liu, "User Preference-Based Demand Response for Smart Home Energy Management Using Multiobjective Reinforcement Learning," in IEEE Access, vol. 9, pp. 161627-161637, 2021, . [CrossRef]
- S. Zhou, Z. Hu, W. Gu, M. Jiang and X. -P. Zhang, "Artificial intelligence based smart energy community management: A reinforcement learning approach," in CSEE Journal of Power and Energy Systems, vol. 5, no. 1, pp. 1-10, March 2019, . [CrossRef]
- F. Alfaverh, M. Denaï and Y. Sun, "Demand Response Strategy Based on Reinforcement Learning and Fuzzy Reasoning for Home Energy Management," in IEEE Access, vol. 8, pp. 39310-39321, 2020, . [CrossRef]
- A. Mathew, A. Roy and J. Mathew, "Intelligent Residential Energy Management System Using Deep Reinforcement Learning," in IEEE Systems Journal, vol. 14, no. 4, pp. 5362-5372, Dec. 2020, . [CrossRef]
- A. Forootani, M. Rastegar and M. Jooshaki, "An Advanced Satisfaction-Based Home Energy Management System Using Deep Reinforcement Learning," in IEEE Access, vol. 10, pp. 47896-47905, 2022, . [CrossRef]
- Y. Liu, D. Zhang and H. B. Gooi, "Optimization strategy based on deep reinforcement learning for home energy management," in CSEE Journal of Power and Energy Systems, vol. 6, no. 3, pp. 572-582, Sept. 2020, . [CrossRef]
- L. Yu et al., "Deep Reinforcement Learning for Smart Home Energy Management," in IEEE Internet of Things Journal, vol. 7, no. 4, pp. 2751-2762, April 2020, . [CrossRef]
- I. Zenginis, J. Vardakas, N. E. Koltsaklis and C. Verikoukis, "Smart Home’s Energy Management Through a Clustering-Based Reinforcement Learning Approach," in IEEE Internet of Things Journal, vol. 9, no. 17, pp. 16363-16371, 1 Sept.1, 2022, . [CrossRef]
- N. Kodama, T. Harada and K. Miyazaki, "Home Energy Management Algorithm Based on Deep Reinforcement Learning Using Multistep Prediction," in IEEE Access, vol. 9, pp. 153108-153115, 2021, . [CrossRef]
- Y. Ye, D. Qiu, X. Wu, G. Strbac and J. Ward, "Model-Free Real-Time Autonomous Control for a Residential Multi-Energy System Using Deep Reinforcement Learning," in IEEE Transactions on Smart Grid, vol. 11, no. 4, pp. 3068-3082, July 2020, . [CrossRef]
- C. Huang, H. Zhang, L. Wang, X. Luo and Y. Song, "Mixed Deep Reinforcement Learning Considering Discrete-continuous Hybrid Action Space for Smart Home Energy Management," in Journal of Modern Power Systems and Clean Energy, vol. 10, no. 3, pp. 743-754, May 2022, . [CrossRef]
- F. Härtel and T. Bocklisch, "Minimizing Energy Cost in PV Battery Storage Systems Using Reinforcement Learning," in IEEE Access, vol. 11, pp. 39855-39865, 2023, . [CrossRef]
- Parvini, M., Javan, M., Mokari, N., Arand, B., & Jorswieck, E. (2021). AoI Aware Radio Resource Management of Autonomous Platoons via Multi Agent Reinforcement Learning. 2021 17th International Symposium on Wireless Communication Systems (ISWCS), 1-6. [CrossRef]
- I. Jendoubi and F. Bouffard, "Multi-agent hierarchical reinforcement learning for energy management," Applied Energy, vol. 332, 120500, 2023, ISSN 0306-2619. [Online]. Available: https://. [CrossRef]
- A. Arora, A. Jain, D. Yadav, V. Hassija, V. Chamola and B. Sikdar, "Next Generation of Multi-Agent Driven Smart City Applications and Research Paradigms," in IEEE Open Journal of the Communications Society, vol. 4, pp. 2104-2121, 2023, . [CrossRef]
- Kim H, Kim S, Lee D, Jang I. Avoiding collaborative paradox in multi-agent reinforcement learning, ETRI Journal 43 (2021), 1004–1012. [CrossRef]
- M. Ahrarinouri, M. Rastegar and A. R. Seifi, "Multiagent Reinforcement Learning for Energy Management in Residential Buildings," in IEEE Transactions on Industrial Informatics, vol. 17, no. 1, pp. 659-666, Jan. 2021, . [CrossRef]
- X. Xu, Y. Jia, Y. Xu, Z. Xu, S. Chai and C. S. Lai, "A Multi-Agent Reinforcement Learning-Based Data-Driven Method for Home Energy Management," in IEEE Transactions on Smart Grid, vol. 11, no. 4, pp. 3201-3211, July 2020, . [CrossRef]
- Lu, R., Bai, R., Luo, Z., Jiang, J., Sun, M., & Zhang, H. (2021). Deep Reinforcement Learning-Based Demand Response for Smart Facilities Energy Management. IEEE Transactions on Industrial Electronics, 69, 8554-8565. [CrossRef]
- Lu, R., Li, Y., Li, Y., Jiang, J., & Ding, Y. (2020). Multi-agent deep reinforcement learning based demand response for discrete manufacturing systems energy management. Applied Energy. [CrossRef]
- Guo, G., & Gong, Y. (2023). Multi-Microgrid Energy Management Strategy Based on Multi-Agent Deep Reinforcement Learning with Prioritized Experience Replay. Applied Sciences. [CrossRef]
- Ye, Y., Tang, Y., Wang, H., Zhang, X., & Strbac, G. (2021). A Scalable Privacy-Preserving Multi-Agent Deep Reinforcement Learning Approach for Large-Scale Peer-to-Peer Transactive Energy Trading. IEEE Transactions on Smart Grid, 12, 5185-5200. [CrossRef]
- S. Lee and D. -H. Choi, "Federated Reinforcement Learning for Energy Management of Multiple Smart Homes With Distributed Energy Resources," in IEEE Transactions on Industrial Informatics, vol. 18, no. 1, pp. 488-497, Jan. 2022, . [CrossRef]
- Deshpande, K., Möhl, P., Hämmerle, A., Weichhart, G., Zörrer, H., & Pichler, A. (2022). Energy Management Simulation with Multi-Agent Reinforcement Learning: An Approach to Achieve Reliability and Resilience. Energies. [CrossRef]
- Hossain, M., & Enyioha, C. (2023). Multi-Agent Energy Management Strategy for Multi-Microgrids Using Reinforcement Learning. 2023 IEEE Texas Power and Energy Conference (TPEC), 1-6. [CrossRef]
- Pigott, A., Crozier, C., Baker, K., & Nagy, Z. (2021). GridLearn: Multiagent Reinforcement Learning for Grid-Aware Building Energy Management. ArXiv, abs/2110.06396. [CrossRef]
- Chen, T., Bu, S., Liu, X., Kang, J., Yu, F., & Han, Z. (2022). Peer-to-Peer Energy Trading and Energy Conversion in Interconnected Multi-Energy Microgrids Using Multi-Agent Deep Reinforcement Learning. IEEE Transactions on Smart Grid, 13, 715-727. [CrossRef]
- Xu, X., Jia, Y., Xu, Y., Xu, Z., Chai, S., & Lai, C. (2020). A Multi-Agent Reinforcement Learning-Based Data-Driven Method for Home Energy Management. IEEE Transactions on Smart Grid, 11, 3201-3211. [CrossRef]
- Samadi, E., Badri, A., & Ebrahimpour, R. (2020). Decentralized multi-agent based energy management of microgrid using reinforcement learning. International Journal of Electrical Power & Energy Systems, 122, 106211. [CrossRef]
- Fang, X., Zhao, Q., Wang, J., Han, Y., & Li, Y. (2021). Multi-agent Deep Reinforcement Learning for Distributed Energy Management and Strategy Optimization of Microgrid Market. Sustainable Cities and Society, 74, 103163. [CrossRef]
- B.-C. Lai, W. -Y. Chiu and Y. -P. Tsai, "Multiagent Reinforcement Learning for Community Energy Management to Mitigate Peak Rebounds Under Renewable Energy Uncertainty," in IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 6, no. 3, pp. 568-579, June 2022, . [CrossRef]
- "Tesla Motors Club, 'Charging efficiency,' Tesla Motors Club Forum, 2018. [Online]. Available: https://teslamotorsclub.com/tmc/threads/charging-efficiency.122072/. [Accessed: 4-1-2024].".
- MathWorks, "Model a House Heating System," MathWorks, 2024. [Online]. Available: https://www.mathworks.com/help/simulink/ug/model-a-house-heating-system.html#responsive_offcanvas.
- Gillespie, D. T. (1992). Continuous Markov processes. In D. T. Gillespie (Ed.), Markov Processes (pp. 111-219). Academic Press. [CrossRef]
- Jiang, J.-J., He, P., & Fang, K.-T. (2015). An interesting property of the arcsine distribution and its applications. Statistics & Probability Letters, 105, 88-95. [CrossRef]
- Nweye, Kingsley; Sankaranarayanan Siva; Nagy, Gyorgy Zoltan, 2023, "The CityLearn Challenge 2022". [CrossRef]
- Joe Hasell (2023) - “Measuring inequality: what is the Gini coefficient?” Published online at OurWorldInData.org. Retrieved from: 'https://ourworldindata.org/what-is-the-gini-coefficient' [Online Resource].
- E. Pritchard, B. Borlaug, F. Yang, and J. Gonder, "Evaluating Electric Vehicle Public Charging Utilization in the United States using the EV WATTS Dataset," presented at the 36th Electric Vehicle Symposium and Exposition (EVS36), Sacramento, CA, USA, Jun. 11-14, 2023. Preprint, NREL, National Renewable Energy Laboratory, Oct. 2023. [Online]. Available: www.nrel.gov/publications.
- Nagy, Gyorgy Zoltan, 2021, "The CityLearn Challenge 2021", Texas Data Repository, V1; weather_data.tab [fileName], UNF:6:ErXpO6j8iUg/4iEVsNtavg== [fileUNF]. [CrossRef]
Figure 2.
Average Training Rewards for RL Algorithms.
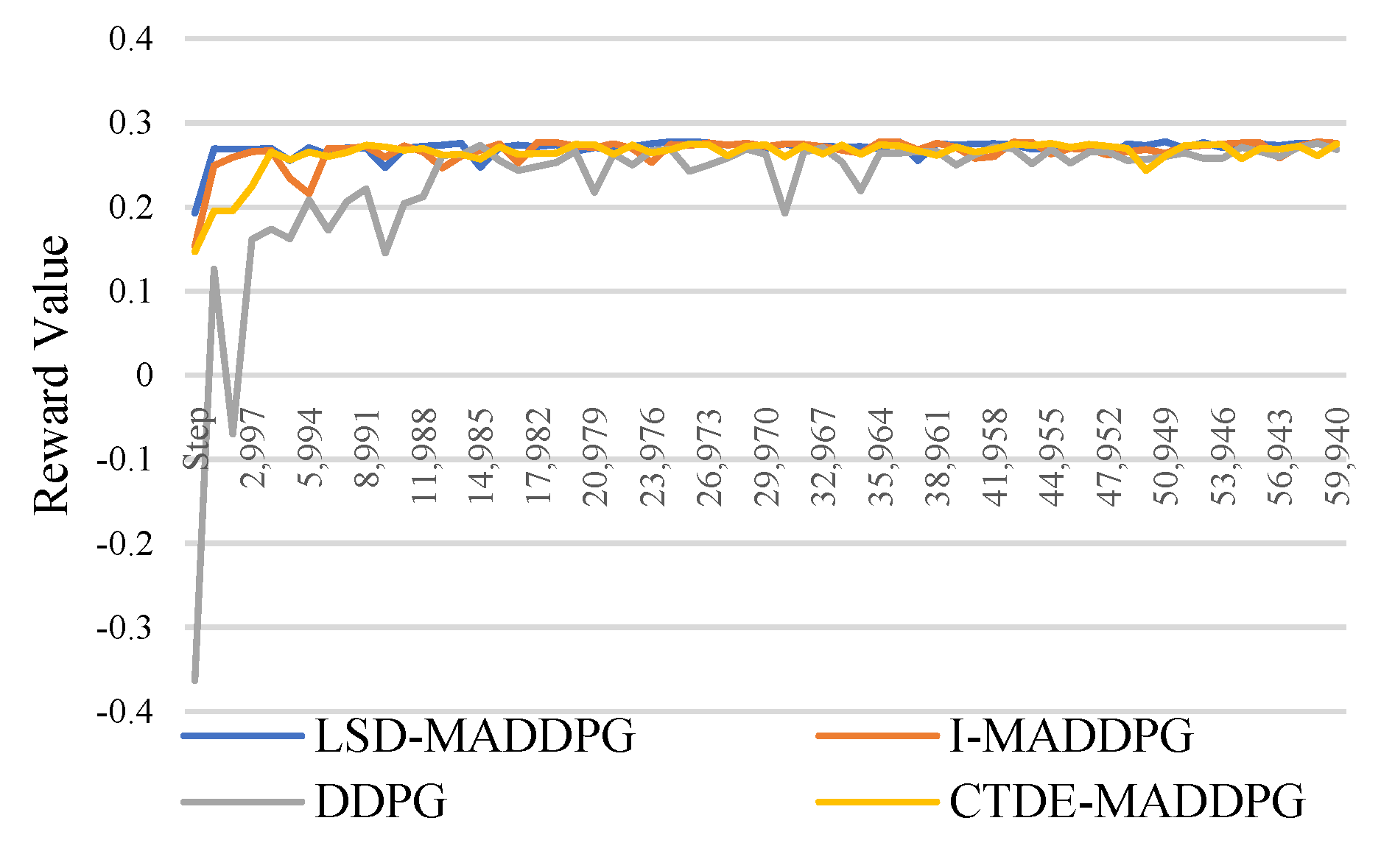
Figure 3.
Performance comparison of controllers for individual buildings across rewards, costs, charge, and peak contribution including (a) DDPG, (b) CTDE, (c) I-MADDPG (d) LSD-MADDPG.
Figure 3.
Performance comparison of controllers for individual buildings across rewards, costs, charge, and peak contribution including (a) DDPG, (b) CTDE, (c) I-MADDPG (d) LSD-MADDPG.
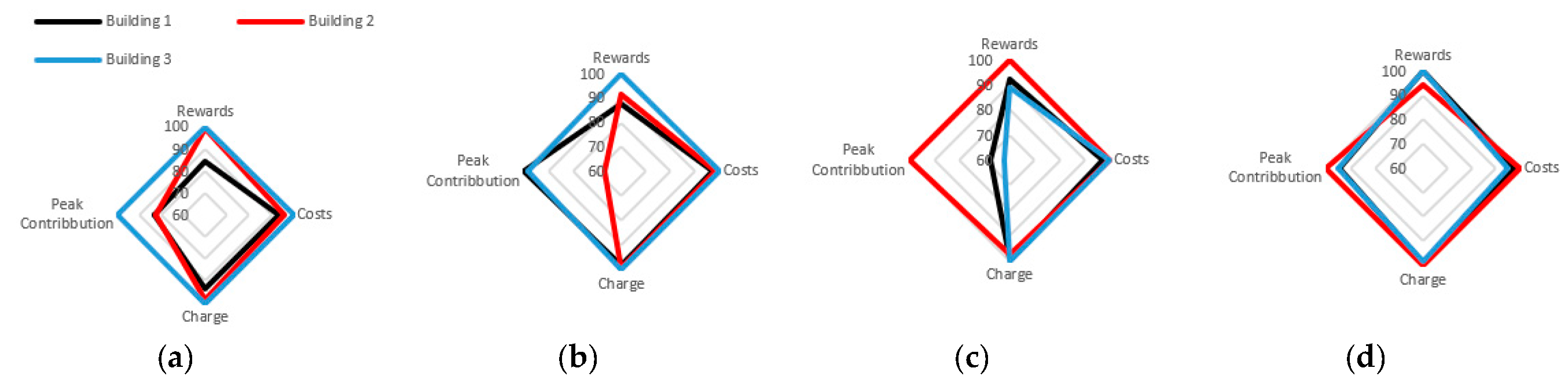
Figure 4.
Energy Consumption of (a) CTDE-MADDPG and (b) LSD-MADDPG Comparison.
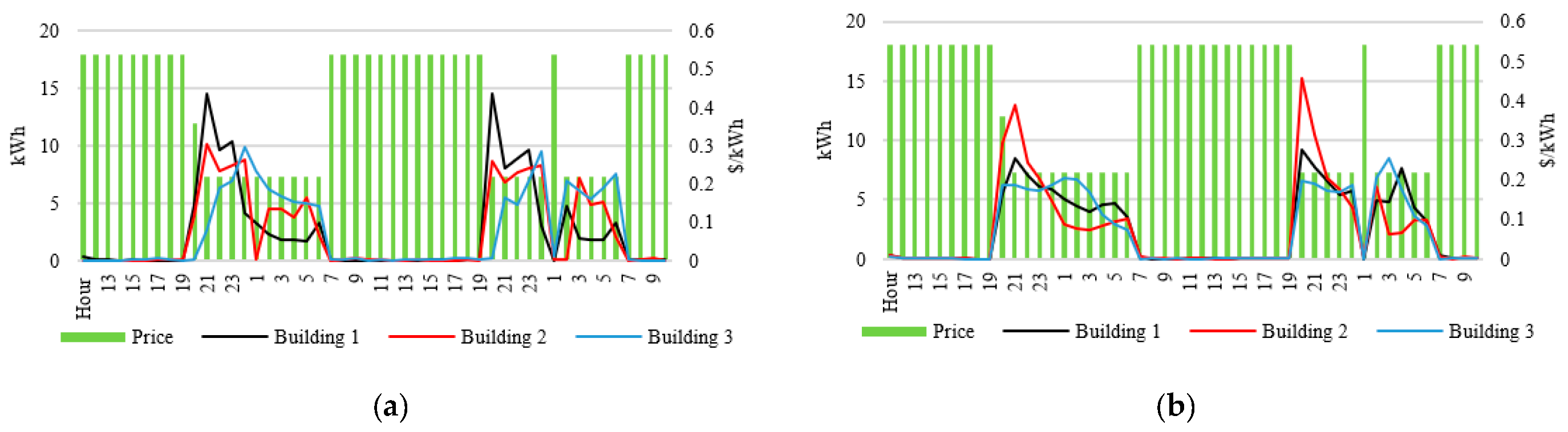
Figure 5.
Average RL Rewards during Training.
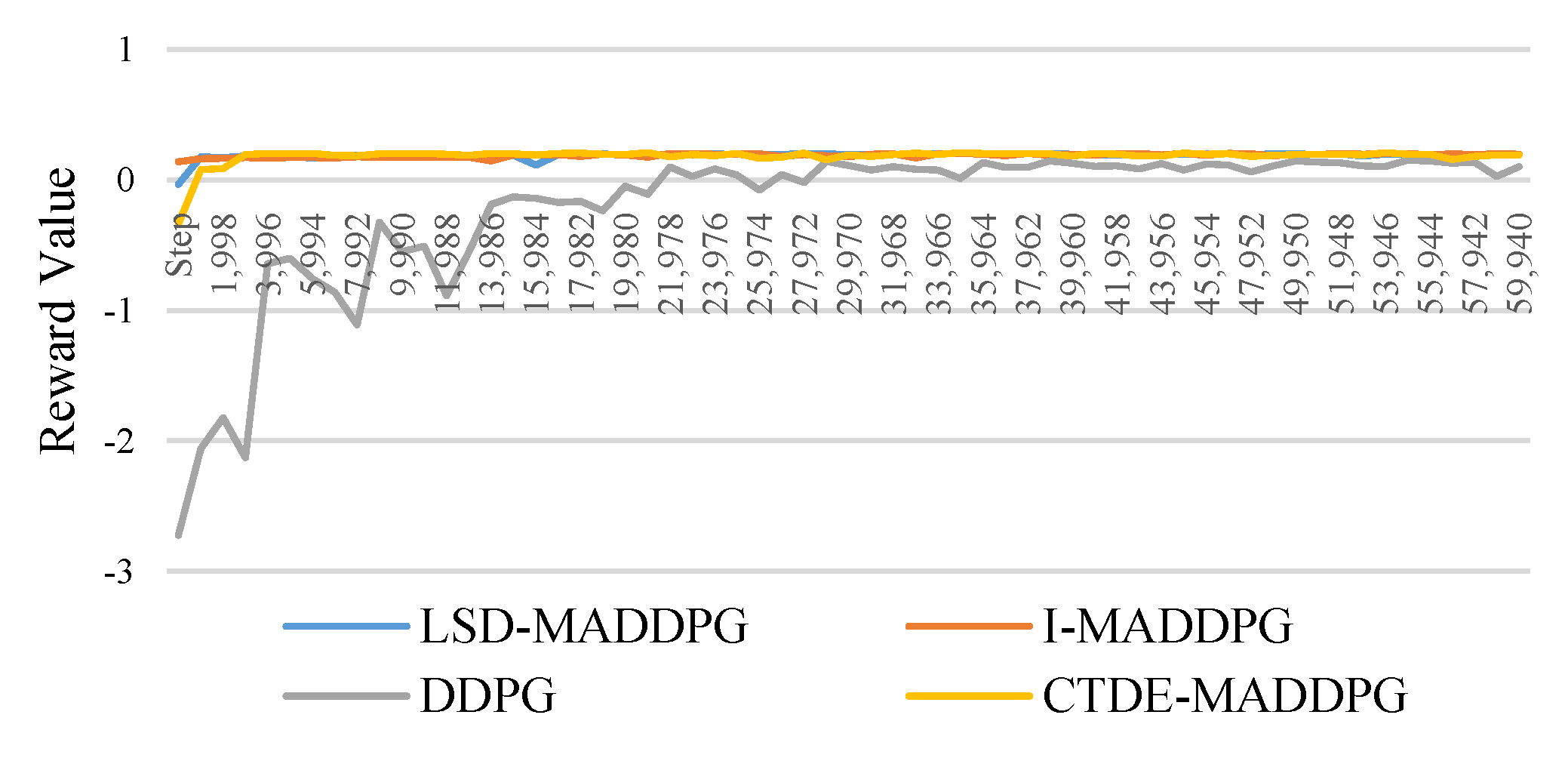
Table 1.
Training Hyperparameters.
| Variable | MARL | |
|---|---|---|
|
1 2 3 4 5 6 7 8 9 |
Total Timesteps Episode Length Learning Rate Actor Learning Rate Critic Noise-rate Gamma Tau Buffer-size Batch-size |
260,000 48 1e-4 1e-3 0.1 0.95 0.01 5e5 256 |
Table 2.
Specifications for Buildings and Energy Systems.
| Building Attributes | Value |
|---|---|
| 0.0001 minute· degree/joule | |
| 1005.4 joule/kilogram·degree | |
| 50, | |
| 1778.4 kilogram | |
| 60 kilogram/minute | |
| 1.5 kW,17 kW | |
| 100 kW | |
| 600 kWm | |
| 5 |
Table 3.
Evaluation Results on 3 Buildings.
| NC | DDPG | CTDE | I-MADDPG | LSD-MADDPG | |
|---|---|---|---|---|---|
| Average Peak (kW) | 51.28 | ● 43.20 | ● 27.30 | 31.96 | ● 31.03 |
| Total Cost ($) | 191.92 | ● 79.59 | ● 82.40 | 83.23 | ● 84.48 |
| Charge (%) | 100 | ● 89 | 90 | ● 92 | ● 91 |
| Peak Contribution | 31.35 | ● 36.67 | ● 43.17 | 41.68 | ● 43.46 |
| Total Reward | 6.63 | ● 34.36 | ● 38.72 | 38.06 | ● 38.69 |
| Gini Coeff | 0.0 | ● 0.0372 | 0.0293 | ● 0.0264 | ● 0.0125 |
Table 4.
Building Type and Attributes.
| Buildings | Thermal Characteristics | Charger Characteristics | ||||||
|---|---|---|---|---|---|---|---|---|
| Attributes | ||||||||
| Building 1 | 1e-4 | 50 | 14 | 4.8 | 1778 | 300 | 10 | 50 |
| Building 2 | 8.33e-5 | 55 | 14 | 60 | 2500 | 420 | 15 | 75 |
| Building 3 | 6.66e-4 | 60 | 15 | 90 | 3200 | 600 | 20 | 100 |
| Building 4 | 5.83e-5 | 65 | 15 | 120 | 4500 | 900 | 25 | 120 |
| Building 5 | 5e-4 | 70 | 16 | 150 | 5500 | 1200 | 30 | 150 |
| Building 6 | 4.16e-4 | 75 | 16 | 180 | 6500 | 1500 | 35 | 200 |
| Building 7 | 3.33e-5 | 80 | 14 | 210 | 7500 | 1800 | 40 | 250 |
| Building 8 | 6.66e-5 | 65 | 15 | 72 | 2800 | 720 | 18 | 85 |
| Building 9 | 5.83e-5 | 55 | 15 | 108 | 4000 | 1080 | 22 | 125 |
Table 5.
Peak And Off-Peak Monthly Pricing.
| Time of Day | Hours | $/kWh | Day Type |
|---|---|---|---|
| Winter (November – February) | |||
| Off-Peak | 22:00 – 05:59 | $0.09 | Every day |
| On-Peak | 17:00 – 19:59 | $0.20 | Monday - Friday |
| On-Peak | 06:00 – 08:59 | $0.20 | Monday - Friday |
| Mid-Peak | Other hours | $0.12 | Monday - Friday |
| Mid-Peak | All hours | $0.12 | Saturday-Sunday |
| Summer (May – August) | |||
| Off-Peak | 22:00 – 05:59 | $0.09 | Every day |
| On-Peak | 12:00 – 17:59 | $0.20 | Monday - Friday |
| Mid-Peak | Other hours | $0.12 | Monday - Friday |
| Mid-Peak | All hours | $0.12 | Saturday-Sunday |
| Transitional (March, April, September, October) | |||
| Off-Peak | 22:00 – 05:59 | $0.09 | Every day |
| Mid-Peak | Other hours | $0.12 | Every day |
Table 6.
Hourly EV Presence Probability and Day Classification.
| Day | Building 1 | Building 2 | Building 3 | Building 4 | Building 5 | Building 6 | Building 7 | Building 8 | Building 9 | |||||||||
| Hour | % | Hour | % | Hour | % | Hour | % | Hour | % | Hour | % | Hour | % | Hour | % | Hour | % | |
| Weekday | 0-6 | 95 | 0-6 | 92 | 0-6 | 85 | 0-8 | 10 | 0-8 | 5 | 0-8 | 5 | 0-23 | 80 | 0-8 | 20 | 0-6 | 90 |
| 7-16 | 10 | 7-16 | 20 | 7-16 | 30 | 9-16 | 80 | 9-16 | 85 | 9-16 | 90 | 0-23 | 80 | 9-16 | 80 | 7-16 | 15 | |
| 17-23 | 90 | 17-23 | 95 | 17-23 | 95 | 17-23 | 10 | 17-23 | 10 | 17-23 | 5 | 0-23 | 80 | 17-23 | 20 | 17-23 | 95 | |
| Weekend | 0-23 | 95 | 0-23 | 95 | 0-23 | 90 | 0-23 | 100 | 0-23 | 5 | 0-23 | 20 | 0-23 | 80 | 0-23 | 10 | 0-23 | 95 |
| Holiday | 0-23 | 95 | 0-23 | 100 | 0-23 | 100 | 0-23 | 100 | 0-23 | 5 | 0-23 | 20 | 0-23 | 80 | 0-23 | 10 | 0-23 | 100 |
Table 7.
Controller Performance Comparison.
| Controller | Mean Reward | Standard Deviation |
|---|---|---|
| LSD-MADDPG | 0.203 | 0.0184 |
| I-MADDPG | 0.188 | 0.0102 |
| CTDE-MADDPG | 0.187 | 0.0341 |
| DDPG | 0.0291 | 0.308 |
Table 8.
Controller Evaluation Case II.
| NC | DDPG | CTDE | I-MADDPG | LSD-MADDPG | |
|---|---|---|---|---|---|
| Total Community Charge | 100% | 0% | 50% | 57% | 83% |
| Reward | -101.65 | 66.31 | 277.22 | 340.89 | 438.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








