Prerpints.org logo
Preprint
Article

Multi-Phase Adaptive Recoding: An Analogue of Partial Retransmission in Batched Network Coding

Altmetrics

Downloads

51

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 September 2024

Posted:

01 October 2024

You are already at the latest version

Alerts
Abstract
Batched network coding (BNC) is a practical realization of random linear network coding (RLNC) designed for reliable network transmission in multi-hop networks with packet loss. By grouping coded packets into batches and restricting the use of RLNC within the same batch, BNC resolves the issue of RLNC that has high computational and storage costs at the intermediate nodes. A simple and common way to apply BNC is to fire and forget the recoded packets at the intermediate nodes, as BNC can act as an erasure code for data recovery. Due to the finiteness of batch size, recoding strategy is a critical design that affects the throughput, the storage requirements and the computational cost of BNC. The gain of the recoding strategy can be enhanced with the aid of a feedback mechanism, however the utilization and development of this mechanism is not yet standardized. In this paper, we investigate a multi-phase recoding mechanism for BNC. In each phase, recoding depends on the amount of innovative information remained at the current node after the transmission of the previous phases was completed. Relevant information can be obtained via hop-by-hop feedback, then a more precise recoding scheme that allocates networking resources can be established. Unlike hop-by-hop retransmission schemes, the reception status of individual packets does not need to be known, and packets to be sent in the next phase may not be the lost packets in the previous phase. Further, due to the loss-tolerance feature of BNC, it is unnecessary to pass all innovative information to the next node. This study illustrates that multi-phase recoding can significantly boost the throughput and reduce the decoding time as compared with the traditional single-phase recoding approach. This opens new window in developing better strategies for designing BNC, rather than sending more batches in a blind manner.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Networks and Communications

1. Introduction

Multi-hop wireless network is an emerging trend of network topology. They can be found in various scenarios including Internet of things, sensor networks, vehicle ad hoc networks, smart lamppost networks, etc. Wireless links can be easily interfered by other wireless signals and undesirable environmental constraints and events. A packet with a mismatched checksum is regarded as a corrupted packet and is dropped by the network node. In other words, in traditional networking that adopts end-to-end retransmission, the destination node can receive a packet only when this packet is correctly transmitted through all network links. This probability diminishes exponentially with the number of hops.
The widely-adopted reliable communication protocol, TCP, is not designed for wireless communications. For example, packet loss in wireless communications may not be caused by congestion, but can be attributed to interference and temporary shadowing. However, such a packet loss event will trigger the TCP congestion control mechanism, as a result reduce the transmission rate. Variations of TCP such as ATCP [2] were proposed to handle relevant packet loss scenarios. Advanced technologies such as Aspera [3] will only send feedback and retransmission request when a packet is lost. However, these TCP-alike protocols are still end-to-end protocols. In other words, the default store-and-forward strategy is applied at the intermediate network nodes and an end-to-end retransmission is adopted. Any packet can reach the destination node only if it has not been lost at any network link. In a multi-hop wireless network (with packet loss), the end-to-end retransmission approach may further degrade the system performance due to the high chance of losing retransmitted packet at one of the lossy links.

1.1. Network Coding Approaches

To truly enhance the performance of multi-hop wireless communications with packet loss and a large number of hops, the intermediate network nodes have to adopt a strategy other than forwarding. Random linear network coding (RLNC) [4] is a realization of network coding [5,6] that allows the intermediate network nodes to transmit new packets generated by the received packets. Previous works showed that RLNC can achieve the capacity of networks with packet loss for a wide range of scenarios [4,7,8,9,10,11]. Instead of forwarding, recoding (i.e., re-encoding) is performed at the intermediate network nodes, which generates recoded packets by linearly combining the received packets randomly. A direct implementation of the above RLNC scheme has a few technical problems and constraints. First, each intermediate network node has to buffer all the received packets, which may consume a huge amount of memory. Second, a coefficient vector being attached to each packet for recording the recoding operations is essential for decoding, however the length of the vector can be very long when the number of input packets is large, and this induces a significant consumption of network resources. Third, the destination node has to solve a big dense system of linear equations, which consumes significant computational resource for Gaussian elimination [12].
To resolve these several problems, a generation-based RLNC was proposed in [13]. In that approach, the input packets are first partitioned into multiple disjointed subsets called the generations. RLNC is then applied to each generation independently. In particular, data in a generation cannot be decoded using packets from another generation. The information carried by a generation has to be completely received in order to recover the data. This approach can be viewed as applying RLNC to multiple pieces of data independently, however optimal theoretical rate cannot be achieved. Practical concerns and solutions regarding generation-based RLNC were discussed and proposed in numerous studies, such as smaller decoding delay and complexity [14,15,16,17,18,19], input packet size selection [20,21,22,23,24], and coefficient overhead reduction [25,26,27].
Towards the optimal rate, overlapped subsets of input packets were considered [28,29,30,31]. More sophisticated approaches restrict the application of RLNC to small subsets of coded packets generated from the input packets [32,33,34,35,36,37]. The coded packets can be generated by LDPC [34,35], generalized fountain codes [36,37], etc. This application of coding theory in network coding leads to another variant of RLNC called batched network coding (BNC). The small subsets of coded packets are called batches. In early literature, a batch is also known as a class [28], a chunk [29] or a segment [38]. A notable difference of BNC from the generation-based RLNC is that BNC decodes the batches jointly such that the decoder does not need to receive all the packets within every batch.
The original RLNC can be regarded as a “BNC with a single batch”, so that we can perform recoding on the data until the transmission is completed. When there are multiple batches, one has to specify the number of recoded packets to be generated for each batch. The information carried by each batch, known as the “rank” of the batch, jointly affects the throughput of BNC. More specifically, the achievable rate of BNC is upper bounded by the expectation of the ranks of the batches arriving at the destination node [39]. Therefore, our goal is to design a recoding scheme that preserves more “ranks” across the batches.

1.2. Recoding of Batched Network Coding

The simplest recoding scheme for BNC is known as the baseline recoding, which generates the same number of recoded packets for all batches regardless of their ranks. Due to its simple and deterministic structure, it appears in many BNC designs and analyses such as [40,41,42]. However, the throughput cannot be optimized [43] as the scheme assigns too many recoded packets for those low-rank batches. Adaptive recoding [38,44,45] is an optimization framework for deciding the number of recoded packets to be sent in order to enhance the throughput. The framework depends only on the local information at each node, thus is capable of being applied distributively and adopted for more advanced formulations [46,47,48].
On the other hand, systematic recoding [43,49] is a subsidiary recoding scheme that forwards the received linearly independent recoded packets at a node (i.e., those packets that carry innovative rank to the node) and regards them as the recoded packets generated by the node itself. This way, fewer recoded packets have to be generated and transmitted later on, thus potentially reduce the delay of receiving a batch at the next node as well as the time taken for decoding. The number of extra recoded packets to be generated is independent of systematic recoding, but is related to the results of baseline or adaptive recoding. Theoretically speaking, the throughput of systematic recoding is better than generating all recoded packets by RLNC, though the benefit is indistinguishable in practice [49]. The actual enhancement in decoding time, however, is not well-studied.
Although many works focus on the recoding of BNC, they consider a fire-and-forget approach: The reception status of the recoded packets generated by the current node is not taken into consideration. This fire-and-forget approach can be useful in extreme applications when feedback is expensive or not available, such as deep-space [50,51,52] and underwater communications [53,54,55]. However, the use of feedback is very common in daily networking applications. For fire-and-forget adaptive recoding, feedback can be used to update the channel condition for further transmission in adaptive recoding [45]. However, it was also shown in [45] that although the throughput can be enhanced, the gain is insignificant. Therefore, another better way of making use of feedback for BNC has to be sorted out.

1.3. Contributions of This Study

In this paper, we consider the use of “reception status” as a feedback for the previous node. As every recoded packet is a random linear combination of the existing packets, all recoded packets of the same batch has the same importance with respect to information carriage. In other words, the “reception status” is not the status for each individual packet, but is a piece of information that can represent the rank of the batch.
From the reception status, the node can infer the amount of “innovative” ranks that is still capable of providing the next node. Thus, the node may start another phase of transmission for sending these innovative ranks by recoding, where the number of recoded packets in this phase depends on the innovative ranks. The throughput can be enhanced because this approach can be regarded as “partial” hop-by-hop retransmission. Partial retransmission is emphasized in this context because in BNC, not all ranks (or packets) in a batch are necessarily to be received for data recovery purpose. The “retransmitted” packets, which are recoded packets generated by random linear combinations, are likely to be different from what the node has previously sent. On the other hand, due to recoding, more packets apart from the innovative rank of a batch can be sent before receiving the feedback. These features of BNC makes the concept of “retransmission” different from the conventional one.
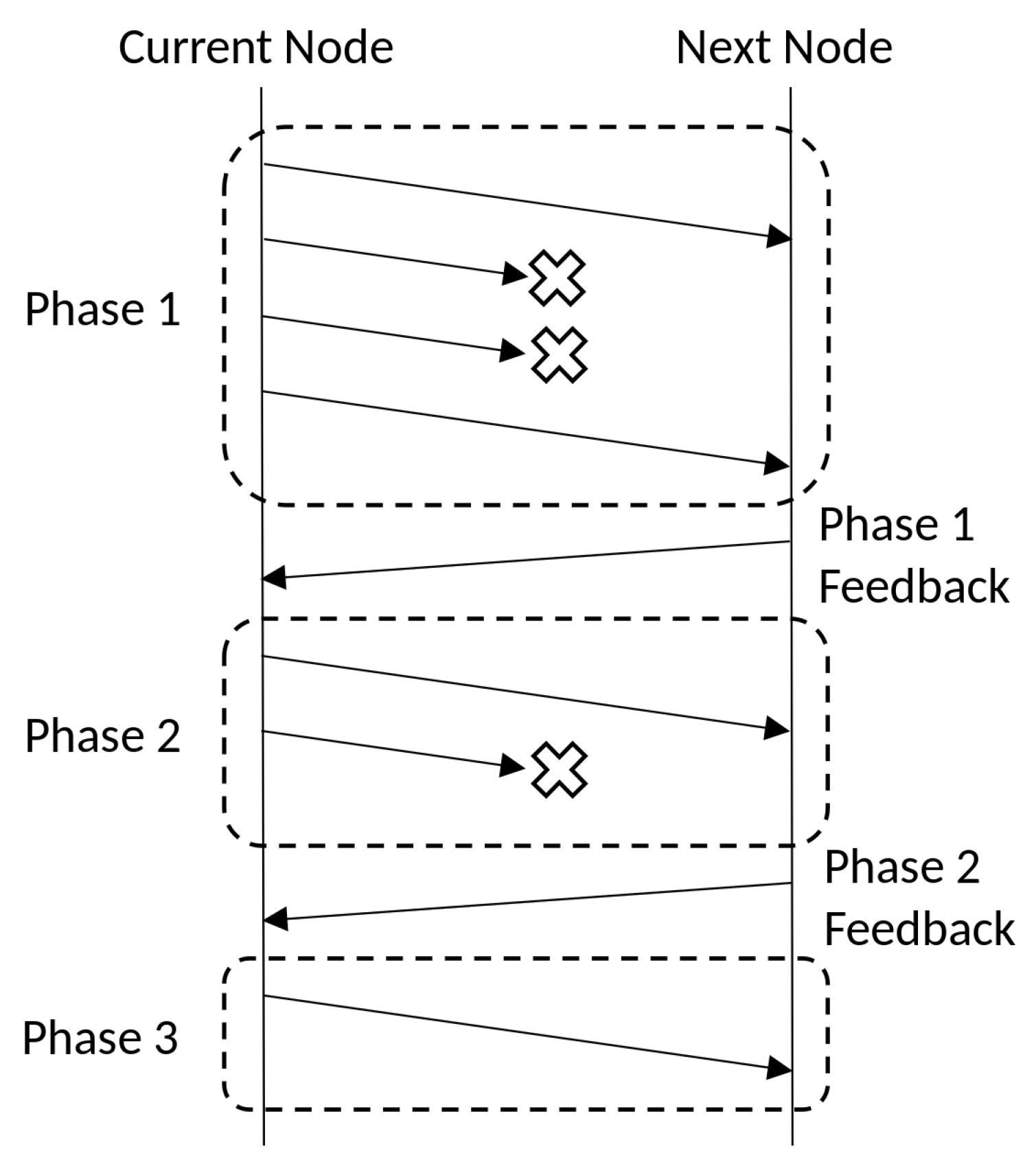
In general, one can perform more than two phases of recoding, i.e., multi-phase recoding. To understand the idea of “phase”, we first illustrate in Figure 1 a three-phase recoding. To transmit a batch, the current node begins phase 1 and sends a few recoded packets. The number of recoded packets depends on the recoding scheme, which will be discussed in Section 3. The lost packets are marked by crosses in Figure 1. After the current node sends all phase 1 packets to the next node, the next node sends a feedback packet for phase 1, which describes the reception status of the batch. According to the feedback packet, the current node infers the amount of “ranks” of the batch that can still be provided to the next node, i.e., the innovative rank of the batch, and then the transmission of phase 2 will begin. The number of recoded packets depends on the innovative rank inferred. After the current node has sent all phase 2 packets, the next node gives a feedback for phase 2. Lastly, the current node starts phase 3, and discards the batch afterwards. Although the reception state after the last phase seems not useful as it will not trigger a new phase, it can be used for synchronization in the protocol design. Details can be found in Section 3.4.
Although the idea looks simple, the main difficulty arises from the allocation of expected number of packets to be sent in each phase. This problem does not exist in generation-based RLNC, as BNC does not require the next node to receive all the ranks. The optimization problem is a generalization of the adaptive recoding framework with high dependence between phases.
The first contribution of this study lies on the formulation and investigation of the throughput of multi-phase recoding. As a tradition in BNC literature, the throughput is defined as the expected value of the rank distribution of the batches arriving at the destination node, i.e., the theoretical upper-bound of the achievable rate [39]. This is because there exists BNC (e.g., BATS codes [37]) that can achieve a close-to-optimal rate. The throughput is the objective to be maximized in the framework of adaptive recoding. However, the full multi-phase problem is hard to be optimized in general, thus, we formulate a relaxed problem as a baseline for comparison. For the two-phase relaxed problem, we also propose a heuristic so that we can approximate the solution efficiently.
The throughput defined for BNC does not consider the time needed for decoding. It is a measurement of the amount of information carried by the transmissions. Yet, decoding time is a crucial factor in Internet of things and real-time applications. When the previous node has finished sending all recoded packets of the current batch, it will be an appropriate time to start recoding a batch in traditional BNC, as this arrangement can maximize the throughput (i.e., expected rank) [56,57]. With systematic recoding, the received linearly independent recoded packets are directly forwarded to the next node, thus the number of recoded packets to be generated at later stages is reduced. Although this approach can potentially reduce the decoding time, its generalization into a multi-phase variation to get aligned with multi-phase recoding scheme is necessary, which lays down the second contribution of this study.
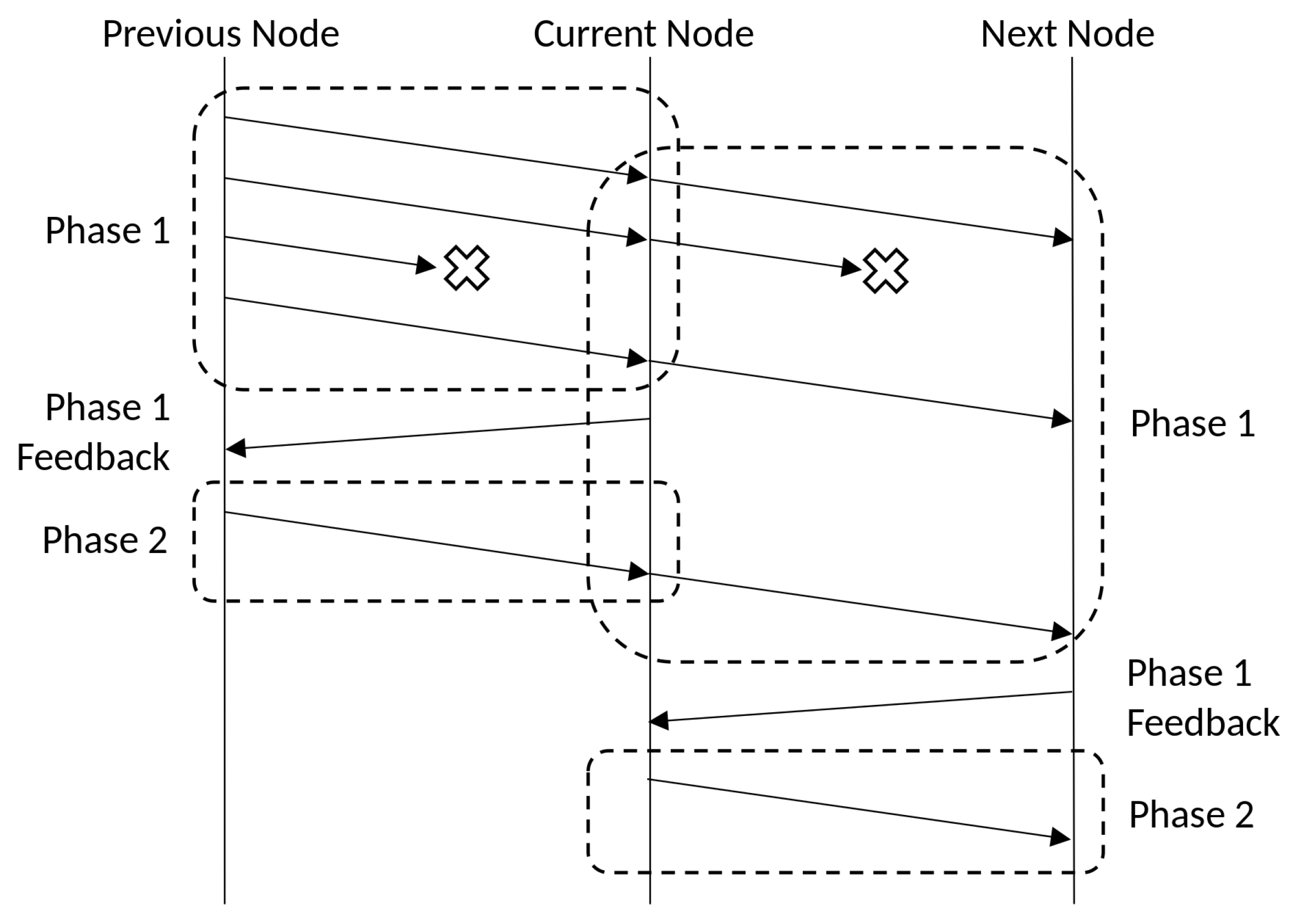
An example of two-phase variation of systematic recoding is illustrated in Figure 2. The flow of the phases between the previous and the current nodes is the same as that shown in Figure 1. When the current node receives a linearly independent recoded packet, it forwards the packet to the next node directly. Starting from phase 2, the nodes (both the previous and the current nodes) generate new recoded packets by RLNC to avoid (with high probability that) having the same packet arriving at the next node again. Except the last phase, the number of recoded packets is the same as the innovative rank in this phase, thus the idea is similar as the original systematic recoding. In the last phase, a fire-and-forget adaptive recoding is applied to complete the batch transmission process. There might be many idling time intervals between the current and the next nodes in the figure, but this can be attributed to the consideration of a single batch (as shown in the figure) During these time intervals, packets of other batches can be sent to utilize the link, and a more detailed discussion can be found in Section 3.4. Although the throughput is not optimized, the multi-phase systematic recoding problem can be solved very efficiently, therefore, it can be adopted in systems that the number of recoded packets per phase cannot be precomputed in advance.
The third contribution lies on the description of a baseline protocol that supports multi-phase recoding. The technical shortcoming of the existing protocols for BNC such as [43,57,58] is that they assume certain sequential order of the batches to determine whether no more packets of a batch will be received in the future. This way, one can determine when the batch recoding process can be started. When it comes to the multi-phase scenario, instead of waiting for the completion of all phases of a batch before transmitting the packets of another batch, one can interleave the phases of different batches to reduce the amount of idling time intervals. However, the sequential order of the batches is then messed up. When the multi-phase variant of systematic recoding is enforced, the systematic recoded packet can be transmitted at any time, which induces more chaos to the sequential order. In our protocol design, the problem of deciding the number of recoded packets per batch per phase is separated from the protocol, so that one can apply different multi-phase recoding schemes for comparison. This protocol is modified from the minimal protocol for BNC [43], and has inherited its simple structure. The purpose of this protocol is to give a preliminary idea for real-world deployment of the multi-phase recoding strategy.

1.4. Paper Organization

The organization of this paper is as follows. The background of BNC and the formulation of the adaptive recoding framework are described in Section 2. This formulation aims for a fire-and-forget strategy, i.e., a one-phase adaptive recoding scheme. Next, the optimization model of multi-phase adaptive recoding is described in Section 3. The general problem in Section 3.1 is complex and hard to be solved due to the high dependency between phases. Therefore, a relaxed model is formulated in Section 3.2 and a heuristic to efficiently solve the two-phase problem is proposed. After that, the mixed use of systematic recoding and multi-phase recoding are investigated in Section 3.3. This version is easy to be solved, and it gives a lower bound on the other multi-phase recoding models. Next, the design of a protocol that supports multi-phase recoding is described in Section 3.4. At last, the numerical evaluations of the throughput and the decoding time are presented in Section 4, and then the study is concluded in Section 5.

2. Traditional Adaptive Recoding

Although there are many possible routes to connect a source node and a destination node, only one route will be selected for each packet, thus line networks are the fundamental building blocks to describe the transmission. A line network is a sequence of network nodes where network links only exist between two neighboring nodes. A recoding scheme for line networks can be extended for general unicast networks and certain multicast networks [37,38]. On the other hand, in scenarios such as bridging the communications of remote areas, street segments of smart lamppost networks, deep space [51,52] and deep sea [54,55] communications, the network topologies are naturally a full or segments of multi-hop line networks. Therefore, we only focus on line networks in this paper. To further simplify the analysis, we consider independent packet loss at each link. This assumption was also made in many BNC literature such as [35,37,38,41,59].

2.1. Batched Network Coding

Denote by Z and Z + the sets of integers and positive integers respectively. Suppose we want to send a file from a source node to a destination node via a multi-hop line network. The data to be transmitted is divided into a set of input packets of the same length. Each input packet is regarded as a column vector over a finite field. An unsuitable choice of input packet size has significant implications as we need to pad useless symbols to the file [60]. We can apply the heuristic proposed in [61] to select a good input packet size. We consider a sufficiently large field size so that we can make an approximate assumption that two random vectors over this field are linearly independent of each other. This assumption is common in network coding literature such as [47,62,63,64]. This way, any n random vectors in an r-dimensional vector space can span a min { n , r } -dimensional vector space with high probability.
The source node runs a BNC encoder to generate batches. Each generated batch consists of M ∈ Z + coded packets, where M is known as the batch size. Each coded packet is a linear combination of a subset of the input packets. The formation of the subset depends on the design of the BNC. Take BATS codes [37,49], which is a matrix generalization of fountain codes [65], as an example. The encoder samples a predefined degree distribution to obtain a degree, where the degree is the number of input packets contributed to the batch. Depending on the application, there are various ways to formulate the degree distribution [66,67,68,69,70,71,72,73,74]. According to the degree, a set of packets is randomly chosen from the input packets.
The encoding and decoding of batches form the outer code of BNC. As a general description, let S be a matrix formed by juxtaposing the input packets, and G be a width-M generator matrix of a batch. Each column in the product of S a n d G corresponds to a packet of the batch.
A coefficient vector is attached to each of the coded packet. The juxtaposition of the coefficient vectors in a freshly generated batch is an M × M full-rank matrix, e.g., an identity matrix [57,58]. The rank of a batch at a node is defined as the dimension of the vector space spanned by the coefficient vectors of the packets of the batch at the node. In order words, by juxtaposing the coefficient vectors of the packets of a batch at the node to form a matrix H , the matrix rank of H is the rank of the batch at this node. At the source node, every batch has rank M.
Recoding is performed at any non-destination node, which is known as the inner code of BNC. That is, we can also apply recoding to generate more packets at the source node before transmitting them to the next node. Simply speaking, recoding generates recoded packets of a batch by applying RLNC on the packets of the batch at the node. Let c i and v i be the coefficient vector and the payload of the i-th packet in the batch respectively. A new recoded packet generated by RLNC has a coefficient vector ∑ i β i c i and payload ∑ i β i v i , where β i ’s are randomly chosen from the field. The number of recoded packets depends on the recoding scheme [38,41,42,46,47].
Before generating new recoded packets, the packets of a batch on hand can be considered as part of the recoded packets. This strategy is called systematic recoding [43,49], which is independent of the decision on the number of recoded packets to be sent. A more refined version is that only the linearly independent packets of a batch are being forwarded. This way, we would not forward too many “useless” packets if the previous node generates excessive recoded packets.
The destination node runs a BNC decoder, where the decoding method depends on the BNC, e.g., Gaussian elimination, belief propagation and inactivation [75,76]. The ranks of the batches at the destination node form a sufficient statistics to the performance of the BNC [39,49].

2.2. Expected Rank Functions

The distribution of the ranks of the batches is closely related to the throughput of BNC. Hence, the expectation of the rank distribution is a core component in recoding strategy. We first describe the formulation of this expectation at the next network node.
Let Bin ( n , p ) be a binomial distribution with failure probability p. Its probability mass function where x ∈ Z is defined as
Bin ( n , p ; x ) = n x ( 1 − p ) x p n − x if x = 0 , 1 , … , n , 0 otherwise .
We further define a variant of Bin ( n , p ) , denoted by Bin ↩ ( n , p , c ) , which we called the condensed binomial distribution.1 Its probability mass function is defined as
Bin ↩ ( n , p , c ; x ) = Bin ( n , p ; x ) if x = 0 , 1 , … , c − 1 , ∑ i = c n Bin ( n , p ; i ) if x = c , 0 otherwise
for x ∈ Z . The hooked arrow symbolizes that we move the probability masses of the tail towards where the arrows point to. The parameter k is called the condensed state of the distribution.
We can interpret these distributions this way. Let p be the packet loss rate of the outgoing channel. Assume the packet loss events are independent. The random variable of the number of received packets of a batch at the next node when the current node sends n packets of this batch follows Bin ( n , p ) , while the random variable of the rank of this batch at the next node follows Bin ↩ ( n , p , r ) when this batch has rank r at the current node.
Let V and V ′ be the vector spaces spanned by (the coefficient vectors of) the packets of a batch at the current node and the next node respectively. The “rank” of the batch the current node can still provide the next node is the “useful” information of the batch at the current node. This concept, known as the innovative rank, was adopted in [64,77], although the context there is for handling overhearing networks. Formally, it is defined as dim ( V + V ′ ) − dim ( V ′ ) . Before the current node sends any packet to the next node, V ′ is an empty space. In this case, the innovative rank is the same as the rank of the batch. That is, for a fire-and-forget recoding scheme, the rank equals the innovative rank.
The goal of recoding is to retain as much “rank” as possible. In a distributed view, we want to maximize the expected rank of the batches at the next node, which is the core idea of adaptive recoding. Denote by E ( r , t ) the expected rank of a batch at the next node when this batch has innovative rank r at the current node and the current node sent t recoded packets. That is,
E ( r , t ) = ∑ i = 0 t Bin ( t , p ; i ) min { i , r } = ∑ i = 0 M i Bin ↩ ( t , p , r ; i ) .
This is called the expected rank function. As in [44], we extend the domain of t from the set of non-negative integers to the set of non-negative real numbers by linear interpolation as
E ( r , t ) = ( 1 − ϵ ) E ( r , ⌊ t ⌋ ) + ϵ E ( r , ⌊ t ⌋ + 1 ) ,
where ϵ = t − ⌊ t ⌋ . That is, we first send ⌊ t ⌋ packets, and then the fractional part of t represents the probability that we send one more packet. For simplicity, we also define in a similar manner that
Bin ↩ ( t , p , r ; i ) = ( 1 − ϵ ) Bin ↩ ( ⌊ t ⌋ , p , r ; i ) + ϵ Bin ↩ ( ⌊ t ⌋ + 1 , p , r ; i ) .
With the formulation of expected rank functions, we can then discuss the formulation of adaptive recoding.

2.3. Traditional Adaptive Recoding Problem (TAP)

We now discuss the adaptive recoding framework, which we call the Traditional Adaptive recoding Problem (TAP) in this paper. Let R be the random variable of the (innovative) rank of a batch. When the node receives an (innovative) rank-r batch, it sends t r recoded packets to the next node. As we cannot use the outgoing link indefinitely for a batch, there is a “resource” limited for the transmission. This resource, denoted by t avg , is the average number of recoded packets per batch, which is an input to the adaptive recoding framework. Depending on the scenario, this value may be jointly optimized with other objectives [46,77].
From [44], we know that if the packet loss pattern is a stationary stochastic process, e.g., the Bernoulli process we used in this paper for independent packet loss, then the expected rank function E ( r , t ) is concave with respect to t. Further, under this concavity condition, the adaptive recoding problem that maximizes the average expected rank at the next node can be written as:
max { t i } i = 0 M ∑ r = 0 M Pr ( R = r ) E ( r , t r ) s . t . ∑ r = 0 M Pr ( R = r ) t r = t avg .
Our multi-phase recoding formulations in the remaining text of this paper are constructed based on (TAP). For ease of reference, we reproduce in Algorithm 1 the greedy algorithm for solving TAP [44] with initial condition embedded. In the algorithm, Δ r , t is defined to be E ( r , t + 1 ) − E ( r , t ) , which can be calculated via dynamic programming or regularized incomplete beta functions [45].
Preprints 119867 i001
As a remark, when there is insufficient resource for forwarding, i.e., E [ R ] ≥ t avg , any feasible solution satisfying t r ≤ r is an optimal solution of (TAP), and the optimal objective value is ( 1 − p ) t avg . This is stated in the following lemma, which is a continuous analogue of [78, Lemma 2].
Lemma 1. 
When E [ R ] ≥ t avg , then any feasible solution satisfying t r ≤ r is an optimal solution of (TAP), and the optimal objective value is ( 1 − p ) t avg .
Proof. 
According to [44, Corollary 2], all Δ r , t have the same value when t < r for all r. On the other hand, we know that Δ r + 1 , t > Δ r , t for all t ≥ r > 0 from [44, Theorem 1]. In other words, as Algorithm 1 selects those largest Δ · , · until the resources depletes, we conclude that it will terminate with t r ≤ r for all r. As E ( r , t r ) = ( 1 − p ) t r for t r ≤ r , the objective value is ∑ r = 0 M Pr ( R = r ) ( 1 − p ) t r = ( 1 − p ) t avg .    □

3. Multi-Phase Adaptive Recoding

The idea of an S-phase transmission is simple: In phase i, for every batch having innovative rank r i at the beginning of this phase, we generate and transmit t i , r i recoded packets. For simplicity, we call this innovative rank the phase i innovative rank of the batch. Afterwards, the phase i transmission is completed. If i < S , the next node calculates the total rank of the batch formed by all the received packets of this batch from phase 1 to phase i. By sending this information back to the current node, the current node can calculate the phase ( i + 1 ) innovative rank of the batch, i.e., the rank of the batch at the current node minus that at the next node. Then, the current node starts the phase ( i + 1 ) transmission. We can see that besides S, the main component under our control to optimize the throughput is the number of recoded packets to be generated and transmitted in each phase.
For one-phase transmission, the problem reduces to the fire-and-forget TAP. In this case, the number of recoded packets can be obtained via the traditional adaptive recoding algorithm due to the fact that the phase 1 innovative rank of a batch is the same as the rank of this batch at the current node, because the next node knows nothing about this batch yet. In the following text, we investigate the number of recoded packets in multi-phase transmission.

3.1. Multi-Phase General Adaptive Recoding Problem (GAP)

To formulate the optimization problem for multi-phase transmission, we first derive the probability mass functions of the innovative rank distributions. Let R i be the random variable of the phase i innovative rank. In the following, we write Pr ( R i = r i ) as Pr ( r i ) to simplify the notation. Note that R i + 1 depends on the phase i innovative rank and the number of recoded packets t i , · to be sent. When all t i , · are given, R 1 → R 2 → … → R S forms a Markov chain. Therefore, we have
Pr ( r i ) = ∑ r 1 , r 2 , … , r i − 1 Pr ( r 1 ) ∏ j = 1 i − 1 Pr ( r j + 1 ∣ r j ) = ∑ r 1 , r 2 , … , r i − 1 Pr ( r 1 ) ∏ j = 1 i − 1 Bin ↩ ( t j , r j , p , r j ; r j − r j + 1 ) ,
where each index r 1 , r 2 , … , r i − 1 in the summation starts from 0 to M.
Recall that the principle of adaptive recoding is to maximize the average expected rank at the next node such that the average number of recoded packets per batch is t avg . The average number of recoded packets per batch can be obtained by
∑ r 1 , r 2 , … , r S Pr ( r 1 , r 2 , … , r S ) ∑ i = 1 S t i , r i = ∑ i = 1 S ∑ r i Pr ( r i ) t i , r i .
Note that the r i in t i , r i is the index of the outer summation, which sums from 0 to M. Let R ¯ be the random variable of the rank of the batch at the next node after the current node completes the phase S transmission.
Theorem 1. 
E [ R ¯ ] = ∑ i = 1 S ∑ r i Pr ( r i ) E ( r i , t i , r i ) .
Proof. 
The probability mass function of R ¯ is
Pr ( R ¯ = k ) = ∑ r 1 , r S Pr ( r 1 , r S ) Bin ↩ ( t S , r S , p , r S ; k − ( r 1 − r S ) ) .
Hence, E [ R ¯ ] equals
  ∑ k = 0 M ∑ r 1 , r S Pr ( r 1 , r S ) Bin ↩ ( t S , r S , p , r S ; k − ( r 1 − r S ) ) k = ∑ r 1 , r S Pr ( r 1 , r S ) ( r 1 − r S + E ( r S , t S , r S ) ) = ∑ r 1 , r 2 , … , r S Pr ( r 1 , r 2 , … , r S ) ∑ i = 1 S − 1 ( r i − r i + 1 ) + ∑ r S Pr ( r S ) E ( r S , t S , r S ) = ∑ i = 1 S − 1 ∑ r i Pr ( r i ) ∑ r i + 1 Bin ↩ ( t i , r i , p , r i ; r i − r i + 1 ) ( r i − r i + 1 ) + ∑ r S Pr ( r S ) E ( r S , t S , r S ) = ∑ i = 1 S ∑ r i Pr ( r i ) E ( r i , t i , r i ) .
Let T i = ( t i , r ) r = 0 M and T = ⋃ i = 1 S T i . We first model an S-phase General Adaptive recoding Problem (GAP) that jointly optimizes all the phases:
max T ∑ i = 1 S ∑ r i Pr ( r i ) E ( r i , t i , r i ) s . t . ∑ i = 1 S ∑ r i Pr ( r i ) t i , r i = t avg .
Any S-phase optimal solution is a feasible solution of the S ′ -phase for S ′ > S , thus increasing the phase would not give a worse throughput. In this model, it is not guaranteed that maximizing the outcomes of a phase would benefit the latter phases, i.e., it is unknown that whether a suboptimal phase would lead to a better overall objective. This dependency makes the problem challenging to solve.

3.2. Multi-Phase Relaxed Adaptive Recoding Problem (RAP)

To maximize the throughput of BNC, we should maximize the expected rank of the batches at the destination node. However, it is unknown that whether a suboptimal decision at an intermediate node would lead to a better throughput at the end. To handle this dependency, TAP relaxes the problem into maximizing the expected rank at the next node. We can see that this dependency is very similar to that we have in GAP. By adopting a similar idea, we relax the formulation of GAP by separating the phases into an S-phase Relaxed Adaptive recoding Problem (RAP):
max α i ≥ 0 ∑ i = 1 S max T i ∑ r i Pr ( r i ) E ( r i , t i , r i ) s . t . ∑ i = 1 S α i = t avg , ∑ r i Pr ( r i ) t i , r i = α i , ∀ i = 1 , 2 , … , S .
This relaxation gives a lower bound of (GAP) for us to understand the throughput gain. Also, by knowing α i , RAP becomes S individual TAP’s with different t avg ’s. That is, we can solve individual phases independently by Algorithm 1 when α i ’s are fixed.
Although the formulation of RAP looks like that it can be solved by considering all Δ · , · among the phases altogether and then applying Algorithm 1. Unluckily, it is not the case. Consider a two-phase problem: The expected rank achieved by phase 1 increases when we increase some t 1 , r for some r ≠ 0 , but at the same time the distribution of R 2 is changed. After that, the expected rank achieved by phase 2 decreases according to the following theorem, which can be proved by heavily using the properties of adaptive recoding and the first-order stochastic dominance of binomial distributions. If the decrement is larger than the increment, then the overall objective decreases, which means that we should increase some t 2 , r ′ for some r ′ ≠ 0 instead, although Δ r ′ , t 2 , r ′ may be smaller than Δ r , t 1 , r .
Theorem 2. 
If the resource for phase ( i + 1 ) remains the same or is decreased when some t i , r , r ≠ 0 , are increased, then the expected rank achieved by phase ( i + 1 ) in the objective of RAP decreases.
Proof. 
See Appendix A.    □
Below is a concrete example. Let M = 4 , the source node sends 4 packets per batch, and the packet loss rate is 10 % . We consider the node right after the source node. At this node, let t avg = 4 and p = 10 % , i.e., the same setting as the source node. This way, both nodes have the same set of values of Δ r , t . We run a brute-force search for ( α 1 , α 2 ) with a step size of 0.001 . The solution is T 1 = ( 0 , 1 , 2 , 3 , 4 ) , T 2 = ( 0 , 1 , 2.9263 , 4 , 5 ) , when corrected to 4 decimal places. For our channel settings, we can use some properties of Δ r , t proved in [45]. First, Δ r , t = 1 − p when t < r , and Δ r , t < 1 − p when r ≠ 0 . Therefore, we can perform a similar greedy algorithm as that in Algorithm 1, starting from T 1 ′ = T 2 ′ = ( 0 , 1 , 2 , 3 , 4 ) . Next, there is another property that Δ 4 , 4 > Δ 3 , 3 > Δ 2 , 2 > Δ 1 , 1 > Δ 0 , 0 = 0 . Now, the algorithm finds the largest Δ r , t i , r , which is Δ 4 , 4 . There is a freedom to choose that Δ 4 , 4 in phase 1 or in phase 2. We can see that in T 2 , we have t 2 , 4 = 5 . This means that the Δ 4 , 4 in phase 2 is chosen. According to the greedy algorithm again, we should choose the next largest Δ r , t i , r , which is the Δ 4 , 4 in phase 1. However, we can see that t 1 , 4 = 4 , but t 2 , 3 = 4 > 3 . That is, in order to achieve an optimal solution, we need to choose Δ 3 , 3 in phase 2 instead of the larger Δ 4 , 4 in phase 1. In other words, we cannot group all Δ · , · among the phases altogether and then apply Algorithm 1 to obtain an optimal solution.
Up to this point, we know that the hardness of RAP is raised from the selection of α i . Our simulation shows that two-phase RAP already has a significant throughput gain, therefore we propose an efficient bisection-like heuristic for two-phase RAP in Algorithm 2 for practical deployment. The heuristic is based on our observations that the objective of RAP looks like unimodal with respect to α 1 . Note that although we solve TAP multiple times in the algorithm, we can reuse the previous output of TAP by applying the tuning scheme in [44], so that we do not need to repeatedly run the full Algorithm 1.
Preprints 119867 i002
Before we continue, we discuss a subtle issue in adaptive recoding here. Consider α i < E [ R i ] = ∑ r i Pr ( r i ) r i . That is, the amount of resource is too less so that it is insufficient to send a basis of the innovative rank space. For simplicity, we call the packets in this basis the innovative packets. Recall that any feasible solution where t i , r ≤ r is an optimal solution for this phase. However, different optimal solutions can lead to different innovative rank distributions in the next phase. This issue actually also occurs when there are more than one r having the same value of Δ r , t r in the general case, but it was ignored in previous works.
In this paper, we consider the following heuristic. First, we get the set of candidates of r, i.e., arg max r ∈ { 0 , 1 , 2 , … , M } Δ r , t r . If it is the case discussed above where the amount of resource is too less, then this set would be { 1 , 2 , 3 , … , M } . Next, our intuition is that we should let those with smaller t r to send more recoded packets. Although they have the same importance in terms of expected rank, their packets in average, i.e., the expected rank of the batch (at the next node) divided by t r , possess a different importance. This means that it is more risky for us to lose a packet of that batch with smaller t r . At last, our another intuition is that, among the r’s with the same t r , we should let the higher rank one to send more recoded packets so that the shape of the rank distribution at the next node is skewer towards the higher rank side, i.e., potentially more information (rank) is retained. To conclude, we have r = max arg min r ′ ′ ∈ arg max r ′ ∈ { 0 , 1 , 2 , … , M } Δ r ′ , t r ′ t r ′ ′ .

3.3. Multi-Phase Systematic Adaptive Recoding Problem (SAP)

We now investigate a constrained version of GAP. In systematic recoding, we forward the received linearly independent packets of a batch to the next node. That is, the number of packets we forwarded is the rank of the batch. As a multi-phase analogue of systematic recoding, in each phase, the number of packets we “forwarded” is the innovative rank of the batch of that phase. However, except the first phase, the so-called “forwarded” packets are generated by RLNC so that we do not need to learn and detect which packets sent by the previous phases are lost during the transmission process.
We now formulate the S-phase Systematic Adaptive recoding Problem (SAP), where for each batch, the node sends the innovative packets to the next node in all phases except the last one. That is, except the last phase, we have t i , r = r for all r, where these phases are called the systematic phases. For the last phase, we perform adaptive recoding on the phase S innovative rank with the remaining resource. By imposing the systematic phases as constraints to (GAP), we obtain
max T S ∑ r S Pr ( r S ) E ( r S , t S , r S ) + ∑ i = 1 S − 1 ∑ r i Pr ( r i ) E ( r i , r i ) s . t . ∑ r S Pr ( r S ) t S , r S + ∑ i = 1 S − 1 ∑ r i Pr ( r i ) r i = t avg .
When ∑ i = 1 S − 1 ∑ r i Pr ( r i ) r i > t avg , i.e., there is insufficient resources to perform the first ( S − 1 ) phases, (SAP) has no feasible solution. Thus, we need to choose a suitable S in practice. On the other hand, as the variables are all for the last phase, we can regard SAP as a single-phase problem, thus it has the same form as TAP. That is, SAP can be solved by Algorithm 1.
When (SAP) has a feasible solution, then the optimal solution of (SAP) is a feasible solution of (GAP). As SAP is easier to solve as compared to RAP, by investigating higher-phase SAP, we can obtain a lower bound on the performance of higher-phase GAP. Let R ˜ i be the random variable of the phase i innovative rank where all the previous phases are systematic phases. For the first phase, define R ˜ 1 = R 1 . Then, R ˜ 1 → R ˜ 2 → … → R ˜ S forms a Markov chain.
For any k ∈ Z + , systematic recoding uses t k , r k = r k . That is, we have Bin ↩ ( r k , p , r k ; · ) = Bin ( r k , p ; · ) . The following lemma and theorem give the formulae on the performance of SAP.
Lemma 2. 
Assume ∑ i = 1 k − 1 ∑ r i Pr ( r i ) r i ≤ t avg , i.e., there is enough resources to perform ( k − 1 ) systematic phases, then E [ R ˜ k ] = p k − 1 E [ R 1 ] .
Proof. 
By using (1), we have
E [ R ˜ k ] = ∑ r k r k Pr ( r k ) = ∑ r 1 , r 2 , … , r k r k Pr ( r 1 ) ∏ j = 1 k − 1 Bin ( r j , p ; r j − r j + 1 ) .
We prove this lemma by induction. When k = 1 , we have E [ R ˜ 1 ] = E [ R 1 ] = p ( 1 ) − 1 E [ R 1 ] . Assume E [ R ˜ k ] = p k − 1 E [ R 1 ] for some k ∈ Z + . For the case of k + 1 , we have
E [ R ˜ k + 1 ] = ∑ r 1 , r 2 , … , r k + 1 r k + 1 Pr ( r 1 ) ∏ j = 1 k Bin ( r j , p ; r j − r j + 1 )   = ∑ r 1 , r 2 , … , r k Pr ( r 1 ) ∑ r k + 1 r k + 1 Bin ( r k , p ; r k − r k + 1 ) ∏ j = 1 k − 1 Bin ( r j , p ; r j − r j + 1 )   = p ∑ r 1 , r 2 , … , r k r k Pr ( r 1 ) ∏ j = 1 k − 1 Bin ( r j , p ; r j − r j + 1 )   = p ( k + 1 ) − 1 E [ R 1 ] .
□
Theorem 3. 
Assume ∑ i = 1 k ∑ r i Pr ( r i ) r i ≤ t avg , i.e., there is enough resources to perform k systematic phases, then the resources consumed by these k phases is 1 − p k 1 − p E [ R 1 ] , and the average expected rank at the next node is ( 1 − p k ) E [ R 1 ] .
Proof. 
We first prove the amount of resources consumed. When k = 1 , the resources consumed is ∑ r 1 r 1 Pr ( r 1 ) = E [ R 1 ] = 1 − p ( 1 ) 1 − p E [ R 1 ] . Assume that the resources consumed by k phases is ∑ i = 1 k ∑ r i r i Pr ( r i ) = 1 − p k 1 − p E [ R 1 ] . When there are k + 1 phases, the resources consumed is
∑ i = 1 k + 1 ∑ r i r i Pr ( r i ) = 1 − p k 1 − p E [ R 1 ] + E [ R ˜ k + 1 ] = ( a ) 1 − p k 1 − p E [ R 1 ] + p k E [ R 1 ] = 1 − p ( k + 1 ) 1 − p E [ R 1 ] ,
where (a) follows Lemma 2. This part is proved by induction.
Next, we prove the expected rank (at the next node) by induction. Note that for any r ∈ { 0 , 1 , 2 , … } , we have E ( r , r ) = ( 1 − p ) r . When k = 1 , the expected rank is ∑ r 1 Pr ( r 1 ) E ( r 1 , r 1 ) = ( 1 − p ( 1 ) ) E [ R 1 ] . Assume that the expected rank after k phases is ∑ i = 1 k ∑ r i Pr ( r i ) E ( r i , r i ) = ( 1 − p k ) E [ R 1 ] . When there are k + 1 phases, the expected rank is
  ∑ i = 1 k + 1 ∑ r i Pr ( r i ) E ( r i , r i ) = ( 1 − p k ) E [ R 1 ] + ∑ r k + 1 Pr ( r k + 1 ) E ( r k + 1 , r k + 1 ) = ( 1 − p k ) E [ R 1 ] + ( 1 − p ) E [ R ˜ k + 1 ] = ( b ) ( 1 − p k ) E [ R 1 ] + ( 1 − p ) p k E [ R 1 ] = ( 1 − p ( k + 1 ) ) E [ R 1 ] ,
where (b) follows Lemma 2 as well. The proof is then completed. □
An intuitive meaning of the above statements is as follows. Every systematic phase remains p portion of innovative rank on average, which is the average rank lost during the transmission. Therefore, after ( k − 1 ) systematic phases, the expectation of innovative rank remained is p k − 1 portion of E [ R 1 ] . The resources consumed by k systematic phases is the sum of the expected innovative rank in all the phases, which is ( 1 + p + p 2 + … + p k − 1 ) E [ R 1 ] = 1 − p k 1 − p E [ R 1 ] . The average expected rank at the next node is the part that is not innovative, i.e., E [ R 1 ] − p k E [ R 1 ] by Lemma 2.
When k → ∞ , the resources consumed is E [ R 1 ] 1 − p . This means that if E [ R 1 ] 1 − p ≤ t avg , then there are always enough resources to perform more systematic phases. Otherwise, we can only perform S ′ systematic phases where, according to Theorem 3, S ′ is the largest integer satisfying 1 − p S ′ 1 − p E [ R 1 ] ≤ t avg . In other words, we have
S ′ = log p 1 − ( 1 − p ) t avg E [ R 1 ] .
Note that if there is remaining resources, we need to apply TAP for one more phase in our setting.
Corollary 1. 
Consider SAP with the highest possible number of systematic phases. Then, E [ R ¯ ] = min { ( 1 − p ) t avg , E [ R 1 ] } .
Proof. 
If E [ R 1 ] ≤ ( 1 − p ) t avg , then we do not have an upper limit on the number of systematic phases. By Theorem 3, we know that E [ R ¯ ] = lim k → ∞ ( 1 − p k ) E [ R 1 ] = E [ R 1 ] .
Now, we consider E [ R 1 ] > ( 1 − p ) t avg . Let S ′ = ⌊ log p ( 1 − ( 1 − p ) t avg E [ R 1 ] ) ⌋ . According to Theorem 3, the expected rank after S ′ systematic phases is ( 1 − p S ′ ) E [ R 1 ] . The remaining resources after S ′ systematic phases is t avg ′ : = t avg − 1 − p S ′ 1 − p E [ R 1 ] . In the ( S ′ + 1 ) phase, there is insufficient resources to send a basis of the innovative rank space. We gain ( 1 − p ) t avg ′ expected rank in this phase. Combining with the expected rank, we have
E [ R ¯ ] = ( 1 − p S ′ ) E [ R 1 ] + ( 1 − p ) t avg ′   = 1 − p S ′ E [ R 1 ] + ( 1 − p ) t avg − 1 − p S ′ 1 − p E [ R 1 ]   = ( 1 − p ) t avg .
The proof is then completed by combining the two cases above. □
This corollary shows that when there is enough resources, ∞-phase SAP is “lossless”. This is not surprising as the ∞-phase SAP can be regarded as a complete hop-by-hop retransmission scheme. More specifically, if the packet loss rate p is the same at all the links and t avg = M at all the non-destination nodes, then ( 1 − p ) t avg is the capacity of the network before normalization, and it can be achieved by SAP.
Although we say ∞ phases, the constraint in SAP states that every batch sends t avg packets on average. That is, it is unlikely to have a very large number of systematic phases before a batch has no more innovative ranks. The following theorem provides an upper bound on this expected stopping time.
Theorem 4. 
Let U be the random variable for the smallest number of systematic phases required such that a batch reaches 0 innovative rank. For k ≥ 1 ,
Pr ( U = k ) = ∑ r 1 Pr ( r 1 ) ( 1 − p k ) r 1 − ( 1 − p k − 1 ) r 1 .
Also, Pr ( U = 0 ) = Pr ( R 1 = 0 ) . Further, E [ U ] < E [ R 1 ] 1 − p .
Proof. 
See Appendix B. □
We will see from the numerical evaluations in Section 4 that two-phase, or at most three-phase, is already good enough in practice.

3.4. Protocol Design

In a fire-and-forget recoding approach, i.e., one-phase recoding, the minimal protocol is very simple. Every BNC packet consists of a batch ID (BID), a coefficient vector, and a payload [43,57,58]. Besides acting as a batch identifier, the BID is also being used as a seed for the pseudorandom generator, so that the encoder and the decoder can agree with the same random sequence. Depending on the BNC design, this random sequence may be used for describing how a batch is being generated. The coefficient vector records the network coding operations. That is, it describes how a recoded packet is being mixed by random linear combination. At last, the payload is the data carried by the packet. To travel through the existing network infrastructure, the BNC packet is encapsulated by other network protocols for transmission [57,58,79]. In more complicated designs, there are control packets and control mechanisms besides the data packets [80], but it is beyond the scope of this paper.
We can see that there is no feedback packet required in the minimal protocol. To maximize the information carried by each recoded packet in a batch, recoding is done when no packet of this batch will be received anymore. In order to identify that the previous node has transmitted all recoded packets of a batch without using feedback, the minimal protocol assumes that the batches are transmitted sequentially and there is no out-of-order packet across batches, so that when a node receives a packet from a new batch (with a new BID), we can start recoding the original batch.
In case there are out-of-order packets across batches, a simple way to handle this is to assume an ascending order of BID, so that we can detect and discard the out-of-order packets. This way, the protocol does not rely on feedback. However, to support multi-phase recoding, we need to know the reception state of the batches at the next node, thus we must introduce feedback packets in the protocol.
We modify from the minimal protocol this way. For the BNC packets (data packets), we also attach a list of BID–phase pairs that the node has finished sending all recoded packets of the corresponding phases of these batches. That is, the next node can start recoding the corresponding phase and send a feedback packet back to the current node. The number of recoded packets depends on the innovative rank of the batch, which is determined by the multi-phase recoding optimization problems. The BID–phase pair will be removed from the list when the next node notifies the reception state of this information.
The feedback packet consists of a list of BID–phase–rank triples. When the node receives a BID–phase pair, it sends an acknowledgment of receiving this BID–phase pair together with the rank of the batch with this BID at this node, i.e., a BID–phase-rank triple. A triple will be removed from the list when the corresponding BID–phase pair no longer appears in the incoming BNC packets, i.e., the previous node has received the acknowledgment. The feedback packet is constantly sent from a node like a heartbeat message to combat against feedback packet loss.
For a bidirectional transmission scenario, this list of triples can be sent together with the BNC packets. Certainly, we can separate these lists from the data packets and send them as control messages. This way, we can have a better flexibility on the length of the payload, as the length of a BNC packet is usually limited by the protocols that encapsulate it, e.g., 65 , 507 bytes for UDP over IPv4. To reduce the computational overhead due to the reassembling of IP fragments at every node for recoding, the length may further be limited within the size of a data-link frame.
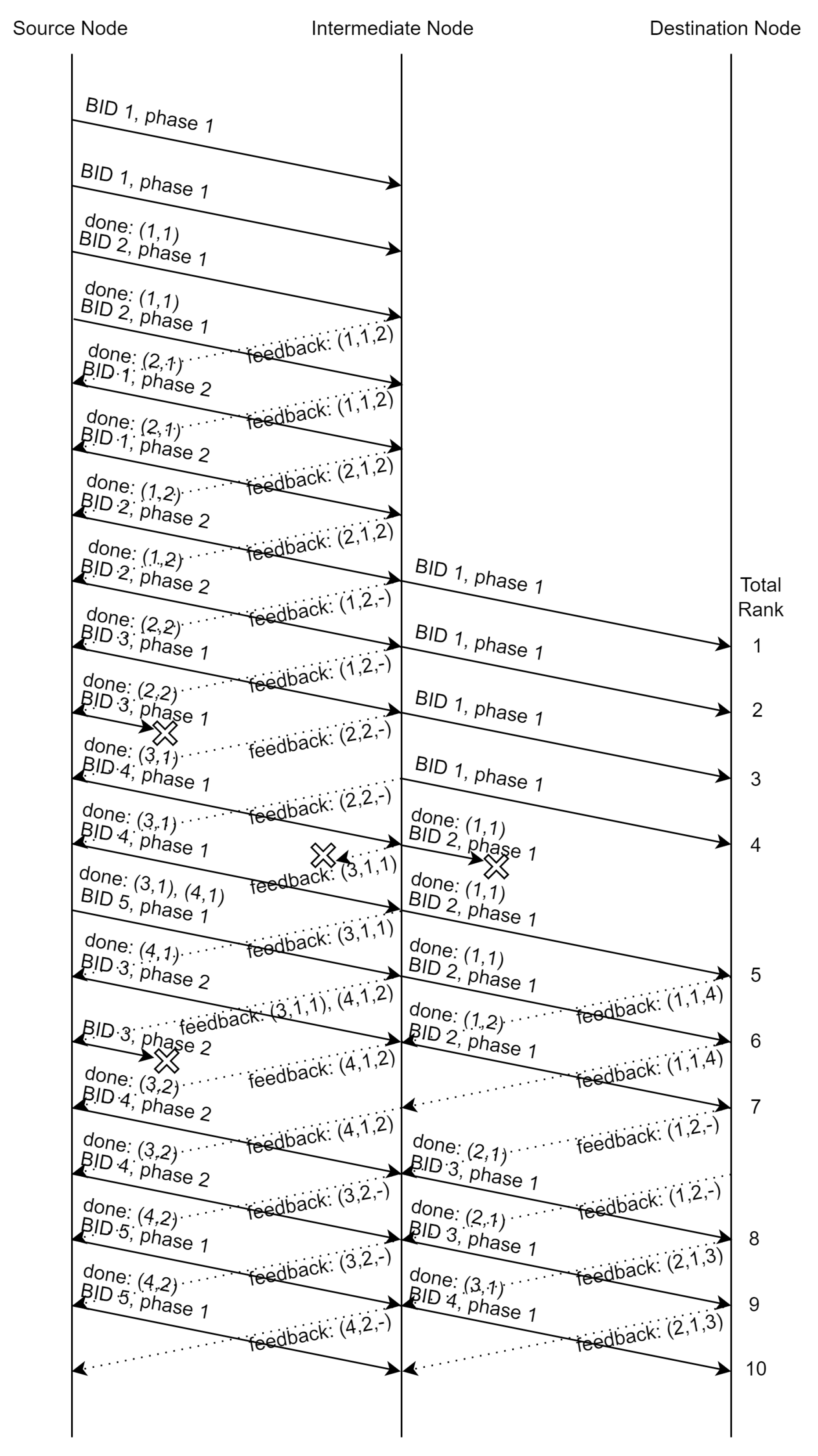
With these modifications, the timing for recoding is no longer depending on the sequential order of BIDs. To demonstrate how the protocol works, we consider a two-hop network (a source node, an intermediate node, and a destination node) with the following settings. We divide the timeline into synchronized timeslots. Each node can send one BNC packet to the next node at each individual timeslot. At the same time, each node can send one feedback packet to the previous node. A transmission will be received at the next timeslot. Assume a node can react to the received BID–phase pairs and BID–phase–rank triples immediately. Also, assume that a feedback packet is sent at every timeslot when acknowledgment is needed. Each BNC packet and feedback packet have independent probability to be lost during transmission. The batch size and the average number recoded packets for all phases at each node are both 4, i.e., M = t avg = 4 . We consider the flow of the packets until the destination node receives a total rank of 10.
Figure 3 illustrates an example flow of the protocol without adopting multi-phase systematic recoding. Consider two-phase recoding: At the beginning, the BNC packets sent by the source node do not include the list of BID–phase pairs. After finishing phase 1 of the first batch, the BID–phase pair ( 1 , 1 ) is attached to the next BNC packet. The intermediate node gives feedback about the rank of the batch it received. When the source node receives the feedback for BID 1 phase 1, it will not attach this information again in the upcoming BNC packets. This way, the intermediate node can make use of the BID–phase pairs attached to the received BNC packets to identify whether the source node has received the feedback message or not. As feedback packet can also be lost, the intermediate node constantly sends feedback messages to the source node. A similar process is done between the intermediate node and the destination node. We can see in the figure that the intermediate node did not start phase 2 of the second batch (BID 2). This is because the innovative rank of the batch at the intermediate node after phase 1 is 0. The destination node cannot gain any rank by receiving more recoded packets of this batch. Right after that, the intermediate node has nothing to be transmitted, thus an idle timeslot is induced.
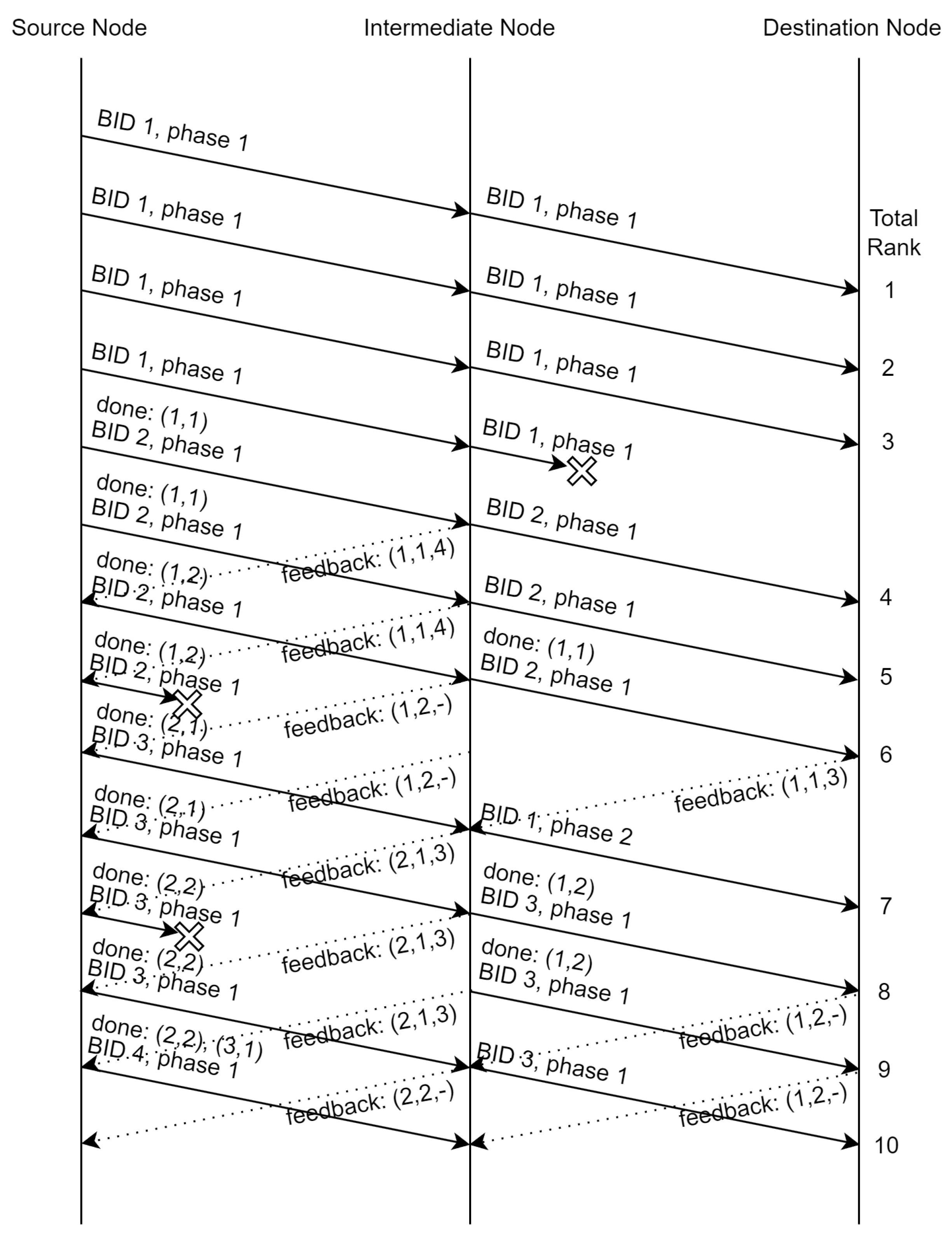
We illustrate another example in Figure 4. This time we adopt two-phase SAP: The source node sends 4 packets per batch in phase 1. As the average number of recoded packets t avg = 4 , the source node sends nothing in phase 2. Therefore, we can see that once the source node receives the feedback of BID 1 phase 1 from the intermediate node, it sends the BID–phase pair ( 1 , 2 ) directly, which indicates the end of BID 1 phase 2. Notice that if we configure with a larger value of t avg , the source node will send packets in phase 2 if some of the phase 1 packets are lost. These extra packets will be regarded as phase 1 systematic packets sent from the intermediate node. The intermediate node sends the BID–phase pair ( 1 , 1 ) after knowing that the source node has finished sending phase 2 of the first batch. In the figure, one phase 1 packet of the first batch forwarded by the intermediate node is lost. After receiving the feedback from the destination node, the intermediate node sends a phase 2 packet of this batch, and the systematic packets for BID 3 phase 1 is deferred by 1 timeslot.

4. Numerical Evaluations

In this section, we evaluate the throughput (i.e., the expected rank arriving at the node) and the decoding time of multi-phase recoding. We consider a multi-hop line network where all the links share the same packet loss rate p = 10 % , 20 % or 30 % . The feedback packets in the evaluation of decoding time has the same packet loss rate as the BNC packets. We choose a batch size M = 4 or 8 in the evaluation, with t avg = M at each node.

4.1. Throughput

We first show the normalized throughput of different schemes, defined as the average total rank received at the node divided by M. This scales the throughput to the range [ 0 , 1 ] . Recall that the throughput in BNC literature only measures the amount of information carried by the packets, and it does not reflect the decoding time.
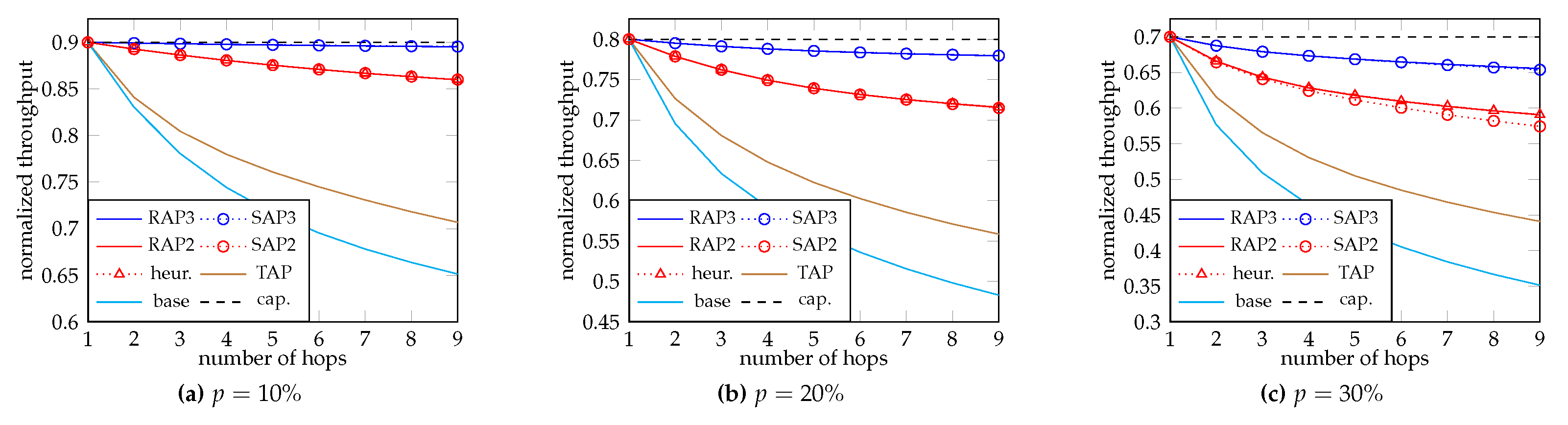
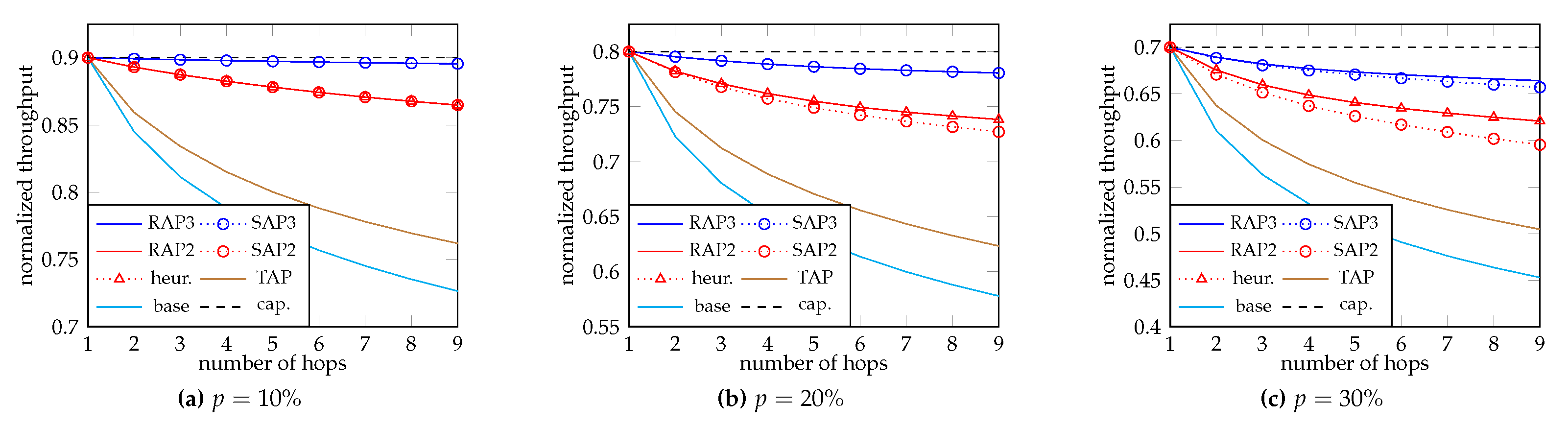
Figure 5 and Figure 6 show the cases when M = 4 and 8 respectively. The blue plots “RAP3” and “SAP3” correspond to three-phase RAP and three-phase SAP respectively. The red plots “RAP2”, “SAP2” and “heur.” correspond to two-phase RAP, two-phase SAP and the heuristic Algorithm 2 respectively. The brown plot “TAP” is the fire-and-forget adaptive recoding in [38,44]. The cyan plot “base” is the (fire-and-forget) baseline recoding where every batch sends M recoded packets regardless of the rank. At last, the black dashed plot “cap.” is the capacity of the network, which is achievable by hop-by-hop retransmission till successful reception (which omits the resources constraint).
From the plots, we can see that when the loss rate p is small, SAP and RAP achieve nearly the same throughput. The difference between RAP and SAP can be observed when p becomes larger. The reason is that for SAP, there is too much remaining resources for the last phase. That is, we send too many “useless” packets in the last phase, so it is beneficial to allocate more resources to the previous phases. Note that it is not common to have a large independent packet loss rate because we can change the modulation to reduce the loss rate. On the other hand, we observe that the throughput of two-phase RAP and that given by Algorithm 2 are nearly the same, which implicates the accuracy of our heuristic.
To show the throughput gain, we take M = 4 and p = 10 % as an example. At the 9-th hop, the throughput gain of two-phase RAP (and SAP) from fire-and-forget adaptive recoding and baseline recoding are 21.67 % and 32.03 % respectively. The throughput of three-phase RAP (and SAP) is very close to the capacity. This also suggests that instead of sending more batches, the inner code can help combating the loss efficiently when feedback is available.

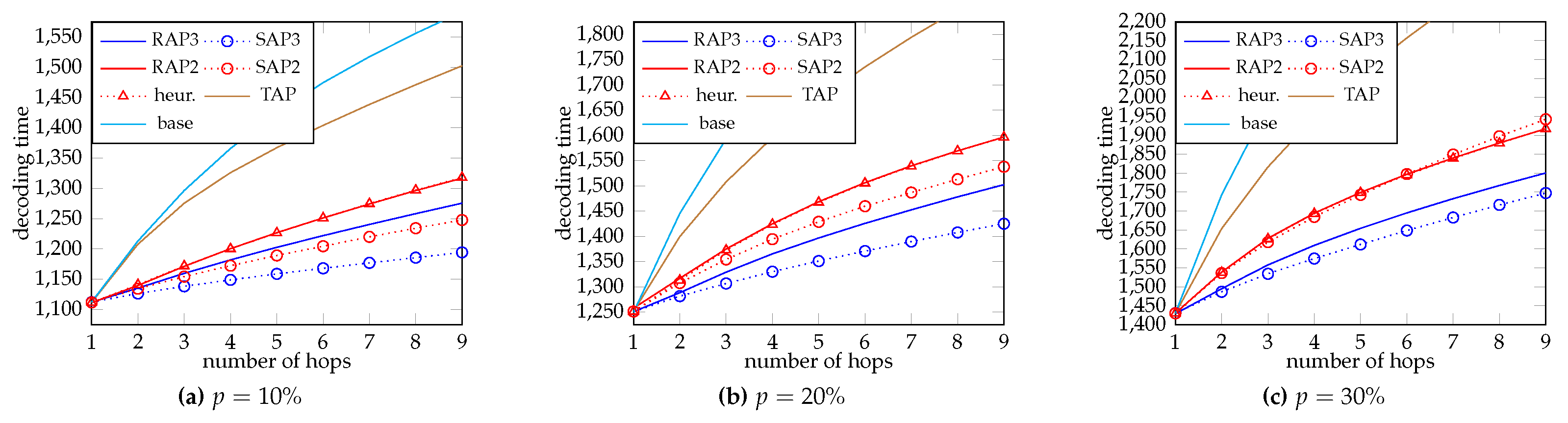
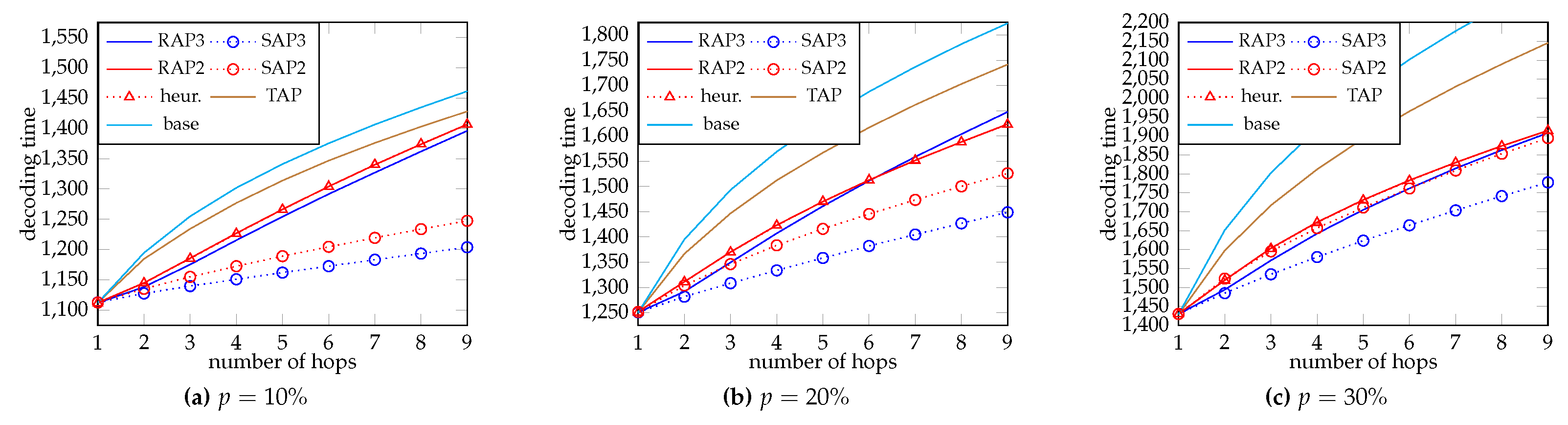
4.2. Decoding Time

Next, we evaluate the decoding time. We apply the protocol in Section 3.4, and make the same assumptions used for Figure 3 and Figure 4. Suppose a node can recover the data when the total rank reaches F = 1000 . The number of timeslots required for decoding is plotted in Figure 7 and Figure 8, respectively for M = 4 and 8. We use the same legend as that described in the last subsection, except that there is no curve for the “capacity”.
We can see that two-phase RAP (RAP2) and the heuristic (heur.) give almost the same decoding time, which again confirms the accuracy of our heuristic. The gain of SAP in decoding time becomes smaller in general when the loss rate p is larger. With a large p, SAP might give a longer decoding time than that without using systematic recoding. The reason is that we have allocated too much resources to the last phase of SAP, which leads to a poorly optimized strategy. When there are more phases, less resources is allowed to the last phase, thus we can still observe an improvement of decoding time for three-phase SAP. For RAP, the difference between decoding time for two- and three- phases is smaller when M becomes larger. When M is larger, more idling timeslots are induced by deferring recoding after notifying by the previous node that all the packets of the batch for the phase has been transmitted. We cannot conclude whether using more phases is better or not when M becomes larger. However, this can be partially compensated by SAP. We can see that three-phase SAP still works well when p = 30 % . Yet, this result suggests that instead of focusing on optimizing the throughput solely, we should also consider the decoding time and the behavior of the protocol in future works of BNC.
We want to point out that there could be many possible solutions for RAP achieving almost the same throughput. However, a significant difference may be observed when applying these solutions for evaluating the decoding time. Due to the limited precision for floating-point numbers, it is possible to obtain a bad solution for decoding time though there is almost no difference in throughput. Therefore, we suggest to allocate resources to early phases when the difference in throughput is smaller than a threshold, so that early phases have more chances to send more innovate packets. Further, the enhancement of the encoding and decoding framework throughout the recoding process can be achieved with advanced statistical models, e.g., [81]. We will leave all these optimal strategies and model development as open problems.

5. Conclusion

Previous literature in BNC did not consider multi-phase transmission. When feedback is available, the fire-and-forget strategy is not the best choice. How to make use of the feedback for BNC is still an open problem, as there are too many different components involved in the deployment of BNC in real systems.
In this paper, we investigated one possible use of feedback for adaptive recoding, together with a preliminary protocol design that can support multi-phase recoding. The information carried by the feedback is the rank of the batch at the node, which is simply a small integer. From our numerical evaluations, we can see that multi-phase recoding has a significant throughput gain when compared with the traditional fire-and-forget scheme. By simulating the decoding time, we found that the conventional throughput optimization for BNC may not be able to reflect the delay induced by the protocol and the recoding scheme. This suggests that in future works, the decoding time might be a more important objective to be optimized than the throughput, and it is likely to be a joint optimization problem with the design of the protocol. We also highlight a message that instead of making more transmissions, one direction to enhance the efficiency of BNC is to craft a well-designed inner code and feedback mechanism, as proposed in this study.

6. Patents

The multi-phase recoding algorithms can be found in the U.S. patent application 17/941,921 filed on Sept. 9, 2022 [82].

Author Contributions

Conceptualization, H.H.F.Y. and M.T.; methodology, H.H.F.Y. and M.T.; software, H.H.F.Y.; validation, H.H.F.Y., M.T. and H.W.L.M.; formal analysis, H.H.F.Y.; investigation, H.H.F.Y.; writing—original draft preparation, H.H.F.Y. and H.W.L.M.; writing—review and editing, H.H.F.Y. and H.W.L.M.; supervision, H.H.F.Y. and M.T.; project administration, H.H.F.Y., All authors have read and agreed to the published version of the manuscript.

Acknowledgments

Part of the work of Hoover H. F. Yin was done when he was with n-hop technologies Limited and the Institute of Network Coding, The Chinese University of Hong Kong.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
BNC Batched network coding
RLNC Random linear network coding
LDPC Low-density parity-check code
BATS code Batched sparse code
TCP Transmission control protocol
ATCP Adhoc TCP
TAP Traditional adaptive recoding problem
GAP Multi-phase general adaptive recoding problem
RAP Multi-phase relaxed adaptive recoding problem
SAP Multi-phase systematic adaptive recoding problem
BID Batch ID
UDP User datagram protocol
IPv4 Internet protocol version 4

Appendix A. Proof of Theorem 2

Let { t i , r } r = 0 M be the solution for phase i RAP, and { t i , r ′ } r = 0 M be that after we increase the resource for phase i. According to Algorithm 1, we have t i , r ′ ≥ t i , r for all r.
Let X r ∼ Bin ( t i , r , p ) and Y r ∼ Bin ( t i , r ′ , p ) . We have Y r first-order stochastically dominates X r [83], denoted by Y r ⪰ X r . That is, Pr ( Y r ≥ s ) ≥ Pr ( X r ≥ s ) for all s. For X r ↩ ∼ Bin ↩ ( t i , r , p , r ) and Y r ↩ ∼ Bin ↩ ( t i , r ′ , p , r ) , their cumulative distributions are the same as that of X r and Y r respectively from 0 to r − 1 . At r, we have Pr ( Y r ↩ ≥ r ) = Pr ( X r ↩ ≥ r ) = 1 . Therefore, Y r ↩ ⪰ X r ↩ .
Let X and Y be the random variables of the phase ( i + 1 ) innovative rank when the solutions for the phase i RAP are { t i , r } r = 0 M and { t i , r ′ } r = 0 M respectively. We have X = ∑ r i Pr ( r i ) ( r i − X r i ↩ ) ⪰ ∑ r i Pr ( r i ) ( r i − Y r i ↩ ) = Y .
Suppose the resource allocated to phase ( i + 1 ) is fixed. Let { t i + 1 , r } r = 0 M and { t i + 1 , r ′ } r = 0 M be the solution of phase i + 1 RAP when the phase ( i + 1 ) innovative ranks are X and Y respectively. According to [44], we have t i + 1 , a > t i + 1 , b and t i + 1 , a ′ > t i + 1 , b ′ for all a > b . Hence, by [44], we have E ( a , t i + 1 , a ) ≥ E ( b , t i + 1 , a ) ≥ E ( b , t i + 1 , b ) . Similarly, we have E ( a , t i + 1 , a ′ ) ≥ E ( b , t i + 1 , b ′ ) .
Due to optimality, we know that
∑ r Pr ( X = r ) E ( r , t i + 1 , r ) ≥ ∑ r Pr ( X = r ) E ( r , t i + 1 , r ′ ) .
On the other hand, we have
∑ r Pr ( X = r ) E ( r , t i + 1 , r ′ ) ≥ ∑ r Pr ( Y = r ) E ( r , t i + 1 , r ′ )
because X ⪰ Y if and only if E [ F ( X ) ] ≥ E [ F ( Y ) ] for any increasing function F [84]. Therefore, we conclude that under the same available resources for phase ( i + 1 ) , the expected rank achieved at the next node by phase ( i + 1 ) RAP when the phase ( i + 1 ) innovative rank is X is no smaller than that when the phase ( i + 1 ) innovative rank is Y. Finally, if we reduce the resources for phase ( i + 1 ) , according to Algorithm 1, the expected rank achieved at the next node decreases, which completes the proof of this theorem.

Appendix B. Proof of Theorem 4

Once the batch reaches 0 innovative rank, the innovative rank in the later phases will all be 0. Hence, Pr ( R ˜ k = 0 ) is the probability that the batch reaches 0 innovative rank after the transmission of some phases before entering the k-th systematic phase. Thus, Pr ( U = k ) = Pr ( R ˜ k + 1 = 0 ) − Pr ( R ˜ k = 0 ) for k ≥ 1 . A special case is that U = 0 , which means that the batch has 0 rank at the very beginning, so we have Pr ( U = 0 ) = Pr ( R 1 = 0 ) .
For k ≥ 1 , by (2), we have Pr ( R ˜ k + 1 = 0 ) equals
  ∑ r 1 , r 2 , … , r k Pr ( r 1 ) ∏ j = 1 k − 1 Bin ( r j , p ; r j − r j + 1 ) Bin ( r k , p ; r k − 0 ) = ∑ r 1 , r 2 , … r k − 1 Pr ( r 1 ) ∏ j = 1 k − 2 Bin ( r j , p ; r j − r j + 1 ) ∑ r k = 0 r k − 1 r k − 1 r k ( 1 − p ) r k − 1 − r k p r k ( 1 − p ) r k = ∑ r 1 , r 2 , … r k − 1 Pr ( r 1 ) ∏ j = 1 k − 2 Bin ( r j , p ; r j − r j + 1 ) ( 1 − p ) r k − 1 ( 1 + p ) r k − 1 = ∑ r 1 , r 2 , … r k − 2 Pr ( r 1 ) ∏ j = 1 k − 3 Bin ( r j , p ; r j − r j + 1 ) ∑ r k − 1 = 0 r k − 2 r k − 2 r k − 1 ( 1 − p ) r k − 2 p r k − 1 1 − p 2 1 − p r k − 1 = ∑ r 1 , r 2 , … r k − 2 Pr ( r 1 ) ∏ j = 1 k − 3 Bin ( r j , p ; r j − r j + 1 ) ( 1 − p ) r k − 2 1 − p 3 1 − p r k − 2 = … = ∑ r 1 Pr ( r 1 ) ( 1 − p ) r 1 1 − p k 1 − p r 1 = ∑ r 1 Pr ( r 1 ) ( 1 − p k ) r 1 .
Hence, for k ≥ 1 , we have
Pr ( U = k ) = ∑ r 1 Pr ( r 1 ) ( 1 − p k ) r 1 − ( 1 − p k − 1 ) r 1 .
To complete the proof, notice that
E [ U ] = ∑ r 1 Pr ( r 1 ) ∑ k = 1 ∞ k ( 1 − p k ) r 1 − ( 1 − p k − 1 ) r 1   = ∑ r 1 Pr ( r 1 ) ∑ k = 1 ∞ k ( ( 1 − p k ) − ( 1 − p k − 1 ) ) ∑ i = 0 r 1 − 1 ( 1 − p k ) i ( 1 − p k − 1 ) r 1 − 1 − i   < ∑ r 1 Pr ( r 1 ) ∑ k = 1 ∞ k r 1 ( p k − 1 − p k ) ( 1 − p k ) r 1 − 1   < ∑ r 1 Pr ( r 1 ) r 1 ( 1 − p ) ∑ k = 1 ∞ k p k − 1   = E [ R 1 ] 1 − p .

References

  1. Yin, H.H.F.; Tahernia, M. Multi-Phase Recoding for Batched Network Coding. 2022 IEEE Information Theory Workshop (ITW), 2022, pp. 25–30.
  2. Liu, J.; Singh, S. ATCP: TCP for Mobile Ad Hoc Networks. IEEE Journal on Selected Areas in Communications (JSAC) 2001, 19, 1300–1315. [Google Scholar] [CrossRef]
  3. Xu, Y.; Munson, M.C.; Simu, S. Method and System for Aggregate Bandwidth Control. U.S. 9,667,545, 2017.
  4. Ho, T.; Koetter, R.; Médard, M.; Karger, D.R.; Effros, M. The Benefits of Coding over Routing in a Randomized Setting. 2003 IEEE International Symposium on Information Theory (ISIT), 2003, p. 442.
  5. Ahlswede, R.; Cai, N.; Li, S.Y.R.; Yeung, R.W. Network Information Flow. IEEE Transactions on Information Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
  6. Li, S.Y.R.; Yeung, R.W.; Cai, N. Linear Network Coding. IEEE Transactions on Information Theory 2003, 49, 371–381. [Google Scholar] [CrossRef]
  7. Jaggi, S.; Chou, P.A.; Jain, K. Low Complexity Optimal Algebraic Multicast Codes. 2003 IEEE International Symposium on Information Theory (ISIT), 2003, p. 368.
  8. Sanders, P.; Egner, S.; Tolhuizen, L. Polynomial Time Algorithms for Network Information Flow. 15th Annual ACM Symposium on Parallel Algorithms and Architectures, 2003, pp. 286–294.
  9. Lun, D.S.; Médard, M.; Koetter, R.; Effros, M. On coding for reliable communication over packet networks. Physical Communication 2008, 1, 3–20. [Google Scholar] [CrossRef]
  10. Wu, Y. A Trellis Connectivity Analysis of Random Linear Network Coding with Buffering. 2006 IEEE International Symposium on Information Theory (ISIT), 2006, pp. 768–772.
  11. Dana, A.F.; Gowaikar, R.; Palanki, R.; Hassibi, B.; Effros, M. Capacity of Wireless Erasure Networks. IEEE Transactions on Information Theory 2006, 52, 789–804. [Google Scholar] [CrossRef]
  12. Mak, H.W.L. Improved remote sensing algorithms and data assimilation approaches in solving environmental retrieval problems; The Hong Kong University of Science and Technology, 2019.
  13. Chou, P.A.; Wu, Y.; Jain, K. Practical Network Coding. Annual Allerton Conference on Communication Control and Computing, 2003, Vol. 41, pp. 40–49.
  14. Pandi, S.; Gabriel, F.; Cabrera, J.A.; Wunderlich, S.; Reisslein, M.; Fitzek, F.H.P. PACE: Redundancy Engineering in RLNC for Low-Latency Communication. IEEE Access 2017, 5, 20477–20493. [Google Scholar] [CrossRef]
  15. Wunderlich, S.; Gabriel, F.; Pandi, S.; Fitzek, F.H.P.; Reisslein, M. Caterpillar RLNC (CRLNC): A Practical Finite Sliding Window RLNC Approach. IEEE Access 2017, 5, 20183–20197. [Google Scholar] [CrossRef]
  16. Lucani, D.E.; others. Fulcrum: Flexible Network Coding for Heterogeneous Devices. IEEE Access 2018, 6, 77890–77910. [Google Scholar] [CrossRef]
  17. Nguyen, V.; Tasdemir, E.; Nguyen, G.T.; Lucani, D.E.; Fitzek, F.H.P.; Reisslein, M. DSEP Fulcrum: Dynamic Sparsity and Expansion Packets for Fulcrum Network Coding. IEEE Access 2020, 8, 78293–78314. [Google Scholar] [CrossRef]
  18. Tasdemir, E.; others. SpaRec: Sparse Systematic RLNC Recoding in Multi-Hop Networks. IEEE Access 2021, 9, 168567–168586. [Google Scholar] [CrossRef]
  19. Tasdemir, E.; Nguyen, V.; Nguyen, G.T.; Fitzek, F.H.P.; Reisslein, M. FSW: Fulcrum sliding window coding for low-latency communication. IEEE Access 2022, 10, 54276–54290. [Google Scholar] [CrossRef]
  20. Torres Compta, P.; Fitzek, F.H.P.; Lucani, D.E. Network Coding is the 5G Key Enabling Technology: Effects and Strategies to Manage Heterogeneous Packet Lengths. Transactions on Emerging Telecommunications Technologies 2015, 6, 46–55. [Google Scholar] [CrossRef]
  21. Torres Compta, P.; Fitzek, F.H.P.; Lucani, D.E. On the Effects of Heterogeneous Packet Lengths on Network Coding. European Wireless 2014, 2014, pp. 385–390. [Google Scholar]
  22. Taghouti, M.; Lucani, D.E.; Cabrera, J.A.; Reisslein, M.; Pedersen, M.V.; Fitzek, F.H.P. Reduction of Padding Overhead for RLNC Media Distribution With Variable Size Packets. IEEE Transactions on Broadcasting 2019, 65, 558–576. [Google Scholar] [CrossRef]
  23. Taghouti, M. ; others. Implementation of Network Coding with Recoding for Unequal-Sized and Header Compressed Traffic. 2019 IEEE Wireless Communications and Networking Conference (WCNC), 2019.
  24. Schütz, B.; Aschenbruck, N. Packet-Preserving Network Coding Schemes for Padding Overhead Reduction. 2019 IEEE 44th Conference on Local Computer Networks (LCN), 2019, pp. 447–454.
  25. de Alwis, C.; Kodikara Arachchi, H.; Fernando, A.; Kondoz, A. Towards Minimising the Coefficient Vector Overhead in Random Linear Network Coding. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, pp. 5127–5131.
  26. Silva, D. Minimum-Overhead Network Coding in the Short Packet Regime. 2012 International Symposium on Network Coding (NetCod), 2012, pp. 173–178.
  27. Gligoroski, D.; Kralevska, K.; Øverby, H. Minimal Header Overhead for Random Linear Network Coding. 2015 IEEE international conference on communication workshop (ICCW), 2015, pp. 680–685.
  28. Silva, D.; Zeng, W.; Kschischang, F.R. Sparse Network Coding with Overlapping Classes. 2009 Workshop on Network Coding, Theory, and Applications, 2009, pp. 74–79.
  29. Heidarzadeh, A.; Banihashemi, A.H. Overlapped Chunked Network Coding. 2010 IEEE Information Theory Workshop (ITW), 2010, pp. 1–5.
  30. Li, Y.; Soljanin, E.; Spasojevic, P. Effects of the Generation Size and Overlap on Throughput and Complexity in Randomized Linear Network Coding. IEEE Transactions on Information Theory 2011, 57, 1111–1123. [Google Scholar] [CrossRef]
  31. Tang, B.; Yang, S.; Yin, Y.; Ye, B.; Lu, S. Expander graph based overlapped chunked codes. 2012 IEEE International Symposium on Information Theory (ISIT), 2012, pp. 2451–2455.
  32. Mahdaviani, K.; Ardakani, M.; Bagheri, H.; Tellambura, C. Gamma Codes: A Low-Overhead Linear-Complexity Network Coding Solution. 2012 International Symposium on Network Coding (NetCod), 2012, pp. 125–130.
  33. Mahdaviani, K.; Yazdani, R.; Ardakani, M. Linear-Complexity Overhead-Optimized Random Linear Network Codes. arXiv:1311.2123 2013.
  34. Yang, S.; Tang, B. From LDPC to chunked network codes. 2014 IEEE Information Theory Workshop (ITW), 2014, pp. 406–410.
  35. Tang, B.; Yang, S. An LDPC Approach for Chunked Network Codes. IEEE/ACM Transactions on Networking 2018, 26, 605–617. [Google Scholar] [CrossRef]
  36. Yang, S.; Yeung, R.W. Coding for a network coded fountain. 2011 IEEE International Symposium on Information Theory (ISIT), 2011, pp. 2647–2651.
  37. Yang, S.; Yeung, R.W. Batched Sparse Codes. IEEE Transactions on Information Theory 2014, 60, 5322–5346. [Google Scholar] [CrossRef]
  38. Tang, B.; Yang, S.; Ye, B.; Guo, S.; Lu, S. Near-Optimal One-Sided Scheduling for Coded Segmented Network Coding. IEEE Transactions on Computers 2016, 65, 929–939. [Google Scholar] [CrossRef]
  39. Yang, S.; Ho, S.W.; Meng, J.; Yang, E.H. Capacity Analysis of Linear Operator Channels Over Finite Fields. IEEE Transactions on Information Theory 2014, 60, 4880–4901. [Google Scholar] [CrossRef]
  40. Huang, Q.; Sun, K.; Li, X.; Wu, D.O. Just FUN: A Joint Fountain Coding and Network Coding Approach to Loss-Tolerant Information Spreading. 15th ACM International Symposium on Mobile Ad Hoc Networking and Computing, 2014, pp. 83–92.
  41. Zhou, Z.; Li, C.; Yang, S.; Guang, X. Practical Inner Codes for BATS Codes in Multi-Hop Wireless Networks. IEEE Transactions on Vehicular Technology 2019, 68, 2751–2762. [Google Scholar] [CrossRef]
  42. Zhou, Z.; Kang, J.; Zhou, L. Joint BATS Code and Periodic Scheduling in Multihop Wireless Networks. IEEE Access 2020, 8, 29690–29701. [Google Scholar] [CrossRef]
  43. Yang, S.; Yeung, R.W.; Cheung, J.H.F.; Yin, H.H.F. BATS: Network Coding in Action. Annual Allerton Conference on Communication Control and Computing, 2014, pp. 1204–1211.
  44. Yin, H.H.F.; Tang, B.; Ng, K.H.; Yang, S.; Wang, X.; Zhou, Q. A Unified Adaptive Recoding Framework for Batched Network Coding. IEEE Journal on Selected Areas in Information Theory 2021, 2, 1150–1164. [Google Scholar] [CrossRef]
  45. Yin, H.H.F.; Yang, S.; Zhou, Q.; Yung, L.M.L.; Ng, K.H. BAR: Blockwise Adaptive Recoding for Batched Network Coding. Entropy 2023, 25, 1054. [Google Scholar] [CrossRef] [PubMed]
  46. Dong, Y.; Jin, S.; Chen, Y.; Yang, S.; Yin, H.H.F. Utility Maximization for Multihop Networks Employing BATS Codes with Adaptive Recoding. IEEE Journal on Selected Areas in Information Theory 2021, 2, 1120–1134. [Google Scholar] [CrossRef]
  47. Xu, X.; Guan, Y.L.; Zeng, Y. Batched Network Coding with Adaptive Recoding for Multi-Hop Erasure Channels with Memory. IEEE Transactions on Communications 2018, 66, 1042–1052. [Google Scholar] [CrossRef]
  48. Yin, H.H.F.; Ng, K.H.; Zhong, A.Z.; Yeung, R.W.; Yang, S.; Chan, I.Y.Y. Intrablock Interleaving for Batched Network Coding with Blockwise Adaptive Recoding. IEEE Journal on Selected Areas in Information Theory 2021, 2, 1135–1149. [Google Scholar] [CrossRef]
  49. Yang, S.; Yeung, R.W. BATS Codes: Theory and Practice; Synthesis Lectures on Communication Networks, Morgan & Claypool Publishers, 2017.
  50. Breidenthal, J.C. The Merits of Multi-Hop Communication in Deep Space. 2000 IEEE Aerospace Conference, 2000, Vol. 1, pp. 211–222.
  51. Zhao, H.; Dong, G.; Li, H. Simplified BATS Codes for Deep Space Multihop Networks. 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, 2016, pp. 311–314.
  52. Yeung, R.W.; Dong, G.; Zhu, J.; Li, H.; Yang, S.; Chen, C. Space Communication and BATS Codes: A Marriage Made in Heaven. Journal of Deep Space Exploration 2018, 5, 129–139. [Google Scholar]
  53. Sozer, E.M.; Stojanovic, M.; Proakis, J.G. Underwater Acoustic Networks. IEEE Journal of Oceanic Engineering 2000, 25, 72–83. [Google Scholar] [CrossRef]
  54. Yang, S.; Ma, J.; Huang, X. Multi-Hop Underwater Acoustic Networks Based on BATS Codes. 13th International Conference on Underwater Networks & Systems, 2018, pp. 30:1–30:5.
  55. Sprea, N.; Bashir, M.; Truhachev, D.; Srinivas, K.V.; Schlegel, C.; Sacchi, C. BATS Coding for Underwater Acoustic Communication Networks. OCEANS 2019 - Marseille, 2019, pp. 1–10.
  56. Wang, S.; Zhou, Q.; Yang, S.; Bai, C.; Liu, H. Wireless Communication Strategy with BATS Codes for Butterfly Network. J. Phys.: Conf. Ser. 2022, 2218, 012003. [Google Scholar] [CrossRef]
  57. Yin, H.H.F.; Yeung, R.W.; Yang, S. A Protocol Design Paradigm for Batched Sparse Codes. Entropy 2020, 22, 790. [Google Scholar] [CrossRef]
  58. Yang, S.; Yeung, R.W. Network Communication Protocol Design from the Perspective of Batched Network Coding. IEEE Communications Magazine 2022, 60, 89–93. [Google Scholar] [CrossRef]
  59. Zhang, C.; Tang, B.; Ye, B.; Lu, S. An efficient chunked network code based transmission scheme in wireless networks. Proc. ICC ’17, 2017, pp. 1–6.
  60. Taghouti, M.; Lucani, D.E.; Pedersen, M.V.; Bouallegue, A. On the Impact of Zero-Padding in Network Coding Efficiency with Internet Traffic and Video Traces. European Wireless 2016, 2016, pp. 72–77. [Google Scholar]
  61. Yin, H.H.F.; Wong, H.W.H.; Tahernia, M.; Qing, J. Packet Size Optimization for Batched Network Coding. 2022 IEEE International Symposium on Information Theory (ISIT), 2022, pp. 1584–1589.
  62. Ye, F.; Roy, S.; Wang, H. Efficient Data Dissemination in Vehicular Ad Hoc Networks. IEEE Journal on Selected Areas in Communications (JSAC) 2012, 30, 769–779. [Google Scholar] [CrossRef]
  63. Lucani, D.E.; Médard, M.; Stojanovic, M. Random Linear Network Coding for Time-Division Duplexing: Field Size Considerations. 2009 IEEE Global Telecommunications Conference, 2009, pp. 1–6.
  64. Yin, H.H.F.; Xu, X.; Ng, K.H.; Guan, Y.L.; Yeung, R.W. Analysis of Innovative Rank of Batched Network Codes for Wireless Relay Networks. 2021 IEEE Information Theory Workshop (ITW), 2021.
  65. Luby, M. LT Codes. 43rd Annual IEEE Symposium on Foundations of Computer Science, 2002, pp. 271–282.
  66. Yang, S.; Zhou, Q. Tree Analysis of BATS Codes. IEEE Communications Letters 2016, 20, 37–40. [Google Scholar] [CrossRef]
  67. Yang, S.; Ng, T.C.; Yeung, R.W. Finite-Length Analysis of BATS Codes. IEEE Transactions on Information Theory 2018, 64, 322–348. [Google Scholar] [CrossRef]
  68. Yang, J.; Shi, Z.; Wang, C.; Ji, J. Design of Optimized Sliding-Window BATS Codes. IEEE Communications Letters 2019, 23, 410–413. [Google Scholar] [CrossRef]
  69. Xu, X.; Zeng, Y.; Guan, Y.L.; Yuan, L. Expanding-Window BATS Code for Scalable Video Multicasting Over Erasure Networks. IEEE Transactions on Multimedia 2018, 20, 271–281. [Google Scholar] [CrossRef]
  70. Xu, X.; Guan, Y.L.; Zeng, Y.; Chui, C.C. Quasi-Universal BATS Code. IEEE Trans. Veh. Technol. 2017, 66, 3497–3501. [Google Scholar] [CrossRef]
  71. Xu, X.; Zeng, Y.; Guan, Y.L.; Yuan, L. BATS code with unequal error protection. ICCS, 2016.
  72. Yin, H.H.F.; Wang, J.; Chow, S.M. Distributionally Robust Degree Optimization for BATS Codes. 2024 IEEE International Symposium on Information Theory (ISIT), 2024, pp. 1315–1320.
  73. Mao, L.; Yang, S.; Huang, X.; Dong, Y. Design and Analysis of Systematic Batched Network Codes. Entropy 2023, 25, 1055. [Google Scholar] [CrossRef]
  74. Mao, L.; Yang, S. Efficient Binary Batched Network Coding employing Partial Recovery. 2024 IEEE International Symposium on Information Theory (ISIT), 2024, pp. 1321–1326.
  75. Shokrollahi, A.; Lassen, S.; Karp, R. Systems and Processes for Decoding Chain Reaction Codes through Inactivation. U.S. 6,856,263, 2005.
  76. Shokrollahi, A.; Luby, M. Raptor Codes; Vol. 6, Foundations and Trends in Communications and Information Theory, now, 2011.
  77. Yin, H.H.F.; Xu, X.; Ng, K.H.; Guan, Y.L.; Yeung, R.W. Packet Efficiency of BATS Coding on Wireless Relay Network with Overhearing. 2019 IEEE International Symposium on Information Theory (ISIT), 2019, pp. 1967–1971.
  78. Yin, H.H.F.; Yang, S.; Zhou, Q.; Yung, L.M.L. Adaptive Recoding for BATS Codes. 2016 IEEE International Symposium on Information Theory (ISIT), 2016, pp. 2349–2353.
  79. Zhang, H.; Sun, K.; Huang, Q.; Wen, Y.; Wu, D. FUN Coding: Design and Analysis. IEEE/ACM Transactions on Networking 2016, 24, 3340–3353. [Google Scholar] [CrossRef]
  80. Yang, S.; Huang, X.; Yeung, R.; Zao, J. RFC 9426: BATched Sparse (BATS) Coding Scheme for Multi-Hop Data Transport, 2023.
  81. Mak, H.W.L.; Han, R.; Yin, H.H.F. Application of Variational AutoEncoder (VAE) Model and Image Processing Approaches in Game Design. Sensors 2023, 23, 3457. [Google Scholar] [CrossRef] [PubMed]
  82. Yin, H.F.H.; Tahernia, M. Systems And Methods for Multi-Phase Recoding for Batched Network Coding. U.S. 17/941921, 2022.
  83. Roch, S. Modern Discrete Probability: An Essential Toolkit. Department of Mathematics, University of Wisconsin-Madison, Madison, WI, 2020.
  84. Levy, H. Stochastic Dominance: Investment Decision Making under Uncertainty, 3 ed.; Springer, 2016.
Preprints 119867 g001
Figure 1. An example of three-phase recoding.
Figure 1. An example of three-phase recoding.
Preprints 119867 g001
Preprints 119867 g002
Figure 2. An example of two-phase variation of systematic recoding.
Figure 2. An example of two-phase variation of systematic recoding.
Preprints 119867 g002
Preprints 119867 g003
Figure 3. An example flow of the protocol without adopting multi-phase systematic recoding.
Figure 3. An example flow of the protocol without adopting multi-phase systematic recoding.
Preprints 119867 g003
Preprints 119867 g004
Figure 4. An example flow of the protocol with two-phase systematic recoding.
Figure 4. An example flow of the protocol with two-phase systematic recoding.
Preprints 119867 g004
Preprints 119867 g005
Figure 5. The throughput of BNC when M = t avg = 4 .
Figure 5. The throughput of BNC when M = t avg = 4 .
Preprints 119867 g005
Preprints 119867 g006
Figure 6. The throughput of BNC when M = t avg = 8 .
Figure 6. The throughput of BNC when M = t avg = 8 .
Preprints 119867 g006
Preprints 119867 g007
Figure 7. The decoding time when M = t avg = 4 and F = 1000 .
Figure 7. The decoding time when M = t avg = 4 and F = 1000 .
Preprints 119867 g007
Preprints 119867 g008
Figure 8. The decoding time when M = t avg = 8 and F = 1000 .
Figure 8. The decoding time when M = t avg = 8 and F = 1000 .
Preprints 119867 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated