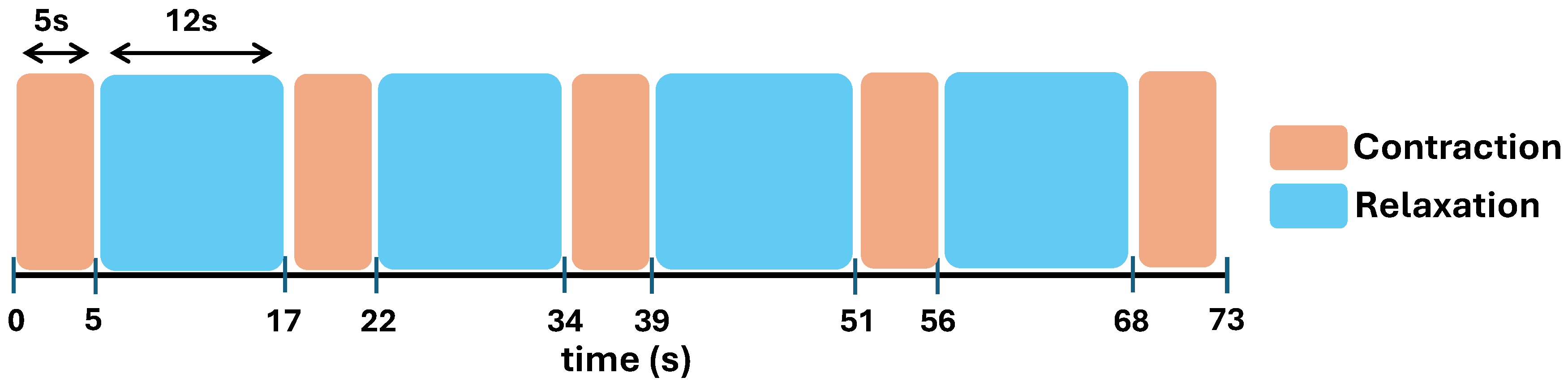Prerpints.org logo
Preprint
Article

Evaluation of Finger Movement Impairment Level Recognition Method Based on Fugl-Meyer Assessment Using Surface EMG

Altmetrics

Downloads

58

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

01 October 2024

Posted:

02 October 2024

You are already at the latest version

Alerts
Abstract
Subjectivity has been an inherent issue in the conventional Fugl-Meyer assessment, which has been the focus of recognition research in several studies. This paper continues our previous work on a recognition method of finger movement impairment levels using EMG. In contrast to our previous work, this paper provided a better recognition result with an improved experimental setting, such as higher sampling frequency and number of EMG channels. A large number of patients was recruited to provide a reliable recognition performance. This paper employed two data processing mechanisms, inter-subject cross-validation (ISCV) and data-scaled inter-subject cross-validation (DS-ISCV), resulting in two evaluation methods. The employed machine-learning algorithms are SVM, random forest (RF), and multi-layer perceptron (MLP). The highest average recall score across impairment levels of 0.73 was achieved by MLP_ISCV in the spherical grasp task. Subsequently, the highest average recall score of non-majority classes of 0.72 was achieved by the SVM_DS-ISCV in the mass extension task. The cross-validation result showed that the proposed method effectively handled the imbalanced dataset without being biased toward the majority class. The proposed method demonstrated the potential to assist doctors in clarifying the finger movement impairment level.
Keywords: 
Subject: Public Health and Healthcare  -   Physical Therapy, Sports Therapy and Rehabilitation

1. Introduction

Stroke is one of the major global health issues, with over 13 million new cases annually and being the second leading cause of mortality and disability worldwide. According to the Global Burden of Disease Study (GBD) in 2016, there is an increase in frequency among younger groups (under 50 years old), depicting the distribution of incidence over different ages. Moreover, the incidence of stroke, along with stroke-related mortality and disability, has increased nearly two-fold from 1990 to 2016 [1]. According to the consequences of disability, muscle dysfunction is the predominant form of impairment following a stroke. Muscle dysfunction significantly worsens the risk of arm paralysis after a stroke and is frequently associated with increased impairment, reduced work capacity, and diminished quality of life. The accumulation of inactive muscle fibers due to dysfunction leads to abnormal muscle activation patterns, such as spastic muscle contractions, that may contribute to further muscle-related disorders [2,3]. Consequently, individuals who have experienced a stroke affecting their arm may struggle to perform daily activities [4].
In order to restore the function of muscle fiber after a stroke, rehabilitation as a routine muscle recovery process is necessary [3,5]. Rehabilitation refers to the combined and coordinated use of medical, social, educational, and occupational measures to retrain a person to the highest level of functional skills [5]. The process of rehabilitation includes the assessment of the patient’s impairment condition. The assessment is intended to observe and evaluate the patient’s actual condition. Therefore, a suitable training and medication program can be specifically arranged for each patient.
Several clinical methods to assess the impairment level of post-stroke patients are currently being employed worldwide. Regarding the assessment of motoric function, the Fugl-Meyer assessment (FMA) is a notable tool as it provides a detailed assessment protocol with a scoring system in most human extremity parts. The Fugl-Meyer scale stands as a groundbreaking quantitative evaluative tool designed to measure sensorimotor stroke recovery. The motor domain function of this tool encompassed major and minor parts of the upper-lower extremities, suggesting the most comprehensive measures of motor impairment following stroke. One of the assessment components is the assessment of a complex motor function, such as finger movement as a minor body part, that is composed of a combination of complex muscles [3]. In the case of finger movement, the Fugl-Meyer assessment of upper extremity (FMA-UE) for hand will be employed. As shown in Table 1, this questionnaire consists of seven finger movement tasks that are Mass Extension (ME), Mass Flexion (MF), Hook Grasp (HG), Thumb Adduction (TA), Pincer Grasp (PG), Cylinder Grasp (CG), and Spherical Grasp (SG). Meanwhile, the impairment level consists of three conditions (i.e, Full, Partial, and None).
The doctor or physiotherapist has an inherent role in the assessment. Several finger movements in FMA-UE are object-dependent tasks that require a patient to hold the object when a doctor performs a tug toward it. This mechanism in the Fugl-Meyer assessment is the conventional method that requires the doctor to observe the impairment level manually through visual and tug inspection. Nevertheless, the inherent role of a doctor in the conventional method raises another issue, such as inherent subjectivity, that also promotes the subjective assessment result. Considering the potential modality to address the subjectivity issue in FMA, electromyography (EMG) is a golden standard for objectively assessing muscle and nervous system function. It’s widely used in rehabilitation and gesture recognition studies [6,7]. However, few studies have examined recognition performance in EMG-related subjective levels.
Our earlier study examined the performance of the EMG-based impairment level recognition method in post-stroke patients for finger movement [8]. We discovered good recognition results on several FMA-based finger movement tasks, highlighting the promising performance of EMG. We also pointed out several crucial shortcomings in the experimental setting, where the number of patients was only 4 with incomplete impairment levels collected, consisting of Full and Partial levels only. Additionally, there were only two EMG channels, and the employed sampling frequency was too small. The occurrence of imbalanced dataset conditions could be addressed with a common resampling method with a SMOTE filter algorithm. The employed machine learning was SVM and RF, with an average accuracy of 67.1 and 64.6, respectively. However, the score couldn’t be generalized due to critical issues in the experimental settings and accuracy bias due to the imbalanced dataset. Consequently, the machine-learning models were at risk of recognizing the person personally instead of the impairment levels. Therefore, an improvement in the experimental setting is required. Another highlighted point was the tendency of imbalance of the collected impairment level target, where one patient can only exhibit one or two levels without certain information prior to assessment.
This paper presents the improved recognition method of FMA’s finger movement impairment level. This paper employed a higher sampling frequency of EMG in data collection. A higher number of EMG channels was employed to accommodate various muscles related to finger movement. A higher number of subjects was recruited to produce reliable machine learning performance. In contrast to the previous experiment, this paper depicted an extremely imbalanced dataset condition due to a higher patient number, suggesting a different resampling method from the previous experiment. This study also discusses the subjective assessment issue of FMA and the doctor’s perspective according to the performance of the machine-learning model. The ultimate goal of this study is to assist a doctor in deciding the patient’s actual impairment level of finger movement. Therefore, this paper also introduces the implementation of the constructed method in a desktop application that can recognize and display the impairment level of each finger movement and output an assessment video. Thus, a doctor or physiotherapist may double-check and evaluate the impairment level separately.

2. Related Research

2.1. Automation of Fugl-Meyer Assessment

Subjectivity and inflexibility are the most crucial issues in the Fugl-Meyer assessment. Several studies have been conducted to overcome the inherent problems. In 2014, a study was conducted on 24 patients with various upper extremity hemiplegia levels after stroke [9]. Support vector regression (SVR) was employed to predict the FMA score of the shoulder-elbow tasks. Another study proposed an automatic acquisition system for one task, pincer grasp, from FMA of the upper extremity of the hand [10]. Several studies have also proposed a recognition system that employed a full set of FMA hand/finger movement tasks, that was finger mass flexion (MF), finger mass extension (ME), hook grasp (HG), thumb adduction (TA), pincer grasp (PG), cylinder grasp (CG), and spherical grasp (SG) [11,12]. Lee et al. constructed a grasping object for each hand-function task, while Formstone et al. employed a muscle-related modality. The aforementioned studies utilized different approaches to addressing the inherent subjectivity of FMA, especially in hand-function tasks, due to the complex movement of the finger and the corresponding muscle. However, most of the aforementioned studies utilized supervised machine learning as the recognition method, where the target learning was the doctor’s subjective assessment. Thus, the subjectivity of FMA couldn’t be eliminated due to the inherent role of a doctor. Furthermore, the doctor’s final decision was to perform further rehabilitation procedures following the assessment.
The subjectivity issue of the FMA could be minimized by conducting multiple assessments. Given the inherent subjectivity in individual patient assessments, performing repetitive assessments may minimize uncertainty and reinforce the doctor’s judgment. Consequently, the repetitive assessment of numerous patients stands to enhance the reliability of assessment outcomes. Furthermore, the integration of sensor technology to objectively capture context information relating to impairment levels has the capacity to increase the precision of assessments of the doctor. This highlights the possibility of achieving accurate subjective assessments through the gathering of extensive training data for a machine learning model. Therefore, the present study encompassed 28 subjects with diverse impairment levels, each undergoing repetitive assessments.

2.2. Employable Sensors in Finger Movement Impairment Level Recognition of Fugl-Meyer Assessment

Several approaches have been conducted to address inherent subjectivity in FMA. Depending on the task of FMA, appropriate modalities should be utilized. The assessment of the non-hand tasks is considered simple as it only comprised a single and long extremity part, such as an arm. Thus, any type of sensor has the potential to record the FMA task activity from this part of the body. Several studies have introduced that the movement activity of non-hand FMA tasks could be captured using proprioceptive and camera-based modalities, such as accelerometer, FSR, and Kinect [9,11,12]. Nevertheless, employing the same sensors in the hand tasks of FMA would be less appropriate, where the corresponding tasks comprised minor parts of the extremities, such as the finger. Therefore, a specific or customized sensor is needed to capture the movement activity of the FMA’s hand tasks. For instance, studies constructed grasping tools embedded with FSR sensors to capture the activity from the finger, especially in pincher grasp [10,12]. The studies indicated that the finger requires a customized sensor to capture its complex movement mechanism due to its small size. However, a customized grasping object embedded with a sensor is limited to the type of movement and the size of the finger.
Another utilizable sensor in the FMA hand tasks is EMG. EMG enables the recording of the complex movement of the finger by capturing the electrical activity of muscles that control the finger [8,11]. Furthermore, EMG may consist of several channels that facilitate the recording of muscle activities of individual finger movement, regardless of the various sizes of fingers and the types of movements. Accordingly, EMG has a prominent potential in capturing the finger activity of the FMA’s hand task as it addresses the limitation of the aforementioned customized grasping object embedded with sensors. In this regard, this paper utilized EMG sensors to capture the finger movement activity of the hand task of FMA.

2.3. Data Imbalance Nature in Actual Patient’s Data Collection Experiment

An imbalanced dataset is a common problem, especially in medicine and rehabilitation field. Several studies have shown the inherent imbalance dataset problem in an experiment with actual subjects or patients. Vijayvargiya et al. encountered imbalance datasets between healthy and unhealthy subjects in knee abnormality detection [13]. Choi et al. proposed a classification method of abnormal electrocardiography (ECG) to address the imbalance dataset [14]. Hasni et al. developed a classification algorithm based on SVM to address the imbalance dataset between normal EMG and neuropathy-myopathy EMG [15]. The studies showed that the imbalanced dataset condition is evident when experimenting with normal and abnormal conditions of the subject.
The FMA experiment is also prone to produce imbalanced datasets. Ideally, the dataset will have balanced data on each impairment level. In the actual situation, the number of data depends on the availability of patients in a rehabilitation facility. This situation highlights the tradeoff in the number of patients across different impairment levels in the data collection experiment, with some levels having an abundance of patients and others fewer in number. Additionally, a patient may exhibit multiple levels of impairment in repetitive tasks, which may pose a risk of reducing the number of data for minority classes. Furthermore, this condition limits further evaluation of patient characteristics, as there is also an imbalance in information such as age and gender. In this paper, we present evidence of an imbalanced dataset of FMA’s impairment levels and propose a recognition method regardless of the patient’s characteristics variation.

3. Proposed Method

In this section, we propose an improved recognition method to detect the impairment level of finger movement based on the Fugl-Meyer assessment in a non-ideal condition of imbalanced datasets.

3.1. Inclusion Criteria of Subject

Prior to recruiting the subject, several criteria must be strictly followed. All subjects must be partially impaired in one arm and able to maintain the sitting position either on a chair or wheelchair by themselves. The subjects are not congenital stroke patients and have no permanent finger injury. According to the assessment by a rehabilitation doctor, the subject must have undergone at least three months of the rehabilitation program. All subject criteria nd experiment procedures were approved by the ethical committee of Airlangga University Hospital, Surabaya, Indonesia (No. 125/KEP/2023).

3.2. Instruments

This paper employed a total of four channels of the EMG sensor from two TSND151 and AMP151 sensors (ATR-Promotion Inc., Japan). TSND151 is a compact wireless multi-function sensor that is embedded in inertial measurement unit sensors (IMU) and an external terminal of 16-bit analog-digital input. Regarding EMG measurement, the external terminal was connected to the AMP151, which was an extended amplifier specified for biological signals. The sampling frequency was set to a maximal setting of 1000 Hz with a 1000 signal amplification. Other instruments were related to the FMA task for finger movement, such as a pen, a piece of paper, a cylinder, and a tennis ball.

3.3. Electrode Attachment

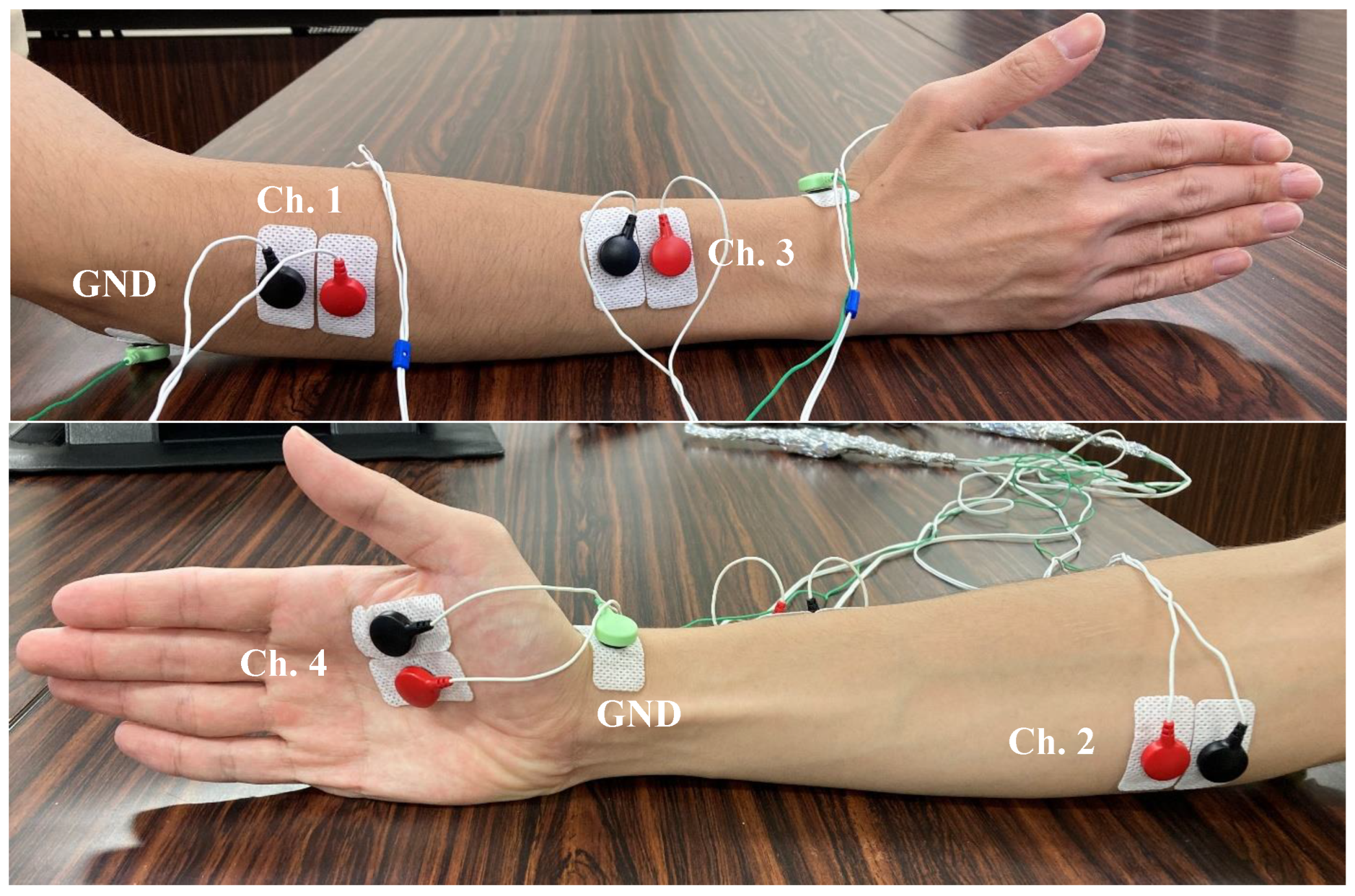
In this paper, we improved the data collection process by capturing the EMG signal from 4 extrinsic and intrinsic muscle activities, whereas the previous experiment only captured 2 extrinsic forearm muscle activities [8]. The attachment location of the electrodes was the Extensor digitorum muscle (Channel 1), Flexor digitorum muscle (Channel 2), Extensor pollicis brevis muscle (Channel 3), and Flexor pollicis brevis muscle (Channel 4). Channel 1–3 are extrinsic muscles and channel 4 is intrinsic muscle [16]. The utilization of intrinsic muscle must be taken into consideration due to its potential to provide a prominent EMG signal of a specific hand finger. The muscle of channel 4 was selected due to its high relative importance in providing an EMG signal of pinch-related movement [17]. The location of muscle attachment is shown in Figure 1.

3.4. Data Processing Flow

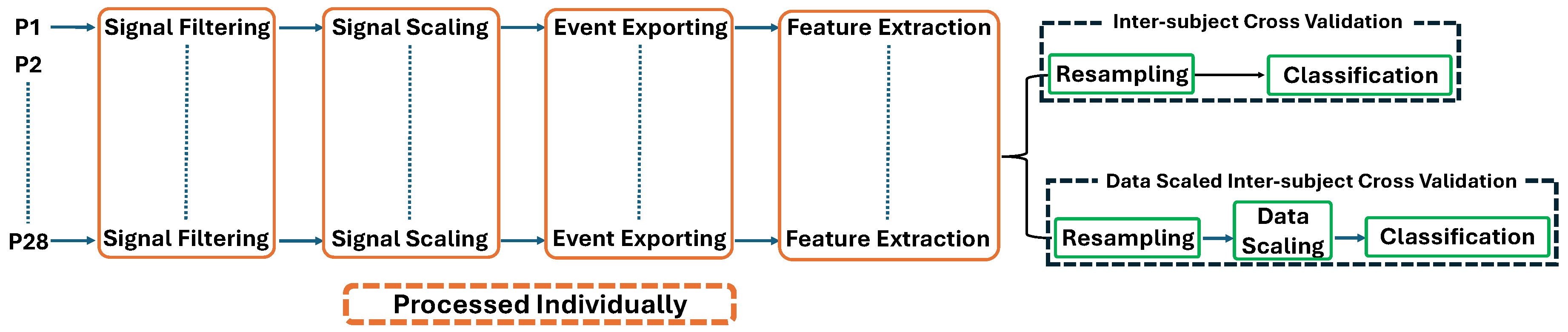
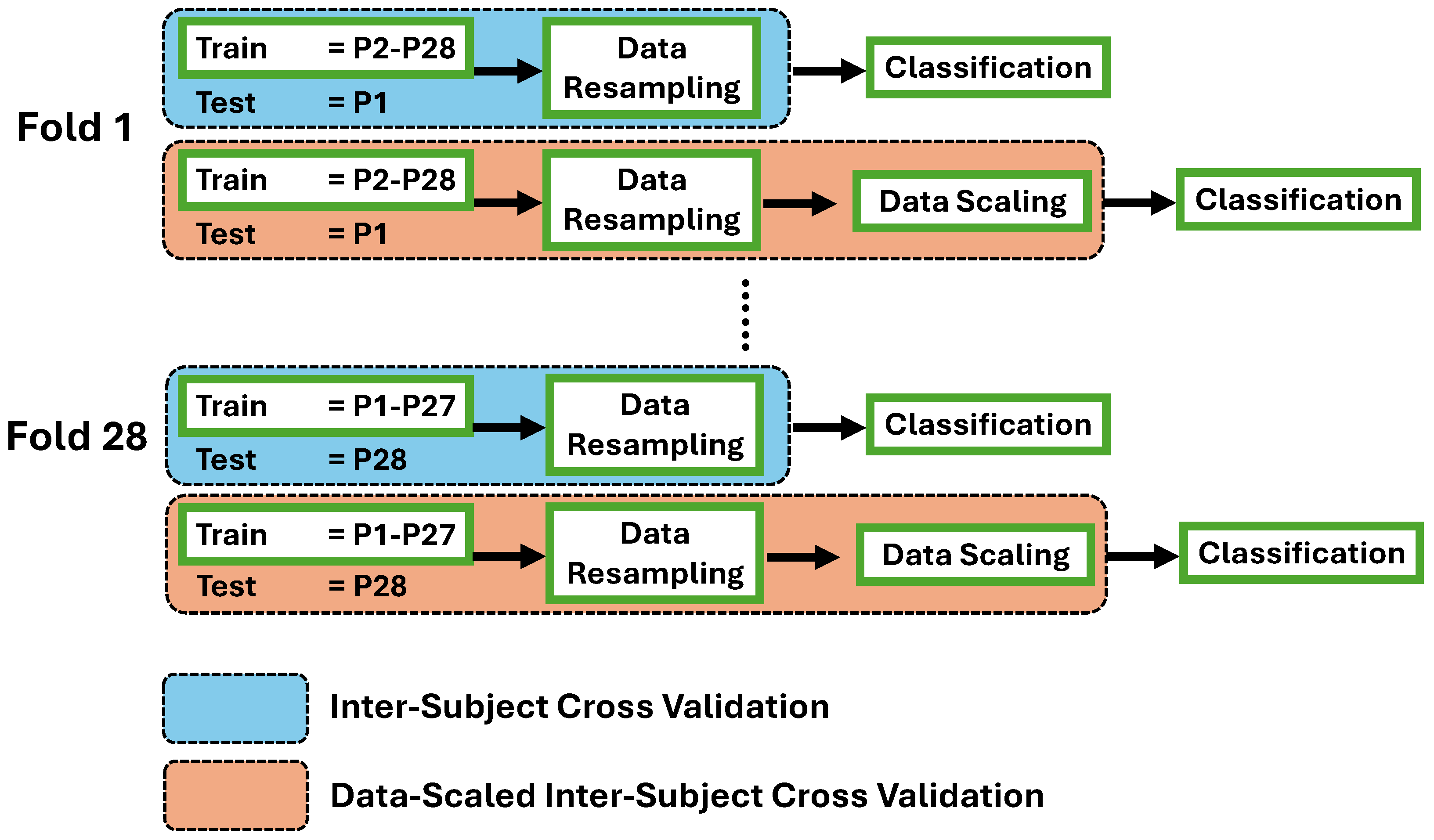
The data was processed to be prepared as machine learning input. The flow encompassed several steps: signal filtering, signal scaling, movement event exporting, and feature extraction. Following the feature extraction process, two mechanisms were conducted to evaluate the performance of machine learning models. The first mechanism was inter-subject cross-validation (ISCV), which consisted of a data resampling process to address imbalanced dataset conditions. This was followed by directly deploying the data into machine learning after the feature extraction step. Another mechanism was data-scaled inter-subject cross-validation (DS-ISCV), which added data scaling prior to the classification process. The signal filtering process until feature extraction was performed individually for each participant’s data. Subsequently, the classification process of both mechanisms was performed using inter-subject cross-validation. Finally, this paper observed and analyzed the classification outcome of both mechanisms for each FMA-based movement task. The data process flow is shown in Figure 2.

3.4.1. Signal Filtering

Motion artifacts, baseline, and power line interference are major noise sources in EMG signals [18,19]. The frequency of power line interference is typically at 50 Hz, depending on the location. The range of baseline and motion disturbances was between 0 and 20 Hz. The power line interference also tends to induce harmonic noises that yield high spikes at the multiplication of 50 Hz, which is observable in the frequency domain. A common process to address this problem is to perform a signal-filtering technique. In the previous experiment, a Butterworth high-pass filter was able to generate a clean signal [8]. Nevertheless, the conventional digital filter still leaves undesirable noise within a non-muscle-contracting signal, such as a relaxed event.
One commonly used digital filtering method is wavelet denoising (WD). In contrast to Butterworth filters that produce flat or smooth frequency responses, WD applies wavelet transform to decompose the signal into frequency components with matched resolutions [20]. Consequently, unlike Butterworth filters, WD offers superior time-frequency localization, ensuring the retention of precise signal features while minimizing noise. The process of wavelet denoising involves an initial decomposition of the signal through a wavelet transform (WT), followed by applying appropriate thresholds to the detail coefficients. This step entails setting all coefficients below the associated thresholds to zero. Subsequently, the denoised signal is reconstructed based on the modified detail coefficients [21].
Parameter selection of wavelet denoising is very important. Preserving the muscle-contracting amplitude of the EMG signal is mandatory while eliminating undesirable noises. Additionally, addressing the non-stationary behavior of EMG signals remains a challenge. Thus, selecting incorrect parameters may result in poor noise removal or elimination of important amplitudes. 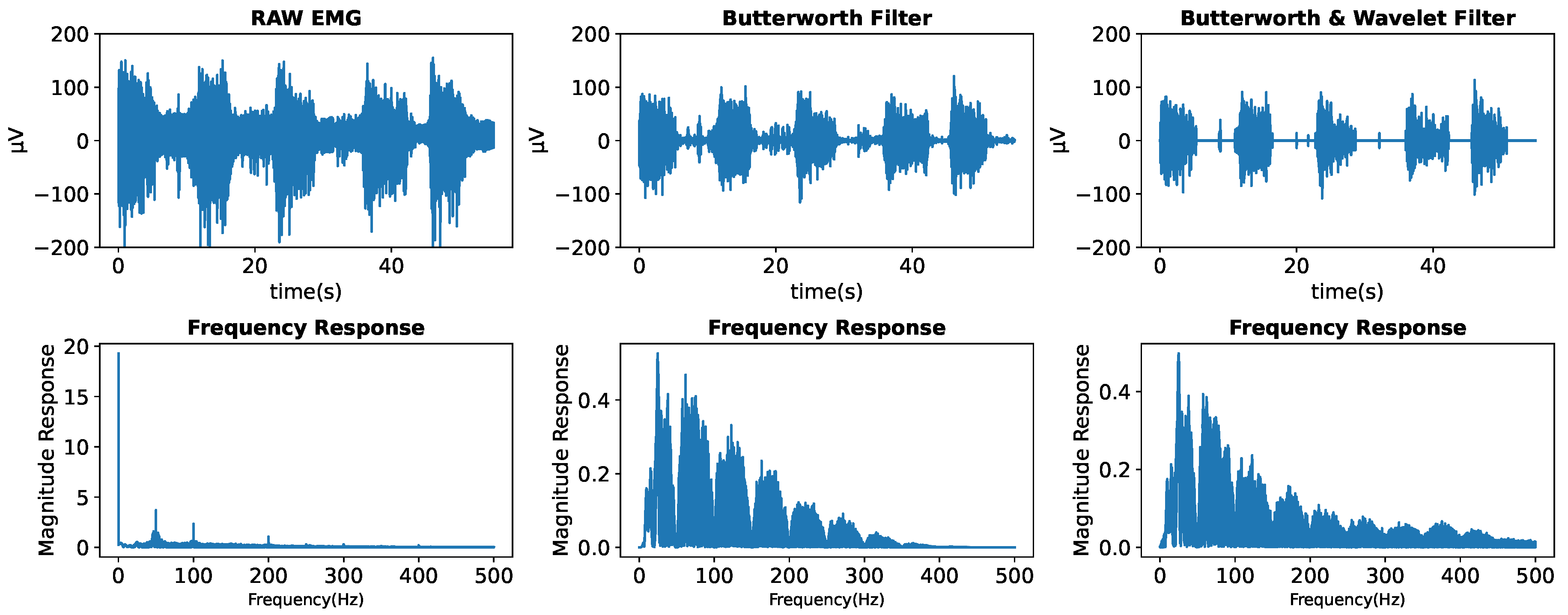A study investigated the optimum wavelet function to identify and denoise the EMG signal [22]. According to the study findings, the Daubechies1 (db1 or haar) wavelet with a hard transformation at 0 dB signal-to-noise ratio (SNR) achieved the best denoising performance. In this paper, we combined the Butterworth filter and wavelet denoising technique. We employed the high-pass and bandstop Butterworth filters to eliminate the specific frequency of the noises. The wavelet filter with the db1 function, hard transformation, and decomposition level 1 were employed to eliminate the remaining noises within the relaxed event signal. Figure 3 illustrates the result after the signal filtering process

3.4.2. Signal Scaling

The EMG represents the combined motor unit action potentials during contraction, recorded at a specific electrode location. The surface EMG voltage potential is greatly influenced by various factors, which differ among individuals and may also change over time within the same individual. Consequently, the amplitude of the EMG signal is ineffective for group comparisons or monitoring over extended durations [23]. To address this issue, several studies stated that a scaling method such as signal normalization or standardization effectively reduced the differences between records within and across subjects [23,24,25]. Several studies have introduced a signal scaling method of z-score normalization to improve the consistency of EMG signals [8,23,26,27,28,29]. This paper employed the z-score method as the EMG signal scaling. The z-score method scales the signal instances by removing the mean feature and scaling it to unit variance.

3.4.3. Event Exporting and Feature Extraction

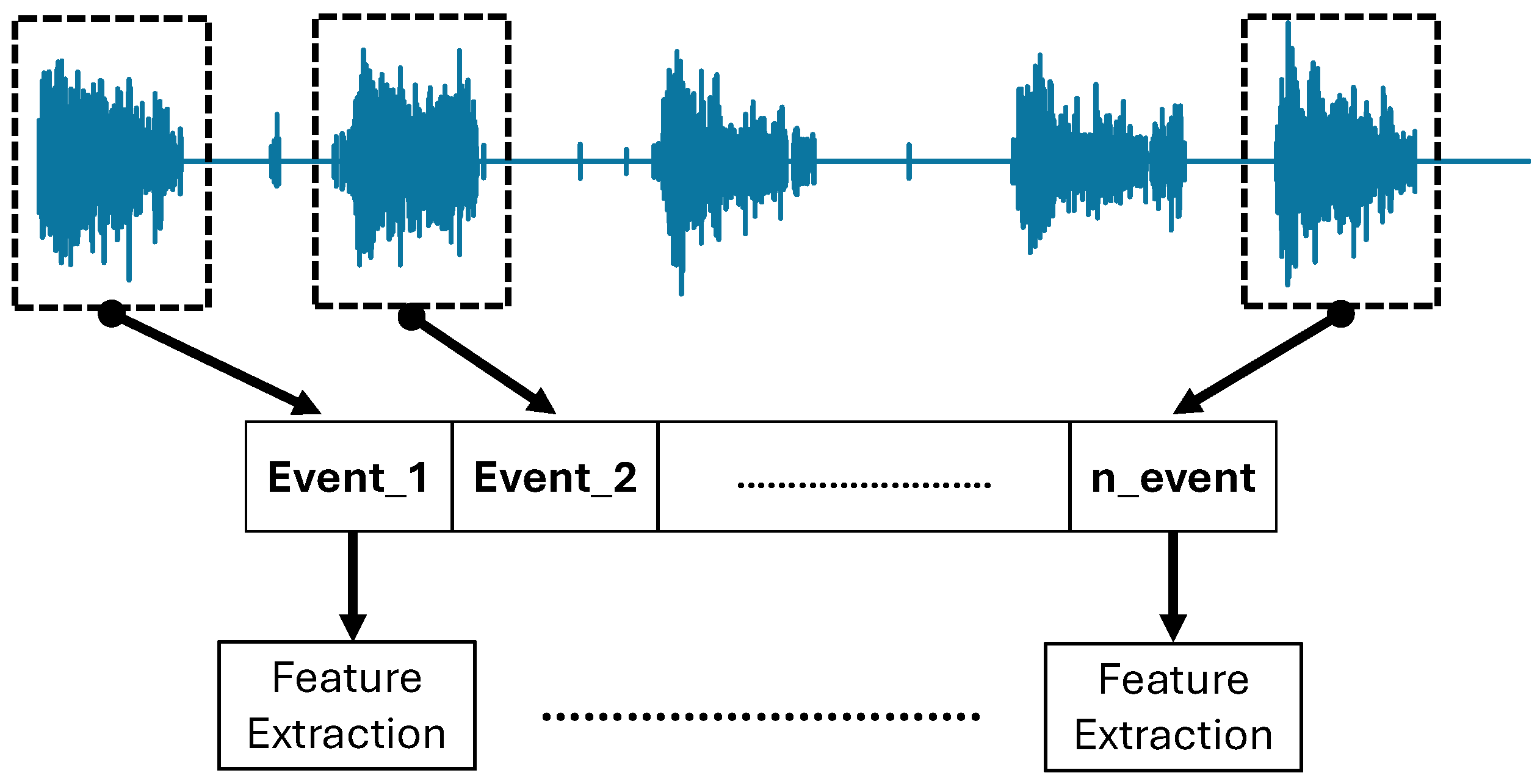
Following the signal filtering process, the EMG signal still consisted of all events of FMA movement tasks, including the relaxation period. Separating task-related amplitude with a relaxed state is important to avoid undesirable data deployment in the feature extraction process and machine learning algorithms, such as the relax-related signal. In the following step, feature extraction was conducted on each exported event separately. As a result, only the EMG signal corresponding to a task-related event was extracted. The illustration of the event exporting and feature extraction process is depicted in Figure 4.
Many features have been introduced for recognition purposes, where time and frequency domain features were mainly employed due to their simplicity, lower computational cost, and promising recognition results. In the previous experiment, seven time-domain features and one frequency-domain feature were employed [8]. The extracted features were mean absolute value (MAV), variance (VAR), root-mean-square (RMS), waveform length (WL), slope sign change (SSC), zero crossing (ZC), Willison amplitude (WAMP), and mean power frequency (MPF). Many studies have utilized these features to provide the amplitude, complexity, and frequency characteristics from EMG signal [30,31,32,33]. However, in the case of impairment level recognition, the amplitude-related features can potentially have a marginal difference in both within and inter-participants. Therefore, emphasizing the complexity-related features potentially provides distinct information between impairment levels.
Several studies have introduced features that depict the complexity of EMG signals. Thongpanja et al. and Oo et al. utilized the Skewness feature to provide complexity information from EMG [34,35]. The skewness measures the asymmetry of a variable within a distribution. A zero skewness signifies a symmetric distribution, while positive skewness indicates a right-skewed distribution, and vice versa [34]. Another promising feature that provides complexity information for EMG is Shannon entropy. This feature describes a signal’s irregularity, complexity, and unpredictability characteristics [36]. Furthermore, the inherent non-stationary nature of the EMG signal potentially has strong feedback with the entropy feature [37]. Typically, a higher value of Shannon entropy of EMG represents a good muscle condition, where a lot of muscle motor units contribute to producing muscle contraction and high amplitude and randomized EMG signal. On the contrary, an impaired muscle makes it difficult to exhibit an EMG signal, resulting in a low value of Shannon entropy. In this regard, this paper employed several features to focus more on the complex characteristics of EMG, consisting of 5 time-domain features and one frequency-domain feature that was waveform length (WL), zero crossing (ZC), mean absolute value (MAV), skewness, Shannon entropy, and mean power frequency (MPF).

3.5. Data Resampling and Scaling

Data resampling was performed to address the imbalance issue in the train datasets, as shown in Figure 5. The famous resampling approaches include oversampling, undersampling, and both combinations. Incorrect selection of the resampling method may lead to invalid classification results. In this paper, the actual number and value of the minority class are important as they correspond to the actual impairment level of the patient. Several studies have shown the promising performance of undersampling approaches to maintain the number of minority classes and produced decent classification results [38,39,40]. This paper utilized a random oversampling approach using the Imblearn library in Python with a sampling strategy to resample all classes except the minority class.
The data scaling was performed for the second mechanism in the following step, as shown in Figure 5. Data scaling is a common measure of treating data before handing it to machine learning algorithms. This technique is particularly useful in managing diverse scales of the data input and improving the performance of machine learning models. One of the data scaling techniques is z-score scaling, where some use a z-score normalization or standardization term. The z-score scales the data instances by removing the unit mean and dividing it by the unit variance. Several studies have proven the performance of z-score in enhancing classification accuracy and efficiency. Al-Faiz et al. showed that the z-score scaling decreased the number of epochs required for the learning network [41]. Suma et al. found an improved accuracy after z-score scaling [42]. Long et al. showed that the classification performance was significantly improved after z-score scaling [43].

3.6. Classification

In the previous experiment, we built machine learning models using the support vector machine (SVM) and random forest (RF) algorithms [8]. Despite being known as traditional machine learning, these algorithms are capable of recognizing complex patterns in the field of EMG-related classification [44,45,46,47]. Both algorithms are based on the support vector and ensemble-type architectures, respectively. In this paper, we employed an additional algorithm of multi-layer perceptron (MLP), a neural network architecture. The machine-learning model was built on each FMA movement task to ensure that the final output of each model is focused on the impairment level of finger movement. As shown in Figure 5, there are two mechanisms of data processing flow, resulting in two classification results of the first (ISCV) and second (DS-ISCV) mechanisms for each machine-learning model. In the present paper, the machine-learning models pertaining to the second mechanism will be denoted as SVM_scaled, RF_scaled, and MLP_scaled.
A Python library named scikit-learn was employed to implement the machine learning models. The parameter of each machine-learning algorithm was pre-determined, where the SVM utilized a poly kernel of degree 3, the regularization parameter of 3, and the gamma parameter of one divided by the number of features. Regarding the random forest, the employed number of trees is 700 with a Gini criterion, and the maximum depth of the tree is 15. Lastly, the parameter of MLP is 100 hidden layer sizes, an activation function of rectification, a maximum iteration of 200, a stochastic gradient-based optimizer, an alpha parameter of 1e-4, an initial learning rate of 1e-4 with an adaptive method, and a stopping tolerance of 1e-7.

3.7. Evaluation

This paper evaluated the performance of the employed machine-learning models through the inter-subject cross-validation method. The inter-subject cross-validation process was performed due to the type of data where a patient can exhibit only one or two impairment levels for a movement task. In this paper, the inter-subject cross-validation procedure encompassed the classification process and the prior data preparation processes, as shown in Figure 2. The objective of this approach was to properly classify inter-subject cross-validation, especially in the train-test dataset selection, and evaluate the outcome of the machine learning models. The illustration of the inter-subject cross-validation approach is shown in Figure 5. The ISCV mechanism encompassed the data resampling and classification, while DS-ISCV included the data scaling process after resampling. The first cross-validation fold encompassed selecting the test data from subject number 1 and the remaining as a training dataset. Subsequently, the last fold utilized test data from subject number 28 and the remaining as a training dataset.

4. Data Collection Experiment

This section presents the procedure for the data collection experiment, including the preparation of the subject and the data collection protocol.

4.1. Subject

The participants comprised 28 stroke patients, 17 males and 11 females, who were over 18 years old. Subject selection was based on random sampling according to inclusion criteria mentioned in Section 3.1, where the patient, who never underwent a Fugl-Meyer assessment, was requested to participate in the experiment on the day of their rehabilitation program in the Airlangga University Hospital. All subjects and their relatives were explained all experiment procedures, and they voluntarily agreed to participate. The subjects sat on a chair or wheelchair by themselves or with the help of relatives or clinicians. Prior to the experiment, the subject was explained all of the experiment protocols and learned the FMA-based finger movement as shown in Table 1.

4.2. Experiment Protocol

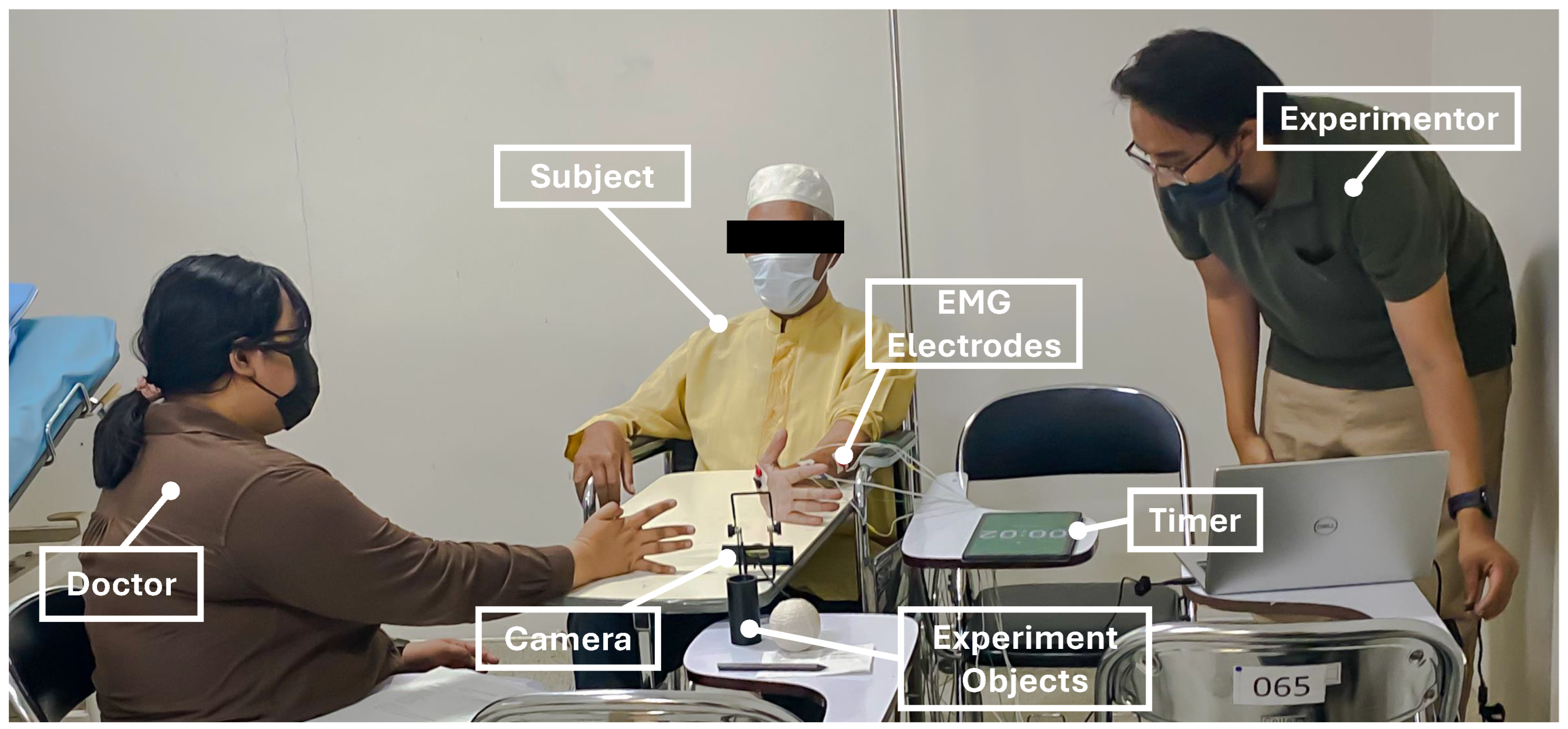
During the experiment, four channels of EMG sensors were attached to the subject’s forearm and palm on the impaired side, where a cleaning measure with an alcohol swab was performed prior to attachment toward the skin area of the electrode attachment position. A doctor sat before the subject to assess and give finger movement instructions. As shown in Figure 7, the assessed finger movement encompassed Mass Flexion (MF), Mass Extension (ME), Hook Grasp (HG), Thumb Adduction (TA), Pincer Grasp (PG), Cylinder Grasp (CG), and Spherical Grasp (SG). The subject was instructed to perform an FMA-based finger movement for 5 s with 5 repetitions. This repetition approach was intended to observe the stability of the patient’s finger movement to achieve a reasonable assessment. Simultaneously, the doctor observed the exhibited finger movement and performed the assessment accordingly. Additionally, the patient was instructed to move only the finger part while the doctor performed a tug toward the experiment objects. This measure was intended to produce a proper assessment from the doctor. In this paper, the doctor’s assessment was utilized as the ground truth for the employed machine learning models. The experimental environment is shown in Figure 6
One session of finger movement assessment encompassed five repetitions of one finger movement. A 12-second relaxation or resting period was given within movement repetitions. However, a preferable resting period within repetition may be given arbitrarily based on the doctor’s instruction. Subsequently, the subject was given a preferable resting period before moving to another finger movement task. This setting was implemented to avoid muscle fatigue that influences the stability of the exhibited EMG [30]. Additionally, an experimenter held a timer to guide the movement repetitions to avoid any mistakes. Simultaneously, the EMG signal of the subject and the experiment video will be recorded throughout the data collection process. The illustration of movement repetitions with the corresponding resting periods is shown in Figure 8.

5. Result

This section demonstrates the presence of an inherent imbalanced dataset in the actual patient experiment. Consequently, recall scores between ISCV and DS-ISCV are compared. Furthermore, the recall score of non-majority classes is evaluated. Finally, detailed cross-validation results of the best machine-learning model for each finger movement task are shown. Each result includes the recall score of the actual target class and the misclassification rate of the other target classes.

5.1. Movement Event Data

As mentioned in Section 4, there are 28 subjects where each subject was instructed to perform each finger movement task with 5 repetitions. In conclusion, the total number of movement events for one task with 5 repetitions across 28 subjects would be 140, and the total number of all 7 FMA finger movement tasks across 28 subjects would be 980. However, some movement events were removed due to the subject’s undesirable hand movement, and unstable conditions occurred in the EMG signal, resulting in poor waveform shape. The final movement events after data removal are shown in Table 2
As shown in Table 2, the movement events of subjects P8 in ME, P2 in PG, and P5 in SG were completely removed. Consequently, the classification of these movements comprised only 27-fold cross-validation. On the other hand, several subjects have less than 5 events in some movement tasks after data removal. The total number of movement events in Table 2 shows evidence of an imbalanced dataset, where the majority class is the Full level in all movement tasks. The Partial level was the minority class in ME, MF, HG, CG, and SG, whereas the None level was in TA and PG. Furthermore, there is a large difference in the number of majority and minority classes with an average of 92±10 events.
Following the data collection experiment, the EMG data underwent a data processing step, as shown in Figure 2. Following the feature extraction step with a 500 ms window size and a 100 ms window step, the processed EMG data were extracted to be prepared as machine-learning input. The number of data points of each movement task and impairment level are shown in Table 3.

5.2. Recognition Performance

A well-known metric such as accuracy may provide misleading information in the imbalanced dataset. The bias of the score toward the majority class accuracy causes the issue. Thus, this paper evaluated recognition performance using an average of recall metrics to minimize bias due to an imbalanced dataset. The average of recall encompassed calculating the recall on each impairment level after concatenating the actual and prediction levels in the inter-subject cross-validation, followed by calculating the overall average across impairment levels. Additionally, the average recall score of minority classes is also presented.
Table 4 shows that the cell in grey color represents the highest recall score of each movement. Four out of seven movements passed recall of 0.50, that was mass extension (ME), hook grasp (HG), pincer grasp (PG), and spherical grasp (SG). Additionally, the machine learning models of ISCV and DS-ISCV performed well according to the movement, where the highest recall was achieved by SVM of the second mechanism (SVM_DS-ISCV) in MF, the first mechanism of MLP (MLP_ISCV) in HG, SVM_DS-ISCV in TA, SVM_ISCV in PG, MLP_ISCV in CG, and MLP_ISCV in SG. However, SVM_DS-ISCV and MLP_ISCV in ME shared the same recall score of 0.70. In this case, the average recall score of the minority classes of Partial and None levels must be observed.
The average recall score of non-minority classes in Table 5 was calculated from the Partial and None levels. In the ME movement, the SVM_DS-ISCV marked the highest score, referring to the best model for recognizing non-majority classes. However, different outcomes occurred in HG and TA, where MLP_DS-ISCV achieved the highest recall score of non-majority classes for both movements. There was a marginal difference in the overall (Table 4) and non-majority classes (Table 5) recall scores on the HG movement. This was due to the trade-off between the recognition of majority and non-majority classes. In the TA movement, despite the highest score of SVM_DS-ISCV in Table 4, the non-majority classes result showed the highest score in MLP_DS-ISCV. This condition was due to the high recall score on the majority class of TA. Considering the importance of the non-majority classes, this paper shows the best model for each movement task with a dagger(†) symbol in Table 5.
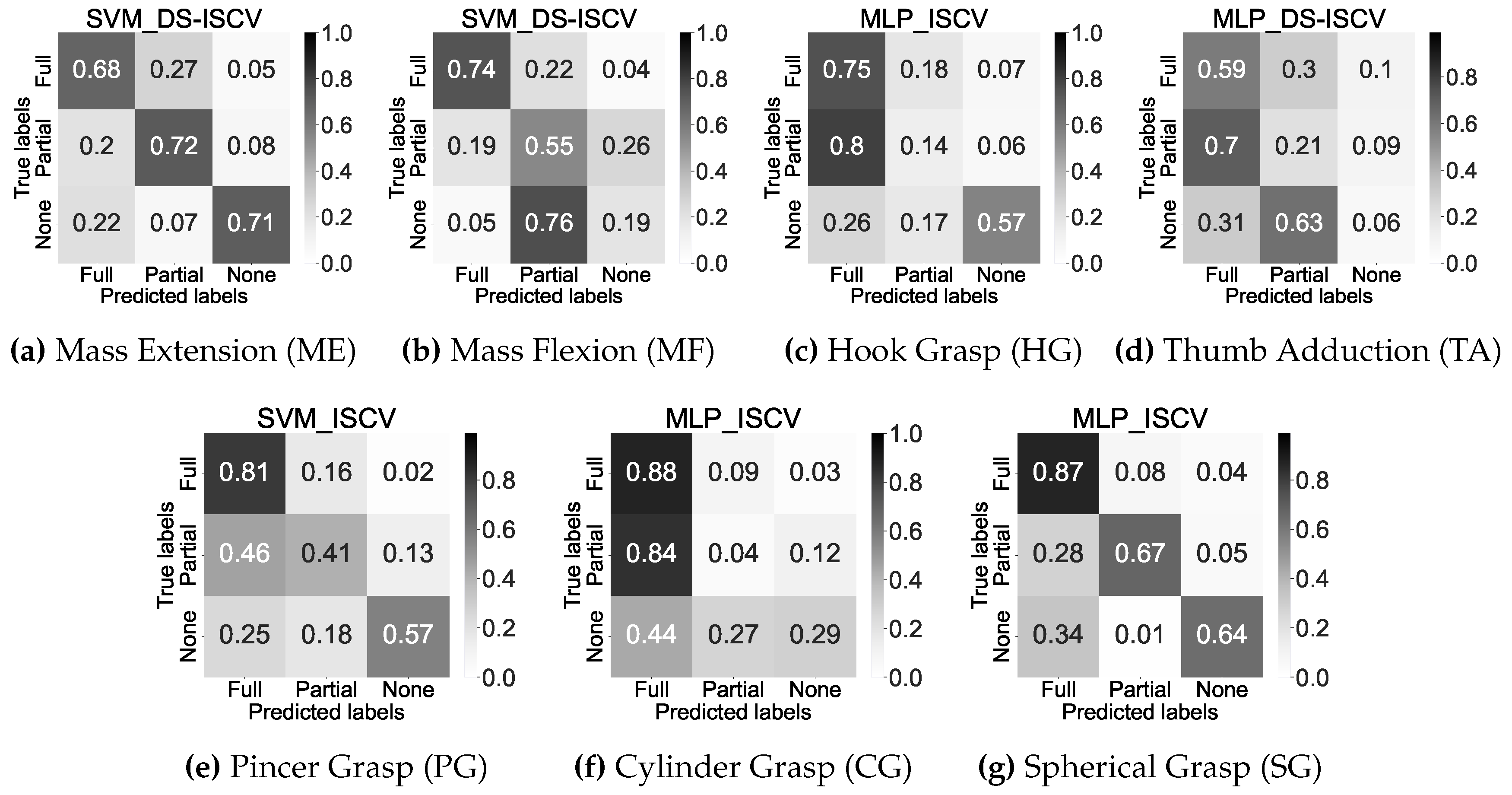
Figure 9 shows the detailed information of concatenated confusion matrices on each movement after inter-subject cross-validation. In general, decent recognition performances were achieved by the SVM_DS-ISCV of ME and MLP_ISCV of SG followed by SVM_ISCV of PG, as shown in Figure 9a, Figure 9g, and Figure 9e respectively. Figure 9b and Figure 9c show decent performance on two impairment levels on the SVM_DS-ISCV of MF and MLP_ISCV of HG, respectively. In contrast, the remaining shows a correct classification of the majority class only.

5.3. Portion of Classification Outcome Across Impairment Levels in Inter-Subject Cross-Validation

Figure 9 shows the general information of correct-incorrect classification after concatenating the classification outcome across the subjects. This section presents the detailed classification outcome of each cross-validation fold, including the misclassification rate across impairment levels. In this paper, the misclassification rate of each cross-validation fold was calculated from the false positive rate, and the classification outcome of the corresponding impairment level was the recall score. Therefore, the classification portion can be observed using these metrics as shown in Table 6.
In Table 6, the recall score for the actual level is shown in black, while the false positive rate for other levels is shown in red for each fold. Each row corresponds to a specific fold in the inter-subject cross-validation, as illustrated in Figure 5. In contrast to Figure 9, which showcases the concatenated confusion matrices subsequent to cross-validation, the classification portion offers detailed insight into discerning the misclassification trends of each movement. Consequently, this allows for a comprehensive evaluation of the performance of the best machine-learning models on each movement. Most movements show the misclassification that results in the recall score below 0.5 occurring between Full and Partial levels in ME, HG, TA, PG, and CG. On the other hand, misclassification between Partial and None levels occurred in MF, whereas misclassification between None and Full levels in SG.

5.4. Comparison Recognition Performance with Previous Experiment

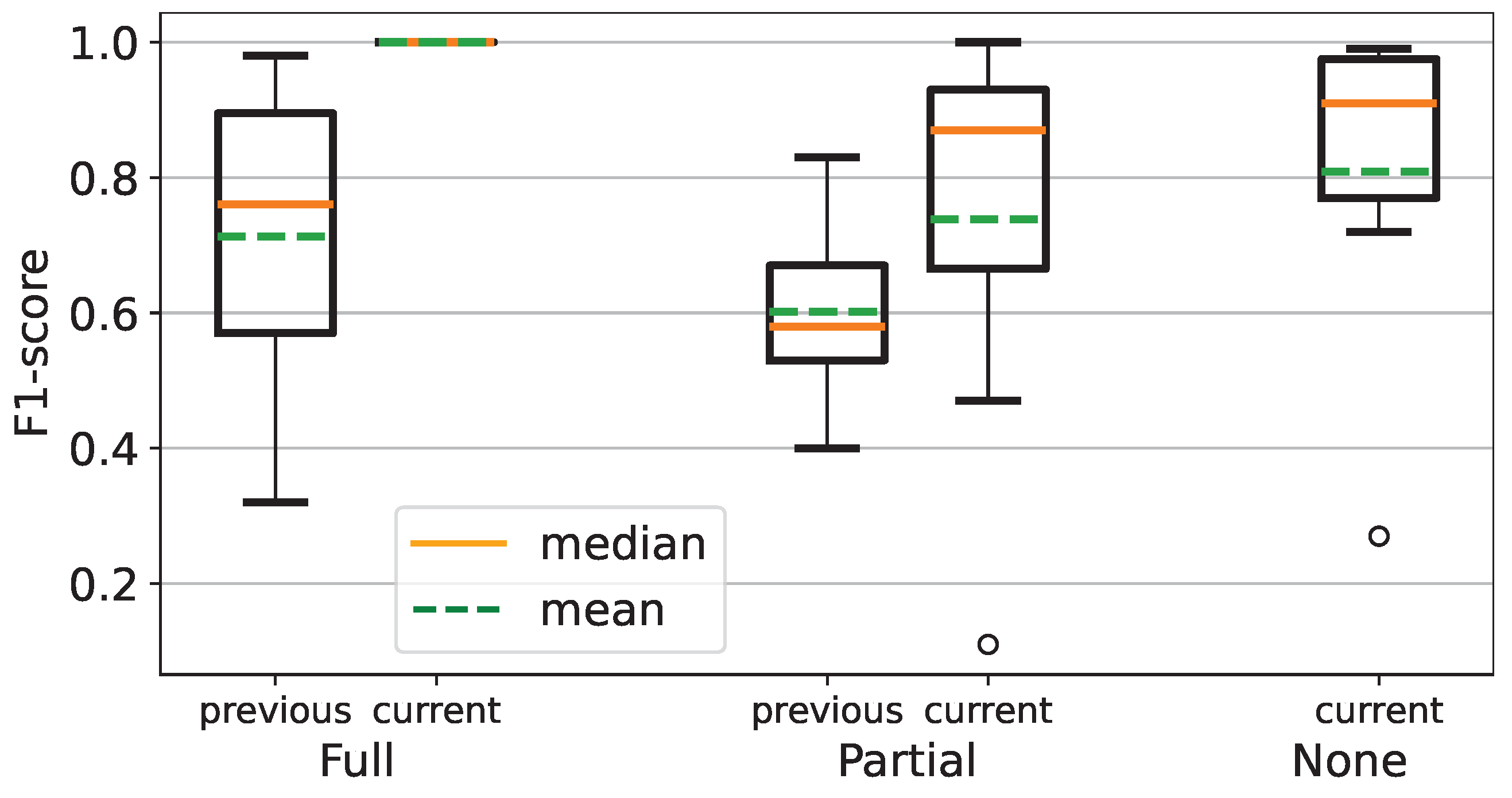
This paper presents an improved recognition method for finger movement impairment levels based on FMA. In the previous experiment, the F1 Score of each impairment level was utilized as the evaluation metric. The previous experiment only comprised a holdout method of the data-splitting process, where the dataset was split into 50% of train and test datasets. However, this paper comprised the leave-one-out cross-validation, where the subject’s data represented the number of observations for data splitting. Accordingly, despite being indirectly incomparable to the previous experiment, we employed the F1-score of the best fold of inter-subject cross-validation for comparison.
In the previous paper, the impairment level of None was not acquired, as shown in Table 7. Therefore, only Full and Partial levels were utilized in this paper. MF achieved the lowest F1 score, whereas TA achieved the highest. In the current experiment result, the lowest F1 score was CG, whereas PG achieved the highest, as shown in Figure 8. This result shows the F1 scores in Table 8 have higher values than the recall score in Table 6. Figure 10 shows that the F1 score of the current experiment is superior to the previous experiment.

6. Discussion

This paper presents a method for recognizing finger movement impairment levels of FMA using EMG in an imbalanced dataset. The discussion delves into the recognition performance of FMA impairment levels within an imbalanced dataset and an inherently subjective environment. Furthermore, the correlation between inherent subjectivity in conventional assessment and the resulting misclassification is discussed.

6.1. Recognition Performance of Imbalanced Dataset

According to Table 3, the minority class of the Partial level occurred in ME, MF, HG, CG, and SG, while the TA and PG had the minority class of None level. Theoretically, the imbalanced dataset will drive the recognition of the minority class toward the majority class [48]. Based on the result shown in Figure 9 and Table 6, there is no correlation between the minority class and the misclassification issue. This finding infers that the proposed method has performed decently in addressing the imbalanced condition of the dataset. Additionally, the employed data processing flow of the ISCV mechanism excludes the data scaling process, and the DS-ISCV mechanism demonstrates its individual contribution. Based on Table 5, the best machine-learning model of the DS-ISCV mechanism was achieved by SVM_DS-ISCV and MLP_DS-ISCV in ME, MF, and TA, whereas the ISCV mechanism machine-learning model achieved the highest score on the rest of the movements.

6.2. Comparison with Previous Experiment

In the previous experiment, the data processing method comprised the data scaling only [8]. Consequently, the result of this study is indirectly incomparable to the previous study. Therefore, selecting the best F1 score of each impairment level from the cross-validation fold was utilized to match the holdout method of the previous experiment. Furthermore, this paper evaluates recognition performance in inter-subject cross-validation settings and addresses the imbalanced dataset issue, which is not explicitly stated in the aforementioned related research [9,10,11,12]. In the previous experiment, the employed features were focused on the statistical and amplitude characteristics of EMG [8], while this paper emphasizes the complexity characteristics of the EMG signal.
Compared to recall metric, which is suitable for imbalanced datasets, several F1-scores in this study showed higher values due to the contrary nature of precision in the F1-score. Consequently, it may not represent the actual performance of the employed machine-learning model. According to this metric, the current experiment result is superior to the previous experiment, as shown in Figure 10.

6.3. Subjectivity Issue of Fugl-Meyer Assessment

In this paper, the doctor’s manual assessment result served as the target learning of the employed supervised machine-learning models. Therefore, a decent recall score corresponds to a decent performance following the doctor’s assessment result. However, as mentioned in the related research on FMA impairment level recognition, the conventional assessment of FMA is prone to subjectivity issues [8,9,10,11,12]. The interaction between Full and None levels exhibits distinct boundaries, whereas the interaction between Full and Partial levels, or Partial and None levels, tends to yield uncertain and subjective assessment results. This ambiguity arises from an indistinct boundary at the Partial level, which behaves like a transitional phase between the None and Full levels, as shown in Table 1.
According to the result, the proposed method showed an interaction in the misclassification rate between Full and Partial levels in ME, HG, TA, PG, and CG. Furthermore, misclassification between Partial and None levels also occurred in MF. This condition showed that the proposed method provides different assessment results according to the muscle information aspect. Furthermore, the employed EMG features comprised both amplitude-related features and frequency and complexity features, as mentioned in Section 3.4.3. Therefore, the proposed method may assist the doctor or physiotherapist in clarifying the patient’s impairment level in uncertain assessment conditions.

6.4. Limitation and Future Work

This paper addressed the inherent subjectivity of FMA assessment using the impairment level recognition method using EMG. Consequently, the system is limited in its output of impairment level according to muscle information. Additionally, various uncontrollable anatomical and physiological factors, such as age and gender variations, anatomical characteristics influencing electrode attachment, and the potential presence of atrophy or fibrosis in the muscle, pose challenges in EMG settings. However, aside from muscle information, the FMA requires the dexterity of the fingers in executing tasks, as shown in Table 1. Consequently, several subjects with different finger dexterity profiles may be recognized as identical due to marginal differences in EMG signal. Therefore, to comprehensively recognize the impairment level of finger movement, an additional modality will be utilized to capture the finger movement profile of each participant.

7. Desktop Application

This paper also presents the use case of the proposed method in actual assessment using a desktop application. This study aims to assist the doctor in making more accurate judgments by employing a biosignal modality of EMG to perform the FMA of finger movement automatically. The implementation of this study requires the doctor to perform a manual assessment, especially in the object-grasping task. Simultaneously, the system automatically assesses the impairment level through the muscle information of EMG. Finally, the doctor may double-check the system’s output before deciding the impairment level of a patient.
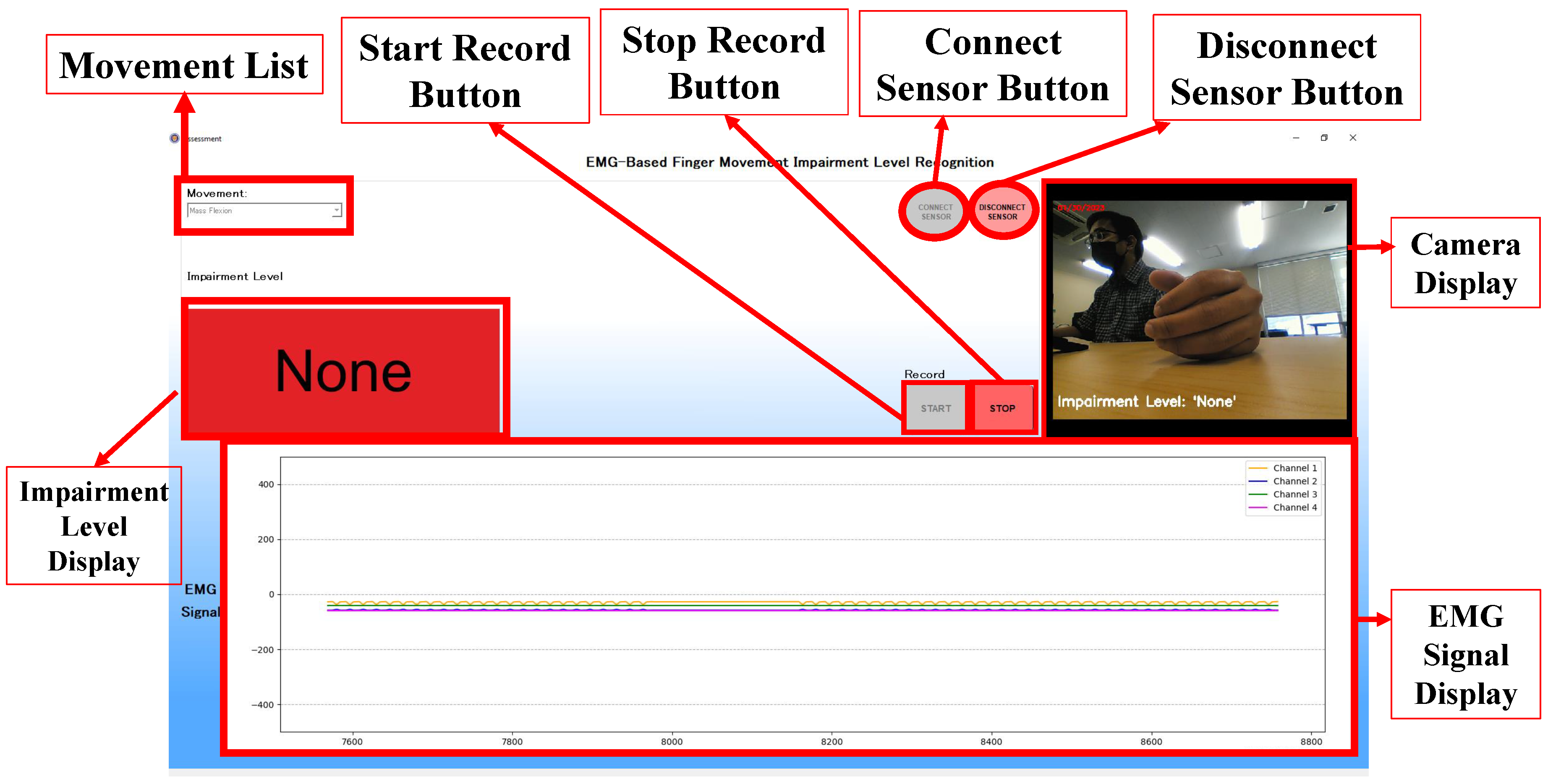
Figure 11 shows the desktop application’s assessment window with several features. The movement list feature consists of a list of FMA finger movements where each item corresponds to the selected machine-learning model. The connect and disconnect buttons control the connection between sensors and the application. Start and stop record buttons control the impairment level recognition and camera recording processes. The impairment level will be displayed in the Impairment Level Display. A camera display will show and record the finger movement. Lastly, the signal obtained from the sensors will be displayed in the EMG signal Display. The assessment window mainly implements the proposed method to output an impairment level of the FMA finger movements. As shown in Figure 11, a display shows a None impairment level with a red background. This impairment level was produced through several processes in the proposed method that were adjusted for real-time assessment inside the application.
The first process of the application workflow was to store the EMG signal from 4 channels individually into an object with a size of 1000 instances. This process was intended to fix the size of EMG data to 1000 instances. The stored EMG data were then filtered using both Butterworth and wavelet filters. Subsequently, the data were extracted with 5 time-domain features and one frequency-domain feature as explained in Section 3.4.3. Following the feature extraction process. The last process is to input the data into the established machine-learning model to output the impairment level. The established machine-learning models were connected with the finger movement item inside the movement list features. Therefore, the model will be automatically selected when the user chooses a finger movement item inside the feature.
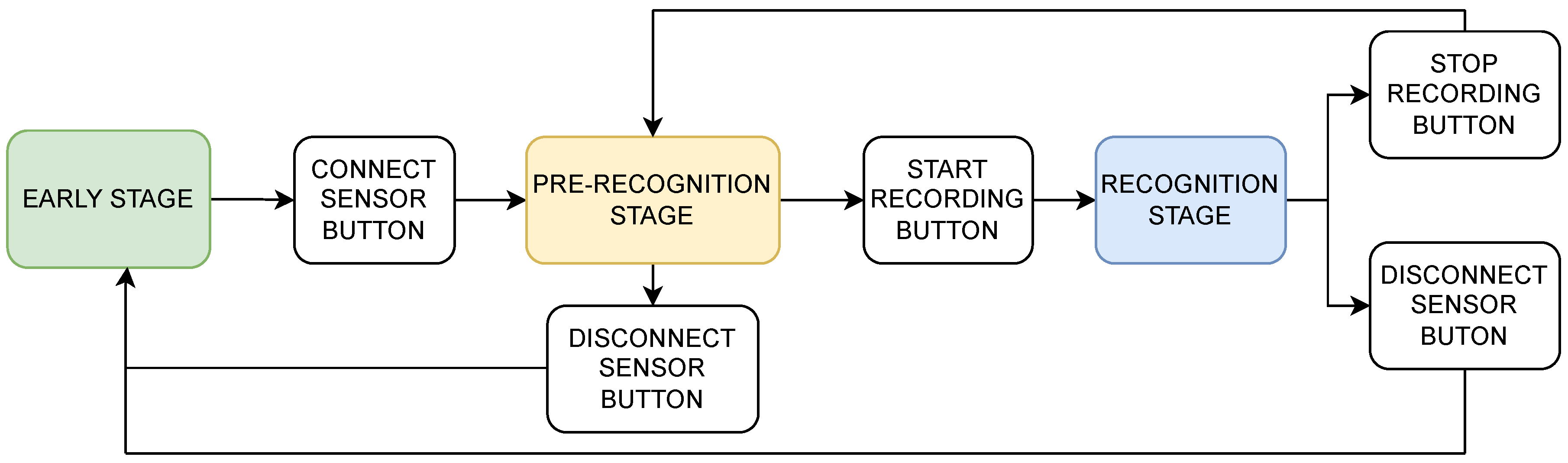
The assessment window consists of several stages, the early stage, the pre-recognition stage, and the recognition stage, which are intended to help the user run the assessment comfortably, as shown in Figure 12. At this stage, the camera display, the green push button for connecting to sensors, and the combo box for finger movement selection are enabled. Meanwhile, the other features are automatically disabled. This stage has a function to facilitate the user adjusting the camera position for the assessment, connecting the application to the EMG sensors, and selecting a finger movement to be assessed. In addition, each item in the list of finger movements is connected with the selected machine-learning model that will be utilized in the recognition stage.
The next stage is the pre-recognition stage. This stage starts after the user clicks the connect-sensor push button and the sensor connection with the application is successfully established. At this stage, several features that correspond to several functions are enabled. The first enabled feature is the plot widget to display the EMG signal. In this feature, the user may check the displayed EMG signal for each channel. With this feature, the doctor may also check for an error in the resulting EMG signal when the patient performs any movement. Therefore, an adjustment in the position of the electrodes or other necessary action to obtain a proper EMG signal is feasible. In addition, the selection of the finger movement is still feasible before the recognition stage. Another enabled feature is the green start-record push button to start the recognition and video recording process. If the user wishes to finish the assessment, the red disconnect sensor push button is enabled at this stage.
Following the command from the start-record push button, the recognition stage is started. The corresponding impairment level information is also transferred into the displayed video at this stage. Therefore, the video displayed in the recognition stage will simultaneously show the assessment date and impairment level. Furthermore, the video recorded on the PC allows the doctor to review the impairment level of the corresponding finger movement outside the desktop application.
At this stage, the user has two options to proceed with the assessment window. The first option is to stop the assessment for the current movement and start another movement. In this option, the user may press the stop-record button and enter the pre-recognition stage. Subsequently, the user can select different movements in the movement list and press the green start-record button to start the assessment. The other option is to finish all of the assessments. Finally, the user may press the red stop-record and disconnect sensor buttons in this option.

8. Conclusion

In this paper, we proposed a recognition method of finger movement impairment levels of FMA using EMG to address the subjectivity issue in an imbalanced dataset condition. The evaluation results of inter-subject cross-validation showed that both data processing mechanisms contribute to addressing the imbalanced dataset condition and subjectivity issue of FMA. The recognition results showed that the SVM and MLP of both mechanisms outperformed the RF model in all FMA tasks. Subsequently, the misclassification rate mainly occurred between Full and Partial levels. Despite moderate recall scores in some movement tasks, this finding highlights the subjectivity issue in conventional assessment. It assists the doctor in making a proper judgment through EMG-based recognition in an uncertain assessment condition. Finally, this paper introduces the desktop application that outputs an assessment video embedded with the system’s impairment level result.

Author Contributions

Conceptualization, A.R.S.S.P., A.O., Y.D.P., R.R., T.T. and M.T.; methodology, A.R.S.S.P., A.O. and T.T.; software, A.R.S.S.P.; validation, A.R.S.S.P..; formal analysis, A.R.S.S.P. and T.T.; investigation, A.R.S.S.P.; resources, A.R.S.S.P.; data curation, A.R.S.S.P. and Y.D.P.; writing—original draft preparation, A.R.S.S.P.; writing—review and editing, A.R.S.S.P., A.O., R.R. and T.T.; visualization, A.R.S.S.P.; supervision, A.O., T.T. and M.T.; project administration, A.R.S.S.P., A.O., R.R., T.T. and M.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study was conducted following ICH–GCP standards and CIOMS–WHO guidelines 2016 (Protocol No. UA-02-23144) and approved by the Ethical Committee of Airlangga University, Surabaya, Indonesia (125/KEP/2023).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data are not publicly published due to ethical restrictions.

Acknowledgments

The authors appreciate the great cooperation of all subjects, clinicians, and all parties supporting the experiment in the Airlangga University Hospital.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ISCV Inter-subject Cross Validation
DS-ISCV Data-Scaled Inter-Subject Cross Validation
SVM Support Vector Machine
RF Random Forest
MLP Multi-layer Perceptron
FMA Fugl-Meyer Assessment
ME Mass Extension
MF Mass Flexion
HG Hook Grasp
TA Thumb Adduction
PG Pincer Grasp
CG Cylinder Grasp
SG Spherical Grasp

References

  1. GBD 2016 Neurology Collaborators. Global, regional, and national burden of neurological disorders, 1990-2016: a systematic analysis for the Global Burden of Disease Study 2016. Lancet Neurol. 2019, 18, 459–480. [Google Scholar] [CrossRef] [PubMed]
  2. Marciniak, C. Poststroke Hypertonicity: Upper Limb Assessment and Treatment. Top. Stroke Rehabil. 2011, 18, 179–194. [Google Scholar] [CrossRef] [PubMed]
  3. Gladstone, D.J.; Danells, C.J.; Black, S.E. Poststroke Hypertonicity: The Fugl-Meyer Assessment of Motor Recovery after Stroke: A Critical Review of Its Measurement Properties. Neurorehabil. Neural Repair 2002, 16, 232–240. [Google Scholar] [CrossRef] [PubMed]
  4. Nam, H.U.; Huh, J.S.; Yoo, J.N.; Hwang, J.M.; Lee, B.J.; Min, Y.S.; Kim, C.H.; Jung, T.D. Effect of Dominant Hand Paralysis on Quality of Life in Patients With Subacute Stroke. Ann. Rehabil. Med. 2014, 38, 450–457. [Google Scholar] [CrossRef]
  5. Dombovy, M.L.; Sandok, B.A.; Basford, J.R. Rehabilitation for Stroke: A Review. Stroke 1986, 17, 363–369. [Google Scholar] [CrossRef]
  6. Kotov-Smolenskiy, A.M.; Khizhnikova, A.E.; Klochkov, A.S.; Suponeva, N.A.; Piradov, M.A. Surface EMG: Applicability in the Motion Analysis and Opportunities for Practical Rehabilitation. Hum. Physiol. 2021, 47, 237–247. [Google Scholar] [CrossRef]
  7. Jaramillo-Yánez, A.; Benalcázar, M.E.; Mena-Maldonado, E. Real-Time Hand Gesture Recognition Using Surface Electromyography and Machine Learning: A Systematic Literature Review. Sensors 2020, 20, 2467. [Google Scholar] [CrossRef]
  8. Sugiharto, A.R.; Tsuchida, S.; Pawana, I.P.A.; Terada, T.; Tsukamoto, M. EMG-Based Recognition Method of Finger Movement Impairment Level in Post-Stroke Patients Based on Fugl-Meyer Assessment. JBINS 2022, 8, 425–433. [Google Scholar]
  9. Wang, J.; Yu, L.; Wang, J.; Guo, L.; Gu, X.; Fang, Q. Automated Fugl-Meyer Assessment Using SVR Model. In Proceedings of the 2014 IEEE International Symposium on Bioelectronics and Bioinformatics, Chung Li, Taiwan, 11–14 April 2014. [Google Scholar]
  10. Alsayed, A.; Kamil, R.; Ramli, H.; As’arry, A. An Automated Data Acquisition System for Pinch Grip Assessment Based on Fugl Meyer Protocol: A Feasibility Study. Journal of Applied Sciences 2020, 10, 3436. [Google Scholar] [CrossRef]
  11. Formstone, L.; Pucek, M.; Wilson, S.; Bentley, P.; McGregor, A.; Vaidyanathan, R. Myographic Information Enables Hand Function Classification in Automated Fugl-Meyer Assessment. In Proceedings of the 2019 9th International IEEE/EMBS Conference on Neural Engineering (NER), San Fransisco, USA, 20–23 March 2019. [Google Scholar]
  12. Lee, S.; Lee, Y.S.; Kim, J. Automated Evaluation of Upper-Limb Motor Function Impairment Using Fugl-Meyer Assessment. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2018, 26, 125–134. [Google Scholar] [CrossRef]
  13. Vijayvargiya, A.; Prakash, C.; Kumar, R.; Bansal, S.; Tavares, J.M.R. Human knee abnormality detection from imbalanced sEMG data. Biomedical Signal Processing and Control 2021, 66, 102406. [Google Scholar] [CrossRef]
  14. Coi, S.; Seo, H.C.; Cho, M.S.; Joo, S.; Nam, G.B. Performance Improvement of Deep Learning Based Multi-Class ECG Classification Model Using Limited Medical Dataset. IEEE Engineering in Medicine and Biology Society Section 2023, 11, 53185–53194. [Google Scholar]
  15. Hasni, H.; Yahya, N.; Asirvadam, V.S.; Jatoi, M.A. Analysis of Electromyogram (EMG) for Detection of Neuromuscular Disorders. In Proceedings of the 2018 International Conference on Intelligent and Advanced System (ICIAS), Kuala Lumpur, Malaysia, 13–14 August 2018. [Google Scholar]
  16. Anatomy, Shoulder and Upper Limb, Hand Muscles. Available online: https://www.ncbi.nlm.nih.gov/books/NBK537229/ (accessed on day month year).
  17. Adewuyi, A.; Hargrove, L.; Kuiken, T. An Analysis of Intrinsic and Extrinsic Hand Muscle EMG for Improved Pattern Recognition Control. Journal of IEEE Transactions on Neural Systems and Rehabilitation Engineering 2016, 24, 485–494. [Google Scholar] [CrossRef] [PubMed]
  18. Luca, C.J.D.; Gilmore, L.D.; Kuznetsov, M.; Roy, S.H. Filtering the Surface EMG Signal: Movement Artifact and Baseline Noise Contamination. Journal of Biomechanics 2010, 43, 1573–1579. [Google Scholar] [CrossRef]
  19. Wang, J.; Tang, L.; Bronlund, J.E. Surface EMG Signal Amplification and Filtering. International Journal of Computer Applications 2013, 82, 15–22. [Google Scholar] [CrossRef]
  20. Bansal, M.; Sharma, R.; Grover, P. Performance evaluation of Butterworth Filter for Signal Denoising. International Journal of Electronics & Communication Technology (IJECT) 2010, 1. [Google Scholar]
  21. Ahsan, M.R.; Ibrahimy, M.I.; Khalifa, O.O. VHDL Modelling of Fixed-point DWT for the Purpose of EMG Signal Denoising. In Proceedings of the 2011 Third International Conference on Computational Intelligence, Communication Systems and Networks, Bali, Indonesia, 26–28 July 2011. [Google Scholar]
  22. Phinyomark, A.; Limsakul, C.; Phukpattaranont, P. Optimal Wavelet Functions in Wavelet Denoising for Multifunction Myoelectric Control. ECTI Transactions on Electrical Engineering, Electronics, and Communications 2009, 8, 43–52. [Google Scholar] [CrossRef]
  23. Sousa, A.S.; Tavares, J.M.R. Surface electromyographic amplitude normalization methods: A review. Electromyography: new developments, procedures and applications 2012, 20, 1–19. [Google Scholar]
  24. Sabri, M.; Miskon, M. F.; Yaacob, M. R.; Basri, A.; Soo, Y.; Bukhari, W. MVC BASED NORMALIZATION TO IMPROVE THE CONSISTENCY OF EMG SIGNAL. Journal of Theoretical and Applied Information Technology 2014, 65, 336–343. [Google Scholar]
  25. Botelho, A.L.; Gentil, F.H.U.; Sforza, C.; Da Silva, M.A.M.R. Standardization of the Electromyographic Signal Through the Maximum Isometric Voluntary Contraction. The Journal of Craniomandibular & Sleep Practice 2011, 29, 23–31. [Google Scholar]
  26. Tanaka, T.; Nambu, I.; Maruyama, Y.; Wada, Y. Sliding-Window Normalization to Improve the Performance of Machine-Learning Models for Real-Time Motion Prediction Using Electromyography. Sensors 2022, 22, 5005. [Google Scholar] [CrossRef] [PubMed]
  27. Shuman, B.R.; Schwartz, M.H.; Steele, K.M. Electromyography Data Processing Impacts Muscle Synergies during Gait for Unimpaired Children and Children with Cerebral Palsy. Front. Comput. Neurosci. 2017, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
  28. Beck, T.W.; Housh, T.J.; Cramer, J.T.; Mielke, M.; Hendrix, Russell. The influence of electrode shift over the innervation zone and normalization on the electromyographic amplitude and mean power frequency versus isometric torque relationships for the vastus medialis muscle. Journal of Neuroscience Methods 2008, 169, 100–108. [Google Scholar] [CrossRef] [PubMed]
  29. AlQudah, A.; Barioul, R.; Lweesy, K.; Elkhalil, H.; Ibbini, M.; Kanoun, O. Electrical Impedance Myography Measurements for Gesture Recognition Data Normalization. In Proceedings of the 2022 International Workshop on Impedance Spectroscopy (IWIS), Chemnitz, Germany, 27–30 September 2022. [Google Scholar]
  30. Qing, Z.; Lu, Z.; Cai, Y.; Wang, J. Elements Influencing sEMG-Based Gesture Decoding: Muscle Fatigue, Forearm Angle and Acquisition Time. Sensors 2021, 21, 7713. [Google Scholar] [CrossRef]
  31. Lee, K.H.; Min, J.Y.; Byun, S. Electromyogram-Based Classification of Hand and Finger Gestures Using Artificial Neural Networks. Sensors 2021, 22, 225. [Google Scholar] [CrossRef]
  32. Phinyomark, A.; Limsakul, C.; Phukpattaranont, P. EMG Feature Extraction for Tolerance of White Gaussian Noise. In Proceedings of the International Workshop and Symposium Science Technology (I-SEEC), Nong Khai, Thailand; 2008. [Google Scholar]
  33. Wang, J.; Cao, D.; Wang, J.; Liu, C. Action Recognition of Lower Limbs Based on Surface Electromyography Weighted Feature Method. Sensors 2021, 21, 6147. [Google Scholar] [CrossRef]
  34. Thongpanja, S.; Phinyomark, A.; Quaine, F.; Laurillau, Y.; Limsakul, C.; Phukpattaranont, P. Probability Density Functions of Stationary Surface EMG Signals in Noisy Environments. IEEE Transactions on Instrumentation and Measurement 2016, 65, 2016. [Google Scholar] [CrossRef]
  35. Oo, T.; Phukpattaranont, P. Signal-to-Noise Ratio Estimation in Electromyography Signals Contaminated with Electrocardiography Signals. Fluctuations and Noise Letters 2020, 19, 2050027. [Google Scholar] [CrossRef]
  36. Bein, B. Entropy. Best Practice & Research Clinical Anaesthesiology 2006, 20, 101–109. [Google Scholar]
  37. Bendat, J.; Piersol, A. Random Data: Analysis and Measurement Procedures, 3rd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
  38. Dendamrongvit, S.; Kubat, M. Undersampling Approach for Imbalanced Training Sets and Induction from Multi-label Text-Categorization Domains. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Berlin, Heidelberg; 2009. [Google Scholar]
  39. Tusell-Rey, C.C.; Camacho-Nieto, O.; Yáñez-Márquez, C.; Villuendas-Rey, Y. Customized Instance Random Undersampling to Increase Knowledge Management for Multiclass Imbalanced Data Classification. Sustainability 2022, 14, 14398. [Google Scholar] [CrossRef]
  40. Ratnasari, A.P. Performance of Random Oversampling, Random Undersampling, and SMOTE-NC Methods in Handling Imbalanced Class in Classification Models. International Journal of Scientific Research and Management (IJSRM) 2024, 12, 494–501. [Google Scholar] [CrossRef]
  41. Al-Faiz, M.Z.; Ibrahim, A.A.; Hadi, S.M. THE EFFECT OF Z-SCORE STANDARDIZATION ON BINARY INPUT DUE THE SPEED OF LEARNING IN BACK-PROPAGATION NEURAL NETWORK. Iraqi Journal of Information and Communications Technology (IJICT) 2018, 1, 42–48. [Google Scholar] [CrossRef]
  42. Suma, V.R.; Renjith, S.; Ashok, S. l Judy, M.V. Analytical Study of Selected Classification Algorithms for Clinical Dataset. Indian Journal of Science and Technology 2016, 9, 1–9. [Google Scholar] [CrossRef]
  43. Long, X.; Fonseca, P.; Haakma, R.; Foussier, J.; Aarts, R.M. Automatic detection of overnight deep sleep based on heart rate variability: A preliminary study. In the Proceedings of the 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 2014.
  44. Toledo-Pérez, D.C.; Rodríguez-Reséndiz, J.; Gómez-Loenzo, R.A.; Jauregui-Correa, J.C. Support Vector Machine-Based EMG Signal Classification Techniques: A Review. Journal of Applied Science 2019, 9, 4402. [Google Scholar] [CrossRef]
  45. Oskoei, M.A.; Hu, H. Support Vector Machine-Based Classification Scheme for Myoelectric Control Applied to Upper Limb. IEEE Transactions on Biomedical Engineering 2008, 55, 1956–1965. [Google Scholar] [CrossRef]
  46. Al-Sharu, W.N.; Alqudah, A.M. Enhancing Prediction of Prosthetic Fingers Movement Based on sEMG using Mixtures of Features and Random Forest. International Journal of Recent Technology and Engineering 2019, 8, 289–294. [Google Scholar] [CrossRef]
  47. Li, Z.; Guan, X.; Zou, K.; Xu, C. Estimation of Knee Movement from Surface EMG Using Random Forest with Principal Component Analysis. Electronics 2019, 9, 43. [Google Scholar] [CrossRef]
  48. KrishnaVeni, C.V.; Rani, T.S. On the Classification of Imbalanced Datasets. International Journal of Computer Science & Technology 2011, 2, 145–148. [Google Scholar]
Preprints 120006 g001
Figure 1. Electrode Attachment Position.
Figure 1. Electrode Attachment Position.
Preprints 120006 g001
Preprints 120006 g002
Figure 2. Diagram of Data Processing Flow.
Figure 2. Diagram of Data Processing Flow.
Preprints 120006 g002
Preprints 120006 g003
Figure 3. EMG Signal Filtering Process.
Figure 3. EMG Signal Filtering Process.
Preprints 120006 g003
Preprints 120006 g004
Figure 4. Event Exporting and Feature Extraction Process.
Figure 4. Event Exporting and Feature Extraction Process.
Preprints 120006 g004
Preprints 120006 g005
Figure 5. Inter-Subject Cross-Validation Data Processing and Classification
Figure 5. Inter-Subject Cross-Validation Data Processing and Classification
Preprints 120006 g005
Preprints 120006 g006
Figure 6. Experiment Environment Setting.
Figure 6. Experiment Environment Setting.
Preprints 120006 g006
Preprints 120006 g007
Figure 7. Finger Movement Tasks of FMA.
Figure 7. Finger Movement Tasks of FMA.
Preprints 120006 g007
Preprints 120006 g008
Figure 8. One Session of Finger Movement Assessment.
Figure 8. One Session of Finger Movement Assessment.
Preprints 120006 g008
Preprints 120006 g009
Figure 9. Concatenated Normalized Confusion Matrices of The Best Machine-Learning Models of Each Movement After Inter-Subject Cross-Validation
Figure 9. Concatenated Normalized Confusion Matrices of The Best Machine-Learning Models of Each Movement After Inter-Subject Cross-Validation
Preprints 120006 g009
Preprints 120006 g010
Figure 10. Boxplot of F1 Scores of Previous and Current Experiments.
Figure 10. Boxplot of F1 Scores of Previous and Current Experiments.
Preprints 120006 g010
Preprints 120006 g011
Figure 11. Assessment Window of Desktop Application.
Figure 11. Assessment Window of Desktop Application.
Preprints 120006 g011
Preprints 120006 g012
Figure 12. User Flow of Assessment Window with the Corresponding Trigger Button.
Figure 12. User Flow of Assessment Window with the Corresponding Trigger Button.
Preprints 120006 g012
Table 1. Motor Domain Function of Fugl-Meyer Assessment for Finger Movement [3].
Table 1. Motor Domain Function of Fugl-Meyer Assessment for Finger Movement [3].
Movement Full (2) Partial (1) None (0)
Mass Extension full active extension some, but not active extension no extension
Mass Flexion full active flexion some, but not active flexion no flexion occurs
Hook Grasp maintains position against resistance can hold position but weak cannot be performed
Thumb Adduction can hold paper against a tug can hold paper but not against tug cannot be performed
Pincher Grasp can hold a pencil against a tug can hold pencil but not against tug cannot be performed
Cylinder Grasp can hold cylinder against a tug can hold cylinder but not against tug cannot be performed
Spherical Grasp can hold a ball against a tug can hold ball but not againts tug cannot be performed
Table 2. Summary of Movement Events (F: Full, P: Partial, N: None; ME: Mass Extension, MF: Mass Flexion, HG: Hook Grasp, TA: Thumb Adduction, PG: Pincer Grasp, CG: Cylinder Grasp, SG: Spherical Grasp).
Table 2. Summary of Movement Events (F: Full, P: Partial, N: None; ME: Mass Extension, MF: Mass Flexion, HG: Hook Grasp, TA: Thumb Adduction, PG: Pincer Grasp, CG: Cylinder Grasp, SG: Spherical Grasp).
ME MF HG TA PG CG SG
Subject F P N F P N F P N F P N F P N F P N F P N
P1 5 5 5 5 5 5 5
P2 5 3 4 3 5 4
P3 5 5 5 5 5 5 5
P4 5 5 3 5 5 5 5
P5 5 5 2 2 1 3 2 2
P6 5 4 1 5 5 5 5 5
P7 5 5 5 5 5 5 5
P8 3 2 5 5 5 5
P9 5 5 5 5 5 5 5
P10 5 5 5 5 5 5 5
P11 5 5 5 5 5 5 5
P12 5 5 5 4 1 2 3 5 5
P13 4 5 5 5 2 3 5 5
P14 5 5 5 5 5 5 5
P15 5 5 5 5 5 5 5
P16 5 5 5 5 5 5 5
P17 4 1 5 5 5 2 3 5 5
P18 5 5 5 5 5 5 5
P19 5 5 5 5 5 5 5
P20 5 5 5 5 5 5 5
P21 5 5 5 5 5 5 5
P22 5 5 5 5 5 5 5
P23 5 5 2 5 5 5 5
P24 5 5 5 5 5 5 5
P25 5 5 5 5 5 5 5
P26 5 5 2 3 5 2 5
P27 5 5 5 5 5 5 5
P28 5 5 5 5 5 5 5
Total 94 11 29 102 9 25 104 9 14 97 25 13 94 25 13 117 7 10 109 10 15
Table 3. Total of Data Point After Feature Extraction Process Across Subjects.
Table 3. Total of Data Point After Feature Extraction Process Across Subjects.
Movement Impairment Level
Full Partial None
ME 4246 491 1288
MF 4601 431 1145
HG 4522 382 640
TA 4083 1001 614
PG 4013 1156 604
CG 5264 320 476
SG 4825 438 689
Table 4. Average Recall Score of Inter-Subject Cross-Validation (Grey: Highest Recall Score of Each Movement).
Table 4. Average Recall Score of Inter-Subject Cross-Validation (Grey: Highest Recall Score of Each Movement).
ISCV DS-ISCV
Movement SVM RF MLP SVM RF MLP
ME 0.61 0.61 0.70 0.70 0.62 0.64
MF 0.40 0.44 0.40 0.49 0.46 0.44
HG 0.46 0.46 0.50 0.46 0.43 0.49
TA 0.27 0.33 0.25 0.35 0.31 0.29
PG 0.60 0.50 0.45 0.48 0.50 0.50
CG 0.32 0.33 0.40 0.34 0.33 0.33
SG 0.49 0.42 0.73 0.46 0.42 0.56
Table 5. Average Recall Score of Inter-Subject Cross-Validation in Non-Majority Classes (Grey: Highest Recall Score of Each Movement; †: Selected Machine-Learning Model).
Table 5. Average Recall Score of Inter-Subject Cross-Validation in Non-Majority Classes (Grey: Highest Recall Score of Each Movement; †: Selected Machine-Learning Model).
ISCV DS-ISCV
Movement SVM RF MLP SVM RF MLP
ME 0.5 0.49 0.64 0.72† 0.49 0.57
MF 0.15 0.21 0.18 0.37† 0.24 0.27
HG 0.25 0.24 0.35† 0.25 0.19 0.36
TA 0.07 0.12 0.08 0.10 0.10 0.14†
PG 0.49† 0.29 0.28 0.26 0.29 0.37
CG 0.03 0.00 0.16† 0.05 0.00 0.09
SG 0.29 0.18 0.65† 0.26 0.18 0.42
Table 6. Portion of Classification Across Impairment Levels in Inter-Subject Cross-Validation (Red: False Positive Rate Score).
Table 6. Portion of Classification Across Impairment Levels in Inter-Subject Cross-Validation (Red: False Positive Rate Score).
Test ME MF HG TA PG CG SG
Data Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level
(fold) Level F P N Level F P N Level F P N Level F P N Level F P N Level F P N Level F P N
P1 F 0.78 0.19 0.03 F 1.00 0.01 0.00 F 0.92 0.04 0.04 P 0.65 0.28 0.06 F 0.97 0.02 0.02 F 0.92 0.08 0.00 F 0.79 0.12 0.09
P2 F 0.05 0.00 0.95 F 0.13 0.83 0.04 F 0.53 0.12 0.35 F 0.10 0.28 0.61 F 0.82 0.02 0.17 F 0.93 0.07 0.00
P3 F 0.99 0.01 0.00 F 0.70 0.25 0.05 F 0.32 0.68 0.00 F 0.04 0.13 0.83 F 0.17 0.64 0.19 F 0.23 0.77 0.00 F 0.98 0.02 0.00
P4 F 0.71 0.20 0.09 F 0.14 0.84 0.02 F 1.00 0.00 0.00 F 0.00 0.99 0.00 F 0.68 0.32 0.00 F 0.99 0.00 0.01 F 0.69 0.08 0.23
P 0.00 0.00 1.00 P 0.00 1.00 0.00
P5 N 0.10 0.04 0.86 N 0.03 0.88 0.09 N 0.00 0.01 0.99 N 0.00 0.99 0.01 P 0.00 1.00 0.00 P 0.66 0.00 0.34
F 0.19 0.42 0.34
P6 P 0.23 0.77 0.00 P 0.10 0.77 0.34 F 0.13 0.25 0.61 F 0.75 0.19 0.05 P 0.91 0.09 0.00 F 0.69 0.22 0.10 F 0.67 0.33 0.00
P7 N 0.26 0.00 0.74 N 0.02 0.86 0.12 N 0.00 0.17 0.83 N 0.00 1.00 0.00 N 0.00 0.38 0.62 N 0.47 0.52 0.01 N 0.05 0.01 0.94
P8 P 0.03 0.89 0.08 F 0.09 0.00 0.91 F 0.00 0.89 0.11 F 0.97 0.02 0.00 F 0.94 0.00 0.06 F 0.76 0.00 0.24
P9 P 0.22 0.75 0.03 F 1.00 0.00 0.00 F 0.91 0.07 0.02 P 0.66 0.30 0.03 F 0.77 0.21 0.03 F 1.00 0.00 0.00 F 0.74 0.09 0.16
P10 F 0.11 0.89 0.00 F 0.77 0.23 0.00 F 0.67 0.33 0.00 F 0.03 0.97 0.00 F 0.99 0.01 0.00 F 1.00 0.00 0.00 F 0.98 0.03 0.00
P11 F 1.00 0.00 0.00 F 0.68 0.32 0.00 F 0.98 0.01 0.01 F 0.02 0.98 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00
F 0.92 0.06 0.02 F 1.00 0.00 0.00
P12 F 0.81 0.19 0.00 F 0.98 0.02 0.00 F 0.98 0.00 0.02 P 1.00 0.00 0.02 P 1.00 0.00 0.00 F 0.84 0.05 0.12 F 1.00 0.00 0.00
P 0.69 0.00 0.26
P13 N 0.70 0.04 0.26 N 0.03 0.97 0.00 N 0.88 0.00 0.12 P 0.83 0.07 0.10 N 0.69 0.05 0.31 F 0.91 0.00 0.09 N 1.00 0.00 0.00
P14 F 0.95 0.05 0.00 F 0.97 0.02 0.00 F 1.00 0.00 0.00 F 0.99 0.01 0.00 F 1.00 0.00 0.00 F 0.98 0.02 0.00 F 1.00 0.00 0.00
P15 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 0.67 0.14 0.19 F 1.00 0.00 0.00 F 1.00 0.00 0.00
Data Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level Actual Predicted Level
(fold) Level F P N Level F P N Level F P N Level F P N Level F P N Level F P N Level F P N
P16 F 0.42 0.58 0.00 F 0.36 0.61 0.03 F 0.98 0.01 0.01 F 0.25 0.75 0.00 F 0.78 0.19 0.03 F 0.19 0.81 0.00 F 0.61 0.39 0.00
F 0.08 0.81 0.23 F 1.00 0.00 0.00
P17 P 0.00 0.34 0.23 F 0.05 0.70 0.25 F 0.46 0.54 0.00 F 0.62 0.38 0.00 P 0.87 0.13 0.00 F 0.76 0.06 0.18 F 0.81 0.02 0.16
P18 N 0.00 0.04 0.96 P 0.32 0.27 0.41 P 0.88 0.11 0.01 P 0.65 0.12 0.23 P 0.08 0.37 0.55 P 0.92 0.06 0.02 P 0.23 0.76 0.01
P19 F 0.19 0.74 0.07 F 1.00 0.00 0.00 F 0.78 0.00 0.22 F 0.99 0.01 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 0.95 0.02 0.04
P20 F 0.68 0.32 0.00 F 0.93 0.07 0.00 F 0.97 0.03 0.00 F 0.32 0.61 0.07 F 0.86 0.14 0.00 F 0.96 0.00 0.04 F 0.84 0.16 0.00
P21 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 0.94 0.06 0.00 F 0.84 0.16 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00
P22 F 0.97 0.00 0.04 F 0.97 0.03 0.00 F 0.48 0.00 0.52 F 0.94 0.00 0.06 F 0.99 0.01 0.00 F 1.00 0.00 0.00 F 0.60 0.40 0.00
P23 N 0.17 0.00 0.83 N 0.06 0.51 0.44 N 0.50 0.47 0.03 N 0.81 0.03 0.15 N 0.25 0.06 0.69 N 0.42 0.01 0.57 N 0.02 0.03 0.95
P24 F 0.99 0.00 0.00 F 0.97 0.03 0.00 F 0.86 0.12 0.01 F 0.60 0.40 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 0.97 0.02 0.01
P25 F 0.93 0.07 0.00 F 1.00 0.00 0.00 F 0.97 0.03 0.00 F 0.99 0.01 0.00 F 0.07 0.93 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00
P26 N 0.21 0.27 0.51 N 0.11 0.59 0.30 P 0.15 0.85 0.00 P 0.79 0.21 0.00 P 0.00 1.00 0.00 F 0.93 0.07 0.00 P 0.33 0.58 0.09
P27 F 0.86 0.12 0.02 F 0.94 0.06 0.00 F 0.96 0.00 0.04 F 0.91 0.09 0.00 F 0.76 0.24 0.00 F 0.96 0.03 0.01 F 0.94 0.06 0.00
P28 F 0.00 1.00 0.00 F 0.89 0.09 0.02 F 1.00 0.00 0.00 F 0.96 0.04 0.00 F 1.00 0.00 0.00 F 1.00 0.00 0.00 F 0.98 0.02 0.00
Table 7. F1-Score of Previous Experiment Result.
Table 7. F1-Score of Previous Experiment Result.
Best Impairment Level
Movement Machine-Learning Full Partial None
ME SVM 0.60 0.58
MF SVM 0.32 0.54
HG SVM 0.54 0.52
TA SVM 0.98 0.83
PG RF 0.90 0.40
CG RF 0.89 0.60
SG SVM 0.76 0.74
Average 0.71 0.60
Table 8. Highest F1-Score of Selected Inter-Subject Cross Validation Fold of Current Experiment Result.
Table 8. Highest F1-Score of Selected Inter-Subject Cross Validation Fold of Current Experiment Result.
Movement Best Impairment Level
Machine-Learning Full Partial None
ME SVM_DS-ISCV 1.00 0.87 0.98
MF SVM_DS-ISCV 1.00 0.94 0.99
HG MLP_ISCV 1.00 0.92 0.91
TA MLP_DS-ISCV 1.00 0.47 0.27
PG SVM_ISCV 1.00 1.00 0.82
CG MLP_ISCV 1.00 0.11 0.72
SG MLP_ISCV 1.00 0.86 0.97
Average 1.00 0.74 0.81
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated