A Fusion Navigation System of Security Robot Based on Millimeter Wave Radar and Inertial Sensor

Preprint

Article

A Fusion Navigation System of Security Robot Based on Millimeter Wave Radar and Inertial Sensor

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 October 2024

Posted:

02 October 2024

You are already at the latest version

Alerts

Abstract

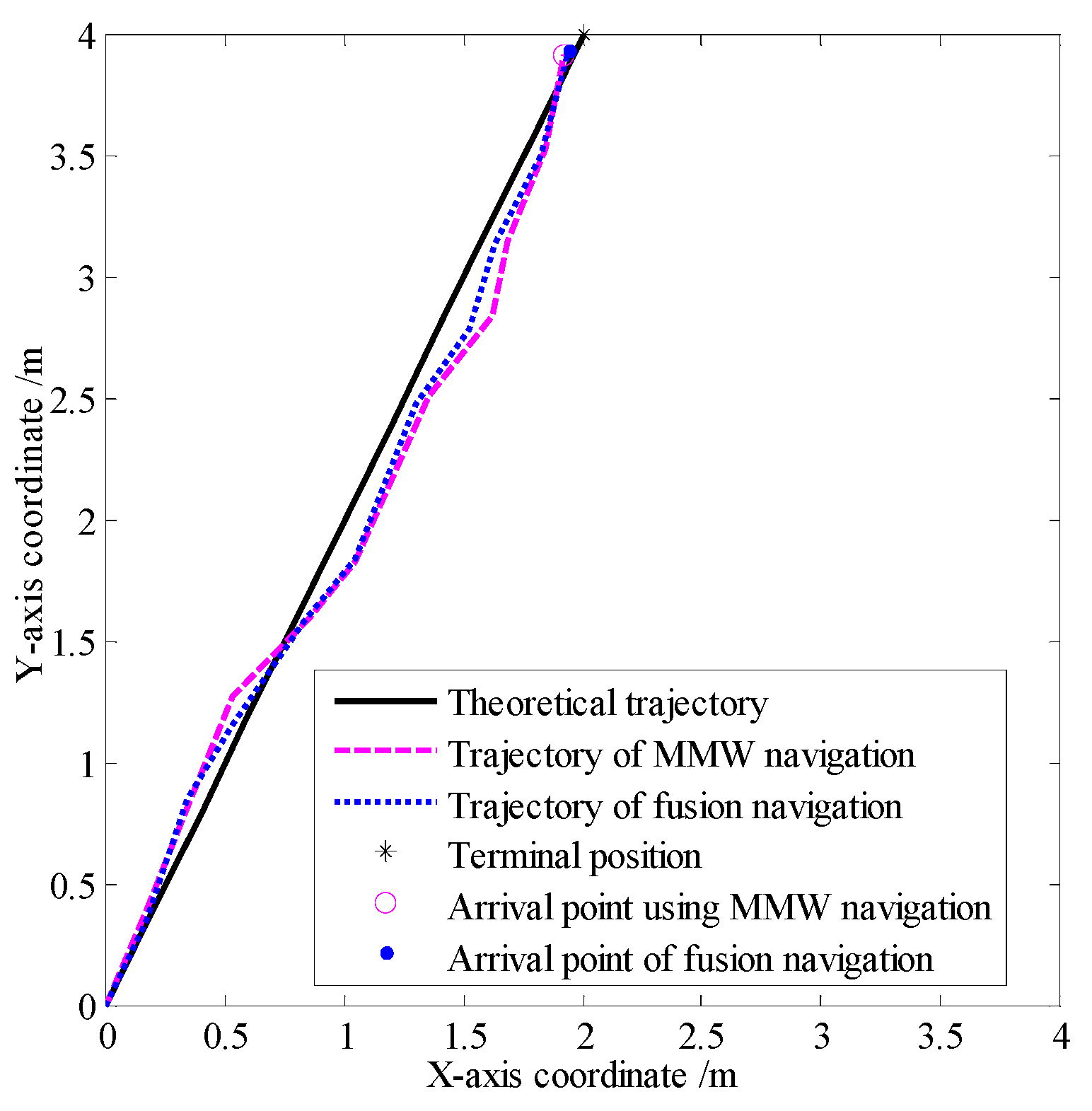
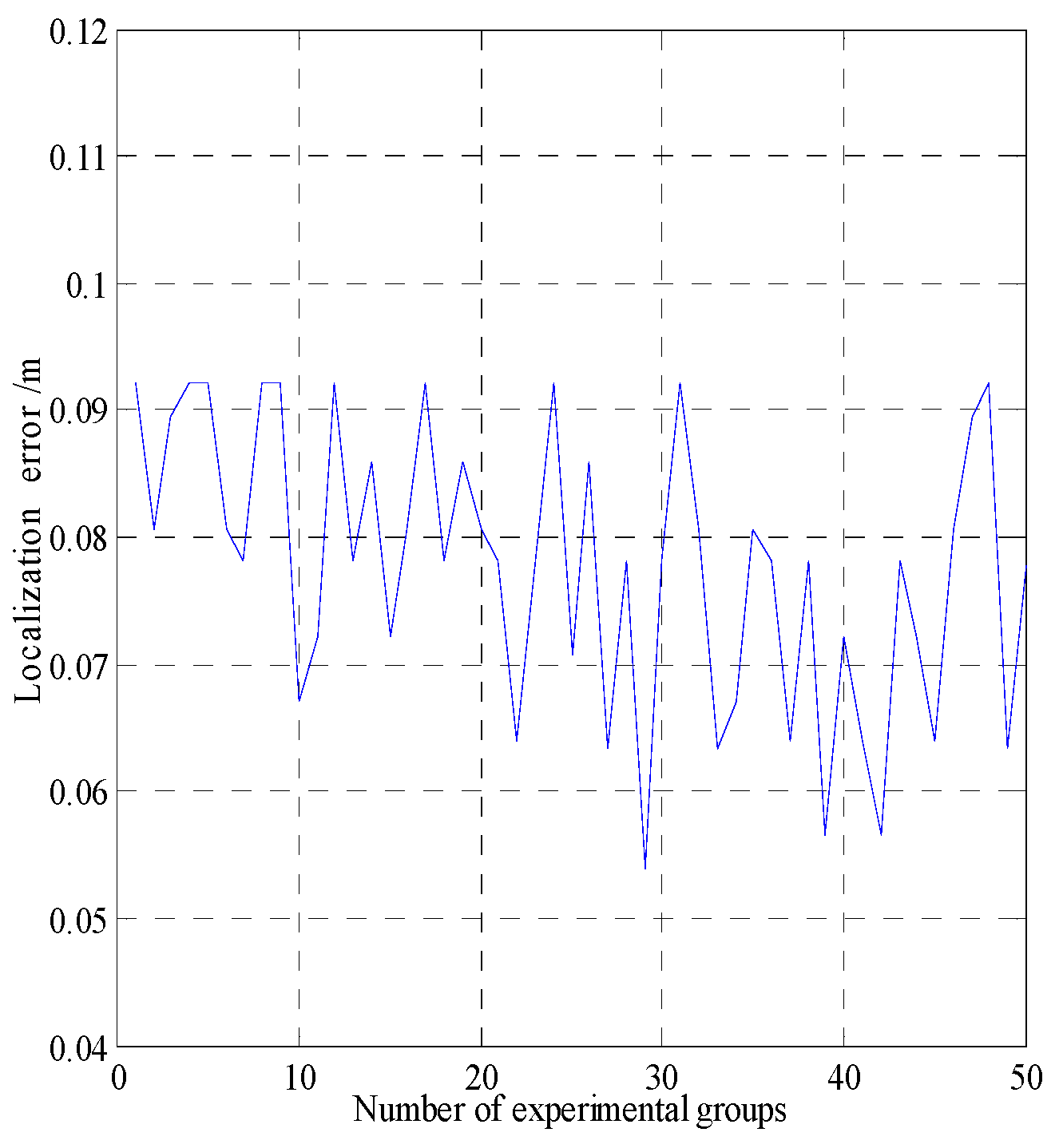
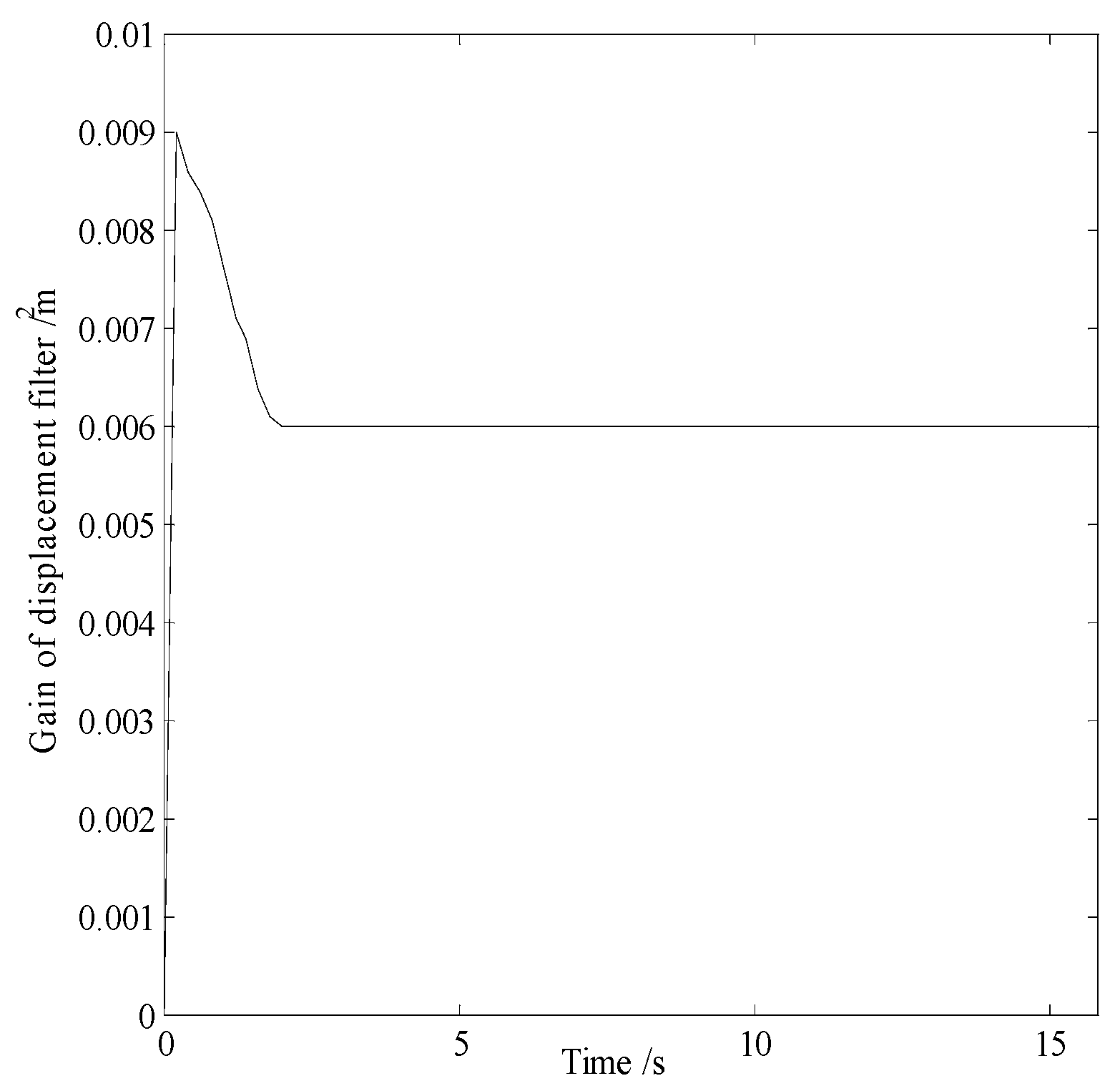
In smog and dust environments, vision and laser-based navigation methods can not be used effectively for controlling the movement of a robot. Autonomous operation of a security robot can be achieved in such environments by using millimeter wave (MMW) radar for the navigation system. In this study, an approximate center method under sparse point cloud is proposed, and a security robot navigation system based on millimeter wave radar is constructed. To improve the navigation accuracy of the robot, inertial navigation of the robot is integrated with MMW radar. Based on the concept of inertial navigation, the state equation for the motion principle of the robot is deduced. According to principle of MMW navigation, the measurement equation is derived, and the kinematics model of the robot is constructed. Further, by applying the Kalman filtering algorithm, a fusion navigation system of the robot based on MMW and inertial navigation is proposed. The experimental results show that the navigation error is close to the error of the navigation system with only MMW in the initial stage. With iterations of the filtering algorithm, the gain matrix converges gradually, and the error of the fusion navigation system decreases, leading to the stable operation of the robot. The localization error of the fusion navigation system is approximately 0.08 metre, and the navigation accuracy is better than that of the navigation system with only MMW radar.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Security robots are intelligent agents that perform dangerous tasks on behalf of humans [1,2] in adverse environments such as smog and dust. To enable the autonomous movement of the robot, the position of the robot must be obtained and it movement be controlled in real time; therefore, navigation technology is a key technology of the robot [3,4]. Laser-based and vision-based navigation are common methods for mobile robot navigation [5,6]. For instance, the university of Luxembourg [7] utilized Lidar to construct and optimize in real-time a three layered Situational Graph that includes a robot tracking layer where the robot poses are registered, a metric-semantic layer with features such as planar walls and novel topological layer constraining the planar walls using higher-level features such as corridors and rooms. This graph can be used for robot navigation. Zou et al. [8] analyzed the characteristics and performance of different Lidar simultaneous localization and mappings and summarized their application to indoor navigation. Although cartographic navigation accuracy is high, over time, cartographers will consume more and more memory to store newly constructed maps. Another study [9] proposed a maples visual navigation system for biped humanoid robots. In this method, information is extracted from color images using deep reinforcement learning to derive motion commands. In addition, a robot navigation system using a Kinect sensor and the concept of transfer learning based on convolutional neural networks was proposed [10]. These studies indicate that laser and visual navigation technologies are widely used and have high precision.

However, in case of working environments such as smog or dust, achieving a precise laser positioning focus point is difficult due to the disturbance of air density [11]. In a dust environment, the environmental information cannot be fully collected using visual sensors, thus hindering the application of a visual navigation method [12]. To realize effective navigation of robots in smog and dust environments, a sensor with strong anti-interference ability needs to be studied. MMW, with a frequency band of 30-300 GHz, have characteristics of both infrared and microwaves, thus possessing the characteristics of strong anti-interference ability, low power consumption, strong penetration, and high Doppler frequency [13]. Therefore, application of MMW radar in smog and dust environments has navigation of robots in the smog environment [14]. The results indicated that the resolution of detection targets using MMW is better than that using optical sensors. Laser navigation cannot be used for robots in a mine environment according to the analysis in [15]; hence, in that study, the technology of simultaneous location and mapping using MMW was proposed to realize autonomous navigation of robots. The triangulation method based on frequency-modulated MMW radar was first proposed in [16]. By scanning the robot with an MMW radar, the distribution information of point clouds was obtained; further, a cut-clustering method was used to effectively reduce the ranging error and localization error caused by the volume of the robot. Based on that method, the security robot navigation system was designed, which was experimentally confirmed to realize autonomous operation of the robot in smog and dust environments, with a localization error of approximately 0.11 m.

While performing dangerous tasks, the robot is usually required to reach the target point as accurately as possible [17]. For example, the robot needs to be accurately moved to a specific position during the task of cleaning of dangerous and flammable objects [18]. One of the effective ways to improve the working efficiency of the robot is to improve its localization accuracy. Combining MMW radar and other sensors is an effective method to improve navigation accuracy [19]. Inertial and other navigation methods are commonly combined with MMW. For example, Li et al. [20] proposed an architecture based on the recurrent convolutional neural network, which combines laser and inertial data to achieve high-precision positioning of the robot. An integrated autonomous relative navigation method based on vision and inertial measurement unit (IMU) data fusion was proposed in [21]. The experimental results showed that this method has high accuracy and robustness. A navigation system based on low-cost vision and inertial fusion and using the extended Kalman filter (EKF) algorithm was proposed in [22]; experiments revealed a navigation accuracy of approximately 0.3 m. In general, inertial sensors are not affected by external environment and have strong anti-interference ability and good navigation accuracy within a short time [23]. Therefore, inertial sensors can also be used in smog and dust environments. A navigation method combining frequency-modulated continuous-wave (FMCW) radar and an inertial odometer was proposed in [24]. FMCW radar is fixed on the carrier, and its navigation error increases with the increase of the robot’s moving distance. In [25,26], a depth fusion method of MMW attitude estimation and other sensors was proposed to accurately estimate the motion trajectory of the carrier; in this method also, the MMW radar is fixed to the carrier.

Fixing the MMW radar on the carrier may increase the navigation error gradually with the moving distance. In this study, the MMW radar is placed in the carrier motion space, the position of the robot is measured by the triangular positioning method, and the positioning accuracy is improved by incorporating inertial sensor information. In this paper, based on inertial navigation theory and frequency-modulated MMW navigation theory, the state equation and the measurement equation of the robot are constructed. Then, the Kalman been researched. A comparative study was conducted on the filtering algorithm is designed, and the fusion navigation method is proposed. Autonomous navigation of the robot in smog and dust environments is achieved with high accuracy. This paper’s contributions are summarized as follows:

1) In order to obtain the approximate geometric center of the target under the sparse point cloud, based on the point cloud information of the millimeter wave radar, an approximate center method based on the sparse point cloud is proposed.

2) In order to solve the navigation problem of security robots in the smoke and dim environment, a navigation algorithm based on millimeter wave and inertial information fusion is constructed.

3) The hardware platform of the security robot based on millimeter wave and inertial navigation fusion is designed.

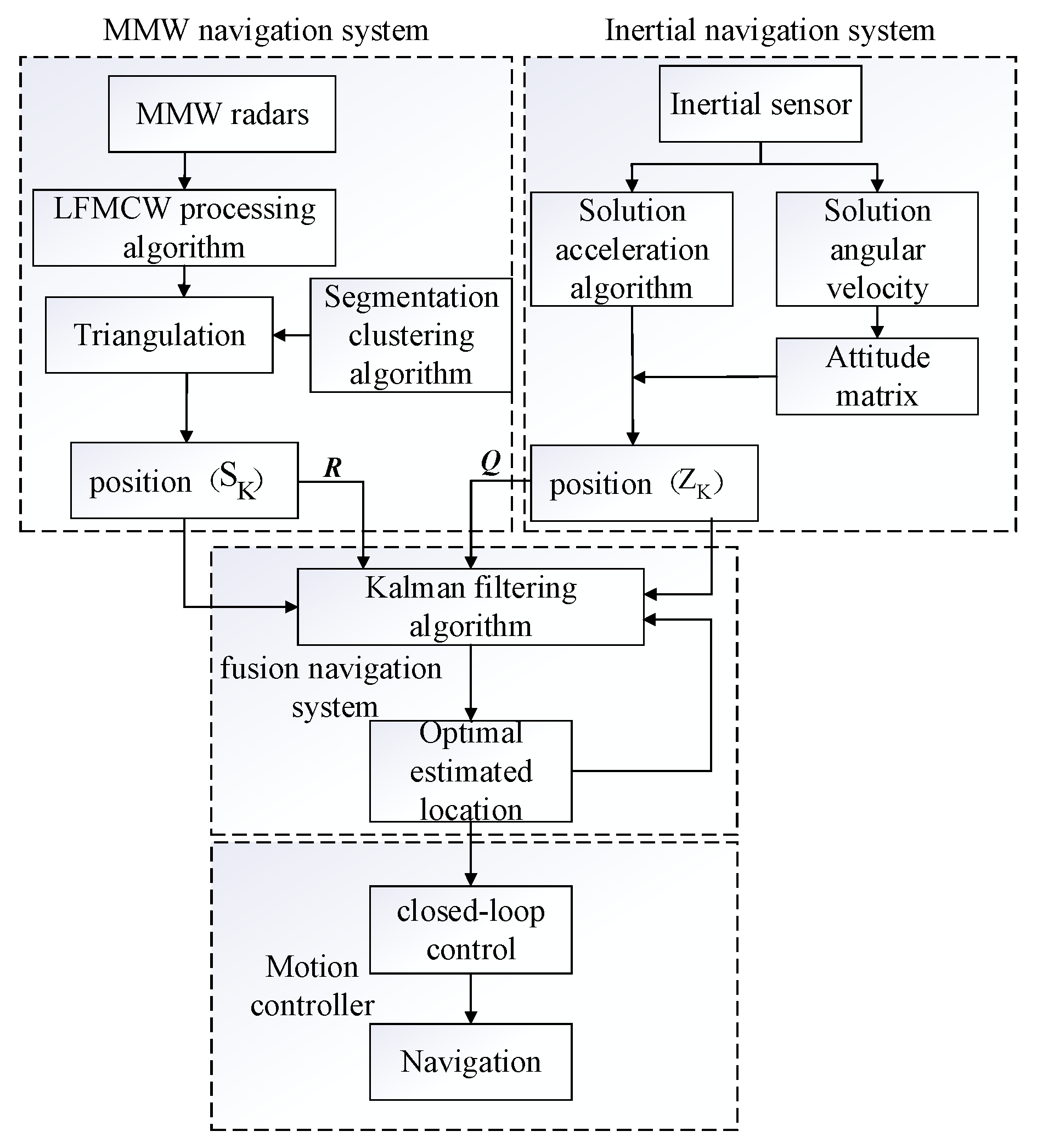
2. Design of Navigation System

Prior to establishing the mathematical model of the fusion navigation system, it is necessary to study the basic principles of the MMW navigation system and inertial navigation system (INS).

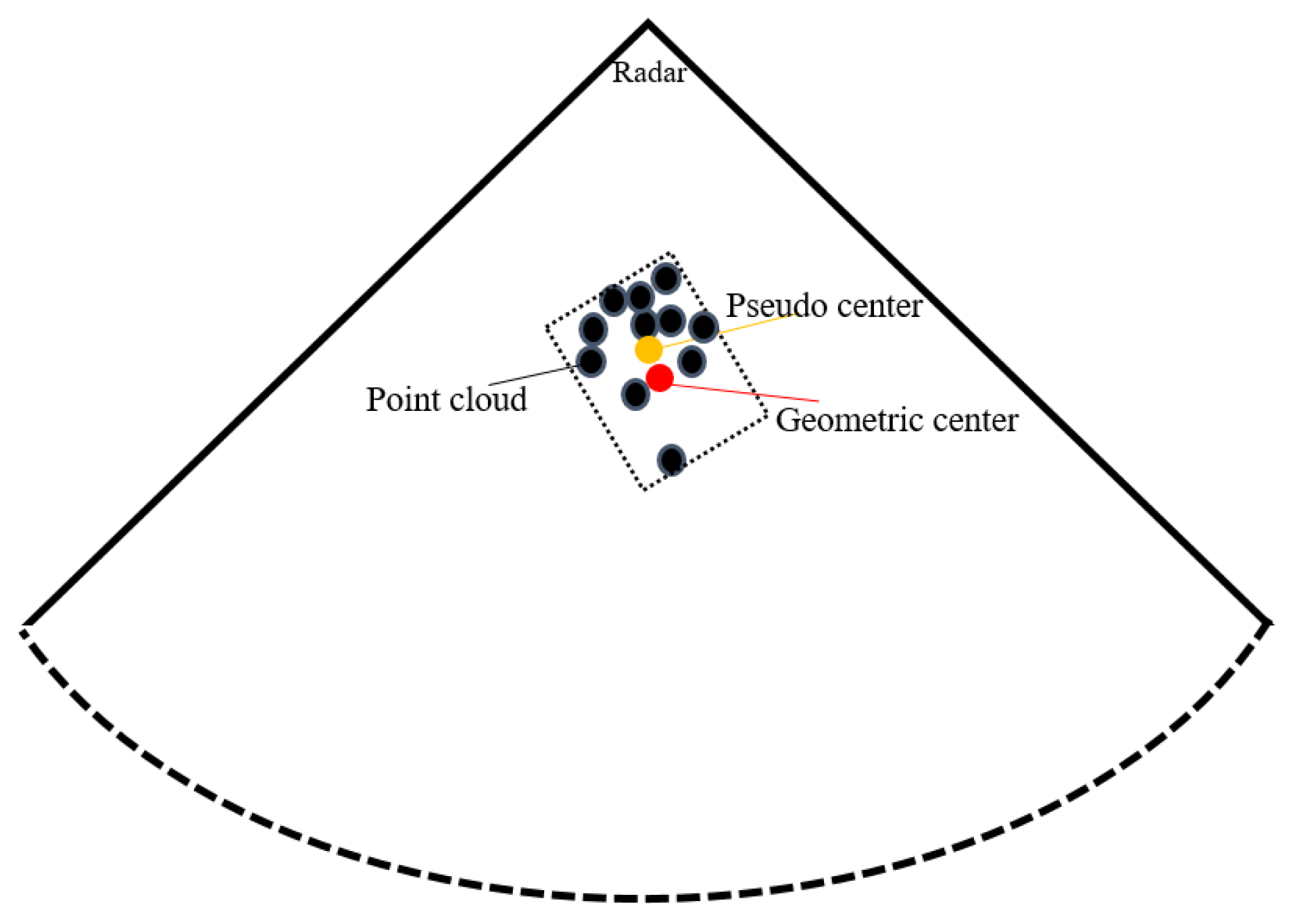
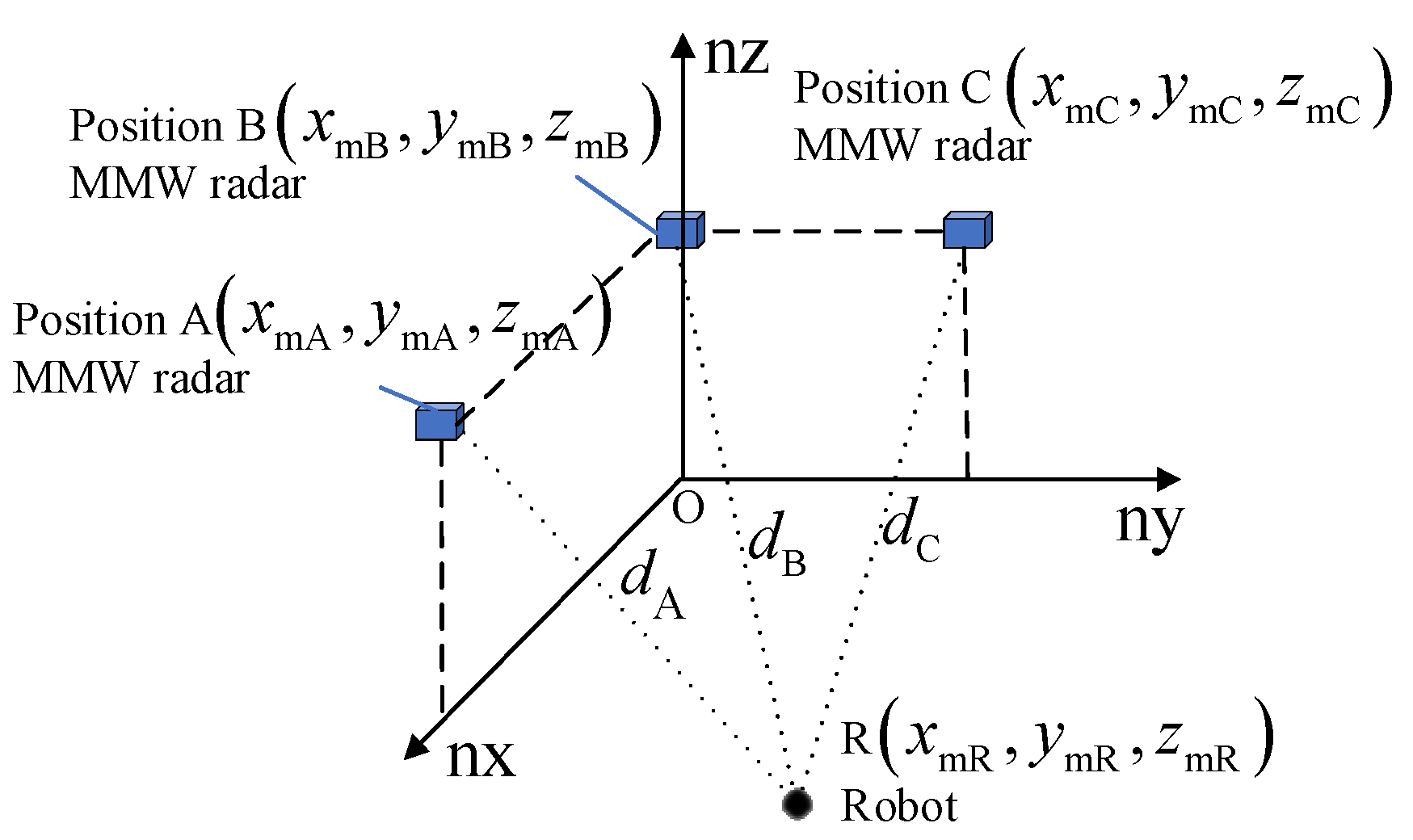
2.1. MMW Navigation System

The basic principle of the MMW navigation system is based on the distance between the MMW radars and the robot, obtained using triangulation to calculate and control the position of the robot.

After normalizing the signal amplitude of a millimeter wave radar, the transmitted signal and the echo signal reflected back at the distance d are:

\{\begin{matrix} X_{trans} (t) = \cos (2 π f_{0} t + π μ t^{2}) \\ X_{rec} (t) = \cos [2 π f_{0} (t - Δ τ) + π μ {(t - Δ τ)}^{2}] \end{matrix}

(1)

In the formula,

f_{0}

is the starting frequency of millimeter wave radar frequency modulated continuous wave.

μ

is the modulation slope.

Δ t = 2 d / c

is the time delay.

c

is the speed of light.

d

is the distance between the measured object and the MMW radar. The complex signal

X_{m i x} (t)

obtained by mixing the received signal with the transmitted signal is:

\begin{array}{l} X_{mix} (t) = \exp [\frac{j (4 π μ d t)}{c} + \\ j (\frac{2 d}{c}) (2 π f_{0} - \frac{2 π μ d}{c})] \end{array}

(2)

The instantaneous frequency

f_{i}

of the signal is:

f_{i} = \frac{1}{2 π} \frac{d [\frac{4 π μ d t}{c} + \frac{2 d}{c} (2 π f_{0} - \frac{2 π μ d}{c})]}{d t} = \frac{2 μ d}{c}

(3)

According to Formula (3), the instantaneous frequency is proportional to the distance. By sampling the echo signal and using fast Fourier transform processing, the target distance corresponding to the peak position of

f_{i}

is:

d = f_{i} c T_{m} / 2 Δ F

(4)

where

Δ F

is the bandwidth of the modulated signal, and

T_{m}

is the modulation period.

For the

i

-th signal source received by the 1st array element of the radar M array elements, it can be obtained through Nyquist sampling:

\begin{array}{l} \begin{matrix} X_{l} (t) = \sum_{i = 1}^{N} A_{T} A_{R} S_{i} (t - τ_{l i}) + N_{l} (t) \end{matrix} \\ l = 1, 2, \dots, M \begin{matrix} i = 1, 2, \dots, N \end{matrix} \end{array}

(5)

Where

X_{l} (t)

is the ADC sampling frequency of the

l

-th signal of

Χ (t)

A_{T} A_{R}

is the gain of the first array element to the

i

-th signal, and

N_{l} (t)

is the additive noise of the first array element.

S_{i} (t - τ_{l i})

refers to the signal from the

i

-th signal to the lth array element under the delay of

τ_{l i}

. The expression of delay is:

τ_{k i} = (d_{k} \sin θ_{i}) / c \begin{matrix} k = 1, 2, \dots, l, M \end{matrix}

(6)

Where

d_{k}

is the position of the array element, and

θ_{i}

is the azimuth of a signal source and the radar. According to Formulas (3) and (4), the

\sum_{i = 1}^{N} A_{T} A_{R} S_{i} (t - τ_{k i})

of M array elements is simplified as follows:

\sum_{i = 1}^{N} A_{T} A_{R} S_{i} (t - τ_{k i}) \approx \sum_{i = 1}^{N} A_{T} A_{R} S_{i} (t) \exp (- j ω_{0} τ_{k i})

(7)

Where

ω_{0}

is the frequency of the received signal. Let the

\exp (- j ω_{0} τ_{k i})

of Formula (5) be transformed to obtain:

\begin{array}{l} α (θ_{i}) = \exp (- j ω_{0} τ_{M i}) = \\ \exp (- j ω_{0} x_{k} \sin θ_{i} / c) \end{array}

(8)

Utilize Capon algorithm:

P (θ) = 1 / [α^{H} (θ) R^{- 1} α (θ)]

(9)

Where

R = Χ (t) \cdot Χ^{H} (t) / L

, and L is the number of snapshots.

P (θ)

is the set spectral range, which is from positive 90 degrees to negative 90 degrees. Search the spectral peak of one dimension of

P (θ)

, and the abscissa corresponding to the peak is the azimuth

θ

, so as to obtain the azimuth of the signal.

Based on the expression to measure the quality of radar received signal:

SNR = \frac{σ P_{t} G_{TX} G_{RX} λ^{2} T_{meas}}{{(4 π)}^{3} d^{4} K_{m} T F}

(10)

Where SNR is the signal-to-noise ratio.

σ

is the scattering cross-section.

P_{t}

is the radar output power.

G_{TX}

and

G_{RX}

are the antenna receiving and transmitting power.

λ

is the signal wavelength.

T_{meas}

is the pulse modulation time.

d

is the distance between the radar and the target.

T

is the temperature.

F

is the radar internal noise coefficient, and

K_{m}

is the antenna noise coefficient.

According to Formula (10), the signal-to-noise ratio of the processed signal is inversely proportional to the fourth power of the distance and is proportional to the radar cross-section. Therefore, the number of target point clouds will be unevenly distributed due to the distance between the reflector and the radar. If the mean value of these point clouds is directly processed, the geometric center distance between the radar and the target will be offset, as shown by the yellow dots in Figure 1:

For this kind of situation, this paper proposes an approximate center method under a sparse point cloud. The set of radial distance between the point cloud and radar is:

d = [d_{1}, d_{2}, \dots, d_{M}]

(11)

The set of angle between the point cloud and radar is:

θ = [θ_{1}, θ_{2}, \dots, θ_{M}]

(12)

The set of point cloud between radar and robot is:

p (d, θ) = [p_{1} (d_{1}, θ_{1}), p_{2} (d_{2}, θ_{2}), \dots, p_{M} (d_{M}, θ_{M})]

(13)

Assume that the maximum angle range of the radar is

ϖ

,and the maximum detection range is

l

, and divide Figure 1:

\{\begin{cases} ϖ_{m - 1} - ϖ_{1} = (m - 1) Δ ϖ \\ l_{e - 1} - l_{1} = (e - 1) Δ l \end{cases}

(14)

Where

ϖ_{1}

is the starting angle scale value.

ϖ_{M - 1}

is the ending angle scale value.

m - 1

is the division multiple, and

Δ ϖ

is the angle division interval.

l_{1}

is the starting distance scale.

l_{M - 1}

is the ending distance scale value.

Δ l

is the distance division interval, and

e - 1

is the division multiple. Its composition range is:

K_{m e} = (m - 1) \times (e - 1)

(15)

According to the distribution of in, it can be divided into G parts, and its expression is:

\{\begin{matrix} G (M_{m}, D_{d}) = [G_{1} (d, θ), G_{2} (d, θ), \dots, G_{m} (d, θ)] \\ G_{1} (d, θ) \cup G_{2} (d, θ) \cup \dots \cup G_{m} (d, θ) = p (d, θ) \\ G (M_{m}, D_{d}) \subseteq K_{m e} (m, e) \end{matrix}

(16)

Where

G_{1} (d, θ), G_{2} (d, θ), \dots, G_{m} (d, θ)

represents all subsets in the

G (M_{m}, D_{d})

region, and the set elements of Formula 10 are distributed in the G region. After calculating the mean value of each subset of the G region, we can get:

d_{p} = \frac{E [G_{1} (d, θ)] + E [G_{2} (d, θ)] + \dots + E [G_{m} (d, θ)]}{G}

(17)

According to Formula 17, the approximate geometric center distance between the radar and the target can be obtained.

Then, three radars are arranged to form the scheme of triangulation, as shown in Figure 2.

As shown in the Figure 2, three radars are placed at points A, B, and C in the navigation coordinate system, and their coordinates are

(x_{mA}, y_{mA}, z_{mA})

(x_{mB}, y_{mB}, z_{mB})

(x_{mC}, y_{mC}, z_{mC})

, respectively. The distances from points A, B, and C to the robot are

d_{A}

d_{B}

, and

d_{C}

respectively. R

(x_{mR}, y_{mR}, z_{mR})

based on the basic principles of triangulation can be obtained.

2.2. Strapdown Inertial Navigation System

In the strapdown INS, the gyroscope and accelerometer are fixed on the robot, with their axes consistent with the carrier body coordinate system, the x-axis is aligned with the direction of the robot’s movement; the direction of the z-axis is perpendicular to the ground, and the direction of the y-axis is determined by the right-hand rule. Using the gyroscope, the attitude matrix of the robot is obtained by measuring the angular motion information. The acceleration of the robot in the navigation coordin, ate system can be expressed as:

[\begin{matrix} a_{nx} \\ a_{ny} \\ a_{nz} \end{matrix}] = [\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix}] [\begin{matrix} a_{bx} \\ a_{by} \\ a_{bz} \end{matrix}] - [\begin{matrix} 0 \\ 0 \\ g \end{matrix}]

(18)

Where

C_{11} = \cos β \cos ψ

C_{12} = \cos β \sin ψ

C_{13} = - \sin β

C_{21} = \sin γ \sin β \cos ψ - \cos γ \sin ψ

C_{22} = \sin γ \sin β \cos ψ + \cos γ \cos ψ

C_{23} = \sin γ \cos β

C_{31} = \cos γ \sin β \cos ψ + \sin γ \sin ψ

C_{32} = \cos γ \sin β \sin ψ - \sin γ \cos ψ

C_{33} = \cos γ \cos β

, g is the gravity acceleration,

γ

β

, and

ψ

are the rotation angles of the robot along the x, y, and z axes, respectively.

{[\begin{matrix} a_{bx} & a_{by} & a_{bz} \end{matrix}]}^{T}

is the acceleration of the robot in the carrier body coordinate system, while

{[\begin{matrix} a_{nx} & a_{ny} & a_{nz} \end{matrix}]}^{T}

is the acceleration of the robot in the navigation coordinate system. To combine the two navigation systems, the inertial navigation coordinate system is consistent with the MMW navigation coordinate system.

The velocity of the robot can be obtained by integrating

{[\begin{matrix} a_{nx} & a_{ny} & a_{nz} \end{matrix}]}^{T}

, and the position of the robot can be obtained by integrating the velocity. Due to the noise in

{[\begin{matrix} a_{bx} & a_{by} & a_{bz} \end{matrix}]}^{T}

, the velocity and position data of the robot are reliable for a short time, and the errors in the data are divergent with increasing time.

3. Fusion Navigation System

An MMW navigation system can work in smog and dust environments and has the characteristics of nondivergence of positioning errors. A strapdown INS has good short-term accuracy, can be integrated with the MMW navigation system to improve the positioning accuracy of the robot, and can provide localization data for the system in a short time when the MMW signal is blocked.

To realize the fusion of the MMW and the INS, it is necessary to study the state equation and measurement equation, thereby constructing a mathematical model of the fusion system.

3.1. State Equation

In the strapdown INS,

T

is the sampling time,

Δ v

is the velocity variation, which is detected using accelerometer.

indicates the difference in velocity at the (k−1)-th and k-th moments. From k-1 to k, the average value of acceleration

{\overline{a}}_{n (k - 1)}

in navigation coordinate is:

{\overline{a}}_{n (k - 1)} = \frac{Δ v_{k}}{T}

(19)

{\overline{a}}_{nx (k - 1)}

{\overline{a}}_{ny (k - 1)}

and

{\overline{a}}_{nz (k - 1)}

represent the average acceleration of the robot along the

n_{x}

n_{y}

and axes respectively. The position of the robot can be expressed as:

\{\begin{matrix} x_{R (k)} = x_{R (k - 1)} + \frac{1}{2} T^{2} {\overline{a}}_{nx (k - 1)} \\ y_{R (k)} = y_{R (k - 1)} + \frac{1}{2} T^{2} {\overline{a}}_{ny (k - 1)} \\ z_{R (k)} = z_{R (k - 1)} + \frac{1}{2} T^{2} {\overline{a}}_{nz (k - 1)} \end{matrix}

(20)

Where

x_{R (k)}

y_{R (k)}

and

z_{R (k)}

represent the position of the robot along the

n_{x}

n_{y}

and

n_{z}

axes at time k.

x_{R (k - 1)}

y_{R (k - 1)}

and

z_{R (k - 1)}

represent the position of the robot along the

n_{x}

n_{y}

and

n_{z}

axes at k-1 time. These average accelerations are consisted of true values and noises. Let

{\overline{a}}_{nx (k - 1)}

{\overline{a}}_{ny (k - 1)}

and

{\overline{a}}_{nz (k - 1)}

represent the true values of the average accelerations, Equation (18) can be expressed as:

[\begin{matrix} x_{R (k)} \\ y_{R (k)} \\ z_{R (k)} \end{matrix}] = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x_{R (k - 1)} \\ y_{R (k - 1)} \\ z_{R (k - 1)} \end{matrix}] + [\begin{matrix} \frac{T^{2}}{2} & 0 & 0 \\ 0 & \frac{T^{2}}{2} & 0 \\ 0 & 0 & \frac{T^{2}}{2} \end{matrix}] [\begin{matrix} {\overline{a}}^{'}_{nx (k - 1)} \\ {\overline{a}}^{'}_{ny (k - 1)} \\ {\overline{a}}^{'}_{nz (k - 1)} \end{matrix}] + [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} w_{x (k - 1)} \\ w_{y (k - 1)} \\ w_{z (k - 1)} \end{matrix}]

(21)

Where

w_{x (k - 1)}

w_{y (k - 1)}

and

w_{z (k - 1)}

represent the noise of the accelerometer along the

n_{x}

n_{y}

and

n_{z}

axes from k-1 to k.

In the navigation system, the position coordinate of the robot is an important state quantity.

R_{k} = {[\begin{matrix} x_{R (k)} & y_{R (k)} & z_{R (k)} \end{matrix}]}^{T}

is a state quantity at k, and

R_{k - 1} = {[\begin{matrix} x_{R (k - 1)} & y_{R (k - 1)} & z_{R (k - 1)} \end{matrix}]}^{T}

is a state quantity at k−1. The discrete-time state equation is shown in the following equation:

R_{k} = Φ R_{k - 1} + Λ {\overline{V}}_{k - 1} + ϒ w_{k - 1}

(22)

Where

Φ = diag [\begin{matrix} 1 & 1 & 1 \end{matrix}]

is the state transition matrix.

Λ = d i a g [\begin{matrix} Δ T & Δ T & Δ T \end{matrix}]

is the control transition matrix.

ϒ = diag [\begin{matrix} 1 & 1 & 1 \end{matrix}]

is the noise coefficient matrix.

w_{k - 1} = {[\begin{matrix} w_{x (k - 1)} & w_{y (k - 1)} & w_{z (k - 1)} \end{matrix}]}^{T}

is the state noise.

3.2. Measurement Equation

In addition, the position of the robot is obtained by the MMW navigation system. Because the navigation system consists of noise interference the position of the robot at k can be given as follows:

[\begin{matrix} x_{mR (k)} \\ y_{mR (k)} \\ z_{mR (k)} \end{matrix}] = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x_{R (k)} \\ y_{R (k)} \\ z_{R (k)} \end{matrix}] + [\begin{matrix} υ_{x (k)} \\ υ_{y (k)} \\ υ_{z (k)} \end{matrix}]

(23)

Where

{[\begin{matrix} x_{mR (k)} & y_{mR (k)} & z_{mR (k)} \end{matrix}]}^{T}

is the only observed quantity. Therefore, the measurement equation of the system is:

Z_{k} = H R_{k} + υ_{k}

(24)

Where

H = diag [\begin{matrix} 1 & 1 & 1 \end{matrix}]

is the measurement matrix, and

υ_{k} = {[\begin{matrix} υ_{x (k)} & υ_{y (k)} & υ_{z (k)} \end{matrix}]}^{T}

is the measurement noise.

3.3. Noise

In Equation (20),

w_{k - 1}

is related to the noise of the accelerometer. Without considering environmental vibration and large temperature changes, the noise of the accelerometer can be expressed as [27]:

{δ a = Δ}_{a} + C_{a} + η_{a}

(25)

Where

Δ_{a}

represents the zero drift of the accelerometer,

C_{a}

represents the fixed error caused by the installation of the accelerometer and other factors, and represents the measurement noise of the accelerometer, which is Gaussian white noise. The compensation method is usually used to approximately eliminate

Δ_{a}

and

C_{a}

In this case, the noise of the accelerometer is mainly random white noise and can be derived as follows:

a_{n} \approx η_{a}

(26)

Therefore,

w_{k - 1}

in Equation (20) is an approximate white noise variable, and its mathematical expectation is as follows:

E (w_{x (k - 1)}) = E (w_{x (k - 1)}) = E (w_{x (k - 1)}) \approx 0

(27)

In Equation (25),

E

represents the mathematical expectation of random variables; then the variance matrix

w_{k - 1}

Q_{k - 1}

is:

Q_{k - 1} = [\begin{matrix} D (w_{x (k - 1)}) & 0 & 0 \\ 0 & D (w_{y (k - 1)}) & 0 \\ 0 & 0 & D (w_{z (k - 1)}) \end{matrix}]

(28)

where represents the variance of random variables.

In Equation (22),

υ_{k}

is the measurement error of the MMW navigation system. It has the characteristics of Gaussian white noise [16], and its mathematical expectation is as follows:

E (υ_{x (k)}) = E (υ_{y (k)}) = E (υ_{z (k)}) = 0

(29)

The measurement noise covariance matrix

G_{k}

of the system is as foliows:

G_{k} = [\begin{matrix} D (υ_{x (k)}) & 0 & 0 \\ 0 & D (υ_{y (k)}) & 0 \\ 0 & 0 & D (υ_{z (k)}) \end{matrix}]

(30)

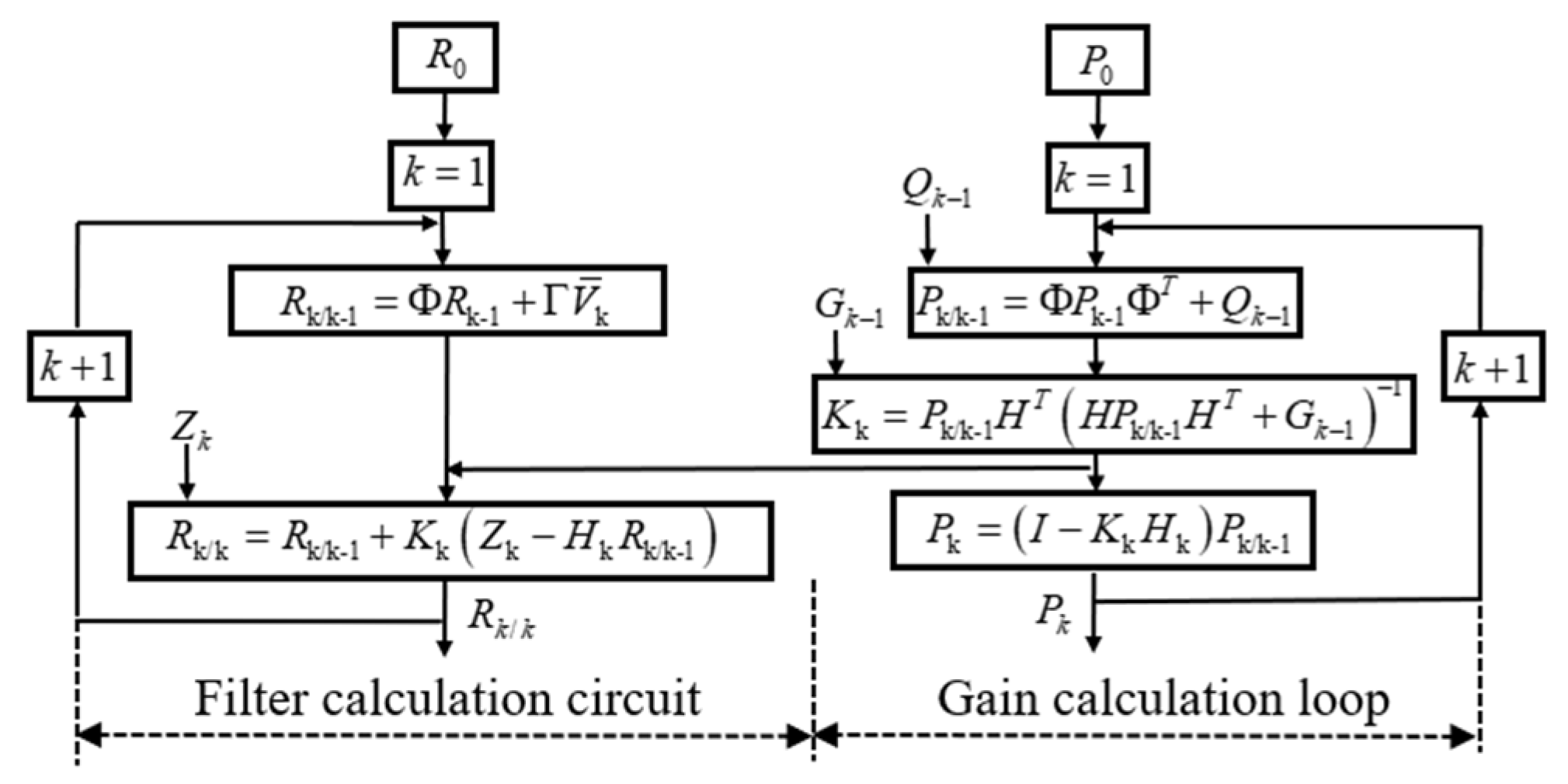
3.4. Filtering Algorithm

The measurement equation is established according to the millimeter wave navigation system, the state equation is established according to the motion state of the system, and the position information of the robot is fused using the Kalman filter algorithm. The algorithm and information interaction are shown in Figure 3:

Algorithm Integrated navigation using Kalman filter approach

1: At k, the predicted position coordinate

R_{k / k - 1}

of the robot can be deduced as follows:

R_{k / k - 1} = Φ R_{k - 1} + Γ {\overline{V}}_{k}

2: The mean square error of the estimate is:

P_{k / k - 1} = Φ P_{k - 1} Φ^{T} + Q

P_{k - 1}

is the best estimation error covariance at k−1.

3: The Kalman filter gain can be obtained:

K_{k} = P_{k / k - 1} H^{T} {(H P_{k / k - 1} H^{T} + G)}^{- 1}

4: The optimal estimation position coordinate of the robot can be obtained as follows:

R_{k / k} = R_{k / k - 1} + K_{k} (Z_{k} - H_{k} R_{k / k - 1})

5: The mean square error between the optimal estimated position coordinate and the true position coordinate is given by

P_{k} = (I - K_{k} H_{k}) P_{k / k - 1}

4. Experiment and Analysis

To verify the effectiveness of the proposed fusion navigation system based on MMW radar and the INS, an experimental device of the system is designed.

4.1. Experimental Equipment

Experimental setup of the proposed fusion navigation system is shown in Figure 4.

In Figure 4, the navigation coordinate system

O_{n} X_{n} Y_{n} Z_{n}

is constructed on a 4 m × 4 m green carpet. The X, Y, and Z axes are orthogonal to each other at point O. Three MMV radars A, B, and C are placed on three tripods, and their position coordinates are

(- 0.5, 3, 1)

(2, - 1, 1)

, and

(2.5, 5.5, 1)

respectively. Three high-speed data differential signal lines with USB 3.0 are connected between the radars and a server, and communication between the server and the robot is achieved by a wireless module. The motion controller of the robot is an STM32 development board.

In the experimental scheme, IWR1642 radars (Texas Instruments, the United States) are used in the MMW navigation system; each radar has a working frequency band of 77–81 GHz, as shown in Figure 5.

An MTi-30 strapdown inertial sensor (Xsens, the Netherlands) is used for the INS, as shown in Figure 6.

In the design scheme, transmission and processing of information are as shown in Figure 7.

According to the figure, the robot position is output by the MMW radar and the INS. However, the output signal contains noise; therefore, the Kalman filter algorithm is used in the fusion navigation system to estimate the optimal position of the robot. Then, this information is transmitted to the motion controller. Closed-loop control is performed in the controller according to current and the target position coordinate.

4.2. Experimental Parameters

Parameters of the MMW navigation system

The elevation angle of the radar is set to 10°.The radar’s minimum signal-to-noise ratio threshold is set to 45. The radar communication baud rate is set to 921600. The range of the radar’s horizontal opening angle is −60° to 60°, and the range of the pitching angle is −19° to 19°. The noise covariance matrix of the MMW navigation system is:

G_{k} = diag [\begin{matrix} {(0.11)}^{2} & {(0.11)}^{2} & 0 \end{matrix}]

(31)

Parameters of the INS

The standard full range of the gyroscope is 450°/s, and the bias stability in operation is 10°/h. The accelerometer is 200 m2/s, and the bias stability in operation is 15 µg. The sampling frequency of MTi-30 is 50 Hz. MTi-30 outputs the attitude angle and velocity variation. In the experiment, the zero drift of the MTi-30 accelerometer was collected by making MTi-30 static for 10 min; was then compensated. Based on the zero bias stability characteristics of gyroscopes and accelerometers, an INS error model is established to obtain the value of Q.

Parameters of the fusion navigation system

Control period of the system: The two systems are fused per 0.2 s. The initial position

R_{0} = {[\begin{matrix} 0 & 0 & 0 \end{matrix}]}^{T}

The initial covariance matrix

P_{0} = {[0]}_{3 \times 3}

Parameters of robot motion control

The length, width, and height of the four-wheel driving mobile robot are 45, 42, and 48 cm, respectively. Total mass is approximately 5.8 kg, and the maximum movement speed is approximately 1.2 m/s. The four motors are the MD36N planetary gear motor. The core control chip of the robot is STM32F103RCT6. The software platform of the robot is the Free-RTOS operating system.

Parameters of robot motion control

The communication baud rate of the wireless module is 921600. The communication protocol of the wireless module is the UDP protocol.

Environment parameters

Smog is created using 20 cigarette cakes; a cigarette cake is about 6.8 cm in diameter, 1 cm in thickness, and 58 g in weight; it is mainly composed of ammonium chloride, flour, and rosin. The indoor light is insufficient, as shown in Figure 8.

4.3. Experimental Results and Analysis

In order to verify the effectiveness of the proposed algorithm, a test experiment of the approximate center method based on sparse point clouds was conducted first. In the experiment, the environment first uses a radar to measure the geometric center of the robot, and compares the two methods. The two methods are direct mean processing and approximate center method for sparse point clouds. The geometric center of the robot is measured with a 1mm accuracy scale and calculated using mathematical formulas. The experimental results are shown in Figure 9:

The blue dots in the image are the point clouds projected by the robot under the millimeter wave coordinate system after being scanned by the millimeter wave radar. The red dot is the reference geometric center point of the robot. The yellow point is the geometric center point obtained by directly processing the mean value of the blue point, and the purple point is the approximate geometric center point of the robot obtained by using the approximate center method of sparse point clouds.

According to Figure 9, it can be intuitively found that the center method based on sparse point clouds is closer to the geometric center of the robot than the direct mean method.

According to the above experimental parameters and methods, experiments were conducted on the fusion navigation of the robot based on the MMW radar and inertial navigation.

Straight motion paths

The initial coordinates of the robot were (0,1,0) and (0,0,0) for straight navigation paths 1 and 2, which satisfy the expressions

y = 0.5 x + 1

and

y = 2 x

respectively. The target position coordinates were set to (4,3,0) and (2,4,0), respectively. The experimental results are shown in Figure 10 and Figure 11, respectively.

In Figure 10 and Figure 11, the solid line represents the theoretical trajectory of the robot. The long-dashed line represents the actual trajectory of the robot based on the MMW navigation system. The short-dashed line represents the actual trajectory of the robot based on the fusion navigation system. To further study the fusion navigation system error of the robot in the linear navigation path, additional 50 sets of experiments were conducted for each path. The navigation error is defined as the difference between the coordinates of the actual point reached by the robot and those of the target point. The error data are shown in Figure 12 and Figure 13, respectively, for navigation paths 1 and 2.

For the results shown in Figure 10 and Figure 11, the gain matrix and covariance matrix of the system are shown in Figure 14 and Figure 15, respectively.

According to Figure 14 and Figure 15, the initial system gain is 0, and diagonal value of the initial covariance matrix is 0. When the gain reaches 0.778, the diagonal value of the covariance matrix is 0.009. After eight sampling iterations, the system gain is 0.631, the diagonal value of the covariance matrix is 0.006, and the system tends to be stable.

To accurately obtain the error value of the fusion navigation system, 100 sets of experiments were conducted, and the average localization error was obtained. This error is compared with the average localization error of 100 experimental errors of the MMW navigation system, as shown in Table 1.

According to Table 1, the fusion localization error is approximately 0.083 m, which is lower than the error of the MMW navigation system.

Curved motion paths

The initial coordinates of the robot were (0.5,0,0) and (0,0,0), for the curved navigation paths 1 and 2, which satisfy the expressions

y = 0.5 x^{2} + 0.9 x + 0.5

and

y = 0.5 x^{2}

, respectively. The target position coordinates were set to (3.4,3.22,0) and (2.8,3.92,0), respectively. The experimental results are shown in Figure 16 and Figure 17, respectively.

In Figure 16 and Figure 17, the solid line represents a theoretical trajectory of the robot. The long-dashed line indicates the actual trajectory of the robot using the MMW navigation system. The short-dashed line indicates the actual trajectory of the robot using the fusion navigation system. To further study the fusion navigation system error of the robot in the curved navigation path, additional 50 sets of experiments were conducted for each path, and the error data are shown in Figure 18 and Figure 19, respectively.

For the experimental results shown in Figure 16 and Figure 17, the gain matrix and covariance matrix of the system are shown in Figure 20 and Figure 21, respectively.

According to Figure 20 and Figure 21, the initial value of the system gain is 0, and the diagonal value of initial covariance matrix is 0; when the gain reaches 0.778, the diagonal value of the covariance matrix is 0.009. After 8 sampling periods, the system gain is 0.631, the diagonal value of the covariance matrix is 0.006, and the system tends to be stable.

To accurately obtain the error value of the fusion navigation system, 100 sets of experiments were conducted, and average the localization error is obtained. This error is compared with the average localization error of 100 experimental errors of the MMW navigation system, as shown in Table 2.

According to Table 2, the fusion localization error is approximately 0.086 m, which is lower than the error of the MMW navigation system.

In the initial stage of the fusion navigation system, the trajectory of the robot is close to that of the MMW navigation system. With the convergence of the gain value of the fusion navigation algorithm, the trajectory of the robot becomes closer to the theoretical trajectory. When the number of iterations of the fusion algorithm is more than eight, the error decreases, resulting in more stable operation of the robot, than that with the MMW navigation system. Finally, the robot reaches the terminal position according to the set navigation path. The average error accuracy of fusion navigation system after a number of experiments is approximately 0.08 m. Therefore, the fusion navigation system based on the MMW radar and INS has smaller error and higher precision than the MMW navigation system.

5. Conclusions

To achieve autonomous operation of a robot in smog and dust environments and to improve its navigation accuracy, a fusion navigation system based on the MMW radar and INS was proposed. Three MMW radars were placed in the motion space of the robot, and the triangulation method was used to realize the navigation of the robot in the smog and dust environment. The experimental results confirmed that the navigation error was close to the error of navigation system with only the MMW radar in the initial stage. After eight iterations of the filtering algorithm, the gain matrix converged gradually and the error of the fusion navigation system decreased, resulting in a stably operating robot. The localization error of the fusion navigation system was approximately 0.08 m, which confirmed better navigation accuracy than the navigation system with only MMW. The difference between this method and satellite navigation is that MMW uses signal frequency processing to calculate the distance between the radar and the robot, which avoids the need to consider the time difference between the transmitted signal and the received signal. Further, when more MMW radar devices are arranged, the robot can operate autonomously in a larger space.

Acknowledgments

The authors gratefully acknowledge the contribution of Key Research and Development Project of Anhui Province [202004a0502001]; The work is also supported by Collaborative Innovation Projects of Anhui Province [GXXT -2023- 020] and [GXXT -2023- 076], Key Research and Development Project of Wuhu [2023yf083].

References

C. G. Hobart et al., “Achieving Versatile Energy Efficiency With the WANDERER Biped Robot,” IEEE Trans. Robot. 36(3), 959-966. [CrossRef]
Y. Chang et al., “LAMP 2.0: A Robust Multi-Robot SLAM System for Operation in Challenging Large-Scale Underground Environments,” IEEE Robot. Autom. Lett. 7(4), 9175-9182. [CrossRef]
Z. Zhou et al., “Navigating Robots in Dynamic Environment With Deep Reinforcement Learning,” IEEE T INTELL TRANSP. 23(12), 25201-25211.
Hu Dai, Rui Zheng, Xiaolu Ma, et al. Adaptive Tracking Strategy for the Positioning of Millimeter-wave Radar Security Robots. IEEE Sensors Journal, 2024, 24(13): 21321-21330 . [CrossRef]
Q. Tao, Z. Hu, G. Lai, et al. SMLAD: Simultaneous Matching, Localization, and Detection for Intelligent Vehicle From LiDAR Map With Semantic Likelihood Model[J]. IEEE Transactions on Vehicular Technology, 2024, 73(2): 1857-1867.
F. Penizzotto, E. Slawinski and V. Mut, “Laser Radar Based Autonomous Mobile Robot Guidance System for Olive Groves Navigation,” IEEE Lat. AM. Trans. 6(1), 191–198. [CrossRef]
H. Bavle, J. L. Sanchez-Lopez, M. Shaheer, J. Civera and H. Voos, “Situational Graphs for Robot Navigation in Structured Indoor Environments,” IEEE Robotics and Automation Letters. 7(4), 9107-9114. [CrossRef]
Q. Zou, Q. Sun, L. Chen, B. Nie and Q. Li, “A Comparative Analysis of LiDAR SLAM-Based Indoor Navigation for Autonomous Vehicles,” IEEE T INTELL TRANSP. 23(7), 6907-6921. [CrossRef]
K. Lobos-Tsunekawa, F. Leiva and J. Ruiz-del-Solar, “Visual Navigation for Biped Humanoid Robots Using Deep Reinforcement Learning,” IEEE Robot. Autom. Lett. 3 (4), 3247–3254. [CrossRef]
S. P. P. da Silva, J. S. Almeida, E. F. Ohata, J. J. P. C. Rodrigues, V.H. C. de Albuquerque and P. P. Rebouças Filho, “Monocular Vision Aided Depth Map from RGB Images to Estimate of Localization and Support to Navigation of Mobile Robots,” IEEE Sensors J. 20(20), 12040-12048. [CrossRef]
M. Ijaz, Z. Ghassemlooy, J. Pesek, O. Fiser, H. Le Minh and E. Bentley, “Modeling of Fog and Smoke Attenuation in Free Space Optical Communications Link Under Controlled Laboratory Conditions,” Journal of Lightwave Technology. 31(11), 1720-1726. [CrossRef]
Valada, J. Vertens, A. Dhall and W. Burgard, “AdapNet: Adaptive semantic segmentation in adverse environmental conditions,” 2017 IEEE International Conference on Robotics and Automation (ICRA) (IEEE, 2017) pp. 4644-4651.
W. Li, R. Chen, Y. Wu et al. Indoor Positioning System Using a Single-Chip Millimeter Wave Radar[J]. IEEE Sensors Journal, 2023, 23(5): 5232-5242.
“Environmental sensing using millimeter wave sensor for extreme conditions,” 2015 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR) (IEEE, 2015) pp. 1-7.
X Zh Chen et al., “Development of millimeter wave radar imaging and SLAM in underground coal mine environment,” Journal of China Coal Society. 45(6), 2182-2192.
Rui Zheng, Fangdong Li, “Navigation system of security mobile robot based on FM millimeter wave,” Chinese Journal of Scientific Instrument. 42(3), 105-113.
J. Undug, M. P. Arabiran, J. R. Frades, J. Mazo and M. Teogangco, “Fire Locator, Detector and Extinguisher Robot with SMS Capability,” 2015 International Conference on Humanoid, Nanotechnology, Information Technology,Communication and Control, Environment and Management (HNICEM) (IEEE, 2015) pp. 1-5.
S. Zhang, W. Wang, N. Zhang and T. Jiang, “ LoRa Backscatter Assisted State Estimator for Micro Aerial Vehicles with Online Initialization,” IEEE Trans. Mobile Comput. 21(11), 4038-4050. [CrossRef]
Xiaochuan Zhao, Qingsheng Luo and Baoling Han, “Survey on robot multi-sensor information fusion technology,” 2008 7th World Congress on Intelligent Control and Automation (WCICA) (IEEE, 2008) pp. 5019-5023.
C. Li, S. Wang, Y. Zhuang and F. Yan, “Deep Sensor Fusion Between 2D Laser Scanner and IMU for Mobile Robot Localization,” IEEE Sensors J. 21(6), 8501-8509. [CrossRef]
W. Liu, S. Wu, Y. Wen and X. Wu, “Integrated Autonomous Relative Navigation Method Based on Vision and IMU Data Fusion,” IEEE Access 8, 51114-51128. [CrossRef]
E. I. Al Khatib, M. A. K. Jaradat and M. F. Abdel-Hafez, “Low-Cost Reduced Navigation System for Mobile Robot in Indoor/Outdoor Environments,” IEEE Access 8, 25014-25026. [CrossRef]
E. T. Benser, “Trends in inertial sensors and applications,” 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) (IEEE, 2015) pp. 1-4.
C. Doer and G. F. Trommer, “An EKF Based Approach to Radar Inertial Odometry,” 2020 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI) (IEEE, 2020) pp. 152-159.
Y. Almalioglu, M. Turan, C. X. Lu, N. Trigoni and A. Markham, “Milli-RIO: Ego-Motion Estimation With Low-Cost Millimetre-Wave Radar,” IEEE Sensors J. 21(3), 3314-3323. [CrossRef]
Lu C X, Saputra M R U, Zhao P, et al. “milliEgo: single-chip mmWave radar aided egomotion estimation via deep sensor fusion,” Proceedings of the 18th Conference on Embedded Networked Sensor Systems (CENSS) (2020) pp. 109-122.
H. Guang-Lin, T. Si-Qian, S. Qiang and Z. Pian, “Research on Calibration and Parameter Compensation of MEMS Inertial Sensors Based on Error Analysis,” IEEE Fifth Int. Symposium on Computational Intelligence and Design (ISCID) (IEEE, 2012) pp. 325-329.

Figure 1. Radar point cloud distribution (red is the geometric center of the target, and yellow is the point cloud information after mean processing).

Figure 2. Millimeter wave triangulation navigation scheme.

Figure 3. Integrated navigation filtering algorithm and block diagram.

Figure 4. Construction and experimental setup of the safety simulation robot platform based on the fusion of the millimeter wave radar and the inertial navigation system. The carrier in the figure is a four omnidirectional (mecanum) wheels robot.

Figure 5. Model of an IWR1642 millimeter wave radar along with the position of the chip and antenna.

Figure 6. Reference position of the MTi-30 inertial navigation system.

Figure 7. Information transmission and processing of the fusion navigation system.

Figure 8. Experimental scene with smoke.

Figure 9. Radar point cloud distribution and processed approximate geometric center point distribution. (a) Experimental result 1. (b) Experimental result 2.

Figure 10. Straight path 1.

Figure 11. Straight path 2.

Figure 12. Localization error of linear navigation path 1.

Figure 13. Localization error of linear navigation path 2.

Figure 14. Gain variation of linear navigation path 1.

Figure 15. Covariance matrix variation of linear navigation path 2.

Figure 16. Curved navigation path 1.

Figure 17. Curved navigation path 2.

Figure 18. localization error of curved path 1.

Figure 19. localization error of curved path 2.

Figure 20. Gain variation of curved path 1.

Figure 21. Covariance matrix variation of curved path 2.

Table 1. Error analysis of robot navigation in straight paths.

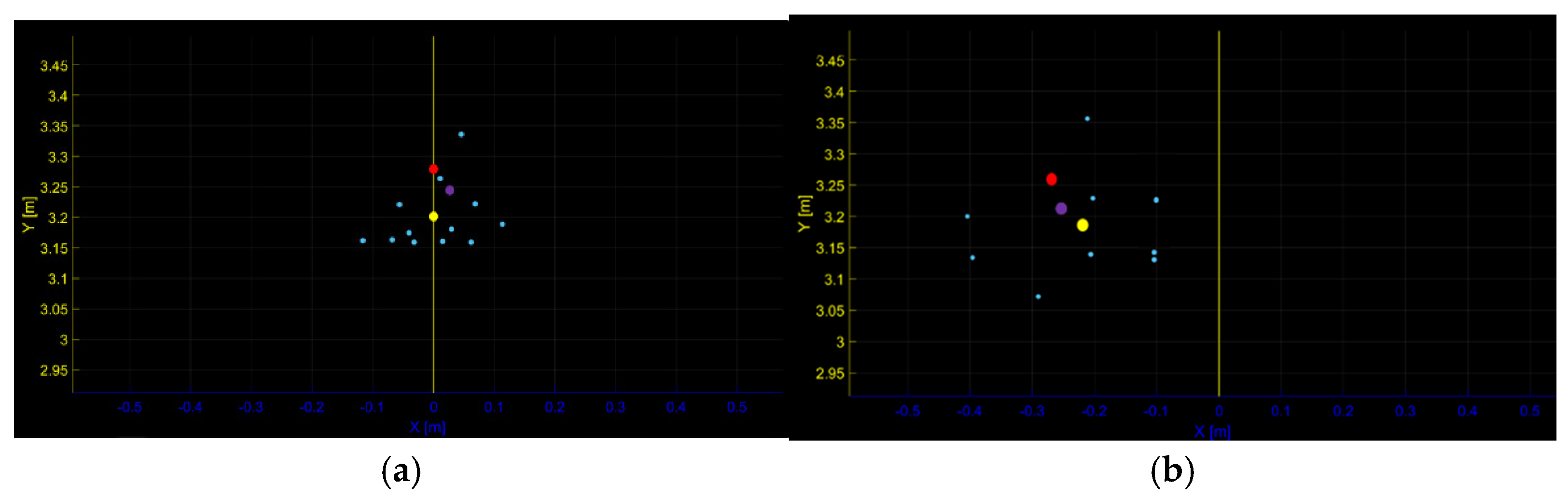
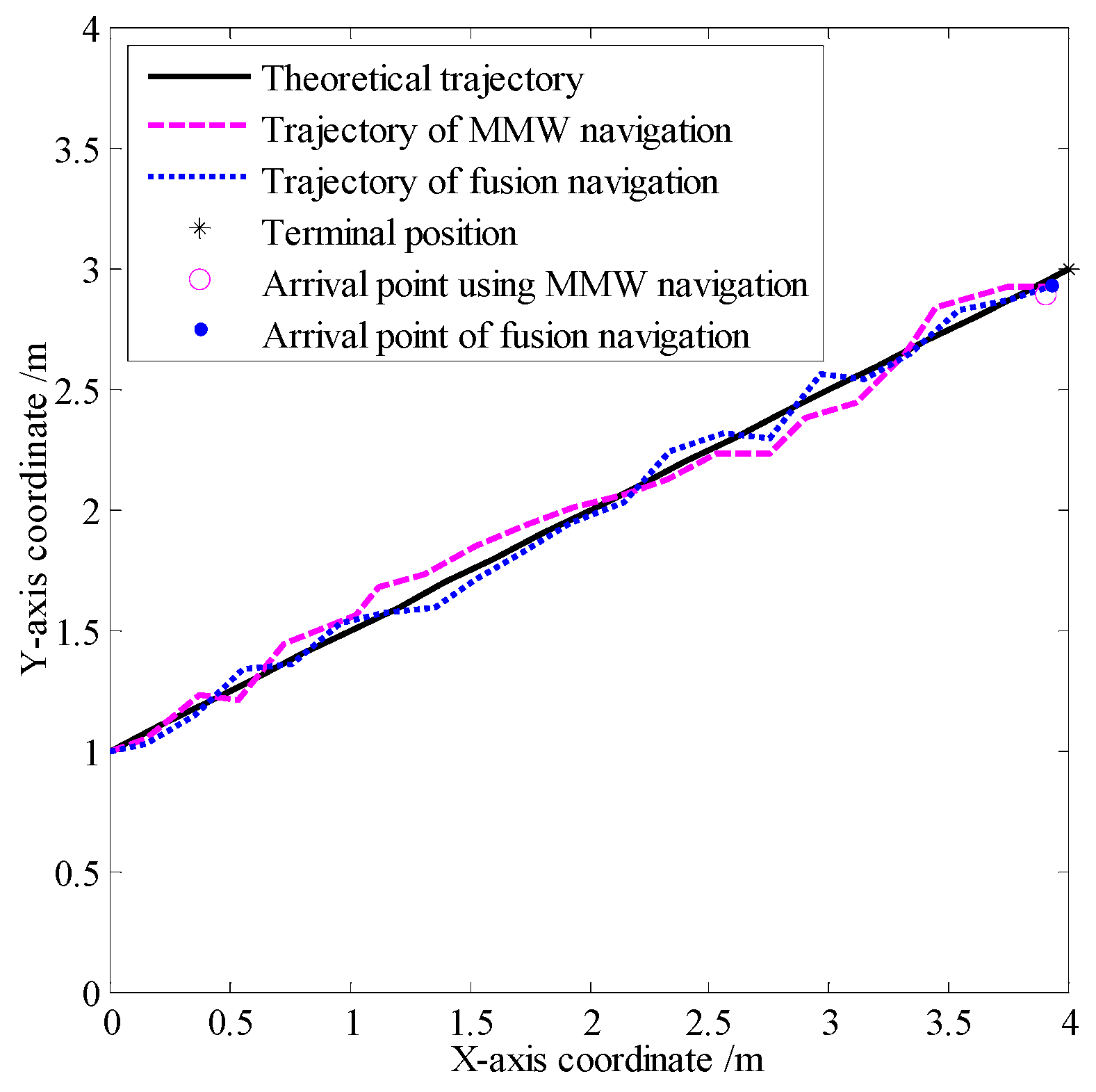
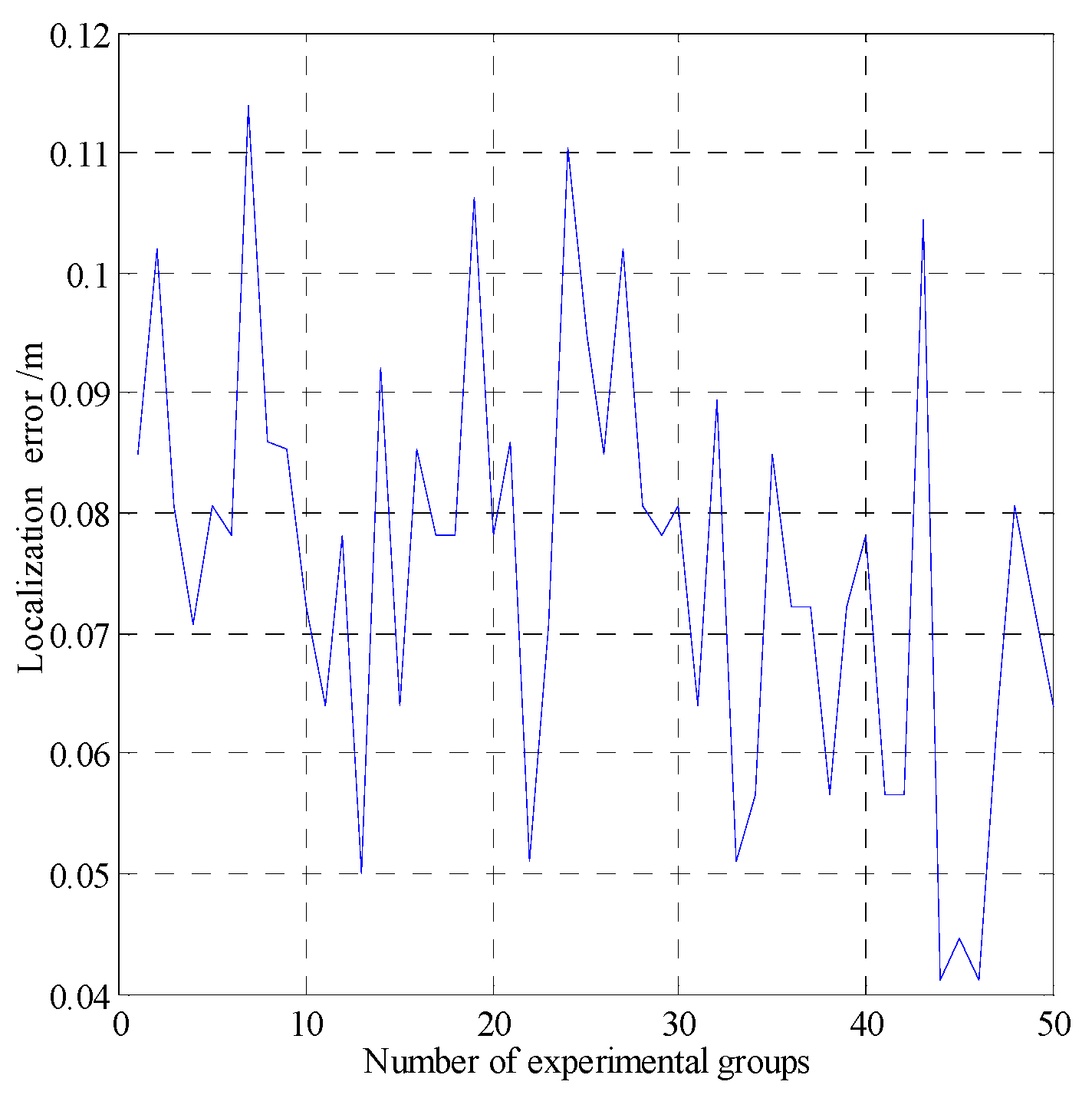
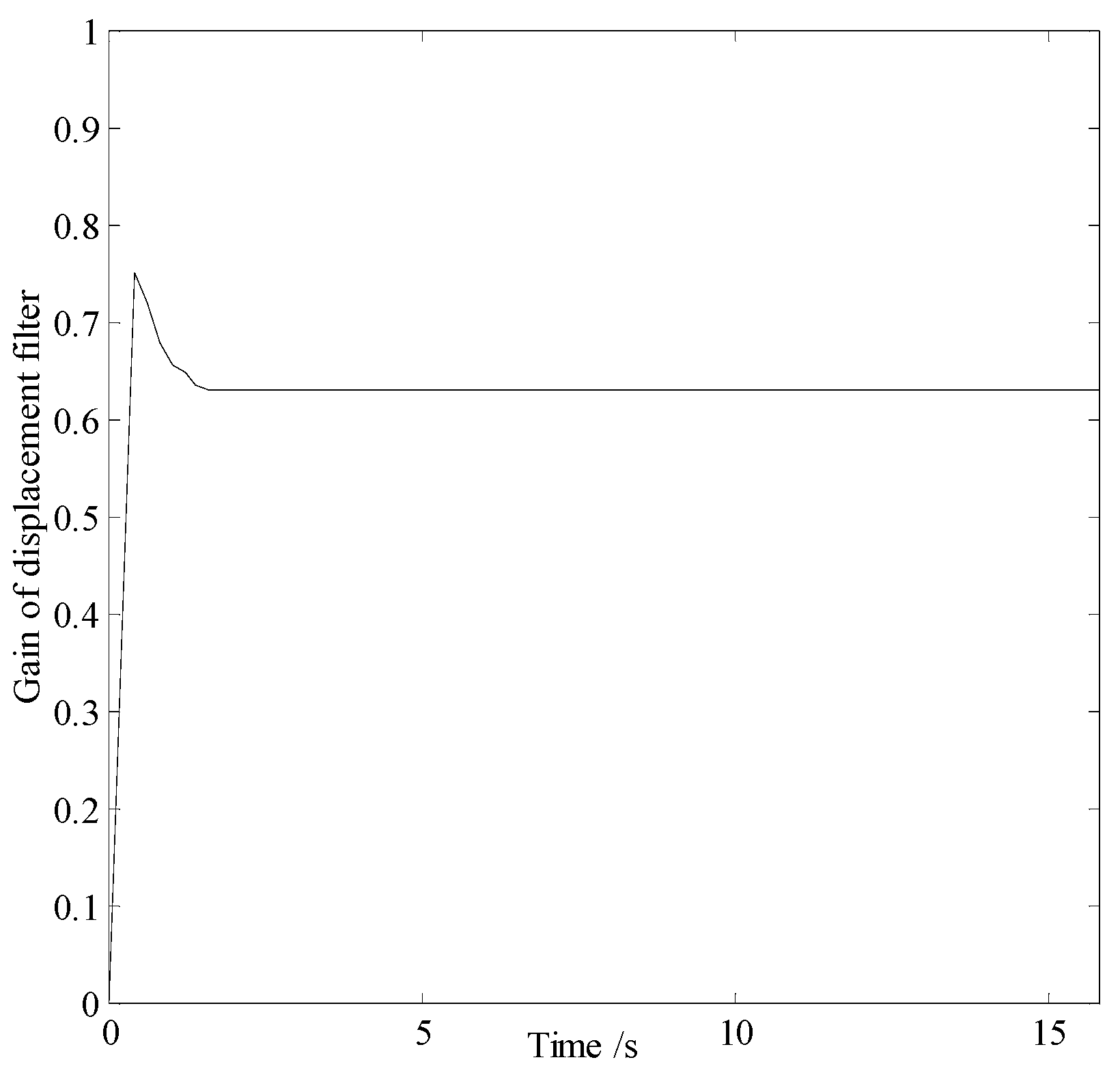
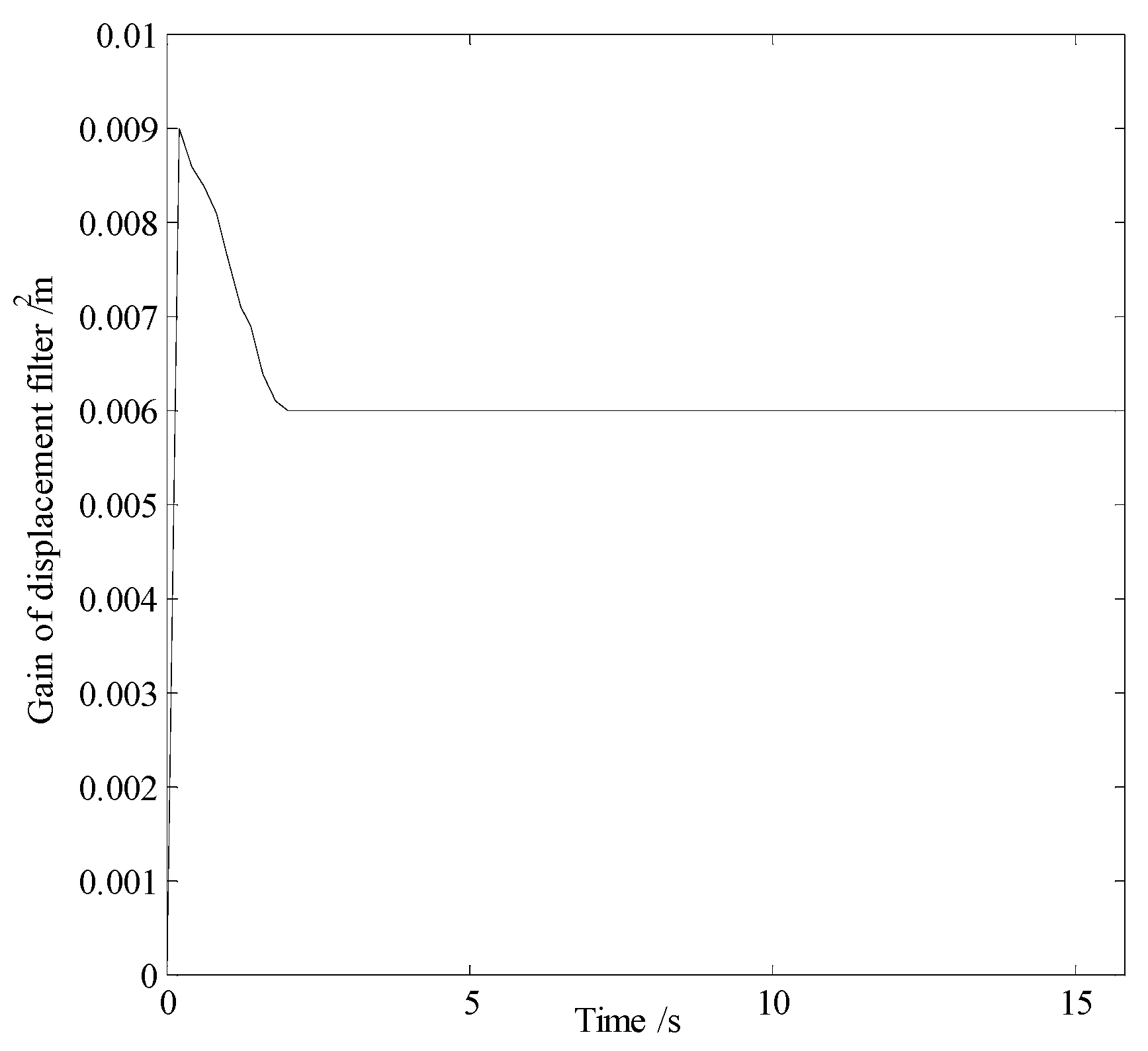
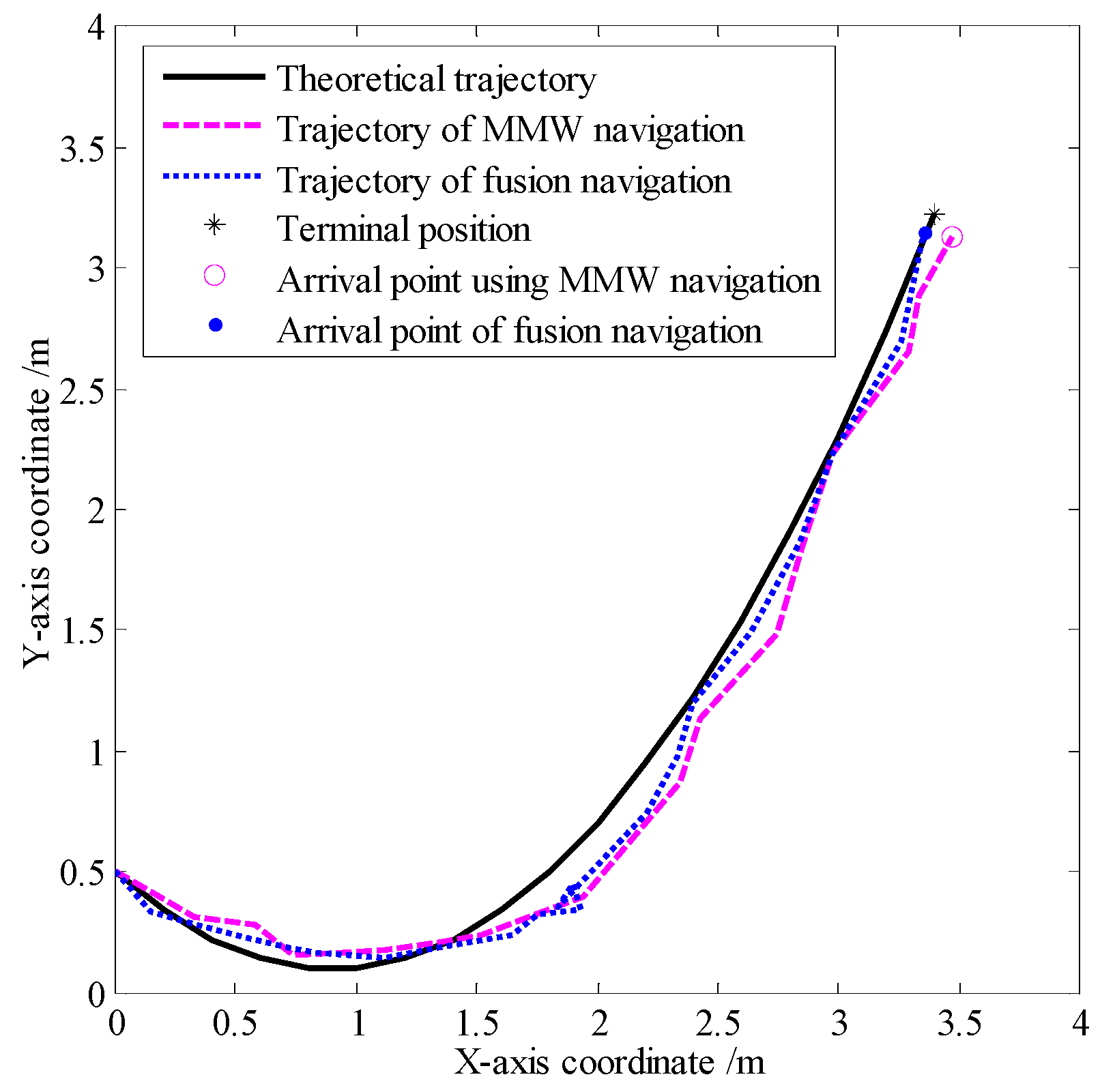
	Localization error
Error of the MMW navigation system	0.11
Errors of the fusion navigation system	0.083

Table 2. Error analysis of robot moving path as curve.

	Localization error
Error of the MMW navigation system	0.11
Errors of the fusion navigation system	0.086

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Fusion Navigation System of Security Robot Based on Millimeter Wave Radar and Inertial Sensor

Abstract

1. Introduction

2. Design of Navigation System

2.1. MMW Navigation System

2.2. Strapdown Inertial Navigation System

3. Fusion Navigation System

3.1. State Equation

3.2. Measurement Equation

3.3. Noise

3.4. Filtering Algorithm

4. Experiment and Analysis

4.1. Experimental Equipment

4.2. Experimental Parameters

4.3. Experimental Results and Analysis

5. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe