Prerpints.org logo
Preprint
Article

The Effect of an Anisotropic Scattering Rate on the Magnetoresistance of a Metal: A Cuprate-Inspired Analysis

Altmetrics

Downloads

60

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 October 2024

Posted:

02 October 2024

You are already at the latest version

Alerts
Abstract
Inspired by the phenomenology of high-critical-temperature superconducting cuprates, we investigate the effect of an anisotropic scattering rate on the magnetoresistance of a metal, relying on Chambers’ solution to the Boltzmann equation. We find that if the scattering rate is enhanced near points of the Fermi surface with a locally higher density of states, an extended regime is found magnetoresistance that varies linearly with the magnetic field. We then apply our results to fit the experimental magnetoresistence of La1.6-xNd0.4SrxCuO4 and speculate about the possible source of anisotropic scattering.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

Introduction

The anomalous properties of the metallic state of high-critical-temperature superconducting cuprates is an intensely debated subject of investigation in condensed matter physics. The most noticeable anomalies are an extended temperature range in which a linear-in-temperature electrical resistivity ρ ( T ) is observed [1,2,3], anomalous power laws and a scaling dependence of the imaginary part of the electron self-energy Im Σ ( ω , T ) = T S ( ω / T ) [4,5], which is mirrored in a similar scaling dependence of the AC conductivity σ ( ω , T ) [6,7,8,9,10,11], at least over a certain frequency range, a seemingly divergent specific heat coefficient C v / T [12], which seems to be mirrored by a seemingly divergent carrier mass [11], as extracted by finite frequency extrapolation of the optical mass, and an extended range of magnetic fields where a linear dependence of the magnetoresistance on the magnetic field is observed [2,13].
There is no microscopic theory that captures all the above rich phenomenology. The phenomenological theory of the marginal Fermi liquid [4] poses the scaling form of the imaginary part of the electron self-energy as a fundamental property and derives a wealth of consequences, such as a divergent quasiparticle mass, but there is not yet a microscopic model of interacting electrons that behaves as a marginal Fermi liquid. Other scenarios invoke the proximity to a quantum critical point. In these theories, the critical fluctuations near the quantum critical point couple with the electrons, endowing them with non-Fermi-liquid properties. The main problem with these theories is that the most convincing candidates as quantum critical points in cuprates are associated with an ordering at finite wavelength, i.e., finite characteristic wave vector q c . These are antiferromagnetic order [14,15], that is indeed found in the parent insulating compound and extends to small doping [16], and charge order, in the form of incommensurate charge density waves [17], for which there is now clear evidence in all families of cuprates [18]. However, since the electrons that are strongly scattered by the critical fluctuations are found on the Fermi surface, at those isolated spots that are connected by the characteristic wave vector q c (hot spots). All the other electrons are only weakly scattered and form a Fermi liquid that short-circuits the non-Fermi-liquid transport properties of the very few hot electrons [19].
Recently, an alternative scenario was proposed in which the Fermi liquid properties gently shrink with reducing the temperature, as a result of the coupling of the electrons to fluctuations with finite characteristic wave vector that are nearly (but not exactly) critical and get overdamped at low temperature [20]. The experimental evidence for such fluctuations in cuprates was recently provided by resonant inelastic X-ray scattering (RIXS) experiments [21,22] that showed that besides nearly critical charge density waves (CDWs), characterized by a narrow peak in the spectra, charge excitations with much broader spectral features are observed. These excitations, called charge density flutuations (CDFs), have a characteristic wave vector q c very close to the wave vector of CDWs, and must therefore have a similar origin, but do not show any tendency to become critical, do not compete with supercondcutivity, and extend on temperature and doping ranges much broader than those in which CDWs are observed. CDFs are excitations with sufficiently low characteristic energy to be a strong source of scattering for the electrons. At the same time, being characterized by broad spectra in momentum space, they mediate a scattering that is essentially isotropic on the Fermi surface, thus escaping the fate of theories with hot spots. It was shown that the imaginary part of the electron self-energy resulting from the scattering mediated by CDFs resembles that of a marginal Fermi liquid, although the ω / T scaling is eventually violated due the non-critical character of CDFs, and the resulting electrical resistivity is linear in temperature above the superconducting critical temperature [23,24].
The question then arises about the transport properties in the presence of a magnetic field. Inspired by a crucial observation of the authors of Refs. [13,25], that points towards an important role of an anisotropic scattering mechanism in producing a magnetoresistance that is linear in the magnetic field over a wide range, we want to systematically investigate the magnetotransport properties of electrons in the presence of a scattering rate that is anisotropic along the Fermi surface. We shall not make any assumption about the origin and nature of such an anisotropic scattering and limit ourselves to discuss the various regime as a function of the different model parameters. This study is a preliminary but necessary step towards any attempt to incorporate CDFs into the theory of magnetotransport in cuprates. In the concluding part of this piece of work we shall try to speculate about the possible source of anisotropic scattering and its connection to nearly-frozen CDF domains.

Dependence of the Conductivity Tensor on the Magnetic Field

In order to calculate the dependence of electrical conductivity on the magnetic field, we adopt a semiclassical approach, within the framework of Boltzmann transport theory. Having in mind the case of high- T c superconducting cuprates as a case study, our calculation applies to a layered system with tetragonal symmetry (for which we set the lattice spacing to 1), and we specialize to the case of a magnetic field perpendicular to the layers. The conductivity tensor for such a system, in the presence of a transverse magnetic field, is a 2 × 2 matrix such that the two diagonal components are equal to each other, as are the two off-diagonal components. The conductivity tensor is therefore determined only by the two components diagonal and off-diagonal, which we indicate with σ x x and σ x y , respectively. To determine the magnetic field dependence of these two quantities without any a priori assumption on the ratio between the scattering rate and the cyclotron frequency, we rely on Chambers’ solution to the Boltzmann equation [26]:
σ x x ( B ) = 2 e 2 v uc ∮ F S v k F ( 0 ) , x ∫ − ∞ 0 e − ∫ t 0 d t ′ τ ( k F ( t ′ ) ) v k F ( t ) , x v k F ( t ) d t d k 4 π 2 , σ x y ( B ) = 2 e 2 v uc ∮ F S v k F ( 0 ) , x ∫ − ∞ 0 e − ∫ t 0 d t ′ τ ( k F ( t ′ ) ) v k F ( t ) , y v k F ( t ) d t d k 4 π 2 ,
where where e is the absolute value of the electron charge, B is the z-component of the transverse magnetic field B , v k is the magnitude of the electron group velocity v k : = ∇ k ξ k , where ξ k is the electron band dispersion law, while v k , x and v k , y refer instead to the two components of v k (we set ℏ = 1 ). The quantity denoted by v uc is the volume of the three-dimensional unit cell of the layered system, so according to our units it is simply the inter-layer distance in units of the in-plane lattice spacing. This quantity plays no role in our further calculations. Since our goal is to evaluate how the scattering anisotropy along the Fermi surface can affect the magnetotransport properties of the system, we consider an angle-dependent elastic scattering rate that does not violate the tetragonal symmetry of the system. In particular, we adopt a scattering rate of the same form proposed in Refs. [13,25]:
1 τ ( k F ) = 1 τ is + 1 τ an | cos ( 2 ϕ k F ) | ν ,
where ϕ k F denotes the angle that the Fermi surface vector k F makes with the positive x-semiaxis in the first Brillouin zone. In our analysis, we are not going to study the behavior of the conductivity as a function of temperature, therefore we do not need to separate the elastic and the inelastic components in the scattering rates 1 / τ is and 1 / τ an . The dependence on the magnetic field in equations (1) comes into play through the time evolution of the vector k F ( t ) . This time evolution is governed the standard equation of motion for an electron in a uniform electric and magnetic field:
d k d t = − e E + v k × B .
where k , E and v k lie on the lattice plane, while B is orthogonal. However, since we are not interested in non-linear effects in the electrostatic field, we can set E = 0 at this level. It is worth noting that, according to the system of units we are using, the quantity e B is dimensionless. In fact, the magnetic field B can be conveniently expressed in units of B 0 : = ℏ / ( e a 2 ) (where a is the in-plane lattice spacing), which is equal to 1 / e in our units. We define the magnetoresistance such that it vanishes at B = 0 :
MR ( B ) : = σ x x ( 0 ) σ x x ( B ) − 1 .
Our main goal is to show how the magnetoresistance depends on the three scattering rate parameters appearing in equation (2), namely 1 / τ is , 1 / τ an and ν . The band dispersion of the electron system that we are going to study is that given by tight-binding, for which we only consider the first three hopping parameters:
ξ k = − 2 t cos ( k x ) + cos ( k y ) − 4 t ′ cos ( k x ) cos ( k y ) − 2 t ′ ′ cos ( 2 k x ) + cos ( 2 k y ) − μ .
The chemical potential μ is adjusted to fix the number of electrons per unit cell 1 − p . Details about the solution of equation 3, to be incorporated in equations 1, as well as a Fourier analysis of the scattering rate in equation 2, are given in the appendices.

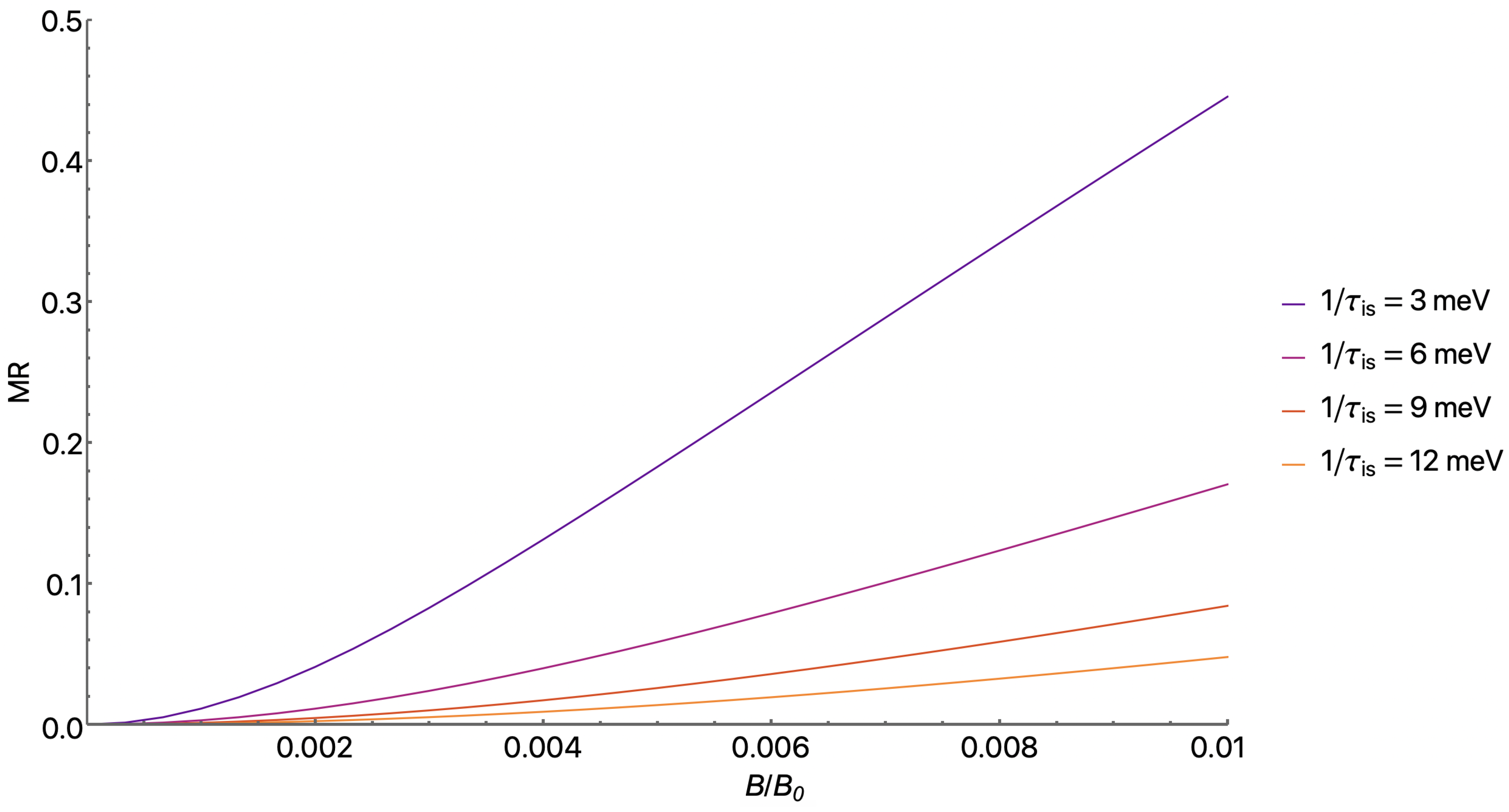
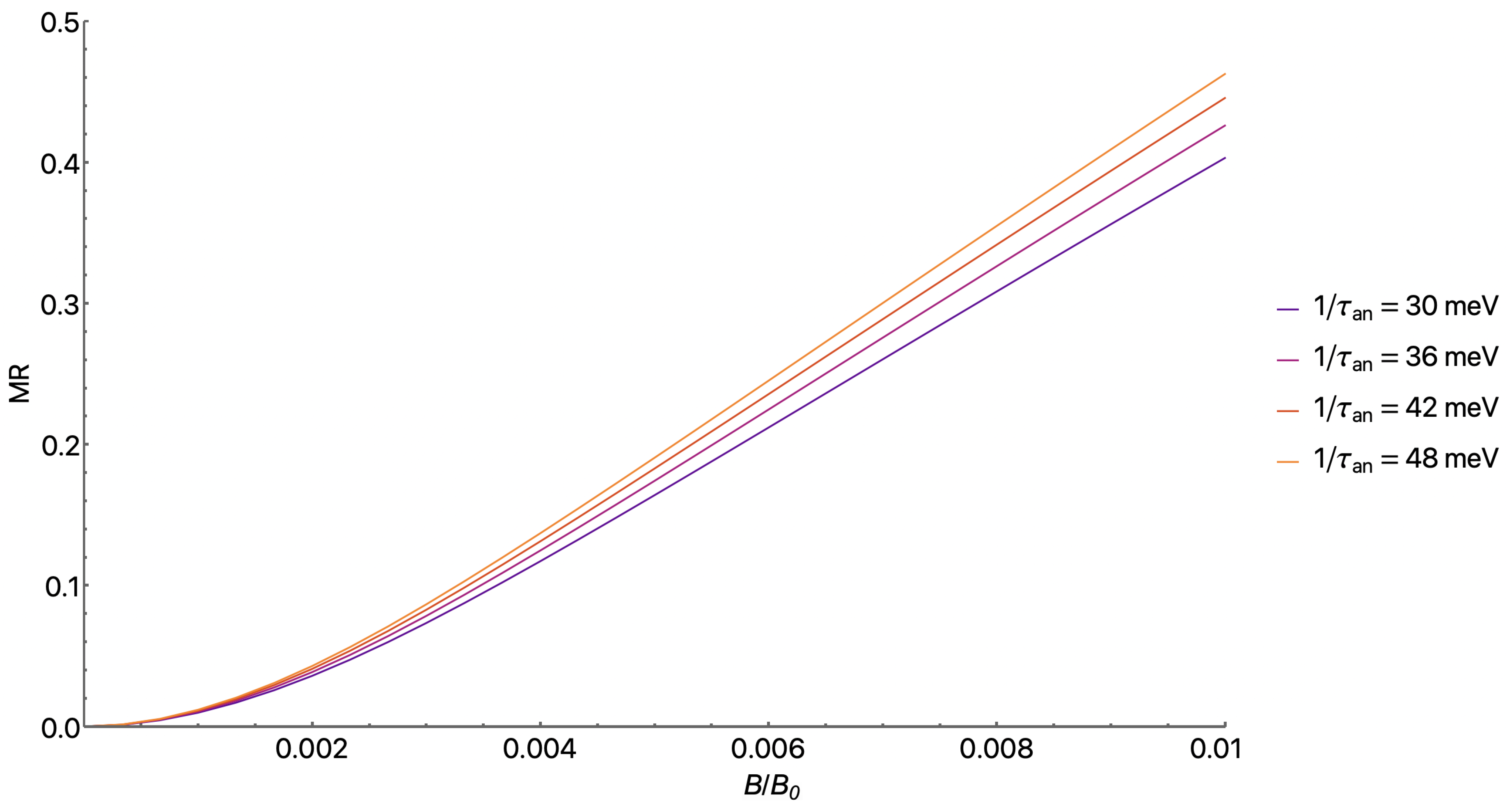
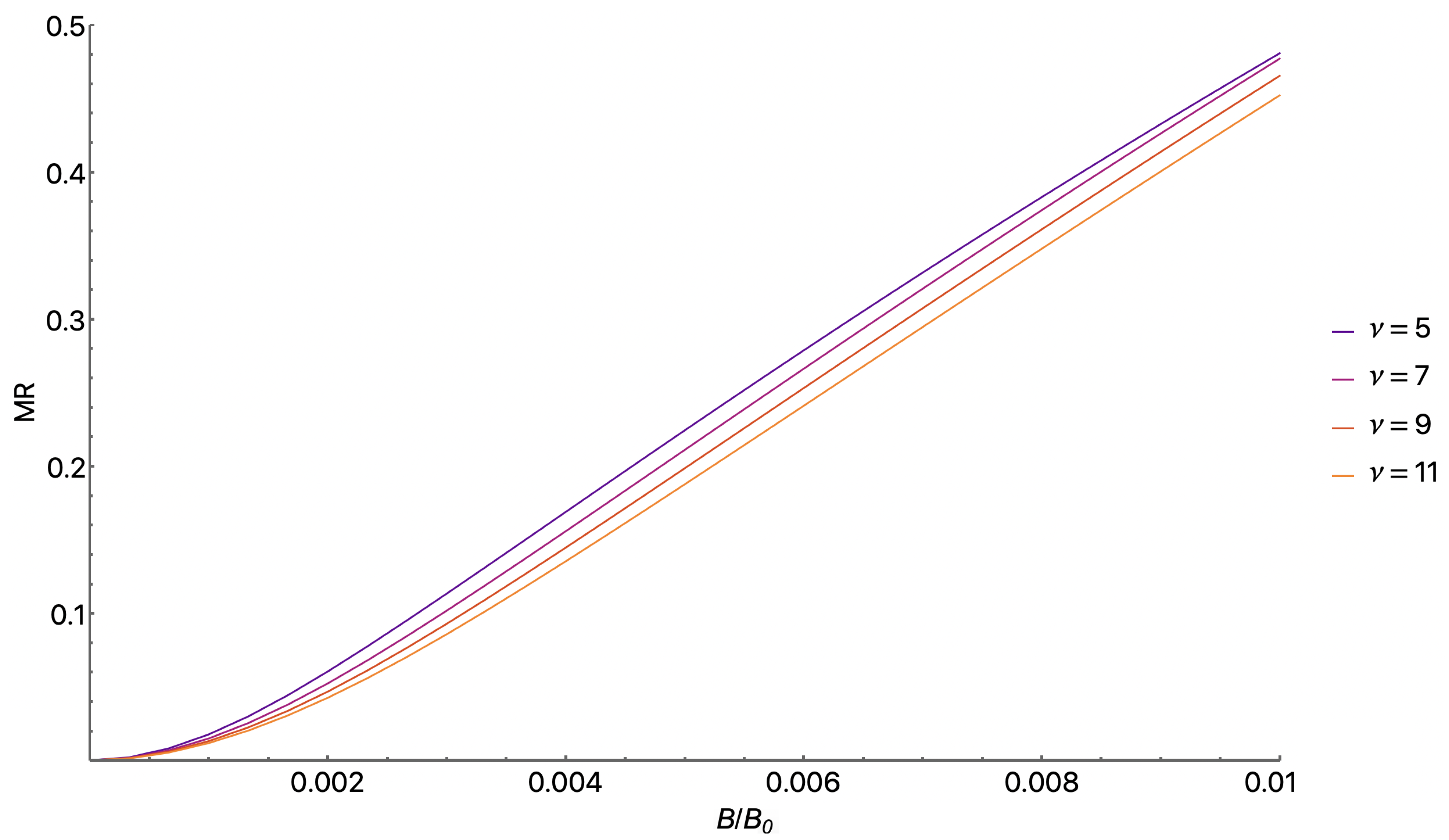
Effect of the Anisotropic Scattering

For the study we are going to conduct, we fix the following set of parameters:
t = 200 meV , t ′ = − 0.135 t = − 27 meV , t ′ ′ = 0.065 t = 13 meV , p = 0.248 .
This set is quite similar to that proposed in Refs. [13,25]. The first problem we are going to face is how the magnetoresistance is affected by the isotropic component of the scattering. In order to estimate of the overall contributions of the two terms that make up our scattering rate, we can average the total scattering rate over a full 2 π angle:
1 τ avg : = 1 2 π ∫ 0 2 π d ϕ k F τ ( k F ) = 1 τ is + 1 τ an f ( ν ) , with f ( ν ) : = Γ ν + 1 2 π Γ ν 2 + 1 ,
where Γ ( z ) is the Euler Gamma function. The dimensionless function f ( ν ) is a strictly decreasing function of ν for non-negative values of its argument, such that it is equal to 1 when ν = 0 and goes as 1 / ν for ν → ∞ . In the absence of a magnetic field, if the total scattering is dominated by a single characteristic scattering rate, Boltzmann transport theory predicts a resistivity that is essentially linear in that scattering rate. The addition of an external magnetic field generally provides a subleading correction to this dependence. For this reason, we expect the quantity MR ( B ) , beyond its dependence on the magnetic field B, to be essentially linear in 1 / τ avg , due to the presence of ρ x x ( 0 ) in the denominator. The trend of magnetoresistance as a function of B, for several values of 1 / τ is , is shown in Figure 1. All the curves in the figure exhibit a crossover between a quadratic and a linear regime, and the scale at which this crossover occurs increases with 1 / τ is . We also observe that the value of the curves increases as 1 / τ is increases, according to an approximately linear relationship at high magnetic fields. It is worth noting that, with the values we have set for the anisotropic part of the scattering ( 1 / τ an = 42 meV and ν = 12 ) and with the range we have chosen for the isotropic one (between 3 meV and 12 meV), the quantity 1 / τ avg is dominated by its isotropic component, this is the reason why the linearity between MR ( B ) and 1 / τ avg roughly reduces to a linearity between MR ( B ) and 1 / τ is .
Let us now analyze the effect of the anisotropic component of the scattering, namely how MR ( B ) is influenced by the two parameters 1 / τ an and ν . We first observe that these two parameters play a different role within the expression for 1 / τ ( k F ) : while 1 / τ an controls the relative weight between the isotropic and anisotropic parts of the scattering rate, ν determines the shape of the anisotropic part. For this reason, we expect that the effect of varying 1 / τ an will be somewhat similar to that of varying 1 / τ is , with the main difference that the dependence of the magnetoresistance on the former will be significantly weaker than that on the latter for ν large enough, as its contribution is significantly suppressed by the factor f ( ν ) . These observations are confirmed by our numerical calculation, the plot of which is shown in Figure 2. An important qualitative difference with Figure 1 is that, in the second case, the curves seem to grow as 1 / τ an increases. The reason is that the scattering rate 1 / τ an has a much weaker effect on ρ x x ( 0 ) than 1 / τ is , weak enough to allow the increase in resistivity due to the magnetic field to (slightly) outweigh the increase in zero-field resistance.
More interesting is the effect of varying the value of ν , graphically reported in Figure 3. As we have already mentioned, the increase of ν leads on the one hand to a sharper anisotropy of the scattering rate, but on the other hand it attenuates the contribution of the anisotropic component compared to the isotropic one. This is why the increase in ν has an effect somewhat opposite to the increase in 1 / τ an , as is evident by comparing Figure 2 and Figure 3. The most interesting aspect of this plot, differently from what we observed in Figure 1 and Figure 2, is that the linear parts of the curves appear to have essentially the same slope, and are therefore distinguished from each other mainly by the scale at which the crossover between the quadratic and linear regimes occurs. In particular, linearity appears to be more stable as ν decreases. However, for excessively low values of ν a deviation from linearity is observed at high magnetic fields, in favor of a sublinear trend.

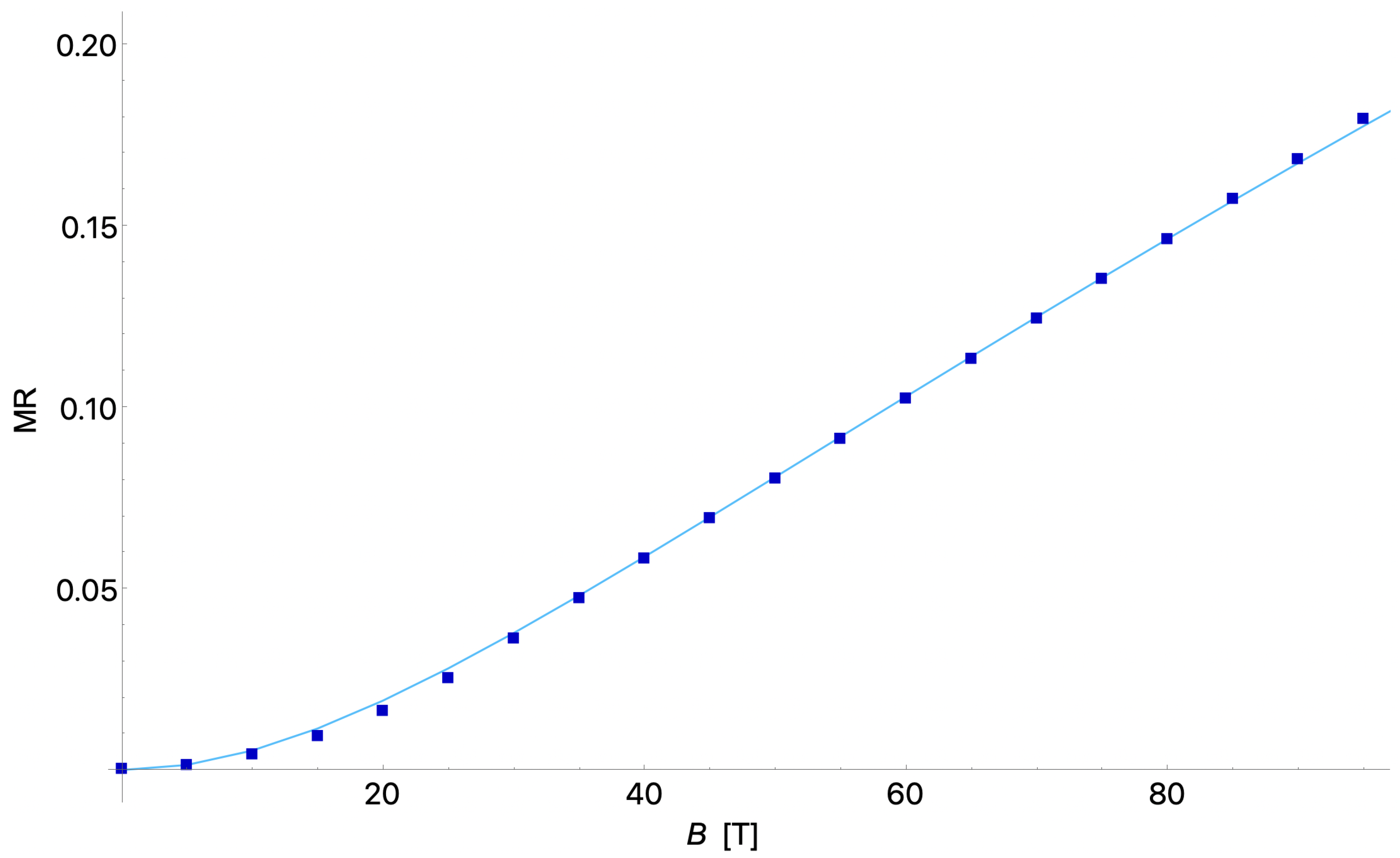
Discussion and Conclusions

For the sake of concreteness, for comparison with experimental data, we will adopt the same set of parameters that we already used to fit the resistivity data for La1.6-xNd0.4SrxCuO4 [24,27], whose experimental estimate is provided in Ref. [28]:
t = 435 meV , t ′ = − 50 meV , t ′ ′ = 38 meV , p = 0.24 .
With this set of parameters, we get μ ≃ − 350 meV . Moreover, in order to have a direct comparison with the experimental data, it is necessary to express the magnetic field in standard SI units. For this reason, it is necessary to fix the value of a, and consequently that of B 0 . By setting a = 3.8 Å [29,30], we get B 0 ≃ 4.56 e 3 T . The fit of the experimental data, shown in Figure 4, provided the following set of values:
1 τ is = 17.7 meV , 1 τ an = 39 meV , ν = 4 .
The set of parameters we have chosen not only allows a good fit of the experimental magnetoresistance curve, but is also consistent with our previous fit for the resistivity data [24,27]. In fact, the value of ρ x x ( 0 ) that we obtain with the expression for 1 / τ ( k F ) given by (2) with the chosen parameters is the same as that obtained by setting 1 / τ ( k F ) equal to the constant value 2 Γ 0 with Γ 0 = 13.7 meV , which is the value we set to fit La1.6–xNd0.4SrxCuO4 resistivity data in absence of magnetic field. We notice, in passing, that the extended linear behavior as a function of B is obtained here for a scattering rate rather less anisotropic than that suggested in Ref. [13]. Another important consequence of the mechanism underlaying an extended linear dependence of the magnetoresistance on the magnetic field, discussed in this piece of work, is that temperature and magnetic field enter the theory in independent manners, so there is no reason to expect B / T scaling of the magnetoresistance. Any observed scaling must necessarily be approximate and somewhat accidental.
So far, we limited ourselves to identifying the range of parameters that are apt to describe the magnetoresistance of cuprates. The task of incorporating CDFs in the theory is beyond the scope of this piece of work, as it requires to specify, both in 1 / τ is and in 1 / τ an , the elastic and anelastic contributions, the latter governing the temperature dependence of the transport properties, which will be the object of future investigations. However, here we wish to speculate about the possible source of anisotropic scattering and its connection to CDFs.
To extend the linear-in-temperature electrical resistivity down to very low temperatures, as it is observed in cuprates when superconductivity is suppressed by a magnetic field, we were recently led to consider a theory in which the damping of CDFs increases with lowering the temperature, and diverges at T = 0 (at a specific doping or in some doping range) [24,27]. This theory allows indeed to extend the linear temperature dependence of the resistivity to low temperatures. Furthermore, the electrons coupled to these overdamped CDFs form a shrinking Fermi liquid [20], that reproduces most of the phenomenology of the marginal Fermi liquid, with the important difference of yielding a quasiparticle mass that stays finite. The divergent specific heath coefficient C v / T is obtained instead as a direct contribution of overdamped CDFs. When trying to identify the source of this overdamping, one is led to consider some kind of incipient glassy behavior for the CDFs, following an approach inspired to Ref. [31]. It is then tempting to imagine that some elongated nanoscopic CDF domains get prematurely frozen, and contribute to the elastic part of the anisotropic scattering rate, responsible for the linear magnetoresistence, whereas the remaining dynamical overdamped CDFs contribute to the inelastic part of the isotropic scattering rate, responsible for the linear-in-temeprature resistivity. This scenario is currently under investigation.

Funding

We acknowledge financial support from the Ateneo Research Projects of the University of Rome Sapienza: Competing phases and non-equilibrium phenomena in low-dimensional systems with microscopic disorder and nanoscale inhomogeneities (n. RM12117A4A7FD11B), Models and theories from anomalous diffusion to strange-metal behavior (n. RM12218162CF9D05), Non-conventional aspects for transport phenomena and non-equilibrium statistical mechanics (n. RM123188E830D258).

Acknowledgments

We acknowledge fruitful conversations with M. Grilli and G. Seibold.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CDFs Charge density fluctuations
CDW Charge density waves
RIXS Resonant Inelastic X-ray Scattering

Appendix A. Equation of Motion of an Electron in a Transverse Magnetic Field

We calculate the conductivity tensor neglecting nonlinear effects in the electric field, but keeping the full dependence on the magnetic field (at least, at magnetic fields low enough to apply a semiclassical approach). The equation of motion for the electron is therefore obtained by setting E = 0 in (3):
d k d t = − v k × e B .
This equation can be expressed either in Cartesian coordinates ( k x , k y ) or in polar coordinates ( k , ϕ ) as follows:
d k x d t = − e B v y , d k y d t = e B v x , 1 k d k d t = − e B k x v y − k y v x k x 2 + k y 2 , d ϕ d t = e B k x v x + k y v y k x 2 + k y 2 ,
where in the last two equations k x = k cos ϕ and k y = k sin ϕ . Since the integral that defines the electrical conductivity is restricted to the Fermi surface, the various wave-vectors that appear are uniquely identified by their angle with respect to the positive x-semiaxis of the first Brillouin zone. Consequently, the only relevant equation of motion is the one for ϕ . Once ϕ is found, the corresponding k is adjusted so that k is on the Fermi surface. We point out that the angular variable ϕ varies continuously along the entire Fermi surface only if this is closed around the Γ point, namely when it crosses both axes of the first Brillouin zone, k x = 0 and k y = 0 . For the case of an open Fermi surface, it is convenient to work with the angular variable φ , defined as the angle taken from the M point starting from the negative y-semiaxis, taken as positive if oriented clockwise (see Figure A1). The equation of motion for φ is then:
d φ d t = e B π − k x + 2 π θ ( − k x ) v x + π − k y + 2 π θ ( − k y ) v y π − k x + 2 π θ ( − k x ) 2 + π − k y + 2 π θ ( − k y ) 2 ,
where θ ( · ) is the Heaviside step function. The quantity k j + 2 π θ ( − k j ) (with j = x , y and k j ∈ [ − π , π ] ) can be interpreted as a Fermi surface vector if the Fermi surface is traced around the M point instead of around the Γ point. Also notice that the sign of π − k j + 2 π θ ( − k j ) is the same as that of k j , this implies that the sign of d ϕ / d t is the same as d φ / d t , as it should. Moreover, we point out that all the functions in this expression are well defined, since in the case of an open Fermi surface with tetragonal symmetry neither k x nor k y can ever vanish.
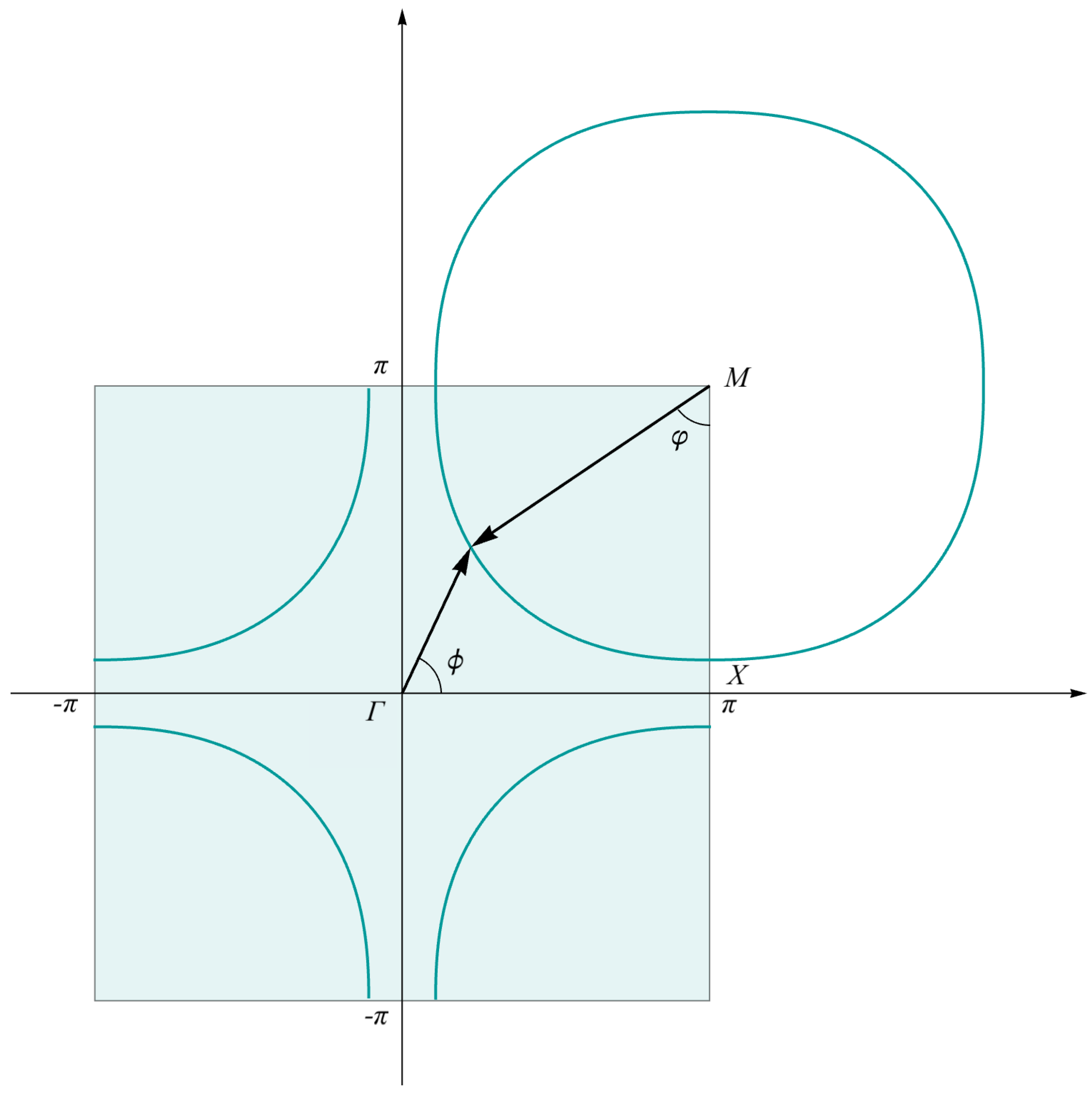
Preprints 119954 g0a1
Figure A1. Graphical display of angles ϕ and φ for an open Fermi surface.
Figure A1. Graphical display of angles ϕ and φ for an open Fermi surface.
Preprints 119954 g0a1

Appendix B. Harmonic Analysis of the Anisotropic Component of the Scattering Rate

The Fourier series expansion of the function | cos ( 2 ϕ ) | ν provides the following result:
| cos ( 2 ϕ ) | ν = 1 2 a 0 + ∑ n = 1 ∞ a n cos ( 4 n ϕ ) ,
where:
a n = Γ ( ν + 1 ) Γ n − ν 2 2 ν − 1 π Γ n + 1 + ν 2 cos n + ν + 1 2 π .
This is a quite general expression, which works for any real ν ≥ 0 . Notice the asymptotic behavior:
Γ n − ν 2 Γ n + 1 + ν 2 ∼ 1 n ν + 1 for n → ∞ ,
which ensures that the previous series is always convergent for any ν > 0 . A very interesting expression can be found when ν is an even non-negative integer. In this case, we can express it as 2 m , where m ∈ N 0 . The expression for a generic coefficient a n is:
a n = 2 1 − 2 m 2 m m − n for 0 ≤ n ≤ m , 0 for n > m ,
which shows that only a finite number of harmonics contributes to reconstruct the original function, as required by appropriate trigonometric identities. In particular, for the trivial case ν = m = 0 the only non-zero term is a 0 = 2 , as we expect since in this case our function becomes constant.

References

  1. Dagotto, E. Correlated electrons in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 763–840. [Google Scholar] [CrossRef]
  2. Giraldo-Gallo, P.; Galvis, J.A.; Stegen, Z.; Modic, K.A.; Balakirev, F.F.; Betts, J.B.; Lian, X.; Moir, C.; Riggs, S.C.; Wu, J.; et al. Scale-invariant magnetoresistance in a cuprate superconductor. Science 2018, 361, 479–481. [Google Scholar] [CrossRef]
  3. Legros, A.; Benhabib, S.; Tabis, W.; Laliberté, F.; Dion, M.; Lizaire, M.; Vignolle, B.; Vignolles, D.; Raffy, H.; Li, Z.Z.; et al. Universal T-linear resistivity and Planckian dissipation in overdoped cuprates. Nat. Phys. 2019, 15, 142. [Google Scholar] [CrossRef]
  4. Varma, C.M.; Littlewood, P.B.; Schmitt-Rink, S.; Abrahams, E.; Ruckenstein, A.E. Phenomenology of the normal state of Cu-O high-temperature superconductors. Phys. Rev. Lett. 1989, 63, 1996. [Google Scholar] [CrossRef]
  5. Damascelli, A.; Hussain, Z.; Shen, Z.-X. Rev. Mod. Phys. 2003, 75, 473. [CrossRef]
  6. El Azrak, A.; Nahoum, R.; Bontemps, N.; Guilloux-Viry, M.; Thivet, C.; Perrin, A.; Labdi, S.; Li, Z.Z.; Raffy, H. Infrared properties of YBa2Cu3O7 and Bi2Sr2Can-1CunO2n+4 thin films. Phys. Rev. B 1994, 49, 9846. [Google Scholar] [CrossRef]
  7. van der Marel, D.; Molegraaf, H.J.A.; Zaanen, J.; Nussinov, Z.; Carbone, F.; Damascelli, A.; Eisaki, H.; Greven, M.; Kes, P.H.; Li, M. Quantum critical behaviour in a high-Tc superconductor. Nature 2003, 425, 271. [Google Scholar] [CrossRef]
  8. van der Marel, D.; Carbone, F.; Kuzmenko, A.B.; Giannini, E. Scaling properties of the optical conductivity of Bi-based cuprates. Annals of Physics 2006, 321, 1716. [Google Scholar]
  9. Hwang, J.; Timusk, T.; Gu, G.D. Doping dependent optical properties of Bi2Sr2CaCu2O8+δ. J. Phys.: Condens. Matter 2007, 19, 125208. [Google Scholar] [CrossRef]
  10. van Heumen, E.; Feng, X.; Cassanelli, S.; Neubrand, L.; de Jager, L.; Berben, M.; Huang, Y.; Kondo, T.; Takeuchi, T.; Zaanen, J. Strange metal electrodynamics across the phase diagram of Bi2-xPbxSr2-yLayCuO6+δ cuprates. Phys. Rev. B 2022, 106, 054515. [Google Scholar] [CrossRef]
  11. Michon, B.; Berthod, C.; Rischau, C.W.; Ataei, A.; Chen, L.; Komiya, S.; Ono, S.; Taillefer, L.; van der Marel, D.; Georges, A. Reconciling scaling of the optical conductivity of cuprate superconductors with Planckian resistivity and specific heat. Nature Communications 2023, 14, 3033. [Google Scholar] [CrossRef]
  12. Michon, B.; Girod, C.; Badoux, S.; Kačmarčík, J.; Ma, Q.; Dragomir, M.; Dabkowska, H.A.; Gaulin, B.D.; Zhou, J.S.; Pyon, S.; et al. Thermodynamic signatures of quantum criticality in cuprate superconductors. Nature 2019, 567, 218–222. [Google Scholar] [CrossRef]
  13. Ataei, A.; et al. Electrons with Planckian scattering obey standard orbital motion in a magnetic field. Nat. Phys. 2022, 18, 1420–1424. [Google Scholar] [CrossRef]
  14. Chakravarty, S.; Halperin, B.I.; Nelson, D.R. Low-temperature behavior of two-dimensional quantum antiferromagnets. Phys. Rev. Lett. 1988, 60, 1057. [Google Scholar] [CrossRef]
  15. Lee, P.A.; Nagaosa, N.; Wen, X. Doping a Mott Insulator: Physics of High Temperature Superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. [Google Scholar] [CrossRef]
  16. Vaknin, D.; Sinha, S.K.; Moncton, D.E.; Johnston, D.C.; Newsam, J.M.; Safinya, C.R.; King, H.E., Jr. Antiferromagnetism in La2CuO4-y. Phys. Rev. Lett. 1987, 58, 2802. [Google Scholar] [CrossRef]
  17. Castellani, C.; Di Castro, C.; Grilli, M. Singular Quasiparticle Scattering in the Proximity of Charge Instabilities. Phys. Rev. Lett. 1995, 75, 4650. [Google Scholar] [CrossRef]
  18. Arpaia, R.; Ghiringhelli, G. Charge Order at High Temperature in Cuprate Superconductor. J. Phys. Soc. Japan 2021, 90, 111005. [Google Scholar] [CrossRef]
  19. Hlubina, R.; Rice, T.M. Resistivity as a function of temperature for models with hot spots on the Fermi surface. Phys. Rev. B 1995, 51, 9253. [Google Scholar] [CrossRef]
  20. Mirarchi, G.; Grilli, M.; Seibold, G.; Caprara, S. The Shrinking Fermi Liquid Scenario for Strange-Metal Behavior from Overdamped Optical Phonons. Condens. Matter 2024, 9, 14. [Google Scholar] [CrossRef]
  21. Arpaia, R.; Caprara, S.; Fumagalli, R.; De Vecchi, G.; Peng, Y.Y.; Andersson, E.; Betto, D.; De Luca, G.M.; Brookes, N.B.; Lombardi, F.; et al. Dynamical charge density fluctuations pervading the phase diagram of a Cu-based high-Tc superconductor. Science 2019, 365, 906–910. [Google Scholar] [CrossRef]
  22. Arpaia, R.; Martinelli, L.; Sala, M.M. : et al. Signature of quantum criticality in cuprates by charge density fluctuations. Nat Commun 2023, 14, 7198. [Google Scholar] [CrossRef]
  23. Seibold, G.; Arpaia, R.; Peng, Y.Y.; Fumagalli, R.; Braicovich, L.; Di Castro, C.; Grilli, M.; Ghiringhelli, G.C.; Caprara, S. Strange metal behaviour from charge density fluctuations in cuprates. Commun. Phys. 2021, 4, 7. [Google Scholar] [CrossRef]
  24. Mirarchi, G. et al., The strange-metal behavior of cuprates. Condens. Matter 2022, 7, 22. [Google Scholar] [CrossRef]
  25. Grissonnanche, G. et al., Linear-in-temperature resistivity from an isotropic Planckian scattering rate. Nature 2021, 595, 667–672. [Google Scholar] [CrossRef]
  26. Chambers R., G. The Kinetic Formulation of Conduction Problems. Proc. Phys. Soc. A 1952, 65, 458. [Google Scholar] [CrossRef]
  27. Caprara, S. et al., Dissipation-driven strange metal behavior. Commun. Phys. 2022, 5, 10. [Google Scholar] [CrossRef]
  28. Meevasana, W. et al. Hierarchy of multiple many-body interaction scales in high-temperature superconductors. Phys. Rev. B 2007, 75, 174506. [Google Scholar] [CrossRef]
  29. Biškup, N. et al. Atomic-resolution studies of epitaxial strain release mechanisms in La1.85Sr0.15CuO4/La0.67 Ca0.33MnO3 superlattices. Phys. Rev. B 2015, 91, 205132. [Google Scholar] [CrossRef]
  30. Dragomir, M. et al. Materials preparation, single-crystal growth, and the phase diagram of the cuprate high-temperature superconductor La2-xSrxCuO4. Phys. Rev. Materials 2020, 4, 114801. [Google Scholar] [CrossRef]
  31. Dzero, M.; Schmalian, J.; Wolynes, P.G. in Structural Glasses and Supercooled Liquids: Theory, Experiment, and Applications, P. G. Wolynes, V. Lubchenko, Eds. (Wiley, 2012), pp. 193-222. [CrossRef]
Preprints 119954 g001
Figure 1. Magnetoresistance as a function of B for several values of 1 / τ is , at fixed 1 / τ an = 42 meV and ν = 12 .
Figure 1. Magnetoresistance as a function of B for several values of 1 / τ is , at fixed 1 / τ an = 42 meV and ν = 12 .
Preprints 119954 g001
Preprints 119954 g002
Figure 2. Magnetoresistance as a function of B for several values of 1 / τ an , at fixed 1 / τ is = 3 meV and ν = 12 .
Figure 2. Magnetoresistance as a function of B for several values of 1 / τ an , at fixed 1 / τ is = 3 meV and ν = 12 .
Preprints 119954 g002
Preprints 119954 g003
Figure 3. Magnetoresistance as a function of B for several values of ν , at fixed 1 / τ is = 3 meV and 1 / τ an = 42 meV .
Figure 3. Magnetoresistance as a function of B for several values of ν , at fixed 1 / τ is = 3 meV and 1 / τ an = 42 meV .
Preprints 119954 g003
Preprints 119954 g004
Figure 4. Plots of the magnetoresistence experimental data (dots) and theoretical fit (solid line) for La1.6–xNd0.4SrxCuO4, at p = 24 % and T = 30 K . The experimental data are taken from ref. [13].
Figure 4. Plots of the magnetoresistence experimental data (dots) and theoretical fit (solid line) for La1.6–xNd0.4SrxCuO4, at p = 24 % and T = 30 K . The experimental data are taken from ref. [13].
Preprints 119954 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated