Prerpints.org logo
Preprint
Article

Options for Performing DNN-Based Causal Speech Denoising Using the U-Net Architecture

Altmetrics

Downloads

65

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 September 2024

Posted:

03 October 2024

You are already at the latest version

Alerts
Abstract
Speech enhancement technology seeks to improve the quality and intelligibility of speech signals degraded by noise, particularly in telephone communications. Recent advancements have focused on leveraging deep neural networks (DNN), especially U-Net architectures, for effective denoising. In this study, we evaluate the performance of a 6-level skip-connected U-Net constructed using either conventional convolution activation blocks (CCAB) or innovative global local former blocks (GLFB) across different processing domains: temporal waveform, short-time Fourier transform (STFT), and short-time discrete cosine transform (STDCT). Our results indicate that the U-Nets can receive better signal-to-noise ratio (SNR) and perceptual evaluation of speech quality (PESQ) when applied in the STFT and STDCT domains, with comparable short-time objective intelligibility (STOI) scores across all domains. Notably, the GLFB-based U-Net outperforms its CCAB counterpart in metrics such as CSIG, CBAK, COVL, and PESQ, while maintaining fewer learnable parameters. Furthermore, we propose domain-specific composite loss functions, considering the acoustic and perceptual characteristics of the spectral domain, to enhance the perceptual quality of denoised speech. Our findings provide valuable insights that can guide the optimization of DNN designs for causal speech denoising.
Keywords: 
Subject: Computer Science and Mathematics  -   Signal Processing

1. Introduction

Most recorded speech signals are affected by noise, which degrades quality and hinders intelligibility. Speech enhancement techniques aim to maximize the perceptual quality of speech signals disturbed by background noise and reverberation. Background noise may include environmental sounds and instrumental interference, while reverberation occurs due to reflections in the transmission path. Although both types of noise can coexist and complicate the denoising task, effective solutions are achievable using deep neural networks (DNN) [1,2], which aim to predict clean speech from corrupted inputs. To this end, the scope of discussion in this study will be limited to speech denoising without losing generality.
Speech denoising is crucial for applications such as audio and video calls, hearing aids, and automatic speech recognition systems. While traditional statistical signal processing approaches have addressed this problem for years, recent research has shifted towards machine learning techniques that learn from real-world data. Following the success of deep learning in various classification and regression tasks [3], there has been a growing interest in applying DNNs for speech denoising.
The core concept of DNN-based speech denoising involves training models to learn the complex mapping from noise-corrupted speech representations to their clean counterparts. This kind of approach offers two significant advantages: (1) it operates without requiring knowledge of the statistical properties of the speech and noise, and (2) it can handle fast-varying non-stationary noise. Several effective DNN architectures have emerged, with the U-Net becoming a prominent choice for speech denoising. Initially designed for biomedical image segmentation [4], the U-Net has proven highly adaptable and effective for speech applications [2,5,6,7,8]. Its U-shaped structure comprises an encoder and a decoder linked by a bottleneck. The encoder compresses input data into a lower-dimensional representation, capturing essential features, while the decoder reconstructs the data to its original dimensions with improved output. The U-Net architecture preserves high-resolution features, facilitates hierarchical feature extraction, supports efficient training, and enhances generalization, making it a powerful tool in DNN-based speech denoising.
When employing U-Net for speech denoising, the input can be represented in various forms, such as time-domain waveforms or spectral transformations (STFT and STDCT). Previous studies often focused on a specific domain and adjusted the U-Net’s structure for optimization. However, discussions on the applicability of a U-Net model across multiple domains remain scarce. This paper aims to develop a versatile U-Net model and evaluate its denoising efficacy on narrowband speech sampled at 8 kHz. Through comparative analyses of experimental results, we hope to identify the domain that offers the greatest advantages for effective speech denoising.
The contributions of this paper are threefold. Firstly, we establish a comparison framework for assessing U-Net performance across different processing domains. Secondly, our examination of classical and advanced U-Nets justifies the design choices for layer configurations, facilitating a balance between model complexity and computational efficiency. Thirdly, upon identifying the optimal domain for DNN-based speech denoising, we explore the use of composite loss functions to enhance perceptual quality further.
The remainder of this paper is structured as follows: Section 2 outlines recent technical developments in the field. Section 3 discusses the U-Net architecture for speech denoising, including network design, causality implementation, input arrangements, and loss functions across domains. Section 4 presents experimental settings and performance evaluations. Conclusions are drawn in Section 5.

2. Related Works and Research Planning

Early DNN-based speech denoising methods often utilized time-frequency representations to analyze spectral features over time [5]. Recent trends indicate that incorporating phase information can significantly enhance speech quality [9,10]. As the phase information exists in the raw temporal waveform and its spectral transformation as well, DNN-based phase-aware speech denoising can be carried out straightforwardly using the speech waveform as the input [11,12,13]. For the denoising process conducted in the spectral domain [2,5,6,7,8], the short-time Fourier transform (STFT) presentation with the real and imaginary (or RI for short) components arranged in sequence is most popular.
DNN-based speech enhancement can be implemented in the form of mapping or masking. The masking approach estimates a suppression gain for each target value [2,14], while mapping directly predicts the output values [5,15,16]. Although the masking approach provides an auxiliary constraint that improves consistency with desired outputs, its advantages diminish as DNNs become more proficient.
Causality is crucial for real-time applications, as it ensures that DNNs only utilize past and present features. Two common methods for implementing causal DNN-based speech denoising include recurrent networks [17,18] (such as long short-term memory, LSTM [19]) and frame-buffering techniques that compile past frame data into a buffer to guide the DNN during denoising [20,21].
A well-defined loss function is essential for training DNNs in speech denoising, as it quantifies the alignment between the DNN’s predictions and target outputs. Here, the goal is to minimize noise while preserving original speech characteristics, balancing the trade-off between denoising and potential speech distortion. Recent advancements in loss functions that optimize both magnitude and phase spectra show promise [9]. Additionally, power compression has proven beneficial in enhancing denoising performance [22].
In this study, we adopt the frame-buffering approach to construct two representative causal U-Nets (classical and advanced) to evaluate the most suitable processing domain for speech denoising. The classical U-Net utilizes multi-level layers of conventional convolution and activation, while the advanced U-Net employs global local former blocks (GLFB) as introduced in [23]. After identifying the optimal domain, we will develop domain-specific loss functions tailored to the domain’s characteristics.

3. Speech Denoising

Based on the discussions above, we elaborate on the processing framework, DNN architecture, input arrangement, and loss function required for subsequent investigation.

3.1. Processing Framework

A noisy speech y [ n ] is commonly modeled as the sum of clean speech x [ n ] and additive noise z [ n ] , i.e.,
y [ n ] = x [ n ] + z [ n ]
Since y [ n ] may vary in length, the denoising process is generally performed using a frame-based overlap-and-add (OLA) method. That is, the noisy speech signal y [ n ] is first divided into frames of fixed length, each overlapping with its adjacent frames, and then weighted by a window w [ n ] , expressed as follows:
y w ( m ) [ n ] = y n + m L s w [ n ]   for   0 ≤ n ≤ L f − 1 ; 0 ≤ m ≤ M − 1.   = y [ i ] w i − m L s   for   i = n + m L s ; 0 ≤ i ≤ ( M − 1 ) L s + L f − 1.  
where y w ( m ) [ n ] denotes the windowed noisy speech signal at the m t h frame. L f represents the frame length and L s corresponds to the shift distance for each succeeding frame. Thus, the length of the overlap portion for two adjacent frames is L f − L s . The function w [ n ] has the periodic form of the Hamming window:
w [ n ] = 0.54 − 0.46 cos 2 π n L f , n = 0 , 1 , ⋯ , L f − 1 ; 0 , otherwise .
After frame partition, y w ( m ) [ n ] in a short time frame can be fed into the DNN model to perform denoising, and the result generated by the DNN is the denoised speech signal, termed y ^ w ( m ) [ n ] . Assembling the denoised speech signals in all frames altogether results in a complete speech segment. Notably, during the re-synthesis stage of the OLA, we have to rescale the amplitude synchronously, as follows:
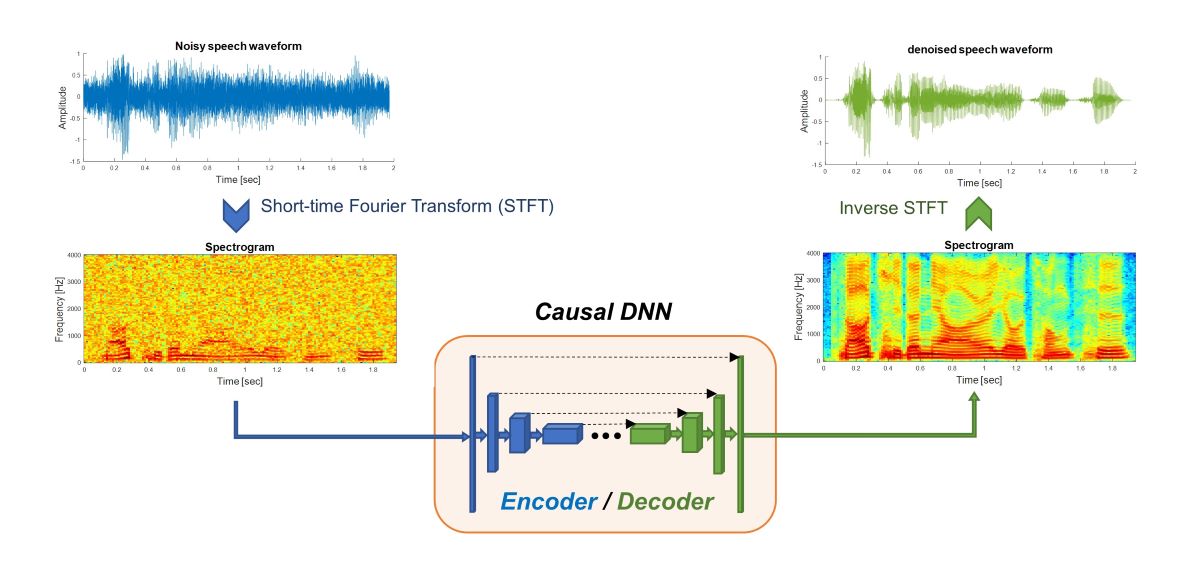
y ^ [ i ] = ∑ m = 0 M − 1 y ^ w ( m ) [ n ] n = i − m L s ∑ m = 0 M − 1 w i − m L s = ∑ m = 0 M − 1 y ^ ( i ) w i − m L s ∑ m = 0 M − 1 w i − m L s
where y ^ ( i ) denotes the denoised output. The denominator in the above expression is meant to restore the amplitude to the original regardless of which window is used. Figure 1 illustrates the concept of DNN-based speech denoising in the temporal domain, where the DNN is responsible for mapping y w ( m ) [ n ] to y ^ w ( m ) [ n ] in each frame.
If the processed object for the DNN is a sequence of spectral components, a common practice is to convert the windowed speech signal y w ( m ) [ n ] using discrete Fourier transform (DFT). The resulting output is widely known as the STFT representation, termed Y D F T ( m ) [ k ] :
Y D F T ( m ) [ k ] = ∑ n = 0 L f − 1 y w ( m ) [ n ] e − i 2 π L f k n ,   k = 0 , 1 , 2 , ⋯ , L f − 1 .
A well-designed DNN is supposed to retrieve the clean STFT coefficient, i.e., X D F T ( m ) [ k ] , from the noisy source, i.e., Y ^ D F T ( m ) [ k ] . This is equivalent to assuming that Y ^ D F T ( m ) [ k ] ≈ X D F T ( m ) [ k ] . To obtain the denoised speech signal, one must first convert Y ^ D F T ( m ) [ k ] to y ^ w ( m ) [ n ] through inverse DFT, as below, and then plug y ^ w ( m ) [ n ] into Formula (4).
y w ( m ) [ n ] = 1 L f ∑ k = 0 L f − 1 Y D F T ( m ) [ k ] e − i 2 π L f k n ,   n = 0 , 1 , 2 , ⋯ , L f − 1 .
STDCT is another option besides STFT. In case the denoising DNN operates in the STDCT domain, the input changes from y w ( m ) [ n ] to its DCT transformation Y D C T ( m ) [ k ] , defined below:
Y D C T ( m ) [ k ] = 2 L f   ∑ n = 0 L f − 1 y w ( m ) [ n ] 1 1 + δ [ k ] cos π k L f n + 1 2 ,   k = 0 , 1 , 2 , ⋯ , L f − 1 .
where δ [ k ] denotes the Kronecker delta function.
Similar to the situation in the STFT domain, the processed STDCT coefficients Y ^ D C T ( m ) [ k ] need to be converted to waveform sequences before applying the OLA (i.e., Eq. (4)) to retrieve the denoised speech signal. The formula for converting Y D C T ( m ) [ k ] to y w ( m ) [ n ] is defined as the following:
y w ( m ) [ n ] = 2 L f   ∑ k = 0 L f − 1 Y D C T ( m ) [ k ] 1 1 + δ [ n ] cos π n L f k + 1 2 ,   n = 0 , 1 , 2 , ⋯ , L f − 1 .

3.2. DNN Architecture

The U-Net architecture is widely recognized for its effectiveness in denoising tasks. Building on previous discussions, we propose a 6-level skip-connected U-Net for our experiments, implementing it with two distinct component modules: the CCAB and the more advanced GLFB.
Our classical U-Net implemented with CCABs is based on [6] and [23], with two essential modifications. Firstly, we replace masking estimation with direction mapping at the final output. Secondly, by referring to the principle for causal speech denoising in [21], we incorporate a frame buffer to collect input data from the current and past seven frames, expanding the input from one-dimensional sequences to two-dimensional (2D) feature maps. The other setups include the use of a frame length L f of 256 and a shift distance L s of 64, resulting in a 32 ms window span with an 8 ms stride, causing a 40 ms delay in real-time processing. Consequently, the input to the U-Net is an array of size 256 × 8 .
The main architecture of the classical U-Net, depicted in Figure 2, features symmetrical encoder and decoder structures [6,23], each comprising six layers of CCABs. Each submodule on the encoder side contains a convolution followed by layer normalization [24] and a leaky rectified linear unit (ReLU) [25], while the convolution is changed to a transposed convolution in the decoder. Figure 3 presents the CCABs used in the classical U-Net. A two-layer dense block [26] is added at the encoder-decoder junction to enhance latent feature integration. In Figure 2, we also label the hyperparameter settings of involved convolutions in form of “F: kernel size, output channels, S: strides.”
The contracting path of the encoder compresses the input features into a compact representation. Meanwhile, the expanding path of the decoder reconstructs the target output. Feature maps that capture local details from previous layers in the contracting path are concatenated with the upsampled feature maps in the expanding pipeline via skip connections.
Before feeding the data into the encoder, we additionally project the input features into higher dimensional space, i.e., keeping the size of the feature map unchanged but increasing the number of channels. The number of channels in the feature map is doubled for every two down-sampling layers and halved for every two up-sampling layers. Another projection layer at the terminal end is responsible for projecting the denoised features back into a single-channel output.
The advanced U-Net retains the overall architecture but replaces CCABs with GLFBs developed in [23]. The GLFB has the same structural features as the transformer architecture [27], signified by its global and local modeling. As depicted in Figure 4, the global section involves pointwise convolution, depth-wise separable convolution, gating, and channel attention, and the local section mainly involves pointwise convolutions and gating. Inside the GLFB, the gating mechanism aims to replace the commonly used activation function. Figure 4 illustrates the detailed composition involved in a GLFB. Because the input and output within a GLFB have the same dimension, addition-based skip connections are therefore used in the advanced U-Net to maintain dimensional consistency. Furthermore, the advanced U-Net requires auxiliary down-sampling and up-sampling for feature extraction and expansion, utilizing convolution with a kernel size of 2 and a stride of 2 for down-sampling and pixel-shuffle [28] for up-sampling. Figure 5 shows such configurations.
While smaller kernel sizes in GLFB stacks can reduce parameters, our focus remains on optimizing denoising performance rather than minimizing model size. We retain the exact kernel sizes of the convolutional filters in the classical U-Net. Still, the advanced U-Net with GLFBs significantly reduces learnable parameters from 612K to 238.6K, achieving 39% memory savings. Notably, the above U-Net structure (either classical or advanced) is adaptable for spectral and temporal-domain denoising tasks, using STFT or STDCT inputs and inverse transformations to reconstruct speech waveforms.

3.3. Input Arrangements

Input arrangement is crucial to the learning speed and ultimate performance of the U-Net. As indicated earlier in the introduction, both temporal and spectral representations of noisy speech can be adopted as input for denoising tasks. When performing speech denoising in the temporal domain, the input consists solely of sequences of noisy speech waveforms. Figure 6 illustrates the input arrangement in the temporal domain. When considering a transformed domain, the noisy speech signals must be converted into the designated domain. For instance, the STDCT sequence is obtained by applying Eq. (7) to a frame of the noisy speech signal. Since an STDCT sequence contains only real values, it can directly serve as input for the U-Net. Figure 7 shows the input arrangement of STDCT coefficients.
The situation is somewhat different when using STDFT coefficients as the U-Net’s input, as STDFT coefficients consist of complex values with conjugate symmetry in their first and second halves. Let us assume the number of points used in the DFT equals the frame length. Due to the conjugate symmetry of the STFT coefficients, only half of the coefficients are needed to conserve all available information. For a DFT sequence with an even length, the coefficients corresponding to the direct current (DC) and Nyquist frequency (NF) only have real values and require special attention in data arrangement. Researchers typically adopt the first half of the DFT coefficients plus one extra (i.e., NF) as input. However, this arrangement appears redundant, as the imaginary parts of both ends are essentially null. To address this issue, we take the first half of the DFT coefficients as input, arranging each coefficient’s real and imaginary parts in alternating order to form a real-value sequence [29].
Additionally, we insert the real NF value into the imaginary position of the DC term. The final arrangement is shown in Figure 8. This arrangement maintains a consistent input dimension regardless of the domain selected for denoising, allowing the proposed U-Net to be applied across various domains without the need for dimensional rescaling.

3.4. Loss Functions

Loss functions are critical for training DNNs because they guide the optimization process and determine how well a DNN performs by gauging the difference between the ideal values and its predictions. It can be shown that, regardless of the chosen domain for speech denoising, the utility of mean squared error (MSE) in computing the gradient for parameter updating has the same effect. We justify this argument through Parseval’s theorem. Let ξ [ n ] denote the difference between denoised y ^ w [ n ] and clean speech x w [ n ] in a single frame. Furthermore, Ξ D F T [ k ] = D F T ξ [ n ] and Ξ D C T [ k ] = D C T ξ [ n ] are the results of applying DFT and DCT to ξ [ n ] . Here, we have omitted the frame index in superscript while discussing the data within the same frame. According to Parseval’s theorem [30], the MSE of ξ [ n ] , Ξ D F T [ k ] , and Ξ D C T [ k ] are essentially congruent.
L M S E y ^ w [ n ] , x w [ n ] = 1 L f ∑ n = 0 L f − 1 y ^ w [ n ] − x w [ n ] 2 = 1 L f ∑ n = 0 L f − 1 ξ 2 [ n ]                   = 1 L f ⋅ 1 L f ∑ k = 0 L f − 1 Ξ F F T [ k ] 2 = 1 L f ⋅ 1 L f ∑ n = 0 L f − 1 Y ^ D F T [ k ] − X D F T [ k ] 2 = 1 L f   L M S E Y ^ D F T [ k ] , X D F T [ k ]                   = 1 L f ∑ k = 0 L f − 1 Ξ D C T [ k ] 2 = 1 L f ∑ n = 0 L f − 1 Y ^ D C T [ k ] − X D C T [ k ] 2 = L M S E Y ^ D C T [ k ] , X D C T [ k ]
Based on the above derivation, we can employ MSE as a universal loss function when comparing and analyzing U-Net’s performance in heterogeneous domains.

4. Experiment and Performance Evaluation

4.1. Datasets for Model Training

In our experiments, the speech samples were sourced from the Centre for Speech Technology Voice Cloning ToolKit (CSTR VCTK) Corpus [31], which includes utterances from 56 individuals (28 males and 28 females). We utilized recordings from 54 of these individuals, each contributing approximately 400 sentences, as training material. The recordings of the remaining two (one male and one female) were set aside for testing. Originally sampled at 48 kHz, these files were down-sampled to 8 kHz for our tests. Noise data were incorporated from the Diverse Environments Multi-channel Acoustic Noise Database (DEMAND) [32], featuring six categories of ambient noise, each with three distinct recordings. During training, noise was randomly mixed with speech at signal-to-noise ratios (SNR) of -5, 5, 10, and 15 dB. For real-time speech denoising, we employed the OLA method with L f = 256 and L s   = 64 at a frame updating rate of 125 times per second, ensuring that processing for each frame was completed within 8 milliseconds.
During the training phase, two percent of our data served as the validation set. We selected the Adam optimizer and processed mini-batches of 2048 observations. The training process was empirically set at a maximum of 60 epochs. The best model was identified based on the lowest validation loss. We conducted the above model training in MATLAB®, utilizing an NVIDIA® 3090 GPU to accelerate processing speed.

4.2. Performance Evaluation

We evaluated the performance of the proposed U-Nets across different domains, focusing on the speech quality and intelligibility of the denoised output. The speech enhancement metrics used included CSIG, CBAK, COVL (proposed by Hu and Loizou [33]), and the Perceptual Evaluation of Speech Quality (PESQ) [34]. CSIG rates speech signal quality, CBAK assesses background noise distortion, and COVL evaluates overall quality—all on a scale from 1 (poor) to 5 (excellent). The PESQ metric ranges from -0.5 to 4.5, with higher scores indicating better speech quality. Additionally, we used the short-time objective intelligibility (STOI) metric [35], ranging from 0 to 1 in terms of percentage, to assess speech intelligibility.
Our tests involved corrupting clean speech with 18 different noise types at initial SNRs of -2.5, 2.5, 7.5, and 12.5 dB. We repeated each test ten times to minimize variation and averaged the results for consistency. According to the results presented in Table 1, the U-Net’s performance in enhancing SNR and improving speech quality and intelligibility was robust across all tested domains, with slight variations. For the classical U-Net constructed using CCABs, the SNR improvement was noteworthy for low SNR conditions where the SNR level jumps from -2.5 dB to above 13 dB. By contrast, the improvement is less than 8 dB when the initial SNR is 12.5 dB. Notably, the advanced U-Net model, equipped with GLFBs, generally outperformed the classical model with CCABs. Improvements of approximately 0.48 dB in SNR and 0.033 in PESQ scores were observed for the input taken from the STFT domain, and the gains were 0.42 dB in SNR and 0.041 in PESQ for the input taken from the STDCT domain.
Our findings suggest that the U-Net’s performance was comparably strong in both the STFT and STDCT domains, with marginal superiority to that attained directly using time sequences in the temporal domain. Furthermore, metrics sensitive to the Fourier spectra, like CSIG, CBAK, and COVL, also demonstrated an apparent preference for the STFT and STDCT domains over the temporal domain. This adaptability and performance consistency underline the potential of U-Net architectures for a broad range of audio processing applications.

4.3. Further Considerations of Loss Function in the STFT and STDCT Domains

The results in Table 1 demonstrate that the U-Net architecture is practical and efficient for speech enhancement. The performance discussed in the previous section is based on training U-Nets using MSE as the loss function. In DNN-based speech denoising, loss functions that integrate magnitude constraints with complex spectral optimization are commonly used to enhance speech quality and intelligibility. Additionally, power compression has been employed to improve the estimated speech quality further. Given the proposed U-Nets’ superior performance in the STFT and STDCT domains, we apply techniques in [9,22] to refine the loss function, potentially improving speech quality further:
L c o m p Y ^ D F T [ k ] , X D F T [ k ] = α L M S E _ M a g | Y ^ D F T , β [ k ] | , | X D F T , β [ k ] | + ( 1 − α ) L M S E _ R I Y ^ D F T , β [ k ] , X D F T , β [ k ]
with Y ^ D F T , β [ k ] and X D F T , β [ k ] defined as
Y ^ D F T , β ( k ) = Y ^ D F T [ k ] β Y ^ D F T [ k ] Y ^ D F T [ k ] = Y ^ D F T [ k ] Y ^ D F T * [ k ] β / 2 Y ^ D F T [ k ] Y ^ D F T [ k ] Y ^ D F T * [ k ] ; X β ( k ) = X D F T [ k ] β X D F T [ k ] X D F T [ k ] = X D F T [ k ] X D F T * [ k ] β / 2 X D F T [ k ] X D F T [ k ] X D F T * [ k ] .
In the above context, the subscript β attached to a DFT coefficient indicates the exponent used to modify the magnitude. A β value between 0 and 1 not only aligns with human auditory perception of sound intensity but also reduces the dynamic range of spectral coefficients, thus enhancing network estimation. Parameter α represents a mixing ratio for combining the magnitude loss L M S E _ M a g ( ⋅ ) and the STFT-RI loss L M S E _ R I ( ⋅ ) . The resulting loss function, termed L c o m p Y ^ D F T ( k ) , X D F T ( k ) and referred to as composite mean squared error (CMSE), is formulated on the understanding that human auditory perception aligns more closely with a logarithmic scale, and the sensitivities to spectral magnitudes and phases differ. Values of α = 0.5 and β = 0.5 have been reported to achieve satisfactory results [9,22].
Liu et al. [23] employed a similar approach with STDCT coefficients. They used a composite loss function comprising two loss values: the MSE loss calculated from absolute STDCT values and the MSE loss derived from the original polar values. Following the expression outlined in Eq. (10), we formulate the composite loss function in the STDCT domain as follows:
L c o m p Y ^ D C T [ k ] , X D C T [ k ] = α L M S E _ M a g | Y ^ D C T , β [ k ] | , | X D C T , β [ k ] | + ( 1 − α ) L M S E _ P o l a r Y ^ D C T , β [ k ] , X D C T , β [ k ]
with Y ^ D C T , β [ k ] and X D C T , β [ k ] defined as
Y ^ D F T , β ( k ) = sgn Y ^ D C T [ k ] ⋅ Y ^ D C T [ k ] β ; X β ( k ) = sgn X D C T [ k ] ⋅ X D C T [ k ] β .
where sgn ( ⋅ ) denotes the sign function.
Our experiments assessed the effects of four combinations of α and β. Specifically, the combination (α,β)=(0,1) directly applies MSE to the target coefficients. The setting (α,β)=(0.5,1), which concurrently minimizes the magnitude and phase spectra, replicates the original parameters used in prior studies [9]. The combination (α,β)=(0,0.5) solely considers power compression factors, whereas (α,β)=(0.5,0.5) engages both magnitude estimation and phase recovery with power compression integrated. The choice of α and β at 0.5 reflects their proven efficacy in STFT-based speech denoising applications, anticipating similar results with the STDCT sequences.
Both classical and advanced U-Net models were retrained and evaluated under the above four settings. As shown in Table 2 and Table 3, trends in response to adjustments in α and β were similar across both U-Net configurations. Modifying either α or β independently showed minimal impact on all evaluated metrics. Metrics from the advanced U-Net, which incorporates GLFBs, generally surpassed those from the classical U-Net. Our experimental results indicate that simultaneously optimizing phase and magnitude spectra without considering power compression actually lowered perceived quality. Also, applying power compression alone (α,β)=(0,0.5) can only yield minor improvements. However, combining power compression with balanced magnitude and phase adjustments significantly enhanced speech quality, with improvements of 0.093 and 0.102 in PESQ for the classical U-Net in the STFT and STDCT domains, respectively.
Further data analyses from Table 2 and Table 3 highlight the advantages of substituting CCABs with GLFBs within the U-Net framework, regardless of compared indicators. GLFBs employ several state-of-the-art techniques, including the MetaFormer architecture, channel attention, gating mechanism, and depthwise separable convolution, all contributing to performance enhancements. Aside from depthwise separable convolution, the specific impact of these techniques warrants further investigation.

5. Conclusions

This study evaluates a 6-level U-Net constructed with either CCABs or GLFBs to assess the efficacy of DNN-based speech denoising across various domains. To ensure causality, the U-Net employs a frame-buffering mechanism that collects feature sequences from the current and previous seven frames. Our experimental results demonstrate consistent enhancements in CSIG, CBAK, COVL, and PESQ for U-Nets operating in the STFT and STDCT domains, outperforming those in the temporal domain. Importantly, the U-Net built with GLFBs features fewer learnable parameters and enhanced denoising efficiency. Given the compatibility of STDCT and STFT with perceptual-based loss functions, we explored domain-specific composite loss functions to improve perceptual quality further. Notable improvements in PESQ and STOI scores were observed when accounting for factors like power compression and the trade-off between spectral magnitudes and phases.
In future work, we plan to expand the capabilities of our denoising DNN based on these findings. Although the proposed U-Net significantly enhances speech quality, the output remains narrowband at 8 kHz. Our next objective is to integrate super-resolution techniques into the denoising DNN to obtain high-quality 32- or even 48-kHz wideband speech.

Author Contributions

Conceptualization, Hwai-Tsu Hu; Data curation, Hwai-Tsu Hu and Tung-Tsun Lee; Formal analysis, Hwai-Tsu Hu; Funding acquisition, Hwai-Tsu Hu; Investigation, Hwai-Tsu Hu and Tung-Tsun Lee; Project administration, Hwai-Tsu Hu; Resources, Hwai-Tsu Hu and Tung-Tsun Lee; Software, Hwai-Tsu Hu and Tung-Tsun Lee; Supervision, Hwai-Tsu Hu; Validation, Hwai-Tsu Hu; Visualization, Hwai-Tsu Hu; Writing—original draft, Hwai-Tsu Hu; Writing—review & editing, Hwai-Tsu Hu and Tung-Tsun Lee.

Funding

This research work was supported by the National Science and Technology Council, Taiwan (R.O.C.) under Grants NSTC 112-2221-E-197-026 and 113-2221-E-197-024.

Data Availability Statement

The speech and noise datasets analyzed during this study are accessible from the CSTR VCTK Corpus [https://www.kaggle.com/datasets/muhmagdy/valentini-noisy (accessed on 24 September 2024)] and DEMAND database [https://www.kaggle.com/datasets/chrisfilo/demand?resource=download (accessed on 24 September 2024)], respectively. The programs implemented in MATLAB® code are available upon reasonable request.

Acknowledgments

This article is a revised and expanded version of a paper entitled “Suitable domains for causal speech denoising using DNN with U-Net architecture”, which was presented at the 7th International Conference on Knowledge Innovation and Invention 2024 (ICKII 2024), Nagoya, Japan, August 16-18, 2024.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Sun, Y.; Wang, W.; Chambers, J.A.; Naqvi, S.M. Enhanced Time-Frequency Masking by Using Neural Networks for Monaural Source Separation in Reverberant Room Environments. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), 3-7 Sept. 2018, 2018. pp. 1647–1651.
  2. Choi, H.-S.; Heo, H.; Lee, J.H.; Lee, K. Phase-aware Single-stage Speech Denoising and Dereverberation with U-Net. ArXiv 2020, abs/2006.00687. [Google Scholar]
  3. Sarker, I.H. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Computer Science 2021, 2, 420. [Google Scholar] [CrossRef]
  4. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. ArXiv 2015, abs/1505.04597. [Google Scholar]
  5. Tan, K.; Wang, D. Learning Complex Spectral Mapping With Gated Convolutional Recurrent Networks for Monaural Speech Enhancement. IEEE/ACM Trans. on Audio, Speech, and Language Processing 2020, 28, 380–390. [Google Scholar] [CrossRef]
  6. Choi, H.-S.; Kim, J.-H.; Huh, J.; Kim, A.; Ha, J.-W.; Lee, K. Phase-aware Speech Enhancement with Deep Complex U-Net. ArXiv 2019, abs/1903.03107. [Google Scholar]
  7. Li, A.; Liu, W.; Zheng, C.; Fan, C.; Li, X. Two Heads are Better Than One: A Two-Stage Complex Spectral Mapping Approach for Monaural Speech Enhancement. IEEE/ACM Trans. on Audio, Speech, and Language Processing 2021, 29, 1829–1843. [Google Scholar] [CrossRef]
  8. Yuan, W. A time–frequency smoothing neural network for speech enhancement. Speech Communication 2020, 124, 75–84. [Google Scholar] [CrossRef]
  9. Luo, X.; Zheng, C.; Li, A.; Ke, Y.; Li, X. Analysis of trade-offs between magnitude and phase estimation in loss functions for speech denoising and dereverberation. Speech Communication 2022, 145, 71–87. [Google Scholar] [CrossRef]
  10. Azarang, A.; Kehtarnavaz, N. A review of multi-objective deep learning speech denoising methods. Speech Communication 2020, 122, 1–10. [Google Scholar] [CrossRef]
  11. Pandey, A.; Wang, D. Dense CNN With Self-Attention for Time-Domain Speech Enhancement. IEEE/ACM Trans. on Audio, Speech, and Language Processing 2020, 29, 1270–1279. [Google Scholar] [CrossRef]
  12. Défossez, A.; Synnaeve, G.; Adi, Y. Real Time Speech Enhancement in the Waveform Domain. ArXiv 2020, abs/2006.12847. [Google Scholar]
  13. Germain, F.G.; Chen, Q.; Koltun, V. Speech Denoising with Deep Feature Losses. In Proceedings of the Interspeech, 2018.
  14. Erdogan, H.; Hershey, J.R.; Watanabe, S.; Roux, J.L. Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 19-24 April 2015, 2015. pp. 708–712.
  15. Kulmer, J.; Mahale, P.M.B. Phase Estimation in Single Channel Speech Enhancement Using Phase Decomposition. IEEE Signal Processing Letters 2015, 22, 598–602. [Google Scholar] [CrossRef]
  16. Lu, X.; Tsao, Y.; Matsuda, S.; Hori, C. Speech enhancement based on deep denoising autoencoder. In Proceedings of the Interspeech; 2013. [Google Scholar]
  17. Zhao, H.; Zarar, S.; Tashev, I.; Lee, C.H. Convolutional-Recurrent Neural Networks for Speech Enhancement. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 15-20 April 2018, 2018. pp. 2401–2405.
  18. Tan, K.; Wang, D. A Convolutional Recurrent Neural Network for Real-Time Speech Enhancement. In Proceedings of the Interspeech, Hyderabad, India, 2-6 September; 2018; pp. 3229–3233. [Google Scholar]
  19. Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
  20. Mirsamadi, S.; Tashev, I.J. Causal Speech Enhancement Combining Data-Driven Learning and Suppression Rule Estimation. In Proceedings of the Interspeech; 2016. [Google Scholar]
  21. Park, S.R.; Lee, J. A Fully Convolutional Neural Network for Speech Enhancement. In Proceedings of the Interspeech 2017, Stockholm, Sweden; 2017; pp. 1993–1997. [Google Scholar]
  22. Li, A.; Zheng, C.; Peng, R.; Li, X. On the importance of power compression and phase estimation in monaural speech dereverberation. JASA Express Letters 2021, 1. [Google Scholar] [CrossRef]
  23. Liu, L.; Guan, H.; Ma, J.; Dai, W.; Wang, G.-Y.; Ding, S. A Mask Free Neural Network for Monaural Speech Enhancement. ArXiv 2023, abs/2306.04286. [Google Scholar]
  24. Ba, J.; Kiros, J.R.; Hinton, G.E. Layer Normalization. ArXiv 2016, abs/1607.06450. [Google Scholar]
  25. Maas, A.L. Rectifier Nonlinearities Improve Neural Network Acoustic Models. 2013.
  26. Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 21-26 July 2017; 2017; pp. 2261–2269. [Google Scholar]
  27. Vaswani, A.; Shazeer, N.M.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Neural Information Processing Systems; 2017. [Google Scholar]
  28. Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016, 1874–1883. [Google Scholar]
  29. Hu, H.-T.; Tsai, H.-H.; Lee, T.-T. Suitable domains for causal speech denoising using DNN with U-Net architecture. In Proceedings of the 7th International Conference on Knowledge Innovation and Invention 2024 (ICKII 2024), Nagoya, Japan, August 16-18; 2024. [Google Scholar]
  30. Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H. Signals & systems, 2nd ed.; Prentice Hall: Upper Saddle River, N.J., 1997. [Google Scholar]
  31. Valentini-Botinhao, C.; Wang, X.; Takaki, S.; Yamagishi, J. Investigating RNN-based speech enhancement methods for noise-robust Text-to-Speech. In Proceedings of the Speech Synthesis Workshop; 2016. [Google Scholar]
  32. Thiemann, J.; Ito, N.; Vincent, E. The Diverse Environments Multi-channel Acoustic Noise Database (DEMAND): A database of multichannel environmental noise recordings. Journal of the Acoustical Society of America 2013, 133, 3591–3591. [Google Scholar] [CrossRef]
  33. Hu, Y.; Loizou, P.C. Evaluation of Objective Quality Measures for Speech Enhancement. IEEE Trans. on Audio, Speech, and Language Processing 2008, 16, 229–238. [Google Scholar] [CrossRef]
  34. ITU-T, R.P. Methods for subjective determination of transmission quality International Telecommunications Union: Geneva, Switzerland, 1996.
  35. Taal, C.H.; Hendriks, R.C.; Heusdens, R.; Jensen, J. An Algorithm for Intelligibility Prediction of Time–Frequency Weighted Noisy Speech. IEEE Trans. on Audio, Speech, and Language Processing 2011, 19, 2125–2136. [Google Scholar] [CrossRef]
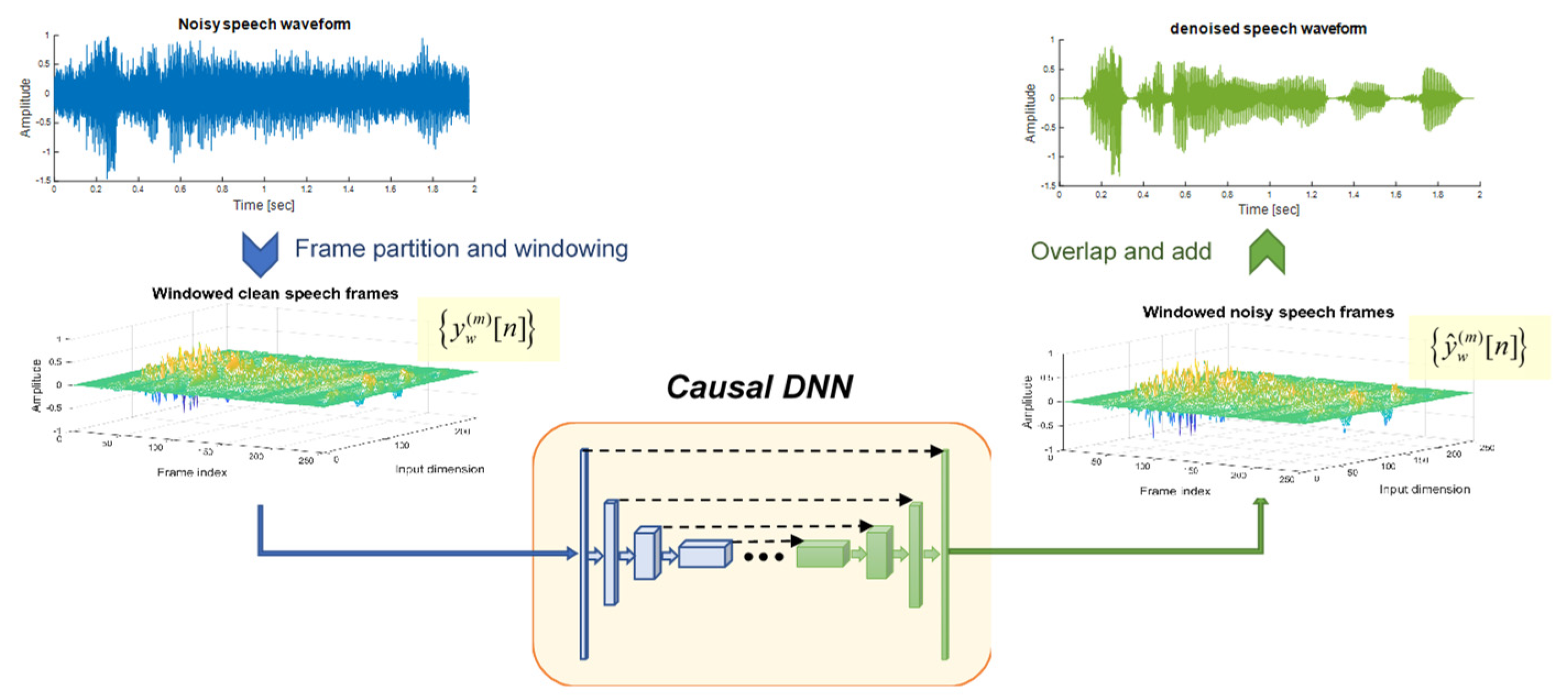
Preprints 119822 g001
Figure 1. Speech denoising through deep neural networks in the temporal domain.
Figure 1. Speech denoising through deep neural networks in the temporal domain.
Preprints 119822 g001
Preprints 119822 g002
Figure 2. Network architecture for the proposed U-Net.
Figure 2. Network architecture for the proposed U-Net.
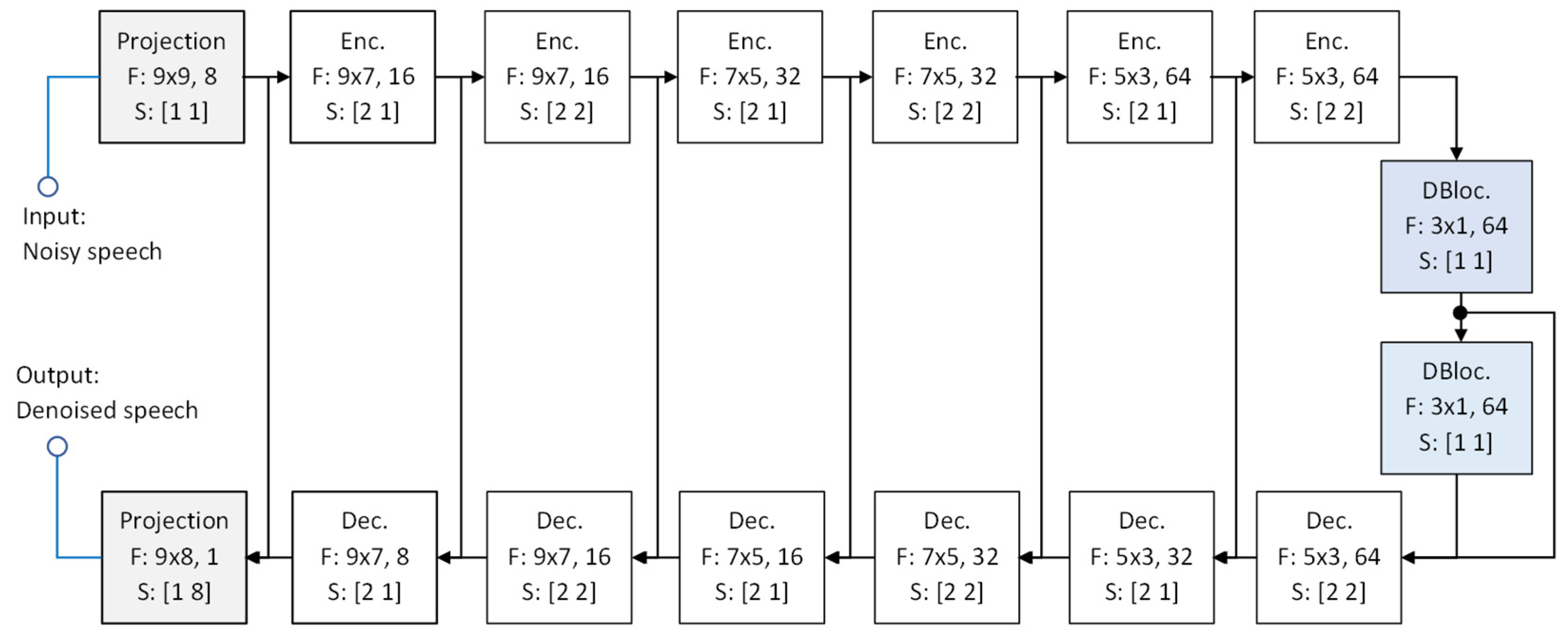
Preprints 119822 g002
Preprints 119822 g003
Figure 3. CCABs used in the encoder and decoder sides of the classical U-Net.
Figure 3. CCABs used in the encoder and decoder sides of the classical U-Net.
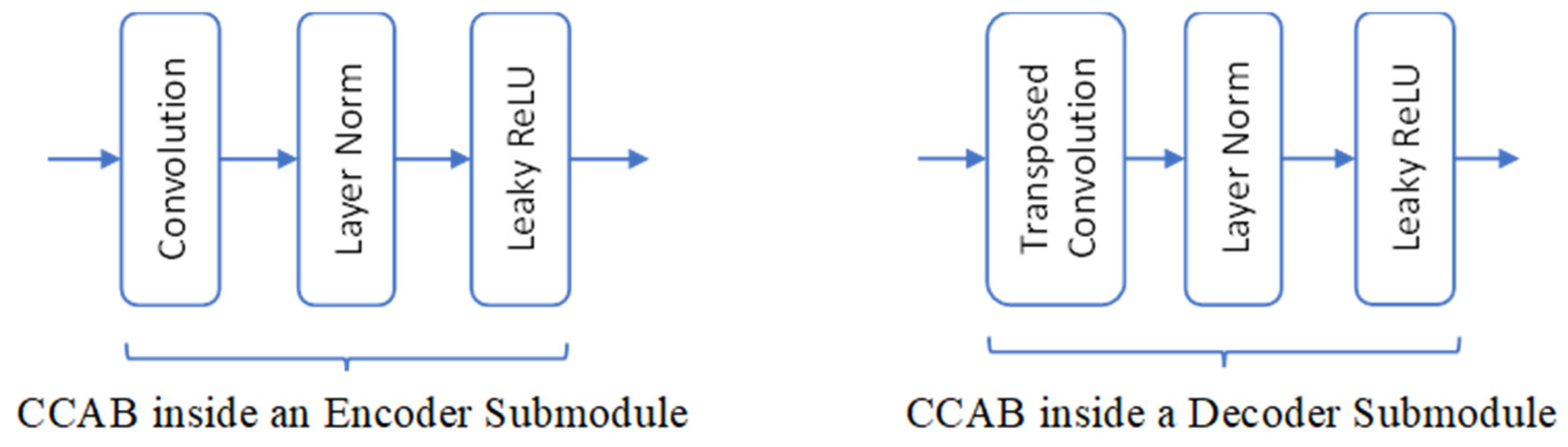
Preprints 119822 g003
Preprints 119822 g004
Figure 4. The composition of GLFB.
Figure 4. The composition of GLFB.
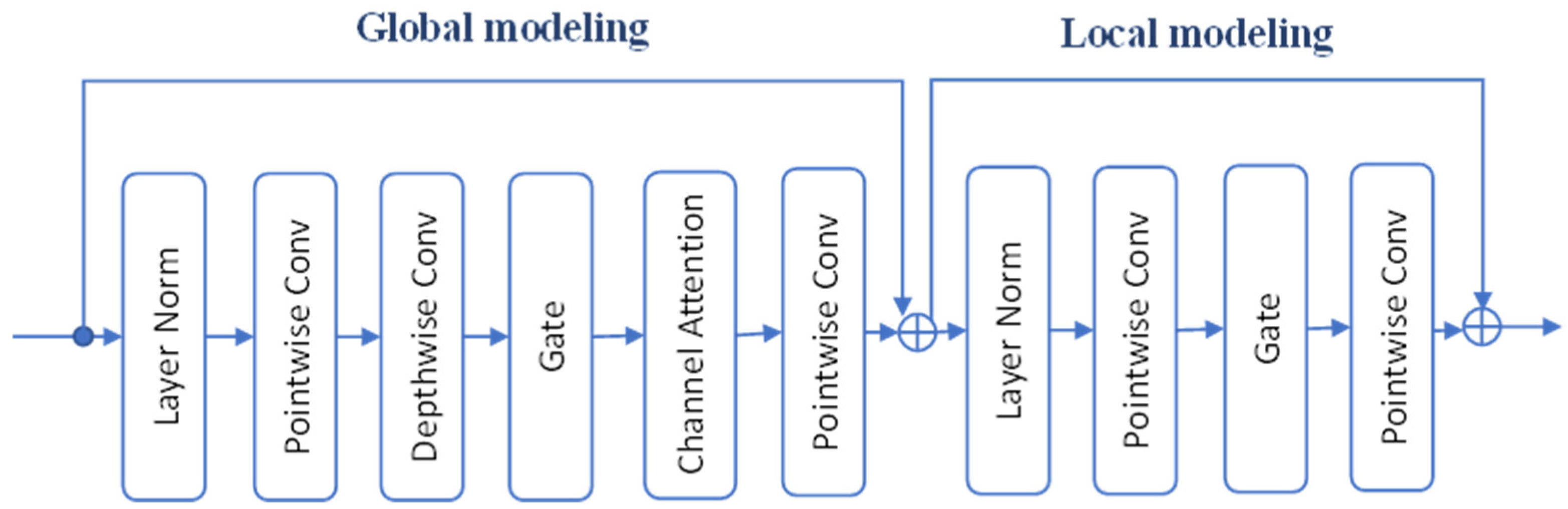
Preprints 119822 g004
Preprints 119822 g005
Figure 5. Encoder and decoder submodules used in the advanced U-Net.
Figure 5. Encoder and decoder submodules used in the advanced U-Net.
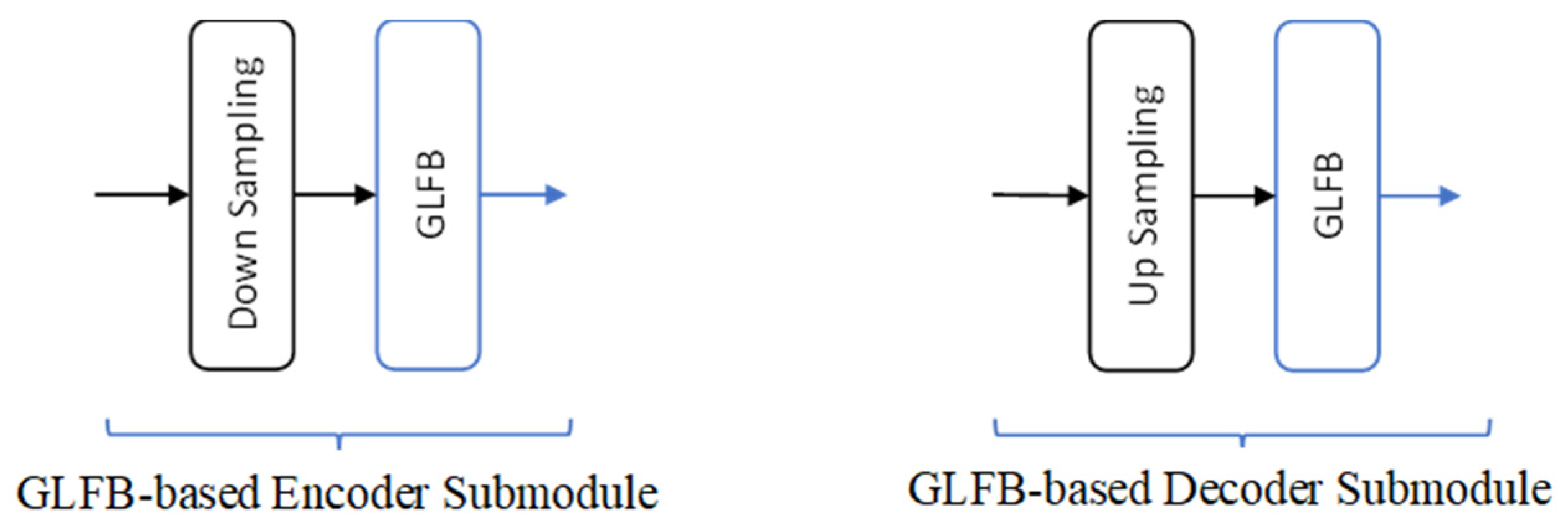
Preprints 119822 g005
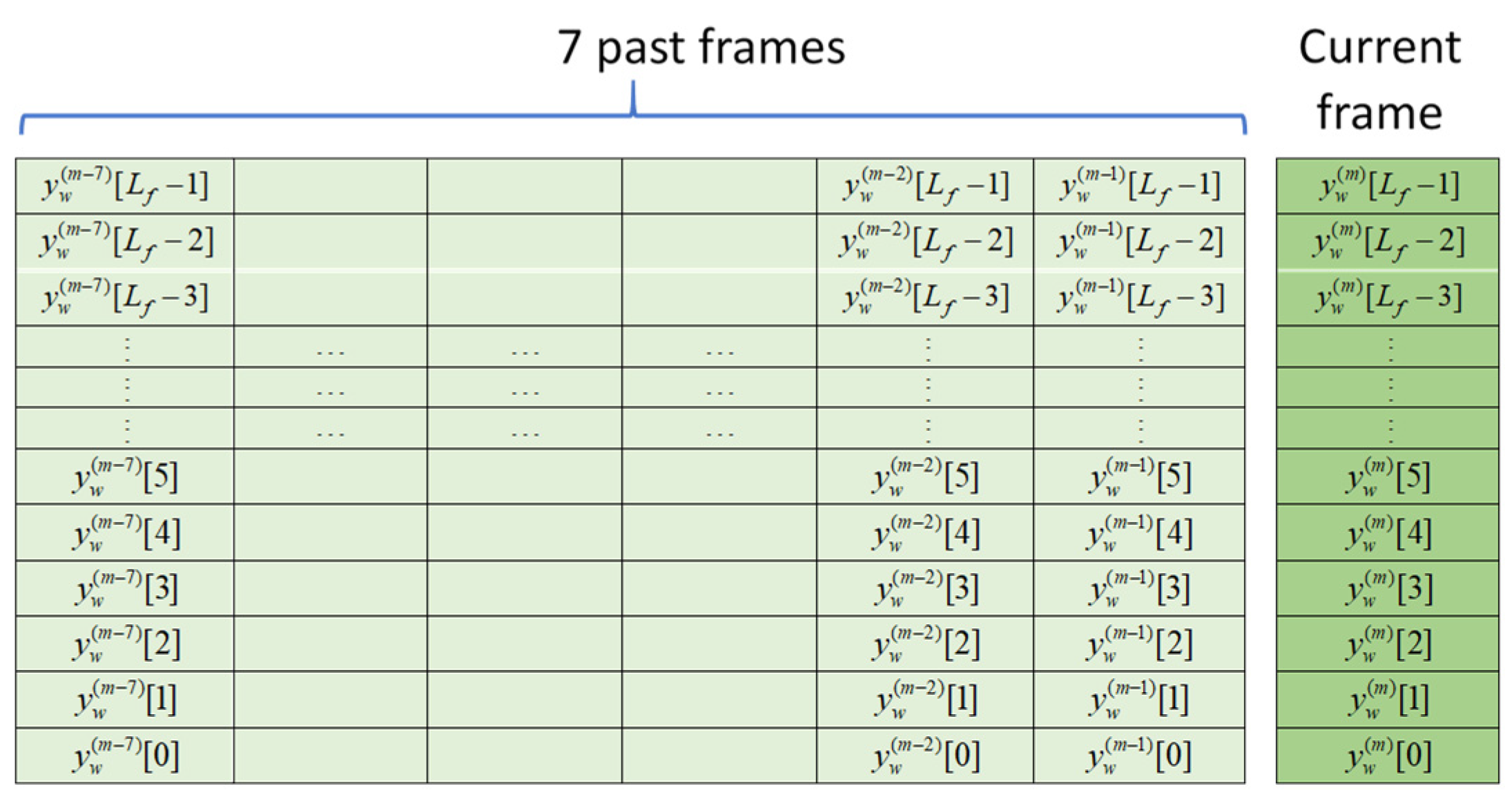
Preprints 119822 g006
Figure 6. U-Net’s input adopted in the temporal domain.
Figure 6. U-Net’s input adopted in the temporal domain.
Preprints 119822 g006
Preprints 119822 g007
Figure 7. U-Net’s input adopted in the STDCT domain.
Figure 7. U-Net’s input adopted in the STDCT domain.
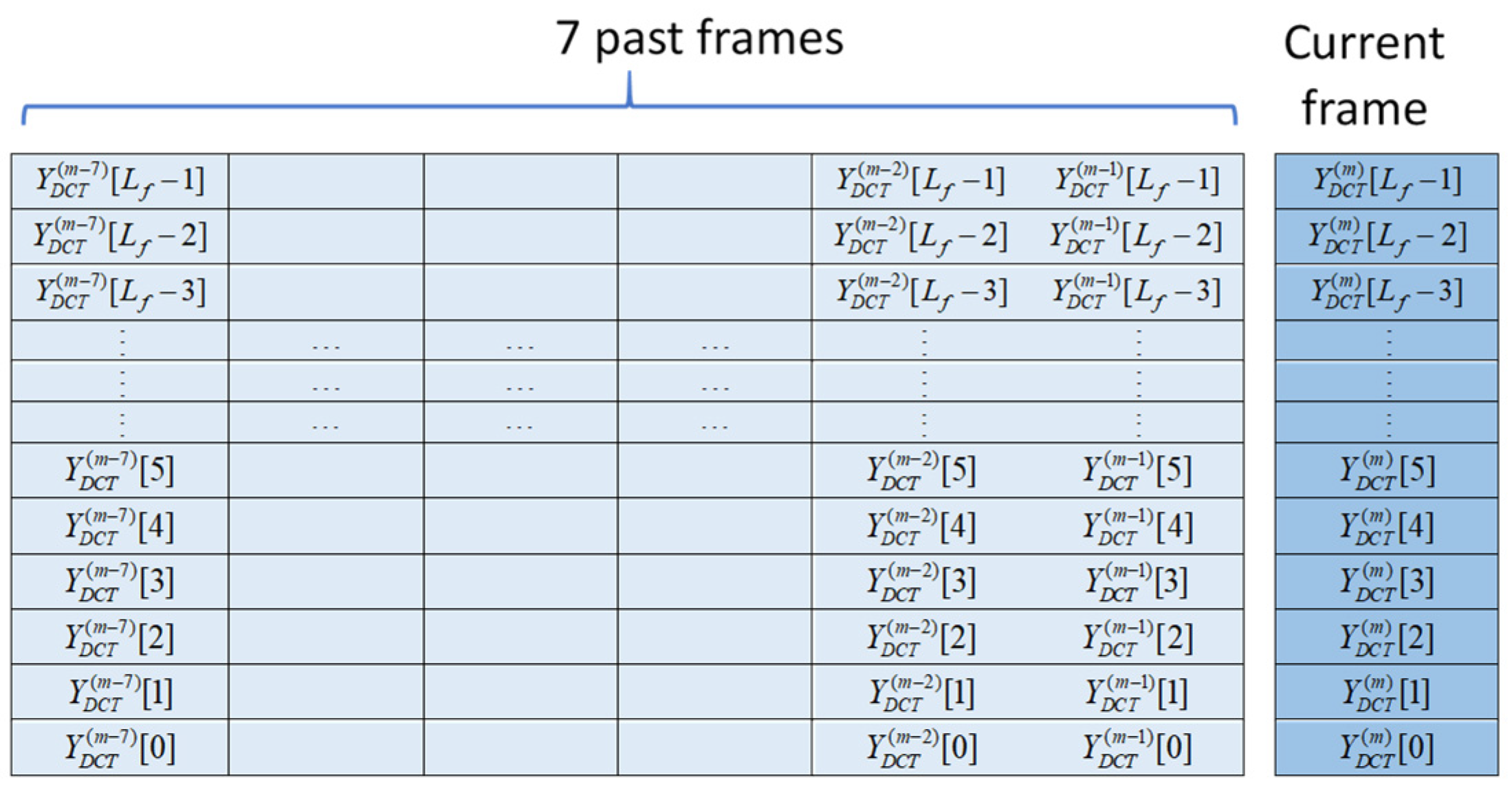
Preprints 119822 g007
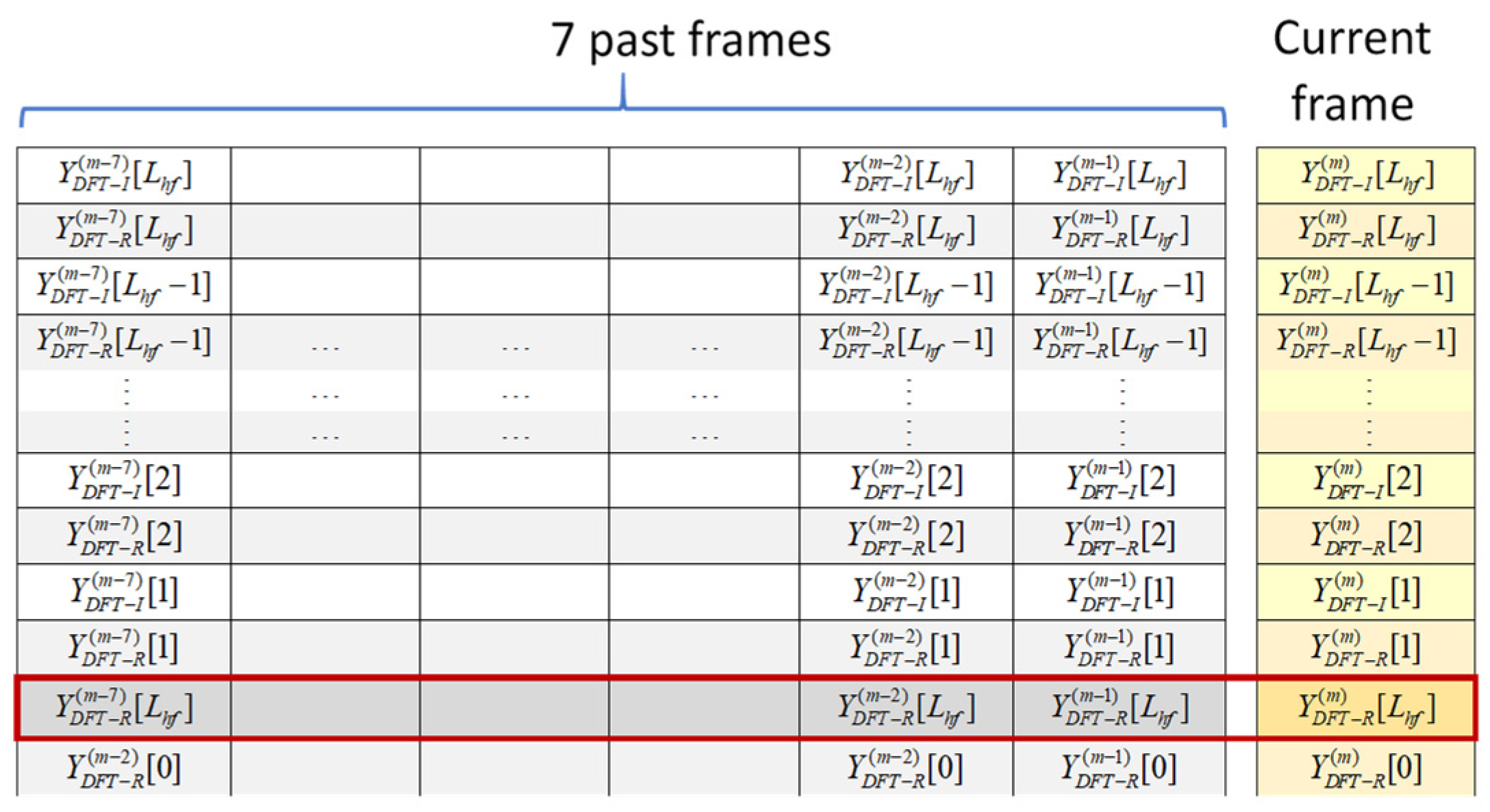
Preprints 119822 g008
Figure 8. U-Net’s input adopted in the STFT domain.
Figure 8. U-Net’s input adopted in the STFT domain.
Preprints 119822 g008
Table 1. Performance comparison for the classical and advanced U-Nets operating in the STFT, STDCT, and temporal domains.
Table 1. Performance comparison for the classical and advanced U-Nets operating in the STFT, STDCT, and temporal domains.
Input type Initial
SNR 		Classical U-Net withCCABs Advanced U-Net with GLFBs
Resulting
SNR (dB)		 CSIG CBAK COVL PESQ STOI (%) Resulting
SNR (dB)		 CSIG CBAK COVL PESQ STOI (%)
STFT-RI sequences –2.5 dB 12.97 3.460 3.055 3.091 2.811 80.59 13.73 3.495 3.114 3.132 2.851 81.69
2.5 dB 15.96 3.941 3.372 3.496 3.097 85.69 16.51 3.948 3.410 3.515 3.123 86.39
7.5 dB 18.37 4.322 3.624 3.814 3.323 89.03 18.75 4.334 3.660 3.838 3.355 89.65
12.5 dB 20.45 4.618 3.854 4.072 3.518 91.45 20.69 4.632 3.887 4.097 3.549 91.99
Average 16.94 4.085 3.476 3.618 3.187 86.69 17.42 4.102 3.518 3.646 3.220 87.43
STDCT sequences –2.5 dB 13.04 3.458 3.062 3.096 2.821 80.85 13.79 3.506 3.122 3.149 2.878 81.95
2.5 dB 16.04 3.940 3.375 3.498 3.102 85.81 16.53 3.964 3.421 3.533 3.145 86.53
7.5 dB 18.38 4.345 3.626 3.830 3.332 89.14 18.66 4.358 3.666 3.858 3.370 89.68
12.5 dB 20.50 4.661 3.861 4.101 3.535 91.61 20.67 4.660 3.890 4.116 3.562 92.00
Average 16.99 4.101 3.481 3.631 3.198 86.85 17.41 4.122 3.525 3.664 3.239 87.54
Waveform sequences –2.5 dB 13.40 3.338 3.014 2.996 2.739 81.18 13.45 3.313 3.009 2.980 2.734 81.13
2.5 dB 15.96 3.784 3.297 3.364 2.992 85.61 16.17 3.761 3.306 3.355 3.000 85.81
7.5 dB 18.21 4.178 3.547 3.690 3.218 88.80 18.30 4.152 3.543 3.673 3.218 88.88
12.5 dB 20.05 4.492 3.771 3.958 3.418 91.13 20.13 4.469 3.761 3.942 3.418 91.06
Average 16.90 3.948 3.407 3.502 3.092 86.68 17.01 3.924 3.405 3.487 3.092 86.72
Table 2. Performance comparison for the classical and advanced U-Nets in the STFT domain with four loss functions exploiting the power compression and trade-off between magnitude estimation and phase recovery.
Table 2. Performance comparison for the classical and advanced U-Nets in the STFT domain with four loss functions exploiting the power compression and trade-off between magnitude estimation and phase recovery.
Loss function
( α , β ) 		Initial
SNR 		Classical U-Net with CCABs Advanced U-Net with GLFBs
Resulting
SNR (dB)		 CSIG CBAK COVL PESQ STOI (%) Resulting
SNR (dB)		 CSIG CBAK COVL PESQ STOI (%)
(0, 1) –2.5 dB 12.97 3.460 3.055 3.091 2.811 80.59 13.73 3.495 3.114 3.132 2.851 81.69
2.5 dB 15.96 3.941 3.372 3.496 3.097 85.69 16.51 3.948 3.410 3.515 3.123 86.39
7.5 dB 18.37 4.322 3.624 3.814 3.323 89.03 18.75 4.334 3.660 3.838 3.355 89.65
12.5 dB 20.45 4.618 3.854 4.072 3.518 91.45 20.69 4.632 3.887 4.097 3.549 91.99
Average 16.94 4.085 3.476 3.618 3.187 86.69 17.42 4.102 3.518 3.646 3.220 87.43
(0.5, 1) –2.5 dB 12.75 3.638 3.053 3.190 2.809 81.02 13.58 3.737 3.125 3.277 2.876 82.41
2.5 dB 15.65 4.052 3.349 3.548 3.076 85.82 16.23 4.110 3.399 3.604 3.126 86.83
7.5 dB 18.00 4.388 3.600 3.843 3.305 89.21 18.46 4.424 3.635 3.880 3.339 89.91
12.5 dB 20.15 4.655 3.834 4.085 3.499 91.65 20.44 4.675 3.859 4.109 3.526 92.07
Average 16.64 4.183 3.459 3.666 3.172 86.92 17.18 4.237 3.504 3.718 3.217 87.81
(0, 0.5) –2.5 dB 13.30 3.298 3.024 2.973 2.758 80.37 13.82 3.397 3.098 3.062 2.821 81.36
2.5 dB 16.27 3.837 3.375 3.442 3.107 85.67 16.63 3.930 3.427 3.517 3.153 86.30
7.5 dB 18.63 4.318 3.666 3.844 3.396 89.25 18.84 4.389 3.701 3.903 3.434 89.58
12.5 dB 20.52 4.679 3.912 4.156 3.627 91.70 20.72 4.739 3.944 4.207 3.666 92.02
Average 17.18 4.033 3.494 3.604 3.222 86.75 17.50 4.114 3.542 3.672 3.269 87.32
(0.5, 0.5) –2.5 dB 13.08 3.750 3.120 3.267 2.844 81.14 13.93 3.901 3.222 3.402 2.949 82.65
2.5 dB 16.04 4.206 3.448 3.677 3.171 86.25 16.66 4.312 3.520 3.777 3.259 87.24
7.5 dB 18.44 4.569 3.715 4.007 3.442 89.74 18.89 4.639 3.769 4.078 3.509 90.30
12.5 dB 20.50 4.848 3.954 4.268 3.663 92.18 20.90 4.907 4.004 4.331 3.727 92.67
Average 17.01 4.343 3.559 3.805 3.280 87.32 17.59 4.440 3.629 3.897 3.361 88.21
Table 3. Performance comparison for the classical and advanced U-Nets in the STDCT domain with four loss functions exploiting the power compression and trade-off between magnitude estimation and phase recovery.
Table 3. Performance comparison for the classical and advanced U-Nets in the STDCT domain with four loss functions exploiting the power compression and trade-off between magnitude estimation and phase recovery.
Loss function
( α , β ) 		Initial
SNR 		Classical U-Net with CCABs Advanced U-Net with GLFBs
Resulting
SNR (dB)		 CSIG CBAK COVL PESQ STOI (%) Resulting
SNR (dB)		 CSIG CBAK COVL PESQ STOI (%)
(0, 1) –2.5 dB 13.04 3.458 3.062 3.096 2.821 80.85 13.79 3.506 3.122 3.149 2.878 81.95
2.5 dB 16.04 3.940 3.375 3.498 3.102 85.81 16.53 3.964 3.421 3.533 3.145 86.53
7.5 dB 18.38 4.345 3.626 3.830 3.332 89.14 18.66 4.358 3.666 3.858 3.370 89.68
12.5 dB 20.50 4.661 3.861 4.101 3.535 91.61 20.67 4.660 3.890 4.116 3.562 92.00
Average 16.99 4.101 3.481 3.631 3.198 86.85 17.41 4.122 3.525 3.664 3.239 87.54
(0.5, 1) –2.5 dB 12.91 3.642 3.077 3.206 2.837 81.28 13.19 3.700 3.103 3.245 2.857 81.79
2.5 dB 15.92 4.077 3.385 3.580 3.114 86.27 16.10 4.090 3.395 3.591 3.123 86.50
7.5 dB 18.26 4.412 3.627 3.870 3.334 89.48 18.38 4.407 3.632 3.871 3.341 89.67
12.5 dB 20.30 4.676 3.852 4.108 3.524 91.68 20.41 4.667 3.857 4.105 3.528 91.99
Average 16.85 4.202 3.485 3.691 3.202 87.18 17.02 4.216 3.497 3.703 3.212 87.48
(0, 0.5) –2.5 dB 13.09 3.345 3.035 3.008 2.776 80.32 13.79 3.401 3.099 3.065 2.828 81.41
2.5 dB 16.06 3.845 3.376 3.448 3.107 85.60 16.55 3.913 3.420 3.506 3.155 86.25
7.5 dB 18.43 4.314 3.658 3.841 3.390 89.10 18.84 4.384 3.703 3.902 3.440 89.58
12.5 dB 20.42 4.687 3.908 4.160 3.626 91.67 20.68 4.740 3.943 4.209 3.670 91.98
Average 17.00 4.048 3.494 3.614 3.225 86.67 17.47 4.109 3.541 3.670 3.273 87.30
(0.5, 0.5) –2.5 dB 13.23 3.792 3.141 3.303 2.877 81.48 13.80 3.889 3.208 3.386 2.934 82.40
2.5 dB 16.03 4.229 3.452 3.695 3.188 86.34 16.63 4.313 3.516 3.774 3.254 87.06
7.5 dB 18.52 4.591 3.726 4.026 3.460 89.73 18.86 4.636 3.764 4.072 3.503 90.13
12.5 dB 20.48 4.862 3.957 4.280 3.674 92.08 20.87 4.903 4.000 4.324 3.720 92.52
Average 17.07 4.368 3.569 3.826 3.300 87.40 17.54 4.435 3.622 3.889 3.353 88.03
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated