1. Introduction
The quality factors of inductor (L) and capacitor (C) are small at the millimeter wave (mmWave). Therefore, designing an ultra-low phase noise (PN) LC voltage-controlled oscillator (VCO) that adheres to the stringent integrated jitter specification for the beyond 5G communication systems is tough. The cascade local oscillator (LO) generator structures of a lower-frequency synthesizer and a frequency multiplier (FM) have been recently published [
1,
2,
3,
4,
5] to accomplish the jitter performance. The main goals of the lower-frequency synthesizer are to provide the best in-band phase noise (PN) and the finest channel resolution performances.
A multiplying delay-locked loop (MDLL), a subsampling phase-locked loop (SSPLL), and an injection-locked PLL (ILPLL) are good candidate topologies to achieve ultra-low in-band PN.
Figure 1(a) shows a phase edge combined (EC)-based MDLL block diagram. Output frequency (
fout) can be expressed as N×
fin/2, where N is an even integer number of delay cells in a voltage-controlled delay line (VCDL). Therefore, the MDLL channel resolution would be
fin. The biggest advantage of the MDLL is that it is free from jitter accumulation, which will improve the in-band PN. However, N is strictly difficult to program because the delay unit number in a VCDL must be changed. Therefore, its channel programmability is limited [
6,
7,
8,
9].
Both the SSPLL and ILPLL (
Figure 1(b) and
Figure 1(c)) have the same channel resolution (
fin) but require extra frequency tracking loops (FTLs) for locking the output frequency as N×
fin. After the target frequencies are tuned, the FTLs are turned off, and their lock states are maintained by a subsampling phase detector (SSPD) for the SSPLL and cascade connection of a digitally-controlled delay line (DCDL) and a pulse width controller for the ILPLL. Therefore, their in-band PNs will be improved because in-band PN sources are no longer multiplied by N
2 when transferred to the PLL outputs [
10,
11,
12]. However, neither the SSPLL nor the ILPLL is suitable for high-magnitude multiplication, N, because it is difficult to design a reliable SSPD and DCDL as N is increased [
13,
14,
15,
16]. Consequently, the number of possible programmable channels is also restricted.
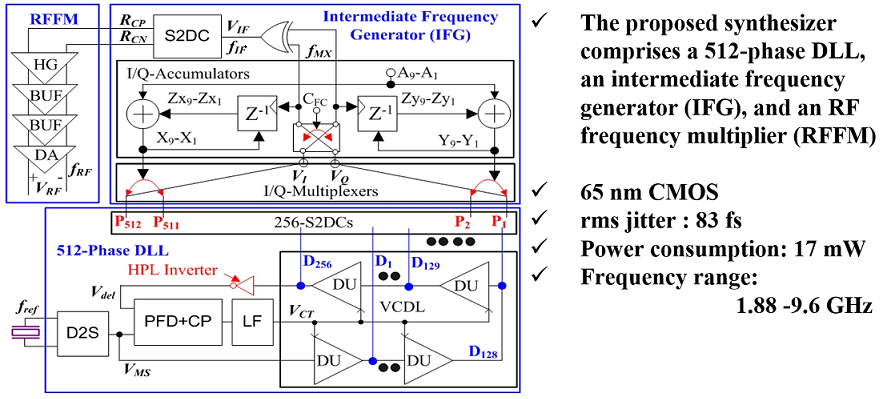
This paper presents a new cascade topology of a DLL-based synthesizer and an FM for a lower-frequency synthesizer. The DLL-based synthesizer consists of a 512-phase DLL and an intermediate frequency generator (IFG), providing a wide IF band. The IF band is up-converted to the RF band by the programmable high-frequency multiplication factor (FMF) RFFM. Therefore, the proposed synthesizer can provide ultra-low in-band PN, a channel resolution that is finer than the input frequency (fin), ultra-low out-band PN, and a wide frequency band. The proposed synthesizer is fabricated in a 65-nm CMOS process, and the active die area is 0.6 mm2. The total power consumption is 15 mW without counting a 50 Ω driving amplifier (DA) power consumption. Recent 5G LO research papers have achieved their rms jitter performances while using signal generators as reference clocks. However, our main purpose is to implement the optimum LO module solution for 5G+ wireless communication systems composed of the proposed synthesizer and currently available state-of-the-art reference external oscillators. When a 156.25 MHz micro-electro-mechanical systems (MEMS) differential oscillator (SiT9501) is applied as the reference clock, the LO module output frequency range is 1.88–9.96 GHz, and its channel resolution range is 3.698–38.609 MHz. The integrated rms jitter from 12 kHz to 20 MHz is 83 fs.
The rest of this paper is organized as follows: In section II, a new synthesizer topology is introduced. Its components are explained as well as their functionalities. Then, the proposed synthesizer output frequency range and channel resolution equations are presented. Finally, the synthesizer’s phase noise analysis and the benefits are presented. Section III shows core building block schematics. The core circuitries are analyzed and verified through simulations. Also, the design procedure for the target output frequency range is talked about in detail. Furthermore, the synthesizer’s adjacent harmonic rejection ratio analysis and simulation are presented last. The proposed synthesizer chip fabrication and printed circuit board (PCB) environment for testing the chip are shown in Section IV. Moreover, the synthesizer’s power consumption is summarized, and the DA output matching and capacitor bank (Cbank) calibration are discussed. Finally, the test measurements of core specifications are reported. The summary and comparative analysis with recently published synthesizers are presented in Section V.
4. Fabrication and Measurement
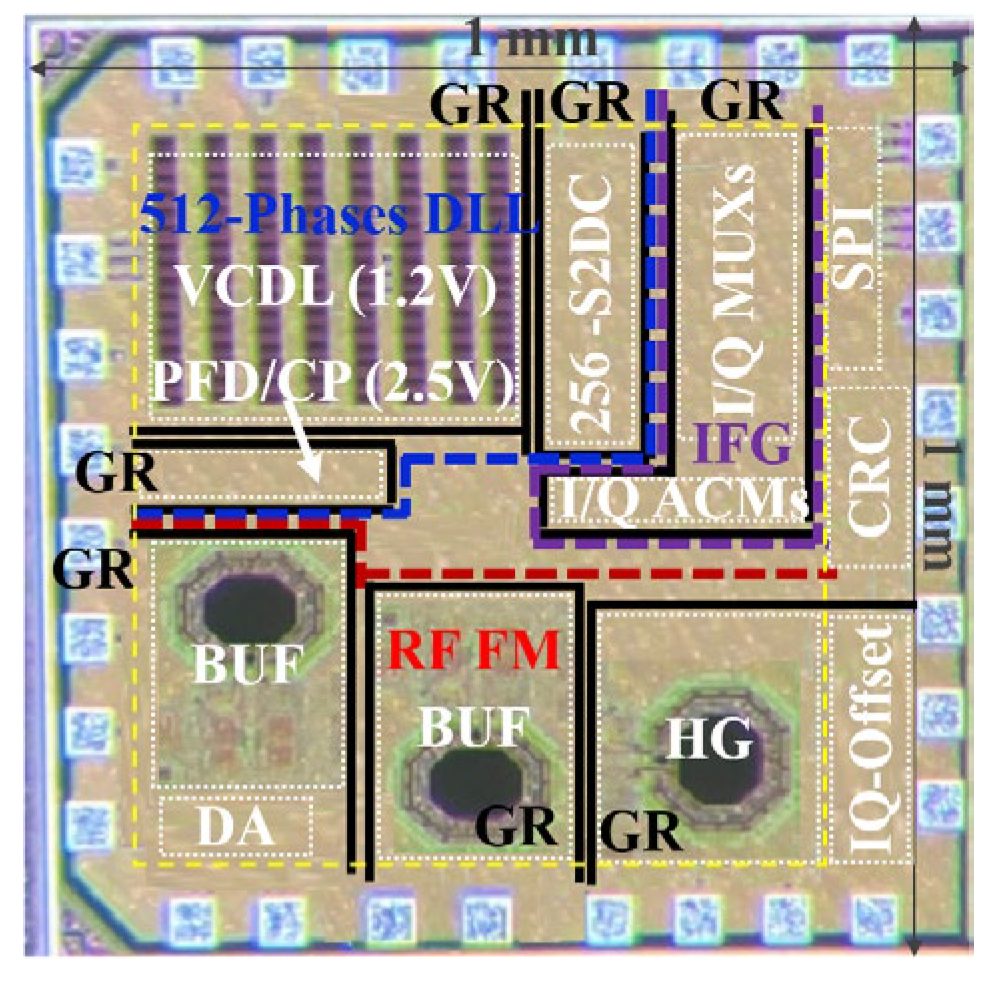
The proposed synthesizer is fabricated in a 65-nm CMOS technology and its active die size is approximately 0.6 mm
2 as shown in
Figure 24 (yellow-dotted box). Almost 35 % of the die area is occupied by the 512-phase DLL (blue-dotted boundary), and the RFFM occupies roughly 40 % (red-dotted boundary). The last 15 % of the active die area is for the IFG (purple-dotted boundary). The total die area is 1 mm
2 including central reference current, SPI, IQ-offset, and I/O pads.
As described in [
27], about 42 dB substrate isolation within 100-μm apart two points with only one 30-μm width guard ring is reported. Since each building block has a wider than 30-μm guard ring width in
Figure 24, the substrate isolation within 100-μm apart would be expected to be more than 42 dB due to multilateral isolations. This is why we try to assign separate power supply, ground, and guard ring (GR) for each building block as much as possible even though GR occupies an extra die area.
Three separate pairs of power supply and ground are allocated for the building blocks in the 512-phase DLL. The power supply voltage is 2.5 V for the PFD+CP to obtain enough headroom. However, the power supply voltage for VCDL and the 256-S2DC is 1.2V for the smallest die area and the lowest average power consumption in the 65-nm process. There is no level shifter required between the CP and VCDL because the CP drives the DU’s varactor, whose maximum potential difference can be bigger than 2.5 V. Each pair of power supply and ground is separated by an individual GR, preventing mutual interference with one another.
The IFG has one pair of power supply and ground for its building blocks of I/Q-multiplexers and I/Q-accumulators and has wide a GR to prevent especially the reference clock harmonics (N×fref) from interfering.
A separate pair of 1.2 V power supply and ground is individually applied for the HG and the BUFs in the RFFM because the mutual interferences through the power supply and ground are so sensitive to the HRR performance. While the DA shares the ground with the 2nd BUF, the DA power supply is separated from the BUF power supply to distinguish the DA power consumption from that of the BUF.
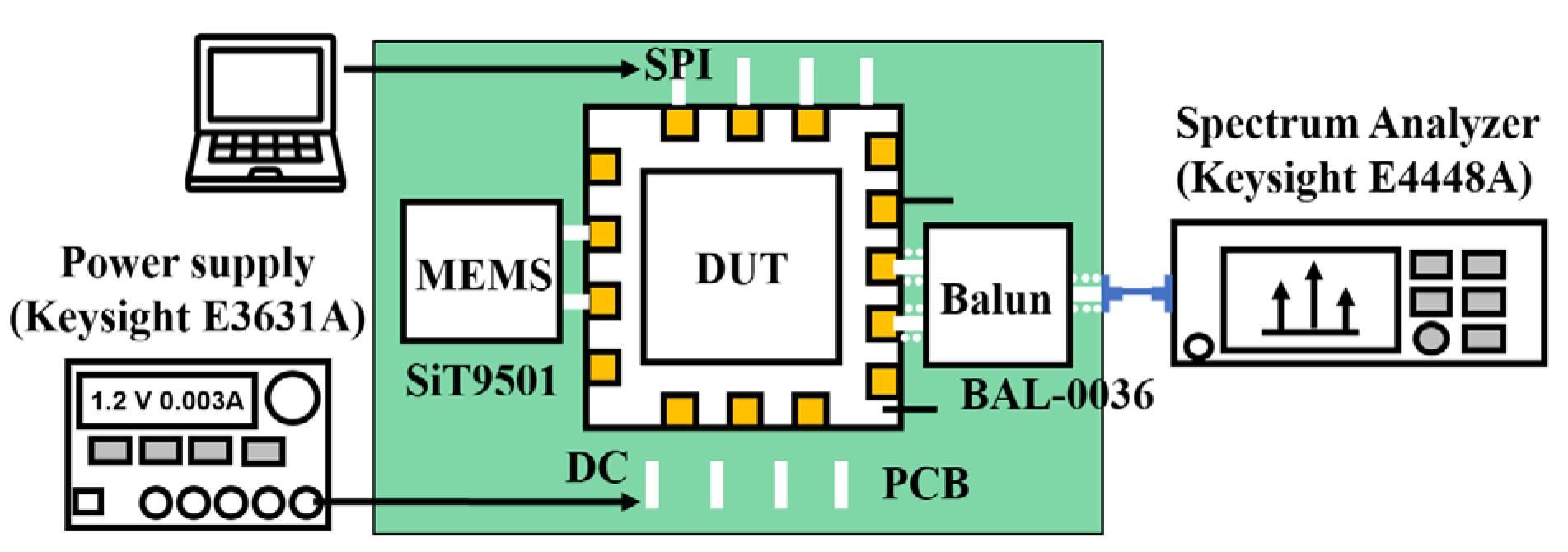
The laboratory test environment is shown in
Figure 25. An external MEMS differential oscillator (SiT9501) is used as a 156.25 MHz reference clock, and its integrated rms jitter from 12 kHz to 20 MHz is as low as 70.629-fs according to the datasheet. Applying a Keysight E3631A as the power supply, the fabricated chip can be evaluated by programming the CPU to control the device under test through SPI. A Keysight E4446A spectrum analyzer measures the presented synthesizer output.
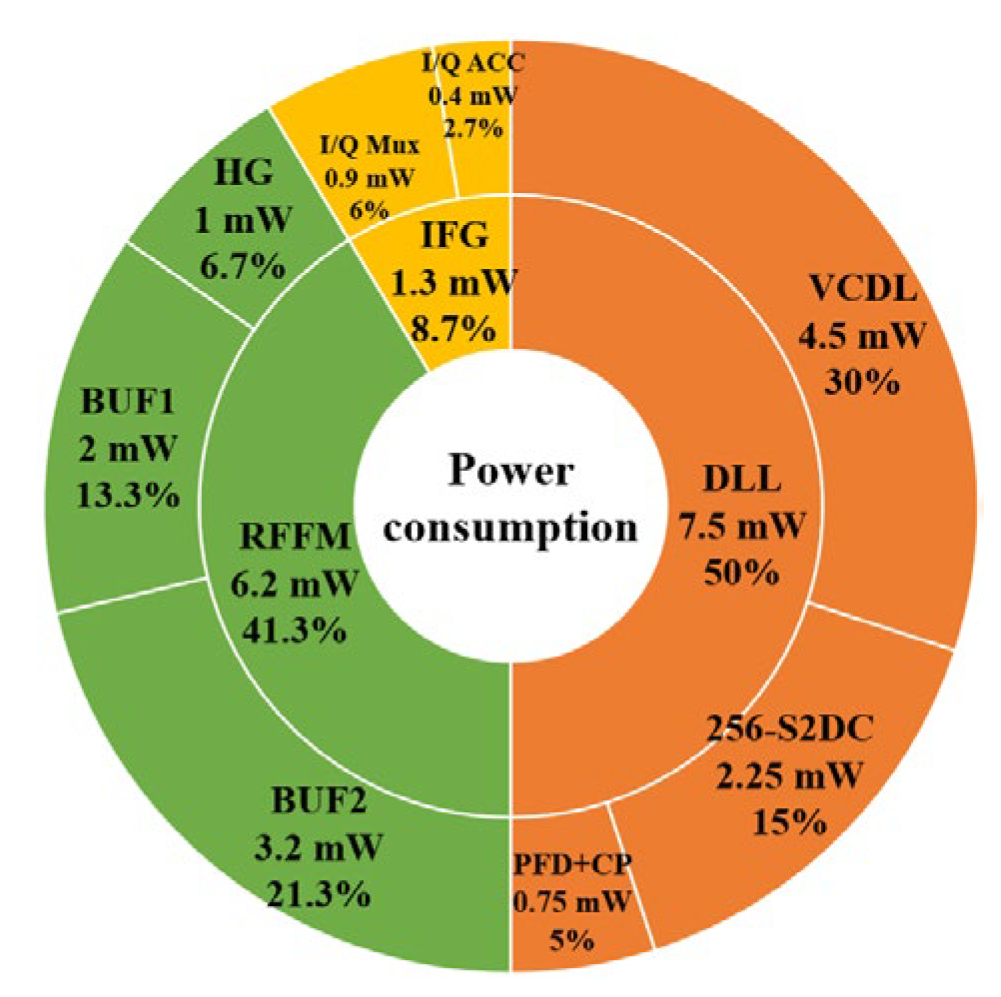
The proposed synthesizer consumes 15 mW. More than 50 % of the total power consumption is allocated to the 512-phase DLL. Even though they are digital circuitries, the average power consumption of the VCDL is approximately 35 % of the total power consumption to perform low PN. However, the 256-S2DCs power consumption is 15 % because it is less sensitive to PN contribution. The power consumption of PFD+CP is 5%. The IFG and RFFM power consumptions are 1.3 and 6.2 mW, respectively. The power consumption of each building block is summarized as shown in
Figure 26.
As mentioned in Section I, the proposed synthesizer is the first building block of the recent cascade LO chain for a 5G
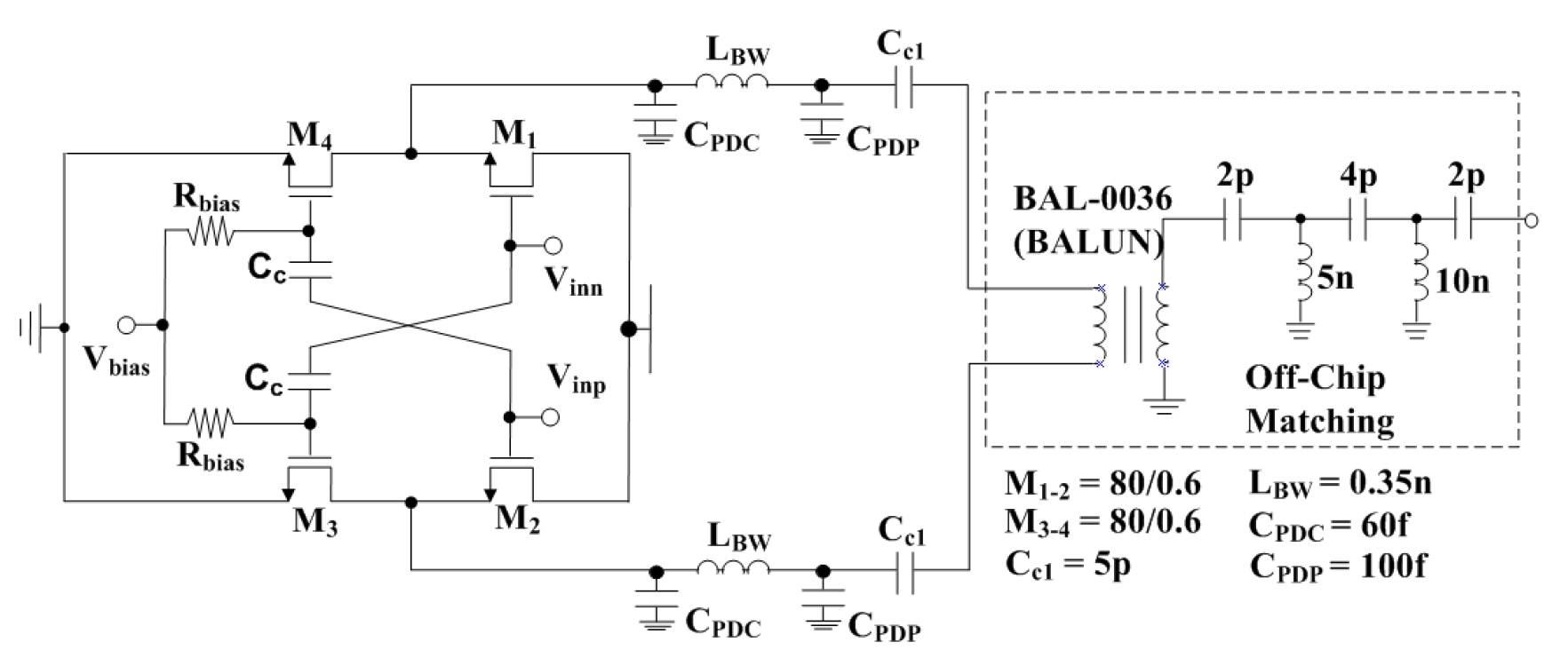
+ wireless communication system. Therefore, the synthesizer will drive the mmWave FM, whose impedance is normally bigger than 50 Ω. For only driving 50 Ω, a simple differential push-pull topology DA for wideband output matching is integrated. As shown in
Figure 27, the DA is matched to 50 Ω through external balun (BAL-0036) and two cascade stages of the C-L-C pi-match.
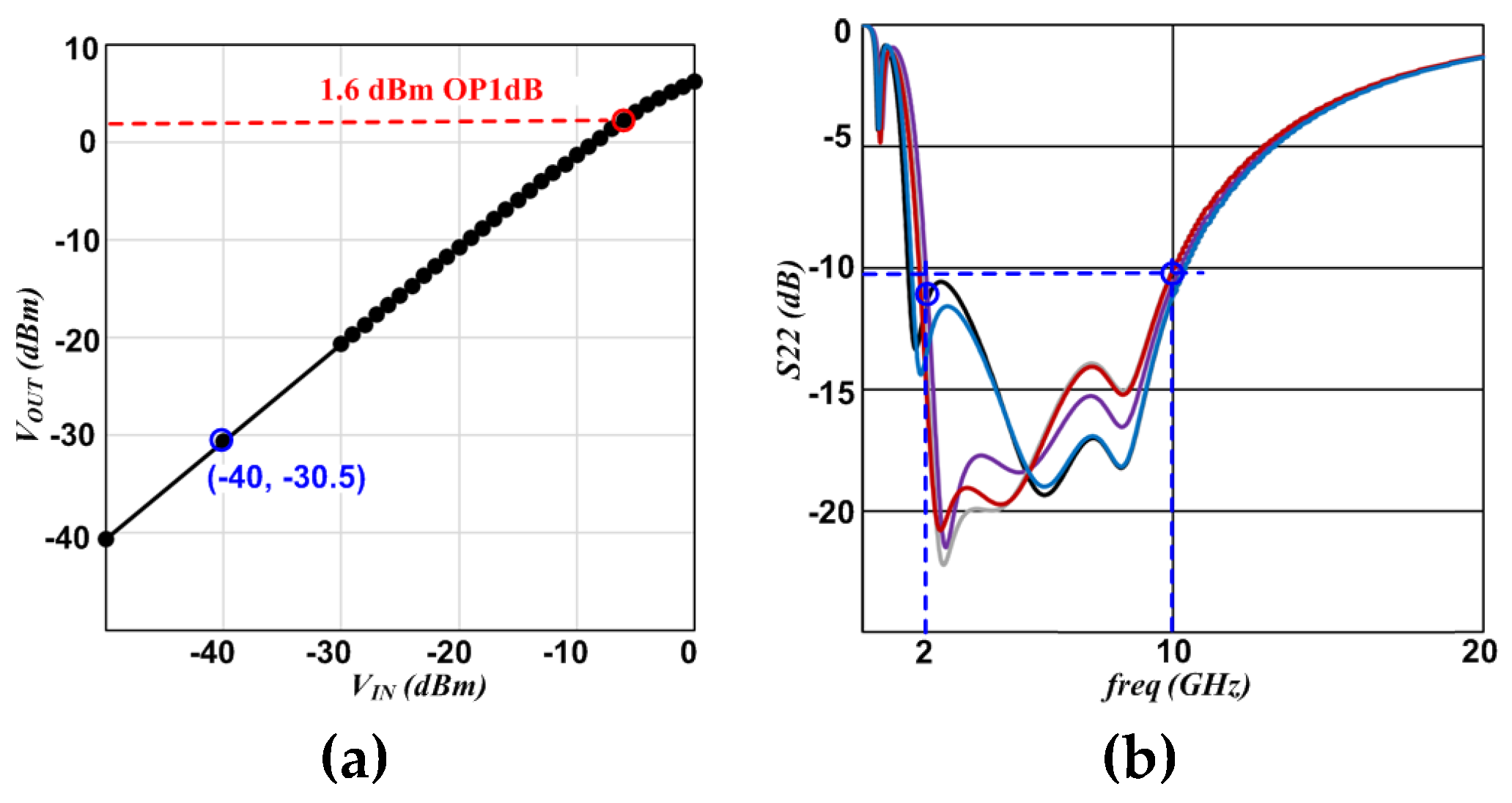
Figure 28(a) shows the simulation plot of the DA output (
VOUT) versus input (
VIN). The DA power gain is 9.5 dB and the output 1-dB compression point (OP1dB) is 1.6 dBm when it consumes 6 mW, which is enough to set the -8 dBm balun output without causing the significant signal distortion by the DA.
Five sample chips (Chip#1–Chip#5) have been mounted on a PCB by chip-on-board and successfully tested for evaluating performances. The DA output is placed as close to the PCB pad as possible so that the bonding wire inductor (0.35 nH L
BW in
Figure 27) would be the smallest.
Figure 28(b) shows the S22 measurements of the sample chips, whose worst S22 is less than −10 dB for the target measurement frequency band of 1.8–10 GHz.
The C
bank magnitude of programming the resonant frequency would be shifted over the process variation. Therefore, the auto-calibration of C
bank is required to promote an efficient mass production yield.
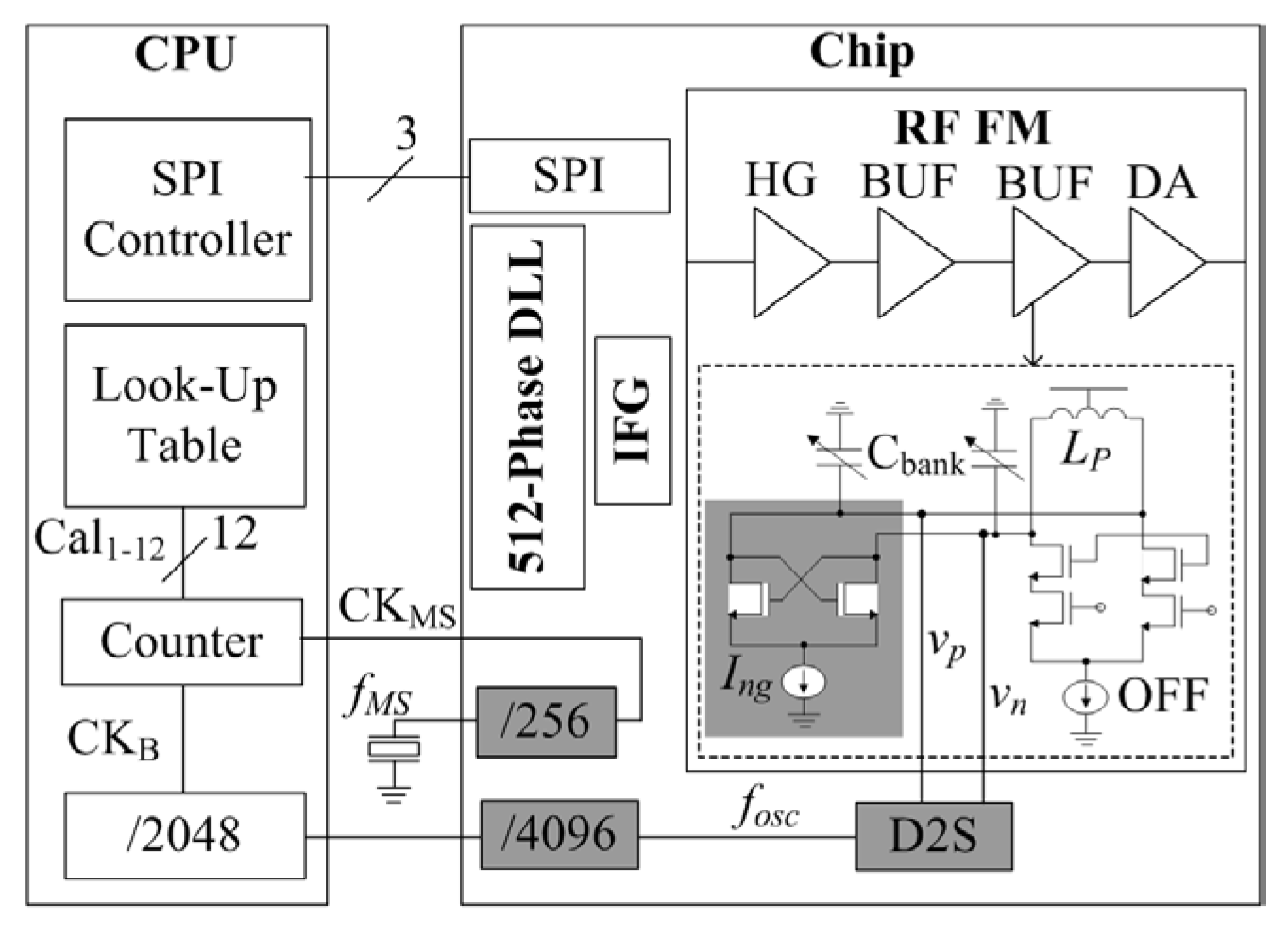
Figure 29 shows the proposed calibration block diagram. As soon as calibration starts, all building blocks are turned off, except those highlighted in the shaded boxes of the digital 256-FD, digital 4096-FD, CMOS differential-to-single (D2S), and the negative-g
m pair of the second BUF. Applying enough current of
Ing forces the positive feedback to oscillate, and its frequency,
fosc, can be expressed as
where
Cpa is the all-parasitic capacitance between
vp and
vn.
CP is expressed as
Dk and are complement binary bits. COFFk and CPk are defined in (12) and (14). fosc is down-converted to CKB by 4096-FD and 2048-FD, and the external MEMS frequency, fMS, is down-converted to CKMS by 256-FD. The counter output in the CPU is updated at the CKMS rate for the CKB period. The final counted value, Cal1-12, for each Cbank state is stored in a look-up table.
Unfortunately, the CMOS D2S would be a complicated topology to handle the wide frequency band of 1.8–10 GHz, which leads to a huge die area. Therefore, the calibrated frequency band is limited up to 2.2 GHz to minimize the D2S die area.
Table 1 shows the calibrated Cal
12-Cal
1 magnitudes in decimals (
Caldec) when the C
bank states are intentionally set to oscillate at approximately 2.0, 2.05, 2.10, 2.15, and 2.20 GHz for Chip#1. The oscillation frequency can be estimated from the calibrated
Caldec as
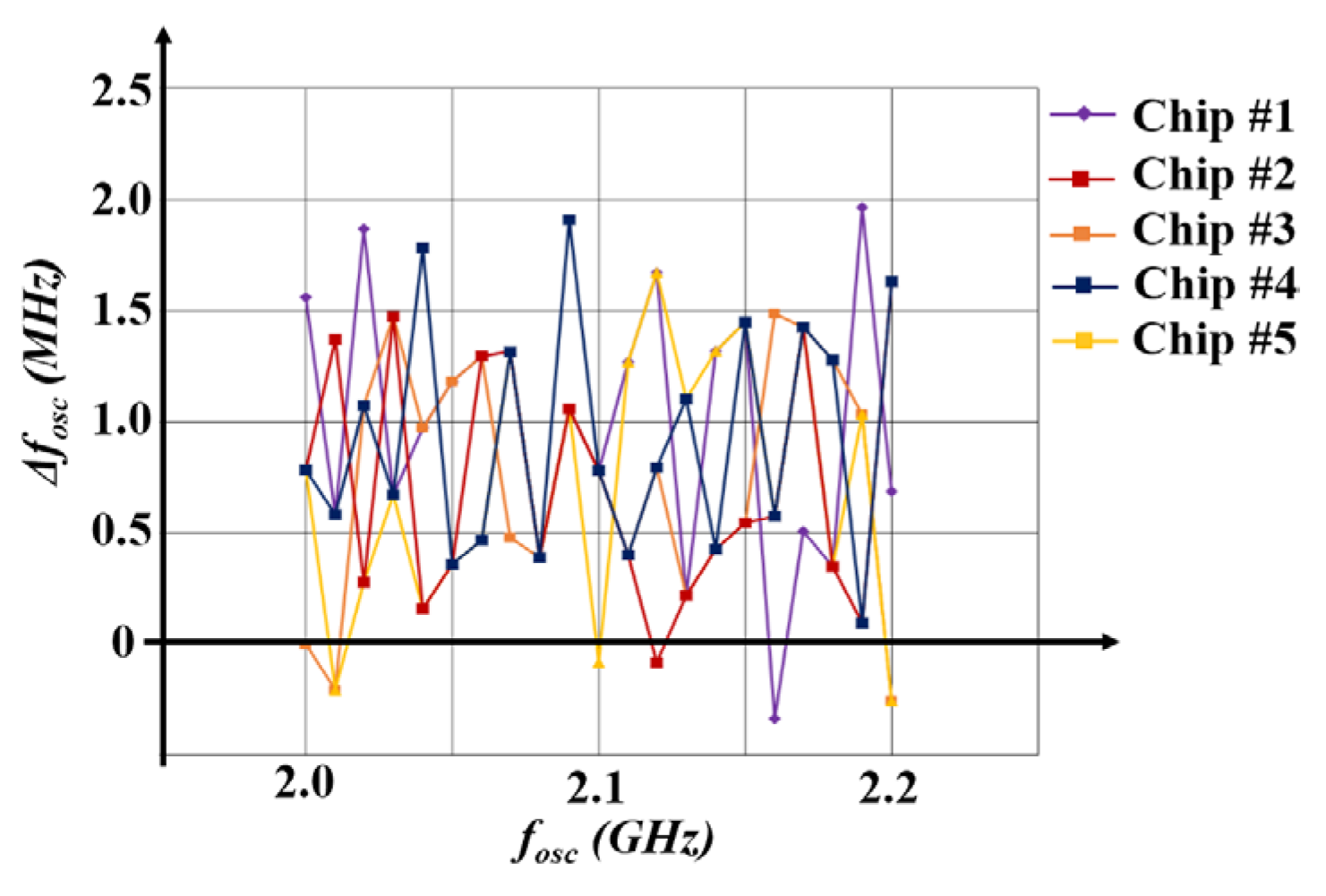
Figure 30 shows the graph of the frequency difference (
Δfosc) between measured (
fosc) and calibrated (
fc-osc) frequencies versus
fosc for all five test chips. The maximum frequency deviation is less than 0.2 % (= 2MHz / 2GHz × 100%), meaning all the tested five chips have an approximately equal C
bank value.
Assuming that the
LP-process variation is trivial and that all capacitances are changed linearly in the same direction over process variations, (21) can be rewritten as
The capacitive process coefficient
) can be calculated by deriving (24) as
where
CP-TT and
Cpa-TT are the capacitances at the TT process. Therefore,
αC represents how much the capacitance deviates from that at the TT process. If
αC is bigger than 1.2, the tested chip is close to the SS process. On the contrary, it is close to the FF process if
αC is smaller than 0.8. Using
αC the required SPI C
bank state of the resonant frequency greater than 2.2 GHz can be estimated.
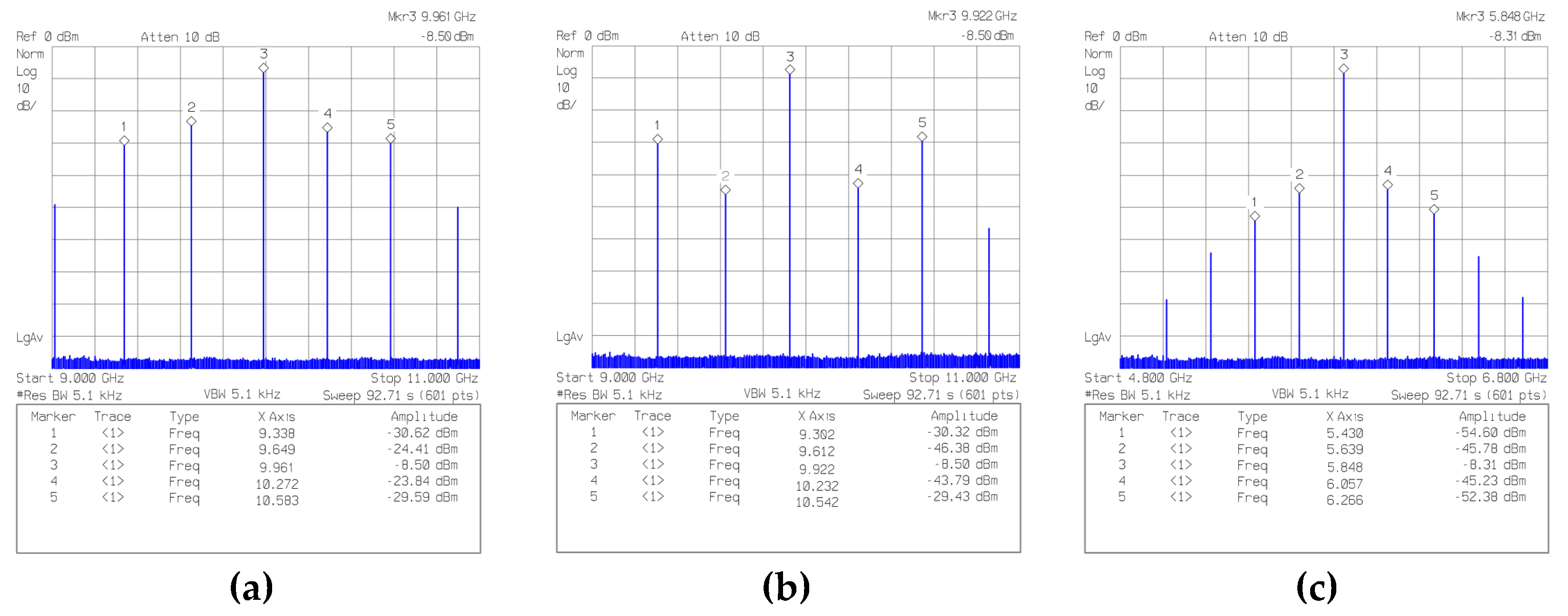
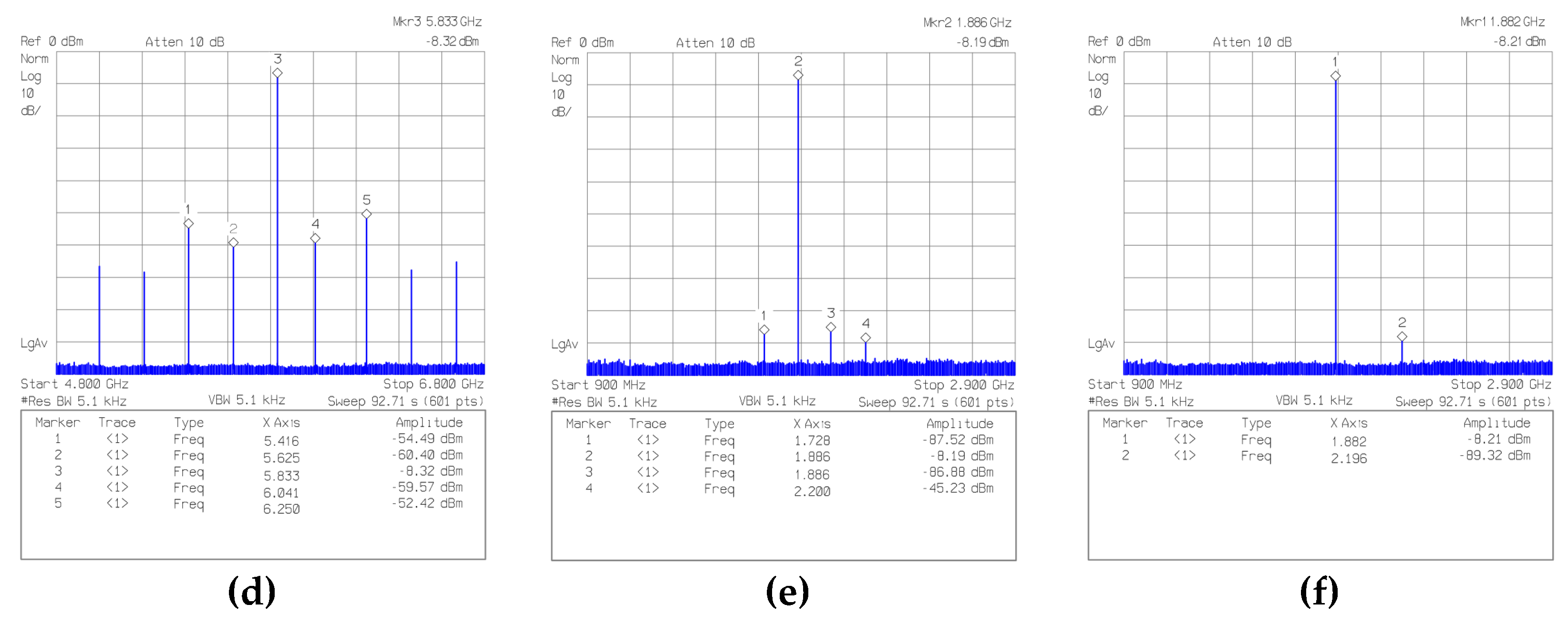
The output spectral measurements for Chip#1, when
ACM is programmed as 1, 2, 127, 128, 253, and 254, are shown in
Figure 31. The output frequency range is 1.882–9.961 GHz, which is close to the simulated range of the TT process.
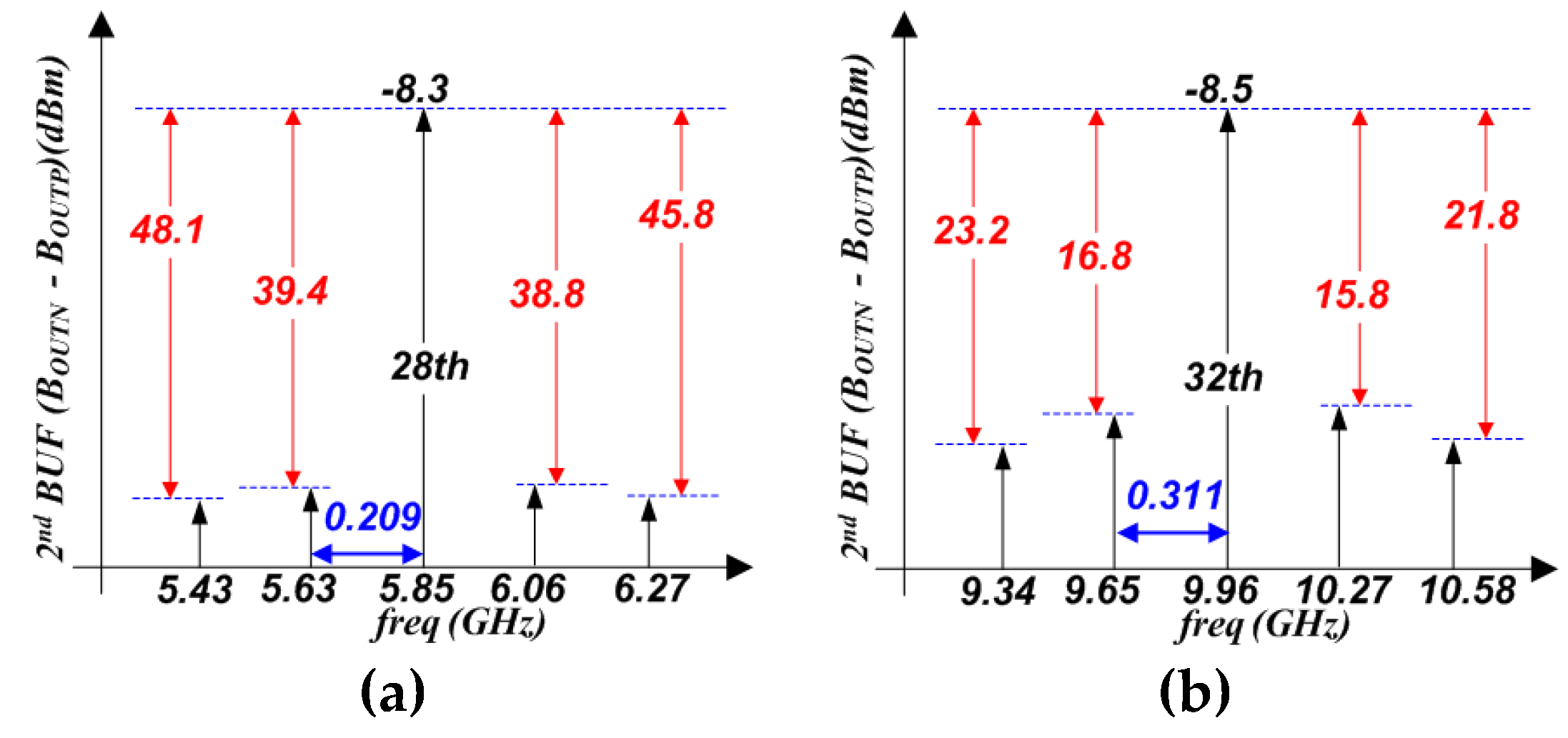
The worst adjacent HRRs happen when
ACM = 1 (
Figure 31(a)) and
ACM = 2 (
Figure 31(b)) resonating with the
LP-C
bank on the 32nd harmonic of
fIF. Unlike the HRR for
ACM = 1, the dominant HRR when
ACM = 2 happens at ±2×
fIF because the duty cycle offset of
VIF is zero. Nonetheless, there are noticeable spurious tones at ±
fIF from the wanted harmonic. The main cause of these spurious tones is the HG differential mismatches. Intentionally introducing the current mismatch between the positive and negative paths of the HG might reduce the HG differential mismatch, but the detailed schematic and analysis are omitted in this article.
The proposed synthesizer output spectra resonating the
LP-C
bank on the 28th and 12th harmonics when
ACM = 127 and
ACM = 253 are shown in
Figure 31(c) and
Figure 31(e), respectively. As expressed in (2),
fIF decreases as
ACM increases. The adjacent offset frequencies are 208.877 and 157.171 MHz for
ACM = 127 and
ACM = 253, respectively. The corresponding output frequencies are 5.848 GHz (= 28×208.877 MHz) and 1.886 GHz (= 12×157.171 MHz). For
ACM = 128 and
ACM = 254, the HRRs at ±
fIF are better compared with the HRRs for
ACM = 127 and
ACM = 253 as shown in
Figure 31(d) and
Figure 31(f).
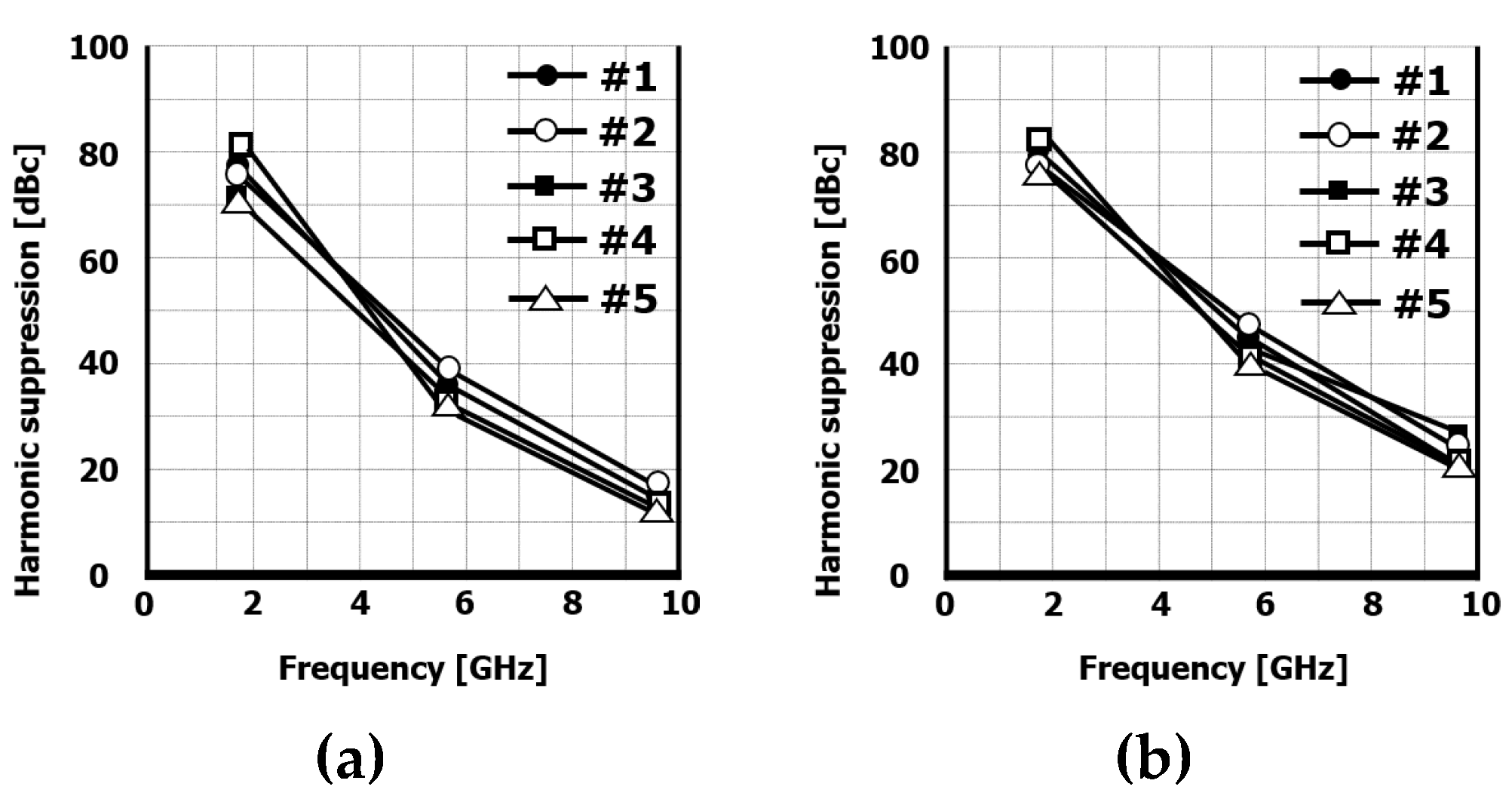
Figure 32 (a) and
Figure 32(b) show all the measured worst HRRs of the sampled chips for
ACM = 1, 127, and 253 and
ACM = 2, 128, and 254, respectively. The HRR performance tendency is maintained as explained in the previous section, which leads to the HRR at a lower resonant frequency being better than that at a higher one. However, all the measured HRRs are slightly deteriorated compared with those from HRR simulations. These HRR gaps are considered owing to all the harmonics of the fundamental tone coupled to the synthesizer output through the same substrate in addition to the HG differential mismatch.
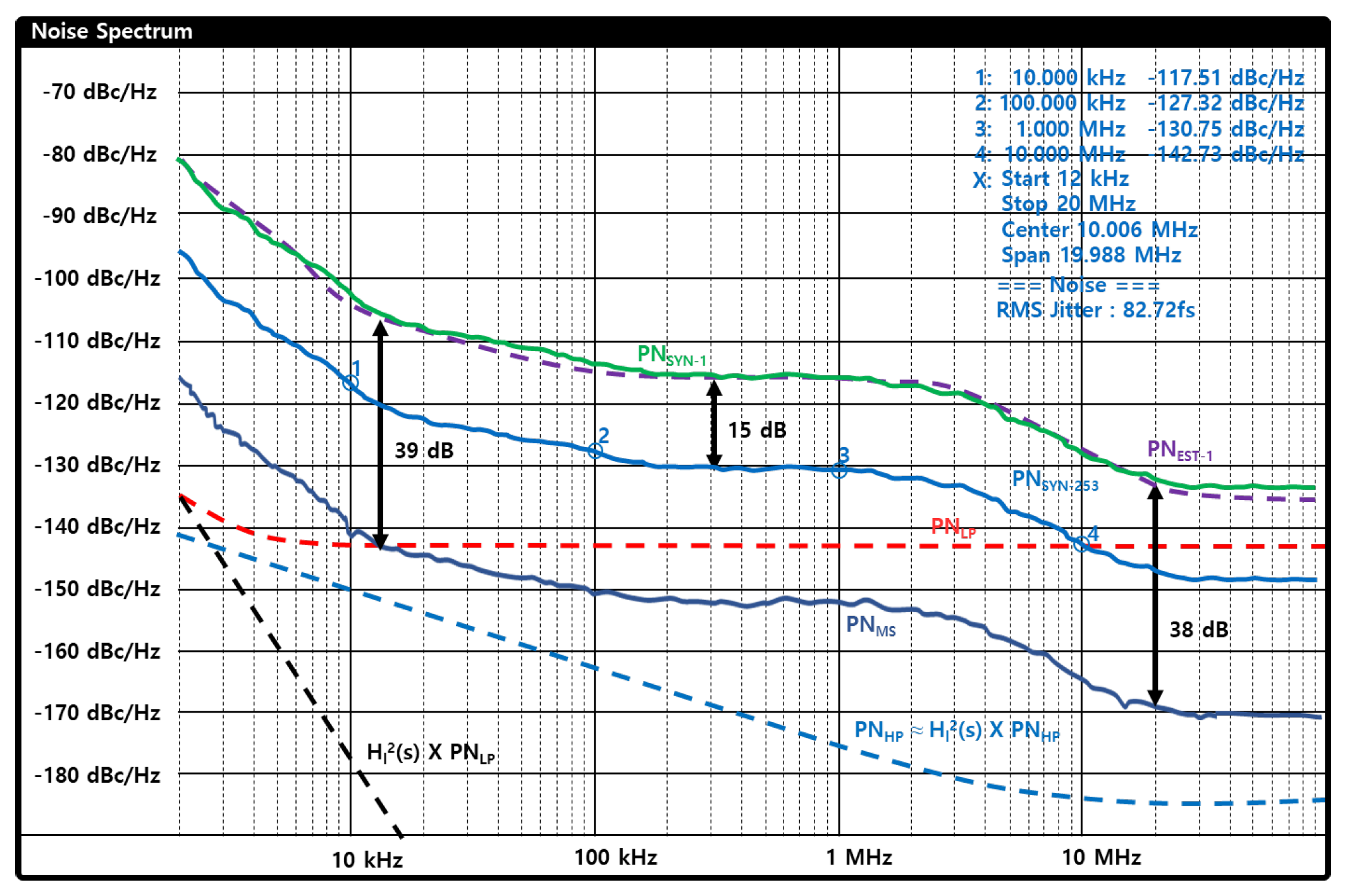
The synthesizer PN measurements (PN
SYN-1 and PN
SYN-253) are shown in
Figure 33 for
ACM = 1 and
ACM = 253, with corresponding FMFs between
fMS and
fRF of 63.751 (=9.96/0.15625) and 12.071 (=1.89/0.15625). All the dotted curves are simulated PNs. The measured MEMS oscillator PN (PN
MS) is drawn to distinguish the PN degradation between
fMS and
fref. The integrated rms jitter of
fMS from 12 kHz to 20 MHz is 72 fs, which is 1.4 fs degraded compared with the jitter in the SiT9501 datasheet.
When
ACM = 1, the estimated synthesizer PN (PN
EST-1) is simply the multiplication of FMF
2 and PN
SUM. PN
SUM = PN
MS + PN
LPHl2(s) + PN
HP×
Hh2(s), where
H1(s) and
Hh(s) are LPF and HPF NTFs as defined in (6). Also, PN
LP is the PN simulation of PFD+CP (
Figure 10), and PN
HP is the PN simulation of DU
128 shown in
Figure 13. Since PN
LP is bigger than PN
HP, the 3-dB DLL loop bandwidth is set low enough for optimizing the synthesizer rms jitter from 12 kHz to 20 MHz. PN
SYN-1 green curve is PN measurement when the DLL 3-dB bandwidth is 100 Hz.
As shown in
Figure 33, the estimated PN (PN
EST-1) is close to the measured PN (PN
SYN-1), proving that the most dominant noise sources are PFD+CP and VCDL. Moreover, the PN differences between PN
SYN-1 and PN
MS are approximately 39 and 38 dB at 12 kHz and 20 MHz offsets, respectively, which are only 3 and 2 dB bigger than the mathematical PN degradation due to frequency multiplication between
fRF and
fMS. The PN difference between PN
SYN-1 and PN
SYN-253 is 15 dB, close to the mathematical PN degradation (20 log (9.96/1.886)). The measured rms jitters of PN
SYN-1 and PN
SYN-253 integrated from 12 kHz to 20 MHz are 82.65 and 82.72 fs, which is a jitter degradation of approximately 10.7 fs compared with the measured integrated jitter of PN
MS (72 fs). In other words, more than 87 % of the presented synthesizer’s rms jitter comes from the reference clock.
Table 2 shows the rms jitter measurements of 12k-20MHz for all five test chips. Also, the rms integrated for 1k-100MHz have been measured, and which average rms jitters are 107.606 and 107.634 fs at 1.89 and 9.96 GHz, respectively. The jitter degradation is only 9.2 fs compared with the integrated PN
MS (98.0 fs) of 1k-100MHz.
5. Summary and Conclusion
To achieve the stringent jitter performance of a beyond 5G LO generator, the cascade structures of a low-frequency synthesizer and FM have been actively researched in the recent decade. If an mmWave FM is noiseless, the FM output jitter equals the lower synthesizer jitter. Therefore, the lower-frequency synthesizer integrated rms jitter must be less than the LO generator target specification. Otherwise, without a PN filter function, the FM output integrated rms jitter cannot achieve the jitter specification.
ILPLL and SSPLL have been successfully developed for the lower-frequency synthesizer to enhance in-band PN by removing the frequency divider in the feedback path. However, VCO jitters in both ILPLL and SSPLL are still accumulated over the injection and subsampling clock periods. Therefore, the output PNs are degraded enough to affect the integrated rms jitter performance, particularly for a wide integrated frequency band. Moreover, their channel resolutions and frequency ranges are poorer than those of the classical Integer-N PLL (CINPLL). In addition, they normally require extra circuitries to program the output frequency and prevent them from losing lock states.
In this article, a new DLL-based synthesizer topology is introduced. The 512 phases (P
1-P
512) are equally spaced by a 512-phase DLL (
Figure 2). The I/Q multiplexer outputs (
VI and
VQ) are initially connected to P
I and P
Q. Next,
VI and
VQ switched to P
I±ACM and P
Q±ACM, where
ACM is the programmable input magnitude of the I/Q accumulator. As keeping switch by
ACM, the period of
VI and
VQ would be (512 ± 2
ACM)×
td, where
td =
TMS/512. Therefore, the fundamental frequency (
fIF) of the XOR output (
VIF) can be derived as (2).
If
VI and
VQ switch only to the phase lag signal, equation (2) can be rewritten as
Equation (26) shows that
fIF can be programmed as a fractional multiple of
fMS (=
fref) similar to CFNPLL output frequency,
fCFN, as
where
K and
M are integers. And, its channel resolution is
fref /
M which is normally smaller than the proposed synthesizer channel resolution defined in (4). On the contrary, the proposed synthesizer provides a finer channel resolution than ILPLL, SSPLL, and CINPLL by setting
Normally, a CFNPLL provides fractional spurs close to an output frequency, which degrades integrated jitter somewhat. In addition, the ΔΣ modulator in the feedback path of CFNPLL contributes a quite bit of integrated jitter. However, the proposed synthesizer removes the above-mentioned penalties for fractional multiplication due to the fixed fractional multiplication.
Recently, injection-locked frequency multipliers (ILFMs) have proven to be an efficient topology for unwanted harmonic suppression. However, ILFMs suffer from a narrow injection-locked frequency range. Moreover, they may require additional circuitries to maintain the lock state, particularly for high-order harmonic injections.
The synthesizer implemented in this paper has the same FM topology as the one reported in [
26], but the presented FM is optimized to achieve the maximum frequency range using the smallest switch and capacitor sizes. The output resonant frequency is tuned by varying the C
bank magnitude while keeping the same parallel inductor (
LP) and equivalent resistance (
REQ). Therefore, the highest quality factor (Q) of the
LP-C
bank load can be achieved at the lowest resonant frequency because Q is proportional to the square root of the total capacitance magnitude. Consequently, the HRR performance is degraded as the wanted frequency is increased.
Table 3 shows the specification comparison of state-of-the-art synthesizers with the proposed synthesizer. While [
23] and [
28] provide the rms jitter integrated from 10 kHz to 30 MHz, the other references including this work have measured rms jitter integrated from 1 kHz to 100 MHz. The active die area of [
19] and [
21] is the smallest (0.2 mm
2). Synthesizers proposed in [
19] and [
22] consume a relatively low power. The jitter performance of [
21] is only 58.2 fs, which is the smallest. The synthesizer proposed in [
28] provides the widest frequency bandwidth.
For fair performance comparison, two figure-of-merits (FoMs) are introduced. FoM
1 and FoM
2 are defined at the bottom of
Table 3. FoM
1 includes integrated rms jitter and power consumption, which are used for all the references. FoM
2 is added to include frequency bandwidth percentage in the comparison metric. As a result, the synthesizer implemented in [
19] accomplishes the best FoM
1. Still, this work achieves the best FoM
2, which might mean the proposed synthesizer performs outstanding overall compared with the other state-of-the-art synthesizers.
Figure 1.
Block diagrams: (a) MDLL; (b) SSPLL; (c) ILPLL.
Figure 1.
Block diagrams: (a) MDLL; (b) SSPLL; (c) ILPLL.
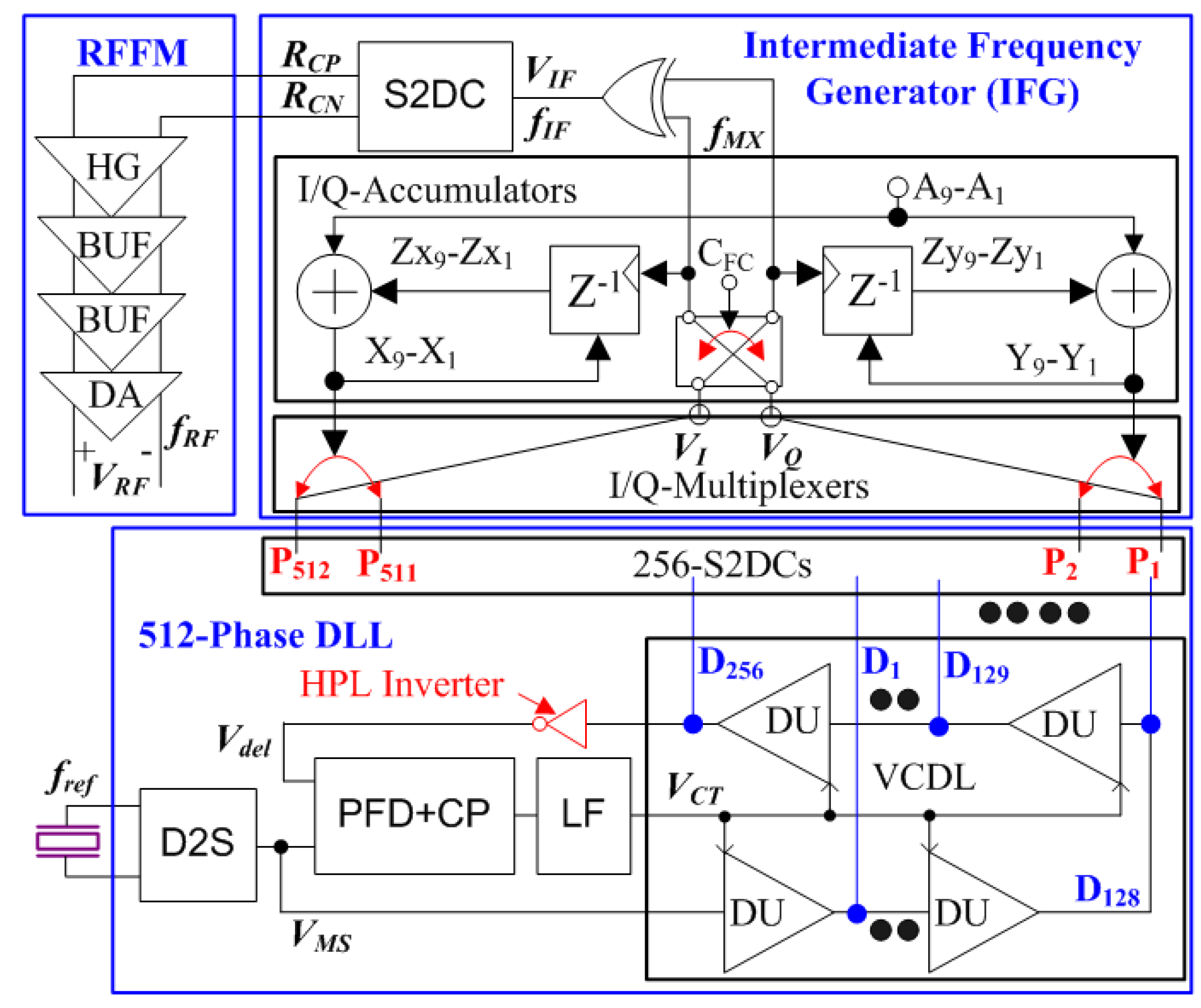
Figure 2.
The proposed synthesizer block diagram.
Figure 2.
The proposed synthesizer block diagram.
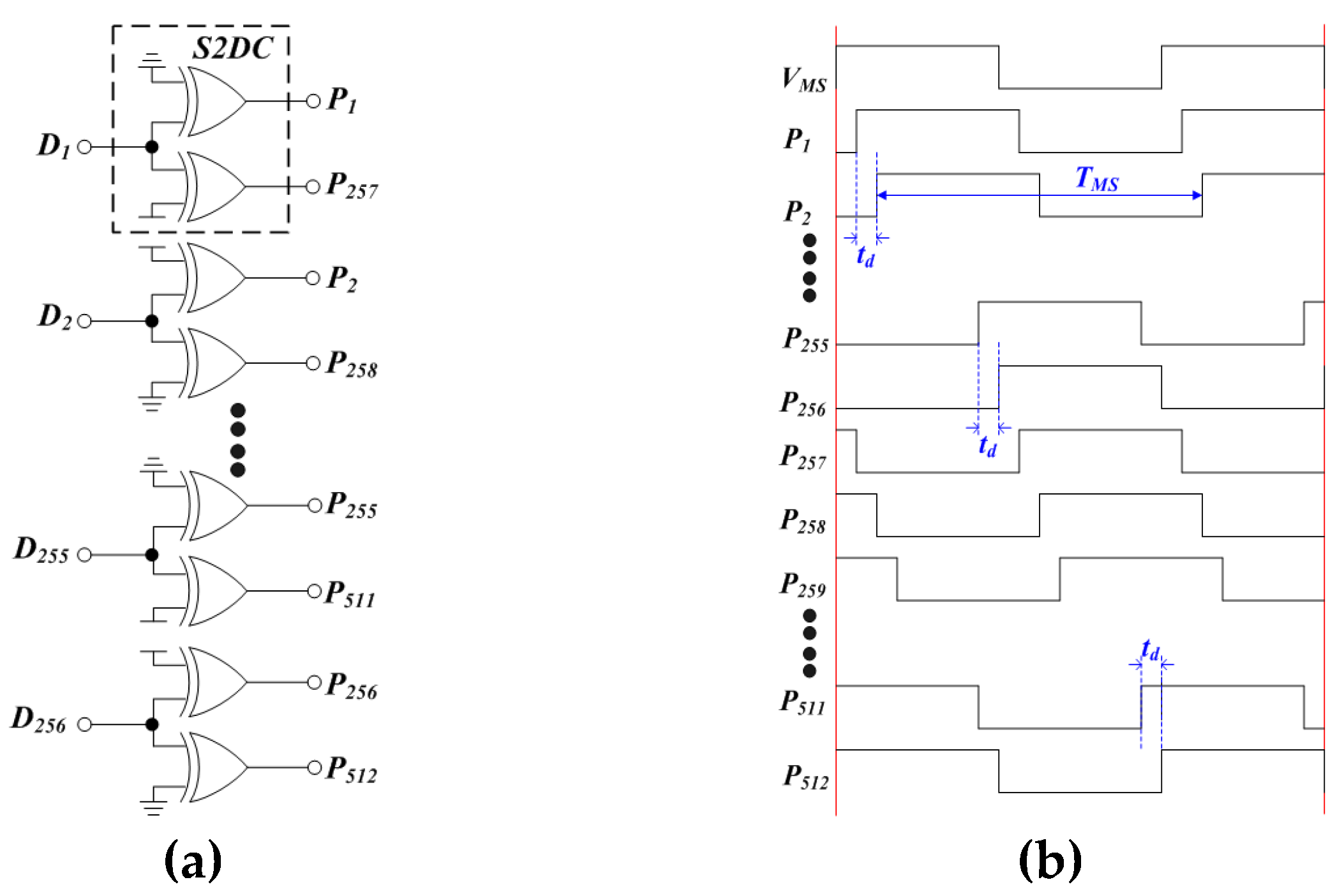
Figure 3.
256-S2DCs (a) Schematic. (b) Output waveforms.
Figure 3.
256-S2DCs (a) Schematic. (b) Output waveforms.
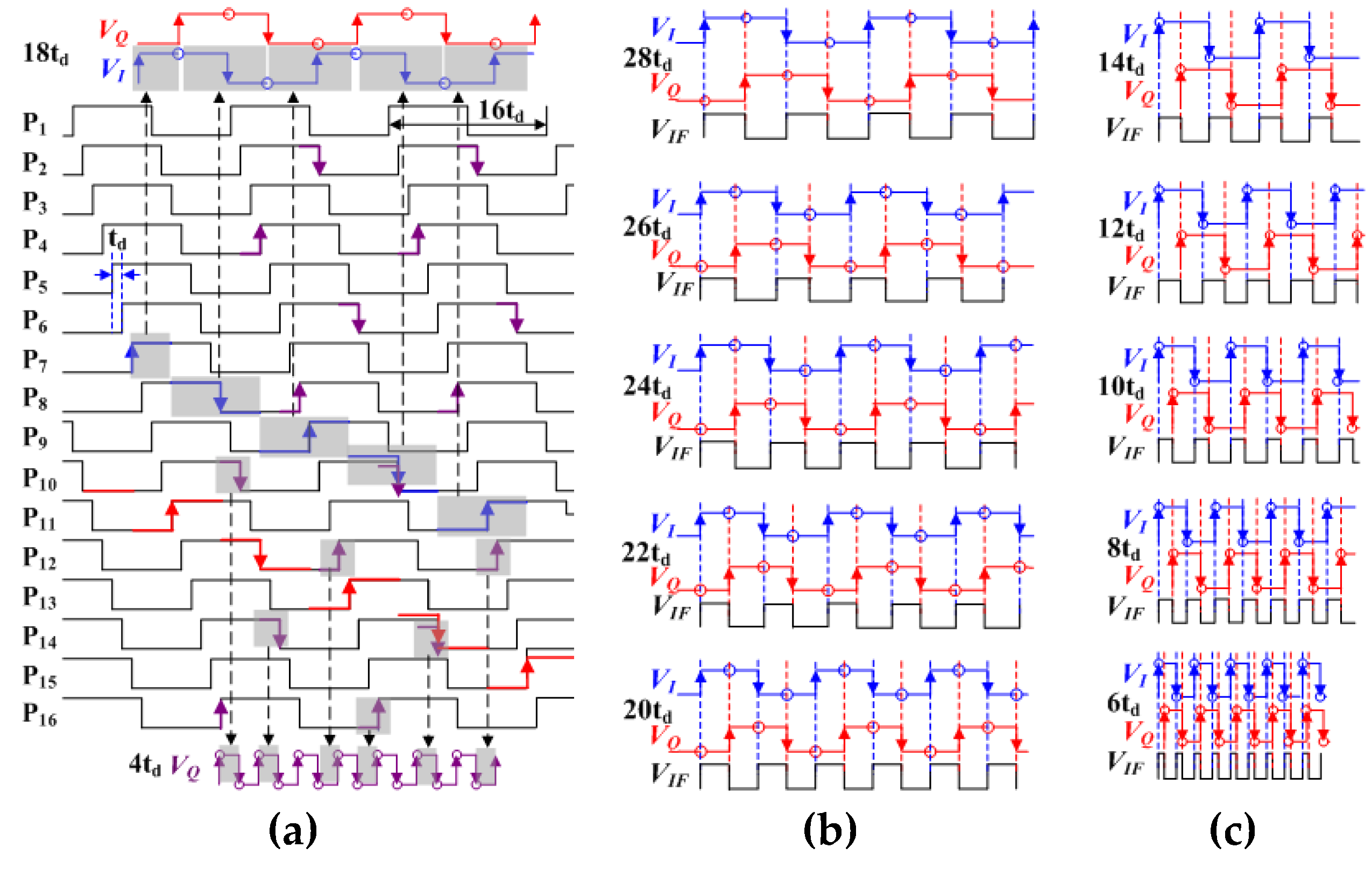
Figure 4.
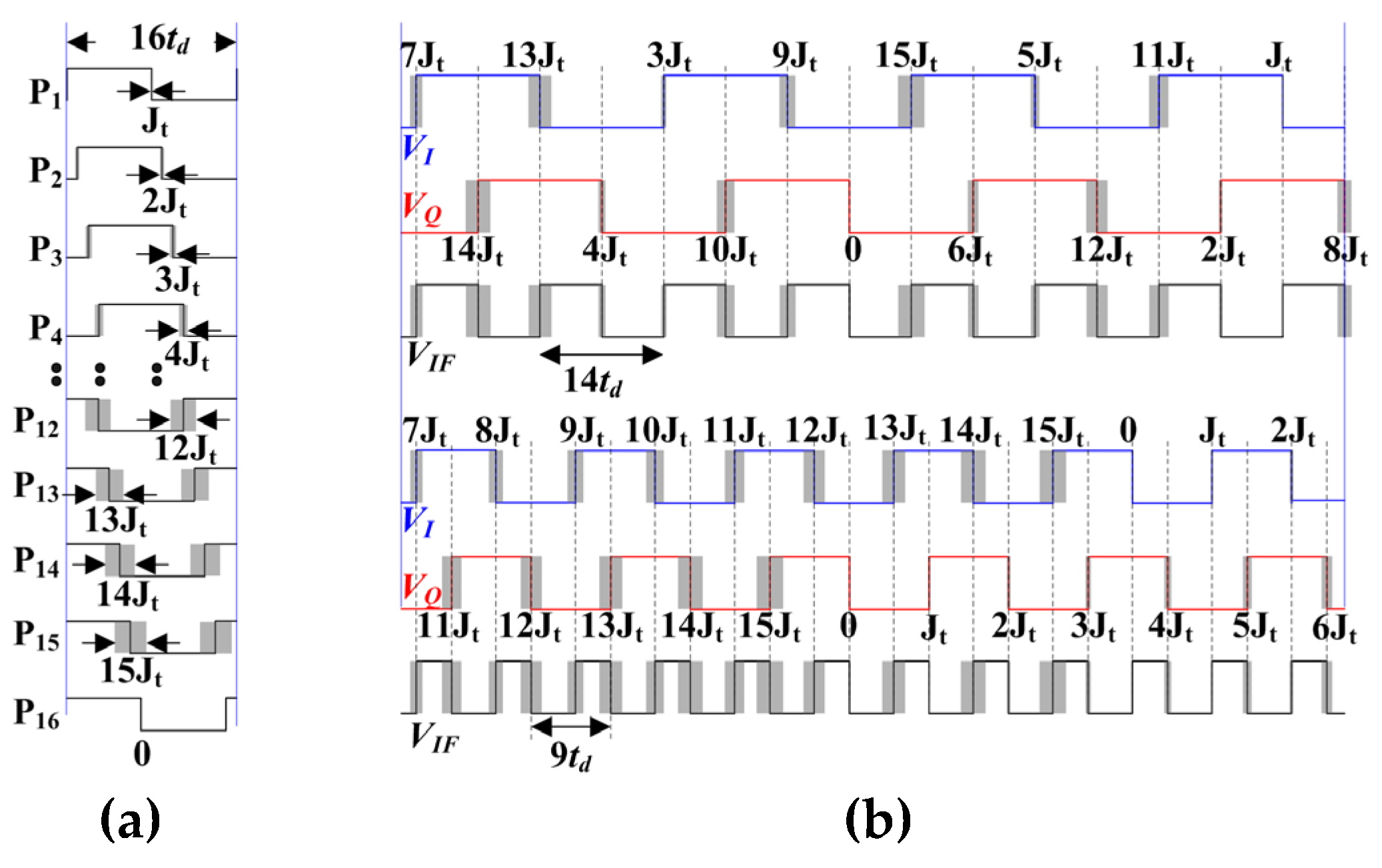
(a) P1-P16, VQ and VI (18td period), and VQ (4td period) pulses. (b) VQ, VI, and VIF pulses when ACM = 2-6 and switching to phase lag. (c) VQ, VI, and VIF pulses when ACM = 1-5 and switching to phase lead.
Figure 4.
(a) P1-P16, VQ and VI (18td period), and VQ (4td period) pulses. (b) VQ, VI, and VIF pulses when ACM = 2-6 and switching to phase lag. (c) VQ, VI, and VIF pulses when ACM = 1-5 and switching to phase lead.
Figure 5.
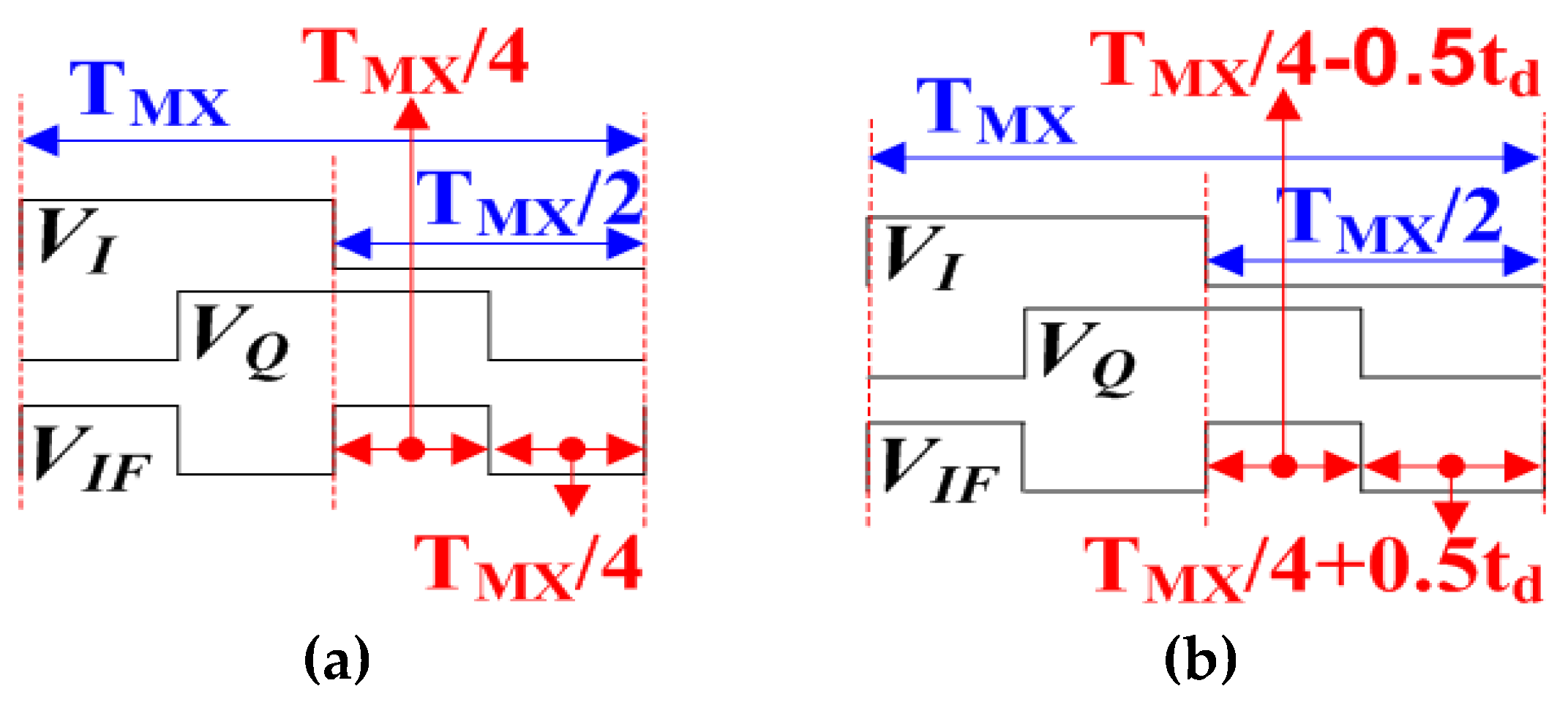
VIF, VI, and VQ waveforms. (a) VIF is 50% duty cycle. (b) VIF are ±0.5td duty cycle offsets from the 50 % duty cycle.
Figure 5.
VIF, VI, and VQ waveforms. (a) VIF is 50% duty cycle. (b) VIF are ±0.5td duty cycle offsets from the 50 % duty cycle.
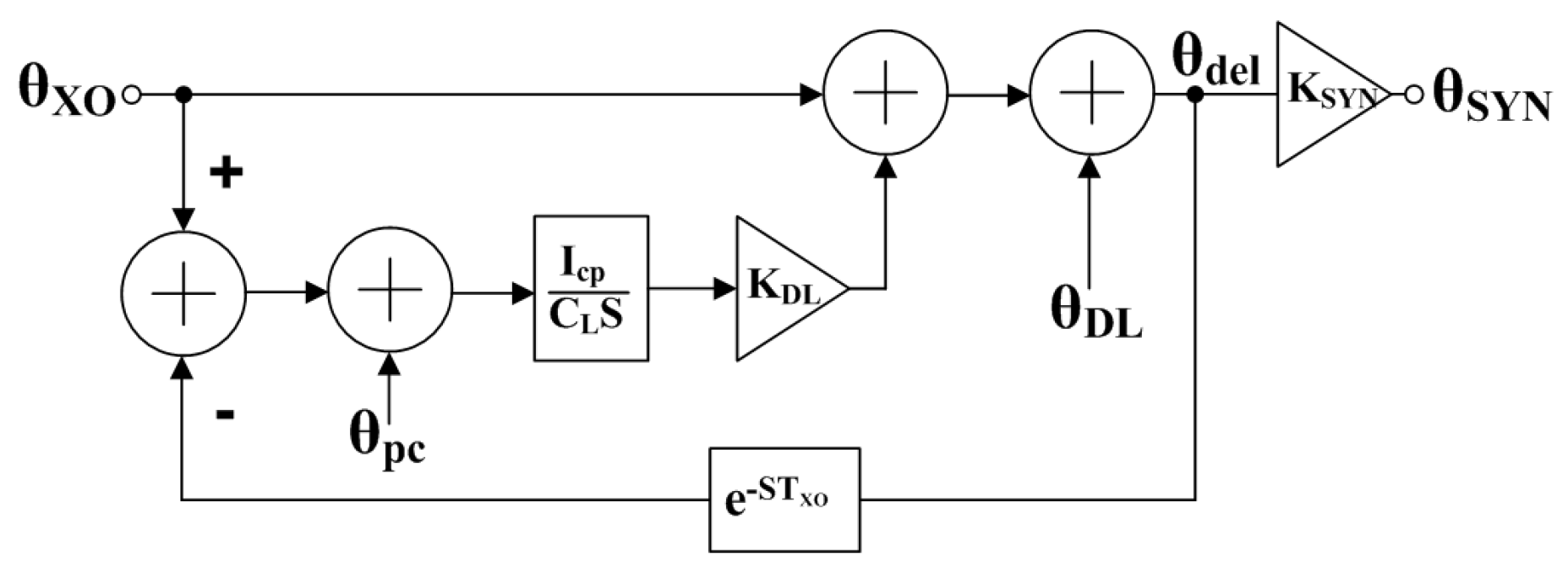
Figure 6.
Phase noise sources of the proposed synthesizer.
Figure 6.
Phase noise sources of the proposed synthesizer.
Figure 7.
Clock waveforms of (a) Ideal reference. (b) Jitter accumulated VCO.
Figure 7.
Clock waveforms of (a) Ideal reference. (b) Jitter accumulated VCO.
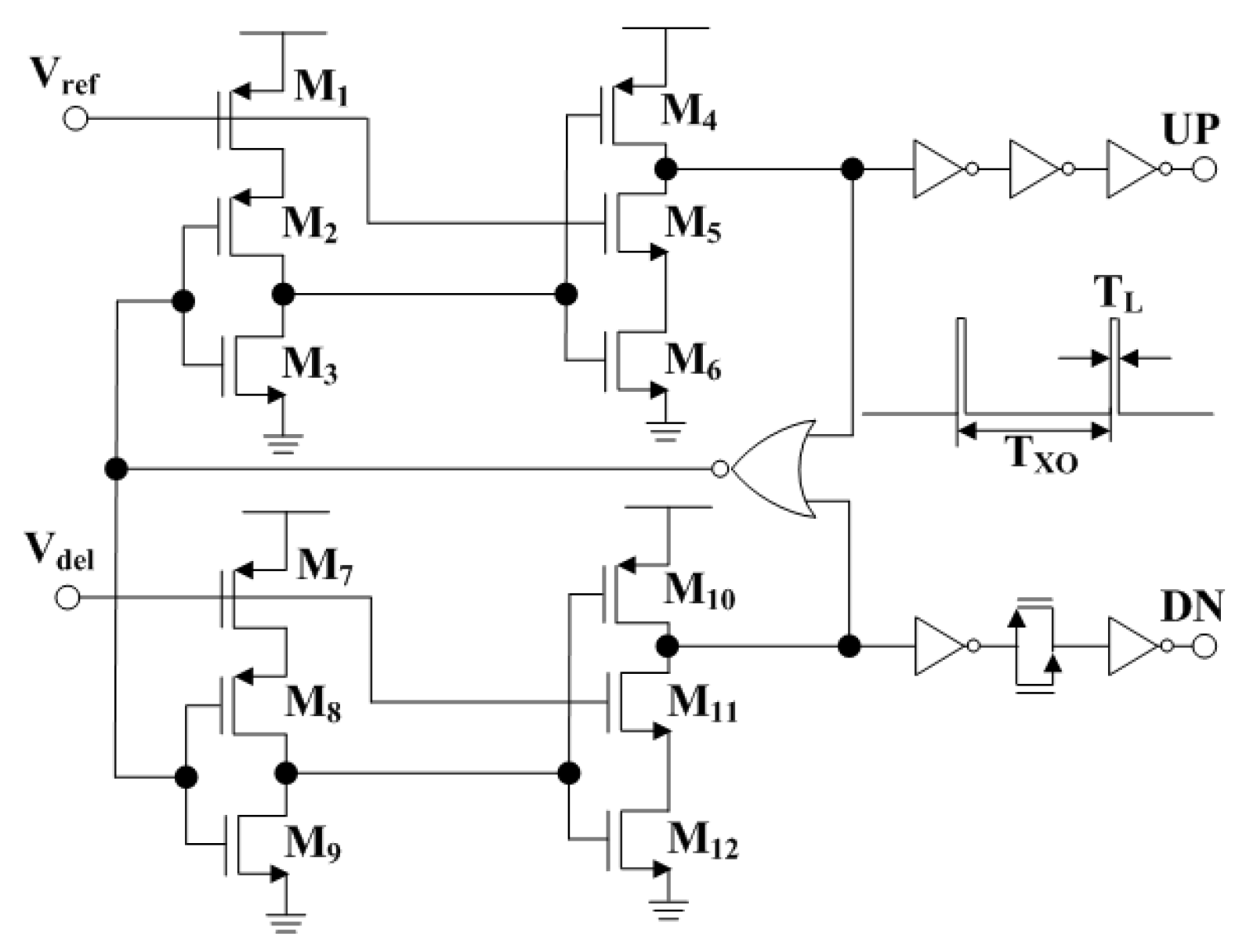
Figure 8.
TSPC PFD schematic.
Figure 8.
TSPC PFD schematic.
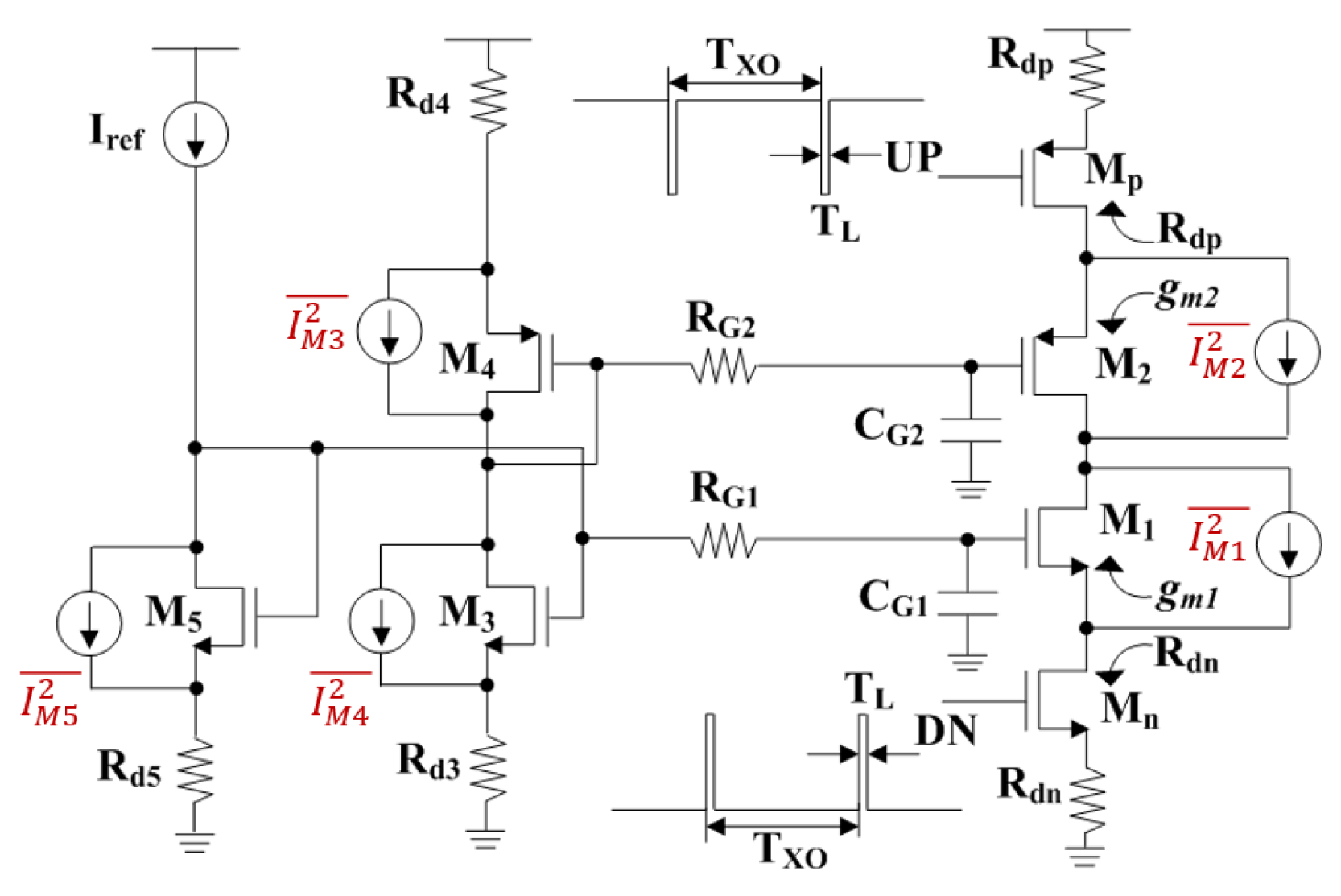
Figure 9.
Charge pump schematic.
Figure 9.
Charge pump schematic.
Figure 10.
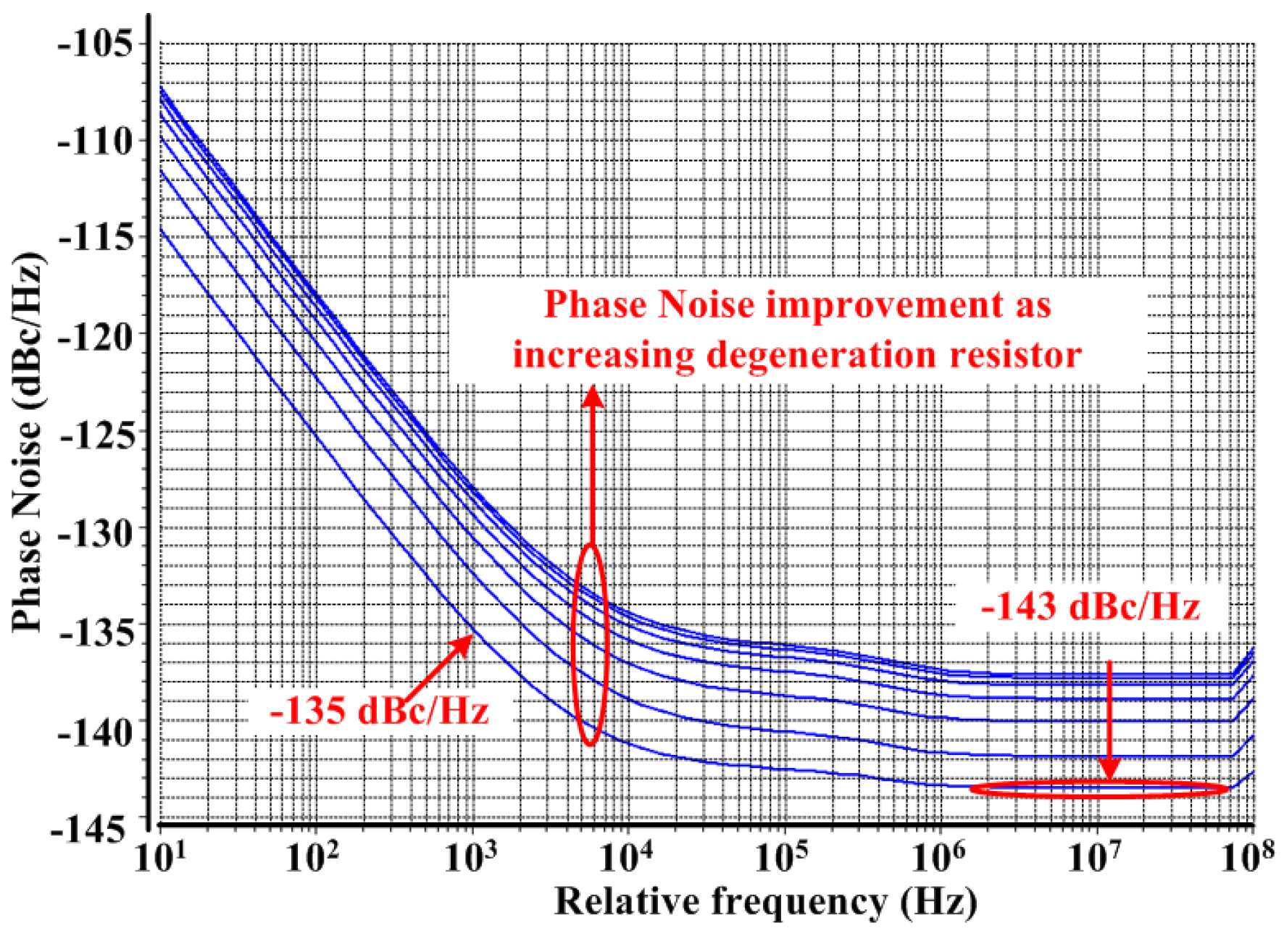
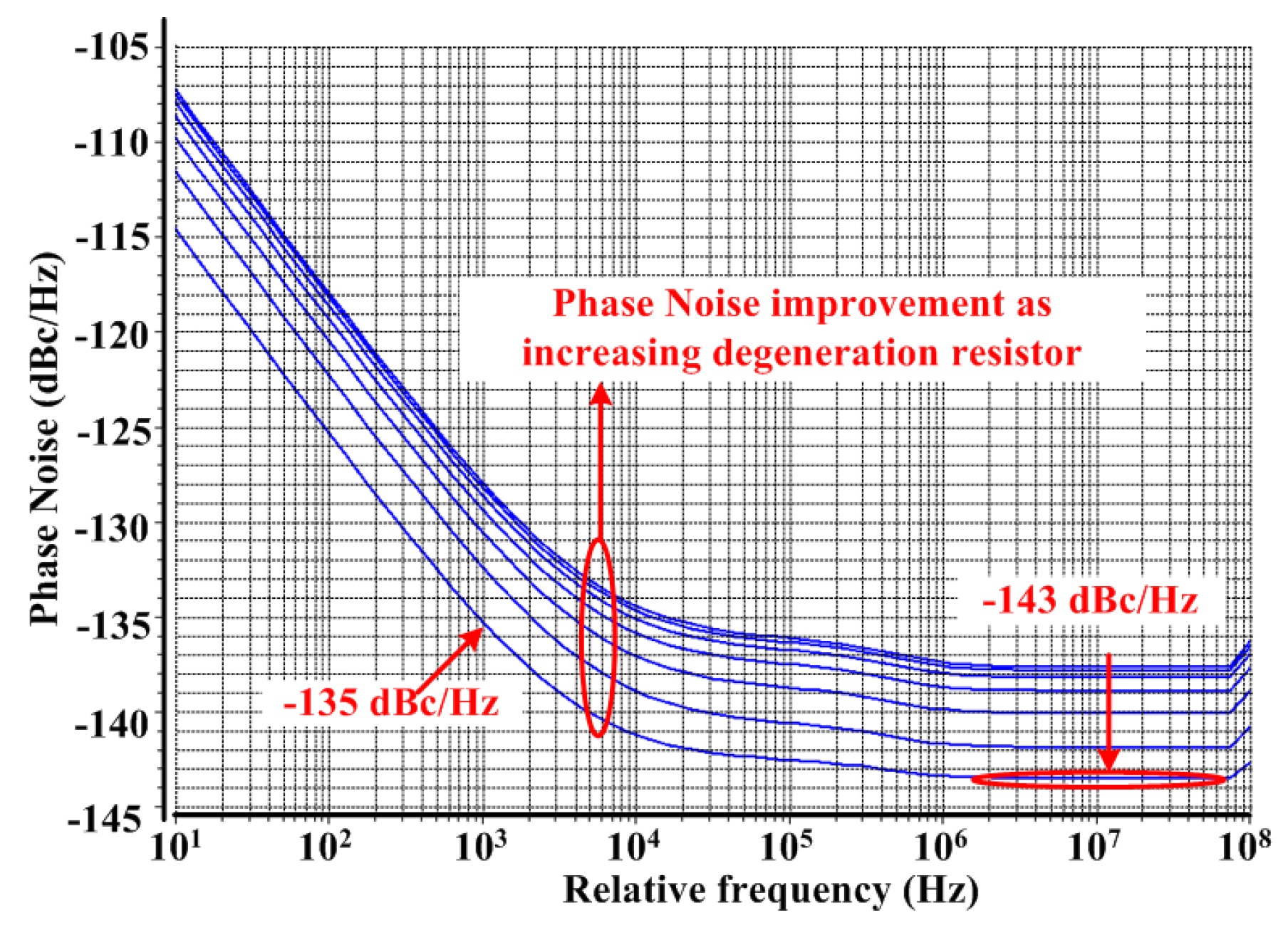
The proposed PFD+CP PN simulations increase Rdn and Rdp as 62.5, 125, 250, 500, 1000, 2000, and 4000 Ω.
Figure 10.
The proposed PFD+CP PN simulations increase Rdn and Rdp as 62.5, 125, 250, 500, 1000, 2000, and 4000 Ω.
Figure 11.
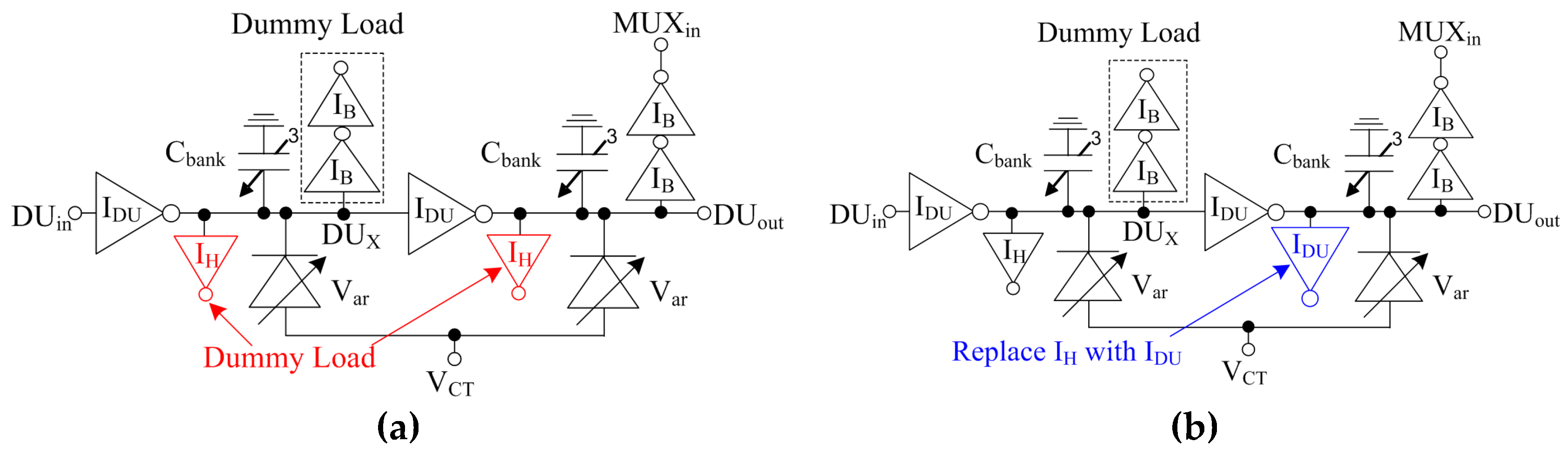
Proposed schematic. (a) The first 255 DUs. (b) The last DU in the VCDL DU chain.
Figure 11.
Proposed schematic. (a) The first 255 DUs. (b) The last DU in the VCDL DU chain.
Figure 12.
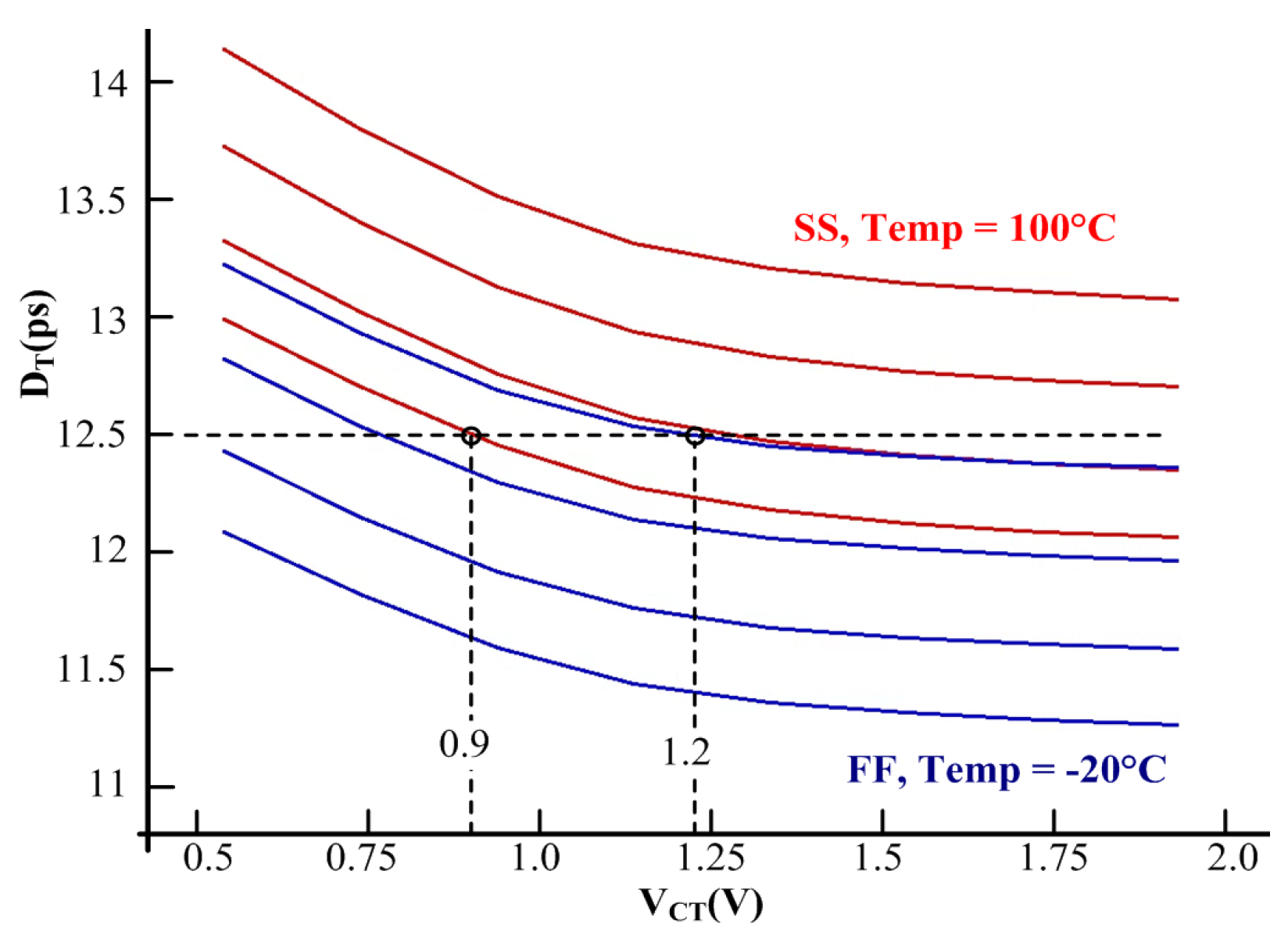
DU SS/100ºC and FF/−20ºC simulation.
Figure 12.
DU SS/100ºC and FF/−20ºC simulation.
Figure 13.
PN simulations on DU16, DU32, DU48, DU64, and DU80 (blue curves) and estimated PN curve (red) on DU256.
Figure 13.
PN simulations on DU16, DU32, DU48, DU64, and DU80 (blue curves) and estimated PN curve (red) on DU256.
Figure 14.
(a) Jitter added P1-P16 waveforms. (b) Jitter added VPSP VPSN, and VXOR pulses for 14td (top) and 9td (bottom).
Figure 14.
(a) Jitter added P1-P16 waveforms. (b) Jitter added VPSP VPSN, and VXOR pulses for 14td (top) and 9td (bottom).
Figure 15.
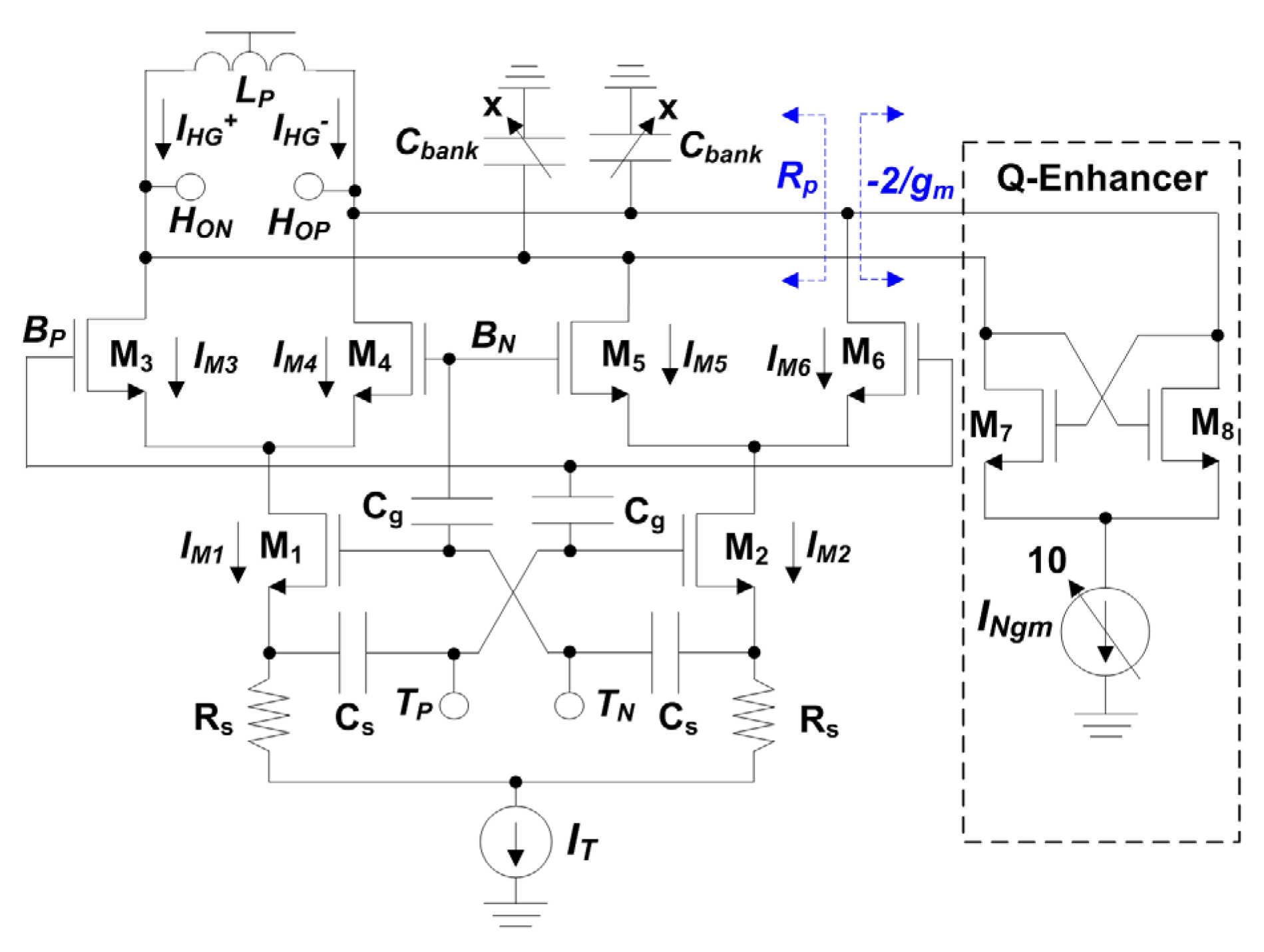
Harmonic generator schematic.
Figure 15.
Harmonic generator schematic.
Figure 16.
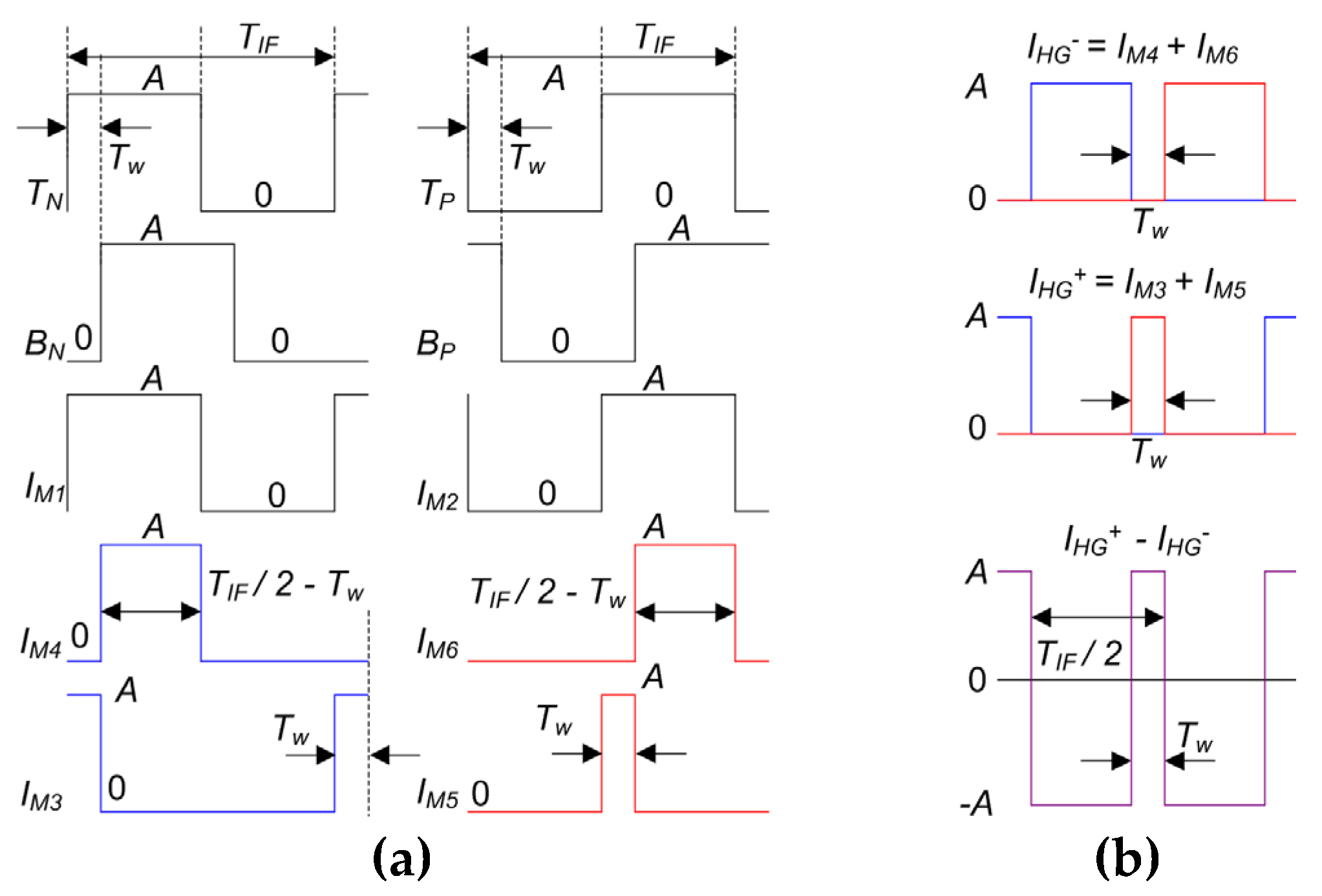
Proposed HG ideal. (a) Internal voltage and current pulses. (b) Single and differential output current pulses.
Figure 16.
Proposed HG ideal. (a) Internal voltage and current pulses. (b) Single and differential output current pulses.
Figure 17.
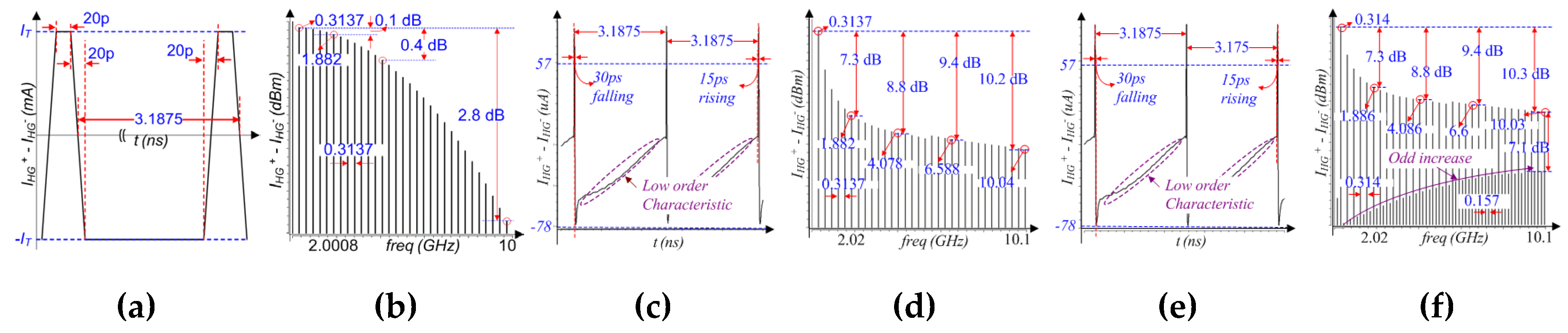
Ideal (IHG+ − IHG-). (a) Pulse. (b) Spectrum. For ACM = 254, simulated (IHG+ − IHG-). (c) Pulse. (d) Spectrum. For ACM = 253, simulated (IHG+ − IHG-). (e) Pulse. (f) Spectrum.
Figure 17.
Ideal (IHG+ − IHG-). (a) Pulse. (b) Spectrum. For ACM = 254, simulated (IHG+ − IHG-). (c) Pulse. (d) Spectrum. For ACM = 253, simulated (IHG+ − IHG-). (e) Pulse. (f) Spectrum.
Figure 18.
(a) HG output LP-Cbank. (b) Equivalent parallel LP-Cbank. (b) When all M1–M10 are turned on. (c) When all M1-M10 are turned off.
Figure 18.
(a) HG output LP-Cbank. (b) Equivalent parallel LP-Cbank. (b) When all M1–M10 are turned on. (c) When all M1-M10 are turned off.
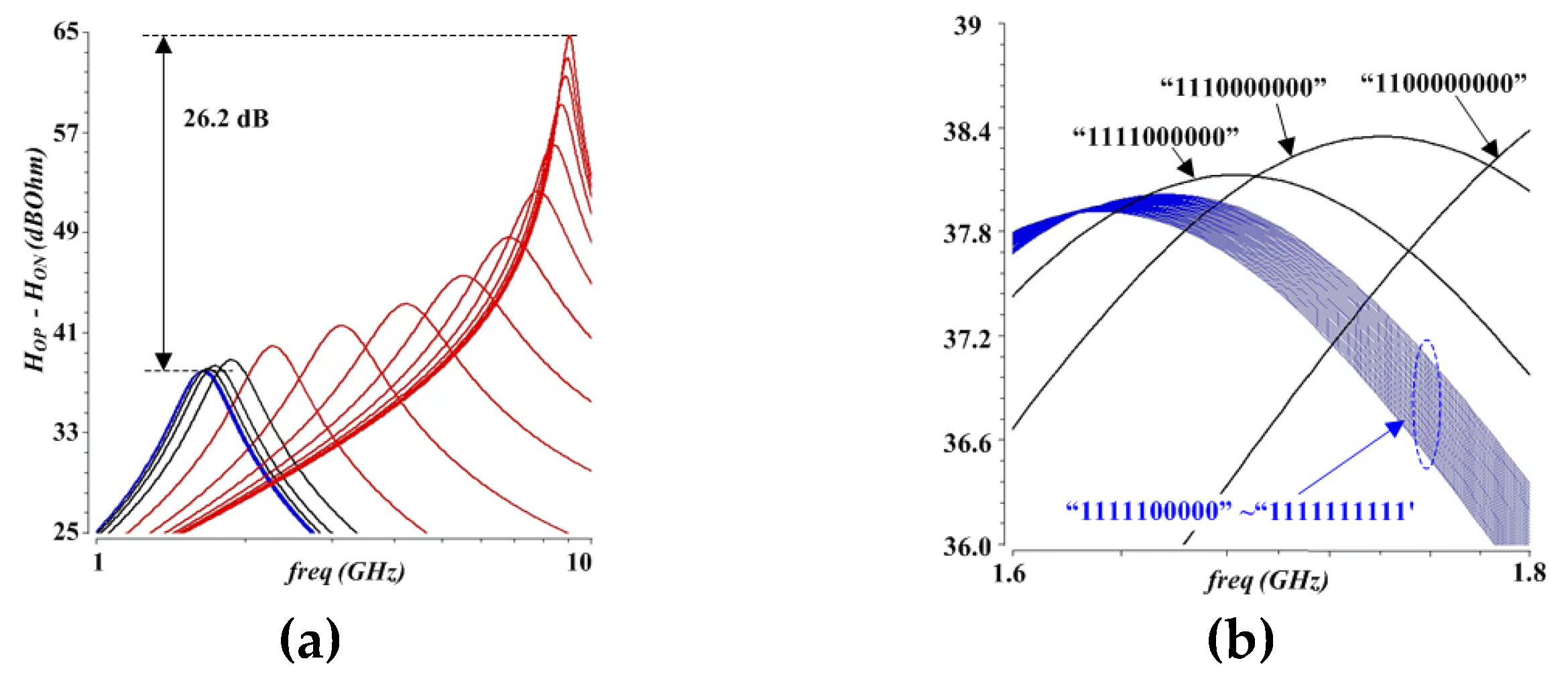
Figure 19.
HG differential output (HOP – HON) impedance simulations. (a) TT process at 25°C. (b) Zoomed simulations.
Figure 19.
HG differential output (HOP – HON) impedance simulations. (a) TT process at 25°C. (b) Zoomed simulations.
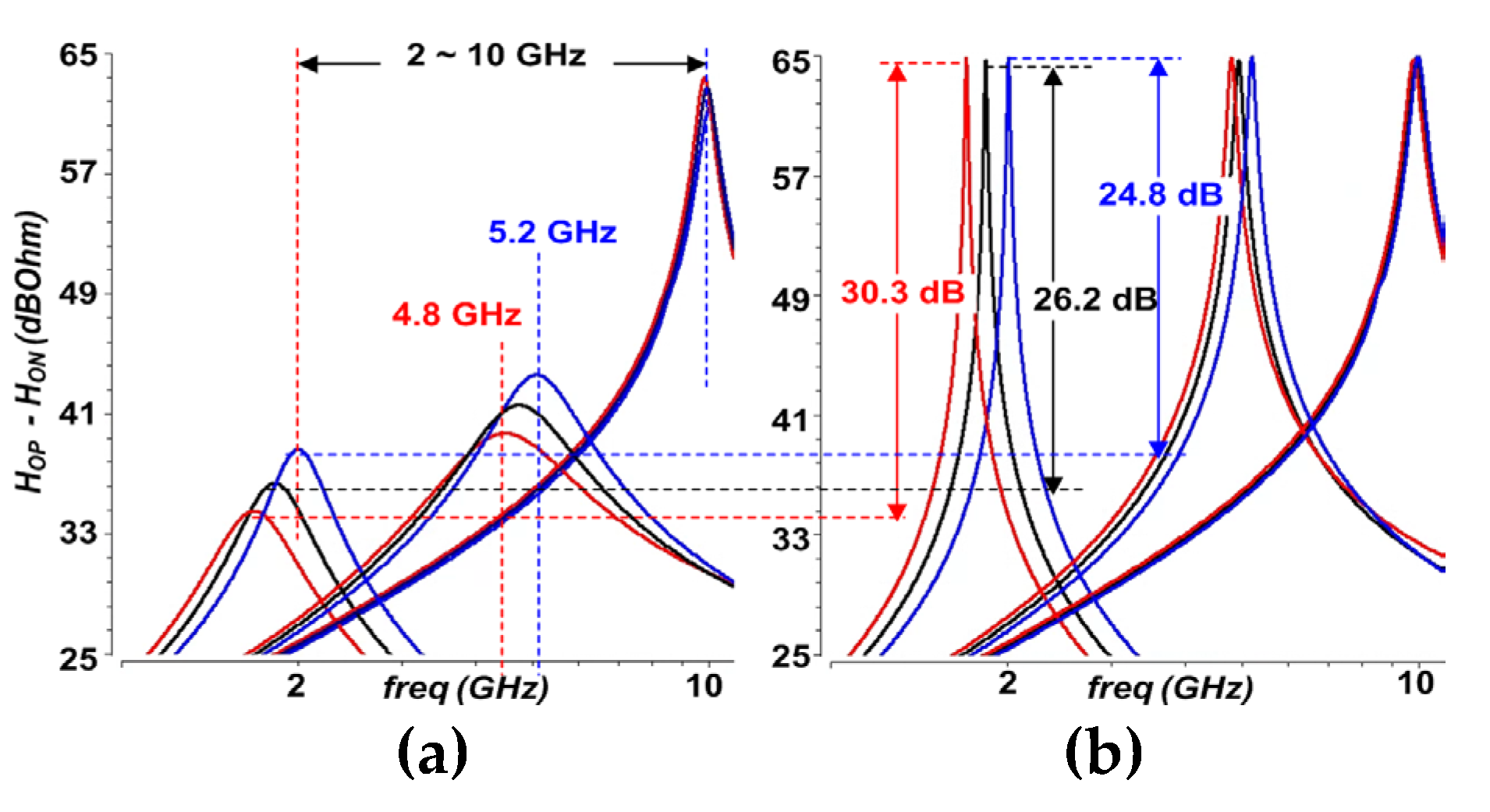
Figure 20.
HG differential output (HOP – HON) AC simulation for FF, TT, and SS processes. (a) Without negative-gm. (b) With negative-gm compensation.
Figure 20.
HG differential output (HOP – HON) AC simulation for FF, TT, and SS processes. (a) Without negative-gm. (b) With negative-gm compensation.
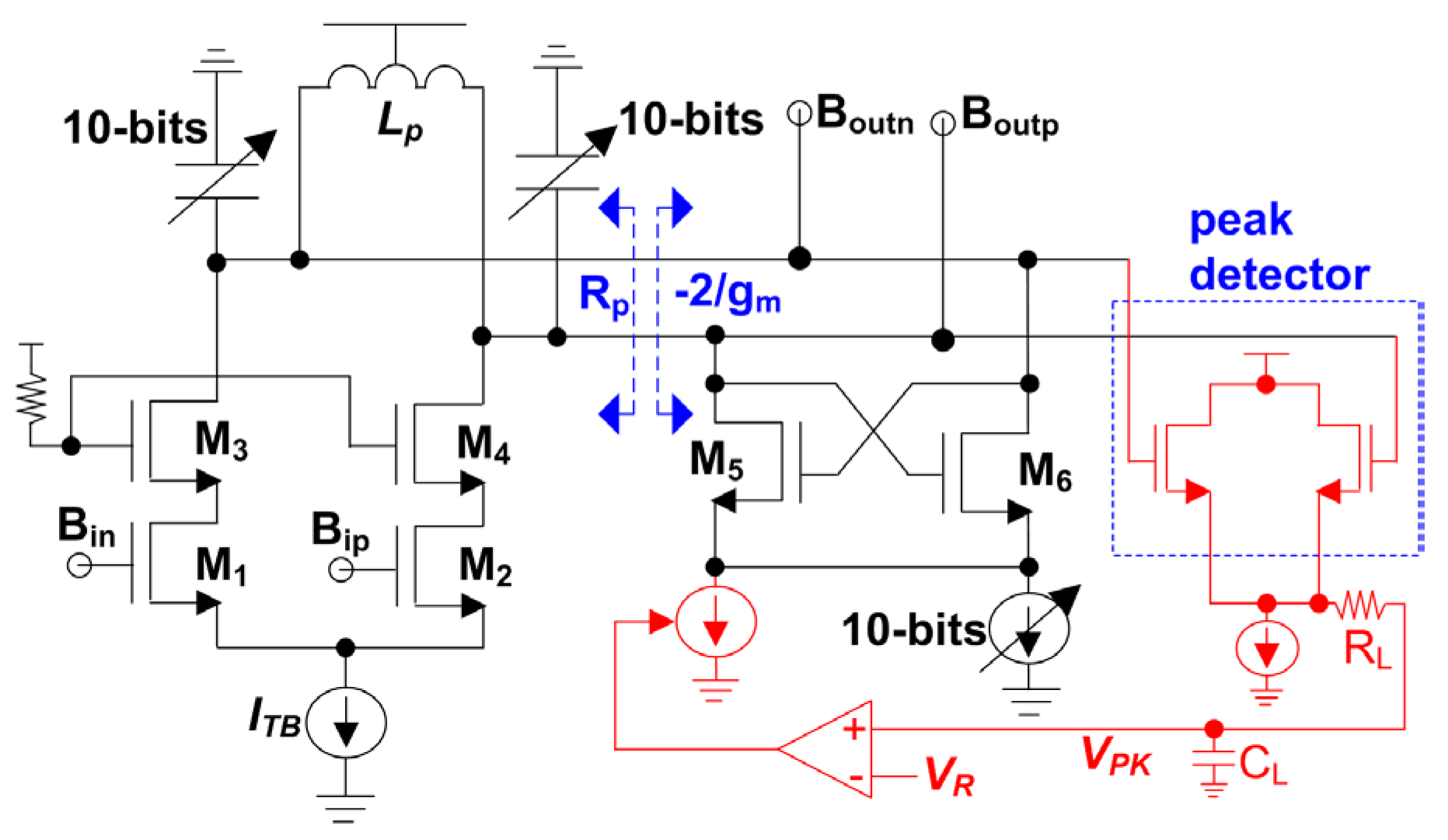
Figure 21.
Schematic of a buffer with an ACACL.
Figure 21.
Schematic of a buffer with an ACACL.
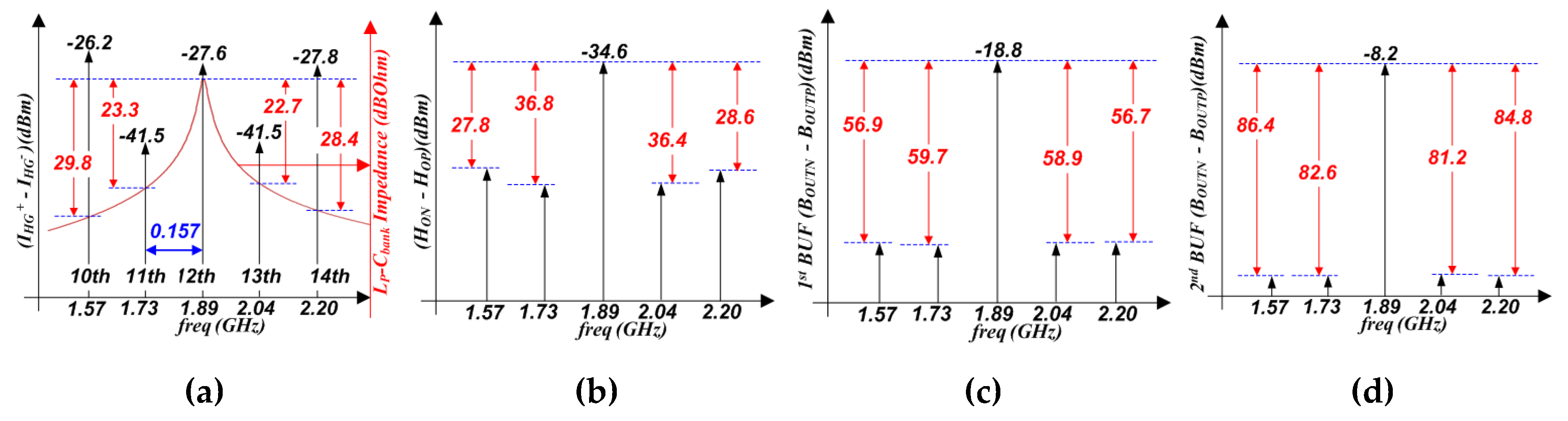
Figure 22.
For ACM = 253. (a) (IHG+ − IHG-) spectrum. (b) HG output spectrum. (c) First BUF output spectrum. (d) Second BUF output spectrum.
Figure 22.
For ACM = 253. (a) (IHG+ − IHG-) spectrum. (b) HG output spectrum. (c) First BUF output spectrum. (d) Second BUF output spectrum.
Figure 23.
The second BUF output spectrum. (a) ACM = 127. (b) ACM = 1.
Figure 23.
The second BUF output spectrum. (a) ACM = 127. (b) ACM = 1.
Figure 24.
Photograph of the proposed synthesizer.
Figure 24.
Photograph of the proposed synthesizer.
Figure 25.
Test environment block diagram.
Figure 25.
Test environment block diagram.
Figure 26.
Test environment block diagram.
Figure 26.
Test environment block diagram.
Figure 27.
Driver amplifier with external output matching.
Figure 27.
Driver amplifier with external output matching.
Figure 28.
DA. (a) OP1dB simulation. (b) S22 measurements of chip#1 ~ chip#5.
Figure 28.
DA. (a) OP1dB simulation. (b) S22 measurements of chip#1 ~ chip#5.
Figure 29.
Capacitor bank (Cbank) calibration block diagram.
Figure 29.
Capacitor bank (Cbank) calibration block diagram.
Figure 30.
Oscillating frequency calibration error.
Figure 30.
Oscillating frequency calibration error.
Figure 31.
The synthesizer output spectrum waveform. (a) ACM =1 and RFFMF =32. (b) ACM =2 and RFFMF =32. (c) ACM =127 and RFFMF =28. (d) ACM =128 and RFFMF =28. (e) ACM =253 and RFFMF =12. (f) ACM =254 and RFFMF =12.
Figure 31.
The synthesizer output spectrum waveform. (a) ACM =1 and RFFMF =32. (b) ACM =2 and RFFMF =32. (c) ACM =127 and RFFMF =28. (d) ACM =128 and RFFMF =28. (e) ACM =253 and RFFMF =12. (f) ACM =254 and RFFMF =12.
Figure 32.
The synthesizer output worst HRRs. (a) ACM = 1, 127, and 253. (b) ACM = 2, 128, and 254.
Figure 32.
The synthesizer output worst HRRs. (a) ACM = 1, 127, and 253. (b) ACM = 2, 128, and 254.
Figure 33.
The synthesizer PN curves of 1.89 and 9.96 GHz.
Figure 33.
The synthesizer PN curves of 1.89 and 9.96 GHz.
Table 1.
Counter Output.
Cbank
D10-D1
|
Cal12-Cal1 Magnitude in decimal (Caldec) |
| Chip#1 |
Chip#2 |
Chip#3 |
Chip#4 |
Chip#5 |
| 1101010101 |
2561 |
2562 |
2561 |
2560 |
2560 |
| 1100101011 |
2499 |
2498 |
2499 |
2499 |
2499 |
| 1100000101 |
2400 |
2400 |
2439 |
2438 |
2439 |
| 1011100001 |
2382 |
2383 |
2382 |
2382 |
2383 |
| 1011000000 |
2328 |
2328 |
2328 |
2329 |
2327 |
Table 2.
RMS jitter measurement.
Table 2.
RMS jitter measurement.
| |
Chip#1 |
Chip#2 |
Chip#3 |
Chip#4 |
Chip#5 |
| RMS Jitter [fs] @ 1.89 [GHz] |
82.651
|
83.121
|
82.141
|
81.841
|
83.741
|
| 107.62
|
107.92
|
107.432
|
107.122
|
107.982
|
| RMS Jitter [fs] @ 9.96 [GHz] |
82.721
|
83.541
|
82.341
|
82.211
|
84.131
|
| 107.572
|
107.832
|
107.482
|
107.242
|
108.052
|
Table 3.
Comparison with state-of-the-art synthesizer.
Table 3.
Comparison with state-of-the-art synthesizer.
| Parameter |
[19] |
[20] |
[21] |
[22] |
[23] |
[28] |
This work |
| Tech. |
65mm
CMOS |
28mm
CMOS |
28mm
CMOS |
65mm
CMOS |
65mm
CMOS |
65mm
CMOS |
65mm
CMOS |
| fref [MHz] |
50.0 |
125.0 |
500.0 |
150.0 |
200.0 |
10 |
156.3 |
| fout [GHz] |
12–14.5 |
18.9–22.3 |
11.9–14.1 |
3–3.7 |
24–28.2 |
0.1–5 |
1.88–9.96 |
| Frequency Bandwidth [%] |
18.9 |
16.5 |
16.9 |
20.9 |
16.1 |
192.2 |
136.5 |
| rms jitter [fs] |
83.0
(1k-100M) |
71.8
(1k-100M) |
58.2
(1k-100M) |
135.0
(1k-100M) |
65.4
(10k-30M) |
9601
(10k-30M) |
107.6
(1k-100M) |
| Active Die area [mm2] |
0.2 |
0.5 |
0.2 |
0.4 |
0.5 |
1.44 |
0.6 |
| Power consumption [mW] |
7.7 |
36.0 |
18.0 |
9.5 |
14.5 |
21 |
17.0 |
| FoM12
|
-252.8 |
-247.3 |
-252.1 |
-247.6 |
-252.1 |
-227.1 |
-246.9 |
| FoM23
|
-265.5 |
-259.5 |
-264.4 |
-260.8 |
-264.1 |
-250.0 |
-268.25 |