Preprint
Article
Harnessing Regression Models to Optimize Project Duration Estimation and Reduce Delays in South African Infrastructure Development
Altmetrics
Downloads
60
Views
28
Comments
0
This version is not peer-reviewed
Submitted:
02 October 2024
Posted:
03 October 2024
You are already at the latest version
Alerts
Abstract
Accurately estimating project duration is critical for the successful delivery of construction projects, particularly in the dynamic and resource-constrained environment of South Africa. This study aims to assess the key factors influencing construction project duration in the South African context through the development of a regression model. By analyzing data from a diverse range of construction projects, the research identifies significant variables such as project size, complexity, location, resource availability, and stakeholder involvement that contribute to delays or expedited completion. The regression model is designed to quantify the impact of these factors, offering a predictive tool that can enhance project planning and scheduling accuracy. The findings provide valuable insights for project managers, contractors, and policymakers, enabling them to make informed decisions that optimize project timelines and improve the overall efficiency of the construction industry in South Africa.
Keywords:
Subject: Engineering - Architecture, Building and Construction
1. Introduction
The construction industry is crucial to South Africa's economic development, significantly impacting infrastructure expansion and job creation. Nonetheless, one of the sector's ongoing challenges is accurately estimating project durations [1,2]. Timely project completion is vital for managing costs, allocating resources, and ensuring stakeholder satisfaction [3]. Unfortunately, delays are common, leading to increased costs, wasted resources, and strained stakeholder relationships [4]. Despite the need for precise completion timelines, accurate estimation of contract completion remains elusive [5]. As mentioned by Vandervoode et al [6] success in construction is often measured by completing projects within the specified time frame, budget, and quality standards, while avoiding accidents. This success reflects the level of project management control and competence. However, persistent project management issues indicate ongoing difficulties. Effective project control involves detailed planning of activities, labor, materials, and equipment, as well as supervision and task allocation [7]. These elements require stringent management to ensure the project meets its design specifications. Various stakeholders, including clients, contractors, designers, and external influences, play a role in project delivery. In South Africa, the challenge of estimating project duration is exacerbated by several contextual factors such as fluctuating economic conditions, varying resource availability, regulatory complexities, and diverse geographical and environmental factors [8,9]. The industry's dynamic nature, characterized by multiple stakeholders, diverse project scales, and varying levels of technological adoption, further complicates duration estimation [10].
Construction projects are unique in their durations and associated costs, which are crucial for evaluating project efficiency and quality, and consequently, broader societal development [11]. The inherent unpredictability of these projects creates significant challenges in adhering to schedules and budgets. This unpredictability arises from the unique nature of construction operations, making construction management complex and multifaceted. Each project’s distinctiveness often leads to temporal and financial unpredictability, hindering progress and complicating the management of construction activities [12]. Unanticipated instability challenges the successful execution and timely delivery of projects within budgetary constraints [4,7]. Variability in construction operations is driven by factors such as project site, clientele, regulatory environment, workforce, machinery, technology, subcontractors, expertise, and project team dynamics, making project analysis and management complex [3,11]. Achieving project completion within budget remains a significant challenge, with cost overruns increasing proportionally with project complexity [13]. To address this issue, this study aims to examine the key factors affecting construction project duration in South Africa by developing a regression model. By analyzing a detailed dataset of construction projects, the research intends to pinpoint the most influential variables impacting project timelines. These variables will be incorporated into a regression model to create a robust tool for more accurate duration predictions.
This is vital because accurate forecasting of construction costs and timelines at the project’s outset is crucial[4]. Inaccurate predictions, whether too high or too low, can lead to budget overruns and suboptimal outcomes, such as failure to meet quality standards and delays [1,14]. Soft computing techniques are particularly suited for modeling time-cost constraints in construction projects due to the non-specific patterns caused by environmental and logistical factors, as well as non-linear and discrete dependencies [15]. As construction projects become increasingly complex and time-consuming, traditional supervision methods may fall short. In these scenarios, computer simulation techniques can be beneficial for addressing such challenges. It is advisable to use historical or current data when there is no expectation of significant changes to the fundamental assumptions of the modeling process [14]. Additionally, leveraging professional expertise is a practical approach for adjusting inputs that may fluctuate due to unforeseen changes in underlying factors. The results of this study are expected to offer valuable insights into the factors that drive construction timelines in the South African context. Moreover, the regression model developed through this research could serve as a practical tool for project managers, contractors, and policymakers, helping them make informed decisions that optimize project duration and improve the overall efficiency and effectiveness of the construction industry in South Africa. Section 1 introduces the study, providing context for its background and highlighting its significance and potential benefits in addressing current infrastructure challenges. Section 2 presents a literature review, contextualizing existing studies and critically examining key issues that inform and guide this research. Section 3 details the methodological approach employed to address the research questions and issues identified. Section 4 presents the study's results, which are further discussed and analyzed in Section 5. Finally, Section 6 concludes the study by offering recommendations and discussing its limitations.
2. Literature Review
Project Duration/Time Delays in the Construction Industry
Project duration refers to the estimated end date of a project, given a specific start date, and represents when the project is expected to be completed [16,17]. It is important to distinguish project duration from total project effort, as these are not interchangeable metrics[14,18]. There is no direct correlation between time and effort; simply adding more team members may only reduce the project duration up to a point, after which it could lead to increased duration and costs. Many construction projects fail to meet their original completion dates, a common issue across various types of construction work worldwide [19,20].
Late project delivery has significant repercussions for all stakeholders involved. For project owners, delays mean a postponed start for asset operations, which can result in missed business opportunities, a loss of competitive advantage, delayed returns on investment, and reduced profits [21,22,23]. For contractors, late completion can lead to contractual penalties, prolonged resource allocation, decreased productive capacity, and increased indirect and overhead costs [24]. Subcontractors face challenges in resource planning, as delays can lead to inaccurate projections and potential overlaps with other projects. End users, particularly those living nearby or directly affected by construction, often experience discomfort and disappointment due to delayed project delivery [25,26,27]. While academic research has proposed various risk and uncertainty management theories for construction projects, these are often conceptual and based on analytical models that are rarely implemented in practice. Construction is an information-intensive industry, and complete project definitions are not always available at the start, leading to uncertainty [28,29]. Effective management of this uncertainty is crucial, especially in fast-track projects where design and production processes are integrated. Fast-tracking involves overlapping sequential activities to compress the project schedule, allowing construction to begin on phases even before the overall project design is complete [30,31]. This method aims to shorten the construction time by starting work on designed portions as soon as they are ready.
Although delays can sometimes have positive effects, such as reducing activity costs through more efficient resource allocation, these benefits typically accrue to contractors, while other stakeholders suffer the negative impacts [32,33]. Weather is consistently cited as a frequent and detrimental cause of project delays. Unresolved claims due to weather-related issues can escalate into legal disputes and prolonged work stoppages, extending beyond the initial weather disruption [33,34]. The primary goal of fast-tracking in construction projects is to achieve earlier project completion, making it essential to structure an appropriate contracting strategy that supports this objective. Several models have been developed to optimize the use of construction crews, thereby minimizing project duration and/or cost, particularly in repetitive construction projects [35,36].
The total project duration is a crucial indicator of how effectively resources are managed to deliver project outcomes within the required quality standards [37]. In practice, baseline project schedules are vulnerable due to uncertainties in activity durations and costs [30]. Therefore, accurate duration prediction is vital both in the initial baseline scheduling and when updating interim baseline schedules during project execution [38]. Effective risk management, which includes identifying, analyzing, mitigating, and monitoring risks, plays a key role in ensuring that a project is completed on time and within budget [39]. Managing risks associated with project schedules and costs is an integral part of efficient project management [40]. Delays, often recurring and complex, remain a significant challenge in construction projects and are a common issue in construction claims, arising from a wide range of causes.
Analytical Methods in Construction Project Duration Estimation
In both developing and industrialized countries, deviations from planned time schedules are a common issue in construction projects [41,42]. Various factors during the construction period disrupt the systematic flow of work, leading to time-based anomalies and ultimately impacting project timelines [43]. Given the construction industry's significant role in a country's macro-economic structure, understanding the impact of timely project completion on the allocated budget is crucial [28]. Project duration serves as a key metric for measuring the efficiency of project implementation. Traditionally, construction managers have relied on deterministic scheduling techniques to plan and estimate project durations [44]. However, these techniques are known to consistently underestimate project durations. While deterministic methods offer advantages such as ease of learning, straightforward output interpretation, and lower computational demands, they also have notable limitations [44]. They often fail to account for variability in activity durations, which can lead to inaccuracies in duration estimates.
Alternative methods, like Stochastic Network Analysis, have been explored as potential solutions [45]. These methods can provide more accurate duration estimates by considering variability and uncertainties. However, they are less frequently adopted due to their computer-intensive nature, the need for extensive historical data, limited contextual applicability, and the requirement for specialized skills that many practitioners lack [36]. The construction industry frequently experiences projects that end later and cost more than initially planned [46]. The literature identifies several causes for these issues, with poor planning and project control practices being a recurring factor in late projects. Deterministic scheduling techniques, despite their advantages, often fall short due to their failure to address variability in activity durations [47]. This variability, defined as the difference between the actual and planned durations of a project activity, is a major source of inaccuracy in these traditional techniques. Thus, addressing this limitation is essential for improving project duration estimates and overall project management [48]. Deterministic scheduling techniques, which assume constant activity durations, often rely on average duration estimates to create project schedules. While these methods are straightforward and require less computational effort, they tend to underestimate project durations, especially when activities are performed in parallel. This underestimation arises from the merge event bias, where the maximum completion time of parallel activities is generally higher than the average of the individual activity durations. This phenomenon is analogous to the challenge of calculating the maximum of multiple random variables, a problem extensively studied in stochastic network analysis (SNA) [49].
SNA addresses this by modeling activity durations with various statistical distributions and generating numerous duration values through simulations to compute a representative project duration. This approach allows for the creation of a statistical distribution of project durations, from which the average and standard deviation can be derived [50]. Delays and cost overruns are severe and persistent problems in construction projects. Late completions lead to budget overruns and missed potential income, while early completions may result in cost extensions due to overstaffing. The definition of a "successful" project often hinges on completing it within the planned schedule, budget, and quality standards [14]. One of the main reasons for the lack of an analytical solution in schedule networks is the absence of statistical distributions that are both sum-stable and max-stable [51]. In series, activity durations are added, while in parallel, the maximum of several path durations needs to be calculated. Because no distribution fits both criteria, approximate methods are required [35]. To address these challenges and enable probabilistic inferences about project durations, the Project Evaluation and Review Technique (PERT) was introduced over 60 years ago [15]. PERT uses three-point estimates (optimistic, most likely, and pessimistic) to calculate the average project duration and standard deviation based on the longest critical path [49]. However, PERT has been criticized for underestimating average project duration and overestimating standard deviation due to its assumptions about the existence of a single critical path [13].
Despite these limitations, PERT remains popular in project management. Researchers have extensively analyzed and refined PERT's assumptions and procedures, including the accuracy of estimates and the incorporation of time-cost trade-offs [22,49]. Notably, the Graphical Evaluation and Review Technique (GERT) developed by Pritsker in 1966 aimed to address PERT's fundamental issues, such as merge event bias, but required Monte Carlo simulation due to its complexity [5,15]. More recently, M-PERT, a technique proposed by Ballesteros-Pérez et al., integrates some of GERT’s principles and allows for manual calculation of project duration averages and standard deviations, though it can be time-consuming for large networks [52]. Overall, while various extensions of PERT and other methods address specific limitations, they often do so by increasing complexity and calculation time.
3. Research Method
This study employs a quantitative research approach to analyze project duration data using regression models to optimize duration estimation and reduce delays in South African infrastructure projects. The primary goal is to identify patterns and relationships between project characteristics (such as project type, sector, and the extension indicator) and the resulting project durations. The analysis is based on historical project data, which includes a variety of project types, sectors (government and private), and whether or not project durations were extended [53]. The data was then subjected to regression analysis to assess the significance and predictive power of these variables in estimating project timelines [54,55]. This approach is well adopted in previous studies [56]. Other studies have also utilized linear regression and multiple regression [28,44]. Data for this study was sourced from a construction management database, which contains records of completed infrastructure projects across different sectors in South Africa. The dataset includes 61 projects, each with the following key variables:
- Project Type (e.g., schools, hostels, industrial buildings)
- Number of Projects (for each type)
- Average Project Duration (in months)
- Sector (Government or Private)
- Extension Indicator (whether the project required an extension or not)
The data were extracted and prepared for analysis by categorizing the projects according to the variables and calculating average durations. The projects in the database spanned a range of types, including school buildings, hostels, industrial facilities, offices, and residential buildings. This diversity of project types provides a robust foundation for identifying generalizable trends. Variables such as the average duration by project type and sector, and the presence of an extension were used to provide an initial understanding of the variability in project durations [57,58]. A linear regression model was applied to determine the impact of the independent variable (e.g., project type, sector, and extension) on project duration. The dependent variable is the average project duration in months [59].
The regression output was evaluated using, Multiple R, R Square, Adjusted R Square, Standard Error, ANOVA as done in other studies [60]. The regression analysis also included an ANOVA (Analysis of Variance) test to examine the overall significance of the model [61]. The F-statistic was used to evaluate whether the independent variables significantly contributed to explaining the variation in project duration [62]. A p-value of less than 0.05 was considered statistically significant, indicating that at least one predictor variable had a meaningful impact on project duration [63]. The coefficient estimates from the regression model were interpreted to determine the specific effect of each independent variable on project duration [64,65]. A positive coefficient suggests that the predictor variable is associated with longer project durations, while a negative coefficient would indicate a shorter duration [66]. The t-statistic and p-values were examined to assess whether the coefficients were statistically significant at the 5% level [66]. Although this study provides valuable insights into the relationship between project characteristics and duration, it is limited by the relatively small sample size of 61 projects. Additionally, the dataset only includes completed projects, which may introduce survivorship bias, as incomplete or delayed projects were not accounted for [53]. Furthermore, other important predictors of project duration, such as contractor experience, project funding, and weather-related delays, were not included in this analysis but could be considered in future research to improve the predictive power of the regression model [67]. This research was conducted using secondary data, and no personal or sensitive information was included in the dataset. All data were anonymized and used in compliance with data protection regulations to ensure confidentiality and ethical handling of project information. The statistical analysis was conducted using Microsoft Excel and SPSS, with Excel used to manage and organize the data and SPSS for regression analysis. These tools facilitated the calculation of descriptive statistics, ANOVA, and regression outputs necessary for the study's findings.
4. Results and Discussion
When it comes to the execution of a building project, success can be defined as the building's completion within the allotted time frame, staying under budget, meeting quality requirements, and experiencing no accidents. This shows the degree of project management control as well as a gauge of competency [68]. The study's findings, aimed at developing a model to optimize project duration estimation and reduce delays in South African infrastructure development, are based on an analysis of 65 infrastructure projects across the country. The projects were categorized according to several key variables, including provincial location, type of contract used, original contract sum, construction duration in months, approved extensions of time (in months), extensions granted with associated costs, approved variation orders, final contract sum, project size (band), project type, and type of client (public or private).
The breadth of this dataset provides a powerful way to build a complex regression model that takes many project timeline drivers into account. The study provides useful information about understanding the relationships between these variables and their implications to identify the reasons for time overruns and likely cost escalation. The model is designed not only to enhance the accuracy of project duration estimates, but also to predict possible submission delays that might take place, thus providing predictive findings which in turn could be employed to plan accurately and carry out infrastructure projects in a more proactive manner. The inclusion of both contract-related variables (such as variation orders and extensions of time) and external factors (such as provincial differences and client type) ensures a holistic approach to understanding project inefficiencies. The ultimate goal is to provide stakeholders with actionable recommendations to streamline project management processes, reduce delays, and enhance the overall efficiency of South African infrastructure development.
- 4.1 Province-Based Duration Variability
As shown in Figure 1 below, the figure illustrates considerable variability in average project durations across different provinces. For instance, Free State has the highest average project duration of 20 months, while Mpumalanga has the lowest at 12 months based on the project information gathered. This suggests that project timelines vary significantly across regions in South Africa were the study was conducted. Regression models could help in identifying the factors responsible for these variations—whether due to resource availability, logistical challenges, or governance factors—and in forecasting more accurate project durations for future developments. Provinces with a higher number of projects, such as Free State (35 projects) and Northern Cape (13 projects), show relatively higher or moderate average durations. However, Gauteng, despite having only 2 projects, has a relatively long average duration of 18 months. This indicates that project volume alone doesn't explain duration, suggesting the need for more sophisticated indicators in a regression model, such as project type which is discussed in subsequent sections and also suggested in other studies [69,70]. Regression models can be used to analyze the relationship between the number of projects and their average durations. The variability in project durations despite a lower number of projects (as seen in Gauteng and North West) could point to other influencing factors beyond the number of projects, which regression can model (e.g., project management strategies, regulatory issues, labor productivity, etc.).
4.2 Correlation Between Project Value and Duration
There appears to be a general trend where larger project values correspond to longer average durations. For instance, projects in the 30,000,000 to 40,000,000 range have an average duration of 26.08 months, the longest in the dataset, while smaller projects in the 0 to 10,000,000 range have the shortest average duration of 9.60 months. This is expected since higher project value often indicates a bigger scope and thus indicating greater time required. This suggests that higher-value projects tend to be more complex and require more time to complete, likely due to larger scopes, more sophisticated engineering challenges, or extended approval processes. However, this relationship isn't strictly linear. For instance, projects in the 40,000,000 to 50,000,000 range have a slightly shorter average duration (24.18 months) than those in the 30,000,000 to 40,000,000 range, despite their higher value. Additionally, projects valued between 50,000,000 and 100,000,000 have a shorter average duration of 16.50 months. This highlights potential inefficiencies or factors not directly tied to project value, suggesting the need for more nuanced models to understand the drivers of delays. From the data, we can observe that while increasing project value often leads to longer project durations, the marginal increase in duration becomes less significant at higher values. For example, the jump from 0 to 10,000,000 projects to 10,000,000 to 20,000,000 only results in a 0.9-month increase in average duration, while the increase from 20,000,000 to 30,000,000 sees a much larger difference of 3.63 months. However, at higher values, such as between 40,000,000 and 50,000,000, the increase in duration is more modest. This may indicate that once certain economies of scale or project management efficiencies are achieved, the time-to-value ratio improves, a useful insight for optimizing project timelines [71]. This is vital for government and private entities involved in infrastructure development, helping them understand the relationship between investment and time to completion [72]. This can also guide budget allocation and resource management, ensuring that projects are completed on time and within budget, thereby minimizing costly delays [73]. This is shown diagrammatically in Figure 2 below.
4.3 Variation in Project Types and Durations
The nature of a project can have a considerable impact on the estimated completion time. For example, schools, despite being numerous, have relatively long durations, indicating that the complexity or the scale of the school projects may contribute to delays. As shown in Figure 3 below, significant variations in the average duration across different project types. For example, Schools (the most frequently undertaken projects, with 51 instances) have an average duration of 18.33 months, while Security Cluster projects, though fewer in number (2), exhibit a much shorter average duration of 7 months. Industrial projects (1 instance) and Student residences (1 instance) exhibit relatively longer average durations at 17 months and 19 months, respectively, which may be due to their complex infrastructure needs or longer approval and construction timelines. It’s notable that Schools constitute the largest number of projects (51), yet their average duration (18.33 months) is higher than projects with fewer instances, like Hostels (11.33 months). This could indicate that a higher number of similar projects doesn’t necessarily lead to time efficiencies, possibly due to factors such as bureaucracy, resource limitations, or variability in project specifications. The complexity of a project type appears to correlate with longer project durations as seen in previous studies [18]. For instance, Student residences and Industrial projects, which tend to involve specialized infrastructure and strict building regulations, exhibit longer durations (19 and 17 months, respectively). Meanwhile, Security clusters, which likely involve simpler structures or smaller scopes, are completed more quickly (7 months).
4.4 Project Extension Impact on Duration
The presence of an extension signifies elongated project duration from estimated timelines, indicating time and cost overrun. Projects that do not require extensions exhibit a more predictable and efficient timeline, while those that experience delays, reflected by the need for an extension, suffer from significant time overruns. By incorporating this variable, the model can help predict whether a project is at risk of needing an extension, based on factors such as project type, location, initial contract sum, and other relevant indicators. This will allow project managers to implement mitigation strategies proactively, reducing the likelihood of delays. The general project extension impact on duration is shown below in Figure 4. The large difference in duration between projects with and without extensions suggests that the factors leading to project extensions—such as scope changes, unforeseen challenges, resource constraints, or contractor inefficiencies—should be examined more closely. Identifying patterns in the projects that require extensions could enhance the accuracy of predictive models. For example, if certain project types or sizes are more likely to experience extensions, these projects could be flagged for closer monitoring from the outset. The stark difference in project durations points to significant opportunities to reduce delays. Projects that do not require extensions have a considerably lower average duration, suggesting that effective project planning, risk management, and resource allocation at the initial stages can prevent the need for extensions [74].
4.5 Sector-Wise Duration Comparison
Figure 5 shows that government projects have an average duration of 18 months, while private projects have a shorter average duration of 12 months. This indicates a significant difference in how long projects take to complete depending on the sector. The fact that government projects take longer on average suggests the presence of specific challenges within the public sector that may contribute to delays, such as bureaucratic processes, extended approval times, or more complex stakeholder management [75,76]. The fact that government projects take longer on average suggests the presence of specific challenges within the public sector that may contribute to delays, such as bureaucratic processes, extended approval times, or more complex stakeholder management [77,78,79]. Public procurement is often subject to complex tendering procedures that can introduce delays in the start or continuation of a project. Government projects may involve multiple layers of decision-makers and stakeholders, leading to delays in approvals and the execution of changes [80,81].
4.6 Regression Models
The regression statistics as seen in Table 1 provides critical insights into the strength and reliability of the regression model in explaining the variability of project durations. Multiple R, also known as the correlation coefficient, measures the strength and direction of the linear relationship between the independent variables (project characteristics, contract type, value) and the dependent variable (project duration). Multiple R: The correlation coefficient between the observed and predicted values. It ranges in value from 0 to 1. A value of 0.315949 indicates a weak positive correlation between the predictors and project duration. This suggests that while there is a positive relationship between the variables, the predictors only explain a small proportion of the variation in project durations. there are potentially many other unconsidered factors affecting project duration that could be considered such as unforeseen delays, project complexity, contractor performance, or external influences like political or economic conditions. Adjusted R Square adjusts the R Square value for the number of predictors in the model, giving a more accurate picture of the model's explanatory power, especially when multiple variables are used. The Standard Error measures the average distance that the observed values fall from the regression line. A value of 11.62519 indicates a relatively high level of error or variability in the project duration predictions. Given the standard error, we can infer that the model’s predictions for project duration have a typical error of about 11 months, which is substantial, particularly in the context of construction projects where timelines are critical. This suggests the need for further refinement to increase precision. The model is based on 61 observations (projects), which is a reasonable sample size for exploratory analysis.
- ANOVA Results
In Table 2, the data reveals that the total degrees of freedom are 60, corresponding to the total number of observations minus 1. There are 59 degrees of freedom for the residuals, showing the number of data points minus the number of predictors (60 total data points - 1 predictor). The total variability in the project durations combining the explained and unexplained variation reveals that it is well explained by the independent variables. the ANOVA (Analysis of Variance) table provides key insights into the overall fit and significance of the regression model. The F-statistic and p-value (1.31%) suggest that the regression model provides statistically significant insights into project duration. Even though the model explains only a small portion of the total variance (as indicated by the R-squared in the earlier analysis), it is nonetheless a meaningful model for predicting project duration based on the included variable. This significance implies that regression models can be a useful tool for predicting project duration, helping to identify patterns that might reduce delays in South African infrastructure projects [82].
The table of coefficients as shown in Table 3 provides crucial insights into how well the independent variable (represented as X Variable 1) influences the dependent variable (project duration). The coefficient 10.86 intercept represents the estimated project duration when the independent variable (X Variable 1) is zero. In this case, the intercept suggests that, on average, the baseline project duration is 10.86 units (months or another relevant time frame) when no changes are introduced by the predictor variable. The standard error of 2.94 indicates the level of variability or uncertainty in the estimate of the intercept. This implies that the predicted baseline duration can fluctuate by about 2.94 units around the estimated 10.86.
T-statistic = 3.69 and P-value = 0.00049: The t-statistic of 3.69 and the corresponding p-value of 0.00049 (less than 0.05) indicate that the intercept is statistically significant. This means that the baseline project duration is not occurring by random chance but is a meaningful value in the context of your model. Confidence Interval (Lower 95% = 4.9753, Upper 95% = 16.7419): The 95% confidence interval shows that the true intercept is likely to lie between 4.98 and 16.74 units. This range represents the degree of uncertainty in the baseline project duration estimate. Standard Error = 8.21226E-08: The small standard error shows a very low degree of variability in the coefficient estimate, indicating high precision in this particular estimate. t-statistic = 2.5579 and P-value = 0.0131: The t-statistic of 2.56 and the corresponding p-value of 0.0131 suggest that the relationship between the independent variable and project duration is statistically significant at the 5% level. Although the coefficient is very small, the p-value indicates that the variable still has some meaningful effect on project duration. Confidence Interval (Lower 95% = 4.57323E-08, Upper 95% = 3.74386E-07): The confidence interval indicates that the true value of the coefficient for the independent variable likely lies between 4.57E-08 and 3.74E-07. This very small range reflects the low magnitude of the predictor's effect on project duration.
While the coefficient of X Variable 1 is extremely small (close to zero), the p-value of 0.0131 indicates that the independent variable has a statistically significant relationship with project duration. This could imply that the independent variable has an influence, albeit a very minor one, on predicting project timelines. In practice, this means that even small adjustments related to the predictor could have a slight impact on project duration, though not dramatically. The intercept shows that the baseline duration of projects, assuming no other factors are involved, is approximately 10.86 units (e.g., months). Understanding the baseline gives infrastructure developers a starting point for estimating project timelines, which could help in better scheduling and resource allocation to prevent delays. The small coefficient and significant p-value suggest that regression models can help in fine-tuning project duration estimates, even when the variables seem to have minor effects. The significance of the variable means that regression models could still be useful in forecasting durations by capturing even small, yet consistent, patterns. However, to optimize project duration estimation more effectively, it would be beneficial to explore additional or alternative predictor variables. The nearly negligible impact of the current variable on project duration indicates that there may be more influential factors (such as project complexity, contractor experience, or regulatory delays) that should be incorporated into the model. The confidence intervals for both the intercept and the independent variable show a range of values that could provide useful benchmarks for infrastructure projects. The narrow interval for the predictor variable, while very small in magnitude, reflects the precision in estimating its effect. This precision could be helpful when scaling the model to more complex datasets or adding more predictors to enhance the regression's predictive power. Since the regression model has highlighted that even very small predictors can have statistically significant effects on project duration, this suggests that tracking and monitoring minor project factors (such as slight adjustments in materials, workforce efficiency, or daily productivity) could lead to incremental improvements in project timelines. In the broader context of South African infrastructure development, this kind of data-driven insight could be leveraged to make cumulative adjustments that ultimately reduce delays.
This residual plot shown in Figure 6 below is related to the performance of a regression model, specifically focusing on the fit between the predicted values (based on "X Variable 1") and the actual observed values. In terms of the residual distribution and model accuracy, the residuals represent the difference between observed and predicted values. Ideally, for a well-fitted regression model, residuals should be randomly scattered around zero without any clear pattern. In this graph, most residuals are close to zero, but a few are significantly far from zero, especially between R5,000.00 and R6,000.00, where we see large positive residuals. This suggests that the model is generally capturing the relationship between the independent variable and the project duration but fails to capture certain trends, potentially at higher values of "X Variable 1." For infrastructure project estimation, this may indicate underperformance or miscalculation for larger or more expensive projects. This is identified as a limitation in the study. Unaccounted factors influencing project delays or cost discrepancies in South African infrastructure development is shown in unaccounted factors influencing project delays or cost discrepancies in South African infrastructure development. To reduce delays, it might be important to address these uncertainties by including these variables.
As seen in Figure 7 below, the Normal Probability Plot, is typically used to assess whether a dataset follows a normal distribution. This plot provides insight into the distribution of residuals (errors) or actual vs. predicted project durations. The plot exhibits a sharp upward deviation towards the right side, indicating that the data does not follow a perfect straight line. This suggests non-normality in the dataset. The extreme deviation at higher percentiles (around the 90th percentile and above) indicates the presence of outliers or potentially skewed data, meaning certain projects experience much longer delays than others. In the context of South African infrastructure development, this graph reflects irregular delays in certain projects (extreme outliers), perhaps due to unpredictable factors like administrative bottlenecks, environmental conditions, or political issues.
Figure 8 showcases the line fit plot showing the relationship between an independent variable, project-related factors and Y (the project duration or delay) in a regression model. The orange line represents the predicted values of Y from the regression model. The line is relatively flat, indicating that the regression model predicts relatively constant values of Y across different levels of X Variable 1. This suggests that X Variable 1 has a limited or weak influence on the predicted Y values in the current regression model. In other words, this variable alone does not significantly explain the variability in project duration or delays but can integrate other variables. The blue diamonds represent the actual observed Y values. There is considerable scatter around the predicted Y values, especially at higher levels of X Variable 1. This indicates that the actual project durations or delays vary much more than the regression model predicts. There are significant deviations from the predicted values, particularly at higher ranges of X Variable 1 (e.g., at R400,000 and above). This suggests that the regression model may be underestimating the actual values, particularly for higher project costs or other factors represented by X Variable 1.
According to the study, the regression model performed well and consistently in predicting the length of projects while accounting for a number of variables as seen in other studies [56,62]. The research investigation's conclusions will be of great use in helping to make decisions that will ensure the project outputs meet the necessary quality standards [83,84].The study's conclusions will offer project managers, customers, and other construction stakeholders advice on how to successfully manage and carry out projects within the allocated spending limit and time frame [83,85]. It is advised that more study be done, especially in the area of using soft computing methods to fully assess the multicollinearity amongst factor variables [86]. This is essential in fostering an inclusive approach in how we conceptualise and deliver infrastructure in developing countries [87,88]. One common issue with construction investments is divergence from a predetermined time schedule, which arises in both industrialised and developing nations. In building projects, time extensions are a very important and persistent issue. A project's late completion causes it to go over its construction budget, which was set aside at the beginning of the project, and it also delays the potential revenue that the created facility could generate. Construction projects are deemed "successful" provided they are finished within the allotted time, budgeted cost, and defined quality standards, even though some adjustments to the time schedule can typically be made in response to client demands. In actuality, the owner, contractor, subcontractors, or certain technical, legal, and natural issues may lead the overall project duration to exceed the estimated bounds of the scheduled time. Since public institutions (i.e., owners) fund the majority of large-scale, high-budget construction projects, it is likely that they will struggle to make progress payments on time. As a result, main contractors may fail to pay their suppliers, in-house employees, and subcontractors on time [45,89]. Poor productivity, shoddy craftsmanship, and inadequate human resource planning appear to be concerning indicators of the domestic construction industry in terms of labor-based variables [90,91]. One way to gauge how well a project is being implemented is to look at its duration. Projects carried out through top-down institutional arrangements were more likely to take a lengthy time than those carried out through bottom-up institutional arrangements, according to a comparable study conducted in China [92]. The results provide knowledge that clients and their delivery managers can use to effectively manage a sizable amount of uncertainty in projects where the client prefers a collaborative delivery-management approach and project information is not sufficiently available for the contractor to price the project meaningfully at the beginning of construction [37]. It can be difficult to schedule repetitive construction projects in a way that maximises the use of several concurrent workers and strategically arranges their work to reduce project duration and expense.
Government-funded projects with a top-down approach proved to be more efficient than those with a top-down approach that involved village funding. on bottom-up projects, no conclusion was reached on which source of funding—village or private developer—was responsible for the shorter project duration [49,93].
The length of the project was also determined by other factors, such as the city, the characteristics of the project, the year it started, the number of families engaged, the size of the temporary relocation fee, and the procedures used to choose moved housing, calculate the temporary relocation cost, and determine the relocation area [94,95]. Several studies have highlighted the need for sustainable infrastructure to address societal impact [88] [96,97]. However, this remains a challenge when buildings are not delivered within time and cost and therefore calls for the imperative of considering digital technologies in delivery of infrastructure to aid prompt delivery[98,99].
5. Conclusions, Implications and Recommendations
The analysis demonstrates that the regression model is statistically significant in explaining the relationship between the independent variable and project duration, though there is still much unexplained variability. The coefficients table reveals that while the independent variable (X Variable 1) has a minimal effect on project duration, it is still statistically significant, suggesting that regression models can be useful for capturing small but meaningful relationships in predicting project timelines. The baseline duration estimate and the narrow confidence intervals for the predictor variables suggest that even minor adjustments can have practical implications in improving project duration estimation. To optimize regression models for reducing delays in South African infrastructure development, the inclusion of more impactful variables will be crucial for better precision and stronger predictive power.
6. Limitations and Areas for Future Studies
While the model is significant, the large residual sum of squares (7973.55) and high mean square error (135.14) suggest that a substantial amount of variability in project duration is still unexplained. This points to a need for additional variables that could better capture the complexities of infrastructure project timelines. Variables such as contractor experience, material availability, weather patterns, and regulatory delays may improve the model’s predictive power. Notwithstanding this, since the model shows a statistically significant relationship between the independent variable and project duration, it can be used to forecast project durations with some degree of confidence. This could be beneficial for project managers in mitigating delays by adjusting timelines and resources based on early predictions. To fully harness regression models for optimizing project duration estimation and reducing delays in South African infrastructure development, future research should focus on incorporating more variables that reflect the diverse and complex factors affecting construction timelines. With improvements, this model can become a valuable tool for infrastructure project managers to predict and prevent delays. The residual plot reveals both the strengths and weaknesses of the current regression model used to predict project durations. While the model performs reasonably well for smaller-scale projects, it struggles with larger projects, leading to inaccuracies in prediction. For South African infrastructure development, improving the model by addressing outliers, heteroscedasticity, and including more relevant variables could lead to better project duration estimates and, subsequently, fewer delays. The skewness and outliers in this study serves as an areas for future studies to utilize alternative regression methods like robust regression or quantile regression to better handle the data's characteristics. This would involve investigating the causes of the most extreme delays and refining model by incorporating additional predictors that may explain the observed non-normality (such as regulatory delays or supply chain issues).
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, M.S.R and M.S.R.; methodology, M.S.R.; software, M.S.R.; validation, M.S.R.,.; formal analysis, M.S.R.; investigation, M.S.R.; resources, M.S.R.; data curation, M.S.R.; writing—original draft preparation, M.S.R.; writing—review and editing, M.S.R.; visualization, M.S.R.; supervision, M.S.R.; project administration, M.S.R.; funding acquisition, M.S.R. All authors have read and agreed to the published version of the manuscript.” Please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.
Data Availability Statement
Data available upon request.
Conflicts of Interest
Declare conflicts of interest or state “The authors declare no conflicts of interest”.
References
- Rizaee, S.; Lei, Z. Duration Estimation of a Heavy Industrial Scaffolding Project: A Case Study. J. Constr. Eng. Manag. 2024, 150. [Google Scholar] [CrossRef]
- ElMenshawy, M.; Marzouk, M. Automated BIM Schedule Generation Approach for Solving Time–Cost Trade-off Problems. Eng. Constr. Archit. Manag. 2021, 28, 3346–3367. [Google Scholar] [CrossRef]
- Abeyasinghe, M. C. L.; Greenwood, D. J.; Johansen, D. E. An Efficient Method for Scheduling Construction Projects with Resource Constraints. Int. J. Proj. Manag. 2001, 19, 29–45. [Google Scholar] [CrossRef]
- Nevett, G.; Goodrum, P. M.; Littlejohn, R. L. Understanding the Effect of Bid Quantities, Project Characteristics, and Project Locations on the Duration of Road Transportation Construction Projects during Early Stages. Transp. Res. Rec. 2020, 2675, 121–134. [Google Scholar] [CrossRef]
- Sadeghi, N.; Dehghani, M. S.; Ingolfsson, A. Choice of Probability Distributions for Activity Durations in Project Networks with Limited Sample Size. J. Constr. Eng. Manag. 2024, 150. [Google Scholar] [CrossRef]
- Vandevoorde, S.; Vanhoucke, M. A Comparison of Different Project Duration Forecasting Methods Using Earned Value Metrics. Int. J. Proj. Manag. 2006, 24, 289–302. [Google Scholar] [CrossRef]
- Akin, F. D.; Damci, A.; Arditi, D. Optimum Finance-Based Scheduling. J. Constr. Eng. Manag. 2024, 150. [Google Scholar] [CrossRef]
- Laryea, S.; Watermeyer, R.; Govender, N. The Influence of Fees on the Quality of Professional Services in South Africa. In Proceedings of the Institution of Civil Engineers - Management, Procurement and Law; 2020. [CrossRef]
- Ballesteros-Pérez, P.; Smith, S. T.; Lloyd-Papworth, J. G.; Cooke, P. Incorporating the Effect of Weather in Construction Scheduling and Management with Sine Wave Curves: Application in the United Kingdom. Constr. Manag. Econ. 2018, 36, 666–682. [Google Scholar] [CrossRef]
- Yang, J.-B.; Chen, Y.-H. Enhanced ESM Approach for Duration Forecasting in Delayed Projects. Ain Shams Eng. J. 2024, 15. [Google Scholar] [CrossRef]
- Al Haj, R. A.; El-Sayegh, S. M. Time-Cost Optimization Model Considering Float-Consumption Impact. J. Constr. Eng. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Mahdi Hosseinian, S.; Arjomand, A.; Li, C. Q.; Zhang, G. Developing a Model for Assessing Project Completion Time Reliability during Construction Using Time-Dependent Reliability Theory. J. Constr. Eng. Manag. 2022, 148. [Google Scholar] [CrossRef]
- Diamantas, V. K.; Kirytopoulos, K. A.; Leopoulos, V. N. Project’s Duration Prediction: Traditional Tools or Simulation? World Rev. Entrep. Manag. Sustain. Dev. 2007, 3, 317–333. [Google Scholar] [CrossRef]
- Bhardwaj, M.; Rana, A.; Sharma, N. K. How Software Size Influence Productivity and Project Duration. Int. J. Electr. Comput. Eng. 2019, 9, 2006–2017. [Google Scholar] [CrossRef]
- Koulinas, G. K.; Xanthopoulos, A. S.; Tsilipiras, T. T.; Koulouriotis, D. E. Schedule Delay Risk Analysis in Construction Projects with a Simulation-Based Expert System. Buildings 2020, 10. [Google Scholar] [CrossRef]
- Zeng, X.; Yu, Y.; Yang, S.; Lv, Y.; Sarker, M. N. I. Urban Resilience for Urban Sustainability: Concepts, Dimensions, and Perspectives. Sustain. 2022, 14. [Google Scholar] [CrossRef]
- van Niekerk, J.; Wium, J.; de Koker, N. The Value of Data from Construction Project Site Meeting Minutes in Predicting Project Duration. Built Environ. Proj. Asset Manag. 2022, 12, 738–753. [Google Scholar] [CrossRef]
- Hegab, M. Y.; Smith, G. R. Delay Time Analysis in Microtunneling Projects. J. Constr. Eng. Manag. 2007, 133, 191–195. [Google Scholar] [CrossRef]
- Barrientos-Orellana, A.; Ballesteros-Pérez, P.; Mora-Melia, D.; González-Cruz, M. C.; Vanhoucke, M. Stability and Accuracy of Deterministic Project Duration Forecasting Methods in Earned Value Management. Eng. Constr. Archit. Manag. 2022, 29, 1449–1469. [Google Scholar] [CrossRef]
- Hasan, M. F.; Mohammed, S. R. Factors Affecting Time and Cost Trade-off in Multiple Construction Projects. Arch. Civ. Eng. 2022, 68, 549–561. [Google Scholar] [CrossRef]
- Irwanto, R.; Rahayu, T.; Panudju, A. T. Artificial Neural Networks for Construction Project Cost and Duration Estimation. Rev. d’Intelligence Artif. 2023, 37, 1449–1460. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; Cerezo-Narváez, A.; Otero-Mateo, M.; Pastor-Fernández, A.; Zhang, J.; Vanhoucke, M. Forecasting the Project Duration Average and Standard Deviation from Deterministic Schedule Information. Appl. Sci. 2020, 10. [Google Scholar] [CrossRef]
- Maharaj, R.; Musonda, I.; Onososen, A. Construction Organisation’s Planning and Implementation: The Case Between Conceptualization and Implementation Teams. Springer 2023, 245. [Google Scholar] [CrossRef]
- Mahamid, I. Analysis of Schedule Deviations in Road Construction Projects and the Effects of Project Physical Characteristics: J. Financ. Manag. Prop. Constr. 2017, 22, 192–210. [Google Scholar] [CrossRef]
- Kim, Y.; Asce, S. M.; Kim, H.; Asce, M.; Murphy, R.; Lee, S.; Asce, M.; Ahn, C. R.; Asce, A. M. Delegation or Collaboration : Understanding Different Construction Stakeholders ’ Perceptions of Robotization. J. Manag. Eng 2022, 38, 1–12. [Google Scholar] [CrossRef]
- Lee, J.; Hyun, H. Multiple Modular Building Construction Project Scheduling Using Genetic Algorithms. J. Constr. Eng. Manag. 2019, 145. [Google Scholar] [CrossRef]
- Babalola, J.; Onososen, A. O. Quantity Surveyors’ Competencies in the Emerging Green Building Adoption. Lagos J. Environ. Stud. 2022, 11, 52–60. [Google Scholar]
- Sapti, M.; Pancapalaga, W.; Widari, W. Managing Risk of Construction Projects to Enhance Project Performance Delivery. J. Sains dan Seni ITS 2019, 53, 1689–1699. [Google Scholar]
- Onososen, A. O.; Musonda, I.; Moyo, T.; Muzioreva, H. Digital Twin Technology in Health, Safety, and Wellbeing Management in the Built Environment. In Smart and Resilient Infrastructure For Emerging Economies: Perspectives on Building Better; Musonda, I., Mwanaumo, E., Onososen, A., Moyo, T., Eds.; CRC Press LLC, 2024; p 7. [CrossRef]
- Kazaz, A.; Ulubeyli, S.; Tuncbilekli, N. A. Causes of Delays in Construction Projects in Turkey. J. Civ. Eng. Manag. 2012, 18, 426–435. [Google Scholar] [CrossRef]
- Ferlito, T.-L.; Musonda, I.; Tjebane, M. M.; Onososen, A. O. Systematic Literature Review on Sustainable Construction Strategies for the Development of Affordable Housing. In The Twelfth International Conference on Construction in the 21st Century (CITC-12; 2022; pp 195–203.
- Fagbenro, R.; Oyediran, O. S.; Onososen, A. O. Consulting Business Workflow and Design Performance Metrics for BIM Based Construction Design in Nigeria. ECS Trans. 2022, 107, 1029. [Google Scholar] [CrossRef]
- Oruc, S.; Dikbas, H. A.; Gumus, B.; Yucel, I. The Impact of Climate Change on Construction Activity Performance. Buildings 2024, 14. [Google Scholar] [CrossRef]
- Little, R. G.; Loggins, R. A.; Wallace, W. A. Building the Right Tool for the Job: Value of Stakeholder Involvement When Developing Decision-Support Technologies for Emergency Management. Nat. Hazards Rev. 2015, 16. [Google Scholar] [CrossRef]
- Lin, J. C.-W.; Lv, Q.; Yu, D.; Srivastava, G.; Chen, C.-H. Optimized Scheduling of Resource-Constraints in Projects for Smart Construction. Inf. Process. Manag. 2022, 59. [Google Scholar] [CrossRef]
- Zwikael, O.; Cohen, Y.; Sadeh, A. Non-Delay Scheduling as a Managerial Approach for Managing Projects. Int. J. Proj. Manag. 2006, 24, 330–336. [Google Scholar] [CrossRef]
- Turkoglu, H.; Polat, G.; Akin, F. D. Crashing Construction Projects Considering Schedule Flexibility: An Illustrative Example. Int. J. Constr. Manag. 2023, 23, 619–628. [Google Scholar] [CrossRef]
- Musonda, I.; Onososen, A. O.; Moyo, T.; Tjebane, M. M. COVID-19 and Shock Events in the AEC Sector-Perspectives on Mitigating Measures. In Construction Safety, Health and Well-being in the COVID-19 era; Manu, P., Cheung, C., Yunusa-Kaltungo, A., Emuze, F., Saurin, T. A., Hadikusumo, B. H. W., Eds.; Routledge: New York, 2023. [Google Scholar] [CrossRef]
- Moyanga, D.; Ojo, L. D.; Awodele, O. A.; Ogunsemi, D. R. Prioritizing the Survival Determinants of Quantity Surveying Firms in Economic Contraction. Eng. Constr. Archit. Manag. 2023. [Google Scholar] [CrossRef]
- Ogunsemi, D. R.; Jagboro, G. O. Time-Cost Model for Building Projects in Nigeria. Constr. Manag. Econ. 2006, 24, 253–258. [Google Scholar] [CrossRef]
- Tjebane, M. M.; Musonda, I.; Onososen, A.; Ramabodu, M. Challenges for the Implementation of Sustainable Construction Practices in Developing Countries: A Bibliometric. In Advances in Information Technology in Civil and Building Engineering: Proceedings of ICCCBE 2022-Volume 2; 2023; p 109. [CrossRef]
- Pawan, P.; Lorterapong, P. A Fuzzy-Based Integrated Framework for Assessing Time Contingency in Construction Projects. J. Constr. Eng. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Ren, L.; Li, P.-P.; Zhao, Y.-G. An Efficient and Effective Method for Reliability Assessment of Project Duration. Qual. Technol. Quant. Manag. 2023, 20, 689–706. [Google Scholar] [CrossRef]
- Berlin, S.; Raz, T.; Glezer, C.; Zviran, M. Comparison of Estimation Methods of Cost and Duration in IT Projects. Inf. Softw. Technol. 2009, 51, 738–748. [Google Scholar] [CrossRef]
- Abdelbasset, E.; Hassan, A.; Amer, N. H.; Khalifa, Y. A. Optimizing the Number of Crews Working in Parallel and Their Work Sequence to Minimize Project Duration and Cost for Repetitive Construction Projects. Innov. Infrastruct. Solut. 2023, 8. [Google Scholar] [CrossRef]
- Le, C.; Jeong, H. D. Determining Highway Project Contract Time from Project Duration Estimates. J. Leg. Aff. Disput. Resolut. Eng. Constr. 2023, 15. [Google Scholar] [CrossRef]
- Malik, T. H. Temporal and Social Distances of the Estimated Duration of R&D Projects in the Biopharma Industry. Technol. Forecast. Soc. Change 2024, 208. [Google Scholar] [CrossRef]
- Jaśkowski, P.; Sobotka, A. Scheduling Construction Projects Using Evolutionary Algorithm. J. Constr. Eng. Manag. 2006, 132, 861–870. [Google Scholar] [CrossRef]
- Ock, J.-H.; Han, S.-H. Measuring Risk-Associated Activity’s Duration: A Fuzzy Set Theory Application. KSCE J. Civ. Eng. 2010, 14, 663–671. [Google Scholar] [CrossRef]
- Arabpour Roghabadi, M.; Moselhi, O. Optimized Crew Selection for Scheduling of Repetitive Projects. Eng. Constr. Archit. Manag. 2020, 28, 1517–1540. [Google Scholar] [CrossRef]
- Türkakın, O. H.; Manisalı, E.; Arditi, D. Delay Analysis in Construction Projects with No Updated Work Schedules. Eng. Constr. Archit. Manag. 2020, 27, 2893–2909. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; Sanz-Ablanedo, E.; Cerezo-Narváez, A.; Lucko, G.; Pastor-Fernández, A.; Otero-Mateo, M.; Contreras-Samper, J. P. Forecasting Accuracy of In-Progress Activity Duration and Cost Estimates. J. Constr. Eng. Manag. 2020, 146. [Google Scholar] [CrossRef]
- Mulenga, M. J. Explaining Cost Overruns on Construction Projects in Gauteng Province, South Africa. 2016.
- Riedel, E.; Al-Keim, A. Strategies to Reduce Cost Overruns and Schedule Delays in Construction Projects. Walden Diss. Dr. Stud. 2017, 159. [Google Scholar]
- Youssefi, I.; Celik, T. Optimized Approach toward Identification of Influential Cost Overrun Causes in Construction Industry. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2023, 9. [Google Scholar] [CrossRef]
- Nuako, F.; Ghansah, F. A.; Adusei, T. Critical Success Factorsfor Cost Overrun Minimization in Public Construction Projects in Developing Countries: The Case of Ghana. Constr. Innov. 2024. [Google Scholar] [CrossRef]
- Famiyeh, S.; Amoatey, C. T.; Adaku, E.; Agbenohevi, C. S. Major Causes of Construction Time and Cost Overruns: A Case of Selected Educational Sector Projects in Ghana. J. Eng. Des. Technol. 2017, 15, 181–198. [Google Scholar] [CrossRef]
- Sweis, G. J. Factors Affecting Time Overruns in Public Construction Projects: The Case of Jordan. Int. J. Bus. Manag. 2013, 8, 120–129. [Google Scholar] [CrossRef]
- Dzvimbo, M. A.; Mashizha, T. M.; Zhanda, K.; Mawonde, A. Promoting Sustainable Development Goals: Role of Higher Education Institutions in Climate and Disaster Management in Zimbabwe. Jamba J. Disaster Risk Stud. 2022, 14. [Google Scholar] [CrossRef]
- Mulalo, R.; Ibrahimu, K.; Nwobodo-Anyadiegwu, E. Project Cost Overrun in the South African Construction Sector: A Case Study of Johannesburg Metropolis. Proc. Int. Conf. Ind. Eng. Oper. Manag. 2018, 2018, 1263–1270. [Google Scholar]
- Sinesilassie, E. G.; Tabish, S. Z. S.; Jha, K. N. Critical Factors Affecting Schedule Performance. Eng. Constr. Archit. Manag. 2017, 24, 757–773. [Google Scholar] [CrossRef]
- Annamalaisami, C. D.; Kuppuswamy, A. Managing Cost Risks: Toward a Taxonomy of Cost Overrun Factors in Building Construction Projects. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7. [Google Scholar] [CrossRef]
- Mabaso, M. Risk Identification in Megaprojects and Its Impacts on Project Management Constraints in Civil Engineering and Construction Companies. 2022, No. November.
- Gunduz, M.; Nielsen, Y.; Ozdemir, M. Fuzzy Assessment Model to Estimate the Probability of Delay in Turkish Construction Projects. J. Manag. Eng. 2015, 31. [Google Scholar] [CrossRef]
- Onososen, A. O.; Musonda, I.; Onatayo, D.; Tjebane, M. M.; Saka, A. B.; Fagbenro, R. K. Impediments to Construction Site Digitalisation Using Unmanned Aerial Vehicles (UAVs). Drones 2023, 7, 45. [Google Scholar] [CrossRef]
- Mukuka, M.; Aigbavboa, C.; Thwala, W. Understanding Construction Projects’ Schedule Overruns in South Africa. ICCREM 2015 - Environ. Sustain. Build. - Proc. 2015 Int. Conf. Constr. Real Estate Manag. 2015, 591–602. [CrossRef]
- Gondia, A.; Siam, A.; El-Dakhakhni, W.; Nassar, A. H. Machine Learning Algorithms for Construction Projects Delay Risk Prediction. J. Constr. Eng. Manag. 2020, 146, 1–16. [Google Scholar] [CrossRef]
- Oshungade, Oluwaseun Olumide, D. K. A Comparative Study of Causes and Effects of Project Delays and Disruptions in Construction Projects in the South African Construction Industry : City of Johannesburg As a Case Study. 2016, 168.
- Wang, X.; Wang, X.; Huang, Y. Chinese Construction Worker Reluctance toward Vocational Skill Training. J. Eng. Des. Technol. 2019, 17, 155–171. [Google Scholar] [CrossRef]
- Szewczyk, B.; Radziszewska-Zielina, E. IT-Based Control and Assessment of Partnering Relations in Construction Projects. Autom. Constr. 2020, 116. [Google Scholar] [CrossRef]
- Maltese, S.; Tagliabue, L. C.; Cecconi, F. R.; Pasini, D.; Manfren, M.; Ciribini, A. L. C. Sustainability Assessment through Green BIM for Environmental, Social and Economic Efficiency. Procedia Eng. 2017, 180, 520–530. [Google Scholar] [CrossRef]
- Olawumi, T. O.; Chan, D. W. M. Developing Project Evaluation Models for Smart Sustainable Practices Implementation in Construction Projects: A Comparative Study between Nigeria and Hong Kong. Eng. Constr. Archit. Manag. 2022, 29, 1522–1552. [Google Scholar] [CrossRef]
- Malkina, M.; Rogachev, D. Financial Contagion of Russian Companies during the COVID-19 Pandemic. J. Corp. Financ. Res. 2023, 17, 55–71. [Google Scholar] [CrossRef]
- Freeman, J.; Hancock, L. Energy and Communication Infrastructure for Disaster Resilience in Rural and Regional Australia. Reg. Stud. 2017, 51, 933–944. [Google Scholar] [CrossRef]
- Loewenberger, P. A.; Newton, M.; Wick, K. Developing Creative Leadership in a Public Sector Organisation. Int. J. Public Sect. Manag. 2014, 27, 190–200. [Google Scholar] [CrossRef]
- Liphadzi, M.; Musonda, I.; Onososen, A. O. The Use of Building Information Modelling Tools for Effective Waste Management: A Systematic Review. In World Building Congress,IOP Conf. Ser.: Earth Environ. Sci. 1101 062001; IOP, 2022. [CrossRef]
- Rodrigues, I. L. The Role of Construction Companies in Modern Housing. Precol’s Footprint in Late Colonial Angola. In 17th International Docomomo Conference - Modern Design: Social Commitment and Quality of Life, Proceedings; C.J., S., M.P., F., A., T., U., P., Eds.; Docomomo, 2022; pp 276–286.
- Azasu, S.; Adewunmi, Y.; Babatunde, O. South African Stakeholder Views of the Competency Requirements of Facilities Management Graduates. Int. J. Strateg. Prop. Manag. 2018, 22, 471–478. [Google Scholar] [CrossRef]
- Makhathini, N.; Musonda, I.; Onososen, A. Utilisation of Remote Monitoring Systems in Construction Project Management. In Construction in 5D: Deconstruction, Digitalization, Disruption, Disaster, Development.; Haupt, T.C., Akinlolu, M., Simpeh, F., Amoah, C., Armoed, Z., Ed.; Springer, 2023. [CrossRef]
- Akinradewo, O.; Oke, A.; Aigbavboa, C.; Mashangoane, M. Willingness to Adopt Robotics and Construction Automation in the South African Construction Industry. In Proceedings of the International Conference on Industrial Engineering and Operations Management; 2018.
- Ebekozien, A.; Aigbavboa, C.; Samsurijan, M. S.; Radin Firdaus, R. B.; Ayo-Odifiri, S. O.; Amadi, G. C. An Appraisal of Guidelines and Practices for Municipal Infrastructure Support Agent to Execute Labour-Intensive Construction Projects in South Africa. Prop. Manag. 2024, 42, 70–85. [Google Scholar] [CrossRef]
- Ebekozien, A.; Aigbavboa, C. O. Improving Quantity Surveying Education through Continually Updating Curriculum Digitalisation to Meet Industry Requirements. J. Eng. Des. Technol. 2023. [Google Scholar] [CrossRef]
- Manfren, M.; Tagliabue, L. C.; Re Cecconi, F.; Ricci, M. Long-Term Techno-Economic Performance Monitoring to Promote Built Environment Decarbonisation and Digital Transformation—A Case Study. Sustain. 2022, 14. [Google Scholar] [CrossRef]
- Onososen, A. O.; Musonda, I. Research Focus for Construction Robotics and Human-Robot Teams towards Resilience in Construction: Scientometric Review. J. Eng. Des. Technol. 2022. [Google Scholar] [CrossRef]
- Onososen, A.; Musonda, I. Perceived Benefits of Automation and Artificial Intelligence in the AEC Sector: An Interpretive Structural Modeling Approach. Front. Built Environ. 2022, 61. [Google Scholar] [CrossRef]
- Ajayi, A.; Oyedele, L.; Owolabi, H.; Akinade, O.; Bilal, M.; Davila Delgado, J. M.; Akanbi, L. Deep Learning Models for Health and Safety Risk Prediction in Power Infrastructure Projects. Risk Anal. 2020, 40, 2019–2039. [Google Scholar] [CrossRef]
- Tucker, R. L. Japanese Construction Industry. Autom. Constr. 1992, 1, 27–34. [Google Scholar] [CrossRef]
- Onososen, A.; Osanyin, O.; Adeyemo, M. Drivers and Barriers to the Implementation of Green Building Development. PM World J. 2019, 9, 1–15. [Google Scholar]
- Yap, J. B. H.; Skitmore, M.; Lim, Y. W.; Loo, S.-C.; Gray, J. Assessing the Expected Current and Future Competencies of Quantity Surveyors in the Malaysian Built Environment. Eng. Constr. Archit. Manag. 2022, 29, 2415–2436. [Google Scholar] [CrossRef]
- Khanh, H. D.; Kim, S. Y.; Khoa, N. Van; Tu, N. T. The Relationship between Workers’ Experience and Productivity: A Case Study of Brick Masonry Construction. Int. J. Constr. Manag. 2021, 0, 1–10. [Google Scholar] [CrossRef]
- Onososen, A.; Musonda, I.; Ramabodu, M.; Dzuwa, C. Task Performance to Understand the Effectiveness of Visualisation Technology-Based Training for Human-Drone Interaction Learning. In Advances in Information Technology in Civil and Building Engineering. ICCCBE 2022. Lecture Notes in Civil Engineering, vol 358.; Skatulla, S., Beushausen, H., Eds.; Springer Nature Switzerland: Switzerland, 2023; pp 297–310. [CrossRef]
- Yuan, D.; Yau, Y.; Hou, H.; Liu, Y. Factors Influencing the Project Duration of Urban Village Redevelopment in Contemporary China. Land 2021, 10. [Google Scholar] [CrossRef]
- Dixon, R.; McGregor, A. Grassroots Development and Upwards Accountabilities: Tensions in the Reconstruction of Aceh’s Fishing Industry. Dev. Change 2011, 42, 1349–1377. [Google Scholar] [CrossRef]
- Santos, R.; Costa, A. A.; Silvestre, J. D.; Vandenbergh, T.; Pyl, L. BIM-Based Life Cycle Assessment and Life Cycle Costing of an Office Building in Western Europe. Build. Environ. 2020, 169. [Google Scholar] [CrossRef]
- Ju, W.; Wu, J.; Kang, Q.; Jiang, J.; Xing, Z. Fire Risk Assessment of Subway Stations Based on Combination Weighting of Game Theory and TOPSIS Method. Sustain. 2022, 14. [Google Scholar] [CrossRef]
- Hokkeling, J. Towards Construction 4.0: An Assessment on the Potential of Digital Twins in the Infrastructure Sector. Univ. Twente 2020, 1–120.
- Tjebane, M. M.; Musonda, I.; Onososen, A.; Ramabodu, M. Challenges for the Implementation of Sustainable Construction Practices in Developing Countries: A Bibliometric Review. In Advances in Information Technology in Civil and Building Engineering. ICCCBE 2022. Lecture Notes in Civil Engineering, vol 358. Springer,; Skatulla, S., Beushausen: Switzerland, 2023. [CrossRef]
- Bhattacharya, S.; Chatterjee, A. Digital Project Driven Supply Chains: A New Paradigm. Supply Chain Manag. 2021, 2, 283–294. [Google Scholar] [CrossRef]
- Tjebane, M. M.; Musonda, I.; Onososen, A.; Ramabodu, M. Unravelling the State of the Art of Blockchain Development for Improved Infrastructure Delivery in the Built Environment: A Bibliometric Review. In Advances in Information Technology in Civil and Building Engineering. ICCCBE 2022. Lecture Notes in Civil Engineering, vol 358. Springer, Cham; Skatulla, S., Beushausen, H., Eds.; Springer: Switzerland, 2023. [CrossRef]
Figure 1.
Province-Based Duration Variability.
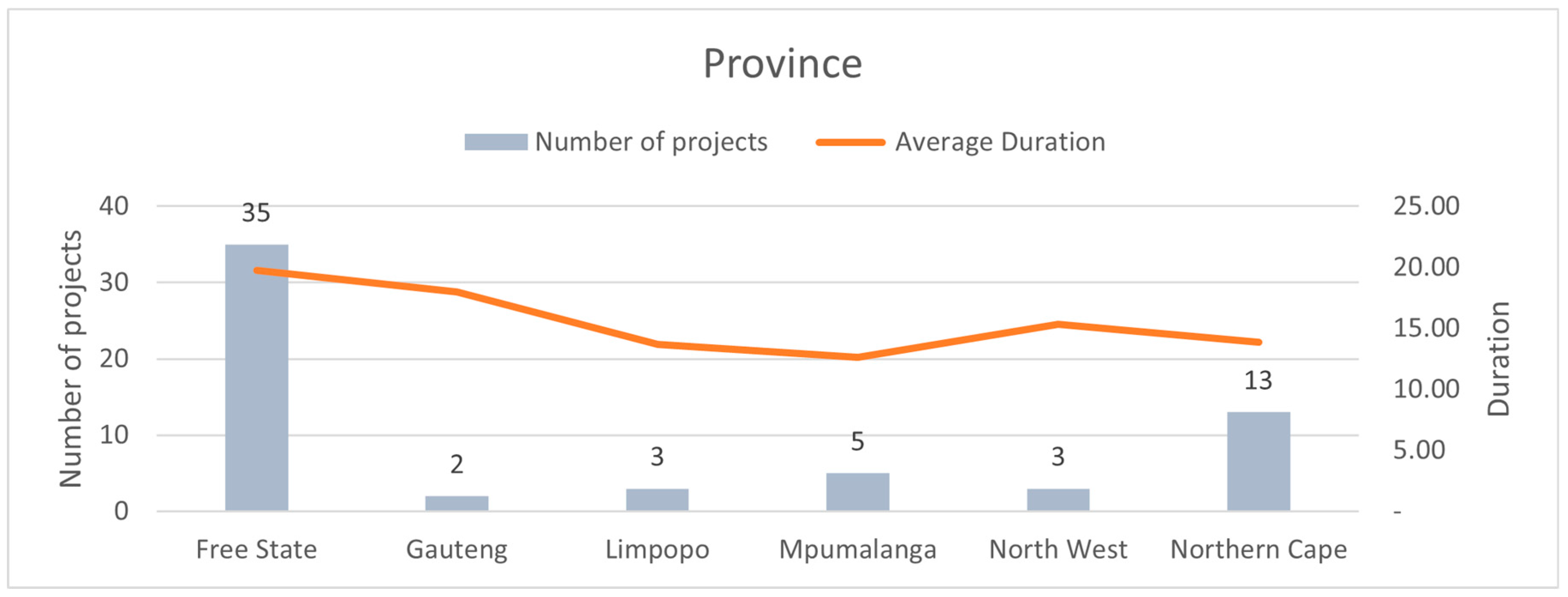
Figure 2.
Correlation Between Project Value and Duration.
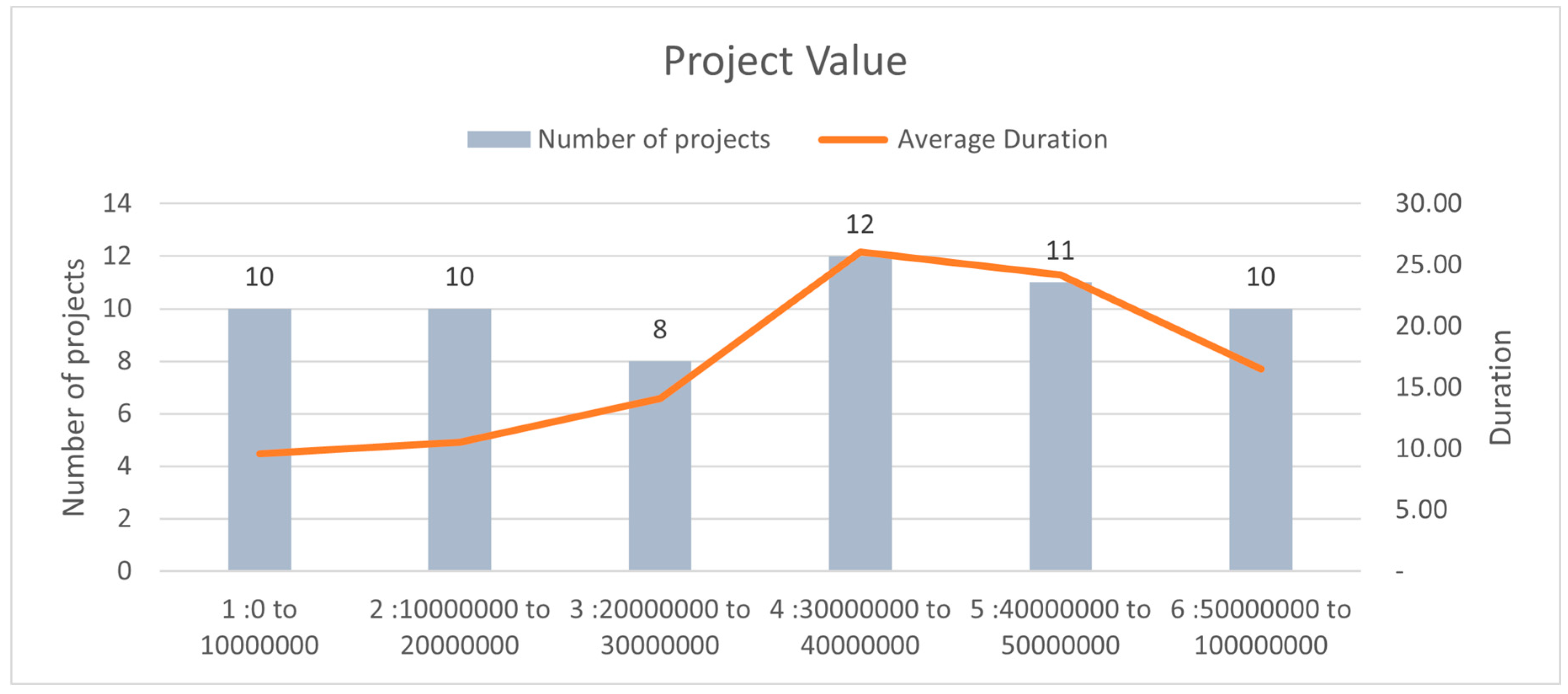
Figure 3.
Variation in Project Types and Durations.
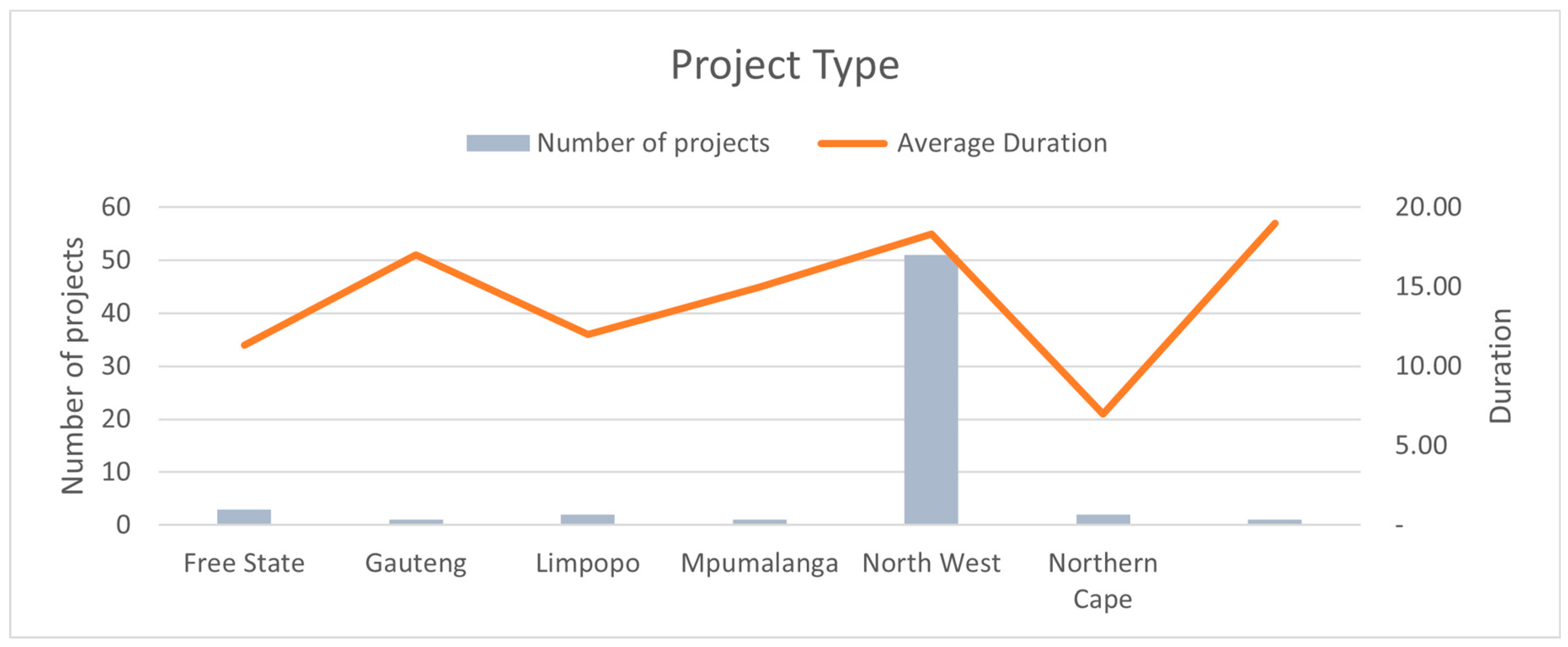
Figure 4.
Project Extension Impact on Duration.
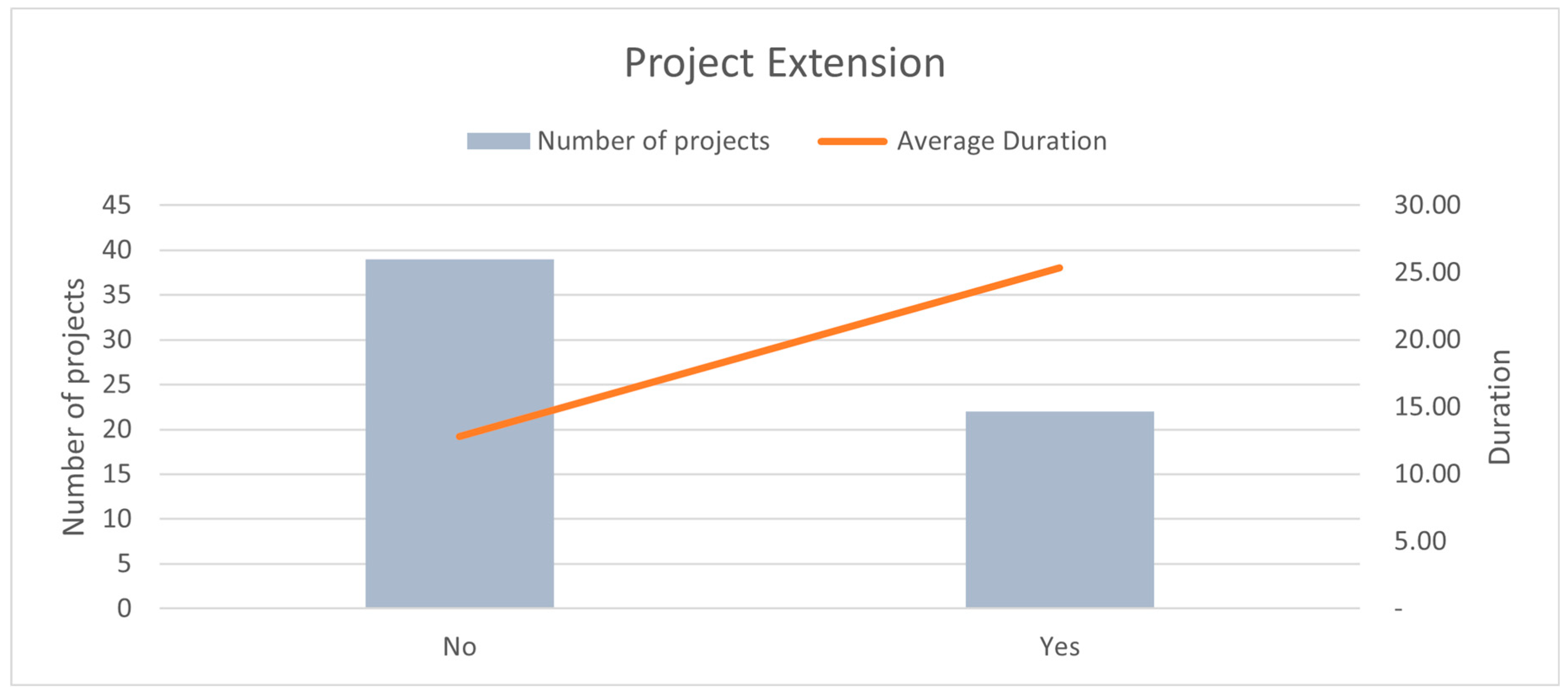
Figure 5.
Sector-Wise Duration Comparison.
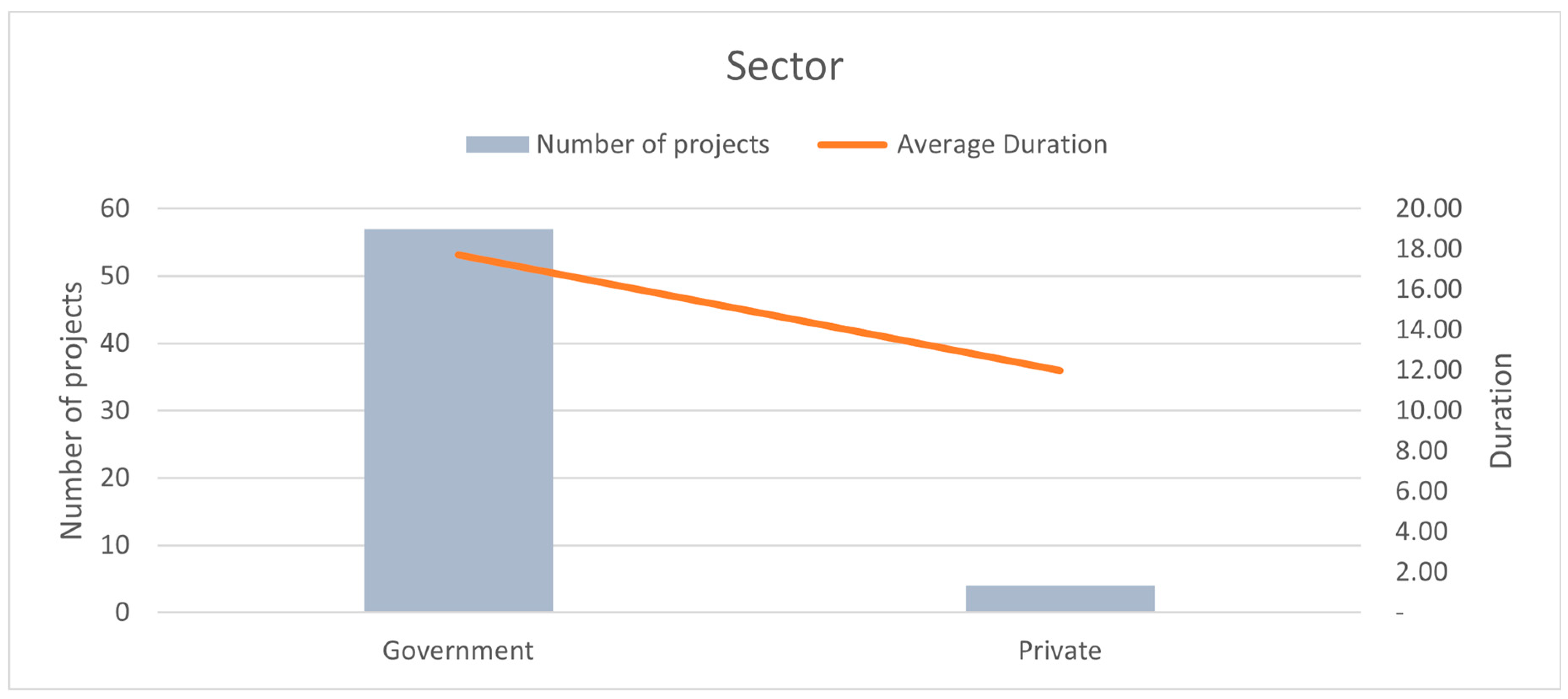
Figure 6.
Residual Plot.
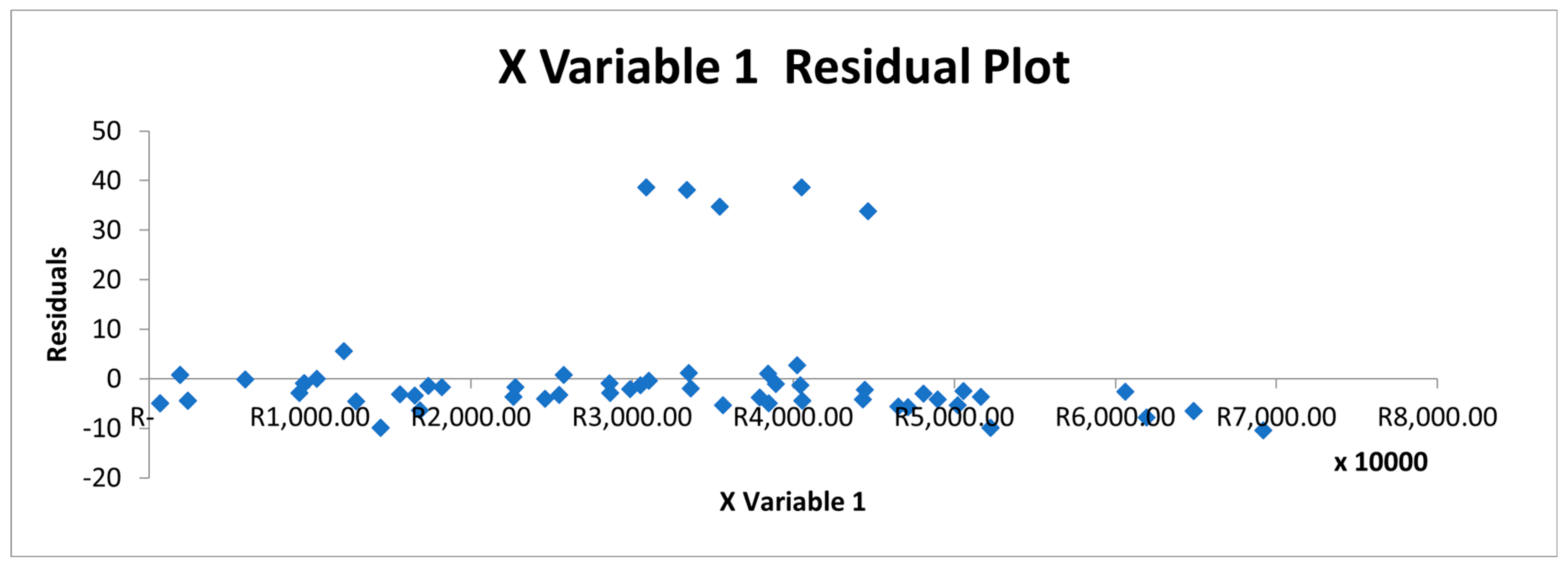
Figure 7.
Normal Probability Plot.
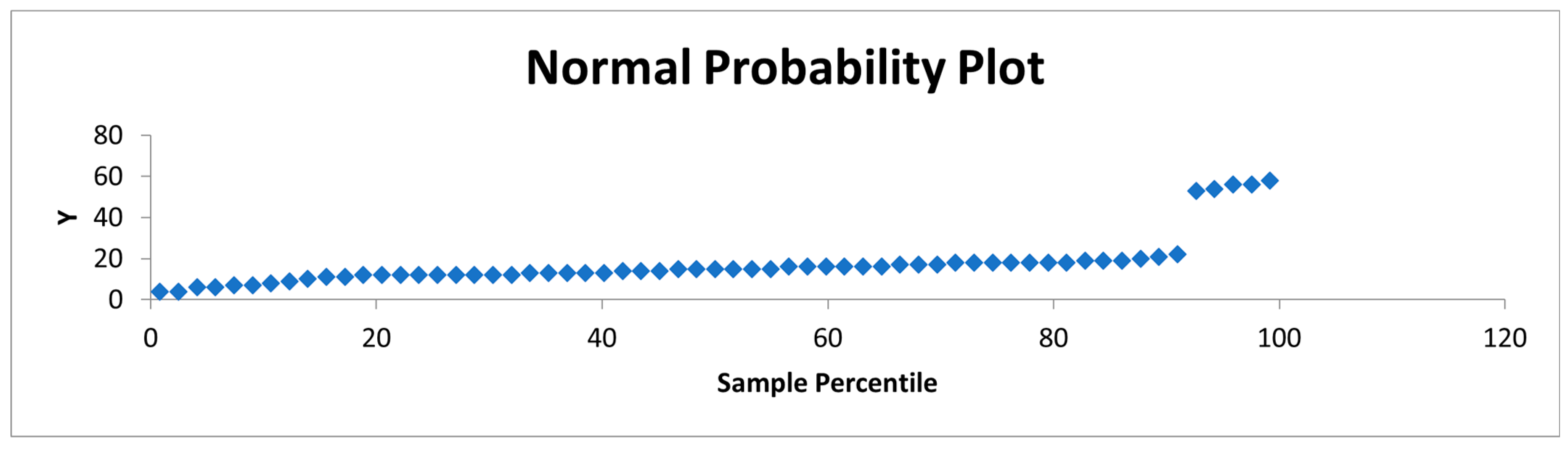
Figure 8.
Line Fit Plot.
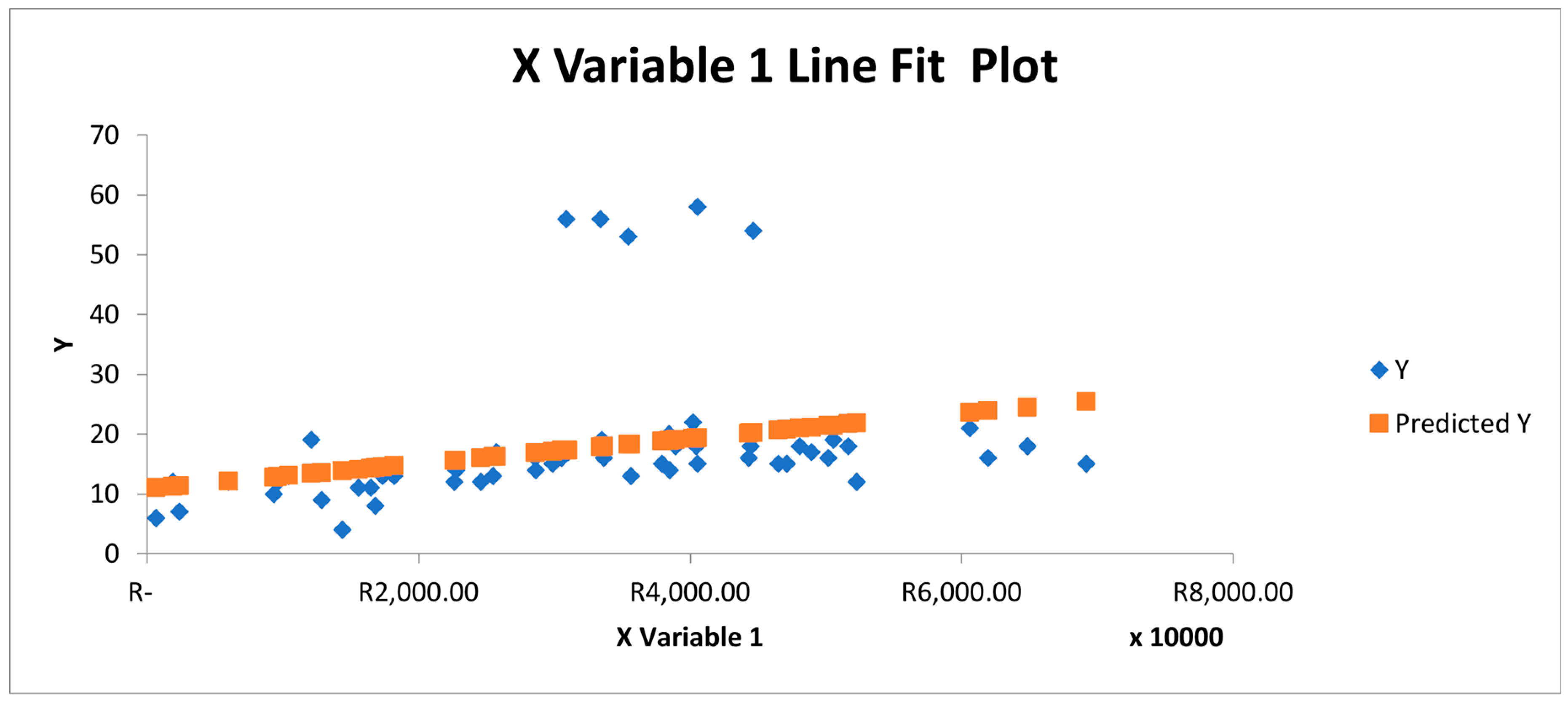
Table 1.
Regression Statistics.
| Regression Statistics | |
| Multiple R | 0.315949 |
| R Square | 0.099824 |
| Adjusted R Square | 0.084566 |
| Standard Error | 11.62519 |
| Observations | 61 |
Table 2.
ANOVA.
| ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 1 | 884.2156 | 884.2156 | 6.542718177 | 1.31% |
| Residual | 59 | 7973.555 | 135.145 | ||
| Total | 60 | 8857.77 |
Table 3.
Coefficients.
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | Lower 95,0% | Upper 95,0% | |
| Intercept | 10.85858 | 2.940175 | 3.693176 | 0.000486005 | 4.975306335 | 16.74186 | 4.975306 | 16.74185974 |
| X Variable 1 | 0.0000% | 8.21E-08 | 2.557874 | 0.013120283 | 4.57323E-08 | 3.74E-07 | 4.57E-08 | 3.74386E-07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





