The Mathematics of Plato's Psychophysics of Colour

Preprint

Article

The Mathematics of Plato's Psychophysics of Colour

Altmetrics

Downloads

Views

Comments

Paul Redding^*

This version is not peer-reviewed

Submitted:

03 October 2024

Posted:

03 October 2024

You are already at the latest version

Alerts

Abstract

Aristotle is often looked to as providing a potentially appropriate model for a naturalistic human psychology that is able to reconcile the commonly opposed normative or “manifest” and factual or “scientific” images of the world. In contrast, this paper argues for the greater relevance of Plato’s comparatively neglected approach, exploring this in the context of a psychophysics of colour perception—a topic still resistant to formalization in modern science. While Plato’s natural philosophy is often dismissed as caught up in a fanciful pre-scientific approach based on the “harmonies” of Pythagorean music theory (the so-called “music of the spheres”), it is argued that such Pythagorean harmony theory had actually provided Plato with the rudiments of contemporary mathematical tools useful for the study of colour phenomena, tools such as projective geometry, linear algebra, algebraic topology, and graph theory. It is argued that Plato’s approach to the psychophysics of colour underlies the colour phenomena discovered by Goethe in the nineteenth century, phenomena that are consistent with modern mathematical analyses of order. It is Plato, not Aristotle, whose work is suggestive of a successful psychophysical approach to colour.

Keywords:

Subject: Arts and Humanities - Philosophy

1. Introduction

Many practicing natural scientists would no doubt be puzzled by the continuing interest among psychologists and philosophers in the psychological studies of Aristotle. Modern science is generally conceived to have, in the seventeenth century, liberated itself from Aristotelian natural philosophy: why then should, four centuries later, investigators return to his writings? One particular reason for such continuing interest has to do with the contrast between what Wilfrid Sellars had described as between the “manifest” and “scientific” images of the world and the role of humans within it [1]. While modern western culture from the 17^th century has generally been marked by the rise of the naturalistic view onto ourselves, this has left significant problems, such as accounting those aspects of ourselves which we take for granted in pursuing the naturalistic point of view itself.

From the naturalistic point of view we are simply complex mechanisms, but in the context of our conceptions of ourselves as investigators of the world, we think of and treat ourselves and others as rational, in the sense of accountable to rational norms. Such norms are presupposed in all scientific debate but seen from the scientific viewpoint such norms are ontologically peculiar entities that have no discernible place in the world of facts. Sellars had contrasted the modern stance in this way with that found within classical philosophy in which norms and ideals were first conceived by Plato as other-worldly entities (Ideas) but which Aristotle had “brought down to earth” with the idea of the intelligible forms of empirical things. In this sense, Aristotle had become the “great defender of the manifest image” in the classical world [2] (110). It should not be surprising then, that topics within Aristotle’s distinctly philosophical psychology have remained a continuing source of interest. Here especially, can be included his account of sensory perception in which experience plays a central role in the formation of the knowledge, upon which animals, and thus we rational animals, are considered to act in the world.i

While perception is the activity of a rational psyche which, for Aristotle, as the form of the body is nevertheless understood as embedded in natural processes of the world—an approach to mind and body different to the characteristic dualism of mind and world and found typically in Descartes and other early modern philosophers. Thus, some have found within Aristotle’s approach to sensory perception one that, while in line with the “manifest” view of ourselves, might still be complementary to natural scientific approaches. Thus, Aristotle has been discussed as anticipating modern “functionalist” and “cognitive scientific” approaches to the mind as developed in the second half of the twentieth century [4,5].

In this paper, however, I pursue in a similar spirit, an approach to the “psychophysics” of colour perception not of Aristotle but of Plato, and specifically an approach informed by the mathematics that Plato had adopted from contemporary Pythagorean mathematicians and natural philosophers. This takes us into territory that goes against the grain of contemporary comparative evaluations of these two philosophers, as Aristotle is thought to be the more “naturalistic” of the two and closer to modern empirical science in his investigations of the world. Indeed, the direction taken by Platonic thought that I will be pursuing is standardly taken as exemplifying one of the most non-scientific paths leading out of the ancient world, as it involves the generalization of the mathematical theory of musical harmony that the Pythagoreans had extended to astronomy, giving rise to the peculiar tradition of the “music of the spheres”—a notion already dismissed by Aristotle as false and mere metaphor [6] (290b12–14). In contrast, I will be arguing that what is found in Plato is the type of anticipation of an applied mathematical approach to the realm of order that has blossomed in mathematics over the last two centuries. Using some of these developments it will be argued that such a Platonic “harmonically” based approach to colour can address problems in thinking about the nature of colour of the sort thematized by Ludwig Wittgenstein throughout his career and that continue to be relevant today.

In this task I follow a number of recent interpreters, such as Samuel Scolnicov [7], Kenneth Sayre [8], and Charles Kahn [9], in treating Plato’s dialogue, the Parmenides, as a work revealing the problems Plato had come to grasp as immanent within the “theory of Ideas” of his own middle-period dialogues. This had led Plato to undertaking a refashioning of this theory in his post-Parmenidean works, the Sophist, Statesman, Timaeus, Philebus, Laws, and Epinomis.ii As stressed by Kahn [9], a general feature of these late works, most explicit in the Timaeus, was a turn towards the type of natural philosophy more typical of pre-Socratic philosophers, with a central aspect of this naturalistic turn being his adoption of Pythagorean mathematics, especially that of the Pythagorean natural philosopher Philolaus of Croton, on whom the views of Plato’s fictional Timaeus may have been based [10]. All in all, I will be arguing that more success might be expected in the realm of the psychophysics of colour from Plato’s relatively neglected late mathematically influenced philosophy than from the massively investigated and comparatively non-mathematical approach of Aristotle.iii

In Section 2, I start with a dimension of Aristotle’s approach to colour that would be the position criticised by Newton in his groundbreaking studies that would lead to the modern physics of colour. This was Aristotle’s explicitly “modificationalist” account, put forward predominantly in Sense and Sensibilia [12]. This had led to Aristotle’s attempting to articulate the field of colour using an analogy to the differentiation of sound into musical consonances and dissonances. Such an approach, I suggest, had drawn upon the same Pythagorean considerations on which Plato had drawn in his late dialogues, and in sections 3 and 4, given problems within Aristotle’s account, an alternative Platonic approach is reconstructed on the basis of Plato’s use of the harmonic ratios in the Timaeus. Beneath these structures taken from the domain of music was a simple but powerful mathematical structure, something like that now called a “group homomorphism”, which was able to be extended to considerations of space in ways that were not simply the application of a “musical metaphor”. While Aristotle’s own application of the musical structure to colour perception would encounter intractable problems, when this is done from a Platonic point of view an approach to the logical articulation of “colour space” similar to that found two millennia later in the attempt of Johann Wolfgang von Goethe to revive Aristotle’s modificationalist account [13] (Goethe 1988). After the logical revolution of the early twentieth century, Ludwig Wittgenstein, deeply influenced by his reading of Goethe’s theory of colour, would argue for the inadequacy of the contemporary logic of colour concepts [14,15,16]. Efforts to address such problems have been taken up by logicians in the last two decades. Building on such approaches, the Platonic infrastructure of Goethe’s theory of colour is shown in section 5.

2. From Aristotelian to Late Platonic Psychophysics

Aristotle’s theory of colour perception was multifaceted. He is most known for his “perceptual realism” [17,18], but here I wish to focus on his so-called “modificationalist” account that, up to the seventeenth century, had remained dominant and would be that against which Newton would launch his own ground-breaking physical approach to colour [19,20]. In relation to this modificationalist approach, Aristotle had suggested parallels between the visual perception of colour and the auditory perception of musical tones, a parallel, I suggest, that Aristotle had taken from the contemporary Platonic culture of the time, and perhaps Plato himself.

In Aristotle’s modificationalist theory of colour, as found across the works Sense and Sensibilia, Meteorology, and On Generation and Corruption, colours are conceived as modifications of white or “brightness” via a mixture with black or “darkness”, revealing the fact that, as Sorabji points out, “a number of Greek colour words did double duty. They were used as much to denote the brilliance of a colour as to denote its hue” [21] (294).iv Kalderon sums up Aristotle’s theory and the history on which it builds:

That white and black, or light and dark, are the primary colours, the colours in terms of which all other colours are explained, is an ancient doctrine, arguably of Homeric roots, that Parmenides and Empedocles share. Aristotle follows them in this. Moreover, Aristotle takes over from Parmenides and Empedocles the idea that light and dark are contraries that constitute the extreme ends of an ordered range of sensible qualities. Moreover, he emphasizes Empedocles’ contribution to this tradition in claiming that it is the ratio of light and dark when combined that determines an intermediary colour. [2] (120)

In On the Soul [22], the home of his perceptual realism, Aristotle had been mainly focussed on how colour as an objective qualification of a substance is able to be matched by a similar sensation in the psyche, allowing the property of the distant object to be known. In Sense and Sensibilia, however, he is more concerned with the ontological question of specifying what “colour is, or sound, or odour, or savour … the point of our present discussion is to determine what each sensible object must be in itself, in order to produce actual sensation” [12] (439a10-17). He then proceeds to discuss three hypotheses concerning how the colours may be generated out of the combination of white and black understood in three ways: first, as juxtaposed, next superposed, and then as mixed.

Concerning the first hypothesis, as found in Empedocles, he notes that “it is conceivable that the white and the black should be juxtaposed in quantities so minute that either separately would be invisible, though the joint product would be visible; and that they should thus have the other colours for resultants. Their product could, at all events, appear neither white nor black; and, as it must have some colour, and can have neither of these, this colour must be of a mixed character—in fact, a species of colour different from either” [12] (439b20-30). After airing objections he considers the second hypothesis with its focus on the way objects appear through some non-totally transparent medium, as when “sun, which in itself appears white … takes a crimson hue when beheld through a fog or a cloud of smoke” [12] (440a12).v Again considering objections, Aristotle turns to a third hypothesis upon which he settles. This concerns a combination by mixture that he says has been dealt with “generally in its most comprehensive aspect” in his earlier “treatise on mixture” [12] (440b4), presumably, On Generation and Corruption [24].

In this work the qualities of white and black are treated as opposing states of a substance, each capable of affecting and being affected by the contrary state of another substance.vi Thus, black and white are considered as at the extremes of a sensory continuum in the way that hot and cold are similarly located at the ends of a continuum of intermediary sensory states. In the case of hot and cold, contact with a hot body, for example, will warm a cold one, the resulting state of which will be some intermediate mixture of hot and cold.vii On this model, black and white will be conceived of as the extremes of a continuum, with the “intermediate colours” spread out between them and determined by the ratios of white and black in each in a way analogous to that of hot and cold.

Many obvious problems present themselves, not the least of which is one raised by many interpreters (e.g., [21] (293); [2] (92)): why is it that mixtures of black and white do not simply produce an array of shades of grey, producing the general experience of a grey-scaled world? Where does the distinctive array of coloured hues actually come from? Moreover, and connected with the indeterminacy of the semantics of colour words noted above, what are we to make of the odd status of black as a privation [steresis] of white? The language of mixing suggests something substantive, something like black die mixed with white,viii but steresis suggests simple absence of white.

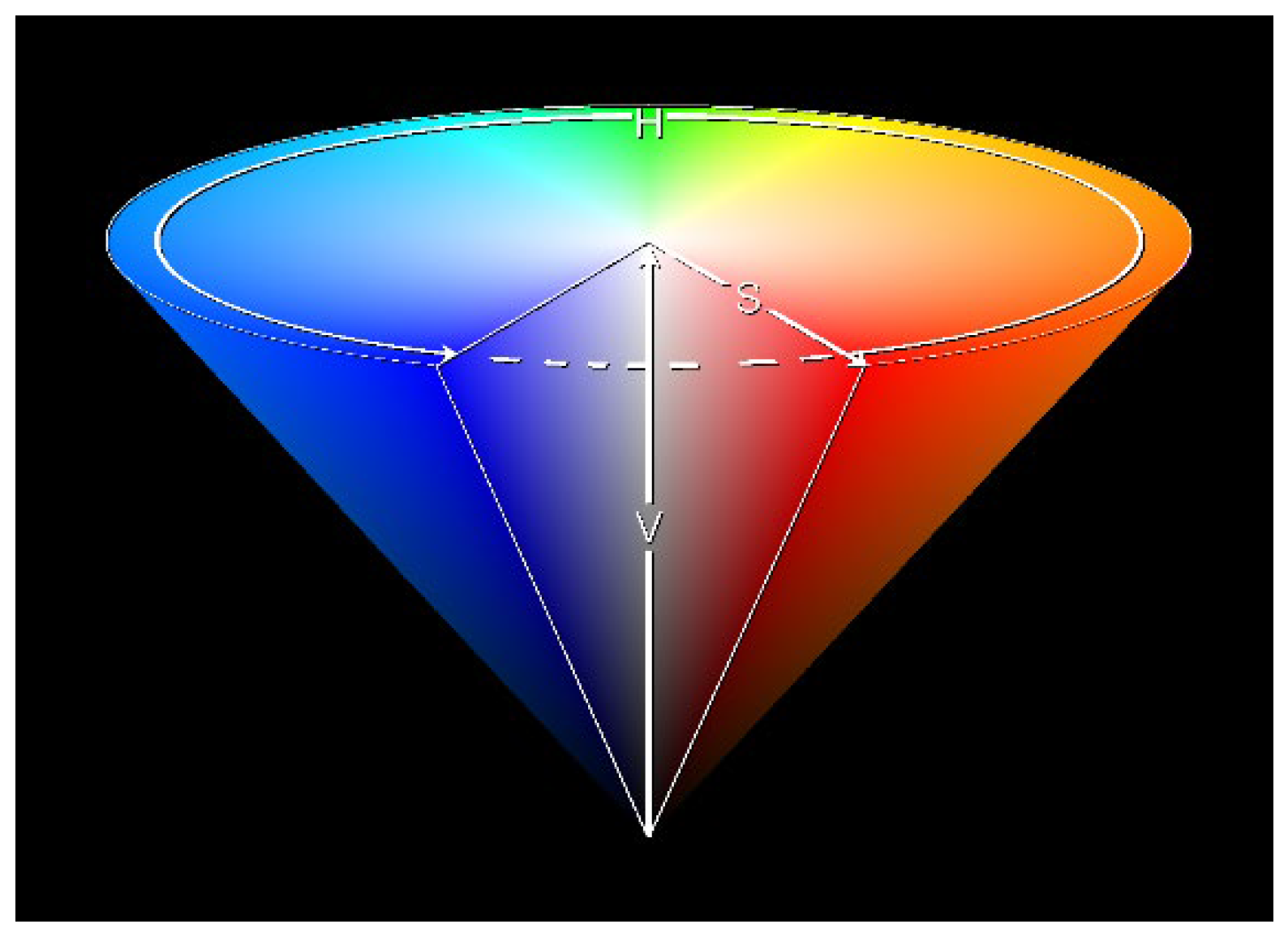
Leaving such problems to one side I want to focus on a more specific problem: even if one accepts that the intermediaries stretching from white to black are somehow coloured rather than grey, how does one find some appropriate order for them? Aristotle’s idea of the different secondary colours resulting from specific ratios of white and black within the mixture suggests that the colours be ordered in terms of their degree of brightness, with purple, for example, being closer to black and yellow closer to white. But the colours themselves can surely vary in brightness or darkness while still retaining their distinctive hue. The secondary colours need an independent ordering principle distinct from the issue of brightness. In the “Munsell” colour system established in the early twentieth century and based on psychological studies of perceived similarity between colour patches [27], the parameters of hue, saturation and brightness, are taken to be independently varying features of light, as illustrated in Figure 1.

One thing about the differentiations of colour seems clear, in that they cannot, as the Cambridge logician W. E. Johnson argued a century ago, be thought to be ordered according to Aristotle’s own genus-species hierarchy. That is, different colours such as red and green cannot be thought of as “species” of the more general genus, “colour”, as red cannot be distinguished from green by the presence of absence of some specifying characteristic, in the way that the genus “animal” can be distinguished into the species “human” and “non-human” according to the presence or absence of a specification such as “rational”[28] (ch. 11); c.f, [2] (175).x I suggest that within Sense and Sensibilia, at least hints towards a possible alternative to the genus/species articulation is provided by the actual ratios of black and white constituents of colour offered by Aristotle when he notes that “they may be juxtaposed in the ratio of 3 to 2, or of 3 to 4, or in ratios expressible by other numbers; while some may be juxtaposed according to no numerically expressible ratio, but according to some incommensurable relation of excess or defect …” [12] (439b20-30). These actual ratios, as Aristotle makes clear, derive from Pythagorean harmonic theory:

Accordingly, we may regard all these colours as analogous to concords, and suppose that those involving numerical ratios, like the concords in music, may be those generally regarded as most agreeable; as, for example, purple, crimson, and some few such colours, their fewness being due to the same causes which render the concords few. The other compound colours may be those which are not based on numbers. Or it may be that, while all colours whatever are based on numbers, some are regular in this respect, others irregular; and that the latter, whenever they are not pure, owe this character to a corresponding impurity in their numerical ratios. This then is one way to explain the genesis of intermediate colours” [12] (439b30-440a6).

As Richard Sorabji has pointed out, the origin of this extension of the model of musical concords [symphoniai] to colour was presumably not Aristotle himself:

How much of the foregoing scheme is Aristotle’s and how much did he inherit? Oskar Becker has suggested that the rational/irrational division stems from Archytas and Eudoxus, while the alternative regular/irregular division is due to Philolaus, Plato, and the Old Academy. Konrad Gaiser thinks that … the mathematical ideas were already being worked on in the Academy before Aristotle wrote about them. A. E. Taylor detects a Pythagorean source. In fact, it is hard to say how much is due to Aristotle. He certainly learnt from others the theories that the remaining colours are produced from black and white by juxtaposition or by superimposition, while the substitution of chemical mixture for juxtaposition and superimposition is his own. [21] (297).

Certainly, that the ratios 3:2 and 4:3 represented two concords in Pythagorean harmonic theory, the diatessaron, literally “through four”, in modern terminology, the “perfect fourth”, as in C to F, and the diapente, “through five” or the “perfect fifth”, as in C to G, when the extremes of the interval of the octave (diapason, “through all”), C to C, were represented by the ratio of 1:2, had been well established before Aristotle’s time. The earliest recorded version is found in Philolaus of Croton [10] (ch 1), [29] (ch. 10), an approximate contemporary of Socrates, and it was then developed by his former student, Archytas of Tarentum, a contemporary and friend of Plato [29] (ch. 11). The idea, however, had seemingly gone back well before them.xi This Pythagorean element would be taken up and transformed by Plato in the dialectical method of his late dialogues.

While critical of Pythagorean metaphysical claims, Aristotle had used the results of Pythagorean natural science throughout his work (c.f., [30] (ch. 12)). But his understanding of Pythagorean science and, especially, the mathematics in which it was based seems to have been limited [31] (24–26), as revealed here by his misconstrued analogy between colours and concords. What are or are not “agreeable” in Pythagorean music theory are not tones per se but combinations of tones, the combination of concordant notes C and F or C and G, for example. But Aristotle is here talking not about agreeable combinations of colours, but the colours themselves considered in isolation. Here I suggest that Aristotle’s analogy, with its reference to numerical ratios was probably based on some extant model circulating in Plato’s Academy during the years he was a member—a model he only partially understood. There are certainly the rudiments of such a model in Plato’s Timaeus as well as that of the well-known extension of Pythagorean music theory to astronomy. In the following section, on the basis of these I pursue what a properly Platonic application of the harmonic model to colour might actually look like.

3. Late Platonic Physics and the Rational Surrogates of Ideal Numbers

Sometime in the centuries before Plato and Aristotle it had been established experimentally by Pythagorean mathematicians that when the length of a vibrating string was halved, the pitch of the tone emitted was raised one octave producing a note heard as being in unison with the first. Dividing the string again in half, produced a note another octave above the original. In short, the sequence of octaves, 1, 2, 3, 4 … was associated with the sequence of lengths 1, 1/2, 1/4, 1/8 …. Otherwise put, octaves ordered in a potentially infinite increasing “arithmetic” sequence were correlated with line lengths ordered in a decreasing “geometric” one. When the members of the arithmetic sequence are considered in relation to the inverses of those of the geometric, the correlation now becomes between the arithmetic sequence 1, 2, 3, 4, … and the geometric sequence now ordered, … 1/8, 1/4, 1/2, 1, 2, 4, 8, ….xii With some modifications, each set of numbers might be thought to form the basis of an algebraic group, the first underlying the operation of addition and the second, multiplication.xiii In modern group theory, two such groups are related by a “group homomorphism” when elements of one group structure are mapped onto those of a different one. So understood, the elements of an additive structure of the type a + b = c would be mapped systematically onto those of a multiplicative structure, d⋅e = f.

Group theory was only formally developed in the nineteenth century, but such a homomorphism between additive and multiplicative groups had been exploited since the seventeenth century, for example, in logarithmic tables, via which long multiplications could be approximated by simpler additions. The Greeks had seemingly exploited the correlations of their own harmonic scales in much the same way, this peculiar alignment of these two different infinite sequences allowing particular relations to be set up between smaller sequences of three terms of each. For three consecutive terms of an arithmetic sequence, the “mean” or “middle term”, equal to half the sum of the extremes, could be correlated with the equivalent “geometric” mean of two terms in a geometric sequence, which is calculated as the square root of the product of the two extremes. The arithmetic mean of two terms, however, also has an inverse, called the harmonic mean. It would be correlations between these three means that would be exploited in harmonic theory and its extension to astronomy.

Within harmonic theory itself, dividing a string geometrically had been found to produce a sequence of octaves, but it had been discovered that dividing a string so as to find consonant tones within an octave was somewhat more complicated. It might be thought that dividing the octave geometrically would produce analogous concords but this solution for the Pythagoreans was stymied. Finding the geometric mean of an interval between extremes a and b encounters the problem that, for the Greeks, if the product a⋅b was itself a non-square number, there was no number or ratio of numbers able to represent the geometric mean of a and b, a magnitude represented in the modern system of “real numbers” as the square root of the product, √a⋅b.xiv Thus, it had been discovered, possibly by Hippasus himself, that continuous and discrete magnitudes were incommensurable in that no ratio of numbers was equivalent to the ratios between some geometrically defined particular line-lengths, such as those of the side and diagonal of a square. The same applies to the geometric mean of an octave represented by the extremes 1 and 2. In any case, actually dividing the string “geometrically” in this way produces a highly dissonant interval, the modern “tritone” as in C to F#.xv

Rather, it was found that within the octave a concord, the diapente, coincided with the arithmetic mean of the octaval extremes, such that if the octave were represented as the interval between 1 and 2, the string would be divided in the ratio of 3:2. A further concordant note, the diatessaron, was found when the string was divided by the ratio 4:3, at the so-called harmonic mean.xvi These two means are related in that the harmonic mean is the mathematical inverse of the arithmetic mean, just as 4:3 is the inverse of 3:2 when both are thought to divide the interval between 1 and 2. Expressed algebraically, a is the arithmetic mean of the extremes m and n when a = (m+n)/2, while the harmonic mean simplifies to the equation h = 2m.n/(m+n).

As can be seen in this example, unlike the geometric mean of the natural numbers 1 and 2, which is irrational, the harmonic and arithmetic means of any two natural numbers will always be able to be specified as ratios of natural numbers. Just as a homomorphism exists between the groups of addition and multiplication over the natural numbers, the product of the ratios 4:3 and 3:2 (the number 2) equals the sum of the intervals, as the fourth and fifth, qua steps in the scale, sum to the octave.

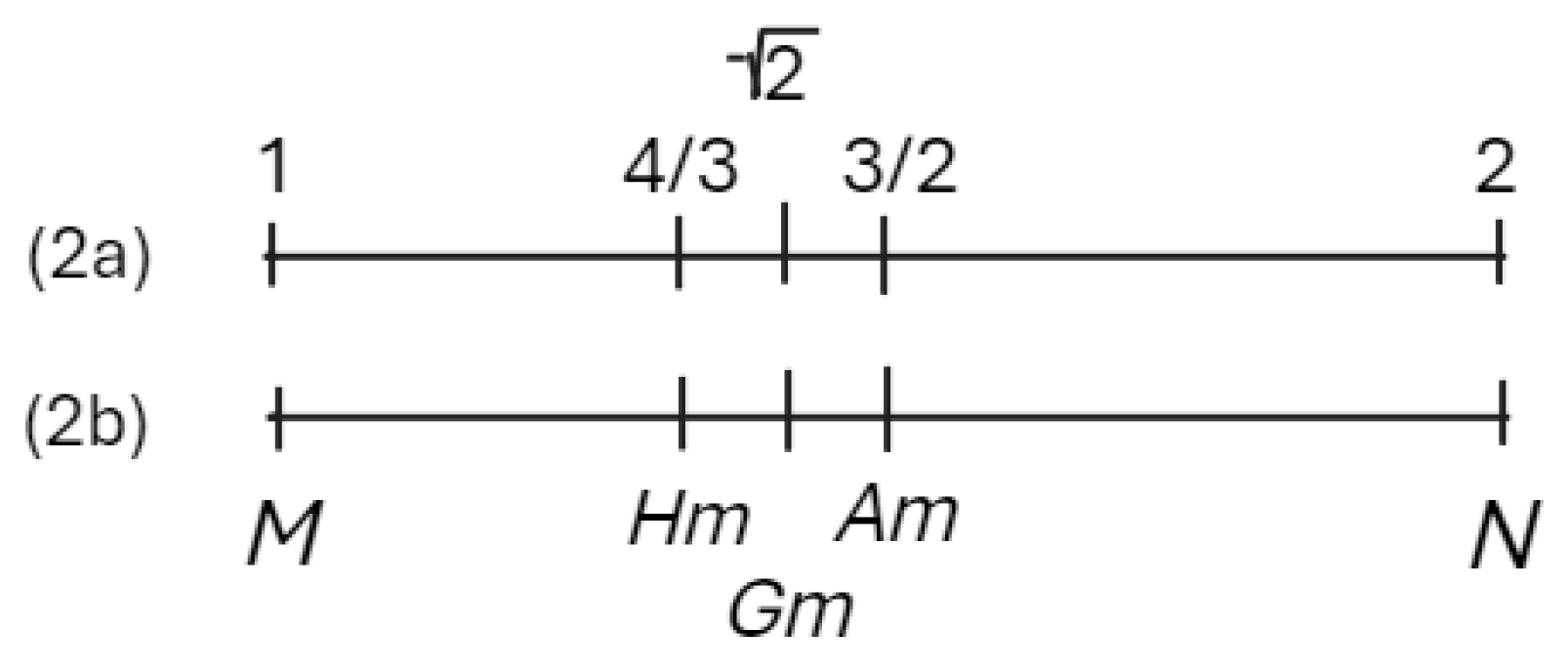
These underlying relations allowed the sequence of the two octaval extremes separated by the two concords, 1, 4:3, 3:2, 2—known to the Greeks as the “harmonia” or “musical tetraktys”—to possess very distinct mathematical properties. For example, the pair of rational means, the arithmetic and harmonic, can function as the basis of an algorithm for giving approximate values to the irrational number (or Greek non-number), √2, as its value falls close to midway between the harmonic and arithmetic means of 1 and 2, as in Figure 2 below.

Using decimal notation, it can be appreciated that, 1.41421… (an approximation of the value of √2 given by any smartphone app) falls roughly midway between 1.3333 … (4/3, the harmonic mean of 1 and 2) and 1.5 (3/2, the arithmetic mean of 1 and 2). Even more striking, however, is the fact that this process can be iterated in that taking the harmonic and arithmetic means of the original harmonic and arithmetic means, results in a smaller range of possible values and so giving a much closer approximation to the value needed (1.41176… < √2 < 1.41666…).The idea of the process being repeated indefinitely now allows a conception of the value of √2 as the limit of a converging pair of potentially infinite series, in much the same way as irrational numbers would come to be understood later in modern European culture.xvii

The musical tatraktys, sometimes expressed in the form of whole numbers as 6, 8, 9, and 12,xviii would be described in the late “Platonic” work, Epinomis, as having been “granted to the human race by the blessed choir of the Muses and has bestowed upon us the use of concord and symmetry to promote play in the form of rhythm and harmony” [33] (991b). Something of the importance that this for the author is clarified by the discussion of the role of mathematics in astronomy and its teaching in the passage that precedes this statement.

Number theory, “the study of numbers in their own right, as opposed to numbers that possess bodies” is described as the first topic to be taught, followed by geometry and stereometry [33] (990c-d). Both geometry and stereometry involve, however, “the assimilation by reference to plane surfaces of numbers that are not by nature similar to one another”. What were not “similar” here were those “incommensurable” magnitudes of arithmetic (numbers) and geometry and stereometry (the continuous magnitudes of lines, areas and volumes). “What people who look into these matters and understand them find divine and miraculous”, notes the author, “is how nature as a whole moulds sorts and kinds according to each proportion, with reference to the power that is always based on the double and the power opposite to this [the half]” [33] (990e-991a). What the “reference” is to here is the geometric proportion, a:b :: b:c which was held to be a type of divine ideal by which magnitudes could be related. However, the passage continues, “the sequence that gives the mean of the double [i.e., the geometric mean] involves both the mean that exceeds the smaller and is exceeded by the larger by an equal amount, and the mean that exceeds one of the extremes by the same fraction of that extreme as the fraction of the other extreme by which it is exceeded by that extreme” [33] (991a). These two other means so “involved” with the geometric mean are the arithmetic mean and the harmonic mean respectively, as they had been defined by Philolaus. Why do these two other means need to have a role here, and why cannot the geometric mean suffice for the measurements of astronomy?

Clearly it is “the assimilation by reference to plane surfaces of numbers” that is relevant. Without the modern system of real numbers, geometric means cannot be calculated for non-square numbers, and so numbers cannot simply be “assimilated” to geometrical figures in order to measure plane surfaces. Some means of working with rational approximations to such “irrational” numbers (that is, numbers without a numerical ratio) is required. It is in relation to this apparent shortcoming of Greek mathematics, I suggest, that lies the significance of the musical tetraktys, acting like a group homomorphism and providing the basis for a mechanically applied algorithm for the calculation of a rational approximation to an “irrational” number, in this case, of the “number” √2.xix

The Greeks had adopted algorithms of this sort for the calculation of algebraic irrationals from earlier Mesopotamian mathematics [34],xx and it is now also known that Mesopotamia had been the source of the Pythagoreans’ harmonic ratios themselves [36]. It is difficult to believe, given its divine status as a gift from the Muses, that the Pythagoreans had not grasped the algorithmic potential of the musical tetraktys itself. Indeed, the dialectical method of science as found in Plato’s late dialogues is described in his Philebus in much the same way as a “gift of the gods to men” [37] (16c).

The approach to mathematics with a focus on its application to the empirical world as reflected in the Epinomis shows a definite departure from that found earlier in the Republic, a change in line with the more nature-philosophical orientation of the later works [9]. In the Republic Book VII, Socrates had set out the mathematical curriculum for future leaders that would eventually lead to the study of dialectic [38] (525b–531c).xxi While the sequence is much the same as in the Epinomis—arithmetic, geometry, stereometry, astronomy and harmonicsxxii—the focus in this classic middle-period work is much more on mathematics understood as a “pure” rather than “applied” discipline, with the main consideration being the role of mathematics in leading “the soul forcibly upward and compel[ling] it to discuss the numbers themselves, never permitting anyone to propose for discussion numbers attached to visible or tangible bodies” [38] (525d). Here there is little or no consideration of actual calculation in relation to this, with calculation [logismos] being generally dismissed as relevant only to “tradesmen and retailers, for the sake of buying and selling” [38] (525c). In short, Plato’s attitude to mathematics in the Republic is focused on the conceptual definition of numbers rather than their roles in calculation. From such a purely conceptual point of view, the ratio between the diagonal and side of a square is perfectly well defined: it is numerically equivalent to the ratio of two “numbers”: that which when multiplied by itself would result in the number 2, and the number 1. In this sense, the irrational and so non-computable number, our √2, is a number that “can be grasped only in thought and can’t be dealt with in any other way”. Such a “number” is perfectly fitted for “turning the soul around, away from becoming and towards truth and being” [38] (525c), but not for everyday use.

This is the role standardly associated with mathematics in interpretations of Plato’s philosophy, in which Plato’s transcendent realm of Ideas is contrasted with Aristotle’s this-worldly realm of “informed” matter, but it is a role that had been modified in the late works where Plato had become more concerned with knowledge applicable to the realm of becoming: the type of knowledge relevant to astronomy considered as natural philosophy and reliant on the application of numbers to continuous magnitudes to allow measurement and calculation. This represents a shift in Plato’s attitude to include the computational dimension of mathematics to augment the earlier purely conceptual dimension, adding a “structuralist” dimension to the very notion of number, as numbers now come to be specified in terms of their computational relations to other numbers.xxiii In contrast, Aristotle would retain the more conceptualist or “logicist” approach to mathematics in that one is supposedly able to abstract away from both the continuous magnitudes of geometry and the discrete magnitudes of arithmetic so as to reach their purely logical determinations.xxiv This structuralist modification of Plato’s earlier conception of mathematics is also apparent in the work of his fictional astronomer, Timaeus, in the dialogue bearing his name, revealing the influence of the earlier Pythagorean natural philosopher Philolaus, on whom Plato may have modelled the figure of Timaeus himself.

4. The Mathematics and Physics of Timaeus and Philolaus

In the Timaeus, Timaeus recounts the “likely story [eikos logos]” of the genesis of the cosmos by the actions of the Demiurge.xxv When he first “began to put the body of the universe together, the god came to make it out of fire and earth”—elements responsible for its visibility and tangibility respectively [41] (31b). But, he adds, the combination of two things requires “a third … some bond between the two that unites them” and for such a purpose, the “best” or “fairest” bond [desmon de kallistos] is one that makes a unity of itself together with the things bonded by it, and this in the nature of things is best accomplished by proportion. For whenever of three numbers which are either solids or squares the middle term between any two of them is such that what the first term is to it, it is to the last, and, conversely, what the last term is to the middle, it is to the first, then, since the middle term turns out to be both first and last, and the last and the first likewise both turn out to be middle terms, they will all of necessity turn out to have the same relationship to each other, and, given this, will all be unified. [41] (31b–32a.xxvi

Things are further complicated, however, by the fact of the body of the universe being three-dimensional, since: solids are never joined together by just one middle term but always by two. Hence the god set water and air between fire and earth, and made them as proportionate to one another as was possible, so that what fire is to air, air is to water, and what air is to water, water is to earth. He then bound them together and thus he constructed the visible and tangible universe. This is the reason why these four particular constituents were used to beget the body of the world, making it a symphony of proportion. [41] (32b–c).

The “proportion” [analogia] referred to in the first passage is standardly taken to be a reference to the geometric proportion, a:b :: b:c, generally regarded by the Greeks as being the ideal bond for binding parts into a whole, and this geometric proportion is repeated in the second paragraph but now extended to a fourth term, such that the relations of fire, to air, to water, to earth are ordered by a continuing geometric sequence, fire: air :: air : water :: water : earth.

With this there appears here to be an implicit reference to the well-known “Delian problem” of finding the length of the side of a cube needed to double the volume of another cube [42] (vol I, 334–336).xxvii The problem had a long pre-history and Hippocrates of Chios (circa 470 – circa 410) had shown that the problem of the duplication of a cube could be reduced to that of finding two geometric means between the lengths of two lines, one twice the length of the other.xxviii However, this second puzzle to which the first had been reduced was “not less difficult” [42] (vol 1, 336).xxix Plato had purportedly set this as a problem for members of his academy and various solutions had been offered.xxx However, “as it turned out, all their solutions were theoretical, and no one of them was able to give a practical construction for ordinary use” (pseudo-Eratosthenes, quoted in [42] (vol. I, 335). As Plato had become clear in his later dialogues, that a mathematical problem has a theoretical solution does not ensure that it can be used for practical construction: numbers as conceptually defined entities need to be connected to devices by which they can be specified for practical application. The existence of this computational dimension to the ratios with which the universe can be explored is insisted upon in Timaeus’s account of the structuring of the cosmic body, which belongs to the domain of becoming rather than the purely intelligible realm of eternal being.

As Kalderon points out, the Demiurge constructs the cosmos working from an intelligible model that is “unchanging and uniform” [11] (21), but this does not entail that these unchanging and uniform forms are actually realized in the completed work. The “fairest bond” referred to seems to be that of the ideal model, and according to the second passage, after the Demiurge has made the four elements “as proportionate to one another as was possible” he is said to have then “bound them together”. If the Timaeus genuinely belongs to Plato’s late period, then one should expect that, as specified by the formula of Epinomis 990e–991a, the arithmetic and harmonic means—those actual world practical surrogates of the inapplicable geometric proportion—should play a role in the binding of the parts of the cosmos into a whole. As Timaeus’s speech progresses, we find that this, indeed, is the case.

When later discussing the Demiurge’s construction of the necessarily embodied soul (Psyche) of the cosmos (which, it turns out, actually precedes the construction of the body [41] (Timaeus 34b)), Timaeus says that “in between the being that is indivisible and always changeless, and the one that is divisible and comes to be in the corporeal realm, [the Demiurge] mixed a third, intermediate form of being, derived from the other two” [41] (Timaeus 35a). There follows a confusing list of different but similar “mixtures” between the “Same and … the Different, in between their indivisible and their corporeal, divisible counterparts”. A type of dough-like substance results which the Demiurge then divides into parts whose sizes form a series of square and cube numbers starting with 2 and 3, thus 2, 3, 4 [22], 9 [32], 8 [23], 16 [42], 27 [33], but he then went on to “fill the double and triple intervals by cutting off still more proportions from the mixture and placing these between them, in such a way that in each interval there were two middle terms”. These middle terms are now specified as the harmonic mean (“one exceeding the first extreme by the same fraction of the extremes by which it was exceeded by the second”) and the arithmetic (“the other exceeding the first extreme by number equal to that by which it was exceed by the second” [41] (36a)) respectively. Thus, “these connections produced intervals of 3:2, 4:3, and 9:8 within the previous intervals”.xxxi In retrospect, it would seem that what Timaeus is referring to with the “fairest bond” had been, as with the “symphony of proportion”, not the geometric mean itself, the role of which had been that of the ideal model of which the realized bond was a worldly expression. The fairest bond itself, as later neo-Platonists had proposedxxxii was the mathematical structure realized in the musical tetraktys.

With this, Timaeus’s cosmic ontology bears a clear relation to the harmonic based cosmology of the Pythagorean natural philosopher Philolaus of Croton [10] (149–150), to whose ideas Plato alludes in the Philebus [37] (16d and 23c). Philolaus, a rough contemporary of Socrates and member of the “mathematici” or mathematical Pythagoreans is the first known advocate of the internal division of the octave by inverse harmonic and arithmetic means [44] (165)—the two means inserted within the intervals of the three-dimensional solid constructed on the ideal model of the geometric proportion in the Timaeus.

In the opening sentences of Philolaus’s book, On Nature,xxxiii Nature is described as “fitted together [harmozein] out of unlimited things (apeiron) and limiting ones (perainonton), both the whole world and everything in it” [44] (155). This is later expanded upon:

[I]t would have been impossible for any of the things that exist and are known by us to come to be if the being of the things out of which the world is constituted, both the limiting ones and unlimited ones, did not exist. But since the principles [archai] existed, not being similar nor related as kindred, it would have been impossible for them to be arranged in a world if a harmony had not supervened, in whatever way this came about. [44] (157-159)

There is no need for harmony among things “that are similar (omoiai) and related as kindred (omophiloi)”, but for those not so similar and related, “it is necessary that these be connected by this kind of harmony if they are going to maintain themselves in the world” [44] (159). In introducing the new “Philolaic method” of dialectic in the Philebus [45], Socrates suggests making “a division of everything that actually exists now in the universe into two kinds, or if this seems preferable, into three” and reintroduces an earlier reference to the Philolaic pair of “the unlimited and the limit” [37] (23c). “Let us now take these as two of the kinds, while treating the one that results from the mixture of these two as our third kind”. He then adds a fourth to Philolaus’s three, the two archai and their mixture: “Look at the cause of this combination of those two together, and posit it as my fourth kind in addition to those three” [37] (23c–d). Positing the mixture as the result of a cause, the role traditionally given to Ideas, thus links such mixture to Ideas as more traditionally conceived. It is in this sense that the mixture of the limit and the unlimited is posited as the worldly imperfect equivalent or paradigm (paradigma) of the Idea that is unable to itself be realized in the actual world.

The “unlimited”, Socrates continues a little further along, is “whatever seems to us to become ‘more and less’, or susceptible to ‘strong and mild’ or ‘too much’ and all of that kind, all that we ought to subsume under the genus of the unlimited as its unity […] for whatever is dispersed and split up into a multitude, we must try to work out its unifying nature as far as we can” [37] (24e-25b).xxxiv In contrast, it would seem that limit has characteristics of discrete multitudes as what is not found in the unlimited includes “the equal” and “equality”, and “things like ‘double’, and all that is related as number to number or measure to measure”. All these belong to limit and will help put “an end to the conflicts that are among opposites, making them commensurate [symmetra] and harmonious [symphona] by imposing a definite number on them” [37] (25e). But the harmonic ratios for Plato are not tightly bound to their musical origins as they had been for Philolaus. As Huffman notes [10] (150), while Timaeus (Plato) closely follows the ratios of Philolaus’s musical scale in the Timaeus, he never mentions their musical origins. This clearly signals that for Plato, musical harmonies had merely been the contingent forms in which these abstract mathematical proportions had been discovered. The proportions themselves are in no sense essentially musical. Their application to the cosmos does not imply, as it would for Kepler in his Harmonices Mundi of 1619, for example [47], that the planets emit harmonious heavenly chords in their movement about the earth.

In Plato’s middle period, the problem had been how to link the clearly incommensurable realms of being and becoming, and Timaeus describes the Demiurge’s task in this way: It is a matter of mixing “a third, intermediate form of being, derived from the other two”, that is, the realms of “the being that is indivisible and always changeless, and the one that is divisible and comes to be in the corporeal realm” [41] (35a). But this structure represents how things are seen from the divine perspective of the Demiurge, the “model” used to guide the construction. From the perspective of beings living within the empirical cosmos of becoming, the two archai are no longer being and becoming, conceived as independently cognizable, but the limit and the unlimited. That is, being and becoming are no longer primitives to be “mixed”: rather their opposition is to be understood as an instance of the more general opposition between the commensurable and the incommensurable. Moreover, we now possess a concrete instance of how this opposition might be resolved into a “mediated unity” within the realm of becoming. It is the specifically inverted relation between the arithmetic and harmonic means that stands as a this-worldly equivalent to the other-worldly ideal relation between the terms of a geometric proportion.

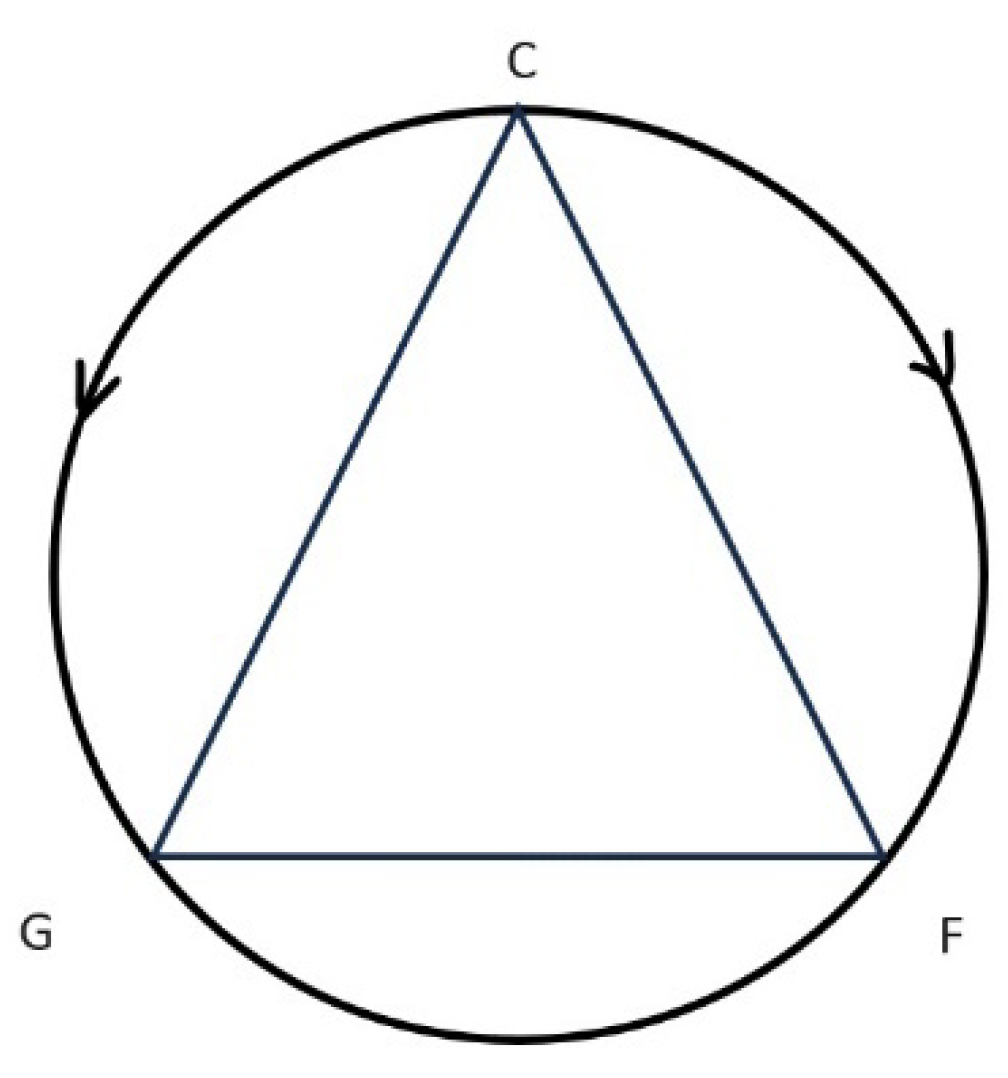
Treating the worldly “fairest bond” in this way, we might represent Plato’s cosmos by a diagram that shows how the four elements of the cosmos (or, alternatively, its four dimensions: point, line, plane, volume) might be understood as a unity of harmonic principles. If we think of the circle below as the clockwise movement of a note x through its octaval interval (C to C), it will pass through two means, the harmonic (F) and the arithmetic (G). If the metric of this circular path is itself an arithmetic one, the sum of the arithmetic and harmonic means is equal to one cycle, the octave itself. Were the metric of the path to be a geometric one, however, it is the product of these means that becomes equivalent to one circuit. Moreover, if the circuit is traced in an anti-clockwise direction representing the descending movement of x from C to the lower C, the interval of C to G now represents a fourth and C to F a fifth. Moreover, Plato would have been aware that different music modes could be generated by an octave starting at any particular note. Such a figure suggests a much stronger reading of the relation in which all three terms of the fairest bond “have the same relationship to each other, and, given this, will all be unified” as this will set a pattern which will no longer hold simply for three numbers that are “either solids or squares”, but for all natural numbers, square, solid or otherwise.

Figure 3. Octave circle with complementary fourth and fifths.

In modern mathematical approaches to the topic of order such as found in graph theory, this simple structure might be represented as a non-directed graph consisting of three vertices (C, F. G) with three connecting edges (CF, FG, and GC).xxxv It would be the fact that such a simple structure is capable of further development, I suggest, that underlies the harmonic “research program” that Kalderon identifies as behind Aristotle’s attempt in Sense and Sensibilia to extend the harmonic intervals to colours.xxxvi While Aristotle’s approach to “mixture” does not accommodate such expansion, Plato’s does.

Elsewhere I have argued for the fruitfulness of that program in that the modern discipline of “projective geometry”, developed briefly in the seventeenth century but then forgotten and revived around the turn of the nineteenth century, had generalized the musical tetraktys to a double-ratio called the “harmonic cross-ratio” and that had provided this form of non-Euclidean geometry’s fundamental “invariant” [48]. For our purposes here, however, in the Timaeus one gets at least some hints as to how this program may have been conceived as extending into a psychophysical theory of colour, as later flirted with unsuccessfully by Aristotle.

5. Platonic Colour Theory as Developed in Goethe’s Zur Farbenlehre: A Sketch

After the discussion of the cosmic soul in the Timaeus we learn how the Demiurge had left it to his/her progeny to fashion the souls of mortal beings. Something of the psychological structure of the world-soul will provide a model for those of mortals, but those of mortals will have additional features not needed by the world-soul. Unlike the world-soul, those of mortals are each individually embodied and thereby located within some specific place within the cosmos and so are in need of external senses like eyes and ears and external organs like hands or feet with which to interact with their surroundings. As located in a living body the mortal soul, as Plato underlines, is reliant on that body’s healthy functioning. Thus, such healthy functioning becomes a precondition to the proper functioning of the finite soul qua soul—that is, to its capacity to approximate the ideals which have been used as model for its construction. This results in a picture in which aspects of the epistemological significance of the sense organs are to be considered in a generally pragmatic way as found in Aristotle, but the difference separating late Plato and Aristotle here is crucial. In Aristotle’s hylomorphic translation of Plato’s middle-period theory of Ideas, normative Ideas are brought into the actual world itself, giving empirical things a teleological character. But Plato retains the element of generalized incommensurability missing in Aristotle.xxxvii What are found in the actual world are not Ideas themselves but their imperfect surrogates, surrogates modelled on the way that the perfect octaval interval is represented within the octave by its two concordant surrogates. This is the general context in which Plato’s late psychophysics of colour must be understood.

In relation to the structural features of colour provided by their mathematical model, the details of the physical mechanisms within which these are realized in Plato are not so important. As for his theory of sight, Plato had a mixed “extramissionist” and “intromissionist” approach—in the former, fiery rays being emitted from the eye to interact with the microstructure of objects, thereby being sent back to the eye.xxxviii The emitted “ray of sight” is contracted by the action of the larger micro-objects upon which it falls (those cubic shapes from which earth is constructed) and it is similarly dilated by the action of the smaller ones (the smaller, sharper tetrahedra, from which fire is composed). Abstracting from the detail, Plato’s approach is more like the modern approach of Newton and Locke in that the causes of colour experience are not themselves be considered independently coloured as they are for Aristotle’s perceptual realism. Rather, colour experience is conceived from a holistic or relational point of view, such that the qualities of the distinct colours can be thought of as a product of principles of order operating within a closed sensory domain producing contrasts and affinities. These, however, can be related analogically to other domains and so colour distinction will be “‘cousin’ to what is cold or hot in the case of the flesh, and, in the case of the tongue, with what is sour, or with all those things that generate heat and that we have therefore called ‘pungent’. So black and white, it turns out, … are really the same as these other properties, though in a different class, which is why they present a different appearance” [41] (Timaeus 67d–e).xxxix One such case from a different class will be the characteristic consonances and dissonances of aural perception. All such sensory domains require a fundamental opposition, and in the case of colour it is that of white and black thought of as correlating with dilation and contraction respectively of the rays of sight, emitted by and then reflected back to the eye.

Recall the fundamental problems facing Aristotle’s application of the musical harmonies to the array of colours in finding some intelligible order among the hues in their difference to that to be found on the linear continuum stretching from white to black. Aristotle had been forced to think of colours as somehow correlating with the ratio of black and white purportedly mixed in them—“mixtures”, it would seem, that like the mixtures of black and white in grey, are conceived as simple, arithmetical sums. Within the properly Platonic framework, however, there are two means implicated, the harmonic and arithmetic means, which stand as the inversely related intra-worldly surrogates of an ideal geometric structure. The general principle here, I have suggested, is a generalization of the way that, within an octave, the harmonic and arithmetic means stand as opposed surrogates for the more ideal geometric mean that defines the perfect unison holding between octaves. Transferred to the model of a colour continuum somehow conceived as stretching from white to black, one must search for a structure involving pairs of inversely related ratios that reproduce something of the ideal meta-opposition of black and white itself—that is, multiply coloured analogues to this primordial opposition.

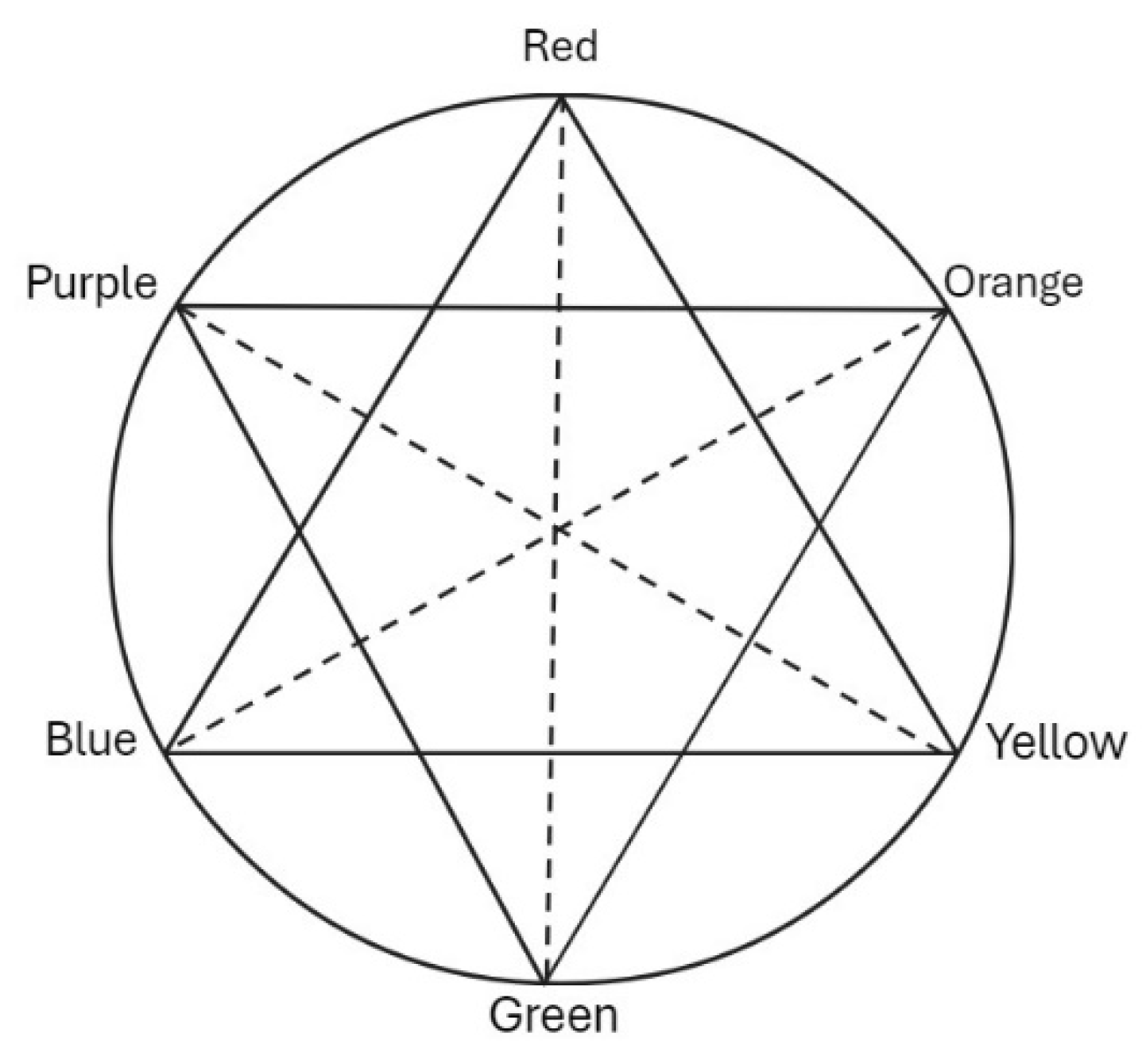
One manifestation of such a Platonic solution, I suggest, is to be found in the structure that Goethe would offer in the nineteenth century in his alternative to Newton’s linear array of hues produced via refraction of sunlight through a prism. In contrast to Newton and conceiving of himself as reviving Aristotle’s modificationalist account of colour, Goethe would appeal to a hexagonal arrangement of six colours in which each would face what is perceived as their aesthetic complement across the three diagonals: red facing green; purple facing yellow; and orange facing blue.xl Conceiving of this structure as a combination of two inverted triangles, Goethe thus would replace Newton’s single spectrum with two tri-coloured spectra, one light and one dark. While Goethe’s inspiration may have been Aristotle’s modificationalism, the underlying structural framework of his hexagon would be Platonic rather than Aristotelian.

Figure 4. Goethe’s colour hexagon/circle (as given in the 1840 English translation, Goethe’s Theory of Colours [49] (plate 1, Figure 3).

From the perspective of modern theories of colour, Goethe is now generally considered as having misconceived the status of his colour theory by thinking of it as a physical theory on the same level as Newtons. But conceived as a psychophysical theory, attempting to capture relations among how colours look to an embodied, located perceiver, with those colours’ characteristic contrasts and complements—that is, qua theoretical elaboration of the associated “manifest” image—Goethe was on steadier ground. In 1860, the Scottish physicist James Clerk Maxwell would demonstrate that all colours could be generated from weighted mixtures of three “primary colours”, red, green, and blue. Then in 1878, the German physiologist, Ewald Hering would propose an “oppositional” theory of colour perception in which the retinal photoreceptive cells respond to two colour contrasts, red-green and yellow-blue. Hering’s two types of cells would later be expanded to three,xli and Maxwell’s triad of primary colours would thus be joined by an inverse triad involved in “subtractive” rather than additive processes—cyan, yellow and magenta.xlii Of course there is no sense in which Plato could have anticipated this type of detailed knowledge. Rather, what his mathematical model allowed concerned something about the particular formal relations articulating such contingent worldly processes. This is the type of structure that concerned Wittgenstein in the first half of the twentieth century and that came to be investigated with the resources of modern logic and logic diagrams in its second half [14]. Wittgenstein insisted that the relevant structures belonged to “grammar”, that is, the patterns of contingent human “language games”. The Platonic approach, in contrast, looks to the human practices underlying mathematics.

In the 1960s, the French logician Robert Blanché [50] (Blanché 1966), had extended into a hexagon a modal interpretation of the traditional square of opposition—a diagrammatic representation of Aristotle’s judgment forms from On Interpretation [51].xliii Blanché added two new vertices to produce six modal judgment types: necessarily p; impossibly p; not impossibly p; not necessarily p; contingently p; and not-contingently p. More recently, using the resources of Boolean algebra, Blanché’s hexagon has been extended from modal logic to Goethe’s colour hexagon as well as to the psychological structures of affective psychical dispositions by Dany Jaspers [52], and Jean-Yves Béziau [53]. Parallels across such diverse domains suggests a type of invariance across essentially incommensurable contents, much as suggested by Plato’s references to structured experiential “cousins” [41] (67d–e).

These modern mathematical and logical approaches can be traced back to Leibniz’s proposal to counter the “analytic” or “coordinate” geometry of Descartes and Fermat with a rival “analysis situs” or analysis of situation [54]. The issue for Leibniz concerned the relation of continuous geometrical magnitudes to discrete numbers, in that he opposed Descartes’s reduction of geometrical shapes to algebraic functions over the “real numbers”. His alternative, in line with his “relativistic” analysis of space, was a more non-reductionist approach establishing a “new relation between algebra and geometry” leading to an evolution of the two fields as “henceforth intrinsically linked in a dialectical process” [55] (237).xliv Such an approach would be manifest in the nineteenth century with the development of disciplines such as projective geometry, linear algebra, and algebraic topology.xlv The spirit of such developments was clearly in the Platonic tradition’s “assimilation by reference to plane surfaces of numbers that are not by nature similar to one another” [33] (990c-d). In order to capture something of those recent attempts to articulate the structure of Goethe’s colour hexagon we might proceed via the juxtaposition of two diagrams (Figure 4a,b below), as linked by the logician John Martin.xlvi

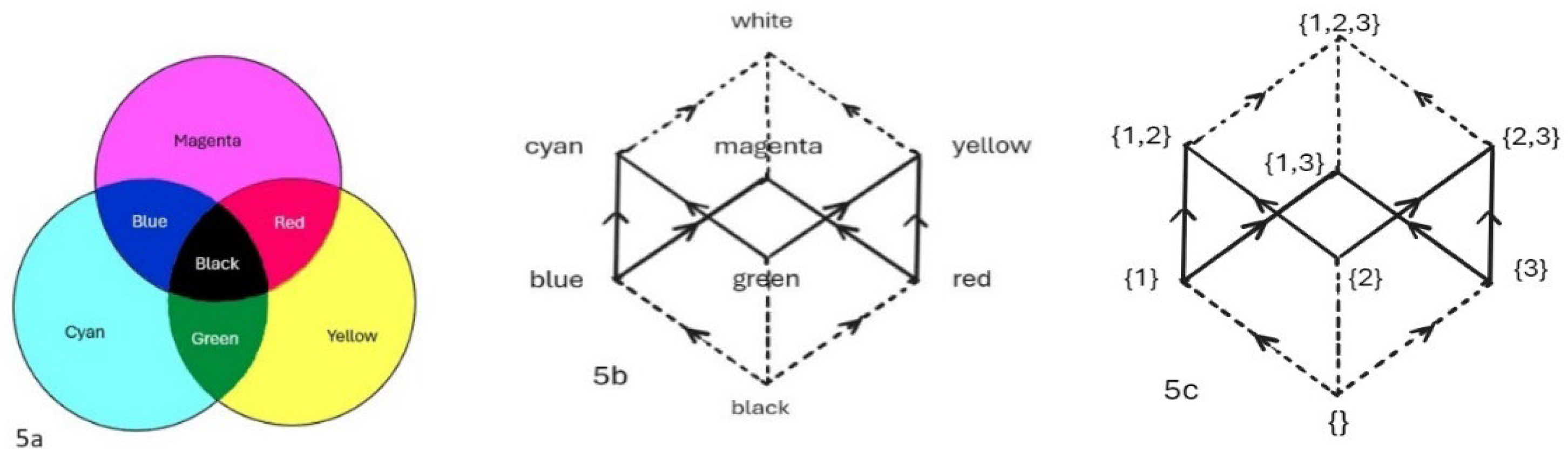
Figure 5. a: A Venn diagram showing the additive logic of colour; 4b: a Hasse diagram of colour transitions; 4c, a Hasse diagram as partial order on the power set of the set {1, 2, 3}.

Figure 4a could be read as a realistic image representing overlapping magenta-, cyan- and yellow-coloured filters seen against a white background as in modern colour theory. Read in this way, it is easy to appreciate how the superposition of the three coloured filters can generate red from magenta and yellow, green from yellow and cyan, blue from cyan and magenta, and black from magenta, cyan and yellow. But it can also be read as a type of Venn diagram showing the combinatory possibilities of these three colours, which might in turn be translated into a Hasse diagram, a “directed acyclic graph” composed of “vertices” and oriented “edges” of the type of graph used by Beziau and Jaspers to configure Goethe’s arrangement of colour relations. The central portion of 4b itself constitutes a “sub-graph” that is isomorphic with Goethe’s colour hexagon.

A “Hasse diagram” gives diagrammatic representation to a “partially ordered set” (“poset”), a “partial order” (here represented by the edges of the graph) on a set of elements (represented by vertices) being defined by relationships that are reflexive, antisymmetric and transitive.xlvii Abstracting from concrete applications of this underlying structure, the partial order can be understood as holding among the (power) subsets of a three-element set. For example, for the set {1, 2, 3} there will be eight subsets: {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, these being arranged as the vertices of a directed acyclic graph such that the set represented by each vertex is contained in the set above it.xlviii In the schematized “musical tetraktys”, the major opposition was between the additive and multiplicative operations separating “intra-octaval” and “extra-octaval” relations. Here also, additive and multiplicative operations are implicitly present by virtue of the underlying set-theoretic operations of union (∪) and intersection (∩). While the vertex {1} instantiates the intersection of those of {1,2} and {1,3} above it, the vertex {1,3} instantiates the union of {1} and {3} below it. Apart from the top vertex, the vertices {1,2}, {1,3}, and {2,3} also instantiate the “disjunctive union”, (∆), of those below them. Disjunctive union is the set-theoretical operation underlying addition,xlix while intersection is the set theoretical operation underlying multiplication. As in the musical tetraktys, a complex interrelation between additive and multiplicative operations exists in relation to Goethe’s colour hexagon.

Translating between the Venn and Hasse colour diagrams (Figure 4a,b), however, involves a switch in the conception of colours themselves. In the Venn diagram colours are represented as discrete entities, separated by borders of abrupt change, while the natural way to interpret the Hasse diagram is to regard the edges as colour continua stretching between two point-like extremes, as when cyan, located at one extreme, can be imagined to gradually blend into green, located at the other, or alternatively, in another direction, to gradually blend into blue. Where the original colours of the Venn diagram do not share a border there will be no continuous transitioning in the Hasse diagram between vertices without passing through an intermediary colour.l In a lecture in 1930, Wittgenstein would refer to a “colour octahedron”,li as meant to show why “we can speak of a greenish blue but not a greenish red” [58] (8), and he would continue to be concerned about this issue twenty years later in Remarks on Color [14] (pt I, §§ 10, 11, 14, 21; pt II, §§27, 30, 52). Wittgenstein would maintain the overall attitude that this was basically a matter of the contingencies of how we speak: the colour octahedron is “really a part of grammar, not of psychology” [58] (8). Plato’s adaption of Philolaus’s method, however, links the contingencies of Wittgenstein’s somewhat algorithmic conception of “following a rule” with the intelligible rule itself. And this abstract structure itself has a concrete model, with the intra-octaval concords standing as intra-octaval surrogates for a non-representable ideal unison.

With the six colours now represented more schematically as the vertices of a graph as in Figure 4b, of which white and black are the upper and lower bounds, we can appreciate how there exist a total of 10 “mini-spectra” (black–blue ; black–red; black–green; blue–cyan; blue–magenta; green–cyan; green–yellow; cyan–white; yellow–white; and magenta–white),lii in which there exists a continuous transition (edge) between any two neighbouring extremes (directly connected vertices). Each of these ten continua may now be thought to be isomorphic to a one-dimensional graph joining white to black through a continuum of greys. Further, it can be appreciated that in the graph these edges of continuous colour transition can be arranged end-to-end so as to provide paths via which one can transition between two non-directly contiguous colours via the intermediary of a third, as when one passes from black to cyan through blue. The branching, however, allows alternative paths, as that from black to cyan through green. With the focus on colour continua, a new meaning is given to the discrete “primary colours”—red, green, blue and cyan, magenta and yellow now representing those points on the colour continuum where branching can be seen to occur.

All in all, there are six alternate paths that can be constructed passing from black to, ultimately, white: black-green-yellow-white; black-green-cyan-white; black-blue-cyan-white; black-blue-magenta-white; black-red-magenta-white; and black-red-yellow-white. Here, the existence of these “two means” between the ultimate extremes should give us pause, as this is exactly what Plato had described in his account of the relations of three-dimensional space as well those among the four elements of the cosmos: fire, air, water and earth. The “symphony of proportion” structuring these domains was reflected into the structure of the world soul itself and, from there, into the particularized souls of mortals. We should not be surprised to find it cropping up in the psychophysics of the colour perception of those mortals. But note that the Hasse diagram, while depicted as planar, could equally be understood as instantiating a cube in three-dimensional space.liii Were we to think of such a cube as having edges of one unit, the paths between adjacent “colours” would thus be of equal length, and so commensurate, but would also be incommensurable with any attempt to plot a direct path from black to white along the “body diagonal” of the cube, as for a cube of side of length x units, the diameter would have a length of √3x units. Once more, within the space created via the master opposition of white to black, that opposition itself cannot find direct representation within that space. The opposition of black and white must be represented by a multitude of surrogate oppositions, via which a path from one extreme to the other can be plotted.

The Platonic space of colour indeed turns out to be “cousin” to all similar oppositional structures that had been first expressed in the Pythagoreans’ musical tetraktys.

6. Conclusions

On the approaches of the interpreters followed here, Plato, in his late writings, had built upon and transformed the method of the Pythagorean natural philosopher Philolaus in an effort to make Ideas relevant to understanding the empirical world. While the concern of the Pythagorean mathematicians had originally been focused upon the problem of the incommensurability between discrete and continuous magnitudes, Philolaus had used the idea of a non-reductive mixture of the incommensurable and commensurable as itself fundamental—a tri-partite unity based on that achieved between the geometric, arithmetic, and harmonic means within the production of musical consonances. In Plato’s middle-period dialogues, a type of conceptual incommensurability had been regarded a consequence of the radically opposed domains of being and becoming, but in the late dialogues the idea of a mediated “mixture” of these emerges as a generalization of Philolaus’s method.

Specifically, these concerned the establishment of relations between elements of two incommensurable domains: one interior, closed domain and the other, a higher-level surrounding domain understood as giving expression to ideals in relation to structures within the former. In the musical tetraktys there was a peculiar relation between the intra-octaval consonant intervals, the fourth and the fifth, each as the inverse of the other, and the extra-octaval “ideal” unison of octaval intervals themselves. In relation to the inability to apply the geometric mean within the octave, the intra-octaval concords could be understood as the imperfect but practically applicable surrogates of the ideal geometric division. Understanding these structures as more general than the actual musical relations in the context of which they were discovered, Plato could envisage a more general research programme applying, not only to the investigation of the structure of the cosmos itself, but also to the structure of the psyches of finite mortal beings shaped on the model of the psyche of the cosmos itself.

Goethe’s investigation of colour phenomena can then be interpreted as a development of Plato’s research program rather than the approach of Aristotle with which it is usually identified. The forms of modern mathematics dealing with order and in terms of which Goethe’s colour hexagon has been explained might be seen to stretch back via Leibniz’s “analysis situs” ultimately to the approach sketched in the Platonist’s Epinomis involving “the assimilation by reference to plane surfaces of numbers that are not by nature similar to one another” [33] (990c-d).

Funding

This research received no external funding.

Notes

i	Alan Code captures the related pragmatic and epistemic aspects of colour perception for Aristotle when he writes: “Indeed, for Aristotle visual information is the most useful sensory information for an animal when it comes to coping with the needs of life and survival. Physical objects are coloured, and by seeing their colours together with the shapes and sizes and motions that accompany them animals are able to keep track of objects, and to distinguish by visual appearance food, water, predators and prey. Of course, in intelligent creatures the information acquired through sight and the other senses is the indispensable starting point for various sorts of knowledge, culminating ultimately in scientific understanding” [3] (237).
ii	The Epinomis is generally thought not to have been authored by Plato, but by a follower, possibly Phillip of Opus. I will be working on the presumption that, given the coherence of the views expressed in those passages in the Epinomis discussed here with Plato’s other post-Parmenidean works, that they accurately reflect Plato’s own late views.
iii	One recent exception to this comparative neglect is that of Mark Kalderon [11] (2023). While the views here are generally in line with Kalderon’s, I provide a much more specific account of the role of the Pythagorean “harmonic means” in Plato’s account of colour.
iv	Sorabji gives the examples of white and black: “Leukon means bright, or light-coloured, as much as it means white. And melan means dark-coloured, as much as it means black” [21] (294).
v	In Meteorology Book 3, Aristotle appeals to this as an explanation of rainbows, noting that “bright light through a dark medium or on a dark surface (it makes no difference) looks red. […] so, too, the sun appears red through smoke and mist” [23] (374a3-4). It is clear he thinks this relevant to his theory of the senses: “We must recognize, as we have said, and lay down first, that white colour on a black surface or seen through a black medium gives red; second, that sight when strained to a distance becomes weaker and less; third, that black is in a sort the negation of sight; an object appears black because sight fails; so everything at a distance looks blacker, because sight does not reach it. The theory of these matters belongs to the account of the senses, which are the proper subjects of such an inquiry” [23] (374b9–17).
vi	In his Categories, colours are classified as affective or dispositional qualities [25] (9a29–9b9). Among the substances in which changes can be induced are the psyches of perceivers—in the case of colour, the affection being via affecting the colour of the fluid of the eye.
vii	The very same change will be reflected in the psyche of a perceiving subject, the coldness of a cold body inducing a felt coldness in the psyche of an embodied subject, mediated by the cooling of that subject’s own body. This affection was at the heart of the perceptual realism of his On the Soul, but had given rise to purported existence of form without matter in the case of the affected psyche itself.
viii	The fundamental colours of white and black in turn align with Aristotle’s two substantive extremes, fire and earth, leaving air and water transparent. In Metaphysics book 5, Aristotle breaks down the four elements further into qualitative determinations, fire being hot and dry, air hot and wet, water cold and wet, and earth cold and dry [26] (1014a26ff). This suggests parallel determinations of white and black as something like qualitative constituents of fire and earth that flow into the intervening elements of air and water to be mixed.
ix	Image, Creative Commons Licence, File:HSV cone 2.png - Wikimedia Commons (https://commons.wikimedia.org/wiki/File:HSV_cone_2.png).
x	Johnson was an older colleague of Wittgenstein at Cambridge.
xi	Legend had attributed the discoveries of the basic harmonic ratios to Pythagoras himself, but they were more likely made in the first part of the fifth century by the first of the “mathematical” Pythagoreans, Hippasus of Metapontum [10] (147–148).
xii	A Greek geometric sequence could be extended indefinitely leftward from 1 by ratios, the equivalent of fractions. Lacking zero and negative numbers, however, an arithmetic sequence could not be similarly extended leftwards, however.
xiii	As indicated, some “modifications” are required. Strictly, Greek arithmetic, lacking zero and negative numbers, could not embody an additive group structures, lacking an identity element and the inverses needed for subtraction. The multiplicative group was closer, however, because the use of ratios of whole natural numbers gives a place to division as the inverse of multiplication, and the identity element, 1, is present.
xiv	“Irrational numbers” were not recognized as numbers until the sixteenth century.
xv	From the seventeenth century, the Pythagorean tonal system would come to be replaced by the modern “equal tempered” system allowing “geometric” division within the octave, dividing the octave into twelve equal steps of geometric increments of the ratio 1: ¹²√2. This, of course, required a very different number system than that available to the Greeks.
xvi	As defined by Archytas of Tarentum, in the arithmetic, “the first exceeds the second is the same as that by which the second exceeds the third” while the mean is harmonic the terms are such that “by that part of itself [by which] the first term exceeds the second one, by this part of the third term the middle term exceeds the third one” [32] (42).
xvii	While the “real numbers” had been accepted since the seventeenth century, a proper definition in terms of limits would wait until the nineteenth century with the work of the likes of Cauchy, Weierstrass and Dedekind. For the Greeks, the notion of infinite meant simply, able to be repeated without any ultimate resting place.
xviii	This, of course, is simply the earlier sequence in which each of the terms is multiplied by 6.
xix	Some argue that such a shortcoming is only apparent, in that for practical purposes, we too, despite modern definitions of irrational numbers, must rely on algorithms to give approximations that can be used in calculation. One simply cannot add or multiply any number by √2 itself. (I am grateful to Norman Wildberger at the University of New South Wales for emphasising this often ignored fact.)
xx	Novak reports on the algorithm using “side and diagonal numbers” for the calculation of rational approximations for √2 [35] (81–82).
xxi	It is clear that in the Republic, Plato conceives of astronomy as a mathematical rather than empirical discipline: “We should consider the decorations in the sky to be the most beautiful and most exact of visible things, seeing that they embroidered on a visible surface. But we should consider their motions to fall far short of the true ones—motions that that are really fast or slow as measured in true numbers, that trace out true geometrical figures, that are all in relation to one another, and that are the true motions of things carried along in them. And these, of course, must be grasped by reason and thought, not by sight” [38] (529b–d). This view changed after the Parmenides.
xxii	Harmonics is not explicitly listed in the Epinomis although its principles are, as noted above, implicit in the discussion of geometry and stereometry.
xxiii	Debates between advocates of conceptualism and computationalism in mathematics have recently become manifest given the growth of theories of machine computation over the last century (see, for example, [39]. One should not forget, however, that “computers” have been around since the origins of mathematics, computers having been once exclusively human.
xxiv	In the Posterior Analytics, Aristotle describes a recent change in thinking about ratios and proportions. A certain law pertaining to ratios—the law of alternation—he describes as once having been proven separately “for things as numbers and as lines and as solids”. Clearly this difference had reflected belief in their incommensurability—in Aristotle’s terminology, their belonging to different kinds of magnitude. However, now, he adds, “it is proved universally; for it did not belong to things as lines or as numbers, but as this which they presuppose to belong universally” [40] (74a18-24). That to which they are meant to belong universally is clearly some purely logical higher genus of quantity, under which the natural numbers of arithmetic and the continuous magnitudes of geometry might themselves be considered to stand as different species, revealing Aristotle’s “conceptualist”, or in modern terms “logicist” approach to mathematical truth. Unlike Plato’s late philosophy, Aristotle’s hylomorphic metaphysics shows no influence of the mediated duality of Philolaus. In the words of Scolnicov, his is a “metaphysics of homogeneity” [7] (19–20).
xxv	While this has traditionally been understood as lowering the epistemic status of the account to something like “probable”, Kalderon has argued for a semantic connection to the idea of its subject matter is a likeness, in this case, the account of the actual cosmos of the realm of becoming is a likeness to an ideal [11] (25–28). In the terminology used here, Timaeus’s empirical universe is a surrogate of a practically inapplicable ideal mathematical structure.
xxvi	Kalderon explains the way the three terms in a geometric proportion can each play the role of first, middle and last by invoking the fact that the proportion itself holds in reverse (first : middle :: middle : last → last : middle :: middle : last) and then by the fact the order can be reversed within each ratio (first : middle :: middle : last → middle : first :: last : middle) [11] (43). Below I suggest that Plato had another, stronger “proportion” in mind.
xxvii	According to Plutarch, the citizens of Delos had been set this task by the oracle of Delphi and had taken it to Plato, who had referred it to the three of the leading mathematicians of the time, Eudoxus, Archytas and Menaechmus.
xxviii	For an account of Hippocrates’ reduction of the cube root to two mean proportional of the interval 1 to 2, see [43] (ch 2.3.
xxix	Hippocrates seems to be the first Greek mathematician to reduce a problem to easier sub-problems.
xxx	For the various solutions offered by Eudoxus, Archytas and Menaechmus and later mathematicians, see [42] (vol. I, 336-370.
xxxi	The interval 9:8 is equal to the difference between the fourth and fifth, thus effectively representing one complete tone, as in F to G. The mathematics of these intervals, derived from Philolaus, was not perfect, and Plato is clearly aware of this and intends it. After inserting the arithmetic and harmonic means, and then the tone, a further small ratio, 256:243, a semitone in the Pythagorean system, is added because in the business of filling the gaps “a small portion” is left over each time. These numbers are by their very conception only approximations.
xxxii	Interpretations of the bond as the musical tetraktys can be found in Proclus, Nicomachus of Gerasa and Iamblicus. Regarding Plato’s specification of the bond at Timaeus 31b – 32a, Kalderon notes that here Plato’s “Greek is beset by syntactic and lexical ambiguities that divide interpreters” [11] (43).
xxxiii	C.f., the opening sentences of Philolaus’s book, On Nature, “Nature in the world was fitted together [harmozein] out of unlimited things (apeiron) and limiting ones (perainonton), both the whole world and everything in it” [44] (155).
xxxiv	Certainly not all interpreters have taken the apeiron in this way as linked to mathematical continuity. Here I follow Karasmantis [46] (390–393).
xxxv	Modern graph theory has deep connections with other realizations of Leibniz’s analysis situs such as algebraic topology, and finds many applications in the sciences.
xxxvi	C.f., Kalderon describes Aristotle’s appeal to the harmonic intervals thus: “This is less an account than the beginnings of one … less a theory than a research program. Given the empirical success of ancient acoustical theory, the role of ratio or harmony in the respected opinions of the wise, and his own experience gleaned from dialectical engagement with the endoxa, Aristotle most likely felt that there were good reasons to believe that this research program could in fact be carried out. But the De Sensu account is not the result of that program, merely its statement” [2] (127).
xxxvii	In Philolaus’s mediated duality of the limit, the unlimited, and their mixture, limit and the unlimited remain distinct despite their combination in mixture. The triad itself must be understood holistically.
xxxviii	Kalderon calls Timaeus’s view an “interactionist” account: “On Timaeus’ account, extramission, the emanation of fire within, makes possible the subsequent intromission, the reception of chromatic affection. The fire emanating from within and the compounding of the visual body are not only physiologically significant, as conditions on the reception of the bodily affection, but are psychologically significant as well. In looking one orients oneself so that the object of perception comes into view” [11] (196).
xxxix	Once again, Plato’s “really the same .. though in a different class” suggests something like the type of weak equivalence found in a homomorphism between different groups.
xl	The idea of an aesthetic complement between colours parallels the felt notion of belonging together found between concords.
xli	These are the cones responding to light of long, middle, and short wavelengths, and associated with reflected red light, green light, and blue light respectively. Hering’s contrasts would later be explained in terms of the “opponent processing” achieved by the neuronal “wiring” of the retina, where stimulation of one type of colour cone suppresses the response of surrounding cones of with opposing colour types, the responses of which would have countered that of the first colour cone.
xlii	These two triads will be familiar to many as the red, green, and blue pixels of a colour television screen employing and additive process and the cyan, magenta and yellow coloured inks of a colour printer serving its “subtractive” process.
xliii	Such diagrams were suggested by Apuleius in the second century CE and Boethius in the sixth.
xliv	Dorier here discusses Leibniz’s proposal specifically in relation to Grassmann’s “vector space theory” (or “linear extension theory”, which, when linked to Cayley’s matrix arithmetic, would lead to modern “linear algebra”).
xlv	In early developments of each of these three areas Leibniz’s idea of an “analysis situs” would be invoked.
xlvi	I have adapted these diagrams from Martin [56] 2003, where they are used for the different purpose of illuminating the role of privative negation in Aristotle.
xlvii	It is usual to display the orientation of the edges as going from below to above.
xlviii	In set theory, the empty set, {}, is taken as contained in every set.
xlix	The disjunctive union of sets A and B, also called the symmetric difference, is defined as the union minus the intersection, (A∪B) − (A∩B).
l	One could not go between green and blue, for example, without passing through black.
li	This was seemingly adopted from the Austrian psychologist, Alois Höfler [57]. Höfler’s octahedron was based on Hering’s idea of two pairs of opposing primary colours.
lii	Note that white and black themselves must play two distinct roles here. As each is in a binary relation with three colours they are part of the colour system, but as the über opposition, each defined in terms of the other, they are outside the system itself.
liii	Such Hasse diagrams are now often considered in this three-dimensional way, as shown by Hans Smessaert [59].

Data Availability Statement

No new data were created or analyzed in this study. Data are contained within the article.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The author declares no conflicts of interest.

References

Sellars, W. Philosophy and the Scientific Image of Man. In the Space of Reasons: Selected Essays of Wilfrid Sellars; Scharp, K., Brandom, R.B., Eds.; Harvard University Press: Cambridge, MA., USA, 2007; pp. 369–408. [Google Scholar]
Kalderon, M.E. Form without Matter: Empedocles and Aristotle on Color Perception; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
Code, A. Aristotelian Colors as Causes. In Meaning and Being: Festschrift for Julius Moravcsik; Follesdall, D., Woods, J., Eds.; College Publications: London, UK, 2008; pp. 235–242. [Google Scholar]
Nussbaum, M.C.; Putnam, H. Changing Aristotle’s Mind. In Essays on Aristotle’s De Anima; Nussbaum, M.C., Oksenberg Rorty, A., Eds.; Clarendon Press: Oxford, UK, 1992; pp. 27–56. [Google Scholar]
Stedman, J.N. Aristotle and Modern Cognitive Psychology and Neuroscience: An Analysis of Similarities and Differences. Jnl. Mind and Behavior. 2013, 34, 121–132. [Google Scholar]
Aristotle. On the Heavens. Stocks, L.J. Trans. In The Complete Works of Aristotle: The Revised Oxford Translation; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 447–511. [Google Scholar]
Scolnicov, S. Plato’s Parmenides, translated with introduction and commentary by Samuel Scolnicov; University of California Press: Berkeley, CA, USA, 2003. [Google Scholar]
Sayre{XE "Sayre"}, K. Plato{XE "Plato"}’s Late Ontology – A Riddle Resolved. With a new Introduction and the Essay “Excess and Deficiency at Statesman 283C–285C”; Parmenides Publishing: Las Vegas, NV, USA, 2007. [Google Scholar]
Kahn, C.H. Plato and the Post-Socratic Dialogue: The Return to the Philosophy of Nature; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
Huffman, C. Philolaus of Croton: Pythagorean and Presocratic; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
Kalderon, M.E. Cosmos and Perception in Plato's Timaeus: In the Eye of the Cognitive Storm; Routledge: Abingdon, UK, 2023. [Google Scholar]
Aristotle. Sense and Sensibilia. Beare, J.I., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 693–713. [Google Scholar]
Goethe, J. W, von. Scientific Studies; Miller D. Ed. and Trans.; Princeton University Press: Princeton, NJ, USA, 1988. [Google Scholar]
Wittgenstein, L. Remarks on Colour; Anscombe, G.E. M, Ed.; McAlister, L., Schättle, M., Trans., Eds.; University of California Press: Berkeley, CA, USA, 1977. [Google Scholar]
Gierlinger, F.A.; Riegelnik, S. (Eds.) Wittgenstein on Colour; De Gruyter: Berlin, DE, 2014. [Google Scholar]
Silva, M. (Ed.) Colours in the Development of Wittgenstein’s Philosophy; Palgrave Macmillan: Cham, CH, 2017. [Google Scholar]
Broadie, S. Aristotle’s Perceptual Realism. Southern. Jnl. Phil. 1993, 31, 137–159. [Google Scholar] [CrossRef]
Caston, V. Aristotle on the Reality of Colours and Other Perceptible Qualities. Res Phil. 2018, 95, 35–68. [Google Scholar] [CrossRef]
Newton{ XE “Newton,Issac” }, I. Opticks: Or, A Treatise of the Reflections, Refractions, Inflections and Colours of Light; Based on the Fourth Edition, London, 1730; Dover: NY, USA, 2012. [Google Scholar]
Zemplén, G.A. Newton’s Rejection of the Modificationalist Tradition. In Form, Zahl, Ordnung; Seising, R., Folkets, M., Hashagen, W., Eds.; Franz Steiner: Stuttgart, DE, 2004; pp. 481–502. [Google Scholar]
Sorabji, R. Aristotle, Mathematics, and Colour. Class. Quarterly 1972, 22, 293–308. [Google Scholar] [CrossRef]
Aristotle. On the Soul. Smith, J.A., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 641–692. [Google Scholar]
Aristotle. Meteorology. Webster, E.W., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 555–625. [Google Scholar]
Aristotle. On Generation and Corruption. Joachim, J.J., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 513–554. [Google Scholar]
Aristotle. Categories. Ackrill, J.L., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 3–24. [Google Scholar]
Aristotle. Metaphysics. Ross, W.D., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 1552–1728. [Google Scholar]
Munsell, A.H.; Cleland, T.M. A Grammar of Color: Arrangements of Strathmore Papers in a Variety of Printed Color Combinations According to the Munsell Color System; The Strathmore Paper Company: Mittineague, MA, USA, 1921. [Google Scholar]
Johnson{ XE “Johnson:William Ernest” }, W.E. Logic. Part I. Cambridge University Press: Cambridge, UK, 1921 .
Barker{ XE "Barker" }, A. The Science of Harmonics in Classical Greece; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
Brumbaugh{ XE "Brumbaugh,Robert" }, R. S. Platonic Studies in Greek Philosophy: Form, Arts, Gadgets, and Hemlock; State University of New York Press: Albany, 1989. [Google Scholar]
Gibson, S. Aristoxenus{ XE "Aristoxenus" } of Tarentum and the Birth of Musicology; Routledge: New York, NY, USA, 2005. [Google Scholar]
Barker{ XE "Barker" }, A. (Ed.) Greek Musical Writings. Volume II. Harmonic and Acoustic Theory; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
Plato. Epinomis. McKirahan, RD., Trans. In Complete Works; Cooper, J.M., Ed.; Hackett: Indianapolis, IN, USA, 1997; pp. 1617–1633. [Google Scholar]
Zellini, P. The Mathematics of the Gods and the Algorithms of Men: A Cultural History. Carnell, S., Segre, E., Eds.; Allen Lane: London, UK, 2020. [Google Scholar]
Novak, J.A. Plato and the Irrationals, part 1. Apeiron 1992, 16, 71–85. [Google Scholar]
Kilmer, A. D. The Musical Instruments from Ur and Ancient Mesopotamian Music. Expedition 1998, 40, 12–19. [Google Scholar]
Plato. Philebus. Frede, D., Trans. In Complete Works; Cooper, J.M., Ed.; Hackett: Indianapolis, IN, USA, 1997; pp. 398–456. [Google Scholar]
Plato. Republic. Grube, G.M.A.; Reeve, C.D.C., Trans. In Complete, Works, Cooper, J.M., Eds.; Hackett: Indianapolis, IN, USA, 1997; pp. 971–1223. [Google Scholar]
Fillion, N. Conceptual and Computational Mathematics. Phil. Math. 2019, 27, 199–218. [Google Scholar] [CrossRef]
Aristotle. Posterior Analytics. Barnes, J., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 114–166. [Google Scholar]
Plato. Timaeus. Zeyl, D.J., Trans. In Complete Works; Cooper, J.M., Ed.; Hackett: Indianapolis, IN, USA, 1997; pp. 1224–1291. [Google Scholar]
Heath, T. A History of Greek Mathematics, 2 volumes; Clarendon Press: Oxford, UK, 1921. [Google Scholar]
Parrochia, D. Mathematics and Philosophy; John Wiley and Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
Laks, A. , Most, G.W., Eds and trans. Early Greek Philosophy: Western Greek Thinkers, Part 1; Harvard University Press: Cambridge, MA, USA, 2016. [Google Scholar]
Huffman, C. The Philolaic Method: The Pythagoreanism Behind the Philebus. In Before Plato: Essays in Ancient Greek Philosophy VI; Preus A. Ed.; State University of New York Press: Albany, NY, USA, 2001; pp. 67–85. [Google Scholar]
Karasmantis, V. Continuity and Incommensurability in Ancient Greek Philosophy and Mathematics. In Socratic, Platonic and Aristotelian Studies: Essays in Honor of Gerasimos Santas; Anagnostopoulos, G., Ed.; Springer: Dordrecht, NL, 2011; pp. 389–399. [Google Scholar]
Kepler, J. The Harmony of the World; Aiton, E.J. , Duncan, A.M., Field, J.V., Trans; American Philosophical Society: Philadelphia, PA, USA, 1997. [Google Scholar]
Redding, P. Conceptual Harmonies: The Origins and Relevance of Hegel’s Logic; University of Chicago Press: Chicago, IL, USA, 2023. [Google Scholar]
Goethe, J.W. von. Theory of Colours; Eastlake, C.L. Trans., Ed.; M.I.T. Press: Cambridge, MA, USA, 1970. [Google Scholar]
Blanché{ XE "Blanché,Robert" }, R. Structures intellectuelles. Essai sur l’organisation systématique des concepts; Vrin: Paris, Fr, 1966. [Google Scholar]
Aristotle. De Interpretatione. Ackrill, J.L., Trans. In The Complete Works of Aristotle: The Revised Oxford Translation, In Two Volumes; Barnes, J., Ed.; Princeton University Press: Princeton, NJ, USA, 1984; pp. 25–38. [Google Scholar]
Jaspers, D. Logic and Colour. Log. Universalis 2012, 6, 227–248. [Google Scholar] [CrossRef]
Béziau J-Y. 2017. A Chromatic Hexagon of Psychic Dispositions. In How Colours Matter to Philosophy; Silva, M., Ed.; Springer: Cham, CH, 2017. [Google Scholar]
De Risi, V. Analysis Situs, the Foundations of Mathematics, and a Geometry of Space. In The Oxford Handbook of Leibniz, Antognazza, M.R., Ed.; Oxford University Press: Oxford, UK, 2018; pp. 247–258. [Google Scholar]
Dorier, J.-L. A General Outline of the Genesis of Vector Space Theory. Hist. math. 1995, 22, 227–261. [Google Scholar] [CrossRef]
Martin, J.N. All Brutes are Subhuman: Aristotle and Ockham on Private Negation. Synthese 2003, 134, 429–461. [Google Scholar] [CrossRef]
Wilde, T. The 4th dimension. Wittgenstein on colour and imagination. In Persons. An Interdisciplinary Approach. Papers of the 25th International Wittgenstein Symposium; Kanzian, C., Quitterer, J., Runggaldier, E., Eds.; Kirchberg am Wechsel: Austrian Ludwig Wittgenstein Society, 2002; pp. 284–286. [Google Scholar]
Wittgenstein, L. Lectures: Cambridge 1930-1932. From notes of John King and Desmond Lee; Lee, D., Ed.; Blackwell: Oxford, UK, 1980. [Google Scholar]
Smessaert, H. On the 3d visualisation of logical relations. Log. Universalis 2009, 3, 303–332. [Google Scholar] [CrossRef]

Figure 1. the three independent variable features of colour: hue, saturation, and value (brightness), according to the Munsell system.ix.

Figure 2. a: the musical tetraktys, b: the division of interval MN by the harmonic, geometric and arithmetic means.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Mathematics of Plato's Psychophysics of Colour

Abstract

1. Introduction

2. From Aristotelian to Late Platonic Psychophysics

3. Late Platonic Physics and the Rational Surrogates of Ideal Numbers

4. The Mathematics and Physics of Timaeus and Philolaus

5. Platonic Colour Theory as Developed in Goethe’s Zur Farbenlehre: A Sketch

6. Conclusions

Funding

Notes

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe