Prerpints.org logo
Preprint
Article

The Design of Highly Reflective All-Dielectric Metasurfaces Based on Diamond Resonators

Altmetrics

Downloads

71

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 October 2024

Posted:

04 October 2024

You are already at the latest version

Alerts
Abstract
All-dielectric metasurfaces offer a low-loss alternative to plasmonic metasurfaces. We proposed the configuration for high-reflectivity all-dielectric metasurfaces based on single-crystal diamond (SCD) resonators on fused silica substrate and conducted simulations to optimize and analyse such configuration via FDTD solver. We utilized GMR as design principles to select the configuration and the substrate material, and analyzed the scattering properties of a single SCD resonator by multipole decomposition. Then we have demonstrated that both the cylindrical resonators in square lattice and frustum-shaped resonators in hexagonal lattice can achieve near-unity reflectivity (> 99.99%) and ultra-low absorption (< 0.001%) at 795 nm, the typical alkali-metal laser wavelength. Additionally, we have demonstrated that such design is quite tolerant to fabrication errors and further supports its potential for realistic applications. To expand the functionality of such devices across multiple wavelengths, a dual-band high-reflectivity meta-surfaces at 744 nm and 828 nm has also been designed. Our work is quite useful for designing diamond-based highly reflective mirrors, paving the way for low-loss all-dielectric reflective metasurfaces in high-power laser applications.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Metasurfaces provide a way to manipulate light by precisely arranging sub-wavelength structures and fine-tuning the parameters of these structures on a flat substrate [1,2,3]. By sophisticatedly designing the 2D-arrays, metasurfaces show the capability of controlling the phase, amplitude, and polarization of the light [4,5], resulting in a wide range of applications, such as imaging [6], holography [7], quantum optics [8], spectrometry [9], and structured light [10]. One important application of interest is the highly reflective mirrors, which often use all-dielectric nanomaterials taking their advantages of the low-loss property and enhanced resonance [11]. Such devices are also referred to as perfect reflectors because they can achieve near-unity reflectivity at certain wavelengths by properly selecting the geometries of resonant nano-structures [12,13,14,15] and precisely arranging their positions [16]. For example, Slovick et al. has presented a structure of square-latticed Si cubes on SiO 2 substrate with over 99.999% reflectivity and less than 0.001% absorptivity at 1 . 5   μ m in simulation [12]. Based on the principles of this work, cylindrical silicon resonators were experimentally demonstrated to achieve a reflectance of 99.9% at 1450 n m [13]. Further, large-scale dielectric reflectors with frustums in hexagonal lattices applying the same material were fabricated and demonstrated to show 99.7% reflectivity at 1530 n m [14].
To better guide the design of the highly reflective metasuraces, one can mainly follow the principles of guided-mode resonance (GMR) [17,18,19]. The GMR gives a physical picture of how the incident light diffracts and propagates in a grating waveguide slab. By optimizing the parameters of the grating layer, it is possible to select the diffracted light at certain mode to achieve the constructive interference [17], which comes from the electromagnetic resonances within the nanostructures of the grating [20,21,22]. In order to have a deeper insight of the physics, the effective medium theory [12,13,14,23,24,25,26] and the multipole decomposition method [27,28,29] are often used to help the analysis. Following the effective medium theory, one can first calculate the effective permittivity and permeability via the scattering-parameters (S-parameter) [12,25], and correspondingly acquire the effective impedance and refractive index, which directly show the properties of the grating layer. On the other hand, electromagnetic resonances in the grating layer result in the scattered fields of electric and magnetic multipole. Through the multipole decomposition, the scattering cross-sections (SCSs) of different resonant modes can be quantitatively calculated, which reveals the contributions of various electromagnetic dipoles, quadrupoles, or higher-order multipoles [28].
In recent years, metasurface reflectors have also been demonstrated to show a high laser induced damage threshold (LIDT) under high-power lasers, using single-crystal diamonds (SCDs) as the material [15]. Because such materials have excellent optical and thermal properties: relatively high refractive index ( n = 2 . 4 ), wide bandgap ( 5 . 5   e V ), and most importantly, the highest thermal conductivity ( 2200 W / K / m at room temperature) [30]. Atikian et al. fabricated a diamond-based metasurface by angled-etching nanostructures into "golf tee"-shaped columns, achieving over 98% reflectivity at 1070 n m and damage-free operation under 10 k W continuous-wave laser with the spot diameter at 750 μ m . [15]. Another advantage of SCDs is that they have extremely low absorption at a broad range of light spectrum, possessing the potential for shorter wavelengths, e.g. visible or even ultraviolet light [30]. Therefore, the diamond-based metasurfaces have the potential to be used for high-power alkali lasers [31], whose typical wavelength is at 795 n m . Moreover, the etching (vertical and angled) of diamond pillars has been achieved in the study by Atikian et al [15], demonstrating the potential of more diamond-based metasurface designs in fabrication.
In this paper, we present the design of a diamond-based metasurface, which can achieve near-unity reflectivity at 795 n m . First, we utilize GMR as design principles to select the configuration and the substrate material of desired, and analyse the scattering properties of a single SCD resonator by multipole decomposition. Then, we select two configuration of cylinders in square lattice and frustums in hexagonal lattice, and by optimizing the geometries of cylinders in square lattice in simulation we can maximize reflectivity while minimizing absorption. Next, we adjust the geometries of the square-latticed cylinder to obtain dual-band reflectivity for certain applications. For the designs above, analyses of electromagnetic fields, effective medium properties and geometrical parameter sweepings are conducted to enhance the understanding of the optimized structures.

2. The Principles for Designing the Perfect Reflector

2.1. Guided-Mode Resonance

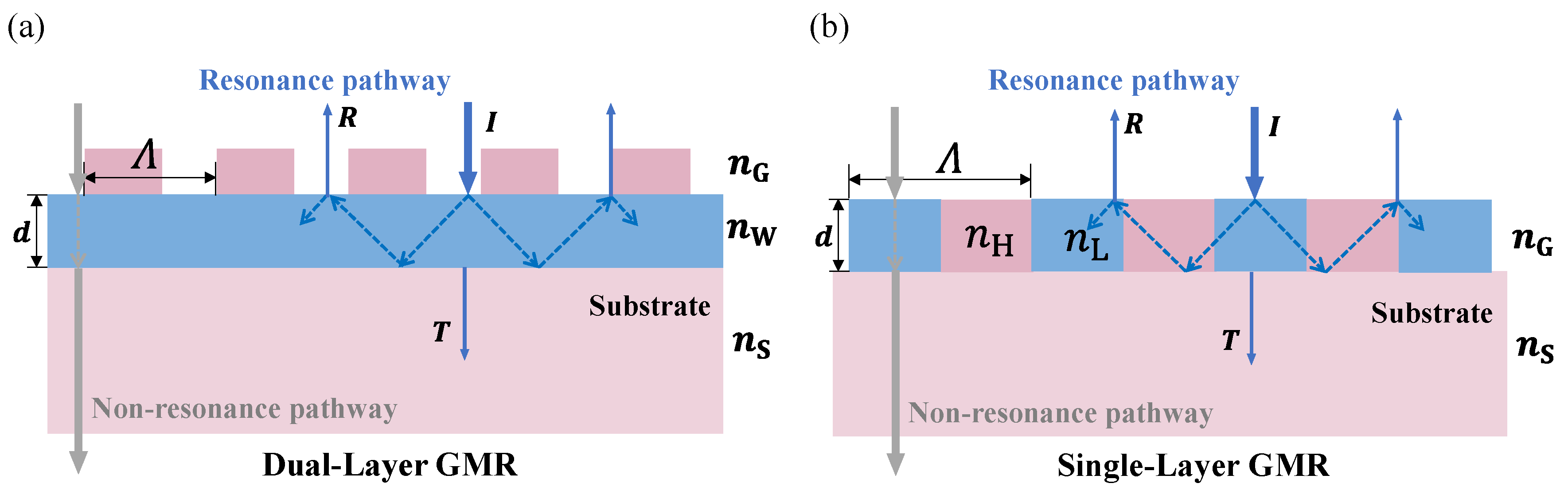
As mentioned before, GMR is a fundamental principle used to design metasurfaces with high reflectivity [18]. Figure 1 (a) presents the schematic of a dual-layer GMR, a grating layer ( n G layer) and a waveguide layer ( n W layer), with a normal incident light at the intensity of I and its reflected and transmitted light (in solid blue). The incident light is first diffracted by the grating layer, and is going to be coupled into the waveguide layer (in dashed blue) when meeting the resonance condition. Here, GMR occurs because the incident light and the waveguide mode constructively interference, resulting in the reflectivity R approaching near-unity and the transmission T near-zero. Otherwise, the light would transport directly through the two functional layers as well as the substrate ( n S layer) (in solid gray). There is another way of realizing GMR by using a a single-layer configuration, as illustrated in Figure 1 (b). The grating layer can also act as the waveguide as long as the higher refractive index of the grating n H , the lower index n L and optical thickness d of the grating structure are carefully optimized [19,32,33]. Here, n G represents the effective refractive index of the same layer of the grating and the waveguide. The single-layer GMR configuration can simplify the metasurface structure and facilitate dissipating heat [15,19].
The metasurfaces, commonly seen as a semi-finite-thickness slab, can be treated as an effective homogeneous medium, with the effective complex permittivity ε * and the effective permeability μ * expressed as ε ′ + i ε ″ and μ ′ + i μ ″ respectively [34]. Following the effective medium theory, the perfect reflection can be achieved while the Eq. (1a) and Eq. (1b) are both satisfied.
ε ′ / μ ′ < 0
ε ″ μ ′ = ε ′ μ ″
The first condition in Eq. (1a) requires the real parts of the permittivity and permeability to have opposite signs, which is easily satisfied at the resonate wavelength of electric or magnetic resonances. Although the second condition in Eq. (1b) appears more strict, it can be satisfied at certain conditons. Particularly, it is more easily to be satisfied in all-dielectric materials with low loss, since the imaginary part of ε * and μ * are approaching zero [12,13]. Therefore, we can verify whether our design is indeed a perfect reflector judging by the two conditions above, of which the permittivity ε * and permeability μ * can be extracted from the S-parameter via simulation [23,24,25,26].
As mentioned before, the SCDs are the perfect candidate as the grating layer for metasurface reflector that can endure high-power lasers, but the materials for the substrate should also be thoroughly considered in order to meet our purpose. We propose the single-layer GMR configuration, using SCDs as the resonant layer with the effective index denoted as n G . Here, the high refractive index equals to that of the SCDs, i.e. n H = n SCD , and the low refractive index is that of the air ( n L = n air ). And in this paper we have chosen the fused silica (silicon dioxide, SiO 2 ) as the substrate mainly for the two reasons below. First, its refractive index is lower than that of SCDs, meeting the conditions of the GMR theory. And second, silica has relatively high LIDT due to its extremely low thermal expansion coefficient, making it possible for high-power-laser applications [35]. Last but not least, the diamond coating on SiO 2 substrates can be achieved using Microwave Plasma Chemical Vapor Deposition technique (MPCVD) [36].

2.2. The Multipole Decomposition

To fully understand the behavior of light scattering and reflection in these resonant structures, it is essential to decompose the scattering field into multipole components for the complexity of electromagnetic field [29]. Multipole decomposition is a crucial method for analyzing the complex electromagnetic fields of scattering, which can separate the contributions of electric dipole (ED), magnetic dipole (MD), electric quadrupole (EQ), magnetic quadrupole (MQ), and higher-order multipoles. It effectively simplifies the description of the field, facilitating the analysis of the field distribution, which helps guide the design of highly reflective metasurfaces [29,37,38].
The electric far-field scattered by an electric and a magnetic dipole (scalar projection) can be written as Eq. (2a) and Eq. (2b) [37].
E ED z = E p e i π e i ω ED t z z − k ED z
E MD z = E m e i π θ z e i ω MD t z z − k MD z
Here, E p ( E m ) represents the amplitudes of the fields scattered by electric (magnetic) dipoles. The phase factor e i π accounts for a phase shift observed during dipole excitation at resonance. The function θ [ z ] is a Heaviside step function, i.e. θ [ z ] = 0 for z < 0 and θ [ z ] = 1 for z > 0 , which describes the antisymmetric behavior of the magnetic dipole resonance [37]. The functions E ED ( z ) and E MD ( z ) present the properties shown as below.
E ED ( − z ) = E ED ( z )
E MD ( − z ) = − E MD ( z )
The incident field E 0 interact with the scattered field E p or E m , ending up with interference. When E 0 = E p or E m , the destructive interference occurs in the forward (transmitted) direction, and a standing wave is generated in the backward (reflected) direction. Particularly, when only ED and MQ contribute to the scattering field, the node of the standing wave is exactly at the surface of the reflector, exhibiting the same behavior of a perfect electric conductor (PEC), and therefore it can also be defined as the generalized electric mirror. In contrast, when the contribution purely comes from MD and EQ, an anti-node (instead of a node) should form at the surface of the mirror, which is referred to as the generalized magnetic mirrors [22,37].
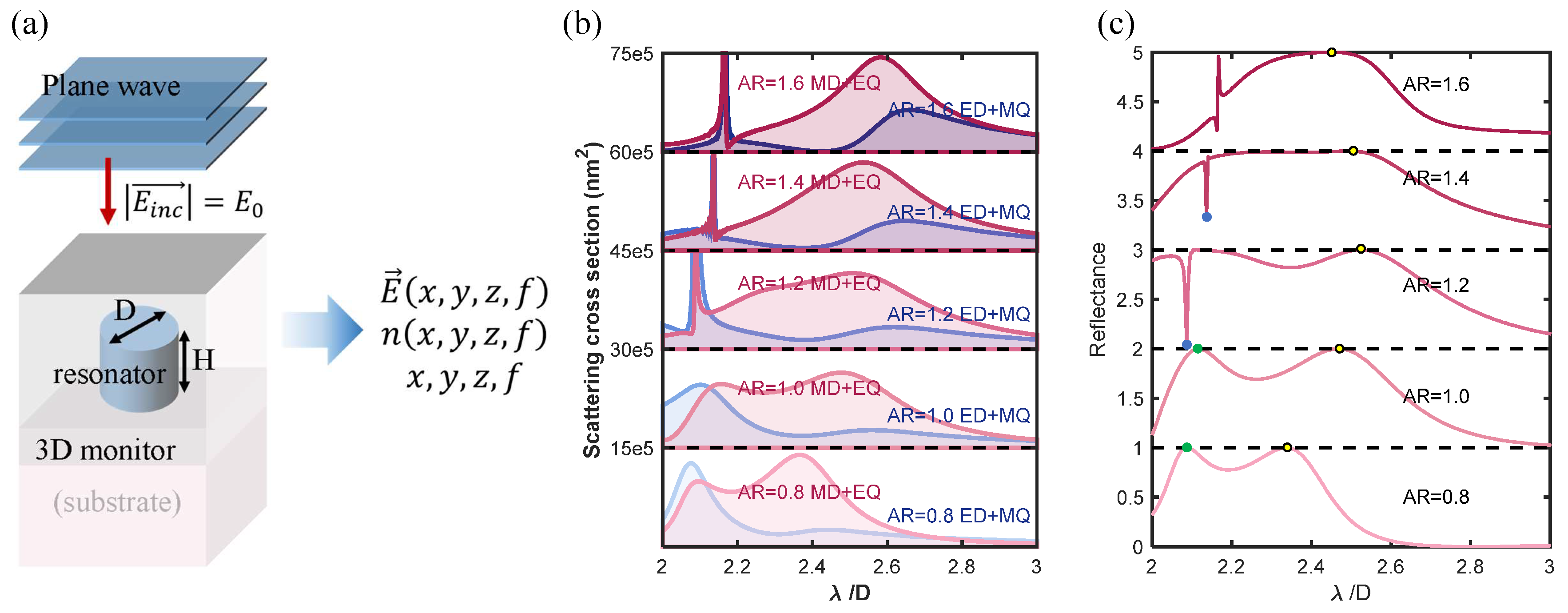
Here, we start from the simplest cylindrical geometry structure of diamond metasurfaces, seen in Figure 2 (a). According to [39], the resonance wavelengths of ED and MD in a cylindrical resonator depend on the aspect ratio ( A R ), which is defined as A R = H / D , where H and D represents the height and diameter of the cylinder respectively. Here, the simulations are conducted by 3D finite-difference time-domain solvers (FDTD, Lumerical Solutions, Inc.) and a total field scattered field (TFSF) source is used to analyze the scattering properties. The SCSs along with the wavelength λ can be numerically calculated, and the peaks are shown at certain wavelengths, representing electric or magnetic resonance. By analysing the wavelength difference of the peaks, an optimized geometry is determined with H = 370 n m and P = 900 n m , where P (pitch) represents the center-to-center distance between adjacent diamond columns. Figure 2 (b) illustrates the SCS for a diamond cylinder resonator without substrate, with A R ranging from 0.8 to 1.6. The calculation of the SCS relies on Hinamoto’s work [27], and it requires the results of electric fields and refractive indices, which varies with the spatial position (x, y, z) and the light frequency f. Shown in Figure 2 (b), the resonant modes happen at the certain wavelength peaks (see Table 1 in the supplementary materials), forming either generalized electric mirror (generated by ED+MQ) or generalized magnetic mirror (generated by MD+EQ).
To further investigate the collective response of the diamond resonators, the reflective spectra at square-latticed configuration have been calculated, as shown in Figure 2 (c). Corresponding to the SCSs, these illustrate that the yellow points of high-reflectivity are mainly the results of MD+EQ, while the peaks in green are the results of both ED+MQ and MD+EQ. However, for A R = 1 . 2 and 1 . 4 , there are sharp drops of the spectra at λ / D around 2.1. This is because the scattering field of different poles interference destructively [40], resulting in the energy localized in the resonators without emitting electromagnetic radiation, which have a high Q-factor [41].

3. Results and Analysis

3.1. Cylindrical Resonators in Square Lattices

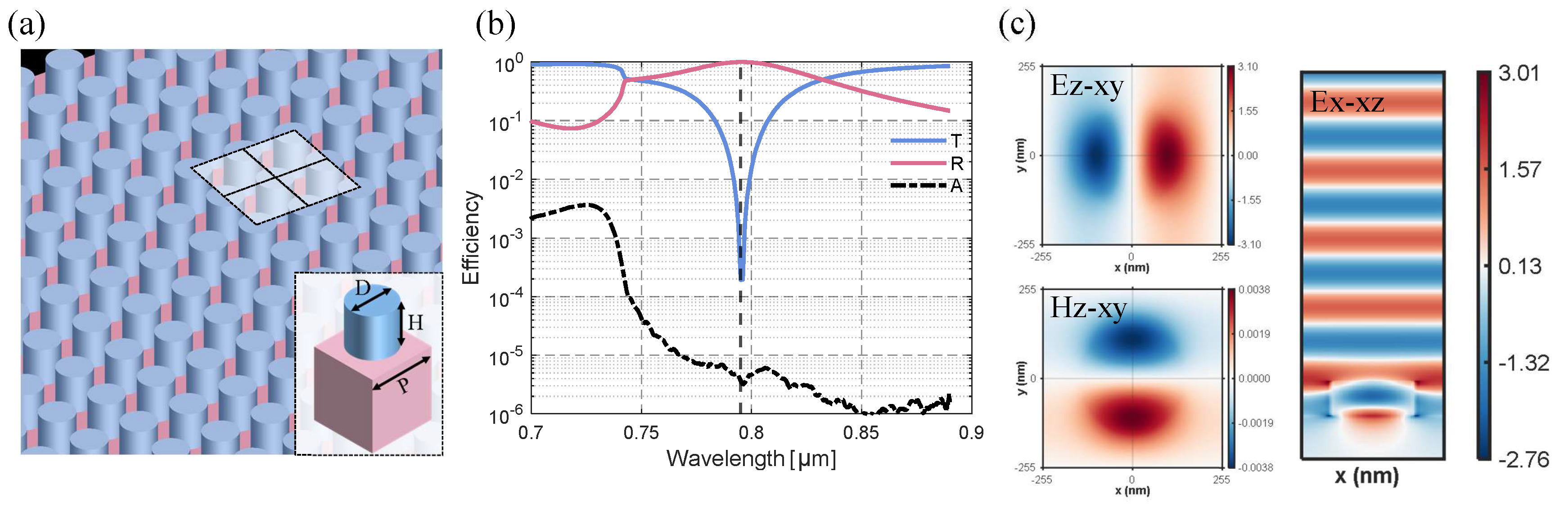
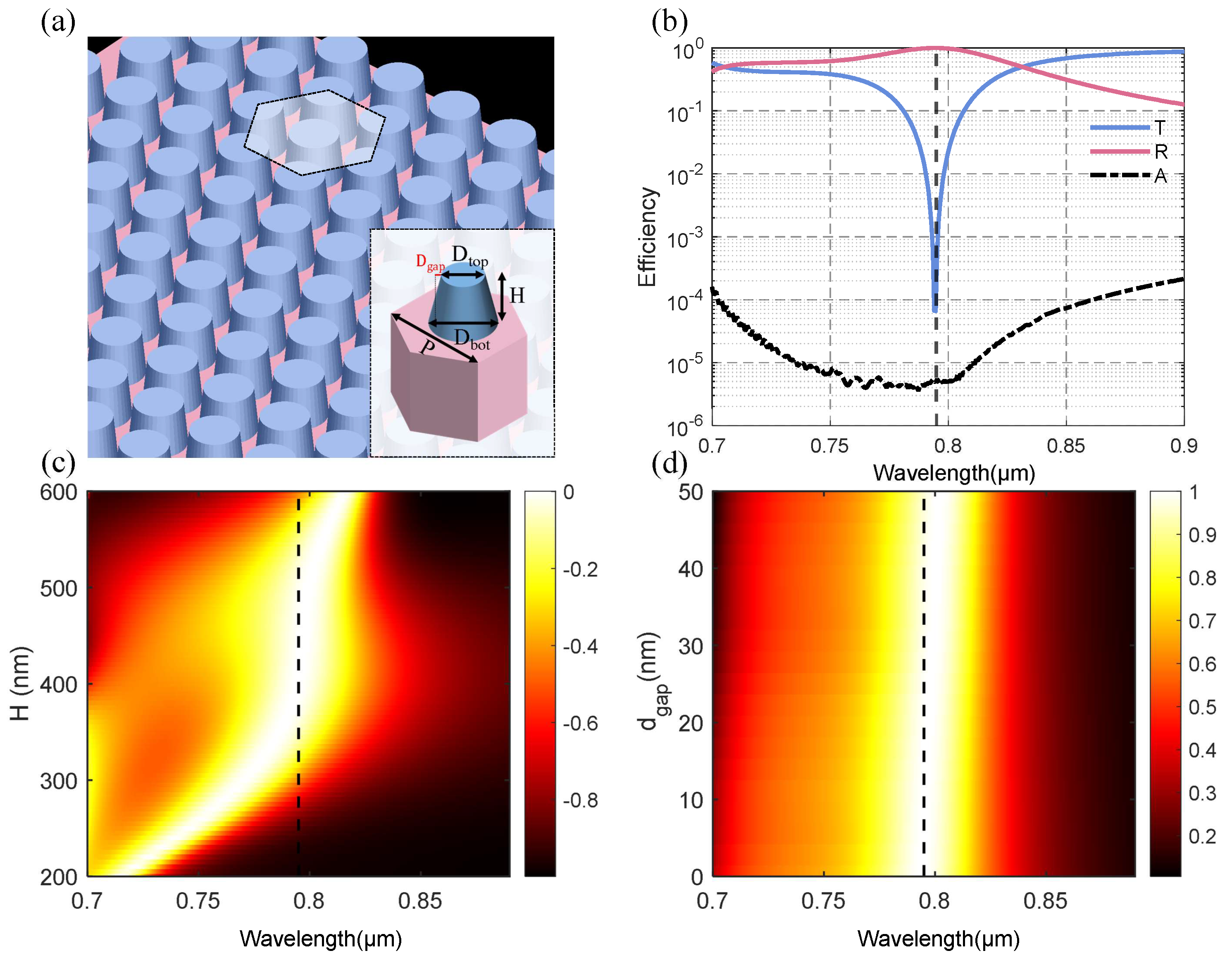
Based on the guidelines above, we can begin to design our all-dielectric metasurfaces with high reflectivity by using diamond resonators and silica substrates. Figure 3 (a) shows the schematic of diamond cylindrical resonators in square lattices. Simulations were performed at vertical incidence for p-polarized planwave at the wavelength between 700 n m and 890 n m . Figure 3 (b) presents the efficiencies of reflectivity, transmission, and absorption along with the wavelength, at the optimized parameters of D = 304   n m , H = 400   n m and P = 510   n m . It is clearly seen that at 795 n m the reflectivity exceeds 99.99% and absorbance is below 0.001%, behaving as a perfect reflector. The electromagnetic fields at 795 n m were calculated, as displayed in Figure 3 (c). It shows the electric field E z (left-top) and magnetic field H z (left-bottom) in the xy-plane, revealing the simultaneous presence of both ED and MD resonances respectively. The right diagram in Figure 3 (c) presents the E x field in the xz-plane, and a half-wave loss in the backward propagation direction is observed here [22]. Therefore, ED is the main contribution of the scattering field, where the metasurface exhibits the behaviour of an electric mirror. Additionally, the field enhancement is predominantly localized within the diamond resonators. This reveals that most of the electromagnetic energy is confined in the diamond layer, rather than being dissipated into the silica substrate, which can minimize thermal damage that may affect the metasurface performance.
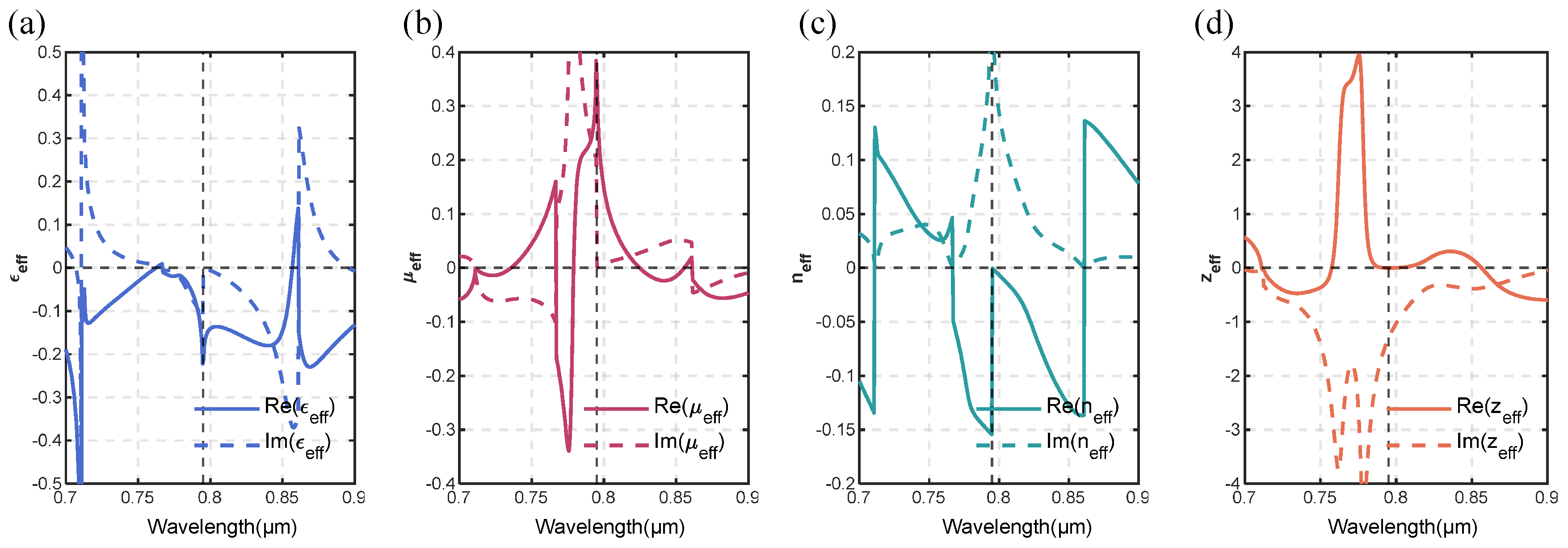
Then we have calculated the effective medium properties of the functional layer by S-parameters in FDTD solver. The results are shown in Figure 4, with the effective permittivity ( ε * = ε ′ + i ε ″ ), magnetic permeability ( μ * = μ ′ + i μ ″ ), refractive index ( n * = n ′ + i n ″ ) and impedance ( z * = z ′ + i z ″ ). Figure 4 (a,b) shows that for wavelength near 795 n m , ε ′ < 0 and μ ′ > 0 , so the condition for perfect reflection in Eq. (1a) is satisfied. Meanwhile, the imaginary parts ε ″ and μ ″ change the signs at the resonance wavelength 795 n m , so that ε * and μ * are purely real; this meets the condition in Eq. (1b). As shown in Figure 4 (c), the imaginary part of the refractive index ( n ″ ) is proved to be maximized to prevent evanescent tunneling across the slab while the real part of the refractive index ( n ′ ) equals to zero. In Figure 4 (d) we also note that the real part of impedance approaches zero at 795 n m , which is corresponding to a reflectivity of unity.
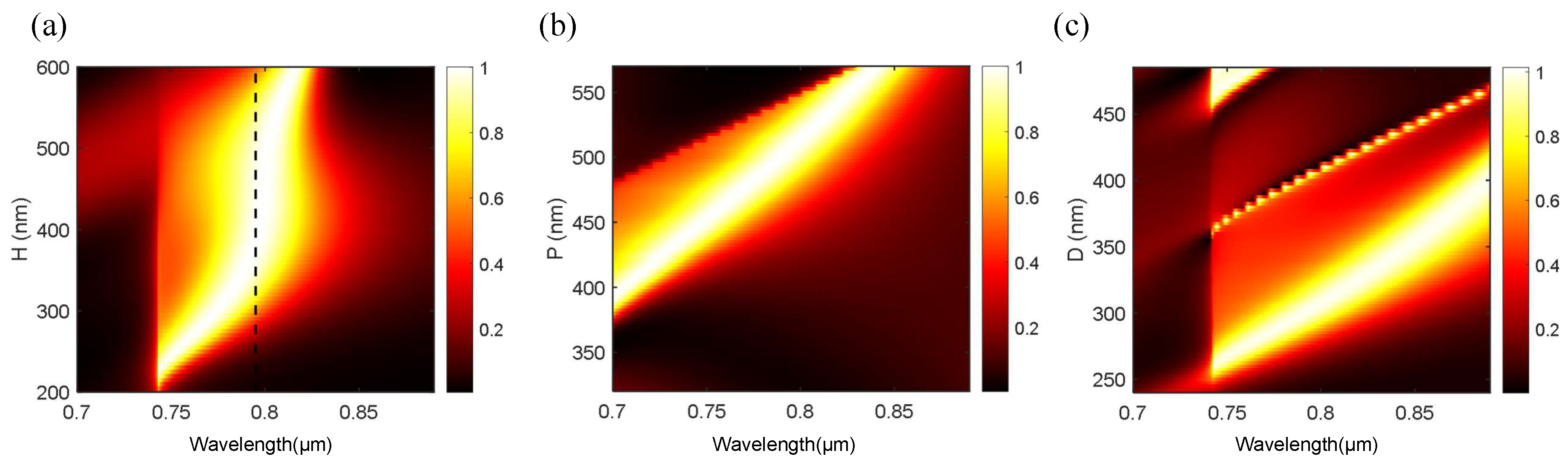
To analyze the impact of structural errors on the reflection spectrum, we conducted parameter sweeping for the three structural parameters (H, D and P) at the range of 700 n m to 890 n m , and the reflective spectra results are shown in Figure 5. As shown in Figure 5 (a), the reflectivity is higher than 98 % when H is between 360 n m and 470 n m , providing high tolerance for the thickness of diamond film. It is advantageous for fabrication, because the highly precise control of cylindrical height is costing, as the realization of the film requires the heteroepitaxial growth of SCDs on a silica substrate. In contrast, the high-reflectivity peak redshifts to a significant degree with the growth of P and a given pitch P supports only a single resonance mode as seen in Figure 5 (b). Figure 5 (c) shows that variations in cylinder diameter D result in multiple reflective peaks, each representing a different resonance mode. During the etching process in fabrication, P can be controlled with relatively high precision, while the cylinder diameter D is easily influenced by the vertical precision of etching processes. Therefore, more precise control of D is needed.

3.2. Frustums in Hexagonal Lattices

In order to mimic the vertical errors of the cylindrical etching processes, the resonators often adopt a frustum-shape with a smaller top and larger base, rather than maintaining a perfectly cylindrical profile [14]. On the other hand, the hexagonal lattice exhibiting six-fold symmetry (C6) have higher symmetry, resulting in the advantages of compactness, wide-angle response and broad photonic bandgap, compared with the square lattices, which possesses only four-fold symmetry (C4) [16,42,43]. Consequently, we ultimately designed a metasurface reflector based on the hexagonal lattices of diamond frustums and the schematic is shown in Figure 6 (a). Here, P is the distance of adjacent frustums, while H, D top and D bot represent the height, the top diameter and bottom diameter of the frustum.
Simulations were performed at vertical incidence for p-polarized planwave at the wavelength between 700 n m and 900 n m . Figure 6 (b) presents the efficiencies of reflectivity, transmission, and absorption along with the wavelength, at the optimized parameters of D top = 292   n m , D bot = 318   n m , H = 400   n m and P = 552   n m . It is clearly seen that at 795 n m the reflectivity exceeds 99.99% and absorbance is below 0.001%, behaving as a perfect reflector.
To further analyze the impact of structural errors on the reflection spectrum, we conducted parameter sweeping for the structural parameters H and D gap (see Eq. 4b) at the range of 700 n m to 890 n m and the reflective spectra results are shown in Figure 6 (c-d).
D avg = D top + D bot 2
D gap = D bot − D avg = D avg − D top
From Figure 6 (c), the spectral position of resonance redshifts with H growing but also remains greater than 98 % at the range of 370 - 500 n m which has a better robustness to the cylinders in square lattices. However, as shown in Figure 6 (d), when we make D avg (see Eq. 4a) constant, the spectrum changes little when D gap is less than 50 nm. For frustums, the errors of D top and D bot come from the lack of precision in the electron beam lithography and etching process. But by slightly changing the input diameter of the cylinders, we can make D avg equal to the theoretical value of D, in order to compensate the resonance shift induced by machining errors.

3.3. Dual-Band High Reflectivity

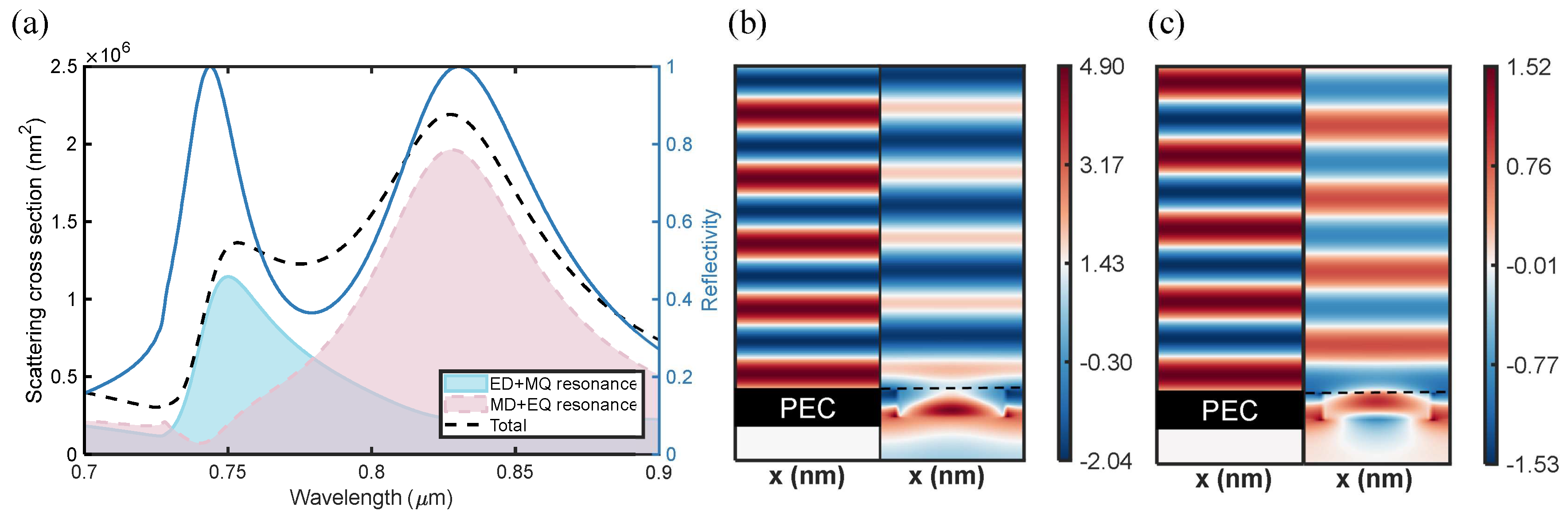
The metasurface can not only be designed for single-peak high reflectivity, but can also be optimized for dual-band high-reflectivity, holding the potential for applications that utilize lasers at two or more wavelengths, e.g. optical tweezers [44]. Here we focuse on cylindrical diamond resonators in square lattices. After adjusting the geometries, we have achieved near-unity reflectance at the wavelengths of 744 n m and 828 n m when D = 380   n m , H = 300   n m and P = 500   n m , and the reflective spectrum is shown in Figure 7(a) in solid blue line. To further analyse the dual-band reflector, we have computed the SCSs of the ED+MQ, MD+EQ and the combination of their total scattering, as shown in Figure 7(a). It is observed that the first reflection peak at 744 n m primarily corresponds to an electric resonance, while the second reflection peak at 828 n m is mainly due to a magnetic resonance.
To explain the high reflectance at the two wavelengths from the perspectives of electric and magnetic mirrors, we conducted electromagnetic field analysis at the reflective peaks. At 744 n m , the electric field E xz closely resembles the reflective behaviour of PEC, because the electric field reflected at the surface experiences a half-wave loss, which is presented in Figure 7(b). In contrast, at the 828 n m wavelength, the magnetic mirror does not exhibit a half-wave loss presented in Figure 7(c).

4. Conclusion

In this paper, we have conducted the design and analysis of highly reflective all-dielectric metasurfaces based on SCD resonators via FDTD simulations. First, utilizing GMR theory and multipole decomposition, we have acquired the preliminary values of the geometrical parameters ( H = 370   n m and P = 900   n m ) in a single diamond cylinder resonator for high refection at 795 n m . Then, we have designed two single-peak highly reflective configurations. The first is based on cylindrical resonators in square lattice, and we have achieve near-unity reflectivity (greater than 99.99%) and minimal absorption (below 0.001%) after optimization ( D = 304   n m , H = 400   n m and P = 510   n m ), as the design behaves as a general electric mirror judging from the electromagnetic field. And considering the fabrication errors, we have swept the geometries of H, P and D, and found that H has strong robustness to the reflection spectrum, tolerating an error of approximately 100 n m . The second is the frustum-shaped resonators in hexagonal lattices ( D top = 292   n m , D bot = 318   n m , H = 400   n m and P = 552   n m ) and it also achieved 99.99% reflectivity as well as good robustness of height H. Moreover, we have found that the adjustment of D avg can compensate the errors of cylindrical D. For the two designs above, the reflective spectra within our simulated wavelength range change slightly with the height H of the columns. It is a good robustness because in fabrication the total thickness variation (TTV) is less than 30 nm (see Figure 8). Finally, we have demonstrated a dual-band high-reflectivity metasurfaces at 744 n m and 828 n m based on cylinders in square lattices, which are mainly resulted by ED+MQ and MD+EQ resonances respectively.
This work paves the way for low-loss all-dielectric reflective metasurfaces in high-power laser applications. For example, our method can be extended to other wavelengths, particularly in the infrared range, where a broader bandwidth is possible. Moreover, by selecting more complex pillar structures, such as cross-shaped or H-shaped columns, more design dimensions are provided, allowing for dual-band or even multi-band frequency control [16]. Using materials with higher refractive indices, large-angle oblique incidence for mirrors with high reflectivity can also be achieved [14].

Author Contributions

Conceptualization, Z.X.(Zhongyang Xing) and Z.X.(Zhongjie Xu); Formal Analysis, J.Z.; Methodology, J.L.; Software, J.L.; Validation, Z.X.(Zhongyang Xing); Data curation, J.L.; writing—original draft preparation, Z.X.(Zhongyang Xing) and J.L.; writing—review and editing, Z.X.(Zhongyang Xing) and J.L.; supervision, X.C., J.Z. and Z.X.(Zhongjie Xu); funding acquisition, J.Z. and Z.X.(Zhongyang Xing).All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (12204541), the Science and Technology Innovation Program of Hunan Province (2021RC3083), and the High-level Talents Programs of National University of Defense Technology.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data will be made available on request.

Acknowledgments

We thank Prof. Yueqiang Hu and Dr. Shaozhen Lou from Hunan University, Research Fellow. Mingcheng Panmai from Nanyang Technological University and Xinye Liao from National University of Defense Technology for the useful discussions.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
GMR Guided Mode Resonance
FDTD Finite-Difference Time-Domain
SCD Single-Crystal Diamond
ED Electric Dipole
MD Magnetic Dipole
EQ Electric Quadrupole
MQ Magnetic Quadrupole
TFSF Total Field Scattered Field
AR Aspect Ratio
SCS Scattering Cross-Section
PEC Perfect Electron Crystallograph

References

  1. Zheludev, N.I.; Kivshar, Y.S. From Metamaterials to Metadevices. Nature Mater 2012, 11, 917–924. [CrossRef]
  2. Liu, Y.; Zhang, X. Metamaterials: A New Frontier of Science and Technology. Chem. Soc. Rev. 2011, 40, 2494. [CrossRef]
  3. Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat Optics with Dispersion-Engineered Metasurfaces. Nat Rev Mater 2020, 5, 604–620. [CrossRef]
  4. Chen, H.T.; Taylor, A.; Nanfang, Y. A review of metasurfaces: physics and applications. Reports on Progress in Physics 2016, p. 076401.
  5. Quan, Y.; Qin, G.; Linsen, C.; Yi, Z.; Yuhang, Y.; Xun, C.; Shuming, W.; Shining, Z.; Zhenlin, W. Recent advanced applications of metasurfaces in multi-dimensions. Nanophotonics 2023, pp. 2295–2315.
  6. Fröch, J.E.; Huang, L.; Tanguy, Q.A.; Colburn, S.; Zhan, A.; Ravagli, A.; Seibel, E.J.; Böhringer, K.F.; Majumdar, A. Real time full-color imaging in a Meta-optical fiber endoscope. eLight 2023, p. 13.
  7. Ren, H.R.; Fang, X.Y.; Jang, J.; Burger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nature Nanotechnology 2020, p. 948.
  8. Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to–orbital angular momentum conversion of light. Science 2017, 358, 896–901. [CrossRef]
  9. Zhang, Z.; Liu, Y.; Wang, Z.; Zhang, Y.; Guo, X.; Xiao, S.; Xu, K.; Song, Q. Folded Digital Meta-Lenses for on-Chip Spectrometer. Nano letters 2023, pp. 3459–3466.
  10. Ni, Y.; Chen, S.; Wang, Y.; Tan, Q.; Xiao, S.; Yang, Y. Metasurface for Structured Light Projection over 120° Field of View. Nano Letters 2020, pp. 6719–6724.
  11. Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [CrossRef]
  12. Slovick, B.; Yu, Z.G.; Berding, M.; Krishnamurthy, S. Perfect Dielectric-Metamaterial Reflector. Phys. Rev. B 2013, 88, 165116. [CrossRef]
  13. Moitra, P.; Slovick, B.A.; Gang Yu, Z.; Krishnamurthy, S.; Valentine, J. Experimental Demonstration of a Broadband All-Dielectric Metamaterial Perfect Reflector. Applied Physics Letters 2014, 104, 171102. [CrossRef]
  14. Moitra, P.; Slovick, B.A.; li, W.; Kravchencko, I.I.; Briggs, D.P.; Krishnamurthy, S.; Valentine, J. Large-Scale All-Dielectric Metamaterial Perfect Reflectors. ACS Photonics 2015, 2, 692–698. [CrossRef]
  15. Atikian, H.A.; Sinclair, N.; Latawiec, P.; Xiong, X.; Meesala, S.; Gauthier, S.; Wintz, D.; Randi, J.; Bernot, D.; DeFrances, S.; Thomas, J.; Roman, M.; Durrant, S.; Capasso, F.; Lončar, M. Diamond Mirrors for High-Power Continuous-Wave Lasers. Nat Commun 2022, 13, 2610. [CrossRef]
  16. Doiron, C.F.; Brener, I.; Cerjan, A. Realizing Symmetry-Guaranteed Pairs of Bound States in the Continuum in Metasurfaces. Nat Commun 2022, 13, 7534. [CrossRef]
  17. Magnusson, R.; Wang, S.S. New Principle for Optical Filters. Applied Physics Letters 1992, 61, 1022–1024. [CrossRef]
  18. Wei, CY (Wei, C.; Liu, SJ (Liu, S.; Deng, DG (Deng, D.; Shen, J (Shen, J.; Shao, JD (Shao, J.; Fan, ZX (Fan, Z. Electric field enhancement in guided-mode resonance filters. Optics letters 2006, pp. 1223–1225.
  19. Sang, T.; Wang, Z. Study on Guided-Mode Resonance Optical Devices; Tongji University Press, 2020.
  20. Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric Gradient Metasurface Optical Elements. Science 2014, 345, 298–302. [CrossRef]
  21. Liu, W.; Kivshar, Y.S. Generalized Kerker Effects in Nanophotonics and Meta-Optics [Invited]. Opt. Express 2018, 26, 13085. [CrossRef]
  22. Liu, W. Generalized Magnetic Mirrors. Phys. Rev. Lett. 2017, 119, 123902. [CrossRef]
  23. Smith, D.R.; Schultz, S.; Markoš, P.; Soukoulis, C.M. Determination of Effective Permittivity and Permeability of Metamaterials from Reflection and Transmission Coefficients. Phys. Rev. B 2002, 65, 195104. [CrossRef]
  24. Smith, D.R.; Schurig, D. Electromagnetic Wave Propagation in Media with Indefinite Permittivity and Permeability Tensors. PHYSICAL REVIEW LETTERS 2003, 90. [CrossRef]
  25. Smith, D.R.; Vier, D.C.; Koschny, Th.; Soukoulis, C.M. Electromagnetic Parameter Retrieval from Inhomogeneous Metamaterials. Phys. Rev. E 2005, 71, 036617. [CrossRef]
  26. Arslanagic, S.; Hansen, T.V.; Mortensen, N.A.; Gregersen, A.H.; Sigmund, O.; Ziolkowski, R.W.; Breinbjerg, O. A Review of the Scattering-Parameter Extraction Method with Clarification of Ambiguity Issues in Relation to Metamaterial Homogenization. IEEE Antennas Propag. Mag. 2013, 55, 91–106. [CrossRef]
  27. Hinamoto, T.; Fujii, M. MENP: An Open-Source MATLAB Implementation of Multipole Expansion for Nanophotonics. OSA Continuum 2021, 4, 1640. [CrossRef]
  28. Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. An Electromagnetic Multipole Expansion beyond the Long-Wavelength Approximation. Optics Communications 2018, 407, 17–21. [CrossRef]
  29. Terekhov, P.D.; Babicheva, V.E.; Baryshnikova, K.V.; Shalin, A.S.; Karabchevsky, A.; Evlyukhin, A.B. Multipole Analysis of Dielectric Metasurfaces Composed of Nonspherical Nanoparticles and Lattice Invisibility Effect. Phys. Rev. B 2019, 99, 045424. [CrossRef]
  30. Holly, C.; Traub, M.; Hoffmann, D.; Widmann, C.; Brink, D.; Nebel, C.E.; Gotthardt, T.; Sözbir, M.C.; Wenzel, C. Monocrystalline CVD-diamond optics for high-power laser applications. SPIE LASE, 2016.
  31. Krupke, W.F. Diode Pumped Alkali Lasers (DPALs)—A Review (Rev1). Progress in Quantum Electronics 2012, 36, 4–28. [CrossRef]
  32. Magnusson, R.; Ding, Y. Spectral-band engineering with interacting resonant leaky modes in thin periodic films. Proceedings of the SPIE - The International Society for Optical Engineering 2004, pp. 119–129.
  33. Sang, T (Sang, T.; Wang, ZS (Wang, Z.; Wang, L (Wang, L.; Wu, YG (Wu, Y.; Chen, LY (Chen, L. Resonant excitation analysis of sub-wavelength dielectric grating. JOURNAL OF OPTICS A-PURE AND APPLIED OPTICS 2006, pp. 62–66.
  34. Lalanne, P.; Lemercier-Lelanne, D. Depth dependence of the effective properties of subwavelength gratings. Journal of the Optical Society of America 1997, pp. 450–458.
  35. Yu, X.; Yang, W.; Shen, C.; Tao, W.; Deng, X. Polarization beam combining by fused silica subwavelength grating. Optics Communications 2024, p. 130135.
  36. Li, Y.; Hao, X.; Dai, B.; Shu, G.; Zhao, J.; Zhang, S.; Liu, X.; Wang, W.; Liu, K.; Cao, W.; Yang, L.; Zhu, J.; Han, J. Research Progress on High Rate and High Quality Growth of MPCVD Single Crystal Diamond. Journal of Synthetic Crystals 2020, pp. 979–989.
  37. Kruk, S.; Kivshar, Y. Tailoring Transmission and Reflection with Metasurfaces. In Dielectric Metamaterials; Elsevier, 2020; pp. 145–174.
  38. Savinov, V.; Fedotov, V.A.; Zheludev, N.I. Toroidal Dipolar Excitation and Macroscopic Electromagnetic Properties of Metamaterials. Physical Review B 2014, 89, 205112. [CrossRef]
  39. Campione, S.; Liu, S.; Basilio, L.I.; Warne, L.K.; Langston, W.L.; Luk, T.S.; Wendt, J.R.; Reno, J.L.; Keeler, G.A.; Brener, I.; Sinclair, M.B. Broken Symmetry Dielectric Resonators for High Quality Factor Fano Metasurfaces. ACS Photonics 2016, 3, 2362–2367. [CrossRef]
  40. Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating Anapole Modes in Dielectric Nanoparticles. Nature Communications 2015, 6, 8069. [CrossRef]
  41. Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound States in the Continuum. Nature Reviews Materials 2016, 1, 16048. [CrossRef]
  42. Vaidya, S.; Benalcazar, W.A.; Cerjan, A.; Rechtsman, M.C. Point-Defect-Localized Bound States in the Continuum in Photonic Crystals and Structured Fibers. Phys. Rev. Lett. 2021, 127, 023605. [CrossRef]
  43. Wang, X.; Wang, J.; Zhao, X.; Shi, L.; Zi, J. Realizing Tunable Evolution of Bound States in the Continuum and Circularly Polarized Points by Symmetry Breaking. ACS Photonics 2023, 10, 2316–2322. [CrossRef]
  44. Bustamante, C.J.; Chemla, Y.R.; Liu, S.; Wang, M.D. Optical Tweezers in Single-Molecule Biophysics. Nat Rev Methods Primers 2021, 1, 25. [CrossRef]
Preprints 120221 g001
Figure 1. Dual-layer and single-layer GMR designs for high-reflectivity metasurfaces. (a) Schematic illustration of the dual-layer GMR design, where n G is the effective refractive index of grating layer, n W is the refractive index of waveguide layer, and n S is for the substrate. The blue and gray lines show the pathway of resonance and non-resonance relatively. Here, Λ is the grating period and d represents the thickness of waveguide layer. I, R, T are the intensity of incident, reflected and transmitted light. (b) The single-layer GMR structure where the grating layer function as waveguide layer as well. Here, n H is the higher refractive index and n L is the lower.
Figure 1. Dual-layer and single-layer GMR designs for high-reflectivity metasurfaces. (a) Schematic illustration of the dual-layer GMR design, where n G is the effective refractive index of grating layer, n W is the refractive index of waveguide layer, and n S is for the substrate. The blue and gray lines show the pathway of resonance and non-resonance relatively. Here, Λ is the grating period and d represents the thickness of waveguide layer. I, R, T are the intensity of incident, reflected and transmitted light. (b) The single-layer GMR structure where the grating layer function as waveguide layer as well. Here, n H is the higher refractive index and n L is the lower.
Preprints 120221 g001
Preprints 120221 g002
Figure 2. SCSs and reflectance spectrum of diamond resonators in square lattices by 3D FDTD solvers. (a) Schematic of the FDTD simulation setup for a single diamond resonator embedded in air, using a total field scattered field (TFSF) source to calculate the SCSs. (b) SCS of generalized electric mirror (ED+MQ) and magnetic mirror (MD+EQ) for A R = 0 . 8 , 1 . 0 , 1 . 2 , 1 . 4 , 1 . 6 . (c) Reflective spectrum of diamond resonators arrays in square lattices for A R = 0 . 8 , 1 . 0 , 1 . 2 , 1 . 4 , 1 . 6 .
Figure 2. SCSs and reflectance spectrum of diamond resonators in square lattices by 3D FDTD solvers. (a) Schematic of the FDTD simulation setup for a single diamond resonator embedded in air, using a total field scattered field (TFSF) source to calculate the SCSs. (b) SCS of generalized electric mirror (ED+MQ) and magnetic mirror (MD+EQ) for A R = 0 . 8 , 1 . 0 , 1 . 2 , 1 . 4 , 1 . 6 . (c) Reflective spectrum of diamond resonators arrays in square lattices for A R = 0 . 8 , 1 . 0 , 1 . 2 , 1 . 4 , 1 . 6 .
Preprints 120221 g002
Preprints 120221 g003
Figure 3. (a) Simulation schematic of diamond cylindrical resonators arranged in a square lattice, where Dis the diameter of cylinder while H is the height, and P represents the distance of adjecent cylinders. (b) Reflectivity, transmission, and absorption plotted on a logarithmic scale with D = 304   n m , H = 400   n m and P = 510   n m . R is reflectance, T stands for transmittance and A is absorption. (c) The electric field E z and magnetic field H z in the xy-plane, and the E x field in the xz-plane. Colors indicate the electric field amplitude.
Figure 3. (a) Simulation schematic of diamond cylindrical resonators arranged in a square lattice, where Dis the diameter of cylinder while H is the height, and P represents the distance of adjecent cylinders. (b) Reflectivity, transmission, and absorption plotted on a logarithmic scale with D = 304   n m , H = 400   n m and P = 510   n m . R is reflectance, T stands for transmittance and A is absorption. (c) The electric field E z and magnetic field H z in the xy-plane, and the E x field in the xz-plane. Colors indicate the electric field amplitude.
Preprints 120221 g003
Preprints 120221 g004
Figure 4. Effective medium properties of diamond metasurface mirror. (a) Effective permittivity ( ε eff ) as a function of wavelength. Re( ε eff ) represents the real part of ε eff and Im( ε eff ) represents the imaginary part of ε eff . (b) Effective permeability ( μ eff ) as a function of wavelength. Re( μ eff ) represents the real part of μ eff and Im( μ eff ) represents the imaginary part of μ eff . (c) Effective refractive index ( n eff ) as a function of wavelength. Re( n eff ) represents the real part of n eff and Im( n eff ) represents the imaginary part of n eff . (d) Effective impedance ( z eff ) as a function of wavelength. Re( z eff ) represents the real part of z eff and Im( z eff ) represents the imaginary part of z eff .
Figure 4. Effective medium properties of diamond metasurface mirror. (a) Effective permittivity ( ε eff ) as a function of wavelength. Re( ε eff ) represents the real part of ε eff and Im( ε eff ) represents the imaginary part of ε eff . (b) Effective permeability ( μ eff ) as a function of wavelength. Re( μ eff ) represents the real part of μ eff and Im( μ eff ) represents the imaginary part of μ eff . (c) Effective refractive index ( n eff ) as a function of wavelength. Re( n eff ) represents the real part of n eff and Im( n eff ) represents the imaginary part of n eff . (d) Effective impedance ( z eff ) as a function of wavelength. Re( z eff ) represents the real part of z eff and Im( z eff ) represents the imaginary part of z eff .
Preprints 120221 g004
Preprints 120221 g005
Figure 5. Sweeping map of cylinder diamond resonantors in square lattices at the wavelength between 700 nm and 890 nm. (a) Cylinder height from 200 nm-600 nm. Colors indicates the reflectivity. (b) Pitch in the square lattice from 310 nm-570 nm. (c) Cylinder diameter from 240 nm-490 nm.
Figure 5. Sweeping map of cylinder diamond resonantors in square lattices at the wavelength between 700 nm and 890 nm. (a) Cylinder height from 200 nm-600 nm. Colors indicates the reflectivity. (b) Pitch in the square lattice from 310 nm-570 nm. (c) Cylinder diameter from 240 nm-490 nm.
Preprints 120221 g005
Preprints 120221 g006
Figure 6. Frustum-shaped diamond resonantors in hexagonal lattices. (a) Simulation schematic of diamond frustum-shaped resonators arranged in a hexagonal lattice.Here, H is the height, and P represents the distance of adjacent frustums, while D top represents the top diameter of the frustum and D bot is the bottom. (b) Reflectivity, transmission, and absorption plotted on a logarithmic scale with D top = 292   n m , D bot = 318   n m , H = 400   n m and P = 552   n m . (c) Sweeping map of frustum height, showing that the design remains robust within the height range of 380 nm to 480 nm. Colors indicates the reflectivity. (d) Sweeping map of D gap (half the gap between the top and bottom diameters of the frustum), showing how increasing the diameter affects the reflection spectrum.
Figure 6. Frustum-shaped diamond resonantors in hexagonal lattices. (a) Simulation schematic of diamond frustum-shaped resonators arranged in a hexagonal lattice.Here, H is the height, and P represents the distance of adjacent frustums, while D top represents the top diameter of the frustum and D bot is the bottom. (b) Reflectivity, transmission, and absorption plotted on a logarithmic scale with D top = 292   n m , D bot = 318   n m , H = 400   n m and P = 552   n m . (c) Sweeping map of frustum height, showing that the design remains robust within the height range of 380 nm to 480 nm. Colors indicates the reflectivity. (d) Sweeping map of D gap (half the gap between the top and bottom diameters of the frustum), showing how increasing the diameter affects the reflection spectrum.
Preprints 120221 g006
Preprints 120221 g007
Figure 7. Cylindrical diamond resonantors in square lattices and electric fields at two high-reflectivity wavelength, compared with PEC. (a) Reflectivity spectrum and SCS of ED+MQ and MD+EQ resonances, showing dual-band reflectivity peaks at 744 nm and 828 nm. (b) The electric field E x field in the xz-plane at 744 n m compared with PEC, showing a half-wave phase loss, indicating the behavior of an generalized electric mirror. (c) The electric field E x field in the xz-plane at 828 n m compared with PEC, showing a half-wave phase loss, where no half-wave phase loss is observed, demonstrating the characteristics of a generalized magnetic mirror.
Figure 7. Cylindrical diamond resonantors in square lattices and electric fields at two high-reflectivity wavelength, compared with PEC. (a) Reflectivity spectrum and SCS of ED+MQ and MD+EQ resonances, showing dual-band reflectivity peaks at 744 nm and 828 nm. (b) The electric field E x field in the xz-plane at 744 n m compared with PEC, showing a half-wave phase loss, indicating the behavior of an generalized electric mirror. (c) The electric field E x field in the xz-plane at 828 n m compared with PEC, showing a half-wave phase loss, where no half-wave phase loss is observed, demonstrating the characteristics of a generalized magnetic mirror.
Preprints 120221 g007
Preprints 120221 g008
Figure 8. The AFM test results for the four test points over a scan area of 10 mm × 10 mm. Measurements were taken at two locations: the center and the edge of the film on two separate samples, providing a total of four data points.
Figure 8. The AFM test results for the four test points over a scan area of 10 mm × 10 mm. Measurements were taken at two locations: the center and the edge of the film on two separate samples, providing a total of four data points.
Preprints 120221 g008
Table 1. SCSs of the two peaks for different AR values and multipoles
Table 1. SCSs of the two peaks for different AR values and multipoles
Peaks 1 Peaks 2
Multipole AR λ / D SCS ( × 10 5 nm 2 ) λ / D SCS ( × 10 5 nm 2 )
ED+MQ 0.8 2.0761 12.679 2.4374 2.5640
1.0 2.0991 9.5938 1.5586 2.6994
1.2 2.0871 132.10 2.6196 3.3584
1.4 2.1361 1761.5 2.6456 4.5045
1.6 2.2652 605.26 2.6607 6.3820
MD+EQ 0.8 2.0951 9.9177 2.3654 13.946
1.0 2.1552 9.7153 2.4765 11.432
1.2 2.0881 18.442 2.5025 11.549
1.4 2.1361 618.95 2.5365 13.930
1.6 2.1652 282.97 2.5816 14.364
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated