Prerpints.org logo
Preprint
Article

Comparing the Relative Efficacy of Generalized Estimating Equations, Latent Growth Curve Modeling, and Area Under the Curve with a Repeated Measures Discrete Ordinal Outcome Variable

Altmetrics

Downloads

78

Views

126

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 October 2024

Posted:

04 October 2024

Read the latest preprint version here

Alerts
Abstract
Researchers are often interested in the effects of change in one variable on change in a second variable, requiring the repeated measures of two variables. There are several multivariate statistical methods appropriate for this research design, including generalized estimating equations (GEE) and latent growth curve modeling (LGCM). Both methods allow for variables that are not continuous in measurement level and not normally distributed. More recently, researchers have begun to employ area under the curve (AUC) as a viable alternative when the nature of change is less important than the overall effect of time on repeated measures of a random variable. The research showed that AUC is an acceptable alternative to LGCM with repeated measures of a continuous and a zero-inflated Poisson random variable. However, less is known about its performance relative to GEE and LGCM when the repeated measures are ordinal random variables. Further, no study to our knowledge has compared AUC to LGCM or GEE when there are two longitudinal processes. We thus compared AUC to LGCM and GEE, assessing the effects of repeated measures of psychological distress on repeated measures of smoking. Results suggest AUC performed equally well to both methods, although missing data management is an issue with both AUC and GEE.
Keywords: 
Subject: Public Health and Healthcare  -   Public Health and Health Services

1. Introduction

Statistical analysis options for repeated measures designs vary depending upon the nature of the outcome variable assessed. When the outcome variable (dependent variable) is continuous and normally distributed (multivariate normal), there are more analysis options than when the dependent variable is discrete. Most students taking statistics courses in undergraduate or even some graduate programs learn little about the different statistical analysis methods available for dealing with repeated measures designs, especially when the dependent variable is discrete. The longitudinal data analysis method they are most likely to encounter is repeated measures ANOVA (RM-ANOVA). Although providing some flexibility, such as the ability assess differences among time points, and shape of change over time in a posthoc analysis (e.g., linear or quadratic), RM-ANOVA has limitations when compared to more advanced multivariate statistical methods such as Generalized Estimating Equations (GEE) and Latent Growth Curve Modeling (LGCM). Both of these methods, however, have advantages and disadvantages as well. A more recent method beginning to be employed in the assessment of repeated measures of a variable of interest is area under the curve (AUC). Researchers are now assessing its comparative effectiveness in relation to these methods.
GEE is a multivariate method that has several advantages over RM-ANOVA [1,2]. First, unlike RM-ANOVA, GEE permits repeated measure variables to be discrete or continuous. Second, there is no need to specify the multivariate distribution as the aim is parameter estimation instead of model testing, and GEE provides normally distributed and consistent parameter estimates with no more than specification of the correct mean structure [3]. RM-ANOVA, by contrast, assumes the repeated measures are multivariate normally distributed [4]. Third, GEE permits the selection of the appropriate correlation structure (i.e., the correlations among the repeated measures), and efficiency of parameter estimates does not suffer from an incorrectly specified correlation structure. RM-ANOVA assumes the correlations between measures remains constant [5]. Further, GEE permits estimation of more complicated relations in a single model, such as when one desires to explore the relation between two repeated measures variables (e.g., the effect of change in one variable on change in a second variable). Assessing the effects of time varying covariates is not easily available in RM-ANOVA, although one can format the data to permit the use of a time varying covariate [6].
Equation 1 presents a basic GEE cumulative logit model with three covariates (x1 through x3; the number of covariates employed in the present study), where the logit is the link function relating the covariates to the repeated-measures outcome variable Yit, j is the level of the ordinal variable Y, where j ranges from 1 to J-1, and t represents time (i.e., the unit of time for the repeated measures). Equation 2 is the general cumulative logit model relating the vectors of predictor variables (X) and parameters (β), to the vector of outcomes (Y), with the mean structure being the probability of the jth level of the ordinal outcome variable y for individual i at time t (equation 3) [3].
l o g i t p r y i t ≤ j = β 0 j + β 1 x i 1 + β 2 x i 2 + β 3 x i 3 + β 4 t
l o g i t p r Y i t ≤ j / X i t = β ′ X i t
E ( Y i t / X i t ; β ) = μ i t 1 , … , μ i t J − 1 ′ , w h e r e   μ i t ( m u ) = p r O i t = j / X i t ; β ,   a n d   O i t   i s   t h e   o r d i a l   r e s p o n s e   1,2 , 3 , … J   f o r   i n d i v i d u a l   i   a t   t i m e   t
While there are indeed many advantages to GEE over RM-ANOVA, limitations include the inability to test models and compare different models since GEE lacks a likelihood function. Further, the treatment of missing data is a question. With GEE, one assumes that data are missing completely at random (MCAR), meaning that the available cases are a random sample of all cases (absent missing data) [3,7,8]. Although plausible, MCAR is less likely than the data being missing at random (MAR). When the data are MAR, this indicates that missingness is related to a predictor variable (or predictor variables) or prior measures of the dependent variable. This is a less-restrictive assumption. Although there are extensions that facilitate modeling with missing data in GEE that are not MCAR [9,10], these are less likely to be employed in a naïve analysis.
Another issue related to modeling discrete dependent variables in GEE is the use of correlation coefficients to represent the relations among the repeated measures. Simulation studies suggest that the best measure of association among repeated measures of discrete data is the local odds ratio (LOR) rather than correlation coefficients [11,12]. Although we did not address this limitation in our GEE analysis in this study, as our aim is to conduct a simple (naïve) analysis that most researchers would do, it is noted that there are more efficient ways to estimate associations than correlation coefficients.
Many of the restrictions encountered with GEE are not met when using LGCM with repeated measures data. LGCM is a multivariate method that employs unobserved (latent) variables to represent initial level (baseline) and rate of change from baseline (trend) [13,14]. Equation 4 presents the relations among the latent and observed variables in a prototypical LGCM with ordinal data [15].
y = ν + Λ η + ε ,
w h e r e   y   i s   a   v e c t o r   o f   o b s e r v e d   o r d i n a l   o u t c o m e s ,   v   i s   a   v e c t o r   o f   r e g r e s s i o n   i n t e r c e p t s ,
Λ l a m b d a   i s   a   m a t r i x   o f   f a c t o r   l o a d i n g s   r e l a t i n g   t h e   o b s e r v e d   v a r i a b l e s   t o   t h e   v e c t o r   o f
l a t e n t   v a r i a b l e s   η , a n d   ε e p s i l o n   i s   a   v e c t o r   o f   r e s i d u a l s
Equation 5 clarifies equation 4 with respect to three repeated measures, the number of repeated measures employed in the present study.
y i 1 y i 2 y i 3 = 0 0 0 + 1 0 1 1 1 2 × η 0 η 1 + ε i 1 ε i 2 ε i 3
Working from left to right, we have a vector of ordinal outcome variables for participant i at time t, for the T=3 time points. On the right side of the equation, we have a vector of regression intercepts, set to equal zero. The Λ matrix includes the factor loadings for the intercept factor (first column) and the slope factor (second column). The intercept loadings are set to 1, indicating an unchanged relation between the intercept and the repeated measures. The unit increasing factor loadings in the second column suggest linear growth over time. The next vector includes the two factors (η; eta), the first representing the intercept factor, and the second representing a linear trend factor. If we had proposed a quadratic trend, there would have been a third factor term. For a cubic trend, there would have been a fourth factor term. The final vector represents the residual, one for each time point. These are assumed to be uncorrelated, although at times researchers may correlate them to improve model fit to the data. This is generally not recommended, however [16,17,18].
The latent variables (η) underlying the observed ordinal variables are continuous, not discrete. To capture progression across increasing levels of the ordinal variable, LGCM uses thresholds (τ; tau). Thresholds are cut points in a continuum representing propensities to progress from one ordinal category to the next in an observed variable [15,19]. To assess change over time, these thresholds are constrained to equality across time points. As such, a change in the proportion of participants across the various levels of an ordinal variable, increasing from a lower to a higher category over time, results in an increased propensity to cross thresholds to higher levels of the dependent variable.
With respect to the latent variables, they are assumed to be multivariate normally distributed, with a mean α (alpha) and variance/covariance ψ (psi; equation 6) [15,19]. The residuals are assumed to normally distributed with a mean 0 and variance θ (theta; equation 7). For a very detailed presentation on LGCM with ordinal data, see the Mehta et al. reference [15]. See also Masyn et al. reference [19]. For a general introduction to growth modeling, see Duncan and Duncan [13].
η = M V N α , ψ
ε = N ( 0 , θ )
LGCM also permits researchers to assess the effect of potential predictor variables on baseline and trend factors. In addition, one can assess the effects of another repeated measures variable on repeated measures of the dependent variable, what is commonly known as an associative (parallel) processes LGCM [20]. This could involve, for instance, assessment of the effects of baseline level for one process on a trend for a second process, and trend to trend effects. We represent effects on the growth factors in equation 8.
η = α + Γ ξ + Β η + ζ , w h e r e   α   i s   t h e   i n t e r c e p t ,
Γ ( G a m m a )   i s   a   m a t r i x   o f   c o e f f i c i e n t s   r e l a t i n g   o b s e r v e d   p r e d i c t o r s   t o   t h e   l a t e n t   v a r i a b l e s ,
ξ X i   i s   t h e   v e c t o r   o f   o b s e r v e d   p r e d i c t o r   v a r i a b l e s ,
Β   i s   a   m a t r i x   o f   c o e f f i c i e n t s   r e l a t i n g   t h e   l a t e n t   v a r i a b l e s   η   t o   o n e   a n o t h e r ,
a n d   ζ   Z e t a   i s   t h e   v e c t o r   o f   r e s i d u a l s
Advantages of LGCM include a likelihood function, allowing for model comparisons. In addition, one can test multiple hypotheses, exploring the effects of predictors on repeated measures of a dependent variable. Moreover, one can assess the effects of initial level and rate of change on other outcome variables, whether latent or observed. Further, like GEE, one can assess change on a variety of levels of a dependent variable, whether continuous or discrete. Another advantage of LGCM, not shared by GEE, is how it handles missing data. Unlike GEE, which assumes MCAR, LGCM assumes data are MAR. This is a far more tenable assumption. Using Full Information Maximum Likelihood (FIML) estimation for parameter estimates, LGCM uses all available data on the dependent variables to estimate parameters [21]. Thus, it has the same sample size as GEE, but with a less-restrictive assumption.
Despite the advantages of both methods, conducting GEE and LGCM requires more than a rudimentary understanding of statistics. Moreover, although not necessarily the case for GEE, one needs specific software to conduct LGCM (e.g., Mplus). This can be an unnecessary impediment to researchers if they are interested in the assessment of longitudinal processes but not in the impact of selected covariates on rates of change, or the shape of development (e.g., linear, quadratic, or cubic). For instance, a researcher may wish to assess whether males or females differ in psychological distress (PD) over multiple timepoints, but not whether males differ from females in the rate of change in PD from baseline, or whether change in PD is linear or quadratic in nature. Further, one important limitation with LGCM and GEE alike is related to the nature of ordinal variables, the type of discrete random variable we are employing in our analysis. When modeling with an ordinal random outcome variable (Y) with k categories, one assumes proportional odds, such that the odds related to a set of predictor variables (X) remains constant when comparing different levels of the dependent variable [22,23,24,25]. This is seen in equation 1, where we predict the log odds (logit) of being in category ≤ j versus > j given a set of predictor variables (x). However, this assumption may not always hold in practice, meaning that multinomial logistic regression instead of ordinal logistic regression is the more appropriate analysis option.
One alternative method that researchers are beginning to investigate as a viable alternative for longitudinal data analysis is area under the curve (AUC). With this method, one merely calculates the area under the curve generated by the repeated measures. Equation 9 presents the calculation of area under the curve for repeated measures analysis, what is known as AUC with respect to the ground [26,27,28]. Employing the trapezoid rule for calculating AUC across T timepoints, we have
A U C g r o u n d = y 2 + y 1 2 × x 2 − x 1 + y 3 + y 2 2 × x 3 − x 2 + … + y T + y T − 1 2 × x T − x T − 1 ,
w h e r e   y t   i s   t h e   y − a x i s   v a l u e   a n d   x t   i s   t h e   x − a x i s   v a l u e   a t   t i m e p o i n t   t
If we let ti represent our intervals xt - xt-1, there will be one less interval than time points (equation 10).
A U C g r o u n d = ∑ i = 1 T − 1 y i + 1 + y i 2 × t i
If the intervals are constant in length, equation 10 reduces to equation 11
A U C g r o u n d = ∑ i = 1 T − 1 t 2 y i + 1 + y i
Researchers have shown that AUC performs as well as LGCM when the data are continuous or discrete counts [26,27]. However, to our knowledge no study has yet compared AUC to GEE or LGCM using discrete ordinal random variables.
AUC has several advantages over GEE and LGCM. First, instead of multiple dependent variables to form growth curves, AUC is a single variable that can be employed in simpler statistical methods such as regression analysis, t-tests, and ANOVAs, as well as multivariate methods such as structural equation modeling (SEM). Second, one does not need advanced statistical knowledge to understand AUC, although some basic knowledge about distributions (e.g., normal or Poisson) is a plus. Further, there is no need to consider issues such as the proportional odds assumption when calculating AUC, as the primary concern is the area created by the different rectangles covering the mass or density for the T-1 intervals.
Despite these advantages, there are some key limitations. First, in calculating AUC without any modifications, individuals missing data at a given timepoint are deleted listwise, meaning the entire record for that participant is expunged, resulting in a potentially drastic reduction in sample size. As such, AUC assumes data are MCAR, and data imputation methods are necessary to reduce the number of missing cases. Second, one must write syntax to calculate AUC for repeated measures designs at this point, and this may be difficult for those with limited experience with syntax and coding. Acknowledging these limitations though, AUC may provide a useful alternative to other repeated measures statistical methods. As such, the purpose of the present study was to assess the relative efficacy of AUC compared to GEE and LGCM using real data from a publicly-available data source. Using data from the Panel Study of Income Dynamics (PSID) transition to adulthood (TA) study, and all three data analysis methods, we assessed the impact of repeated measures of a continuous predictor variable, psychological distress, on repeated measures of an ordinal dependent variable, nicotine use, both measured in 2017, 2019, and 2021.
Rational for selecting these variables. In this study, we assessed the relation between psychological distress and smoking in older adolescents and young adults (ages 18-24). Smoking is the leading cause of preventable disease and death in the United States [29], and while combustible cigarette smoking has decreased in recent years, e-cigarette smoking (vaping) has been on the rise, and both remain serious risk factors for poor health outcomes [30,31]. A potential reason for smoking in older adolescents and young adults is the rising prevalence of mental health issues [32]. Nicotine can temporarily relieve symptoms of mental illness, such as anxiety and depression, and many people suffering from these issues may use it to self-medicate, leading to nicotine dependence [33,34,35,36]. In the long term, however, smoking can increase susceptibility to anxiety and the severity of depression, exacerbating poor mental health [36,37]. Thus, studying the relation between psychological distress and smoking in older adolescents and young adults may help to find solutions to both problems. Finally, we also controlled for race and education level, as these are two factors that are known to affect smoking status [38].

2. Materials and Methods

Participants and procedures. Participants were drawn from a total sample size of n=4222 young adults (18-24 years old) at each of three data collection waves (2017, 2019, and 2021) who were taking part in the Panel Study of Income Dynamics (PSID) Transition to Adulthood (TA) supplement. Started in 1968, the PSID is the longest continuously running cohort study [39]. Although its original purpose was to understand the intergenerational transmission of poverty, subsequent data collections have included a variety of variables covering health and other experiential domains. The final sample sizes per analysis differed due to missing data and its treatment in each statistical method, with 2510 participants for the GEE, and 2511 participants for LGCM and AUC, after multiple imputation for the AUC analysis. The large number of participants missing per wave resulted from the transitional nature of this supplement. Participants age out and new participants enter the TA sample during each data collection wave. However, we were only interested in following the same participants (cohort) across the data collection waves to meet our aim. We found that the three waves selected maximized our cohort size, as adding additional waves resulted in a drastic decrease in sample size.
Instrumentation. To estimate use of nicotine across time, we generated a four-level ordinal variable from two PSID questions related to one’s nicotine use behavior (i.e., “Do you smoke cigarettes?” and “Have you ever vaped?”). Values are 0 – Does not use a nicotine product, neither combustible cigarettes(smoking) nor electronic cigarette (e – cigarette; vaping), 1 – vaped or vapes, 2 – smokes, 3 – vaped/vapes and smokes). We assessed psychological distress with a variable that is the sum of six five-point (0 through 4) Likert-style questions asking how often in the past month the respondent felt nervous, hopeless, restless, everything an effort, too sad, and worthless. Scores ranged from 0 to 24 points. Finally, we controlled for race (0 – non-White, 1 – White) and education (0 – greater than a high school education, 1 – high school education or less).
Data analysis methods. We conducted GEE, LGCM, and AUC. Our GEE analysis included four predictor variables, the time varying covariate psychological distress, the two time-invariant covariates education and race (both measured at 2017), and time (i.e., data collection wave). We also included two interaction terms, one each for the time invariant covariates; race by time and education by time. This allowed us to assess whether the effects of 2017 education and race smoking, if any, changed across time.
For the LGCM, we conducted an associated-processes model, with one process for repeated measures of psychological distress, and a second process for smoking. Each LGCM included two factors, one for intercept and one for a linear trend. In each LGCM, we controlled for the effects of the time invariant covariates, education and race, on the baseline level and linear trend factors. We also controlled for the effect of baseline level of the opposite LGCM on each trend factor (i.e., the effect of baseline smoking on psychological distress trend, and the effect of baseline psychological distress on smoking trend). Finally, we assessed the effect of psychological distress trend on smoking trend. To assess the fit of our LGCM to the data, we used chi-share test of model fit, the Comparative Fit Index (CFI), Root Mean Square Error of Approximation (RMSEA), and Standardized Root Mean Residual (SRMR). Heuristics for good fit include a non-significant chi-square, CFI ≥ 0.95, RMSEA ≤ 0.05, and SRMR ≤ 0.06 [40,41,42].
For AUC, we employed multiple regression analysis to assess the effects of psychological distress AUC on smoking AUC, controlling for race and education, both measured at 2017.

3. Results

3.1. Descriptive Statistics

Table 1 presents the descriptive statistics for our sample, including missing data per variable.

3.2. GEE

Table 2 presents the results of the GEE analysis. Psychological distress and time had significant and positive effects on nicotine use. Converting the logits (log odds) to odds ratios, each unit increase in psychological distress across the three time points was associated with a 5% increase in the odds of progressing to a higher level of smoking, from not smoking to smoking both combustible and e-cigarettes (OR=1.053; 95% CI=1.029, 1.078). Compared to baseline (time 1; 2017), time 2 (2019) and time 3 (2021) were associated with a 34% (OR=1.34; 95% CI=1.174, 1.531) and over two-fold (OR=2.054; 95% CI=1.711, 2.467) increase in the odds of progressing to a higher level of smoking, respectively.

3.3. LGCM

Table 3 presents the results of the associated processes LGCM analysis. The model fit the data fairly well, χ2(df=15)=184.613, p<0.001; CFI=0.990; RMSEA=0.067, 90%CI=0.059, 0.076; SRMR=0.043. These results indicate acceptable fit, with the exception of the significant chi-square, suggesting some model misfit that is amplified by the larger sample size [43]. The RMSEA, was above the 0.06 cutoff for good fit, suggesting acceptable fit but not necessarily good fit. Regarding model effects, baseline psychological distress had a significant and positive effect on smoking trend (b=0.037, z=6.777, p<0.001). The trend-to-trend path from psychological distress to smoking distress, however, was not significant (p=0.259).

3.4. AUC

Table 4 presents the results of the AUC multiple regression analysis, for the original sample based on listwise deletion of missing data (n=1095) and the multiple imputation sample (n=2511). Figure 1 presents the standardized residual plots for the initial sample (panel a), and each of the five imputations (panels b – f) from the multiple imputation runs. Figure 2 presents the residual plots of the standardized residuals for the initial sample (panel a) and each of the five imputations (panels b – f) from the multiple imputation runs. Looking at the regression assumptions, the standardized residuals peak at lower values, with higher values approaching normality, suggesting most participants have lower levels of smoking (Figure 1), and there is apparent homoscedasticity when looking at the variance of the residuals (Figure 2). Given that as sample size increases, however, there is convergence in distribution of standardized variables to the standard normal distribution (central limit theorem)[44], possible violations of the normality assumption are unlikely. Further, there was no difference in the pattern of results between the two samples (Table 4). However, we will look at the multiple imputation sample as its sample size is comparable to the sample sizes for the GEE and the LGCM analyses. Psychological distress had a significant and positive effect on smoking (b=0.033, t=7.189, p < 0.0001).

3.5. Comparing the Three Methods

In all three methods, psychological distress had a significant effect on smoking. The only difference was in how the effects are partitioned in LGCM. With LGCM, we were able to explore the effects of baseline psychological distress on smoking trend, and the effect of psychological distress trend on smoking trend. Because of this partitioning, we saw that only the effect of baseline distress on smoking trend was significant. As such, initial levels of psychological distress have the greatest impact on progression to higher levels of smoking, with no further impact from change in distress with time. Regarding the two covariates race and education in the LGCM, being White versus non-White, and having a high school education or less versus a greater education, were associated with higher levels of smoking at baseline, but had the inverse effect on rate of change from baseline (i.e., a negative effect on smoking trend). This indicates a possible ceiling effect for these variables, meaning that their effect was strong initially, leaving little room for additional growth.
In contrast to the results for the LGCM, neither race nor education had a significant effect on smoking in the GEE analysis. The AUC results were more similar to those seen with LGCM, with both covariates having significant and positive effects on smoking.

3. Discussion

The aim of the present study was to compare three multivariate methods for analyzing repeated measures data, GEE, LGCM, and AUC. The results of all three methods agreed on the positive effects of psychological distress on smoking, with LGCM being able to partition the effects between baseline level and trend. This is a key difference among the methods, and suggests that researchers interested in understanding how different facets of growth in a longitudinal process, whether initial level or rate of change, affect each other may be best served by LGCM over the other two methods. For researchers interested in overall effects, it seems that AUC provides the most reasonable choice, as it incorporates the entirety of change within a single variable, whether a predictor or an outcome variable. Nevertheless, the handling of missing data in AUC and GEE can be problematic, especially if one is not well versed in handling missing data using methods such as multiple imputation.
Even though the aim of this study was to compare performance among the three different statistical methods, the finding that psychological distress was associated with an increase in the propensity to smoking with all three methods is noteworthy. A potential reason for this robust association is that psychological distress may cause individuals to smoke as way to self-medicate for symptoms of mental illness. Based on the findings from each method, it would appear that psychological distress predisposes one to nicotine use, and that the effect persists across time. This is seen with the significant effect of baseline distress on LGCM, trend along with a non-significant effect from psychological distress trend to smoking trend. This result is mirrored by the effect of psychological distress on smoking in both GEE and AUC, two methods that essentially aggregate change into a single variable (long-format data structure in GEE, calculation in AUC).
Another interesting contrast that mirrors the effects seen with psychological distress is seen when comparing the effects of education and race on smoking in LGCM and AUC. Both results mirror what is seen with distress, as there appears to be a ceiling effect for race and education in LGCM, and a clear positive effect for the two covariates with AUC. This highlights the greater ability to partition effects with LGCM. It is notable that neither variable had a significant effect on smoking using GEE, neither on its own or as an interaction term with time. More research is needed comparing these different methods to better understand the nature of such differing effects.
Like all studies, there are several limitations to our work. First, our smoking variable was generated based on the available questions. The questions related to vaping were not as well defined as those for combustible cigarette smoking, at times failing to delineate past from current use. Second, the low prevalence of smoking in this sample may have affected the results. Third, we only controlled for two variables, education and race. However, as the aim of this study was to compare the three methods, we did not find it necessary to go beyond two control variables. Researchers interested in better understanding the relation between psychological distress and smoking should include additional control variables. These limitations noted, this study adds to recent studies that suggest that AUC is a viable alternative method for assessing longitudinal data, especially when the research aim is to understand overall effects rather than partitioning effects by baseline level and trend. Nevertheless, all three methods are useful for researchers interested in assessing change, with AUC being the most accessible in our opinion. The next steps are to develop programs to calculate AUC regardless of the number of repeated measures, develop an equation that incorporates baseline to asses change, without allowing for negative values, and adding the ability to account for missing data through multiple imputation without the researcher having to write additional code.

Author Contributions

Conceptualization, D.R. and R.Y.; methodology, D.R.; software, D.R.; validation, D.R. and J.U.; formal analysis, D.R.; investigation, D.R. and R.U.; resources, D.R., R.V. and J.U.; data curation, D.R.; writing—original draft preparation, D.R., R.V. and J.U.; writing—review and editing, D.R., R.V. and J.U.; visualization, D.R.; supervision, D.R. and J.U.; project administration, D.R. and J.U. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study did not require ethical approval.

Informed Consent Statement

This study used publicly available data, and therefore did not require informed consent.

Data Availability Statement

The data employed in this study are from the Panel Study of Income Dynamics (PSID), data center, https://simba.isr.umich.edu/default.aspx. Direct access to the specific dataset employed for this study is available from the first author.

Acknowledgments

We would like to thank the International Research Institute of North Carolina for providing additional support for article searches and other guidance during this process.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Zeger, S.L.; Liang, K.-Y.; Albert, P.S. Models for longitudinal data: a generalized estimating equation approach. Biometrics 1988, 1049–1060. [Google Scholar] [CrossRef]
  2. Liang, K.-Y.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
  3. da Silva, J.L.; Colosimo, E.A.; Demarqui, F.N. A general GEE framework for the analysis of longitudinal ordinal missing data and related issues. Statistical Modelling 2019, 19, 174–193. [Google Scholar] [CrossRef]
  4. Rodriguez, D. Core Statistic: Practial Knowledge for the Health Sciences, 2nd ed.; Kendall Hunt: Dubuque, IA, 2024. [Google Scholar]
  5. Schober, P.; Vetter, T.R. Repeated Measures Designs and Analysis of Longitudinal Data: If at First You Do Not Succeed-Try, Try Again. Anesthesia and analgesia 2018, 127, 569–575. [Google Scholar] [CrossRef] [PubMed]
  6. How can I do repeated measures ANOVA with covariates in SPSS? Available online: https://stats.oarc.ucla.edu/spss/faq/how-can-i-do-repeated-measures-anova-with-covariates-in-spss/ (accessed on September 19, 2024).
  7. Little, R.J.; Rubin, D.B. Statistical analysis with missing data; John Wiley & Sons, 2019; Volume 793. [Google Scholar]
  8. Lipsitz, S.R.; Fitzmaurice, G.M.; Weiss, R.D. Using Multiple Imputation with GEE with Non-monotone Missing Longitudinal Binary Outcomes. Psychometrika 2020, 85, 890–904. [Google Scholar] [CrossRef]
  9. Robins, J.M.; Rotnitzky, A.; Zhao, L.P. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the american statistical association 1995, 90, 106–121. [Google Scholar] [CrossRef]
  10. Yang, C.; Diao, L.; Cook, R.J. Adaptive response-dependent two-phase designs: Some results on robustness and efficiency. Statistics in Medicine 2022, 41, 4403–4425. [Google Scholar] [CrossRef]
  11. Zhou, X.; Xu, R.; Elashoff, D. Local odds ratio is more efficient than correlation coefficient for modeling longitudinal ordinal data. In Proceedings of the Joint Statistical Meetings, Baltimore, MD; 2017. [Google Scholar]
  12. Touloumis, A.; Agresti, A.; Kateri, M. GEE for multinomial responses using a local odds ratios parameterization. Biometrics 2013, 69, 633–640. [Google Scholar]
  13. Duncan, T.E.; Duncan, S.C. An introduction to latent growth curve modeling. Behavior therapy 2004, 35, 333–363. [Google Scholar]
  14. Duncan, T.E.; Duncan, S.C. The ABC’s of LGM: An introductory guide to latent variable growth curve modeling. Social and personality psychology compass 2009, 3, 979–991. [Google Scholar] [CrossRef]
  15. Mehta, P.D.; Neale, M.C.; Flay, B.R. Squeezing interval change from ordinal panel data: latent growth curves with ordinal outcomes. Psychological methods 2004, 9, 301. [Google Scholar] [CrossRef] [PubMed]
  16. Hermida, R. The problem of allowing correlated errors in structural equation modeling: concerns and considerations. Computational Methods in Social Sciences 2015, 3, 5–17. [Google Scholar]
  17. MacCallum, R.C.; Roznowski, M.; Necowitz, L.B. Model modifications in covariance structure analysis: the problem of capitalization on chance. Psychological bulletin 1992, 111, 490. [Google Scholar] [CrossRef]
  18. Goffin, R.D. Assessing the adequacy of structural equation models: Golden rules and editorial policies. Personality and Individual Differences 2007, 42, 831–839. [Google Scholar] [CrossRef]
  19. Masyn, K.E.; Petras, H.; Liu, W. Growth curve models with categorical outcomes. Encyclopedia of criminology and criminal justice 2014, 2013. [Google Scholar]
  20. Rodriguez, D. Research Methods; Kendall Hunt Publishing Company: Dubuque, IA, USA, 2021. [Google Scholar]
  21. Schminkey, D.L.; von Oertzen, T.; Bullock, L. Handling missing data with multilevel structural equation modeling and full information maximum likelihood techniques. Research in Nursing & Health 2016, 39, 286–297. [Google Scholar]
  22. Liu, A.; He, H.; Tu, X.M.; Tang, W. On testing proportional odds assumptions for proportional odds models. General Psychiatry 2023, 36. [Google Scholar] [CrossRef]
  23. Brant, R. Assessing proportionality in the proportional odds model for ordinal logistic regression. Biometrics 1990, 1171–1178. [Google Scholar] [CrossRef]
  24. McCullagh, P. Regression models for ordinal data. Journal of the Royal Statistical Society: Series B (Methodological) 1980, 42, 109–127. [Google Scholar] [CrossRef]
  25. Agresti, A. Categorical data analysis; John Wiley & Sons, 2012; Volume 792. [Google Scholar]
  26. Rodriguez, D. Assessing area under the curve as an alternative to latent growth curve modeling for repeated measures zero-inflated poisson data: a simulation study. stats 2023, 6, 354–364. [Google Scholar] [CrossRef]
  27. Rodriguez, D. Area under the curve as an alternative to latent growth curve modeling when assessing the effects of predictor variables on repeated measures of a continuous dependent variable. Stats 2023, 6, 674–688. [Google Scholar] [CrossRef]
  28. Pruessner, J.C.; Kirschbaum, C.; Meinlschmid, G.; Hellhammer, D.H. Two formulas for computation of the area under the curve represent measures of total hormone concentration versus time-dependent change. Psychoneuroendocrinology 2003, 28, 916–931. [Google Scholar] [CrossRef] [PubMed]
  29. Cornelius, M.E. Tobacco product use among adults–United States, 2021. MMWR. Morbidity and mortality weekly report 2023, 72. [Google Scholar] [CrossRef] [PubMed]
  30. Pierce, J.P.; Luo, M.; McMenamin, S.B.; Stone, M.D.; Leas, E.C.; Strong, D.; Shi, Y.; Kealey, S.; Benmarhnia, T.; Messer, K. Declines in cigarette smoking among US adolescents and young adults: indications of independence from e-cigarette vaping surge. Tobacco Control 2023, tc-2022-057907. [Google Scholar] [CrossRef] [PubMed]
  31. Bandi, P.; Star, J.; Minihan, A.K.; Patel, M.; Nargis, N.; Jemal, A. Changes in E-Cigarette Use Among U.S. Adults, 2019–2021. American Journal of Preventive Medicine 2023, 65, 322–326. [Google Scholar] [CrossRef]
  32. Becker, T.D.; Arnold, M.K.; Ro, V.; Martin, L.; Rice, T.R. Systematic Review of Electronic Cigarette Use (Vaping) and Mental Health Comorbidity Among Adolescents and Young Adults. Nicotine & Tobacco Research 2020, 23, 415–425. [Google Scholar] [CrossRef]
  33. Romm, K.F.; Cohn, A.M.; Wang, Y.; Berg, C.J. Psychosocial predictors of trajectories of dual cigarette and e-cigarette use among young adults in the US. Addictive Behaviors 2023, 141, 107658. [Google Scholar] [CrossRef]
  34. Moustafa, A.F.; Testa, S.; Rodriguez, D.; Pianin, S.; Audrain-McGovern, J. Adolescent depression symptoms and e-cigarette progression. Drug and alcohol dependence 2021, 228, 109072. [Google Scholar] [CrossRef]
  35. Collins, S.; Hoare, E.; Allender, S.; Olive, L.; Leech, R.M.; Winpenny, E.M.; Jacka, F.; Lotfalian, M. A longitudinal study of lifestyle behaviours in emerging adulthood and risk for symptoms of depression, anxiety, and stress. Journal of Affective Disorders 2023, 327, 244–253. [Google Scholar] [CrossRef]
  36. Rodriguez, D.; Moss, H.B.; Audrain-McGovern, J. Developmental Heterogeneity in Adolescent Depressive Symptoms: Associations With Smoking Behavior. Psychosomatic Medicine 2005, 67. [Google Scholar] [CrossRef]
  37. Zimmermann, M.; Chong, A.K.; Vechiu, C.; Papa, A. Modifiable risk and protective factors for anxiety disorders among adults: A systematic review. Psychiatry Research 2020, 285, 112705. [Google Scholar] [CrossRef] [PubMed]
  38. Wang, G.; Wu, L. Healthy people 2020: social determinants of cigarette smoking and electronic cigarette smoking among youth in the United States 2010–2018. International journal of environmental research and public health 2020, 17, 7503. [Google Scholar] [CrossRef] [PubMed]
  39. Panel Study of Income Dynamics, public use dataset. 2012.
  40. Cangür, Ş.; Ercan, I. Comparison of model fit indices used in structural equation modeling under multivariate normality. 2015. [Google Scholar]
  41. MacCallum, R.C.; Browne, M.W.; Sugawara, H.M. Power analysis and determination of sample size for covariance structure modeling. Psychological methods 1996, 1, 130. [Google Scholar] [CrossRef]
  42. Shi, D.; Lee, T.; Maydeu-Olivares, A. Understanding the Model Size Effect on SEM Fit Indices. Educational and Psychological Measurement 2019, 79, 310–334. [Google Scholar] [CrossRef]
  43. McNeish, D. Should we use F-tests for model fit instead of chi-square in overidentified structural equation models? Organizational Research Methods 2020, 23, 487–510. [Google Scholar] [CrossRef]
  44. Zhang, X.; Astivia, O.L.O.; Kroc, E.; Zumbo, B.D. How to think clearly about the central limit theorem. Psychological Methods 2023, 28, 1427. [Google Scholar] [CrossRef]
Preprints 120258 g001
Figure 1. Standardized residual plots for the original sample with missing data (panel a), and the five imputed samples (panels b – f).
Figure 1. Standardized residual plots for the original sample with missing data (panel a), and the five imputed samples (panels b – f).
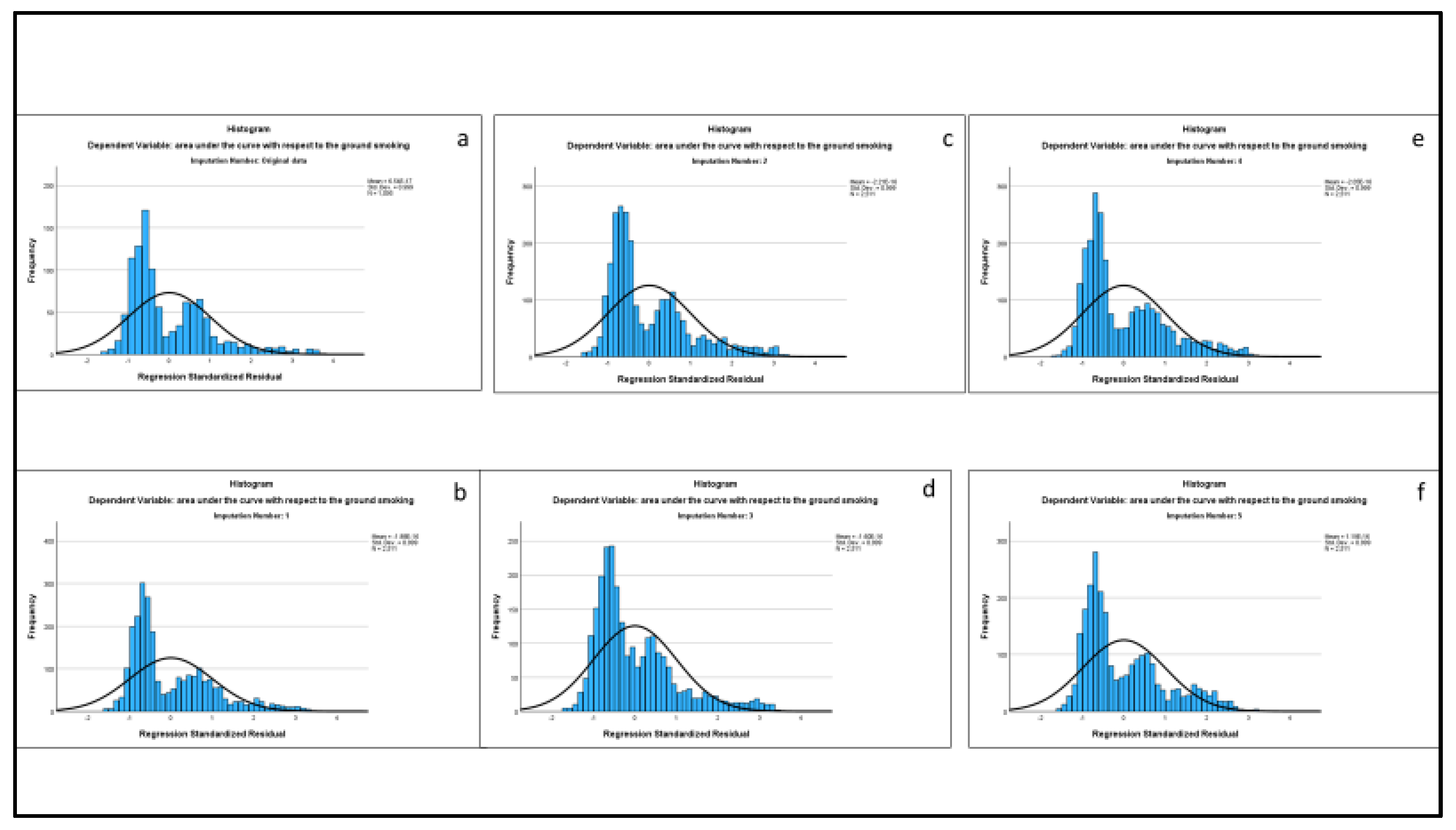
Preprints 120258 g001
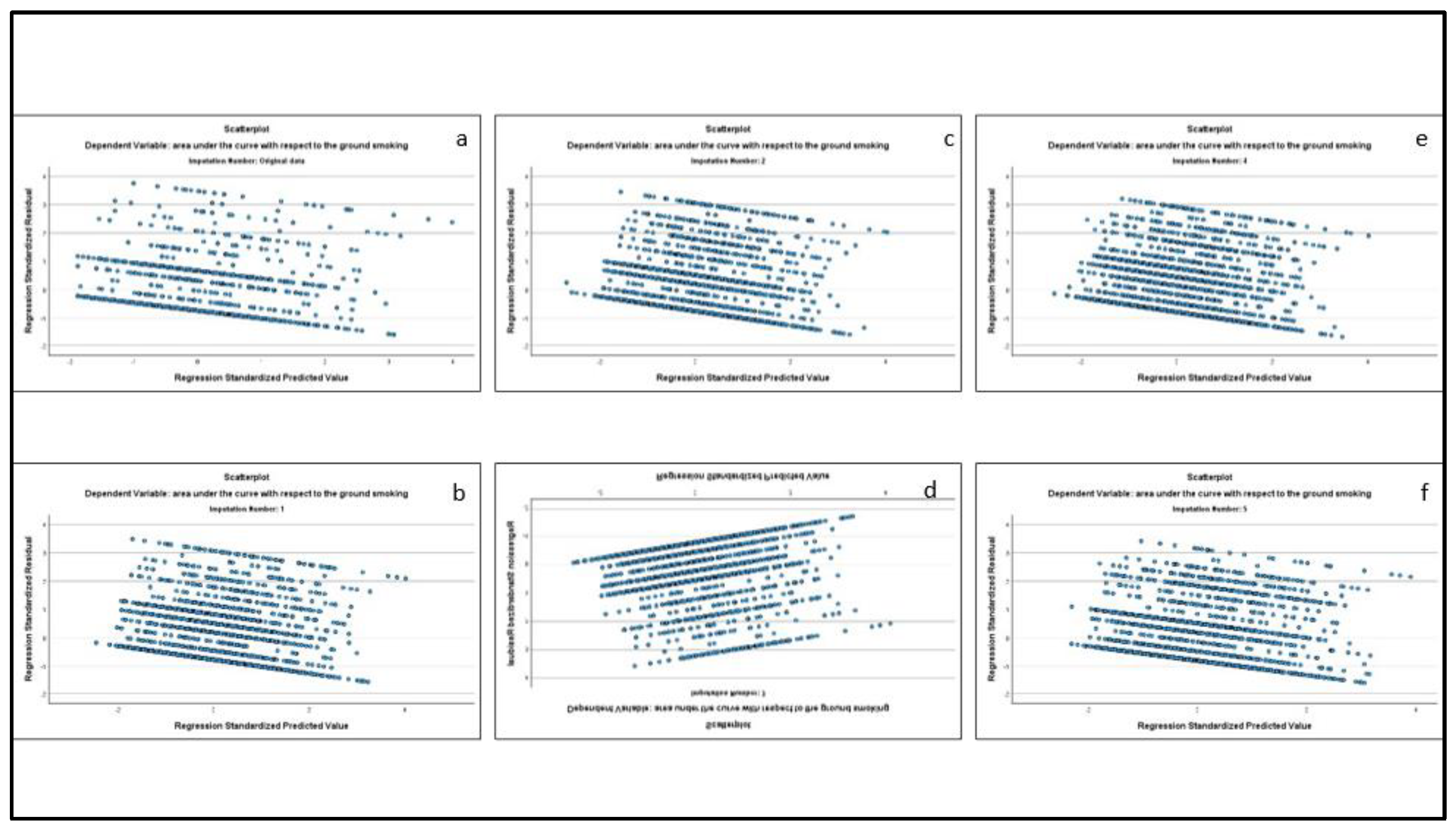
Preprints 120258 g002
Figure 2. Residual plots for the original sample (panel a) and the five imputed samples from the multiple imputation (panels b – f).
Figure 2. Residual plots for the original sample (panel a) and the five imputed samples from the multiple imputation (panels b – f).
Preprints 120258 g002
Table 1. Descriptive statistics.
Table 1. Descriptive statistics.
Discrete variables
Variable Level N %
Race White 1097 26.0
Non-White 1414 33.5
System missing 1711 40.5
Education ≤High School 1055 25.0
>High School 1471 34.8
System missing 1696 40.2
Nicotine use 2017 Does not smoke 1674 39.6
Vapes/vaped 473 11.2
Smokes 185 4.4
Smokes and vapes/vaped 188 4.5
System missing 1702 40.3
Nicotine use 2019 Does not smoke 1642 38.9
Vapes/vaped 642 15.2
Smokes 122 2.9
Smokes and vapes/vaped 142 3.4
System missing 1674 39.6
Nicotine use 2021 Does not smoke 1438 34.1
Vapes/vaped 729 17.3
Smokes 54 1.3
Smokes and vapes/vaped 88 2.1
System missing 1913 45.3
Continuous variables
Variable N Mean SD
Distress 2017 2512 4.91 4.00
System missing 1710
Distress 2019 2519 6.10 5.35
System missing 1703
Distress 2021 2309 6.72 5.73
System missing 1913
Table 2. GEE results (n=2510).
Table 2. GEE results (n=2510).
Variable B SE 95% CI
Lower Upper Wald p-value
≤High school 0.139 0.2258 -0.304 0.581 0.377 0.539
White race 0.191 0.2368 -0.273 0.655 0.651 0.420
Psychological distress 0.052 0.0116 0.029 0.075 20.274 <0.001
Time 3 0.720 0.0932 0.537 0.903 59.705 <0.001
Time 2 0.293 0.0677 0.160 0.426 18.759 <0.001
High school*Time 3 0.117 0.1174 -0.113 0.347 0.994 0.319
High school*Time 2 0.053 0.0868 -0.117 0.223 0.378 0.539
Race*Time 3 -0.143 0.1161 -0.371 0.084 1.519 0.218
Race*Time 2 -0.049 0.0838 -0.213 0.115 0.342 0.559
Table 3. LGCM results (n=2511).
Table 3. LGCM results (n=2511).
Intercept Slope
Smoking
b SE z-value p-value b SE z-value p-value
Distress slope - - - - 0.011 0.01 1.129 0.259
Distress intercept - - - - 0.037 0.005 6.777 <0.001
High school 0.364 0.05 7.363 <0.001 -0.082 0.027 -3.063 0.002
White 0.251 0.049 5.095 <0.001 -0.058 0.027 -2.176 0.03
Psychological distress
b SE z-value p-value b SE z-value p-value
Smoke slope - - - - - - - -
Smoke intercept - - - - -0.008 0.055 -0.138 0.89
HS 0.295 0.159 1.852 0.064 0.226 0.152 1.488 0.137
WHITE 0.164 0.16 1.023 0.306 0.379 0.151 2.514 0.012
Table 4. AUC.
Table 4. AUC.
Original data (N=1,095) Multiple imputation (n=2,511)
Predictor b SE t-value p-value b SE t-value p-value
Intercept 0.335 0.053 6.314 p<0.001 0.498 0.085 5.845 0.000
High school 0.451 0.050 8.989 p<0.001 0.512 0.069 7.392 0.000
White 0.317 0.050 6.358 p<0.001 0.286 0.066 4.309 0.000
AUC distress 0.033 0.003 11.102 p<0.001 0.033 0.005 7.189 0.000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated