New Predictive Model for the Computation of Reinforced Concrete Column Shear Strength

Preprint

Article

New Predictive Model for the Computation of Reinforced Concrete Column Shear Strength

Altmetrics

Downloads

Views

Comments

Anthos Ioannis Ioannou^*

David Galbraith,Nikolaos Bakas,

George Markou,

John Bellos

Anthos Ioannis Ioannou^*

David Galbraith,Nikolaos Bakas,

George Markou,

John Bellos

This version is not peer-reviewed

Submitted:

03 October 2024

Posted:

08 October 2024

You are already at the latest version

Alerts

Abstract

The assessment methods for estimating the behavior of the complex mechanics of reinforced concrete (RC) structural elements were primarily based on experimental investigation, followed by collective evaluation of experimental databases from the available literature. There is still a lot of uncertainty in relation to the strength and deformability criteria that have been derived from tests due to the differences in the experimental test setups of the individual research studies that are being fed into the databases used to derive predictive models. This research work focuses on structural elements that exhibit pronounced strength degradation with plastic deformation and brittle failure characteristics. The study’s focus is on evaluating existing models that predict the shear strength of RC columns, which take into account important factors including the structural element’s ductility and axial load, as well as the contributions of specific resistance mechanisms like that of concrete, transverse, and longitudinal reinforcement. Significantly improved predictive models are proposed herein through the implementation of machine learning (ML) algorithms on refined datasets. Three ML models, LINREG, POLYREG-HYT, and XGBoost-HYT-CV, were used to develop different predictive models that were able to compute the shear strength of RC columns. According to the numerical findings, POLYREG-HYT and XGBoost-HYT-CV derived models outperformed other ML models in predicting the shear strength of rectangular RC columns with the correlation coefficient having a value R greater than 99% and minimal errors. It was also found that the newly proposed predictive model derived a 2-fold improvement in terms of the correlation coefficient compared to best available equation in the international literature.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Following the development of Performance–Based Assessment (PBA) frameworks, between 1995 and 2010, practical evaluation of the seismic behavior of reinforced concrete (RC) structures became a priority when accounting for a large number of existing RC buildings in urban centers. Earthquakes that occurred in the last 30 years affected urban regions such as Loma-Prieta (1989), Northridge (1994, California), Athens (1999, Parnitha), Izmit (1999, Turkey), ChiChi (1999), L’Aquila (2009, Italy), Haiti (2010), Kahramanmaras (2023, Turkey), etc., all highlighted the catastrophic potential and risk to human life imparted by old construction. Damage was more intense in RC buildings with soft storeys.

For the first time in this period, the explicit interest in the literature is focused on the drift capacity of columns at collapse. A large number of studies have been published thus far, attempting to quantify the deformation capacity of columns, with reference to the seismic risk presented by existing construction. In particular, crucial parameters that affect the seismic behavior of this type of element at advanced stages of deformation are of significant importance, especially when elements with inadequate steel reinforcing configurations that represent old-type practices are evaluated.

An important factor responsible for the dispersion of results is the perceived insensitivity of the analytical models to some critical parameters that control the onset of failure. In columns controlled by flexural yielding before failure (flexure-shear elements), the load-carrying capacity against horizontal load is generally controlled by flexure. On the other hand, the deformation capacity is generally much lower than that specified by the analytical models, which superimpose a limiting envelope on the resistance curve. This approach aims to effectively control the interplay between shear and flexure after yielding, based on the ratio

V_{n} (μ) / V_{f l e x}

, by limiting drift capacity which is suggested in KAN.EPE., 2014. Flexural strength is hardly the only controlling variable; for example, strength loss in lap splices, exacerbated by cyclic deformation reversals may alter the hierarchy expressed by the preceding ratio. For these reasons, the estimation of the shear capacity of RC columns is still an open problem that requires further investigation and the development of more accurate design formulae.

For the purposes of this study, a dataset was obtained from the PEER database of columns by Berry et al. (2004), which included an extensive collection of tests gathered from published experimental studies. The type of failure of the RC column specimens was thoroughly examined and served as the primary criterion for inclusion in the selected dataset. The extracted data were then utilized to compare the existing proposed models for shear strength calculations with the reported values, allowing for an assessment of the model’s predictive accuracy.

Design codes like ASCE/SEI 41-13, EN1998-3, 2005, and Pardalopoulos et al. (2013) all specify useful formulae for determining the shear strength of RC columns. Meanwhile, numerous researchers (Aschheim and Moehle, 1992; Lynn and Moehle, 1996; Sezen and Moehle, 2004; Elwood and Moehle, 2003; Priestley et al., 1996) developed formulae for calculating the shear strength of RC columns. Comparing experimental tests and equations between the aforementioned criteria and proposed models, however, revealed a discrepancy (ASCE/SEI 41-13; EN1998-3, 2005; Pardalopoulos et al., 2013). Additionally, a number of formulae that had been suggested in earlier research had limitations in particular situations, such as short, rectangular RC columns with light transverse reinforcement (Tran and Li, 2014). Due to their numerous coefficients, only a few models were even challenging in application techniques (Aval et al., 2017). The existing models that are used to assess the shear strength of RC columns were supplemented and improved using an optimization methodology in order to enhance the investigation. The proposed model, which was created using machine learning methods, is contrasted with the models proposed by ASCE/SEI 41-13, EN1998-3, 2005, and Pardalopoulos et al. (2013).

2. Crucial Behaviour Parameters

A qualifying criterion for the type of failure and the behavior of RC columns is the yielding of the longitudinal reinforcement before the occurrence of shear failure. (Shear failure is identified by transverse reinforcement yielding precluding other inadequacies such as lap-splice failure). If longitudinal bar yielding precedes stirrup yielding, the failure is described as of flexure-shear type, whereas if the sequence is reversed, the failure is referred to as brittle-shear. For the brittle-shear type of failure the drift capacity is particularly small and in any case is less than the nominal yielding drift

θ_{y}

of the element.

Because flexural yielding is the benchmark reference in assessment procedures, the drift at the onset of longitudinal bar yielding is needed to define all other forms of failure by comparison. Thus,

θ_{y}

is calculated either by member analysis (i.e., Response 2000), or according to Greek Code for Interventions (KANEPE, 2017)) and the EN 1998-3, 2005. Alternatively, mechanics-based relationships may be used (i.e.,

θ_{y} = \frac{1}{3} . φ_{y} . L_{s}

, where

φ_{y} = m i n \{2.1 \frac{ε_{y}}{h}, \frac{0.75 ε_{c 0}}{χ}\},

and χ the height of the compression zone that equals to

ξ d

, and

L_{s}

is the shear span and h the cross-sectional height). The values of drift where brittle failures are developed are obtained from

θ = θ_{y} \frac{V_{n}}{V_{f l e x}}

, where

V_{n}

is the member shear strength and

V_{f l e x}

, is the flexural strength calculated from the yielding moment of the critical section divided by the shear span (Pardalopoulos et al., 2011). It is noted that in the case of shear failure before flexural yielding, the ratio

\frac{V_{n}}{V_{f l e x}} \leq 1

. The shear strength

, V_{n}

for the needs of seismic assessment are obtained from EN1998-3, 2005, Pardalopoulos et al., (2013), ASCE/SEI 41-13 and respectively, using mean values for material strengths as shown in Table 1.

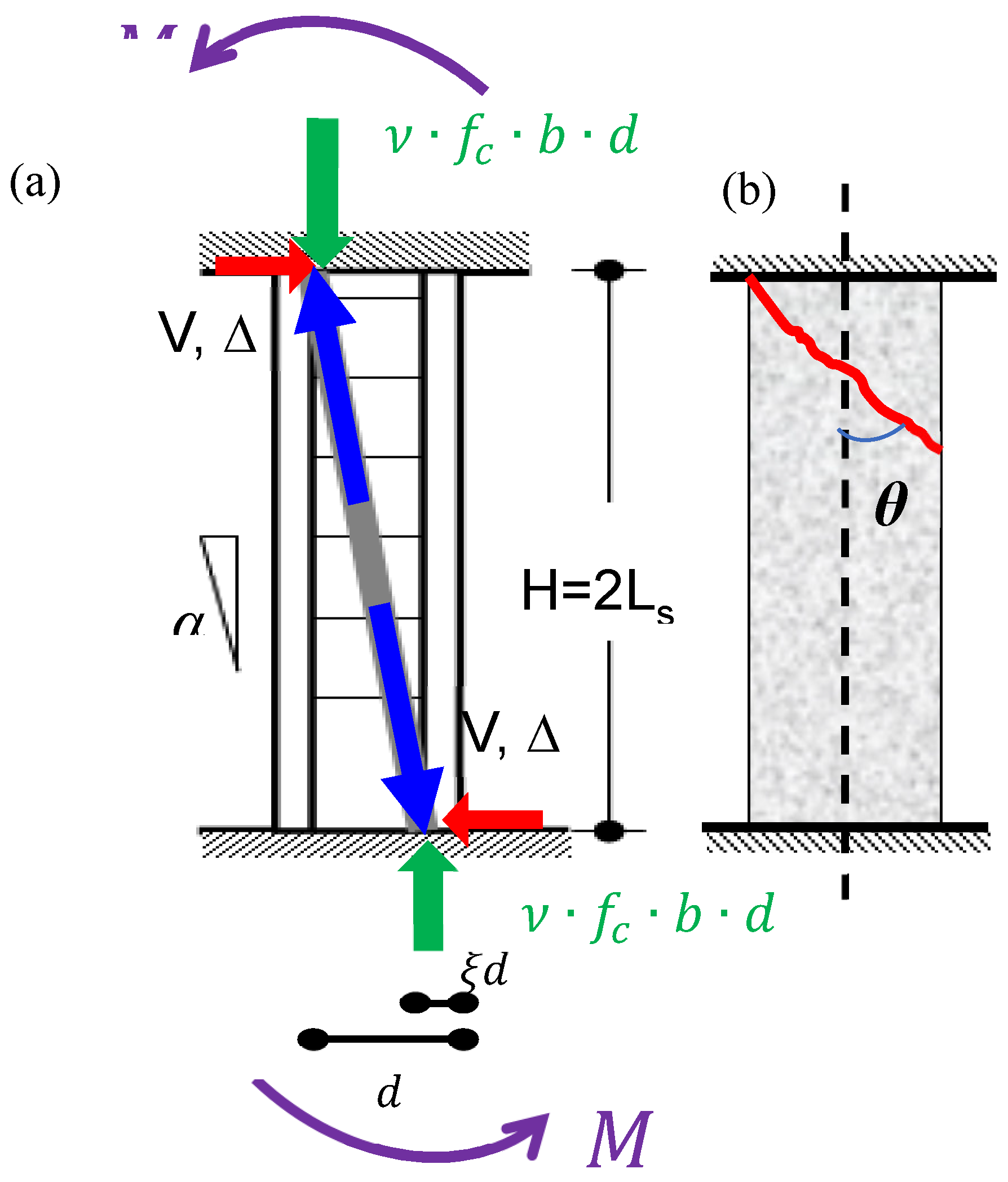
Ioannou et al. 2018 considered the EN1998-3, 2005 expressions and the model of Pardalopoulos et al. (2013) with some additional modifications that had been proposed earlier. First, the concrete contribution term is taken as per the Tureyen and Frosh (2003) approach where the underlying assumption is that shear transfer in cracked sections under cyclic loading occurs mainly in the compression zone of the member. As for the second, the axial load contribution is accounted for, provided that the axial load ratio exceeds a lower limit of 0.1 (the sign convention used is compression positive). This is performed to ensure that cracks in the compression zone are closed and that the force component transferred may be non-trivial. In the case of the third, the number of stirrups activated in the V_w term is determined from the inclination of the critical crack plane measured with reference to the longitudinal axis, θ_v which is usually not taken as 45^ο as it is assumed from previous available models in the literature [cotθ_v = 1] but rather, it depends on the axial load magnitude acting on the section (Figure 1(b)).

Relevant studies that have applied the above-mentioned framework have been conducted by Aschheim and Moehle, 1992; Lynn and Moehle, 1996; Sezen and Moehle, 2004; Elwood and Moehle, 2003; Priestley et al., 1996. Regarding the proposed relationship from Pardalopoulos et al. (2013), for consistency with fundamental principles, a correction has been proposed at a later stage where the effective concrete section area contributing to the shear strength at the critical section is equal to the area of compression zone, and therefore the

0.5 \sqrt{f_{c}'} \cdot (0.8 A_{c})

is replaced with

0.4 \sqrt{f_{c}'} \cdot (χ \cdot b)

(Tureyen and Frosch, 2003) – at this point, the compression zone height is taken equal to χ = ξd (Berry et al., 2004).

Consequently, for the model considered, the contribution of the transverse reinforcement (V_w) is taken into consideration as long as it has been confirmed that at least one stirrup meets the critical sliding plane. Finally, all terms are reduced with increasing displacement ductility through a postulated reduction factor

0.7 \leq η (μ_{Δ}) \leq 1

3. Dataset Collection

The dataset employed in the current investigation was composed of 74 specimens featuring old-type steel reinforcing setups. The reporting of a pure shear or flexure-shear failure, which meant that longitudinal reinforcement yielding occurred before the observed shear failure, was the criterion for evaluating the specimen’s selection. This is a consequence of the circumstance that in that case, a reduction in shear strength was more prominent when the resistance envelope curve’s maximum shear force value was exceeded during a corresponding increase in drift. More specifically, 44 specimens showed a flexure-shear type of failure whereas 30 specimens failed in shear. Axial failure and drift during shear might also be more clearly identified. A few of the specimens were taken from databases that have been published and accessible by Berry et al. (2004) and Kim et al. (2019). The data collection is shown in Table 2.

The cross-section’s height

h

, width

b

, and element shear span

L_{s}

are geometric dimensions that are usually used for the development of predictive models. It’s important to note that the column’s aspect ratio

\frac{L_{S}}{d}

varies from 1.0 to 4.8, covering short and slender RC columns. The concrete cover c, reinforcement details such as the transverse reinforcement diameter

d_{b w}

, the spacing of the transversal reinforcements, the longitudinal reinforcement ratio

ρ_{t o t}

, and the transversal reinforcing bar ratio

ρ_{w}

, are additional parameters that are included in the dataset. The uniaxial compressive strength of the concrete

f_{c}^{'}

and the yield strength of the longitudinal reinforcement

f_{y l}

and transverse reinforcing bars

f_{y w}

make up the material properties. The values of

f_{c}^{'}

vary from 16 to 86 MPa, which covers the case of high-strength concrete materials. Moreover, the crucial parameters such as the axial load P (superstructural loads) and the maximum experimental shear strength

V_{e x p, m a x} (k N)

are considered in the dataset.

4. Machine Learning Algorithms

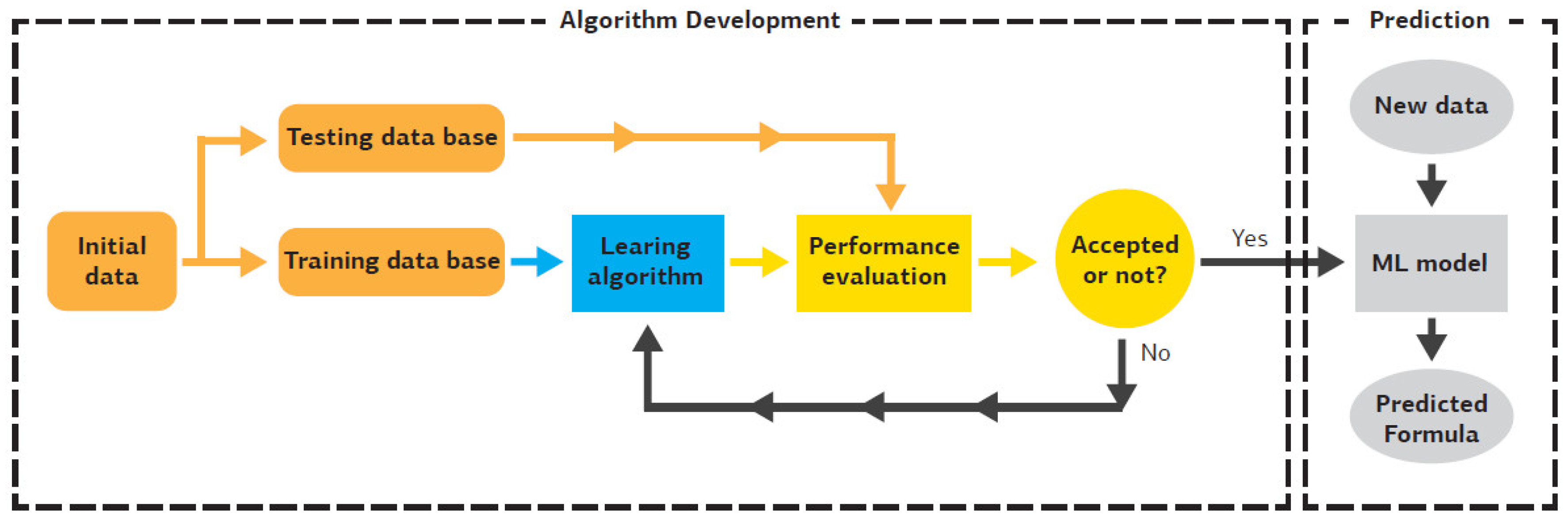
Thai (2022) stated that ML is the process of educating a computer system (ML model) on how to produce an accurate prediction when provided with new data. A typical ML flow chart for predictive modeling is shown in Figure 2. The computer system is educated to be able to gain knowledge and develop until its performance is met by applying a learning algorithm and initial data. As a result, both the effectiveness of the learning algorithm and the properties of the initial data have a significant impact on how accurate an ML model is. Building an ML model involves three basic steps: setting up the database, training the model, and assessing it.

The input and output variables that make up an ML model’s initial data are given as features (input variables) and labels (output variables), which are referred to in ML terminology. A structure’s geometric dimensions and material properties, for example, are categorized as features when forecasting how the structure will behave, whereas its maximum strength and ductility are employed as independent variables. For improved performance, some ML algorithms demand that all input data be scaled in the [0,1] range (Chollet, 2017). Initial data are divided into training and testing groups at random to evaluate the performance of ML models. It is important to note here that in order to determine the numerical performance and accuracy of a predictive model, error metrics are used such as the mean absolute error (MAE) and mean squared error (MSE).

In a range of scientific areas, including simulation-based engineering research, the usage of ML algorithms has grown significantly in recent years (Markou et al., 2024). ML algorithms are a very promising tool for tackling computationally challenging issues given their predictive abilities have been demonstrated in several applications. Different techniques are used to produce answers that cannot be reached by standard numerical procedures. Some of the often-used ML numerical techniques are random forest, gradient boosting (Breiman, 2001), and ANNs (Bakas et al., 2019). These models, however, are frequently too sophisticated to be effectively deployed and tested in practical situations. Improved ML approaches have recently been created in order to solve these shortcomings (Gravett et al., 2021 and AlHamaydeh et al., 2022).

The present research investigation has employed the following techniques:

➢: Linear Regression (LRegr): The simplest regression model in ML is called linear regression, and it assumes that the relationship between the input and output variables is best described by a straight line (linear function). This method is used as a base numerical technique, and it is compared to the more advanced ML algorithms.
➢: Nonlinear Regression (NLRegr): In nonlinear regression, Ruckstuhl (2016) states that functions with nonlinear parameters are utilized. Such a function was frequently drawn from theory. Markou et al. (2024) proposed the POLYRG-HYT that has advanced predictive features, thus it is adopted herein for the needs of the numerical analysis.
➢: Extreme Gradient Boosting (XGBoost): The XGBoost algorithm was proposed by Chen and Guestrin (2016) in order to accelerate the GBM algorithm, which is currently highly difficult to implement owing to its sequential model training. XGBoost uses numerous strategies for surpassing GBM in speed. For example, the randomization technique is used to reduce overfitting and increase training speed. Compressed column-based structure is also used to store data to reduce the cost of sorting which is the most time-consuming part of tree learning. For the needs of this research work, the XGBoost-HYT-CV is adopted as it was presented by Markou et al. (2024).

According to Markou et al. (2024), the proposed tuning for the case of the XGBoost-HYT-CV is performed for the following significant training parameters:

Maximum Number of XGBoost Rounds ∈ [10, 20, . . . , 1000],
Maximum tree depth ∈ [1, 7, 15],
Learning Rate Eta ∈ [0.05, 0.2, 0.5],
Colsample_bytree ∈ [0.5, 1],
Subsample ∈ [0.5, 1].

5. Investigation of the Proposed and Existent Formulae

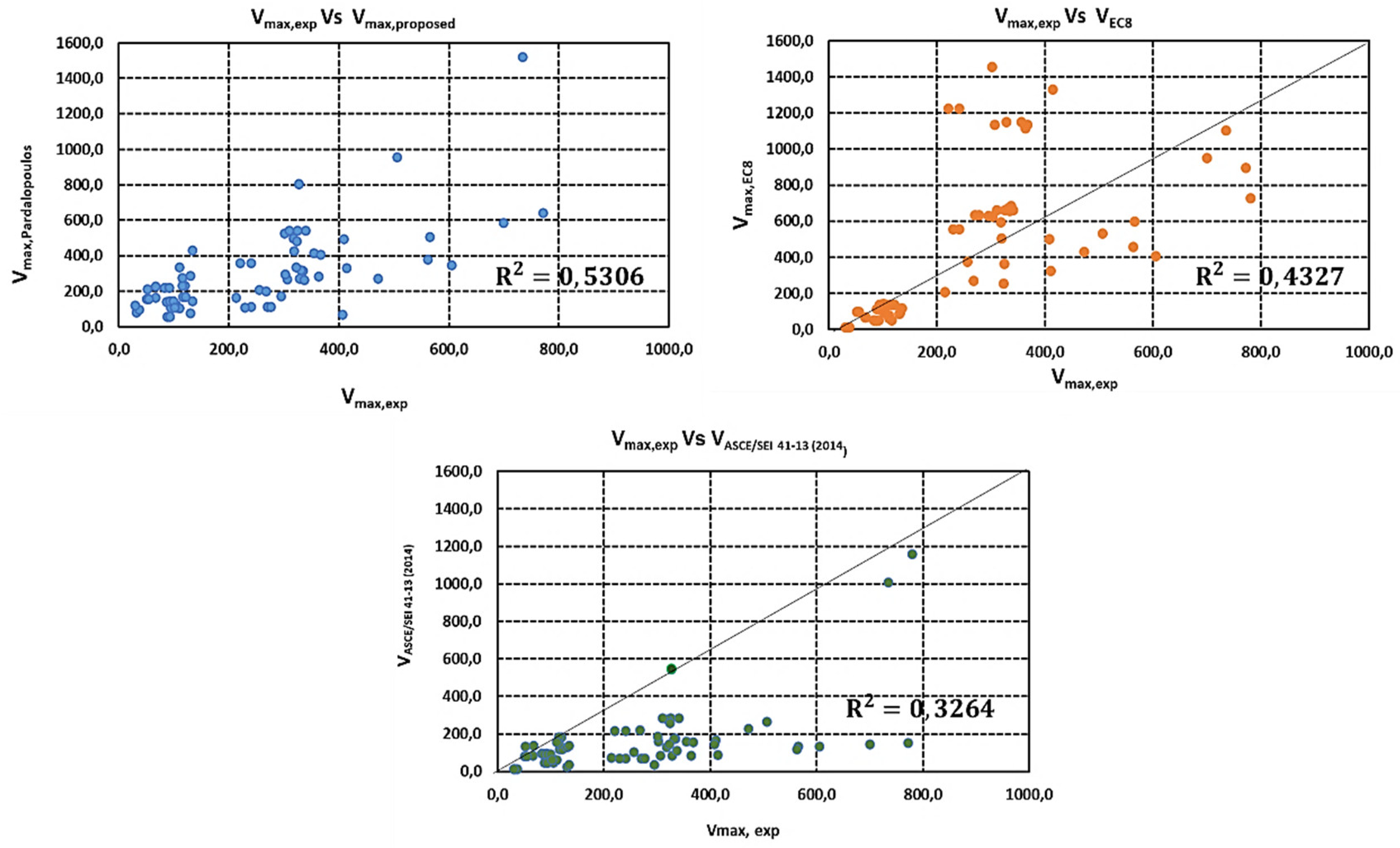
Figure 3 demonstrates a comparison between experimental results from the dataset presented in Table 2 and the proposed models from EN1998-3 (2005), Pardalopoulos et al. (2013) and ASCE/SEI 41-13 (2014) for the shear strength evaluation of the under study RC columns. The objective of the study was to propose an improved model utilizing a numerical technique as described in the next section by confirming the consistency of the under-study models in terms of experimental RC column shear or flexure-shear failures.

The 45° line in Figure 3 represents the equal value correlation, while the points above and below indicate instances where the analytical estimate differs from the corresponding experimental value. Deviations from the equal value line suggest poor predictive accuracy, whereas consistent overestimation highlights the need for a safety factor. It is evident that the Pardalopoulos et al. (2013) model has a correlation coefficient of R = 0.54, which is higher than that of the current EN1998-3 (2005) model (R = 0.43) and the corresponding ASCE/SEI 41-13 (2014) model which derived a correlation coefficient R = 0.33. This underscores the necessity for improving maximum shear strength estimates.

5.1. Proposed Predictive Models

The basic principles of POLYREG-HYT ML algorithm are based on the polynomial regression approach with hyperparameter tuning (Ioannou et al., 2023) and are targeted at the construction of nonlinear terms composed of different combinations of independent variables up to the 3rd degree. The approach may automatically derive the optimal predictive model while avoiding overfitting by selecting nonlinear characteristics that correspond to the lowest prediction error.

95, 90, 85, and 80 percent of the data were used to train the POLYREG-HYT algorithm (Markou et al., 2024) by identifying relative relationships. The remaining 5, 10, 15, and 20 percent, respectively, were used to evaluate the performance of the numerically obtained shear strength equations (testing dataet). In a cross-validation context, this process was repeated five times using randomly permuted subsets of the training set. It must be noted herein that all analyses were performed through the use of the nbml software (Markou et al., 2024) that is written in Python.

Three datasets were utilized in the parametric investigation performed for the needs of this research work. The first matched the independent variables in Pardalopoulos et al. (2013), the other matched the independent variables in EN1998-3 (2005) and the last matched the independent variables of ASCE/SEI 41-13 (2014). Five iterations of the POLYREG-HYT algorithm were run for every train-test split ratio. The performance of POLYREG-HYT and Linear Regression (LRegr) algorithms was assessed by means of a comparative study of the obtained data. The correlation coefficient (R) and the mean absolute percentage error (MAPE) were used to assess the predictions made by the predictive models.

After running the ML algorithm, three predictive models were obtained as can be seen in Eqs 1, 2 and 3 that correspond to the POLYREG-HYT. The three equations correspond to the three different datasets described above (i. EN1998-3, 2005, ii. Pardalopoulos et al., 2013 and iii. ASCE/SEI 41-13, 2014).

According to the numerical results, using the POLYREG-HYT method and analyzing dataset 1 (based on EN1998-3, 2005 variables), we determined that the optimal split ratio to be 90/10%. The highest R values achieved were 98.44% for training and 99.4% for testing, with a MAPE value of 17.7% on the test dataset. For dataset 2 (based on the Pardalopoulos et al. (2013) model variables), the best split ratio was again found to be 90/10%. In this case, the training and testing R were 95.26% and 99.65%, respectively, with a MAPE of 13.9%. Finally, for dataset 3 (based on ASCE/SEI 41-13, 2014 variables), the optimal split ratio was the same as before (90/10%), where the R values obtained were 99.14% for training and 99.0% for testing, with a MAPE of 15.5% same on the testing dataset.

\begin{matrix} V_{e x p, 1} = - 4.51614 \cdot 10^{- 1} \cdot h + 1.83925 \cdot 10^{- 2} \cdot ρ_{t o t} \cdot s + 1.77130 \cdot 10^{- 1} \cdot d - 3.67223 \cdot 10^{- 1} \cdot a_{d} \cdot s \\ + 2.69541 \cdot 10 \cdot ρ_{t o t} + 1.72100 \cdot 10 \cdot d_{b l} + 4.41065 \cdot 10^{- 1} \cdot b \cdot ρ_{w} - 2.63221 \cdot 10^{- 4} \cdot V_{r}^{2} + 1.22815 E \cdot \\ 10^{- 1} \cdot d_{b w} \cdot s + 2.38053 \cdot 10^{- 2} \cdot h \cdot f_{c}^{'} + 3.25673 \cdot 10^{- 1} \cdot V_{r} + 6.82692 \cdot 10^{- 4} \cdot A_{t r} \cdot f_{y w} \cdot - 9.40552 \cdot \\ 10^{- 1} f_{c}^{'} \cdot d_{b w} + 1.99045 \cdot 10 * c * ρ_{w} - 3.70053 \cdot 10 \cdot ρ_{w}^{2} + 8.01932 \cdot 10 \cdot v - 8.63480 \cdot 10 \cdot c \cdot v + \\ 4.64570 \cdot 10^{- 4} \cdot f_{y l} \cdot s + 9.46359 \cdot 10^{- 5} \cdot P \cdot V_{r} + 2.91722 \cdot 10^{- 3} \cdot f_{y l} \cdot f_{c}^{'} + 1.09822 \cdot 10^{- 4} \cdot d \cdot P - \\ 8.39975 \cdot 10^{- 1} \cdot a_{d} \cdot f_{c}^{'} w h e r e P i n K N \end{matrix}

(1)

\begin{matrix} V_{e x p, 2} = 4.50889 \cdot 10^{- 3} \cdot f_{y l} \cdot s + 1.23497 \cdot 10 \cdot h + 3.49000 \cdot 10 \cdot a_{d} - 1.11066 \cdot 10 \cdot d + 2.97440 \cdot 10 \cdot \\ ρ_{t o t} - 9.80018 \cdot 10^{- 5} \cdot A_{t r}^{2} + 4.30251 \cdot 10^{- 4} \cdot P \cdot 0.4 \cdot ξ \cdot b \cdot d \cdot \\ f_{c}^{'} + 1.59616 \cdot 10^{- 3} \cdot s \cdot 0.4 \cdot ξ \cdot b \cdot d \cdot f_{c}^{'} - 3.91027 \cdot 10^{- 1} \cdot A_{t r} - 2.49454 \cdot 10 \cdot s + 3.61139 \cdot 10 \cdot 0.4 \cdot ξ \cdot b \cdot d \cdot f_{c}^{'} + 3.58780 \cdot 10^{- 1} \cdot V_{r} - \\ 1.34864 \cdot 10 \cdot a_{d} \cdot 0.4 \cdot ξ \cdot b \cdot d \cdot f_{c}^{'} + 1.78231 \cdot 10^{- 2} \cdot f_{c}^{'} \cdot A_{t r} + 1.46317 \cdot 10^{- 4} \cdot f_{y l} \cdot V_{r} - 2.12422 \cdot \\ 10^{- 3} \cdot h \cdot f_{y l} + + 1.77066 \cdot 10^{- 2} \cdot d \cdot d_{b l} - 2.05816 \cdot 10^{- 1} \cdot v * V_{r} + 1.17495 10^{- 1} \cdot d_{b w} \cdot s - 2.04027 \cdot \\ 10^{- 1} \cdot a_{d} \cdot f_{c}^{'} - 4.38284 \cdot 10 \cdot a_{d} \cdot v + 6.14056 \cdot 10 \cdot d_{b w} - 3.24594 \cdot 10^{- 2} \cdot v \cdot P - 1.11574 \cdot 10 \cdot d_{b w}^{2} + \\ 1.18462 \cdot 10^{- 1} \cdot f_{y w} \cdot v - 9.82636 \cdot 10 \cdot d_{b w} \cdot v w h e r e P i n K N \end{matrix}

(2)

\begin{matrix} V_{e x p, 3} = 1.17316 \cdot 10^{2} a_{d} - 6.90891 \cdot 10^{- 1} \cdot d - 1.26582 \cdot 10 \cdot c + 3.39341 \cdot 10^{- 1} \cdot f_{y l} - 4.92902 \cdot 10 \cdot \\ a_{d} \cdot ρ_{t o t} - 1.96488 \cdot 10 \cdot d_{b w} + 1.48838 \cdot 10 \cdot V_{c} + 5.59181 \cdot 10 \cdot c \cdot ρ_{t o t} + 1.60358 \cdot 10^{- 1} \cdot d \cdot d_{b w} - \\ 2.39573 \cdot 10^{- 1} \cdot c \cdot f_{c}^{i} - 4.45350 \cdot 10 \cdot c \cdot v + 1.39423 \cdot 10^{- 2} \cdot h \cdot f_{c}^{i} + 9.45579 \cdot 10^{- 3} \cdot h \cdot V_{c} - 9.21490 \cdot \\ 10^{- 2} \cdot b \cdot a_{d} + 2.81197 \cdot 10^{- 1} \cdot f_{y w} + 4.43107 \cdot 10^{- 2} \cdot c \cdot c - 2.95561 \cdot 10^{- 2} \cdot d_{b w} \cdot f_{y w} \end{matrix}

(3)

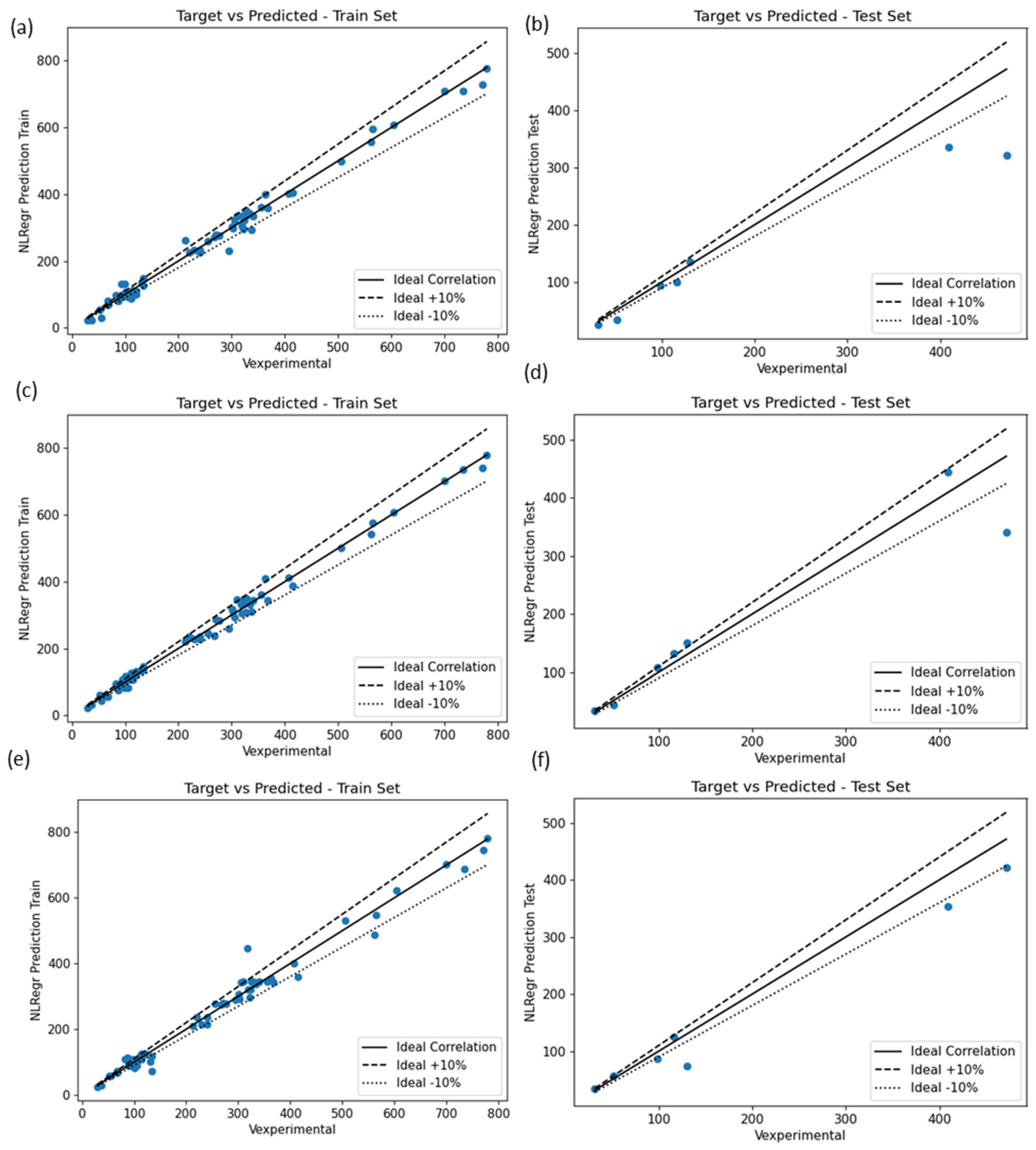
Figure 4 shows the results of the numerically derived models during the testing and training of POLYREG-HYT for the case of the three datasets. It is easy to observe that a strong correlation was achieved by examining the correlation between the relationships of the experimental values versus those derived from the formulae for each scenario. It is also worth noting that, despite the fact that the newly developed predictive models differ significantly from the original models proposed in the international literature (especially the number of terms), the proposed formulae were able to not only predict the shear strengths accurately, but to provide with a 2-fold improvement in terms of correlation when compared with the three previously proposed predicrive equations (i. EN1998-3, 2005, ii. Pardalopoulos et al., 2013 and iii. ASCE/SEI 41-13, 2014). This highlights the numerical superiority of the adopted ML algorithm of POLYREG-HYT that has the ability to provide us with a closed form solution (Markou et al., 2024).

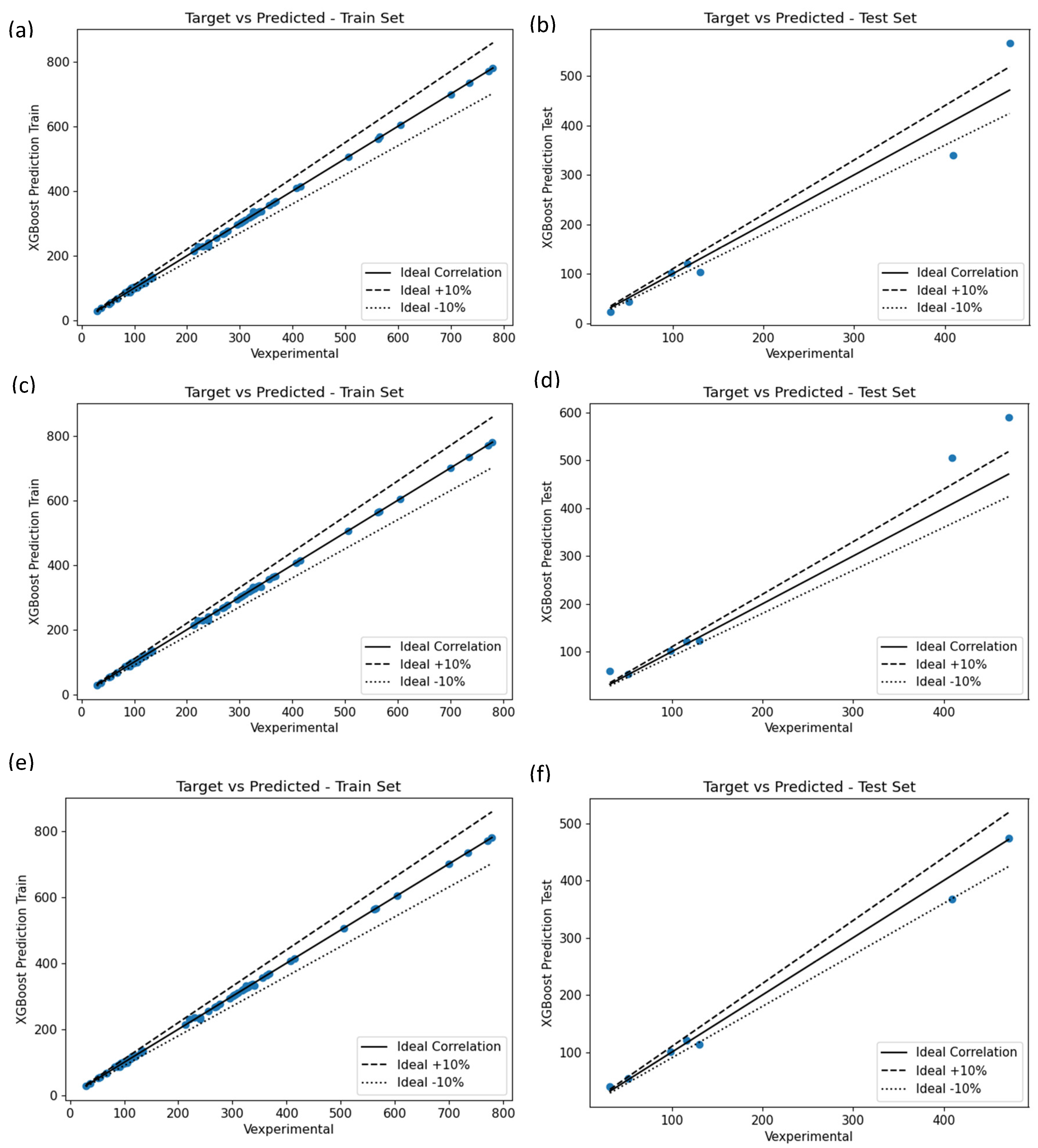
To enhance the accuracy of the predictive models, XGBoost-HYT-CV (Markou et al., 2024) was employed in addition to the POYREG-HYT and LRegr. The results for the test and training datasets using XGBoost-HYT-CV are presented in Figure 5 and Table 3, Table 4 and Table 5. These findings demonstrate that the advanced ML method achieved the highest correlation coefficient values between experimental and predicted results. Specifically, Figure 5 and Table 3, Table 4 and Table 5 showcase the outcomes of applying XGBoost-HYT-CV to the three dataset with a 90/10% test-train ratio.

Based on the correlation coefficient R values and the values of the MAPE error metric presented in Table 3, Table 4 and Table 5, the dataset developed based on Pardalopoulos et al. (2013) derived the highest correlation coefficient value (R = 99.65%) when using the ML algorithm of XGBoost-HYT-CV. The ASCE/SEI 41-13, 2014 dataset follows with a correlation coefficient of 99.58% and an error of 8.95% (on the test dataset). Lastly, the EN 1998-3, 2005-prepared dataset derived an optimum correlation coefficient value of 98,45% and an error of 17.7% for the case of the POLYREG-HYT ML algorithm followed by a 97% correlation coefficient and a corresponding 15.3% MAPE value for the case of XGBoost-HYT-CV. It is easy to observe that even though the POLYREG-HYT managed to derive a higher correlation coefficient (1.45% higher) compared to the one obtained by XGBoost-HYT-CV, the latter was able to result a lower MAPE value when used on the test dataset.

5.2. Sensitivity Analysis

Sensitivity analysis was performed to evaluate the effect of a specific input on the target variable. According to Hariri-Ardebili (2018), ML is a particular kind of artificial intelligence that “learns” as it finds new patterns in data and develops techniques to enhance decision-making based on knowledge concealed in large datasets. Sensitivity analysis may be applied to both the ML tasks of classification and regression.

To allow for the permutation of only one feature around its given values, all features at certain values (i.e., 25%, Median, and 75% quantiles) are maintained fixed as soon as the trained models are formed. The matching sensitivity curves for every feature and every trained model are obtained after these values are established in training mode. Therefore, it is possible to determine the equivalent influence of each input feature on the target variable, which is shown in a summarized manner in Figure 6.

It is important to note at this point that given its superior predictive performance, XGBoost-HYT-CV (used on the Pardalopoulos et al., 2013 dataset) was selected to perform the sensitivity analysis shown in Figure 6. This numerically developed predictive model exhibited the highest correlation coefficient, lowest MAPE, and the most accurate predictions on the test dataset. Additionally, the sensitivity analysis across all three datasets revealed a consistent hierarchy of parameter importance, reinforcing the credibility of the Pardalopoulos et al. (2013) dataset.

The sensitivity analysis, as illustrated in Figure 6, reveals key parameters that are consistent with previous research findings, thus strengthening the conclusions derived from the numerical findings of this research work. According to Figure 6, the primary factors influencing the shear strength of RC columns include the compressive zone height, specimen geometry, axial load ratio, concrete cover, longitudinal and transverse reinforcement percentages, effective depth, stirrup yield stress, transverse reinforcement area within diagonal cracks, stirrup spacing, and the aspect ratio.

Furthermore, these findings align with prior studies focused solely on the experimental evaluation of shear strength in older-style RC structural elements. Sezen and Mohele (2004) demonstrated that the shear strength of lightly reinforced rectangular columns is notably influenced by variables such as aspect ratio, axial load, amount of transverse reinforcement, and deformation ductility requirements.

6. Conclusion

The present study investigated the strength and deformation parameters defining the mechanical behavior of RC columns under lateral sway such as what is occurring during seismic loading, focusing on the details of the failure mechanisms of columns. A carefully chosen collection of specimens from the experimental database that highlights the behavior of columns experiencing shear failure after flexural yielding was assembled to study the parametric sensitivity of the examined data, while at the same time, an evaluation of existing relationships for the limit state failure in strength term was carried out (shear mechanism failure and bearing capacity at failure).

To develop a predictive model for RC columns, a dataset of 74 samples was employed to train a polynomial regression model optimized through hyperparameter tuning. The resulting predictive formula, when using POLYREG-HYT, outperformed existing models in the literature, achieving a correlation coefficient R of 99.1% compared to 53.1%, 43.3%, and 32.6% for the case of the EN1998-3, Pardalopoulos et al., and ASCE/SEI 41-13 predictive models, respectively.

Furthermore, the XGBoost-HYT-CV ML algorithm was found to derive the most accurate predictive model reaching a correlation coefficient R 99.65% when used on the test dataset. This corresponds to a 2.3 times improved correlation coefficient compared to the EN1998-3 model and almost 2 times improvement compared to the Pardalopoulos et al. 2013 predictive model. This hihglights the numerical superiority of the proposed predictive model when used to compute the shear strength of RC columns.

Finally, it must be noted that the preparation of the dataset foresaw the use of specific experimental results that followed a specific type of failure. Given that ML algorithms have the ability to provide with complicated connections between the input and output features, future work will foresee the use of larger datasets for the development of enhanced predictive models that will not be limited by the type of shear failure of the RC column nor any geometrical restraints. This research work will allow the development of universal predictive models that will allow Civil Engineers to be able to compute the ultimate shear strength of RC columns without the need of making any adjustments or assumptions when using the predictive models.

References

Yu, B.; Liu, S.; Li, B. Probabilistic Calibration for Shear Strength Models of Reinforced Concrete Columns. J. Struct. Eng. 2019, 145 (5), 04019026. [CrossRef]
Tureyen, A. K. and Robert, J. F. Concrete Shear Strength: Another Perspective. ACI Structural Journal 2003, 100 (5). https://doi. org/10. 14359/12802.
Tran, C.T.N.; Li, B. Shear strength model for reinforced concrete columns with low transverse reinforcement ratios. Adv. Struct. Eng. 2014, 17, 1373–1385.
Thai, H.-T. Machine Learning for Structural Engineering: A State-of-the-Art Review. Structures 2022, 38, 448–491. [CrossRef]
Sun, B.; Liu, H.; Zhou, S.; Li, W. Evaluating the Performance of Polynomial Regression Method with Different Parameters during Color Characterization. Mathematical Problems in Engineering 2014, 2014, 1–7. [CrossRef]
Shaw, P.; Greenstein, D. and Lerch, J. et al., “Intellectual ability and cortical development in children and adolescents,” Nature, vol. 440, no. 7084, pp. 676–679, 2006.
Sezen, H.; Moehle, J. P. Shear Strength Model for Lightly Reinforced Concrete Columns. J. Struct. Eng. 2004, 130 (11), 1692–1703. [CrossRef]
Sezen, H. and Moehle, J. P. Seismic Behavior and Modeling of Reinforced Concrete Building Columns, University of California, 2002.
Sattar, S. Sensitivity Analysis of Reinforced Concrete Structures:: A Comprehensive Review; NIST TN 2254; National Institute of Standards and Technology: Gaithersburg, MD, 2023; p NIST TN 2254. [CrossRef]
Ruckstuhl, A. Introduction to Nonlinear Regression; IDP Institut f ̈ ur Datenanalyse und Prozessdesign ZHAW Z ̈ urcher Hochschule f ̈ ur Angewandte Wissenschaften, 2016.
Priestley, M. J. N.; Verma, R.; Xiao, Y. Seismic Shear Strength of Reinforced Concrete Columns. Journal of Structural Engineering 1994, 120 (8), 2310–2329. [CrossRef]
Pardalopoulos, S. J.; Thermou, G. E.; Pantazopoulou, S. J. Rapid Preliminary Seismic Assessment Methodology for Non-Conforming Reinforced Concrete Buildings. 2011, 17.
Pardalopoulos, S. J.; Thermou, G. E.; Pantazopoulou S. J. Preliminary Seismic Assessment Method for Identifying R. C. Structural Failures. In Computational Methods in Earthquake Engineering; Springer Dordrecht Heidelberg New York London, Vol. 2, 2013.
Murphy, K. P. Machine Learning: A Probabilistic Perspective; Adaptive computation and machine learning series; MIT Press: Cambridge, MA, 2012.
Markou, G.; Bakas, N. P. Prediction of the Shear Capacity of Reinforced Concrete Slender Beams without Stirrups by Applying Artificial Intelligence Algorithms in a Big Database of Beams Generated by 3D Nonlinear Finite Element Analysis. Computers and Concrete 2021, 28 (6), 433–447. [CrossRef]
Markou, G., Bakas, N.P., Chatzichristofis, S.A. and Papadrakakis, M. (2024), General Framework of High-Performance Machine Learning Algorithms: Application in Structural Mechanics, Computational Mechanics, Volume 73, pages 705–729. [CrossRef]
Lynn, A. C. and Moehle, J. P. Seismic Evaluation of Existing Reinforced Concrete Building Columns. Thesis, University of California at Berkley, California, 2001.
Kim, C.-G.; Park, H.-G.; Eom, T.-S. Cyclic Load Test and Shear Strength Degradation Model for Columns with Limited Ductility Tie Details. J. Struct. Eng., 145 (2), 04018249, 2019. [CrossRef]
Ioannou, A.; Pantazopoulou. S. J., G., S.; Illampas, R. Limit States Behaviour (or Failure) of Reinforced Concrete Columns; Hellenic Concrete Conference, 2018.
Ioannou, A. I.; Bakas, B.; Markou, G.; Westhuizen V. D. A. M.; Pantazopoulou S. J.; Petrou M. F.; Charmpis D. C. Prediction of Reinforced Concrete Columns Limit States Using Machine Learning Algorithms. In COMPDYN 2023; Athens, Greece, 2023.
Hariri-Ardebili M. Risk, reliability, resilience (R3) and beyond in dam engineering: A state-of-the-art review. International journal of disaster risk reduction, 2018, 31:806–831.
Gravett, Z. D., Mourlas, C., Taljaard V. L., Bakas P. N., Markou, G. and Papadrakakis, M. (2021), New Fundamental Period Formulae for Soil-Reinforced Concrete Structures Interaction Using Machine Learning Algorithms and ANNs, Soil Dynamics and Earthquake Engineering, 144 (2021), 106656.
European Committee for Standardization. EN 1998-3:2005, Design of Structures for Earthquake Resistance – Part 3: Assessment and Retrofitting of Buildings, 2005.
Elwood, K. J.; Moehle, J. P. Drift Capacity of Reinforced Concrete Columns with Light Transverse Reinforcement. Earthquake Spectra 2005, 21 (1), 71–89. [CrossRef]
Design Team for the Composition of Greek Regulations for Assessment, Retrofit and Strengthening of Existing Reinforced Concrete Structures, Harmonization of KA. NE. ΠΕ. with Eurocodes, Athens, 2017.
Chollet F. Deep learning with Python: Manning; 2017.
Chen, T. Guestrin, C. XGBoost: A scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2016. p. 785–94.
Chen, T. Guestrin, C. XGBoost: A scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2016. p. 785–94.
Breiman, L. Random forests, Machine learning 45 (1) (2001) 5–32,.
Biskinis D.; Roupakias G. K.; Fardis M.N. Degradation of Shear Strength of RC Members with Inelastic Cyclic Displacements. ACI Structural Journal 2004, 101 (6), 773–783.
Bezanson, J.; Edelman, A.; Karpinski. S., S., V. B. Julia: A Fresh Approach to Numerical Computing. 59 (1), 65–98, 2017. [CrossRef]
Berry, M. Parrish, M.; Eberhard, M. PEER Structural Performance Database User’s Manual (Version 1.0). 44, 2004.
Bentz, E.; Collins, M. P., Response 2000 User’s Manual,Version 1. 1., September 2001.
Bakas, N. P; Langousis, A.; Nicolaou M.; Chatzichristofis, S. A. A gradient free neural network framework based on universal approximation theorem, arXiv preprint arXiv:1909.13563, (2019).
Aval, S. B.; Ketabdari, H.; Gharebaghi, S.A. Estimating Shear Strength of Short Rectangular Reinforced Concrete Columns Using Nonlinear Regression and Gene Expression Programming. Structures 2017, 12, 13–23. [CrossRef]
Aschheim, M.; Moehle, J. P. Shear Strength and Deformability of RC Bridge Columns Subjected to Inelastic Cyclic Displacements. California Department of Transportation March 1992.
ASCE/SEI 41-13, 2014, Seismic Evaluation and Retrofit of Existing Buildings, American Society of Civil Engineers, Reston, VA.
Anthos, I. Ioannou. Seismic Behavior and Assessment of Reinforced Concrete Elements with Brittle Details & Retrofitting Using Engineered Cementitious Composites. Ph.D. Dissertation, University of Cyprus, Nicosia, 2022.
AlHamaydeh, M.; Markou, G.; Bakas N.; and Papadrakakis, M. Ai-based shear capacity of frp-reinforced concrete deep beams without stirrups, Engineering Structures 264 (2022).114441.

Figure 1. EN model for the contribution of the diagonal strut to shear strength (a) Definition of the strut angle, and (b) definition of the critical crack angle, θ_v.

Figure 2. Usual ML flow chart (Thai, 2022).

Figure 3. Correlation of experimental corrected maximum shear strength data vs. model predictions as (a) Proposed model by Pardalopoulos et al. (2013); (b) Proposed model by EN1998-3, 2005 and (c) Proposed model by ASCE/SEI 41-13 (2014).

Figure 4. Correlation between experimental shear strengths and numerically predicted values using the POLYREG-HYT method based on the following models: (a), (b) EN1998-3 (2005): Training and testing datasets; (c) and (d) Pardalopoulos et al. (2013): Training and testing datasets and (e) and (f) ASCE/SEI 41-13 (2014): Training and testing datasets.

Figure 5. Comparison of numerically predicted shear strengths using XGBoost-HYT-CV to experimental values and proposed model predictions (a, b) EN1998-3, 2005 dataset (c, d) Pardalopoulos et al., 2013 dataset and (e, f) ASCE/SEI 41-13, 2014 dataset.

Figure 6. A bar chart-based sensitivity analysis to assess the impact of different variables in the Pardalopoulos et al. (2013) dataset on model output.

Table 1. Typical shear strength models for shear critical R.C. columns.

References	Description of Models
EN1998-3, 2005	$V_{n}^{E} = V_{c} + V_{w} + V_{N} = η^{Ε} (μ) \cdot 0.16 \sqrt{f_{c}} (0.8 A_{c}) [\max \{0.5, 100 ρ_{t o t}\}] \cdot (1 - 0.16 \cdot \min \{5, \frac{L_{s}}{h}\})] + η^{Ε} (μ) \frac{A_{s t} f_{t t} (d - d^{'})}{s} + m i n \{N, 0.55 A_{c} f_{c}'\} \cdot \tan α$
	Where $η^{Ε} (μ) = (1 - 0.05 \min (5, μ_{Δ}^{p l}))$
Pardalopoulos et al., (2013)	$V_{n} = 0.4 ξ b d \sqrt{f_{c}'} + λ \cdot ν \cdot (b d f_{c}) \tan α + A_{s t} f_{y t} \frac{d (1 - ξ)}{s} \cdot \cot θ_{v}$ $θ_{v} = 4 5^{o} f o r ν \leq 0.10 θ_{v} = 4 5^{ο} - 1 5^{ο} . \frac{ν}{0.25} \geq 3 0^{ο} f o r ν \geq 0 .$
ASCE/SEI 41-13 (2014)	$V_{n} = η (μ_Δ) \cdot {(V}_{s} + V_{c}) = η (μ_Δ) [0.5 \cdot \sqrt{f_{c}^{'}} \sqrt{1 + \frac{N_{u}}{0.5 \cdot \sqrt{f_{c}^{'}} \cdot A_{g}}}] \frac{0.8 {\cdot A}_{g}}{\frac{L_{s}}{d}} + η (μ_Δ) \frac{A_{s t} {\cdot f}_{y t} \cdot d}{s} 0.7 \leq η (μ_Δ) \leq 1$

Table 2. Basic parameters and experimental shear strengths of 74 sets of shear critical columns.

	Reference	Test	$L_{s}$ (mm)	$b$ (mm)	$h$ (mm)	$c$ (mm)	$d_{b w}$ (mm)	$s$ (mm)	$ρ_{w}$ (%)	$ρ_{t o t}$ (%)	$f_{y l}$ (MPa)	$f_{y w}$ (MPa)	$f_{c}^{'}$ (MPa)	$P$	$V_{e x p . m a x} (k N)$
	Reference	Test	$L_{s}$ (mm)	$b$ (mm)	$h$ (mm)	$c$ (mm)	$d_{b w}$ (mm)	$s$ (mm)	$ρ_{w}$ (%)	$ρ_{t o t}$ (%)	$f_{y l}$ (MPa)	$f_{y w}$ (MPa)	$f_{c}^{'}$ (MPa)	( $k N$ )	$V_{e x p . m a x} (k N)$
1	Lynn et al. (1996)	3SLH18	1473,0	457,0	2946,0	38,1	9,5	457,0	0,1	3,0	331,0	400,0	25,6	503,0	270,0
2	Lynn et al. (1996)	3CMD12	1473,0	457,0	2946,0	38,1	9,5	305,0	0,2	3,0	331,0	400,0	27,7	1512,0	355,0
3	Lynn et al. (1996)	3CMH18	1473,0	457,0	2946,0	38,1	9,5	457,0	0,1	3,0	331,0	400,0	27,7	1512,0	328,0
4	Henkhaus et al. 2013	B1	736,5	457,0	1473,0	35,0	9,5	457,0	0,1	1,5	455,0	490,0	20,0	1545,5	565,5
5	Henkhaus et al. 2013	B2	736,5	457,0	1473,0	35,0	6,4	203,0	0,1	1,5	455,0	455,0	19,3	1531,7	317,2
6	Henkhaus et al. 2013	B3	736,5	457,0	1473,0	35,0	9,5	457,0	0,1	1,5	455,0	490,0	22,1	969,3	562,3
7	Henkhaus et al. 2013	B4	736,5	457,0	1473,0	35,0	9,5	457,0	0,1	2,5	441,0	490,0	24,1	2164,3	771,2
8	Henkhaus et al. 2013	B5	736,5	457,0	1473,0	35,0	9,5	457,0	0,1	2,5	441,0	490,0	23,4	2248,1	699,4
9	Henkhaus et al. 2013	B6	1473,0	457,0	2946,0	35,0	9,5	305,0	0,2	2,5	490,0	469,0	27,6	634,1	334,2
10	Henkhaus et al. 2013	B7	1473,0	457,0	2946,0	35,0	9,5	305,0	0,2	2,5	490,0	469,0	28,3	650,1	331,7
11	Henkhaus et al. 2013	B8	1473,0	457,0	2946,0	35,0	9,5	305,0	0,1	2,5	490,0	469,0	29,0	666,2	336,7
12	Zhou et al. 1987	104-08	160,0	160,0	320,0	12,5	5,0	40,0	0,7	2,2	341,0	559,0	19,8	406,0	82,7
13	Zhou et al. 1987	114-08	160,0	160,0	320,0	12,5	5,0	40,0	0,7	2,2	341,0	559,0		406,0	91,3
14	Kim et al. 2018	SBd2	1200,0	400,0	1200,0	40,0	12,7	165,0	0,4	2,5	571,0	500,0		870,4	340,2
15	Kim et al. 2018	SBd4	1200,0	400,0	1200,0	40,0	12,7	82,0	0,8	2,5	571,0	500,0		870,4	326,9
16	Kim et al. 2018	SCd2	1200,0	400,0	1200,0	40,0	12,7	165,0	0,4	2,5	571,0	500,0		870,4	325,4
17	Kim et al. 2018	SDd2	1200,0	400,0	1200,0	40,0	12,7	165,0	0,4	2,5	571,0	500,0		512,0	319,0
18	Kim et al. 2018	SDd4	1200,0	400,0	1200,0	40,0	12,7	82,0	0,8	2,5	571,0	500,0		870,4	326,9
19	Kim et al. 2018	RFd2	1200,0	250,0	1200,0	40,0	9,5	105,0	0,8	2,4	566,0	530,0		870,4	220,2
20	Nagasaka 1982	HPRC10-63	300,0	200,0	600,0	12,0	5,5	35,0	0,7	1,3	371,0	344,0		146,9	86,9
21	Arakawa et al. 1989	OA2	225,0	180,0	450,0	10,0	4,0	64,3	0,2	3,1	340,0	249,0		189,6	130,6
22	Arakawa et al. 1989	OA5	225,0	180,0	450,0	10,0	4,0	64,3	0,2	3,1	340,0	249,0		475,8	134,0
23	Umehara and Jirsa 1982	CUS	455,0	410,0	910,0	25,0	6,0	89,0	0,3	3,0	441,0	414,0		533,2	322,7
24	Umehara and Jirsa 1982	CUW	455,0	230,0	910,0	25,0	6,0	56,0	0,3	3,0	441,0	414,0		533,2	255,3
25	Umehara and Jirsa 1982	2CUS	410,0	410,0	230,0	25,0	6,0	89,0	0,3	3,0	441,0	414,0		1069,4	409,4
26	Bet et.al. 1985	1_1	305,0	305,0	305,0	25,0	6,0	210,0	0,2	2,4	462,0	414,0		289,3	213,6
27	Aboutaha et al. 1999	SC3	457,2	457,2	914,4	38,0	9,5	406,4	0,1	1,9	434,0	400,0		0,0	407,0
28	Aboutaha et al. 1999	SC9	914,4	914,4	457,2	38,0	9,5	406,4	0,1	1,9	434,0	400,0		0,0	604,5
29	Sokoli and Ghannoum(2016)	CS-60	457,2	457,2	457,2	38,1	16,0	140,0	1,5	4,7	464,0	472,0		290,0	779,6
30	Sokoli and Ghannoum (2016)	CS-100	457,2	457,2	457,2	38,1	10,0	114,0	0,7	2,9	700,0	820,0		1806,0	734,6
31	Lynn et al. (1996)	2CLH18	457,0	457,0	457,0	38,1	9,5	457,0	0,1	2,0	331,0	400,0		503,0	240,8
32	Lynn et al. (1996)	3CLH18	457,0	457,0	457,0	38,1	9,5	457,0	0,1	3,0	331,0	400,0		503,0	277,0
33	Lynn et al. (1996)	2SLH18	457,0	457,0	457,0	38,1	9,5	457,0	0,1	2,0	331,0	400,0		503,0	229,0
34	Lynn et al. (1996)(lap splice)	2CMH18	457,0	457,0	457,0	38,1	9,5	457,0	0,1	3,0	331,0	400,0		1512,0	306,0
35	Lynn et al. (1996)(lap splice)	3SMD12	457,0	457,0	457,0	38,1	9,5	305,0	0,2	3,0	331,0	400,0		1512,0	367,0
36	Matchulat et al. 2005	Sp.1	457,0	457,0	457,0	39,7	9,5	460,0	0,3	2,5	441,3	372,3		2159,5	414,0
37	Matchulat et al. 2005	Sp.2	457,0	457,0	457,0	39,7	9,5	460,0	0,3	2,5	441,3	372,3		1663,0	363,2
38	Sezen and Moehle 2002	Specimen 1	457,0	457,0	457,0	65,1	9,5	304,8	0,2	2,5	434,4	476,0		665,4	302,5
39	Sezen and Moehle 2002	Specimen 2	457,0	457,0	457,0	65,1	9,5	304,8	0,2	2,5	434,4	476,0		2666,1	301,0
40	Sezen and Moehle 2002	Specimen 4	457,0	457,0	457,0	65,1	9,5	304,8	0,2	2,5	434,4	47,0		664,7	294,6
41	Wight and Sozen 1973	40.033a(East)	152,0	152,0	305,0	32,0	6,3	127,0	0,3	2,5	496,0	345,0		188,2	98,8
42	Wight and Sozen 1973	40.033a(west)	152,0	152,0	305,0	32,0	6,3	127,0	0,3	2,5	496,0	345,0		188,2	101,3
43	Wight and Sozen 1973	40.048.(East)	152,0	152,0	305,0	32,0	6,3	89,0	0,5	2,5	496,0	345,0		177,9	104,6
44	Wight and Sozen 1973	40.048(West)	152,0	152,0	305,0	32,0	6,3	89,0	0,5	2,5	496,0	345,0		177,9	98,5
45	Wight and Sozen 1973	40.033(East)	152,0	152,0	305,0	32,0	6,3	127,0	0,3	2,5	496,0	345,0		177,6	94,2
46	Wight and Sozen 1973	40.033(West)	152,0	152,0	305,0	32,0	6,3	127,0	0,3	2,5	496,0	345,0		177,6	104,9
47	Wight and Sozen 1973	25.033(East)	152,0	152,0	305,0	32,0	6,3	127,0	0,3	2,5	496,0	345,0		110,6	87,9
48	Wight and Sozen 1973	25.033(West)	152,0	152,0	305,0	32,0	6,3	127,0	0,3	2,5	496,0	345,0		110,6	93,3
49	Wight and Sozen 1973	40.067(East)	876,0	152,0	305,0	32,0	19,0	64,0	0,7	2,5	496,0	345,0	33,4	178,1	93,1
50	Wight and Sozen 1973	40.067(West)	876,0	152,0	305,0	32,0	19,0	64,0	0,7	2,5	496,0	345,0	33,4	178,1	99,4
51	Wight and Sozen 1973	40.147(East)	875,0	152,0	305,0	32,0	19,0	64,0	1,5	2,5	496,0	317,0	33,5	178,6	119,8
52	Wight and Sozen 1973	40.147(West)	875,0	152,0	305,0	32,0	19,0	64,0	1,5	2,5	496,0	317,0	33,5	178,6	114,7
53	Wight and Sozen 1973	40.092(East)	875,0	152,0	305,0	32,0	19,0	102,0	0,9	2,5	496,0	317,0	33,5	178,6	115,9
54	Wight and Sozen 1973	40.092(West)	875,0	152,0	305,0	32,0	19,0	102,0	0,9	2,5	496,0	317,0	33,5	178,6	121,0
55	Ohue et al. 1985	2D16RS	400,0	200,0	200,0	11,0	16,0	50,0	0,6	2,0	369,0	316,0	32,0	183,0	110,6
56	Ohue et al. 1985	4D13RS	400,0	200,0	200,0	12,0	13,0	50,0	0,6	2,7	370,0	316,0	29,9	183,0	101,4
57	Zhou et al. 1987	124-08	160,0	160,0	160,0	12,5	9,5	40,0	1,8	2,2	341,0	559,0	19,8	406,0	115,0
58	Zhou et al. 1987	204-08	320,0	160,0	160,0	12,5	9,5	40,0	0,7	2,2	341,0	559,0	21,1	432,7	66,5
59	Zhou et al. 1987	223-09	320,0	160,0	160,0	12,5	9,5	40,0	1,8	2,2	341,0	559,0	21,1	486,1	67,4
60	Zhou et al. 1987	302-07	480,0	160,0	160,0	12,5	9,5	40,0	0,7	2,2	341,0	559,0	28,8	516,8	51,2
61	Zhou et al. 1987	312-07	480,0	160,0	160,0	12,5	9,5	40,0	0,6	2,2	341,0	559,0	28,8	516,8	54,9
62	Zhou et al. 1987	322-07	480,0	160,0	160,0	12,5	9,5	40,0	1,0	2,2	341,0	559,0	28,8	516,8	51,8
63	Amitsu et al. 1991	CB060C	323,0	278,0	278,0	28,0	28,0	52,0	0,9	4,1	441,0	414,0	46,3	2633,6	505,6
64	Xiao and Martirossyan 1998	HC4-8L16-T6-0.1P	508,0	254,0	254,0	13,0	15,9	51,0	1,6	2,5	510,0	449,0	86,0	532,6	267,6
65	Xiao and Martirossyan 1998	HC4-8L16-T6-0.2P	508,0	254,0	254,0	13,0	15,9	51,0	1,6	2,5	510,0	510,0	86,0	1065,3	324,1
66	Kim et al. 2018	Sad2	1200,0	400,0	400,0	40,0	25,4	165,0	0,4	2,5	571,0	500,0	32,0	870,4	310,3
67	Kim et al. 2018	RGd2	1200,0	250,0	640,0	40,0	22,2	105,0	0,8	2,4	566,0	530,0	32,0	870,4	240,8
68	Nagasaka 1982	HPRC19-32	300,0	200,0	200,0	12,0	12,7	20,0	1,2	1,3	371,0	344,0	21,0	294,0	110,7
69	Zhou et al. 1985	No.806	80,0	80,0	80,0	10,0	6,0	80,0	0,4	1,8	336,0	341,0	32,3	124,0	31,6
70	Zhou et al. 1985	No. 1007	80,0	80,0	80,0	10,0	6,0	80,0	0,4	1,8	336,0	341,0	34,0	152,3	36,7
71	Zhou et al. 1985	No.1309	80,0	80,0	80,0	10,0	6,0	80,0	0,4	1,8	336,0	341,0	32,8	188,9	29,6
72	Imai and Yamamoto 1986	No 1	825,0	500,0	400,0	37,0	22,0	100,0	0,3	2,7	318,0	336,0	27,1	390,2	471,3
73	Ono et al. 1989	CA025C	300,0	200,0	200,0	19,0	9,5	70,0	0,8	2,1	361,0	426,0	25,8	265,2	130,0
74	Ono et al. 1989	CA060C	300,0	200,0	200,0	19,0	9,5	70,0	0,8	2,1	361,0	426,0	25,8	635,7	133,8
Νotation : L_s= element shear span; b= section width; h= section height; c= concrete cover; d_bw= transverse reinforcement diameter; s= transverse reinforcement spacing; ρ_w= geometrical transverse reinf. ratio in the direction of seismic action; ρ_tot= longitudinal reinforcement ratio; f_yl= longitudinal reinforcement yielding stress; f_yw= transverse reinforcement yielding stress; f’_c= concrete compressive strength; P= axial load; V_exp.max= experimental shear force

Table 3. Error metric evaluation for various machine learning algorithms on the EN1998-3, 2005 dataset, using a 90/10 train-test split.

MODEL	DATASET	R	MAPE	MAMPE	MAE	RMSE
POLYREG-HYT	Train	0,99490	0,07903	0,05084	13,224	18,4979
LREGR	Train	0,96821	0,19220	0,13054	33,9533	45,8741
XGBOOST-HYT-CV	Train	0,99987	0,01225	0,00644	1,67587	2,92632
POLYREG-HYT	Test	0,98448	0,17764	0,20863	38,9874	63,9059
LREGR	Test	0,84845	0,42230	0,33075	61,8105	92,0577
XGBOOST-HYT-CV	Test	0,97007	0,15299	0,16567	30,9598	46,2470

Table 4. Error metric evaluation for various machine learning algorithms on the Pardalopoulos et al., 2013 dataset using a 90/10 train-test split.

MODEL	DATASET	R	MAPE	MAMPE	MAE	RMSE
POLYREG-HYT	Train	0,99647	0,06761	0,04623	12,0254	15,3862
LREGR	Train	0,97552	0,16353	0,11609	30,1960	40,3127
XGBoost-HYT-CV	Train	0,99989	0,00913	0,00495	1,28678	2,72715
POLYREG-HYT	Test	0,95266	0,13873	0,16834	31,4586	52,3988
LREGR	Test	0,87672	0,49074	0,30313	56,6489	85,0794
XGBoost-HYT-CV	Test	0,99652	0,21500	0,19804	37,0085	59,0950

Table 5. Error metric evaluation for various machine learning algorithms on the ASCE/SEI 41-13, 2014 dataset using a 90/10 train-test split.

MODEL	DATASET	R	MAPE	MAMPE	MAE	RMSE
POLYREG-HYT	Train	0,99001	0,08229	0,06268	16,3040	25,8498
LREGR	Train	0,97806	0,14642	0,10738	27,9311	38,2091
XGBoost-HYT-CV	Train	0,99988	0,00958	0,00532	1,38284	2,86823
POLYREG-HYT	Test	0,99140	0,15463	0,14728	27,5236	36,1777
LREGR	Test	0,92665	0,25136	0,23429	43,7839	62,0201
XGBoost-HYT-CV	Test	0,99575	0,08957	0,06142	11,4780	17,5487

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

New Predictive Model for the Computation of Reinforced Concrete Column Shear Strength

Abstract

1. Introduction

2. Crucial Behaviour Parameters

3. Dataset Collection

4. Machine Learning Algorithms

5. Investigation of the Proposed and Existent Formulae

5.1. Proposed Predictive Models

5.2. Sensitivity Analysis

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe