Prerpints.org logo
Preprint
Article

Reliability Analysis of Developing Programs for Converting MIDAS GEN to ANSYS Models Based on Python

Altmetrics

Downloads

72

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 October 2024

Posted:

07 October 2024

You are already at the latest version

Alerts
Abstract
The reasonableness and accuracy of engineering design are often assessed through the use of a variety of structural design analysis software, which are then compared and verified. However, it is challenging for a single analysis software to meet the diverse and complex design requirements. In order to meet the specific engineering requirements, it is necessary to convert the MIDAS result model into an ANSYS structural model and conduct a nonlinear analysis and simulation in ANSYS. Nevertheless, the existing interface is unable to facilitate direct conversion of the model. Accordingly, this paper presents a Python-based ANSYS APDL program that enables the complete conversion of MIDAS GEN structural models to ANSYS finite element models. The program is capable of converting a range of data, including material, section, element, connection, load, node mass, constraint, time history function, and so forth. The program is capable of converting specific connection units, including elastic and general connection units. Additionally, the beam-column section direction, beam end freedom release, rigid element, and special anti-rocking structure of the structure can be considered. Ultimately, the theatre model is transformed. Following a comparison of the analysis results, it was found that the mass and mode of the model before and after the transformation were essentially identical. The maximum error of the first six orders of the structure is 2.95%, with the structural displacement under gravity load remaining essentially unchanged. The research and analysis demonstrate the accuracy and reliability of the MIDAS GEN conversion ANSYS program. The conversion program significantly reduces the time required for direct modeling in ANSYS, enhancing work efficiency. The study has considerable practical significance for the seismic sway design and analysis of buildings based on vibration isolation design.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

In line with the ongoing advancement of China’s social and constructional landscape, there has been a notable rise in the expectations of the general public with regard to construction. Concurrently, there has been a notable increase in the prevalence of intricate structural designs. Consequently, ensuring the safety of complex structures represents a significant challenge for engineers. The utilization of commercial structural design and analysis software, including PKPM, YJK, Revit, ETABS, SAP2000, MIDAS, ANSYS, ABAQUS, and others, enables engineers to implement the design and verification of complex structures. MIDAS and some software are relatively straightforward to operate, facilitate the creation of models, and can perform fundamental structural analysis. However, their capabilities in nonlinear analysis are limited. ANSYS, for instance, exhibits enhanced analysis capabilities. Nevertheless, its operational and modeling procedures are intricate, which would considerably augment the analytical workload. Furthermore, to validate the precision of the software’s analysis outcomes, the structural design process frequently employs a range of software for comparative analysis. It is challenging for a single software to fulfill the requirements of structural design and analysis [1].
The ANSYS structural analysis software offers seven distinct types of analysis, including static analysis, eigenvalue buckling analysis, modal analysis, harmonic response analysis, transient dynamic analysis, spectral analysis, and explicit dynamic analysis. Furthermore, specialized analyses can be performed, including failure analysis, composite material analysis, and fatigue analysis [2]. The nonlinear analysis capability of ANSYS is particularly robust. ANSYS is frequently employed for the simulation of highly nonlinear analysis in the process of structural design and analysis [3,4]. In addition, modeling and analysis parameter settings are very flexible in ANSYS, which enables the software to be utilized for complex structural analysis in numerous projects [5,6,7]. A comparison of ANSYS with other design software, such as MIDAS, has demonstrated that ANSYS produces more accurate results and is therefore better suited to meeting the design requirements [8,9,10].
Nevertheless, the interactive functionality of the ANSYS interface is applicable to a wide range of scenarios. Furthermore, modeling directly in ANSYS is an extremely inefficient process that is a waste of time. To address the issue of model conversion across different software platforms, numerous software applications offer model conversion interfaces that facilitate the development of models in other software with greater ease. However, the software comes with a function that does not cover all design software. And many model conversion needs are still not met. For this reason, some scholars have researched and developed many model conversion programs and interfaces. For ANSYS software, it can implement the conversion between Revit to ANSYS, SAP2000 to ANSYS, CAD to ANSY, etc. Feng [11] used the interface program developed by the Revit API interface to realize the information conversion between Revit and ANSYS software. What’s more, a cell high-rise building was converted. ZHOU [12] used the BIM model and finite element analysis and the secondary development of the interface program written to achieve the exchange of information between Revit and ANSYS software. ZHAO et al. [13] realized the model conversion between Revit and ANSYS software and verified its feasibility through a basement project. He [14] designed and realized the data conversion of building structure from the IFC model to the ANSYS structural analysis model. The veracity and dependability of the mapping model and the overarching program framework were validated through the utilization of an arithmetic example. Ma [1] realized the model transformation from SAP2000 to ANSYS based on a Python program and verified the model accuracy through two arithmetic examples. YANG et al. [15] used Auto LISP language, C language, HP-GL drawing language, and APDL language to construct interfaces between ANSYS, MIDAS, and AutoCAD.
The concept of model conversion between different software has been proposed by numerous scholars and has led to the development of numerous conversion programs. However, the majority of these programs focus on the conversion between Revit and ANSYS. Conversely, there is a paucity of model conversion programs between MIDAS and ANSYS, and the related research is still relatively scarce. The discrepancies between different models are significant, with some units being unique and their functions varying. This necessitates a model-specific analysis.
In light of the aforementioned considerations, this paper seeks to address the necessity for research into the transformation and analysis of engineering models in practice. The MIDAS GEN data file management file is analyzed based on the Python language. In consideration of the diverse attributes of the structure and the requisite unit conversions, the ANSYS modeling is conducted using the APDL language, and the MIDAS GEN conversion ANSYS model program is developed. It is expected that the MIDAS GEN structural analysis model can be fully transformed into the ANSYS finite element model, which saves the time of direct modeling in ANSYS and improves work efficiency.

2. Model Conversion Requirements

2.1. Overview of the Project

The total site area of the performing arts center under construction is 15,000 square meters, while the total floor area is 72,000 square meters. The facility’s primary functions are to serve as a theatre and a space for performing arts, in addition to providing related support facilities and equipment. The theater has about 1800 seats, 4 underground floors, 5 local underground floors, and 6 floors above ground. The building’s height is 38m above ground. The plan of the first floor of the performing arts center is shown in Figure 1. The project site is situated in close proximity to the existing underground railway system, as well as the planned future extension of this line. The closest distance between them is about 20m. The project adopts steel spring vibration isolation bearings. For the theater and performing arts space, it adopts a vibration isolation design. Also, it sets vertical and horizontal vibration isolation joints between the structure and the surrounding public space to become an independent structural unit. The structural model of the vibration isolation area of the theater is shown in Figure 2 and Figure 3. The main part of the structure adopts a reinforced concrete seismic wall, with a plan length of 83.4 m, a width of 61 m and a total structural height of 62 m. The large-span roof at the top of the main stage adopts the arrangement of steel beams, with a span of 24 m. With a span of 35 m, the top of the auditorium adopts the steel truss structure.
It is necessary to conduct vibration isolation and seismic analysis of the theatre vibration isolation zone. The vibration isolation device not only fulfills the requisite criteria for vibration isolation but also demonstrates adequate seismic performance under seismic action. After arranging the steel spring support, the vertical stiffness of the structure becomes weaker and the swaying phenomenon is more obvious under seismic action. Bu Longgui of Beijing Architectural Design Institute proposed a vibration isolation device anti-seismic sway structure (Patent No.: ZL202320619498.4 [16]). To verify the anti-rocking performance of the anti-rocking structure, it is applied in the vibration isolation model for ground vibration analysis to analyze the anti-rocking effect of the device. Due to the special mechanical properties of the anti-rocking structure, it is not possible to perform equivalent simulations in MIDAS software. Therefore, ANSYS is used for finite element analysis.
Since there is no existing program to convert the finite element model completely, the MIDAS to ANSYS program was written in Python.

2.2. Model Conversion

In this theater model, a multitude of components need to be converted. These include materials, sections, nodes, line units, surface units, elastic connection units, general connection units, node masses, constraints, loads, and engineering (seismic) vibration time-range functions are included. Among these, there are some special units and attributes that require particular attention during the conversion process.
(1) Steel Spring Vibration Isolation Bearings
The steel spring vibration isolation bearing in the steel spring exhibits two distinct characteristics: vertical stiffness and horizontal stiffness. In the MIDAS model, the horizontal stiffness is divided into Y-axis and Z-axis stiffness, according to the direction of the unit. Consequently, it is necessary to identify the characteristics of the spring unit in ANSYS for the purposes of simulation.
(2) Anti-rocking Construction
The anti-rocking device is illustrated in Figure 4. The bearing is primarily composed of an upper cover plate, a lower bottom plate, a steel spring, a steel sleeve, a steel rod, and a ball hinge bearing. By setting only the tensile steel rod, the steel rod is pulled and the vertical stiffness of the bearing is increased when the upper structure is rocking. Thereby the anti-rocking stiffness of the structure is increased, the anti-overturning moment is added, the vertical displacement of a single bearing is reduced and the rocking response of the structure is suppressed.
The force-displacement curve of the anti-rocking device is shown in Figure 5. The force-displacement curve exhibits a “flag” shape. Prior to the spring generating upward displacement, the overall stiffness of the bearing is the vertical stiffness k1 of the steel spring. Following the pulling of the steel tie rod, the overall stiffness of the bearing is constituted by the sum of the vertical stiffness of the steel spring and the axial tensile stiffness of the steel tie rod k1 + k2. Subsequent to the yielding of the steel tie rod, the overall stiffness of the bearing is once again represented by the vertical stiffness of the steel spring k1.
The mechanical properties of the structure are special. In addition to the initial clearance of the steel tie rod, it is essential to determine the stiffness of the steel tie rod and consider its yield characteristics. However, in MIDAS GEN, it is not possible to set relevant units or connections for accurate simulation. Therefore, it may be necessary to utilize alternative software for corresponding analysis. Finally, ANSYS software is selected, but units must also be sourced within ANSYS which meets the characteristics of an anti-rocking device for simulation.

3. MIDAS to ANSYS Program

The programming language Python provides an efficient high-level data structure that can be easily and effectively used for object-oriented programming. This feature makes it simple and easy to read. In this paper, the program of MIDAS GEN to ANSYS is written by Python, which can transform the MIDAS GEN model into an ANSYS model. The program conversion process is illustrated in Figure 6.

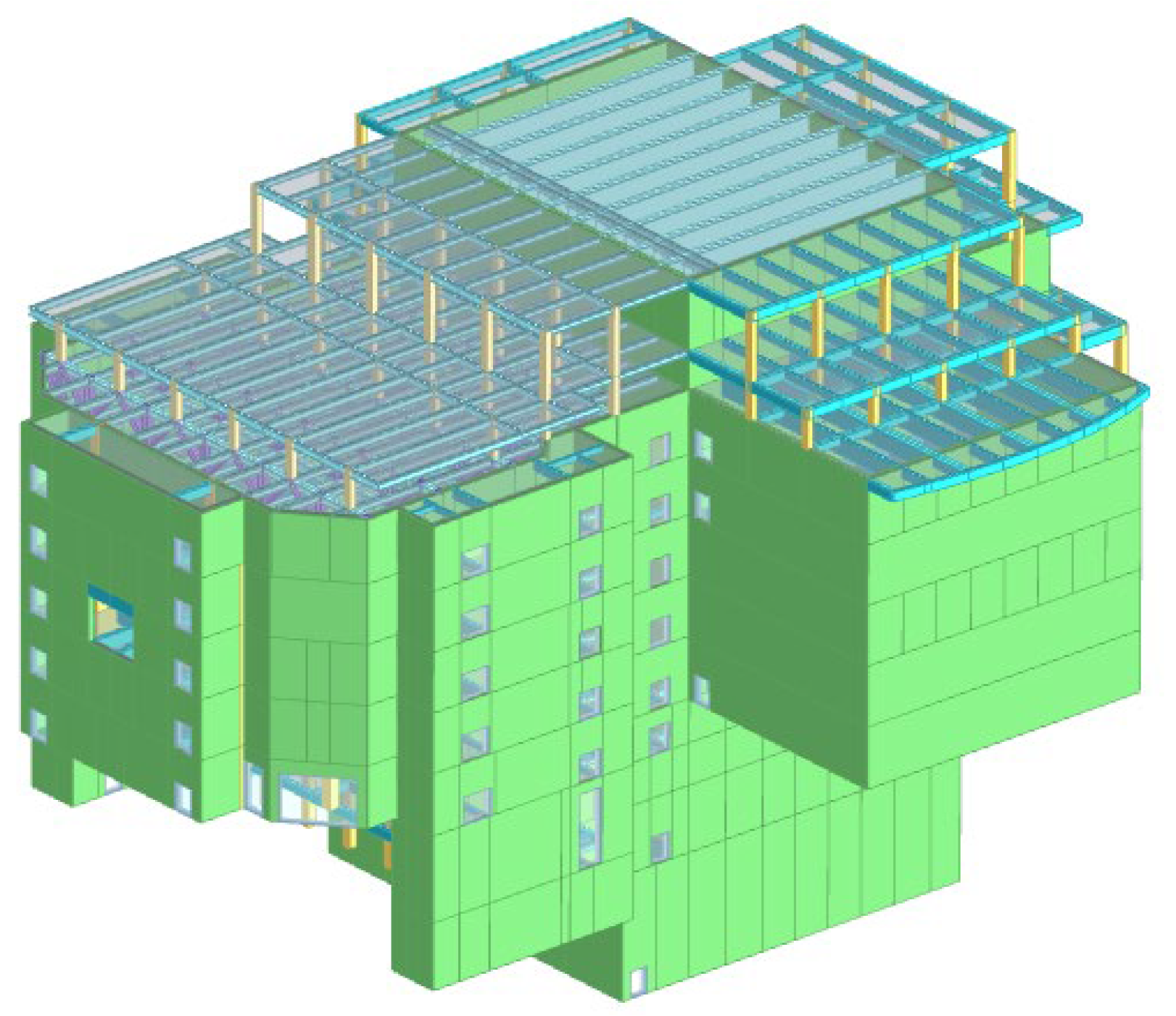
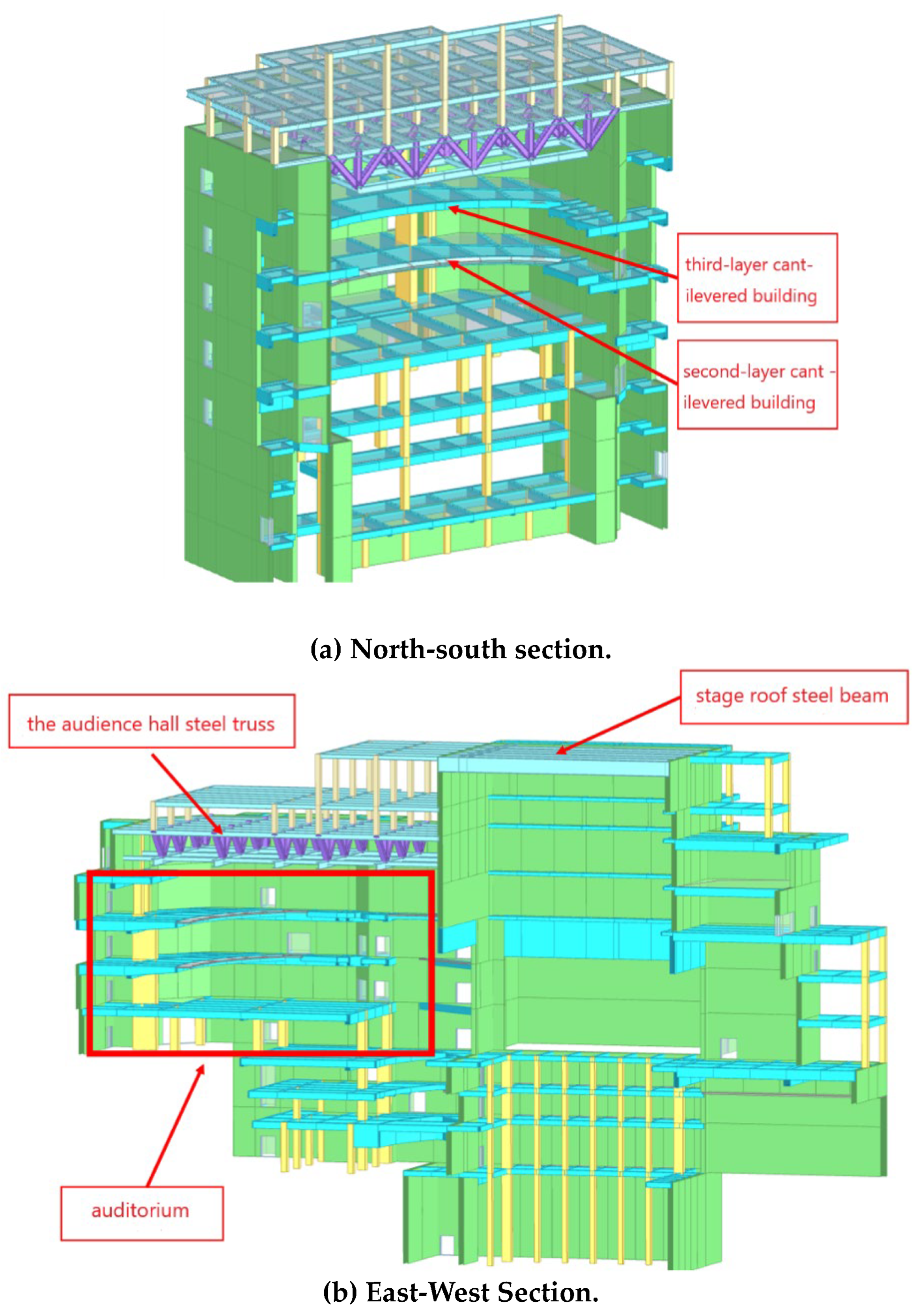
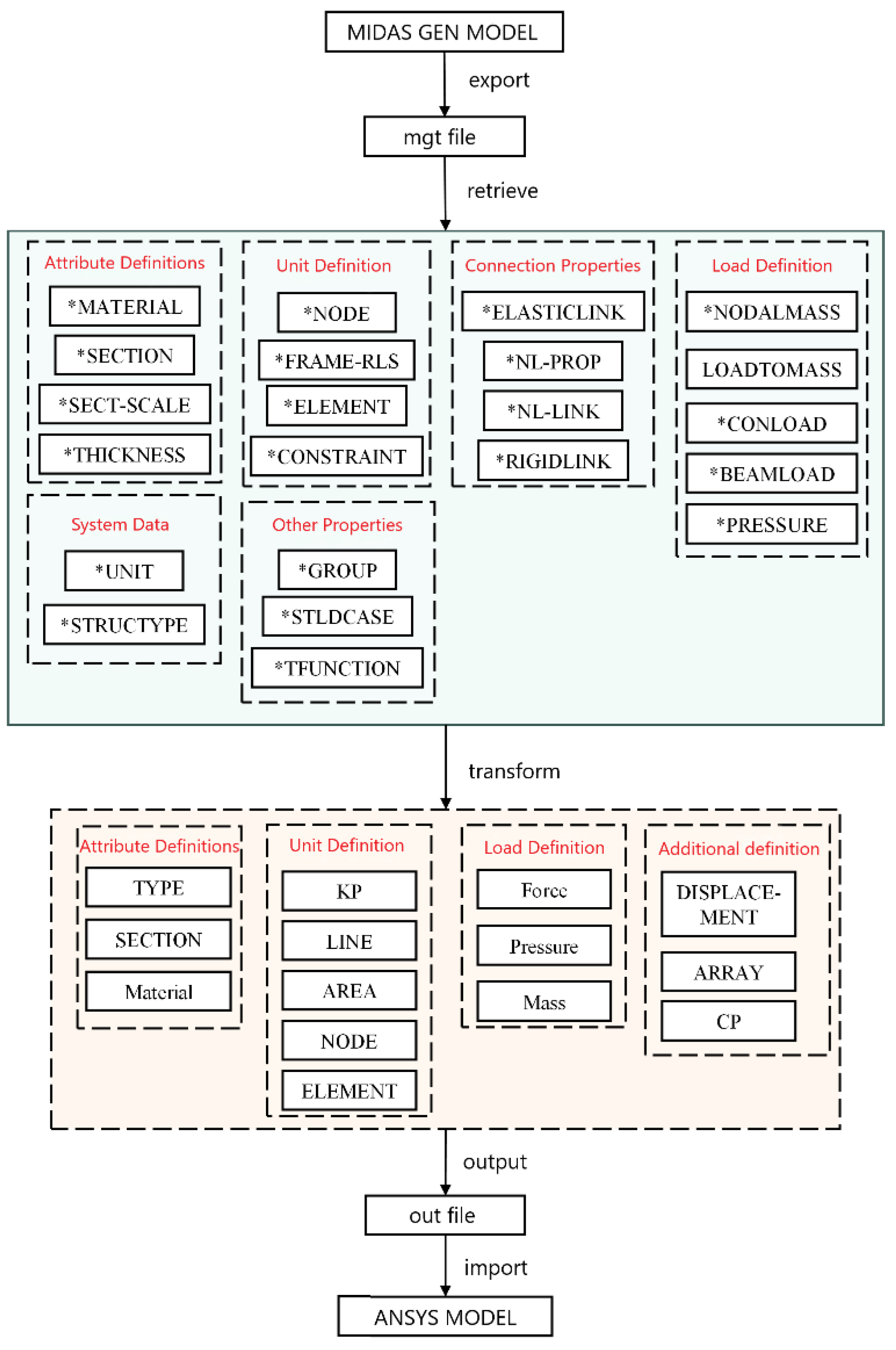
3.1. Software Features

The conversion program is capable of importing and reading the MDIAS GEN data file. By analyzing, processing and integrating the program data, the APDL command streams out a file that ANSYS can read is exported, thereby enabling the rapid modeling of ANSYS. The specific conversion functions are as follows:
(1) The structural properties include the material, section, section parameter scaling, wall thickness and so on. For some special sections, such as national standard hot rolled section steel or custom sections, manual input is required and automatic conversion cannot be achieved.
(2) The nodes in MIDAS are converted to the key points in ANSYS, resulting in a one-to-one correspondence between the two. The beam-plate element is converted into a line and area in ANSYS. The program automatically selects the corresponding element type. Generally, the BEAM188 element is used for the beam and column, while the SHELL181 element is used for the wall and plate. The mesh size of each unit can be modified according to the user’s specifications. The key points, lines and surfaces can be further divided into finite element meshes.
(3) Special element transformations, such as node mass, elastic connection element, general connection element, etc. The mass of the joint is simulated by the MASS21 element in ANSYS, and the elastic connection element uses the COMBIN14 element. However, the elastic connection unit and the general connection unit play different roles in MIDAS and possess a multitude of functions. Therefore, it is imperative to correspond to different unit settings according to the attributes of the different units.
(4) Setting the release beam end constraint in MDIAS GEN to realize the hinge of the beam and column. Creating the rigid domain can also be converted to the ANSYS model through the program.
(5) The transformation of a variety of load conditions, such as node load, beam-column distribution load, plate and shell uniform load, etc. A variety of working conditions need to be grouped and converted to generate different models or simple load files.
(6) Time history function conversion is also a function. ARRAY is used to store time history data in ANSYS. For different time history waves or vibration waves, multiple ARRAYs can be used for storage and the time history wave can be pre-scaled by setting the scaling coefficient.

3.2. Key Issues Addressed

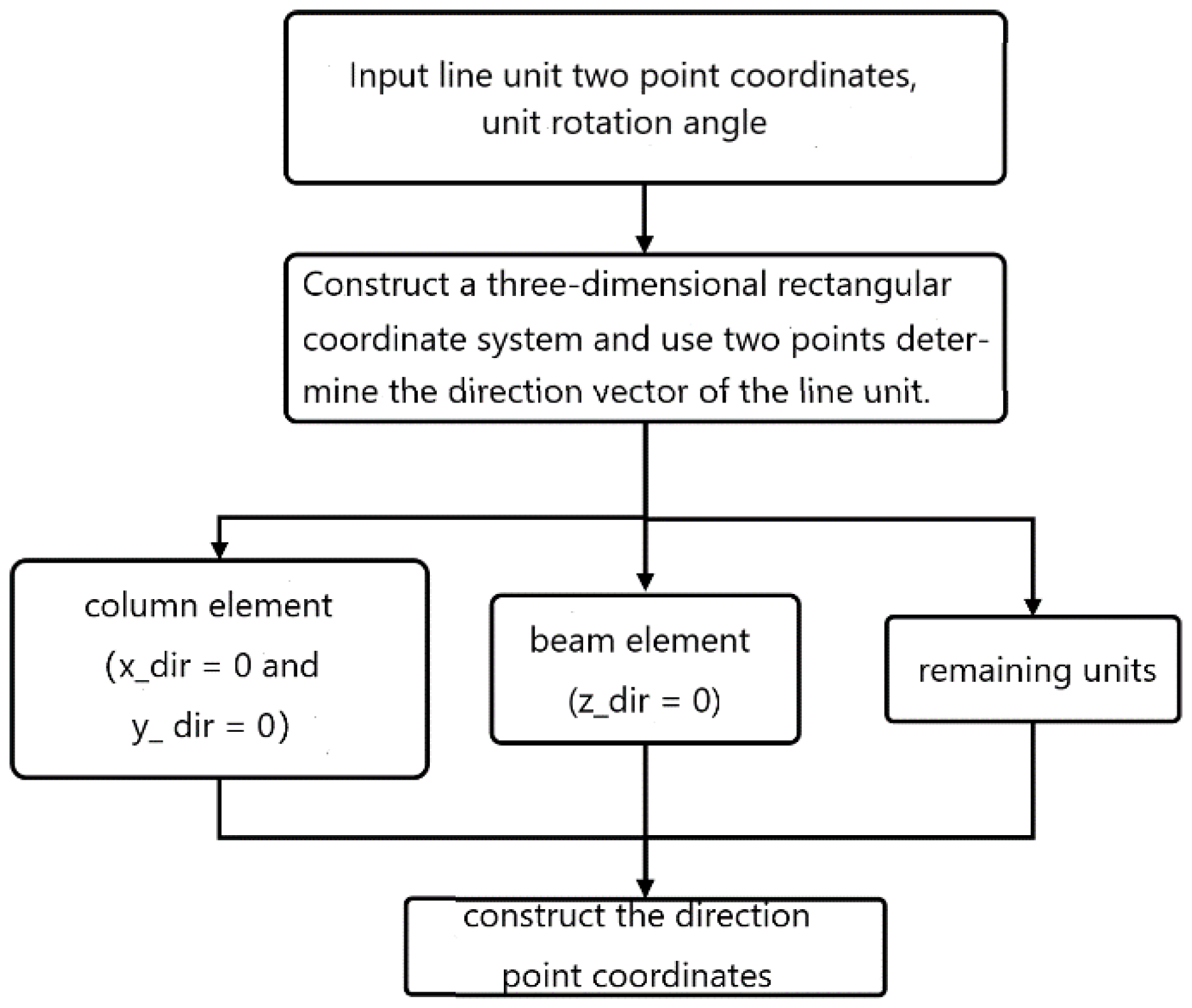
(1) Line unit 3 axis direction
In ANSYS, the line element (BEAM188) must be defined with specific key points to determine the 3-axis direction of the section. In MIDAS, there is a corresponding element angle corresponding to it and the 3-axis direction can be adjusted. The three-axis direction determination rules of the two are the same, but there is only a component β angle in MIDAS GEN [17]. In ANSYS, the data must be converted into a unit direction point, which requires further construction. The direction point construction process is shown in Figure 7.
In the above steps, x_dir, y_dir and z_dir are the three coordinate values of the direction vector of the line element respectively. If x_dir = 0 and y_dir = 0, the direction vector is perpendicular to the Z axis and is identified as a cylindrical element. The z_dir = 0 indicates that the direction vector is parallel to the XY plane and is identified as a beam element. After the classification of the unit, it is more important to find the vector corresponding to the zero rotation angle of the line unit, which means to find a vertical line through the line unit in the plane (OXY plane, OXZ plane, OYZ plane )where the line unit is located. Finally, the final direction vector and direction key points are determined according to different rotation angles. The method for calculating the direction point vector is given below. Vector1, Vector2 and Angle are the line unit direction vector, the vertical vector of the line unit direction vector and the unit rotation angle [18] respectively.
Algorithm 1: getAngleVector
Input: vector1: a three-dimensional vector in space [x1, y1, z1], vector2: a three-dimensional vector in space [x2, y2, z2], angle: target angle (in radians) between the resulting vector and vector2
1. If length(vector1) = 3 or length(vector2) = 3
2. Calculate dot_product = vector1[0]*vector2[0] + vector1[1]*vector2[1] + vector1[2]*vector2[2]
3. Calculate product_length = sqrt((vector1[0]**2 + vector1[1]**2 + vector1[2]**2) * (vector2[0]**2 + vector2[1]**2 + vector2[2]**2))
4. Calculate cos_angle = dot_product / product_length
5. Calculate delta_angle = angle - acos(cos_angle)
6. Calculate new vector coordinates:
x = cos(delta_angle)*vector2[0] + sin(delta_angle)*vector1[0]
y = cos(delta_angle)*vector2[1] + sin(delta_angle)*vector1[1]
z = cos(delta_angle)*vector2[2] + sin(delta_angle)*vector1[2]
7. Find max_ = max(abs(x), abs(y), abs(z))
8. Normalize vector coordinates:
x’ = x / max_
y’ = y / max_
z’ = z / max_
9. Return result_vector = [x’, y’, z’]
10. Else if return None
11. End if
12. End
(2) Rigid domain problem
In structural modeling, some short beams and short columns are used to connect two components, which are often replaced by rigid rods in software. At the same time, in the process of grid division of plate wall elements, there will also be some elements with very small areas or extremely irregular shapes. The size of these line and surface elements is very small compared with other elements, which will greatly affect the calculation speed of the software. Especially when the display dynamics analysis is carried out in LS-DYNA, the minimum element size is directly related to the software calculation speed [19,20]. To reduce its influence, the above unit can be set as a rigid unit in the ANSYS modeling process, which means that the material property is set to be rigid.
For the line element, the distance between the two nodes is calculated as the length of the line element. And the length of the line element is less than the limit value, which can be set as the rigid element. For the surface element, the area less than the limit is set as the rigid element. In addition, some units with extremely irregular shapes, are also set as rigid units, such as a large aspect ratio and a very small angle between the edges. The above units are determined by the ratio of the area to the square of the longest diagonal.
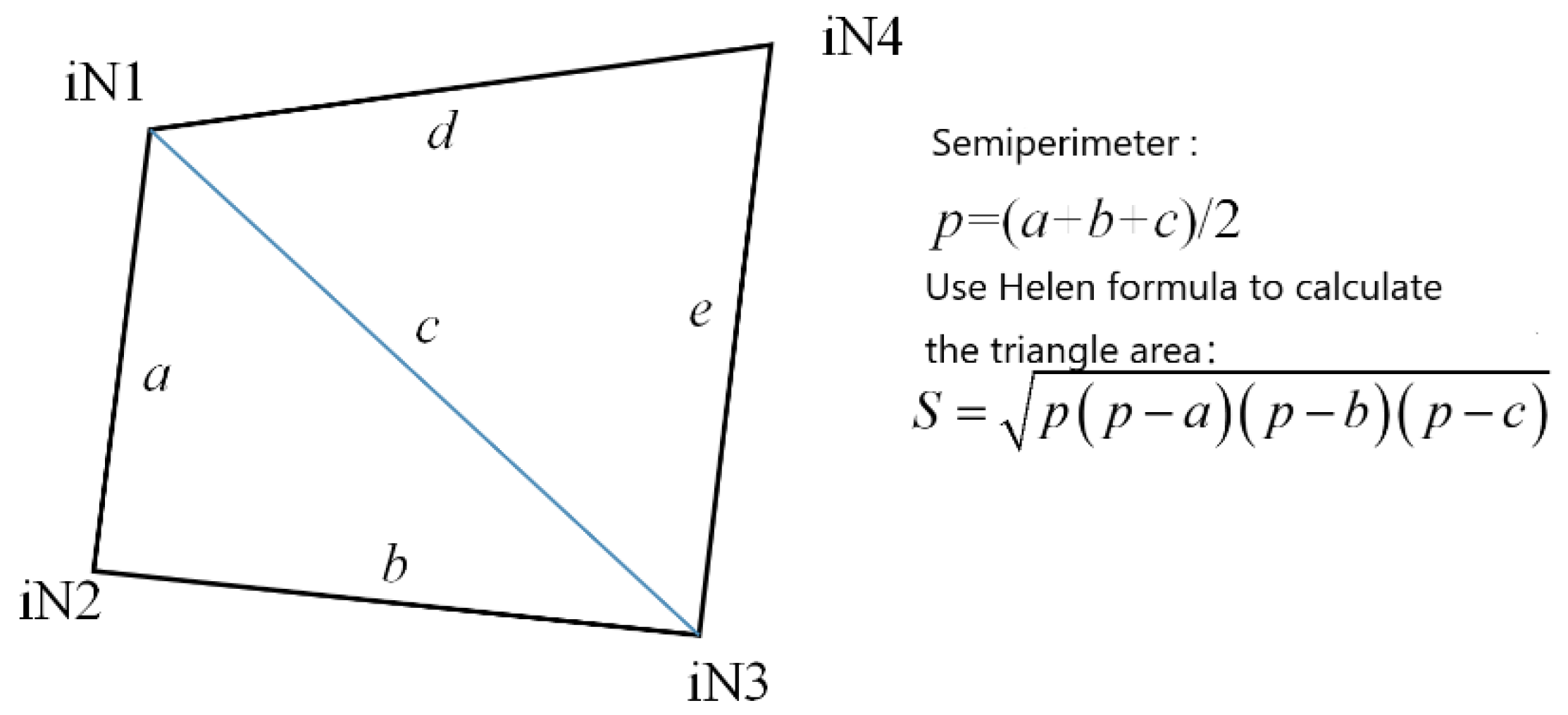
However, if two minimal elements contain common nodes, they cannot be set as two independent rigid elements. Therefore, it is necessary to combine these two independent rigid elements into one rigid element, which means setting the same rigid material properties. The above operation must iterate through all the rigid elements. Then find out the elements with common nodes for grouping and set the rigid material. A Python program is listed below that uses Helen’s formula to calculate the area of the specified four points (Figure 8) and the ratio of the longest diagonal.
Algorithm 2: CalculateAreaAndLengthRatio
Input: iN1, iN2, iN3, iN4: coordinates of four points in 3D space (e.g., iN1 = [x1, y1, z1])
Output: BI: ratio of the area to the square of the longest diagonal; S: total area of the quadrilateral
1. Extract coordinates from input points:
x1, y1, z1 = iN1
x2, y2, z2 = iN2
x3, y3, z3 = iN3
x4, y4, z4 = iN4
2. Calculate edge lengths and diagonal lengths:
a = sqrt((x2-x1)**2 + (y2-y1)**2 + (z2-z1)**2) // Length of edge between N1 and N2
b = sqrt((x3-x2)**2 + (y3-y2)**2 + (z3-z2)**2) // Length of edge between N2 and N3
c = sqrt((x3-x1)**2 + (y3-y1)**2 + (z3-z1)**2) // Diagonal length between N1 and N3
d = sqrt((x4-x1)**2 + (y4-y1)**2 + (z4-z1)**2) // Length of edge between N1 and N4
e = sqrt((x4-x3)**2 + (y4-y3)**2 + (z4-z3)**2) // Length of edge between N3 and N4
l1 = c // Diagonal length between N1 and N3
l2 = sqrt((x4-x2)**2 + (y4-y2)**2 + (z4-z2)**2) // Diagonal length between N2 and N4
3. Calculate the longest diagonal length:
l = max(l1, l2)
4. Calculate areas of two triangles using Heron’s formula:
p1 = (a + b + c) / 2
p2 = (d + e + c) / 2
S1 = sqrt(p1 * (p1 - a) * (p1 - b) * (p1 - c)) // Area of triangle N1N2N3
S2 = sqrt(p2 * (p2 - d) * (p2 - e) * (p2 - c)) // Area of triangle N1N3N4
5. Calculate total area of the quadrilateral:
S = S1 + S2
6. Calculate the ratio of the area to the square of the longest diagonal:
BI = S / (l**2)
7. Return the area ratio and total area:
return [BI, S]
(3) Beam end bending moment release
In the structure, some truss elements or hinged beam elements need to release the endpoint bending moment, which also needs to be considered in the ANSYS modeling. The line element node has six degrees of a freedom and the node overlap means that the two units are rigidly connected. Some special processing can be used to release the degree of freedom of the node, so as to achieve the purpose of hinge.
BEAM44 and BEAM188 / 189 are three units in ANSYS with freedom release function. And their release modes are different. The BEAM188 / 189 unit uses the ENDRELEASE command to release the degree of freedom. While BEAM44 uses KEYOPT(7) to release the degrees of freedom by releasing the ‘ stiffness matrix ‘. In addition, the hinge can also be set by coupling the degree of freedom. The two units set two coincident nodes at the coincident node. Then couple the translational degree of freedom of the two coincidence nodes and release the rotational degree of freedom. The purpose of the hinge can be achieved [2].
The BEAM44 unit is used in this program for the unit that is to release the degree of freedom. For different situations, such as unilateral hinges and hinges on both sides, different BEAM44 unit types are set. KEYOPT (7) sets the corresponding parameters (Table 1). KEYOPT(7) needs to be superimposed when multiple degrees of freedom are released. For example, KEYOPT(7) = 11 if the rotational degrees of freedom around the Y-axis and Z-axis are to be released.
(4) Element loads
The conversion program can realize the conversion of nodal loads, beam loads and pressure loads. In addition, considering the load combination problem under various working conditions, various load conditions can be selectively converted in the process of program conversion and different partial coefficients can be set.
The node load is applied to the key points of the structure and is applied using the ‘FK’ command. The uniform load of the beam can only be applied to the element using the ‘On Beams ‘ command in ANSYS and the uniform load cannot be applied to the online element. The shell load is applied using the ‘ SFA ‘ command.
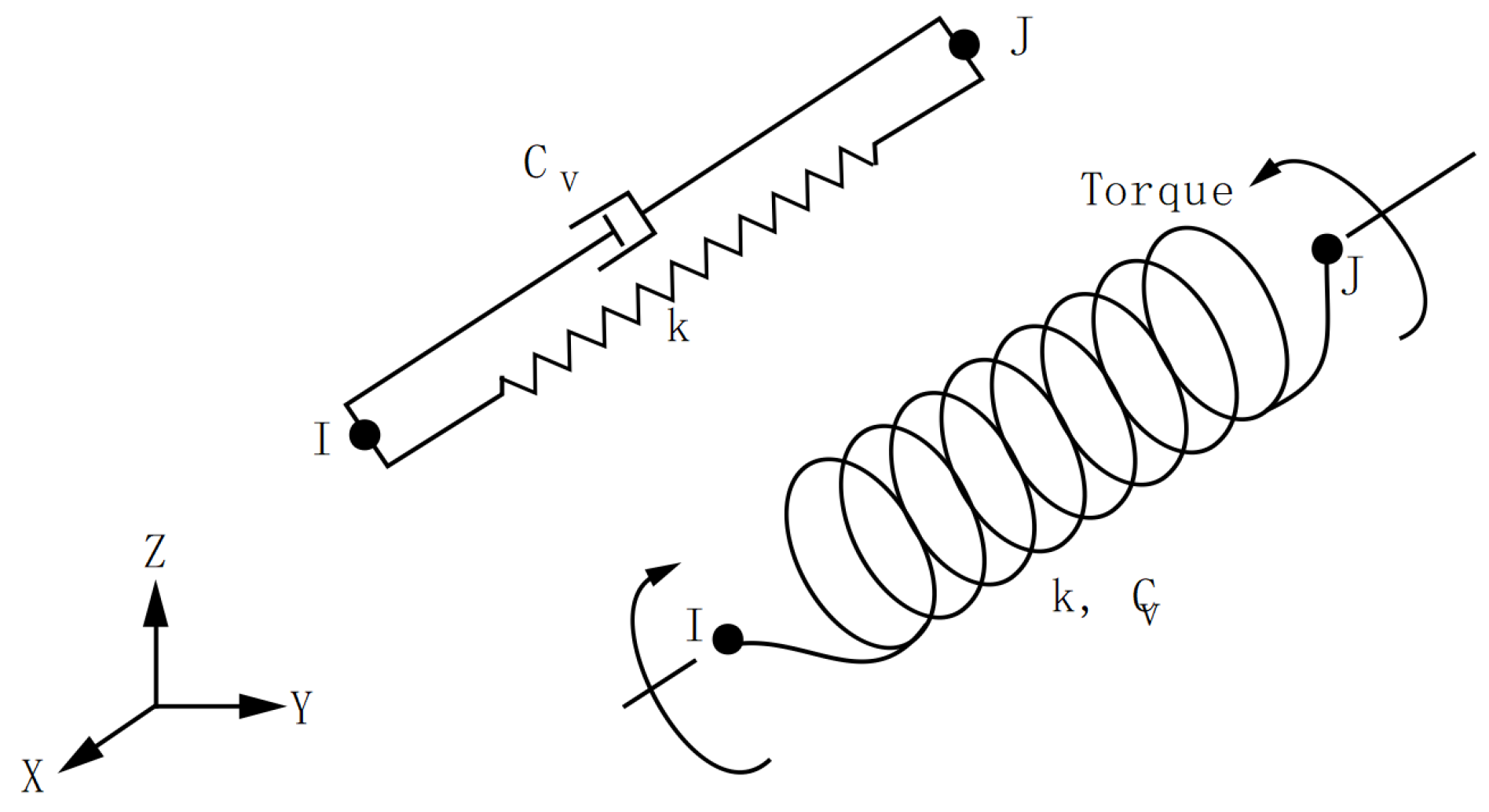
(5) Simulation of elastic connection unit
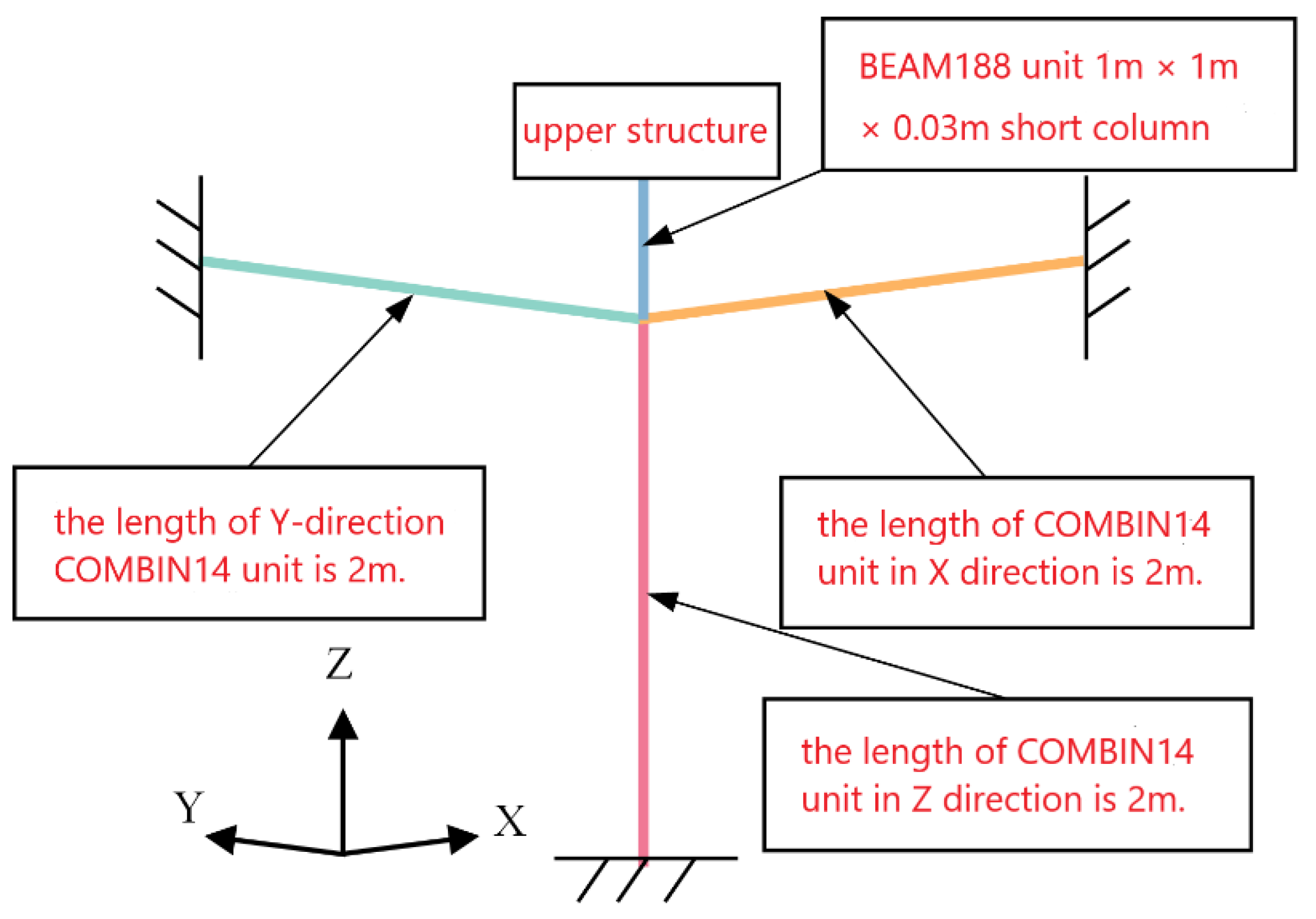
In MIDAS, the steel spring in the structure is simulated by the elastic connection element. Different stiffness of the element can be set in three dimensions [21]. In the ANSYS model, there is no corresponding element to adjust the three-dimensional stiffness. Wen [22] analyzed the elastic connection element of MIDAS and the COMBIN14 element of ANSYS. And found that for the axial expansion torsion problem, the two are similar to the stiffness matrix of ordinary beam element, which can be simulated by COMBIN14 element. However, only one-dimensional stiffness can be set. In ANSYS, three COMBIN14 elements are used for the simulation. Without considering the element damping, the schematic diagram of the COMBIN14 element is shown in Figure 9 [23,24]. The original spring connection node is stretched downward into a short column of 1.0m × 1.0m × 0.03m. The short column is short, while its cross section and the stiffness are large. It can be considered as a rigid rod. Three COMBIN14 elements are arranged along the X, Y and Z directions. The element length is 2m and the stiffness is distributed axially, as shown in Figure 10.
However, the elastic connection unit plays different roles in different models. In this theater model, the elastic connection unit simulates the spring. And it is possible to connect the components. If the elastic connection is used for the connection between the components, the two nodes can be connected by coupling degrees of freedom. Different conversion methods can be set according to different needs.
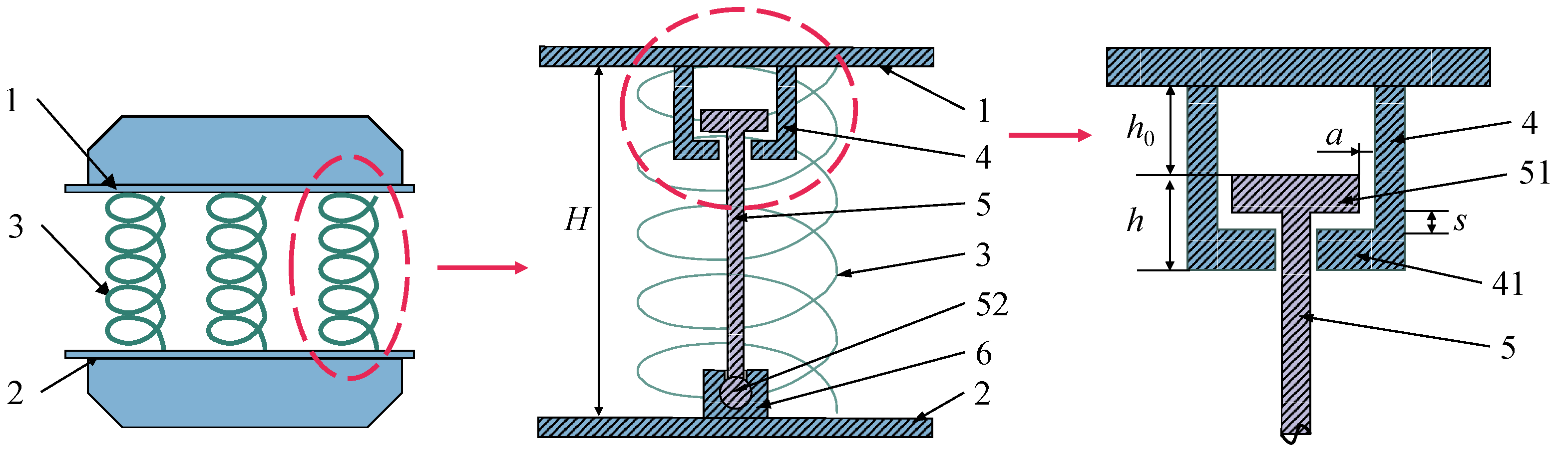
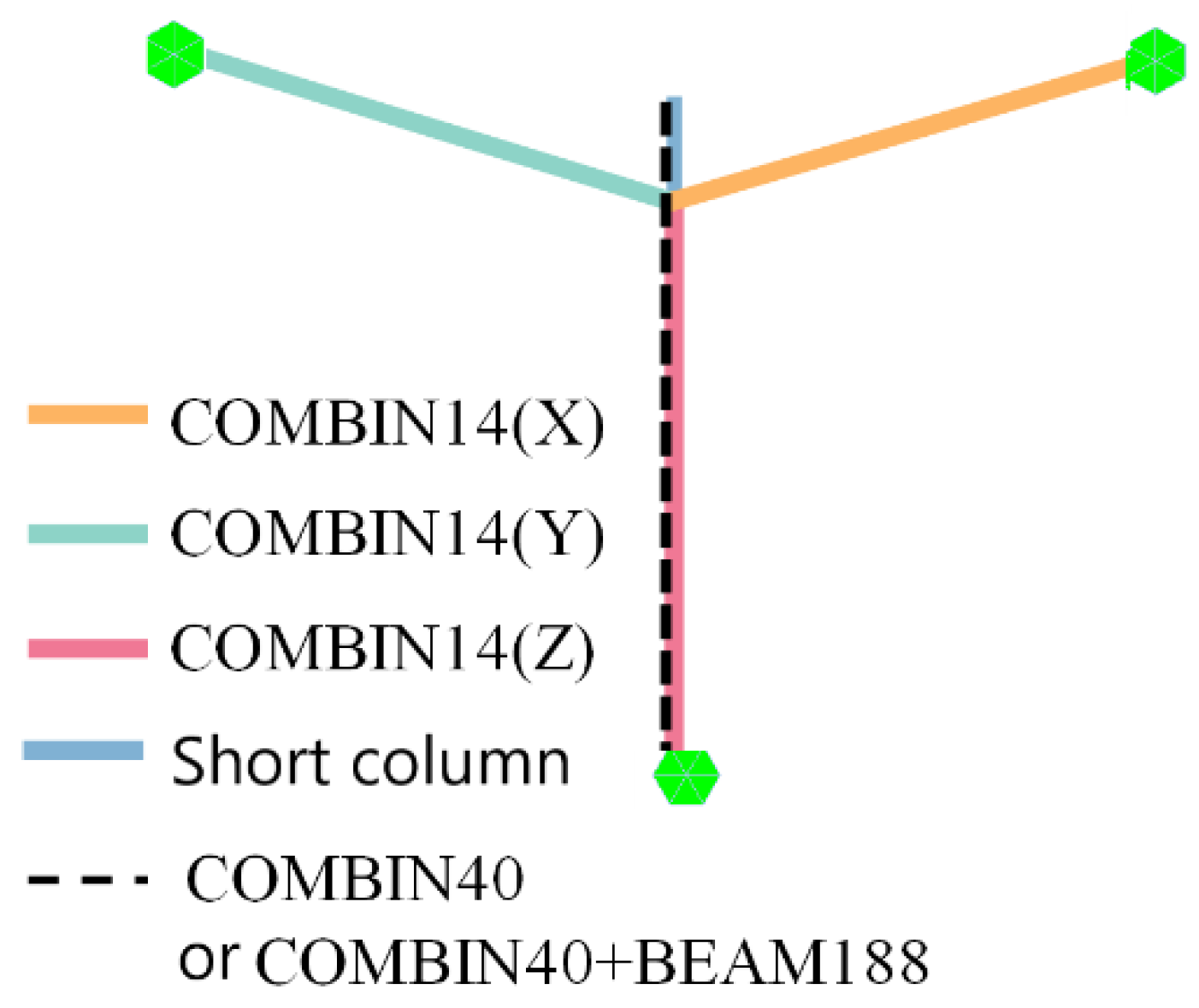
(6) Anti-rocking structure simulation
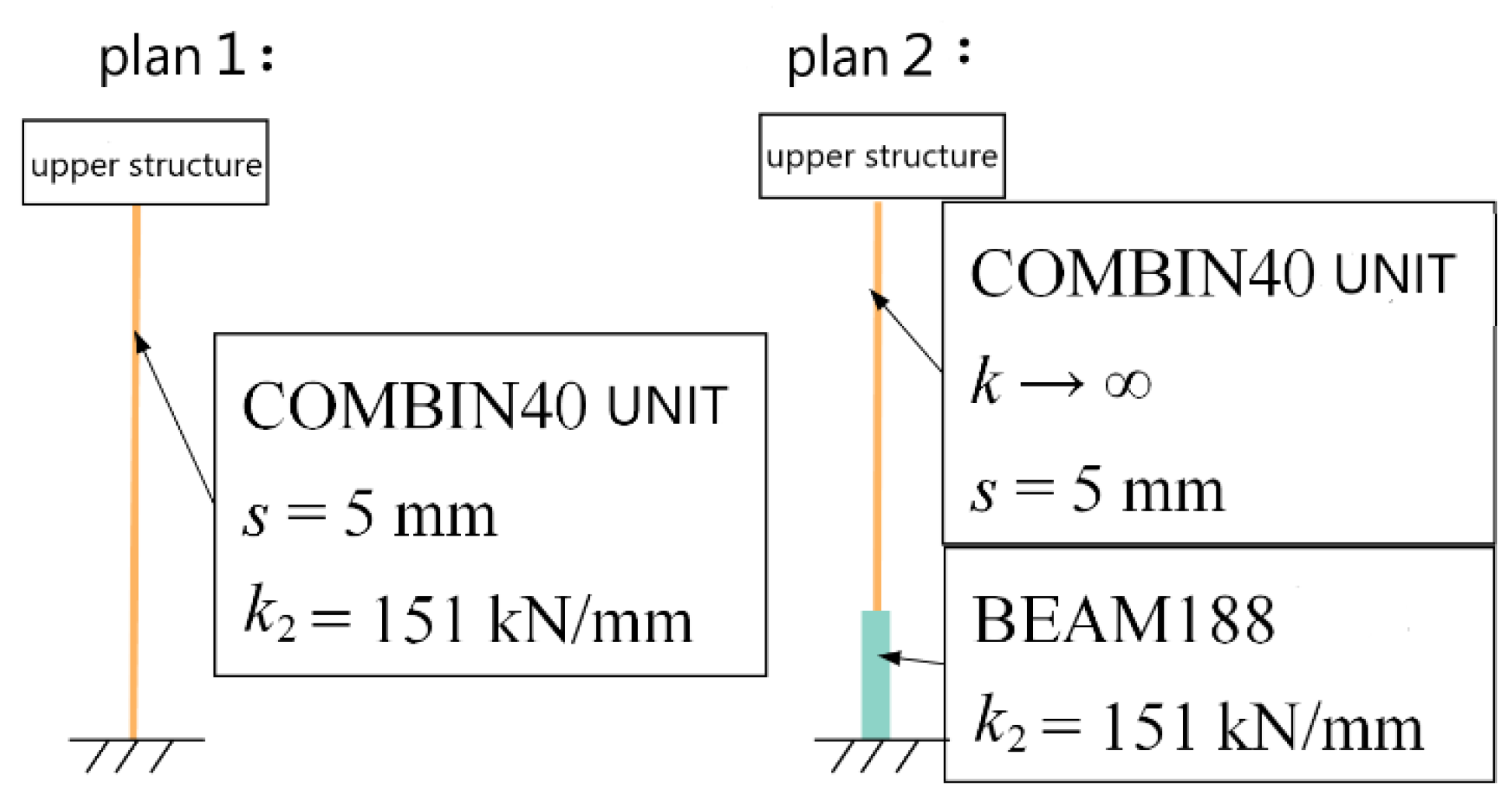
The mechanical properties of the anti-rocking structure are special. The stiffness and yield strength of the steel tie rod need to be adjusted, considering the initial play of the steel tie rod. Two simulation schemes of the anti-rocking structure are proposed, as shown in Figure 11. Scheme 1 is simulated by a single COMBIN40 element and scheme 2 is simulated by COMBIN40 + BEAM188 plastic beam element in series.
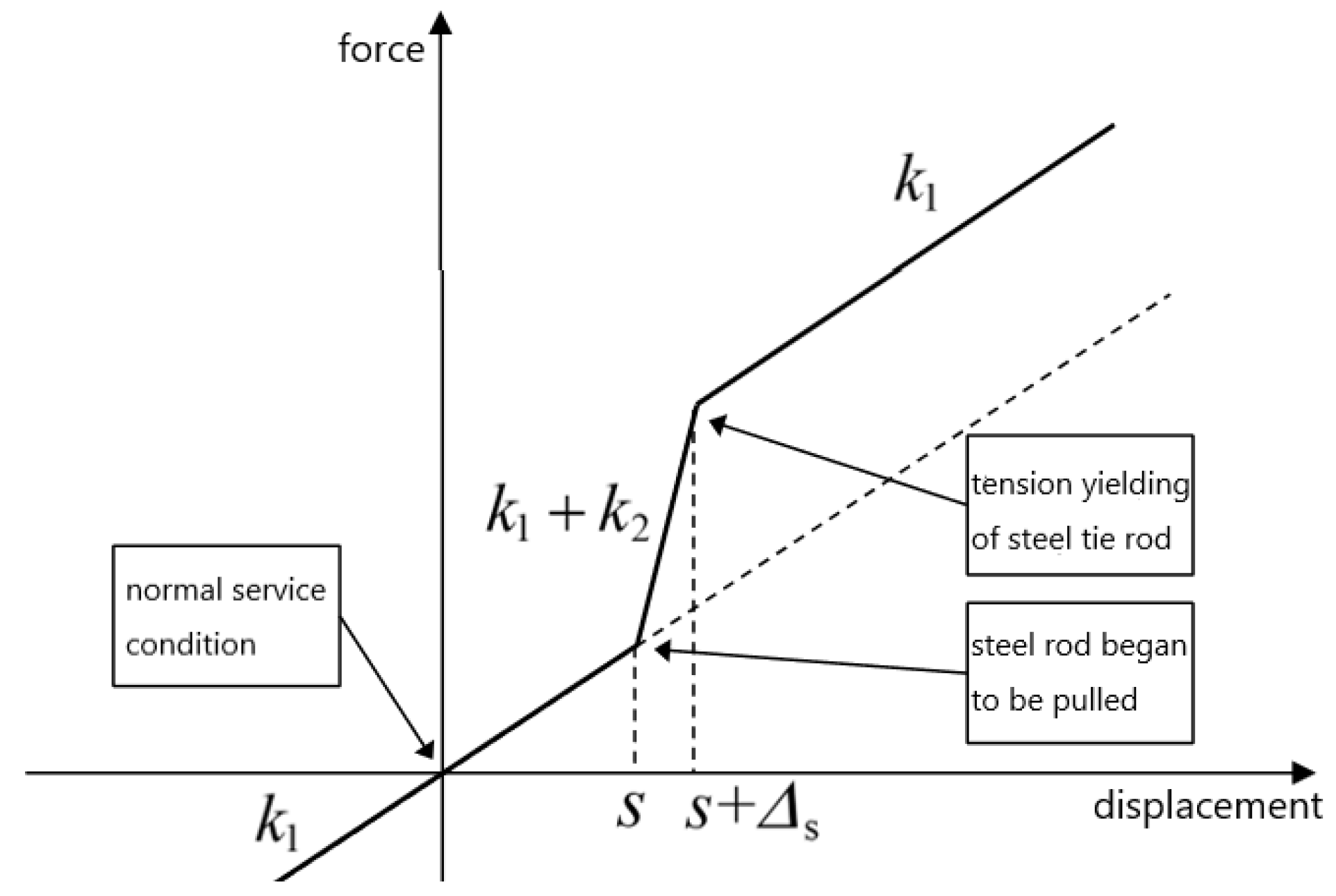
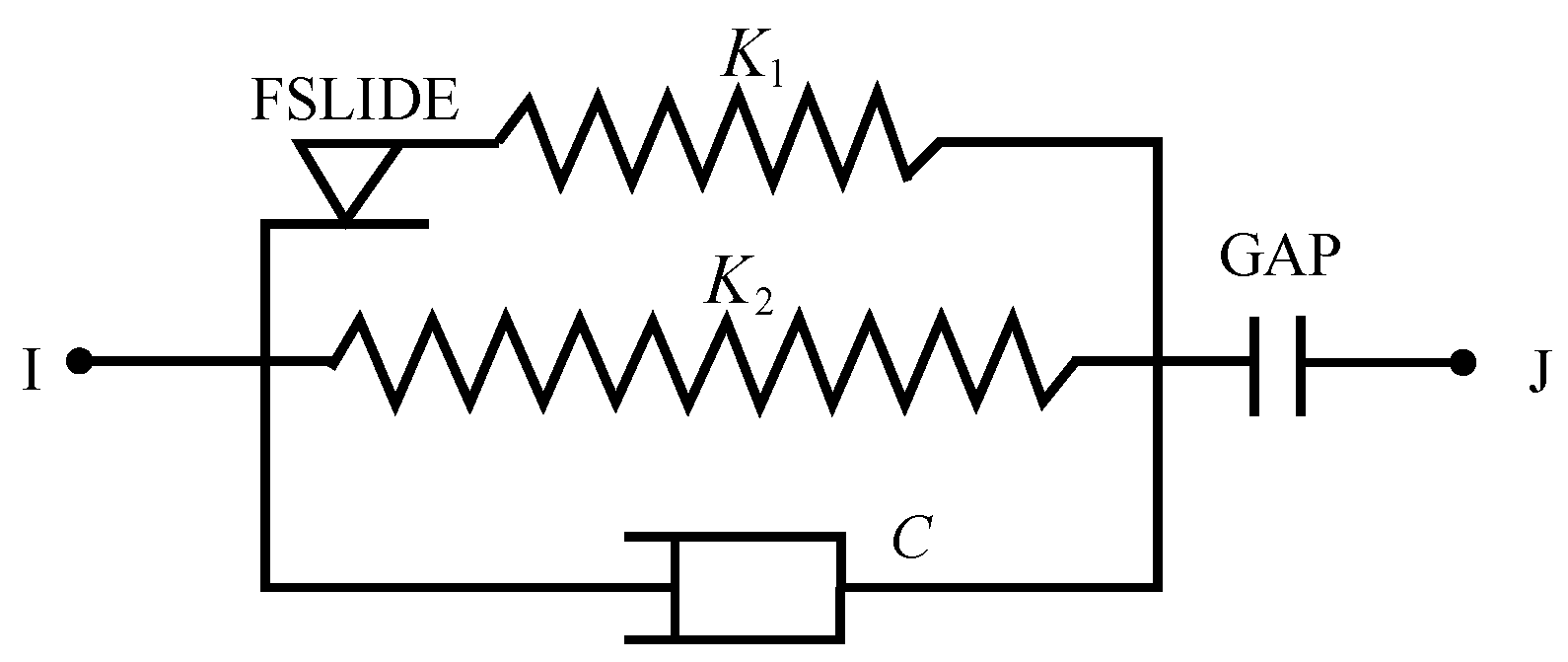
The element properties of COMBIN40 are shown in Figure 12 [23]. The element includes initial gap, element stiffness (k1) and (k2), element slip force and element damping(C). The element stiffness can be used to simulate the stiffness of the steel tie rod. The element slip force can be used to approximate the yield force of the steel tie rod and the element initial gap can be used to simulate the initial gap of the steel tie rod. COMBIN40 whose stiffness is set to a maximum value only considers the initial clearance of the steel tie rod. It is considered to be a rigid rod and the element stiffness is provided by the BEAM188 element. Using the bilinear element and the Von Mises yield criterion, the element yield can be considered.
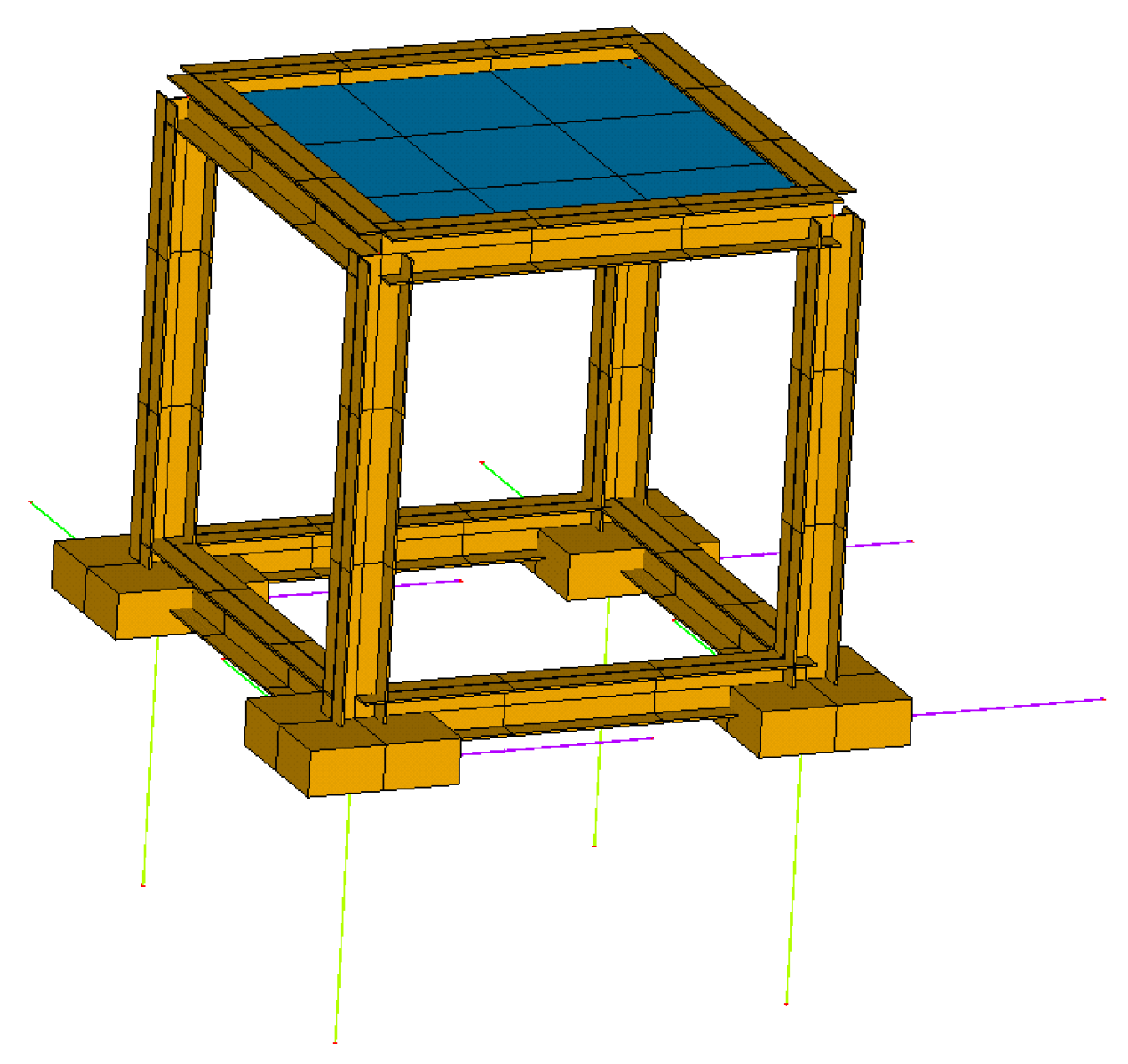
To analyze the difference between the actual analysis results of the two schemes, a three-dimensional frame model is established in ANSYS, as shown in Figure 13 and Figure 14. The anti-rocking structure is arranged according to the two schemes and the dynamic time history analysis is carried out. The ground motion time history wave adopts the Taft wave and the acceleration is loaded in three directions.
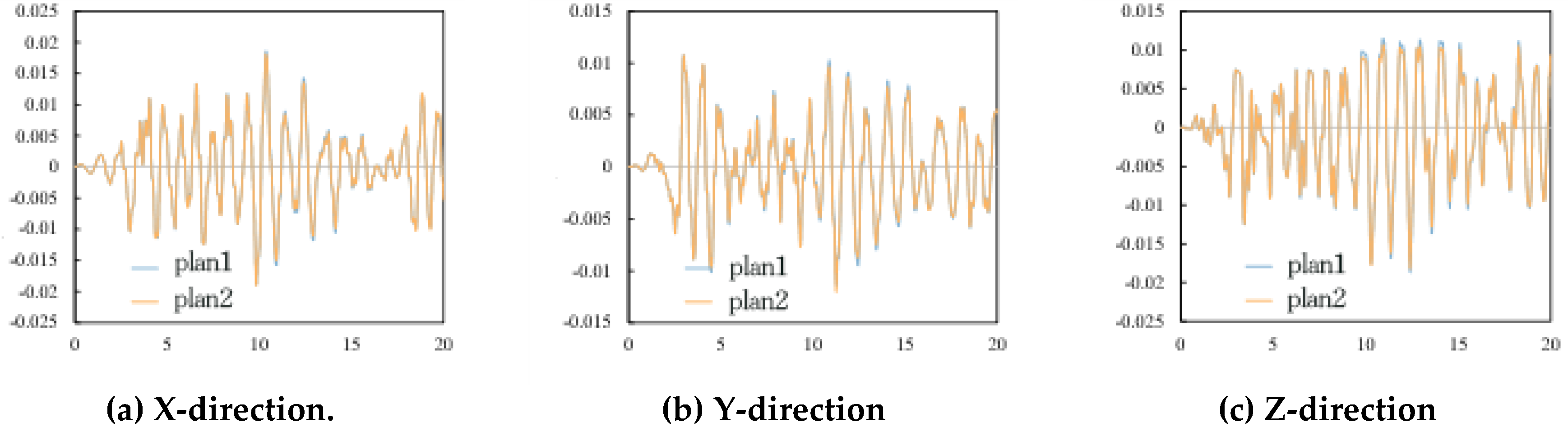
Figure 15 illustrates the vertical displacement curves of the bearings in the two layout schemes. As illustrated in the diagram, upon the initial application of the seismic wave, the three-way displacement curves of the No. 4 bearing unit in the two scheme models exhibit a high degree of coincidence. As the steel rod is subjected to continuous tensile strain, the peak displacement of the two is observed to differ. However, the discrepancy is not significant. The maximum discrepancy in displacement in the X and Y directions is 1.0% and 1.8%, respectively. The maximum discrepancy in the Z-direction displacement is 7.25%. A comparison of the three-dimensional displacement curves of X, Y and Z reveals that as the seismic wave loading time is extended continuously, the degree of coincidence between the displacement curves of the two schemes increases once more. Ultimately, the displacement curves converge. This may be attributed to the failure of the steel tie rod in the anti-rocking structure, which may have been caused by excessive stretching. Following the failure of the steel tie rod, the anti-rocking device will cease to function, resulting in a gradual alignment of the displacement curve. Furthermore, the values of X, Y and Z three-way displacements in the non-overlapping section of the curve in Scheme 1 are higher than those in Scheme 2. This indicates that the limiting effect of the anti-rocking device on the vertical displacement of the bearing and the anti-rocking effect of the device are underestimated when only the COMBIN40 element is used.
Nevertheless, when compared with the analysis results of Scheme 1 and Scheme 2, it can be observed that the difference between the node displacement and the anti-rocking effect is not significant. Furthermore, Scheme 2 is capable of more realistically and accurately simulating the anti-rocking device. However, both the COMBIN40 spring element and the BEAM188 plastic beam element in the second scheme are nonlinear elements, which makes achieving convergence in the calculation process a significant challenge. At the same time, the calculation time for the two groups of models is markedly disparate. Under the two groups of schemes, the finite element calculation time for the small model in Figure 13 is approximately 10 minutes and 2 hours, respectively. Therefore, the difference is considerable. The first scheme can greatly reduce the software calculation time.
In summary, it is more feasible and effective to use the first scheme to simulate the anti-rocking device. The Python conversion program encompasses the necessary programs for both schemes, which can be selected based on the specific requirements.

4. Analysis of Model Transformation Results

The theater model has been converted from the MIDAS GEN model to the ANSYS model using the Python conversion program. The anti-rocking device has been selected as the simulation scheme in Figure 11. The MIDAS GEN model of the theater structure is shown in Figure 16 (a) and the converted ANSYS model is shown in Figure 16 (b).
Figure 17 displays the displacement of the structure under the influence of a gravitational load. The largest vertical displacement of the roof truss of the auditorium is 7.61 cm and 6.58 cm, respectively. The difference between the two results is 14 %. The vertical displacement range of the spring bearing of the vibration isolation layer in the MIDAS GEN model is 29.9-31.3 mm, while in the ANSYS model it is 29.7-31.6 mm. The calculation results are relatively close, which is consistent with the theoretical compression of the spring bearing of 30 mm.
The results of the structural mass and modal analysis, conducted using the ANSYS and MIDAS GEN software, are presented in Table 2. The mass of the model structure is considered a representative value for the structural gravity load, which means 1.0*dead load + 0.5*live load. The two values are 60320 tons and 60325 tons, respectively, with a difference of only 0.01 %. As the load has been converted to the joint mass in MIDAS GEN and only the joint mass has been converted in ANSYS, the quality results are highly consistent. The modal analysis method in MIDAS GEN and ANSYS adopts the subspace iteration method. Because there are many local vibrations of the beam in the MIDAS GEN structure (the 3rd to 10th modes), the modal results of the two models do not completely correspond. However, upon adjusting the structural vibration mode in accordance with the corresponding mode, it is evident that the first six natural vibration periods of the two model structures are the same. The maximum error is 2.95% and the average error is 0.9%.
Figure 18 and Figure 19 are the main vibration modes of MIDAS and ANSYS structural models, respectively. The first-order vibration mode of the structure demonstrates the overall Y-direction translation, with the Y-direction mass participation coefficients equaling 81.9% and 81.7%, respectively. The second-order vibration mode of the structure demonstrates the overall X-direction translation, with the X-direction mass participation coefficients are 86.5% and 76.5%, respectively. The 11th-order mode of the MIDAS GEN model corresponds to the third-order mode of the ANSYS model, which shows the overall rotation around the Z axis. Furthermore, the mass participation coefficients in the ROTZ direction are 99% and 85.07%, respectively. The 12th-order mode of the MIDAS GEN model corresponds to the 4th-order mode of the ANSYS model, which depicts overall Z-direction translation. The Z-direction mass participation coefficients are 57.39% and 80.8%, respectively. The results of the MIDAS GEN and ANSYS analyses are comparable. The 3rd to 10th modes of the MIDAS GEN structural model represent local beam element vibration, whereas the ANSYS model does not calculate these modes.
The results of the above analysis demonstrate that the parameters of the MIDAS GEN and ANSYS models are essentially identical. The ANSYS model after program conversion is more accurate. The accuracy and reliability of the conversion program are also verified. The conversion program significantly reduces the workload of direct modeling in ANSYS, improves work efficiency and provides a certain reference for future engineering design analysis.

5. Conclusion

In this paper, a MIDAS GEN conversion ANSYS program is developed to meet the needs of model conversion for a theater structure based on Python and ANSYS APDL language. The program is capable of effectively converting a MIDAS GEN structural model to an ANSYS structural model, thereby reducing the time required for modeling while enhancing the reliability of the resulting analysis. The research and analysis verify the accuracy and reliability of the MIDAS GEN conversion ANSYS program. The conversion program greatly saves the time of direct modeling in ANSYS and improves work efficiency and the study is of great practical significance for the anti-seismic sway design and analysis of buildings based on vibration isolation design.
(1) The program can read the material, section, unit, connection, load, node mass, constraint, time history function and other model data in the mgt file. After the program analysis and conversion, the command stream file that can be identified by ANSYS is derived, so as to realize the rapid establishment of the ANSYS model.
(2) The program is capable of converting specific connection units, including elastic and general connection units. However, it should be noted that some adjustments may be required depending on the specific functions of the unit in question, particularly in the context of actual conversion applications.
(3) The conversion program can also consider the conversion of the 3-axis direction of the beam-column element section, the release of the degree of freedom at the beam end, the rigid element, the steel spring and the special anti-rocking structure of the structure.
(4) A MIDAS GEN theater model was subjected to a transformation. A comparison of the analysis results of the two models revealed that the quality and mode of the model were essentially unchanged before and after the transformation. The maximum error of the first six orders of the structure was only 2.95%, and the structural displacement under gravity load was also essentially identical.

Author Contributions

Conceptualization, M.Z.; methodology, Y.Y. and K.F.; software, K.F.; validation, Y.Y.; formal analysis, K.F. and J.Z.; investigation, Y.Y.; resources, Y.Y., M.Z. and K.F.; data curation, K.F.; writing—original draft preparation, Y.Y., K.F. and J.Z.; writing—review and editing, M.Z.; visualization, Y.Y.; supervision, M.Z.; project administration, M.Z.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.

References

  1. Ma Xiaoping. Research on the transformation technology and software development of SAP2000 to ANSYS model based on Python. Railw. Stand. Des. 2024, 68, 167–177. [Google Scholar]
  2. Wang Xinmin. Numerical Analysis of ANSYS Engineering Structure; People’s Transportation Publishing House: Beijing, China, 2007. [Google Scholar]
  3. Zhuo Zhiying. Elastoplastic time history analysis of complex steel structures; Yunnan University: China, 2015. [Google Scholar]
  4. Hu Haohua. Dynamic characteristics and seismic performance analysis of concrete-filled steel tubular railway arch bridge; Shijiazhuang Railway University: China, 2013. [Google Scholar]
  5. Ma Fu, Cheng Xinghua. Beam frame supported shear wall structure based on the ANSYS finite element static analysis of beam-type transfer floor. Adv. Mater. Res. 2013, 2621, 508–510. [Google Scholar]
  6. Han Zebin, Zhang Yongping, Zhang Yonghua. Static and dynamic analysis of long-span spatial steel structure based on ANSYS. IPPTA: Q. J. Indian Pulp Pap. Tech. Assoc. 2018, 30, 190–198. [Google Scholar]
  7. Adriana Ionescu, Madalina Calbureanu, Mihai Negru. Static and dynamic simulation in the seismic behavior of a building structure using ANSYS program. Int. J. Mech. 2013, 7, 210–217. [Google Scholar]
  8. Jiang Lizhong, Feng Yuling, ZhouWangbao, et al. Vibration characteristic analysis of high-speed railways simply supported beam bridge-track structure system. Steel Compos. Struct. 2019, 31, 591–600. [Google Scholar]
  9. Chen Ming, Qian Ying, Zeng Qianwang, et al. Finite element analysis of a steel structure landscape bridge based on ANSYS and MIDAS CIVIL: The Fourth National Steel Structure Bridge Technology Innovation Conference, Zhengzhou, Henan, China, 2023.
  10. Deng Xue. Design and mechanical property analysis of the suspendome structure in Tianjin cycling gymnasium for east Asian games; Tianjin University: China, 2012. [Google Scholar]
  11. Feng Dawei. Research on interface development between BIM model and mechanical structure analysis; Chang ‘an University: China, 2019. [Google Scholar]
  12. Zhou H, He X, Leng Xiaoyong. Development and application of a Revit-ANSYS model transformation interface: The 11th Asian Conference on Rock Mechanics (ARMS11), Beijing, 2021. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 072058. [Google Scholar] [CrossRef]
  13. Zhao Xiaoyu, Chen Zihan, Yu Siling, et al. Research on model transformation automation based on Revit and ANSYS. Yangtze River Inf. Commun. 2021, 34, 119–121. [Google Scholar]
  14. He Shixin. One-way data mapping from the IFC model of building structure to ANSYS structural analysis model; Huazhong University of Science and Technology: China, 2020. [Google Scholar]
  15. Wang Yang, Wang Shuhong, Xue Zhao, et al. Interface design between ANSYS, Midas and AutoCAD for numerical modelling of the tunnel; Third International Conference on New Development in Rock Mechanics and Engineering (NDRM’2009) & Sanya Forum for the Plan of City and City Construction, Sanya: Hainan, China, 2009. [Google Scholar]
  16. Beijianyuan Architectural Design Shenzhen Co., Ltd. A kind of anti-seismic rocking structure of vibration isolation device: CN219569240U.
  17. Liang Jiongfeng. In Midas/Gen Structure Finite Element Analysis and Application; Institute of Technology Press, 2016.
  18. Yu Xiaomei, Li Zhen, Zheng Xiangwei, et al. Python Data Analysis Case Tutorial; Tsinghua University Press: Beijing, China, 2022. [Google Scholar]
  19. Liu Chengqing. In Analysis of Seismic, Impact and Progressive Collapse Resistance of ANSYS / LS-DYNA Engineering Structure; Architecture & Building Press, 2014.
  20. LS-DYNA Dev. LS-DYNA KEYWORD USER’S MANUAL VOLUME I.
  21. Liu Hongbo. MIDAS Gen Software Foundation and Practical Tutorial; Tianjin University Press: Tianjin, China, 2020. [Google Scholar]
  22. Wen Junbo. Discussion on the stiffness matrix of commonly used connection elements in finite element; Zhengzhou University: China, 2022. [Google Scholar]
  23. ANSYS, Inc. Ansys User’s Guide; ANSYS, Inc.: USA, 2012. [Google Scholar]
  24. Xiong Lingfang, Shi Binbin. Numerical Analysis Method and Calculation Example of ANSYS Engineering Structure Part 2: Structural Dynamics and Structural Nonlinear Problems; China Railway Publishing House: Beijing, China, 2015. [Google Scholar]
Preprints 120365 g001
Figure 1. Rendering diagram of the art center.
Figure 1. Rendering diagram of the art center.
Preprints 120365 g001
Preprints 120365 g002
Figure 2. The model of the theater vibration isolation area.
Figure 2. The model of the theater vibration isolation area.
Preprints 120365 g002
Preprints 120365 g003
Figure 3. Section of theater vibration isolation area.
Figure 3. Section of theater vibration isolation area.
Preprints 120365 g003
Preprints 120365 g004
Figure 4. Schematic diagram of anti-rocking device under earthquake [16]. 1- top plate; 2- base plate; 3- steel spring; 4- steel sleeve; 5- steel rod; 6- ball hinge base; 41- Steel sleeve inward flange; 51- steel tie rod T-flange; 52- steel tie rod lower ball head.
Figure 4. Schematic diagram of anti-rocking device under earthquake [16]. 1- top plate; 2- base plate; 3- steel spring; 4- steel sleeve; 5- steel rod; 6- ball hinge base; 41- Steel sleeve inward flange; 51- steel tie rod T-flange; 52- steel tie rod lower ball head.
Preprints 120365 g004
Preprints 120365 g005
Figure 5. Force-displacement curve of anti-rocking bearing device.
Figure 5. Force-displacement curve of anti-rocking bearing device.
Preprints 120365 g005
Preprints 120365 g006
Figure 6. Flow chart of model transformation.
Figure 6. Flow chart of model transformation.
Preprints 120365 g006
Preprints 120365 g007
Figure 7. Line element direction point construction.
Figure 7. Line element direction point construction.
Preprints 120365 g007
Preprints 120365 g008
Figure 8. The area calculated by Heron’s formula.
Figure 8. The area calculated by Heron’s formula.
Preprints 120365 g008
Preprints 120365 g009
Figure 9. Schematic diagram of COMBIN14 element.
Figure 9. Schematic diagram of COMBIN14 element.
Preprints 120365 g009
Preprints 120365 g010
Figure 10. The schematic diagram of steel spring simulation scheme.
Figure 10. The schematic diagram of steel spring simulation scheme.
Preprints 120365 g010
Preprints 120365 g011
Figure 11. Simulation scheme of steel tension rod.
Figure 11. Simulation scheme of steel tension rod.
Preprints 120365 g011
Preprints 120365 g012
Figure 12. Schematic diagram of COMBIN40 element.
Figure 12. Schematic diagram of COMBIN40 element.
Preprints 120365 g012
Preprints 120365 g013
Figure 13. Three-dimensional frame model.
Figure 13. Three-dimensional frame model.
Preprints 120365 g013
Preprints 120365 g014
Figure 14. Arrangement of anti-rocking structure.
Figure 14. Arrangement of anti-rocking structure.
Preprints 120365 g014
Preprints 120365 g015
Figure 15. Displacement-time curve of the node.
Figure 15. Displacement-time curve of the node.
Preprints 120365 g015
Preprints 120365 g016
Figure 16. FE model of MIDAS GEN and ANSYS.
Figure 16. FE model of MIDAS GEN and ANSYS.
Preprints 120365 g016
Preprints 120365 g017
Figure 17. Structural displacement under gravity load.
Figure 17. Structural displacement under gravity load.
Preprints 120365 g017
Preprints 120365 g018
Figure 18. Results of MIDAS GEN mode analysis.
Figure 18. Results of MIDAS GEN mode analysis.
Preprints 120365 g018
Preprints 120365 g019
Figure 19. Results of ANSYS mode analysis.
Figure 19. Results of ANSYS mode analysis.
Preprints 120365 g019
Table 1. KEYOPT(7) of BEAM44.
Table 1. KEYOPT(7) of BEAM44.
KEYOPT(7) 1 10 100 1000 10000 100000
freedom release ROTZ ROTY ROTX DZ DY DX
Table 2. Comparison of structural quality and cycle.
Table 2. Comparison of structural quality and cycle.
Model MIDAS ANSYS differential
structural mas (W/t) 60320 60325 0.01%
structural period
(T/s)		 first period 0.808 0.800 0.95%
second period 0.743 0.737 0.88%
third period 0.580 0.578 0.27%
fourth period 0.381 0.392 2.95%
fifth period 0.367 0.365 0.34%
sixth period 0.358 0.358 0.04%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated