1. Introduction
Mathematical models are essential in science and engineering for approximating and solving real-world problems. These models, which include linear, algebraic, and differential equations, help simulate and understand complex systems based on practical observations. In structural mechanics, they are crucial for predicting material stress, strain, and deformation in design and manufacturing. Numerical methods like the Finite Element Method (FEM) have become indispensable for solving such models, particularly for problems involving complex domains, varying material properties, or nonlinear behaviors that make analytical solutions challenging [
1].
The FEM provides approximate solutions by discretizing a system into smaller, manageable parts called finite elements. This subdivision allows for accurate representation of complex geometries and is computationally efficient. However, while FEM is widely applied, its comparative performance as a generalization of other methods, such as the Rayleigh-Ritz method, particularly in terms of approximation accuracy and computational efficiency, is a topic of continued research.
1.1. Research Objectives
This study aims to address the following questions:
How do the Rayleigh-Ritz and finite element methods compare in solving boundary value problems?
What are the sources of error in each method, and how do they affect the accuracy of the solutions?
To what extent can the use of linear elements in FEM impact the overall performance in comparison to the Rayleigh-Ritz method?
1.2. Scope and Methodology
The study will involve solving a boundary value problem using both the Rayleigh-Ritz method and the linear element approach of the finite element method. The accuracy of the approximations will be compared through graphical illustrations and numerical analysis. Sources of error, including element approximation and domain discretization, will be identified and evaluated. While FEM will be explored using linear elements, more advanced elements such as quadratic or cubic will not be considered in this analysis. Additionally, the study will focus solely on static, linear problems and will not account for dynamic or nonlinear behavior, which could be addressed in future research.
1.3. Paper Structure
The remainder of this paper is structured as follows:
Section 2 reviews the methodology of the research using the finite element method and variational principles.
Section 3 outlines the mathematical formulation of both methods for the boundary value problem under consideration.
Section 4 presents the comparative analysis of the results, including error estimation and graphical illustrations.
Section 5 discusses the findings, and
Section 6 concludes the study with suggestions for further research and practical implications.
2. Method
2.1. Weighted Integrals
In almost all approximate methods used to determine the solution of differential and integral equations, we seek a solution in the form
where
u represents the solution of a differential equation and associated boundary conditions, and
is its approximation that is represented as a linear combination of unknown parameters
and known functions
of position
x in the domain
on which the problem is posed. We shall shortly discuss the conditions on
. The approximate solution
is completely known only when
are known. Thus, we must find a means to determine
such that
satisfies the differential equation at every point
x of the domain
and conditions on the boundary
of
, then
, which is the exact solution of the problem. Of course, approximate methods are not about problems for which exact solutions can be determined by some methods of mathematical analysis: the role of approximate methods is to find an approximate solution of problems that prove difficult to obtain analytically. [
2]
When the exact solution cannot be determined, the alternative is to find a solution
that satisfies the governing equations in an alternative way. In the process of satisfying the governing equations approximately, we obtain(not accidentally but by planning)
N algebraic relations among the
N parameters
. For example, consider the problem of solving the differential equation
subjected to the boundary conditions
where
, and
are known functions,
and
are known parameters, and
is the function to be determined. We now seek an approximate solution over the entire domain
by substituting
into Equation (
1) such that
We shall consider how to solve such equations later. The equation requires the approximate solution
to satisfy the differential equation in the weighted-integral sense,
where
R is called the residual defined as
and
is called a weight function.
2.2. Development of Weak Forms
There are three steps in the development of the weak form of any differential equation.
Step 1: This step is the same as in a weighted-residual method. Move all terms of the differential equation to one side (so that it reads
), multiply the entire equation with a function
, and integrate over the domain
of the problem
Recall that the expression in the square brackets is not identically zero since
u is replaced by its approximation,
. Mathematically, in Equation (
2), the error in the differential equation (due to the approximation of the solution) is made zero in the weighted integral sense.
Step 2: While the weighted integral statement, Equation (
2), allows us to obtain the necessary number
of algebraic relations among
for
N different choices of the weight function
w, it requires that the approximation functions
be such that
is differentiable as many times as needed in the original differential equation and satisfies the specified boundary conditions. So, it makes sense to shift half of the derivatives from
u to
w so that both are differentiated equally, and we have weaker continuity requirements on
. The resulting integral form is known as the weak form.
Step 3: The third and last step of the weak formulation is to impose the actual boundary conditions of the problem under consideration. It is here that we require the weight function
w to vanish at boundary points where the essential boundary conditions are specified, i.e.,
w is required to satisfy the homogeneous form of the specified essential boundary conditions of the problem [
1].
2.3. Linear and Bilinear Functionals
Linear and bilinear functionals are fundamental concepts in functional analysis and variational methods, including the Rayleigh-Ritz method, which is used to approximate solutions to boundary value problems (BVPs). These functionals play a key role in formulating and solving the variational form of the governing differential equations. [
3] A linear functional L maps a function u from a vector space into real numbers
, such that:
for any scalars
and functions
In the Rayleigh-Ritz method, linear functionals are typically associated with external forces, boundary conditions, or source terms in the governing equations. A bilinear functional, B(u,v), maps two functions u and v from a vector space into real numbers
, and it is linear in each argument:
for any scalars
and functions
In boundary value problems, bilinear functionals often represent the energy terms in the system, such as the potential energy in elasticity or other physical quantities. The Rayleigh-Ritz method is based on variational principles, where the objective is to minimize a functional (often representing the total energy of the system) to find an approximate solution to a BVP. This is done by approximating the solution as a linear combination of trial functions and applying the variational principle. In the variational formulation of a boundary value problem, the solution satisfies a weak form of the governing differential equations. This weak form is expressed using bilinear and linear functionals as shown below:
where
is the second-order differential equation for the system, B(u,v) is the bilinear functional representing the system’s internal energy, and L(u) is the linear functional representing external forces. In the Rayleigh-Ritz method, the trial solution u(x) is expressed as a linear combination of known basis functions
where
are unknown coefficients to be determined. Substituting this into the variational form leads to a system of algebraic equations for
, which are obtained by minimizing the functional:
These functionals transform the original problem into an optimization problem, where the weak form is minimized to approximate the solution.
2.4. A Brief Look at the Finite Element Method
The finite element method (FEM) is a numerical technique for solving problems which are described by partial differential equations. The finite element method is a technique in which a given domain is represented as a collection of simple domains, called finite elements, so that it is possible to systematically construct the approximation functions needed in a variational or weighted-residual approximation of the solution of a problem over each element [
4]. Thus, the finite element method differs from the traditional Ritz, Galerkin, least-squares, collocation and other weighted residual methods in the manner in which the approximation functions are constructed. But this difference is responsible for the following three basic features of the finite element method:
Division of whole domain into sub-domains that enable a systematic derivation of the approximation functions as well as representation of complex domains.
Derivation of approximation functions over each element.
Assembly of elements is based on the continuity of the solution and balance of internal fluxes; the assemblage of elements results in a numerical analog of the mathematical model of the problem being analyzed [
2].
2.4.1. Discretization of the Domain
In the finite element method, the domain
of the problem is divided into a set of subintervals i.e., line elements, called finite elements. A typical element is denoted
and it is located between points A and B with coordinates
and
(i.e, of length
). The reason for dividing a domain into a set of sub-domains is twofold. First, domains of most systems by design are a composite of geometrically materially different parts, and the solution on these sub-domains is represented by different functions that are continuous at the interfaces of these sub-domains. Therefore, it is appropriate to seek approximation of the solution over each sub-domain. Second, approximation of the solution over each element is simpler than its approximation over the entire domain. However, the number of elements into which the total domain is divided in a problem depends mainly on the geometry of the domain and on the desired accuracy of the solution [
5].
2.4.2. Derivation of Element Equations
In the finite element method, we seek an approximate solution to Equation (
1) over each finite element. The polynomial approximation of the solution within a typical finite element
is assumed to be of the form
where
are the values of the solution
at the nodes of the finite element
, and are the approximation functions over the element. Next, we develop the algebraic equations among the unknown parameters, like the Ritz and Galerkin method. The main difference here is that we work with a finite element (i.e., sub-domain) as opposed to the total domain. This step results in a matrix equation of the form
, which is called the finite element model of the original equation [
1]. The derivation of finite element equations involves the following three steps:
Construct the weighted-residual or weak form of the differential equation.
Obtain an approximate solution over a typical finite element.
Derive the finite element equations by substituting the approximate solution into the weighted-residual or weak form.
To obtain the weak form, we multiply the governing differential Equation (
1) with a weight function
w and integrate over a typical element which results into
The last step is to identify the primary and secondary variables of the weak form. This requires us to classify the boundary conditions of each differential equation into essential (or geometric) and natural (or force) boundary conditions. The classification is made uniquely by examining the boundary term appearing in the weak form (Equation (
6)),
The coefficient of the weight function
w in the boundary expression is called a secondary variable. The dependent unknown
u in the same form as the weight function
w appearing in the boundary expression is termed a primary variable. For the model at hand, the primary variable is
u while the secondary variable is
. For a typical lone element, we have four boundary conditions
where
and
mimic the compressive force and tensile force for the axial deformation of a bar respectively. If we select
such that it automatically satisfies the end conditions
and
, then it remains that we include the remaining conditions:
in the weak form. Using Equation (
11), the weak form becomes
The finite element model based on the weak form in Equation (
12) is called the weak form Galerkin finite element model. [
6]
2.4.3. Assemblage of Element
The final aspect of finite element analysis is to assemble all the finite elements. In deriving the element equations, we isolated a typical element (the eth element) from the mesh and formulated the variational problem (or weak form) and developed its finite element model. To obtain the finite element equations of the total problem, we must put the elements back into their original positions. In putting the elements with their nodal degrees of freedom back into their original positions, we must require that the solution is uniquely defined (i.e., u is continuous) and their source terms are balanced at the points where elements are connected to each other. Please note, if the variable u is not continuous, we do not impose its continuity; but in the problem studied the primary variable is assumed to be continuous [?]. The assembly of elements is carried out by imposing the following two conditions:
- 2.
For the same three elements, the balance of secondary variables at connecting nodes requires
where
I is the global node number assigned to the nodal point that is common to the three elements and
is the value of externally applied source, if any (otherwise zero).
3. Main Section
In this study, we shall consider a boundary value problem as given in the equation below:
with boundary conditions,
where
and
are given data where
Young’s Modulus,
Cross Sectional Area.
3.1. Variational Method for Solving Boundary Value Problems (Ritz Method)
To approach this problem, we choose the approximate solution in the form
with
. Then, we construct the weak form by moving all the terms to only one side of the differential equation such that we have
.
Then, multiply Equation (
21) by a weight function
and integrate over the domain
. Doing this, we have
Integrating the term
by parts, we have
Substituting Equation (
22) into Equation (
21) then,
Applying our boundary conditions,
Equation (
24) is called the weak form of the equation. The word weak refers to the weakened continuity of
u, which is required to be twice differentiable in the weighted integral statement Equation (
21) but only once differentiable in Equation (
24).
The variational problem and quadratic functional can be expressed in the form:
where
By minimizing the quadratic functional using the relation
and solving, we have
Setting
. let
and substituting
into Equation (
26), we have
Differentiating with respect to the
’s, we have
Also,
satisfies boundary conditions of the differential equation.
For the choice of the approximation functions in Equation (
29), the matrix coefficients
and vector coefficients
can be computed as follows:
for
. We shall consider the one, two parameter approximations.
For , we have and .
The one-parameter Rayleigh-Ritz solution us given by
For
, we have
Solving the linear equation using Crammer’s rule, we obtain
The two parameter Ritz solution is given by:
3.2. Using the Finite Element Analysis
We recall the problem
with boundary conditions,
where
and
are given data.
We divide the domain over two subdivisions i.e., we have two finite elements. Using the Ritz method, we obtain the weak form over each subdivision which is given as
Following our previous assumption, we set
. The coefficient matrix over a finite element is given as
Since the weak form over an element is equivalent to the differential equation and the natural boundary conditions, the approximate solution
of (Equation (
5)) is required to satisfy only the end conditions
and
. We seek the approximate solution
in the form of algebraic polynomials. For the weak form in Equation (
37), the minimum polynomial order of
is linear (which is what we are going to employ to solve this problem).
where
and
are constants. Dividing into subdivisions with end points
and
, we have
Solving both equations simultaneously, we have
Substituting
and
in Equations (
45) and (46) into Equation (
42), we have
Comparing Equation (
47) with Equation (
5), we have
We can then compute Equation (38) and Equation (39) by evaluating the integrals. We have
and so on.
The coefficient or stiffness matrix is given as
The coefficient matrix of the two linear finite elements with
is
The co-efficients
are evaluated as
Element
.
Element
.
The assembled equation is given as
where
denote force at the nodes with
Therefore, the assembled equation becomes
According to the boundary condition,
and
. Therefore, solving for
, we have the solution:
.
4. Results
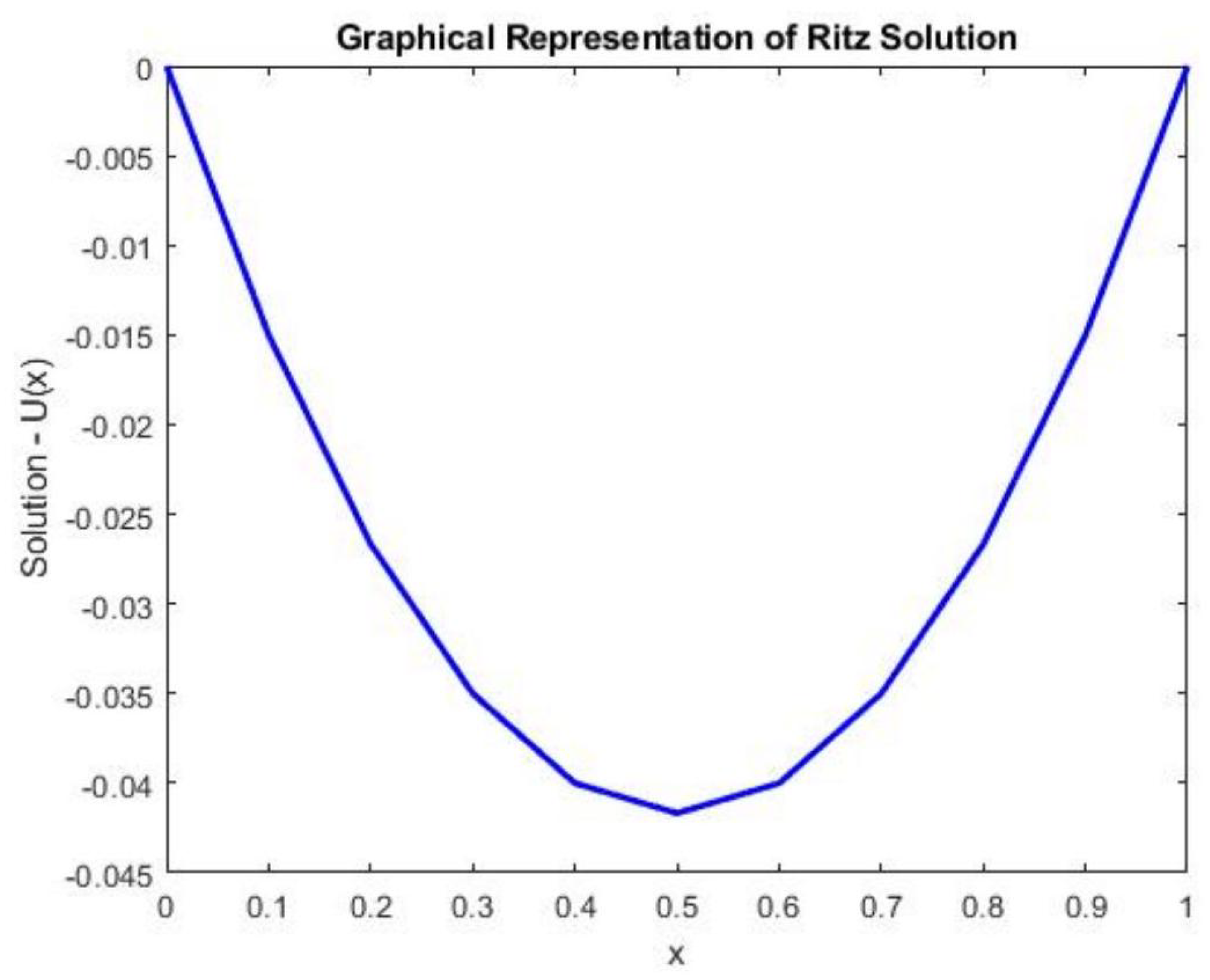
Figure 1.
The Graphical Representation of Rayleigh-Ritz Solution.
Figure 1.
The Graphical Representation of Rayleigh-Ritz Solution.
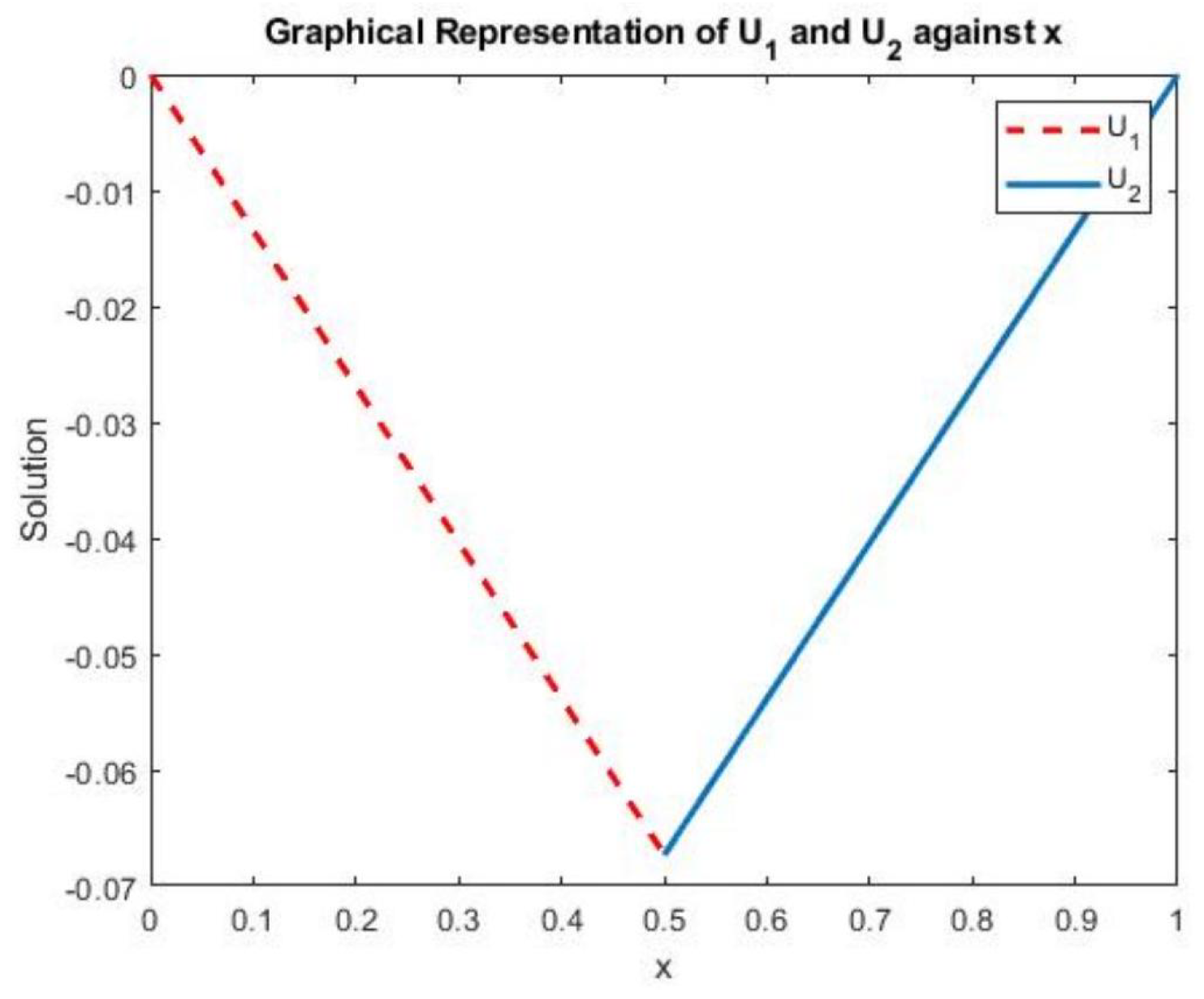
Figure 2.
Graph of the Finite Element Method in Two Subdivisions.
Figure 2.
Graph of the Finite Element Method in Two Subdivisions.
5. Discussion
A systematic study of the steps involved in the finite element formulation of a model second order differential equation in single variable was presented. The study introduces the basic principles of the finite element method and applied to problems in one dimension. Taking a close look at
Table 1, we discover that the values obtained using the finite element method is reasonably close to those obtained using the Ritz method. This shows that the finite element method is equivalent to the use of the Rayleigh-Ritz method with a piecewise polynomial approximation to the displacement. The approximation is defined through a finite set of nodal values that constitute the degrees of freedom of the problem.
6. Conclusions
In using the finite element method, the use of quadratic element is highly recommended for higher studies compared to the use of linear element for a better and more accurate solution. Also, in this research work, the domain was divided into two subdivisions to avoid too much computation. It is recommended that the domain be split into as many subdivisions as possible.
Acknowledgments
I appreciate Dr. Samuel A. Borokinni for his supervision of this paper and his invaluable support and guidance throughout the research process. Dr. Borokinni went above and beyond, dedicating countless extra hours to ensure that this document met the highest standards. I am truly grateful for his unwavering commitment and mentorship.
References
- Reddy, J. An Introduction to the Finite Element Method; McGraw-Hill, 1993.
- Courant, R. ; others. Variational methods for the solution of problems of equilibrium and vibrations. Lecture notes in pure and applied mathematics 1994, pp. 1–1.
- Logan, D.L. A first course in the finite element method, 5th. Kanada Cengage Learn 2011.
- Babuska, I. Survey lectures on the mathematical foundations of the finite element method. The Mathematical Foundations of the Finite Element Method with Applications to Partial Differential Equations 1972, pp. 3–359.
- Kiritsis, D.; Emmanouilidis, C.; Koronios, A.; Mathew, J. Engineering Asset Management: Proceedings of the Fourth World Congress on Engineering Asset Management (WCEAM) 2009; Springer Science & Business Media, 2011.
- Hrennikoff, A. Solution of problems of elasticity by the framework method 1941.
Table 1.
Comparison between the solutions of Rayleigh-Ritz and Finite Element Methods.
Table 1.
Comparison between the solutions of Rayleigh-Ritz and Finite Element Methods.
| |
Ritz Solution |
|
FEM |
| x |
|
|
Linear Element |
| 0.0 |
0.00 |
0.00 |
0.00 |
| 0.1 |
−0.00150 |
−0.0089 |
−0.0135 |
| 0.2 |
−0.0267 |
−0.0185 |
−0.0269 |
| 0.3 |
−0.0350 |
−0.0279 |
−0.0404 |
| 0.4 |
−0.0400 |
−0.0359 |
−0.0538 |
| 0.5 |
−0.0417 |
−0.0417 |
−0.0673 |
| 0.6 |
−0.0400 |
−0.0441 |
−0.0538 |
| 0.7 |
−0.0350 |
−0.0421 |
−0.0404 |
| 0.8 |
−0.0267 |
−0.0348 |
−0.0269 |
| 0.9 |
−0.0150 |
−0.0211 |
−0.0135 |
| 1.0 |
0.00 |
0.00 |
0.0 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).