Prerpints.org logo
Preprint
Article

Pressure-Induced Graphene-like Si Layer in Ductile RuSi2 with Ambient-Pressure Superconductivity and High Hardness

Altmetrics

Downloads

92

Views

58

Comments

0

supplementary.pdf (547.72KB )

Submitted:

06 October 2024

Posted:

07 October 2024

You are already at the latest version

Alerts
Abstract
Of particular interest is the serendipity of distinctive nonmetallic layered frameworks with the stoichiometry of 1:2 in the binary metallic compounds within inorganic chemistry and materials science. This not only gives rise to the unexpected properties, especially the distinguished superconductivity, as reflected in MgB2, MoB2, NaC2, LaP2 and CeP2, but also strengthens the cognition of the elemental contributions. Although various investigations on the superconducting performances in the alkali, alkaline-earth and rare-earth metal disilicides containing the silicon layers have been reported, the pursuit of superconductors with silicon-planar framework in transition metal disilicides remain unknown up to now. In the present work, crystal structure searches and first-principles calculations were thoroughly conducted in RuSi2 within the pressure range of 0-300 GPa to uncover the novel structures, incredible silicon building block and the amazing properties. The ground orthorhombic Cmca-RuSi2 phase at ambient pressure is a semiconductor with the band gap of 0.485 eV, whose hardness can reach 31.7 GPa. Even more intriguingly, the high-pressure orthorhombic Cmcm-RuSi2 configuration with the fabulous graphene-like silicon-layer, which can be theoretically stabilized with the transformation pressure of 50.97 GPa, can be unexpectedly recovered to ambient pressure. Electron-phonon coupling calculations unravels that it possesses the metallic trait with an estimated Tc value of 1.43 K at 75 GPa, which increases to 10.07 K under ambient pressure. The enhanced Tc stems from the increased density of states at the Fermi level and associated with the coupled vibrations between Ru and the planar Si layer. Meanwhile, the hardness value for Cmcm-RuSi2 is 26.8 GPa under ambient pressure, which further results from the three-dimensional covalent Ru-Si and Si-Si building blocks. The coexistence of superconductivity and high hardness in the Cmcm-RuSi2 configuration under ambient pressure will pave the way for delving into more binary transition-metal silicides and correlated ternary silicides with the profound silicon layers.
Keywords: 
Subject: Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

Last decade has witnessed the exuberant development of superconductor, which discloses a variety of advanced superconductor materials. Among these superconductors, a class of binary compound constituted by rich nonmetallic and metallic elements has garnered climbing interest from academic and industrial communities not only due to the considerable superconducting transition temperature Tc but also owing to the unprecedented nonmetallic polymetric configurations. In the binary hydride superconductors, the special H24, H29, H32 and H36 clathrate structures were verified in CaH6 [1,2], YH9 [3,4], LaH10 [5,6] and CeH18 [7] with the near or even above room-temperature Tc values of 205 K (172 GPa), 262 K (182 GPa), 250 K (170 GPa), and 329 K (350 GPa), respectively. Recently, another A-15 type structure of Pm-3n-Lu4H23 [8] was further proposed with a measured Tc value of 71 K (218 GPa), which consists of a combined clathrate structure of H20 and H24 cage. This idea stems from the Si clathrate structures in Ba8Si46 [9,10] with the low-temperature properties. The high temperature Tcs in these hydrogen clathrate structures are closely associated with sodalite H clathrate structure, because the stretching and rocking vibrations of H atoms within H-cage contribute to strong electron-phonon coupling. Apart from the three dimensional (3D) hydrogen cage structure in the binary hydrogen-rich superconductor, two unpredictable hydrogen configurations with high Tcs enter into the scientists’ horizon, which not only contains one-dimensional (1D) nanotubes in HfH9 (110 K, 200 GPa) [11] and H7 chains in GaH7 (~100 K, 200−300 GPa) [12], but also consists of the momentous two-dimensional (2D) layered configurations. These 2D layered structures can be typified by the wavy H layer containing the edge-sharing pea-like H18 ring in LiH4 (93.6 K, 100 GPa) [13], exotic layered structure composed of quasimolecular H2 and linear H3 units in KH6 (58.6−69.8 K, 166 GPa) [14], puckered hexagonal honeycomb of H atoms sandwiched between slabs of atomic Fe and H atoms in FeH5 (51 K, 130 GPa) [15], hydrogen pentagraphenelike structure in HfH10 (213−234 K, 250 GPa) [16] and H9 nonagon in XH15 (X = Ca, Sr, Y and La) [17] with the estimated high Tc values of 189 K at 200 GPa, 139 K at 300 GPa, 208 K at 220 GPa and 113 K at 200 GPa, respectively. Although the breakthroughs in achieving high transition temperature Tc have breathed new life into the pursuit of room-temperature superconductivity, the extremely high pressures (usually surpassing 100 GPa) in synthesizing these hydride-based superconductors involving diamond anvil cell (DAC) necessitates the use of culet with the small sample size ranging from 40 to 80 μm [18]. Nevertheless, the small sample size conduces to the weak magnetic measurements challenging and makes precise temperature control difficult. On the other hand, the DAC for the synthesis were always broken during depressurization owing to the hydrogen embrittlement [19,20]. Both aspects are expected to get rid of the hydride superconductor under high pressure, which portends the advent of other non-H building blocks in binary metal compounds under lower or even atmospheric pressures.
In the binary compounds containing metal and non-H light element (B, C, N and P), a variety of researchers endeavored to dig into their superconductivity and extraordinary nonmetallic frameworks, especially for 2D planar motifs. The planar nonmetallic skeleton is of great interest due to the spectacular properties, such as distinct superconductivity. Starting from metal borides, MgB2 (at 1atm) [21] and MoB2 (under 100 GPa) [22] within the identical P6/mmm symmetry possess the highest and second highest Tcs of corresponding 39 and 32 K because of the 2D graphitic boron layer among the metal borides. In the metal carbides, the predicted superconducting critical temperature Tc for NaC2 [23] could approach ~42 K at 80 GPa with the existence of hexagonal rings, which is slightly higher that of MgB2 [21]. Moreover, YC2 was also theoretically verified to be a good superconductor with the estimated Tc value of 2.9 K [24], characterized by the 2D graphite sheet. Importantly, the KN2 [25] monolayer presents a unique superconducting trait with an estimated critical temperature (Tc) of 4.3 K under ambient condition. Furthermore, the particular novel planar N4 unit gives rise to the phonon-mediated superconductivity with the Tc value of 4−8 K in P63/mcm-FeN2 [26]. Last but not least, the I4/mmm-KP2 [27] configuration with puckered phosphorus layer is predicted to have the superconducting critical temperature Tc of 22 K under 5 GPa. Moreover, the calculated Tc values for CeP2 [28] under ambient pressure (Tc = 30.77 K) and LaP2 [29] at 11 GPa (Tc = 22.2 K), regarded as the the highest and second highest Tcs among those of already known binary transition-metal phosphorus, which should be attributed to the graphene-like P layer. From the anterior discussions, two recognizable traits for these binary metal compounds with superb superconductivity fade into our sight, the stoichiometry of 1: 2 and the nonmetallic layered framework (B, C, N and P). In consequence, to uncover more marvelous superconductors, we need to achieve more fresh structures containing the nonmetallic layer fabrications in this category of compounds.
Surrounded by B, C, N and P elements in the periodic table of elements, Si is a common but useful element for a great number of fields, such as integrated circuits and solar cells. Contrary to the semiconductor properties of silicon at ambient pressure, the metal silicides possess the superconducting properties in consequence of its various intriguing motifs (e.g. 3D cages and 2D buckled layers). In the 3D silicon cage system, Ba8Si46 [30] consists of a combination of Si20 and Si24 cages linked by sharing a pentagonal face with the estimated Tc of 8 K at ambient pressure while Ba24Si100 [31] contains Si20 cage with the Tc value of 1.4 K at the pressure of 1.5 GPa. Subsequent experiment proposed that LaSi10 [32] is deemed as a superconductor with Tc = 6.7 K. Moreover, the superconducting critical temperature of P6/m-NaSi6 [33] is estimated to be 13.1 K with the silicon clathrate configuration, in which all Si atoms form simple hexagonal open channels and guest Na atoms fill the channels. Apart from the 3D silicon clathrate configurations, another extraordinary example of graphite-like 2D-structured sub-network are metal disilicides in the form of MSi2, where M represents the metal atom. This kind compound is very stable and multifunctional and can be chemically modified by oxidation, which further could induce novel silicon framework such as layered silicon, silicon clathrates and other silicon allotropes after removing the metals. More interestingly, the superconducting phenomenon can be achieved in such layered silicides, which hence stimulate the experimental and theoretical discoveries of the interesting superconductivity in MSi2. In the alkali-metal disilicides, RbSi2 [34] with the trigonal EuGe2-type phase (space group: P-3m1, 164), characterized by the hexagonal honeycomb structure, was predicted to have the Tc value of 9 K. For the alkaline-earth metal disilicides, three layered phases in MgSi2 [35,36] namely, the R-3m phase at 0 GPa, Imma phase at 10 GPa and P6/mmm phase at 20 GPa were predicted to possess the superconducting critical temperature Tc values of ~7, ~6.9 and ~7 K, respectively. CaSi2 [37,38] is transformed to the hexagonal AlB2-type structure (space group: P6/mmm, 191) with the graphite-like Si layers at 15 GPa in experiment, which displays a superconducting transition at 14 K. Moreover, the high pressure of BaSi2 [39] with the EuGe2-type layered configuration is a superconductor with the experimentally measured Tc value of 6.8 K. In rare-earth metal disilicides, LaSi2 [40] is considered as a superconductor with the tetragonal ThSi2-type (I41/amd, 141) layered structure, which has the superconducting Tc value of 2.5 K. Recently, another theoretical group studied the superconductivity of the binary Y−Si system and pointed out that the estimated Tc value of Imma-YSi2 [41] with the apparent layered structure is 0.5 K at 50 GPa. Based on the anterior superconductivity discussions, the layered structures in metal disilicides MSi2 cover alkali, alkaline-earth and rare-earth metal disilicides. Nevertheless, a distinct category of metal disilicides, namely, transition metal disilicides may be neglected in previous investigations, which arouses our interest in the quest for the layered structures with exceptional superconductivity in transition-metal disilicides.
Chemical substitution is one of the diverse routes in chemical pressure, which can tune the structures and properties of materials [42,43]. Following on this method, we replace alkali, alkaline-earth and rare-earth metal with the considered transition metal in MSi2. As is generally known, ruthenium element is located in the VIII group of the periodic table and is a typical transition metal element, which is selected as a representative transition metal. According to the experiment, there are four compounds (e.g., RuSi [44,45], Ru2Si3 [45,46,47], Ru4Si3 [45,46] and RuSi2 [48]) in the binary Ru-Si system under atmospheric pressure. Zhang et al. theoretically predicted three stable compounds in the binary Ru-Si system at ambient pressure, namely, RuSi, Ru2Si3 and RuSi2 through the CALYPSO crystal structure prediction method in combination with first-principles [49]. Both experiment and theory confirm the stable existence of RuSi, Ru2Si3 and RuSi2 in Ru-Si system under ambient pressure, which exhibit the semiconductor characters with narrow band gaps. RuSi consists of two polymorphic types, in other words, the FeSi-type phase with space group of P213 at low temperature and the CsCl-type phase with space group of Pm-3m at high temperature [50]. Ru2Si3 crystallizes in the orthorhombic Pbcn configuration [45,46,47]. More importantly, RuSi2 was reported experimentally for the first time and analyzed theoretically with three possible phases, tetragonal α-RuSi2 (P4/mmm), orthorhombic β-RuSi2 (Cmca) and cubic γ-RuSi2 (Fm-3m) [51]. Recently, Zhang et al theoretically confirmed that the component RuSi2 with the Cmca phase is stable in the convex hull of the binary Ru−Si system based on the CALYPSO crystal research method and first-principles [49]. However, the exploration on RuSi2 has focused only on the structures and electronic properties under the atmospheric pressure in spite of the fantastic silicon framework and unexpected properties possibly existing under the high pressure condition, for example, the novel structures with superconductivity. High pressure is an effective methodology to induce the structural transition of materials, bringing about the variation of the properties [52,53], for instance, the evolution from insulator or semiconductor to metallicity or superconductivity. Moreover, RuSi undergoes a structural transition from FeSi-type to CsCl-type cubic structure at 0.28 GPa, accompanied by the semiconductor-metal conversion [50]. These two aspects enhance our confidence in pursuing the novel structures with superconductivity in RuSi2 under high pressure. Impressed by the layered structures with the alkali, alkaline-earth and rare-earth metal disilicides discussed above, two questions has been lingering in my mind. could the novel phases appear for RuSi2 under high pressure? Furthermore, if novel structures could stabilized under high pressure, could the high-pressure phases contain the layered silicon motifs with the superconductivity and superb hardness?
To resolve the aforementioned two problems, we performed an extensive study on the potential RuSi2 configurations over the pressure range of 0−300 GPa by applying an unbiased CALYPSO method combined with first-principles calculations. Herein, we report an absolutely novel RuSi2 configuration with the orthorhombic Cmcm symmetry under high pressure, composed of a graphene-like silicon-layer with one centered ruthenium atom. More intriguingly, this configuration can be quenchable after releasing the pressure down to ambient pressure. The Cmcm-RuSi2 structure exhibits the superconducting character with the superconducting critical temperature of 10.07 K at ambient pressure, which is the second highest temperature among the MSi2 (M = metal) silicides (R-3m-CaSi2, 14 K) [38]. In addition, its Vicker hardness value can reach 26.76 GPa, makes it become a rarely hybrid material that simultaneously behaves the superconducting property and high hardness under atmospheric pressure. This investigation provide a new pathway for the design of hard superconductors in transition-metal silicides, which will arouse the interest of the experimental researchers in synthesizing transition metal disilicides and measuring related properties.

2. Computational Method

The structure searches of RuSi2 materials under high pressure are based on the particle swarm optimization (PSO) algorithm as implemented in the crystal structure prediction CALYPSO code [54,55], which has successfully predicted the ambient-pressure and high-pressure structures of various systems [56,57,58,59]. In the pressure range of 0−300 GPa, we implemented the structure searches with unit cells including up to four formula units (f.u.). The structural geometrical optimization, electronic structure, Bader charge, electron localization functions (ELF) [60,61] and elastic constants calculations were performed through density functional theory in the Vienna ab initio simulation package (VASP) [62] within the Perdew−Burke−Ernzerhof (PBE) exchange correlation function of generalized gradient approximation (GGA) [63,64]. The Projector-Augmented Wave (PAW) [65] method was adopted to treat 4d75s1 and 3s23p2 as valence electrons for Ru and Si atoms, respectively. In addition, the cutoff energy of 800 eV for the plane-wave basis expansion of the electronic wave functions was implemented and appropriate Monkhorst−Pack k meshes for sampling in the Brillouin zone were set to ensure that all the enthalpy calculations were well converged to better than 1 meV/atom [66]. The crystal orbital Hamilton population (COHP) method was applied in LOBSTER code [67,68]. The phonon and electron-phonon coupling (EPC) matrix elements were calculated within density functional perturbation theory (DFPT) as implemented in the QUANTUM ESPRESSO package [69] with a kinetic cutoff energy of 80 Ry. In the first Brillouin zone, we have selected k-point meshes for Cmcm-RuSi2 phase of 12 × 12 × 12 at 1 atm and 10 × 10 × 10 at 25, 50 and 75 GPa, respectively. The q-point meshes for Cmcm-RuSi2 phase were set to 3 × 3 × 3 at 1 atm and 5 × 5 × 5 at 25, 50 and 75 GPa, respectively.

3. Results and Discussion

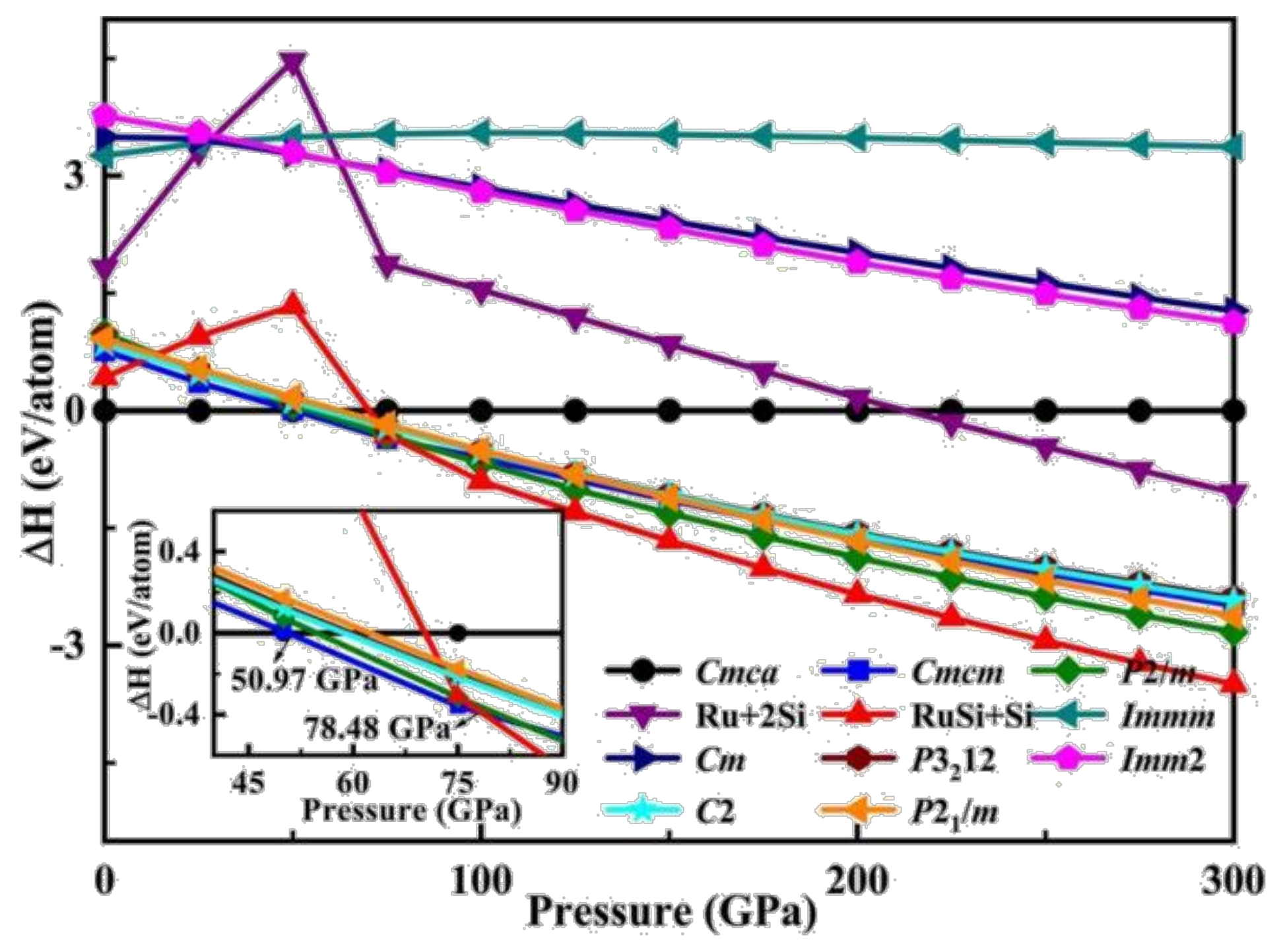
3.1. Structural Transition and Dynamical Stability

In the first instance, in order to determine the structural transition sequence and potential stable structures for RuSi2 under high pressure, we carried out the CALYPSO code for thoroughly crystal structure searches. As a result, nine candidate low-energy structures with space groups of Cmca, Cmcm, P2/m, Immm, Cm, P3212, Imm2, C2 and P21/m were predicted at the pressure range of 0−300 GPa. The structural diagrams, together with detailed structural parameters of nine candidate phases under ambient pressure are summarized in Figure S1 and Table S1 of the Supplementary Information (SI). The previously known Cmca [49,70] and Immm [71] structures of transition metal disilicide RuSi2 were successfully reproduced by our structure searches, demonstrating the reliability of the CALYPSO method. Subsequently, we constructed the enthalpy-pressure (H−P) curves of the low-energy phases and presented two possible decomposition routes (Ru + 2Si and RuSi + Si) with respect to Cmca phase, as shown in Figure 1. The phase stability of RuSi2 compound is established at various pressures by judging the enthalpy difference relative to the solid constituent elements and stable compounds (i.e. Ru, Si solid phase, and RuSi compound). The corresponding known stable elements P63/mmc for Ru [72], Fd-3m, P63/mmc, and Fm-3m for Si [73], and compounds P213 and Pm-3m for RuSi [44,45,74] under corresponding pressures were achieved from the previous literature. According to Figure 1, RuSi2 adopts the orthorhombic β-FeSi2 type configuration (space group: Cmca) as ground-state structure under ambient pressure, which is consistent with the previous experimental observations and theoretical researches [49,51,75]. As the pressure increases, the RuSi2 is found to crystallize in another orthorhombic Cmcm phase, which is energetically favored over the Cmca-RuSi2 above 50.97 GPa and maintains its stability up to 79.15 GPa. Noticeably, this Cmcm-RuSi2 configuration is absolutely distinctive from previously reported metal disilicides MSi2, such as hexagonal P6/mmm-type phase in MgSi2 [35,36] and CaSi2 [37,38], trigonal P-3m1 phase in RbSi2 [34] and alkaline-earth metal disicides, trigonal I41/amd phase in LaSi2 [40], rhombohedral R-3m phase in MgSi2 [35,36], and orthorhombic Imma in MgSi2 [35,36] and YSi2 [41] Hence, this orthorhombic Cmcm phase is predicted to be a high-pressure ground-state structure in metal disilicides in the present work for the first time. Above 79.15 GPa, the RuSi2 compound decomposes into RuSi + Si. Additionally, the considered pressure dependence of RuSi2 decomposition reaction proves that RuSi2 will not decompose into Ru + 2Si within the pressure range of 0−78.48 GPa (see Figure 1). Thus, compressing RuSi and Si is a potential synthetic route for RuSi2 crystal. The above analysis demonstrates the thermodynamical stability of Cmca-RuSi2 and Cmcm-RuSi2 phases and provides their potential synthetic routes, which will stimulate the experimental synthesis. Subsequently, we focus on the structural, chemical bonding, electronic, superconducting and mechanical characters for the Cmca-RuSi2 and Cmcm-RuSi2 phases.
To probe into the dynamical stability of two thermodynamical stable structures under specific pressures, we have computed their phonon dispersion curves (see Figure S2 and Figure 7). It is evidently found that both the Cmca-RuSi2 phase at atmospheric pressure and the Cmcm-RuSi2 phase at the pressure range of 0−75 GPa are dynamically stable, as there is no imaginary frequency in the whole Brillouin zone. Although the Cmcm-RuSi2 structure can be acquired under high pressure, it can be recovered to ambient pressure condition, thereby render it applicable in practical settings. Subsequently, we mainly focus on the the structural, chemical bonding, electronic, superconducting and mechanical features for the Cmca-RuSi2 and Cmcm-RuSi2 phases under atmospheric pressure.

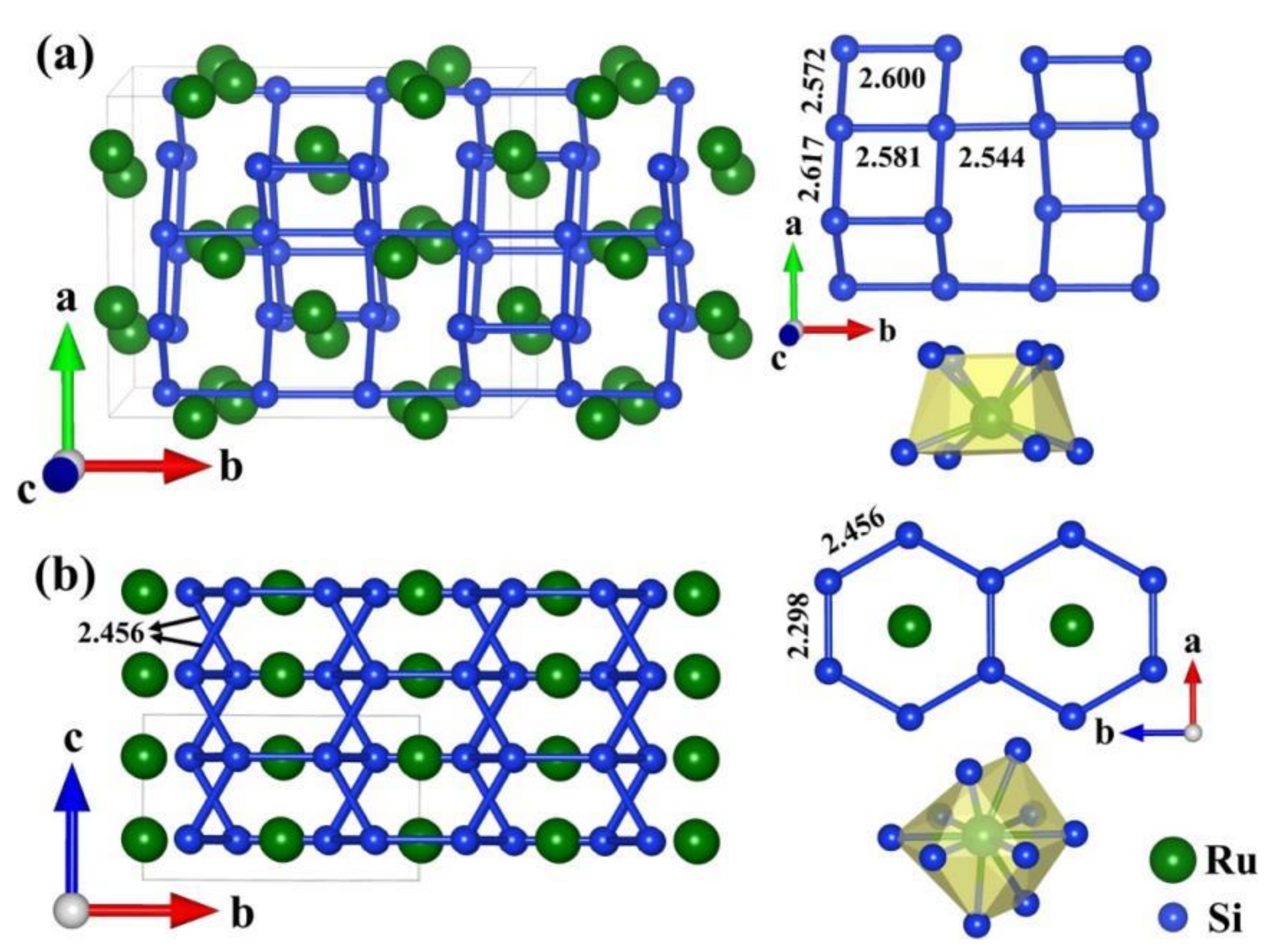
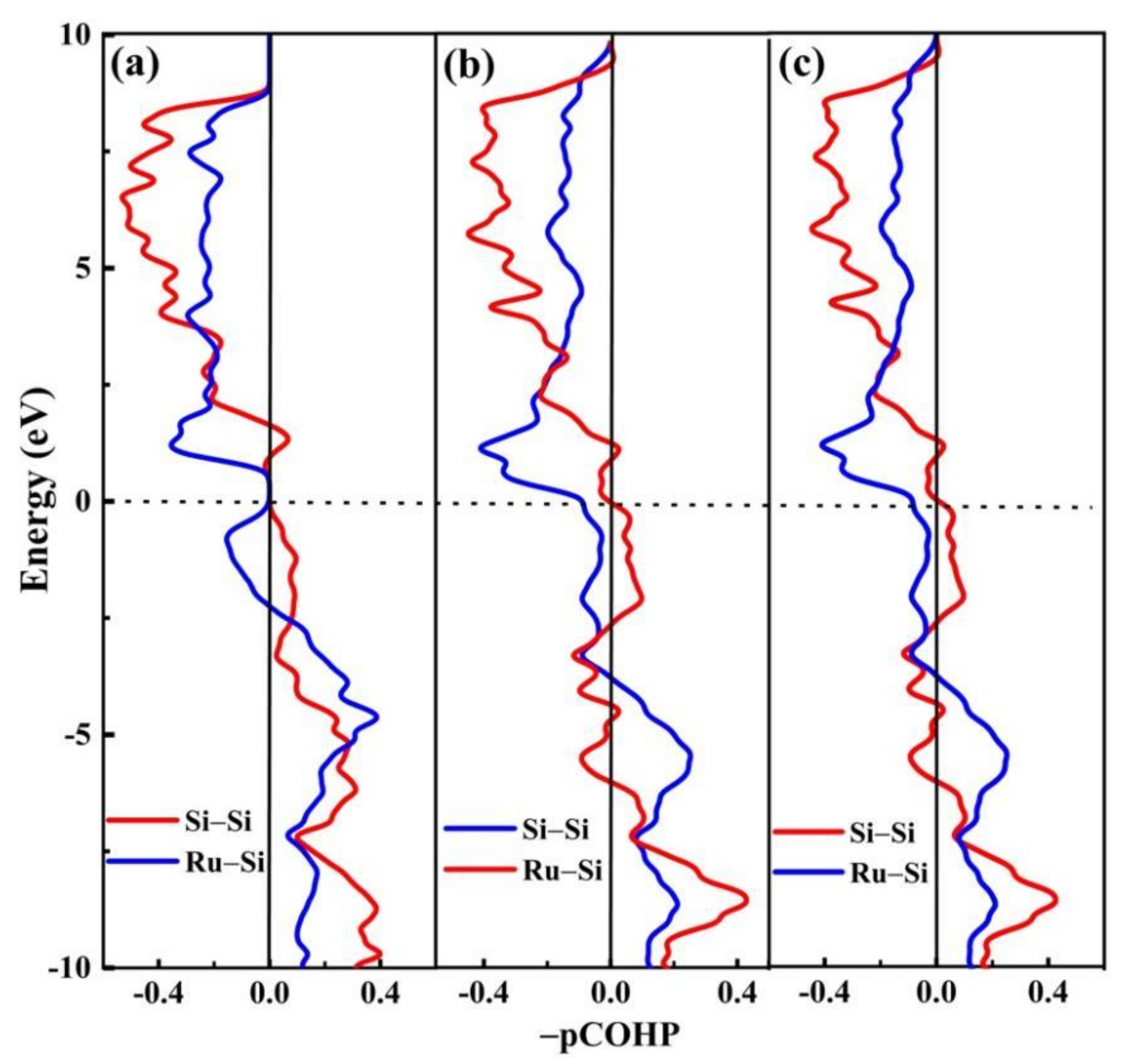
3.2. Structural Character and Bonding Essence

The crystal structure diagrams for the Cmca-RuSi2 phase at 1 atm and the Cmcm-RuSi2 phase at 75 GPa were distinctly depicted in Figure 2 and homologous structural parameters were tabulated in Table S2. From Table S2, the lattice parameters (a = 10.170 Å, b = 8.108 Å, and c = 8.209 Å) of Cmca-RuSi2 excellently align with previous results (a = 10.223 Å, b = 8.133 Å, and c = 8.250 Å) [49,51,75]. In this structure, there are two inequivalent Si atoms located at the Wyckoff sites 16g (0.372, -0.778, 0.057) and 16g (0.127, -0.551, 0.225), respectively, with Si-Si separations varying from 2.54 to 2.62 Å. All the Si atoms form a ladder-like Si-network framework with the planar quadrangle along the b axis and the angle between the nearest three Si atoms is nearly 90°. The shortest Si-Si distance (2.54 Å) is marginally longer than the those of Si (2.22 Å) atoms, d-Si (2.35 Å) [76], and allotrope Cmcm-Si24 (2.33-2.41 Å) [76], but comparable to those of C49-WSi2 [77] (2.56 Å) and B31-RhSi (2.53-2.69 Å) [78], expounding the contribution of Si-Si covalent bond to the structure construction. This result can be evidenced by the electron localization function (ELF) for the Cmca-RuSi2 under ambient pressure, as displayed in Figure 3(a) and 3(b), which precisely describes the electron localization between Si atoms. Besides, each Ru atom is coordinated by eight Si atoms, forming a “RuSi8” building block with Ru-Si separation range of 2.45-2.52 Å. The shortest Ru-Si distance (2.45 Å) is slightly longer than the sum of the covalent bond radii of Ru (1.25 Å) and Si (1.11 Å) atoms, indicating the covalent Ru-Si bond, which can be demonstrated by ELF in Figure 3a,b as well. For the Cmcm-RuSi2 phase at 75 GPa, the lattice parameters are a = 6.693 Å, b = 4.052 Å and c = 3.866 Å, where Ru atoms occupying the Wyckoff sites 4c (-0.500, 0.307, 0.750) are neighbored by equivalent Si atoms locating at 8g (-0.832, 0.316, 0.750) sites. More charmingly, the Cmcm-RuSi2 phase contains two interpenetrating honeycomb-like silicon-layer along the c-axis, which forms the silicon hexagonal ring with one metal atom Ru located at the center of hexagonal ring in the a-b plane, disclosing that metallic atom and nonmetallic silicon layer are in the same flat. This layered feature is distinct from previously reported planar structures, such as MgB2 [21], MoB2 [22], NaC2 [23], YC2 [24], CeP2 [28] and LaP2 [29], where the hexagonal-ring nonmetallic layer and metallic atom generate two alternate layers and are distributed in different flats. In silicon hexagonal-ring, the there are two kinds of Si-Si bond lengths, corresponding to 2.298 and 2.461 Å, while the Si-Si bond length between the silicon layers is 2.456 Å. These three Si-Si bond lengths are elongated into 2.417, 2.668 and 2.655 Å, respectively, when the pressure decreases to the ambient pressure. Additionally, ten silicon atoms are coordinated around one Ru atom, forming a distorted RuSi10 dodecahedron with four different Ru-Si bond lengths of 2.347, 2.431, 2.435 and 2.440 Å at 75 GPa, compared with the elongated Ru-Si bond separations of 2.523, 2.615, 2.554 and 2.683 Å under atmospheric pressure. Both of Si-Si and Ru-Si bond distances provide an explanation of the Si-Si and Ru-Si covalent bonds in the Cmcm-RuSi2 crystal at ambient pressure and high pressure, which can also be substantiated by the electron localization in the intermediate regions of the Si-Si and Ru-Si bonds, as depicted in Figure 3c–f. In short, based on the overall analyses of bond length and ELF, the Cmca-RuSi2 and Cmcm-RuSi2 phases under ambient pressures as well as the Cmcm-RuSi2 phase under high pressure are characterized by a combination of the covalent Ru-Si and Si-Si bonds.
The formation of strong covalent Ru−Si and Si−Si interactions in these two stable configurations of RuSi2 can be quantitatively disclosed through the calculated crystal orbital Hamilton population (COHP) curves and integral crystal orbital Hamilton population (ICOHP) at the Fermi level, as displayed in Figure 4. The calculated ICOHP values for Ru−Si and Si−Si pairs in Cmca-RuSi2 under 1 atm are −1.84 and −2.41 eV for per pair, respectively. Moreover, the predicted ICOHP values for the Ru−Si bonds in Cmcm-RuSi2 at 1 atm and 75 GPa is −1.66 and −1.68 eV for per pair, respectively, with the corresponding ICOHP values of the Si−Si pairs −2.25 and −2.23 eV for per pair. Afterward, the predicted ICOHP values for the Si−Si pairs (−2.41, −2.25 and −2.23 eV for per pair) in both RuSi2 structures are comparable to those of covalent Si−Si pairs in Na4Si24 (−2.544 eV/pair) [76], P−P pairs in LaP2 (−2.32 eV/pair) [29], P1−P2 pairs in Ce2P3 (−2.41 eV/pair) [28], B2−Β2 pairs in LiB4 (−2.55 eV/pair) [79] and B2−Β2 pairs in NaB4 (−2.55 eV/pair) [80], reconfirming strong covalent Si−Si bond in both configurations. From the consequences above, it can be conspicuously found summarized into two aspects. On the one hand, the strength of the covalent Si−Si bond is stronger than that of the Ru−Si covalence in both RuSi2 configurations as the estimated ICOHP values for the Si−Si pairs are slightly lower than those of the Ru−Si pairs. On the other hand, compared with the layered Cmcm-RuSi2 phase, Cmca-RuSi2 possesses the stronger Ru−Si and Si−Si covalent bonds, which should be the main driving force that the Cmca-RuSi2 phase have more magnificent incompressibility than the Cmcm-RuSi2 structure.

3.3. Electronic Structure and Superconductive Property

To further delve into the electronic structures of the Cmca-RuSi2 phase at 1 atm as well as the Cmcm-RuSi2 phase at 1 atm and 75 GPa, we calculated their electronic band structure (BS) and density of states (DOS), as constructed in Figure 5. Note that the Cmca-RuSi2 structure under ambient pressure displays a semiconductor behavior characterized by a direct band gap of 0.485 eV, in conformity with the preceding theoretical calculations reported by Zhang et al [49]. On the contrary, as the pressure increase, the conduction band and the valence band of Cmcm-RuSi2 phase pass through the Fermi level (EF) and overlap, implying its metallic character. In reality, a semiconductor-metal transformation or metallization occurs under high pressure, along with the structural transition from Cmca-RuSi2 to Cmcm-RuSi2. This phenomenon metallization induced by high pressure can also be appreciated in other systems, such as MgH2 [81], CaLi2 [82] and SiH4 [83]. Moreover, the Cmcm-RuSi2 phase still maintains the metallic characteristic when the pressure is released into the ambient pressure, as shown in Figure 5(b). On the other hand, the semi-conductive and metallic traits in Cmca-RuSi2 and Cmcm-RuSi2 can be elucidated in the right side of Figure 5a–c. On the basis of the total and partial density of states (TDOS and PDOS) of both RuSi2 structures, it is obviously achieved that the Ru-4d state make the dominant contribution to TDOS. Apart form the Ru-4d state contribution, the Si-3p state also contributes to TDOS at a certain extent. The hybridization effect between the Ru-4d and Si-3p states near both sides of the EF disclose the Ru-Si covalent bond in both RuSi2 phases, which in excellent accord with the previous analyses of bond length, ELF, and COHP. Eventually, the chemical bonding in the Cmca-RuSi2 and Cmcm-RuSi2 configurations comprises a complex combination of the covalent Ru-Si and Si-Si bonds with the Si-Si bond stronger than that of the Ru-Si bonding. More noticeably, as presented in the left sides of Figure 3b,c, the electronic BS exhibits multiple characters in proximity to EF, comprising of the hole pockets around T/S/U points, electron pockets around Z/S points and flat band along the Y-S-X direction. In view of the atypical BS, we further dig into the topological structure of Fermi surfaces (see Figure 6), which serve to unveil the electronic performance at the EF. The emerge of three bands in Cmcm-RuSi2 indicates excellent electrical conductivity and the third band should be attributed to the flat band along the Y-S-X, further secured by the decreased energy approaching the EF at the ambient pressure. These electronic traits proposed from the BS and Fermi surfaces have been comprehensively investigated and deemed as imperative signs for superconductivity.
Kindled by the metallic and significant band structure characters in Cmcm-RuSi2 under ambient and high pressures coupled with the outstanding superconductivity in the layered framework in MgB2 [21], MoB2 [22], NaC2 [23], KP2 [27], CeP2 [28], and LaP2 [29] as well as alkali, alkaline-earth and rare-earth metal disilicides, analogous to the Cmcm-RuSi2 phase, we assume that the layered Cmcm-RuSi2 structure should be a promising superconductor. Subsequently, we calculated the phonon dispersion curves, the projected phonon density of states (PHDOS) and Eliashberg spectral function α2F(ω) together with the electron−phonon integral constant λ of Cmcm-RuSi2 at 1 atm, 25 GPa, 50 GPa, and 75 GPa with the intention of illuminating their potential superconductivity, presented in Figure 7. As analysed above, its dynamical stability could be verified within the pressure range of 0−75 GPa as a consequence of the absence of imaginary phonon frequency throughout the whole Brillouin zone at 1 atm, 25 GPa, 50 GPa, and 75 GPa. In the PHDOS, the phonon vibrational modes of Cmcm-RuSi2 can mainly be divided into three districts on the basis of the phonon region. The vibrations of Ru atoms mainly contribute to the low-frequency phonon regions (< 9 THz), while the high-frequency phonon modes (10−15 THz) are associated with silicon layers because of Ru atom heavier than Si atom. It is worthy noting that the intermediate-frequency branches stem from the coupled vibrations of Ru atom and Si layer. For the EPC parameter λ, the low-frequency vibrations by Ru atoms around below 9 THz contribute 82.4%, 77%, 74% and 67.5% at 1 atm, 25 GPa, 50 GPa and 75 GPa of the total λ, respectively, while the high-frequency phonon bands above 10 THz associated with light Si atom vibrations only account for 13.2%, 19.7%, 20.5% and 22.5% in Cmcm-RuSi2, respectively. In addition, the corresponding coupled vibrations from Ru atoms and Si layer contribute 4.4%, 3.3%, 6.5% and 10% at 1 atm, 25 GPa, 50 GPa and 75 GPa of the total λ, respectively. This directly denotes that the vibrations from Ru atoms combined with the coupled vibrations between Ru atoms and Si layers play significant roles in the superconductivity of Cmcm-RuSi2.
The electron-phonon coupling parameters λ, logarithmic average phonon frequency ωlog, electron density of states at the Fermi level N(Ef) and superconducting transition temperature Tc of Cmcm-RuSi2 at 1 atm, 25 GPa, 50 GPa and 75 GPa were also calculated in Table 1. The superconducting critical temperature Tc values are estimated by using the Allen–Dynes modified McMillan equation:
T c = ω bg 1.2 exp 1.04 1 + λ λ − μ * 1 + 0.62 λ
where, the Coulomb pseudopotential parameters μ* are set to typical 0.10 and 0.13, respectively. As summarized in Table 1, the predicted EPC parameter λ for the Cmcm-RuSi2 crystal is 0.4 at 75 GPa and displays a monotonous decrease with the increment of the pressure. Accordingly, the maximal EPC parameter λ value of 0.91 emerges in Cmcm-RuSi2 under ambient pressure, which is comparable to 0.93 for RaSi2 at 0 GPa, 1.1 for CaSi2 at 0 GPa, 0.92 for Al2Si3 at 10 GPa, 1.01 for P63/mmc-Y3Si, but larger than 0.81 for P6/mmm-MgSi3 at 0 GPa, 0.808 for Cmmm-Si4 at ambient pressure, 0.897 for P6/m-NaSi6 at 0 GPa, 0.799 P6/m-Si6 at 0 GPa. To compare with the former binary conventional superconductors, we draw a overall diagram which displays a combination of the Tc and stabilized pressure for established superconductors, as shown in Figure 8. Additionally, the detailed Tc values
For the conventional superconductors at different pressures are summarized in Table S3. It is undoubtedly found that the Cmcm-RuSi2 structure are estimated to be 10.07 K at atmospheric pressure, which is comparable to 13.7 K in MgSi3 , 13 K in P6/m-NaSi6 and 12 P6/m-Si6 at 0 GPa, 14 K for CaSi2 at 15 GPa, 10.5 K for P6/mmm-CeP2 at 16.5 GPa, and 13.6 K for CrB2 at 60.7 GPa, but higher than other transition metal disilicides, such as RbSi2 (9 K) [34], MgSi2 (~7 K) [35,36], BaSi2 (6.8 K) [39], LaSi2 (2.5 K) [40] and YSi2 (0.5 K, 50 GPa) [41]. In short, the novel Cmcm-RuSi2 configuration at ambient pressure possesses the secondarily highest Tc among the binary metal disilicides, merely lower than that of CaSi2 (14 K) under 15 GPa. In addition, it is worthy mentioning that the superconducting critical temperature Tc in Cmcm-RuSi2 is significantly higher than those of the corresponding metallic Cmcm-Si4 (2.2 K) [87] and Ru (0.51 K) [91,92] at ambient pressure, which tremendously advance the superconductivity for the related elemental substances.
The investigation of the variation trends with the increasing pressure serve as an appropriate pathway for a deeper understanding of the superconductivity driven in Cmcm-RuSi2, as intuitively exhibited Figure 9. Regarding the broad stable pressure range obtained in Cmcm-RuSi2, we have implemented calculations to estimate its pressure-dependent superconductivity. As the pressure decreases, a successive increase presents in the Tc values, eventually reaching 10.07 K at atmospheric pressure. Manifestly, two substantial parameters (λ and ωlog) play a vital role in determining Tc, displaying the contrasting trends with pressure. The increment in Tc with decreasing pressure results from the synchronous enhancement in λ, which dominates the evolution of Tc with pressure. The growth in λ should be related to the increasing DOS at the Fermi energy upon the reducing pressure, which further originate from the decrease of charges of Ru-4d orbital transferred from silicon layer, as tabulated in Table S4. In the Cmcm-RuSi2 phase, one Ru atom gain 1.38 e at 75 GPa and reduces to 1.06 e under ambient pressure. The charge transferred from nonmetallic Si to metallic Ru is feasible for the reason that the electronegativity value of Si (1.90) element is lower than that of Ru element according to the periodic table of the elements. The anion character in metallic element Ru is rarely seen in binary metal silicides. In contrast, the reducing process of ωlog with the decreasing pressure should be attributed to the elongation of Si−Si bonds within the configuration. Upon the reducing compression, the variation trend of λ (increment) and ωlog (diminution) is similar to those in Ce2P3, CeP2 [28]and Sc2P [93].
As the representative superconductor in the component of 1:2 in binary metallic compounds, MgB2 encompasses a similar honeycomb B layer, differing from Cmcm-RuSi2. It is necessary to unlock the discrepancy in the structural characters, electronic properties, the superconducting mechanism and Tc values between both phases at ambient pressure. In regard to the structural trait, the honeycomb B layer and Mg atoms are located in the alternate layers along the c axis in MgB2 whereas the graphene-like Si layer and the Ru atoms are in the same plane with Ru atom sited at the center of the Si hexatomic ring. In the case of the metallic character, MgB2 mainly stems from the B-2p orbital while the current Cmcm-RuSi2 should be ascribed to the Ru-4d state. The high frequency for MgB2 derives from the graphene-like B layer with the superconductivity of MgB2 dominated by the electron-phonon coupling of B atoms [94], while the transition Ru-4d orbital electrons also take part in the coupling. This comparison not only points toward a possibility to uncover different superconducting sources in the traditional prototype phases, such as H3S, CaH6 and LaH10, but also widens the cognition of the elemental contributions in superconductivity. As for the Tc value, MgB2 is higher than Cmcm-RuSi2, which can be summarized as the following reasons: (a) The MgB2 has an open B layer without the B−B interlayer covalence while Cmcm-RuSi2 contains an closed Si layer with the interlayer covalent Si−Si bond; (b) the bond strength of Si-Si bond in Cmcm-RuSi2 is weaker than that of MgB2, as demonstrated by the calculated ICOHP (−2.25 per pair Si−Si in comparison with −6.92 per pair B−B); (c) the ωlog value for Cmcm-RuSi2 is lower than that of MgB2 (167.97 Κ with respect to 450 Κ) [94], which results from the lower phonon frequencies of Ru and Si atoms lower than those of Mg and B atoms, as related to the larger atomic mass of Ru and Si, respectively.

3.4. Mechanical Property and Hardness

With the high development in the superconductor, it necessitates the eminent mechanical property and hardness integrated with spectacular ductility. The elastic constants for the Cmca-RuSi2 and Cmcm-RuSi2 phases at 1 atm in conjunction with the Cmcm-RuSi2 configuration under ambient pressure and 75 GPa were computed through the identical strain−stress means [95], as corroborated in Table 2. Both phases are dynamically stable under focused pressures as they satisfy the mechanical stability criteria for the orthorhombic crystal system [96]. Thereafter, the homologous shear modulus G, bulk modulus B, B/G, Young’s modulus E and Poisson’s ratio ν of both phases can be attainable from the elastic constants based on the Voigt–Reuss–Hill (VRH) method [97] (see Table 2). In the Cmca-RuSi2 configuration under ambient pressure, the current estimated elastic constants Cij, bulk modulus B, shear modulus G, Young’s modulus E and Poisson’s ratio v are in conformity with the prior theoretical consequens [49], clarifying that the methodology utilized in present work is convincing. Generally speaking, the C11, C22 and C33 values in material denote the resistance to compression along the corresponding a-, b- and c-axis. From Table 2, Cmcm-RuSi2 under 75 GPa possesses ultra-high C11, C22 and C33 values, which are much higher than those of P6/mmm-ScB2 [98], explaining that this phase behaves excellent incompressibility along a-, b- and c-axis. The calculated B, G and E values of Cmcm-RuSi2 under 75 GPa are 410.13, 184.99 and 482.44 GPa, respectively, which are significantly higher than those of the Cmca-RuSi2 phase at ambient pressure (B, G and E values are 173.53 , 107.99 and 268.30 GPa, respectively), corroborating that this phase transition induced by compression enhances the mechanical properties of RuSi2 crystal to a great extent. Moreover, the value of B/G can estimate the brittle or ductile manner of a solid: a high ratio of B/G (> 1.75) indicates the ductility, while a low ratio (< 1.75) indicates the brittleness according to the Pugh criterion [99,100]. For transition metal silicides, the improvement of ductility can greatly improve their industrial work efficiency, because their actual productions as high-temperature materials are limited by their own brittleness [101,102,103]. As listed in Table 2, the the B/G value of Cmca-RuSi2 at 1 atm is 1.61, uncovering the brittle nature whereas the B/G values of Cmcm-RuSi2 at 1 atm and 75 GPa are 2.03 and 2.22, corresponding to ductile character, respectively. This phenomenon confirms the brittle-to-ductile transformation in RuSi2, accompanied by the structural transformation under high pressure, which is analogous to NbSi2 [104] and MoN2 [105].
Hardness should be characterized as a substantial mechanical property of a material and can be used to measure the ability to resist local deformation, especially plastic deformation, indentation or scratches. In addition, the orientation bond in a material is an important index to measure its hardness, and it can be expressed by Pugh’s ratio G/B [99,100]. A larger G/B value corresponds to a higher hardness. As summarized in Table 2, the G/B values of Cmca-RuSi2 and Cmcm-RuSi2 phases under atmospheric pressure are 0.64 and 0.49, respectively. However, Gao et al. indicated that the vital problem in digging into the hardness of materials is how to describe the strength of internal bonds of the materials. Thus, we further probe into the hardness values of both structures employing the hardness model proposed by Gao et al [106,107]. The Vickers hardness could be calculated with the following formula:
H ν = { ∏ μ 740 P μ V b μ − 5 3 n μ } 1 ∑ n μ
where
V b μ = d μ 3 / ∑ d v 3 N b μ
where μ labels all different types of covalent bonds in the system, P μ is the Mulliken overlap population of the μ type bond, ν b μ is its volume, n μ is the number of μ type bonds, d μ is its bond length, and N b μ is the bond number of type μ per unit volume. On account of the aforementioned empirical equation, the estimated hardness values of Cmca-RuSi2 and Cmcm-RuSi2 phases reach 31.74 and 26.76 GPa, respectively (see Table 3). The hardness value of Cmca-RuSi2 under ambient pressure is consistent with the previous theoretical results [49]. The predicted Hv values of Cmca-RuSi2 (31.74 GPa) and Cmcm-RuSi2 (26.76 GPa) are comparable to the experimental measurements of β-SiC (34 GPa) [106], BP (33 GPa) [108], TiC (32 GPa) [109] β-Si3N4 (30 GPa) [109] and transition metal disilicide WSi2 (28.5 GPa) [110], but higher than elemental solid Si (12 GPa) [106]. Hence, it can be concluded that both Cmca-RuSi2 and Cmcm-RuSi2 are potential high hardness materials. In comparison with Cmcm-RuSi2, Cmca-RuSi2 has a higher hardness, which can be ascribed to the stronger Ru-Si and Si-Si covalent bonds and better orientation than those of Cmcm-RuSi2.

4. Conclusions

To sum up, our comprehensive first-principles structure searches in RuSi2 within the pressure range of 0−300 GPa have disclosed the emerge of the peculiar Cmcm-RuSi2 phase at 50.97 GPa. This Cmcm-RuSi2 configuration contain an extraordinary graphene-like silicon layer, which is dynamically stable and simultaneously leads to exceptional superconductivity and high hardness under ambient pressure, despite it is recovered from the high pressure. On the one hand, its predicted Tc value could reach 10.07 K at ambient pressure, comparable to the previous proposed P6/m-NaSi6 (13 K) and CaSi2(14 K)。On the other hand, the Vickers hardness value is 26.76 GPa, which is comparable to WSi2 (28.5 GPa). Furthermore, its excellent conductivity stem from the the strong interaction between Ru-4d electrons and the phonons B−B and coupled Ru−Si vibrations, while its high hardness can be ascribed to the 3D robust Ru−Si and Si−Si directional covalent framework. In addition, the Cmcm-RuSi2 phase is a ductile material. The ambient-pressure ground Cmca phase is a narrow-gap semiconductor with a estimated hardness of 31.7 GPa.
The special graphene-like silicon layer in the transition-metal disilicides Cmcm-RuSi2 phase broaden the existing silicon-layer space beyond alkali, alkaline-earth and rare-earth metal disilicides. The removal of metal atoms can be utilized to acquire silicon framework such as layered silicon, silicon clathrates and other silicon allotropes. This mode has uncovered a succession of novel elemental structures, such as I4/mmm-B4, Pm-B17 [80] and P6/m-Si6 [33], which is destined to promote the quest for the analogous silicon laminar structures and distinct silicon motifs (eg. 3D silicon clathrate framework and 1D silicon chains) in elemental silicon and transition-metal silicides. On the other hand, this layered network in Cmcm-RuSi2 provide a wonderful bedding for adding light element adatoms to layered superconductors, which could enhance the superconductivity for the parent Cmcm-RuSi2 configuration. This method has been practically employed recently to improve the superconductivity in very diverse ultrathin materials, ranging from monolayer MgB2 to truly 2D atomic sheets doped graphene and transition metal dichalcogenides.
The Cmcm-RuSi2 structure has the secondarily highest superconducting transition temperature among the metal disilicides, MSi2 (M = metal), merely lower than that of CaSi2 (14 K), which facilitate the in-depth investigation on the superconductivity mechanism in the metal disilicides in both theory and experiment.
The anion transition-metal in Cmcm-RuSi2 is rarely reported in preceding binary compounds that contains metal and nonmetal elements, which widens the physical and chemical cognition.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org., Figure S1: Nine structures of RuSi2 at ambient pressure. The red and green spheres represent Ru and Si atoms, respectively; Figure S2: The phonon dispersion curves of Cmca-RuSi2 at ambient pressure.

Author Contributions

Supervision, C.Z., Y.J. and W.S.; Formal analysis, K.G. and W.S.; Investigation, C.Z. and Y.W.; Writing, C.Z. and Y.W.; Review and editing, Y.J. and W.S.; Calculation, Y.W., M.L., F.Y. and W.S.; Visualization, Y.W., M.L. and F.Y.; Funding acquisition, K.G. and Y.J. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China (No. 2023YFB3712300), National Natural Science Foundation of China (11804031), Key Science and Technology Foundation of Gansu Province (No. 22JR5RA095) and ‘Light of West China’ Program of CAS.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article and Supplementary Information.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wang, H.; Tse, J.S.; Tanaka, K.; Iitaka, T.; Ma, Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. USA 2012, 109, 6463–6466. [Google Scholar] [CrossRef] [PubMed]
  2. Ma, L.; Wang, K.; Xie, Y.; Yang, X.; Wang, Y.; Zhou, M.; Liu, H.; Yu, X.; Zhao, Y.; Wang, H.; Liu, G.; Ma, Y. High-temperature superconducting phase in clathrate calcium hydride CaH6 up to 215 K at a pressure of 172 GPa. Phys. Rev. Lett. 2022, 128, 167001. [Google Scholar] [CrossRef] [PubMed]
  3. Du, M.; Li, Z.; Duan, D.; Cui, T. Superconducting phases of YH9 under pressure. Phys. Rev. B 2023, 108, 174507. [Google Scholar] [CrossRef]
  4. Kong, P.; Minkov, V.S.; Kuzovnikov, M.A.; Drozdov, A.P.; Besedin, S.P.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Prakapenka, V.B.; Chariton, S.; Knyazev, D.A.; Greenberg, E.; Eremets, M.I. Superconductivity up to 243 K in the yttrium-hydrogen system under high pressure. Nat. Commun. 2021, 12, 5075. [Google Scholar] [CrossRef]
  5. Errea, I.; Belli, F.; Monacelli, L.; Sanna, A.; Koretsune, T.; Tadano, T.; Bianco, R.; Calandra, M.; Arita, R.; Mauri, F.; Flores-Livas, J.A. Quantum crystal structure in the 250-kelvin superconducting lanthanum hydride. Nature 2020, 578, 66–69. [Google Scholar] [CrossRef]
  6. Geballe, Z.M.; Liu, H.; Mishra, A.K.; Ahart, M.; Somayazulu, M.; Meng, Y.; Baldini, M.; Hemley, R.J. Synthesis and stability of lanthanum superhydrides. Angew. Chem. Int. Ed. 2018, 57, 688–692. [Google Scholar] [CrossRef]
  7. Zhong, X.; Sun, Y.; Iitaka, T.; Xu, M.; Liu, H.; Hemley, R.J.; Chen, C.; Ma, Y. Prediction of above-room-temperature superconductivity in lanthanide/actinide extreme superhydrides. J. Am. Chem. Soc. 2022, 144, 13394–13400. [Google Scholar] [CrossRef]
  8. Li, Z. ; He, X. ; Zhang, C. ; Lu, K. ; Min, B.; Zhang J.; Zhang, S.; ZhaoJ.; Shi, L.; Peng, Y.; Feng, S.; Deng, Z.; Song, J.; Liu, Q.; Wang, X.; Yu, R.; Wang, L.; Li, Y.; Bass, J.D.; Prakapenka, V.; Chariton, S.; Liu, H.; Jin, C.; Sci. Superconductivity above 70 K observed in lutetium polyhydrides. China Phys. Mech. 2023, 66, 267411.
  9. Yamanaka, S.; Enishi, E.; Fukuoka, H.; Yasukawa, M. High-Pressure synthesis of a new silicon clathrate superconductor, Ba8Si46. Inorg. Chem. 2000, 39, 56–58. [Google Scholar] [CrossRef]
  10. Imai, M.; Kikegawa, T. In situ observation of the formation of Si clathrate Ba8Si46 at high pressure and high temperature. Inorg. Chem. 2008, 47, 8881–8883. [Google Scholar] [CrossRef]
  11. Gao, K.; Cui, W.; Chen, J.; Wang, Q.; Hao, J.; Shi, J.; Liu, C.; Botti, S.; Marques, M.A.L.; Li, Y. Superconducting hydrogen tubes in hafnium hydrides at high pressure. Phys. Rev. B 2021, 104, 214511. [Google Scholar] [CrossRef]
  12. Liu, M.; Cui, W.; Shi, J.; Hao, J.; Li, Y. Superconducting H7 chain in gallium hydrides at high pressure. Phys. Chem. Chem. Phys. 2023, 25, 7223–7228. [Google Scholar] [CrossRef] [PubMed]
  13. Li, X.; Guo, Z.; Zhang, X.; Yang, G. Layered hydride LiH4 with a pressure-insensitive superconductivity. Inorg. Chem. 2024, 63, 8257–8263. [Google Scholar] [CrossRef] [PubMed]
  14. Zhou, D.; Jin, X.; Meng, X.; Bao, G.; Ma, Y.; Liu, B. and Cui, T.; Ab initio study revealing a layered structure in hydrogen-rich KH6 under high pressure. Phys. Rev. B. 2012, 86, 0147118. [Google Scholar] [CrossRef]
  15. Wang, Y.; Chen, S.; Guo, J.; Huang, X.; Cui, T. Absence of superconductivity in I4/mmm-FeH5: experimental evidence. Phys. Chem. Chem. Phys. 2024, 26, 7371–7376. [Google Scholar] [CrossRef]
  16. Xie, H.; Yao, Y.; Feng, X.; Duan, D.; Song, H.; Zhang, Z.; Jiang, S.; Redfern, S.A.T.; Kresin,V. Z.; Pickard, C. J.; Cui, T. Hydrogen pentagraphenelike structure stabilized by hafnium: a high-temperature conventional superconductor. Phys. Rev. Lett. 2020, 125, 217001. [CrossRef]
  17. Chen, Y.; Liu, Z.; Lin, Z.; Jiang, Q.; Du, M.; Zhang, Z.; Song, H.; Xie, H.; Cui, T.; Duan, D. High Tc superconductivity in layered hydrides XH15 (X = Ca, Sr, Y, La) under high pressures. Front. Phys. 2022, 17, 103–109. [Google Scholar] [CrossRef]
  18. Jiang, Q.; Chen, L.; Du, M.; Duan, D. A perspective on reducing stabilizing pressure for high-temperature superconductivity in hydrides. J. Phys.: Condens. Matter 2024, 36, 493002. [Google Scholar] [CrossRef]
  19. Song, J.; Curtin, W.A. Atomic mechanism and prediction of hydrogen embrittlement in iron curtin. Nat. Mater. 2013, 12, 145–151. [Google Scholar]
  20. Dwivedi, S.K.; Vishwakarma, M. Hydrogen embrittlement in different materials: A review. Int. J. Hydrogen Energ. 2018, 43, 21603–21616. [Google Scholar] [CrossRef]
  21. Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef] [PubMed]
  22. Pei, C.; Zhang, J.; Wang, Q.; Zhao, Y.; Gao, L.; Gong, C.; Tian, S.; Luo, R.; Li, M.; Yang, W.; Lu, Z.Y.; Lei, H.; Liu, K.; Qi, Y. Pressure-induced superconductivity at 32 K in MoB2. Natl. Sci. Rev. 2023, 10, nwad034. [Google Scholar] [CrossRef] [PubMed]
  23. Yang, Q.; Zhao, K.; Liu, H.; Zhang, S. Superconductive sodium carbides with pentagon carbon at high pressures. J. Phys. Chem. Lett. 2021, 12, 5850–5856. [Google Scholar] [CrossRef] [PubMed]
  24. Feng, X.; Lu, S.; Pickard, C.J.; Liu, H.; Redfern, S.A.T.; Ma, Y. Carbon network evolution from dimers to sheets in superconducting ytrrium dicarbide under pressure. Commun. Chem. 2018, 1, 85. [Google Scholar] [CrossRef]
  25. Yang, Q.; Zhao, Y.; Jiang, X ; Wang, B.; Zhao, J.; Mater, J. Unconventional stoichiometric two-dimensional potassium nitrides with anion-driven metallicity and superconductivity. Chem. C 2024, 12, 103–109.
  26. Chen, Y.; Cai, X.; Wang, H.; Wang, H.; Wang, H. Novel triadius-like N4 specie of iron nitride compounds under high pressure. Sci. Rep. 2018, 8, 10670. [Google Scholar] [CrossRef]
  27. Liu, Y.; Wang, C.; Kong, X.; Duan, D. Stability and superconductivity of K–P compounds under Pressure. Inorg. Chem. 2017, 56, 12529–12534. [Google Scholar] [CrossRef]
  28. Li, X.; Bergara, A.; Zhang, X.; Li, F.; Liu, Y.; Yang, G. Superconducting Ce2P3 and CeP2 with an interesting planar P layer. J. Mater. Chem. C 2024, 12, 2526–2533. [Google Scholar] [CrossRef]
  29. Li, X.; Zhang, X.; Yang, Z.; Liu, Y.; Yang, G. Pressure-stabilized graphene-like P layer in superconducting LaP2. Phys. Chem Chem. Phys. 2022, 24, 6469–6475. [Google Scholar] [CrossRef]
  30. Connétable, D.; Timoshevskii, V.; Masenelli, B.; Beille, J.; Marcus, J.; Barbara, B.; Saitta, A.M.; Rignanese, G.-M. Superconductivity in doped sp3 semiconductors: the case of the clathrates. Phys. Rev. Lett. 2003, 91, 247001. [Google Scholar] [CrossRef]
  31. Rachi, T.; Yoshino, H.; Kumashiro, R.; Kitajima, M.; Kobayashi, K.; Yokogawa, K.; Murata, K.; Kimura, N.; Aoki, H.; Fukuoka, H.; Yamanaka, S.; Shimotani, H.; Takenobu, T.; Iwasa, Y.; Sasaki, T.; Kobayashi, N.; Miyazaki, Y ; Saito, K.; Guo, F.; Kobayashi, K.; Osaka, K.; Kato, K.; Takata, M,; Tanigaki1, K. Superconductivity and physical properties of Ba24Si100 determined from electric transport, specific-heat capacity, and magnetic susceptibility measurements. Phys. Rev. B 2005, 72, 144504.
  32. Yamanaka, S.; Izumi, S.; Maekawa, S.; Umemoto, K. Phase diagram of the La–Si binary system under high pressure and the structures of superconducting LaSi5 and LaSi10. J. Solid. State. Chem. 2009, 182, 1991–2003. [Google Scholar] [CrossRef]
  33. Sung, H.-J.; Han, W.H.; Lee, I.-H.; Chang, K.J. Superconducting open-framework allotrope of silicon at ambient pressure. Phys. Rev. Lett. 2018, 120, 157001. [Google Scholar] [CrossRef] [PubMed]
  34. Flores-Livas, J.A; Sanna, A. Spintronics: Superconductivity in intercalated group-IV honeycomb structures. Phys. Rev. B. 2015, 91, 054508. [Google Scholar] [CrossRef]
  35. Huan, T.D. Spintronics: Pressure-stabilized binary compounds of magnesium and silicon. Phys. Rev. Mater. 2018, 2, 023803. [Google Scholar] [CrossRef]
  36. Zha, D.-B.; Jiang, P.; Huang, H.-M.; Li, Y.-L. Spintronics: Refined phase diagram and kagome-lattice superconductivity in Mg-Si system. Phys. Rev. Mater. 2023, 7, 114805. [Google Scholar] [CrossRef]
  37. Bordet, P.; Affronte, M.; Sanfilippo, S.; Nunez-Regueiro, M.; Laborde, O.; Olcese, G.L.; Palenzona, A.; LeFloch, S.; Levy, D.; Hanfland, M. Spintronics: Structural phase transitions in under high pressure. Phys. Rev. B. 2000, 62, 11392–11397. [Google Scholar] [CrossRef]
  38. Sanfilippo, S.; Elsinger, H.; Nunez-Regueiro, M.; Laborde, O.; LeFloch, S.; Affronte, M.; Olcese, G.L.; Palenzona, A. Spintronics: Superconducting high pressure CaSi2 phase with Tc up to 14 K. Phys. Rev. B. 2000, 61, R3800–R3803. [Google Scholar] [CrossRef]
  39. Imai, M.; Hirata, K.; Hirano, T. Spintronics: Superconductivity of trigonal BaSi2. Physica C 1995, 245, 12–14. [Google Scholar] [CrossRef]
  40. Satoh, T.; Asada, Y.J. Spintronics: Superconductivity of LaSi2. Phys. Soc. Japan. 1970, 28, 263–263. [Google Scholar] [CrossRef]
  41. Zhang, J.; Chen, G.; Liu, H. Spintronics: Stable structures and superconductivity in a Y-Si system under high pressure. J. Phys. Chem. Lett. 2021, 12, 10388–10393. [Google Scholar] [CrossRef] [PubMed]
  42. Hilleke, K.P.; Zurek, E. Rational Design of Superconducting Metal Hydrides via Chemical Pressure Tuning. Angew. Chem. Int. Ed. 2022, 61, e202207589. [Google Scholar] [CrossRef] [PubMed]
  43. Flores-Livas, J.A.; Debord, R.; Botti, S.; Miguel, A.S.; Pailhès, S.; Marques, M.A.L. Spintronics: Superconductivity in layered binary silicides: A density functional theory study. Phys. Rev. B. 2011, 84, 184503. [Google Scholar] [CrossRef]
  44. Buschinger, B.; Geibel, C.; Diehl, J.; Weiden, M.M.; Guth, W.; Wildbrett, A.; Horn, S.; Steglich, F. Spintronics: Preparation and low temperature properties of FeSi-type RuSi. J. Alloy. Compd. 1997, 256, 57–60. [Google Scholar] [CrossRef]
  45. Perring, L.; Bussy, F.; Gachon, J.C.; Feschotte, P. The ruthenium-silicon system. J. Alloy. Compd. 1999, 284, 198–205. [Google Scholar] [CrossRef]
  46. Opahle, I.; Madsen, G.K.H.; Drautz, R. High throughput density functional investigations of the stability, electronic structure and thermoelectric properties of binary silicides. Phys. Chem. Chem. Phys. 2012, 14, 16197–16202. [Google Scholar] [CrossRef]
  47. Wolf, W.; Bihlmayer, G.; Blügel, S. Electronic structure of the Nowotny chimney-ladder silicide Ru2Si3. Phys. Rev. B 1997, 55, 6918–6926. [Google Scholar] [CrossRef]
  48. Ivanenko, L.; Behr, G.; Spinella, C.R.; Borisenko, V.E. RuSi2: evidence of a new binary phase in the ruthenium-silicon system. J. Cryst. Growth 2002, 236, 572–576. [Google Scholar] [CrossRef]
  49. Zhang, C.; Kuang, X.; Jin, Y.; Lu, C.; Zhou, D.; Li, P.; Bao, G.; Hermann, A. Prediction of stable ruthenium silicides from first-principles calculations: stoichiometries, crystal structures, and physical properties. ACS Appl. Mater. Inter. 2015, 7, 26776–26782. [Google Scholar] [CrossRef]
  50. Xiong, Z.; Wang, X.; Cao, L.; Wang, J.; Yu, J.; Yin, H.; Wang, X.; Ma, J. Structural stability, phase transition, electronic, elastic and thermodynamic properties of RuX (X= Si, Ge, Sn) alloys under high pressure. J. Alloy. Compd. 2017, 693, 440–447. [Google Scholar] [CrossRef]
  51. Ivanenkoa, L.I.; Shaposhnikova, V.L.; Filonova, A.B.; Krivosheevaa, A.V.; Borisenkoa, V.E.; Migasb, D.B.; Migliob, L.; Behrc, G.; Schumannc, J. Electronic properties of semiconducting silicides: fundamentals and recent predictions. Thin solid films 2004, 461, 141–147. [Google Scholar] [CrossRef]
  52. Zhang, L.; Wang, Y.; Lv, J.; Ma, Y. Materials discovery at high pressures. Nat. Rev. Mater. 2017, 2, 1–16. [Google Scholar] [CrossRef]
  53. Miao, M.; Sun, Y.; Zurek, E.; Lin, H. Chemistry under high pressure. Nat. Rev. Chem. 2020, 4, 508–527. [Google Scholar] [CrossRef]
  54. Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
  55. Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
  56. Wang, W.; Zhang, C.; Jin, Y.; Li, S.; Zhang, W.; Kong, P.; Xie, C.; Du, C.; Liu, Q.; Zhang, C. Structural, mechanical and electronic properties and hardness of ionic vanadium dihydrides under pressure from first-principles computations. Sci. Rep. 2020, 10, 8868. [Google Scholar] [CrossRef]
  57. Wang, Y.; Jin, Y.; Yang, F.; Zhang, J.; Zhang, C.; Kuang, F.; Ju, M.; Li, S.; Cheng, S. Prediction of potential high-temperature superconductivity in ternary Y-Hf-H compounds under high pressure. Sci. Rep. 2024, 14, 17670. [Google Scholar] [CrossRef]
  58. Jin, Y.; Huang, W.; Zhang, J.; Li, S.; Cheng, S.; Sun, W.; Ju, M.; Zhang, C. An unexpectedly stable Y2B5 compound with the fractional stoichiometry under ambient pressure. Arab. J. Chem. 2023, 16, 104546. [Google Scholar] [CrossRef]
  59. Wang, Y.; Zhang, C.; Zhang, J.; Li, S.; Ju, M.; Sun, W.; Dou, X.; Jin, Y. A ten-fold coordinated high-pressure structure in hafnium dihydrogen with increasing superconducting transition temperature induced by enhancive. Chinese Phys. B 2023, 32, 527–534. [Google Scholar] [CrossRef]
  60. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  61. Savin, A.; Jepsen, O.; Flad, J.; Andersen, O.K.; Preuss, H.; Schnering, H.G. Electron localization in solid-state structures of the elements: the diamond structure. Angew. Chem., Int. Ed. Engl. 1992, 31, 187–188. [Google Scholar] [CrossRef]
  62. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [CrossRef] [PubMed]
  63. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  64. Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
  65. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  66. Monkhorst, H.J.; Pack, J.D. Special points for brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  67. Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
  68. Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. LOBSTER: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef]
  69. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; Corso, A.D.; Gironcoli, S.; Fabris, S.; Fratesi, G.; Gebauer, R.; Gerstmann, U.; Gougoussis, C.; Kokalj, A.; Lazzeri, M.; Martin-Samos, L.; Marzari, N.; Mauri, F.; Mazzarello, R.; Paolini, S.; Pasquarello, A.; Paulatto, L.; Sbraccia, C.; Scandolo, S.; Sclauzero, G.; Seitsonen, A.P., Smogunov, A.; Umari, P.; Wentzcovitch, R.M. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 2009, 21, 395502.
  70. Opahle, I.; Parma, A.; McEnary, E.J.; Drautz, R.; Madsen, G.KH. High-throughput study of the structural stability and thermoelectric properties of transition metal silicides. New J. Phys. 2013, 15, 105010. [Google Scholar] [CrossRef]
  71. Siegrist, T.; Hulliger, F.; Travaglini, G. The crystal structure and some properties of ReSi2. J. Alloy. Compd. 1983, 92, 119–129. [Google Scholar] [CrossRef]
  72. Cynn, H.; Klepeis, J.E.; Yoo, C.S.; Young, D.A. Osmium has the lowest experimentally determined compressibility. Phys. Rev. Lett. 2002, 88, 135701. [Google Scholar] [CrossRef] [PubMed]
  73. Shen, G.; Ikuta, D.; Sinogeikin, S.; Li, Q.; Zhang, Y.; Chen, C. Direct observation of a pressure-induced precursor lattice in silicon. Phys. Rev. Lett. 2012, 109, 205503. [Google Scholar] [CrossRef] [PubMed]
  74. Vocado, L.; Price, G.D.; Wood, I.G. Crystal structure, compressibility and possible phase transitions in Ɛ-FeSi studied by first-principles pseudopotential calculations. Acta Cryst. 1999, B55, 484–493. [Google Scholar] [CrossRef]
  75. Shaposhnikov, V.L.; Filonov, A.B.; Krivosheeva, A.V.; Ivanenko, L.I.; Borisenko, V.E. Structural, electronic and optical properties of a new binary phase–ruthenium disilicide. Phys. Stat. Sol. (b) 2005, 242, 2864–2871. [Google Scholar] [CrossRef]
  76. Kim, D.Y.; Stefanoski, S.; Kurakevych, O.O.; Strobel, T.A. Synthesis of an open-framework allotrope of silicon. Nat. Mater. 2015, 14, 169–173. [Google Scholar] [CrossRef]
  77. Pan, Y.; Jing, C.; Wu, Y. The structure, mechanical and electronic properties of WSi2 from first-principles investigations. Vacuum 2019, 167, 374–381. [Google Scholar] [CrossRef]
  78. Wang, J.; Kuang, X.; Jin, Y.; Lu, C.; Huang, X. Theoretical investigation on the structural phase transition, elastic properties and hardness of RhSi under high pressure. J. Alloy Compd. 2014, 592, 42–47. [Google Scholar] [CrossRef]
  79. Wang, Q.; Li, H.; Wei, J.; Zhong, T.; Zhu, L.; Zhang, X.; Liu, H.; Zhang, S. Hardness and superconductivity in tetragonal LiB4 and NaB4. J. Chem. Phys. 2023, 159, 234707. [Google Scholar] [CrossRef]
  80. Zhang, S.; Du, X.; Lin, J.; Bergara, A.; Chen, X.; Liu, X.; Zhang, X.; Yang, G. Superconducting boron allotropes. Phys. Rev. B. 2020, 101, 174507. [Google Scholar] [CrossRef]
  81. Zhang, C.; Sun, G.; Wang, J.; Lu, C.; Jin, Y.; Kuang, X.; Hermann, A. Prediction of novel high-pressure structures of magnesium niobium dihydride. ACS Appl. Mater. Interfaces 2017, 9, 26169–26176. [Google Scholar] [CrossRef] [PubMed]
  82. Matsuoka, T.; Debessai, M.; Hamlin, J.J.; Gangopadhyay, A.K.; Schilling, J.S. Pressure-Induced superconductivity in CaLi2. Phys. Rev. Lett. 2008, 100, 197003. [Google Scholar] [CrossRef]
  83. Chen, X.-J.; Wang, J.-L.; Struzhkin, V.V.; Mao, H.; Hemley, R.J.; Lin, H.-Q. Superconducting behavior in compressed solid with a layered structure. Phys. Rev. Lett. 2008, 101, 077002. [Google Scholar] [CrossRef] [PubMed]
  84. Weller, T.E. Weller, T.E.; Ellerby, Mark.; Saxena, S.S.; Smith, R.P.; Skipper, N.T. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nat. Phys. 2005, 1, 39–41. [Google Scholar] [CrossRef]
  85. Yang, Q.P.; Zhang, H.M.; Zhao, J.J.; Jiang, X. Probing the superconductivity limit of Li-doped graphene. Adv. Funct. Mater. 2024, 2406023. [Google Scholar] [CrossRef]
  86. Liao, Z.W.; Yi, X.W.; You, J.Y.; Gu, B.; Su, G. Family of binary transition metal pnictide superconductors. Phys. Rev. B 2023, 108, 014501. [Google Scholar] [CrossRef]
  87. Kang, Y.-Gu.; Lee, I.-H.; Han, M.J.; Chang, K.J. Spintronics: Ab initio prediction of nontrivial topological band and superconductivity in stable metallic Si allotropes at ambient pressure. Phys. Rev. Mater. 2021, 5, 104802. [Google Scholar] [CrossRef]
  88. Wu, L.L.; Wan, B.; Liu, H.Y.; Gou, H.Y.; Yao, Y.S.; Li, Z.P.; Zhang, J.W.; Gao, F.M.; Mao, H-k. Spintronics: Coexistence of superconductivity and superhardness in beryllium hexaboride driven by inherent multicenter bonding. J. Phys. Chem. Lett. 2016, 7, 4898–4904. [CrossRef]
  89. Fu, Y.; Li, F.; Zhang, X.H.; Zhang, S.L.; Liu,Y.; Yang, G.C. Superconducting ScP4 with a novel phosphorus framework. Appl. Phys. A 2022, 128, 318. [CrossRef]
  90. Sananda, B.; Kreisel, A.; Valadkhani, A.; Dürrnagel, M.; Schwemmer, T.; Thomale, R.; Valentí, R.; Mazin, I.I. Hybrid s-wave superconductivity in CrB2. Phys. Rev. B 2023, L020501. [Google Scholar]
  91. Schilling, J.S. Studies in superconductivity at extreme pressures. Physica C 2007, 460, 182–185. [Google Scholar] [CrossRef]
  92. Hamlin, J.J. Superconductivity in the metallic elements at high pressures. Physica C 2015, 514, 59–76. [Google Scholar] [CrossRef]
  93. Zhao, K.; Wang, Q.; Li, H.; Gao, B.; Wei, S.; Zhu, L.; Xu, H.; Liu, H.; Zhang, S. Superconductivity in dense scandium-based phosphides. Phys. Rev. B 2023, 108, 174513. [Google Scholar] [CrossRef]
  94. Kortus, J.; Mazin, I.I.; Belashchenko, K.D.; Antropov, V.P.; Boyer, L.L. Superconductivity of Metallic Boron in MgB2. Phys. Rev. Lett. 2001, 86, 4656–4659. [Google Scholar] [CrossRef]
  95. Lu, C.; Kuang, X.Y.; Wang, S.J.; Zhao, Y.R.; Tan, X.M. Theoretical investigation on the high-pressure structural transition and thermodynamic properties of cadmium. Europhys. Lett. 2010, 91, 16002. [Google Scholar] [CrossRef]
  96. Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
  97. Connétable, D.; Thomas, O. First-principles study of the structural, electronic, vibrational, and elastic properties of orthorhombic NiSi. Phys. Rev. B 2009, 79, 094101. [Google Scholar] [CrossRef]
  98. Shein, I.R.; Ivanovskii, A.L. Elastic properties of mono-and polycrystalline hexagonal AlB2-like diborides of s, p and d metals from first-principles calculations. J. Phys.: Condens. Matter 2008, 20, 415218. [Google Scholar] [CrossRef]
  99. Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Jian, M. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
  100. Haines, J.; Léger, J.M.; Bocquillon, G. Synthesis and design of superhard materials. Annu. Rev. Mater. Res. 2001, 31, 1–23. [Google Scholar] [CrossRef]
  101. Pan, Y.; Wang, S.L.; Zhang, X.; Jia, L.H. First-principles investigation of new structure, mechanical and electronic properties of Mo-based silicides. Ceram. Int. 2018, 44, 1744–1750. [Google Scholar] [CrossRef]
  102. Todai, M.; Hagihara, K.; Kishida, K.; Inui, H.; Nakano, T. Microstructure and fracture toughness in boron added NbSi2 (C40)/MoSi2 (C11b) duplex crystals. Scr. Mater. 2016, 113, 236–240. [Google Scholar] [CrossRef]
  103. Zhang, G.H.; Sun, G.D.; Chou, K.C. A novel process to prepare MoSi2 by reaction between MoS2 and Si. J. Alloy Compd. 2017, 694, 480–488. [Google Scholar] [CrossRef]
  104. Pu, D.L.; Pan, Y. Influence of high pressure on the structure, hardness and brittle-to-ductile transition of NbSi2 ceramics. Ceram. Int., 2021, 47, 2311–2318. [Google Scholar] [CrossRef]
  105. Ding, L.P.; Shao, P.; Zhang, F.H.; Lu, C.; Huang, X.F. Prediction of molybdenum nitride from first-principle calculations: crystal structures, electronic properties, and hardness. J. Phys. Chem. C 2018, 122, 21039–21046. [Google Scholar] [CrossRef]
  106. Gao, F.M.; He, J.L.; Wu, E.D.; Liu, S.M.; Yu, D.L.; Li, D.C.; Zhang, S.Y.; Tian, Y.J. Hardness of covalent crystals. Phys. Rev. Lett. 2003, 91, 015502. [Google Scholar] [CrossRef]
  107. Gao, F.M. Theoretical model of intrinsic hardness. Phys. Rev. B 2006, 73, 132104. [Google Scholar] [CrossRef]
  108. Andrievski, R.A. Superhard materials based on nanostructured high-melting point compounds: achievements and perspectives. Int. J. Refract. Met. Hard Mater. 2001, 19, 447–452. [Google Scholar] [CrossRef]
  109. Guo, X.J.; Li, L.; Liu, Z.Y.; Yu, D.L.; He, J.L.; Liu, R.P.; Xu, B.; Tian, Y.J.; Wang, H.T. Hardness of covalent compounds: Roles of metallic component and d valence electrons. J. Appl. Phys. 2008, 104, 023503. [Google Scholar] [CrossRef]
  110. Yan, H.Y.; Wei, Z.T.; Zhang, M.G.; Wei, Q. Exploration of stable stoichiometries, ground-state structures, and mechanical properties of the W-Si system. Ceram. Int. 2020, 46, 17034–17043. [Google Scholar] [CrossRef]
Preprints 120376 g001
Figure 1. The enthalpy curves for nine low-energy candidate phases and two considered decomposition routes with respect to Cmca phase. The inset shows the specific decomposition pressure of RuSi2.
Figure 1. The enthalpy curves for nine low-energy candidate phases and two considered decomposition routes with respect to Cmca phase. The inset shows the specific decomposition pressure of RuSi2.
Preprints 120376 g001
Preprints 120376 g002
Figure 2. Crystal structures of two stable RuSi2 phases. The green and blue spheres represent Ru and Si atoms, respectively. (a) Cmca-RuSi2 at 1 atm, and (b) Cmcm-RuSi2 at 75 GPa.
Figure 2. Crystal structures of two stable RuSi2 phases. The green and blue spheres represent Ru and Si atoms, respectively. (a) Cmca-RuSi2 at 1 atm, and (b) Cmcm-RuSi2 at 75 GPa.
Preprints 120376 g002
Preprints 120376 g003
Figure 3. The 3D and 2D electron localization functions (ELF) of two stable RuSi2 phases. (a) and (b) (001) plane for the Cmca-RuSi2 at 1 atm, (c) and (d) (001) plane for the Cmcm-RuSi2 at 1 atm, and (e) and (f) (001) plane for the Cmcm-RuSi2 at 75 GPa. The green and blue spheres represent Ru and Si atoms, respectively.
Figure 3. The 3D and 2D electron localization functions (ELF) of two stable RuSi2 phases. (a) and (b) (001) plane for the Cmca-RuSi2 at 1 atm, (c) and (d) (001) plane for the Cmcm-RuSi2 at 1 atm, and (e) and (f) (001) plane for the Cmcm-RuSi2 at 75 GPa. The green and blue spheres represent Ru and Si atoms, respectively.
Preprints 120376 g003
Preprints 120376 g004
Figure 4. The crystal orbital Hamilton population (COHP) curves of two stable RuSi2 phases. (a) Cmca-RuSi2 at 1 atm, (b) Cmcm-RuSi2 at 1 atm, and (c) Cmcm-RuSi2 at 75 GPa. The dotted vertical line at 0 eV represents Fermi energy level.
Figure 4. The crystal orbital Hamilton population (COHP) curves of two stable RuSi2 phases. (a) Cmca-RuSi2 at 1 atm, (b) Cmcm-RuSi2 at 1 atm, and (c) Cmcm-RuSi2 at 75 GPa. The dotted vertical line at 0 eV represents Fermi energy level.
Preprints 120376 g004
Preprints 120376 g005
Figure 5. Electronic band structures and density of states (DOS) of two stable RuSi2 phases. (a) Cmca-RuSi2 at 1 atm, (b) Cmcm-RuSi2 at 1 atm, and (c) Cmcm-RuSi2 at 75 GPa.
Figure 5. Electronic band structures and density of states (DOS) of two stable RuSi2 phases. (a) Cmca-RuSi2 at 1 atm, (b) Cmcm-RuSi2 at 1 atm, and (c) Cmcm-RuSi2 at 75 GPa.
Preprints 120376 g005
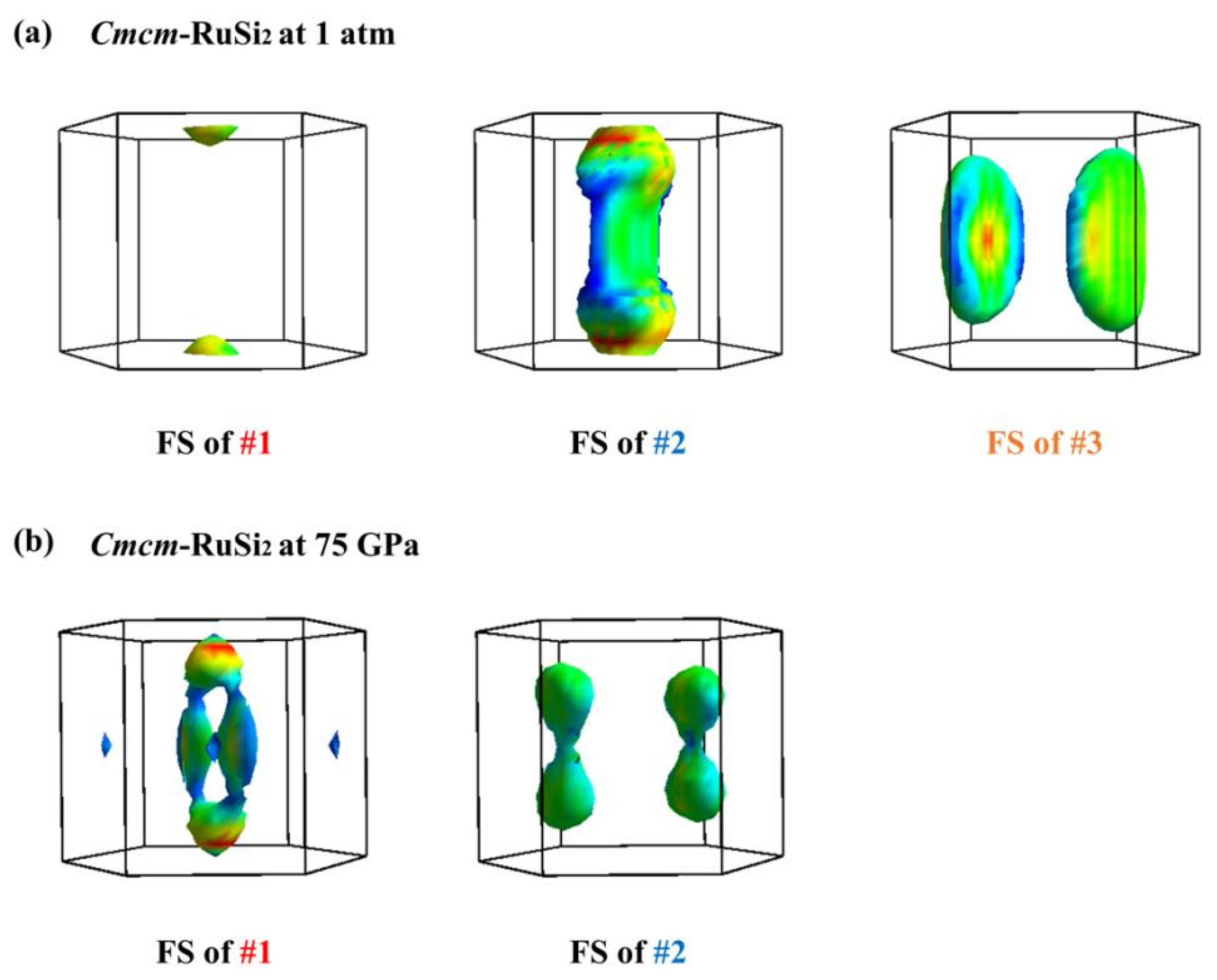
Preprints 120376 g006
Figure 6. The nested Fermi surfaces for the Cmcm-RuSi2 configuration at (a) 1atm and (b) 75 GPa.
Figure 6. The nested Fermi surfaces for the Cmcm-RuSi2 configuration at (a) 1atm and (b) 75 GPa.
Preprints 120376 g006
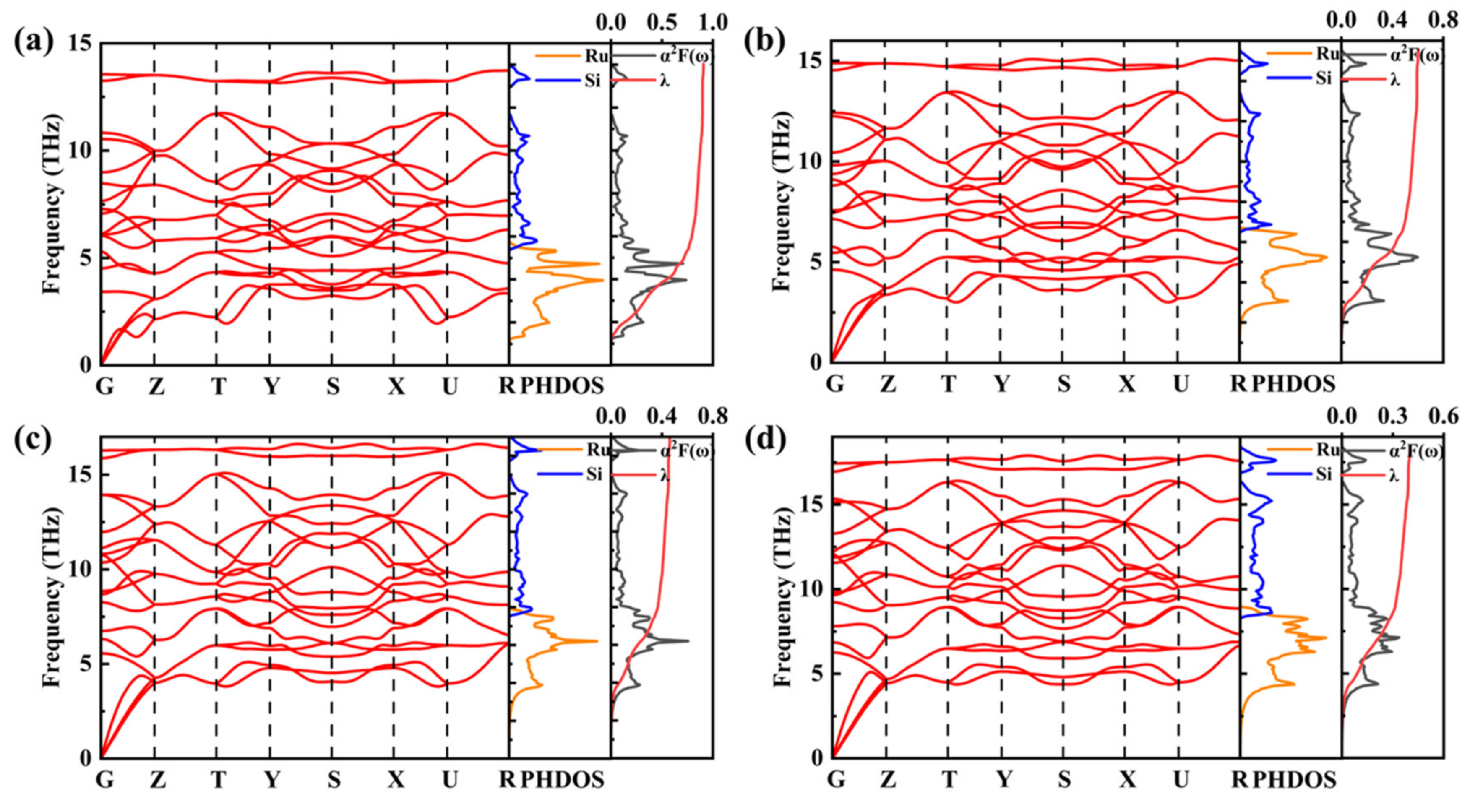
Preprints 120376 g007
Figure 7. The phonon dispersion curves, the projected phonon density of states (PHDOS) and Eliashberg spectral function α2F(ω) together with the electron−phonon integral constants λ(ω) of (a) Cmcm-RuSi2 at 1 atm, (b) Cmcm-RuSi2 at 25 GPa, (c) Cmcm-RuSi2 at 50 GPa, and (d) Cmcm-RuSi2 at 75 GPa.
Figure 7. The phonon dispersion curves, the projected phonon density of states (PHDOS) and Eliashberg spectral function α2F(ω) together with the electron−phonon integral constants λ(ω) of (a) Cmcm-RuSi2 at 1 atm, (b) Cmcm-RuSi2 at 25 GPa, (c) Cmcm-RuSi2 at 50 GPa, and (d) Cmcm-RuSi2 at 75 GPa.
Preprints 120376 g007
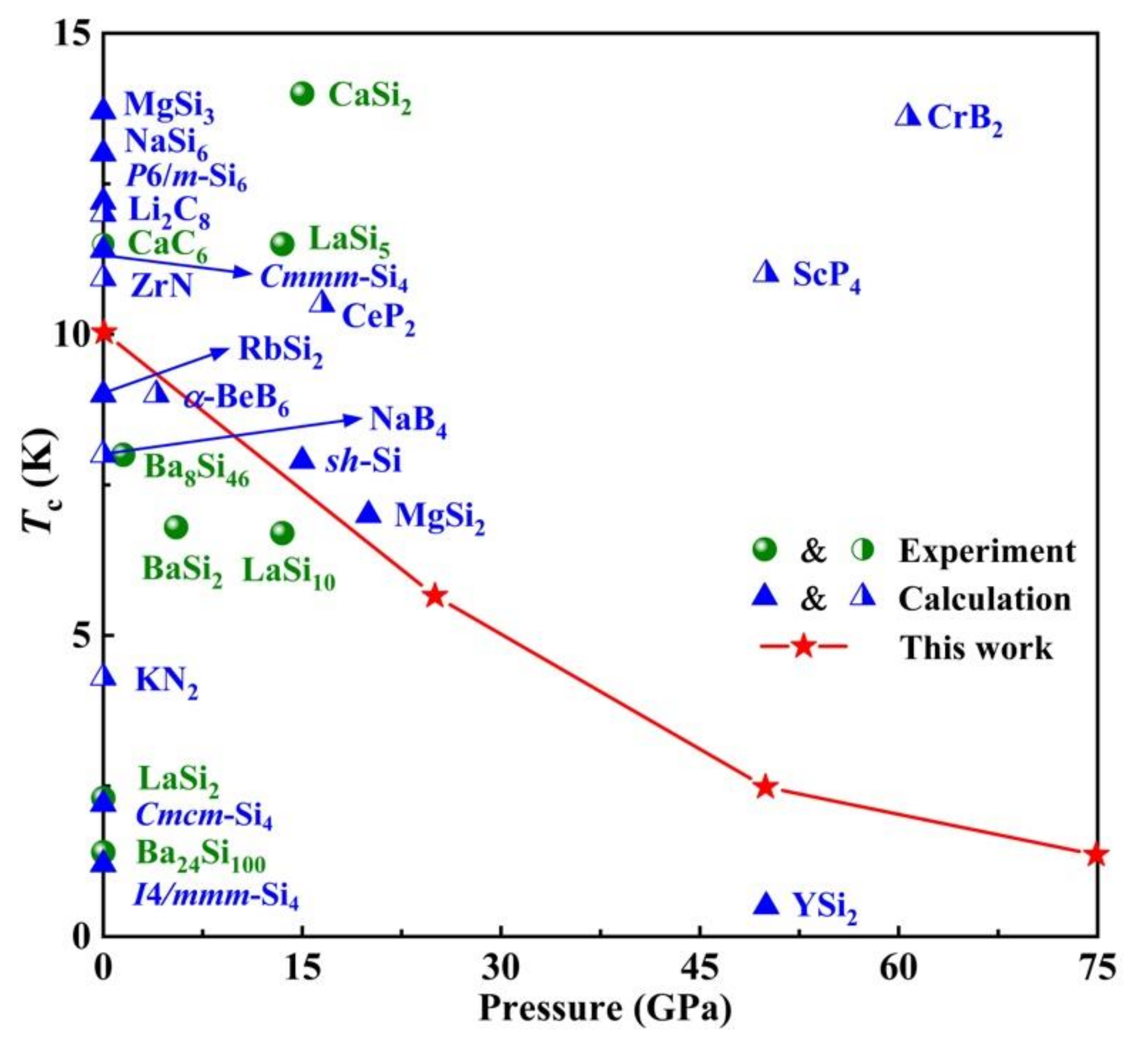
Preprints 120376 g008
Figure 8. Pressure dependence of Tc values for typical superconductors. The green filled and half-filled circles stand for the Tc values of well-known metal silicides and other binary compounds in experiment, respectively [9,10,11,32,38,39,40,84]. The blue filled and half-filled triangles denote the Tc values of well-known metal silicides and other binary compounds in theory, respectively [25,33,35,41,43,85,86,87,88,89,90]. The red filled stars the Tc values (μ* = 0.1) of the Cmcm-RuSi2 configuration at four different pressures.
Figure 8. Pressure dependence of Tc values for typical superconductors. The green filled and half-filled circles stand for the Tc values of well-known metal silicides and other binary compounds in experiment, respectively [9,10,11,32,38,39,40,84]. The blue filled and half-filled triangles denote the Tc values of well-known metal silicides and other binary compounds in theory, respectively [25,33,35,41,43,85,86,87,88,89,90]. The red filled stars the Tc values (μ* = 0.1) of the Cmcm-RuSi2 configuration at four different pressures.
Preprints 120376 g008
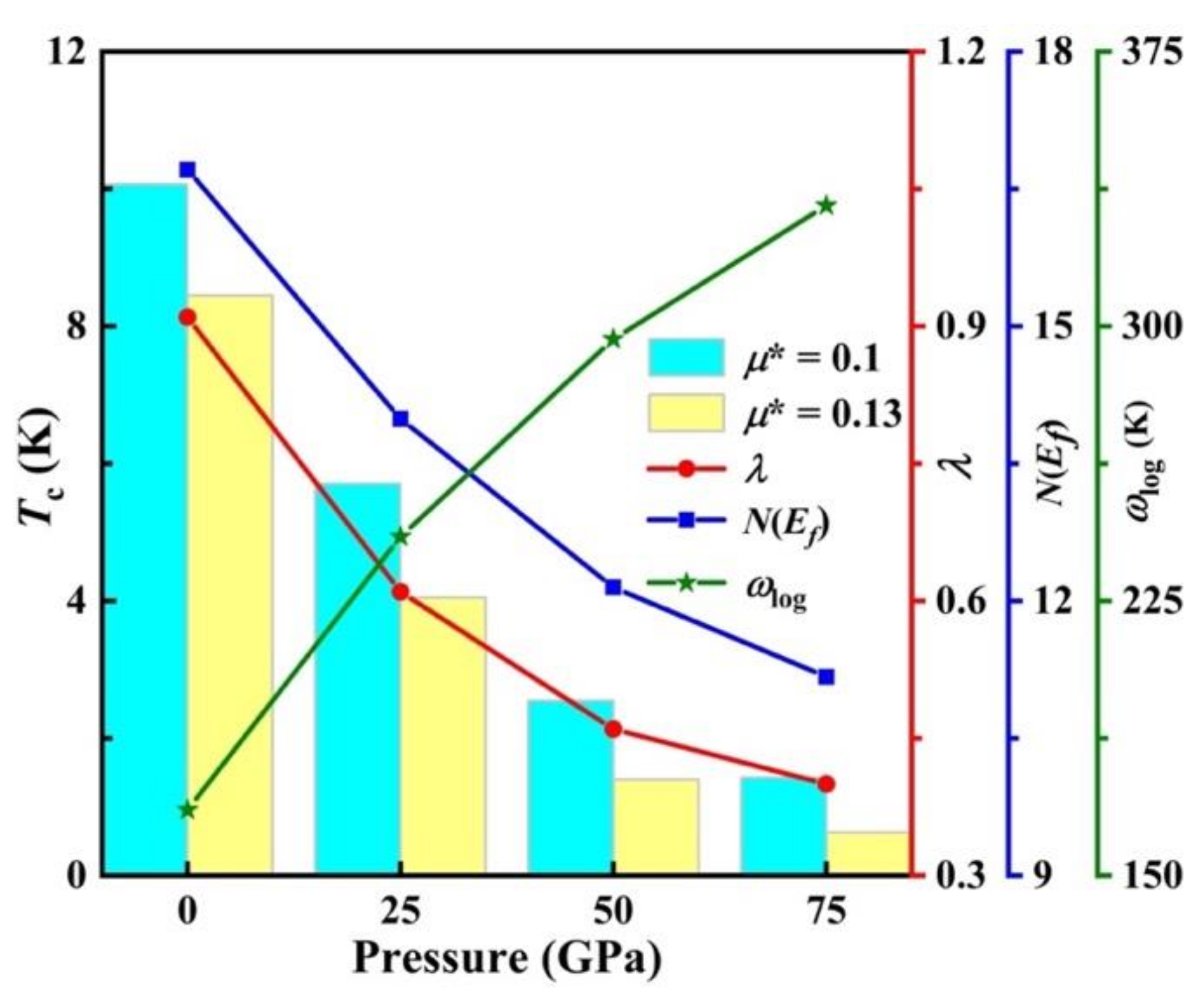
Preprints 120376 g009
Figure 9. Calculated electron-phonon coupling parameters λ, electronic density of states at the Fermi level N(Ef) (states/spin/Ry/Unit Cell), logarithmic average phonon frequency ωlog (K), and superconducting transition temperature Tc (K) in Cmcm-RuSi2 phase as a function of pressure with μ* = 0.10 and 0.13.
Figure 9. Calculated electron-phonon coupling parameters λ, electronic density of states at the Fermi level N(Ef) (states/spin/Ry/Unit Cell), logarithmic average phonon frequency ωlog (K), and superconducting transition temperature Tc (K) in Cmcm-RuSi2 phase as a function of pressure with μ* = 0.10 and 0.13.
Preprints 120376 g009
Table 1. Calculated electron-phonon coupling parameters λ, electronic density of states at the Fermi level N(Ef) (states/spin/Ry/Unit Cell), logarithmic average phonon frequency ωlog (K), and superconducting transition temperature Tc (K) of Cmcm-RuSi2 at 1 atm, 25 GPa, 50 GPa and 75 GPa, respectively.
Table 1. Calculated electron-phonon coupling parameters λ, electronic density of states at the Fermi level N(Ef) (states/spin/Ry/Unit Cell), logarithmic average phonon frequency ωlog (K), and superconducting transition temperature Tc (K) of Cmcm-RuSi2 at 1 atm, 25 GPa, 50 GPa and 75 GPa, respectively.
Structure Pressure ωlog N (Ef) λ Tc
μ* = 0.10 μ* = 0.13
Cmcm-RuSi2 1 atm 167.97 16.71 0.91 10.07 8.45
25 GPa 242.56 13.99 0.61 5.71 4.05
50 GPa 296.50 12.15 0.46 2.55 1.40
75 GPa 332.95 11.17 0.40 1.43 0.63
Table 2. Elastic constants Cij (GPa), shear modulus G (GPa), bulk elastic modulus B (GPa), B/G, Young’s modulus E (GPa) and Poisson’s ratio ν of two stable RuSi2 structures.
Table 2. Elastic constants Cij (GPa), shear modulus G (GPa), bulk elastic modulus B (GPa), B/G, Young’s modulus E (GPa) and Poisson’s ratio ν of two stable RuSi2 structures.
Pressure Space group C11 C22 C33 C44 C55 C66 C12 C13 C23 G B B/G E ν
1 atm Cmca 271 336 327 103 111 122 115 90 112 107.99 173.53 1.61 268.30 0.24
1 atm Cmcm 389 288 292 85 90 69 96 112 128 89.28 181.20 2.03 230.05 0.29
75 GPa Cmcm 836 676 594 149 173 188 261 246 298 184.99 410.13 2.22 482.44 0.30
Table 3. Calculated bond parameters and Vickers hardness Hv (GPa) of two stable structures.
Table 3. Calculated bond parameters and Vickers hardness Hv (GPa) of two stable structures.
bond P n d (Å) Vb (Å3) Hv (GPa)
Cmca Ru-Si 0.38 16 2.452 2.955 31.7
0.30 16 2.458 2.977 28a
0.35 16 2.460 2.984
0.41 16 2.460 2.986
0.36 16 2.467 3.010
0.30 16 2.484 3.072
0.30 16 2.500 3.131
0.27 16 2.523 3.219
Si-Si 0.33 8 2.541 3.289
0.32 16 2.570 3.402
0.28 8 2.576 3.428
0.27 8 2.598 3.514
0.31 16 2.612 3.574
0.18 8 2.689 3.898
0.20 16 2.693 3.913
Cmcm Ru-Si 2.23 8 2.226 6.367 26.8
0.32 4 2.242 6.513
Si-Si 0.37 4 2.293 6.967
a Reference [49]. 0.76 4 2.307 7.095
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated