Preprint
Article
Dynamic Time Warping as Elementary Effects Metric for Morris-based Global Sensitivity Analysis of High-dimension Dynamical Models
Altmetrics
Downloads
54
Views
56
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity
Submitted:
05 October 2024
Posted:
07 October 2024
You are already at the latest version
Alerts
Abstract
This work focused on demonstrating the use of dynamic time warping (DTW) as metric for the elementary effects computation in Morris-based global sensitivity analysis (GSA) of model parameters in multivariate dynamical systems. One of the challenges of GSA on multivariate time-dependent dynamics is the modeling of parameter perturbation effects propagated to all model outputs while capturing time-dependent patterns. The study establishes and demonstrates the use of DTW as metric of elementary effects across the time domain and the multivariate output domain, which are all aggregated together via the DTW cost function into a single metric value. Unlike the commonly studied coefficient-based functional approximation, and covariance decomposition methods, this new DTW-based Morris GSA algorithm implements curve alignment via dynamic programing for cost computation in every parameter perturbation trajectory, which captures the essence of “elementary effect” in the original Morris formulation. This new algorithm eliminates approximations and assumptions about the model outputs while achieving the objective of capturing perturbations across time and the array of model outputs. The technique was demonstrated using ordinary differential equation (ODE) system of a mixed-order adsorption kinetics, Monod-type microbial kinetics, and the Lorenz attractor for chaotic solutions. DTW as Morris-based GSA metric enables the modeling of parameter sensitivity effects on the entire array of model output variables evolving in time domain resulting to parameter rankings attributed to the entire model dynamics.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
1. Motivations
Sensitivity analysis (SA) is important in the development and application of dynamical models due to several reasons [1,2]: (i) understanding model behavior - SA helps in understanding how changes in model parameters affect the overall behavior of the system; (ii) identifying critical parameters - sensitivity analysis identifies which parameters have the most significant impact on model outputs allowing modelers to focus on accurately estimating these critical parameters, improving the model’s reliability; (iii) model validation and confidence building - SA aides in building confidence in the model by demonstrating the robustness of the model and highlighting areas where more precise data is needed; (iv) guiding data collection – SA informs data collection efforts by determining which parameters require more accurate measurements resulting to more efficient use of resources and time during data collection; (v) exploring uncertainty - SA allows modelers to explore the effects of uncertainty in parameter values on the model predictions. Performing SA on high-dimensional dynamical models has been a challenge due to the functional nature of data, i.e., information is a sequence of data [2]. Handling such functional data during SA has been the focus of numerous studies that can be grouped into two main categories: (1) elementary effects of coefficients of basis functions [3,4,5], and (2) variance decomposition [5,6]. However, it is computationally prohibitive to apply these prior SA techniques separately on each time-dependent output in high-dimensional dynamical models [7]. This work provides a solution to this challenge by establishing the theory and demonstrating the use of dynamic time warping (DTW) as metric of elementary effects in Morris-based global SA (GSA). Originated in time series analysis, DTW algorithm measures the similarity between two sequential data by determining their optimal alignment or matching via dynamic programming [8]. The sequences are "warped" non-linearly in the time dimension to determine a measure of their similarity, which is the alignment path with the minimal cost [9]. This makes DTW a fitting technique to be the generalized metric of the Morris GSA for dynamical models that exhibit a range of linear and non-linear effects of parameters. We propose DTW as elementary effects metric for Morris-based GSA of high-dimension dynamical models.
2. The Proposed DTW-based Metric of Elementary Effects for Dynamical Systems
Our proposed SA scheme, we call DTW-based Morris GSA, can be visualized using Figure 1 and Table 1. Due to determination of minimal cost of alignment, DTW determines not only the path to align the paired sequences but also the optimal cost value to align the sequences [8]. After alignment via dynamic programming, the difference between the two sequences (or perturbation in the context of SA) is computed using distance measure like Euclidean distance and aggregated by taking the mean of the distances we denote as as shown in Equation (1), where is the length of the th alignment path and is the total number of paired alignment paths. This makes the optimal cost of alignment as a measure of perturbation between the two sequences, which is equivalent to the “elementary effect” in the original Morris GSA [10]. This leads us to the following proposition.
- Proposition. We take the dynamic time warping (DTW) cost of alignment between pairs of sequential model outputs as the “elementary effect” to be used in the Morris GSA. By adding conditioning on the multiple outputs, e.g., via normalization along each output dimension, the DTW cost of all model outputs may then be aggregated together, e.g., via summation, averaging, etc., to compute a single metric of model perturbation between two parameter settings; hence, a single metric of perturbation across all model outputs is computed per parameter trajectory in the Morris GSA.
This proposed SA scheme implements a functional computation of the elementary effect because DTW takes into account the entire sequential data in every model output pair to compute the cost of alignment. In contrast to the prior algorithms implementing basis functions approximation [3] and variance decomposition [6], DTW-based Morris GSA does not approximate the model outputs nor make assumptions on the sequential data (normality of residuals, independence, etc.) in computing SA index. This makes our proposed algorithm to be the first GSA on dynamical models that does not approximate the model perturbations. We show in this paper the workflow on how to implement a DTW-based Morris GSA.
3. Notations and Formulations for DTW-based Morris GSA
We first present the original Morris formulation to have a reference for the new approach in our proposed DTW-based Morris GSA. Then we show the modifications of the formulations to implement the DTW cost as the new elementary effect metric.
3.1. Original Morris GSA Formulation
The Morris GSA involves the computation of the SA index using the fundamental measure of “elementary effect” as representation of model output perturbations relative to the corresponding parameter perturbations. Let us denote the model outputs (high-dimensional) of the system of differential equations to be , and the model parameters to be . So, the system of ordinary differential equations (ODEs) for the dynamical system evolving in time is represented as follows with the function :
Note that we are generalizing the ODE model by assuming to be composed of coupled ODEs where the ’s may exhibit relations among each other via the mathematical definition of . To compute “elementary effect”, each parameter in is varied across levels in the space of the parameters according to Morris sampling approach [10,11]. The region of Morris sensitivity sampling is a -dimensional -level grid. Each parameter being perturbed by an amount has its own elementary effect (Equation (3)) on the model outputs [11], but the original Morris formulation is valid only at a particular th time-point in the time-sequence.
The Morris sensitivity index for th parameter is then computed and we denote the SA index as (Equation (4)). High level of indicates high SA index, which means very sensitive model outputs relative to parameter perturbations. Note that several prior works were done to extend this original Morris formulation to try to capture the elementary effects across the entire sequence of , but these works implemented approximations of the sequential data of model outputs as pointed out in the introduction section. This paper proposes the DTW-base Morris GSA that eliminates the approximations while achieving the goal of capturing the perturbation patterns across .
3.2. DTW-Based Morris GSA Formulation
Our proposed DTW-based Morris builds on the formulations of the original Morris as shown above by replacing the computation of elementary effect with the DTW alignment cost, which captures the perturbations in the model outputs across the time sequence . This means that the model outputs are now functions of both and , i.e., , when computing the elementary effect. We simplify the notation by replacing the numerator expression representing the perturbation in the model outputs with the DTW cost when the parameter is perturbed by , which we simply denote as (see Figure 1 also). That is, we define the new elementary effect as measured by the cost of DTW alignment as shown in Equation (5). The SA index, , is computed in the same manner as the original Morris approach but using the as shown in Equation 6. For correct aggregation of the costs across all model outputs into a single value, model outputs are normalized within each dimension in (see Table 1 for this step on the Algorithm 1) prior to computing ; hence, prior to computing .
3.3. Assertion: The Original Morris GSA is a Special Case of DTW-Based Morris GSA
This new formulation of SA index computation from DTW-based elementary effect is a generalization of the original Morris elementary effect when the DTW-based Morris is applied on a single time point . This naturally follows from the definition of the DTW-based elementary effect as discussed above. This means the original Morris GSA is a special case of one time-point implementation of our proposed DTW-based Morris GSA.
4. Methodology
4.1. Pseudo-Code of Implementing DTW-based Morris GSA
The implementation of DTW-based Morris GSA in this study was done by setting different levels of random number generator index, which varies the sampling trajectories for the model parameters. Table 2 summarizes the workflow for this implementation.
4.2. Python Code Implementation: DTW-Morris GSA Python Module
The popular programming language Python was used to implement the computations for this DTW-based Morris GSA. The code scripts are maintained in the open-access online GitHub repository of the paper. For ease of use and readability of the codes and workflow in this paper, the Python codes were also organized in Jupyter Notebook files, which are also available in the same repository. See Data Availability section for more information.
4.3. Example Time-Series Dynamical Models Tested
The set of examples chosen for the testing of the proposed algorithm showcases a progression of the complexity of the dynamical models. The first example involves a single model output, the second example involves three model outputs, and the third example involves a set of solutions to chaotic systems. This progression allows the evaluation of the advances the proposed algorithm brings and also allows for the elucidation of potential limitations.
4.3.1. Example 1: Mixed-Order Adsorption Kinetics—Single-Output Dynamics
The first example tested is the mixed-order adsorption kinetics model involving a single differential equation of the adsorption capacity () [12,13]. Following is the set of ODE system (Equation (7)) for this adsorption dynamics. There are three parameters in the model and all are subjected to GSA via the proposed algorithm: = first-order rate constant, = second-order rate constant, and = adsorption capacity at equilibrium [14].
4.3.2. Example 2: Microbial Growth Kinetics—Multiple-Output Dynamics
The second example tested is a Monod-type microbial kinetics that models the growth of microbial cells (), the depletion of the substrate () during biogrowth, and the production of extracellular product () during biogrowth. That is, having three dimensions with each variable expressed in its ODE form with respect to time . The specific model used is for the conversion of glucose to ethanol by Saccharomyces cerevisiae [15]. Following is the set of differential-algebraic ODE system for this biogrowth dynamics. There are six parameters in the model and all are subjected to GSA via the proposed algorithm: = cell natural death rate constant, = substrate-per-cell yield coefficient, = product-per-cell yield coefficient, = substrate saturation constant, = cell maintenance utilization coefficient, and = maximum specific growth rate. The model is shown in Equation (8a–g).
where:
4.3.3. Example 3: Lorenz Attractor—A Set of Chaotic Solutions
The third example tested is the Lorenz attractor ODE system [16] that is commonly used as benchmark ODE for similar works on the analysis of dynamical models due to its characteristic chaotic behavior that occurs at certain combinations of model parameter values [17]. The Lorenz system is a foundational dynamical model in the areas of chaos theory and weather modeling such as atmospheric convection [18]. The Lorenz ODE system consists of three variables we denote as = rate of convection, = rate of horizontal temperature variation, and = rate of vertical temperature variation. Following is the set of differential-algebraic ODE system for this chaos dynamics. That is, having three dimensions with each variable expressed in its ODE form with respect to time . There are three parameters in the model and all are subjected to GSA via the proposed algorithm: , , and , which are parameters respectively proportional to the Prantl number, Rayleigh number, and certain physical dimensions of the atmospheric layer itself [17]. The model is shown in Equation (9a–c).
4.4. Analysis and Aggregation of Model Parameter Sensitivities
Existing data analysis and data aggregation techniques are used to evaluate the performance of the proposed DTW-based Morris GSA, and to make conclusions about the sensitivities of model parameters in Example 1, Example 2, and Example 3. For each run of the DTW-based Morris algorithm, the parameter sensitivity values are used to rank the parameters with Rank 1 assigned to the most sensitive (highest value). With the seed index of the random number generator (RNG) varied in the study of each model, a set of parameter ranking is created for every RNG index. After running the set total of varied RNG index (Algorithm 2), a set of parameter rank list is consequently created. Graphical analysis on the parameter rank list is done to evaluate sensitivity trends. Finally, a set of rank-aggregation techniques is implemented on each model parameter rank list to computationally determine the overall ranks of the parameters. The techniques include: Borda’s rank aggregation method (Borda), and Cross Entropy Monte Carlo rank aggregation method (CEMC) , which are all implemented using an existing R-package ‘TopKLists’ [19].
5. Results and Discussion
The results show the successful implementation of our proposed DTW-based Morris GSA for high-dimensional dynamical models.
5.1. Example 1: Mixed-Order Adsorption Kinetics—Single-Output Dynamics
The results are shown in Figure 2. The sample adsorption kinetics curves Figure 2A follow the typical patterns of adsorption of various adsorbate-adsorbent pairs. The rank-aggregation results (Figure 2B,C) on the parameter SA index rankings show consistent overall rankings of the parameters with as top-1 indicating it is the most sensitive model parameter. Parameter is top-2 and as the least sensitive parameter being top-3.
5.2. Example 2: Microbial Growth Kinetics—Multiple-Output Dynamics
The results are shown in Figure 3. The sample microbial kinetics curves in Figure 3A follow the typical patterns of cell growth (), substrate consumption (), and product accumulation (). Evident in Figure 3B is the effect of normalizing the model outputs along each output dimension. That is, consists of curves of normalized based on the lower-bound and upper-bound values of : . The same was done on the other model outputs: and . This normalization is critical step to be done to make sure the succeeding aggregation of the across all model outputs is correct. This normalization step has been coded in our Python script implementing DTW-based Morris GSA.
The rank-aggregation results (Figure 3C,D,E) on the parameter SA index rankings show consistent overall rankings of the four most sensitive parameters via the Borda method (Figure 3D): as top-1, as top-2, as top-3, and as top-4. On the other hand, the lower-rank parameters , and changed overall ranking depending on the rank-aggregation metric - mean, geometric mean, and L2-norm (Figure 3D). The CEMC method results to almost the same overall parameter ranking aggregation as Borda except for the parameter as top-1, and as top-2 (Figure 3E).
5.3. Example 3: Lorenz Attractor: A Set of Chaotic Solutions
The results are shown in Figure 4. The sample Lorenz attractor curves shown in Figure 4A,B follow the typical patterns of Lorenz chaotic solutions. An example for the normalized model output is shown Figure 4C. The rank-aggregation results (Figure 4D,E) on the parameter SA index rankings show consistent overall rankings of the parameters with as top-1 indicating it is the most sensitive model parameter. Parameter is top-2 and as the least sensitive parameter being top-3. Amid being a complex dynamical model due to its chaotic nature, the Lorenz Attractor was conveniently subjected to the DTW-based Morris GSA. After a careful search of the literature, we concluded that this is the first time that parameters sensitivities were computed for the Lorenz Attractor dynamical model, which is an indication of the potential of our proposed approach.
6. Conclusions
DTW-based Morris GSA can successfully determine parameter sensitivities of high-dimensional dynamical models. The results verify the capabilities of our prosed DTW-based Morris GSA. The findings also open the possibilities of extending the technique to more complex dynamical systems and to other areas that may benefit from the computational capabilities of the technique.
Data Availability Statement
The Python package and Jupyter Notebook files used to implement the DTW-based Morris GSA developed in this paper is provided as an open-source material through the GitHub repository of the project: https://github.com/dhanfort/DTW_based_Morris_GSA.git.
Acknowledgments
This work was conducted with the support of the Energy Institute of Louisiana (EIL) at the University of Louisiana at Lafayette. We are greatly appreciative of EIL’s administrative staff Sheila Holmes for making things happen when research projects face challenges during implementation.
References
- Murray-Smith, D.J. Sensitivity Analysis for Model Evaluation. In Testing and Validation of Computer Simulation Models: Principles, Methods and Applications, Murray-Smith, D.J., Ed. Springer International Publishing: Cham, 2015; pp. 49–60. [CrossRef]
- Zhang, K.; Lu, Z.; Cheng, K.; Wang, L.; Guo, Y. Global sensitivity analysis for multivariate output model and dynamic models. Reliability Engineering & System Safety 2020, 204, 107195. [Google Scholar] [CrossRef]
- Campbell, K.; McKay, M.D.; Williams, B.J. Sensitivity analysis when model outputs are functions. Reliability Engineering & System Safety 2006, 91, 1468–1472. [Google Scholar] [CrossRef]
- Fortela, D.L.B.; Farmer, K.; Zappi, A.; Sharp, W.W.; Revellame, E.; Gang, D.; Zappi, M. A Methodology for Global Sensitivity Analysis of Activated Sludge Models: Case Study with Activated Sludge Model No. 3 (ASM3). Water Environment Research 2019, 91, 865–876. [Google Scholar] [CrossRef]
- Cosenza, A.; Mannina, G.; Vanrolleghem, P.A.; Neumann, M.B. Global sensitivity analysis in wastewater applications: A comprehensive comparison of different methods. Environmental Modelling & Software 2013, 49, 40–52. [Google Scholar] [CrossRef]
- Gamboa, F.; Janon, A.; Klein, T.; Lagnoux, A. Sensitivity indices for multivariate outputs. Comptes Rendus Mathematique 2013, 351, 307–310. [Google Scholar] [CrossRef]
- Li, L.; Papaioannou, I.; Straub, D. Efficient global sensitivity analysis method for dynamic models in high dimensions. International Journal for Numerical Methods in Engineering 2024, 125, e7494. [Google Scholar] [CrossRef]
- Gold, O.; Sharir, M. Dynamic Time Warping and Geometric Edit Distance: Breaking the Quadratic Barrier. ACM Trans. Algorithms 2018, 14, Article–50. [Google Scholar] [CrossRef]
- Jeong, Y.-S.; Jeong, M.K.; Omitaomu, O.A. Weighted dynamic time warping for time series classification. Pattern Recognition 2011, 44, 2231–2240. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environmental Modelling & Software 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. Journal of Hazardous Materials 2020, 390, 122156. [Google Scholar] [CrossRef]
- Mikolajczyk, A.P.; Fortela, D.L.B.; Berry, J.C.; Chirdon, W.M.; Hernandez, R.A.; Gang, D.D.; Zappi, M.E. Evaluating the Suitability of Linear and Nonlinear Regression Approaches for the Langmuir Adsorption Model as Applied toward Biomass-Based Adsorbents: Testing Residuals and Assessing Model Validity. Langmuir 2024, 40, 20428–20442. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. A general kinetic model for adsorption: Theoretical analysis and modeling. Journal of Molecular Liquids 2019, 288, 111100. [Google Scholar] [CrossRef]
- Fogler, H.S. Chapter 9: Reaction Mechanisms, Pathways, Bioreactions, and Bioreactors. In Elements of Chemical Reaction Engineering, 6 ed.; Pearson: 2021.
- Lorenz, E.N. Deterministic Nonperiodic Flow. Journal of Atmospheric Sciences 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Springer-Verlag New York Inc.: New York, 1982. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Kesarkar, A.; Zeng, X.; Atlas, R. The Dual Nature of Chaos and Order in the Atmosphere. In Atmosphere, 2022; Vol. 13.
- Schimek, M.G.; Budinska, E.; Ding, J.; Kugler, K.G.; Svendova, V.; Lin, S.; Pfeifer, B. TopKLists: Inference, Aggregation and Visualization for Top-K Ranked Lists. CRAN (Comprehensive R Archive Network): 2022; 10.32614/CRAN.package.TopKLists.
Figure 1.
Schematic on how DTW is implemented for each pair of model parameter perturbation. (A) The resulting data sequences (time curves) of model output between two pairs of parameter settings constitute one trajectory of perturbation (deviation). (B) Each pair of perturbed curves undergoes DTW alignment computation achieved by applying dynamic programming. (C) The DTW cost of alignment, , represents the deviation between the curves.
Figure 1.
Schematic on how DTW is implemented for each pair of model parameter perturbation. (A) The resulting data sequences (time curves) of model output between two pairs of parameter settings constitute one trajectory of perturbation (deviation). (B) Each pair of perturbed curves undergoes DTW alignment computation achieved by applying dynamic programming. (C) The DTW cost of alignment, , represents the deviation between the curves.

Figure 2.
Results in implementing the DTW-based Morris GSA on a single-output dynamics using the example of mixed-order adsorption kinetics. (A) Example natural curves from the simulated adsorption kinetics. (B) descriptive summary of the model parameter ranking based in SA index. (C) Borda method and CEMC method rank-aggregation results.
Figure 2.
Results in implementing the DTW-based Morris GSA on a single-output dynamics using the example of mixed-order adsorption kinetics. (A) Example natural curves from the simulated adsorption kinetics. (B) descriptive summary of the model parameter ranking based in SA index. (C) Borda method and CEMC method rank-aggregation results.
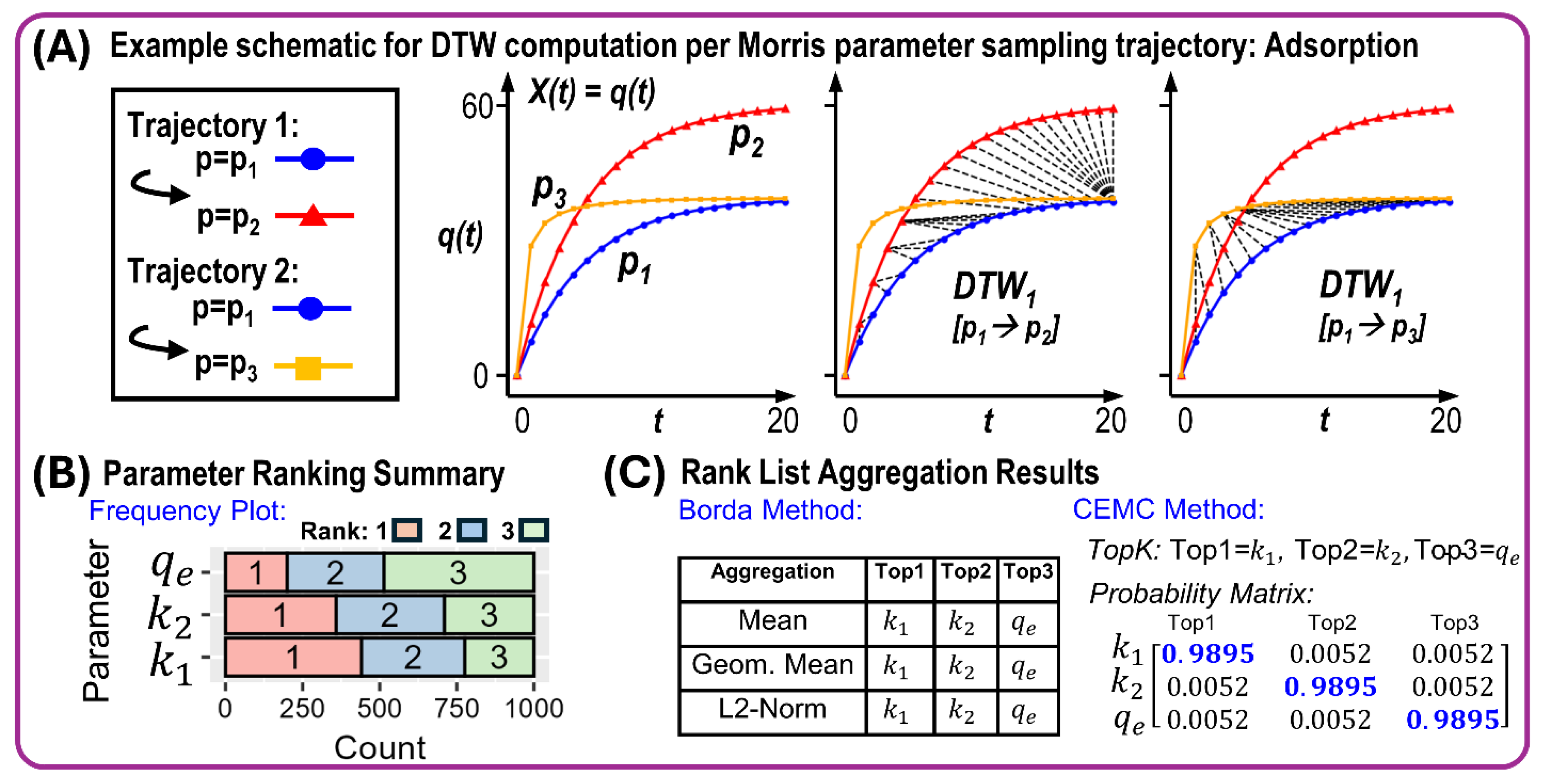
Figure 3.
Results in implementing the DTW-based Morris GSA on a multiple-output dynamics using the example of microbial growth kinetics. (A) Example natural curves from the simulated Monod-type microbial kinetics. (B) example of the normalized model outputs annotated with the optimally aligned path for each trajectory. (C) descriptive summary of the model parameter ranking based in SA index. (D) Borda method rank-aggregation results. (D) CEMC rank-aggregation results.
Figure 3.
Results in implementing the DTW-based Morris GSA on a multiple-output dynamics using the example of microbial growth kinetics. (A) Example natural curves from the simulated Monod-type microbial kinetics. (B) example of the normalized model outputs annotated with the optimally aligned path for each trajectory. (C) descriptive summary of the model parameter ranking based in SA index. (D) Borda method rank-aggregation results. (D) CEMC rank-aggregation results.
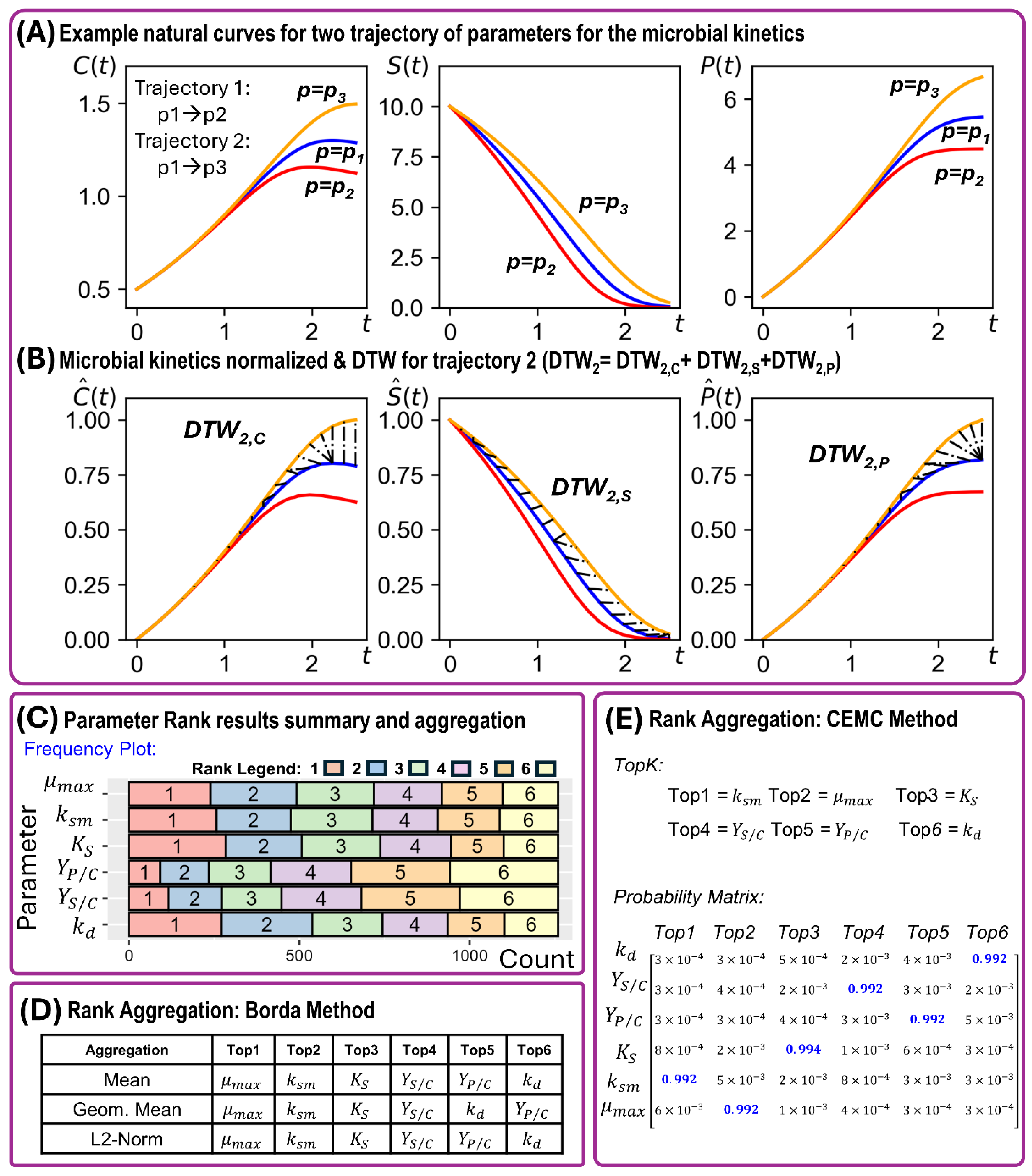
Figure 4.
Results in implementing the DTW-based Morris GSA on a set of chaotic solutions using the example for the Lorenz Attractor. (A) Example natural curves from the simulated Lorenz Attractor. (B) 3D rendering of the model outputs. (C) normalized curves prior to computation of DTW alignment cost. (D) descriptive summary of the model parameter ranking based in SA index. (E) Borda method and CEMC method rank-aggregation results.
Figure 4.
Results in implementing the DTW-based Morris GSA on a set of chaotic solutions using the example for the Lorenz Attractor. (A) Example natural curves from the simulated Lorenz Attractor. (B) 3D rendering of the model outputs. (C) normalized curves prior to computation of DTW alignment cost. (D) descriptive summary of the model parameter ranking based in SA index. (E) Borda method and CEMC method rank-aggregation results.
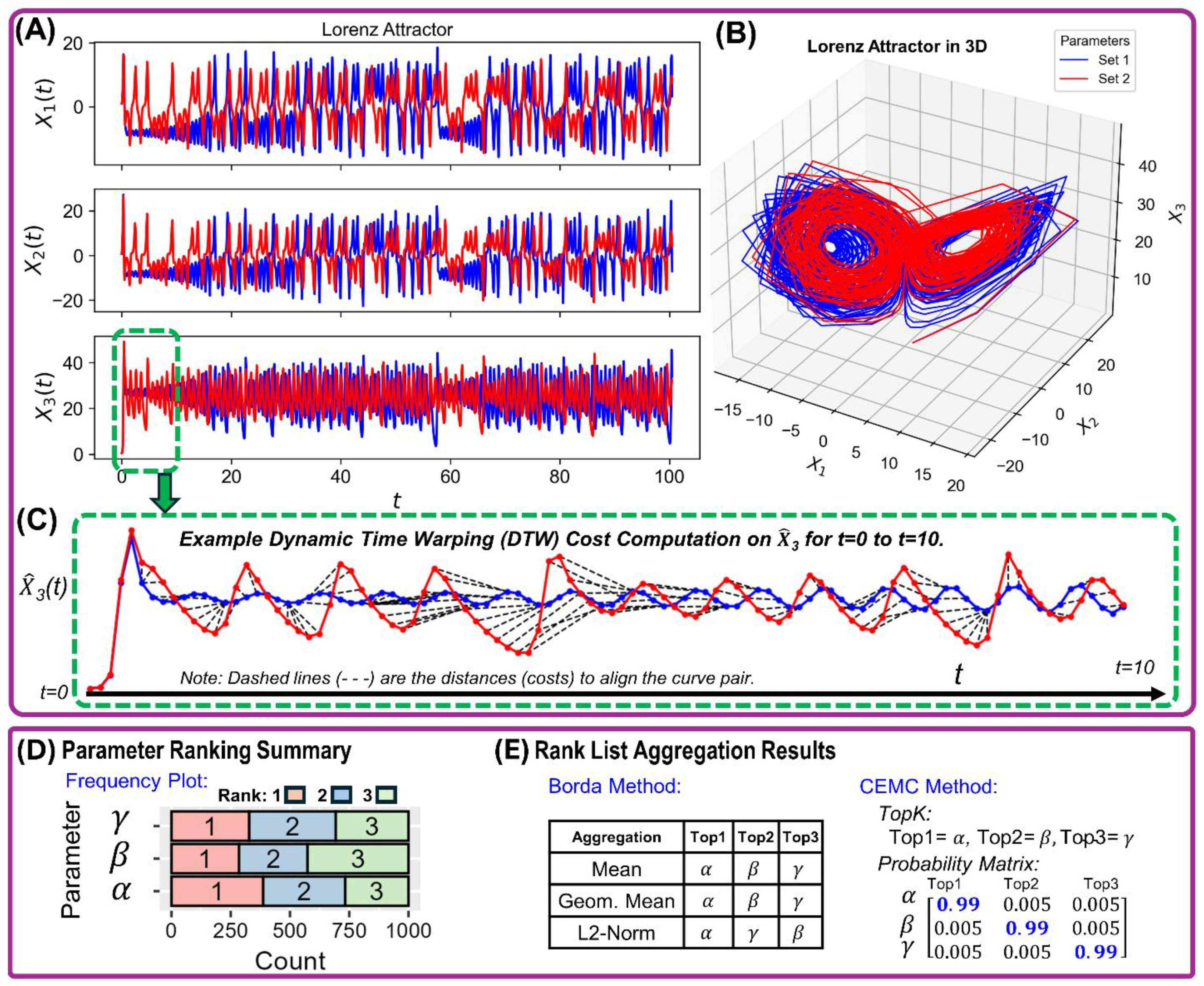
Table 1.
Pseudocode of the Dynamic Time Warping (DTW)-based Morris GSA.
|
Algorithm 1: DTW-based Morris GSA This is the core DTW-based Morris GSA. Note: The algorithmic innovation in this current work from base Morris algorithm are in Step 3. Steps: 1. Initialize the grid jump (Δ), and the number of trajectories (r) of each parameter. 2. Simulate model for each trajectory and collect all model output vectors: 2.1. Randomly generate a starting point in the input parameter space 2.2. Simulate model across random trajectories of input parameter: 2.2.1. Perturb the parameter by , keeping others constant. 2.2.2. Run the model with the original and perturbed inputs and collect sequential data of model outputs. 3. Calculate the elementary effect each parameter per trajectory step via DTW: 3.1. Normalize model output vectors according to each model output’s high and low values. 3.2. Calculate the elementary effect for each parameter per trajectory step via DTW: 3.2.1. Compute DTW cost () then the elementary effect in each pair of original and perturbed model output. 3.2.2. Compute the average of the elementary effects of each parameter across all model output dimensions. 4. Calculate the mean () of the elementary effects for each parameter across all trajectories. This number is the SA index for each model parameter subject to GSA. 5. Rank the parameters based on the mean to identify the most influential model parameters ones. |
Table 2.
Pseudocode of the implementation of DTW-based Morris GSA studies for high-dimensional dynamical models.
Table 2.
Pseudocode of the implementation of DTW-based Morris GSA studies for high-dimensional dynamical models.
|
Algorithm 2: Implement DTW-based Morris GSA at Varying Randomization This is the implementation-level algorithm for the DTW-based Morris GSA. Note: RNG seed randomization affects step 2.1 and 2.2 in Algorithm 1. Steps: 1. Generate a set of seed index for the random number generator (RNG) 2. Collect instances of parameter sensitivity ranks via Algorithm 1: DTW-based Morris GSA 2.1. Implement Algorithm 1: DTW-based Morris GSA for each seed index. 2.2. Append each parameter ranking results until all RNG seed are implemented. 3. Apply descriptive statistics and aggregation on the all parameter sensitivity ranks. 4. Apply a set of rank-aggregation techniques to computationally determine the overall ranks of the parameters. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







