Preprint
Article
A New Paradigm in AC Drive Control: Data Driven Based Control by Learning of the High Efficiency Data Set. Generalizations and Applications to a PMSM Drive Control System
Altmetrics
Downloads
77
Views
33
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
04 October 2024
Posted:
07 October 2024
You are already at the latest version
Alerts
Abstract
This paper presents a new means to control the processes, which involve the electric energy conversion. Electric machines fed by electronic converters provide the useful power defined by the inner product of two generalized energetic variables: the effort and the speed. The novelty of the paper idea is to control the desired energetics variables by a direct Data Driven Control (DDC) law in terms of the pair effort, speed and corresponding voltage controls of the electronic converter. It must be mentioned that the same desired useful power might be obtained with different controls at different efficiencies. The regularization problem was solved by selecting from a knowledge database, the maximum efficiency operation points. Knowing a reasonable number of optimal efficiency operation points, an interpolative Radial Base Function (RBF) control was built up. The RBF algorithm can find by interpolation the optimal controls for any admissible operation points of the process. The control scheme developed for this purpose has an inner DDC loop, that perform the converter control based on measured speed and demanded torque by the outer loop which handles the speed. A comparison of the DDC with the Model Predictive Control (MPC) schemas highlights the advantages of the new proposed control.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Electric Drive Systems (EDSs) have getting a real interest in the least decades by developing advanced technologies in digital processors, signals proceedings and power systems. The main benefits provide by developing EDSs can be summarized as follows: fast transients, high power density, large range of speed and power, low cost, safety operation, robustness, modular components etc.
Increasing number of EDSs applications (see automotive) implies new control techniques to improve the performances of the energy conversion process. Firstly, the efficiency improving of the EDSs can be done from the conception phase, when there is selected the Permanent Magnet Synchronous Machine (PMSM) that presents a high efficiency as a consequence of the using of modern technologies of manufacturing of permanent magnets. Secondarily, the increasing of the EDSs with PMSM may be obtained by using an adequate optimal control law designed by a certain methodology.
The traditional control strategies are based on the physical equations of the process model, for example the common used in EDSs are: Field Oriented Control (FOC) with the mathematical model in an appropriate coordination frame which it is used by an adequate decoupled control changes for torque and flux, the loops being usually designed with classical PI linear controllers [1,2], Direct Torque Control (DTC) – a bang to bang control implemented by hysteresis controllers [2] and Model Predictive control (MPC) which uses a future control sequence obtained by the process model predictor in the aim to find the best control law sequence by minimising a knower objective function [3].
The specific particularity of the advanced EDSs is that the input voltage and frequency are not directly applied from the power grid, which presents fixed values. The command is obtained by using a power interface represented by a power electronic invertor, which allows the giving variable values of voltage and frequency for obtaining the imposed performances [4]. This task is crucial for met the advanced results, which can improve the close loop performance of the EDSs [5,6].
In the least years, the MPC control strategy has been extensively developed and improved, being an actual motivation for research and industry [7-11]
]]. More advanced studies are dedicated to improve the control results, taking into account the nonlinear magnetic circuit [12], advanced optimization method [13], robustness [14] or fault tolerant capability [15], respectively. However, MPC strategy is strongly based on the model of the process, which in practice can differs from the one of the real system, leading to the worsening of the control performances.
In EDSs, the Artificial Intelligence Methods (AIMs) are well approached on control system. Thus, the torque minimization was successfully obtained by using Neural Network (NN) method [16], the Radial Basis Function Proportional-Integral-Derivative (RBF-PID) controller developed in [17] leads to improve the tracking results and an iterative learning control strategy reduce the torque ripple [18]. More advanced AIMs can be founded in the survey [19].
The Reinforcement Learning (RL) is an advance popular framework used to control systems and devices in a wide range of applications because of its ability to autonomously find control polices to achieve a desired goal without assuming that the environment are known. Thus, in [20] it is proved that the actual methods of deep RL leads to obtain a suitable control structure of the adaptive controller. Further, a low-complexity gradient descent solution with backtracking iteration approach for MPC Quadratic Programming (QP) problem leads by minimizing to reduce the number of the searched control inputs and improve the control performances [21]. In spite of the various benefits obtained by AIMs, these control advanced algorithms require a large amount of hardware and software resources.
A new trend in the control theory applications is based on data-driven control (DDC) that discusses the transition from Model-Based Control (MBC) applications to Model-Free Control (MFC) adaptive structures, involving the learning in a given control framework context [22,23,24,25]. The DDC method is an advanced strategy that can learn the dynamics [26], or can let to obtain different formulations via regularizations and relaxations methods, bridging the direct and indirect data driving control [27]. Indirect data driven control is formulated as bi-level optimization problem. That is, first a model fitted from the data in the inner identification, before the model is used to control the outer problem. Model is used for many reasons: first is the availability of powerful analysis and design of the control methods. Another advantages is that the models are very compressed compared to the data driven representation. At least, for more details about stabilization, optimality, and robustness behavior of DDC see [28].
Also, it can be mention that there can be obtained predictive control applications, which are directly obtained from the data set, which does not include all the main features of the classical predictive control strategy, as: integrator that ensure a offset-free control, the constraint handling, feed forward action, and disturbance control model, which make the strategy to be more versatile for real-time applications [29]. Furthermore, an algorithm designed for control an unknown stochastic linear time-invariant systems illustrate the high closed-loop performance obtained by data-enabled predictive control strategy which has a novel robust distribution [30]. A simultaneous MPC and DDC strategy with relaxed assumption on the model in a proper framework shows how a no convex optimal problem is transformed into a one with convex constraints [31]. The input-mapping based data-driven model predictive control is successful used for systems with bounded disturbance [32] or for advance learning [33]. For generalization, in [34] is discussed a data-enabled predictive control parametric algorithm that combined the identification method obtained by a learning procedure and a control one of the dynamical systems, resulting in an equivalent MPC formulation, which is valid for both linear time-invariant system, which is directly applied, and for nonlinear systems, that requires a regularization procedure.
As expected, an emerging technology on control system development may be based on both DDC and MPC strategies. Although, EDSs with represent a rapid process for control applications, with the help of the advance sensors and adequate numerical signal processing there can be collected and processed a large amount of data that is sufficient for implementing the DDC solution. Thus, based on White-Box (WB) modeling estimation by least squares technique, in [35] a DDC-MPC method is proposed for current controlling of PMSM, that leads to compensate the modeling errors and, to improve the control performance for both dynamic and steady-state regimes. In relatively recent paper [36,37], it has been shown the transition from the classical model-based approach towards data-driven optimal control strategies, which take into account the model predictive control paradigm, leading to develop the data-enabled predictive control. At least, in the reference [38] it is shown that a fractional PI controller for a PMSM drive can be obtained by a DDC algorithm in certain practical conditions.
MPC strategy and then recently starting by DDC have done many successfully solved problems. An important issue in the EDSs with PMSM is related on the efficiency improving by control means. In literature [39,40,41] can be founded various solution for improving the efficiency of EDSs with PMSM. Most of them are based on the modeling of the power losses with algebraic relation, taking into account some specific constants of materials. The minimize of an analytic cost function with constraints will give the optimal solution that ensures a high efficiency. This approach has an elegant mathematical description, but also many limitations: the constants of the materials depend of the magnetic/electric fields, there are losses that cannot be modeled analytically (abnormal losses) and many methods are designed for partial losses.
Finally, there is an extensive literature focusing on the MFC strategy (philosophy). Research started early in 1956 through the project [42] “A proposal for the Dartmouth Summer Research Project on Artificial Intelligence” by J. McCarthy, Dartmouth College, M. L. Minsky, Harvard University, N. Rochester, IBM Corporation, C. E. Shannon, Bell Telephone Corporation. It is concluded in this research project: ‘’if a machine can do a job, then an automatic calculator can be programmed to simulate the machine’’. Paraphrasing we can say mutatis mutandis: if a classic automatic control based on a physical model can control a process, then an informatic system can control the same process without a physical model. This is the main philosophy followed in the paper to show how a MBC strategy offers good enough possibilities to develop a MFC in certain energetic constraint. The addresing paper made a transion from the MBC to MFC in the DDC paradigme for high performance objective.
For a large set of the phisical processes the main controlled quantities are effort and flow. Their product represents the useful power. In the paper we develop a new technique to find adequate controls of the effort and flow in terms of maximum efficiency, that is the minimum losses. These appropriates controls are extracted from an aprioric DataBase (DB) in terms of required effort and measured speed. The aprioric DB contains mainly the steady state measurements in the open loop tests for: the speed, the effort and the corresponding controls. An RBF interpolativ system is trained so that, based on an few set of the optimal experimental data, to exctract the controls for any desired speed and flow. In the on line operation of the process the initial DB is adaptive. An on line optimisation system search the new optomal controls when the process parameters are changed. DB are free from process parameters and in consecace from the process model.
The paper shows that an informatic system based on an experimental database, without knowing the parameters of the process, can do the same job as a MPC control system with multiple advantages. Thus, we propose a new combined linear PID and DDC, where the control variables are directly obtained from an experimental database by a RBF methodology. The key of DDC is to find the relation of the energetic variables with the control variables, by a RBF -NN interpolative surfaces. These surfaces are built with a set of the optimal experimental support points extracted from a large knowledge database.
In the following, we demonstrate that the proposed combined linear PID and the RBF-NN methodology can successfully dynamically simulate EDSs with PMSM, controlled by the MPC methodology, without knowing any parameters of the motor or driven process.
Respecting the state of art, in the paper there are proposed the following new contributions:
- (i)
- A new combined linear and DDC control methodology that uses the process control variables obtained from an experimental database built by a RBF methodology.
- (ii)
- In the case of the EDSs, the combined control methodology is in terms of an outer time domain PID control of speed and an inner implicit RBF control loop.
- (iii)
- The inner control loop is based on an experimental database, which contains the optimal controls corresponding to any speed and torque of process operation points. The control law is in implicit form that is a set a steady state process operation points.
- (iv)
- The RBF methodology compresses the set of all admissible operation points by network architecture, with a few optimal data basis functions.
- (v)
- We present a novel control scheme in which the demanded effort by the PI controller and measured speed are the input for the RBF inner loop. The output of the inner loop is the inverter’s modulator input, which select the proper inverter’s voltage vector sequence of the invertor.
- (vi)
- The inner RBF control loop is adaptive, that is the inverter control is temperature dependent because the parameters of the process changes with motor is temperature.
The organization of this paper is structured as follows. Thus, in the Section II is presented how is obtained a data free control algorithm based on the physical modeling of the processes. The section III is dedicated to DDC of AC drives, where the illustrative application of PMSM drive control is done. The comparative results obtained by MPC and DDC techniques are presented in Section IV. At last, in Section V there were summarized the main benefits obtained by the proposed novelty control method.
2. Problem Statement. From Classical Physical Modeling of Energy Conversion Flow to Data Free Model Control
2.1. Problem Statement
The energy conversion flow is an essential objective for ensuring of the social and economic stability. In industry and residence, many applications are designed to deal with the macroscopic energy conversion that implies three main types of fields: electromagnetics, mechanics and thermodynamics (Figure 1).
Starting from these energy conversion possibilities, in practice there can be developed different conversion processes subject of adequate constraints.
In the various physical processes like electrical, mechanical, hydro- or thermal, the desired useful work is universally characterized by a pair of energetic variables: the effort e (t) and flow s (t). The inner product of these generalized variables is the instantaneous useful power:
The different forms of primary power p1(t), can be converted in useful forms by various means. Let be η the efficiency of the power conversion process. Then, primary power p1(t) is easily obtained:
If, for example, we refer to a mechanical process of motion which develop a useful force fu and a linear velocity v, the motion being described in external (cartesian) coordinates, then we have e = fu, and s = v. If the motion is rated to the drive motor shaft, then e = m and s = ω, where m is the developed torque and ω the angular speed. In the case of an electrical process, the electrical voltage represented in the complex domain, e=u and the corresponding current s= i. Similarly, in the case of Hydro, Ventilation, Air Conditioning (HVAC) processes, the pressure e=P and the flow rate s=Q.
Usually, the above energetic macroscopic process are well-modeled by the actual intrinsic physical theories. In the control theory, the using of this model with lumped parameters have some vulnerabilities: high sensitivity to parameter variations, incomplete modeling of some loss components, linearity on a small range, low control accuracy at high frequencies etc. However, the analytic modeling has the advantage of simplicity, being in many approaches a starting point in the developing of advanced control methods.
The transition from MBC to model MFC is illustrated in Figure 2. For this aim it is considerate a combined PI and inner control (cascaded or not) for a given process described by adequate physical model equations.
The inner control is switched from MBC to MFC whenever is necessary, giving on the output the control u as is suggested in Figure 2(a).
In the first stage exposed in Figure 2(b), the inner control is switched to MBC. At this step, there selected a collection of the main data in steady-steate regime that coresponds to the high efficiency, grouped in:
where has been considerate that in steady-state regime we have eref=e.
Now, the next step is the designing of the MFC controller. This controller has a interpolative-adaptive structure with a vraiable structure, being able to learn from MBC data, having as input the data stored (3) in a sufficient number, and the output u*MFC as is shown in Figure 2(c). The MFC algorithm is trainned in a open structure, and has the ability to learn from the experince given by MBC
Having closed the trainning phase of MFC, the testing phase in done in the close loop structure as is indicated in Figure 2(d).
The transition from MBC to MFC depends of the process that is subject of control strategy. This procedure may be applied to the process with complex, nonlinear and multivariable structure.
2.2. The DDC Strategy of the Energy Conversion Process
The MFC tehnique represents a modern approach with a large applicability in practice. From MFC control techniques, a particular direction are described by DDC strategy which is developed in the following.
The numerical processing of the signals that refers to the training phase are carried out with the MBC strategy, which is why the MBC acronym will be ignored in the symbolization of signals, distinguishing between the acronyms DDC and MPC whenever is necessary.
The state model of this nonlinear deterministic conversion processes is described by:
The state x, control input u and output y, respectively, are restricted to the sets of adequate dimensions: ,and . Further, in the vector θ(t) there are comprised the parameter of the process. The nonilinearty of the state model (3) is emphases by the nonlinear functions f and g.
Let us to adopt the fallowing outputs variables:
By usually discretizing techniques, the corresponding discrete state space model of the plant (4) becomes:
where the discrete states x(k), control inputs u(k), and outputs y(k) are matrices of appropriate sizes.
Also, in (6) ξ is the discrete noise of the process, while Ts represents the sampling time period.
The control problem to be solved is definited according to: seek for a control u(t) that will bring a desired useful work:
when the input of the system is suppyled by the energy:
with a natural condition resulted from (2):
such as for any other control, which also bring the same work E2, the energy E1 is larger:
In other words, we assume that for a given desired pair of the generalized variables e(t) and s(t), there exist a bounded control u(t) and a bounded cost criterion, which can be espressed either in a contionous set formulation:
or in a discrete representation:
where there has been used the mean square error: .
Also, in the cost formulation (11)-(12) there is used the Total Harmonic Distorsion THD factor that is a measure of harmonic distortion, computed by:
where and represent the Root Mean Square (RMS) values of fundamental and harmonics components of the effort e, respectively.
For the same desired work (7) the final cost C which is lower, has better control u. The interval (t1-t0) length is a time window with the required energy E2 (6), where t1/0 represents the end/start time.
It can be mention that the input power may be either positive or negative , as the power is delivered or received by the process.
The first term from (11)-(12) refers at the control quality in the control horizon N length and the second terms, respectively, refers to the input energy.
The numerical computation has a large aplicalbility in data computation. For our approach we define cost – solving problem based on (12) as follows:
where the constraints E2 and η ensure the uniqueness of the optimal cost problem.
The process model (4) is in time domain, having an explicit form. A more convenient approach is developed in the following.
We introduce the implicit control law:
In the model (15) the ouput of the process was reduce in terms of the generalized variables pair (e,s), and the corresponding input is . In consequence, the output variables p1, p2 are free, being unconstrained, which shows the control law G is not unique. A regularization procedure is effectuated by selecting from the set (e,s) corresponding to the maximum efficiency power operation points.
The command law of the process results from the explicit model (15):
Let consider a time window for requested output trajectories of the both generalized variables:
By eliminate the time from relations (16) we have the implicit representation:
Each discrete point kTs , with k=1,...,Nobs, where Nobs is the number of observations points, on the trajectory (17) in the generalized variables (e, s) plane, has the input controls which represents the supports points for the control surfaces:
The surfaces (19) in the continuous domain represent the endless set of steady state operation points. Any stable operating point (e,s) is correlated with the corresponding’s controls (u1,u2). A trajectory of motion (16) in the permissible range, beginning in a stable initial state (e0,s0) and reaching the final state (ef,sf), passes through an countless set of intermediate energy states, since in classical physics it is admitted that states of physical processes can vary only continuously. By using digital process control techniques, the set of states travelled from the initial state to the final state becomes countable due to sampling operations. An exhaustive condition of stability of process controlled by the two fundamental energy quantities, effort e and velocity (flow) s is as follows: if the speed control loop is stable in the sense that the required effort eref is on the control surfaces (19), the operating points on the motion path will be stable. Through the sampling process, stability is reduced, the longer the sampling period.
Generalizing we can say that the multivariable control law (19) can be generated with the required precision, by means of a known set of operating points of the process:
Through an interpolation algorithmassociated with thedatabase, for any current value, a value is generated which approximates the control law relation (15), so that:
The control law is determined by means of an experimental data set and some continuity and smoothing properties of the surfaces (15), which are specific properties of energetic inertial processes.
In summary, the control law has the form:
with properties:
The RBF-NN is largely used in control system
]]. A typical RBF-NN structure used for obtaining the input plant command is depicted in Figure 3.
The RBF-NN is used for two objectives, as training and testing:
where by RBF has been denoted the function of the neural network.
Having a classical structure, the RBF is organized in three levels of layers as input, hiden and output, respectively. Moreover, the weights obtained in the testing step are grouped in:
The output of the RBF-NN is given by a linear combination:
where the activation function is given by Gaussian distribution
having the parameters σ and μ which are the basis width vector and center points of Gaussian function, respectively.
Also, the input Gaussian function is represented by set:
Enhancing the RBF depicted in Figure 3, in Figure 4 is illustrated the combined control structure of a generic process, that involves an outer explicit flow control loop and a inner multivariable data driven control loop.
The fundamental operation key of the DDC schema is the knowlage database. This database containes a large set of process operation points, from which are limited steady-state ones. In the block scheme from Figure 3, the actual values of control, output, effort and flow is comprised in the set:
where y(k) is the output of the process, and N is the number of colected data.
The next task is to select a suficient number of steady-state points from all the operation points from,
For obtaining the suficient number of steady-state points contained in the set, the operator used for data extraction will be symbolized by “°”.
Supplimentary, as input data, there are considered the aprioric informations included in the set:
where: rated specification of the process are contained in the set , envirovment and design requirments which are contained in the sets and , respectively.
The input control data set will be computed based on both aprioric information and process data. In fact, the design of the required database is quite complex, and will be presented in the next section for the case of a concrete application. However, stating from the inputs of knowledges and datathe output of the database is
where byhas been represented a numerical operator used for data processing in the database.
The proposed PI and combinated DCC structure is illustrated ub Figure 4.
The trainning phase designing of DDC strategy is depicted in Figure 4(a), where are highlited the main steps of DDC algorithm, while the testing phase made in close loop structure is represented in Figure 4(b).
The DDC control structure from Figure 4(b) is desined for tracking the output of the process sDDC(k) to its reference sref-DDC(k) by using a linear PI controller, having the output eref-DDC(k) bounded into the limits -/+emax.
The control data set contains the maximum efficiency operation points selected from the knowledge database. The interpolation algorithm AF find the actual control u(k) based on demanded effort e(k)ref and the measured flow s(k).
We assume that all points (19), also referred as nodes, or “support points” are distinct and not collinear. Due to the intrinsic nature of the energy conversion process, the DDC law (15) is geometrically represented as continuous differentiable surfaces which allows to find an interpolation algorithm such that these surfaces passes exactly through each experimental points (18). The maximum efficiency operation points (e,s) is selected from the knoulagy database by a grid (direct) search method. These methodology involve setting up of grids in the input space (e,s) and evaluating the power efficiency of each grid point. The operation point that corresponds to the maimum efficiency was considered the best solution.
Two interpolation methods that are widely used in different application fields (in areas such as computer graphics, physical modeling, geographic information systems, medical imaging, and more), have been adopted. We used two basic methods: Delaunay triangulation and related methods and RBF-NN interpolation.
Let be a set of data and we wont to find a rule which allows us to deduce information about the process we are studying at locations differet from those at wich we are obtained our measurements.
The interpolated value of a point, other than support points, was obtained by local interpolation techniques with the three nearby points. One widely used approach is Delaunay triangulation of data and the Voronoi diagram of a set of points, which is the dual of the first approach (Delaunay triangulation).
The RBF network has its origin in performing the interpolation of a set of data points in a multidimensional compact domain to an arbitrary accuracy, given sufficient number of data points. It has a network architecture with weighed basis functions. The solution is optimal by minimizing a functional containing a regularization terms. The RBF method compresses a very large volume of data, with the help of a much smaller number of weighted basic functions in the training process. In the exam (assessing) stage, the RBF network returns any point in the field covered by the data used in the training stage by an interpolation process of the weighted basis function. The discrete model of the control law is practically non-inertial, because the control u(k) at the current step k is obtained by accessing the fast interpolation algorithm:
where Td is the desired final time of the motion trajectories.
The new control methodology of the energy conversion process in terms of the effort and flow was represented in Figure 4. The objectives (10)-(11) are accomplished by two control loops: a MIMO inner control loop in terms of desired effort eref(t) and measured flow s(t) and an outer classical PI speed control loop.
3. The DDC of AC drive. Illustrative Case Study: The DDC of a PMSM Drive System
The control method proposed in the privious section has the ability to offers a new alternative of the classical methods which are based on the model accuracy. The novel approach is model free, being suitable for a large class of applications.
In the following, we begin with the principle of the DDC scheme applied to AC drives. Afterwards, there is done an illustrative application for a PMSM driving systems controlled according to the methodology developed in this paper. As MBC method has been selected the MPC strategy due to benefits of providing an optimal solution without any frequency modulator.
3.1. The DDC Principle of AC Drives
AC drives are founded in a large area of applications due to their height-performances resulted in dynamic regime.
Usually, the cascade control structure of AC drives is used to separate the different dynamics of electrical and mechanical parts, respectively, and then to have an independent control of each loop.
In addition to the advance control law, an important attention is paid for the electronic power inverter used to obtain the voltage supply. This aspect will be largely approached in the following sections.
This section is dedicated to the DDC principle applied to AC drives.
As mention in the second section, the DDC method is based on a learning technique. For our approach, the learning is based on the collected data from MPC strategy running.
The stages on DDC design are illustrated in Figure 5.
It is starting from a cascade structure, having the well-known quantities: speed (actual and reference), torque (reference), voltage and current (components). A brief description of each stage can be done as follows:
- a.
- Stage I: Stored data from MPC cascade control running. In this stage there are selected a limited data obtained from MPC cascade running in steady-state regime for: speed, torque, voltage and current. Further, from this there is imposed the constraint of high efficiency, resulting in the stored data;
- b.
- Stage II: Training of DDC strategy. The stored data obtained on the previous stage serves as a base in this training stage for DDC design which is done in a open structure. Usually, the stored data are numerically processed in the order to improve the main features: efficiency, robustness, tracking and disturbance rejection. This objectives are done by using a DB which offers multiple possibilities of data processing;
- c.
- Stage III: Testing of DDC method. Learning from the previous stage, the DDC strategy is able to operate in any point required by the application of AC drive. The DDC method are implemented with no cascade control structure as is shown in the figure.
The DDC strategy may be a emergence solution in the actual AC drives whose model parameters sensitivity is still reported as an open problem.
Nevertheless, an important objective it represented by the improving of the efficiency in various scenarios.
Usually, the electrical parameters of the model of AC drives are subject of variations as dependence of exogenous conditions that can differ with environment conditions: temperature, external fields, altitude etc. In this can there must be studied the robustness of the DDC strategy under these circumstances.
3.2. DDC of the PMSM Drive System
The PMSM drives are largely used in the adjustable applications that require high performance control performances and high efficiency. A conventional structure used in practice includes a two level power electronic inverter as in Figure 6. On this input of the power electronic inverter is usually ensured a constant DC bus voltage UDC which is provided by a DC bus circuit that contains a DC link voltage and a voltage rectifier. The main feature of this power structure is that the discrete logic commnad Sabc={Sa,Sb,Sc} applied on the top switches {1,3,5} is negated applied to the bottom switches {4,6,2}.
The power inverter discrete command is provided by the control structure that is developed in the following.
3.2.1. Plant Modeling: PMSM and Power Inverter
Naturally, the model of PMSM is developed in the three-phase coodinates (a,b,c). This model has a complex structure, being difficult to be used in the practical close-loop control applications. A first approach to avoid this drawback is to use ortogonal fixed coordinate (α,β) that offer some improvments. At last, the ortogonal transfomation in a moving system reference frame (d,q) provides the highest benefits of the model of PMSM for close loop applications. Indeed, the usual FOC tehnique appied to PMSM is done by align the space vector of PM flux with a north pole of the rotor of PMSM.
Figure 7.
Space vector diagrame of a PMSM with rotor system frame orientation .
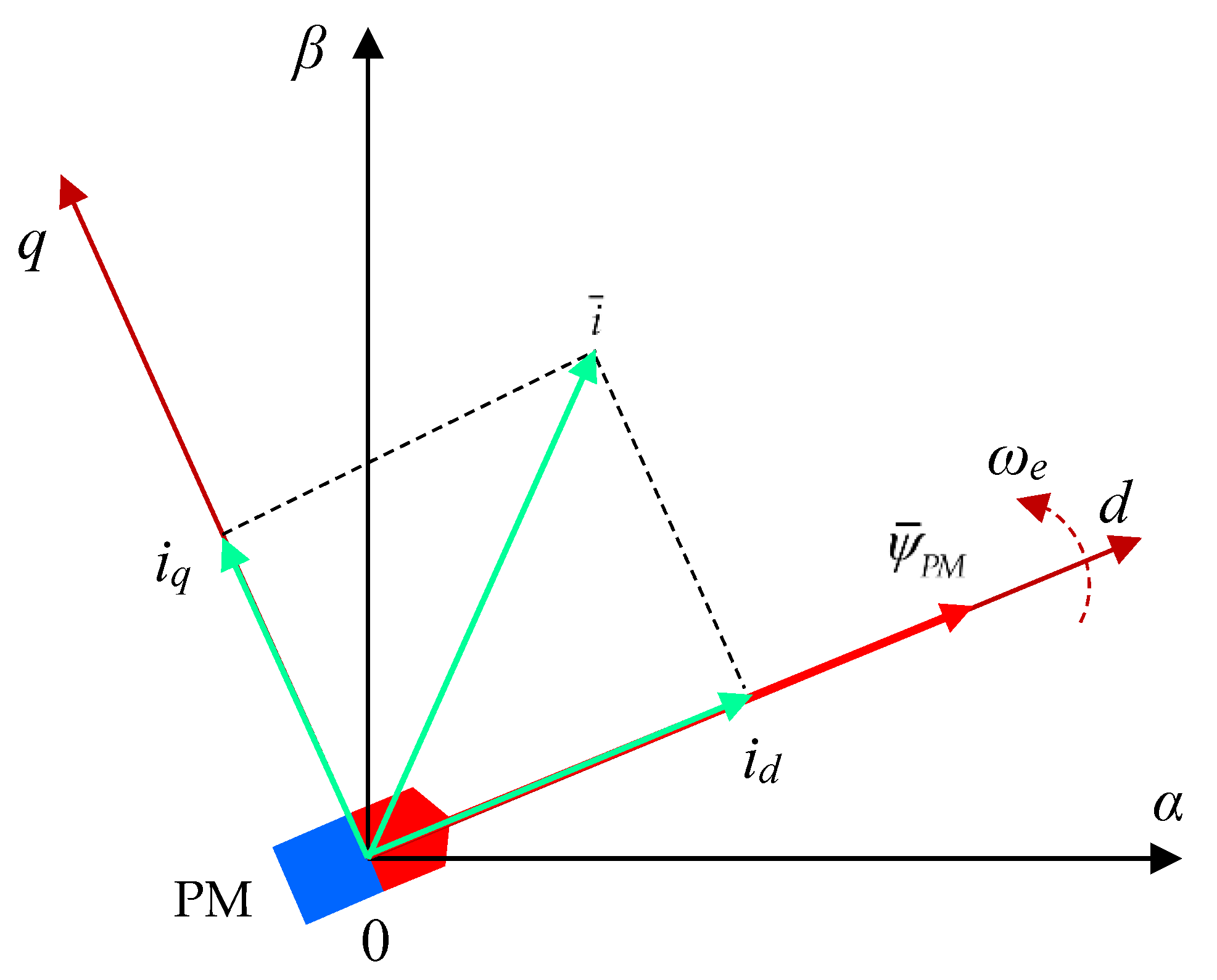
In addition, the stator current components (id,iq) of space vector current admits to be colinear and perpendicular with the PM flux direction. The both space vectors as PM flux and current rotates with the electrical speed ωe.
For this kind of application, the pair of flow and effort mention above in the privious section it corresponds to torque and angular speed:
The PMSM model obtained by FOC principle is composed by the currents and the motion equations [8]:
where: (ud,uq),(id,iq) and (Ld,Lq) are voltages, currents and inductances, all expressed in (d,q) coordinates, (ωe, ωm) are electrical and mechanical angular speed, respectively, Rs denoted the stator resistance, ψPM represents the permanent magnet flux, m and mℓ are the electromagnetic and load torques, respectively, and the group of constants represented by zp,J and μf that are poles pairs, total inertia of drive and friction factor, respectively.
The system (35) – (36) was completed by introducing the expressions of the electromagnetic torque, magnetic flux components, input and output power, respectively, as follows:
where u and i are the phasors of voltage and current, respectively, i* represents the complex-conjugate phasor of current, and by Re{◦} is denoted the real part of the applied quantity.
The equivalent circuit scheme of the PMSM based on the dq current model (35) is depicted in Figure 8, where has been introduced the total ElectroMotive Force (EMF) force components:
The Equations (34) – (38) describe the so-called dq model of the PMSM drive system. Based on the dq model there is designed the control structure in a propper maner. However, the physical operation of PMSM is done in the natural three-phase system reference frame. To obatin the desired quantities there are used the Clarke and Park direct/indirect transformations, respectively, of the quantity λ=u,i,ψ, as follows:
where vector-matrix quantities used are:
and the involved matrix-tranformations are given by:
The power invertor command will be supplied by the finite set values Sabc which contains the optimal logical values requited for obtaining inverter control.
Based on finite set values Sabc the model of the two-level power inverter provides the three-phase voltages:
where the power inverter matrix model is:
3.2.2. MPC with Finite Set
The DDC method is developed by using the main features of the MPC strategy that provides a command law which corresponds to voltage of the inverter, computed by a switching functions set. In this strategy, the main variables as current, voltage and electromagnetic torque are discretized on every time instant by forward Euler forward method, that gives to a generic variable z(t) the next fist-time derivative linear approximation:
Taking into account Euler forward approximation method, the first-time derivate of current (35) becomes:
Now, from the first-time derivate of current (37), the predictive electromagnetic torque results:
The one-step-ahead MPC law is an optimal solving problem defined as follows:
where emfrated is the rated back motion EMF computed by:
with the back EMF constant:
the index i corresponds to the combination of switching state Sabc (see below the Table 1).
A better ilustration of the voltage space vector of the power inverter and their hexagonal bounds is done in Figure 9.
In the dq system reference frame, the components of the space vector for the eight possible states are obtained in a vector-matrix representation:
Further, in Figure 10 is presented the cascade control structure, with a PI speed control in an outer loop and a MPC multivariable inner current control loop for the electronic power converter which supply the PMSM. The PI speed control is designed via the classical pole placement method [45].
The electrical energy provided from the power grid is of fixed values of voltage and frequency. By and adevate osition there is osition a DC voltage. The DC-bus voltage UDC is filtred by a passive Low Pass Filter (LPF) represented by a high value capacitor C, obtaining a constant value of the DC-bus voltage UDC=cst.
The PI controller is used for osition the mechanical speed ωmMPC its reference ωmref-MPC. For the MPC formulation of the inner loop, there are measured the three-phase current (a,b,c), and then by the Park/Clarke transformations are successively obtained the dq MPC current idqMPC(k)=[idMPC(k) iqMPC(k)]T . Further, based on (48) is obtained the current prediction idqMPC(k+1)=[idMPC(k+1) iqMPC(k+1)]T. Now,the MPC problem defined according to (50) will give optimal switching combinations SabcMPC. For the future computations, there is additionally calculated the voltages udqMPC(k)=[udMPC(k) uqMPC(k)]T based on a switch-voltage transformation S/u.
It can be mentioned that the mecanical speed ωmMPC is not directly measured. Firstly, there is measured the osition of the rotor αmMPC(k) by an encoder (E), and then by derivation is obtained the actual mechanical speed ωmMPC(k).
3.2.3. DDC Law of PMSM
The main idea of DDC strategy is to learn from a well-known MBC method whose performances has been already proved. In this sense, the DDC method of a PMSM drive is developed by selecting a DB containing the data provided by MPC law. Following the metodology developed for DDC in the sens of the maximum energy conversion process objective, for PMSM the output is given by speed and torque , while the control by dq voltage . In this conext, the training sequence becomes:
Also, for the PMSM drive the training matrix of the RBF-NN is composed by speed and dq volage of the reduced model (high efficiency points extraction):
The training phase of the DDC controller is depicted in Figure 11. As mention above, the entire metodology is based on the the learning of the experience of the high-value efficiency steady-state data provided by MPC strategy.
The set of aprioric informations includes rated data of PMSM, power inverter load and other components, envirovment and design requirments of EDSs.
Once training is done, the DDC control structure may be done as in Figure 12. The output of the DDC controller is given by the dq voltage . The optimal set of the switching functions combinations is then obtained by a command shaping block.
To have a succinct description, in Figure 13 is depicted a schematic representation of the DDC control structure. The main controllers as PI and DDC are highlighted. The DDC algorithm is represented in a sequential structure, where the command shaping has an internal computing loop. The DDC algorithm has a complex structure. A first stage is the searching on the DB the corresponding command. Once finded, an internal computing programming loop is designed. Further, there are compared the command and the feedback (that is also an optimal value) , resulting an error which is then integrated obtaining the the voltage control that acts as input in the searching block. Finally, there is obtained switching functions develivred by DDC method that will feed the gate of the inverter.
More detailes will presented later in the pseudocode format of the DDC method.
3.2.4. Design of the DDC Database
The input data in DB is initially done from the MPC operation, selected from the high efficiency values. After that, the data are processed according to various criteria. Hence, the acronym MPC will be substituted, making the distinction between MPC and DDC whenever is necessary.
The operation of a PMSM drive depends on the required mechanical speed domain limits. Generally, there are possible three situation that show how torque and outer power varies vs. mechanical speed:
where: ωm,b is the based mechanical speed which corresponds to the rated one (ωm,b=ωmN), and ωm,max represent the maximal mechanical speed.
In Figure 14 are illustrated the torque – speed characteristics of a PMSM drive system. Until base speed ωm < ωm,b, the operation of PMSM is done on constant torque in region I. In the region II, where the power becomes constant, there is used field-weakening technique. At last, the critical operation done for ωm < ωm,max must be avoided (region III) for ensuring a safety operation.
Let be Ω,M, P and H the sets of sets of torque, power, and their orresponding efficiency:
where Nω/m/p/h is the number of points of each set.
As can be easlier oserver from Figure 14, some of the different paris of speed-torque (ωmj,mj) or speed – power (ωmj,P2j) corresponds to the same value of efficiency. That means that the solution is not unique.
Considering that all the sets (57) – (60) has the same number of points , there are introduced the next sets obtained by cartesian product:
Now, there can be definited the following multi-valued maps:
whose points are contained in the sets:
To avoid the efficiency multi-valued representation, we select the high efficiency points that corresponds to each point, defining the functions:
where the maximal efficiency vector is :
and the contained sets are given by:
An illustrative representation of the transformation of te multi-valued map of the efficiency vs torque/power into a single-valued functions of a PMSM drive characteristics is depicted in Figure 15.
An essential objective is the design of the DB. Generally, there are few steps that must be followed in the order to obtain high computation accuracy as it is suggested in Figure 16.
Succinctly, the main followed steps can be described as:
- I.
- Storage grid of high efficiency data. At this step there are collected the main data set in the steady-state regime and knowledge which corresponds to a high efficiency value stored in
- II.
- Database grid learning. The database sets are extended by a learning process, adding new points contained in the set:
- III.
- Application to data grid searching. It is checked that the added new points corresponds to the real operation for open loop applications.
- IV.
- Close loop data grid control. Finally, the designed database grid is introduced in the desired close loop application from Figure 16.
These steps can be changed/improved depending on the desired objectives. For example, exogenous quantities may have a high influence on the system which are not on thermodynamic equilibrium.
Numerical computations of the quantities delivered by DB are affected by errors and noises. The DDC strategy is a searching discrete – interpolative method of the best solution within learning data bounds.
In the order to improve the acuarcy of data processing there is used a moving window filter, whose output is given by:
where Lw is the filter length, n is the current sample, and the input samples (nonfiltered) and output samples (filtred), respectively, are:
where .
The moving window filter structure is represented in Figure 17. The input samples are introducd by using the unit-delay operator Δ. On the output is obtained an average value of the moving samples.
As can be observed from (75) – (76) the filtred qunatities are voltage, torque and mechanical speed. Based on this, further there result the filering of both input and output powers of PMSM. Finally, the filtred powers are used to compute the efficincy, that do not contains high numerical noises and errors.
3.2.5. DDC Matlab Implementation
The DDC of the PMSM is implemented in Matlab simulation environment, tacking into account the main programming features of this software pakage.
To obtain a high analysis, in the paper is made up a comparasion between the MPC method and DDC strategy of the PMSM drive.
MPC Algorithm
The basic idea of the model predictive control for the PMSM fed by the simplest inverter with two voltage levels, having eight available state voltage switching vectors vi (Table 1) is the following: the torque and speed can be controlled by direct selecting a proper switching invertor’s voltage vector based on the machine parametric predictive model and an appropriate cost function g.
The objective of the Algorithm 1 represented in pseudocode format from Figure 12 is to give to reader the necessary tools to understand the simulations results and to replicate the implementation of the exposed algorithms thinking in Matlab environment.
The switching vector vopt , that was predicted to provide the most favourable process behaviour, i. e, the one that minimize the objective function g, is considered to be optimal and is generated by the inverter, applying directly the corresponding switch functions svs=[ Sa, Sb, Sc ].
The parameters of the motor and the driven process are included in the vector (electromagnetic parameters). After initialisations of the finite states for the swithching vector (lines 1,2) and the rated values and state variables, the main iteration loop are opend (line 8).
The model requires the actual state variables to be recalled from the previous sampling period state.
Figure 18.
The pseudocode format of the MPC algorithme of a PMSM drive control.

The electrical and mechanical parameters respectively, and , of the plant are grouped in the electromechanically set of parameters, as follows:
The MPC algorithm starts with the initializing the main data used in the computing loop.
A first programing syntax is developed for implement the PI speed controller:
where the reference /actual mechanical speed is,denotes the maximal value of the electromagnetic torque, and Kp/i are the parameters of the PI controller. The PI_control generates the required value of torque reference (set point) mref.
The relation (78) describes a typical programing syntax that contain the Input/Output sets of quantities. This type of programing syntax structure was fallowed in the rest of the paper.
The MPC strategy takes as input the voltages vd/q, the previous measured currents , the electromecanical set of parameters and sampling time instant of MPC calculated around ten times higher then the simulation discretizing one:
Thinking in the Matlab environment implementation, the function which simulate the PMSM model has as the input the controls (ud,uq) - the components of the supply voltage, the old states, the load torque and the electomagnetique parameters and as the outputs - the current components (id,iq), the electomagnetique torque m and the angular velocity ωm:
Finally, the programs were grouped and compacted in a software application of the proposed control structure.
The equations of the physical model (80) are in the continuous time domain. The variables of the model take values in the real domain. In fact the PMSM is supplied by the power electronic inverter which provide in the simplest case, a eight finite switching state vector:
The components (ud, uq) takes values on the set vdq. For this reason, these quantities must be shaped. According to the principle algorithm of the power inverter command, within each sampling period Ts, the components (vdopt,vqopt) and the duration d (0 <d> Ts) are calculated so that the machine currents resulting from switching supply voltage has to be as close as possible to the ideal sinusoidal form of the three-phase currents:
which admits the syntax:
The command algorithm used by MPC control is implicit, that is different from classical version. Within each sampling period Ts, the command algorithm looks for the optimal components (vdopt,vqopt), which minimizes the g criterion function:
This function provides the variables of the process at the current sampling period. The filter is implemented by the function Mouving_Average, having the input the switching voltage vector components (vdopt,vqopt), length of the window of the filter L and the sample time period Ts, providing the output of the moving window that corresponds to the filtered inputs (udftr, uqftr):
The numerical data calculated at each step Ts are stored in the DB named Data_Base_1, which will continue to be used in DDC Algorithm presented in the next section.
3.4.2. DDC Algorithm
The DDC controls (ud, uq) are directly obtained from DB with (Figure 11) by the interpolation techniques RBF – NN exposed in the seconnd section. The control low was generated by means of a known set of operating points of the process (55) through an interpolation technique (25). The resulting Algorithm 2 of the DDC strategy in pseudocode format is depicted in Figure 19 that schematically is given by Figure 13. The main common programing syntax from MPC and DDC has the same significance.
In first line there is loaded the data from database DB1, created with the MPC algorithm (Figure 18), where the support points of the control surfaces are described by:
As mention before, the control system is designed in two stages. In the the first, by MPC software are simulated a set of motion trajectories. In database DB1 are stored in a set of grided operation points of the process. Based on DB1 is simulated the DDC algorithm with which they were obtained the results presented in the paper.
There is a particularity of the electric drive systems, because the controls udq(k) must be shaped by the switching vector vdq of the power inverter (81). The setof operating points of the process (55) is essential for the efficiency of the energy conversion system with power electronic converter and electric machine. In that aim we selected from a large database a few set of the optimal energy operation points defined by the speed, torque, votltge control of power converter, input and output powers.
The parameters Pem (line 5) are used for the offline simulation of the process. The online operation of the control algorithm is parameters free. These is the main advantage of the DDC method.
In the main loop there are called the following functions:
- The PI_control which calculate the actual torque set point mref using the measured past speed ωmold and the speed set point ωmref, and the tunning parameters Kp and Ki ;
- The matlab RBF_Interpolant function which interpolate the control surfaces (24) by scattered support points contained in DB 1;
- The function Process_Model which calculate the actual process variables (id,iq,m,ω,) and the powers p1,p2.
The control u(a)= ud(a)+juq(a) are the query of the actual points (ωmold, mref) for the surfaces Fd and Fq . These controls are sampled from the continuous time domain. The inverter is controlled by the finite states switching functions svs . The transformation of the controls ud and uq from continuous time domain in the finite states domain of the inverter’s switching vectors vd and vq is a synthesis process.
The actual control u(a) at the step a is synthetized by a finite set of the switching vectors v=vd+jvq as follows
where Hm is the horizon of modulation and each vopt(k) vectors are determinates with a searching procedure, minimizing the g criteria function. The dimension of the Hm horizon was chosen by analogy with the classical modulation.
4. Illustrative Case Study of DDC of a PMSM Drive System
An industrial PMSM from a drive system supplied by a power inverter is used to illustrate the proposed DDC approach by comparison with the MPC control in the order to check the optimal energy operation. The PMSM rated data are depicted in Table 2.
The illustrative case study is done in Matlab-Simulink software in command-line line implementation programs. For simulation it has been adopted the sampling time period Ts=10-4s. Also, the speed loop is designed by choosing a linear control law implemented by PI controller designed by pole placement method, resulting the parameters Kpω=30 and Kiω=0.1. As aprioric data there are considerate the PMSM parameters (Table 2), rated data for a conventional power invertor with DC link voltage UDC=520V, the PMSM operate in a closed room.
A first objective is the designing of database used for DDC steategy based on the high efficiency data colected from the MPC stratefy running of PMSM. The second aim is to check the results of a comparative analysis obtained by MPC and DCC in rated conditions. To study a high impact of the DDC method, a third scope is to made a comparative analysis of the reults obtained via MPC and DCC strategies in mismatch conditions. Finally, a performance comparative analysis of the privious results obtained via MPC and DDC strategies for rated and mismach conditions is done in the order to demonstrate that the developed DDC method in the paper is a relevant topic for future research.
4.1. Database Learning Design
The essential point in DDC method is the DB design. Firstly, there are the bootstrap DB obtained from process design theoretical data and parametric offline of the process.
From this large knowledge and data DB we extracted the control (working) DB. The control DB containes a few optimal efficiency steady-state opearation points of the process (around 250), obtained in exagenous conditions. In our case the exagenous conditions are the ambiental temperature T0 and rated flux ψPM. Tacking into account the ambiental conditios the control becomes:
In consequence, the control DB must be extracted, and the RBF interpolation block will have four inputs and two outputs controls.
In this paper we applied the direct searching corrections of the controls in the sens of maximum energy efficiency.This corections are global or local.
A gridded experimental data points was obtained by simulating the MPC control algorithm, providing an admissible set of the operation points of the process selected in steady-state regime for the highest efficiency values.
There were adopted voltage global correction on the entire DB:
where the factors kd=1.04 and kq=1 are selected in the order to improve the DDC performances.
The local DB corection are applied around a steady-state points. This kinds of corrections are applied mainly online in steady-state operation, in the sense of searching the maximum energy efficiency, in the actual exogenous conditions,
Based on this set experimental data, in Figure 20 it was built the discrete implicit surfaces of the high efficiency DDC control law , which contains around 250 points of steady-state higher efficiency operation given by MPC strategy.
4.2. Study on Rated Data Conditions
In this section is provided a compartive analysis of the results obtained via MPC and DDC in rated conditions provided by the model parameters of PMSM from Table 2.
Adopting a speed step reference of , in Figure 23 is depicted the speed tracking results obtained by MPC and DDC strategies. The speed provided by DDC method ad MPC one present close responses, but the DDC has a sensible lower transient regime.
The current results provided by MPC and DDC strategies are illustrated in Figure 24. In the case of d-axis current component, the MPC law offers a small value then the corresponding one of DDC law in absolute values. After a different dynamic regime, the q-axis current component presents close values in steady state regime for for both DDC and MPC controllers.
On the shaft of the PMSM dtive is applied a step load torque . The load and electromagnetic torques provided by MPC/DDC laws are represented in Figure 25. Excepting the startup process, in dynamic regime the electromagnetic torque obtained by DDC si smaller then one given by MPC . However, the speed transient leads to have a higher dynamic torque regime for DDC method.
Figure 26 indicates the voltages obtained by both MPC and DDC strategies and . As a consequnce of the increasing of the q-axis voltage component provided by DB, this difference is seened in the figure, having . For d-axis, the votage component have closed values for MPC and DDC strategies.
To have a concrete appreciation of the current tracking or voltage delivered by the control system of PMSM, in the following there are evaluated the current/voltage magnitude computed according to:
which are graphically illustrated in Figure 27 and Figure 28. It can be seen that, after the startup, during the transient regime the DDC method provide a lower value then de corresponding one given by MPC strategy , and in steady-state regime becomes grater .
The efficiency of PMSM obtained by MPC and DDC control strategies in depicted in Figure 29. As expected, the new control technology provides advanced benefits as parameter free and high efficiency objective. Thus, the dynamic efficiency compared with the classical one steady state efficiency is greater.
To evaluate the efficiency of the PMSM on the enitre simulation domain, there is used the average efficiency defined according to:
which is graphically represented in Figure 30.
Finally, it is important to ases the phase currents. Since the PMSM has a symmetric mecahical and electrical structure, the system of currents is also symetrical, which is why only the current on the first phase will be represented as in Figure 31. The peak of the phase current proided by DDC method has a high value then one given by MPC law.
A first conclusion is that the DDC strategy may operate without any mathematical model, being also parameter-free. The key of DDC strategy operation is related on database design, learning process and available computational resources. A more important appreciation is that DDC improve both tracking refecences and efficiency. However, the DDC strategy remains stable in the imposed simulation scenario.
3.3. Study on Mismatch Conditions
Often, in practice the dq PMSM model with constant lumped parameters is just an idealization which cannot always be fulfilled.
In the following is considered there the next variations of the parameters of the dq model of PMSM due to demagnetization and temperature increasing, respectively, as follows:
otherwise, all the conditions remain unchanged.
In this case, the speed tracking results obtained by MPC and DDC strategies ate illustrated in Figure 32. Now, again, the speed obtained by DDC strategy has a shorter dynamic regime then the one given by MPC law. The speed response is even better than the one obtained in the rated scenario. For MPC strategy, the results get worse once with parameters mismatch.
For current results given by MPC and DDC laws, both transient and steady-state regimes are different as is depicted in Figure 33. The d-axis current component delivered by MPC controller and the one of DDC law in have different values in dynamic regime, and closed in steady-state regime. On q-axis, the current given by MPC and DDC have different values in both dynamic and steady-state regime.
Applying the same step load torque , the load and electromagnetic torques obtained by MPC/DDC strategies have different dynamics as is graphically depicted in Figure 34. The dynamic torque given by DDC has a higher value then the one provided by MPC , but acts in a short transient. Thus, the evolution of electromagnetic torques is done with different dynamics until the main disturbance represented of the load torque is rejected.
The voltages provided by both MPC and DDC strategies and are shown in Figure 35. On d-axis, the voltage components present appropiate values, with small differences in dynamic regime. Important differences are founded on q-axis, where has a significant value, mainly in steady-state regime.
The magnitude of current and voltage are represented in Figure 36 and Figure 37, respectively. The current magnitude obtained by DDC law is allways smaller then the one given by MPC algorithm . Mostly, a significant increasing of the voltage magnitude for DDC algorithm then MPC controller is obtained .
The efficiency of PMSM obtained by DDC law is substantially increased the the one provided by and DDC strategy in both dynamic and steady state regimes, as illustrated in Figure 38. This is a consequnce of the fact that DDC method is designed by using the high-efficincy data colected from MPC operation. This is a major objective done in this robust scenario.
As expected the average efficiency for the entire simulation time is increased for DDC method as is graphically depicted in Figure 39.
In this scenario, the phase current obtained by DDC strategy has a smaller peak value then the one delivered by MPC algorithm in both transient and steady-state regimes as is shown in Figure 40. However, a small peak value will generate reduced power losses, and then the increasing of the efficiency of PMSM. The DDC strategy is designed by using a database learning that no not contain overcurrents, feature which will maintain the phase current into a minimal range.
The study developed in this section shows the results given by DDC strategy under robustness conditions of PMSM parameters mismatch. The main objective of the efficiency increasing has been successfully shown. However, this objective leads secondary to decrease the dynamic regime of speed tracking. Compared with MPC strategy, the DDC law requires a higher voltages magnitude/components which must take into account the voltage limit levels of the PMSM drive. Also, the DDC strategy leads to obtain a smaller peak value of the phase current that will generate lower level of power losses.
3.4. Comparative analysis of MPC and DDC results
The proposed DDC method proves to have a stable operation on the rated an mismatch cases and, also offers several benefits. For a relevant comparison of the above discussed cases, there are used the next criteria:
- -
- Settling time of the mechanical speed – tst;
- -
- Average efficiency on the entire simulation time– ηav;
- -
- Peak value of the a phase current in steady-state regime– Iapk;
- -
- THD of the a phase current computed in steady-state regime, for ten harmonics, including the fundamental of the frequency 55.66 Hz, for a comman time domain pf MPC and DDC strategies, 4-5 s time.
The comparative results based on the above criteria of the MPC and DDC strategies are summarized in Table 3.
It is obvious that in both tests, compared with MPC law, the DDC strategy leads to decreasing of the settling time of the mechanical speed . In rated conditions there is is obatined a small diffrence, but in the mismatch test the DDC method leads to a setting time with 61% lower then the one obtained by MPC strategy, which is a high advantage. For rated conditions, the increasing of the average efficiency is small for DDC strategy , being around 1.2 % from the one resulted in rated conditions with MPC controller. A high increasing of the DDC average efficiency , about 11 % results for mismatch test, which is the major successfully, achieved objective. In addition, the peak value of the phase current for rated conditions is smaller for DDC, , and higher in the mismatch case . As a consequnce of interpolation and digital signal processing, the THD of the phase current obtained by DDC law remais low for both rated/mismach cases studied.
We can conclude that DDC strategy persevere better the high efficiency objective in the both rated and robust scenarios then the classical MPC law. Nevertheless, the settling of speed responses has been also improved in the both tests.
Finally, it should be noticed the results of the performances presented in Table 3 are open to be improved since the results depends on the learning process and on software and hardware available resources.
5. Conclusions
The many faces of the macroscopic energy conversion systems may be characterized by a set of generalized variables as effort and flow. This approach allows a physical – based mathematical equation modeling developed in the order to increase the efficiency of energy conversion.
In spite of the high performances of actual devices and actuators for the energy transformation, there are enough resources for the improvements of their efficiency, especially in the operation points at low effort and high flow or respectively at high effort and high flow.
A transition from MBC to MFC is required for ensuring the non-sensitive control approach.
The idea of the paper is to build the surfaces of the DDC law in terms of effort and flow. Starting from a large knowledge DB we built a control DB containing a reasonable optimal efficiency steady state operation points of the process. A RBF interpolative system has been trained in order to extract from this surfaces the controls demanded for any operation points. It results that the control efficiency is largely dependent from the consistency of the colected data.
The AC drives is a field that emphasis the largely developed fast process in industry and residence. The performances of this DDC method were evaluated based on a PMSM drive system simulated by MPC methodology. The DB was built in Matlab simulation environment using a specific algorithm for the MPC control of PMSM drive and the algorithm of DDC. The comparison criteria were the efficiency of the energy process conversion (the ratio of the output and input powers), the quality of the control for speed and effort and the current THD. Due to the PMSM windings resistance variations and to the degree of the magnetic circuit depreciations during the time, the DDC efficiency control is better than MPC control, because the MPC is model parameters dependent.
In many research papers in the field has been demonstrated that the direct DDC strategy is superior in reduction the bias whereas the indirect MPC one gives beter variance. The results shown in Figure 36 and Figure 38 confirm the fact that the MPC control gives better variance but the DDC gives beter efficiency and bias to process parameters modifications.
Our DDC technique, being process parameters free is more general then classical process model control as MPC, in the sense that does not depend on the nature of process (electromagnetic , thermic or mechanic). If we reefer on the electric driven systems, DDC technic is the same for all type of motors (asynchronous, synchronous or others).
The DDC method with appropriately designed management make possible to realize a high level of the energy transformation quality that is fast dynamic response, high energy efficiency and low parametric sensitivity.
The muliple aspects disscused and successfully solved in the paper shows that the novel tehnology developed in the paper is still an open problem which can provides realistic improved results in a future promissing approach.





Author Contributions
Conceptualization, M.C. and I.B.; methodology, I.B. (Ion Bivol); software, M.C. (Madalin Costin); validation, M.C. and I.B.; formal analysis, I.B.; investigation, I.B.; resources, M.C.; writing—original draft preparation, M.C.; writing—review and editing, I.B.; visualization, M.C.; supervision, I.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported under Contract no. RF 2462/31.05.2024 “Performance Evaluation of a Novel Control Strategy for Electromagnetic Energy Conversion Processes based on RBF-NN techniques, by comparison with Established MPC-type Methods, with respect to PMSM Motors” from “Supporting and Developing Research, Innovation and Technology Transfer activities at the University “Dunărea de Jos” of Galați”.
Data Availability Statement
Data availability is not applicable to this article as the study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sul, S.K. Control of Electric Machine Drive Systems, John Wiley and Sons: Hoboken, NJ, USA, 2011.
- Vas, P. Sensorless Vector and Direct Torque Control, Oxford University Press, NY, USA, 1998.
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives, John Wiley & Sons, Ltd.: West Sussex, UK, 2012.
- Holtz, J. Advanced PWM and predictive control—An overview. IEEE Trans. Ind. Electron. 2016, 63, 3837–3844. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, K. Implementation of a direct control algorithm for induction motors based on discrete space vector modulation. IEEE Trans. Power Electron. 2000, 15, 769–777. [Google Scholar] [CrossRef]
- Vafaie, M.; Dehkordi, B.; Moallem, P.; Kiyoumarsi, A. Minimizing torque and flux ripples and improving dynamic response of PMSM using a voltage vector with optimal parameters. IEEE Trans. Ind. Electron. 2015, 63, 3876–3888. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J. I.; Franquelo, L.G.; Rodriguez, J.; Young, H. A.; Marquez, A.; Zanchetta, P. Predictive control: a review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Rodríguez, J.; Kennel, R.M.; Espinoza, J.R.; Trincado, M.; Silva, C.A.; Rojas, C.A. High-performance control strategies for electrical drives: An experimental assessment. IEEE Trans. Ind. Electron. 2011, 59, 812–820. [Google Scholar] [CrossRef]
- Zhang, K.; Fan, M.; Yang, Y.; Zhu, Z.; Garcia, C.; Rodriguez, J. Field enhancing model predictive direct torque control of permanent magnet synchronous machine. IEEE Trans. Energy Convers. 2021, 36, 2924–2933. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: an engineering perspective. Int J Adv Manuf Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Richter, J.; Doppelbauer, M. Predictive trajectory control of permanent-magnet synchronous machines with nonlinear magnetic. IEEE Trans. Ind. Electron. 2016, 63, 3915–3924. [Google Scholar] [CrossRef]
- Djerioui, A.; Houari, A.; Machmoum, M.; Ghanes, M. Grey wolf optimizer-based predictive torque control for electric buses applications. Energies 2020, 13, 5013. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Abbaszadeh, A.; Rodriguez, J. Robustness improvement of predictive current control using prediction error correction for permanent-magnet synchronous machines. IEEE Trans. Ind. Electron. 2016, 63, 3458–3466. [Google Scholar] [CrossRef]
- Hu, F.; Luo, D.; Luo, C.; Long, Z.; Wu, G. Cascaded robust fault-tolerant predictive control for PMSM drives. Energies 2018, 11, 3087. [Google Scholar] [CrossRef]
- Singh, B.; Jain, P.; Mittal, A.P.; Gupta, J.R.P. Torque ripples minimization of DTC IPMSM drive for the EV propulsion system using a neural network. J. Power Electron. 2008, 8, 23–34. [Google Scholar]
- Wang, W.; Liu, Y.; Chen, H.; Gao, J.; Zhu, S.; Zhou, R. Improved Rotor Flux-Based SMO and RBF-PID Control Strategy for PMSM. Actuators 2023, 12, 327. [Google Scholar] [CrossRef]
- Qian, W.; Panda, S.K.; Xu, J.X. Torque ripple minimization in PM synchronous motors using iterative learning control. IEEE Trans. Power Electron. 2004, 19, 272–279. [Google Scholar] [CrossRef]
- Wang, G.; Xie, J.; Wang, S. Application of Artificial Intelligence in Power System Monitoring and Fault Diagnosis. Energies 2023, 16, 5477. [Google Scholar] [CrossRef]
- Schenke, M.; Kirchgassner, W.; Wallscheid, O. Controller design for electrical drives by deep reinforcement learning: A proof of concept. IEEE Trans. Ind. Informat. 2020, 16, 4650–4658. [Google Scholar] [CrossRef]
- Xie, H.; Wang, F.; Xun, Q.; He, Y.; Rodriguez, J.; Kennel, R. A low-complexity gradient descent solution with backtracking iteration approach for finite control set predictive current control. IEEE Trans. Ind. Electron. 2020, 69, 4522–4533. [Google Scholar] [CrossRef]
- Prag, K.; Woolway, M.; Celik, T. Toward data-driven optimal control: a systematic review of the landscape. IEEE Access 2022, 10, 32190–32212. [Google Scholar] [CrossRef]
- Hou, Z. S.; Wang, Z. From model-based control to data-driven control: survey, classification and perspective. Inf. Sci. 2013, 235, 3–35. [Google Scholar] [CrossRef]
- Markovsky, I.; Dörfler, F. Behavioral systems theory in data-driven analysis, signal processing, and control. Annu. Rev. Control 2021, 52, 42–64. [Google Scholar] [CrossRef]
- Markovsky, I.; Dörfler, F. Data-driven dynamic interpolation and approximation. Automatica 2022, 135, 110008. [Google Scholar] [CrossRef]
- Hao, W. Data-Driven Control with Learned Dynamics. Ph.D. Dissertation, Clemson University, South Carolina, USA, August 2020. [Google Scholar]
- Dörfler, F.; Coulson, J.; Markovsky, I. Bridging direct and indirect data-driven control formulations via regularizations and relaxations. IEEE Trans. Autom. Control 2023, 68, 2023. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. Formulas for data-driven control: stabilization, optimality, and robustness. IEEE Trans. Autom. Control 2020, 65, 909–924. [Google Scholar] [CrossRef]
- Kadali, R.; Huang, B.; Rossiter, A. A data driven subspace approach to predictive controller design. Control Eng. Pract. 2003, 11, 261–278. [Google Scholar] [CrossRef]
- Coulson, J.; Lygeros, J.; Dorfler, F. Distributionally robust chance constrained data-enabled predictive control. IEEE Trans. Autom. Control 2021, 67, 3289–3304. [Google Scholar] [CrossRef]
- Abolpour, R.; Khayatian, A.; Dehghani, M. Simultaneous model prediction and data-driven control with relaxed assumption on the model. ISA Transactions 2024, 145, 225–238. [Google Scholar] [CrossRef]
- Yang, L.; Ma, A.; Li, D.; Xi, Y. Input-mapping based data-driven model predictive control for unknown linear systems with bounded disturbances. Automatica 2023, 153, 111056. [Google Scholar] [CrossRef]
- Yang, L.; Li, D.; Ma, A.; Xi, Y.; Pu, Y.; Tan, Y. Input-mapping based data-driven model predictive control for unknown linear systems via online learning. International Journal of Robust and Nonlinear Control 2022. [Google Scholar] [CrossRef]
- Coulson, J.; Lygeros, J.; Dorfler, F. Data-Enabled Predictive Control: In the Shallows of the DeePC. In Proceedings of the 18th European Control Conference (ECC), Naples, Italy, 25-28 June 2019; pp. 307–312. [Google Scholar]
- Brosch, A.; Hanke, S.; Wallscheid, O.; Bocker, J. Data-driven recursive least squares estimation for model predictive current control of permanent magnet synchronous motors. IEEE Trans. Power Electron. 2021, 36, 2179–2190. [Google Scholar] [CrossRef]
- Carlet, P. G.; Favato, A.; Bolognani, S.; Dörfler, F. Data-driven continuous-set predictive current control for synchronous motor drives. IEEE Trans. Power Electron. 2022, 37, 6637–6646. [Google Scholar] [CrossRef]
- Carlet, P. G.; Favato, A.; Torchio, R.; Toso, F.; Bolognani, S.; Dörfler, F. Real-time feasibility of data-driven predictive control for synchronous motor drives. IEEE Trans. Power Electron. 2023, 38, 1672–1682. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, X.; Song, B.; Zhou, X.; Guo, Y. Data-driven adaptive fractional order PI control for PMSM servo system with measurement noise and data dropouts. ISA Transactions 2018, 75, 172–188. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Zhang, C.; Li, L.; Zhang, J.; Wang, M. Maximum Efficiency per Torque Control of Permanent-Magnet Synchronous Machines. Appl. Sci. 2016, 6, 425. [Google Scholar] [CrossRef]
- Cavallaro, C.; Tommaso, A.O.; Miceli, R.; Raciti, A.; Galluzzo, G.R.; Trapanese, M. Efficiency Enhancement of Permanent-Magnet Synchronous Motor Drives by Online Loss Minimization Approaches. IEEE Trans. Ind. Electron. 2005, 52, 1153–1160. [Google Scholar] [CrossRef]
- Ni, R.G.; Xu, D.G.; Wang, G.L.; Ding, L.; Zhang, G.Q.; Qu, L.Z. Maximum Efficiency Per Ampere Control of Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2015, 62, 2135–2143. [Google Scholar] [CrossRef]
- McCarthy, J.; Minsky, M.L.; Rochester, N.; Shannon, C.E. A Proposal for the Dartmouth Summer Research Project on Artificial Intelligence, August 31, 1955. AI Magazine. 27, 4 (Dec. 2006), 12.
- Liu, J. Radial Basis Function (RBF) neural network control for mechanical systems: design, analysis and Matlab simulation. Springer Science & Business Media, 2013.
- Kaminski, M. Nature-Inspired Algorithm Implemented for Stable Radial Basis Function Neural Controller of Electric Drive with Induction Motor. Energies 2020, 13, 6541. [Google Scholar] [CrossRef]
- Astrom, K.J.; Wittenmark, B. Computer-Controlled Systems: Theory and Design, 3rd ed. Prentice Hall: Upper Saddle River, NJ, USA, 1997.
Figure 1.
The diagram of the macroscopic energy flow conversion.
Figure 2.
The transion from MBC to MFC.
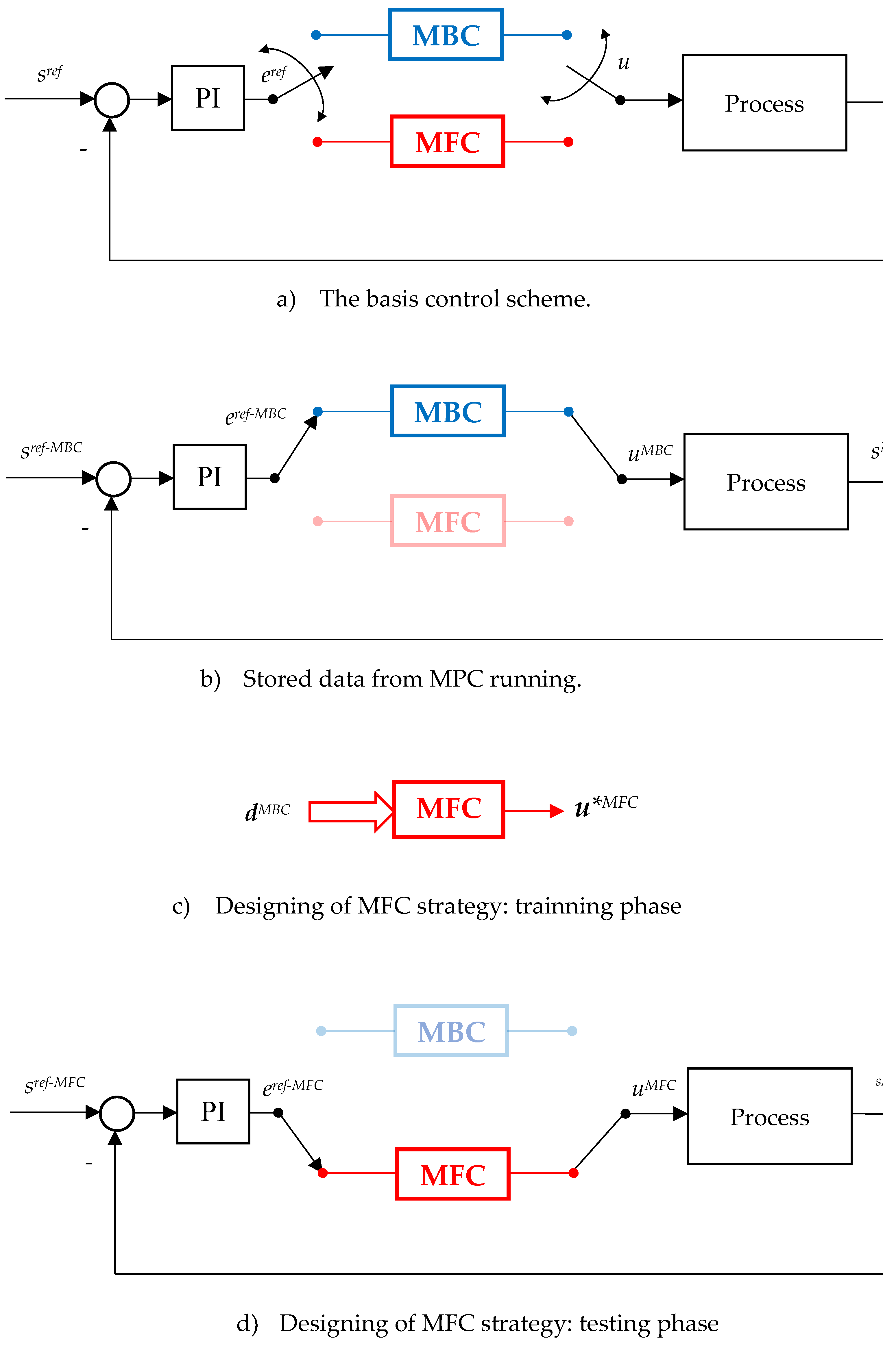
Figure 3.
The RBF-NN used for obtaining the plant input.
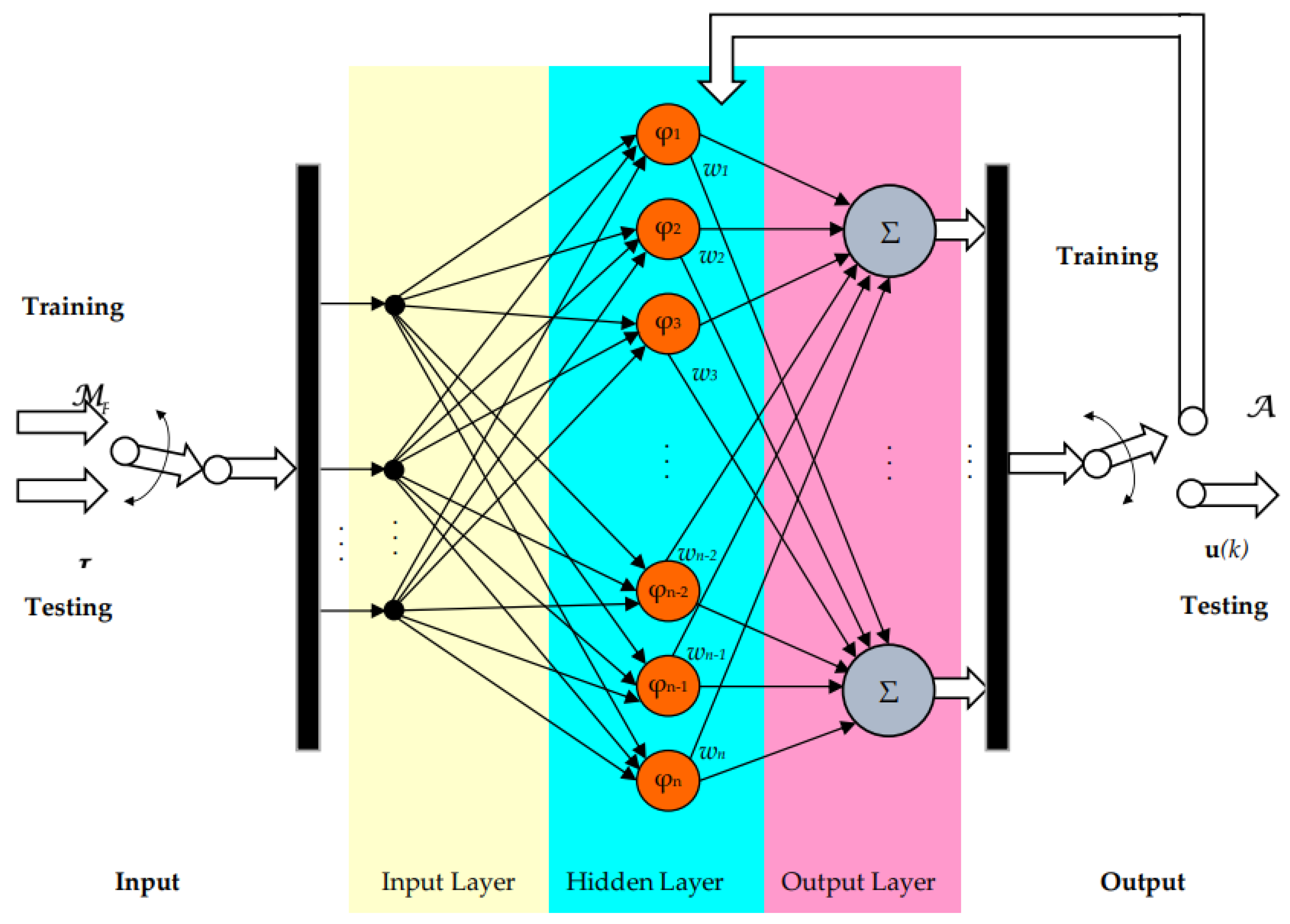
Figure 4.
A combined control structure with linear PI outer control loop and DDC inner control.
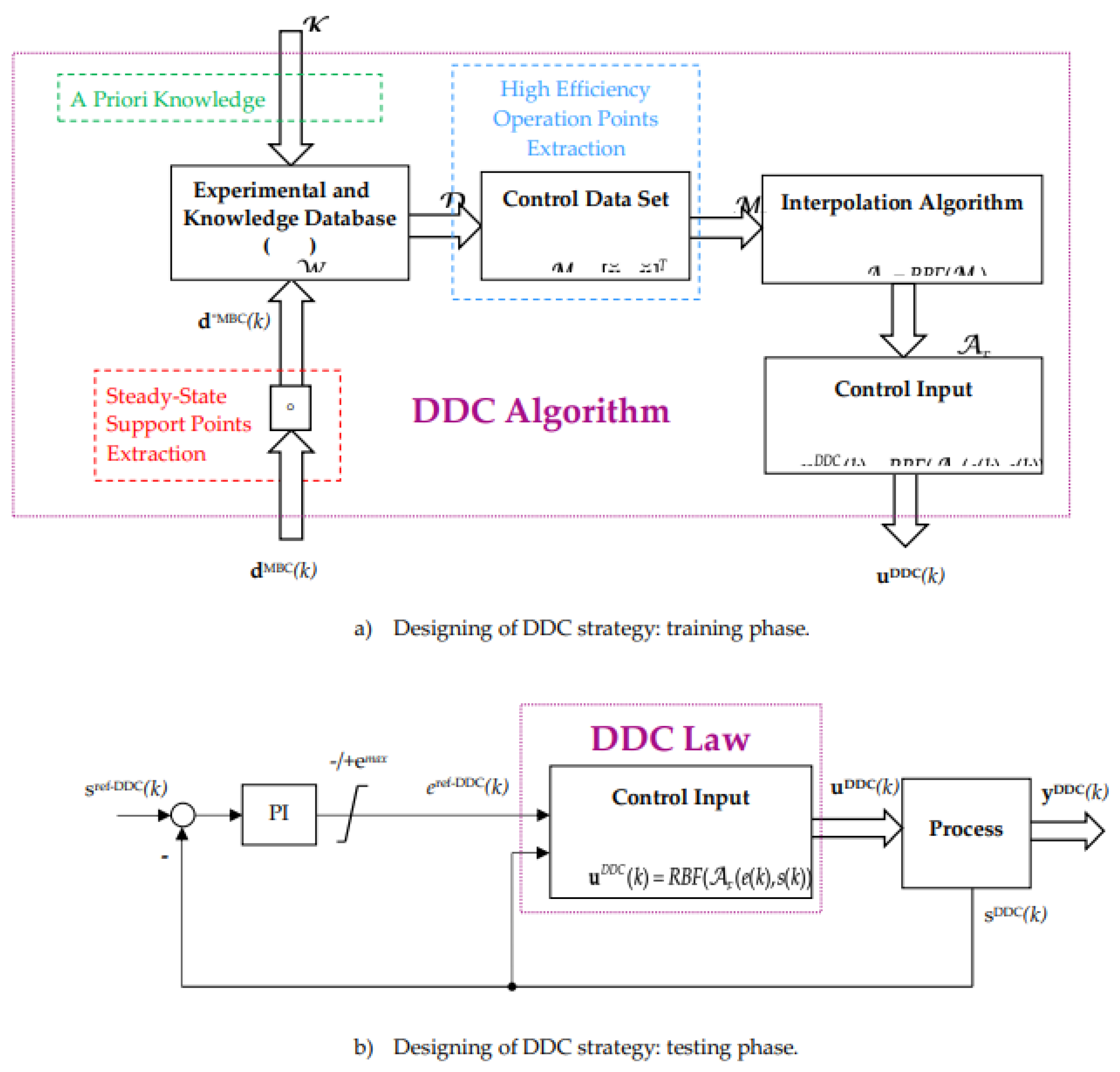
Figure 5.
The principle of the DDC strategy applied to an AC motor.
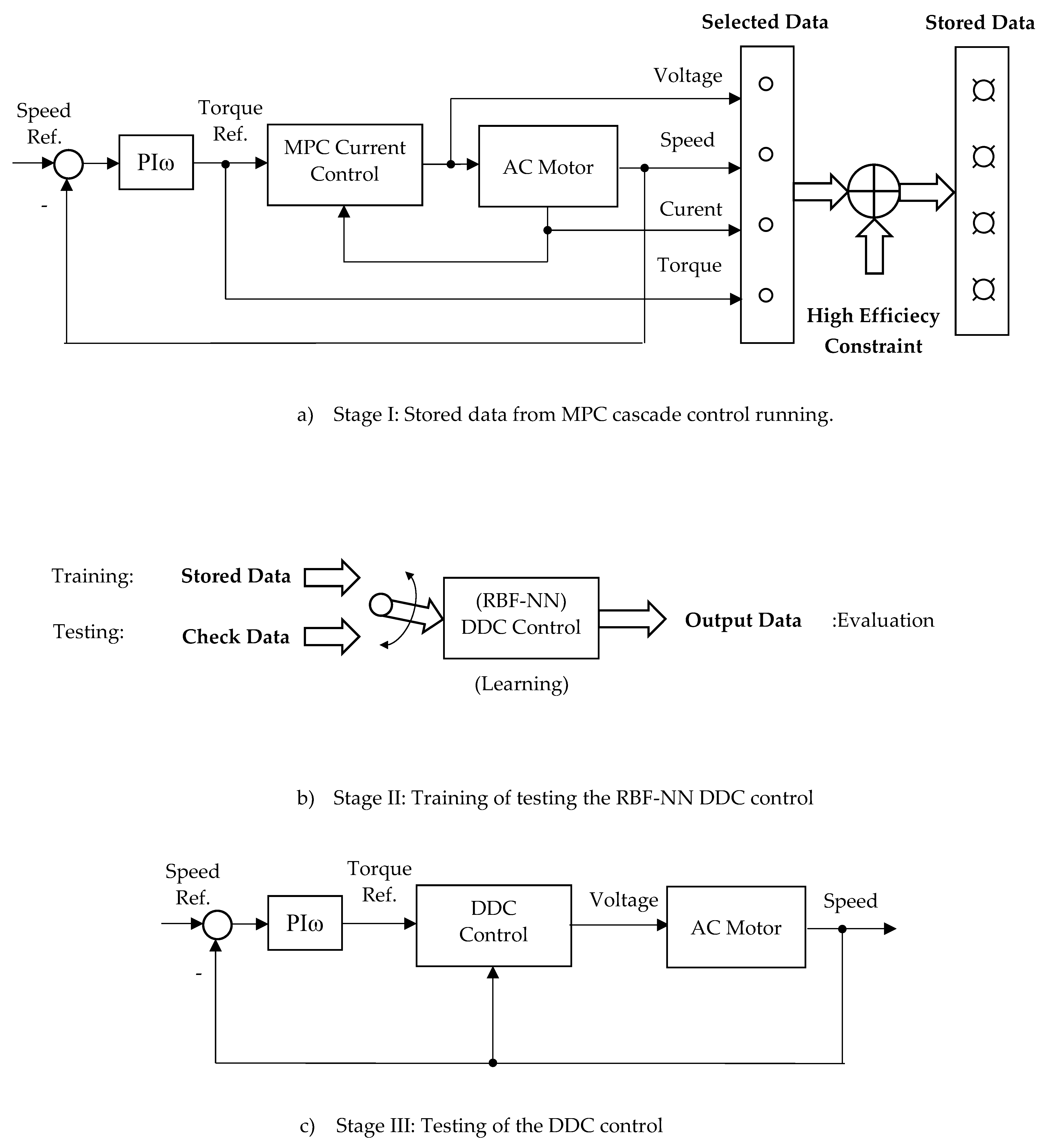
Figure 6.
Power structure of the PMSM drive. .
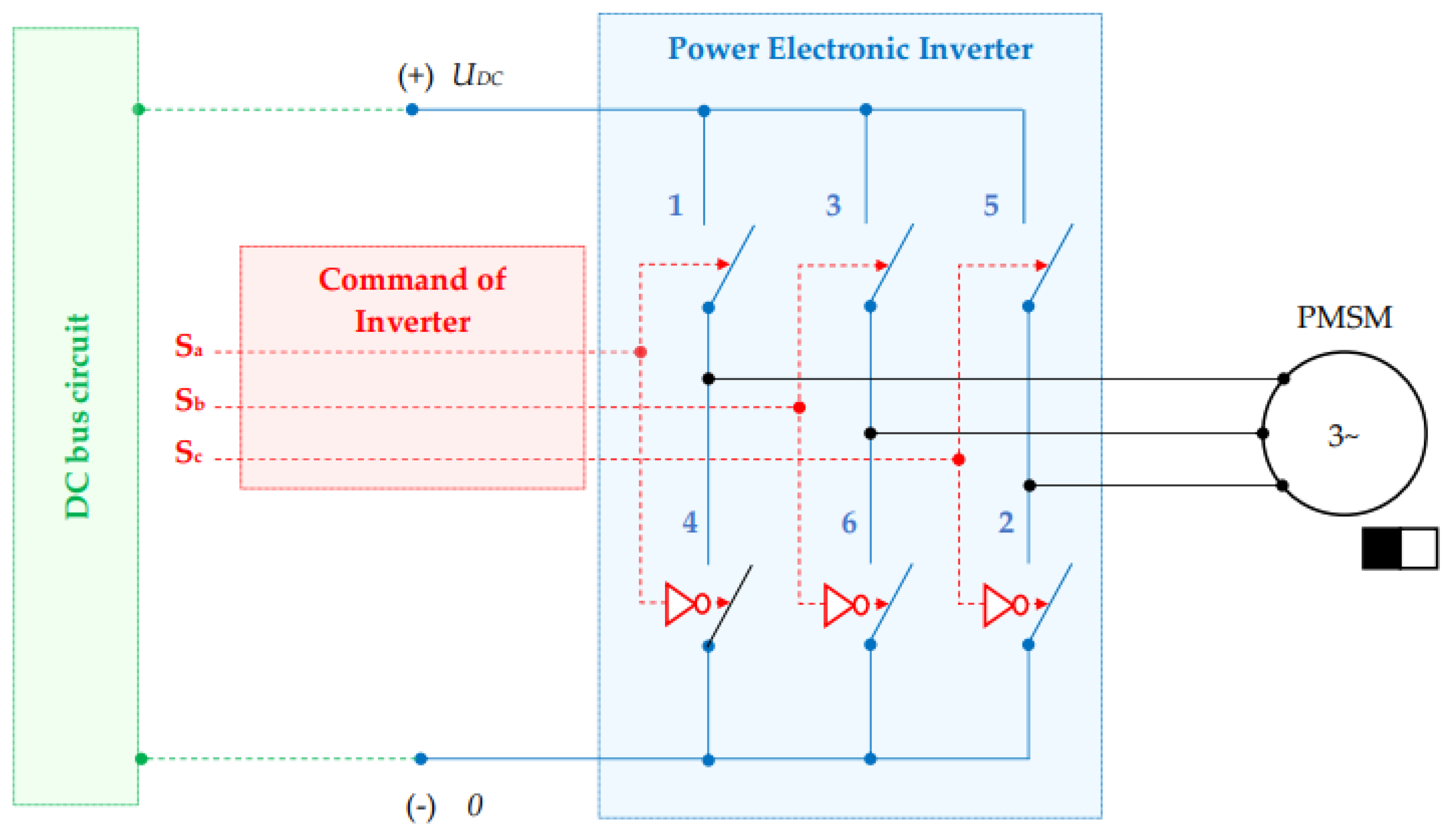
Figure 8.
The dq equivalent circuit scheme of PMSM.
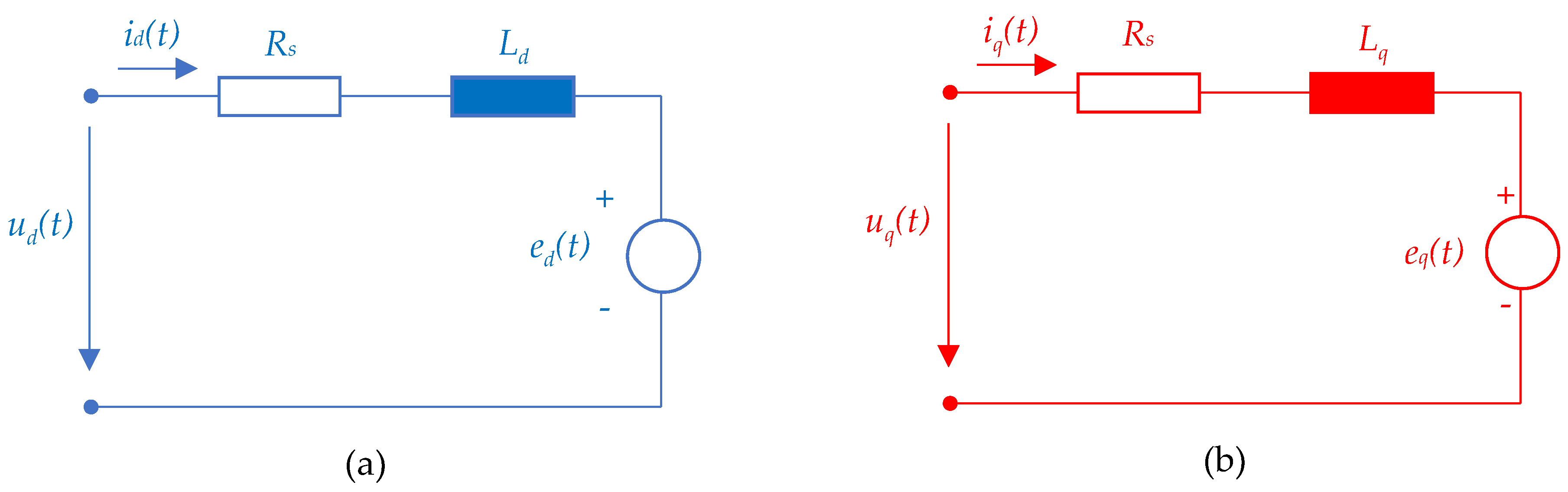
Figure 9.
The voltage space vector according to their coresponding switching states.
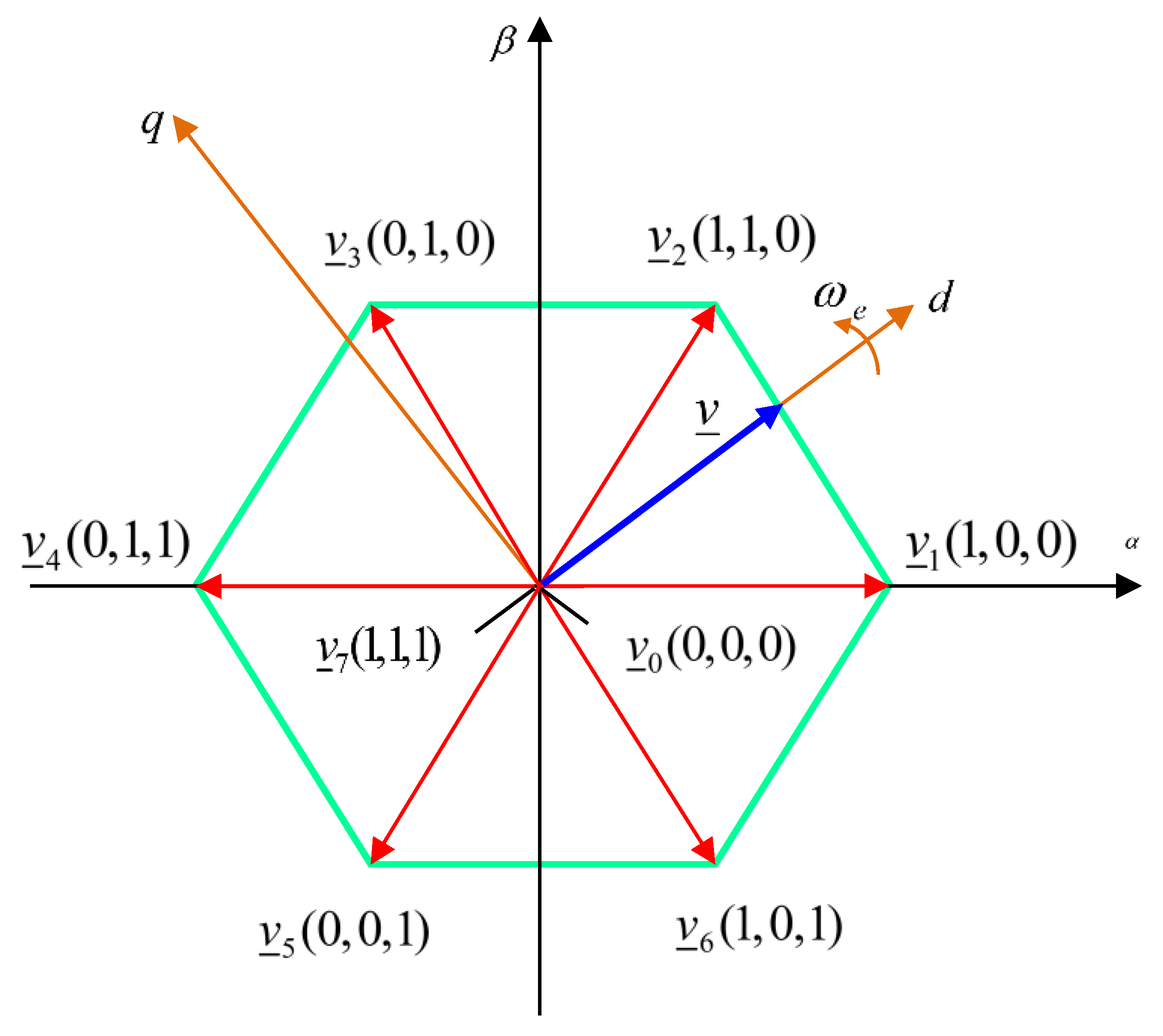
Figure 10.
The MPC control PMSM drive.
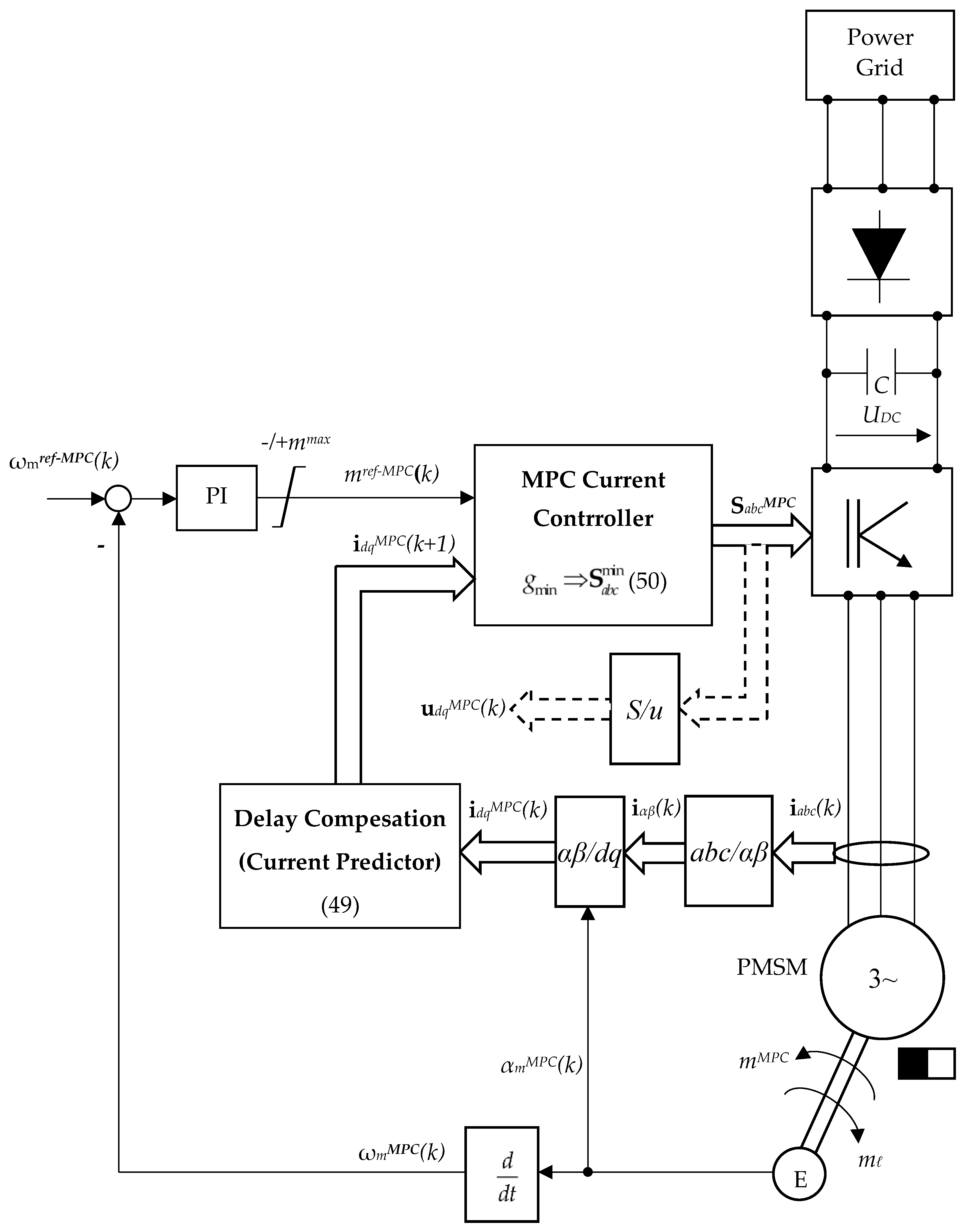
Figure 11.
Training phase of the DDC controller of PMSM.
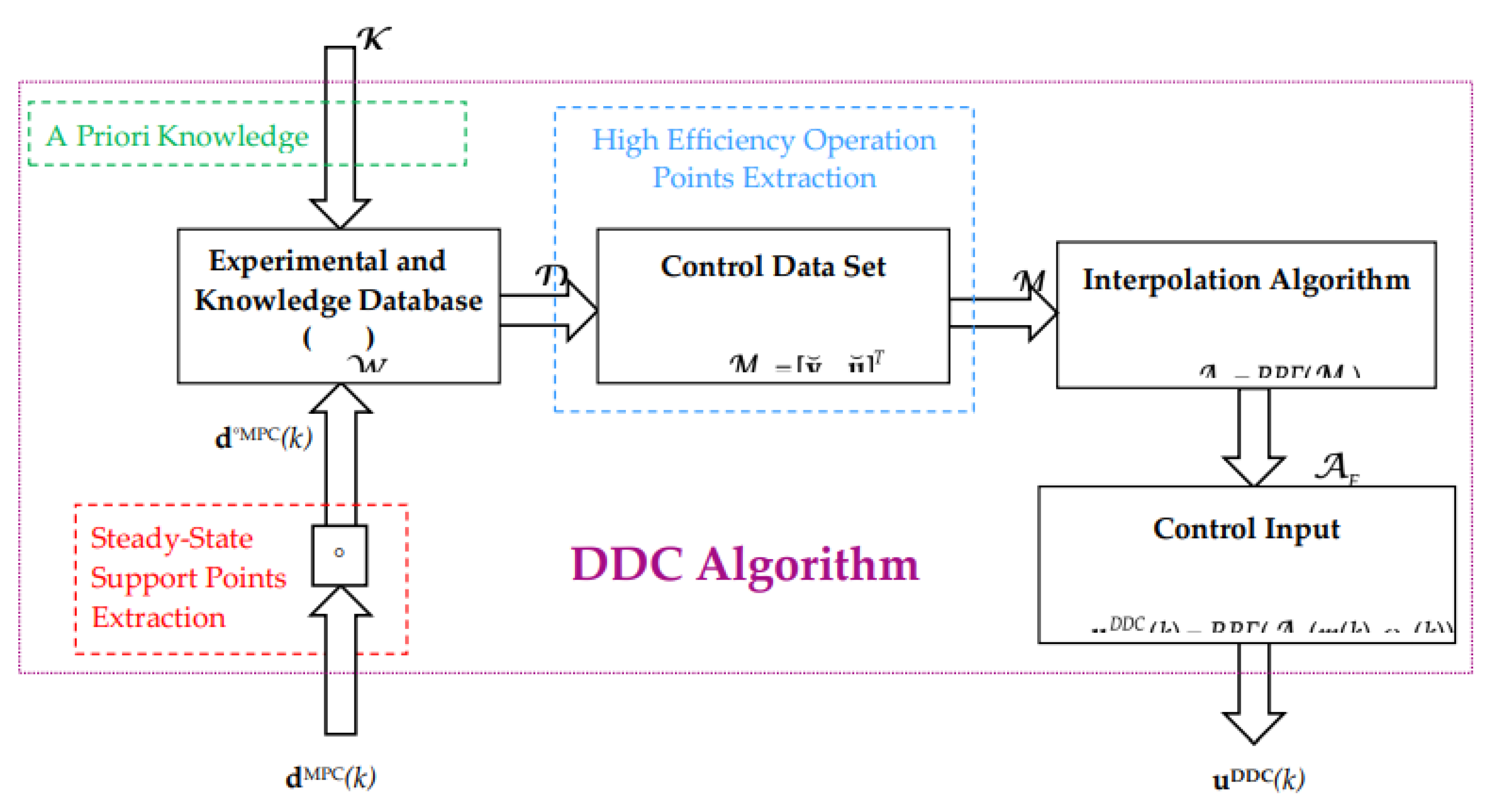
Figure 12.
The DDC control sctructure of a PMSM drive.
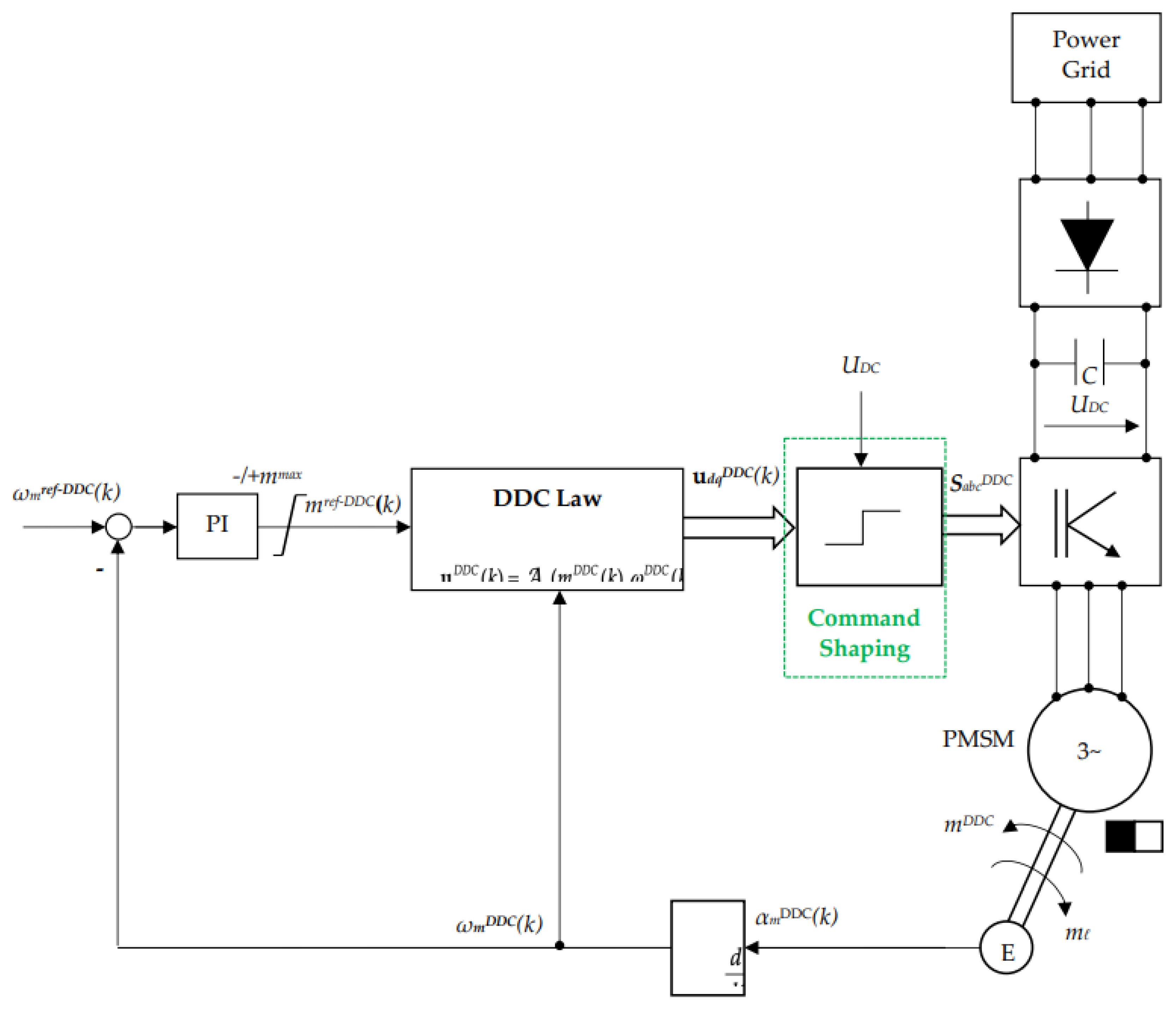
Figure 13.
A schematic representation of the DDC control of the PMSM drive system.
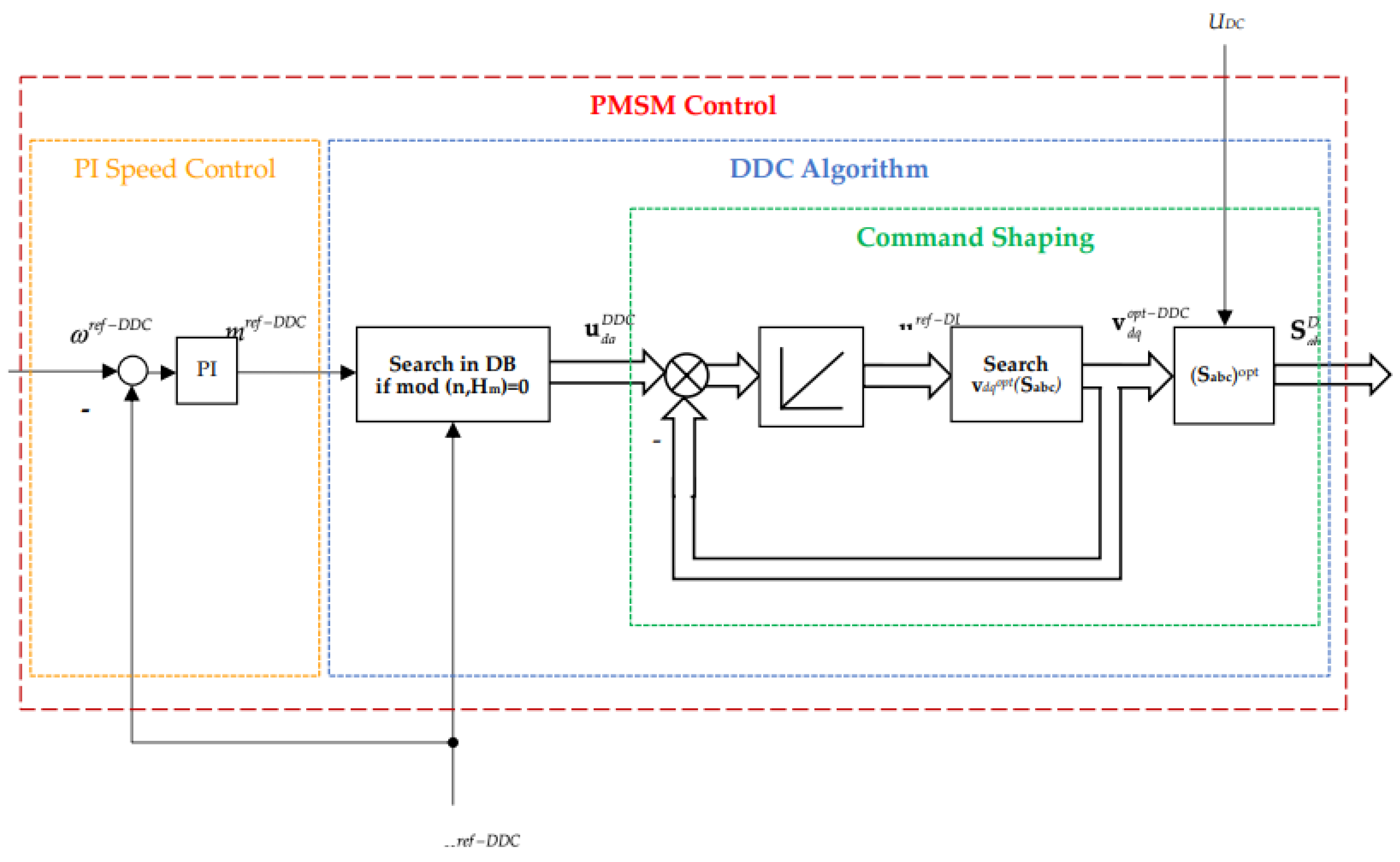
Figure 14.
The torque—speed characteristics under iso-efficiency curves of a PMSM drive.
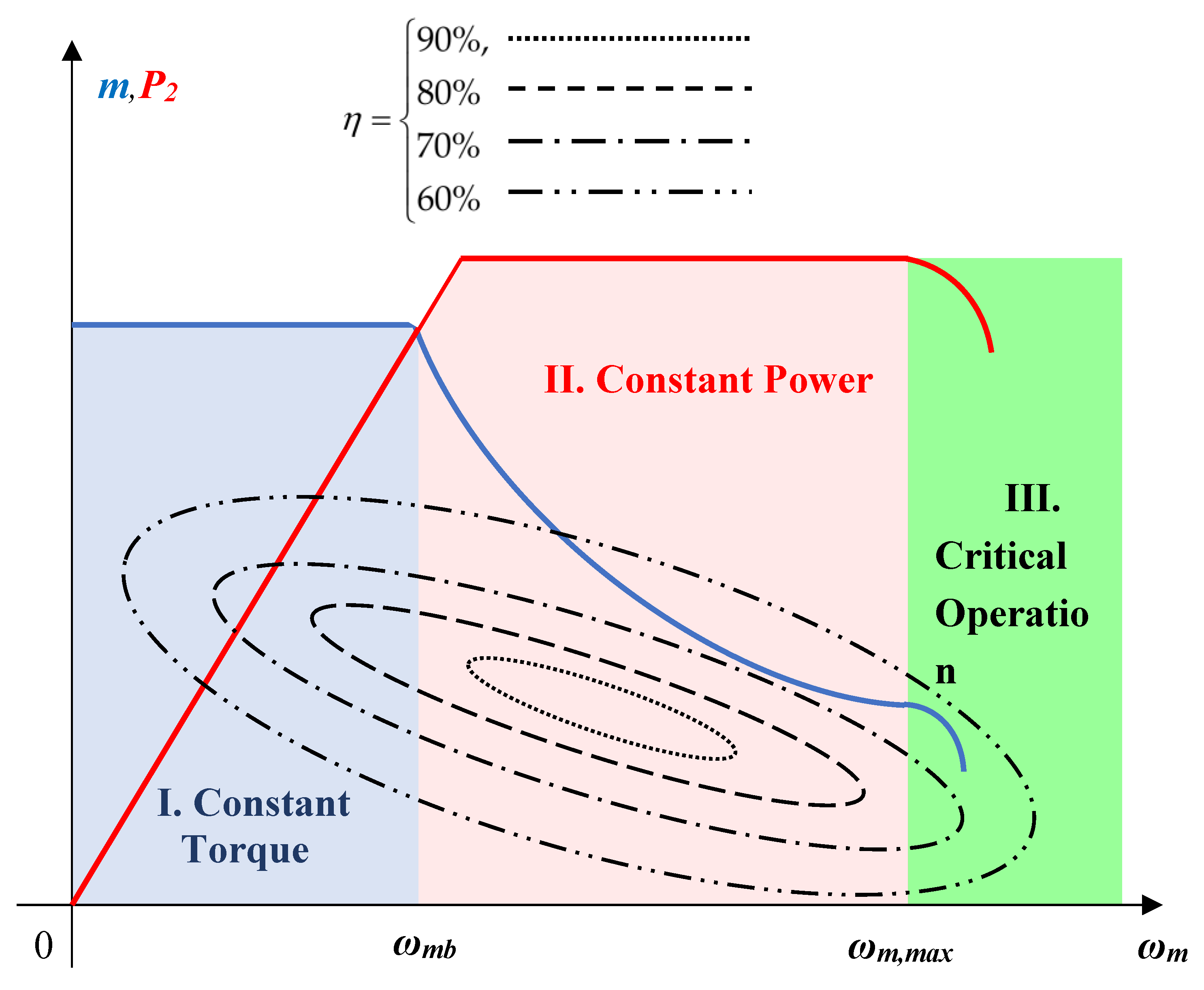
Figure 15.
Transformation of the multi-valued efficiency map into a single-valued function.
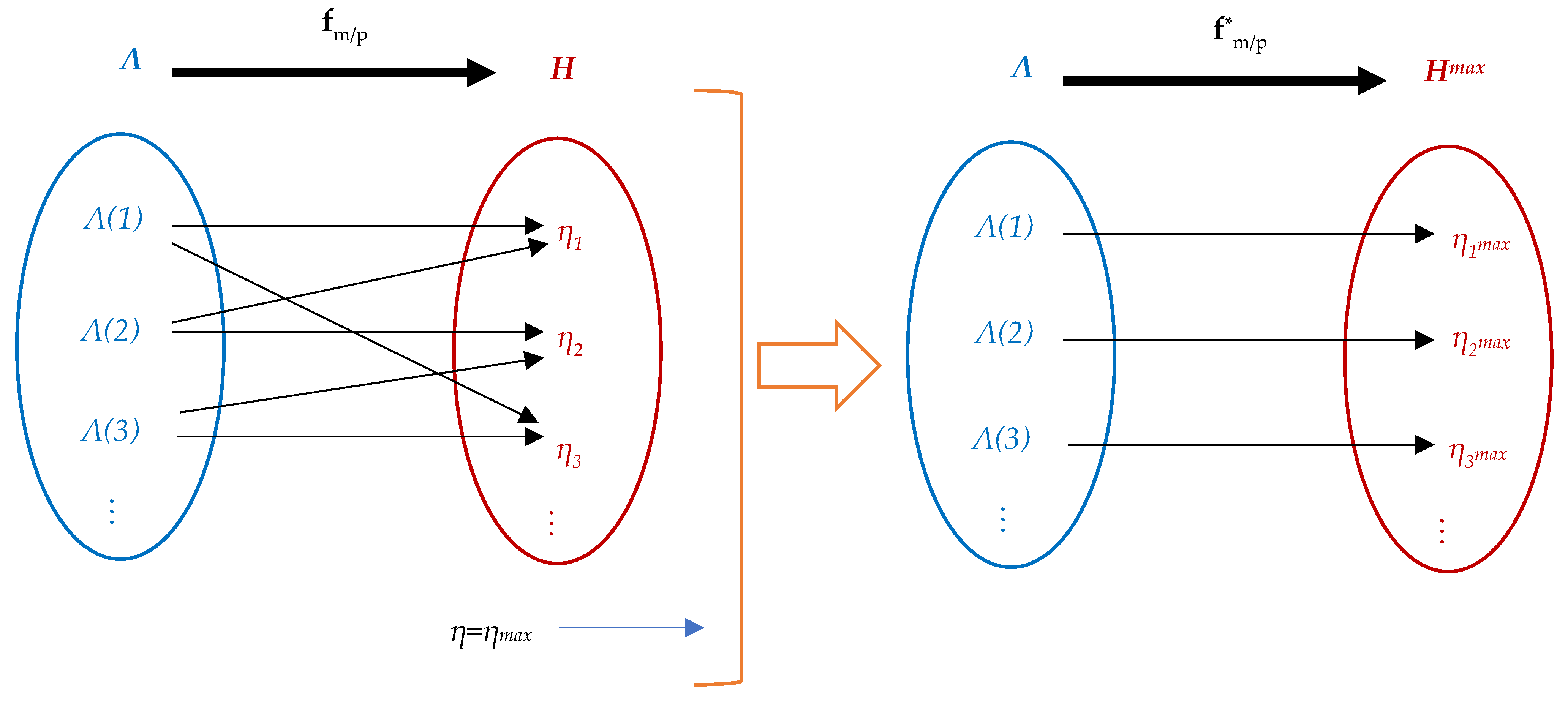
Figure 16.
The database grid steps design of close loop applications.
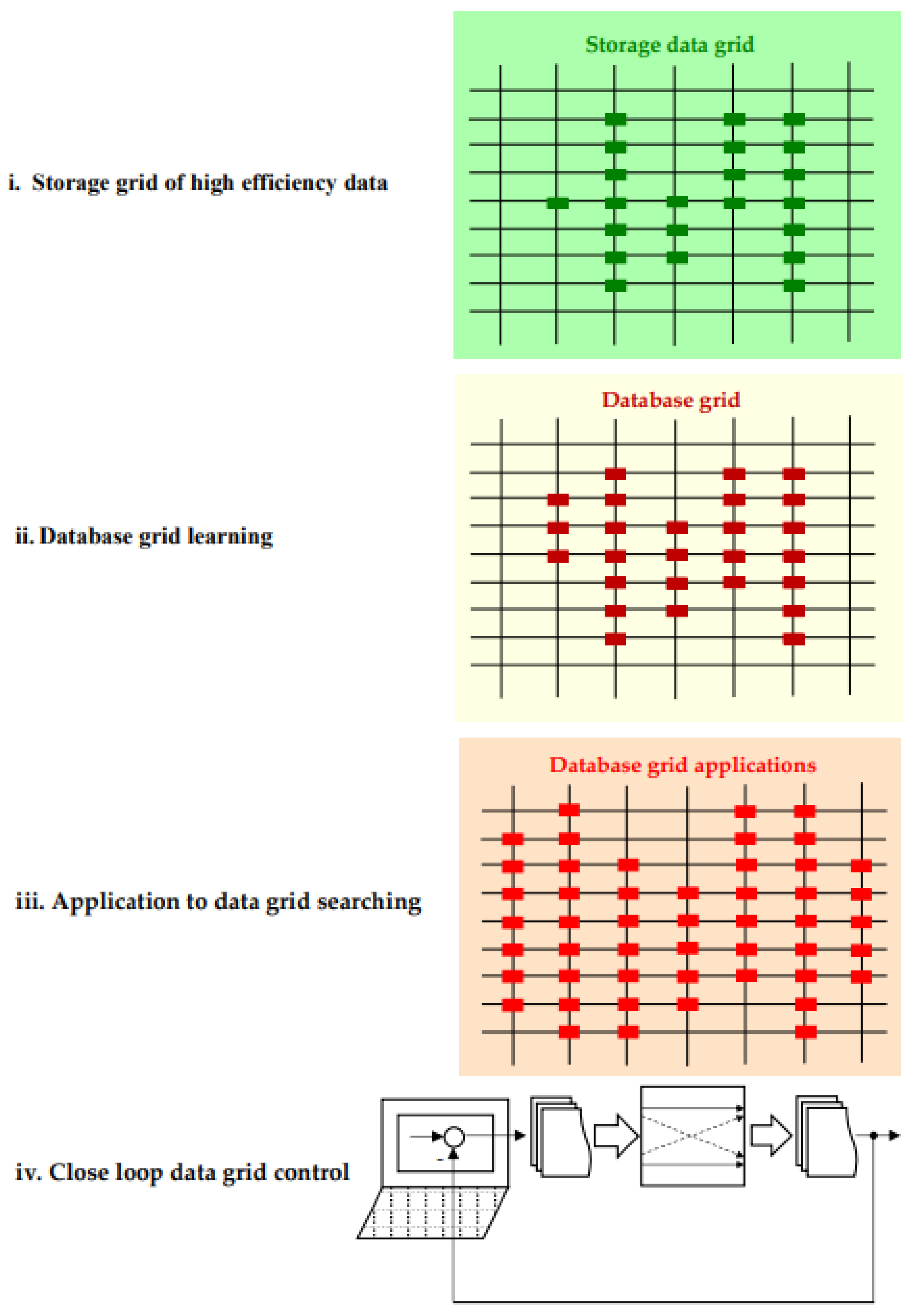
Figure 17.
The moving window filter structure.

Figure 19.
The DDOC control algorithm of a PMSM drive control.

Figure 20.
The efficiency surface vs. speed and torque.
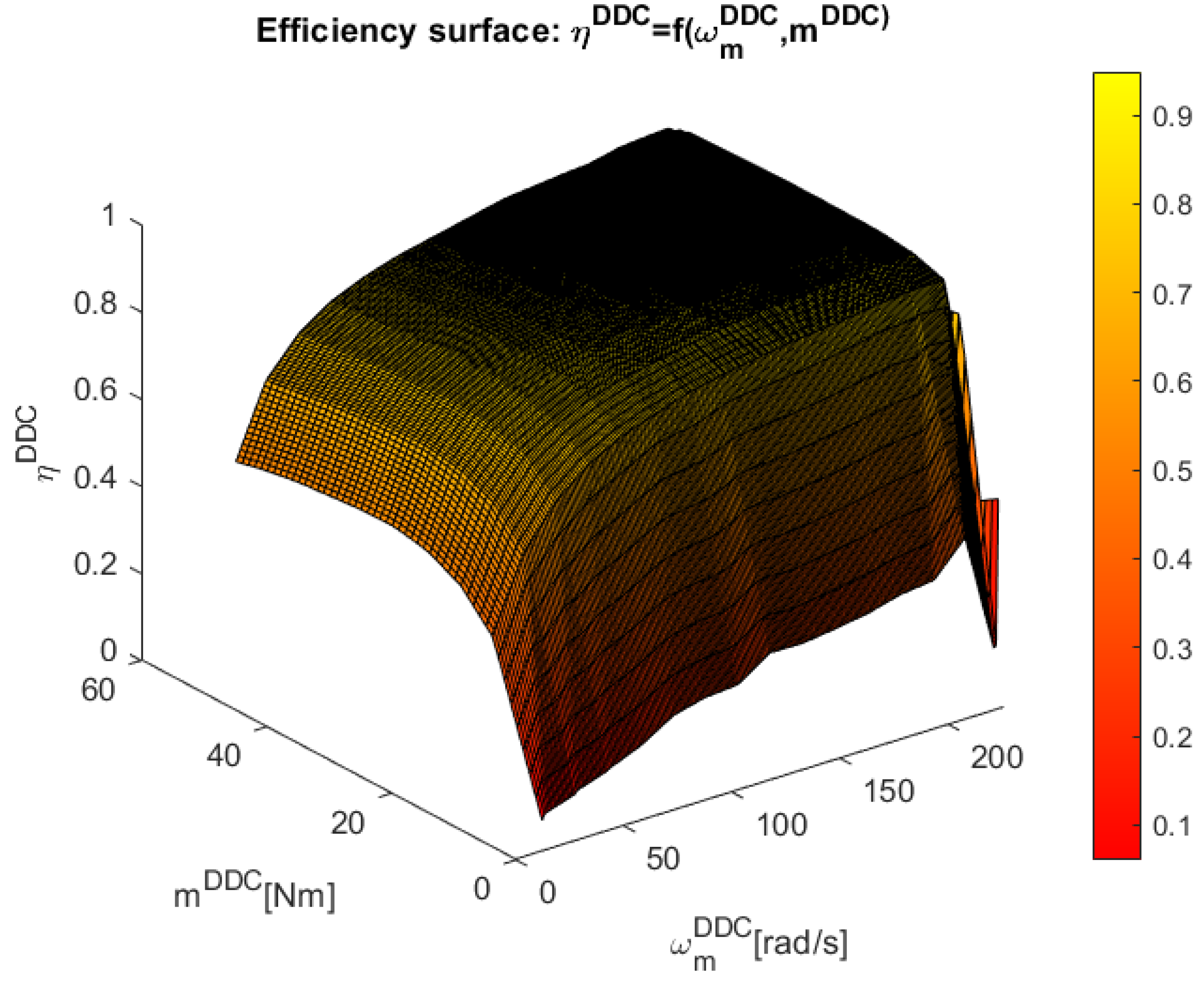
Figure 21.
The d-axis voltage surface vs. speed and torque.
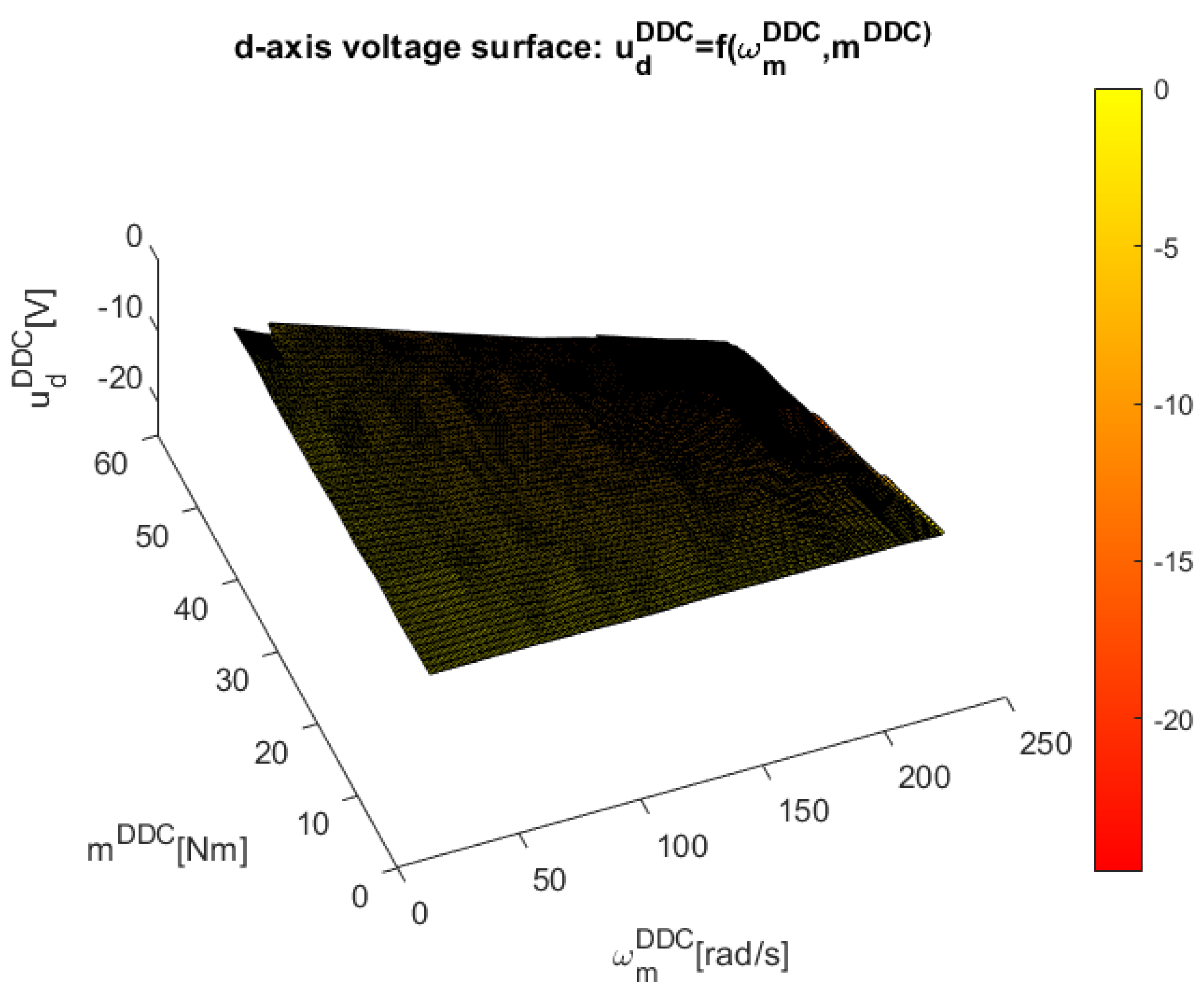
Figure 22.
The q-axis voltage surface vs. speed and torque.
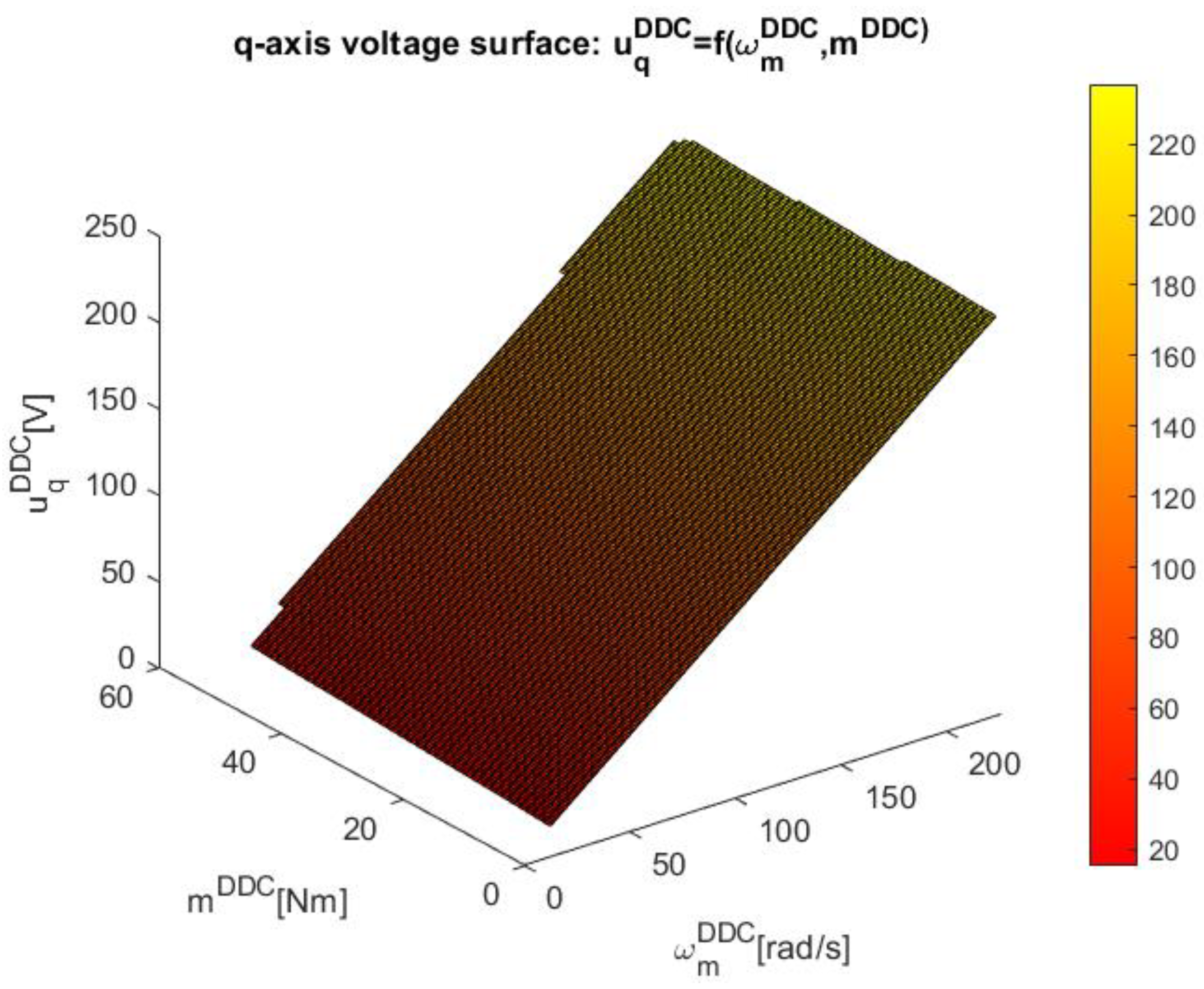
Figure 23.
The speed tracking results obtained for MPC and DDC control strategies.
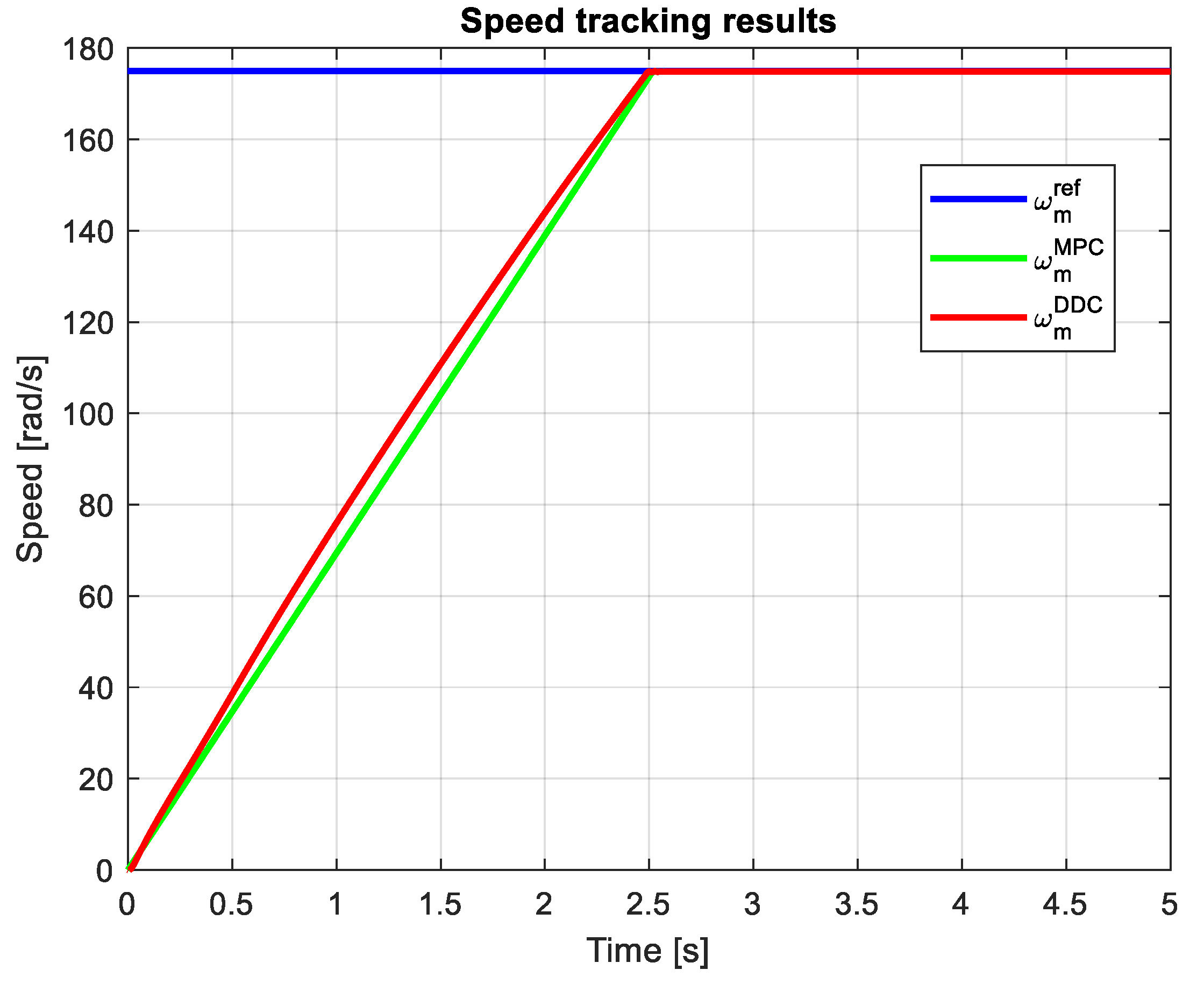
Figure 24.
The current results obtained for MPC and DDC control strategies.
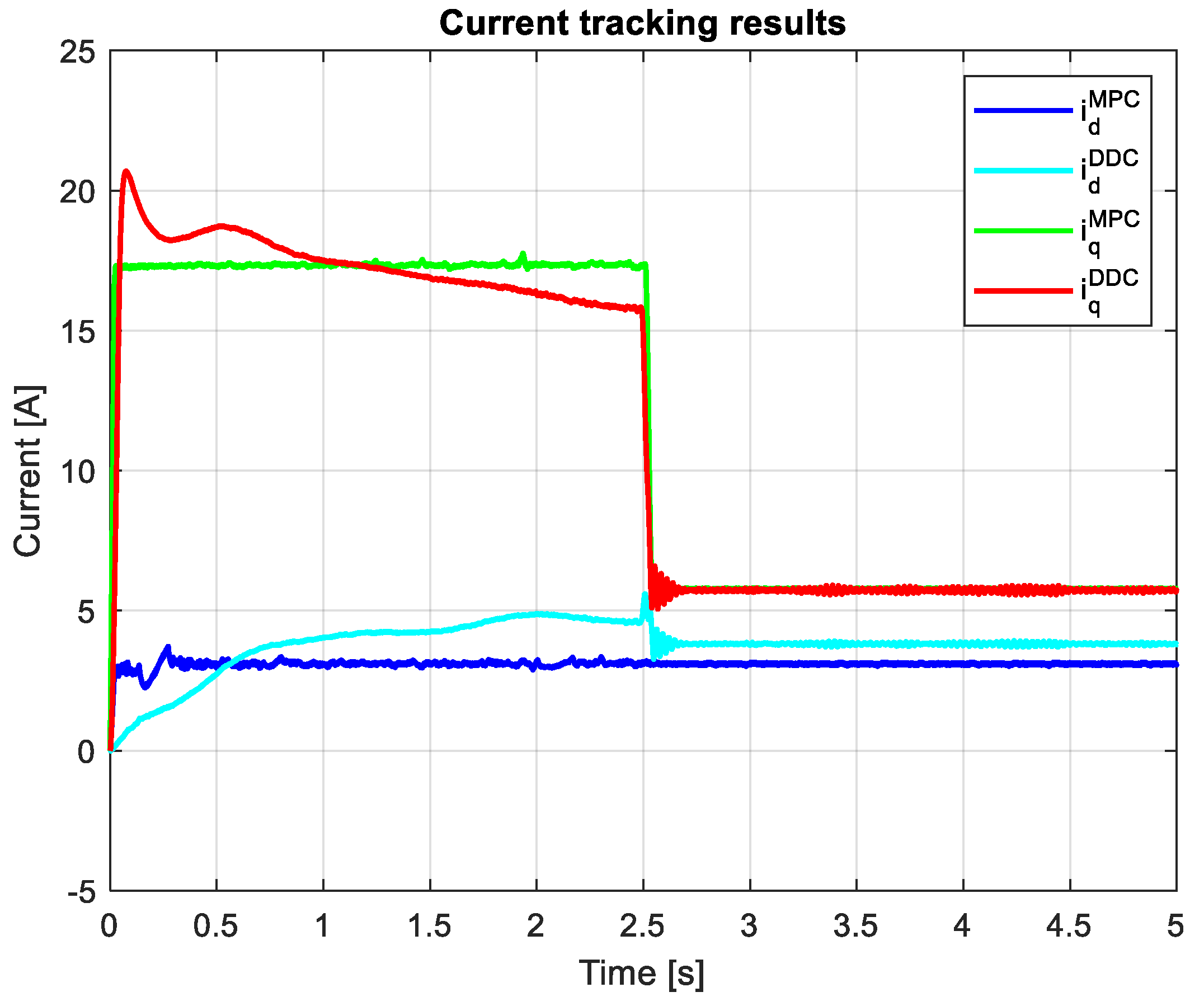
Figure 25.
Load and electromagnetic torques for MPC and DDC control strategies.
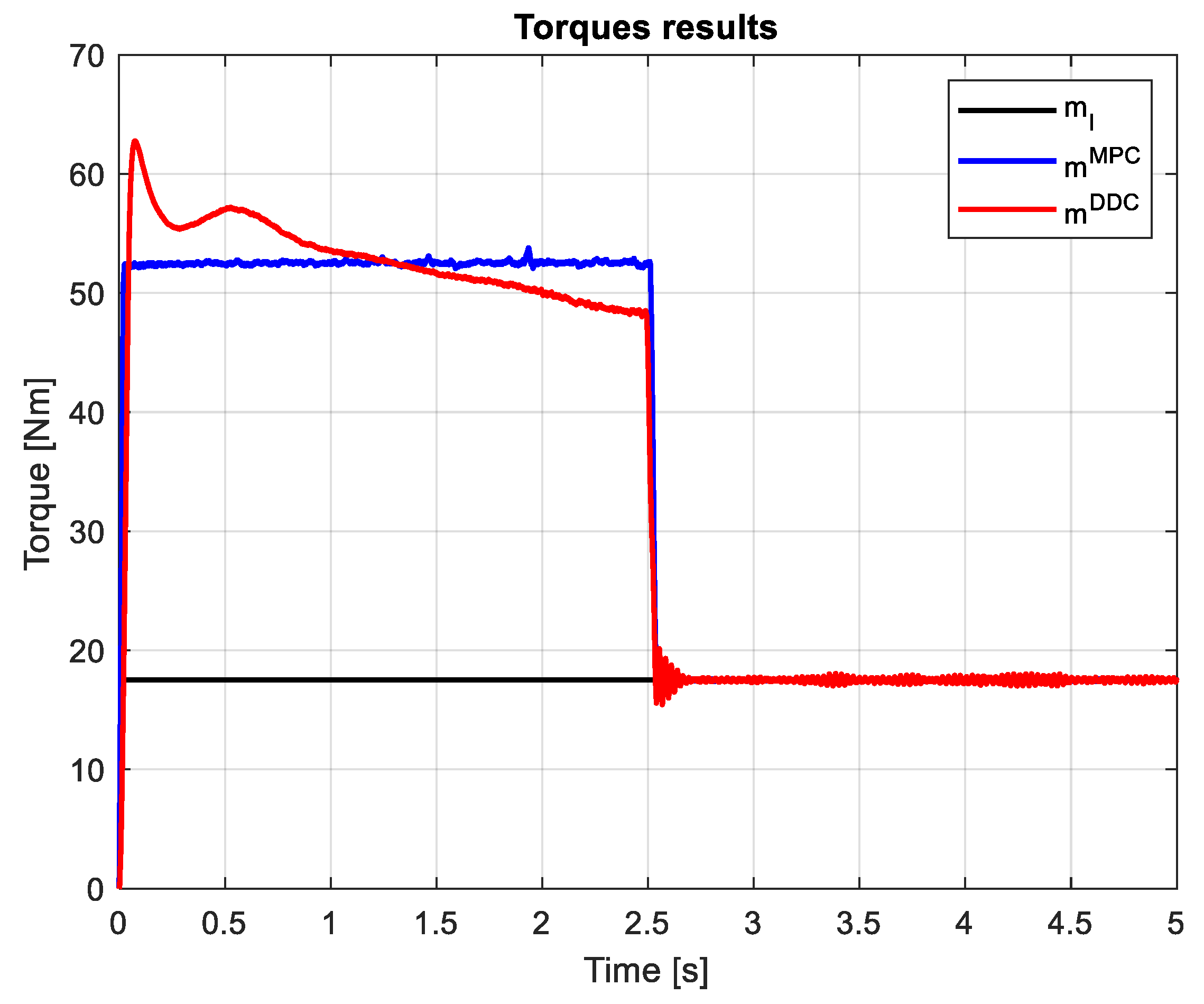
Figure 26.
Voltage components for MPC and DDC control strategies.
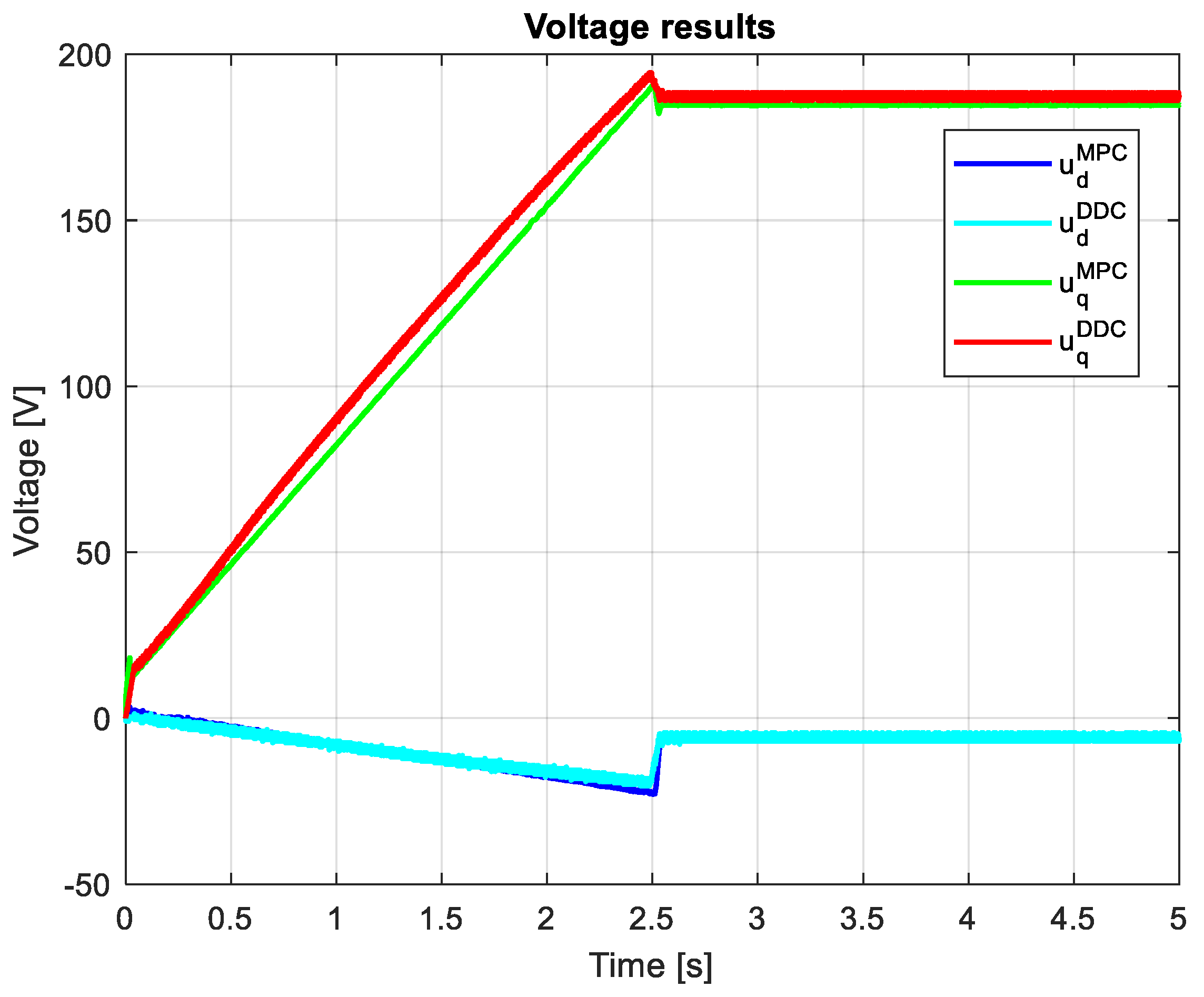
Figure 27.
Current magnitude for MPC and DDC control strategies.
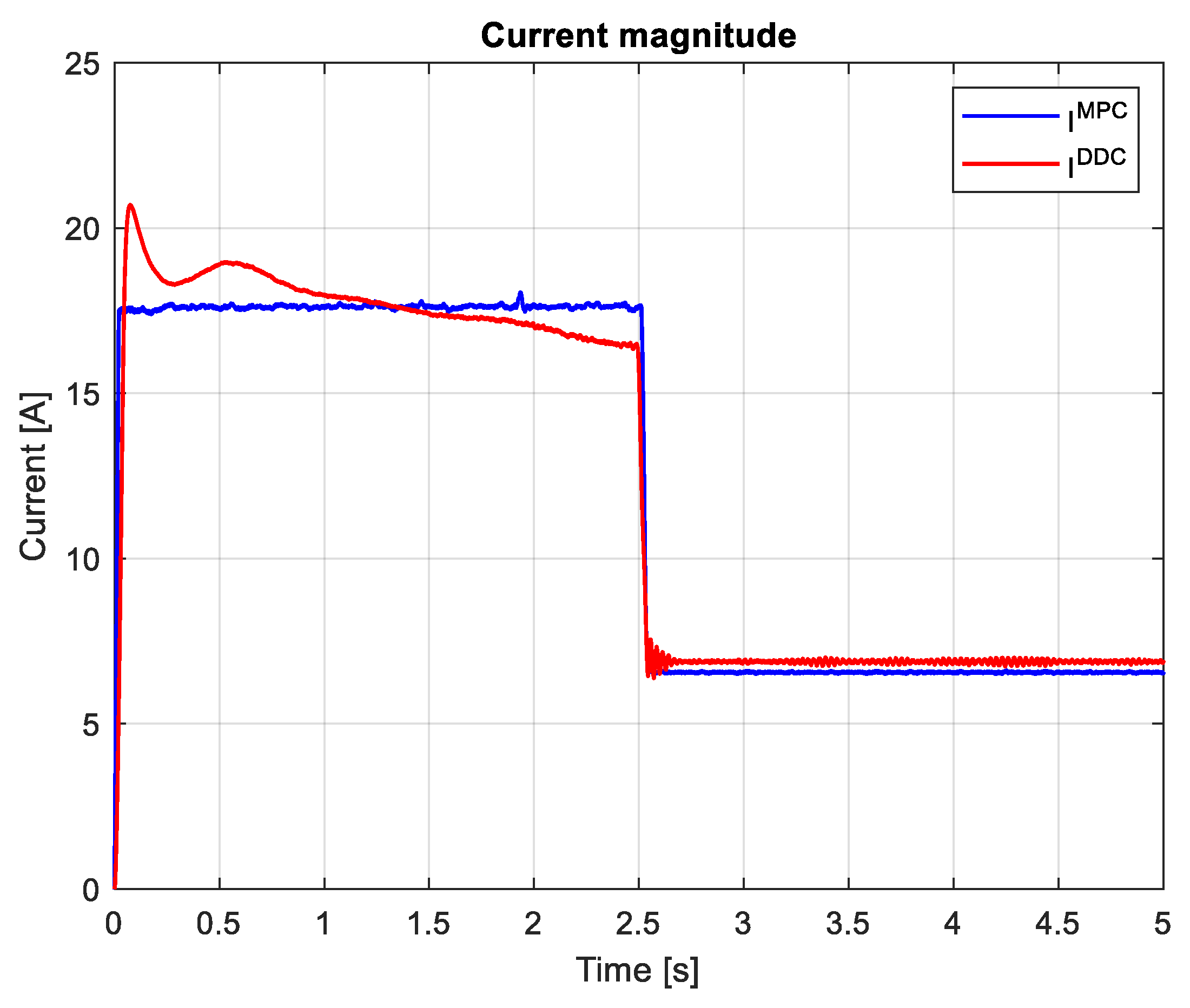
Figure 28.
Voltage magnitude for MPC and DDC control strategies.
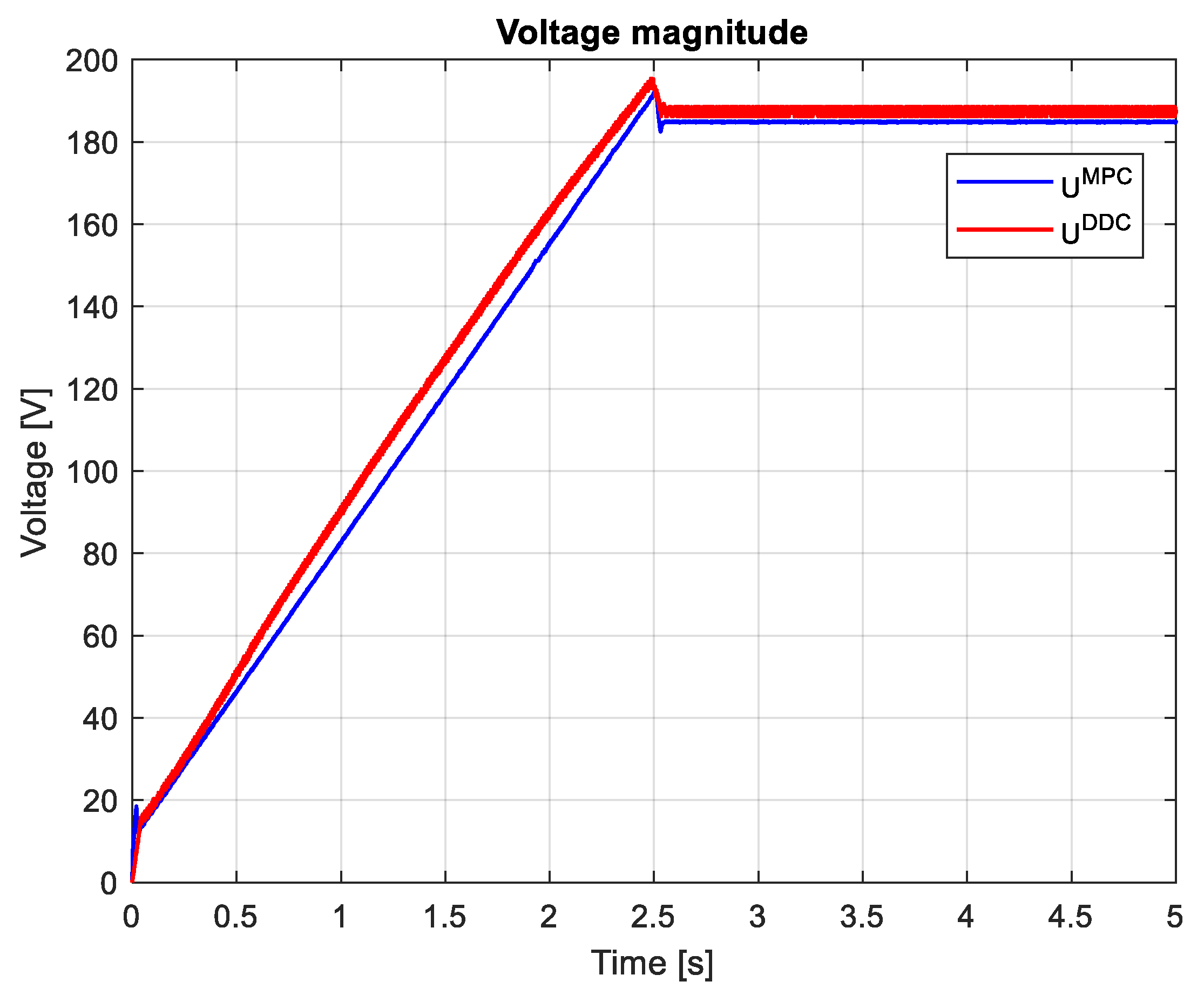
Figure 29.
Efficiency of PMSM for MPC and DDC control strategies.
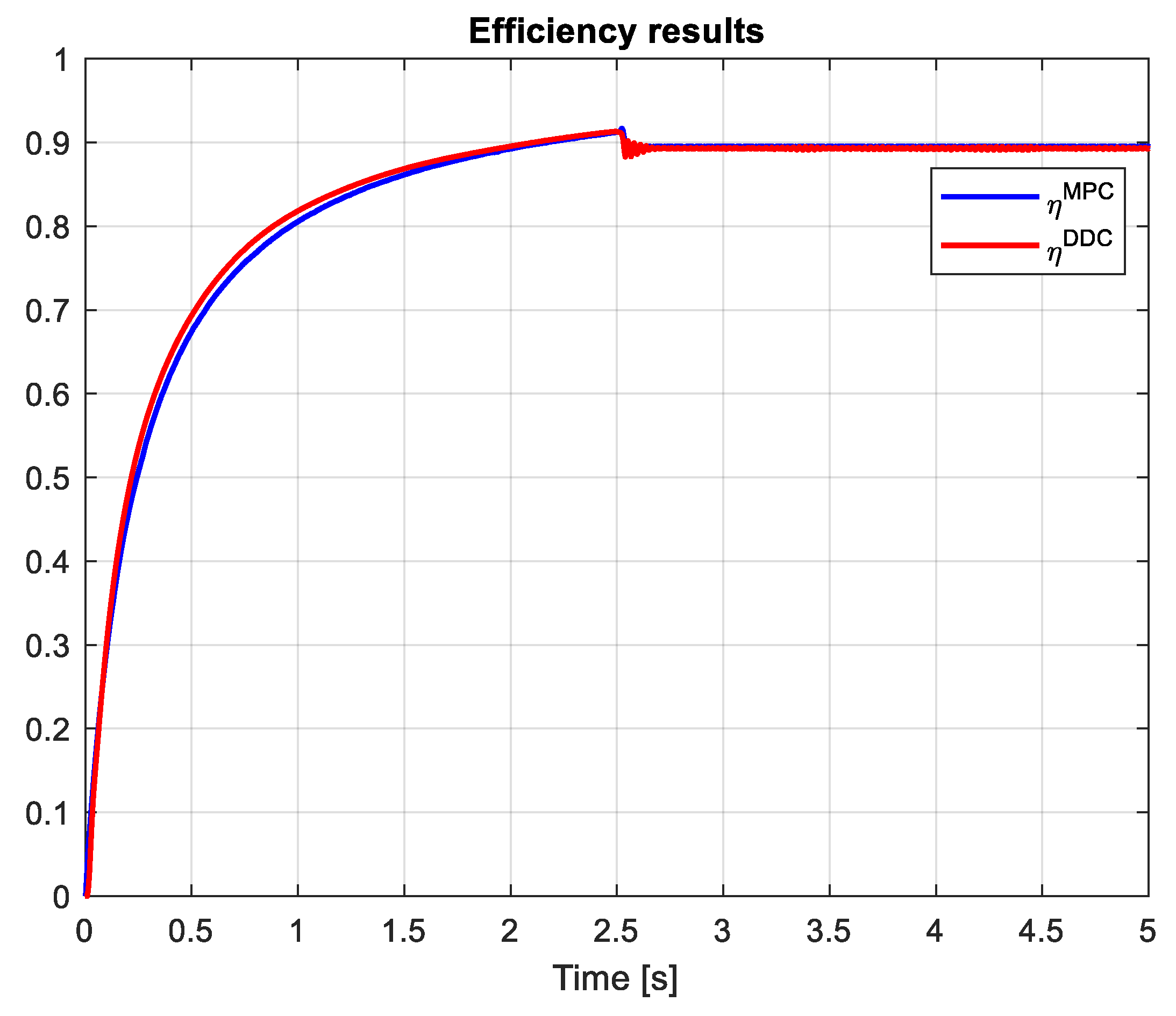
Figure 30.
Average efficiency of PMSM for MPC and DDC control strategies.
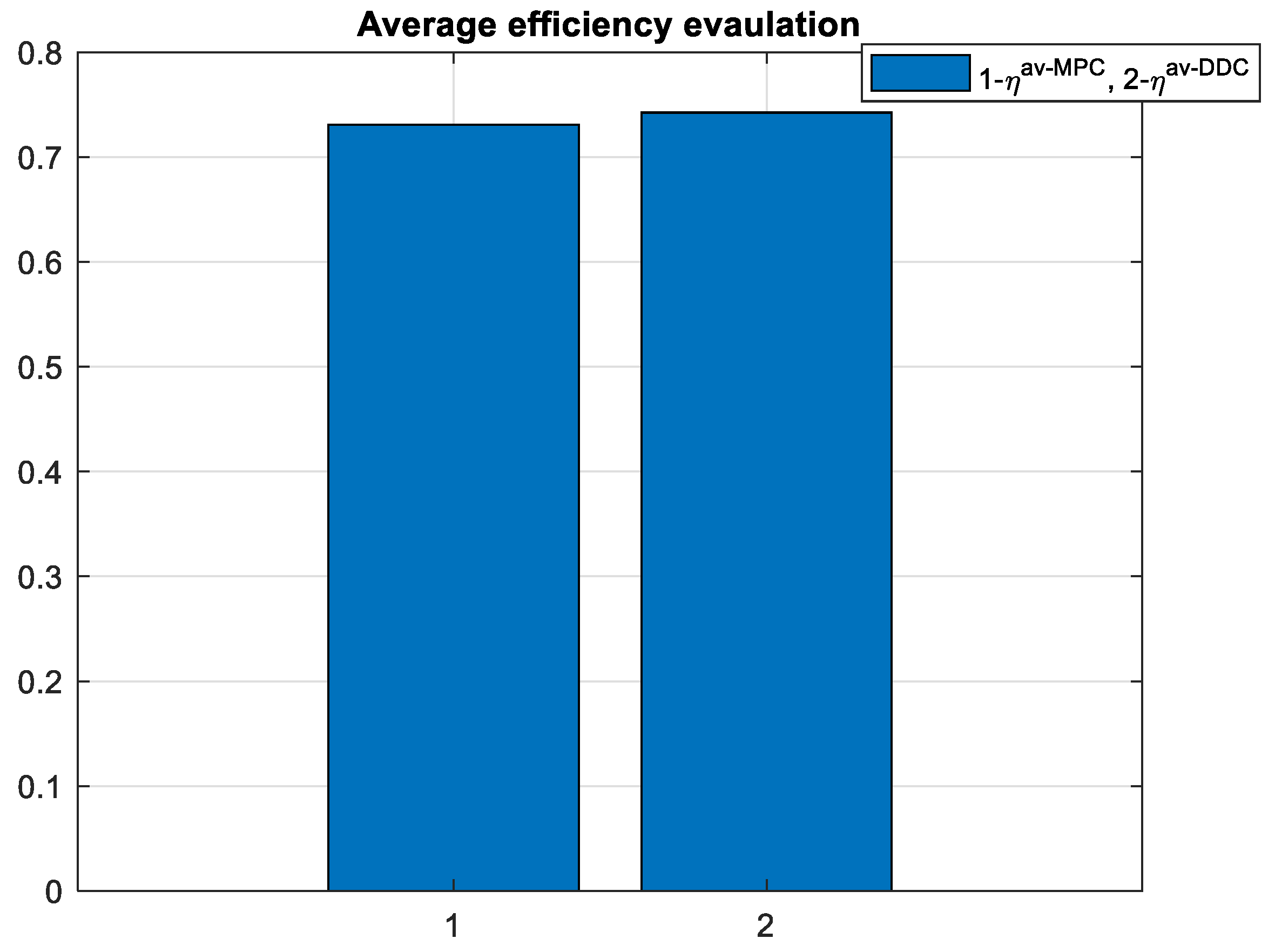
Figure 31.
Phase current of PMSM for MPC and DDC control strategies.
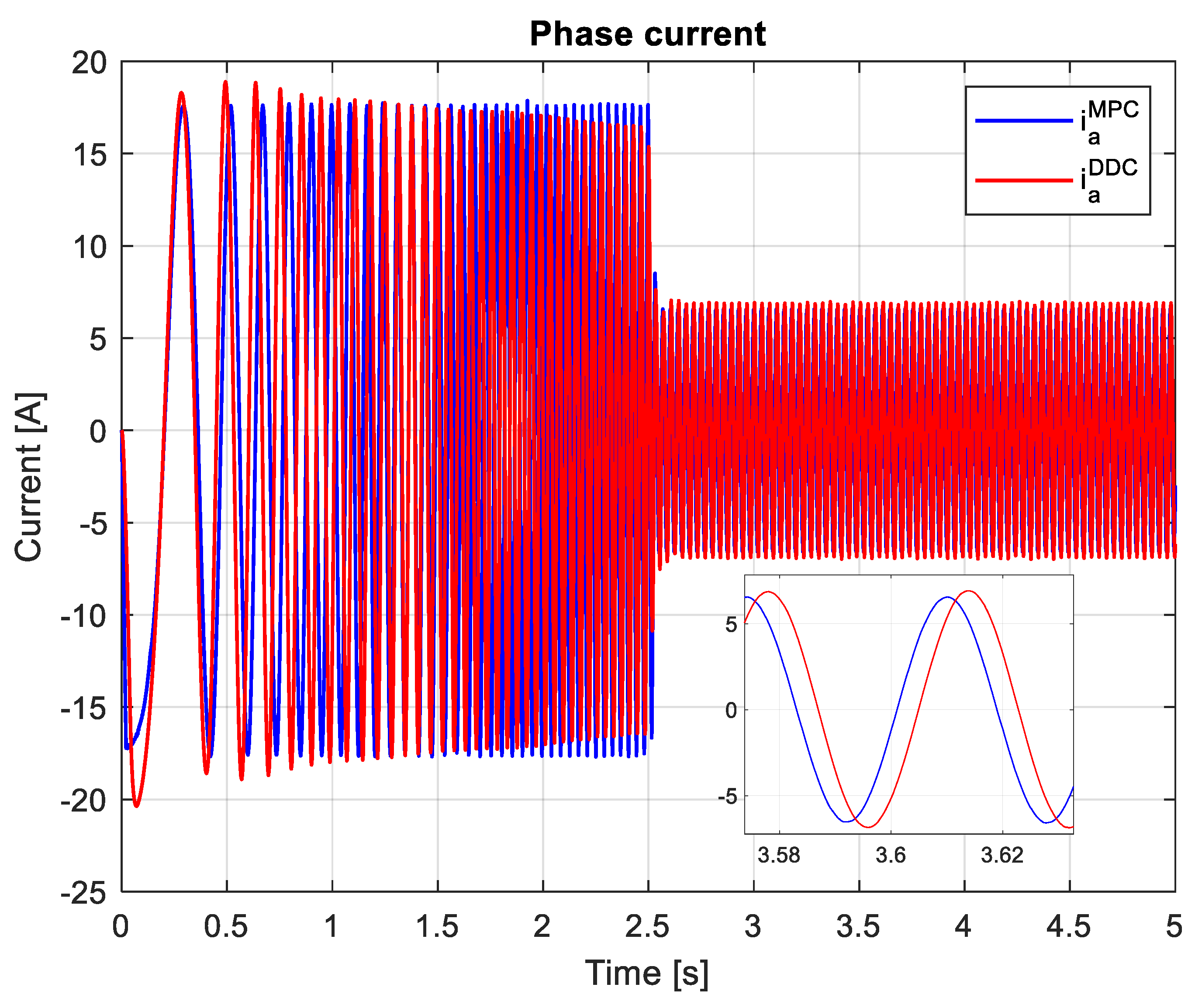
Figure 32.
The tracking results of speed obtained via MPC and DDC control laws.
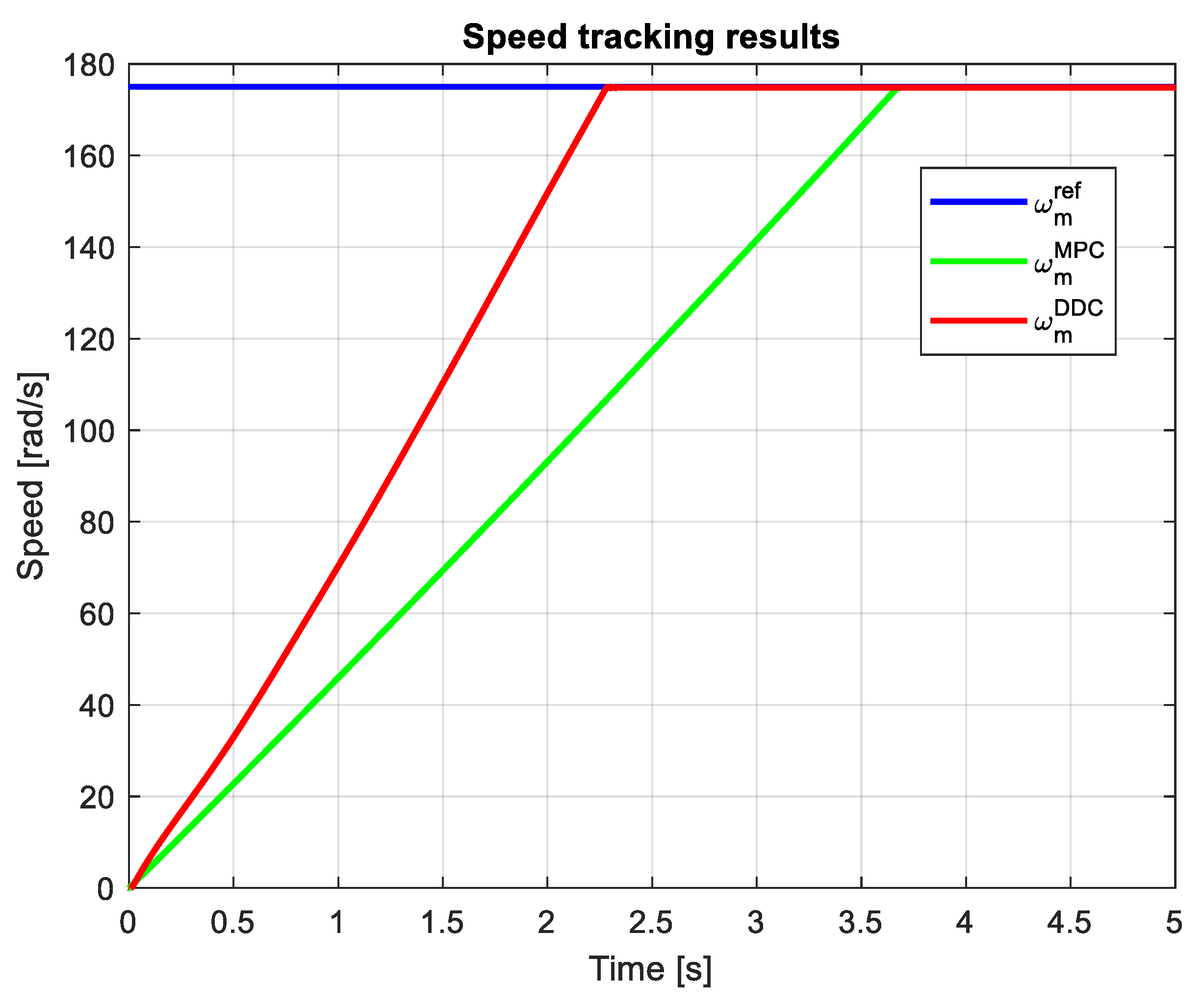
Figure 33.
The dq current obtained for MPC and DDC control laws.
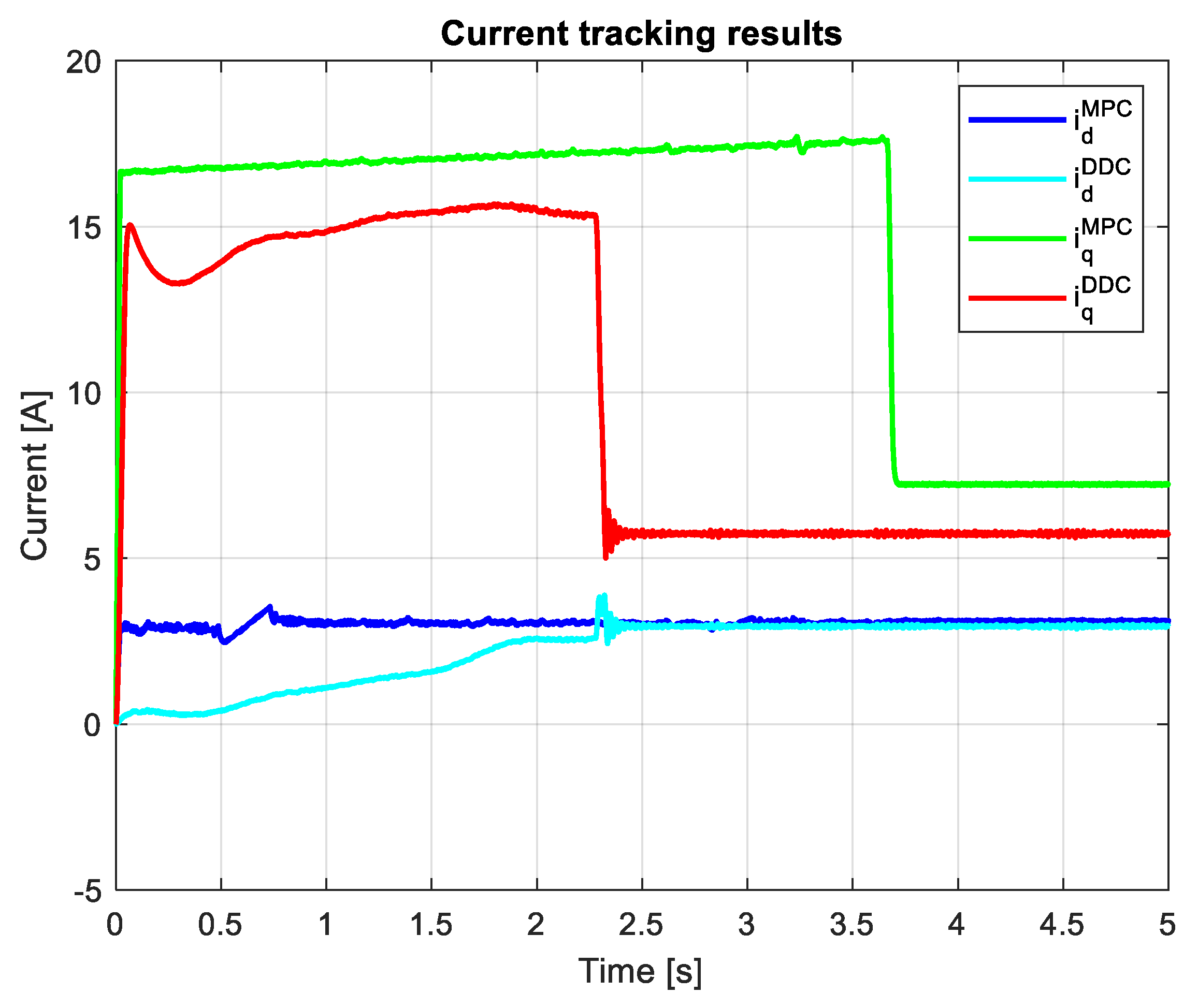
Figure 34.
Load torque disturbance rejection for MPC and DDC control strategies.
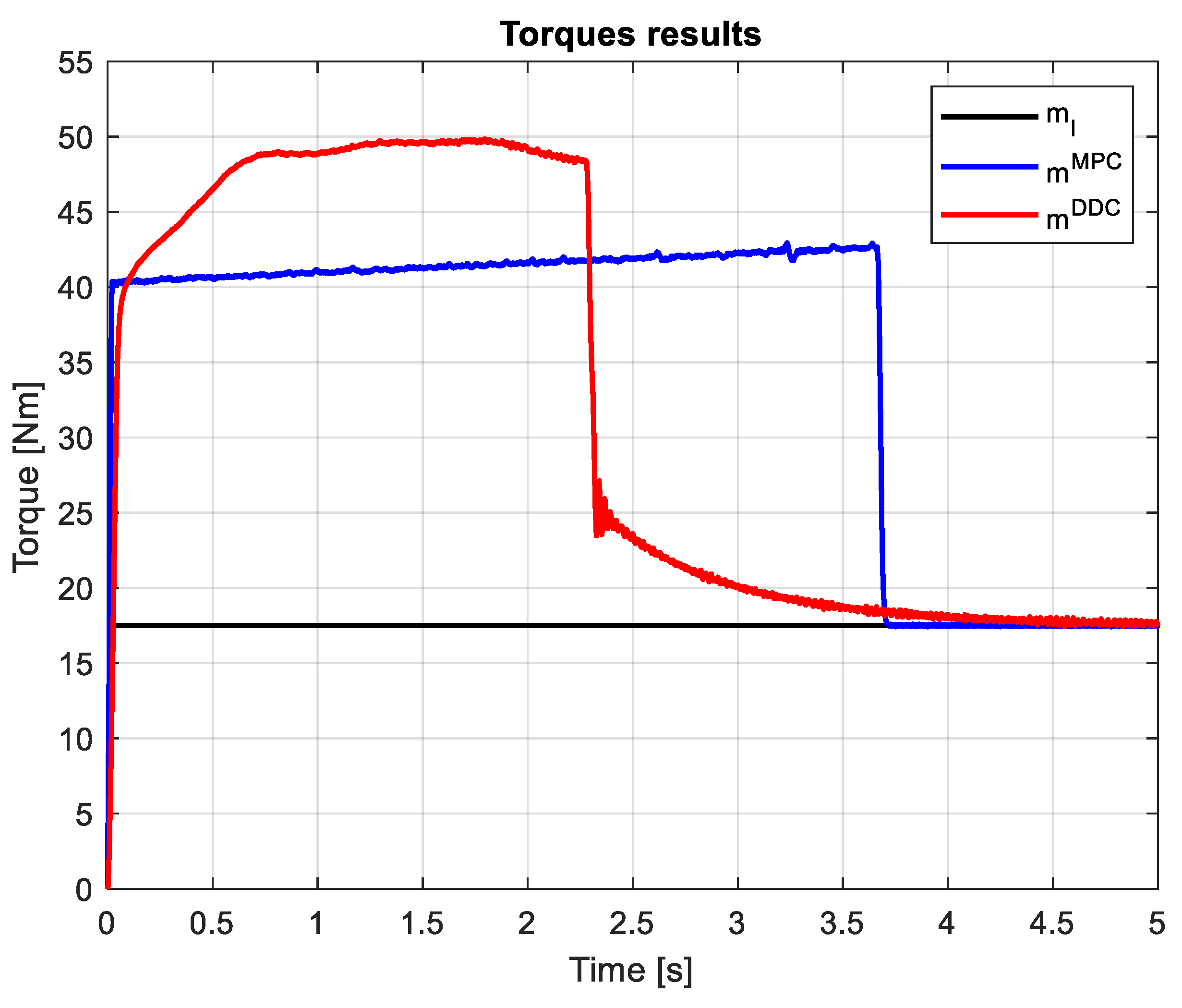
Figure 35.
Voltage obtained by MPC and DDC control strategies.
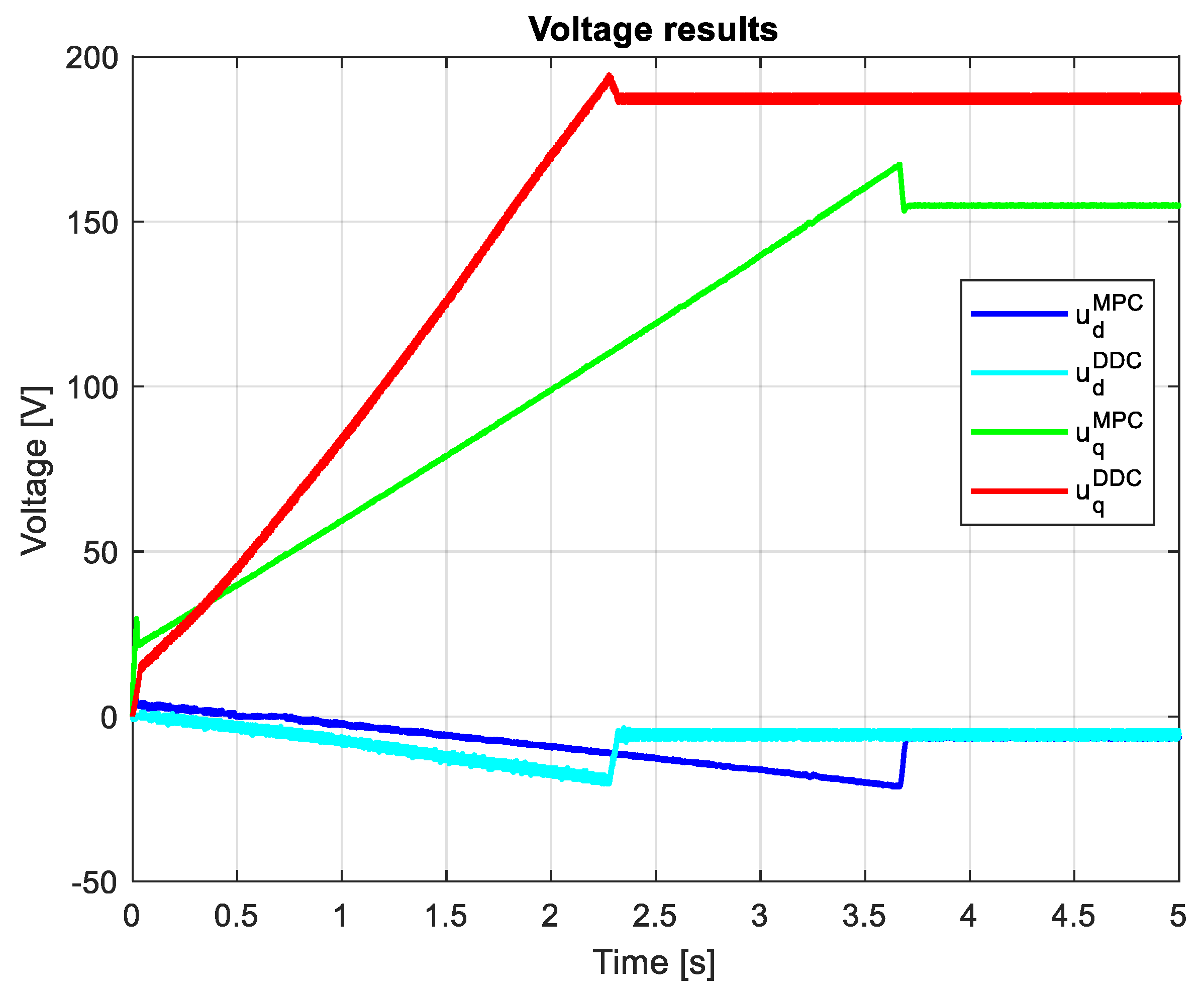
Figure 36.
Current magnitude given by MPC and DDC control algorithms.
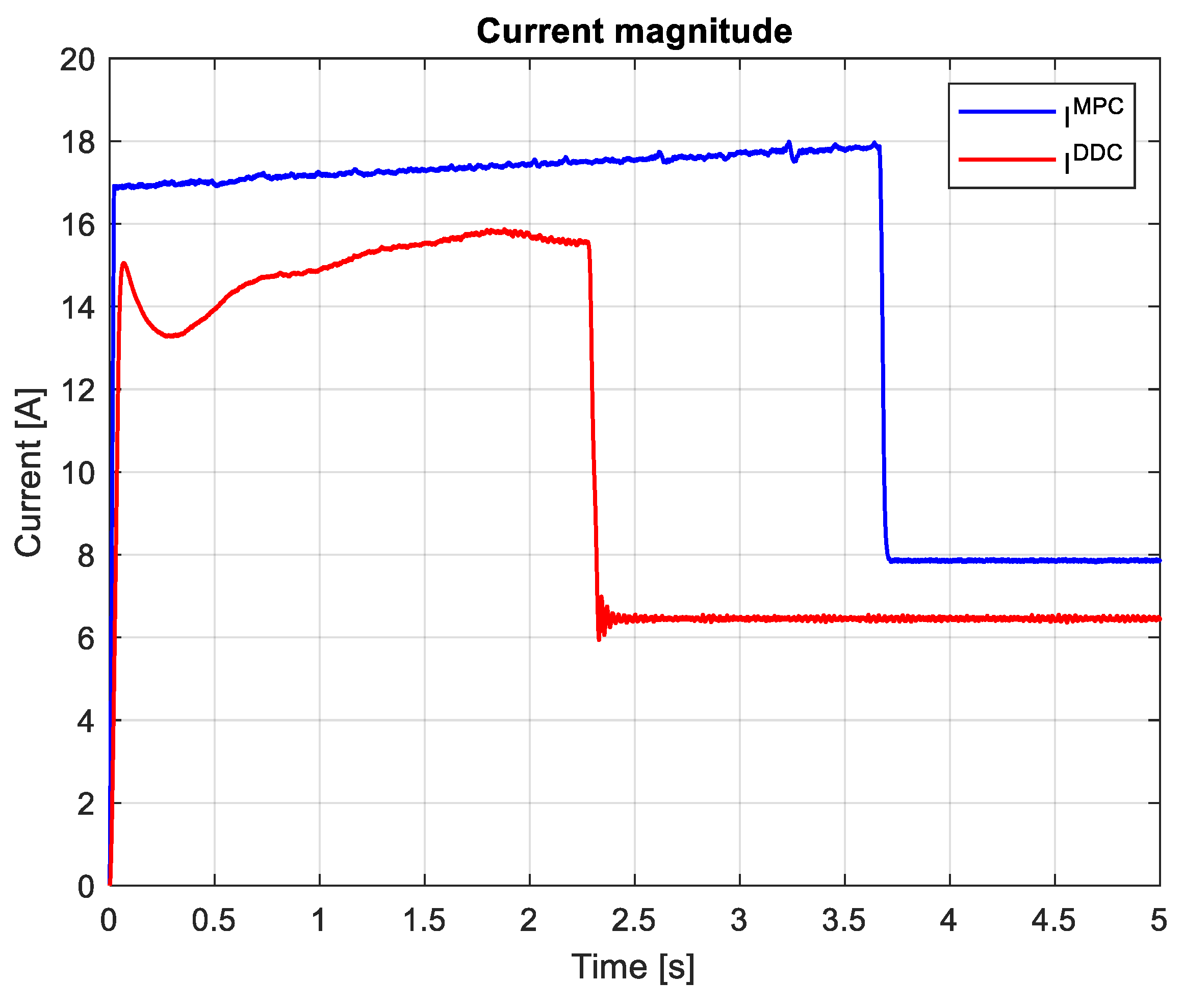
Figure 37.
Voltage magnitude given by MPC and DDC control algorithms.
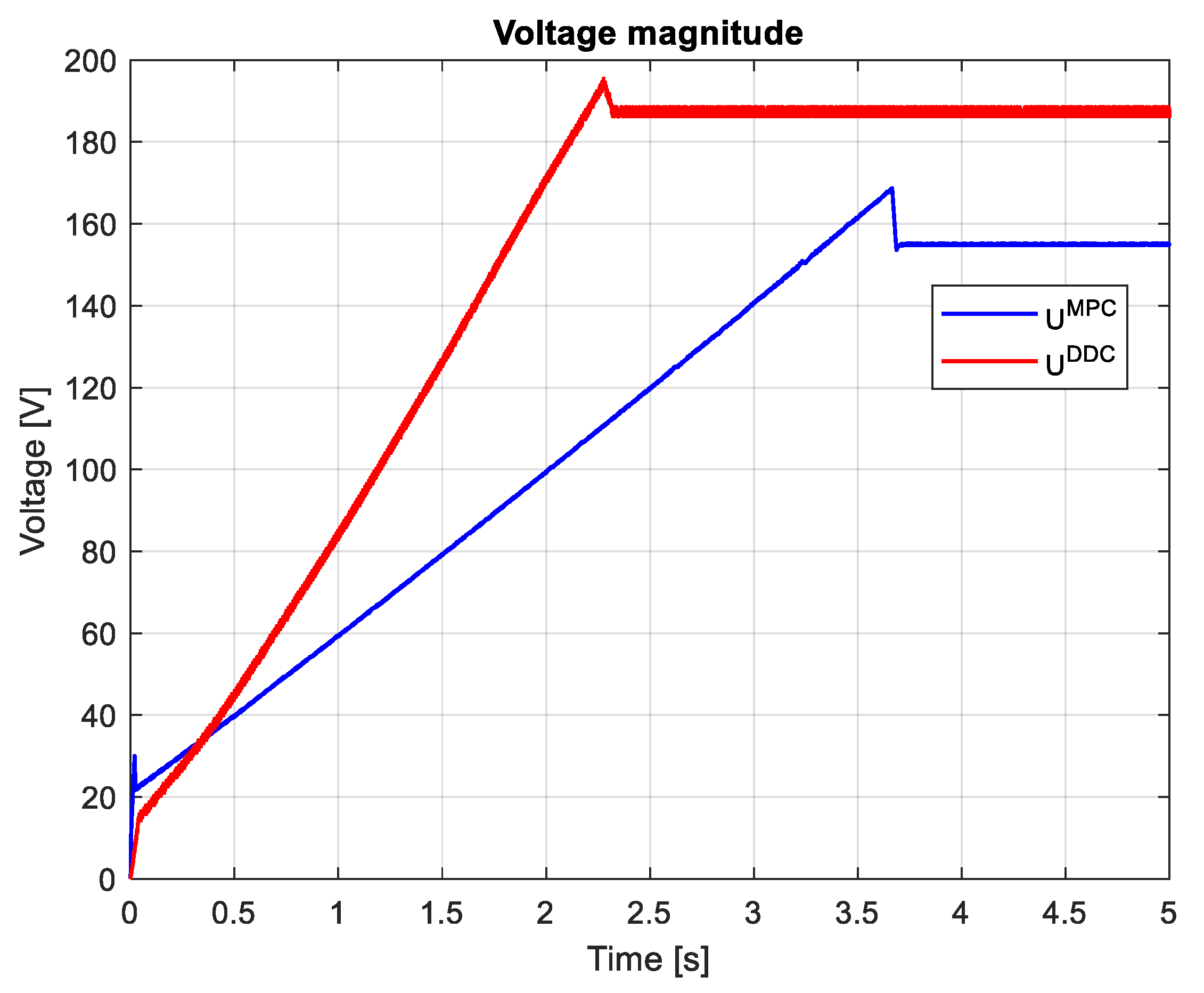
Figure 38.
Efficiency of PMSM obtained by using MPC and DDC control algorithms.
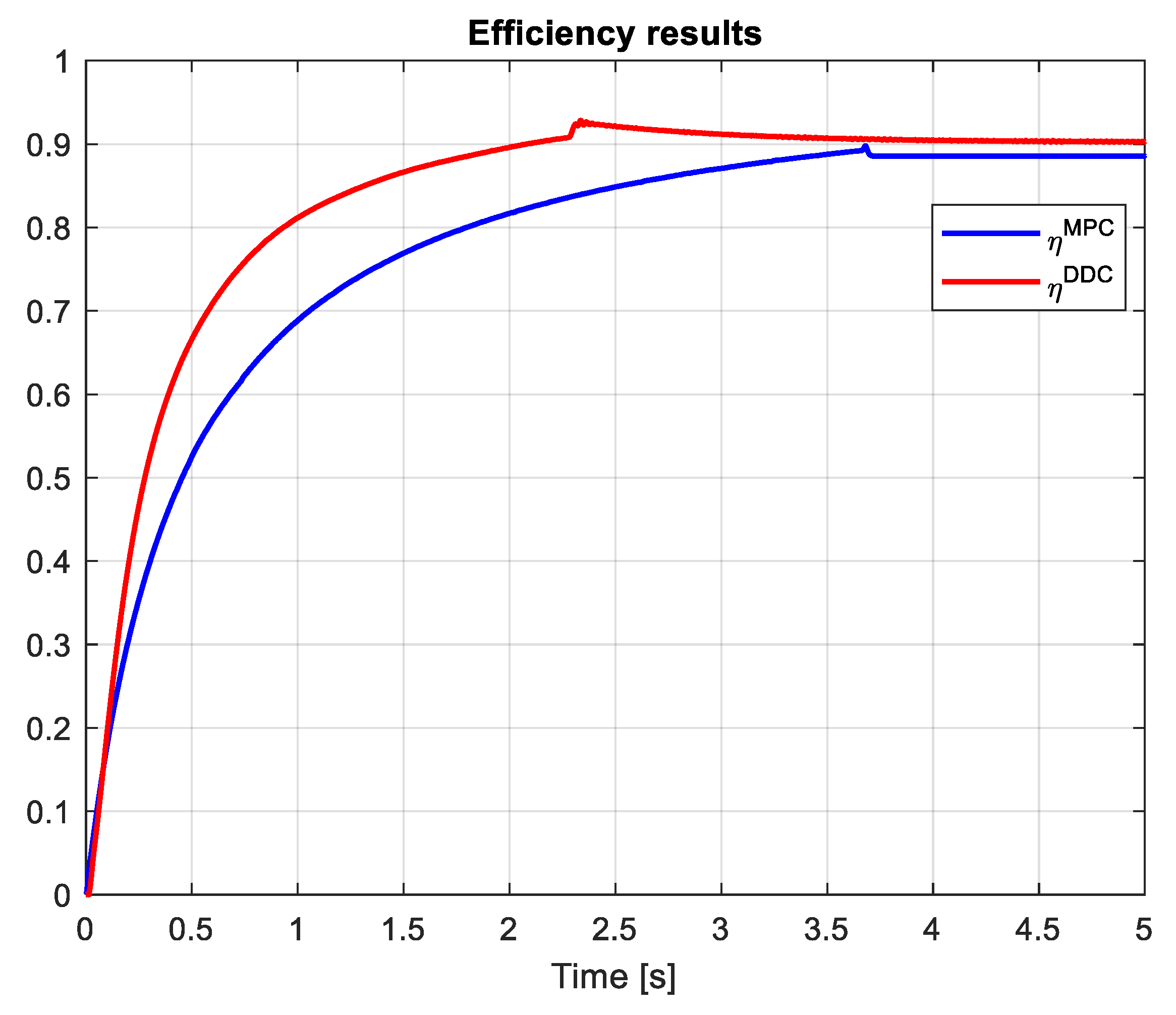
Figure 39.
Average efficiency of PMSM provided by using MPC and DDC control algorithmes.
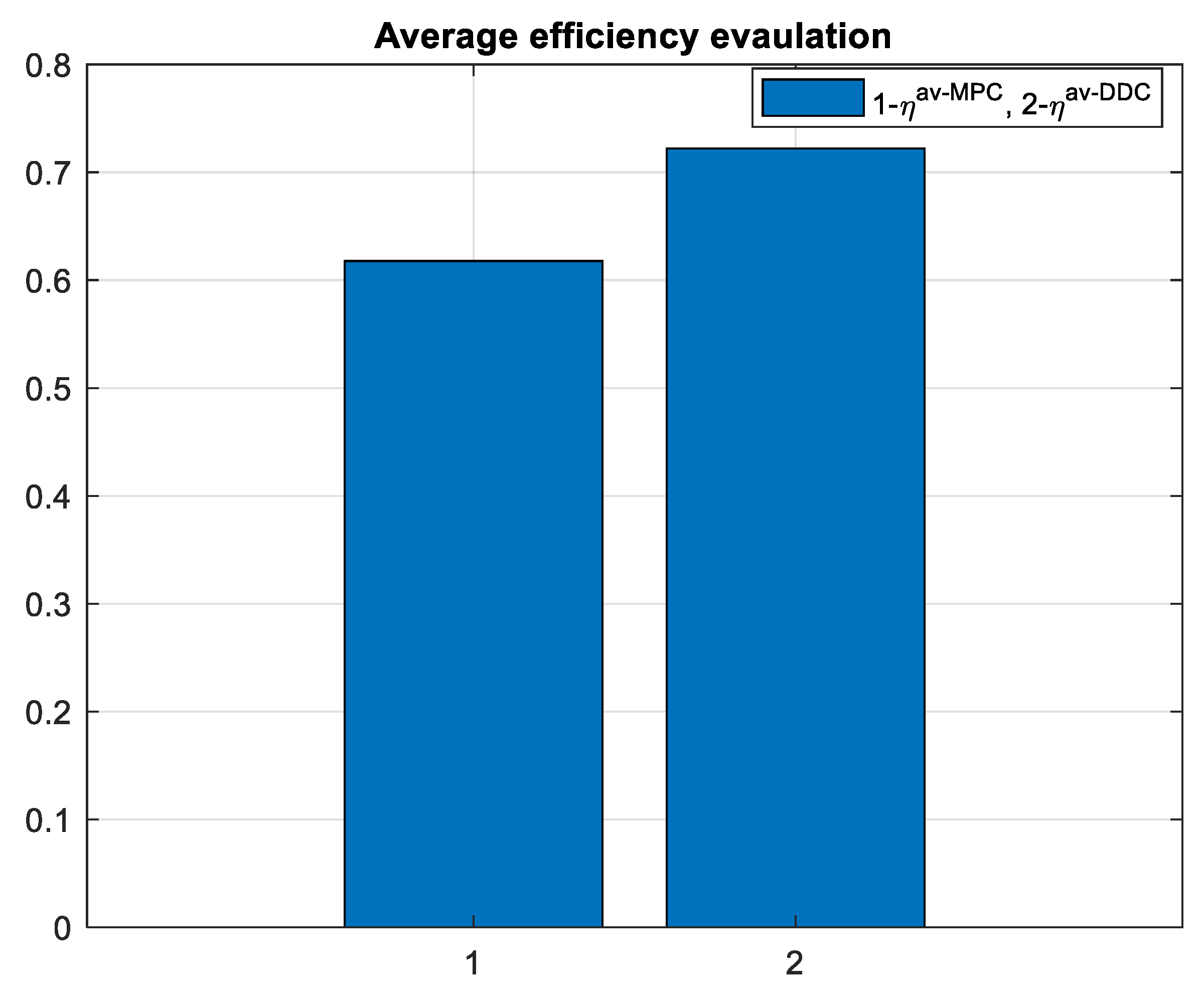
Figure 40.
Phase current for MPC and DDC control algotihms.
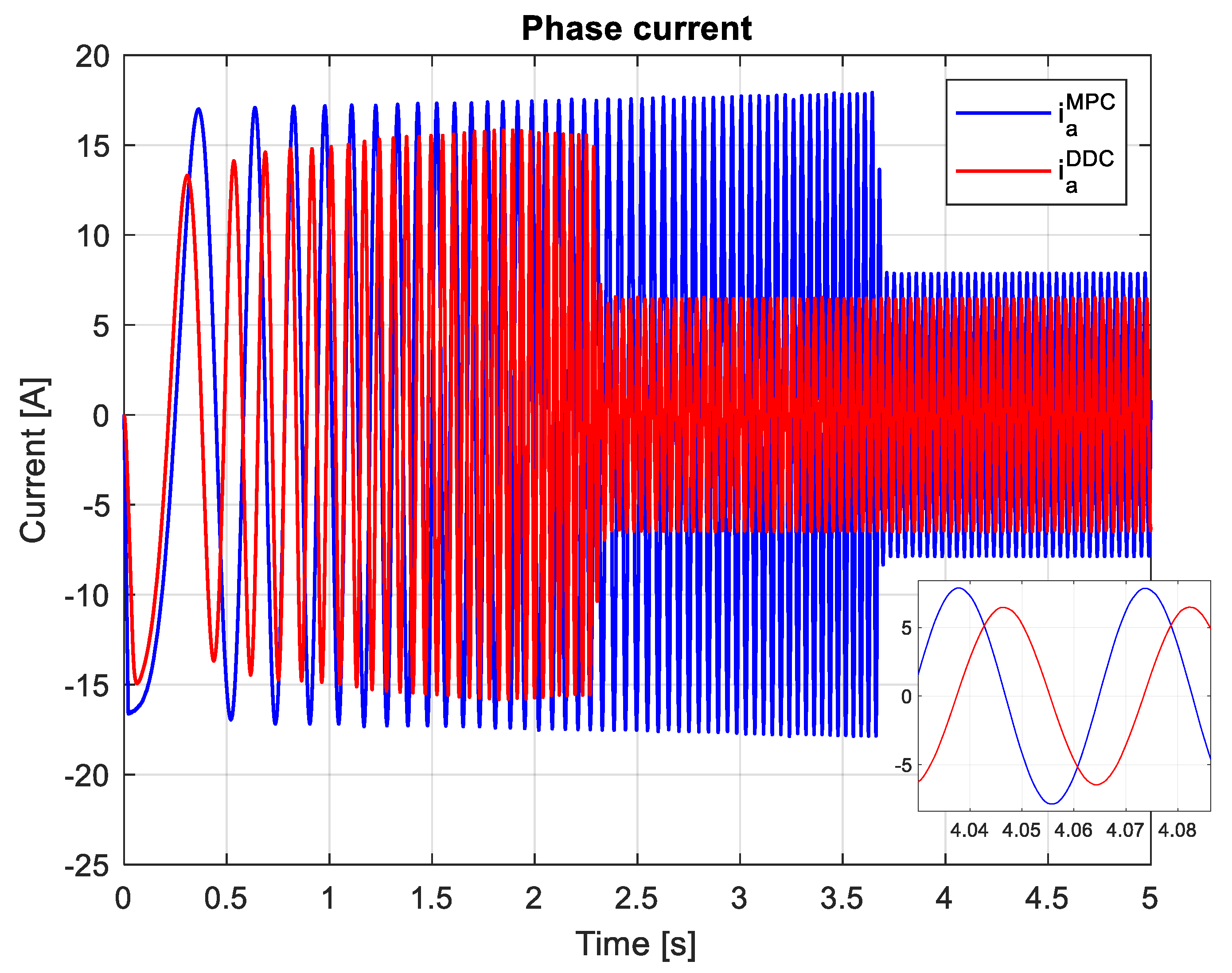
Table 1.
The voltage space vector according to their corresponding switching function.
| Index i | Sabc | Voltage space vector |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Table 2.
PMSM rated specifications data.
| Symbol | Description | Values |
|---|---|---|
| PN [W] | Rated power | 5500 |
| UN [V] | Rated voltage | 325 |
| mN [Nm] | Rated torque | 35 |
| IN [A] | Rated current | 10.6 |
| ωmN [rad/sec] | Rated speed | 157 |
| Rs [Ω] | Rotor resistence | 0.65 |
| Ld [H] | Direct axis inductance | 0.0082 |
| Lq [H] | Quadrature axis inductance | 0.0082 |
| J[kg∙m2] | Total inertia of the PMSM drive | 0.5 |
| zp | Stator pole pairs | 2 |
Table 3.
The comparative evaluation of MPC and DDC strategies.
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






