Forecasting Hydropower with Innovation Diffusion Models: A Cross-Country Analysis

Preprint

Brief Report

Forecasting Hydropower with Innovation Diffusion Models: A Cross-Country Analysis

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Farooq Ahmad,

Livio Finos

Mariangela Guidolin^*

Farooq Ahmad,

Livio Finos

Mariangela Guidolin^*

This version is not peer-reviewed

Submitted:

07 October 2024

Posted:

08 October 2024

You are already at the latest version

Alerts

Abstract

Hydroelectric power is one of the most essential renewable energy sources in the world. In addition to generating electricity, hydropower offers other benefits such as flood control, irrigation assistance, and clean drinking water. In this study, we examine the evolution of hydropower in the context of energy transition with a forecasting analysis. We analyze time series data of hydropower generation from 1965 to 2023 and apply Innovation Diffusion Models as well as other models such as Prophet and ARIMA for comparison. The models are evaluated for different geographical regions, namely the North, South, and Central American countries, the European countries, and the Middle East with Asian countries, to determine their effectiveness in predicting trends in hydropower generation. The models' accuracy is assessed using Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE). Through this analysis, we find that, on average, the GGM model outperforms the Prophet and ARIMA models, and is more accurate than the Bass Model. This analysis underscores the critical role of precise forecasting in energy planning and suggests further research to validate these results and explore other factors influencing the development of hydroelectric generation.

Keywords:

Subject: Business, Economics and Management - Econometrics and Statistics

1. Introduction

The increase in the world population is directly related to an increase in energy consumption, especially electricity [1,20]. This increased demand for energy, if not met sustainably, can harm the environment, particularly due to air pollution and climate change effects [22] deriving from the burning of fossil fuels such as coal and natural gas [20]. However, fossil fuels, including coal, oil, and natural gas, still serve as primary energy sources worldwide [13]. To contrast this reliance on fossil fuels, interest in renewable energy sources has recently increased significantly worldwide [5]. Renewable energy includes sources that naturally regenerate, such as hydroelectric, solar, wind, and geothermal energy. These sources are far more sustainable and environmentally friendly compared to fossil fuels. With technological advancements, particularly with the initiation of the Fourth Industrial Revolution, the adoption of renewable energy sources is expected to soar. This shift is crucial for alleviating the effects of climate change, greenhouse gas emissions, and increasing energy costs [18].

Hydropower, one of the oldest and most well-researched renewable energy sources, has a history of nearly 150 years. Despite its longstanding presence, innovation in hydropower remains vibrant, with current efforts centered on enhancing plant flexibility via improvements in turbine design, operational strategies, and digitalization. These innovations are intended to help hydropower plants better address the needs of modern power systems, which encounter more variable energy demands and a growing share of intermittent renewable sources. Reservoir-type hydropower plants, in particular, are well-equipped to offer the necessary emissions-free flexibility for today’s power systems [17]. This critical renewable energy source leverages the power of rivers and reservoirs, playing an essential role in electricity supply, particularly in nations with limited resources [28]. Hydropower is an economical and environmentally friendly option for energy production, providing numerous additional benefits such as flood control, irrigation support, and clean drinking water, alongside electricity generation [24]. These characteristics make hydropower an appealing and deserving candidate for increased attention and investment [2]. This explains why hydroelectricity generation rose by nearly 70 TWh (close to 2%) in 2022, reaching 4300 TWh. In fact, hydropower remains the largest renewable electricity source, producing more than all other renewable technologies combined, and is expected to remain the world’s largest source of renewable electricity generation into the 2030s. Therefore, it will continue to play a critical role in decarbonizing the power system and improving system flexibility. It is also acknowledged that, without major policy changes, global hydropower expansion is expected to slow down this decade. The contraction results from slowdowns in the development of projects in China, Latin America, and Europe. However, increasing growth in Asia Pacific, Africa, and the Middle East partly offset these declines. Increasingly erratic rainfall due to climate change is also disrupting hydro production in many parts of the world. In the Net Zero Emissions by 2050 Scenario, hydropower maintains an average annual generation growth rate of nearly 4% from 2023 to 2030, aiming to supply approximately 5500 TWh of electricity per year. As stated in [17] in the last five years the average growth rate was less than one-third of what is required, signaling a need for significantly stronger efforts, especially to streamline permitting and ensure project sustainability. Hydropower plants should be recognized as a reliable backbone of the clean power systems of the future and supported accordingly.

Starting from these pieces of evidence, our study aims to analyze the role of hydroelectric data in countries’ energy transition using the approach of Innovation Diffusion Models [9]. The literature on the application of innovation diffusion models for energy growth processes has been developing significantly in recent years and our paper aims to contribute to this direction. We propose a cross-country analysis of hydropower generation, provide some forecasts based on Innovation Diffusion Models [9], and compare their performance with typical time series models such as ARIMA models [16] and Prophet model [29].

The rest of the paper is organized as follows: Section 2 offers a review of the existing literature, setting the stage by discussing previous research and developments relevant to hydropower. Section 3 outlines the data sources and methods employed in this study. Section 4 presents a detailed analysis and discussion of the results, interpreting the findings concerning current challenges and opportunities for hydropower. Finally, Section 5 provides concluding remarks, summarizing the key insights of the study and offering recommendations for future research and policy actions to enhance the role of hydropower in sustainable energy systems.

2. Background Literature

In the hydroelectric generation forecasting literature, various statistical, econometric, machine learning, and hybrid models have been widely used. These methods differ in methodology, complexity, and performance [15]. The most widely used methods for forecasting hydroelectric generation have been linear time series models such as ARIMA models and their different extensions [8]. For example, in a study using data from India, the authors used ARIMA models to model and forecast hydroelectric generation, which accounted for more than 60% of global renewable energy [19]. The study used various ARIMA models to analyze historical data from 1971-1972 to 2019-20. The researchers determined that the ARIMA(1,1,1) model with drift was suitable to forecast the energy demand of the country. In [25], ARIMA models were used with monthly data obtained from the Son La hydroelectric plant in Vietnam, covering the period from January 2015 to December 2019. Similarly, in [23], data from the official site of the Electricity Regulation and Control Agency (ARCONEL) were analyzed for the years 2000 to 2015, focusing on monthly reports on energy production from hydroelectric plants in Ecuador. The results indicated that the

A R I M A (1, 1, 1) x {(0, 0, 1)}_{12}

model, which incorporated seasonality, best fits the time series data, allowing for forecasts of energy production for one to twelve months ahead. This model was trained using data from 2000 to 2014 and validated with data from January to December 2015, and its forecast for 2020 suggested an increase in monthly production, with actual values falling within the confidence intervals of the ARIMA model’s predictions with annual seasonality.

In [30], the authors introduced a new gray combination optimization model to forecast China’s hydropower generation, using data from 2000 to 2020. They split the data into a training set (2000 to 2015) and a test set (2016 to 2020). The TDGM (three-parameter discrete grey model) outperformed ARIMA and SVM (Support Vector Machines) [?], achieving a low Mean Relative Forecast Percentage Error (MRFPE). Forecast results indicated that China’s hydropower generation could reach 1687.738 billion kWh by 2025, reflecting a 24.5% increase from 2020. In [21], the authors presented a novel ensemble forecast model to predict medium to long-term wind and hydroelectric generation, using data from November 2010 to December 2020. The model involved three phases: Phase I combined ARIMA and Bi-LSTM predictions, Phase II incorporated forecasts for seasonal and off-season periods using the Deliberate Search Algorithm (DSA), and Phase III merged the predictions from both phases. The results showed that the Mean Absolute Error (MAE) for wind and hydropower ranged from 1.97% to 5.52% and 2.3% to 6.42%, respectively, while the Root Mean Square Error (RMSE) ranged from 2.7% to 7.8% and from 2.63% to 8.4%, for timeframes from one week to the next year.

In this paper, we propose to use the different approaches of Innovation Diffusion Models to describe and predict the growth of hydroelectric power. This choice relies on a well-established stream of literature that has employed diffusion models to study renewable energy sources, to understand the dynamics underlying energy transition by using both univariate (see for instance [10]) and bivariate models (see [4]). Recent reviews of this literature may be found for instance in [9], [3], [4], [27].

However, the analyses proposed in the literature have typically focused on renewable energy sources like wind and solar ([10]), whereas hydroelectricity has not been studied in much detail. Moreover, the studies using innovation diffusion models have tried to describe the patterns of growth of these energy technologies, without paying much attention to their forecasting ability compared to other models. In this paper, we try to fill this gap by focusing on hydropower data with a forecasting analysis.

3. Materials and Methods

In this section, we provide details of the data used in the analysis and the models that have been employed for forecasting. Specifically, we offer a description of the Bass, GGM, Prophet models, and ARIMA models.

3.1. Data

The analysis proposed in this paper is based on data from the Energy Institute Statistical Review [6], which covers multiple countries. In North Africa, limited data are in stark contrast to the various start years of hydroelectric projects in different regions, with some countries launching their efforts recently as 2011.

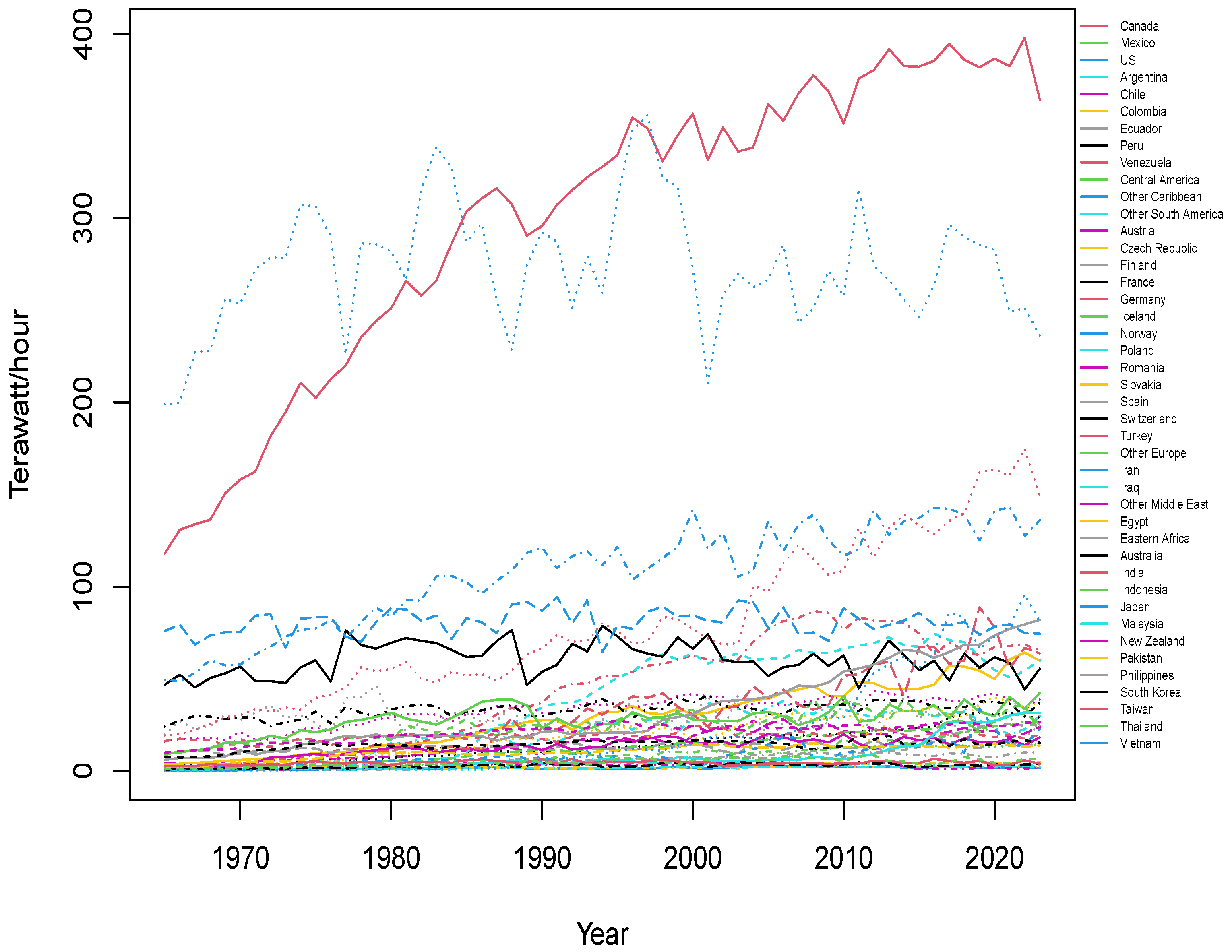
Figure 1 shows hydroelectric generation data for each country considered from 1965 to 2023. The figure indicates that, unlike other countries, Canada and the US have generated a substantial amount of electricity from hydropower, while most countries have maintained similar generation levels. It may be also noticed that India and Norway have significantly increased their hydroelectricity generation, whereas some countries have reduced their reliance on this source.

To analyze the evolution of hydropower in these countries, we have employed a variety of models, starting from diffusion models, namely the Bass model 3.2.1 and GGM 3.2.3, whose performance will be compared with other concurrent models, namely Prophet and ARIMA models.

3.2. Models

This section is dedicated to a description of the models used for the forecasting analysis.

3.2.1. Bass Model

The Bass model (BM) presents a depiction of the life cycle of an innovation, showing the stages of introduction, growth, maturity, and decline. It is crucial to note that this model was initially developed in the realm of marketing science and aims to demonstrate the evolution of a new product’s growth over time, but then it was found out that it is suitable also for studying the diffusion of energy technologies [9]. The model operates on the assumption that two primary sources of information influence consumption decisions: external factors such as the media and advertising, and internal factors such as imitation and learning from others. One notable advantage of the BM is its ability to effectively explain the initial phase of diffusion, which is attributed to the presence of innovators. There is a significant body of literature on the role of innovators, also known as early adopters [26]. However, it is the BM that explicitly accounts for their role. The BM is formally represented by a first-order differential equation.

z^{'} (t) = [p + q \frac{z (t)}{m}] [m - z (t)], t > 0

(1)

Where

z (t)

is the cumulative number of adoptions at time t,

z^{'} (t)

is defined as the variation over time of adoptions. m is the market potential, the maximum number of realizable sales within the diffusion, and its value is assumed to be constant throughout the entire process.

m - z (t)

is proportional to the residual market. The residual market is affected by the coefficients p and q. Parameter p, called innovation coefficient, represents the effect of the external influence, due to the mass media communication and advertising. Parameter q, called imitation coefficient, is the internal influence, whose effect is modulated by the ratio

z (t) / m

. Parameters p and q are utilized to measure the two distinct classifications of consumers mentioned earlier, namely the innovators and the imitators.

The closed-form BM solution can be expressed as

z (t) = m \frac{(1 - e^{- (p + q) t})}{(1 + \frac{q}{p} e^{- (p + q) t})} t > 0

(2)

Three parameters m, p, and q define the dynamics of the diffusion process in terms of cumulative sales, or

z (t)

, in Equation (2). The market potential m, is a scale parameter that enables the modeling of the diffusion process in absolute terms, whereas parameters p and q, as in Equation (2), act on the speed of diffusion.

z (t)

, as given by Equation (2) for a range of parameter values p and q. The cumulative process, as can be seen, has an s-shaped pattern and approaches saturation, denoted by the parameter m, at varying rates based on the values of the parameters p and q [9].

3.2.2. Dynamic Market Potential

After conducting a comprehensive examination of the research conducted by [12], it becomes evident that there exists a potential to generalize the concept of BM taking into account the dynamic nature of the market potential. In light of this, it is possible to formulate the variable

m (t)

in a way that accurately depicts the inherent complexities and fluctuations associated with market dynamics.

z^{'} (t) = m (t) [p + q \frac{z (t)}{m (t)}] [1 - \frac{z (t)}{m (t)}] + m^{'} (t) \frac{z (t)}{m (t)}, t > 0

(3)

Equation (3) characterizes the instantaneous adoptions

z^{'} (t)

as a sum of a BM with

m (t)

and a factor

m^{'} (t) z (t) / m (t)

, which allocates a fraction of the market potential variation

m^{'} (t)

z^{'} (t)

, specifically the growth rate

z (t) / m (t)

. Within Equation (3), the market potential variation

m^{'} (t)

impacts the instantaneous adoptions

z^{'} (t)

, which can either be positive and reinforcing if

m (t)

is increasing, or negative if

m (t)

is decreasing. This demonstrates that the adoption of a product receives an additional advantage from an expanding market potential, while a declining market weakens the process. Equation (3) can be conveniently rearranged as follows.

\frac{z^{'} (t) m (t) - z (t) m^{'} (t)}{m^{2} (t)} = {[\frac{z (t)}{m (t)}]}^{'} = [p + q \frac{z (t)}{m (t)}] [1 - \frac{z (t)}{m (t)}]

(4)

The generalization of BM, where the function

m (t)

depends on time, has closed-from-solution,

z (t) = m (t) \frac{(1 - e^{- (p + q) t})}{(1 + \frac{q}{p} e^{- (p + q) t})}

(5)

Equation (5) clearly demonstrates that

m (t)

is an independent function that influences the dynamics of the diffusion process, represented by parameters p and q. The specific form of

m (t)

can vary depending on the assumptions made about the market potential. In [12] and [11] certain structures for

m (t)

have been proposed. The GGM is based on one of these possibilities.

3.2.3. GGM

In [12] authors postulated a specific specification for

m (t)

, under the assumption that the growth of the market potential is contingent upon a communication process regarding the new product. This process typically precedes the adoption phase and serves the purpose of “building” the market. More precisely, the dynamic market potential

m (t)

is defined according to a structure that resembles a Bass model,

m (t) = K \sqrt{\frac{1 - e^{(p_{c} + q_{c}) t}}{1 + \frac{q_{c}}{p_{c}} e^{(p_{c} + q_{c}) t}}}

(6)

In Equation (6), the parameters

p_{c}

and

q_{c}

govern the communication process. The parameter

p_{c}

characterizes the behavior of innovative consumers who initiate discussions about the new product, while

q_{c}

represents the forces that propagate the information, causing it to become “viral”. The parameter K shows the asymptotic behavior of

m (t)

when all informed consumers ultimately become adopters. The GGM exhibits the following cumulative structure

z (t) = K \sqrt{\frac{1 - e^{(p_{c} + q_{c}) t}}{1 + \frac{q_{c}}{p_{c}} e^{(p_{c} + q_{c}) t}}} \frac{1 - e^{(p_{s} + q_{s}) t}}{1 + \frac{q_{s}}{p_{s}} e^{(p_{s} + q_{s}) t}}, t > 0

(7)

In Equation (7), the cumulative adoptions,

z (t)

, are depicted as the product of two distinct phases, namely, the communication phase with parameters

p_{c}

and

q_{c}

, and the adoption process with parameters

p_{s}

and

q_{s}

3.2.4. Prophet Model

In [29] the authors proposed an innovative model able to handle time series with nonlinear trend, seasonality, and other possible effects appearing in the data. The mathematical components of the Prophet model are defined as,

y (t) = g (t) + s (t) + h (t) + ϵ_{t}

(8)

In Equation (8)

g (t)

is the trend function that models non-periodic changes in the value of the time series,

s (t)

represents periodic changes (e.g., weekly and yearly seasonality), and

h (t)

represents the effects of holidays that occur on potentially irregular schedules over one or more days. The error term

ϵ_{t}

represents any idiosyncratic changes that are not accommodated by the model, for which we assume that

ϵ_{t}

is normally distributed. In this approach, both the nature of the time series (piece-wise trends, multiple seasonality, floating holidays) as well as the challenges involved in forecasting are accounted for. The first one is nonlinear growth denoted by

g (t)

in Equation (8). This sort of growth is typically modeled by the logistic growth model, defined as

g (t) = \frac{C}{a + e x p (- k (t - m))}

(9)

where C is the carrying capacity, k the growth rate, and m an offset parameter. If the trend is linear then the growth model is defined as

g (t) = (k + a {(t)}^{T} δ) t + (m + a {(t)}^{T} γ)

Whereas before k is the growth rate,

δ

has the rate adjustments, m is the offset parameter, and

γ_{j}

is set to

- s_{j} δ_{j}

to make the function continuous.

s_{j}

is defined as the change points. The seasonality effect is approximated by a standard Fourier series given as,

s (t) = \sum_{n = 1}^{N} [a_{n} cos (\frac{2 π n t}{P}) + b_{n} sin (\frac{2 π n t}{P})]

(10)

In Equation (10), N is the count of Fourier components, P shows periods, and

a_{n}

b_{n}

represents Fourier coefficients. The above components then amalgamate into an additive model. The effect of

h (t)

on holidays and events that provide predictable shocks often does not follow any specific periodic pattern [29].

3.2.5. Auto-Regressive Integrated Moving Average Model (ARIMA)

One of the traditional statistical techniques that is used frequently for time series forecasting is the ARIMA model (Auto Regressive Integrated Moving Average) [16]. To model and predict time series data, it integrates moving average (MA), differencing (I), and autoregressive (AR) components. ARIMA models accommodate trends and seasonality, as well as linear relationships within the data. A general ARIMA model can be written as

y_{t}^{'} = c + ϕ_{1} y_{t - 1}^{'} + \dots + ϕ_{p} y_{t - p}^{'} + θ_{1} ε_{t - 1} + \dots + θ_{q} ε_{t - q} + ε_{t},

(11)

where

y_{t}^{'}

is the differenced series, and the “predictors” on the right-hand side include both lagged values of

y_{t}

and lagged error terms. We call this an ARIMA(

p, d, q

) model, where

$p =$ order of the autoregressive part;
$d =$ degree of first differencing involved;
$q =$ order of the moving average part.
$ε =$ is called the white nose and is assumed to be independent and identically distributed variables sampled from a normal distribution with zero mean.

To form more complicated models, the backshift notation is often used. For example, Equation (11) can be written in backshift notation as

(1 - ϕ_{1} B - \dots - ϕ_{p} B^{p}) {(1 - B)}^{d} y_{t} = c + (1 + θ_{1} B + \dots + θ_{q} B^{q}) ε_{t}

(12)

Where

(1 - ϕ_{1} B - \dots - ϕ_{p} B^{p})

A R (p)

part,

{(1 - B)}^{d}

is d differences, while

(1 + θ_{1} B + \dots + θ_{q} B^{q})

is MA(q) part. Selecting appropriate values for p, d, and q can be difficult, but usually, this is performed by using selection criteria such as the AIC or error measures like the Root Mean Squared Error (RMSE) [16].

3.3. Evaluation Metrics

Three evaluation metrics are considered to measure the performance of the selected models after careful consideration: Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE).

3.3.1. Mean Absolute Error (MAE)

MAE works on averaging the squared discrepancies between expected and actual values. The Mean Absolute Error, or MAE, provides a quantitative assessment of prediction accuracy while highlighting the greater errors [16].

MAE = \frac{1}{n} \sum_{i = 1}^{n} (| y_{i} - {\hat{y}}_{i} |)

(13)

3.3.2. Root Mean Squared Error (RMSE)

To understand RMSE, it is necessary to first show the formula for Mean Squared Error (MSE). MSE calculates the average of the squared discrepancies between the predicted and actual values. It provides a quantitative assessment of prediction accuracy, with a greater emphasis on larger errors [7].

MSE = \frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}

(14)

Taking the square root of the MSE gives the Root Mean Squared Error (RMSE):

RMSE = \sqrt{MSE}

(15)

3.3.3. Mean Absolute Percentage Error (MAPE)

The MAPE averages percentage difference between the expected and actual values is measured by MAPE (Mean Absolute Percentage Error), which offers a comparative assessment of predicting accuracy [14].

MAPE = \frac{100 %}{n} \sum_{i = 1}^{n} |\frac{y_{i} - {\hat{y}}_{i}}{y_{i}}|

(16)

4. Results

In the results section, we evaluate the effectiveness of the models proposed in predicting hydropower generation data. This evaluation examines how well each model captures the observed patterns and trends in hydroelectric generation in different regions and periods. We consider metrics such as goodness of fit, accuracy, and predictive capability to identify the model that most accurately represents the data. The detailed findings are presented in the following subsections.

4.1. American Countries

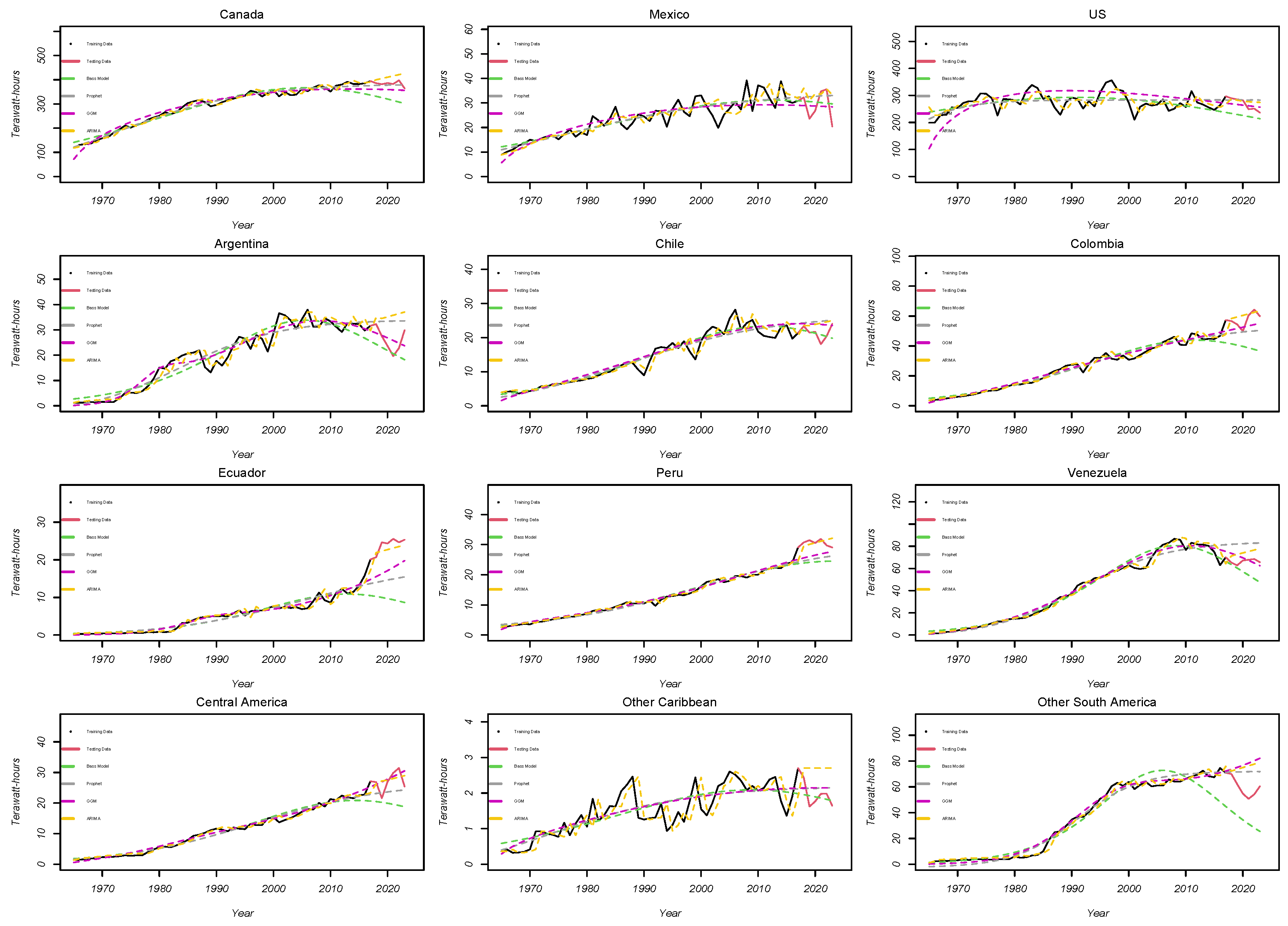
In Figure 2, we illustrate a comparison between four forecasting models—Bass, Prophet, ARIMA, and GGM using data from American countries spanning the years 1965 to 2023. This dataset is split into a training set of 52 points (marked in black) and a test set of 7 points (marked in red), allowing us to assess each model’s performance across various contexts. The figure demonstrates the performance of each model in the countries analyzed. We may notice that the Bass model, displayed in green, generally underestimates data during rapid growth periods but performs well in countries like Mexico, where the data has a peak followed by a decline. Conversely, the GGM, shown in purple, often surpasses the Prophet (blue) and ARIMA (yellow) models, especially in North American countries such as Mexico and the US. This highlights that the GGM may be better suited for capturing complex trends and regional dynamics. The Prophet model is more accurate in scenarios of continuous growth but tends to misinterpret fluctuating data, resulting in either overestimation or underestimation. This behavior is seen consistently across different datasets. The Bass model once again underestimates during rapid growth but performs well in regions like the Caribbean, Chile, and Argentina, where data peaks followed by a decline. In contrast, the GGM consistently outperforms the Prophet and ARIMA models, particularly in Argentina, Ecuador, the Caribbean, and Venezuela. Although these visual insights are valuable, they must be supported by quantitative evaluations for a thorough assessment. Further analysis using quantitative metrics from the model-fitting results section is necessary to validate these observations and provide a complete evaluation of the models’ performance.

4.2. European Countries

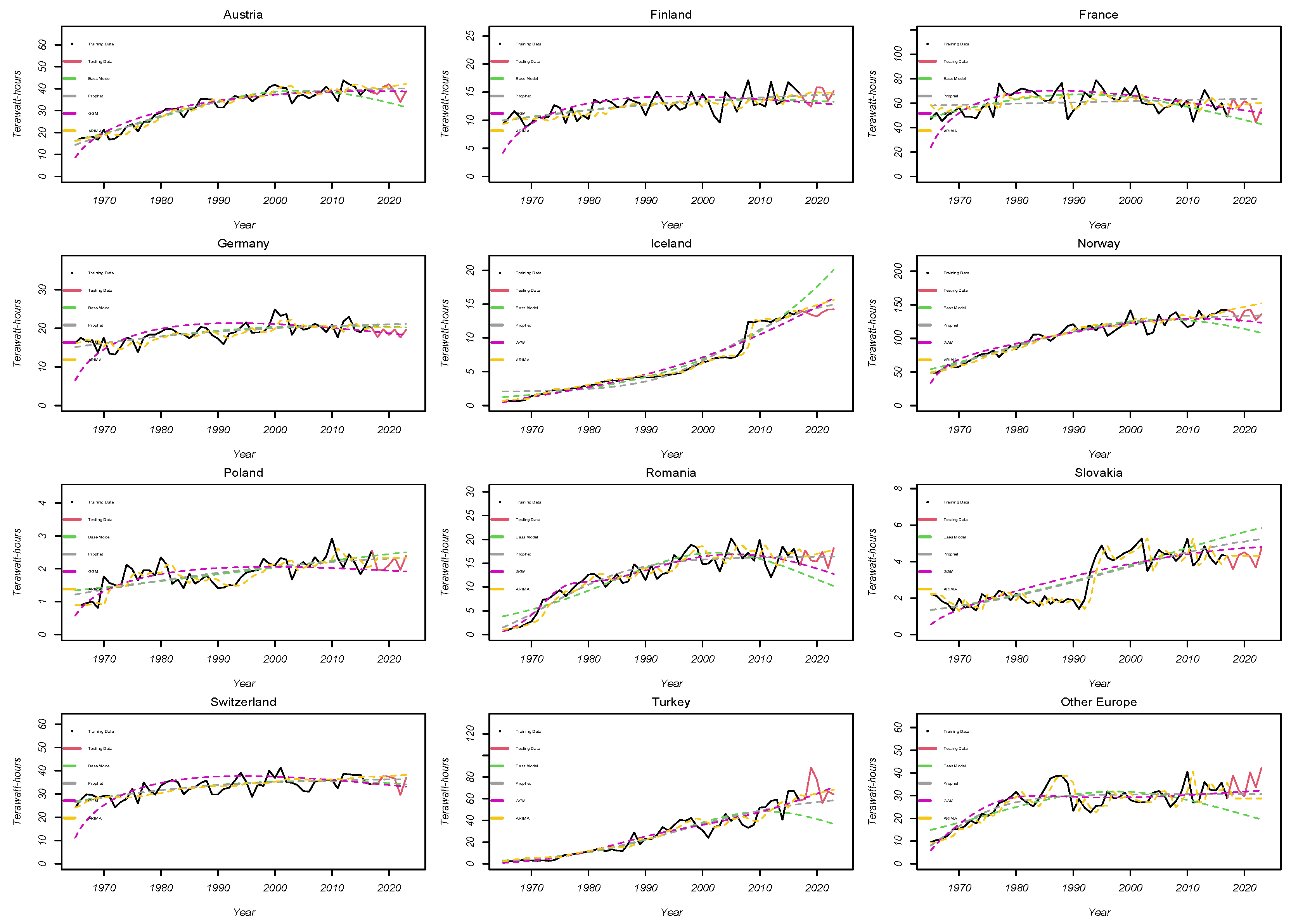
Figure 3 shows a comparative analysis of the models applied to data from European countries. In the European case, it is evident the difficulty in determining the best-performing model due to the striking similarity in the hydroelectric generation patterns in these developed nations. This uniformity in hydroelectric power output causes all models to closely fit the data. Figure 3 illustrates that almost all models are in close agreement with the data, suggesting stability and minimal fluctuations in hydroelectric production in these European countries. To better assess the performance of the models, specific countries with more significant deviations have been selected. For instance, in Austria, the GGM and Prophet models exhibit similar performance, while the Bass model underestimates the data. In contrast, in countries like Iceland, where hydroelectric production is on the rise, all models overestimate the data. However, the GGM shows the closest alignment with the original data among the four models. Visually, the GGM’s performance is notably better compared to the Bass and Prophet models in most countries. This analysis will include more metrics to provide a clearer distinction between models, helping to identify the most precise and reliable model to forecast hydroelectric generation in European countries.

4.3. Asian and Middle East Countries

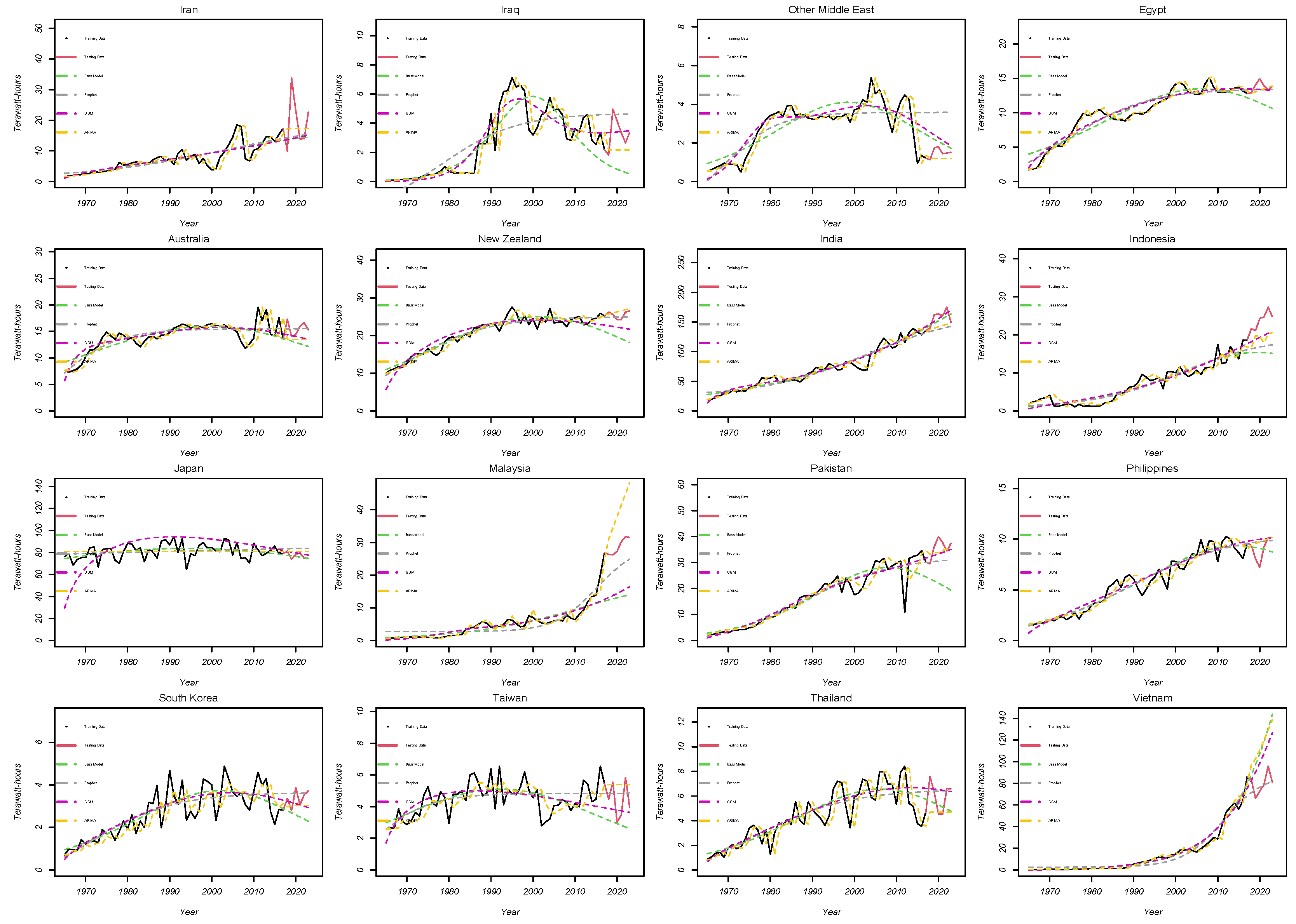
Figure 4 presents the alignment results of the hydroelectric generation model for Middle Eastern and Asian countries where data is available. Since hydroelectric generation in the Middle Eastern region tends to be lower compared to other regions, we combined the Middle Eastern countries for a more coherent analysis. The results show that in Middle Eastern countries, particularly in Iran, all models performed similarly. However, in Iraq and Egypt, the GGM model outperformed the others significantly, while the Bass and Prophet models occasionally either overestimated or underestimated hydroelectric generation. To further refine this analysis, we will evaluate performance metrics to determine which model offers the best predictive ability.

In contrast, Figure 4 also highlights the fit of the model for hydroelectric generation in Asian countries, including Australia, where substantial investments in hydroelectric projects have led to significant increases over time. Although most models fit the data well, there are noticeable performance differences. For instance, the GGM generally outperforms the Prophet and Bass models across most countries, except Vietnam, where performance varies. Similarly to the Middle Eastern countries, the Bass and Prophet models sometimes overestimate or underestimate hydroelectric generation. To complete this analysis, performance metrics will be considered to identify the best model in terms of prediction ability.

4.4. Evaluation Metrics

Table 1 presents the average performance metrics, namely Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE), for the evaluated models. The Bass model demonstrates an average MAE of approximately 9.7652, indicating that on average the model deviates about 9.7652 units from the actual hydropower generation values. The corresponding average RMSE of 10.456 reflects the typical magnitude of errors, while the MAPE, averaging around 24.525%, represents the average percentage deviation of the model predictions from the actual hydroelectric generation values. However, the GGM exhibits superior performance with an average MAE of approximately 5.1979, indicating smaller deviations from the actual hydroelectric generation values compared to the Bass model. The average RMSE of 5.898 suggests smaller errors in magnitude, and the MAPE, averaging 15.498%, indicates a lower average percentage deviation from the actual values. Regarding model performance, the Prophet Model shows moderate results, with an average MAE of approximately 5.216, falling between the Bass Model and the GGM. The corresponding average RMSE of 6.0988 represents the typical magnitude of errors, while the MAPE, averaging around 18.796%, represents the average percentage deviation from the actual hydroelectric generation values. The ARIMA model also shows strong performance, with an average MAE of approximately 5.788. This suggests smaller deviations from the actual values compared to the Bass model. The average RMSE of 6.7488 indicates the typical error magnitude, and the MAPE, averaging 16.1219%, suggests a lower average percentage deviation from the actual values. Overall, the GGM demonstrates superior performance compared to the Bass, ARIMA, and Prophet models in terms of average error metrics, suggesting that it may be the most accurate model for predicting hydropower generation in the evaluated dataset.

Table 2 presents a comparison of the mean absolute percentage error (MAPE) for the four models. The rows represent the models being evaluated, while the columns denote the models they are compared against. Starting with the Prophet model, it outperformed the Bass model in 30 of the 43 countries evaluated. Furthermore, Prophet did better than the ARIMA model in 21 countries and surpassed GGM in 17 countries. Next, looking at the ARIMA model, we see that it was outperformed by the Prophet model in 22 countries. The Bass Model outperformed ARIMA in 31 countries, and GGM did better in 17 countries. However, the GGM showed impressive results. It outperformed the Prophet model in 26 countries, the Bass model in 33 countries, and the ARIMA model in 26 countries. This highlights GGM’s consistent performance across different regions. The Bass Model had more mixed results. It was outperformed by the Prophet model in 13 countries, by the GGM in 10 countries, and by the ARIMA model in 12 countries.

From these results, it is clear that GGM generally has a lower MAPE, which indicates that it provides more accurate forecasts for hydropower data compared to the other models. This suggests that GGM is the most reliable model for predicting hydroelectric generation in various countries, making it a valuable tool for energy planning and forecasting.

By examining these comparisons, we can see that, while each model has its strengths, GGM consistently delivers the most accurate predictions. This analysis underscores the importance of selecting the right model for forecasting to ensure effective energy planning and management (the Appendix provides a detailed breakdown of the results).

5. Conclusions

The global community is currently grappling with critical challenges posed by climate change and the increasing demand for reliable, sustainable energy sources. The shift to renewable energy is widely considered a primary solution to these urgent issues. As a result, accurately predicting the rise of renewable energy sources has become essential for effective energy planning and management. Among these, hydroelectric still plays a central role.

Our research conducted an in-depth analysis of hydropower generation data from 43 countries, which we categorized into five distinct regions, covering the years 1965 to 2023. This extensive data set allowed us to evaluate and compare various models for forecasting hydroelectric production patterns in different geographic regions, including the Americas, Africa, Europe, Asia, and the Middle East. Significant variations in data generation were observed within each region. To address this, we used a train-test data split, using 53 data points for training and 6 points for testing, out of a total of 59.

In highly developed countries, maintaining consistent levels of power generation is challenging due to various factors, while in less developed countries, power generation tends to increase over time. From our graphical analysis, we observed notable changes in power generation in certain countries. The ARIMA model performed well in these scenarios, while the Bass model was more effective with increasing datasets. The Prophet model generated clear graphs with stable data, and the GGM model outperformed the others in cases with small variations in power generation, whether increasing or decreasing.

Among the models studied, the GGM consistently proved superior in accurately predicting hydroelectric power generation. It effectively captured complex nonlinear patterns in the data, and its performance was validated through quantitative metrics such as mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE). On average, across all countries, the GGM model (5.1979 MAE, 5.8983 RMSE, and 15.4978 MAPE) slightly outperformed the Prophet (5.2163 MAE, 6.0988 RMSE, and 18.7966 MAPE) and ARIMA (5.7881 MAE, 6.7488 RMSE, and 16.1219 MAPE) models and was significantly more accurate than the Bass Model (9.7652 MAE, 10.4561 RMSE, and 24.5253 MAPE). In all countries examined, the GGM consistently achieved lower MAPE scores than other models, demonstrating its greater reliability and precision in the prediction of hydroelectric generation.

Although the Bass model showed notable success in specific countries with distinctive data trends, such as Chile and regions in eastern Africa, the GGM outperformed all other models in a broader range of regions and conditions.

In summary, the findings of our analysis show an interesting ability of the GGM to capture the evolutionary patterns of hydropower in most analyzed countries. This opens a new perspective on the use of this kind of model, which has been generally employed with descriptive purposes [9], rather than predictive. In this sense, hydropower data have offered the possibility to deal with a variety of patterns, with a growing trend, with a flat, or, in some cases, with a declining behavior for which a sufficiently flexible structure is necessary. Whereas the Bass Model does not have this flexibility, the GGM can capture the nonlinearities of the data efficiently. These findings highlight the critical importance of models like the GGM in enhancing our understanding and forecasting capabilities in the context of energy transitions. The insights gained from these models can equip policymakers and energy planners to make more informed decisions, steering their countries toward sustainable energy futures on a global scale.

Author Contributions

Conceptualization, M.G., F.A. and L.F.; methodology, M.G.; software, M.G.; validation, F.A., M.G., and L.F.; formal analysis, F.A., and M.G.; investigation, M.G., and L.F.; resources, F.A. and M.G.; data curation, F.A.; writing–original draft preparation, F.A. and M.G.; writing–review and editing, M.G and F.A.; visualization, F.A. and M.G.; supervision, M.G., and L.F.; project administration, F.A., G.M., and L.F.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data used in this study is available at https://www.energyinst.org/statistical-review

Conflicts of Interest

The authors declare no conflicts of interest.

Table A1. Overall models results.

Country	Model	MAE	MSE	RMSE	MAPE
Canada	BM	66.0842697	4504.8002387	67.1178087	17.2188732
	GGM	24.4790566	689.5971616	26.2601821	6.3296417
	Prophet	10.1587427	130.9905848	11.4451118	2.6491495
	ARIMA	30.1045593	1144.9760207	33.8374943	7.9536895
Mexico	BM	5.2454048	33.5386168	5.7912535	20.2788509
	GGM	5.2638338	32.0753076	5.6635066	19.3594590
	Prophet	5.3898187	48.1223380	6.9370266	22.6726527
	ARIMA	5.3937792	47.4668499	6.8896190	22.6722391
US	BM	41.9250130	1974.4022465	44.4342463	15.4393961
	GGM	16.5125208	293.9787199	17.1458076	6.1989374
	Prophet	20.3072578	739.1742449	27.1877591	8.2243748
	ARIMA	16.4344742	472.9964088	21.7484806	6.6508693
Argentina	BM	5.0460849	39.3179516	6.2704028	17.9021872
	GGM	3.5565751	17.1466323	4.1408492	14.3646525
	Prophet	7.4901847	75.2792764	8.6763631	32.6302025
	ARIMA	9.6669316	114.1637288	10.6847428	41.3217673
Chile	BM	1.4997635	4.5428143	2.1313879	6.9577939
	GGM	2.5056871	9.4229953	3.0696898	12.5504025
	Prophet	3.2257494	14.4774182	3.8049203	16.0332807
	ARIMA	2.6240310	10.9359677	3.3069575	13.1871190
Colombia	BM	18.4774657	374.9943061	19.3647697	31.4826222
	GGM	5.5118651	36.9241645	6.0765257	9.3132428
	Prophet	8.0729056	83.5419017	9.1401259	13.4896407
	ARIMA	3.9614912	26.2897768	5.1273557	7.3376092
Ecuador	BM	14.7008842	220.3509188	14.8442217	60.4232303
	GGM	6.6170600	45.1676416	6.7206876	27.2925960
	Prophet	9.4465509	90.9595007	9.5372690	38.8338915
	ARIMA	1.6990184	3.1618271	1.7781527	6.9788381
Peru	BM	6.2932649	40.7851161	6.3863226	20.4936958
	GGM	3.8855863	17.3878519	4.1698743	12.5751891
	Prophet	5.0903552	27.7682123	5.2695552	16.5320012
	ARIMA	1.3965065	2.8074849	1.6755551	4.6407140
Venezuela	BM	10.6717530	157.5804984	12.5531071	15.9292858
	GGM	4.4761906	29.4964444	5.4310629	6.8774296
	Prophet	16.2060473	265.5713985	16.2963615	24.5748624
	ARIMA	8.4555605	75.9650872	8.7157953	12.8184292
Central America	BM	7.2916267	64.8107618	8.0505131	25.8424549
	GGM	2.5196772	10.1968499	3.1932507	10.1386136
	Prophet	3.8625350	19.7255155	4.4413416	13.6563005
	ARIMA	2.5228483	9.5054117	3.0830848	9.9951753
Other Caribbean	BM	0.2223351	0.0666057	0.2580809	11.4291869
	GGM	0.3374809	0.1347491	0.3670818	18.8181172
	Prophet	0.3338083	0.1316452	0.3628294	18.5875380
	ARIMA	0.7977321	0.7133839	0.8446205	44.6848357
Other South America	BM	25.6681849	686.3453703	26.1981940	43.6293782
	GGM	18.9569180	427.9374278	20.6866485	34.0270408
	Prophet	12.9704927	209.1748393	14.4628780	23.4705416
	ARIMA	16.9093777	347.9695683	18.6539424	30.4604138

Country	Model	MAE	MSE	RMSE	MAPE
Austria	BM	5.4462594	35.4085258	5.9505063	13.7619874
	GGM	1.8915194	6.3805977	2.5259845	5.0426955
	Prophet	2.3036428	8.4475921	2.9064742	6.2538154
	ARIMA	2.9182853	14.0803561	3.7523801	7.9773424
Czech Republic	BM	0.1859873	0.0584269	0.2417166	9.5312934
	GGM	0.1856165	0.0584217	0.2417059	9.5394358
	Prophet	0.2360734	0.0917547	0.3029104	12.6215928
	ARIMA	0.2622903	0.0869694	0.2949058	12.3345700
Finland	BM	1.3664158	2.7834548	1.6683689	9.0884168
	GGM	1.5660685	3.7213446	1.9290787	10.3300331
	Prophet	1.2295043	1.6839889	1.2976860	8.7788720
	ARIMA	1.2198664	1.9634556	1.4012336	8.9658790
France	BM	11.0141810	149.3647609	12.2214877	18.5493976
	GGM	5.7548662	40.5020560	6.3641226	10.3617908
	Prophet	7.1390507	89.6719836	9.4695292	14.1733833
	ARIMA	5.8163152	60.7172215	7.7921256	11.2178639
Germany	BM	1.5881680	3.4403264	1.8548117	8.7309180
	GGM	0.9718622	1.0544572	1.0268677	5.1690873
	Prophet	2.2771408	6.0335442	2.4563274	12.4003265
	ARIMA	1.4781678	3.0324464	1.7413921	8.1353358
Iceland	BM	4.2146884	19.2031891	4.3821443	30.5155443
	GGM	1.0431425	1.3488512	1.1614005	7.5607219
	Prophet	0.7045184	0.6009440	0.7752058	5.1561171
	ARIMA	1.1865707	1.5349012	1.2389113	8.6416974
Norway	BM	22.3395177	552.3940465	23.5030646	16.2979338
	GGM	10.2275571	139.3417575	11.8043110	7.3584154
	Prophet	6.5525203	48.6022193	6.9715292	4.8479555
	ARIMA	12.6250792	214.7500321	14.6543520	9.6042767
Poland	BM	0.3303318	0.1353097	0.3678446	16.2736275
	GGM	0.1861305	0.0711348	0.2667110	8.0822982
	Prophet	0.2154036	0.0652897	0.2555185	10.7285196
	ARIMA	0.2317687	0.0767290	0.2770000	11.5604302
Romania	BM	4.9826463	27.7820157	5.2708648	29.8400631
	GGM	2.6815349	9.8874835	3.1444369	15.6545919
	Prophet	1.3915730	2.2479552	1.4993183	8.6646793
	ARIMA	1.3473533	3.0170228	1.7369579	8.8558633
Slovakia	BM	1.4677063	2.3046143	1.5180956	36.3304547
	GGM	0.5577166	0.4780515	0.6914127	14.4784880
	Prophet	0.9258432	1.0150172	1.0074806	23.3135901
	ARIMA	0.3487080	0.1960251	0.4427472	8.9073703
Spain	BM	4.8372902	39.5747504	6.2908466	22.2596955
	GGM	9.7003960	124.0123650	11.1360839	43.1468892
	Prophet	4.9742992	41.5867009	6.4487751	22.9461819
	ARIMA	4.8192681	36.8795948	6.0728572	21.8419873
Switzerland	BM	2.6132591	8.5664982	2.9268581	7.5833502
	GGM	3.0125261	10.6347716	3.2610998	8.5523374
	Prophet	1.9552595	8.5733463	2.9280277	6.0794828
	ARIMA	2.3194117	13.5686762	3.6835684	7.3122751
Turkey	BM	28.4400760	924.2676053	30.4017698	39.9405230
	GGM	9.9675826	171.1472200	13.0823247	13.4455122
	Prophet	12.1743337	267.9655743	16.3696541	15.7275200
	ARIMA	9.3296113	155.8771469	12.4850770	12.5526322
Other Europe	BM	14.9316052	248.9817963	15.7791570	40.1621697
	GGM	5.0266596	38.9922987	6.2443814	12.8857958
	Prophet	5.8329177	51.2867408	7.1614762	14.9191503
	ARIMA	7.4257156	75.9957521	8.7175542	19.2168466

Country	Model	MAE	MSE	RMSE	MAPE
Iran	BM	6.9845990	94.0041205	9.6955722	29.8907715
	GGM	6.9621666	91.2623229	9.5531316	30.1792819
	Prophet	6.9486845	86.4862953	9.2998008	31.1460150
	ARIMA	7.0090000	69.7343173	8.3507076	36.9366992
Iraq	BM	2.5826157	7.7512828	2.7841126	72.8283569
	GGM	0.8142556	1.0241314	1.0119938	28.5069276
	Prophet	1.3566285	2.5682044	1.6025618	53.8265823
	ARIMA	1.3311835	2.4834816	1.5759066	35.3691181
Other Middle East	BM	0.4954593	0.3513755	0.5927693	36.5357261
	GGM	0.6865652	0.5995384	0.7742986	49.5678705
	Prophet	2.0667063	4.3259500	2.0798918	141.9515216
	ARIMA	0.3383080	0.1461239	0.3822616	21.0196483
Egypt	BM	2.5110039	6.9451962	2.6353740	17.9827015
	GGM	0.6452614	0.6113224	0.7818711	4.5618663
	Prophet	0.6421577	0.6217804	0.7885305	4.5254181
	ARIMA	0.6122890	0.6886871	0.8298717	4.2852172
Eastern Africa	BM	0.7572179	0.9703197	0.9850481	1.0499911
	GGM	0.6716996	0.9471116	0.9731966	0.9361015
	Prophet	5.2784516	40.4743566	6.3619460	6.7510398
	ARIMA	6.4304142	52.6912961	7.2588771	8.3140052
Australia	BM	2.7970137	9.3485534	3.0575404	17.4598564
	GGM	1.7075183	4.1138105	2.0282531	10.4882302
	Prophet	1.0355469	1.3720416	1.1713418	6.6322687
	ARIMA	2.1032379	5.7853018	2.4052654	12.9935551
India	BM	10.8661305	139.3920315	11.8064403	6.7774007
	GGM	9.4595922	128.0283392	11.3149609	6.0529437
	Prophet	19.9960172	507.5936439	22.5298390	12.2355462
	ARIMA	15.4506733	347.9091390	18.6523226	9.3586446
Indonesia	BM	8.6518393	79.3014666	8.9051371	35.5816079
	GGM	4.3706414	21.0994345	4.5934121	17.8933986
	Prophet	7.0656199	53.0799937	7.2856018	29.0442821
	ARIMA	4.8304685	26.8643168	5.1830799	19.7830646
Japan	BM	2.1477368	6.7294859	2.5941253	2.7466141
	GGM	2.5287287	10.9769519	3.3131483	3.3744494
	Prophet	6.7437972	53.2167127	7.2949786	8.8918553
	ARIMA	4.0173795	23.6275183	4.8608146	5.3466671
Malaysia	BM	15.6746804	249.1243383	15.7836732	54.1055571
	GGM	14.1350465	201.5822452	14.1979662	48.8989211
	Prophet	6.3201616	40.7913102	6.3868075	21.8257963
	ARIMA	10.8076573	130.9042179	11.4413381	36.7537446
New Zealand	BM	6.1320725	39.4782035	6.2831683	23.8990721
	GGM	3.3648502	12.4139614	3.5233452	13.0549705
	Prophet	1.0648053	1.2768798	1.1299910	4.1288790
	ARIMA	1.0896510	1.7940917	1.3394371	4.3811396
Pakistan	BM	14.2613183	220.9642790	14.8648673	38.9999476
	GGM	3.1400424	13.7241215	3.7046081	8.5777542
	Prophet	5.5001061	37.5695582	6.1294011	14.7370059
	ARIMA	2.9634511	11.8654716	3.4446294	8.2557543
Philippines	BM	1.0149268	1.4040747	1.1849366	11.7601556
	GGM	1.0009784	1.9877948	1.4098918	12.6727268
	Prophet	0.9157312	1.5913179	1.2614745	11.5093363
	ARIMA	0.7970325	1.4894786	1.2204420	10.2586298
South Korea	BM	0.8503699	0.9464235	0.9728430	23.8664714
	GGM	0.4354003	0.2775283	0.5268096	12.3352467
	Prophet	0.3419239	0.1828225	0.4275775	11.0047753
	ARIMA	0.4476506	0.2740110	0.5234606	12.5720995

Country	Model	MAE	MSE	RMSE	MAPE
Taiwan	BM	1.5197248	3.3751510	1.8371584	30.9698589
	GGM	0.9684150	1.4439601	1.2016489	20.3520254
	Prophet	1.0213260	1.2629225	1.1237982	26.6071623
	ARIMA	1.2032583	2.0592151	1.4349966	33.3744756
Thailand	BM	1.2782954	1.9572457	1.3990160	20.3053724
	GGM	0.9296723	1.4679627	1.2115951	18.2717879
	Prophet	0.8890638	1.4179258	1.1907669	17.3762354
	ARIMA	1.4399657	3.0686854	1.7517664	21.3886357
Vietnam	BM	34.4984843	1478.5136118	38.4514449	43.9377585
	GGM	24.2945265	767.5679138	27.7050160	31.2298631
	Prophet	6.6473449	76.9770441	8.7736563	8.0971371
	ARIMA	36.7219175	1513.9384908	38.9093625	47.0253358

References

Aminifar, F.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A.; Al-Turki, Y. The proliferation of solar photovoltaics: Their impact on widespread deployment of electric vehicles. IEEE Electrification Magazine, 2020; 8, 79–91. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9185064.
Bakis, R. The current status and future opportunities of hydroelectricity. Energy Sources, Part B, 2007; 2, 259–266. https://www.tandfonline.com/doi/pdf/10.1080/15567240500402958.
Bessi, A.; Guidolin, M.; Manfredi, P. Diffusion of renewable energy for electricity: An analysis for leading countries. In International Conference on Time Series and Forecasting, 2021, 291–305, Springer. https://link.springer.com/chapter/10.1007/978-3-031-14197-3_19.
Bessi, A.; Guidolin, M.; Manfredi, P. The role of gas on future perspectives of renewable energy diffusion: Bridging technology or lock-in? Renewable and Sustainable Energy Reviews, 2021, 152, 111673. https://www.sciencedirect.com/science/article/pii/S1364032121009473.
de Freitas Cavalcanti, J. T.; de Lima, J. G.; do Nascimento Melo, M. R.; Monteiro, E. C. B.; Campos-Takaki, G. M. Fossil fuels, nuclear energy and renewable energy. Seven Editora, 2023. https://sevenpublicacoes.com.br/index.php/editora/article/view/1693.
Energy Institute, Statistical Review of World Energy. Energy Institute, 2024. Available at: https://www.energyinst.org/statistical-review. 2024-06-17.
Geem, Z. W.; Roper, W. E. Energy demand estimation of South Korea using artificial neural network. Energy Policy, 2009, 37, 4049–4054. https://www.sciencedirect.com/science/article/pii/S0301421509003218.
Ghadimi, N.; Akbarimajd, A.; Shayeghi, H.; Abedinia, O. Two stage forecast engine with feature selection technique and improved meta-heuristic algorithm for electricity load forecasting. Energy, 2018, 161, 130–142. https://www.sciencedirect.com/science/article/pii/S0360544218313859.
Guidolin, M. Innovation Diffusion Models: Theory and Practice. John Wiley & Sons, 2023. https://www.wiley.com/en-au/Innovation+Diffusion+Models%3A+Theory+and+Practice-p-9781119756231.
Guidolin, M.; Mortarino, C. Cross-country diffusion of photovoltaic systems: Modelling choices and forecasts for national adoption patterns. Technological Forecasting and Social Change, 2010, 77, 279–296. https://www.sciencedirect.com/science/article/pii/S0040162509000997.
Guseo, R.; Guidolin, M. Cellular automata with network incubation in information technology diffusion. Physica A: Statistical Mechanics and its Applications, 2010, 389, 2422–2433. https://www.sciencedirect.com/science/article/pii/S0378437110001317.
Guseo, R.; Guidolin, M. Modelling a dynamic market potential: A class of automata networks for diffusion of innovations. Technological Forecasting and Social Change, 2009, 76, 806–820. https://www.sciencedirect.com/science/article/pii/S0040162508001807.
He, P.; Ni, X. Renewable energy sources in the era of the fourth industrial revolution: A perspective of civilization development. In Journal of Physics: Conference Series, 2022, 2301, 012030. IOP Publishing. https://iopscience.iop.org/article/10.1088/1742-6596/2301/1/012030/meta.
Herrera, G. P.; Constantino, M.; Tabak, B. M.; Pistori, H.; Su, J.-J.; Naranpanawa, A. Long-term forecast of energy commodities price using machine learning. Energy, 2019, 179, 214–221. https://www.sciencedirect.com/science/article/pii/S036054421930708X.
Huang, J.; Tang, Y.; Chen, S. Energy demand forecasting: Combining cointegration analysis and artificial intelligence algorithm. Mathematical Problems in Engineering, 2018, 1–13. https://onlinelibrary.wiley.com/doi/full/10.1155/2018/5194810.
Hyndman, R. J.; Athanasopoulos, G. Forecasting: Principles and Practice. OTexts, 2018. https://otexts.com/fpp3/.
International Energy Agency, “Hydroelectricity,” International Energy Agency, Available online: https://www.iea.org/energy-system/renewables/hydroelectricity ( Aug. 30, 2024).
Kabeyi, M. J. B.; Olanrewaju, O. A. Sustainable energy transition for renewable and low carbon grid electricity generation and supply. Frontiers in Energy Research, 2022, 9, 1032. https://www.frontiersin.org/journals/energy-research/articles/10.3389/fenrg.2021.743114/full.
Karumanchi, H.; Mathew, S. Forecasting of hydropower generation of India using autoregressive integrated moving average model. Journal of Algebraic Statistics, 2022, 13, 3124–3128. https://publishoa.com/index.php/journal/article/view/991.
Lizunkov, V.; Politsinskaya, E.; Malushko, E.; Kindaev, A.; Minin, M. Population of the world and regions as the principal energy consumer. International Journal of Energy Economics and Policy, 2018, 8, 250–257. https://www.zbw.eu/econis-archiv/bitstream/11159/2120/1/1028134991.pdf.
Malha n, P.; Mittal, M. A novel ensemble model for long-term forecasting of wind and hydropower generation. Energy Conversion and Management, 2022, 251, 114983. https://www.sciencedirect.com/science/article/pii/S0196890421011596.
Malhotra, R. Fossil energy: Introduction. In Fossil Energy, 2020, 1–4. https://link.springer.com/referenceworkentry/10.1007/978-1-4939-9763-3_920.
Mite-León, M.; Barzola-Monteses, J. Statistical model for the forecast of hydropower production in Ecuador. International Journal of Renewable Energy Research, 2028, 8, 1130–1137. https://www.sciencedirect.com/science/article/abs/pii/0040162577900312.
Office of Energy Efficiency & Renewable Energy, Title of the document or webpage. U.S. Department of Energy, 2022. Available at: https://www.energy.gov/eere. 2024-08-27.
Polprasert, J.; Nguyen, V. A. H.; Charoensook, S. N. Forecasting models for hydropower production using ARIMA method. In 20219th International Electrical Engineering Congress (IEECON),2021 197–200. IEEE. https://ieeexplore.ieee.org/abstract/document/9440293.
Rogers, E. M. Diffusion of Innovations, New York: The Free Press, 2003. https://www.taylorfrancis.com/chapters/edit/10.4324/9780203887011-36/diffusion-innovations-everett-rogers-arvind-singhal-margaret-quinlan.
Savio, A.; De Giovanni, L.; Guidolin, M. Modelling energy transition in Germany: An analysis through ordinary differential equations and system dynamics. Forecasting, 2022, 4, 438–455. https://www.mdpi.com/2571-9394/4/2/25.
Shamout, M. D.; Khamkar, K. A.; Lal, A.; Danaiah, P.; Mukasheva, A.; Kaushik, N. Hydropower technology as a renewable energy source of power generation and its effect on environment sustainability. In 2022 International Interdisciplinary Humanitarian Conference for Sustainability (IIHC),2022 1017–1020. IEEE. https://ieeexplore.ieee.org/abstract/document/10059855.
Taylor, S. J.; Letham, B. Forecasting at scale. The American Statistician, 2018, 72, 37–45. https://www.tandfonline.com/doi/full/10.1080/00031305.2017.1380080.
Zeng, B.; He, C.; Mao, C.; Wu, Y. Forecasting China’s hydropower generation capacity using a novel grey combination optimization model. Energy, 2023, 262, 125341. https://www.sciencedirect.com/science/article/pii/S0360544222022241.

Figure 1. Hydroelectricity generation by all countries

Figure 2. American countries: model fits and forecasting

Figure 3. European countries: model fits and forecasting

Figure 4. Asian and Middle East countries: model fits and forecasting

Table 1. Model comparison based on MAE, RMSE, and MAPE.

Model	MAE	RMSE	MAPE
BM	9.765295	10.456071	24.52534
GGM	5.197930	5.898378	15.49786
Prophet	5.216293	6.098824	18.79666
ARIMA	5.788099	6.748870	16.12192

Table 2. Model comparison based on MAPE. The rows represent the models being evaluated, while the columns denote the models being compared against.

	Prophet	ARIMA	BM	GGM
Prophet	0	21	30	17
ARIMA	22	0	31	17
BM	13	12	0	10
GGM	26	26	33	0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Forecasting Hydropower with Innovation Diffusion Models: A Cross-Country Analysis

Abstract

1. Introduction

2. Background Literature

3. Materials and Methods

3.1. Data

3.2. Models

3.2.1. Bass Model

3.2.2. Dynamic Market Potential

3.2.3. GGM

3.2.4. Prophet Model

3.2.5. Auto-Regressive Integrated Moving Average Model (ARIMA)

3.3. Evaluation Metrics

3.3.1. Mean Absolute Error (MAE)

3.3.2. Root Mean Squared Error (RMSE)

3.3.3. Mean Absolute Percentage Error (MAPE)

4. Results

4.1. American Countries

4.2. European Countries

4.3. Asian and Middle East Countries

4.4. Evaluation Metrics

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe