Preprint
Review
Carbon, Corporate Forestry and Conservation: Struggles for Science in Sustainability and Benchmarks
Altmetrics
Downloads
149
Views
41
Comments
1
This version is not peer-reviewed
Submitted:
07 October 2024
Posted:
08 October 2024
You are already at the latest version
Alerts
Abstract
To help limit further climate change, science must be robust and the best available, because it provides insight and understanding, of our impacts and reparations. Although strong standards are part of science, human frailties and facets of society also contribute. Initially, science aided industrialisation of forests, and conservation-oriented science followed. Some early data and methods suit both purposes, but there are different needs, dimensions and scales to consider. Science struggles to blend these frontiers and societal features, such that peer review cannot be the only quality control. Examples are reviewed in depth under two main headings: sustainability and benchmarks. The main arena is a target for industry and conservation: mixed-forests in Tasmania, Australia. Common flaws leading to faulty conclusions were: mis-representing and not noticing earlier studies, inadequately accounting for spatial dimensions and time, and inappropriate benchmarks or error margins when making comparisons. Example results after refinements are: carbon stocks are not sustained within several cycles of first logging primary forest, succession to rainforest may not reduce carbon more than logging cycles, and the proclaimed highest-carbon site is a common peak. Recognizing the carbon legacy and industrial use together through time is necessary for consideration of alternatives and consequent climate-change mitigation.
Keywords:
Subject: Environmental and Earth Sciences - Environmental Science
1. Introduction
To prevent further climate change
becoming entrenched, humanity must turn around its trend in carbon emissions by
applying only ‘robust science’ or ‘the best available science’, i.e., by
applying the scientific process correctly
[1]
. Anthropogenic climate change, which is the warming and extreme
weather resulting from our carbon emissions, is forecast to become more
frequent
[2,3]
. Science
is important for preventing further climate change because greenhouse gas
emissions can be more effectively reduced when they can be better quantified,
when their origin can be more precisely attributed, and when the effectiveness
of interventions can be forecast
[4]
. Also, information on what will be the most profitable
interventions should be an output of science. Science is a human product and
therefore cannot be viewed as somehow infallible, perfectly managed, and devoid
of typical human flaws: and similarly for its deployment. The quality of
scientific research, is established through a set of standards for
experimentation and a sequence of protocols for publishing completed work. This
makes science different to many other human activities but it merges with them,
and they with it. This paper reviews some frontiers of science and shows some
flaws where that science is blended with other characteristics of society: it
shows, how to amend the science and the relevance of the new results. This work
examines science that is related to carbon dynamics of forests. The first
frontier considered is sustainability of forest use and its benchmarks
(reference points), which is examined via soil carbon and biomass, and the
second is extreme dimensions in forests and its benchmark, used for determining
conservation. Some commonalities between these two are the forest type, high
public interest, and appropriate benchmarks for use in comparisons of carbon
stocks when making decisions.
Carbon and its measurement
benchmarks are important in understanding climate change because carbon
circulates through forests and the atmosphere, but goes from the forests to the
atmosphere sooner if there are extreme disturbances. The focus here is on
science that is relevant to the logging of forests that do not have evidence of
previous industrial-scale disturbance, generally called logging of ‘primary’
forests (hereafter, logging). It is a type of land conversion, as it converts
primary forest to land with a repeated tree cropping process (logging cycles
leading to perpetual, young secondary forest), though it is not conversion in
the vernacular usage of the term, which is conversion to non-forest. There is a
related term with which the reader may be familiar: ‘oldgrowth’ forest, which
is forest dominated by older trees and naturally fallen coarse woody debris on
the ground, typical of old primary forests of that type. Some primary forests
are oldgrowth forests, and vice-versa. Other oldgrowth forests are those that
have undergone considerable anthropogenic disturbance but have essentially recovered
and now have the structural components typical of a later growth-stage. This
follows the definitions of Barredo, et al.
[5]
.
Scientists measure the stores and
flow of carbon that were in primary forests and any carbon that is later
sequestered when the main timber species is regenerated on-site. The carbon may
be, for example, in the soil, in wood products, waterways, younger trees, and
in waste material, and some will accumulate in the atmosphere as greenhouse
gasses. Owing to the many processes and the range of locations involved, there
are ample opportunities for both flaws and erudition in the applicable science,
and therefore, both flaws and mastery in the style of carbon management adopted
by society.
Any blemishes in science, may go
unnoticed and are part of the information feedstock for the general public,
media, politicians, advocacy organisations (such as environmental NGOs and
timber industry representative bodies). The blemishes in
climate-change-mitigation science can insinuate themselves into policy and
on-ground actions, so it is best to solve them. In a review of the knowledge,
perceptions and claims of people who many might expect to be at the forefront
of environmental knowledge, namely forestry students and forestry workers, Pernica
[6]
found that the
majority of their information on ecology and the consequences of environmental
deterioration was obtained from mass media, especially television (84%). The
groups mentioned above are mostly non-scientists, who may not be able to
determine which are the most valid scientific facts, and they may not be
interested in looking deeper. When comparing the capabilities and
responsibilities of ecologists and journalists, Kirkpatrick
[7]
concludes that it is the
responsibility of the media and conservation organisations to translate the
results of ecological research into wider communication and action. An
alternative view is that while scientists have to maintain their own integrity,
they should contribute directly to public debates, and also educate the public
about objectivity and scientific abuse
[8]
. Donald and Graves
[9]
describe how a fact checking organisation worked with the social
media company Meta, to help ensure correct information regarding climate change
is delivered to the public. (Some people currently rely on their ‘feed’— a
software-generated daily compilation of information in social media, in place
of reading a newspaper). Although there are fake-news detection algorithms
[10]
, the bottom line may be the
veritableness of what scientists provide as feedstock. A major aim of the
present work is to assess the use of science and data, to reveal some of the
flaws, and to adopt a perspective that includes a larger scale, and thereby
indicate amelioration and its impact.
What is typically considered by
the general public as climate change science, is the impact of people’s
greenhouse gas emissions on the climate. Despite the above mention of flaws,
compared with some other facets of climate change science, humans’ net impact
on the climate has been determined to a high degree of quality and accuracy,
even though sometimes publicly disputed, i.e., ‘climate change denial’
[11–13]
. Scientists have worked on
several other aspects of anthropogenic climate change, e.g.,: (1) how our
activities increase greenhouse gas emissions; (2) our future emissions; (3)
reducing our emissions and their impact (called ‘climate change mitigation’);
(4) climate change’s past and future impacts on the environment; and (5) ways
in which the effects of anthropogenic climate change on the environment, induce
even more emissions and further increase climate change (i.e., positive
feedback)
[14,15]
.
Any science outputs of numeric
values have error margins, which is what some scientists call ‘precision’ or
‘uncertainty’. Some people misinterpret ‘uncertainty’ as meaning that
scientists have misgivings about the fundamentals
[3]
. As a preliminary
consideration, it is important to note that error margins are from two main
sources. The first source is the accuracy in reading a single value using an
instrument. These are often listed as ± after a value and there are established
formula for determining their influence after numerous mathematical operations
on data [e.g., 16]. The second source is the imprecision in ascertaining a
value from nature by multiple readings, such as from different locations. Each
reading may be influenced differently by various characteristics (some unknown)
that were not accounted for by using a control experiment. Many scientific
reports on forests only account for the second type of error margin such as by
citing standard deviations on values. But both types can be important when
making comparisons against benchmarks, as considered in the last example in
this review. Eighty years ago, new statistical tools, such as standard
deviation and the regression equation, being incorporated into forest
mensuration for forestry professionals, to the benefit of their profession
[17]
. Although computer software
for the application of those tools continues to be made easier to use, aversion
to overstating the implications of statistical measures has been voiced
[18,19]
. Validation of comparisons
in this paper do not rely on those statistical methods for comparing against benchmarks.
More-basic scientific protocols remain constant however, such as error analysis
for individual measurements.
Omissions and inaccuracies in the
development and use of science arise for several reasons (some of which are
examined in this review), such as:
- (1)
- (2)
- there are knowledge hiatuses between and within scientific disciplines, such as between forest carbon modellers and product life-cycle-inventory modellers [22].
- (3)
- the multidisciplinary wavefront of scientific knowledge, may not advance in a coordinated manner, instead its components progress disjointedly [23], possibly leaving a gap which misses some reality.
- (4)
- some relevant science may be either: considered irrelevant or not currently a priority [e.g., off-site effects, 24]; forgotten over the course of time by scientists; or not picked up in literature searches.
- (5)
- some relevant factors may not be programmed, or are incorrectly programmed, into modelling software, which consequently produces incorrect forecasts [25].
- (6)
- although many fields of science involve no public quarrels, some scientists work in areas where controversy and advocacy occur [23], such as at the junction of nature conservation and forestry, and the controversy may lead to unintentional bias in experimental design or interpretation. Advocacy may arise from a personal preference or may be a workplace requirement. For example, the State forestry agency in Tasmania, Australia (Sustainable Timber Tasmania), when advertising for a carbon and ecosystem services analyst said that advocacy and public relations were a duty in the role:
‘Support advocacy and internal and
external knowledge translation on forest management, carbon and climate
change.’
[26]
Fortunately, there is a consensus
for scientific publications that there should be no bias in the application of
scientific standard protocols
[8,27–31]
. Sometimes however, it is left to the filter of peer review, to
detect and correct for bias.
This paper looks at struggles with
the correctness, relevance and timing of science, which needs to be robust and
‘the best available science’
[1]
, in other words: good science. Defining such science, is necessary.
The first consideration must be the purpose of science, because that reveals
why it needs to be correct. Fundamentally, a reliable understanding of what is
around any being augments their usual subconscious decision making, because
when needing to stay safe and healthy, it adds to their decision making and
allows more judicious choices
[32]
. Correct information and explanations allow one to be more
productive in a range of circumstances, including adapting to new locations and
with new materials. Science allows explanations of phenomena that aren’t
immediately obvious, which in turn allows development of technology and
materials for a vast array of purposes. Correct explanations are just as
important today, away from primeval evolutionary demands and in a
post-development world, for example in how to manage forests and various
resources, in relation to anthropogenic climate change and materials for use
[9,33]
.
One major purpose of science, is
revealing logical, robust reasons for observations, based on more-fundamental
robust insights. In this context, robustness of science means that it is
resilient to different tests (rather than just being serendipitously correct
once), and that it does not provide unobserved information when within the
bounds of what it was devised to represent. In philosophical terms, science
should provide ‘grounded beliefs’
[34]
. The starting point is therefore with the most basic and simple of
observable facts, such as mathematics, then applied mathematics in the form of
physics, up through chemistry and then application of that in biology and
medicine, all the way building robustly upon what is established below. For
example, the cross-sectional area of a tree trunk is approximated by a
mathematical formula using the constant π (from mathematics), and applied
mathematics and physics are used in instruments to measure the other dimensions
of a tree (or to fell it), allowing a calculation of its timber volume, habitat
value, wind resistance, and carbon content. Applied sciences are also used to
turn some of the tree into paper or to measure how much carbon is kept out of
the atmosphere and for how long, if the tree remains intact. The stepwise
understanding of science, where each small step is soundly based and verified
through scientific protocols, allows people to understand more complex
observations including those of our global impact. Understanding causes gives
us the opportunity to try and adjust our future. This basic purpose for
science, when applied to mitigation (i.e., limiting) of anthropogenic climate
change, is summarised in an edict from Francis Bacon:
“Human knowledge and human power
meet in one; for where the cause is not known the effect cannot be produced.”
[35]
The steps of science, which form
progress in understanding, are written in scientific publications and computer
programs that allow people elsewhere to build on what has been substantiated by
others:
‘His notebooks indicate that
scientific imagining is a human characteristic that might appear in any age but
that without the organized companionship of like-minded people, science does
not advance’, [
[36]
p105].
Scientific knowledge advances for
some individuals in isolation (e.g., Leonardo Da Vinci about 500 years ago),
but more generally in contemporary times the broader topic and its application
advance faster when networked
[37]
. Publication allows: ‘speculations, theories, hypotheses,
observations, and indications of knowledge which still need to be examined and
discussed scientifically’
[38]
. Scientific writing originated at least 3,500 years ago, with
Babylonian astronomy written in cuneiform on stone tablets. In contrast,
dissemination and quality control of contemporary science is very closely
linked with the publication process in scientific journals. That process began
about 360 years ago, with Sir Christopher Wren founding The Royal Society in
London, which still publishes major scientific journals today, such as the
Transactions of the Royal Society series. Quality control of science is also
established at a governmental level and by research establishments in many
countries. For example, the Australian government has established a code for
responsible conduct of research and published several guides to it, focussing
on, for example: peer review of research, managing and investigating breaches
of the Australian code, and managing data and information
[39]
. The code describes
institutional responsibilities and individuals’ appropriate behaviour that can
foster ‘an honest, ethical and conscientious research culture’ to provide a
framework for developing high-quality research.
The most common check of research
quality is by peer review of manuscripts submitted to journals or conferences
for publication. Editors in publishing companies (e.g., Elsevier, MDPI,
Springer, Sage, and Taylor and Francis) select usually two or three people to
perform a peer review and they are provided with guidelines on how to conduct
it. The reviewers should be impartial experts in the topic of the manuscript
and they should check its content for aspects such as: appropriate referencing
of the scientific literature, originality, relevance, soundness of methodology,
informative diagrams, sufficient background for reproducibility by other
scientists, and conclusions supported by the data
[40,41]
. The major outcome is advancement
of science and global distribution of reliable information. The peer review
process is subject to typical human frailties however, and therefore yields a
minor, secondary outcome: less-reliable or less-applicable (limited scope)
information, which may have wide negative impacts when combined with some other
public influences
[41–43]
. This review seeks to improve some of that secondary outcome. After
publication, rebuttals by other scientists may add some quality control in some
circumstances and in extreme cases withdrawal of a published paper may occur.
Part of this review has the framework of a rebuttal and part is a synthesis of
detail.
Thus far, the explanation of
science may appear more like the processes within a computer, and with
alternatives being only of lower quality. But both are important, and synergy
between the two is productive. There is something else that makes good science
but is hard to measure: imagination. It is required for theorising, discovery,
experimental design, and conceiving alternative explanations or common links,
etc. Using, as an example, the discovery of the concept that planets and stars
etc. are formed by the condensation of matter, the historian Webster says:
‘It will be seen that patient,
plodding investigation does not form the whole of science, a place exists in it
for the widest flights of the scientific imagination.’, [
[44]
p675].
This can be exemplified by:
‘Progress in science comes from
not looking at Nature at face value, but understanding some voyage of discovery
to reveal a different viewpoint. From this new vantage, the landscape takes on
new aspects and dimensions, leading to fresh insights and new satisfactions.
With this vision, the next step is perhaps even more fulfilling—predicting what
can be seen from a higher standpoint.’, [
[45]
, p1].
his review does not gauge
imagination, but it does bring various work together using a perspective from a
bigger scale, hopefully to ameliorate earlier flaws and advance science. In
places the information presented in this paper is complex, but context is
provided and linked to overarching themes. For the reader to get the most
benefit from the present work, a quote from an early proponent of the
scientific approach, that helped guide collating information for this paper, is
relevant:
“Read not to contradict and
confute, nor to believe and take for granted, nor to find talk and discussion,
but to weigh and consider.” [
[46]
, p158]
The main part of this review
begins by describing the major forest type (
Section 2
) examined later in
the examples of science improvement, and then its industrial usage (
Section 3
). This includes
considering corporate strategy and some missed science. Then the dynamics of
soil carbon are discussed, as they relate to forestry activities (
Section 4
). This establishes
the background science necessary to investigate some aspects of science that
have been missed in reports relevant to carbon dynamics, forestry and
conservation. Examples are given where published interpretations have not
sufficiently considered spatial and time dimensions. The sustainability of
forestry operations is considered and previously missed aspects of science
related to benchmarks are detailed (
Section
5
), to provide new perspectives. The second part of the
review (
Section 6
)
examines claims for extraordinary dimensions (including carbon stocks) of a
particular forest stand, that was broached for purposes of conservation.
Finally, positive ways forward are summarised.
2. Mixed-forests in Tasmania, Australia: A Target of Industry and then Conservation
The most-often used forest-type
example in this work is the main target of the forest industry in Australia in
recent decades: mixed-forest in Tasmania. Although a relatively remote country,
Australia was the leading supplier of export woodchips for paper production in
the Asia-Pacific until 2010, with the majority of hardwood woodchips sourced
from its southernmost State of Tasmania, which was Australia’s major wood
product by volume
[47]
.
Tasmania has the highest proportion of forest cover amongst Australian States;
its forests have on average a higher biomass than other States; and its
southern central, high-biomass forests have been an industry focus. For over a
century Tasmania played a major role in the international wood products trade,
initially for lumber and then for newsprint and then the hardwood pulp market
for paper products
[47–49]
:
‘TASMANIA possesses, amongst other
wonderful natural advantages, extensive Forests of valuable Hardwood, and for
its area has the largest supply of timber available for export of all the
Australian States. … of which the extent of country estimated to be under
Forest is one-fourth, or about four million acres, consisting of some of the
finest timber in the world… The principal Hardwood Forests lie within a radius
of 60 miles of Hobart, the Capital, in Southern Tasmania, where the greater quantity
of better timber is to be found, although there are many extensive beds of fine
timber in the North-Western and Western Districts of the Island.’
[48]
Mixed-forest is a major part of an
early pulpwood logging concession in the central southern Tasmania, in the
Styx, Florentine and Tyenna Valleys
[49–51]
. Prior to logging, the majority of that mixed-forest was oldgrowth
primary forest. The areas with Eucalyptus regnans as the eucalypt
component were initially the main target
[52]
.
In Australia, ‘tall open-forest’
has its tallest stratum >30 m high, creating a canopy cover of 30–70%
[53]
. In Tasmania, such forest, the
‘wet-eucalypt’ forest, is subdivided into ‘wet-sclerophyll’ and ‘mixed-forest’
[54,55]
. The mixed-forest is a form
of rainforest
[56]
,
with a closed rainforest understory below an open eucalypt canopy (
Figure 1
). One could avoid
confusion with the more common type of mixed-forest globally—an
angiosperm-gymnosperm mix, by using the term ‘clopen forest’ for the Tasmanian
mixed-forest. ‘Clopen’ is a term used to describe something that is both open
and closed, such as clopen sets, in set theory.
Common rainforest tree species in
the mixed-forest are: Nothofagus cunninghamii f. Hook. (myrtle beech/
myrtle), Atherosperma moschatum Labill. (sassafras) and some Phyllocladus
aspleniifolius Labill. (celery-top pine). This type of mixed-forest is
common in Tasmania and predominates whenever the eucalypt species is Eucalyptus
regnans (swamp gum/ mountaint ash). Other common eucalypt species in the
mixed forest are E. obliqua (stringy-bark, messmate), E.
delegatentsis (gum-top stringy bark/ alpine ash, previously E. gigantea),
and further from the central ecotone: E. globulus (Tasmanian blue gum).
Mixed-forest was previously common in Victoria, where it is now rare and
termed ‘ecotone’ forest
[57,58]
. In Australia, mixed-forest also occurs in the States of New South
Wales and Queensland, but in narrower patches and with the eucalypts emergent
mostly over sub-tropical or tropical rainforest rather than temperate
rainforest
[55,59]
.
In Tasmania the largest
mixed-forest ecotone is located between lower-water-balance eucalypt forest of
the dry east coast woodlands and the higher-rainfall, lower-fire-frequency,
west-coast temperate rainforest
[55]
. Here, in between, fire is naturally infrequent but just frequent
enough to regenerate large areas of eucalypts once every few centuries. The
edge of the ecotone is not sudden, but incorporates more-frequent fire on its
border with the more fire-prone forests, and less fire on its border with the
wetter forests and swamplands, with accompanying fragmentation and subtle
differences in species distribution. This ecotone in Tasmania is much wider
than alpine treeline ecotones, and is more similar in size and genesis to some
of the ecotonal forests of the cerrado/Amazon rainforest transition, the
northern Brazilian Amazon or the Rainy Zone of western China; but by fitting
within Tasmania it is much smaller than the forest tundra ecotone of northern
Quebec
[60–63]
.
Another similarity of the mixed-forest
ecotone with some other ecotonal forests globally, is that the species from the
adjoining forest types have adapted synergistically to each other. For example,
the rainforest trees can grow on the buttresses of the tall mature eucalypts,
as hemi-epiphytes, using the stemflow [of rainfall] of the Eucalyptus
regnans, and the eucalypt using the low flammability of the rainforest
trees to allocate energy into vertical growth rather than into growing thick
bark up the trunk or lignotubers for survival through fire (
Figure 1
.a) [
[59,64–66,67]
Figure
S2
,68].
In relation to carbon accounting,
it is important to mention an aspect of the mixed-forests which makes them
unique amongst eucalyptus forests in Australia, as it relates to fine-scale
carbon concentration. Being of a maritime climate
[69]
, sudden downpours in central
Tasmania are often accompanied by strong winds of micro-fronts which means the
rainfall is inclined rather than vertical. If one can imagine rainfall at a
steep angle in
Figure 1
.a, it can be visualised how the tall vertical expanse of leaves of
the dispersed, mature eucalypts intercepts a larger portion of rain before it
reaches the closed rainforest canopy in between them, than if the rain fell
vertically. The steep angle of the eucalypt branches, and relatively smooth
bark (amongst eucalypt species) of the E. regnans, channels it towards
the trunk, and subsequently a wavy wall of water flows over the buttress zone,
which both the eucalypts and their hemi-epiphytes use. This stemflow is not
observed on the rainforest trees between the eucalypts. Thus, carbon from
biomass (through root decomposition and exudates) and dissolved organic carbon
in the stemflow, concentrate carbon in the soil close to the eucalypts. When
these mature eucalypts eventually die, the hemi-epiphytes and moss are notably
absent from their buttresses. The different characteristics described above
which combine to produce this stemflow process and its effects in Tasmanian
mixed-forests, have been observed separately in other forests globally, though
not reported in unison
[70–76]
.
Figure 1.
Canopy stratification of mixed-forest: open Eucalyptus regnans (~72 m high) above closed myrtle and sassafras canopy. Seen from edge of logging coupe SX009C, Styx Valley, Tasmania. (a) tallest eucalypt in foreground: DBH= 4.56 m with mature myrtle hemi-epiphyte joint up to 5.4 m height on the right-hand side and sassafras joint up to 4.7 m on left hand side; (b) drone view from above closed, lower canopy (courtesy of Darren Turner), tall tree on RHS is same E. regnans tree as in (a) on LHS. (c) at ground-level: myrtle, sassafras and ferns in-between mature E. regnans.
Figure 1.
Canopy stratification of mixed-forest: open Eucalyptus regnans (~72 m high) above closed myrtle and sassafras canopy. Seen from edge of logging coupe SX009C, Styx Valley, Tasmania. (a) tallest eucalypt in foreground: DBH= 4.56 m with mature myrtle hemi-epiphyte joint up to 5.4 m height on the right-hand side and sassafras joint up to 4.7 m on left hand side; (b) drone view from above closed, lower canopy (courtesy of Darren Turner), tall tree on RHS is same E. regnans tree as in (a) on LHS. (c) at ground-level: myrtle, sassafras and ferns in-between mature E. regnans.

Another aspect of the buttress
region of mature eucalypt trees in the mixed-forest warrants mentioning because
it relates to allometric equations later in this paper. Tree diameter at 1.3 m
from the ground on the high side of the tree (diameter at breast height, DBH)
is often used as a variable in allometric equations for tree biomass, carbon or
timber volume; and as a measure of growth in long-term inventory plots.
(Heights other than 1.3 m may be used in other countries
[77]
). Spurs develop in the
buttress region which link the main trunk to large lateral roots. Cross
sections of the buttress region show much folding of the sapwood zone (
Figure 2
.b). In smaller trees,
such as the Hawthorn example in
Figure 2
.a, this only occurs near ground level. There is a difference of
scale which needs to be appreciated in developing science applying to this part
of the eucalypt trees. Maximum DBHs observed for E. delegatensis, E.
globulus, E. obliqua and E. regnans (in alphabetical order) are
5.73, 5.6, 6.53, and 10.78 m in DBH; with maximum heights of 90, 94, 91 and 132
m tall respectively, and wood volumes (not accounting for the possibility of
internal hollows) of larger specimens in the high 300s to mid 400s m3
[78–87]
. The E.
obliqua or E. regnans of DBH 2.92 m in
Figure 1
.b was therefore of
modest size but it showed the deep folding of growth layers at least to 2 m up
the trunk. The folding has been observed up to 15.4 m above ground (
Figure 3
.c)
[67]
and it could possibly occur
anywhere in the buttress region. That region on E. regnans is evident as
the only area aboveground of rough bark, and which can extend up to ~18 m
[80]
, e.g., the trunk of a E.
regnans tree of DBH 6 m may still have a buttress-spread component of 5% at
14 m height [
[88]
Equation 5]. Thus, this part of the mature eucalypts in mixed-forest is in
between what is typically considered as trunk and roots in smaller trees.
Figure 2.
Structure of lower tree trunk extending to lateral roots. (a) Urban hawthorn (Crataegus hybrid) Hobart, cut at ground level, diameter= ~0.42 m, scale bar= 0.5 m (b) Sector of cross-section of partially hollowed E. regnans or E. obliqua in logging coupe (operational logging unit) after eucalypt regeneration burn, Styx Valley, DBH 2.92 m, cut near 1.3 m (courtesy of David Green), then pinned in place, dried and sanded. Gaps between lobes due to wood shrinkage and enclosed bark that fell away. Scale bar on left= 1 m. Note wood grain pattern in the lobes such that cambium and phloem are both near the centre of the trunk and on the outside. Insets show chainsawing (top) and fresh solid surface (bottom).
Figure 2.
Structure of lower tree trunk extending to lateral roots. (a) Urban hawthorn (Crataegus hybrid) Hobart, cut at ground level, diameter= ~0.42 m, scale bar= 0.5 m (b) Sector of cross-section of partially hollowed E. regnans or E. obliqua in logging coupe (operational logging unit) after eucalypt regeneration burn, Styx Valley, DBH 2.92 m, cut near 1.3 m (courtesy of David Green), then pinned in place, dried and sanded. Gaps between lobes due to wood shrinkage and enclosed bark that fell away. Scale bar on left= 1 m. Note wood grain pattern in the lobes such that cambium and phloem are both near the centre of the trunk and on the outside. Insets show chainsawing (top) and fresh solid surface (bottom).
Due to wind stresses the spurs in
the buttress region may become pronounced, with flutes in between them
[89]
. The amount of non-circularity
at 1.3 m height is usually about 20%, but is more variable in middle-sized
trees, for example E. regnans of DBH 4±1 m [
[67]
Figure 9
]. Consequently the amount of carbon in trees of that size will have
more uncertainty when derived from allometric equations based on DBH. An
example of a more mature tree with a more circular buttress, is the Chapel tree
in the Styx Valley, Tasmania (DBH= 6.03, height= 80.1 m, in 2012) (
Figure 3
.a-b). Such numerous
complexities increase error margins in carbon accounting when mature trees are
included. If there is a trunk hollow, then due to the deep folding of the
cambium zone, growth may occur inwards, into the hollow space, as well as on
the outside of the tree (
Figure 3
.). This has been observed up to at least 15.4m aboveground (the
example mentioned above). The occurrence of internal growth adds to the error
margins based on allometric equations. If there is no hollow in the buttress
region, which appears to be rare in recent times
[67]
, and the cross-section
minimally non-circular, then growth may be even and fully represented by the
DBH.
Figure 3.
Tree growth with only partial contribution to increase in the external diameter, after hollow formation. (a) Virtual slice at 1.3 m above ground of 3D model of a E. regnans (the Chapel Tree, Styx Valley) DBH 6.03 m, showing minimal buttress spurs and internal growth—the small circle near the entrance to the hollow is a young stem stalk, formed while surrounding wood was decomposing. (b) photo of the same tree showing new growth and hollow. (c) A cross-section of a E. regnans tree at 15.4 m above ground, felled during logging, coupe SX019i, showing new internal growth, including bark, but inside trunk hollow. DBH 3.84 m. Exterior of buttress did not suggest internal hollow, but at 1.3 m aboveground the tree was ~50% hollow.
Figure 3.
Tree growth with only partial contribution to increase in the external diameter, after hollow formation. (a) Virtual slice at 1.3 m above ground of 3D model of a E. regnans (the Chapel Tree, Styx Valley) DBH 6.03 m, showing minimal buttress spurs and internal growth—the small circle near the entrance to the hollow is a young stem stalk, formed while surrounding wood was decomposing. (b) photo of the same tree showing new growth and hollow. (c) A cross-section of a E. regnans tree at 15.4 m above ground, felled during logging, coupe SX019i, showing new internal growth, including bark, but inside trunk hollow. DBH 3.84 m. Exterior of buttress did not suggest internal hollow, but at 1.3 m aboveground the tree was ~50% hollow.

Evidence of large eucalyptus trees
in mixed-forest without trunk hollows was secured after they were felled, e.g.,:
the ‘Helms tree’ with a DBH of 6.37 m from the Tyenna Valley
[51]
, age ~390 years; and the
‘Maydena butt log’, with a DBH of 4.08 m (~40 years after it was felled and
assuming it was felled at 1.3 m above ground), on permanent exhibit, Tyenna
Valley, Tasmania (
Figure 5
). Hollows gradually increase in size, such that the large trees
don’t usually die suddenly (except by severe fire or logging) but if they do,
their carbon stock does not suddenly change, except in severe fire or if after
felling and milling, a substantial portion of the waste material (‘mill
residue’) is burnt. Although the incorporation of gradual hollow development
(with tree decomposition) into carbon accounting is only about two decades old,
the phenomenon is global, and was mentioned long ago, e.g.,:‘The monarch oak,
the patriarch of trees,
Shoots rising up and spreads by
slow degrees;
Three centuries he grows, and
three he stays.
Supreme in state, and in three
more decays.’, Dryden
[90]
adapted from Chaucer’s 14th century ‘The Knight’s Tale’ in ‘The
Canterbury Tales’.
and: ‘…its dimensions at the time
of writing as thirty feet in circumference on the outside and twenty feet round
the hollow within…’, [
[91]
p60].
Figure 5.
Similar-sized trees with varying hollow size, relating to different carbon stocks. (a) A buttress region (‘butt’) log of DBH ~4.08 m, on permanent display in the Tyenna Valley, showing a nearly 100% solid cross section. 1 m quadrat for qualitative scale only. Photographed in 2002, logged c1965, bark has decomposed and some timber has shrunk, revealing folding of cambium layers in the buttress region. (b) 3D model of a logged and burnt E. regnans of DBH 4.18 m with ~25% of the carbon lost from the buttress region, in the Styx Valley, developed in earlier work [67,92]. The hollow had no entrance point in the buttress region (so the hollow was not indicated externally). Such 3D models allow: more accurate measurements (e.g., by burl removal); and with sufficient samples, allowed new data types and formation of new allometric equations for C accounting.
Figure 5.
Similar-sized trees with varying hollow size, relating to different carbon stocks. (a) A buttress region (‘butt’) log of DBH ~4.08 m, on permanent display in the Tyenna Valley, showing a nearly 100% solid cross section. 1 m quadrat for qualitative scale only. Photographed in 2002, logged c1965, bark has decomposed and some timber has shrunk, revealing folding of cambium layers in the buttress region. (b) 3D model of a logged and burnt E. regnans of DBH 4.18 m with ~25% of the carbon lost from the buttress region, in the Styx Valley, developed in earlier work [67,92]. The hollow had no entrance point in the buttress region (so the hollow was not indicated externally). Such 3D models allow: more accurate measurements (e.g., by burl removal); and with sufficient samples, allowed new data types and formation of new allometric equations for C accounting.

A unique attribute of the mature
stage of the forests is a concentration of soil organic carbon (SOC) that is
not usually measured. It is under large tree trunks or tree buttresses, where
it is principally derived from decomposing roots and is usually much more
concentrated and deeper in the profile than in between trees
[92]
. Its expansion with tree
growth is shown in
Figure 6
. The thick layer of reddish-brown lignomor (decomposed,
structure-less wood Green, et al.
[93]
), which is nearly 50% carbon, is derived from decomposing coarse
roots (
Figure 7
),
Figure 6.
Tree growth of a E. regnans and associated concentrated soil organic carbon. Drawing based on Figure 2.b in Dean, et al. [92], but with separated growth stages and extra detail. Aboveground shape drawn from taper formulae adjusted for ground slope [88], roots drawn from observations and literature [67,80]. For the older tree, two scenarios are portrayed: on the left the trunk remains undecomposed and on the right-hand-side the tree has hollowed out.
Figure 6.
Tree growth of a E. regnans and associated concentrated soil organic carbon. Drawing based on Figure 2.b in Dean, et al. [92], but with separated growth stages and extra detail. Aboveground shape drawn from taper formulae adjusted for ground slope [88], roots drawn from observations and literature [67,80]. For the older tree, two scenarios are portrayed: on the left the trunk remains undecomposed and on the right-hand-side the tree has hollowed out.
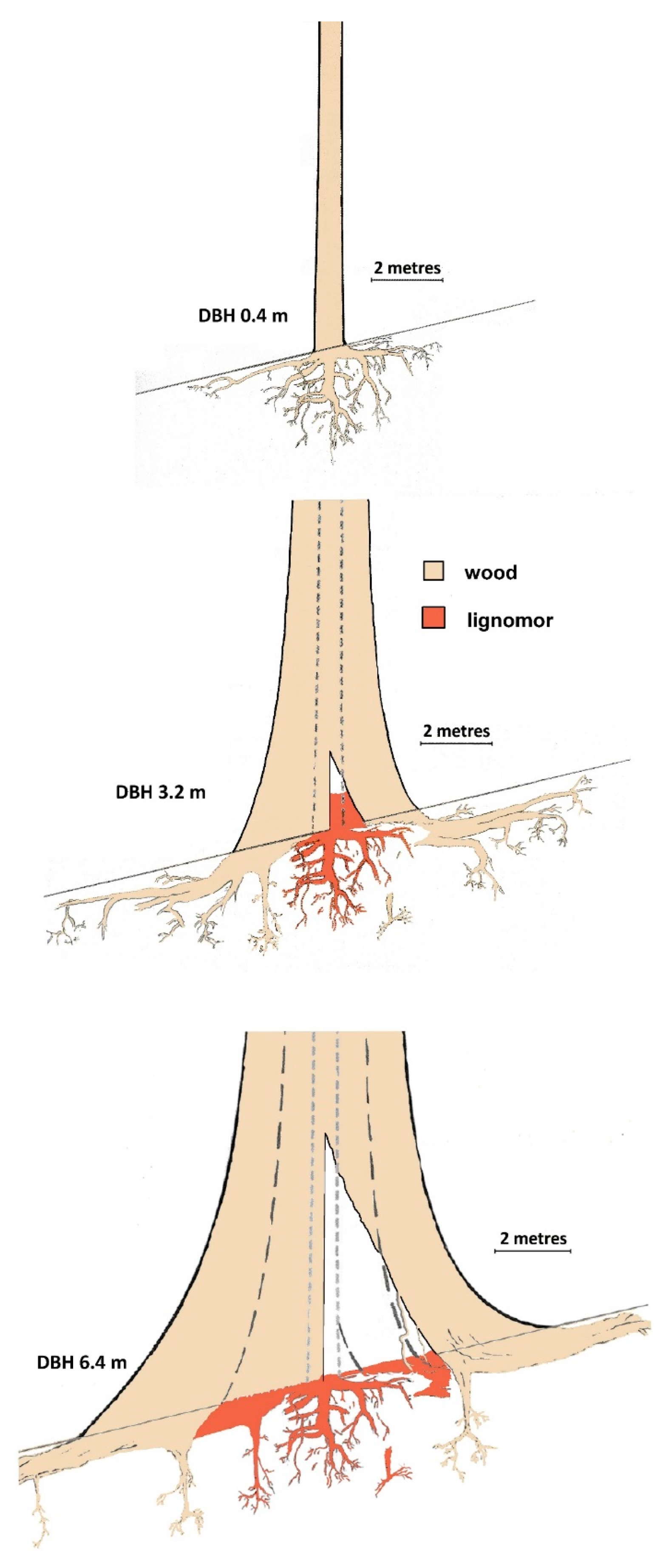
Figure 7.
Examples of stages shown in Figure 6. (a) 3D model of an ~0.6 m DBH tree trunk and parts of central tap root and lateral roots (no decomposition), (b) lower part of a 3.11m DBH tree filled with lignomor from trunk decomposition (handle of the 2 m long soil auger is visible), (c) the edge of the bowl of ligniform from a burnt and fallen tree, showing contrast with surrounding soil, (d) pushed over, burnt and wind-rowed medium-sized trunk in a plantation showing large hollow, I pushed over and burnt medium-sized trunk with small hollow, coupe SX004c (photo: Melinda Lambourne), and (f) measuring 0.9 m deep pit in bowl of lignomor under live, hollow E. regnans, l(DBH 6.08 m).
Figure 7.
Examples of stages shown in Figure 6. (a) 3D model of an ~0.6 m DBH tree trunk and parts of central tap root and lateral roots (no decomposition), (b) lower part of a 3.11m DBH tree filled with lignomor from trunk decomposition (handle of the 2 m long soil auger is visible), (c) the edge of the bowl of ligniform from a burnt and fallen tree, showing contrast with surrounding soil, (d) pushed over, burnt and wind-rowed medium-sized trunk in a plantation showing large hollow, I pushed over and burnt medium-sized trunk with small hollow, coupe SX004c (photo: Melinda Lambourne), and (f) measuring 0.9 m deep pit in bowl of lignomor under live, hollow E. regnans, l(DBH 6.08 m).

In order to refer to the different
tree sizes and stand structures in Tasmanian forests, when considering tallies
of timber, carbon or stand-type distribution, it is sometimes useful to use a
categorisation system developed by the timber industry. It was used heavily in
the Tasmanian State-wide mapping of forests by aerial photography
interpretation, and the categories are consequently called API types
[52,94,95]
. In mature stands,
eucalypt tree heights are categorised by the acronyms En, corresponding
to dominant height classes: E1: > 55 m, E2: 41 to 55 m, E3: 27 to 41 m, E4:
15 to 27 m, E5: < 15 m
[52,94]
. Eucalypt canopy closures are categorised by crown cover as
follows: a=90–100%, b=70–90%, c=50–70%, and d=10–50%
[94]
. Some of the common rainforest
or rainforest understorey types are M+, M- and S, referring to rainforest with
myrtles usually > 25 m height, 8–25 m height and scrub, respectively. Thus,
for example, a moderately tall mixed-forest stand with a strong rainforest
understorey could be labelled as E2b.M+. API types also refer to many other
characteristics, such as the year of ‘regeneration’ for logging operational
units with a known date for reseeding of the eucalypt species, or if an area
has been strongly affected by wildfire. This allows a range of investigations
using GIS (geographic information systems).
3. Industry Activity, Science and Conservation in Mixed-Forest
The Materials and Methods should
be described with sufficient details to allow others to replicate and build on
the published results. Please note that the publication of your manuscript
implicates that you must make all materials, data, computer code, and protocols
associated with the publication available to readers. Please disclose at the
submission stage any restrictions on the availability of materials or
information. New methods and protocols should be described in detail while
well-established methods can be briefly described and appropriately cited.
3.1. Allocation of the Southern Central Mixed-Forest Area to Industry
To gain public order and curtail
slash-and-burn activity in Tasmania, the government initially set aside 22,000
ha of forest for industrial forestry, then a further 38,000 ha in the early 20th
century, then up to 594,000 ha by 1938, of which 46% was pulpwood concessions
for private companies to produce newsprint, to save buying it from Canada
[48,50]
. Only 12% of the large area
of forest was allocated to pulpwood concessions (~81,000 ha) was allocated to
national parks and scenic reserves. Half of that reserved area was ‘in isolated
positions where the land is of poor quality’ (Counsel, E. A. : Annual Report of
Surveyor General and Secretary for Lands, 1906.
[50]
). Part of the large concession
allocation was the Florentine and Styx Valleys’ 162,000 ha pulpwood concession.
Prior to logging it was mostly even-aged E. regnans—dominated
mixed-forest
[55,96,97]
. Some of that concession included land that was previously in the
nearby Mt Field national park
[98]
. These generally ‘mature to over-mature’ stands (in forestry
terminology) were to provide a century-long new industry sourcing pulpwood,
converting them from primary forest into secondary forest with further logging
cycles
[52,99,100]
.
Only 0.22% (365 ha) of that area was initially reserved from logging
[101]
. That small reservation was
to conserve 11 particular botanical and cultural assets: ‘To provide for values
other than wood production such as recreation, fauna, flora, stream protection
and historical site.’ [Appendix 10 in
[52]
]. After nearly a century of industrial usage, new species and
substances in the vestiges of that concession area are still being discovered
[102–105]
. Linking logged and
unlogged areas of forest, to enable animal recolonisation ,was not undertaken
in that concession area
[106]
.
3.2. Historically Missed Science, Filling the Void, and Arising Controversy
One of the earliest portrayals of
Australia featured its fauna by 19th century scientists and artists
(e.g., Eugene von Gerard, John Gould, Gustav Muchel and Georges Waterhouse).
Large areas of native vegetation were drastically altered by industry before
some of that fauna could be adequately studied in regions less often accessed,
such as in tree canopies, below-ground, and in relation to a forest’s 3D
structure [e.g., [107,108-113]].
Public controversy about
conversion of Australian mature, primary forests to even-aged, eucalypt logging
cycles, mounted in the 1970s, simultaneously with the upsurge in logging for
woodchip exports
[114]
.
Dargavel
[115]
states
that one part of that controversy was because foresters understood the forest
well scientifically, for timber management purposes, but he separates out
ecology as a branch of science for which “the foresters’ knowledge was limited
and partial”. At the time, foresters were aware of a deficiency in the
knowledge of ecology of eucalypt forests related to timber production,
specifically the relationships between species distribution, soil and
microclimatic factors, and how species react to different environmental factors
and pathogens
[116]
.
Scientists have been experimenting in forests for over 200 years, studying such
characteristics as forest soil moisture and the effects of forests on local
climate
[117]
. But
when public pressure forced some of their environmental concerns into logging
plans it “caught Australia’s forest services by surprise”, as they were
‘unprepared and unskilled for planning in the much more complex and
controversial situations that arose’
[118]
. More research on some aspects of ecology was precipitated by a
combination of stakeholder factors: the forest owners (the public) became more
interested in forest management following the peak extraction for woodchips in
Australia, the forest industries were approaching the vestiges of primary
forests in their original logging concessions, and privatisation of plantations
meant a change in research funding.
In Tasmania, in the mid-twentieth
century peer reviewed scientific publications were mainly on silviculture and
logging methods but included some aspects of local ecology
[55,119–121]
. Ecology has only in
the last four decades begun to be part of forest management
[122]
. For all intents and
purposes, the focus meanwhile had been on productivity goals
[123]
. For example, Keith, et
al.
[124]
, with
reference to the availability of allometric equations, note there is ‘a bias
towards production forest species and small trees’, and the lack of data for
large trees means assessment of mature forests is hampered. Globally, for the
late-twentieth and early twenty-first centuries, a bibliographic analysis of
science publications revealed several trends in forest research. From 1956–2019
there was a trend of less research on sustained-yield to an increase in forest
ecology
[125]
; and in
the second half of the period 1970–2005 compared with the first half, there
were an increased number of publications on ecology of tropical rainforests,
landscape habitat fragmentation, elevated CO2, and climate change
[23]
. Currently, a wide range of
research topics related to forestry is primarily funded by the Australian
federal government’s CSIRO, Australian Research Council and Rural Industries
Research & Development Corporation; some State government departments; and
more independently, at universities. The major focus is still on the
traditional topics of silviculture and wood products but also the renewed one
of ecology, plus the newer topics of the carbon cycle and the life-cycle of
wood-products. The legacy of the historical bias in application of science to
forests is that current-day society struggles to integrate ecological concepts
into government policies on industrial forestry: even amidst anthropogenic
climate change the two appear immiscible.
The partitioning of forest
components in science is not only from wood production. Biodiversity of forests
has traditionally been studied in terms of the numbers of individual species or
types of ecosystems, and their spatial distribution over map projections, i.e.,
within two dimensions (2D) [e.g.,
[126,127,128]
]. Forest ecosystems are still often catalogued or described
according to the most common tall plant species present [e.g.,
[129,130]
]. This could be because
people undertaking science are generally very much non-arboreal, diurnal,
surface-based and traversing the vertical axis (above or below ground) is not a
region to which they are intricately accustomed [e.g.,
[107,131,132]
]
. They rely on specially designed tools or local indigenous people,
to measure outside of their 2D oecumene [e.g.,
[133,134]
]. For example, regarding
public demands on State-organised forestry in Australia, Dargavel
[115]
states:
‘What the foresters lacked the
most was detailed knowledge about the arboreal wildlife, and even their casual
knowledge was limited because much of the wildlife is nocturnal, when most
foresters have gone home.’
This was reiterated in 2022–23,
when it was noted that the State forest agency for Victoria stated it was too
dangerous to survey for nocturnal fauna at nighttime, though it was done by
academic scientists [
[135]
, p38-39].
Consequently, the 3D aspect of
forest biodiversity has historically come in as a poor second in scientific
reports. Biodiversity of forest canopies was recorded in the late 20th
century but the technology of that era didn’t allow sufficient expanse in 2D,
for the data collection to encompass 2D heterogeneity
[132]
. This century though,
scientific endeavour is burgeoning in the vertical dimension, at least
aboveground, and with significant findings: for example, canopy insect diversity
from DNA in rainfall or from climbing using modern apparatus [136-138.
[136–138]
, canopy structure of mature forests using long-boom tower cranes or
LiDAR
[139,140]
,
taking advantage of logging to compress 3D habitat information into 2D
[141]
, and contrasts in animal
diversity between measurements from the ground and from the canopy— sometimes
with previously unrecognised differences between before and after logging
[142–148]
. Most of the science reviewed in the first part of this paper, is
on the negative vertical axis, namely soil carbon effects, because recent work
there has resulted in controversy.
3.3. Public vs. Industrial Interest, in Determining Scientific Endeavours
In Australia, most State
governments manage timber extraction from the public forests as a ‘government
trading enterprise’, or ‘government business enterprise’, or ‘state business
corporation’, each based on the model of corporations. These enterprises are
the cores of what were previously the State forestry departments. The
administration of the more-peripheral parts varies between the States (e.g.,
either privatised, contracted out or handled by a different government
department). Each corporation has two main areas of activity that may overlap spatially:
use of existing forests (native-forest logging) and planting forests before
using them (plantation and native-regeneration forestry). South Australia, the
Northern Territory and the Australian Capital Territory don’t have government
commercial native forest logging enterprises, just plantations.
Globally, government management of
forests has always been intertwined with the forest industries, with access to
primary forests remaining controversial
[149,150]
. When public objections rose steeply in Australia there was a
desire in the forest industry to avoid conflicts similar to those experienced
in the U.S.A., which had reduced the power of the industry. In order to
maintain forestry’s control over public forests in Australia, Florence
[116]
suggested that localised
environmental considerations, including ecology and maintenance or enhancement
of non-timber values, be factored into logging plans, and that the essence of
the precautionary principle be followed. But this recommendation was not heeded
to any notable degree, and not such that it mollified biologists or
conservationists. Instead, another avenue expanded: Australian forest
industries have directed a greater amount of funding away from research and
into marketing, including public relations (PR) through representative bodies
such as Forest and Wood Products Australia (FWPA)
[151]
. Here, the Bernays
[152]
definition of PR is followed:
as ‘the attempt, by information, persuasion, and adjustment, to engineer public
support for an activity, cause, movement or institution.’
More generally, the divisive
ambience that pervades society, with regards to existing large industries and
carbon emissions, climate change, industrial land use and conservation, is part
of humanity’s larger struggle of industrialisation vs. environment. The
struggle between forestry causes and environmental causes includes: industries’
and conservationists’ public relations, corporate defences against
environmentalists, government alignments, litigation, forestry blockades,
animal rights activism, industrial crime and corruption, environmental damage
and human fatalities [e.g., [7,153,154-168]]. For any large industry that
interacts with the environment, a portion of humanity may see that industry as
an aggressor against the environment and therefore react, but that reaction may
surprise the industry who in turn see the public’s reaction as a force against
which they must act, and that may entail public relations exercises
[169]
. Both sides may refute each
other’s PR
[170,171]
.
Within this paper some scientific reports are described which are aligned with
PR campaigns, and detail is examined in order to improve the science and help
to resolve outstanding issues.
The process of scientific
publication in journals, can be used both by people preferring a particular
industrial development and by people preferring conservation. But
conservation-oriented scientific studies more often seem to be reactionary,
purely in response to industry’s impacts, rather than science driven for the
need to know about nature before using it. For example, research interest in
ecology in Victoria (a State of Australia) is strongly correlated to the amount
of wood products a forest has yielded, more-so than to the financial returns
from logging. Bennett and Adams
[172]
suggested this was due to logging intensity— its associated
environmental impacts and opportunities for study, or that more people settled
near the more-productive areas [and thus were closer to such logging]. One
technique is to use science to produce benchmarks for ‘ecological importance’
and species endangerment. These combine with public preference to determine
policy
[173]
. One such
study is reviewed below (
Section 6
).
Corporate responsibility (CR) is
multifaceted, including, inter alia, responsibility to shareholders, financial
sustainability, and corporate social responsibility (CSR). CR may require a
corporation to adjust the market place (called ‘market management’ or ‘issues
management’
[174]
)
through a range of strategies, not only in trade competition but even such
processes as eliminating standards bodies and alternative products, and
modification of government regulation
[175,176]
. Within that process, some corporations may subvert some of the
parts of science that support conservation but that will cause adverse
financial performance (e.g., by sidelining, omitting or discrediting its
relevance or veracity): and more generally, a range of methods may be used to
align science to satisfy the needs of a large organisation
[114,166,177]
.
Often science only occurs after
corporations have begun to implement their proposals. This science sometimes
provides clarification, may assess alternatives, or may investigate side
effects. Just as a conservation organisation may not feel obliged to consider
the financial implications of nature conservation, so too, a corporation may
not devise methods of resource use that entail comprehensive environmental
knowledge and long-term protection of the environment, unless demanded by their
stakeholders [e.g.,
[176]
]. Thus, science may simply not be considered prior to, for example,
industrial activities that produce carbon emissions. In this context, this
review looks at some scientific publications that may inadvertently function as
part of industry’s more-general, issues management
[174]
.
Goals of corporate responsibility
have moved from solely profit to include social and environmental concerns,
towards CSR and the development of a ‘social license’ for corporate activity.
From the late 1990s major international organisations such as the European
Commission and the United Nations urged large corporations to include CSR in
their core strategies, in consultation with stakeholders
[178,179]
. Centuries ago the
various benefits of forests made the general public a stakeholder in forestry
and forests [
[180]
p
10,
[181]
p xi].
Sustainability is currently one of the expectations critical to social license,
and part of this review examines how that expectation is met.
The World Bank suggests that sustainability
should be included in CSR but doesn’t specify if that is environmental
sustainability, and some companies interpret sustainability as meaning business
viability
[182,183]
.
Some industries rely on the older targets and methods of corporate
responsibility, against a background of legal requirements which have not
shifted markedly to reflect CSR. For example, when solutions for the global
syndemic (the combination of the obesity, undernutrition and climate change
pandemics) were reviewed, a change in management of CSR was recommended:
‘Corporate social responsibility
efforts, which are too often marketing exercises, need to evolve into a
stronger accountability model, in which targets and performance criteria are
independently specified, monitored, and publicly shared.’
[184]
In corporate forestry, one PR
mechanism is ‘generic marketing’, where plantation forestry and logging of
primary forests are not differentiated in marketing material. It is designed to
counterbalance ‘anti-logging activism and competition for market share’ [e.g.,
[185–187]
]. This avoids recognising
the legacy carbon from the primary forest by considering the secondary forest
as long-term plantation land, but the legacy carbon is considered in this
review.
A more-general industrial public
relations tool is to embellish knowledge gaps in controversial areas, such as
exaggerating the significance of scientific uncertainty, or even creating it
[188]
. When applied to climate
change it increases the momentum of avoidance of climate change mitigation by
humanity
[12,189,190]
.
Knowledge gaps need to be handled carefully in scientific endeavours, else the
science created may be lopsided, which may lead to lopsided policy. For
example, change in soil organic carbon (ΔSOC) with logging hasn’t been studied
to the same precision as change in biomass, and thus ignoring it in financial
accounting is appropriate, due to insufficient precision for investment.
However, not accounting for it in scientific forecasts is an omission, as both
the value and the error margin could be mentioned. In this review, the ΔSOC
accompanying conversion of primary forest to secondary forest with logging
cycles is considered, and contrasted against its omission.
3.4. Conservation in the Mixed-Forests
Although conserving forests from
industrial activity is often dressed as a recent idea, it is centuries or
millennia old. Ancient civilisations such as those of Greece, Rome, India,
China and Maya also exercised forms of forest conservation, reforestation and
plantations, though for more local benefit and society-oriented reasons than
are the national parks of today
[191–194]
. These conservation initiatives were concomitant with neighbouring
major forest attrition, deforestation and related land degradation issues, and
consequent adjustments to societies
[191,195–197]
. Forest conservation was suggested in the 13th and 14th
centuries in England, to keep forests intact for some people’s needs, in the
face of flora and fauna attrition by local residents
[198]
. More forest conservation was
later proposed in that same region, but for forest amenity’s sake, and again to
counteract attrition by local residents
[198]
. Sourcing of forest products by local people was mainly for local
usage, but also for selling further afield. In the late eighteenth and early
nineteenth century, forest conservation, less damaging use of forests and even
reforestation, was proposed in Brazil, due to: land becoming far less
productive after slash and burn agriculture, possibly medicinally important
plant species being lost, alternative uses for the timber, and important fauna
species declining
[199]
.
As early as 1925 there was public
disquiet about the misleading information in forest industry PR
[200]
, such as against the notion
that forests cannot regrow and maintain themselves without human intervention
by logging:
‘A forest may and often does
maintain itself unimpaired century after century. If this were not so, why was
a large part of this country covered with magnificent forest with trees several
to many centuries old when the first settlers came? Can we doubt that it
would still be so but for human interference?...No more nonsense can be
disseminated than the idea that if we do not hurry up and cut the rest of our
dwindling pernicious supply of timber the forests are going to fall down and
rot like a crop of weeds. … We shall never get any real conservation in this
country until people wake up to a realization of how the tentacles of
commercial interests have penetrated, not only the branches of our government,
but also most of the conservation organizations.’
[200]
Similar reasoning is published by
advocates of corporate forestry today, when they imply that mixed-forest will
turn into lower-carbon-stock rainforest and emit carbon if not logged [e.g.,
[201]
]. We examine the carbon
balance for that process in this review.
All remnant primary forest on
public land in Australia, is currently sought after by both the forest
industries and those interested in conservation. National parks and other
reserved forest land such as world heritage areas, have become newly contested
land
[202]
. The goal
is represented through industry mantras such as ‘a shared vision’
[203,204]
. A media release by
Forestry Australia (previously Institute of Foresters Australia) included:
‘The paper Reshaping forest
management in Australia to provide nature-based solutions to global challenges,
by Dr William Jackson and other members of the IFA/AFG, says it is time to move
beyond the era of conflict and develop more holistic approaches that encompass
all forest values, such as water, biodiversity, tourism and forest products,
across the landscape.’
[205]
In contrast, the article they cite
states:
‘To be clear, active management is
not a call for commercial timber harvesting in national parks and conservation
reserves.’
[206]
Overall, conservation of primary
forests did not prevail in Australia because “The forest industry had the
financial advantage in being able to have offices and professional lobbyists at
a level the environmental movement could never match. It presented itself as
the defender of employment, in ways that were as specious as the appealing
pictures and that were also persuasive.”
[115]
. Demand grew to conserve some more forest from timber felling
following intensification of logging in Australia for export pulpwood in the
1970s and 1980s, which peaked in the 90s and included further forays into
national parks
[207,208]
. Consequently, in the 1980s some forest neighbouring pulpwood
concessions in Tasmania and some national park land were assigned World
Heritage status
[209]
.
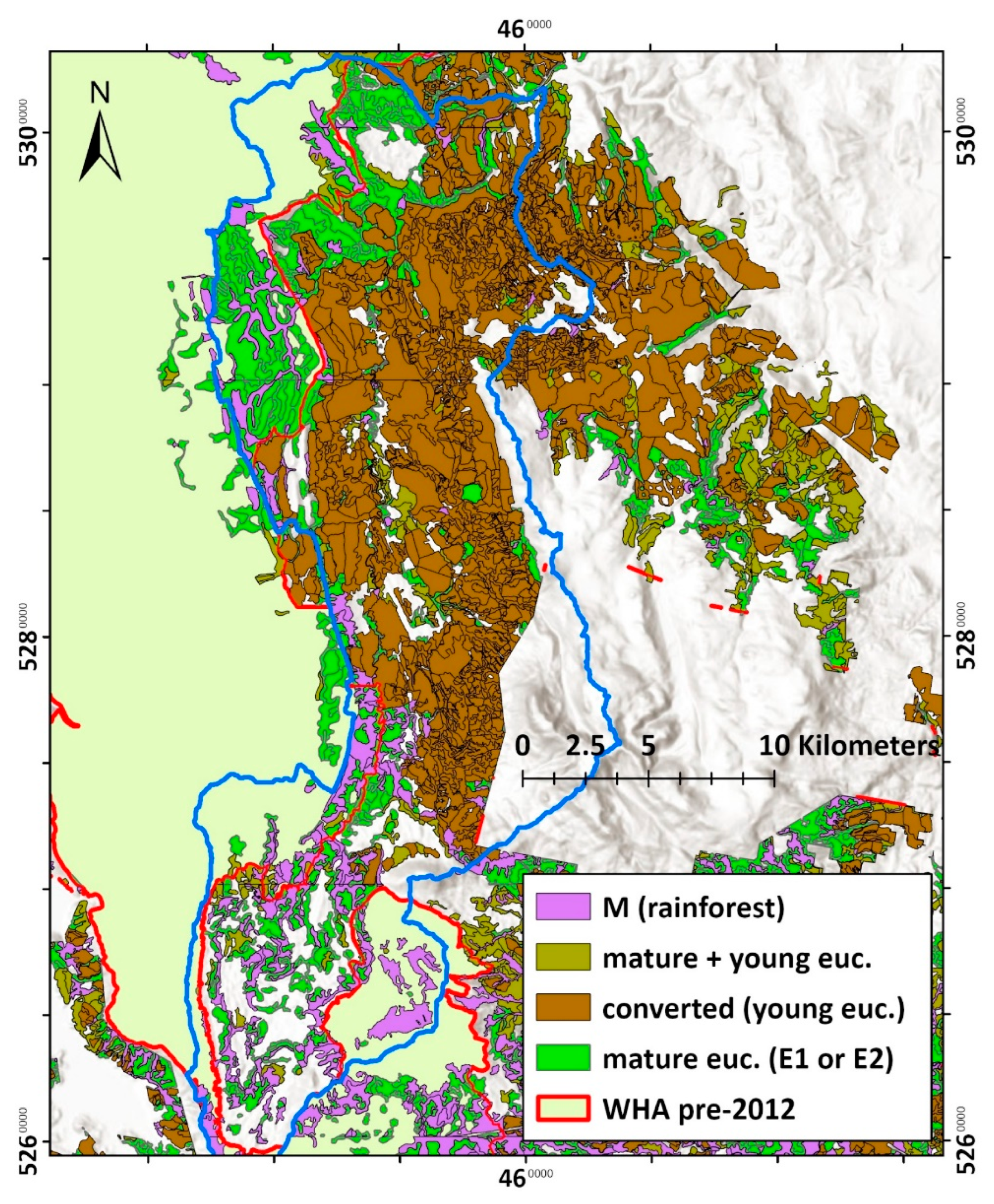
The most notable of these was an area of tall, mature mixed-forest (with 41–80
m tall eucalypts) intermingled with myrtle-dominated rainforest, bordering the
northwest side of the Florentine Valley (
Figure
8
). Without such reservation, designed by Kirkpatrick,
it would have met the same fate as nearly all the mixed-forest in that valley—
clearfell logging conversion to young, production forest cycles (
Figure 8
). This century, the
public’s awareness of dwindling primary forest acreage in the concessions
caused further demand for World Heritage assignments, even including land that
had earlier been selectively logged
[210]
. The extension was achieved and some its components are described
below.
Figure 8.
Logging extent (brown) in the Florentine Valley catchment (blue outline) as of 2012. Note the area of mature, tall mixed-forest (bright green) in the top left of the Florentine Valley that was reserved from logging and allocated into the World Heritage Area (yellow with red outline). Forest type mapping was from aerial photography interpretation by the State forestry agency, Forestry Tasmania. Projection: GDA 1994, MGA, Zone 55.
Figure 8.
Logging extent (brown) in the Florentine Valley catchment (blue outline) as of 2012. Note the area of mature, tall mixed-forest (bright green) in the top left of the Florentine Valley that was reserved from logging and allocated into the World Heritage Area (yellow with red outline). Forest type mapping was from aerial photography interpretation by the State forestry agency, Forestry Tasmania. Projection: GDA 1994, MGA, Zone 55.
4. Dynamics of Soil Carbon Relevant to Measuring Forestry Effects
4.1. Time Periods for Measurement of Change in SOC
In the last thirty years, there
has been an approximately 12-fold increase in interest soil related to climate
change, followed by 10-fold for soil-and-biodiversity, and then to a much
lesser extent, ~5.5-fold increase for soil organic carbon specifically;
soil-and-logging, soil-and-ecosystems and soil-and-silviculture
[211]
.
The change in soil organic carbon
(ΔSOC) accompanying industrial forestry is gradually being measured more
comprehensively. The time required for change is a complicating factor that
must be considered when designing experiments aiming to detect ΔSOC. It is
necessary to consider the spatiotemporal dynamics of SOC so that the different
results from various experiments on SOC can be interpreted. Most experiments so
far have been conducted over time periods such as 1 to 50 years after logging,
which is when decomposition of the fresh logging debris creates a peak in SOC.
These periods have been considered to be short, medium or even long-term
[212–214]
.
The upper mineral soil is most
responsive to surface changes. For example, it shows a short-term peak in SOC
after a brief, disturbance-driven decline, after both logging and fire [
[215]
,
Figure 4
, [216-218]].
Therefore, experiments examining only surface soil are more likely to indicate
change, if done at timescales typical of many experiments (the 1-to-50 years
mentioned above).
Change in SOC, over most of the
soil profile, in response to long-term change in forest biomass (not just a
single disturbance such as a wildfire), has a time scale longer than that of a
human generation and therefore longer than most experiments— typically several
centuries to millennia
[215,219]
. The fact that SOC changes so much slower than does biomass, has
been offered as an explanation, along with natural spatiotemporal variability,
as to why many experiments have not found any ΔSOC due to forestry activities
[220]
. The reasons for the
relatively slow change in SOC are three-fold:
- (a)
- coarse tree roots take time to grow and then decompose to contribute to soil carbon stocks, and it is the new tree stock for which one requires a corresponding value of SOC;
- (b)
- the half-life of the slowly decomposing part of SOC, which forms the majority of total SOC, is in the order of several centuries [e.g., [221]], which is much longer than that of biomass and therefore its change is also slower; and
- (c)
Due to differences in water
availability and temperature, decomposition of molecules that reside in the
soil and were derived from trees, is likely to be faster in tropical climates
and slower in more-polar climates. The timescales involved over the whole soil
profile are exhibited in carbon isotope measurements of carbon age at different
depths
[223,227]
. For
example, in a warm, moist tropical environment for 0.7 to 1 m depths:
‘In deep layers, the age
distribution reveals the small but non-negligible direct incorporation of
photosynthetically fixed carbon through deep roots or soluble carbon (for the
youngest carbon), and the predominance of carbon that is older than 1,000
years.’
[223]
In this environment, mid-level
(0.2 to 0.7 m) has SOC of mostly intermediate ages of 100 to 1,000 years, which
leaves the surface soil as the most responsive to change
[223,227]
. In a temperate forest,
mean SOC ages were <60, 100 and 550 years for the Ah horizon (uppermost
mineral soil), 0–0.1 m and 0.1–0.3 m depths, respectively
[227]
. In temperate forests, SOC
turnover times of ~200 years have been observed to be long enough to prevent
detection of management effects in experiments spanning only several decades
[225]
. This confirms the notion
that experiments to detect change even as high up as 0.1–0.3 m, need to sample
over several centuries to measure ΔSOC.
For the purpose of modelling the
carbon cycle for carbon accounting, the change in SOC due to the short-term
activity of logging, including the intense regeneration burn, can be considered
separately from the longer-term effect of reduced biomass after logging. There
are multiple effects around the time of logging, such as additions to SOC from
the extra charcoal (if there is burning) and decomposing timber
[228]
. The timber, bark and leaves
left on site after logging is collectively called ‘forest residue’ or ‘logging
residue’ in forest industry terminology. For calculation purposes, the loss
from soil turbation during logging, post-logging grading for plantations, and
fire due to clearfell, burn and sow (CBS) type logging, must also be separated,
from the additions from logging residue. This separation requires care in
experimental design because the factors are best measured separately— the
contributing factors must be discerned in the data collected.
The SOC in the soil profile can be
divided into categories called pools, where a pool is a group of organic
compounds whose stability is delineated by having a similar half-life, and some
of the pools may contribute their carbon to each other or directly to carbon in
the atmosphere [e.g.,
[229]
]. In general, for the soil profile, the half-time for sequestration
or loss of SOC is mathematically equal to the half-life of the slowest changing
SOC pool that forms a substantial part of the SOC stock [
[230,231]
, p43]. This means that
the time it takes for SOC to reach a long-term steady-state equilibrium, that
corresponds to the prevalent, long-term-average biomass cover is proportional
to the half-life of the slow SOC pool.
A simple calculation can show how
long it takes to achieve some sort of equilibrium in SOC, depending on that
slow SOC pool: assuming first order kinetics, such as simple exponential decay
of soil carbon, the time to 95% of the long-term steady state, is
ln(0.05)/(ln(0.5) (= 4.3) times the half-life of the slow SOC pool. This is the
mathematical reason why the initialisation period (‘spin-up’ time) of soil
carbon models is usually from around 1,000 to 3,000 years, and longer periods
can provide more certainty
[232–235]
.
This time scale, of around 1,000
years or more, is not unique to assessing ΔSOC with land cover change: it
appears elsewhere in the science of anthropogenic climate change. It is the
period after which, if we promptly and completely stop adding our greenhouse
gas emissions to the atmosphere, anthropogenic warming and atmospheric CO2
will notably begin to dissipate (though in this case it is related mostly to
the atmosphere-ocean C exchange)
[236,237]
. Thus, there are two reasons to be aware of that time scale when
considering our impacts, both past and future.
This temporal characteristic of
the slow SOC pool also means that multi-century and millennial time spans are
necessary for ΔSOC experiments that aim to determine the effect on the whole
soil profile due to long-term change in the forest biomass, such as conversion
to logging cycles to produce wood products or bioenergy, reforestation,
afforestation, or long-term change in fire regime. Also due to such time
scales, long-term averages must be used when calculating the effects using
modelling/simulation/forecasting studies. It is the new, long-term-average SOC,
either modelled, or observed through space-for-time substitution studies, that
must be used to represent the real effects of management. To shortcut that long
duration, one could claim that no change will occur lower down in the soil
profile where half-lives are longer, but that would be denying that the SOC
originated from trees.
From these time scales, rather
than from the viewpoint of an individual person’s typical experiment, the first
50 years after logging, mentioned at the beginning of this section, is short-term.
4.3. Linking ΔSOC to Change in Biomass, and Measuring It
Broadscale datasets where SOC can
be compared against forest biomass, and where other factors are normalised,
show that SOC is positively correlated with forest biomass per unit area
[238,239]
. Thus, where
time-averaged, long-term biomass is reduced by intensive logging then it would
be expected that SOC must also decrease. A long-term decline in SOC with
subsequent harvest cycles over several centuries is because there’s less wood
available (compared with the primary forest), both from fallen branches and
trunks and from coarse roots of those trunks, to decompose into soil carbon
[240–243]
. That is the biological
perspective, and it is mirrored in computer models, where mass is stored in
matrices for live biomass carbon, dead biomass carbon, SOC pools and the
atmosphere, with periodic movement of carbon between them according to
half-lives of the pools.
Within the numerous findings from
experiments on intensive logging and SOC that were reviewed in Dean, et al.
[239]
, any seeming inconsistency
from the positive correlation can be explained. For example, upon examining
purportedly paired sites Leuschner, et al.
[244]
found a long-term drop in SOC
over a few centuries of logging but did not find a correlation between SOC and
biomass. However, their ‘low’ biomass values were not time averaged over the
logging cycle but were near the end of the cycle and on average, statistically
close to the primary forest values. Assuming a Chapman-Richards type growth
function, the time average biomass for the logging cycle is more likely to be ~2/3
of the biomass at the time of logging. That lower value would have been more
likely to reveal a positive correlation between biomass and SOC. Because of the
laggardness of ΔSOC, average values over longer time periods are better
indicators than values at a point in time. They are also more relevant to the
effects of land use on climate change.
There are of course natural,
long-term changes in SOC
[245]
that create a background against which one would observe the trend
due to intensive logging. Where some of the forest biomass due to logging is
moved off site, is not burnt as mill waste, and becomes a wood-product, then
eventually decomposes in landfill, it can contribute to off-site SOC. For the
mathematics of carbon accounting, this off-site SOC should be added to the
forest’s on-site SOC.
The question arises, when will the
ΔSOC due to management, become measurable by experimentation? Several cycles of
reduced growth and decomposition under conditions of reduced biomass [due to
logging of primary then secondary forest], are needed to change SOC
sufficiently for it to show up empirically
[239]
. One can merge the outputs from different reports shown in
Figure 2
of Dean, et al.
[239]
based on cycle number of the
secondary-forest logging [models from: [47,241,242,246-248]]. To normalise the
different data sets along the time axis, the common logging cycle duration was
chosen as 80 years. The merged data provide a rough estimate of the fate of SOC
for a range of species, range of soil depths and range of cycle lengths as a
function of logging cycle number. This average trend can be formulated in
equation form (Eq1) using Eureqa
[249,250]
(portrayed in
Figure 9
):
SOC% = 1,965/(14.92 + lc) + 8.944sqrt(0.0875 + lc) – 34.21
where SOC%= percentage of
the original, long-term-average, primary forest SOC, lc= logging cycle
[number] from 1 to 35 cycles (i.e., up to 2,800 years since first logging), R2=
0.95, Correlation coefficient= 0.97, Maximum error= 32.05, Mean squared error=
11.92, Mean absolute error= 1.475, Coefficients= 3.
Figure 9.
Change in SOC, as a percent of the time-averaged-mean of the original primary forest SOC, versus cycle number of logging the secondary forest, with 0 being the logging of the primary forest. This average line was from data from the models in Figure of Dean, et al. [239] cited in the main text here; data were first converted to the relative time through each logging cycle.
Figure 9.
Change in SOC, as a percent of the time-averaged-mean of the original primary forest SOC, versus cycle number of logging the secondary forest, with 0 being the logging of the primary forest. This average line was from data from the models in Figure of Dean, et al. [239] cited in the main text here; data were first converted to the relative time through each logging cycle.
The model outputs merged to create
Figure 9
had
cycle lengths from 50 to 100 years. For other cycle lengths the curve may
extend or contract depending on the time balance between coarse root growth,
and root and SOC decomposition, within each cycle. Other causes of variation in
the curve will be, for example, the local environment, species, and logging
procedures.
Quantitatively, Equation 1 and the
curve in
Figure 9
indicate that after 3 cycles of intensive logging there will be a 9% drop in
SOC, 18% after 6 cycles, and 30% after 12 cycles. The trend implies that even
where people are no longer logging primary forest, they will still be losing
carbon if persisting with logging of the secondary forest, except after many
centuries. In contrast, conversion of forest to cropland can incur a similar
ΔSOC after only ~20 years
[251]
, making it much easier to measure, but even there, the decline
continues in subsequent years before levelling off [
[230]
,
Figure 8
,
[252–254]
]. The gradual decline in
Figure 9
reveals that in order
to measure ΔSOC with scientific significance, one may need to measure over
several logging cycles. SOC shows a peak in the first cycle due to
decomposition of the large amount of debris from primary-forest logging (unless
it is mostly burnt), so it is pointless trying to detect ΔSOC that soon. This
explains why many review papers indicate ambivalence about ΔSOC with logging,
which is echoed in the finding of Leuschner, et al.
[244]
that: ‘… the long management
history of nearly all Central European forests often hinders the detection of
legacy effects, unless true primeval forests are used as a reference.’
A few studies have observed the
cumulative effects of several logging cycles, which allows comparison with
Figure 9
. Leuschner, et al.
[244]
, for the upper soil profile
down to 0.5 m depth report a 13.5% drop in SOC after ‘several’ centuries of
logging (which may correspond to three or four cycles). However, that change
was averaged over three different locations then converted to a percentage,
whereas if the percentages had been calculated first for each of the three
locations and then those averaged, the result might differ in magnitude. For
the upper soil profile down to 0.55 m Ferré, et al.
[255]
note a drop in SOC of ~40%
over 3 or 4 logging cycles over 37 years, but that includes soil manipulation
through ploughing and fertiliser addition. For the upper soil profile down to
0.6 m, Vario, et al.
[256]
reported a drop in SOC of up to -24% for the second logging cycle.
These changes are comparable with the trends shown in
Figure 9
but are higher in
magnitude, considering the number of logging cycles passed.
An example of the ambivalence
arising from short-term experiments is in a recent review of ΔSOC, with
different anthropogenic activities
[245]
. Their overall finding concurred with that of Dean, et al.
[239]
, in that intensive logging of
a primary forest followed by repeated logging cycles decreases soil carbon
compared with the earlier, long-term average for the primary forest. However,
they found that the change was mostly in the topsoil, whereas if allowing
sufficient time for the whole soil profile to match that of the new forest
cover, then that whole profile is more likely to change (as lower down changes
more slowly). Conversely, another recent examination of ΔSOC with logging,
though only thinning, which considered mostly short-term experiments
[257]
, could not find any
statistically significant effects of logging. On considering the dynamics
described above, short-term and surface-soil experiments cannot possibly show
the long-term, whole-profile effects on SOC from logging. Thus, although Lei,
et al.
[257]
, cited Dean,
et al.
[239]
, they
didn’t take onboard the timelines for assessing change mentioned therein.
Most chronosequence studies
compare forest SOC at different ages since the first logging, against the SOC
of primary forest, but only for one logging cycle [[258-260],e.g.,
[261,262]
]. There are few
experiments on ΔSOC that span several logging cycles. They would probably use
space-for-time substitution, but the non-equivalence between sites is the bane
of such experiments. Often, one of the pairs has already been considered
inferior for resource extraction. Undeveloped land has a long history of being
less productive than developed land
[50,263–266]
. It will be difficult to find data in the form of equivalent paired
sites, to compare with the modelling in
Figure
9
. A typical example is presented here. For selective
logging over about two centuries (i.e., no definitive cycles) Christophel, et
al.
[267]
found an
increase in the upper mineral soil to 0.3 m depth and a decrease in the organic
layer above, and combined there is a net decrease with the logging. However,
the paired sites may not have been equivalent because the mineral soil in the
unmanaged forest sites had ‘larger stone contents’
[267]
. Regarding that comparison of
sties, the increase in stoniness % volume for the primary forests compared with
the managed sites, averaged across the three locations in Christophel, et al.
[267]
, for the Ah, AB and BC
horizons was 14%, 10% and 21%, respectively. These amounts are enough to
indicate that the productivity on the sites could be different and if so, then
the organic matter returns to the soil will also be different. Also, as
sampling an equivalent mass of soil when making SOC comparisons is sometimes
necessary
[268]
, the
soil sampling depth would need to be between 10% and 21% deeper than -0.3 m in
the stonier primary forest.
It is often inappropriate to
ignore earlier land cover when portraying the carbon forecast for forestry,
because of the centuries required for SOC stock to reach a new dynamic
equilibrium [e.g.,
[230,269,270,271]
]. In ecology, where there is a major disturbance followed by a
long-term change, and the flora and fauna species take time to reach a new
equilibrium, that period is called ‘relaxation time’
[272,273]
. That same term will be adopted
here, for the forest soil organic carbon to adjust after conversion from the
long-term average of a primary forest to that of the long-term secondary forest
under logging cycles.
There are ~2 Mha of plantations in
Australia, and ~5 Mha of mostly hardwood production forest on public land, plus
between 22 and 108 Mha of privately owned or leased forest but most of which is
not commercially viable
[274–276]
. Most of that 7 Mha of forest production land was primary forest
prior to logging. And as Australia only began converting primary forests about
200 years ago, much of that area is still in the first few cycles, and
consequently Australia has much more carbon to emit within the relaxation time
[if it continues logging on that land].
An appropriate baseline
corresponding to somewhere within the relaxation time must be included when
showing a carbon forecast for a particular activity. It is often not included
in bioenergy and forest carbon accounts
[277]
. Indeed, forest debris, waste from mills and almost any timber from
forests is called ‘renewable energy’ and burning it is considered ‘carbon
neutral’ by many corporate forestry proponents, because the trees can be
regrown [e.g.,
[278]
].
But this neglects the decreasing soil carbon during the relaxation time. Time
segments and baselines from within the relaxation time could be included in
corporate carbon accounting. If the date of the original forest conversion to
logging cycles is known, then one can estimate where in
Figure 9
the current logging
is acting. This would allow up-to-date life-cycle-analysis calculations for the
carbon footprint of recent wood products, which could be conveyed to customers
or used in national accounts.
As a corollary to the long-term
emission upon conversion of primary forest to logging cycles, another
perspective is offered by considering the time taken to replenish emitted
carbon. Long relaxation times are also required upon soil recovery, for
definitive results— to separate the signal from the background noise. Recovery
requires several generations of trees to grow and decompose to sequester the
carbon into the soil, as shown in the model output in
Figure 10
(adapted from Dean,
et al.
[230]
). For
diagrammatic simplicity, the SOC depletion in this example is from
deforestation, rather than from logging cycles. The modelled SOC in
Figure 10
starts at 0 Mg ha-1
before any vegetation contributes carbon to it, to show the spin-up time for
models (mentioned above), but less time would be needed where there is nearly
as much legacy carbon as in the future forest. The ripples are due to sudden
death of the stand (such as from a s)and-replacing fire) but the same overall
shape of the sequestration and emission occurs when modelled as annual
contributions of SOC to the soil
[230]
.
Figure 10.
Output from a simple model in Microsoft-Excel: a three-pool SOC system with half-lives of 2, 50 and 500 years where SOC was created from decomposing roots of trees that died and regrew every 200 years. Colours differentiate successive generations of trees. After ~3,000 years there was deforestation and the site left barren for 200 years (e.g., a wide forest road). Recovery of SOC took nearly 1,500 years (the ‘relaxation time’) because several generations of forest had to regrow, mature, and decompose, to supply new SOC.
Figure 10.
Output from a simple model in Microsoft-Excel: a three-pool SOC system with half-lives of 2, 50 and 500 years where SOC was created from decomposing roots of trees that died and regrew every 200 years. Colours differentiate successive generations of trees. After ~3,000 years there was deforestation and the site left barren for 200 years (e.g., a wide forest road). Recovery of SOC took nearly 1,500 years (the ‘relaxation time’) because several generations of forest had to regrow, mature, and decompose, to supply new SOC.
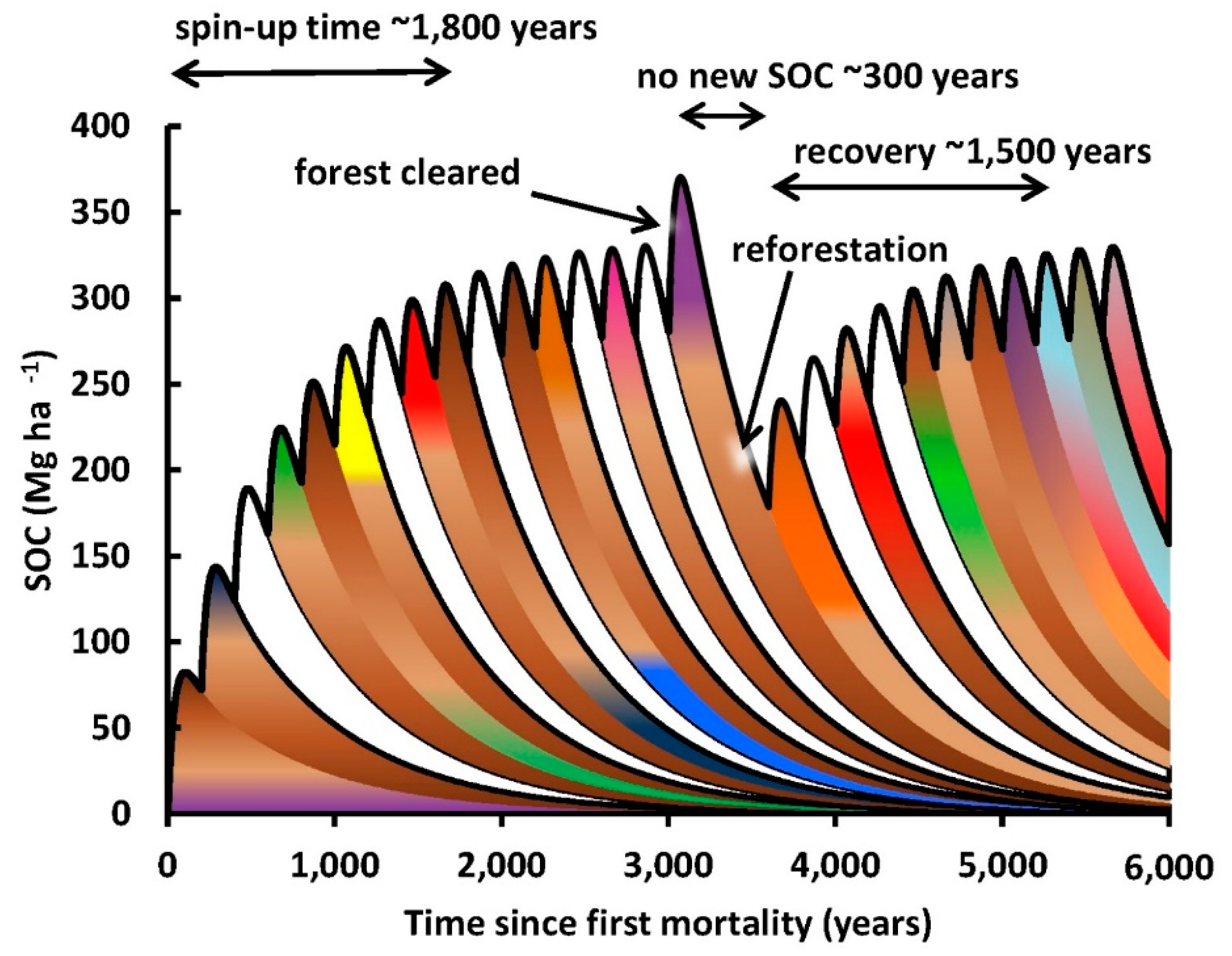
4.4. Points of Reference for SOC Measurement
4.4.1. Difficult Locations: Under Large Trees and Deeper Down
Another reason for ambiguity over
ΔSOC with logging of primary forests is that, before logging, SOC is not
usually measured under large tree trunks where it is usually more concentrated
and deeper in the profile than in between trees, nor is it measured under large
coarse woody debris (CWD)
[92,279]
(
Figure 7
). Therefore, pedogenic patches
[279]
of concentrated SOC could be missed before logging. During logging
the large stumps and CWD are sometimes upturned, broken or bulldozed aside,
such that the lignomor underneath is accessible to random soil sampling (
Figure 7
.d-e). Approximately
4% of the SOC could be missed prior to logging because of this difference in
measurement before and after logging [
Figure
11
in
[92]
]. This could cause inaccuracy and imprecision, or introduce bias
when assessing the impact of land use on SOC.
Depth is another inadequately
represented dimension when measuring SOC
[224,261]
. The international, minimum recommended depth for measuring SOC
change is 0.3 m, principally for international comparisons
[280]
, with a more general
recommendation of 1 m
[281]
. Depending on the tree species, soil profile and fragmentation of
bedrock, the roots and therefore a substantial portion of the SOC from
decomposition of old roots or infiltration of surface water containing tree
carbon, can be below a metre depth
[92,224,282–291]
. The depth for SOC measurement should be guided by such factors
[224,290–292]
.
To measure 90% of SOC in a
mixed-forest in Tasmania it was necessary to include soil down to ~1.6 m depth
[92]
. The depth to include at least
95% of the root biomass for Eucalyptus species is often over 2 m or
deeper where the soil depth or fracturing of bedrock permits
[92,282]
(
Figure 11
.c). For a site in
the Brazilian Amazon where SOC was measured to -10 m, only 21% of the SOC was
in the top 0.3 m, ~50% to -1 m, and 16% was below -3 m
[293]
. Where soil or bedrock and
species permit, roots of woody species extend to 10–20 m depth
[294,295]
, which will create
pedogenic high-SOC patches after root decomposition.
The stoniness of many forest soils
is often an impediment to SOC sampling. The location in
Figure 11
(a) and (b) with a
very thin layer (~0.2 m) of mineral soil supported forests of Eucalyptus
regnans and Eucalyptus obliqua, though only to ~45 m height, rather
than the 75 m typical of mixed-forests. Tree roots can occupy fissures up to
several metres in bedrock and decompose there (
Figure 11
.c), creating soil
and adding SOC, and contributing to translocation of water that may contain
dissolved organic carbon from above [e.g.,
[296]
]. The inclusion of this characteristic in carbon modelling, is
suggested based on experimental evidence of likely forest root decomposition in
weathered and fractured bedrock plus underground transportation of some of that
resultant carbon as dissolved organic carbon
[289]
. Organic carbon in fractures in weathered bedrock, even granitic,
is linked to root distribution. The rock surface in the fractures (to < 0.02
m thickness) can contain associated soil carbon
[297]
. The fraction of root mass in
bedrock (and hence the soil carbon derived directly from root decomposition
there) naturally depends on, for example, the depth of the A and B soil
horizons, tree species, climate, tree age, water distribution, and bedrock type
[298–300]
.
Figure 11.
(a) and (b): thin soils with large boulders that would prohibit typical soil sampling to more than about 0.2 m depth. The amount of total SOC may be similar to that for other Eucalyptus regnans and E. obliqua forests of equal long-term-average biomass in that climate, and would need to be included in carbon modelling of land use. Photographed during clearfell cable logging of primary forest in coupe WE008e, near Mt. Wedge, Tasmania. (c) Roots descending over 5 m into fractured bedrock in dry schlerophyll forest, South Australia, exposed during mining. When these trees die (apart from those exposed) some of the root carbon will form local SOC.
Figure 11.
(a) and (b): thin soils with large boulders that would prohibit typical soil sampling to more than about 0.2 m depth. The amount of total SOC may be similar to that for other Eucalyptus regnans and E. obliqua forests of equal long-term-average biomass in that climate, and would need to be included in carbon modelling of land use. Photographed during clearfell cable logging of primary forest in coupe WE008e, near Mt. Wedge, Tasmania. (c) Roots descending over 5 m into fractured bedrock in dry schlerophyll forest, South Australia, exposed during mining. When these trees die (apart from those exposed) some of the root carbon will form local SOC.

In a critique of a soil carbon GIS
and modelling study by Dean and Wardell-Johnson
[301]
, McIntosh, et al.
[302]
referred to three reports on
soil organic carbon in northern Tasmania
[303–305]
, as being available as points of reference for comparison for SOC
down to 1 m depth, i.e., they purportedly formed benchmarks. These three
reports will be examined here to portray aspects of SOC measurement appropriate
for use in the calculation of land use effects on the carbon cycle and for
comparison with carbon-cycle modelling.
The soil depths studied in Grant,
et al.
[303]
, for
example, are only to between 0.8 and 1.2 m depth and many have a ‘+’ sign on
the last measurement. Additionally, there were some methodological issues
because the experiments were not originally designed for spatial carbon
assessment. They had been instigated to determine soil suitability for
plantations
[306]
.
Those methodological issues are explored here. Part of peer review is to make
sure that standard scientific protocols have been followed. Science that gets
published without peer review is called ‘grey literature’ and therefore using
it as a basis for the next advance in science is viewed as meaning that the
next step might possibly be more dubious than if using peer-reviewed science as
a basis. The three 1995 Tasmanian reports
[303–305]
were such grey literature. Consequently, checks would have been
appropriate on how applicable their data is to scientific assessment of spatial
carbon accounting, under the scientific peer review process.
That ‘+’ sign indicates that the
soil profile continued deeper than was sampled, therefore, it is likely that
there was more carbon to be tallied than that reported. Such a comparison
against modelled SOC values is often not valid because the values derived from
modelling, such as in Dean and Wardell-Johnson
[301]
, which used CAR4D, include
SOC to wherever it may have been translocated, such as down into the fractures
of bedrock, or laterally offsite by groundwater or streams. Due to the limited
data available, in modelling the carbon cycle in CAR4D, the entire soil profile
(including fractured or semi-permeable bedrock) is treated as homogenous:
undifferentiated laterally or depth-wise
[301,307]
. Some modelling software accounts for SOC to only 0.3 m, for highly
calibrated sites or it uses very generalised profiles, or tweaks the
carbon-compound half-lives or emission pathways to match SOC to 0.3 m, for
example in FullCAM [
[308]
; S. H. Roxburgh, CSIRO, personal communnication, 2021].
McIntosh, et al.
[302]
referred to the modelled
total of 685 Mg ha-1 for the case study #1 site in Dean and
Wardell-Johnson
[301]
,
which was a E. regnans-dominated forest (introduced in
[307]
) as being:
‘…more than twice the maximum measured
soil C value under E. regnans available to these authors in 2010 which
was 273 Mg.ha-1 in the previously mentioned Stronach profile
[21]
.’
The SOC values in McIntosh, et al.
[302]
were only
tallied to 1 m depth rather than for the full profile as in carbon modelling,
which suggests that the 273 Mg ha-1 for the Stronach site in Grant,
et al.
[303]
(the
reference ‘
[21]
’ cited
in McIntosh, et al.
[302]
) had also been truncated to 1 m depth from its reported 305 Mg ha-1
to 1.2 m.
Values of SOC for the full profile
can be estimated by fitting simple exponentials to reported empirical SOC data
using equations of the form:
cumulative_SOC = g [1 − exp(bz)]
where z is depth in metres
(negative below 0); Dean, et al.
[92]
. If z is lower than where SOC was measured, then the extrapolation
relies on there being soil or rocks that can adsorb SOC occurring lower in the
profile, or DOC or colloidal SOC being carried deeper or sideways. From soil
sampling in McIntosh, et al.
[302]
, the site of highest SOC had 304–326 Mg ha-1 to 1 m
depth. Extrapolation using Equation 2 for this site gives ~498 Mg ha-1.
This value is closer than their declared benchmark of 273 Mg.ha-1,
to the temporal average of 685 Mg ha-1 for site #1 modelled in Dean
and Wardell-Johnson
[301]
, which was for the entire soil profile and any translocated SOC.
Additionally, site #1 in Dean and
Wardell-Johnson
[301]
had above-average, long-term, live biomass, as shown later in this paper, and
therefore could be expected to have above-average SOC, whereas the sites in Grant,
et al.
[303]
are more
likely to have been average. The live biomass for mature E. regnans
stands can vary greatly, e.g., 262–647
→
697–1053
[57,77,92,309]
, and is possibly
related to the ‘site index’ (forestry terminology for potential wood volume at
a particular age). If this difference persists in particular locations over
successive generations of E. regnans trees, then by the positive
relationship between aboveground biomass and soil carbon [mentioned above],
there should be an equivalent range of SOC between those stands. On a pro-rata
basis the variation in biomass found in Dean, et al.
[92]
for stands of approximately
equal maturity, corresponds to a variation in SOC of 184-to-455 Mg ha-1
(across the average of 330 Mg ha-1).
Regarding suitable points of
reference, there were other SOC data available back in 2010, from soil carbon
accounting experiments in E. regnans-dominated forests: data from
Victoria
[258]
had
been used to calibrate the model ‘CAR4D’
[307]
. For those sites, there was an estimated 1,300 to 3,000 Mg ha-1
to 10 to 20 m depths, and a measured average of 650 Mg ha-1 to 1 m
depth
[258]
. The SOC
in CAR4D was modelled as being less than at those Victorian sites, concomitant
with the frequently shallower soils in the Styx Valley, Tasmania. Now that SOC
data from experiments designed for carbon accounting are available for E.
regnans-dominated forests in Tasmania
[92,302,310]
, CAR4D can be recalibrated.
4.4.2. Difficult Locations: Coarser Components
Not only dimensions need to be
considered comprehensively but also other parts of the soil. Many, though not
all, experiments involving sampling of SOC in soil have not measured the carbon
in firm particles greater than 2 mm width
[290,311]
. The reason for this may be because: (a) they were considered
chemically unable to bind to organic carbon
[290,312]
, (b) some researchers may do it simply to align with an established
protocol, or (c) the harder fragments can be more difficult to grind in
preparation for elemental analysis. But the practice can miss out on
substantial portions of SOC, resulting in underestimations for some forests and
possibly incorrect calibration of carbon dynamics models
[290,312,313]
. Significant amounts
of organic carbon can be dissolved into stones or adsorbed on their weathering
surfaces, with significant contribution to total SOC
[314–316]
.
Where there has been forest fires
or post-logging burns, there may be pieces of charcoal as well as coarse
mineral fragments. Without any post-logging burn, Hopmans, et al.
[317]
found SOC to 0.3 m depth was
209 Mg.ha-1: with and without post-logging burns the amount of SOC
in charcoal and rocks >2 mm width was 42% and 29% of the total SOC,
respectively
[317]
. In
forests with occasional fire but no post logging burns Buma, et al.
[318]
found that the SOC to 0.1 m
depth contained ~16% charcoal in the >2 mm fraction. Holub and Hatten
[213]
and Harrington, et al.
[319]
also sampled
carbon in material >2 mm width but only up to 4.75 mm width.
Charcoal is more likely to be near
the surface (unless in buried sediments) and coarse stony fragments are more
likely to be closer to the bedrock
[313]
. It is logical to include such carbon pools in forest carbon
accounting related to climate change. The organic carbon associated with
charcoal and mineral fragments is inherently included in earlier modelling work
[47,235,269]
and was
measured empirically in Dean, et al.
[92]
. Discarding and not counting the organic carbon in the >2 mm
charcoal and rock fragments in the soil, could be one of the reasons for the lower
SOC benchmark suggested by McIntosh, et al.
[302]
.
Soil may also contain very old
organic carbon that is not derived from the current or recent forest biomass,
but from ‘fossil’ carbon in soil derived from sedimentary bedrock
[320,321]
. This could complicate
modelling of forest carbon dynamics and measuring the effects of
land-use-change. Organic matter found in rocks and soil during forest carbon
accounting experiments originating from the forest should ideally be
differentiated from that from shale, some sandstone and mudstone etc (such as
the grey or black varieties). Radiocarbon dating, radiocarbon natural
abundances (Δ14C), or carbon isotope ratios (δ13C) may
allow such differentiation
[322]
.
4.4.3. Soil Sampling Specific for SOC Accounting
Apart from just the depth aspect,
it is worth considering those 1995 Tasmanian purportedly benchmark studies more
closely in different dimensions, especially as there has been further
developments in science now that spatial soil carbon accounting is a common
goal. When considering points of reference (benchmarks) for comparisons, one
must consider possible bias and error margins. One of the aspects that has
progressed considerably in the last few decades to reduce bias and error
margins is elemental analysis of soils [e.g.,
[323,324]
]. The three 1995 Tasmania reports used a modified Walkley-Black
(WB) method for carbon assay but without any mention of a correction factor:
‘These have been determined using
the Walkley and Black colorimetric method (Rayment and Higginson 1992).’ [
[325]
, p18], plus:
‘The procedure is that described
by Rayment and Higginson (1992) using 0.5 M sodium dichromate (Na2Cr2O7.2H2O).
Read absorbance using the “Cecil spectrophotometer CE 292”. Determine organic
carbon values from plotted standard curve of absorbance verses organic carbon
(%)’
[306]
The WB method may not measure all
the organic carbon in the soil, depending on the chemical structure of the
organic molecules, and on how they are bound in the soil, which in turn is
dependent on for example, climate, soil type, parent rock type, tree species
and land management
[326–328]
. And it may not measure the carbon in charcoal, as is necessary in
forest carbon accounting. The WB method relies on oxidation of organic carbon,
under moderate heat generated by the action of aqueous sulfuric acid, with
accompanying reduction of Cr6+ to Cr3+, but the oxidation
of carbon may be incomplete. Which is why the USA Forest Service recommends
that the method should not be used
[329]
.The amount of oxidised carbon is determined by titration for Cr6+
or by colorimetry of the Cr3+, or simply by measuring the amount of
CO2 released. The recommended correction factor, which is a
multiplier, is usually near 1.3 but calibration for specific environments and
land use may require multipliers nearer 1.7
[330]
. For some Tasmanian plantations Wang, et al.
[331]
found that the WB method
detected 97% of the carbon found by using an Elemental Analyzer and therefore
no substantial multiplier was needed, but that may have been due to the
younger, loosely bound carbon
[332]
, and possibly as the plantations may have been sprayed with
atrazine (which contains organic carbon and may not have been bound strongly to
the soil). One modified-WB method uses heat to oxidise more of the carbon and
thus requires a lower multiplier
[327]
, but the heat method was not used in the 1995 Tasmania reports,
though sodium dichromate dihydrate was used instead of potassium dichromate. Meersmans,
et al.
[327]
recommend
calibrating the WB method for different soils and land use. Any use of a
multiplier in the three 1995 Tasmania reports, was not reported, and the same
colorimeter absorbance vs carbon curve may’ve been used for all samples, thus
rendering them quite imprecise for spatial carbon accounting.
Another increase in uncertainty
occurs when the soil bulk density is either not calculated or not reported, in
a method appropriate for soil carbon accounting. The three 1995 Tasmania reports
that McIntosh, et al.
[302]
suggested should be points of reference, provided the concentration
of carbon in the soil as wt% from the fine, sieved soil, but the reported bulk
density was the weight of the whole sample, including stones and roots, divided
by the volume of the entire sample
[306]
. To use such data for spatial SOC calculations requires
recalculating the density of the fine soil fraction using any reported stone
and root volumes and weights. However, the volume of stone and roots was
reported within wide ranges for the different horizons in the soil types in the
area, and not precisely for the specific sample from which carbon or bulk
density were measured. For soil carbon accounting it is necessary to subtract
from the weight and volume of the soil core, the weight and volumes (in
quantitative terms for each sample) of any material in the core that isn’t
measured as part of the fine soil
[333–335]
. If the carbon in any of those components was derived from the
forest biomass then it can be included later in the carbon accounting.
Preferably, the bulk density and carbon concentration should be determined from
the same sample
[336]
.
Therefore, in those three 1995 Tasmanian reports, the volume and weight of soil
within each sample volume could only be determined semi-quantitatively, and consequently
with substantial error margins.
To illustrate the error margins
introduced by that earlier methodology, a few examples from the three 1995
Tasmanian reports will be processed here. The amount of roots was given as, for
example, ‘many medium roots’ in an A1 and a B1 horizon, ‘abundant fine roots’
in an A1 horizon and ‘common coarse roots’ in a B2t horizon. The stone content
of the soil was given in more quantitative terms; for example: 2–10% granite
(20-60 mm fragments) and 10–20% granite (60-200mm fragments) in a B1 horizon,
0–<2% basalt in an A1 horizon, and 20–50% sandstone in a B2 horizon. If one
assumes the average densities for such rock types
[337]
, and assumes that the bulk
density was measured with the average amount of stone volume for a particular
horizon (e.g., 35% sandstone for a horizon with 20–50% sandstone by volume)
then the measured bulk density can be adjusted to give an effective one.
However, insufficient detail was provided for a quantitative adjustment for the
root volume.
By thus accounting for stone
volume, the total soil carbon for four example soil types ‘Cuckoo’, ‘Kapai’,
‘Stronach’ and ‘Maweena’ which host wet-eucalypt forests, in Grant, et al.
[303]
reduces from 402, 344, 305,
and 331 Mg ha-1 respectively (to the measured depths of 1.2, 1, 1.2
and 0.96 m respectively) to 180, 244, 297, and 112 Mg ha-1
respectively. I.e., reductions of between 2 and 66 %. Due to imprecision in
stone content alone, the error margin for total SOC after adjusting for stone
content, is up to ~±18%. It would be higher if including error margins in the
rock densities, and if the root volumes were quantified in a similar style.
4.4.4. Comparing Carbon Stocks across Climates and Time Periods
In Australian forests, and indeed
globally, SOC generally increases with rainfall (assuming other factors being
equal)
[338–340]
. The
largest concentration of Tasmanian rainforests is in the west and northwest of
Tasmania, which is a higher rainfall zone (on average) than where the tall-open
forests in Tasmania are
[301,341]
. Therefore, Tasmanian rainforest could be expected, on average, to
have higher SOC values than the tall-open forest. The GIS analysis in Dean and
Wardell-Johnson
[301]
,
based on national SOC and rainfall layers, and a Tasmania vegetation layer,
shows this to be the case: 2218 and 1559 mm yr-1 and 369 and 271 Mg
ha-1, respectively for rainforest and tall-open forest. Likewise,
the fraction of Tasmanian rainforest in close vicinity to tall-open forest in
Tasmania is expected to have lower SOC than the average rainforest. That close
proximity, lower-rainfall location (average 1241 mm yr-1) is where McIntosh,
et al.
[302]
measured
SOC in the two forest types, and found an average value of 102 Mg ha-1
to -0.3 m depth for rainforest. When critiquing Dean and Wardell-Johnson
[301]
and comparing the two values
for rainforest SOC, McIntosh, et al.
[302]
appeared to not take into account the difference in climate, and
wrote:
‘…the unreferenced 369 Mg.ha-1
of C at 0–30 cm depth quoted by Dean and Wardell-Johnson (
[27]
,
Table 1
) for rainforest soils
in Tasmania is over three times too high…’.
Many of the western Tasmanian
rainforest soils in western Tasmania [which is where rainforests are
concentrated] are organosols, with an average SOC of 450 Mg ha-1 to
0.47 m depth
[342]
.
Assuming equal SOC distribution over that depth gives 287 Mg ha-1 to
0.3 m. Or alternatively, application of a simple exponential falloff with depth
(Equation 2 above), gives 311 Mg ha-1 to 0.3 m depth. If the soil
profiles and bedrock allowed SOC to venture much deeper than 0.3 m, then
extrapolating to the full profile gives SOC as 1200 Mg ha-1. The
value of 369 Mg ha-1 in Dean and Wardell-Johnson
[301]
is 19% higher than the value
of 311 Mg ha-1 found empirically by di Folco and Kirkpatrick
[342]
. Such a difference is
reasonable, considering that the GIS data used was a nation-wide layer.
As described above, the
mixed-forest and rainforest each have their own ideal geographical ranges, with
some spatial overlap if fire history permits. On pedogenesis timescales,
rainforest sites in close proximity to mixed-forest sites, are possibly often
occupied by mixed-forest, and vice-versa. The overlap, in the absence of
logging, ebbs and flows with the vagaries of fire
[119]
. There was still decomposing
eucalypt debris in several of the rainforest plots studied by McIntosh, et al.
[302]
and some contained live
eucalypts:
‘While rainforest sites contained
negligible quantities of live eucalypt boles (small eucalypts were encountered
in just 3 rainforest sites), they contained significant quantities of eucalypt
CWD (
Table 2
).
Eucalypts contributed 27% of total CWD volume and 29% of total CWD C-mass in
rainforests.’
[201]
,
Thus, considering the timescales
involved for change in SOC compared with those for biomass change, as described
above, the experiment in McIntosh, et al.
[302]
was not really designed for their stated objective of
differentiating between the SOC in mixed-forest and in rainforest. Moreover,
these timescales may mean that such a differentiation in SOC of the ecotone
region does not exist; it may only exist in the regions where rainforest and
tall-open forest do not swap locations over time, and this would match with the
data to-date, in the reports discussed above.
The blurred spatio-temporal
boundary between mixed-forest and rainforest is in part because coarse woody
debris and especially soil carbon, representative of either forest type,
persists to a degree depending on its half-life. This material constitutes
‘legacy carbon’
[343,344]
(
Figure 12
). Empirical studies attempting to contrast SOC stocks in rainforest
and mixed-forest in close proximity, will thus be unproductive until the
transition between the two is almost complete for all forest attributes,
include soil.
Figure 12.
Fallen E. regnans logs spanning Cliff Creek, Styx Valley, Tasmania. The creek is centred in a 200 m wide gully mapped as API-type rainforest. The logs are remnants of previous mixed-forest. This contrast typifies the blurred spatio-temporal boundary between mixed-forest and rainforest, being in-between from a carbon dynamics perspective. The gully is not rainforest from a carbon perspective, even though living eucalyptus trees are absent.
Figure 12.
Fallen E. regnans logs spanning Cliff Creek, Styx Valley, Tasmania. The creek is centred in a 200 m wide gully mapped as API-type rainforest. The logs are remnants of previous mixed-forest. This contrast typifies the blurred spatio-temporal boundary between mixed-forest and rainforest, being in-between from a carbon dynamics perspective. The gully is not rainforest from a carbon perspective, even though living eucalyptus trees are absent.

When rainforest and mixed-forest
are in close proximity, and may interchange location over time, then it is
appropriate to consider the effect on differences in biomass, rather than on
SOC. For the purposes of carbon accounting for climate change effects, this
should be considered over long time periods, to get the overall impact. A long-term,
time-based average carbon stock, has equivalences to a landscape-level average
at one point in time, if numerous instances of forests of different ages are
present across the landscape. Here the claim by Moroni, et al.
[201]
that net carbon will decrease
and stay that way if mixed-forest is not logged but allowed to mature and go
through succession to pure rainforest is re-examined, but over a long enough
time period to get representative, time-averaged carbon stock:
‘As Tasmania’s wet forests
transition from mixed forest to rainforest they can be expected to lose more
than half their total (live + dead, standing + downed) bole wood volume and
biomass as smaller dimension rainforest trees replaced the larger eucalypts. …
Certainly, setting aside Tasmanian wet eucalypt forest to store C will not
deliver the usual long term C accumulation benefits common to forests elsewhere
and maximizing landscape level C-stocks is likely to require periodic
disturbance to maintain the C-dense eucalypts in the landscape.’
[201]
The ’periodic disturbance’ in that
extract most likely implies fire and/or logging. Prior to industrialisation and
without Aboriginal burning (though burning on the far east coast may have
trickled effects across to the centre of the island), mixed-forests occupied
large areas in Tasmania (such as in the logging concession areas) and therefore
they do not need logging to exist. The Primary mixed-forest has been the foundation
of export-scale commercial forestry in Tasmania for nearly a century because of
its eucalypt content. Whereas extraction reconnaissance projects for rainforest
areas, such as in northwest Tasmania, have found logging to be either
uncommercial or to require low extraction fractions to maintain forest health [[345-347,348],
p37-38]. Thus there are at least two possible reasons for the controversy over
benefits of the two alternative forest types. Prior to industrialisation in the
area of the logging concessions, there were sufficient periodic disturbances of
perhaps once every several hundred years in the form of wildfire, e.g., 450 to
500 years
[349,350]
to
maintain a dominance of mixed-forest. Higher-frequency disturbance at such
intensity is not necessary.
More fire is inevitable in the
future with anthropogenic climate change
[351,352]
, so the chances of succession to rainforest, or maintenance of
rainforest, are less likely than normal. Rainforest attrition is forecast with
climate change
[353]
,
which will put neighbouring mixed-forests in Tasmania at risk (rather than the
risk coming from replacement by rainforest). Rainforest species in mixed-forest
have an intrinsic benefit in the face of climate change: they protect carbon in
the wider landscape from fire
[354]
. CBS logging can create poor regeneration of the rainforest species
and create stands more favourable to pulpwood than sawlog production (i.e.,
shorter wood-product half-life and therefore add to climate change)
[355–357]
. As the seed source for
the rainforest understory becomes restricted spatially with fragmentation of
mixed-forest
[357]
,
further logging will make it more-difficult to regain primary-forest carbon
levels, which will also contribute to climate change. The importance of primary
forests in climate change policy has been re-iterated, with policy initiatives
broached for their conservation
[358]
. Limiting forest fragmentation and general anthropogenic
disturbance is likely to help maintain existing mesic micro-environments that protect
against drying-out under climate change and thus against fire. At least 50% of
rural fires in Australia are of anthropogenic origin [e.g.,
[359,360]
]. Eliminating that
ignition source and managing combustible material near infrastructure, such as
roadside grassland and farmland
[361]
, would help reduce forest carbon losses under climate change.
The difference in biomass
accompanying the succession from mixed-forest to rainforest matches the typical
case for forest succession, where the pioneer (coloniser) species is fast
growing and has appreciable initial biomass
[362,363]
. Whereas Moroni, et al.
[201]
call it ‘unusual ecology’. In mixed-forest the coloniser species
are eucalypts, e.g., Eucalyptus regnans. The issue of decline in biomass
with forest succession was covered numerically and graphically in Dean, et al.
[235]
, and it was mentioned that
landscape-level carbon stocks in biomass can decline if: ‘the understorey,
which dominates the later stages of succession, has a lesser biomass than the
maximum for the E. regnans dominated forest’.
To illustrate possible dynamics of
carbon in biomass of rainforest succession and to compare it against logging,
two simulations were run using CAR4D (
Figure
13
), with two levels of understorey biomass: one very
low and one higher but still only at around 20% of total stand biomass at the
time of logging. Rainforest understorey can contribute 50% of total biomass
prior to onset of substantial eucalypt senescence in mixed-forest
[364]
. Due to the low precision of
understorey allometrics, no definitive quantitative result is shown in
Figure 12
, but even when
including wood-products, it is not necessarily the case that harvesting cycles
store more carbon than long-term rainforest.
McIntosh, et al.
[302]
measured and compared
standing biomass in the two forest types. They had a mixed-forest:rainforest
biomass ratio of 1:0.45. The two scenarios in
Figure 13
have ratios of
1:0.48 and 1:0.72. The first of those is close to that of McIntosh, et al.
[302]
. In both cases, the long-term
rainforest average total carbon does not go below the long-term logging average
carbon (where the carbon is summed across biomass and wood products). That is
because rainforest total carbon doesn’t oscillate as much as that of a logged
forest. The magnitudes in the frequent oscillations must be averaged over time,
with an average that is lower than the peaks, which most likely correspond to
the point at which they would be logged.
The long-term average C in biomass
in rainforest can exceed the long-term eucalypt logging-cycle carbon (including
wood-products) if it is a third or more of the biomass of mature wet-eucalypt
primary forest (
Figure 13
.a). The C in biomass of rainforest understorey only needs to be
about 15% of the C in biomass of primary mixed-forest at the time of logging,
if the two forest types are to be equivalent in terms of C. However, it needs
to be at least 20%, if upon succession it is to exceed the mixed-forest carbon
(
Figure 13
.b). If
comparing the long-term carbon stocks of pure rainforest and mixed-forest, then
the long-term rainforest carbon only needs to be more than half of peak
mixed-forest carbon at the time of logging of primary mixed-forest, if it is to
substantially exceed long-term mixed-forest carbon (
Figure 13
.b).This is due to
the more-frequent low carbon periods in mixed-forest than in rainforest. Note
that this 50% requirement is very different to the 100% requirement implied in McIntosh,
et al.
[302]
and Moroni,
et al.
[201]
.
Considering the error margins involved in modelling the carbon stocks of the
two forest types and wood products, although
Figure 13
.b shows rainforest
carbon exceeding logged mixed-forest carbon, in the long-term, it’s likely that
it is not definitive at this stage: more accurate and precise data are needed.
Rather than considering the
rainforest understorey biomass within mixed-forest as a representation of what
the pure rainforest will be like after succession, there’s an additional
possible change upon succession that will increase rainforest biomass. Gilbert
[55]
noted that rainforest biomass
is slightly smaller in mixed-forest than in pure rainforest but added that it
was difficult to find sites of equivalent productivity, from which a
significant comparison could be made. Notably though, paired
mixed-forest/rainforest sites in northwest Tasmania were found to have higher
rainforest wood volumes in the rainforest members
[365]
. Thus, some of the eucalypt
biomass may be replaced by rainforest biomass upon succession, which would make
rainforest have a slightly higher advantage than indicated in
Figure 13
. Though another
explanation for this increase in biomass for pure rainforest is that it could
usually occupy higher site-index (more productive) sites than does
mixed-forest.
Figure 13.
Simulated aboveground carbon stocks of forest succession and logging scenarios including wood products, typical of Site-1 in Dean, et al. [47], for primary-forest and harvesting cycles (modelled using CAR4D). Important for comparisons: time-based averages of total carbon (including wood products)— dashed horizontal lines. (Solid curve=total carbon in biomass plus wood products; dashed green curve=understorey biomass; dotted red curve=E. regnans biomass, purple solid horizontal lines= total carbon stock at time of logging.) The rainforest understorey filled space between senescing eucalypts which succeeded to rainforest; afterwards intense wildfire with seeding from nearby E. regnans. New mixed-forest grows to age 320 years, then logged (parameters as in Dean, et al. [47]). Rainforest biomass was set to a maximum of ~1/3 (a) and ~1/2 (b) of peak of the mixed-forest— corresponding to 15% and 22% (respectively) of stand-level biomass at time of primary-forest logging. In (a) long-term rainforest biomass= ~half that of the time-averaged mixed-forest biomass and equal to that of the harvest cycles (including wood-products). In (b) long-term rainforest biomass= ~time-averaged mixed-forest biomass and greater than that of the harvesting cycles (including wood-products).
Figure 13.
Simulated aboveground carbon stocks of forest succession and logging scenarios including wood products, typical of Site-1 in Dean, et al. [47], for primary-forest and harvesting cycles (modelled using CAR4D). Important for comparisons: time-based averages of total carbon (including wood products)— dashed horizontal lines. (Solid curve=total carbon in biomass plus wood products; dashed green curve=understorey biomass; dotted red curve=E. regnans biomass, purple solid horizontal lines= total carbon stock at time of logging.) The rainforest understorey filled space between senescing eucalypts which succeeded to rainforest; afterwards intense wildfire with seeding from nearby E. regnans. New mixed-forest grows to age 320 years, then logged (parameters as in Dean, et al. [47]). Rainforest biomass was set to a maximum of ~1/3 (a) and ~1/2 (b) of peak of the mixed-forest— corresponding to 15% and 22% (respectively) of stand-level biomass at time of primary-forest logging. In (a) long-term rainforest biomass= ~half that of the time-averaged mixed-forest biomass and equal to that of the harvest cycles (including wood-products). In (b) long-term rainforest biomass= ~time-averaged mixed-forest biomass and greater than that of the harvesting cycles (including wood-products).
4.5. ΔSOC with Logging Burns and Disturbance by Machinery
Measuring the change in SOC
accompanying land management is difficult, and for the forestry activity of
logging even more so because of natural forest heterogeneity (the pedogenic
patchwork, Stutz and Lang
[279]
) and the hodgepodge disturbances by logging machinery. The intense
burn of logging debris (‘residue’) in CBS-type logging adds even more
variability, but sufficient experimental evidence has been accumulating to
infer definitive effects
[366–372]
. It must be noted, that for carbon-cycle modelling purposes such as
determining values to include in computer software, the effects of the CBS
activity are considered separately to the additions to SOC that occur
afterwards from logging residue over longer time periods. The measured values
of ΔSOC accompanying these relatively short-term interactions for different
forest types range from -6% to -50%, but this is only for the upper soil
surface, to a depth of no more than 0.15 m
[239]
. The burn appears to oxidise SOC to no more than ~-0.1 m
[367]
, where there is no logging
residue or roots penetrating the soil. The fraction of the total SOC pool
emitted, depends on the depth distribution of SOC. That fraction can be
estimated for E. regnans-dominated forests in two locations where the
depth distribution of SOC has been reported. The equations for the profile
in-between trees for locations in Tasmania and Victoria are
given by:
where cumulative_SOC is the
cumulative SOC in Mg·ha-1 to a certain depth z, in metres
(negative below-ground). Equation 3 is for the Styx, Tyenna and Florentine
valleys in Tasmania from Fig 9.b and Supporting
Table S2
in Dean, et al.
[92]
, and Equation 4 is for
Toolangi in the Great dividing Range, Victoria from
Figure 11
in Polglase, et al.
[258]
.
Percentage drops in SOC for the
upper soil surface are collated in
Table
1
in Dean, et al.
[239]
. The second datum for Pennington, et al.
[367]
in that table needs to be
corrected to ΔSOC=13.4% down to 0.1 m depth. The values for ΔSOC then range
from -37% to 0.02 m depth to an average of -30% to 0.15 m depth. There are on
average, greater emissions of SOC closer to the surface (R2=0.67 for
a straight line fit of ΔSOC versus depth). Applying Equations 3 and 4 to the 10
data points in that table, allows the fraction of total SOC residing near the
surface to be calculated, which in turn allows calculation of the average ΔSOC
from the felling disturbance and CBS burns, across the whole soil profile, as
3.6(2.5)% and 4.1(2.8)% respectively (standard deviations in brackets), i.e.,
~4% loss of SOC from the soil profile due to the CBS burn.
The soil bulk density near the
surface increases during logging (from disturbance by machinery), and again
during the post-logging burn
[367,373]
. Pennington, et al.
[367]
found an increase in bulk density of 15% to 0.1 m depth due to the
CBS burn alone. As a result of the common process of measuring to a fixed depth
before and after logging activities, the increase in bulk density means that
more mineral soil from deeper down is contained in the sample after logging. It
too would have lost some SOC as its volume has decreased, which would increase
the SOC loss for the whole profile to possibly more than 4%. The soil
compaction and turbation indicate a need for additional care in experimental
design and interpretation.
The estimated short-term drop in
SOC from successive CBS logging events, used in modelling in CAR4D was 2.5% per
cycle
[47,301]
, which
is conservative compared with the ~4% calculated above. A sensitivity modelling
analysis showed that if the emission per cycle goes from 2.5% to 5% then the
long term ΔSOC due to converting primary forest to logging cycles goes from
-48% to -57%
[47]
,
which is a substantial difference. Therefore, both pinning down the effect
better, and working on its future prevention, are important for climate change
mitigation.
Previously in CAR4D the ΔSOC with
each CBS event was erroneously set at -10%
[307]
. The error arose from applying a measured drop in the surface soil
(0.2 m depth) found by Polglase, et al.
[258]
to the whole profile, instead of calculating its proportion of the
whole profile, as done above here. Using the corrected CAR4D, the long-term
(over 1.5 millennia) drop in SOC with conversion of a primary forest stand of E.
regnans mixed-forest to logging cycles, case study #1 in Dean and
Wardell-Johnson
[301]
was 47%. This was a correction of the earlier estimate of 87% in
[307]
.
Absolute values of ΔSOC are
important to carbon trading and determining the net effect on climate change
from management. However, it is the percentage that is most important when
comparing different land uses: it indicates what fraction of an ecosystem is
being lost, and whether one land use constitutes an emission relative to
another. The percentage loss of SOC with conversion of primary forest to
logging cycles does not change if the initial stocks are lower: the long-term
loss upon logging is linearly proportional to the pre-logging long-term average
SOC stock [
Figure 5
a in
[47]
].
Without recalibrating CAR4D, a
simple calculation can show the effect of the recently improved data on SOC
stocks for E. regnans-dominated forests in Tasmania, on the absolute
value of ΔSOC. If the SOC value of 330 Mg ha-1 from Dean, et al.
[92]
, is used as the pre-logging
SOC for site-1 in Dean, et al.
[47]
(which was also case study #1 in Dean and Wardell-Johnson
[301]
), then the long-term C
emission upon conversion to logging cycles of average tall-open forests
State-wide in Tasmania from 2010-to-2030 is 52(±26) Megatonnes of CO2-e
instead of the 66(±33) in Dean and Wardell-Johnson
[301]
. The change in SOC with
logging for the low end— case study #2 in Dean and Wardell-Johnson
[301]
(a low biomass
wet-sclerophyll forest)— remains as stated because the SOC stock was given
simply as a typical fraction of biomass (and the change in biomass is
unaltered).
5. Sustainability Interpretation for Corporate Forestry
The World Bank suggests that
sustainability should be included in corporate social responsibility (CSR) but
doesn’t specify if that is environmental sustainability, and some companies
interpret sustainability as meaning business viability
[182,183]
. Some corporations rely
on the older targets and methods of corporate responsibility and issue
sustainability rhetoric, against a background of legal and financial
requirements which have not shifted markedly to reflect a changed meaning of
CSR [
[374]
, p17-18].
For example, when solutions for the global syndemic (the combination of the
obesity, undernutrition and climate change pandemics) were reviewed, a change
in management of CSR was recommended:
‘Corporate social responsibility
efforts, which are too often marketing exercises, need to evolve into a
stronger accountability model, in which targets and performance criteria are
independently specified, monitored, and publicly shared.’
[184]
From the point of view of
sustainability of the wood stock, the primary aim in the Tasmanian pulpwood
concessions was to provide mill pulpwood and the second aim was a quota of
sawmill timber. For scheduling log supply for the pulp mill, the rotation age
was set at 80 years
[52]
. That period has passed but primary forest, both inside and outside
of the concession area, are still a target of corporate forestry, and logging
of primary forest vestiges within the concession area still occurs. Indeed, the
impossibility of sustainability was recognised early on by industry (namely
Australian Newsprint Mills, grantees of the Styx/Florentine concession), and
there was no original claim to sustainability:
‘Since the growing stock is
dominated by a large quantity of overmature timber, the sustainable yield which
could be cut from a “normal” succession of age classes on all sites has little
relevance in determining the allowable cut for the present level of industry.’
[52]
.
This is straightforward logic
where clearfelling is used, but in some locations sustained yield is still
claimed but redefined: the ‘primary forest premium’ referring to an accepted
loss for secondary forest logging, such as 50% compared with the primary forest
[375]
.
One practical step towards
sustainability is to treat the resource as valuable. An example where this has
not occurred is in the logging of large trees such as from mixed-forests in
Tasmania: as early as the mid-1950s, while surveying forests in the Styx Valley
for sawlog and pulpwood it was noticed that ~10% shattered on felling
[376]
. Even in contemporary times
no large trees, or even sections of them, are lowered to the ground gently,
thus wasting some potential sawlog timber. Also, a few large trees may be
dynamited (with substantial timber shattering) if the feller cannot find a safe
exit route after chain-sawing (e.g., coupe WE008e, pers. obs., 2004). The
existence of cable logging and climbing arborists in Tasmania indicates the
technology exists to keep logs intact.
Environmental sustainability is a
widely accepted policy, and is often part of CSR
[374,377]
. ‘Sustainability’ is part
of the latest name of the Tasmanian State forest agency: ‘Sustainable Timber
Tasmania’. Previous names were the ‘Forestry Department’, ‘Forestry Commission’
and ‘Forestry Tasmania’. But the resource extraction method involving primary
forests in the original pulpwood concession boundaries is fundamentally
unchanged from the mid-20th century, except that for some logging, the CBS
process has been more dispersed across a larger area via ‘aggregate retention’.
Sustained yield has not been achieved, for the reason described by industry in
the last quote above. The name change does however fit in with the corporate
concept of forestry, by promoting sustainability as part of market engineering
[378]
.
‘Aggregate retention’, is
essentially clearfell but with vestigial islands of forest
[379,380]
. The burn intensity is
lower but the islands are sometimes burnt
[379]
, which may not reduce the total carbon emissions. Without a
reduction in the annual log quota, the dispersion of clearfell means an
increased number of logging units and road area (increased forest
fragmentation), which in turn means an increased area of forest subject to edge
effects and escaped burns. Larger trees are more susceptible to fatalities at
forest edges, where windspeeds are higher; the edges may have less SOC; and
roadsides increase drying-out and grass cover, which can help the spread of
fire
[381–386]
.
With regards to sustainability of
forest carbon levels, the Tasmanian Regional Forest Agreement (RFA) mentioned a
need to manage the forests in a way that maintained or enhanced the carbon
within the carbon cycle and that research priorities included the estimation of
the impact of logging and fire on the carbon cycle
[387]
. The New South Wales (NSW,
another State in Australia) RFA was more general by denoting environmentally
sustainable logging as an objective that required long-term commitment. The NSW
concept of sustainability included maintenance of forests’ capacity for:
‘formation of soil, energy flows and the carbon, nutrient and water cycles,
fauna and flora communities and their interactions’, biomass production,
ecologically sustainable extraction levels, and minimisation of deleterious
effects
[388]
.
Overall, when including ecosystem
ecology as part of sustainability, it has not yet been established in absolute
terms by State-managed, corporate forestry in Australia
[389]
. For plantations in
Queensland in 1997 procedures that were still being implemented included: minimum
tillage to reduce soil erosion (and associated loss of organic compounds), and
watercourse and riparian vegetation protection; and the effects of retention of
logging residue on a rage of processes were still being investigated
[390,391]
. For native Eucalyptus
marginata (jarrah)-dominated forests in Western Australia, as of 2004, more
felling for timber had occurred than could be regrown, i.e., sustained yield
had not been achieved for a significant period, larger trees had been targeted,
with accompanying biodiversity loss
[108]
.
Sustainability at the species level
can also be considered. In contrast to the natural, spatial occurrence of the
different eucalypt species of the Styx/Florentine pulpwood concession, logging
focussed on E. regnans: shown by the areas logged of different species
by 1976. From the 1950s to the 1970s, 63% of the oldgrowth area logged was of E.
regnans. Initially, the Concession was only 19% E. regnans [by
area], and 49% E . obliqua, and 23% E. obliqua) (data in ANM
[52]
). Therefore, the ratio of
logged E. regnans versus availability in the concession was 3.4-to-1.
The same ratios for the other species logged were: E delegatensis—0.82:1,
E obliqua—0.5:1, and other sundry species—0.083:1. Tasmanian State
forest was still being high-graded for E. regnans from 1999 to 2009
[47]
.
The preference for E. regnans
was initially because E. regnans was the most suitable for pulping,
having the least fraction of material to be initially discarded in primary
processing
[52,392]
.
‘The species has proved
particularly suitable for pulping and has been used to provide a good quality,
easily bleachable soda pulp on the one hand and, on the other, a sulphate pulp
which has been used for the manufacture of kraft paper. It also forms the basis
of the Australian newsprint industry because it has been found to be the one
eucalypt species which is most satisfactory for grinding.’
[392]
.
From 1941 to 1957 the sourced
timber was 90% oldgrowth E. regnans, until changes in the pulping
process allowed the use of other mature eucalypt species, reducing the mature E.
regnans requirement to 75%, and further changes in 1971 allowed the use of
regrowth timber including some acacia, reducing mature E. regnans
requirements to 50% by 1979
[52]
.
Analysis of data in ANM
[52]
, shows that tree height,
rather than species alone, was a factor in species selection in the
Styx/Florentine logging concession. Stand descriptions therein refer to the API
types (described in
Section 2
) for the eucalypts in the stands. For the three main eucalypt
species present in the concession area, eucalypt category E1 was logged in
preference to category E2 (
Table 1
). For example, the ratio of E1 to E2 in the area of oldgrowth E.
delegatensis present was 1:7.0, but the ratio in the area logged was 1:1.4,
i.e., less E2 was logged less than if logging areas across stands of E1 and E2 E.
delegatensis had been selected randomly. This preference for logging the
taller height categories means that the forests were high graded based on tree
height. Data on the areas of remnant oldgrowth for the different species in
1976 in the Styx and Florentine Valleys
[52]
, show that E. regnans is twice as likely to be in category
E1 than E2, whereas E. delegatensis is 7 times more likely to be in E2
than in E1, and E. obliqua is 5 times more likely to be in E2 than in E1
(
Table 1
.(a)).
Thus, there were two fronts of high-grading: species (owing to compatibility
with the pulping process adopted) and height. Thus E. regnans has been depleted
the most.
Table 1.
Ratios of areas of different species relative to those in height category E1. Based on data in ANM [52]. Each species was normalised with respect to E1 separately and for parts 1.a and 1.b separately. (a) Oldgrowth as of 1976, and (b) oldgrowth logging from 1953–1976. Comparing 1.a and 1.b shows that the taller height categories were preferentially logged.
Table 1.
Ratios of areas of different species relative to those in height category E1. Based on data in ANM [52]. Each species was normalised with respect to E1 separately and for parts 1.a and 1.b separately. (a) Oldgrowth as of 1976, and (b) oldgrowth logging from 1953–1976. Comparing 1.a and 1.b shows that the taller height categories were preferentially logged.
| (a) | |||
| E. reg | E. del | E. obl | |
| E1 | 1 | 1 | 1 |
| E2 | 0.53 | 7.0 | 5.4 |
| E3 | 0.0051 | 2.9 | 5.2 |
| E4 | 0.00023 | 0.11 | 0.21 |
| (b) | E. reg | E. del | E. obl |
| E1 | 1 | 1 | 1 |
| E2 | 0.18 | 1.4 | 2.7 |
| E3 | 0.013 | 0.17 | 3.1 |
| E4 | 0 | 0 | 0 |
In the later 1970s there was
already possible evidence of over logging of E. regnans: E. regnans
seed was scarce and some areas of previous E. regnans oldgrowth were
re-seeded with other eucalypt species such as E. delegatensis
[393]
. This may have exacerbated
the situation by converting areas to a different species. This process appeared
to be still continuing in 2011. The non-E. regnans species are of lower
carbon stocks (on average). The average amount of pulpwood per hectare for
oldgrowth in the concession, as of 1976, for E. delegatensis and average
E. obliqua stands was 15% and 29% less than for E. regnans,
respectively [data in
[52]
]. Species, site productivity and provenance of seed, can influence
biomass
[394]
.
Therefore, with the historical high-grading of E. regnans having removed
the taller trees and there being a seed shortage, remaining seed for manual
coupe regeneration of E. regnans may come from areas where the genetic
provenance is shorter.
Taller trees have been targeted
globally, despite their disproportionately greater contribution to
climate-change-mitigation and ecosystem processes, and despite their decline
due to climate change
[395–398]
. This would gradually reduce local carbon storage, in a similar way
to the reduction in animal body or targeted component size, due to people
hunting larger individuals
[399,400]
.
5.1. Applying a Missing Baseline
When developing and publishing the
results of carbon accounting models, the system boundaries for material flow
must be acknowledged, without which unfactored emissions or double accounting
may occur
[4,401]
.
This lack of clarity may lead to knowledge gaps and publication of erroneous
information
[4]
. A
baseline (reference point, a benchmark) of 0 Mg ha-1 for carbon
stock (i.e., omitting legacy carbon such as soil carbon and logging residue— a
blank slate) is often portrayed in carbon-oriented promotional material for
forestry [e.g.,
[402]
,
Figure 10
]. In
Figure 14
.a promotional
material from Forest & Wood Products Australia (a forestry representative
body) is shown with a baseline of 0 Mg ha-1, i.e., as though
forestry management starts on a blank slate. In this review paper, the process
was simulated using CAR4D. Parameters in CAR4D were generously set to a
logging-cycle length of 90 years and with wood-product half-lives of 80 years
for sawlog and 4 years for pulpwood. These half-lives include those of mill
residues, some of which are routinely incinerated within a year of logging.
Also, these longer half-lives are a proxy for some of the wood-products
contributing to SOC in landfill, while noting that the methane produced there
(which has a higher global warming potential than CO2) may
counterbalance the longevity of that pool [
[403,404]
, p98-102]. Emissions from local and international freighting of the
wood-products, and thinning between full harvests, were omitted from the
simulations. The same simulation was run again but with the benchmark being the
original primary forest biomass and SOC instead of starting with them at 0 Mg
ha-1 (
Figure 14
.c and Fig 14.b respectively). The largest difference in results
between the two simulations is due to the neglect of the legacy SOC of the
primary forest, in the corporate forestry version. The overall trend in carbon
stock was down instead of up, when the legacy carbon was included. A zero or
unnaturally low baseline for forest SOC is also used in some scientific
calculations for assessment of forest bioenergy climate change effects, though
it is often disclosed as such [e.g.,
[405,406]
]. Ignoring the legacy SOC would be more appropriate for plantation
establishment on long-cleared land or in some of the forests in Europe
considered by
[407]
,
where logging has occurred for many centuries, but not for primary forest
conversion to logging cycles. Therefore, the promotional material with a
benchmark of 0 Mg ha-1 could be an example of generic marketing.
The numerical output from CAR4D
for the simulations showed that for recovery of total carbon stock to that of
the time-averaged, original primary-forest, then wood-product half-lives would
have to be increased to 400 and 20 years for sawlog and pulpwood respectively,
including for mill residues. It would be difficult to achieve such half-lives.
But if they could be achieved, then the recovery would take ~1260 years. During
that time, the drop in SOC would be counterbalanced by carbon in the wood
products. Meanwhile however, emissions due to the steadily decreasing SOC would
contribute to climate change and consequently also to climate-change positive
feedback [globally].
Similarly, life-cycle-analyses
(LCA) that claim emission offsets for burning wood waste [from logging, i.e.,
‘forest residue’ or ‘mill residue’] for energy require accounting of the C
balance of logging, and comparison with other energy sources such as
hydroelectricity, wind and solar power. Comparable system boundaries in the LCA
must be used for any comparison with substitutable materials
[408]
. The emissions in processing
and delivering the wood-product must be considered
[409]
, just as they are in
determining the C-footprint of other industrial products. LCA will include:
diesel usage during logging, in haulage [e.g.,
[410]
] and in international
freighting; mill energy usage for virgin- and recycled-products; and NOx
emissions. Such additional emissions could be high in the current market
situation, as wood-product movement occurs from Tasmania to Japan, then to
China and other countries, and then sometimes back to China for recycling
[411]
, though that latter move has
been limited by some countries in recent years.
Figure 14.
(a) Pamphlet advertisement by Forest & Wood Products Australia, using graph from Ximenes, et al. [[402] Figure 10] and not from DAFF & BRS as stated in the advertisement— emphasises the temporarily increasing wood-product pool— giving the illusion of increases ad infinitum. It ignores the primary forest legacy carbon. (b) and (c): output from CAR4D for Site-1 in Dean, et al. [47], drawn in ‘stacked-area’ format: (b) ignoring the primary forest carbon (i.e., zero baseline), and (c) not ignoring primary forest carbon. Style (b) would be more appropriate to use for plantations on long-cleared land or where logging has occurred for several centuries, but not for the LUC of primary forest conversion to logging cycles.
Figure 14.
(a) Pamphlet advertisement by Forest & Wood Products Australia, using graph from Ximenes, et al. [[402] Figure 10] and not from DAFF & BRS as stated in the advertisement— emphasises the temporarily increasing wood-product pool— giving the illusion of increases ad infinitum. It ignores the primary forest legacy carbon. (b) and (c): output from CAR4D for Site-1 in Dean, et al. [47], drawn in ‘stacked-area’ format: (b) ignoring the primary forest carbon (i.e., zero baseline), and (c) not ignoring primary forest carbon. Style (b) would be more appropriate to use for plantations on long-cleared land or where logging has occurred for several centuries, but not for the LUC of primary forest conversion to logging cycles.
Forestry is not the only land use
where legacy SOC from the previous forest makes a large difference to a carbon
footprint. A major difference was found when accounting for legacy SOC when
previously forested land was used for grain crops
[412]
. Those authors considered
that inclusion to aid realism, though requiring more work and providing
location-dependent outcomes for the land managers. That difference coincides
with considering where along the time axis in
Figure 9
, a particular logging
cycle may be; giving a different future drop in SOC depending on when the
accounting begins.
5.2. New Regulation Regarding Sustainability
The most logical way to address
the lack of scientific knowledge about the environmental impact of intensive
forest logging is firstly to acknowledge it and secondly use the precautionary
principle. In this vein there is a recent step towards an intent of sustainability
by the ‘Standards Reference Committee SRC AS/NZS 4708’ in a proposed update to
forest practices standards. It includes the precautionary principle applied to
cultural, economic, environmental (including the carbon cycle) and social
sustainability
[413]
.
The proposal was for Australian and New Zealand forestry, by a committee
comprised of forest industry representatives, academic institutions, government
agencies and unions. It applies to all threats of serious or irreversible
environmental damage (in their definition). However, soil carbon is not
mentioned specifically, and the emphasis for soil sustainability appears to be
on avoiding erosion. With respect to carbon the proposed standard, states:
‘The average carbon stock on the
defined forest unit shall be maintained or increased over successive harvest
cycles.’
and one of the allowable
conditions for forest conversion is that it:
‘does not destroy areas of
significantly high carbon stock; … ’
The first condition suggests that
there might be a method of forest conversion to logging cycles that is contrary
to what normally occurs (compare with
Figure
9
and
Figure 14
.b). The second condition most likely refers to areas where the land
is converted to plantation, orchards or long-term non-forest uses.
Additionally, as corporate forestry claims sustainability [e.g.,
[414]
] but rarely measures a site’s
soil carbon prior to logging or in the long-term, then a management activity is
unlikely to forecast emission of an area’s carbon. Nevertheless, this latter
condition would be a significant statement towards forest carbon sustainability
if: (a) applied to conversion of primary forests to logging cycles, (b)
‘destroy’ is interpreted as either rearranged or only partially eliminated, and
(c) a list of forest stands with high carbon stock can be created. This latter
condition links across to the second part of this review paper where such a
list is considered.
5.3. Terminology Hinging on Sustainability
A subtle forestry industry public
relations tool is renaming activities to give the indication of
more-sustainable operations, such as calling the burning of waste from
timber-mills ‘re-use’ or ‘recycling’ [e.g.,
[415]
]. Other popular name changes are to label forests simply as
biomass; the felled or still-standing timber that is not hauled out, as
‘residue’; coarse woody-debris and dead hollow trees as ‘fuel’; and the word
‘harvesting’ in place of ‘logging’ for primary forests (
Figure 15
)
[416]
. The original meaning of
harvest was to collect from a crop that one has sown. This renaming occurs
elsewhere in society too, such as harvesting rainwater and wild seaweed, but rarely
to fossil fuels. The change over time can be seen in the journal Australian
Forestry, published by Taylor & Francis. Early on ‘harvesting’ was used
only for plantations, which matched with its dictionary definition (
Figure 15
). One of the first
uses of it for primary forests was in the pulp and paper industry c1960, during
the controversy over whether or not to leave Melbourne’s water catchment as
primary forest, and the resolution was for more investment in a public
relations campaign, in research, and in logging
[417–419]
. The number of articles
in Australian Forestry including the words ‘logging’ and ‘harvesting’ has grown
over time (
Figure 15
), indicating more attention to that part of resource extraction but
the growth rate for the use of the word ‘harvesting’ has nearly doubled that
for ‘logging’ (0.79(0.05) and 0.34(0.06) respectively; standard errors in
brackets). The two growth rates are significantly different: the probability of
them being the same is P= 3.6x10-8, in a Student’s t-test
distribution. Their usage within a scientific paper is not mutually exclusive
however, for example there are still logging roads and log trucks, not
harvesting roads and harvest trucks, but, for example, selective-logging is now
often termed selective-harvesting, in primary forests.
The terminology towards
sustainability has been more embellished, where it is often claimed that
wood-products sequester carbon (and therefore logging helps prevent climate
change)
[420–426]
.
Whereas as the carbon sequestration, from gas to solid, was actually performed
by the trees.
Figure 8.
Change in use of the words ‘logging’ and ‘harvesting’ from 1936 to 2022, in the journal Australian Forestry. Data were obtained by using the search function on the journal home page and GoogleScholar©. The word ‘harvesting’ has increased ~twice as much as the word ‘logging’, since the journal started in 1936. Initially ‘harvesting’ was exclusively for plantations, then it was increasingly for logging primary forests.
Figure 8.
Change in use of the words ‘logging’ and ‘harvesting’ from 1936 to 2022, in the journal Australian Forestry. Data were obtained by using the search function on the journal home page and GoogleScholar©. The word ‘harvesting’ has increased ~twice as much as the word ‘logging’, since the journal started in 1936. Initially ‘harvesting’ was exclusively for plantations, then it was increasingly for logging primary forests.
5.4. Product Substitution for Sustainability
Using timber instead of some other
building construction materials, including timber from primary forests, has
been suggested as being more sustainable, as it has lower carbon emissions—the
‘substitution effect’ in considering the carbon footprint of logging— but most
of these comparisons have not noted products with lower emissions than timber [e.g.,
[427,428]
]. For
example, the products most frequently compared against timber are standard
concrete (using ordinary Portland cement), steel and aluminium. Whereas
lower-carbon-footprint forms of concrete, which can also have superior
structural properties (for example), appear to not be mentioned in those
substitution comparisons
[429–432]
. Additionally, when comparing building products, the recycling and
durability of steel and aluminium (which reduces their carbon footprint over
time) does not appear to be included. Another criticism has been that temporal
characteristics of substitution are often not compared in a practical sense
[429]
. In the 1970s, in several
annual reports, the Tasmanian State forest agency mentioned that sales of sawn
eucalypt timber were adversely affected by, for example: concrete slabs for
housing, particle board, plywood, low-cost imported timbers, low rates of
housing construction, and Pinus radiata from interstate [e.g.,
[433]
]. This suggests that a trade
perspective could still be involved to some degree in some of the comparisons.
An aspect that has frequently been
disregarded when comparing the carbon footprint of timber and concrete building
materials is that concrete slowly re-sequesters carbon by carbonising
(reverting back to calcium carbonate by reacting with CO2 in the
air, in the presence of moisture), and it can be recycled to some degree
[434–439]
. Conversely, structural
timber can only release carbon to the atmosphere, it cannot sequester carbon. A
more-recent comparison did include concrete carbonisation (including the peak
carbonisation upon building demolition) and steel recycling but still found
less emissions when using timber. There was still a point to be considered
though, because they had assumed substituting the burning of fossil fuels by
burning forestry residue and wood from demolitions
[406]
but did not compare against
using renewable energy such as solar power had been used (instead of burning
wood), not even by the year 2216, when newer technologies will be generating
base-load power
[440]
.
More comprehensive comparisons are necessary before sustainability by product
substitution can be claimed, at least for countries such as Australia with
ample renewable energy and relatively recent primary forest conversion.
Science relevant to
climate-change-mitigation got entangled in corporate strategy in the 1970s,
when a forest industry PR organisation in the USA promoted the phrase ‘trees
are the renewable resource’. That increased public approval of the industry
from 34% to 55%
[441]
.
Forest & Wood Products Australia recently promoted the trade marked brand
‘The Ultimate Renewable’ for both plantation and native forest timber under the
one umbrella, with social media and online free TV advertisements
[442]
. The only detail on
renewability and sustainability offered on The Ultimate Renewable website is:
‘…native forest managers renew their forests through natural or artificial
reseeding’, and readers are referred to check forest certification: all
State-level logging agencies are certified to some degree
[443,444]
. Part of the proof of
renewability lies in the scientific data on life-cycle assessment of the
products, which Hansen and Juslin
[176]
state should be provided by corporations as part of their
environmental responsibility. This would lead back to the requirement for more
scientific detail.
A recent review of the dependence
of global warming potential of building products found that the details of the
life-cycle assessment that were included, such as through modelling parameters,
made a significant difference to the balance
[445]
. The ISO 14067:2018 standard for life-cycle analysis mentions that
land use effects on soil carbon should be included, though not necessarily so
for the original forest conversion. A time span of 90% of the time taken for
SOC to reach equilibrium after land-use-change, is recommended for assessing
the upper soil profile under agricultural crops. Modelling shows that this
approach makes a difference to the findings of life-cycle assessment of
products
[446,447]
. Following
this ISO 14067:2018 recommendation and using the relaxation time (mentioned
earlier), then the modelling duration should be at least ~1,000(±500) years,
for the full soil profile for forest conversion from primary to secondary
forests with intensive management (when at least 40% of biomass is removed per
logging cycle).
5.5. Sustainability with Regards to Soil Carbon
Stewart
[448]
theorised that forestry can
partake in climate change mitigation, through, for example, maintaining optimum
tree cover, extending wood-product half-life, and not burning logging residue;
and he mentioned that whole-tree harvesting would deplete soil carbon. Harmon,
et al.
[269]
mathematically verified these postulates, with forecasts that the conversion of
primary forests to logging cycles decreases the long-term C stock, even when
including the carbon in wood products. Later modelling confirmed the concerns
first voiced in the late 1970s: long-term, intensive logging, especially when
accompanied by slash burning or removals for bioenergy, depletes forest SOC,
and nitrogen and phosphorus in the soil
[47,239,240,449–453]
.
Just before that safeguard cautioning
in the 1970s, the Australian Government published an environmental appraisal of
the woodchip (pulpwood) industry, including for carbon emissions from soil:
‘Some concern has been expressed
about the environmental effect of increased carbon dioxide levels in the
atmosphere as a result of increased soil respiration associated with clear
felling. However, this effect is negligible both in relation to the magnitude
of the grand cycles of carbon dioxide and oxygen in and across the ocean
surfaces, and by comparison to the similar effect of the large-scale burning of
fossil fuels in the past century.’
[106]
This appraisal missed the issue
that it is not so much the change in soil ‘respiration’ but the long-term-average
reduced input of carbon to the soil from biomass (
Figure 9
).
Sustainability for industries
using biological systems was first mentioned in forestry, in the 18th century,
describing sustained timber yield over consecutive logging cycles
[454]
. In the 1960s the concept was
expanded by the US Forest Service to include ‘all the benefits from the land’
and some foresters concurred that sustainability had to incorporate more forest
attributes than wood volume alone
[455]
. In 1992 the Australian government concluded that sustainability
for forestry must include ‘keeping options open for the future and adopting a
precautionary approach to potentially irreversible consequences of particular
uses.’ However, in the early 1990s there was little evidence of Australian
forestry interpreting the meaning of sustainability to include the land’s soil
carbon stock, though that must be part of true sustainability
[456,457]
. Consequently, it was
considered that claims of ecological sustainability in Australia ‘should be
viewed with considerable scepticism’
[456]
.
Monitoring of soil carbon by the
forest industry is not currently a legal requirement, only a suggestion. It was
not until the end of the 21st century that soil carbon was measured in the
context of carbon accounts for corporate forestry. A review of eight technical
standards for ascribing the carbon footprint of wood products used for building
[458]
found that five
did not mention soil and the others included it only if there was a land use
change, and one of these (ISO 14067:2013) mentioned ongoing research into
change in soil carbon. Conversion of primary forest to secondary forest, is
often not regarded as a land use change. Additionally, there is low precision
on values for forest SOC stocks, and consequently more uncertainty for ΔSOC,
including the modelling of the impact of climate change feedback on it
[459,460]
.
One protocol has a more
comprehensive consideration of sustainability: SNV-REDD+
[461]
. It requires measurement and
comparison of SOC but the time period is not mentioned and the maximum depth of
analysis is only the IPCC’s 0.3 m
[280]
. Reference is made to the IPCC 2006 standards
[462]
, which were intended
primarily for national-level accounting, where the default time period for SOC
change is only 20 years— much shorter than relaxation time for the full soil
profile.
For calculating the carbon
footprint of bioenergy, incorporation of SOC dynamics has been recommended
[463–465]
. Modelling ΔSOC for
bioenergy, from agricultural crops, using longer time spans (e.g., up to 200
years) and more depth of the soil profile (down to 1 m) made a ‘huge impact’ on
the results
[466]
. A
global forecast for using bioenergy from forest biomass to replace fossil
fuels, which included SOC to 1 m depth and typical SOC half-lives, found that
the global pool of SOC would significantly decline and that there was
negligible climate benefit
[453]
. Alternatively, secondary forests and plantations are sometimes
compared against a benchmark of 0 Mg ha-1, with consequently no
negative effect on SOC mentioned
[402,467,468]
. Parameterisation of soil carbon models from measurement of SOC taken
while legacy carbon is present, but incorrectly attributed, can induce
inaccurate forecasts by: suggesting low carbon stocks of the pre-disturbance
forest, short half-lives of the slow SOC pool, and too-high SOC values in the
disturbed forest
[469]
.
To date, knowledge on the fate of
soil carbon upon conversion of primary forests to logging cycles has not been
reflected in policy, but there are indications of a slow and partial
recognition of its importance. In a review of which pools are measured in which
financial carbon accounting protocols, the fate of soil carbon is either listed
as ongoing research or assumed to be zero change
[458]
. Early in the 21st century,
for the routine updates of one national forest inventory (namely Sweden), it
was recognised that more information on the existing soil carbon stock was
needed so that any change could be included in reports
[470]
. Around the same time, in a
review on the sustainability of logging, with a focus on building materials,
attention to the fate of soil carbon is recommended:
‘For harvested wood products
(HWPs) there are additional considerations regarding the impacts associated
with forestry operations, which may include issues associated with land use
change, as well as impacts upon soil carbon and the ecosystem services that
forests provide, in addition to harvestable timber. … Because up to twice as
much wood material is removed from the forest when timber is used in buildings,
it is important to include the fate of these wood by-products in any study
(i.e., is this material used for energy, is a proportion left in the forest as
soil improvement?). If surplus wood is left in the forest after harvesting
operations, it is essential to consider the fate of this material with respect
to GHG emissions.’
[471]
Although the science of reported
climate change effects has not been examined in this paper, it is relevant to
mention one item here. Climate change is forecast to increase fire frequency in
southern Tasmania
[352]
. Any carbon storage that was increased earlier due to the direct
effect of higher atmospheric CO2 concentration [e.g.,
[472]
] would be lost by the future
fires. Repeated burning is correlated with reducing a forest to a savannah or
shrubland state, and reducing a savannah to grassland
[473–476]
. This is the trend that
one can expect as climate change progresses. Soil nutrient losses are higher
with more intense or higher frequency fire, and feedback leads to a more
fire-prone ecosystem and reduced soil nutrients
[477]
. Over several millennia the
process can dramatically alter the soil type, for example by reducing clay
content by eluviation
[477]
, and a higher proportion of more labile SOC
[478]
. This will reduce
site-quality and therefore long-term C storage, which in turn constitutes
positive feedback to climate change [e.g.,
[479,480]
]. Although the 30% decline in SOC stock in Tasmanian mixed-forests
and rainforests was modelled by correlation with climate changes occurring by
2100
[301]
, in that
modelling SOC was a proxy for biomass C, assuming a positive correlation
[238,239]
, with the decline based
on the biomass’s response to climate change. Owing to the long relaxation time
for SOC (described above), the time for the forecast decline in SOC
[301]
, would most likely be
manifested long after the year 2100, and not within a century as reported
there. It is the biomass that could decline by 30% by 2100 and the SOC would
follow but much more slowly.
5.6. Bioenergy and Sustainability
Bioenergy is one of the few topics
in the forestry realm where there could be said to be a true debate, because
there is an ample amount of scientific literature representing the for and
against arguments, and the topic is discussed between politicians
[481–483]
. Nevertheless, regardless
of the against arguments, the trade in forest carbon for bioenergy is already
well underway in many jurisdictions.
The claim of sustainability when
burning forests for energy relies on timber regrowing and reabsorbing emitted
greenhouse gasses
[278]
, whereas burnt fossil fuels don’t become fossil fuels again as
readily. However, Ter-Mikaelian, et al.
[484]
explains how the claim that
this generally produces climate-change-mitigation, is an oversimplification.
Some obvious contraindications are:
- (1)
- Any substitution for fossil fuels may, at least in part, instead be substituting for renewable energy such as solar, wind-power or hydroelectricity. (Which is a point often ignored, e.g., Gustavsson, et al. [406].)
- (2)
- The effect of logging primary forest on soil carbon stock has often been discounted, though it is sometimes acknowledged that primary forests should not be used for bioenergy production [e.g., [485]].
- (3)
- The time required for forest regrowth is longer than currently required for climate change mitigation. Instead, algae have a growth duration (hours to days) that is more relevant to climate change mitigation than is that of trees (years to decades, to centuries) [486].
- (4)
- If forest bioenergy greatly decreases energy prices then some people may increase their energy consumption.
- (5)
- As described above, sustained yield from conversion of primary forest to secondary logging cycles, cannot occur. Similarly therefore, most of the burnt biomass is not recoverable.
- (6)
- Product substitution that provides avoided emissions is sometimes mistakenly treated as carbon removal from the atmosphere [487].
If the balance being considered is
only that between the emissions from burning fossil fuels and those from
burning forest biomass, the review by Giuntoli, et al.
[488]
found that the balance
depends on details, such as the market response to increasing wood price. The
replacement ratio may not be 1:1 for various reasons
[488]
. There are also other
industrially driven factors such as increased logging due to bioenergy profits,
logging intensification, average stand-age reduction, increased logging frequency,
change in lumber use towards fuelwood, and change in species planted
[488]
. Regarding ‘change in lumber
use’ for example, Giuntoli, et al.
[488]
noted that logging residues such as bark and stumps, may contain
impurities and therefore not be of suitable quality for fuel pellets, and so
pulpwood will be burnt instead. The authors of that review also found that the
support for pro-bioenergy from forests relied on better use of forests and
increasing forest area, but the evidence for these is weak. ‘In general, our
review finds that all studies that project a large role of forest bioenergy in
climate change mitigation rely on too optimistic assumptions, at times even
unrealistic.’
In paper mills, ventures to
increase wood particle recovery, decrease toxic effluent, and increase
fossil-fuel substitution, have often led to either equivalent or increased GHG
emissions [e.g.,
[489]
].
Notably, from a climate-change-mitigation perspective, Mathieu, et al.
[490]
found that it was better to
burn waste paper than to place it in landfill, though that burning was used to
substitute for fossil fuels, and substitution using cleaner energy was not
assessed.
Stewart
[448]
discussed the pros and cons
of bioenergy from forests in terms of fossil fuel substitution but renewable
energy such as wind or solar was not as popular in the 1970s so he may not have
been aware that bioenergy might inadvertently be substituting for those too. He
recommended that the bioenergy feedstock come from used rather than fresh,
timber and paper. If the recommendations of Stewart
[448]
had been implemented or
empirically investigated, then the forest industry would have been able to
mitigate climate change more successfully.
Since the short-cycle eucalyptus
pulpwood output from tropical countries began to dominate the global pulpwood
market, the demand for pulpwood from Australia has declined, and in its place,
proponents of the forest industries and the Australian government have
considered using native forest residues for bioenergy, and have even referred
to it as ‘green’ hydrogen
[491–495]
. Whereas actual ‘green’ hydrogen can be produced by desalination of
seawater using solar or wind power [e.g.,
[496]
].
The greenness of green hydrogen
depends on the carbon footprint of its production, and if derived from biomass
then it depends on either: (a) pyrolysis or gasification of the biomass
[497–499]
, or (b) the electricity
derived from biomass burnt to hydrolyse water to make the hydrogen. Forest
residues from native forests in Australia include non-sawlog biomass, such as
non-target tree species in clearfell logging sites (such as rainforest
species), pulpwood, sawmill offcuts, sawdust and pulp-mill residues.
Since the era of Stewart
[448]
, the Australian forest
industry has supported intensive forest usage:
‘Popular concern in some quarters
that timber harvest or other professionally acceptable forest management practices
may seriously deplete the forest soils of nutrients has no scientific basis.
The harvest of trees and even limbs at infrequent intervals removes relatively
low amounts of soil nutrients per hectare on an annual basis- far less than the
suburbanite removes by his annual raking and disposal of leaves. Nutrients are
replaced in forests that have been cut by decomposition of material that
remains and through other natural processes. Only the most remote likelihood
exists that soils of native forests would be significantly depleted by normal
levels of timber harvest (possibly excepting sandy soils of very low nutrient
status and where phosphate fertilizer application is already coming into
routine use). Further, numerous scientific observations by soil specialists
lend no support to assertions that forest soils may be irrevocably depleted of
nutrients by clearcut harvests at reasonable intervals. In such a remote case
that soil deficiency did occur, it could readily be corrected by application of
fertilizer as is routinely done in modern agriculture.’
[106]
The Australian government has
most-recently announced that burning native forest residues for bioenergy will
not be considered renewable energy, but that curtailing of emissions could be
reversed by an alternative government, or by direct gasification of forest
residues
[500]
.
Diverse opportunities exist for energy production for humans without having to
burn trees or fossil fuels, such as hydrogen production by solar-powered
catalysis of water splitting, or with more efficient energy transduction: from
genetically modified micro-algae
[501–503]
.
Advocates of bioenergy also appear
to rely on the claim that forests are ‘sustainably managed’. However, that
characteristic is usually assumed rather than proven, for example:
‘Holistic assessments show that
forests managed according to sustainable forest management principles and
practices (around one billion hectares globally, of which over 420 million
hectares are certified; UNECE FAO, 2019) can contribute to climate change
mitigation by providing bioenergy and other forest products that replace
GHG-intensive materials and fossil fuels, and by storing carbon in the forest
and in long-lived forest products.’
[504]
In that review of approaches to bioenergy
assessment, entitled ‘Applying a science-based systems perspective…’, Cowie, et
al.
[504]
set out to
clarify the ‘significant role that bioenergy can play in displacing fossil
fuels’. They cited a review by Achat, et al.
[505]
. That review found that
forest soil carbon declines when removing harvest residues for bioenergy.
However, Cowie, et al.
[504]
did not refer to that mention of reduced soil carbon, but to its
mention of the potential drop in forest productivity with excessive residue
removal.
Examination of UNECE
[506]
, which was cited in Cowie, et
al.
[504]
for the
>420 million hectares ‘certified’ as sustainably managed, showed that the
certification of 424 Mha is by the Forest Stewardship Council (FSC) and the
Programme for Endorsement of Forest Certification (PEFC). Such certification
schemes recommend conservation of general soil attributes (e.g., by avoiding
erosion and compaction) but do not require maintenance of soil carbon stocks
[507]
. Therefore in the review by Cowie,
et al.
[504]
there was
no evidence of sustainability of soil carbon stocks, although they claimed
general sustainability over very large areas, and therefore on their logic,
they also claimed that climate change mitigation via bioenergy was practicable
from those areas.
The reliance on certification
schemes is echoed in Aguilar, et al.
[481]
where the Sustainable Biomass Program is mentioned as a
certification system relying in turn on systems such as FSC and PEFC. They
studied sustainability but over only 12 years. Prudently, they emphasised this
empirical limitation of only a 12-year condition analysis (i.e., too short a
duration for representative and measurable ΔSOC).
It was difficult to trace the one
billion sustainably managed hectares mentioned in Cowie et al. (2021)’s, in UNECE
[506]
but there was a
1.7 billion hectares. This was forests in the ‘UNECE region’ that is part of
the UN’s Sustainable Development Goal for 2030, which is designed to be part of
the intended ‘circular economy’ and part of the UN’s aims to address climate
change and to ‘regenerate and sustainably manage natural resources’. This area
increased from 1.7 billion hectares in 2020 to 2.1 billion hectares in 2020
(i.e., 43 and 54% of the world’s forests respectively)
[508,509]
. However, Siry, et al.
[509]
, in reference to the original
1.7 billion hectares, refer to the management intensity and protection as
‘moot’ (i.e., questionable) because there wasn’t enough data to suggest good
management. The mere existence of forestry plans does not mean sustainability,
and indeed the area of actual sustainable management globally (a subset of the
area with management plans) could not be assessed in 2010 as there was
insufficient data on definitions, criteria and assessment methods
[510]
. The management of the 2.1
billion hectares simply refers to land under nationally- or community-approved
forest management plans that last for at least 5 years
[511]
. It’s likely that the
sustainability part of those plans depends on the blank slate (benchmark of 0
Mg ha-1) concept for SOC, or that they don’t consider SOC. But the
initial starting conditions must be considered when assessing the carbon
balance of forest management
[512]
. Thus the large area of sustainably managed forest, in Cowie, et
al.
[504]
, does not
exist. That removes one of the bases for their logic in claiming that
sustainable forest use exists, from which bioenergy can be extracted.
The emphasis on sustainable
management is echoed in UNECE
[506]
:
‘The EU’s revised Renewable Energy
Directive (RED II, 2018/2001/EU) entered into force in December 2018 (European
Commission, 2019). …Specific to forest biomass, RED II notes that biofuels,
bioliquids and biomass fuels produced from forest biomass should minimize the
risk of unsustainable practices. …To ensure the sustainable harvesting of
biomass, RED II requires the regeneration of harvested areas, special attention
for areas designated for protective purposes, the conservation of biodiversity,
and the tracking of carbon stocks. Thus, primary-sourced forest biomass should
be harvested following sustainable forest management principles implemented
through national laws or best management practices at the level of sourcing
areas. Operators should take appropriate steps to minimize the risk of using
unsustainable forest biomass for the production of bioenergy. … Wood is a cost
effective and potentially renewable source of energy, which can supply a big
share of global heat if the natural resource base is sustainably managed,
including the environmental and social dimensions.’
[506]
The references to claims of actual
sustainability appear to be circular in that the UNECE cite Cowie, et al.
[504]
and vice-versa:
‘The sustainability of wood-pellet
production in the United States southeast destined for the EU and the United
Kingdom continues to be debated in public media and other forums (e.g., Popkin,
2021; Hodgson, 2021). Science-based reports assessing the integrity of carbon
pools from forests used to procure fibre for pelletization suggest that carbon
stocks are not being negatively affected, and new demand could contribute to
the growth and regrowth of wood fibres (Aguilar et al., 2020; Cowie et al.,
2021).’
[513]
The UNECE reflects on different
regional criteria regarding sustainability of forest management and lists
different criteria for inspiration
[514]
. Among them are the Montréal Process and the Forest Europe
criteria. The 2015 version of the Montréal Process indicators separate soil
conservation (‘resource protection’) into Criterion 4, and carbon conservation
[515]
into Criterion 5, both of
which are qualitative. Criterion 5 merely reiterates the forest industry
initiatives, though more mildly by using the word ‘may’, that wood products may
be more sustainable than ‘manufacturing products that have significant carbon
footprints’ and that forest biomass may ‘offset the need to burn fossil fuels’
[515]
. The demand is that the
contribution to global carbon cycles is retained
[516]
. It does however, state that
the criteria will be periodically reviewed to reflect advances in knowledge.
The Montréal Process Technical
notes provide more detail. For soil in Criterion 4 each country’s report is
merely obliged to summarise how they met best management practices and their
efforts to monitor compliance
[516]
. For carbon in Criterion 5 forest managers are referred to the IPCC
and UNFCC for guidance on assessment
[516]
. For both criteria countries are told that ‘Useful data may be
obtained from government, university, industry, and research organisation
sources.’. This again seems circular for assessing industry’s carbon footprint.
It fundamentally relies on accepted standards of practice and in these there is
no indication of a requirement to measure or model soil carbon over a timescale
appropriate to its half-life or its depth distribution. Likewise, the Forest
Europe criteria reflect the requirement that the contribution to the carbon
cycle be maintained:
‘Criterion 1: Maintenance and
Appropriate Enhancement of Forest Resources and their Contribution to Global
Carbon Cycles… 1.4 Forest Carbon. Carbon stocks and carbon stock changes in
forest biomass, forest soils and in harvested wood products. …
Criterion 2: Maintenance of Forest
Ecosystem Health and Vitality… 2.2 Soil condition. Chemical soil properties
(pH, CEC, C/N, organic C, base saturation) on forest and other wooded land
related to soil acidity and eutrophication, classified by main soil types’
[514]
The paucity of ΔSOC measurement in
relation to forestry and bioenergy, and the consequent absence of a thorough
check on SOC sustainability, has had a major effect on outcomes. There is hope
for a check on soil carbon sustainability, if the Forest Europe criteria are
enforced over long-term effects: measurement or modelling of soil carbon stocks
over appropriate time scales may then be undertaken.
5.6.1. Carbon Modelling Example
One of the few models of the
bioenergy carbon footprint that includes soil organic carbon and decomposition
of root and aboveground biomass was in an assessment for a power station in New
South Wales (NSW) in Australia
[517]
. The question was whether biomass should be sourced from native
forests for bioenergy. The author submitted the report as an independent expert
witness while working for the Department of Primary Industries
[518]
. That submission formed a
counterbalance to those from the government’s Environmental Protection
Authority and the local Council. Cowie
[517]
claims that the burning of forest biomass produces less greenhouse
gasses compared with burning fossil fuels and will cause net carbon
sequestration over 80 years. The claim is stated to rely on ‘sustainably
managed forests’ and science:
‘Switching from coal to
sustainably-harvested woody biomass as an energy source reduces atmospheric CO2
over time scales relevant to climate stabilisation. … Sustainable forest
management ensures that annual biomass removals do not exceed annual forest
growth. The forest carbon stock is therefore stable; the same quantity of CO2
is released as is sequestered by the forest each year, so there is no net
transfer of carbon from the forest to the atmosphere.’ Cowie
[517]
The majority of the biomass (70%)
is to come from ‘plantation and native forest harvest residues’
[517]
. That native forest biomass
is from two sources: wood that normally would be pulpwood from native forests,
and trees from ‘land clearing and other approved activities’, 44% and 56% by
weight, respectively
[519]
. The single largest component (56%), land clearing, is usually
deforestation for livestock farming. The second largest component (44%) is from
native forest logging (public and private forests, 60% and 40% respectively, HRL
Technology Group
[519]
).
Cowie
[517]
modelled
the carbon accounts for one logging cycle of tall open native forest from 2020
to 2100 using the computer software, FullCAM
[308,520]
.
In the modelling by Cowie (2021)
her
Figure 2
,
shows the soil carbon drop by a net 20% during the 100 year logging cycle (from
45 Mg ha-1 to 36 Mg ha-1), and it does not recover,
regardless of whether or not biomass is extracted for bioenergy. Therefore,
although not shown in her report, after two rotations it would be lowered
further, and so on. Considering the timescales taken to recover SOC (
Figure 10
above), the proposed
logging and burning, according to the modelling of Cowie
[517]
, will create a long-term
carbon debt. However Cowie
[517]
overtly states that the only requirement for sustainability is that
biomass is replenished. Thus, the SOC loss appears to be ignored.
The biomass stock, as modelled in Cowie
[517]
, recovers after
about 75 to 80 years, but that is greater than the usual logging-cycle-length
for that region of 50 to 60 years
[521]
. In the normal scenario of integrated harvesting ‘the crown, stump,
bark, leaves, small branches etc. are left in forest for biodiversity and
forest health’
[519]
.
This would not occur under bioenergy extraction and therefore, ‘forest health’
may suffer too, which would be a second reduction in sustainability.
6. Benchmarks for Conservation Directives
There are sometimes rebuttals
between authors of science whose publications have findings that support
more-conservative use of nature instead of prevalent logging methods and
vice-versa, for example: Poynter and Ryan
[522]
vs. Keith, et al.
[523]
and Lindenmayer and Sato
[524]
; Dean
[525]
vs. Moroni, et al.
[526]
; and Sterman, et al.
[527]
vs. Prisley, et al.
[528]
. In this section I analyse detail to check for validity, and
highlight sources of likely discord in a recent pro-conservation paper by Sanger
and Ferrari
[529]
,
related to climate change mitigation and biodiversity conservation. Hearsay
suggests that paper may have been subject to controversy, although it is not
yet reported in the scientific literature. The paper broached, for the first
time, a carbon stock competition in Tasmania and claimed to win it, at a
particular site:
‘The current study represents the
highest measured carbon stock for a forest in Tasmania (
Table 1
), with measurements
well over previous studies.’
In Sanger and Ferrari
[529]
the authors also claimed to
have undertaken the most comprehensive study of carbon stock assessment in
Tasmania to date.
This paragraph summarises some of
their study’s pitfalls, with details provided below. For example, it did not
compare their tally with existing reports of total carbon for other sites in
Tasmania as the authors said that to the best of their knowledge they did not
exist. To gauge earlier work on Tasmania’s forests, their study did compare
their biomass-only tally with that of some other studies, but some were missed.
More importantly from a science perspective, comparisons were not placed on a
level footing. Also, incorrect statements were made about which carbon pools
were studied in some reports. They undertook some measurements in more detail,
by tree climbing to measure the girth higher up the trunk and on branches for some
of the trees in their study plot, rather than relying as heavily on taper
formulas and allometric equations as in many other studies. However, their
method of girth measurement that was published in public internet media, showed
unnecessary flaws compared with the standard technique. Additionally, selection
of some of the allometric equations they used appears unfounded, and their soil
carbon analysis was not comprehensive compared with other contemporary
measures, which is contrary to one of their claims. Overall, some standard
scientific protocols were not followed, which contributed to their study not
being an example of robust science, nor of the best available science. To
provide a carbon comparison on a level footing, detail is provided below of recalculation
of the carbon stocks represented in Sanger and Ferrari
[529]
and several earlier studies.
Another reason for presenting such a carbon comparison here, is that the
process in itself, provides valuable, general insights into some aspects of the
use of science for forest carbon accounting more generally.
6.1. Measurement of Carbon Stocks by Using Proxies
Studying the sums or changes in
the carbon stocks of Tasmanian forests, has only occurred during the last forty
years, roughly, and sometimes as a biproduct of a different investigation [e.g.,
[368]
]. Therefore,
actual carbon data are scarce. Different attributes of nature pique scientific
interest at different times, depending on society’s needs, such as for resource
extraction, atmospheric amelioration (as currently for climate change
mitigation), drinking water runoff, or interest in a specific animal species.
But for whatever forest attribute is in vogue, there are usually other data
that can be transformed or used as a proxy. For example Johnson
[530]
noted that data on the change
in soil carbon with forest management was often in reports that focussed on
other nutrients. For carbon in trees, a long-standing proxy for carbon is
merchantable timber volume, to which a ‘biomass expansion factor’ (BEF) is
applied to include the carbon in the unmerchantable, aboveground parts of a
tree
[531]
. This
method misses some carbon in other parts of the forest stand however, if some
species felled during logging contribute to forest biomass but are
unmerchantable (such as some rainforest species amongst eucalyptus species), or
if their merchantability varies with market demand. It also has a high error
margin unless the BEF is tailored to each stand, which is rarely done.
In their carbon account of
Tasmanian wet-sclerophyll forests, Moroni and Lewis
[532]
used a biomass expansion
factor of 1.46, and added soil carbon values from similar soils elsewhere. That
BEF value came from Snowdon, et al.
[533]
, where it was derived by reassessment of earlier reported data for
Australian native forests in general [e.g.,
[534]
]. Many of the allometric ratios presented in the review by Grierson
et al.
[534]
were
based on the whole of the stem and not just on the merchantable portion, so the
BEFs should be higher than theirs if based on the merchantable part only. To
account for that difference, in their assessment of the C stock for the whole
of State forest in Tasmania, MBAC
[535]
multiplied by an expansion factor of 1.25, to represent the wood in
the entire stem, before applying the 1.46 expansion factor to get to the whole
of the aboveground mass of the tree, and then a third expansion factor of 1.29
to account for unlogged trees in the forest stand. However, most of the data in
reports such as Grierson et al.
[534]
, were from quite young trees, e.g., less than 100 years old and so
the BEFs for mature forests should be lower
[536]
. This is because relatively more biomass is in the trunk for mature
forest trees and therefore more of the total is merchantable (unless senescence
is well established). Consequently, Snowdon et al.
[533]
used a lower limit of 25
years for their data collation for BEF. Possibly these two biases of whole-stem
and mature-age cancel out to some degree. The average BEF given in Grierson et
al.
[534]
for the most
common eucalyptus species in the tall wet-sclerophyll forests of Tasmania,
namely E. regnans, E. obliqua and E. delegatensis, was
1.32 but the average age was only 43 years. Limiting this to stands older than
24 years gives an average BEF of 1.28 (and the average age of those trees as 61
years), but that is based on entire stem volume and not just the merchantable
part of the stem. This is lower than the 1.46 used in Moroni and Lewis
[532]
, but there’s insufficient
information to give a definitive adjustment to it. For tall-open eucalyptus
forests, in the Farm Forestry Toolbox, a computer program designed for tree
growers and merchants in Tasmania
[537]
, for expanding from whole stem biomass to aboveground biomass, the
default BEF is 1.313. Alternatively, based on weights from destructive sampling
of small, Tasmanian E. obliqua (average DBH of 0.683 m for 44 trees) Ximenes,
et al. [
[538]
Table 4
&
Table 10
] reported data
yielding BEFs of 1.43 and 1.58, depending on the merchantability of stem wood
in the crown for pulpwood. They also showed that in that particular stand, the
BEF might increase for larger trees. BEFs can range from 1.25 for a
high-quality stand with sawlog and pulpwood extraction to 5.0 for a low-quality
stand with sawlog usage only [
[533]
, p xiv]. Therefore, the value of 1.46 might be sufficiently
conservative and appropriate to use for average, larger trees. In general
however, the use of BEFs will introduce large error margins for carbon
accounting unless empirically derived for a particular forest stand, as in
Ximenes et al.
[538]
.
Even for different species within a stand, the BEF can vary significantly
[539]
.
An early eucalypt sawlog inventory
(1922) for tall forests in Tasmania measures 32 transects covering 124 ha of
the Florentine Valley
[540]
. But that dataset is difficult to compare with more-contemporary
surveys as the BEFs cannot be estimated without knowing the historical
merchantability criteria for eucalyptus sawlogs. The more-contemporary BEF that
was applied by Moroni and Lewis
[532]
, caters for both sawlog and pulpwood being extracted.
After that 1920s sawlog inventory,
in the pulpwood era records were kept by Australian Newsprint Mills during
logging of the Styx/Florentine pulpwood concession
[541]
. In the midst of that
activity, a detailed inventory of small plots in the Styx, Florentine and
Tyenna valleys, in terms of tree species, sizes and ages, was undertaken to
show related forest types on sites of different productivity and in different
stages of ecological succession from mixed-forest to rainforest
[55]
. In that exposition there were
three plots of mixed-forest and two of rainforest. Those data included girths
of trees and were therefore amenable to carbon inventory, because allometric
equations based on DBH can be applied, without relying on an expansion factor.
The highest biomass representatives were selected from each of the two main
forest types, to provide a comparison with total C found in Sanger and Ferrari
[529]
[where it was claimed they
had the highest carbon reported in Tasmania], and to provide another datum for
the mixed-forest vs. rainforest comparison (detailed above). The mixed-forest
stand was 0.149 ha by Road 10 in the Florentine Valley and dominated by
even-aged E. regnans, older than 300 years. The rainforest was ‘transect
A’, 0.116 ha by Road 7 in the Florentine Valley and some of its trees were
older than 500 years. A range of allometric equations was tested to see what
difference they made to the totals (
Table
2
). The largest rainforest trees in the two stands were
assigned 25% senescence, regardless of whether or not the allometric equations
already had senescence incorporated (to ensure conservative carbon stocks). To
get 20% and 15% senescence in the eucalypts, the stand age in Eq. 8 of Dean, et
al.
[307]
was set at
317.49 years and then 299.575 years, respectively. In the final comparison with
Sanger and Ferrari
[529]
, the eucalypts were assigned 15% senescence, because although there
was no crown loss, the crowns were ‘stag headed’, which indicated some demise
compared with being in their prime. Although not stated in Gilbert
[55]
, his description suggests the
API phototype for the mixed-forest plot would be E1c.M+, and that the
rainforest plot was M+.
Table 2.
Carbon stocks (Mg ha-1) to 4 significant figures, of live biomass [including roots, root/shoot ratio= 0.15]. Based on data in Gilbert [55] for: (a) mixed-forest by Road 10, Florentine Valley; and (b) rainforest tree species in the same mixed-forest on the first row, and on the second row: rainforest by Road 7, Florentine Valley. Different allometric equations for understorey go from left to right across the table: ‘und’ in (a) and (b); and go from top to bottom down the table for Eucalyptus regnans: ‘Er’ in (a). Allometric equations were sought from the following publications: ‘D2020’= Dean, et al. [92] with the root C corrected as mentioned in the main text, Eq. 7; ‘D2003/2006’= Dean, et al. [307] or Dean and Roxburgh [88] which are equal to within 4 significant figures for this forest stand; ‘D2003’= Dean, et al. [307]; ‘D2011’= Dean, et al. [542] with half of the sums corresponding to incorrectly adjusted general rainforest tree equation in Keith, et al. [124] to get temperate rainforest trees (my error, not theirs); ‘D2011 corr.’= Dean, et al. [542] corrected; ‘K2000 temperate’= temperate rainforest from Keith, et al. [124]; ‘K2000 general’= general rainforest from Keith, et al. [124]; ‘newrainforest_C’= new rainforest allometric equation introduced in this text (Eq. 11).
Table 2.
Carbon stocks (Mg ha-1) to 4 significant figures, of live biomass [including roots, root/shoot ratio= 0.15]. Based on data in Gilbert [55] for: (a) mixed-forest by Road 10, Florentine Valley; and (b) rainforest tree species in the same mixed-forest on the first row, and on the second row: rainforest by Road 7, Florentine Valley. Different allometric equations for understorey go from left to right across the table: ‘und’ in (a) and (b); and go from top to bottom down the table for Eucalyptus regnans: ‘Er’ in (a). Allometric equations were sought from the following publications: ‘D2020’= Dean, et al. [92] with the root C corrected as mentioned in the main text, Eq. 7; ‘D2003/2006’= Dean, et al. [307] or Dean and Roxburgh [88] which are equal to within 4 significant figures for this forest stand; ‘D2003’= Dean, et al. [307]; ‘D2011’= Dean, et al. [542] with half of the sums corresponding to incorrectly adjusted general rainforest tree equation in Keith, et al. [124] to get temperate rainforest trees (my error, not theirs); ‘D2011 corr.’= Dean, et al. [542] corrected; ‘K2000 temperate’= temperate rainforest from Keith, et al. [124]; ‘K2000 general’= general rainforest from Keith, et al. [124]; ‘newrainforest_C’= new rainforest allometric equation introduced in this text (Eq. 11).
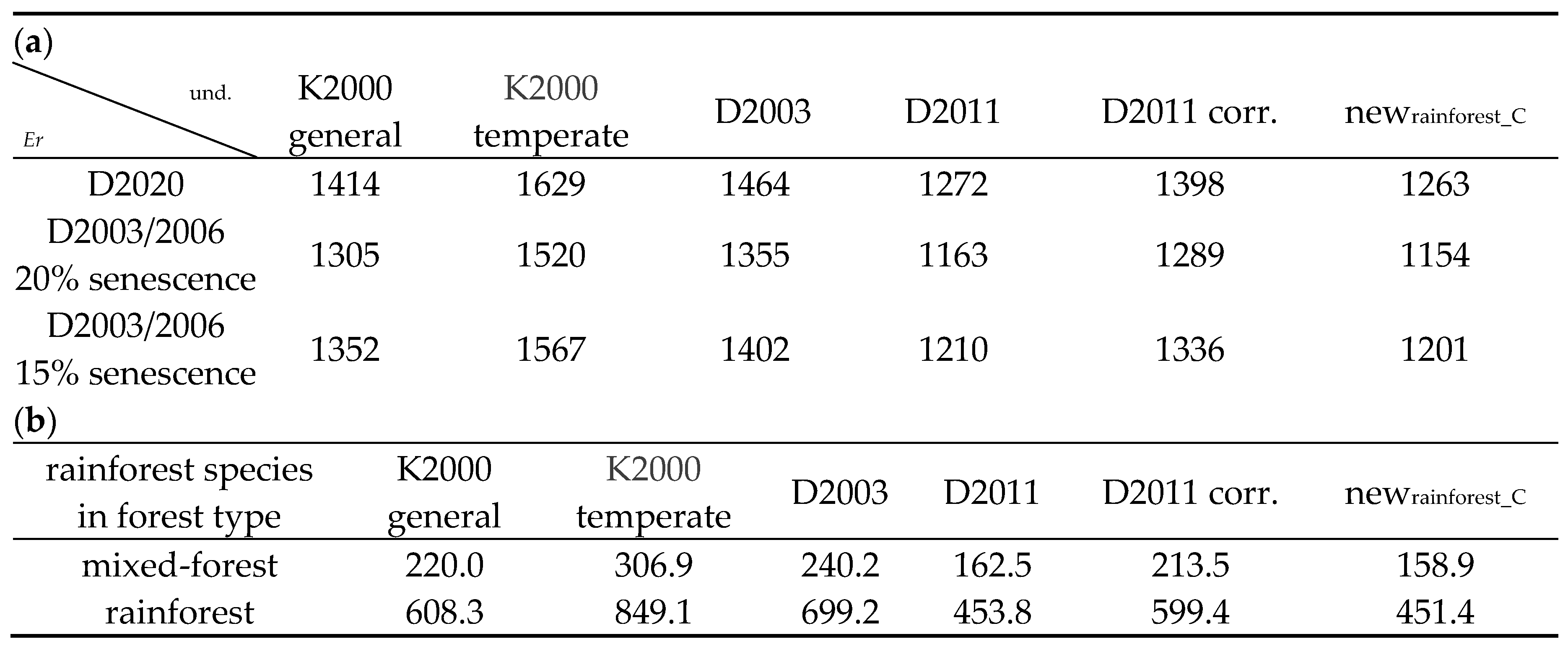 |
The different allometric equations
used to produce
Table 2
are explained in the next section. The root/shoot ratio used was
0.15, throughout, as Gilbert
[55]
noted that the trees were mature.
6.2. Suitable Allometric Equations for Carbon in Tree Biomass
Root mass is rarely measured
directly, as it is usually more difficult for people to measure things
below-ground than aboveground, similar to the difficulty with measuring higher
up a tree (section 5.3). Consequently, tallying carbon often relies on assumed
root:shoot ratios. For a given environment, as a tree matures, this ratio
usually decreases. Throughout many carbon assessments in Tasmania a root:shoot
ratio of 0.25:1 has been assumed, though the lower one of 0.15:1 was modelled
for mature trees
[307]
,
and the even lower one of 0.136:1 is the default for tall-open eucalyptus
forests in the Farm Forestry Toolbox
[537]
. The value of 0.15:1 is an average of relevant literature values
[67]
. In tall-open forest, through
a complex empirical and modelling process for one individual mature understorey
tree a root:shoot ratio of 0.18 (±0.05):1 was found
[67]
. The data ranges suggest that
in mixed-forests, 0.15:1 could be a suitable root:shoot ratio for both mature
eucalypts and understorey rainforest trees. Therefore, it has been adopted in
this report and, for the purposes of comparing carbon stocks, we convert other
people’s reported values to that figure, where possible.
The allometric equations for Eucalyptus
regnans, from Dean, et al.
[307]
and Dean and Roxburgh
[88]
, only produced a difference in stand-level C stocks for living
biomass at the 5th significant figure, (e.g., 1201.2 and 1201.4 respectively,
for the 15% eucalypt senescence scenarios with the new rainforest equation, Eq.
11) and therefore they were combined into one row in the table. The equation
for Eucalyptus regnans in Dean, et al.
[92]
was specific to their study site in that the upper limit was in
terms of the maximum live tree size observed and its degree of senescence.
However, in production of that equation I had made the mistake of multiplying
the root biomass twice by 0.47 instead of once, to get carbon. Therefore, the
carbon stock reported in Dean, et al.
[92]
was a little lower than it should have been, and it requires the
following multiplier before use:
(1 + 0.15) ÷ (1 + (0.47 × 0.15)) = 1.07426436
and the corrected allometric
equation in full becomes:
where Eregnans_C
is mass of carbon for the whole tree in Mg and DBH is in m.
The allometric equations for Eucalyptus
regnans in Dean, et al.
[307]
and Dean and Roxburgh
[88]
differ only for stem volume, with more data being used to derive
the equation in the newer report. The older equation
[307]
is:
where Vol_max= 380 m3,
DBH_mid= 4.3 m, k= 2.57, V is the stem volume in m3
and DBH is in m, and the newer one
[88]
is :
where Vol_max= 1100 m3,
V is the stem volume in m3 and DBH is in m. In both cases the
equations for the other tree components and a user-adjustable senescence in the
form of a two-parameter sigmoid function, are given in Dean, et al.
[307]
, with the influence of growth
parameters for different sites explained in Dean, et al.
[235]
.
Figure 9.
Comparison of different eucalyptus allometric equations, shown at two scales, from (a) larger to (b) smaller trees. For the equations that didn’t include root mass, it was added with a root:shoot ratio of 0.15:1. Equations’ species and references: ‘Ed 2011’= Eucalyptus delegatensis [542] but with the root portion corrected, as described in the main text; ‘Eo K2000 temperature’= E. obliqua [124]; ‘Eo W2021’= E. obliqua [543]; ‘Er D2003’= E. regnans [307], with m= 400 years and k= -6; ‘Er S2015’= E. regnans [77]; ‘Er X2018’= E. regnans [544]; ‘Er D2020’= E. regnans [92] with the root C corrected as mentioned in the main text, Eq. 7; ‘Er mid= 600, k= -6’= E. regnans [88] with an older-age but faster senescence than for Er D2003, to show flexibility of that equation.
Figure 9.
Comparison of different eucalyptus allometric equations, shown at two scales, from (a) larger to (b) smaller trees. For the equations that didn’t include root mass, it was added with a root:shoot ratio of 0.15:1. Equations’ species and references: ‘Ed 2011’= Eucalyptus delegatensis [542] but with the root portion corrected, as described in the main text; ‘Eo K2000 temperature’= E. obliqua [124]; ‘Eo W2021’= E. obliqua [543]; ‘Er D2003’= E. regnans [307], with m= 400 years and k= -6; ‘Er S2015’= E. regnans [77]; ‘Er X2018’= E. regnans [544]; ‘Er D2020’= E. regnans [92] with the root C corrected as mentioned in the main text, Eq. 7; ‘Er mid= 600, k= -6’= E. regnans [88] with an older-age but faster senescence than for Er D2003, to show flexibility of that equation.
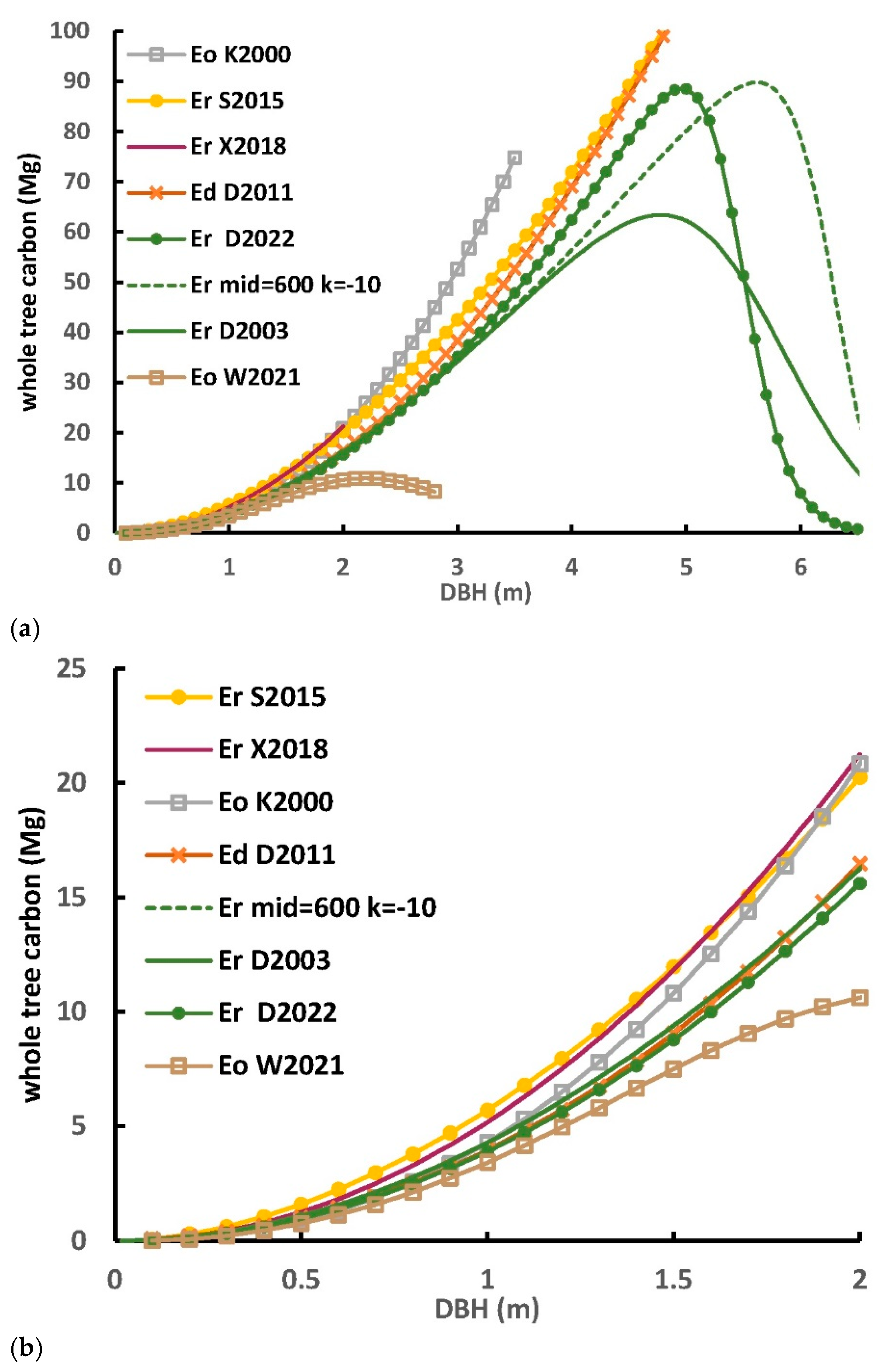
In
Figure 9
it can be seen that
the two allometric equations for E. obliqua diverge more sharply than do
the other equations. The higher one, Eo K2000, was the average from four
different environments. The highest biomass stand of those four was from an
atypical poorer site
[124]
, but noted as having much less disturbance than the other three
stands: it made the average allometric trend to higher values. The lower curve
for E. obliqua in
Figure 9
,
[543]
,
was from one site with a history of relatively frequent fire
[350]
, being in the Huon district,
in southern Tasmania, which had a longer history of agriculture, logging and
urbanisation than did the Styx Valley in south-central Tasmania
[545]
. Indeed, the final dip in
that lower-yielding equation was based on one tree alone, of DBH 2.74 m, with
the next-smallest tree having a DBH of 2.02 m which is near the peak in the
curve
[546]
. That
allometric equation was therefore mostly based on the stem taper of
non-senesced trees whereas the larger trees had lost their crowns and thus
weren’t represented by it (Tim Wardlaw, Sustainable Timber Tasmania, pers.
comm., 2024). This is an example of where equations developed from a small
number of data, and therefore possibly containing a couple of extremes, may
produce equations with limited applicability, and potentially low-accuracy
results if applied beyond their bounds, whereas a greater range of input data
is more likely to yield a more generally applicable equation.
Possible error margins from using
allometric equations can be inferred from the range of trends in
Figure 9
(b). For example, for
a young, mature E. obliqua tree of a relatively small diameter of DBH
1.5 m, the allometric equation of Keith, et al.
[124]
gives the carbon mass of
10.806 Mg whereas that of Wardlaw
[543]
gives 7.500 Mg. If one couldn’t choose between the two equations
and had to select the average, then the error margin [about the mean] is
1.65 Mg, which is a relative error
of 19%. If calculating a site’s carbon by adding up the carbon in each tree,
for perhaps 20 such trees per hectare, then that relative error is transferred
directly to the total carbon content. For larger trees, usually fewer data go
into construction of the allometric equation and therefore its uncertainty is
higher. The error margin is also higher for larger trees due to estimating the
degree of senescence, or when devising the allometric equation-- how much
senescence was incorporated into it for which DBH? Error margins also get added
from such things as measurement errors in the plot size, land slope and DBH
measurement. The discrepancy between the Er D2023 and Er D2020 allometric
equations for E. regnans (in
Figure
9
) and that of Sillett, et al.
[77]
is nearly as great as for that
between the E. obliqua equations, but that may be because Sillett, et
al.
[77]
didn’t
include internal hollows as a tree ages (for those that have them). The
allometric equation from Ximenes, et al.
[544]
for aboveground biomass of E. regnans was based on direct
weighing and therefore included carbon loss accompanying senescence, but it was
only for trees with DBH ≤2 metres, and no internal hollows were noticed (F.
Ximines, Dept. of Primary Industries, New South Wales, pers. comm. 2024). That
equation yields carbon content close to that of Sillett, et al.
[77]
for young E. regnans
trees, and makes the equations Er D2023 and Er D2020 look conservative.
For commercial forestry work over
a larger area in Tasmania, an equation for E. obliqua stem volume (the
merchantable part of the tree) was developed by State forestry, but it was
based on both DBH and tree height and represented the stem taper (which was
integrated to give volume)
[547]
. In typical commercial forestry it is important to quantify the
stem, rather than the branches, because the branches are not sold. The DBH
values of specimens used to calibrate that taper model ranged up to 3 m, which
means it could be useful in carbon accounting. Tree height is not a reliable
variable for the more-mature eucalypt trees for several reasons: (a) they may
lose different amounts of the crown, from senescence, (b) short, stout trees,
growing in more open conditions will have developed extra branch mass whereas
trees in stands that have not thinned much will accrue greater height, (d)
trees that have only recently lost their crowns have not yet invested in the
extra branch mass typical of short, stout trees, (e) extra complexity will be
added as a stand thins with old age, neighbouring trees may (or may not) have
fallen and so the extra light reaching the tree allows a large branch mass to
develop, without the tree increasing height but with increase in DBH. One
outcome of the range of circumstances is that trees of larger DBH (i.e., E.
regnans of 5–8 m) are often shorter
[80]
.
Thus, for useful allometric
equations, a large range of data are needed including for the large trees
experiencing a range of factors, rather than relying on extrapolation. Data on
an extensive range of small, medium and large E. regnans trees in the
Styx, Florentine and Arve valleys of Tasmania and in various historical
records, provided the input for the carbon accounting software CAR4D, which was
used for forecasting, spatial analysis, and analysis of industry and fire
effects, over long time periods
[88,307]
.
The allometric equation for E.
regnans from Sillett, et al.
[77]
keeps increasing for higher DBH, because it doesn’t account for
eventual decline with advanced age, such as internal stem-wood decomposition (hollows)
from typical senescence or fire. The allometric equation for E. delegatensis
from Dean, et al.
[542]
initially also keeps increasing within the range of DBHs for which
it was applied but it is of sigmoidal form and therefore reaches an asymptote.
It was partly constructed from an allometric based on data restricted to DBH of
3.5 m from Keith, et al.
[124]
for E. obliqua. But other contributing parts for that
equation for E. delegatensis included an allometric equation with senescence
(for E. regnans), so it will be constrained. Also, senescence was
subtracted on a tree-by-tree basis before tallying the stand totals in Dean, et
al.
[542]
. Therefore,
the forest carbon stocks would not have been overestimated.
An appraisal of allometric
equations for the rainforest species in mixed-forest in Tasmania is necessary.
Destructive sampling for specific species could give more accurate data for the
rainforest understorey than volumes based on stem taper functions, and such
sampling has been undertaken as part of commercial inventory. The first
species-specific allometric equations for the rainforest understorey species in
mixed-forest were developed by the Forestry Commission [of Tasmania] from
rainforest in the South Arthur River area of northwest Tasmania
[347]
. Although they didn’t specify
the exact range of tree sizes examined, their plots included mature rainforest
across sites of different productivities. The maximum heights for myrtle trees
on the more productive, well drained, sites was typically around 37 m but could
be up to 45 m
[347,548]
. Their equations give the volume of wood in stems under the bark as
a function of DBH and height, but they did not publish a formula for tree
height. Such volumes were processed as part of this review to yield aboveground
carbon. Height was parameterised as a function of DBH from trees on a 1 ha plot
at State forestry’s research plot at Warra in southern Tasmania. The commonly
used expansion factor of 1.46
[533]
was used, and a basic density of 0.5 Mg m-3
[543]
. Individual tree data in that
dataset from Warra were reported as part of Australia’s Terrestrial Ecosystem
Research Network (TERN) project
[546]
, but there the allometric equation for myrtle volume used was that
for a different species— New Zealand mountain beech (Nothofagus solandri
var. cliffortioides)
[549]
, and the basic density used to convert to carbon was 0.58 Mg m-3.
The reason for choosing a different species in the TERN report was not stated
and it gave stem volumes (and hence tree carbon) that were only 76.5% as high
as those for Tasmanian myrtle, from Walker and Candy
[347]
. The TERN data from Warra
were re-processed but using the allometric equation for myrtle volume from Walker
and Candy
[347]
. The
DBH range was notably restricted at the Warra site. For example, the maximum
DBH and heights of myrtle were 0.448 m and 29.4 m respectively, which are
smaller than for those observed in the Styx and Florentine valleys, and the
earlier work in NW Tasmania. Therefore, any comparison between the relevant
allometric equations for the different sites can only be done at the low end of
the size spectrum. But the TERN data do offer a potentially more accurate
benchmark in that range against which to compare any non-species-specific
rainforest understorey allometric equations. The height as a function of DBH
equation from the Warra data in Wardlaw
[543]
was developed from a much more restricted dataset than the Walker
and Candy
[347]
equation for volume. Therefore, to the Warra dataset of 100 points for myrtle,
a range of other DBHs and heights for myrtle were added to derive a new
equation for height as a function of DBH, for myrtle trees: 2 data points from
the literature
[548]
,
8 from my own historical data collection Tasmania-wide, and 6 from citizen
science by Wilderness Society volunteers (
[92,542,550]
). These extra data had a maximum DBH of 2.39 m, and a maximum
height 48 m. The new equation was constrained to match the curvature of the Wardlaw
[543]
equation for
myrtle trees at low DBH by including in a mathematical regression, the 79
DBH-height data point pairs reported in Wardlaw
[546]
where the height had been
calculated from their equation rather than measured in the field. The new
equation, of Chapman-Richards growth-function format, was refined using Labfit
[551]
:
where height is the tree height in
m, DBH is in cm, a= 35.9377 (SD 0.8331) m, P(t)<0.001, b= 5.4261 (SD 0.2688)
cm P(t)<0.001, adjR2= 0.75, Df= 117 (though less in reality due
to using some calculated heights from Wardlaw
[546]
), and P< 3 x 10-8. Note that this function has
essentially reached its asymptote when DBH values are as low as 1.5 m, and
therefore it could reasonably be used for DBH values larger than the 2.39 m in
the data set. This equation was used to get DBH-height pairs for input to the Walker
and Candy
[347]
equation for myrtle stem volume, combined with the expansion factor 1.46 and
density 580 Kg m-3
[546]
, and a root/shoot ratio of 0.15, to extend the allometric comparison
process for tree carbon of rainforest understorey trees (
Figure 10
).
Non-species specific (generic)
allometric equations for the biomass of Australian rainforest trees were
published in Keith, et al.
[124]
and given in terms of an adjustment to a global standard for rainforests
for two different regions in Australia: sub-tropical and temperate. My error in
Dean, et al.
[542]
was
in subtracting the adjustment to get from global rainforest to Australian
temperate rainforest, rather than adding it. The mathematical form of those
equations in Keith, et al.
[124]
was log-log and although an upper limit on DBH wasn’t stated, the
formula was only graphed for trees with DBHs between 0.1 and 1.0 m. For wider
trees, the biomass would possibly have increased unrealistically due to the
exponential form of the equation. Therefore, two different approaches were
subsequently used. Firstly, in Dean, et al.
[307]
, an allometric equation was developed which gave biomasses matching
those for temperate rainforest understorey from Keith, et al.
[124]
up to 1 m DBH (
Figure 10
(b)), but then
instead of increasing exponentially for higher DBHs it was made to approach an
asymptote by making it a sigmoid function (
Figure 10
(a)). Secondly, in Dean,
et al.
[542]
, the
allometric from Keith, et al.
[124]
was averaged with the allometric equation for rainforest trees of Dean,
et al.
[307]
(which
was halved to ensure conservative values). Although the second method still
would increase exponentially, the combination gave reasonable values for DBHs
up to about 3 m (
Figure 10
(a)). Note that the maximum DBH for understorey rainforest trees in
the data in Gilbert
[55]
was about 2 m, which means that carbon stocks in
Table 2
that use the Keith, et
al.
[124]
equations
are most likely too high, which leaves the newrainforest_C as being
more likely to be applicable.
For rainforest understorey trees
there is an adjustment necessary, to a published allometric equation, due to an
error I had made in the formulation of the allometric equation in Dean, et al.
[542]
, which was pointed out to me
by Barrie May (pers. comm., CO2 Australia Ltd., 2012) during his
calculations for a report on Tasmanian carbon stocks
[550]
. My error was to subtract the
adjustment to get from global rainforest to Australian temperate rainforest in Keith,
et al.
[124]
, rather
than add it. The effect was that the carbon stocks reported in Dean, et al.
[542]
were below what they should
have been. I corrected that error for the comparison of different C studies
here and the corresponding allometric equation is labelled ‘D2011 corr.’ in
Table 2
. The error has most
impact near DBH 0.5 m [and is less for other values of DBH]. If that erroneous
process was applied to the stands in Gilbert
[55]
, it would have made an ~9.5% reduction in the stand totals for
mixed-forest, and an ~24% reduction for both the rainforest understorey and the
pure rainforest (
Table 2
).
Figure 10.
Comparison of different rainforest understorey allometric equations, shown at different scales, from (a) larger to, (b) medium, to (c) smaller trees. For the equations that didn’t include root mass, it was added with a root:shoot ratio of 0.15:1. ‘K2000 temperate’= temperate rainforest [124]; ‘K2000 general’= general rainforest [124]; ‘K200 temperate inc.’= incorrect adjustment to the general rainforest tree equation in Keith, et al. [124] to get rainforest trees (my error, not theirs); ‘D2003’= [307]; ‘half D2003’= D2003 divided by 2; ‘ave’= average of D2003 and K2000 temperate; ‘rain_new’= Eq. 11, new rainforest allometric equation introduced here; ‘Walker & Candy (1982)’= [347] using height derived from Eq. 10 introduced here, density of 0.58 Mg m-3, and expansion factor of 1.46; ‘sassafras TERN’= sassafras [546].
Figure 10.
Comparison of different rainforest understorey allometric equations, shown at different scales, from (a) larger to, (b) medium, to (c) smaller trees. For the equations that didn’t include root mass, it was added with a root:shoot ratio of 0.15:1. ‘K2000 temperate’= temperate rainforest [124]; ‘K2000 general’= general rainforest [124]; ‘K200 temperate inc.’= incorrect adjustment to the general rainforest tree equation in Keith, et al. [124] to get rainforest trees (my error, not theirs); ‘D2003’= [307]; ‘half D2003’= D2003 divided by 2; ‘ave’= average of D2003 and K2000 temperate; ‘rain_new’= Eq. 11, new rainforest allometric equation introduced here; ‘Walker & Candy (1982)’= [347] using height derived from Eq. 10 introduced here, density of 0.58 Mg m-3, and expansion factor of 1.46; ‘sassafras TERN’= sassafras [546].
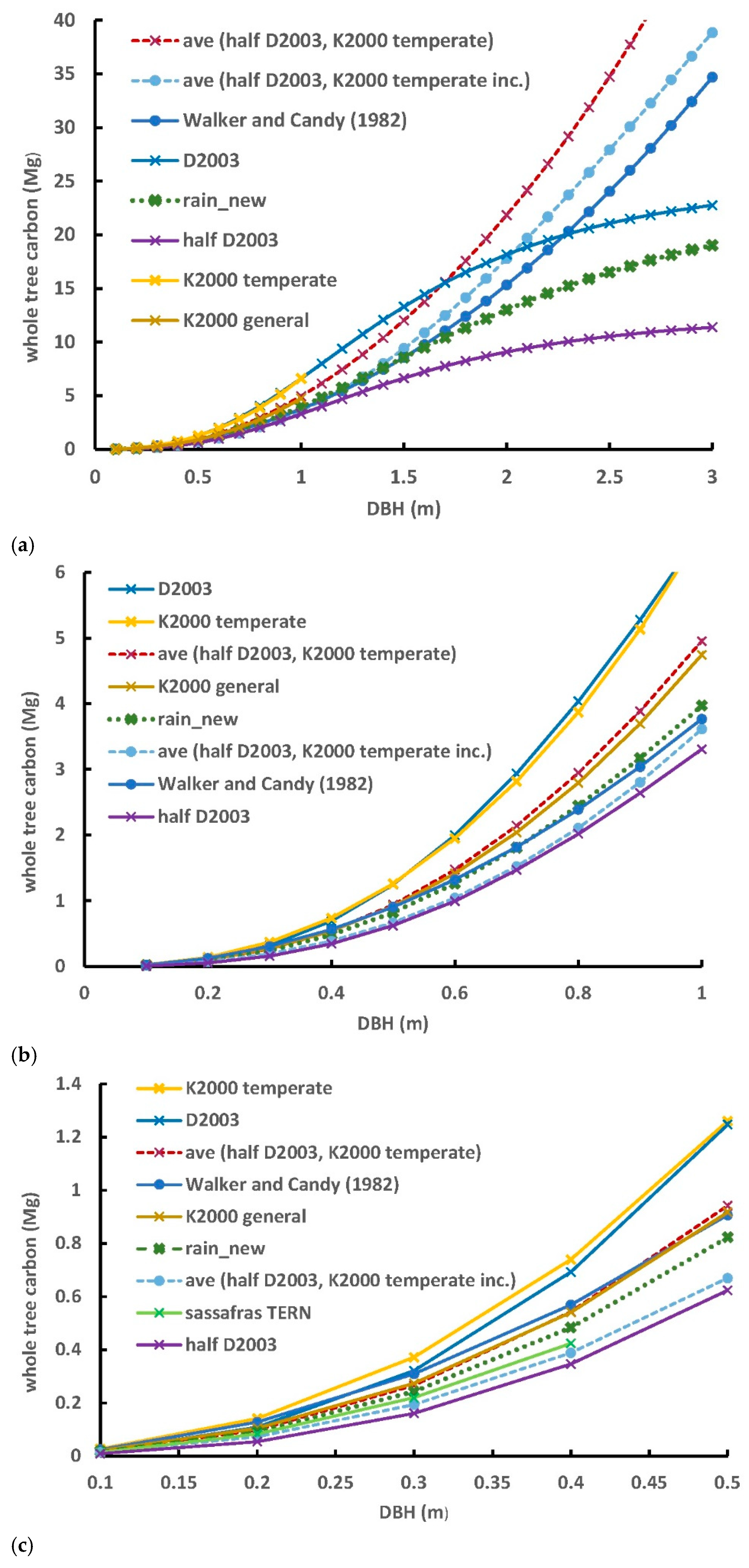
The Walker and Candy
[347]
equation is another that
forecasts exponentially increasing volumes with DBH (
Figure 10
.(a)) and therefore
it too cannot be used for the larger-DBH myrtle trees. The myrtles with larger
DBHs that I have observed in mixed-forest in Tasmania (such as over 2 m)
usually have increased hollow volume, both above and belowground,
representative of senescence, and therefore their C content approaches an
asymptote. To represent the additional scientific knowledge gained over the
last 20 years, shown in
Figure 10
, the allometric equation for C in rainforest understorey trees from
Dean, et al.
[307]
was
remodelled to give a new equation:
where newrainforest_C
is the carbon in the whole understorey rainforest tree in Mg and DBH is in m.
The multiplier ‘1.15’ represents the root/shoot ratio, and the ‘0.5’ multiplier
represents carbon being half of the biomass. This equation can be applied to
all DBH ranges of rainforest trees measured in mixed-forests for typical carbon
inventories in Tasmania. The carbon stock derived by this equation is much
lower than that from the temperate rainforest understory allometric equation
from Keith, et al.
[124]
, and only slightly higher than that from Walker and Candy
[347]
plus the expansion factor,
and it is therefore conservative. It will eventually approach the same
asymptote as in Dean, et al.
[307]
but only for higher DBH values than observed. At low DBH (< 0.5
m) it gives less carbon than does the Walker and Candy
[347]
process but more carbon than
does the equation for sassafras from Wardlaw
[546]
. But that latter equation assumes a cone above 1.3 m and it is
therefore quite approximate, and sassafras is relatively shade tolerant so has
a high branch volume and therefore its corresponding expansion factor is
probably higher than the 1.46 used in that work.
As with the graphs of the
allometric equations for eucalypts (
Figure
9
) it is worth gauging the precision (or error margins)
of allometric equations for the understorey species from
Figure 10
. For example, for a
tree of DBH 0.5 m: there’s a variation between the equations of ~33%. The
difference between curves gives an indication of the possible error margins
that can be assigned to the total rainforest understorey carbon in a
mixed-forest or rainforest study site. The wide error margin is another reason
why the newrainforest_C allometric equation was chosen for
use rather than that of Keith, et al.
[124]
in tallying carbon stocks for the comparison process. In this way,
the total, even if still with a high error margin, could not be viewed as
excessive, and indeed for trees of DBH 1 m, it is in the lower half of the
spread of carbon values.
6.3. Inventories of Carbon at the Landscape Scale
A major, publicly available
inventory of the primary tall-eucalypt forests in Tasmania was by ANM
[52]
, to describe the forests in terms
of merchandise, namely the pulpwood and possibly sawlog merchantable volumes in
the Styx/Tyenna/Florentine pulpwood concession area. Some details from this
assessment were given in
Section 2
above. As pulpwood uses more of the stem of a mature eucalypt tree
than does sawlog alone, then a BEF can be applied to process the merchantable
volume data of ANM
[52]
into carbon in live biomass of the forest stand. Appendix 4 in ANM
[52]
gives yields [of pulpwood plus
sawlogs] in terms of Mg per hectare for oldgrowth forests in the concession,
based on ‘recent production records’ from ‘various contractors’ over the period
1976 to 1977.
The yields were grouped under the
API types (see section 2), grouped by eucalypt height and canopy coverage. The
yields reported were for greenwood as delivered to the pulp mill and were not
for dry biomass. This is confirmed by the density they found when comparing
volumes with weights at the mill: 1.057 Mg m-3, which they used for
calculating spatial yield tables and annual extraction rates [52 p10 & 21].
Therefore, to get those yields of greenwood mass to dry biomass (before
dividing by 2 to get carbon) they must be multiplied by the basic density of E.
regnans (which was the main timber logged from which the yields were
obtained) and divided by 1.057. The basic density of 0.5124 Mg m-3
[307]
was used here, being for E.
regnans, as it was the main timber logged from which the yields were
obtained
[52]
. The
usual expansion factor of 1.46 was applied, to get whole aboveground mass and a
factor 1.15 to include roots. The product was then multiplied by 1.29 to
include the trees in the coupe that were not logged, such as those considered
unmerchantable, or on stream banks, or killed in escaped regeneration burns
[535]
(to give column 5 in
Table 3
). This may account to
some degree for rainforest trees which not taken off-site but just felled or
burnt (not all species were pulped). The values thus derived are in
Table 3
, where the phototypes
were also grouped to match the grouping used in a Tasmania-wide forest C
assessment by Moroni, et al.
[552]
: column 5 in
Table 3
.
If the reported yields in ANM
[52]
are processed differently,
there is a strong similarity in C stocks for some API-types with those reported
by Moroni, et al.
[552]
. If it is assumed that ANM’s reported yields were for dry timber
(not green timber), and the carbon in roots is not added, and no 1.29
non-merchantable-tree-factor is applied, then one obtains the values in column
6 of
Table 3
.
Numeric values from Moroni, et al.
[552]
were not available directly but were read off their graphs, with an
error of about +/-10 Mg ha-1
[553]
and are given in column 7 in
Table 3
. By comparing columns
6 and 7 it appears that values of C stock in live biomass for E1a and b, E1c and
d, and E2c and d in Moroni, et al.
[552]
, are identical [within error margins] to the C in aboveground live
biomass derived from the reported yields in ANM
[52]
but assuming they were for dry
biomass and not adding root mass. However, Moroni, et al.
[552]
describe their method as:
‘Total standing tree volume
(standing gross bole volume) was estimated from sample plot data collated in
2007 from >3500 permanent and temporary inventory plots. …
Standing-tree bole volumes are converted to forest C mass as described below.
Bole volumes of all standing living and dead trees of all species were
multiplied by a basic density of 500 kg m−3
[31]
allowing biomass to be
estimated. Total above-ground live-tree biomass (bole, branches and foliage)
was estimated from live bole biomass by multiplying by an expansion factor of
1.46
[32]
. Root
biomass was included by multiplying total above-ground biomass by 1.25.’
It is not possible to tell if the
similarity for those three averaged API types (columns 6 and 7 in
Table 3
) is coincidence or
not. But if they were calculated from the same data set then the carbon values
in Moroni, et al.
[552]
are missing the carbon in roots and are thus too low. Similarly, the
carbon values may also be too low because it’s likely that some rainforest
species such as myrtle and sassafras, or some portion of them, may not have
been tallied in the ANM inventories, as only eucalypts and Acacia dealbata
(silver wattle) were pulped in that era
[52]
. But, conversely, if the carbon values in Moroni, et al.
[552]
were calculated from that ANM
[52]
data set then
they will be too high as the original data were for green wood (including
moisture). Regardless, the values for the different API types in
Table 3
are averages over
hundreds of hectares and thus unlikely to represent local peaks such as in Sanger
and Ferrari
[529]
.
Table 3.
Oldgrowth merchantable timber yields (pulpwood + sawlog) from the Styx/Florentine concession [52], converted to spatial C density, and compared with Tasmanian forest carbon stocks from Moroni, et al. [552]. AG= aboveground, PA= API type averaged. Units Mg ha-1 = tonnes per hectare.
| API type | ANM [52] green yield (Mg ha-1) |
yield x 1.46 x 0.5 = AG C (Mg ha-1) | PA | ANM [52] yield, expanded C with roots (Mg ha-1) | PA AG C assumingdry yield(Mg ha-1) | Moroni, et al. [552 Figure 3] C in biomass (Mg ha-1) |
| E1a | 718 | 524.1 | E1a, E1b | 340 | 473 | 470 |
| E1b | 578 | 421.9 | ||||
| E1c | 699 | 510.2 | E1c, E1d | 232 | 322 | 319 |
| E1d | 183 | 133.7 | ||||
| E2a | 514 | 394.8 | E2a, E2b | 310 | 432 | 285 |
| E2b | 641 | 467.95 | ||||
| E2c | 361 | 263.5 | E2c, E2d | 175 | 244 | 244 |
| E2d | 307 | 224.1 |
Forest stands with peaks in carbon
content may not be reported as high volumes in logging records as the trees may
not be merchantable, e.g., due to strong senescence when pulpwood is not
marketable. In the pulpwood era one of the highest merchantable volumes
reported was 150,000 super feet [hoppus] per acre
[96,541]
. This was converted to C
in Mg ha-1, using a value for logs of 0.0030045 to convert super
feet to m3
[554]
, converting to per hectare, and using the same multiplication
factors as for column 5 in
Table 3
, giving: 618 Mg ha-1 of carbon in live biomass
(including roots). Two example stands with this C stock had areas of 0.81 ha
and 11 ha, of predominantly 100 to 150–160 year old E. regnans
mixed-forest with API-type E1a* (i.e., eucalypts over 76 m high and 70–100%
eucalyptus crown cover— high stand density), on steep slopes, in coupe L.38 in
Lords block, Florentine valley
[541]
. They were clearfell logged then burnt (CBS), from 1959 to 1962, so
will not reach the same carbon content until the year ~2120, and only if
unlogged and if climate change allows a similarly productive and fire-free
climate there until then. The stands were considered ‘young’ mixed-forest as
the rainforest understorey, although up to ~30–37 m high, was not well
developed, but would have developed broader, denser crowns, as the eucalypts
underwent self-thinning [and if they had not been logged]
[555]
. This carbon stock is nearly
double the average for the E1a API-type and the logging record refers to the
site as ‘extremely productive’. It demonstrates that the broader forest
averages, even within one API-type, cannot compete with smaller sites for high
carbon stocks.
Now that some of the variety in allometric equations and expansion factors has been shown, it is an appropriate point to describe what must be compared when gauging contenders for the status of highest carbon stocks in Tasmania, as claimed by Sanger and Ferrari [529] for their study plot. The C stock in live biomass (above and below ground) from their Table 2 is 916 Mg ha-1. The error margin on that value can be partly gleaned from the standard deviation between the data on their 4 transects in their Table B2: ~50% of the mean. No error margin is mentioned for the C in their individual trees with DBH >2.5 m, so it would have to be estimated from the imprecision in allometric equations, such as +/- 20%, from the derivation of the equations shown above in this section. There is also an accrued error from imprecision in each measurement made in the forest (section 2). Overall, as a rough guide, one could reasonably assume +/- 25% error, (229 Mg ha-1), which makes the reported C in live biomass including roots, in Sanger and Ferrari [529] between 687 and 1145 Mg ha-1. Therefore, as a rough guide for comparison with other reports, one must check if the C in live plant biomass in that other data is at least: (a) 687 Mg ha-1 if the root:shoot ratio used is 0.25:1; or (b) 632 Mg ha-1 if the root:shoot ratio used is 0.15:1; or (c) 549 Mg ha-1 if only aboveground C in live plant biomass is reported. Where possible, the root:shoot ratio in other data were converted to 0.15:1, to put all data sets on the same footing. There will also be error margins on the other data, so any overlap could be from two directions. If there is overlap then the two data points are indistinguishable. In reports where dead biomass and soil carbon are also reported, they can provide more detail and possibly more certainty in the comparison. One must also consider the area of forest measured, as it is easier to get a high carbon value in a small, non-randomly located plot (e.g., a 0.05 ha study plot centred around a non-senesced tree of DBH 5 m), than in a larger area such as 5,000 ha, which by its nature, must be more medium. In this, comparing size of study areas could however lead to an unintentional bias, because Sanger and Ferrari [529] stated that their study area was not randomly located but selected because ‘it had the highest density of large trees that were safe for climbing’.
6.4. The First Direct Carbon Assessments in Tasmanian Tall Forests
The first, intentionally carbon-oriented assessment of temperate mixed-forests in Tasmania was by Dean, et al. [307] with a mixed empirical-simulation study. Some useful milestones in forest carbon studies prior to that were Olson [556] and Harmon, et al. [269] in the USA, and Grierson, et al. [557] and Polglase, et al. [258] in Victoria, Australia. The latter two were in similar forests to that in Tasmania [307], and related data for such forests were reported earlier [e.g., 55,80,83,558]. Dean, et al. [307] parameterised the allometric equations for E. regnans and understorey species with their own data plus historical data from both Victoria and Tasmania. The high-end data were from Tasmania as the larger trees and older forest stands had long-since been logged out of Victoria. Differences in E. regnans between the two States were accounted for in parameterisation, such as the fact that they generally grow slower in Tasmania but last longer (Adrian Goodwin, Forestry Tasmania, pers. Comm. 2002). Dean, et al. [307] measured and modelled live biomass (including for example, non-circularity of stems and internal decomposition from senescence), and modelled dead biomass (fallen and standing) and soil carbon [including any translocated SOC]. However, Sanger and Ferrari [529] appear to have not known of that earlier work (even though they cited data from a conference paper which drawn from the original paper), nor of a later report by Moroni and Lewis [532] which also included all the same main carbon pools:
“To the authors’ knowledge, no studies from Tasmania have estimated the carbon from the whole forest ecosystem, including soil carbon”, Sanger and Ferrari [529].
Additionally, Sanger and Ferrari [529] state that root biomass was not included in the values given in Dean and Roxburgh [88], although it was explicitly included. A standard of science writing is to correctly represent earlier work when mentioning it. Errors are part of humanity but the collection of citing errors in Sanger and Ferrari [529] becomes an issue if the statements about earlier work are used as part of a foundation of further work by others, through the ‘amplification’ effect [559].
The values for most of the different carbon pools were not stated explicitly in Dean, et al. [307] but, as done with some other studies, they can be read off graphs, in this case their Figure 3.4. The specific growth and decomposition in that study were parameterised to simulate those observed in a 20 ha, E. regnans-dominated stand with API-type ‘E2d.M-‘ in logging coupe SX004C in the Styx Valley, Tasmania. Notably, the growth simulation had the standing biomass in E. regnans peaking near 215 years of age while the understorey biomass was still low, which matches with the relative portions measured earlier in mixed-forest [55]. Their graph also provided the carbon stock values for when the stand age reached 321 years, which was when the coupe was logged. The carbon stocks for those two ages are listed in Table 4(a).
The soil organic carbon (SOC) pool in that study was for the full soil profile (including any soil carbon that was translocated vertically or horizontally); therefore values will be higher than those measured to a specific depth. Moreover, it is not directly comparable with the SOC measured in Sanger and Ferrari [529] which was to only 0.3 m depth— that would require knowledge of the rate of change in SOC with depth. It can be misleading to compare the carbon stock of different soil types based only on the upper soil profile, to ≤ 0.3 m because the steepness of the falloff of SOC with depth can vary substantially between soil types. A soil with higher SOC above 0.3 m may have less SOC for the full profile than a soil with less above 0.3 m [e.g., Figure 2 in 560]. Considering the different uncertainties, to derive a value for SOC so that the total carbon stocks can be compared, a direct method is to treat the value to 0.3 m depth as a fraction of the total SOC. In Polglase, et al. [258] it was only ~25% of the total, and in Dean, et al. [92] it was <33% of the total. As a first approximation, for the SOC for Dean, et al. [307] to only -0.3 m, it will be assumed to be 30% of the total SOC derived from CAR4D: 179 Mg ha-1 (Table 4). Some further adjustment may be needed because in Dean, et al. [307] the SOC was higher than that of other Tasmanian forest studies because (as stated above) it was based on values from E. regnans forests in Victoria [258]. The half-life of SOC in the model CAR4D would need to be decreased to bring that total SOC back down near typical Tasmanian values to 0.3 m depth. In the absence of that recalibration of CAR4D, when making a comparison with Sanger and Ferrari [529], it is possible to simply instead adopt a value from elsewhere: the value for SOC to -0.3 m as in Dean, et al. [92]: 108 Mg ha-1, which will be introduced below.
In CAR4D trees died gradually as part of self-thinning, and once completely dead they fell and were in the CWD carbon pool. Therefore, there was no separate carbon pool for stags, for comparison with studies where one is measured.
For another comparison of data with Sanger and Ferrari [529], listed in Table 4(b) is carbon in live biomass for a small, 0.341 ha patch of E. obliqua-dominated ~450 year old oldgrowth within logging coupe WR005D within the State forestry’s Warra Long-Term Ecological Research site from Dean and Roxburgh [88]. For both sites the forest age was determined by tree ring counts from celery-top pine (Phyllocladus aspleniifolius) (Kathryn Allen, dendrochronologist, pers. Comm., 2002, 2004; method given in Allen, et al. [561]).
In that first attempt at simulating change in C stocks with time in mixed-forest [307], although the modelled understorey matched observations during the mixed forest stage, in the succession to rainforest stage it eventually surpassed the carbon content of the E. regnans, by an incorrect extrapolation, e.g., after 350 years reaching ~850 Mg ha-1 vs. 533 Mg ha-1, respectively. This contravenes earlier evidence [55], and consequently the understorey biomass was halved in subsequent use of that model. The mixed-forest vs. rainforest comparison was performed by several other authors [201,302,550], all showing that a mixed-forest has peak in biomass carbon that surpasses the peak rainforest carbon, as in Figure 13 above. These different data sets, are useful to review here because they provide further examples of C stocks to compare with Sanger and Ferrari [529].
The next publicly reported assessment of carbon stock for a specific location in Tasmanian forests was for a commercial enterprise, but for carbon credits rather than timber [562], and no SOC was tallied. That forest was in a less productive area than the central pulpwood concessions, and the location had already been selectively logged. Therefore biomass was lower, and it was not a contender with Sanger and Ferrari [529] for high carbon stocks. Nevertheless, both aboveground live and dead biomass (including coarse woody debris) were measured, and reported in terms of carbon, so it qualified for entrance and could have been in the list of existing carbon studies in Tasmania by the latter authors. Several other carbon credit projects followed but they were also on low productivity land (and therefore relatively low carbon stocks) compared with the central pulpwood area in State forests [e.g., 563].
The next carbon study to be published for a specific location in Tasmanian State forests was for 7.656 ha of a E. delegatensis-dominated mixed-forest within the planned logging coupe, FO044A in the Florentine valley, [542]. The API-type of the forest was E1 and E2 with 1–90 % eucalypt tree canopy coverage (Table 5). The understorey was mostly tall myrtle rainforest (M+) but shorter or just scrub in places. There was a wide range of biomass spatially across the area. Aboveground plant biomass, dead and alive, was measured (including assignment of 25% senescence (loss) for the eucalyptus trees) and reported in terms of carbon stock: 622(180) Mg ha-1 (standard deviation amongst the different plots in brackets). As mentioned above, allometric equations were developed for E. delegatensis and rainforest understorey in that work. Following further development of the equation for rainforest understorey in the present work (Eq. 11), updated carbon stocks for that location are presented here (Table 5). The new total for aboveground carbon (living plus dead plant biomass) is only 3% higher than published earlier. The average plot size was ~0.77 ha, which is large enough to represent a forest stand, and therefore the carbon contents are listed separately for each plot, as some could be contenders for locations of high carbon.
6.5. Government-Commissioned Carbon Assessments of Specific Forest Types
For the part of their consultancy that compared carbon in mix-forest and rainforest, May, et al. [550] reported three main separate data collections, the first two spanned the Styx, Florentine and Tyenna Valleys. The first included measurement of live and dead plant biomass. The second study additionally included measurement of SOC to 0.45 m depth, so the carbon pools measured were mainly the same as those in Sanger and Ferrari [529], and indeed sites were chosen in both studies that were viewed as having high carbon stocks. In the second one, live and dead biomass were reported in terms of volume, which were converted to mass of C here. Unfortunately though, the second study was discontinued and didn’t reach the peer review stage. In neither of these first two studies were the allometric equations used for eucalyptus species published. In both studies, their mixed-forest and rainforest plots were purportedly environmentally equivalent pairs. The mixed-forest and rainforest areas in such proximity are related by fire spread. Fire is less likely (and thereby less likely to convert rainforest to mixed-forest) in damper spots (such as due to shade or topographic water flow), or spots sheltered from the main wind direction on typical days of extreme fire danger. Whereas, only if the fire spread was random, could the two components in any one pair be genuinely environmentally equivalent. Additionally, some plots delineated as rainforest still contained live and/or dead eucalypts, so were still at the intermediate phase between mixed-forest and rainforest.
The third study was based on aboveground live and dead plant biomass data donated by The Wilderness Society and additionally included data from northwest Tasmania. In these three studies in May, et al. [550] there was no mention of tree roots and therefore it assumed in the present work that root carbon was not included in their tallying.
In the first study in May, et al. [550] there were sixteen each of mixed-forest and rainforest 0.1257 ha plots (totalling 2.01 ha for each forest type). The mixed-forest plots were E1a, E1b, E2a or E2b API-types and randomly positioned. Those categories were written in May, et al. [550] in terms of forest categories FC1 and FC3, with the translation to APIs given in Moroni, et al. [552].) Therein, field data were converted to spatial carbon stocks using the Farm Forestry Toolbox [537]. The allometric equations for E. regnans and E. delgatensis in that software are listed as confidential, being from Forestry Tasmania, and they were not publicly available. Therefore, they cannot be compared with other equations as in Figure 9 or Figure 10. A taper equation was available for E. obliqua [564], but taper equations alone cannot account for branches or internal trunk hollows. Allometric equations for rainforest understorey were developed by May, et al. [550] but not published. The carbon contents provided in May, et al. [550] are therefore only listed here verbatim. After ~50 years of commercial logging in the area since Gilbert [55], it seems unlikely that the carbon contents of the semi-randomly positioned plots across such a large area could be examples of peak carbon. Indeed, the eucalypts measured were below median size for the region, with the highest DBH being 2.6 m, and the tallest eucalypt being 55 m high. i.e., small-to-medium in size for mature eucalypts. Therefore it cannot be seen how any of their plots could be of the stated E1 type as the average mature eucalypt height for that category must be between 55 and 76 m [52,94]. Nevertheless, in their processed data, although the average carbon mass found in live plant biomass of 373 Mg ha-1 is no contender against Sanger and Ferrari [529] for the highest reported carbon in Tasmania, the mass at individual plots in Figure 110 of May, et al. [550] showed four likely candidates. Data was extracted from their Figure 110 to an accuracy of about ±10 Mg ha-1, and root carbon was added (root:shoot ratio= 0.15:1). Study-area-averages for dead biomass were also added: standing trees (with root carbon)= 120.75 Mg ha-1, and CWD= 23 Mg ha-1 (Table 6). The API-types of the forests were oldgrowth E1a, E1b, E2a and E2b, with a range of understorey types but the data points could not be matched to API-types using their Figure 110.
In the second study in May, et al. [550], the intention was to have a mixed-forest plot measured at each of 5 locations and 6 rainforest plots measured across 2 locations. But it was only possible to measure and report on two sites. Each plot had a maximum size of 0.1256 ha. Stem volume was calculated using unpublished allomeric equations from Forestry Tasmania, and converted to mass using a basic density of 0.5 Mg m-3, and scaled up to whole, aboveground tree carbon using the BEF of 1.46. That mass was halved to get aboveground carbon in live plant biomass (Table 6). Standing dead timber for this second study was not reported separately. The CWD was also reported in terms of volume. This was converted to mass of carbon, assuming an average density of 0.335 Mg m-3 as in Grove, et al. [565] and in the State-level section of May, et al. [550]: giving 100(±38) Mg ha-1. Soil carbon was reported down to 0.45 m depth rather than 0.3 m depth: 89(±58) Mg ha-1 in the mixed-forest, which, if assuming the same proportional decline with depth as for the in-between-tree zone as in Dean, et al. [92], gives 67(±43) Mg ha-1, to -0.3 m.
The third study in May, et al. [550], for three locations in Tasmania, partly overlapped with Dean, et al. [542] and Dean, et al. [92] in the Florentine and Styx Valleys respectively, in that most of the unprocessed data came from the same source. In the Styx Valley though, only half the data had been collected in time for May, et al. [550] [compared with what was used in Dean, et al. [92]] and the site-specific allometric equation hadn’t been developed. The allometric equations used in the third study of May, et al. [550] were from Dean, et al. [542] except that for understorey trees the temperate rainforest equation of Keith, et al. [124] was used. For the Florentine Valley component, the results from Dean, et al. [542] were given to May, et al. [550] for them to report and so that area won’t be re-listed here. The results for the northwest Tasmania region within the third study are not contenders with for a high carbon area and so won’t be further mentioned. That leaves only the Styx Valley results from the third study to portray here. To put that rainforest carbon on a level playing field with the other studies (i.e., newrainforest_C from Eq. 11), a pro-rata correction was applied to the results from the erroneous allometric equation used, as suggested from Table 2. (a correction of -48.2%). It is unknown how much senescence they modelled for the eucalyptus trees in the Styx Valley data so their values are reported verbatim here (Table 6I).
6.6. The State Forest Agency’s Carbon Assessments of Specific Forest Types
Chronologically, the next report on carbon stocks in Tasmania was by Moroni and Lewis [532], with values that could be contenders with Sanger and Ferrari [529] for high carbon. These wet-sclerophyll forests studied were in the Huon district, southern Tasmania, with API-types E2c and/or E2d (the lower category in Table 3) and they were mature E. obliqua—dominated [532]. Live and dead aboveground plant biomass were measured for six 0.2 ha plots. The fire history was not stated. Biomass for standing live trees was calculated from unpublished allometric equations for bole [merchantable stem] volume, and the BEF applied was 1.46. Root carbon was estimated with a root:shoot ratio of 0.25:1. Soil carbon was reported to a possibly variable depth depending on the particular soil type, as it was retrieved from values for purportedly similar soils in the north of Tasmania, that were described in the three 1995 Tasmanian reports mentioned above [303,304,305]. In Moroni and Lewis [532] the SOC amounts were compared with those modelled by the program Fullcam [566,567], which only models to 0.3 m depth, so it may be that the original empirical values were trimmed to that level.
The individual carbon pools for the six plots were not tabulated but there were graphs of total C, debris C, and live biomass: data were extracted from those graphs with an accuracy of ~+/- 4 Mg ha-1, and after reaggregation, the reconstructed site averages only differed from those reported by +/- 3 Mg ha-1 (meaning there was a minimal transcription error). From these data, and the fact that each plot had been attributed the same SOC of 179 Mg ha-1, it was possible to derive the values for the other C pools for each plot. From this vantage point it was possible to change the root:shoot ratio from 0.25:1 to 0.15:1, for comparison with the other reported values in this section (Table 7). This lowered the site average total C by 6%. Notably, the site average live plant biomass is similar to that in Table 4(a) for the E2d.M- site in Dean, et al. [307]. The site average of 634(187) Mg ha-1 is approximately two standard deviations higher than the value of 244 Mg ha-1 for the State-wide E2c,E2d average in Moroni, et al. [552].
6.7. A comprehensive Carbon Assessment Including More Soil Carbon Detail
The next scientific publication on carbon stocks for tall eucalypt forest of Tasmania reported live and dead biomass and soil carbon for plots in the Styx Valley and partly in the Tyenna Valley [92]. Sanger and Ferrari [529] stated that they only reported soil carbon. The site averages for the different pools were reported but for the carbon in living trees, plot-level values were shown in their Figure 12(a) [92]. There are two plots which looked in that figure like possible contenders for having the highest carbon stocks in Tasmania.
Dean, et al. [92] calculated SOC to the full depth of where it transcended down through the soil, rocks and interstitial spaces, by extrapolation of the upper changes in SOC with depth. Additionally, SOC was measured separately close to the larger eucalyptus tree trunks, both above and below ground, and for the soil (lignomor) in the softer, more decomposed logs. The overall value was 330 Mg ha-1 to 90% of the maximum SOC (or 367 Mg ha-1 in total). The error margin, in terms of standard deviation, on that value can be estimated as 25% (82.5 Mg ha-1), from the various measurements and formulations that went into its derivation. For the purposes of comparison with Sanger and Ferrari [529], the soil organic carbon which had been allocated from half of the soft-log mass in Dean, et al. [92], was reattributed to the general CWD pool. For comparison with the value of 149 (SD 103) Mg ha-1 from Sanger and Ferrari [529], the value of SOC that will be used from Dean, et al. [92] to 0.3 m depth, will be that for ground away from trees, it is that derived from data in Dietrich [310]: 108(SD 10) Mg ha-1. This is notably less than a third of the total SOC.
A site-specific allometric equation for E. regnans, which included senescence, was developed in Dean, et al. [92] (see section 6.2). Some of the plots, with lower overall live biomass, contained some E. delegatensis and E. obliqua trees, and the corresponding equations mentioned above (section 6.2) were used to calculate C in biomass for those trees. Here, we have recalculated the understorey biomass using Eq. 11. Values are summarised in Table 8 but without the SOC pool.
6.8. Placing the Pro-Conservation Report on a Level Playing Field
Where possible, for the purpose of comparing carbon stocks, the root:shoot ratio of 0.15:1 has been applied to other data collections mentioned in this section. Consequently, that must also be done to the data reported in Sanger and Ferrari [529]. Also for making an equitable comparison, some of the other factors used in that report must be adjusted: (a) account for ground slope, (b) use the new rainforest allometric equation, and (c) use species specific wood densities and allometric equations for the eucalyptus trees where possible.
There are firstly some possibly larger matters to address though in Sanger and Ferrari [529] regarding what appears to be their particular adoption of standard scientific processes, for example (a) citing of earlier work, (b) error margins; (c) accounting for senescence in the larger trees, especially trunk hollows; (d) some missing information; and I comparing results with those in earlier work. Those will be addressed these here. The issue of incorrect citing of earlier literature was discussed above and will only be mentioned again with respect to tree hollows etc.
When citing the equations used from Dean, et al. [542], except in one instance, Sanger and Ferrari [529] transcribed them verbatim, even copying errors in the original work (some of which had been corrected in a corrigendum). For example, Eq3 in Dean, et al. [542] for the temperate rainforest understorey aboveground biomass:
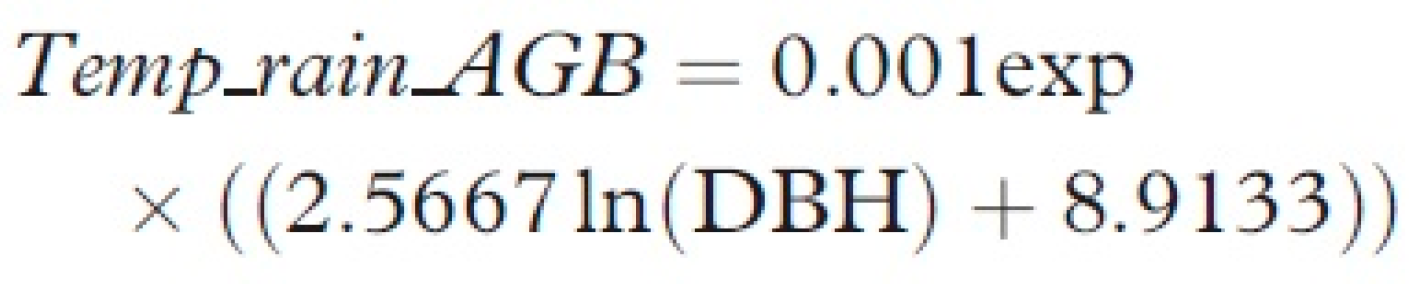
was copied as:
“UAGB = 0.001exp x (2.5667 ln (DBH) + 8.9133)”, Sanger and Ferrari [529],
where the multiplication sign, ‘X’, after ‘exp’ is incorrect mathematical syntax. And the ‘0.01’ in Eq. 2 in Dean, et al. [542] was transcribed verbatim but had been corrected to 0.1 in the corrigendum [568]. The corrigendum was uncited so it may have been inadvertently missed. The exception to their verbatim transcriptions was the allometric equation for E. delegatensis, namely Eq. 2 in Dean, et al. [542]:
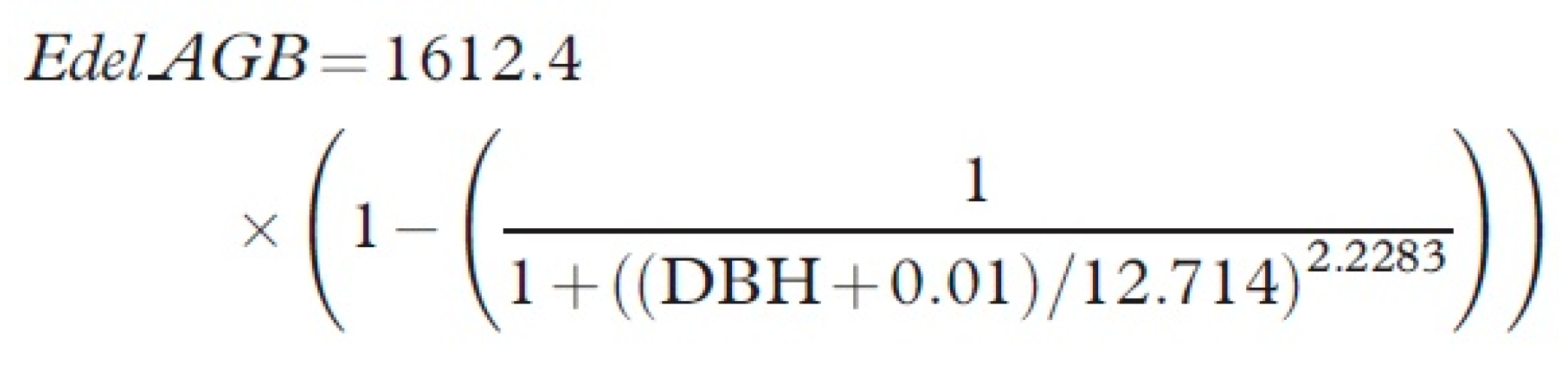
which was transcribed as:
‘EAGB = 1612.4 x (1- (1/ 1 + ((DBH + 0.01)/12.714)2.2283)’, [529].
The ‘del’ is missing in the transcription. Notably Sanger and Ferrari [529] describe it as being an ‘averaging allometric equation’ for ‘eucalypt trees’, whereas in Dean, et al. [542] it is specifically described as being designed for the aboveground biomass of E. delegatensis trees. An allometric equation developed for one species has been erroneously stated as generic for all eucalyptus species. That would mislead readers about the earlier publication and might result in other people copying that error for their own calculations further afield, while citing the original publication (the amplification effect). A possible reason for the error is that Sanger and Ferrari [529] wanted an equation that would suit any eucalypt species in their study plot. Such a generic equation was already available, at least for trees of DBH ≤ 1 m [124], and it could have been adopted and modified for senescence in trees with larger DBH values, following for example Dean, et al. [92], possibly using individual tree data [124,543,544].
Some information missing from Sanger and Ferrari [529] is the species names for the trees measured and modelled. This is important in deciding parameters for carbon accounting. Only the eucalypt species present in the larger 98 ha surrounding their ~2 ha study plot are mentioned. One could assume the species in the study plot are the same as in the larger 98 ha, but in Sanger and Ferrari [529] their choice of allometric equations suggests a subset. In the surrounding 98 ha of forest there were E. regnans, E. obliqua and E. globulus, with no mention of E. delegatensis being present (though they used an allometric equation developed for that species), whereas in the public media, the first author, Sanger, stated:
‘What makes it really special ... is that there are giant trees from four different species of eucalypt tree,…’ [569]
There are strong links between the publication, Sanger and Ferrari [529], an internet Facebook page and a commercial internet site run by a company called the ‘The Tree Projects’ [570,571]. On that commercial site E. delegatensis is mentioned as being in the larger forest stand, and only E. obliqua , E. regnans and E. globulus are featured on their Facebook site [571]. This is helpful but some uncertainty remains as to the species present in their study plot.
There could be a difference in species between their plot and the surrounds because: (a) they only measured 2% (by area) of the ‘Grove of Giants’ (their name for the 100 ha total), and (b) the average height of the trees with DBH over 2.5 m that they measured was 56 m (maximum height 72 m, and maximum DBH 5.12 m) whereas the surrounds have some trees near 80 m tall and a maximum DBH > 6 m. Thus, maybe a higher proportion of the trees in their plot were E. obliqua or their plot was more senesced than the surrounds. But this cannot be determined, especially as it can’t be determined whether the latitude and longitude provided for their plot refers to the centre, or a corner, or just somewhere in the larger 100 ha expanse. The URL web data link for ‘the data that support the findings’ provided in Sanger and Ferrari [529] does not lead to a web page, and when contacted, the journal’s administration didn’t provide an alternative URL.
Typically in scientific papers on forest carbon, the tree species are mentioned in the Introduction or Methods sections. An even more useful place to mention them in this case [529], would have had been in their Table B1, where the individual DBHs were listed for trees with DBH >2.5 m. As the species in the understorey were not mentioned, they cannot provide a clue about the fire history and thus the likely eucalypt assemblage. However, the company’s website provides geographic coordinates for the walking trail in the ‘Grove of Giants’ and overlaying that with the State forest agency’s API-type map of 1984, gives the API types as E1b.S.ER and E1c.S. The ‘S’ indicates scrub (understorey < 15 m) and the ‘ER’ indicates young (regenerated) eucalypts present with the oldgrowth trees. Photos of trees being measured on the company’s Facebook page supports these API types, and a range of eucalyptus and understorey species [571]. In a traverse along the recommended walking trail in the ‘Grove of Giants’ by J. Kirkpatrick (University of Tasmania, pers. Comm., 2024) myrtle, sassafras, celery-top pine and Tasmanian Laurel (Anopterus glandulosus) were seen in the understorey, making it young rainforest understorey, rather than scrub. It had possibly begun to mature, since the State forestry’s aerial photography. In summary, the relative concentration of different eucalypt species in the study plot of Sanger and Ferrari [529] cannot be determined from any of the information publicly available. Therefore, the error margin on the study plot’s carbon content could be increased further.
Their choice of mixing different allometric equations for different parts of their data processing of the eucalyptus trees in Sanger and Ferrari [529], namely for E. regnans from Sillett, et al. [572] and E. delegatensis from Dean, et al. [542], seems unnecessary, and could possibly lead to some bias, causing inaccuracy in the carbon stocks. For small eucalyptus trees in southern Tasmania (where the ‘Grove of Giants’ is) Bowling [573] found that for small regrowth eucalyptus trees (mostly with DBH < 0.64 m) the volume (for a given DBH and height) does not vary much between species, though some trends in deviation from the norm were noticed. With more data for each species, some definitive trends appear. For example, even for trees of the same DBH (1 m) and height (58 m), the wood volume in the stem, from integrating under their taper equation curves (Figure 11), for E. obliqua [574], E. delegatensis [574], and E. regnans [88], is 13.3, 12.5 and 12.0 m3 respectively— a spread of about 10%. The taper equation for E. obliqua mentioned above by Goodwin [547], gave a volume of 12.8 m3, and could have been graphed in Figure 11 but was not because in the mid-section it was too close to the curve for E. delegatensis. (For people who might use these equations, I just mention here that there’s a typographical erro) in Goodwin [547] which could cause confusion: the equations for α2 and α3 in the parabolic part of the ta)er, are actually for α3 and α2, respectively.)
Furthermore, Ilic [575] gave the basic densities of E. obliqua, E. delegatensis and E. regnans as 580, 524 and 485 Kg m-3, respectively. This reinforces the sequence of decreasing mass that was indicated by the taper equations for equal-dimensioned trees in that species sequence. When normalised to the mass for E. obliqua, the mass ratios for that sequence are: 1: 0.850: 0.756. This gives a value to the imprecision (error margin) associated with not identifying the species— possibly up to about ±12 %. Wood density is an important contributor to carbon calculations when applying an allometric equation that is otherwise intended to be generic across species [576].
Additionally, E. regnans are commonly known to be, on average, the more-buttressed of the ash-type eucalypts, which could induce a potential extra error margin if mixing allometric equations between species. There is minimal information available for allometric equations of non-plantation E. globulus, (which are likely to be in the study plot of Sanger and Ferrari [529]) and it is considered an area of necessary research, but young specimens have an average basic density near 600 Kg m-3 [577].
Figure 11.
Different stem shapes of some eucalyptus species with the same DBH (1 m) and height (58 m), based on taper equations, showing difference in underbark wood volume, which yield a volume range of ~10%. The roughness for E. regnans near the top of the buttress region is because its taper equation was for over-bark shape, and the bark becomes thinner there.
Figure 11.
Different stem shapes of some eucalyptus species with the same DBH (1 m) and height (58 m), based on taper equations, showing difference in underbark wood volume, which yield a volume range of ~10%. The roughness for E. regnans near the top of the buttress region is because its taper equation was for over-bark shape, and the bark becomes thinner there.
The benefit for Sanger and Ferrari [529] from choosing an allometric equation for E. delegatensis for their smaller trees is that it gives a medium volume. But if their trees were mostly E. obliqua or E. globulus, then they may have underestimated the volumes, or overestimated them if they were E. regnans.
Accounting for senescence in older trees is important when determining carbon stocks [307,309,578]. Sanger and Ferrari [529] state that they used an equation for E. regnans, from Sillett, et al. [572] to calculate missing carbon due to hollows etc.:
‘Internal decay was factored by equations to predict occurrence and volume of decay related to tree size was also derived from Sillett et al. (2010).’
However, in ‘Sillett et al. (2010)’ it is explicitly mentioned that internal decay was not accounted for, which was confirmed with its lead author: ‘Our published numbers for EURE do not account for hollows or decay’ (Steve Sillett, Cal. Poly. Humboldt, pers. Com. 2023). Consequently, to put carbon stocks on a level playing field for comparison purposes, some carbon must be subtracted from that apportioned to the larger trees in Sanger and Ferrari [529]. There is no reason to believe that the eucalypts in the plot of Sanger and Ferrari [529] had less hollows than those with which they are being compared here, such as in the Styx and Florentine Valleys. Both senescence and fire, and their combination, will increase the likelihood of lost carbon from the tree trunks. Therefore, it is shown here, how at least as much fire has occurred in the locality of the ‘Grove of Giants’, as in the Styx and Florentine Valleys.
Fire can increase hollows beyond that from normal senescence, especially in the buttress region or an existing hollow, because of turbulent flow. Turbulent flow, will in places, increase the speed of passing air and therefore delivers more oxygen, which pushes the exothermic reaction forward, creating a hotter, larger and longer burn. For a tree trunk this increases loss of carbon compared with wood decomposition alone. Such a fire is shown in Figure 12 after a light, prescribed burn of surrounding buffel grass in central Australia.
Figure 12.
Intense fire due to turbulent flow in tree hollow River Red gum (Eucalyptus camaldulensis), following a light, prescribed burn of feral agricultural grass (Cenchrus ciliaris) in Todd River, central Australia. Carbon was still being emitted the following day after the grass had long-since self-extinguished. Similar release of carbon and hollow enlargement could occur for ground-level forest fires.
Figure 12.
Intense fire due to turbulent flow in tree hollow River Red gum (Eucalyptus camaldulensis), following a light, prescribed burn of feral agricultural grass (Cenchrus ciliaris) in Todd River, central Australia. Carbon was still being emitted the following day after the grass had long-since self-extinguished. Similar release of carbon and hollow enlargement could occur for ground-level forest fires.

Strong evidence of fire in the region of the ‘Grove of Giants’ is that there are young eucalypts in the stand (the ‘ER’ in the API type) and that the understorey is not mature. Additionally, in the nearby Warra ecological research site, which also has a history of recent fire, the mature eucalypts were noted to be ‘almost invariably hollow, or at least heavily decayed at their centre’ [350]. Comparing maps for the ‘Grove of Giants’ region and the Styx Valley show that the creek lines have quite different vegetation: no rainforest gullies surrounding the ‘Grove of Giants’ whereas they prevail in the Styx Valley. In the former the gullies contain eucalypts <110 years old and mature eucalypts, possibly constituting wet-eucalypt forest rather than rainforest (Figure 13).
Figure 13.
Indicators from vegetation of more frequent fire near the study area of (a) Sanger and Ferrari [529] with mature and young eucalypts in the creek lines (black square= study plot), compared with (b) the central Styx Valley with rainforest in the creek lines. Hence probably more hollow development in the mature eucalypts in (a). Blue lines= creeks and rivers. Vegetation categories based on API types from State forest agency maps.
Figure 13.
Indicators from vegetation of more frequent fire near the study area of (a) Sanger and Ferrari [529] with mature and young eucalypts in the creek lines (black square= study plot), compared with (b) the central Styx Valley with rainforest in the creek lines. Hence probably more hollow development in the mature eucalypts in (a). Blue lines= creeks and rivers. Vegetation categories based on API types from State forest agency maps.
Several of the trees in the photos of the ‘Grove of Giants’ showed indicators for deep basal cavities [570,571]. In three dimensions they are clearer. For example, a 3D model based on aerial LiDAR of one of the largest E. globulus trees in the larger 100 ha surrounding their study plot, shows two deep basal fissures and higher up a deep stem indentation, which could lead to an internal basal hollow [579].
One of the largest E. regnans trees measured in Tasmania in the last 20 years, the ‘El Grande’ tree (which I measured to have a DBH of 6.19 m), had a stem volume of 406 m3 but had internal stem hollows, which may have reduced that wood volume by up to 40%, down to 244 m3 [77]. The measured volume for the E. globulus tree [mentioned in the last paragraph], when not accounting for stem hollows was 325 m3 [569]. But this could be much lower if the internal losses are similar to that in the El Grande tree. In Sanger and Ferrari [529] crown loss is already taken into account for the trees with DBH >2.5 m as the calculations include tree height. Dean, et al. [542] subtracted 25% from the eucalypt mass to account for internal hollows. Combining the two influences, it is reasonable to subtract 15% from the values in Sanger and Ferrari [529] from the trees with DBH >2.5 m, to place their plot’s total carbon on a level playing field for comparison purposes. Although this may sound like maligning of the larger trees, it is only to prevent overestimation of their carbon stock, and it does not detract from their numerous other values such as wind attenuation, carbon storage and cycling, local climate moderation and unique ecological contributions.
The variation in hollow occurrence described in section 2 suggests that in the absence of definitive detail, one must allow for a balanced and adjustable degree of hollowing. Other than assuming an average internal decomposition which can be adjusted for location [307], other methods are destructive sampling [124] [but then the tree dies] and coring. The latter method was used by Sillett, et al. [580] for individual Coast redwood (Sequoia sempervirens) and for stand-level carbon accounting they modelled the shape of trunk internal decay for trees with DBH > 2 m, through reductions in wood density..
Ground slope was not mentioned in Sanger and Ferrari [529]. Slope doesn’t usually make much difference to soil organic carbon calculation [other than depth calculation on steep slopes] because the cores or pits are dug vertically, and the extrapolation to a hectare is done assuming the surface of the collected sample is horizontal. On very steep slopes however, one may not be digging only downwards but, from the soil’s perspective, sideways too, and therefore measuring more of the topsoil, giving higher carbon stocks than due. Sloping ground makes a difference to the biomass calculation, as the projected plot area is reduced, which increases the calculated carbon in biomass per hectare, by the secant of the cosine of the slope. Using GoogleEarth Pro©, the typical slope in the ‘Grove of Giants’ was found to be about 20% or 11°, which increases carbon in biomass by about 2%, from the values reported in Sanger and Ferrari [529]. The projected plot area becomes 1.914 ha rather than the original 1.95 ha. The ground slope from a cross-section of the 3D model from LiDAR data of the large E. Globulus [581] was 9(±1)°,which would increase carbon in biomass by 1.2%. In Sanger and Ferrari [529], there was initially some uncertainty about the plot that they had laid out, because it was twice described as 100 x 130 m, once as 150 x 130, twice as 19,500 m3, and once as 2 ha. On balance that is 4:2 in favour of 150 x 130 m, which was used in the recalculations here, before adjusting for slope.
In each measurement of trunk diameter there is an error margin when reading a distance off the tape. This type of error margin is usually taken as ± two tenths of the minimum graduation mark on the measuring device, but it also depends on a user’s experience level. People who routinely measure tree diameters have acquired habits that reduce error in placement of the tape before any reading is taken, such as sliding the tape to-and-fro a few times to make sure it has achieved the minimum local girth. Other basics include making sure the tape is perpendicular to the axis of the trunk or branch, and that it is not over any local swelling such as from a burl or branch development, but rather below or above it (or both, and then the average taken). Such information was passed on to the citizen science crew for the group measurements made in some earlier work [e.g., 92,542]. From photographs in public media on the internet however, it appears to have not been passed on to the arborists deployed for data collection in Sanger and Ferrari [529]. There were instances of tapes over substantial amounts of shed bark from higher up the tree, tapes not level for trunk and DBH measurements, tape over part of a burl, and a tape over a large branch-collar [569,571]. These all add apparent wood volume, rather than simply increasing the error margins. Measurements were taken off some photos in the public media that showed incorrect measurement technique in citizen science data collection in the ‘Grove of Giants’ [569,571 19-December-2022, 19-January-2023, 23-February-2023]. The angle from perpendicular [to the trunk axis] on diameter measurements was between 5 and 9°, giving an extra trunk volume (locally) of ~0.4 and 1.6% respectively. The extra diameter over the bark strands from higher up the trunk was ~5%, which translates directly to the same percentage of extra volume. The placing of the tape over the branch collar gave an extra volume (locally) of ~21%. It cannot be established if the examples provided in public media were exceptions or the typical procedure adopted. A rough estimate from the non-perpendicular diameter tapes may be, overall, conservatively in the order of 1%, which is insubstantial. If it was as high as 5% on average then that would be a significant factor when comparing carbon stocks. Most humans are outside of their normal 2D oecumene (as discussed in section 3) when climbing tall trees and this makes measurement more difficult, but practice of standard measurement techniques can help overcome difficulties and ensure less error in measurement. Regardless of the errors in measurement, due to the uniqueness of tree climbing, allowing public access to the data (by activating the mentioned data repository link in their paper) would have enefitted science by allowing improvement to existing allometric equations.
Having described several studies and summarised their data in the tables above, they can now be compared with the carbon stocks derived by Sanger and Ferrari [529], but only after adjustment of the latter for common allometric equations, wood density, senescence; and ground slope.
To summarise the differences between the reassessed and original calculations in Sanger and Ferrari [529], the multiplication factors are explained here. To convert from my earlier erroneous understorey allometric that they used, to the newly developed one here, without knowledge of their individual DBH measurements, I applied the ratio from Table 2(b) for the mixed-forest site assessment of Gilbert [55]: 158.9/162.5 = 0.97785 (which decreases biomass). The root:shoot ratio of 0.15 was used rather than the 0.25 in Sanger and Ferrari [529] (which decreases biomass). A wood density of 512.4 Kg m-3 was used rather than their 520 Kg m-3. I applied an 11° ground slope to the wood measurements (which increases live and dead biomass). And I applied a 15% senescence to eucalyptus trees with DBH > 2.5 m if their height was less than the typical 75 m (assuming, in the absence of other information, that the trees are E. regnans) and some senescence had already been deducted by measurement of reduced height (another reduction of live plant biomass). The results are shown in Table 9.
It is worth noting the effect of different amounts of senescence in the large trees. Assuming no senescence in the larger trees, other than that originally measured (by reduced crown mass), increases the C in study-wide live biomass by 9.9 % from 742.2 to 815.5 Mg ha-1, whereas assuming 20% senescence in the larger trees decreases C in study-wide live biomass by only 3.3%, to 717.8 Mg ha-1. This gives another indication of likely error margins.
The error margins for the biomass values from Sanger and Ferrari [529] were earlier described as ±25%, and the corresponding absolute values for the adjusted data are shown in Table 9. The error margins assigned to their values for CWD and soil organic carbon to 0.3 m depth [in that table] were the standard error (standard deviation divided by square root of sample size (namely 4)) found experimentally. Those standard deviations could be reduced by collecting more data. But to decrease the error margins in the biomass carbon values, more intensive experimental procedures would be needed, and if still using allometric equations, then more experiments to get relevant ones, such as for mature E. globulus (if present).
6.9. Comparison of the Carbon Stocks from Different Reports
In Figure 14, the first comparison of the carbon stocks in the study plot of Sanger and Ferrari [529] with other studies, is of living plant biomass, then studies that included other pools too are shown, such as dead plant biomass and SOC. For the graphs, the tally from Sanger and Ferrari [529] was set as the benchmark to compare others against, as they claimed to have the most carbon reported in Tasmania. For ease of visualisation in the graphs error margins have only been applied to that tally from Sanger and Ferrari [529], but further on the influence of equivalent error margins on all the data being compared, is examined. There are of course error margins associated with the other reports, some of which may be as high or higher than those in Sanger and Ferrari [529]. The graphs are simpler this first way though, when there are many data points, and therefore they are easier to interpret.
The data points from reports that are centred below the lower error margin of Sanger and Ferrari [529]) are not shown in the graphs and in the table, in order to be conservative with showing possible competitors. This is also partly because, with science at its current level of development and field sampling so limited, forest-based carbon data for the tall eucalypt forests are generally too imprecise to warrant closer interrogation.
Although it is generally not permitted in scientific journal publications to show both graphs and tables of the same data, it is done so here because they provide different information. The graphs provide a useful visualisation of the distribution of values whereas Table 10 is useful for providing data for further work, such as in future comparisons. Often when retrieving data for this paper (and earlier ones) it has been necessary to use the software Datagrabber [582] to extract information from graphs, a process which adds its own error margins, in addition to those in the original data. Thus, in the interests of science both types are provided here, and it is suggested that it be considered as a scientific standard.
Figure 14.
Comparison of carbon stocks in different pools, from Sanger and Ferrari [529] with those from other studies. The horizontal dashed lines are the error margins for Sanger and Ferrari [529], from Table 9. The code name is shown in column 4 of Table 10. In (c) the points that didn’t have SOC measurements adding to their total C, but still got within the error margins of Sanger and Ferrari [529] with all its pools, are shown as grey squares. Point G59 did not have debris or SOC measured, but still was within the margins in all figures.
Figure 14.
Comparison of carbon stocks in different pools, from Sanger and Ferrari [529] with those from other studies. The horizontal dashed lines are the error margins for Sanger and Ferrari [529], from Table 9. The code name is shown in column 4 of Table 10. In (c) the points that didn’t have SOC measurements adding to their total C, but still got within the error margins of Sanger and Ferrari [529] with all its pools, are shown as grey squares. Point G59 did not have debris or SOC measured, but still was within the margins in all figures.
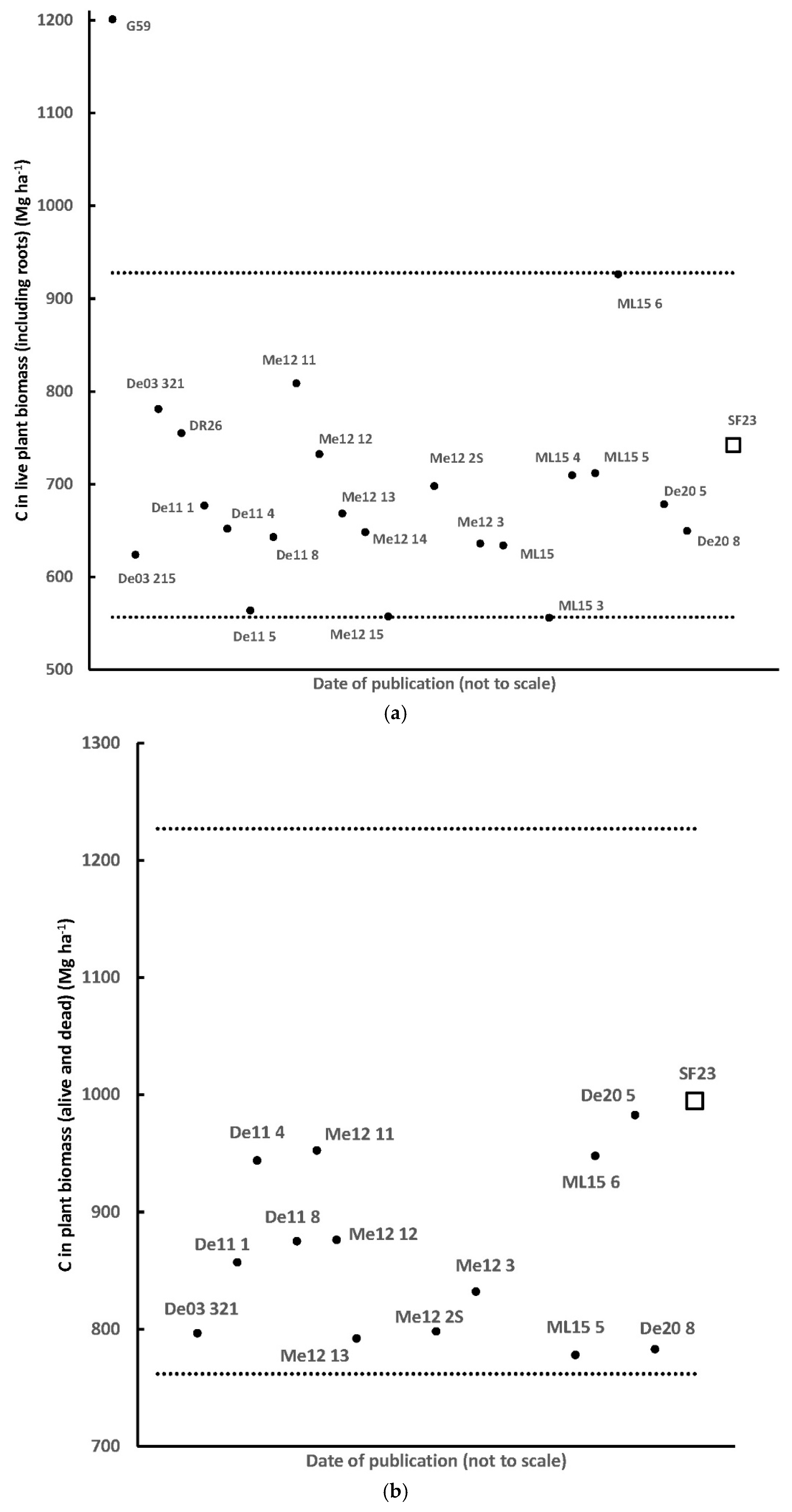
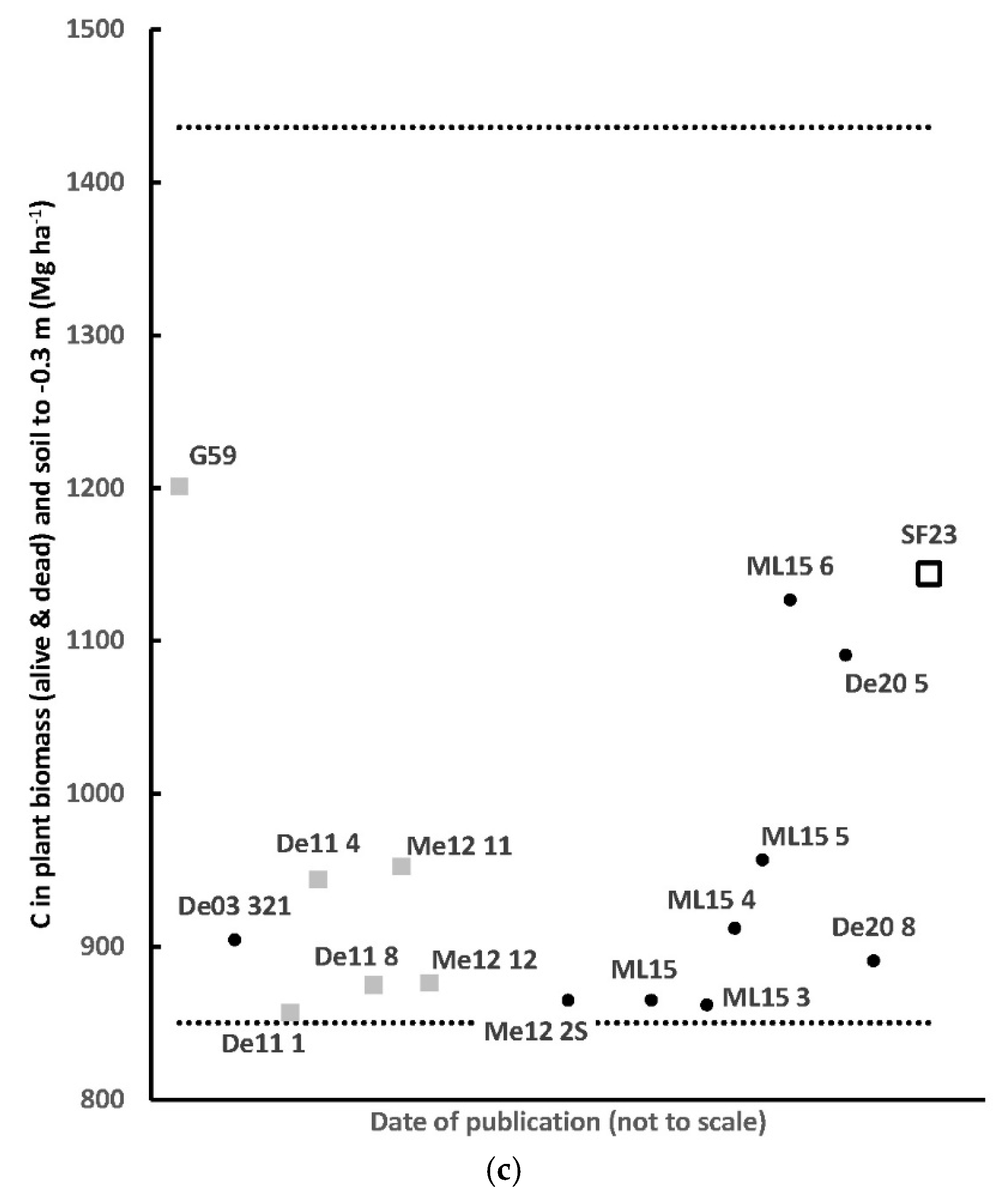
Table 10.
Summary of carbon stocks, to 3 significant figures, for different pools that are within the error margins of those in Sanger and Ferrari [529] and therefore indistinguishable from them; plus projected area and aerial photo interpretation (API) type. Note that the area may not necessarily be the maximum area, merely a sample, except for Dean, et al. [307] where the 20 ha is mostly modelled but with an empirical base for the whole stand.
Table 10.
Summary of carbon stocks, to 3 significant figures, for different pools that are within the error margins of those in Sanger and Ferrari [529] and therefore indistinguishable from them; plus projected area and aerial photo interpretation (API) type. Note that the area may not necessarily be the maximum area, merely a sample, except for Dean, et al. [307] where the 20 ha is mostly modelled but with an empirical base for the whole stand.
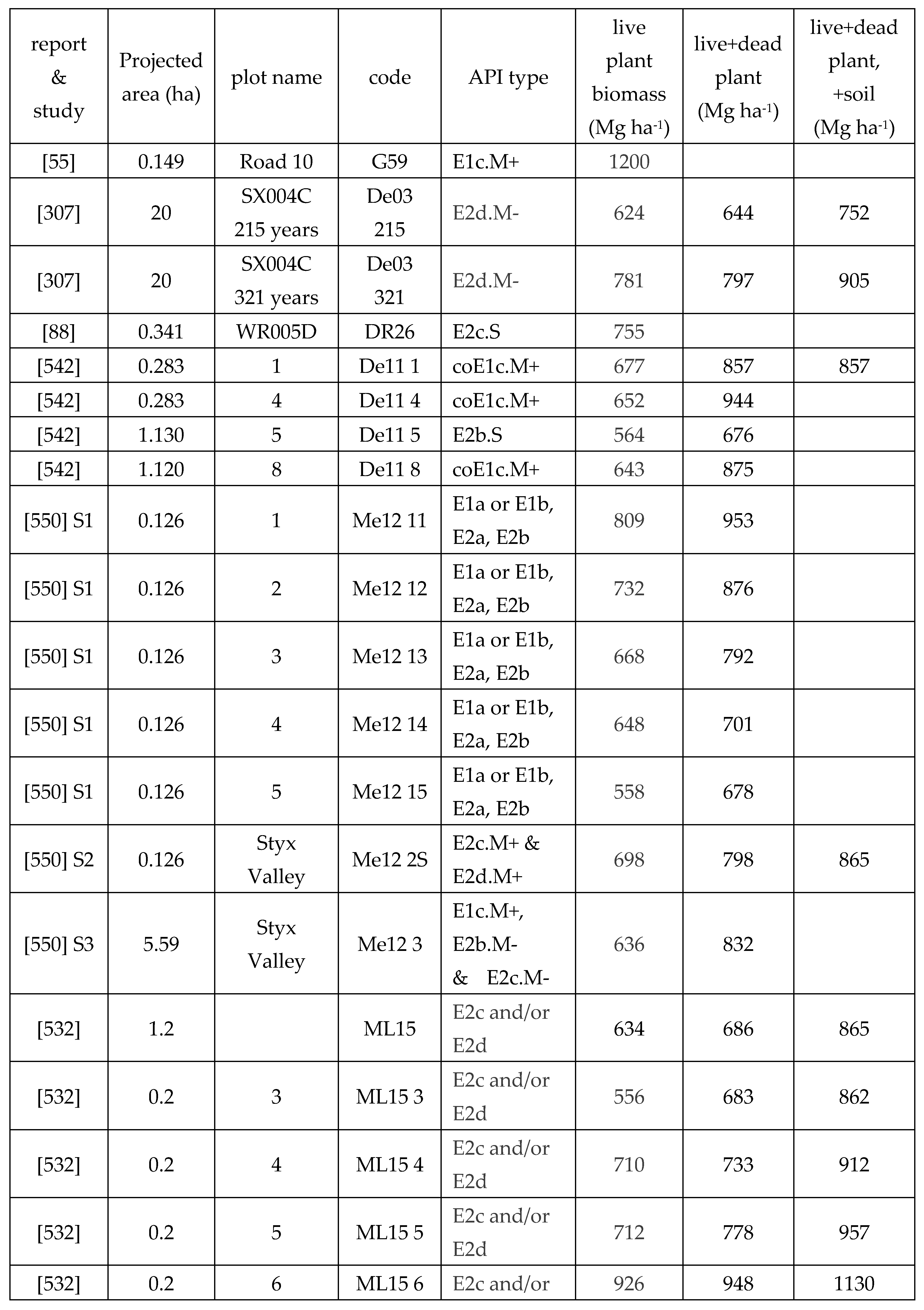 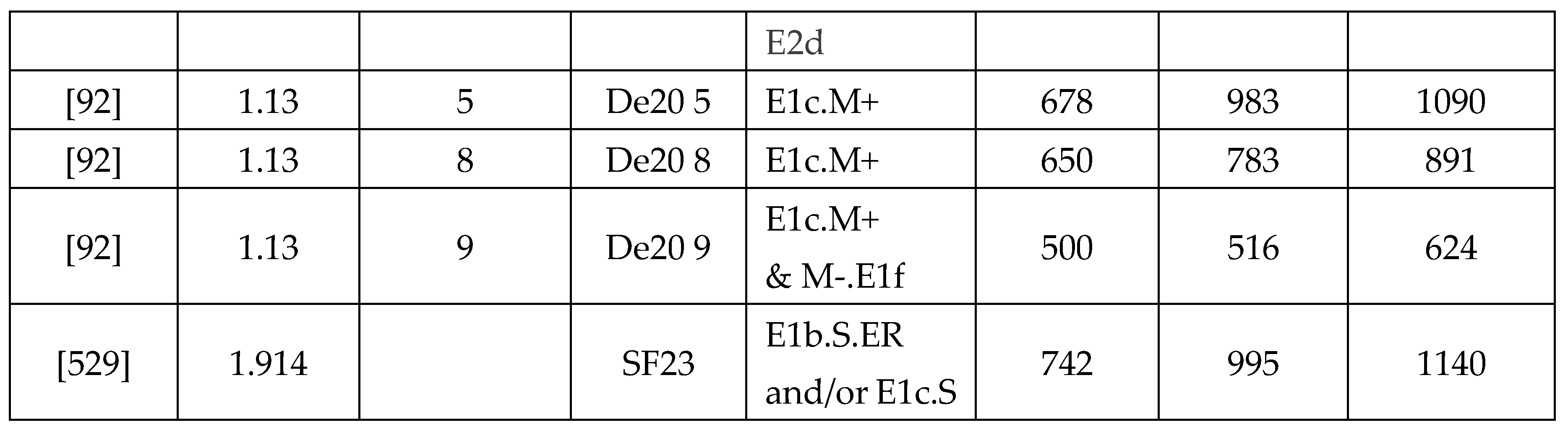
|
In Figure 14 the error margins are allocated only to the benchmark datum, namely the tally in Sanger and Ferrari [529]. The error margin for the biomass pool (alive and dead) was set at ±25%. If the same error had been set for the total carbon at their site then the contenders would only have to reach [100% minus 25% which is] 75% of the total, to be indistinguishable from it. If the benchmark and all the contenders have the same error margins as each other, then what percentage of the benchmark do the contenders have to reach to be indistinguishable from that benchmark? The answer, which is the error margins on the benchmark and on the test reports, is not 12.5% (25 divided by 2). It is given by the following equation:
where em_perc is the error margin on both the benchmark and the test report (the contender) as a percentage (equal on both) and test_perc is what percentage of the benchmark datum, the test report datum has to reach to be indistinguishable from the benchmark. If the report datum plus the em_perc error margin surpasses the benchmark datum minus the em_perc error margin, then the benchmark and test are indistinguishable. Also, if one subtracts em_perc from the benchmark datum and adds it to the test report datum, and if the two results are equal then the two datums are indistinguishable.
From Equation 12, the value equivalent to ±25% error on the benchmark Sanger and Ferrari [529] but none on the test reports, is 2500/175= ±14.28571% error margin on the benchmark and on the test reports. All the reports mentioned in this section were tested, by assigning that error margin to both them and to the benchmark, and the result was the same as in Table 10 and Figure 14. As people are used to the base 10 system and multiples of it, for the sake of making visualisation easier, the ±14.28571% can be approximated to ±15%. It then should become obvious to people who routinely work in forest carbon accounting, that this error margin (15% on all reports, or ±25% on only the benchmark) is conservative. For example, consider the errors, starting with running a tape measure through a forest on a hillside, placing a tape at 1.3 m aboveground around the buttress of mature trees, reading the tape, and the errors in allometric equations (such as can be inferred from Figure 9 and Figure 10) and errors in estimating the degree of senescence, in trees that are afflicted.
If one knows the error margin on both the test report and benchmark and wants to know what fraction of the benchmark a test report has to reach to be comparable with it, then that is given by:
where em_perc and test_perc are as in Eq. 12. For example, if the error margin on both reports is 20% then the test report datum only has to be 80/1.2 = 66.666 (reoccurring) % of the benchmark datum to be indistinguishable from it. The two latter equations incidentally represent an arc of a circle of radius √(1502+1502) and the various possibilities are best shown in Figure 15.
Figure 15.
Relationship between the fraction of the benchmark report datum that a test report has to reach (%), and the error margins on both reports (%) for the two reports, for them to be indistinguishable. This simplifies comparisons of various reports if one can assume equal error margins for them. The curve is given mathematically in Equations 12 and 13.
Figure 15.
Relationship between the fraction of the benchmark report datum that a test report has to reach (%), and the error margins on both reports (%) for the two reports, for them to be indistinguishable. This simplifies comparisons of various reports if one can assume equal error margins for them. The curve is given mathematically in Equations 12 and 13.
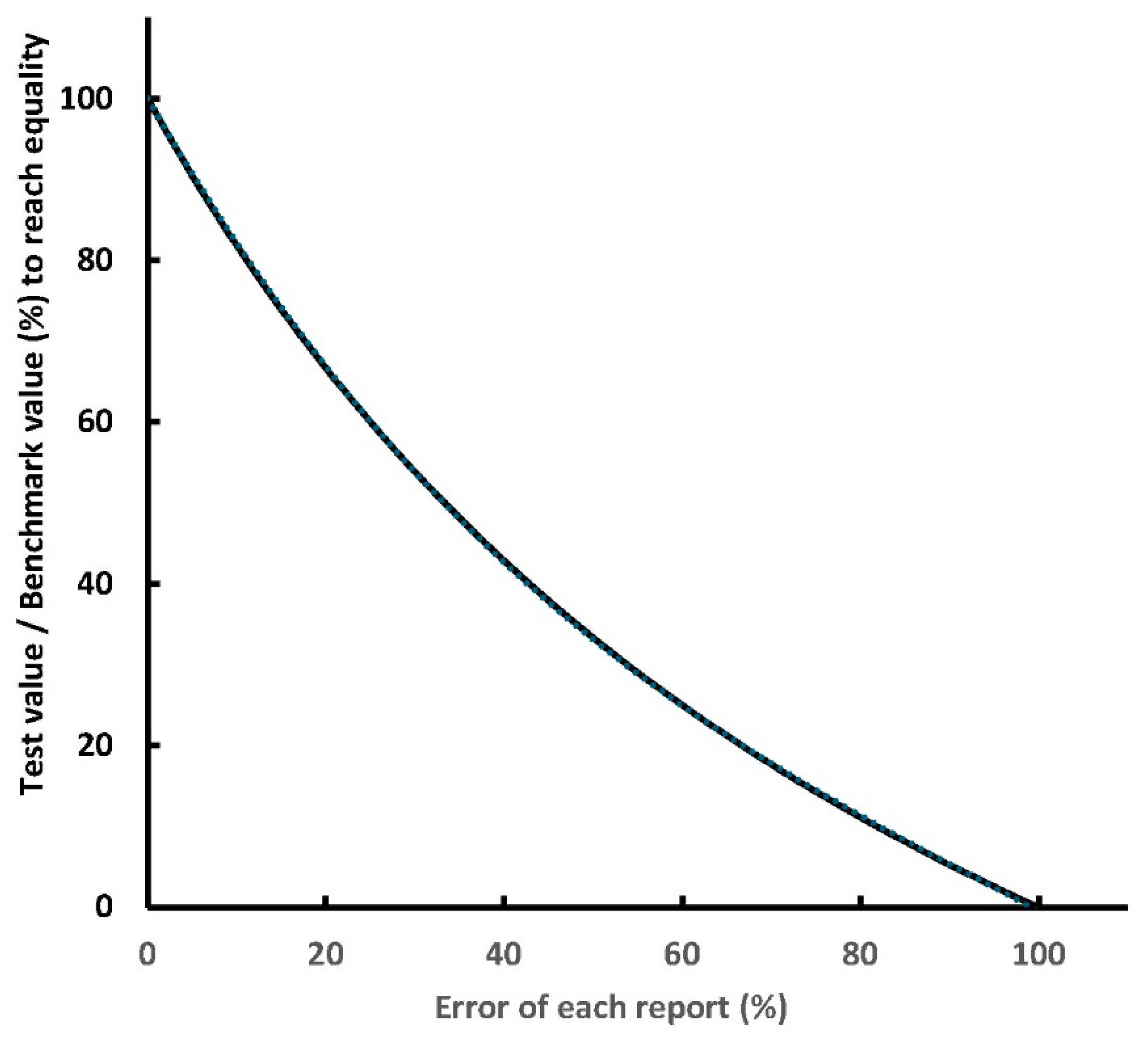
The error margins for these data types, as mentioned in section 2, are partly genuine error margins, in the physics sense, and partly indicative of natural variation in biology. Most often in biology the former type are not shown, only the latter, which accrues as a range of values due to un-measured influences. Other places that genuine measurement errors are not mentioned are, for example, in financial matters, such as a domestic electricity bill, because then one could apply an equivalent margin when paying it. In biology the natural variation is usually assumed to be much larger than the measurement error and it is the only one cited, usually in the form of a standard deviation or standard error, as in the soil carbon value in Sanger and Ferrari [529]. That method assumes that sufficient samples have been acquired to include all relevant effects, and that similar effects operate elsewhere. However, when making comparisons, such as of carbon stocks, then stating an indicative error margin is much more important, the measurement error should be included too. Therefore, the overall ~±15% error margin that is used here (or the ±25% on only the benchmark) is conservative.
The SOC in different studies was measured to different depths. To provide a comparison it was therefore necessary to trim the depth of soil being considered to the minimum, which was -0.3 m in Sanger and Ferrari [529] and possibly also in Moroni and Lewis [532]. Although Sanger and Ferrari [529] claimed to be the most comprehensive carbon study of Tasmanian forests they did not measure as deeply as did some others, didn’t include SOC in moist stones and only had four sample points, but they did understand that latter shortcoming. Their soil carbon section was better than some of the earlier reports in that it used elemental analysis for carbon rather than the Walkley-Black method and it did include carbon in large charcoal particles. In future work, if for different locations it becomes routine to examine SOC further down or laterally, and significantly different amounts of SOC are there or have been translocated by water, then the competition would have to be rerun and it may provide better discrimination.
Regarding the competition declared by Sanger and Ferrari [529] of the highest carbon stocks in Tasmania— Figure 14 shows that they are no longer the clear winners, but approximately equal with several other sites. Additionally, if SOC and CWD had been measured for the site in Gilbert [55], then it may have the most carbon. The large error margins and natural variability in the current state of carbon accounting science for mature forests mean that many different sites are indistinguishable (Figure 14), a situation that was also noted in forest carbon comparisons nearly 20 years ago [88], though detail has improved since then.
One must also consider the size of the area sampled and its randomness of selection. The 20 ha for the site in Dean, et al. [307] is the largest in Table 9, but that was mostly a simulation study, so it can be disregarded. Several carbon studies didn’t reach the contenders table, perhaps because of their larger size. That leaves, from Table 9, the area of 5.59 ha for the Styx Valley part of Study 3 in May, et al. [550] as the only study site larger than the 1.914 ha of Sanger and Ferrari [529]. But the allometric equations used in the former study may not be comparable, e.g., the high-yielding temperate rainforest equation of Keith, et al. [124] may have been used. Notably, some of the same raw data were used in both May, et al. [550] and Dean, et al. [92], but the tally was lower in the latter study, which also included a larger area.
The 0.149 ha site in the Florentine Valley of Gilbert [55], measured before almost the entire valley was logged, has arguably the highest carbon stock to date for a Tasmania forest, but a relatively small area. However, it was possibly selected because, rather than being an extreme case, it was representative of high biomass forests that existed prior to logging. Logging records or the Styx and Florentine Valleys show that typical forest stands of specific height cohort and with a high wood volume were typically each from 1 to 15 ha in size [541]. The average size of the stands of the same forest type, E1c.M+ as measured in Gilbert [55], from the aerial phototype mapping of Forestry Tasmania, was ~21 ha (standard deviation 29 ha). These figures give a likely indication for the extent of the stand in Gilbert [55]. Nevertheless, neither that study nor Sanger and Ferrari [529] had selected their study plots totally at random within a forest type. Random site selection is partly interchangeable with studying a larger area, and so the Study 3 in May, et al. [550] with its larger area comes into consideration again, but it still raises scepticism for the reasons mentioned earlier. Overall then, the benchmark and contenders in Table 9 and Figure 14 remain indiscernible, except possibly for the larger area in Sanger and Ferrari [529], i.e., unless the size of their plot was also non-random, not just its location. If the size was not random, then for a more level comparison the area limits of forest stands sampled in the other studies in Table 9 would need to be determined. On balance, questions that consequently arise are: how much of the ‘Grove of Giants’ is represented by the ~1.9% of it sampled; is the majority of it much lower C, equivalent or higher? and similarly for the surrounds of other sites in Table 9.
A pertinent question from a carbon conservation perspective is: where else in Tasmania are there high carbon forests? Table 10 indicates that it’s likely to be in forests with either E1 or E2 phototype and with at least a 20% crown cover of eucalypts. For example, there is an area of forest similar in size and appearance, as seen from GoogleEarth ©, similar to the ‘Grove of Giants’, ~3.2 km to the north. Further afield, using an API-type map of 2012 from the Tasmanian State forestry agency, there was ~42,400 ha of either mature E1 or E2 with eucalypt crown coverage of at least 50%, left standing within Tasmania’s original southern central pulpwood concession boundaries. After the logging and the WHA extension of the late 1980s there was ~32,700 ha left in State forest and after further logging and the 2013 WHA extension there was ~13,300 ha left in State forest to be logged. From GIS analysis of the 2012 data, logging appears to have been concentrated in the Florentine, Tyenna and Styx Valleys and the largest contiguous stands of primary, mature E1 and E2 forest that now remain, are in at the northern and southern extremities of the original pulpwood concession, such as near the ‘Grove of Giants’, a little to north in the Russell River area, further south in the Kermandie catchment and north of the main Florentine catchment near Wayatinah. As the conservation activities for the ‘Grove of Giants’ stand show, conservation effort appears to have switched from the centre of the Florentine and Styx pulpwood concession since some of that central part of it formed part of the WHA extension of 2013. Its focus has recently intensified on the large individual trees, perhaps because both the general public and the State forest agency have revealed a sensitivity on that topic, and because the large trees are probably emblems of contrast with current human civilisation. They are current levers to gain conservation areas— but smaller and smaller examples become icons as the larger ones fall to various effects of the inexorable human consumption of nature. How then to most expediently identify the prominent stands? Apart from simply walking through Tasmania’s forests, LIDAR is currently a common remote sensing method for determining tree height and this could be combined with stand density (the forestry term for the number of trees per hectare) to find likely stands of high carbon stock, but it would need ground-truthing to determine the degree of hollow formation in the trees. Height alone may not be sufficient though for high carbon mass and biodiversity. Stand density will play a part in carbon accumulation but may detract from biodiversity. For example the highest concentration of the tallest trees was in the Andromeda block in the Styx Valley Kostoglou [87], but their diameters were below average, which indicated a high stand density even when mature— they may have germinated from an atypically intense burn which limited early regeneration of the rainforest understorey and later growth of large hemi-epiphytes. When viewing sites with potentially high carbon mass, there will be a trade-off between stand density (including old and recent fire effects), senescence (which may be accompanied by regeneration to for mixed-aged stands and more carbon, as in Keith, et al. [309]) and basal diameter (which can allow dominance of the carbon tally from a few individuals), and it’s likely that site contention can only be solved through thorough measurement.
6.10. The Proclamation of Giant Trees and HIGH carbon
There may be a few reasons for trying to find a specific forest site with a high carbon mass or ‘high carbon’, such as: (a) to describe the nature in a particular region, (b) to help calibrate and parameterise a carbon forecasting model for a particular forest type as a function of age, (c) to add to the database of the global carbon distribution, (d) to alert and motivate members of the public who are interested in conserving such sites, (e) to describe the limits on how much carbon stock can be sustained overtime and for how long, and (f) it is likely to be a target of corporate forestry as merchantable biomass is more concentrated and it is therefore of public interest to calculate the anthropogenic carbon emissions.
From comments in Sanger and Ferrari [529] and by the TallTreeProjects in public media [570,571] it can be inferred that they align most strongly with option (d). An example is the frequent use of a strong adjective ‘ultra-large’:
‘Ultra-large trees (>2.5 m DBH) were measured throughout the entire plot and smaller trees, understory and coarse woody debris were measured within four transects within the plot following methodology adapted from Keith et al. (2014; Figure 1).’ [529]
Also, in their Table B2 they refer to smaller trees as: ‘Large trees (1–2.5 m DBH)’. The maximum dimensions of some typical eucalypts in such forests were given in section 2. The maximum tree dimensions in Sanger and Ferrari [529] are a DBH of 5.12 m, a height of 72 m, and a volume of 254 m3—not ‘ultra-large’, but near the median in diameter and average height, if E. regnans. In Sanger and Ferrari [529] any tree with a DBH >2.6 m is called ‘ultra-large’. That prompts the question as to what genuinely large trees could be termed. Trees in tall open forests in Tasmania were first publicly called giants when their forests were allocated to newspaper production: the E. regnans—dominated forests of the Styx/Tyenna/Florentine pulpwood concession: ‘Giant trees will build new industry. Newsprint from Tasmanian forests’ [100]. But that was in a newspaper (not a scientific paper), where titles are designed to attract readership, for financial competitiveness. The terminology ‘ultra’ may have been for public relations purposes, to create a vision of something unprecedented and extraordinary, to prompt support for conservation. The commercial attention to the high organic mass of the site has consequently moved from developing products from it [through logging and milling] and inadvertently breaking down its molecules into smaller ones such as atmospheric greenhouse gasses, to commercial tourism with the molecular structure in its current configuration.
Use of the internet in forest-use controversies is not new however, but the ease of publication of videos and photographs is more recent. In the early 1990s a public ‘listserver’ could be used, which was the precursor of the modern-day Facebook discussion group. Listservers could not be accessed on mobile phones at the time, only via computer, and without digital photographs and video data on that publication medium, there was much less public viewing and consequently less public interest.
Some other tools used in Sanger and Ferrari [529] are also revealing. The name ‘Grove of Giants’ may be an adaptation of the ‘Grove of Titans’, which is a stand of Coastal Redwoods (Sequoia sempervirens) in northern California with a high mass of carbon that has been the subject of extensive scientific study and is part of Jedediah Smith Redwoods State Park. It was named in 1998 and initially studied for canopy ecology then later for carbon content and the number of people visiting it has increased significantly via internet social media [580,583,584]. The redwoods form more of a true grove however, by the definition of the word, as the forest floor is much barer than in the ‘Grove of Giants’. There are other similarities between the tall trees of Tasmania and the redwoods of the USA: they’ve both had tree carbon studied by tree climbing and they’ve both been the focus of corporate forestry for timber extraction [100,572,585 p106]. The competitive declaration for a high carbon stock is also not new but appears to have been initiated by Keith, et al. [309] for E. regnans—dominated forests in Victoria (Australia), with the title ‘Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests’, which can be compared with the title “The Grove of Giants: Tasmanias’ most carbon-dense forest” from Sanger and Ferrari [529]. That global claim for Victorian E. regnans, similarly didn’t include error margins in their comparison, and the carbon stock was possibly surpassed by S. sempervirens forests in several locations, depending on error margins [580]. Error margins have been included in some carbon comparisons [e.g., 586 Figure 4, 587 Table 3].
The area surrounding the study plot of Sanger and Ferrari [529] has larger trees, e.g., a E. globulus of diameter 5.35 m and height ~80 m [588]. Advancement of conservation however didn’t require measurement of carbon in that larger area— the strong public media presence induced the State forest agency to reserve the surrounding area from logging [589]. But there is likely to be [carbon] leakage— the State forestry agency is likely to log primary forest elsewhere instead, with less media attention, to get that same timber volume, if it still has the same annual quota to fulfil. A media report says that this did indeed occur [589].
7. Conclusions
Several possible flaws in science were examined above and corrections provided, including: mis-citing scientific literature, inadequate literature review, not recognising relevant spatial dimensions and time, and inappropriate or missing benchmarks. The peer review process for scientific publications is only part of quality control. Added to that is a background of science developed for specific purposes, but with purposes that are in the process of change as human society expands and depletes parts of the biosphere. These three items (flaws, history and changing purpose) combine to create a struggle for science. Although it is always disheartening to realise a flaw in one’s published work, in the longer term it is to the benefit of the reputation of science to note flaws in scientific studies and to provide corrections. It must be done for both industry-promoting science and for conservation-promoting science, as in this review. This approach can help to assure the public and other scientists that extra quality control is being performed, above the peer review process. This in turn should allow more confidence by the public in findings of science, such as when it reveals trends not physically observed within a typical human lifetime, for example the many different contributions to anthropogenic climate change and its acceleration. This in turn should permit more climate change mitigation activities.
There has so far been insufficient awareness of the value of nature to prevent its continuing decline [590]. For appreciation of humanity’s impact on forests so far, and the ongoing legacy of anthropogenic climate change that current and future generations will attend to [590], it is necessary for the public to recognise the dimensions and composition of forests that we have changed, and what vestiges of them remain. For appropriate recognition of that legacy, overplaying of remaining tree size or overshadowing what has been removed before, must be avoided and corrected, as indeed must underestimation of carbon stocks by not counting parts that are difficult to measure. Better accounting can help appropriate recognition, which could in turn help avoid premature forest conversion to greenhouse gasses. All the dimensions, current and past, need to be viewed upon one time axis, otherwise each successive generation of people may believe that they are operating without an undercurrent (they may assume the 0 Mg ha-1 benchmark) and that the vestigial primary forests can provide them with resources similar what their predecessors used. This belief can be promoted in part by the term sustainability, which as shown in this paper, has not been achieved for industrial use of Australian forests. Instead, the legacy which constitutes the background must be visible and acknowledged, to show the situation in a comprehensive light, and this will in turn show that many extractions from nature, are cumulative rather than unique.
The uncertainties and error margins examined above mean that numerous improvements are needed in scientific data to help improve recognition and interpretation of nature, such as for climate change forecasts and climate change mitigation. For example, more data on the physical and chemical routes and precision for carbon fluxes associated with decomposing trees and wood products (including, for example, recycled paper), and the translocation of SOC vertically and horizontally via water flow. The current work showed that more effort is required to increase knowledge about soil carbon stocks and change, which concurs with Makarieva, et al. [591]. More applied research could also be invested in recycling of wood products and determining their LCA, including building materials and paper, to reduce demand for forest conversion [592]. Some change to science is also needed, to ensure that an extra layer of quality control is enacted for some topics, such as the forest carbon cycle. This could be in part, through increased deposition of data at the publication stage, as is done in some other fields. Possibly also, society in general can add to the available data by recording basic data for all medium to large trees. This is done to a degree already in some places, such as for urban street trees. Forest agencies can partake by, for example, recording data on all trees felled during logging, merchantable or not.
Some comment on climate change mitigation and forestry is appropriate, in the context of this paper. If less area of primary forest is to be converted to secondary forest logging cycles, and the corresponding carbon emission is to be reduced, then in the short-term either the timber volume quota must be addressed, or swapped to plantation-grown timber [135 p213-214], and supplemented with recycled timber. A different solution appears from a more comprehensive viewpoint: the continually increasing global human population within a limited area that is currently shared with other species [593], suggests that there is no reason to assume that other plants and animals can provide the raw materials necessary for humans into the future. Therefore, a longer-term source of materials such as timber, from other than forests or plantations must be sought, such as synthetic timber. This is underway and although partly adopted, is currently more at the research than the production stage. It is often based on recycled plastics rather than on copying the molecular structure of wood, although the meso-scale (> nanometre) has been copied, with promising results [e.g., 594,595,596]. (With plastic-like products one must of course have a 100% non-discard policy, due to their effects on other species.) A related product, with a similar precipitating cause, is synthetic food such as cultured protein, for human consumption, but that is also still under development [597]. This swap of resource inputs, may span both ‘degrowth’ and ‘green growth’ concepts [598], as it maintains productivity and supply. More applied research could also be invested in recycling of wood products and determining their LCA, including building materials and paper, to reduce demand for forest conversion [592]. Makarieva, et al. [591] recommend not using ‘intact forests’ for timber production but instead for climate control, as they still have that innate capacity, which is provided through balances between ecosystem components. They recommend that timber be sourced from areas where the genetics of the original ecosystem are unavailable to recreate the ecosystem within reasonable timeframes, e.g., plantations and other cropland, as such locations have already lost their climate control ability. These alternative routes will be part of the mix to accompany improvements in science.
Funding
This research received no external funding.
Data Availability Statement
Any raw data supporting the conclusions of this article will be made available by the author on request, except GIS data which was from a commercial source.
Acknowledgments
The author would like to thank: Richard Doyle for help interpreting the older soil surveys; Andrew Norton for discussions on bioenergy; Jamie Kirkpatrick for comments on an earlier version of the manuscript and on approaches to science; Forestry Tasmania for access to forests, documents and data; Fabio Ximenes and Stephen Sillett for discussions on their work; and the University of Tasmania for access to software and their library.
Conflicts of Interest
The author declares no conflicts of interest.
References
- UNFCCC. Nationally determined contributions under the Paris Agreement. In Proceedings of the Conference of the Parties serving as the meeting of the Parties to the Paris Agreement. Third session, Glasgow, Scotland, 2021; p. 42.
- Stoddard, I.; Anderson, K.; Capstick, S.; Carton, W.; Depledge, J.; Facer, K.; Gough, C.; Hache, F.; Hoolohan, C.; Hultman, M.; et al. Three decades of climate mitigation: Why haven’t we bent the global emissions curve? Annual Review of Environment and Resources 2021, 46, 653–689. [Google Scholar] [CrossRef]
- Jamieson, D. Reason in a Dark Time. Why the Struggle Against Climate Change Failed.; Oxford University Press: New York, USA, 2014; p. 288. [Google Scholar]
- Kennelly, C.; Berners-Lee, M.; Hewitt, C.N. Hybrid life-cycle assessment for robust, best-practice carbon accounting. Journal of Cleaner Production 2019, 208, 35–43. [Google Scholar] [CrossRef]
- Barredo, J.I.; Brailescu, C.; Teller, A.; Sabatini, F.M.; Mauri, A.; Janouskova, K. Mapping and assessment of primary and old-growth forests in Europe; Publications Office of the European Union: Luxembourg, 2021; Volume EUR 30661 EN, p. 43. [Google Scholar]
- Pernica, M. Forestry students and workers and their attitudes towards the environment. Journal of Forest Science 2004, 50, 47–54. [Google Scholar] [CrossRef]
- Kirkpatrick, J.B. The politics of the media and ecological ethics. In Ecology for Everyone. Communicating ecology to scientists, the public and the politicians, Wills, R., Hobbs, R., Eds.; Surrey Beatty & Sons: Sydney, 1998; pp. 36–41. [Google Scholar]
- Higgins, P.A.T.; Chan, K.M.A.; Porder, S. Bridge over a philosophical divide. Evidence & Policy 2006, 2, 249–255. [Google Scholar] [CrossRef]
- Donald, R.; Graves, L. Making them pay: Comparing how environmental facts matter in two accountability contexts. New Media & Society 2024, 14614448241279250. [Google Scholar] [CrossRef]
- Kozik, R.; Pawlicka, A.; Pawlicki, M.; Choraś, M.; Mazurczyk, W.; Cabaj, K. A meta-analysis of state-of-the-art automated fake news detection methods. IEEE Transactions on Computational Social Systems 2024, 11, 5219–5229. [Google Scholar] [CrossRef]
- Cook, J.; Oreskes, N.; Doran, P.T.; Anderegg, W.R.L.; Verheggen, B.; Maibach, E.W.; Carlton, J.S.; Lewandowsky, S.; Skuce, A.G.; Green, S.A.; et al. Consensus on consensus: a synthesis of consensus estimates on human-caused global warming. Environmental Research Letters 2016, 11, 1–7. [Google Scholar] [CrossRef]
- Dunlap, R.E. Climate change skepticism and denial: an introduction. American Behvioural Scientist 2013, 57, 691–698. [Google Scholar] [CrossRef]
- Oreskes, N.; Conway, E.M. Merchants of Doubt: How a Handful of Scientists Obscured the Truth on Issues from Tobacco Smoke to Global Warming; Bloomsbury Publishing: London, 2010; p. 274. [Google Scholar]
- Anderegg, W.R.L.; Trugman, A.T.; Badgley, G.; Anderson, C.M.; Bartuska, A.; Ciais, P.; Cullenward, D.; Field, C.B.; Freeman, J.; Goetz, S.J.; et al. Climate-driven risks to the climate mitigation potential of forests. Science 2020, 368, 1–9. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Dufresne, J.-L.; Cox, P.M.; Rayner, P. How positive is the feedback between climate change and the carbon cycle? Tellus B 2003, 55, 692–700. [Google Scholar] [CrossRef]
- Kovalyuk, B.P.; Skorenkyy, Y.L.; Nikiforov, Y.M. Physics Laboratory; Ternopil Ivan Puluj National Technical University: Ternopil, Ukraine, 2016; p. 130. [Google Scholar]
- Bruce, D.; Schumacher, F.X. Forest Mensuration; McGraw Hill: New York, 1942. [Google Scholar]
- Halsey, L.G. The reign of the p-value is over: what alternative analyses could we employ to fill the power vacuum? Biology Letters 2019, 15, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Leo, G.D.; Sardanelli, F. Statistical significance: p value, 0.05 threshold, and applications to radiomics—reasons for a conservative approach. European Radiology Experimental 2020, 4, 1–8. [Google Scholar] [CrossRef]
- Gibson, C.C.; Ostrom, E.; Ahn, T.K. The concept of scale and the human dimensions of global change: a survey. Ecological Economics 2000, 32, 217–239. [Google Scholar] [CrossRef]
- Cash, D.W.; Adger, W.N.; Berkes, F.; Garden, P.; Lebel, L.; Olsson5, P.; Pritchard, L.; Young, O. Scale and cross-scale dynamics: governance and information in a multilevel world. Ecology and Society 2006, 11, 1–12. [Google Scholar] [CrossRef]
- Newell, J.P.; Vos, R.O. Accounting for forest carbon pool dynamics in product carbon footprints: Challenges and opportunities. Environmental Impact Assessment Review 2012, 37, 23–36. [Google Scholar] [CrossRef]
- Neff, M.W.; Corley, E.A. 35 years and 160,000 articles: a bibliometric exploration of the evolution of ecology. Scientometrics 2009, 80, 657–682. [Google Scholar] [CrossRef]
- Seppelt, R.; Dormann, C.F.; Eppink, F.V.; Lautenbach, S.; Schmidt, S. A quantitative review of ecosystem service studies: approaches, shortcomings and the road ahead. Journal of Applied Ecology 2011, 48, 630–636. [Google Scholar] [CrossRef]
- Lautenbach, S.; Mupepele, A.-C.; Dormann, C.F.; Lee, H.; Schmidt, S.; Scholte, S.S.K.; Seppelt, R.; Teeffelen, A.J.A.v.; Verhagen, W.; Volk, M. Blind spots in ecosystem services research and challenges for implementation. Regional Environmental Change 2019, 19, 2151–2172. [Google Scholar] [CrossRef]
- NRMjobs; SST. Advert ID: 20015822. Sustainable Timber Tasmania. Carbon & Ecosystem Services Analyst.; NRMjobs: Aldgate, South Australia, 2023. [Google Scholar]
- Rohlf, D.J. Scientists, agendas, and litigation: a response to Peery et al. Frontiers in Ecology and the Environment 2019, 17, 555–556. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Jones, G.; Redpath, S.M.; Franklin, A.B.; Simberloff, D.; Turner, M.G.; Radeloff, V.C.; White, G.C.; Peery, M.Z. Reinforcing the concept of agenda-driven science: a response to Rohlf. Frontiers in Ecology and the Environment 2019, 17, 556–557. [Google Scholar] [CrossRef]
- Noon, B.R.; Murphy, D.D. CASE STUDY 3 Management of the Spotted Owl: The Interaction of Science, Policy, Politics, and Litigation. In Principles of Conservation Biology, Carroll, G.K.M.C.R., Ed.; Sinauer Associates, Inc.: Sunderland, Massachusetts, 1994; pp. 380–388. [Google Scholar]
- Wilhere, G.F.; Maguire, L.A.; Scott, M.; Rachlow, J.L.; Goble, D.D.; Svancara, L.K. Conflation of values and science: response to Noss et al. Conservation Biology 2012, 26, 943–944. [Google Scholar] [CrossRef] [PubMed]
- Noss, R.F.; Dobson, A.P.; Baldwin, R.; Beier, P.; Davis, C.R.; Dellasala, D.A.; Francis, J.; Locke, H.; Nowak, K.; Lopez, R.; et al. Bolder thinking for conservation. Conservation Biology 2012, 26, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Budaev, S.; Jørgensen, C.; Mangel, M.; Eliassen, S.; Giske, J. Decision-making from the animal perspective: Bridging ecology and subjective cognition. Frontiers in Ecology and Evolution 2019, 7, 1–14. [Google Scholar] [CrossRef]
- Waisbord, S. Intertwining science journalism with (post)development. Journalism Studies 2024, 25, 575–582. [Google Scholar] [CrossRef]
- McKay, R.T.; Dennett, D.C. The evolution of misbelief. Behavioural and Brain Sciences 2009, 32, 493–561. [Google Scholar] [CrossRef]
- Bacon, F. Novum Organum Scientarium; Wirceburgi: Würzburg, Germany, 1779 edition, 1620. [Google Scholar]
- Bolles, E.B. Galileo’s Commandment. An Anthology of Great Science Writing; Little Brown and Company: London, 1999; p. 485. [Google Scholar]
- Fortunato, S.; Bergstrom, C.T.; Börner, K.; Evans, J.A.; Helbing, D.; Milojević, S.; Petersen, A.M.; Radicchi, F.; Sinatra, R.; Uzzi, B.; et al. Science of science. Science 2018, 359, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Beck, C. Quality control in science. Available online: https://www.mpg.de/12138624/quality-control-in-science (accessed on 19 September 2024).
- National Health and Medical Research Council, A.R.C. , Universities Australia,. Australian Code for the Responsible Conduct of Research 2018; Commonwealth of Australia: Canberra, Australia, 2018; p. 7. [Google Scholar]
- Elsevier. How to conduct a review. Available online: https://www.elsevier.com/en-au/reviewer/how-to-review (accessed on.
- National Academies of Sciences Engineering and Medicine. Reproducibility and Replicability in Science; The National Academies Press: Washington, D.C, 2019; p. 257. [Google Scholar]
- Kusumoto, F.M.; Bittl, J.A.; Creager, M.A.; Dauerman, H.L.; Lala, A.; McDermott, M.M.; Turco, J.V.; Taqueti, V.R.; Fuster, V. Challenges and controversies in peer review. Journal of The American College of Cardiology 2023, 82, 2054–2062. [Google Scholar] [CrossRef]
- Eckert, M. Safeguarding peer review to ensure quality at scale; Frontiers Media SA, Switzerland: Lausanne, Switzerland, 2024. [Google Scholar]
- Webster, H. History of the Modern World; D. C. Heath & Co.: Boston, USA, 1930; p. 881. [Google Scholar]
- Fraser, G. The New Physics for the Twenty-First Century; Cambridge University Press: Cambridge, England, 2006; p. 548. [Google Scholar]
- Bacon, F. Essays Civil and Moral; Cassell: London, 1905; p. 192. [Google Scholar]
- Dean, C.; Wardell-Johnson, G.W.; Kirkpatrick, J.B. Are there any circumstances in which logging primary wet-eucalypt forest will not add to the global carbon burden? Agricultural and Forest Meteorology 2012, 161, 156–169. [Google Scholar] [CrossRef]
- Lewin, D.W. The Eucalypti Hardwwod Timbers of Tasmania, and the Tasmanian Ornamental and Softwood Timbers. A Descriptive Treatise on their Commerical Uses, with Reports on their Durability.; Gray Brothers: Hobart, Tasmania, 1906; p. 139. [Google Scholar]
- Wood, L.J.; Kirkpatrick, J.B. The allocation of rights to public forests in Tasmania: a geographical critique. Applied Geography 1984, 4, 215–234. [Google Scholar] [CrossRef]
- Gray, H.R. State forests of the Empire: Tasmania. Empire Forestry Journal 1939, 18, 202–211. [Google Scholar]
- Helms, A.D. A giant eucalypt (Eucalyptus regnans) Nichols Spur, Junee, Derwent Valley, Tasmania. Australian Forestry 1945, 9, 24–28. [Google Scholar]
- ANM. Working Plan For Concession Area Of Australian Newsprint Mills Limited In The Derwent Valley; Australian Newsprint Mills Limited, Boyer: Boyer, Tasmania, 1979; p. 45. [Google Scholar]
- Specht, R.L. Vegetation. In The Australian Environment’, 4th ed.; Leeper, G.W., Ed.; CSIRO and Melbourne University Press: Melbourne, 1970. [Google Scholar]
- Kirkpatrick, J.B.; Peacock, R.J.; Cullen, P.J.; Neyland, M.G. The Wet Eucalypt Forests of Tasmania; Tasmanian Conservation Trust Hobart: Hobart, 1988. [Google Scholar]
- Gilbert, J.M. Forest succession in the Florentine Valley, Tasmania. papers and Proceedings of the Royal Society of Tasmania 1959, 93, 129–151. [Google Scholar] [CrossRef]
- Kirkpatrick, J.B.; DellaSala, D.A. Temperate Rainforests of Australasia. In Temperate and Boreal Rainforests of the World: Ecology and Conservation, DellaSala, D.A., Ed.; Island Press: Washington DC, 2011; pp. 195–212. [Google Scholar]
- Fedrigo, M.; Kasel, S.; Bennett, L.T.; Roxburgh, S.H.; Nitschke, C.R. Carbon stocks in temperate forests of south-eastern Australia reflect large tree distribution and edaphic conditions. Forest Ecology and Management 2014, 334, 129–143. [Google Scholar] [CrossRef]
- Petrie, A.H.K.; Jarrett, P.H.; Patton, R.T. The vegetation of the Blacks' Spur region: A study in the ecology of some Australian mountain eucalyptus forests: I. The mature plant communities. Journal of Ecology 1929, 17, 223–248. [Google Scholar] [CrossRef]
- Ash, J. The location and stability of rainforest boundaries in north-eastern Queensland, Australia. Journal of Biogeography 1988, 15, 619–630. [Google Scholar] [CrossRef]
- Zhuang, P.; Gao, X.-M. The concept of the Rainy Zone of West China and its significane to the biodiveristy conservation of China. Biodiversity Science 2002, 10, 339–344. [Google Scholar]
- Barni, P.E.; Manzi, A.O.; Condé, T.M.; Barbosa, R.I.; Fearnside, P.M. Spatial distribution of forest biomass in Brazil’s state of Roraima, northern Amazonia. Forest Ecology and Management 2016, 377, 170–181. [Google Scholar] [CrossRef]
- Asselin, H.; Payette, S. Late Holocene opening of the forest tundra landscape in northern Québec, Canada. Global Ecology and Biogeography 2005, 14, 307–313. [Google Scholar] [CrossRef]
- Marques, E.Q.; Marimon-Junior, B.H.; Marimon, B.S.; Matricardi, E.A.T.; Mews, H.A.; Colli, G.R. Redefining the Cerrado–Amazonia transition: implications for conservation. Biodiversity and Conservation 2020, 29, 1501–1517. [Google Scholar] [CrossRef]
- Clarke, P.J.; Lawes, M.J.; Midgley, J.J.; Lamont, B.B.; Ojeda, F.; Burrows, G.E.; Enright, N.J.; Knox, K.J.E. Resprouting as a key functional trait: how buds, protection and resources drive persistence after fire. New Phytologist 2013, 197, 19–35. [Google Scholar] [CrossRef] [PubMed]
- Casson, P.B. The forests of western Tasmania. Australian Forestry 1952, 16, 71–86. [Google Scholar] [CrossRef]
- Dixon, D. A taxonomic revision of the Australian Ficus species in the section Malvanthera (Ficus subg. Urostigma: Moraceae). Telopea 2003, 10, 125–153. [Google Scholar] [CrossRef]
- Dean, C.; Kirkpatrick, J.B.; Osborn, J.; Doyle, R.B.; Fitzgerald, N.B.; Roxburgh, S.H. Novel 3D-geometry and models of the lower regions of large trees for use in carbon accounting of primary forests. AoB Plants 2018, 10, 1–19. [Google Scholar] [CrossRef]
- Furlaud, J.M.; Prior, L.D.; Williamson, G.J.; Bowman, D.M.J.S. Fire risk and severity decline with stand development in Tasmanian giant Eucalyptus forest. Forest Ecology and Management 2021, 502, 1–17. [Google Scholar] [CrossRef]
- Kirkpatrick, J.B.; Brown, M.J. A numerical analysis of Tasmanian higher plant endemism. Botanical Journal of the Linnean Society 1984, 88, 165–183. [Google Scholar] [CrossRef]
- Frost, E.E.; Levia Jr., D. F. Hydrologic variation of stemflow yield across co-occurringdominant canopy trees of varying mortality. Ecohydrology 2014, 7, 760–770. [Google Scholar] [CrossRef]
- Levia Jr., D. F.; Frost, E.F. A review and evaluation of stemflow literature in the hydrologic and biogeochemical cycles of forested and agricultural ecosystems. Journal of Hydrology 2003, 274, 1–29. [Google Scholar] [CrossRef]
- Levia Jr., D. F.; Van Stan, I.I.J.T.; Inamdar, S.P.; Jarvis, M.T.; Mitchell, M.J.; Mage, S.M.; Scheick, C.E.; McHale, P.J. Stemflow and dissolved organic carbon cycling: temporal variability in concentration, flux, and UV-Vis spectral metrics in a temperate broadleaved deciduous forest in the eastern United States. Canadian Journal of Forest Research 2012, 42, 207–216. [Google Scholar] [CrossRef]
- Van Stan II, J.T.; Siegert, C.M.; Levia Jr., D. F.; Scheick, C.E. Effects of wind-driven rainfall on stemflow generation between codominant tree species with differing crown characteristics. Agricultural and Forest Meteorology 2011, 151, 1277–1286. [Google Scholar] [CrossRef]
- Oyarzún, C.E.; Godoy, R.; Staelens, J.; Donoso, P.J.; Verhoest, N.E.C. Seasonal and annual throughfall and stemflow in Andean temperate rainforests. Hydrological Processes 2011, 25, 623–633. [Google Scholar] [CrossRef]
- Levia, D.F.; Germer, S. A review of stemflow generation dynamics and stemflow-environment interactions in forests and shrublands. Reviews of Geophysics 2015, 53, 673–714. [Google Scholar] [CrossRef]
- Terra Marcela d.Castro Nunes, S.; de Mello, C.R.; de Mello, J.M.; de Oliveira, Vinícius A.; Nunes, Matheus H.; Silva, Vinícius O.; Rodrigues, André F.; Alves, Geovane J. Stemflow in a neotropical forest remnant: vegetative determinants, spatial distribution and correlation with soil moisture. Trees 2018, 32, 1–13. [Google Scholar] [CrossRef]
- Sillett, S.C.; Van Pelt, R.; Kramer, R.D.; Carroll, A.L.; Koch, G.W. Biomass and growth potential of Eucalyptus regnans up to 100 m tall. Forest Ecology and Management 2015, 348, 78–91. [Google Scholar] [CrossRef]
- Maiden, J.H. Forestry Handbook. Part Il. Some of the Principal Commercial Trees of New South Wales; Forest Department of New South Wales: Sydney, 1917; p. 224. [Google Scholar]
- McIntosh, D. National Register of Big Trees. Australia's Champion Trees. 2018.
- Ashton, D.H. The root and shoot development of Eucalyptus regnans F. Muell. Australian Journal of Botany 1975, 23, 867–887. [Google Scholar] [CrossRef]
- Herrmann, W. Vulnerability of Tasmanian giant trees. Australian Forestry 2006, 69, 285–298. [Google Scholar] [CrossRef]
- Williams, J.L.; Lindenmayer, D.; Mifsud, B. The largest trees in Australia. Austral Ecology 2023, 48, 653–671. [Google Scholar] [CrossRef]
- Galbraith, A.V. Mountain Ash (Eucalyptus regnans F. van Mueller): a General Treatise on its Silviculture, Management, and Utilization; Government Printer: Melbourne, 1937; p. 51. [Google Scholar]
- Hickey, J.E.; Kostoglou, P.; Sargison, G.J. Tasmania’s tallest trees. Tasforests 2000, 12, 105–122. [Google Scholar]
- Ferguson, K.V.M. Some Statistics of Timber Yields from Virgin Stands of White Mountain Ash. Australian Forestry 1948, 12, 13–15. [Google Scholar] [CrossRef]
- Law, G. Distant affinities. The challenges facing temperate forests in World Heritage Areas (USA, Slovakia and Japan). Report to the Winston Churchill Memorial Trust of Australia, December 2011, 2010; 67.
- Kostoglou, P. A survey of ultra tall eucalypts in southern Tasmania. A report to Forestry Tasmania; Forestry Tasmania: Hobart, Australia, 2000; p. 22. [Google Scholar]
- Dean, C.; Roxburgh, S.H. Improving visualisation of mature, high-carbon-sequestering forests. Forest Biometry, Modelling and Information Sciences 2006, 1, 48–69. [Google Scholar]
- Julin, K.R.; Farr, W.A. Stem Fluting of Western Hemlock in Southeast Alaska; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, Oregon, 1989; p. 8. [Google Scholar]
- Dryden, J. Palamon and Arcite. In Fables Ancient and Modern; 1700.
- Rodgers, J. The English Woodland; Batsford: London, 1941; p. 132. [Google Scholar]
- Dean, C.; Kirkpatrick, J.B.; Doyle, R.B.; Osborn, J.; Fitzgerald, N.B.; Roxburgh, S.H. The overlooked soil carbon under large, old trees. Geoderma 2020, 376, 1–20. [Google Scholar] [CrossRef]
- Green, R.N.; Trowbridge, R.L.; Klinka, K. Towards a Taxonomic Classification of Humus Forms. Forest Science, Monograph 1993, 29, 1–49. [Google Scholar] [CrossRef]
- Stone, M.G. Forest-type mapping by photointerpretation: A multi-purpose base for Tasmania’s forest management. Tasforests 1998, 10, 15–32. [Google Scholar]
- Hickey, J.; Davis, S.; Wardman, R.; Harris, J. How much rainforest is in Tasmania? A better answer to a difficult question. Tasforests 1993, 5, 13–24. [Google Scholar]
- ANM. The forests of the Concession. Newsprint Log, Australian Newsprint Mills Pty. Ltd. 1947, 2, 21–25. [Google Scholar]
- Irby, I.G. Report of the Forestry Department for the Year Ended 30th June, 1922; Forestry Department: Hobart, Tasmania, 1922; Volume 27. [Google Scholar]
- Quarmby, D. Old forests and Tasmania's early national parks movement. In Proceedings of the Australia's Ever-changing Forests V. Proceedings of the Fifth National Conference on Australian Forest History, Hobart, Tasmania, 2002; pp. 197–208.
- The Mercury. Newsprint Industry. Area of Timber Supply for Papr Making. The Mercury 1937, p. 9.
- The Mercury. Giant trees will build new industry. Newsprint from Tasmanian forests. The Mercury Friday, 23 September 1938 1938, p. 8.
- ANM. The forests of the concession. Newsprint Log (Australian Newsprint Mills Pty. Ltd., Tasmania) 1959, 15, 21–25. [Google Scholar]
- Dean, C.; Horn, E. Dean, C.; Horn, E. A hard, high-carbon, lignomor with conchoidal fracture: cunnite, from mature myrtle beech (Nothofaus cunninghamii (Hook. f.) Oerst.). Geoderma 2019, In Press. [CrossRef]
- Noordeloos, M.; Gates, G.M. Preliminary studies in the genus Entoloma in Tasmania – II. Cryptogamie, Mycologie 2009, 30, 107–140. [Google Scholar]
- Mesibov, R. The millipede genus Tasmaniosoma Verhoeff, 1936 (Diplopoda, Polydesmida, Dalodesmidae) from Tasmania, Australia, with descriptions of 18 new species. ZooKeys 2010, 41, 31–80. [Google Scholar] [CrossRef]
- Eberhard, S.; Giachino, P.M. Tasmanian Trechinae and Psydrinae (Coleoptera, Carabidae): a taxonomic and biogeographic synthesis, with description of new species and evaluation of the impact of Quaternary climate changes on evolution of the subterranean fauna. Subterranean Biology 2011, 9, 1–72. [Google Scholar] [CrossRef]
- Crane, W.J.B. Natural Environmental Aspects of Forest Management. In Economic and Environmental Aspects of the Export Hardwood Woodchip Industry, Cromer, D.A.N., Lamb, V.J.E.I.D., McArthur, A.G., Welsey, D., Girdlestone, J.N., Eds.; Australian Government: Canberra, Australia, 1975; Volume 2, pp. 43–76. [Google Scholar]
- Bauhus, J. Rooting Patterns of Old-Growth Forests: is Aboveground Structural and Functional Diversity Mirrored Belowground. In Old-Growth Forests. Function, Fate and Value, Wirth, C., Gleixner, G., Heimann, M., Eds.; Ecological Studies; Springer-Verlag: Berlin Heidelberg, 2009; pp. 211–229. [Google Scholar]
- Calver, M.; Wardell-Johnson, G.W. Sustained Unsustainability? An evaluation of evidence for a history of overcutting in the Jarrah forests of Western Australia and its consequences for fauna conservation. In Conservation of Australia's Forest Fauna, 2nd ed.; Lunney, D., Ed.; Royal Zoological Society of NSW: Sydney, Australia, 2004; pp. 94–114. [Google Scholar]
- Lindenmayer, D.B.; Cunningham, R.B.; Tanton, M.T.; Nix, H.A.; Smith, A.P. The conservation of arboreal marsupials in the montane ash forests of the central highlands of victoria, south-east Australia: III. The habitat requirements of leadbeater's possum Gymnobelideus leadbeateri and models of the diversity and abundance of arboreal marsupials. Biological Conservation 1991, 56, 295–315. [Google Scholar]
- Galbraith, A.V. The disastrous forest fires of January 1939, in Victoria. Empire Forestry Journal 1939, 18, 10–18. [Google Scholar]
- Law, B.S. The ecology of bats in south-east Australian forests and potential impacts of forestry practices: a review. Pacific Conservation Biology 1996, 2, 363–374. [Google Scholar] [CrossRef]
- Newell, G.R. Responses of Lumholtz's tree-kangaroo (Dendrolagus lumholtzi) to loss of habitat within a tropical rainforest fragment. Biological Conservation 1999, 91, 181–189. [Google Scholar] [CrossRef]
- Kirkpatrick, J.B. Big history of land clearance and deforestation. Journal of Big History 2024, 7, 1–18. [Google Scholar] [CrossRef]
- Kirkpatrick, J.B. The growthist/greenie ritual conflict and the nature of the argument— the example of the woodchip export EIS. In Proceedings of the Institute of Australian Geographers' Conference, Perth, Australia, 1987, 10-18 May 1986; pp. 312–318. [Google Scholar]
- Dargavel, J. Views and perspectives: Why does Australia have ‘forest wars’? International Review of Environmental History 2018, 4, 33–51. [Google Scholar] [CrossRef]
- Florence, R.G. Resource use and biological and environmental planning for eucalypt forest management. Australian Forestry 1972, 36, 147–153. [Google Scholar] [CrossRef]
- Fedotova, A. Forestry experimental stations: Russian proposals of the 1870s. Centaurus 2014, 56, 254–274. [Google Scholar] [CrossRef]
- Dargavel, J. Integration within the model: A new era for Australian forest planning. Impact Assesment 1990, 8, 101–118. [Google Scholar] [CrossRef]
- Cremer, K.W. Eucalypts in rain forest. Australian Forestry 1960, 24, 120–126. [Google Scholar] [CrossRef]
- Cremer, K.W. Studies on problems of regeneration of Eucalyptus regnans in Tasmania. University of Tasmania, 1966.
- Frankcombe, D.W. The regeneration burn. Appita 1966, 19, 127–132. [Google Scholar]
- Paul, E.A.; Robertson, G.P. Ecology and the agricultural sciences: a false dichotomy. Ecology 1989, 70, 1594–1597. [Google Scholar] [CrossRef]
- Puettmann, K.J.; Wilson, S.M.; Baker, S.C.; Donoso, P.J.; Drössler, L.; Amente, G.; Harvey, B.D.; Knoke, T.; Lu, Y.; Nocentini, S.; et al. Silvicultural alternatives to conventional even-aged forest management - what limits global adoption? Forest Ecosystems 2015, 2, 1–16. [Google Scholar] [CrossRef]
- Keith, H.; Barrett, D.; Keenan, R. Review of allometric relationships for estimating woody biomass for New South Wales, the Australian Capital Territory, Victoria, Tasmania and South Australia; Australian Greenhouse Office: 2000; p. 119.
- Polinko, A.; Coupland, K. Paradigm shifts in forestry and forest research: a bibliometric analysis. Canadian Journal of Forest Research 2020, 51, 127–135. [Google Scholar] [CrossRef]
- Kirkpatrick, J.B.; Brown, M.J. Planning for Species Conservation. In Nature Conservation: Cost Effective Biological Surveys and Data Analysis, Margules, C.R., Austin, M.P., Eds.; CSIRO: Canberra, Australia, 1991; pp. 83–89. [Google Scholar]
- Dumbrell, A.J.; Clark, E.J.; Frost, G.A.; Randell, T.E.; Pitchford, J.W.; Hill, J.K. Changes in species diversity following habitat disturbance are dependent on spatial scale: theoretical and empirical evidence. Journal of Applied Ecology 2008, 45, 1531–1539. [Google Scholar] [CrossRef]
- Elton, C.S. The structure of invertebrate populations inside neotropical rain forest. Journal of Animal Ecology 1973, 42, 55–104. [Google Scholar] [CrossRef]
- Specht, R.L.; Specht, A. Species richness of sclerophyll (heathy) plant communities in australia the influence of overstorey cover. Australian Journal of Botany 1989, 37, 337–350. [Google Scholar] [CrossRef]
- Mittelbach, G.G. A matter of time for tropical diversity. Nature 2017, 550, 51–52. [Google Scholar] [CrossRef]
- Hu, Y.; Kelly, L.T.; Gillespie, G.R.; Jessop, T.S. Lizard responses to forest fire and timber harvesting: Complementary insights from species and community approaches. Forest Ecology and Management 2016, 379, 206–215. [Google Scholar] [CrossRef]
- Perry, D.R.; Williams, J. The tropical rain forest canopy: A method providing total access. Biotropica 1981, 13, 283–285. [Google Scholar] [CrossRef]
- Basset, Y.; Novotny, V.; Miller, S.E.; Pyle, R. Quantifying biodiversity: Experience with parataxonomists and digital photography in Papua New Guinea and Guyana. BioScience 2000, 50, 899–908. [Google Scholar] [CrossRef]
- Carr, A.; Zeale, M.R.K.; Weatherall, A.; Froidevaux, J.S.P.; Jones, G. Ground-based and LiDAR-derived measurements reveal scale-dependent selection of roost characteristics by the rare tree-dwelling bat Barbastella barbastellus. Forest Ecology and Management 2018, 417, 237–246. [Google Scholar] [CrossRef]
- Lindenmayer, D.B. The Forest Wars; Allen & Unwin: Crows Nest, New South Wales, Australia, 2024; p. 267. [Google Scholar]
- Macher, T.-H.; Schütz, R.; Hörren, T.; Beermann, A.J.; Leese, F. It's raining species: Rainwash eDNA metabarcoding as a minimally invasive method to assess tree canopy invertebrate diversity. Environmental DNA 2023, 5, 3–11. [Google Scholar] [CrossRef]
- Blakely, T.J.; Harding, J.S.; Didham, R.K. Distinctive aquatic assemblages in water-filled tree holes: a novel component of freshwater biodiversity in New Zealand temperate rainforests. Insect Conservation and Diversity 2012, 5, 202–212. [Google Scholar] [CrossRef]
- Bar-Ness, Y.D.; Kirkpatrick, J.B.; McQuillan, P.B. Age and distance effects on the canopy arthropod composition of old-growth and 100-year-old Eucalyptus obliqua trees. Forest Ecology and Management 2006, 226, 290–298. [Google Scholar] [CrossRef]
- Ishii, H.T.; Tanabe, S.-i.; Hiura, T. Exploring the relationships among canopy structure, stand productivity, and biodiversity of temperate forest ecosystems. Forest Science 2004, 50, 342–355. [Google Scholar] [CrossRef]
- Dalagnol, R.; Wagner, F.H.; Emilio, T.; Streher, A.S.; Galvão, L.S.; Ometto, J.P.H.B.; Aragão, L.E.O.C. Canopy palm cover across the Brazilian Amazon forests mapped with airborne LiDAR data and deep learning. Remote Sensing in Ecology and Conservation 2022, 8, 601–614. [Google Scholar] [CrossRef]
- Gibbons, P.; Lindenmayer, D.B.; Barry, S.C.; Tanton, M.T. Hollow selection by vertebrate fauna in forests of southeastern Australia and implications for forest management. Biological Conservation 2002, 103, 1–12. [Google Scholar] [CrossRef]
- Pedley, S.M.; Oxbrough, A.; Martin, R.D.; Irwin, S.; Kelly, T.C.; O’Hallora, J. Can ground-based assessments of forest biodiversity reflect the biological condition of canopy assemblages? Forest Ecology and Management 2016, 359, 190–198. [Google Scholar] [CrossRef]
- Straw, N.A.; Williams, D.T.; Fielding, N.J.; Jukes, M.; Connolly, T.; Forster, J. The influence of forest management on the abundance and diversity of hoverflies in commercial plantations of Sitka spruce: the importance of sampling in the canopy. Forest Ecology and Management 2017, 406, 95–111. [Google Scholar] [CrossRef]
- Whitworth, A.; Braunholtz, L.D.; Huarcaya, R.P.; MacLeod, R.; Beirne, C. Out on a limb: arboreal camera traps as an emerging methodology for inventorying elusive rainforest mammals. Tropical Conservation Science 2016, 9, 675–698. [Google Scholar] [CrossRef]
- Whitworth, A.; Beirne, C.; Huarcaya, R.P.; Whittaker, L.; Rojas, S.J.S.; Tobler, M.W.; MacLeod, R. Human disturbance impacts on rainforest mammals are most notable in the canopy, especially for larger-bodied species. Biodiveristy Research 2019, 25, 1166–1178. [Google Scholar] [CrossRef]
- Dumbrell, A.J.; Hill, J.K. Impacts of selective logging on canopy and ground assemblages of tropical forest butterflies: Implications for sampling. Biological Conservation 2005, 125, 123–131. [Google Scholar] [CrossRef]
- Malcolm, J.R. Comparative abundances of neotropical small mammals by trap height. Journal of Mammalogy 1991, 72, 188–192. [Google Scholar] [CrossRef]
- Corcoran, E.; Denman, S.; Hamilton, G. Evaluating new technology for biodiversity monitoring: Are drone surveys biased? Ecology and Evolution 2021, 11, 6649–6656. [Google Scholar] [CrossRef] [PubMed]
- Delabre, I.; Boyd, E.; Brockhaus, M.; Carton, W.; Krause, T.; Newell, P.; Wong, G.Y.; Zelli, F. Unearthing the myths of global sustainable forest governance. Global Sustainability 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Hughes, J.D. How the ancients viewed deforestation. Journal of Field Archeology 1983, 10, 435–441. [Google Scholar] [CrossRef]
- Kile, G.A.; Nambiar, E.K.S.; Brown, A.G. The rise and fall of research and development for the forest industry in Australia. Australian Forestry 2014, 77, 142–152. [Google Scholar] [CrossRef]
- Bernays, E.L. The theroy and practice of public relations: a résumé. In The Engineering of Consent, 1st ed.; Bernays, E.L., Ed.; University of Oklahoma Press: Norman, Oklahoma, 1955; pp. 3–4. [Google Scholar]
- Krien, A. Into the Woods. The Battle for Tasmania's Forests; Black inc.: Melbourne, 2012; p. 316. [Google Scholar]
- Kirkpatrick, J.B. The political ecology of biogeography. Journal of Biogeography 2000, 27, 45–48. [Google Scholar] [CrossRef]
- Clarkson, R.B. Tumult in the Mountains: Lumbering in West Virginia 1770–1920.; McClain Printing Company: Parson, West Virginia, 1964. [Google Scholar]
- Ajani, J. The Forest Wars; Melbourne University Press: Melbourne, 2007; p. 362. [Google Scholar]
- Medimorec, S.; Pennycook, G. The language of denial: text analysis reveals differences in language use between climate change proponents and skeptics. Climatic Change 2015, 1–9. [Google Scholar] [CrossRef]
- Hanson, D.; White, R. Rhetorics of environmental routinisation in one Australian company's annual reports. Australian Journal of Social Issues 2003, 38, 477–493. [Google Scholar] [CrossRef]
- McCright, A.M.; Dunlap, R.E. Anti-reflexivity: The American Conservative Movement’s Success in Undermining Climate Science and Policy. Theory, Culture & Society 2010, 27, 100–133. [Google Scholar] [CrossRef]
- Sneddon, J.N.; Soutar, G.N.; Lee, J.A. Exploring wool apparel consumers’ ethical concerns and preferences. Journal of Fashion Marketing and Management 2014, 18, 169–186. [Google Scholar] [CrossRef]
- Bayldon, W.; Narishetty, S.; Rose, G.D.; Rothwell, J.; Mills, P.C. Effects of eight vehicles on transdermal lidocaine penetration in sheep skin in vitro. Journal of Veterinary Pharmacology and Therapeutics 2013, 37, 151–160. [Google Scholar] [CrossRef] [PubMed]
- Vidot, A.; Conifer, D. Investigation launched into claims Australian cattle were slaughtered with sledgehammer in Vietnam. 2015.
- Winter, C.; Poole, L. Animals Australia allege camel cruelty while live export company loads ship in Adelaide. 2014.
- Fuller, K.; Razaghi, T. Scholarship to honour the life of Glen Turner; Australian Broadcasting Corporation: 13-February-2015 2015.
- Woodburn, J. Moree shooting: Farmer continued firing as environmental officer tried to flee, court told; Australian Broadcasting Corporation: 06-August-2014 2014.
- Bradshaw, C.J.A.; Ehrlich, P.R. Killing the Koala and Poisoning the Prairie. Australia, America, and the Environment; The University of Chicago Press: Chicago, 2015; p. 235. [Google Scholar]
- INTERPOL. Global Forestry Enforcement. Strengthening Law Enforcement Cooperation Against Forestry Crime; Lyon, France, 2019; p. 11.
- INTERPOL. Forestry crime: targeting the most lucrative of environmental crimes; Lyon, France, 14-December-2020 2020.
- Halaj, D.; Báliková, K.; Brodrechtová, Y. The perception of an image of the state forest enterprise by general public in chosen region of the Slovak Republic. Journal of Forest Science 2022, 68, 26–34. [Google Scholar] [CrossRef]
- Poynter, M. Timber shortage decades in the making, but being worsened by 'save-the-forests' political ideology. Available online: https://www.onlineopinion.com.au/view.asp?article=21548 (accessed on.
- Ajani, J. Is using native forests for energy really carbon-neutral?; The Conversation, 22-December-2011 2011.
- Bennett, L.T.; Adams, M.A. Ecological effects of harvesting in Victoria's native forests: quantification of research outputs. Australian Forestry 2004, 67, 212–221. [Google Scholar] [CrossRef]
- Czech, B.; Krausman, P.R.; Borkhataria, R. Social construction, political power, and the allocation of benefits to endangered species. Conservation Biology 1998, 12, 1103–1112. [Google Scholar] [CrossRef]
- Heath, R.L. Corporate Issues Management: Theoretical Underpinnings and Research Foundations. In Public Relations Research Annual, Grunig, J.E., Grunig, L.A., Eds.; Lawrence Erllbaum Associates, Inc.: Hillsdale, New Jersey, 1990; Volume 2, pp. 29–65. [Google Scholar]
- Jaworski, B.; Kohli, A.K.; Sahay, A. Market-driven versus driving markets Journal of the Academy of Marketing Science 2000, 28, 45-54.
- Hansen, E.; Juslin, H. Marketing of forest products in a changing world. New Zealand Journal of Forestry Science 2005, 35, 190–204. [Google Scholar]
- Saltelli, A. Why science’s crisis should not become a political battling ground. Futures 2018, 104, 85–90. [Google Scholar] [CrossRef]
- Li, N.; Puumalainen, K.; Toppinen, A. Managerial perceptions of corporate social and financial performance in the global forest industry. The International Forestry Review 2014, 16, 319–338. [Google Scholar] [CrossRef]
- Latapí Agudelo, M.A.; Jóhannsdóttir, L.; Davídsdóttir, B. A literature review of the history and evolution of corporate social responsibility. International Journal of Corporate Social Responsibility 2019, 4, 1–23. [Google Scholar] [CrossRef]
- Fernow, B.E. What is Forestry; Government Printing Office: Washington, D.C., 1891; p. 52.
- Knuchel, H. Planning and Control in the Managed Forest; Oliver & Boyd: Edinburgh, 1953. [Google Scholar]
- World Bank Institute. Public Policy for Corporate Social Responsibility. e-conference, July 7-25, 2003.
- Blowfield, M. Corporate Social Responsibility: reinventing the meaning of development? International Affairs 2005, 81, 515–524. [Google Scholar] [CrossRef]
- Swinburn, B.A.; Kraak, V.I.; Allender, S.; Atkins, V.J.; Baker, P.I.; Bogard, J.R.; Brinsden, H.; Alejandro, C.; Schutter, O.D.; Devarajan, R.; et al. The global syndemic of obesity, undernutrition, and climate change: The Lancet Commission report. The Lancet 2019, 393, 791–846. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R. Marketing of forestry and its products: a NSW perspective. Australian Forestry 2006, 69, 161–166. [Google Scholar] [CrossRef]
- COAG. National Climate Change and Commercial Forestry Action Plan 2009–2012, Council of Australian Governments, Canberra, Australia.; Canberra, Australia., 2009; p. 24.
- The CIE. Forest and Wood Products Australia Generic Marketing Promotions, Evaluation. Discussion Paper; The Centre for International Economics: Canberra and Sydney, 2015; p. 69. [Google Scholar]
- Michaels, D. Doubt is Their Product. How Industry's Assault on Science Threatens Your Health; Oxford University Press: New York, 2008; p. 371. [Google Scholar]
- Hobson, K.; Niemeyer, S. “What sceptics believe”: The effects of information and deliberation on climate change scepticism. Public Understanding of Science 2013, 22, 396–412. [Google Scholar] [CrossRef] [PubMed]
- McDonald, R.I.; b, H.Y.C.; Newell, B.R. Personal experience and the ‘psychological distance’ of climate change: An integrative review. Journal of Environmental Psychology 2015, 44, 109–118. [Google Scholar] [CrossRef]
- Pant, V.K.; Singh, R. A review of social forestry practices in ancient India (neolithic time to 6th Century CE). Utkal Historical Research Journal 2021, 34, 57–66. [Google Scholar]
- Nipunage, D.S.; Kulkarni, D.K. Deo-rahati: an ancient concept of biodiversity conservation. Asian Agri-History 2010, 14, 185–196. [Google Scholar]
- Lentz, D.L.; Hockaday, B. Tikal timbers and temples: ancient Maya agroforestry and the end of time. Journal of Archaeological Science 2009, 36, 1342–1353. [Google Scholar] [CrossRef]
- Evans, J. The History of Tree Planting and Planted Forests. In Planted Forests. Uses, Impacts & Sustainability, Evans, J., Ed.; Food and Agriculture Oranisation of the United Nations: Wallingford, U.K, 2009; p. 213. [Google Scholar]
- Hughes, J.D. Ancient deforestation revisited. Journal of the History of Biology 2011, 44, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.E. A Practical Treatise on Tree Culture in South Australia; Spiller, South Australian Government: Adelaide, South Australia, 1881; p. 116. [Google Scholar]
- Yang, J.; Liu, L.; Roberts, H.; Liu, Z.; Song, L.; Zhang, P. Holocene flood records and human impacts implied from the pollen evidence in the Daming area, North China Plain. Frontiers in Earth Science 2024, 12, 1–12. [Google Scholar] [CrossRef]
- Short, B. Conservation, class and custom: lifespace and conflict in a nineteenth-century forest environment. Rural History 1990, 10, 127–154. [Google Scholar] [CrossRef]
- Pádua, J.A. 'Annihilating Natural Productions': nature's economy, colonial crisis and the origins of Brazilian political environmentalism (1786-1810). Environment and History 2000, 6, 255–287. [Google Scholar] [CrossRef]
- Van Name, W.G. Anti-conservation propaganda. Science 1925, 61, 415–416. [Google Scholar] [CrossRef] [PubMed]
- Moroni, M.T.; Musk, R.; Wardlaw, T.J. Forest succession where trees become smaller and wood carbon stocks reduce. Forest Ecology and Management 2017, 393, 74–80. [Google Scholar] [CrossRef]
- Baxter, T.I. Whither forests of the Tasmanian Wilderness World Heritage Area? Australian Environment Review 2014, 29, 112–117. [Google Scholar]
- IFA IFG. Submission to the Victorian Regional Forest Agreements Major Event Review Following the 2019-20 Bushfires; The Institute of Foresters of Australia and Australian Forest Growers: Melbourne, Australia, 2021; p. 20. [Google Scholar]
- Australian Forest Products Association. Forest industries applaud Coalition election commitments to drive innovation and modern manufacturing timber jobs. News, Media Release 14-April-2022. Available online: https://ausfpa.com.au/forest-industries-applaud-coalition-election-commitments-to-drive-innovation-and-modern-manufacturing-timber-jobs/ (accessed on 7 November 2022).
- Abbott, D. A new shared vision for Australia’s forests. Media Release. 17 March 2021. Available online: https://www.forestry.org.au/media-release-a-new-shared-vision-for-australias-forests/ (accessed on 13 May 2023).
- Jackson, W.; Freeman, M.; Freeman, B.; Parry-Husbands, H. Reshaping forest management in Australia to provide nature-based solutions to global challenges. Australian Forestry 2021, 84, 50–58. [Google Scholar] [CrossRef]
- Norton, T.W. Conserving biological diversity in Australia's temperate eucalypt forests. Forest Ecology and Management 1996, 85, 21–33. [Google Scholar] [CrossRef]
- Kiernan, K. Conservation, timter and perceived values at Mt Field, Tasmania. In Proceedings of the Australia's Ever-changing Forests V. Proceedings of the Fifth National Conference on Australian Forest History, Hobart, Tasmania, 2002; pp. 209–227.
- Kirkpatrick, J.B. Conservation Worrier. DE Press Inc.: Hobart, Tasmania, 2017; pp. 133-142.
- Hitchcock, P. Independent Verification Group Forest Conservation Report 5A Verification of the Heritage Value of ENGO- Proposed Reserves. 2012, 308.
- Knoepp, J.D.; Adams, M.B.; Harrison, R.; West, L.; Laseter, S.H.; Markewitz, D.; Richter, D.D. ; Jr., M.A.C. History of forest soils knowledge and research. In Global Change and Forest Soils. Cultivating Stewardship of a Finite Natural Resource, Busse, M., Giardina, C.P., Morris, D.M., Page-Dumroese, D.S., Eds.; Developments in Soil Science; Elsevier: 2019; Volume 36, pp. 43-55.
- Grand, S.; Lavkulich, L.M. Effects of Forest Harvest on Soil Carbon and Related Variables in Canadian Spodosols. Soil Science Society of America Journal 2012, 76, 1816. [Google Scholar] [CrossRef]
- Holub, S.M.; Hatten, J.A. Soil carbon storage in Douglas-fir forests of western Oregon and washington before and after modern timber harvesting practices. Soil Science Society of America Journal 2019, 83, S175–S186. [Google Scholar] [CrossRef]
- Dietzen, C.A.; Marques, E.R.G.; James, J.N.; Bernardi, R.H.A.; Holub, S.M.; Harrison, R.B. Response of deep soil carbon pools to forest management in a highly productive Andisol. Soil Science Society of America Journal 2017, 81, 970–978. [Google Scholar] [CrossRef]
- Andrieux, B.; Beguin, J.; Bergeron, Y.; Grondin, P.; Paré, D. Drivers of postfire soil organic carbon accumulation in the boreal forest. Global Change Biology 2018, 2018, 1–20. [Google Scholar] [CrossRef]
- Li, J.; Pei, J.; Liu, J.; Wu, J.; Li, B.; Fang, C.; Nie, M. Spatiotemporal variability of fire effects on soil carbon and nitrogen: A global meta-analysis. Global Change Biology 2021, 27, 4196–4206. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Cui, X.; Sang, Y.; Song, J. Changes in soil organic carbon and total nitrogen as affected by primary forest conversion. Forest Ecology and Management 2020, 463, 1–12. [Google Scholar] [CrossRef]
- James, J.; Page-Dumroese, D.; Busse, M.; Palik, B.; Zhang, J.; Eaton, B.; Slesak, R.; Tirocke, J.; Kwon, H. Effects of forest harvesting and biomass removal on soil carbon and nitrogen: Two complementary meta-analyses. Forest Ecology and Management 2021, 485, 1–19. [Google Scholar] [CrossRef]
- Hibbard, K.A.; Schimel, D.S.; Archer, S.; Ojima, D.S.; Parton, W. Grassland to woodland transitions: integrating changes in landscape structure and biogeochemistry. Ecological Applications 2003, 13, 911–926. [Google Scholar] [CrossRef]
- Jandl, R.; Lindner, M.; Vesterdal, L.; Bauwens, B.; Baritz, R.; Hagedorn, F.; Johnson, D.W.; Minkkinen, K.; Byrne, K.A. How strongly can forest management influence soil carbon sequestration? Geoderma 2007, 137, 253–268. [Google Scholar] [CrossRef]
- Laub, M.; Demyan, M.S.; Nkwain, Y.F.; Blagodatsky, S.; Kätterer, T.; Piepho, H.-P.; Cadisch, G. DRIFTS band areas as measured pool size proxy to reduce parameter uncertainty in soil organic matter models. Biogeosciences 2020, 17, 1393–1413. [Google Scholar] [CrossRef]
- Chen, J.; Cui, H.-Y.; Jia, B.; Gang, S.; Li, Y.; Li, F.-C.; Mou, X.M.; Li, X.G. Soil sampling depth matters in assessing the impact of shrubification on soil organic carbon storage in grazed alpine meadows. Geoderma 2022, 426. [Google Scholar] [CrossRef]
- Balesdent, J.; Basile-Doelsch, I.; Chadoeuf, J.; Cornu, S.; Derrien, D.; Fekiacova, Z.; Hatté, C. Atmosphere–soil carbon transfer as a function of soil depth. Nature 2018, 559, 559–602. [Google Scholar] [CrossRef]
- Callesen, I.; Harrison, R.; Stupak, I.; Hatten, J.; Raulund-Rasmussen, K.; Boyle, J.; Clarke, N.; Zabowski, D. Carbon storage and nutrient mobilization from soil minerals by deep roots and rhizospheres. Forest Ecology and Management 2016, 359, 322–331. [Google Scholar] [CrossRef]
- Krueger, I.; Schulz, C.; Borken, W. Stocks and dynamics of soil organic carbon and coarse woody debris in three managed and unmanaged temperate forests. European Journal of Forest Research 2017, 136, 123–137. [Google Scholar] [CrossRef]
- Fontaine, S.; Barot, S.; Barré, P.; Bdioui, N.; Mary, B.; Rumpel, C. Stability of organic carbon in deep soil layers controlled by fresh carbon supply. Nature 2007, 450, 277–280. [Google Scholar] [CrossRef] [PubMed]
- Wäldchen, J.; Schulze, E.-D.; Schöning, I.; Schrumpf, M.; Sierra, C. The influence of changes in forest management over the past 200years on present soil organic carbon stocks. Forest Ecology and Management 2013, 289, 243–254. [Google Scholar] [CrossRef]
- Lucas-Borja, M.E.; R. Ortega; I. Miralles; P. A. Plaza-Álvarez; J. González-Romero; E. Peña-Molina; Moya, D.; D. A. Zema; J. W. Wagenbrenner; J. de las Heras. Effects of wildfire and logging on soil functionality in the short-term in Pinus halepensis M. forests. European Journal of Forest Research 2020, 139, 935–945. [CrossRef]
- Parton, W.J.; Stewart, J.W.B.; Cole, C.V. Dynamics of C, N, P and S in grassland soils: a model. Biogeochemistry 1988, 5, 109–131. [Google Scholar] [CrossRef]
- Dean, C.; Roxburgh, S.H.; Harper, R.J.; Eldridge, D.J.; Watson, I.W.; Wardell-Johnson, G.W. Accounting for space and time in soil carbon dynamics in timbered rangelands. Ecological Engineering 2012, 38, 51–64. [Google Scholar] [CrossRef]
- Olson, J.S. Forest Studies. In Health Physics Division Annual Progress Report for Period Ending July 31, 1959, 15th ed.; ORNL, Ed.ORNL, Ed.; Health and Safety TID-4500; U. S. Atomic Energy Commission: Washington D.C, 1959; Volume ORNL-2806, pp. 37–54. [Google Scholar]
- Peltoniemi, M.; Thürig, E.; Ogle, S.; Palosuo, T.; Schrumpf, M.; Wutzler, T.; Butterbach-Bahl, K.; Chertov, O.; Komarov, A.; Mikhailov, A.; et al. Models in country scale carbon accounting of forest soils. Silva Fennica 2007, 41, 575–602. [Google Scholar] [CrossRef]
- Hudiburg, T.W.; Higuera, P.E.; Hicke, J.A. Fire-regime variability impacts forest carbon dynamics for centuries to millennia. Biogeosciences 2017, 14, 3873–3882. [Google Scholar] [CrossRef]
- Xia; Luo; Wang; Weng; Hararuk. A semi-analytical solution to accelerate spin-up of a coupled carbon and nitrogen land model to steady state. Geoscientific Model Development 2012, 5, 1259–1271. [CrossRef]
- Dean, C.; Roxburgh, S.H.; Mackey, B.G. Forecasting landscape-level carbon sequestration using gridded, spatially adjusted tree growth. Forest Ecology and Management 2004, 194, 109–129. [Google Scholar] [CrossRef]
- Solomon, S.; Plattner, G.-K.; Knutti, R.; Friedlingstein, P. Irreversible climate change due to carbon dioxide emissions. Proceedings of the National Academy of Sciences 2019, 106, 1704–1709. [Google Scholar] [CrossRef]
- Frölicher, T.L.; Joos, F. Reversible and irreversible impacts of greenhouse gas emissions in multi-century projections with the NCAR global coupled carbon cycle-climate model. Climate Dynamics 2010, 35, 1439–1459. [Google Scholar] [CrossRef]
- Augusto, L.; Boča, A. Tree functional traits, forest biomass, and tree species diversity interact with site properties to drive forest soil carbon. Nature Communications 2022, 13, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Dean, C.; Kirkpatrick, J.B.; Friedland, A.J. Conventional intensive logging promotes loss of organic carbon from the mineral soil. Global Change Biology 2017, 23, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kershaw, J.A., Jr.; Oliver, C.D.; Hinckley, T.M. Effect of harvest of old growth Douglas-fir stands and subsequent management on carbon dioxide levels in the atmosphere. Journal of Sustainable Forestry 1993, 1, 61–77. [Google Scholar] [CrossRef]
- Johnson, K.; Scatena, F.N.; Pan, Y. Short- and long-term responses of total soil organic carbon to harvesting in a northern hardwood forest. Forest Ecology and Management 2010, 259, 1262–1267. [Google Scholar] [CrossRef]
- Liski, J.; Ilvesniemi, H.; Mäkelä, A.; Starr, M. Model analysis of the effects of soil age, fires and harvesting on the carbon storage of boreal forest soils. European Journal of Soil Science 1998, 49, 407–416. [Google Scholar] [CrossRef]
- Jandl, N.; Jandl, R.; Schindlbacher, A. Future management options for cembran pine forests close to the alpine timberline. Annals of Forest Science 2018, 75, 1–12. [Google Scholar] [CrossRef]
- Leuschner, C.; Feldmann, E.; Pichler, V.; Glatthorn, J.; Hertel, D. Forest management impact on soil organic carbon: A paired-plot study in primeval and managed European beech forests. Forest Ecology and Management 2022, 512, 1–9. [Google Scholar] [CrossRef]
- Mayer, M.; Prescott, C.E.; Abaker, W.E.A.; Augusto, L.; Cécillon, L.; Ferreira, G.W.D.; James, J.; Jandl, R.; Katzensteiner, K.; Laclau, J.-P.; et al. Tamm Review: Influence of forest management activities on soil organic carbon stocks: A knowledge synthesis. Forest Ecology and Management 2020, 466, 1–25. [Google Scholar] [CrossRef]
- Peckham, S.D.; Gower, S.T. Simulated long-term effects of harvest and biomass residue removal on soil carbon and nitrogen content and productivity for two Upper Great Lakes forest ecosystems. Global Change Biology Bioenergy 2011, 3, 135–147. [Google Scholar] [CrossRef]
- Wang, F.; Mladenoff, D.J.; Forrester, J.A.; Blanco, J.A.; Scheller, R.M.; Peckham, S.D.; Keough, C.; Lucash, M.S.; Gower, S.T. Multimodel simulations of forest harvesting effects on long-term productivity and CN cycling in aspen forests. Ecological Applications 2014, 24, 1374–1389. [Google Scholar] [CrossRef] [PubMed]
- Seely, B.; Welham, C.; Kimmins, H. Carbon sequestration in a boreal forest ecosystem: results from the ecosystem simulation model, FORECAST. Forest Ecology and Management 2002, 169, 123–135. [Google Scholar] [CrossRef]
- Cardoso, P.; Borges, P.A.V.; Carvalho, J.C.; Rigal, F.; Gabriel, R.; Cascalho, J.; Correia, L. Automated discovery of relationships, models and principles in ecology. bioRxiv 2015, 8. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Poeplau, C.; Don, A.; Vesterdal, L.; Leifeld, J.; Wesemael, B.V.; Schumacher, J.; Gensior, A. Temporal dynamics of soil organic carbon after land-use change in the temperate zone – carbon response functions as a model approach. Global Change Biology 2011, 17, 2415–2427. [Google Scholar] [CrossRef]
- Beheshti, A.; Raiesi, F.; Golchin, A. Soil properties, C fractions and their dynamics in land use conversion from native forests to croplands in northern Iran. Agriculture, Ecosystems and Environment 2012, 148, 121–133. [Google Scholar] [CrossRef]
- Huon, S.; Rouw, A.d.; Bonté, P.; Robain, H.; Valentin, C.; Lefèvre, I.; Girardin, C.; Troquer, Y.L.; Podwojewski, P.; Sengtaheuanghoung, O. Long-term soil carbon loss and accumulation in a catchment following the conversion of forest to arable land in northern Laos. Agriculture, Ecosystems and Environment 2013, 169, 43–57. [Google Scholar] [CrossRef]
- Wei, X.; Shao, M.; Gale, W.J.; Zhang, X.; Li, L. Dynamics of aggregate-associated organic carbon following conversion of forest to cropland. Soil Biology & Biochemistry 2013, 57, 876–883. [Google Scholar] [CrossRef]
- Ferré, C.; Comolli, R.; Leip, A.; Seufert, G. Forest conversion to poplar plantation in a Lombardy floodplain (Italy): effects on soil organic carbon stock. Biogeosciences Discussions 2014, 11, 9601–9627. [Google Scholar] [CrossRef]
- Vario, C.L.; Neurath, R.A.; Friedland, A.J. Response of Mineral Soil Carbon to Clear-Cutting in a Northern Hardwood Forest. Soil Science Society of America Journal 2014, 78, 309. [Google Scholar] [CrossRef]
- Lei, L.; Xiao, W.; Zeng, L.; Frey, B.; Huang, Z.; Zhu, J.; Cheng, R.; Li, M.-H. Effects of thinning intensity and understory removal on soil microbial community in Pinus massoniana plantations of subtropical China. Applied Soil Ecology 2021, 167, 1–10. [Google Scholar] [CrossRef]
- Polglase, P.; Adams, M.; Attiwill, P.M. Measurement and Modelling of Carbon Storage in a Chronosequence of Mountain Ash Forests: Implications for Regional and Global Carbon Budgets; Report commissioned by the State Electricity Commission, Victoria: Melbourne, Australia, 1994; p. 61. [Google Scholar]
- He, J.; Dai, Q.; Xu, F.; Peng, X.; Yan, Y. Variability in carbon stocks across a chronosequence of masson pine plantations and the trade-off between plant and soil systems. Forests 2021, 12, 1–15. [Google Scholar] [CrossRef]
- Law, B.E.; Sun, O.J.; Campbell, J.; S. Van Tuyl; Thornton, P.E. Changes in carbon storage and fluxes in a chronosequence of ponderosa pine. Global Change Biology 2003, 9, 510–524. [CrossRef]
- Diochon, A.; Kellman, L.; Beltrami, H. Looking deeper: An investigation of soil carbon losses following harvesting from a managed northeastern red spruce (Picea rubens Sarg.) forest chronosequence. Forest Ecology and Management 2009, 257, 413–420. [Google Scholar] [CrossRef]
- Martin, J.L.; Gower, S.T.; Plaut, J.; Holmes, B. Carbon pools in a boreal mixedwood logging chronosequence. Global Change Biology 2005, 11, 1883–1894. [Google Scholar] [CrossRef]
- Squires, A. Parks and Woodland in Medieval Leicestershire 1086-1530. In Leicestershire Landscapes, Bowman, P., Liddle, P., Eds.; Leicestershire Museums Archaeological Fieldwork Group Monographs; No. 1; Leicestershire Museums Archaeological Fieldwork Group: University of Leicester, England, 2004; pp. 141–153. [Google Scholar]
- Mendel, L.C.; Kirkpatrick, J.B. Historical progress of biodiversity conservation in the protected-area system of Tasmania, Australia. Conservation Biology 2002, 16, 1520–1529. [Google Scholar] [CrossRef]
- Scott, J.M.; Davis, F.W.; Mcghie, R.G.; Wright, R.G.; Groves, C.; Estes, J. Nature reserves: Do they capture the full range of America’s biological diversity? Ecological Issues in Conservation 2001, 11, 999–1007. [Google Scholar] [CrossRef]
- Kayanja, F.I.B.; Byarugaba, D. Disappearing forests of Uganda: The way forward. Current Science 2001, 81, 936–947. [Google Scholar]
- Christophel, D.; Spengler, S.; Schmidt, B.; Ewald, J.; Prietzel, J. Customary selective harvesting has considerably decreased organic carbon and nitrogen stocks in forest soils of the Bavarian Limestone Alps. Forest Ecology and Management 2013, 305, 167–176. [Google Scholar] [CrossRef]
- Gifford, R.M.; Roderick, M.L. Soil carbon stocks and bulk density: spatial or cumulative mass coordinates as a basis of expression? Global Change Biology 2003, 9, 1507–1514. [Google Scholar] [CrossRef]
- Harmon, M.E.; Ferrel, W.K.; Franklin, J.F. Effects on carbon storage of conversion of old-growth forests to young forests. Science 1990, 247, 699–702. [Google Scholar] [CrossRef] [PubMed]
- Sathre, R.; O'Connor, J. Meta-analysis of greenhouse gas displacement factors of wood product substitution. Environmental Science and Policy 2010, 13, 104–114. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Laurance, W.F. A history of hubris – Cautionary lessons in ecologically sustainable forest management. Biological Conservation 2012, 151, 11–16. [Google Scholar] [CrossRef]
- Diamond, J.M. Biogeographic kinetics: estimation of relaxation times for avifaunas of southwest Pacific Islands. PNAS 1972, 69, 3199–3203. [Google Scholar] [CrossRef]
- Kuussaari, M.; Bommarco, R.; Heikkinen, R.K.; Helm, A.; Krauss, J.; Lindborg, R.; Öckinger, E.; Pärtel, M.; Pino, J.; Rodà, F.; et al. Extinction debt: a challenge for biodiversity conservation. Trends in Ecology ad Evolution 2009, 24, 564–571. [Google Scholar] [CrossRef]
- MPIGA. Australia’s State of the Forests Report. Five-yearly report 2008. Montreal Process Implementation Group for Australia and National Forest Inventory Steering Committee.; Bureau of Rural Sciences: Canberra, 2008; p. 250. [Google Scholar]
- Thompson, D.; Connell, M. Issues in Assessing the Sustainability of Private Native Forestry; RIRDC Publication No. 09/031; Canberra, 2009; p. 40.
- Downham, R.; Gavran, M. Australian plantation statistics 2019 update; Australian Bureau of Agricultural and Resource Economics and Sciences: Canberra, 2019; p. 15. [Google Scholar]
- Brander, M.; Ascui, F.; Scott, V.; Tett, S. Carbon accounting for negative emissions technologies. Climate Policy 2021, 21, 699–717. [Google Scholar] [CrossRef]
- Laurijssen, J.; Marsidi, M.; Westenbroek, A.; Worrell, E.; Faaij, A. Paper and biomass for energy? The impact of paper recycling on energy and CO2 emissions. Resources, Conservation & Recycling 2010, 54, 1208–1218. [Google Scholar] [CrossRef]
- Stutz, K.P.; Lang, F. Forest ecosystems create pedogenic patchworks through woody debris, trees, and disturbance. Geoderma 2023, 429, 1–12. [Google Scholar] [CrossRef]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories. Volume 4 Agriculture, Forestry and Other Land Use; National Greenhouse Gas Inventories Programme, IGES: Japan, 2006. [Google Scholar]
- FAO. Measuring and modelling soil carbon stocks and stock changes in livestock production systems: Guidelines for assessment. Version 1.; Food and Agriculture Organisation of the Uniten Nations: Rome, Italy, 2019; p. 145. [Google Scholar]
- Sochacki, S.J.; Ritson, P.; Brand, B.; Harper, R.J.; Dell, B. Accuracy of tree root biomass sampling methodologies for carbon mitigation projects. Ecological Engineering 2017, 98, 264–274. [Google Scholar] [CrossRef]
- Salisbury, E.J. Stratification and hydrogen-ion concentration of the soil in relation to leaching and plant succession with special reference to woodlands. Journal of Ecology 1922, 9, 220–240. [Google Scholar] [CrossRef]
- Marsden, C.; Nouvellon, Y.; Laclau, J.-P.; Corbeels, M.; McMurtrie, R.E.; Stape, J.L.; Epron, D.; Maire, G.l. Modifying the G’DAY process-based model to simulate the spatial variability of Eucalyptus plantation growth on deep tropical soils. Forest Ecology and Management 2013, 301, 112–128. [Google Scholar] [CrossRef]
- Rui, G.; Yike, W.; Ning, A.; Changhai, L.; Qiaoyu, Z.; Fangfang, Q. Characteristics and inflluencing factors of deep soil orgnaic carbon in characteristic economic forests in Northern Shaanxi. Journal of Forest and Environment 2021, 41, 464–470. [Google Scholar] [CrossRef]
- Wade, A.M.; Richter, D.D.; Medjibe, V.P.; Bacon, A.R.; Paul R., Heine; White, L.J.T.; Poulsen, J.R. Estimates and determinants of stocks of deep soil carbon in Gabon, Central Africa. Geoderma 2019, 341, 236–248. [Google Scholar] [CrossRef]
- Jia, X.; Wu, H.; Shao, M.a.; Huang, L.; Wei, X.; Wang, Y.; Zhu, Y. Re-evaluation of organic carbon pool from land surface down to bedrock on China’s Loess Plateau. Agriculture, Ecosystems and Environment 2020, 293. [Google Scholar] [CrossRef]
- Germon, A.; Laclau, J.-P.; Robin, A.; Jourdan, C. Tamm Review: Deep fine roots in forest ecosystems: Why dig deeper? Forest Ecology and Management 2020, 466, 1–16. [Google Scholar] [CrossRef]
- Tune, A.K.; Druhan, J.L.; Wang, J.; Bennett, P.C.; Rempe, D.M. Carbon dioxide production in bedrock beneath soils substantially contributes to forest carbon cycling. Journal of Geophysical Research: Biogeosciences 2020, I25, 1–13. [Google Scholar] [CrossRef]
- Gross, C.D.; Harrison, R.B. The case for digging deeper: Soil organic carbon storage, dynamics, and controls in our changing world. Soil Systems 2019, 3, 1–24. [Google Scholar] [CrossRef]
- Nepstad, D.C.; Carvalho, C.R.d.; Davidson, E.A.; Jlpp, P.H.; Lefebvre, P.A.; Negrelros, G.H.; Sllva, E.D.d.; Stone, T.A.; Trumbore, S.E.; Vieira, S. The role of deep roots in the hydrological and carbon cycles of Amazonian forests and pastures. Nature 1994, 372, 666–669. [Google Scholar] [CrossRef]
- Smith, P.; Soussana, J.F.; Angers, D.; Schipper, L.; Chenu, C.; Rasse, D.P.; Batjes, N.H.; Egmond, F.v.; McNeill, S.; Kuhnert, M.; et al. How to measure, report and verify soil carbon change to realize the potential of soil carbon sequestration for atmospheric greenhouse gas removal. Global Change Biology 2019, 26, 219–241. [Google Scholar] [CrossRef]
- Strey, S.; Boy, J.; Strey, R.; Welpelo, A.; Schönenberg, R.; Schumann, C.; Guggenberger, G. Digging deeper: The value of deep soil carbon for potential REDD+ projects in tropical forest communities in Amazonia. Erdkunde 2017, 71, 231–239. [Google Scholar] [CrossRef]
- Archer, N.A.L.; Quinton, J.N.; Hess, T.M. Below-ground relationships of soil texture, roots and hydraulic conductivity in two-phase mosaic vegetation in South-east Spain. Journal of Arid Environments 2002, 52, 535–553. [Google Scholar] [CrossRef]
- Jackson, R.B.; Banner, J.L.; Jobbágy, E.G.; Pockman, W.T.; Wall, D.H. Ecosystem carbon loss with woody plant invasion of grasslands. Nature 2002, 418, 623–626. [Google Scholar] [CrossRef]
- Shaler, N.S. The Origin and Nature of Soils; U.S. Geological Survey: Washington, D.C., 1892; Volume 4, part I.
- Frazier, C.S.; Graham, R.C. Pedogenic transformation of fractured granitic bedrock, southern California. Soil Science Society America Journal 2000, 64, 2057–2069. [Google Scholar] [CrossRef]
- Nie, Y.; Chen, H.; Ding, Y.; Yang, J.; Wang, K. Comparison of rooting strategies to explore rock fractures for shallow soil-adapted tree species with contrasting aboveground growth rates: a greenhouse microcosm experiment. Frontiers in Plant Science 2017, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Robles, U.; Arredondo, T.; Huber-Sannwald, E.; Ramos-Leal, J.A.; Yépez, E.A. Technical note: Application of geophysical tools for tree root studies in forest ecosystems in complex soils. Biogeosciences 2017, 14, 5343–5357. [Google Scholar] [CrossRef]
- Sehhati, M.T.; Sepehr, A.; Ekhtesasi, M.R.; Goudie, A. The eco-geomorphological roles of rocky deep crevices for water supply on arid zone mountain slopes (case study: Mehriz–Yazd, Iran). Environmental Earth Sciences 2015, 74, 493–504. [Google Scholar] [CrossRef]
- Dean, C.; Wardell-Johnson, G. Old-growth forests, carbon and climate change: functions and management for tall open-forests in two hotspots of temperate Australia. Plant Biosystems 2010, 144, 180–193. [Google Scholar] [CrossRef]
- McIntosh, P.D.; Hardcastle, J.L.; Klöffel, T.; Moroni, M.; Santini, T.C. Can carbon sequestration in tasmanian “wet” eucalypt forests be used to mitigate climate change? Forest succession, the buffering effects of soils, and landscape processes must be taken into account. International Journal of Forestry Research 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Grant, J.C.; Laffan, M.D.; Hill, R.C. Soils of Tasmanian State Forests 2. Forester Sheet. Soils Bulletin 2; Forestry Tasmania: Hobart, Australia, 1995; p. 247. [Google Scholar]
- Hill, R.B.; Laffan, M.D.; Grant, J.C. Soils of Tasmanian State Forests 3. Forth Sheet. Soils Bulletin 3; Forestry Tasmania: Hobart, Australia, 1995; p. 317. [Google Scholar]
- Laffan, M.D.; Grant, J.C.; Hill, R.C. Soils of Tasmanian State Forests 1. Pipers Sheet. Soils Bulletin 1; Forestry Tasmania: Hobart, Australia, 1995; p. 272. [Google Scholar]
- Herbert, A.; Hill, M.D.L.R.C.; Grant, J.C. Laboratory procedures for soil analysis and preparation of plant materials, Soils Technical Report No. 2, Second ed.; Forestry Tasmania: Hobart, Australia, 1995; p. 22. [Google Scholar]
- Dean, C.; Roxburgh, S.H.; Mackey, B.G. Growth Modelling of Eucalyptus regnans for Carbon Accounting at the Landscape Scale. In Modelling Forest Systems, Amaro, A., Reed, D., Soares, P., Eds.; CABI Publishing: Wallingford, Oxford, U.K, 2003. [Google Scholar]
- Paul, K.I.; Roxburgh, S.H. FullCAM: building capability via data informed parameters. Accurately tracking forest carbon from biomass to soil. Report for Department of the Environment and Energy.; CSIRO Agriculture: Canberra, Australia, 2017; p. 65. [Google Scholar]
- Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proceedings of the National Academy of Sciences of the United States of America 2009, 106, 11635–11640. [Google Scholar] [CrossRef]
- Dietrich, P. Carbon stocks in coarse woody debris and soil in the mixed forests and the rainforests in southern Tasmania. MSc, Technische Universität, Dresden, Germany, 2012.
- Batjes, N.H. Total carbon and nitrogen in the soils of the world. European Journal of Soil Science 1996, 47, 151–163. [Google Scholar] [CrossRef]
- G. Corti; Ugolini, F.C.; Agnelli, A.; Certini, G.; Cuniglio, R.; Berna, F.; Sanjurjo, M.J.F. The soil skeleton, a forgotten pool of carbon and nitrogen in soil. European Journal of Soil Science 2002, 53, 283–298. [CrossRef]
- Rivard, R.; Kimpe, C.R.D. Propriétés de quelques sols riches en graviers dans la région de Québec. Canadian Journal of Soil Science 1980, 60, 263–273. [Google Scholar] [CrossRef]
- Harrison, R.B.; Adams, A.B.; Licata, C.; Flaming, B.; Wagoner, G.L.; Carpenter, P.; Vance, E.D. Quantifying Deep-Soil and Coarse-Soil Fractions: Avoiding Sampling Bias. Soil Science Society America Journal 2003, 67, 1602–1606. [Google Scholar] [CrossRef]
- Zabowski, D.; Whitney, N.; Gurung, J.; Hatten, J. Total soil carbon in the coarse fraction and at depth. Forest Science 2011, 57, 11–18. [Google Scholar] [CrossRef]
- Basile-Doelsch, I.; Balesdent, J.; Rose, J. Are interactions between organic compounds and nanoscale weathering minerals the key drivers of carbon storage in soils? Environmental Science and Technology 2015, 49, 3997–3998. [Google Scholar] [CrossRef]
- Hopmans, P.; Bauhus, J.; Khanna, P.; Weston, C. Carbon and nitrogen in forest soils: Potential indicators for sustainable management of eucalypt forests in south-eastern Australia. Forest Ecology and Management 2005, 220, 75–87. [Google Scholar] [CrossRef]
- Buma, B.; Poore, R.E.; Wessman, C.A. Disturbances, their interactions, and cumulative effects on carbon and charcoal stocks in a forested ecosystem. Ecosystems 2014, 17, 947–959. [Google Scholar] [CrossRef]
- Harrington, A.; Holub, S.M.; Bauer, C.; Ashley, E.; Steel. The distribution of tree roots in Douglas-fir forests in the Pacific Northwest in relation to depth, space, coarse organic matter and mineral fragments. Northwest Science 2017, 91, 326–343. [CrossRef]
- Keller, C.K.; Bacon, D.H. Soil respiration and georespiration distinguished by transport analyses of vadose CO2, 13CO2, and 14CO2. Global Biogeochemical Cycles 1998, 12, 361–372. [Google Scholar] [CrossRef]
- Blair, N.E.; Leithold, E.L.; Ford, S.T.; Peeler, K.A.; Holmes, J.C.; Perkey, D.W. The persistence of memory: The fate of ancient sedimentary organic carbon in a modern sedimentary system. Geochimica et Cosmochimica Acta 2003, 67, 63–73. [Google Scholar] [CrossRef]
- Ishikawa, N.F.; Tayasu, I.; Yamane, M.; Yokoyama, Y.; Sakai, S.; Ohkouchi, N. Sources of dissolved inorganic carbon in two small streams with different bedrock geology: Insights from carbon isotopes. Radiocarbon 2015, 57, 439–448. [Google Scholar] [CrossRef]
- Qi, M.; Chen, S.; Wei, Y.; Zhou, H.; Zhang, S.; Wang, M.; Zheng, J.; Rossel, R.A.V.; Chang, J.; Shi, Z.; et al. Using visible-near infrared spectroscopy to estimate whole-profile soil organic carbon and its fractions. Soil & Environmental Health 2024, 2, 1–9. [Google Scholar] [CrossRef]
- Shamrikova, E.V.; Vanchikova, E.V.; Kyzyurova, E.V.; Zhangurova, E.V. Methods for measuring organic carbon content in carbonate-containing soils: A review. Eurasian Soil Science, 2024, Vol. 57, No. 3, pp. 380–394 2024, 57, 380–394. [Google Scholar] [CrossRef]
- Grant, J.C.; Laffan, M.D.; Hill, R.B.; Neilsen, W.A. Forest Soils of Tasmania. A Handbook for Identification and Management; Forestry Tasmania: Hobart, Australia, 1995; p. 189. [Google Scholar]
- De Vos, B.; Lettens, S.; Muys, B.; Deckers, J.A. Walkley–Black analysis of forest soil organic carbon: recovery, limitations and uncertainty. Soil Use and Management 2007, 23, 221–229. [Google Scholar] [CrossRef]
- Meersmans, J.; Van Wesemael, B.; Van Molle, M. Determining soil organic carbon for agricultural soils: a comparison between the Walkley & Black and the dry combustion methods (north Belgium). Soil Use and Management 2009, 25, 346–353. [Google Scholar] [CrossRef]
- Fernandes, R.B.A.; Afonso de Carvalho Junior, I.; Silva Ribeiro Junior, E.; Mendonça, E.d.S. Comparison of different methods for the determination of total organic carbon and humic substances in Brazilian soils. Revista Ceres 2015, 62, 496–501. [Google Scholar] [CrossRef]
- Pearson, T.R.H.; Brown, S.L.; Birdsey, R.A. Measurement Guidelines for the Sequestration of Forest Carbon. General Technical Report NRS-18; Forest Service, United States Department of Agriculture: Pennsylvania, USA, 2007; p. 44. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total Carbon, Organic Carbon and Organic Matter. In Methods of Soil Analysis. Part 3. Chemical Methods-SSSA Book Series no. 5, Sparks, D.L., Page, A.L., Helmke, P.A., Loeppert, R.H., Soltanpour, P.N., Tabatabai, M.A., Johnston, C.T., M.E., S., Eds.; Soil Sceince Society of Amerrica and American Society of Agronomy: Madison, Wisconsin, 1996; pp. 961–1010. [Google Scholar]
- Wang, X.J.; Smethurst, P.J.; Herbert, A.M. Relationships between three measures of organic matter or carbon in soils of eucalypt plantations in Tasmania. Australian Journal of Soil Research 1996, 34, 545–553. [Google Scholar] [CrossRef]
- Olayinka, A.; Adebayo, A.; Amusan, A. Evaluation of organic carbon oxidation efficiencies of a modified wet combustion and Walkley-Black procedures in Nigerian soils. Communications in Soil Science and Plant Analysis 1998, 29, 2749–2756. [Google Scholar] [CrossRef]
- McKenzie, N.; Ryan, P.; Fogarty, P.; Wood, J. Sampling, measurement and analytical protocols for carbon estimation in soil, litter and course woody debris. Technical Report No. 14, National Carbon Accounting System; Commonwealth of Australia: Canberra, 2000; p. 52. [Google Scholar]
- Poeplau, C.; Vos, C.; Don, A. Soil organic carbon stocks are systematically overestimated by misuse of the parameters bulk density and rock fragment content. Soil 2017, 3, 61–66. [Google Scholar] [CrossRef]
- Mehler, K.; Schöning, I.; Berli, M. The importance of rock fragment density for the calculation of soil bulk density and soil organic carbon stocks. Soil Science Society of America Journal 2014, 78, 1186–1191. [Google Scholar] [CrossRef]
- Conen, F.; Zerva, A.; Arrouays, D.; Jolivet, C.; Jarvis, P.; Grace, J.; Mencuccini, M. The carbon balance of forest soils: detectability of changes in soil carbon stocks in temperate and boreal forests. In The Carbon Balance of Forest Biomes, Griffiths, H., Jarvis, P., Eds.; Garland Science/BIOS Scientific Publishers: Southampton, U.K, 2004; Volume 9, pp. 233–247. [Google Scholar]
- Seigel, H.O. A Guide to High Precision Land Gravimetric Surveys; Scintrex Limited: Concord, Ontario, Canada, 1995; p. 132. [Google Scholar]
- Bennett, L.T.; Hinko-Najera, N.; Aponte, C.; Nitschke, C.R.; Fairman, T.A.; Fedrigo, M.; Kasel, S. Refining benchmarks for soil organic carbon in Australia’s temperate forests. Geoderma 2020, 368. [Google Scholar] [CrossRef]
- Post, W.M.; Emanuel, W.R.; Zinket, P.J.; Stangenberger, A.G. Soil carbon pools and world life zones. Nature 1982, 298, 156–159. [Google Scholar] [CrossRef]
- Jobággy, G.J.; Jackson, R.B. The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecological Applications 2002, 10, 423–436. [Google Scholar] [CrossRef]
- Australian Forestry Council. FORWOOD: report of the Forestry and Wood-based Industries Development Conference 1974. In Proceedings of the Forestry and Wood-based Industries Development Conference, Canberra, Australia, 1974.
- di Folco, M.-B.; Kirkpatrick, J.B. Organic soils provide evidence of spatial variation in human-induced vegetation change following European occupation of Tasmania. Journal of Biogeography 2013, 40, 197–205. [Google Scholar] [CrossRef]
- Harmon, M.E. Carbon sequestration in forests. Addressing the scale question. Journal of Forestry 2001, 99, 24–29. [Google Scholar] [CrossRef]
- Harmon, M.E. Woody Detritus Mass and its Contribution to Carbon Dynamics of Old-Growth Forests: the Temporal Context. In Old-growth Forests: Function, Fate and Value. Ecological studies, C., W., G., G., M., H., Eds.; Springer-Verlag: New York, 2009; pp. 159–190. [Google Scholar]
- Mesibov, R. Review of the Deep Red Myrtle Resource in Tasmania; Ferguson, I.S., Ed.; Forestry Tasmania: Hobart, Tasmania, Australia, 2002; p. 56.
- Elliott, H.J.; Hickey, J.E.; Jennings, S.M. Effects of selective logging and regeneration treatments on mortality of retained trees in Tasmanian cool temperate rainforest. Australian Forestry 2005, 68, 274–280. [Google Scholar] [CrossRef]
- Walker, B.B.; Candy, S. Investigating methods of assessing rainforest in Tasmania. In Proceedings of the Tasmanian Rainforests. Recent Research Results, Hobart, Tasmania; 1982; pp. 7–34. [Google Scholar]
- Duncan, F. Tasmania's Vegetation and its Response to Forest Operations. Working Paper 6. Background information additional to the Environmental Impact Statement on Tasmanian Woodchip Exports Beyond 1988. EIS Study Group.; Tasmanian Government Printer: Hobart, Tasmania, 1985; p. 127. [Google Scholar]
- Wood, S.W.; Hua, Q.; Allen, K.J.; Bowman, D.J.M.S. Age and growth of a fire prone Tasmanian temperate old-growth forest stand dominated by Eucalyptus regnans, the world's tallest angiosperm. Forest Ecology and Management 2010, 260, 438–447. [Google Scholar] [CrossRef]
- Hickey, J.E.; Su, W.; Rowe, P.; Brown, M.J.; Edwards, L. Fire history of the tall wet eucalypt forests of the Warra ecological research site, Tasmania. Australian Forestry 1999, 62, 66–71. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Kolden, C.A.; Abatzoglou, J.T.; Johnston, F.H.; Werf, G.R.v.d.; Flannigan, M. Vegetation fires in the Anthropocene. Nature Reviews Earth & Environment 2020, 1, 500–515. [Google Scholar] [CrossRef]
- Fox-Hughes, P.; Harris, R.; Lee, G.; Grose, M.; Bindoff, N. Future fire danger climatology for Tasmania, Australia, using a dynamically downscaled regional climate model. International Journal of Wildland Fire 2014, 23, 309–321. [Google Scholar] [CrossRef]
- Riddington, M. Victoria’s rainforests and the potential impacts of a changing climate. The Victorian Naturalist 2014, 131, 209–218. [Google Scholar]
- Lindenmayer, D.B.; Hobbs, R.J.; Likens, G.E.; Krebs, C.J.; Banks, S.C. Newly discovered landscape traps produce regime shifts in wet forests. PNAS 2011, 108, 15887–15891. [Google Scholar] [CrossRef] [PubMed]
- Taplin, R.E.; Tighe, P.J.; Hill, A.H.; Hoystead, P.A.; McCuaig, A. Temperate rainforest species and forest regeneration in the Hastings forest region of the southern forests, Tasmania. In The Rainforest Legacy. Australian National Rainforest Study. Special Australian Heritage Publication, Werren, G., Kershaw, P., Eds.; Australian Government Publishing Service: Canberra, 1991; Volume 7. [Google Scholar]
- Jordan, G.J.; Patmore, C.; Duncan, F.; Luttrell, S.D. The effects of fire intensity on the regeneration of mixed forest tree species in the Clear Hill/ Mount Wedge area. Tasforests 1992, 4, 25–38. [Google Scholar]
- Tabor, J.; McElhinny, C.; Hickey, J.; Wood, J. Colonisation of clearfelled coupes by rainforest tree species from mature mixed forest edges, Tasmania, Australia Forest Ecology and Management 2007, 240, 13-23.
- Mackey, B.; DellaSala, D.A.; Kormos, C.; Lindenmayer, D.; Kumpel, N.; Zimmerman, B.; Hugh, S.; Young, V.; Foley, S.; Arsenis, K.; et al. Policy options for the world’s primary forests in multilateral environmental agreements. Conservation Letters 2015, 8, 139–147. [Google Scholar] [CrossRef]
- Forestry Tasmania. 2000 Annual Report. Forestry Tasmania; Forestry Tasmania: Hobart, Tasmania, Australia, 2001; p. 62. [Google Scholar]
- Bryant, C. Understanding bushfire trends in deliberately lit vegetation fires in Australia; Government, A., Ed.; Australian Institute of Criminology, Australian Government: Canberra, 2008; Volume 27, p. 618.
- Enright, N.J.; Fontaine, J.B. Climate change and the management of fire-prone vegetation in southwest and southeast Australia. Geographical Research 2013, 52, 34–44. [Google Scholar] [CrossRef]
- Hall, G.M.J.; Hollinger, D.Y. Simulating New Zealand forest dynamics with a generalized temperate forest gap model. Ecological Applications 2000, 10, 115–130. [Google Scholar] [CrossRef]
- Hiltner, U.; Huth, A.; Fischer, R. Importance of succession in estimating biomass loss: Combining remote sensing and individual-based forest models. Biogeosciences. Discussions 2020, preprint. [Google Scholar] [CrossRef]
- Green, G. Esperance 74D (EP074D) Logging Coupe Inventory; Timber Workers for Forests: Hobart, Tasmania, 2002. [Google Scholar]
- FORTECH. Study No. 2 Rainforest in the Northwest of Tasmania; Forestry Technical Services Pty Ltd: Canberra, ACT, 1982; p. 153. [Google Scholar]
- Rab, M.A. Soil physical and hydrological properties following logging and slash burning in the Eucalyptus regnans forest in southeastern Australia. Forest Ecology and Management 1996, 84, 159–176. [Google Scholar] [CrossRef]
- Pennington, P.I.; Laffan, M.; Lewis, R.; Otahal, P. Assessing the long-term impacts of forest harvesting and high intensity broadcast burning on soil properties at the Warra LTER Site. Tasforests 2001, 13, 291–298. [Google Scholar]
- Ellis, R.C.; Graley, A.M. Gains and losses in soil nutrients associated with harvesting and burning eucalypt rainforest. Plant and Soil 1983, 74, 437–450. [Google Scholar] [CrossRef]
- Tomkins, I.B.; Kellas, J.D.; Tolhurst, K.C.; Oswin, D.A. Effects of fire intensity on soil chemistry in a eucalypt forest. Australian Journal of Soil Research 1991, 29, 25–47. [Google Scholar] [CrossRef]
- Antos, J.A.; Halpern, C.B.; Miller, R.E.; Cromack, K., Jr.; Halaj, M.G. Temporal and Spatial Changes in Soil Carbon and Nitrogen After Clearcutting and Burning of an Old-Growth Douglas-Fir Forest. Research Paper PNW-RP-552; Forest Service, United States Department of Agriculture: Portland, Oregon, USA, 2003; p. 28. [Google Scholar]
- Jiménez Esquilín, A.E.J.; Stromberger, M.E.; Massman, W.J.; Frank, J.M.; Sheppard, W.D. Microbial community structure and activity in a Colorado Rocky Mountain forest soil scarred by slash pile burning. Soil Biology and Biochemistry 2007, 39, 1111–1120. [Google Scholar] [CrossRef]
- Bormann, B.T.; Homann, P.S.; Darbyshire, R.L.; Morrissette, B.A. Intense forest wildfire sharply reduces mineral soil C and N: the first direct evidence. Canadian Journal of Forest Research 2008, 38, 2771–2783. [Google Scholar] [CrossRef]
- Rab, M.A. Changes in physical properties of a soil associated with logging of Eucalyptus regnans forest in southeastern Australia. Forest Ecology and Management 1994, 70, 215. [Google Scholar] [CrossRef]
- Camilleri, Mark A. Corporate Sustainability, Social Responsibility and Environmental Management. An Introduction to Theory and Practice with Case Studies; Springer Nature: Cham, Switzerland, 2017; p. 195.
- Putz, F.E.; Romero, C.; Sist, P.; Schwartz, G.; Thompson, I.; Roopsind, A.; Ruslandi, R.; Medjibe, V.; Ellis, P. Sustained timber yield claims, considerations, and tradeoffs for selectively logged forests. PNAS Nexus 2022, 1, 1–7. [Google Scholar] [CrossRef]
- Crane, A.H. Assessment of A.N.M. Concession-Upper Styx Area, Assessment of A.N.M. mature forest 1956/57. Report from Chief Commissioner, Forestry Commission Tasmania. 1957, 8.
- Bansal, P.; Song, H.-C. Similar but not the same: Differentiating corporate sustainability from corporate responsibility. Academy of Management Annals 2017, 11, 105–149. [Google Scholar] [CrossRef]
- Han, X.; Hansen, E. From a production orientation to a stakeholder orientation: the evolution of marketing sophistication in private, multi-site U.S. sawmills. In Proceedings of the Proceedings of the 55th International Convention of Society of Wood Science and Technology, Beijin, China, 27-31-August-2012, 2012; pp. 1–10.
- Chuter, R. Feasibility of burning debris from wet eucalypt forests harvested to an aggregated retention prescription; Forestry Tasmania: Hobart, Tasmania, Australia, 2007; p. 31. [Google Scholar]
- Neyland, M.; Hickey, J.; Beadle, C.; Bauhus, J.; Davidson, N.; Edwards, L. An examination of stocking and early growth in the Warra silvicultural systems trial confirms the importance of a burnt seedbed for vigorous regeneration in Eucalyptus obliqua forest. Forest Ecology and Management 2009, 258, 481–494. [Google Scholar] [CrossRef]
- Shen, C.; Ma, L.; Hu, J.; Huang, L.; Chen, Y.; Guan, D. Soil carbon storage and its determinants in forest fragments of differentiated patch size. Forests 2019, 10, 1–13. [Google Scholar] [CrossRef]
- Bae, J.; Ryu, Y. The magnitude and causes of edge effects on soil organic carbon stocks within and across urban to rural forest patches. Landscape and Urban Planning 2021, 215, 1–11. [Google Scholar] [CrossRef]
- Zeng, H.; Peltola, H.; Talkkari, A.; Venäläinen, A.; Strandman, H.; Kellomäki, S.; Wang, K. Influence of clear-cutting on the risk of wind damage at forest edges. Forest Ecology and Management 2004, 2003, 77–88. [Google Scholar] [CrossRef]
- Dupont, S.; Brunet, Y. Impact of forest edge shape on tree stability: a large-eddy simulation study. Forestry 2008, 81, 299–315. [Google Scholar] [CrossRef]
- Franklin, J.F.; Forman, R.T.T. Creating landscape patterns by forest cutting: Ecological consequences and principles. Landscape Ecology 1987, 1, 5–18. [Google Scholar] [CrossRef]
- Narayanaraj, G.; Wimberly, M.C. Influences of forest roads on the spatial patterns of human- and lightning-caused wildfire ignitions. Applied Geography 2012, 32, 878–888. [Google Scholar] [CrossRef]
- Commonwealth of Australia & TAS. Consolidated Tasmanian Regional Forest Agreement; Commonwealth of Australia and Tasmanian governments,: 1997; p. 84.
- Commonwealth of Australia & NSW. Regional Forest Agreement for Southern New South Wales; Commonwealth of Australia and the State of New South Wales: 2001; p. 110.
- Brown, A.J. Collaborative governance versus constitutional politics: decision rules for sustainability from Australia’s South East Queensland forest agreement. Environmental Science & Policy 2002, 5, 19–32. [Google Scholar] [CrossRef]
- Costantini, A.; Dunn, G.M.; Grimmett, J.L. Towards sustainable management of forest plantations in south-east Queensland. II: Protecting soil and water values during second rotation Pinus plantation management. Australian Forestry 1997, 60, 226–232. [Google Scholar] [CrossRef]
- Costantini, A.; Grimmett, J.L.; Dunn, G.M. Towards sustainable management of forest plantations in south-east Queensland. I: Logging and understorey residue management between rotations in steep country Araucaria cunninghamii plantations. Australian Forestry 1997, 60, 218–225. [Google Scholar] [CrossRef]
- ANM. The properties of Australian Timbers. Mountain Ash. Newsprint Log, Australian Newsprint Mills Pty. Ltd. 1947, 2, 7–9. [Google Scholar]
- Forestry Commission. Silviculture Manual; Forestry Commission of Tasmania: Hobart, Tasmania, 1978; p. 124. [Google Scholar]
- Spencer, B.; Mazanec, R.; Abadi, A.; Gibberd, M.; Zerihun, A. Flowering phenology in a Eucalyptus loxophleba seed orchard, heritability and genetic correlation with biomass production and cineole: breeding strategy implications. Nature Scientific Reports 2020, 10, 1–16. [Google Scholar] [CrossRef]
- Enquist, B.J.; Abraham, A.J.; Harfoot, M.B.J.; Malhi, Y.; Doughty, C.E. The megabiota are disproportionately important for biosphere functioning Nature Communications 2020, 11, 1-11. [CrossRef]
- Ali, A.; Wang, L.-Q. Big-sized trees and forest functioning: Current knowledge and future perspectives. Ecological Indicators 2021, 127. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Laurance, W.F.; Franklin, J.F. Global decline in large old trees. Science 2012, 1305. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Laurance, W.F. The ecology, distribution, conservation and management of large old trees. Biological Reviews 2016, 92. [Google Scholar] [CrossRef] [PubMed]
- Allendorf, F.W.; Hard, J.J. Human-induced evolution caused by unnatural selection through harvest of wild animals. PNAS 2009, 106, 9987–9994. [Google Scholar] [CrossRef] [PubMed]
- Coltman, D.W.; O’Donoghue, P.; Jorgenson, J.T.; Hogg, J.T.; Strobeck, C.; Festa-Bianchet, M. Undesirable evolutionary consequences of trophy hunting. Nature 2003, 426, 655–658. [Google Scholar] [CrossRef] [PubMed]
- Strømman, A.H.; Peters, G.P.; Hertwich, E.G. Approaches to correct for double counting in tiered hybrid life cycle inventories. Journal of Cleaner Production 2009, 17, 35–43. [Google Scholar] [CrossRef]
- Ximenes, F.A.; Robinson, M.; Wright, B. Forests, wood and Australia's carbon balance; Forest and Wood Products Research and Development Corporation, C.R.C.f.G.A., Ed.; Forest and Wood Products Research and Development Corporation (Australian Government): Melbourne, 2008; p. 20. [Google Scholar]
- Pingoud, K.; Perälä, A.-L.; Pussinen, A. Carbon dynamics in wood products. Mitigation and Adaptation Strategies for Global Change 2001, 6, 91–111. [Google Scholar] [CrossRef]
- Dean, C. Land Use and Carbon Dynamics in Woody Ecosystems. PhD, Univeristy of Tasmania, Hobart, Tasmania, 2017.
- Ågren, G.I.; Hyvönen, R. Changes in carbon stores in Swedish forest soils due to increased biomass harvest and increased temperatures analysed with a semi-empirical model. Forest Ecology and Management 2003, 174, 25–37. [Google Scholar] [CrossRef]
- Gustavsson, L.; Nguyen, T.; Sathre, R.; Tettey, U.Y.A. Climate effects of forestry and substitution of concrete buildings and fossil energy. Renewable and Sustainable Energy Reviews 2021, 136, 1–15. [Google Scholar] [CrossRef]
- Schulze, E.D.; Bouriaud, O.; Irslinger, R.; Valentini, R. The role of wood harvest from sustainably managed forests in the carbon cycle. Annals of Forest Science 2022, 79, 1–13. [Google Scholar] [CrossRef]
- Horne, R.; Grant, T.; Verghese, K. Life Cycle Assessment. Principles, Practice and Prospects; CSIRO Publishing: Collingwood, Victoria, Australia, 2009; p. 175. [Google Scholar]
- Ingerson, A. Carbon storage potential of harvested wood: summary and policy implications. Mitigation, Adaptation Strategies for Global Change 2011, 16, 307–323. [Google Scholar] [CrossRef]
- May, B.; England, J.R.; Raison, R.J.; Paul, K.I. Cradle-to-gate inventory of wood production from Australian softwood plantations and native hardwood forests: Embodied energy, water use and other inputs. Forest Ecology and Management 2012, 264, 37–50. [Google Scholar] [CrossRef]
- Stafford, B. Environmental Aspects of China's Papermkaing Fiber Supply, Forest Trends: Hobart, Australia, 2007.
- Joensuu, K.; Rimhanen, K.; Heusala, H.; Saarinen, M.; Usva, K.; Leinonen, I.; Palosuo, T. Challenges in using soil carbon modelling in LCA of agricultural products—the devil is in the detail. The International Journal of Life Cycle Assessment 2021, 26, 1764–1778. [Google Scholar] [CrossRef]
- Responsible Wood. AS/NZS 4708:202X. Sustainable forest management—requirements. Stage: Public Comment Draft; Responsoble Wood: New Farm, Queensland, 2020; p. 84. [Google Scholar]
- Tasmanian Timber Promotions Board. Tasmanian Timber. Tasmanian Oak, 2023.
- Rosen, K.; Lovett, S. Statement of Enviornmental Effects. Bombala Sawmill Modification 3. Dongwha Australia. 2018, 229. [Google Scholar]
- Schultz, B. Language and the natural environment. In The Ecolinguistics Reader: Language, Ecology and Environment, Fill, A., Mülhäusler, P., Eds.; Continuum: London, 2001; pp. 109–114. [Google Scholar]
- Leslie, A.J. logging of catchments-- the Victorian problem. Australian Forestry 1962, 26, 45–49. [Google Scholar] [CrossRef]
- IFA. The utilization of timber resources in the watersheds of Victoria. Tendered by W. G. Chandler for the Victorian Division of the Australian Institute of Foresters. Australian Forestry 1959, 23, 110–113. [Google Scholar] [CrossRef]
- Leslie, A.J. The pulp and paper industry in relation to state forestry in Australia. Australian Forestry 1954, 18, 50–57. [Google Scholar] [CrossRef]
- Stanturf, J.A.; Jones, S.B.; Ticknor, W.D. Managing Industrial Forestland in a Changing Society. Journal of Forestry 1993, 91, 6–11. [Google Scholar] [CrossRef]
- Hetemäki, L.; Hänninen, R. Outlook for Finland’s Forest Industry Production and Wood Consumption for 2015 and 2020. 2009, 11.
- Tardif, P.; O'Connor, J. Selling Wood Products to the Green Building Market. 2013, 2.0, 83.
- Reid, H.; Huq, S.; Inkinen, A.; MacGregor, J.; Macqueen, D.; Mayers, J.; Murray, L.; Tipper, R. Using Wood Products to Mitigate Climate Change: A Review of Evidence and Key Issues for Sustainable Development. 2004, 90.
- Pingoud, K.; Ekholm, T.; Sievänen, R.; Huuskonen, S.; Hynynen, J. Trade-offs between forest carbon stocks and harvests in a steady state – a multi-criteria analysis. Journal of Environmental Management 210, pp. 96–103, 2018 2017, 210, 96–103. [Google Scholar] [CrossRef]
- Deheza, M.; N’Goran, C.; Bellassen, V. What Incentives To Climate Change Mitigation Through Harvested Wood Products In The Current French Policy Framework? (Summary). 2014, Climate Report No 47.
- Fernholz, K. Sustainable Forestry: Renewable Materials Storing Carbon. In Proceedings of the Building Sustainably: From Forestland Management to Carbon-Positive, Healthy Buildings, online, 2020, 20-October-2020; p. 13. [Google Scholar]
- Naqvi, M.; Yan, J.; Dahlquist, E. Black liquor gasification integrated in pulp and paper mills: A critical review. Bioresource Technology 2010, 101, 8001–8015. [Google Scholar] [CrossRef]
- Lippke, B.; Oneil, E.; Harrison, R.; Skog, K.; Gustavsson, L.; Sathre, R. Life cycle impacts of forest management and wood utilization on carbon mitigation: knowns and unknowns. Carbon Management 2011, 2, 303–333. [Google Scholar] [CrossRef]
- Harmon, M.E. Have product substitution carbon benefits been overestimated? A sensitivity analysis of key assumptions. Environmental Research Letters 2019, 14, 1–8. [Google Scholar] [CrossRef]
- Guo, P.; Meng, W.; Du, J.; Stevenson, L.; Han, B.; Bao, Y. Lightweight ultra-high-performance concrete (UHPC) with expanded glass aggregate: Development, characterization, and life-cycle assessment. Construction and Building Materials 2023, 371, 1–14. [Google Scholar] [CrossRef]
- Kulasuriya, C.; Vimonsatit, V.; Dias, W.P.S. Performance based energy, ecological and financial costs of a sustainable alternative cement. Journal of Cleaner Production 2021, 287, 1–8. [Google Scholar] [CrossRef]
- Khalil, A.; Wang, X.; Celik, K. 3D printable magnesium oxide concrete: towards sustainable modern architecture. Additive Manufacturing 2020, 33, 1–9. [Google Scholar] [CrossRef]
- Forestry Commission. Timber Production and Marketing. In Report for year 1978-1979; State Government of Tasmania: Hobart, Tasmania, 1979; pp. 10–11. [Google Scholar]
- Villagrán-Zaccardi, Y.A.; Marsh, A.T.M.; Sosa, M.E.; Zega, C.J.; Belie, N.D.; Bernal, S.A. Complete re-utilization of waste concretes–Valorisation pathways and research needs. Resources, Conservation & Recycling 2022, 177, 1–16. [Google Scholar] [CrossRef]
- Shah, I.H.; Miller, S.A.; Jiang, D.; Myers, R.J. Cement substitution with secondary materials can reduce annual global CO2 emissions by up to 1.3 gigatons. Nature Communications 2022, 13, 1–11. [Google Scholar] [CrossRef]
- Kjellsen, K.O.; Guimaraes, M.; Nilsson, Å. The CO2 Balance of Concrete in a Life Cycle Perspective. Nordic Innovation Centre Project NI-project 03018; Danish Technological Institute: 2005.
- Cao, Z.; Myers, R.J.; Lupton, R.C.; Duan, H.; Sacchi, R.; Zhou, N.; Miller, T.R.; Cullen, J.M.; Ge, Q.; Liu, G. The sponge effect and carbon emission mitigation potentials of the global cement cycle. Nature Communications 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Verbeck, G.J. Carbonation of Hydrated Portland Cement. ASTM Special Technical Publication 205.; Research and Development Laboratories of the Portland Cement Association: Chicago, Illinois, 1958; p. 20. [Google Scholar]
- Xi, F.; Davis, S.J.; Ciais, P.; Crawford-Brown, D.; Guan, D.; Pade, C.; Shi, T.; Syddall, M.; Lv, J.; Ji, L.; et al. Substantial global carbon uptake by cement carbonation. Nature Geoscience 2016, 9, 880–883. [Google Scholar] [CrossRef]
- Giuliani, U.; Grazian, S.; Alotto, P.; Agostini, M.; Bustreo; Zollino, G. Nuclear Fusion impact on the requirements of power infrastructure assets in a decarbonized electricity system. Fusion Engineering and Design 2023, 192, 1–8. [CrossRef]
- Heath, R.L. A rhetorical approach to zones of meaning and organizational prerogatives. Public Relations Review 1993, 19, 141–155. [Google Scholar] [CrossRef]
- FWPA. About; Forest & Wood Products Australia: Melbourne, Australia, 2023; p. 3. [Google Scholar]
- FWPA. FAQs; Forest & Wood Products Australia: Melbourne, Australia, 2023; p. 3. [Google Scholar]
- Wood, R. Find Certified; Responsible Wood: Kedron, Queensland, Australia, 2023. [Google Scholar]
- Morris, F.; Allen, S.; Hawkins, W. On the embodied carbon of structural timber versus steel, and the influence of LCA methodology. Building and Environment 2021, 206, 1–10. [Google Scholar] [CrossRef]
- Bessou, C.; Benoist, A.; Tailleur, A.; Godard, C.; Gac, A.; Cour, J.L.d.l.; Boissy, J.; Mischler, P. Accounting for land use contribution to climate change in agricultural LCA: Which methods? In Which impacts? In Proceedings of the Global food challenges towards sustainable consumption and production, Bangkok, Thailand, 2018, 17-19-October-2018; pp. 1–4. [Google Scholar]
- Sevenster, M.; Luo, Z.; Eady, S.; Grant, T. Including long-term soil organic carbon changes in life cycle assessment of agricultural products. The International Journal of Life Cycle Assessment 2020, 25, 1231–1241. [Google Scholar] [CrossRef]
- Stewart, P.J. Forestry for carbon dioxide fixation. The Commonwealth Forestry Review 1978, 57, 263–266. [Google Scholar]
- Raison, R.J.; Khanna, P.K.; Crane, W.J.B. Effects of intensified harvesting on rates of nitrogen and phosphorus removal from Pinus radiata and eucalyptus forests in Australia and New Zealand. New Zealand Journal of Forestry Science 1982, 12, 394–403. [Google Scholar]
- Dewar, R.C.; McMurtrie, R.E. Sustainable stemwood yield in relation to the nitrogen balance of forest plantations: a model analysis. Tree Physiology 1996, 16, 173–182. [Google Scholar] [CrossRef]
- Donald, D.G.M. Silviculture and yield. South African Forestry Journal 1987, 141, 45–52. [Google Scholar] [CrossRef]
- Forsius, F.; Akujärvi, A.; Mattsson, T.; Holmberg, M.; Punttila, P.; Posch, M.; Liski, J.; Repo, A.; Virkkala, R.; Vihervaara, P. Modelling impacts of forest bioenergy use on ecosystem sustainability: Lammi LTER region, southern Finland. Ecological Indicators 2015, 65, 66–75. [Google Scholar] [CrossRef]
- Ahamer, G. Why biomass fuels are principally not carbon neutral. Energies 2022, 15, 1–39. [Google Scholar] [CrossRef]
- Kuhlman, T.; Farrington, J. What is sustainability? Sustainability 2010, 2, 3436–3448. [Google Scholar] [CrossRef]
- Smith, J.H.G. An economic view suggests that the concept of sustained yield should have gone out with the crosscut saw. The Forestry Chronicle 1969, 45, 167–171. [Google Scholar] [CrossRef]
- Doley, D. Session Review. Forests and the global environment. Australian Forestry 1993, 56, 317–326. [Google Scholar] [CrossRef]
- Vance, E.D. Agricultural site productivity: principles derived from long-term experiments and their implications for intensively managed forests. Forest Ecology and Management 2000, 138, 369–396. [Google Scholar] [CrossRef]
- Tellnes, L.G.F.; Ganne-Chedeville, C.; Dias, A.; Dolezal, F.; Hill, C.A.S.; Zea Escamilla, E. Comparative assessment for biogenic carbon accounting methods in carbon footprint of products: a review study for construction materials based on forest products. iForest : Biogeosciences and Forestry 2017, 10, 815–823. [Google Scholar] [CrossRef]
- Hararuk, O.; Xia, J.; Yiqi Luo1. Evaluation and improvement of a global land model against soil carbon data using a Bayesian Markov chain Monte Carlo method. Journal of Geophysical Research: Biogeosciences 2014, 119, 403–417. [CrossRef]
- Metsaranta, J.M.; Shaw, C.H.; Kurz, W.A.; Boisvenue, C.; Morken, S. Uncertainty of inventory-based estimates of the carbon dynamics of Canada’s managed forest (1990–2014). Canadian Journal of Forest Research 2017, 47, 1082–1094. [Google Scholar] [CrossRef]
- Subedi, B.P.; Pandey, S.S.; Pandey, A.; Eak Bahadur Rana; Bhattarai, S.; Banskota, T.R.; Charmakar, S.; Tamrakar, R. Forest Carbon Stock Measurement: guidelines for measuring carbon stocks in community-managed forests, Second ed.; Asia Network for Sustainable Agriculture and Bioresources; Federation of Community Forest Users, Nepal; International Centre for Integrated Mountain Development; Norwegian Agency for Development Cooperation: Kathmandu, Nepal, 2011; p. 67.
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories. Volume 4 Agriculture, Forestry and Other Land Use, Chapter 2 Generic Methodologies Applicable to Multiple Landuse Categories; National Greenhouse Gas Inventories Programme, IGES: Japan, 2006; p. 59. [Google Scholar]
- Liu, W.; Yu, Z.; Xie, X.; Gadow, K.v.; Peng, C. A critical analysis of the carbon neutrality assumption in life cycle assessment of forest bioenergy systems. Environmental Reviews 2018, 26, 93–101. [Google Scholar] [CrossRef]
- Fan, Y.V.; Klemeš, J.J.; Ko, C.H. Bioenergy carbon emissions footprint considering the biogenic carbon and secondary effects. International Journal of Energy Research 2021, 45, 283–296. [Google Scholar] [CrossRef]
- Albers, A.; Collet, P.; Benoist, A.; Hélias, A. Back to the future: dynamic full carbon accounting applied to prospective bioenergy scenarios. International Journal of Life Cycle Assessment 2020, 25, 1242–1258. [Google Scholar] [CrossRef]
- Petersen, B.M.; Knudsen, M.T.; Hermansen, J.E.; Halberg, N. An approach to include soil carbon changes in life cycle assessments. Journal of Cleaner Production 2013, 52, 217–224. [Google Scholar] [CrossRef]
- Paul, K.I.; Polglase, P.J.; Richards, G.P. Predicted change in soil carbon following afforestation or reforestation, and analysis of controlling factors by linking a C accounting model (CAMFor) to models of forest growth (3PG), litter decomposition (GENDEC) and soil C turnover (RothC). Forest Ecology and Management 2003, 177, 485–501. [Google Scholar] [CrossRef]
- Cowie, A.L.; Smith, P.; Johnson, D. Does soil carbon loss in biomass production systems negate the greenhouse benefits of bioenergy? Mitigation and Adaptation Strategies for Global Change 2006, 11, 979–1002. [Google Scholar] [CrossRef]
- Wutzler, T.; Reichstein, M. Soils apart from equilibrium – consequences for soil carbon balance modelling. Biogeosciences 2007, 4, 125–136. [Google Scholar] [CrossRef]
- Fridman, J.; Holm, S.; Nilsson, M.; Nilsson, P.; Ringvall, A.H.; Ståhl, G. Adapting National Forest Inventories to changing requirements – the case of the Swedish National Forest Inventory at the turn of the 20th century. Silva Fennica 2014, 48, 1–29. [Google Scholar] [CrossRef]
- Hill, C.A.S. The Environmental Consequences Concerning the Use of Timber in the Built Environment. Frontiers in Built Environment 2019, 5, 1–10. [Google Scholar] [CrossRef]
- Berry, S.L.; Roderick, M.L. Changing Australian vegetation from 1788 to 1988: effects of CO2 and land-use change. Australian Journal of Botany 2006, 54, 325–338. [Google Scholar] [CrossRef]
- Banfai, D.S.; Bowman, D.J.M. Dynamics of a savanna-forest mosaic in the Australian monsoon tropics inferred from stand structures and historical aerial photography. Australian Journal of Botany 2005, 53, 185–194. [Google Scholar] [CrossRef]
- Bond, W.J.; Woodward, F.I.; Midgley, G.F. The global distribution of ecosystems in a world without fire. New Phytologist 2005, 165, 525–538. [Google Scholar] [CrossRef] [PubMed]
- Cloudsley-Thompson, J.L. Desert expansion and the adaptive problems of the inhabitants. In Environmental Physiology of Desert Animals, Hadley, N.F., Ed.; Dowden, Hutchinson and Ross: Stroudsburg, Pennsylvania, 1975; pp. 255–268. [Google Scholar]
- Specht, R.L. Changes in the Eucalypt Forest of Australia as a Result of Human Disturbance. In The Earth in Transition: Patterns and Processes of Biotic Impoverishment, Woodwell, G.M., Ed.; Cambridge Univesity Press: New York, 1990; pp. 177–197. [Google Scholar]
- McIntosh, P.D.; Laffan, M.D.; Hewitt, A.E. The role of fire and nutrient loss in the genesis of the forest soils of Tasmania and southern New Zealand. Forest Ecology and Management 2005, 220, 185–215. [Google Scholar] [CrossRef]
- Gill, R.A. Influence of 90 years of protection from grazing on plant and soil processes in the subalpine of the Wasatch Plateau USA. Rangeland Ecology and Management 2007, 60, 88–98. [Google Scholar] [CrossRef]
- Gough, C.M.; Vogel, C.S.; Harrold, K.H.; George, K.; Curtis, P.S. The legacy of harvest and fire on ecosystem carbon storage in a northern temperate forest. Global Change Biology 2007, 13, 1935–1949. [Google Scholar] [CrossRef]
- Williams, R.J.; Bradstock, R.A.; Cary, G.J.; Enright, N.J.; Gill, A.M.; Liedloff, A.C.; Lucas, C.; Whelan, R.J.; Andersen, A.A.; Bowman, D.J.M.S.; et al. The impact of climate change on fire regimes and biodiversity in Australia—a preliminary assessment. 2009, 257.
- Aguilar, F.X.; Mirzaee, A.; McGarvey, R.G.; Shifey, S.R.; Burtraw, D. Expansion of US wood pellet industry points to positive trends but the need for continued monitoring. Nature Scientific Reports 2020, 10, 1–17. [Google Scholar] [CrossRef]
- Mai-Moulin, T. Sustainable bioenergy pathways. Conditions to move forward; Copernicus Institute of Sustainable Development, Utrecht University: Utrecht, The Netherlands, 2020; p. 279. [Google Scholar]
- Johnson, F.X.; Roman, M. Biofuels Sustainability Criteria. Relevant issues to the proposed Directive on the promotion of the use of energy from renewable sources; European Parliament: Bruxelles, 2008; p. 33. [Google Scholar]
- Ter-Mikaelian, M.T.; Colombo, S.J.; Chen, J. The burning question: Does forest bioenergy reduce carbon emissions? A review of common misconceptions about forest carbon accounting. Journal of Forestry 2015, 113, 57–68. [Google Scholar] [CrossRef]
- Giuntoli, J.; Barredo, J.I.; Avitabile, V.; Camia, A.; Cazzaniga, N.E.; Grassi, G.; Jasinevičius, G.; Jonsson, R.; Marelli, L.; Robert, N.; et al. The quest for sustainable forest bioenergy: win-win solutions for climate and biodiversity. Renewable and Sustainable Energy Reviews 2022, 159, 1–20. [Google Scholar] [CrossRef]
- Benemann, J.R. CO2 mitigation with microalgae systems. Energy Conservation and Management 1997, 38, S475–S479. [Google Scholar] [CrossRef]
- Terlouw, T.; Bauer, C.; Rosa, L.; Mazzotti, M. Life cycle assessment of carbon dioxide removal technologies: a critical review. Energy & Environmental Science 2021, 14, 1701–1721. [Google Scholar] [CrossRef]
- Giuntoli, J.; Searle, S.; Jonsson, R.; Agostini, A.; Robert, N.; Amaducci, S.; Marelli, L.; Camia, A. Carbon accounting of bioenergy and forest management nexus. A reality-check of modeling assumptions and expectations. Renewable and Sustainable Energy Reviews 2020, 134, 1–21. [Google Scholar] [CrossRef]
- Menzes, G.B.; Golkar, T.; Moo-Young, H.H. Pulp and paper mill effluents management. Water Environment Research 2011, 83, 1525–1531. [Google Scholar] [CrossRef]
- Mathieu, F.; François, N.; Nicolas, R.; Frédéric, M. Quantifying the impact of forest management on the carbon balance of the forest-wood product chain: A case study applied to even-aged oak stands in France. Forest Ecology and Management 2012, 279, 176–188. [Google Scholar]
- Milani, D.; Kiani, A.; McNaughton, R. Renewable-powered hydrogen economy from Australia’s perspective. International Journal of Hydrogen Energy 2020, 45, 24125–24145. [Google Scholar] [CrossRef]
- AECOM; ARNEA. Australia's Off-grid Clean Energy Market. Research Paper; Canberra, Australia, 2014; p. 133.
- SFM. Bioenergy: How the Timber Industry is Contributing to Growth in Renewables. Available online: https://sustainableforestmanagement.com.au/growth-in-renewable-bioenergy/ (accessed on 7 October 2024).
- Bioenergy Australia. About Bioenergy. Available online: https://www.bioenergyaustralia.org.au/about/ (accessed on 7 October 2024).
- Aalde, H.; Gonzalez, P.; Gytarsky, M.; Krug, T.; Kurz, W.A.; Ogle, S.; Raison, J.; Schoene, D.; Ravindranath, N.H.; Carle, J.B.; et al. IPCC Guidelines for National Greenhouse Gas Inventories. Chapter 4, Forest Land. Institute for Global Environmental Strategies: Hayama, Japan, 2006; pp. 4.1-4.83.
- Wang, C.; Walsh, S.D.C.; Weng, Z.; Haynes, M.W.; Summerfield, D.; Feitz, A. Green steel: Synergies between the Australian iron ore industry and the production of green hydrogen. International journal of hydrogen energy 2023, 48, 32277–32293. [Google Scholar] [CrossRef]
- Brown, D.; Rowe, A.; Wild, P. Techno-economic comparisons of hydrogen and synthetic fuel production using forest residue feedstock. International Journal of Hydrogen Energy 2014, 39, 12551–12562. [Google Scholar] [CrossRef]
- Balat, H.; Kırtay, E. Hydrogen from biomass-- Present scenario and future prospects. International Journal of Hydrogen Energy 2010, 35, 7416–7426. [Google Scholar] [CrossRef]
- Nurdiawati, A.; Urban, F. Decarbonising the refinery sector: A socio-technical analysis of advanced biofuels, green hydrogen and carbon capture and storage developments in Sweden. Energy Research and Social Science 2022, 84, 1–16. [Google Scholar] [CrossRef]
- Australian Government. Native Forest Wood Waste removed from Renewable Energy Target, Media Release, 16-December-2022 The Honourable Chris Bowen MP, Minister for Climate Change and Energy: Canberra, 2022.
- Ardo, F.M.; Lim, J.W.; Ramli, A.; Lam, M.K.; Kiatkittipong, W.; Abdelfattah, E.A.; Shahid, M.K.; Usman, A.; Wongsakulphasatch, S.; Sahrin, N.T. A review in redressing challenges to produce sustainable hydrogen from microalgae for aviation industry. Fuel 2022, 330, 1–11. [Google Scholar] [CrossRef]
- Gupta, A.; Likozar, B.z.; Jana, R.; Chanu, W.C.; Singh, M.K. A review of hydrogen production processes by photocatalytic water splitting e From atomistic catalysis design to optimal reactor engineering. International Journal of Hydrogen Energy 2022, 47, 33282–33307. [Google Scholar] [CrossRef]
- Rosero-Chasoy, G.; Rodríguez-Jasso, R.M.; Aguilar, C.N.; Buitrón, G.; Chairez, I.; Ruiz, H.A. Green hydrogen production: a critical review. In Green Approach to Alternative Fuel for a Sustainable Future, Shah, M.p., Ed.; Elsevier: Cambridge, MA, USA, 2023; pp. 381–390. [Google Scholar]
- Cowie, A.L.; Berndes, G.; Bentsen, N.S.; Brandão, M.; Cherubini, F.; Egnell, G.; George, B.; Gustavsson, L.; Hanewinkel, M.; Harris, Z.M.; et al. Applying a science-based systems perspective to dispel misconceptions about climate effects of forest bioenergy. Global Change Biology - Bioenergy 2021, 13, 1210–1231. [Google Scholar] [CrossRef]
- Achat, D.L.; Deleuze, C.; Landmann, G.; Pousse, N.; Ranger, J.; Augusto, L. Quantifying consequences of removing harvesting residues on forest soils and tree growth – A meta-analysis. Forest Ecology and Management 2015, 348, 124–141. [Google Scholar] [CrossRef]
- UNECE. Forest Products Annual Market Review 2018-2019; UNECE and FAO: Geneva, 2019. [Google Scholar]
- Forest Stewardship Council. Guidance for Demonstrating Ecosystem Services Impacts. FSC-GUI-30-006 V1-1 EN. 2021.
- FAO; UNEP. The State of the World’s Forests 2020. Forests, biodiversity and people.; Food and Agriculture Organization of the United Nations: Rome, 2020; p. 214. [Google Scholar]
- Siry, J.P.; Cubbage, F.W.; Ahmed, M.R. Sustainable forest management: global trends and opportunities. Forest Policy and Economics 2005, 7, 551–561. [Google Scholar] [CrossRef]
- FAO. Global Forest Resources Assessment 2010. Main Report. FAO Forestry Paper 163; Food and Agriculture Organization of the United Nations: Rome, 2010. [Google Scholar]
- FAO. Forest Resources Assessment 2000. Food and Agriculture Organization of the United Nations: University of Michigan, 2001; p. 479.
- Krankina, O.N.; Harmon, M.E. The impact of intensive forest management on carbon stores in forest ecosystems. World Resource Review 1994, 6, 161–177. [Google Scholar]
- UNECE. Forest Products Annual Market Review 2020-2021; United Nations Economic Commission for Europe: Geneva, 2021; p. 86. [Google Scholar]
- Linser, S.; O'Hara, P. Guidelines for the Development of a Criteria and Indicator Set for Sustainable Forest Management. Geneva Timber and Forest Discussion Paper 73; Lugov, D.C.A., Ed.; United Nations and Food and Agriculture Organization of the United Nations: Geneva, Switzerland, 2019; p. 91. [Google Scholar]
- MPWG. The Montréal Process. Criteria and Indicators for the Conservation and Sustainable Management of Temperate and Boreal Forests; Research Institute of Forestry, Chinese Academy of Forestry, Beijing, China: Beijing, China, 2015; p. 31. [Google Scholar]
- MPWG. Montréal Process Criteria and Indicators for the Conservation and Sustainable Management of Temperate and Boreal Forests. Technical Notes on Implementation of the Montréal Process Criteria and Indicators. Criteria 1- 7. Third Edition, June 2009. Revised July 2014.; 2014; p. 101.
- Cowie, A.L. Expert report on Climate Change and Ecologically Sustainable Development matters Land and Environment Court Proceedings 2021/00128111; Department of Primary Industries, New South Wales: New South Wales, Australia, 2021; p. 35. [Google Scholar]
- NSW Parliament. Legislative Council. 2019-20-21. First Session of the Fifty-Seventh Parliament. Questions and Answers. No 597. 2021, Friday 1 October 2021, 19.
- HRL Technology Group. Redbank Power Station QA/QC, Supply Chain and Material Handling. Addendum Report; HRL Technology Group Pty Ltd: Mulgrave, VIC, Australia, 2021; p. 45. [Google Scholar]
- Richards, G.P. The FullCAM Carbon Accounting Model: Development, Calibration and Implementation for the National Carbon Accounting System. NCAS Technical Report No. 28. Parts 1 and 2.; Australian Greenhouse Office: Canberra, Australia, 2001; p. 61. [Google Scholar]
- Ximenes, F.; Coburn, R.; McLean, M.; Samuel, J.; Cameron, N.; Law, B.; Threllfall, C.; Wright, K.; Macintosh, S. North Coast Residues. A project undertaken as part of the 2023 North Coast Forestry Project; NSW Department of Primary Industries: Sydney, Australia, 2017; p. 66. [Google Scholar]
- Poynter, M.; Ryan, M. Leadbeater’s possum and Victoria’s Central Highlands’ forests: flawed science and environmental activism as drivers of forest management change. Australian Foresty 2018, 81, 250–272. [Google Scholar] [CrossRef]
- Keith, H.; Lindenmayer, D.; Mackey, B.; Blair, D.; Carter, L.; McBurney, L.; Okada, S.; Konishi-Nagano, T. Managing temperate forests for carbon storage: impacts of logging versus forest protection on carbon stocks. Ecosphere 2014, 5, art75. [Google Scholar] [CrossRef]
- Lindenmayer, D.B.; Sato, C. Hidden collapse is driven by fire and logging in a socioecological forest ecosystem. PNAS 2018, 115, 5181–5186. [Google Scholar] [CrossRef] [PubMed]
- Dean, C. Creative Carbon Accounting—A Reply to “TheWood, the Trees, or the Forest? Carbon in Trees in Tasmanian State Forest: A Response to Comments”. International Journal of Forestry Research 2012, 2012, 762080. [Google Scholar] [CrossRef]
- Moroni, M.T.; Kelley, T.H.; McLarin, M.L.; Read, S.M. The Wood, the Trees, or the Forest? Carbon in Trees in Tasmanian State Forest: A Response to Comments. International Journal of Forestry Research 2012, 2012, 1–6. [Google Scholar] [CrossRef]
- Sterman, J.D.; Siegel, L.; Rooney-Varga, J.N. Reply to comment on ‘Does replacing coal with wood lower CO2 emissions? Dynamic lifecycle analysis of wood bioenergy’. Environmental Research Letters 2018, 13, 1–8. [Google Scholar] [CrossRef]
- Prisley, S.P.; Gaudreault, C.; Lamers, P.; Stewart, W.; Miner, R.; Junginger, H.M.; Oneil, E.; Malmsheimer, R.; Volk, T.A. Comment on ‘Does replacing coal with wood lower CO2 emissions? Dynamic lifecycle analysis of wood bioenergy’. Environmental Research Letters 2018, 13. [Google Scholar] [CrossRef]
- Sanger, J.C.; Ferrari, A. The Grove of Giants: Tasmania's most carbon-dense forest. Austral Ecology 2023, 48, 1245–1251. [Google Scholar] [CrossRef]
- Johnson, D.W. Effects of forest management on soil carbon storage. Water, Air and Soil Pollution 1992, 64, 83–120. [Google Scholar] [CrossRef]
- Brown, S.; Lugo, A.E. Biomass of tropical forests: A new estimate based on forest volumes. Science 1984, 223, 1290–1293. [Google Scholar] [CrossRef]
- Moroni, M.T.; Lewis, T. Comparing measured and modelled eucalypt forest carbon stocks. Technical Report 01/2015; Forestry Tasmania: Hobart, Australia, 2015; p. 25. [Google Scholar]
- Snowdon, P.; Eamus, D.; Gibbons, P.; Khanna, P.K.; Keith, H.; Raison, R.J.; Kirschbaum, M.U.F. Synthesis of Allometrics, Review of Root Biomass and Design of Future Woody Biomass Sampling Strategies. Techincal Report No. 17.; Australian Greenhouse Office, Commonwealth of Australia: Canberra, Australia, 2000; Volume 17. [Google Scholar]
- Grierson, P.F.; Adams, M.A.; Attiwill, P.M. Estimates of Carbon Storage in the above-ground biomass of Victoria's Forests. Australian Journal of Botany 1992, 40, 631–640. [Google Scholar] [CrossRef]
- MBAC. Forestry Tasmania’s Carbon Sequestration Position; MBAC Consulting Group Pty. Ltd.: Melbourne, Australia, 2007; p. 43. [Google Scholar]
- Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass estimation methods for tropical forests with applications to forest inventory data. Forest Science 1989, 35, 881–902. [Google Scholar] [CrossRef]
- PFT; Goodwin, A. N. Farm Forestry Toolbox Version 5.3.8b; Private Forests Tasmania: Hobart, Tasmania, 2016. [Google Scholar]
- Ximenes, F.A.; Gardner, W.D.; Kathuria, A. Proportion of above-ground biomass in commercial logs and residues following the harvest of five commercial forest species in Australia. Forest Ecology and Management 2008, 256, 335–346. [Google Scholar] [CrossRef]
- Setiahadi, R. Comparison of individual tree aboveground biomass estimation in community forests using allometric equation and expansion factor in Magetan, East Java, Indonesia. Biodiversitas 2021, 22, 3899–3909. [Google Scholar] [CrossRef]
- Lawrence, A.G.S. Assessment of Florentine Valley. In Annual Report, Irby, I.G., Ed.; Forestry Department: Hobart, Tasmania, 1922; Volume 27, pp. 14-18 + maps.
- ANM. ANM. Australian Newsprint Mills. Unpublished logging coupe registers for the Florentine, Tyenna and Styx Valleys. Forestry Tasmania Library, Hobart, Tasmania; c1960.
- Dean, C.; Fitzgerald, N.B.; Wardell-Johnson, G.W. Pre-logging carbon accounts in old-growth forests, via allometry: An example of mixed-forest in Tasmania, Australia. Plant Biosystems 2011, 146, 223–236. [Google Scholar] [CrossRef]
- Wardlaw, T. Measuring a fire. The story of the January 2019 fire told from measurements at the Warra supersite, Tasmania. Fire 2021, 4, 1–18. [Google Scholar] [CrossRef]
- Ximenes, F.A.; Kathuria, A.; McLean, M.; Coburn, R.; Sargeant, D.; Ryan, M.; Williams, J.; Boer, K.; Mo, M. Carbon in mature native forests in australia: The role of direct weighing in the derivation of allometric equations. Forests 2018, 9, 1–26. [Google Scholar] [CrossRef]
- Dargavel, J.B. The Development of the Tasmanian Wood Industries: a Radical Analysis. Australian National University, Canberra, Australia, 1982.
- Wardlaw, T. Warra Tall Eucalypt Stem Diameter, Height and Aboveground Woody Biomass Data. Version 1.0. Terrestrial Ecosystem Research Network. (Dataset). TERN: 2022.
- Goodwin, A.N. A taper equation for Eucalyptus obliqua. In Proceedings of the Integrating Forest Information Over Space and Time. IUFRO S4.01 Mensuration, Growth and Yield and S4.02 Forest Resource Inventory, Canberra, Australia, 1992, 13-17-January-1992; pp. 454–467. [Google Scholar]
- APPM. Evaluation of South Arthur River Myrtle with Decay as a Pulpwood Resource. Unpublished report by Australian Pulp and Paper Mills, Burnie, Tasmania, deposited with the Forestry Commission. 1980, 46, plus photos, maps and data sheets.
- Harcombe, P.A.; Allen, R.B.; Wardle, J.A.; Pratt, K.H. Spatial and temporal patterns in stand structure, biomass, growth, and mortality in a monospecific Nothofagus solandrivar. cliffortioides (Hook, f.) Poole Forest in New Zealand. Journal of Sustainable Forestry 1997, 63, 313–345. [Google Scholar] [CrossRef]
- May, B.; Bulinski, J.; Goodwin, A.; Macleod, S. Tasmanian Forest Carbon Study. Report was commissioned by the State Government through the Tasmanian Climate Change Office.; CO2 Australia Limited: 2012; p. 372.
- da Silva, W.; da Silva, C.P. LABFit Curve Fitting Software. v7.2.48; Brazil, 2015.
- Moroni, M.T.; Kelley, T.H.; McLarin, M.L. Carbon in Trees in Tasmanian State Forest. International Journal of Forestry Research 2010, 2010, 1–13. [Google Scholar] [CrossRef]
- Dean, C. Comment on ‘Carbon in Trees in Tasmanian State Forest’. International Journal of Forestry Research 2011, 2011, 1–10. [Google Scholar] [CrossRef]
- Wickett, H.C. The measurent of logs and methods of stating their volumes. In Proceedings of the Australian Timber Industry Stabilisation Conference, Karunda, Queensland, 1960, 26-30 September 1960; p. 6. [Google Scholar]
- Gilbert, J.M. Regeneration of the Eucalypts. PhD, University of Tasmania, Hobart, Tasmania, Australia, 1958.
- Olson, J.S. Energy storage and the balance of producers and decomposers in ecological systems. Ecology 1963, 44, 322–331. [Google Scholar] [CrossRef]
- Grierson, P.F.; Adams, M.A.; Attiwill, P.M. Carbon Storage in Soil and in Forest Products; School of Botany, University of Melbourne: Parkville, Victoria, Australia, 1991; p. 42. [Google Scholar]
- Ashton, D.H. The development of even-aged Stands of Eucalyptus regnans F. Muell. in central Victoria. Australian Journal of Botany 1976, 24, 397–414. [Google Scholar] [CrossRef]
- Ngatuvai, M.; Autrey, C.; McKenny, M.; Elkbuli, A. Significance and implications of accurate and proper citations in clinical research studies. Annals of Medicine and Surgery 2021, 72, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Dincă, L.C.; Dincă, M.; Vasile, D.; Spârchez, G.; Holonec, L. Calculating organic carbon stock from forest soils. Notulae Botanicae Horti Agrobotanici Cluj-Napoca 2015, 43, 568–575. [Google Scholar] [CrossRef]
- Allen, K.; Francey, R.; Michael, K.; Nunez, M. A structural time series approach to the reconstruction of Tasmanian maximum temperatures. Environmental Modelling & Software 1999, 14, 261–274. [Google Scholar] [CrossRef]
- REDD Forests Pty. Ltd. Reducing Carbon Emissions by Protecting a Native Forest in Tasmania; Sydney, New South Wales, Australia, 2009; p. 95. [Google Scholar]
- Forests Alive Pty. Ltd. New Leaf Carbon Project; Sydney, New South Wales, Australia, 2013; p. 143.
- Goodwin, A.N. A taper equation for Eucalyptus obliqua. In Proceedings of the IUFRO Conference (S 4.01, Mensuration, Canberra, Australia, 13-17 January 1992, 1992, Growth and Yield) on Integrating Forest Informatoin Over Space and Time; pp. 454–467.
- Grove, S.J.; Stamm, L.; Barry, C. Log decomposition rates in Tasmanian Eucalyptus obliqua determined using an indirect chronosequence approach. Forest Ecology and Management 2009, 258, 389–397. [Google Scholar] [CrossRef]
- Brack, C.L.; Richards, G.; Waterworth, R. Integrated and comprehensive estimation of greenhouse gas emissions from land systems. Sustainable Science 2006, 1, 91–106. [Google Scholar] [CrossRef]
- Waterworth, R.M.; Richards, G.P. Implementing Australian forest management practices into a full carbon accounting model. Forest Ecology and Management 2008, 255, 2434–2443. [Google Scholar] [CrossRef]
- Dean, C.; Fitzgerald, N.B.; Wardell-Johnson, G.W. Errata. Corrigendum. Plant Biosystems 2012, 146, 487. [Google Scholar] [CrossRef]
- Abbott, S. Photographing 'world's biggest blue gum' to shine light on 500 yo giant in logging coupe; Hobart, Australia, 04-November-2022 2023.
- Sanger, J.; Pearce, S. The Tree Projects. Available online: https://www.thetreeprojects.com/ (accessed on 07-October-2024).
- Sanger, J.; Pearce, S. The Tree Projects Facebook page. Available online: https://www.facebook.com/thetreeprojects (accessed on 07-October-2024).
- Sillett, S.C.; Van Pelt, R.; Koch, G.W.; Ambrose, A.R.; Carroll, A.L.; Antoine, M.E.; Mifsud, B.M. Increasing wood production through old age in tall trees. Forest Ecology and Management 2010, 259, 976–994. [Google Scholar] [CrossRef]
- Bowling, P.J. A volume table for regrowth of some Tasmanian eucalypts. Australian Forestry 1951, 15, 87–95. [Google Scholar] [CrossRef]
- Bi, H. Trigonometric variable-form taper equations for Australian eucalypts. Forest Science 2000, 46, 397–409. [Google Scholar] [CrossRef]
- Ilic, J. Woods of eucalyptus — part1. Distinguishing three species from the ash group (E. regnans, E. delegatensis and E. obliqua). IAWA Journal 1997, 18, 27–36. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Duque, W.B.C.D.A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; Henry, M.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Global Change Biology 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Ilic, J.; Boland, D.; McDonald, M.; Downes, G.; Blakemore, P. Woody Density Phase 1 — State of Knowledge. Technical Report No. 18; Australian Greenhouse Office, Commonwealth of Australia: Canberra, 2000; p. 218. [Google Scholar]
- Brack, C. Not everything that can be counted counts. Australian Forestry 2014, 77, 75–77. [Google Scholar] [CrossRef]
- Calders, K.; D’hont, B.; Hambrecht, L.; Lucieer, A.; Pearce, S. Lathamus Keep, Tasmania - 3D model by Q-ForestLab (Ghent University) (@CAVElab_UGent); Universiteit Gent: Ghent, Belgium, 2024. [Google Scholar]
- Sillett, S.C.; Pelt, R.V.; Carroll, A.L.; Jim Campbell-Spickler; Antoine, M. E. Aboveground biomass dynamics and growth efficiency of Sequoia sempervirens forests. Forest Ecology and Management 2020, 458, 1–43. [Google Scholar] [CrossRef]
- Calders, K.; D’hont, B.; Hambrecht, L.; Lucieer, A.; Pearce, S. High Res Slice of Lathamus Keep, Tasmania - 3D model by Q-ForestLab (Ghent University) (@CAVElab_UGent); Universiteit Gent: Ghent, Belgium, 2024. [Google Scholar]
- Roxburgh, S.H.; DataGrabber. Software Downloads. Available online: http://www.steverox.info/software_downloads.htm (accessed on 9 November 2010).
- Sillett, S.C. Tree crown structure and vascular epiphyte distribution in Sequoia sempervirens rain forest canopies. Selbyana 1999, 20, 76–97. [Google Scholar]
- Voigt, C. Impacts of Social Trails around Old-Growth Redwood Trees in Redwood National and State Parks. Humboldt State University, Arcata, California, 2016.
- Erwin, K. Fragile Majesty. The Battle for North America's Last Great Forest; The Mountaineers: Seattle, WA, USA, 1989; p. 272. [Google Scholar]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Zutta, W.S.B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; Petrova, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. PNAS 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Kurtz, B.C.; Almeida, T.M.H.d.; Coelho, M.A.N.; Deccache, L.S.J.; Tortorelli, R.M.; Gonzaga, D.R.; Madureira, L.K.; Guedes-Oliveira, R.; Barros, C.F.; Siqueira, M.F.d. Quantifying the carbon stocks in urban trees: The Rio de Janeiro Botanical Garden as an important tropical carbon sink. Journal of Zoological and Botanical Gardens 2024, 5, 579–589. [Google Scholar] [CrossRef]
- TWS. Victoria's Giant Trees. Tall and Big Tree news: From Victoria, Tasmania and occasionally other places!
- Holmes, A. Tasmania expands native logging harvest area as other states wind back; Australian Broadcasting Corporation: Hobart, Tasmania, Australia, 04-July-2023 2023. [Google Scholar]
- Hayward, M.W.; Meyer, N.F.V.; Balkenhol, N.; Beranek, C.T.; Bugir, C.K.; Bushell, K.V.; Callen, A.; Dickman, A.J.; Griffin, A.S.; Haswell, P.M.; et al. Intergenerational inequity: Stealing the joy and benefits of nature from our children. Frontiers in Ecology and Evolution 2022, 10, 1–6. [Google Scholar] [CrossRef]
- Makarieva, A.M.; Nefiodov, A.V.; Morozov, V.E.; Aleynikov, A.A.; Vasilov, R.G. Science in the vanguard of rethinking the role of forests in the third millennium: comments on the draft concept of the federal law "Forest Code of the Russian Federation". Forest Science Issues 2020, 3, 1–19. [Google Scholar] [CrossRef]
- Yu, B.; Fingrut, A. Sustainable building design (SBD) with reclaimed wood library constructed in collaboration with 3D scanning technology in the UK. Resources, Conservation & Recycling 2022, 186, 1–12. [Google Scholar] [CrossRef]
- Hayward, M.W. Problems with the World's Ecosystems: the Future and Attempts to Mitigate Decline. In The Living Planet: the State of the World's Wildlife, Maclean, N., Ed.; Cambridge University Press: Cambridge, England, 2023; pp. 349–367. [Google Scholar]
- Kamite, M. Compounding method for high quality building materials using fine-powder ligneous refuse technology. Transactions of the Materials Research Society of Japan 2001, 26, 817–820. [Google Scholar]
- Santos, G.; Esmizadeh, E.; Riahinezhad, M. Recycling construction, renovation, and demolition plastic waste: Review of the status quo, challenges and opportunities. Journal of Polymers and the Environment 2024, 32, 479–509. [Google Scholar] [CrossRef]
- Tao, J.; Tahmasebi, P.; Kader, M.A.; Feng, D.; Sahimi, M.; Evans, P.D.; Saadatfar, M. Wood biomimetics: Capturing and simulating the mesoscale complexity of willow using cross-correlation reconstruction algorithm and 3D printing. Materials & Design 2023, 228, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Jiang, L.; Zhang, L.; Raghavan, V.; Wang, J. A comprehensive review on novel synthetic foods: Potential risk factors, detection strategies, and processing technologies. Comprehenisve Reviews in Food Science and Food Safety 2024, 23, 1–32. [Google Scholar] [CrossRef]
- Komatsu, H.; Rappleye, J. Well-being in times of decline: The feasibility and effectiveness of degrowth for sustainability. Journal of Future Studies 2024, 29, 59–72. [Google Scholar] [CrossRef]
Table 4.
Carbon stocks (Mg ha-1) to 3 significant figures, live biomass includes roots (root/shoot ratio of 0.15) from: (a) from Figure 3.4 in Dean, et al. [307] from measurements and modelling in computer program CAR4D. Values read from the published figure are to +/-15 Mg ha-1, and (b) from [Table 1. in 88] a 450 year old oldgrowth E. obliqua-dominated stand.
Table 4.
Carbon stocks (Mg ha-1) to 3 significant figures, live biomass includes roots (root/shoot ratio of 0.15) from: (a) from Figure 3.4 in Dean, et al. [307] from measurements and modelling in computer program CAR4D. Values read from the published figure are to +/-15 Mg ha-1, and (b) from [Table 1. in 88] a 450 year old oldgrowth E. obliqua-dominated stand.
| (a). | ||||||||
| E. regnans age (years) | E. regnans | Understorey | Standing live | Dead trees, CWD & litter | Plant biomass (alive & dead) | SOC to -0.3 m | Total | |
| 215 | 553 | 70.8 | 624 | 20.3 | 644 | 197 | 1310 | |
| 321 | 438 | 343 | 781 | 15.5 | 796 | 197 | 1450 | |
| (b) | ||||||||
| E. obliqua | Understorey | Standing live | ||||||
| 733 | 22.5 | 755 | ||||||
Table 5.
Carbon stocks to 3 significant figures, of live and dead plant biomass [including roots with root:shoot = 0.15:1, and 25% senescence for the eucalyptus trees] derived from data collected in Dean, et al. [542] and using the updated allometric equations described above. The value in brackets for the site average carbon is the standard deviation from the plots, and the values in brackets for the individual plots are standard deviations accompanying the derivation of allometric equations used in the calculations— both ~28%. In the API-types: ‘co’=cut over (earlier selective logging), and ‘S’= scrub.
Table 5.
Carbon stocks to 3 significant figures, of live and dead plant biomass [including roots with root:shoot = 0.15:1, and 25% senescence for the eucalyptus trees] derived from data collected in Dean, et al. [542] and using the updated allometric equations described above. The value in brackets for the site average carbon is the standard deviation from the plots, and the values in brackets for the individual plots are standard deviations accompanying the derivation of allometric equations used in the calculations— both ~28%. In the API-types: ‘co’=cut over (earlier selective logging), and ‘S’= scrub.
| Plot # | phototype | projected area (ha) | C in live biomass (Mg ha-1) | C dead plant biomass (Mg ha-1) | C in live and dead plant biomass (Mg ha-1) |
| 1 | coEc1.M+ | 0.283 | 677 | 180 | 857 (240) |
| 2 | coEc1.M+ | 0.283 | 328 | 198 | 526 (147) |
| 3 | coEc1.M+ | 0.283 | 386 | 138 | 524 (147) |
| 4 | coEc1.M+ | 0.283 | 652 | 293 | 944 (264) |
| 5 | E2b.S | 1.13 | 564 | 112 | 676 (189) |
| 6 | E2f.M+ | 1.12 | 327 | 145 | 472 (132) |
| 7 | E2b.S | 1.12 | 410 | 88 | 498 (140) |
| 8 | coEc1.M+ | 1.12 | 643 | 232 | 875 (245) |
| 9 | E2d.M- | 1.12 | 451 | 108 | 559 (157) |
| 10 | coEc1.M+ | 0.908 | 344 | 171 | 515 (144) |
| site | 7.66 | 478(142) | 166(62) | 645 (180) |
Table 6.
Carbon stocks (Mg ha-1) in aboveground carbon pools from May, et al. [550] to 4 significant figures, of live and dead plant biomass, with added roots (root/shoot ratio of 0.15) and using the updated allometric. The values in brackets for the site average carbon pools are the standard deviations amongst the six plots. (a) live above ground derived from their Figure 110 (plus roots) and for totals: with carbon in dead biomass. (a) First study, spanning the Styx, Tyenna and Florentine Valleys. For the site averages the figures in brackets are the standard deviations from the 16 plots. (b) Second study, one site in each of the Styx and Florentine valleys. (c) Third study, Styx Valley.
Table 6.
Carbon stocks (Mg ha-1) in aboveground carbon pools from May, et al. [550] to 4 significant figures, of live and dead plant biomass, with added roots (root/shoot ratio of 0.15) and using the updated allometric. The values in brackets for the site average carbon pools are the standard deviations amongst the six plots. (a) live above ground derived from their Figure 110 (plus roots) and for totals: with carbon in dead biomass. (a) First study, spanning the Styx, Tyenna and Florentine Valleys. For the site averages the figures in brackets are the standard deviations from the 16 plots. (b) Second study, one site in each of the Styx and Florentine valleys. (c) Third study, Styx Valley.
| (a) | |||||||
| plot # | C in live biomass | Total (live plus dead above- and below-ground biomass) | |||||
| 1 | 808.7 | 952.5 | |||||
| 2 | 732.4 | 876.2 | |||||
| 3 | 668.4 | 812.2 | |||||
| 4 | 648.4 | 792.1 | |||||
| 5 | 557.5 | 701.2 | |||||
| 6 | 534.0 | 677.8 | |||||
| 7 | 408.1 | 551.8 | |||||
| 8 | 364.3 | 508.1 | |||||
| 9 | 357.1 | 500.8 | |||||
| 10 | 338.9 | 482.7 | |||||
| 11 | 255.2 | 398.9 | |||||
| 12 | 247.5 | 391.2 | |||||
| 13 | 244.5 | 388.3 | |||||
| 14 | 236.9 | 380.6 | |||||
| 15 | 226.0 | 369.7 | |||||
| 16 | 213.2 | 357.0 | |||||
| average | 429(201) | 573(201) | |||||
| (b) | |||||||
| location | PI type | C in live biomass | Total (live plus dead above- and below-ground biomass) | ||||
| Styx Valley | E1c.M+ or E1d.M+ | 636 | 736 | ||||
| Florentine Valley | E1a.M+ or E1b.M+ | 523 | 623 | ||||
| (c) | |||||||
| C in live biomass | C in dead biomass | Total (live plus dead above- and below-ground biomass) | |||||
| 780 | 196 | 977 | |||||
Table 7.
Carbon stocks (Mg ha-1) to 4 significant figures, live and dead plant biomass [including roots, root/shoot ratio= 0.15] derived from figures in Moroni and Lewis [532] and using the updated allometric. The values in brackets for the site average carbon pools are the standard deviations amongst the six plots. Note that the ‘total’ C includes their value for SOC of 179 Mg ha-1 down to an unstated depth, possibly to -0.3 m.
Table 7.
Carbon stocks (Mg ha-1) to 4 significant figures, live and dead plant biomass [including roots, root/shoot ratio= 0.15] derived from figures in Moroni and Lewis [532] and using the updated allometric. The values in brackets for the site average carbon pools are the standard deviations amongst the six plots. Note that the ‘total’ C includes their value for SOC of 179 Mg ha-1 down to an unstated depth, possibly to -0.3 m.
| plot # | C in live biomass | Debris | total C |
| 1 | 397.2 | 24.70 | 600.9 |
| 2 | 508.2 | 47.43 | 734.7 |
| 3 | 556.1 | 126.9 | 862.0 |
| 4 | 709.6 | 23.46 | 912.0 |
| 5 | 711.9 | 65.97 | 956.8 |
| 6 | 926.2 | 21.71 | 1127 |
| site | 634(187) | 52(41) | 866(182) |
Table 8.
Carbon stocks (Mg ha-1) to 3 significant figures, of live and dead plant biomass [including roots, root/shoot ratio= 0.15] and soil carbon, derived from Dean, et al. [92]. The value in brackets for the site average carbon is the standard deviation from the 10 plots. Some plots straddled two API-types: both are shown.
Table 8.
Carbon stocks (Mg ha-1) to 3 significant figures, of live and dead plant biomass [including roots, root/shoot ratio= 0.15] and soil carbon, derived from Dean, et al. [92]. The value in brackets for the site average carbon is the standard deviation from the 10 plots. Some plots straddled two API-types: both are shown.
| Plot # | phototype | projected area (ha) | live biomass | dead biomass | total biomass |
| 1 | M- & E1c.M+ | 1.11 | 474.1 | 45.92 | 520.0 |
| 2 | E2b.M- | 1.11 | 298.5 | 187.3 | 485.7 |
| 3 | E1c.M+ | 1.11 | 256.8 | 150.4 | 407.2 |
| 4 | E1c.M+ | 1.13 | 547.9 | 90.43 | 638.4 |
| 5 | E1c.M+ | 1.13 | 678.3 | 304.5 | 982.7 |
| 6 | E2c.M- | 1.11 | 399.4 | 64.61 | 464.0 |
| 8 | E1c.M+ | 1.11 | 649.6 | 133.2 | 792.7 |
| 9 | E1c.M+ & M-.E1f | 1.12 | 500.1 | 16.04 | 516.2 |
| 10 | M- & E1c.M+ | 1.12 | 409.8 | 109.1 | 518.9 |
| 11 | E1c.M+ | 1.11 | 402.9 | 83.31 | 486.2 |
| site | 11.16 | 462(137) | 119(83) | 580(176) |
Table 9.
Carbon stocks in different pools, from Sanger and Ferrari [529] but adjusted as described in the main text, to enable comparison on a level footing with other studies in Tasmanian. The error margins for live plant biomass are ±25%, and the error margins for coarse woody debris (standing and fallen, CWD) and soil organic carbon (SOC) to 0.3 m depth, were one standard error of their empirically determined variability.
Table 9.
Carbon stocks in different pools, from Sanger and Ferrari [529] but adjusted as described in the main text, to enable comparison on a level footing with other studies in Tasmanian. The error margins for live plant biomass are ±25%, and the error margins for coarse woody debris (standing and fallen, CWD) and soil organic carbon (SOC) to 0.3 m depth, were one standard error of their empirically determined variability.
| Carbon pool | C (Mg ha-1) | lower error margin | upper error margin |
| aboveground in trees > 2.5 m DBH | 369.6 | 277.2 | 462.1 |
| aboveground in trees from 1 to 2.5 m DBH | 120.4 | 90.27 | 150.4 |
| aboveground in understorey trees | 155.4 | 116.5 | 194.2 |
| roots | 96.81 | 72.61 | 121.0 |
| CWD | 252.6 | 205.1 | 299.4 |
| SOC to -0.3 m | 149 | 88.5 | 209 |
| live aboveground plant biomass | 645.4 | 484.0 | 806.7 |
| live plant biomass | 742.2 | 556.7 | 927.8 |
| total (plant biomass, plus SOC to -0.3 m) | 1144 | 850.2 | 1436 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





