Prerpints.org logo
Preprint
Article

Mechanical Properties of Two-Dimensional Metal Nitrides: Numerical Simulation Study

This version is not peer-reviewed.

Submitted:

08 October 2024

Posted:

09 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
It is expected that two-dimensional (2D) metal nitrides (MNs), consisting of the elements of the 13th group of the periodic table and nitrogen, namely aluminium nitride (AlN), gallium nitride (GaN), indium nitride (InN) and thallium nitride (TlN) have enhanced physical and mechanical properties, due to a honeycomb graphene-like atomic arrangement, characteristic to these compounds. The basis for the correct design and improved performance of nanodevices and complex structures based on 2D MNs of the 13th group is the understanding of the mechanical response of their components. In this context, a comparative study to determine the elastic properties of metal nitride nanosheets was carried out making use of the nanoscale continuum modelling (or molecular structural mechanics) method. The differences in the elastic properties (surface Young´s and shear moduli, and Poisson´s ratio) found for 2D 13th group MNs are attributed to the bond length of the respective diatomic hexagonal lattice. The results obtained contribute to a benchmark in the evaluation of mechanical properties of AlN, GaN, InN and TlN monolayers by analytical and numerical approaches.
Keywords: 
Subject: 
Engineering  -   Mechanical Engineering

1. Introduction

Two-dimensional (2D) metal nitrides (MNs) are attractive emergent materials with important forthcoming applications in advanced electronics, light industry, energy storage and strain engineering [1,2]. Compounds of elements from the 13th group of the periodic table, such as aluminium (Al), gallium (Ga), indium (In) and thallium (Tl), with nitrogen (N) are representatives of the MNs family, and their 2D allotropes exhibit planar hexagonal graphene-like lattice [3,4]. For this reason, 2D aluminium nitride (AlN), gallium nitride (GaN), indium nitride (InN) and thallium nitride (TlN) nanostructures, are envisioned to have superior physical and mechanical properties compared to those of respective bulk counterparts [4,5]. Hexagonal aluminium nitride (h-AlN), gallium nitride (h-GaN) and indium nitride (h-InN) are wide gap semiconductors and are capable of emitting light in green, blue and UV diapasons [6]. This makes h-AlN, h-GaN and h-InN promising materials in applications such as solid-state light-emitting devices (LED) and high-speed field-effect transistors (FETs) [4,7,8]. On the other hand, hexagonal thallium nitride (h-TlN) has a small or rather negative energy band gap [5,9]. The latter denotes a material with a very small overlap between the bottom of the conduction band and the top of the valence band. Such materials are commonly known as semimetals, which is the case of h-TlN. This points to h-TlN as a suitable candidate for infrared optical devices [10]. Among 2D MNs, nanosheets (NSs) of aluminium nitride, gallium nitride and indium nitride were already synthesized. The greatest success was achieved in the fabrication of AlN and GaN nanosheets. Aluminium nitride nanosheets (AlNNSs) growth methods include chemical vapor deposition (CVD) [11], molecular beam epitaxy (MBE) [12], physical vapour transport (PVT) [13] and metal–organic chemical vapour deposition (MOCVD) [14]. The developments of the growth of gallium aluminium nanosheets (GaNNSs), in addition to CVD [15] and MOCVD [16] techniques, owe to electrochemical etching (ECE) [17], UV-assisted electroless chemical etching [18] and ammonolysis of liquid metal derived oxides [19]. The latter was also used to produce indium nitride nanosheets (InNNSs) [19]. The MBE [20] and MOCVD [21] techniques were also employed to synthesize InNNSs. Thallium nitride nanosheets (TlNNSs) have not yet been synthesized and 2D TlN is only in the focus of computational investigations, so far [4,5,10].
Moreover, in the work of Singh et al. [22] computational synthesis of the hexagonal AlN, GaN and InN monolayers was suggested, based on ab initio density functional theory (DFT) calculations. The results are helpful to establish suitable synthesis conditions for 2D MNs, including identifying the best substrates for their growth and stabilization.
A key to the accurate design and improved performing of innovative nanodevices and systems based on two-dimensional MNs is understanding the mechanical behaviour of their constituents. To the best of our knowledge, the mechanical response of the MN nanosheets has only been investigated theoretically up to now. To this end, most research has resorted to ab initio DFT calculations and molecular dynamics (MD), which are encompassed in atomistic approaches. The ab initio DFT method, which is suitable for a small number of atoms and requires substantial computational resources, was used in the works of Jafari et al. [23], Peng et al. [24], Kourra et al. [25] and Lv et al. [26] to assess the elastic properties of AlN nanosheets. Tuoc et al. [27] and Fabris et al. [28] employed the same approach to study the mechanical behaviour of GaN nanosheets, and Ahangari et al. [29] used it for the same type of study of AlNNSs and GaNNSs. Also, ab initio DFT calculations were employed in two works by Peng at al. [30,31] to assess the elastic constants of InNNSs [30] and TlNNSs [31]. Regarding the evaluation of the elastic properties of AlN, GaN and InN nanosheets, Luo et al. [32] and Faraji et al. [33] also used ab initio DFT calculations. Although the ab initio DFT approach is established as more accurate method than MD, the latter is more cost-effective for large atomic configurations. The MD method requires potential functions for modelling the interactions between the 13th group and nitrogen atoms, the choice of which, to a large extent, influences the results. Rouhi et al. [34] studied the mechanical response of the GaN nanosheets, carrying out MD simulations with Tersoff-Brenner (TB) potential function. Singh et al. [35] determined the elastic constants of AlNNSs, GaNNSs and InNNSs, employing the TB potential to describe the interatomic interactions in respective diatomic nanostructure. In a MD simulation study with Tersoff-like potentials, Le [36] evaluated the tensile properties of aluminium nitride, gallium nitride and indium nitride NSs. Sarma et al. [37] investigated the mechanical behaviour of GaN nanosheets using Stillinger–Weber (SW) potential in their MD simulation study.
In addition to resource consuming atomistic approaches, the nanoscale continuum modelling (NCM) method has been used for modelling the mechanical behaviour of 2D MNs. The NCM, also called molecular structural mechanics (MSM) approach, has proven to be a fast and reliable method for evaluating the mechanical properties of 1D and 2D nanostructures with graphene and graphene-like lattices due to its simplicity and straightforward mathematical formulation in contrast to the atomistic approaches (see, for example [38,39,40,41]). The NCM/MSM approach is based on the connection between the molecular structure and solid mechanics in such a way that the bonds between 13th group (Al, Ga, In, Tl) and N atoms are represented as elastic elements, most often beams or springs. Le [42] derived a closed-form solution within the NCM/MSM approach, to calculate the Young´s modulus of aluminium nitride NSs. Ben et al. [2] assessed the maximum stress and tensile strain of AlNNSs, GaNNSs and InNNSs using the respective closed-form expressions, within the scope of the NCM/MSM method. Using the same approach, Giannopoulos et al. [43] modelled the interatomic bonding between Ga and N atoms as spring elements to study the tensile behaviour of GaN nanosheets. In two their works Sakharova et al. [44,45] in the framework of the NCM/MSM method, interatomic bonds were represented as beam elements to evaluate the Young´s modulus of square InNNSs [44], and Young´s and shear moduli of AlNNSs and GaNNSs, over a wide range of their aspect ratios [45].
It is worth noting that there is a certain inconsistency in the elastic properties of 2D MNs reported in the literature. Also, it can be concluded that research on the mechanical behaviour of 2D metal nitrides is not systematized to date and focuses mainly on AlNNSs and GaNNSs, while studies, which include two other representatives of MNs, are less frequent (InNNSs) or very rare (TlNNSs).
The aim of the current work is to carry out a systematic comparative study on the evaluation of the surface Young´s and shear moduli, and Poisson´s ratio of aluminium nitride, gallium nitride, indium nitride and thallium nitride nanosheets (AlNNSs, GaNNSs, InNNSs and TlNNSs). With this purpose, a three-dimensional finite element (FE) model was built under the NCM/MSM approach. In view of the lack of information on the value of nanosheet thickness for MNs, the surface elastic moduli were selected for analysis in this study. It is expected that the present work will contribute to the knowledge of the mechanical response of the two-dimensional metal nitrides and unlock new perspectives of their applications in novel nanodevices.

2. Materials and Methods

2.1. Modeling of the Elastic Behaviour of MN Nanosheets

The bonds between atoms of the diatomic MN lattices were modelled as equivalent beam elements within the scope of the NCM/MSM approach. The resulting equivalent continuum structure is characterised by the tensile, E b A b , bending, E b I b , and torsional, G b J b , rigidities of the beams, which are linked to the molecular structure of the nanosheet, through bond stretching, k r , bond bending, k θ , and torsional resistance, k τ , force field constants, as follows [46]:
E b A b = l k r ,   E b I b = l k θ ,   G b J b = l k τ ,
where, A b = π d 2 / 4 is the cross-section area, I b = π d 4 / 64 is the moment of inertia, and J b = π d 4 / 32 is the polar moment of inertia of beam element, which has a circular cross-section and diameter d, and l is the beam length, equal to the bond length of the diatomic metal nitride nanostructures, a M - N .
Equations (1) permit calculating the input parameters for the numerical simulation making use of the k r , k θ , and k τ force field constants. For the metal nitrides under study, the bond stretching, k r , and bond bending, k θ , force constants values are scarce in the literature. Consequently, in the current work, the bond stretching and bond bending force constants were assessed by the method based on analytical expressions from the molecular mechanics (MM) for the surface Young's modulus, E s , and the Poisson's ratio, ν . The E s and ν , values can be obtained using DFT calculations or experimentally. The k r and k θ force field constants are related to E s and ν through the following expressions [47]:
E s = 4 3 k r k θ k r a M - N 2 2 + 9 k θ ν = k r a M - N 2 – 6 k θ k r a M - N 2 + 18 k θ .
The bond stretching, k r , and bond bending, k θ , force constants are assessed by solving the system of equations (2), as follows:
k r = 3 E s 3 1 - ν ,
k θ = E s a M - N 2 2 3 1 + 3 ν .
The bond length, a M - N , the surface Young's modulus, E s , and the Poisson's ratio, ν , required for computing the bond stretching, k r , and bending, k θ , force constants (Equations (3) and (4)) together with their calculated values are shown in Table 1. The torsional resistance force constant, k τ , was obtained basing on DREIDING force field [48], which allow describing the torsional behaviour of the diatomic nanostructure based only on the hybridization of the atoms. The value of k τ is also presented in Table 1.
The knowledge of the values of k r , k θ , and k τ (Table 1) permits calculating the geometrical and elastic properties of the beams (input values for the numerical simulation) by Equations (1), assuming that a M - N = l, as shown in Table 2.

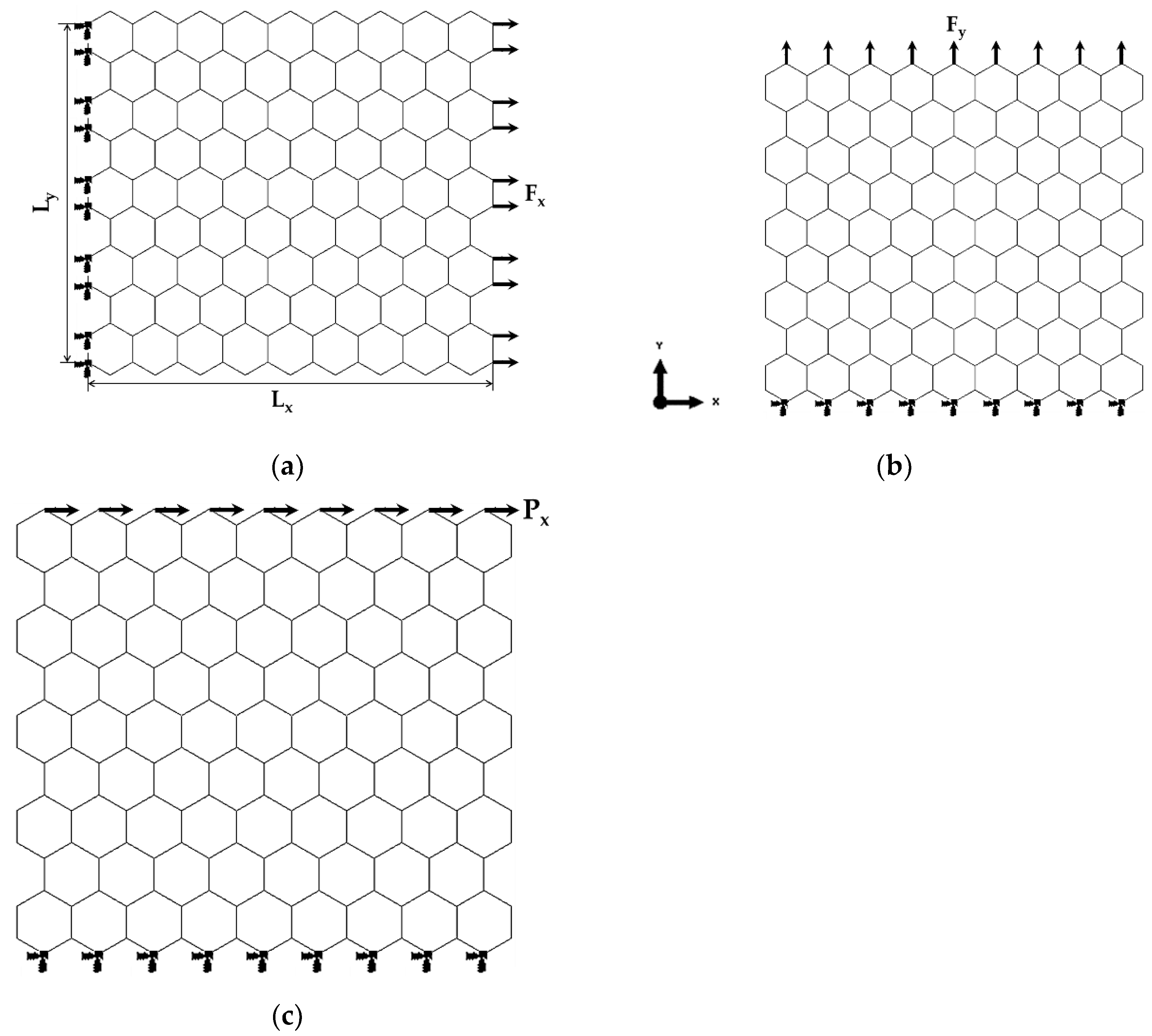
2.2. Finite Element Analysis and Elastic Properties of MN Nanosheets

Square single-layer AlNNSs, GaNNSs, InNNSs and TlNNSs nanosheets with dimensions ≈ 15×15 nm2 were studied. This size of NS was chosen to ensure that the NSs mechanical response is independent of their size, since the elastic properties of square nanosheets have been shown to be nearly constant with increasing the NS side lengths, with an exception of the range of small NSs [45,49]. The finite element (FE) meshes of the MN nanosheets were obtained in the form of the Program Database files, using the Nanotube Modeler© software. The bond lengths for FE meshes of AlNNSs and GaNNSs, a Al - N = 0.183 nm and a Ga - N = 0.195 nm, respectively, were assumed as defined by the Nanotube Modeler© program. For InNNSs and TlNNSs, the bond lengths a In - N = 0.206 nm [3] and a Tl - N = 0.2154 nm [4] were respectively adopted. The next step was to convert the Program Database files to a format usable by ABAQUS® FE code, resorting to the in-house application InterfaceNanosheets.NS [49]. Afterwards, the abovementioned code was used to perform finite element analysis (FEA) of the elastic response of MN nanosheets under numerical tensile and in-plane shear tests.
To simulate the elastic behaviour of NSs along the x-direction, an axial tensile load, F x , is applied to the edge nodes of the NS right side, leaving the opposite side fixed (Figure 1a). The Young´s modulus along the x-axis, E x , is determined as [40]:
E x   =   F x L x u x L y t n ,
where u x is the NS axial displacement (elongation in the x-direction) taken from FEA; L x and L y are the NS side lengths (see, Figure 1a); t n is the nanosheet thickness.
In turn, based on the results of the tensile test used to assess E x , the Poisson´s ratio, ν xy , is evaluated as follows [40]:
ν xy = u y L x u x L y ,
where u y is transversal displacement, measured in the FEA, at x = L x / 2 .
Similarly, to simulate tension along the y-direction, an axial force, F y , is applied to the nodes of the NS upper side, leaving the lower side fixed (Figure 1b). The Young´s modulus along the y-axis, E y , is determined as follows [40]:
E y   =   F y L y v y L x t n ,
where v y is the NS axial displacement in the y-direction, taken from FEA.
The two tensile loading conditions of the MN nanosheets, as shown in Figure 1a and Figure 1b, represent zigzag and armchair configurations, respectively.
To simulate the in-plain shear test, the shear load, P x , is applied to the NS upper side, leaving the edge nodes of the NS bottom side fixed (Figure 1c). Consequently, the NS shear modulus, G xy , is calculated as follows [40]:
G xy   =   P x γ xy L x t n ,   γ xy =   t a n s x L y ,
where s x is the displacement along x-axis, taken from the FEA and measured in the nanosheet central part; L x and L y are the NS side lengths (see, Figure 1a); t n is the NS thickness.
In the current study, assuming the lack of knowledge of the value of t n for the MNs, the surface Young’s and shear moduli, E s x , E sy and G sxy (the product of the respective elastic modulus by the NS thickness) were calculated instead of E x , E y and G xy . To this end, Equations (6) – (8) are transformed as follows:
E s x = E x t n = F x L x u x L y ,
E sy = E y t n = F y L y v y L x ,
G sxy = G xy t n = P x γ xy L x .

3. Results and Discussion

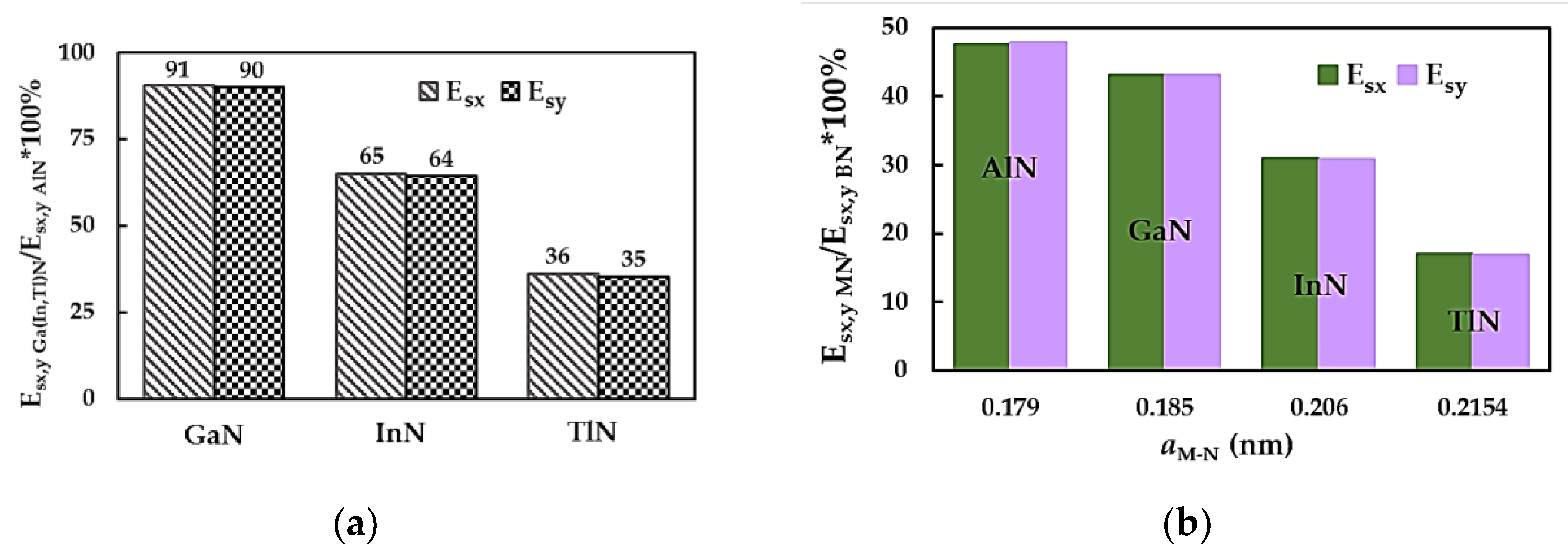
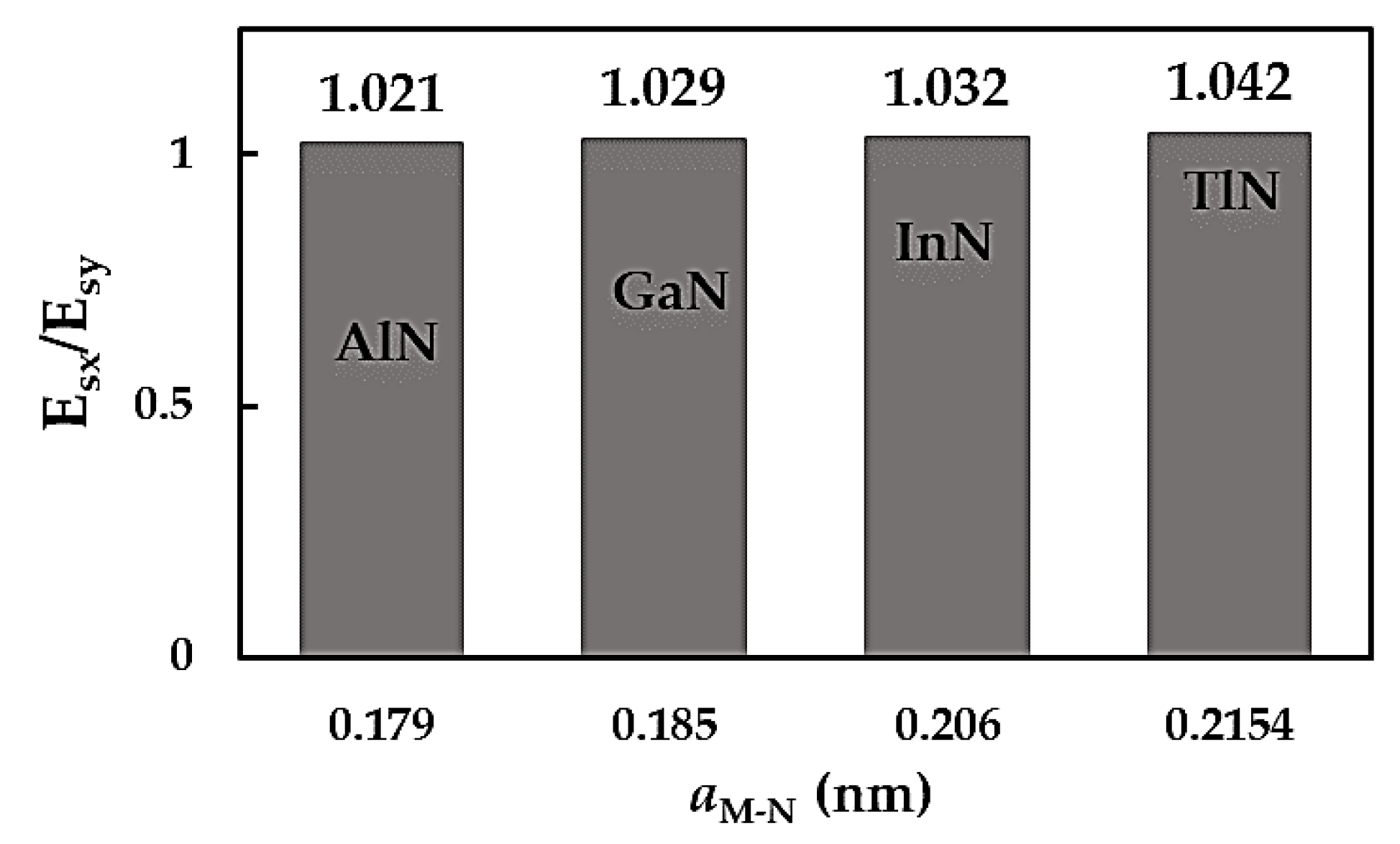
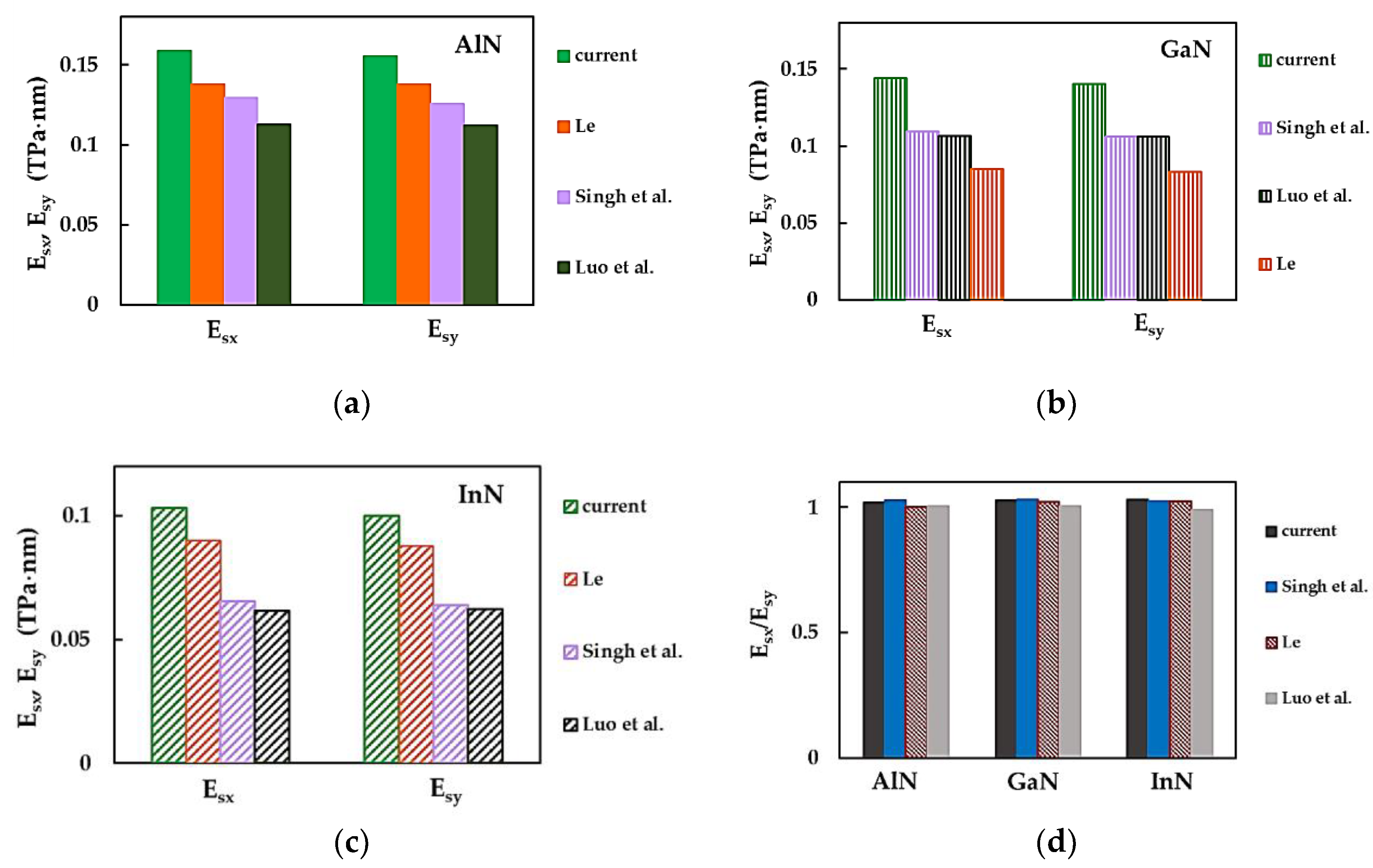
3.1. SurfaceYoung´s Moduli and Poisson´s Ratio of MN Nanosheets

The surface Young’s moduli of metal nitride NSs in the x-direction (zigzag configuration), E sx , and in the y-direction (armchair configuration), E sy , were calculated by Equations (9) and (10), respectively, using the tensile simulation results. The values of E sx and E sy as a function of the bond length, a M - N , are shown in Figure 2a and Figure 2b, respectively, for AlN, GaN, InN and TlN nanosheets. The surface Young’s moduli, E sx , y , of 2D MNs decreases with increasing of the a M - N value. The smaller the interatomic bond length, the higher the E sx , y value. Thus, the highest surface Young´s modulus is observed for NSs of AlN. The average E sx , y values for GaNNSs, InNNSs and TlNNSs are approximately 90%, 65% and 36%, respectively, of that calculated for AlNNSs (see, Figure 3a). In order to understand how best to use metal nitride monolayers in the construction of novel nanodevices, the surface Young´s moduli, E sx , y , of AlNNSs, GaNNSs, InNNSs and TlNNSs, normalized by those for boron nitride nanosheets (BNNSs) are plotted in Figure 3b. Boron (B) is a non-metal, which belongs to the 13th group of the periodic table as metals Al, Ga, In and Tl, and hexagonal boron nitride (h-BN) is an insulator with remarkable mechanical properties, similar to graphene [50,51]. The surface Young´s moduli of BNNSs for the zigzag and armchair configurations, calculated from the Young´s modulus results of Sakharova et al. [49], E sx = 0.334 TPa⋅nm and E sy = 0.324 TPa⋅nm, respectively, were considered for comparison purpose.
As shown in Figure 3b, the E sx , y values of AlNNSs, GaNNSs, InNNSs and TlNNSs are about 48%, 43%, 31% and 17%, respectively, of the BNNSs surface Young’s moduli. Even the most mechanically resistant of the MNs group, the aluminium nitride NSs, have the E sx , y values, which are almost twice lower than those of boron nitride NSs. This must be taken into consideration when developing novel applications, involving MN monolayers. To take better advantage of the electronic, optical and thermal properties of 2D metal nitrides without compromising robustness and operation of nanodevices and systems, the MN nanosheets, especially those with weaker tensile properties such as InNNSs and TlNNSs, should be combined with, for example, BNNSs or graphene. It is worth noting that the surface Young´s moduli of 2D nanostructures formed by 13th group-nitride compounds are close to those of their 1D counterparts, i.e. nanotubes (NT) [52]. Thus, both 1D and 2D allotropes can be exploited in design and manufacturing of innovative nanodevices, without losing their strength and durability.
It can be observed that the surface Young's modulus of the MN nanosheets is to some extent higher for the zigzag configuration than for the armchair configuration, E sx > E sy , which indicates an anisotropy of AlNNSs, GaNNSs, InNNSs and TlNNSs. In a previous study by the authors [49], such anisotropic behaviour was reported for the case of BNNSs and was explicated by dissimilar stresses necessary for elongation of the hexagonal lattice along the x- and y-directions; this is because the atomic arrangement for zigzag configuration differs from that of the armchair configuration, with respect to the applied axial load. The anisotropic NSs behaviour can be quantified by the ratio between the surface Young´s moduli in zigzag and armchair directions, E sx / E sy . The evolution of the E sx / E sy ratio for 2D MN nanostructures with their bond length, a M - N , is shown in Figure 4.
The E sx / E sy ratio increases from 1.021 (AlNNSs) to 1.042 (TlNNSs) with increasing bond length, a Al - N = 0.179 nm < a Ga - N = 0.185 nm < a In - N = 0.206 nm < a Tl - N = 0.215 nm. It can be concluded that the metal nitride nanosheets exhibit a mild anisotropy regardless of the compound that forms the 2D MN nanostructure.
For comparison purposes, the current surface Young’s moduli, E sx and E sy , and their ratio, E sx / E sy , together with the respective results from the literature are plotted in Figure 5, for AlN, GaN and InN nanosheets. A reasonable concordance (difference ≈ 14%) is observed when the E sx , y values, calculated in the present study for AlNNSs and InNNSs, are compared with those reported by Le [36], who used the analytical expression obtained within the NCM/MSM method. The surface Young´s moduli evaluated by Singh et al. [35] for GaNNSs and InNNSs are in a very good agreement with the respective E sx , y values, assessed by Luo et al. [32] (see, Figure 5b,c). To this end, Singh et al. [35] employed MD simulations with TB potential function to describe the interactions between Ga (In) and N atoms, while Luo et al. [32] used the ab initio DFT calculations.
Regarding the ratio between the surface Young’s moduli in the zigzag and armchair directions, Le [36] for AlNNSs and Luo et al. [32] for AlNNSs and GaNNSs found that E sx / E sy ≈ 1, which suggests an isotropic behaviour of these MN nanosheets (see, Figure 5d). On the other hand, Le [36] reported the anisotropic behaviour for GaNNSs and InNNSs, and Luo et al. [32] for InNNSs. In the latter case, the ratio E sx / E sy < 1 occurs. According to Singh et al. [35], the AlNNSs, GaNNSs and InNNSs under study are transversely anisotropic. For all metal nitride NSs from Figure 5d, which demonstrate anisotropic behaviour, except for the InNNSs studied by Luo et al. [35], the surface Young´s modulus in the zigzag direction is slightly higher than in the armchair direction, E sx > E sy , i.e. E sx / E sy > 1. The current E sx / E sy ratios for aluminium nitride, gallium nitride and indium nitride NSs are in a good agreement (the biggest difference of 0.87%) with those reported in the literature, meaning a mild nanosheet anisotropy in the transversal direction.
Figure 6 compares the current average values of the surface Young´s modulus, calculated by E sNS = E sx + E sy / 2 , for InNNSs and TlNNSs with those reported by Peng et al. [30,31]. The choice of InN and TlN nanosheets was due to the fact that the comprehensive comparison of the E sNS moduli for AlNNSs and GaNNSs with the results available in the literature has been performed by the authors in previous work [45].
Currently used NCM/MSM approach leads to higher E sNS values for InNNSs and TlNNSs when compared with the respective results from the works [30,31,33]. Faraji et al. [33] and Peng et al. [30] assessed the surface Young´s modulus of InNNSs resorting to Vienna ab initio simulation package (VASP) for the ab initio DFT calculations. Both studies implemented the generalized gradient approximation (GGA) parameterized by the Perdew– Burke– Ernzerhof (PBE) functional to describe the exchange–correlation energy. Although the calculation approach is similar, it leads to different surface Young´s modulus results for InNNSs. Figure 5a-c and Figure 6 shows a noticeable scattering of the surface Young´s modulus values of MN nanosheets, as well a lack of the results, especially for thallium nitride NSs.
The metal nitrides NSs Poisson´s ratio, ν xy , calculated by Equation (6), is shown in Figure 7a as a function of the diatomic structure bond length, a M - N . The value of ν xy of metal nitride NSs increases nearly twofold, from 0.12 (AlNNSs) to 0.25 (TlNNSs), with increasing of a M - N . The Poisson´s ratio for AlNNSs, GaNNSs and InNNSs consists about 48%, 57% and 73%, respectively, of ν xy obtained for TlNNSs, as shown in Figure 7b.
Figure 8 compares the current Poisson´s ratio results with those from the literature for MN nanosheets. The values of ν xy calculated in the present study for AlNNSs, GaNNSs, InNNSs and TlNNSs are considerably lower than those evaluated by Luo et al. [32], Singh et al. [35], Faraji et al. [33] and Peng et al. [30,31].
A good agreement is observed between the ν xy values assessed by Luo et al. [32] and Singh et al. [35], with differences of ≈ 2.9%, 2.2% and 3.7% for AlNNSs, GaNNSs and InNNSs, respectively. In both studies the atomistic approach was used, although Luo et al. [32] has calculated the Poisson´s ratio employing the VASP within ab initio DFT method and GGA-PBE for the exchange–correlation energy, and Singh et al. [35] used MD simulations with TB potential to this end. It is worth noting that Faraji et al. [33], who used the same calculation methodology as Luo et al. [32], obtained the values of ν xy being ≈ 58%, 58% and 54%, of those by Luo et al. [32], for the corresponding AlN, GaN and InN nanosheets.
Despite the values of the Poisson´s ratio reported by Luo et al. [32], Singh et al. [35] and Faraji et al. [33] for AlN, GaN and InN nanosheets are different from those currently computed, the evolution trends of ν xy with the bond length, a M - N , are comparable. As seen in Figure 8a, the values of ν xy for AlNNSs, GaNNSs and InNNSs obtained by Luo et al. [32], Singh et al. [35] and Faraji et al. [33], increase when a M - N increases, although the Poisson´s ratios for AlNNSs and GaNNSs are similar. This can be explained by close values of the bond length, a Al - N and a Ga - N , used in these studies [32,33,35].
It can be concluded from Figure 8 that, for metal nitride NSs, there is a scarcity and spread of the Poisson´s ratio values. Considerably more ν xy results are necessary to build a reliable benchmark for ascertaining this elastic property by theoretical methods.

3.2. Surface Shear Modulus of MN Nanosheets

The evolution of the surface shear modulus, G sxy , for AlNNSs, GaNNSs, InNNSs and TlNNSs, calculated with aid of Equation (11), as a function of the respective bond length, a M - N , is shown in Figure 9. G sxy decreases from 0.029 TPa⋅nm (AlNNSs) to 0.012 TPa⋅nm (TlNNSs), when the value of a M - N increases.
Figure 10a facilitates the comparison of the surface shear modulus results for the metal nitrides NSs under study, G sxy , of GaNNSs, InNNSs and TlNNSs, by normalizing by that of AlNNSs, which has the biggest G sxy value among the MNs group. The surface shear modulus of GaN, InN and TlN nanosheets is about 96%, 67% and 40%, respectively, of G sxy of aluminium nitride NSs. As can be noticed from the results shown in Figure 10a, the surface shear moduli of AlNNSs and GaNNSs have close values.
Similar to the case of the surface Young´s modulus of MN nanosheets (see, Figure 3b), their surface shear modulus was compared with that of boron nitride NSs, as shown in Figure 10b. G sxy calculated for AlNNSs, GaNNSs, InNNSs and TlNNSs are ≈ 45%, 43%, 30% and 18%, respectively, of the BNNSs surface shear modulus. To better understand the current results of the surface shear modulus, G sxy , values for metal nitride NSs are plotted together with the surface shear modulus of the respective NTs, G sNTs , in Figure 11. The values of G sNTs were taken from previous work by the authors [52] and, similar to the current study, were obtained resorting to the numerical simulation within the NCM/MSM approach. To complete the comparison, the G sxy and G sNTs values of boron nitride NSs [49] and NTs [39] are also plotted in Figure 11.
Contrasting the surface Young´s moduli of NTs and NSs of the 13th group – nitride compounds (see, 3.1. SurfaceYoung´s moduli and Poisson´s ratio of MN nanosheets), the nanotubes surface shear modulus is 2.5, 2.2, 2.0, 1.9, 1.6 times bigger than G sxy of boron nitride, aluminium nitride, gallium nitride, indium nitride and thallium nitride nanosheets, respectively. It can be concluded that NSs (2D nanostructures) based on the nitride compounds have inferior shear properties when compared to their 1D (NTs) counterparts. This should be taken into account in design of nanodevices and systems, where higher mechanical resistance of the constituents to the applied shear stress is required.
As far as we know, results on the surface shear modulus for MN nanosheets are scarce or even non-existent (the case of TlNNSs) in the literature. Figure 12 compares the current values of the surface shear modulus for AlNNSs, GaNNSs and InNNSs with those from the works by Luo et al. [32] and Singh et al. [35].
The G sxy value calculated in the present study for InNNSs shows a very good concordance when compared to those reported by Singh et al. [35] and Luo et al. [32], with the respective differences of about 0.9% and 5.6%. For AlNNSs and GaNNSs, the current value of G sxy is considerably lower (in a range of 30% to 49%) than those assessed by Singh et al. [35] and Luo et al. [32]. In these studies, the differences between the surface shear moduli are 10.0%, 4.8% and 6.1% for AlN, GaN and InN nanosheets, respectively. The decreasing trend in the evolution of the surface shear modulus with increasing bond length is observed in the current work, similar to the results reported by Singh et al. [35] and Luo et al. [32] (see Figure 12). In short, the scarcity of G sxy values in the literature to date does not allow pertinent conclusions to be drawn with regard to the mechanical response of the metal nitride NSs under shear loading. Furthermore, more shear modulus results are required to establish a reference for evaluating the shear elastic properties of MN nanosheets by theoretical approaches. The present study attempts to fill this gap.

4. Conclusions

In the current work, the elastic properties (surface Young’s and shear moduli, and the Poisson´s ratio) of 2D metal nitrides with graphene-like lattice (AlNNSs, GaNNSs, InNNSs and TlNNSs) were evaluated, basing on the NCM/MSM method. To the best of our knowledge, this systematic comparative study, which comprises all metals of the 13th group of the periodic table, was performed for the first time. The main conclusions are given below.
The surface Young’s and shear moduli, and the Poisson´s ratio of AlN, GaN, InN and TlN nanosheets are sensitive to the bond length of the honeycomb diatomic arrangement. The surface Young´s and shear moduli decrease, while the Poisson´s ratio increases, with increasing interatomic bond length.
The surface Young’s modulus of AlNNSs, GaNNSs, InNNSs and TlNNSs is, at least, half of that obtained for boron nitride or graphene nanosheets. This result should be taken into account during the design of prospective complex systems and nanodevices, where 2D metal nitride nanostructures are considered as potential constituents.
It was shown that the surface shear modulus of the 2D nitride nanostructures (NSs) is about two times lower than that observed for their 1D counterparts (NTs), indicating weaker mechanical properties of the nitride nanosheets under in-plane shear loading.
The results achieved represent a substantial input to the knowledge and determination of the elastic properties of metal nitride nanosheets by analytical and numerical approaches.

Author Contributions

Conceptualization, N.A.S. and A.F.G.P.; methodology, N.A.S. and J.M.A.; investigation, N.A.S. and A.F.G.P.; software, J.M.A.; formal analysis, N.A.S., J.M.A. and A.F.G.P.; writing - original manuscript, N.A.S.; writing - review and editing, all the authors. All authors have read and agreed to publish this version of the manuscript.

Funding

This research is sponsored by FEDER funds through the program COMPETE—Programa Operacional Factores de Competitividade—and by national funds through FCT, Fundação para a Ciência e a Tecnologia, under the projects CEMMPRE - UIDB/00285/2020 and ARISE - LA/P/0112/2020

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author after obtaining permission of authorized person.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Zheng, F.; Xiao, X.; Xie, J.; Zhou L.; Li, Y.; Dong, H. Structures, properties and applications of two-dimensional metal nitrides: from nitride MXene to other metal nitrides. 2D Mater. 2022, 9, 022001. [CrossRef]
  2. Ben, J.; Liu, X.; Wang, C.; Zhang, Y.; Shi, Z.; Jia, Y.; Zhang, S.; Zhang, H., Yu, W.; Li D.; Sun, X. 2D III-Nitride Materials: Properties, Growth, and Applications. Adv. Mater. 2021, 33, 2006761.
  3. Şahin, H.; Cahangirov, S.; Topsakal, M.; Bekaroglu, E.; Akturk, E.; Senger, R.T.; Ciraci, S. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations. Phys. Rev. B 2009, 80, 155453. [CrossRef]
  4. Ye, C.; Peng, Q. Mechanical Stabilities and Properties of Graphene-like 2D III-Nitrides: A Review. Crystals 2023, 13, 12. [CrossRef]
  5. Elahi, S.M.; Farzan, M.; Salehi, H.; Abolhasani, M.R. An investigation of electronic and optical properties of TlN nanosheet and compare with TlN bulk (Wurtzite) by first principle. Optik 2016, 127, 9367 – 9376. [CrossRef]
  6. Vurgaftman, I.; Meyer, J.R. Band parameters for nitrogen-containing semiconductors. J. Appl. Phys. 2003, 94, 3675 – 3696. [CrossRef]
  7. Wu, K.; Huang, S.; Wang W.; Li, G. Recent progress in III-nitride nanosheets: properties, materials and applications. Semicond. Sci. Technol. 2021, 36, 123002. [CrossRef]
  8. Wang, Z.; Wang, G.; Liu, X.; Wang, S.; Wang, T.; Zhang, S.; Yu, J.; Zhao G.; Zhang, L. Two-dimensional wide band-gap nitride semiconductor GaN and AlN materials: properties, fabrication and application. J. Mater. Chem. C 2021, 9, 17201–17232. [CrossRef]
  9. Zaoui, A. Plane wave pseudopotential study of ground state properties and electrochemical description of thallium nitride. Mater. Sci. Eng.B 2003, 103, 258 – 261. [CrossRef]
  10. Abdullah, N.R..; Abdullah, B.J.; Gudmundsson, V. Electronic and optical properties of metallic nitride: A comparative study between the MN (M = Al, Ga, In, Tl) monolayers. Solid State Commun. 2022, 346, 114705. [CrossRef]
  11. Zhang, X.; Liu, Z.; Hark, S. Synthesis and optical characterization of single-crystalline AlN nanosheets. Solid State Commun. 2007, 143, 317–320. [CrossRef]
  12. Borisenko, D.P.; Gusev, A.S.; Kargin, N.I.; Komissarov, I.V.; Kovalchuk N.G.; Labunov, V.A. Plasma assisted-MBE of GaN and AlN on graphene buffer layers. Jpn. J. Appl. Phys. 2019, 58, SC1046. [CrossRef]
  13. Yang, F.; Jin, L.; Sun, L.; Ren, X.; Duan, X.; Cheng, H.; Xu, Y.; Zhang, X.; Lai, Z.; Chen, W.; Dong H.; Hu, W. Free-standing 2D hexagonal aluminum nitride dielectric crystals for high-performance organic field-effect transistors. Adv. Mater. 2018, 30, 1801891. [CrossRef]
  14. Wang, W.L.; Zheng, Y.L.; Li, X.C.; Li, Y.; Zhao, H.; Huang, L.G.; Yang, Z.C.; Zhang X.N.; Li, G.Q. 2D AlN layers sandwiched between graphene and Si substrates. Adv. Mater. 2019, 31, 1803448. [CrossRef]
  15. Chen, Y.X.; Liu, K.L.; Liu, J.X.; Lv, T.R.; Wei, B.; Zhang, T.; Zeng, M.Q.; Wang Z.C.; Fu, L. Growth of 2D GaN single crystals on liquid metals. J. Am. Chem. Soc. 2018, 140, 16392–16395. [CrossRef]
  16. Wang, W.L.; Li, Y.; Zheng, Y.L.; Li, X.C.; Huang L.G.; Li, G.Q. Lattice structure and bandgap control of 2D GaN grown on graphene/Si heterostructure. Small 2019, 15, 1802995. [CrossRef]
  17. Zhang, Z.; Zhang, S.; Zhang, L.; Liu, Z.; Zhang, H.; Chen, J.; Zhou, Q.; Nie, L.; Dong, Z.; Pan, G. Honeycomb-like gallium nitride prepared via dual-ion synergistic etching mechanism using amino acid as etchant. Chem. Phys. Lett. 2021, 773, 138588. [CrossRef]
  18. ElAfandy, R.T.; Majid, M.A.; Ng, T.K.; Zhao, L.; Cha, D.; Ooi, B.S. Exfoliation of threading dislocation-free, single-crystalline, ultrathin gallium nitride nanomembranes. Adv. Funct. Mater. 2014, 24, 2305–2311. [CrossRef]
  19. Syed, N.; Zhang, Y.; Zheng, G.; Wang, L.; Russo, S.P.; Esrafilzadeh, D.; McConville, C.F.; Kalantar-Zadeh, K.; Daeneke, T. Wafer-Sized Ultrathin Gallium and indium nitride nanosheets through the ammonolysis of liquid metal derived oxides. J. Am. Chem. Soc. 2019, 141, 104 – 108. [CrossRef]
  20. Wang, X, Che, S.-B.; Ishitani, Y.; Yoshikawa, A.; Sasaki, H.; Shinagawa, T., Yoshida, S. Polarity inversion in high Mg-doped In-polar InN epitaxial layers. Appl. Phys. Lett. 2007, 91, 081912. [CrossRef]
  21. Pécz, B.; Nicotra, G., Giannazzo, F., Yakimova, R., Koos, A.; Georgieva, A.K. Indium Nitride at the 2D Limit. Adv. Mater. 2021, 33, 2006660. [CrossRef]
  22. Singh, A.K.; Zhuang, H.L.; Hennig, R.G. Ab initio synthesis of single-layer III-V materials. Phys. Rev. B 2014, 89, 245431.
  23. Jafari, H.; Ravan, B.A.; Faghihnasiri, M. Mechanical and electronic properties of single-layer TiN and AlN under strain. Solid State Commun. 2018, 282, 21–27. [CrossRef]
  24. Peng, Q.; Chen, X.-J. Liu, S.; De, S. Mechanical stabilities and properties of graphene-like aluminium nitride predicted from first-principles calculations. RSC Adv. 2013, 3, 7083–7092.
  25. Kourra, M.H.; Sadki, K.; Drissi, L.B.; Bousmina, M. Mechanical response, thermal conductivity and phononic properties of group III-V 2D hexagonal compounds. Mater. Chem. Phys. 2021, 267, 124685. [CrossRef]
  26. Lv, S.-J.; Yin, G.-X.; Cui, H.-L.; Wang, H.-Y. Electronic, vibrational, elastic, and piezoelectric properties of H-, F-f Functionalized AlN sheets. Phys. Status Solidi B 2021, 258, 2100216.
  27. Tuoc, V.N.; Lien, L.T.H; Huan, T.D.; Trung, N.N. Structural, electronic and mechanical properties of few-layer GaN nanosheet: A first-principle study. Mater. Trans. 2020, 61, 1438–1444. [CrossRef]
  28. Fabris, G.S.L.; Paskocimas, C.A.; Sambrano, J.R.; Paupitz, R. One- and two-dimensional structures based on gallium nitride. J. Solid State Chem. 2021, 303, 122513. [CrossRef]
  29. Ahangari, M.G.; Fereidoon, A.; Mashhadzadeh, A.H. Interlayer interaction and mechanical properties in multi-layer graphene, Boron-Nitride, Aluminum-Nitride and Gallium-Nitride graphene-like structure: A quantum-mechanical DFT study. Superlattices Microstruct. 2017, 112, 30–45. [CrossRef]
  30. Peng, Q.; Sun, X.; Wang, H.; Yang, Y.; Wene, X.; Huang, C.; Liu, S.; De, S. Theoretical prediction of a graphene-like structure of indium nitride: A promising excellent material for optoelectronics. Appl. Mater. Today 2017, 7, 169 – 178. [CrossRef]
  31. Peng, Q.; Liang, C.; Ji, W.; De, S. A First Principles Investigation of the Mechanical Properties of g-TlN. Model. Numer. Simulat. Mater. Sci. 2012, 2, 76–84.
  32. Luo, Z.J.; Yang, Y.F.; Yang, X.Z.; Lv, B.; Liu, X.F. The mechanical properties and strain effect on the electronic properties of III-nitride monolayers: ab-initio study. Mater. Res. Express 2019, 6, 115915. [CrossRef]
  33. Faraji, M.; Bafekry, A.; Fadlallah, M.M.; Jappor, H.R.; Nguyen, C.V.; Ghergherehchi, M. Two-dimensional XY monolayers (X = Al, Ga, In; Y = N, P, As) with a double layer hexagonal structure: A first-principles perspective. Appl. Surf. Sci. 2022, 590, 152998. [CrossRef]
  34. Rouhi, S.; Pourmirzaagha, H.; Bidgoli, M.O.; Molecular dynamics simulations of gallium nitride nanosheets under uniaxial and biaxial tensile loads. Int. J. Mod. Phys. B 2018, 32, 1850051. [CrossRef]
  35. Singh, S.; Raj, B.M.R.; Mali, K.D.; Watts, G. Elastic Properties and nonlinear elasticity of the noncarbon hexagonal lattice nanomaterials based on the multiscale modelling. J. Eng. Mater. Technol. 2021, 143, 021006. [CrossRef]
  36. Le, M.-Q. Atomistic Study on the tensile properties of hexagonal AlN, BN, GaN, InN and SiC sheets. J. Comput. Theor. Nanosci. 2014, 11, 1458–1464. [CrossRef]
  37. Sarma, J.V.N.; Chowdhury, R.; Jayaganthan, R. Mechanical behavior of gallium nitride nanosheets using molecular dynamics. Comput. Mater. Sci. 2013, 75, 29–34. [CrossRef]
  38. Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Fernandes, J.V. Developments in the evaluation of elastic properties of carbon nanotubes and their heterojunctions by numerical simulation. AIMS Mater. Sci. 2017, 4, 706 – 737. [CrossRef]
  39. Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Chaparro, B.M.; Fernandes, J.V. On the Determination of Elastic Properties of Single-Walled Boron Nitride Nanotubes by Numerical Simulation. Materials 2021, 14, 3183. [CrossRef]
  40. Tapia, A.; Cab, C.; Hernández-Pérez, A.; Villanueva, C.; Peñuñuri, F.; Avilés, F. The bond force constants and elastic properties of boron nitride nanosheets and nanoribbons using a hierarchical modeling approach. Physica E 2017, 89, 183–193. [CrossRef]
  41. Georgantzinos, S.K.; Kariotis, K.; Giannopoulos, G.I.; Anifantis, N.K. Mechanical properties of hexagonal boron nitride monolayers: Finite element and analytical predictions. Proc. IMechE C J. Mech. Eng. Sci. 2020, 234, 4126–4135. [CrossRef]
  42. Le, M.-Q. Prediction of Young’s modulus of hexagonal monolayer sheets based on molecular mechanics. Int. J. Mech. Mater. Des. 2015, 11, 15 – 24. [CrossRef]
  43. Giannopoulos, G.I.; Georgantzinos, S.K. Tensile behavior of gallium nitride monolayer via nonlinear molecular mechanics. Eur. J. Mech. A Solids. 2017, 65, 223–232. [CrossRef]
  44. Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M.; Chaparro, B.M.; Fernandes, J.V. On the determination of elastic properties of indium nitride nanosheets and nanotubes by numerical simulation. Metals 2023, 13, 73. [CrossRef]
  45. Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Chaparro, B.M.; Parreira, T.G.; Fernandes, J.V. Numerical Evaluation of the Elastic Moduli of AlN and GaN Nanosheets. Materials 2024, 17, 799. [CrossRef]
  46. Li, C.; Chou, T.W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487 – 2499. [CrossRef]
  47. Genoese, A.; Genoese, A.; Rizzi, N. L.; Salerno, G. Force constants of BN, SiC, AlN and GaN sheets through discrete homogenization. Meccanica 2018, 53, 593 – 611.
  48. Mayo, S.L.; Barry D. Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897 – 8909. [CrossRef]
  49. Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M. A Study of the mechanical behaviour of boron nitride nanosheets using numerical simulation. Nanomaterials 2023, 13, 2759. [CrossRef]
  50. Zeng, H.; Zhi, C.; Zhang, Z.; Wei, X.; Wang, X.; Guo, W.; Bando, Y.; Golberg, D. “White Graphenes”: Boron Nitride Nanoribbons via Boron Nitride Nanotube Unwrapping. Nano Lett. 2010, 10, 5049 – 5055.
  51. Nadeem, A.; Ali Raza, M.; Maqsood, M.F.; Ilyas, M.T.; Westwood, A.; Rehman, Z.U. Characterization of boron nitride nanosheets synthesized by boron-ammonia reaction. Ceram. Int. 2020, 46, 20415 – 20422. [CrossRef]
  52. Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M.; Chaparro, B.M.; Parreira, T.G.; Fernandes, J.V. On the Determination of Elastic Properties of Single-Walled Nitride Nanotubes Using Numerical Simulation. Materials 2024, 17, 2444. [CrossRef]
Preprints 120594 g001
Figure 1. Schematic representation of the loading and boundary conditions for TlNNS: (a) tensile loading in the x- direction (zigzag configuration); (b) tensile loading in the y-direction (armchair configuration); (c) in-plane shear loading in the x-direction.
Figure 1. Schematic representation of the loading and boundary conditions for TlNNS: (a) tensile loading in the x- direction (zigzag configuration); (b) tensile loading in the y-direction (armchair configuration); (c) in-plane shear loading in the x-direction.
Preprints 120594 g001
Preprints 120594 g002
Figure 2. Surface Young´s modulus, as a function of the bond length, a M - N , of the diatomic NS structure, for (a) the zigzag configuration, E sx , and (b) the armchair configuration, E sy , of MN nanosheets.
Figure 2. Surface Young´s modulus, as a function of the bond length, a M - N , of the diatomic NS structure, for (a) the zigzag configuration, E sx , and (b) the armchair configuration, E sy , of MN nanosheets.
Preprints 120594 g002
Preprints 120594 g003
Figure 3. Comparison of the surface Young´s moduli, E sx , y , of (a) GaNNSs, InNNSs and TlNNSs with those of AlNNSs; (b) metal nitride NSs with those of BNNSs [49].
Figure 3. Comparison of the surface Young´s moduli, E sx , y , of (a) GaNNSs, InNNSs and TlNNSs with those of AlNNSs; (b) metal nitride NSs with those of BNNSs [49].
Preprints 120594 g003
Preprints 120594 g004
Figure 4. Ratio between the surface Young´s moduli in the zigzag and armchair directions, E sx / E sy , as a function of the bond length, a M - N , for MN nanosheets.
Figure 4. Ratio between the surface Young´s moduli in the zigzag and armchair directions, E sx / E sy , as a function of the bond length, a M - N , for MN nanosheets.
Preprints 120594 g004
Preprints 120594 g005
Figure 5. Comparison of the current surface Young´s moduli, E sx , y , of (a) AlNNSs, (b) GaNNSs, (c) InNNSs; and (d) E sx / E sy ratio for the MNs from figures (a,b,c) with those available in the literature [32,35,36].
Figure 5. Comparison of the current surface Young´s moduli, E sx , y , of (a) AlNNSs, (b) GaNNSs, (c) InNNSs; and (d) E sx / E sy ratio for the MNs from figures (a,b,c) with those available in the literature [32,35,36].
Preprints 120594 g005
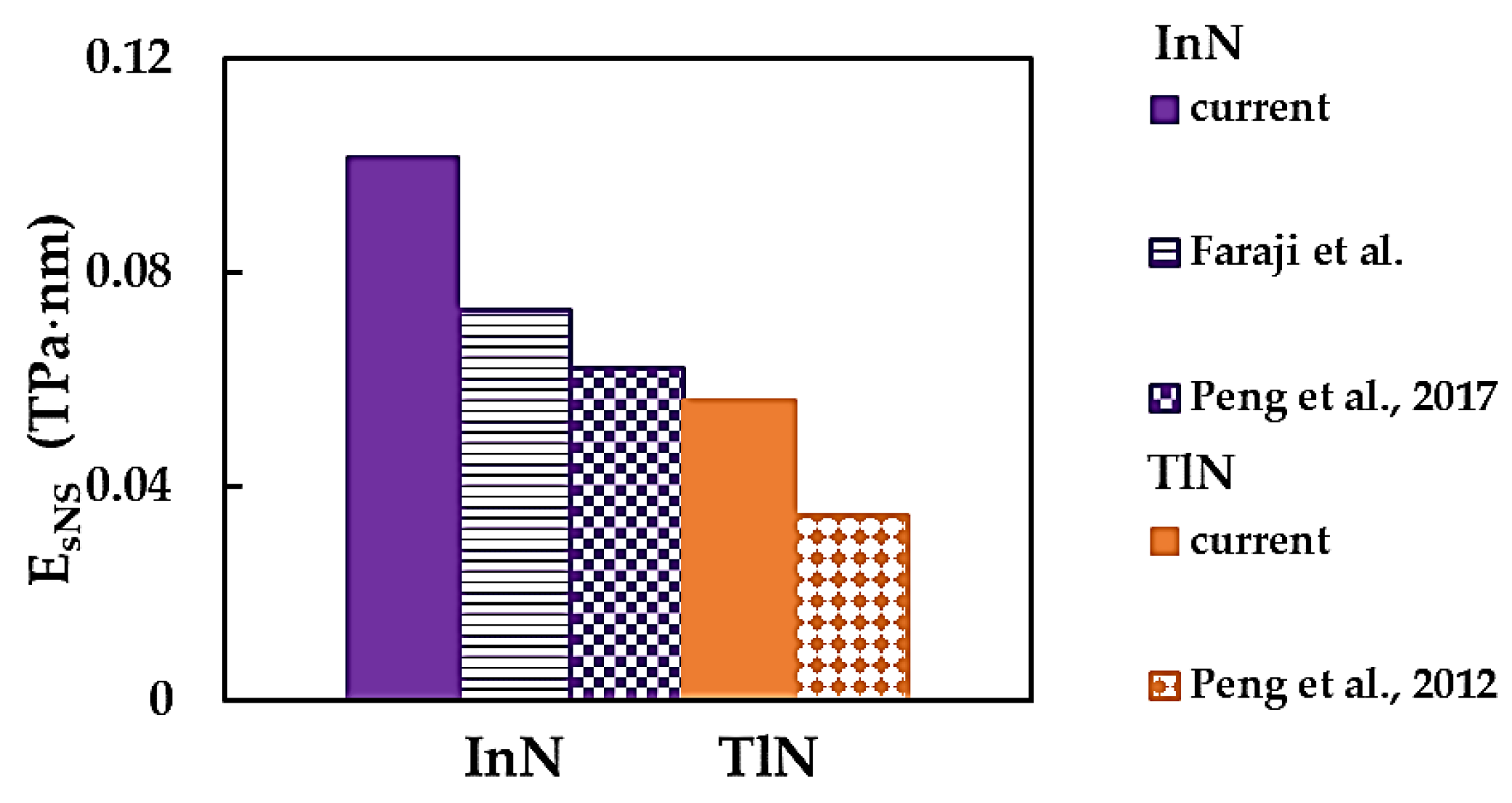
Preprints 120594 g006
Figure 6. Comparison of the current surface Young´s modulus, E sNS , for InNNSs and TlNNSs with those from the studies of Faraji et al. [33] and Peng et al. (2012, 2017) [30,31].
Figure 6. Comparison of the current surface Young´s modulus, E sNS , for InNNSs and TlNNSs with those from the studies of Faraji et al. [33] and Peng et al. (2012, 2017) [30,31].
Preprints 120594 g006
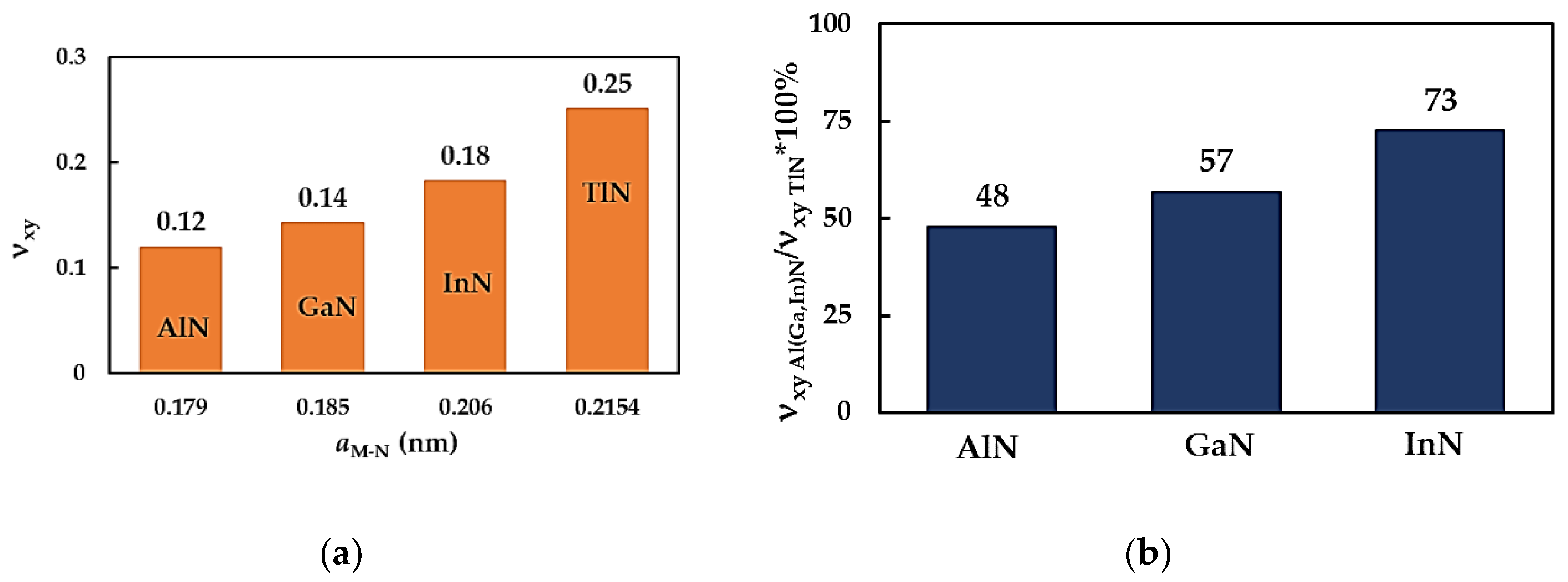
Preprints 120594 g007
Figure 7. (a) Evolution of the Poisson´s ratio, ν xy , of MN nanosheets, as a function of the bond length, a M - N ; (b) Comparison of the ν xy values for AlNNSs, GaNNSs and InNNSs with that of TlNNSs.
Figure 7. (a) Evolution of the Poisson´s ratio, ν xy , of MN nanosheets, as a function of the bond length, a M - N ; (b) Comparison of the ν xy values for AlNNSs, GaNNSs and InNNSs with that of TlNNSs.
Preprints 120594 g007
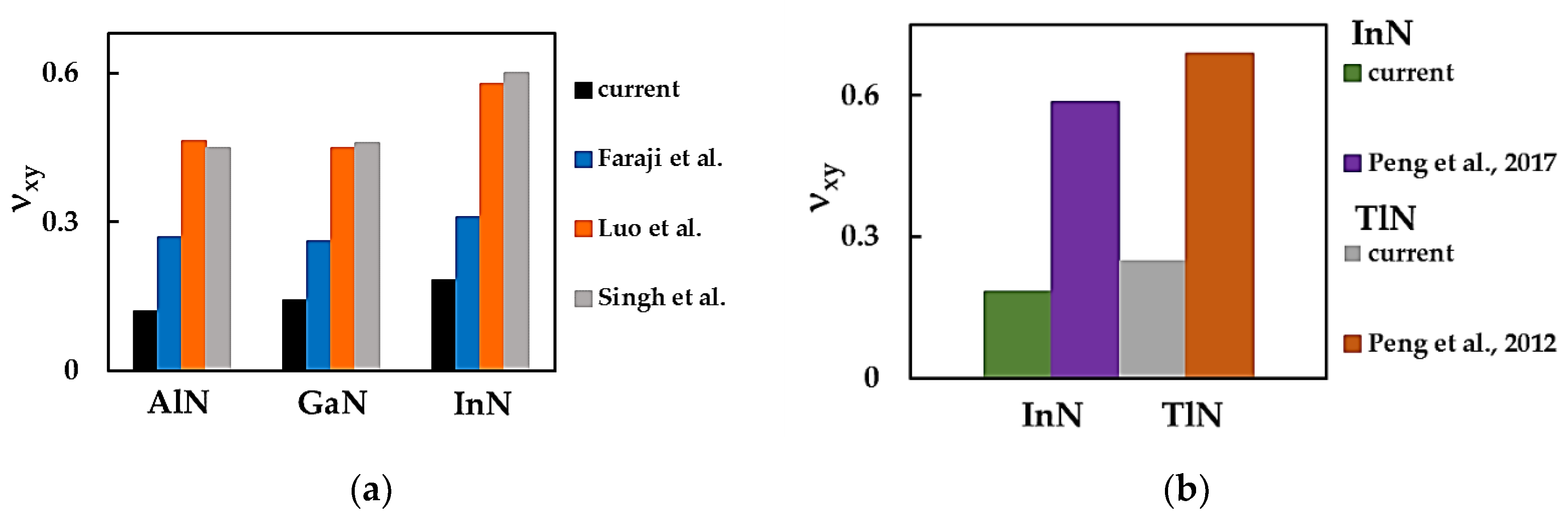
Preprints 120594 g008
Figure 8. Comparison of the Poisson´s ratio, ν xy , of (a) AlNNSs, GaNNSs and InNNSs, (b) InNNSs and TlNNSs with respective values from the literature [30,31,32,33,35].
Figure 8. Comparison of the Poisson´s ratio, ν xy , of (a) AlNNSs, GaNNSs and InNNSs, (b) InNNSs and TlNNSs with respective values from the literature [30,31,32,33,35].
Preprints 120594 g008
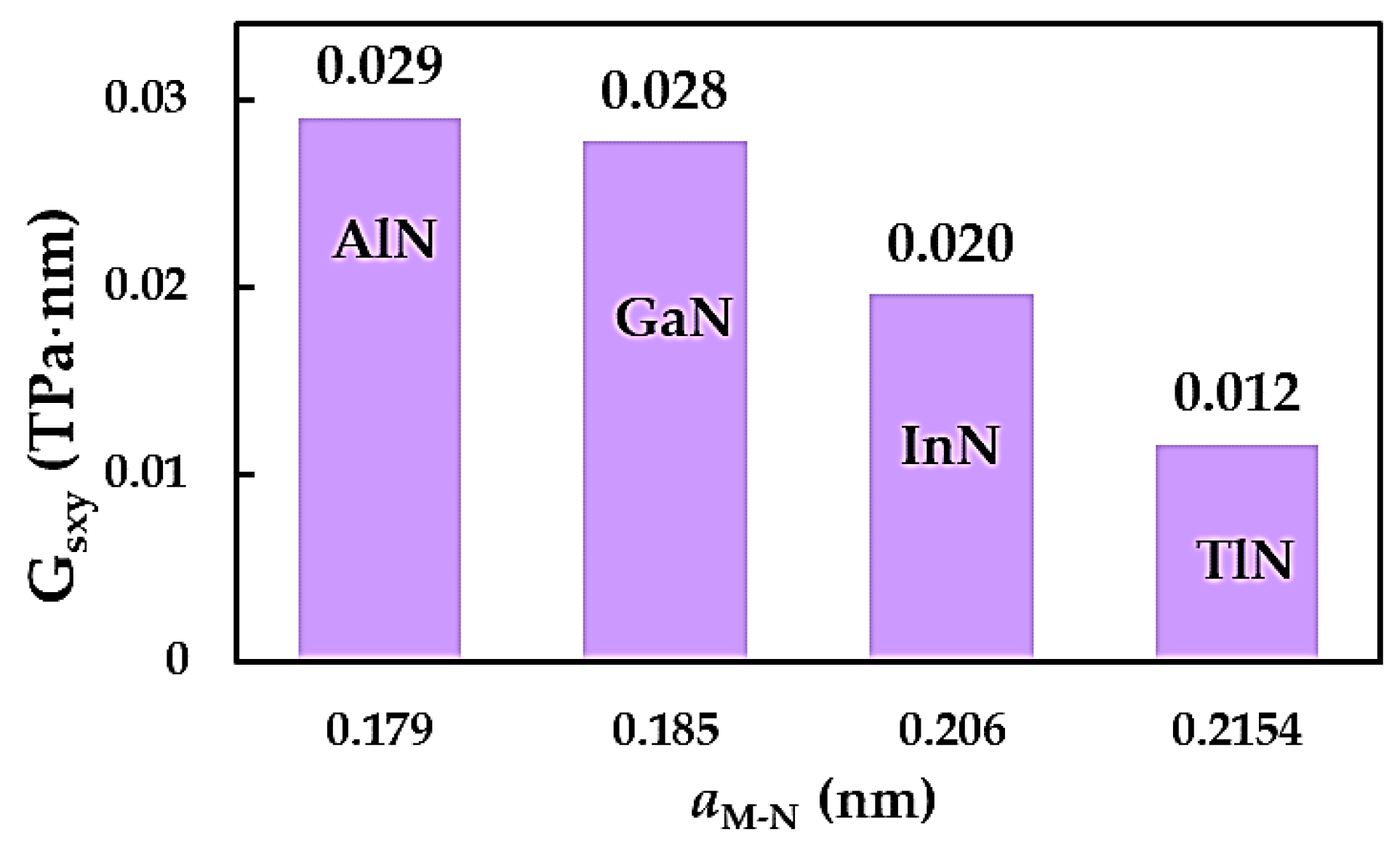
Preprints 120594 g009
Figure 9. Evolution of the surface shear modulus, G sxy , of the MN nanosheets as a function of the respective bond length, a M - N .
Figure 9. Evolution of the surface shear modulus, G sxy , of the MN nanosheets as a function of the respective bond length, a M - N .
Preprints 120594 g009
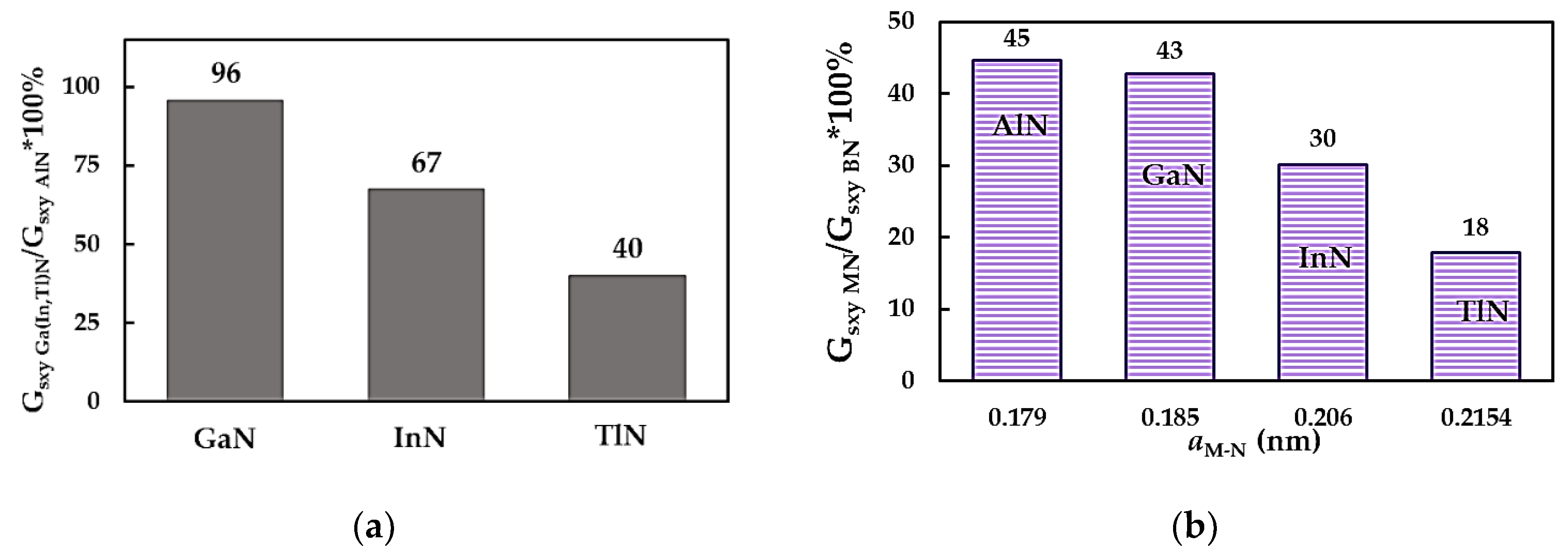
Preprints 120594 g010
Figure 10. Comparison of the surface shear modulus, G sxy , of (a) GaNNSs, InNNSs and TlNNSs with that of AlNNSs; (b) the metal nitride NSs with that of the BNNSs [49].
Figure 10. Comparison of the surface shear modulus, G sxy , of (a) GaNNSs, InNNSs and TlNNSs with that of AlNNSs; (b) the metal nitride NSs with that of the BNNSs [49].
Preprints 120594 g010
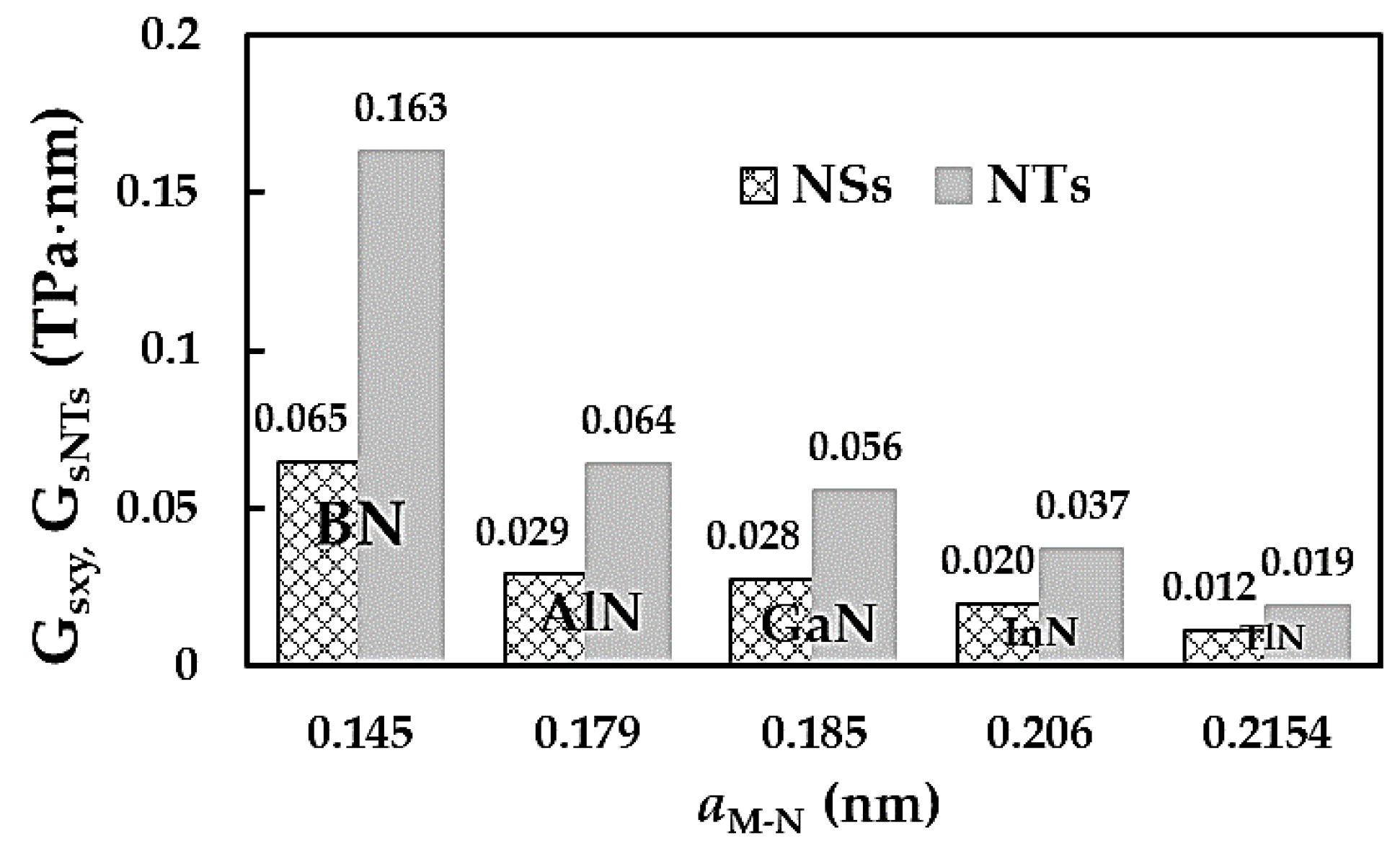
Preprints 120594 g011
Figure 11. Comparison of the surface shear modulus, G sxy , of the 13th group - nitride NSs with the shear modulus, G sNTs , of the homologous NTs [52]. G sxy and G sNTs for BN nanosheets and nanotubes are from [39,49], respectively.
Figure 11. Comparison of the surface shear modulus, G sxy , of the 13th group - nitride NSs with the shear modulus, G sNTs , of the homologous NTs [52]. G sxy and G sNTs for BN nanosheets and nanotubes are from [39,49], respectively.
Preprints 120594 g011
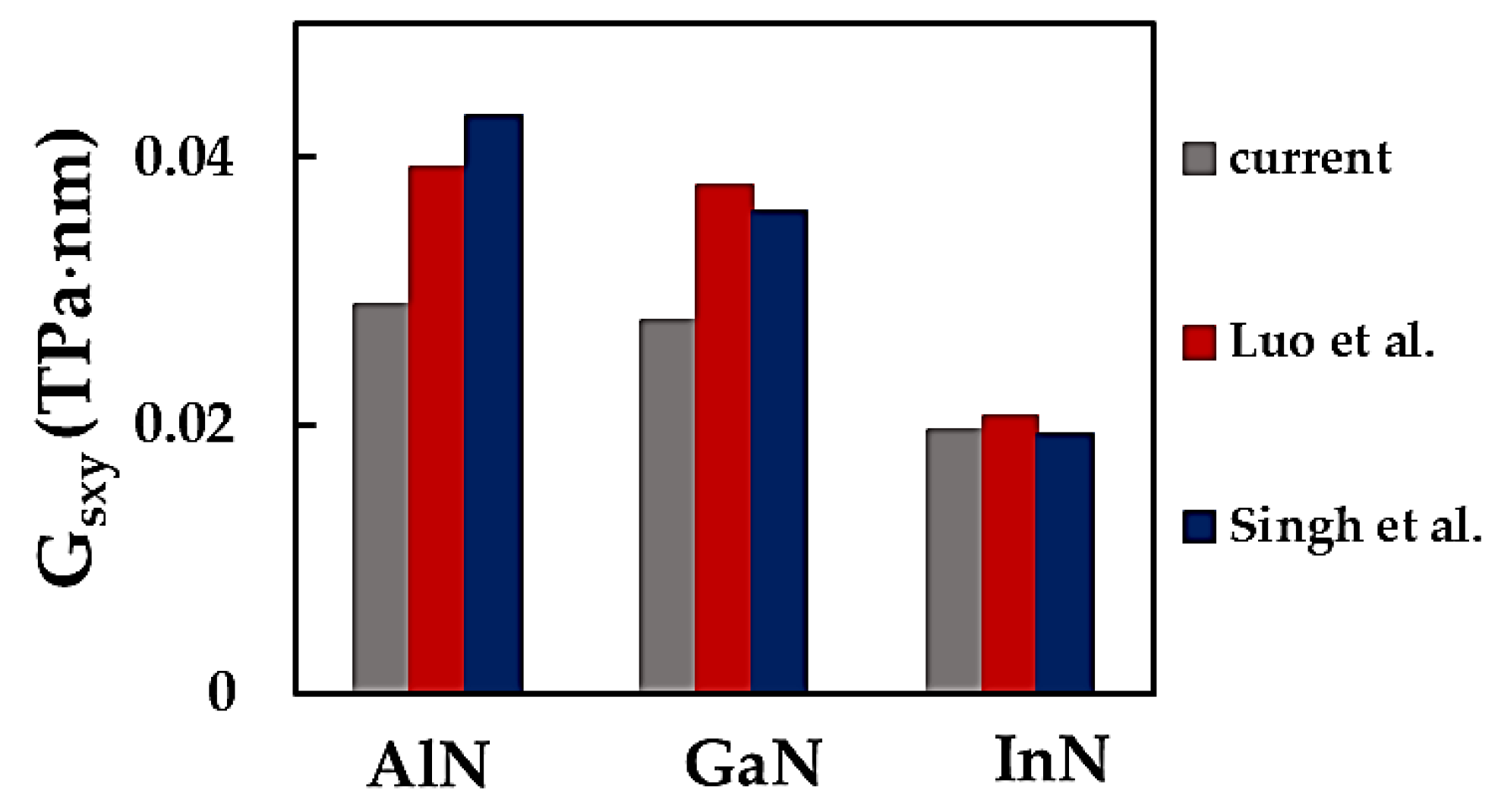
Preprints 120594 g012
Figure 12. Comparison of the current surface shear modulus, G sxy , of AlNNSs, GaNNSs and InNNSs.
Figure 12. Comparison of the current surface shear modulus, G sxy , of AlNNSs, GaNNSs and InNNSs.
Preprints 120594 g012
Table 1. Bond length, surface Young's modulus, Poisson's ratio, and k r , k θ and k τ force field constants for AlN, GaN, InN and TlN nanosheets.
Table 1. Bond length, surface Young's modulus, Poisson's ratio, and k r , k θ and k τ force field constants for AlN, GaN, InN and TlN nanosheets.
Compound a M - N , nm [3] Es, nN/nm [3] ν [3] k r , nN/nm k θ , nN⋅nm/rad2 k τ , nN⋅nm/rad2
AlN 0.179 116 0.46 372 0.451 0.625
GaN 0.185 110 0.48 366 0.445
InN 0.206 67 0.59 283 0.296
TlN 0.2154* 34.5* 0.689* 192 0.151
* Values from Ye and Peng [4].
Table 2. Geometrical and elastic properties of the beams, together with their respective formulation, as input parameters for numerical simulation.
Table 2. Geometrical and elastic properties of the beams, together with their respective formulation, as input parameters for numerical simulation.
Compound diameter,
d, nm		 Formulation Young´s modulus,
Eb, GPa		 Formulation shear modulus,
Gb, GPa		 Formulation Poisson ’ s   ratio ,   ν b  
AlN 0.1392 d = 4 k θ k r 4374 E b = k r 2 l 4 π k θ 3032 G b = k r 2 k τ l 8 π k θ 2 0.46 [3]
GaN 0.1395 4437 3113 0.48 [3]
InN 0.1294 4432 4674 0.59 [3]
TlN 0.1120 4200 8712 0.689 [4]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated