Prerpints.org logo
Preprint
Article

Complex Order Derivation and Integration of Functions

Altmetrics

Downloads

56

Views

13

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Modeling, Stability, and Control of Dynamic Systems and Their Applications

Submitted:

08 October 2024

Posted:

09 October 2024

You are already at the latest version

Alerts
Abstract
Some mathematical problems reach such complexity that their solution and engineering interpretation is no longer possible, or at least extremely difficult for researchers without the use of artificial intelligence tools. Mathematical relations for such problems are very difficult to interpret. In connection with the development of means for mathematical calculations, such problems have partially lost their relevance. However, new problems can be posed in mathematics, for which the existing means of mathematical calculations may still be insufficient. Presumably, such problems include the problem of differentiation and integration to a complex degree. Derivation of various functions is widely used in many branches of mathematics, technology, and science. Historically, derivation was known for cases where the exponent index of the degree of derivation was a positive integer value, which meant the multiplicity of taking the derivation operation. Later, this operation was extended with the notion that the exponent index can also be negative, which means multiple integration. Derivation to a negative power is defined as integration, and integration to a negative power is defined as derivation. Later, the concept of the possibility of fractional (non-integer) derivation and, accordingly, fractional integration was developed and widely used. This extension of the mathematical tool proved to be of considerable practical value, since it permits the design and implementation of more efficient controllers for systems having negative feedback, for instance. Publications about taking the derivative to a purely imaginary degree have already appeared, but, apparently, the question of differentiation was also discussed in the literature, in which the degree of taking the derivative would be expressed by a complex number. The article suggests an approach to solving this problem, which may not have been discussed yet. If this complex number, denoting the degree of differentiation, has a positive real part, the operation is better called a special form of differentiation, but if the real part of the degree of differentiation is negative, then the operation is more consistent with the concept of integration. Formally, inverting the exponent of the degree of differentiation turns the operation into integration and vice versa. Throughout history, it has been repeatedly confirmed that mathematics occasionally solves problems that at the time of their discovery have no obvious applied value; however, the development of the theory is valuable in and of itself, even if there is currently no obvious applied value for such development. In addition, experience has shown that every new mathematical tool will ultimately be applied to a significant practical issue.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Signal derivation is widely used in automatic control systems. Derivation is one of the most common types of signal processing along with integration and filtering. Filtering can also be represented as one of the forms of linear transformation based on derivation or integration, as well as on the algebraic summation of signals or their various fragments. Linear signal conversion operations have the advantageous difference from non-linear conversion operations that, as a rule, the signal-to-noise ratio, as a minimum, almost does not deteriorate during their execution, while this indicator can deteriorate sharply and irrevocably when performing nonlinear conversion operations. If the filtering operation at the same time suppresses those frequency regions where the signal is weak or should not occur at all, leaving without suppression or even enhancing those frequency regions that are of the greatest interest, since the signal is expected to appear in them, then the signal-to-noise ratio in the entire band of the received signal even increases if it is evaluated by signs of signal energy in the entire remaining frequency band. Some students sometimes even characterize this action as an increase in the signal-to-noise ratio, although in fact it is more correct to say that such filtering simply suppresses noise in those frequency ranges where there is no useful part of the signal, or where it is not required for further processing of the entire signal in the aggregate. Derivation, integration and filtering are also widely used in signal processing to identify control objects, that is, to determine the mathematical models of controlled objects. Also, for the purposes of control, it was necessary to modify the concept of derivation, expanding it to such concepts as fractional derivation and integration. This extension proved to be very useful. This article considers further possibilities of expanding the concept of derivation.
Some mathematical problems reach such complexity that their solution and engineering interpretation is no longer possible, or at least extremely difficult for researchers without the use of artificial intelligence tools. Mathematical relations for such problems are very difficult to interpret. In connection with the development of means for mathematical calculations, such problems have partially lost their relevance. However, new problems can be posed in mathematics, for which the existing means of mathematical calculations may still be insufficient. Presumably, such problems include the problem of differentiation and integration to a complex degree.
The differential calculus has become one of the most important mathematical tools in many fields of science and technology. Initially, for the operation of derivation, the definition was given for simple derivation, that is, derivation to the first degree. Further, by induction, the concept was given for any integer order of derivation as the corresponding number several consecutive derivations of. The inverse operation, called integration, can be thought of as derivation to a negative power. Thus, the exponent of the degree of derivation was defined as a positive integer, which meant the multiplicity of taking the differentiation operation. With the development of mathematics, later this operation was extended by the assumption that the exponent can be negative.
This means multiple integration. Derivation to a negative power is defined as integration, and integration to a negative power can be defined as derivation. Subsequently, mathematicians posed and positively resolved the concept of the possibility of fractional derivation, and, accordingly, fractional integration [1,2,3,4,5,6,7]. It turned out that this extension of the mathematical apparatus has a fairly important applied value. For example, this allows making more accurate mathematical models of viscoelastic materials for large extension [8]. Also, such a fractional derivation makes it possible to design and implement more efficient controllers for systems with negative feedback [9,10,11,12]. Regulators using fractional derivation and integration received a special name – PIλDµ-regulators [13,14,15,16]. Here P, I and D mean the proportional, integrating, and derivative links, respectively, and the exponents indexes λ and µ are fractional values, which is greater than zero but less than unit [17,18,19,20]. Publications on this topic continue, their number is growing every year [21,22,23,24].
Publications on taking the derivative to a purely imaginary degree have already appeared [25,26,27], it cannot be ruled out that the question of derivation, in which the degree of taking the derivative would be expressed by a complex number, has also already been discussed in the literature, there are indications of this [28,29,30,31]. Of course, if mathematicians have solved the problem of derivation to an imaginary degree, then, according to fairly clear rules, it can be argued that derivation to a complex degree can be derived as a consequence from the concepts of derivation to an imaginary degree and derivation to a real degree (moreover, both of these derivation indices can be non-integer). In this paper, we propose a different way to solve this problem, while we do not undertake to discuss which of the methods is simpler, we cannot even check whether the results of applying two different methods coincide. Throughout history, it has been repeatedly confirmed that mathematics occasionally solves problems that at the time of their discovery have no obvious applied value; however, the development of the theory is valuable in and of itself, even if there is currently no obvious applied value for such development. In addition, experience has shown that every new mathematical tool will ultimately be applied to a significant practical issue.
This paper discusses the question of how to interpret derivation to complex degree. If this complex value is inversed, then such operation can be interpreted as integration to a complex degree. Derivation can be treated as kind of integration with the use of the inverted complex index of it respectively to the original index of the degree of derivation.

2. Statement of the Problem

We will discuss time functions, since operations with time functions are most important in signal theory.
Let there be a time function
f t .
For this function, the concept of derivative can be introduced
Υ t = f ′ ( t ) = d f ( t ) / d t .
This derivative is interpreted as the rate of change of the function, it is defined through the limit:
Υ ( t ) = lim ∆ t → 0 ⁡ ( ∆ f t ∆ t ) .
The derivative operator can be denoted with the corresponding symbol
p = d / d t .
Some authors argue that this symbol cannot be treated like an ordinary algebraic factor, but it is allowed to use it in this form, that is, relation (2) can be rewritten in the following form:
Υ t = p f t .
Using this symbol, one can also conditionally write integration, which is defined as follows:
θ ( t ) = ∫ − ∞ t f ( τ ) d τ .
A simplified notation of the integration operation in this case will be as follows:
θ t = p − 1 f t .
Zero can also be included in this series, i. e. lack of derivative:
f t = p 0 f t .
Double derivative is taking the derivative twice
Υ ′ t = f ″ ( t ) = d d f t d t / d t .
There is a special notation for this operation.
Υ ′ ( t ) = d 2 f ( t ) / d t 2 .
This relationship can be rewritten as follows:
Υ ′ t = p 2 f t .
Here the action with the symbolic derivation operator (4) is used, which can also be written in the following form:
Υ ′ ( t ) = ( d d t ) 2 f ( t ) .
The double integration can be defined in a similar way
Ψ t = ∫ − ∞ t θ τ d τ = ∫ − ∞ t [ ∫ − ∞ t f ( τ ) d τ ] d σ .
The specified cumbersome relation (13) in symbolic form can be written quite simply:
Ψ t = p − 2 f t .
On this basis, it is possible to define taking the derivative of any integer number of times:
p n f t = d n f ( t ) d t n .
Taking into account the definition for negative and zero degrees of derivation in relation (15), the exponent n can take any finite integer value, including negative values and zero.
n = 0 , ± 1 , ± 2 , … ± ∞ .
In other words, the exponent belongs to the set of integers:
n ∈ Z .
Here Z is the set of integers.
Let us pay attention to the essential difference between the concept of n-fold derivation and raising the result of derivation to the power n.
p n f t ≠ p f t n .
Thus, the problem statement is divided into two subtasks.
Problem. It is necessary to define the mathematical operation of taking the derivative of the power c = a + bi, where i is an imaginary unit, c is a complex number, a, b are real coefficients.

3. Method for Solving the Problem

The method for solving the problem is to use the Laplace transform, which allowed giving a mathematically precise definition of the concept of fractional derivation and fractional integration.
A deep justification for replacing the derivative symbol with a letter designation with subsequent actions with this designation according to the rules of algebra is available in the mathematical apparatus of the Laplace transform. Indeed, in the case of applying the Laplace transform to some function, we obtain the Laplace mapping from this function:
L f t ↔ F s .
Here L{·} is the Laplace transform, s is the argument of the Laplace function, and F(s) is the Laplace transformation (image) of the function f(t) [25,26,27].
The Laplace transform is defined as follows:
F s = L f ( t ) = ∫ 0 ∞ e − s t f ( t ) d t .
For this transformation, it is known that if instead of the original function f(t) its derivative Υ ( t ) is used, then the result of the transformation will be equal to the result of the transformation from the original function, multiplied by the argument s:
L Υ ( t ) = s · L f t .
There is a similar rule for the integral: if instead of the original function f(t) its integral Ψ(t) is used, then the result of the transformation will be equal to the result of the transformation from the original function, divided by the argument s:
L Ψ ( t ) = 1 s · L f t .
These relations are not only analogous to the corresponding relations with the symbolic notation of the derivation operation, they also provide a way to understand how the result of fractional derivation or fractional integration can be calculated. And this, in turn, legalizes this operation, since it can be determined mathematically, exactly and uniquely.
Indeed, for example, half derivation is such an action with the function f(t), which will give a new function, the result of the Laplace transformation from which will give the product of the transformation from the original function and the Laplace argument to the power of one second:
L d 1 / 2 d t 1 / 2 f ( t ) = s 1 / 2 · L f t .
Thus, one can define what it means to take the operation of derivation or integration to any rational degree, i.e. the exponent, which, according to relation (17), we attributed to the set of integers, we can now refer to the set of real numbers R, namely:
L d m d t m f ( t ) = s m · L f t .
n ∈ R .
Fractional derivation and integration are widely known, it is used, for example, when designing a controller [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].
In connection with the task set, it is advisable to use the apparatus of the Laplace transform to define the concept of imaginary and complex derivation, i. e. derivation to an imaginary and complex degree.

4. The Result of Solving the Problem

This paper aims to solve the fundamental mathematical question: “Is it permissible to use numbers from the set of complex numbers as exponents of the derivation operator?” An intermediate question is to define how derivation to an imaginary degree should be treated.
Based on the methodology discussed in the previous section, we can write
L d i d t i f ( t ) = s i · L f t .
Therefore, we know what the Laplace transform of the imaginary derivation of the function f(t) should exist. Therefore, we can define an imaginary derivation as such a transformation of a function that, after transforming it according to Laplace, gives the Laplace transformation of the original function, multiplied by the argument of the Laplace function to the indicated imaginary power. This gives a mathematical relation to define the imaginary differentiation operation:
d i d t i f t = L − 1 s i · L f t .
Here L-1{·} is the inverse Laplace transform, which is defined as follows:
L − 1 F ( s ) = 1 2 π i lim ω → ∞ ⁡ ∫ σ + i ω σ − i ω e − s t F ( s ) d s .
Since the operation of the Laplace transform L{·} in (27) is defined by relation (20), just as the operation of the inverse Laplace transform L-1{·} is defined by relation (28), thus the operation (27) is completely defined, the result of this operation is unique.
Problem 2 can be solved in two ways. Firstly, through a definition of the form (27) with the argument i replaced by the argument c = a + bi, and secondly, we can pass to the required relation through the relations for calculating the complex power of a complex number through the real and imaginary powers of this number. The second way seems to be more complicated, so it is not considered here.
Thus, the complex power derivative of a differentiable function can be defined as follows:
d c d t c f t = 1 2 π i lim ω → ∞ ⁡ ∫ σ + i ω σ − i ω [ e − s t s c · ∫ 0 ∞ e − s t f t d t ] d s .

5. Discussion

The formulation of the question may at first glance seem to be of no importance for the theory, and the result obtained in the form of relation (27) does not demonstrate obvious practical significance today. However, the theoretical question posed by us has the right to be posed, and the proposed solution of this problem is undoubted from a mathematical point of view, since undoubted initial relations are used.
Publications about the derivative to the imaginary or even, perhaps, to the complex degree have already appeared. Dear reviewers pointed out to us that such issues have long been considered and resolved, in particular, with reference to publications [25,26,27,28,29,30,31]. Not all of these publications are available in the public domain, but, for example, the entire issue of the journal Mathematics of the MDPI publishing house, devoted to non-integer differentiation, to which these reviewers referred [26], was studied by us quite carefully, nothing like derivation in the imaginary or even more so in the complex degree in this journal was not found. It can only be noted that even non-integer derivation, to which the entire issue of the journal is devoted, is a very complex mathematical problem, for the solution of which many methods are proposed, both theoretical and numerical, including various methods of approximation. Apparently, the problem of derivation to a complex power is not as simple as some reviewers point out, and we did not find publications with a solution to this problem in the public domain. Maybe they were looking in the wrong place, we proceed from the fact that such publications do exist, and it is possible that they, among other things, are in the list we indicated [25,27,28,29,30,31].
Of course, if mathematicians have solved the problem of derivation to an imaginary degree, then, according to fairly clear rules, it can be argued that derivation to a complex degree can be derived as a consequence from the concepts of derivation to an imaginary degree and derivation to a real degree (moreover, both of these derivation indices can be non-integer). In this article, we propose a different way to solve this problem, while we do not undertake to discuss which of the methods is simpler, we cannot even check whether the results of applying two different methods coincide.
In some cases, certain conventions are used in mathematics, as, for example, it was accepted that the factorial of zero is equal to one, since in this case many formulas take on the simplest form. But we could agree on another solution, the community of mathematicians could agree that the factorial of zero is equal to zero, 0! = 1, since by definition the factorial of an integer M is the product of all integers from one to this number M, i. e. M! = 1·2·…M, that is, the number M must be included in the product, and if the product of integers includes zero, then the result is zero. We do not in any way deny that the factorial of zero is equal to one, and we do not propose to cancel this agreement, we only point out that even in such an exact science as mathematics, there can be not only an exact proof of one consequence from another, but also at some stages an agreement. We did not find a way to compare the results of two methods for calculating the derivative to a complex degree - known and proposed by us. We only assume that the method we propose has not yet been published or discussed. At the same time, we are convinced that the method we propose must be correct, since it is based on the correct ratios, properly applied. It would be interesting to know that the results would not match, and it would be equally interesting to see that the results would match.
In relation (27), it is possible to set various specific types of the function f(t), which will allow one to obtain various specific examples of the imaginary and complex differentiation of these functions. The simplest, apparently, will be calculated such operations with respect to harmonic, power and exponential functions.

6. A Look at the Problem from the Standpoint of the Theory of Automatic Control

In the theory of automatic control, fractional derivation and integration are also used, which is noted above and is confirmed by the already given bibliography [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Traditional integration arises when considering, for example, a first order equation, which is the simplest low pass filter. The most common integrating chain can be described, for example, by the following Laplace transfer function:
Y s = a 0 b 0 + b 1 s X s .
We can obtain the frequency response of this system if we replace the argument of the Laplace transform s with the complex argument of the Fourier transform, i. e. we make the following substitution:
s → i ω .
The transfer function, strictly speaking, is equal to the square root of the quadratic form, i.e. we must first get the following relation
Y i ω = a 0 b 0 + b 1 i ω X i ω .
Then the ratio of the output value to the input value should be multiplied by the complex conjugate number and take the square root of the result. We’ll get:
Y ω X ( ω ) = a 0 ( b 0 ) 2 + ( b 1 ω ) 2 .
This transfer function clearly breaks down into five different ranges. First, in the case
ω ≪ b 0 b 1 ,
that is, in the case when
b 0 ≫ b 1 ω ,
under the root, you can approximately leave only the second term, which is easily taken out from under the root. In this case, we can roughly write:
Y ω X ( ω ) ≈ a 0 b 0 .
That is, in the indicated frequency range, the transfer function is practically unchanged; when the frequency of the input signal changes, the amplitude of the output signal does not change at all. This section can be called a section of proportional transmission of the input signal. Secondly, in the case
ω ≫ b 0 b 1 ,
that is, in the case when
b 0 ≪ b 1 ω ,
under the root, you can approximately leave only the second term, which is easily taken out from under the root. In this case, we can roughly write:
Y ω X ( ω ) ≈ a 0 b 1 ω .
That is, in the specified frequency range, the transfer function decays inversely with the frequency increase factor. For example, if the input frequency is increased by a factor of four, then the output signal will also decrease by a factor of four, and so on.
This section can be called the section on which the signal undergoes integration.
Thirdly, there is a small frequency range in which
ω ≈ b 0 b 1 ,
that is, in the case when these quantities are approximately comparable
b 0 ≈ b 1 ω .
In this case, there is something in between the previous two cases, that is, in the specified frequency range, the transfer function decays by an amount average between the two previous options, which is approximately inversely proportional to the square root of the frequency increase. For example, if the input frequency is quadrupled, the output signal will be halved. This section can be called the half-integration section. Thus, half-integration is not a mathematical fiction, but a very real action that exists in practice.
Fourth, there is a segment of the transition from zero to half integration.
Fifthly, there is a section of transition from a half transition to a whole.
These two sections give all examples of intermediate states of non-integer integration, but not in a large frequency range, but in small regions.
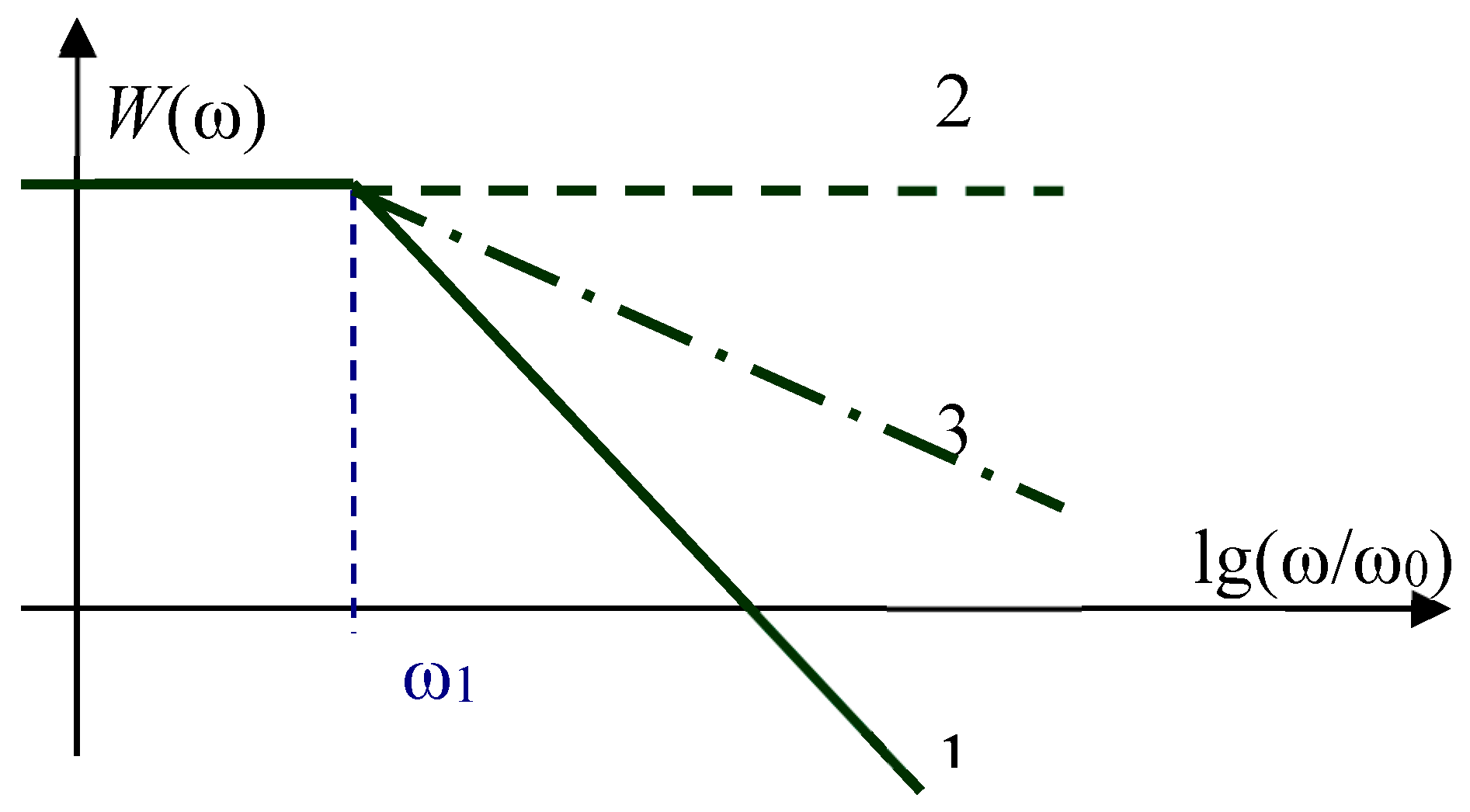
In addition, if we build a logarithmic frequency response of such an integrating link, that is, the dependence of the output signal on frequency at a unit amplitude of this input signal, then we can see that it breaks up into the indicated five sections. Approximately, this graph can only be depicted in the form of segments corresponding to the first and second sections, as shown by line 1 in Figure 1, and the other three differ from this approximate graph by no more than 3 dB. Line 2 in this Figure shows the graph if there were no integration. Line 3 is the algebraic mean between these two lines and shows the half-integration plot. From this fact, we can conclude that half integration can approximately be approximated by a function that is the geometric mean between integer integration and no integration, however, this approximation well models only the dependence of the output signal amplitude, but it is not accurate, and for the phase characteristic, the dependence is simpler, so it should not be argued that half-integration can be obtained as a geometric mean.
Thus, at least for harmonic signals, it can be argued that the amplitude of half of the integral of the signal is approximately equal to the geometric mean of the amplitude of the original signal and the amplitude of the integral of this signal:
d 1 2 d t 1 2 X t 2 ≈ | X ( t ) | · d d t X t .
Similarly, it can be shown that the phase shift at half derivation is equal to the arithmetic mean between the phase shift of the original signal and the phase shifts of the fully integrated signal. So harmonic signal
X t = A t c o s ⁡ ( ω t )
It can be represented as a projection of a rotating vector onto the abscissa axis, while the amplitude of this vector is equal to the amplitude of the signal (41), and the angle of rotation of the vector is equal to the phase (41), which corresponds to the traditional vector representation of harmonic signals, that is:
X t = A t e i ω t = A ( t ) e i φ t ⁡ .
The integral of (41) has the following form:
Y t = 1 ω A t cos ⁡ ω t − π 2 = B ( t ) e i θ ( t )
Here, new notations are introduced for the new amplitude and the new phase.
In other words, the amplitude decreases in proportion to the frequency, and the phase shift is π/2. In the case of half integration, the amplitude will decrease by a value equal to the root of the frequency, and the phase shift will be half as much:
Y 0.5 t ≈ 1 ω A t c o s ⁡ ( ω t − π 4 )
In terms of relations (42), (43), we can write:
Y 0.5 t ≈ A t B ( t ) e i θ ( t ) + φ ( t ) / 2 ⁡ .
This relation is not significant for mathematics, since it is not a strictly mathematical definition of the concept of a half derivative, however, it can be quite useful for approximate calculations, and also, in our opinion, it is quite useful for an engineering idea of ​​what is half derivative. This relationship can also be criticized from the position that the operations of integration and differentiation are linear operations. In accordance with this, the operations of non-integer integration and differentiation must also be linear operations. Relationship (45) does not look linear in any way.
From the practice of automatic control, the approximation of half or even non-integer integration in the operator domain (in the Laplace transform domain) is known by the following approximate relation [24]:
Y λ s = 1 s λ ≈ K I ∏ i = 0 N − 1 ( 1 + s z i ) ∏ i = 0 N − 1 ( 1 + s p i ) .
Here zi and pi are coefficients that increase symmetrically from the lowest to the highest value; for example, pi = k·pi, zi = k·zi, p0 ≠ z0 [24].
This relationship is clearly linear, but it is also clearly approximate. Therefore, it should be emphasized that relation (27), given above, is the best definition of non-integer differentiation both from the point of view of accuracy and from the point of view of the definition of the concept of multiple integration.
A non-integer integration can be defined in two ways. First, it can be defined as the result of integer integration of a quantity obtained by non-integer differentiation. Secondly, it can be defined as the result of non-integer differentiation of the quantity obtained by integer integration. Thirdly, it can be defined by analogy with relation (27), namely:
Y λ t = 1 2 π i lim ω → ∞ ⁡ ∫ σ + i ω σ − i ω [ e − s t s − λ · ∫ 0 ∞ e − s t X t d t ] d s .
Similar reasoning can be carried out with respect to the fractional derivation of relations (41) and (42). The derivative of the signal (41) has the following form:
Z t = d X t d t = ω A t c o s ⁡ ( ω t + π 2 )
We also introduce the notation
D t = ω A t .
ϑ t = φ t + π 2 .
In these terms, relation (48) can be rewritten as follows:
Z t = d X t d t = D t c o s ⁡ ( ϑ ( t ) )
In vector representation we get:
Z t = D t e i ϑ ( t ) .
The half derivative in this case can be represented approximately by the following relation:
Z 0.5 t ≈ A ( t ) D t e i [ ϑ t + φ t ] / 2
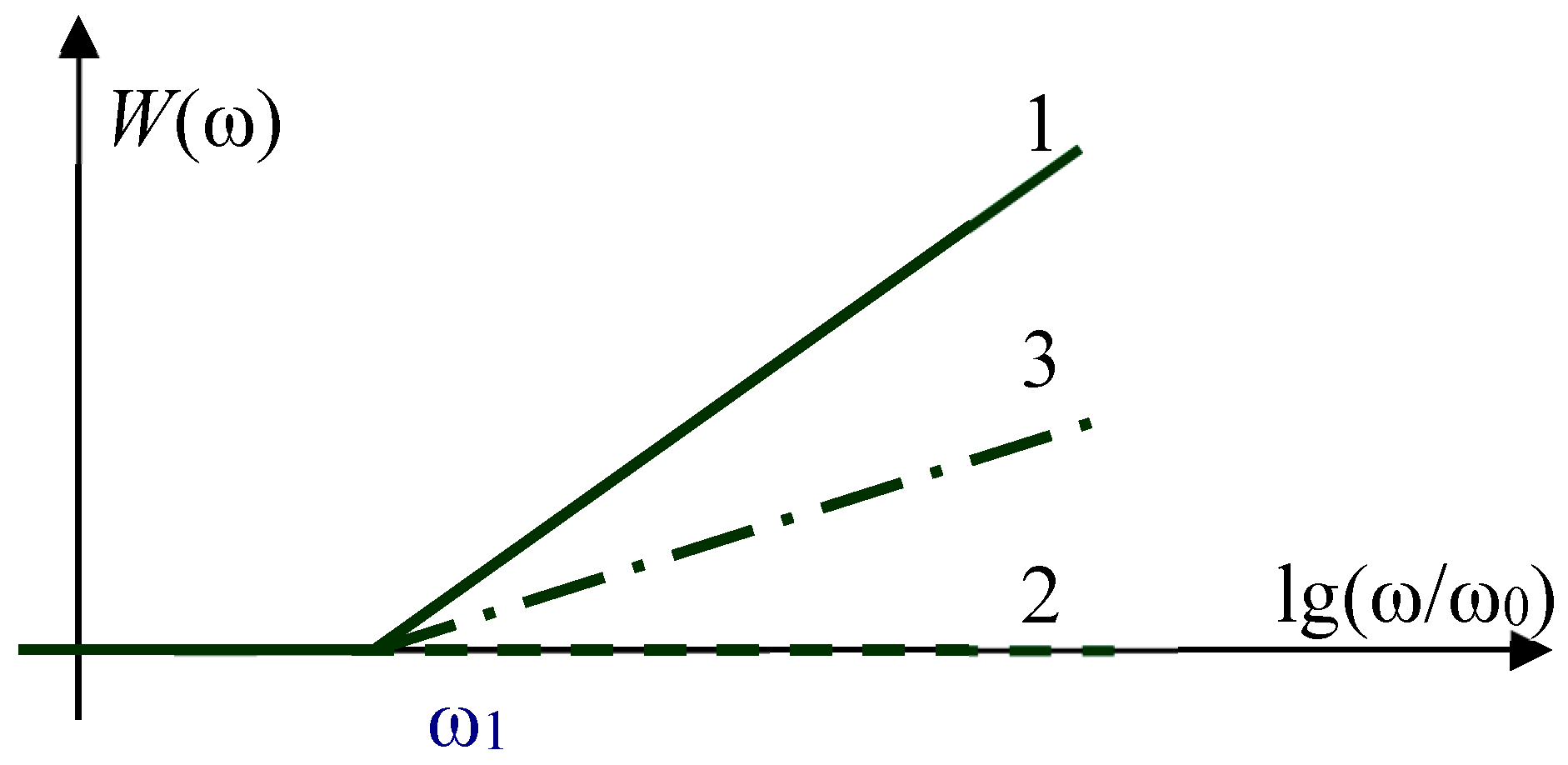
The above relation (53) is also not strictly mathematically justified, it is interesting from an engineering point of view as one of the options for understanding what half derivation is. Relation (27) is a rigorous definition. To illustrate the technical derivation obtained on the differentiating chain, as well as the lack of derivation and half derivation, a graph of a similar logarithmic frequency response, similar to the graph in Figure 1, can be shown. This graph is shown in Figure 2.
Thus, with regard to fractional derivation and fractional integration, there are quite a lot of different concepts that do not contradict each other. The concept discussed above is the most intuitive from the standpoint of an engineering approach, although it is not perfect. The concept based on relation (46) is most convenient for implementation and for mathematical modeling using, for example, software tools such as MATLAB Simulink, VisSim, SimInTech, or other similar software tools. The concept based on relation (27), in our opinion, is the best from all positions, since it is both intuitively understandable at the engineering level and flawless from a mathematical point of view. However, we currently find it difficult to name an algorithm that would allow us to calculate fractional derivative or fractional integral of a function that is input to a digital device in real time in the form of separate samples. Such an algorithm can certainly be implemented based on relation (46) or close to it. The expediency of applying the algorithm according to relations (45) or (53) is not essential, since a simple expression is obtained only for the case of exactly half derivation or half integration, while relation (46) allows you to set an arbitrary fractional derivation or integration exponent. Apparently, a rather urgent task for artificial intelligence would be to find simple algorithms for calculating non-integer derivatives and fractional integrals directly from relations (27) and (47). In this regard, the task of calculating and visually interpreting the derivative to a complex power by relation (27) or the integral to a complex power by relation (47) is also not so acute, but quite relevant.

7. Conclusion

This paper considers new tasks for artificial intelligence tools on the example of derivation and integration in a complex degree. The mathematical definition for these operations in the form (27) and (47) was first introduced through the direct and inverse Laplace transforms. For the practical application of these relationships and the visual interpretation of these operations for the purpose of understanding at the engineering level, it is desirable to use artificial intelligence tools that exceed the capabilities of traditional mathematical computing packages. From the standpoint of the further development of this direction, one can indicate an interesting approach in terms of the use of hypercomplex numbers. As is known, hypercomplex numbers are called a special form of complex numbers, where there are generally four terms, one of which is the real part of the number, and the other three are imaginary components. It is reliably known that hypercomplex numbers can be successfully used for signal processing [36], for solving problems of managing multichannel objects [37], and for using fuzzy logic [38]. All this is an indispensable mathematical apparatus for heuristic methods used in artificial intelligence. Consideration of the possibility of derivation and integration to a degree, which is expressed by a hypercomplex number, will expand the tools of this mathematical apparatus. The application of Laplace transformations in the space of hypercomplex numbers should have its own extension, respectively, the simple use of relations (27) and (47) will probably not give the required result, however, these relations can be taken as the basis for further reasoning.

References

  1. Podlubny, I. Fractional Order Systems and PIλDµ Controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [CrossRef].
  2. Maamri, N.; Trigeassou, J. C. Integration of Fractional Differential Equations without Fractional Derivatives," 2021 9th International Conference on Systems and Control (ICSC), 2021, pp. 429-435. [CrossRef]
  3. Mbodje, B.; Montseny, G.; Boundary fractional derivative control of the wave equation, in IEEE Transactions on Automatic Control, vol. 40, no. 2, pp. 378-382, Feb. 1995. [CrossRef]
  4. Trigeassou, J.; Maamri N.; Oustaloup, A. Automatic initialization of the Caputo fractional derivative, 2011 50th IEEE Conference on Decision and Control and European Control Conference, 2011, pp. 3362-3368. [CrossRef]
  5. Paola, M. Di; Pinnola F. P.; Spanos P. D. Analysis of multi-degree-of-freedom systems with fractional derivative elements of rational order, ICFDA’14 International Conference on Fractional Differentiation and Its Applications 2014, 2014, pp. 1-6. [CrossRef]
  6. Ionescu C. M.; Ionescu F. D. Power law and fractional derivative models can measure analgesia, 2014 IEEE International Conference on Automation, Quality and Testing, Robotics, 2014, pp. 1-4. [CrossRef]
  7. Wei, X.; Liu D.; Boutat D. Caputo fractional derivative estimation for a class of signals satisfying a linear differential equation, 2015 34th Chinese Control Conference (CCC), 2015, pp. 4598-4603. [CrossRef]
  8. Fukunaga, M.; Shimizu, N. Fractional derivative models of viscoelastic materials for large extension, ICFDA’14 International Conference on Fractional Differentiation and Its Applications 2014, 2014, pp. 1-5. [CrossRef]
  9. Leu, J.F.; Tsay, S.Y.; Hwang, C. Design of Optimal Fractional Order PID Controllers. J. Chin. Inst. Chem. Eng. 2002, 33, 175–179.
  10. Stanisławski, R.; Rydel, M.; Li, Z. A New Reduced-Order Implementation of Discrete-Time Fractional-Order PID Controller. IEEE Access 2022, 10, 17417–17429. [CrossRef]. [CrossRef]
  11. Zhmud, V.; Dimitrov, L.; Nosek, J. Automatic Control Systems. New Concepts and Structures of Regulators; RuScience: Moscow, Russia, 2018; p. 84.
  12. Shekher, V.; Rai, P.; Prakash, O. Tuning and Analysis of Fractional Order PID Controller. Int. J. Electron. Electr. Eng. 2012, 5, 11–21.
  13. Dumlu, A.; Ayten, K. Real time fractional-order control technique for coupled tank liquid level control process. Int. J. Adv. Appl. Sci. 2017, 4, 127–132. [CrossRef]. [CrossRef]
  14. Dorcak, L.; Terpak, J.; Papajova, M.; Dorcakova, F.; Pivka, L. Design of the fractional-order PIλDµ controllers based on the optimization with self-organizing migrating algorithm. Acta Montan. Slovaca 2007, 12, 285–293.
  15. Abraham, A.; Biswas, A.; Das, S.; Dasgupta, S. Design of Fractional Order PIλDµ Controllers with an Improved Differential Evolution. Available online: http://www.softcomputing.net/gecco2008_abraham.pdf (accessed on 21 January 2022).
  16. Das, S.; Pan, I.; Gupta, A. Improved Model Reduction and Tuning of Fractional Order PIλDµ Controllers for Analytical Rule Extraction with Genetic Programming. ISA Trans. 2012, 51, 237–261. [CrossRef] [PubMed].
  17. Bettoua, K.; Charef, A. Control quality enhancement using fractional PIλDµ controller. Int. J. Syst. Sci. 2009, 40, 875–888. [CrossRef].
  18. El-Khazali, R. Fractional-order PIλDµ controller design. Comput. Math. Appl. 2013, 66, 639–646. [CrossRef].
  19. Ranganayakulu, R.; Uday, B.B.; Rao, A.; Patle, D. A comparative study of fractional order PIλ/PIλDµ tuning rules for stable first order plus time delay processes. Resour. Effic. Technol. 2016, 2, 136–152. [CrossRef]. [CrossRef]
  20. Pan, Z.; Wang, X.; Hoang, T.; Chen, Y.; Tian, L. Design and Application of Fractional Order PIλDµ Controller in Grid-Connected Inverter System. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017.
  21. Puangdownreong, D. Optimal PIλDµ Controller Design Based on Spiritual Search for Wind Turbine Systems. Int. J. Innov. Comput. Inf. Control 2019, 15, 2259–2273.
  22. Tytiuk, V.; Chornyi, O.; Baranovskaya, M.; Serhiienko, S.; Zachepa, I.; Tsvirkun, L.; Kuznetsov, V.; Tryputen, N. Synthesis of a Fractional-Order PIλDµ-controller for a Closed System of Switched Reluctance Motor Control. Ind. Control Syst. 2019, 2, 35–42. [CrossRef].
  23. Mohammed, R. Quadrotor Control Using Fractional-Order PIλDµ Control. JACET 2019, 5, 1–10.
  24. Zhmud, V.; Dimitrov, L. Using the Fractional Differential Equation for the Control of Objects with Delay. Symmetry 2022, 14, 635. [CrossRef]
  25. Kilbas, A. A., Srivastava, H.M., Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematical Studies, Vol.204, Elsevier (North-Holland) Science Publishers, Amsterdam, London and New York, 2006. https://www.elsevier.com/books/theory-and-applications-of-fractional-differential-equations/kilbas/978-0-444-51832-3.
  26. Fractional Calculus: Theory and Applications. Edited by F. Mainardi. https://www.mdpi.com/books/pdfdownload/book/755. [CrossRef]
  27. Ross, B. (Ed.). The fractional calculus and its application, in: Lecture notes in mathematics, vol.475, Springer-Verlag, Berlin, 1975.
  28. Baleanu, D., Machado, J.A.T., Luo, A.C.J. Fractional Dynamics and Control, Springer Science, 2012. http://rentals.springer.com/product/9781461404576. [CrossRef]
  29. Bertram Ross, Francis H. Northover, A use for a derivative of complex order in the fractional calculus, 9(4),(1977), 400-406;
  30. Bai, Z., Lu, H. Positive solutions for a boundary value problem of nonlinear fractional differential equation, J. Math. Anal. Appl. 311 (2005), 495-505. https://www.sciencedirect.com/science/article/pii/S0022247X05001733. [CrossRef]
  31. Neamaty, A., Yadollahzadeh, M., Darzi, R. On fractional differential equation with complex order. Progr. Fract. Differ. Appl 1.3 (2015): 223-227. https://www.naturalspublishing.com/files/published/173ze8c3p6e39t.pdf.
  32. Wang, Y.; Chen, G. Formalization of Laplace Transform in Coq, 2017 International Conference on Dependable Systems and Their Applications (DSA), 2017, pp. 13-21. [CrossRef]
  33. Erfani, S.; Ahmadi, M. Fundamentals of generalized Laplace transform techniques for linear time-varying systems, ISSCS 2011 - International Symposium on Signals, Circuits and Systems, 2011, pp. 1-4. [CrossRef]
  34. Adams, J. L.; Veillette, R. J.; Hartley T. T.; Adams, L. I. Restrictions on the inverse Laplace transform for fractional-order systems," ICFDA’14 International Conference on Fractional Differentiation and Its Applications 2014, 2014, pp. 1-8. [CrossRef]
  35. Fulton, D. Explaining complex power, in IEEE Power Engineering Review, vol. 19, no. 6, pp. 47-, June 1999. [CrossRef]
Preprints 120589 g001
Figure 1. Logarithmic frequency response example of an aperiodic link (real integrator) – line 1, a proportional link – line 2, and a link that performs real half integration – line 3.
Figure 1. Logarithmic frequency response example of an aperiodic link (real integrator) – line 1, a proportional link – line 2, and a link that performs real half integration – line 3.
Preprints 120589 g001
Preprints 120589 g002
Figure 2. Logarithmic frequency response example of a real derivation link – line 1, a proportional link – line 2, and a link that performs real half derivation – line 3.
Figure 2. Logarithmic frequency response example of a real derivation link – line 1, a proportional link – line 2, and a link that performs real half derivation – line 3.
Preprints 120589 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated