Prerpints.org logo
Preprint
Article

Automatic Defects Recognition of Lap Joint of Unequal Thickness Based on X-ray Image Processing

Altmetrics

Downloads

64

Views

29

Comments

0

This version is not peer-reviewed

Nondestructive Testing and Evaluation

Submitted:

08 October 2024

Posted:

09 October 2024

You are already at the latest version

Alerts
Abstract
It is difficult to automatically recognize defects using digital image processing method in X-ray radiograph that tested from lap joint of unequal thickness plates. The continuous change of the wall thickness for the lap joint workpiece brings about the very different gray levels in X-ray background image. Besides, due to the shape and fixturing of the workpiece, the distribution of the weld seam in the radiograph is not vertical and results in an existence of a certain angle with the vertical direction. This makes it difficult for automatic defect detection and localization. In this paper, a method of X-ray image correction based on invariant moments is presented to solve the problem. In addition, an automatic defect detection method combined of image noise suppression, background removal, image segmentation and mathematical morphology is introduced. The results show that the proposed method can effectively recognize the gas pores in lap joint of unequal thickness and it is suitable for automatic detection.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

Welding as a manufacturing technique has been widely used in industry. In order to avoid structural failure, it is necessary to conduct reliability inspection of welding quality [1]. X-ray examination has become prevalent across welding, additive manufacturing, and numerous other manufacturing processes [2,3,4]. As these industries undergo rapid advancements [5], X-ray inspection proves invaluable due to its capacity to yield immediate and intuitive outcomes, facilitating the swift identification of volumetric flaws [6,7,8]. The artificial way to review the X-ray film is a common manner to the quality examination for welding. Images consist of the inside of the inspected specimen, which obtained from inspection devices[9].At present, the commonly used X-ray testing technologies include film method, real-time imaging method and X-ray computed tomography(CT)[10,11,12]. X-ray inspection is the most intuitive approach for the non-destructive testing (NDT) of flat weldment [13,14,15,16], pipeline [17,18] to avoid pipeline safety accidents.
In the area of X-ray inspection evaluation, manual evaluation is currently the primary method employed, which imposes high technical requirements on the inspectors. Furthermore, prolonged work can lead to visual fatigue among inspectors, making this method unsuitable for evaluating large volumes of radiographic films. To address the need for efficient evaluation, automatic defect recognition technology has emerged. In recent years, defect detection based on machine recognition has seen enormous progress. For example, the application of Support Vector Machines (SVM) in weld defect defection of X-ray images is receiving more and more attention, which has led to the rapid development of weld automatic detection [19,20,21]. Other automatic defect recognition methods based on neural network, such as Convolutional Neural Networks (CNNs) [22,23] and dual-graph interactive consistency reasoning network (DGICR-Net) [24] have been researched. These methods are conducive to improving the reliability of weld defect detection in X-ray images. However, due to the complexity and limitations of imaging conditions, objects and algorithms, there are still many problems to be further studied in practical applications [25,26]. In particular, when the welded structure to be detected is complex, higher requirements are put forward for the detection.
Automatic recognition of defects in radiographic inspection of lap welds on plates of unequal thickness remains challenging. This is primarily due to the variation in the thickness of the workpiece, and this leads to differences in the grayscale of the image background and continuous changes in the grayscale of the weld zone, making defect recognition based on image threshold segmentation difficult. In terms of reducing the impact caused by background gray levels, x-ray radiography methodology [27] and infrared thermography [28] haven been researched to increase the signal-to-noise ratio (SNR) of the weld region image, which can enhance the recognition rate of defects. In terms of image correction, a standard X-ray digital radiographic data acquisition procedure and optimized radiographic exposure conditions has been carried out to suppress the structural noise [29].
In order to fulfil automatic defect detection in lap joint of unequal thickness plates, we first preprocessed the original radiograph to obtain an image in which the lap joint weld is vertically distributed. In subsequent work, several image processing methods such as noise suppression, background removal, image segmentation and mathematical morphology have been introduced. At last, the X-ray image of lap joint of unequal thickness plates, defects are automatically extracted.

2. X-ray Inspection System and Weld Specimen Preparation

The MU2000 X-ray real-time imaging system produced by the YXLON Company of Germany is adopted. The weld specimen used in this work are two low-carbon steel plates with unequal thickness in lap joint structure. The thickness of the plates are 4mm and 2mm respectively. Figure 1(a) shows the geometric form of the specimen, and Figure 1(b) shows the appearance of the actual weldment.
Figure 2 shows the overall testing system combining with defects testing methods used in this paper. In this paper, the weldment is placed on a stage with a three-axis rotation system and is radiographed by the X-ray source. The generated radiographic information is transmitted to the computer through the detector. Defects in the images received can be successively detected through a series of digital imaging processing techniques including：image correction based on moment invariant, noise suppression based on wavelet, image segmentation based on threshold and mathematical morphology.

3. Methodology

3.1. Principle of X-ray Radiographic Testing

In radiographic method, radiation from a source falls on the specimen to be radiographed. The transmitted intensity through the specimen is recorded on a detecting medium such as film on the other side of the specimen. Intensity of radiation beam decreases exponentially with the thickness x of the specimen. In radiographic testing, attenuation in the specimen can be calculated by using the following expression (1):
I = I 0 B − μ x
where I = intensity of radiation emerging out of the specimen, I0 = intensity of radiation without specimen, μ = linear attenuation coefficient per unit thickness and B = build up factor which depends on energy of the source, attenuating material and its thickness.

3.2. X-ray Radiographic Image Correction

To facilitate the automatic defect detection, the distribution of weld seam in radiograph is better to be vertical. However, in the process of specimen placing and clamping before X-ray radiography, the spatial position of the weld seam to be tested is uncertain due to factors such as shapes of specimen and fixture. In addition, the mechanical error of the system transmission mechanism, among other factors, easily causes specimens to be positioned variably, like weld seams offset from the center or vertically arranged welds having an inclination angle with gravity. As shown in Figure 3, there is a certain tilt angle α between weld seam and gravity direction, affecting the effective implementation of subsequent image processing methods.
In order to eliminate this effect, a method based on moment invariant is used to calculate the inclination angle. Then, rigid transformation is introduced to translate the original radiograph, correct the inclination angle and fulfil image correction.

3.2.1. Moment Invariant

Moments invariants have been widely used in pattern recognition and digital image processing since M.K.Hu proposed the theorem in 1962. This research proved that moment invariant has the invariance of rotation and translation. In order to better study the various properties of moments, researchers have also given a variety of definitions of moments, such as Zemike moments, wavelet moments and so on.
For Hu moments, if the digital image function is piece-wise continuous and has non-zero values in a finite part of the x, y plane, the existence of its p + q t h order moment m p q can be proved. And it can also be proved that m p q is uniquely determined by f ( x , y ) ; conversely, f ( x , y ) can also be uniquely determined by m p q . It should be reminded that finiteness assumption is essential for the uniqueness theorem, otherwise the conclusion may not hold. The (p+q)th order moment of in summation form can be defined as (2):
m p q = ∑ m = 1 M ∑ n = 1 N x p y q f x , y
where ( x , y ) can be defined as pixel coordinate， f ( x , y ) is the gray scale function for ( x , y ) . Form expression (2), it is easy to define the central moments in terms of moment invariant. It is well known that central moment do not change under translation of coordinates. Therefore, the p + q t h central moment of f ( x , y ) can be defined as (3)：
μ p q = ∑ m = 1 M ∑ n = 1 N x − x ¯ p y − y ¯ q f ( x , y )
where p , q = 0 , 1 , … , ( x ¯ , y ¯ ) is the barycentric coordinates, x ¯ = m 10 / m 00 , y ¯ = m 01 / m 00 . The first four orders of central moments can be deducted: μ 00 = m 00 ≡ μ , μ 01 = μ 10 = 0 , μ 20 = m 20 − μ x ¯ , μ 11 = m 11 − μ y ¯ , μ 02 = m 02 − μ y ¯
The p + q t h normalized central moment η p q can be defined as expression (4):
η p q = μ p q / μ 00 r
where r = 1 + ( p + q ) / 2 .
Any geometrical pattern or alphabetical character can always be represented by a density distribution function, with respect to a pair of axes fixed in the visual field. In terms of X-ray radiograph, the gray scale level of the image can be regarded as the density distribution function of the pattern. Based on uniqueness theorem mentioned above, the pattern can also be represented by its two-dimensional moments m p q , with respect to a pair of fixed axes. Furthermore, if these central moments are normalized in size by using the similitude moment invariants, then the set of moment invariants can still be used to characterize the particular pattern. Obviously, normalized moments are independent of the pattern position in the visual field and also independent of the pattern size. Therefore, the inclination angle can be calculated based on invariant theorem.
For a two-dimensional image, represents the gray level center of the image in the horizontal direction, represents gray level center of the image in the vertical direction. The inclination angle θ that minimizes the second-order central moment can be expressed by the following function (5):
θ = 1 2 a r c t a n 2 μ 11 μ 20 − μ 02
The x’, y’ axes determined by any particular values of θ satisfying (5) is called the principal axes of the pattern. With added restrictions, θ can be determined uniquely. Moments determined for such a pair of principal axes are independent of orientation. μ 02 is the extension of the image in the horizontal direction; μ 20 is the extension of the image in the vertical direction; represents the inclination of the image: when μ 11 > 0 , the image is inclined to the upper left; otherwise, when μ 11 < 0 , the image is inclined to the upper right.
Result of the previous calculation, namely the value of inclination angle θ , is the basis of performing subsequent image processing methods. To fulfil image correction, a suitable translation algorithm is necessary.

3.2.2. Rigid Body Translation

When correcting an image, it is often necessary to transform it accordingly. Rigid body translation means that the distance between two points in the transformed image remains the same as the previous image after transformation. Image contour is an important information for feature extraction, the contour of the specimen is regarded as a rigid body in order to utilize the properties, and the positioning information of the object can be represented by the calculation of the image contour features.
When the image to be processed is rotated and in need of correction，the following rigid body transformation formula (6) (7) (8)can be used：
x y = c o s ∆ θ − s i n ∆ θ s i n ∆ θ c o s ∆ θ x y + ∆ x ∆ y
∆ θ = θ − ∆ θ m
∆ x ∆ y = x c ' y c ' − x c y c
x c , y c is the centroid coordinate of the original image, θ m is the angle between the main axis and the positive direction of the x axis; x c ' , y c ' is the centroid coordinate of the translated image; ∆ x is the displacement required to register the previous image with the template image, where θ is the angle between the main axis and the positive direction of the x axis. Figure 4 shows the schematic diagram of the overall image correction steps．

3.3. Defect Detection in X-ray Radiographic

The transitional region refers to the area between the target and the background. It is a special region, which not only can separate different regions based on boundary attributes, but also its width and area both are non-zero values. Due to the change of thickness, the radiograph of lap joints presents continuous grayscale distribution in the welding area, which is in line with the characteristics of transitional region. Compared with non-transitional region, the changes in grayscale of transitional region are more frequent and dramatic. These results are caused by the change of thickness in fillet weld seam combining defects and noise. Given an radiograph with limited grayscale level, the targets segmented can be divided into extended targets and weak targets according to the proportion of the size. In this case, the weld seam is the extended target, and defect is the weak target. The sudden change of grayscale level in the continuous transitional region represents the existence of defects.
After transforming the original radiograph, the weld seam is vertically distributed along the longitude of the image. Also, the horizontal grayscale distribution changes regularly according to the change of thickness. In order to identify defects, noisy suppression based on wavelet threshold is carried out first as image pre-processing. Based on that, the simulation of background image can be obtained. The purpose of simulating the background is to eliminate the sudden change in linear grayscale level caused by the existence of defects. After that, the method of least squares is used to fit the grayscale curve of the weld seam in the processed image. Then, the foreground image is obtained by subtracting the transformed image and the fitted background simulation. At last, the foreground image is processed based on iterative segmentation and mathematical morphology, and the weak target, namely the defects in the X-ray radiograph can be finally extracted. Figure 5 shows the flow diagram of digital image processing.

3.3.1. Noise Suppression

The industrial television inspection system based on the image intensifier can display the defect status of the specimen in real time, which is suitable for dynamic inspection. However, as the X-ray radiation go through the image intensifier, the information of the radiograph is easily disturbed. Therefore, the test results of the real-time detection system present low sensitivity and high noise level. In terms of noise suppression, methods based on wavelet and wavelet transformation have been widely used. At present, the commonly used noise suppression methods include wavelet module maximum, nonlinear wavelet transform threshold and noise reduction based on wavelet transformation. Threshold filtering is the simplest filtering method. Its basic principle is to compare the amplitude of the wavelet coefficient with a preset threshold. If the wavelet coefficient is lower than the preset threshold, it is set to 0; on the contrary, if the wavelet coefficient is higher than the preset threshold, it is retained. Wavelet threshold method is a simple method with low computational cost and has great potential practicability in image processing. The implementation procedure of the algorithm is as follows:
(1) Select the appropriate wavelet and wavelet decomposition level N, each will obtain the wavelet coefficients of low-frequency components and high-frequency components, that is, approximation signals and detail signals. Continue to perform wavelet decomposition on approximation signals, and obtain a set of wavelet coefficients;
(2) Perform quantization processing based on the threshold method on the wavelet coefficients obtained by decomposition to estimated wavelet coefficients;
(3) Using the estimated wavelet coefficients to perform inverse wavelet transform, in other words wavelet reconstruction, to obtain a noise-suppressed image.

3.3.2. Background Removal

Several regions account for the change of thickness, including the thick plate region, the overlapping region of the two plates, the non-linear thickness change in the weld seam region and the thin plate region. Figure 6a shows the target region of the joint. Figure 6b shows the continuous change of grayscale of the background of the image. Since the grayscale of the weld area changes continuously in the x direction, the grayscale of possible defects may be submerged in the grayscale value of the background image, as shown in Figure 6c,d. It can be seen that the unique grayscale distribution of the image brings difficulties to detect defects. Therefore, the method of background image filtering is suitable for automatic defect detection. Assuming that the original grayscale distribution of the radiograph is P i , j , the line grayscale distribution b i of the background image B ( i , j ) is obtained by using the matrix column vector mean, as shown in formula (9).
b i = 1 y ∑ j = 1 y P ( i , j ) , i = 1 , 2 , 3 , … , x
The formula of calculating the grayscale F ( i , j ) of foreground image is shown in formula (10)
F ( i , j ) = P ( i , j ) − B i , j , i = 1 , 2 , 3 , … , x , j = 1 , 2 , 3 , … , y
Figure 6f shows that after background removal, the grayscale distribution of the foreground image contains defects, noise and small proportion of background resistance.

3.3.3. Image Segmentation

According to the grayscale histogram of the image, the optimal threshold can be calculated using mathematical statistics. Also, the iterative method as follows is used to solve the image segmentation threshold:
(1) Set the program terminal parameter λ 0 , at the same time select a suitable threshold value λ 1 base on grayscale distribution;
(2) Segment the image with λ 1 and all pixels can be divided into two sets: set A includes pixels with greater grayscale value than λ 1 ; set B includes pixels with smaller grayscale value than λ 1 ;
(3) Calculate the average grayscale value of each set and get τ 1 , τ 2 , the new threshold λ 2 can be obtained by the following expression (11)
λ 2 = τ 1 + τ 2 / 2
(4) Terminate the program when the optimal threshold is found, which satisfy the constrain formula (12)
λ 1 − λ 2 < λ 0
Otherwise, repeat procedure (1) ~ (3) until the optimal threshold is found.

3.3.4. Mathematical Morphology

Post-processing based on mathematical morphology is performed after image segmentation, using structural units to assign the values to the central element. The basic operations are erosion and dilation. Opening operation and closing operation are two important operations in morphology. The opening operation is to erode and then dilate, which can generally smooth the contour of the image. Contrary to the opening operation, the closing operation is dilation first and then erosion, which can fuse the narrow gaps in the image and fill the gaps in the contour. Suppose A is a binarized ray image, and B is a selected structuring element, then A is opened by structural element B which is defined as formula (13):
A ∘ B = A Θ B ⊕ B
Where ( A Θ B ) is defined as erosion in expression (14):
( A Θ B ) = x B x ⊆ A
Similarly, the closing operation is defined as formula (15):
A • B = A ⊕ B Θ B
Where A ⊕ B is defined as dilation in expression (16):
A ⊕ B = x B ^ X ∩ A ⊆ ϕ
In this paper, the structural unit B is defined as expression (17):
B = 0 1 0 1 1 1 0 1 0

4. Experimental Results and Analysis

4.1. Image Pre-Processing

The original radiograph obtained is shown in Figure 7(a). The weld occupies a large proportion in the whole image, and the welding seam area is inclined at a small angle. The thickness of the weld varies nonlinearly and continuously along the plates’ thickness direction, resulting in a continuous change in the grayscale of the acquired radiograph. As welding speed varies, alterations in wire feeding speed and other process factors lead to changes in the amount of cladding, affecting the width and height of the weld. Furthermore, the presence of defects significantly alters the grayscale of the radiograph, making the overall scenario more complex. This brings difficulties to automatic defect identification. The weld area is initially obtained through ROI recognition on the original radiograph for subsequent processing.
Firstly, the radiograph is binarized. In this paper, image binarization employs an iterative thresholding approach to determine a threshold value, which is then utilized to isolate the weld area from the analyzed image. The extraction of weld edges is facilitated by the Canny algorithm, which leverages the Laplacian operator to discern between prominent and subtle edges by applying two distinct thresholds. This methodology selectively includes weak edges only when they are contiguous to stronger ones, thereby minimizing noise interference and enhancing the detection of genuine, faint edges compared to alternative methods. In the binarized image extracted from the weld area, the weld inclination angle is calculated to be 3.1º according to the invariant moment theory and the result is presented in Figure 7(b). On this basis, the image is corrected, and the results are shown in Figure7 (c) and (d). It can be seen from the correction results that the corrected image well maintains the characteristics of the original radiograph, and detail information is not lost during the rotation process. This provides the basis for the later image processing, defect recognition and extraction.

4.2. Automatic Defects Detection

The corrected image shown in Figure 7(d) is subjected to wavelet-based noise suppression processing to obtain Figure 8(a), which removes high-frequency noise components in the image. Using the noise-suppressed image to estimate the image background, and obtain the background image, as shown in Figure 8(b). The foreground image obtained by subtracting the corrected image and the background image shown in Figure 7(d) is shown in Figure 8(c). The foreground image is composed of defect images, noise points and residual background components. The foreground image is further processed by image threshold segmentation based on iterative method, and the background residue and noise points in the image are filtered out to obtain Figure 8(d). Finally, the operations of expansion, corrosion, opening and closing based on mathematical morphology are performed to filter out isolated noise points, separate adhesion targets, and realize automatic defect identification. The results are shown in Figure 8(e).
The method proposed enables automatic defect recognition, sizing, measurement, and localization utilizing image processing techniques without the need for extensive samples or training, such as that required by machine learning.

5. Conclusion

(1) The characteristics of X-ray inspection digital images of lap weld structures of unequal thickness plates are analyzed and researched. Firstly, the variation in the thickness of the workpiece leads to differences in the grayscale of the image background and continuous changes in the grayscale of the weld zone. Secondly, the position of the weld seam in the radiograph is not vertical and the place of it is uncertain.
(2) To facilitate the automatic defect detection, the distribution of weld seam in radiograph is first preprocessed to be vertical. First, moment invariant is introduced to calculate the inclination angle. Then, rigid body transformation is applied to fulfil image correction. The preprocessing of original radiograph provided a solid foundation for subsequent work.
(3) Based on preprocessing, a background removal method through background simulation was applied to the image. This resulted in obtaining the radiographic foreground image through background removal.。
(4) Through threshold segmentation and mathematical morphology, a binary image of defects is obtained. The automatic recognition of defects in X-ray radiograph of lap joint of unequal thickness plate was achieved.
(5) The proposed method can achieve automatic recognition, sizing, measuring and locating of defects, which is a image processing-based method that does not require a large amount of samples and training such as machine learning.

Author Contributions

Conceptualization, D.C. and H.L.; methodology, D.C., Z.W. and H.L.; software, Z.W.; validation, Z.W.; formal analysis, Z.W. and H.L.; investigation, Z.W.; resources, D.C.; data curation, Z.W. and H.L.; writing—original draft preparation, Z.W.; writing—review and editing, D.C., Z.W. and H.L.; visualization, Z.W.; supervision, D.C.; project administration, D.C.; funding acquisition, D.C. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgements

This research was funded by National Natural Science Foundation of China（52375328）and CGN-HIT Advanced Nuclear and New Energy Research Institute (CGN-HIT202310). The authors are grateful to Qingsheng Li, Qiang Guo, Weigang Su and Tao Jia for providing testing block and helpful discussions on topics related to this work.

Conflicts of Interest

Author Haichun Liu was employed by the company PipeChina Engineering Quality Supervision and Inspection Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. José A; Santiago P; Juan V; Manuel D. Advanced Comparison of Phased Array and X-rays in the Inspection of Metallic Welding. Materials, 2022, 15, 7108. [Google Scholar] [CrossRef] [PubMed]
  2. Guoxiang X; Pengfei L; Lin L; Qingxian H; Jie Z; Xiaoyan G; Baoshuai D. Influence of Arc Power on Keyhole-Induced Porosity in Laser + GMAW Hybrid Welding of Aluminum Alloy: Numerical and Experimental Studies. Materials 2019, 12, 1328. [CrossRef]
  3. Masoud S ;Martin S ;Thomas K ;Norbert H ;Bernhard R. A Review of Non-Destructive Testing(NDT) Techniques for Dfect Detection: Application to Fusion Welding and Future Wire Arc Additive Manufacturing Process. Metals, 2022,15,3697. [CrossRef]
  4. DebRoy T ;Wei H L ;Zuback J S ;Mukherjee T ; Elmer J W ;Milewski J O ;Beese A M ;Wilson-Heid A ;De A ;Zhang W. Additive manufacturing of metallic components – Process, structure and properties. Progress in Materials Science, 2018, 92,112-224. [CrossRef]
  5. Andrew E ;Athanasios T ;Yevgen G. Very High Cycle Fatigue of Welds: A Review. Metals,2023,13,1860. [CrossRef]
  6. Rozemarijn V ;Andreas Fouras ;Colin J ;Nickolas P. Innovations in thoracic imaging: CT, radiomics, AI and x-ray velocimetry. RESPIROLOGY, 2022,27,10,818-833. [CrossRef]
  7. Max F ;Ronay A ; Yung-Tsun T L ;Kincho H L. Detection and Segmentation of Manufacturing Defects with Convolutional Neural Network and Transfer Learning. Smart and Sustainable Manufacturing Systems,2018,2,1. [CrossRef]
  8. Zimu X ;Ki-Young S ;Madan M G. Development of a CNN edge detection model of noised X-ray images for enhanced performance of non-destructive testing. Measurement,2021,174. [CrossRef]
  9. Zeng JL ;Zou YR ;Du D ;Chang BH ;Pan JL. Research on a visual weld detection method based on invariant moment. INDUSTRIAL ROBOT-THE INTERNATIONAL JOURNAL OF ROBOTICS RESEARCH AND APPLICATION,2015,42,2,117-128. [CrossRef]
  10. Diana C ;Sabin M ;Muhammad A M ;Mihail Lungu ;Ioana P ;Adrian S ;Cosmin D ; Ion T ;Andrei C P. Use of X-ray Computed Tomography for Assessing Defects in Ti Grade 5 Parts Produced by Laser Melting Deposition. Metals,2020,10,1408. [CrossRef]
  11. Isabel D ;Thomas F ; Lovre K O ;Matej V. Brief Review on Experimental and Computational Techniques for Characterization of Cellular Metals. Metals,2020,10,726. [CrossRef]
  12. Katsunori M ;Wataru Y ;Margie O; Atsushi M. Evaluation of gratings for X-ray and neutron phase imaging techniques by using x-ray projection microscope. INTERNATIONAL WORKSHOP ON X-RAY AND NEUTRON PHASE IMAGING WITH GRATINGS,2012,1466,193-198. [CrossRef]
  13. Gilbert A C ;Nils B ;Stephan A ;Frédéric D G ; René G ;Nathalie B. Advanced Non-Destructive in Situ Characterization of Metals with the French Collaborating Research Group D2AM/BM02 Beamline at the European Synchrotron Radiation Facility. Metals,2019,9,352. [CrossRef]
  14. Gábor V ;Antal G ;Inge U ;Ildikó S ;Ferenc G ;Rachid C. Nondestructive Investigation of Neutron Irradiation Generated Structural Changes of Reactor Steel Material by Magentic Hyteresis Method. Metals,2020,10,642. [CrossRef]
  15. Wei T ;Stylianos C ;Caleb M S ;Roger G.M ;Robert H. Study of Mechanical Properties, Microstructure, and Residual Stresses of AISI 304/304L Stainless Steel Submerged Arc Weld for Spent Fuel Dry Storage Systems. Metals,2024,14,262. [CrossRef]
  16. Yoshihiko H; Daisuke K; Masataka O; Mizuki A; Takuya O; Yoshiaki M; Hidetoshi F; Yuichiroh K; Hironao M; Kenji A. X-ray Radiography Inspection of Pores of Thin Aluminum Foam during Press Forming Immediately after Foaming. Metals,2021,11,1226. [CrossRef]
  17. Weichao Q ;Shaohua D ;Lin C ;Qingying R. Image enhancement method for low-light pipeline weld X-ray radiographs based on weakly supervised deep learning. NDT&E International,2024,143. [CrossRef]
  18. Hardik D V ;Kush P M ; Vishvesh B ;Bharat D. Processing and evaluation of dissimilar Al-SS friction welding of pipe configuration: Nondestructive inspection, properties, and microstructure. Measurement,2021,167. [CrossRef]
  19. Ying W ;Hui G. Weld Defect Detection of X-ray Images Based on Support Vector Machine. IETE Technical Review, 2014,31,2,137-142. [CrossRef]
  20. Abdelhak M ;Fakhita R. Fast segmentation method for defects detection in radiographic images of welds. 2009 IEEE/ACS INTERNATIONAL CONFERENCE ON COMPUTER SYSTEMS AND APPLICATIONS,2009,1,857-860. [CrossRef]
  21. Yan W ; Yi S ;Peng L; Hao W. Detection of line weld defects based on multiple thresholds and support vector machine. NDT&E International, 2008,41,517-524. [CrossRef]
  22. Zhenhui T ;Engang T ;Yongxiong W ;Licheng W ;Taicheng Y. Nondestructive Defect Detection in Castings by Using Spatial Attention Bilinear Convolutional Neural Network. Industrial Information,2021,17. [CrossRef]
  23. Marek S ;Krzysztof S ;Ewa K. Detection of Flaws in concrete Using Ultrasonic Tomography and convolutional Neural Networks. Materials,2020,13,1557. [CrossRef]
  24. Xiaoyuan L ;Jinhai L ;Huanqun Z ;Huaguang Z ;Xiankai S. DGICR-Net: Dual-Graph Interactive Consistency Reasoning Network for Weld Dfect Recognition With Limited Labeled Samples. Instrumentation and Measurement, 2024,73. [CrossRef]
  25. Bassam G N M ;Mouna A ; Mohammed H M ;Boualem M ; Željko B ; Rami S ; Sorour A A. Inspection of internal erosion-corrosion of elbow pipe in the desalination station. Engineering Failure Analysis,2019,102,293-302. [CrossRef]
  26. Yasir Z ;Vineet T ;Nasir R ;Amjad A ;Rajwali K ;Ali A ;Kashif I ;Saiful I ;Tao W. Electrical and Optical Properties of Indium and Lead Co-Doped Cd0.9Zn0.1Te. Metals,2021,14,5825. [CrossRef]
  27. Das H ;Kunar A ;Rajkumar K V ;Saravanan T ;Jayakumar T ;Tapan K P. Nondestructive Evaluation of Friction Stir-Welded Aluminum Alloy to Coated Steel Sheet Lap Joint. Journal of Materials Engineering and Performance, 2015,24,11. [CrossRef]
  28. Saravanan T ;Lahiri B B ;Arunmuthu K ;Bagavathiappan S ;Sekhar A S;Pillai V P M;Philip J ;Rao B P C ;Jayakumar T. Non-Destructive Evaluation of Friction Stir Welded Joints by X-ray Radiography and Infrared Thermography. Procedia Engineering,2014,86,469-475. [CrossRef]
  29. Saravanan T ;Mahadevan S ;Mukhopadhyay C K. An improved quality assessment of fuel pin end plug welds using digital X-ray radiography. Digital Radiography, 2020,62. [CrossRef]
Preprints 120571 g001
Figure 1. Preparation for weld specimen.
Figure 1. Preparation for weld specimen.
Preprints 120571 g001
Preprints 120571 g002
Figure 2. Overall testing system and defect testing methods.
Figure 2. Overall testing system and defect testing methods.
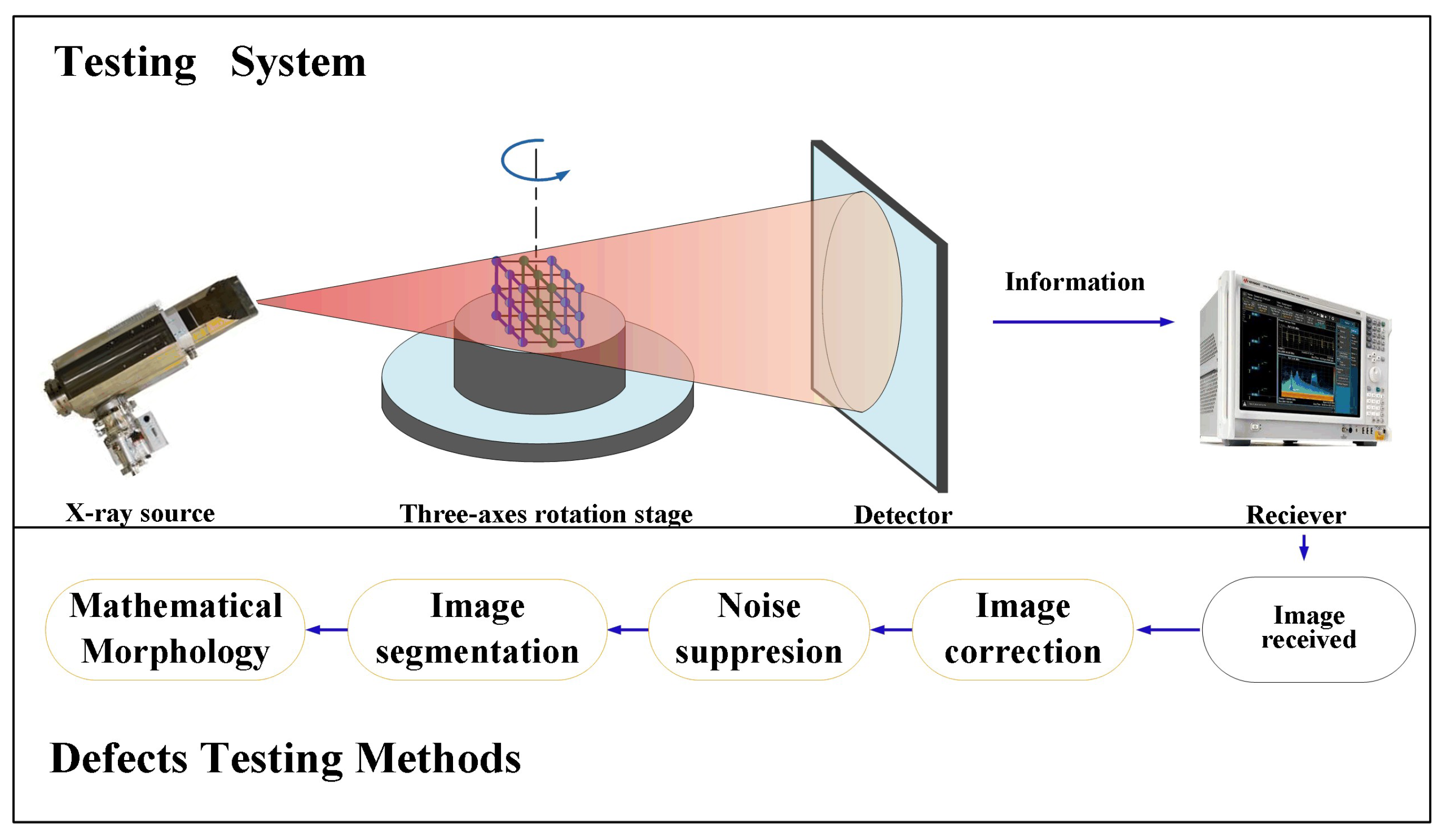
Preprints 120571 g002
Preprints 120571 g003
Figure 3. Positioning of the weld under testing.
Figure 3. Positioning of the weld under testing.
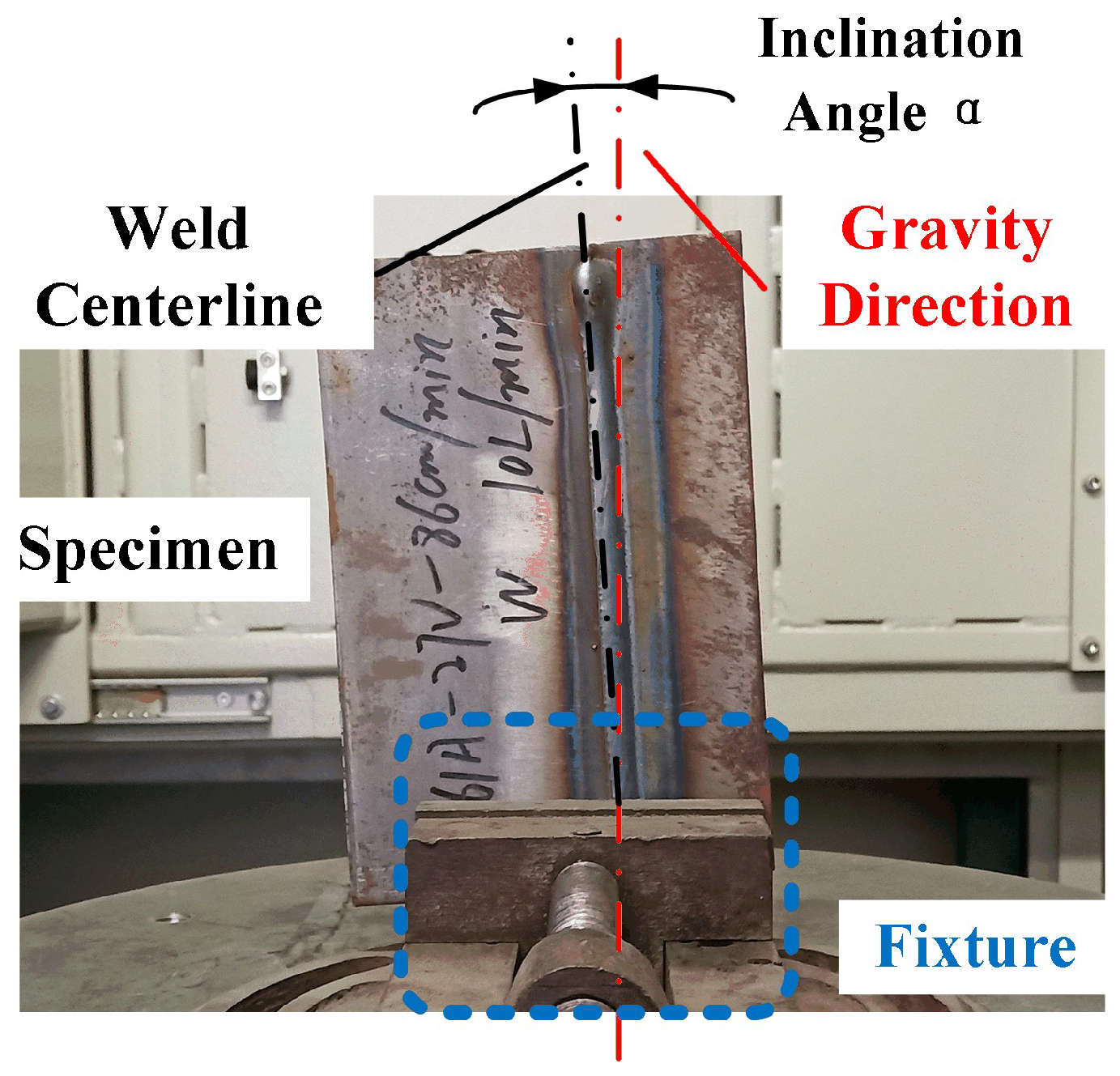
Preprints 120571 g003
Preprints 120571 g004
Figure 4. Image correction steps.
Figure 4. Image correction steps.
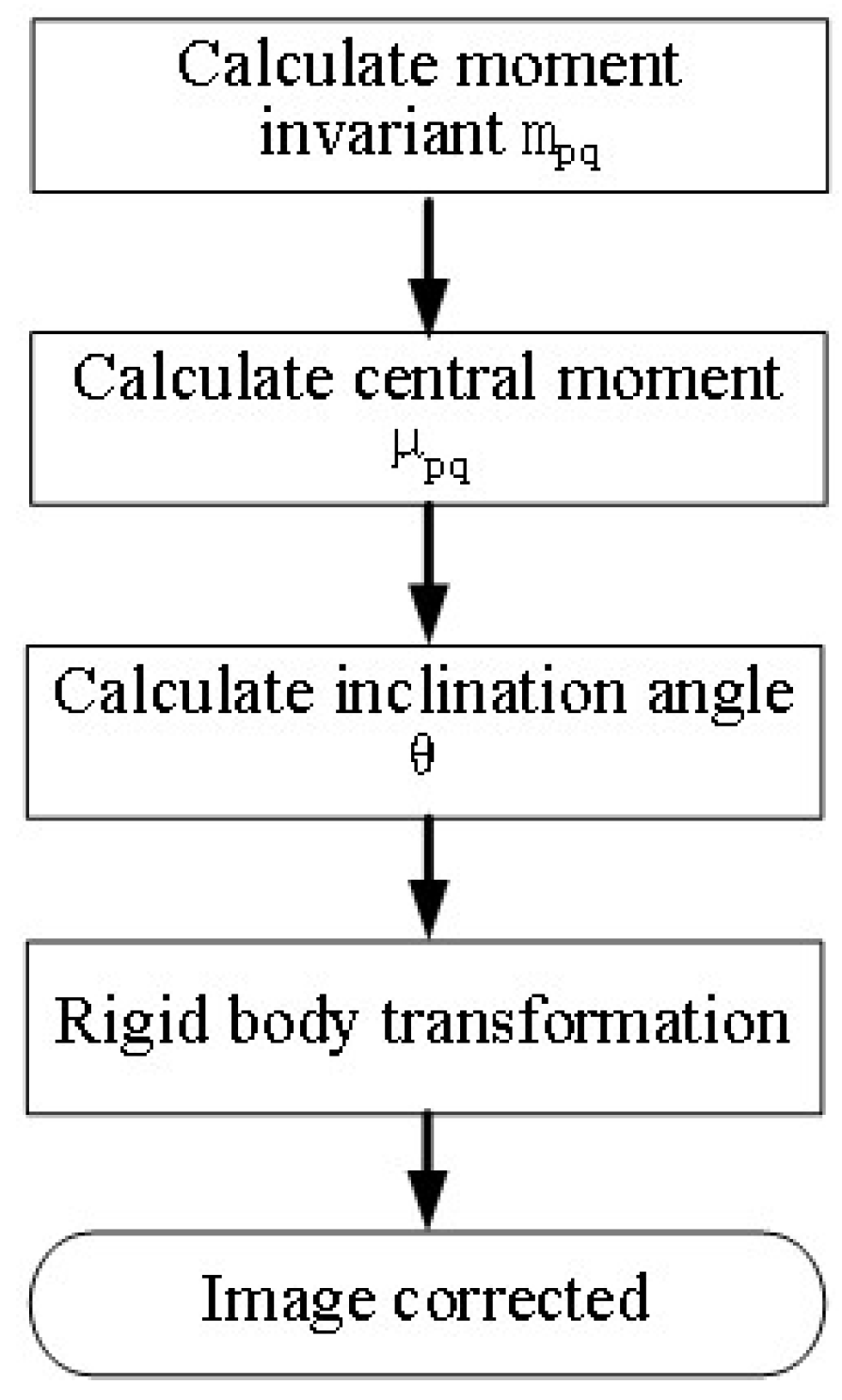
Preprints 120571 g004
Preprints 120571 g005
Figure 5. Digital image processing for defect detection.
Figure 5. Digital image processing for defect detection.
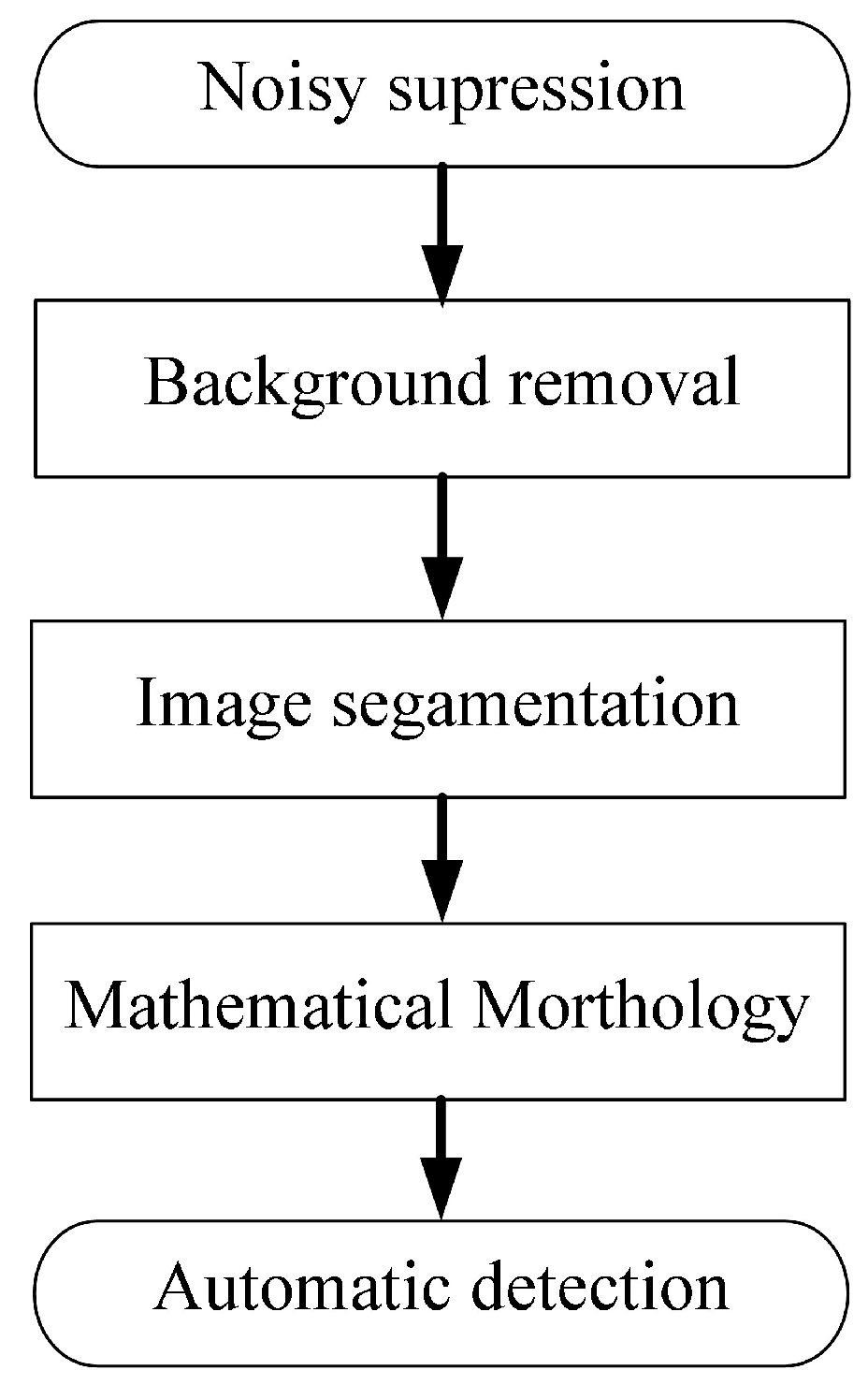
Preprints 120571 g005
Preprints 120571 g006
Figure 6. Background removal.
Figure 6. Background removal.
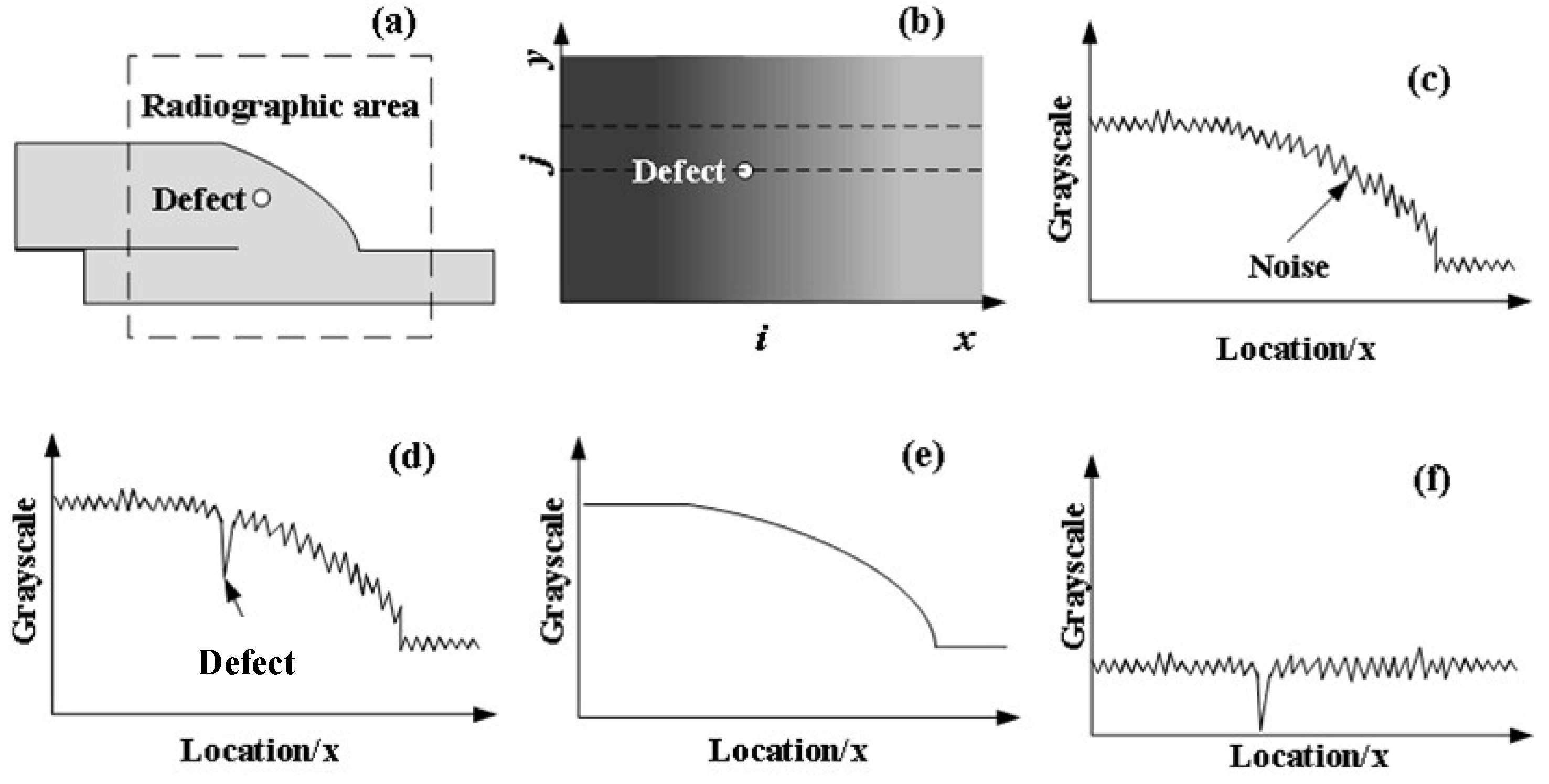
Preprints 120571 g006
Preprints 120571 g007
Figure 7. Image correction. (a) Original radiograph (b) Contour extraction (c) Image correction (d) Image corrected.
Figure 7. Image correction. (a) Original radiograph (b) Contour extraction (c) Image correction (d) Image corrected.
Preprints 120571 g007
Preprints 120571 g008
Figure 8. Defect detection. (a)Noise suppression (b) Background image (c) Foreground image (d) Image segmentation (e) Mathematical morphology.
Figure 8. Defect detection. (a)Noise suppression (b) Background image (c) Foreground image (d) Image segmentation (e) Mathematical morphology.
Preprints 120571 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated