Preprint
Article
Theory of Unification of the Interactions of Fundamental Forces: SU(3) x SU(2) --> U(1)
Altmetrics
Downloads
208
Views
103
Comments
0
This version is not peer-reviewed
Submitted:
08 October 2024
Posted:
09 October 2024
You are already at the latest version
Alerts
Abstract
Here, using the theory of electrical modelling of the neutron and proton as a three-phase alternating current electrical generator, we will begin the path to demonstrate that the interactions of electromagnetic forces, weak force and strong force that are part of the standard model, can be described by a single electromagnetic force interaction, in other words: SU(3) x SU(2) --> U(1). We will also hypothesize two particles that would give rise to gravitons. It is the interactions of the quarks (U, Û, D, ^D) that dominate the dynamics; They are responsible for the origin of bosons (photons, gluons, W⁺, W⁻, Z⁰, gravitons and Higgs boson).
Keywords:
Subject: Physical Sciences - Theoretical Physics
1. Introduction
We are going to study electromagnetic interactions; weak interactions, responsible for nuclear decay and strong interactions, responsible for the formation of neutrons and protons and their constituents. We are going to analyse all of this from the point of view of symmetries, as if nature tried to impose symmetries so that we could understand the subatomic world. All this culminated or crystallized with the creation of the standard model.
Using the symmetries, we can represent the interactions using the following equation:
SU(3) x SU(2) x U(1)
Using the theory from the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron; we are going to demonstrate that we can reduce the symmetries SU(3) x SU(2) x U(1) into a single symmetry which we can represent in the following equation:
SU(3) x SU(2) → U(1)
Let's quote this phrase attributed to Feinman
``What is not prohibited is mandatory´´
If there is not something that explicitly prohibits it, the particles have to do it, or in other words, if something does not happen it is because there is a conservation law behind it that prevents it and that conservation law is generally associated with a symmetry and a quantum number.
Taking this idea into account, we will try to reduce the symmetries of the standard model to a single equivalent electromagnetic symmetry, thus simplifying the standard model and its interactions to a single electromagnetic interaction.
To be clear, the idea is to develop an alternative and complementary model to the standard model of particle physics that will help us in future developments and research.
It is also important to state that the theory of the electrical model of the neutron and the proton as a three-phase alternating current electrical generator, allows us to lay the foundations for a future quantum theory of gravity.
This model is a very powerful tool, it uses quarks as vectors; This allows us to model the neutron and proton as three-phase alternating current electrical generators. It also allows us to represent force carriers such as the photon, the gluon, the W⁺ boson, the W⁻ boson and the Z⁰ boson, as quark interactions. With this new interpretation we are generalizing the standard model.
In the paper: Proton Decay and Inverse Neutron Decay; we can predict the subatomic particles: Dproton, Protoniu, Dneutron and Neutroniumd; through the use of vector mathematics, which allows us to notice the powerful tool we have in our hands.
We must consider the use of vector models in particle physics, as a complement to the standard model, this will allow us to develop theoretical physics by leaps and bounds.
In the following example we are going to consider the importance of vector mathematics:
Example: a real black hole is characterized by the following parameters,
- Mass
- Spin
- Electric charge
When we say that a black hole is charged, all physicists hold their heads and think that it is impossible, this happens because they think in a scalar way; But what would happen if we think vector-wise, in a composite particle formed by elementary particles with a positive charge but whose net charge is zero. Obviously, if the black hole is formed by these particles, its net charge will also be zero, although the elementary particles that constitute it are positively charged.
In this simple example we have seen the importance of introducing vector thinking into particle physics.
It is precisely this vector thinking that will allow us to introduce the bases for creating a vector model of the graviton.
1.1. Analysis of the Equation E = mc²
Let's start from Einstein's most famous equation, E = mc²; this will allow us to make a series of assumptions, which will be our basis in the development of this paper, both for the particles that belong to the standard model and the particles of gravity.
We are going to skip all of Dirac's mathematical development and analyse the following equation:
E = (+/-) mc² (1)
The correct interpretation of this equation will provide us with very valuable information, which we will use to develop our theory.
Next, we are going to start our interpretation:
a) We are going to analyse equation (1), from the point of view of the electric charge.
a.1) The sign (+) in equation (1) tells us that there is a positive charge, which can be matter or antimatter. Example, U quark.
a.2) The sign (-) of equation (1) tells us that there is a negative charge, which can be matter or antimatter. Example, U quark.
a.3) There is a third possibility, neutral charge or no charge, in other words matter and antimatter without charge. This would be the case of neutrinos.
b) We are going to analyse equation (1), from the point of view of the mass.
b.1) The sign (+) of the equation tells us that there is a force of attraction for matter (matter & antimatter).
Example, anti de Sitter space, ADS.
b.2) The sign (-) of the equation tells us that there is a repulsive force for matter (matter & antimatter)
Example, De sitter space, DS, expansion of the universe.
Now that we have concluded our preliminary analysis, we are going to propose the following hypotheses:
- (1)
- Here, we hypothesize the existence of elementary particles that have mass and also have a positive charge. These particles are included in the standard model and are characterized by having spin ½. An example, Up quark.
- (2)
- Here, we hypothesize the existence of elementary particles that have mass and also have a negative charge. These particles are included in the standard model and are characterized by having spin ½. An example, Down quark.
- (3)
- Here, we hypothesize the existence of elementary particles that have mass and have a neutral charge. These particles are included in the standard model and are characterized by having spin ½. An example, electron neutrino.
These particles are part of our standard model, when we talk about particles implicitly, we also refer to the existence of their antiparticles. With the exception of leptons that can be found in isolation in nature, quarks or fermions cannot be found in isolation in nature due to their quantum property of colour, they form more complex structures such as bosons, neutrons, protons, etc.
- (1)
- Here we hypothesize the existence of sub-particles or elementary quanta that have mass and can also have a positive, negative or neutral charge. These sub-particles are not included in the standard model. Generally, elemental quanta never remain individually with a positive, neutral or negative charge, they form particles such as the Up and Down quark.
- (2)
- Here, we hypothesize the very existence of the structure of space-time which is quantized and acts as a support for all particles and sub-particles described in hypotheses 1), 2), 3) and 4). A turning point in the structure of space-time is the Planck longitude. Above the Planck length we are in the domain of the 4 fundamental interactions, electromagnetic force, weak force, strong force and gravitational force. Below the Planck length, we are inside a black hole, in the domain of gravitational force.
These 5 hypotheses will support all our theoretical development in this paper.
1.2. Summary of the Theory of Three-Phase Alternating Current Electric Generators
We are going to make a short introduction to understand the theory of three-phase alternating current electrical generators, this theory is very important to understand the context and be able to relate the concepts of matter, antimatter, left-handed particles and right-handed particles.
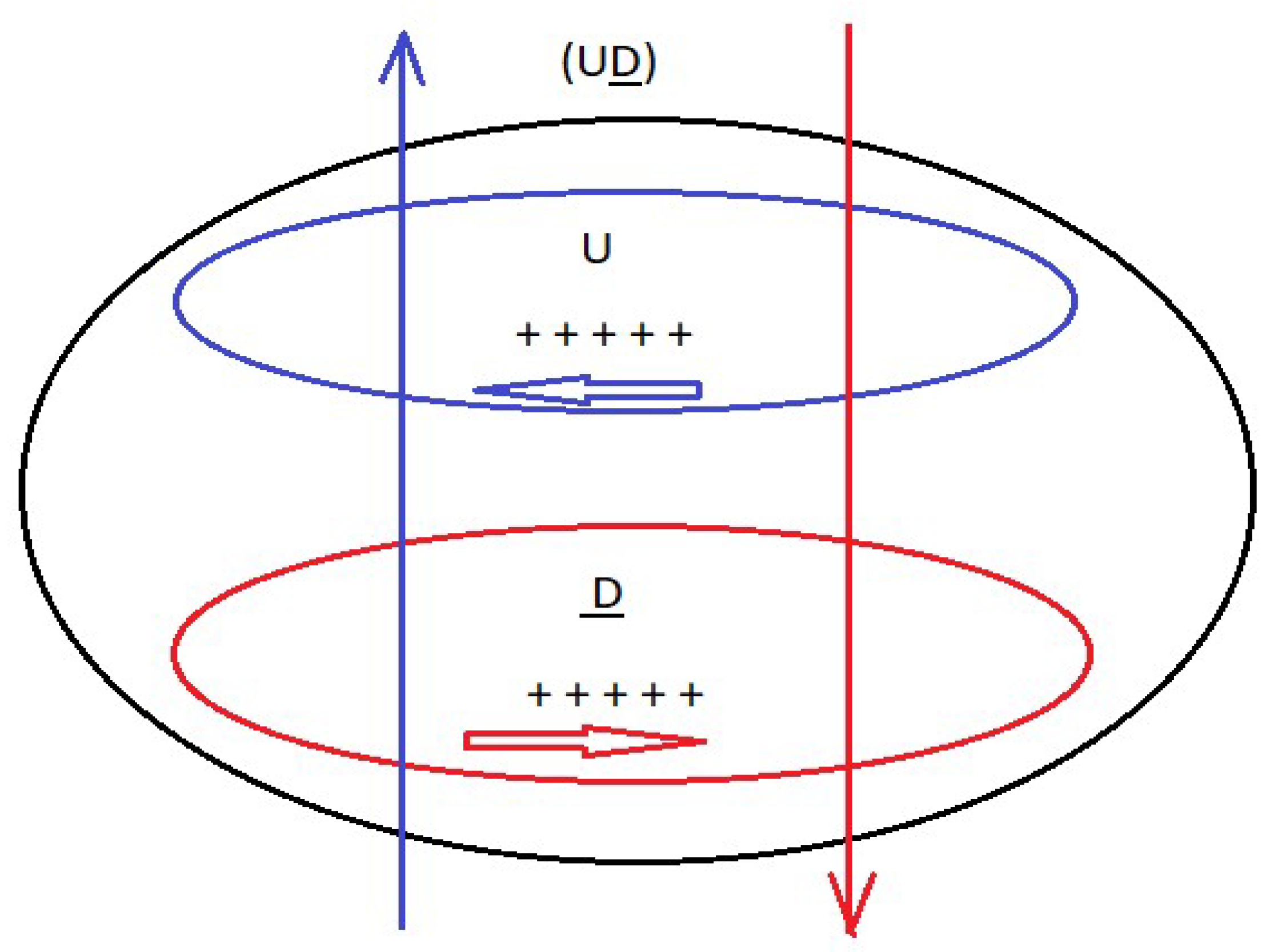
Here we put forward the hypothesis for a neutron, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quark-gluon interaction. See figure 1
Where D corresponds to the D quark and D corresponds to the D antiquark.
Where U corresponds to the U quark and U corresponds to the U antiquark.
The gluon interaction is given by (R, B, G) and (R, B, G).
Here we put forward the hypothesis for a proton, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quark-gluon interaction. See figure 2.
If we look at figure 3 and figure 4, which correspond to the electrical circuit of a three-phase generator, we see that the electrical circuit of a neutron represented in figure 1 and the electrical circuit of a proton represented in figure 2, have an identical diagram. Basically, the difference is the following, in a three-phase generator, the pairs, XX', YY' and ZZ' have the same frequency and in the case of a proton and neutron the DD pairs have twice the frequency of the UU pairs.
In analogy to what happens in a generator, in the proton and the neutron, the DD dipoles vibrate at approximately twice the frequency of the UU dipoles. Continuing with the analogy, the dipoles, XX', YY' and ZZ' in a generator would be analogous to the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton.
If we consider that the voltages, VL1, VL2 and VL3 are the result of rotating the rotor, which produces a variation of the magnetic field and ends up inducing and generating the voltages in the stator, continuing with the analogy, we can say that the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, is the result of a variable magnetic field that is generated from the interaction of quarks and anti-quarks with gluons, precisely this mechanism makes protons and neutrons generate their mass and are self-sustaining, this is the mechanism that allows the existence of hadrons.
The dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, are also out of phase with a phase angle that we are going to determine, the nomenclature of the gluons (R, B, G) and (R, B, G) serves to remind us that the Interactions between quarks and gluons are vectors.
Now we are going to analyse figure 5.
If we look at figure 5, we see that in red, green and blue the sinusoidal lines of tension generated in the stator of the three-phase electric generator are drawn.
By construction of the generator stator, the sine waves marked in red, green and blue are out of phase by 120 degrees.
We are going to analyse the sinusoidal voltage marked in red VL2.
If we look at figure 5, the voltage value that VL2 takes between 0 degrees and 180 degrees is positive, positive half-cycle. However, between 180 degrees and 360 degrees, the voltage value of VL2 is negative, negative half-cycle.
If we return to our analogy between the neutron and the proton with electrical generators; We can consider that the upper or positive semi-cycle corresponds to matter and the lower or negative semi-cycle corresponds to antimatter. It is a very nice analogy.
This analogy is very important, it is telling us that matter and antimatter are always linked, twinned. However, QCD theory does not treat matter and antimatter in a twinned manner and discriminates matter over antimatter.
In my personal opinion, QCD describes half of the story, it excludes antimatter from history. Precisely this perception is what led me to develop the theory of the neutron and the proton as a three-phase alternating current generator, in which matter and antimatter are included in the theory.
Next, we are going to describe a new analogy.
To do this we are going to run the generator like an engine.
A generator works in the following way: a generator is made up of a rotor and a stator. The stator is fixed. The magnetic field is located in the rotor. When the rotor rotates, it produces a variation in the magnetic field that induces a current and a voltage in the stator. The voltage and current in the stator are what we use. If the generator is three-phase, then the generated voltages can be represented by (R, S, T).
A motor works in the following way: the motor is made up of a stator and a rotor. If it is a three-phase motor then the voltage (R, S, T) is applied to the stator. This voltage (R, S, T) that is applied to the stator is analogous to that in figure 5. This voltage generates a current and therefore generates an induced field in the rotor that causes the rotor to rotate. This is the operating principle of an engine described in a simplified way.
The importance in this analogy is the following, if we apply a voltage (R, S, T) to the stator, we will assume that the rotor rotates to the left, this corresponds to the left-handed particles; However, if we make a phase change and apply the voltage (R, T, S) to the motor stator, then the rotor rotates to the right, this corresponds to right-handed particles.
In these two simple analogies we have compared matter, antimatter, left-handed particles and right-handed particles with the operation of electrical generators.
These analogies that we have described here will represent the base guide for the development of this paper.
2. Nuclear Phenomenology - Sum of Spins ½ of Subatomic Particles
We are not going to carry out the mathematical development, we are going to put the final results and we are going to focus on the application.
Spin 1/2 particles, Definition of Isospin:
Isospin is a symmetry associated with interchangeability or coupling between spin 1/2 particles.
Later we are going to describe the concept of symmetry, in particular we are going to analyse the SU(2) and SU(3) symmetries in order to compare them with our model that we are going to develop below.
We are going to represent the quantum states of spin 1/2 particles in the following way:
│↑ >, │↓ > (2)
Let's represent the superposition states:
│↑ > (+⁄-) │↓ > (3)
These operators have a certain algebra or commutation relationship.
Isospin:
│↑ > ≡ │1⁄2, 1⁄2 ˃ (4)
We consider this subatomic particle that has spin 1/2 and projection 1/2.
│↓ > ≡ │ 1⁄2, - 1⁄2 ˃ (5)
We consider this subatomic particle that has spin 1/2 and projection – 1/2.
Now we are going to apply the following algebraic operation and we are going to calculate the results:
│↑ ↑ > ≡ │1, 1 ˃ (6)
│↓ ↓ > ≡ │ 1, - 1 ˃ (7)
(1 ⁄ √2) x │↑↓ + ↓↑ > ≡ │1,0 > (8)
(1 ⁄ √2) x │↑↓ - ↓↑ > ≡ │0,0 > (9)
Example of a phenomenon where the proton and the neutron behave like two states of the same particle:
│p >, │n >
where p corresponds to the proton and n corresponds to the neutron.
The superposition states correspond to:
│p > (+/-) │n >
│p > ≡ │1/2, 1/2 >
│n > ≡ │1/2, -1/2 >
│pp > ≡ │1, 1 >
│nn > ≡ │1, -1 >
(1/√2) │pn + np > ≡ │1, 0 >
(1/√2) │pn - np > ≡ │0, 0 >
Using this same procedure, we are going to apply the spin ½ addition mechanism to the U, U, D and D quarks.
We are going to extend or generalize the symmetry of the neutron and the proton to the other particles, especially to the particles (U, U, D, D).
- (1)
- Sum of quark U and anti-quark U
│U >, │U >
where U corresponds to the quark U and U corresponds to the anti-quark U.
The superposition states correspond to:
│U > (+/-) │U >
│U > ≡ │1/2, 1/2 > (10)
│U > ≡ │1/2, -1/2 > (11)
│UU > ≡ │1, 1 > (12)
│UU > ≡ │1, -1 > (13)
(1/√2) │UU + UU > ≡ │1, 0 > (14)
(1/√2) │UU - UU > ≡ │0, 0 > (15)
We can write equation 14 as follows:
(1/√2) │UU + UU > ≡ │1, 0 >
│UU + UU > ≡ │2, 0 >
│UU > + | UU > ≡ │1, 0 > + │1, 0 >
│UU > ≡ │1, 0 > (14a)
│UU > ≡ │1, 0 > (14b)
- (2)
- Sum of quark D and anti-quark D
│D >, │D >
where D corresponds to the quark D and D corresponds to the anti-quark D.
The superposition states correspond to:
│D > (+/-) │D >
│D > ≡ │1/2, 1/2 > (16)
│D > ≡ │1/2, -1/2 > (17)
│DD > ≡ │1, 1 > (18)
│DD > ≡ │1, -1 > (19)
(1/√2) │DD + DD > ≡ │1, 0 > (20)
(1/√2) │DD - DD > ≡ │0, 0 > (21)
We can write equation 14 as follows:
(1/√2) │DD + DD > ≡ │1, 0 >
│DD + DD > ≡ │2, 0 >
│DD > + | DD > ≡ │1, 0 > + │1, 0 >
│DD > ≡ │1, 0 > (20a)
│DD > ≡ │1, 0 > (20b)
- (3)
- Sum of quark U and anti-quark D
│U >, │D >
where U corresponds to the quark U and D corresponds to the anti-quark D.
The superposition states correspond to:
│U > (+/-) │D >
│U > ≡ │1/2, 1/2 > (22)
│D > ≡ │1/2, -1/2 > (23)
│UU > ≡ │1, 1 > (24)
│DD > ≡ │1, -1 > (25)
(1/√2) │UD + DU > ≡ │1, 0 > (26)
(1/√2) │UD - DU > ≡ │0, 0 > (27)
- (4)
- Sum of quark D and anti-quark U
│D >, │U >
where D corresponds to the quark D and U corresponds to the anti-quark U.
The superposition states correspond to:
│D > (+/-) │U >
│D > ≡ │1/2, 1/2 > (28)
│U > ≡ │1/2, -1/2 > (29)
│DD > ≡ │1, 1 > (30)
│UU > ≡ │1, -1 > (31)
(1/√2) │DU + UD > ≡ │1, 0 > (32)
(1/√2) │DU - UD > ≡ │0, 0 > (33)
We are going to follow the following rule for spins:
Left-handed particles
Rule 1, for matter:
| MATTER | |||
| CHARGE | SPIN | SPIN | CHARGE |
| ← | ← | ||
| - 1/3 e | D | U | 2/3 e |
| 1/3 e | D | U | - 2/3 e |
| → | → | ||
Rule 2, for antimatter:
| ANTIMATTER | |||
| CHARGE | SPIN | SPIN | CHARGE |
| ← | ← | ||
| 1/3 e | D | U | - 2/3 e |
| - 1/3 e | D | U | 2/3 e |
| → | → | ||
Right-handed particles
Rule 3, for matter:
| MATTER | |||
| CHARGE | SPIN | SPIN | CHARGE |
| → | → | ||
| - 1/3 e | D | U | 2/3 e |
| 1/3 e | D | U | - 2/3 e |
| ← | ← | ||
Rule 4, for antimatter:
| ANTIMATTER | |||
| CHARGE | SPIN | SPIN | CHARGE |
| → | → | ||
| 1/3 e | D | U | - 2/3 e |
| - 1/3 e | D | U | 2/3 e |
| ← | ← | ||
Example:
│U > ≡ │1/2, 1/2 >
│U > ≡ │1/2, -1/2 >
Using rule 1 for matter we have: for the quark U, we see that the spin is 1/2 and its angular projection that results from applying the left-hand rule is also 1/2, it is telling us that the magnetic field in the inside of the coil is upward. For the antiquark U, we see that the spin is 1/2 and its angular projection that results from applying the left-hand rule is also -1/2, this is telling us that the magnetic field inside the loop is downwards.
Now that we have established a spin rule, we are going to perform the following interactions between quarks.
- (5)
- Sum of quark D and anti-quark U
│D >, │U >
where D corresponds to the quark D and U corresponds to the anti-quark U.
The superposition states correspond to:
│D > (+/-) │U >
│D > ≡ │1/2, 1/2 > (34)
│U > ≡ │1/2, -1/2 > (35)
│DU > ≡ │1, -1 > (36)
If we add the spin of the D quark (equation 34) and the spin of the U antiquark (equation 35), the sum of the spins would have to give us:
│DU > ≡ │1,0 >
However, the correct sum of the spins is represented by equation 36.
Equation 36 can be interpreted as follows:
If we consider the D quark, the spin rule tells us that the D quark generates an upward magnetic flux; If we consider the U antiquark, the U antiquark generates a downward magnetic flux; If we consider that the magnetic flux of the U antiquark is greater than the flux generated by the D quark, the resulting magnetic field flux is directed downwards.
This can also be interpreted in the following way:
(1/√2) │DU + UD > ≡ │1, 0 >
│DU + UD > ≡ │2, 0 >
│DU > + │UD > ≡ │1, -1 > + │1, 1 >
│DU > ≡ │1, -1 >
│UD > ≡ │1, 1 >
- (6)
- Sum of quark U and anti-quark D
│U >, │D >
where U corresponds to the quark U and D corresponds to the anti-quark D.
The superposition states correspond to:
│U > (+/-) │D >
│U > ≡ │1/2, 1/2 > (37)
│D > ≡ │1/2, -1/2 > (38)
│UD > ≡ │1, 1 > (39)
If we add the spin of the U quark (equation 37) and the spin of the D antiquark (equation 38), the sum of the spins would have to give us:
│UD > ≡ │1,0 >
However, the correct sum of the spins is represented by equation 39.
Equation 39 can be interpreted as follows:
If we consider the U quark, the spin rule tells us that the U quark generates an upward magnetic flux; If we consider the D antiquark, the D antiquark generates a downward magnetic flux; If we consider that the magnetic flux of the U quark is greater than the flux generated by the D antiquark, the resulting magnetic field flux is directed upwards.
This can also be interpreted in the following way:
(1/√2) │UD + DU > ≡ │1, 0 >
│UD + DU > ≡ │2, 0 >
│UD > +│ DU > ≡ │1, 1 > + │1, -1 >
│UD > ≡ │1, 1 >
│DU > ≡ │1, -1 >
Taking into account what has been developed, we are going to define the following particles:
│p > ≡ │1/2, 1/2 >
│n > ≡ │1/2, -1/2 >
│ν > ≡ │1/2, 0 >
│ν > ≡ │1/2, 0 >
│νν > ≡ │1, 0 >
│e⁻ > ≡ │1/2, 1/2 >
│e⁺ > ≡ │1/2, -1/2 >
│ e⁻e⁺ > ≡ │1, 0 >
│U > ≡ │1/2, 1/2 >
│U > ≡ │1/2, -1/2 >
│D > ≡ │1/2, 1/2 >
│D > ≡ │1/2, -1/2 >
│UU > ≡ │1, 0 >
│UU > ≡ │1, 1 >
│UU > ≡ │1, -1 >
│DD > ≡ │1, 0 >
│DD > ≡ │1, 1 >
│DD > ≡ │1, -1 >
│UD > ≡ │1, 1 >
│DU > ≡ │1, -1 >
│DU > ≡ │1, -1 >
│UD > ≡ │1, 1 >
(1/√2) │UD + DU > ≡ │2, 0 >
(1/√2) │UD - DU > ≡ │0, 0 >
(1/√2) │DU + UD > ≡ │1, 0 >
(1/√2) │DU - UD > ≡ │0, 0 >
These are the base particles, with which we are going to work.
Example:
- (a)
- We make two protons collide and we obtain deuterium plus the particle π⁺. Exceeding a certain energy threshold, one of the protons transforms into a neutron plus the pion (+), the neutron unites with the proton and transforms into deuterium.
p + p → d + π⁺ < Ɣʹ, 1, 1| Uᵗ | Ɣ, 1, 1>
d ₁ H², (1, 1) → (1/ √2) |pn – np > ≡ |0, 0 >
We observe that deuterium couples to isospin (0) and its projection is also zero (0).
If we analyse the initial state, we see that the sum of the two protons couple with isospin 1 and their projection also 1; If we analyse the final state, we see that the deuterium does not contribute to the sum, therefore for symmetry to be preserved, the π⁺particle has to have isospin 1 and projection 1.
π⁺, │UD > ≡ │1, 1 >
- (b) We collide two neutrons and obtain deuterium plus the particle π⁻. Once a certain energy threshold is exceeded, one of the neutrons transforms into a proton plus the pion (-), the proton joins the neutron and becomes deuterium.
n + n → d + π⁻ < Ɣʹ, 1, -1| Uᵗ | Ɣ, 1, -1>
d → ₁ H ², (1, 1) → (1/ √2) |pn – np > ≡ |0, 0 >
We observe that deuterium couples to isospin (0) and its projection is also zero (0).
If we analyse the initial state, we see that the sum of the two neutrons couples with isospin (1) and its projection (-1); If we analyse the final state, we see that deuterium does not contribute to the sum, therefore for symmetry to be preserved, the π⁻ particle has to have isospin (1) and projection (-1).
π⁻, │DU > ≡ │1, -1 >
- (c) We collide neutrons against protons and obtain deuterium plus the particle π⁰.
n + p → d + π⁰ < Ɣʹ, 1, 0| Uᵗ | Ɣ, 1, 0>
d → ₁ H ², (1, 1) → (1/ √2) |pn – np > ≡ |0, 0 >
We observe that deuterium couples to isospin (0) and its projection is also zero (0).
If we analyse the initial state, we see that the sum of the neutron plus the proton couples with the isospin (1) and its projection (0); If we analyse the final state, we see that deuterium does not contribute to the sum, therefore for symmetry to be preserved, the π⁰ particle has to have isospin (1) and projection (0).
π⁰, │UU > ≡ │1, 0 >
π⁰, │DD > ≡ │1, 0 >
3. Standard Model
The standard model is divided into fermionic and bosonic particles. Among the fermionic particles we have quarks and leptons.
All fermionic particles have spin 1/2.
Bosonic particles, according to their interaction, are divided in the following way:
Electromagnetic force interaction: photons
Strong force interaction: gluons
Weak force interaction: W (+/-) boson and Z boson
Gravitational force interaction: graviton!!!!
Higgs field interaction: Higgs boson
Figure 6.
– Standard model.

4. β⁻Decay Analysis
We are going to try to find a relationship between the fermionic particles of the standard model and the messenger or bosonic particles.
We know that fermionic particles have spin 1/2 and bosonic particles have spin 1 except for the Higgs boson which has spin 0.
To find the relationship between fermions and bosons we are going to use the β⁻ decay model, developed in the paper: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron.
Neutron → Proton + e⁻ + ṽ + ∆E (40)
Vector analysis of βˉ decay
Figure 7, Figure 8 and Figure 9 are used in the vector analysis of the decay of the neutron into proton:
From the vector diagram the following table is obtained:
Table 1 shows that the total energy involved in β⁻ decay corresponds to IEtI = 385.37 MeV/c².
In order to find a relationship between fermions and bosons, we are going to analyse the 9 interactions in Table 1 one by one.
Direct interactions:
- (i)
- [R(DD)R]n → [R(DD)R]p
There is a neutral current in (RR), which adds mass, which causes the mass of [R(DD)R]n to reach the value of (R(DD)R)p.
Let's remember that gluons (RR) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that (R(DD)R)n has a mass of: 84.69 MeV/c²
If we look at figure 8, we see that (R(DD)R)p has a mass of: 103.81 MeV/c²
In figure 9, we see that there is a potential difference that gives rise to E1, therefore what is really produced is a neutral electric current that makes (R(DD)R)n → (R(DD)R)p , as shown in table 2 in green.
- (ii)
- [B(DD)B]n → [B(UU)B]p
There is a non-neutral current in (BB), that removes mass, that causes the mass of [B(DD)B]n to reach the value of [B(UU)B]p
Let's remember that gluons (BB) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that (B(DD)B)n has a mass of: 84.69 MeV/c²
If we look at figure 8, we see that (B(UU)B)p has a mass of: 48.28 MeV/c²
In figure 9, we see that there is a potential difference that gives rise to E2, therefore what really occurs is the decay of the quarks (DD) into quarks (UU) which makes B(DD)B]n → [B(UU)B]p as shown in table 3 in green.
Here we are going to carry out the following reasoning, for this we are going to use the following graph:
If we look at the graph in figure 10, there is a mass value between 2.2 Mev/c² and 4.7 Mev/c² marked with x, in blue, which corresponds to zero charge (0 e).
Let's give an interpretation to this graph that relates the D quark to the U quark.
We see that for 0 Mev/c² it corresponds to a charge of zero, 0 e. As the mass increases, the charge also increases, reaching 2.2 Mev/c², with a charge of +2/3 e, which corresponds to the U quark. We continue adding mass, but now we add negative charge until we reach a value of null charge or zero charge, we do not know this mass value and we denote it with an X. We continue adding mass and negative charge until we reach a mass of 4.7 Mev/c² and a charge of - 1/3 e, which corresponds to the D quark.
We are going to hypothesize that quarks (D, D) are composite particles within which the elementary particles (U, U) are contained.
- (iii)
- [G(UU)G]n → [G(UU)G]p
There is a neutral electric current in (GG), that adds up to mass, that causes the mass of [G(UU)G]n to reach the value of [G(UU)G]p
Let's remember that gluons (GG) do not exist, it simply tells us that the exchange of quarks (UU) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that (G(UU)G)n has a mass of: 39.39 MeV/c²
If we look at figure 8, we see that (G(UU)G)p has a mass of: 48.28 MeV/c²
In figure 9 we see that there is a potential difference E3, therefore what is really produced is a neutral electric current that makes [G(UU)G]n → [G(UU)G]p as shown in table 4 in green.
Cross interactions:
- (iv) [R(DD)B]n → [R(DU)B]p
there are two electric currents that removes mass, that causes the mass of [R(DD)B]n to reach the value of [R(DU)B]p
There is a neutral electric current of D quarks in the direction of R.
There is an electric current of D antiquarks in the direction of B.
Let's remember that gluons (RB) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that [R(DD)B]n has a mass of: 100.45 MeV/c²
If we look at figure 8, we see that [R(DU)B]p has a mass of: 48.28 MeV/c²
In figure 9 we see that there is a potential difference E4, we observe that there is a neutral electric current in the direction of R that goes from the quark Dn → Dp and we also observe in the direction of B the decay of the quark Dn → Up; Therefore, what really occurs is that [R(DD)B]n → [R(DU)B]p as shown in table 5 in green.
We can represent this transformation in the following way:
D → U + e⁺ + ʋ
In this interaction: [R(DD)B]n → [R(DU)B]p; We observe that U antiquark, positrons and neutrinos are produced.
- (v) [R(DU)G]n → [R(DU)G]p
there are two neutral electric currents that adds up to mass, that causes the mass of [R(DU)G]n to reach the value of [R(DU)G]p
There is a neutral electric current of D quarks in the direction of R.
There is a neutral electric current of U antiquarks in the direction of G.
Let's remember that gluons (RG) do not exist, it simply tells us that the exchange of quarks (DU) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that [R(DU)G]n has a mass of: 100.45 MeV/c²
If we look at figure 8, we see that [R(DU)B]p has a mass of: 125.54 MeV/c²
In figure 9, we see that there is a potential difference E5; If we observe in the direction of R, we see that there is a neutral electric current that goes from Dn → Dp and if we observe in the direction of G, we also observe that there is a neutral electric current that goes from Un →Up; Therefore, what really occurs is that [R(DU)G]n →[R(DU)G]p as shown in table 6, in green.
- (vi)
- [B(DD)R]n → [B(UD)R]p
there are two electric currents that adds up to mass, that causes the mass of [B(DD)R]n to reach the value of [B(UD)R]p.
There is an electric current of D quarks in the direction of B.
There is a neutral electric current of D antiquark in the direction of R.
Let's remember that gluons (BR) do not exist, it simply tells us that the exchange of quarks (DD) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that [B(DD)R]n has a mass of: 100.45 MeV/c²
If we look at figure 8, we see that [B(UD)R]p has a mass of: 165.38 MeV/c²
In figure 9, we see that there is a potential difference E6, note that in the direction of B the D quark decays into the U quark, D → U; Also note that in the direction of R there is a neutral electric current between the U quarks, U -- > U; Therefore what really occurs is that [B(DD)R]n --> [B(UD)R]p as shown in table 7 in green.
We can represent this transformation in the following way:
D → U + e⁻ + ʋ
In this interaction: [B(DD)R]n → [B(UD)R]p; We observe that U quark, electron and antineutrinos and are produced.
- (vii)
- [B(DU)G]n → [B(UU)G]p
there are two electric currents that removes mass that causes the mass of [B(DU)G]n to reach the value of [B(UU)G]p.
There is an electric current of D quarks in the direction of B.
There is a neutral electric current of U antiquark in the direction of G.
Let's remember that gluons (BG) do not exist, it simply tells us that the exchange of quarks (DU) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that [B(DU)G]n has a mass of: 100.45 MeV/c²
If we look at figure 8, we see that [B(UU)G]p has a mass of: 97.78 MeV/c²
In figure 9, we see that there is a potential difference E7. If we look in the direction of B, the D quark decays into the U quark, D --> U; If we look in the direction of G, there is a neutral electric current between the U antiquarks, U --> U; Therefore, what is actually produced is [B(DU)G]n →[B(UU)G]p as show in table 8, in green.
We can represent this transformation in the following way:
D → U + e⁻ + ʋ
In this interaction: [B(DU)G]n → [B(UU)G]p; We observe that U quark, electron and antineutrinos are produced.
- (viii)
- G(UD)R → G(UD)R
There are two neutral electric currents that adds up to mass that causes the mass of [G(UD)R]n to reach the value of [G(UD)R]p.
There is a neutral electric current of U quarks in the direction of G.
There is a neutral electric current of D antiquark in the direction of R.
Let's remember that gluons (GR) do not exist, it simply tells us that the exchange of quarks (UD) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that [G(UD)R]n has a mass of: 164.47 MeV/c²
If we look at figure 8, we see that [G(UD)R]p has a mass of: 202.80 MeV/c²
In figure 9, we see that there is a potential difference E8. If we observe in the direction of G, there is a neutral current that goes from the Un quark to the Up quark, Un --> Up; If we observe in the direction of R, there is a neutral electric current that goes from the Dn antiquark to the Dp antiquark, Dn --> Dp; Therefore, what really occurs is that [G(UD)R]n → [G(UD)R]p as shown in table 9, in green.
- (ix) G(UD)B → G(UU)B
There are two electric currents that removes mass that causes the mass of [G(UD)B]n to reach the value of [G(UU)B]p.
There is a neutral electric current of U quarks in the direction of G.
There is a electric current of D antiquarks in the direction of B.
Let's remember that gluons (GB) do not exist, it simply tells us that the exchange of quarks (UD) is vector and has a magnitude and angle that must be respected.
If we look at figure 7, we see that [G(UD)B]n has a mass of: 164.47 MeV/c²
If we look at figure 8, we see that [G(UU)B]p has a mass of: 97.78 MeV/c²
In figure 9, we see that there is a potential difference E9, if we look in the direction of G we see that there is a neutral electric current that goes from the Un quark to the Up quark, Un → Up; If we look in the direction of B, we see that the Dn antiquark decays into the Up antiquark, Dn → Up; Therefore, what really occurs is that [G(UD)B]n → [G(UU)B]p as shown in table 10, in green.
We can represent this transformation in the following way:
D → U + e⁺ + ʋ
In this interaction: G(UD)B → G(UU)B; We observe that U antiquark, positrons and neutrinos are produced.
We observe that in table 3 (E2), an electron and a positron are emitted; in table 5 (E4), a positron is emitted; in table 7 (E6), an electron is emitted; in table 8 ((E7), an electron is emitted and finally in table 10 (E9), a positron is emitted. The important thing in our analysis is the net emission, which we will demonstrate below that it consists of the emission of an electron and an electron antineutrino.
Origin of the electron
To determine the origin of the electron, we are going to analyse figure 2 and 3.
In Figure 2 and 3, we see that the neutron and proton interactions are divided into direct interactions and cross interactions.
If we analyze the direct interaction in the decay of the neutron → proton, we observe that the dipole [B(DD)B]n --> [B(UU)B]p undergoes transformations.
E2 = [B(DD)B]n → [B(UU)B]p = 36.41 MeV/c²
When analyzing the cross interaction, we observe that the following dipoles undergo transformations,
E4 = [R(DD)B]n → [R(DU)B]p = 80.75 MeV/c²
E6 = [B(DD)R]n → [B(UD)R]p = 72.87 MeV/c²
E7 = [B(DU)G]n → [B(UU)G]p = 41.35 MeV/c²
E9 = [G(UD)B]n → [G(UU)B]p = 68.93 MeV/c²
We observe that in the dipoles E2, E4, E6, E7 and E9; transformations occur in the BB interaction.
Using table 1, we are going to make the following graphs:
The interactions that occur in RR and GG are neutral currents that do not produce transformations in the quarks.
The interactions in BB produce transformations in the quarks.
Now we are going to try to interpret the values given in table 11, in BB interactions.
In table 1, we observe that the interaction at B = 36.41. If we compare with the interaction B in table 11, we observe that there is a difference of 0.95 MeV/c²
In table 1, we observe that the interaction at B = 36.41. If we compare with the interaction B in table 11, we observe that there is a difference of 36.41 MeV/c²
The difference between the BB interactions is given by:
ΔBB = 36.41 MeV/c² - 35.46 MeV/c² = 0.95 MeV/c²
This difference in mass or energy given by ΔBB = 0.95 MeV/c², It is what gives rise to the electron.
Origin of the antineutrino
We are going to represent the neutrino and antineutrino in the following way:
│ν > ≡ │1/2, 0 >
│ν > ≡ │1/2, 0 >
Let us observe that the neutrino and antineutrino have spin 1/2 and zero angular projection (0).
We know that neutrinos have very small mass, therefore they can transport energy and transfer it through their linear momentum. Let's remember that neutrinos are particles that have no electrical charge.
An example occurs when an antineutrino interacts with an electron and changes the speed of the electron and its angle. The change in speed of the electron produces a change in energy and therefore a change in its mass.
The interaction of the antineutrino with the electron acts as a neutral current, which causes the electron to change its speed, its energy and therefore its mass.
We are going to perform the following analysis on βˉ decay. 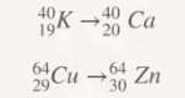
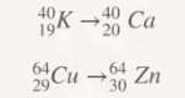
Initially, the decay of potassium into calcium was analysed and it was observed that a neutron transformed into a proton and emitted an electron. The decay of copper into Zinc was also analysed and again it was observed that a neutron transformed into a proton and emitted an electron, that is:
n →p + e⁻
A → B + e⁻
Where A is the parent nucleus, B is the daughter nucleus and e⁻ is the electron.
Let's represent this in the following way, 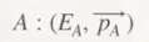
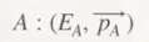
Where A is a quadruple-vector and represents the parent nucleus, Eᴀ is the energy and Pᴀ represents the ordinary impulse in (X, Y, Z). 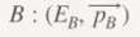
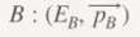
Where B is a quadruple-vector and represents the daughter nucleus, Eв is the energy and Pв represents the ordinary impulse in (X, Y, Z). 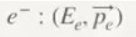
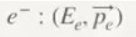
Where e⁻ is a quadruple-vector and represents the electron, Ee is the energy and Pe represents the ordinary momentum in (X, Y, Z).
Now if I stand at the centre of mass, that is, at the parent nucleus, we have:
Pᴀ = 0; Eᴀ = mᴀ
Pв = - Pe
The process is defined by these equations.
We now consider the following equations: 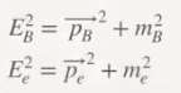
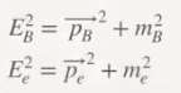
We can determine the value of Ee.
However, what was observed is that Ee is not fixed, it is variable and represents a continuous spectrum, which at that time violated the law of conservation of energy and momentum. This led to the postulation of a new particle that they called antineutrino.
This particle, the antineutrino, allowed the conservation of energy, impulse and lepton number.
To determine the origin of the antineutrino on βˉ decay, we are going to analyse figure 7, 8 and 9.
Let's remember that we are using the theory: modelling a neutron and proton as a three-phase alternating current electric generator.
In the previous item we analysed the origin of the electron, we observed that it is related to BB interactions.
We observe that the dipoles E2, E4, E6, E7 and E9; They are involved in the BB interactions that give rise to the electron.
However, if we analyze table 2 to table 10, we observe that there are neutral electric currents.
Let's analyze table 2 again,
If we look at figure 7, we see that (R(DD)R)n has a mass of: 84.69 MeV/c²
If we look at figure 8, we see that (R(DD)R)p has a mass of: 103.81 MeV/c²
In figure 9, we see that there is a potential difference E1, therefore what is really produced is a neutral electric current (DD) that goes from (R(DD)R)n → (R(DD)R)p, as show in table 12 in green.
If we analyse in the RR direction, we observe that there are no changes in flavour in the DD quark, there is only a change in mass that goes from 84.69 MeV/c² in the neutron to 103.81 MeV/c² in the proton. We could attribute this mass variation to the interaction of neutrinos and antineutrinos that act as neutral currents.
If we observe in the direction of R, the change in mass D quarks, is attributed to the neutrinos, if we observe in the direction of R, the change in mass D antiquarks, is attributed to the antineutrinos.
Now let's analyse table 8.
If we look at figure 7, we see that [B(DU)G]n has a mass of: 100.45 MeV/c²
If we look at figure 8, we see that [B(UU)G]p has a mass of: 97.78 MeV/c²
In figure 9, we see that there is a potential difference E7, therefore what is really produced is a electric current (DU) that goes from [B(DU)G]n → [B(UU)G]p as show in table 13, in green.
If we analyse in the direction of B, we observe that there is a change in flavour in the D quark, which transforms into the U quark; If we analyse in the direction of G, we observe that there is no change in flavour in the U antiquark.
The cross interaction is related to the direct interaction, therefore the change of flavour in the direction of B, in which the D quark transforms into the U quark in Table 13, is related to the origin of the electron. However, in the G direction, there is no change in flavour in the U antiquark, this is related to a current of antineutrinos.
Here, it is necessary to make the following comment.
We are going to use the following equation:
n → p + e⁻ + ν
If we bombard neutrons with neutrinos in a nuclear reactor, we obtain protons and electrons. We can represent this in the following equation:
ν +n → p + e⁻
However, if we bombard neutrons with antineutrinos in a nuclear reactor, we do not obtain protons and electrons. We can represent this in the following equation:
 → p + e⁻
→ p + e⁻Now let's analyse table 10.
If we look at figure 7, we see that [G(UD)B]n has a mass of: 164.47 MeV/c²
If we look at figure 8, we see that [G(UU)B]p has a mass of: 97.78 MeV/c²
In figure 9, we see that there is a potential difference E9, therefore what is really produced is a electric current (UD) that goes from [G(UD)B]n → [G(UU)B]p as show in table 14, in green.
In table 14, if we analyse in the direction of G, we observe that there is no change in flavour in the U quark. If we analyse in the direction of B, we observe that there is a change in flavour in the D antiquark, which becomes a U quark.
The cross interaction is related to the direct interaction, therefore the flavour change in the direction of B, in which the D antiquark transforms into the U antiquark in Table 14, is related to the origin of the positron. However, in the G direction, there is no flavour change in the U quark, this is related to a current of neutrinos.
In table 13, we clearly see that when the D quark transforms into a U quark, there is an associated neutral antineutrino current.
In table 14, we clearly see that when the D antiquark transforms into a U antiquark, there is an associated neutral neutrino current.
When we analyse the origin of the electron, we determine that in the BB interaction, there is a net mass value corresponding to 0.95 MeV/c², which gives rise to the electron and therefore has associated a neutral current corresponding to the antineutrino, as can be seen in table 13. Therefore, the emission of the electron is associated with the emission of an antineutrino, in the process in which a neutron decays into a proton.
By analysing the decay of a neutron into a proton in beta decay, we determine the importance of the neutral currents of neutrinos and antineutrinos; They help us configure the direct and cross interactions inside the proton.
We are going to propose a model that explains the process by which neutrinos and antineutrinos are created.
`In the following figure, we will recall the proposed model for the D and D antiquark.
In Figure 12, we are proposing that the D quark is a composite particle, in which the U quark and neutrinos are included.
In Figure 13, we are proposing that the D antiquark is a composite particle, in which the U antiquark and the antineutrinos are included.
We are going to write the βˉ decay as a function of the D quark and the U quark.
D → U + e⁻ + ν
We are going to perform the following calculation:
We are going to calculate the mass of the neutrino for the temperature of the electron.
T = 5.93 10 ⁹ K
E = K x T
E = 1.38 10⁻²³ x 5.93 10 ⁹ K = 8.18 10 ⁻¹⁴
E = 8.18 10 ⁻¹⁴ J
E = h x f; f = E / h
f = 8.18 10 ⁻¹⁴ / 6.63 10⁻³⁴
f = 1.23 10²⁰ Hz
c = λ x f; λ = c/f = 3 10⁸ / 1.23 10²⁰
λ = 2.43 10 ⁻¹² m
M(neutrino) = h / (λ x C) = 6.63 10⁻³⁴ / (2.43 10 ⁻¹² x 3 10⁸)
M(neutrino) = 0.909 10 ⁻³⁰ = 9.09 10⁻³¹ kg
These calculations also hold true for antineutrinos.
We have shown that if we consider the temperature of the electron T = 5.93 10 ⁹ K, the mass of the antineutrino is exactly equal to the mass of the electron. It is important to remember that the linear momentum of the electron is different from the linear momentum of the antineutrino.
|Pe| ≠ |Pν| → Me.Ve ≠ Mν.Vν
The calculations that we are going to carry out below are approximate calculations, we want to determine the number of neutrinos that are emitted when a D quark decays into a U quark.
Md = 8.55 10⁻³⁰ kg
Mu = 4.10 10 ⁻³⁰ kg
Me = 9.10 10 ⁻³¹ kg, T = 5.93 10 ⁹ K
Mν = Me = 9.10 10 ⁻³¹ kg, T = 5.93 10 ⁹ K
Δ = Md – Mu = 4.45 10 ⁻³⁰ kg
Qν = Δ / Mν = 4.45 10 ⁻³⁰ kg / 9.10 10 ⁻³¹ kg = 0.489 10 = 5
These calculations are telling me that at the temperature at which βˉ decay of the neutron into a proton occurs, the mass of the antineutrino is approximately the mass of the electron.
If we consider an intermediate temperature between the U quark and the electron, possibly the mass corresponding to Δ = 4.45 10 ⁻³⁰ kg is divided into two, one for the electron and another for the antineutrino and not in 5 as the calculation carried out.
Now when the antineutrino reaches the temperature of empty space, that is, 2.7 K, it is evident that its mass takes on the value we know, Mν = 1.6 10 ⁻³⁶ kg, or perhaps even lower.
These calculations show us the importance of considering the temperature at which particle interactions occur.
Mν = Mν = 1.6 10 ⁻³⁶ kg, T = 2.55 10⁴ K
Mν = Mν = 9.10 10 ⁻³¹ kg, T = 5.93 10 ⁹ K
In this simple analysis we have replaced the quantum model of QCD with the electrical model of a three-phase alternating current electrical generator. Quarks and gluons are used in the QCD model; In the electrical model as a three-phase alternating current electrical generator, the interactions are carried out through quarks and antiquarks, the gluons are only indicative notations to remind us that we are working with vectors with module and phase, as happens in an electrical generator.
4.1. Neutron Analysis
For our analysis we will need the following figure:
In figure 14, we observe that there are 9 dipoles, 3 dipoles belong to interaction 1 or direct interaction and 6 dipoles belong to interaction 2 or crossed interaction.
Interaction 1
Dipole 1, is represented by R(DD)R, which generates a neutral quark electric current (DD) in the RR direction, in phase.
R(DD)R →│DD > ≡ │1, 0 >
Dipole 2, is represented by B(DD)B, which generates a neutral quark electric current (DD) in the BB direction, in phase.
B(DD)B →│DD > ≡ │1, 0 >
Dipole 3, is represented by G(UU)G, which generates a neutral quark electric current (UU) in the GG direction, in phase.
G(UU)G →│UU > ≡ │1, 0 >
The quark current (DD) in the RR and BB directions can escape confinement by generating photons.
The quark current (UU) in the GG direction can escape confinement by generating photons.
This can be seen when we analyse the B⁻ decay.
Interaction 2
Dipole 4 is represented by R(DD)B, which generates two quark electric currents (DD), one electric current in the R direction, D quarks; the other electric current in the B direction, D antiquarks. Both currents are out of phase.
R(DD)B →│DD >
Dipole 5 is represented by R(DU)G, which generates two quark electric currents (DU), one electric current in the R direction, D quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
R(DU)G →│DU >
Dipole 6 is represented by B(DD)R, which generates two quark electric currents (DD), one electric current in the B direction, D quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
B(DD)R →│DD >
Dipole 7 is represented by B(DU)G, which generates two quark electric currents (DU), one electric current in the B direction, D quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
B(DU)G →│DU >
Dipole 8 is represented by G(UD)R, which generates two quark electric currents (UD), one electric current in the G direction, U quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
G(UD)R →│UD >
Dipole 9 is represented by G(UD)B, which generates two quark electric currents (UD), one electric current in the G direction, U quarks; the other electric current in the B direction, D antiquarks. Both currents are out of phase.
G(UD)B →│UD >
If we analyse the dipoles of interaction 2, we see that they are crossed interactions which generate two quark currents that are characterized by being out of phase, they are not in phase. These currents are confined to the neutron.
In this simple analysis we have replaced the quantum model of QCD with the electrical model of the neutron as a three-phase alternating current electrical generator. In the QCD model, quarks and gluons are used to represent the interactions in the neutron; In the electrical model of the neutron as a three-phase alternating current electrical generator, the interactions in the neutron are carried out through quarks and antiquarks, the gluons are just indicative notations to remind us that we are working with vectors with module and phase, as happens in an Electric generator.
4.2. Proton Analysis
For our analysis we will need the following figure:
In figure 15, we observe that there are 9 dipoles, 3 dipoles belong to interaction 1 or direct interaction and 6 dipoles belong to interaction 2 or crossed interaction.
Dipole 1, is represented by R(DD)R, which generates a quark electric current (DD) in the RR direction, in phase.
R(DD)R →│DD > ≡ │1, 0 >
Dipole 2, is represented by B(UU)B, which generates a quark electric current (UU) in the BB direction, in phase.
B(UU)B →│UU > ≡ │1, 0 >
Dipole 3, is represented by G(UU)G, which generates a quark electric current (UU) in the GG direction, in phase.
G(UU)G →│UU > ≡ │1, 0 >
The quark current (DD) in the RR directions can escape confinement by generating photons.
The quark current (UU) in the BB and GG direction can escape confinement by generating photons.
This can be seen when we analyse the B⁻ decay.
Interaction 2
Dipole 4 is represented by R(DU)B, which generates two quark electric currents (DU), one electric current in the R direction, D quarks; the other electric current in the B direction, U antiquarks. Both currents are out of phase.
R(DU)B →│DU >
Dipole 5 is represented by R(DU)G, which generates two quark electric currents (DU), one electric current in the R direction, D quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
R(DU)G →│DU >
Dipole 6 is represented by B(UD)R, which generates two quark electric currents (UD), one electric current in the B direction, U quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
B(UD)R →│UD >
Dipole 7 is represented by B(UU)G, which generates two quark electric currents (UU), one electric current in the B direction, U quarks; the other electric current in the G direction, U antiquarks. Both currents are out of phase.
B(UU)G →│UU >
Dipole 8 is represented by G(UD)R, which generates two quark electric currents (UD), one electric current in the G direction, U quarks; the other electric current in the R direction, D antiquarks. Both currents are out of phase.
G(UD)R →│UD >
Dipole 9 is represented by G(UU)B, which generates two quark electric currents (UU), one electric current in the G direction, U quarks; the other electric current in the B direction, U antiquarks. Both currents are out of phase.
G(UU)B →│UU >
If we analyse the dipoles of interaction 2, we see that they are crossed interactions which generate two quark currents that are characterized by being out of phase, they are not in phase. These currents are confined to the proton.
In this simple analysis we have replaced the quantum model of QCD with the electrical model of the proton as a three-phase alternating current electrical generator. In the QCD model, quarks and gluons are used to represent the interactions in the proton; In the electrical model of the proton as a three-phase alternating current electrical generator, the interactions in the proton are carried out through quarks and antiquarks, the gluons are just indicative notations to remind us that we are working with vectors with module and phase, as happens in an Electric generator.
4.3. Analysis of the Interactions of Quarks in β⁻ Decay, Neutrons and Protons.
If we analyse the interactions of β⁻ Decay, the neutron and the proton, we conclude that all the interactions we observe are reduced to only six interactions:
Direct interaction
(DD) → │DD > ≡ │1, 0 >, in phase. (41)
(UU) → │UU > ≡ │1, 0 >, in phase (42)
Cross interactions
(DU) → │DU >, out of phase (43)
(UD) → │UD >, out of phase (44)
(DD) → │DD >, out of phase (45)
(UU) → │UU >, out of phase (46)
Direct interactions are very important, they can escape confinement and are part of the electromagnetic charge carriers that we call photons and the neutral currents that correspond to the Z boson.
Suppose the D quark and the D antiquark rotate in the (x, y) plane; We say that they are in phase when their spin or magnetic moment are aligned on the Z axis. We can see this in equation 41.
Suppose the U quark and the U antiquark rotate in the (x, y) plane; We say that they are in phase when their spin or magnetic moment are aligned on the Z axis. We can see this in equation 42.
If we have the interaction of a quark and an antiquark and the spin or its resulting magnetic moment is not on the Z axis, we say that it is out of phase, we can see this in equation 43, 44, 45 and 46.
Cross interactions are important because they give rise to W⁺ bosons, W⁻ bosons and Z bosons. They cannot escape confinement, they decay.
If we analyse the strong force, we observe that the gluons disappear.
Strong force interactions are replaced by direct interactions and cross interactions; The markers (R, B, G) and (R, B, G) simply indicate that the direct and crossed interactions are vector and have magnitude and angle that must be respected. The quantum number that represents the colour disappears.
We observe that the electrical modelling of a neutron and proton as a three-phase alternating current electrical generator is a reductionist, simplifying model; It allows us to reduce weak and strong force interactions to simple electromagnetic interactions.
Finally, it is important to highlight that the bosons corresponding to electromagnetic interactions, weak and strong corresponding to photons, W⁺, W⁻ bosons, Z bosons and gluons are replaced by quark interactions corresponding to (U, U, D, D).
In the theory that corresponds to the electrical modelling of a neutron or a proton as a three-phase generator of alternating current, the bosons as we know them disappear, they are transformed into quark interactions (U, U, D, D). Thinking about force interactions in vector form allows us to reduce and simplify the standard model. This becomes a phenomenal, very important advance.
Figure 16.
– (DD).
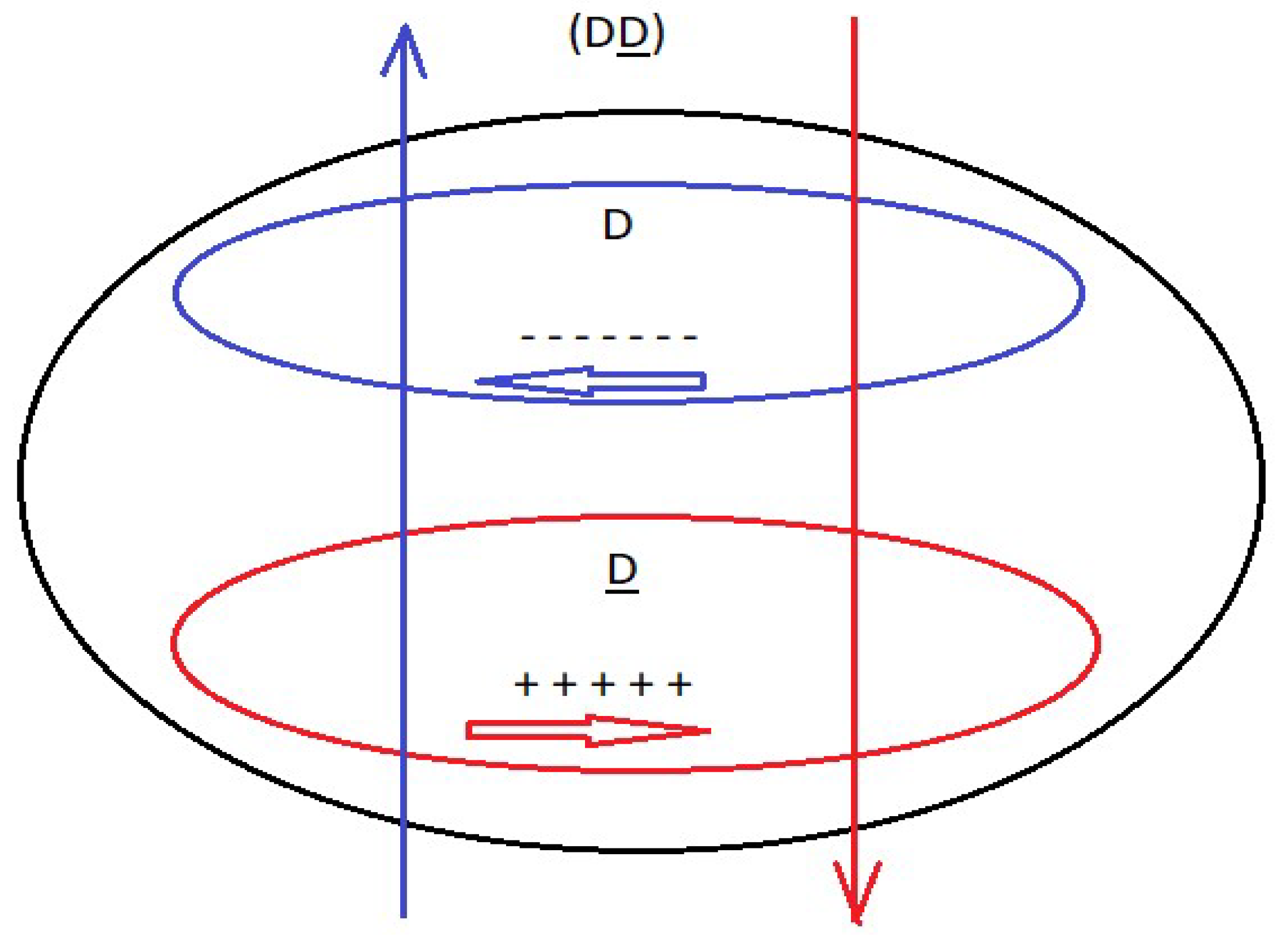
Figure 17.
– (UU).
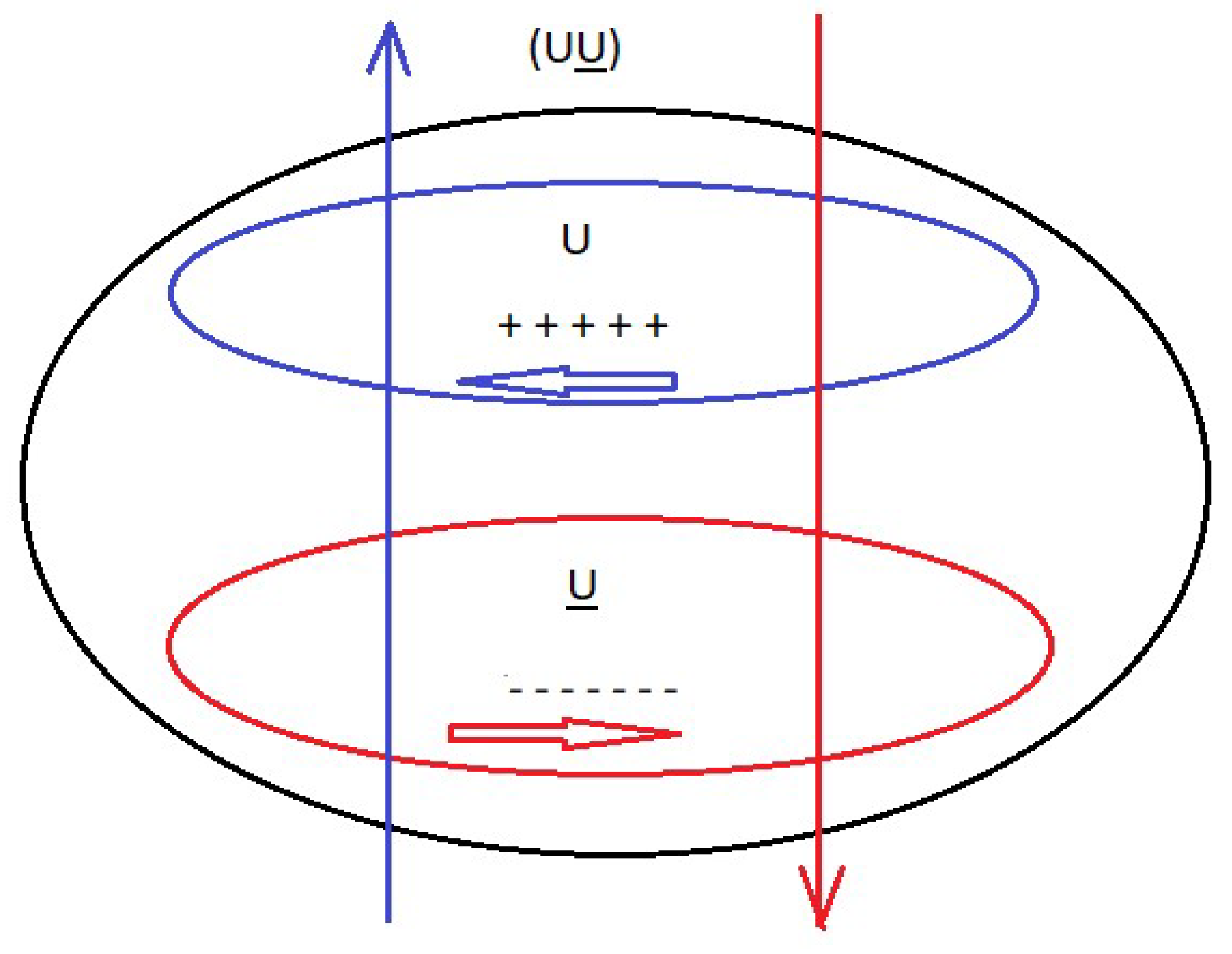
Figure 18.
– (DU).
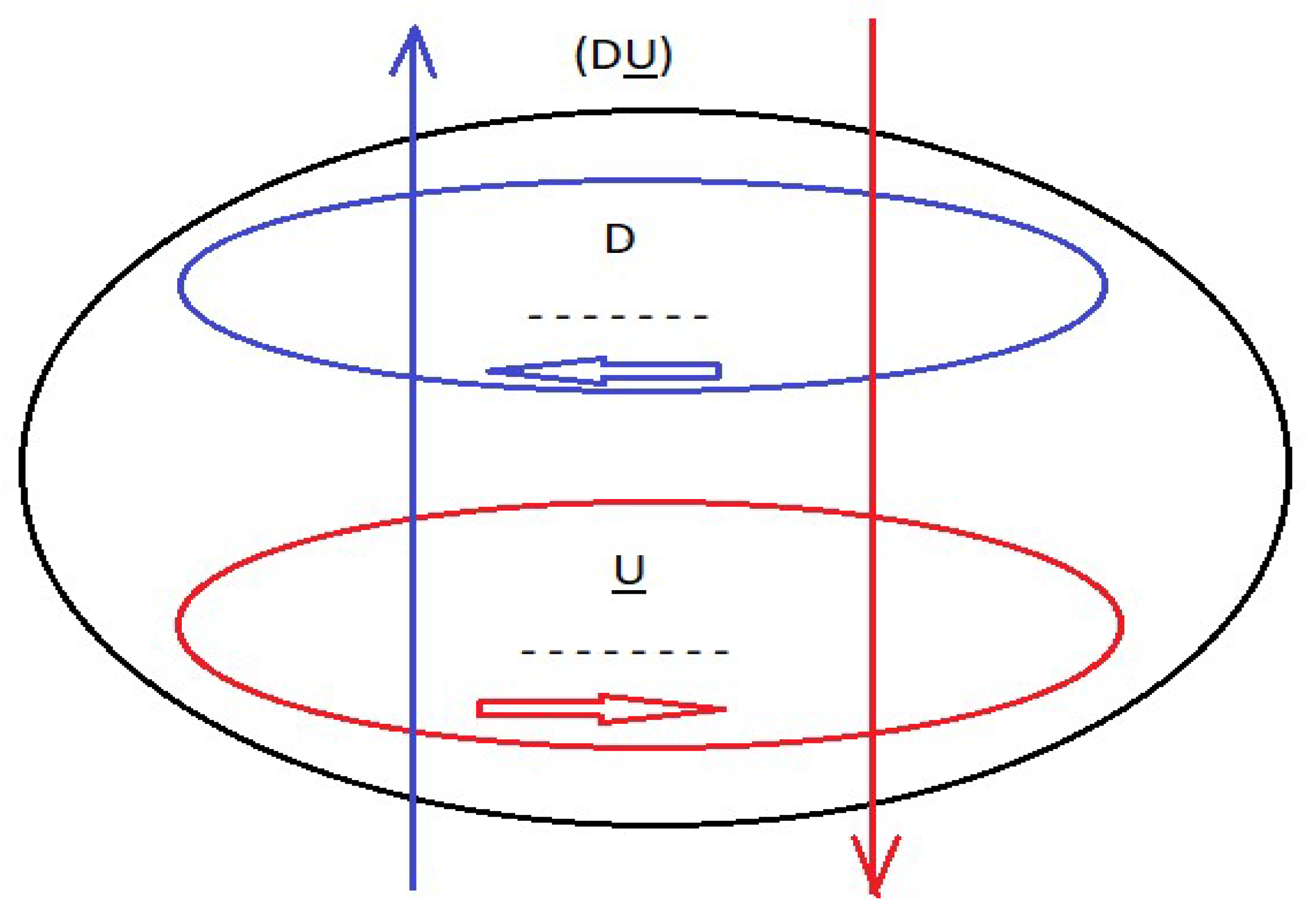
Figure 19.
– (UD).
5. Application of the Model and Results
5.1. Analysis of the Proposed Models for the Photon
In the paper: Generalization of the standard model. Theory of Everything (TOE), we have proposed a generalized model for the photon. Here, in this paper, we are going to delve into our model and propose specific models for the photon with their respective examples.
Main characteristics of photons:
Mass = 0
Electric charge = 0
Spin = 1
Next, we will hypothesize and propose the following model for photons:
- (DD) → │DD > ≡ │1, 0 >
- (UU) → │UU > ≡ │1, 0 >
We are going to highlight that photons are part of the group of gluons. It is important to note that the photons (DD) are in phase. The photons (UU) are also in phase.
Photon modelled as quarks (DD)
- I)
- First analysis:
Figure 20.
– Feynmann diagram, (a) emission of a photon by an electron (b) absorption of a photon by an electron.
Figure 20.
– Feynmann diagram, (a) emission of a photon by an electron (b) absorption of a photon by an electron.
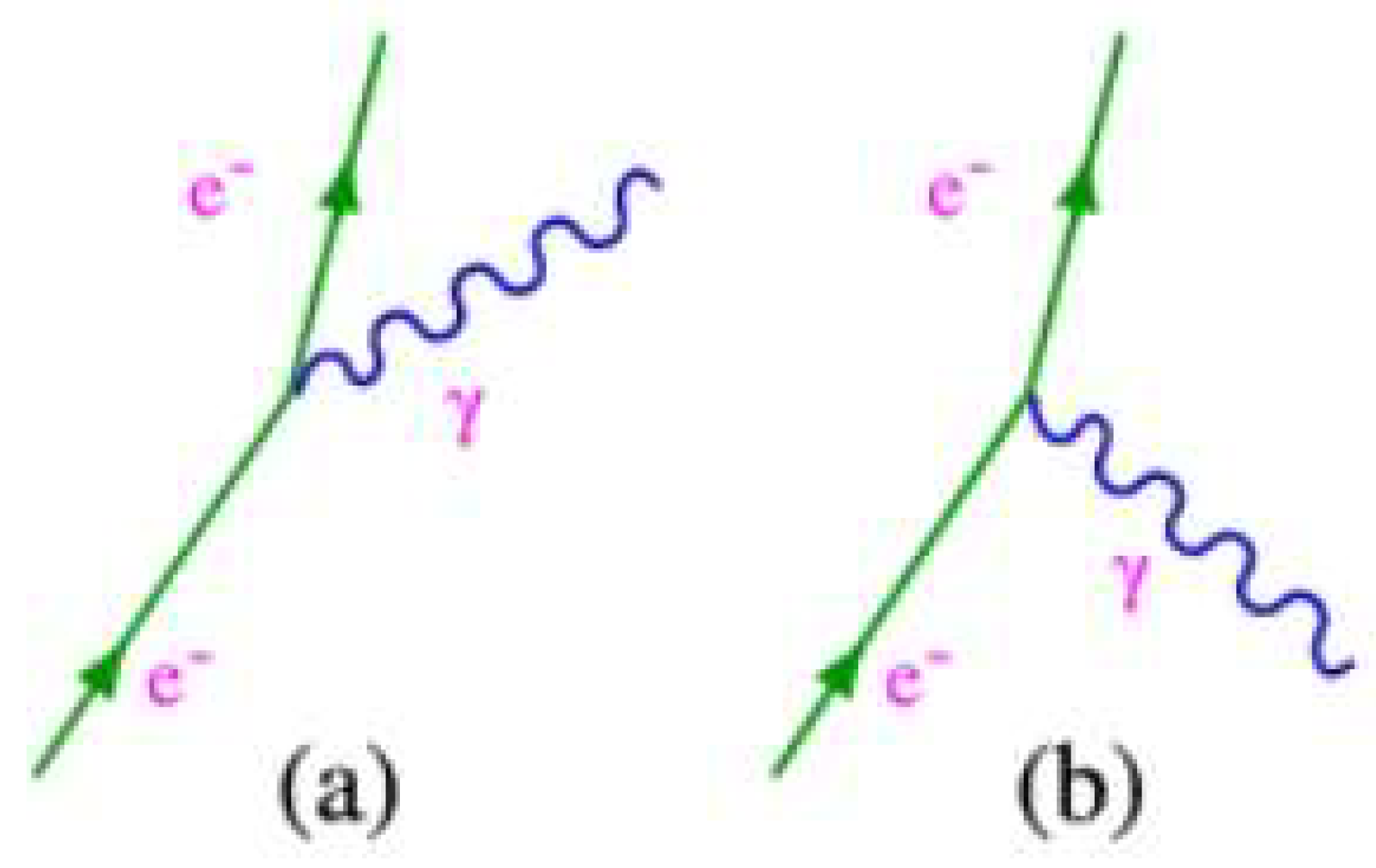
This can be exemplified with the electrons that orbit around an atom, as they gain or lose energy, the electrons jump from their orbits and can even escape from the atom.
If we analyse β⁻ Decay, specifically the interaction [B(DD)B]n → [B(UU)B]p, which we can represent in table 3; We conclude that the energy involved in the emission or absorption of a photon by an electron is distributed partly in the electron and partly in the nucleus of the atom. Let us remember that electrons are attached to the nucleus through the exchange of photons.
- II)
- Second analysis:
Figure 21.
- (c) emission of a photon by a positron (d) absorption of a photon by a positron.
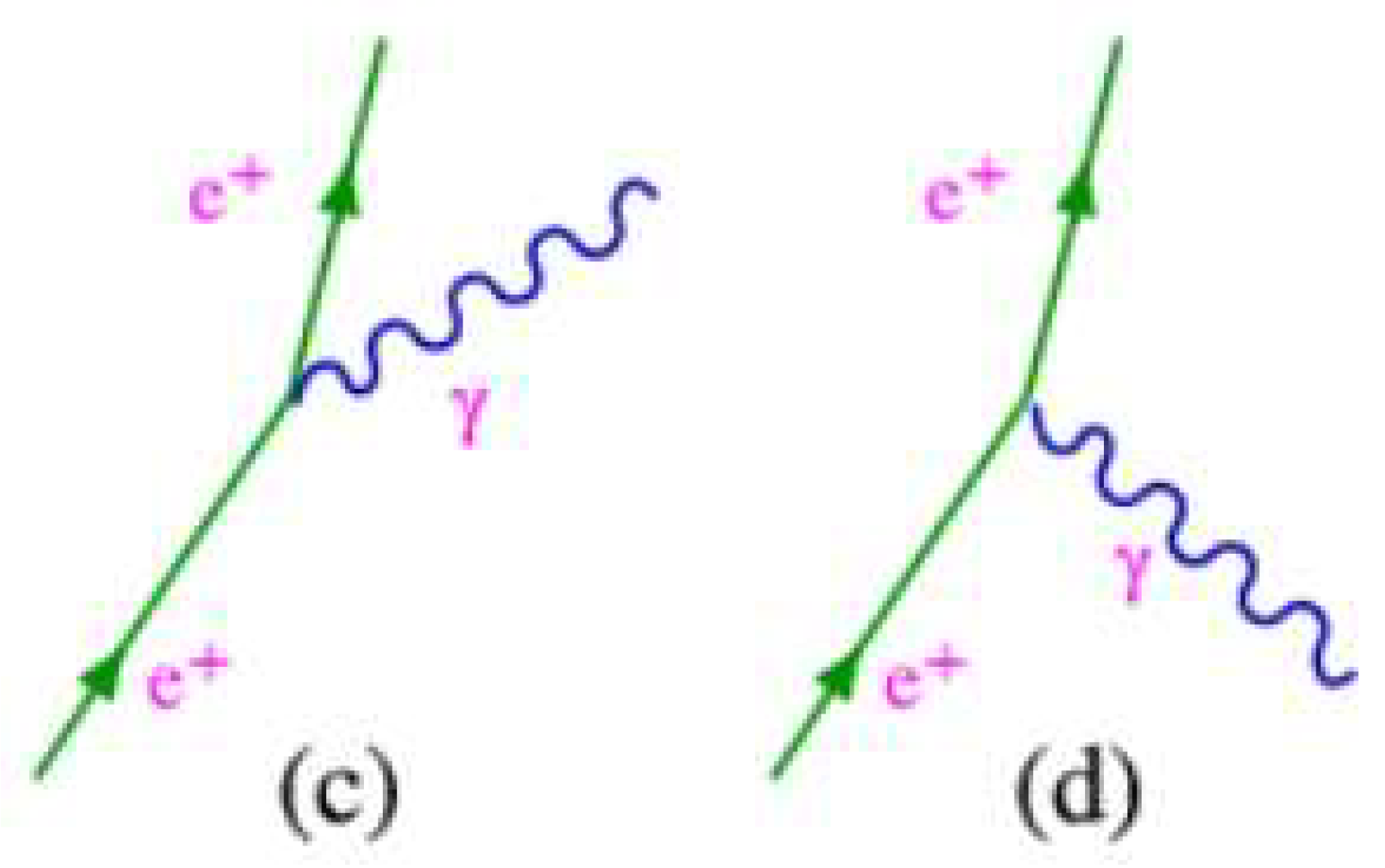
Considering antimatter, this can be exemplified by positrons orbiting an antiatom, as they gain or lose energy, the positrons jump out of their orbits and can even escape the antiatom.
If we analyse β Decay, specifically the interaction [B(DD)B]n → [B(UU)B]p, We conclude that the energy involved in the emission or absorption of a photon by an positron is distributed partly in the positron and partly in the nucleus of the antiatom. Let us remember that the positrons are linked to the antiatom through the exchange of photons.
- III)
- Third analysis:
Figure 22.
– Feynmann diagram, (e) a photon creates an electron and positron, (f) an electron and a positron create a photon.
Figure 22.
– Feynmann diagram, (e) a photon creates an electron and positron, (f) an electron and a positron create a photon.
This interaction can be observed in particle colliders, it is more intuitive to understand. In particle collisions, a photon (DD) can decay into an electron and a positron. The same thing happens if we make electrons and positrons collide, these collisions can create photons (DD).
To finish this item, these three interactions can be understood by considering the photo as the combination of quarks (DD).
IV) Fourth analysis: Photon modelled as quarks (UU)
To begin our analysis, let's consider the following figure:
Let's analyse figure 23, in which protons are made to collide at high speeds, this causes the fusion of a top quark with a top antiquark to generate a Higgs boson, this Higgs boson decays in a couple of bottom and anti-bottom bosons, which decay into a pair of photons, this is what we really measure in the detection of the Higgs Boson.
Here, we are going to hypothesize the following, when the interaction of the D quark with the D antiquark occurs, the resulting interaction is analogous to the interaction in figure 23, the resulting interaction is shown in figure 24, where the fusion of the D quark and the D antiquark produces a Higgs boson, which in turn decays into a pair of U quark and U antiquark and this in turn produces a pair of photons.
If the diagram in figure 24 is true, we wonder, could there be three families of Higgs bosons?
Figure 24 represents an example of how we can produce photons formed by quark (UU).
5.2. Analysis of the Proposed Models for the Gluons
In the paper: Generalization of the standard model. Theory of Everything (TOE), we have proposed a generalized model for the gluons. Here, in this paper, we are going to delve into our model and propose specific models for the gluons with their respective examples.
If we analyse figure 14, corresponding to the neutron, and figure 15, corresponding to the proton, we observe that we can represent the gluons by combining the following markers (R, B, G), which represents matter and (R, B, G) which represents antimatter.
The combination of these markers tells us the number of gluons that exist, 9 in total.
Next, we are going to describe the existing gluon combinations:
(RR), (BB), (GG), (RB), (RG), (BR), (BG), (GR) and (GB)
This is the number of gluons proposed in the paper: Generalization of the standard model. Theory of everything (TOE).
These gluons had the following characteristics:
Mass = 0
Electric charge = 0
Colour charge = yes
Spin = 1
However, in this paper we make the following hypothesis:
Here, working with the theory of the neutron and proton as a three-phase alternating current electric generator, we hypothesize that (R, B, G) and (R, B, G) are simply markers that tell us that the interactions between quarks have magnitude and angles that must be met, as happens in an electric generator.
In other words, gluon interactions reduce to interactions between quarks.
This implies that in the strong interaction the colour charge disappears and is transformed into simple electromagnetic interactions.
Strong interaction → Electromagnetic interaction
The strong interaction reduces to 6 combinations of quark interactions. Below we are going to list these 6 combinations.
Direct interactions
- (DD) → │DD > ≡ │1, 0 >
- (UU) → │UU > ≡ │1, 0 >
These interactions that correspond to the strong force are analogous to the electromagnetic interaction that gives rise to photons.
We can explain this in the following way, when a neutron decays into a proton, and this in turn traps the electron and forms the Hydrogen atom; It is the electron that is linked to the nucleus of the atom through the exchange of photons.
Initially, the gluon (DD) was part of the neutron, after the decay of the neutron into a proton, that gluon (DD) is transformed into a photon and becomes part of the binding energy between the electron and the nucleus of the atom.
The interactions of the quarks (DD) and (UU) are the only ones that can escape the confinement of an atom.
Cross interactions
- (DU) → │DU >
- (UD) → │UD >
- (DD) → │DD >
- (UU) → │UU >
These interactions that correspond to the strong force are analogous to the electromagnetic.
The interactions of the quarks (DU), (UD), (DD) and (UU) cannot escape confinement.
The property that the electric charge is different from zero allows W⁻ bosons to be produced during β⁻ decay and W⁺ bosons to be produced during β⁺ decay.
It is important to see how the strong and weak-electromagnetic force interactions can be reduced to six quark interactions given by equations 41, 42, 43, 44, 45 and 46.
It is important to highlight the following, when we work with the theory of electrical modeling of the proton and neutron as a three-phase alternating current generator, our model includes matter and antimatter together. However, in the standard model, there is one equation that determines matter and another for antimatter; For example, when we model a neutron or proton, we consider only matter and not antimatter.
I think that the theory corresponding to the electrical modeling of a neutron and proton as a three-phase alternating current electrical generator would be a very important complement to the standard model, it would help us develop particle physics in leaps and bounds and discover the great mysteries that we have today, thanks to his visionary ideas.
The theory corresponding to the electrical modeling of the neutron and proton as a three-phase alternating current electrical generator, in addition to being a complement to the theory of the standard model of particle physics, is a generalization of the same, simply because it includes matter and antimatter, directly in their interactions.
5.3. Analysis of the Proposed Models for the Gravitons
When we analyse the standard model, we see that it does not include gravity.
Here, we are going to develop a model of the graviton using vector thinking, that is, we are going to use the theory of modelling a neutron and proton as a three-phase alternating current electric generator, which will allow us to develop a model for the graviton.
Vector thinking is a very powerful tool. Vector thinking allows us to imagine a black hole formed by positively charged particles (U quark) or negatively charged particles (D quark) but whose resulting net charge is zero, in perfect balance.
What is a black hole? A black hole is a body in which the electromagnetic force interactions, weak force interactions and strong force interactions have been disconnected; There is only the gravitational force.
Saying that only the gravitational force exists inside a black hole is the way to follow to discover the graviton particle.
For this, we are going to mention the paper: Analysis of the Kerr-Newman Diagram. Unravelling the interior of a black Hole; in which we define two types of black holes.
First black hole model formed by D quark
If we analyse figure 25, we observe that the black hole is formed by neutroniumd particles, which contain D quark in a special configuration that is characterized because the resulting net charge is zero. The interior of the black hole is made up of matter, it does not contain antimatter.
Second black hole model formed by U quark
If we analyze figure 26, we observe that the black hole is formed by protoniu particles, which contain U quark in a special configuration that is characterized because the resulting net charge is zero. The interior of the black hole is made up of matter, it does not contain antimatter.
Continuing along our path, we observe that the minimum fundamental particles inside black holes correspond to the D quark and the U quark.
However, we also said, when a black hole forms, antimatter is ejected out of the black hole into space-time; Therefore, we must consider and include the D antiquark and the U antiquark in our theory of the graviton.
Here, we are going to hypothesize that the (U, U, D, D) quarks are the fundamental particles that contribute to the existence of the graviton.
We are going to represent the quantum states in the following way:
│U > ≡ │1/2, 1/2 > (47)
│U > ≡ │1/2, -1/2 > (48)
│D > ≡ │1/2, 1/2 > (49)
│D > ≡ │1/2, -1/2 > (50)
Using the quantum states described in equation 47, 48, 49 and 50; We are going to use the following expressions to calculate the different models for gravitons.
│↑ ↑ > ≡ │1, 1 ˃
│↓ ↓ > ≡ │ 1, - 1 ˃
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 >
Model 1 for gravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│U > ≡ │1/2, 1/2 >
│U > ≡ │1/2, -1/2 >
│UU + UU > ≡ |UU > + |UU > = │1, 0 > + │1, 0 > =│2, 0 >
│UU + UU > ≡ │2, 0 > (51)
Model 2 for gravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│D > ≡ │1/2, 1/2 >
│D > ≡ │1/2, -1/2 >
│DD + DD > ≡ |DD > + |DD > = │1, 0 > + │1, 0 > =│2, 0 >
│DD + DD > ≡ │2, 0 > (52)
Here, we have hypothesized the existence of two graviton particles, given by equation 51 and 52; We observe that in all of them, their spin corresponds to 2 but their angular projection is zero.
If we add the spins of the graviton particle formed by two U quak and two U antiquark or of the graviton particle formed by two D quark and Two D antiquark, the spin of the resulting particle is 2, as can be seen in equations 51 and 52.
What is more difficult to imagine or visualize is the sum of the angular momentum projection of the four particles equal or zero (0). If the angular momentum projection of the 4 particles is in phase, aligned on the Z axis, the angular momentum of the two U quarks is up and the angular momentum of the two U antiquarks are down, the resulting angular momentum is zero.
However, after carrying out a rigorous analysis, we came to the conclusion that graviton models 1 and 2 are not viable.
Model 3 for gravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│UD + DU > ≡ |UD > + |DU > = │1, 1 > + │1, -1 > =│2, 0 >
│UD + DU > ≡ │2, 0 > (53)
Model 4 forgravitons:
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 >
│↑↓ + ↓↑ > ≡ │2,0 >
│DU + UD > ≡ |DU > + |UD > = │1, -1 > + │1, 1 > =│2, 0 >
│DU + UD > ≡ │2, 0 > (54)
After carrying out a rigorous analysis, we came to the conclusion that graviton models 3 and 4 are viable.
From now on we are going to use model 3 and 4 to represent gravitons.
If we analyze our model, we observe that photons are made up of quarks (U, U, D, D); The same happens with the W(+), W(-), Z bosons, gluons and gravitons. Absolutely all bosons are made up of quarks (U, U, D, D).
Taking into account what was stated above, that all bosons of gauge corresponding to the forces of strong, weak and electromagnetic interactions are formed by quarks (U, U, D, D); It is assumed that the graviton is also made up of quarks (U, U, D, D), this is the reason why we define gravitons according to equations 53 and 54.
Another reason is the quantum fluctuation that exists in the fabric of space-time; virtual particles that are born and disappear, let's assume that these virtual particles are the result of the creation and decay of gravitons, specifically gravitons formed by D quarks and D antiquarks.
A third reason is related to the behavior of the graviton with respect to the photon, we can see this in table 16 and table 17; At low temperatures the mass of the graviton is approximately equal to the mass of the photon, as the temperature increases, the mass of the graviton is less than 10²⁰ times the mass of the photon; this is due to the differences that exist between the magnetic field and the electric field of the photon and graviton, as a function of temperature.
Until now, detecting gravitons with the intention of discovering a new exotic particle has been very difficult in the particle collider at the LHC at CERN. With the definition of the graviton given by equations 53 and 54; I think that it may be much easier to design an experiment at the LHC at CERN that allows us to detect quarks (U, U, D, D), or some of their associated disintegrations, in such a way that allows us to identify gravitons in particle collisions.
When we analyze bodies like the moon, earth, sun, white dwarf stars, neutron stars and black holes; absolutely all the bodies we know; All the mentioned bodies have a mass and therefore an associated gravity. They are the quarks (U, U, D, D), the reason for the link between the mass of the body and its associated gravity.
Knowing that gravitons are made up of quarks (U, U, D, D), it is easier to imagine the relationship between the mass of the bodies, their associated gravity and the curvature of space-time.
Knowing that gravitons are made up of quarks (U, U, D, D), it is now easy for us to imagine and understand the sea of virtual particles that exist in the fabric of space-time, which is the result of decays and formation of gravitons.
Now that we know that gravitons are made up of quarks (U, U, D, D), we can conclude that gravity is a force and affirm that gravitons are the gauge bosons of the gravitational force.
Next, we are going to show that gravity is a force.
To do this, we are going to resort to the theory developed in the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant.
In the analysis of this theory, we show that the Boltzmann constant is variable. There is a Boltzmann constant that we all know and that I call the electromagnetic Boltzmann constant and a variable or effective Boltzmann constant that I call the gravitational Boltzmann constant. We also show that Boltzmann's constant is related to the curvature of space-time.
Kв = 1.38 10⁻²³ J/K, for flat spacetime
Where Kв is called the electromagnetic Boltzmann constant.
1.38 10⁻²³ J/K > Kв-effective > 1.78 10⁻⁴³ J/K, for curved space-time
Where Kв-effective is called the gravitational Boltzmann constant.
In the following table we are going to calculate the curvature and the force of gravity exerted by the bodies mentioned above (earth, sun, white dwarf star, neutron stars and black holes).
The calculations of the values represented in table 1 are found in the paper: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant.
In table 15, it can be seen that there is a relationship between the Boltzmann constant Kв-effective, the curvature of space-time and gravity.
In the following graph, we are going to demonstrate why gravity is a force!!!!
If we look at figure 27, in the upper part we represent the flat space-time by a straight line and we mark that space-time by a point which we designate as A.
Now, we imagine that we can bring the sun and we place it in the center of flat space-time, curving it. We can see this in the drawing represented at the bottom. Now we see that the sun curves space-time and also contracts it, we can see this because point A moves to the right and the location of point A at the beginning corresponds to point B. In other words, the presence of curved mass and contracts space time.
The stretching of space-time between point A and B produces a force F; from this simple example we can show that Newton was right, gravity is a force and the bosons that transport gravity exist and are the gravitons defined in equation 53 and 54.
The force F, which stretches space-time from Point B to Point A, is responsible for keeping our feet on the ground, for the fall of bodies, for the rotation of bodies, etc.
From another point of view, we can also see gravity as the curvature of space-time, the greater the curvature, the greater gravity and the greater the stretching of space-time.
Next, through images we will try to interpret what happens to space-time as the force of gravity increases.
If we look at figure 27, we see that for the sun, table 15 shows us that gravity is of the order of g = 2.73 10² m/s²; If we now consider a neutron star, the gravity is of the order of g = 2.0 10¹² m/s². When a black hole of three solar masses forms, the value of gravity corresponds to g = 5.0 10¹² m/s²; In this last condition, space-time reaches the Planck length.
In all these situations, we observe that as the mass increases, gravity increases, therefore the force of gravity and the curvature of space-time; This is indicating to us that there is a compression of space-time, we can see this in figure 27.
A special condition occurs when a black hole of three solar masses is formed, in this condition the length of space-time reaches the Planck length.
As the black hole grows, that is, its mass increases, space-time experiences two forces, a compression force and a torsion force, we can see this in figure 28.
As the black hole grows, the Planck length, which initially has the shape of a rod, as shown in Figure 28, transforms into a spring similar to a corkscrew; The compression force produces a force of gravity towards the interior of the black hole, towards the center. The torsion force produces a tangential force that generates rotation in black holes. This tangential or torsion force is responsible for the origin of dark matter.
Lp = Lpɛ = 1.61 10⁻³⁵ m;
Where Lpɛ is Electromagnetic Planck length
1.61 10⁻³⁵ m > Lpɢ > 1.28 10⁻⁵⁴ m
Where Lpɢ is Gravitational Planck length
When the black hole reaches its critical mass, it disintegrates and transforms into a white hole (Big Bang). The Planck length that was compressed, after disintegration tends to reach its normal value and the immense energy released gives rise to cosmic inflation.
In the following table, we are going to analyze how gluon varies with temperature. Gluon is understood as the quark interactions given by equations 41, 42, 43, 44, 45 and 46.
All the calculations presented in table 16 are developed in the paper: Electrical-quantum modeling of the neutron and proton as a three-phase alternating current electrical generator. Determination of the number of quarks-antiquarks-gluons and gravitons, inside a neutron.
In the following table, we are going to analyze how graviton varies with temperature. Graviton is understood as the quark interactions given by equations 53 and 54.
All the calculations presented in table 17 are developed in the paper: Electrical-quantum modeling of the neutron and proton as a three-phase alternating current electrical generator. Determination of the number of quarks-antiquarks-gluons and gravitons, inside a neutron.
We are going to analyse the behaviour of the mass of the gluon and the graviton as a function of temperature, we are going to make a comparison to obtain important conclusions.
If we analyze tables 16 and 17, for a temperature less than 2 K, we see that the mass of the gluon coincides with the mass of the graviton.
- For a temperature T < 2 K, we have:
T = 1.57 10⁻¹⁰ K, gluon mass = 2.35 10⁻⁵⁰ kg; graviton mass = 2.40 10⁻⁵⁰ kg
T = 1.57 10⁻⁵ K, gluon mass = 2.35 10⁻⁴⁵ kg; graviton mas = 2.40 10⁻⁴⁵ kg
T = 1.57 10⁰ K, gluon mass = 2.35 10⁻⁴⁰ kg; graviton mass = 2.40 10⁻⁴⁰ kg
We observe that as the temperature increases, the mass of the gluon and graviton also increases.
We observe that for a temperature below 2 kelvins, the mass of the gluon is approximately equal to the mass of the graviton.
- We will analyze the temperature range between T = 2 K and T = 10¹³ K
We observe that as the temperature increases, the mass of the gluon also increases.
T = 1.57 10⁰ K, gluon mass = 2.35 10⁻⁴⁰ kg
T = 1.57 10¹³ K, gluon mass = 2.35 10⁻²⁷ kg
However, the same does not happen with the mass of the graviton; in the interval we are analyzing, we observe that the mass of the graviton decreases.
T = 1.57 10⁰ K, graviton mass = 2.40 10⁻⁴⁰ kg
T = 10¹³ K, graviton mass = 1.92 10⁻⁴⁷ kg
We observe for a temperature of T = 10¹³ K, the difference between the mass of the gluon and the graviton is of the order 10²⁰.
If we look at tables 16 and 17, we see that this difference 10²⁰, is maintained in the temperature range between T = 10⁶ K and T = 10¹³ K.
- We will analyze the temperature range T > 10¹³ K
Above T > 10¹³ K, we observe that as the temperature increases, the mass of the gluon also increases.
T = 1.57 10¹³ K, gluon mass = 2.35 10⁻²⁷ kg
T = 1.57 10²⁶ K, gluon mass = 2.35 10⁻¹⁴ kg
Above T > 10¹³ K, we observe that as the temperature increases, the mass of the graviton also increases.
T = 10¹³ K, graviton mass = 1.92 10⁻⁴⁷ kg
T = 10²⁶ K, gluon mass = 1.92 10⁻³⁴ kg
If we look at tables 16 and 17, we see that this difference 10²⁰, is maintained in the temperature range between T = 10¹³ K and T = 10²⁶ K.
In conclusion, for a temperature higher than T > 10⁶ K, the mass difference between the gluon and the graviton is of the order of 10²⁰. For a temperature lower than T < 10⁰ K, the mass of the gluon and that of the graviton are approximately equal or coincident. There is a temperature interval between T = 10⁰ K and T = 10⁶ K, in which the difference between the mass of the gluon and that of the graviton widens between 10⁰ and 10²⁰.
It is possible to explain the difference, 10²⁰, between the mass of the gluon and the graviton, simply by considering their origin, as shown below:
Quark interactions, gluons:
- (DD) → │DD > ≡ │1, 0 >, in phase
- (UU) → │UU > ≡ │1, 0 >, in phase
- (DU) → │DU >, out of phase
- (UD) → │UD >, out of phase
- (DD) → │DD >, out of phase
- (UU) → │UU >, out of phase
Quark interactions, gravitons:
- │UD + DU > ≡ │2, 0 >, in phase
- │DU + UD > ≡ │2, 0 >, in phase
In figure 29, we observe the graviton model given by │UD + DU > ≡ │2, 0 >; We observe that it is a graviton that has a positive net charge, however it has spin 2 and zero angular projection. If we analyze from the point of view of the electric field, the upper and lower coils exert a repulsive force; If we analyze from the point of view of the magnetic field, the upper and lower coil exert an attractive force. It is important to highlight that UD corresponds to the internal coils and DU corresponds to the external coils. The direction of rotation of the arrows is obtained by applying rule 1 and 2 for matter and antimatter (left-handed particles).
In figure 30, we observe the graviton model given by │DU + UD > ≡ │2, 0 >; We observe that it is a graviton that has a negative net charge, however it has spin 2 and zero angular projection. If we analyze from the point of view of the electric field, the upper and lower coils exert a repulsive force; If we analyze from the point of view of the magnetic field, the upper and lower coil exert an attractive force. It is important to highlight that DU corresponds to the internal coils and UD corresponds to the external coils. The direction of rotation of the arrows is obtained by applying rule 1 and 2 for matter and antimatter (left-handed particles).
If we compare the interactions of the quarks that we denote as gluons with the interactions of the quarks which we denote as gravitons, we can see that gluons are made up of two elements, a quark and an antiquark; However, gravitons are made up of four elements, 2 quarks and 2 antiquarks.
This difference is very important, it is telling us the reason for the stability of gravitons, because the electromagnetic force is 10⁴⁰ times greater than the gravitational force.
We are going to comment on why we defined the graviton according to equation 53 and 54; Its definition is related to the virtual particles that exist in space-time. When we excite space-time, generally by the Heisenberg principle, a set of pairs of virtual particles are produced, particles and their antiparticles, that is the main reason for the definition given for the graviton.
Vacuum fluctuations should not be interpreted as small quantum violations of the principle of conservation of energy.
We could have defined the graviton as the sum of the following quarks (UUUU) or (DDDD), but this last definition does not coincide with the sea of virtual particles that exist in space-time. By this we mean that gravitons are responsible for the existence of virtual particles.
It is also worth mentioning, the definition of graviton that we have adopted, represented in equations 53 and 54, is telling us that space-time is made up of matter and antimatter, it is telling us that there is no imbalance between matter and antimatter and that all matter and antimatter are in perfect balance in the universe.
We can also observe this difference if we compare the mass of gluons as a function of temperature, table 16, with the mass of gravitons as a function of temperature, table 17.
Up to this point, using the electrical model of the neutron and the proton as an alternating current electrical generator, we have proposed a model that corresponds to graviton particles. We have also shown that the bosons corresponding to the electromagnetic, weak, strong and gravitational forces can be described by (U, U, D, D) quarks.
It is important to make it clear that the bosons that represent the standard model corresponding to the interactions of the electromagnetic, weak and strong forces are born from the equations denoted as 55, 56, 57 and 58, including the Higgs boson.
It is also necessary to highlight that the model proposed for gravitons is also born from equation 57.
For this we use as a premise that bosons are the result of the combination of fermions. Taking into account the above, from the point of view of color, nature requires that the wave function of Hadrons be antisymmetrical, that is, singlet, without color. It is also important to highlight that nature demands of us, from the point of view of spin and flavor, that the wave function of Hadrons be symmetrical, behaving like bosons.
│↑ ↑ > ≡ │1, 1 ˃ (55)
│↓ ↓ > ≡ │ 1, - 1 ˃ (56)
(1⁄√2) │↑↓ + ↓↑ > ≡ │1,0 > (57)
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 > (58)
5.3. Analysis of the Proposed Models for the Higgs Boson
To hypothesize the model corresponding to the Higgs boson, we are going to work with equation 58.
Model 1 for the Higgs boson
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 >
│↑↓ - ↓↑ > ≡ │0,0 >
│UD - DU > ≡ |UD > - |DU > = |UD > + |DU > =│1, 1 > - │1, -1 > =│0, 0 >
│UD - DU > ≡ |UD > + |DU > │0, 0 > (59)
Model 2 for the Higgs boson
(1⁄√2) │↑↓ - ↓↑ > ≡ │0,0 >
│↑↓ - ↓↑ > ≡ │0,0 >
│DU - UD > ≡ |DU > - |UD > = |DU > + |UD > =│1, -1 > - │1, 1 > =│0, 0 >
│DU - UD > ≡ |DU > + |UD > │0, 0 > (60)
In equation 59 and 60, we observe model 1 and 2 of the Higgs boson as a combination of quarks (U, U, D, D).
Note that in both models represented in equation 59 and 60; The Higgs boson is not stable, its decay is approximately immediate.
If we analyze equation 59, we observe that the upper loop is formed by the U quark, with charge (+) and the D quark, with charge (-); Both are annihilated instantly.
If we analyze equation 59, we observe that the lower loop is formed by the D antiquark, with charge (+) and the U antiquark, with charge (-); both are also instantly annihilated.
In other words, the Higgs boson formed by equation 59 is not stable, it decays instantly. This condition in which we affirm that the Higgs boson decays instantly is very important, too important.
We are going to explain the importance of the meaning of the decay of the Higgs Boson. When the Higgs Boson decays, the important thing is not the Higgs boson, it is the Higgs field, it is the Higgs potential, it is the temperature it generates; There is the importance of the decay of the Higgs Boson, in temperature. Let us remember that there is a relationship between temperature, energy, frequency and Boltzmann's constant; given by the following equations.
E = h x ν (61)
E = Kв x T (62)
Equation 61 and 62 tell us that for a given energy or temperature, space-time has a certain frequency or wavelength and a certain effective Boltzmann constant.
Here is the importance of the Higgs Boson, the combination of frequency (wavelength), temperature (energy) and the effective Boltzmann constant which is related to temperature; They are the fundamental pillars to form the elementary particles that form the standard model, which constitute the three families of quarks and leptons.
La combinación de los quarks (U, U, D, D) que dan origen al bosón de Higgs, el cual se desintegra instantáneamente; crean las condiciones para que se originen las partículas elementales que forman el modelo estándar.
The mechanism by which the elementary particles of the model are formed is developed in the paper: Generalization of the Standard Model. Theory of Everything (T.O.E.)
The analysis we carried out for model 1 of the Higgs boson is also valid for model 2 of the Higgs boson.
6. Symmetries in Particles
In physics, symmetry is defined as an operation to which it is applied to a state or system and leaves it invariant.
U, Symmetry operation
If we apply the symmetry operator U to the Ψ function, it transforms it into the Ψʹ function, simply by applying the operator.
| Ψ > → | Ψʹ > = U | Ψ >
Now if I transform my state and also transform the rest of the universe, with the same transformation operator; It is to be expected that the expectation values are the same.
< Φ | Ψ >
We can interpret this from the point of view of probabilities.
| < Φ | Ψ > |² = | < Φʹ | Ψʹ > |² = | < Φ | Uᵗ U | Ψ > |²
The probability of the untransformed states is the same as the probability of the transformed states. I can express the transformed states in terms of the symmetry operators, which leads me to the following condition.
Uᵗ U = I → The operator U has to be unitary.
A characteristic that we are going to ask of all symmetry operators is that they be unitary transformations.
Noether's theorem
It tells me that for every symmetry my system had there would have to be a conserved quantity. In quantum mechanics, Noether's theorem relates symmetries to conservation laws.
Symmetry of spatial translations, P → Conservation of linear momentum
symmetry of spatial rotations, L → Conservation of angular momentum
Symmetry of temporal translations, H → Conservation of energy
Symmetry of phase transformations, e → Conservation of charge
Isospin symmetry, I → Conservation of isospin
`In general, symmetry transformations generate mathematical groups, which satisfy the following conditions:
- The identity function, must be an element of the group
- The inverse function, must be an element of the group
- Let there be associativity
- If the group of transformations is commutative it is said to be an abelian group, if the group of transformations is non-commutative it is said to be non-abelian.
Symmetry groups
U(n), unitary group nxn; Example, group U(1), complex phase transformations.
SU(n), unitary group nxn + determinant = 1; Example, SU(2), Isospin / weak interactions; SU(3), strong interactions.
Representation of the group SU(2) of dimension 2
For SU(2), the fundamental representation is given by two base 2 elements, as shown below:
 , fundamental representation.
, fundamental representation.Considering these elements of base 2, of dimension 2, I am going to define the following generators.
Where σ₁, σ₂ and σ₃, are the Pauli matrices, which satisfy a certain commutation relation.
The elements of the group (transformations) would be given by the following equation:
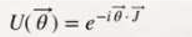
The elements of the group, which would be the unitary matrices with a determinant equal to 1 and order 2x2, would be given by the exponential of the generator; The transformations are the matrices U that materialize the rotations which are applied to the two spin (1/2) projections.
Representation of the group SU(2) of dimension 3
For SU(2) of dimension 3, the representation is given by three base 3 elements, as shown below:
Now, I have 3 generators ĵ of dimension 3 x 3, which satisfy the following commutation relation.
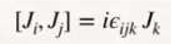
And the elements of the group are the transformations or matrices U that I build with the generators.
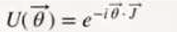
Combination of two spins ½ in SU(2), dimension 2; I get:
2 ⊗ 2 = 3ѕ + 1ᴀ
Combination of three spins ½ in SU(2), dimension 3; I get:
2 ⊗ 2 ⊗ 2 = 4ѕ + 2мѕ + 2мᴀ
Representation of the group SU(3) of dimension 3
For SU(3) of dimension 3, the representation is given by two base 3 elements, as shown below:
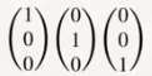 , fundamental representation.
, fundamental representation.The group SU(3) are 3x3 unitary matrices with determinate equal to 1.
The SU(2) generators of dimension 3x3 are different from the generators of SU(3) dimension 3x3.
The SU(3) generators of dimension 3x3, which I need to describe a transformation, are going to be different from the SU(2) generators of dimension 3x3 and we are also going to need more generators, a total of 8.
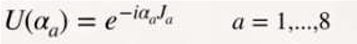
The elements of the group, which would be the unitary matrices with a determinant equal to 1 and order 3x3, would be given by the exponential of the generator; The transformations are the matrices U that materialize the rotations which are applied to the three spin (1/2) accoupling.
The generators of SU(3) are called Gell-Mann matrices.
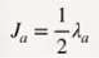 Where λa are Gell-Mann matrices.
Where λa are Gell-Mann matrices.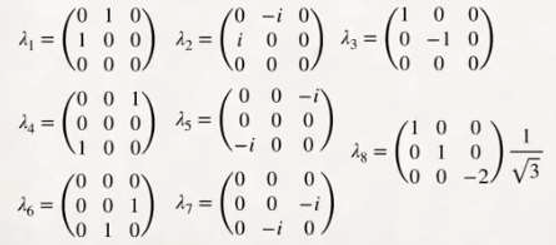
Combination of two spins ½ in SU(3); I get:
3 ⊗ 3 = 6ѕ + 3ᴀ
Combination of three spins ½ in SU(3); I get:
3 ⊗ 3 ⊗ 3 = 10ѕ + 8мѕ + 8мᴀ + 1ᴀ
Isospin, electric charge and strangeness
Correlation between electric charge and isospin:
- i)
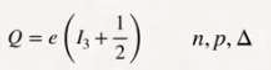
- ii)
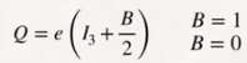 B = 1, baryons; B = 0, mesons.
B = 1, baryons; B = 0, mesons.
ii) includes baryons and mesons and does not include strange particles.
- iii)
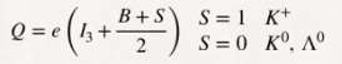
iii) includes baryons, mesons and particles with strangeness.
Quark model (1964)
Use SU(3) symmetry where the elements are the quarks (u, d, s).
3 ⊗ 3 ⊗ 3 = 10ѕ + 8мѕ + 8мᴀ + 1ᴀ
3 ⊗ 3 = 8ѕ + 1ᴀ
To accept this quark model, the following premises had to be met:
- Quarks have to have a fractional electric charge.
- Individual quarks never occur in isolation.
- Quarks only combine in three or as quarks and antiquarks.
Example 1:
Figure 41.
- Particle classification.
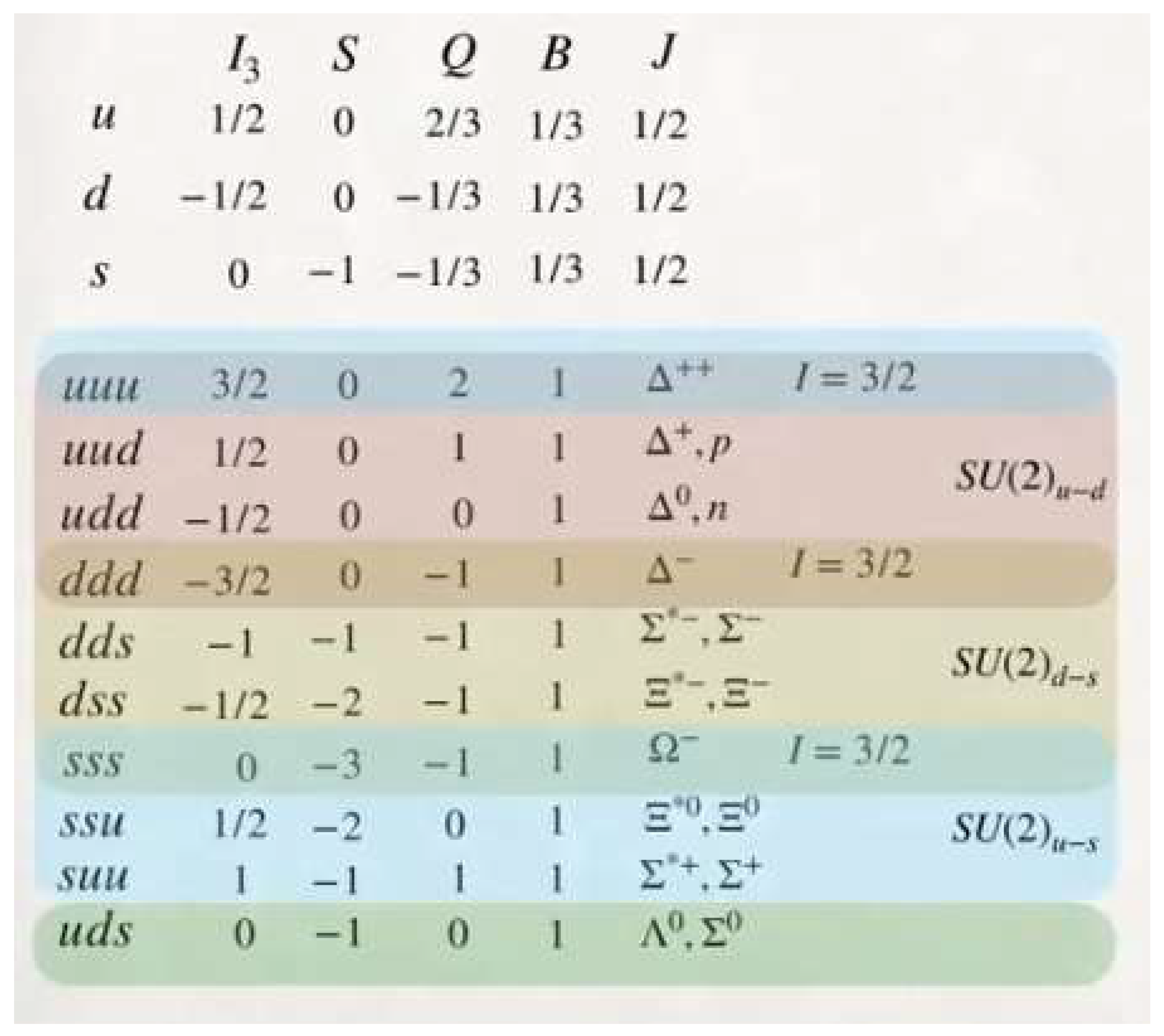
Example 2:
Figure 42.
- Meson.
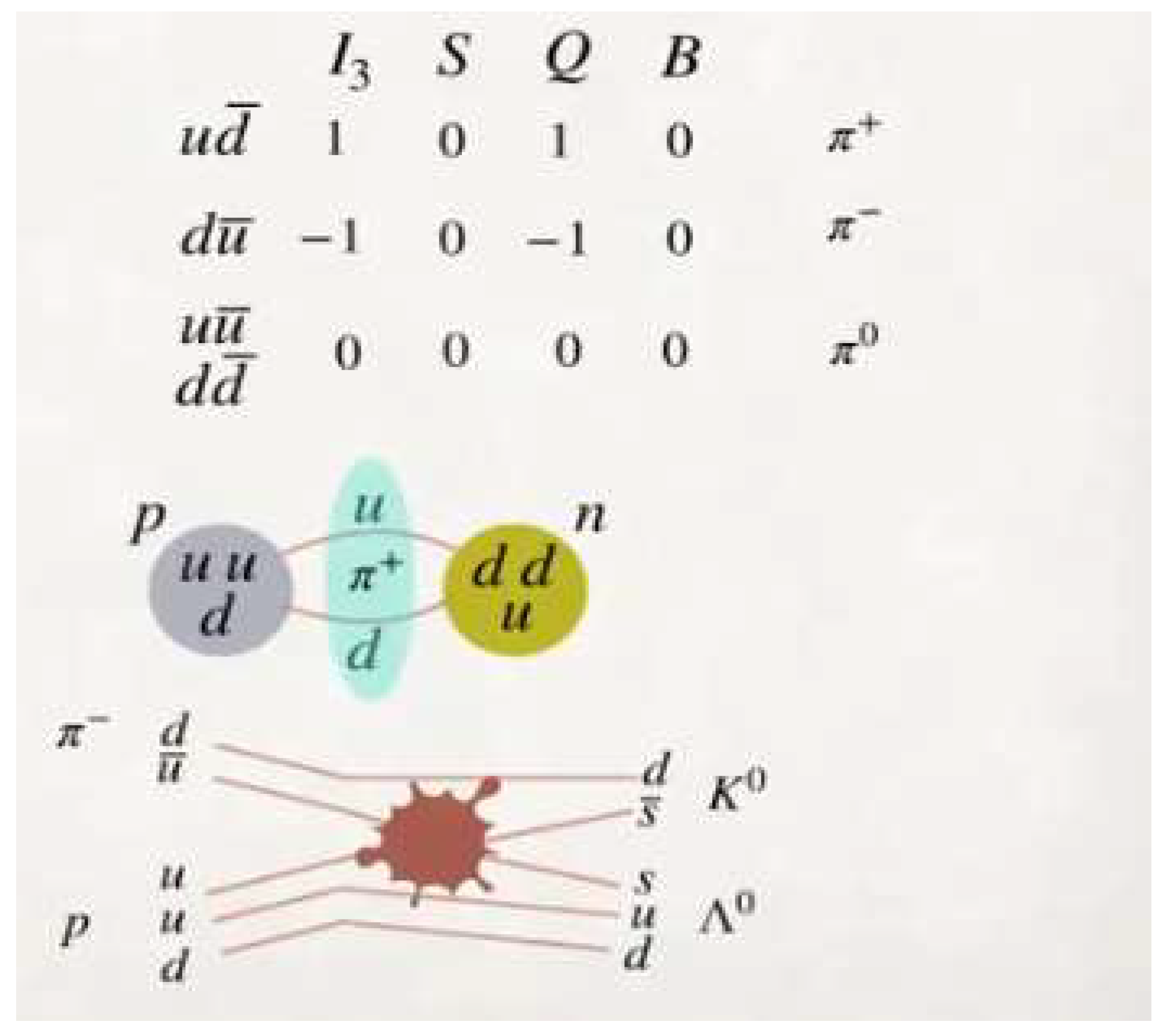
In Figure 41 and 42, we have generalized the isospin theory of the proton and neutron to the particles (u, d, s).
Figure 43.
- Functions SU(2) and SU(3) that have symmetry defined under permutations.
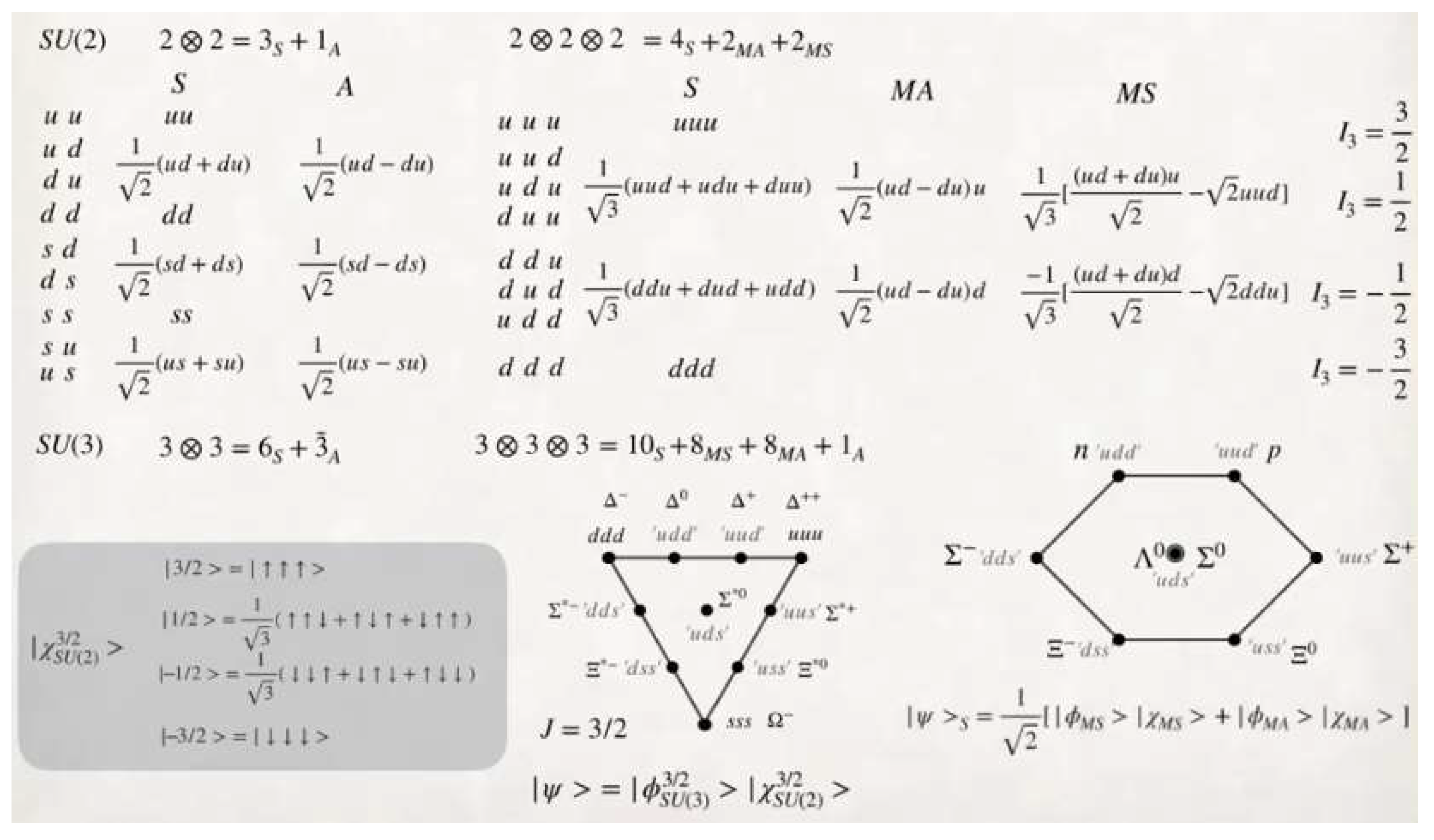
5.4. Fermions, Bosons, Spin and Color Symmetry
Bosons: Particles that are described by symmetric wave functions due to the exchange of positions of the particles. They obey the Bose-Einstein statistics.
Example: Bose-Einstein condensate.
Fermions: Particles that are described by antisymmetric wave functions due to the exchange of position of the particles. They obey the Fermi-Dirac statistics.
Example: The filling of the layers around the nucleus to form atoms, obeying the Pauli principle.
Now we are going to carry out a brief analysis of the magnetic moment of the particles.
Magnetic moment
Let us remember that the Dirac equation predicts the magnetic moment of elementary particles, it predicts what the spin of elementary fermionic particles would be.
For example, it predicts the magnetic moment of the electron or muon to nine significant digits.

The equation for the magnetic moment tells us that it is proportional to the electric charge and inversely proportional to the mass. We use natural units.
However, the prediction fails for the neutron and the proton. We know that this is because the neutron and proton are not elementary particles.
We can approximately calculate the relationship of the magnetic moment of the quarks.
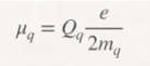
Where μq is the magnetic moment of a quark.
With this we can create operators that allow us to calculate the ratio of the magnetic moment of the proton and the neutron.
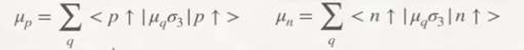
where μp is the magnetic moment of the proton and μn is the magnetic moment of the neutron.
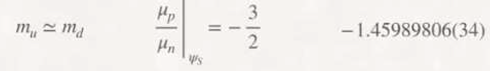
Let us observe that the quotient of the magnetic moments of the proton and the neutron gives me as a result of the calculation an error of the order of 3%, without knowing the mass of the U quark and the D quark, as long as I use a flavor and spin wave function totally symmetrical.
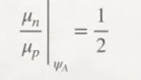
If I use a completely asymmetric flavor and spin wave function, the result is not correct and not even the sign agrees.
This tells us that the way in which the flavor and spin of the quarks combine inside the protons and neutrals is symmetrical in the face of perturbations.
Color symmetry
Now we are going to analyze the color symmetry, we are going to analyze what ant-symmetrizes the wave function; In other words, how can I put together a totally antisymmetric wave function.
For this we are going to draw the following equations:
3 ⊗ 3 ⊗ 3 = 10ѕ + 8мѕ + 8мᴀ + 1ᴀ
Let us observe that in the combination of three particles with spins ½, SU(3), already exists a singlet state defined as 1ᴀ, whose wave function is totally antisymmetric.
3 ⊗ 3 = 8ѕ + 1ᴀ
Let us also observe that in the combination of 2 particles with spins ½, SU(3), there already exists a singlet state defined as 1ᴀ, whose wave function is totally antisymmetric.
Now, I postulate that quarks have a quantum number that has SU(3) symmetry, different from the flavor and spin that makes the combinations of quarks in hadrons and mesons anti-symmetrize the wave function.
I am expressing the following:
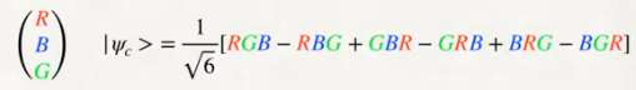
This tells us that the way the color of the quarks combine within the protons and the neutrals is anti-symmetric to perturbations.
Let us observe that the fundamental representation of the quarks is given by (R, B, G) and that the combination of the quarks that gives me a completely anti-symmetric wave function is represented in the equation above.
A spin singlet is a state that has no spin or projection.
A color singlet is an essentially colorless state.
This is telling me that the wave function of hadrons has no color, that is, mesons and baryons are colorless combinations.
This is telling me that nature demands that the hadron wave function be antisymmetric, singlet, colorless.
This is one of the reasons why quarks cannot exist in isolation.
This is also telling us that the lowest energy state corresponds to the singlet state.
In conclusion, the interactions of quarks inside protons and neutrons abhor explicit color, they always combine in singlets, whose wave function is antisymmetric, which correspond to the minimum energy state.
Example:
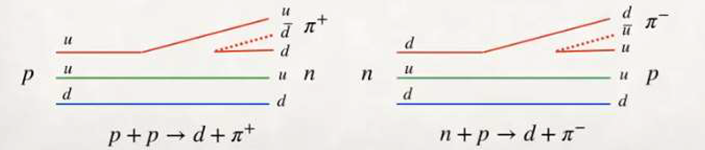
Here, color symmetry is represented in that both processes represent colorless singlets.
Now we can understand the SU(3) symmetry which predicts what the interactions between quarks would be like.
Here, we reach a point where it becomes inevitable to compare the bases on which the entire theory of QCD quantum chromodynamics of SU(3) symmetry is based and the theory that corresponds to the neutron and proton model, as an electric generator of alternating current, three-phase.
Nature requires that the wave function of hadrons be asymmetrical, that they behave as colorless singlets, that is, that baryons and mesons reach their minimum energy state.
We have verified that this premise is fulfilled in the SU(3) theory of quantum chromodynamics, but with a very important reservation, it is developed only for matter and does not contemplate antimatter.
However, if we analyze the theory of the proton and neutron as a three-phase alternating current generator; It also meets the premise, but there is a very important difference with respect to the QCD theory, it includes matter and antimatter.
In my humble personal opinion, I believe that we must consider both complementary theories, taking advantage of everything they can provide us to enrich science.
With this I am meaning the following; When we analyze beta minus decay, in the conventional theory everything is represented as a black box. The neutron represents the input and the output represents the proton, electron and antineutrino. However, in the black box there is no theory that explains what really happens in the decay of the neutron into a proton. This is where the theory of modeling the neutron and proton as a three-phase alternating current electrical generator comes into play, providing a logical explanation of what could really happen with the interactions of quarks in the decay of the neutron into a proton; in other words, this theory explains to us what really happens inside the black box.
I think that the theory of modeling the proton and neutron as a three-phase alternating current electric generator should be considered very seriously and used as a complement to the theory of QCD.
Taking into account everything we have developed in this paper, we could generalize the theory of modeling a neutron and proton as a three-phase alternating current electric generator and consider including SU(2) in the generalization.
Let us remember that QED quantum electrodynamics unites SU(2) with U(1)
QED → SU(2) x U(1)
I think we have started a path in which SU(3) symmetries and SU(2) symmetries can be represented by a single U(1) symmetry, where all interactions included in the standard model can be represented by a single electromagnetic interaction; We can also include gravity.
SU(3) x SU(2) → U(1)
We can express this as follows:
Quark interactions, gluons:
- (DD) → │DD > ≡ │1, 0 >, in phase.
- (UU) → │UU > ≡ │1, 0 >, in phase.
- (DU) → │DU >, out of phase.
- (UD) → │UD >, out of phase.
- (DD) → │DD >, out of phase.
- (UU) → │UU >, out of phase.
Quark interactions, gravitons:
- │UD + DU > ≡ │2, 0 >, in phase.
- │DU + UD > ≡ │2, 0 >, in phase.
Let's note that all the interactions that are included in the standard model can be represented by 6 bosons that we define as gluons.
Also note that the interaction that corresponds to the gravitational force is represented by two bosons that we define as gravitons.
Note that both gluons and gravitons are made up of quarks (U, U, D, D).
Now we are going to give a 3.0 explanation of the subtle difference that exists between the electromagnetic force and the gravitational force.
For this, we are going to need Einstein's field equation of general relativity or eventually, the Maldacena correspondence.
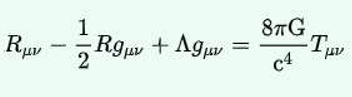
ADS = CFT
The right side of both equations corresponds to matter or energy and is under the domain of the strong, weak and electromagnetic interaction forces.
Let us remember again that the theory of electrical modeling of a proton and neutron as a three-phase alternating current generator reduces strong and weak interactions to simple electromagnetic interactions, we can express this as follows:
SU(3) x SU(2) → U(1)
Therefore, in both equations we have; On the left side the interactions of the gravitational force, which represents the curvature of space-time; on the right side the interactions of the electromagnetic force, which represents matter or energy. This equality is fulfilled as long as the gravitons and the carriers of the electromagnetic force, the gluons, are made up of the fundamental bricks of the universe, the quarks (U, U, D, D).
This is very important; we are saying that space-time and matter (energy) are made up of the same fundamental bricks.
We are saying that gravity is matter (energy), as long as they are made up of quarks (U, U, D, D); Only under this condition are the Einstein field equation of General Relativity and the Maldacena correspondence true.
Now we are going to carry out a new analysis adopting another point of view.
To do this we are going to adopt the following premises:
- (i)
- Nature requires that the wave function of spin 1/2 baryons with respect to flavor and spin, combine symmetrically in the face of permutations.
- (ii)
- Nature requires that the wave function of the Hadrons, with respect to color, combine in an antisymmetric way in the face of permutations.
If we observe any corner of the universe, we see that practically all matter is made up of baryons, therefore the wave function that characterizes the baryons with respect to color is antisymmetric when faced with permutations. If we look under the magnifying glass of the quantum number that represents color, the wave function that represents the baryons is singlet, it has no color; In other words, the baryons are in a state of minimum energy, with this we are wanting to affirm that the energy of their individual constituents is greater than the energy of the whole. premise ii) is met.
When we say that the baryons are in a state of minimum energy, it leads us to premise i), that is, we are referring to the wave function, with respect to flavor and spin, which is symmetric in the face of permutations.
Saying that its state is of minimum energy and that its wave function is symmetry in the face of permutations, with respect to flavor and spin, means that its behavior is analogous to that of bosons, this is very important and we are going to explain it in the following example.
Example:
D quarks are fermions, they have color, which is why they cannot exist in a free state in nature. D quarks join with a D antiquark to form a photon (DD), that is, a Boson. The boson has a wave function that is symmetric under permutations and has no color, a singlet state.
If we analyze gravitons, they are also bosons, that is, their wave function is symmetrical in the face of permutations (flavor and spin) and they have no color, that is, they are singlets.
To conclude, gravitational interactions and electromagnetic interactions are totally equivalent, both interactions are the result of interactions between quarks (U, U, D, D).
When we say that space-time is flat, we are saying that space-time has an effective Boltzmann constant Kʙɛ = 1.38 10⁻²³ J/K.
Under these conditions the matter content is reduced to the graviton content.
As the temperature increases, the quantities of virtual particles that make up space-time increase, the decay of gravitons gives rise to matter; As the temperature continues to increase, material structures such as the Earth, stars, white dwarfs, neutron stars and black holes begin to form, all types of celestial material bodies that we know; This causes the Boltzmann constant to reach its minimum value Kʙԍ = 1.78 10⁻⁴³ J/K.
Let us remember that the maximum curvature of space-time is reached for a Boltzmann constant equal to Kʙԍ = 1.78 10⁻⁴³ J/K, this occurs when a black hole forms.
Now we are going to analyze a celestial body, an ideal neutron star, we are going to assume that this neutron star is made up only of neutrons.
We know that neutrons are made up of quarks (U, U, D, D); therefore, we can say that the neutron star forms a pocket of quarks (U, U, D, D).
Now we are going to analyze from the point of view of the curvature of space-time, we know that the curvature of the space-time of a neutral star is approximately the curvature of the space-time of a black hole and corresponds to a Boltzmann constant in the order of Kʙn = 1.78 10⁻⁴¹ J/K.
In table 15, we see that the curvature of space-time for a neutron star is in the order of 10¹⁹ times the curvature corresponding to flat space-time, it is very large, therefore its gravity is also very large.
In figure 27 we observe that a body that has mass and curves space-time produces a stretching of space-time due to its contraction, this generates a force and is what we call gravitational force.
In summary, we could represent the neutron star as a bag of compacted quarks (U, U, D, D) that has a very large gravity, that is, it produces a fairly large stretching of space time; in other words, the number of gravitons that surround the neutron star is also large, therefore the number of quarks (U, U, D, D).
Another way of looking at it is the following, we said that we can represent the neutron star as a compact bag of quarks (U, U, D, D), surrounded by a space-time whose gravity is very great. Let us remember that space-time is made up of gravitons, that is, quarks (U, U, D, D); by saying that the curvature of space-time is great, we are saying that its gravity is great and therefore the number of gravitons is also great.
This is telling us that there is a continuity in the quantity of quarks (U, U, D, D) if we consider the interior of the neutron star as we move away, this quantity decreases and consequently the gravitational force decreases. This continuity is given by the existence of gravitons and is represented by the curvature of space-time that we call gravity.
Therefore, we can affirm that space-time represents a sea of gravitons (bosons) formed by quarks (U, U, D, D).
To conclude, the quarks (U, U, D, D) are those that dominate the dynamics that determine the origin of matter and antimatter and the interactions of the strong, weak electromagnetic and gravitational force. They are the fundamental bricks on which the entire universe we know is based. In this dynamic, we can also include dark matter and dark energy, which we can also say is dominated by quark interactions (U, U, D, D).
Additional comment:
In a talk at a conference dedicated to the 100th birthday of Erwin Schrödinger, Chen Ning Yang quoted from a lecture on quantum mechanics given by Paul Dirac. The topic here is the non-commutability of operators, often presented as the essential feature of quantum theory in the literature. Dirac said:
“The question arises whether the noncommutation is really the main new idea of quantum mechanics. Previously I always thought it was but recently I have begun to doubt it and to think that maybe from the physical point of view, the noncommutation is not the only important idea and there is perhaps some deeper idea, some deeper change in our ordinary concepts which is brought about by quantum mechanics.”
Dirac then continued, according to Yang, as follows:
“So, if one asks what is the main feature of quantum mechanics, I feel inclined now to say that it is not noncommutative algebra. It is the existence of probability amplitudes which underlie all atomic processes. Now a probability amplitude is related to experiment but only partially. The square of its modulus is something that we can observe. That is the probability which the experimental people get. But besides that, there is a phase, a number of modulus unity which can modify without affecting the square of the modulus. And this phase is all important because it is the source of all interference phenomena but its physical significance is obscure. “
7. Conclusions
Here, we have laid the bases, the foundations, from which we will be able to describe, using a single interaction force, the particle physics that describes the standard model and the interaction of the gravitational force.
Using the theory of electrical modelling of the neutron and proton as a three-phase alternating current electrical generator, we have demonstrated in a pragmatic way, without being rigorous, that the interactions of the weak and strong electromagnetic forces that are part of the standard model, can be replaced by a single electromagnetic interaction.
SU(3) x SU(2) → U(1)
We have hypothesized that the electromagnetic, weak and strong force interactions that are part of the standard model can be replaced by quark interactions (U, U, D, D); which are described below.
Quark interactions, gluons:
- (DD) → │DD > ≡ │1, 0 >, in phase.
- (UU) → │UU > ≡ │1, 0 >, in phase.
- (DU) → │DU >, out of phase.
- (UD) → │UD >, out of phase.
- (DD) → │DD >, out of phase.
- (UU) → │UU >, out of phase.
We have proposed the model of two particles that correspond to gravitons, which correspond to interactions of quarks and antiquarks as described in the following equations:
Quark interactions, gravitons:
- │UD + DU > ≡ │2, 0 >, in phase.
- │DU + UD > ≡ │2, 0 >, in phase.
Let's remember that when we say that it is in phase, it means that the spin or angular projection on the Z axis is aligned. Out of phase, means that the spin or angular projection is not aligned to the Z axis.
It is important to note that the interaction of the gravitational force can also be replaced by interactions of quarks and antiquarks (U, U, D, D).
To conclude, the theory that corresponds to the electrical model of the neutron and the proton as a three-phase alternating current electrical generator, allows us to write all the bosons (photon, gluon, graviton, W⁺, W⁻, Z⁰ and Higgs) as simple quark and antiquarks interactions (U, U, D, D).
About the authors
HECTOR GERARDO FLORES (ARGENTINA, 1971). I studied Electrical Engineering with an electronic orientation at UNT (Argentina); I worked and continue to work in oil companies looking for gas and oil for more than 25 years, as a maintenance engineer for seismic equipment in companies such as Western Atlas, Baker Hughes, Schlumberger, Geokinetics, etc.
Since 2010, I study theoretical physics in a self-taught way.
In the years 2020 and 2021, during the pandemic, I participated in the course and watched all the online videos of Cosmology I and Cosmology II taught by the Federal University of Santa Catarina UFSC (graduate level).
MARIA ISABEL GONÇALVEZ DE SOUZA (Brazil, 1983). I studied professor of Portuguese language at the Federal University of Campina Grande and professor of pedagogy at UNOPAR University, later I did postgraduate, specialization. I am currently a qualified teacher and I work for the São Joao do Rio do Peixe Prefecture, Paraiba. I am Hector's wife and my studies served to collaborate in the formatting of his articles, corrections, etc; basically, help in the administrative part with a small emphasis in the technical part analyzing and sharing ideas.
HARSHIT JAIN (India, 2008) I was born on July 14, 2008, into a loving family. My father, Ajitendra Kumar Jain, and my mother, Preeti Jain, have been incredibly supportive throughout my life and education. I grew up in Lalitpur, where I attended Jawahar Navodaya Vidyalaya (JNV) for my high school education.
My passion for learning has always driven me toward subjects that explore the mysteries of the universe. I have a particular interest in physics, biology, cosmology, and mathematics. This interest led me to the Pacific Institute of Cosmology, where I am currently pursuing advanced studies in these fields.
One of the most significant influences on my academic journey has been Professor Padhi, a renowned scholar who works with several professors who hold the prestigious title of Fellow of the Royal Society (FRS). His mentorship has been invaluable, guiding me through complex concepts and encouraging me to delve deeper into research.
Throughout my studies, I've engaged in various research projects, some of which have challenged conventional thinking and opened new avenues for exploration. These experiences have not only honed my analytical skills but also strengthened my resolve to contribute meaningfully to the scientific community.
In summary, I am Harshit Jain, a young scientist with a passion for discovery. My journey is just beginning, but I'm excited about the endless possibilities that lie ahead. I owe much of my success to my supportive family, dedicated mentors, and the enriching educational environments I've been fortunate to be a part of. I look forward to continuing my research and making meaningful contributions to the fields I hold dear.
Conflicts of Interest
The authors declares that there are no conflicts of interest.
References
- Flores, H. G. (2023). RLC electrical modelling of black hole and early universe. Generalization of Boltzmann's constant in curved spacetime. J Mod Appl Phys. 2023; 6(4):1-6. Flores, https://www.preprints.org/manuscript/202305.2246/v3.
- Flores, H.G.; Gonçalvez de Souza, M.I. Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant. Preprints 2023, 2023090301. [CrossRef]
- Gerardo Flores, H.; Gonçalves de Souza, M. I. Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron. Preprints 2023, 2023102076. [CrossRef]
- Gerardo Flores, H.; Jain, H.; Gonçalves de Souza, M. I. Proton Decay and Inverse Neutron Decay. Preprints 2024, 2024050023. [Google Scholar] [CrossRef]
- GERADORES DE CORRENTE ALTERNADA Universidad Federal Rio Grande do Norte UFRN – Apostille. https://docente.ifrn.edu.br/heliopinheiro/Disciplinas/maquinas-acionamentos-eletricos/apostila-de-maquinas-de-cc.
- Eisberg Resnick, Física Cuántica.
- Eyvind, H. Wichmann. Física cuántica.
- Sears – Zemansky. Física Universitaria con Física Moderna Vol II.
- M. Tinkham, Group Theory and Quantum Mechanics, McGraw-Hill, New York, 1964.
- P.H.E. Meijer, E. Bauer (2004) Group Theory: The Application To Quantum Mechanics (Dover).
- M. Hamermesh (1962) Group theory and its application to physical problems (Dover).
- Aula 02: circuitos Trifásicos. Universidad Federal de Parana, UFPR. https://www.eletrica.ufpr.br/sebastiao/wa_files/te344%20aula%2002%20-%20circuitos%20trifasicos_(2).pdf.
- Circuitos Trifasicos Universidad de São Paulo, USP. https://edisciplinas.usp.br/pluginfile.php/5335698/mod_resource/content/1/Slides%231.pdf.
- Gabriel Vinicius Vian. Introdução à Eletrodinâmica e Cromodinâmica Quântica. UNIVERSIDADE FEDERAL DA FRONTEIRA SUL, CAMPUS REALEZA.CURSO DE FÍSICA – LICENCIATURA – 2022 https://rd.uffs.edu.br/bitstream/prefix/5440/1/VIAN.pdf.
- Jefferson Taneo Shida Gonçalves. Introdução à QCD, Fundamentos e aplicações na física do LHC. Universidade Federal do Rio Grande - Instituto de Matemática, Estatística e Física. Rio Grande, 2017 https://imef.furg.br/images/stories/Monografias/Fisica_bacharelado/2017/2017-2_Jefferson_Shida.pdf.
- Michelangelo, L. Mangano. INTRODUCTION TO QCD CERN, TH Division, Geneva, Switzerland https://cds.cern.ch/record/454171/files/p41.pdf.
- P. Z. Skands. Introduction to QCD. Theoretical Physics, CERN, 1211 Geneva 23, Switzerland. School of Physics & Astronomy, Monash University, Clayton VIC 3800, Australia Updated: July, 2017 https://arxiv.org/pdf/1207.2389.pdf.
- Thomas Gehrmann and Bogdan Malaescu. Precision QCD Physics at the LHC. Annual Review of Nuclear and Particle Science. https://www.annualreviews.org/docserver/fulltext/nucl/72/1/annurev-nucl-101920-014923.pdf?expires=1711222185&id=id&accname=guest&checksum=718297BFB633C2F332DE04F95BB9CFE2.
- François Gieres. ABOUT SYMMETRIES IN PHYSICS. Institut de Physique Nucleaire de Lyon, IN2P3/CNRS, Universit´e Claude Bernard. 43, boulevard du 11 novembre 1918, F - 69622 - Villeurbanne CEDEX https://arxiv.org/pdf/hep-th/9712154.
- Stefano Disca, Roberto Demaria, Lorenzo Formaggio INTRODUCTIVE EXERCISES TO QUANTUM FIELD THEORY https://arxiv.org/pdf/2406.01393.
- Valentin Benedetti, Horacio Casini, Javier M. Magán ABJ anomaly as a U(1) symmetry and Noether’s theorem Instituto Balseiro, Centro Atómico Bariloche 8400-S.C. de Bariloche, Río Negro, Argentina https://arxiv.org/pdf/2309.03264.
- John L. Friedman Notes on Gravitational Physics Department of Physics, University of Wisconsin-Milwaukee; May 17, 2024. https://arxiv.org/pdf/2308.09826.
- James T. Wheeler SU(3) × SU(2) × U(1): The residual symmetry of extended conformal gravity. Utah State University, Logan, UT 84322; November 13, 2018 https://arxiv.org/pdf/hep-th/9109033.
- Logan Nye Entangled Origins of SU(3) × SU(2) × U(1): Emergence of Gauge Symmetries in the Standard Model Carnegie Mellon University file:///C:/Users/55839/Downloads/Entangled_Origins_of_SU_3__x_SU_2__x_U_1___Emergence_of_Gauge_Symmetries_the_Standard_Model_Nye.pdf.
- Thomas Görnitz, Goethe-Universität Frankfurt am Main · Institut für Didaktik der Physik. Uwe Schomäcker, Technische Universität Braunschweig · Institut für Mathematische Physik. The Structures of Interactions: How to Explain the Gauge Groups U(1), SU(2) and SU(3) file:///C:/Users/55839/Downloads/2016_Structures_of_interactions_GrnitzSchomcker_Res_gate.pdf.
- Lucas Carvalho Simões Quebra Espontânea da Simetria Quiral em Modelos de Yukawa-Higgs Universidade Federal do Espírito Santo – UFES, Programa de Pós-Graduação em Física. 5 de abril de 2019, Vitória - ES, Brasil. https://sappg.ufes.br/tese_drupal//tese_13252_Disserta%E7%E3o%20Lucas%20Sim%F5es%20-%20PPGFis.pdf.
- Jean-Bernard Zuber Invariances in Physics and Group Theory M2/International Centre for Fundamental Physics. https://www.lpthe.jussieu.fr/~zuber/Cours/InvariancesGroupTheory-2014.pdf.
- Matthew Robinson Book: Symmetry and the Standard Model Mathematics and Particle Physics https://www.docdroid.net/QGtZ58X/matthew-robinson-auth-symmetry-and-the-standard-model-mathematics-and-particle-physics-2011-springer-verlag-new-york-libgenlc-pdf#page=4.
- Scott Willenbrock Symmetries of the Standard Model Department of Physics, University of Illinois at Urbana-Champaign, February 2, 2008. https://arxiv.org/pdf/hep-ph/0410370.
- J. Zupan Introduction to flavor physics Department of Physics, University of Cincinnati, Cincinnati, Ohio, USA https://cds.cern.ch/record/2702255/files/939-4115-1-PB.pdf.
- Álvaro Pastor-Gutiérrez(1,2), Jan M. Pawlowski(2,3) and Manuel Reichert(4) The Asymptotically Safe Standard Model: From quantum gravity to dynamical chiral symmetry breaking 1 Max-Planck-Institut für Kernphysik P.O. Box 103980, D 69029, Heidelberg, Germany 2 Institut für Theoretische Physik, Universität Heidelberg, Philosophenweg 16, 69120 Heidelberg, Germany 3 ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung mbH, Planckstr. 1, 64291 Darmstadt, Germany 4 Department of Physics and Astronomy, University of Sussex, Brighton, BN1 9QH, U.K. https://scipost.org/SciPostPhys.15.3.105/pdf.
- Gustavo Garcia de Melo Simetria conforme e covariância galileana Universidade de Brasília, 2015. http://icts.unb.br/jspui/bitstream/10482/19882/1/2015_GustavoGarciaMelo.pdf.
- FILIPE JOAQUIM Introduction to particle Physics https://indico.cern.ch/event/1328014/contributions/6081852/attachments/2922272/5129762/Joaquim%20Aula%204.pdf.
- Noether’s Theorem CERN https://indico.cern.ch/event/106673/contributions/1306809/attachments/20980/30332/Natal_Lectures_Part_III.pdf.
- Igor R. Klebanov Joseph Henry Laboratories, Princeton University, Princeton, New Jersey 08544 Edward Witten Institute for Advanced Study, Olden Lane, Princeton, New Jersey 08540 AdS/CFT Correspondence and Symmetry Breaking https://arxiv.org/pdf/hep-th/9905104.
- Erin Blauvelt,a; Laura Engelbrecht,b; and Kurt Hinterbichler,c a: Department of Physics, Lehigh University, Bethlehem, PA, 18018. U.S.A. b: Institute for Theoretical Physics, ETH Zürich, Wolfgang-Pauli-Strasse 27, 8093, Zürich, Switzerland. c: CERCA, Department of Physics, Case Western Reserve University, 10900 Euclid Ave, Cleveland, OH 44106, U.S.A. Shift Symmetries and AdS/CFT file:///C:/Users/55839/Downloads/Shift_Symmetries_and_AdSCFT.pdf.
- Michaelmas 2014, Prof. N. Manton Symmetries, Fields and Particles University of Cambridge https://www.damtp.cam.ac.uk/user/examples/3P2.pdf.
- Howard Georgi Book: Lie Algebras in Particle Physics Cambridge, MA; May, 1999. https://library.oapen.org/bitstream/handle/20.500.12657/50876/9780429967764.pdf.
- CHONG LEONG ONG SUPERSYMMETRIC MODELS FOR QUARKS AND LEPTONS WITH NONLINEARLY REALIZED E8 SYMMETRY * Submitted to Physical Review D Stanford Linear Accelerator Center https://www.slac.stanford.edu/pubs/slacpubs/3250/slac-pub-3459.pdf.
- Thomas T. Dumitrescu. Lectures on Generalized Symmetries and Phases of Gauge Theory Lectures at IHES Summer School (June/July 2024) on Symmetries and Anomalies, June 26, 2024. https://indico.math.cnrs.fr/event/11080/attachments/4585/8220/Lecture%20Notes_DumitrescuT.pdf.
- Elina Rischke Symmetries in Quantum Mechanics and Particle Physics. Frankfurt Digital Summer School 2021 https://itp.uni-frankfurt.de/~drischke/Script_Symmetries_GU2021.pdf.
- Goran Senjanović; Alejandra Melfo Introductory Course Standard Model of particle physics https://www2.physik.uni-muenchen.de/lehre/vorlesungen/sose_22/Introduction-to-Physics-of-Neutrinos/Materials/SMcourse.pdf.
- IAN LIM SYMMETRIES, FIELDS, AND PARTICLES https://lim.physics.ucdavis.edu/teaching/files/sfp-notes-partiii.pdf.
- GABRIEL J. H. KHAN WHAT IS NOETHER’S THEOREM? https://math.osu.edu/sites/math.osu.edu/files/Noether_Theorem.pdf.
- Juan Maldacena The symmetry and simplicity of the laws of physics and the Higgs boson Institute for Advanced Study, Princeton, NJ 08540, USA https://arxiv.org/pdf/1410.6753.
- Juan Maldacena The Illusion of Gravity https://www.ias.edu/sites/default/files/sns/sciam-maldacena-3a.pdf.
Figure 1.
- Electrical model of the neutron considering matter and antimatter.
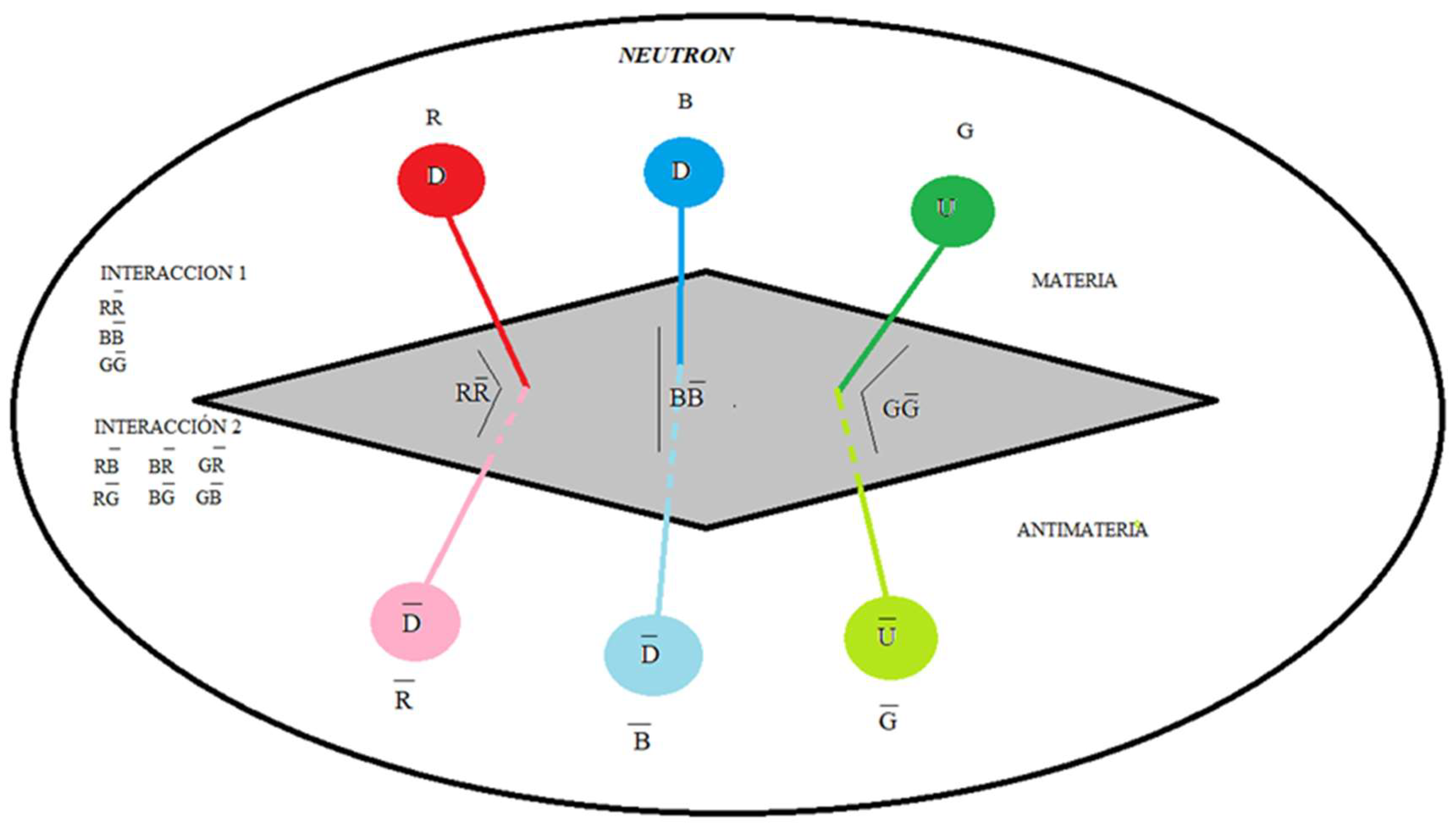
Figure 2.
- Electrical model of the proton considering matter and antimatter.
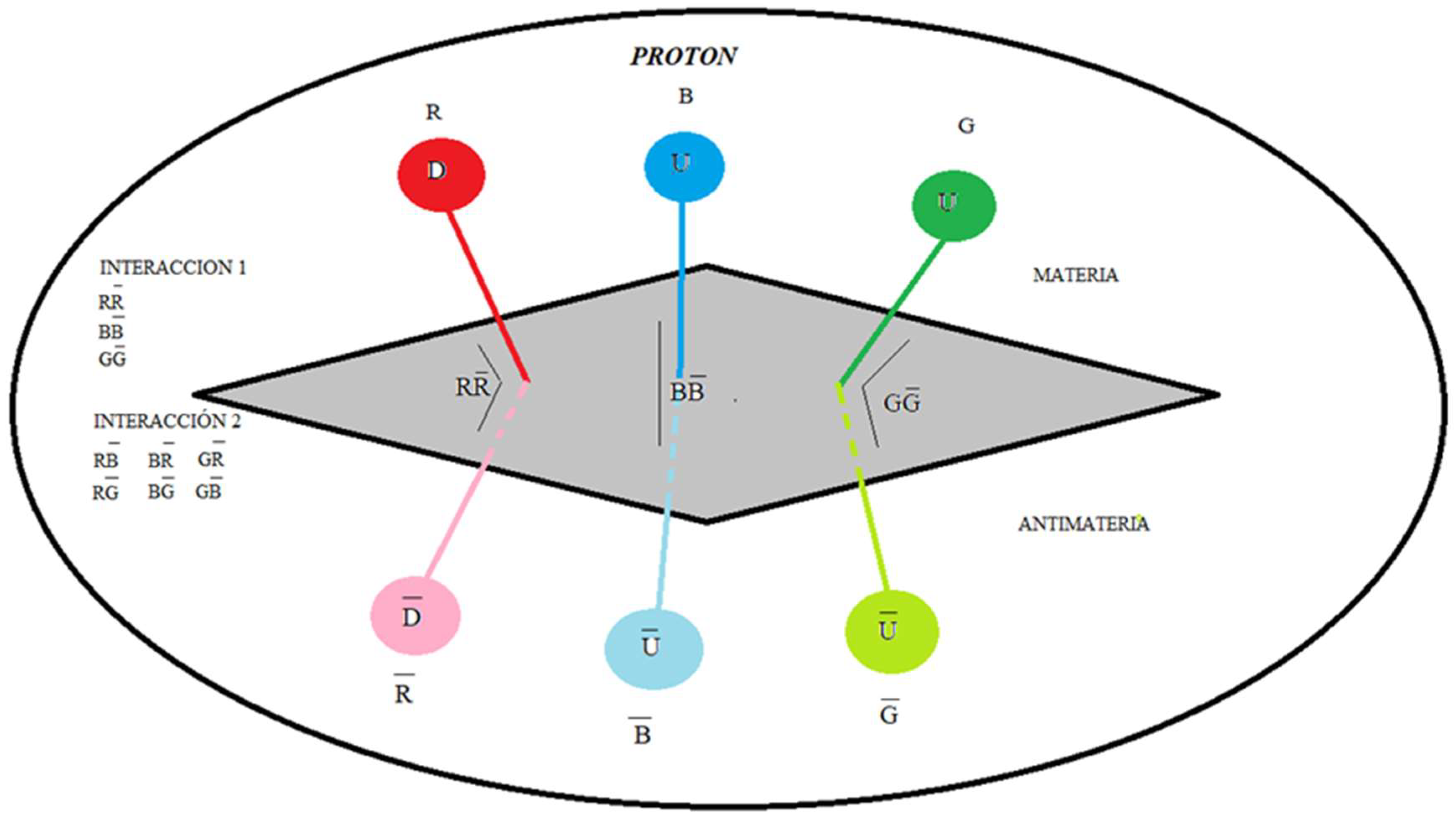
Figure 3.
– Three phase generator.
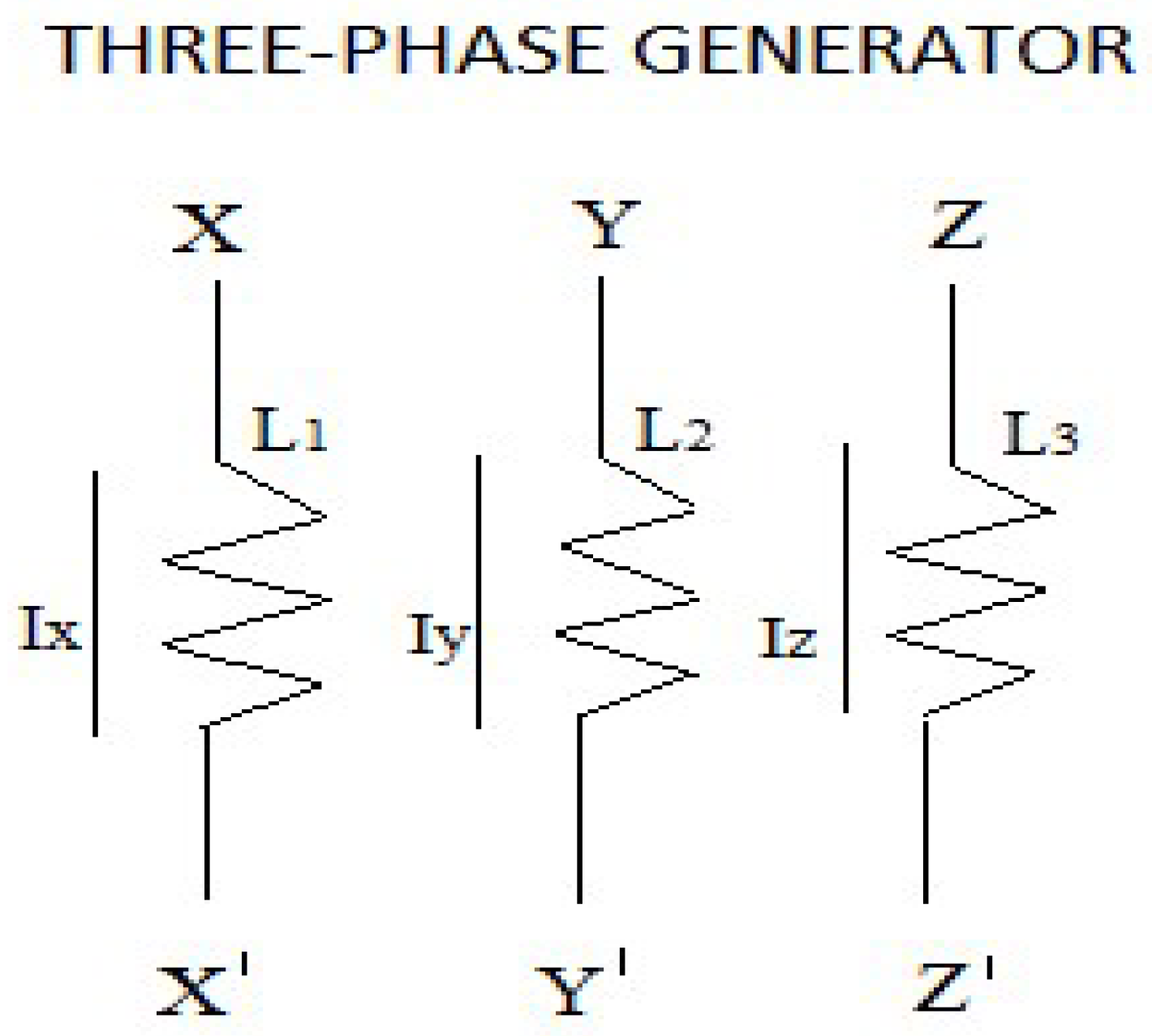
Figure 4.
– Three phase generator.
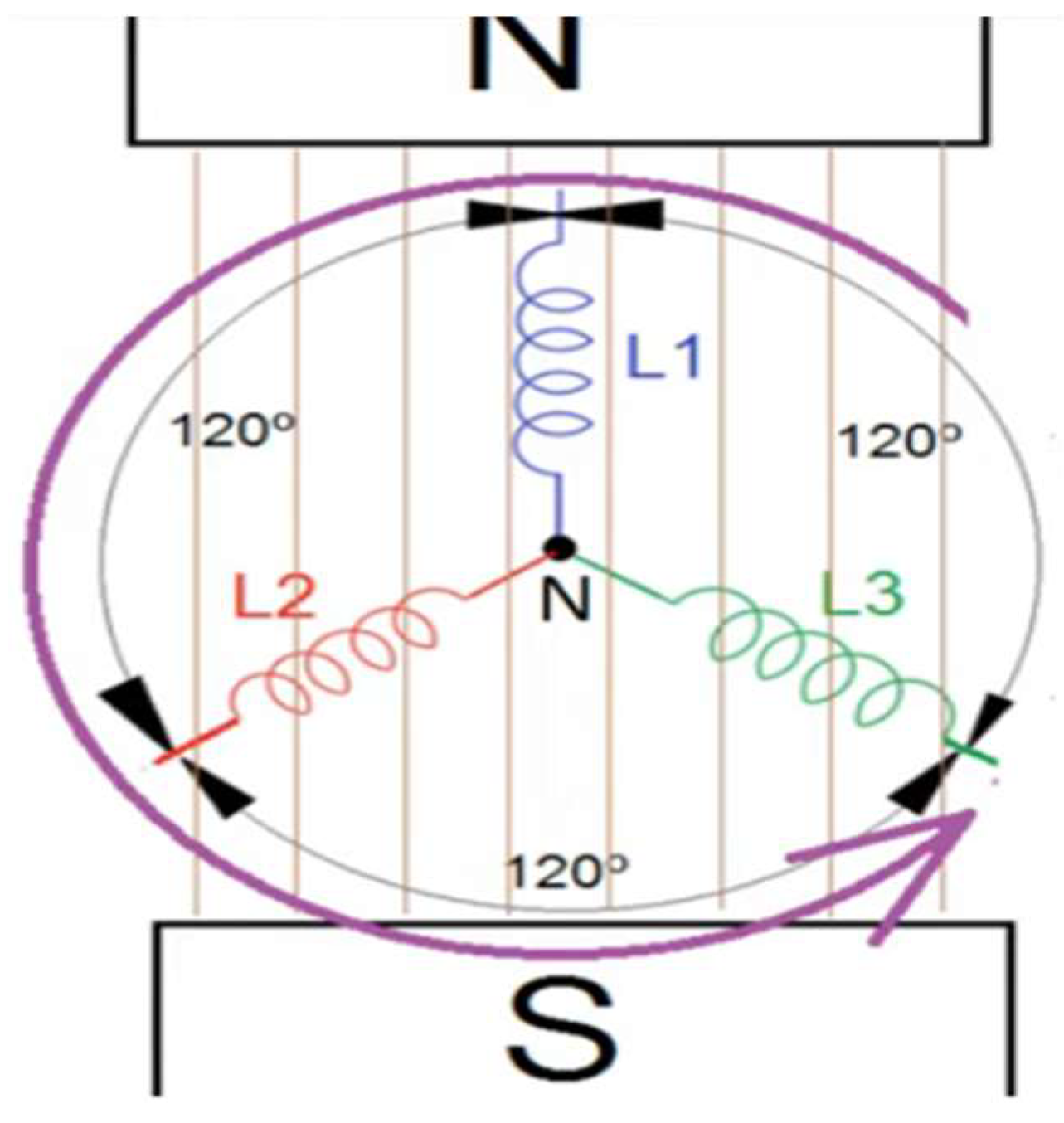
Figure 5.
- Three-phase voltage generated with a phase shift of 120 degrees.
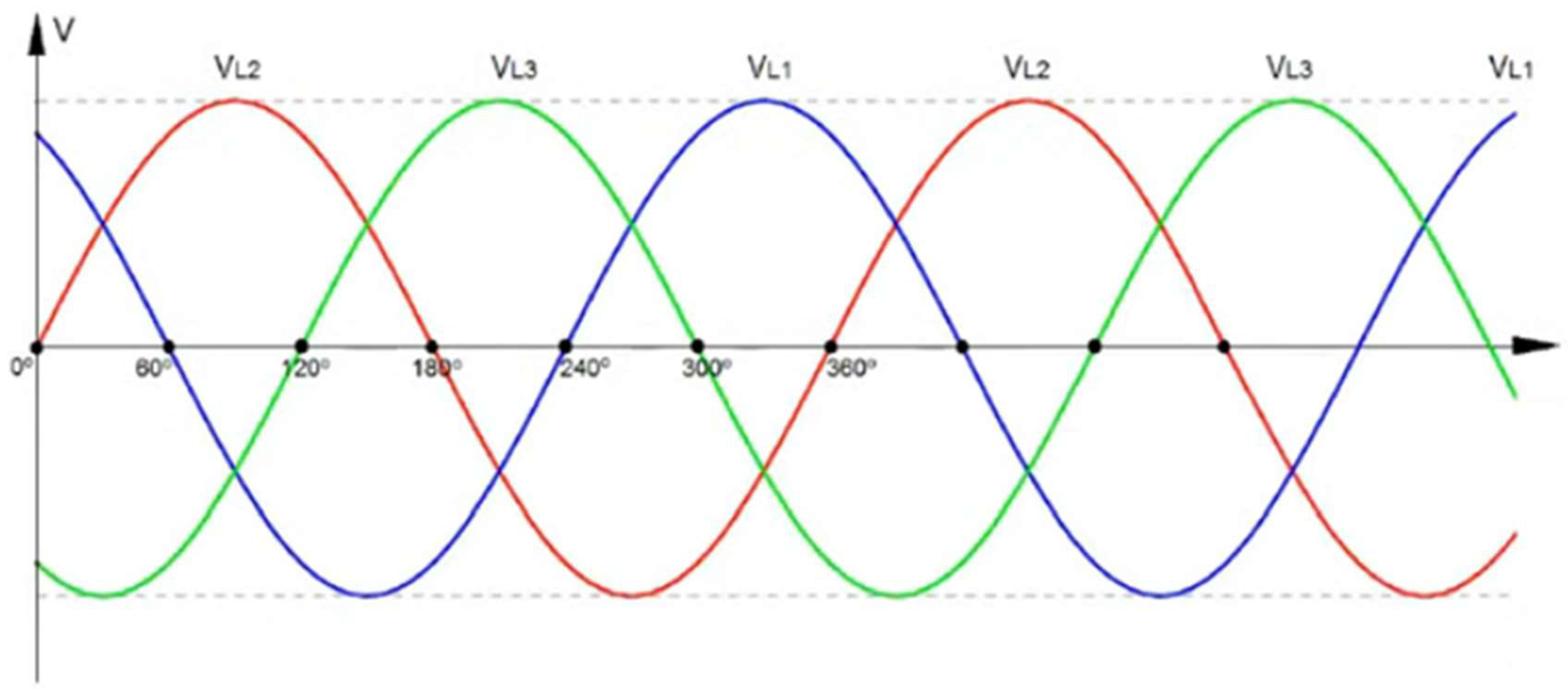
Figure 7.
– Neutron.
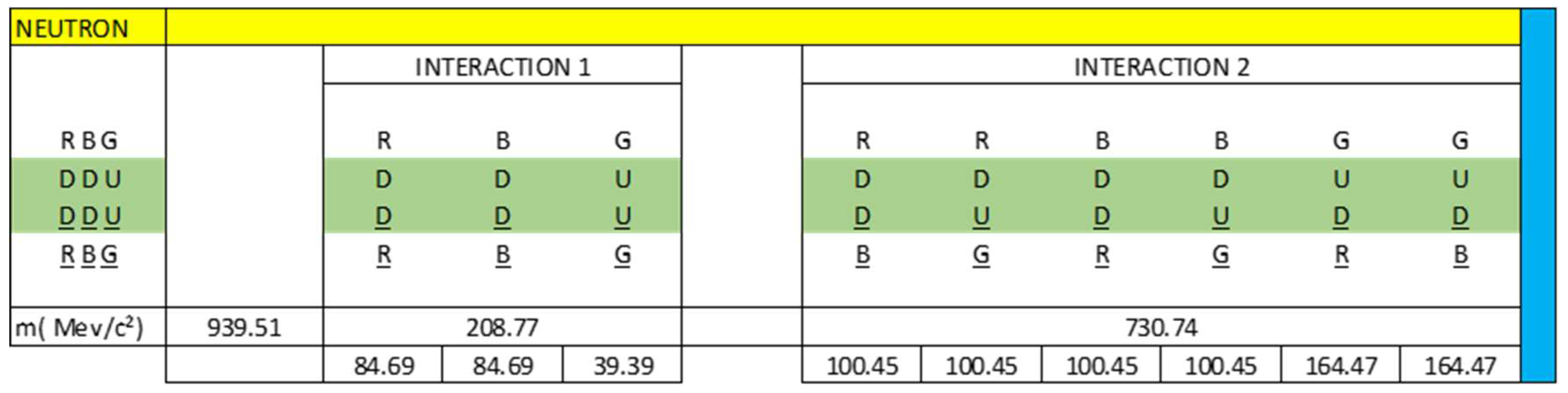
Figure 8.
– Proton.
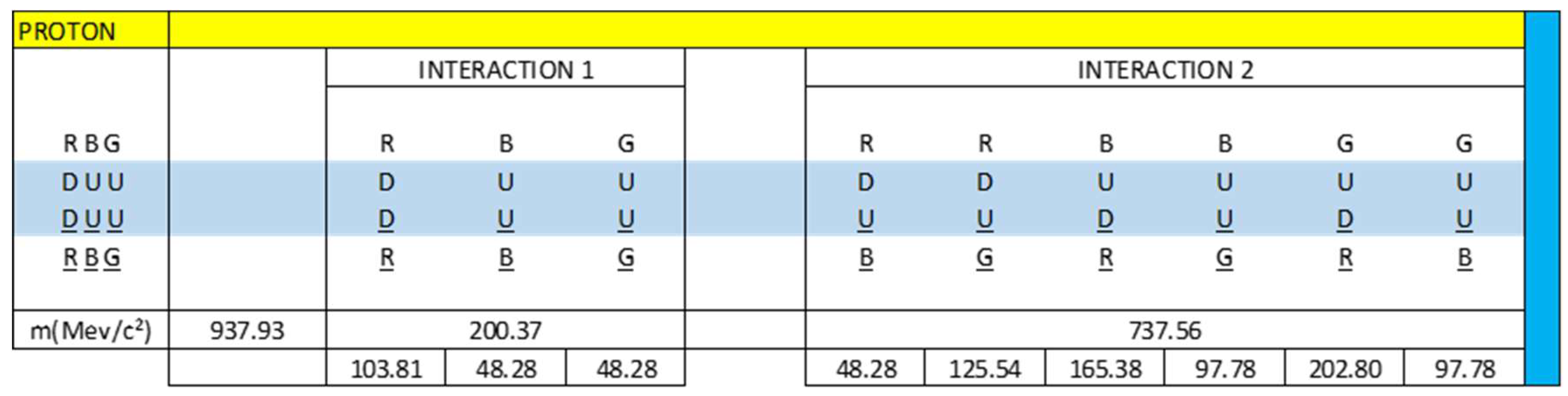
Figure 9.
- Vector diagram of β⁻ Decay.
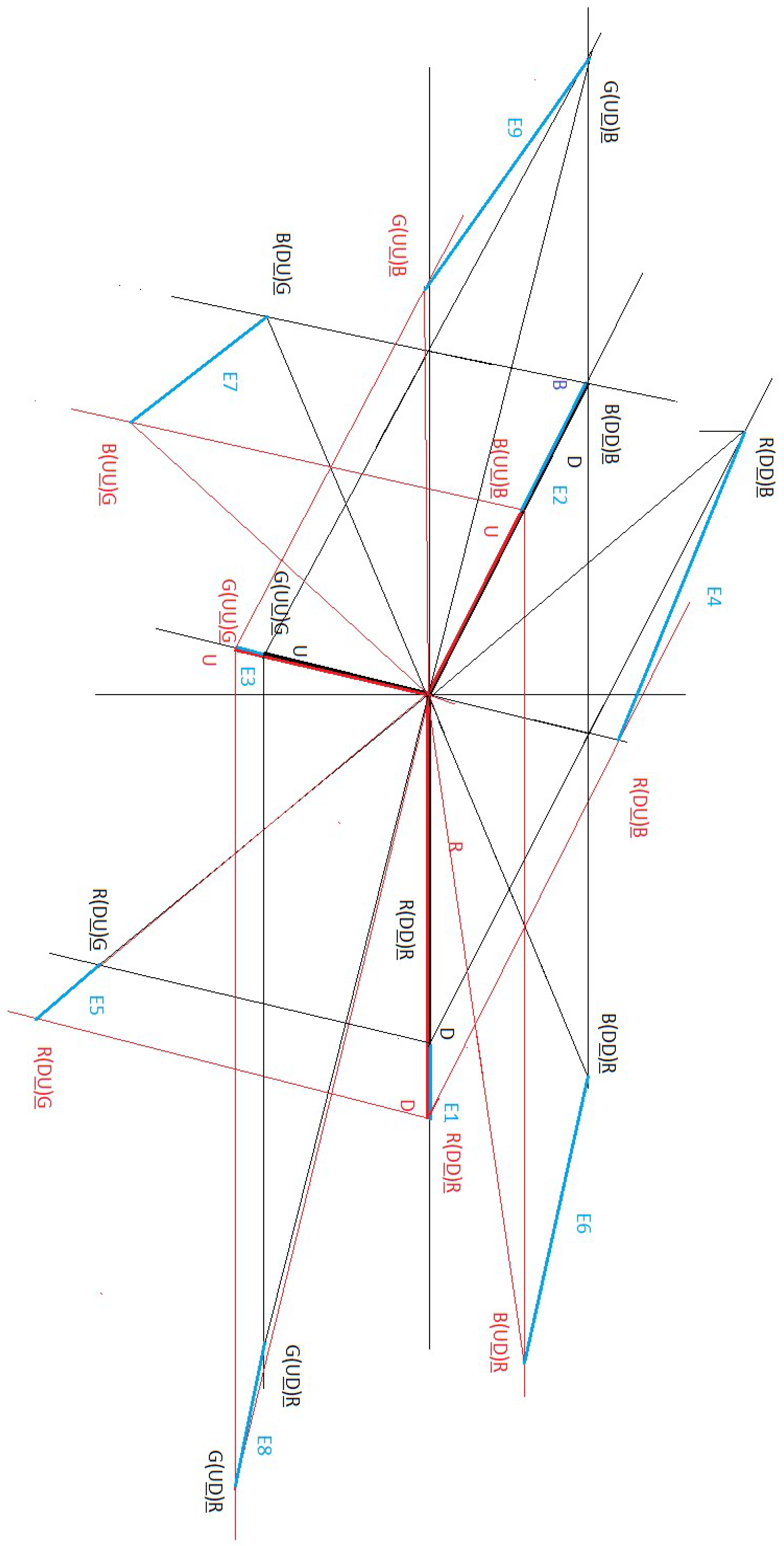
Figure 10.
- Mass distribution vs charge distribution.

Figure 11.
- Mass distribution vs charge distribution.

Figure 12.
- Mass distribution vs charge distribution.

Figure 13.
- Mass distribution vs charge distribution.

Figure 14.
– Neutron.
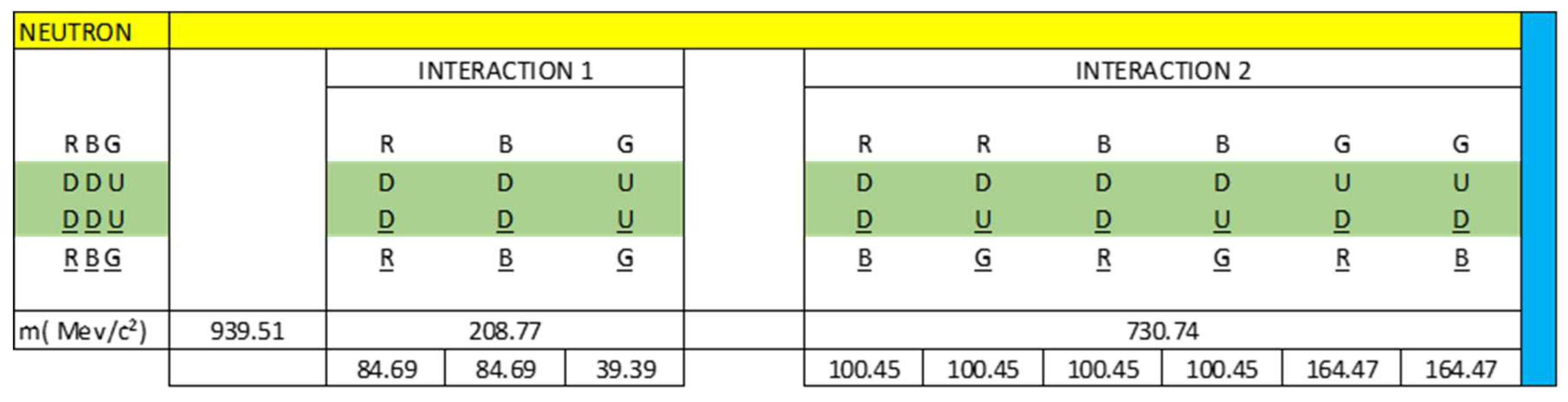
Figure 15.
– Proton.
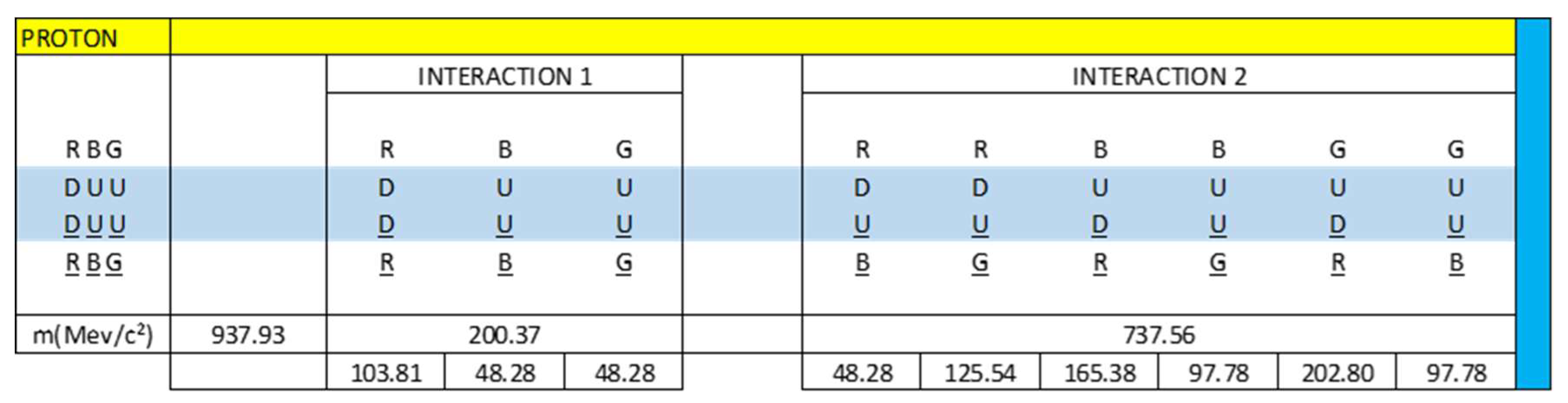
Figure 23.
- Collision of protons produces the Higgs boson which is detected by the detection of photons.
Figure 23.
- Collision of protons produces the Higgs boson which is detected by the detection of photons.
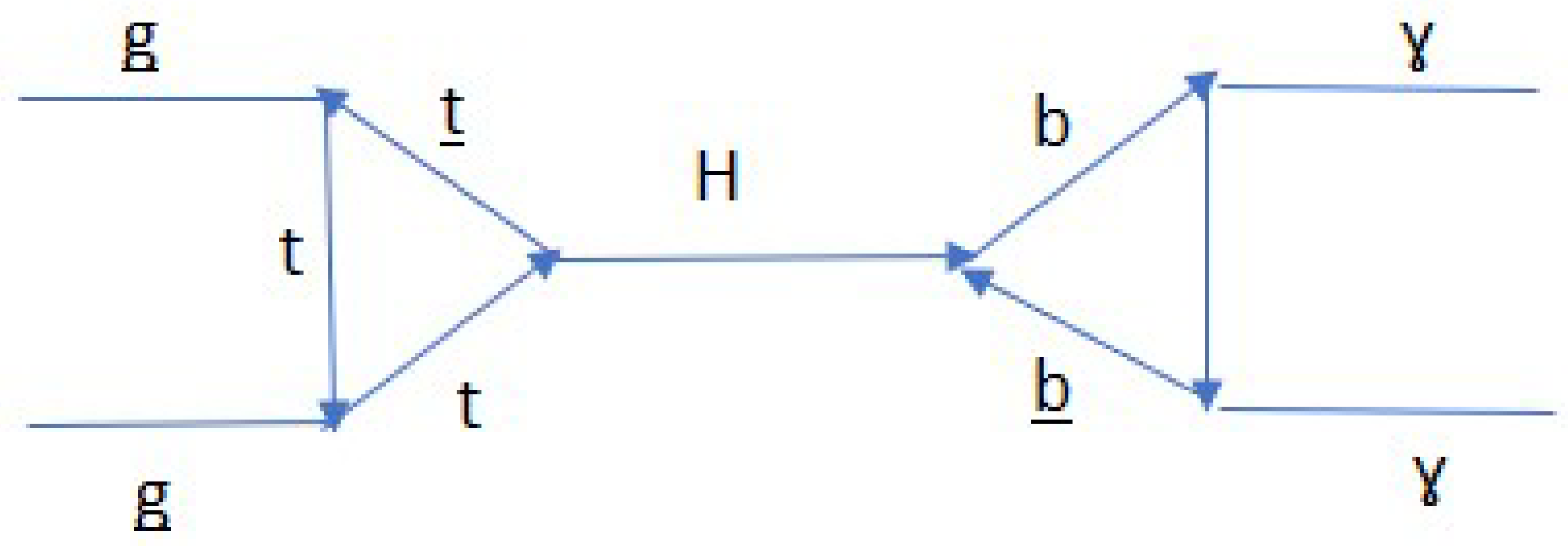
Figure 24.
- Collision of D & D Quarks produces the Higgs boson which is detected by the detection of photons.
Figure 24.
- Collision of D & D Quarks produces the Higgs boson which is detected by the detection of photons.
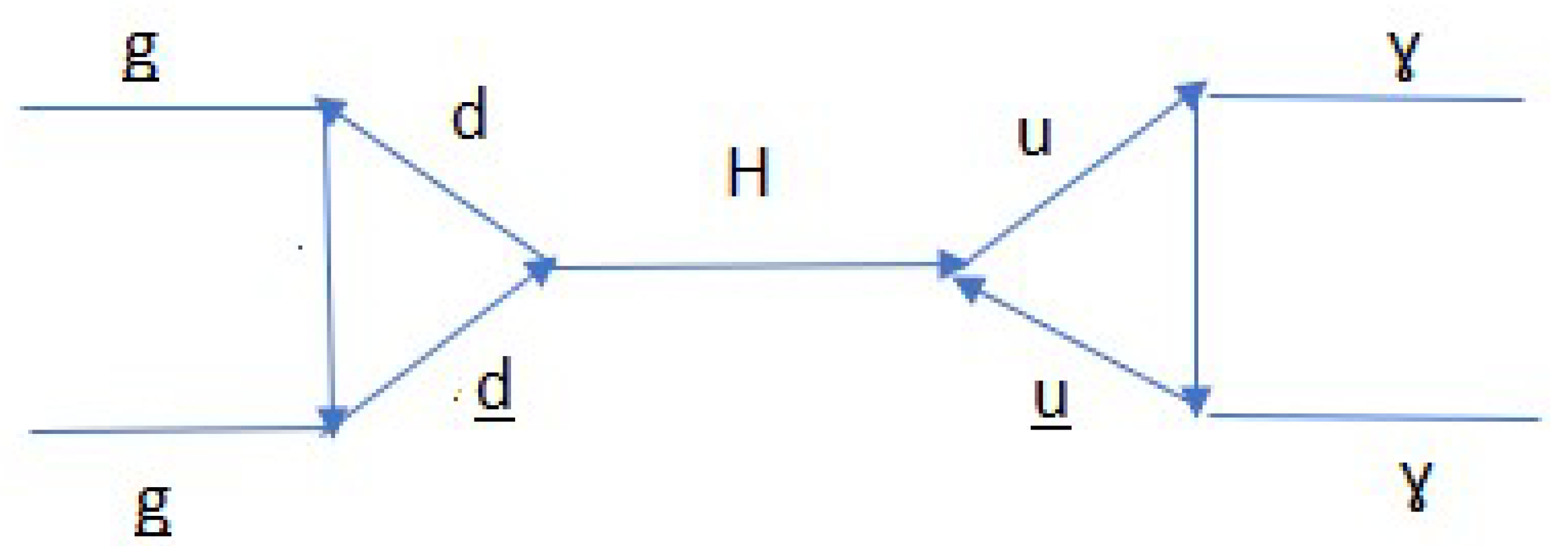
Figure 25.
- black hole formed by Neutroniumd particles.
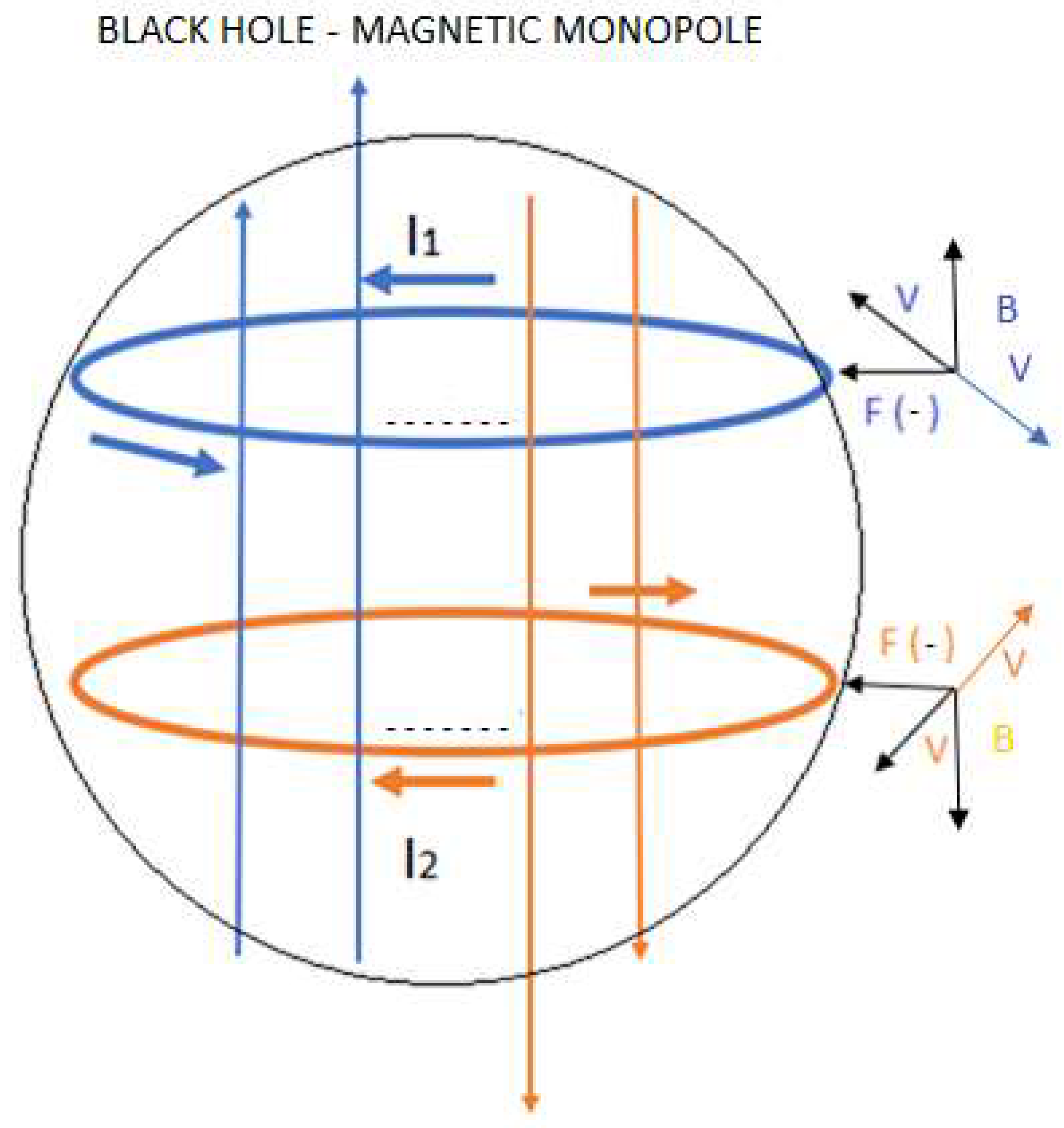
Figure 26.
- black hole model formed by protoniu particles.
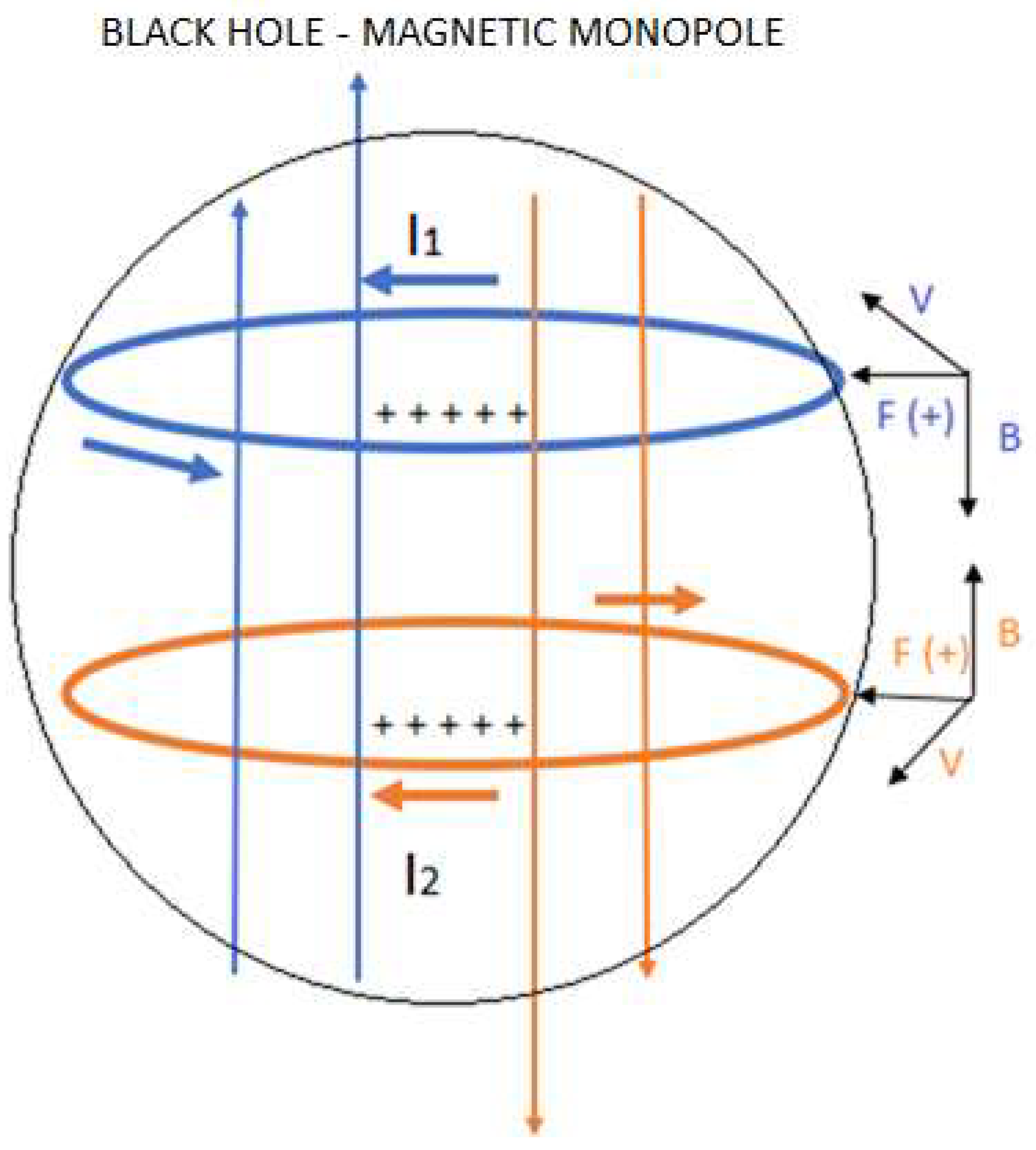
Figure 27.
- Gravity is a force.
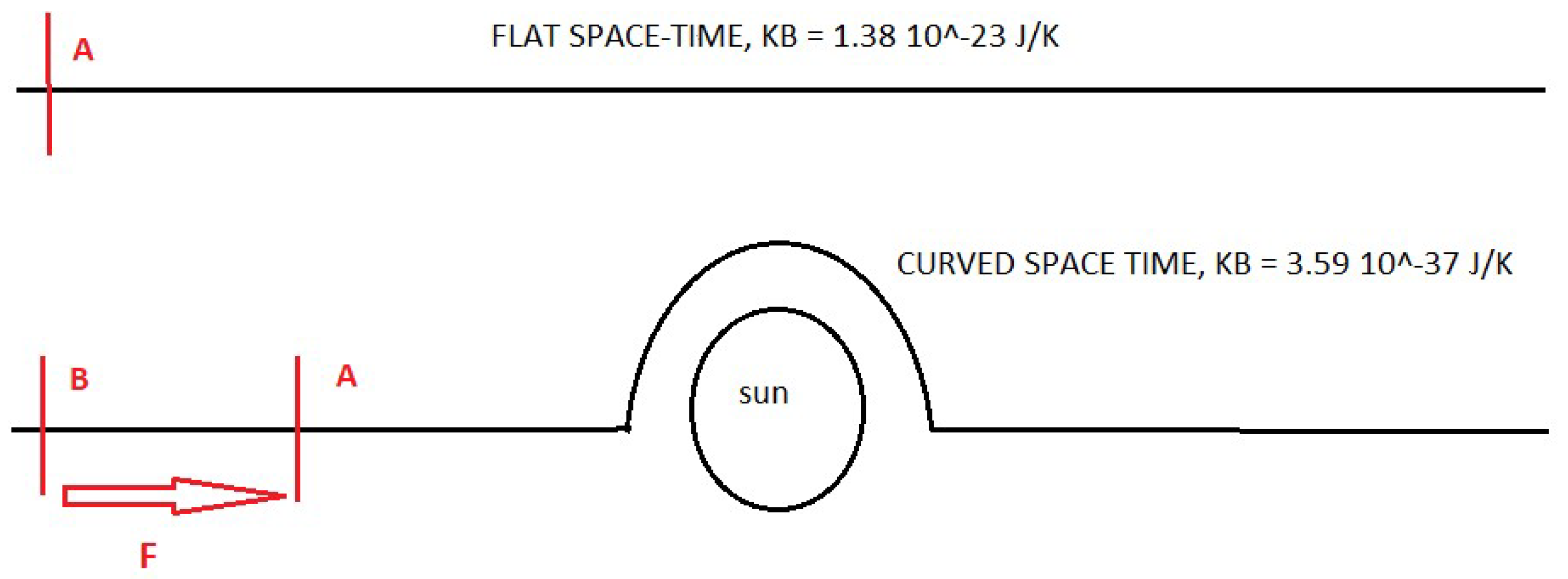
Figure 28.
- compression and torsion forces that act in space-time corresponding to a Planck length inside a black hole.
Figure 28.
- compression and torsion forces that act in space-time corresponding to a Planck length inside a black hole.
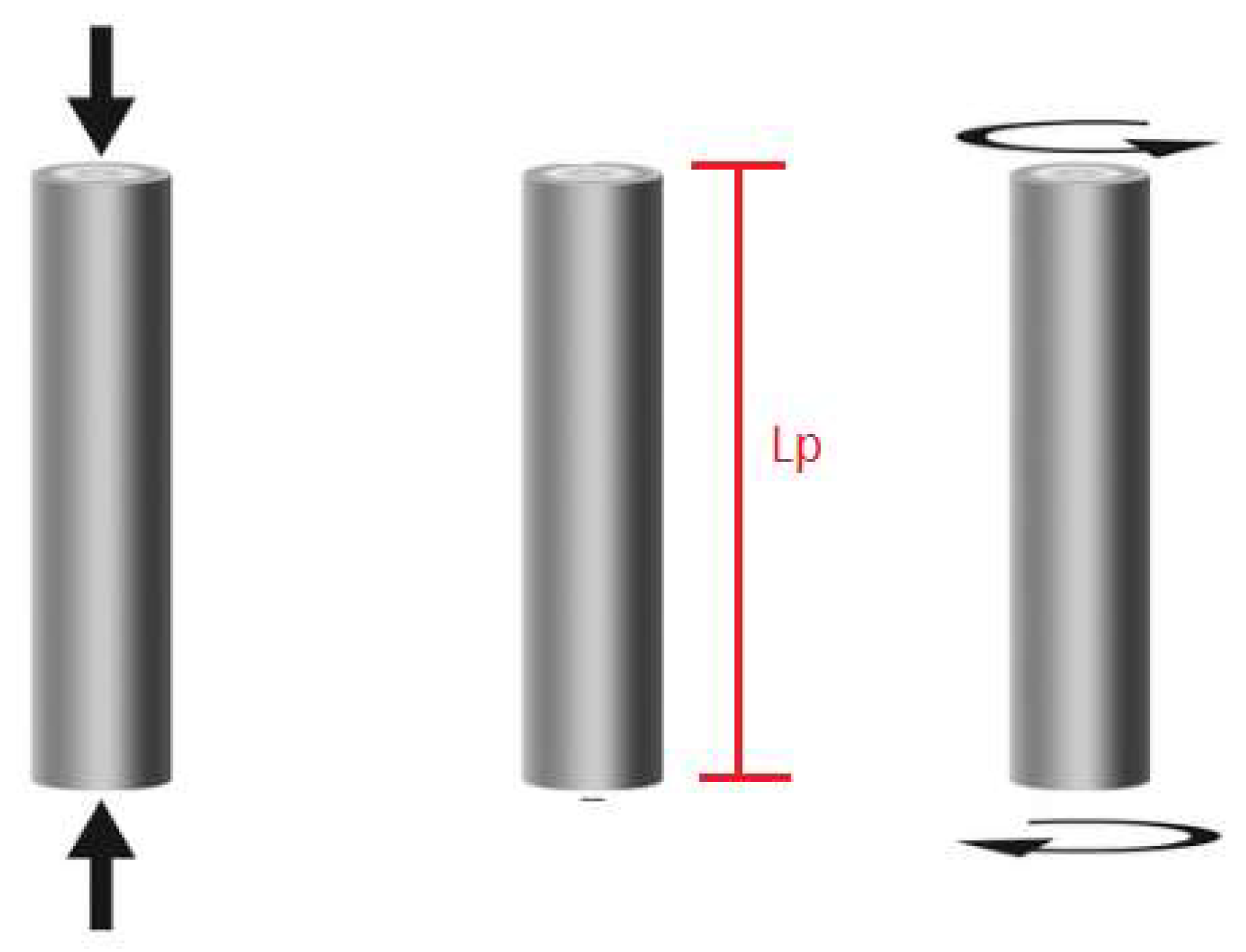
Figure 29.
-│UD + DU > ≡ │2, 0 >.
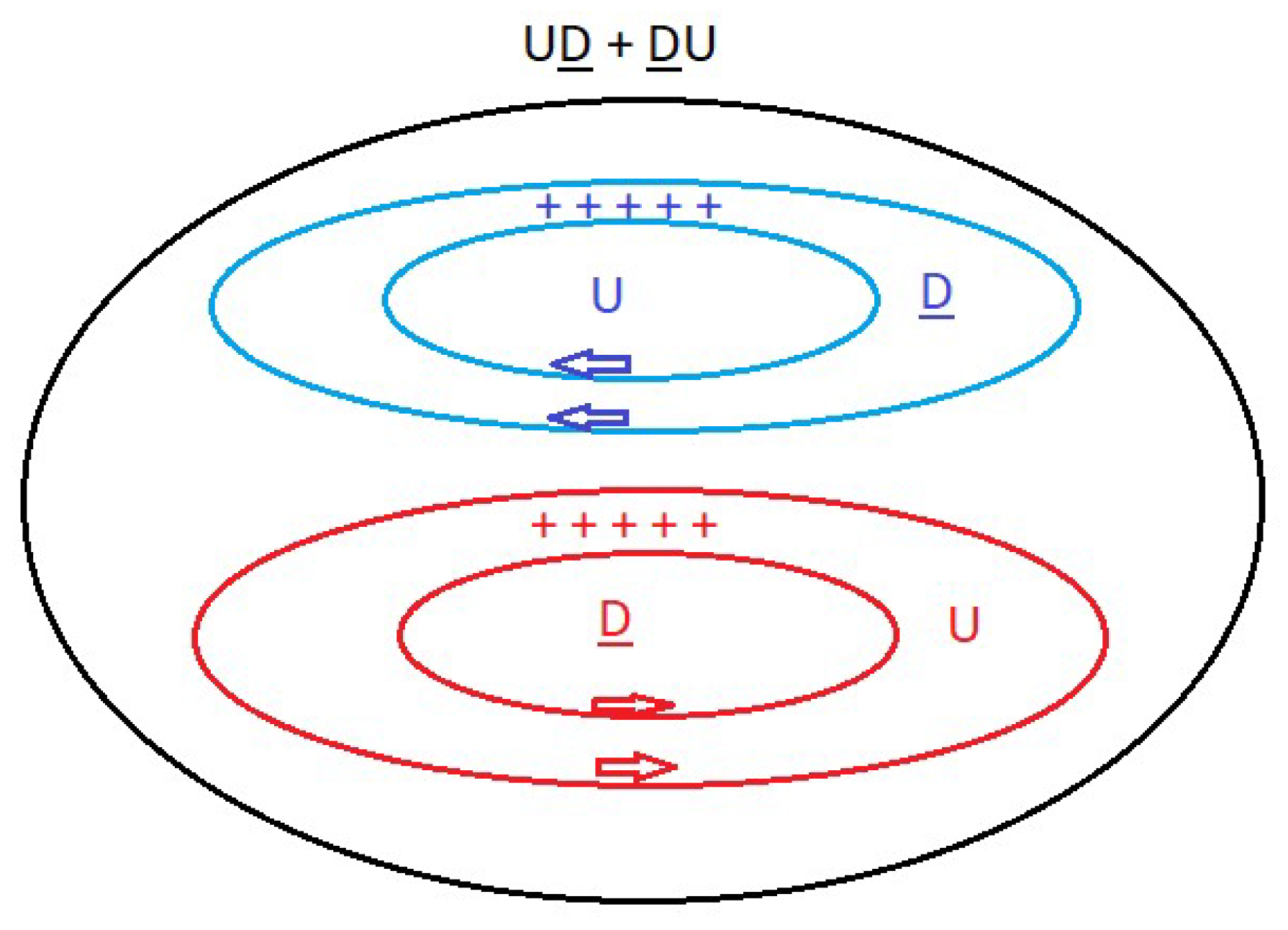
Figure 30.
-│DU + UD > ≡ │2, 0 >.
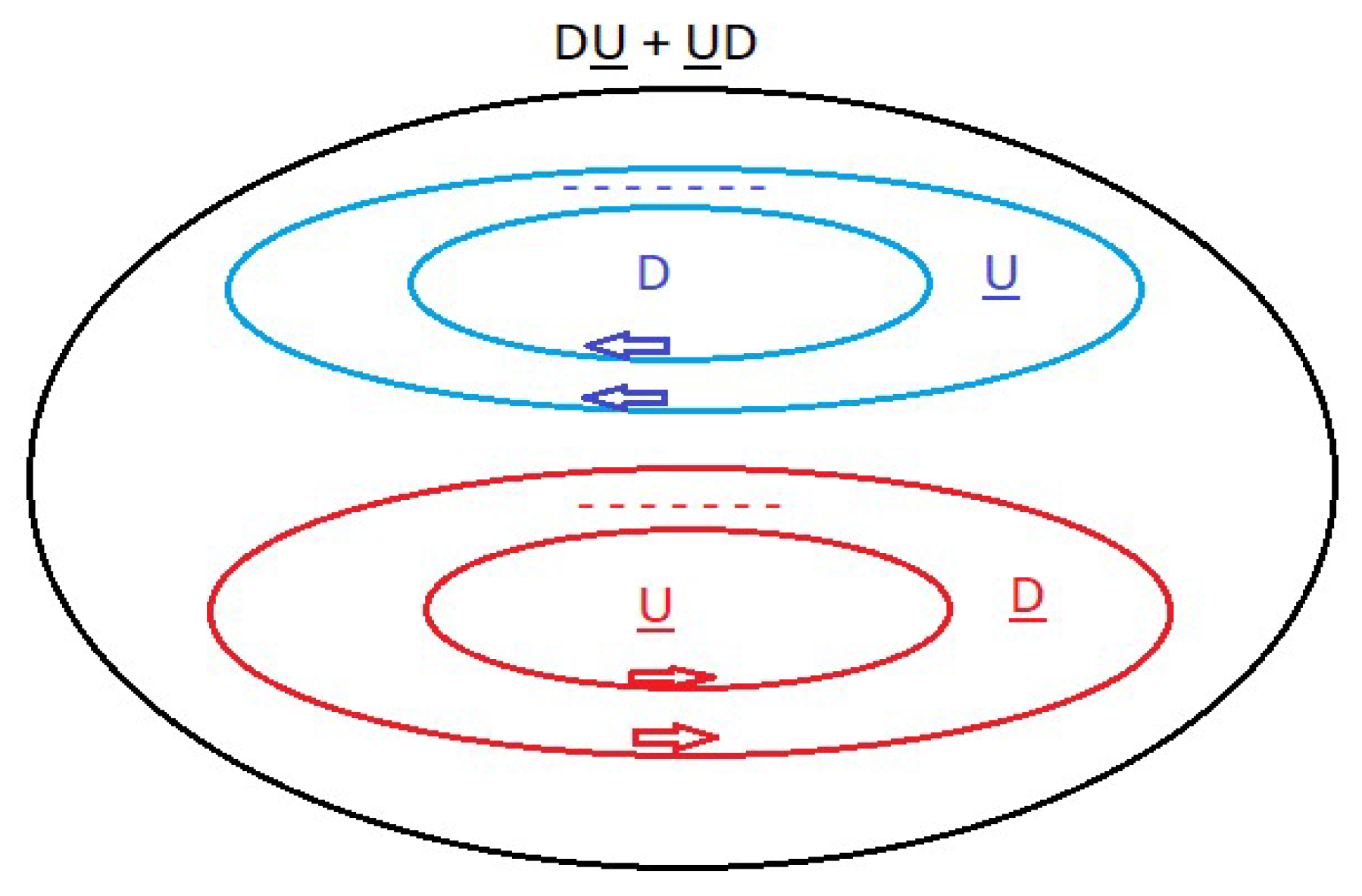
Table 1.
β⁻ Decay.
| βˉ DECAY | |||
| NEUTRON | PROTON | INTERACTION | INTERACTION (MeV/c²) |
| R(DD)R | R(DD)R | E1 = 1.94 | IE1I = 19.12 |
| B(DD)B | B(UU)B | E2 = 3.69 | IE2I = 36.41 |
| G(UU)G | G(UU)G | E3 = 0.9 | IE3I = 08.89 |
| R(DD)B | R(DU)B | E4 = 8.2 | IE4I = 80.75 |
| R(DU)G | R(DU)G | E5 = 2 | IE5I = 19.69 |
| B(DD)R | B(UD)R | E6 = 7.4 | IE6I = 72.87 |
| B(DU)G | B(UU)G | E7 = 4.2 | IE7I = 41.35 |
| G(UD)R | G(UD)R | E8 = 3.8 | IE8I = 37.42 |
| G(UD)B | G(UU)B | E9 = 7 | IE9I = 68.93 |
| TOTAL INTERACTION | IEtI = 385.37 MeV/c² | ||
Table 2.
- Electric current (DD) in green, between (R(DD)R)n and (R(DD)R)p.
| 84.69 MeV/c² | E1 = 19.12 MeV/c² | 103.81 MeV/c² |
| N | --> | P |
| R | R | |
| D | D | D |
| D | D | D |
| R | R |
Table 3.
- Electric current (DD) in green, between (B(DD)B)n and (B(UU)B)p.
| 84.69 MeV/c² | E2 = 36.41 MeV/c² | 48.28 MeV/c² |
| N | --> | P |
| B | B | |
| D | D | U |
| D | D | U |
| B | B |
Table 4.
- Electric current (UU) in green, between (G(UU)G)n and (G(UU)G)p.
| 39.39 MeV/c² | E3 = 8.89 MeV/c² | 48.28 MeV/c² |
| N | --> | P |
| G | G | |
| U | U | U |
| U | U | U |
| G | G |
Table 5.
- Electric current (DD) in green, between (R(DD)B)n and (R(DU)B)p.
| 100.45 MeV/c² | E4 = 80.75 MeV/c² | 48.28 MeV/c² |
| N | --> | P |
| R | R | |
| D | D | D |
| D | D | U |
| B | B |
Table 6.
- Electric current (DU) in green, between (R(DU)G)n and (R(DU)G)p.
| 100.45 MeV/c² | E5 = 19.69 MeV/c² | 125.54 MeV/c² |
| N | --> | P |
| R | R | |
| D | D | D |
| U | U | U |
| G | G |
Table 7.
- Electric current (DD) in green, between [B(DD)R]n and [B(UD)R]p.
| 100.45 MeV/c² | E6 = 72.84 MeV/c² | 165.38 MeV/c² |
| N | --> | P |
| B | B | |
| D | D | U |
| D | D | D |
| R | R |
Table 8.
- Electric current (DU) in green, between [B(DU)G]n and [B(UU)G]p.
| 100.45 MeV/c² | E7 = 41.35 MeV/c² | 97.78 MeV/c² |
| N | --> | P |
| B | B | |
| D | D | U |
| U | U | U |
| G | G |
Table 9.
- Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
| 164.47 MeV/c² | E8 = 37.42 MeV/c² | 202.80 MeV/c² |
| N | --> | P |
| G | G | |
| U | U | U |
| D | D | D |
| R | R |
Table 10.
- Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
| 164.47 MeV/c² | E9 = 68.93 MeV/c² | 97.78 MeV/c² |
| N | --> | P |
| G | G | |
| U | U | U |
| D | D | U |
| B | B |
Table 11.
- Analysis of BB interactions.
| R | R | B | B | G | G |
| MeV/c² | MeV/c² | MeV/c² | MeV/c² | MeV/c² | MeV/c² |
| 80.75 | 72.87 | 72.87 | 80.75 | 68.93 | 41.35 |
| 41.35 | 68.93 | ||||
| 114.22 | 149.68 | ||||
| 149.68 - 114.22 = 35.46 | |||||
Table 12.
- Electric current (DD) in green, between (R(DD)R)n and (R(DD)R)p.
| 84.69 MeV/c² | E1 = 19.12 MeV/c² | 103.81 MeV/c² |
| N | --> | P |
| R | R | |
| D | D | D |
| D | D | D |
| R | R |
Table 13.
- Electric current (DU) in green, between [B(DU)G]n and [B(UU)G]p.
| 100.45 MeV/c² | E7 = 41.35 MeV/c² | 97.78 MeV/c² |
| N | --> | P |
| B | B | |
| D | D | U |
| U | U | U |
| G | G |
Table 14.
- Electric current (UD) in green, between [G(UD)R]n and [G(UD)R]p.
| 164.47 MeV/c² | E9 = 68.93 MeV/c² | 97.78 MeV/c² |
| N | --> | P |
| G | G | |
| U | U | U |
| D | D | U |
| B | B |
Table 15.
- We can observe in table 14, according to the state of matter, how the Kв, frequency, wavelength, etc, vary.
Table 15.
- We can observe in table 14, according to the state of matter, how the Kв, frequency, wavelength, etc, vary.
| Earth | Flat space-time | Curved space-time | units |
|---|---|---|---|
| Kʙ (Boltzmann´s constant) | 1.38 10ˉ²³ | 2.97 10ˉ²⁸ | (J/K) |
| f (frequency) | 1.25 10¹⁴ | 2.69 10⁹ | Hz |
| λ (wavelength) | 2.4 10ˉ⁶ | 0.11 | m |
| second of arc | 1.85 10ˉ¹² | 8.49 10ˉ⁸ | m |
| Cv (curvature) | 1 | 4.58 10⁴ | times |
| g (gravity) | 9.81 | m/s² | |
| Sun | Flat space-time | Curved space-time | units |
| Kʙ (Boltzmann´s constant) | 1.38 10ˉ²³ | 3.59 10ˉ³⁷ | (J/K) |
| f (frequency) | 3.12 10¹⁷ | 8.1 10³ | Hz |
| λ (wavelength) | 9.61 10ˉ¹⁰ | 3.7 10⁴ | m |
| second of arc | 7.41 10ˉ¹⁶ | 0.0285 | m |
| Cv (curvature) | 1 | 3.84 10¹³ | times |
| g (gravity) | 2.73 10² | m/s² | |
| White dwarf star | Flat space-time | Curved space-time | units |
| Kʙ (Boltzmann´s constant) | 1.38 10ˉ²³ | 1.97 10ˉ³⁷ | (J/K) |
| f (frequency) | 4.12 10¹⁷ | 5.74 10³ | Hz |
| λ (wavelength) | 0.72 10ˉ⁹ | 5.224 10³ | m |
| second of arc | 5.55 10ˉ¹⁶ | 0.0403 | m |
| Cv (curvature) | 1 | 7.2 10¹³ | times |
| g (gravity) | 4.7 10⁶ | m/s² | |
| Neutron star | Flat space-time | Curved space-time | units |
| Kʙ (Boltzmann´s constant) | 1.38 10ˉ²³ | 2.42 10ˉ⁴² | (J/K) |
| f (frequency) | 2.084 10²² | 3.655 10³ | Hz |
| λ (wavelength) | 1.43 10ˉ¹⁴ | 8.207 10⁴ | m |
| second of arc | 1.1 10ˉ²⁰ | 0.0633 | m |
| Cv (curvature) | 1 | 5.75 10¹⁸ | times |
| g (gravity) | 2.0 10¹² | m/s² | |
| Black hole | Flat space-time | Curved space-time | units |
| Kʙ (Boltzmann´s constant) | 1.38 10ˉ²³ | 1.78 10ˉ⁴³ | (J/K) |
| f (frequency) | 2.084 10²³ | 2.688 10³ | Hz |
| λ (wavelength) | 1.439 10ˉ¹⁵ | 1,11 10⁵ | m |
| second of arc | 1.108 10ˉ²¹ | 0.0856 | m |
| Cv (curvature) | 1 | 7.72 10¹⁹ | times |
| g (gravity) | 5.0 10¹² | m/s² |
Table 16.
– Variation of the mass of gluons with temperature.
 |
Table 17.
– Calculation of the mass of the graviton as a function of temperature.
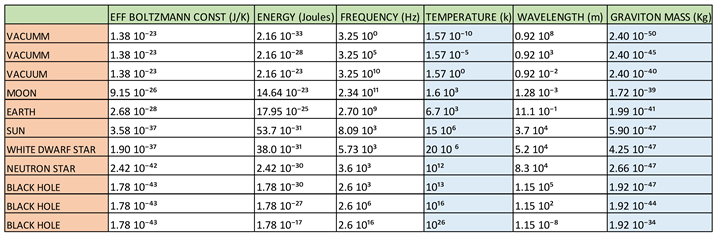 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







