Preprint

Article

Crouch Gait Recognition in the Anatomical Space using Synthetic Gait Data

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Juan-Carlos Gonzalez-Islas

Omar-Arturo Dominguez-Ramirez^*

Omar Lopez-Ortega

Jonatan Pena Ramirez

Juan-Carlos Gonzalez-Islas

Omar-Arturo Dominguez-Ramirez^*

Omar Lopez-Ortega

Jonatan Pena Ramirez

This version is not peer-reviewed

Submitted:

08 October 2024

Posted:

09 October 2024

You are already at the latest version

Alerts

Abstract

Crouch gait is one of the most common gait abnormalities. In the literature, there are few works related to the crouch gait recognition. In this work, we aim at the integration of a framework for multiclass crouch gait recognition using synthetic eight-DoF model gait data in anatomical space. The main contribution of our study is the joint function generator algorithm, which could be used to generate other physiological signals; and the gait data validation stage. In addition, we use a feature selection method and a body region segmentation approach to improve classification performance. We generated a gait dataset containing 25 join functions of each DoF for each gait class (4 crouched and normal). The algorithms that we evaluated for classification were: K-nearest neighbors (kNN), Naive Bayes (NB), discriminant analysis (DA), decision trees (DT), and an artificial neural network (ANN). We calculated the metrics: accuracy (Acc), recall (R), specificity (SP), precision (P) and the F-measure (FM) to asses the classification performance. In general, for this work, the best algorithms were discriminant analysis and artificial neural networks. The main results of the proposed recognition framework provide evidence that can be used in real clinical settings to diagnose and make decisions about treatments related to crouch gait diseases.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Crouch gait (CG) is one of the most common gait abnormalities, often seen in stroke, cerebral palsy (CP), spastic diplegic, and quadriplegic patients [1]. Crouch gait is characterized by excessive flexion of the hips, knees, and ankles during the stance phase, significantly reducing the range of motion of the joints and timing in the gait cycle [2,3]. Therefore, treatments and assistive technologies are required to prevent the worsening of the crouch posture and subsequent functional deterioration [4].

Most articles in the literature base the analysis of crouch gait only on knee flexion [5,6,7,8,9]. In fact, generally not only in the crouh, gait analysis is developed using only the sagittal plane [10]. Since CG is clinically recognized as a complex multi-joint and multiplanar gait disorder [11], it is necessary to consider movements of the hip, ankle, and even the pelvis in the 3 anatomical planes.

On the other hand, computational kinematic modeling is useful for simulating human gait and determining abnormalities based on the gait pattern [12]. In this way, the evaluation of two musculoskeletal models in children with crouch gait is presented in [13]. Using this approach, mild, moderate and severe crouch gait of patients with cerebral palsy has been simulated in [14]. In addition, in [15] the simulation of the effect of muscle activations on the performance of a knee prosthesis of a person with a crouch gait was presented.

In addition, the data from the analysis of the crouch gait are large, multivariable, and multidimensional, making it necessary to use the gait recognition approach to detect gait abnormalities [16]. In this sense, cluster analysis was applied using the gait kinematics data of the lower limbs, pelvis, and trunk to assess children with cerebral palsy [10]. Finally, [7], presented a gait classification method for subjects with cerebral palsy. The features of the gait data from the sagittal plane were used as input into a cluster analysis based on k-means to determine five homogeneous groups. These groups were labeled, in order of increasing gait pathology: i) mild crouch with mild equinus, ii) moderate crouch, iii) moderate crouch with anterior pelvic tilt, iv) moderate crouch with equinus, and v) severe crouch.

Furthermore, an adaptive wavelet extreme learning machine (AW-ELM) has been applied to classify (accuracy up to 91%) crouch gait categories in four patients with hemiplegia and healthy [17]; but the number of participants in this study is not statistically significant. Most studies in patients with crouch gait focus on estimating muscular behavior and force evaluation; however, few have addressed kinematic modeling and recognition [13].

For any gait recognition system, the availability of adequate data is an essential requirement, especially for supervised methods. The size of the gait data set must be large enough to reflect the variety of factors. So far, existing work on the generation of gait and physiological data sets is still far from this objective [18,19]. A possible solution to these problems is to use realistic synthetic data generated from computational and mathematical models [20,21]. Using synthetic data for training learning models is a recent strategy to address missing data [22]. In terms of gait, data sets of silhouettes for a game engine [23] or joint functions for controlling prosthetic legs [24] have recently been generated.

To address the limitations and opportunities mentioned above, in this work we present a general framework for crouch gait recognition. Multiclass recognition was performed using synthetic gait data in anatomical space using the eight-DoF multijoint and multiplanar model presented in a previous work [25]. The research question that we have addressed is: is it possible to recognize multiclass crouch gait in the anatomical space using gait synthetic data? The main contribution of this work is the framework approach for crouch gait recognition and the synthetic joint function generator.

2. Materials and Methods

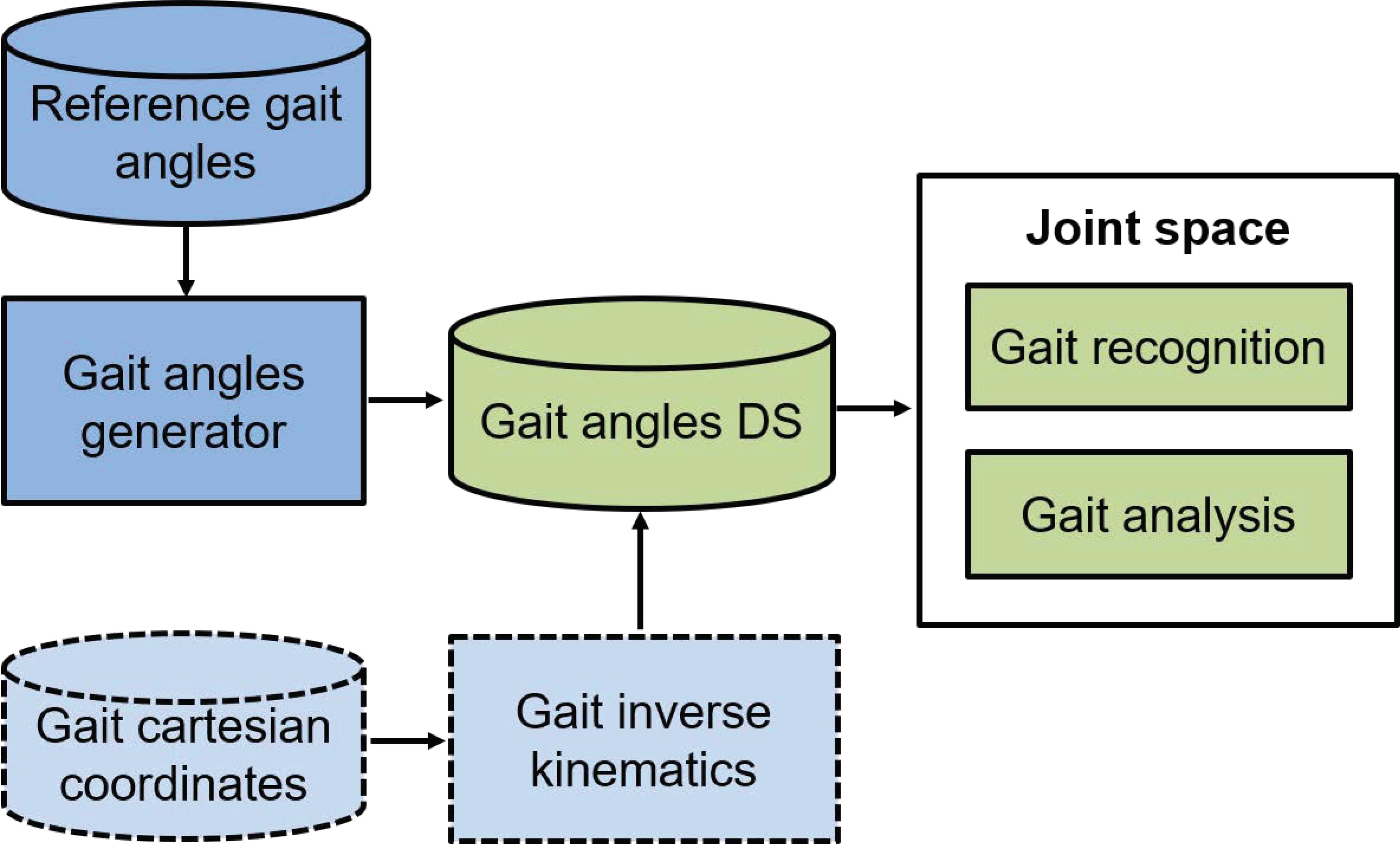
The general framework used in this work to recognize crouch gait is shown in Figure 1. We propose two main approaches. The first one considers the availability of the gait joint signals, in which in this case the signals are generated synthetically. The second approach contemplates the calculation of the joint coordinates from the Cartesian coordinates, using the inverse kinematics method proposed in [25]. In this work, we only explore the first proposal.

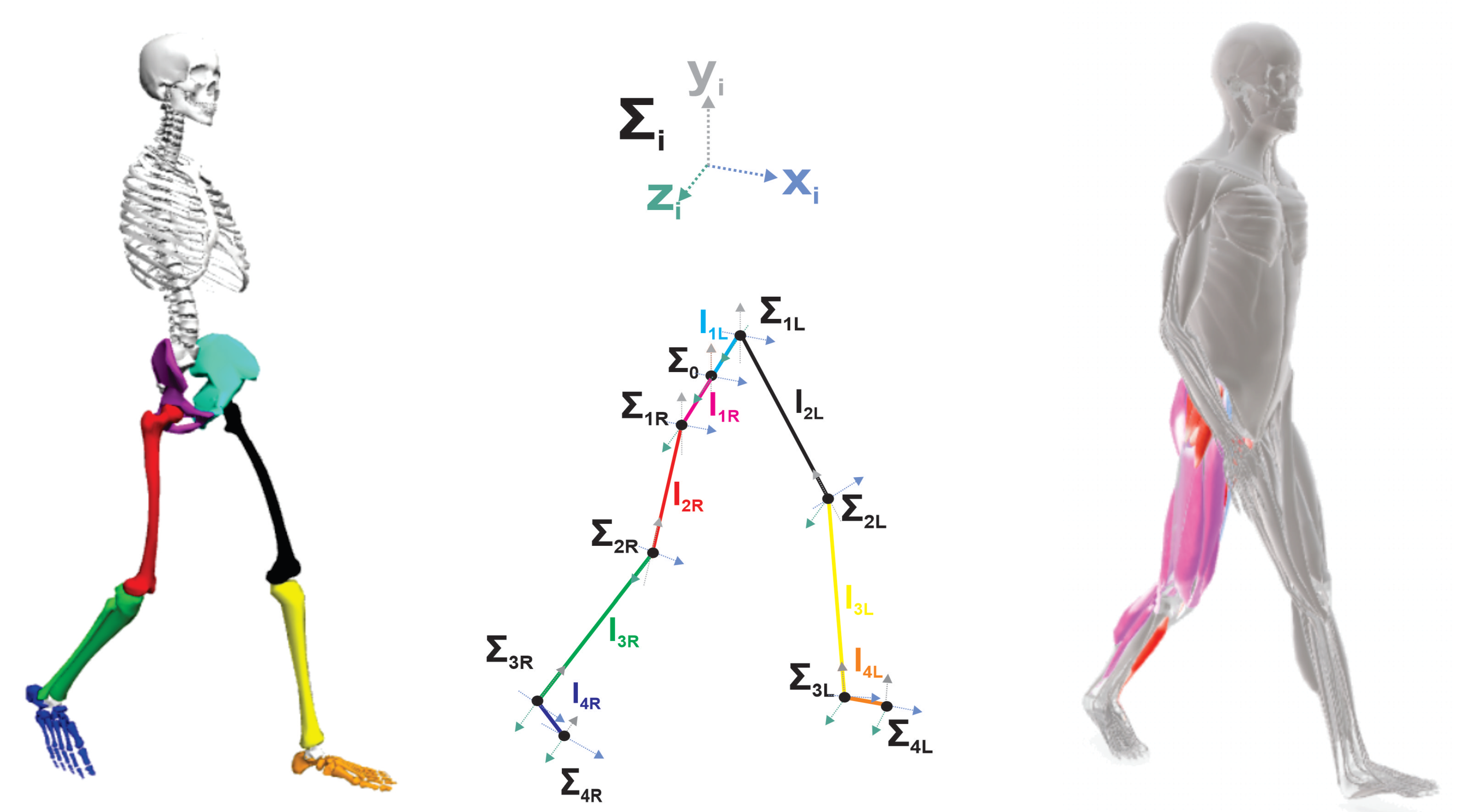
The model of the lower limbs during the gait cycle that we use is a reduction of the conventional gait model [26]. Figure 2 shows the proposed eight-DoF multiplanar and multijoint system. The model considers the lower limbs as eight rigid body segments as follows: right pelvis (

l_{1 R}

), left pelvis (

l_{1 L}

), right femur (

l_{2 R}

), left femur (

l_{2 L}

), right tibia (

l_{3 R}

), left tibia (

l_{3 L}

), right foot (

l_{4 R}

) and left foot (

l_{4 L}

). Meanwhile, the corresponding joint functions, rotation axis and reference frame for the eight motions are: pelvic rotation (

q_{1}

Σ_{0}

y_{0}

), pelvic list (

q_{2}

Σ_{0}

x_{0}

), right hip flexoextension (

q_{3 R}

Σ_{1 R}

z_{1 R}

), left hip flexoextension (

q_{3 L}

Σ_{1 L}

z_{1 L}

), right knee flexoextension (

q_{4 R}

Σ_{2 R}

z_{2 R}

), left knee flexoextension (

q_{4 L}

Σ_{2 L}

z_{2 L}

), right ankle dorsi/plantar flexion (

q_{5 R}

Σ_{3 R}

z_{3 R}

) and left ankle dorsi/plantar flexion (

q_{5 L}

Σ_{3 L}

z_{3 L}

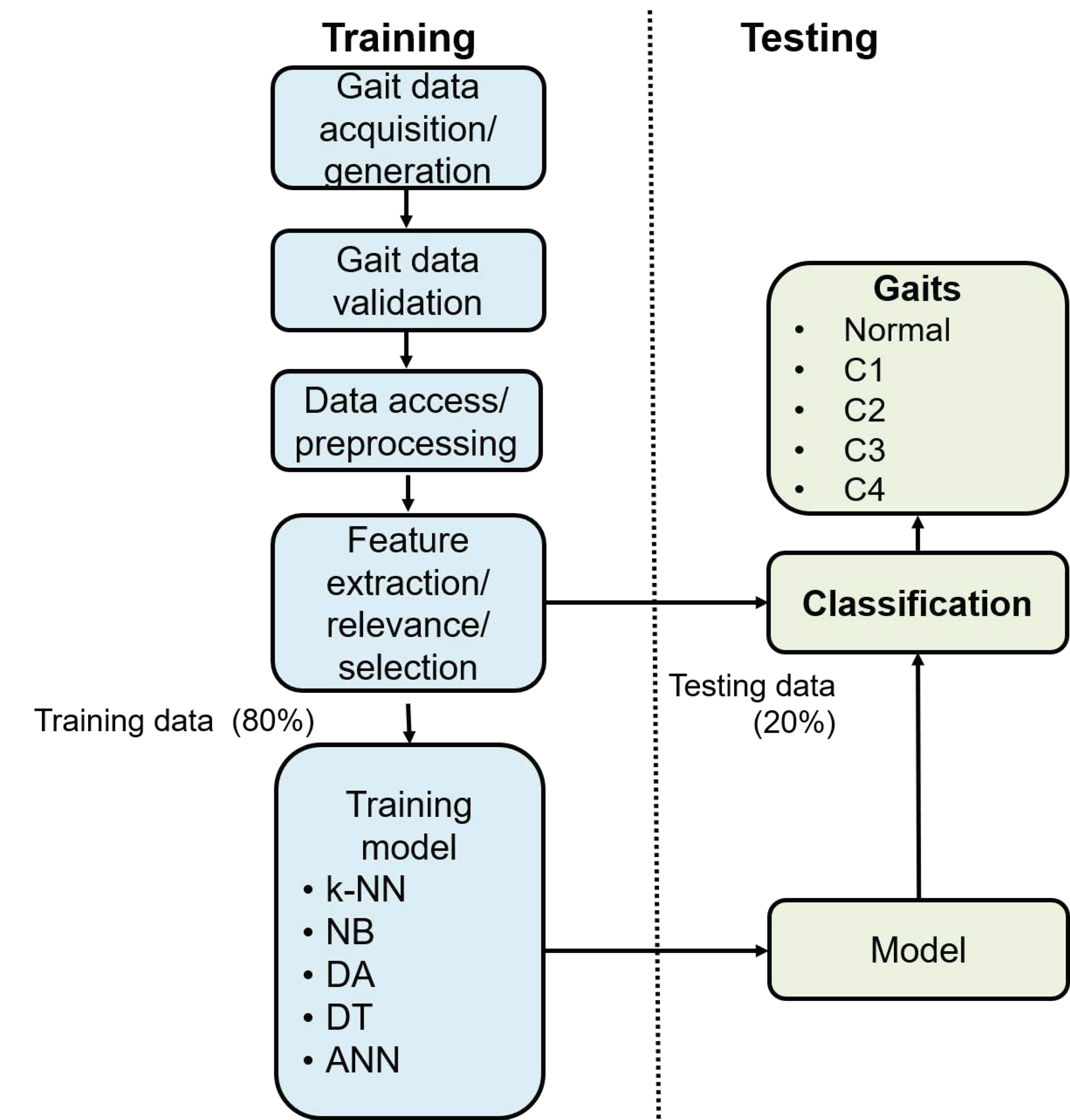
Gait recognition is an approach to assess and compare different gait performances of different users based on the gait pattern. For the grouch gait recognition approach, we consider four levels of crouch severity: crouch 1 (C1), crouch 2 (C2), crouch 3 (C3), crouch 4 (C4), and normal gait (N). The initial eight joint functions taken as signal references for the five gaits (Figure 1) were obtained from the dataset of the well-known model

2392 - O p e n S i m

[28]. However, for the crouch gait recognition framework proposed in this work, one signal for each joint variable is not sufficient, so we implemented a synthetic joint function generator. Gait angles are stored in a gait angles dataset to be subsequently used as input in the acquisition stage. The framework of a gait recognition system consists of different modules, as shown in Figure 3 [29].

2.1. Gait Data Acquisition

The first step of any gait recognition system is the data acquisition module, which is used to collect human gait data. Generally, there are four ways to do it, marker-based, non marker-based, floor sensors, and wearable sensors [30]. 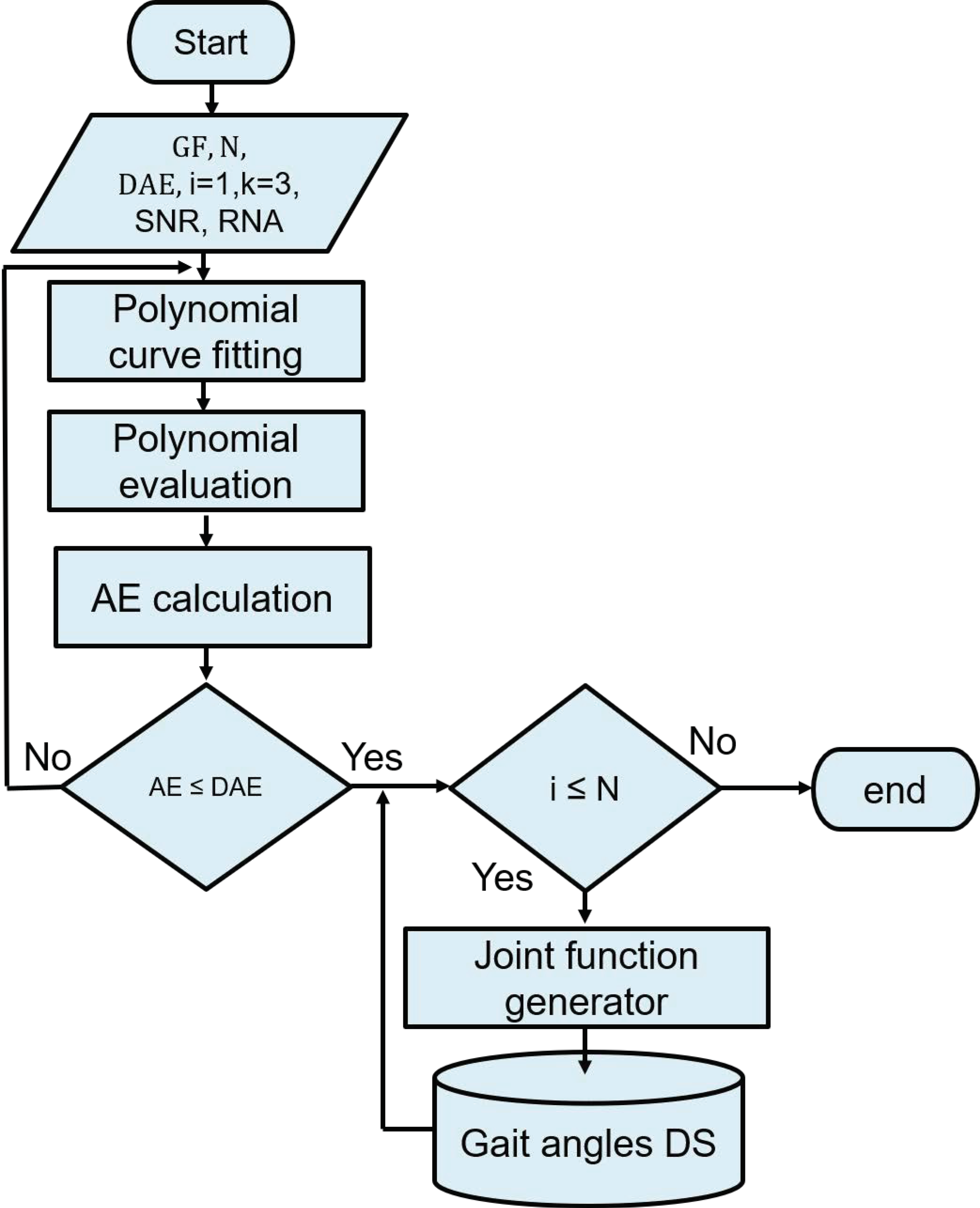To address the lack of a crouch gait dataset of real patients available to evaluate and validate our approach; In this work, in the first stage, we propose the generation of synthetic gait data based on reference joint functions [28]. The flowchart of the gait joint functions generator is shown in Figure 4, where, GJF: gait joint function, N: number of desired joint functions, DAE: desired approximation error, AE: approximation error, K: polynomial degree, RNA: random noise amplitude and SNR: signal noise relationship.

Given any joint function

q_{i}

, the initial point of the algorithm is to fit a polynomial curve to obtain the coefficients of a polynomial

p (x)

of degree k that is the best fit to the joint function. Subsequently, the polynomial

p (x)

is evaluated at each point in x, where x in this case is the array of samples from the gait cycle. Next, we calculate the mean square error (MSE) (AE), between

q_{i}

and the evaluation of

p (x)

, and if

A E \leq D A E

, the process is repeated until the stop condition is met. The degree of polynomial k is inversely proportional to the error associated with the desired error

D A E = 0.2

. A small error generates a greater degree of polynomial, which increases the mathematical complexity and thus the computational cost during the evaluation.

The function applied to fit the polynomial curve returns a polynomial

p (x)

(synthetic joint function) of degree k that is a best fit (in the least-squares sense) for the data in

q_{i}

. The coefficients of

p (x)

(1) are of descending powers, and the number of coefficients is

k + 1

p (x) = p_{1} x^{k} + p_{2} x^{k - 1} + . . . + p_{k} x + p_{k + 1},

(1)

The fitting function uses x to form Vandermonde matrix V with

k + 1

columns and

m = l e n g t h (x)

rows, resulting in the linear system

(\begin{matrix} x_{1}^{k} & x_{1}^{k - 1} & \dots & 1 \\ x_{2}^{k} & x_{2}^{k - 1} & \dots & 1 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ x_{m}^{k} & x_{m}^{k - 1} & \dots & 1 \end{matrix}) (\begin{matrix} p_{1} \\ p_{2} \\ ⋮ \\ p_{k + 1} \end{matrix}) = (\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{m} \end{matrix}) .

(2)

The fitted polynomial is considered the polynomial generator of the join function, which is used as a base function to synthesize the joint functions. In Table 1 we present the degree of the fitted polynomial for each joint function of the five gaits.

The degree of the fitted polynomial is related to the complexity of the joint function. In this case, the more complex is the dorsiplantar function of C2, while the simplest is the list of C4. Then, we generate joint functions

N = 50

for each gait (N, C1, C2, C3, and C4). Figure 5 shows the eight joint functions of the five gait classes during a gait cycle [28].

In order to provide the coefficients of the generating polynomials for the normal gait, Table 2 summarizes the values of the fitted polynomial coefficients for the 8 DoF of the joint functions for a normal gait.

Subsequently, to generate the joint function dataset of the five gaits with the eight movements, the coefficients of the polynomial generator are modified using normally distributed random numbers and evaluated in x. In addition, to simulate real world random disturbances that can occur in practical systems, we add that white Gaussian noise is used in signal processing , where the signal noise relationship was defined previously

S N R = 20

Finally, each joint synthetic function is stored. To validate our generator approach, we developed a test z only on the eighth normal gait functions, where the null hypothesis

H_{0}

: A synthetic normal function has the same statistical distribution as the reference normal function; and the alternative hypothesis

H_{1}

: A synthetic normal function has a different statistical distribution than the reference normal function. The value of statistical significance established for all cases is

α = 0.05

. In all cases, the null hypothesis was accepted. Table 3 summarizes the minimum and maximum values of the eight references to joint functions during a gait cycle [28], which is useful for local analysis if each joint is evaluated independently or by each lower limb. Also, it makes possible to develop a global multiplanar analysis; however, to determine a global pattern to classify each crouch gait abnormalities, it necessary apply a gait recognition framework as is in this study.

2.2. Gait Data Validation

Most of the machine learning work focuses on improving the accuracy and efficiency of training and inference algorithms, but little addresses the problem of monitoring the quality and validity of raw data. Errors in input data can determine poor performance in accelerating and assessing the precision of the framework [31]. Therefore, in this work, we perform the statistical test z to confirm that the data sets generated for each type of gait are statistically different [32].

Thus, using the brute force method in the data sets of the five types of gait, we established

H_{0}

: the synthetic joint angles of the test gait are outliers from the synthetic joint angles of the reference gait; and the alternative hypothesis

H_{1}

: the synthetic joint angles of the test gait have a different statistical distribution than the synthetic joint angles of the reference gait. The value of statistical significance established for all cases is

α = 0.05

. Table 4 summarizes the z values of the ten combinations between gait types.

For this approach, one of the gait dataset of each type was taken as a reference, and the other gait dataset of the other typo was used as a test. For example, in the first case, normal gait is the reference and crouch 1 is the test (N-C1), and the z value is

- 3.57

. The p values depending on the z values, to

q_{1}

q_{4 R}

q_{4 L}

and

q_{5 L}

lead to rejection

H_{0}

, that is, the data sets of the five datasets of joint functions have a statistically different distribution from each other. However, with respect to

q_{2}

q_{3 R}

q_{3 L}

and

q_{5 R}

in one case for each, C1-C3, C2-C3 and C1-C4, respectively, we accept

H_{0}

. This implies that for those cases the data sets are not statistically different. In Figure 6 we can visualize and compare using the distributions boxplots of the data from the five angles for each joint function.

2.3. Data Access and Preprocessing

Gait data access and preprocessing are the next steps after data acquisition [33]. In this work, the raw data contain a dataset with 250 joint angle functions, 50 per each gait class. Subsequently, the preprocessing stage is useful for integrating, cleaning, transforming, and reducing data. Because we do not have incomplete, noisy, multivariable data or with many elements for each function, we do not perform any of these actions at this stage.

2.4. Feature Extraction and Selection

In order to identify the individuals corresponding to the five classes of gait in a general and non-redundant way, it is required in the gait recognition system to extract useful features from the raw data [30]. To this end, we calculate the arithmetic mean (AM), standard deviation (STD) [34], root mean square value (RMS). In addition, as a novel feature, we propose the shape factor (SF), which is based on the waveform of the join angle function and is calculated from (3).

S F = \frac{R M S}{\frac{1}{M} \sum_{i = 1}^{M} | q_{i} |},

(3)

where the RMS value is calculated as

R M S = \sqrt{\frac{1}{M} \sum_{i = 1}^{M} {|q_{i}|}^{2}} .

(4)

where M is the length of the joint angle function. From each gait example in the feature extraction stage, we obtain a, array with 32 features, containing the four metrics for the eight joint angles. But, this initial approach makes the system tend to overfitting. Table 5 summarizes the average values of each feature for each joint angle function for each gait type. Therefore, we proposed a classification based on 3 different areas of the body such as pelvic (

q_{1}

and

q_{2}

), right lower limb (

q_{3 R}

q_{4 R}

and

q_{5 R}

) and left lower limb (

q_{3 L}

q_{4 L}

and

q_{5 L}

). It makes possible a local classification and analysis. Hence, now, each example only contains the four features of the corresponding angles.

Then, for the feature selection stage, we determine the relevance of each of the features and, based on a

t h r e s h o l d = 0.4

, we only select the most important features using neighborhood component analysis for classification. Finally, we use the selected features for the training stage.

2.5. Training Classification Model

The gait dataset containing the five gait for each class was randomly partitioned into two sets, where 80% for training and 20% as test data. For the supervised classification training stage, we use the algorithms: K-nearest neighbors, Naive Bayes, discriminant analysis, decision trees, and an artificial neural network. In order to evaluate the algorithm performance, we test each trained model, and the metrics that we used were: accuracy (Acc), recall (R), specificity (SP), precision (P) and the F-measure (FM) [35], using the following equations, respectively.

Accuracy (Acc)

$A c c = \frac{T P + T N}{T P + T N + F P + F N} \times 100$

(5)
Recall or sensitivity (R)

$R = \frac{T P}{T P + F N} \times 100$

(6)
Specificity (SP)

$S P = \frac{T N}{T N + F P} \times 100$

(7)
Precision (P)

$P = \frac{T P}{T P + F} \times 100$

(8)
F-measure (F)

$F = \frac{2 \times P \times R}{P + R_{i}} \times 100,$

(9)

where TP: true positives, TN: true negatives, FP: false positives y FN false negatives.

3. Results and Discussion

In this work, we propose multiclass recognition of crouch gait based on three body sections such as the pelvic (

q_{1}

and

q_{2}

), the right lower limb (

q_{3 R}

q_{4 R}

and

q_{5 R}

) and the left lower limb (

q_{3 L}

q_{4 L}

and

q_{5 L}

). The experimental results for each classification algorithm were calculated using a k-fold cross-validation with

k = 10

. Table 6 and Table 7 present the results of accuracy (Acc), recall (R), specificity (SP), precision (P), and F-measure (FM) using the first body section with K-nearest neighbors (kNN), Naive Bayes (NB), discriminant analysis (DA), decision trees (DT) and an initial neural network (ANN), respectively.

The metrics were calculated using a multiclass confusion matrix. The algorithm with the best accuracy to correctly predict the outcome of the pelvic section for N, C1, C2, and C3 is DA, except that for C4 it is ANN. Sensitivity or recall (R) is the probability of correctly identifying the gait in people characterized by this type of gait. The best performance on the recall for the five gaits is DA. Precision is the rate of relevant instances among retrieved instances, which implies the probability of correctly classifying specific crouch individuals as general subjects with this condition. Specificity, on the other hand, is the true negative rate. These are the negative cases that the algorithm has classified as corresponding to other gaits. Precision refers to the distance from the measurement result to the true value. The algorithm with the best precision is DA for the five gaits. The F measure is a measure of predictive performance and the DA is the best algorithm in this way, while, KNN has the lowest performance. Table 8 and Table 9 show the performance using a similar approach, but using the body section of the right lower limb.

As we can see in Table 8 and Table 9 related with the righ lower limb body section, the performance for the five gait types with the five metrics increases. This is because now it is considered an articular function for more and before the feature selection stage derived from the feature relevance there are 4 more predictors, which improves the classification performance. For normal, crouch1, crouch 3 and crouch 4 gaits, the best performance is achieved by NB, while for crouch 2 is by KNN. In the same sense, to evaluate the classification performance by regions, Table 10 and Table 11 summarize the results for the 5 gaits and the five metrics using the left lower limb body region.

As we can visualize the results in Table 10 and Table 11, in general the performance of the 5 algorithms for the 5 metrics increases using the body region of the left lower limb, and discriminant analysis is the best algorithm. Finally, we analyze the global performance of the algorithms for each metric, Table 12 summarizes the average performance of the algorithms to classify the 5 gaits by body region.

Considering average performance, for accuracy the algorithm best evaluated in the pelvic and left regions is DA with 96.96 and 99.52%, respectively, while in the right region it is NB 99. 52%. The algorithm with the worst performance is KNN for the 3 cases. Regarding recall and specificity, the best performance was achieved in a similar way to the accuracy for the pelvic and left region, only for the left region, the algorithm with the best performance is NB with 98.59% and 99.70%, respectively. A similar performance occurs with the precision and f-measure, DA being the algorithm with the best performance for the first and third regions, and NB with 98. 79% and 98. 61%, respectively, for the region of the right lower limb.

4. Conclusions

This paper presents a framework for multiclass crouch gait recognition in anatomical space using synthetic data. Anatomical space metrics are useful for establishing normal gait ranges as a pattern to assess gait objectively. The main contribution of this work is the novel algorithm used to generate synthetic joint functions, which could be used to synthesize other physiological signals from body systems. On the other hand, the features that we used in the feature extraction stage are the arithmetic mean, standard deviation, root mean square, and, in a novel way, the shape factor are sufficient to classify the crouch gait with high performance. In addition, to the 8 DoF model used as the basis for this work, which reduces the level of instrumentation required; the feature relevance and selection method used in this work allows one to reduce computational complexity, optimizing the classification results. The body region approach used for classification allows us to avoid overfitting and also develops a global and local analysis. In general, regarding the accuracy using the pelvic and lower limb regions the best algorithm was DA, while in right lower limb was ANN, which implies none algorithm has the best performance for each problem and the metric used as a reference depends of the objective of the study.

Finally, this proposed classification framework can be used to define homogeneous groups of subjects with crouch gait, which can help diagnose and make decisions about treatments related to crouch gait diseases. In addition, the signal generation approach can be used as a reference in the control of robotic systems for rehabilitation purposes. Although the framework has obtained interesting results, some areas of opportunity may remain for future research. In this sense, this framework could be used for recognizing another kind of abnormal gaits, as well as the use of other spatio-temporal and in the frequency domain metrics. Ultimately, we intend to develop a crouch gait recognition system in the work space..

Author Contributions

Conceptualization, J.-C.G.-I. and O.-A.D.-R.; methodology, J.-C.G.-I., O.-A.D.-R. and O.L.-O.; software, J.-C.G.-I.; validation, J.-C.G.-I. and O.L.-O.; formal analysis, J.-C.G.-I., O.-A.D.-R. and J.P.-R.; investigation, J.-C.G.-I. and O.-A.D.-R; resources, J.-C.G.-I. and O.-A.D.-R.; data curation, O.L.-O. and J.P.-R.; writing—original draft preparation, J.-C.G.-I. and O.-A.D.-R.; writing—review and editing, O.L.-O. and J.P.-R.; visualization, J.-C.G.-I.; supervision, O.L.-O. and J.P.-R.; project administration, O.-A.D.-R.; funding acquisition, O.-A.D.-R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available on request.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

DoF	Degrees of fredom
kNN	K-nearest neighbors
NB	Naive Bayes
DA	discriminant analysis
DT	decision trees
ANN	artificial neural networks
Acc	accuracy
R	recall
SP	specificity
P	precision
FM	F-measure
CG	crouch gait
CP	Cerebral palsy
AW-ELM	adaptive wavelet extreme learning machine
GJF	gait joint function
DAE	desired approximation error
AE	approximation error
RNA	random noise amplitude
SNR	signal noise relationship

References

Bumbard, K.B.; Herrington, H.; Goh, C.H.; Ibrahim, A. Incorporation of torsion springs in a knee exoskeleton for stance phase correction of crouch gait. Applied Sciences 2022, 12, 7034. [Google Scholar] [CrossRef]
Brunner, R.; Frigo, C.A. Control of Tibial Advancement by the Plantar Flexors during the Stance Phase of Gait Depends on Knee Flexion with Respect to the Ground Reaction Force. Bioengineering 2023, 11, 41. [Google Scholar] [CrossRef] [PubMed]
Miller, F. Crouch Gait in Cerebral Palsy. Cerebral Palsy 2020, 1489–1504. [Google Scholar]
Shideler, B.L.; Bulea, T.C.; Chen, J.; Stanley, C.J.; Gravunder, A.J.; Damiano, D.L. Toward a hybrid exoskeleton for crouch gait in children with cerebral palsy: Neuromuscular electrical stimulation for improved knee extension. Journal of neuroengineering and rehabilitation 2020, 17, 1–14. [Google Scholar] [CrossRef] [PubMed]
O’Sullivan, R.; Marron, A.; Brady, K. Crouch gait or flexed-knee gait in cerebral palsy: Is there a difference? A systematic review. Gait & Posture 2020, 82, 153–160. [Google Scholar]
Morais Filho, M.C.d.; Kawamura, C.M.; Lopes, J.A.F.; Neves, D.L.; Cardoso, M.d.O.; Caiafa, J.B. Most frequent gait patterns in diplegic spastic cerebral palsy. Acta Ortopédica Brasileira 2014, 22, 197–201. [Google Scholar] [CrossRef]
Rozumalski, A.; Schwartz, M.H. Crouch gait patterns defined using k-means cluster analysis are related to underlying clinical pathology. Gait & posture 2009, 30, 155–160. [Google Scholar]
Van der Krogt, M.M.; Doorenbosch, C.A.; Harlaar, J. Muscle length and lengthening velocity in voluntary crouch gait. Gait & posture 2007, 26, 532–538. [Google Scholar]
Wren, T.A.; Rethlefsen, S.; Kay, R.M. Prevalence of specific gait abnormalities in children with cerebral palsy: influence of cerebral palsy subtype, age, and previous surgery. Journal of Pediatric Orthopaedics 2005, 25, 79–83. [Google Scholar]
Abbasi, L.; Rojhani-Shirazi, Z.; Razeghi, M.; Raeisi-Shahraki, H. Kinematic cluster analysis of the crouch gait pattern in children with spastic diplegic cerebral palsy using sparse K-means method. Clinical Biomechanics 2021, 81, 105248. [Google Scholar] [CrossRef]
Galey, S.A.; Lerner, Z.F.; Bulea, T.C.; Zimbler, S.; Damiano, D.L. Effectiveness of surgical and non-surgical management of crouch gait in cerebral palsy: A systematic review. Gait & posture 2017, 54, 93–105. [Google Scholar]
González-Islas, J.; Domínguez-Ramírez, O.A.; López-Ortega, O. Biped gait analysis based on forward kinematics modeling using quaternions algebra. Revista mexicana de ingeniería biomédica 2020, 41. [Google Scholar]
Ravera, E.P.; Beret, J.A.; Riveras, M.; Crespo, M.J.; Shaheen, A.F.; Catalfamo Formento, P.A. Assessment of two musculoskeletal models in children with crouch gait. In Proceedings of the Biomedical Engineering and Computational Intelligence: Proceedings of The World Thematic Conference—Biomedical Engineering and Computational Intelligence, BIOCOM 2018. Springer, 2020, pp. 13–23.
Brandon, S.C.; Thelen, D.G.; Smith, C.R.; Novacheck, T.F.; Schwartz, M.H.; Lenhart, R.L. The coupled effects of crouch gait and patella alta on tibiofemoral and patellofemoral cartilage loading in children. Gait & posture 2018, 60, 181–187. [Google Scholar]
Guess, T.M.; Razu, S. Musculoskeletal modeling of crouch gait. In Proceedings of the 2018 3rd Biennial South African Biomedical Engineering Conference (SAIBMEC). IEEE; 2018; pp. 1–4. [Google Scholar]
Rani, V.; Kumar, M. Human gait recognition: A systematic review. Multimedia Tools and Applications.
Adil, S.; Al Jumaily, A.; Anam, K. AW-ELM-based Crouch Gait recognition after ischemic stroke. In Proceedings of the 2016 5th International Conference on Electronic Devices, Systems and Applications (ICEDSA). IEEE; 2016; pp. 1–4. [Google Scholar]
Ciucu, R.I.; Seriţan, G.C.; Dragomir, D.A.; Cepişcă, C.; Adochiei, F.C. ECG generation methods for testing and maintenance of cardiac monitors. In Proceedings of the 2015 E-Health and Bioengineering Conference (EHB). IEEE; 2015; pp. 1–4. [Google Scholar]
Cheng, Y.; Zhang, G.; Huang, S.; Wang, Z.; Cheng, X.; Lin, J. Synthesizing 3d gait data with personalized walking style and appearance. Applied Sciences 2023, 13, 2084. [Google Scholar] [CrossRef]
Gaidon, A.; Wang, Q.; Cabon, Y.; Vig, E. Virtual worlds as proxy for multi-object tracking analysis. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp.; pp. 4340–4349.
Martinez-Gonzalez, P.; Oprea, S.; Garcia-Garcia, A.; Jover-Alvarez, A.; Orts-Escolano, S.; Garcia-Rodriguez, J. Unrealrox: an extremely photorealistic virtual reality environment for robotics simulations and synthetic data generation. Virtual Reality 2020, 24, 271–288. [Google Scholar] [CrossRef]
Li, M.; Martin, A.E. Using System Identification and Central Pattern Generators to Create Synthetic Gait Data. IFAC-PapersOnLine 2022, 55, 432–438. [Google Scholar] [CrossRef]
Kim, M.; Hargrove, L.J. Generating synthetic gait patterns based on benchmark datasets for controlling prosthetic legs. Journal of neuroengineering and rehabilitation 2023, 20, 115. [Google Scholar] [CrossRef]
Dou, H.; Zhang, W.; Zhang, P.; Zhao, Y.; Li, S.; Qin, Z.; Wu, F.; Dong, L.; Li, X. Versatilegait: a large-scale synthetic gait dataset with fine-grainedattributes and complicated scenarios. arXiv, 2021; arXiv:2101.01394. [Google Scholar]
Gonzalez-Islas, J.C.; Dominguez-Ramirez, O.A.; Lopez-Ortega, O.; Peña-Ramirez, J.; Ordaz-Oliver, J.P.; Marroquin-Gutierrez, F. Crouch Gait Analysis and Visualization Based on Gait Forward and Inverse Kinematics. Applied Sciences 2022, 12, 10197. [Google Scholar] [CrossRef]
Baker, R.; Leboeuf, F.; Reay, J.; Sangeux, M.; et al. The conventional gait model-success and limitations. Handbook of human motion.
Biodigital. Walk cycle, 2024. https://human.biodigital.com/dashboard.html, Last accessed on 2024-09-26.
Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS computational biology 2018, 14, e1006223. [Google Scholar] [CrossRef]
Singh, J.P.; Jain, S.; Arora, S.; Singh, U.P. Vision-based gait recognition: A survey. Ieee Access 2018, 6, 70497–70527. [Google Scholar] [CrossRef]
Wan, C.; Wang, L.; Phoha, V.V. A survey on gait recognition. ACM Computing Surveys (CSUR) 2018, 51, 1–35. [Google Scholar] [CrossRef]
Breck, E.; Polyzotis, N.; Roy, S.; Whang, S.; Zinkevich, M. Data Validation for Machine Learning. In Proceedings of the MLSys; 2019. [Google Scholar]
Stine, R.; Foster, D. Statistics for Business: Decision Making and; Addison-Wesley, 2011.
Paluszek, M.; Thomas, S. MATLAB machine learning; Apress, 2016.
Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. Human activity recognition on smartphones using a multiclass hardware-friendly support vector machine. In Proceedings of the Ambient Assisted Living and Home Care: 4th International Workshop, IWAAL 2012, Proceedings 4. Vitoria-Gasteiz, Spain, 3-5 December 2012; Springer, 2012; pp. 216–223. [Google Scholar]
Jun, K.; Lee, Y.; Lee, S.; Lee, D.W.; Kim, M.S. Pathological Gait Classification Using Kinect v2 and Gated Recurrent Neural Networks. IEEE Access 2020, 8, 139881–139891. [Google Scholar] [CrossRef]

Figure 1. Framework for crouch gait analysis and recognition of the crouch gait in anatomical space.

Figure 2. 8 DoF gait kinematics model. Right (Eskeletal model), center (open kinematic chain) and left (3D anatomical gait cycle representation) [12,27].

Figure 3. Workflow for the crouch gait recognition in the anatomical space.

Figure 4. Flowchart of the gait joint functions generation algorithm.

Figure 5. Gait joint angles for the eight movements for the five gaits. Green (N), blue (C1), red (C2), black (C3) and magenta (C4) [28].

Figure 6. Statistical distribution of the dataset of five gait classes for each joint function.

Table 1. Degree of the fitted polynomial for each joint function

q_{i}

of the five gaits.

Table 1. Degree of the fitted polynomial for each joint function

q_{i}

of the five gaits.

Gaits	$q_{1}$	$q_{2}$	$q_{3 R}$	$q_{4 R}$	$q_{4 R}$	$q_{3 L}$	$q_{4 L}$	$q_{5 L}$
N	8	8	11	13	19	9	16	18
$C 1$	13	7	10	15	16	10	17	16
$C 2$	11	8	12	8	12	14	12	25
$C 3$	10	9	11	9	9	17	20	10
$C 4$	13	6	11	14	11	12	15	17

Table 2. Coefficients of the 8 fitted polynomials related to the joint angles (JA) normal gait.

Degree	$q_{1}$	$q_{2}$	$q_{3 R}$	$q_{4 R}$	$q_{4 R}$	$q_{3 L}$	$q_{4 L}$	$q_{5 L}$
0	2.55	-0.61	24.54	-16.70	-4.07	-8.23	-1.68	9.83
1	7.40	23.49	21.75	7.22	-4.84	17.98	-483.51	236.07
2	-492.37	-1472.05	-1369.65	-722.66	-7670.96	-14597.64	48218.72	-34696.65
3	5544.54	14185.41	22725.49	24034.68	161661.15	458524.13	-2253486.62	1504465.30
4	-26216.01	-59323.86	-241392.15	-154960.95	-1767801.57	-8046722.75	56425115.24	-35800895.63
5	61950.47	130871.89	1399106.93	469784.71	12194158.15	83268450.62	-862057667.9	508490937
6	-77761.28	-158286.79	-4761956.61	-789262.96	-55670796.21	-551813305.7	8772028344	-4687249980
7	49728.93	99084.50	9980083.31	754677.56	172033407.9	2489659884	-6.2E10	29838603312
8	-12763.75	-25082.45	-13020755.88	-385074.79	-363732411.8	-7945107407	3.28E+11	-1.36E+11
9	0	0	10298543.96	81518.01	525222063.2	18341337557	-1.28E+12	4.63E+11
10	0	0	-4520035.13	0	-508420218.7	-30965724446	3.83E+12	-1.18E+12
11	0	0	845028.27	0	315197063.8	38256307914	-8.74E+12	2.27E+12
12	0	0	0	0	-113039758.2	-34210329856	1.53E+13	-3.33E+12
13	0	0	0	0	17830308.13	21563269103	-2.07E+13	3.67E+12
14	0	0	0	0	0	-9089398136	2.12E+13	-3.00E+12
15	0	0	0	0	0	2300657105	-1.62E+13	1.75E+12
16	0	0	0	0	0	-264524081.1	8.95E+12	-6.98E+11
17	0	0	0	0	0	0	-3.37E+12	1.68E+11
18	0	0	0	0	0	0	7.73E+11	-1.9E10
19	0	0	0	0	0	0	-8.2E10	0

Table 3. Maximum and minimum range of movement (ROM) in degrees of the eight joint angles for the five gaits.

	Normal		Crouch 1		Crouch 2		Crouch 3		Crouch 4
JA	Min	Max	Min	Max	Min	Max	Min	Max	Min	Max
$q_{1}$	-3.57	2.56	0.02	11.56	-29.01	-6.14	-24.5	-2.31	28.86	45.37
$q_{2}$	-4.10	4.42	-8.12	-2.27	-5.54	6.05	-9.52	-0.84	-24.92	-14.8
$q_{3 R}$	-16.82	25.26	18.29	54.36	14.23	42.54	9.89	45.91	17.25	64.45
$q_{4 R}$	-58.25	-2.27	-68.75	-57.64	-73.46	-54.91	-47.27	-26.25	-72.13	-37.31
$q_{5 R}$	-14.07	10.75	13.07	34.16	-24.15	-8.2	-39.07	-29.96	13.55	29.48
$q_{3 L}$	-16.82	25.26	29.90	58.78	-6.99	28.55	-6.44	31.28	33.51	59.40
$q_{4 L}$	-58.25	-2.27	-81.97	-55.32	-55.86	-39.10	-39.76	-12.06	-67.43	-31.68
$q_{5 L}$	-14.07	10.75	6.89	29.31	-9.56	17.96	-3.66	15.10	-1.06	9.30

Table 4. Statistical z-values for the eight joint angles of the five gaits of the z test.

Gaits	$q_{1}$	$q_{2}$	$q_{3 R}$	$q_{4 R}$	$q_{4 R}$	$q_{3 L}$	$q_{4 L}$	$q_{5 L}$
$N, C 1$	-12.12	12.47	-67.14	85.51	-40.72	-68.55	80.28	-36.012
$N, C 2$	30.31	-0.63	-47.45	82.77	31.49	-6.50	50.78	-3.59
$N, C 3$	24.35	9.41	-46.24	35.27	61.57	-13.13	2.44	-6.20
$N, C 4$	-64.40	34.69	-81.16	64.44	-38.64	-68.15	47.96	-6.58
$C 1, C 2$	43.38	-15.85	20.50	-2.55	72.63	72.73	-33.20	32.82
$C 1, C 3$	37.29	-3.70	21.76	-46.77	102.88	64.96	-87.62	30.17
$C 1, C 4$	-53.44	26.87	-14.59	-19.61	2.09	0.46	-36.38	29.8
$C 2, C 3$	-5.22	11.99	0.88	-51.92	29.47	-6.78	-52.18	-2.60
$C 2, C 4$	-82.97	42.18	-24.77	-20.03	-68.71	-63.06	-3.05	-2.98
$C 3, C 4$	-80.65	32.53	-30.69	31.83	-100.02	-46.95	43.71	-0.38

Table 5. Gait features average, arithmetic mean (AM), standard deviation(STD), root mean square (RMS) and shape factor (SF).

	Normal				Crouch 1				Crouch 2				Crouch 3				Crouch 4
JA	AM	STD	RMS	SF	AM	STD	RMS	SF	AM	STD	RMS	SF	AM	STD	RMS	SF	AM	STD	RMS	SF
$q_{1}$	-0.65	2.28	2.35	1.09	6.22	3.14	6.97	1.11	-16.49	7.53	18.12	1.09	-12.70	7.25	14.60	1.15	35.34	5.08	35.70	1.01
$q_{2}$	0.21	2.32	2.31	1.29	-6.01	1.89	6.30	1.04	0.76	4.09	4.14	1.09	-5.60	2.58	6.16	1.09	-20.15	3.29	20.42	1.01
$q_{3 R}$	8.02	15.35	17.18	1.12	38.44	13.39	40.69	1.05	30.08	9.46	31.52	1.04	29.53	10.84	31.44	1.06	44.78	15.19	47.26	1.05
$q_{4 R}$	-19.98	18.32	26.99	1.35	-64.36	2.86	64.43	1.00	-62.51	6.22	62.82	1.00	-37.68	5.05	38.01	1.00	-53.25	9.85	54.15	1.01
$q_{5 R}$	1.08	6.47	6.50	1.25	23.66	6.81	24.62	1.04	-16.86	5.05	17.59	1.04	-33.24	1.95	33.30	1.00	22.69	4.11	23.05	1.01
$q_{3 L}$	8.02	15.35	17.18	1.12	46.47	10.35	47.60	1.02	12.81	13.10	18.28	1.19	15.51	11.89	19.51	1.15	45.26	8.26	46.01	1.01
$q_{4 L}$	-19.98	18.32	26.99	1.35	-67.83	8.29	68.34	1.00	-49.29	4.82	49.52	1.00	-21.60	9.11	23.43	1.08	-47.32	11.39	48.66	1.02
$q_{5 L}$	1.08	6.47	6.50	1.25	20.32	6.19	21.23	1.04	2.50	8.55	8.87	1.21	5.07	6.17	7.97	1.27	4.75	3.29	5.77	1.18

Table 6. Classification performance of 5 gaits using pelvic section with KNN, NB and DA.

	KNN					NB					DA
Metric	N	C1	C2	C3	C4	N	C1	C2	C3	C4	N	C1	C2	C3	C4
Acc	92.60	92.20	92.20	92.80	93.40	94.40	97.00	96.80	94.20	95.60	97.80	98.20	95.80	96.6	96.40
R	83.06	79.29	83.62	86.98	79.43	88.01	98.32	87.48	88.59	84.24	92.75	95.16	91.88	91.40	92.25
SP	95.18	95.41	94.66	94.41	97.23	96.36	96.634	98.59	95.70	98.70	99.01	98.98	97.03	98.26	97.27
P	79.90	81.95	82.56	78.54	88.87	88.52	90.22	91.65	85.45	95.30	95.69	96.41	88.69	92.30	90.41
FM	79.87	80.18	81.84	81.73	80.77	86.84	93.85	88.86	85.68	89.01	93.98	95.63	89.84	91.50	90.79

Table 7. Classification performance of 5 gaits using using pelvic section with DT and ANN.

	DT					ANN
Metric	N	C1	C2	C3	C4	N	C1	C2	C3	C4
Acc	92.80	93.20	93.60	95.00	93.40	95.00	95.00	95.20	96.20	97.40
R	80.64	81.00	80.91	86.20	84.32	88.58	83.38	92.14	91.05	90.32
SP	95.82	96.12	96.26	97.55	94.78	96.78	97.71	95.99	97.52	98.72
P	81.24	81.36	84.16	89.57	77.25	86.38	90.35	85.10	91.01	93.80
FM	80.65	80.19	81.81	86.91	80.054	86.85	86.08	88.06	90.61	91.58

Table 8. Classification performance of 5 gaits using right lower limb body section with KNN, NB and DA.

	KNN					NB					DA
Metric	N	C1	C2	C3	C4	N	C1	C2	C3	C4	N	C1	C2	C3	C4
Acc	99.20	99.20	99.80	98.60	99.20	99.60	99.80	99.60	99.20	99.40	99.40	96.2	95.4	98.6	98.00
R	97.55	97.00	99.23	99.00	97.67	97.98	100.00	100.00	94.97	100.00	99.09	91.94	87.62	96.09	94.56
SP	99.75	99.75	100.00	98.55	99.75	100.00	99.76	99.50	100.00	99.26	99.50	97.47	97.36	99.24	98.72
P	99.09	98.75	100.00	94.42	99.09	100.00	99.00	98.04	100.00	96.92	98.09	90.56	90.00	96.87	94.95
FM	98.22	97.78	99.60	96.40	98.28	98.94	99.47	98.96	97.31	98.37	98.56	90.99	88.32	96.46	94.55

Table 9. Classification performance of 5 gaits using right lower limb body section with DT and ANN.

	DT					ANN
Metric	N	C1	C2	C3	C4	N	C1	C2	C3	C4
Acc	99.40	99.00	99.20	99.00	99.40	98.00	97.00	97.56	99.40	96.20
R	98.09	97.63	98.00	99.41	98.04	96.33	99.17	100.00	99.17	98.20
SP	99.74	99.50	99.50	98.92	99.77	98.52	96.63	97.09	99.52	97.14
P	99.23	98.18	98.00	96.98	98.57	94.57	91.35	93.57	98.00	92.43
FM	98.60	97.81	98.00	98.14	98.19	95.03	93.95	95.47	98.45	94.14

Table 10. Classification performance of 5 gaits using using left lower limb with KNN, NB and DA.

	KNN					NB					DA
Metric	N	C1	C2	C3	C4	N	C1	C2	C3	C4	N	C1	C2	C3	C4
Acc	99.40	98.60	99.60	98.60	99.80	98.60	99.20	98.60	99.60	98.80	99.80	99.60	100.00	99.40	100.00
R	100.00	98.57	97.98	95.00	99.00	94.31	100.00	95.84	98.33	97.08	98.57	98.26	100.00	100.00	100.00
SP	99.26	98.61	100.00	99.50	100.00	99.51	99.01	99.23	99.76	99.20	100.00	100.00	100.00	99.26	100.00
P	96.92	97.06	100.00	97.14	100.00	97.14	96.36	97.27	98.89	97.60	100.00	100.00	100.00	96.90	100.00
FM	98.37	97.74	98.94	95.88	99.47	95.58	98.04	96.50	98.50	97.18	99.23	99.09	100.00	98.36	100.00

Table 11. Classification performance of 5 gaits using using left lower limb with DT and ANN.

	DT					ANN
Metric	N	C1	C2	C3	C4	N	C1	C2	C3	C4
Acc	98.80	99.20	99.40	99.60	99.40	98.40	97.80	98.40	98.60	98.20
R	96.33	97.26	99.00	98.57	99.41	94.43	96.14	93.52	95.66	97.23
SP	99.23	99.74	99.50	99.72	99.52	99.22	98.05	99.47	99.26	98.54
P	97.28	99.17	98.04	99.33	98.00	97.40	91.31	98.40	96.92	94.14
FM	96.68	98.13	98.44	98.89	98.59	95.64	93.59	95.63	96.08	95.31

Table 12. lassification performance average of the 5 gaits for all algorithms and 3 regions (pelvic, right and left lower limbs.

	Pelvic ( $Q_{1}$ and $Q_{2}$ )					Right lower limb ( $Q_{3 R}$ , $Q_{4 R}$ and $Q_{5 R}$ )					Left lower limb ( $Q_{3 L}$ , $Q_{4 L}$ and $Q_{5 L}$ )
Metric	KNN	NB	DA	DT	ANN	KNN	NB	DA	DT	ANN	KNN	NB	DA	DT	ANN
Acc	92.64	95.60	96.96	93.60	95.76	99.20	99.52	97.52	99.20	97.63	99.20	98.96	99.76	99.28	98.28
R	82.47	89.33	92.69	82.61	89.10	98.09	98.59	93.86	98.23	98.53	98.11	97.11	99.36	98.11	95.40
SP	95.38	97.19	98.11	96.10	97.34	99.56	99.70	98.46	99.48	97.78	99.47	99.34	99.85	99.54	98.91
P	82.36	90.23	92.70	82.72	89.33	98.27	98.79	94.09	98.19	93.99	98.22	97.45	99.38	98.36	95.64
FM	80.88	88.85	92.34	81.92	88.64	98.06	98.61	93.77	98.15	95.41	98.08	97.16	99.34	98.14	95.25

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer