Prerpints.org logo
Preprint
Review

Modelling Carbon-Based Nanomaterials (CNMs) and Derived Composites and Devices

This version is not peer-reviewed.

Submitted:

09 October 2024

Posted:

10 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
A review of different modelling techniques, specifically in the framework of carbon-based nanomaterials (CNMs, including nanoparticles as graphene and carbon nanotubes - CNTs) and the composites and devices that can be derived from them, is presented. The article highlights the multiscale nature of these types of materials and systems, which require different approaches depending on the type, size, internal structure/configuration of the material and properties of interest. Far from attempting to cover the entire spectrum of models, this review examines a wide range of analysis and simulation techniques, highlighting their potential use, some of their weaknesses and strengths, and presenting the latest developments and some application examples. Specifically, this paper shows how electronic, atomistic, mesoscopic, continuum and system models can be used to study and design CNMs, to predict different properties and responses of materials, or even to study devices such as sensors. This review has been performed within the framework of COST Action EsSENce (High-performance Carbon-based composites with Smart properties for Advanced Sensing Applications – CA19118).
Keywords: 
Subject: 
Physical Sciences  -   Applied Physics

1. Introduction

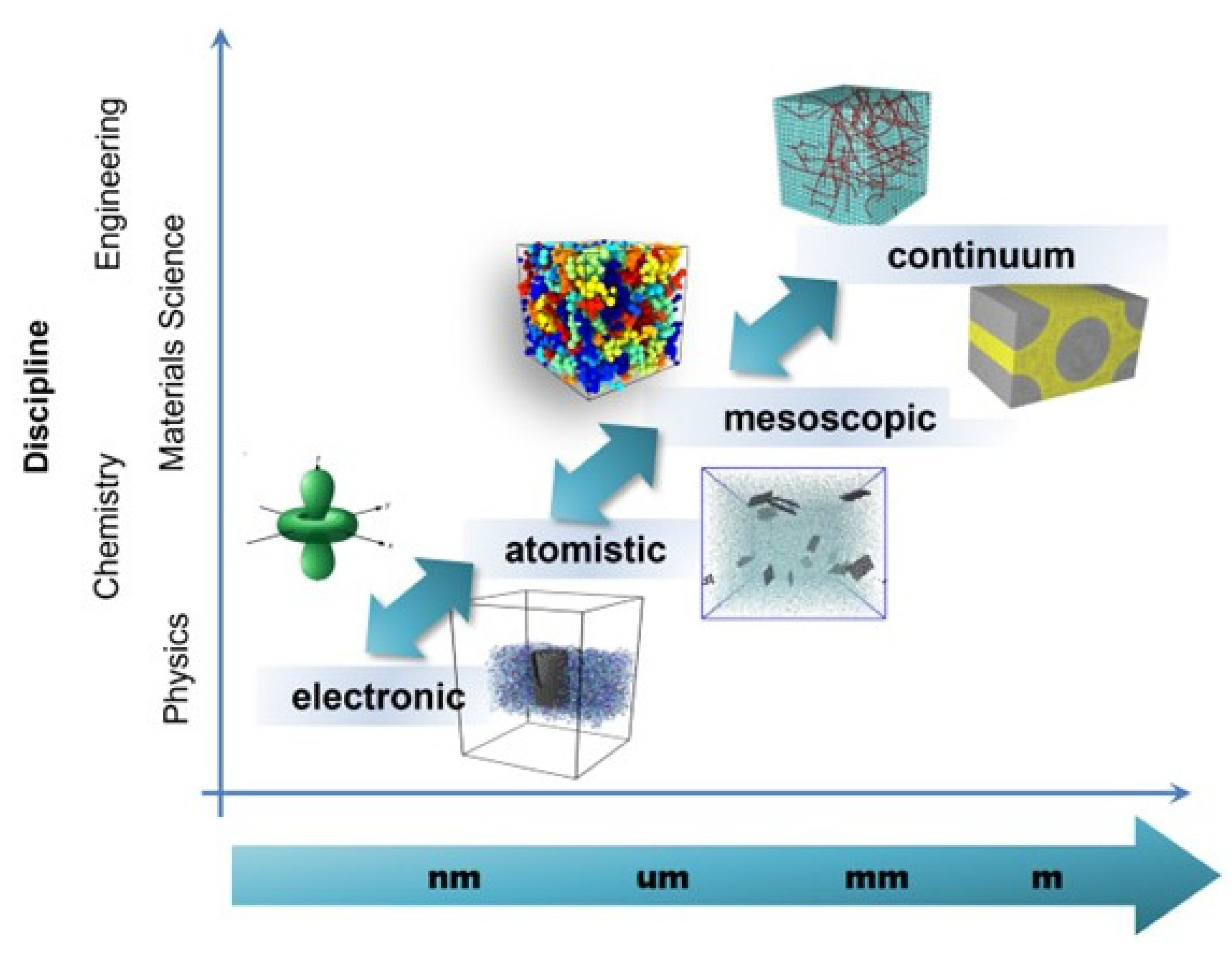
Recent advances in analytical and computational modelling enable the prediction and understanding of material properties and responses on scales ranging from the electronic/atomistic, through the microstructure or transitional, and up to the continuum (Figure 1). Multiscale material modelling is based on a systematic reduction of the degrees of freedom at different length scales in which a material can be described. Connections between these scales are established either by parametrization, by grouping (i.e., coarse graining) or homogenization procedures. These different scales in the description of materials have historically been associated with different disciplines, from physics to engineering, including chemistry and materials science (Figure 1). 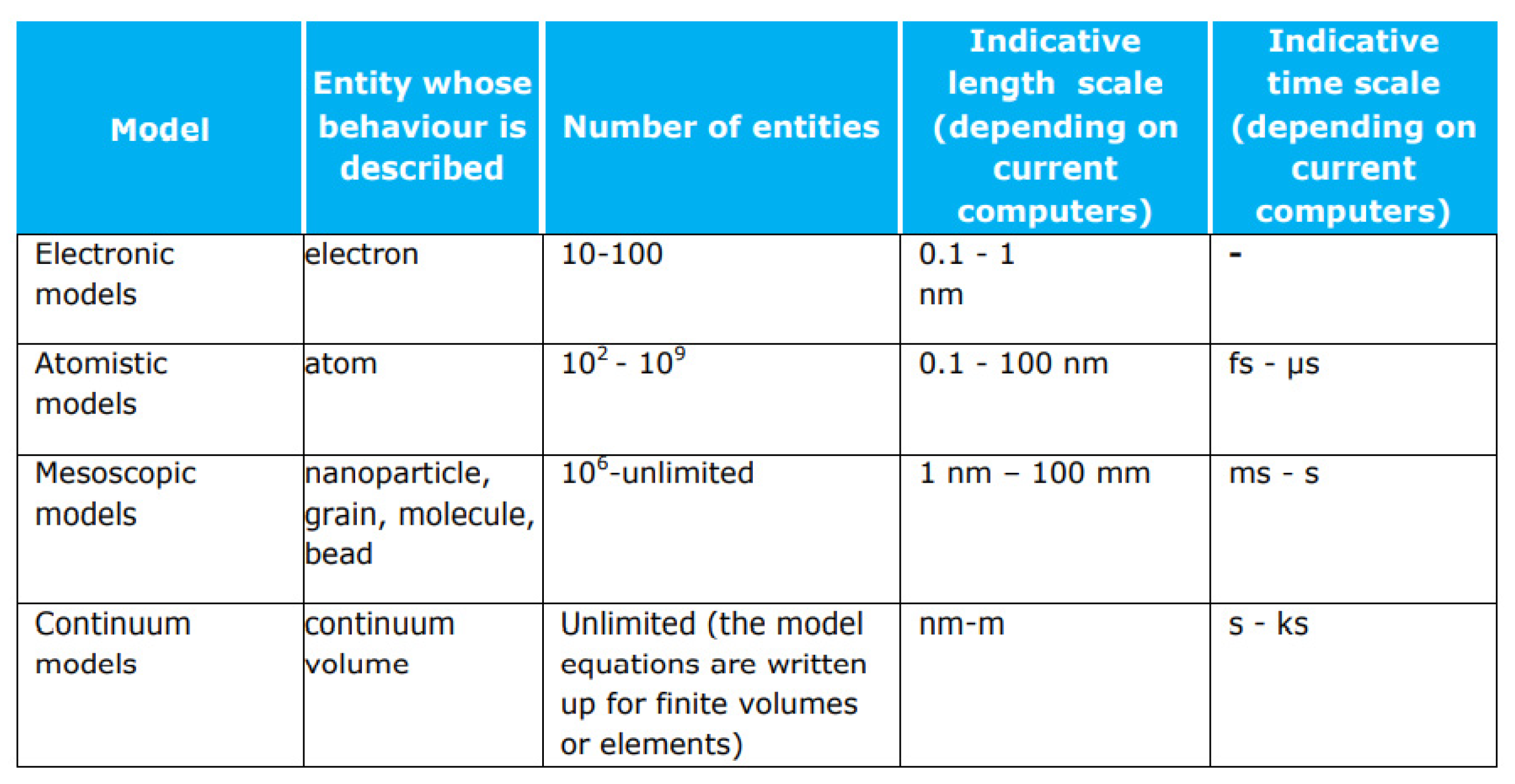Each scale can be studied by means of different types of models (electronic, atomistic, mesoscopic and continuum), which employ distinct basic entities and usually work in different ranges of timescales and number of entities (Figure 2). However, the scale and type of model do not have a one-to-one correspondence, since there are areas of overlapping regarding the models that can be employed for a specific analysis.
This report presents a review of different modelling strategies and methodologies used in the field of carbon-based nanoparticles (graphene, carbon nanotubes—CNTs, nanofibers, etc.), carbon-based nanomaterials (CNMs) and devices (such as sensors) that can be obtained from these materials. Within this framework, the variety of models, methods and applications is extremely wide, and getting a full picture in a condensed report is hard-to-reach. This review, then, aims to cover some of the key modelling approaches usually employed at different length and time scales, ending with a discussion on a specific type of sensor, derived from these carbon-based materials, as an example of device-level modelling. This leads to the four main sections that constitute the present document.
At the lower scale, the first type of models focuses on electronic calculations, theoretical studies of single-particle and collective excitations. These models are relevant for photonics, plasmonic and nano-electronics applications. At the next level, molecular dynamics (MD) models enable the study of material properties/responses that are mainly dominated by interactions between atoms or molecules, defined through force fields. These models help in predicting mechanical, thermal, surface properties, and other physical properties such as density, viscosity, or glass transition temperature; they are used transversally in the design of materials and nanocomposites for a wide range of applications. At the continuum level, modelling is typically employed to predict the macroscopic-homogenized properties of materials by considering the constituents as a continuous medium rather than as discrete particles. Compared with the latter, MD models provide detailed atomic-level information but are limited to small systems due to computational constraints. Continuum models, on the other hand, can handle much larger systems but lack the detailed description of atomic or molecular interactions. These models can also be used to predict different types of properties (again mechanical, thermal, electrical, acoustic, and other physical properties). Certain kinds of products and devices need to be modelled as systems instead, which might require a combination of different type of properties and physics. Each system has its own requirements, which can lead to the integration of different sub-models. At this scale, as an application example relevant to sensors, this review focuses on the modelling and simulation of graphene field effect transistors (GFET) devices and circuits.
This review has been performed within the framework of COST Action EsSENce (High-performance Carbon-based composites with Smart properties for Advanced Sensing Applications—CA19118), funded by the European Cooperation in Science and Technology (COST). The EsSENce COST Action aimed to construct an international scientific & technological innovation hub focusing on advanced composite materials reinforced with CNMs for sensing applications. Particularly, working group WG5 deals with the modelling of materials and sensing mechanisms, identified as a key area to support the development of CNMs, advanced high-performance composites, and their implementation into products and devices. Thus, the objective is to exemplify and promote i) the use of “standard” or widely shared modelling protocols, or ii) the development/application of new modelling approaches. In addition, a second goal is to identify some of the needs in this field, considering both experimental characterization (needed to feed or validate the models) and the modelling perspective.

2. Theoretical Modelling of Interactions of Charged Particles with Graphene-Based Nanomaterials and Their Composites

Graphene is the best known and the most explored two-dimensional (2D) material. It is the world’s thinnest and strongest material, with the highest electrical and thermal conductivity known. Due to its outstanding physical, chemical, electrical and optical properties, graphene shows great potential in many fields, including sensors.
In nanoscale devices graphene typically appears in stacks separated by insulating layers of finite thickness [2,3,4], which usually support strong Fuchs-Kliewer or optical surface phonon modes [5]. Those phonon modes are active in the terahertz (THz) to mid-infrared (mid-IR) frequency range and can dampen the Dirac plasmon in doped graphene which operates in the same frequency range [6], or can hybridize with it [7]. As a prototype of layered nanostructures involving doped graphene sheets, a sandwich-like composite which consists of two layers of graphene separated by an insulating layer was studied and it was found that the structure supports a variety of interesting plasmon-phonon hybrid modes in the THz to mid-IR frequency range [8]. An insulating layer of sapphire (aluminum oxide, Al2O3) was chosen because it is often used as a dielectric spacer in experiments [9,10,11,12,13,14]. The effective dielectric function of the system was obtained by using a local dielectric function for the bulk Al2O3 and by using two approaches within the random phase approximation for graphene’s electronic response: an ab initio method based on the time-dependent density functional theory calculations and a method based on the massless Dirac fermion approximation for graphene π bands.
The most efficient way to probe the plasmon-phonon hybridization between graphene and the nearby insulator(s) is by means of an externally moving charged particle. Such hybridization has an effect on the energy loss of an incident particle [15], as well as on the resulting wake effect in the induced electrostatic potential [16]. The wake potential (the total potential in the plane of the upper graphene sheet) induced by an external charged particle moving parallel to the graphene-Al2O3-graphene composite system (Figure 3) was investigated in Ref. [17]. The distance of the charged particle from the top graphene, the thickness of the Al2O3 layer, and the doping density (i.e., Fermi energy) of graphene were fixed at their respective typical values. The effects of variations of all those parameters were studied in Ref. [18].
The plasmon-phonon hybridization also has an impact on the stopping force (the dissipative force which opposes the particle’s motion) and the image force (the perpendicularly oriented conservative force which bends the particle’s trajectory towards the upper graphene sheet). A thorough analysis of the stopping and image forces on a charged particle moving parallel to the graphene-Al2O3-graphene composite was performed in Ref. [19], covering broad ranges of the particle speeds and distances, as well as the doping densities of the two graphene sheets. It should be noted that the stopping force is the negative of the usual stopping power, whereas the image force is related to the familiar image potential.
Note that the wake effect and the stopping and image forces were previously investigated theoretically in free-standing and supported graphene [15,16,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39].
In the last few years van der Waals (vdW) heterostructures based on graphene and hexagonal boron nitride (hBN) layers with different stacking modes have attracted a great deal of interest because of their potential applications [40,41,42,43,44,45,46,47,48]. Graphene/hBN vdW heterostructures were studied very recently in Refs. [49,50].
Electron energy loss spectroscopy (EELS) is a commonly used experimental technique for investigating electronic and plasmonic properties of 2D materials and vdW heterostructures [51,52,53]. Theoretical modelling of the experimental EELS data for free-standing (single and multilayer) graphene sheets obtained by (scanning) transmission electron microscope is presented in Refs. [54,55,56,57], whereas the theoretical modelling of the experimental EELS data for monolayer graphene supported by different substrates is given in Refs. [58,59,60,61].
Acoustic plasmon (AP) in graphene or in graphene-dielectric-metal structure has been studied very intensively in the last few years [62,63]. In Ref. [64] the authors focused on the AP in graphene doped by alkali metals and demonstrated that two isoelectronic systems, KC8 and CsC8, support substantially different plasmonic spectra: the KC8 supports a sharp Dirac plasmon (DP) and a well-defined AP, while the CsC8 supports a broad DP and does not support an AP at all. These findings could be very useful in the area of chemical or biological sensing [65,66].

3. Molecular Dynamics Applied to CNM Properties Prediction

Molecular Dynamics (MD) is a computational method to simulate the behavior of atoms and molecules over time. In an MD simulation, the trajectories of atoms (considered as rigid spheres) and molecules are determined by numerically solving Newton’s equations of motion. Forces between particles are calculated by exploiting calibrated interaction potentials (force fields), and from these forces the accelerations, velocities, and subsequent positions of the atoms are determined [67]. For materials science, MD provides detailed insights into phenomena that would otherwise be difficult to observe directly, such as diffusion, phase transitions, interfacial effects, and mechanical behavior at the nanoscale.
One of the key aspects of MD simulations lies in the force fields, which are mathematical models used to calculate interactions between atoms due to the presence of covalent bonds (bonded interactions) and electrostatic forces (Coulomb/Van der Waals, non-bonded interactions) [68]. In MD simulations of CNMs, some specific force fields have gained prominence [69]:
  • The Adaptive Intermolecular Reactive Bond Order (AIREBO) potential is tailored for carbon systems and describes long-range van der Waals interactions and torsional effects. It is versatile for modelling both sp2 and sp3 hybridized carbon structures [70]. AIREBO might not perform well for systems with significant charge transfer or in the case of interactions with elements outside its parameterization.
  • Tersoff potential considers both the distance between atoms (bond lengths) and their relative orientation (bond angles) to provide a detailed representation of the complex interactions that occur in carbon-based materials [71]. This potential may not be ideal for modelling weak interactions, and it might require recalibration for systems different from its original parameterization.
  • ReaxFF is a reactive force field capable of simulating bond formation and breaking during MD simulations. This dynamic nature is achieved by not predefining specific bond types but allowing the system to evolve based on atomic positions and interactions. Due to its reactive nature, ReaxFF can be computationally demanding. It also requires careful system-specific parameterization to ensure reliable results, e.g., in the case of condensed carbon phases [72].
  • Machine Learning (ML) interatomic potentials differ from traditional ones, as they do not depend on fixed mathematical formulas. Instead, they learn representations of the potential energy surface of the system through trainings based on lower-scale simulations. Several implementations for certain carbon forms with near DFT-level accuracy have been reported in the literature, e.g., Gaussian Approximation Potential (GAP) [73], hybrid neural network potential [74], GAP-20 potential for various crystalline phase of carbon and amorphous carbon [75]. Furthermore, MACE—a transferable force field for organic molecules created using ML trained on first-principles reference data—was recently implemented [76]. Despite the good accuracy of current ML-based force fields in predicting the properties of carbon allotropes, various challenges still exist, especially regarding the description of mechanical properties and the curation of reliable training datasets.
MD is well-suited for investigating various properties of CNMs and composites made thereof [77]. The mechanical properties of these materials, for example, can be determined through MD simulations that allow the stresses and strains experienced by the system to be evaluated [78]. In these tests, a strain is systematically applied to the system, and the resulting stress responses of the material are recorded, thus providing information on its elastic constants, tensile strength, and potential fracture points [79]. For instance, simulations of cellulose nanocrystal-graphene composites revealed enhanced mechanical properties due to covalent bonding and van der Waals interactions [80]. Similarly, MD analyses of single-walled carbon nanotubes (SWCNT) have demonstrated Young’s moduli in agreement with experimental values, showcasing their exceptional mechanical strength and stiffness [81]. However, these simulations face some challenges, as the simulated strain rates should be much higher than those typically found in experimental setups to provide meaningful results in a feasible computational time. Another technique for analyzing the mechanical properties of a material is nanoindentation, which involves the simulation of a virtual indenter pressing on the surface and allows the hardness and localized stress response to be derived [82]. For example, nanoindentation MD simulations on polymer nanocomposites highlighted the effect of nanoparticle interactions and temperature on mechanical reinforcement [83] The results, though, can be influenced by the chosen shape of the indenter and the interaction potentials utilized. Pull-out tests simulations [84] and density profile analysis [85], on the other hand, are valuable aids in characterizing the interface region between a CNM and the surrounding environment (e.g., the polymer in the case of composites), which is a key interaction region that strongly determines the properties of the composite material. These analyses provide useful insights into the mechanisms of load transfer through materials and interfacial adhesion behavior.
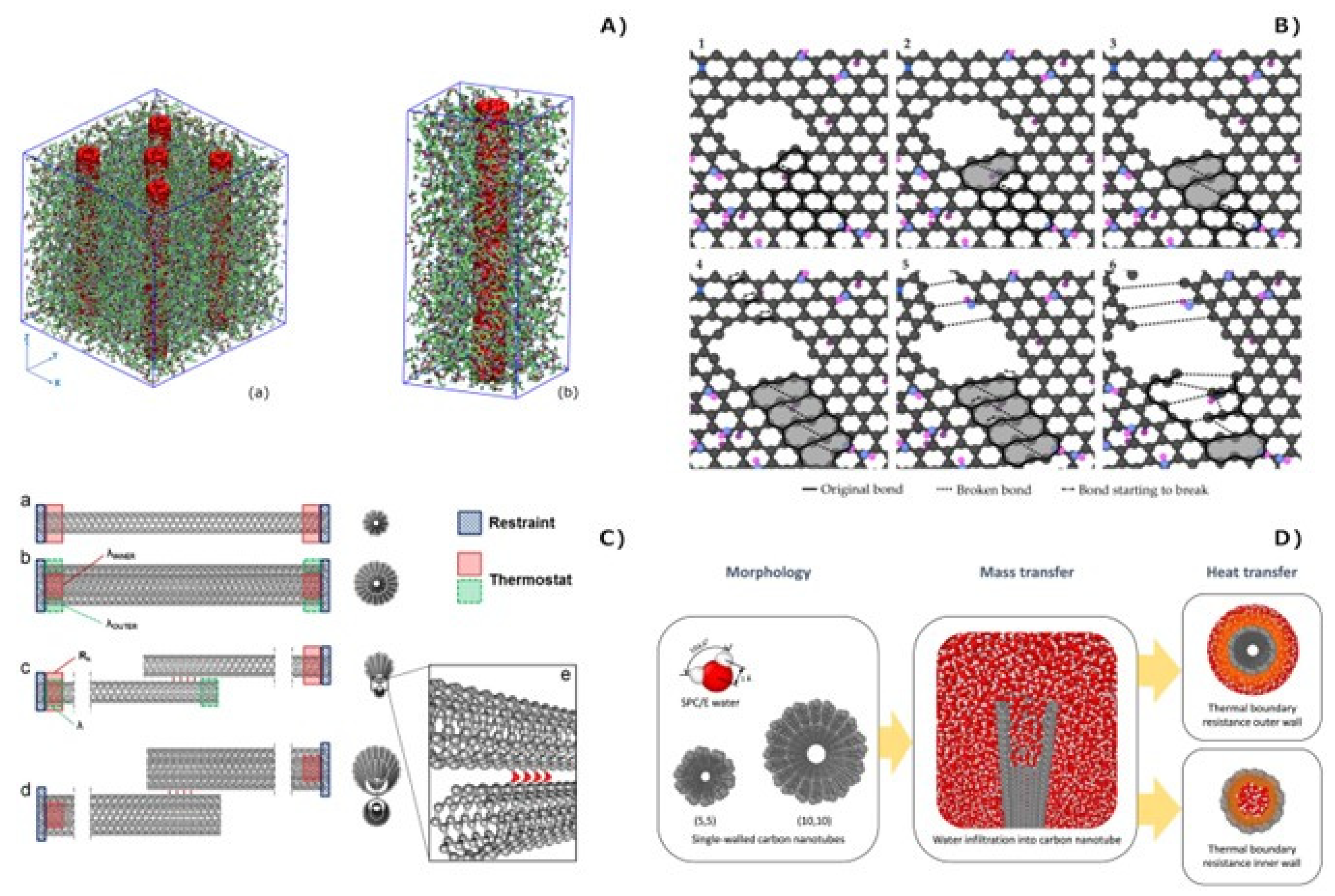
The thermal properties of CNMs can be explored using various protocols [86,87]. In the Non-equilibrium Molecular Dynamics (NEMD) technique, for instance, a temperature gradient is established within the simulation domain, thus enabling the calculation of thermal conductivity [88]. NEMD was employed to calculate the thermal conductivity of multi-walled CNTs with different geometrical features, such as diameter, length, chirality, and number of walls [89]. Still, this method entails an issue, as the artificial imposition of a gradient might not realistically replicate actual experimental scenarios. The Equilibrium Molecular Dynamics (EMD) method offers another approach, relying on the analysis of heat current fluctuations within a system at equilibrium. A notable example involves the use of EMD simulations to determine the thermal conductivity of graphene nanoribbons [90]. By employing the Green-Kubo method, researchers studied the effects of ribbon width, edge roughness, and hydrogen termination on thermal conductivity. The results showed that smooth edges yield the highest conductivity, while edge roughness significantly reduces it. However, EMD often requires extended simulation times. Another critical thermal property that can be computed by MD simulations is the thermal boundary resistance (TBR, also known as Kapitza resistance, originating from phonon scattering in the presence of defects or interfaces) [91]. As carbon nanomaterials are often embedded into other materials (e.g., polymeric matrices, fluids), understanding the efficiency of heat transfer across these interfaces becomes vital [92]. Both NEMD and EMD protocols offer quantitative insights into this property. Furthermore, theoretical models such as the Acoustic Mismatch Model and the Diffuse Mismatch Model, informed by inputs from MD simulations, provide complementary perspectives on TBR [93].
For thermodynamic properties, MD simulations lean on specialized techniques, like free energy calculations. Properties such as adhesion can be probed using advanced sampling methods, such as umbrella sampling and metadynamics [85], but these techniques often require care in choosing the force field and can be computationally burdensome. The wetting properties of CNMs are fundamental as well for optimizing their performance in suspensions and composites. Wettability, quantified by contact angle measurements, can indeed affect the dispersion of CNMs in various solvents, along with the ability of polymers to spread and adhere to CNMs thus influencing the mechanical and thermal properties of the composite [94]. At the atomistic level, two main approaches are used to measure the contact angle. The free energy perturbation (FEP) method involves calculating the free energy changes to determine the interaction parameters between a liquid and a surface [95]. This approach allows the interaction parameters to be calibrated and the work of adhesion and friction coefficients to be evaluated. In the second method, called the droplet method, a liquid droplet is placed on the tested surface and allowed to relax until equilibrium is reached [96]. The contact angle is then measured by analyzing the shape of the droplet along the three-phase contact line [97]. The latter approach is widely used to study the effects of surface roughness and interfacial properties. For instance, MD simulations revealed that difunctional epoxy and cyanate ester resins exhibit high wettability on CNT surfaces, while polyether ether ketone resins show poor wetting properties [98]. Graphene oxide, due to its hydrophilic functional groups, generally offers better wettability than pristine graphene, improving dispersion and interfacial bonding in polymer matrices [99]. Additionally, carbon nanoparticle coatings synthesized through controlled flame deposition can be tailored from hydrophilic to superhydrophobic states by adjusting synthesis conditions, which optimize surface interactions and enhances composite performance [100].
Other type of properties that can also be studied through MD models are the dielectric ones (dielectric constants, relaxion) using specific approaches as the dipole moment fluctuation method [101].
While offering mechanistic insights into the properties and behavior of CNMs, MD simulations do not lack challenges. For instance, MD approaches typically operate within specific temporal (fs to µs) and spatial (nm to µm) scales, and phenomena outside these scales might not be detected and analyzed effectively [102]. Moreover, the choice of the force field can significantly impact the results, as not all force fields describe the intricate interactions in nanomaterials with the same accuracy [103]. Furthermore, high-resolution simulations, especially those involving long timescales or large systems, can be computationally demanding, requiring substantial resources and time. The imposition of periodic boundary conditions, instead, can lead to artifacts in the results, especially if the size of the simulated system is not large enough compared to the phenomena under observation [104]. Finally, the rates used in simulations (e.g., thermal or mechanical ones), due to computational constraints, often exceed experimental rates, potentially leading to discrepancies between numerical and experimental data [105].
Looking ahead, the MD research landscape on CNMs presents promising prospects [106]. One of the most significant improvements in recent years has been the development of enhanced force fields. Ongoing research in this area aims to refine these force fields specifically for carbon nanomaterials, with the goal of increasing the accuracy in predicting their properties. Moreover, the growing popularity of multiscale modeling as a robust approach offers significant opportunities: by linking/coupling MD with other simulation methodologies, such as electronic, mesoscopic and/or continuum models [107], researchers aim to bridge the spatiotemporal gaps between scales. Yet, one of the most transformative shifts in the field of molecular dynamics is probably the integration of data-driven approaches within MD simulations. The support of machine learning and artificial intelligence is not merely augmenting computational efficiency, but it is reshaping the paradigms of simulations. These tools offer optimized parameter selections, predictive capabilities, and the prospect of devising new force fields. Lastly, shared efforts between experimentalists and computational researchers are fostering iterative refinements in simulation methodologies. This synergy is guiding MD studies closer to experimental observations, ensuring a more harmonized understanding of CNMs.

4. Continuum Models

At the next level within the multiscale materials modelling framework, continuum models are powerful tools for predicting the properties of nanocomposites. These models consider the microstructure of the nanocomposite, including the size, shape, and distribution of the nanoparticles, to predict the macroscopic-homogenized properties of the material. Continuum models can be used to predict different types of properties or responses: mechanical, thermal, electrical, acoustic, among other physical properties.
There are basically three types of continuum models: analytical, semi-analytical and numerical. The most common analytic models used for nanocomposites are based on the early work of Eshelby on ellipsoidal inclusions on an infinite elastic matrix, such as the relevant Mori-Tanaka’s mean field approach, which introducing as a hypothesis that each particle sees as far field the average matrix strain, allowed the application to non-diluted concentrations, calculating the properties of the composite by a physical combination of the properties of the nanoparticles and the matrix, weighted by their respective volume fractions. Other type of analytical models are the self-consistent models (SCM), where each nanoparticle in the nanocomposite is embedded in a matrix that has the same properties as the nanocomposite itself (this leads to a system of coupled equations that must be solved numerically); In general, these models can be solved relatively quickly compared with other approaches, making them useful for initial approximations and quick calculations. Despite this, as it is reported later, more and more advanced models are being developed attempting to capture complex geometric and material aspects. There are hundreds of works in the literature applying these models to determine standard fiber-based composites properties first, and later applied also to nanocomposites, for example considering the matrix-particle interphase as a third material phase constituent. In this sense, interesting references comparing/reviewing all these methods are the article of Y. Wang and Z. Huang [108], the chapter of Yehia A. Bahei-El-Din about Averaging Models of Fibrous Composites in [109], and the recent publication of A. Elmasry, W. Azoti, S. El-Safty and A. Elmarakbi that presents a review comparing different models for effective properties calculation of nano- and micro-composites [110]. Works focused on mechanical properties include: i) nanocomposites’ stiffness prediction (i.e., response in the elastic range), as the research done by M.M. Shokrieh, M. Esmkhani, Z. Shokrieh and Z. Zhao for an epoxy resin modified with graphene nanoplatelets [111], the work presented by A. Chiminelli and M. Laspalas for an epoxy resin modified with MWCNTs [112], the work of A. Singh and D. Kumar studying the influence of the functionalization of graphene nanoplatelets in the elastic properties of a modified polyethylene [113] or a more recent work of D. Shin, I. Jeon and S. Yang for graphene modified PET [114]; ii) non-linear behavior and strength predictions of CNMs, as the approach proposed by J. Nafar Dastgerdi, G. Marquis and M. Salimi introducing interfacial damage/debonding processes in CNTs reinforced polymers [115] or the model developed by W. Azoti and A. Elmarakbi applied to a graphene platelets GPL-reinforced polymer PA6 composite (Generalized Mori-Tanaka) [116]. Other works/studies can be found about the utilization of this type of analytic approaches to develop more advanced models introducing viscoelasticity [117] or creep effects [118], among others. Overall, good correlations with experimental results are obtained for the elastics properties especially at low nanoparticles concentrations, while at higher concentration more significant deviations are usually observed. This is generally explained due to interactions between the nanoparticles at high contents that produce non-homogeneous dispersions and agglomerations. For predictions in the non-linear regime and in terms of strength, it is generally seen that the results are strongly dependent on the particle/polymer interface representation and on the aspect ratios of the particles. This also observed in the modelling of other type of properties of nanocomposites (thermal, electrical, acoustic…). For example, in the work published by J. Shao et al. [119] for predicting dielectric properties of polymers modified with nanoparticles, the Knott model was modified with the Tanaka formula for hybrid particles to take into consideration the interphase region. Obviously, the issues mentioned at high concentrations are also present in these cases. Apart from this, these models are valuable to evaluate different functionalization of carbon-based nanoparticles.
In addition to the models mentioned above, some semi-empirical analytical models are also well-known for composites, starting with the classical rule of mixture, evolving to Chamis’ model and the Halpin–Tsai’s model (as a simplified version of the SCM), and leading to more advanced models introducing (again) elastoplasticity (approaches to yield stress and linearization methods [108]). The Halpin–Tsai approach for aligned reinforcement has been employed widely for the analysis of graphene-based nanocomposites [120]. In this sense, works as the ones developed by Weon et al. [121], Chong et al. [122] and Zarasvand and Golestanian [123] can be highlighted. In the last, the nonlinear tensile stress-strain behavior of randomly-distributed graphene nanocomposites have been obtained, presenting a good correlation with experimental results in the whole range of the stress-strain curves. In a work published by M. Yang et al. [124], the Halpin-Tsai model was adapted to quantitatively characterize the effect of temperature on the yield strength of nanofiller-reinforced polymer-matrix nanocomposites. Compared with the classical ones, the model showed better agreement with the available experimental data from sub-zero temperature to the full glass transition region. Progressing with elastoplasticity, several Non-linear Mean Field Methods have been developed from the elastic ones, the Tangent and Secant approaches being the most known. Some reference publications implementing these methods are the ones of Doghri [125,126]. An advantage of these models is the straightforward implementation. They also allow to study more complex loading cases than other models, including cyclic loads.
Semi-analytical methods are based on global constitutive equations that are evaluated from the local scale using analytic/explicit relations that link the microscopic and the macroscopic properties. Analytical relations are usually dependent on mean field procedures. The best known is the Transformation fields analysis (TFA). It connects analytical and computational approaches by a computational evaluation of the localization operators. The main concept is replacing the plastic strain field with piecewise uniform fields to reduce the number of macroscopic internal variables. Thereby, a set of reduced constitutive relations for the heterogeneous material can be established, leading to a computational time reduction compared to full numerical models [110]. Reference works of this type of model are the ones published by Dvorak [127,128]. A more recent work published by I.Al. Khattab and M. Sinapius present an interesting implementation of the TFA model as a user routine integrated into RVE-micro scale model [129]. The results reveal that the TFA is a proper method for solving inelastic deformation and other incremental problems in heterogeneous media with many interacting inhomogeneities on a nanoscale level.
Finally, numerical continuum micromechanics models, such as the finite element method (FEM), are considered also powerful approaches for CNMs modelling. In numerical approaches, an acknowledged constitutive model (elasticity, viscoelasticity, elastoplasticity, viscoplasticity…) is assumed in a Representative Volume Element (RVE) to induce an explicit macroscopic model. On one hand, these models allow to introduce more accurate description of the materials nano-morphology [130]. This is one of the limitations of analytic models, that usually require an idealization of the nanoreinforcements’ shape, representing them as discs, cylinders or spheres. On the other hand, these models allow to introduce complex nonlinear multi-phase material behaviors. The main disadvantages of finite elements are computational costs, size dependency of the results and limitations in the development of RVEs with high inclusions volume concentrations and aspect ratios.
RVE based models apply to statistically homogeneous materials. They can be used as repeating unit cell (RUC) when the (nano)composite has a periodic microstructure. Sufficient number of randomly distributed fibers or particles to be contained in the RVE is needed so that the microstructure of a composite could be reflected precisely [108]. This is also linked with the size of the volume studied. Various works reflect the importance of defining a proper RVE size [131]. In this sense, it happens that a larger RVE size gave better prediction accuracy but resulted in lower computational efficiency. Finally, the boundary conditions are a critical aspect in RUC models, and they have to be defined carefully to represent properly the effect of the reinforcements/particles distribution patterns and the loads applied.
Some first reference publications that can be found about RVE and FEM to estimate properties of polymer nanocomposites are the works of Liu and Chen [132,133]. Particularly, they studied the elastic properties of CNT-reinforced polymers. Chwał and Muc [134,135] applied a similar approach with various boundary conditions to calculate the mechanical properties of SWCNT-polymer nanocomposite. More recent works present a combination of this type of FE continuum models with MD, in similar way to the multi-scale framework presented in this report. For example, recently Barakat et al. published an article where the distribution of mechanical properties of graphene-based polymer nanocomposites is computed using a micro-meso up to macro hierarchical computational approach employing non-equilibrium atomistic MD simulations and continuum FE models [136]. In the same line, the work published by Muhammad et al. can be highlighted [137], where not only mechanical but thermal properties are predicted for graphene-reinforced epoxies. For SWCNT-polymer nanocomposites, Malague et al. proposed a procedure to assess size effects using the atomistic simulations and equivalent continuum model with a large number of CNTs [138].
Elastic RVE/RUC models can be extended to nonlinear cases, providing that the nonlinear constitutive laws for the constituents are available. For example, based on a three-dimensional RVE model, Yuan and Lu [139] conducted a numerical investigation on the elastoplastic behavior of carbon nanotubes (CNTs) reinforced polymer composites. A. Zarasvand et al. [140] also conducted experimental, numerical, and micromechanical studies to determine the nonlinear behavior of CNT-reinforced polymer. When non-linear constitute behaviors are considered, FEM approaches become computationally consuming. To address this limitation, several numerical strategies with reduced computational effort have been developed. Examples are the Voronoi Cell Finite Element Method (VCFEM) [141,142], the Generalized Method of Cells (GMC) [143], and the Finite Volume Direct Averaging Micromechanics (FVDAM) [144,145,146].
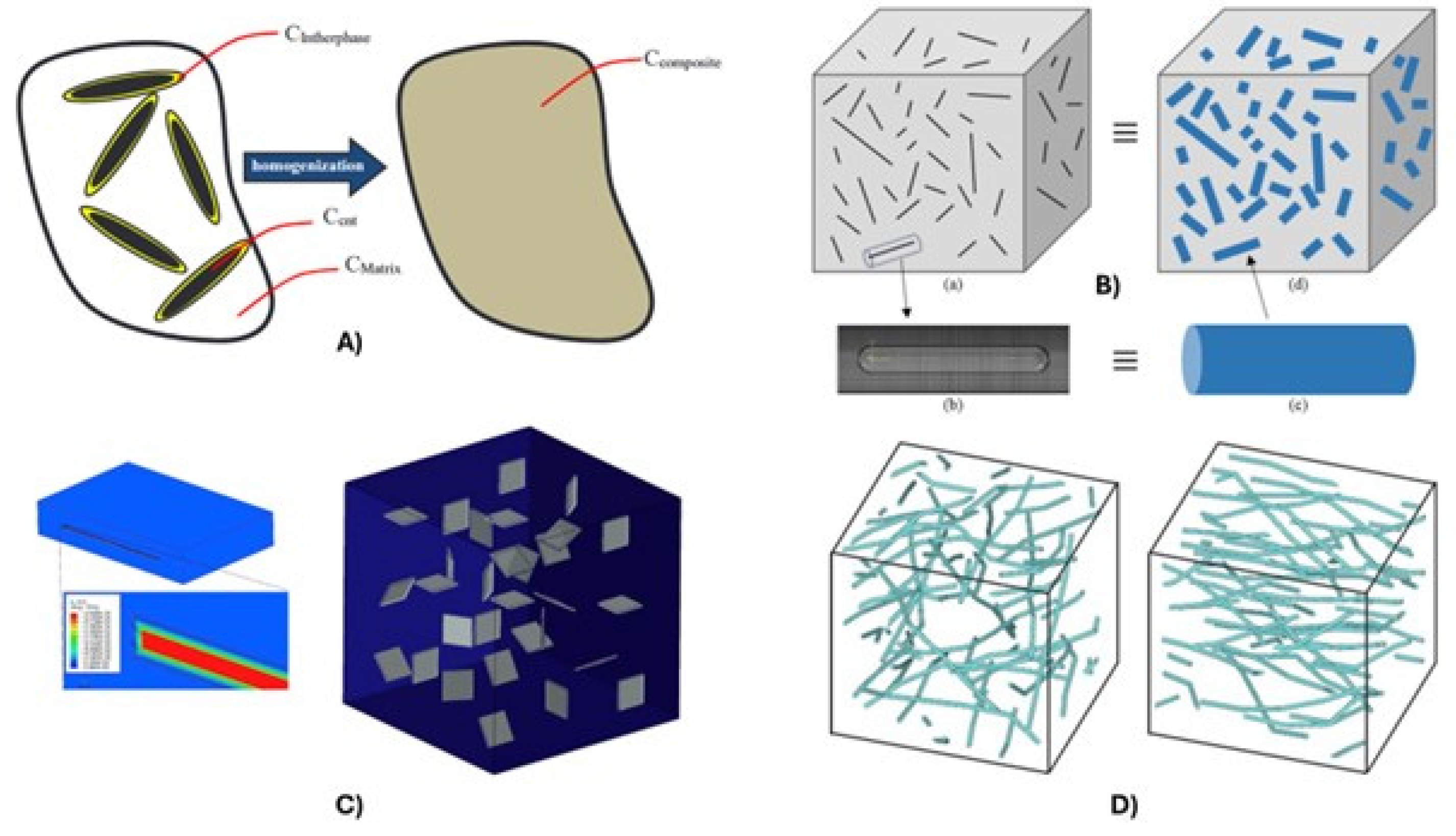
Preprints 120741 g005
Figure 5. Examples of continuum models to study CNMs. A) Mean field homogenization scheme [112], B) Combined FE and analytic Mori-Tanaka models for CNT reinforced polymer taking into account viscoelastic properties [117], C) Utilization of Halpin–Tsai approach for Graphene Nanoplatelet reinforced epoxy [123] and D) REV/FEM models analyses considering elastoplasticity for wavy and random CNTs distribution in nanocomposites [139].
Figure 5. Examples of continuum models to study CNMs. A) Mean field homogenization scheme [112], B) Combined FE and analytic Mori-Tanaka models for CNT reinforced polymer taking into account viscoelastic properties [117], C) Utilization of Halpin–Tsai approach for Graphene Nanoplatelet reinforced epoxy [123] and D) REV/FEM models analyses considering elastoplasticity for wavy and random CNTs distribution in nanocomposites [139].
Preprints 120741 g005

5. CNM Devices—Graphene Field Effect Transistors

When we arrive to discuss carbon nanomaterial devices that can be considered mature enough to be used in sensing systems, one of the most used configurations is based upon graphene field effect transistors (G-FET). High frequency applications have been in a first time a major goal for this class of devices, and a series of interesting results reporting the fabrication of research level devices working in the GHz domain were published in the 2010’s years [147,148,149,150]. Anyway, the problems that were initially addressed for the graphene transistors to replace silicon MOSFET as the choice alternative for commercial high-performance logic and high frequency electronics [151], prevented until now their large-scale adoption for this class of applications.
As a follow up, the intense research work realized during these years has produced many interesting results, experimental and theoretical as well, that have permitted a good insight into the physic mechanism of the GFET structures, paving the way to the definition of an application playground in the biosensing domain, avoiding the HF requirements of a G-FET based ASIC project. A nice summary of the present state of this approach can be found in the recently published review paper of S. Szunerits [152]. According to the authors not only graphene is proposed for FET biosensing applications, but also other 2D materials like metal dichalcogenides, hexagonal boron nitride or black phosphorus have been investigated for FET gate-channel technology. Indeed, graphene maintains his position as a first-choice material commercial applications for low term potential.
Although it is not currently available on the market, it may be foreseen that the use of GFET circuitry will soon find commercial application in wearable flexible sensing systems [153], in Point-Of-Care systems [154,155], and even in skin bioelectronics for health monitoring [156] exploiting its mechanical/electrical properties together with biocompatibility characteristics. Advanced experimental results in this field have been recently presented for applications of major interest, like, for example, cancer monitoring [157], COVID19 screening [158] or glucose monitoring in diabetic patients [159].
While no clinical validation has yet been performed, the proposed technology for these important biomedical playgrounds has been fully demonstrated in laboratory environment. The next step still needed for allowing the fabrication of large-scale point-of-care biosensing systems is the definition of a reproducible fabrication process, integrated with standard silicon CMOS technology. Once some variability can be expected from the fabrication condition, modelling and simulation will play a major role in the G-FET circuitry design. Looking at the recent past, modelling and simulation of GFET device and circuits, in a variety of configurations has certainly given an important contribution to the actual advanced state of the art for design and fabrication.
Regarding the electrical properties, a model to calculate the DC characteristics of large-area graphene field-effect transistors was presented initially by Thiele and Schwierz [160]. This paper opened the door to the heuristic approach of correlating the experimental results with the specific characteristics of the graphene material, like the sheet carrier density and transport properties. More specifically, the Thiele&Schwierz model suc-cessfully describe the experimental DC behavior of the drain current (Id), as a func-tion of the Drain-Source Voltage (Vds), for different Gate Source voltage (Vgs), using a reduced set of parameters about the device geometry like the gate length (L) and width (W), the insulator thickness (tox), drain and source contact resistances (Rs, Rd), together with material properties like charge mobilities in the graphene channel, sheet carrier density, carrier saturation velocity.
As a general description, a G-FET has a structure that can be thought similar to a thin film transistor (TFT), where the 2D graphene layer is used for channel forming. The traditional approach for the electrical simulation of semiconductor FET devices is based on the drift-diffusion model, including the Poisson equation [161]. Following an approach similar to the one proposed by Thiele&Schwierz, yet including the standard drift-diffusion approach, a Verilog compact model suitable for circuit level design model based of the drift and diffusion scheme has been presented and made freely available by Landauer [162]. The main problem for the direct application of this model to the G-FET structure is the definition of the charge mobility value, that in a 2D material can be largely affected by the presence of impurities, lattice defects and substrate quality. A nice approach to this problem was recently described by Nastasi [163]. They describe extensively the physical and numerical model, including the model for the mobility and its dependence on the applied electric field, and the results obtained on a top gate configuration described by a 2D geometry.
The approach directed to modelling the behavior of the device when embedded in a more general circuit is of major importance when the target application is related to the sensing of some specific bio-element. From this point of view, the correlation between material properties and electrical behavior and output extraction is the main objective of any modelling task. The G-FET structure better suited for targeting the sensing of biomolecules (such as proteins and nucleic acids) in biological fluids, is the co-planar and liquid-immersed-gate configuration, which is effectively largely preferred in biological G-FET design. This configuration overcomes the standard top-gate or bottom-gate inherited by the flat panel semiconductor industry and presents a new challenge for modelling and simulation approach. The main results of this activity have the production of G-FET models suitable to be used in a circuit simulator, to support the fabrication of complete G-FET based circuit for biosensing applications. A dual gate G-FET model for circuit simulation, suitable to be used for biosensing use, was presented by Umoh. The main value of this model is the direct application in a SPICE implementation, in a traditional configuration settling on standard FET SPICE model parameters, used internally to calculate junction resistances and capacitances. Within this context, Jmai [164] presented a model freely distributed in its MATLAB and Verilog implementation, allowing the user to select an appropriate topology for a system-level design suitable to be used in real life applications. Once again, the charge mobilities are a main parameter that need to be assessed as a function of the fabrication condition. As already mentioned, considering the multiscale concept, these models at system level can be fed with results obtained from models at lower scales, in the specific case of GFETs for example to determine the dielectric properties that are required. In this way, the nanocomposite properties can be investigated and designed with MD or continuum models and these results can be introduced in the transistor model for device optimization.
As a matter of fact, from the biosensing point of view, it is possible to assume that the presence of the target bio-element on the graphene surface would be the main driving cause for the mobility fluctuation, and the correspondent variation of the drain current of the transistor. This observation focusses the modelling attention on a differential current extraction, targeting the information about the presence of the biomarkers, instead that the mobility value itself. The model for the dual gate configuration is directly extendible to the liquid gate configuration, and from a high-er-application-level approach, Fuente-Zapico has adapted the Synopsys Sentaurus Commercial TCAD suite for the simulation of a liquid gate graphene field effect transistor, GFET, used as antibody-based biosensor [165]. In this work the authors have successfully included the liquid electrolyte, the antibody functionalization of the graphene surface and the biomarkers trapping effects, reporting application driven parameters to the current-voltage characteristics, calculated in a standard commercial device-circuit simulator.
As a bottom line, it must be outlined that The Graphene Flagship’s 2D Experimental Pilot Line (2D-EPL), has been offering, starting in 2022, prototyping services to academics, SMEs and companies which can benefit from the progresses of graphene related materials integration with silicon [166]. The 2D-EPL provide in a multi-project wafer run (MPW) for G-FET circuit including a top/bottom contact with an optional local or global back and liquid gate. Directed to Bio/Gas/Chemical sensors this MPW include a stand-alone G-FET circuit as well as a fully CMOS integration.
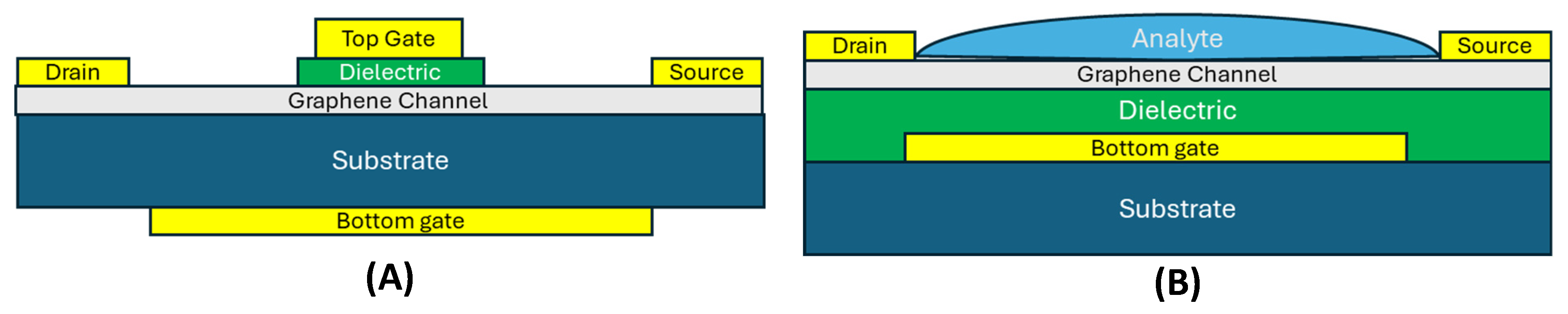
Preprints 120741 g006
Figure 5. G-FET in a typical dual gate configuration (A) and for biosensing application with the analyte in contact with the graphene layer (B). The application of a voltage at the liquid analyte permits a state-of-the-art dual liquid gate configuration.
Figure 5. G-FET in a typical dual gate configuration (A) and for biosensing application with the analyte in contact with the graphene layer (B). The application of a voltage at the liquid analyte permits a state-of-the-art dual liquid gate configuration.
Preprints 120741 g006

6. Conclusions

A review of different modelling strategies and methodologies used within the framework of carbon-based nanoparticles (graphene, carbon nanotubes—CNTs, nanofibers, etc.), and carbon-based nanomaterials (CNMs) and devices (as sensors) that can be obtained from these materials has been presented. The range of modelling and simulation techniques generally employed covers from electronic to continuum models, passing through atomistic and meso-scale. For each case, their typical uses, some of their weaknesses and strengths, and the latest developments are presented, including application examples and key references. Sometimes, multi-scale workflows are required, where these different models and scales are sequentially linked as part of a single analysis. Modelling devices require multi-physics models, integrating different phenomena that can be present simultaneously. Then, system type models are used. In this sense, the modelling of G-FET for sensing applications is included in this review, as specific example of carbon-based devices.
As regards the theoretical study of interactions of charged particles with graphene-based nanomaterials, a mathematical framework for studying such interactions uses various response functions of such materials as an input, which may be available from analytical phenomenological models, ab initio calculations, or even experimental data from optical spectroscopies. This allows various research groups to quickly develop reliable models for analyzing plasmonic properties of layered nanostructures including graphene, which can be used to predict the properties for novel designs of such structures.
Regarding molecular dynamics models, they are typically used to investigate various properties of CNMs at the atomistic scale, thus helping to predict their physico-chemical behavior and optimize their performance for specific applications. MD simulations can provide valuable insights into the thermomechanical properties of car-bon-based structures (e.g., thermal conductivity or elastic constants) and interface interactions in composite materials, yielding increasingly accurate results due to ongoing research efforts and the integration of data-driven approaches.
Continuum models include mainly analytical, semi-analytical and numerical approaches. Analytical models can be solved relatively quickly and often provide a clear and straightforward understanding of the underlying physics and insights into the relationships between different variables and parameters. However, sometimes they are limited in terms of the geometrical complexity that they can address. Numerical models can partially deal with these issues, but are constrained by their computational cost, size dependency of the results and restrictions in the development of RVEs with high inclusions volume concentrations and aspect ratios. Overall, good reproducibility of the properties of the materials are obtained especially at low nanoparticles concentrations, even for non-linear and time dependent responses, while at higher concentration more significant deviations are usually observed. This is generally explained due to interactions between the nanoparticles at high contents that produce non-homogeneous dispersions and agglomerations. For mechanical properties predictions in the non-linear regime or in terms of strength, it is generally seen that the results are strongly dependent on the particle/polymer interface representation and on the aspect ratios of the particles. Similar influences are also observed for other types of properties, such as thermal ones.
Finally, electrical behavior of G-FET, their analysis and design can be supported through Spice and Verilog models made freely available by the authors. The theoretical formulation of such models is available in literature and the main simulation software houses are starting to include them in their commercial packages. We can expect, for the next future, the introduction of integrated models, describing mechanical, thermal electrical and optical models, addressing the sensing applications where this class of devices can offer breakthrough solutions. Modelling techniques are powerful tools to support materials research in the development of novel applications, particularly in the case of carbon-based materials and their derived composites and devices. It provides the key information for identifying new materials, tailoring materials and/or design materials for structures and systems.

Author Contributions

Conceptualization, A.C., I.R., M.F and A.F.; Methodology, A.C., I.R., M.F and A.F.; Resources, A.C., I.R., M.F, M.Fe, M.L, A.K, M.P and A.F.; Writing—Original Draft Preparation, A.C., I.R., M.F, M.Fe, M.L, A.K, M.P and A.F.; Writing—Review & Editing, A.C., I.R., M.F, M.Fe, M.L, A.K, M.P and A.F.. All authors have read and agreed to the published version of the manuscript.

Funding

For the authors of affiliation1, the writing of the article has been done with the support of the European Regional Development Fund (ERDF). I.R. and A.K. acknowledge funding by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (Contract No. 451-03-66/2024-03/200017). For Authors of affiliation 4, 5 by the Portuguese FCT program, Center of Technology and Systems (CTS) UIDB/00066/2020/UIDP/00066/2020 and by FCT project ASER-META 2022.07694.PTDC.

Acknowledgments

This review has been elaborated with the support of the COST Action “High-performance Carbon-based composites with Smart properties for Advanced Sensing Applications” (EsSENce), with contract number CA19118. A.C. and M.L. acknowledge the support of the European Regional Development Fund (ERDF) for the article writing. I.R. and A.K. thank Professor Zoran L. Mišković for useful discussions and invaluable advice.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Commission), D.-G. for R. and I. (European; Baas, A.F. de What Makes a Material Function?: Let Me Compute the Ways : Modelling in H2020 LEIT NMBP Programme Materials and Nanotechnology Projects : Sixth Version; Publications Office of the European Union, 2017; ISBN 978-92-79-63185-6.
  2. Yan, H.; Li, X.; Chandra, B.; Tulevski, G.; Wu, Y.; Freitag, M.; Zhu, W.; Avouris, P.; Xia, F. Tunable Infrared Plasmonic Devices Using Graphene/Insulator Stacks. Nat. Nanotechnol. 2012, 7, 330–334. [Google Scholar] [CrossRef]
  3. Gomez-Diaz, J.S.; Moldovan, C.; Capdevila, S.; Romeu, J.; Bernard, L.S.; Magrez, A.; Ionescu, A.M.; Perruisseau-Carrier, J. Self-Biased Reconfigurable Graphene Stacks for Terahertz Plasmonics. Nat. Commun. 2015, 6, 6334. [Google Scholar] [CrossRef]
  4. Francescato, Y.; Giannini, V.; Yang, J.; Huang, M.; Maier, S.A. Graphene Sandwiches as a Platform for Broadband Molecular Spectroscopy. ACS Photonics 2014, 1, 437–443. [Google Scholar] [CrossRef]
  5. Ong, Z.-Y.; Fischetti, M.V. Theory of Interfacial Plasmon-Phonon Scattering in Supported Graphene. Phys. Rev. B 2012, 86, 165422. [Google Scholar] [CrossRef]
  6. Yan, H.; Low, T.; Zhu, W.; Wu, Y.; Freitag, M.; Li, X.; Guinea, F.; Avouris, P.; Xia, F. Damping Pathways of Mid-Infrared Plasmons in Graphene Nanostructures. Nat. Photonics 2013, 7, 394–399. [Google Scholar] [CrossRef]
  7. Fei, Z.; Andreev, G.O.; Bao, W.; Zhang, L.M.; McLeod, A.S.; Wang, C.; Stewart, M.K.; Zhao, Z.; Dominguez, G.; Thiemens, M.; et al. Infrared Nanoscopy of Dirac Plasmons at the Graphene–SiO2 Interface. Nano Lett. 2011, 11, 4701–4705. [Google Scholar] [CrossRef]
  8. Despoja, V.; Djordjević, T.; Karbunar, L.; Radović, I.; Mišković, Z.L. Ab Initio Study of the Electron Energy Loss Function in a Graphene-Sapphire-Graphene Composite System. Phys. Rev. B 2017, 96, 075433. [Google Scholar] [CrossRef]
  9. Ye, L.; Yuan, K.; Zhu, C.; Zhang, Y.; Zhang, Y.; Lai, K. Broadband High-Efficiency near-Infrared Graphene Phase Modulators Enabled by Metal–Nanoribbon Integrated Hybrid Plasmonic Waveguides. Nanophotonics 2022, 11, 613–623. [Google Scholar] [CrossRef]
  10. Yao, W.; Tang, L.; Nong, J.; Wang, J.; Yang, J.; Jiang, Y.; Shi, H.; Wei, X. Electrically Tunable Graphene Metamaterial with Strong Broadband Absorption. Nanotechnology 2021, 32, 075703. [Google Scholar] [CrossRef]
  11. Shiga, K.; Komiyama, T.; Fuse, Y.; Fukidome, H.; Sato, A.; Otsuji, T.; Uchino, T. Electrical Transport Properties of Gate Tunable Graphene Lateral Tunnel Diodes. Jpn. J. Appl. Phys. 2020, 59, SIID03. [Google Scholar] [CrossRef]
  12. Shirdel, M.; Mansouri-Birjandi, M.A. A Broadband Graphene Modulator Based on Plasmonic Valley-Slot Waveguide. Opt. Quant. Electron. 2020, 52, 36. [Google Scholar] [CrossRef]
  13. Shirdel, M.; Mansouri-Birjandi, M.A. Broadband Graphene Modulator Based on a Plus-Shaped Plasmonic Slot Waveguide. Appl. Opt. 2019, 58, 8174–8179. [Google Scholar] [CrossRef]
  14. Liu, M.; Yin, X.; Zhang, X. Double-Layer Graphene Optical Modulator. Nano Lett. 2012, 12, 1482–1485. [Google Scholar] [CrossRef]
  15. Allison, K.F.; Mišković, Z.L. Friction Force on Slow Charges Moving over Supported Graphene. Nanotechnology 2010, 21, 134017. [Google Scholar] [CrossRef]
  16. Marinković, T.; Radović, I.; Borka, D.; Mišković, Z.L. Probing the Plasmon-Phonon Hybridization in Supported Graphene by Externally Moving Charged Particles. Plasmonics 2015, 10, 1741–1749. [Google Scholar] [CrossRef]
  17. Despoja, V.; Radović, I.; Karbunar, L.; Kalinić, A.; Mišković, Z.L. Wake Potential in Graphene-Insulator-Graphene Composite Systems. Phys. Rev. B 2019, 100, 035443. [Google Scholar] [CrossRef]
  18. Kalinić, A.; Radović, I.; Karbunar, L.; Despoja, V.; Mišković, Z.L. Wake Effect in Interactions of Ions with Graphene-Sapphire-Graphene Composite System. Phys. E 2021, 126, 114447. [Google Scholar] [CrossRef]
  19. Kalinić, A.; Despoja, V.; Radović, I.; Karbunar, L.; Mišković, Z.L. Stopping and Image Forces Acting on a Charged Particle Moving near a Graphene-Al2O3-Graphene Heterostructure. Phys. Rev. B 2022, 106, 115430. [Google Scholar] [CrossRef]
  20. Radović, I.; Hadžievski, Lj.; Bibić, N.; Mišković, Z.L. Dynamic-Polarization Forces on Fast Ions and Molecules Moving over Supported Graphene. Phys. Rev. A 2007, 76, 042901. [Google Scholar] [CrossRef]
  21. Radović, I.; Hadžievski, Lj.; Mišković, Z.L. Polarization of Supported Graphene by Slowly Moving Charges. Phys. Rev. B 2008, 77, 075428. [Google Scholar] [CrossRef]
  22. Gumbs, G.; Huang, D.; Echenique, P.M. Comparing the Image Potentials for Intercalated Graphene with a Two-Dimensional Electron Gas with and without a Gated Grating. Phys. Rev. B 2009, 79, 035410. [Google Scholar] [CrossRef]
  23. Allison, K.F.; Borka, D.; Radović, I.; Hadžievski, Lj.; Mišković, Z.L. Dynamic Polarization of Graphene by Moving External Charges: Random Phase Approximation. Phys. Rev. B 2009, 80, 195405. [Google Scholar] [CrossRef]
  24. Radović, I.; Borka, D.; Mišković, Z.L. Wake Effect in Doped Graphene Due to Moving External Charge. Phys. Lett. A 2011, 375, 3720–3725. [Google Scholar] [CrossRef]
  25. Gumbs, G.; Roslyak, O.; Huang, D.; Balassis, A. Spectroscopic Characterization of Gapped Graphene in the Presence of Circularly Polarized Light. J. Mod. Opt. 2011, 58, 1990–1996. [Google Scholar] [CrossRef]
  26. Borka, D.; Radović, I.; Mišković, Z.L. Dynamic Polarization of Graphene by Moving External Charges: Comparison with 2D Electron Gas. Nucl. Instrum. Methods B 2011, 269, 1225–1228. [Google Scholar] [CrossRef]
  27. Despoja, V.; Dekanić, K.; Šunjić, M.; Marušić, L. Ab Initio Study of Energy Loss and Wake Potential in the Vicinity of a Graphene Monolayer. Phys. Rev. B 2012, 86, 165419. [Google Scholar] [CrossRef]
  28. Radović, I.; Borka, D.; Mišković, Z.L. Dynamic Polarization of Graphene by External Correlated Charges. Phys. Rev. B 2012, 86, 125442. [Google Scholar] [CrossRef]
  29. Radović, I.; Borka Jovanović, V.; Borka, D.; Mišković, Z.L. Interactions of Slowly Moving Charges with Graphene: The Role of Substrate Phonons. Nucl. Instrum. Methods B 2012, 279, 165–168. [Google Scholar] [CrossRef]
  30. Radović, I.; Borka, D.; Mišković, Z.L. Wake Effect in Interactions of Dipolar Molecules with Doped Graphene. Phys. Lett. A 2013, 377, 2614–2620. [Google Scholar] [CrossRef]
  31. Marinković, T.; Radović, I.; Borka, D.; Mišković, Z.L. Wake Effect in the Interaction of Slow Correlated Charges with Supported Graphene Due to Plasmon–Phonon Hybridization. Phys. Lett. A 2015, 379, 377–381. [Google Scholar] [CrossRef]
  32. Shi, X.; Lin, X.; Gao, F.; Xu, H.; Yang, Z.; Zhang, B. Caustic Graphene Plasmons with Kelvin Angle. Phys. Rev. B 2015, 92, 081404. [Google Scholar] [CrossRef]
  33. Chaves, A.J.; Peres, N.M.R.; Smirnov, G.; Mortensen, N.A. Hydrodynamic Model Approach to the Formation of Plasmonic Wakes in Graphene. Phys. Rev. B 2017, 96, 195438. [Google Scholar] [CrossRef]
  34. Kolomeisky, E.B.; Straley, J.P. Kelvin-Mach Wake in a Two-Dimensional Fermi Sea. Phys. Rev. Lett. 2018, 120, 226801. [Google Scholar] [CrossRef] [PubMed]
  35. Zhang, Y.; Jiang, W. Pseudomagnetic Field Modulation of Stopping Power for a Charged Particle Moving above Graphene. Phys. Plasmas 2018, 25, 072107. [Google Scholar] [CrossRef]
  36. Li, M.; Qu, G.-F.; Wang, Y.-Z.; Zhu, Z.-S.; Shi, M.-G.; Zhou, M.-L.; Liu, D.; Xu, Z.-X.; Song, M.-J.; Zhang, J.; et al. Interaction of H2+ Molecular Beam with Thin Layer Graphene Foils. Chin. Phys. B 2019, 28, 093401. [Google Scholar] [CrossRef]
  37. He, X.-L.; Zhang, Y.-Y.; Mišković, Z.L.; Radović, I.; Li, C.-Z.; Song, Y.-H. Interactions of Moving Charge with Supported Graphene in the Presence of Strain-Induced Pseudomagnetic Field. Eur. Phys. J. D 2020, 74, 18. [Google Scholar] [CrossRef]
  38. Bai, X.-J.; Zhang, Y.-Y.; Mišković, Z.L.; Radović, I.; Li, C.-Z.; Song, Y.-H. The Effects of Pseudomagnetic Fields on Plasmon–Phonon Hybridization in Supported Graphene Probed by a Moving Charged Particle. Plasmonics 2021, 16, 1089–1098. [Google Scholar] [CrossRef]
  39. Preciado Rivas, M.R.; Moshayedi, M.; Mišković, Z.L. On the Role of the Energy Loss Function in the Image Force on a Charge Moving over Supported Graphene. J. Appl. Phys. 2021, 130, 173103. [Google Scholar] [CrossRef]
  40. Mylnikov, D.A.; Kashchenko, M.A.; Kapralov, K.N.; Ghazaryan, D.A.; Vdovin, E.E.; Morozov, S.V.; Novoselov, K.S.; Bandurin, D.A.; Chernov, A.I.; Svintsov, D.A. Infrared Photodetection in Graphene-Based Heterostructures: Bolometric and Thermoelectric Effects at the Tunneling Barrier. npj 2D Mater. Appl. 2024, 8, 34. [Google Scholar] [CrossRef]
  41. Abdelsalam, H.; Sakr, M.A.S.; Teleb, N.H.; Abd-Elkader, O.H.; Zhilong, W.; Liu, Y.; Zhang, Q. Highly Efficient Spin Field-Effect Transistor Based on Nanographene and hBN Heterostructures: Spintronic and Quantum Transport Properties. Chin. J. Phys. 2024, 90, 237–251. [Google Scholar] [CrossRef]
  42. Khanin, Yu.N.; Vdovin, E.E.; Morozov, S.V.; Novoselov, K.S. Coulomb Correlation Gap at Magnetic Tunneling between Graphene Layers. JETP Lett. 2023, 118, 433–438. [Google Scholar] [CrossRef]
  43. Tian, B.; Li, J.; Chen, M.; Dong, H.; Zhang, X. Synthesis of AAB-Stacked Single-Crystal Graphene/hBN/Graphene Trilayer van Der Waals Heterostructures by In Situ CVD. Adv. Sci. 2022, 9, 2201324. [Google Scholar] [CrossRef] [PubMed]
  44. Lu, L.; Zhang, B.; Ou, H.; Li, B.; Zhou, K.; Song, J.; Luo, Z.; Cheng, Q. Enhanced Near-Field Radiative Heat Transfer between Graphene/hBN Systems. Small 2022, 18, 2108032. [Google Scholar] [CrossRef] [PubMed]
  45. Hu, C.; Deng, A.; Shen, P.; Luo, X.; Zhou, X.; Wu, T.; Huang, X.; Dong, Y.; Watanabe, K.; Taniguchi, T.; et al. Direct Imaging of Interlayer-Coupled Symmetric and Antisymmetric Plasmon Modes in Graphene/hBN/Graphene Heterostructures. Nanoscale 2021, 13, 14628–14635. [Google Scholar] [CrossRef]
  46. Song, S.-B.; Yoon, S.; Kim, S.Y.; Yang, S.; Seo, S.-Y.; Cha, S.; Jeong, H.-W.; Watanabe, K.; Taniguchi, T.; Lee, G.-H.; et al. Deep-Ultraviolet Electroluminescence and Photocurrent Generation in Graphene/hBN/Graphene Heterostructures. Nat. Commun. 2021, 12, 7134. [Google Scholar] [CrossRef]
  47. Wang, L.; Liu, J.; Ren, B.; Song, J.; Jiang, Y. Tuning of Mid-Infrared Absorption through Phonon-Plasmon-Polariton Hybridization in a Graphene/hBN/Graphene Nanodisk Array. Opt. Express 2021, 29, 2288–2298. [Google Scholar] [CrossRef]
  48. Cheng, X.; Zhou, X.; Tao, L.; Yu, W.; Liu, C.; Cheng, Y.; Ma, C.; Shang, N.; Xie, J.; Liu, K.; et al. Sandwiched Graphene/hBN/Graphene Photonic Crystal Fibers with High Electro-Optical Modulation Depth and Speed. Nanoscale 2020, 12, 14472–14478. [Google Scholar] [CrossRef]
  49. Golenić, N.; de Gironcoli, S.; Despoja, V. Optically Driven Plasmons in Graphene/hBN van Der Waals Heterostructures: Simulating s-SNOM Measurements. Nanophotonics 2024, 13, 2765–2780. [Google Scholar] [CrossRef]
  50. Golenić, N.; de Gironcoli, S.; Despoja, V. Tailored Plasmon Polariton Landscape in Graphene/Boron Nitride Patterned Heterostructures. npj 2D Mater. Appl. 2024, 8, 37. [Google Scholar] [CrossRef]
  51. Rossi, A.W.; Bourgeois, M.R.; Walton, C.; Masiello, D.J. Probing the Polarization of Low-Energy Excitations in 2D Materials from Atomic Crystals to Nanophotonic Arrays Using Momentum-Resolved Electron Energy Loss Spectroscopy. Nano Lett. 2024, 24, 7748–7756. [Google Scholar] [CrossRef]
  52. Govyadinov, A.A.; Konečná, A.; Chuvilin, A.; Vélez, S.; Dolado, I.; Nikitin, A.Y.; Lopatin, S.; Casanova, F.; Hueso, L.E.; Aizpurua, J.; et al. Probing Low-Energy Hyperbolic Polaritons in van Der Waals Crystals with an Electron Microscope. Nat. Commun. 2017, 8, 95. [Google Scholar] [CrossRef]
  53. Roslyak, O.; Gumbs, G.; Huang, D. Energy Loss Spectroscopy of Epitaxial versus Free-Standing Multilayer Graphene. Phys. E 2012, 44, 1874–1884. [Google Scholar] [CrossRef]
  54. Borka Jovanović, V.; Radović, I.; Borka, D.; Mišković, Z.L. High-Energy Plasmon Spectroscopy of Freestanding Multilayer Graphene. Phys. Rev. B 2011, 84, 155416. [Google Scholar] [CrossRef]
  55. Wachsmuth, P.; Hambach, R.; Kinyanjui, M.K.; Guzzo, M.; Benner, G.; Kaiser, U. High-Energy Collective Electronic Excitations in Free-Standing Single-Layer Graphene. Phys. Rev. B 2013, 88, 075433. [Google Scholar] [CrossRef]
  56. Wachsmuth, P.; Hambach, R.; Benner, G.; Kaiser, U. Plasmon Bands in Multilayer Graphene. Phys. Rev. B 2014, 90, 235434. [Google Scholar] [CrossRef]
  57. Djordjević, T.; Radović, I.; Despoja, V.; Lyon, K.; Borka, D.; Mišković, Z.L. Analytical Modeling of Electron Energy Loss Spectroscopy of Graphene: Ab Initio Study versus Extended Hydrodynamic Model. Ultramicroscopy 2018, 184, 134–142. [Google Scholar] [CrossRef]
  58. Radović, I.; Borka, D.; Mišković, Z.L. Theoretical Modeling of Experimental HREEL Spectra for Supported Graphene. Phys. Lett. A 2014, 378, 2206–2210. [Google Scholar] [CrossRef]
  59. Politano, A.; Radović, I.; Borka, D.; Mišković, Z.L.; Chiarello, G. Interband Plasmons in Supported Graphene on Metal Substrates: Theory and Experiments. Carbon 2016, 96, 91–97. [Google Scholar] [CrossRef]
  60. Politano, A.; Radović, I.; Borka, D.; Mišković, Z.L.; Yu, H.K.; Farías, D.; Chiarello, G. Dispersion and Damping of the Interband π Plasmon in Graphene Grown on Cu (111) Foils. Carbon 2017, 114, 70–76. [Google Scholar] [CrossRef]
  61. Despoja, V.; Radović, I.; Politano, A.; Mišković, Z.L. Insights on the Excitation Spectrum of Graphene Contacted with a Pt Skin. Nanomaterials 2020, 10, 703. [Google Scholar] [CrossRef]
  62. Chi, J.; Zhao, X.; Wang, L.; Yang, Z. Polymer-Integrated Acoustic Graphene Plasmon Resonator for Sensitive Detection of CO2 Gas. J. Phys. D: Appl. Phys. 2024, 57, 335102. [Google Scholar] [CrossRef]
  63. Wu, Z.; Xu, Z. Understanding and Probing of Sub-Femtometer Resolutions Utilizing Acoustic Plasmon Resonances in Graphene-Dielectric-Metal Hybrid-Structures. Opt. Laser Technol. 2023, 162, 109305. [Google Scholar] [CrossRef]
  64. Marušić, L.; Kalinić, A.; Radović, I.; Jakovac, J.; Mišković, Z.L.; Despoja, V. Resolving the Mechanism of Acoustic Plasmon Instability in Graphene Doped by Alkali Metals. Int. J. Mol. Sci. 2022, 23, 4770. [Google Scholar] [CrossRef] [PubMed]
  65. Zhu, C.; Du, D.; Lin, Y. Graphene and Graphene-like 2D Materials for Optical Biosensing and Bioimaging: A Review. 2D Mater. 2015, 2, 032004. [Google Scholar] [CrossRef]
  66. Zhu, A.Y.; Cubukcu, E. Graphene nanophotonic sensors. 2D Mater. 2015, 2, 032005. [Google Scholar] [CrossRef]
  67. Allen, M.P. Introduction to Molecular Dynamics Simulation; NIC series; John von Neumann Institute for Computing: Jülich, 2004; ISBN 978-3-00-012641-3. [Google Scholar]
  68. Torkaman-Asadi, M.A.; Kouchakzadeh, M.A. Atomistic Simulations of Mechanical Properties and Fracture of Graphene: A Review. Computational Materials Science 2022, 210, 111457. [Google Scholar] [CrossRef]
  69. Qian, C.; McLean, B.; Hedman, D.; Ding, F. A Comprehensive Assessment of Empirical Potentials for Carbon Materials. APL Materials 2021, 9, 061102. [Google Scholar] [CrossRef]
  70. Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A Reactive Potential for Hydrocarbons with Intermolecular Interactions. The Journal of Chemical Physics 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
  71. Tersoff, J. Empirical Interatomic Potential for Carbon, with Applications to Amorphous Carbon. Phys. Rev. Lett. 1988, 61, 2879–2882. [Google Scholar] [CrossRef]
  72. Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF Potential for Carbon Condensed Phases and Its Application to the Thermal Fragmentation of a Large Fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef]
  73. Deringer, V.L.; Csányi, G. Machine Learning Based Interatomic Potential for Amorphous Carbon. Phys. Rev. B 2017, 95, 094203. [Google Scholar] [CrossRef]
  74. Wen, M.; Tadmor, E.B. Hybrid Neural Network Potential for Multilayer Graphene. Phys. Rev. B 2019, 100, 195419. [Google Scholar] [CrossRef]
  75. Rowe, P.; Deringer, V.L.; Gasparotto, P.; Csányi, G.; Michaelides, A. An Accurate and Transferable Machine Learning Potential for Carbon. The Journal of Chemical Physics 2020, 153, 034702. [Google Scholar] [CrossRef] [PubMed]
  76. Kovács, D.P.; Moore, J.H.; Browning, N.J.; Batatia, I.; Horton, J.T.; Kapil, V.; Witt, W.C.; Magdău, I.-B.; Cole, D.J.; Csányi, G. MACE-OFF23: Transferable Machine Learning Force Fields for Organic Molecules 2023.
  77. Srivastava, R.; Fasano, M.; Nejad, S.M.; Thielemann, H.C.; Chiavazzo, E.; Asinari, P. 3 Modeling Carbon-Based Smart Materials. In Carbon-Based Smart Materials; Charitidis, C.A., Koumoulos, E.P., Dragatogiannis, D.A., Eds.; De Gruyter, 2020; pp. 33–80 ISBN 978-3-11-047913-3.
  78. Sáenz Ezquerro, C.; Laspalas, M.; García Aznar, J.M.; Castelar Ariza, S.; Chiminelli, A. Molecular Modelling of Graphene Nanoribbons on the Effect of Porosity and Oxidation on the Mechanical and Thermal Properties. J Mater Sci 2023, 58, 13295–13316. [Google Scholar] [CrossRef]
  79. Li, Y.; Wang, Q.; Wang, S. A Review on Enhancement of Mechanical and Tribological Properties of Polymer Composites Reinforced by Carbon Nanotubes and Graphene Sheet: Molecular Dynamics Simulations. Composites Part B: Engineering. [CrossRef]
  80. Zhang, X.; Chen, Z.; Lu, L.; Wang, J. Molecular Dynamics Simulations of the Mechanical Properties of Cellulose Nanocrystals—Graphene Layered Nanocomposites. Nanomaterials 2022, 12, 4170. [Google Scholar] [CrossRef]
  81. Zang, J.-L.; Yuan, Q.; Wang, F.-C.; Zhao, Y.-P. A Comparative Study of Young’s Modulus of Single-Walled Carbon Nanotube by CPMD, MD and First Principle Simulations. Computational Materials Science 2009, 46, 621–625. [Google Scholar] [CrossRef]
  82. Kirca, M.; To, A.C. Mechanics of CNT Network Materials. In Advanced Computational Nanomechanics; John Wiley & Sons, Ltd., 2016; pp. 29–70 ISBN 978-1-119-06892-1.
  83. Patil, S.P. Nanoindentation of Graphene-Reinforced Silica Aerogel: A Molecular Dynamics Study. Molecules 2019, 24, 1336. [Google Scholar] [CrossRef]
  84. Huang, F.; Zhou, S. Molecular Dynamics Simulation of Coiled Carbon Nanotube Pull-Out from Matrix. International Journal of Molecular Sciences 2022, 23, 9254. [Google Scholar] [CrossRef]
  85. Sáenz Ezquerro, C.; Laspalas, M.; Chiminelli, A.; Serrano, F.; Valero, C. Interface Characterization of Epoxy Resin Nanocomposites: A Molecular Dynamics Approach. Fibers 2018, 6, 54. [Google Scholar] [CrossRef]
  86. Mohammad Nejad, S.; Srivastava, R.; Bellussi, F.M.; Chávez Thielemann, H.; Asinari, P.; Fasano, M. Nanoscale Thermal Properties of Carbon Nanotubes/Epoxy Composites by Atomistic Simulations. International Journal of Thermal Sciences 2021, 159, 106588. [Google Scholar] [CrossRef]
  87. Bigdeli, M.B.; Fasano, M. Thermal Transmittance in Graphene Based Networks for Polymer Matrix Composites. International Journal of Thermal Sciences 2017, 117, 98–105. [Google Scholar] [CrossRef]
  88. Fasano, M.; Bozorg Bigdeli, M.; Vaziri Sereshk, M.R.; Chiavazzo, E.; Asinari, P. Thermal Transmittance of Carbon Nanotube Networks: Guidelines for Novel Thermal Storage Systems and Polymeric Material of Thermal Interest. Renewable and Sustainable Energy Reviews 2015, 41, 1028–1036. [Google Scholar] [CrossRef]
  89. Bellussi, F.M.; Sáenz Ezquerro, C.; Laspalas, M.; Chiminelli, A. Effects of Graphene Oxidation on Interaction Energy and Interfacial Thermal Conductivity of Polymer Nanocomposite: A Molecular Dynamics Approach. Nanomaterials 2021, 11, 1709. [Google Scholar] [CrossRef]
  90. Evans, W.J.; Hu, L.; Keblinski, P. Thermal Conductivity of Graphene Ribbons from Equilibrium Molecular Dynamics: Effect of Ribbon Width, Edge Roughness, and Hydrogen Termination. Applied Physics Letters 2010, 96, 203112. [Google Scholar] [CrossRef]
  91. Dias, F.S.; Machado, W.S. The Effects of Computational Time Parameter in the Thermal Conductivity of Single-Walled Carbon Nanotubes by Molecular Dynamics Simulation. Computational Condensed Matter 2018, 15, 21–24. [Google Scholar] [CrossRef]
  92. Casto, A.; Vittucci, M.; Vialla, F.; Crut, A.; Bellussi, F.M.; Fasano, M.; Vallée, F.; Del Fatti, N.; Banfi, F.; Maioli, P. Experimental Optical Retrieval of the Thermal Boundary Resistance of Carbon Nanotubes in Water. Carbon 2024, 229, 119445. [Google Scholar] [CrossRef]
  93. Chen, J.; Xu, X.; Zhou, J.; Li, B. Interfacial Thermal Resistance: Past, Present, and Future. Rev. Mod. Phys. 2022, 94, 025002. [Google Scholar] [CrossRef]
  94. Casto, A.; Bellussi, F.M.; Diego, M.; Del Fatti, N.; Banfi, F.; Maioli, P.; Fasano, M. Water Filling in Carbon Nanotubes with Different Wettability and Implications on Nanotube/Water Heat Transfer via Atomistic Simulations. International Journal of Heat and Mass Transfer 2023, 205, 123868. [Google Scholar] [CrossRef]
  95. Leroy, F.; Liu, S.; Zhang, J. Parametrizing Nonbonded Interactions from Wetting Experiments via the Work of Adhesion: Example of Water on Graphene Surfaces. J. Phys. Chem. C 2015, 119, 28470–28481. [Google Scholar] [CrossRef]
  96. Bellussi, F.M.; Roscioni, O.M.; Rossi, E.; Cardellini, A.; Provenzano, M.; Persichetti, L.; Kudryavtseva, V.; Sukhorukov, G.; Asinari, P.; Sebastiani, M.; et al. Wettability of Soft PLGA Surfaces Predicted by Experimentally Augmented Atomistic Models. MRS Bulletin 2023, 48, 108–117. [Google Scholar] [CrossRef]
  97. Provenzano, M.; Bellussi, F.M.; Morciano, M.; Asinari, P.; Fasano, M. Method for Predicting the Wettability of Micro-Structured Surfaces by Continuum Phase-Field Modelling. MethodsX 2023, 11, 102458. [Google Scholar] [CrossRef] [PubMed]
  98. Bamane, S.S.; Gaikwad, P.S.; Radue, M.S.; Gowtham, S.; Odegard, G.M. Wetting Simulations of High-Performance Polymer Resins on Carbon Surfaces as a Function of Temperature Using Molecular Dynamics. Polymers 2021, 13, 2162. [Google Scholar] [CrossRef]
  99. Xu, K.; Zhang, J.; Hao, X.; Zhang, C.; Wei, N.; Zhang, C. Wetting Properties of Defective Graphene Oxide: A Molecular Simulation Study. Molecules 2018, 23, 1439. [Google Scholar] [CrossRef]
  100. Griffo, R.; Di Natale, F.; Minale, M.; Sirignano, M.; Parisi, A.; Carotenuto, C. Analysis of Carbon Nanoparticle Coatings via Wettability. Nanomaterials 2024, 14, 301. [Google Scholar] [CrossRef] [PubMed]
  101. Yang, X. D. , Chen, W., Ren, Y., & Chu, L. Y. Exploring dielectric spectra of polymer through molecular dynamics simulations. Molecular Simulation 2022, 48, 935–943. [Google Scholar] [CrossRef]
  102. Manolis, G.D.; Dineva, P.S.; Rangelov, T.; Sfyris, D. Mechanical Models and Numerical Simulations in Nanomechanics: A Review across the Scales. Engineering Analysis with Boundary Elements 2021, 128, 149–170. [Google Scholar] [CrossRef]
  103. Chmiela, S.; Sauceda, H.E.; Müller, K.-R.; Tkatchenko, A. Towards Exact Molecular Dynamics Simulations with Machine-Learned Force Fields. Nat Commun. 2018, 9, 3887. [Google Scholar] [CrossRef]
  104. Yang, J.Z.; Li, X. Comparative Study of Boundary Conditions for Molecular Dynamics Simulations of Solids at Low Temperature. Phys. Rev. B 2006, 73, 224111. [Google Scholar] [CrossRef]
  105. Koyanagi, J.; Takase, N.; Mori, K.; Sakai, T. Molecular Dynamics Simulation for the Quantitative Prediction of Experimental Tensile Strength of a Polymer Material. Composites Part C, 2020; 2. [Google Scholar] [CrossRef]
  106. Ciccotti, G.; Dellago, C.; Ferrario, M.; Hernández, E.R.; Tuckerman, M.E. Molecular Simulations: Past, Present, and Future (a Topical Issue in EPJB). Eur. Phys. J. B 2022, 95, 3. [Google Scholar] [CrossRef]
  107. Muhammad, A.; Srivastava, R.; Koutroumanis, N.; Semitekolos, D.; Chiavazzo, E.; Pappas, P.-N.; Galiotis, C.; Asinari, P.; Charitidis, C.A.; Fasano, M. Mesoscopic Modeling and Experimental Validation of Thermal and Mechanical Properties of Polypropylene Nanocomposites Reinforced By Graphene-Based Fillers. Macromolecules 2023, 56, 9969–9982. [Google Scholar] [CrossRef]
  108. Wang, Y.; Huang, Z. Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study. Materials 2018, 11, 1919. [Google Scholar] [CrossRef] [PubMed]
  109. Bahei-El-Din, Y.A. 1.17 Multiscale Mechanics of Composite Materials and Structures. In Comprehensive Composite Materials II; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier: Oxford, 2018; ISBN 978-0-08-100534-7. [Google Scholar]
  110. Elmasry, A.; Azoti, W.; El-Safty, S.A.; Elmarakbi, A. A Comparative Review of Multiscale Models for Effective Properties of Nano- and Micro-Composites. Progress in Materials Science 2023, 132, 101022. [Google Scholar] [CrossRef]
  111. Shokrieh, M.M.; Esmkhani, M.; Shokrieh, Z.; Zhao, Z. Stiffness Prediction of Graphene Nanoplatelet/Epoxy Nanocomposites by a Combined Molecular Dynamics–Micromechanics Method. Computational Materials Science 2014, 92, 444–450. [Google Scholar] [CrossRef]
  112. Laspalas, M.; Chiminelli, A.; Sáenz-Ezquerro, C.; Serrano, F.; Valero, C. Analysis of the Elastic Properties of CNTs and Their Effect in Polymer Nanocomposites. MATEC Web of Conferences 2018, 188, 01018. [Google Scholar] [CrossRef]
  113. Singh, A.; Kumar, D. Effect of Functionalization on the Elastic Behavior of Graphene Nanoplatelet-PE Nanocomposites with Interface Consideration Using a Multiscale Approach. Mechanics of Materials 2019, 132, 18–30. [Google Scholar] [CrossRef]
  114. Shin, D.; Jeon, I.; Yang, S. Multiscale Modeling Assessment of the Interfacial Properties and Critical Aspect Ratio of Structurally Defected Graphene in Polymer Nanocomposites for Defect Engineering. European Journal of Mechanics—A/Solids, 1047. [Google Scholar] [CrossRef]
  115. Nafar Dastgerdi, J.; Marquis, G.; Salimi, M. Micromechanical Modeling of Nanocomposites Considering Debonding and Waviness of Reinforcements. Composite Structures 2014, 110, 1–6. [Google Scholar] [CrossRef]
  116. Azoti, W.; Elmarakbi, A. Constitutive Modelling of Ductile Damage Matrix Reinforced by Platelets-like Particles with Imperfect Interfaces: Application to Graphene Polymer Nanocomposite Materials. Composites Part B: Engineering. [CrossRef]
  117. Shajari, A.R.; Ghajar, R.; Shokrieh, M.M. Multiscale Modeling of the Viscoelastic Properties of CNT/Polymer Nanocomposites, Using Complex and Time-Dependent Homogenizations. Computational Materials Science 2018, 142, 395–409. [Google Scholar] [CrossRef]
  118. Hassanzadeh-Aghdam, M.K. Evaluating the Effective Creep Properties of Graphene-Reinforced Polymer Nanocomposites by a Homogenization Approach. Composites Science and Technology 2021, 209, 108791. [Google Scholar] [CrossRef]
  119. Shao, J.; Zhou, L.; Chen, Y.; Liu, X.; Ji, M. Model-Based Dielectric Constant Estimation of Polymeric Nanocomposite. Polymers 2022, 14, 1121. [Google Scholar] [CrossRef]
  120. Young, R.J.; Kinloch, I.A.; Gong, L.; Novoselov, K.S. The Mechanics of Graphene Nanocomposites: A Review. Composites Science and Technology 2012, 72, 1459–1476. [Google Scholar] [CrossRef]
  121. Weon, J.-I.; Sue, H.-J. Effects of Clay Orientation and Aspect Ratio on Mechanical Behavior of Nylon-6 Nanocomposite. Polymer 2005, 46, 6325–6334. [Google Scholar] [CrossRef]
  122. Chong, H.M.; Hinder, S.J.; Taylor, A.C. Graphene Nanoplatelet-Modified Epoxy: Effect of Aspect Ratio and Surface Functionality on Mechanical Properties and Toughening Mechanisms. J Mater Sci 2016, 51, 8764–8790. [Google Scholar] [CrossRef]
  123. Alasvand Zarasvand, K.; Golestanian, H. Investigating the Effects of Number and Distribution of GNP Layers on Graphene Reinforced Polymer Properties: Physical, Numerical and Micromechanical Methods. Composites Science and Technology 2017, 139, 117–126. [Google Scholar] [CrossRef]
  124. Yang, M.; Li, W.; Zhao, Z.; He, Y.; Zhang, X.; Ma, Y.; Dong, P.; Zheng, S. Micromechanical Modeling for the Temperature-Dependent Yield Strength of Polymer-Matrix Nanocomposites. Composites Science and Technology 2022, 220, 109265. [Google Scholar] [CrossRef]
  125. Doghri, I.; Ouaar, A. Homogenization of Two-Phase Elasto-Plastic Composite Materials and Structures: Study of Tangent Operators, Cyclic Plasticity and Numerical Algorithms. International Journal of Solids and Structures 2003, 40, 1681–1712. [Google Scholar] [CrossRef]
  126. Wu, L.; Doghri, I.; Noels, L. An Incremental-Secant Mean-Field Homogenization Method with Second Statistical Moments for Elasto-Plastic Composite Materials. Philosophical Magazine 2015, 95, 3348–3384. [Google Scholar] [CrossRef]
  127. Dvorak, G.J. Transformation Field Analysis of Inelastic Composite Materials. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences. [CrossRef]
  128. Dvorak, G.J.; Benveniste, Y. On Transformation Strains and Uniform Fields in Multiphase Elastic Media. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences. [CrossRef]
  129. Khattab, I.Al.; Sinapius, M. Multiscale Modelling and Simulation of Polymer Nanocomposites Using Transformation Field Analysis (TFA). Composite Structures 2019, 209, 981–991. [Google Scholar] [CrossRef]
  130. Pontefisso, A.; Mishnaevsky, L. Nanomorphology of Graphene and CNT Reinforced Polymer and Its Effect on Damage: Micromechanical Numerical Study. Composites Part B: Engineering. [CrossRef]
  131. Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the Size of the Representative Volume Element for Random Composites: Statistical and Numerical Approach. International Journal of Solids and Structures 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
  132. Chen, X.L.; Liu, Y.J. Square Representative Volume Elements for Evaluating the Effective Material Properties of Carbon Nanotube-Based Composites. Computational Materials Science 2004, 29, 1–11. [Google Scholar] [CrossRef]
  133. Liu, Y.J.; Chen, X.L. Evaluations of the Effective Material Properties of Carbon Nanotube-Based Composites Using a Nanoscale Representative Volume Element. Mechanics of Materials 2003, 35, 69–81. [Google Scholar] [CrossRef]
  134. Chwał, M.; Muc, A. Transversely Isotropic Properties of Carbon Nanotube/Polymer Composites. Composites Part B: Engineering. [CrossRef]
  135. Chwał, M. Numerical Evaluation of Effective Material Constants for CNT-Based Polymeric Nanocomposites. Advanced Materials Research 2014, 849, 88–93. [Google Scholar] [CrossRef]
  136. Barakat, M.; Reda, H.; Chazirakis, A.; Harmandaris, V. Investigating the Mechanical Performance of Graphene Reinforced Polymer Nanocomposites via Atomistic and Continuum Simulation Approaches. Polymer 2023, 286, 126379. [Google Scholar] [CrossRef]
  137. Muhammad, A.; Sáenz Ezquerro, C.; Srivastava, R.; Asinari, P.; Laspalas, M.; Chiminelli, A.; Fasano, M. Atomistic to Mesoscopic Modelling of Thermophysical Properties of Graphene-Reinforced Epoxy Nanocomposites. Nanomaterials 2023, 13, 1960. [Google Scholar] [CrossRef]
  138. Malagù, M.; Goudarzi, M.; Lyulin, A.; Benvenuti, E.; Simone, A. Diameter-Dependent Elastic Properties of Carbon Nanotube-Polymer Composites: Emergence of Size Effects from Atomistic-Scale Simulations. Composites Part B: Engineering. [CrossRef]
  139. Yuan, Z.; Lu, Z. Numerical Analysis of Elastic–Plastic Properties of Polymer Composite Reinforced by Wavy and Random CNTs. Computational Materials Science 2014, 95, 610–619. [Google Scholar] [CrossRef]
  140. Alasvand Zarasvand, K.; Golestanian, H. Determination of Nonlinear Behavior of Multi-Walled Carbon Nanotube Reinforced Polymer: Experimental, Numerical, and Micromechanical. Materials & Design 2016, 109, 314–323. [CrossRef]
  141. Gai, W.; Zhang, R.; Guo, R. Two-Scale Modeling of Composites Damage with Voronoi Cell Finite Element Method for Microscale Computation. Composite Structures 2022, 291, 115659. [Google Scholar] [CrossRef]
  142. Ghosh, S.; Lee, K.; Moorthy, S. Multiple Scale Analysis of Heterogeneous Elastic Structures Using Homogenization Theory and Voronoi Cell Finite Element Method. International Journal of Solids and Structures 1995, 32, 27–62. [Google Scholar] [CrossRef]
  143. Pineda, E.J.; Bednarcyk, B.A.; Waas, A.M.; Arnold, S.M. Progressive Failure of a Unidirectional Fiber-Reinforced Composite Using the Method of Cells: Discretization Objective Computational Results. International Journal of Solids and Structures 2013, 50, 1203–1216. [Google Scholar] [CrossRef]
  144. Cavalcante, M.A.A.; Pindera, M.-J. Finite-Volume Enabled Transformation Field Analysis of Periodic Materials. Int. J. Mech. Mater. Des. 2013, 9, 153–179. [Google Scholar] [CrossRef]
  145. Cavalcante, M.A.A.; Pindera, M.-J. Generalized FVDAM Theory for Elastic–Plastic Periodic Materials. International Journal of Plasticity 2016, 77, 90–117. [Google Scholar] [CrossRef]
  146. Cavalcante, M.A.A.; Khatam, H.; Pindera, M.-J. Homogenization of Elastic–Plastic Periodic Materials by FVDAM and FEM Approaches—An Assessment. Composites Part B: Engineering, 1713. [Google Scholar] [CrossRef]
  147. Zhang, Y.; Andersson, M.A.; Stake, J. A 200 GHz CVD Graphene FET Based Resistive Subharmonic Mixer. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS); IEEE: San Francisco, CA, May, 2016; pp. 1–4. [Google Scholar]
  148. Wu, Y.; Jenkins, K.A.; Valdes-Garcia, A.; Farmer, D.B.; Zhu, Y.; Bol, A.A.; Dimitrakopoulos, C.D.; Zhu, W.; Xia, F.; Avouris, Ph.; et al. State-of-the-Art Graphene High-Frequency Electronics. Nano Letters 2012, 12, 3062–3067. [Google Scholar] [CrossRef]
  149. Lin, Y.-M.; Jenkins, K.; Farmer, D.; Valdes-Garcia, A.; Avouris, P.; Sung, C.-Y.; Chiu, H.-Y.; Ek, B. Development of Graphene FETs for High Frequency Electronics.; 2009. 1 December. [CrossRef]
  150. Habibpour, O.; Vukusic, J.; Stake, J. A 30-GHz Integrated Subharmonic Mixer Based on a Multichannel Graphene FET. IEEE Transactions on Microwave Theory and Techniques 2013, 61, 841–847. [Google Scholar] [CrossRef]
  151. Schwierz, F. Graphene Transistors: Status, Prospects, and Problems. Proceedings of the IEEE 2013, 101, 1567–1584. [Google Scholar] [CrossRef]
  152. Szunerits, S.; Rodrigues, T.; Bagale, R.; Happy, H.; Boukherroub, R.; Knoll, W. Graphene-Based Field-Effect Transistors for Biosensing: Where Is the Field Heading To? Anal. Bioanal. Chem. 2024, 416, 2137–2150. [Google Scholar] [CrossRef] [PubMed]
  153. Wang, X.; Liu, Z.; Zhang, T. Flexible Sensing Electronics for Wearable/Attachable Health Monitoring. Small 2017, 13, 1602790. [Google Scholar] [CrossRef]
  154. Wang, C.; Liu, M.; Wang, Z.; Li, S.; Deng, Y.; He, N. Point-of-Care Diagnostics for Infectious Diseases: From Methods to Devices. Nano Today 2021, 37, 101092. [Google Scholar] [CrossRef]
  155. Prattis, I.; Hui, E.; Gubeljak, P.; Kaminski Schierle, G.S.; Lombardo, A.; Occhipinti, L.G. Graphene for Biosensing Applications in Point-of-Care Testing. Trends Biotechnol 2021, 39, 1065–1077. [Google Scholar] [CrossRef]
  156. Wang, Y.; Haick, H.; Guo, S.; Wang, C.; Lee, S.; Yokota, T.; Someya, T. Skin Bioelectronics towards Long-Term, Continuous Health Monitoring. Chem. Soc. Rev. 2022, 51, 3759–3793. [Google Scholar] [CrossRef] [PubMed]
  157. Xiao, L.; Li, K.; Liu, B.; Tu, J.; Li, T.; Li, Y.-T.; Zhang, G.-J. A pH-Sensitive Field-Effect Transistor for Monitoring of Cancer Cell External Acid Environment. Talanta 2023, 252, 123764. [Google Scholar] [CrossRef]
  158. Alnaji, N.; Wasfi, A.; Awwad, F. The Design of a Point of Care FET Biosensor to Detect and Screen COVID-19. Sci. Rep. 2023, 13, 4485. [Google Scholar] [CrossRef]
  159. Huang, C.; Hao, Z.; Qi, T.; Pan, Y.; Zhao, X. An Integrated Flexible and Reusable Graphene Field Effect Transistor Nanosensor for Monitoring Glucose. Journal of Materiomics 2020, 6, 308–314. [Google Scholar] [CrossRef]
  160. Thiele, S.; Schwierz, F. Modeling of the Steady State Characteristics of Large-Area Graphene Field-Effect Transistors. Journal of Applied Physics 2011, 110, 034506. [Google Scholar] [CrossRef]
  161. Selberherr, S. Analysis and Simulation of Semiconductor Devices; Springer: Vienna, 1984; ISBN 978-3-7091-8754-8. [Google Scholar]
  162. Landauer, G.M.; Jiménez, D.; González, J.L. An Accurate and Verilog-A Compatible Compact Model for Graphene Field-Effect Transistors. IEEE Transactions on Nanotechnology 2014, 13, 895–904. [Google Scholar] [CrossRef]
  163. Nastasi, G.; Romano, V. A Full Coupled Drift-Diffusion-Poisson Simulation of a GFET. Communications in Nonlinear Science and Numerical Simulation 2020, 87, 105300. [Google Scholar] [CrossRef]
  164. Jmai, B.; Silva, V.; Mendes, P.M. 2D Electronics Based on Graphene Field Effect Transistors: Tutorial for Modelling and Simulation. Micromachines 2021, 12, 979. [Google Scholar] [CrossRef]
  165. Fuente-Zapico, E.; Martínez-Mazon, P.; Carlos Galdón, J.; Márquez, C.; Navarro, C.; Donetti, L.; Sampedro, C.; Gamiz, F. Simulation of BioGFET Sensors Using TCAD. Solid State Electronics 2023, 208, 108761. [Google Scholar] [CrossRef]
  166. Multi Project Wafer Runs Available online:. Available online: https://graphene-flagship.eu/industrialisation/pilot-line/multi-project-wafer-runs/ (accessed on 27 August 2024).
Preprints 120741 g001
Figure 1. Multi-scale materials modelling approach. Discipline vs. Length Scale.
Figure 1. Multi-scale materials modelling approach. Discipline vs. Length Scale.
Preprints 120741 g001
Preprints 120741 g002
Figure 2. Material models, entity, length scale and time scale [1].
Figure 2. Material models, entity, length scale and time scale [1].
Preprints 120741 g002
Preprints 120741 g003
Figure 3. Material Diagram of the graphene-Al2O3-graphene heterostructure with point charge Ze moving with constant speed v at a fixed distance above the top graphene.
Figure 3. Material Diagram of the graphene-Al2O3-graphene heterostructure with point charge Ze moving with constant speed v at a fixed distance above the top graphene.
Preprints 120741 g003
Preprints 120741 g004
Figure 4. Examples of atomistic models used to study carbon structures. (A) Epoxy resin boxes reinforced by (a) 5 single-walled carbon nanotubes (SWCNTs) and (b) one SWCNT [87]. (B) Dislocation formation during stretching simulation of a graphene oxide nanoribbon model [78]. (C) Investigation of the thermal properties of (a) SWCNTs, and (b) double-walled carbon nanotubes (DWCNTs) composed of two coax-ial SWCNTs [88]. (D) Effect of surface wettability on heat and mass transfer at the interface between water and CNTs [93].
Figure 4. Examples of atomistic models used to study carbon structures. (A) Epoxy resin boxes reinforced by (a) 5 single-walled carbon nanotubes (SWCNTs) and (b) one SWCNT [87]. (B) Dislocation formation during stretching simulation of a graphene oxide nanoribbon model [78]. (C) Investigation of the thermal properties of (a) SWCNTs, and (b) double-walled carbon nanotubes (DWCNTs) composed of two coax-ial SWCNTs [88]. (D) Effect of surface wettability on heat and mass transfer at the interface between water and CNTs [93].
Preprints 120741 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated