Prerpints.org logo
Preprint
Article

A Conservative and Compact Finite Difference Scheme for the Sixth-Order Boussinesq Equation with the Surface Tension

Altmetrics

Downloads

33

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 October 2024

Posted:

10 October 2024

You are already at the latest version

Alerts
Abstract

In this study, we propose a conservative and compact finite difference scheme designed to preserve both the mass change rate and energy for solving the sixth-order Boussinesq equation with the surface tension. Theoretical analysis confirms that the proposed scheme achieves second-order accuracy in temporal discretization and fourth-order accuracy in spatial discretization. The solvability, convergence, and stability of the difference scheme are rigorously established through the application of the discrete energy method. Additionally, a series of numerical experiments are conducted to illustrate the effectiveness and reliability of the conservative scheme for long-time simulations.

Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

The numerical solution of partial differential equations (PDEs) represents a fundamental component in numerous scientific and engineering applications. In recent years, there has been a growing emphasis on the development of high-order finite difference methods aimed at improving both the accuracy and efficiency of solutions for a wide range of PDEs. A particular area of interest is the Boussinesq equation, which was first introduced by Joseph Boussinesq in 1872 to model nonlinear wave propagation in dispersive media [1]. As a result, this equation has been extensively applied across multiple domains, including the investigation of ion-sound waves in plasma, solitary waves in vascular systems, tsunami waves in oceanography and coastal sciences, as well as pressure waves in liquid-gas bubble mixtures, among others [2,3].
This article investigates the sixth-order Boussinesq equation, taking into account the effects of surface tension, as outlined in [4]:
u t t − k 2 u x x + a 1 u x x x x − a 2 u x x t t − b 1 u x x x x x x + b 2 u x x x x t t + c ( u 2 p ) x x = 0 ,
with the specified initial conditions
u ( x , 0 ) = φ ( x ) , u t ( x , 0 ) = ψ ( x ) .
In this context, the parameters a 1 ≥ 0 , a 2 ≥ 0 , b 1 ≥ 0 and b 2 ≥ 0 are non-negative, while k and c are constants. Furthermore, p ≥ 1 is a positive integer, and φ ( x ) and ψ ( x ) are two specified smooth functions.
Solitary waves have attracted considerable interest across various fields of physics and engineering. Biswas [5] successfully derived an exact solitary wave solution for the Korteweg-de Vries equation, which is characterized by power law nonlinearity and time-varying coefficients. The singular solitary wave solution for the Rosenau-KdV equation is presented in [6], while the specific 1-soliton solution for the Rosenau-KdV-RLW equation is detailed in [7]. Eq. (1) is frequently encountered in numerous mathematical models concerning solitary wave propagation, as emphasized by Lu and Helal [8,9]. Furthermore, Biswas et al. [4] provide a variety of solitary wave, shock wave, and singular solitary wave solutions for the Boussinesq equation (1), which incorporates the effects of surface tension. Under the assumption of solitary wave behavior, it is observed that the solution to the sixth-order Boussinesq equation (1) and its derivatives approach zero as | x | → ∞ , that is [10,11]
lim x → ± ∞ u = 0 , lim x → ± ∞ ∂ n u ∂ x n = 0 , n ≥ 1 ,
then Eq. (1) is linked to the following global conservation law:
d d t ∫ − ∞ + ∞ u ( x , t ) d x = C .
This research focuses on the solitary wave solution and seeks to develop a conservative linear finite difference scheme for the sixth-order Boussinesq equation (1). To effectively implement the numerical method, we analyze a sufficiently large yet finite spatial domain, denoted as [ x l , x r ] , instead of the unbounded interval ( − ∞ , + ∞ ) . This strategy ensures that the solution remains sufficiently small at the boundaries of the domain. Consequently, we consider the following boundary conditions:
u ( x l , t ) = u ( x r , t ) = 0 , u x ( x l , t ) = u x ( x r , t ) = 0 , u x x ( x l , t ) = u x x ( x r , t ) = 0 ,
where 0 ≤ t ≤ T .
The Boussinesq equation and its variants have been thoroughly analyzed through both theoretical and numerical approaches. In the theoretical context, Esfahani and Farah [12] have conducted an investigation into a nonlinear sixth-order Boussinesq equation
u t t − u x x ± u x x x x − u x x x x x x + ( u 2 ) x x = 0 , x ∈ R , t ≥ 0 .
The authors established the local well-posedness of Eq. (4) within the framework of non-homogeneous Sobolev spaces H s ( R ) , where s < 0 and s ∈ R . Following this, Wang and Esfahani [13] conducted an investigation into the sixth-order Boussinesq equation as follows:
u t t − u x x ± u x x x x − u x x x x x x − ( | u | 2 u ) x x = 0 , x ∈ R , t ≥ 0 .
The authors have demonstrated that the problem described by Eq. (5) is globally well-posed within the Sobolev space H s ( R ) , where 3 / 2 and s ∈ R .
In a numerical context, Feng et al. [14] proposed a symmetric three-level implicit difference scheme that exhibits second-order accuracy for the following sixth-order Boussinesq equation
u t t − u x x − u x x x x − 0.4 u x x x x x x − 6 ( u 2 ) x x = 0 .
A linearized stability analysis indicates that the difference scheme, which incorporates a free parameter denoted as θ , exhibits stability for values of θ that are equal to or greater than 1/4. In 2017, Kolkovska and Vucheva [15] introduced a nonlinear second-order difference scheme aimed at addressing the sixth-order Boussinesq problem, as detailed below:
u t t − u x x − β 1 u x x t t + β 2 u x x x x − β 3 u x x x x x x + α ( u 2 ) x x = 0 , u ( x , 0 ) = φ ( x ) , u t ( 0 , x ) = ψ ( x ) , u → 0 , u x x → 0 , u x x x x → 0 , | x | → ∞ .
However, the scheme presented in [15] demonstrates conditional stability, which is dependent on a strict limitation on the subsequent ratio
τ h 2 < 3 β 1 2 1 + 4 β 2 + 16 β 3 , β 1 ≥ 0 , β 2 ≥ 0 , β 3 ≥ 0 .
There exists a significant lack of theoretical analysis regarding the solvability and convergence properties of the scheme proposed by Kolkovska [15]. More recently, Arslan [16] has introduced a novel methodology that combines the differential transform method with the finite difference technique to obtain approximate solutions for singularly perturbed ill-posed problems and sixth-order Boussinesq equations. In a separate study, Zhang et al. [17] introduced a meshless numerical technique known as the generalized finite difference method, which has demonstrated efficacy in addressing enhanced Boussinesq-type equations. This method is particularly advantageous for simulating wave propagation over irregular bottom topographies.
In the field of physics, the principle of conservation of mass and energy holds critical importance. A numerical scheme that fails to uphold local conservation may produce non-physical outcomes [18]. Therefore, the preservation of mass and energy is a fundamental consideration in the development of numerical schemes aimed at solving PDEs. A considerable amount of research has been devoted to the development of conservative finite-difference schemes applicable to various nonlinear wave equations. For instance, Deng et al. [19] proposed energy-preserving finite difference methods that are applicable to systems of nonlinear wave equations in two dimensions. Furthermore, Bayarassou et al. [20] investigated a high-order conservative linearized finite difference scheme for the regularized long wave (RLW)-Korteweg-de Vries equation. Additionally, Hou et al. [21] introduced an energy-preserving, high-order compact finite difference scheme specifically designed for two-dimensional nonlinear wave equations. Nanta et al. [22] presented a wave model that integrates the classical Camassa-Holm equation with the BBM-KdV equation, incorporating dual-power law nonlinearities while ensuring the preservation of energy conservation properties.
This article aims to present a conservative difference scheme for the resolution of the sixth-order Boussinesq problem as defined in Eqs. (1)-(3). Furthermore, the article will examine the solvability, convergence, and stability of the proposed scheme. The problem outlined in Eqs. (1)-(3) holds considerable physical significance.
Theorem 1.
Consider u as the solution to the sixth-order Boussinesq problem defined by Eqs. (1)-(3). Let us denote u t = v x x , and assume that the supplementary boundary conditions are given by v x ( x l , t ) = v x ( x r , t ) = 0 and v x x ( x l , t ) = v x x ( x r , t ) = 0 . Under these conditions, it can be concluded that E ( t ) = E ( 0 ) for all t ∈ [ 0 , T ] , where
E ( t ) = k 2 ∥ u ∥ L 2 2 + a 1 ∥ u x ∥ L 2 2 + a 2 ∥ u t ∥ L 2 2 + b 1 ∥ u x x ∥ L 2 2 + b 2 ∥ u x t ∥ L 2 2 + ∥ v x ∥ L 2 2 − 2 c 2 p + 1 ∫ x l x r u 2 p + 1 d x .
Proof. 
Let u t = v x x . We substitute this expression into Eq. (1) and subsequently take the antiderivative twice. This process results in the following equation:
v t = k 2 u − a 1 u x x + a 2 u t t + b 1 u x x x x − b 2 v x x t t − c u 2 p .
Consequently, we obtain further results
d E d t = 2 ∫ x l x r k 2 u u t + a 1 u x u x t + a 2 u t u t t + b 1 u x x u x x t + b 2 u x t u x t t + v x v x t − c u 2 p u t d x = 2 ∫ x l x r u t k 2 u + a 2 u t t − c u 2 p + a 1 u x u x t + b 1 u x x u x x t + b 2 u x t u x t t + v x v x t d x = 2 ∫ x l x r [ u t v t + a 1 u x x − b 1 u x x x x + b 2 u x x t t + a 1 u x u x t + b 1 u x x u x x t + b 2 u x t u x t t + v x v x t ] d x = 2 ∫ x l x r ( u t v t + v x v x t ) d x + 2 a 1 ∫ x l x r ( u t u x x + u x u x t ) d x + 2 b 2 ∫ x l x r ( u t u x x t t + u x t u x t t ) d x − 2 b 1 ∫ x l x r ( u t u x x x x − u x x u x x t ) d x ≡ 2 ( l 1 + a 1 l 2 + b 2 l 3 − b 1 l 4 ) .
Utilizing the boundary conditions delineated in Eq. (3) along with the additional assumptions, we derive the following results
l 1 = ∫ x l x r ( u t v t + v x v x t ) d x = ∫ x l x r ( v x x v t + v x v x t ) d x = v t v x | x l x r = 0 ,
l 2 = ∫ x l x r ( u t u x x + u x u x t ) d x = u t u x | x l x r = 0 ,
l 3 = ∫ x l x r ( u t u x x t t + u x t u x t t ) d x = u t u x t t | x l x r = v x x u x t t | x l x r = 0 .
Since
∫ x l x r u x x u x x t d x = ∫ x l x r u x x d ( u x t ) = u x t u x x | x l x r − ∫ x l x r u x t u x x x d x = − ∫ x l x r u x t u x x x d x = − ∫ x l x r u x x x d ( u t ) = − u t u x x x | x l x r + ∫ x l x r u t u x x x x d x = − v x x u x x x | x l x r + ∫ x l x r u t u x x x x d x = ∫ x l x r u t u x x x x d x ,
which yields
l 4 = ∫ x l x r ( u t u x x x x − u x x u x x t ) d x = ∫ x l x r u t u x x x x d x − ∫ x l x r u x x u x x t d x = 0 .
Consequently, from Eqs. (8)-(12), we deduce that d E / d t = 0 , which indicates that E ( t ) = E ( 0 ) for t ∈ [ 0 , T ] . This completes the proof. □
It is essential to emphasize that if the parameters a 1 , a 2 , b 1 , b 2 , k, c and the initial conditions φ ( x ) and ψ ( x ) satisfy E ( 0 ) ≥ 0 , then E ( t ) can be defined as the energy at time t. Moreover, the solution to Eqs. (1)-(3) complies with the principle of energy conservation, where
E ( 0 ) = k 2 ∥ φ ∥ L 2 2 + a 1 ∥ φ x ∥ L 2 2 + a 2 ∥ ψ ∥ L 2 2 + b 1 ∥ φ x x ∥ L 2 2 + b 2 ∥ ψ x ∥ L 2 2 + ∥ v x ( x , 0 ) ∥ L 2 2 − 2 c 2 p + 1 ∫ x l x r φ 2 p + 1 d x .
The subsequent sections of this manuscript are organized as follows: In Section (Section 2), we introduce a compact finite difference scheme designed for the resolution of the sixth-order Boussinesq equation (1)-(3). Section (Section 3) rigorously establishes the discrete conservation properties associated with the mass change rate and energy. A comprehensive theoretical analysis addressing the scheme’s solvability, convergence, and stability is presented in Section (Section 4). Section (Section 5) includes numerical experiments that validate the theoretical results. Finally, Section (Section 6) provides a concise summary of the findings.

2. Compact Difference Scheme

In this section, we present a compact and conservative difference scheme specifically developed to tackle the sixth-order Boussinesq problem as delineated in Eqs. (1)-(3). For two positive integers J and N, we define the spatial and temporal discretization parameters as h = ( x r − x l ) / J and τ = T / N , respectively. The uniform grid points are established as x j = x l + j h and t n = n τ , where j = 0 , 1 , … , J and n = 0 , 1 , … , N . We denote U j n ≈ u ( x j , t n ) as the approximation of the function u at the point ( x j , t n ) and
Z h 0 = { U = ( U j ) | U − 2 = U − 1 = U 0 = U 1 = U 2 = U J − 2 = U J − 1 = U J = U J + 1 = U J + 2 = 0 } ,
where − 2 ≤ j ≤ J + 2 . The Sobolev space is defined as described in [23]:
H 0 k ( Ω ) = u ( x ) ∈ H k ( Ω ) : ∂ i u ∂ x i | ∂ Ω = 0 , i = 0 , 1 , 2 , . . . , k − 1 .
We will now proceed to establish the following notations:
( U j n ) x ˜ = 1 h ( U j + 1 n − U j n ) , ( U j n ) x ¯ = 1 h ( U j n − U j − 1 n ) , ( U j n ) x ^ = 1 2 h ( U j + 1 n − U j − 1 n ) , ( U j n ) t ˜ = 1 τ ( U j n + 1 − U j n ) , ( U j n ) t ¯ = 1 τ ( U j n − U j n − 1 ) , ( U j n ) t ^ = 1 2 τ ( U j n + 1 − U j n − 1 ) , U ¯ j n = 1 2 ( U j n + 1 + U j n − 1 ) , U j n + 1 2 = 1 2 ( U j n + 1 + U j n ) , 〈 U n , V n 〉 = h ∑ j = 1 J − 1 U j n V j n , ∥ U n ∥ 2 = 〈 U n , U n 〉 , ∥ U n ∥ ∞ = max 1 ≤ j ≤ J − 1 | U j n | , U n , V n ∈ Z h 0 .
In the subsequent section, we will develop a compact difference scheme for Eqs. (1)-(3). By setting
w = k 2 u x x − a 1 u x x x x + a 2 u x x t t + b 1 u x x x x x x − b 2 u x x x x t t − c u 2 p x x ,
Eq. (1) can be expressed as w = u t t . By utilizing the Taylor expansion for the variable x, we obtain
w j n = k 2 ( U j n ) x ˜ x ¯ − h 2 12 ( ∂ x 4 u ) j n − a 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ − h 2 6 ( ∂ x 6 u ) j n + a 2 ( U j n ) x ˜ x ¯ t ˜ t ¯ − h 2 12 ( ∂ x 4 ∂ t 2 u ) j n + b 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ − h 2 4 ( ∂ x 8 u ) j n − b 2 ( U j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ − h 2 6 ( ∂ x 6 ∂ t 2 u ) j n − c [ ( U j n ) 2 p ] x ˜ x ¯ − h 2 12 ( ∂ x 4 u 2 p ) j n + O ( τ 2 + h 4 ) .
Furthermore, Eq. (Section 2) is associated to
b 1 ( ∂ x 8 u ) j n = − k 2 ( ∂ x 4 u ) j n + a 1 ( ∂ x 6 u ) j n + a 2 ( ∂ x 4 ∂ t 2 u ) j n + b 2 ( ∂ x 6 ∂ t 2 u ) j n + c ( ∂ x 4 u 2 p ) j n + ( ∂ x 2 w ) j n .
Substituting Eq. (15) into Eq. (14) yields
w j n = k 2 ( U j n ) x ˜ x ¯ − a 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ + a 2 ( U j n ) x ˜ x ¯ t ˜ t ¯ + b 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ − b 2 ( U j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ − c [ ( U j n ) 2 p ] x ˜ x ¯ + k 2 h 2 6 ( ∂ x 4 u ) j n − a 1 h 2 12 ( ∂ x 6 u ) j n + a 2 h 2 6 ( ∂ x 4 ∂ t 2 u ) j n − b 2 h 2 12 ( ∂ x 6 ∂ t 2 u ) j n − c h 2 6 ( ∂ x 4 u 2 p ) j n − h 2 4 ( ∂ x 2 w ) j n .
Through the application of second-order accuracy in our approximations, we achieve
U j n = U ¯ j n + O ( τ 2 ) , w j n = ( ∂ t 2 u ) j n = ( U j n ) t ˜ t ¯ + O ( τ 2 ) , ( ∂ x 4 u ) j n = ( U j n ) x ˜ x ¯ x ˜ x ¯ + O ( h 2 ) , ( ∂ x 6 u ) j n = ( U j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ + O ( h 2 ) , ( ∂ x 2 ∂ t 2 u ) j n = ( U j n ) x ˜ x ¯ t ˜ t ¯ + O ( τ 2 + h 2 ) , ( ∂ x 4 ∂ t 2 u ) j n = ( U j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + O ( τ 2 + h 2 ) , ( ∂ x 6 ∂ t 2 u ) j n = ( U j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + O ( τ 2 + h 2 ) , ( ∂ x 4 u 2 p ) j n = [ ( U j n ) 2 p ] x ˜ x ¯ x ˜ x ¯ + O ( h 2 ) .
Consequently, the proposed compact finite difference scheme can be expressed as follows:
( U j n ) t ˜ t ¯ − k 2 ( U ¯ j n ) x ˜ x ¯ + a 1 − k 2 h 2 6 ( U ¯ j n ) x ˜ x ¯ x ˜ x ¯ − a 2 − h 2 4 ( U j n ) x ˜ x ¯ t ˜ t ¯ − b 1 − a 1 h 2 12 ( U ¯ j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯
+ b 2 − a 2 h 2 6 ( U j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + b 2 h 2 12 ( U j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + c [ ( U j n ) 2 p ] x ˜ x ¯ + c h 2 6 [ ( U j n ) 2 p ] x ˜ x ¯ x ˜ x ¯ = 0 ,
U j 0 = φ ( x j ) , ( U j 0 ) t ^ = ψ ( x j ) , 0 ≤ j ≤ J ,
U κ n = 0 , 4 3 ( U κ n ) x ^ − 1 3 ( U κ n ) x ¨ = 0 , 4 3 ( U κ n ) x ˜ x ¯ − 1 3 ( U κ n ) x ^ x ^ = 0 , κ = 0 , J , 0 ≤ n ≤ N .
It is essential to recognize that since U 0 n = 0 , 4 3 ( U 0 n ) x ^ − 1 3 ( U 0 n ) x ¨ = 0 and 4 3 ( U 0 n ) x ˜ x ¯ − 1 3 ( U 0 n ) x ^ x ^ = 0 hold based on Eq. (18), we may proceed with the assumption that U − 2 n = U − 1 n = U 1 n = U 2 n = 0 for the sake of simplicity. Similarly, we can also assume that U J − 2 n = U J − 1 n = U J + 1 n = U J + 2 n = 0 , where j = − 2 , − 1 , J + 1 and J + 2 denote ghost points under the condition 1 ≤ n ≤ N . Consequently, it can be concluded that U n ∈ Z h 0 .
In this context, we employ the following methodology to derive U 1 :
( U j 0 ) t ˜ t ¯ − k 2 ( U ¯ j 0 ) x ˜ x ¯ + a 1 − k 2 h 2 6 ( U ¯ j 0 ) x ˜ x ¯ x ˜ x ¯ − a 2 − h 2 4 ( U j 0 ) x ˜ x ¯ t ˜ t ¯ − b 1 − a 1 h 2 12 ( U ¯ j 0 ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ + b 2 − a 2 h 2 6 ( U j 0 ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + b 2 h 2 12 ( U j 0 ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + c [ ( U j 0 ) 2 p ] x ˜ x ¯ + c h 2 6 [ ( U j 0 ) 2 p ] x ˜ x ¯ x ˜ x ¯ = 0 .
From Eq. (17), we get
1 2 τ ( U j 1 − U j − 1 ) = ( U j 0 ) t ^ = ψ ( x j ) , 0 ≤ j ≤ J ,
that is
U j − 1 = U j 1 − 2 τ ψ ( x j ) , 0 ≤ j ≤ J ,
which yields
( U j 0 ) t ˜ t ¯ = 1 τ 2 ( U j 1 − 2 U j 0 + U j − 1 ) = 2 τ 2 U j 1 − U j 0 − τ ψ ( x j ) = 2 τ 2 U j 1 − φ ( x j ) − τ ψ ( x j ) ,
where 0 ≤ j ≤ J .

3. Discrete Conservative Laws

In this section, we demonstrate that the proposed methodology, as outlined in Eqs. (16)-(18), maintains both the rate of mass change and energy conservation. We will now present a modified version of the previously discussed scheme and define an auxiliary variable V n ∈ Z h 0 that fulfills the following conditions:
( V j n + 1 / 2 ) x ˜ x ¯ = ( U j n ) t ˜ , j = 0 , 1 , . . . , J , n = 0 , 1 , . . . , N − 1 .
Lemma 2.([24,25,26]) For any two discrete functions U , V ∈ Z h 0 , it follows that
〈 U x ˜ x ¯ , U 〉 = − 〈 U x ˜ , U x ˜ 〉 = − ∥ U x ˜ ∥ 2 , 〈 U x ˜ x ¯ , V 〉 = − 〈 U x ˜ , V x ˜ 〉 = 〈 U , V x ˜ x ¯ 〉 , 〈 U x ˜ x ˜ x ¯ x ¯ , U 〉 = ∥ U x ˜ x ¯ ∥ 2 .
Lemma 3.
For any discrete function U ∈ Z h 0 , it follows that
〈 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ , U 〉 = − 〈 U x ˜ x ¯ x ˜ , U x ˜ x ¯ x ˜ 〉 = − ∥ U x ˜ x ¯ x ˜ ∥ 2 .
Proof. 
According to Lemma 2, it can be concluded that
〈 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ , U 〉 = 〈 ( U x ˜ x ¯ x ˜ x ¯ ) x ˜ x ¯ , U 〉 = 〈 U x ˜ x ¯ x ˜ x ¯ , U x ˜ x ¯ 〉 = 〈 ( U x ˜ x ¯ ) x ˜ x ¯ , U x ˜ x ¯ 〉 = − 〈 ( U x ˜ x ¯ ) x ˜ , ( U x ˜ x ¯ ) x ˜ 〉 = − ∥ U x ˜ x ¯ x ˜ ∥ 2 .
This completes the proof. □
Lemma 4.([11,26]) For any discrete function U n ∈ Z h 0 , it follows that
∥ U n ∥ ≤ C ∥ U x ˜ n ∥ , ∥ U n ∥ ∞ ≤ C ∥ U x ˜ n ∥ .
Lemma 5.([11,27]) For any discrete function U n ∈ Z h 0 , it follows that
∥ U x ˜ n ∥ ≤ 4 h 2 ∥ U n ∥ .
Theorem 6.
Let U n ∈ Z h 0 denote the solution to the equations (16)-(18). We define the discrete mass as M n = h ∑ j = 1 J − 1 U j n . Consequently, the rate of change of discrete mass is described by the following equation:
R n ≡ h τ ∑ j = 1 J − 1 ( U j n + 1 − U j n ) = R n − 1 = · · · = R 0 = h ∑ j = 1 J − 1 ψ ( x j ) , 0 ≤ n ≤ N − 1 .
Proof. 
By multiplying Eq. (16) by h and subsequently summing over j from 1 to J, we obtain the following result:
h ∑ j = 1 J − 1 ( U j n ) t ˜ t ¯ − k 2 h ∑ j = 1 J − 1 ( U ¯ j n ) x ˜ x ¯ + a 1 − k 2 h 2 6 h ∑ j = 1 J − 1 ( U ¯ j n ) x ˜ x ¯ x ˜ x ¯ − a 2 − h 2 4 h ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ t ˜ t ¯ − b 1 − a 1 h 2 12 h ∑ j = 1 J − 1 ( U ¯ j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ + b 2 − a 2 h 2 6 h ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + b 2 h 3 12 ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + c h ∑ j = 1 J − 1 [ ( U j n ) 2 p ] x ˜ x ¯ + c h 3 6 ∑ j = 1 J − 1 [ ( U j n ) 2 p ] x ˜ x ¯ x ˜ x ¯ = 0 .
Upon noting that U n ∈ Z h 0 , we can deduce
p 1 = h ∑ j = 1 J − 1 ( U j n ) t ˜ t ¯ = h τ 2 ∑ j = 1 J − 1 ( U j n + 1 − 2 U j n + U j n − 1 ) ,
p 2 = h ∑ j = 1 J − 1 ( U ¯ j n ) x ˜ x ¯ = 1 h ∑ j = 1 J − 1 ( U ¯ j + 1 n − 2 U ¯ j n + U ¯ j − 1 n ) = 1 h ∑ j = 1 J − 1 ( U ¯ j + 1 n − U ¯ j n ) − ( U ¯ j n − U ¯ j − 1 n ) = 1 h ∑ j = 1 J − 1 ( U ¯ j + 1 n − U ¯ j n ) − 1 h ∑ j = 1 J − 1 ( U ¯ j n − U ¯ j − 1 n ) = 1 h ( U ¯ J + 1 n − U ¯ J n ) − ( U ¯ 1 n − U ¯ 0 n ) = 0 ,
p 3 = h ∑ j = 1 J − 1 ( U ¯ j n ) x ˜ x ¯ x ˜ x ¯ = 1 h 3 ∑ j = 1 J − 1 ( U ¯ j + 2 n − 4 U ¯ j + 1 n + 6 U ¯ j n − 4 U ¯ j − 1 n + U ¯ j − 2 n ) = 1 h 3 ∑ j = 1 J − 1 ( U ¯ j + 2 n − U ¯ j + 1 n ) − 3 ( U ¯ j + 1 n − U ¯ j n ) + 3 ( U ¯ j n − U ¯ j − 1 n ) − ( U ¯ j − 1 n − U ¯ j − 2 n ) = 1 h 3 ( U ¯ J + 1 n − U ¯ 2 n ) − 3 ( U ¯ J n − U ¯ 1 n ) + 3 ( U ¯ J − 1 n − U ¯ 0 n ) − ( U ¯ J − 2 n − U ¯ − 1 n ) = 0 ,
p 4 = h ∑ j = 1 J − 1 ( U ¯ j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ = 1 h 5 ∑ j = 1 J − 1 ( U ¯ j + 3 n − 6 U ¯ j + 2 n + 15 U ¯ j + 1 n − 20 U ¯ j n + 15 U ¯ j − 1 n − 6 U ¯ j − 2 n + U ¯ j − 3 n ) = 1 h 5 [ ( U ¯ J + 2 n − U ¯ 3 n ) − 5 ( U ¯ J + 1 n − U ¯ 2 n ) + 10 ( U ¯ J n − U ¯ 1 n ) − 10 ( U ¯ J − 1 n − U ¯ 0 n ) + 5 ( U ¯ J − 2 n − U ¯ − 1 n ) − ( U ¯ J − 3 n − U ¯ − 2 n ) ] = 0 ,
p 5 = h ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ t ˜ t ¯ = 1 h ∑ j = 1 J − 1 ( U j + 1 n − 2 U j n + U j − 1 n ) t ˜ t ¯ = 1 h ∑ j = 1 J − 1 ( U j + 1 n − U j n ) t ˜ t ¯ − 1 h ∑ j = 1 J − 1 ( U j n − U j − 1 n ) t ˜ t ¯ = 1 h ( U J + 1 n − U J n ) − ( U 1 n − U 0 n ) t ˜ t ¯ = 0 .
Similarly, we obtain
p 6 = h ∑ j = 1 J − 1 [ ( U j n ) 2 p ] x ˜ x ¯ = 0 , p 7 = h ∑ j = 1 J − 1 [ ( U j n ) 2 p ] x ˜ x ¯ x ˜ x ¯ = 0 ,
p 8 = h ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ = 0 , p 9 = h ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ = 0 .
By substituting Eqs. (23)-(29) into Eq. (22), we obtain
h ∑ j = 1 J − 1 ( U j n ) t ˜ t ¯ = h τ 2 ∑ j = 1 J − 1 ( U j n + 1 − 2 U j n + U j n − 1 ) = 0 ,
that is
h τ ∑ j = 1 J − 1 ( U j n + 1 − U j n ) = h τ ∑ j = 1 J − 1 ( U j n − U j n − 1 ) ,
which yields R n = R n − 1 = · · · = R 0 .
Additionally, as indicated by Eq. (20), we obtain
R 0 = h τ ∑ j = 1 J − 1 ( U j 1 − U j 0 ) = h τ ∑ j = 1 J − 1 ( U j 0 − U j − 1 ) = h τ ∑ j = 1 J − 1 [ U j 0 − U j 1 + 2 τ ψ ( x j ) ] = − R 0 + 2 h ∑ j = 1 J − 1 ψ ( x j ) ,
which yields R 0 = h ∑ j = 1 J − 1 ψ ( x j ) . This completes the proof. □
Theorem 7.
Let U n ∈ Z h 0 represent the solution to Eqs. (16)-(18) and let V n ∈ Z h 0 denote the solution to Eq. (21). It can be inferred that the discrete energy is conserved, such that E n = E n − 1 = ⋯ = E 0 , where
E n ≡ ∥ V x ˜ n + 1 2 ∥ 2 + k 2 2 ∥ U n + 1 ∥ 2 + ∥ U n ∥ 2 + 1 2 a 1 − k 2 h 2 6 ∥ U x ˜ n + 1 ∥ 2 + ∥ U x ˜ n ∥ 2 + a 2 − h 2 4 ∥ U t ¯ n + 1 ∥ 2 + 1 2 b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ n + 1 ∥ 2 + ∥ U x ˜ x ¯ n ∥ 2 + b 2 − a 2 h 2 6 ∥ U x ˜ t ¯ n + 1 ∥ 2 − b 2 h 2 12 ∥ U t ˜ t ¯ n + 1 ∥ 2 − c h τ 6 ∑ k = 0 n ∑ j = 1 J − 1 ( U j + 1 k ) 2 p + 4 ( U j k ) 2 p + ( U j − 1 k ) 2 p ( U j k + 1 + U j k ) t ¯ ,
where 0 ≤ n ≤ N − 1 .
Proof. 
By computing the inner product of Eq. (16) with V n + 1 2 + V n − 1 2 , we obtain
〈 U t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 − k 2 〈 U ¯ x ˜ x ¯ n , V n + 1 2 + V n − 1 2 〉 + a 1 − k 2 h 2 6 〈 U ¯ x ˜ x ¯ x ˜ x ¯ n , V n + 1 2 + V n − 1 2 〉 − a 2 − h 2 4 〈 U x ˜ x ¯ t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 − b 1 − a 1 h 2 12 〈 U ¯ x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n , V n + 1 2 + V n − 1 2 〉 + b 2 − a 2 h 2 6 〈 U x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 + b 2 h 2 12 〈 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 + c 〈 ( U n ) x ˜ x ¯ 2 p , V n + 1 2 + V n − 1 2 〉 + c h 2 6 〈 ( U n ) x ˜ x ¯ x ˜ x ¯ 2 p , V n + 1 2 + V n − 1 2 〉 = 0 .
Utilizing Lemma 2 and Lemma 3, along with Eq. (21), a simple computation yields
q 1 = 〈 U t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 = 〈 ( V x ˜ x ¯ n + 1 2 ) t ¯ , V n + 1 2 + V n − 1 2 〉 = 1 τ 〈 V x ˜ x ¯ n + 1 2 − V x ˜ x ¯ n − 1 2 , V n + 1 2 + V n − 1 2 〉 = − 1 τ ( ∥ V x ˜ n + 1 2 ∥ 2 − ∥ V x ˜ n − 1 2 ∥ 2 ) ,
q 2 = 〈 U ¯ x ˜ x ¯ n , V n + 1 2 + V n − 1 2 〉 = 1 2 〈 U n + 1 + U n − 1 , ( V n + 1 2 + V n − 1 2 ) x ˜ x ¯ 〉 = 1 2 〈 U n + 1 + U n − 1 , ( U n + U n − 1 ) t ˜ 〉 = 1 2 τ 〈 U n + 1 + U n − 1 , U n + 1 − U n − 1 〉 = 1 2 τ ( ∥ U n + 1 ∥ 2 − ∥ U n − 1 ∥ 2 ) ,
q 3 = 〈 U ¯ x ˜ x ¯ x ˜ x ¯ n , V n + 1 2 + V n − 1 2 〉 = 1 2 〈 ( U n + 1 + U n − 1 ) x ˜ x ¯ , ( V n + 1 2 + V n − 1 2 ) x ˜ x ¯ 〉 = 1 2 〈 ( U n + 1 + U n − 1 ) x ˜ x ¯ , ( U n + U n − 1 ) t ˜ 〉 = 1 2 τ 〈 ( U n + 1 + U n − 1 ) x ˜ x ¯ , U n + 1 − U n − 1 〉 = − 1 2 τ ( ∥ U x ˜ n + 1 ∥ 2 − ∥ U x ˜ n − 1 ∥ 2 ) ,
q 4 = 〈 U x ˜ x ¯ t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 = 〈 ( V x ˜ x ¯ n + 1 2 ) x ˜ x ¯ t ¯ , V n + 1 2 + V n − 1 2 〉 = 1 τ 〈 V x ˜ x ¯ x ˜ x ¯ n + 1 2 − V x ˜ x ¯ x ˜ x ¯ n − 1 2 , V n + 1 2 + V n − 1 2 〉 = 1 τ ( ∥ V x ˜ x ¯ n + 1 2 ∥ 2 − ∥ V x ˜ x ¯ n − 1 2 ∥ 2 ) = 1 τ ( ∥ U t ˜ n ∥ 2 − ∥ U t ˜ n − 1 ∥ 2 ) = 1 τ ( ∥ U t ¯ n + 1 ∥ 2 − ∥ U t ¯ n ∥ 2 ) ,
q 5 = 〈 U ¯ x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n , V n + 1 2 + V n − 1 2 〉 = 1 2 〈 ( U n + 1 + U n − 1 ) x ˜ x ¯ x ˜ x ¯ , ( V n + 1 2 + V n − 1 2 ) x ˜ x ¯ 〉 = 1 2 〈 ( U n + 1 + U n − 1 ) x ˜ x ¯ x ˜ x ¯ , ( U n + U n − 1 ) t ˜ 〉 = 1 2 τ 〈 ( U n + 1 + U n − 1 ) x ˜ x ¯ x ˜ x ¯ , U n + 1 − U n − 1 〉 = 1 2 τ ( ∥ U x ˜ x ¯ n + 1 ∥ 2 − ∥ U x ˜ x ¯ n − 1 ∥ 2 ) ,
q 6 = 〈 U x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 = 〈 ( V x ˜ x ¯ n + 1 2 ) x ˜ x ¯ x ˜ x ¯ t ¯ , V n + 1 2 + V n − 1 2 〉 = 1 τ 〈 V x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n + 1 2 − V x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n − 1 2 , V n + 1 2 + V n − 1 2 〉 = − 1 τ ( ∥ V x ˜ x ¯ x ˜ n + 1 2 ∥ 2 − ∥ V x ˜ x ¯ x ˜ n − 1 2 ∥ 2 ) = − 1 τ ( ∥ U x ˜ t ˜ n ∥ 2 − ∥ U x ˜ t ˜ n − 1 ∥ 2 ) = − 1 τ ( ∥ U x ˜ t ¯ n + 1 ∥ 2 − ∥ U x ˜ t ¯ n ∥ 2 ) ,
q 7 = 〈 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , V n + 1 2 + V n − 1 2 〉 = 〈 ( V x ˜ x ¯ n + 1 2 ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ¯ , V n + 1 2 + V n − 1 2 〉 = 1 τ 〈 V x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n + 1 2 − V x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n − 1 2 , V n + 1 2 + V n − 1 2 〉 = 1 τ ( ∥ V x ˜ x ¯ x ˜ x ¯ n + 1 2 ∥ 2 − ∥ V x ˜ x ¯ x ˜ x ¯ n − 1 2 ∥ 2 ) = 1 τ ( ∥ U t ˜ t ˜ n ∥ 2 − ∥ U t ˜ t ˜ n − 1 ∥ 2 ) = 1 τ ( ∥ U t ˜ t ¯ n + 1 ∥ 2 − ∥ U t ˜ t ¯ n ∥ 2 ) ,
q 8 = 〈 ( U n ) x ˜ x ¯ 2 p , V n + 1 2 + V n − 1 2 〉 = 〈 ( U n ) 2 p , ( V n + 1 2 + V n − 1 2 ) x ˜ x ¯ 〉 = 〈 ( U n ) 2 p , ( U n + U n − 1 ) t ˜ 〉 = 〈 ( U n ) 2 p , ( U n + 1 + U n ) t ¯ 〉 = h ∑ j = 1 J − 1 ( U j n ) 2 p ( U j n + 1 + U j n ) t ¯ = h ∑ k = 0 n ∑ j = 1 J − 1 ( U j k ) 2 p ( U j k + 1 + U j k ) t ¯ − h ∑ k = 0 n − 1 ∑ j = 1 J − 1 ( U j k ) 2 p ( U j k + 1 + U j k ) t ¯ ,
q 9 = 〈 ( U n ) x ˜ x ¯ x ˜ x ¯ 2 p , V n + 1 2 + V n − 1 2 〉 = 〈 ( U n ) x ˜ x ¯ 2 p , ( V n + 1 2 + V n − 1 2 ) x ˜ x ¯ 〉 = 〈 ( U n ) x ˜ x ¯ 2 p , ( U n + U n − 1 ) t ˜ 〉 = 〈 ( U n ) x ˜ x ¯ 2 p , ( U n + 1 + U n ) t ¯ 〉 = h ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ 2 p ( U j n + 1 + U j n ) t ¯ = h ∑ k = 0 n ∑ j = 1 J − 1 ( U j k ) x ˜ x ¯ 2 p ( U j k + 1 + U j k ) t ¯ − h ∑ k = 0 n − 1 ∑ j = 1 J − 1 ( U j k ) x ˜ x ¯ 2 p ( U j k + 1 + U j k ) t ¯ .
As a result, following Eqs. (38) and (39), we arrive at the following conclusions
c 〈 ( U n ) x ˜ x ¯ 2 p , V n + 1 2 + V n − 1 2 〉 + c h 2 6 〈 ( U n ) x ˜ x ¯ x ˜ x ¯ 2 p , V n + 1 2 + V n − 1 2 〉 = c h ∑ k = 0 n ∑ j = 1 J − 1 ( U j k ) 2 p ( U j k + 1 + U j k ) t ¯ + c h 3 6 ∑ k = 0 n ∑ j = 1 J − 1 ( U j k ) x ˜ x ¯ 2 p ( U j k + 1 + U j k ) t ¯ − c h ∑ k = 0 n − 1 ∑ j = 1 J − 1 ( U j k ) 2 p ( U j k + 1 + U j k ) t ¯ − c h 3 6 ∑ k = 0 n − 1 ∑ j = 1 J − 1 ( U j k ) x ˜ x ¯ 2 p ( U j k + 1 + U j k ) t ¯ = c h 6 ∑ k = 0 n ∑ j = 1 J − 1 ( U j + 1 k ) 2 p + 4 ( U j k ) 2 p + ( U j − 1 k ) 2 p ( U j k + 1 + U j k ) t ¯ = c h 6 ∑ k = 0 n − 1 ∑ j = 1 J − 1 ( U j + 1 k ) 2 p + 4 ( U j k ) 2 p + ( U j − 1 k ) 2 p ( U j k + 1 + U j k ) t ¯ .
By substituting Eqs. (31)-(37) and (40) into Eq. (30), we obtain
1 τ ∥ V x ˜ n + 1 2 ∥ 2 + k 2 2 τ ∥ U n + 1 ∥ 2 + 1 2 τ a 1 − k 2 h 2 6 ∥ U x ˜ n + 1 ∥ 2 + 1 τ a 2 − h 2 4 ∥ U t ¯ n + 1 ∥ 2 + 1 2 τ b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ n + 1 ∥ 2 + 1 τ b 2 − a 2 h 2 6 ∥ U x ˜ t ¯ n + 1 ∥ 2 − b 2 h 2 12 τ ∥ U t ˜ t ¯ n + 1 ∥ 2 − c h 6 ∑ k = 0 n ∑ j = 1 J − 1 ( U j + 1 k ) 2 p + 4 ( U j k ) 2 p + ( U j − 1 k ) 2 p ( U j k + 1 + U j k ) t ¯ = 1 τ ∥ V x ˜ n − 1 2 ∥ 2 + k 2 2 τ ∥ U n − 1 ∥ 2 + 1 2 τ a 1 − k 2 h 2 6 ∥ U x ˜ n − 1 ∥ 2 + 1 τ a 2 − h 2 4 ∥ U t ¯ n ∥ 2 + 1 2 τ b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ n − 1 ∥ 2 + 1 τ b 2 − a 2 h 2 6 ∥ U x ˜ t ¯ n ∥ 2 − b 2 h 2 12 τ ∥ U t ˜ t ¯ n ∥ 2 − c h 6 ∑ k = 0 n − 1 ∑ j = 1 J − 1 ( U j + 1 k ) 2 p + 4 ( U j k ) 2 p + ( U j − 1 k ) 2 p ( U j k + 1 + U j k ) t ¯ .
Multiplying Eq. (41) by τ , and subsequently adding the formula
k 2 2 ∥ U n ∥ 2 + 1 2 a 1 − k 2 h 2 6 ∥ U x ˜ n ∥ 2 + 1 2 b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ n ∥ 2
to both sides, we obtain
∥ V x ˜ n + 1 2 ∥ 2 + k 2 2 ∥ U n + 1 ∥ 2 + ∥ U n ∥ 2 + 1 2 a 1 − k 2 h 2 6 ∥ U x ˜ n + 1 ∥ 2 + ∥ U x ˜ n ∥ 2 + a 2 − h 2 4 ∥ U t ¯ n + 1 ∥ 2 + 1 2 b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ n + 1 ∥ 2 + ∥ U x ˜ x ¯ n ∥ 2 + b 2 − a 2 h 2 6 ∥ U x ˜ t ¯ n + 1 ∥ 2 − b 2 h 2 12 ∥ U t ˜ t ¯ n + 1 ∥ 2 − c h τ 6 ∑ k = 0 n ∑ j = 1 J − 1 ( U j + 1 k ) 2 p + 4 ( U j k ) 2 p + ( U j − 1 k ) 2 p ( U j k + 1 + U j k ) t ¯ = ∥ V x ˜ n − 1 2 ∥ 2 + k 2 2 ∥ U n ∥ 2 + ∥ U n − 1 ∥ 2 + 1 2 a 1 − k 2 h 2 6 ∥ U x ˜ n ∥ 2 + ∥ U x ˜ n − 1 ∥ 2 + a 2 − h 2 4 ∥ U t ¯ n ∥ 2 + 1 2 b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ n ∥ 2 + ∥ U x ˜ x ¯ n − 1 ∥ 2 + b 2 − a 2 h 2 6 ∥ U x ˜ t ¯ n ∥ 2 − b 2 h 2 12 ∥ U t ˜ t ¯ n ∥ 2 − c h τ 6 ∑ k = 0 n − 1 ∑ j = 1 J − 1 ( U j + 1 k ) 2 p + 4 ( U j k ) 2 p + ( U j − 1 k ) 2 p ( U j k + 1 + U j k ) t ¯ ,
that is E n = E n − 1 = · · · = E 0 .
In a similar manner, by computing the inner product of Eq. (19) with V 1 2 + V − 1 2 , we obtain
E 0 = ∥ V x ˜ 1 2 ∥ 2 + k 2 2 ∥ U 1 ∥ 2 + ∥ U 0 ∥ 2 + 1 2 a 1 − k 2 h 2 6 ∥ U x ˜ 1 ∥ 2 + ∥ U x ˜ 0 ∥ 2 + a 2 − h 2 4 ∥ U t ¯ 1 ∥ 2 + 1 2 b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ 1 ∥ 2 + ∥ U x ˜ x ¯ 0 ∥ 2 + b 2 − a 2 h 2 6 ∥ U x ˜ t ¯ 1 ∥ 2 − b 2 h 2 12 ∥ U t ˜ t ¯ 1 ∥ 2 − c h τ 6 ∑ j = 1 J − 1 ( U j + 1 0 ) 2 p + 4 ( U j 0 ) 2 p + ( U j − 1 0 ) 2 p ( U j 1 + U j 0 ) t ¯ = ∥ V x ˜ − 1 2 ∥ 2 + k 2 2 ∥ U 0 ∥ 2 + ∥ U − 1 ∥ 2 + 1 2 a 1 − k 2 h 2 6 ∥ U x ˜ 0 ∥ 2 + ∥ U x ˜ − 1 ∥ 2 + a 2 − h 2 4 ∥ U t ¯ 0 ∥ 2 + 1 2 b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ 0 ∥ 2 + ∥ U x ˜ x ¯ − 1 ∥ 2 + b 2 − a 2 h 2 6 ∥ U x ˜ t ¯ 0 ∥ 2 − b 2 h 2 12 ∥ U t ˜ t ¯ 0 ∥ 2 ,
where U j − 1 = U j 1 − 2 τ ψ ( x j ) , 0 ≤ j ≤ J . This completes the proof. □
Theorem 8.
Let φ ( x ) , ψ ( x ) ∈ H 0 2 ( Ω ) , then it follows that the solution U n to Eqs. (16)-(18) satisfies
∥ U n ∥ ≤ C , ∥ U x ˜ n ∥ ≤ C , ∥ U x ˜ x ¯ n ∥ ≤ C , ∥ U n ∥ ∞ ≤ C , ∥ U x ˜ n ∥ ∞ ≤ C , ∥ U x ˜ x ¯ n ∥ ∞ ≤ C , 0 ≤ n ≤ N .
Proof. 
We employ mathematical induction to derive the estimate. From Eq. (17), it can be deduced that ∥ U 0 ∥ ≤ C , ∥ U x ˜ 0 ∥ ≤ C , and ∥ U x ˜ x ¯ 0 ∥ ≤ C . In accordance with Lemma 4, it follows that ∥ U 0 ∥ ∞ ≤ C , ∥ U x ˜ 0 ∥ ∞ ≤ C and ∥ U x ˜ x ¯ 0 ∥ ∞ ≤ C . We proceed under the assumption that
∥ U k ∥ ≤ C , ∥ U x ˜ k ∥ ≤ C , ∥ U x ˜ x ¯ k ∥ ≤ C , ∥ U k ∥ ∞ ≤ C , ∥ U x ˜ k ∥ ∞ ≤ C , ∥ U x ˜ x ¯ k ∥ ∞ ≤ C ,
where k = 1 , 2 , · · · , n . By taking the inner product of Eq. (16) with U t ^ n , we can express the components of the inner product as follows:
〈 U t ˜ t ¯ n , U t ^ n 〉 − k 2 〈 U ¯ x ˜ x ¯ n , U t ^ n 〉 + a 1 − k 2 h 2 6 〈 U ¯ x ˜ x ¯ x ˜ x ¯ n , U t ^ n 〉 − a 2 − h 2 4 〈 U x ˜ x ¯ t ˜ t ¯ n , U t ^ n 〉 − b 1 − a 1 h 2 12 〈 U ¯ x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n , U t ^ n 〉 + b 2 − a 2 h 2 6 〈 U x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , U t ^ n 〉 + b 2 h 2 12 〈 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , U t ^ n 〉 = − c 〈 ( U n ) x ˜ x ¯ 2 p , U t ^ n 〉 − c h 2 6 〈 ( U n ) x ˜ x ¯ x ˜ x ¯ 2 p , U t ^ n 〉 .
By utilizing Lemmas 2 and 3 in conjunction with the Cauchy-Schwarz inequality [24,28], a simple calculation yields
s 1 = 〈 U t ˜ t ¯ n , U t ^ n 〉 = 1 2 τ 〈 U t ¯ n + 1 − U t ¯ n , U t ¯ n + 1 + U t ¯ n 〉 = 1 2 τ ( ∥ U t ¯ n + 1 ∥ 2 − ∥ U t ¯ n ∥ 2 ) ,
s 2 = 〈 U ¯ x ˜ x ¯ n , U t ^ n 〉 = 1 4 τ 〈 U x ˜ x ¯ n + 1 + U x ˜ x ¯ n − 1 , U n + 1 − U n − 1 〉 = − 1 4 τ ( ∥ U x ˜ n + 1 ∥ 2 − ∥ U x ˜ n − 1 ∥ 2 ) ,
s 3 = 〈 U ¯ x ˜ x ¯ x ˜ x ¯ n , U t ^ n 〉 = 1 4 τ 〈 U x ˜ x ¯ x ˜ x ¯ n + 1 + U x ˜ x ¯ x ˜ x ¯ n − 1 , U n + 1 − U n − 1 〉 = 1 4 τ ( ∥ U x ˜ x ¯ n + 1 ∥ 2 − ∥ U x ˜ x ¯ n − 1 ∥ 2 ) ,
s 4 = 〈 U x ˜ x ¯ t ˜ t ¯ n , U t ^ n 〉 = − 〈 ( U x ˜ n ) t ˜ t ¯ , ( U x ˜ n ) t ^ 〉 = − 1 2 τ ( ∥ U x ˜ t ¯ n + 1 ∥ 2 − ∥ U x ˜ t ¯ n ∥ 2 ) , s 5 = 〈 U ¯ x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n , U t ^ n 〉 = 1 4 τ 〈 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n + 1 + U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n − 1 , U n + 1 − U n − 1 〉
= − 1 4 τ ( ∥ U x ˜ x ¯ x ˜ n + 1 ∥ 2 − ∥ U x ˜ x ¯ x ˜ n − 1 ∥ 2 ) ,
s 6 = 〈 U x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , U t ^ n 〉 = 〈 ( U x ˜ x ¯ n ) t ˜ t ¯ , ( U x ˜ x ¯ n ) t ^ 〉 = 1 2 τ ( ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 − ∥ U x ˜ x ¯ t ¯ n ∥ 2 ) ,
s 7 = 〈 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ n , U t ^ n 〉 = − 〈 ( U x ˜ x ¯ x ˜ n ) t ˜ t ¯ , ( U x ˜ x ¯ x ˜ n ) t ^ 〉 = − 1 2 τ ( ∥ U x ˜ x ¯ x ˜ t ¯ n + 1 ∥ 2 − ∥ U x ˜ x ¯ x ˜ t ¯ n ∥ 2 ) , s 8 = 〈 ( U n ) x ˜ x ¯ 2 p , U t ^ n 〉 = − 〈 ( U n ) x ˜ 2 p , U x ˜ t ^ n 〉 = − h ∑ j = 1 J − 1 ( U j n ) x ˜ 2 p ( U j n ) x ˜ t ^ = − h ∑ j = 1 J − 1 ( U j n ) x ˜ 2 p − 1 U j + 1 n + ( U j n ) 2 p − 1 ( U j n ) x ˜ ( U j n ) x ˜ t ^ ≤ h ∥ U x ˜ n ∥ ∞ 2 p − 1 ∑ j = 1 J − 1 | U j + 1 n | · | ( U j n ) x ˜ t ^ | + h ∥ U n ∥ ∞ 2 p − 1 ∑ j = 1 J − 1 | ( U j n ) x ˜ | · | ( U j n ) x ˜ t ^ | ≤ C ( ∥ U n ∥ 2 + ∥ U x ˜ n ∥ 2 + ∥ U x ˜ t ^ n ∥ 2 ) .
Since
U x ˜ t ^ n = 1 2 ( U x ˜ t ¯ n + U x ˜ t ¯ n + 1 ) , ∥ U n ∥ ≤ C ∥ U x ˜ n ∥ ,
then we finally have
s 8 = 〈 ( U n ) x ˜ x ¯ 2 p , U t ^ n 〉 ≤ C ( ∥ U x ˜ n ∥ 2 + ∥ U x ˜ t ¯ n ∥ 2 + ∥ U x ˜ t ¯ n + 1 ∥ 2 ) .
Similarly, we have
s 9 = h 2 〈 ( U n ) x ˜ x ¯ x ˜ x ¯ 2 p , U t ^ n 〉 = h 2 〈 ( U n ) x ˜ x ¯ 2 p , U x ˜ x ¯ t ^ n 〉 = h 3 ∑ j = 1 J − 1 ( U j n ) x ˜ x ¯ 2 p ( U j n ) x ˜ x ¯ t ^ = h ∑ j = 1 J − 1 ( U j + 1 n ) 2 p − 2 ( U j n ) 2 p + ( U j − 1 n ) 2 p ( U j n ) x ˜ x ¯ t ^ ≤ C ( ∥ U n ∥ 2 + ∥ U x ˜ x ¯ t ^ n ∥ 2 ) ≤ C ( ∥ U x ˜ n ∥ 2 + ∥ U x ˜ x ¯ t ¯ n ∥ 2 + ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 ) .
By substituting Eqs. (45)-(53) into Eq. (44), we obtain
1 2 ( ∥ U t ¯ n + 1 ∥ 2 − ∥ U t ¯ n ∥ 2 ) + k 2 4 ( ∥ U x ˜ n + 1 ∥ 2 − ∥ U x ˜ n − 1 ∥ 2 ) + 1 4 a 1 − k 2 h 2 6 ( ∥ U x ˜ x ¯ n + 1 ∥ 2 − ∥ U x ˜ x ¯ n − 1 ∥ 2 ) + 1 2 a 2 − h 2 4 ( ∥ U x ˜ t ¯ n + 1 ∥ 2 − ∥ U x ˜ t ¯ n ∥ 2 ) + 1 4 b 1 − a 1 h 2 12 ( ∥ U x ˜ x ¯ x ˜ n + 1 ∥ 2 − ∥ U x ˜ x ¯ x ˜ n − 1 ∥ 2 ) + 1 2 b 2 − a 2 h 2 6 ( ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 − ∥ U x ˜ x ¯ t ¯ n ∥ 2 ) − b 2 h 2 24 ( ∥ U x ˜ x ¯ x ˜ t ¯ n + 1 ∥ 2 − ∥ U x ˜ x ¯ x ˜ t ¯ n ∥ 2 ) ≤ C τ ( ∥ U x ˜ n ∥ 2 + ∥ U x ˜ t ¯ n ∥ 2 + ∥ U x ˜ t ¯ n + 1 ∥ 2 + ∥ U x ˜ x ¯ t ¯ n ∥ 2 + ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 ) .
Defining
B n = 1 2 ∥ U t ¯ n + 1 ∥ 2 + k 2 4 ( ∥ U x ˜ n + 1 ∥ 2 + ∥ U x ˜ n ∥ 2 ) + 1 4 a 1 − k 2 h 2 6 ( ∥ U x ˜ x ¯ n + 1 ∥ 2 + ∥ U x ˜ x ¯ n ∥ 2 ) + 1 2 a 2 − h 2 4 ∥ U x ˜ t ¯ n + 1 ∥ 2 + 1 4 b 1 − a 1 h 2 12 ( ∥ U x ˜ x ¯ x ˜ n + 1 ∥ 2 + ∥ U x ˜ x ¯ x ˜ n ∥ 2 ) + 1 2 b 2 − a 2 h 2 6 ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 − b 2 h 2 24 ∥ U x ˜ x ¯ x ˜ t ¯ n + 1 ∥ 2 ,
then based on Lemma 5, we can conclude that
B n ≥ 1 2 ∥ U t ¯ n + 1 ∥ 2 + k 2 4 ( ∥ U x ˜ n + 1 ∥ 2 + ∥ U x ˜ n ∥ 2 ) + a 1 4 ( ∥ U x ˜ x ¯ n + 1 ∥ 2 + ∥ U x ˜ x ¯ n ∥ 2 ) + a 2 2 ∥ U x ˜ t ¯ n + 1 ∥ 2 + b 1 4 ( ∥ U x ˜ x ¯ x ˜ n + 1 ∥ 2 + ∥ U x ˜ x ¯ x ˜ n ∥ 2 ) + b 2 2 ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 − k 2 6 ( ∥ U x ˜ n + 1 ∥ 2 + ∥ U x ˜ n ∥ 2 ) − 1 2 ∥ U t ¯ n + 1 ∥ 2 − a 1 12 ( ∥ U x ˜ x ¯ n + 1 ∥ 2 + ∥ U x ˜ x ¯ n ∥ 2 ) − a 2 3 ∥ U x ˜ t ¯ n + 1 ∥ 2 − b 2 6 ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 = k 2 12 ( ∥ U x ˜ n + 1 ∥ 2 + ∥ U x ˜ n ∥ 2 ) + a 1 6 ( ∥ U x ˜ x ¯ n + 1 ∥ 2 + ∥ U x ˜ x ¯ n ∥ 2 ) + a 2 6 ∥ U x ˜ t ¯ n + 1 ∥ 2 + b 1 4 ( ∥ U x ˜ x ¯ x ˜ n + 1 ∥ 2 + ∥ U x ˜ x ¯ x ˜ n ∥ 2 ) + b 2 3 ∥ U x ˜ x ¯ t ¯ n + 1 ∥ 2 .
Consequently, Eq. (54) can be reformulated as follows:
B n − B n − 1 ≤ C τ ( B n + B n − 1 ) , 1 ≤ n ≤ N − 1 .
Assuming that τ is sufficiently small, specifically τ ≤ k − 2 k C with k ≥ 2 , we further obtain
B n ≤ 1 + τ C 1 − τ C B n − 1 ≤ ( 1 + τ k C ) B n − 1 ≤ exp ( k T C ) B 0 .
This indicates that B n is bounded, which leads to the conclusions that ∥ U x ˜ n + 1 ∥ ≤ C and ∥ U x ˜ x ¯ n + 1 ∥ ≤ C as derived from Eq. (55). By applying Lemma 4, we further establish that ∥ U n + 1 ∥ ∞ ≤ C , ∥ U x ˜ n + 1 ∥ ∞ ≤ C , and ∥ U x ˜ x ¯ n + 1 ∥ ∞ ≤ C . This completes the proof. □

4. Solvability, Convergence and Stability

In this section, we examine the solvability, convergence and stability of the previously discussed scheme.
Theorem 9.
The difference scheme outlined in Eqs. (16)-(18) exhibits a unique solution.
Proof. 
According to Eq. (17), it is established that U 0 has a unique solution. To demonstrate the unique solvability of U 1 , we will analyze the homogeneous version of Eq. (19) as detailed below:
1 τ 2 U 1 − k 2 2 U x ˜ x ¯ 1 + 1 2 a 1 − k 2 h 2 6 U x ˜ x ¯ x ˜ x ¯ 1 − 1 τ 2 a 2 − h 2 4 U x ˜ x ¯ 1 − 1 2 b 1 − a 1 h 2 12 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ 1 + 1 τ 2 b 2 − a 2 h 2 6 U x ˜ x ¯ x ˜ x ¯ 1 + b 2 h 2 12 τ 2 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ 1 = 0 .
By computing the inner product of Eq. (56) with U 1 , we obtain
1 τ 2 ∥ U 1 ∥ 2 + k 2 2 ∥ U x ˜ 1 ∥ 2 + 1 2 a 1 − k 2 h 2 6 ∥ U x ˜ x ¯ 1 ∥ 2 + 1 τ 2 a 2 − h 2 4 ∥ U x ˜ 1 ∥ 2 + 1 2 b 1 − a 1 h 2 12 ∥ U x ˜ x ¯ x ˜ 1 ∥ 2 + 1 τ 2 b 2 − a 2 h 2 6 ∥ U x ˜ x ¯ 1 ∥ 2 − b 2 h 2 12 τ 2 ∥ U x ˜ x ¯ x ˜ 1 ∥ 2 = 0 ,
that is
∥ U 1 ∥ 2 + τ 2 k 2 2 + a 2 − h 2 4 ∥ U x ˜ 1 ∥ 2 + τ 2 2 a 1 − k 2 h 2 6 + b 2 − a 2 h 2 6 ∥ U x ˜ x ¯ 1 ∥ 2 + τ 2 2 b 1 − a 1 h 2 12 − b 2 h 2 12 ∥ U x ˜ x ¯ x ˜ 1 ∥ 2 = 0 .
Assuming that the parameters τ and h are sufficiently small, we observe that ∥ U 1 ∥ = 0 , ∥ U x ˜ 1 ∥ = 0 , ∥ U x ˜ x ¯ 1 ∥ = 0 , and ∥ U x ˜ x ¯ x ˜ 1 ∥ = 0 . Consequently, Eq. (19) admits only the trivial solution, indicating that U 1 is uniquely determined.
We subsequently assume that the solutions for U 0 , U 1 , U 2 ,..., U n are uniquely determined, where n ≤ N − 1 . By examining the homogeneous version of Eq. (16) for U n + 1 , we obtain
1 τ 2 U n + 1 − k 2 2 U x ˜ x ¯ n + 1 + 1 2 a 1 − k 2 h 2 6 U x ˜ x ¯ x ˜ x ¯ n + 1 − 1 τ 2 a 2 − h 2 4 U x ˜ x ¯ n + 1 − 1 2 b 1 − a 1 h 2 12 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n + 1 + 1 τ 2 b 2 − a 2 h 2 6 U x ˜ x ¯ x ˜ x ¯ n + 1 + b 2 h 2 12 τ 2 U x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ n + 1 = 0 .
Similarly, by computing the inner product of Eq. (59) with U n + 1 , we obtain
∥ U n + 1 ∥ 2 + τ 2 k 2 2 + a 2 − h 2 4 ∥ U x ˜ n + 1 ∥ 2 + τ 2 2 a 1 − k 2 h 2 6 + b 2 − a 2 h 2 6 ∥ U x ˜ x ¯ n + 1 ∥ 2 + τ 2 2 b 1 − a 1 h 2 12 − b 2 h 2 12 ∥ U x ˜ x ¯ x ˜ n + 1 ∥ 2 = 0 .
which yields ∥ U n + 1 ∥ = 0 , ∥ U x ˜ n + 1 ∥ = 0 , ∥ U x ˜ x ¯ n + 1 ∥ = 0 , ∥ U x ˜ x ¯ x ˜ n + 1 ∥ = 0 . The difference scheme (16)-(18) is demonstrated to possess a unique solution through the application of the method of induction. This completes the proof. □
Theorem 10.
Assuming that φ ( x ) , ψ ( x ) ∈ H 0 2 ( Ω ) and u ∈ C x , t 10 , 4 ( [ x l , x r ] × ( 0 , T ] ) , it can be concluded that the solution U n to Eqs. (16)-(18) converges to the solution u n of the problem defined by Eqs. (1)-(3). Furthermore, the rate of convergence is characterized by O ( τ 2 + h 4 ) in both the ∥ · ∥ and ∥ · ∥ ∞ norms. Specifically, this implies that
∥ u n − U n ∥ ≤ O ( τ 2 + h 4 ) , ∥ u n − U n ∥ ∞ ≤ O ( τ 2 + h 4 ) .
Proof. 
The truncation errors associated with Eqs. (16)-(18) can be expressed as follows:
( u j n ) t ˜ t ¯ − k 2 ( u ¯ j n ) x ˜ x ¯ + a 1 − k 2 h 2 6 ( u ¯ j n ) x ˜ x ¯ x ˜ x ¯ − a 2 − h 2 4 ( u j n ) x ˜ x ¯ t ˜ t ¯ − b 1 − a 1 h 2 12 ( u ¯ j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯
+ b 2 − a 2 h 2 6 ( u j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + b 2 h 2 12 ( u j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + c [ ( u j n ) 2 p ] x ˜ x ¯ + c h 2 6 [ ( u j n ) 2 p ] x ˜ x ¯ x ˜ x ¯ = r j n ,
u j 0 = φ ( x j ) , ( u j 0 ) t ^ = ψ ( x j ) , 0 ≤ j ≤ J ,
u 0 n = u J n = 0 , ( u 0 n ) x ^ = ( u J n ) x ^ = 0 , ( u 0 n ) x ˜ x ¯ = ( u J n ) x ˜ x ¯ = 0 , 0 ≤ n ≤ N .
Through the application of the Taylor expansion, it can be demonstrated that the inequality | r j n | ≤ O ( τ 2 + h 4 ) is valid as both τ and h approach zero, for n ≥ 0 .
Define the error term as e j n = u j n − U j n . By subtracting Eqs. (16)-(18) from Eqs. (61)-(63), we obtain
r j n = ( e j n ) t ˜ t ¯ − k 2 ( e ¯ j n ) x ˜ x ¯ + a 1 − k 2 h 2 6 ( e ¯ j n ) x ˜ x ¯ x ˜ x ¯ − a 2 − h 2 4 ( e j n ) x ˜ x ¯ t ˜ t ¯ − b 1 − a 1 h 2 12 ( e ¯ j n ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ + b 2 − a 2 h 2 6 ( e j n ) x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + b 2 h 2 12 ( u j e ) x ˜ x ¯ x ˜ x ¯ x ˜ x ¯ t ˜ t ¯ + c [ ( u j n ) 2 p − ( U j n ) 2 p ] x ˜ x ¯
+ c h 2 6 [ ( u j n ) 2 p − ( U j n ) 2 p ] x ˜ x ¯ x ˜ x ¯ , e j 0 = 0 , ( e j 0 ) t ^ = 0 , 0 ≤ j ≤ J ,
e 0 n = e J n = 0 , ( e 0 n ) x ^ = ( e J n ) x ^ = 0 , ( e 0 n ) x ˜ x ¯ = ( e J n ) x ˜ x ¯ = 0 , 0 ≤ n ≤ N .
By computing the inner product of Eq. (64) with ( e j n ) t ^ , we obtain
1 2 ( ∥ e t ¯ n + 1 ∥ 2 − ∥ e t ¯ n ∥ 2 ) + k 2 4 ( ∥ e x ˜ n + 1 ∥ 2 − ∥ e x ˜ n − 1 ∥ 2 ) + 1 4 a 1 − k 2 h 2 6 ( ∥ e x ˜ x ¯ n + 1 ∥ 2 − ∥ e x ˜ x ¯ n − 1 ∥ 2 ) + 1 2 a 2 − h 2 4 ( ∥ e x ˜ t ¯ n + 1 ∥ 2 − ∥ e x ˜ t ¯ n ∥ 2 ) + 1 4 b 1 − a 1 h 2 12 ( ∥ e x ˜ x ¯ x ˜ n + 1 ∥ 2 − ∥ e x ˜ x ¯ x ˜ n − 1 ∥ 2 ) + 1 2 b 2 − a 2 h 2 6 ( ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 − ∥ e x ˜ x ¯ t ¯ n ∥ 2 ) − b 2 h 2 24 ( ∥ e x ˜ x ¯ x ˜ t ¯ n + 1 ∥ 2 − ∥ e x ˜ x ¯ x ˜ t ¯ n ∥ 2 ) = τ 〈 r n , e t ^ n 〉 − c τ 〈 [ ( u n ) 2 p − ( U n ) 2 p ] x ˜ x ¯ , e t ^ n 〉 − c τ h 2 6 〈 [ ( u n ) 2 p − ( U n ) 2 p ] x ˜ x ¯ x ˜ x ¯ , e t ^ n 〉 .
According to Lemma 2 and the Cauchy-Schwarz inequality [24,28], it can be concluded that
〈 | [ ( u n ) 2 p − ( U n ) 2 p ] x ˜ x ¯ , e t ^ n 〉 | = 〈 ( u n ) 2 p − ( U n ) 2 p , e x ˜ x ¯ t ^ n 〉 = h ∑ j = 1 J − 1 [ ( u j n ) 2 p − ( U j n ) 2 p ] ( e j n ) x ˜ x ¯ t ^ = h ∑ j = 1 J − 1 e j n ∑ k = 0 2 p − 1 ( u j n ) 2 p − 1 − k ( U j n ) k ( e j n ) x ˜ x ¯ t ^ ≤ C ( ∥ e x ˜ n ∥ 2 + ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 + ∥ e x ˜ x ¯ t ¯ n ∥ 2 ) .
Similarly, we have
h 2 〈 [ ( u n ) 2 p − ( U n ) 2 p ] x ˜ x ¯ x ˜ x ¯ , e t ^ n 〉 = h 2 〈 [ ( u n ) 2 p − ( U n ) 2 p ] x ˜ x ¯ , e x ˜ x ¯ t ^ n 〉 = h 3 ∑ j = 1 J − 1 ( u j n ) 2 p − ( U j n ) 2 p x ˜ x ¯ ( e j n ) x ˜ x ¯ t ^ = h ∑ j = 1 J − 1 ( u j + 1 n ) 2 p − ( U j + 1 n ) 2 p − 2 ( u j n ) 2 p − ( U j n ) 2 p + ( u j − 1 n ) 2 p − ( U j − 1 n ) 2 p ( U j n ) x ˜ x ¯ t ^ ≤ C ( ∥ e x ˜ n ∥ 2 + ∥ e x ˜ x ¯ t ¯ n ∥ 2 + ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 ) .
Furthermore, we get
〈 r n , e t ^ n 〉 = 〈 r n , 1 2 ( e t ¯ n + 1 + e t ¯ n ) 〉 ≤ 1 2 ∥ r n ∥ 2 + 1 4 ( ∥ e t ¯ n + 1 ∥ 2 + ∥ e t ¯ n ∥ 2 ) .
Substituting Eqs. (68)-(70) into Eq. (67), we obtain
1 2 ( ∥ e t ¯ n + 1 ∥ 2 − ∥ e t ¯ n ∥ 2 ) + k 2 4 ( ∥ e x ˜ n + 1 ∥ 2 − ∥ e x ˜ n − 1 ∥ 2 ) + 1 4 a 1 − k 2 h 2 6 ( ∥ e x ˜ x ¯ n + 1 ∥ 2 − ∥ e x ˜ x ¯ n − 1 ∥ 2 ) + 1 2 a 2 − h 2 4 ( ∥ e x ˜ t ¯ n + 1 ∥ 2 − ∥ e x ˜ t ¯ n ∥ 2 ) + 1 4 b 1 − a 1 h 2 12 ( ∥ e x ˜ x ¯ x ˜ n + 1 ∥ 2 − ∥ e x ˜ x ¯ x ˜ n − 1 ∥ 2 ) + 1 2 b 2 − a 2 h 2 6 ( ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 − ∥ e x ˜ x ¯ t ¯ n ∥ 2 ) − b 2 h 2 24 ( ∥ e x ˜ x ¯ x ˜ t ¯ n + 1 ∥ 2 − ∥ e x ˜ x ¯ x ˜ t ¯ n ∥ 2 ) ≤ τ 2 ∥ r n ∥ 2 + C τ ( ∥ e x ˜ n ∥ 2 + ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 + ∥ e x ˜ x ¯ t ¯ n ∥ 2 + ∥ e t ¯ n + 1 ∥ 2 + ∥ e t ¯ n ∥ 2 ) .
Setting
D n = 1 2 ∥ e t ¯ n + 1 ∥ 2 + k 2 4 ( ∥ e x ˜ n + 1 ∥ 2 + ∥ e x ˜ n ∥ 2 ) + 1 4 a 1 − k 2 h 2 6 ( ∥ e x ˜ x ¯ n + 1 ∥ 2 + ∥ e x ˜ x ¯ n ∥ 2 ) + 1 2 a 2 − h 2 4 ∥ e x ˜ t ¯ n + 1 ∥ 2 + 1 4 b 1 − a 1 h 2 12 ( ∥ e x ˜ x ¯ x ˜ n + 1 ∥ 2 + ∥ e x ˜ x ¯ x ˜ n ∥ 2 ) + 1 2 b 2 − a 2 h 2 6 ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 − b 2 h 2 24 ∥ e x ˜ x ¯ x ˜ t ¯ n + 1 ∥ 2 ,
then from Lemma 5, we have
D n ≥ 1 2 ∥ e t ¯ n + 1 ∥ 2 + k 2 4 ( ∥ e x ˜ n + 1 ∥ 2 + ∥ e x ˜ n ∥ 2 ) + a 1 4 ( ∥ e x ˜ x ¯ n + 1 ∥ 2 + ∥ e x ˜ x ¯ n ∥ 2 ) + a 2 2 ∥ e x ˜ t ¯ n + 1 ∥ 2 + b 1 4 ( ∥ e x ˜ x ¯ x ˜ n + 1 ∥ 2 + ∥ e x ˜ x ¯ x ˜ n ∥ 2 ) + b 2 2 ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 − k 2 6 ( ∥ e x ˜ n + 1 ∥ 2 + ∥ e x ˜ n ∥ 2 ) − 1 2 ∥ e t ¯ n + 1 ∥ 2 − a 1 12 ( ∥ e x ˜ x ¯ n + 1 ∥ 2 + ∥ e x ˜ x ¯ n ∥ 2 ) − a 2 3 ∥ e x ˜ t ¯ n + 1 ∥ 2 − b 2 6 ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 = k 2 12 ( ∥ e x ˜ n + 1 ∥ 2 + ∥ e x ˜ n ∥ 2 ) + a 1 6 ( ∥ e x ˜ x ¯ n + 1 ∥ 2 + ∥ e x ˜ x ¯ n ∥ 2 ) + a 2 6 ∥ e x ˜ t ¯ n + 1 ∥ 2 + b 1 4 ( ∥ e x ˜ x ¯ x ˜ n + 1 ∥ 2 + ∥ e x ˜ x ¯ x ˜ n ∥ 2 ) + b 2 3 ∥ e x ˜ x ¯ t ¯ n + 1 ∥ 2 .
Consequently, from Eqs. (71)-(72), we obtain
D n − D n − 1 ≤ τ 2 ∥ r n ∥ 2 + C τ ( D n + D n − 1 ) .
That is
( 1 − C τ ) ( D n − D n − 1 ) ≤ τ 2 ∥ r n ∥ 2 + 2 C τ D n − 1 .
Therefore, if the value of τ is sufficiently small such that the expression 1 − C τ remains positive, then
D n − D n − 1 ≤ C τ ∥ r n ∥ 2 + C τ D n − 1 .
By summing Eq. (73) from 1 to n, we obtain
D n ≤ D 0 + C τ ∑ l = 1 n ∥ r l ∥ 2 + C τ ∑ l = 1 n D l − 1 .
It is essential to note that
τ ∑ l = 1 n ∥ r l ∥ 2 ≤ n τ max 1 ≤ l ≤ n ∥ r l ∥ 2 ≤ T · O ( τ 2 + h 4 ) 2 , D 0 ≤ O ( τ 2 + h 4 ) 2 ,
we subsequently obtain from the Discrete Gronwall’s inequality [29,30] that D n ≤ O ( τ 2 + h 4 ) 2 . This leads to the conclusion that ∥ e x n ∥ ≤ O ( τ 2 + h 4 ) and ∥ e x ˜ n ∥ ≤ O ( τ 2 + h 4 ) . Ultimately, we utilize the findings from Lemma 4 to demonstrate that ∥ e n ∥ ≤ O ( τ 2 + h 4 ) and ∥ e n ∥ ∞ ≤ O ( τ 2 + h 4 ) . This completes the proof. □
We subsequently obtain the following theorem.
Theorem 11.
Under the conditions specified in Theorem 10, the solution U n of the Eqs. (16) -(18) exhibits stability. The analysis is conducted with respect to both the ∥ · ∥ norm and the ∥ · ∥ ∞ norm.

5. Numerical Experiments

In this section, we conduct a series of numerical experiments aimed at assessing the efficacy and accuracy of the theoretical analysis presented in the preceding sections. Following this, we will quantify the corresponding errors utilizing the designated error norms [27,29,31]:
∥ e n ∥ = h ∑ j = 1 J − 1 | u j n − U j n | 2 1 2 , ∥ e n ∥ ∞ = max 1 ≤ j ≤ J − 1 | u j n − U j n | .
Example 1.
Consider the parameters
k = 1 , a 1 = 0 , a 2 = 1 , b 1 = 0 , b 2 = 0 , c = − 1 , p = 1 ,
which is the following improved Boussinesq equation [2,27]
u t t − u x x − u x x t t − ( u 2 ) x x = 0 ,
the solitary wave solution is expressed as follows
u ( x , t ) = A sech 2 1 c 0 A 6 x − x 0 − c 0 t , c 0 = ± 1 + 2 3 A ,
where A, x 0 and c 0 are given constants. The initial conditions may be established by evaluating Eq. (76) and its derivative for t at the point t = 0 :
φ ( x ) = A sech 2 1 c 0 A 6 x − x 0 ,
ψ ( x ) = 2 A A 6 sech 2 1 c 0 A 6 x − x 0 tanh 1 c 0 A 6 x − x 0 .
First, we choose the following parameters:
x 0 = 0 , A = 0.5 , c 0 = 1 + 2 A / 3 , x l = − 60 , x r = 100 , t ∈ [ 0 , 1 ] .
We then compare our findings with the numerical results presented in [2]. The computational accuracy for both temporal and spatial variables is evaluated at T = 1 and is detailed in Table 1 and Table 2, where τ = 0.001 in Table 1 and τ / h = 0.1 in Table 2. The data presented in Table 1 and Table 2 indicate that the current difference scheme (16)-(18) demonstrates significantly superior performance in comparison to the finite volume element scheme described in [2].
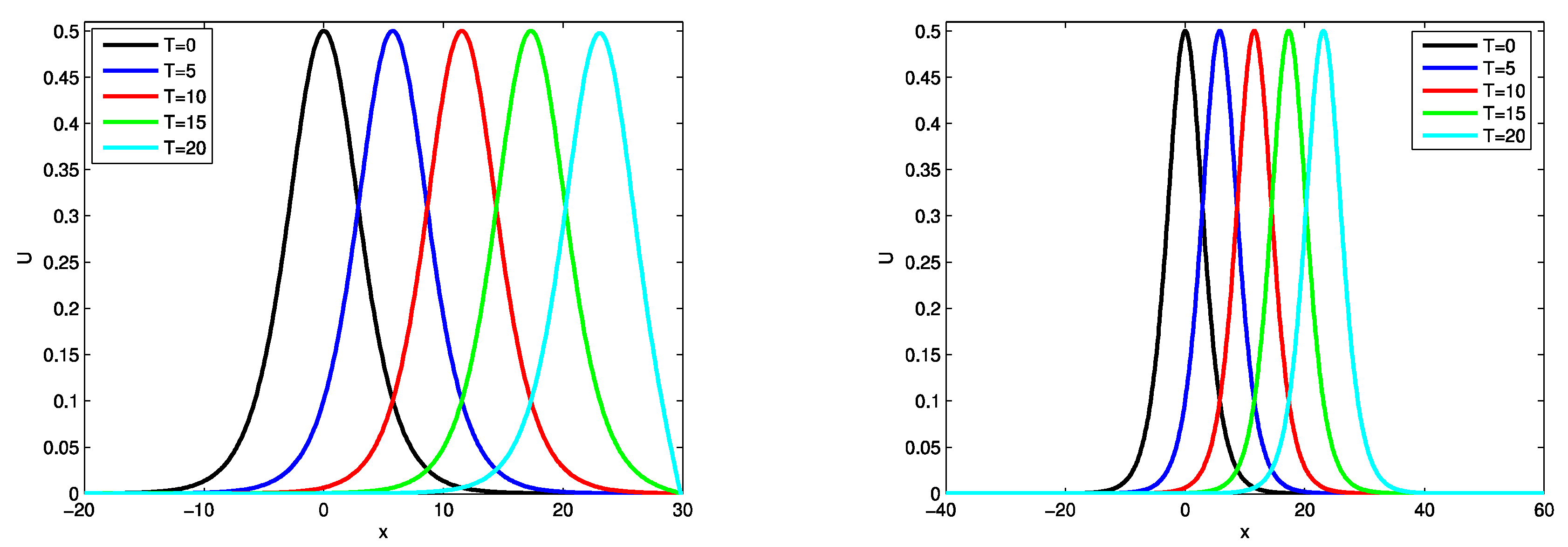
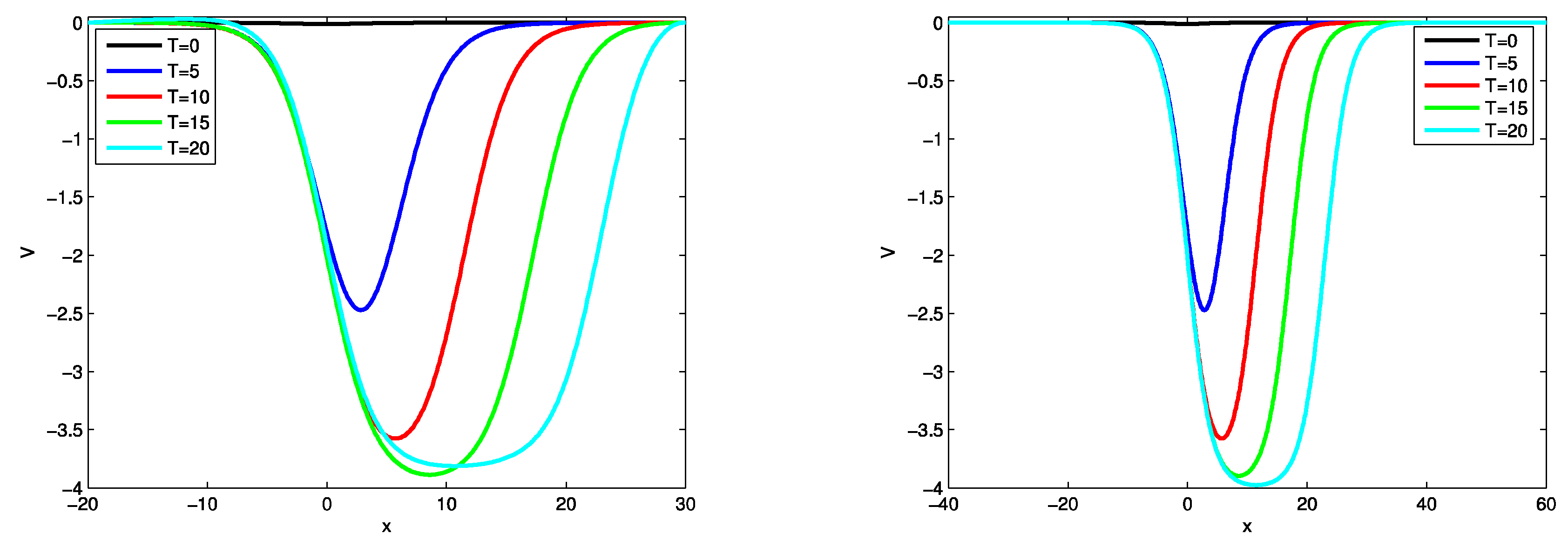
The present analysis investigates the solitary wave and its corresponding numerical solutions, as illustrated in Figure 1. The spatial domain is defined as x ∈ [ − 20 , 30 ] and [ − 40 , 60 ] , with parameters set at h = 0.1 and τ = h 2 at the time instances T = 0 , 5 , 10 , 15 , 20 . Figure 1 indicates that the patterns generated by the current scheme, as described by Eqs. (16)-(18), demonstrate a significant degree of agreement with the solitary wave solutions. Furthermore, the numerical solutions for the auxiliary variable V n , as estimated by Eq. 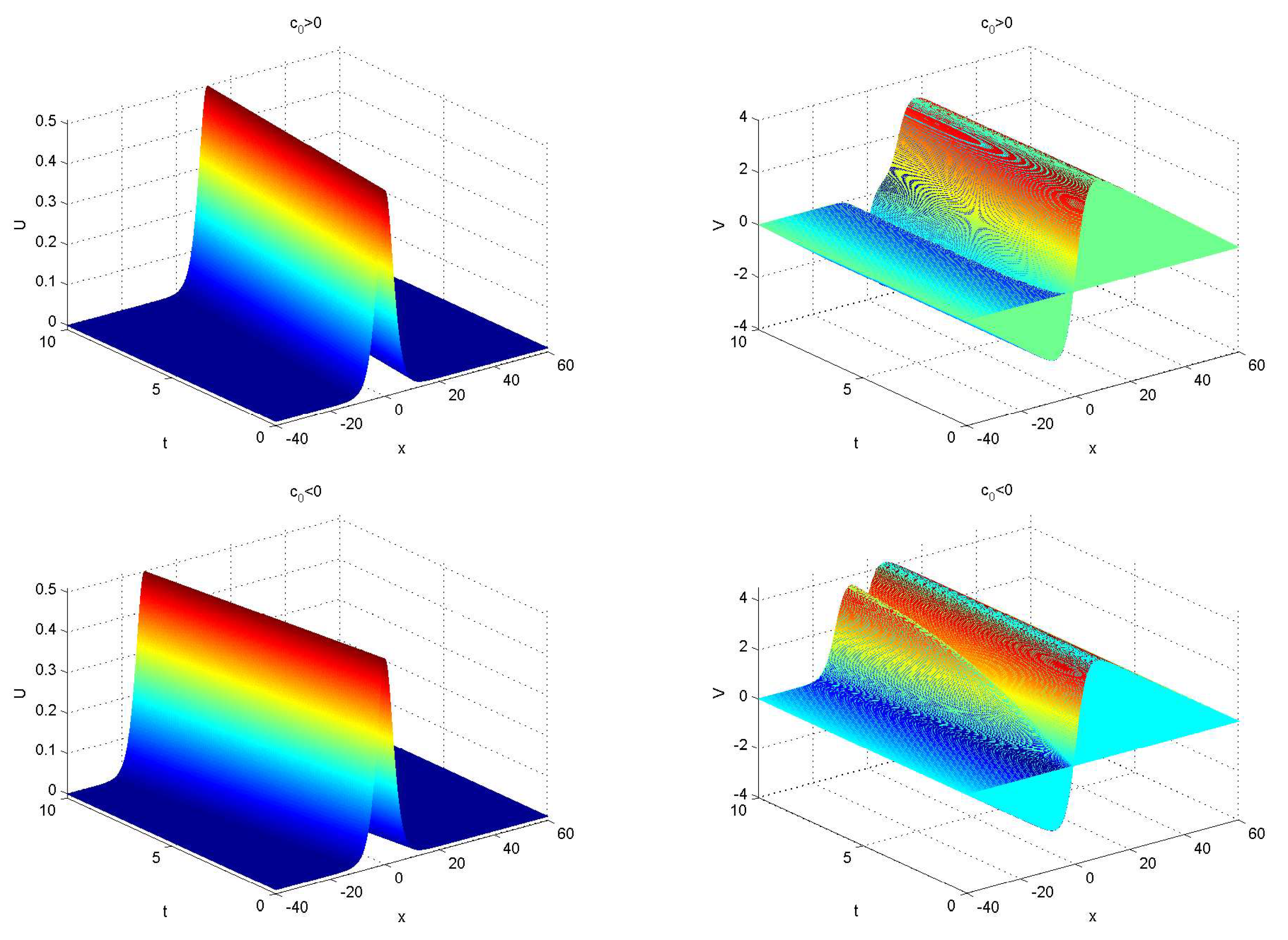(21), are visually represented in Figure 2. The graphs displaying the approximate solutions U n and V n , obtained from the difference scheme (16)-(18) with the parameters x ∈ [ − 40 , 60 ] , h = 0.1 , τ = h 2 , and c 0 = ± 1 + 2 A / 3 at T = 10 , are shown in Figure 3. It is observed that when c 0 > 0 , the solitary wave propagates to the right, while for c 0 < 0 , the solitary wave propagates to the left. These results are consistent with those reported in [27].
Finally, we present the discrete mass M n , the discrete rate of mass change R n and the discrete energy E n at various time intervals, as detailed in Table 3. The parameters are defined with c 0 > 0 , x ∈ [ − 40 , 60 ] , h = 0.1 and τ = h 2 . Analysis of Table 3 indicates that the discrete rate of mass change R n associated with soliton wave propagation is minimal, indicating that the mass change R n is conservative. Additionally, it is noted that the energy E n also exhibits conservative properties.
Example 2.
Consider the parameters
k = 1 , a 1 = 363 169 , a 2 = 2 , b 1 = 1 2 , b 2 = 0 , c = 1 2 , p = 1 ,
which is the sixth-order Boussinesq equation [15]
u t t − u x x − 2 u x x t t + 363 169 u x x x x − 1 2 u x x x x x x + 1 2 ( u 2 ) x x = 0 ,
the solitary wave solution is given by
u ( x , t ) = 210 169 sech 4 x 26 − 97 4394 t .
The initial data are
φ ( x ) = 210 169 sech 4 x 26 ,
ψ ( x ) = 420 28561 2522 sech 4 x 26 tanh x 26 .
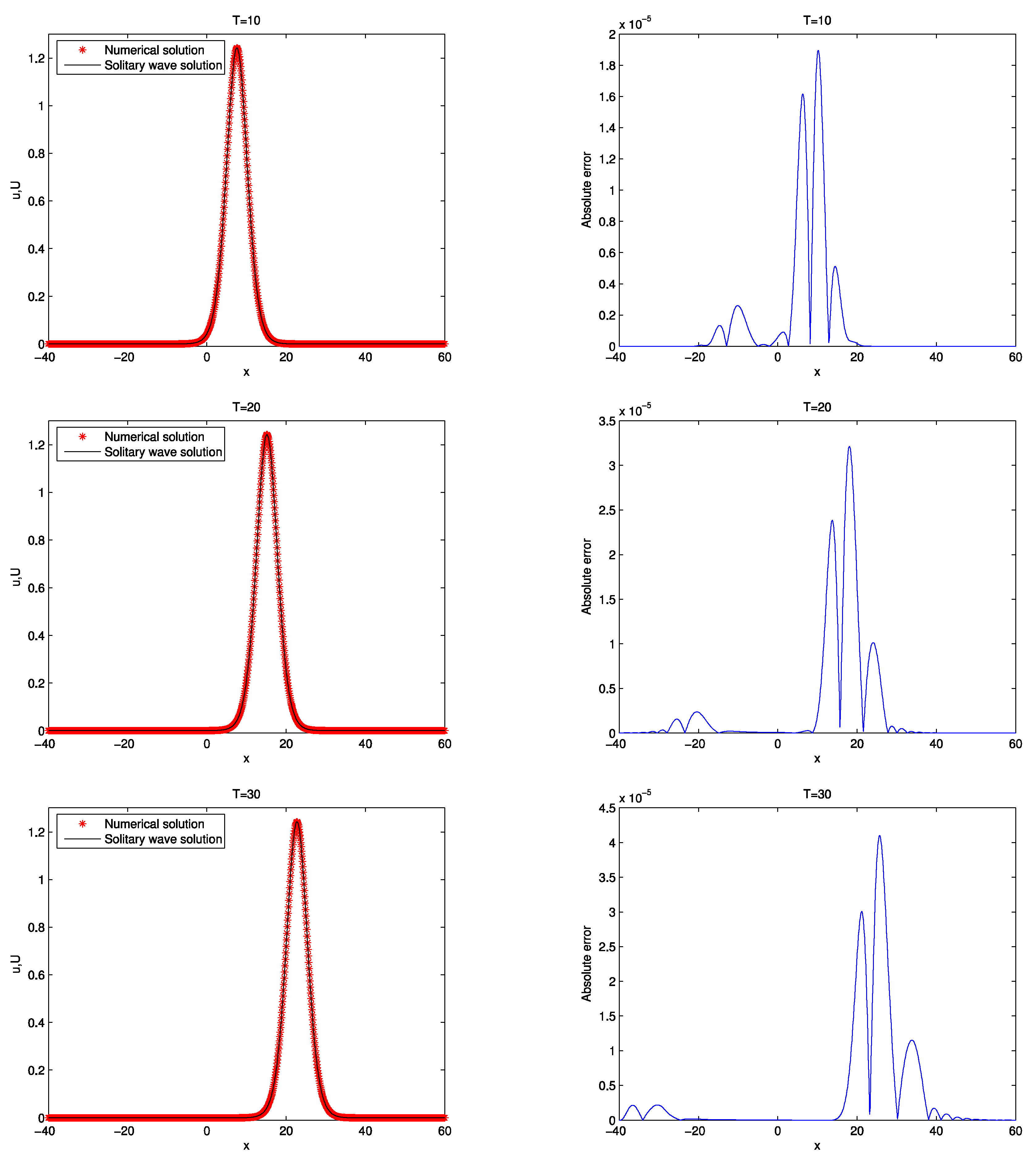
In this example, we first calculate the solution over the spatial domain defined by [ − 40 , 60 ] × [ 0 , 40 ] with a grid size of h = 0.1 and a time step τ = h 2 . The comparison between the solitary wave and the numerical solutions at the time instances T = 10 , 20, and 30 is presented in Figure 4. The results indicate that the errors across all grid points remain below 4.5 × 10 − 5 .
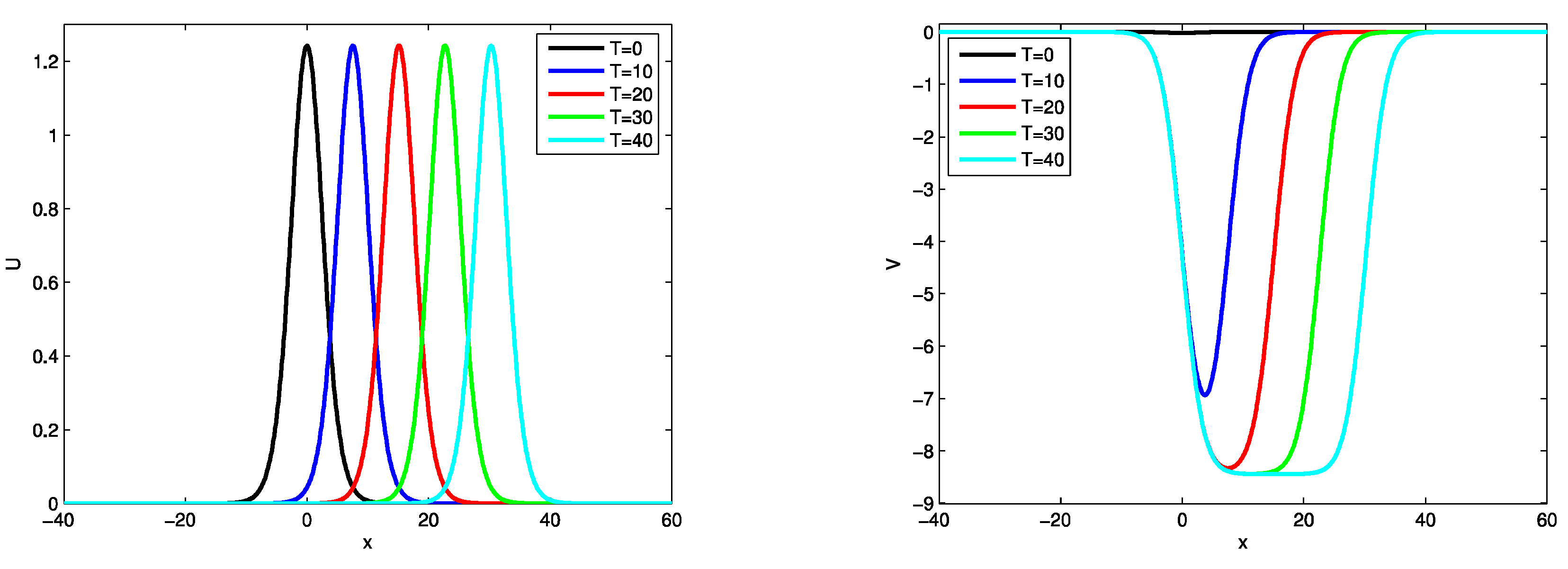
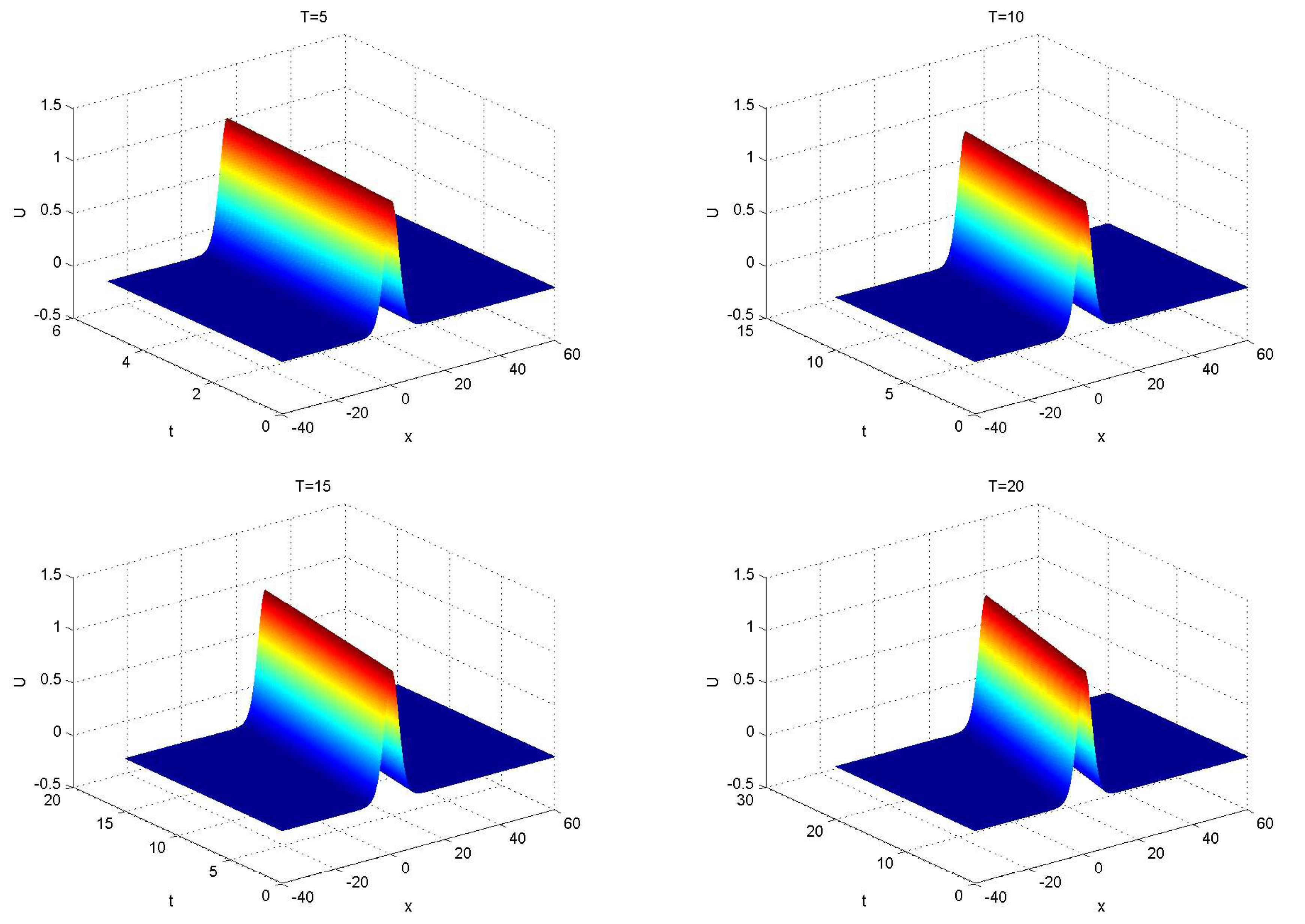
Figure 5 illustrates the numerical solutions at various time intervals, specifically T = 0 , 10, 20, 30, and 40. A detailed analysis of Figure 5 indicates that the wave heights at these specified time points are nearly indistinguishable. Figure 6 presents the graphs of the approximate solutions U n obtained from the current scheme described by Eqs. (16)-(18) at times T = 5 , 10, 15, and 20, with the parameters set to h = 0.1 , τ = h 2 , x l = − 40 and x r = 60 .
Additionally, Table 4 presents a summary of the discrete mass M n , the discrete rate of mass change R n , and the discrete energy E n at various time points T = 0 , 5, 10, 15, and 20. The findings suggest that both the discrete rate of mass change R n and the discrete energy E n exhibit conservative behavior in the discrete sense.
Example 3.
Consider the following sixth-order Boussinesq equation with the effects of surface tension
u t t − k 2 u x x + a 1 u x x x x − a 2 u x x t t − b 1 u x x x x x x + b 2 u x x x x t t + c ( u 2 p ) x x = 0 ,
where a 1 ≥ 0 , a 2 ≥ 0 , b 1 ≥ 0 , b 2 ≥ 0 , p ≥ 1 . In their research, Biswas et al. [4] examined the solitary wave solution corresponding to Eq. (83), that is
u ( x , t ) = A sech 2 2 p − 1 [ B ( x − ν t ) ] ,
where
A = ( 2 p + 1 ) ( b 2 k 2 − b 1 ) 2 c b 2 1 2 p − 1 , B = | 2 p − 1 | 2 b 2 k 2 − b 1 a 1 b 2 − a 2 b 1 , ν = b 1 b 2 .
To perform numerical simulations, the initial conditions can be determined by evaluating Eq. (84) and its derivative at the time point t = 0 , that is
φ ( x ) = A sech 2 2 p − 1 ( B x ) ,
ψ ( x ) = 2 2 p − 1 A B ν sech 2 2 p − 1 ( B x ) tanh ( B x ) .
To demonstrate the efficacy of the present difference scheme, we provide numerical results that pertain to the errors and rates of convergence. The parameters are configured with h = 0.4 and τ = h 2 at time T = 10 , as illustrated in Table 5, where x l = − 40 and x r = 60 . From Table 5, it is evident that the convergence rate achieved by the current finite difference scheme is approximately 4.0, which is consistent with the theoretical order of convergence specified in Theorem 10. 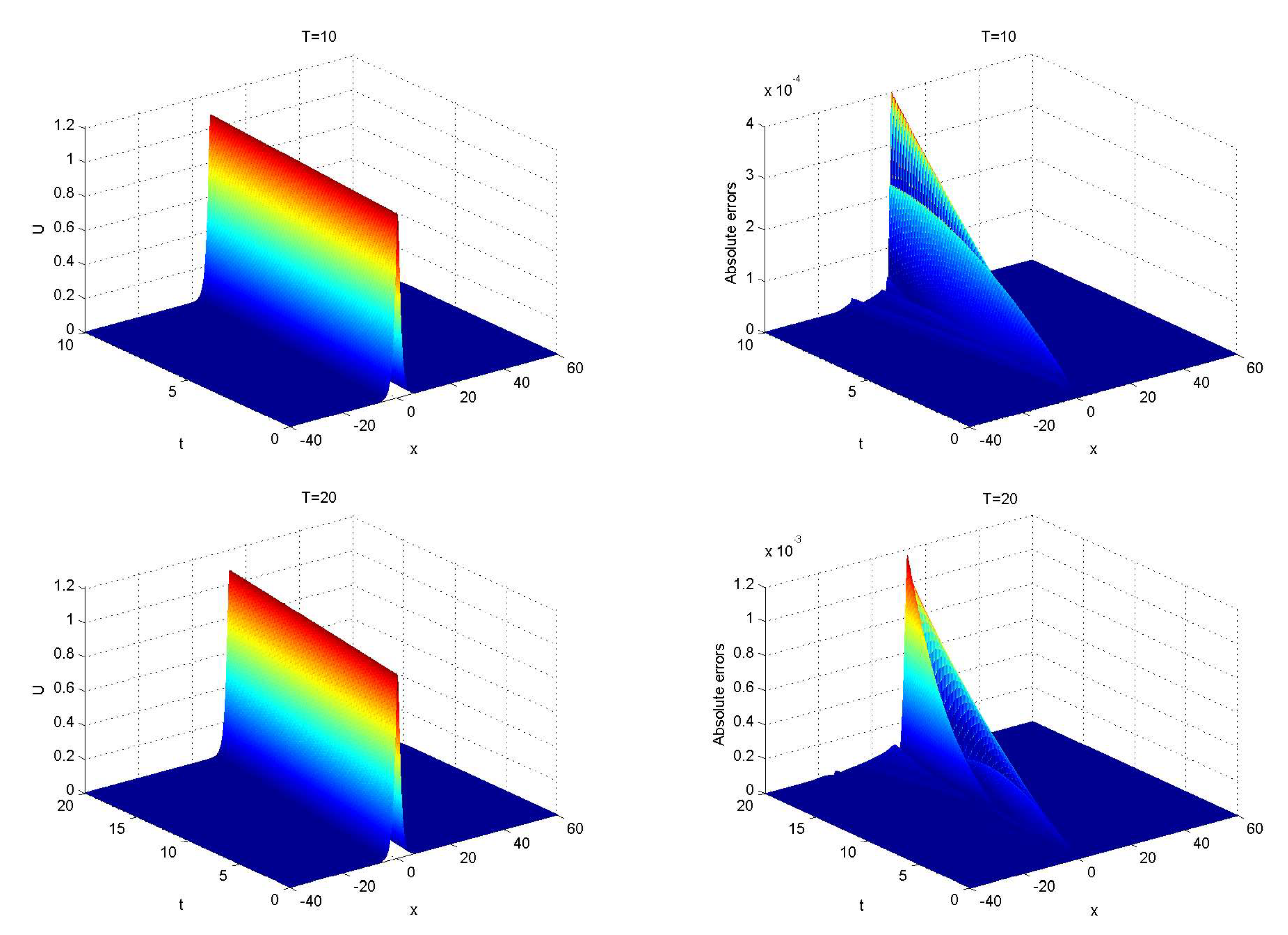Figure 7 depicts the numerical solutions and absolute errors at times T = 10 and 20 with h = 0.1 , τ = h 2 , x l = − 40 , x r = 60 and p = 2 . Furthermore, Table 6 presents additional information regarding the discrete mass M n , the discrete rate of mass change R n and the discrete energy E n at various time intervals T = 0 , T = 5 , T = 10 , T = 15 , T = 20 , T = 25 , and T = 30 . It is clear that both the rate of mass change R n and the energy E n exhibit conservative behavior in the discrete sense.
Furthermore, for p = 1 , Eq. (83) exhibits two conserved quantities [4]:
I 1 = ν 10 ∫ − ∞ ∞ 7 b 2 u x x x 2 − 10 a 2 u x x 2 + 10 u x 2 d x ,
I 2 = 1 30 ∫ − ∞ ∞ − 15 b 1 + 2 b 2 ν 2 u x x x 2 − 15 a 2 ν 2 u x x 2 + 15 c 2 − ν 2 − k 2 u x 2 d x .
Furthermore, for any arbitrary p > 1 , Eq. (83) possesses two conserved quantities [4]:
I 3 = ∫ − ∞ ∞ − 1 3 b 2 u x x x x t + 1 2 a 2 u x x t − u t d x ,
I 4 = ∫ − ∞ ∞ − 1 3 b 2 t u x x x x t + 1 15 b 2 u x x x + 1 2 a 2 t u x x t − 1 6 a 2 u x x − t u t + u d x .
We will evaluate our numerical method by employing these invariants and selecting the approximate values as follows:
I 1 n ˜ = ν h 10 ∑ j = 1 J − 1 7 b 2 2 [ 3 ( U j n ) x ˜ x ¯ x ^ − ( U j n ) x ˜ x ¯ x ¨ ] 2 − 10 a 2 3 [ 4 ( U j n ) x ˜ x ¯ − ( U j n ) x ^ x ^ ] 2 + 10 3 [ 4 ( U j n ) x ^ − ( U j n ) x ¨ ] 2 , I 2 n ˜ = h 30 ∑ j = 1 J − 1 { − 1 2 ( 15 b 1 + 2 b 2 ν 2 ) [ 3 ( U j n ) x ˜ x ¯ x ^ − ( U j n ) x ˜ x ¯ x ¨ ] 2 − 5 a 2 ν 2 [ 4 ( U j n ) x ˜ x ¯ − ( U j n ) x ^ x ^ ] 2 + 5 ( c 2 − ν 2 − k 2 ) [ 4 ( U j n ) x ^ − ( U j n ) x ¨ ] 2 } , I 3 n ˜ = h ∑ j = 1 J − 1 − b 2 9 5 ( U j n ) x ˜ x ¯ x ˜ x ¯ − 2 ( U j n ) x ˜ x ¯ x ^ x ^ t ^ + a 2 6 4 ( U j n ) x ˜ x ¯ − ( U j n ) x ^ x ^ t ^ − ( U j n ) t ^ , I 4 n ˜ = h ∑ j = 1 J − 1 { − b 2 t n 9 5 ( U j n ) x ˜ x ¯ x ˜ x ¯ − 2 ( U j n ) x ˜ x ¯ x ^ x ^ t ^ + b 2 30 [ 3 ( U j n ) x ˜ x ¯ x ^ − ( U j n ) x ˜ x ¯ x ¨ ] + a 2 t n 6 4 ( U j n ) x ˜ x ¯ − ( U j n ) x ^ x ^ t ^ − a 2 18 4 ( U j n ) x ˜ x ¯ − ( U j n ) x ^ x ^ − t n ( U j n ) t ^ + U j n } .
To demonstrate the conservative properties of the current difference scheme represented by Eqs. (16)-(18), we have compiled the invariants I ˜ 1 n , I ¯ 2 n , I ¯ 3 n , I ¯ 4 n , M n , R n and E n at various temporal intervals, as presented in Table 7 and Table 8. The data illustrated in these tables indicate that the conservative quantities I ˜ j n ( j = 1 , 2 , 3 , 4 ) and R n and E n remain approximately constant over a time frame of up to 30 units. Consequently, the compact scheme proposed, as outlined by Eqs. (16)-(18), demonstrates both efficiency and reliability for simulations conducted over long periods.

6. Conclusion

A conservative and compact fourth-order accurate difference scheme has been formulated for the resolution of the sixth-order Boussinesq equation. A thorough analysis of solvability, convergence, and stability has been performed. Numerical results demonstrate that the numerical solution effectively preserves the discrete rates of mass change, denoted as R n , and energy, represented as E n .

Author Contributions

Conceptualization, X. Wang and W. Dai; methodology, W. Dai and A. Biswas; validation, X. Wang; formal analysis, X. Wang; writing—original draft preparation, X. Wang; writing—review and editing,X. Wang and W. Dai; supervision, W. Dai and A. Biswas. All authors have reviewed and agreed to the published version of the manuscript.

Funding

X. Wang was supported by Fujian Provincial Natural Science Foundation of China (No: 2024J01802).

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author, X. Wang, upon reasonable request.

Acknowledgments

We would like to express our sincere gratitude to the anonymous reviewers for their valuable comments and suggestions which greatly enhance the quality of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Boussinesq, J. Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 1872, 17, 55–108. [Google Scholar]
  2. Yan, J.; Deng, D.; Lu, F.; Zhang, Z. A new efficient energy-preserving finite volume element scheme for the improved Boussinesq equation. Appl. Math. Model. 2020, 87, 20–41. [Google Scholar] [CrossRef]
  3. Wang, Q.; Zhang, Z.; Zhang, X.; Zhu, Q. Energy-preserving finite volume element method for the improved Boussinesq equation. J. Comput. Phys. 2014, 270, 58–69. [Google Scholar] [CrossRef]
  4. Biswas, A.; Guzman, J. Vega; Bansal, A.; et al. Solitary waves, shock waves and conservation laws with the surface tension effect in the Boussinesq equation. Proceedings of the Estonian Academy of Sciences. 2023, 72, 17–29. [Google Scholar] [CrossRef]
  5. Biswas, A. Solitary wave solution for KdV equation with power-law nonlinearity and time-dependent coefficients. Nonlinear Dyn. 2009, 58, 345–348. [Google Scholar] [CrossRef]
  6. Razborova, P.; Triki, H.; Biswas, A. Perturbation of dispersive shallow water waves. Ocean Engineering. 2013, 63, 1–7. [Google Scholar] [CrossRef]
  7. Razborova, P.; Kara, Abdul H. ; Biswas, A. Additional conservation laws for Rosenau-KdV-RLW equation with power law nonlinearity by Lie symmetry. Nonlinear Dyn. 2015, 79, 743–748. [Google Scholar] [CrossRef]
  8. Lu, F.; Song, Z.; Zhang, Z. A compact fourth-order finite difference scheme for the improved Boussinesq equation with damping terms. J. Comp. Math. 2016, 34, 462–478. [Google Scholar]
  9. Helal, M. A.; Seadawy, A. R.; Zekry, M. Stability analysis of solutions for the sixth-order nonlinear Boussinesq water wave equations in two-dimensions and its applications. Chinese J. Phys. 2017, 55, 378–385. [Google Scholar] [CrossRef]
  10. Burde, G. I. Solitary wave solutions of the high-order KdV models for bi-directional water waves. Commun. Nonlinear. Sci. Numer. Simulat. 2011, 16, 1314–1328. [Google Scholar] [CrossRef]
  11. Yimnet, S.; Wongsaijai, B.; Rojsiraphisal, T.; Poochinapan, K. Numerical implementation for solving the symmetric regularized long wave equation. Appl. Math. Comput. 2016, 273, 809–825. [Google Scholar] [CrossRef]
  12. Esfahani, A.; Farah, L. G. Local well-posedness for the sixth-order Boussinesq equation. J. Math. Anal. Appl. 2012, 385, 230–242. [Google Scholar] [CrossRef]
  13. Wang, H.; Esfahani, A. Global rough solutions to the sixth-order Boussinesq equation. Nonlinear Anal. 2014, 102, 97–104. [Google Scholar] [CrossRef]
  14. Feng, B.; Kawahara, T.; Mitsui, T.; Chan, Y. Solitary-wave propagation and interactions for a sixth-order generalized Boussinesq equation. Int. J. Math. Math. Sci. 2005, 9, 1435–1448. [Google Scholar] [CrossRef]
  15. Kolkovska, N.; Vucheva, V. Energy preserving finite difference scheme for sixth-order Boussinesq equation. Procedia Eng. 2017, 199, 1539–1543. [Google Scholar] [CrossRef]
  16. Arslan, D. Approximate solutions of singularly perturbed nonlinear ill-posed and sixth-order Boussinesq equations with hybrid method. Bitlis Eren Üniversitesi Fen Bilimleri Dergisi 2019, 8, 451–458. [Google Scholar] [CrossRef]
  17. Zhang, T.; Lin, Z.-H.; Huang, G.-Y.; et al. Solving Boussinesq equations with a meshless finite difference method. Ocean Engin. 2020, 198, 106957. [Google Scholar] [CrossRef]
  18. Zhou, H.; Sheng, Z.; Yuan, G. A conservative gradient discretization method for parabolic equations. Adv. Appl. Math. Mech. 2021, 13, 232–260. [Google Scholar] [CrossRef]
  19. Deng, D.; Liang, D. The energy-preserving finite difference methods and their analyses for system of nonlinear wave equations in two dimensions. Appl. Numer. Math. 2020, 151, 172–198. [Google Scholar] [CrossRef]
  20. Bayarassou, K.; Rouatbi, A.; Omrani, K. Uniform error estimates of fourth-order conservative linearized difference scheme for a mathematical model for long wave. Int. J. Comput. Math. 2020, 97, 1678–1703. [Google Scholar] [CrossRef]
  21. Hou, B.; Liang, D. The energy-preserving time high-order AVF compact finite difference scheme for nonlinear wave equations in two dimensions. Appl. Numer. Math. 2021, 170, 298–320. [Google Scholar] [CrossRef]
  22. Nanta, S.; Yimnet, S.; Poochinapan, K.; Wongsaijai, Ben. On the identification of nonlinear terms in the generalized Camassa-Holm equation involving dual-power law nonlinearities. Appl. Numer. Math. 2021, 160, 386–421. [Google Scholar] [CrossRef]
  23. Wang, X.; Dai, W. A three-level linear implicit conservative scheme for the Rosenau-KdV-RLW equation. J. Comput. Appl. Math. 2018, 330, 295–306. [Google Scholar] [CrossRef]
  24. Wongsaijai, B.; Poochinapan, K.; Disyadej, T. A compact finite difference method for solving the General Rosenau-RLW equation. Int. J. Appl. Math. 2014, 44, 192–199. [Google Scholar]
  25. Mohanty, R. K.; Dai, W.; Han, F. A new high accuracy method for two-dimensional biharmonic equation with nonlinear third derivative terms: application to Navier-Stokes equations of motion. Int. J. Comput. Math. 2015, 92, 1574–1590. [Google Scholar] [CrossRef]
  26. Ye, H.; Liu, F.; Anh, V. Compact difference scheme for distributed-order time-fractional diffusion-wave equation on bounded domains. J. Computat. Phys. 2015, 298, 652–660. [Google Scholar] [CrossRef]
  27. Wongsaijai, B.; Oonariya, C.; Poochinapan, K. Compact structure-preserving algorithm with high accuracy extended to the improved Boussinesq equation. Math. Comput. Simulat. 2020, 178, 125–150. [Google Scholar] [CrossRef]
  28. Zhou, Y. Application of Discrete Functional Analysis to the Finite Difference Methods, International Academic Publishers, Beijing, 1990.
  29. Wang, X.; Dai, W.; Guo, S. A conservative linear difference scheme for the 2D regularized long-wave equation. Appl. Math. Comput. 2019, 342, 55–70. [Google Scholar] [CrossRef]
  30. Tamang, N.; Wongsaijai, B.; Mouktonglang, T.; et al. Novel algorithm based on modification of the Galerkin finite element method to general Rosenau-RLW equation in (2+1)-dimensions. Appl. Numer. Math. 2020, 148, 109–130. [Google Scholar] [CrossRef]
  31. Ucar, Y.; Karaagac, B.; Esen, A. A new approach on numerical solutions of the Improved Boussinesq type equation using quadratic B-spline Galerkin finite element method. Appl. Math. Comput. 2015, 270, 148–155. [Google Scholar] [CrossRef]
Preprints 120683 g001
Figure 1. Solitary wave solutions of u ( x , t ) at T = 0 and numerical solutions at T = 5 , 10, 15, 20, x l = − 20 , x r = 30 (left) and x l = − 40 , x r = 60 (right) for Example 1.
Figure 1. Solitary wave solutions of u ( x , t ) at T = 0 and numerical solutions at T = 5 , 10, 15, 20, x l = − 20 , x r = 30 (left) and x l = − 40 , x r = 60 (right) for Example 1.
Preprints 120683 g001
Preprints 120683 g002
Figure 2. Numerical solutions of the auxiliary variable V at T = 0 , 5, 10, 15, 20, x l = − 20 , x r = 30 (left) and x l = − 40 , x r = 60 (right) for Example 1.
Figure 2. Numerical solutions of the auxiliary variable V at T = 0 , 5, 10, 15, 20, x l = − 20 , x r = 30 (left) and x l = − 40 , x r = 60 (right) for Example 1.
Preprints 120683 g002
Preprints 120683 g003
Figure 3. 3D plots of the numerical solutions U n and V n at T = 10 with x l = − 40 , x r = 60 for Example 1.
Figure 3. 3D plots of the numerical solutions U n and V n at T = 10 with x l = − 40 , x r = 60 for Example 1.
Preprints 120683 g003
Preprints 120683 g004
Figure 4. Numerical and solitary wave solutions and absolute error at T = 10 , 20 and 30 for Example 2.
Figure 4. Numerical and solitary wave solutions and absolute error at T = 10 , 20 and 30 for Example 2.
Preprints 120683 g004
Preprints 120683 g005
Figure 5. Numerical solutions of U and V with h = 0.1 and τ = h 2 at T = 0 , 10, 20, 30, 40, x l = − 40 , x r = 60 for Example 2.
Figure 5. Numerical solutions of U and V with h = 0.1 and τ = h 2 at T = 0 , 10, 20, 30, 40, x l = − 40 , x r = 60 for Example 2.
Preprints 120683 g005
Preprints 120683 g006
Figure 6. 3D plots of the numerical solutions U n at T = 5 , 10, 15 and 20 with h = 0.1 , τ = h 2 , x l = − 40 , x r = 60 for Example 2.
Figure 6. 3D plots of the numerical solutions U n at T = 5 , 10, 15 and 20 with h = 0.1 , τ = h 2 , x l = − 40 , x r = 60 for Example 2.
Preprints 120683 g006
Preprints 120683 g007
Figure 7. Numerical solutions and absolute errors at T = 10 and 20 with h = 0.1 , τ = h 2 , x l = − 40 , x r = 60 , p = 2 for Example 3.
Figure 7. Numerical solutions and absolute errors at T = 10 and 20 with h = 0.1 , τ = h 2 , x l = − 40 , x r = 60 , p = 2 for Example 3.
Preprints 120683 g007
Table 1. Comparative analysis of spatial errors and convergence rates for Example 1.
Table 1. Comparative analysis of spatial errors and convergence rates for Example 1.
h ∥ e n ∥ [2] rate ∥ e n ∥ rate ∥ e n ∥ ∞ [2] rate ∥ e n ∥ ∞ rate
0.4 9.05 × 10 − 4 − 5.44 × 10 − 5 − 4.50 × 10 − 4 − 3.15 × 10 − 5 −
0.2 2.25 × 10 − 4 2.01 3.21 × 10 − 6 4.08 1.13 × 10 − 4 1.99 2.05 × 10 − 6 3.94
0.1 5.62 × 10 − 5 2.00 1.90 × 10 − 7 4.07 2.81 × 10 − 5 2.00 1.19 × 10 − 7 4.09
Table 2. Comparison of the temporal errors and convergence rates for Example 1.
Table 2. Comparison of the temporal errors and convergence rates for Example 1.
h ∥ e n ∥ [2] rate ∥ e n ∥ rate ∥ e n ∥ ∞ [2] rate ∥ e n ∥ ∞ rate
0.04 8.69 × 10 − 4 − 2.76 × 10 − 5 − 4.32 × 10 − 4 − 1.51 × 10 − 5 −
0.02 2.19 × 10 − 4 1.98 6.58 × 10 − 6 2.06 1.10 × 10 − 4 1.97 3.63 × 10 − 6 2.05
0.01 5.53 × 10 − 5 1.99 1.59 × 10 − 6 2.04 2.78 × 10 − 5 1.99 9.04 × 10 − 7 2.00
Table 3. Discrete mass M n , discrete rate of mass change R n and the discrete energy at various time intervals for Example 1.
Table 3. Discrete mass M n , discrete rate of mass change R n and the discrete energy at various time intervals for Example 1.
T M n R n E n
0 3.99999998662202 0.00000000770792 2.59519634357874
5 3.99999998684879 0.00000000748522 2.59519634801190
10 3.99999998721201 0.00000000711875 2.59519636602745
15 3.99999998755727 0.00000000676334 2.59519639725431
20 3.99999998788500 0.00000000641617 2.59519644155837
Table 4. Discrete mass M n , discrete rate of mass change R n and the discrete energy E n with h = 0.1 and τ = h 2 at various time intervals for Example 2.
Table 4. Discrete mass M n , discrete rate of mass change R n and the discrete energy E n with h = 0.1 and τ = h 2 at various time intervals for Example 2.
T M n R n E n
0 8.44807966748734 1.88271050488737 15.35813895730075
5 8.44807966747724 1.88289006817254 15.35813896808486
10 8.44807966744347 1.88285678675310 15.35813901287684
15 8.44807966738941 1.88269314441971 15.35813909109440
20 8.44807966731402 1.88292585889068 15.35813920256866
Table 5. Errors and convergence rates of the current scheme when h = 0.4 and τ = h 2 at T = 10 for Example 3.
Table 5. Errors and convergence rates of the current scheme when h = 0.4 and τ = h 2 at T = 10 for Example 3.
p h , τ h / 2 , τ / 4 h / 4 , τ / 16
∥ e ∥ 1.530067340E-02 9.709362247E-04 5.777896747E-05
p = 1 rate − 3.9780748 4.07076021
∥ e ∥ ∞ 1.015003674E-02 6.556924437E-04 4.127486212E-05
rate − 3.9523219 3.9896839
∥ e ∥ 7.862155174E-02 4.719448787E-03 3.012389794E-04
p = 2 rate − 4.0582346 3.9696380
∥ e ∥ ∞ 7.973541804E-02 4.682164328E-03 3.018001249E-04
rate − 4.0899732 3.9555103
Table 6. Discrete mass M n , discrete rate of mass change R n and the discrete energy E n with h = 0.1 , τ = h 2 and P = 2 at various time intervals for Example 3.
Table 6. Discrete mass M n , discrete rate of mass change R n and the discrete energy E n with h = 0.1 , τ = h 2 and P = 2 at various time intervals for Example 3.
T M n R n E n
0 3.02090976925920 1.52260617289068 8.70669460321910
5 3.02090976827031 1.52400439056038 8.70669481288416
10 3.02090976455933 1.52404485849716 8.70669563361528
15 3.02090975829348 1.52179604152168 8.70669698162941
20 3.02090974941932 1.52420689642572 8.70669874989782
25 3.02090973801432 1.52375610223547 8.70670081739405
30 3.02090972410221 1.52240106874032 8.70670306135933
Table 7. Conservative quantities I ˜ 1 n , I ˜ 2 n and the discrete quantities M n , R n and E n with h = 0.1 , τ = h 2 and p = 1 at various time intervals for Example 3.
Table 7. Conservative quantities I ˜ 1 n , I ˜ 2 n and the discrete quantities M n , R n and E n with h = 0.1 , τ = h 2 and p = 1 at various time intervals for Example 3.
T I ˜ 1 n I ˜ 2 n M n R n E n
0 0.77574398822 0.72568182168 2.99999999979 1.06047283470 3.78558199462
5 0.77574415451 0.72568197184 2.99999999869 1.06079683168 3.78558200635
10 0.77574474392 0.72568250450 2.99999999479 1.06080624484 3.78558205484
15 0.77574571092 0.72568337974 2.99999998836 1.06028637400 3.78558213956
20 0.77574703291 0.72568457913 2.99999997943 1.06084514881 3.78558226063
25 0.77574867931 0.72568607763 2.99999996804 1.06074072374 3.78558241692
30 0.77575061250 0.72568784435 2.99999995426 1.06042851618 3.78558260687
Table 8. Conservative quantities I ˜ 3 n , I ˜ 4 n and the discrete quantities M n , R n and E n with h = 0.1 , τ = h 2 and p = 2 at various time intervals for Example 3.
Table 8. Conservative quantities I ˜ 3 n , I ˜ 4 n and the discrete quantities M n , R n and E n with h = 0.1 , τ = h 2 and p = 2 at various time intervals for Example 3.
T I ˜ 1 n I ˜ 2 n M n R n E n
0 0.00000000879 3.02090976945 3.02090976927 1.52260617358 8.70669460355
5 0.00000001689 3.02090976957 3.02090976906 1.52318643159 8.70669464967
10 0.00000002587 3.02090976979 3.02090976876 1.52365257478 8.70669471985
15 0.00000003535 3.02090977012 3.02090976836 1.52400439292 8.70669481421
20 0.00000004386 3.02090977051 3.02090976788 1.52424172749 8.70669493260
25 0.00000005221 3.02090977097 3.02090976732 1.52436447198 8.70669507504
30 0.00000006009 3.02090977148 3.02090976668 1.52437256971 8.70669524020
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated