Preprint
Article
Loan Approval Prediction Improved by XGBoost Model Based on Four-Vector Optimization Algorithm
Altmetrics
Downloads
75
Views
63
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 October 2024
Posted:
11 October 2024
You are already at the latest version
Alerts
Abstract
This paper discusses an improved XGBoost model based on four-vector optimization algorithm to improve the accuracy of loan approval prediction. Through the analysis of correlation heat maps, we found that there were significant positive and negative correlations among some variables, which laid the foundation for subsequent machine learning analysis. Based on this, we compare the traditional machine learning algorithm with the improved model to evaluate its performance in loan approval forecasting. In the confusion matrix analysis of the training set, the improved XGBoost model demonstrated excellent performance, with all loan approval predictions being correct with 100% accuracy. However, the performance in the test set was slightly different, with 1,182 projects receiving correct loan approval predictions and 99 projects forecasting errors. Of these, 26 projects that should have been predicted to be "unapproved" were incorrectly labeled as "approved," while 73 projects that should have been predicted to be "approved" were incorrectly labeled as "unapproved." These results suggest that we still need to pay attention to the misjudgment of the model in practical application. By synthesizing all model evaluation indicators, we found that the improved XGBoost model based on the four-vector optimization algorithm has a higher accuracy in loan approval prediction than the traditional XGBoost model, with an increase of 1.5%. In addition, the other evaluation indicators also show a trend of significantly better than the traditional model. This study shows that the four-vector optimization algorithm can effectively improve the application effect of XGBoost model in the field of loan approval, and provide more accurate data support and decision-making basis for the financial industry. In the future, we will continue to explore the potential and application prospects of this algorithm in other fields.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
I. Introduction
Loan approval forecasting is an important research direction in the field of fintech, and its background is mainly derived from the risk management challenges faced by banks and financial institutions in the process of loan issuance [1]. With the development of economy and the intensification of market competition, the traditional loan approval method has gradually exposed some problems such as inefficiency and inaccurate risk assessment. This not only affects the customer application experience, but also increases the risk of default for financial institutions. Therefore, how to effectively evaluate the credit risk of borrowers and improve the efficiency of loan approval has become a hot spot of academic and practical circles.
Machine learning, as a powerful data analysis tool, is playing an increasingly important role in loan approval forecasting. Machine learning algorithms can extract underlying patterns and rules through deep learning of historical data, which gives them significant advantages in credit scoring and risk prediction [2]. Compared to traditional methods, machine learning can handle larger and more complex data sets, and has self-optimizing capabilities, which can constantly adjust the model based on new data to improve the accuracy of predictions.
Specifically, the application of machine learning in loan approval forecasting is mainly reflected in several aspects. First, by using classification algorithms (such as decision trees [3], random forests [4], support vector machines [5], etc.), financial institutions can perform credit ratings on borrowers and classify them into different risk levels. This approach takes into account not only the borrower’s credit history, but also other variables such as income level, type of occupation, social network behavior, etc., to enable a more comprehensive risk assessment.
Second, machine learning can also be used for anomaly detection, that is, to identify potential fraud. In loan applications, some borrowers may provide false information to obtain loans, and machine learning models can reduce the risk of fraud by analyzing the data patterns of applicants and detecting anomalies in time. In addition, through unsupervised learning methods such as cluster analysis, borrowers with similar characteristics can be grouped to provide a basis for the subsequent design of credit products.
Finally, with the development of big data technology, the processing power of real-time data streams is increasing, which provides new opportunities for the application of machine learning in loan approval. For example, with online learning algorithms, financial institutions can update their models in real time to adapt to market changes and changes in user behavior, thus improving the speed and accuracy of decision-making. This flexibility allows banks to respond quickly to market demands while reducing operating costs.
In short, the introduction of machine learning in the background of loan approval prediction research not only improves the scientific and accurate degree of credit decision-making, but also brings innovation and change to the financial industry. This paper improves the XGBoost model based on four-vector optimization algorithm for loan approval prediction, and compares the advantages and disadvantages of the proposed algorithm and the traditional machine learning algorithm in loan approval prediction.
II. Data from Data Analysis
A loan approval dataset is a collection of financial records and related information used to determine whether an individual or organization qualifies for a loan from a lender. It includes various factors such as cibil score, income, employment status, loan term, loan amount, asset value and loan status. This dataset is commonly used in machine learning and data analytics to develop models and algorithms that predict the likelihood of loan approval based on a given feature. Data set web site (https://www.kaggle.com/datasets/architsharma01/loan-approval-prediction-dataset), take some data to show, the results are shown in Table 1.
III. Correlation Analysis
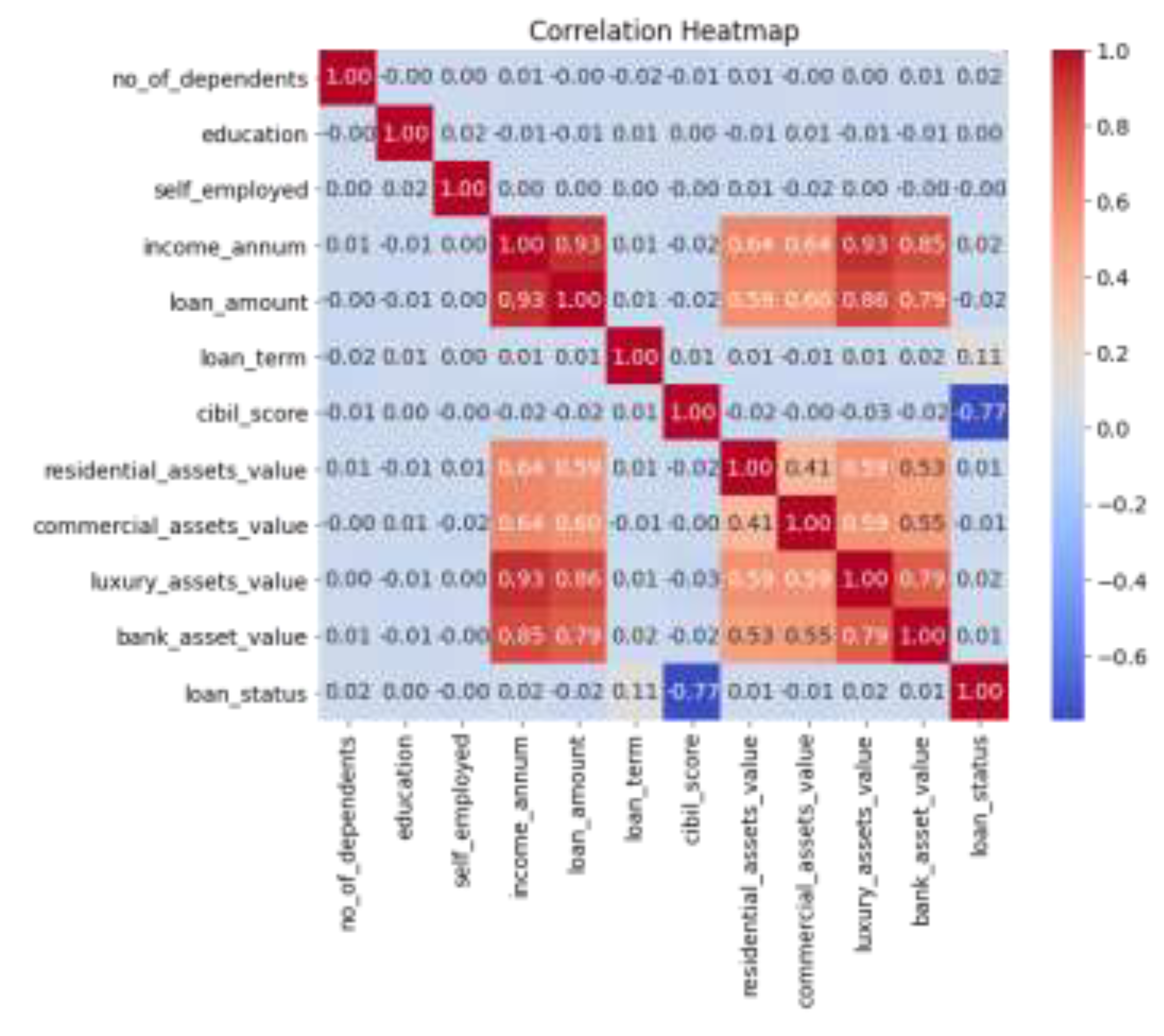
Correlation analysis is a statistical method used to assess the strength and direction of the relationship between two or more variables. Its core principle is to quantify the linear relationship between variables by calculating the correlation coefficient. Correlation coefficients typically range from -1 to 1, where 1 indicates a completely positive correlation, -1 indicates a completely negative correlation, and 0 indicates no linear relationship. In this paper, the correlation analysis of various data is carried out first, and the correlation heat maps of each variable are output. The results are shown in Figure 1.
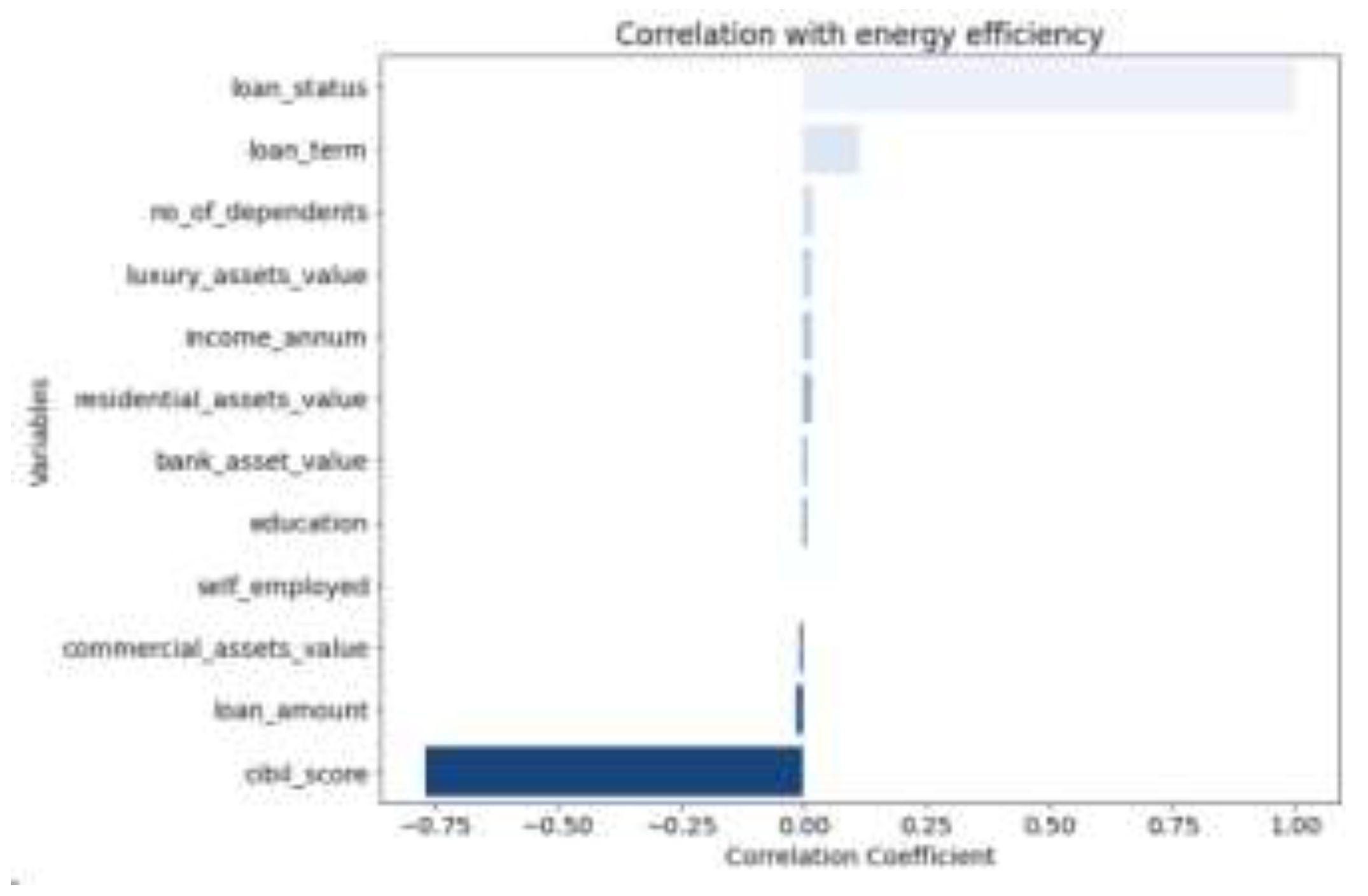
It can be seen from the correlation heat map that there are positive and negative correlations among some variables. The next step of machine learning analysis can be carried out to explore the potential relationship between various variables. Output the correlation ranking between each variable and the target variable, and the results are shown in Figure 2.
IV. Method
A. Four Vector Optimization Algorithm
Four-vector optimization algorithm is a kind of optimization method based on physics and mathematics principle, which is mainly used to solve high dimensional complex problems. The algorithm draws on the four-dimensional space-time concept of relativity and transforms the optimization problem into a process of finding the best solution in the four-dimensional space.
The basic principle of the four-vector optimization algorithm is to represent each solution to be optimized as a four-dimensional vector, usually containing time and three spatial coordinates [6]. This representation enables the algorithm to explore the region of the solution efficiently in multidimensional space. Specifically, the algorithm evaluates the pros and cons of each four-vector solution by defining the fitness function, and uses the dynamic update mechanism to gradually improve these four vectors to approximate the global optimal solution.
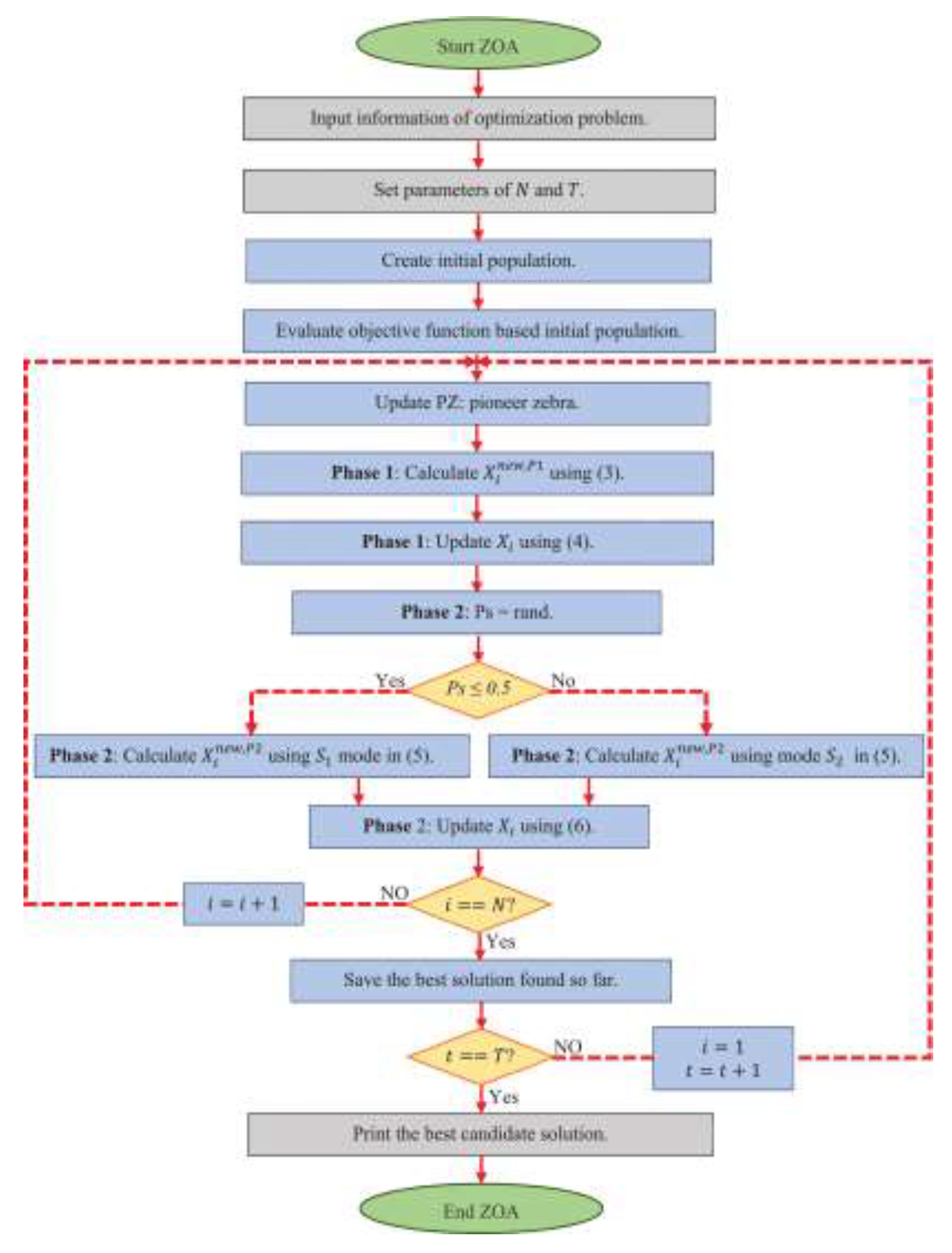
In the execution process, the four-vector optimization algorithm adopts a series of operations, including selection, crossover, mutation, etc., which are similar to genetic algorithm [7]. First, some excellent individuals are randomly selected from the current population as the parents, and then a new generation of individuals is generated through crossover and mutation. Each generation of individuals is evaluated according to a fitness function to retain the better performers and weed out the poor performers. The process iterates until a termination condition is met, such as reaching a preset number of iterations or finding a satisfactory solution. The flow chart of the four-vector optimization algorithm is shown in Figure 3.
In addition, the four-vector optimization algorithm also introduces an adaptive mechanism, which makes the search process dynamically adjust parameters according to the current state, thus improving the convergence speed and global search ability. This flexibility allows the algorithm to handle performs well on complex, multi-peak problems [8].
The algorithm flow of four-vector optimization algorithm can be summarized as the following main steps:
- Initialize the system
Parameter setting: Determine the basic parameters of the algorithm, including population size, maximum number of iterations, fitness threshold, etc.
Generate initial population: Randomly generate a certain number of four-dimensional vectors in the search space as the initial solution. These vectors usually consist of time and three spatial coordinates.
- 2.
- Fitness evaluation
Calculate the fitness function: Calculate the fitness value for each four-dimensional vector (individual), and the fitness function is used to measure the quality of the solution. The higher the fitness value, the better the solution.
- 3.
- Select an operation
Select excellent individuals: Select the best performing individuals from the current population based on fitness values. Common selection methods include roulette selection or tournament selection to ensure that outstanding individuals are retained for the next generation.
- 4.
- Crossover and variation
Cross operation: Randomly pair from selected parent individuals and perform cross operation to generate new individuals. Crossover can be achieved by swapping parts of genes to produce new solutions.
Mutation operation: Mutate newly generated individuals to increase the diversity of the population and avoid premature convergence. Variation usually involves randomly adjusting certain components in a four-dimensional vector.
- 5.
- Refresh the population
Merging old and new individuals: The new individuals after crossing and mutation are merged with the original population, and then the optimal individuals are selected according to the fitness value to form a new population [9].
- 6.
- Check the termination conditions
Termination condition judgment: Check whether the termination condition is met, such as reaching the maximum number of iterations or finding a satisfactory fitness value. If the conditions are met, the algorithm is terminated. Otherwise, return to step 2 to continue the iteration.
- 7.
- Output the result
Output optimal solution: at the end of the algorithm, output the current best four-dimensional vector and its corresponding fitness value, which is the approximate optimal solution of the problem.
B. XGBoost
XGBoost is an efficient algorithm widely used in machine learning competitions and real-world applications, especially when dealing with structured data. The core idea is to build a strong prediction model by integrating multiple weak learners (usually decision trees) to gradually reduce the prediction error of the model. XGBoost is based on the gradient lifting framework, but it has made many important improvements on the basis of the traditional gradient lifting tree (GBM), which has significantly improved its computational efficiency and model performance [10]. The algorithm flow diagram of the XGBoost model is shown in Figure 4.
First, XGBoost adopts the idea of an addition model, where the outputs of multiple weak learners are added together to form a final prediction. In each iteration, XGBoost calculates the loss function based on the predictions of the current model and uses the gradient information to update the model. Specifically, it optimizes each newly added tree by minimizing the loss function so that the new tree corrects the errors of all previous trees. This approach allows each new tree to focus on data points that the previous round of models failed to predict correctly, thus improving the accuracy of the overall model.
Second, XGBoost introduces regularization terms to control model complexity and prevent overfitting. Unlike traditional GBM, XGBoost adds L1 (Lasso) and L2 (Ridge) regularized terms to the objective function, which effectively limits the depth and number of trees, thereby improving the generalization ability of the model. This feature makes XGBoost particularly effective against high-dimensional sparse data, as it can automatically select important features and suppress irrelevant ones.
In addition to the above principles, XGBoost also employs a number of technological innovations to improve training efficiency. For example, it uses parallel computing so that when building each tree, split point searches can be performed on all features simultaneously, which greatly speeds up training. In addition, XGBoost implements cache optimization to further improve computational efficiency by storing data in memory to reduce I/O operations. These techniques enable XGBoost to handle large data sets and maintain high performance in a variety of scenarios.
In addition, XGBoost supports custom loss functions and evaluation metrics, giving users the flexibility to adapt the model to specific problems. In addition, it also provides a variety of functions, such as early stop method, cross-validation, etc., to help users better tune the hyperparameters. This makes modeling with the algorithm relatively easy, even for beginners.
C. Optimization of XGBoost Model Based on Four-Vector Optimization Algorithm
When the four-vector optimization algorithm is applied to XGBoost, the following aspects can be significantly improved:
- Speed up the training process: Since each sample point is represented as a four-dimensional vector containing multiple information, the model can converge to the optimal solution faster. While traditional methods typically require multiple iterations of a data set, the four-vector-based approach can improve efficiency through parallel processing.
- Improve the prediction accuracy: the information of Hessian matrix is introduced to make the model more accurate when adjusting parameters. This higher-order information can help the model better understand the shape of the loss function and make more reasonable decisions.
- Enhance generalization ability: By comprehensively considering more dimensions of information, the four-vector method can effectively reduce the risk of overfitting and improve the generalization ability of the model to new data. Especially in high-dimensional sparse data scenarios, this advantage is particularly obvious.
- Flexibility and scalability: XGBoost, built on a four-vector optimization algorithm, can easily incorporate new features or adjust hyperparameters to suit different data distributions and problem types. This flexibility makes it widely applicable in practical applications.
V. Result
In terms of model parameter Settings, the learning rate is set to 0.1, the maximum depth is set to 10, the subsample ratio is set to 0.5, the column sampling ratio is set to 0.5, the regularization parameter lambda is set to 1, and the alpha is set to 0, which is used to control complexity. The number of iterations is set to 500. A four-vector optimization algorithm is used to adjust these hyperparameters, and the performance of different parameter combinations is evaluated by cross-validation to find the best model configuration. In terms of hardware Settings, the CPU is 32G, the graphics card is 3090, and the experiment is carried out on Matlab R2022a.
In terms of evaluation parameters, this paper uses accuracy, accuracy, recall rate and F1-score to evaluate the model. Accuracy refers to the percentage of the total sample that the model correctly predicts. Accuracy reflects the ability of the model as a whole to classify all samples, but can be misleading when the categories are unbalanced. Accuracy refers to the proportion of samples predicted to be positive that are actually positive. The accuracy rate is concerned with how accurate the model is at predicting positive classes. The return rate refers to the proportion of samples that are actually positive that are correctly predicted to be positive, also known as sensitivity or true rate. The recall rate is concerned with whether the model can identify all true positive classes. F1-score refers to the harmonic average of accuracy rate and recall rate, and is an indicator that considers accuracy and completeness. F1-score is particularly useful when dealing with category imbalances, as it won’t rely solely on accuracy. It provides a balanced perspective, finding a compromise between precision and recall.
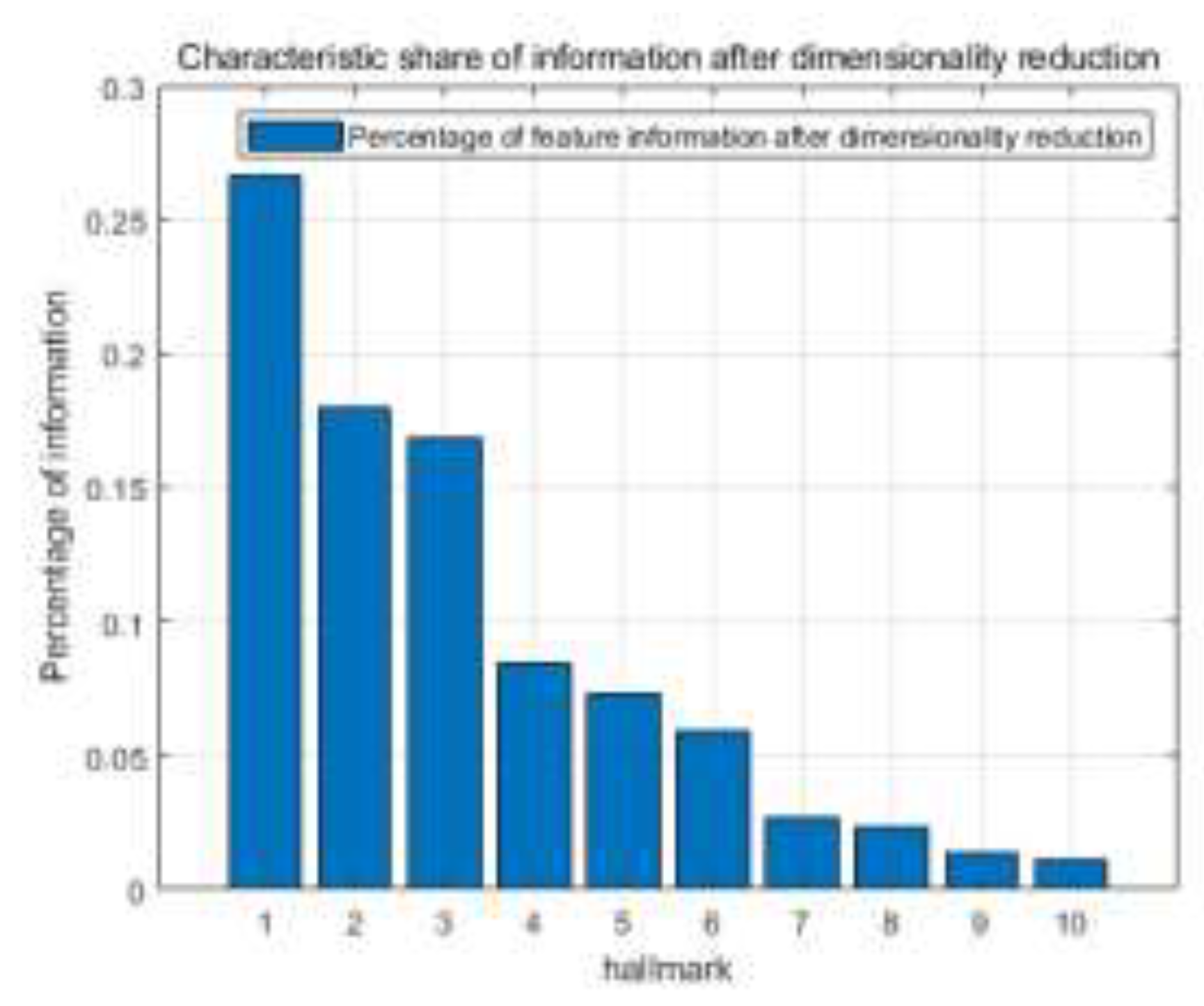
The percentage of feature information after dimensionality reduction is output, as shown in Figure 5.
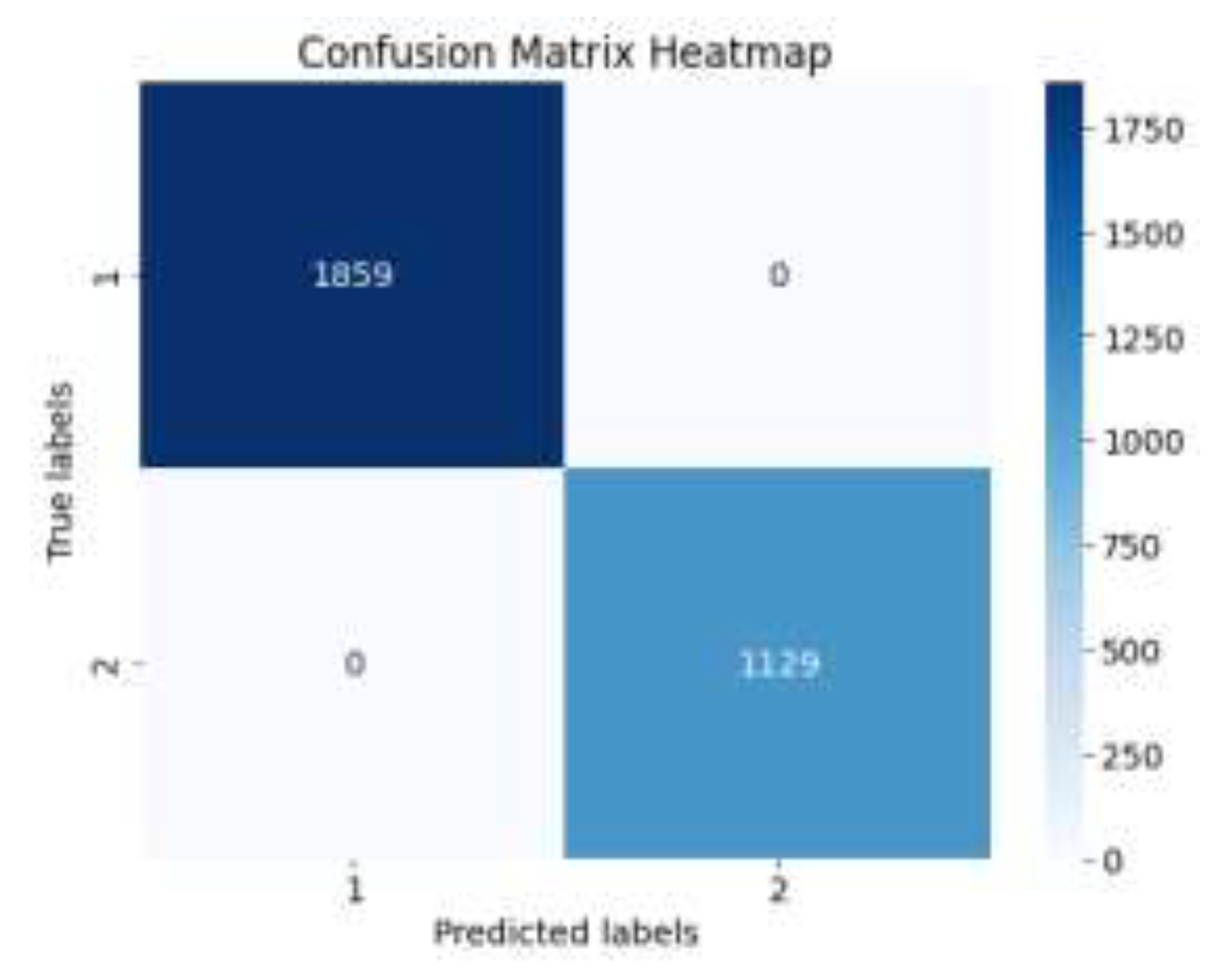
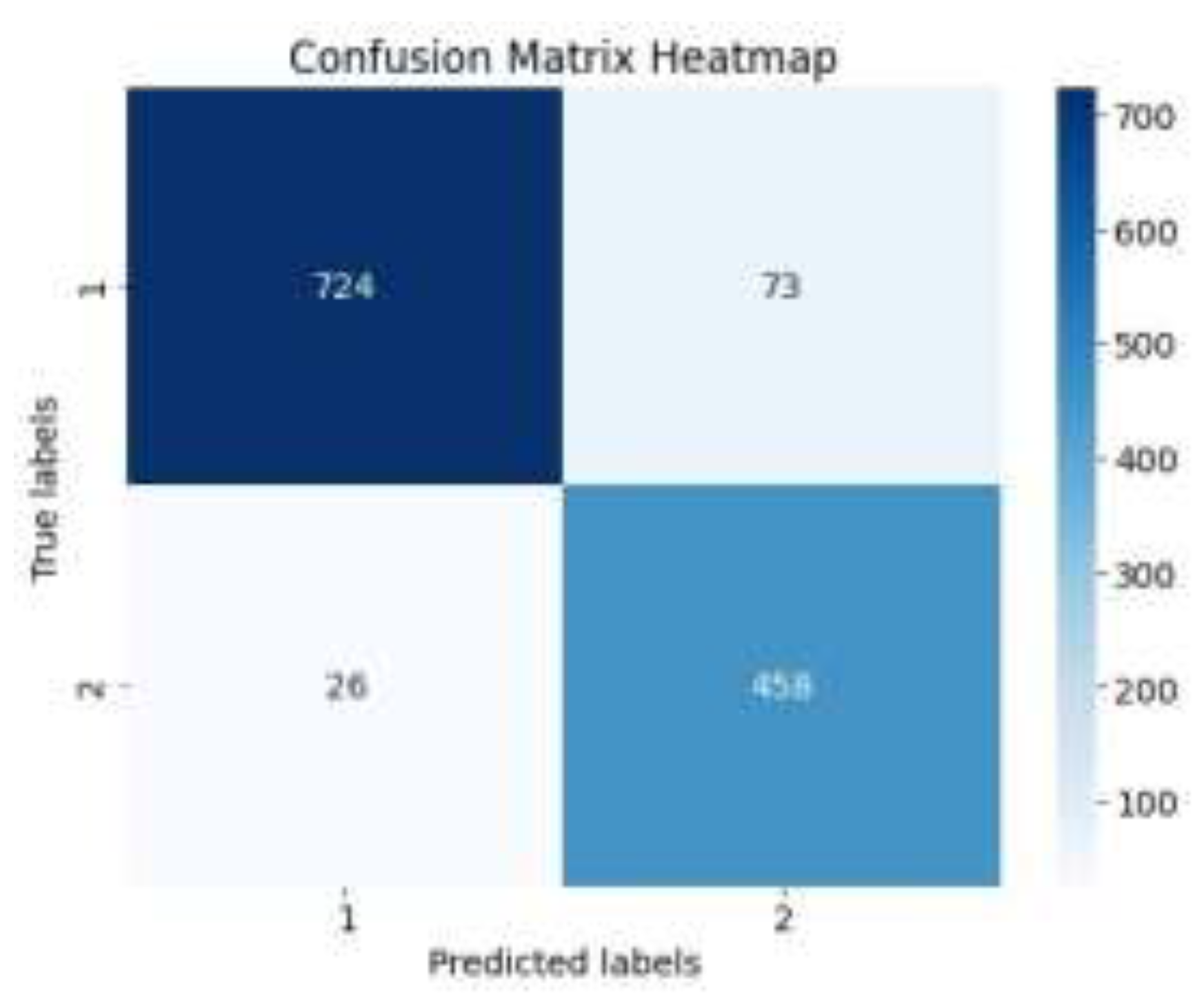
The results of loan approval prediction based on the XGBoost model optimized by the four-vector optimization algorithm in this paper are output. The confusion matrix of the training set prediction is shown in Figure 6, and the confusion matrix of the test set prediction is shown in Figure 7.
According to the confusion matrix of the training set, all the loan approval predictions are correct with an accuracy of 100%.
According to the mixed down matrix of the test set, 1182 project loan approval predictions were correct and 99 project loan approval predictions were unsuccessful, among which 26 projects that should have been predicted as „not approved” were predicted as „approved” and 73 projects that should have been predicted as „approved” were predicted as „not approved”.
The results of XGBoost and the XGBoost model optimized based on the four-vector optimization algorithm in terms of accuracy rate, accuracy rate, recall rate and F1 score are compared, and the evaluation indicators are shown in Table 2.
According to the model evaluation indicators, the accuracy of the XGBoost model optimized based on the four-vector optimization algorithm proposed in this paper is 1.5% higher than that of XGBoost in loan approval prediction, and other indicators are also better than that of XGBoost model.
VI. Conclusion
In this paper, four-vector optimization algorithm is used to improve the XGBoost model, aiming at improving the accuracy and effectiveness of loan approval prediction. In the research process, we first analyzed the correlation between several variables, and revealed the positive and negative correlation of some variables by using heat map. This finding sets the stage for subsequent machine learning analyses, allowing us to select features more specifically and optimize models.
In the model training stage, by constructing the XGBoost model based on the four-vector optimization algorithm, we get a remarkable prediction effect. The confusion matrix of the training set showed that the model achieved 100% accuracy in the loan approval prediction, and all samples were correctly classified. This result shows that the XGBoost model processed by the four-vector optimization algorithm has a strong fitting ability when dealing with complex data.
However, the performance on the test set is slightly different. The confusion matrix showed that 99 of the 1,182 test samples were wrong in their loan approval predictions. Of these, 26 projects that should have been predicted to be “unapproved” were incorrectly labeled as “approved,” while 73 projects that should have been predicted to be “approved” were incorrectly labeled as „unapproved.” These errors suggest that even optimized models still have a degree of uncertainty, which reflects the challenges of data complexity in the area of loan approval.
From the overall performance index, the improved XGBoost model based on the four-vector optimization algorithm is better than the traditional XGBoost model in loan approval prediction, and its accuracy is increased by 1.5%. In addition, other evaluation indicators such as accuracy rate, recall rate and F1-score show comparative advantages. These results fully prove the importance of introducing four-vector optimization algorithm to improve the performance of XGBoost model, and also provide new ideas for the future application of machine learning methods in the field of financial technology.
In summary, the XGBoost model optimized based on the four-vector optimization algorithm presented in this paper shows excellent performance in the loan approval prediction task. Although further refinement is still needed to reduce the misclassification rate, its potential in improving overall accuracy cannot be ignored. In the future, we will continue to explore more advanced methods to further improve the efficiency and accuracy of decision-making in the loan approval process, and provide more reliable data support for financial institutions.
References
- Viswanatha, V., et al. „Prediction of loan approval in banks using machine learning approach.” International Journal of Engineering and Management Research 13.4 (2023): 7-19.
- Uddin, Nazim, et al. „An ensemble machine learning based bank loan approval predictions system with a smart application.” International Journal of Cognitive Computing in Engineering 4 (2023): 327-339. [CrossRef]
- Uddin, Nazim, et al. „An ensemble machine learning based bank loan approval predictions system with a smart application.” International Journal of Cognitive Computing in Engineering 4 (2023): 327-339. [CrossRef]
- Krishnaraj, P., S. Rita, and Jitendra Jaiswal. „Comparing Machine Learning Techniques for Loan Approval Prediction.” Proceedings of the 1st International Conference on Artificial Intelligence, Communication, IoT, Data Engineering and Security, IACIDS 2023, 23-25 November 2023, Lavasa, Pune, India. 2024.
- Sandhu, Harjyot Singh, Varun Sharma, and Vishali Jassi. „Loan Approval Prediction Using Machine Learning.
- Liu, Yaru, and Huifang Feng. „Hybrid 1DCNN-Attention with Enhanced Data Preprocessing for Loan Approval Prediction.” Journal of Computer and Communications 12.8 (2024): 224-241. [CrossRef]
- Kandula, Ashok Reddy, et al. „Comparative Analysis for Loan Approval Prediction System Using Machine Learning Algorithms.” International Conference on Computer & Communication Technologies. Singapore: Springer Nature Singapore, 2023.
- Phan, Chung, Stefano Filomeni, and Kok Seng Kiong. „The impact of technology on access to credit: A review of loan approval and terms in rural Vietnam and Thailand.” Research in International Business and Finance (2024): 102504. [CrossRef]
- Ogundunmade, Tayo P., Adedayo A. Adepoju, and Abdelaziz Allam. „Stock price forecasting: Machine learning models with K-fold and repeated cross validation approaches.” Mod Econ Manag 1 (2022).
- Budiharto, Widodo. „Data science approach to stock prices forecasting in Indonesia during Covid-19 using Long Short-Term Memory (LSTM).” Journal of big data 8 (2021): 1-9.
Figure 1.
Correlation heat maps.
Figure 2.
The correlation ranking between each variable and the target variable.
Figure 3.
The flow chart of the four-vector optimization algorithm.
Figure 4.
The algorithm flow diagram of the XGBoost model.
Figure 5.
The percentage of feature information after dimensionality reduction.
Figure 6.
The confusion matrix of the training set.
Figure 7.
The confusion matrix of the test set .
Table 1.
Selected data sets.
| Cibil score | Commercial assets value | Luxury assets value | Bank asset value | Loan status |
| 778 | 17600000 | 22700000 | 8000000 | 1 |
| 417 | 2200000 | 8800000 | 3300000 | 2 |
| 506 | 4500000 | 33300000 | 12800000 | 2 |
| 467 | 3300000 | 23300000 | 7900000 | 2 |
| 382 | 8200000 | 29400000 | 5000000 | 2 |
| 319 | 8300000 | 13700000 | 5100000 | 2 |
| 678 | 14800000 | 29200000 | 4300000 | 1 |
| 382 | 5700000 | 11800000 | 6000000 | 2 |
| 782 | 800000 | 2800000 | 600000 | 1 |
| 388 | 1400000 | 3300000 | 1600000 | 2 |
| 547 | 4700000 | 9500000 | 3100000 | 1 |
| 538 | 5800000 | 20400000 | 6400000 | 2 |
| 311 | 9600000 | 14600000 | 4300000 | 2 |
| 679 | 16600000 | 20900000 | 5000000 | 1 |
| 469 | 1200000 | 5900000 | 1900000 | 2 |
| 794 | 3900000 | 16400000 | 4400000 | 1 |
Loan_status is the predictor variable, and other variables are the input variables. 1 in loan_status indicates yes, and 2 indicates no.
Table 2.
Model evaluation.
| Model | Accuracy | Precision | Recall | F1 score |
| XGBoost | 0.9227 | 0.9653 | 0.9084 | 0.936 |
| This paper | 0.9071 | 0.952 | 0.8959 | 0.9231 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated