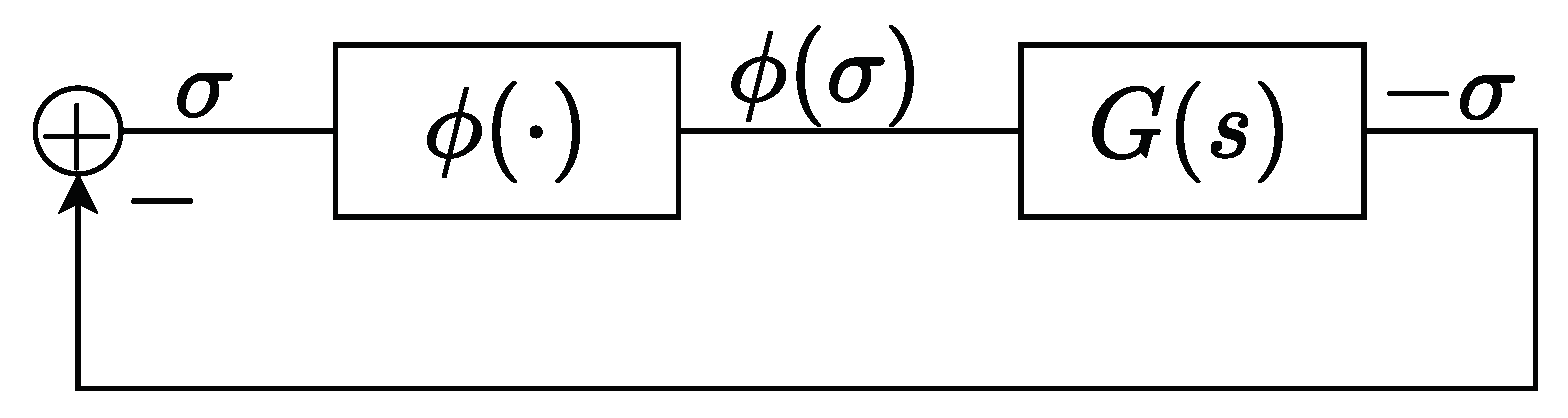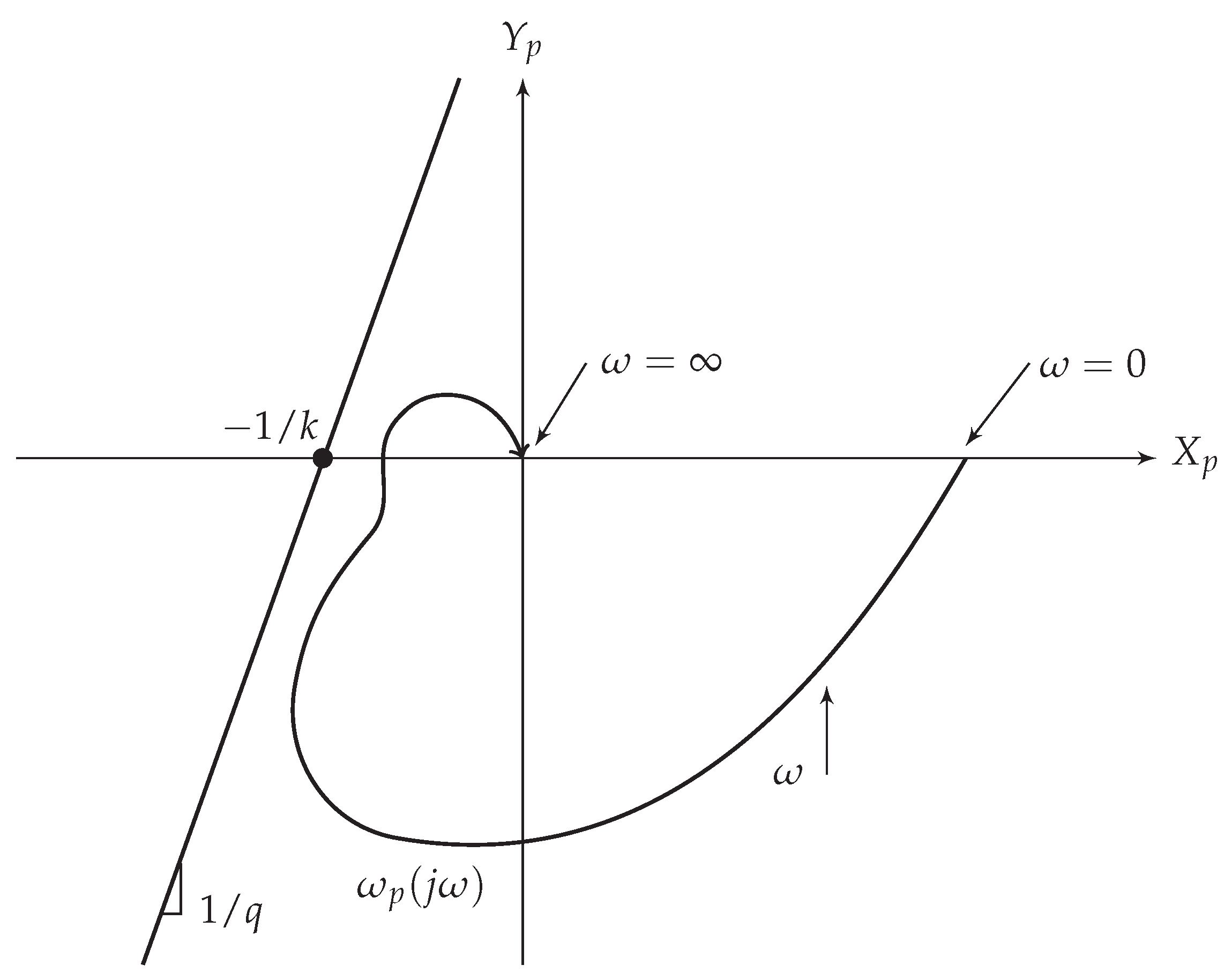Uses of the Popov Stability Criterion for Analyzing Global Asymptotic Stability in Power System Dynamic Models

Preprint

Article

Uses of the Popov Stability Criterion for Analyzing Global Asymptotic Stability in Power System Dynamic Models

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

09 October 2024

Posted:

10 October 2024

You are already at the latest version

Alerts

Abstract

Stability studies remain a crucial aspect of power systems dynamic analysis, and are typically explored in three main categories: numerical methods, linearization techniques, or direct methods, which utilize Lyapunov energy functions. This paper belongs to the third category, and highlights the usefulness of the Popov stability criterion in the analysis of nonlinear power system models. The main advantage of this criterion is that it provides conditions for global asymptotic stability of an equilibrium point, for a nonlinear dynamic system. We show a general method to apply this stability criterion, and examine its uses in several specific applications and case-studies. The results are demonstrated by analyzing the stability of a system that includes a grid-connected storage device and a renewable energy source.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Stability studies remain a crucial aspect of power systems dynamic analysis. Despite the fact that stability problems in power systems have been researched for a very long time [1,2,3], the increasing penetration of renewable energy sources, and the rapidly evolving technological advancements, give rise to more intricate and complex system dynamics, that necessitates a deeper and wider perspective regarding their stability [4,5,6]. The core of the problem lies in the fact that renewable energy sources, such as wind and solar, are inherently intermittent and often unpredictable due to their dependence on environmental conditions. This variability introduces challenges in maintaining a stable frequency within the power grid, a parameter that is crucial for the reliable operation of electrical power systems. Frequency stability is maintained by balancing the supply and demand of power within the grid. However, the intermittent nature of renewable sources can lead to significant deviations if not properly managed. These deviations can cause a range of issues, from minor inefficiencies to severe system failures, including blackouts or damage to sensitive infrastructure. Energy storage systems (ESS) have emerged as a vital solution to address these challenges, providing the necessary flexibility to absorb or release energy in response to fluctuations in supply and demand [7,8,9]. By quickly adjusting their output, ESS can help smooth out the variability in renewable energy generation, thereby stabilizing the frequency of the grid.

Many works in the recent literature study stability problems in power systems, using different approaches. This vast field of research can be divided roughly to three main approaches: Numerical analysis [10,11,12], linearization based techniques [13,14,15,16], and direct methods - which utilize at their core various Lyapunov energy functions [17,18,19]. Considering the direct methods, one may examine for instance, work [20], that presents a theoretical foundation of direct methods for both network-reduction and network-preserving power system models. The authors suggest a systematic procedure for constructing energy functions for both network-reduction and network-preserving power system models, utilizing the “boundary of stability region based controlling unstable equilibrium point” (or BCU) method for commuting the unstable equilibrium point, together with an algorithm for the numerical solution of the direct method. Finally, a practical demonstration of the proposed method for online transient stability assessments on two power systems is outlined. Moreover, paper [21] introduces a novel framework to construct the Region of Attraction (ROA) of a power system centered around a stable equilibrium by using stable state trajectories of the system dynamics. The proposed method leverages a Lyapunov function along with the Gaussian process approach. In addition, a sampling algorithm is designed to reconcile the tradeoffs between the exploitation for enlarging the ROA and the exploration for enhancing the confidence level of the sample region. The writers conduct various simulations and experimental validations to substantiate the assessment approach for the ROA of an IEEE test system with real data. It is demonstrated that the proposed approach can significantly enlarge the estimated ROA compared to previous works.

As described above, a large number of works utilize linearization techniques to study the stability of power systems. Due to the vast amount of research in this field, we naturally review only several representative papers. For example, study [22] investigates the application of a multi-variable nonlinear controller for generators. The proposed controller is based on linearization, and its main goal is to improve the transient stability and voltage regulation under post-fault conditions. Simulation results show the improvement in swing stability and system damping under large disturbances, as well as robust terminal voltage regulation. To continue this line of thinking, researchers in [23] offer a new framework to study integration methods for power systems impacted by delays. They use matrix-pencil theory for numerical stability analysis and accuracy analysis. The proposed approach covers all implicit Runge–Kutta methods for time-delay systems. The authors illustrate the idea through simulations on the IEEE 14-bus system, and consider three examples of implicit integration methods, such as “Backward Euler”, “trapezoidal”, and “2-s Radau IIA”.

As seen in the literature review above, there exist three central approaches to analyze the stability of power system dynamic models, namely - numeric simulations, linearization techniques, and direct methods that utilize a variety of Lyapunov functions. In this paper, we continue the line of thinking represented by this last approach, and propose a new criterion for finding global stability properties of equilibrium points in nonlinear power system models. Our approach is based on the Popov stability criterion, which provides exactly this kind of information. With respect to previous works, the proposed method has the following properties:

With respect to linearization techniques, the proposed approach provides information on the global stability of an equilibrium point of a power system model, rather then on its local stability.
With respect to numerical techniques, the proposed approach provides analytical conditions, which apply generally to the type of system under study.
With respect to direct methods, the proposed approach provides a systematic procedure for applying the Popov stability criterion in various power system models, which has not been used before in this application, and thus enables a systematic analysis of several small-scale systems, as described in the text below.

We present first the general mathematical background, and then proceed with practical applications of this proposed approach.

2. Materials and Methods

2.1. Mathematical Background - The Popov Stability Criterion

The Popov stability criterion applies to nonlinear feedback systems that include a memory-less nonlinear component. Unlike linearization techniques, this criterion provides conditions for global asymptotic stability of an equilibrium point. Consider the following dynamic system:

\begin{matrix} \dot{x} & = A x - b ϕ (σ) \\ σ & = c^{T} x, \end{matrix}

(1)

where A is a constant matrix, b and c are constant vectors, and

ϕ (σ)

is a continuous function of

σ

that describes the nonlinearity. It is assumed that

The eigenvalues of the constant matrix A are in the open left half-plane,
$ϕ (0) = 0$ ,
$0 < ϕ (σ) / σ \leq k < \infty$ , for all $σ \neq 0$ , where k is a positive constant.

The system is described in Figure 1.

Popov’s stability criterion states that an equilibrium point of the dynamic system (1) is globally asymptotically stable if there exist real numbers

q, η

such that the inequality

Re {(1 + j ω q) G (j ω)} + 1 / k \geq η > 0,

(2)

holds for every real

ω \geq 0

. Defining

\begin{matrix} G (s) & = c^{T} {(s I - A)}^{- 1} b, \\ X_{p} (ω) & = Re {G (j ω)}, \\ Y_{p} (ω) & = ω Im {G (j ω)}, \end{matrix}

(3)

one can plot the “Popov plot”, shown in Figure 2. In this figure, if the plot is indeed in the right-half plane defined by the straight line with slope

1 / q

which intersects with x-axis at

- 1 / k

, then the conditions of the Popov criterion hold, and the equilibrium point of (1) is globally asymptotically stable, for every

0 < ϕ (σ) / σ \leq k

. We proceed by describing the implementation of this criterion in power system dynamic models.

2.2. Dynamic Stability of a Synchronous Generator, Connected to a Non-Linear Frequency Dependent Load

Consider a system consisting of a synchronous generator connected to non-linear load. We adopt an idealized model, where all the power generated is transferred without loss directly to the load. The system is described by the following differential equation:

H \frac{d}{d t} ω + D \cdot (ω - ω_{s}) = P_{ref} - P_{load} (ω),

(4)

where

H > 0

represents the moment of inertia of the rotor,

ω

is the electrical frequency of the rotor,

D > 0

stands for the damping coefficient, and without loss of generality,

P_{ref} = P_{load} (ω_{s})

represents the reference power, where

ω_{s}

is the nominal angular velocity. The power consumed by the load is a general non-linear function of the electrical angular frequency

P_{laod} = P_{laod} (ω)

. For the system (4) there is at least one equilibrium point located at

ω = ω_{s}

. It is trivial to verify that linearizing (4) in a small neighborhood of the equilibrium point

ω = ω_{s}

leads to

H \frac{d}{d t} \hat{ω} = - (D + {\frac{d P_{load}}{d ω}|}_{ω = ω_{s}}) \cdot \hat{ω},

(5)

where

\hat{ω} = ω - ω_{s}

, so the equilibrium point

ω = ω_{s}

is locally asymptotically stable if

- D < {\frac{d P_{load}}{d ω}|}_{ω = ω_{s}} .

(6)

We extend here this well-known result by providing a sufficient condition for global asymptotic stability of the equilibrium

ω = ω_{s}

, that is, we provide a condition under which any trajectory

ω (t)

of (4) converges to

ω_{s}

t \to \infty

, from any initial point. Our main claim consists of two parts, and it is the following one:

Theorem 1.

Consider the dynamic system (4) with a load profile

P_{load} (ω)

, which is generally a nonlinear but continuous function of ω. If there exists a constant k such that

- D < \frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}} \leq k

(7)

for all

ω \neq ω_{s}

, then the equilibrium point

ω = ω_{s}

is the only equilibrium point of (4), and it isglobally asymptotically stable .

In addition, if

P_{load} (ω)

is differentiable at

ω_{s}

, and

- D > {(d P_{load} / d ω)|}_{ω = ω_{s}}

, or equivalently

- D > lim_{ω \to ω_{s}} \frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}},

(8)

then the equilibrium

ω = ω_{s}

isunstable .

Proof.

We start by proving the second part of the theorem, the instability condition given in (8). Examine the linearized system described in (5). It is clear that this system has one real pole with value

- D - {\frac{d}{d ω} P_{load} (ω)|}_{ω = ω_{s}}

. A strictly positive pole means that the equilibrium point

ω_{s}

is unstable, thus, the system is unstable if

- D - {\frac{d}{d ω} P_{load} (ω)|}_{ω = ω_{s}} > 0,

(9)

which is the same as

{\frac{d}{d ω} P_{load} (ω)|}_{ω = ω_{s}} < - D,

(10)

and by definition of the derivative, we get

{\frac{d}{d ω} P_{load} (ω)|}_{ω = ω_{s}} = lim_{ω \to 0} \frac{P_{load} (ω_{s} + ω) - P_{load} (ω_{s})}{ω} .

(11)

Now, the following equivalent expression may be used

{\frac{d}{d ω} P_{load} (ω)|}_{ω = ω_{s}} = lim_{ω \to ω_{s}} \frac{P_{load} (ω) - P_{load} (ω_{s})}{ω - ω_{s}} .

(12)

Substituting (12) in (10) results in

lim_{ω \to ω_{s}} \frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}} < - D,

(13)

which completes the proof for the instability condition in (8).

Now, we proceed to prove the first claim in the main theorem, the stability condition given in (7), based on Popov’s criterion. Let us define

ϕ (ω) = P_{load} (ω) - P_{ref}

and

ω \leftarrow ω - ω_{s}

. Substitute these values in (4) to obtain

\frac{d}{d t} ω = - \frac{D}{H} ω - \frac{1}{H} ϕ (ω) .

(14)

Assuming condition (7) is true, we now show that (2) holds. For the choice of

x = ω, A = - D / H, b = 1 / H

and

σ = 1 \cdot ω

, the transfer function of the system is

G (s) = \frac{\frac{1}{H}}{s + \frac{D}{H}} .

(15)

Following, we shall now find

q \in R

and a small and positive constant

η

that satisfy (2). Substitution of (15) in the right expression of (2) results in

Re {(1 + j ω q) G (j ω)} + \frac{1}{k} = \frac{\frac{1}{H}}{{(\frac{D}{H})}^{2} + ω^{2}} (\frac{D}{H} + ω^{2} q) + \frac{1}{k} .

(16)

For the choice of

ω = 0

we can directly choose the lower bound to be

η = \frac{1}{D} + \frac{1}{k} > 0

. Now, by analysing the “Popov plot” we find the values of

q \in R

for which (2) holds. To plot the “Popov plot”, we rely on

\begin{matrix} X_{p} (s = j ω) = Re {G (s = j ω)} = \frac{D}{{(\frac{D}{H})}^{2} + ω^{2}}, \\ Y_{p} (s = j ω) = Im {G (s = j ω)} = \frac{- \frac{1}{H}}{{(\frac{D}{H})}^{2} + ω^{2}} ω^{2} . \end{matrix}

(17)

Notice that by taking

ω \to 0

the resulting point on the “Popov plot” is

(\frac{H^{2}}{D}, 0)

, and for

ω \to \infty

the point on the “Popov plot” is

(0, - \frac{1}{H})

. Between these points the transfer function is continuous and is shaped like a quarter of a circle. By the geometric interpretation of (2), it is sufficient to find a straight line, with a slope of

1 / q

that intersects the x-axis at

- 1 / k

, and is located strictly to the left of the plot of the “Popov plot” of the transfer function. In this case, it is clear that for every choice of a positive slope, the “Popov plot” of the transfer function will be strictly to the right of this straight line, in particular for the value of

q = - 1

. Consequently, if condition (7) holds, then there exist

q \in R

and a small positive constant

η

such that (2) holds, meaning that the equilibrium is globally asymptotically stable, as desired. □

The following corollary can be used to analyze the stability of a typical small power system, in which a synchronous machine is feeding a general frequency dependant impedance

Z (j ω)

Corollary 1.

If the load power is given by

P_{load} (ω) = \frac{{3 | V |}^{2} Re {Z (j ω)}}{{| Z (j ω) |}^{2}},

(18)

where

| V |

is constant,

Re {Z (j ω)}

is bounded from above,

| Z (j ω) |

is bounded from below by a positive constant,

Re {Z (j ω)}, Im {Z (j ω)} \in C^{1}

, and

D > \frac{{3 | V |}^{2}}{ω - ω_{s}} (\frac{Re {Z (j ω_{s})}}{| Z (j ω_{s}) |^{2}} - \frac{Re {Z (j ω)}}{{| Z (j ω) |}^{2}}),

(19)

for all

ω \neq ω_{s}

, then the equilibrium point

ω = ω_{s}

is the only equilibrium point of (4), and it is globally asymptotically stable.

Proof.

To prove this statement, we show that it satisfies the conditions of Theorem 1. Substituting (18) and

P_{ref} = P_{load} (ω_{s})

in Corollary 1 results in

D > - \frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}},

(20)

which yields directly the lower bound:

- D < \frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}} .

(21)

Following, using the fact that

| V |

is constant,

Re {Z (j ω)} \leq k_{1}

, and

0 < k_{2} \leq | Z (j ω) |

, we proceed to determine the upper bound. Examining the expression

\frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}},

(22)

and substituting (18), results in

\frac{{3 | V |}^{2} (\frac{Re {Z (j ω_{s})}}{| Z (j ω_{s}) |^{2}} - \frac{Re {Z (j ω)}}{{| Z (j ω) |}^{2}})}{ω - ω_{s}} .

(23)

For

ω \to 0

and

ω \to \infty

the expression (23) is well defined, and the upper and lower bounds can be calculated directly. Let us denote them by

c_{l}, c_{u}

respectively. In the regions

[0, ω_{s})

and

(ω_{s}, \infty)

the expression (23) is continuous, thus there are no additional extremum points that can be found there. Finally, consider the limit

lim_{ω \to ω_{s}} (\frac{Re {Z (j ω_{s})}}{| Z (j ω_{s}) |^{2}} - \frac{Re {Z (j ω)}}{{| Z (j ω) |}^{2}}) \frac{1}{ω - ω_{s}} .

(24)

We now show that this limit exists, and is finite. That is, our goal is to prove that

lim_{ω \to ω_{s}} (\frac{Re {Z (j ω_{s})}}{| Z (j ω_{s}) |^{2}} - \frac{Re {Z (j ω)}}{{| Z (j ω) |}^{2}}) \frac{1}{ω - ω_{s}} = C .

(25)

We rely on the following assumptions presented in Theorem 1:

There exists $k_{1}$ such that $Re {Z (j ω)} \leq k_{1}$ ,
There exists $k_{2}$ such that $| Z (j ω) | \geq k_{2}$ ,
$Re {Z (j ω)}, Im {Z (j ω)} \in C^{1}$ .

Examining the limit (24) again, application of L’Hopital’s rule results in

lim_{ω \to ω_{s}} \frac{\frac{d}{d ω} (\frac{Re {Z (j ω)}}{{| Z (j ω) |}^{2}})}{\frac{d}{d ω} (ω - ω_{s})} = lim_{ω \to ω_{s}} \frac{(\frac{d}{d ω} Re {Z (j ω)}) {| Z (j ω) |}^{2} - Re {Z (j ω)} (\frac{d}{d ω} {| Z (j ω) |}^{2})}{{| Z (j ω) |}^{4}} .

(26)

Since

Re {Z (j ω)}, Im {Z (j ω)} \in C^{1}

, we have that

| Z (j ω) | = {(Re {Z (j ω)})}^{2} + {(Im {Z (j ω)})}^{2} \in C^{1}

. Hence, the following limits are well defined:

${lim}_{ω \to ω_{s}} \frac{d}{d ω} Re {Z (j ω)} = c_{1}$ ,
${lim}_{ω \to ω_{s}} {| Z (j ω) |}^{2} = c_{2}$ ,
${lim}_{ω \to ω_{s}} Re {Z (j ω)} = c_{3}$ ,
${lim}_{ω \to ω_{s}} \frac{d}{d ω} {| Z (j ω) |}^{2} = c_{4}$ .

Therefore, the original limit we are interested in is equal to

\frac{c_{1} c_{2} - c_{3} c_{4}}{c_{2}^{4}} \equiv C .

(27)

Note that, depending on the system’s parameters, it is possible to get

C > 0

C < 0

. In each case, the value of C is a candidate for upper or lower limit respectively. w.l.o.g. assuming

C > 0

we deduce it is a candidate for the upper bound. Consequently, (22) is bounded by

- D < \frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}} \leq k,

(28)

where

k = max {c_{u}, C}

and

D = c_{l}

. Thereby, the conditions of Theorem 1 holds in this unique case, meaning that

ω = ω_{s}

is indeed the only equilibrium point of (4), and it is globally asymptotically stable. □

2.3. Synchronous Machine Driving a Resistive-Inductive Load

In this case study, we analyze a system in which the nonlinear load has a resistive-inductive behavior. The main claim used for the analysis is Corollary 1. Our aim is to find the minimal value of D which bounds from above the expression (19), which is derived from the active power of the system. For this type of model, the active power is given by

P_{load} = 3 {| V |}^{2} \cdot \frac{R}{R^{2} + {(ω L)}^{2}} .

(29)

Examine the expression

\frac{P_{load} - P_{ref}}{ω - ω_{s}} .

(30)

Substitution of (29) in (30) leads to

\frac{{3 | V |}^{2}}{ω - ω_{s}} (\frac{R}{R^{2} + {(ω_{s} L)}^{2}} - \frac{R}{R^{2} + {(ω L)}^{2}}) .

(31)

Re-writing this equation results in

\frac{1}{ω - ω_{s}} \cdot \frac{ω^{2} - ω_{s}^{2}}{(R^{2} + ω_{s}^{2} L^{2}) \cdot (R^{2} + ω^{2} L^{2})} \cdot 3 {| V |}^{2} R L^{2},

(32)

or alternatively

\frac{ω + ω_{s}}{R^{2} + ω^{2} L^{2}} \cdot \frac{{3 | V |}^{2} R L^{2}}{R^{2} + ω_{s}^{2} L^{2}} .

(33)

Next, we aim to find the minimal value that bounds (33) from above. For this purpose, notice that the expression given in (33) consists of continuous functions of

ω

. Hence, the derivative may be calculated directly and is given by

\frac{{3 | V |}^{2} R}{R^{2} + ω_{s}^{2} L^{2}} \cdot [\frac{- ω^{2} - 2 ω_{s} ω + {(\frac{R}{L})}^{2}}{{(ω^{2} + {(\frac{R}{L})}^{2})}^{2}}],

(34)

which critical points are

r_{1, 2} = - ω_{s} \pm \sqrt{ω_{s}^{2} + {(\frac{R}{L})}^{2}} .

(35)

Since

ω > 0

, the only valid root is

r_{2}

, so to analyze (34) we examine its behavior close to the critical point

r_{2}

. Given that

\frac{{| V |}^{2} R}{R^{2} + ω_{s}^{2} L^{2}} > 0

and

{(ω^{2} + {(\frac{R}{L})}^{2})}^{2} > 0

, it is sufficient to look at the sign of the expression

- ω^{2} - 2 ω_{s} ω + {\frac{R}{L}}^{2}

. When

ω \to r_{2}^{-}

, the derivative (34) is negative, and when

ω \to r_{2}^{+}

, the expression (34) is positive, meaning that

r_{2}

is a maximum point. Consequently, the upper bound may be defined as

D = \frac{\sqrt{ω_{s}^{2} + {(\frac{R}{L})}^{2}}}{R^{2} + {(- ω_{s} + \sqrt{ω_{s}^{2} + {(\frac{R}{L})}^{2}})}^{2} \cdot L^{2}} \cdot \frac{{3 | V |}^{2} R L^{2}}{R^{2} + ω_{s}^{2} L^{2}} .

(36)

This results in a strict upper bound for the expression given in (33). Indeed, the condition given in (19) holds, therefore,

ω_{s}

is the only global asymptotic equilibrium point of the given system, as desired, and a simplified expression is

D = \frac{\sqrt{ω_{s}^{2} + {(\frac{R}{L})}^{2}}}{{\frac{R}{L}}^{2} + {(- ω_{s} + \sqrt{ω_{s}^{2} + {(\frac{R}{L})}^{2}})}^{2}} \cdot \frac{{3 | V |}^{2} R}{R^{2} + ω_{s}^{2} L^{2}} .

(37)

Notice that the active power at the operating point is given by

P^{*} = \frac{{3 | V |}^{2} R}{R^{2} + ω_{s}^{2} L^{2}}

and the reactive power at the operating point is defined as

Q^{*} = \frac{{3 | V |}^{2} ω_{s} L}{R^{2} + ω_{s}^{2} L^{2}}

. We therefore have

\frac{R}{L} = ω_{S} \cdot \frac{P^{*}}{Q^{*}}

. Substituting these terms in (37) produces

D = \frac{\sqrt{ω_{s}^{2} + ω_{s}^{2} \cdot {(\frac{P^{*}}{Q^{*}})}^{2}}}{ω_{s}^{2} \cdot {\frac{P^{*}}{Q^{*}}}^{2} + {(- ω_{s} + \sqrt{ω_{s}^{2} + ω_{s}^{2} \cdot {(\frac{P^{*}}{Q^{*}})}^{2}})}^{2}} \cdot P^{*},

(38)

which is the same as

D = \frac{\sqrt{1 + {(\frac{P^{*}}{Q^{*}})}^{2}}}{{\frac{P^{*}}{Q^{*}}}^{2} + {(- 1 + \sqrt{1 + {(\frac{P^{*}}{Q^{*}})}^{2}})}^{2}} \cdot \frac{P^{*}}{ω_{s}} .

(39)

Re-arranging the terms in the expression above, yields

D = \frac{\sqrt{1 + {(\frac{P^{*}}{Q^{*}})}^{2}}}{{\frac{P^{*}}{Q^{*}}}^{2} + 1 - 2 \sqrt{1 + {(\frac{P^{*}}{Q^{*}})}^{2}} + 1 + {(\frac{P^{*}}{Q^{*}})}^{2}} \cdot \frac{P^{*}}{ω_{s}},

(40)

D = \frac{\sqrt{1 + {(\frac{P^{*}}{Q^{*}})}^{2}}}{{\frac{P^{*}}{Q^{*}}}^{2} + 1 - \sqrt{1 + {(\frac{P^{*}}{Q^{*}})}^{2}}} \cdot \frac{P^{*}}{2 ω_{s}},

(41)

which may be written as

D = \frac{1}{\sqrt{{\frac{P^{*}}{Q^{*}}}^{2} + 1} - 1} \cdot \frac{P^{*}}{2 ω_{s}},

(42)

thereby leading to

D = \frac{Q}{\sqrt{P^{*} + {Q^{*}}^{2}} - Q} \cdot \frac{P^{*}}{2 ω_{s}} .

(43)

In conclusion, using the fact that

{| S |}^{2} = P^{2} + Q^{2}

, the bound on D may be presented in the following way

D = \frac{Q}{| S | - Q} \cdot \frac{P^{*}}{2 ω_{s}} .

(44)

2.4. Synchronous Machine Driving a Lossless Synchronous Motor, with a Quasi-Linear Mechanical Load

Examine the following non-linear load function:

P_{load} (ω) = τ (ω) \cdot ω,

(45)

where

τ (ω)

is given by

\{\begin{matrix} α \cdot ω, & ω \leq ω_{0} \\ α \cdot ω_{0}, & ω > ω_{0} \end{matrix},

(46)

where

α = \frac{P_{ref}}{ω_{s}^{2}}

To prove that

ω = ω_{s}

is indeed the global asymptotic stable point, we aim to prove that the conditions of Theorem 1 hold. We start by analyzing separately the domains

[0, ω_{0}]

and

(ω_{0}, \infty)

. Define two constants for each domain

c_{l} \geq 0, c_{u} > 0

which denote the upper and lower bound of

τ (ω)

accordingly. Following, the global upper and lower bounds are given by

k = max {c_{u}^{1}, c_{u}^{2}}

and

D = min {c_{l}^{1}, c_{l}^{2}}

, where the superscript

i \in {1, 2}

denotes the domain. Consider the domain

[0, ω_{0}]

, the expression that we are interested in is given by

\frac{P_{load} (ω) - P_{ref}}{ω - ω_{s}} .

(47)

Alternatively, we have

\frac{\frac{P_{ref}}{ω_{s}^{2}} \cdot ω^{2} - P_{ref}}{ω - ω_{s}},

(48)

which is equal to

\frac{P_{ref}}{ω_{s}} \cdot \frac{{(\frac{ω}{ω_{s}})}^{2} - 1}{\frac{ω}{ω_{s}} - 1} .

(49)

This can be further simplified as follows:

\frac{P_{ref}}{ω_{s}} \cdot (\frac{ω}{ω_{s}} + 1) .

(50)

Using the extreme value theorem, since the expression (47) is continuous on a closed and bounded interval

[0, ω_{0}]

, it must attain a minimum and maximum values there. Moreover, since the function is monotonic, it is assured it will attain them only once on this interval. Hence, (50) is bounded from below by

c_{l}^{1} = 0

, and since it is monotonically increasing, the maximum value is obtained at

ω_{0}

and equals to

c_{u}^{1} = \frac{P_{ref}}{ω_{s}} \cdot (\frac{ω_{0}}{ω_{s}} + 1)

. Next, looking at the domain

(ω_{0}, \infty)

, substituting (45) in the expression (47) equals to

\frac{\frac{P_{ref}}{ω_{s}^{2}} \cdot ω_{0} \cdot ω - P_{ref}}{ω - ω_{s}},

(51)

which yields

\frac{P_{ref}}{ω_{s}} \cdot \frac{\frac{ω_{0}}{ω_{s}} \cdot \frac{ω}{ω_{s}} - 1}{\frac{ω}{ω_{s}} - 1} .

(52)

Note that

\frac{ω_{0}}{ω_{s}} > 1

since

ω_{0} > ω_{s}

. Hence, the function (52) is continuous and strictly monotonically decreasing on the interval

(ω_{0}, \infty)

, which leads to a lower bound

c_{l}^{2} = \frac{P_{ref}}{ω_{s}} \cdot \frac{{(\frac{ω_{0}}{ω_{s}})}^{2} - 1}{\frac{ω_{0}}{ω_{s}} - 1},

(53)

which reduces to

c_{l}^{2} = \frac{P_{ref}}{ω_{s}} \cdot (\frac{ω_{0}}{ω_{s}} + 1) .

(54)

The upper bound on this interval can be calculated by examining the limit

ω \to \infty

, which is

lim_{ω \to \infty} (\frac{P_{ref}}{ω_{s}} \cdot \frac{\frac{ω_{0}}{ω_{s}} \cdot \frac{ω}{ω_{s}} - 1}{\frac{ω}{ω_{s}} - 1}) = \frac{P_{ref}}{ω_{s}} \cdot \frac{ω_{0}}{ω_{s}} .

(55)

Consequently, we can choose

c_{u}^{2} = \frac{P_{ref}}{ω_{s}} \cdot \frac{ω_{0}}{ω_{s}}

as the upper bound on the current interval. Summarizing, we can globally bound (47) from below by

\begin{matrix} D & = max \{0, \frac{P_{ref}}{ω_{s}} \cdot (\frac{ω_{0}}{ω_{s}} + 1)\} \\ = \frac{P_{ref}}{ω_{s}} \cdot (\frac{ω_{0}}{ω_{s}} + 1), \end{matrix}

(56)

where the global upper bound is

\begin{matrix} k_{0} & = max \{\frac{P_{ref}}{ω_{s}} \cdot (\frac{ω_{0}}{ω_{s}} + 1), \frac{P_{ref}}{ω_{s}} \cdot \frac{ω_{0}}{ω_{s}}\} \\ = \frac{P_{ref}}{ω_{s}} \cdot (\frac{ω_{0}}{ω_{s}} + 1) . \end{matrix}

(57)

This proves that the conditions of Theorem 1 hold, and therefore

ω = ω_{s}

is indeed the global asymptotic equilibrium point, as desired.

3. Numeric Results

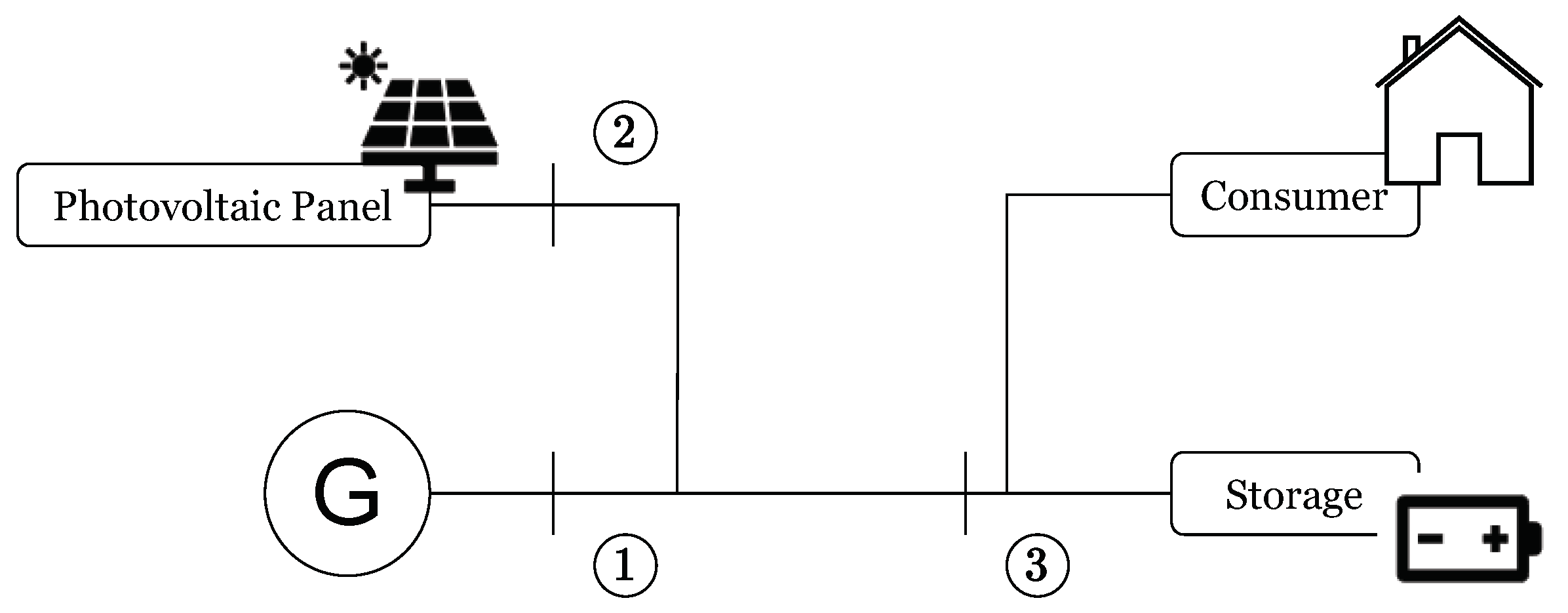
To demonstrate this result, we consider here the classical problem of managing an ideal grid connected storage device, and focus on the behavior of the poles given different values of the damping coefficient of the generator. Consider a microgrid system comprising a grid-connected ideal storage device and a photovoltaic (PV) panel, as illustrated in Figure 3.

The storage device is charged by both the grid and the PV, and supplies an aggregated load characterized by its active power consumption. The load’s active power demand, represented by a continuous, positive function

P_{a} : R_{\geq 0} \to R

, is defined over a finite time interval

[0, T]

, where T is a known constant. The power generated by the PV panel is modeled as a piecewise continuous, non-negative function

P_{p v} : R_{\geq 0} \to R

. The net power consumption of the load is given by

P_{L} (t) = P_{a} (t) - P_{p v} (t)

. The rate of charge or discharge of the storage device is described by

P_{s} (t) = P_{g} (t) - P_{L} (t)

, where

P_{g} : R_{\geq 0} \to R

is the power supplied by the grid, and

P_{s} : R_{\geq 0} \to R

is the power flowing into the storage device. Additionally, the quantities

E_{g} (t), E_{L} (t)

, and

E_{s} (t)

represent the generated energy, the load energy, and the stored energy, respectively. These energy values are derived from their corresponding power functions via the relation

E (t) = \int_{0}^{T} P (τ) d τ

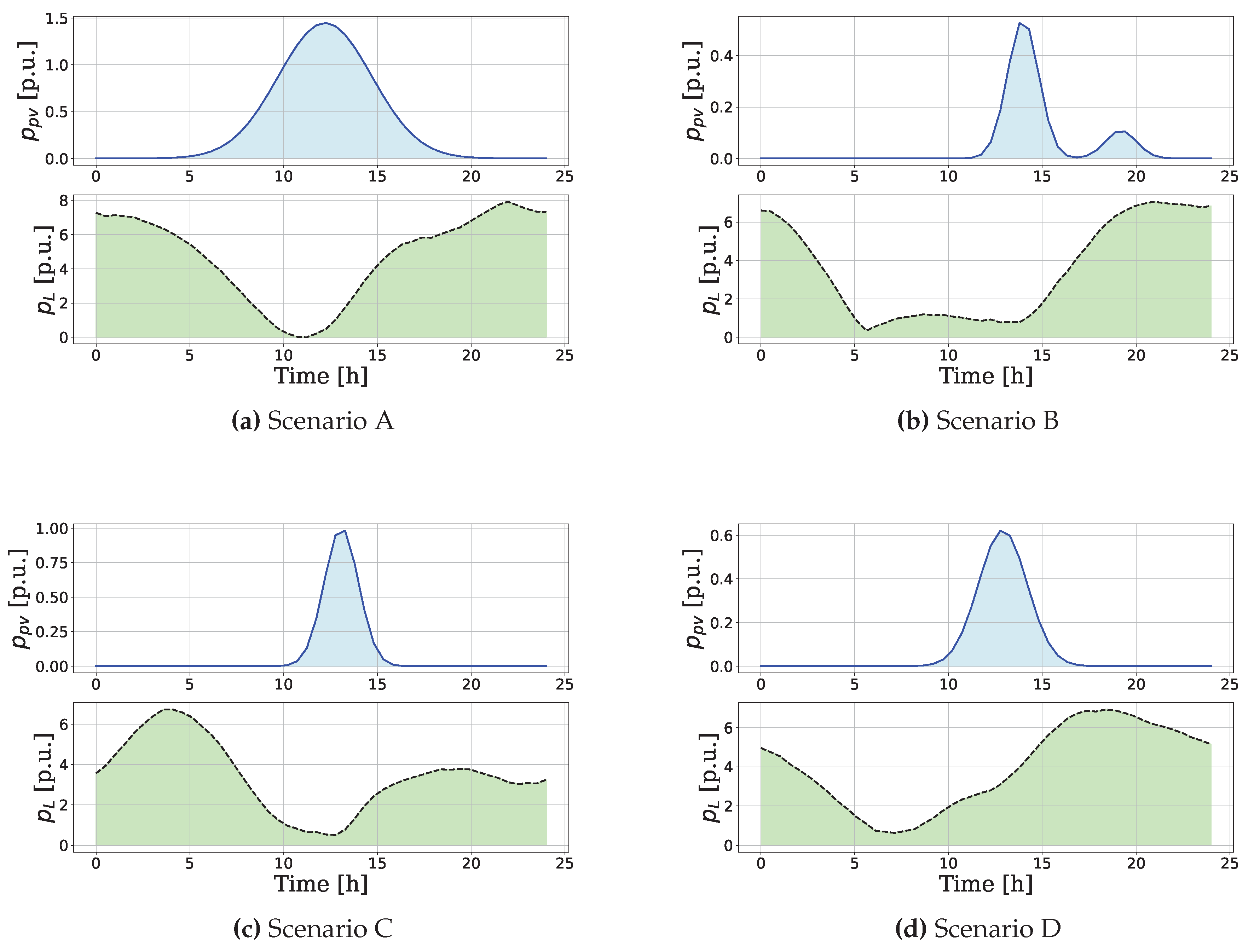
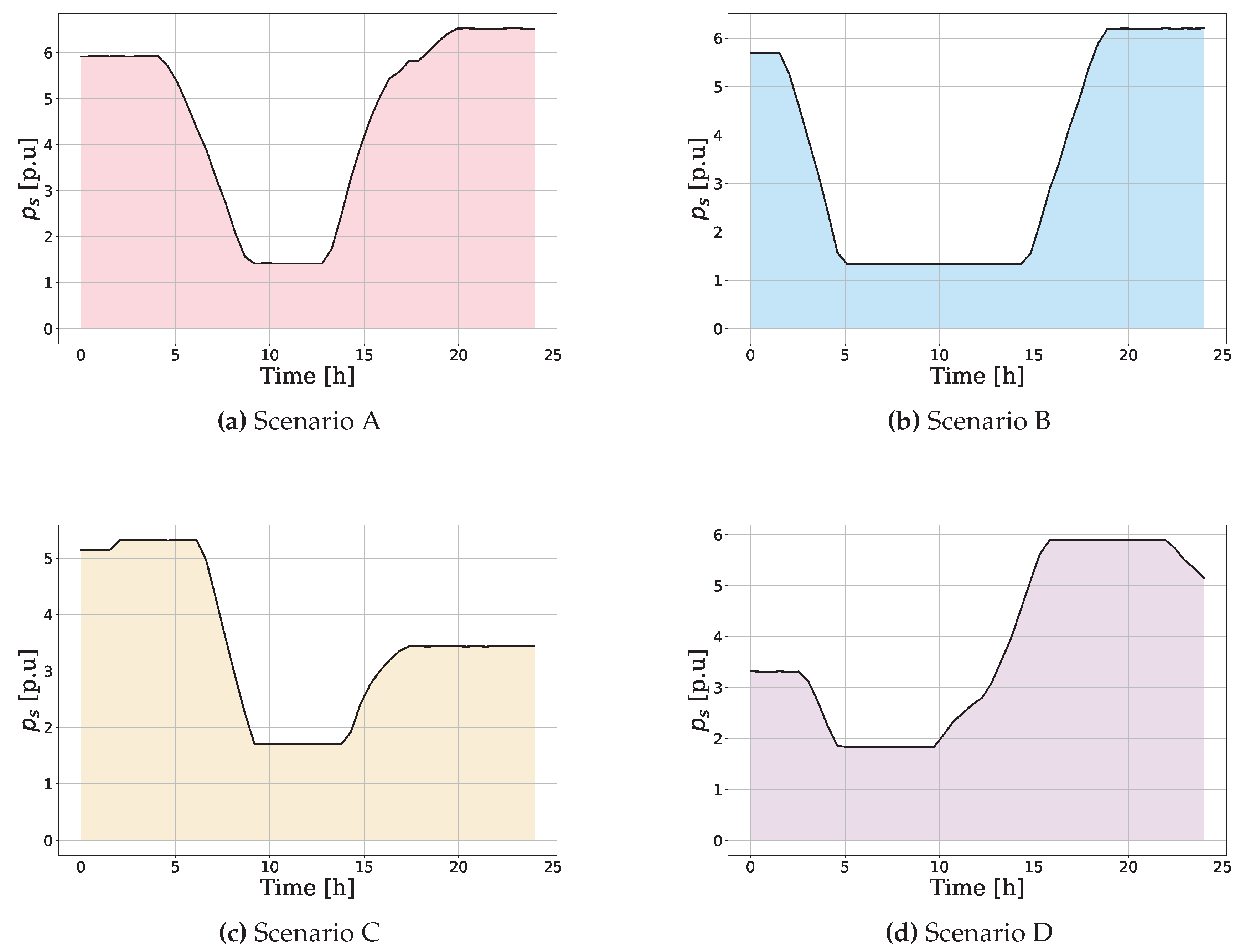
To verify our finding we performed a MATLAB simulation, using Simulink to model the storage device as an R-L circuit, using the idea presented in [24] and the analysis presented in Section 2.3. The solar generation and the consumption profiles are presented in Figure 4.

The critical value of the bound D which defines the stability condition is

D_{t h} = 95.402

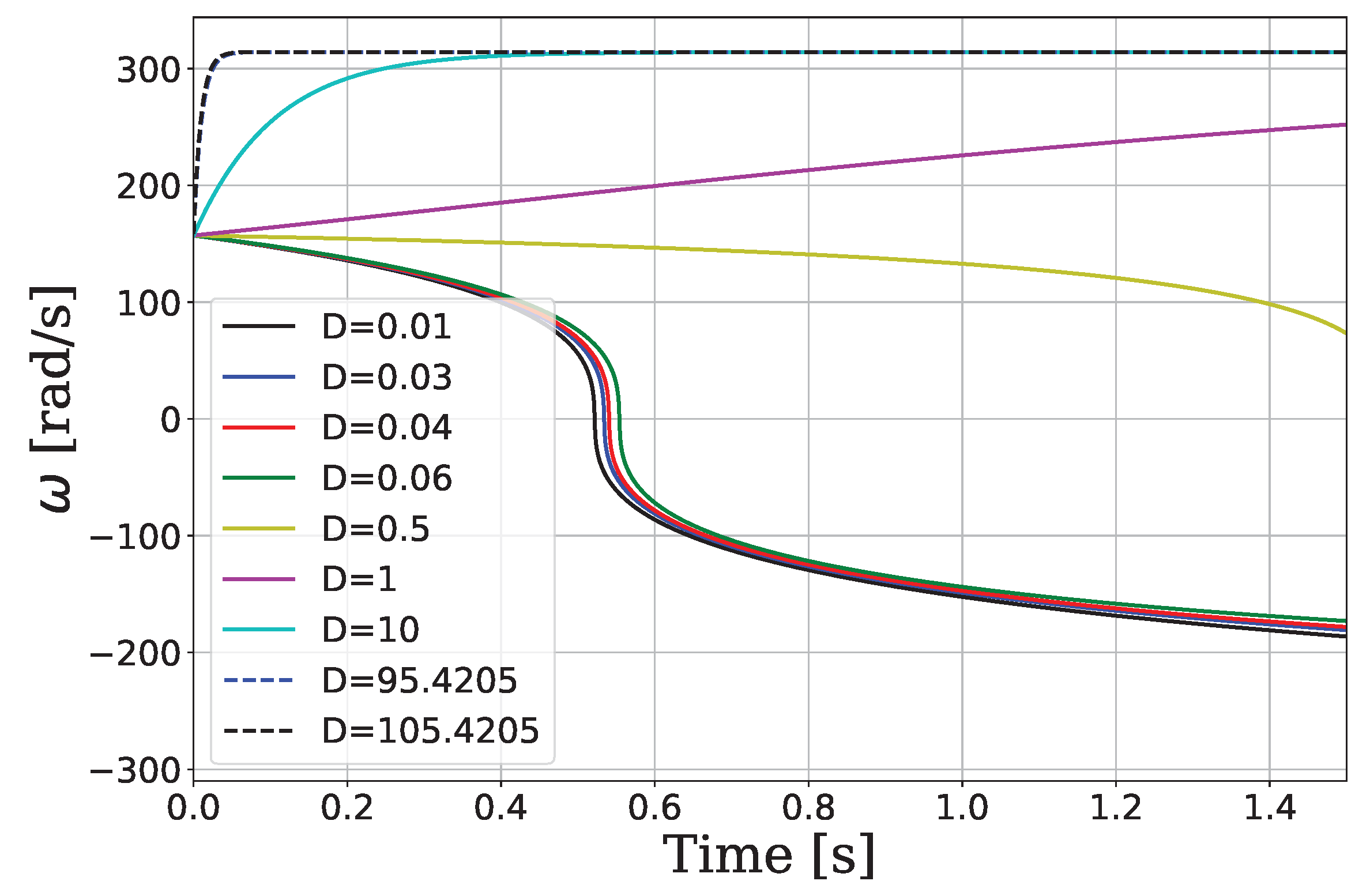
. Performing the simulation for different values of D, shows clearly that for all values of D which are above the threshold value

D_{t h}

, the system is stable and the frequency converges to the globally asymptotically stable point

ω_{s} \approx 314

. On the contrary, for all values of D that are beneath the threshold

D_{t h}

the system diverges. For values of D in which the system is stable, the scheduling policy of the storage device is presented in Figure 5.

Examining Figure 6, it can be observed how for different values of D, the frequency either stabilizes on the unique global stable point

ω_{s}

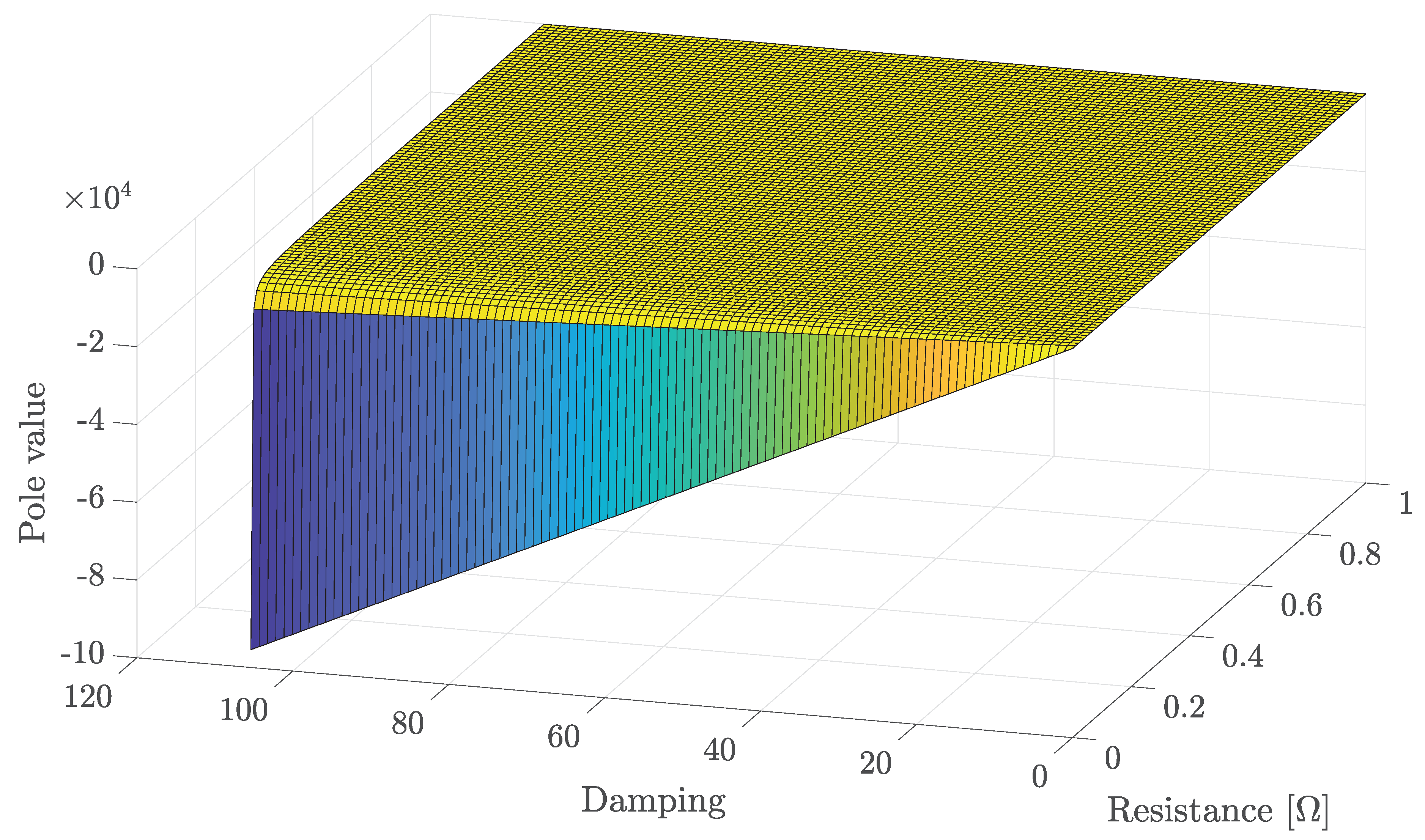
, or diverges. Figure 7 presents how the poles move as the values of the damping coefficient D and the resistance R changes, thus showing the transition of the system from a stable to an unstable state. We examine the following values of the resistance

R = [0.1, 0.5, 1, 5, 10, 100]

in units of

Ω

, and the damping coefficient values tested are

D = [0.01, 0.03, 0.04, 0.06, 0.5, 1, 10, D_{t h}, D_{t h} + 10]

4. Discussion & Conclusions

Stability problems in power systems are typically explored using one of three main approaches: numerical methods, linearization techniques, or direct methods, which utilize Lyapunov energy functions. This paper belongs to the third category, and highlights the usefulness of the Popov stability criterion in the analysis of nonlinear power system models. The main advantage of this criterion is that it provides conditions for global asymptotic stability of an equilibrium point. This stands in contrast to linearization techniques, which only provides conditions for local stability. We show a general method to apply this stability criterion, and examine its uses in several specific applications. More specifically, we examine small power systems such as synchronous machine driving a resistive-inductive load and a synchronous machine driving a lossless synchronous motor, with a quasi-linear mechanical load. Following we rely on a simplified model of a storage device that is powered by a synchronous machine, to analyze the frequency stability for varying system parameters. For instance, we evaluate for which practical parameters of the storage and the synchronous machine, such as the resistance and damping coefficient, the equilibrium is globally asymptotically stable.

Author Contributions

Conceptualization, E.G. and Y.L.; methodology, Y.L; software, E.G. and Y.L.; validation, E.G. J.B and L.K.; formal analysis, E.G. and Y.L.; writing—original draft preparation, E.G.; writing—review and editing, E.G. and Y.L.; visualization, E.G. and J.B.; supervision, Y.L.; Funding acquisition J.B. All authors have read and agreed to the published version of the manuscript.

Funding

The work of J. Belikov was partly supported by the Estonian Research Council grant PRG1463.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The original data presented in the study are openly available in GitHub at https://github.com/ElinorG11/PopovStability.git.

Conflicts of Interest

The authors declare no conflict of interest.

References

Kundur, P. Power System Stability and Control; McGraw-Hill, 1994.
Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; Van Cutsem, T.; Vittal, V. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Transactions on Power Systems 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
Caliskan, S.Y.; Tabuada, P. Compositional Transient Stability Analysis of Multimachine Power Networks. IEEE Transactions on Control of Network Systems 2014, 1, 4–14. [Google Scholar] [CrossRef]
Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Ángel Molina-García. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renewable and Sustainable Energy Reviews 2019, 115, 109369. [Google Scholar] [CrossRef]
Meegahapola, L.; Sguarezi, A.; Bryant, J.S.; Gu, M.; Conde D., E. R.; Cunha, R.B.A. Power System Stability with Power-Electronic Converter Interfaced Renewable Power Generation: Present Issues and Future Trends. Energies 2020, 13. [Google Scholar] [CrossRef]
H. Bevrani, A. Ghosh, G.L. Renewable energy sources and frequency regulation: survey and new perspectives. IET Renewable Power Generation 2010, 4, 438–457. [Google Scholar] [CrossRef]
Golpîra, H.; Atarodi, A.; Amini, S.; Messina, A.R.; Francois, B.; Bevrani, H. Optimal Energy Storage System-Based Virtual Inertia Placement: A Frequency Stability Point of View. IEEE Transactions on Power Systems 2020, 35, 4824–4835. [Google Scholar] [CrossRef]
Mosca, C.; Arrigo, F.; Mazza, A.; Bompard, E.; Carpaneto, E.; Chicco, G.; Cuccia, P. Mitigation of frequency stability issues in low inertia power systems using synchronous compensators and battery energy storage systems. IET Generation, Transmission & Distribution 2019, 13, 3951–3959. [Google Scholar] [CrossRef]
Serban, I.; Teodorescu, R.; Marinescu, C. Energy storage systems impact on the short-term frequency stability of distributed autonomous microgrids, an analysis using aggregate models. IET Renewable Power Generation 2013, 7, 531–539. [Google Scholar] [CrossRef]
Süli, E.; Mayers, D.F. An introduction to numerical analysis; Cambridge university press, 2003.
Nielsen, K.L. Methods in numerical analysis.; MACMILLAN, 1956.
Montoya, O.D.; Gil-González, W. On the numerical analysis based on successive approximations for power flow problems in AC distribution systems. Electric Power Systems Research 2020, 187, 106454. [Google Scholar] [CrossRef]
Socha, L. Linearization methods for stochastic dynamic systems; Springer Science & Business Media, 2007.
Liang, X. Linearization Approach for Modeling Power Electronics Devices in Power Systems. IEEE Journal of Emerging and Selected Topics in Power Electronics 2014, 2, 1003–1012. [Google Scholar] [CrossRef]
Sun, J. Small-Signal Methods for AC Distributed Power Systems–A Review. IEEE Transactions on Power Electronics 2009, 24, 2545–2554. [Google Scholar] [CrossRef]
Persson, J.; Söder, L. Comparison of threes linearization methods. Proceedings of 16th Power System Computation Conference, Power Systems Computation Conference ( PSCC ), 2008;, 2008.
Slotine, J.J.E. Applied nonlinear control; Pearson, 1991.
Isidori, A. Nonlinear control systems: an introduction; Springer, 1985.
Willems, J. Direct method for transient stability studies in power system analysis. IEEE Transactions on Automatic Control 1971, 16, 332–341. [Google Scholar] [CrossRef]
Chang, H.D.; Chu, C.C.; Cauley, G. Direct stability analysis of electric power systems using energy functions: theory, applications, and perspective. Proceedings of the IEEE 1995, 83, 1497–1529. [Google Scholar] [CrossRef]
Zhai, C.; Nguyen, H.D. Estimating the Region of Attraction for Power Systems Using Gaussian Process and Converse Lyapunov Function. IEEE Transactions on Control Systems Technology 2022, 30, 1328–1335. [Google Scholar] [CrossRef]
Kazemi, A.; Motlagh, M.J.; Naghshbandy, A. Application of a new multi-variable feedback linearization method for improvement of power systems transient stability. International Journal of Electrical Power & Energy Systems 2007, 29, 322–328. [Google Scholar] [CrossRef]
Tzounas, G.; Dassios, I.; Milano, F. Small-signal stability analysis of implicit integration methods for power systems with delays. Electric Power Systems Research 2022, 211, 108266. [Google Scholar] [CrossRef]
Yang, J.; Cai, Y.; Pan, C.; Mi, C. A novel resistor-inductor network-based equivalent circuit model of lithium-ion batteries under constant-voltage charging condition. Applied Energy 2019, 254, 113726. [Google Scholar] [CrossRef]

Figure 1. Block diagram of the system.

Figure 2. Popov plot.

Figure 3. System model consisting of a generator and a PV, feeding a non-linear load that includes a storage device.

Figure 4. Solar generation and consumption profiles for various scenarios.

Figure 5. Storage scheduling policies under different scenarios of solar generation and consumption profiles.

Figure 6. Frequency vs. time for different values of the damping coefficient D.

Figure 7. Root-locus for various values of the damping coefficient D and resistance R.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Uses of the Popov Stability Criterion for Analyzing Global Asymptotic Stability in Power System Dynamic Models

Abstract

1. Introduction

2. Materials and Methods

2.1. Mathematical Background - The Popov Stability Criterion

2.2. Dynamic Stability of a Synchronous Generator, Connected to a Non-Linear Frequency Dependent Load

2.3. Synchronous Machine Driving a Resistive-Inductive Load

2.4. Synchronous Machine Driving a Lossless Synchronous Motor, with a Quasi-Linear Mechanical Load

3. Numeric Results

4. Discussion & Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe