Prerpints.org logo
Preprint
Article

Polarizing Magnetic Field Effect on Some Electrical Properties of a Ferrofluid in Microwave Field

Altmetrics

Downloads

60

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 October 2024

Posted:

11 October 2024

You are already at the latest version

Alerts
Abstract
The complex dielectric permittivity, ε (f, H) = εʹ (f, H)- i εʺ (f, H), in the microwave frequency range f, of (0.1 - 3) GHz and polarizing field values H, in the range of (0 - 135) kA/m, was measured for a kerosene-based ferrofluid with magnetite particles. A relaxation process attributed to interfacial type relaxation was highlighted, determining for the first time in the microwave field, the activation energy of the dielectric relaxation process in the presence of the magnetic field, EA(H), in relation to the activation energy in zero field, EA(H=0). Based on the complex permittivity measurements and the Claussius-Mossotti equation, the dependencies on frequency (f), and magnetic field (H), of the polarizability (α) and electrical conductivity (σ), were determined. From the dependence of α(f,H), the electric dipolar moment, p, of the particles in the ferrofluid, was determined. The conductivity spectrum, σ(f,H), was found to be in agreement with Jonscher's universal law and the electrical conduction mechanism in the ferrofluid was explained using both Mott's VRH (variable range hopping) model and CBH (correlated barrier hopping) model. Based on these models and conductivity measurements, the hopping distance, Rh, of the charge carriers and the maximum barrier height, Wm, for the investigated ferrofluid was determined for the first time in the microwave field. Knowledge of these electrical properties of the ferrofluid in the microwave field is useful for explaining the mechanisms of polarization and control of electrical conductivity with an external magnetic field, in order to use ferrofluids in various technological applications in microwave field.
Keywords: 
Subject: Chemistry and Materials Science  -   Electronic, Optical and Magnetic Materials

1. Introduction

Ferrofluids or magnetic liquids represents a colloidal system of single-domain magnetic nanoparticles, dispersed in a carrier liquid and coated with a surfactant to prevent their agglomeration [1,2]. The magnetic and electrical properties of ferrofluids have led to their use in many technological [3] or biomedical [4,5] applications. Several authors have investigated the dielectric properties of ferrofluids in low frequency fields, to highlight the dielectric relaxation processes [6,7,8]. At the same time, the understanding of the polarization phenomena in a ferrofluid was achieved through studies on the static and dynamic behavior of the complex dielectric permittivity at low frequencies, depending on the temperature, frequency or the concentration of the particles in the ferrofluid [9,10,11]. Few works are known regarding the study of the dielectric properties of ferrofluids in the microwave field and the explanation of relaxation and polarization phenomena at these high frequencies. In our previous paper [12], it is shown that the frequency dependence of the complex dielectric permittivity in the microwave range and in a zero polarizing magnetic field can be well described using the Maxwell-Wagner-Sillars theoretical model, valid for heterogeneous dielectrics in the biphasic approximation and applied of the investigated ferrofluid sample.
In this paper, based on measurements on the frequency dependence, f, of the complex dielectric permittivity in the range (0.1 - 3) GHz and at different values ​​of the polarizing magnetic field, H, between (0 - 135) kA/m, in combination with the Claussius-Mossotti equation, we determined for the first time, the frequency and magnetic field dependence of the microwave polarizability, α(f,H), of a kerosene-based ferrofluid sample. Also, the obtained results allowed the determination of the dependence on f, and H, of the electrical conductivity, σ(f, H), of the ferrofluid, this dependence being explained by means of existing theoretical models in the investigated field.

2. Sample and Experimental Setup

The sample used for measurements was a kerosene-based ferrofluid with magnetite nanoparticles, obtained by the chemical co-precipitation method with NH4OH in aqueous solution, and having the density, ρF=1.255 g/cm3. Stabilization with oleic acid was achieved by hydrophobization in the absence of the dispersion medium [13,14,15], the magnetic material thus obtained being then dispersed in kerosene and filtered in a magnetic field gradient, to eliminate aggregates and coarse particles [14,15]. The dependence of the magnetization M on the magnetic field, H of the ferrofluid sample (Figure 1) was determined using an inductive method [16] and it shows a Langevin-type dependence [1].
Based on the dependence M(H), from Figure 1, and the magneto-granulometric analysis of Chantrell [17], we have determined the following magnetic parameters for the ferrofluid sample, assuming the particles to be of spherical shape: the saturation magnetization of the ferrofluid, Msat = 38.7 kA/m; the mean magnetic diameter of a particle, dm = 11.02 nm; the particles concentration, n = 23.11·1022 m−3 and initial susceptibility χin = 2.48. The measurements of the complex dielectric permittivity over the frequency range f = (0.1- 3) GHz and the polarizing magnetic field, H = (0 to 135 kA/m), were performed using the open-circuited (OC) coaxial transmission line technique [18,19] (Hewlett Packard (HP) type), incorporating a coaxial cell, containing the ferrofluid sample, in conjunction with the HP 8753C network analyzer [18,19]. The coaxial cell was placed between the poles of an electromagnet, the axis of cell being perpendicular to the polarizing magnetic field.

3. Results and Discussions

3.1. Complex Dielectric Permittivity

The frequency dependences of the real εʹ and imaginary εʺ components of the complex dielectric permittivity at different H values are shown in Figure 2 a) and b) for the investigated ferrofluid sample.
From Fig. 2 a) it is observed that for each constant value of H, in the range (0 - 135) kA/m, the εʹ component decreases gradually by increasing the frequency from 0.1 GHz to 3 GHz. Regarding the variation with frequency of the εʺ component in Fig. 2 b) it is observed that εʺ shows a maximum at a frequency, fmax between (1-2) GHz, for each H value of the polarizing magnetic field, which indicates the existence of a dielectric relaxation process [20]. Similarly, from Fig. 2 a) and b) it is shown that by increasing H from zero to 24.47 kA/m, both εʹ and εʺ decrease compared to the value corresponding to H=0, after which they start to increase with increasing H, between 24.42 kA/m and 135.45 kA/m. This behavior of the components εʹ(f,H) and εʺ(f,H) depends on the shape of the particles and the orientation of the electric dipoles in the direction of the electric field [21]. In the ferrofluid located in a coaxial line and subjected to a magnetic field perpendicular to the axis of the coaxial line, changes occur in its local structure, forming both small agglomerations of particles and large agglomerations of magnetic particles (so-called condensed-phase droplets) [21], which can coexist with un-aggregated particles. The formation of small agglomerations of particles in the form of a chain in the presence of the magnetic field, as shown in Ref. [22], leads to an increase in the eccentricity of the agglomeration, which results in an increase in both the εʹ and εʺ components, of the complex dielectric permittivity. Due to the large agglomerations of particles in the ferrofluid, their rotation is hindered by the neighbors in the agglomeration, the dielectric behavior of the ferrofluid being like that of a magnetic powder [22,23].
The presence of the magnetic field causes a reduction of the charge carriers on the surface of the particles, so that the electric dipolar moment of the particles decreases compared to the electric dipolar moment of the particle in the absence of the magnetic field, which leads to the decrease of both the real, εʹ, and imaginary component, εʺ, of the complex dielectric permittivity. As a result, in the case of ferrofluids, where there is a combination of the effect of condensed-phase droplets with small agglomerations and non-agglomerated particles, it will lead to the decrease or increase of the components of the complex dielectric permittivity on different domains of magnetic field, as we obtained experimentally in Fig. 2.
As previously mentioned, from Fig. 2b) the εʺ(f, H) component has a maximum for each value of H, which indicates the existence of a interfacial relaxation process, characterized by the relaxation time, τ. Using the fmax values ​​ corresponding to the maximum of the εʺ component for each H value (Fig. 2 b)), in the Debye equation which states that 2πfmaxτ =1 [24], we determined the τ values ​​of the relaxation time, whose dependence on the magnetic field is shown in Figure 3.
As can be seen from Fig. 3, by increasing the field H from 0 to approximately 60 kA/m, the relaxation time τ increases from 0.09 ns to approximately 0.13 ns, then for values ​​H>60 kA/m, τ remains approximately constant at the value of 0.133 ns. If the values ​​of τ(H), corresponding to the εʺ component at all investigated values of H, obeys an Arrhenius-type law, the following relationship can be written:
τ ( H ) = τ 0 ⋅ exp E A ( H ) k T  
where τ0 is a constant; k is the Boltzmann constant; T is the constant room temperature and EA(H) is the activation energy of the relaxation process which depends on the applied magnetic field, H. Considering equation (1), the relaxation time τ (H=0), in the absence of the magnetic field and the relaxation time τ(H≠0), in the presence of the magnetic field, can be written in the form:
τ ( H = 0 ) = τ 0 ⋅ exp E A , 0 k T   , τ ( H ) = τ 0 ⋅ exp E A , h k T  
In relation (2), Ea,0 and Ea,h represent the activation energy of the interfacial relaxation process both in zero field and in the presence of a magnetic field H, respectively, from which we immediately obtain:
Δ E A ( H ) = E A , h − E A , 0 = k T ⋅ ln τ ( H ) τ ( H = 0 )  
This relationship allows the determination (for the first time) of the magnetic field dependence, and the variation of the activation energy of the relaxation process, in the presence of a magnetic field, ΔEa(H), compared to the activation energy in zero field, using the τ values ​​of the relaxation time from Fig. 3. The dependence ΔEa,h(ΔH) is shown graphically in Figure 4.
From Fig. 4, it can be seen that the variation of activation energy of the relaxation process, ΔEa,h increases from 0 meV to approximately 9.3 meV, with increasing of the applied magnetic field, ΔH from 0 kA/m to approximately 60 kA/m, then for values, H>60 kA/m, ΔEa,h remains approximately constant at the value of 9.88 meV. This increase of EA(H), compared to EA(H = 0), can be correlated with the changes that take place in the local structure of the ferrofluid due to the presence of the magnetic field perpendicular to the axis of the coaxial line in which the ferrofluid is located, forming both small agglomerations of particles and condensed-phase droplets [21], in agreement with the dielectric experimental results obtained, in Fig. 2.

3.2. Complex Polarizability

Starting from the Clausius-Mossotti equation [20], in the harmonic regime, as shown in reference [8] for the computing of the real (αʹ) and imaginary (αʺ) components of the complex polarizability, α, of a ferrofluid the following equations were used:
α ′ = 3 ε 0 M ρ F N A ⋅ K ′ , α ″ = 3 ε 0 M ρ F N A ⋅ K ″
In Eq. (4), NA is the Avogadro number; ε0 is the permittivity of free space and M is the molar mass of the ferrofluid. Also, Kʹ and Kʺ represent the real and imaginary components of the complex form of the Clausius-Mossotti factor, K=(ε-1)/(ε+2). Considering the complex form of the dielectric permittivity, ε=εʹ-iεʺ, the components K' and K'' are given by the relations:
K ′ = ε ′ 2 + ε ″ 2 + ε ′ − 2 ε ′ 2 + ε ″ 2 + 4 ε ′ + 4
K ″ = 3 ε ″ ε ′ 2 + ε ″ 2 + 4 ε ′ + 4
Using the values of components εʹ(f, H) and εʺ(f, H) of the complex dielectric permittivity, from Fig. 2 a) and b) with relations (5) and (6) the components Kʹ and Kʺ were computed. The frequency dependence of these components (K' and K''), for different values ​​of the magnetic field, is shown in Figure 5. As can be observed from fig. 5, the frequency dependence of the K' and K'' components of the Clausius-Mossotti complex factor, for different values of H, are similar to the dependencies εʹ(f, H) and εʺ(f, H) of the complex dielectric permittivity (Fig. 2 b)).
To determine the real, α'(f, H), and imaginary, α''(f, H), components of the total complex polarizability, α, using equation (4) and the values K'(f, H) and K''(f, H) from Fig. 5, it is necessary to compute the factor (3ε0M/ρFNA). For this ferrofluid sample, the molar mass M, was computed as shown in Ref. [25], and the obtained value is M=196.73 g/mol. As a results, the value obtained for the factor (3ε0M/ρFNA) is 6.97 ·10−39 F·m2. Consequently, the real, α'(f,H) and imaginary, α''(f,H) components of the total complex polarizability, α, from equation (4), were determined and their frequency dependence at different values ​​of the magnetic field is shown in Figure 6.
In the microwave frequencies range (between 0.1 GHz and 3 GHz), as can be observed from Fig. 6, the component α' decreases for all magnetic field values, and α'' component, presents a maximum at a frequency fmax,α, as in the case of the K'' component of the Clausius-Mossotti complex factor (Fig. 5). At the same time, from Fig. 6 it can be seen that by increasing of H from zero to 24.47 kA/m, both α' and α'' decrease compared to the value corresponding to H=0, after which they start to increase by increasing H from 24.42 kA/m up to 135.45 kA/m.
It is known that [20] the total polarizability can be due to the combined effects corresponding to both electrical conduction losses and different polarization mechanisms: electronic or ionic displacement and dipolar polarization. As shown in Ref. [8], at high frequencies (above 200 kHz), the dipolar orientation mechanism is predominant in the total polarization of the ferrofluid, the polarizability, α’ is given by the relation [20].
α ′ = p 2 3 k T
Using relation (7) and knowing the αʹ values ​​of the polarizability corresponding to each H value of the magnetic field, we determined for the first time the dependence on the magnetic field, H of the electric dipolar moment, p of the ferrofluid nanoparticles, at different frequencies of the microwave field, represented graphically in Figure 7.
As can be seen in Fig. 7, for all investigated microwave frequencies, by increasing the magnetic field from zero to approximately 30 kA/m, the electric dipolar moment decreases to a minimum value, after which it increases with increasing magnetic field. The electric dipolar moment p decreases with increasing frequency, between the approximate values of 6.3 x 10-30 C·m and 5.9 x 10-30 C·m. This result is in agreement with the frequency and magnetic field dependence of the component εʹ(f H) of the complex dielectric permittivity (Fig. 2 a)). In the presence of the magnetic field, there is a decrease in the number of charge carriers on the surface of the particles, so that the electric dipolar moment of the particles decreases compared to the electric dipole moment of the particle in the absence of magnetic field.

3.3. The electrical conductivity

Using the experimental data of the complex dielectric permittivity in Fig. 2 b), the real component σ, of the complex electrical conductivity can be calculated [20] from the relation:
σ ( f , H ) = 2 π f ε 0 ε ″
The frequency dependence of σ, in the microwave range and at different values H of polarizing magnetic field is shown in Figure 8.
As can be observed from Fig. 8, at a constant value H, the conductivity, σ, of the ferrofluid presents a linear region at low frequencies, similar to DC-conductivity (σDC) and a dispersion region, at higher frequencies, corresponding to AC-conductivity (σAC), in accordance with the Jonscher universal law [26], generally known for the variation with frequency and temperature of the electrical conductivity of a sample [27]:
σ ( ω , H ) = σ D C ( H ) + σ A C ( ω , H )
In this work, the temperature is constant and the variation of the conductivity σ, of the ferrofluid was studied as a function of frequency and magnetic field, the result obtained in Fig. 8, agreeing with Jonscher's universal law like a dependence on frequency and temperature of electrical conductivity [27]. As can be seen in Fig. 8, the σDC conductivity does not depend on the frequency but only on the magnetic field H, while the conductivity σAC depends on both the frequency and the field H. In relation (10), according to Jonscher's law [26], the σAC conductivity is given by the relation:
σ A C ( ω , H ) = A 0 ω n ( H )
where n is an exponent dependent on the magnetic field, at constant temperature (0 < n < 1) and A0 is a pre-exponential factor [26,28]. From Fig. 8, the conductivity values ​​σDC(H) were determined for all the measured H values ​​of the magnetic field. Using the experimental values ​​obtained for the static conductivity, σDC(H), we plotted the magnetic field dependence of the static conductivity, σDC(H), as shown in Figure 9.
From figure 9, it is observed that σDC(H), increases when the magnetic field H increases from zero to approximately 30 kA/m, and then decreases with the increase of H from 30 kA/m to 135 kA/m, this behavior agreeing with Mott's VRH theory [29]. The increase in conductivity, σDC, around ​​low magnetic fields, between zero and 30 kA/m, can be attributed to the increase in the mobility of electric charge carriers, which are magnetically activated when H increases [29]. At magnetic fields H above 30 kA/m, the static conductivity decreases with increasing magnetic field, which indicates a decrease in the mobility of charge carriers [29,30]. This behavior of the static conductivity with the magnetic field H can be correlated with the variation of the dielectric permittivity depending on the value ​​of H, from Fig. 2.
In the high frequency range, between (0.8-3) GHz, corresponding to the σAC component of the conductivity (see Fig. 9), by logarithmisation of equation (10), a linear relationship between ln(σAC) and ln(ω) is obtained, graphically represented in Figure 10, at different values ​​of the magnetic field H, applied to the ferrofluid sample. By fitting the experimental dependencies ln(σAC)(ln(ω)), from Fig. 10, it was possible to determine both the exponent n and the parameter A0, corresponding to each H value of the magnetic field, the obtained results being presented in Table 1.
Based the Mott’s variable-range-hopping (VRH) model [29], and the electrical conduction mechanism by hopping of charge carriers [28,31], we established for the first time in the microwave range, the following equation that allows the determination of the hopping distance Rh of the charge carriers, between the localized states.
R h ( H ) = 3 e 4 1 6 π α   k T σ D C 1 − n A 0 n 1 / 2
In Eq. (11), e is the electric charge of the electron and α=109 m-1, represents the degree of localization [29]. Using the obtained values for σDC (Fig. 9), exponent n and parameter A0 (Table 1), with Eq. (11) the values Rh corresponding to each value H of magnetic field, were determined, being listed in Table 1 and the Rh(H) dependence is presented in Figure 11.
As can be seen, from both Table 1 and Fig. 11, the hopping distance, Rh, initially decreases with increasing magnetic field H, applied to the ferrofluid, from 10.27 nm (for H = 0) to 7.43 nm (for H = 24.47 kA/m), after which Rh begins to increase with the increase of H, reaching the value of 16.43 nm corresponding to H=135.45 kA/m. This result shows that the conduction mechanism (DC-conductivity) in the microwave frequency range is established by the hopping of charge carriers between the localized states due to the Mott VRH mechanism [29] inside the ferrofluid magnetite particles; the latter being influenced by the presence of the magnetic field, H. Thus, around ​​low magnetic fields, between zero and approximately 30 kA/m, the decrease in the hopping distance Rh will cause a greater number of charge carriers to participate in the electrical conduction, which leads to the increase electrical conductivity σDC, in this domain of low magnetic field as observed experimentally (see Fig. 9). The increase of the magnetic field H from approximately 30 kA/m to 135 kA/m, causes the increase of the hopping distance Rh which will lead to a smaller number of charge carriers participating in the electrical conduction and therefore to the decrease of the electrical conductivity σDC, as was also obtained experimentally (see Fig. 9).
In the high frequency region, corresponding to the σAC conductivity, the variation with frequency at different H values ​​of the magnetic field (Fig. 9), is like the σAC dependence for different T values ​​of the temperature [32]. As a result, for the analysis of the conduction mechanism at high frequencies, we used the correlated barrier hopping model (CBH) [33], which explains that the dependence σAC(f,H) is due of the short-range hopping of the charge carriers between the sites separated by energy barriers of varied heights [26,31,34]. In a first approximation, from the CBH model, the exponent n is given by the relation:
n = 1 − 6 k T W m
where Wm is the maximum barrier height (equal to the band gap energy) [26]. The dependence of the maximum energy barrier height, Wm(H), versus magnetic field, H, is shown in Figure 12 for the ferrofluid sample.
From figure 12 it can be seen that by increasing the magnetic field H, there is a decrease in the energy of the band gap, Wm, from 2.6 eV (for H=0) to approximately 1.82 eV (for H=135 kA/m), being in agreement with the values of the bandgap energy of magnetite nanoparticles (Fe3O4), obtained by other authors: 1.76 eV [35] and 2.24 eV [36] respectively, at room temperature.

4. Conclusions

The paper reports the effect of the polarizing magnetic field, H, on the polarizability and electrical conductivity of a kerosene-based ferrofluid with magnetite particles, in the microwave range (0.1-3) GHz at different values of H between (0–135) kA/m, using the complex dielectric permittivity measurements.
Based on the experimental measurements of the complex dielectric permittivity, ε(f,H) and Clausius-Mossotti equation, the frequency and magnetic field dependencies in the microwave range, α(f,H), of the complex polarizability of the ferrofluid were determined. Assuming that in the microwave domain, the dipolar mechanism is predominant in the total polarization, from the dependence α(f,H), it was determined for the first time, the electric dipolar moment, p, of the particles in the ferrofluid, depending on the magnetic field H, at different microwave frequencies.
The results show that at all investigated microwave frequencies, by increasing the magnetic field, H from zero to approximately 30 kA/m, the electric dipolar moment p, decreases to a minimum value, after which it increases slightly by increasing the magnetic field, the obtained result being in accordance with the dependence of the εʹ(f,H) component of the complex dielectric permittivity.
The conductivity spectrum, σ(f, H) for each H value, respects the universal Jonscher law showing a region where σ does not depend on frequency, corresponding to σDC conductivity and another region, where σ increases rapidly with frequency, corresponding to σAC conductivity. The results show that σDC(H), increases when H increases from zero to about 30 kA/m, then decreases with the increase of H from 30 kA/m to 135 kA/m, this behavior agreeing with Mott's VRH theory. This variation of the conductivity, σDC, correlates well with the variation of the dielectric permittivity ε(f,H), which can be attributed to the increase or decrease in the mobility of the electric charge carriers, in the ferrofluid, magnetically activated when H increases.
Using the VRH model of Mott and the σDC measurements, we established for the first time in the microwave range, an equation that allows the determination of the hopping distance Rh of the charge carriers, between the localized states. The results show that Rh at the beginning decreases, with increasing H, applied to the ferrofluid, from 10.27 nm (for H = 0) to 7.43 nm (for H = 24.47 kA/m), after which Rh begins to increase with the increase of the magnetic field, up to the value of 16.43 nm corresponding to H=135.45 kA/m, this dependence being correlated with the variation with the H field of the σDC static conductivity.
Based on both the VRH and CBH theoretical models, the maximum height of the energy barrier, Wm, or the band gap energy, was determined for the first time in microwave range,, which decreases by increasing H, from 2.6 eV (for H=0) to 1.82 eV (for H=135 kA/m), in agreement with the values ​​of band gap energy for magnetite nanoparticles obtained by other authors at room temperature.

Author Contributions

Conceptualization, I.M., C.N.M. and P.C.F.; methodology, I.M. and C.N.M.; measurements, P.C.F. and I.M.; supervision: P.C.F.; formal analysis, C.N.M.; investigation, I.M. and C.N.M.; writing-original draft preparation, I.M.; writing—review and editing, I.M., C.N.M. and P.C.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest

References

  1. Rosensweig, R. E. Ferrohydrodynamics; Cambridge University Press: Cambridge, 1985. [Google Scholar]
  2. Odenbach, S. Ferrofluids; Springer 594; Berlin Heidelberg, 2002.
  3. Scherer, C.; Figueiredo Neto, A. M. Ferrofluids: Properties and Applications. Braz. J. Phys. 2005, 35(3A), 718–727. [Google Scholar] [CrossRef]
  4. Lübbe, A. S.; Alexiou, C.; Bergemann, C. Clinical Applications of Magnetic Drug Targeting. J. Surg. Res. 2001, 95(2), 200–206. [Google Scholar] [CrossRef]
  5. Pankhurst, Q. A.; Connolly, J.; Jones, S. K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D: Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
  6. Malaescu, I.; Marin, C.N. Dependence on the temperature of the activation energy in the dielectric relaxation processes for ferrofluids in low-frequency field. J. Magn. Magn. Mater. 2002, 252, 68–70. [Google Scholar] [CrossRef]
  7. Rajnak, M.; Kurimsky, J.; Dolnik, B.; Kopcanský, P.; Tomasovicova, N.; Taculescu-Moaca, E.A.; Timko, M. Dielectric-spectroscopy approach to ferrofluid nanoparticle clustering induced by an external electric field. Phys. Rev. E. 2014, 90(3), 032310. [Google Scholar] [CrossRef] [PubMed]
  8. Marin, C.N.; Fannin, P.C.; Malaescu, I.; Matu, G. Macroscopic and microscopic electrical properties of a ferrofluid in a low frequency field. Phys. Lett. A. 2020, 384(7), 126786. [Google Scholar] [CrossRef]
  9. Malaescu, I.; Marin, C.N. Dielectric behaviour of some ferrofluids in low frequency field, J. Coll. Int. Sci. 2002, 251(1), 73–77. [Google Scholar] [CrossRef]
  10. Derriche, O.; Jorat, L.; Noyel, G.; Monin, J. Magneto dielectric response of a ferrofluid at low temperature. J. Magn. Magn. Mater. 1991, 102(3), 255–260. [Google Scholar] [CrossRef]
  11. Timko, M.; Marton, K.; Tomco, L.; Kiraly, J.; Molcan, M.; Rajnak, M.; Kopcansky, P.; Cimbala, R.; Stoian, F.; Holotescu, S.; Taculescu, A.S. Magneto-dielectric properties of transformer oil based magnetic fluids in the frequency range up to 2 MHz. Magnetohydrodynamics. 2012, 48, 427–434. [Google Scholar]
  12. Fannin, P.C.; Marin, C.N.; Malaescu, I.; Stefu, N. Microwave dielectric properties of magnetite colloidal particles in magnetic fluids. J. Phys.: Condens. Matter 2007, 19, 036104. [Google Scholar] [CrossRef]
  13. Gabor, L.; Minea, R.; Gabor, D. RO Patent, 1994, 108851.
  14. Malaescu, I.; Gabor, L.; Claici, F.; Stefu, N. Study of some magnetic properties of ferrofluids filtered in magnetic field gradient. J. Magn. Magn. Mater. 2000, 222, 8–12. [Google Scholar] [CrossRef]
  15. Susan-Resiga, D.; Malaescu, I.; Marinica, O.; Marin, C.N. Magnetorheological properties of a kerosene-based ferrofluid with magnetite particles hydrophobized in the absence of the dispersion medium. Phys. B: Phys. Cond. Matter 2020, 587, 412150. [Google Scholar] [CrossRef]
  16. Ercuta, A. Sensitive AC hysteresigraph of extended driving field capability. IEEE Trans. Instrum. Measur. 2020, 69(4), 1643–1651. [Google Scholar] [CrossRef]
  17. Chantrell, R.W.; Popplewell, J.; Charles, S.W. Measurements of particle size distribution parameters in ferrofluids, IEEE Trans. Magn. 1978, 14(5), 975–977. [Google Scholar] [CrossRef]
  18. Fannin, P.C.; Perov, P. A.; Charles, S. W. On the resonant frequency of ferrofluids subjected to perpendicular and parallel polarizing fields. J. Phys. D:Appl. Phys 1999, 32, 2367–2370. [Google Scholar] [CrossRef]
  19. Fannin, P.C. Use of Ferromagnetic Resonance Measurements in Magnetic Fluids. J. Mol. Liq. 2004, 114, 79–87. [Google Scholar] [CrossRef]
  20. Scaife, B.K.P. Principles of Dielectrics, Oxford Clarendon Press, 1998.
  21. Fannin, P.C.; Bunoiu, O.M.; Malaescu, I.; Marin, C.N.; Ursu, D. Magnetically tuning microwave propagation parameters in ferrofluids. Eur. Phys. J. E 2021, 44, 83. [Google Scholar] [CrossRef] [PubMed]
  22. Marin, C.N.; Fannin, P.C.; Raj, K.; Socoliuc, V. Magnetodielectric spectroscopy of magnetic fluids. Magnetohydrodynamics. 2013, 49, 270–276. [Google Scholar] [CrossRef]
  23. Zhang, J.; Yuping, D.; Shuqing, L.; Xiaogang, L.; Shunhua, L. The effects of high magnetic field on the morphology and microwave electromagnetic properties of MnO2 powder. J. Solid State Chem. 2010, 183, 1490–1495. [Google Scholar] [CrossRef]
  24. Debye, P. Polar Molecules, The Chemical Catalog Company, New York, 1929.
  25. Marin, C.N.; Malaescu, I.; Savici, A. Investigation of the low frequency polarization mechanisms in magnetic fluids. Acta Phys. Pol. A. 2013, 124(4), 724–727. [Google Scholar] [CrossRef]
  26. Jonscher, A.K. Universal Relaxation Law, 1st ed.; Chelsea Dielectrics Press: London, UK, 1996. [Google Scholar]
  27. Brindusoiu, S.; Poienar, M.; Marin, C.N.; Sfirloaga, P.; Vlazan, P.; Malaescu, I. The electrical conductivity of Fe3(PO4)2·8H2O materials. J. Mat. Sci.: Mat. in Electron 2019, 30, 15693–15699. [Google Scholar] [CrossRef]
  28. Teusdea, A.; Malaescu, I.; Sfirloaga, P.; Marin, C.N. Electric and Dielectric Properties in Low-Frequency Fields of Composites Consisting of Silicone Rubber and Al Particles for Flexible Electronic Devices. Materials. 2022, 15, 2309. [Google Scholar] [CrossRef] [PubMed]
  29. Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials; Clarendon: Oxford, UK, 1979. [Google Scholar]
  30. Ali, H.; Karim, S.; Rafiq, M.A.; Maaz, K.; Rahman, A.U.; Nisar, A.; Ahmad, M. Electrical conduction mechanism in ZnS nanoparticles. J. Alloys Compd. 2014, 612, 64–68. [Google Scholar] [CrossRef]
  31. Hill, R.M. Hopping conduction in amorphous solids. Philos. Mag. 1971, 24, 1307–1325. [Google Scholar] [CrossRef]
  32. Sfirloaga, P.; Poienar, M.; Malaescu, I.; Lungu, A.; Vlazan, P. Perovskite type lanthanum manganite: Morpho-structural analysis and electrical investigations. J. Rare Earths 2018, 36, 499–504. [Google Scholar] [CrossRef]
  33. Elliot, S.R. A.c. conduction in amorphous chalcogenide and pnictide semiconductors. Adv. Phys. 1987, 36, 135–217. [Google Scholar] [CrossRef]
  34. Funke, K. Jump relaxation in solid electrolytes, Prog. Solid State Chem. 1993, 22, 111–195. [Google Scholar] [CrossRef]
  35. Saragi, T.; Depi, B.L; Butarbutar, S.; Permana, B.; Risdiana, R. The impact of synthesis temperature on magnetite nanoparticles size synthesized by co-precipitation method, IOP Conf. Series: J. Phys.: Conf. Series. 2018, 1013, 012190.
  36. Abadiah, N.M.; Yuliantika, D.; Hariyanto, Y.A.; Saputro, R.E.; Masruroh, R.; Taufiq, A.; Soontaranoon, S. Nanostructure, Band Gap, and Antibacterial Activity of Spinel Fe2MO4/OO Magnetic Fluids. IOP Conf. Series: Earth and Environ. Sci 2019, 276, 012064. [Google Scholar]
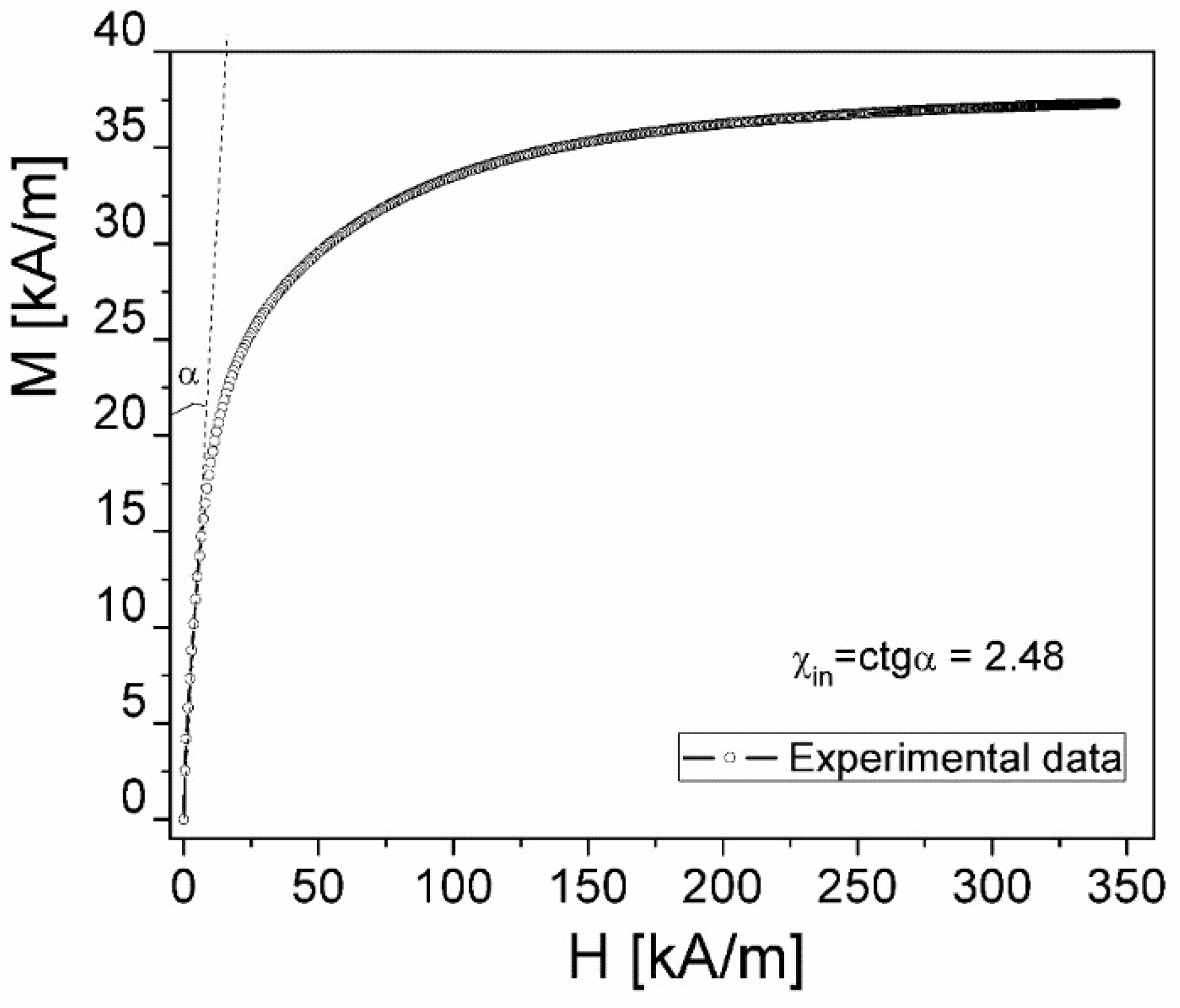
Preprints 120825 g001
Figure 1. Magnetization curve of the ferrofluid sample.
Figure 1. Magnetization curve of the ferrofluid sample.
Preprints 120825 g001
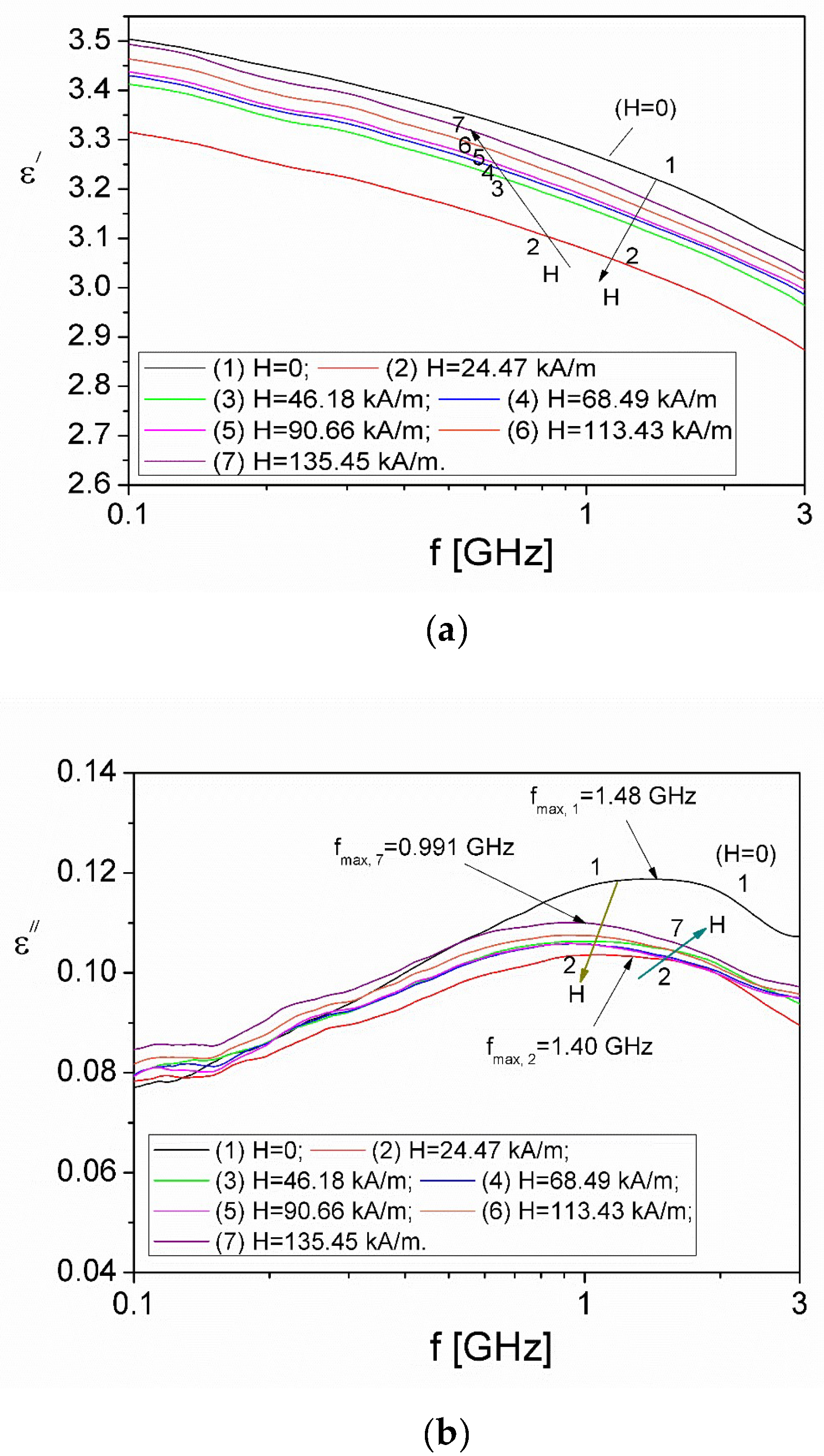
Preprints 120825 g002
Figure 2. a) The frequency and magnetic field dependencies of the real component εʹ, and b) imaginary component εʺ, of the complex dielectric permittivity, for the investigated ferrofluid sample.
Figure 2. a) The frequency and magnetic field dependencies of the real component εʹ, and b) imaginary component εʺ, of the complex dielectric permittivity, for the investigated ferrofluid sample.
Preprints 120825 g002
Preprints 120825 g003
Figure 3. The magnetic field dependence of the relaxation time, of the ferrofluid sample.
Figure 3. The magnetic field dependence of the relaxation time, of the ferrofluid sample.
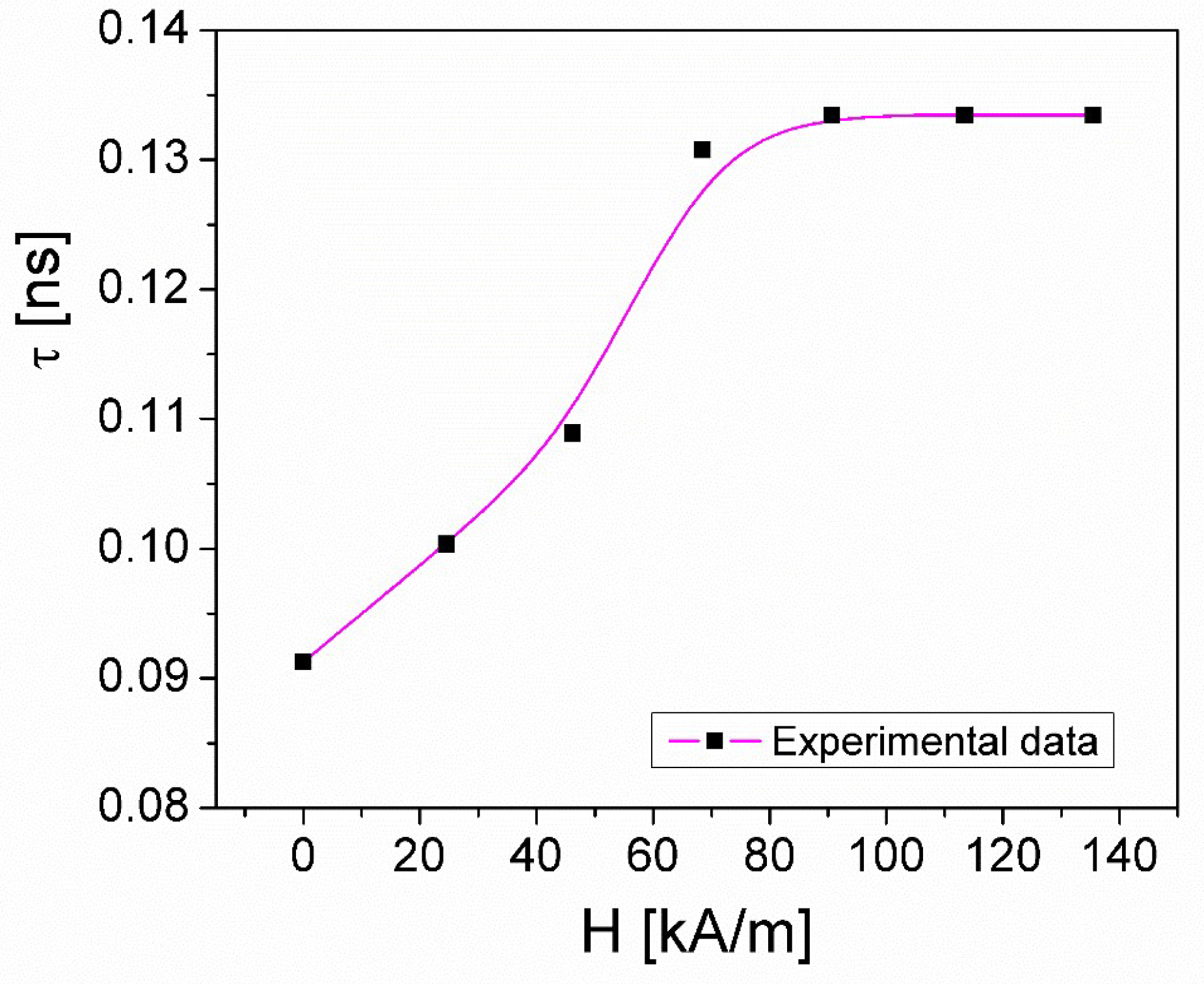
Preprints 120825 g003
Preprints 120825 g004
Figure 4. The dependence on the variation of the magnetic field ΔH, of the variation of the activation energy, ΔEa,h, in the presence of a magnetic field magnetic field.
Figure 4. The dependence on the variation of the magnetic field ΔH, of the variation of the activation energy, ΔEa,h, in the presence of a magnetic field magnetic field.
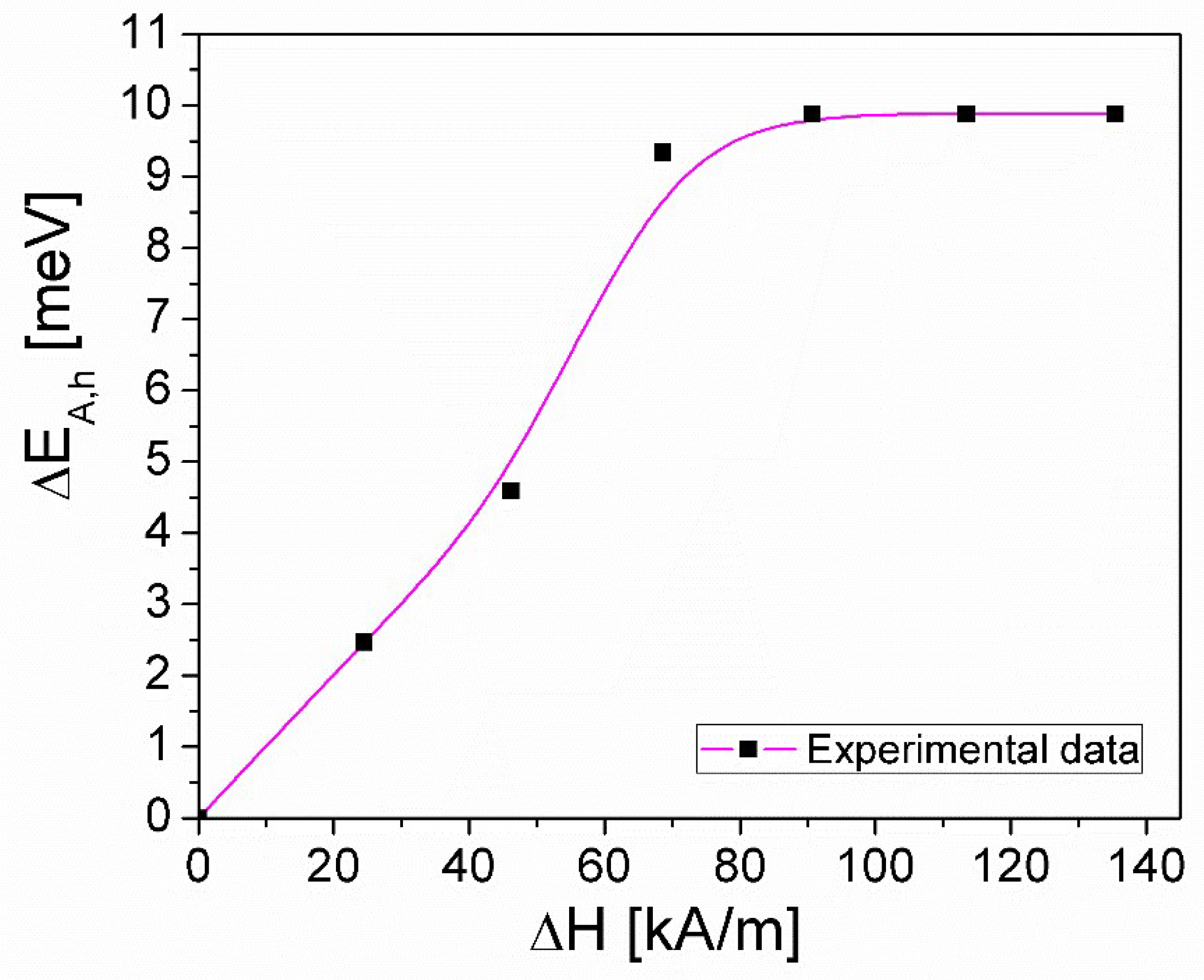
Preprints 120825 g004
Preprints 120825 g005
Figure 5. The frequency and magnetic field dependencies of the (Kʹ) and (Kʹʹ) components of the Clausius-Mossotti complex factor.
Figure 5. The frequency and magnetic field dependencies of the (Kʹ) and (Kʹʹ) components of the Clausius-Mossotti complex factor.
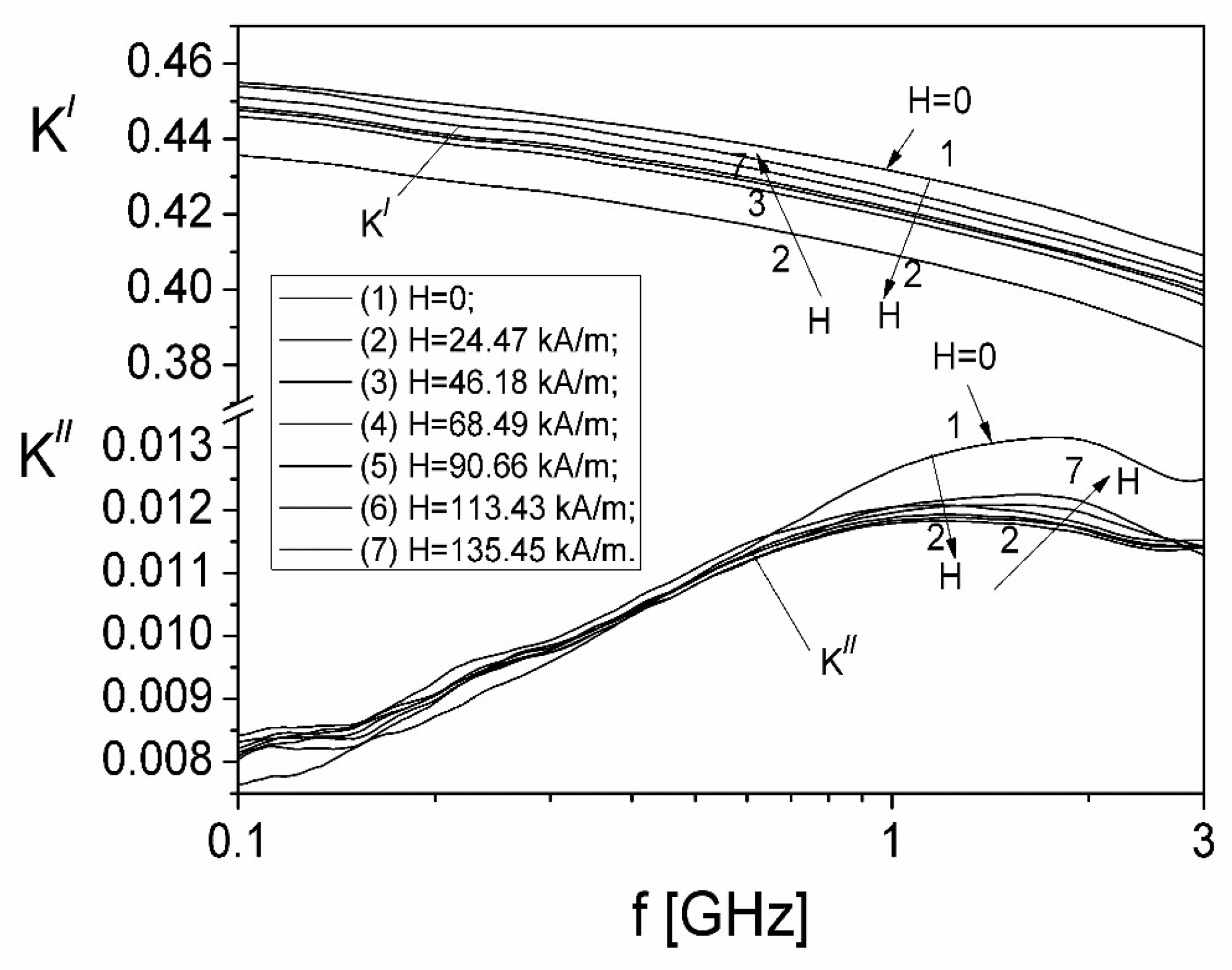
Preprints 120825 g005
Preprints 120825 g006
Figure 6. The frequency and magnetic field dependencies of the (αʹ) and (αʹʹ) components of the complex polarizability.
Figure 6. The frequency and magnetic field dependencies of the (αʹ) and (αʹʹ) components of the complex polarizability.
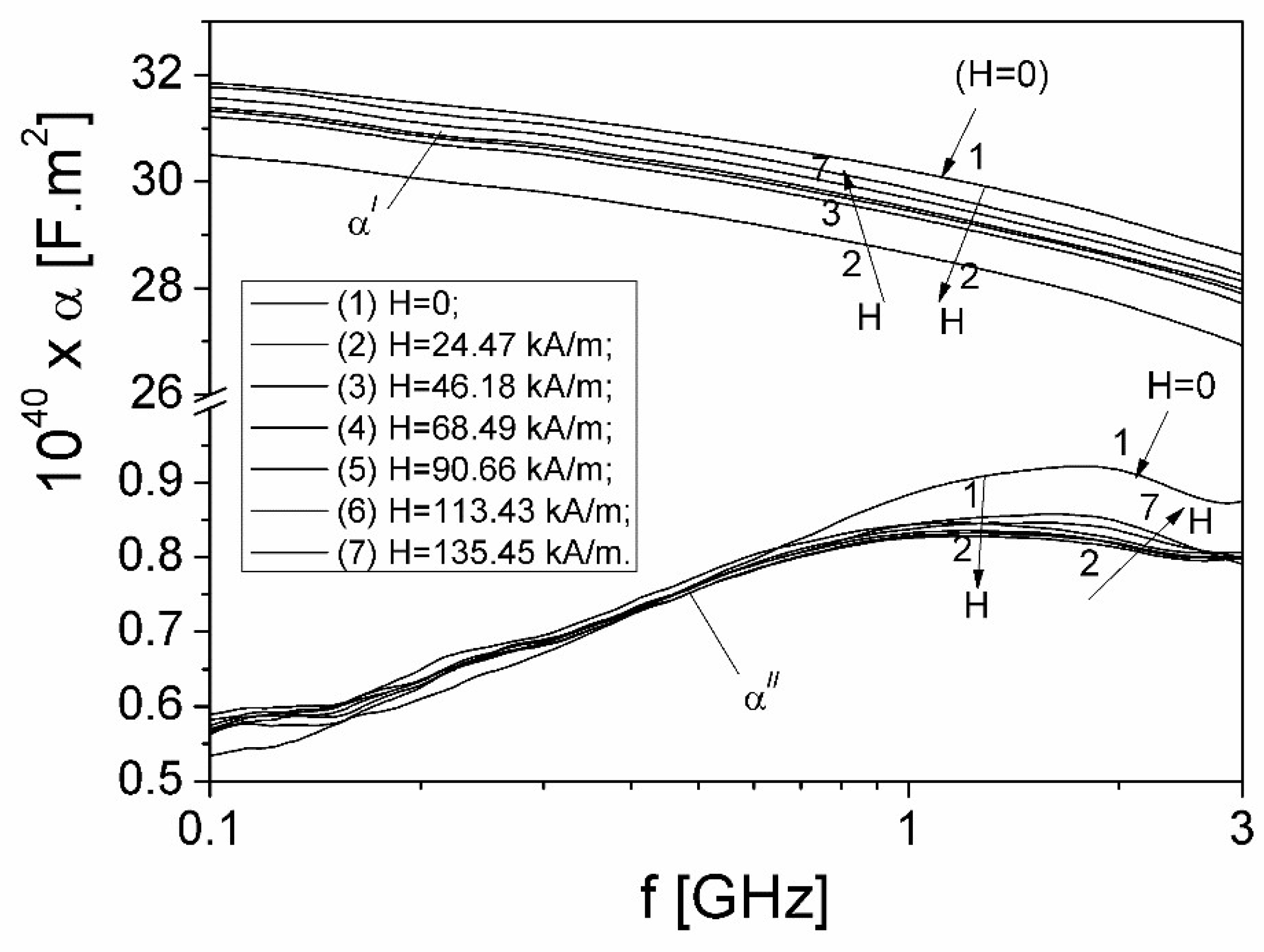
Preprints 120825 g006
Preprints 120825 g007
Figure 7. Magnetic field dependence of the electric dipolar moment of ferrofluid particles at different values of microwave frequencies.
Figure 7. Magnetic field dependence of the electric dipolar moment of ferrofluid particles at different values of microwave frequencies.
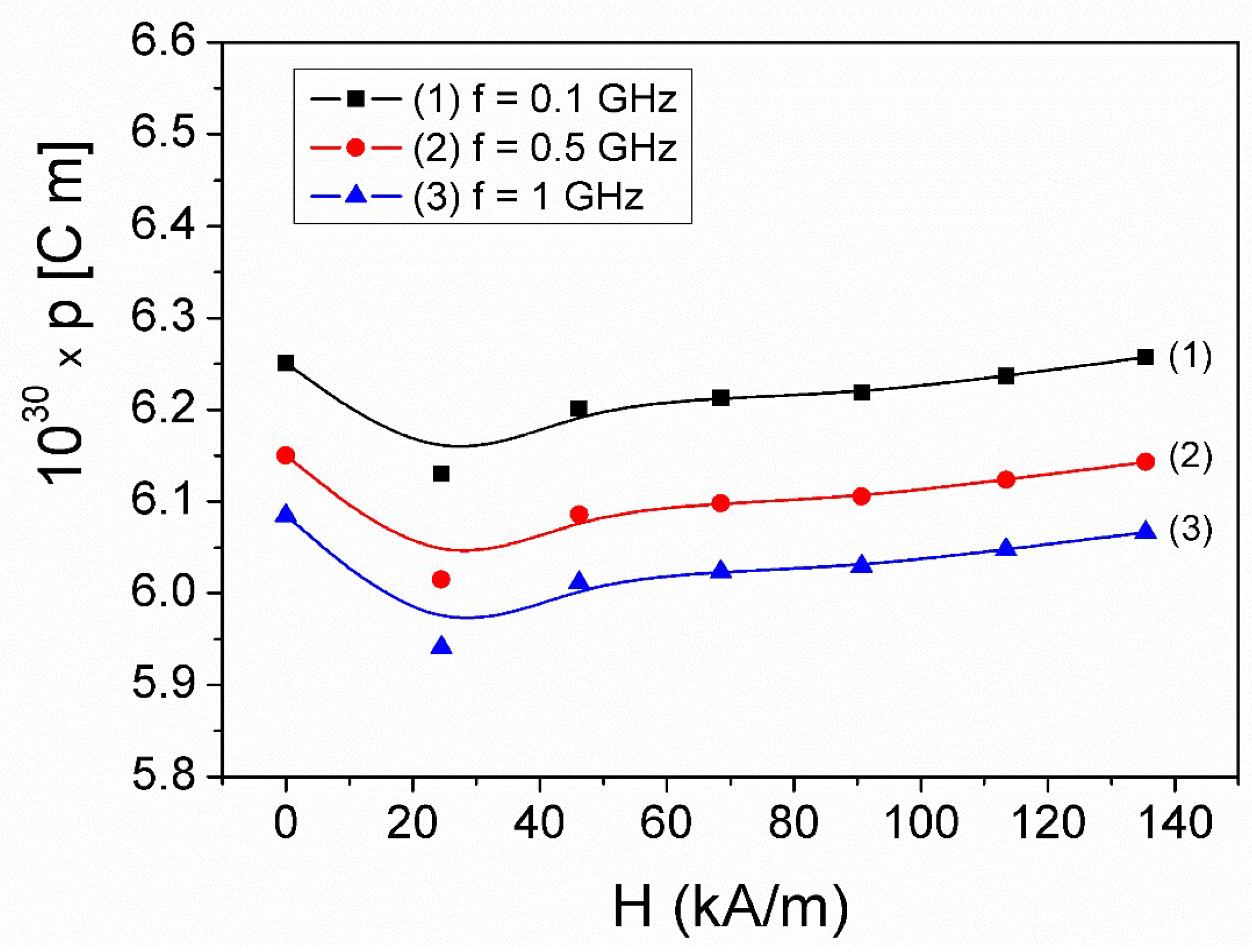
Preprints 120825 g007
Preprints 120825 g008
Figure 8. Frequency dependence of the conductivity, σ, at various values H of magnetic field, for the ferrofluid sample.
Figure 8. Frequency dependence of the conductivity, σ, at various values H of magnetic field, for the ferrofluid sample.
Preprints 120825 g008
Preprints 120825 g009
Figure 9. Magnetic field dependence of the static conductivity, σDC(H), for the ferrofluid sample.
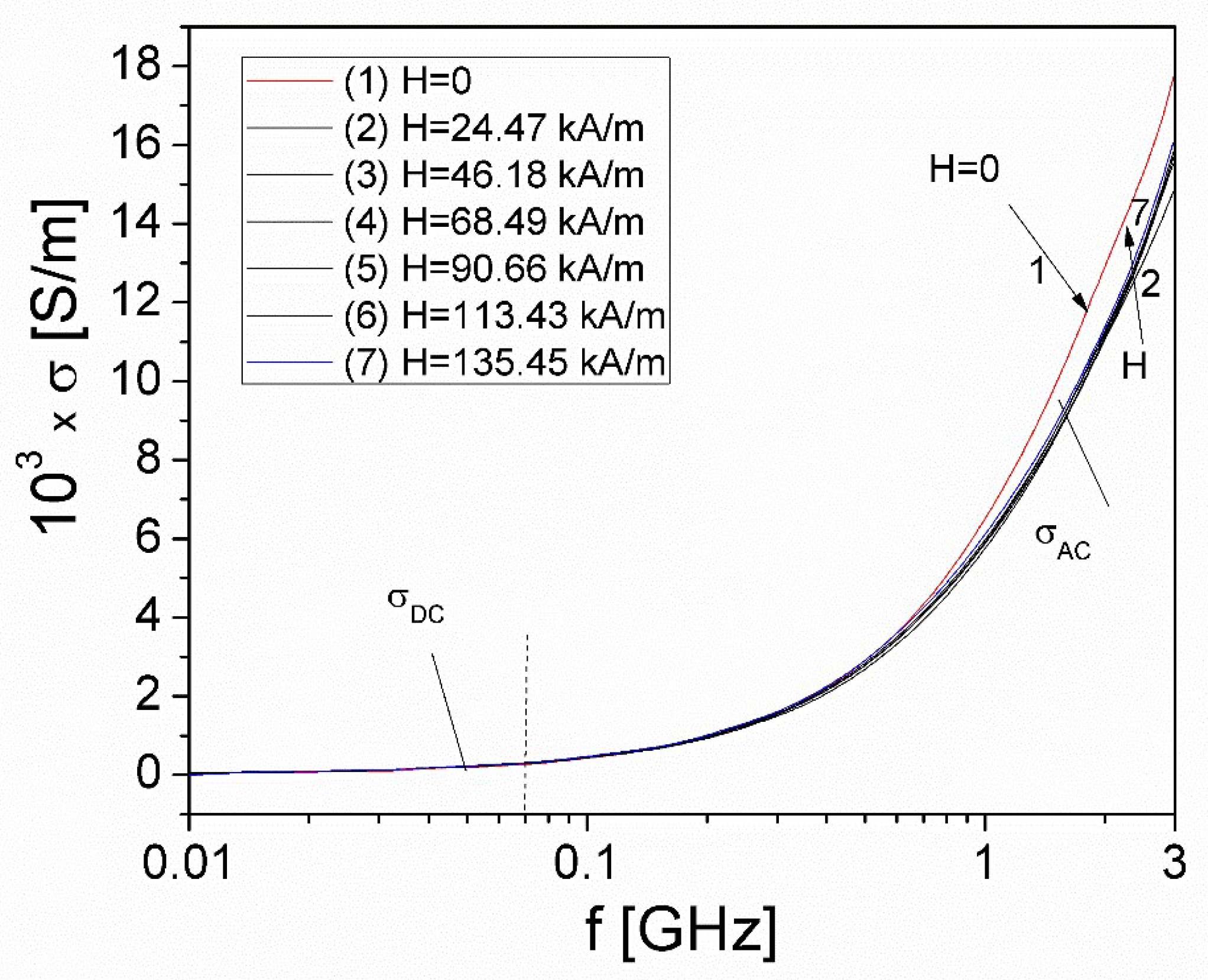
Figure 9. Magnetic field dependence of the static conductivity, σDC(H), for the ferrofluid sample.
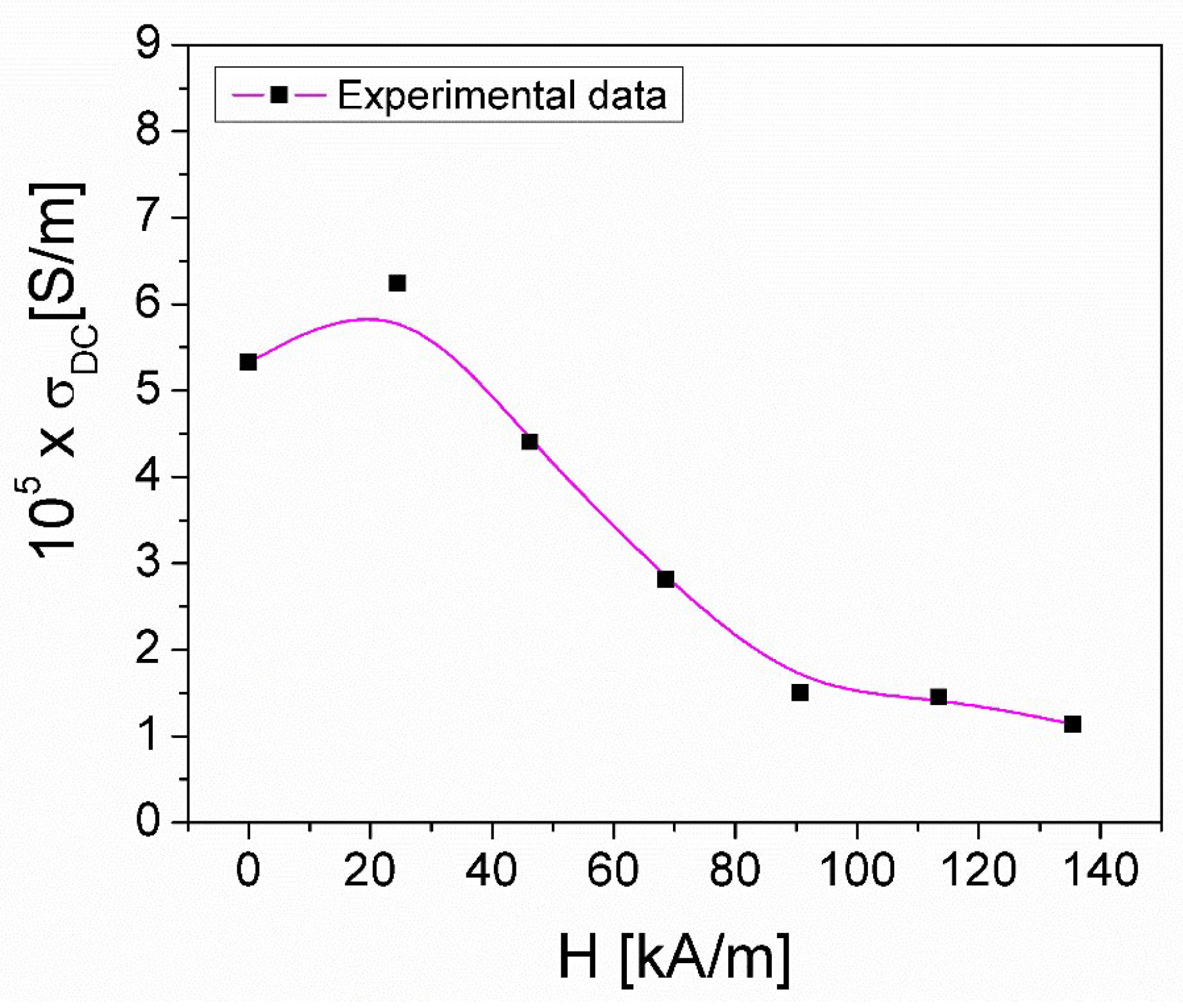
Preprints 120825 g009
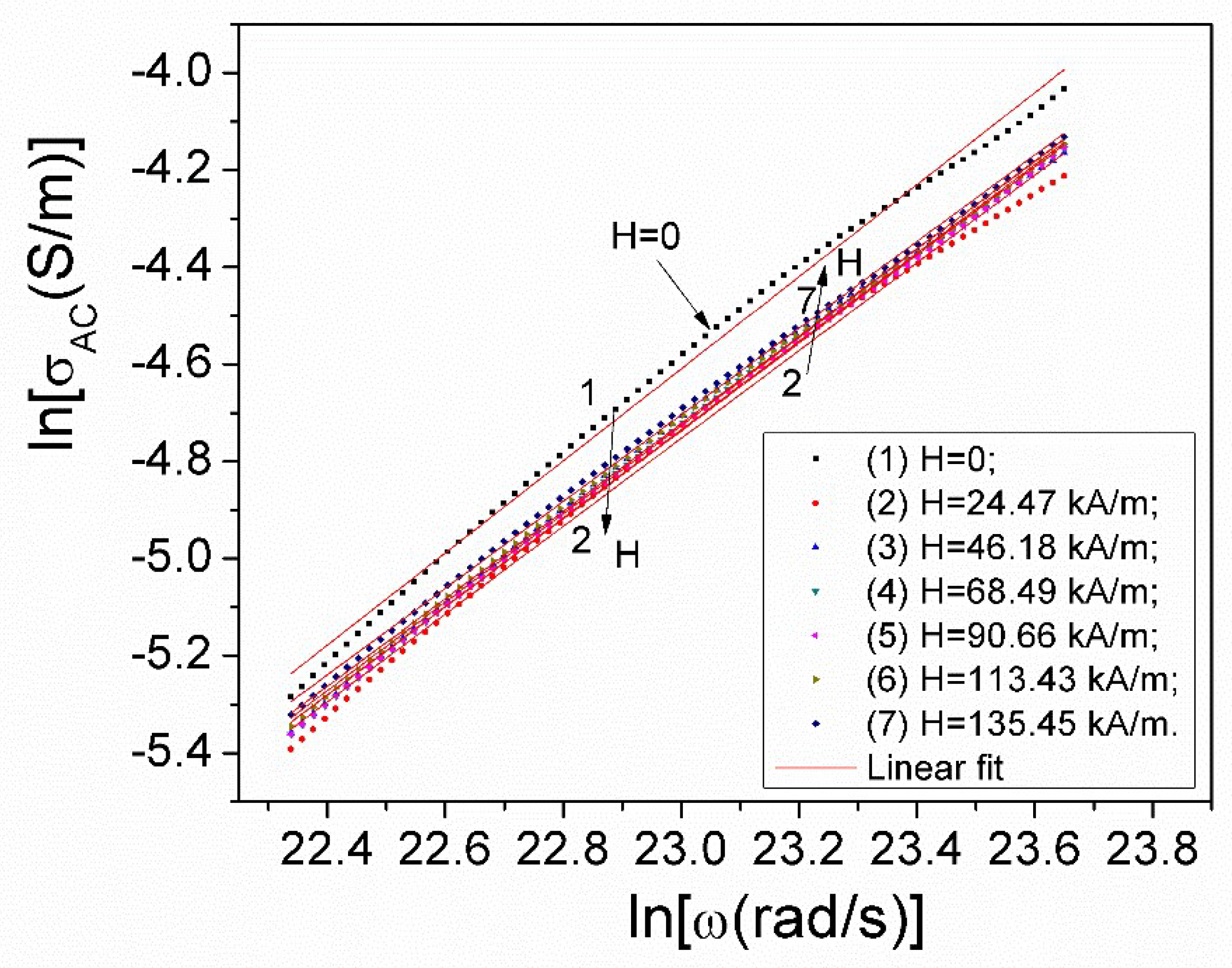
Preprints 120825 g010
Figure 10. The lnσAC(lnω) dependence at different H values of the polarizing magnetic field applied to the ferrofluid sample.
Figure 10. The lnσAC(lnω) dependence at different H values of the polarizing magnetic field applied to the ferrofluid sample.
Preprints 120825 g010
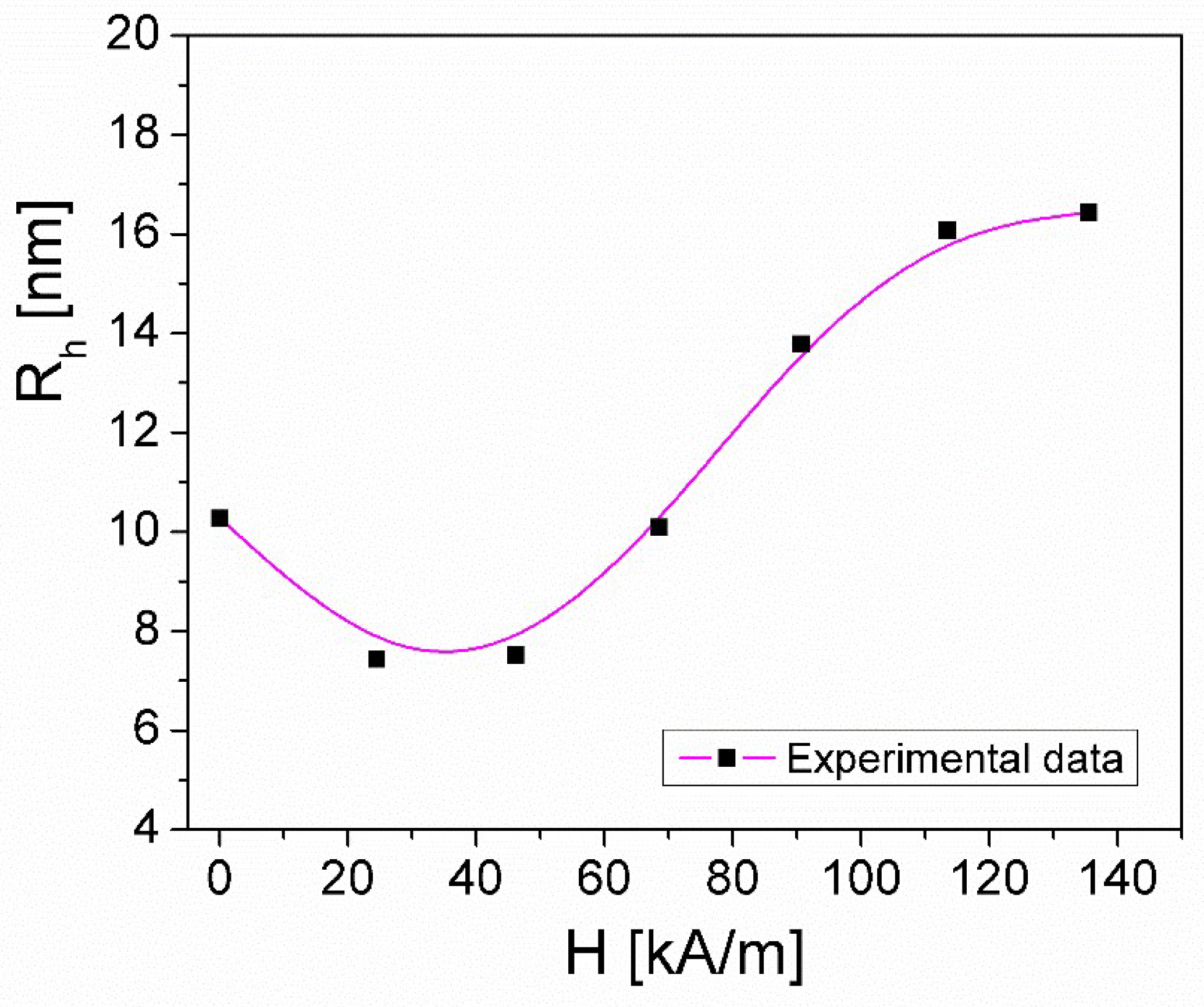
Preprints 120825 g011
Figure 11. Magnetic field dependence of the hopping distance (Rh) of charge carriers from the ferrofluid sample.
Figure 11. Magnetic field dependence of the hopping distance (Rh) of charge carriers from the ferrofluid sample.
Preprints 120825 g011
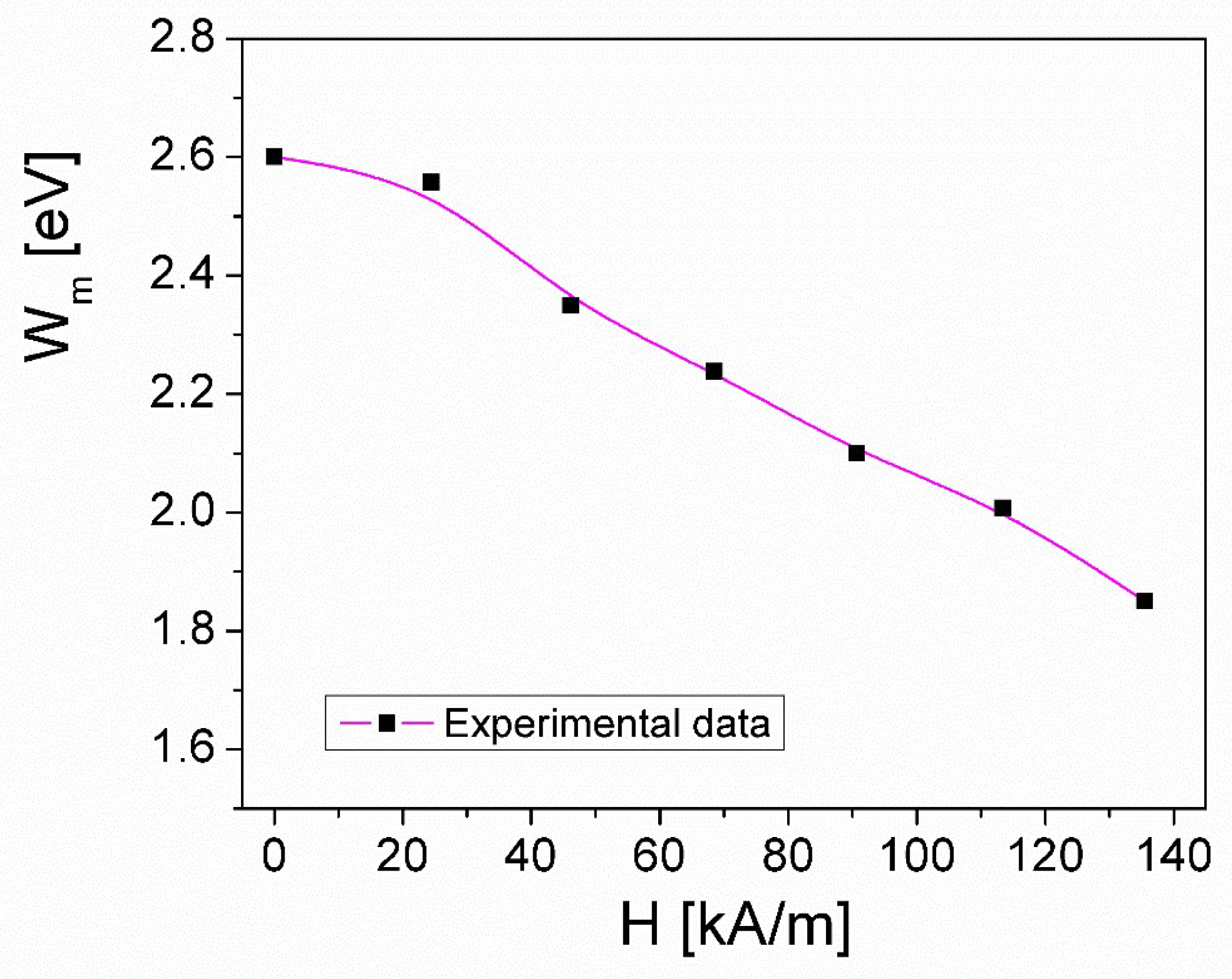
Preprints 120825 g012
Figure 12. Magnetic field dependence of the maximum energy barrier height, Wm(H), of the ferrofluid sample.
Figure 12. Magnetic field dependence of the maximum energy barrier height, Wm(H), of the ferrofluid sample.
Preprints 120825 g012
Table 1. Some parameters of ferrofluid determined from conductivity measurements.
Table 1. Some parameters of ferrofluid determined from conductivity measurements.
Preprints 120825 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated