Prerpints.org logo
Preprint
Article

Superpixel Classification with the Aid of Neighborhood for Water Mapping in SAR Imagery

Altmetrics

Downloads

35

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 October 2024

Posted:

10 October 2024

You are already at the latest version

Alerts
Abstract
Water mapping for satellite imagery has been an active research field for many applications, 1 in particular natural disaster such as flood. Synthetic Aperture Radar (SAR) provides high-resolution 2 imagery without constraint on weather conditions. Single-date SAR approach is less accurate than 3 multi-temporal but can produce results more promptly. This paper proposes novel segmentation 4 schemes that are designed to process both a target superpixel and its surrounding ones for the 5 input for machine learning. We devise MISP-SDT/XGB schemes to generate, annotate, and classify 6 superpixels, and perform land/water segmentation of SAR imagery. These schemes are applied to 7 Sentinel-1 SAR data to examine segmentation performances. Introducing single/mask/neighborhood 8 models in the MISP-SDT scheme and single/neighborhood models in the MISP-XGB, we assess the 9 effects of the contextual information about target and its neighbor superpixels on its segmentation 10 performances. As to polarization, it is shown that the VH mode produces more encouraging results 11 than the VV, which is consistent with previous studies. Also, under our MISP-SDT/XGP schemes 12 the neighborhood models show better performances than FCNN models. Overall, the neighborhood 13 model gives better performances than the single model. Results from attention maps and feature 14 importance scores show that neighbor regions are looked at or used by the algorithms in the neighbor- 15 hood models. Our findings suggest that under our schemes the contextual information has positive 16 effects on land/water segmentation.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Extracting water regions in radar images has been an important field in remote sensing, given the fact that water segmentation has many real-world applications such as ice/snow/oceans monitoring and change detection (CD) in water in dams, lakes, and rivers. It is significant to map water regions promptly and accurately and provide the information about the water regions, especially when a natural disaster like flooding occurs. Nowadays Synthetic Aperture Radar (SAR) data are widely used for providing imagery for water mapping, as the radar technology offers customers weather condition independent, 24/7 available, and high-resolution satellite imagery.
Multi-temporal SAR imagery, where images of a region are made on several diffrent dates [1], can utilize CD as a methodology for flood detection; it uses not only flood imagery but also its pre-/post-flood imagery as reference for flood mapping [2,3]. The behavior of surface water, which shows high temporal variability (the standard deviation of the backscattered intensities) and low minimum backscatter in time series, enables us to use a simple threstholding approach for segmenting water accurately [4]. It is equally true, however, that multi-temporal imagery is not available to be used at any time; we need at least two images (ideally produced under the same conditions except for date) for water mapping. Single-date SAR imagery’s larger uncertainty leaves it behind multi-temporal in accurate extraction, but it is more economical of resources and time; it has therefore an advantage in a situation which needs fast action.
In general, electromagetic (plane) waves have a degree of freedom, e.g. a rotation around the propagation axis. This allows us to have linearly polarization which is eigher vertical (V) or horizontal (H). Considering both transmitted waves and received, we have combinations of V and H such as the vertical-horizontal (Vertical transmit and Horizontal received, VH) mode. Likewise we have VV, HV, and HH. It is thought that the HH mode is more suitable for distinguishing flood regions from non-flood [5,6]. The VV mode is more sensitive than the HH and cross-polarizations (VH, HV) to small-scale roughness of waves on the water surface. The VH component, which makes it easier for us to notice differences between a flood region and a non-flood, is more useful than the VV for detecting flood regions [7,8].
As to algorithms for land/water segmentation (river, lake, flood regions etc) in SAR imagery, thresholding-based approaches have been traditionally used [5]. Its underlying assumption is that the backscattering amplitudes which differ between the Earth’s surface types allows us to classify the points of imagery by setting thresholds in the amplitude histogram. For instance, the surface layer backscatter coefficents of high moistured soil tend to be higher than those of low moistured soil [9]; the amplitude of smooth surface such as calm water regions is low, while rough surface yields a higher amplitude. As a result, water regions are generally darker in SAR imagery [1], and thus a threshold for land regions can be set. At the same time, the thresholds depend on several conditions, that is, wind, incident angle, polarization, speckle noize, and therefore segmentation results are affected by these conditions.
There have been various nonneuralnet machine learning (ML) approaches used for several data source: random forest for Sentinel-1 C-band [10], K-means clustering for Sentinel-1A [11], Fuzzy C-Means clustering for Gaofen-3 and Sentinel-1 [12], Support Vector Machine (SVM) [13], Markov Random Field (MRF) for TerraSAR-X [14], XGBoost for Resourcesat-2 [15]. In addition, several statistical models have been used for Radarsat-2 [16], COSMO-Sky-Med [17], and Sentinel-1 [18].
Also, superpixel-based segmentation approaches have been applied for water mapping. In the superpixel framework, an image which consists of standard pixels is partitioned into groups according to algorithms, and each of the groups has statistically or morphologically meaningful information. In terms of image description, it could be argued, the superpixel representation maintains the same level of detail as the pixel representation, while the latter uses larger computational resources [19]. The framework threfore has potential capability to organize data from imagery faster and focus on more relevent regions.
Superpixel-based approaches have a range of applications: change detection [20], image segmentation [21], automatic target recognition (ATR), extracting water regions and coastlines [22], etc. For segmentation within the framework of superpixel, there has been a variety of superpixel methods especially for optical images; simple linear iterative clustering (SLIC), an edge-based SLIC (ESLIC) [23], pixel intensity and location similarity (PILS) [24], quick shift (QS) [25], and turbo pixels (TP) [26,27]. When it comes to SAR imagery, mixture-based superpixel (MISP) method is robust to SAR imegery’s speckle noise, which facilitates more practical use of the model [28].
Not only non-neuralnet ML models but neuralnet-based models have been applied for water mapping. CNN-based models especially U-Net models have shown good performances in typical evaluation metrics [29] - besides, they have been applied to near-real-time flood detection because of their speed [8].
In relation to encoder-decoder-type architecture, we have seen that the course of evolution of Seq2Seq [30] into Transformer was directed by the alignment model [31] (commonly known as the attention mechanism [32,33]). Compared to CNN and RNN, Transformer has smaller complexity per layer, minimum number of sequential operations, and maxium per lengths [33]. The attention-based models, which make it easier to find distant relations between words in sentences, have shown a brilliant performance in Natural Language Processing and accordingly been widely used in the field. The attention-based models are used in not just NLP but Computer Vision subject. Vision Transformer (ViT) converts an image into a sequence of patches which are used for embeddings, together with positional encoding, so that it can leverage the contextual information about the image [34].
The attention mechanism has been used for improving a neuralnet model’s human interpretability as well. For instance, real driving datasets were analyzed by constructing a visual attention model and computing attention maps to find which parts of the video image were cared by the model [35]. For chest radiograph classification, an attention-based model outperformed GradCAM (gradient-weighted class activation mapping) – it was concluded that, compared to GradCAM, the attention-based model could be more helpful for radiologists in terms of decision making [36]. Also, audio data were classified by an attention-based deep sequence model, where the attention scores were taken advantaged of to visualize which parts of the specrogram were cared [37].
The objective of the present study is to propose novel segmentation schemes whereby contextual information about superpixels is utilized for the input of machine learning to perform land/water segmentation of SAR imagery. This study also assesses our model’s performances in land/water classification, applying our models for Sentinel-1’s flood data [38].
The rest of this paper is organized as follows. Setcion 2 describes the satellite data and its data prosessing for the present study, and presents the method for generating and annotating superpixels. The section also provides schemes which are designed for unstructured/structured input for ML, showing performance indicators for land/water segmentation as well. Section 3 describes the setting of parameters; the section does feature selection for the structured scheme, presenting the results of numerical experiments. The section also makes a qualitative analysis by using attention rollout scores. Section 4 interprets the findings from Section 3. The final section is devoted to our concluding remarks.

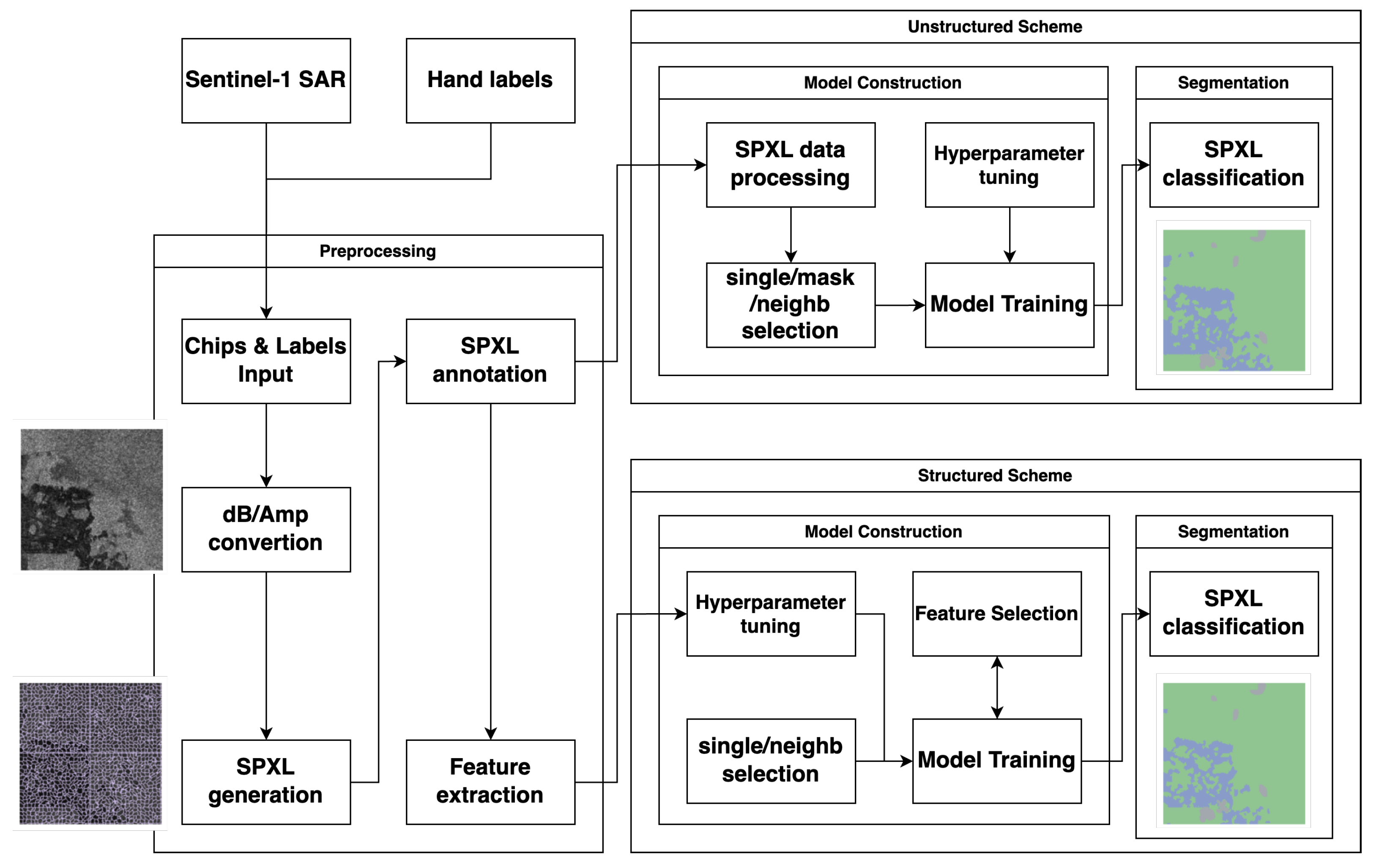
2. Materials and Methods

2.1. Sen1Floods11 Dataset

Sen1floods11 is a dataset which processed the data of 11 flood events during 2016-2019, providing global coverage of 4831 chips of 512x512 pixels [38]. The flood imagery data of the dataset were from Sentinel-1 and Sentinel-2 – the former has VV and VH, and the latter has 13 bands, where the ground resolution is sampled to 10 meters on all bands. In the dataset, 4370 chips were automatically labeled; Otsu’s thresholding algorithm for the histogram from the VH band was used for the Sentinel-1 flood mapping reference, and thresholds of Normalized Difference Vegetation Index (NDVI) and Modified Normalized Difference Water Index (MNDWI) were used for the Sentinel-2. The Sen1floods11 has also 446 chips which were hand labeled by trained remote sening analysis, using a GUI of Google Earth Engine.
The hand labeled chips were treated as high quality data, and their test data were used for performance assessment [38]. The breakdown of the hand-labeled dataset is shown in Table 1, where the dataset contains 252 chips for train, 89 for validation, and 90 for test. Also 15 chips for Bolivia data is included in the hand-labeled dataset. Among them we used train, validation, and test chips.
Here it should be noted that we have 3 types of water area: permanent water (PW), temporaly water (TW), and all water (AW). PW was determined by using the JRC (European Commission Joint Research Centre) surface water dataset [39] which provides surface water observations at 50m resolusion on a monthly basis. The permanent water regions were given as the regions which were detected as water at both the start 1984 and the end 2018 of the dataset [38]. TW is an area temporalily covered by water, and AW is given by the union of TW and PW.

2.2. Data Processing

We now provide a brief description about the whole picture of processing the data. We use Sentinel-1 SAR imagery (chips) and hand-labeled data for training and assessing our models. The values of a chip is converted from dB scale into amplitude. The chip is then divided into four tiles, each of which is 256x256 pixels and used for generation of superpixels. Each superpixel is labeled a land/water superpixel acccording to percentages of land/water pixels in the superpixel. In the present unstructrued scheme, the generated superpixel data are further processed so that the data can be used as the input of our neuralnet model, where either our single or neighborhood framework is selected. Under the single framework, only a target superpixel is given in a training/testing process, while the neighbor provides both a target and its neighbor superpixels. The model is trained after the relating hyperparameters are tuned. Then each superpixel is classified by the model, which leads to segmentation of the chip.
When it comes to our structured scheme, features are extracted from each of the generated superpixels and their values (together with land/water class values) are stored as their corresponding columns in a file. Also our single/neighborhood scheme is adopted; the number of columns under the neighbor is larger than those under the single. Then hyperparameter tuning is performed and a model is trained together with feature selection in order to build an optimal model. The trained model is used for superpixel land/water classification for each superpixel, or equivalently, segmentation is performed. The flow diagram of the data processing is illustrated in Figure 1.

2.3. Superpixel Generation

Suppose a SAR image consists of N pixels and it is divided into K superpixels. Then we assume the conditional probability distribution of the amplitude a n of the n-th pixel given the k-th superpixel is modelled by Nalagami distribution [28]:
p ( a n | μ k , ν k ) = 2 Γ ( ν k ) ν k μ k ν k ( a n ) 2 ν k − 1 e − ν k a n 2 μ k
where μ k , ν k are the Nakagami parameters for the k-th superpixel, and Γ ( x ) is the Gamma function. As to the conditional distribution of the position q n = ( x n , y n ) T of the n-th pixel given the k-th superpixel, it is expressed by divariate normal distribution:
p ( q n | m k , Σ k ) = 1 ( 2 π ) | Σ k | e − 1 2 ( q n − m k ) T Σ k − 1 ( q n − m k )
where the centroid and covariance are m k and Σ k , respectively. We introduce a handy parameter θ k = { μ k , ν k , m k , Σ k } for superpixels.
Assuming that the amplitude and position of a pixel is statistically independent, we introduce a vector f n = ( a n , q n ) T for the n-th pixel. After that, we introduce a K-dimensional label vector z n ∈ R K defined by
z n ∈ { ( 1 , 0 , … , 0 ) T , ( 0 , 1 , 0 , … , 0 ) T , … , ( 0 , … , 0 , 1 ) T } , ( n = 1 , … , N ) ,
where each vector is normalized as ∑ k = 1 K z n , k = 1 . This vector connects a pixel to a superpixel; for example, z 8 = ( 0 , 1 , 0 , … , 0 ) means that the 8th pixel belongs to the 2nd superpixel. The prior distribution for this vector is represented by a multinominal distribution
p ( z n | ω 1 : K ) = ∏ k = 1 K ω k z n , k
where ω 1 , … , ω K are the parameters for the multinominal distribution. The prior of ω 1 : K is
p ( ω 1 : K ) = Γ ( α K ) ( Γ ( α ) ) K ∏ k = 1 K ω k α − 1 ,
where α is the concentration parameter.
Then we optimize these parameters { θ k } 1 , … , K , { ω k } 1 , … , K , { z n } 1 , … , N to obtain the posterior distribution. We deal with it by splitting the divariate distribution-related part and concentration-related: p ( z 1 : N , θ 1 : K , ω 1 : K | f 1 : N ) ∝ p ( f 1 : N | z 1 : N , θ 1 : K ) p ( z 1 : N | ω 1 : K ) . Given that a n and q n are statistically independent, the former is futher splitted by the position-related part and the amplitude-related [28]: p ( f 1 : N | z 1 : N , θ 1 : K ) = ∏ n = 1 N ∏ k = 1 K p ( a n | θ k ) p ( q n | θ k ) z n , k

2.3.1. Block ICM

As to maximum a posteriori (MAP), we have two assumptions: (1) each pixel in a likelihood function is independent (2) each pixel is Markovian. In this case, we can iteratively update the parameters to see the convergence for them. This method, called Iterated Conditional Modes (ICM) [40], allows us to obtain the local minima of the parameters at low computational cost. In the present study, we use a block ICM approach which is faster than conventional ICM, and parameters are updated in the following order [28]:
z n ( t ) = max z n p ( f n | z n , θ 1 : K ( t − 1 ) ) p ( z n | ω 1 : K ( t − 1 ) )
θ k ( t ) = max θ k p ( f 1 : N | z 1 : N ( t ) , θ k )
ω k ( t ) = max ω k p ( z n ( t ) | ω 1 : K ) p ( ω 1 : K )
where t means pseudo-time. That is, we first obtain z n ( t ) , and accordingly we analytically determine { θ k } and { ω k } . Specifically we have
m k ( t ) = 1 | S k | ∑ k ∈ S k q n
for the centroid parameter, and
Σ k ( t ) = 1 | S k | ∑ n ∈ S k ( q n − m k ( t ) ) ( q n − m k ( t ) ) T
for the covariance. As to Nakagami scale parameter, we have μ k ( t ) = 1 | S k | ∑ n ∈ S k a n 2 . When it comes to the Nakagami shape parameter ν k ( t ) , we have the derivative of the likelihood function:
log ν k μ k ( t − 1 ) − ψ ( ν k ) + 2 | S k | ∑ k ∈ S k log a n
where ψ is the digamma function. We then search for the root of it to update the shape parameter.

2.3.2. Superpixel Annotation

After generating superpixels from the given data, we label them land/water according to predefined strategies. That is, the superpixel of which land/water pixels compose more than 68 percent is given as a land/water superpixel.

2.4. Superpixel Classification

The generated superpixels are classified into two major categories, (a) water (b) land. To do this, we use supervized machine learning, considering two types of schemes: unstructured and structured data schemes. Under the unstructured scheme, we use shallow variant models (MISP-SDT) of DeiT-Ti [41], where DeiT is the abbreviation of Data-efficient image Transformer; we use boosting algorithms under the structured scheme.

2.4.1. Unstructured Data Scheme

We present our unstructured data model and the architecture. The generated superpixels are put into tiles; each of them has 72x72x3 pixels. These tiles are augmented through random flips and rotations. We divide a tile image x ∈ R H × W × C ( H = 72 , W = 72 , C = 3 ) into flattened patches x p a t ∈ R N × ( P 2 C ) , where N ( = H W / P 2 ) is the number of patches [34] and P = 6 . The patch sequence and the class label (CLS) emmbedding x C L S ∈ R N are put together, and accordingly the length of the sequence is N + 1 . Then they are embedded by E ∈ R ( P 2 C ) × D , and equipped with positional embedding E p o s ∈ R ( N + 1 ) × D , where D is hidden dimension (latent vector size [34]). This yields the input for the transformer block:
ζ 0 = [ x C L S T ; x p a t E ] + E p o s .
In the transformer block, the input enters layer normalization and multi-head self attention (MSA), and the output of the MSA is added to the input to form an intermediate object ζ ˜ 1 . The intermediate goes into layer normalization and subsequently a Multi-layer Perceptron (MLP) which consists of an nn layer with GELU activation and a dropout layer; the output of the MLP is added to the intermediate to obtain the input ζ 1 for the next transformer block. Likewise we have
ζ ˜ b = M S A ( L a y e r N o r m ( ζ b − 1 ) ) + ζ b − 1 ( b = 1 , 2 , … , B )
ζ b = M L P ( L a y e r N o r m ( ζ ˜ b ) ) + ζ ˜ b
where B is the number of transformer blocks. In the present study, we set B = 8 . Then, the first row (CLS) of ζ B enters the classification head which contains a layer normalization and a linear; land/water classification is performed.
y = C H ( ( ζ B ) 0 , * )
where C H is the classification head, and ( ζ B ) 0 , * is the first row of ζ B .
Single/Mask/Neighborhood models
In the present study, we leverage the color channels R, G, B of the ViT input imagery x H × W × C so that we can incorporate the neighborhood information of a target superpixel into the scheme. To see this, the amplitude data from a raw tif file, its contrast-stretched amplitude, and the information about whether a superpixel is a target one or neghborhood are assigned to R , G , and B, respectively. We then call R, G, and B, the SAR channel, the stretched SAR channel, and the role channel, respectively. In putting the role channel to use in the unstructured scheme, we adopt three approches for the input information about the MISP-SDT: (i) a target superpixel only (ii) a target and its neighborhood regions and masking the role channel (iii) a target and its neighborhood regions.
We call (i), (ii), and (iii) the single model, mask model and neighborhood model. In the single model, the role channel is set 0, and in the SAR and streched channels regions except for a target superpixel are set 0. This means that a target’s surrounding region is treated like a padding. In the mask model, the role channel is set 0. In the neighborhood model, the padding region, the neighborhood region, and the target superpixel region in the role channel are set 0, 0.5, 1.0, respectively. An example of the unstructured input for the single/mask/neighborhood models are shown in Figure 2, where the 1st, 2nd, and 3rd rows represent the inputs for the single, mask, and neighborhood schemes, respectively. In the figure, the SAR, stretched, and role channels for these schemes are shown as well.
Considering these things, we show the architecture of the MISP-SDT and an example of its input in Figure 3.
Attention rollout
We also provide a short explanation of MSA and attention score. Suppose z ∈ R N × D is the input sequence, and the query, key, and value ( q , k , v ∈ R N × D h ) are given by [ q , k , v ] = z U q k v , where U q k v ∈ R D × 3 D h . Typically, we set D h = D / h , where h is the number of heads. Then the self-attention is given as S A ( z ) = W v , where W ∈ R is an attention weight matrix. The weight matrix is explicitly expressed as
W i j = softmax ( q k T / D h ) i j = e x p ( ∑ m = 1 D h q i m k m j / D h ) ∑ e x p ( ∑ m = 1 D h q i m k m j / D h )
Then MSA is given as
M S A ( z ) = [ S A 1 , S A 2 , … , S A h − 1 , S A h ] U M S A ,
where U M S A ∈ R h D h × D . We then move on to attention rollout. Suppose A ( b ) is the attention score matrix for the b-th transformer block. Then, its raw attention is defined by A ( b ) = 0 . 5 ( I + 〈 W a t t , h 〉 h ) , where W a t t , h is the attention matrix of an h-head attention, and usually it is averaged over the heads. Then, given the number of transformer blocks is B, the attention rollout for the attention matrices is obtained by the following recursive calculation [42]:
A ˜ ( b ) = A ( b ) A ˜ ( b − 1 ) ( 0 < b ≤ B − 1 ) A ( b ) ( b = 0 )

2.4.2. Structured Data Scheme

We also consider turning unstructured superpixel data into structured data and using them as inputs for machine learning. It is expected that constructed data from neighborhood superpixels have many NaNs since the number of neighbor superpixels differs between target ones. On top of that, noise and outliers in amplitude could often appear in sar imagery. Also, there could be a case where the ground truth is not so accurate. Taking these things into account, we choose XGBoost [43], which handles sparsity to build tree structures and is robust to outliers, as the algorithm for this case.
Now let us provide a brief explanation about the XGBoost framework. Suppose we have a set of N data points D = { ( x j , y j ) | x j ∈ R m , y j ∈ R , ( j = 1 , … , N ) } , and a function F * maps x to y. Following the typical gradient boosting procedure, we approximate F * by the additive expansion of functions { f k ( x ) } k = 1 , … , t (aka base learner [44]). In the XG tree boosting method, we have
y ^ i ( t ) = y ^ i ( t − 1 ) + f t ( x i ) = ∑ k = 1 t f k ( x i ) ,
after the t-th iteration that constructs a decision tree [43]. The shrinkage parameter η ∈ [ 0 , 1 ] , which each of the base learner functions is multiplied by, is also considered. This parameter beefs up the technical capabilities for training an XGB model to improve its performances, since it disperses the power of each base learner function over future trees [43]. The column subsampling technique is considered as well to run the program faster and address an overfitting issue.
The objective function of the t-th iteration is expressed by the sum of convex loss functions ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) and a regularization term Ω ( f t ) . Expanding the former with regard to y ^ i ( t − 1 ) and retaining by the second-order term, we find
L ( t ) ≃ ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) ) + 1 1 ! · ∂ l ∂ y ^ ( t − 1 ) f t ( x ) + 1 2 ! · ∂ 2 l ∂ ( y ^ ( t − 1 ) ) 2 f t 2 ( x ) + Ω ( f t )
= ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) ) + 1 1 ! g i f t ( x ) + 1 2 ! h i f t 2 ( x ) + Ω ( f t )
where g i = ∂ ∂ y ^ ( t − 1 ) l ( y i , y ^ ( t − 1 ) ) | y ^ ( t − 1 ) = y ^ i ( t − 1 ) , and h i = ∂ ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ ( t − 1 ) ) | y ^ ( t − 1 ) = y ^ i ( t − 1 ) . In the XGBoost regime, the regularization term is given by Ω ( f ) = γ ∑ j = 1 T + 1 2 λ ∑ j = 1 T w j 2 = γ T + 1 2 λ ∑ j = 1 T w j 2 , where T is the number of the leaves of a tree. The objective function is therefore written as [43]
L ( t ) = ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) ) + ∑ j = 1 T ∑ i ∈ I j g i w j + 1 2 ∑ i ∈ I j h i + λ w j 2 + γ T ,
which indicates that the objective function is a convex quadratic function. Obviously it has the minimum at w j = w ^ j = − ∑ i ∈ I j g i ∑ i ∈ I j h i + λ . Substituting this into equation (19) yields the analytic form of it:
L m i n ( t ) = ∑ j = 1 T − ( ∑ i ∈ I j g i ) 2 2 ( ∑ i ∈ I j h i + λ ) + ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) ) + γ T .
In building a tree according to Information Gain(IG), the objective function is utilized as the score function to calculate the IG for determining the splitting point of a node.
When it comes to the structured inputs to the XGB, we extract feature information from a superpixel and represent it as (the row of) a dataframe. For instance, a target superpixel provides us with the 50th percentile, standard deviation of the amplitude, the area of it, and they are named pc50_cent, std_cent, area_cent, respectively. A column is assigned to the values of a feature. Likewise, a neighbor superpixel provides feature columns. Also, we consider the angle between a basis axis and the line segment which is bounded by the x-y median point of a target superpixel and that of a neighbor superpixel. In the process of superpixel generation, a superpixel could become like a set of uncombined islands, and therefore we use the number of the islands as a feature as well. All of the features used in the MISP-XGB models are shown in Table A1 of the appendix.
Feature selection is an important part of building machine learning models, allowing us to train a model faster, have better interpretability, and extend models more easily. There exist several ways to perform feature selection: filter, wrapper, embedded, and hybrid. To some extent, feature selection is embedded into the XGBoost as the tree boosting algorithm automatically picks the sets of features in real terms during the program running – the algorithm uses the feature which maximizes the XGBoost’s information gain for each splitting of a tree. Having said that, it is more desirable to construct an optimal model by conducting feature selection explicitly, because it improves model performance.
Specifically for XGBoost, rank-based feature selection methods were developed [45,46]. In the present study, the feature importance score for each of the features is calculated according to the weight which counts how many times a feature is used for tree splitting. Then the features are arranged in descending order of the importance score. Provided that x is a threshold, the top x percent of the features are then used to train a model to get the validation score. For several different thresholds, the validation scores are calculated to find out an optimal model.

2.5. Performance Metrics

Now that we consider a land/water binary classification problem, we introduce 4 cases in terms of segmentation: True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN). TP is the case where water is correctly predicted, and TN is the case where land is correctly predicted. FP is the case where water is wrongly predicted, and FN is the case where land is wrongly predicted. These terms are important especially when there is a significant imbalance between land and water. We threfore use typical segmentation performance indicators: Accuracy, which is defined by T P + T N T P + T N + F P + F N , Recall (or Sensitivity) T P T P + F N , Presicion T P T P + F P , and the F-1 score (the harmonic mean of Recall and Precision). Intersection over Union (IoU) T P T P + F P + F N , which is known as Critical Success Index (CSI) and commonly used in this sort of segmentation [29], is considered as well.
In the present study, we define IoU (at the chip level) and its average by [47]
I o U s = T P s T P s + F P s + F N s
m I o U = 1 S ∑ s = 1 S I o U s
where S is the total number of the samples, and T P s , F P s , F N s mean the true positive, the false positive, and the false negative for the s-th sample, respectively. We also consider IoU at the pixel level, which is given by I o U = ∑ s = 1 S T P s ∑ s = 1 S ( T P s + F P s + F N s ) [47].

3. Results

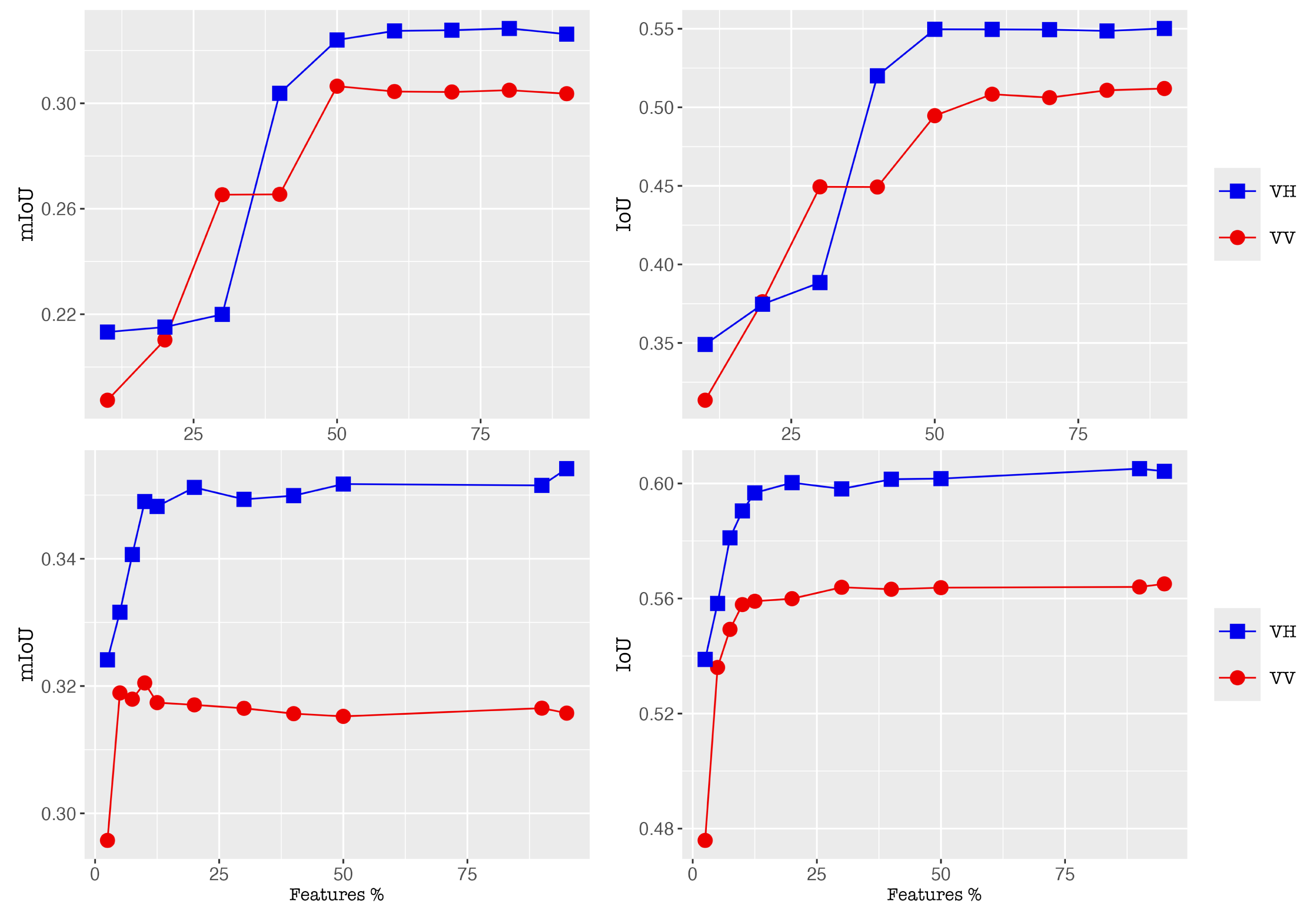
3.1. Parameter Tuning

Numerical experiments were conducted using hand-labeled train data, where the VV mode and VH were used. We basically genarated around 1444 superpixels for a chip, setting the concentration parameter α = 1000000 [28], and iteration parameter 25 for the block ICM.
In carrying out numerical experiments, we tuned relating parameters for the unstructured/structured models. For the unstructured models, the learning rate and weight decay were set 0 . 0005 × B a t c h S i z e 512 and 0.05, respectively. AdamW was chosen as the optimizer [41].
For the structured models, the boosting count and the max depth of a tree were set 1450 and 10, respectively. The learning rate was set 0.0035, and early stopping round was 250. Also, the land-to-water ratio was set 11.319:1 for the weight in order to address the class imbalance issue. The parameter choices and values for the models are presented in Table 2.
It is noted that we excluded NaN region of SAR imagery from performance assessment as our schemes were designed to use SAR imagery, not optical imagery. Also, the numerical experiments were performed within the framework of Tensorflow (2.15.1) under the unstructured scheme, together with NVIDIA Tesla T4 GPU. Under the structured scheme, XGBoost (2.0.3) was used for the numerical experiments.

3.2. Feature Selection

Under the MISP-XGB schemes, we had 19 features and 342 features in the single and neighborhood models, respectively. Setting several different percentage thresholds for the features, we calculated the validation scores to determine an optimal set of the features.
Figure 4 shows how the validation scores converge in relationship to the top x percent of the whole features. The x-axes of the figures represent the top x percent of all features for the single models (upper subfigures) and the top x percent of all features for the neighborhood models (lower); the y-axes show the validation scores which are mIoU (left subfigures) and IoU (right). Each of the subfigures presents the results from the VV mode (red-colored) and the VH (blue).
It can be seen from the upper subfigures that the validation scores start to converge at around the top 50 percent of the single features for the single model in the VV mode. Similarly, convergence starts at around the top 50 percent for the single model in the VH mode. Therefore, the optimal threshold for the feature selection was set 50 percent; namely this amounted to top 9 features to be used for the single model in both VV and VH modes. Likewise, we estimated that the threshold is at around the top 20 percent of the whole features – or equivalently we obtained top 40 features and top 38 features in the VV mode and the VH, respectively, in the neighborhood models.
The features used under the MISP-XGB scheme are presented in Figure A1 in Appendix. In the figure, bar charts in the VV and VH modes are filled with red and blue, respectively – the results from the single (upper subfigure) and neighborhood (lower) models are shown together. From the figure, it can be seen that neighborhood-superpixel features accounted for 60 percent of the top 10 features in the VV mode. They accounted for 90 percent of the top 10 features in the VH modes, which suggests that neighborhood-superpixel features were more frequently used in the VH mode, compared to the VV.

3.3. Experimental Study

The results of the numerical experiments are presented in Table 3. We firstly look at the results from the unstructured scheme. From the table, it can be seen that the neighborhood model generally showed better performances than the single model in the segmentation performance indicators in both polariation modes, except that the recall value of the neighborhood model was worse than that of the single in the VV mode, and the recall value of the neighborhood model was comparable to that of the single model in the VH mode. For both VV and VH, the mask model underperformed the single and neighborhood models except for recall.
Then we go on to the structured scheme. In the VV mode, the neighborhood model generally had better scores than the single model except that the recall value of the neighborhood model was lower than that of the single model. This pattern emerged in the VH mode as well – in this sense the results from both unstructured and structured schemes were in line with each other.
A few of examples of the results from the MISP-SDT scheme are shown in Figure 5, where the SAR imagery (1st subfigure), the segmentation results from the single model (2nd), the neighborhood model (3rd), and the ground truth (4th) for Somalia_94102 (top) and USA_504150 (bottom) are seen. In the figure, land, water, and unknown regions are filled with green, blue, and grey respectively.
When it comes to polarization, the VH mode produced on the whole more encouraging results than the VV; for instance under the unstructured scheme the f1 score and mIoU in the single model were increased from 0.376, 0.292 (VV) to 0.431, 0.338 (VH), respectively. A previous study showed that the precision of the VV component is generally larger than that of the VH – the co-polarized mode got lower scores than the cross-polarized in recall [8]. The finding was in line with our results in terms of precision and recall. These results indicate that the cross-polarized components are more suitable for flood/non-flood segmentation. This is consistent with previous studies.
We then compare our models to others in terms of AW. Table 4 displays a table which draws a comparison between our models and others. In the table, FCNN (fully convolusional neural network) is a CNN-based model [38], where FCNN (HL) and FCNN (S1W) are the models trained on respectively the hand-labeled and Sentinel-1 Weak datasets. Also, AlbuNet-34 (AN-34) is a model architecture developed from the LinkNet which links the input of its encoder block to the output of its conresponding decoder block to retain spatial information [48]. AN-34’s encoder is based on pretrained ResNet-34 [49]. Using summation for the information flow from the encoder to the decoder, AN-34 has fewer parameters than U-Net to gain faster training and inference speed [50]. From the table, it can be seen that the MISP-SDT and MISP-XGB models outperformed these CNN-based models in IoU and mIoU.

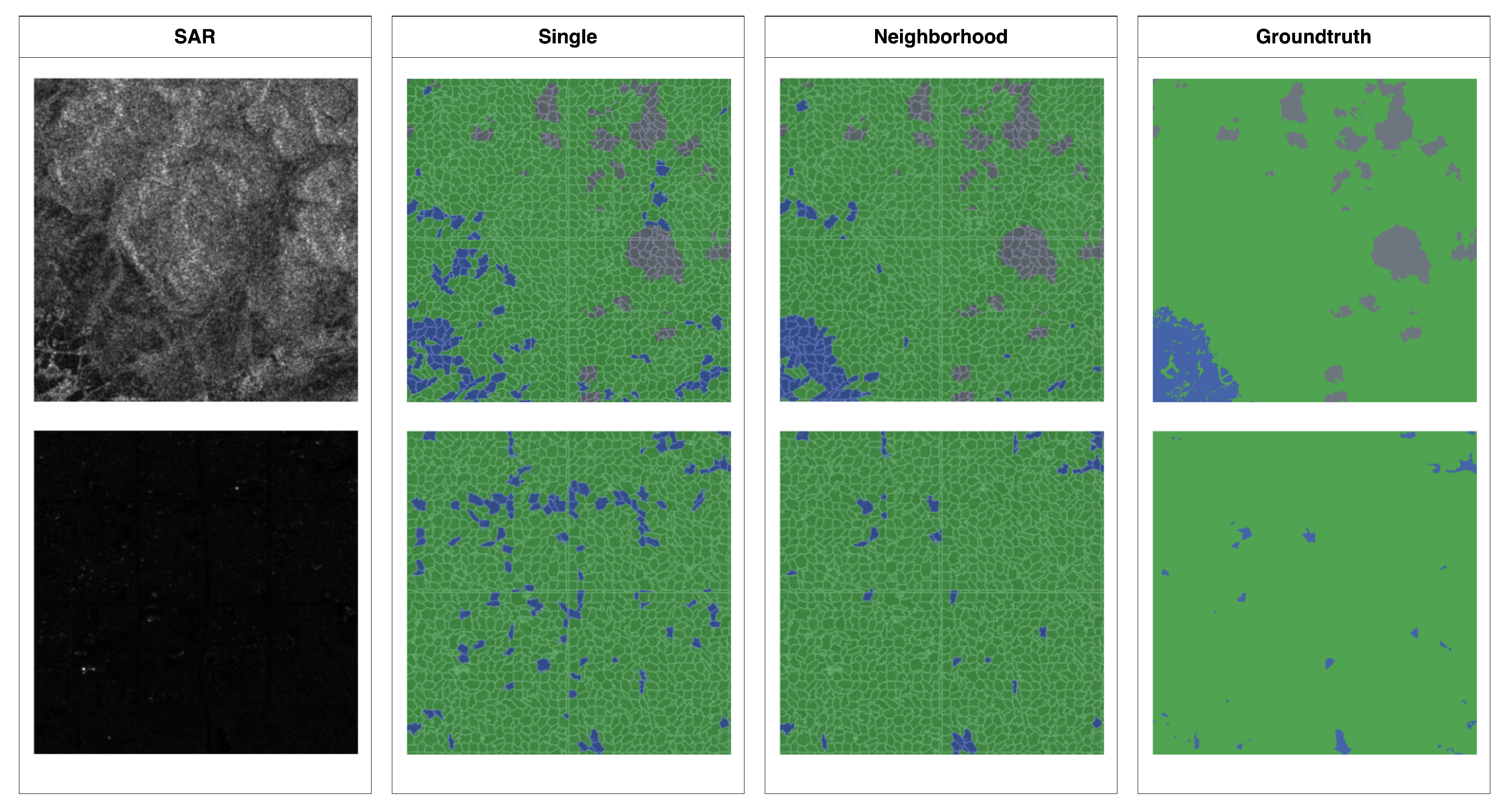
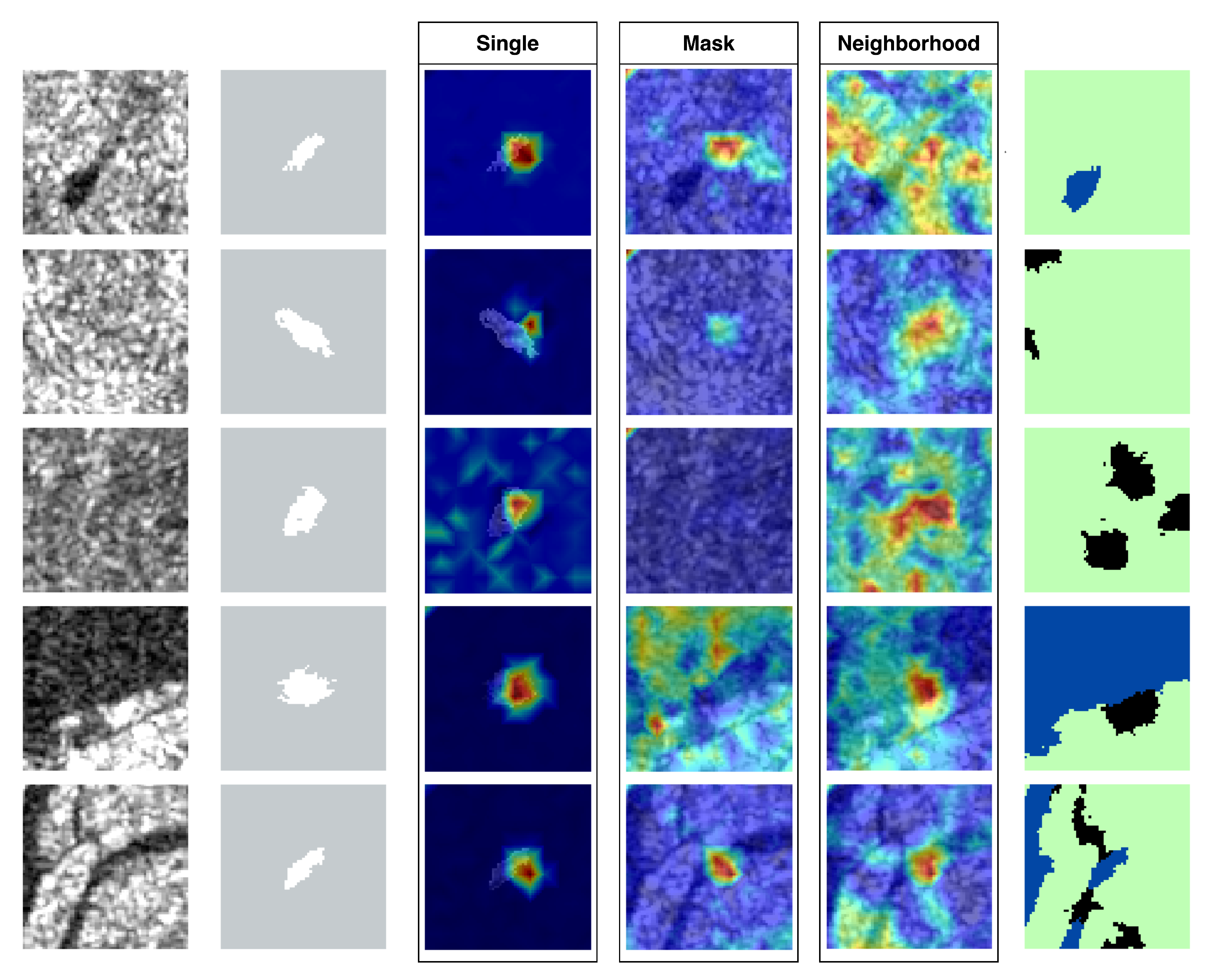
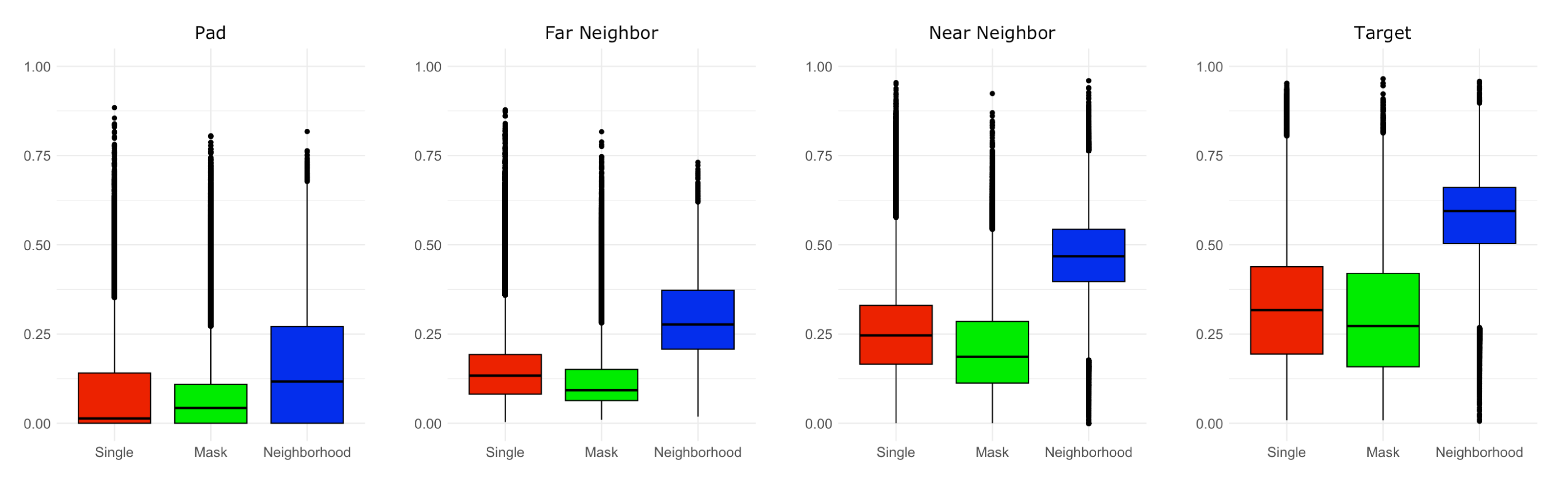
3.4. Qualitative Analysis

Also, we consider how the existence of neighborhood superpixels makes a difference in the unstructured scheme, by utlizing the attention map, where the attention rollout scores relating to CLS label embedding are visualized.
Figure 6 shows several examples of sets of stretched SAR data channel (the 1st column), role channel (2nd), attention map for single (3rd), attention map for mask (4th), attention map for neighborhood (5th), and class label map (the ground truth) (6th). For the class label map, land, water, and unknown regions are represented by green color, blue, and black, respectively. From the subfigures, we see that high score regions (red-colored regions) are mainly overlapped with the target region and its surrounding regions in the single scheme – this suggests that the target and its surrounding regions are more closely looked at by the single model. In terms of the distribution of attention map scores, the mask model showed patterns which were similar to those of the single model, although there exist some exceptions such as a more duffused type or almost uniformly distributed type. Meanwhile, in the neighborhood model, high and reltively high score (light-green-colored regions) regions are spread to the neighborhood regions, suggesting that not only the target and its surrounding regions but the neghborhood regions are cared by the model. Having acknowledged this, it is also crucial to recognize that these are examples of the numerous results of attention rollout scores that were calcuated by the single, mask, and neighborhood models. We look at this more carefully in the discussion section.

4. Discussion

We have seen that the neighborhood model generally outperforms the single model in both VV and VH modes for the MISP-SDT/XGB schemes. In the VV mode, the neighborhood model had better scores than the single model except that the recall values (0.459 in the unstructured scheme and 0.533 in the structured) for the single models were higher than those (0.425 in the unstructured and 0.514 in the structured, respectively) for the neighborhood models. These differences in recall between the single model and the neighborhood were mitigated in the VH mode: the recall values were 0.542 and 0.580 in the single models, compared to those (0.543 and 0.570) in the neighborhood models. That is, they are comparable for the unstructured scheme, and the gap was narrowed for the structured scheme in the VH mode.
As to the polarization, it has been found that the VV models underperformed the VH for both MISP-SDT and MISP-XGB, regardless of whether the model is single or neighbohood. These findings were in line with those of previous studies, supporting the notion that cross-polarized SAR imagery is more suitable for flood detection than the co-polarized. It was also observed that under the MISP-XGB, the results from the neighborhood model showed 6 neighbor features were ranked in the top 10 features in the VV mode; 9 neighbor features were ranked in the top 10 in the VH mode. It could be argued that the VH mode made it easier for the algorithm to utilize neighbor features for the classification, compred to the VV.
We have carried out the qualitative analysis as well; we now introduce a concept of Near Neighbor region to evaluate the results from the qualitative analysis more carefully. Roughly, the Near Neighbor region of a target superpixel is defined to be the vicinity of the target superpixel. More specifically, we define the circle area whose center is the centroid of the target region of a superpixel and the radius is equal to 1.1 times the semi major axis of the target region. Then, we define the Near Neighbor region of the superpixel by the intersection of the inside region of the circle area and the outside region of the target superpixel.
Figure 7 illustrates a few examples of part of SAR imagery (left subfigures), its target/neighbor superpixels (center), and corresponding Target/Near Neighbor/Far Neighbor regions (right). In the right subfigures, Target, Near neighbor, and Far Neighbor regions are filled with white, indigo, and gray, respectively.
Then, we calculated the average of the attention rollout scores for each region (i.e. Padding/Far Neighbor/Near Negihbor/Target), using the single, mask, and neighborhood models for the test VH data.
Figure 8 shows boxplots of the averages of attention rollout scores for Pad (1st subfigure), Far Neighbor (2nd), Near Neighbor (3rd), and Target (4th) regions, where attention rollout scores were min-max normalized on a scale of 0 to 1. In the figure, each subfigure shows the results from the single (red), mask (green), and neighborhood (blue) models. From the figure, it is apparent that for the neighborhood model the attention rollout scores in Target, Near Neighbor, and Far Neighbor regions are the highest, second highest, and third highest, respectively. This pattern emerges from the single and mask models.
It is noticeable that the score for Target region was the highest in the neighborhood model among the four regions – likewise the scores were in the mask and single models. As to the comparison between the three models, the neighborhood, single, and mask models had the highest, 2nd highest, 3rd highest scores, respectively for Target region, and this pattern is similar to those for Far Neighbor and Near Neighbor regions. It could be argued that these findings are related to the fact that the neighborhood model is given more information than the single and mask, and that the mask is not given information about the role of a superpixel.
It is thought that the neighborhood model gains an advantage in terms of segmentation because the model is provided more information about SAR and its stretch, and the roles of regions. These things suggest that the role channel has positive effects on land/water segmentation, allowing the neighborhood model to get an advantage. These findings suggest that contextual information about a target superpixel and its neighbor ones has overall positive effects on classification performanes of the algorithm.

5. Conclusions

We have devised novel superpixel schemes which use the mixture-based superpixel framework for single-date SAR imagery, incorporating the unstructured/structured data of both target and neighbor superpixels into the input for the ML algorithms. Designing the unstructured and structured schemes to annotate and segment target superpixels, we have designed MISP-SDT and MISP-XGB schemes, respectively. We have also developed single/mask/neighborhood models and single/neighborhood models for the unstructured and structured schemes, respectively. Accordingly, our schemes have enabled us to take advantage of contexual information about SAR imagery to segment superpixels.
Our schemes were applied to Sentinel-1 SAR data to examine segmentation performances. The results from the numerical experiments demonstrated that the cross-polarized mode produced better results than the co-polarized, which were consistent with previous studies. Under our MISP-SDT/XGB schemes, where we did not reply on Sentinel-2 optical imagery, the neighborhood models outperformed the FCNN model in IoU and mIoU.
As to models, the neighborhood model as a whole gave better performances than the single; this pattern of numerical results emerged regardless of whether the scheme was unstructured or structured.
We have used attention maps and feature importance scores, demonstrating that neighbor regions were looked at or used by the ML algorithms in the neighborhood models. Our findings suggest that under the unstructured/structured schemes contextual information provided by neighbor superpixels helps the ML algorithms to improve land/water classification performance. As part of future work, we mention that the interpretability of ML could be enhanced by further developing this kind of schemes. Moreover, it will be worthwhile to consider how this sort of schemes could be applied to different research fields and topics.

Data Availability Statement

The Sentinel-1 imagery data used in this article are available in https://github.com/cloudtostreet/Sen1Floods11 .

Acknowledgments

I thank the members of the Space Intelligence Business Division of SKY Perfect JSAT Corporation for helpful comments and excellent research assistance.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
MISP Mixture-based superpixel
ICM Iterated Conditional Modes
CD Change Detection
VV Vertical transmit and Vertical received
VH Vertical transmit and Horizontal received
ML Machine Learning
DeiT Data-efficient image Transformer
MSA Multi-head self-attention
MLP Multi-layer Perceptron
SDT Shallow Deit-Ti
XGB XG boost

Appendix A. Features for MISP-XGB

Table A1 provides names and their explanations in terms of the features for MISP-XGB models under the structured scheme. Basically, the name of each feature consists of two words with one underscore or three words with two underscores. The first word and the last word are the statistical representation and the role, respectively, of a superpixel. For instance, mean_cent and mean_01 are the mean values of a target superpixel and the 2nd neighborhood superpixel, respectively. The exception is Shannon entropy: e.g. shannon_entropy_cs_05 is the Shannon entropy of the contrast-stretched version of the 6th neghborhood superpixel.
Table A1. The feature names and their explanations for the MISP-XGB scheme. The feature names which ends with cent indicate that they are features of target superpixel. For the neighborhood superpixels, ** in the Feature name column represents the numbers: 00, 01, ... 0e, 0f, 10.
Table A1. The feature names and their explanations for the MISP-XGB scheme. The feature names which ends with cent indicate that they are features of target superpixel. For the neighborhood superpixels, ** in the Feature name column represents the numbers: 00, 01, ... 0e, 0f, 10.
Feature name Explanation Model
mean_cent The mean value of a superpixel single/neighb
std_cent The standard deviation of a superpixel
pc25_cent The 25th percentile
pc50_cent The 50th percentile
pc75_cent The 75th percentile
skew_cent The skewness
deg_cent The degree of angle
kurtosis_cent The kurtosis
shannon_entropy_cent The Shannon entropy
area_cent The area
num_islands_cent The number of islands
mean_cs_cent The mean of a contrast-stretched superpixel
std_cs_cent The standard deviation of a contrast-stretched superpixel
pc25_cs_cent The 25th percentile of a contrast-stretched
pc50_cs_cent The median of a contrast-stretched
pc75_cs_cent The 75th percentile of a contrast-stretched
skew_cs_cent The skewness of a contrast-stretched
kurtosis_cs_cent The kurtosis of s contrast-stretched
shannon_entropy_cs_cent The Shannon entropy of a contrast-stretched
mean_** The mean value of the *-th neighborhood of a target superpixel neighb
std_** The standard deviation of the *-th neighborhood of a target superpixel
pc25_** The 25th percentile of the *-th neighborhood of a target superpixel
pc50_** The median of the *-th neighborhood of a target superpixel
pc75_** The 75th percentile of the *-th neighborhood of a target superpixel
skew_** *-th neighborhood’s skewness
deg_** The angle between *-th neighborhood and the base axis
kurtosis_** *-th neighborhood’s kurtosis
shannon_entropy_** *-th neighborhood’s Shannon entropy
area_** *-th neighborhood’s are
num_islands_** The number of islands of the *-th neighborhood of a target superpixel
mean_cs_** The mean of the contrast-stretched *-th neighborhood
std_cs_** The standard deviation of the *-th neighborhood (contrast-stretched)
pc25_cs_** The 25th percentile of the *-th neighborhood (contrast-stretched)
pc50_cs_** The median of the *-th neighborhood (contrast-stretched)
pc75_cs_** The 75th percentile of the *-th neighborhood (contrast-stretched)
skew_cs_** *-th neighborhood’s skewness (contrast stretched)
kurtosis_cs_** *-th neighborhood’s kurtosis (contrast stretched)
shannon_entropy_cs_** *-th neighborhood’s Shannon entropy (contrast stretched)

Appendix B. Feature importance

Figure A1 presents the features which were used under the MISP-XGB scheme and their feature importance scores. The scores were calculated on the basis of weight. In the figure, the upper subfigures were obtained by the single models, and the lower were by the neighborhood models. The results from the VV (left subfigures) and VH (right) modes were shown together.
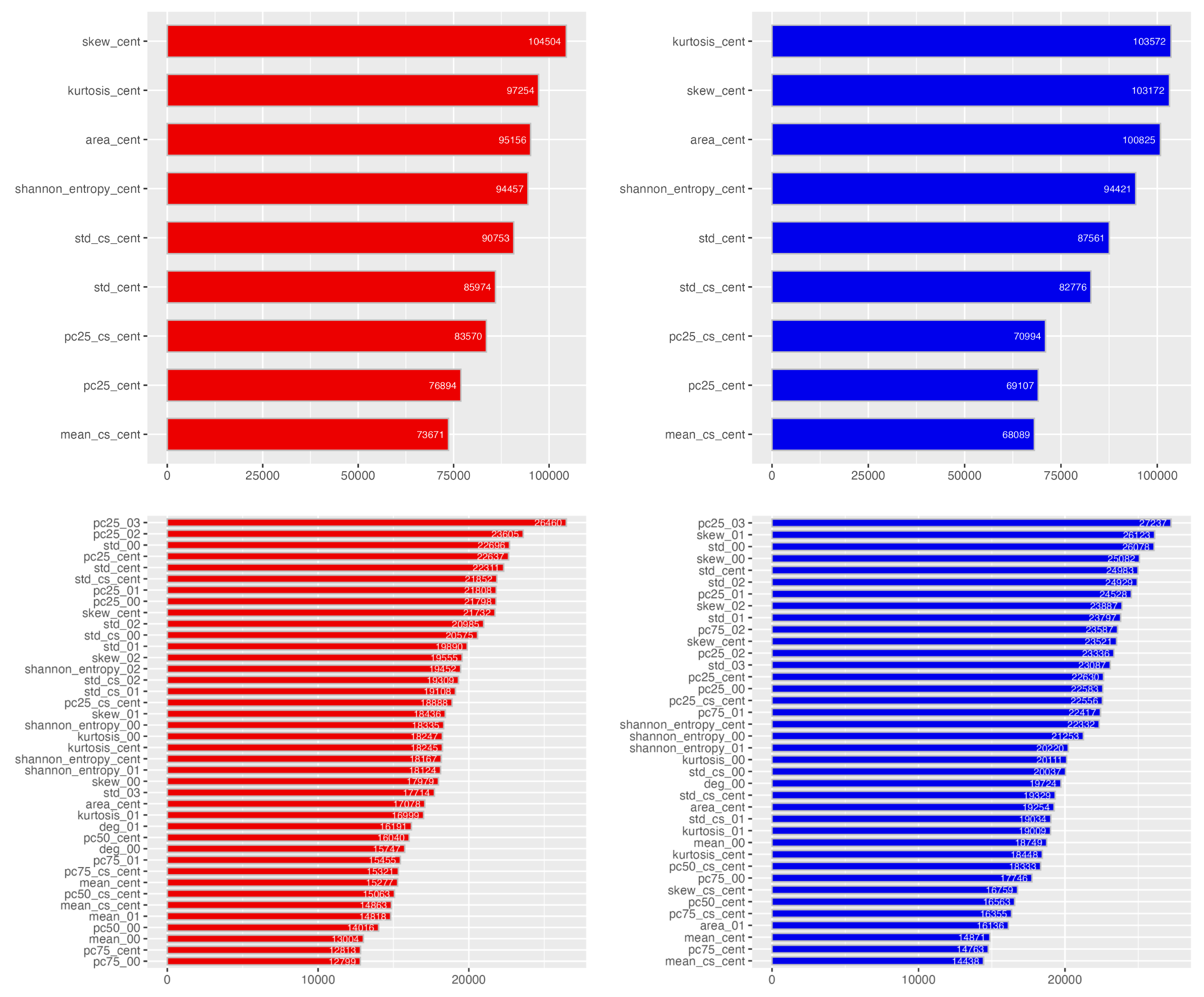
Preprints 120765 g0a1
Figure A1. The features used in the single (upper subfigures) and neighborhood (lower) models under the structured scheme and their feature importance scores calculated on the basis of the weight.
Figure A1. The features used in the single (upper subfigures) and neighborhood (lower) models under the structured scheme and their feature importance scores calculated on the basis of the weight.
Preprints 120765 g0a1

References

  1. Delmeire, S. Use of ERS-1 data for the extraction of flooded areas. Hydrological processes 1997, 11, 1393–1396. [CrossRef]
  2. Matgen, P.; Hostache, R.; Schumann, G.; Pfister, L.; Hoffmann, L.; Savenije, H. Towards an automated SAR-based flood monitoring system: Lessons learned from two case studies. Physics and Chemistry of the Earth, Parts A/B/C 2011, 36, 241–252. [CrossRef]
  3. Giustarini, L.; Hostache, R.; Matgen, P.; Schumann, G.J.P.; Bates, P.D.; Mason, D.C. A change detection approach to flood mapping in urban areas using TerraSAR-X. IEEE transactions on Geoscience and Remote Sensing 2012, 51, 2417–2430. [CrossRef]
  4. Santoro, M.; Wegmüller, U. Multi-temporal synthetic aperture radar metrics applied to map open water bodies. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2013, 7, 3225–3238. [CrossRef]
  5. Manjusree, P.; Prasanna Kumar, L.; Bhatt, C.M.; Rao, G.S.; Bhanumurthy, V. Optimization of threshold ranges for rapid flood inundation mapping by evaluating backscatter profiles of high incidence angle SAR images. International Journal of Disaster Risk Science 2012, 3, 113–122. [CrossRef]
  6. Gulácsi, A.; Kovács, F. Sentinel-1-imagery-based high-resolution water cover detection on wetlands, Aided by Google Earth Engine. Remote Sensing 2020, 12, 1614. [CrossRef]
  7. Matgen, P.; Schumann, G.; Henry, J.B.; Hoffmann, L.; Pfister, L. Integration of SAR-derived river inundation areas, high-precision topographic data and a river flow model toward near real-time flood management. International Journal of Applied Earth Observation and Geoinformation 2007, 9, 247–263. [CrossRef]
  8. Wu, X.; Zhang, Z.; Xiong, S.; Zhang, W.; Tang, J.; Li, Z.; An, B.; Li, R. A Near-Real-Time Flood Detection Method Based on Deep Learning and SAR Images. Remote Sensing 2023, 15, 2046. [CrossRef]
  9. Lang, M.W.; Townsend, P.A.; Kasischke, E.S. Influence of incidence angle on detecting flooded forests using C-HH synthetic aperture radar data. Remote Sensing of Environment 2008, 112, 3898–3907. [CrossRef]
  10. Huang, W.; DeVries, B.; Huang, C.; Lang, M.W.; Jones, J.W.; Creed, I.F.; Carroll, M.L. Automated extraction of surface water extent from Sentinel-1 data. Remote Sensing 2018, 10, 797. [CrossRef]
  11. Wu, L.; Wang, L.; Min, L.; Hou, W.; Guo, Z.; Zhao, J.; Li, N. Discrimination of algal-bloom using spaceborne SAR observations of Great Lakes in China. Remote Sensing 2018, 10, 767. [CrossRef]
  12. Li, N.; Niu, S.; Guo, Z.; Wu, L.; Zhao, J.; Min, L.; Ge, D.; Chen, J. Dynamic waterline mapping of inland great lakes using time-series SAR data from GF-3 and S-1A satellites: A case study of DJK reservoir, China. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2019, 12, 4297–4314. [CrossRef]
  13. Lv, W.; Yu, Q.; Yu, W. Water extraction in SAR images using GLCM and support vector machine. In Proceedings of the IEEE 10th international conference on signal processing proceedings, 2010. [CrossRef]
  14. Martinis, S.; Twele, A. A hierarchical spatio-temporal Markov model for improved flood mapping using multi-temporal X-band SAR data. Remote Sensing 2010, 2, 2240–2258. [CrossRef]
  15. Nagaraj, R.; Kumar, L.S. Multi scale feature extraction network with machine learning algorithms for water body extraction from remote sensing images. International Journal of Remote Sensing 2022, 43, 6349–6387.
  16. Sghaier, M.O.; Foucher, S.; Lepage, R. River extraction from high-resolution SAR images combining a structural feature set and mathematical morphology. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2016, 10, 1025–1038. [CrossRef]
  17. D’Addabbo, A.; Refice, A.; Pasquariello, G.; Lovergine, F.P.; Capolongo, D.; Manfreda, S. A Bayesian network for flood detection combining SAR imagery and ancillary data. IEEE Transactions on Geoscience and Remote Sensing 2016, 54, 3612–3625. [CrossRef]
  18. Asaro, F. A novel statistical-based scale-independent approach to unsupervised water segmentation of SAR images. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2019, pp. 1057–1060. [CrossRef]
  19. Gonzalez, R.C.; Woods, R.E. Digital image processing, fourth ed.; Pearson Education, New York, 2018.
  20. Zhu, L.; Zhang, J.; Sun, Y. Remote sensing image change detection using superpixel cosegmentation. Information 2021, 12, 94. [CrossRef]
  21. Jing, W.; Jin, T.; Xiang, D. Fast Superpixel-based clustering algorithm for SAR image segmentation. IEEE Geoscience and Remote Sensing Letters 2021, 19, 1–5. [CrossRef]
  22. Pappas, O.; Anantrasirichai, N.; Adams, B.; Achim, A. High-resolution Coastline Extraction in SAR Images via MISP-GGD Superpixel Segmentation. In Proceedings of the 2021 CIE International Conference on Radar (Radar). IEEE, 2021, pp. 2525–2528. [CrossRef]
  23. Gharibbafghi, Z.; Tian, J.; Reinartz, P. Modified superpixel segmentation for digital surface model refinement and building extraction from satellite stereo imagery. Remote Sensing 2018, 10, 1824. [CrossRef]
  24. Xiang, D.; Tang, T.; Zhao, L.; Su, Y. Superpixel generating algorithm based on pixel intensity and location similarity for SAR image classification. IEEE Geoscience and Remote Sensing Letters 2013, 10, 1414–1418. [CrossRef]
  25. Ke, J.; Guo, Y.; Sowmya, A. A Fast Approximate Spectral Unmixing Algorithm Based on Segmentation. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2017, pp. 66–72.
  26. Levinshtein, A.; Stere, A.; Kutulakos, K.N.; Fleet, D.J.; Dickinson, S.J.; Siddiqi, K. Turbopixels: Fast superpixels using geometric flows. IEEE transactions on pattern analysis and machine intelligence 2009, 31, 2290–2297. [CrossRef]
  27. Gadhiraju, S.V.; Sahbi, H.; Banerjee, B.; Buddhiraju, K.M. Supervised change detection in satellite imagery using super pixels and relevance feedback. Geomatica 2014, 68, 5–14. [CrossRef]
  28. Arisoy, S.; Kayabol, K. Mixture-based superpixel segmentation and classification of SAR images. IEEE Geoscience and Remote Sensing Letters 2016, 13, 1721–1725. [CrossRef]
  29. Nemni, E.; Bullock, J.; Belabbes, S.; Bromley, L. Fully convolutional neural network for rapid flood segmentation in synthetic aperture radar imagery. Remote Sensing 2020, 12, 2532. [CrossRef]
  30. Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078 2014. [CrossRef]
  31. Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473 2014. [CrossRef]
  32. Luong, M.T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation. arXiv preprint arXiv:1508.04025 2015. [CrossRef]
  33. Ashish, V. Attention is all you need. Advances in neural information processing systems 2017, 30, I.
  34. Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929 2020. [CrossRef]
  35. Kim, J.; Canny, J. Interpretable learning for self-driving cars by visualizing causal attention. In Proceedings of the Proceedings of the IEEE international conference on computer vision, 2017, pp. 2942–2950.
  36. Wollek, A.; Graf, R.; Čečatka, S.; Fink, N.; Willem, T.; Sabel, B.O.; Lasser, T. Attention-based saliency maps improve interpretability of pneumothorax classification. Radiology: Artificial Intelligence 2022, 5, e220187. [CrossRef]
  37. Won, M.; Chun, S.; Serra, X. Toward interpretable music tagging with self-attention. arXiv preprint arXiv:1906.04972 2019. [CrossRef]
  38. Bonafilia, D.; Tellman, B.; Anderson, T.; Issenberg, E. Sen1Floods11: A georeferenced dataset to train and test deep learning flood algorithms for sentinel-1. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 2020, pp. 210–211.
  39. Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [CrossRef]
  40. Besag, J. On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society Series B: Statistical Methodology 1986, 48, 259–279. [CrossRef]
  41. Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the International conference on machine learning. PMLR, 2021, pp. 10347–10357.
  42. Abnar, S.; Zuidema, W. Quantifying attention flow in transformers. arXiv preprint arXiv:2005.00928 2020. [CrossRef]
  43. Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794. [CrossRef]
  44. Friedman, J.H. Stochastic gradient boosting. Computational statistics & data analysis 2002, 38, 367–378. [CrossRef]
  45. Ben Jabeur, S.; Stef, N.; Carmona, P. Bankruptcy prediction using the XGBoost algorithm and variable importance feature engineering. Computational Economics 2023, 61, 715–741. [CrossRef]
  46. Manju, N.; Harish, B.; Prajwal, V. Ensemble feature selection and classification of internet traffic using XGBoost classifier. International Journal of Computer Network and Information Security 2019, 11, 37.
  47. Bai, Y.; Wu, W.; Yang, Z.; Yu, J.; Zhao, B.; Liu, X.; Yang, H.; Mas, E.; Koshimura, S. Enhancement of detecting permanent water and temporary water in flood disasters by fusing sentinel-1 and sentinel-2 imagery using deep learning algorithms: Demonstration of sen1floods11 benchmark datasets. Remote Sensing 2021, 13, 2220. [CrossRef]
  48. Chaurasia, A.; Culurciello, E. Linknet: Exploiting encoder representations for efficient semantic segmentation. In Proceedings of the 2017 IEEE visual communications and image processing (VCIP). IEEE, 2017, pp. 1–4. [CrossRef]
  49. Shvets, A.A.; Iglovikov, V.I.; Rakhlin, A.; Kalinin, A.A. Angiodysplasia detection and localization using deep convolutional neural networks. In Proceedings of the 2018 17th IEEE international conference on machine learning and applications (ICMLA). IEEE, 2018, pp. 612–617. [CrossRef]
  50. Bereczky, M.; Wieland, M.; Krullikowski, C.; Martinis, S.; Plank, S. Sentinel-1-based water and flood mapping: Benchmarking convolutional neural networks against an operational rule-based processing chain. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 2023–2036. [CrossRef]
Preprints 120765 g001
Figure 1. The flow diagram of the data processing.
Figure 1. The flow diagram of the data processing.
Preprints 120765 g001
Preprints 120765 g002
Figure 2. An example of the input for the unstructured scheme, where the 1st, 2nd, and 3rd columns represent the SAR channel, stretched SAR channel, and role channel, respectively. The inputs for the single model (the 1st row), mask model (2nd), and neighborhood model (3rd) are shown together.
Figure 2. An example of the input for the unstructured scheme, where the 1st, 2nd, and 3rd columns represent the SAR channel, stretched SAR channel, and role channel, respectively. The inputs for the single model (the 1st row), mask model (2nd), and neighborhood model (3rd) are shown together.
Preprints 120765 g002
Preprints 120765 g003
Figure 3. Architecture of the MISP-SDT models and an example of input.
Figure 3. Architecture of the MISP-SDT models and an example of input.
Preprints 120765 g003
Preprints 120765 g004
Figure 4. The relations between the top x percent of the all features and the validation scores for the VV mode (red) and the VH (blue). The results from the single models (upper subfigures) and the neighborhood models (lower) are presented. The validation scores are mIoU (left subfigures) and IoU (right).
Figure 4. The relations between the top x percent of the all features and the validation scores for the VV mode (red) and the VH (blue). The results from the single models (upper subfigures) and the neighborhood models (lower) are presented. The validation scores are mIoU (left subfigures) and IoU (right).
Preprints 120765 g004
Preprints 120765 g005
Figure 5. The segmentation results for Somalia_94102 (top) and USA_504150 (bottom). Their SAR imagery (1st subfigure), segmentation results from the single model (2nd), the neighborhood (3rd), and the groundtruth (4th).
Figure 5. The segmentation results for Somalia_94102 (top) and USA_504150 (bottom). Their SAR imagery (1st subfigure), segmentation results from the single model (2nd), the neighborhood (3rd), and the groundtruth (4th).
Preprints 120765 g005
Preprints 120765 g006
Figure 6. Several examples of the sets of stretched SAR channel (the 1st column), role channel (2nd), attention map for single (3rd), attention map for mask (4th), attention map for neighborhood (5th), and class label map (the ground truth) (6th). As to the class label map, land, water, unknown regions are filled with green, blue, and black, respectively.
Figure 6. Several examples of the sets of stretched SAR channel (the 1st column), role channel (2nd), attention map for single (3rd), attention map for mask (4th), attention map for neighborhood (5th), and class label map (the ground truth) (6th). As to the class label map, land, water, unknown regions are filled with green, blue, and black, respectively.
Preprints 120765 g006
Preprints 120765 g007
Figure 7. A few examples of part of SAR imagery (left), its target/neighbor superpixels (center), and its Target/Near Neighbor/Far Neighbor regions (right). Target, Near Neighbor, and Far Neighbor regions are filled with white, indigo, and grey, respectively.
Figure 7. A few examples of part of SAR imagery (left), its target/neighbor superpixels (center), and its Target/Near Neighbor/Far Neighbor regions (right). Target, Near Neighbor, and Far Neighbor regions are filled with white, indigo, and grey, respectively.
Preprints 120765 g007
Preprints 120765 g008
Figure 8. The averages of attention rollout scores for the roles (Pad for 1st subfigure, Far neighbor for 2nd, Near Neighbor for 3rd, Target for 4th) of a superpixel, for the single, mask, neighborhood models.
Figure 8. The averages of attention rollout scores for the roles (Pad for 1st subfigure, Far neighbor for 2nd, Near Neighbor for 3rd, Target for 4th) of a superpixel, for the single, mask, neighborhood models.
Preprints 120765 g008
Table 1. Breakdown of Sen1Flood11 dataset.
Table 1. Breakdown of Sen1Flood11 dataset.
Type Sample size
Train (Hand-labeled) 252
Validation 89
Test 90
Bolivia 15
Table 2. Values/Choices of parameters under the unstructrued/structured schemes.
Table 2. Values/Choices of parameters under the unstructrued/structured schemes.
Scheme Parameter Value/Choice
]7*Unstructured Epochs 80
Learning rate 0.0005 × Batch Size / 512
Batch size 512
Optimizer AdamW
Loss function Cross entropy
Weight decay 0.05
Dropout 0.0
]9*Structured Boosting count 1450
Learning rate 0.0035
max depths of tree 10
Early stopping round 250
Objective function Binary logistic
L1 regularization 0.6
L2 regularization 1.2
Tree method Approx
Column subsample ratio 0.55
Table 3. Numerical results for the hand-labeled training data.
Table 3. Numerical results for the hand-labeled training data.
Pol Scheme Model Accuracy Recall Precision F-1 IoU mIoU
VV Unstr Single 0.916 0.459 0.479 0.376 0.473 0.292
Mask 0.888 0.578 0.362 0.364 0.438 0.274
Neighb 0.926 0.425 0.541 0.403 0.515 0.309
Str Single 0.908 0.533 0.444 0.391 0.462 0.300
Neighb 0.923 0.514 0.479 0.411 0.513 0.319
VH Unstr Single 0.926 0.542 0.468 0.431 0.565 0.338
Mask 0.921 0.574 0.451 0.425 0.536 0.325
Neighb 0.936 0.543 0.497 0.456 0.601 0.357
Str Single 0.924 0.580 0.464 0.439 0.569 0.345
Neighb 0.935 0.570 0.509 0.466 0.608 0.368
Table 4. Comaprison to FCNN and AlbuNet-34 in terms of AW.
Table 4. Comaprison to FCNN and AlbuNet-34 in terms of AW.
Metric FCNN (HL) FCNN (S1W) AlbuNet-34 MISP-SDT MISP-XGB
IoU n/a n/a 0.497 0.601 0.608
mIoU 0.313 0.309 0.347 0.357 0.368
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated