Prerpints.org logo
Preprint
Article

Requirements of Constrictive Binding and Dynamic Systems on Molecular Cages for Drug Delivery

Altmetrics

Downloads

118

Views

96

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 October 2024

Posted:

10 October 2024

You are already at the latest version

Alerts
Abstract
Molecular cages have promising host-guest properties for drug delivery applications. Specifically, guest⊂cage complexes can be used for on-command release of encapsulated guest molecules in response to specific stimuli. This research explores both dynamic and constrictive binding guest⊂cage systems for drug encapsulation and release in biological environments. In dynamic systems, the guest rapidly passes in and out through the portals of the cage, enabling drug delivery in vitro but facing limitations in vivo due to dilution effects that result in guest release. These challenges are addressed by constrictive binding systems, where the guest is trapped in a "gate-closed" state within the cage. In these systems, the on-command release is triggered by a "gate opening" event, which lowers the guest-out energy barrier. The full guest release is achieved when gate opening reduces the cage-guest affinity, making constrictive binding systems more effective for controlled drug delivery. As a result, this study shows that guest⊂cage complexes have suitable properties for drug delivery in biological contexts.
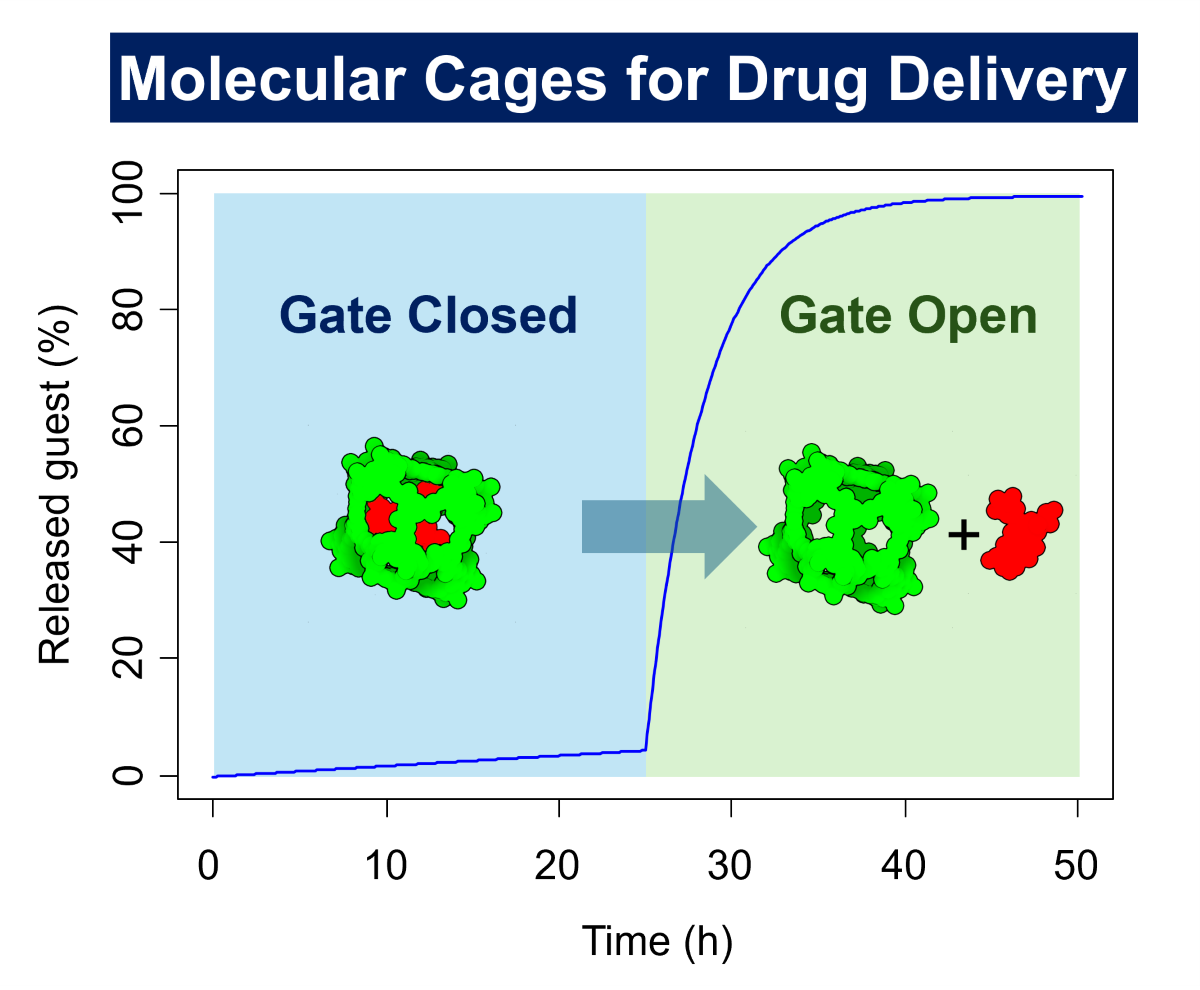
Keywords: 
Subject: Chemistry and Materials Science  -   Medicinal Chemistry

1. Introduction

Molecular cages are supramolecular structures that can isolate guest molecules from the surrounding media by encapsulation in their central cavity, mimicking the encapsulation processes found in biological systems [1,2,3]. In fact, in biology compartmentalization has a vital importance in keeping the living organisms away from equilibrium, resulting in a complex network of non-equilibrium chemical systems [4]. Molecular cages are therefore suitable systems for mimicking these complex functions. The three-dimensional shape of their cavity gives a unique preorganization with enhanced affinity for guests in comparison to related supramolecular architectures such as macrocycles [5,6]. This property makes cages unique species for diverse applications such as catalysis [7,8,9,10,11], sensing of diverse chemical species [12,13,14,15,16,17,18,19], separation of chemicals [20,21,22,23,24], removal of pollutants from water [25,26,27,28], stabilization of chemical species [29,30], biological applications [31,32,33,34,35,36,37,38,39,40], and many others [1,2]. In addition to these properties, molecular cages can be engineered to transport cargo molecules [41] with stimuli-responsive properties to pH [34,42,43] and light [44,45,46,47], among others [48,49,50,51,52,53,54]. Typically, cages are prepared by the thermodynamically controlled self-assembly of metals and ligands to yield metallo-cages or by the self-assembly of only organic ligands to yield pure organic cages [1,2,55,56,57]. To facilitate the design of cages with specific geometries and properties, computational modelling has been extensively used. This allows reducing trial-and-error attempts or predict host-guest properties [58,59,60,61,62,63,64].
Focusing on therapeutic applications of molecular cages, cages are capable of encapsulating drugs, forming inactive guest⊂cage complexes, in which the activity of the drug is restored upon their release from the cage [31,32]. In this area, it is crucial to design cages that efficiently encapsulate drugs and respond to selective stimuli for controlled drug release [34,65,66]. Various systems have been developed for this purpose, most of which rely on equilibrium processes, which present limitations related to dynamic equilibria and drug dissociation when applied in a physiological environment [1,2]. Achieving systems where drugs are kinetically trapped inside the cage, is a challenging task. To accomplish this, the constrictive binding strategy has been proposed in simple host–guest systems, where the guest in–out activation barrier prevents rapid equilibrium between the drug inside the cavity and the external environment. The in-and-out passage of the guest molecule requires heating to widen the portals to create sufficient space [67].
Cram, back in 1991, reported an example of constrictive binding of a 1,1,2,2-tetrachloroethane guest molecule using a fully organic hemicarcerand host [68]. This guest⊂cage complex is stable at room temperature in the solid state or in solution, but slowly decomplexes by heating it at 100–134 °C. The van’t Hoff analysis provided an activation barrier of 24.6 kcal/mol, with a t1/2 value of 18 h at 100 oC. Further studies by Cram showed that the in–out activation barriers are guest-dependent for a series of hemicarcerands, with the larger guests found to have lower activation energies for decomplexing. This is likely due to an increased compression of the cage to accommodate them, which are released upon decomplexation [69]. The relative size of the guest regarding the size of the portals of the cage is a key parameter for successful constrictive binding. If the guests are too small, constrictive binding is ineffective as the guest molecules pass through the portals; if the guests are too large, the energy barrier becomes too high, preventing complexation from occurring [70,71]. Both guest shape and size influence the observed constrictive binding [72]. As a result, the in-and-out kinetics of the guest depend on the cage’s conformation and are also correlated with the cage–guest affinity, where stronger affinity leads to slower kinetics [73]. The binding properties in these guest⊂cage complexes can be described as the combination of intrinsic binding (i.e., free energy difference between the complex and free cage and guest) and the constrictive binding as the additional free energy barrier associated with the guest passing through the portals of the cage (Figure 1) [75]. These systems, in which the guest molecule is trapped inside the cage, and it is only released from it under specific conditions, act as a gating mechanism as described by Houk [74,75,76,77,78].
Metallo-organic cages have the same host–guest behaviour as organic cages. Fujita and his team have shown a “ship in a bottle” entrapment-type synthesis showing that a large labile cyclic silanol, that fits tightly to the cage cavity, prevents its hydrolysis for more than one month [79]. This shows the feasibility of using molecular cages to effectively isolate the encapsulated guest from the surrounding media, highlighting the importance of having a large enough sized guest that cannot pass through the portals of the host. If the size of the guest is smaller than the portal, Raymond showed that the partial dissociation of the host structure can create a portal for in–out guest passage, and the deformation of the host structure can create a dilated aperture for guest passage without any host rupture [80].
Nitschke and his team measured the rate constant for guest uptake (kin) and the association constant (KAss) for Nitschke’s water-soluble Fe4L6 metal–organic cage. We have carefully reanalyzed this data and determined guest release rate constants (kout) as kout= kin/KAss, showing a guest release decrease with guest size. On one side, the guest must have a smaller size than the cavity size (150 Å3) as guests with a size of 135 Å3 or larger do not bind. For smaller guests, the kout decreases with the size of the guest, from 5 ×10–2 s–1 for acetone (73 Å3) to 5 ×10–8 s–1 for cyclohexane (111 Å3). These results show an impressive change of 6 orders of magnitude in the out-rate, changing the release timescale from seconds to months, from the smaller to the larger guest [81].
In this work, we study the thermodynamic and kinetic requirements of guest⊂cage complexes for drug delivery applications. We focus on both, dynamic and constrictive binding systems, analyzing the effects of dilution, binding constant strength, and the activation energy required for the encapsulated guest to escape the cavity of the cage in operational systems.

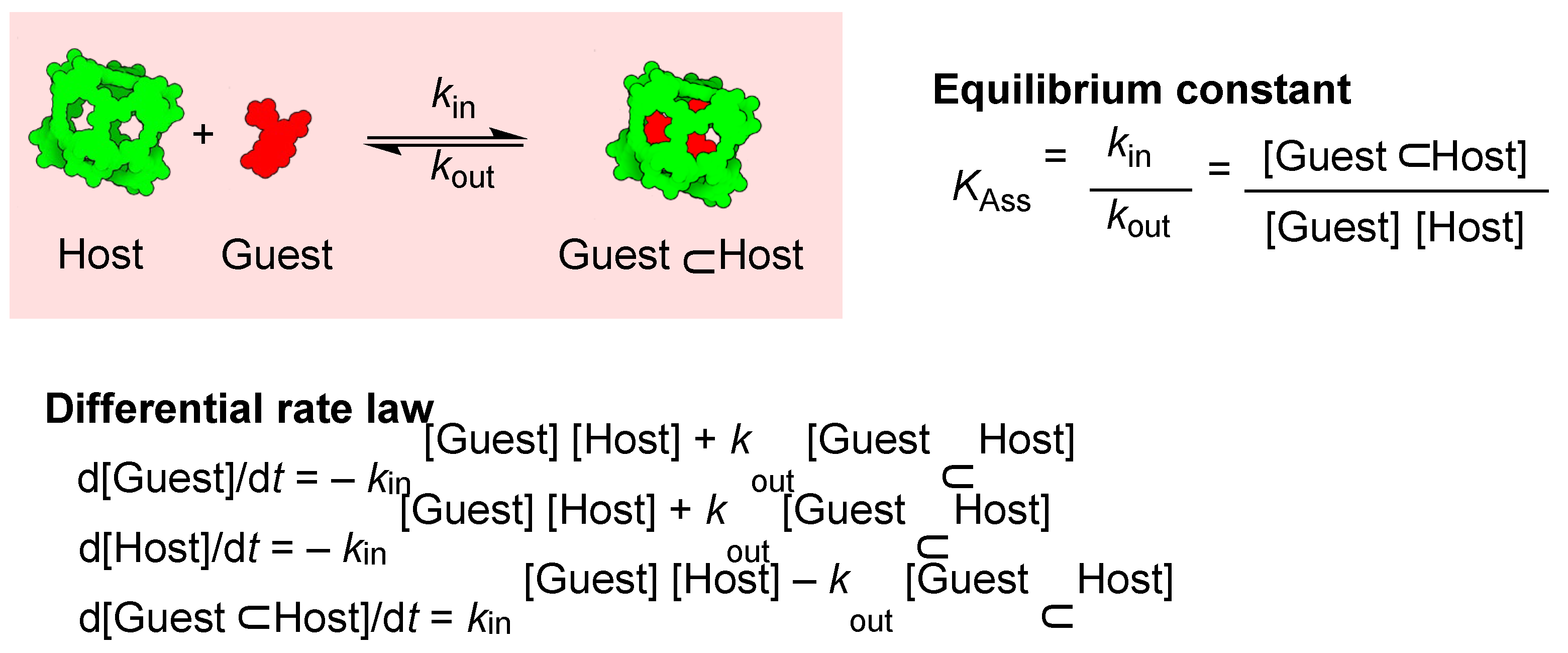
2. Materials and Methods

The molecular encapsulation kinetics and thermodynamics have been obtained using standard 1:1 host–guest binding isotherms. Simulations were performed using the R software [82] and the RStudio software interface [83]. Differential equations, corresponding to the host–guest kinetic models, were solved with the library deSolve using the standard parameters [84]. The Eyring equation was used to convert activation free energy barriers into kinetic constants [85].

3. Results and Discussion

To explore the effects of dilution, binding constant strength, and the guest in–out activation energy, we modelled the host–guest encapsulation process considering the in-and-out processes involved in the encapsulation equilibrium (Figure 2). The in-step of guest encapsulation involves the reaction between a guest molecule and a host molecule; while the step of guest release involves a dissociative mechanism creating an empty cavity. This is a reasonable assumption considering the large host cavity occupancy required by the guest [86,87,88]. The cage formation step is, therefore, a second-order reaction, while the dissociative mechanism for the decomplexation step is a first-order reaction with the corresponding equations described in Figure 2.

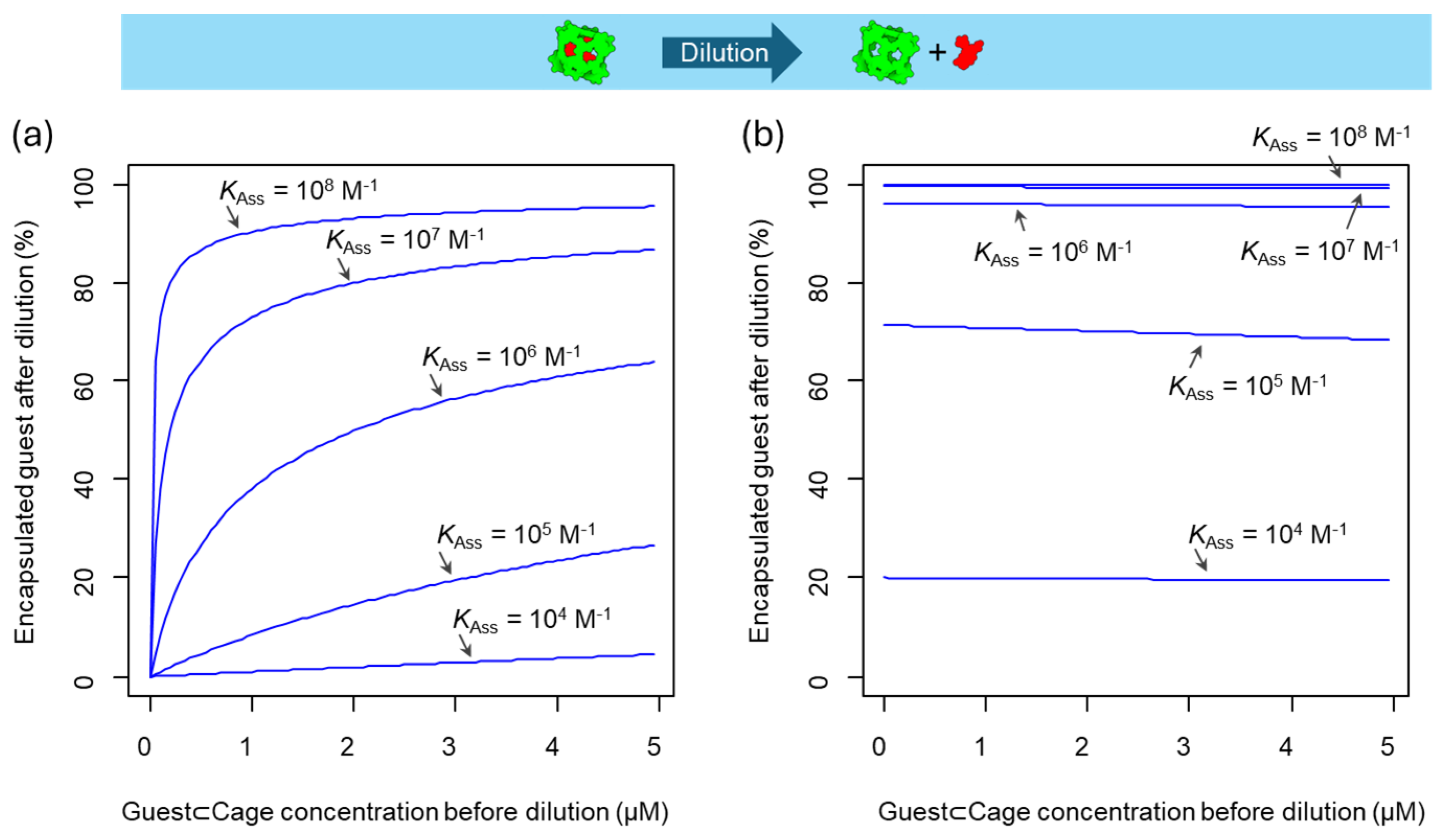
3.1. Effects of Dilution in Guest⊂Cage Complexes

A large number of the reported cage structures in literature have sufficiently large portals that allow the fast entry and exit of guests from the cavity, allowing these systems to operate under equilibrium conditions at room temperature. These systems result in labile guest⊂cage complexes, where the guest can rapidly pass in–out of the cage. When the guest⊂cage complex is diluted, a re-equilibration takes place as dictated by the equilibrium constant, resulting in the guest escaping from the cage cavity. As the required concentrations for biological experiments are usually in the micromolar range, this produces practically no significant binding, unless the binding constant is as high as 106 or 108 M–1. Figure 3a shows the effect of the binding constant on the encapsulation equilibrium, for example, when KAss = 108 M–1 a 4% of the guest is released from the cage at 5 µM concentration, and nearly 40% if KAss = 106 M–1. The amount of encapsulated guest can be increased by using an excess concentration of the cage. According to Le Chatelier principle, the excess of cage shifts the equilibrium towards the formation of the host–guest complex (Figure 3b). For example, when the association constant is 106 M–1 and the concentration of the guest is 5 µM, an increase of cage concentration from 5 µM to 25 µM rises the amount of encapsulated guest from 60% to 95% (from Figure 3a to Figure 3b). Thus, cages with a good affinity towards the guests may be suitable for biological applications by using either equimolar amounts, if the association constant is as high as 108 M–1, or using an excess of the cage to favor encapsulation. Note that, these systems may be suitable for in vitro studies, as it is possible to set up the concentration in the well, but not suitable for in vivo studies, where additional dilution effects will occur. Therefore, to preserve the encapsulated guest in the guest⊂cage complex after dilution, it is necessary to develop systems with constrictive binding.

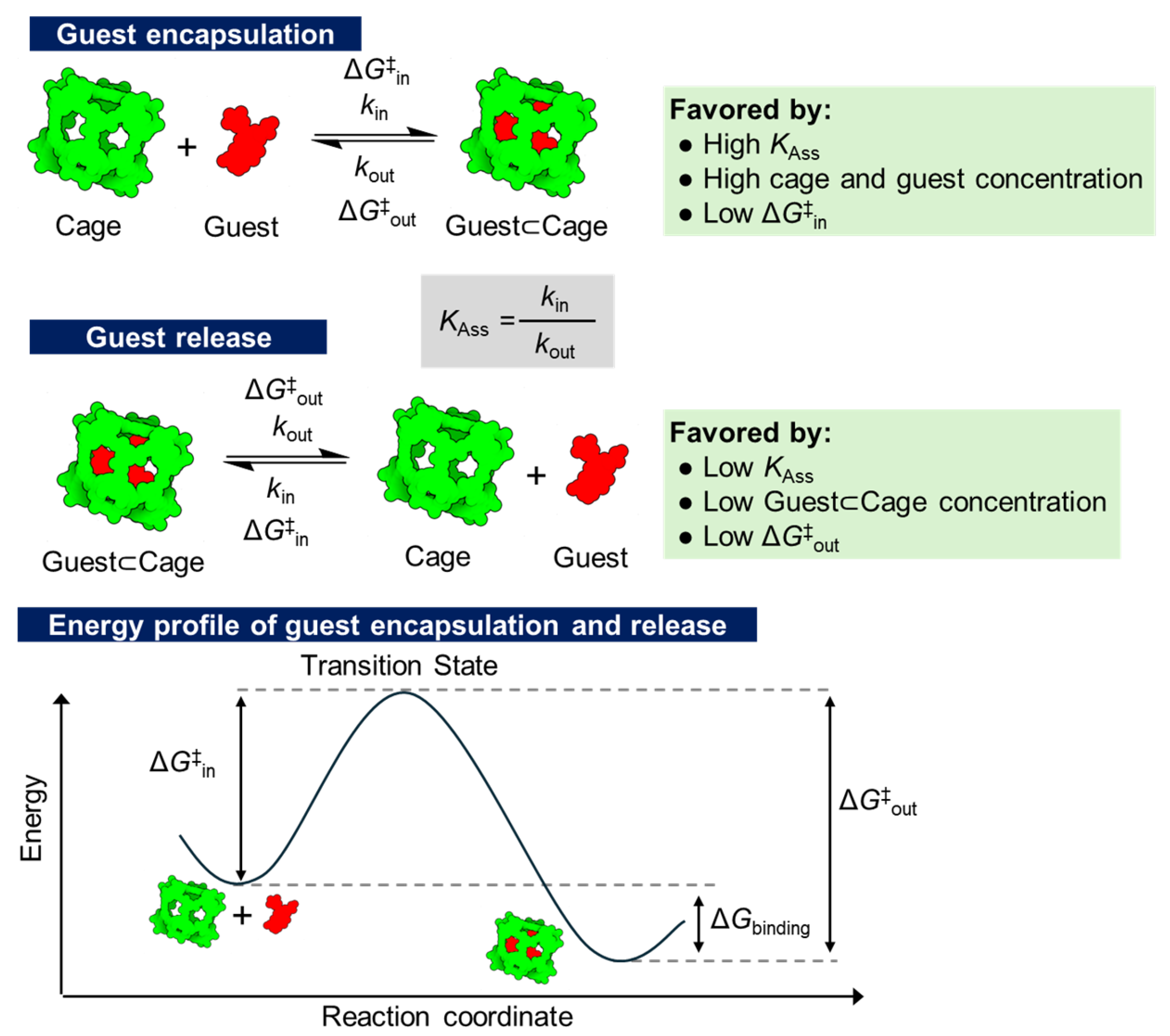
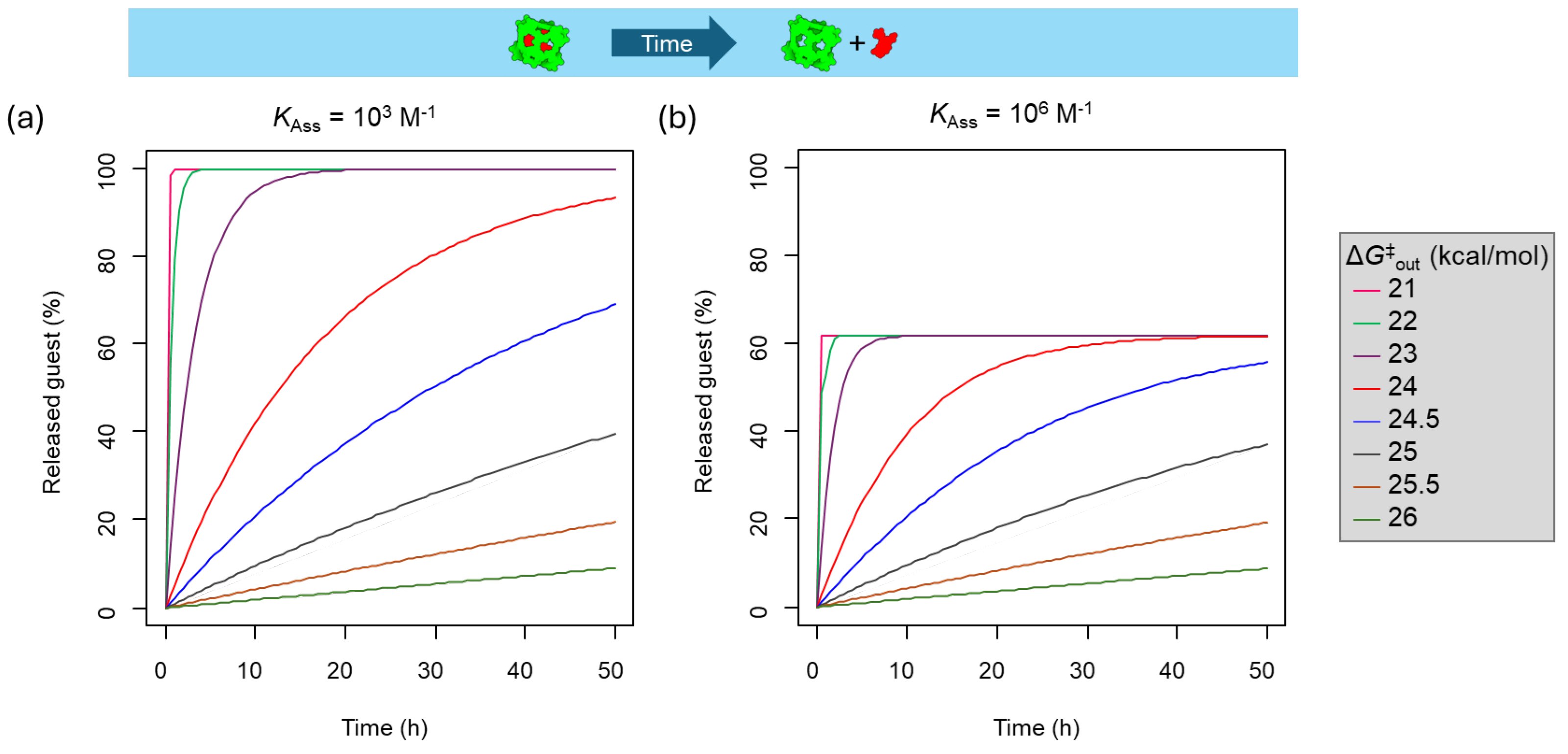
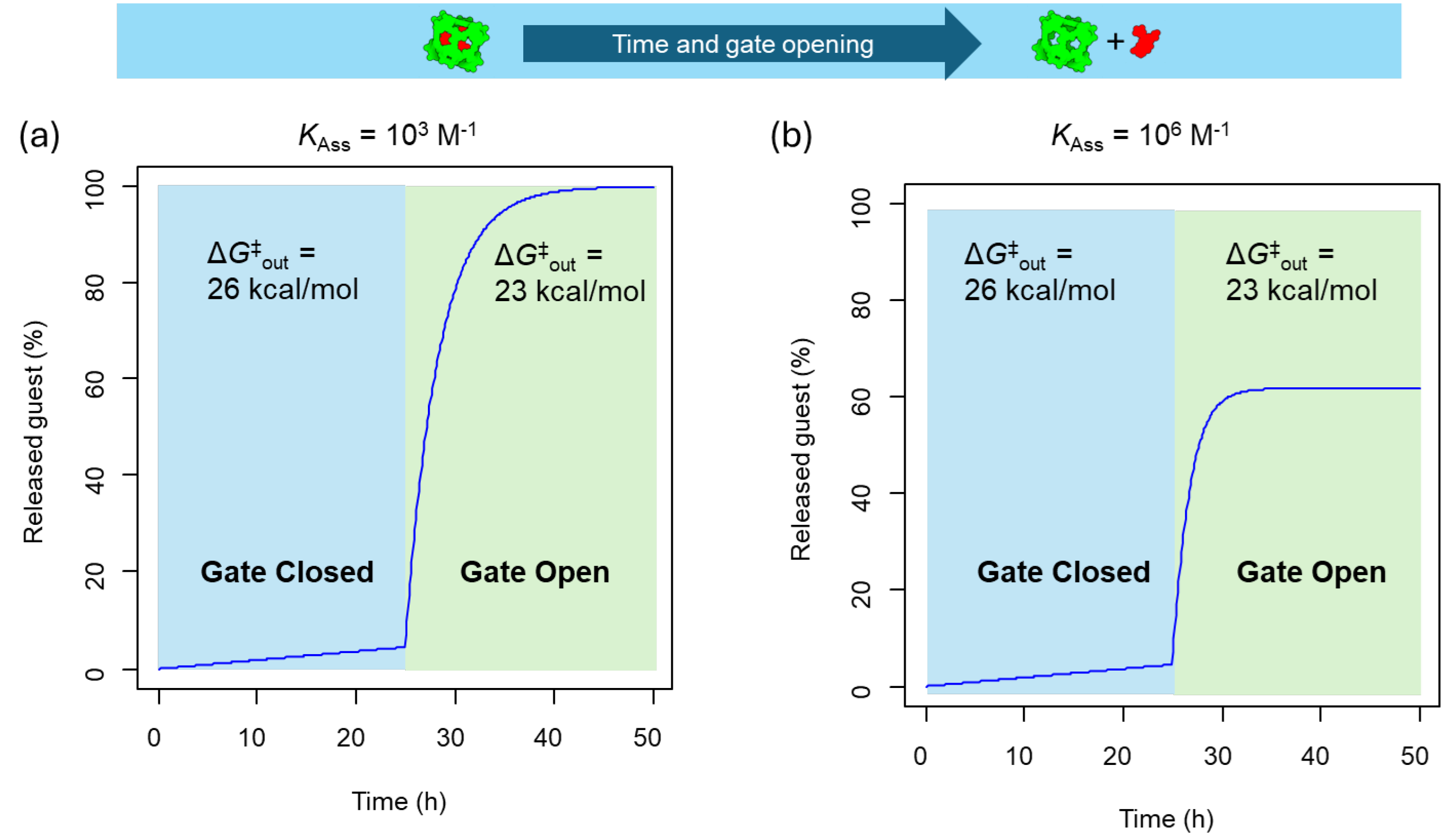
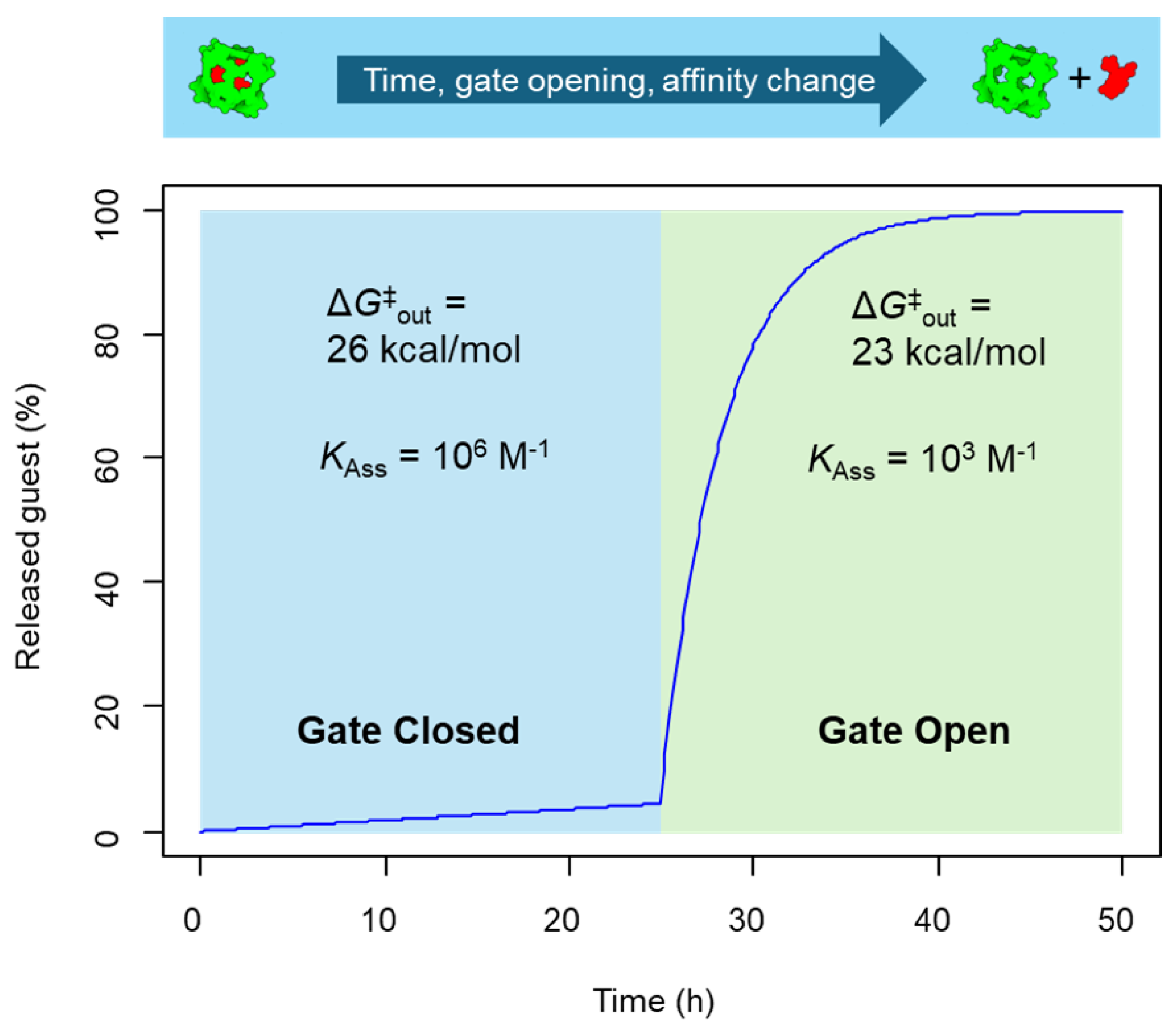
3.2. Energy Barrier for Guest Escaping the Cavity in Guest⊂Cage Complexes

To overcome the limitations of the guest⊂cage complexes that operate under equilibrium conditions, it is necessary to develop kinetically locked guest⊂cage systems, i.e., systems under constrictive binding. We have simulated the guest release from a guest⊂cage complex at different energy barriers and association constants considering an initial guest⊂cage concentration of 1 µM (Figure 4). When the association constant is as low as 103 M–1 and the guest out activation barrier is 23 kcal/mol or lower, a complete release of the guest is achieved in less than 20 h (Figure 4a). If the association constant is 106 M–1, a similar release kinetics dependency with the guest out activation barrier is observed (Figure 4b), but with a significant difference, in this case, the larger affinity results in a significant amount of encapsulated guest when the equilibrium is reached. These results show that guest⊂cage systems with a guest-out activation barrier of at least 25 kcal/mol are suitable to keep 95% of the encapsulated guest for at least 10 h. These inert systems are ideal for achieving the required performance in biological applications, as they will not suffer from the re-equilibration by dilution effects, making them suitable for in vivo studies.
The results from the simulations of Figure 4 demonstrate that guest⊂cage systems with an activation barrier of at least 25 kcal/mol for guest exit are ideal “gate closed” systems, effectively keeping the guest inside the cage. Engineering the structure of cages with stimuli-responsive motifs results in a “gate closed”–“gate open” system for on-command guest release. In these systems, the encapsulated guest is not able to escape from the cavity of the cage in the “gate closed” (i.e., large guest out activation barrier) until a certain stimulus is present that activates the “gate open” state (i.e., low guest-out activation barrier). We have simulated the release of the guest from a guest⊂cage at the concentration of 1 µM with a guest-out activation barrier of 26 kcal/mol. A minimal guest release is observed until the gate opening occurs in response to a specific stimulus that reduces the barrier to 23 kcal/mol (Figure 5). This change in the activation barrier leads to complete guest release when the association constant is 103 M–1 (Figure 5a), and 60% release when the association constant is 106 M–1, due to the equilibrium reached between the host and guest (Figure 5b).
The “gate closed”–“gate open” systems are, therefore, ideal for biological applications due to their release properties. A last aspect to consider is the feasibility of preparing the guest⊂cage complex under chemical synthetic conditions. An effective guest⊂cage synthesis requires a high association constant to drive the formation of the host–guest complex. Therefore, from the synthetic point of view, an association constant of 106 M–1 would be preferred. However, as described in Figure 5b the high guest–cage affinity does not allow the complete release of the guest due to encapsulation equilibrium. Developing a more sophisticated guest⊂cage system that simultaneously produces gate opening and affinity reduction in response to stimuli would be ideal. This can be achieved for example by partial or full cage disassembly. We have simulated using the same conditions described in Figure 5, but adding to the reduction of the guest-out barrier in the “gate open” event a reduction of the association constant (Figure 6). This system has the ideal properties from the synthetic point of view, i.e., a high association constant that facilitates the guest⊂cage formation with a high out activation barrier that prevents the guest from escaping the cavity. Note that synthesis may require heating to achieve a suitable guest rate or to self-assemble the cage around the guest molecule. Then, when the gate is open, a reduction in both, guest-out energy barrier and cage–guest affinity, resulting in a complete guest release. These guest⊂cage have, therefore, ideal properties for in vivo studies.

4. Conclusions

Molecular cages have excellent host–guest properties for drug delivery applications. We have shown that dynamic systems, in which the guest can rapidly pass in–out, can result in a guest⊂cage complex suitable for drug delivery in vitro, with limitations for in vivo experiments due to guest release by dilution effects. These limitations are overcome with constrictive binding guest⊂cage complexes, where the guest is trapped in the cavity of the cage in a “gate closed” state. On-command guest release is therefore achieved by “gate open”, which produces a reduction of the guest-out energy barrier allowing the release of the guest. A complete guest release is achieved when the gate-opening event also produces a reduction in the cage–guest affinity. As a result, this study shows that overall guest⊂cage complexes might have suitable properties for drug delivery in biological environments, yet to achieve this goal molecular cages with the necessary structures and properties to meet the required thermodynamic and kinetic criteria need to be designed. Future work in the field of molecular cages will soon enable the synthesis of molecular cages with constrictive binding of drug molecules with optimal properties for in vivo drug delivery.

Author Contributions

Conceptualization, V.M-C.; methodology, G.M.-G. and V.M-C.; experiments and simulations, V.M-C. and G.M.-G.; writing—original draft preparation, G.M.-G., V.M-C. and R.M-.M.; writing—review and editing, G.M.-G., V.M-C. and R.M-.M.; supervision, V.M-C. and R.M-.M.; project administration, V.M-C. and R.M-.M.; funding acquisition, V.M-C. and R.M-.M. All authors have read and agreed to the published version of the manuscript.

Funding

V. M.-C. acknowledges the financial support from project CIDEGENT/2020/031 funded by the Generalitat Valenciana, project PID2020-113256RA-I00 funded by MICIU/AEI/10.13039/501100011033, and project CNS2023-144879 funded by MICIU/AEI/10.13039/501100011033 and European Union NextGenerationEU/PRTR. R. M.-M. acknowledges the financial support from project PROMETEO CIPROM/2021/007 from the Generalitat Valenciana and project PID2021-126304OB-C41 funded by MICIU/AEI/10.13039/501100011033 and FEDER A way to make Europe.

Data Availability Statement

All data generated or analyzed during this study are included in the manuscript. The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.

Acknowledgments

This research was supported by CIBER (CB06/01/2012), Instituto de Salud Carlos III, Ministerio de Ciencia e Innovación.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Montà-González, G.; Sancenón, F.; Martínez-Máñez, R.; Martí-Centelles, V. Purely Covalent Molecular Cages and Containers for Guest Encapsulation. Chem. Rev. 2022, 122, 13636–13708. [Google Scholar] [CrossRef] [PubMed]
  2. Percástegui, E. G.; Ronson, T. K.; Nitschke, J. R. Design and Applications of Water-soluble Coordination Cages. Chem. Rev. 2020, 120, 13480–13544. [Google Scholar] [CrossRef]
  3. Lewis, J. E. M. Developing Sophisticated Microenvironments in Metal-organic Cages. Trends Chem. 2023, 5, 717–719. [Google Scholar] [CrossRef]
  4. Penocchio, E.; Bachir, A.; Credi, A.; Astumian, R. D.; Ragazzon, G. Analysis of Kinetic Asymmetry in a Multi-Cycle Reaction Network Establishes the Principles for Autonomous Compartmentalized Molecular Ratchets. Chem 2024, 10, 1–12. [Google Scholar] [CrossRef]
  5. Martí-Centelles, V.; Pandey, M. D.; Burguete, M. I.; Luis, S. V. Macrocyclization Reactions: The Importance of Conformational, Configurational, and Template-Induced Preorganization. Chem. Rev. 2015, 115, 8736–8834. [Google Scholar] [CrossRef]
  6. Martí-Centelles, V.; Duarte, F.; Lusby, P. J. Host-Guest Chemistry of Self-Assembled Hemi-Cage Systems: The Dramatic Effect of Lost Pre-Organization. Isr. J. Chem. 2019, 59, 257–266. [Google Scholar] [CrossRef]
  7. Martí-Centelles, V.; Lawrence, A. L.; Lusby, P. J. High Activity and Efficient Turnover by a Simple, Self-Assembled Artificial “Diels-Alderase”. J. Am. Chem. Soc. 2018, 140, 2862–2868. [Google Scholar] [CrossRef]
  8. Pappalardo, A.; Puglisi, R.; Trusso Sfrazzetto, G. Catalysis inside Supramolecular Capsules: Recent Developments. Catalysts 2019, 9, 630. [Google Scholar] [CrossRef]
  9. Piskorz, T. K.; Martí-Centelles, V.; Spicer, R. L.; Duarte, F.; Lusby, P. J. Picking the Lock of Coordination Cage Catalysis. Chem. Sci. 2023, 14, 11300–11331. [Google Scholar] [CrossRef]
  10. Ward, M. D. New Insights into Coordination-cage Based Catalysis. Chem. Commun. 2024, 60, 10464–10475. [Google Scholar] [CrossRef]
  11. Andrews, K. G.; Piskorz, T. K.; Horton, P. N.; Coles, S. J. Enzyme-like Acyl Transfer Catalysis in a Bifunctional Organic Cage. J. Am. Chem. Soc. 2024, 146, 17887–17897. [Google Scholar] [CrossRef] [PubMed]
  12. Luo, K.; Liu, Y.; Li, A.; Lai, Z.; Long, Z.; He, Q. A Tetraphenylethylene-Based Superphane for Selective Detection and Adsorption of Trace Picric Acid in Aqueous Media. Supramol. Chem. 2024, 1–10. [Google Scholar] [CrossRef]
  13. La Cognata, S.; Amendola, V. Recent Applications of Organic Cages in Sensing and Separation Processes in Solution. Chem. Commun. 2023, 59, 13668–13678. [Google Scholar] [CrossRef] [PubMed]
  14. Merli, D.; La Cognata, S.; Balduzzi, F.; Miljkovic, A.; Toma, L.; Amendola, V. A Smart Supramolecular Device for the Detection of t,t-Muconic Acid in Urine. New J. Chem. 2018, 42, 15460–15465. [Google Scholar] [CrossRef]
  15. Ludden, M. D.; Taylor, C. G. P.; Ward, M. D. Orthogonal Binding and Displacement of Different Guest Types Using a Coordination Cage Host with Cavity-Based and Surface-Based Binding Sites. Chem. Sci. 2021, 12, 12640–12650. [Google Scholar] [CrossRef]
  16. Lu, Y.; Wang, S.-M.; He, S.-S.; Huang, Q.; Zhao, C.-D.; Yu, S.; Jiang, W.; Yao, H.; Wang, L.-L.; Yang, L.-P. An Endo-functionalized Molecular Cage for Selective Potentiometric Determination of Creatinine. Chem. Sci. 2024, 14, 14791–14797. [Google Scholar] [CrossRef]
  17. Luo, K.; Liu, Y.; Li, A.; Lai, Z.; Long, Z.; He, Q. A Tetraphenylethylene-Based Superphane for Selective Detection and Adsorption of Trace Picric Acid in Aqueous Media. Supramol. Chem. 2024, 1–10. [Google Scholar] [CrossRef]
  18. Lu, Y.; Wang, S.-M.; He, S.-S.; Huang, Q.; Zhao, C.-D.; Yu, S.; Jiang, W.; Yao, H.; Wang, L.-L.; Yang, L.-P. An Endo-functionalized Molecular Cage for Selective Potentiometric Determination of Creatinine. Chem. Sci. 2024, 15, 14791–14797. [Google Scholar] [CrossRef]
  19. Maitra, P. K.; Bhattacharyya, S.; Purba, P. C.; Mukherjee, P. S. Coordination-induced Emissive Poly-nhc-derived Metallacage for Pesticide Detection. Inorg. Chem. 2024, 63, 2569–2576. [Google Scholar] [CrossRef]
  20. Zhang, D.; Ronson, T. K.; Zou, Y.-Q.; Nitschke, J. R. Metal–organic Cages for Molecular Separations. Nat. Rev. Chem. 2021, 5, 168–182. [Google Scholar] [CrossRef]
  21. Little, M. A.; Cooper, A. I. The Chemistry of Porous Organic Molecular Materials. Adv. Funct. Mater. 2020, 30, 1909842. [Google Scholar] [CrossRef]
  22. Zhang, J.; Xie, S.; Zi, M.; Yuan, L. Recent Advances of Application of Porous Molecular Cages for Enantioselective Recognition and Separation. J. Sep. Sci. 2020, 43, 134–149. [Google Scholar] [CrossRef] [PubMed]
  23. García-Simón, C.; Garcia-Borràs, M.; Gómez, L.; Parella, T.; Osuna, S.; Juanhuix, J.; Imaz, I.; Maspoch, D.; Costas, M.; Ribas, X. Sponge-like Molecular Cage for Purification of Fullerenes. Nat. Commun. 2014, 5, 5557. [Google Scholar] [CrossRef] [PubMed]
  24. Ghosh, A.; Pruchyathamkorn, J.; Fuertes Espinosa, C.; Nitschke, J. R. Light-driven Purification of Progesterone from Steroid Mixtures Using a Photoresponsive Metal–organic Capsule. J. Am. Chem. Soc. 2024, 146, 2568–2573. [Google Scholar] [CrossRef]
  25. Pérez-Ferreiro, M.; Gallagher, Q. M.; León, A. B.; Webb, M. A.; Criado, A.; Mosquera, J. Engineering a Surfactant Trap via Postassembly Modification of an Imine Cage. Chem. Mater. 2024, ASAP. [Google Scholar] [CrossRef]
  26. Wang, Z.; Pacheco-Fernández, I.; Carpenter, J. E.; Aoyama, T.; Huang, G.; Pournaghshband Isfahani, A.; Ghalei, B.; Sivaniah, E.; Urayama, K.; Colón, Y. J.; Furukawa, S. Pore-networked Membrane Using Linked Metal-organic Polyhedra for Trace-level Pollutant Removal and Detection in Environmental Water. Commun. Mater. 2024, 5, 161. [Google Scholar] [CrossRef]
  27. Samanta, J.; Tang, M.; Zhang, M.; Hughes, R. P.; Staples, R. J.; Ke, C. Tripodal Organic Cages with Unconventional CH···O Interactions for Perchlorate Remediation in Water. J. Am. Chem. Soc. 2023, 145, 21723–21728. [Google Scholar] [CrossRef]
  28. Liu, X.; Zhang, Z.; Shui, F.; Zhang, S.; Li, L.; Wang, J.; Yi, M.; You, Z.; Yang, S.; Yang, R.; Wang, S.; Liu, Y.; Zhao, Q.; Li, B.; Bu, X.; Ma, S. Porous Organic Cage as an Efficient Platform for Industrial Radioactive Iodine Capture. Angew. Chem. Int. Ed. 2024, ASAP. [Google Scholar] [CrossRef]
  29. Mal, P.; Breiner, B.; Rissanen, K.; Nitschke, J. R. White Phosphorus is Air-Stable within a Self-Assembled Tetrahedral Capsule. Science 2009, 324, 1697–1699. [Google Scholar] [CrossRef]
  30. Galan, A.; Ballester, P. Stabilization of Reactive Species by Supramolecular Encapsulation. Chem. Soc. Rev. 2016, 45, 1720–1737. [Google Scholar] [CrossRef]
  31. Montà-González, G.; Ortiz-Gómez, E.; López-Lima, R.; Fiorini, G.; Martínez-Máñez, R.; Martí-Centelles, V. Water-Soluble Molecular Cages for Biological Applications. Molecules 2024, 29, 1621. [Google Scholar] [CrossRef]
  32. Tapia, L.; Alfonso, I.; Solà, J. Molecular Cages for Biological Applications. Org. Biomol. Chem. 2021, 19, 9527–9540. [Google Scholar] [CrossRef] [PubMed]
  33. Casini, A.; Woods, B.; Wenzel, M. The Promise of Self-Assembled 3D Supramolecular Coordination Complexes for Biomedical Applications. Inorg. Chem. 2017, 56, 14715–14729. [Google Scholar] [CrossRef] [PubMed]
  34. Montà-González, G.; Bastante-Rodríguez, D.; García-Fernández, A.; Lusby, P. J.; Martínez-Máñez, R.; Martí-Centelles, V. Comparing organic and metallo-organic hydrazone molecular cages as potential carriers for doxorubicin delivery. Chem. Sci. 2024, 15, 10010–10017. [Google Scholar] [CrossRef]
  35. Sun, D.; Feng, X.; Zhu, X.; Wang, Y.; Yang, J. Anticancer Agents Based on Metal Organic Cages. Coord. Chem. Rev. 2024, 500, 215546. [Google Scholar] [CrossRef]
  36. Dou, W.-T.; Yang, C.-Y.; Hu, L.-R.; Song, B.; Jin, T.; Jia, P.-P.; Ji, X.; Zheng, F.; Yang, H.-B.; Xu, L. Metallacages and Covalent Cages for Biological Imaging and Therapeutics. ACS Mater. Lett. 2023, 5, 1061–1082. [Google Scholar] [CrossRef]
  37. Tapia, L.; Pérez, Y.; Carreira-Barral, I.; Bujons, J.; Bolte, M.; Bedia, C.; Solà, J.; Quesada, R.; Alfonso, I. Tuning pH-dependent Cytotoxicity in Cancer Cells by Peripheral Fluorine Substitution on Pseudopeptidic Cages. Cell Rep. Phys. Sci. 2024, 5, 102152. [Google Scholar] [CrossRef]
  38. Mosquera, J.; Henriksen-Lacey, M.; García, I.; Martínez-Calvo, M.; Rodríguez, J.; Mascareñas, J. L.; Liz-Marzán, L. M. Cellular Uptake of Gold Nanoparticles Triggered by Host–Guest Interactions. J. Am. Chem. Soc. 2018, 140, 4469–4472. [Google Scholar] [CrossRef]
  39. Rodríguez, J.; Mosquera, J.; Couceiro, J. R.; Nitschke, J. R.; Vázquez, M. E.; Mascareñas, J. L. Anion Recognition as a Supramolecular Switch of Cell Internalization. J. Am. Chem. Soc. 2017, 139, 55–58. [Google Scholar] [CrossRef]
  40. Hernández-López, L.; Von Baeckmann, C.; Martínez-Esaín, J.; Cortés-Martínez, A.; Faraudo, J.; Caules, C.; Parella, T.; Maspoch, D.; Carné-Sánchez, A. (bio)functionalisation of Metal–organic Polyhedra by Using Click Chemistry. Chem. Eur. J. 2023, 29. [Google Scholar] [CrossRef]
  41. Ling, Q.-H.; Lou, Z.-C.; Zhang, L.; Jin, T.; Dou, W.-T.; Yang, H.-B.; Xu, L. Supramolecular Cage-mediated Cargo Transport. Chem. Soc. Rev. 2024, 53, 6042–6067. [Google Scholar] [CrossRef] [PubMed]
  42. Nakabayashi, K.; Kawano, M.; Fujita, M. pH-Switchable Through-Space Interaction of Organic Radicals within a Self-Assembled Coordination Cage. Angew. Chem. Int. Ed. 2005, 44, 5322–5325. [Google Scholar] [CrossRef] [PubMed]
  43. Sivalingam, V.; Parbin, M.; Krishnaswamy, S.; Chand, D. K. Cage-to-Cage Transformations in Self-Assembled Coordination Cages Using “Acid/Base” or “Guest Binding-Induced Strain” as Stimuli. Angew. Chem. Int. Ed. 2024, 63, e202403711. [Google Scholar] [CrossRef] [PubMed]
  44. Benchimol, E.; Tessarolo, J.; Clever, G. H. Photoswitchable Coordination Cages. Nat. Chem. 2024, 16, 13–21. [Google Scholar] [CrossRef]
  45. Lee, H.; Tessarolo, J.; Langbehn, D.; Baksi, A.; Herges, R.; Clever, G. H. Light-Powered Dissipative Assembly of Diazocine Coordination Cages. J. Am. Chem. Soc. 2022, 144, 3099–3105. [Google Scholar] [CrossRef]
  46. DiNardi, R. G.; Douglas, A. O.; Tian, R.; Price, J. R.; Tajik, M.; Donald, W. A.; Beves, J. E. Visible-Light-Responsive Self-Assembled Complexes: Improved Photoswitching Properties by Metal Ion Coordination. Angew. Chem. Int. Ed. 2022, 61, e202205701. [Google Scholar] [CrossRef]
  47. Kennedy, A. D. W.; DiNardi, R. G.; Fillbrook, L. L.; Donald, W. A.; Beves, J. E. Visible-Light Switching of Metallosupramolecular Assemblies. Chem. Eur. J. 2022, 28, e202104461. [Google Scholar] [CrossRef]
  48. Lewis, J. E. M.; Gavey, E. L.; Cameron, S. A.; Crowley, J. D. Stimuli-responsive Pd2L4 metallosupramolecular Cages: Towards Targeted Cisplatin Drug Delivery. Chem. Sci. 2012, 3, 778–784. [Google Scholar] [CrossRef]
  49. Clegg, J. K.; Cremers, J.; Hogben, A. J.; Breiner, B.; Smulders, M. M. J.; Thoburn, J. D.; Nitschke, J. R. A Stimuli Responsive System of Self-assembled Anion-binding Fe4l68+cages. Chem. Sci. 2013, 4, 68–76. [Google Scholar] [CrossRef]
  50. Clegg, J. K.; Cremers, J.; Hogben, A. J.; Breiner, B.; Smulders, M. M. J.; Thoburn, J. D.; Nitschke, J. R. A Stimuli Responsive System of Self-assembled Anion-binding Fe4l68+cages. Chem. Sci. 2013, 4, 68–76. [Google Scholar] [CrossRef]
  51. Vasdev, R. A. S.; Findlay, J. A.; Garden, A. L.; Crowley, J. D. Redox Active [Pd2L4]4+ Cages Constructed from Rotationally Flexible 1,10-Disubstituted Ferrocene Ligands. Chem. Commun. 2019, 55, 7506–7509. [Google Scholar] [CrossRef] [PubMed]
  52. Lisboa, L. S.; Findlay, J. A.; Wright, L. J.; Hartinger, C. G.; Crowley, J. D. A Reduced-Symmetry Heterobimetallic [PdPtL4]4+ Cage: Assembly, Guest Binding, and Stimulus-Induced Switching. Angew. Chem. Int. Ed. 2020, 59, 11101–11107. [Google Scholar] [CrossRef] [PubMed]
  53. Barber, B. E.; Jamieson, E. M. G.; White, L. E. M.; Mcternan, C. T. Metal-peptidic Cages—helical Oligoprolines Generate Highly Anisotropic Nanospaces with Emergent Isomer Control. Chem 2024, 10, 2792–2806. [Google Scholar] [CrossRef]
  54. Liu, Y.; Liu, F.-Z.; Li, S.; Wang, P.; Wang, J.; Chu, Z.; Zhang, Z.; Yan, K. Guest Release from Coordination Assemblies in the Solid State. Chem 2024, 10, 1502–1515. [Google Scholar] [CrossRef]
  55. Martí-Centelles, V. Kinetic and thermodynamic concepts as synthetic tools in supramolecular chemistry for preparing macrocycles and molecular cages. Tetrahedron Lett. 2022, 93, 153676. [Google Scholar] [CrossRef]
  56. Lewis, J. E. M. Molecular Engineering of Confined Space in Metal–organic Cages. Chem. Commun. 2022, 58, 13873–13886. [Google Scholar] [CrossRef]
  57. Yang, X.; Ullah, Z.; Stoddart, J. F.; Yavuz, C. T. Porous Organic Cages. Chem. Rev. 2023, 123, 4602–4634. [Google Scholar] [CrossRef]
  58. Martí-Centelles, V.; Piskorz, T. K.; Duarte, F. CageCavityCalc (C3): A Computational Tool for Calculating and Visualizing Cavities in Molecular Cages. J. Chem. Inf. Model. 2024, 64, 5604–5616. [Google Scholar] [CrossRef]
  59. Piskorz, T. K.; Martí-Centelles, V.; Young, T. A.; Lusby, P. J.; Duarte, F. Computational Modeling of Supramolecular Metallo-organic Cages-Challenges and Opportunities. ACS Catal. 2022, 12, 5806–5826. [Google Scholar] [CrossRef]
  60. Tarzia, A.; Wolpert, E. H.; Jelfs, K. E.; Pavan, G. M. Systematic Exploration of Accessible Topologies of Cage Molecules via Minimalistic Models. Chem. Sci. 2023, 14, 12506–12517. [Google Scholar] [CrossRef]
  61. Young, T. A.; Gheorghe, R.; Duarte, F. cgbind: A Python Module and Web App for Automated Metallocage Construction and Host–Guest Characterization. J. Chem. Inf. Model. 2020, 60, 3546–3557. [Google Scholar] [CrossRef]
  62. Turcani, L.; Tarzia, A.; Szczypiński, F. T.; Jelfs, K. E. stk: An Extendable Python Framework for Automated Molecular and Supramolecular Structure Assembly and Discovery. J. Chem. Phys. 2021, 154, 214102. [Google Scholar] [CrossRef] [PubMed]
  63. Santolini, V.; Miklitz, M.; Berardo, E.; Jelfs, K. E. Topological Landscapes of Porous Organic Cages. Nanoscale 2017, 9, 5280–5298. [Google Scholar] [CrossRef]
  64. Greenaway, R. L.; Jelfs, K. E. High-throughput Approaches for the Discovery of Supramolecular Organic Cages. ChemPlusChem 2020, 85, 1813–1823. [Google Scholar] [CrossRef]
  65. Yang, Y.; Ronson, T. K.; Teeuwen, P. C. P.; Du, Y.; Zheng, J.; Wales, D. J.; Nitschke, J. R. Guest Binding Is Governed by Multiple Stimuli in Low-symmetry Metal-organic Cages Containing Bis-pyridyl(imine) Vertices. Chem 2024, ASAP. [Google Scholar] [CrossRef]
  66. Gunawardana, V. W. L.; Ward, C.; Wang, H.; Holbrook, J. H.; Sekera, E. R.; Cui, H.; Hummon, A. B.; Badjić, J. D. Angew. Chem. Int. Ed. 2023, 62, e202306722. [Google Scholar] [CrossRef]
  67. Conn, M. M.; Rebek Jr., J. Self-Assembling Capsules. Chem. Rev. 1997, 97, 1647–1668. [Google Scholar] [CrossRef]
  68. Quan, M. L. C.; Knobler, C. B.; Cram, D. J. Constrictive Binding by an Octalactone Hemicarcerand. J. 1991. [Google Scholar] [CrossRef]
  69. Bobbins, T. A.; Cram, D. J. Comparisons of Activation Energies for Guest Escapes from the Inner Phases of Hemicarcerands with Varying Numbers of Bowl-linking Groups. J. Chem. Soc., Chem. Commun. 1995, 15, 1515–1516. [Google Scholar] [CrossRef]
  70. Sheu, C.; Houk, K. N. Molecular Mechanics and Statistical Thermodynamics Studies of Complexes of a Flexible Hemicarcerand with Neutral Guests. J. Am. Chem. Soc. 1996, 118, 8056–8070. [Google Scholar] [CrossRef]
  71. Smulders, M. M. J.; Zarra, S.; Nitschke, J. R. Quantitative Understanding of Guest Binding Enables the Design of Complex Host–guest Behavior. J. Am. Chem. Soc. 2013, 135, 7039–7046. [Google Scholar] [CrossRef]
  72. Cram, D. J.; Jaeger, R.; Deshayes, K. Host-Guest Complexation. 65. Hemicarcerands that Encapsulate Hydrocarbons with Molecular Weights Greater than Two Hundred. J. Am. Chem. Soc. 1993, 115, 9879–10470. [Google Scholar] [CrossRef]
  73. He, S.; Quan, M.; Yang, L.-P.; Au-Yeung, H. Y.; Jiang, W. Kinetic–thermodynamic Correlation of Conformational Changes in Ammonium Complexes of a Flexible Naphthocage. Chem. Sci. 2024. [Google Scholar] [CrossRef] [PubMed]
  74. Houk, K. N.; Nakamura, K.; Sheu, C.; Keating, A. E. Gating as a Control Element in Constrictive Binding and Guest Release by Hemicarcerands. Science 1996, 273, 627–629. [Google Scholar] [CrossRef]
  75. Liu, F.; Helgeson, R. C.; Houk, K. N. Building on Cram’s Legacy: Stimulated Gating in Hemicarcerands. Acc. Chem. Res. 2014, 47, 2168–2176. [Google Scholar] [CrossRef]
  76. Escobar, L.; Escudero-Adán, E. C.; Ballester, P. Guest Exchange Mechanisms in Mono-Metallic PdII/PtII-Cages Based on a Tetra-Pyridyl Calix [4]pyrrole Ligand. Angew. Chem. Int. Ed. 2019, 131, 14277–14281. [Google Scholar] [CrossRef]
  77. Rieth, S.; Hermann, K.; Wang, B.-Y.; Badjić, J. D. Controlling the Dynamics of Molecular Encapsulation and Gating. Chem. Soc. Rev. 2011, 40, 1609–1622. [Google Scholar] [CrossRef]
  78. Ro, S.; Rowan, S. J.; Pease, A. R.; Cram, D. J.; Stoddart, J. F. Dynamic Hemicarcerands and Hemicarceplexes. Org. Lett. 2000, 2, 2411–2414. [Google Scholar] [CrossRef]
  79. Yoshizawa, M.; Kusukawa, T.; Fujita, M.; Yamaguchi, K. Ship-in-a-bottle Synthesis of Otherwise Labile Cyclic Trimers of Siloxanes in a Self-assembled Coordination Cage. J. Am. Chem. Soc. 2000, 122, 6311–6312. [Google Scholar] [CrossRef]
  80. Davis, A. V.; Raymond, K. N. The Big Squeeze: Guest Exchange in an M4L6 Supramolecular Host. J. Am. Chem. Soc. 2005, 127, 7912–7919. [Google Scholar] [CrossRef]
  81. Smulders, M. M. J.; Zarra, S.; Nitschke, J. R. Quantitative Understanding of Guest Binding Enables the Design of Complex Host–guest Behavior. J. Am. Chem. Soc. 2013, 135, 7039–7046. [Google Scholar] [CrossRef]
  82. R Core Team, version 4.0.5. R: A language and environment for statistical computing. R Foundation for Statistical Computing: Vienna, Austria, 2021. Available online: https://www.R-project (accessed on 16 September 2024).
  83. Studio Team. RStudio: Integrated Development for R, version 2022.02.3. RStudio, Inc.: Boston, MA, 2022. Available online: http://www.rstudio.com/ (accessed on 16 September 2024).
  84. Soetaert, K.; Petzoldt, T.; Setzer, R. W. Solving Differential Equations in R: Package deSolve. J. Statist. Soft. 2010, 33, 1–25. [Google Scholar] [CrossRef]
  85. Eyring, H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
  86. Gibb, C. L. D.; Li, X.; Gibb, B. C. Adjusting the Binding Thermodynamics, Kinetics, and Orientation of Guests Within Large Synthetic Hydrophobic Pockets. Proc. Natl. Acad. Sci. 2002, 99, 4857–4862. [Google Scholar] [CrossRef] [PubMed]
  87. Norjmaa, G.; Vidossich, P.; Maréchal, J.-D.; Ujaque, G. Modeling Kinetics and Thermodynamics of Guest Encapsulation into the [M4L6]12– Supramolecular Organometallic Cage. J. Chem. Infor. Model. 2021, 61, 4370–4381. [Google Scholar] [CrossRef]
  88. Prabodh, A.; Sinn, S.; Grimm, L.; Miskolczy, Z.; Megyesi, M.; Biczók, L.; Bräse, S.; Biedermann, F. Teaching Indicators to Unravel the Kinetic Features of Host–guest Inclusion Complexes. Chem. Commun. 2020, 56, 12327–12330. [Google Scholar] [CrossRef]
Preprints 120761 g001
Figure 1. Schematic representation of the encapsulation of a guest molecule driven by the association constant of guest into the molecular cage followed by the corresponding guest release. The equilibrium is shifted to the formation of the guest⊂cage complex or the release of guest depending on concentration, association constant, and energy barriers. The energy profile of both guest encapsulation and release is also shown.
Figure 1. Schematic representation of the encapsulation of a guest molecule driven by the association constant of guest into the molecular cage followed by the corresponding guest release. The equilibrium is shifted to the formation of the guest⊂cage complex or the release of guest depending on concentration, association constant, and energy barriers. The energy profile of both guest encapsulation and release is also shown.
Preprints 120761 g001
Preprints 120761 g002
Figure 2. Dissociative mechanism of a guest⊂cage complex with the corresponding equilibrium constant and differential rate law for the reversible encapsulation reaction.
Figure 2. Dissociative mechanism of a guest⊂cage complex with the corresponding equilibrium constant and differential rate law for the reversible encapsulation reaction.
Preprints 120761 g002
Preprints 120761 g003
Figure 3. Percentage of encapsulated guest at different guest⊂cage concentrations after dilution considering different association constant values. (a) Dilution of a solution containing the guest⊂cage complex. (b) Dilution of a solution containing the guest⊂cage complex and an excess cage with a total cage concentration of 25 µM.
Figure 3. Percentage of encapsulated guest at different guest⊂cage concentrations after dilution considering different association constant values. (a) Dilution of a solution containing the guest⊂cage complex. (b) Dilution of a solution containing the guest⊂cage complex and an excess cage with a total cage concentration of 25 µM.
Preprints 120761 g003
Preprints 120761 g004
Figure 4. Guest release kinetics of from guest⊂cage complexes (1 µM) with different activation barriers for: (a) Guest–cage association constant of 103 M–1, (b) Guest–cage association constant of 106 M–1.
Figure 4. Guest release kinetics of from guest⊂cage complexes (1 µM) with different activation barriers for: (a) Guest–cage association constant of 103 M–1, (b) Guest–cage association constant of 106 M–1.
Preprints 120761 g004
Preprints 120761 g005
Figure 5. Guest release kinetics of from guest⊂cage (1 µM) complexes with an activation barrier of 26 kcal/mol in the gate closed state that is reduced to 23 kcal/mol in the gate open state in response to a stimulus for: (a) Guest–cage association constant of 103 M–1, (b) Guest–cage association constant of 106 M–1.
Figure 5. Guest release kinetics of from guest⊂cage (1 µM) complexes with an activation barrier of 26 kcal/mol in the gate closed state that is reduced to 23 kcal/mol in the gate open state in response to a stimulus for: (a) Guest–cage association constant of 103 M–1, (b) Guest–cage association constant of 106 M–1.
Preprints 120761 g005
Preprints 120761 g006
Figure 6. Guest release kinetics of guest⊂cage (1 µM) complexes with an activation barrier of 26 kcal/mol in the gate-closed state, which is reduced to 23 kcal/mol in the gate-open state in response to a stimulus, with the simultaneous reduction of the guest–cage association constant.
Figure 6. Guest release kinetics of guest⊂cage (1 µM) complexes with an activation barrier of 26 kcal/mol in the gate-closed state, which is reduced to 23 kcal/mol in the gate-open state in response to a stimulus, with the simultaneous reduction of the guest–cage association constant.
Preprints 120761 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated