Prerpints.org logo
Preprint
Article

Experimental Parametric Study on the Primary Efficiency of a Fixed Bottom-Detached Oscillating Water Column Wave Energy Converter in Short-Fetch Sea Conditions

This version is not peer-reviewed.

Submitted:

10 October 2024

Posted:

11 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
The Oscillating Water Column (OWC) represents a highly promising approach for wave energy conversion. This study presents laboratory experiments conducted on a fixed, bottom-detached OWC device to evaluate the impact of various geometric parameters (specifically, turbine damping, front wall draft, and chamber length in the direction of wave propagation) on the device's capture width ratio. Despite the extensive research over the past few decades on OWC devices, most studies and field-tested prototypes have been designed for long-fetch sea conditions. Consequently, these devices tend to be larger in size and have higher rated power outputs. In contrast, short-fetch sea conditions necessitate tuning the OWC to the shorter dominant wave frequencies, which calls for the development of smaller devices and specialized turbines, highlighting the need for focused research. This work specifically addresses short-fetch sea conditions, which are representative of moderate wave climates, such as those found in the Central Mediterranean region. The study identifies a maximum capture width ratio of approximately 73%. The experimental dataset generated can serve as a benchmark for numerical models under these specific conditions and assist in the development of air turbines optimized for effective performance in short-fetch wave climates.
Keywords: 
Subject: 
Engineering  -   Marine Engineering

1. Introduction and Motivations

The Oscillating Water Column (OWC) Wave Energy Converter (WEC) is one of the most promising devices for the exploitation of the wave energy resource (Falcao & Henriques, 2016, Ozkop et al. 2017). It is a rigid structure that incorporates a hollow chamber partially immersed into the sea. The OWC-WEC can be a floating or a fixed device and even if the principle for energy harvesting is the same, the design parameters that play a major role for its optimization are quite different. The present work focuses on fixed OWC-WECs. In this case, the external wave motion propagates its dynamical effects inside the chamber through the lower opening, inducing a pulsating pressure field on the internal water column, causing its oscillation. The oscillation of the water column acts as a piston on the upstanding air column, creating a pulsating pressure field which, in turn, generates an alternating airflow through the conduit connected with the atmosphere. As such, the power of the wave motion is converted in the power of the alternating airflow. The efficiency of this process is called hereafter primary efficiency. Most often, fixed OWC-WECs are proposed as bottom-founded onshore devices. However, a fixed bottom-detached configuration may be more economically viable in deep waters, particularly when supported by piles or integrated into tension-leg moored floating platforms for multipurpose. In this latter case, the frontal and back walls can be asymmetrical, with the frontal wall being relatively short to allow wave-induced dynamic pressure to excite the internal water column, and the back wall being relatively long to intercept most of the wave energy distributed along the water depth. This paper focuses on fixed bottom-detached OWC-WECs."
In any case, the alternating airflow power can be harvested with self-rectifying air turbines (Falcao et al., 2018) and electricity can be generated with electrical generators. This further assembly of devices constitutes the Power Take Off (PTO) component of the OWC-WEC. The alternating airflow could also be rectified by using non-return air valves. This approach, although of proven effectiveness and robustness for small devices e.g. navigation buoys (Masuda, 1971 & Masuda 1986), is unpractical for larger devices (Whittaker et al, 1984; Falcao & Gato, 2012) and was progressively abandoned. The PTO conversion processes have their own efficiency (i.e., the secondary efficiency). To maximize the overall OWC-WEC performance, from waves to wire, the maximization of both the primary and the secondary efficiencies is needed.
Under the excitation of given wave conditions, the dynamics of the water column, and consequently the primary efficiency, depends on its hydrodynamic and inertial properties, which are in turn function of its shape and size (McCormick, 1981; Evans and Porter, 1995; McCormick, 2007). Each water column has its specific natural frequency of oscillation, and the resonant behaviour occurs when the frequency of the incident wave motion approaches the device natural frequency. A possible approach to promote resonance with given wave conditions is that of varying the length of the water column, thus altering its inertial properties. The proposals for L- or U-shaped OWCs (Masuda et al., 1987; Boccotti, 2007), which deviate from the conventional prismatic design, are grounded in this fundamental principle. Moreover, since the wave frequencies are strongly related to the fetch length and the size of the storms that characterize a given sea basin, tuning the OWC size to site-specific wave conditions is fundamental to maximize the primary efficiency.
Concerning the PTO, a given turbine imposes a specific relation between the airflow and the air pressure drop (Falcao et al., 2014), and the water column adapts its dynamics to such conditions. This two-way interaction between water column dynamics and turbine characteristics highlights the complexity of the fluid dynamics affecting primary efficiency. Therefore, designing a turbine that optimizes the airflow-pressure drop relationship to maximize primary efficiency, while operating at its highest possible efficiency, is crucial.
Although the OWC concept for wave energy harvesting was proposed several decades ago, only a limited number of full-size prototypes have been built for research or demonstration purposes (e.g., Ohneada et al., 1991; Ravindran et al. 1991; Heath et al., 2000; Falcao, 2000; Suzuki et al., 2004; Alcorn et al., 2005; Torre-Enciso et al., 2009). Thousands of oceanic buoys with their light powered by the OWC concept have been deployed since 1965 and continued working for decades (Masuda,1971; Whittaker et al., 1985; Falcao & Henriques, 2016). In the following years, many efforts were made to scale-up the size of this device and to harvest a larger amount of wave energy, with the goal of playing a significant role in the renewable energy sector. However, the commercial phase has not been reached yet.
Almost all the studies and the field-tested prototypes of OWC-WEC concern long-fetch sea conditions, i.e. long-waves, therefore the size of the devices and the rated powers are relatively big. In short-fetch sea conditions, tuning the OWC to the characteristic wave frequencies implies the development of smaller devices and specific turbines, and thus, focused research is mandatory. The short-fetch sea condition is the framework of the present work.
Economic, reliability, and operability concerns remain key factors limiting the commercial diffusion of the OWC technology. The development of floating and offshore OWC devices presents additional challenges, including mooring, energy transmission, survivability in extreme waves, and maintenance. Moreover, the development of multifunctional nearshore structures, such has harbour breakwaters embodying OWC or other WECs, assures the sharing of construction costs decreasing the capital and the operational expenses for the energy devices (Mustapa et al., 2017; Vicinanza et al., 2019; Simonetti & Cappietti 2021). As a result, the opportunities to locate nearshore energy hotspots (Iglesias & Carballo, 2010, Vicinanza et al., 2013, Hadadpour et al., 2014; Vannucchi and Cappietti, 2016) and share construction costs with other maritime structures have renewed interest in advancing fixed and nearshore OWC-WEC devices, particularly for niche markets.
The sizing of such kind of OWC-WEC for site-specific wave conditions, along with the optimization of the primary efficiency, appears as one of the most urgent and fundamental improvements to achieve. Further enhancements, such as the development of L- or U-shaped OWC designs (Boccotti, 2007; Arena et al., 2013; Ribeiro e Silva et al., 2016), the use of dielectric elastomer as PTO (Moretti et al., 2015) or the more recent proposals of hybrid devices embodying OWCs with a different WEC concept (Cappietti et al., 2018; Cabral et al., 2020; Simonetti et al., 2022), represent promising directions for further improvements.
Despite the research activities carried out so far on fixed, nearshore OWCs, research at a fundamental level is still needed, particularly concerning the site-specific dimensioning and the optimization of the primary efficiency joined with the optimization of the turbine efficiency. Moreover, as aforementioned, site-specific studies most frequently refer to sea states representative of highly energetic wave climates (e.g. Oceanic ones), characterized by higher and longer waves than those of short fetch (or moderate) wave climate as the Mediterranean or the North Sea.
Laboratory experiments are crucial for analysing the performance of the device, especially in capturing non-linear phenomena, turbulence, and real fluid effects often overlooked in theoretical or numerical approaches. They are also essential for benchmarking and validating Computational Fluid Dynamics (CFD) models, which may be used for refined optimizations OWC-WECs (as shown by Simonetti et al., 2017).
With the aim of contributing to the development of the OWC-WEC and providing the research community with a specific database of laboratory results for benchmarking CFD models, this work focuses on near-shore, fixed, prismatic OWCs equipped with a conventional PTO system (i.e. an air turbine), under short fetch sea conditions. This work also aims to provide the second-order functional relationships between the airflow and the air pressure drop that maximize the primary efficiency. Such second-order functions are proposed to the mechanical engineers’ research community to support the development of efficient self-rectifying impulse turbines able to provide the same functional relations. To the authors’ knowledge, direct measurements of the airflow velocity during the inhalation and exhalation phases are not provided in the literature. The present database includes such measurements, strengthening the possibility of using it to benchmark numerical models.
The paper is structured as follows: an overview previous laboratory experiments on fixed OWCs is given in Section 2. Section 3 describes the laboratory experiments, including the tested OWC models, wave conditions, and the laboratory methodology. Section 4 presents the results, detailing experimental measurements of the key variables that significantly impact the primary efficiency of the OWC. Conclusions and suggestions for future work are summarized in Section 5.

2. State of the Art on Laboratory Tests on Fixed OWC Devices

Early laboratory experiments on two-dimensional fixed OWC are documented by Count et al. (1981), Robinson et al. (1981) and Maeda et al. (1985). In these works, for the first time, the presence of a turbine with non-linear airflow-pressure drop relation was simulated by using orifices and results were compared with linear theory predictions. Sarmento (1992) performed laboratory tests on simple two-dimensional OWC geometries, to assess the validity of linear wave theory predictions (Sarmento and Falcao, 1985). The effect of both linear (e.g., the Wells turbine, Raghunathan 1995) and non-linear (i.e. impulse turbines, McCormick, 1979; Richards & Weiskopf, 1986) PTOs was tested, respectively by using a porous filter and an orifice. This experimental approach has become the standard for laboratory tests in the following years and it is also adopted in the laboratory experiments documented in the present work. In all these early works, simplified geometries were tested under incident waves within the limits of applicability of linear wave theory.
Later, Sarmento (1993) studied the shoreline PICO-power plant on a 1:35 scale model, with the aim to optimize its geometry under irregular waves representative of the wave climate of the installation site (i.e., the Azores islands, therefore long-fetch wave conditions were studied). Also, in this case due to the relatively small-scale ratio, it was preferred to mimic the effect of a Well turbine on the OWC dynamics instead of including a scaled turbine model. This study showed that for an optimized size of the OWC chamber it is possible to find an optimum value of the air pressure drop induced by the turbine, which allows the higher primary efficiency. Moreover, the strong sensitivity of primary efficiency on the OWC front wall draught was highlighted.
Morris-Thomas et al. (2007) also studied the effect of the OWC geometry on the hydrodynamic performance of a shore-based OWC through laboratory tests (at model scale 1:12.5) under the action of regular waves suitable for description by linear wave theory. The tests focused on the effect of front wall draught and thickness on the OWC. A square vent located on the roof of the chamber imposed a second-order relation between the airflow and the pressure drop, simulating the presence of a non-linear turbine. Their results demonstrated that the hydrodynamic performance is not prominently influenced by the front wall thickness, and that, for relatively short waves, the OWC efficiency increases when the front wall draught decreases.
Sheng et al. (2012) investigated the primary efficiency using laboratory tests on a fixed cylindrical OWC under regular waves covering a wide range of wave periods (with a ratio of the OWC diameter to the incident wavelength between 0.2 and 0.015). The sensitivity to different non-linear turbines was studied by simulating each turbine with a circular-shaped vent. Several vents were tested, with ratios between their area and the horizontal area of the water column between 0.5%-2.0%. This study stressed the importance of the OWC dimensions to obtain an appropriate wave energy extraction, confirming as the most relevant parameter the draught of the frontal wall, which strongly influences the OWC natural frequency. The study also highlighted significant practical limitations in sizing the OWC sectional area, recommending that, to prevent sloshing motions, which cause energy losses, the length of the OWC chamber in the direction of the waves should not exceed 1/4 to 1/5 of the incident wavelength.
Lopez et al. (2012); López & Iglesias (2014) and López et al. (2015) used laboratory tests in a wave flume (with a scale factor 1:25) to calibrate and validate a numerical model. The OWC model was tested under both regular waves and irregular waves, with characteristics representative of the western Oceanic coast of Spain, i.e. for long fetch waves. Different non-linear turbines were simulated by means of circular vents on the top cover. They observed that the primary efficiency increases with the wave steepness at low wave frequencies, while decreasing at high wave frequencies. Their results also confirmed the importance of studying the coupling between the chamber and the air turbine effects to optimize the device performance by adapting the turbine specifications to the chamber geometry and the wave climate (as further explored by the same authors employing numerical modelling in Lopez et al., 2015b and Pereiras et al., 2015).
Iturrioz et al. (2014) and (2015) developed and validated a CFD model in the open source code IHFOAM with flume experiments to study the hydrodynamics and pneumatics around a fixed detached OWC. Their laboratory tests were performed with a scale factor 1:30. A set of regular and irregular waves were tested, representative of relatively long-fetch seas (with periods up to 17 s at full scale). Also in this case, different circular vents were used to simulate a non-linear PTO, highlighting the complexity of the flow conditions and relevant differences between the process of air inhalation and exhalation, which could not be simulated by using simplified modelling approaches.
Ning et al. (2016) performed laboratory tests on a fixed OWC model, to assess the effects on the OWC performance of: incident regular wave amplitude, chamber length, front wall draught, non-linear turbine simulated with different circular vent sizes, bottom slope. They explored a range of relative water depth kh (being k the wave number and h the water depth) between 0.85 and 3.6 and wave steepness between 0.006 and 0.1. They found a relevant relation between wave non-linearity and the primary efficiency, with the OWC performance at first increasing with the wave amplitude, reaching a maximum for a certain value and then decreasing. Moreover, they found that when the chamber width increases, the OWC performance increases for low-frequency waves. As observed in many of the previous studies, the front wall draught and the turbine airflow-pressure drop relation strongly affect the device performance. Their study confirmed that a deeper frontal wall leads to a lower resonant frequency and a lower primary efficiency, and that the optimal efficiency occurs for a given airflow-pressure drop relation.
Vyzikas et al. (2016) performed laboratory tests on four different shapes of the OWC device, under regular and irregular waves, to suggest potential shape improvements towards the optimization of the device. In their work, better performance was found when using the so-called U-OWC principle (Boccotti, 2007), with an increase in the capture with ratio up to 30% with respect to the standard OWC, under a specific wave condition. However, since a fixed value of the design parameters (draught, damping, chamber width) was considered for each OWC shape, and under a limited set of weave conditions, further studies are needed to generalize these results.
He et al. (2014) performed laboratory tests at 1:25 model scale on a fixed bottom-detached and pile-supported OWC, focusing particularly on the vortex induced energy losses taking place for different airflow-pressure drop relations of the turbine (i.e., different values of the applied PTO damping) and of the front wall draught. The tested wave conditions (periods, at full scale, between 5 s and 8 s and height of 0.9 m) can be considered representatives of short fetch seas. They found that larger damping levels were preferable to increase the energy extraction and to reduce vortex-induce energy losses.
Elhanafi et al. (2017) performed laboratory tests on three-dimensional 1:50 scale models of bottom-detached tension-legs moored OWCs. The effect of a non-linear air turbine was simulated with the usual approach of circular vents. The set of hydrodynamic conditions tested in the laboratory were representative of Bass Strait in southern Australia, with periods between 7 and 14 s and heights between 2.5 and 5 m (i.e. a relatively long fetch wave climate). The tests were also aimed at validating a CFD model to be used for further analysing the OWC performance (Elhanafi et al., 2017b and 2017c). The impact on the primary efficiency of the airflow-pressure drop relation applied by the turbine and of the device geometry was studied. The authors confirmed again that the turbine characteristics are crucial and fundamentally related to the wave climate, and that an increase in device performance can be achieved by adopting asymmetric back and front walls.
Laboratory experiments at a relatively large scale (1:5-1:9) were performed by Viviano et al. (2016), with the aim of investigating the wave reflection coefficient (in random wave conditions) for OWC integrated into vertical breakwaters. A value of the circular vent size, i.e. of the turbine airflow-pressure relation, which minimize the reflection coefficient (to a value of 0.5) was found. The same dataset was later used to formulate a prediction formulae of wave loads acting on the OWC front wall (Pawitan et al., 2019).
Ashlin et al. (2018) studied an array of five OWCs integrated in a detached breakwater with a set of laboratory tests at 1:20 model scale. They considered regular waves only, and studied the effect of different wavelength, steepness and spacing between the chambers with fixed values of the other design parameters. The authors found relevant three-dimensional effects of wave convergence and focusing in front of the array, causing an increase in the absorbed wave power compared to the case of an isolated device. The importance of wave concentration phenomena has been also experimentally studied by David et al. (2018), who tested a 1:20 scaled model of a bottom-standing OWC with different inclinations of vertical walls located in front of the OWC model resembling collectors to focalize the incident wave energy.
Zabihi et al. (2019) tested a fixed offshore OWC model at scale 1:15, under irregular waves with significant heights between 1.5 and 4.5 m at full scale, and peak periods between 6 and 10 seconds. The authors studied the sensitivity of the primary efficiency to the main design parameters (i.e. front wall draught, turbine damping), highlighting relevant non-linear effects related to the incident wave heights, with lower performance for higher waves. For fixed wave parameters, the shape of the incident wave spectrum was found to affect the primary efficiency, with better performance for Pierson–Moskowitz spectrum rather than JONSWAP spectrum.
Çelik and Altunkaynak (2019) performed a test campaign on a fixed OWC (model scale 1:30) varying the dimeter of the circular vent simulating the turbine, the chamber draught and the incident wave steepness. Regular waves were tested, having at full scale height between 1.2 and 3.6 m and periods of 6 to 10 s. The authors confirmed that the optimal turbine applied damping for the chamber depends on both the incident wave steepness and the chamber draught.
Ning et al. (2019) tested a 1:20 scale model of a fixed, dual-chamber OWC device, assessing the effect of its width, draught, and incoming wave conditions on performance. A fixed-opening circular vent was used to reproduce the turbine behaviour. The tested wave conditions (wave height of 1.2 m and periods ranging between 5 and 10 s at full scale) can be representative of short fetch wave climates. The authors found that dual-chamber devices may have better performance than single-chamber ones, with an increased effective frequency bandwidth. They further stressed the fundamental relevance of sizing the device according to the reference wave climate.
Lopez et al., 2020, performed laboratory tests on a two-dimensional model of a fixed, breakwater-integrated OWC at scale 1:25. The focus of the tests was evaluating air compressibility scale effects (previously discussed, e.g. in Falcao et al., 2014 and Simonetti et al., 2018) for a device equipped with a circular vent -simulated non-linear PTO. For this purpose, the OWC chamber was tested also connected to an external air-volume reservoir. A wide range of wave conditions were tested (heights of 0.5-2 m and periods of 5-15 s at full scale). Differences in the primary efficiency up to 30% due to air compressibility were noticed in such a study. Furthermore, the authors highlighted a significant influence of the turbine-applied damping and the wave height on the efficiency, both governed by the incident wave period.
Liu et al. (2020) performed flume experiments on a fixed rectangular-shaped OWC model (chamber planar size: 0.6 x 0.8 m) including a scaled model of an impulse turbine (with a tip diameter of 11.8 cm), tested at different rotational speeds. Both the primary and the secondary efficiencies were measured, with peak values of 67% and 24% respectively. The authors concluded that, due to manufacturing complexity, the tested turbine size could not be further reduced to match the optimal damping required for the primary efficiency maximization.
Zhao et al., 2021, experimentally investigated the performance of a single, dual and triple chamber fixed OWC, performing Froude-scaled tests at scale 1:20 under regular waves with periods of 5-8 s and height of 1 m. The authors found that the capture width ratio of the multi-chamber device is higher than that of the single chamber configuration. Sun et al., 2023, performed tank tests on a bottom fixed OWC equipped with an orifice (ratio of the orifice area to the horizontal cross-sectional area of the air chamber of 0.66%) to reproduce a quadratic PTO. The authors underlined relevant 3D-effects and a strong sensitivity of the device’s performance to the incident wave direction (with relative decreases in the capture with up to 20% for a variation of 30° in the incident wave direction). More recently, Liu et al. 2024 compared flume and tank tests of a fixed, isolated OWC model Froude-scaled at 1:15, concluding that a decrease of the performance of about 20% was observed in tank tests. The OWC model included a small scale self-rectifying air turbine as PTO, also proposing a correction method to be applied to the turbine performance to account for the unavoidable distortions in the Reyolds number between model and prototype. In this study, however, the size of the turbine model was not optimized to match the OWC chamber optimal functioning, which resulted in a relatively low capture width ratio.
From the previous studies reviewed, it can be stressed that:
i)
The hydrodynamic and energy-harvesting performances are still mainstream in the research related to the OWC devices. Site-specific studies are fundamental, and most of the previous studies refers to long-fetch wave conditions which may be significantly different from short-fetch ones (e.g. those of the Mediterranean or Noth Sea).
ii)
Matching studies between the chamber and PTO damping are still needed, to provide the manufacturer with the target characteristic functioning of the air-turbine to be designed to maximize both the primary and secondary efficiency of the device. Most of the studies on the OWC plant uses the orifice or porous media to represent the PTO, given the scaling issues unavailable for the air-turbine component. In these studies, the PTO is often characterized in terms of opening-ratios only (i.e., the ratio of the area of the orifice to that of the cross section of the OWC chamber). The damping coefficient, establishing the relation between the air chamber pressure and airflow rate, is often disregarded, while it could provide a more meaningful information for the air turbine’s manufacturing.
The present study aims to provide a database which contributes to fulfil such gaps.

3. Description of Laboratory Tests

Laboratory experiments were carried out at the Maritime Engineering Laboratory (LABIMA) of the Civil and Environmental Department (DICEA) of Florence University and the OWC model was tested in the LABIMA Wave-Current Flume 1 (WCF1). The WCF1 is 37 m long, 0.80 m wide and has a maximum operational water depth of 0.60 m. Wave motions are generated by a piston-type wave maker and absorbed at the other end of WCF1 through a porous structure.

3.1. Model Description

The OWC model is a 20 cm wide hollow, prismatic, and rectangular-shaped box with vertical walls. The model was built by using Perspex sheets 8-10 mm thick, to allow the observation of the water column kinematic behaviour inside the OWC chamber during the tests. Moreover, cylindrical vent ducts with a length of 10 cm and different diameters, located on the roof of the model, were used to simulate a set of non-linear PTOs. To avoid air losses affecting the behaviour of the device, the air chamber was made water- and airtight by using silicone as sealing. An assembly composed of three adjacent OWC chambers, equipped with two flaps connected at its sides (9 cm wide each), formed the 78 cm-wide model that was installed and tested in the flume (Figure 1 and Figure 3). The model was firmly connected to a system of rigid steel bars in turn fixed to the flume side walls, forming a stationary assembly of three OWC chambers kept fixed 22 m away from the wave generator. The central OWC chamber was equipped with sensors for measuring the fundamental quantities for the analysis of the primary efficiency.

3.2. Variable Model Design Parameters for the Parametric Study

Owing to their key role, as emerged by the state of the art literature reviewed in Section 2, this work focused on the evaluation of the effect of: i) 3 sizes of the chamber length, W; ii) 3 values of the front wall draught, D and iii) 9 circular vent duct diameters, V, with an aperture equal to 0.5%, 1% and 2% of the OWC horizontal section area (see Section 2.2.1). Overall, 36 OWC alternatives were studied comprising the 9 alternatives in the absence of the vent and each configuration was teste dunder different wave conditions for a total of 288 different tests.
The other design parameters had fixed values, as follows: the chamber width B, was 0.20 m; the freeboard, Fc was 0.16 m above the still water level; the flume water depth was 0.50 m; the OWC was detached from the flume bottom about 0.21 m and the draught of the back wall was 0.29 m below the Still Water Level (SWL).
The draught of the back wall was chosen to allow to intercept about 90% of the incident wave power along the water depth, in the tested wave conditions, promoting the wave reflection, thus amplifying the water column oscillations. The values of fixed and varied design parameters are summarized in Table 1.

3.2.1. PTO Modeling

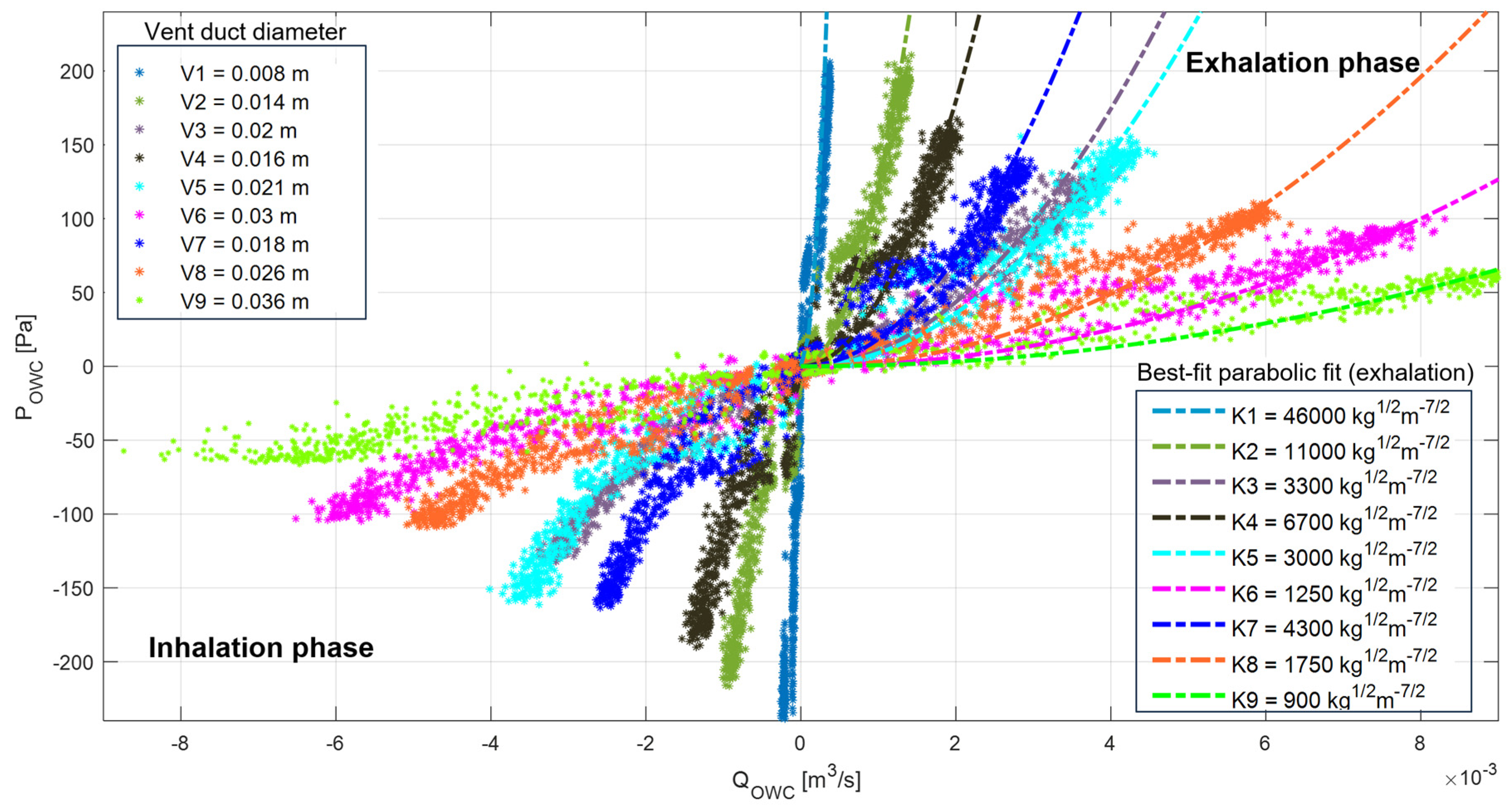
The effect of a self-rectifying impulse turbine, conceived to equip the OWC at the prototype scale, is reproduced using a circular vent duct on the top cover of each OWC chamber. This study investigates different relations between the air pressure drop and the airflow rate, obtained by varying the vent diameter (as in Table 1). By using circular vents, non-linear PTOs having a quadratic relation between the airflow rate, QOWC and the air chamber pressure POWC, were simulated. The experimental measurements of such functional dependence demonstrate the effectiveness of this laboratory technique for reproducing non-linear PTOs. The instantaneous of QOWC and POWC sampled at 50 Hz are depicted in Figure 2. On the base of a second order dependence, is it possible to fully define the PTO associated to each vent duct diameter V as a damping coefficient, K= P O W C / Q O W C (with a determination coefficient R2 higher than 0.8 for each case). It is worth noting that a relevant asymmetry is observed between the inhalation phase and the exhalation phase in the laboratory tests (with K determining the best fit for the exhalation phase always lower than that for the inhalation phase, with relative differences between 7 and 30%). The damping coefficients calculated from the instantaneous values of QOWC and POWC measured in laboratory are reported in Table 2, for both the inhalation and the exhalation phase. In the following, we will refer to the K-value representing the best fit for the exhalation phase only (K1-K9).
Furthermore, the experimental measurements proved that the damping coefficient cannot be correlated to the ratio between the vent duct area and the OWC horizontal section area: even when the same ratio is imposed, the measured damping coefficient (i.e. the simulated PTO) can be extremely different if a different vent duct size is considered. The damping coefficient is very well correlated to the vent duct diameter, as it can also be modelled by the Darcy-Weisbach equation for head pressure losses (Eq. 1).
Δ P ρ g = λ V 1 2 g Q 2 Ω 2  
In the present case Δ P = P O W C and Q = Q O W C and so K = 2 2 ρ λ / π     V − 5 2   , where V is the went duct diameter and λ is function of duct roughness and also of the Reynolds number when the flow regime is not fully turbulent.

3.3. Instrumentation and Data Acquisition

The wave motions time series along the flume were measured by means of six ultrasonic distance sensors (wave gauges, WGs) at a sampling frequency of 1 kHz and positioned as in Figure 3. Such a high sampling frequency was required solely for the measurements of the airflow in the vent duct, which was conducted by using hot-wire anemometers. However, since all sensors were connected to the same the acquisition system, it was preferred to synchronize all the measurements with the same sampling frequency. The first wave gauge (WG1) was placed about 3.5 m from the wave maker, to measure the generated waves, while incident and reflected waves were measured by three wave gauges (WG2, WG3 and WG4) located about one wavelength from the OWC model frontal wall. The transmitted waves were acquired by placing two wave gauges (WG6 and WG7) behind the model. The distance of each wave probe from the model and the wave generator was fixed based on the two-point method, proposed by Goda & Suzuki (1995), to separate incident and reflected waves and to determine their amplitude and phases.
As for the physical processes involved within the device, the central OWC chamber of the OWC array was equipped as follows (Figure 4):
i)
one ultrasonic distance sensor (WG5) to measure the water column oscillations, ηOWC(t) [m];
ii)
one relative pressure transducer (PT), to measure the air pressure drop POWC(t) [Pa] and
iii)
one hot-wire anemometer (HW), to measure the airflow velocity UOWC(t) [m/s].
Preprints 120876 g003
Figure 3. Experimental setup indicating the locations of the OWC model and the wave probes (WG), the hot wire anemometer (HW) and the pressure transducer (PT) along the wave-current flume.
Figure 3. Experimental setup indicating the locations of the OWC model and the wave probes (WG), the hot wire anemometer (HW) and the pressure transducer (PT) along the wave-current flume.
Preprints 120876 g003
Preprints 120876 g004
Figure 4. Sketch of the experimental setup for the investigation of the processes involved within the central OWC of the model segment: wave probe (WG), pressure transducer (PT) and hot-wire anemometer (HW).
Figure 4. Sketch of the experimental setup for the investigation of the processes involved within the central OWC of the model segment: wave probe (WG), pressure transducer (PT) and hot-wire anemometer (HW).
Preprints 120876 g004

3.4. Wave Conditions

The 36 OWC alternatives (27 geometries with different vent diameters and 9 geometries with the vent totally closed) were tested under three regular waves (H=0.04 m and 0.8 s ≤ T ≤ 1.4 s) and five irregular waves (0.02≤Hs≤0.06 m and 0.9≤Tp≤1.1 s), for a total of 288 tests. The characteristics of the waves are shown in Table 3, with H and f being the wave height and the frequency, respectively on a water depth of 0.50 m. The values of the regular and the irregular waves were selected referring to sea states representative of a moderate wave climate site located in the Mediterranean area (central Tuscany), having mean annual wave power of about 3 kW/m. As pointed-out in the reviewed literature, sizing an OWC-WEC for specific sea states is of pivotal importance for enhancing its performance in the exploitation of the wave energy resource. For this reason, the present experimental work was framed in the specific Mediterranean wave conditions, as previously assessed in Vannucchi and Cappietti, 2016.
Each regular wave test had a duration of 60 s (i.e. about 14-20 wave periods). The five irregular waves tested had a duration of 90 s (i.e. about 80-100 wave periods). In each case, a pre-trigger time of 10 s before wave generation was allotted to record the zero values of each sensor. A JONSWAP wave energy spectrum (Hasselmann et al., 1973) was chosen, with a peak enhancement factor, γ=3.3 (representative of fetch-limited wave conditions).
The effective incident wave condition was assessed by generating each wave attach (regular and irregular) in absence of the model in the flume (W0D0V0 tests) and acquiring the wave motion through an ultrasonic wave probe (WG5) located at the centre of the removed model position, i.e. exactly at the same location where the WG embodied into the OWC model measures the oscillation of its internal free surface. For each simulated wave, the characteristic wave parameters were measured by using a time window during which the local wave motion was fully developed and the residual reflected wave motion, coming from the passive absorber located at the end of flume, had not reached the WG position yet. Time domain analysis was used for the regular waves and frequency domain analysis for the irregular waves (Table 3). In the present work, only the analysis of the results obtained for regular wave tests (Wave 1, Wave 2 and Wave 3 in Table 3) are presented.

3.5. Data Acquisition and Analysis

3.5.1. Assessment of the Natural Frequency of the OWC

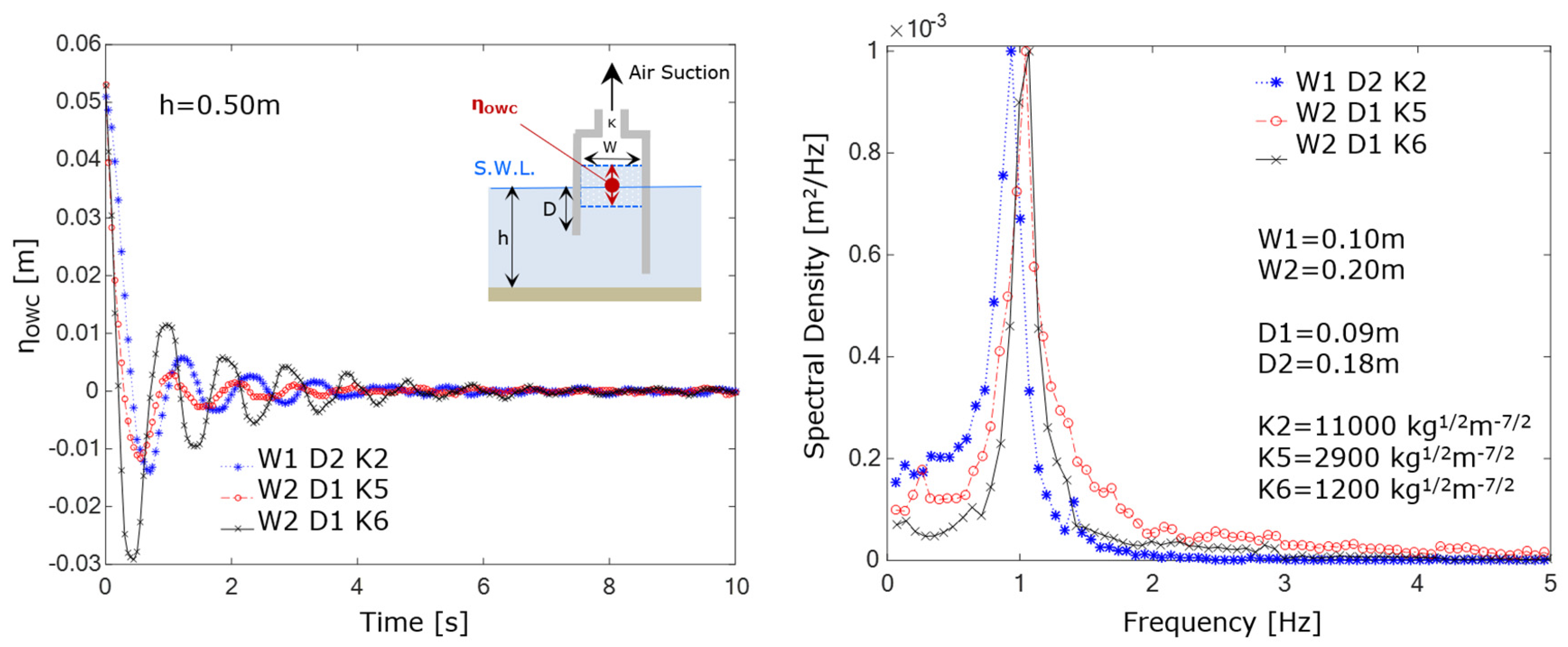
The performance of an OWC, in terms of wave energy harvesting, may be improved by tuning the OWC device to the incident wave frequency. Generally, the resonance frequency of the device is estimated from the draught of its front wall (D) with approximated formula (Evans and Porter, 1995; McCormick 2007). In this study, additional free decay tests (called hereafter RES tests), were performed to assess the natural frequency of each OWC alternative. The use of free decay tests to estimate the OWC resonance frequency is quite limited (Simonetti et al., 2015; Vyzikas et al., 2017b; Çelik and Altunkaynak, 2020). Simonetti et al., 2015, applied a Frequency Domain Analysis (FDA) to the free surface time series to directly estimate the resonant frequency. Vyzikas et al., 2017b and Çelik and Altunkaynak, 2020 used a Logarithmic Decrement Method (LDM), finding small differences between the resonant frequencies computed with FDA and LDM for low levels of applied damping (Vyzikas et al., 2017b).
In this work, RES tests were carried out without wave attacks, imposing a free surface level inside the OWC chamber 0.05 m higher than the external still water level, by air suctioning from the vent duct. After the air suction, the vent duct was closed and then it was suddenly opened allowing the water column to freely oscillate until the equilibrium state was reached. The time series of free surface oscillation, ηOWC, was acquired at a sampling frequency of 20 Hz. Both FDA and LDM were comparatively used. In the FDA, the OWC resonant frequency (fOWC=1/Towc) was determined by Appling a Fast Fourier Transform (FFT) to the recorded water column oscillations time series (as exemplarily depicted in Figure 5. for three cases among the whole set of OWC models tested).
In the LDM, the decay response of the damped oscillating system, the logarithmic decrement δ can be determined as (Eq. 2):
δ = ln ⁡ 1 n x t 0 x t n
where x(t0) and x(tn) are the surface displacement at the first and the last peaks considered, respectively. The damping ratio can be determined by the logarithmic decrement δ as in Eq. (3).
ξ = δ 2 π 2 + δ 2
The damped natural period TdOWC is determined as the average time elapsed between consecutive peaks in the signal (with associated damped natural frequency ωd=2π/TdOWC). The undamped natural frequency is expressed as (Eq. 4)
ω n = ω d 1 − ξ 2
The undamped natural period of the OWC, Tnowc, is consequently obtained as TnOWC=2π/ ω n . For the whole set of tested OWC geometries, the differences obtained in the values of TdOWC and TnOWC are lower than 0.5%, i.e. negligible. Therefore, the natural period of the OWC is hereafter referred to as TOWC only.
The whole set of measured natural periods for each OWC model tested, obtained by applying the FDA and the LDM methods alternatively, are summarized in Table 4. The maximum difference in the TOWC values obtained with the two methods is lower than 5%.
Overall, values of TOWC in the range 0.8-1.3 s (corresponding to natural frequencies fOWC of 0.8-1.3 Hz) were found, confirming the crucial effect of the front wall draught on the natural period of each OWC alternative investigated.
As expected, a decreasing trend of the natural frequency was observed when the front wall draught increased. For given values of W and D, TOWC is relatively insensitive to the damping coefficient K, with a maximum observed variation up to 6%.
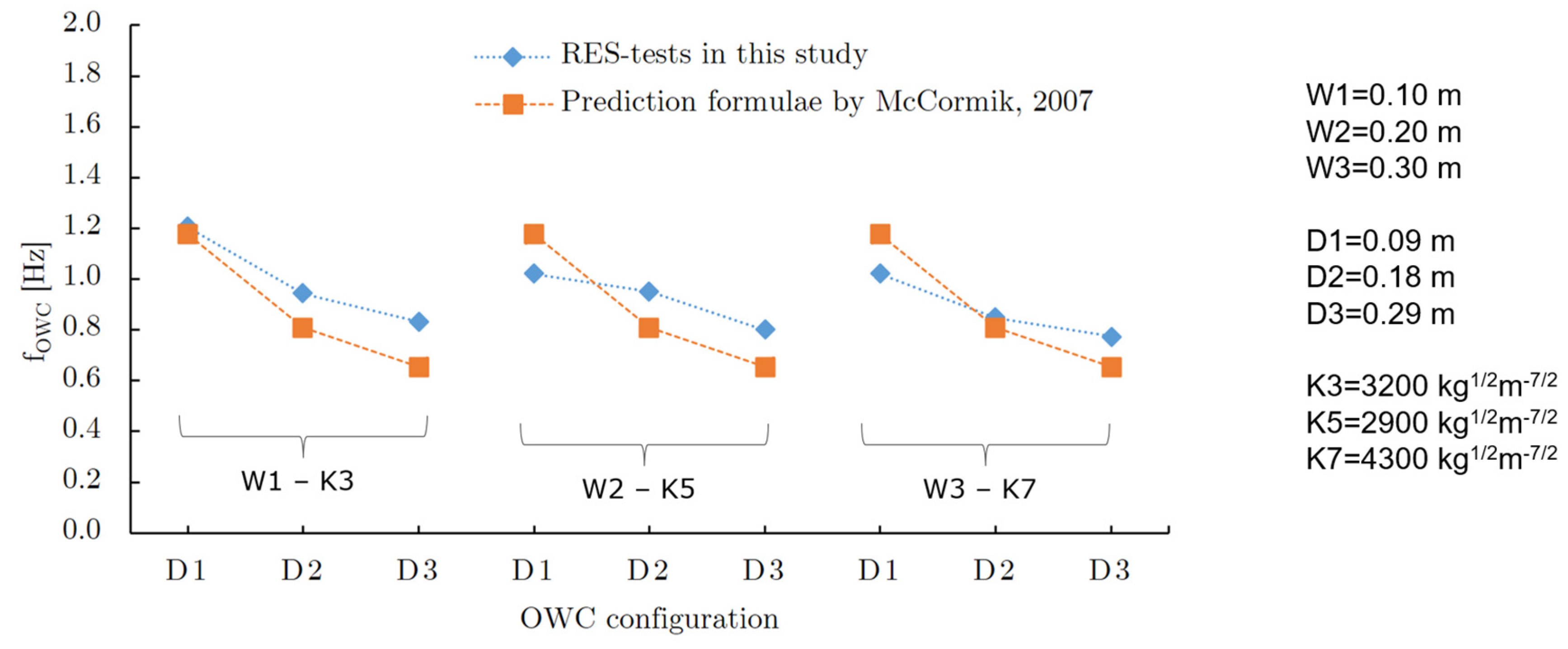
These experimental results are compared with the natural frequency assessed by applying the prediction formula by McCormick (2007), expressed as in Eq. 5.
f O W C = 1 2 π g D + D a
where D is the front wall draught and Da is an additional length due to the added mass of the system, here assumed equal to D, as in Vyzikas et al., 2017. For the three chamber length cases (W1-W3), with different front wall draughts (D1-D3) but comparable damping coefficients (i.e. K3 for W1, K5 for W2 and K7 for W3, when using McCormick formula, it is possible to note an overestimation of the natural frequency (up to 15%) for the chamber lengths W having the smaller draught (D1) and an underestimation (up to 20%) for draughts D2 and D3 (Figure 6).
For the smallest chamber draught D1, the overestimation of fOWC obtained when using Eq. (5) is higher for increasing chamber length W (i.e. for W2 and W3).

3.5.2. Assessment of the OWC Performance in Regular and Irregular Waves

To assess the primary efficiency of the device, many studies refers to the so called Capture Width, CW [m] (Cruz, 2008), defined as the width of the wave front (assuming uni-directional waves) that contains the same amount of power as that absorbed by the device (Price et al., 2009). CW is thus determined as the ratio of the mean absorbed pneumatic power, Πabs, [W] to the averaged wave power associated to the incident waves, Πw, [W/m]:
C W = Π a b s Π w
For regular waves, the period-averaged incident wave power per unit width [W/m], for a generic water depth h, was evaluated according to the linear theory as in Eq. 7:
Π w   r e g = 1 16 ρ g H 2 ω k 1 + 2 k h sinh ⁡ 2 k h
where ρ is the water density, H is the regular wave height, ω is the wave frequency and k is the wave number.
It is worth to stress that the averaged incident wave power, Πw [W/m], is computed by using the acquisitions of the ultrasonic wave probe (WG5) located at the centre of the removed model position (i.e. W0D0V0 tests).
The mean absorbed pneumatic power, Πabs [W], was measured by integrating over the duration of the tests, Ttest, the product of the relative air pressure within the OWC chamber, POWC(t), and air flow rate, QOWC(t), throughout the air turbine as, for instance, in Sarmento, (1993):
Π a b s = 1 T t e s t ∫ 0 T t e s t Q O W C t P O W C t d t
in which the air flow rate QOWC (t) was derived from the time series of air velocity sampled at the centre of the vent duct Umax(t). For this purpose, the average velocity along the duct cross section Uaverage(t) was calculated based on the value of Reynolds number Re. For Re<2400, a laminar pipe flow is assumed, hence Uaverage(t) is calculated as half of Umax(t) while for Re>2400, the flow inside the pipe is assumed to be fully turbulent and a one-seventh power law is used to compute Uaverage(t) from the velocity profile U(x) along the pipe radius R (Eq. 11).
U ( x ) U m a x = 1 − x R 1 / 7
The capture width ratio of the OWC device, CWR, is computed as the ratio of the wave period averaged pneumatic power absorbed by the OWC to the wave period averaged incident wave power, multiplied by the chamber width, B, as defined in Eq. 12:
C W R = C W B
In this study, the chamber width B is fixed at a value of 0.20 m (Table 3).

4. Results and Discussion

With the main purpose of facilitating the understanding of the processes involved within the OWC chamber, the sensitivity analysis of the outcomes achieved for the regular wave tests (Wave 1 to Wave 3 in Table 3), is reported in Section 4.1, Section 4.2 and Section 4.3. The performance of the device, for the different geometry alternatives tested, are discussed in Section 4.4.

4.1. Effect of the OWC Chamber Length

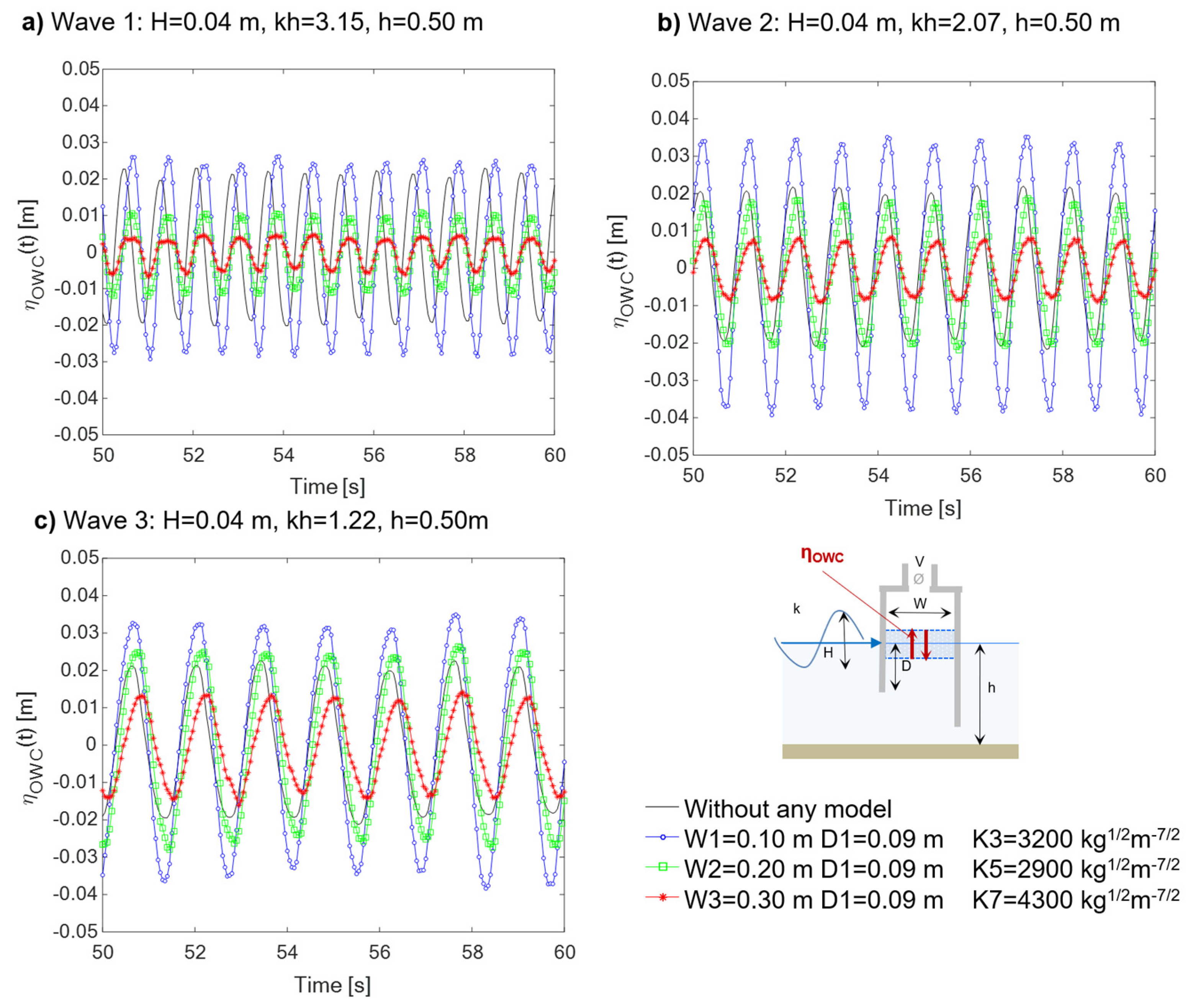
As shown exemplarily in Figure 7, Figure 8 and Figure 9, the effect of chamber length (in wave propagation direction) on the processes inside the OWC is analysed by comparing three OWC geometries characterized by different chamber width (W=0.10-0.30 m), comparable damping coefficients (K3, K5 and K7) and same value of the front wall draught (D1=-0.09 m S.W.L.).
Generally, the water column oscillation measured within the OWC, ηOWC shows an increasing trend with decreasing the chamber length (Figure 7, from W3 to W1). Comparing ηOWC inside the OWC with ηOWC acquired without the OWC model in the flume (black line in Figure 7), it is possible to observe that for all the regular waves tested, the smallest chamber (W1=0.10 m) leads to an amplification of ηOWC. This amplification is directly proportional to the increase of the wavelength from Wave 1 to Wave 3 (Figure 7). With Wave 3, the smallest chamber W1 leads to water column oscillation values approximately 0.03 m higher than that registered without model in the flume. The medium and largest chamber (W2=0.20 m and W3=0.30 m) do not cause an amplification of the free surface motion registered without OWC, however, it is possible to confirm for both that ηOWC increases with increasing the wave period.
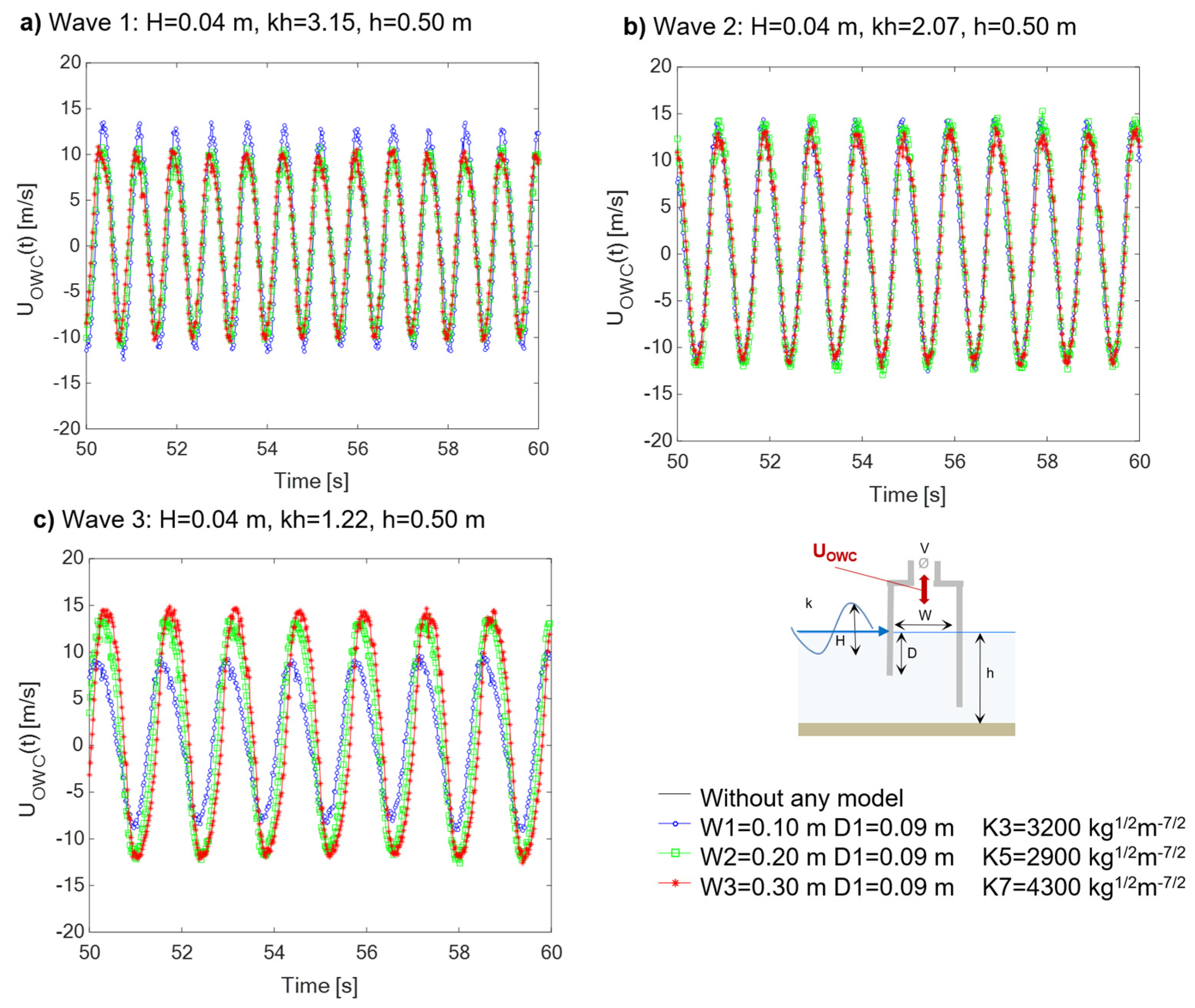
The measurements of, respectively, airflow velocity UOWC(t) acquired within the vent duct (Figure 8) and air pressure measured within the OWC chamber POWC(t) (Figure 9) show a good consistency with the results for the inner water surface elevation, ηOWC(t). Comparing the results obtained for the longest waves (i.e. Wave 3 in Figure 7c and Figure 8c), the airflow velocity UOWC(t) shows a trend directly proportional to the size of the chamber width, but inversely proportional to the inner water surface elevation, ηOWC(t). This could be explained analysing, for convenience, the air volume flux obtained for the same regular wave (e.g. Wave 3), for both the largest chamber (W3) and the smallest chamber (W1). In these cases, the air volume flux is denoted as QW3 and QW1, respectively, and under the hypothesis of air incompressibility, it can be determined as in Eq. 13:
Q W 1 = W 1 · B · η W 1 ( t ) T / 2 ;             Q W 3 = W 3 · B · η W 3 ( t ) T / 2
where W1=0.10 m and W3=0.30 m are the chamber widths to be compared, T=1.4 s is the period of Wave 3 and B=0.20 m is the chamber width perpendicular to the wave propagation direction.
From the air volume flux ratio (Eq. 14), it is possible to highlight the correlation with the water column oscillation registered inside W3 and W1, denoted as ηW3 (t) and ηW1 (t), respectively:
Q W 3 Q W 1 = W 3 · η W 3 ( t ) W 1 · η W 1 ( t )
then, since the ratio W3/W1 is equal to 3 and the ratio ηW3/ ηW1 is approximately 0.4, it is demonstrated that decreasing the inner water surface elevation while increasing the chamber width (Figure 7c) leads to an increase of air volume flux, as in Eq. 15:
Q W 3 = 1.3   Q W 1
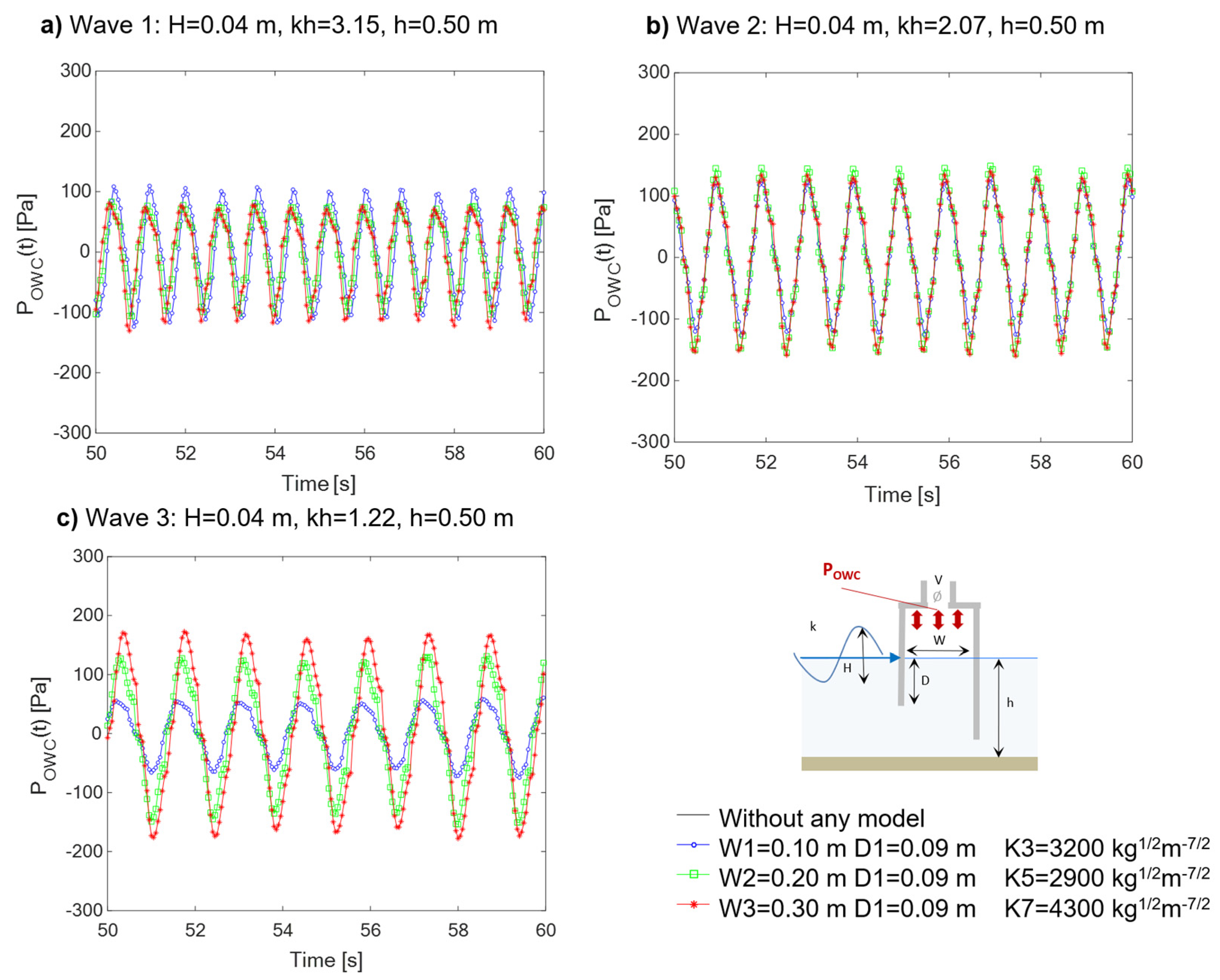
The air pressure oscillations POWC(t) (Figure 9) reveal the same trend as the air volume flux for comparable damping coefficients, due to the second-order dependence between QOWC and POWC. Regarding the outcomes achieved for Wave 1 and Wave 2, a negligible influence of chamber width is observed on UOWC(t) and POWC(t) (Figure 8 a, b and Figure 9 a, b), as the ratio ηW3/ηW1 is about 0.3, and the coefficient in Eq. 15 is approximately equal to 1. However, it is confirmed that the influence of chamber width is strictly correlated to the incident wavelength.
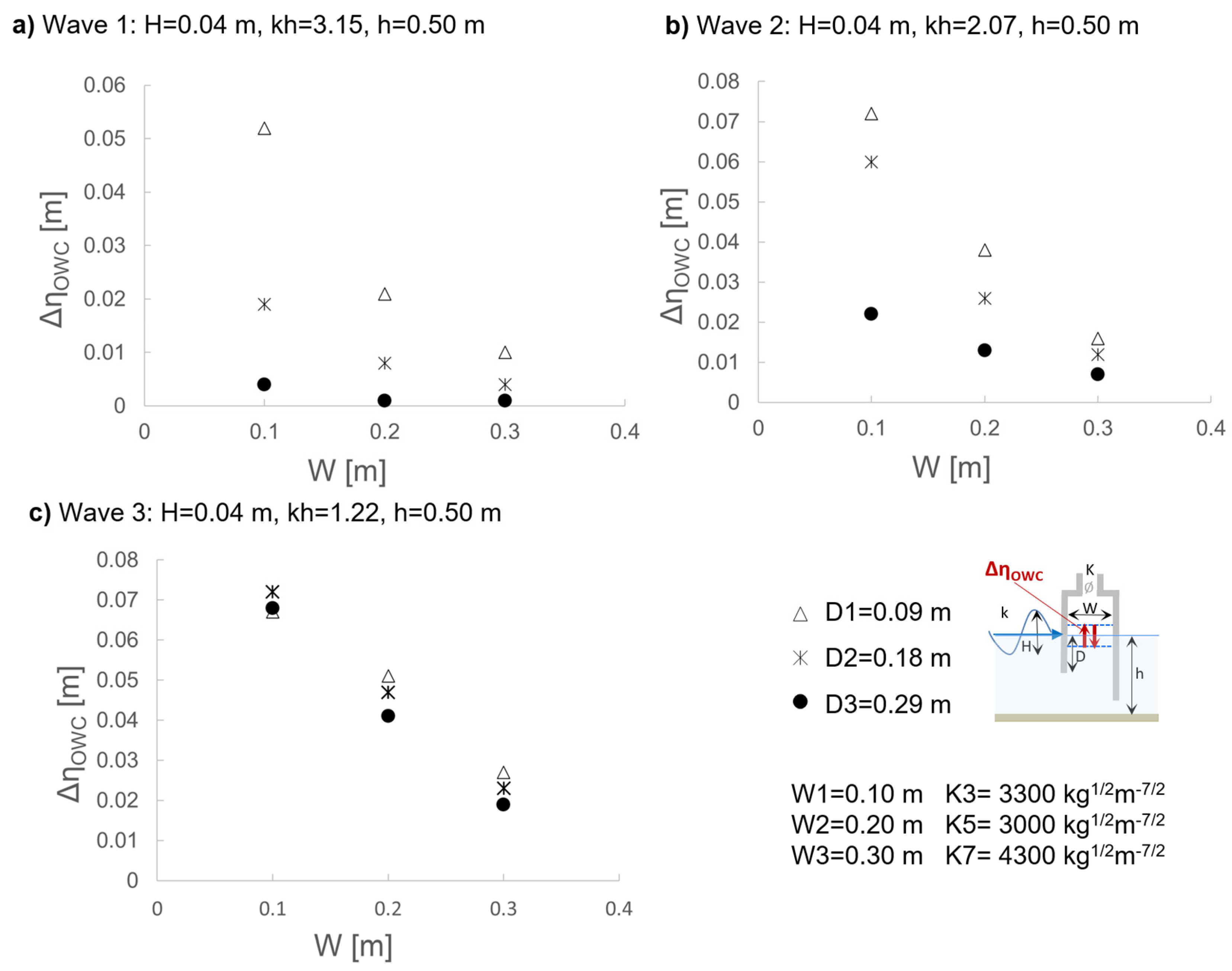
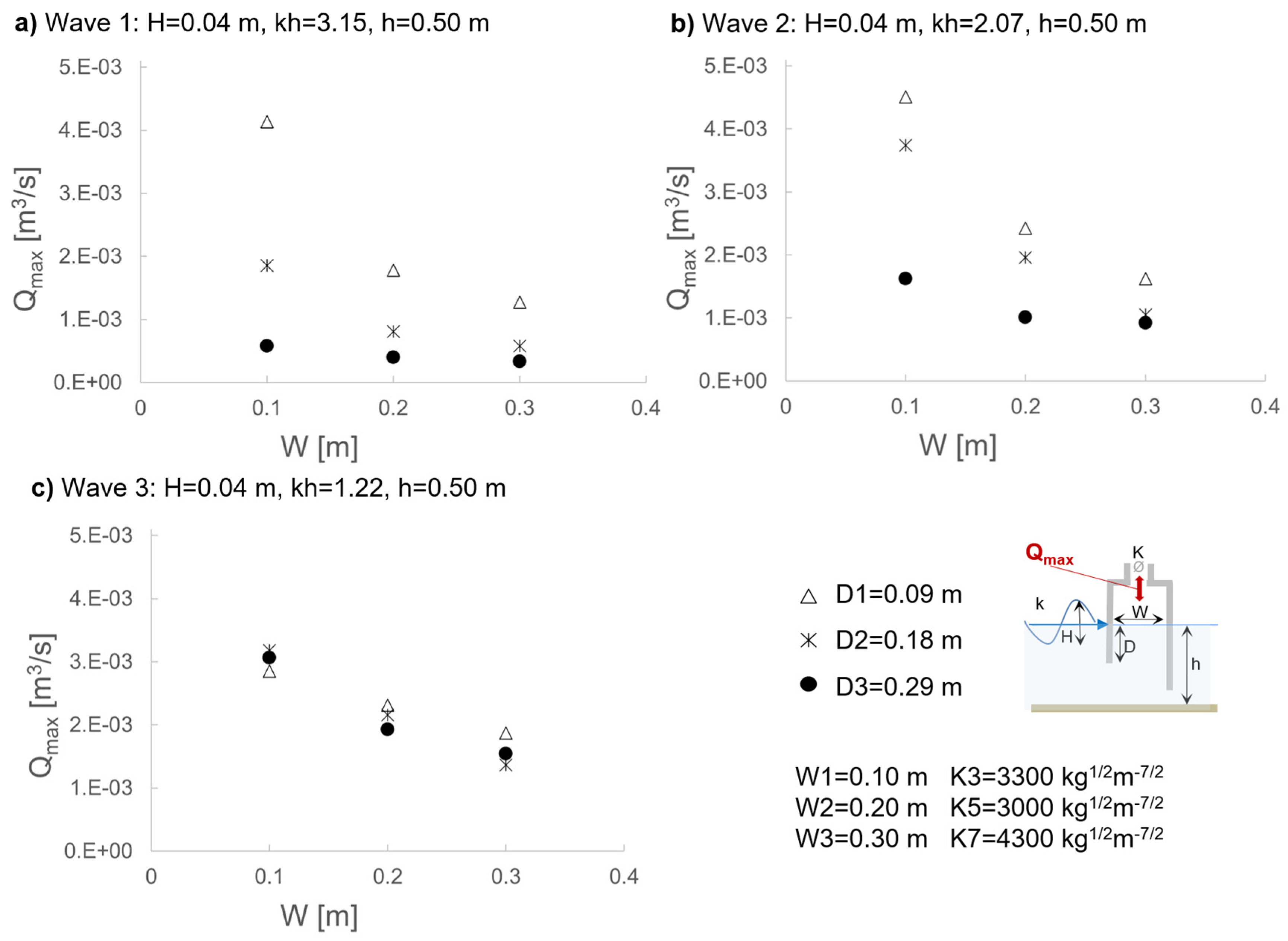
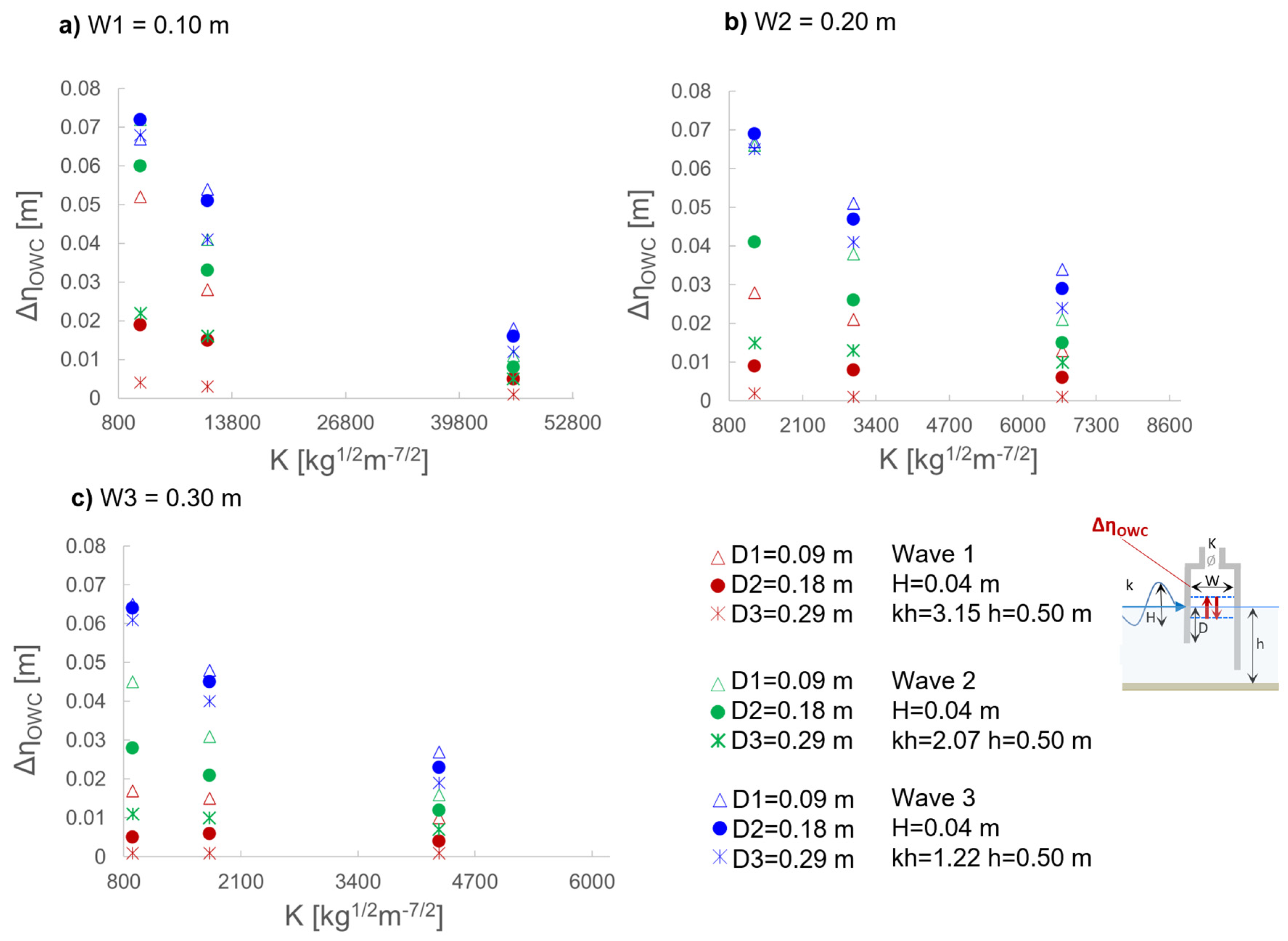
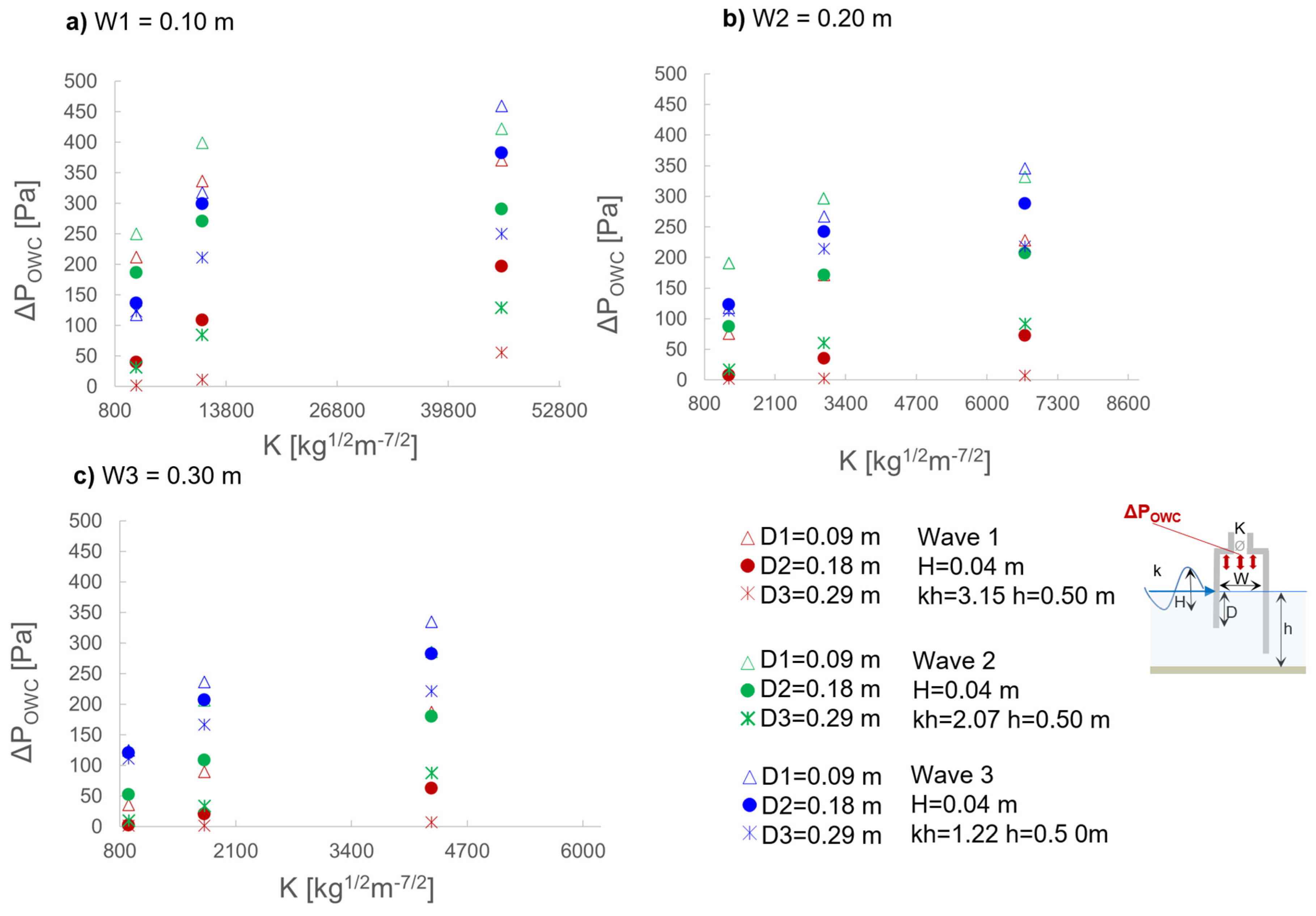
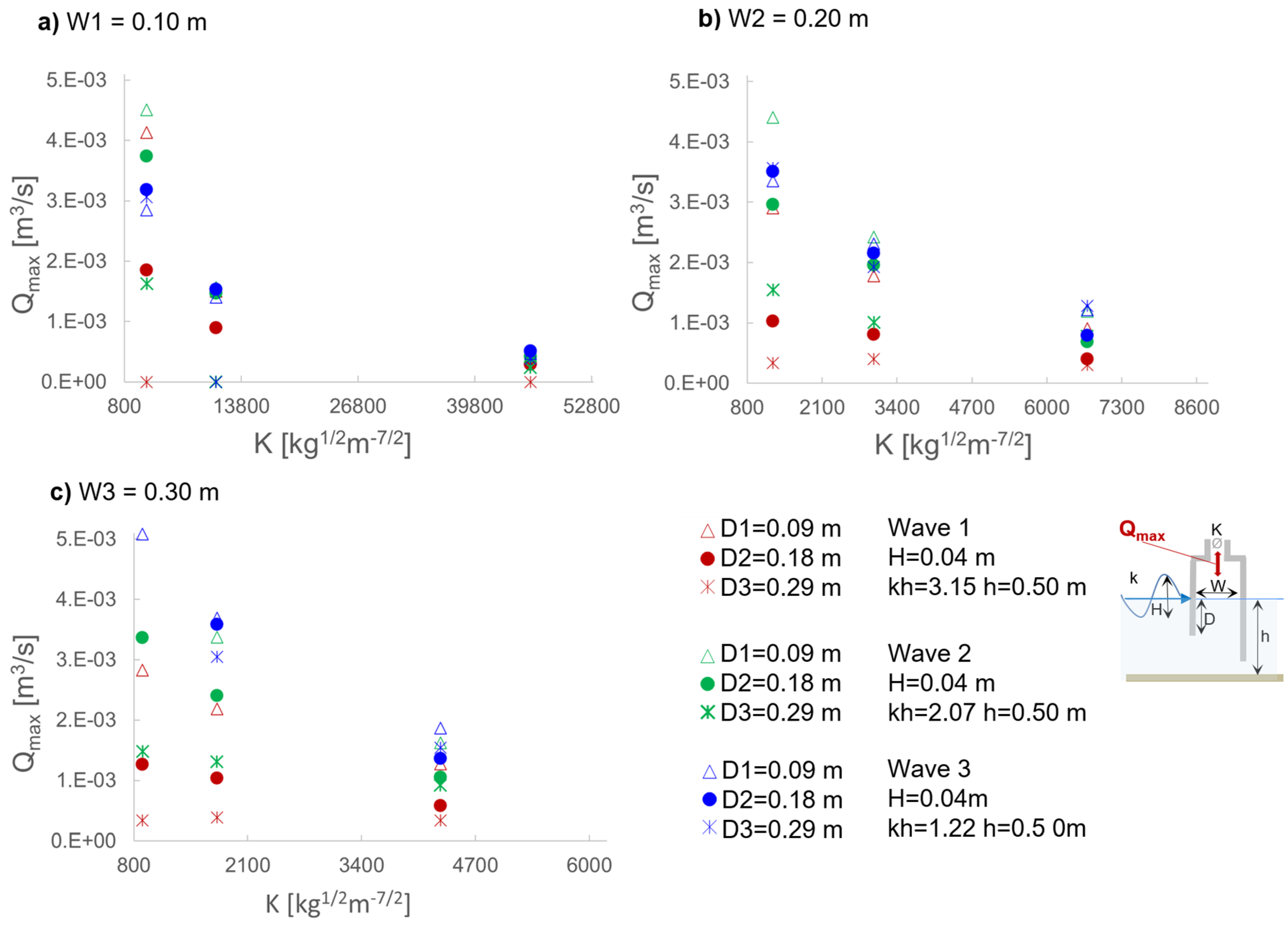
The results obtained for the water surface oscillations amplitude ΔηOWC in the OWC, the air pressure oscillation amplitude ΔPOWC and maximum air volume flux Qmax (obtained from air velocity measurements as detailed in Section 3.5.2) for the tested OWC configurations with comparable damping (K3, K5 and K7) for the three draughts tested (D1-D3) are reported respectively in Figure 10, Figure 11 and Figure 12, which allows extending the considerations made for draft D1 to the other draughts tested.

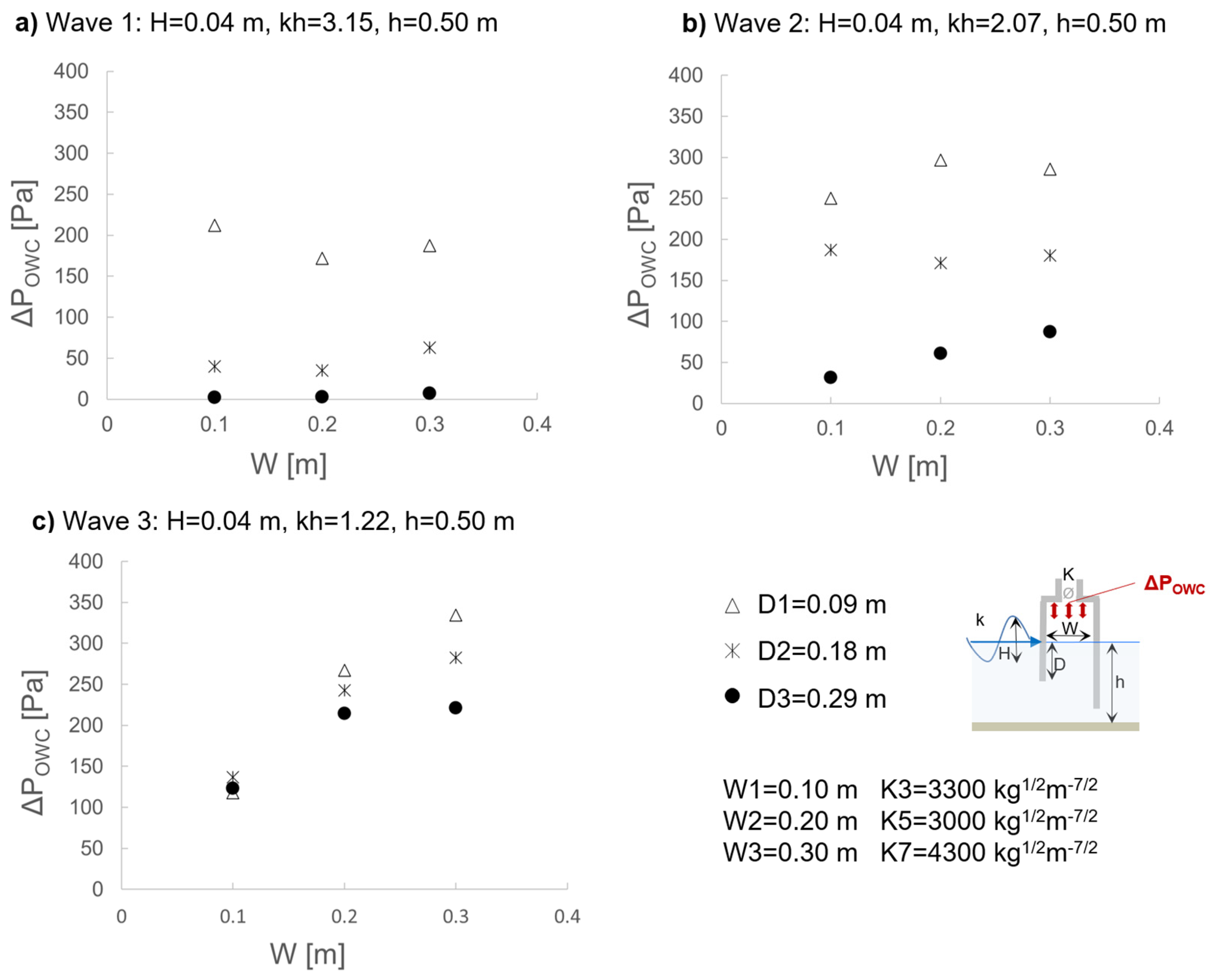
4.2. Effect of the OWC Front Wall Draught

As observed during the free decay RES tests, the front wall draught D is of paramount importance in determining the resonance frequency of the device (i.e. increasing D causes a shift of the OWC resonance frequency towards lower values, as reported in Table 4). Therefore, the front wall draught strongly influences the hydrodynamic processes inside the OWC. To assess this effect, the time series obtained for three OWC models characterized by the same chamber length (i.e. W2=0.20 m) and damping coefficient (i.e. 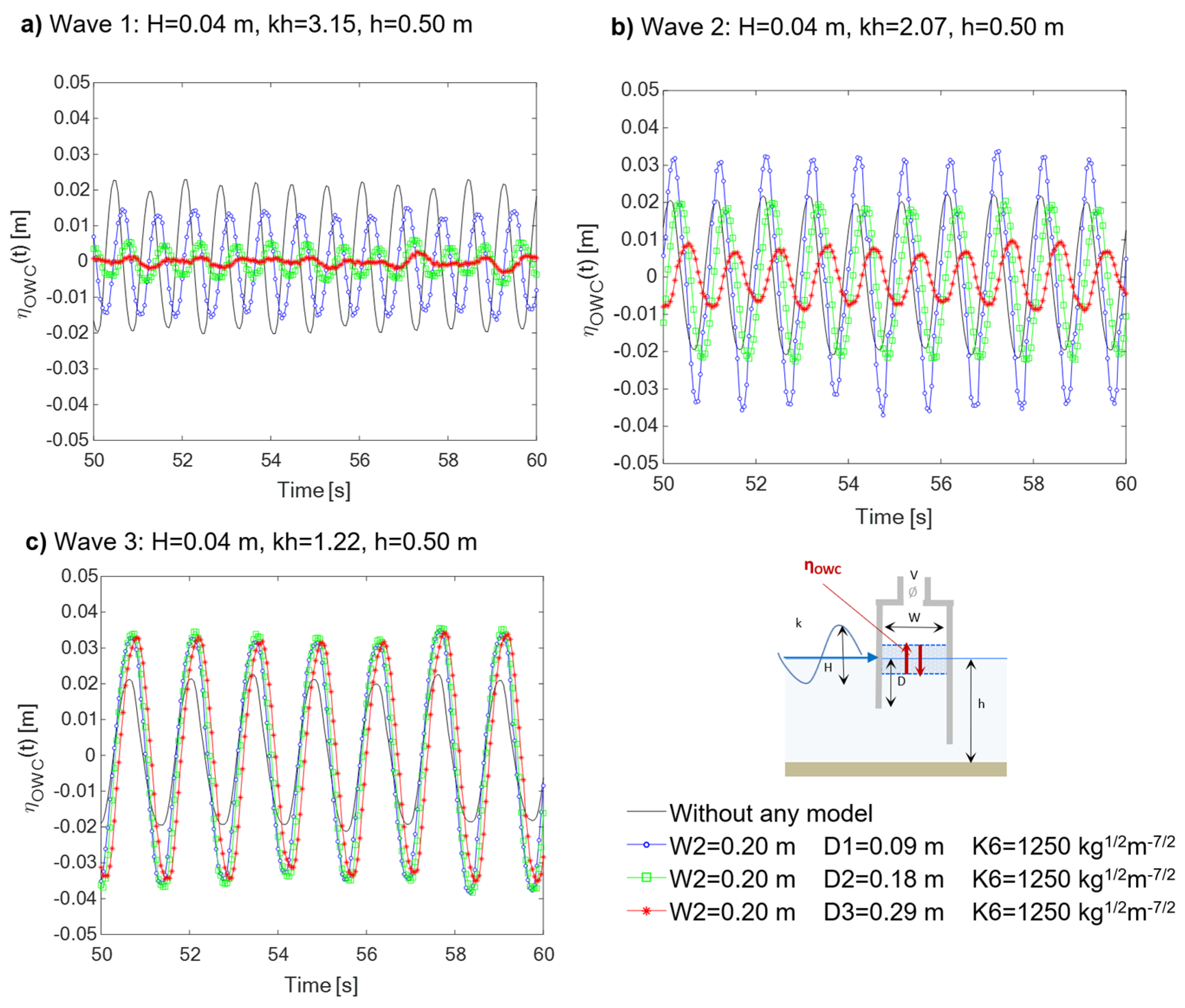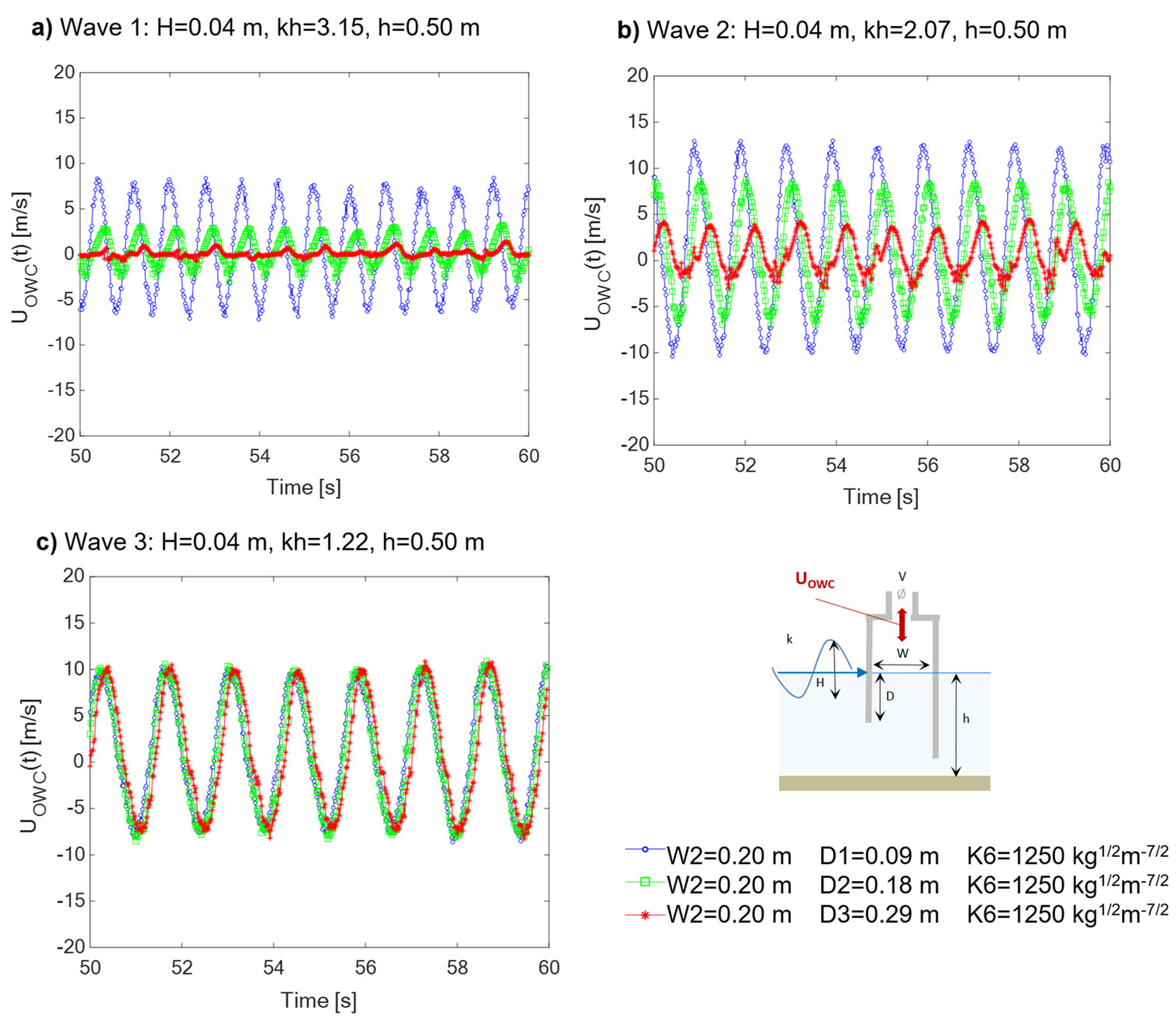K6), but different front wall draughts (D1=-0.09 m, D2=-0.18 m and D3=-0.29 m S.W.L.), are compared in Figure 13.
As expected from the RES tests, it is possible to note that under the shortest and the medium wavelengths (Wave 1 in Figure 13a and Wave 2 in Figure 13b), increasing the submergence of front wall draught leads to a decrease of the water surface elevation ηOWC(t). Instead, with the longest wave (Wave 3 in Figure 13c) the three draughts show a similar effect.
Comparing ηOWC(t) inside the OWC with ηOWC(t) registered without the model (black line in Figure 13), it is possible to observe that with the medium wavelength (Wave 2 in Figure 13b) the shortest front wall draught (D1) leads to an amplification of the water surface elevation of about 0.02 m. The same amplification is observed for the longest wavelength (Wave 3 in Figure 13c), without any relevant distinction between the different front wall draughts investigated.
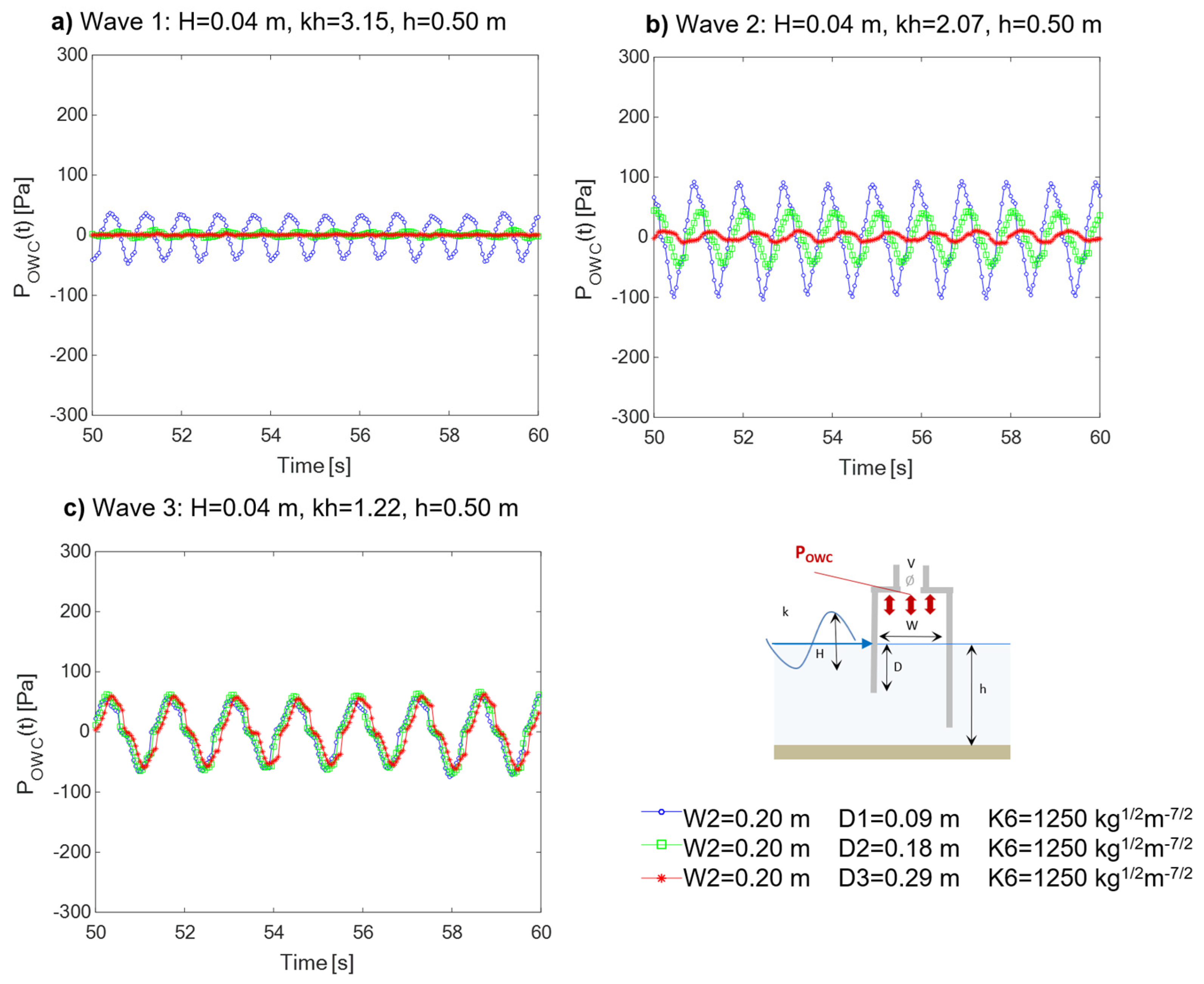
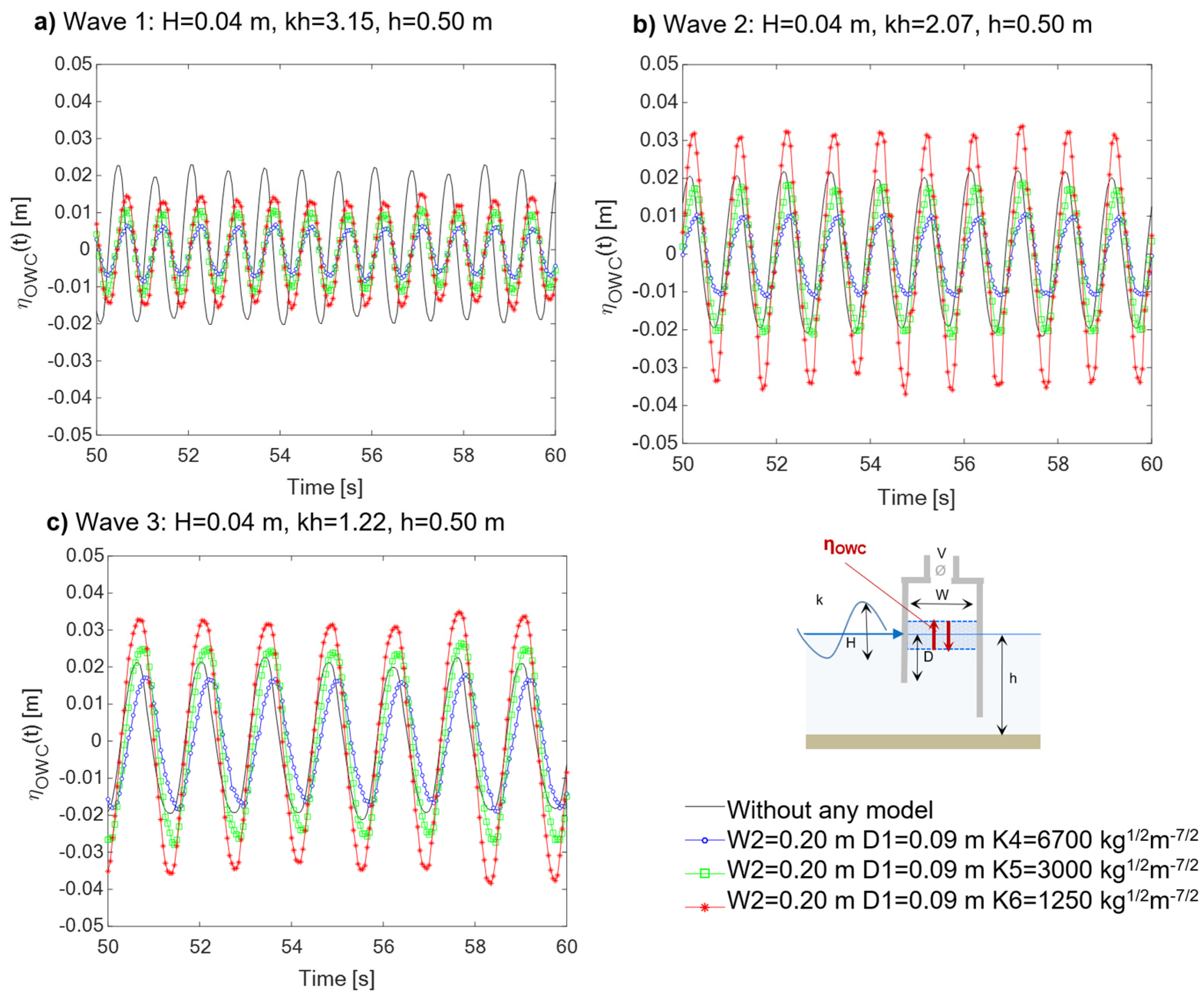
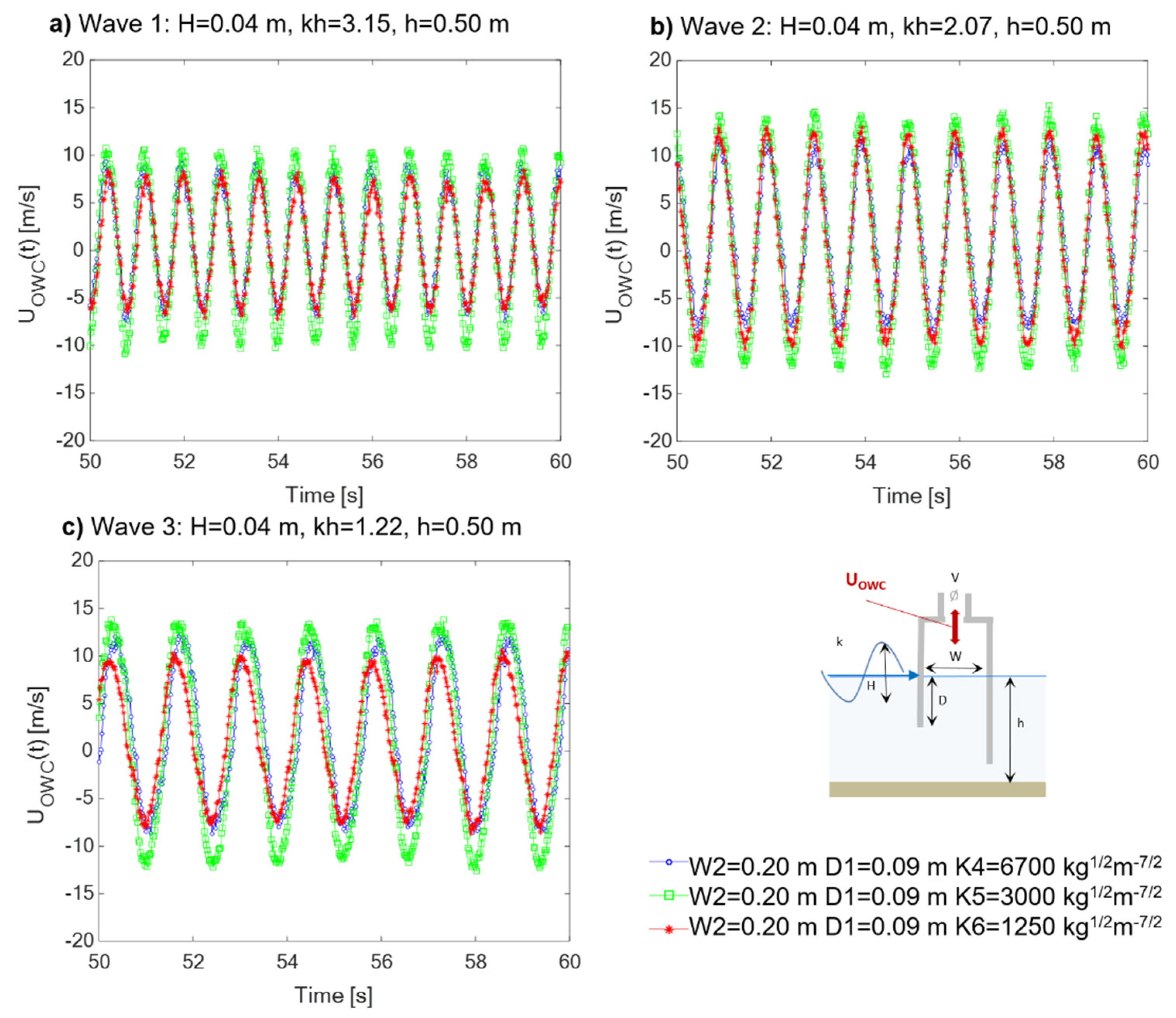
The effect of D observed on ηOWC(t) aligns with the results obtained for air pressure POWC(t) (Figure 14) and airflow velocity UOWC(t) (Figure 15). Generally, except in the case of the longest waves (Wave 3 in Figure 14c, Figure 15c), increasing the submergence of the front wall draft leads to a reduction in POWC (t) and UOWC (t). This could be physically attributed to the wave-induced pressure, which decreases exponentially with increasing depth below the still water level (S.W.L.).
The values of ΔηOWC, ΔPOWC and Qmax for the tested OWC configurations with comparable damping (K3, K5 and K7) for the three draughts tested (D1-D3) in Figs. 10-12 show that, when the chamber length W and damping K are fixed, the impact of varying the draught is limited for the longest wave condition (Wave 3). However, for other wave conditions, increasing the draught D results in a significant reduction in the amplitude of oscillations in the OWC chamber’s monitored quantities. The dependency of the effect of D on the wave periods derives from the balance between the phenomena of approaching resonance when increasing the wave periods for higher draughts of the OWC chamber, and the reduction in wave-induced pressure acting on the OWC as D increases.

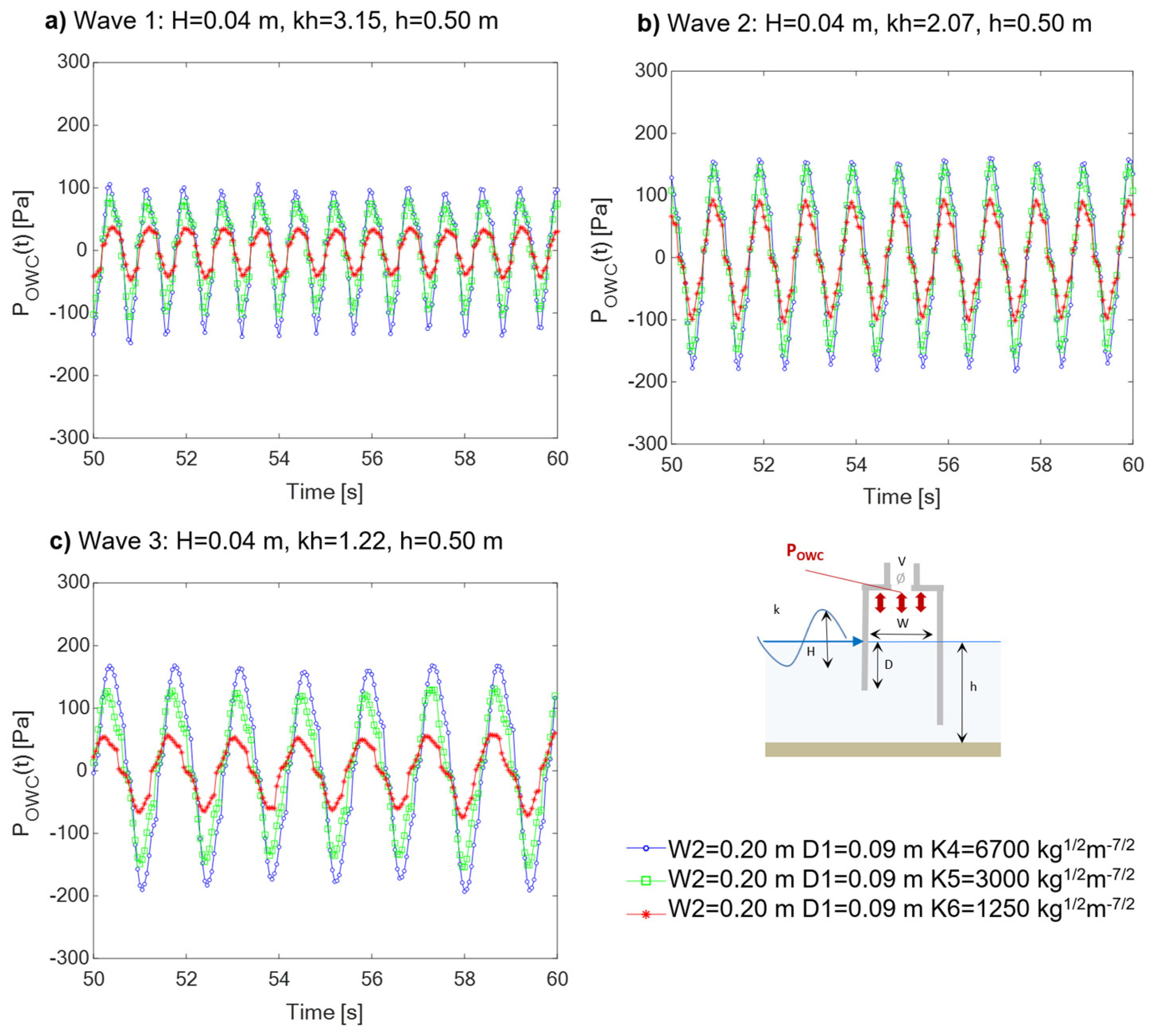
4.3. Effect of the Damping Induced by the PTO

The effect of the damping induced by the air turbine (i.e. the damping coefficient K) can be clearly observed from the results exemplary obtained for the medium chamber length (W2=0.20 m) with the smallest front wall draught (D1=-0.09 m S.W.L.) tested with different the damping coefficients (from K4=6700 kg1/2m-7/2 to K6=1250 kg1/2m-7/2). As expected, higher damping values leads to a decrease of the free surface oscillation ηOWC for all the tested wave cases (Figure 16a-c). For Wave2 and Wave3 (the longest waves), with the lowest damping K5 and K6, an amplification of ηOWC is observed compared to the condition with no model in the flume. For the shortest wave condition (Wave 1 in Figure 16a), the free surface oscillation inside the chamber is always smaller than that in the flume without the model, despite the damping value applied. Air pressure in the chamber, POWC(t) and air velocity in the vent duct, UOWC(t), for the same cases are exemplarily reported in Figure 17 and Figure 18. Fixing the geometrical parameters and wave conditions, higher values of K results in higher air pressure within the OWC chamber. The relative impact of changing the damping value is, however, dependent on the incident wave period: e.g. the relative difference between the maximum air pressure POWC with damping levels K4 and K5 is limited to 7% for Wave2 (Figure 17b), while it is higher than 20% for (Wave 1 and Wave 3).
The results obtained for the water surface oscillations amplitude ΔηOWC in the OWC, the air pressure oscillation amplitude ΔPOWC and maximum air volume flux Qmax (obtained from air velocity measurements as detailed in Section 3.5.2) for all the tested OWC configurations under regular waves are reported respectively in Figure 19, Figure 20 and Figure 21.
Generally, the inner water surface oscillation ΔηOWC and the maximum air volume flux Qmax decrease with increasing K: when K increases from 900 to 46000 kg1/2m-7/2, ΔηOWC decreases from 0.002-0.07 m to 0.001-0.02 m, while Qmax decreases from 3·10-4-5·10-3 m3/s to 3·10-4-1.5·10-3 m3/s (Figure 19 and Figure 21). In contrast, an increasing trend of the inner air pressure oscillations ΔPOWC with increasing the damping coefficient K (Figure 20): ΔPOWC=2-125 Pa for the smallest damping value K9=900 kg1/2 m-7/2 and ΔPOWC=55-460 Pa for the highest damping value K1=46000 kg1/2m-7/2, is observed.
The analysis of the overall dataset confirms what is highlighted in detail for geometry W2D1 in Figure 16, Figure 17 and Figure 18: the relative influence of the damping on the damping on the OWC functioning is different for different wave conditions, with the greatest relative changes observed for the longest wave (Wave 3, in blue in Figure 19, Figure 20 and Figure 21). Such a strong dependence of the effect of damping variations on the incident wave period may be related to the distance from the resonance conditions (which are reported in Tab. 4 for the tested OWC geometries): previous studies suggest that, in off-resonance conditions, the impact of variations of the damping is higher (Simonetti et al, 2017).
Moreover, a progressively smaller rate of the decrease of ΔηOWC and increase of ΔPOWC for increasing damping values can be highlighted, as previously observed also in Simonetti et al., 2017.
Considering that the OWC capture width directly depends on the product of air pressure and airflow velocity, as in Eq. 5, it is therefore evident that an optimal damping value (i.e. a value that maximizes the capture width) exists for each OWC geometry (as also confirmed in previous studies, e.g. in Ning et al., 2016; Simonetti et al., 2017; Lopez et al., 2014).

4.4. Performance of the OWC Device

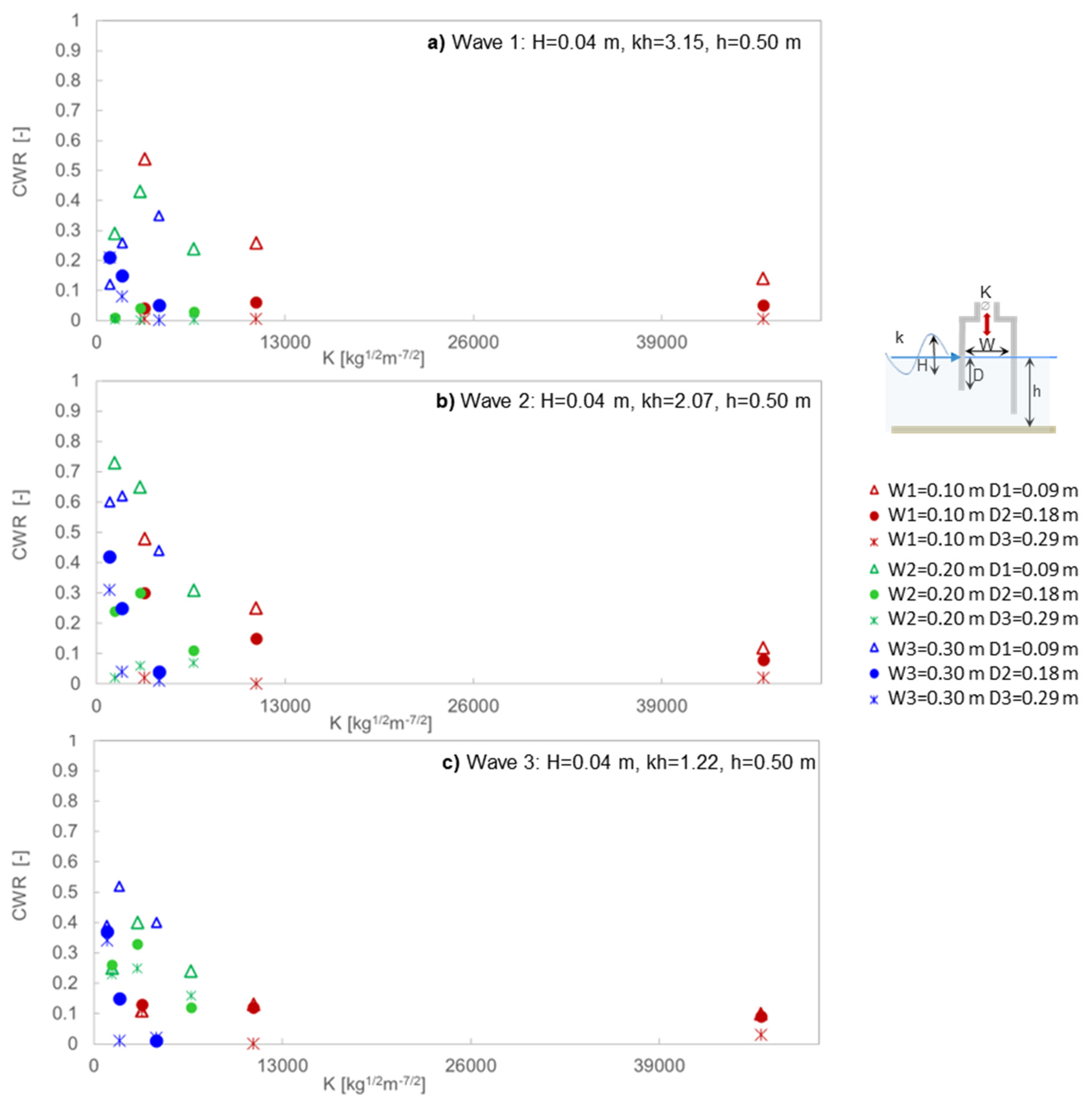
Overall results obtained for the OWC performance, expressed in terms of dimensionless capture width CWR (see Eq. 10) for the tested OWC geometries under regular wave are documented in Figure 22. In this section dimensionless OWC geometry parameters are also used to present the results to generalize the findings (i.e. ratio of the chamber length to the incident wavelength, W/L, and of the front wall draught to the incident wave height D/H).
The highest CWR-values in the experimental tests are obtained for the OWC configurations with the following geometries: W2D1K5 (0.19 m, 0.09 m, 3000 kg1/2m-7/2) and W2D1K6 (0.19 m, 0.09 m, 1250 kg1/2m-7/2). CWR=0.73 is reached for the incident wave with H=0.04 m and T=1s (Wave 2, Figure 22b), while under Wave 1 and Wave 3 CWR is limited to a maximum of 0.55. For fixed values of W and V, lower CWR-values are obtained when increasing the front wall draught D, as expended from the trends in POWC and QOWC discussed in Section 4.2. This result is confirmed by several previous studies, e.g. those by Morris-Thomas et al., 2007 and Ning et al., 2016. Despite the value of the other geometry parameters, CWR values higher than 0.5 are only obtained for the smallest draught (D1). In the configurations with the highest D (D3=0.29 m, D3/H=7.25), CWR < 0.35 for all tested wave conditions is obtained. For a given value of the front wall draught D and of the PTO applied damping K, CWR is always lower for the chamber length W1 (W1/L=0.03-0.09) than for W2 (W2/L=0.07-0.19) and W3 (W3/L=0.11-0.29) (Figure 22). For wave periods T<1 s (i.e. Wave 1, kh= 3.15 with W2/L=0.12-0.19, and W3/L=0.19-0.29), the OWC geometries with chamber width W2 have a CWR about 10% higher than those with chamber W3 (Figure 22a). On the other hand, for OWC geometries with chamber W3, a slightly higher (10%-15%) CWR-value is obtained for wave period T=1.4 s (in the case of Wave 3, with kh=1.2 and W3/λ=0.11, while W1/λ=0.03 and W2/λ=0.07).
Laboratory tests indicate that higher capture width ratios are obtained for relative chamber width W/λ=0.07-0.19, relative front wall draught D/H~2.25 and PTO-applied damping in the range 900-4300 kg1/2m-7/2. For OWC having a similar range of front wall draught values, an optimal relative length of the OWC chamber W/L in the range 0.09-0.012 was also confirmed by several previous studies, e.g. in Vizykas et al., 2017, Simonetti et al., 2017, Chen et al., 2021. A value of the optimal relative chamber length for energy extraction performance around of W/L = 0.10-0.12 was also recently identified for both a fixed, bottom detached for a bottom standing OWC, by Qu et al., 2023 and He et al., 2024, respectively.

5. Conclusions

In the present work, the results of a laboratory tests campaign on a fixed and bottom-detached Oscillating Water Column (OWC) device are presented. The study is aims at providing a knowledge base for the maximization of the performance of the device in terms of its capture width in short-fetch climates by means of laboratory tests at small scale and to provide a new data set for the research community in which 288 different test conditions are available.
The analysis performed on the laboratory results is mainly focussed on investigating the most relevant design parameters (i.e. chamber width W, front wall draught D, and size of the vent simulating the damping of a turbine with a quadratic airflow-pressure relation) affecting the performance of the OWC device. The key results and the implications are summarised as follows:
The natural frequency fOWC of the tested OWC device, as resulting from specifically conceived laboratory tests, is in the range fOWC =0.6-1.0 Hz. The value of fOWC is mainly determined by its front wall draught D.
Increasing values of the damping coefficient K associated with each vent diameter V result in higher inner air pressure POWC, but in lower inner water surface oscillations ηOWC and airflow rate QOWC. An optimal value of damping exists for each geometry of the OWC chamber. In the present study, the optimal PTO-applied damping is in the range 900-4300 kg1/2m-7/2.
For the testes wave conditions and OWC geometries, decreasing the front wall draught D implies an increase of POWC, ηOWC, QOWC, although for the longer wave condition (relative water depth kh=1.22) such differences are strongly attenuated.
Laboratory tests indicate that, for the short-fetch conditions of this study, higher capture width ratios are obtained for relative chamber width W/L=0.07-0.19, relative front wall draught D/H~2.25. A maximum value of capture width ratio of around 73% is found in such conditions.
For the PTO damping K, the present work has identified the range within which, under short-fetch conditions, the optimum for the chamber operation is located. Within this range, turbine manufacturers would need to operate to design a turbine with a quadratic relationship between flow rates and fluxes (i.e. an impulse turbine) that allows for the application of an optimal damping level to the OWC chamber, while simultaneously ensuring satisfactory performance of the turbomachine. Once the optimal turbine is precisely defined, a second-level optimization of the device geometry could be performed, in the vicinity the geometry identified in the present work, which would keep the designed turbomachine and its related damping characteristics fixed while maximizing the chamber's performance under this constraint. It must be mentioned that previous studies have shown that climate change may significantly impact wave energy resources in various locations, affecting both the average and extreme significant wave heights, as well as the intra-annual stability of wave energy. Monthly variations in wave energy are expected to increase across much of the Mediterranean and Atlantic coasts of Europe, potentially doubling in some areas (Sierra et al., 2020; Simonetti & Cappietti, 2024). Therefore, wave energy converters could have to face harsher conditions, raising concerns about their survivability. These aspects should be considered in the future development of WECs. However, for the case of a fixed, detached OWC, Simonetti & Cappietti, 2023 estimated that the relative variation in the optimal dimensions of the device between the present and the future wave climate scenario (projected to 2100) would be limited to 10%
The experimental dataset presented in this work will be made available upon request for numerical model validation.

Author Contributions

Conceptualization, Lorenzo Cappietti; Data curation, Ilaria Crema, Andrea Esposito and Lorenzo Cappietti; Formal analysis, Ilaria Crema, Andrea Esposito and Irene Simonetti; Investigation, Ilaria Crema and Andrea Esposito; Methodology, Ilaria Crema, Irene Simonetti and Lorenzo Cappietti; Resources, Lorenzo Cappietti; Software, Lorenzo Cappietti; Supervision, Lorenzo Cappietti; Validation, Ilaria Crema, Irene Simonetti and Lorenzo Cappietti; Writing – original draft, Ilaria Crema, Irene Simonetti and Lorenzo Cappietti; Writing – review & editing, Irene Simonetti and Lorenzo Cappietti.

References

  1. Alcorn, R., Hunter, S., Signorelli, C., Obeyesekera, R., Finnigan, T., Denniss, T., (2005). Results of the testing of the Energetech wave energy plant at Port Kembla, Energetech Rep.
  2. Arena, F., Fiamma, V., Laface, V., Malara, G. et al., (2013). Installing U-OWC devices along the Italian coasts, in: Proc 32nd Int Conf Ocean Offshore Arct Eng, Nantes, France.
  3. Ashlin, S.J., Sannasiraj, S.A., Sundar, V., (2018). Performance of an array of oscillating water column devices integrated with an offshore detached breakwater, Ocean Engineering, 163, pp. 518-532. [CrossRef]
  4. Boccotti, P., (2007). Comparison between a U-OWC and a conventional OWC, Ocean Engineering, Volume 34, Issues 5–6, 2007, Pages 799-805, ISSN 0029-8018. [CrossRef]
  5. Cabral, T., Clemente, D., Rosa-Santos, P., Taveira-Pinto, F., Morais, T., Belga, F., Cestaro, H., (2020). Performance Assessment of a Hybrid Wave Energy Converter Integrated into a Harbor Breakwater. Energies, 13, 236. [CrossRef]
  6. Cappietti, L., Simonetti, I., Penchev, V., Penchev, P., (2019). Laboratory tests on an original wave energy converter combining oscillating water column and overtopping devices, Advances in Renewable Energies Offshore – Guedes Soares (Ed.) © 2019 Taylor & Francis Group, London, ISBN 978-1-138-58535-5, Lisbon, Portugal. pp 791-796.
  7. Celik, A. Altunkaynak, A., (2019), Experimental investigations on the performance of a fixed-oscillating water column type wave energy converter, Energy, 188. [CrossRef]
  8. Celik, A. Altunkaynak, A., (2020), Determination of hydrodynamic parameters of a fixed OWC by performing experimental and numerical free decay tests, Ocean Engineering, 204, 106827. [CrossRef]
  9. Chen, J., Wen, H., Wang, Y., Wang, G., (2021) A correlation study of optimal chamber width with the relative front wall draught of onshore OWC device, Energy, 225, 120307,ISSN 0360-5442. [CrossRef]
  10. Count, B., Fry, R., Haskell, J., Jackson, N. (1981). The MEL oscillating water column. U.K. Marchwood Eng. Lab. C.E.G.B. Report RD/M/I 157N81.
  11. Cruz, J. (2008) Ocean Wave Energy Current Status and Future Perspectives.
  12. David, D. R., Vallam, S., Annamalaisamy, S. S., 2018, Effect of Harbor Walls on the Efficiency of an Oscillating Water Column, J. Waterway, Port, Coastal, Ocean Eng., 2018, 144(2): 04017043. [CrossRef]
  13. Evans, D., Porter, R., (1995). Hydrodynamic characteristics of an oscillating water column device. Appl. Ocean Res. 17, 155–164. [CrossRef]
  14. Elhanafi, A., Macfarlane, G., Fleming, A. & Leong, Z., (2017). Experimental and numerical investigations on the hydrodynamic performance of a floating–moored oscillating water column wave energy converter. Applied Energy, 205(April), pp.369–390. [CrossRef]
  15. Elhanafi A, Fleming A, MacFarlane G, Leong, Z., (2017b). Numerical hydrodynamic analysis of an offshore stationary–floating oscillating water column–wave energy converter using CFD. Int J Naval Architect Ocean Eng; 9:77–99. [CrossRef]
  16. Elhanafi A, Fleming A, Macfarlane G, Leong Z, (2017c). Underwater geometrical impact on the hydrodynamic performance of an offshore oscillating water column–wave energy converter. Renew Energy; 105:209–31. [CrossRef]
  17. Falcão, A.F.O. (2000), The shoreline OWC wave power plant at the Azores, in: Proc 4th European Wave Energy Conf, Aalborg, Denmark, pp. 42-47.
  18. Falcão, A.F.O. and Gato L.M.C. (2012) Air Turbines. In: Sayigh A, (ed.) Comprehensive Renewable Energy, Vol 8, pp. 111–149. Oxford: Elsevier.
  19. Falcão, A.F.O., Henriques, J.C.C., Gato, L.M.C., Gomes, R.P.F., (2014). Air turbine choice and optimization for floating oscillating-water-column wave energy converter, Ocean Engineering, Volume 75, Pages 148-156, ISSN 0029-8018. [CrossRef]
  20. Falcão, A.F.O. & Henriques, J.C.C., (2014). Model-prototype similarity of oscillating water-column wave energy converters, Int.J.Mar.Energy 6, 18-34. [CrossRef]
  21. Falcão, A.F.O. & Henriques, J.C.C., (2016). Oscillating-water-column wave energy converters and air turbines: A review. Renewable Energy. 85. 1391-1424. [CrossRef]
  22. Falcão, A.F.O., Henriques, J.C.C., Gato, L.M.C., (2018). Self-rectifying air turbines for wave energy conversion: A comparative analysis, Renewable and Sustainable Energy Reviews, Volume 91, Pages 1231-1241, ISSN 1364-0321. [CrossRef]
  23. Goda, Y. & Suzuki, Y. (1995) ‘Estimation of incident and reflected waves in regular wave experiments’, Ocean Engineering, 22(1), pp. 77–86. [CrossRef]
  24. Hadadpour, S., Etemad-Shahidi, A., Jabbari, E., Kamranzad, B., (2014). Wave energy and hot spots in Anzali port, Energy, Volume 74, Pages 529-536, ISSN 0360-5442. [CrossRef]
  25. Hasselmann, K. et al. (1973) ‘Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP)’, Ergnzungsheft zur Deutschen Hydrographischen Zeitschrift Reihe, A(8)(8 0), p. p.95.
  26. He, F. and Huang, Z. (2014) ‘Hydrodynamic performance of pile-supported OWC-type structures as breakwaters: An experimental study’, Ocean Engineering. Pergamon, 88, pp. 618–626. [CrossRef]
  27. He, F., Pan, J.,Lin, Y., Song, M., Zheng, S., (2024) Development of an oscillating water column-type wave absorber for anti-reflection and effective energy extraction, Applied Ocean Research, 144, 103910, ISSN 0141-1187. [CrossRef]
  28. Heath, T, Whittaker, T.J.T., Boake, C.B., (2000). The design construction and operation of the LIMPET wave energy converter (Islay, Scotland), in: Proc 4th European Wave Energy Conf, Aalborg, Denmark, pp. 49-55.
  29. Iglesias, G., Carballo, R., (2010). Wave energy and nearshore hot spots: The case of the SE Bay of Biscay, Renewable Energy, Volume 35, Issue 11, Pages 2490-2500. [CrossRef]
  30. Iturrioz, A. et al. (2014) ‘Time-domain modeling of a fixed detached oscillating water column towards a floating multi-chamber device’, Ocean Engineering, 76, pp. 65–74. [CrossRef]
  31. Iturrioz, A. et al. (2015) ‘Validation of OpenFOAM® for Oscillating Water Column three-dimensional modeling’, Ocean Engineering. Elsevier, 107, pp. 222–236. [CrossRef]
  32. Liu, Z., Xu, C., Qu, N., Cui, Y., Kim, K., (2020). Overall performance evaluation of a model-scale OWC wave energy converter, Renewable Energy, Volume 149, 2020, Pages 1325-1338, ISSN 0960-1481. [CrossRef]
  33. Liu, Z., Xu, C., Kim, K., Zhang, X., Ning, D., (2024) Hydrodynamic and energy-harvesting performance of an isolated oscillating water column device: An experimental study, Coastal Engineering, 189, 104459, ISSN 0378-3839. [CrossRef]
  34. López, I. et al. (2012) ‘Turbine−chamber coupling in an OWC Wave Energy Converter’, Civil Engineering, pp. 1–7.
  35. López, I. and Iglesias, G. (2014) Efficiency of OWC wave energy converters: A virtual laboratory, Applied Ocean Research, 44, pp. 63–70. [CrossRef]
  36. Lopez, I., Pereiras, B., Castro, F., Iglesias, G. (2014)V Optimisation of turbine-induced damping for an OWC wave energy converter using a RANS-VOF numerical model. Appl. Energy 127, 105–114. [CrossRef]
  37. López, I., Castro, A. and Iglesias, G. (2015) Hydrodynamic performance of an oscillating water column wave energy converter by means of particle imaging velocimetry, Energy, 83, pp. 89–103. [CrossRef]
  38. López, I., Carballo, R., Taveira-Pinto, F., Iglesias, G. (2020) Sensitivity of OWC performance to air compressibility, Renewable Energy 145, 1334-1347. [CrossRef]
  39. Maeda, H., Kinoshita, T., Masuda, K., Kato, W. (1985). Fundamental research on oscillating water column wave power absorbers. J. Energy Res. Tech. 150, 81-86. [CrossRef]
  40. Masuda, Y. (1971), Wave-activated generator, in: Int. Colloq Exposition Oceans, Bordeaux, France.
  41. Masuda, Y., McCormick, M.E., (1986). Experiences in pneumatic wave energy conversion in Japan, in: M.E. McCormick, Y.C. Kim (Eds.), Utilization of Ocean Waves e Wave to Energy Conversion, Amer Soc Civil Eng, New York, pp. 1-33.
  42. Masuda, Y., Yamazaki, T., Outa Y. and McCormick, M. (1987). Study of Backward Bent Duct Buoy," OCEANS '87, Halifax, NS, Canada, 1987, pp. 384-389.
  43. McCormick, M.E., (1979). Ocean wave energy concepts. In: Proceedings of MTS-IEEE Oceans 79 Conference, pp. 553–557. San Diego, CA.
  44. McCormick, M. (1981). Ocean Wave Energy Conversion. John Wiley & Sons, New York. [CrossRef]
  45. McCormick, M.E., (2007). Ocean Wave Energy Conversion. Dover publications, New York. [CrossRef]
  46. Moretti, G., Fontana, M. & Vertechy, R., (2015). Model-based design and optimization of a dielectric elastomer power take-off for oscillating wave surge energy converters. Meccanica 50, 2797–2813. [CrossRef]
  47. Morris-Thomas, M. et al. (2007) ‘An Investigation Into the Hydrodynamic Efficiency of an Oscillating Water Column’, Journal of Offshore Mechanics and Arctic Engineering, 129(4), p. 273. [CrossRef]
  48. Mustapa, M.A., Yaakob, O.B., Yasser M. Ahmed, Chang-Kyu Rheem, K.K. Koh, Faizul Amri Adnan, (2017). Wave energy device and breakwater integration: A review, Renewable and Sustainable Energy Reviews, Volume 77, Pages 43-58, ISSN 1364-0321. [CrossRef]
  49. Ning, D. Z. et al. (2016). An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter, Applied Energy. Elsevier Ltd, 168, pp. 636–648. [CrossRef]
  50. Ning, D., Wang, R., Chen, L., Sun, K., (2019). Experimental investigation of a land-based dual-chamber OWC wave energy converter, Renewable and Sustainable Energy Reviews, Volume 105, 2019, Pages 48-60, ISSN 1364-0321. [CrossRef]
  51. Ohneda, H., Igarashi, S., Shinbo, O., Sekihara, S., Suzuki, K., Kubota, H., et al., (1991). Construction procedure of a wave power extracting caisson breakwater, in: Proc 3rd Symp Ocean Energy Utilization, Tokyo, pp. 171-179.
  52. Ozkop E., Altas, I.H., (2017) Control, power and electrical components in wave energy conversion systems: A review of the technologies, Renewable and Sustainable Energy Reviews, Volume 67, Pages 106-115, ISSN 1364-0321. [CrossRef]
  53. Pawitan, K.A., Dimakopoulos, A.S., Vicinanza, D., Allsop, W., Bruce, T., (2019). A loading model for an OWC caisson based upon large-scale measurements, Coastal Engineering, 145, 2019, pp: 1-20, ISSN 0378-3839. [CrossRef]
  54. Pereiras, B., Lopez, I., Castro, F., Iglesias, G., (2015). Non-dimensional analysis for matching an impulse turbine to an OWC (oscillating water column) with an optimum energy transfer, Energy 87, 481-489. [CrossRef]
  55. Price, A.A.E., Dent, C. J. and Wallace, A. R. (2009) On the capture width of wave energy converters, Applied Ocean Research, 31(4), pp. 251–259. [CrossRef]
  56. Qu, M., Yu, D., Li, Y., Gao, Z., (2023) Effect of relative chamber width on energy conversion and mechanical characteristics of the offshore OWC device: A numerical study, Energy, Volume 275, 127372, ISSN 0360-5442. [CrossRef]
  57. Raghunathan, S. (1995). The wells air turbine for wave energy conversion, Prog. Aerospace Sci., 31, pp. 335-386. [CrossRef]
  58. Ravindran,M., Koola,P.M. (1991). Energy from sea waves e the Indian wave energy program, Curr. Sci. 60. 676-680.
  59. Ribeiro de Silva, S., Gomes, R.P.F., Falcão, A.F.O., (2016). Hydrodynamic optimization of the UGEN: Wave energy converter with U-shaped interior oscillating water column, International Journal of Marine Energy, Volume 15, Pages 112-126, ISSN 2214-1669. [CrossRef]
  60. Richards D and Weiskopf FB (1986) Studies with and testing of the McCormick pneumatic wave energy turbine with some comments on PWECS systems. In: McCormick ME and Kim YC (eds.) Utilization of Ocean Waves – Wave to Energy Conversion, pp. 80–102. New York: ASCE.
  61. Robinson, R. N.; Murray, A. 1981: Geometric-wavefield influence on the behaviour of an oscillating water column. In: Proc. Int. Syrup. Hydrodynamics in Ocean Eng. 1067-86. Norwegian Inst. of Tech.
  62. Sarmento, A. J. N. A.; Falco, A. E de O. (1985). Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 150, 467-485.
  63. Sarmento, A. J. N. A. (1992). Wave flume experiments on two-dimensional oscillating water column wave energy devices. Experiments in Fluids. [CrossRef]
  64. Sarmento, A.J. N. A. (1993). Model test optimization of an OWC. International Journal of Offshore and Polar Engineering, 3, pp. 66–72.
  65. Sierra, J.P.; Castrillo, R.; Mestres, M.; Mösso, C.; Lionello, P.; Marzo, L. (2020) Impact of Climate Change on Wave Energy Resource in the Mediterranean Coast of Morocco. Energies, 13, 2993. [CrossRef]
  66. Sheng, W., Lewis, T. and Alcorn, R. (2012). On wave energy extraction of oscillating water column device. International Conference on Ocean Energy, (iii), pp. 1–9.
  67. Simonetti, I., Cappietti, L., El Safti, H., Oumeraci, H. (2015), Numerical modelling of fixed oscillating water column wave energy conversion devices: Toward geometry hydraulic optimization, Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering - OMAE, 2015, 9.
  68. Simonetti, I., Cappietti, L., Elsafti, H., Oumeraci, H., (2017). Optimization of the geometry and the turbine induced damping for fixed detached and asymmetric OWC devices: a numerical study Energy, 139, pp. 1197-1209.
  69. Simonetti, I., Cappietti, L., Elsafti, H., Oumeraci, H., (2018) Evaluation of air compressibility effects on the performance of fixed OWC wave energy converters using CFD modelling, Renew. Energy 119 (2018) 741-753. [CrossRef]
  70. Simonetti, I., Cappietti., L. (2021) Hydraulic performance of oscillating water column structures as anti-reflection devices to reduce harbour agitation, Coastal Engineering, 165, 202, 103837. [CrossRef]
  71. Simonetti, I., Esposito, A., Cappietti, L. (2022) Experimental Proof-of-Concept of a Hybrid Wave Energy Converter Based on Oscillating Water Column and Overtopping Mechanisms, Energies, 15, 8065. [CrossRef]
  72. Simonetti, I.; Cappietti, L. (2024) Projected Trends in Wave Energy Potentials along the European Coasts and Implications for Wave Energy Exploitation (1976–2100). J. Mar. Sci. Eng., 12, 239. [CrossRef]
  73. Simonetti I., Cappietti L., (2023) Mediterranean coastal wave-climate long-term trend in climate change scenarios and effects on the optimal sizing of OWC wave energy converters, Coastal Engineering, 179, 104247, ISSN 0378-3839. [CrossRef]
  74. Sun, Y., Ning, D., Mayon, R., Chen, Q., 2023, Experimental and numerical investigation on hydrodynamic performance of a 3D land-fixed OWC wave energy converter, Applied Ocean Research, 141, 2023, 103805, ISSN 0141-1187. [CrossRef]
  75. Suzuki, M., Arakawa, C., Takahashi, S., (2004). Performance of a wave power generating system installed in breakwater at Sakata port in Japan, in: Proc 14th Int Offshore Polar Eng Conf, Toulon, France.
  76. Torre-Enciso, Y., Ortubia, I., Lopez de Aguileta, L.I., Marques, J. (2009). Mutriku wave power plant: from the thinking out to the reality, in: Proc 8th European Wave Tidal Energy Conf, Uppsala, Sweden, pp. 319-329.
  77. Vannucchi, V., Cappietti, L., 2016, Wave Energy Assessment and Performance Estimation of State of the Art Wave Energy Converters in Italian Hotspots, Sustainability, 8(12), 1300; [CrossRef]
  78. Vicinanza, D., Di Lauro, E., Contestabile, P., Gisonni, G., (2019). Review of Innovative Harbor Breakwaters for Wave-Energy Conversion, Journal of Waterway, Port, Coastal, and Ocean Engineering, 145 (4).
  79. Vicinanza, D., Contestabile, P., Ferrante, V., (2013). Wave energy potential in the north-west of Sardinia (Italy), Renewable energy, Volume 50, 2013, Pages 506-521, ISSN 0960-1481. [CrossRef]
  80. Viviano, A., Naty, S., Foti, E., Bruce, T., Allsop, W., Vicinanza, D., 2016, Large-scale experiments on the behaviour of a generalised Oscillating Water Column under random waves, Renewable Energy, 99, pp. 875-887. [CrossRef]
  81. Vyzikas, T. et al. (2016). Experimental investigation of different geometries of fixed oscillating water column devices, Renewable Energy, 104, pp. 248–258. [CrossRef]
  82. Vyzikas, T., Deshoulieres, S., Giroux, O., Barton, M., Greaves, D., (2017). Numerical study of fixed Oscillating Water Column with RANS-type two-phase CFD model. Renewable Energy, 102, 294-305. [CrossRef]
  83. Whittaker, T.J.T., McIlhagger, D.S., Barr, A.G. (1984). Wells Turbines for Navigation Buoys, Editor(s): JOHN TWIDELL, FIONA RIDDOCH, BILL GRAINGER, Energy for Rural and Island Communities, Pergamon, Pages 289-297, ISBN 9780080305806. [CrossRef]
  84. Whittaker, T. J. T., McPeake, F. A., and Barr, A. G. (1985). The Development and Testing of a Wave-Activated Navigation Buoy With a Wells Turbine. ASME. J. Energy Resour. Technol. June 1985; 107(2): 268–73. [CrossRef]
  85. Zabihi, M., Mazaheri, S., Montazeri Namin, M. (2019), Experimental hydrodynamic investigation of a fixed offshore Oscillating Water Column device, Applied Ocean Research, Volume 85, 2019, Pages 20-33, ISSN 0141-1187. [CrossRef]
  86. Zhao, X., Zhang, l., Li, M., Johanning, L., 2021, Experimental investigation on the hydrodynamic performance of a multi-chamber OWC-breakwater, Renewable and Sustainable Energy Reviews, 150,111512, ISSN 1364-0321. [CrossRef]
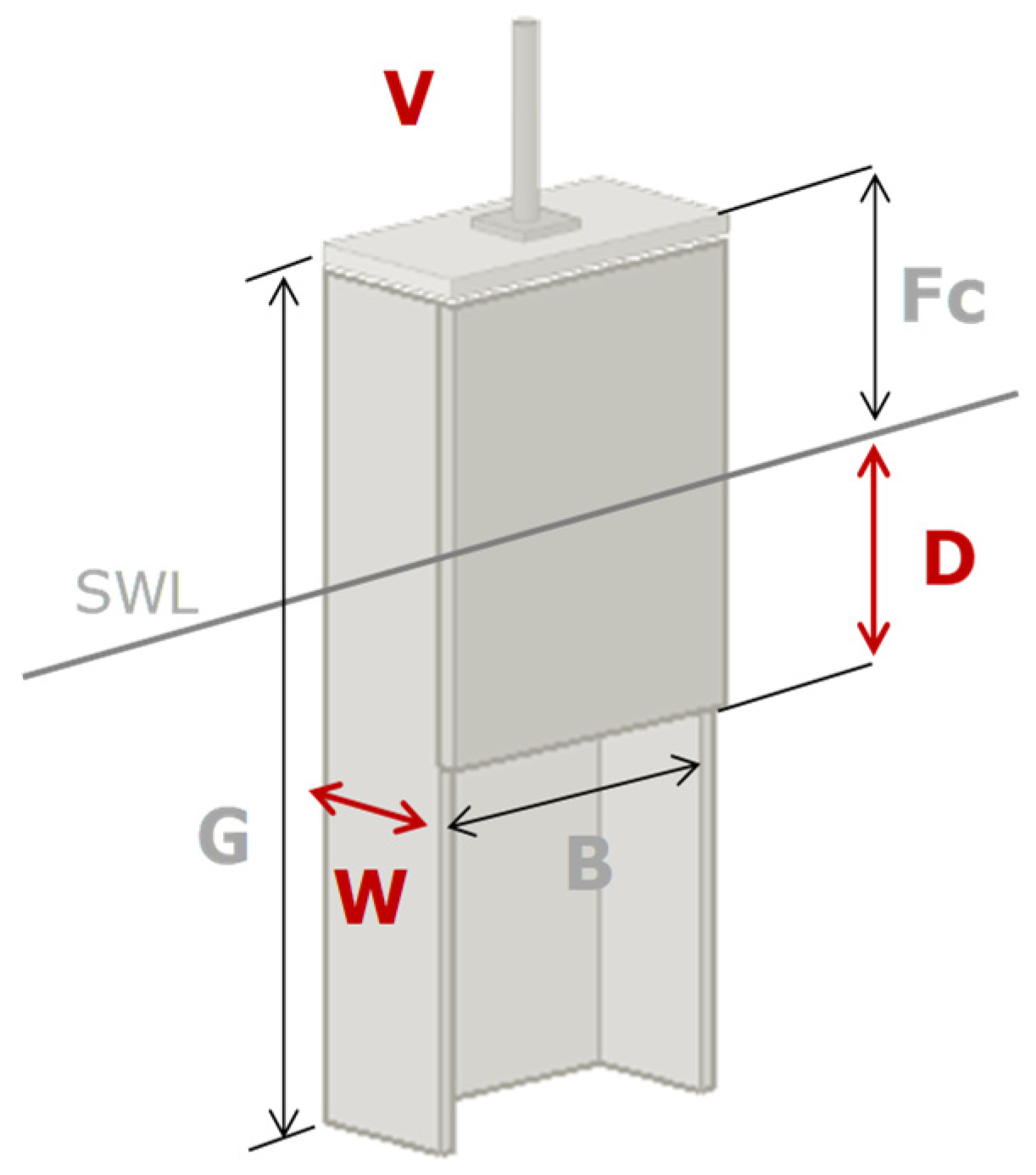
Preprints 120876 g001
Figure 1. Definition sketch for the OWC parameters naming convention. Parameters that were varied in the laboratory tests are marked in red in the definition sketch.
Figure 1. Definition sketch for the OWC parameters naming convention. Parameters that were varied in the laboratory tests are marked in red in the definition sketch.
Preprints 120876 g001
Preprints 120876 g002
Figure 2. Instantaneous values of air volume flux QOWC vs. air chamber pressure POWC for the nine vent duct diameters V with the associated damping coefficients K estimated as best-parabolic fit for the exhalation phase. Data refers to the draft level D2 (Table 1) and to the wave condition H02 (Table 3) only, since acquisitions for other cases are substantially analogous.
Figure 2. Instantaneous values of air volume flux QOWC vs. air chamber pressure POWC for the nine vent duct diameters V with the associated damping coefficients K estimated as best-parabolic fit for the exhalation phase. Data refers to the draft level D2 (Table 1) and to the wave condition H02 (Table 3) only, since acquisitions for other cases are substantially analogous.
Preprints 120876 g002
Preprints 120876 g005
Figure 5. Time series of water level oscillations inside the OWC chamber (a) and Fast Fourier Transform spectra of the induced water surface oscillations (b), exemplarily for the OWC models W1D2K2, W2D1K5 and W2D1K6.
Figure 5. Time series of water level oscillations inside the OWC chamber (a) and Fast Fourier Transform spectra of the induced water surface oscillations (b), exemplarily for the OWC models W1D2K2, W2D1K5 and W2D1K6.
Preprints 120876 g005
Preprints 120876 g006
Figure 6. Natural frequency of the OWC assessed using the prediction formula proposed (McCormick, 2007), compared with the results of RES tests for three chamber lengths, with different front wall draught and turbine damping (K3 for W1, K5 for W2 and K7 for W3).
Figure 6. Natural frequency of the OWC assessed using the prediction formula proposed (McCormick, 2007), compared with the results of RES tests for three chamber lengths, with different front wall draught and turbine damping (K3 for W1, K5 for W2 and K7 for W3).
Preprints 120876 g006
Preprints 120876 g007
Figure 7. Effect of chamber width W on water surface elevation ηOWC(t) compared with η(t) recorded at the same location in the same test without any model (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 7. Effect of chamber width W on water surface elevation ηOWC(t) compared with η(t) recorded at the same location in the same test without any model (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g007
Preprints 120876 g008
Figure 8. Effect of chamber width W on airflow velocity UOWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 8. Effect of chamber width W on airflow velocity UOWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g008
Preprints 120876 g009
Figure 9. Effect of chamber width W on air pressure POWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 9. Effect of chamber width W on air pressure POWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g009
Preprints 120876 g010
Figure 10. Effect of chamber width W and front wall draught D, for comparable damping (i.e. K3 for W1, K5 for W2 and K7 for W3) on air pressure oscillation amplitude ΔηOWC for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 10. Effect of chamber width W and front wall draught D, for comparable damping (i.e. K3 for W1, K5 for W2 and K7 for W3) on air pressure oscillation amplitude ΔηOWC for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g010
Preprints 120876 g011
Figure 11. Effect of chamber width W and front wall draught D, for comparable damping (i.e. K3 for W1, K5 for W2 and K7 for W3) on the air pressure POWC at the centre of the OWC chamber for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 11. Effect of chamber width W and front wall draught D, for comparable damping (i.e. K3 for W1, K5 for W2 and K7 for W3) on the air pressure POWC at the centre of the OWC chamber for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g011
Preprints 120876 g012
Figure 12. Effect of chamber width W and front wall draught D, for comparable damping (i.e. K3 for W1, K5 for W2 and K7 for W3) on maximum air volume flux Qmax in the pipe for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 12. Effect of chamber width W and front wall draught D, for comparable damping (i.e. K3 for W1, K5 for W2 and K7 for W3) on maximum air volume flux Qmax in the pipe for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g012
Preprints 120876 g013
Figure 13. Effect of front wall draught D on water surface elevation ηOWC(t), compared with the η(t), recorded at the same location in the same test without any model (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 13. Effect of front wall draught D on water surface elevation ηOWC(t), compared with the η(t), recorded at the same location in the same test without any model (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g013
Preprints 120876 g014
Figure 14. Effect of front wall draught D, on air pressure POWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 14. Effect of front wall draught D, on air pressure POWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g014
Preprints 120876 g015
Figure 15. Effect of front wall draught D, on airflow velocity UOWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 15. Effect of front wall draught D, on airflow velocity UOWC(t) (time series recorded at the centre of the OWC, for regular wave tests - H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g015
Preprints 120876 g016
Figure 16. Effect of damping K on water surface elevation ηOWC(t) compared with the η(t) recorded at the same location in the same test without any model (time series recorded at the centre of the OWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 16. Effect of damping K on water surface elevation ηOWC(t) compared with the η(t) recorded at the same location in the same test without any model (time series recorded at the centre of the OWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g016
Preprints 120876 g017
Figure 17. Effect of damping K on air pressure POWC(t) (time series recorded at the centre of the OWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 17. Effect of damping K on air pressure POWC(t) (time series recorded at the centre of the OWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g017
Preprints 120876 g018
Figure 18. Effect of damping K on the airflow velocity UOWC(t) (time series recorded at the centre of the OWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 18. Effect of damping K on the airflow velocity UOWC(t) (time series recorded at the centre of the OWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g018
Preprints 120876 g019
Figure 19. Effect of damping coefficient K on water surface oscillations ΔηOWC at the centre of the OWC for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 19. Effect of damping coefficient K on water surface oscillations ΔηOWC at the centre of the OWC for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g019
Preprints 120876 g020
Figure 20. Effect of damping coefficient K on air pressure oscillation amplitude ΔPOWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 20. Effect of damping coefficient K on air pressure oscillation amplitude ΔPOWC, for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g020
Preprints 120876 g021
Figure 21. Effect of damping coefficient K on maximum air volume flux Qmax in the pipe for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Figure 21. Effect of damping coefficient K on maximum air volume flux Qmax in the pipe for regular wave tests (H=0.04 m, kh=1.22-3.15 & h=0.50 m).
Preprints 120876 g021
Preprints 120876 g022
Figure 22. Capture width ratio CWR versus damping K for the regular wave tests (H=0.04 m, kh=1.22-3.15, h=0.50m).
Figure 22. Capture width ratio CWR versus damping K for the regular wave tests (H=0.04 m, kh=1.22-3.15, h=0.50m).
Preprints 120876 g022
Table 1. Fixed and varied design parameters.
Table 1. Fixed and varied design parameters.
FIXED DESIGN PARAMETERS
Notation Description [unit] value
B Chamber width [m] 0.20
G Back wall length [m] 0.45
Fc Freeboard [m] +0.16 S.W.L.
G-Fc Back wall draught [m] 0.29
thfbt Front, back and top cover wall thickness [m] 0.01
ths Side walls thickness [m] 0.008
VARIED DESIGN PARAMETERS
Notation Description [unit] value
W Chamber length [m] W1=0.10
W2=0.20
W3=0.30
D Front wall draught [m] D1=0.09
D2=0.18
D3=0.29
V Vent duct diameter [m] V1=0.008
V2=0.014
V3=0.020
V4=0.016
V5=0.021
V6=0.030
V7=0.018
V8=0.026
V9=0.036
Table 2. Damping coefficients K calculated for each vent duct diameter tested.
Table 2. Damping coefficients K calculated for each vent duct diameter tested.
Vent duct diameter V [m] OWC length W [m] Damping K [kg1/2m-7/2] -
best fit for the exhalation phase 		Damping Kin [kg1/2m-7/2] -
best fit for the inhalation phase
V1=0.008 W1=0.1 K1=46000 Kin1=49000
V2=0.014 W1=0.1 K2=11000 Kin2=15000
V3=0.020 W1=0.1 K3=3300 Kin3=3800
V4=0.016 W2=0.2 K4=6700 Kin4=10000
V5=0.021 W2=0.2 K5=3000 Kin5=3600
V6=0.030 W2=0.2 K6=1250 Kin6=1700
V7=0.018 W2=0.3 K7=4300 Kin7=4900
V8=0.026 W2=0.3 K8=1750 Kin8=2150
V9=0.036 W2=0.3 K9=900 Kin9=1000
Table 3. Incident effective wave parameters as obtained from time domain analysis (for regular waves) and frequency domain analysis (for irregular waves) of wave data acquired during wave tests in absence of the model (water depth 0.50 m).
Table 3. Incident effective wave parameters as obtained from time domain analysis (for regular waves) and frequency domain analysis (for irregular waves) of wave data acquired during wave tests in absence of the model (water depth 0.50 m).
Regular waves
Wave H [m] T [s] f [Hz] kh [-] H/λ [-] Sampling Duration [s]
1 0.042 0.8 1.25 3.15 0.040 70
2 0.043 1.0 1.00 2.07 0.025 70
3 0.042 1.4 0.71 1.22 0.013 70
Irregular waves
Wave* Hs [m] Tp [s] fp [Hz] kh [-] H/λ [-] Duration [s]
4 0.021 0.9 1.11 2.68 0.021 100
5 0.021 1.0 1.00 2.28 0.019 100
6 0.038 1.0 1.00 2.23 0.028 100
7 0.040 1.0 1.00 1.88 0.024 100
8 0.057 1.1 0.91 1.85 0.034 100
*The five irregular waves tested, with Hs and fp being the significant wave height and peak frequency, respectively
Table 4. Natural period of the OWC models considered in the free decay RES tests in this study.
Table 4. Natural period of the OWC models considered in the free decay RES tests in this study.
OWC model TOWC [s] FDA TOWC [s] LDM OWC model TOWC [s] FDA TOWC [s] LDM OWC model TOWC [s] FDA TOWC [s] LDM
W1D1K1 - * - W2D1K4 - 0.98 W3D1K7 - 0.98
W1D2K1 - - W2D2K4 - 1.13 W3D2K7 - 1.18
W1D3K1 - - W2D3K4 1.23 1.25 W3D3K7 - 1.29
W1D1K2 0.82 0.85 W2D1K5 1.00 0.98 W3D1K8 1.03 1.02
W1D2K2 1.05 1.00 W2D2K5 1.10 1.05 W3D2K8 1.10 1.12
W1D3K2 1.21 1.23 W2D3K5 1.30 1.25 W3D3K8 1.20 1.20
W1D1K3 0.83 0.83 W2D1K6 0.92 0.94 W3D1K9 1.04 1.05
W1D2K3 1.06 1.03 W2D2K6 1.10 1.09 W3D2K9 1.10 1.12
W1D3K3 1.20 1.18 W2D3K6 1.20 1.18 W3D3K9 1.19 1.19
*[-] OWC configurations for the free surface oscillation in the RES test was damped too quickly to permit a precise estimation of the OWC natural frequency TOWC.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated