Introduction

1. Resonances in Small, Doublelayered, High-Contrast, Nonlinear Scatterers with Arbitrary Geometry

1.2. Case 1: Single-Layer Kerr Effect

Consider the scattering problem of high contrast small volume, $hB$. The small scatterer has two concentric inner and outer layers, with the latter exhibiting nonlinear Kerr effect.

$$hB=h{B}_{\mathrm{in}}\cup h{B}_{\mathrm{out}}$$

$$\eta \left(x\right)={\chi }_{h{B}_{\mathrm{in}}}\left(x\right){\eta }_{\mathrm{in}}+{\chi }_{h{B}_{\mathrm{out}}}\left(x\right){\eta }_{\mathrm{out}}={\chi }_{h{B}_{\mathrm{in}}}{\displaystyle \frac{{\eta }_{\mathrm{in}}}{h^2}}+{\chi }_{h{B}_{\mathrm{out}}}{\displaystyle \frac{{\eta }_{\mathrm{out}}}{h^2}}$$

$$\beta \left(x\right)={\chi }_{h{B}_{out}}{\displaystyle \frac{{\beta }_0}{h^2}}$$

for constant ${\eta }_0$ and ${\beta }_0$.

Within the context of this new configuration, the operators $T_h$, previously defined by (1), can be expressed as:

$$\begin{array}{cc}\hfill T_h\left(\lambda \right)\left(u\right)\left(x\right)& ={\displaystyle \frac{{\eta }_{in}^0}{4\pi }}{\int }_{B_{in}}{\displaystyle \frac{exp(i\sqrt{\lambda }h|x-y|)}{|x-y|}}u\left(y\right)dy\hfill \\ \hfill & +{\displaystyle \frac{{\eta }_{out}^0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{exp(i\sqrt{\lambda }h|x-y|)}{|x-y|}}u\left(y\right)dy\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{exp(i\sqrt{\lambda }h|x-y|)}{|x-y|}}u\left(y\right){\left|u\left(y\right)\right|}^{2}dy\hfill \end{array}$$

Hence we define the limiting operator, $T_0$, as $h\to 0$ as:

$$\begin{array}{cc}\hfill T_0\left(\lambda \right)\left(u\right)\left(x\right)& ={\displaystyle \frac{{\eta }_{in}^0}{4\pi }}{\int }_{B_{in}}{\displaystyle \frac{u\left(y\right)}{|x-y|}}dy\hfill \\ \hfill & +{\displaystyle \frac{{\eta }_{out}^0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{u\left(y\right)}{|x-y|}}dy\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{u\left(y\right)}{|x-y|}}{\left|u\left(y\right)\right|}^{2}dy\hfill \end{array}$$

As it was introduced in section 1.1, we are solving for the resonances, ${\lambda }_h$, the eigenvalue problem

$${\lambda }_h{T}_h{u}_h=u_h$$

via the limiting eigenvalue problem

$${\lambda }_0{T}_0{u}_0=u_0$$

In other words, we first solve the easier latter equation for $u_0$ and ${\lambda }_0$. Now let us expand $T_h$ by performing Taylor expansion of $h⟼exp\left(i\sqrt{\lambda }h\right|x-y\left|\right)$:

$$\begin{array}{cc}\hfill & T_h\left(\lambda \right)\left(u\right)\left(x\right)=T_0\left(\lambda \right)\left(u\right)\left(x\right)+{\displaystyle \frac{i\sqrt{\lambda }h}{4\pi }}\left({\eta }_{in}^0{\int }_{B_{in}}u\left(y\right)dy\right.\hfill \\ \hfill & \left.+{\eta }_{out}^0{\int }_{B_{out}}u\left(y\right)dy+{\beta }_0{\int }_{B_{out}}u\left(y\right){\left|u\left(y\right)\right|}^{2}dy\right)+\mathcal{O}\left(h^2\right)\hfill \end{array}$$

Evaluating at $u_0$ and ${\lambda }_0$ we obtain:

$$\begin{array}{cc}\hfill & (T_0-T_h\left({\lambda }_0\right))u_0=-{\displaystyle \frac{i\sqrt{{\lambda }_0}h}{4\pi }}\left({\eta }_{in}^0{\int }_{B_{in}}{u}_0\left(y\right)dy\right.\hfill \\ \hfill & \left.+{\eta }_{out}^0{\int }_{B_{out}}{u}_0\left(y\right)dy+{\beta }_0{\int }_{B_{out}}{u}_0^3\left(y\right)dy\right)+\mathcal{O}\left(h^2\right)\hfill \end{array}$$

or

$$(T_0-T_h\left({\lambda }_0\right))u_0=-{\displaystyle \frac{i\sqrt{{\lambda }_0}h}{4\pi }}\left({\eta }_{in}^0{U}_{in}+{\eta }_{out}^0{U}_{out}+{\beta }_0{U}_{out\beta }\right)+\mathcal{O}\left(h^2\right)$$

where

$$U_{in}={\int }_{B_{in}}{u}_0\left(y\right)dy,U_{out}={\int }_{B_{out}}{u}_0\left(y\right)dy$$

and

$$U_{out\beta }={\int }_{B_{out}}{u}_0^3\left(y\right)dy$$

At this point, we are ready to compute ${\lambda }_1$ by executing the expansion asymptotic formula:

$${\lambda }_h={\lambda }_0+{\lambda }_0^2\langle (T_0-T_h\left({\lambda }_0\right))u_0,u_0\rangle +\mathcal{O}\left(h^2\right)$$

(5)

Let

$${\lambda }_h={\lambda }_0+{\lambda }_{1}h+\mathcal{O}\left(h^2\right)$$

It follows that the correction ${\lambda }_1$ is

$${\lambda }_{\mathbf{1}}=-{\displaystyle \frac{\mathbf{i}{\lambda }_{\mathbf{0}}^{\frac{\mathbf{5}}{\mathbf{2}}}}{\mathbf{4}\pi }}\left({\eta }_{\mathbf{in}}^{\mathbf{0}}{\mathbf{U}}_{\mathbf{in}}+{\eta }_{\mathbf{out}}^{\mathbf{0}}{\mathbf{U}}_{\mathbf{out}}+{\beta }_{\mathbf{0}}{\mathbf{U}}_{\mathbf{out}\beta }\right){\mathbf{U}}_{\mathbf{0}}$$

where

$$U_0={\int }_B{u}_0\left(y\right)dy$$

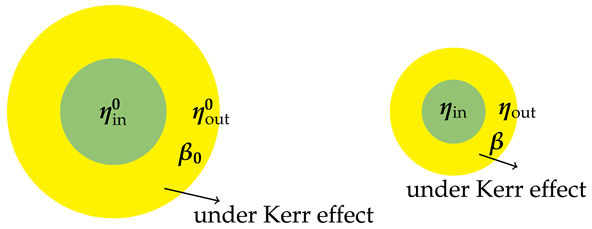
1.3. Case 2: Dual-Layer Kerr Effect

This configuration offers greater flexibility in designing the 3D scatterer, allowing for scenarios with either distinct or identical susceptibility coefficients (${\eta }_{\mathrm{in}}\ne {\eta }_{\mathrm{out}}$ or ${\eta }_{\mathrm{in}}={\eta }_{\mathrm{out}}$) and Kerr coefficients (${\beta }_{\mathrm{in}}\ne {\beta }_{\mathrm{out}}$ or ${\beta }_{\mathrm{in}}={\beta }_{\mathrm{out}}$). All coefficients are assumed to be constant.

$$\beta \left(x\right)={\chi }_{h{B}_{in}}{\displaystyle \frac{{\beta }_{in}^0}{h^2}}+{\chi }_{h{B}_{out}}{\displaystyle \frac{{\beta }_{out}^0}{h^2}}$$

In this case $T_h$ and $T_0$ write:

$$\begin{array}{cc}\hfill T_h\left(\lambda \right)\left(u\right)\left(x\right)& ={\displaystyle \frac{{\eta }_{in}^0}{4\pi }}{\int }_{B_{in}}{\displaystyle \frac{exp(i\sqrt{\lambda }h|x-y|)}{|x-y|}}u\left(y\right)dy\hfill \\ \hfill & +{\displaystyle \frac{{\eta }_{out}^0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{exp(i\sqrt{\lambda }h|x-y|)}{|x-y|}}u\left(y\right)dy\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_{in}^0}{4\pi }}{\int }_{B_{in}}{\displaystyle \frac{exp(i\sqrt{\lambda }h|x-y|)}{|x-y|}}u\left(y\right){\left|u\left(y\right)\right|}^{2}dy\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_{out}^0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{exp(i\sqrt{\lambda }h|x-y|)}{|x-y|}}u\left(y\right){\left|u\left(y\right)\right|}^{2}dy\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill T_0\left(\lambda \right)\left(u\right)\left(x\right)& ={\displaystyle \frac{{\eta }_{in}^0}{4\pi }}{\int }_{B_{in}}{\displaystyle \frac{u\left(y\right)}{|x-y|}}dy\hfill \\ \hfill & +{\displaystyle \frac{{\eta }_{out}^0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{u\left(y\right)}{|x-y|}}dy\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_{in}^0}{4\pi }}{\int }_{B_{in}}{\displaystyle \frac{u\left(y\right)}{|x-y|}}{\left|u\left(y\right)\right|}^{2}dy\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_{out}^0}{4\pi }}{\int }_{B_{out}}{\displaystyle \frac{u\left(y\right)}{|x-y|}}{\left|u\left(y\right)\right|}^{2}dy\hfill \end{array}$$

Similar to case 1, we perform a Taylor expansion of $h⟼exp\left(i\sqrt{\lambda }h\right|x-y\left|\right)$, yielding:

$$\begin{array}{cc}\hfill & T_h\left(\lambda \right)\left(u\right)\left(x\right)=T_0\left(\lambda \right)\left(u\right)\left(x\right)+{\displaystyle \frac{i\sqrt{\lambda }h}{4\pi }}\left({\eta }_{in}^0{\int }_{B_{in}}u\left(y\right)dy\right.\hfill \\ \hfill & \left.+{\eta }_{out}^0{\int }_{B_{out}}u\left(y\right)dy+{\beta }_{in}^0{\int }_{B_{in}}{u\left(y\right)\left|u\left(y\right)\right|}^{2}dy+{\beta }_{out}^0{\int }_{B_{out}}u\left(y\right){\left|u\left(y\right)\right|}^{2}dy\right)+\mathcal{O}\left(h^2\right)\hfill \end{array}$$

Subsequently, the correction ${\lambda }_1$ is derived by evaluating the inner product in equation (5).

$${\lambda }_{\mathbf{1}}=-{\displaystyle \frac{\mathbf{i}{\lambda }_{\mathbf{0}}^{\frac{\mathbf{5}}{\mathbf{2}}}}{\mathbf{4}\pi }}\left({\eta }_{\mathbf{in}}^{\mathbf{0}}{\mathbf{U}}_{\mathbf{in}}+{\eta }_{\mathbf{out}}^{\mathbf{0}}{\mathbf{U}}_{\mathbf{out}}+{\beta }_{\mathbf{in}}^{\mathbf{0}}{\mathbf{U}}_{\mathbf{in}\beta }+{\beta }_{\mathbf{out}}^{\mathbf{0}}{\mathbf{U}}_{\mathbf{out}\beta }\right){\mathbf{U}}_{\mathbf{0}}$$

where

$$U_{in\beta }={\int }_{B_{in}}{u}_0^3\left(y\right)dy,U_{out\beta }={\int }_{B_{out}}{u}_0^3\left(y\right)dy$$

$$U_{in}={\int }_{B_{in}}{u}_0\left(y\right)dy,U_{out}={\int }_{B_{out}}{u}_0\left(y\right)dy,\mathrm{and}{U}_0={\int }_B{u}_0\left(y\right)dy$$

Note that we recover ${\lambda }_1$ in case 1 by setting ${\beta }_{in}^0=0$. Furthermore, setting ${\beta }_{out}^0=0$ provides the formula for ${\lambda }_1$ when only the inner layer exhibits the Kerr effect.

2. Resonances in Small, Multilayered, High-Contrast, Nonlinear Scatterers with Arbitrary Geometry

References

1. Zhou, D.; Biswas, R. Trapping light in solar cells. Journal of Applied Physics 2010, 107, 094501. [Google Scholar]
2. Cummer, S.A.; Christensen, J.; Alu, A. Controlling sound with acoustic metamaterials. Nature Reviews Materials 2016, 1, 1–13. [Google Scholar] [CrossRef]
3. Alu, A.; Engheta, N. Plasmonic materials for optical transformation and invisibility cloaking. Journal of Optics A: Pure and Applied Optics 2007, 10, 093002. [Google Scholar]
4. Meklachi, T.; Schotland, J.C.; Moskow, S. Asymptotic analysis of resonances of small volume high contrast linear and nonlinear scatterers. Journal of Mathematical Physics 2018, 59, 20. [Google Scholar] [CrossRef]
5. Meklachi, T. Theorem of resonance of Small Volume High Contrast multilayered materials. 2022; arXiv:math-ph/2205.00674]. [Google Scholar]
6. Ammari, H.; Millien, P.; Ruiz, M. Mathematical analysis of plasmonic resonances for nanoparticles: the scalar case. Archive for Rational Mechanics and Analysis 2018, 227, 1011–1069. [Google Scholar]
7. Moskow, S. Nonlinear eigenvalue approximation for compact operators. Journal of Mathematical Physics 2015, 56. [Google Scholar] [CrossRef]
8. Ammari, H.; Challa, D.P.; Li, M. Layer potential techniques for the approximation of resonances in high-contrast plasmonic media. SIAM Journal on Mathematical Analysis 2022, 54, 1759–1785. [Google Scholar]
9. Boyd, R.W. Nonlinear optic, Elsevier, 2020.
10. Poutrina, E.; Huang, D.; Urzhumov, Y.; Smith, D.R. Nonlinear and tunable metamaterials. Advanced materials 2010, 22, 867–870. [Google Scholar]
11. Suchkov, S.V.; Dmitriev, A.L.; Dotsenko, I.E.; Levchenko, V.A.; Zaitsev, S.V. Resonant properties of dielectric microspheres with a high refractive index. Journal of the Optical Society of America B 2000, 17, 674–682. [Google Scholar]
12. Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nature Photonics 2011, 5, 523–530. [Google Scholar] [CrossRef]
13. Ma, G.; Yang, M.; Xiao, S.; Yang, Z.; Sheng, P. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Nature materials 2014, 13, 873–878. [Google Scholar] [CrossRef] [PubMed]
14. Dabrowski, A.; Ghandriche, A.; Sini, M. Mathematical analysis of the acoustic imaging modality using bubbles as contrast agents at nearly resonating frequencies. 2020; arXiv:math.AP/2004.07808]. [Google Scholar]
15. Kircher, M.F.; Alcaraz de La Osa, R.; Nelson, B.D.; Manjavacas, A.; Nordlander, P.; Halas, N.J. Resonant infrared nanostructures for sensing, spectroscopy, and optical switching. ACS photonics 2014, 1, 1066–1076. [Google Scholar]
16. Alitalo, P.; Koppens, F.H. Graphene antenna for terahertz photodetection. Nano letters 2015, 15, 4685–4689. [Google Scholar]
17. Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nature materials 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
18. Adams, B.; Li, K.; Meklachi, T. Spectral analysis of scattering resonances with application on high-contrast nanospheres. Letters in Mathematical Physics 2022, 112, 70. [Google Scholar] [CrossRef]