Prerpints.org logo
Preprint
Article

From Fields to Microclimate: Assessing the Influence of Agricultural Landscape Structure on Vegetation Cover and Local Climate in Central Europe

Altmetrics

Downloads

65

Views

46

Comments

0

This version is not peer-reviewed

Submitted:

10 October 2024

Posted:

11 October 2024

You are already at the latest version

Alerts
Abstract
Agricultural intensification through simplification and specialisation has homogenised diverse landscapes, reducing their heterogeneity and complexity. While the negative impact of large, simplified fields on biodiversity is well-documented, the role of landscape structure in mitigating and stabilising climate is becoming increasingly important. Despite considerable knowledge of landscape cover types, the understanding of how landscape structure influences climatic characteristics remains limited. To explore this further, we studied an area along the Czech-Austrian border, where socio-political factors have created stark contrasts in landscape structure, despite similar topography. Using Land Parcel Information System (LPIS) data, we analysed the landscape structure on both sides, and processed eight Landsat 8 and 9 OLI/TIRS scenes from the 2022 vegetation season to calculate vegetation indices (NDVI, NDMI) and microclimatic features (surface temperature, albedo, and energy fluxes). Our findings reveal significant differences between the two regions. Czech fields, with their larger, simpler structure and lower edge density, experience more extreme temperatures and fluctuating energy fluxes, while Austrian fields exhibit greater stability. These patterns are consistent across landscape classes, with Austria’s finer landscape structure providing higher stability throughout the vegetation season. In light of climate change and biodiversity conservation, these results emphasise the need to protect and restore landscape complexity to enhance resilience and environmental stability.
Keywords: 
Subject: Environmental and Earth Sciences  -   Environmental Science

1. Introduction

The structure of the landscape, particularly farmland, has a significant impact on its environment. Since the 1950s, the European landscape has undergone substantial changes due to the intensification of agriculture. The industrial approach to farming often neglects natural aspects, creating an environment more prone to degradation, dependent, and fragile. In many ways, due to the suppression of autoregulatory ecosystem services, the agroecosystems are more dependent on the human input of pesticides, fertilisers, tillage, etc. [1]. The increasing size of monoculture fields has led to the elimination of valuable field edges, which naturally provide shelter for wild organisms and habitats for semi-natural plants. Extensive monoculture fields have replaced the diverse mosaic of land covers with large, homogenised areas growing crops such as wheat, corn, or oilseed rape, which unfortunately often become almost the only crops rotated in the Czech Republic. This simplification of the landscape not only boosts production but also exacerbates the associated problems [2,3].
Large monoculture fields are more vulnerable to pests due to a lack of biodiversity and, consequently, a lack of natural predators [4,5]. This issue leads to the increased use of pesticides and insecticides, further reducing biodiversity and trapping farmers in a vicious cycle. During periods when fields are bare, the soil’s ability to retain and absorb surface water is diminished, disrupting the hydrological cycle [6]. Additionally, the fields are naturally susceptible to erosion due to surface runoff and unrestricted wind flow, which annually removes large portions of fertile topsoil (fine particles), along with its natural fertility [7,8]. An important factor in this context, particularly in the landscape’s hydrological regime, is the widespread installation of field drainage systems [9].
The impact of landscape changes on biodiversity, water runoff, and soil erosion is only one part of the problem. These changes are relatively well-documented. An equally important but often overlooked aspect is the impact of landscape structure changes on the biophysical properties of the surface, which are directly or indirectly related to climate processes. The relationship between landscape structure and surface biophysical properties has been studied from various perspectives. For instance, the "Daisyworld" model by Watson and Lovelock [10] demonstrated the interconnectedness of "Life" and the "Environment." The authors stated, "Regardless of the details of the interaction, the effect of the daisies is to stabilise temperature." Shukla and Mintz [11] described changes in precipitation patterns, surface temperature, and surface pressure in their simulation, comparing Earth with 100% potential evapotranspiration to Earth with no evapotranspiration. Other studies have focused on the impact of vegetation cover on atmospheric circulation (see e.g., [12,13,14,15,16]).
A significant portion of the research in this field focuses on urban areas, where growing populations and urban sprawl intensify the effects of the "Urban Heat Island" (UHI) phenomenon [17,18,19,20]. This poses not only an ecological challenge but also a public health concern, as Central Europe, among other regions, experienced yet another summer of heatwaves [21]. The composition and configuration of urban environments, including green spaces, play a crucial role in cooling cities [22,23]. This phenomenon can also raise questions of environmental justice, as lower-income urban residents are at greater risk of heat stress [24].
Although considerable attention has been given to UHI issues and the bioclimatic functions of various landscape covers, the importance of changes in landscape structure in shaping climatic characteristics still needs to be explored.
The border areas between the Czech Republic and Austria offer a fascinating example of vastly different landscape structures in close proximity. These differences are a function of agricultural policy and landscape management (see e.g., [25,26,27,28,29]). Kupková et al. [30] compared land cover changes along the entire Iron Curtain between 1990 and 2006, observing an increase in heterogeneous agricultural areas on the Czech side due to more complex cultivation patterns, while changes on the Austrian side were minimal. The development of landscape structure between 1952 and 2009 was studied by Sklenička et al. [27], who found that the Czech landscape was more homogeneous compared to the Austrian side, where heterogeneity increased, while it slightly decreased in the Czech Republic over the study period.
Although the relationship between landscape structure and biophysical surface properties has been researched, the farmland context has often been overlooked, with more focus on urban areas or large-scale models. The structure of farmland in the border region between the Czech Republic and Austria has been studied from multiple perspectives, yet no one has asked whether the farmland structure affects the microclimate of these distinctly different neighbouring landscapes. We hypothesise that farmland structure influences the spatial and seasonal characteristics of vegetation patterns (biomass) and landscape microclimatic features, such as surface moisture, surface temperature, and heat fluxes.

2. Materials And Methods

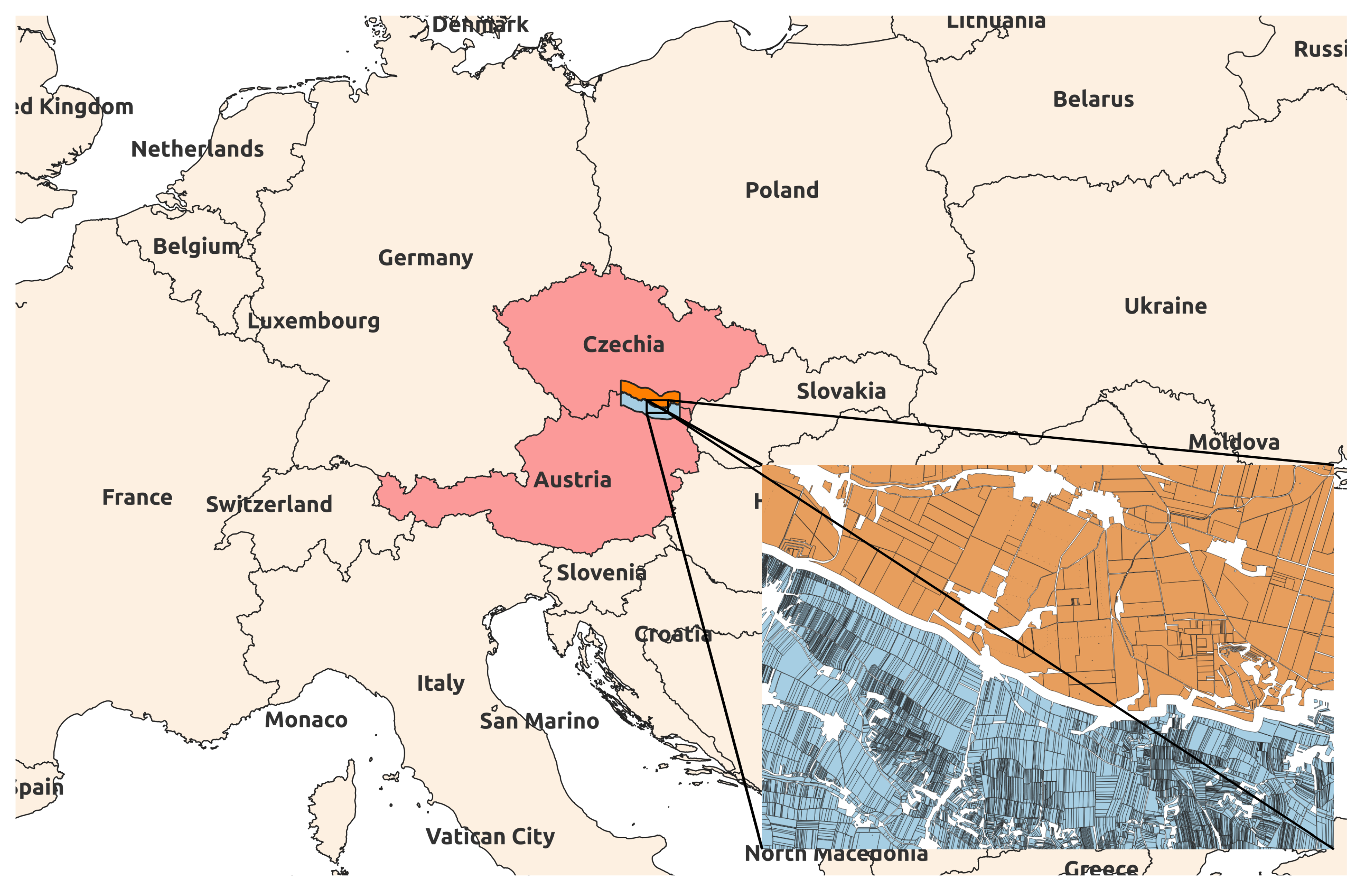
2.1. Area of Interest Description

The aim of selecting the area of interest was to select areas that differ in structure while the topographic and climatic characteristics are the same or very similar and are large enough for the analysis. The Czech-Austrian border area fulfils this assumption, where the landscape has evolved differently in the two countries during the 20th century. This area uniquely contrasts the landscape structures despite the physical proximity and climatic similarities. It is thus an interesting example of how different landscape management can change its characteristics.
The AOI was selected as a 20 km buffer on each side of the border between the Czech Republic and Austria, stretching approximately between 49.17°N, 15.25°E and 48.54°N, 16.66°E (Figure 1). The inner buffer of 100 m in touch with the border was excluded from the dataset to prevent inaccuracies. Based on the irregular border shape, the resulting area of the Czech part of the AOI is smaller, with 144 579 ha, compared to the Austrian with 155 922 ha.
The area is moderately hilly in the western part and flat in the eastern part. The mean elevation of the Czech AOI is 353 m, spanning from 160 m to 770 m with an average slope of 3.77° and a mean aspect of 140.8°. The Austrian AOI has a similar average elevation of 354 m, ranging between 170 m and 731 m, with a mean slope value of 4.18° and mean aspect of 149.28°. The Czech side of the AOI lies over three regions: South Bohemian Region, Vysočina and South Moravian Region and Lower Austria on the Austrian side.
The AOI belongs to the temperate zone, humid continental climate region, subtype Dfb (warm summer subtype) according to the Köppen classification [31]. The long-term average year temperature and precipitation (1991-2020) are 7.9 °C and 677 mm for the western part and 9.4 °C and 561 mm for the eastern part of AOI, respectively [32].
The vegetation cover consists mainly of agricultural non-forest areas. On the Czech side of the AOI, the proportion of forest is 11.3% of the area, and on the Austrian side 10.7%. Built-up areas are a minority on both sides of the AOI. Arable land represents approximately 89% of the agricultural area on the Czech side of the AOI and 81% on the Austrian side. The remainder consists of vineyards, permanent grassland, fallow land and arable grassland. Details are given in the Table 1. The main crops are winter wheat, winter and spring barley, corn and oilseed rape. Only agricultural non-forest fields were selected for the analysis

2.2. Landscape Structure Analysis

The data for the structural analysis were obtained from the Land Parcel Identification System (LPIS) - for Austria, a version last updated on 30 June 2022 [33] and for the Czech Republic version published 31 December 2021 [34]. The data are provided as vector layers, thus, we rasterised them since raster format is used as input for the landscape structure analysis software. Rasterisation was done in QGIS in 2 m resolution, which was an intersection of preserving enough detail with reasonable data size. These layers contain solely farmland areas, leaving out all settlements, forests and infrastructure. The data on the Austrian side had crop information for each plot, yet the Czech data had broader classes. Therefore, we had to reclassify the Austrian data to unify the classes. We selected the most abundant ones (arable land, vineyards, permanent grassland, fallow land and grass cultures on arable land). The farmland as a whole was also characterised (category All, see Table 1). This data has been then processed in the Python library PyLandStats [35] as a successor to the program for “Spatial Pattern Analysis for Categorical Maps” – FRAGSTATS [36] because it was superior in handling our size of data. According to the program documentation, we ran the landscape level analysis for the entire farmland and class level analysis for the individual land cover classes.
Table 1. The summary of the landscape structural characteristics for the Czech (CZ) and Austrian (AT) area calculated using PyLandStats [35].
Table 1. The summary of the landscape structural characteristics for the Czech (CZ) and Austrian (AT) area calculated using PyLandStats [35].
Country All Arable land VVineyeVards Permanent grass Fallow land Grass on field
Total area (ha) CZ 144 579.1 129 187.5 5 132.3 7 981.0 682.4 703.8
AT 155 922.7 126 257.7 8 145.2 4 245.6 7 139.8 8 890.6
Proportion of landscape (%) CZ 100.0 89.4 3.6 5.5 0.5 0.5
AT 100.0 81.0 5.2 2.7 4.6 5.7
Number of patches CZ 13 172.0 7 036.0 1 478.0 3 086.0 601.0 447.0
AT 66 788.0 18 998.0 4 835.0 5 027.0 13 593.0 6 465.0
Patch density CZ 9.1 4.9 1.0 2.1 0.4 0.3
AT 42.8 12.2 3.1 3.2 8.7 4.1
Largest patch index CZ 0.37 0.37 0.04 0.06 0.02 0.02
AT 0.11 0.11 0.03 0.03 0.02 0.02
Total edge (m) CZ 1 551 290.0 1 480 348.0 196 248.0 463 950.0 698 246.0 153 428.0
AT 9 175 832.0 7 109 228.0 1 712 832.0 947 618.0 3 976 782.0 2 732 080.0
Edge density CZ 10.7 10.2 1.4 3.2 4.8 1.1
AT 58.8 45.6 11.0 6.1 25.5 17.5
Area mean (ha) CZ 11.0 18.4 3.5 2.6 1.1 1.6
AT 2.3 6.6 1.7 0.8 0.5 1.4
Area weighted mean (ha) CZ 57.3 62.7 13.8 11.1 8.6 9.4
AT 17.5 20.6 7.0 3.9 1.5 4.2
Area median (ha) CZ 2.26 7.43 1.16 1.12 0.36 0.41
AT 0.38 2.97 0.67 0.38 0.32 0.69
Area range (ha) CZ 531.7 531.7 52.2 92.0 27.5 35.0
AT 164.3 164.3 46.8 40.5 23.9 27.2
Area std. deviation (ha) CZ 22.6 28.5 6.0 4.7 2.9 3.5
AT 5.9 9.6 3.0 1.6 0.7 2.0
Area coef. of variation (ha) CZ 205.5 155.5 172.3 181.1 256.9 222.4
AT 254.8 144.9 177.0 188.8 139.1 143.4

2.3. Weather Data

The meteorological data were used to assume the microclimatic conditions of the AOI and calculate the energy fluxes from the Landsat satellite data (see below). The hourly weather data were obtained from the Meteostat database through RapidAPI portal [37] for the weather station in Tulln, Austria, for the dates corresponding with the satellite data acquisition schedule. We collected data concerning relative humidity and air temperature from this meteorological station. The global radiation values were calculated using GRASS GIS and its function r.sun.incidout in QGIS [38,39].

2.4. Satellite Data Processing

Landsat 8 OLI/TIRS data were used to analyse changes in vegetation cover characteristics, surface temperature and energy balance indices, i.e., evaporative latent heat flux, sensible heat flux, soil heat flux, albedo and evaporative fraction. Satellite data were obtained from the EarthExplorer (USGS), Collection 2 Level 2 product repository for cloud-free or negligible cloud cover days over the area of interest for the 2022 growing season. Images were acquired for 18 May, 3 June, 19 June, 21 July, 30 August, 7 September, 23 September and 25 October.
The spectral reflectance and surface temperature bands were used for further analysis. Detailed information on the characteristics of the data is summarised on the USGS website [40]. SRTM digital terrain model (DMT) data with a spatial resolution of 30 m were used as supplemental data [41]. Any cloud cover was removed from the image using the FMask method [42,43].
Vegetation cover characteristics were assessed through vegetation spectral indices. Changes in vegetation cover were assessed using the Normalized Difference Vegetation Index (NDVI; [44]), corresponding to the amount of biomass [45,46]. The NDVI index was calculated as follows:
N D V I = ρ N I R − ρ R E D ρ N I R + ρ R E D ,
where ρ R E D and ρ N I R are satellite spectral reflectance bands in the red and near-infrared (NIR) regions of the spectrum.
Surface moisture characteristics were evaluated using the Normalized Difference Moisture Index (NDMI, [47]), corresponding to surface moisture. The NDMI index was calculated as follows:
N D M I = ρ N I R − ρ S W I R 1 ρ N I R + ρ S W I R 1 ,
where ρ S W I R 1 is the satellite spectral band in the SWIR spectral regions (Band 6, spectral range 1.57 - 1.65 μ m).
Albedo ( α ; rel.) indicates shortwave radiation exchange at the Earth’s surface. To calculate broad-band albedo, the approach of Liang [48], Liang et al. [49] and Tasumi et al. [50] was used, where albedo is calculated as a linear combination of spectral bands. The coefficients for the individual spectral bands are taken from [51]. The albedo was calculated according to the relation:
α = ∑ b = 1 7 ( ρ s _ b · w b ) ,
where b is the spectral band number, ρ s _ b is the spectral reflectance band and w b is the band coefficient taken from [51].
Evaporative fraction (EF; rel.), sensible heat flux (H; W·m − 2 ), latent heat flux (LE; W·m − 2 ) and ground heat flux (G; W·m − 2 ) were chosen as indicators of energy exchange at the surface. The evaporative fraction represents the ratio of energy used for evaporation to the total energy available in the environment. It is the reciprocal of Bowen’s ratio (the ratio between sensible and latent heat flux, see [52]). It is, therefore, a useful indicator of surface energy conversion and the functional properties of vegetation cover. The gradient model based on the surface energy balance approach [53], which uses the temperature difference in the area of interest, was used for the calculation. The temperature gradient is scaled to range from minimum surface temperature for areas with maximum evapotranspiration intensity to maximum temperature for areas with minimum evapotranspiration level. EF was calculated as follows [53]:
E F = T m a x − T s T m a x − T a ,
where T m a x (°C) is the maximal surface temperature for the AOI, corresponding to the minimal evapotranspiration intensity. T s is surface temperature (°C), and T a (°C) is territorial air temperature for mixing layer level (approx. at 200 m above surface). The territorial air temperature was calculated for the area of interest for the satellite imagery time based on data from the Tulln weather station (see above) and the change in adiabatic gradient based on DMT from the SRTM data layer. The adiabatic gradient considered was 0.65 °C per 100 m elevation.
The latent heat flux, i.e., the flux of energy consumed to evaporate water in the process of evapotranspiration, is, similarly to EF, an indicator of the ability of vegetation to transform solar energy into water vapour and thus limit surface overheating. This is a significant stabilising effect in the landscape (see e.g., [54] for details). The latent heat flux of evaporation was calculated based on the EF and the surface heat balance:
L E = E F · ( R n − G ) ,
where R n is total net radiation ( W·m − 2 ). Details of R n calculation are given in [55].
The sensible heat flux represents the turbulent heat exchange between the surface and the atmosphere, where heat is transferred to the atmosphere and heats it. The sensible heat flux was calculated according to the relationship:
H = R n − G − L E .
The ground heat flux combines the properties of the vegetation cover and the soil characteristics. The empirical approach of Bastiaanssen et al. [56] was used for the calculation:
G = T s α ( 0.0038 α + 0.0074 α 2 ) ( 1 − 0.98 N D V I 4 ) R n .
The QGIS module SEBCS for QGIS [55] was used to calculate spectral vegetation indices, albedo, evaporative fraction and heat fluxes.

2.5. Statistical Analysis

A comparative analysis of hypothesis testing using Student’s t-test was used to statistically compare the observed landscape characteristics on the Czech and Austrian sides of the AOI. The test was chosen with respect to good estimation ability and robustness in case of violation of test assumptions, e.g., data normality. A representative sample size of 200 values for the Czech and Austrian sides of the AOI was selected for each variable testing to avoid statistical error II. The sample size was chosen to preserve the statistical characteristics of the study areas and, at the same time, not to increase the power of the test excessively. Basic statistical variables were also calculated for each variable.

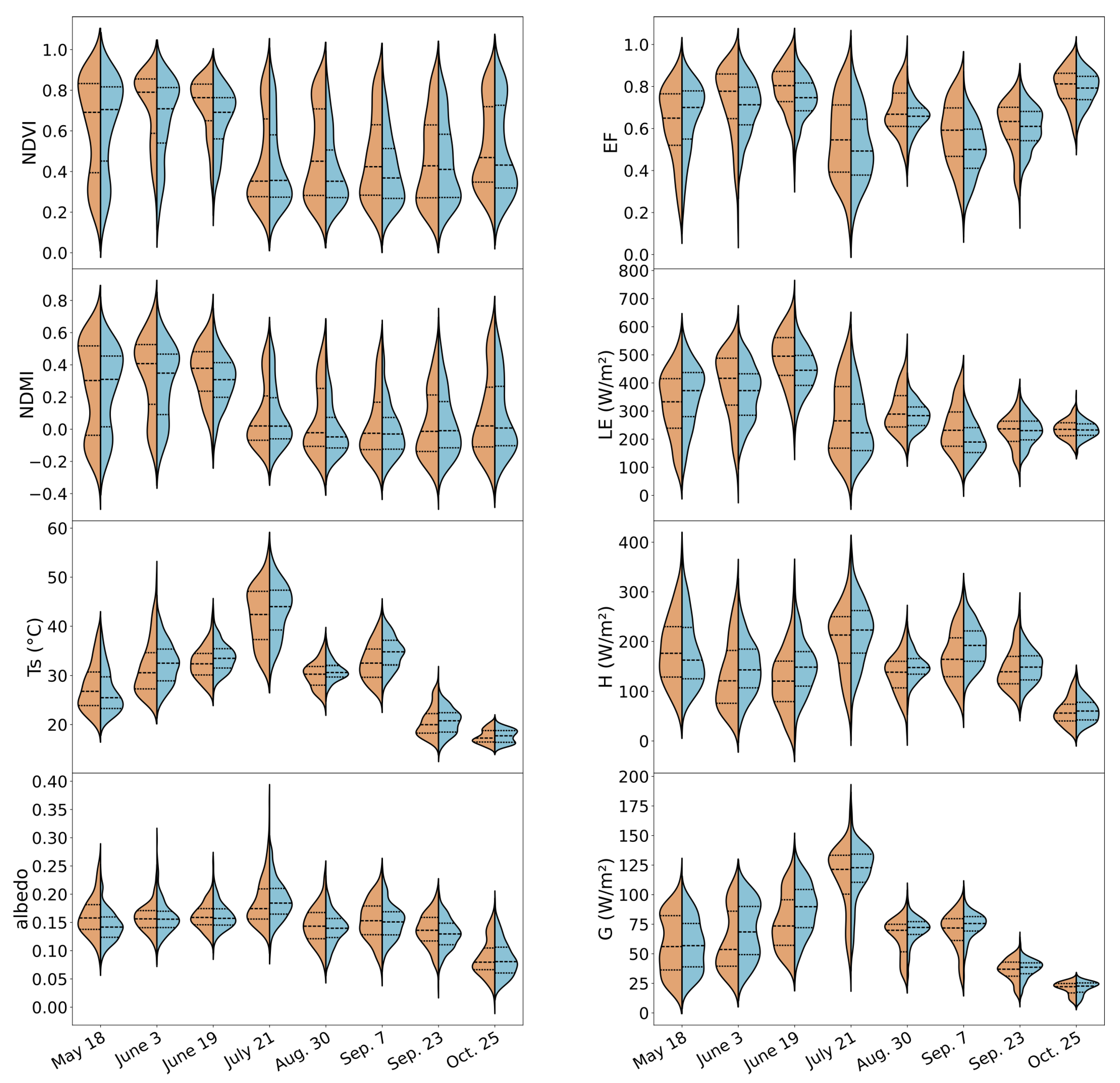
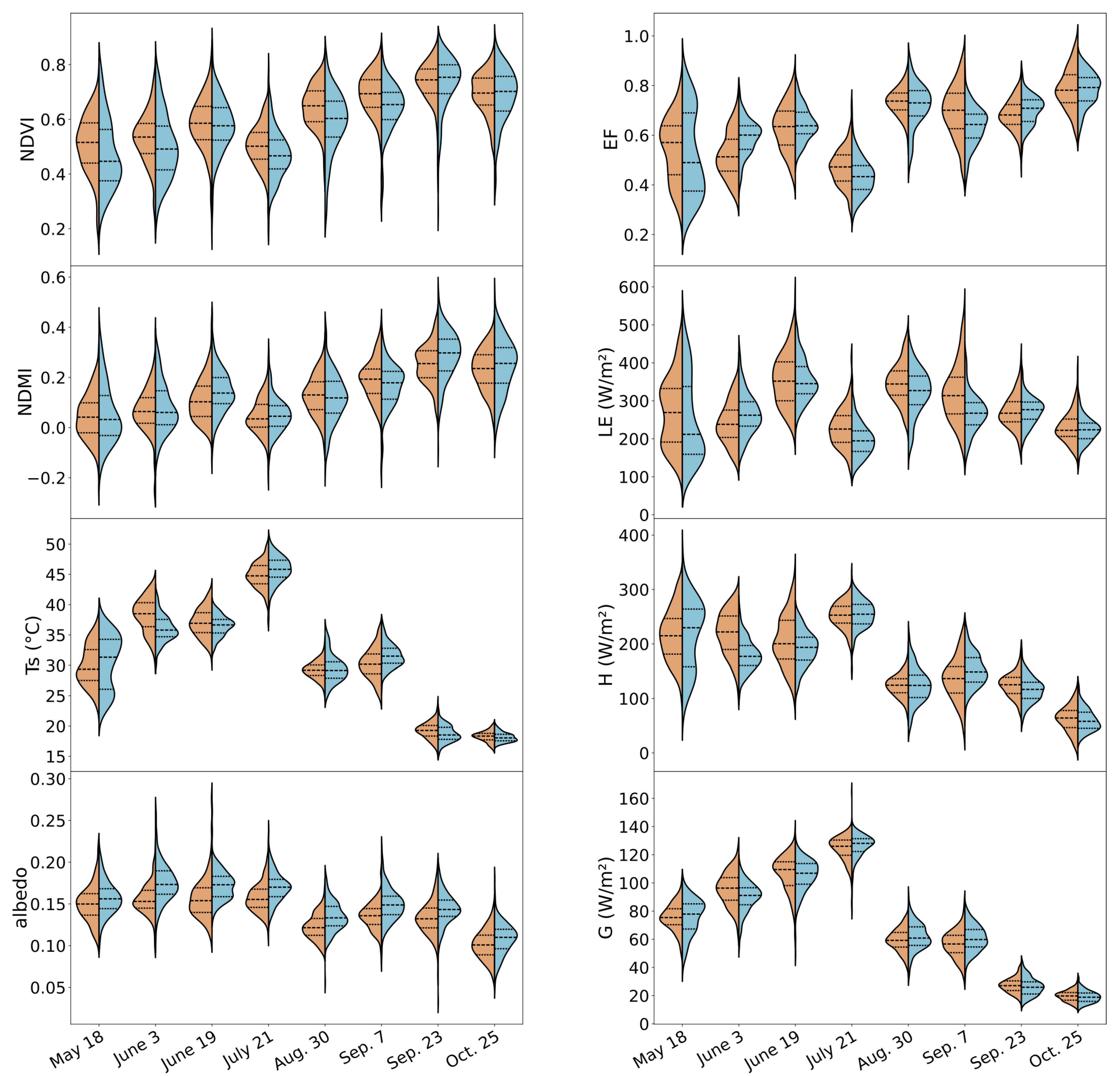
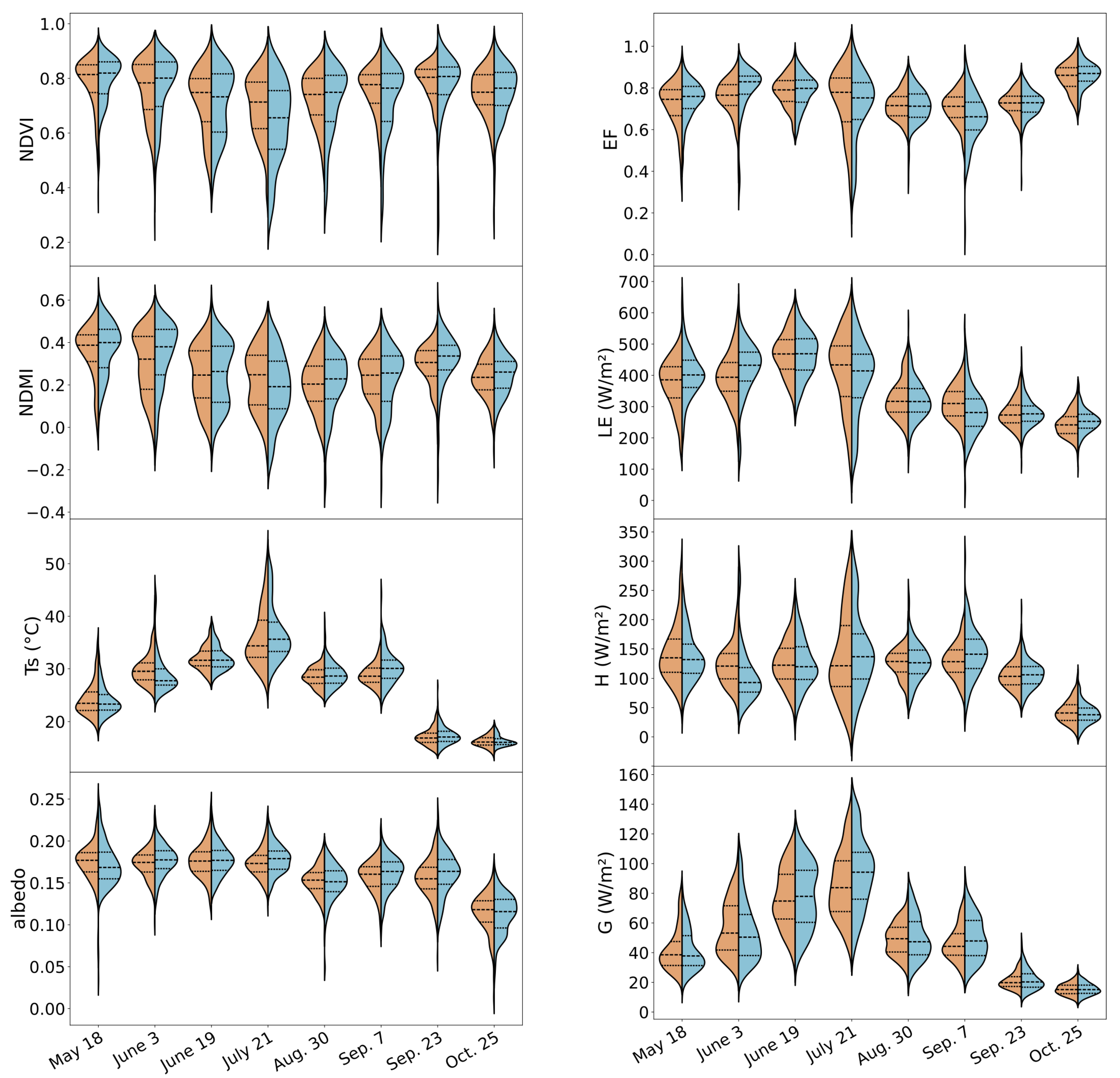
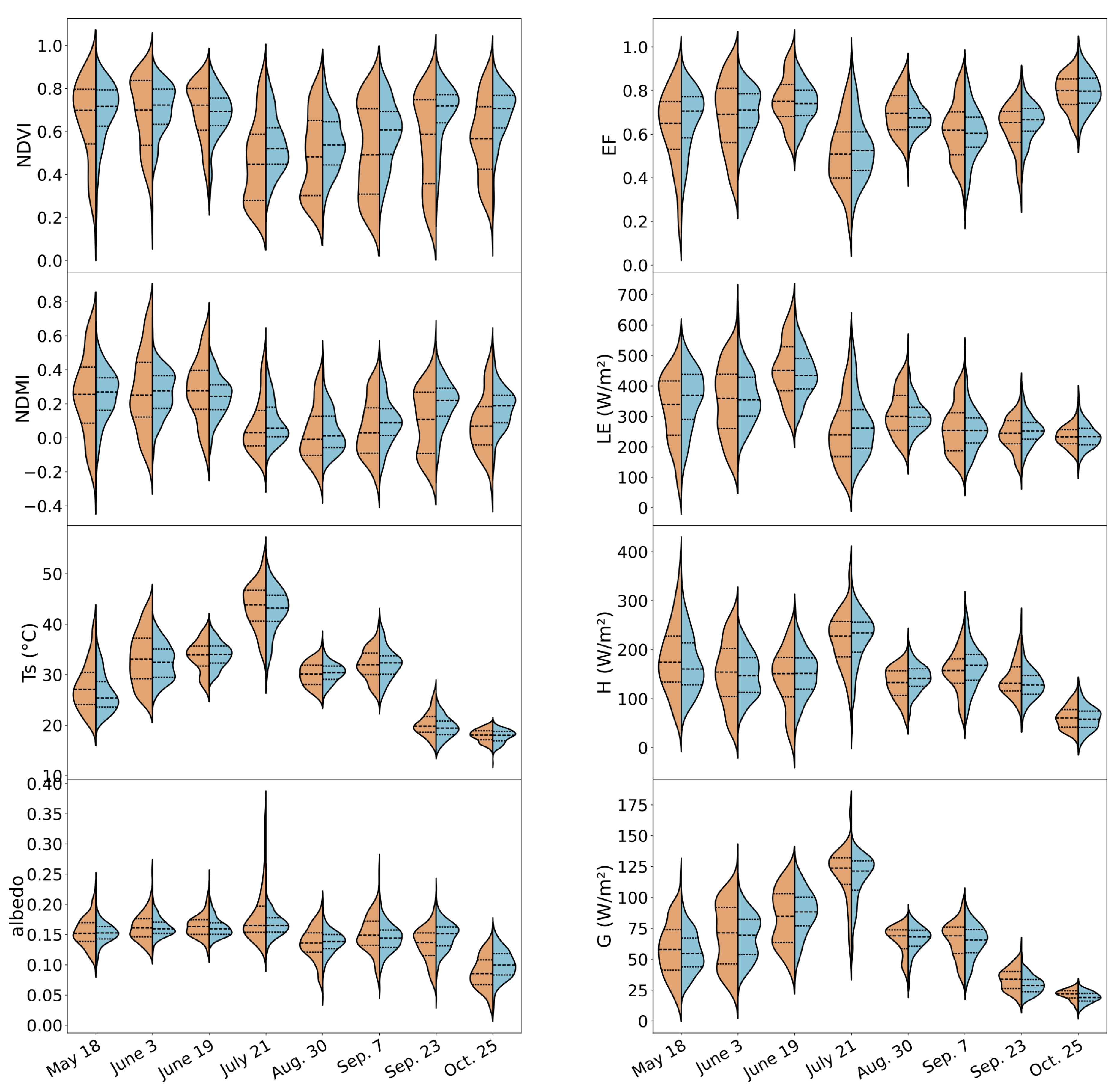
3. Results

3.1. Landscape Structure

The structural analysis proved the vast differences between the Czech and Austrian sides of the border (see summary in Table 1). The total area of each side of the AOI was similar, although not identical, due to the AOI shape (determined by the border buffer). In the end the area on the Czech side (144 000 ha) turned out to be slightly smaller compared to the Austrian side (156 000 ha). Both study areas differ significantly in patch size and shape. The simple patch count suggested differences, with 13 172 patches on the Czech side and 66 788 on the Austrian side. A more informative value for comparing the two AOIs is the patch density, which shows the number of patches relative to the size of the AOI, therefore providing more accurate information when comparing two areas of not identical sizes. In our case, the density of the Czech AOI was 9.1, and the Austrian AOI was 42.8 patches per ha. The largest patch index shows the ratio of the largest patch to the total area with values of 0.37 on the Czech side and 0.11 on the Austrian side.
Another parameter of landscape structure evaluation is the edge characteristics. The total edge is just a plain sum of the edge length in our AOIs; considering the different numbers of patches and different AOI sizes, there are more edges on the Austrian side compared to the Czech side. Edge density is then related to the total areas of each AOI therefore making it more precise for a comparison. The edge density shows a more than 5-fold difference between our Czech area (10.7) and the Austrian area (58.8).
Values of the patch level metrics show the same trends as observed in the densities of patches and edges. The mean patch size in the Czech AOI was 11.0 ha, but it only reached 2.3 in the Austrian one. This was also reflected in the area-weighted mean, which was 57.3 ha for the Czech and only 17.5 ha for the Austrian side. The median plot sizes were 2.26 ha in Czechia and 0.38 ha in Austria. The standard deviations were 22.6 ha (Czechia) and 5.9 ha (Austria), respectively.
Considering the structure of the individual classes of the land cover, we chose categories with the largest proportion of the landscape. We chose arable land, which takes 89.4% of the Czech landscape and 81.0% of the Austrian one. Second, we chose vineyards, which take 3.6% on the Czech side and 5.2% in Austria. Permanent grassland represents 5.5% of the Czech area, yet in Austria, only 2.72%. Another category worth mentioning is the fallow land which takes (sadly) only 0.5% of the Czech agricultural landscape in our AOI but 4.6% of the Austrian (10× more). Another class that is very marginal in Czechia (with 0.5% of the total area) but significant in Austria (with 5.7%) is grass on arable land, which generally indicates animal feed production but on a field instead of a permanent grassland.
From the point of the structure within the chosen classes, we can see similar patterns as we saw with the agricultural landscape as a whole. Focusing on the arable land, we see that the number of patches (7 036 in Czechia versus 18 998 in Austria) and patch density (4.9 patches per ha in the Czech side and 12.2 patches per ha in Austria) are both much larger on the Austrian side. This is then reflected in the other metrics, such as total edge (1 480 km and 7 109 km) or edge density (10.2 vs 45.6 m·ha − 1 ). Furthermore, the mean area of the fields in Czechia reached 18.4 ha, and the mean area in Austria 6.6 ha. Other land cover classes follow the trend. Vineyards, permanent grassland, and fallow land have larger total areas on the Austrian side of the AOI than the grass cover on arable land class and arable land. We can see that in Austria the absence of permanent grassland is compensated by growing grass and animal feed in general more temporally on arable land instead of permanent grass cultures. The relative values such as Patch density or edge density are higher in Austria among all the land cover classes. The mean area size is then larger in Czechia within all of the classes.

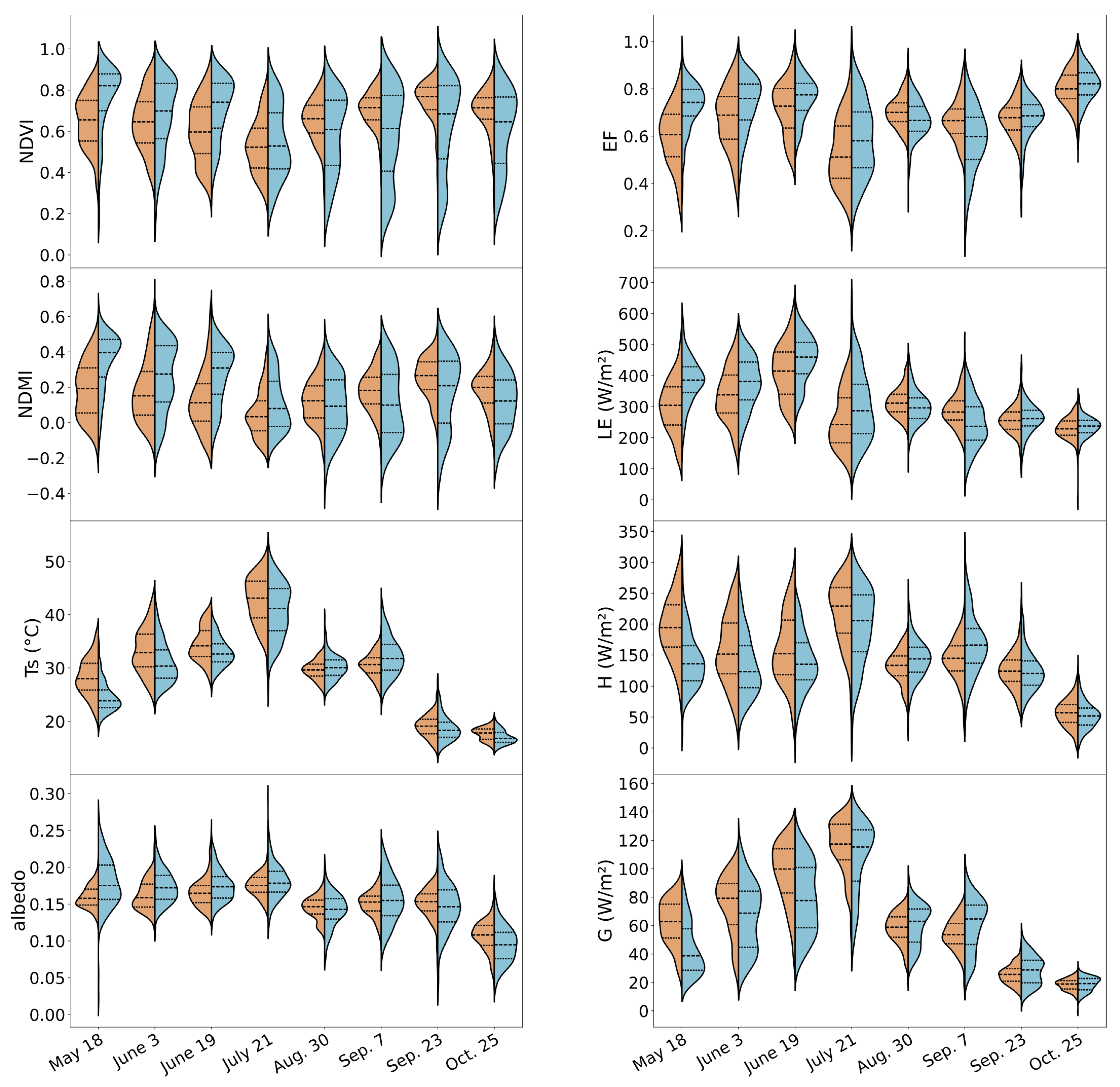
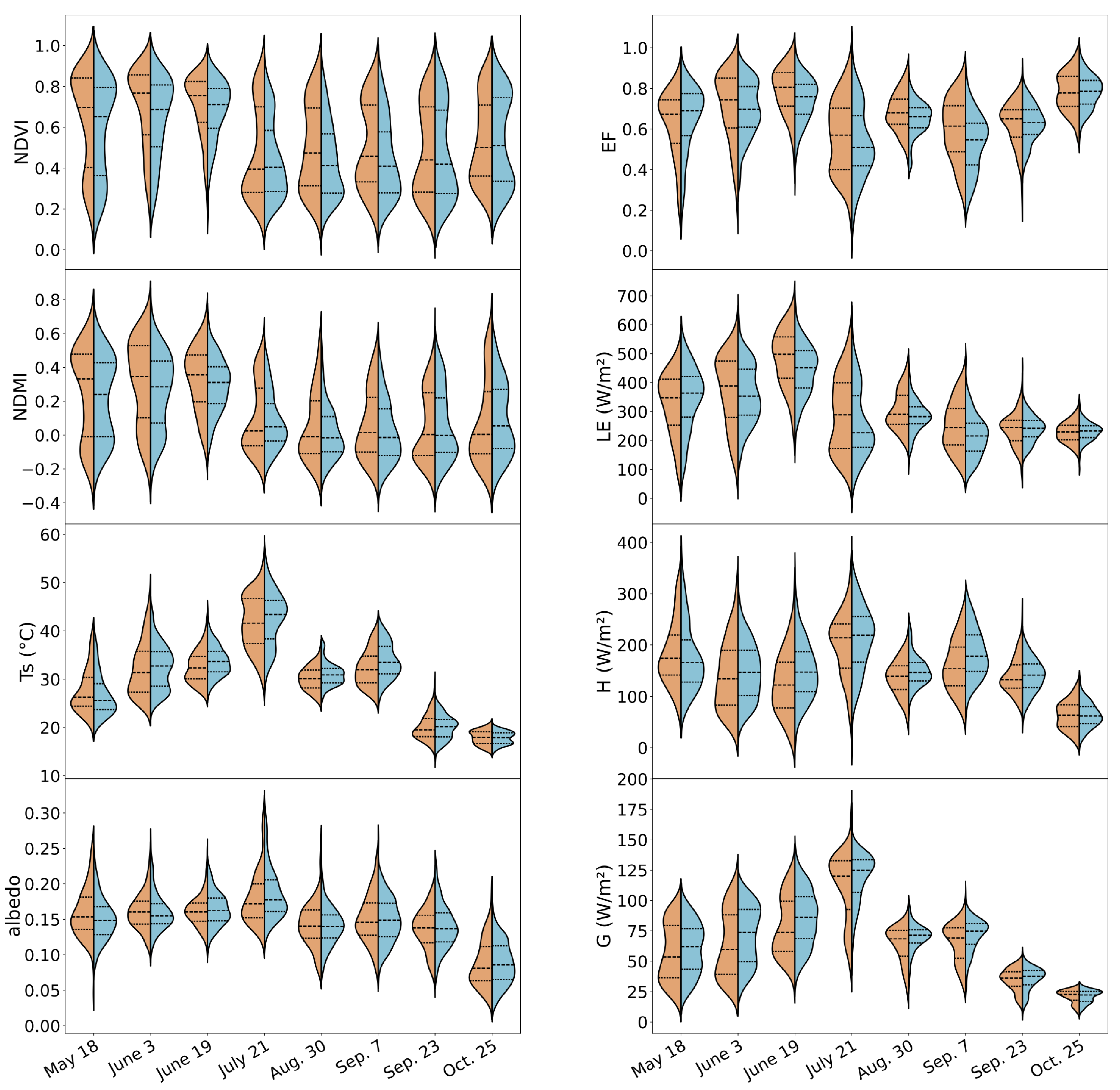
3.2. Energy Fluxes

From the point of the energy dissipation and functional parameters of the surface, we worked with the same classes as in the structural analysis (all agricultural land, arable land, vineyards, permanent grassland, fallow land and grass cover on arable land). The time series analysis for the dates 18 May 2022, 3 June 2022, 19 June 2022, 21 July 2022, 30 August 2022, 7 September 2022, 23 September 2022 and 25 October 2022 gave the following results. The statistical comparison of the Czech and Austrian sides of the AOI summarises Figure 2. The graphical explanation is provided in Figure 3, and Figure A1 to Figure A5 in Appendix.
The NDVI on the Czech side had slightly higher values in six out of eight cases with the exceptions of 21 July and 25 October, where the Austrian side had slightly higher median 0.39 vs 0.40 and 0.50 vs 0.51 respectively (Figure 3). In the class of arable land, we see very similar development (see Figure A1). Worth pointing out is the plot from 30 August, showing on the Czech side a distinct peak in the area of high values around 0.8 which is absent on the Austrian side. Vineyards on the Czech side appear to have higher NDVI values in the spring compared to Austria, yet this trend is reversed later in the season (Figure A2. NDVI values are higher in Austria. On the permanent grassland patches, we see more equal results for both sides. However, there is a trend of very low minimum values on the Czech side early (May, June) and late (October) in the season, and the very opposite, especially on the plots from July through the end of September (Figure A3). Fallow land shows higher NDVI values in all but one case (19 June) on the Austrian side and with a very heterogeneous distribution of values on the Czech side in all of the dates (Figure A4). In the case of the grass cover on arable land, we see higher average values on the Austrian side till 21 July, when both sides have a quite similar shape and average values. Since 30 August, the land cover on the Czech side has a much narrower range of NDVI values with higher median and average in all the other four cases (Figure A5).
The NDMI shows a similar pattern logically following the vegetation index. On the same two dates, the NDMI median was slightly higher, the same as we observed with the NDMI, with a very narrow difference (0.02 and 0.05 on 21 July and 0.004 and 0.05 on 25 October, see Figure 3). On arable land, we see the largest differences in values in June, on 3 June and 19 June, in both cases, with higher values on the Czech side (Figure A1). The rest of the cases had quite similar NDMI values. In vineyards, we see differences in the appearance of the more outlier values, especially on the Austrian side (Figure A2). Overall, this class has quite low values of NDMI, with median values ranging between 0.0 and 0.3. The permanent grassland class has a higher NDMI median in Austria in all but one case on 21 July despite outlier low values, especially the dates 30 August, 7 September and 23 September (Figure A3). The fallow land on the Czech side was reaching more heterogeneous values throughout the whole observed period. In the September and October dates, we also see an increasing difference between the median values with higher values on the Austrian side (Figure A4). For the grass cover on arable land, the value distribution looks in reverse, with a higher value range on the Austrian side, especially from August to October. There are higher median NDMI values on the Austrian side for the first four cases from 18 May to 21 July; in the four following dates, the medians on the Czech side exceed the Austrian (Figure A5).
The surface temperature only reached higher median values in Czechia on the first (18 May) and the last (25 October) of our dates. However, we can see more interesting developments in the distribution of temperatures in the agricultural landscape. For example, in the second case (3 June), the median temperature is higher on the Austrian side (32.15 °C vs 32.70 °C), yet we can see more extremely high values on the Czech side, with surface temperatures reaching over 50 °C (Figure 3). A similar phenomenon also appeared on 23 September, when overall median and mean values were lower in Czechia despite the presence of extremely high values. Solely considering arable land class, we cannot see a dramatic difference from the overall agricultural landscape (Figure A1). We see extremely high surface temperature values in Czechia on 3 June or 23 September, but we can also see lower T s values on the Czech side than in Austria across all cases (best manifested 19 June, 21 July or 7 September). In the patches of vineyards, we see a higher value range in Austria on the first date and 30 August (Figure A2). On the Czech side, we can see an abundance of low outlier values on September 7. Permanent grassland shows high outlier values, mostly on the Austrian side, with 3 June or 7 September, with some values reaching almost 50 °C. However, median values on those cases on both sides were between 27.7 °C and 30 °C (see Figure A3). On fallow land, we see distinctly more uniform value distribution on the Austrian side for the first two cases, with the rest of the observed season keeping the trend, however less pronounced (see Figure A4. The grass cover on arable land has significantly lower values in the first four dates (18 May to 21 July) in Austria and the last two cases (23 September and 25 October). The two dates in the middle (30 August and 7 September) can be characterised by high outlier values on the Austrian side, increasing the median values (for more details, see Figure A5).
Another parameter that we calculated was albedo. In general, the more vegetation there is on the surface and the more complex it is, the lower albedo values we see. Therefore, high albedo values could suggest dry, bare soil. However, high albedo values could also mean senescent crop areas as they are light in colour and low in moisture. On 18 May, 19 June, 30 August, 7 September and 25 October, we observed more of the extremely high values on the Czech side (see Figure 3). On the arable land, albedo differs in the first date (18 May) along with the September dates, with both higher occurrences of higher values and overall median (Figure A1). Albedo values on vineyards were higher in all eight cases throughout the vegetation season (see Figure A2). On the permanent grassland patches, there are low outlier albedo values most pronounced on 18 May, 30 August or 23 September (Figure A3). On 3 June, 21 July and 23 September, we found significantly higher albedo values on the Austrian side. As in the surface temperature case, we can see a much higher uniformity of values on the Austrian side. Despite the distribution differences (most shown on 21 July) the median values differ significantly towards the end of the observed period on the three last cases (September and October). The grass cover on arable land class shows more heterogeneous values on the Austrian side, with higher median values at the beginning of the observed period on the Austrian side and lower by the end of it (see Figure A5).
Evaporative fraction is the fraction of available energy transformed into latent heat. Except for the first and last dates (18 May and 25 October), EF has higher medians and means in all six other cases (3 June 2022, 19 June 2022, 21 July 2022, 30 August 2022, 7 September 2022 and 23 September 2022). The largest difference we can see is on 7 September, with a median of 0.61 on the Czech side and a median of 0.55 on the Austrian side (p < 0.001, see Figure 3). It is worth mentioning that on the Czech side, despite having higher median values on the dates of 3 June and 23 September, we observe extremely low values in the distribution, and this corresponds to the extremely high-temperature values seen on those same dates. On the arable land, the values of the EF have a similar development (see Figure A1). In all eight cases, both the high and low outlier values were found on the Czech side. This is more pronounced in the lower values on 3 June and 23 September and in the higher values, for example, on 30 August or 7 September. In all but the first date, the average and median values of the EF are higher in the Czech Republic. The vineyards have varied, with four dates with higher medians on the Czech side and four dates on the Austrian side. The largest difference can be seen directly on the first date when there are higher values of EF on the Austrian side. Nonetheless, the median and average values are lower on this side due to a peak of low values around 0.4. For more details, see Figure A2). There are very low outliers on the permanent grassland land cover, suggesting some extra dry spots (see Figure A3). This appears to happen on both sides of the border, however it seems to happen more in Austria. Despite the low-value outliers, EF, in all cases, has average values around 0.8. There is a high heterogeneity of the land cover of the fallow land (see Figure A4). The larger differences can be found in the first three dates (from 18 May to 19 June) but also on 30 August. The grass on arable land has higher heterogeneity of values on the Czech side on the first three dates and some very low outlier values (see Figure A5). This distribution changes on 21 July when there is already higher heterogeneity on the Austrian side, and this trend seems to last till the second to last date. The dates 30 August and 7 September have some very low outlier values on the Austrian side, and those are also the only dates with lower average values on the Austrian side.
EF and the latent heat flux have similar development since those two variables are very closely related. The first and last dates have slightly higher median values of latent heat on the Austrian side, and all six of the others have higher median values in Czechia. The September dates (7 September and 23 September) both contain some high outlier values on the Austrian side, however the means in both cases are higher in Czechia (see Figure 3). The largest median difference occurred on 21 July with values 289 W·m − 2 and 227 W·m − 2 and means 290 W·m − 2 and 256 W·m − 2 . The largest difference in mean values was seen on June 19 with CZ mean of 483 W·m − 2 and 442 W·m − 2 , which makes over 40 W·m − 2 difference in the energy dissipation. What we see in the farmland in general, as well as on the arable land alone, is a higher value heterogeneity on the Czech side. On the arable land, this is even more pronounced, and we see high outlier values along with low outlier values more frequently on the Czech side than on the Austrian side, suggesting more surface heterogeneity (best visible on 19 June or 7 July; for more details, see Figure A1). On the patches of vineyards, we found higher latent heat median values on the first date, 18 May, and then from 19 June to 7 September, with the letter also having the greatest heterogeneity sticking out, especially with the high extreme LE values. In the early dates we particularly see that arable land has a much higher latent heat flux than vineyards. For example, on 3 June we see on the vineyards median LE values 237.97 W·m − 2 on the Czech side and 262.04 W·m − 2 on the Austrian side, however on the arable land the median values are 416.58 W·m − 2 and 372.68 W·m − 2 respectively (see Figure A1 and Figure A2). The class of permanent grass varies more on the Austrian side, with both high values (on 18 May) and low outlier values (for example, 3 June). In the case of 7 September, we see both at the same time (see Figure A3). Fallow land has more heterogeneous values of LE such as it had with all the other parameters. Especially on 3 June, 19 June or 7 September, we see a larger range of latent heat values in both high and low extremes on the Czech side (see Figure A4). The grass on arable land class has some very low outliers of LE on 30 August and 7 September on the Austrian side, as we had seen in the evaporative fraction on this land cover. These two cases also have lower overall median and average values of LE in Austria. All the other dates, and especially the first four of them (between 18 May and 21 July), have higher medians on the Austrian side with more low outlier values on the Czech side. For more details, see Figure A5.
The sensible heat flux values have the opposite development to the Latent heat flux and Evaporative fraction. In all but the first and the last dates, we see that the sensible heat values are higher on the Czech side. On 3 June and 23 September, Czechia had higher outlier values despite having lower overall median values (see Figure 3). The fields of arable land show more equality on the Austrian side. The dates 3 June, 30 August or 23 September contain more high extreme values on the Czech side yet again with overall lower median values in all but the first date (18 May). Opposite to the latent heat flux, we see higher median values on the vineyard patches compared to the arable land, especially in the first three cases (see Figure A1 and Figure A2). The permanent grass class has significantly lower median values compared to the vineyards, for example, on 3 June, the Czech and Austrian medians are 120.52 W·m − 2 and 92.93 W·m − 2 respectively, compared to 221.88 W·m − 2 and 176.98 W·m − 2 on vineyards. However, the median values of sensible heat flux are quite low, mainly, the Austrian side shows a great deal of variability with some extreme outlier values reaching almost 350 W·m − 2 , for example, 3 June or 7 September (see Figure A3). On the fallow land we again see greater heterogeneity on the Czech side with values ranging from 0 to 400 W·m − 2 of the sensible heat flux in two cases (on 18 May and 21 July; see Figure A4). The grass on arable land has higher heterogeneity and median values on the 30 August and the 7 September. On the other cases, the medians are lower on the Austrian side, with the largest difference on the first date (18 May) with the medians of 194.40 W·m − 2 and 135.80 W·m − 2 in the Czech and Austrian side (see Figure A5).
The last of the energy fluxes is the ground heat flux, which corresponds to the latent heat flux and the sensible heat flux. However, there is a difference in the first date, 18 May. The only case with the higher G median on the Austrian side is the last one (barely by 0.42 W·m − 2 ). In all the other cases, we see higher overall values of the ground heat flux in the agricultural landscape of the two countries (see Figure 3). Talking solely arable land, the development is quite similar, with all the medians higher on the Austrian side in all cases. On 18 May and on 21 July, the G flux values are quite alike. However, the dates between them (3 June and 19 June) differ significantly between Czechia and Austria. On 30 August and 7 September, the density plots had a similar peak, but we could see more of the low outlier values on the Czech side. For more details, see Figure A1. The vineyards have relatively high ground heat flux values, steadily growing between 18 May and 21 July to suddenly drop on 30 August and get lower in the dates after. Compared to the ground flux values of the permanent grass cover, for example on 3 June the Czech and Austrian medians for vineyards are 96.34 W·m − 2 and 91.11 W·m − 2 respectively and on the permanent grass 53.20 W·m − 2 and 50.44 W·m − 2 (see Figure A2 and Figure A3). There are higher medians on the Austrian side in the peak vegetation dates on 19 June and 21 July, as well as 7 September. As did the other fluxes, the fallow land patches have a high range of ground heat flux values on the Czech side. This trend is noticeable mostly in the first four dates. However, it continues in the last four cases. The arable land with grass cover has more heterogeneity on the Austrian side with a wide range of values in the first four dates (from 18 May till 21 July), in which the median ground heat flux values on the Austrian side are also significantly lower in all four cases (see Figure A5).

4. Discussion

Structure determines a number of functional aspects of the landscape, such as biodiversity, management options, or biophysical properties related to energy exchange and water cycle formation. The Czech-Austrian border region is an interesting example of two landscapes with different structures in the same environment (see Figure 1). The two countries differ in their historical development after the Second World War. Due to the forced socialisation of property by the communist regime from the 1950s onwards (so-called collectivisation) and the desire to maximise the efficiency of agricultural production within co-operative farms, where the maximising yields became the prime agricultural policy objective, the land was merged into large field units [57]. Thus, the landscape structure was completely changed. In Austria, on the other hand, the structure of farms and agricultural areas still follows the historical land tenure and ownership relations.
Czech agriculture, three and a half decades after the end of the communist totalitarian regime (since 1989), has not moved towards small, private farming. Big holdings that replaced the collective farms are holding a grip on Czech agriculture. According to 2020 Eurostat data [58], the top 27.8% of largest farms control 92-93% of the utilised agricultural areas (UAA), which is the second highest result in the EU after Slovakia (with only 17.9% largest farms controlling 92-93% of their UAA). Within the EU, the Czech Republic also stands out in the largest average farm size, according to the Czech Ministry of Agriculture [59]. This value is around 130 ha at the moment, which is a reduction from 152.4 ha in 2010. Nevertheless, this is still significantly more than 89.3 ha in 2007 [60]. However, inflating farm sizes and deflating farm numbers have been stopped or at least paused in the Czech Republic [61].
The development of landscape structure is almost inverse in Austria. Historically, Austria is a land of small farmers, and in the EU context, that can still be said, yet the trend is growing farm sizes. The average holding size grew from 42.6 ha in 2010 to 44.9 ha in 2020 as well as the average utilised agricultural area size (consisting of arable land, kitchen gardens, permanent grassland and permanent crops), which extended from 18.8 ha to 23.6 ha in the same period [62].
The results of the structural analysis of the Czech and Austrian sides of the AOI confirm the difference described above. The average patch size on the Czech side was 11 ha and on the Austrian side 2.3 ha, corresponding to the patch density which is higher on the Austrian side on all the different land covers. The median values of patch sizes are substantially lower, with Czech and Austrian values at 2.2 ha and 0.4 ha on farmland. When focusing solely on the arable land, the mean patch size on the Czech side was 18.4 ha, and on the Austrian side 6.6 ha, i.e., on the Czech side, patch size was three times higher than on the Austrian side. The values of the patch size medians are smaller (7.4 and 3.0 ha). However, the ratio is almost the same as that of the average patch size. The patch size difference corresponds with the other landscape structural features. The Edge density is higher on all six land cover types on the Austrian side. On the entire farmland, the edge density is 5.5 times higher in Austria, and on the arable land alone, it is 4.5 times higher. The patch density is 4.7 times higher on the Austrian side, and the total edge length is 5.9 times higher on the Austrian side (see Table 1).
Larger field sizes have their (partial) justification for the effectiveness of agricultural production. On the other hand, it can have a huge impact on environmental factors and biodiversity. As shown by Al-Amin et al. [63], increasing the size of the field block increases productivity by reducing the relative proportion of time spent on transport, maintenance and preparation and increasing the proportion of time spent on actual work activities. Brunotte and Fröba [64] compared the fuel consumption based on the field size finding a reduction in the fuel demands with a growing field size from 2.5 ha to 60 ha, although over the 60 ha value, the field block size loses the significance in the fuel consumption. On the other hand, large field areas are significantly threatened by wind and water soil erosion, as shown Devátý et al. [7] for areas corresponding with our AOI.
The structural pattern of the landscape, especially field areas, edge areas, and length, is important for the agroecosystem biodiversity. The edges between fields represent the environment for many species. They provide feed and shelter for organisms living within their bounds [65]. For example, the European hare is greatly affected by farmland homogenisation, being forced to increase the home range sizes with the increased field block sizes (decreasing patch and edge densities, respectively). Moreover, the field edges provide sheltering in periods of inactivity or sheltering for leverets as well as providing feed for lactating females, which prefer the natural diet (if available) in the form of wild herbs, grasses and weeds even to the crops [66,67]. This affects all organisms, including invertebrates or plants, and the diversity of original wild species is decreasing due to intensification. Increased farmland homogenisation is connected to population decreases in 52% of common European farmland bird species between the years 1980 and 2020 (such as Alectoris rufa – Red-legged Partridge or Gallinago gallinago – Common Snipe) [68]. Šálek et al. [69] directly compared the diversity of farmland birds in the context of the cross-border Czech and Austrian farmland structure differences. Even though some bird species were not significantly more abundant in Austria, none were more abundant in the Czech Republic, and most of them were more abundant in Austria with overall 1.5-1.6 × more individuals and 1.3-1.5 × more farmland bird species in Austria compared to the Czech Republic.
Although the degree of heterogeneity of farmland structure has been connected to the abundance and diversity of different bird, mammal, insect, and plant species, our subsequent question was: does the farmland structure affect the physical properties of the surface, including energy dissipation? From our observational timeframe starting on 18 May and finishing on 25 October 2022, we see more significant differences in the full vegetation season rather than on the beginning (18 May) and end of it (23 September, 25 October), meaning the differences are most likely caused directly by the farmland management. Between 7 November and 23 November, we saw a steep decline in the differences between our AOI’s Czech and Austrian sides, mainly concerning whole farmland and arable land classes.
When we focus on the amount of vegetation represented by NDVI, the most significant difference between the two sides of AOI we see on the 30 August is the latter part of vegetation season, often harvest time (see Figure 2). Even though the mean values are higher on the Czech side, on the farmland in general, both maximum and minimum values also suggest more extreme situations appear on the Czech side, as shown in the violin plots (see Figure 3 and Appendix). The vegetation cover relates to the surface moisture represented by the NDMI index. When looking at the same late August date, and especially the distribution of the values, we see an absence of NDMI values around 0.4 on the Austrian side, whereas there is a distinct density peak on the Czech side. On a smaller scale, this appears across the cases that correspond closely with the NDVI. Vegetation is important in utilising water on the land surface by providing shade to the bare soil, increasing roughness and cooling [54,70]. Therefore, these two indexes are closely intertwined. Those variables are then related to the surface temperature, which indicates the ability of the surface to dissipate solar energy. The dry surface of the barren soil, despite having higher albedo values due to its surface complexity, is more susceptible to overdrying, overheating and, last but not least, erosion [71]. Looking at the arable land patches, there are significant differences in all but the latest two dates (23 September and 25 October). In the six cases that significantly differ, five have higher maximum surface temperature values on the Czech side (except 21 July), and all six have broader Interquartile ranges, which means a higher occurrence of the extreme surface temperature compared to Austria. Like the maximum temperature, the lowest surface temperature values lay also on the Czech side on the same dates as the maximum values again, except on 21 July, suggesting higher variability of the surface despite having lower averages on the Czech side on five out of six cases.
The lack of vegetation and moisture on the surface lowers the energy spent on evaporation through evapotranspiration, lowering evaporative fraction and raising the surface temperatures. Nonetheless, the energy budget remains the same, shifting the energy dissipation towards raising ground and sensible heat flux instead of the latent heat flux when water and vegetation are present. Therefore, the lower the evaporative fraction, the less energy from this budget is utilised in the water phase transition. Omitting again the last two dates, the evaporative fraction on the arable land has both maximum and minimum values on the Czech side in five out of six cases, confirming more extreme situations appearing on the surface of the Czech farmland where there are spots with highest relative evapotranspiration along spots with lowest relative evapotranspiration coexisting at the same moment. This may result from the large parcel sizes, which are prone to magnifying the extremes.
When exploring the energy fluxes themselves, the latent heat flux is analogical to the previous variables in the sense of higher variability of values on the Czech side and mostly higher mean values. Where vegetation and moisture are available, energy will be dissipated into latent heat through evapotranspiration. As we know, there are spots with more vegetation and more water as well as spots with less vegetation and less water on the Czech side, resulting in more heterogeneous latent heat values. When energy is not transformed into latent heat, it is split approximately in a ratio of 1:2 between the ground heat flux and the sensible heat flux, consequently having the opposite development to the latent heat flux. The ground heat flux had a stable growth between the first four cases, peaking on 21 July on both sides, with the Austrian mean higher in all four cases. On that date (21 July), we see a higher mean on the Austrian side not because of higher values of the ground heat around 125 W·m − 2 but because of the absence of low values around 75 W·m − 2 . This effect can be observed in multiple cases, such as 30 August or 7 September. It corresponds to the previously described variables. Furthermore, the sensible heat flux has a similar distribution of values. This is the energy spent on warming up the surroundings, including objects on the surface, people, animals, plants, and the surface itself [72]. Except on 21 July, the Czech side had similarly lower minimums, higher maximums and larger IQRs on the arable land.
The results show significant instability of the microclimate seasonal development on the Czech side compared to Austrian AOI. The instability of these features, mostly extreme values, is a complex question. However, this could be explained by the differences in the landscape mosaic structure and partly by the ability of the Landsat sensor to be used for analysis. In the scale of the satellite resolution (30 × 30 m), the Austrian landscape is presented by the fine mosaic, which averages and smoothes the microclimatic features. On the other hand, the large field blocks on the Czech side allow the occurrence of high surface temperature, low sensible heat flux, and, as a consequence, large spatial gradients. The important role also plays crop rotation, which tends to simplification mainly in the Czech Republic than in Austria, with the preference for cereals, oilseeds and corn for biogas production (see [73] and [74]). The limited cropping practices often result in the long-term exposure of the land surface, i.e., the absence of vegetation cover. The occurrence of microclimatic extremes, large gradients, limited evapotranspiration, and surface overheating significantly impacts the climate of the surroundings. In a study done by Hesslerová et al. [21], there is an example of a comparison of multiple land covers and their characteristics of energy fluxes. In one case, they compare two football pitches laying just one next to another, whilst one has natural grass cover and the other has artificial grass. These two land covers appear very similar to the eye, yet on the thermal image. There is a difference in surface temperature around 12 °C due to evapotranspiration and the consequent changes in the latent heat flux. In any farmland, it may not be possible to avoid patches without any vegetation cover. Yet, there are ways to mitigate the threats of land without land cover, such as intercropping. There may be another way of regulation in the form of landscape configuration. Large production patches of monocultures can have plenty of biomass and moisture during the peak vegetation. These crops then have a high rate of evapotranspiration, which, as a result, cools down the surface through the dissipation in energy fluxes. Vegetation also increases surface roughness, improving water retention and bolstering erosion prevention. The problem can appear when the crop is at the beginning or the very end of its development. At that moment, the bare soil is mostly uncovered and susceptible to extremes and the larger the patch, the more pronounced the extreme effects are. This is also problematic for many wild living organisms that lack habitats in a situation where there is almost no vegetation on a field exceeding 20 ha. Smaller field sizes lead to higher edge density, which provides natural feed and shelter for various animals. Moreover, the edges provide habitats for wild species of plants, and last but not least, they counteract erosion effects since small patches do not allow fast runoff, hence improving water infiltration and retention.
The cooling effect of vegetation deserves more attention as one of the ecosystem services regulating the meso/micro climate of the landscape. Looking through the prism of climate change and global warming, we talk about increasing temperatures and extreme weather episodes. As global efforts to reduce greenhouse gas emissions fail, we may need other solutions to moderate their impact. The changes in climatic characteristics intensity, such as average air temperature, maxima and minima in the Czech Republic, are significantly higher than the global trend (for more details, see [32,75]). The absence of vegetation can have (arguably) a much higher impact, and the same can apply to extreme precipitation episodes that happen more often. With the changing layout of the precipitation, we see longer periods of drought followed by more intense episodes of precipitation [76,77,78]; nonetheless, dry bare soil has low surface roughness and low infiltration ability, allowing fast surface runoff of the water, causing floods, or at the very least erosion [8,79]. Due to increasing the arable land area, people have been building subsurface drainage systems in the Czech Republic since the 1860s, culminating during collectivisation and continuing even after 1989, being motivated by an undeniable increase in soil fertility. According to existing records, over 1 million hectares of farmland are currently drained in the Czech Republic [9]. This further deepens the drying of the Czech landscape and probably will also in the future, thanks to the very long lifespan of the drainage systems. As our results showed, higher farmland complexity may contribute to tackling the effects of global warming and climate change in reducing extreme weather impacts.

5. Conclusions

This study examined the impact of agricultural intensification and farmland structure on surface parameters and microclimatic conditions along the Czech-Austrian border. Despite similar topography, the regions exhibit stark contrasts in farmland structure due to different socio-political histories: large, homogeneous fields in the Czech Republic resulting from collectivisation and smaller, diverse fields in Austria reflecting traditional land practices.
Our findings reveal that the Czech farmlands, characterised by larger field sizes and fewer edges, experience significant microclimatic instability marked by more pronounced extremes. Specifically, higher extreme surface temperatures, lower surface moisture levels, and greater variability in energy fluxes, including latent heat, sensible heat, and ground heat fluxes, especially during the peak vegetation season. These severe extremes are attributed to the amplification effects of large, uniform fields, compounded by simple crop rotations and extended periods of bare soil exposure. While mean values of these parameters differed between the regions, the heightened extremes on the Czech side were most striking.
In contrast, the Austrian side, with smaller fields and higher edge densities, demonstrated more stable microclimatic conditions with fewer extreme fluctuations. The increased landscape heterogeneity supports better vegetation cover, improved moisture retention, and balanced energy distribution. This environment fosters higher biodiversity, evidenced by greater species richness and abundance of birds, insects, and wild plants. Field edges serve as vital habitats and resources for various organisms, enhancing agroecosystem health.
The study underscores that farmland structure significantly influences not only biodiversity but also the physical properties of the land surface and local climate regulation. Large fields with minimal edges exacerbate environmental challenges like soil erosion, reduced water infiltration, and heightened vulnerability to extreme weather events due to the amplification of microclimatic extremes. Conversely, smaller fields with more edges enhance ecosystem services such as cooling through evapotranspiration and bolster resilience to climate change by mitigating environmental extremes.
Promoting landscape heterogeneity in agricultural practices can yield substantial environmental benefits by reducing the severity of microclimatic extremes and supporting biodiversity. Strategies like decreasing field sizes, diversifying crops, and maintaining edge habitats can alleviate the severe conditions observed in large, homogeneous fields. These practices are particularly relevant amid climate change, where adaptive measures are essential to counteract rising temperatures and shifting weather patterns. Thoughtful landscape management enhances ecosystem services and contributes to global efforts to reduce greenhouse gas emissions and adapt to climate variability.
In summary, our research highlights the crucial role of farmland structure in influencing environmental parameters—particularly the occurrence of environmental extremes—and ecosystem services. By adopting agricultural practices that enhance landscape heterogeneity, it is possible to moderate microclimatic extremes, support biodiversity, and increase the adaptive capacity of agroecosystems to climate change. These insights are vital for policymakers, land managers, and stakeholders aiming to develop sustainable and resilient agricultural landscapes less susceptible to environmental extremes.
The appendix contains graphs of functional landscape characteristics, i.e., vegetation spectral indices (NDVI and NDMI) and microclimatic characteristics, which include surface temperature, albedo, evaporative fraction and heat fluxes. The graphs describe the seasonal pattern of these parameters for each evaluated landscape cover class within the AOI in the Czech Republic and Austria.

Author Contributions

Conceptualisation, J.K. and J.B.; methodology, J.K. and J.B.; formal analysis, J.K.; investigation, J.K.; resources, J.K.; data curation, J.K.; writing—original draft preparation, J.K. and J.B.; writing—review and editing, J.K and J.B.; visualisation, J.K.; supervision, J.B.; project administration, J.B.; funding acquisition, J.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Grant Agency of the University of South Bohemia in České Budějovice, Czech Republic, project No. GAJU 069/2022/Z

Data Availability Statement

All the original data used in the project comes from public sources. The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Preprints 120868 g0a1
Figure A1. The violin plots of individual functional variables for the Arable land in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Figure A1. The violin plots of individual functional variables for the Arable land in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Preprints 120868 g0a1
Preprints 120868 g0a2
Figure A2. The violin plots of individual functional variables for the Vineyards in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Figure A2. The violin plots of individual functional variables for the Vineyards in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Preprints 120868 g0a2
Preprints 120868 g0a3
Figure A3. The violin plots of individual functional variables for the Permanent grassland in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Figure A3. The violin plots of individual functional variables for the Permanent grassland in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Preprints 120868 g0a3
Preprints 120868 g0a4
Figure A4. The violin plots of individual functional variables for the Fallow land in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Figure A4. The violin plots of individual functional variables for the Fallow land in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Preprints 120868 g0a4
Preprints 120868 g0a5
Figure A5. The violin plots of individual functional variables for the Grass on arable land in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Figure A5. The violin plots of individual functional variables for the Grass on arable land in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Preprints 120868 g0a5

References

  1. Oliver, T.H.; Isaac, N.J.B.; August, T.A.; Woodcock, B.A.; Roy, D.B.; Bullock, J.M. Declining resilience of ecosystem functions under biodiversity loss. Nature Communications 2015, 6, 10122. [Google Scholar] [CrossRef] [PubMed]
  2. Bowles, T.M.; Mooshammer, M.; Socolar, Y.; Calderón, F.; Cavigelli, M.A.; Culman, S.W.; Deen, W.; Drury, C.F.; Garcia Y Garcia, A.; Gaudin, A.C.; Harkcom, W.S.; Lehman, R.M.; Osborne, S.L.; Robertson, G.P.; Salerno, J.; Schmer, M.R.; Strock, J.; Grandy, A.S. Long-Term Evidence Shows that Crop-Rotation Diversification Increases Agricultural Resilience to Adverse Growing Conditions in North America. One Earth 2020, 2, 284–293. [Google Scholar] [CrossRef]
  3. Shah, K.K.; Modi, B.; Pandey, H.P.; Subedi, A.; Aryal, G.; Pandey, M.; Shrestha, J. Diversified Crop Rotation: An Approach for Sustainable Agriculture Production. Advances in Agriculture 2021, 2021, 1–9. [Google Scholar] [CrossRef]
  4. Boesing, A.L.; Nichols, E.; Metzger, J.P. Effects of landscape structure on avian-mediated insect pest control services: A review. Landscape Ecology 2017, 32, 931–944. [Google Scholar] [CrossRef]
  5. Thies, C.; Tscharntke, T. Landscape Structure and Biological Control in Agroecosystems. Science 1999, 285, 893–895. [Google Scholar] [CrossRef]
  6. Smets, T.; Poesen, J.; Bochet, E. Impact of plot length on the effectiveness of different soil-surface covers in reducing runoff and soil loss by water. Progress in Physical Geography: Earth and Environment 2008, 32, 654–677. [Google Scholar] [CrossRef]
  7. Devátý, J.; Dostál, T.; Hösl, R.; Krása, J.; Strauss, P. Effects of historical land use and land pattern changes on soil erosion – Case studies from Lower Austria and Central Bohemia. Land Use Policy 2019, 82, 674–685. [Google Scholar] [CrossRef]
  8. Zuazo, V.H.D.; Pleguezuelo, C.R.R. Soil-Erosion and Runoff Prevention by Plant Covers: A Review. In Sustainable Agriculture; Lichtfouse, E., Navarrete, M., Debaeke, P., Véronique, S., Alberola, C., Eds.; Springer Netherlands: Dordrecht, 2009; pp. 785–811. [Google Scholar] [CrossRef]
  9. Tlapáková, L.; Žaloudík, J.; Kolejka, J. Thematic survey of subsurface drainage systems in the Czech Republic. Journal of Maps 2017, 13, 55–65. [Google Scholar] [CrossRef]
  10. Watson, A.J.; Lovelock, J.E. Biological homeostasis of the global environment: The parable of Daisyworld. Tellus B 1983, 35B, 284–289. [Google Scholar] [CrossRef]
  11. Shukla, J.; Mintz, Y. Influence of Land-Surface Evapotranspiration on the Earth’s Climate. Science 1982, 215, 1498–1501. [Google Scholar] [CrossRef]
  12. Segal, M.; Avissar, R.; McCumber, M.C.; Pielke, R.A. Evaluation of Vegetation Effects on the Generation and Modification of Mesoscale Circulations. Journal of the Atmospheric Sciences 1988, 45, 2268–2293. [Google Scholar] [CrossRef]
  13. Pielke, R.A.; Avissar, R. Influence of landscape structure on local and regional climate. Landscape Ecology 1990, 4, 133–155. [Google Scholar] [CrossRef]
  14. Hayden, B.P. Ecosystem feedbacks on climate at the landscape scale. Philosophical Transactions of the Royal Society B: Biological Sciences 1998, 353, 5–18. [Google Scholar] [CrossRef]
  15. Pielke, R.A.; Marland, G.; Betts, R.A.; Chase, T.N.; Eastman, J.L.; Niles, J.O.; Niyogi, D.d.S.; Running, S.W. The influence of land-use change and landscape dynamics on the climate system: Relevance to climate-change policy beyond the radiative effect of greenhouse gases. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2002, 360, 1705–1719. [Google Scholar] [CrossRef]
  16. Nippgen, F.; McGlynn, B.L.; Marshall, L.A.; Emanuel, R.E. Landscape structure and climate influences on hydrologic response. Water Resources Research 2011, 47, 2011WR011161. [Google Scholar] [CrossRef]
  17. Mackey, C.W.; Lee, X.; Smith, R.B. Remotely sensing the cooling effects of city scale efforts to reduce urban heat island. Building and Environment 2012, 49, 348–358. [Google Scholar] [CrossRef]
  18. Favretto, A. Urban Heat Island analysis with Remote Sensing and GIS methods: An application in the Trieste area (North-East of Italy). Bollettino della Società Geografica Italiana 2018, 1, 215–229. [Google Scholar] [CrossRef]
  19. Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bulletin of the American Meteorological Society 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
  20. Debbage, N.; Shepherd, J.M. The urban heat island effect and city contiguity. Computers, Environment and Urban Systems 2015, 54, 181–194. [Google Scholar] [CrossRef]
  21. Hesslerová, P.; Pokorný, J.; Huryna, H.; Seják, J.; Jirka, V. The impacts of greenery on urban climate and the options for use of thermal data in urban areas. Progress in Planning 2022, 159, 100545. [Google Scholar] [CrossRef]
  22. Du, S.; Xiong, Z.; Wang, Y.C.; Guo, L. Quantifying the multilevel effects of landscape composition and configuration on land surface temperature. Remote Sensing of Environment 2016, 178, 84–92. [Google Scholar] [CrossRef]
  23. Connors, J.P.; Galletti, C.S.; Chow, W.T.L. Landscape configuration and urban heat island effects: Assessing the relationship between landscape characteristics and land surface temperature in Phoenix, Arizona. Landscape Ecology 2013, 28, 271–283. [Google Scholar] [CrossRef]
  24. Harlan, S.L.; Brazel, A.J.; Prashad, L.; Stefanov, W.L.; Larsen, L. Neighborhood microclimates and vulnerability to heat stress. Social Science & Medicine 2006, 63, 2847–2863. [Google Scholar] [CrossRef]
  25. Zelinka, V.; Zacharová, J.; Skaloš, J. Analysis of spatiotemporal changes of agricultural land after the Second World War in Czechia. Scientific Reports 2021, 11, 12655. [Google Scholar] [CrossRef]
  26. Bičík, I.; Kupková, L.; Jeleček, L.; Kabrda, J.; Štych, P.; Janoušek, Z.; Winklerová, J. Land use changes in the Czech Republic 1845–2010: socio-economic driving forces; Springer Geography, Springer: Cham, 2015. [Google Scholar]
  27. Sklenička, P.; Šímová, P.; Hrdinová, K.; Šálek, M. Changing rural landscapes along the border of Austria and the Czech Republic between 1952 and 2009: Roles of political, socioeconomic and environmental factors. Applied Geography 2014, 47, 89–98. [Google Scholar] [CrossRef]
  28. Rašín, R.; Chromỳ, P. Land use and land cover development along the Czech-Austrian boundary. In Land use/cover changes in selected regions in the World; Bičík, I., Himiyama, Y., Feranec, J., Eds.; Institute of Geography, Hokkaido University of Education: Asahikawa, 2010. [Google Scholar]
  29. Grešlová, P.; Gingrich, S.; Krausmann, F.; Chromý, P.; Jančák, V. Social metabolism of Czech agriculture in the period 1830–2010. AUC GEOGRAPHICA 2015, 50, 23–35. [Google Scholar] [CrossRef]
  30. Kupková, L.; Bičík, I.; Najman, J. Land cover changes along the iron curtain 1990–2006. Geografie 2013, 118, 95–115. [Google Scholar] [CrossRef]
  31. Belda, M.; Holtanová, E.; Halenka, T.; Kalvová, J. Climate classification revisited: From Köppen to Trewartha. Climate Research 2014, 59, 1–13. [Google Scholar] [CrossRef]
  32. Czech Hydrometeorological Institute. Portál ČHMÚ: Historická data: Počasí: Základní informace (Czech Hydrometeorological Institute Portal: Historical data: Weather: Basic Information). https://www.chmi.cz/historicka-data/pocasi/zakladni-informace, accessed on 2024-09-27.
  33. INSPIRE. INSPIRE Geoportal Österreich. https://geometadatensuche.inspire.gv.at/metadatensuche/inspire/eng/catalog.search#/home, accessed on 2024-09-27.
  34. Ministry of Agriculture of the Czech Republic. Veřejný export dat LPIS. https://mze.gov.cz/public/portal/mze/farmar/LPIS/uzivatelske-prirucky/prirucky-pro-verejny-lpis/export-dat-lpis, accessed on 2024-09-27.
  35. Bosch, M. PyLandStats: An open-source Pythonic library to compute landscape metrics. PLOS ONE 2019, 14, e0225734. [Google Scholar] [CrossRef]
  36. McGarigal, K.; Cushman, S.; Ene, E. FRAGSTATS v4: Spatial Pattern Analysis Program for Categorical Maps. Computer software program produced by the authors. https://www.fragstats.org/, accessed on 2024-09-27.
  37. Meteostat. The Meteostat JSON API. https://rapidapi.com/meteostat/api/meteostat, accessed on 2024-09-27.
  38. Hofierka, J.; Suri, M. ; others. The solar radiation model for Open source GIS: Implementation and applications. Proceedings of the Open source GIS-GRASS users conference, 2002, Vol. 2002, pp. 51–70.
  39. Caha, J. QGIS algorithm - r.sun.incidout — grass_r_sun_incidout. https://jancaha.github.io/r_package_qgis/reference/grass_r_sun_incidout.html, accessed on 2024-09-27.
  40. Earth Resources Observation and Science (EROS) Center. Landsat 8-9 Operational Land Imager / Thermal Infrared Sensor Level-2, Collection 2, 2013. [CrossRef]
  41. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; Seal, D.; Shaffer, S.; Shimada, J.; Umland, J.; Werner, M.; Oskin, M.; Burbank, D.; Alsdorf, D. The Shuttle Radar Topography Mission. Reviews of Geophysics 2007, 45, 2005RG000183. [Google Scholar] [CrossRef]
  42. Qiu, S.; Zhu, Z.; He, B. Fmask 4.0: Improved cloud and cloud shadow detection in Landsats 4–8 and Sentinel-2 imagery. Remote Sensing of Environment 2019, 231, 111205. [Google Scholar] [CrossRef]
  43. Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sensing of Environment 2015, 159, 269–277. [Google Scholar] [CrossRef]
  44. Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sensing of Environment 1979, 8, 127–150. [Google Scholar] [CrossRef]
  45. Swoish, M.; Da Cunha Leme Filho, J.F.; Reiter, M.S.; Campbell, J.B.; Thomason, W.E. Comparing satellites and vegetation indices for cover crop biomass estimation. Computers and Electronics in Agriculture 2022, 196, 106900. [Google Scholar] [CrossRef]
  46. Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. Journal of Plant Physiology 2004, 161, 165–173. [Google Scholar] [CrossRef]
  47. Jin, S.; Sader, S. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sensing of Environment 2005, 94, 364–372. [Google Scholar] [CrossRef]
  48. Liang, S. Narrowband to broadband conversions of land surface albedo I. Remote Sensing of Environment 2001, 76, 213–238. [Google Scholar] [CrossRef]
  49. Liang, S.; Shuey, C.J.; Russ, A.L.; Fang, H.; Chen, M.; Walthall, C.L.; Daughtry, C.S.; Hunt, R. Narrowband to broadband conversions of land surface albedo: II. Validation. Remote Sensing of Environment 2003, 84, 25–41. [Google Scholar] [CrossRef]
  50. Tasumi, M.; Allen, R.G.; Trezza, R. At-Surface Reflectance and Albedo from Satellite for Operational Calculation of Land Surface Energy Balance. Journal of Hydrologic Engineering 2008, 13, 51–63. [Google Scholar] [CrossRef]
  51. Olmedo, G.F.; Ortega-Farías, S.; de la Fuente-Sáiz, D.; Fonseca-Luego, D.; Fuentes-Peñailillo, F. water: Tools and Functions to Estimate Actual Evapotranspiration Using Land Surface Energy Balance Models in R. The R Journal 2016, 8, 352–369. [Google Scholar] [CrossRef]
  52. Bowen, I. The Ratio of Heat Losses by Conduction and by Evaporation from any Water Surface. Physical Review 1926, 27, 779–787. [Google Scholar] [CrossRef]
  53. Suleiman, A.; Crago, R. Hourly and Daytime Evapotranspiration from Grassland Using Radiometric Surface Temperatures. Agronomy Journal 2004, 96, 384–390. [Google Scholar] [CrossRef]
  54. Pokorný, J.; Brom, J.; Čermák, J.; Hesslerová, P.; Huryna, H.; Nadezhdina, N.; Rejšková, A. Solar energy dissipation and temperature control by water and plants. International Journal of Water 2010, 5, 311–336. [Google Scholar] [CrossRef]
  55. Brom, J. SEBCS for QGIS - Module for calculation of energy balance features and vegetation water stress indices; University of South Bohemia in České Budějovice, 2021.
  56. Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. Journal of Hydrology 1998, 212-213, 198–212. [Google Scholar] [CrossRef]
  57. Klug, H.; Gottsmann, F.; Heredia, M. Transboundary landscape structure to determine the environmental situation of traditional land-use activities in Austria and Czech Republic. 10th international conference on information & communication technologies (ICT) in urban planning and spatial development and impacts of ICT on physical space, 2005, pp. 201–206.
  58. EUROSTAT. Farms and farmlands in the European Union - statistics; Statistics Explained 2022, pp.1–9.
  59. Ministry of Agriculture of the Czech Republic. Facts and Data. https://mze.gov.cz/public/portal/en/mze/about-ministry/facts-and-data, accessed on 2024-09-27.
  60. Kowalski, A.; Wigier, M. ; Instytut Ekonomiki Rolnictwa i Gospodarki Żywnościowej., Eds. The common agricultural policy of the European Union: The present and the future: EU member states point of view: Proceedings of the International Scientific Conference "The Common Agricultural Policy of the European Union - the present and the future", 5-7 December 2017, Stare Jabłonki, Poland; Number 73.1 in Monographs of Multi-Annual Programme, Dział Wydawnictw Instytutu Ekonomiki Rolnictwa i Gospodarki Żywnościowej - Państwowego Instytutu Badawczego: Warszawa, 2018. [Google Scholar]
  61. IS StaR. Average size of a section of the arable land block | IS StaR Portal. https://www.sdg-data.cz/en/cr-2030/odolne-ekosystemy/average-size-of-a-section-of-the-arable-land-block, accessed on 2024-09-27.
  62. Peyr, S. FarmStructureSurvey2020:Agriculturalandforestryholdingsincreasedinsize. STATISTICS AUSTRIA, Correctedpressrelease:12.853-151/22 2022, pp.1–2.
  63. Al-Amin, A.K.M.A.; Lowenberg-DeBoer, J.; Franklin, K.; Behrendt, K. Economics of field size and shape for autonomous crop machines. Precision Agriculture 2023, 24, 1738–1765. [Google Scholar] [CrossRef]
  64. Brunotte, J.; Fröba, N. Schlaggestaltung - kostensenkend und bodenschonend; Number 460 in KTBL-Schrift, KTBL, Kuratorium für Technik und Bauwesen in der Landwirtschaft: Darmstadt, 2007. [Google Scholar]
  65. Ševčík, R.; Krivopalova, A.; Cukor, J. Přímý vliv struktury zemědělské krajiny na výměru domovských okrsků zajíce polního: Předběžné výsledky z České republiky. Zprávy lesnického výzkumu 2023, 68. [Google Scholar] [CrossRef]
  66. Schai-Braun, S.C.; Ruf, T.; Klansek, E.; Arnold, W.; Hackländer, K. Positive effects of set-asides on European hare (Lepus europaeus) populations: Leverets benefit from an enhanced survival rate. Biological Conservation 2020, 244, 108518. [Google Scholar] [CrossRef]
  67. Smith, R.K.; Vaughan Jennings, N.; Harris, S. A quantitative analysis of the abundance and demography of European hares Lepus europaeus in relation to habitat type, intensity of agriculture and climate. Mammal Review 2005, 35, 1–24. [Google Scholar] [CrossRef]
  68. Reif, J.; Gamero, A.; Hološková, A.; Aunins, A.; Chodkiewicz, T.; Hristov, I.; Kurlavičius, P.; Leivits, M.; Szép, T.; Voříšek, P. Accelerated farmland bird population declines in European countries after their recent EU accession. Science of The Total Environment 2024, 946, 174281. [Google Scholar] [CrossRef]
  69. Šálek, M.; Kalinová, K.; Daňková, R.; Grill, S.; Żmihorski, M. Reduced diversity of farmland birds in homogenized agricultural landscape: A cross-border comparison over the former Iron Curtain. Agriculture, Ecosystems & Environment 2021, 321, 107628. [Google Scholar] [CrossRef]
  70. Huryna, H.; Pokorný, J. The role of water and vegetation in the distribution of solar energy and local climate: A review. Folia Geobotanica 2016, 51, 191–208. [Google Scholar] [CrossRef]
  71. Ripl, W.; Eiseltová, M. Sustainable land management by restoration of short water cycles and prevention of irreversible matter losses from topsoils. Plant Soil and Environment 2009, 55, 404–410. [Google Scholar] [CrossRef]
  72. Pokorný, J. Dissipation of solar energy in landscape—controlled by management of water and vegetation. Renewable Energy 2001, 24, 641–645. [Google Scholar] [CrossRef]
  73. STATISTICS AUSTRIA. Arable land, permanent grassland. https://www.statistik.at/en/statistics/agriculture-and-forestry/crop-production-and-farming/arable-land-permanent-grassland, accessed on 2024-09-27.
  74. Czech Statistical Office. Agriculture. https://csu.gov.cz/agriculture, accessed on 2024-09-27.
  75. Zahradníček, P.; Brázdil, R.; Štěpánek, P.; Trnka, M. Reflections of global warming in trends of temperature characteristics in the Czech Republic, 1961–2019. International Journal of Climatology 2021, 41, 1211–1229. [Google Scholar] [CrossRef]
  76. Mužíková, B.; Vlček, V.; Středa, T.; others. Tendencies of climatic extremes occurrence in different Moravian regions and landscape types. Acta Universitatis Agriculturae et Silviculturae Mendelianae Brunensis 2011, 59, 169–178. [Google Scholar] [CrossRef]
  77. Potop, V.; Türkott, L.; Kožnarová, V.; Možný, M. Drought episodes in the Czech Republic and their potential effects in agriculture. Theoretical and Applied Climatology 2010, 99, 373–388. [Google Scholar] [CrossRef]
  78. Brázdil, R.; Trnka, M.; Dobrovolný, P.; Chromá, K.; Hlavinka, P.; Žalud, Z. Variability of droughts in the Czech Republic, 1881–2006. Theoretical and Applied Climatology 2009, 97, 297–315. [Google Scholar] [CrossRef]
  79. Kiprotich, P.; Wei, X.; Zhang, Z.; Ngigi, T.; Qiu, F.; Wang, L. Assessing the Impact of Land Use and Climate Change on Surface Runoff Response Using Gridded Observations and SWAT+. Hydrology 2021, 8, 48. [Google Scholar] [CrossRef]
Preprints 120868 g001
Figure 1. The overview map of the area of interest (AOI). The detail shows a landscape structure on both the Czech and Austrian sides of AOI.
Figure 1. The overview map of the area of interest (AOI). The detail shows a landscape structure on both the Czech and Austrian sides of AOI.
Preprints 120868 g001
Preprints 120868 g002
Figure 2. The summary of the landscape biophysical features statistical testing for the Czech and Austrian areas of interest. The Student’s t-test was used for testing. Note: AL – All, AR – Arable land, VY – Vineyards, PG – Permanent grassland, FL – Fallow land, GF – Grass on field
Figure 2. The summary of the landscape biophysical features statistical testing for the Czech and Austrian areas of interest. The Student’s t-test was used for testing. Note: AL – All, AR – Arable land, VY – Vineyards, PG – Permanent grassland, FL – Fallow land, GF – Grass on field
Preprints 120868 g002
Preprints 120868 g003
Figure 3. The violin plots of individual functional variables for the entire Farmland in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Figure 3. The violin plots of individual functional variables for the entire Farmland in the Czech Republic (orange colour) and Austria (blue colour). For each variable, data from eight terms during the vegetative season of 2022 are shown. NDVI – Normalized difference vegetation index; NDMI – Normalized difference moisture index; T s –Surface temperature; EF – Evaporative fraction; LE – Latent heat flux; H – Sensible heat flux; G – Ground heat flux.
Preprints 120868 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated