Preprint
Article
Multi-Camera Rig and Spherical Camera Assessment for Indoor Surveys in Complex Spaces
Altmetrics
Downloads
53
Views
33
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
11 October 2024
Posted:
11 October 2024
You are already at the latest version
Alerts
Abstract
This study compares the photogrammetric performance of three multi-camera systems—two spherical cameras (INSTA 360 Pro2 and MG1) and one multi-camera rig (Ant3D)—to evaluate their accuracy and precision in confined environments. These systems are particularly suited for indoor surveys, such as narrow spaces, where traditional methods face limitations. The instruments were tested for the survey of a narrow spiral staircase within Milan Cathedral and the results were analyzed based on different processing strategies, including different relative constraints between sensors, various calibration sets for distortion parameters, interior orientation (IO), and relative orientation (RO), as well as two different ground control solutions. The study also included a repeatability test. The findings showed that, with appropriate ground control, all systems achieved the target accuracy of 1 cm. In partially unconstrained scenarios, instead, the drift errors ranged between 5 and 10 cm. Performance varied depending on the processing pipelines, but the results suggest that imposing a multi-camera constraint between sensors and estimating both IO and RO parameters during the Bundle Block Adjustment yields the best outcomes. In less stable environments, it might be preferable to pre-calibrate and fix the IO parameters.
Keywords:
Subject: Environmental and Earth Sciences - Remote Sensing
1. Introduction
Fisheye and spherical photogrammetry have become increasingly investigated topics in recent years. Undoubtedly, technological progress has made it possible to have devices with good performance, appreciable image quality, and resolutions sufficient for using such cameras in precision applications, even at affordable costs.
The purpose of this work is to compare three different systems (two spherical cameras and one multi-camera rig) with the aim of defining the levels of accuracy and precision achievable in particularly confined environments, varying the strategies for processing the photogrammetric block. Particular attention is given to the calibration of the multi-camera geometry and the interior orientation and distortion parameters, as well as the subsequent ground control of the block.
Although some researchers [1] had already begun to investigate the possibility of using panoramic photography in close-range photogrammetry in the 1980s, it is only since the late 1990s that the topic has started to gain real interest. This interest has certainly been driven by the increasing availability of the first consumer-grade digital cameras and the growing availability of software for generating panoramic images, coupled with the increasing computing power of personal computers. At the same time, it is important to note that, in those same years, the development and progressive adoption of approaches based on projective geometry in photogrammetry and computer vision provided the theoretical and mathematical foundations to generalize many geometric problems (e.g., coplanarity and collinearity equations, bundle adjustment, resection, etc.) and to apply the same geometric-mathematical model to linear, frame, or spherical cameras [2,3,4,5].
In those years, the main attempts to use spherical photogrammetry mostly consisted of stitching frame images acquired using traditional cameras and optics, mounted on a tripod and moved (rotated) in such a way as to keep fixed the position of the projection center [6,7,8,9]. As technology advanced, dedicated 360-degree cameras began to emerge [10]. These cameras utilized multiple lenses to capture the entire environment simultaneously. However, the real breakthrough occurred just recently with the increased diffusion of virtual reality (VR) technologies [11]. The demand for high-quality 360-degree content to deliver immersive VR experiences led to a surge in consumer-friendly 360-degree cameras, making the technology accessible to a broader audience and lowering the pricing of the hardware [12,13]. Generally, entry- and mid-level 360-degree cameras consist of two opposite-facing fisheye lenses (like the Insta360 One X2 [14,15] or the Ricoh Theta Z1 [16,17]) that capture the entire 360° field of view (FOV), while higher-end cameras incorporate more sensors. See for instance the iSTAR Fusion 360 (4 cameras [18,19]), the Insta360 Titan (8 cameras [20]), or the Panono 360° (36 cameras [21,22]).
As far as photogrammetric processing and 3D reconstruction are concerned, the use of 360-degree cameras is particularly efficient for indoor environments and confined spaces: data collection is much faster and simpler since fewer images are needed to achieve sufficient spatial coverage with high overlap between consecutive images. At the same time, with a single shot, the floor, roof and surrounding walls are captured simultaneously and do not require the camera’s poses to be changed to capture the whole interior geometry of the object. This approach is increasingly popular and has been tested in various acquisition scenarios as an alternative to terrestrial laser scanning and mobile mapping systems [23,24,25].
Usually, processing is done on automatically stitched panoramas. Working with stitched images (e.g., represented using equirectangular projection) has (apparently) several clear advantages: the total number of images is reduced, and a single image can display the entire field of view visible from a specific shooting position. The image is directly usable for visualization purposes (consider Google Street View-like applications or VR environments), making it easy to identify and recognize the various elements in the image. If properly created, the stitched image implicitly defines the geometric constraints to which the different component images are subjected (coincidence of the principal center and fixed relative orientation between the various sensors) and is free from geometric distortions, as these are corrected and removed during the stitching process. It is important to stress, however, that for a correct image stitching operation, the principal center of each individual frame must coincide. This requirement becomes increasingly critical as the distance between the camera and the object to be captured decreases. From this perspective, using a spherical head mount that allows the image sensor to be moved, if properly calibrated, ensures optimal results. On the other hand, systems with multiple sensors that capture the entire scene simultaneously, although more practical and quicker in acquisition, and ensuring substantial synchronization of the various frames, almost never meet this requirement. In [26], Barazzetti et al. investigated fisheye image calibration to improve stitching and tested different stitching software. In the same work the use of the raw fisheye images instead of the single equirectangular projection is hinted to be a viable approach to overcome quite high residuals (between 3 and 8 pixels depending on the software used) in the stitching process. The same approach can be found in [27] and in [28] where it is demonstrated that working with stitched images, in general, gives lower performances in terms of the 3D positional accuracy, but slightly better in terms of completeness and processing time. In [29] the use of equirectangular stitched panoramas instead of using raw fisheye images resulted in considerable drift errors in the image block orientation stage. As reported in [26], due to high reprojection errors from inaccurate image stitching and inaccurate spherical image orientation, meshes and dense point clouds derived from this data tend to be noisy and coarse.
If the generation of spherical/panoramic/equirectangular images is not a fundamental requirement, an alternative approach, while still leveraging the potential of fisheye photogrammetry, is the use of multi-camera rig systems. Even though the types of cameras previously described (from now on called spherical cameras) can be considered multi-camera rig systems as well, in this work we use the term “multi-camera rig” to refer specifically to those systems where, while attempting to capture a 360-degree (or at least 180-degree) view of the scene, the centers of projection of the various sensors are not positioned as close together as possible. Consequently, there is no attempt to obtain a unique spherical image through stitching. These systems are generally more oriented toward professional users, although early iterations were developed with off-the-shelf low-cost action cameras and custom camera rigs. More recently, custom devices have been proposed using specialized hardware for precise synchronization and global shutter sensors. They typically feature higher-quality cameras but inevitably they come with higher costs. In [30], Koehl et al. assembled four GoPro cameras on a rigid bar; in [31] a multi-camera setup with five GitUp cameras is presented. In [32] the authors designed a handheld device with two cameras for agile surveys in archaeological and cultural heritage fields; in [33,34]a system named Ant3D, a handheld device with five cameras for narrow space surveys, is presented; other relevant examples can be found in [35,36,37]. While the inability to create panoramic images may seem a limitation of these systems—and indeed, using a higher number of not stitched together images is often quite impractical for an operator—the fact that the various image sensors have significant baseline distances (ranging from some tens of centimeters to just over a meter) is actually one of their main strengths. In this case, capturing images from a single position allows for a 3D reconstruction of the scene that can also be accurately scaled if the lengths of the individual baselines between the sensors are known.
As previously mentioned, for both types of cameras (spherical and multi-camera rigs), the primary application field—or rather, the field where the advantages of these systems over other types of instruments are most evident—is indoor surveying. This is particularly true for confined spaces or environments similar to them, such as the narrow streets of historical urban centers [15].
The variability of image scale is generally a problem for fisheye photogrammetry. With their wide field of view, it is likely that elements at significantly different distances from the observation point will appear in the frame. This variability is often exacerbated by greater image distortion, especially at the edges of the lens's field of view. Such variability usually leads to greater difficulties in identifying and correctly positioning tie points, which significantly affects the success of image block orientation procedures and the subsequent 3D reconstruction of the object. However, in confined indoor spaces, the problem is much less significant because the object tends to surround the observation point.
Camera calibration and relative orientation constraints are essential for accurate results. The topic is undoubtedly current and, although well-known and studied both theoretically and practically for traditional frame cameras, it has been the subject of numerous studies by various authors in recent years as far as spherical and fisheye cameras are concerned. For instance, Nocerino et al. [38] proposed a methodology to calibrate the Interior Orientation (IO) and Relative Orientation of the camera sensors (RO) of a multi-camera system, while Perfetti and Fassi [39] used self-calibration to compute IO parameters and baselines between cameras.
The challenge of establishing correct and stable ground control of the block is the most significant practical issue when working in particularly confined and meandering environments, as measuring Ground Control Points (GCPs) can be difficult and costly. Typically, image blocks are constrained using well-distributed GCPs or Global Navigation Satellite System (GNSS) camera positioning [40], which are not always feasible in such scenarios. Nevertheless, drift with few ground constraints seems to be an underexplored topic.
As mentioned, the purpose of this work is to compare three different systems (two spherical cameras and one multi-camera rig) with the aim of defining the levels of accuracy and precision achievable in particularly confined environments. The three different instruments are treated as multi-camera rigs, foregoing the possibility of using panoramic images for the first two systems. This is because, given the camera-to-object distances involved, the assumption of coinciding projection centers between the different sensors is not even approximately verified. However, as will be seen, the different geometric configurations of the sensors in the three models require different operational choices for image acquisition.
The paper is organized as follows: Section 2 outlines the case study, detailing the three different systems and the methodologies employed for camera calibration and data processing. Section 3 presents the results. Finally, Section 4 and Section 5 offers a detailed discussion on the accuracy and precision levels achievable by each instrument along with practical recommendations for their optimal use, particularly in terms of data processing strategies and calibration techniques.
2. Materials and Methods
The tests assessing the levels of accuracy and precision achievable with the three instruments were conducted in a particularly challenging confined environment, specifically a spiral staircase (section 2.1). This location was selected because such environments pose significant difficulties and often prove to be prohibitive for traditional surveying techniques. Consequently, such scenarios are ideal for the application of multi-camera systems, which can achieve fields of view ranging from 180° to 360° for each shooting position.
The performance of the three systems (each described in section 2.2) was also evaluated using various calibration sets for distortion parameters, interior orientation, and relative orientation (section 2.3). Validation of the results was performed against a ground truth obtained from a previous photogrammetric survey [23]. However, in these application contexts, providing a ground truth test field is quite challenging, as all current surveying techniques exhibit similar weaknesses concerning drift errors. For this reason, this study also included a repeatability test, comparing the results from three different datasets collected with each instrument.
2.1. Case Study: The Minguzzi Spiral Staircase
The selected case study is a complex architectural environment, specifically the Minguzzi spiral staircase within Milan (Italy) Cathedral (Figure 1). This marble spiral staircase is situated within the right pylon of the cathedral's main facade and spans approximately 25 meters in height. It serves as a connector between three distinct levels of the building: the lower level of the roofs at its upper end, the central balcony of the facade in the middle, and the floor of the church at its base.
The staircase is characterized by extremely low luminance, with poor-quality artificial illumination and only sporadic exterior openings spaced at regular intervals. These openings, relatively large (85 cm) and deep (approximately 2 m) from the interior due to the substantial wall thickness, narrow noticeably towards the exterior, ending as small vertical embrasures (30 cm in width).
The core of the spire features a column made of marble blocks with a diameter of about 40 cm, around which the ramp ascends. The passage left for traversal is extremely narrow, approximately 70 cm wide. This constrained space would pose a significant challenge for any kind of surveying methodology, particularly due to the revolving nature of the staircase, which impedes imaging of the staircase's top from a bottom viewpoint, resulting in limited visibility from any position along the stair and propagating uncertainty. For these reasons the spiral staircase has been used as a test site in previous experiments [27,29,41].
Traditional terrestrial scanner instrumentation proved impractical due to space constraints, and other factors such as limited operational range, shadow areas from tripod legs, and the staircase's spiraling geometry that further complicated data acquisition. While LiDAR-based mobile scanners offer increased flexibility, the dynamic changes in geometric features along the acquisition track would exponentially increase drift error, particularly without efficient loop closures.
Providing accurate GCPs along the staircase – for instance measuring their coordinates using a Total Station – is rather unrealistic due to the limited and constrained space and the short-length intervisibility of subsequent measuring stations. It is worth noting that, also using high precision instruments, large drift errors should be expected in the (open) total station traverse.
Given these challenges, the case study presented an ideal environment to evaluate the multi-camera fisheye photogrammetric systems.
2.2. Equipment
2.2.1. INSTA 360 Pro 2 Spherical Camera
The INSTA 360 Pro2 is a professional-grade 360° camera characterized by its spherical shape, measuring 143 mm in diameter. It is equipped with six cameras, each boasting a resolution of 4000x3000 pixels and F2.4 fisheye lenses with a fixed focal length of 1.88 mm, providing a wide 200° field of view along the sensor's maximum dimension. The sensors are equidistantly posed around the equator, with a relative rotation of 60°, as illustrated in Figure 2b. This arrangement makes the centers of projection of the sensors non-coincident and spaced with relative shifts as reported in Table 1.
The camera simultaneously records raw fisheye images acquired by each sensor (see Figure 5a) and, if enabled, equirectangular images with a resolution of 7680 x 3840 pixels achieved through real-time stitching. Stitched images can also be produced in post-processing using dedicated software like Insta360stitcher, other open-source or commercial software such as PTGui [42] and Autopano [43], or proprietary codes for enhanced distortion correction control. However, from Table 1, it should be noted that the base-length between two consecutive sensors is ca. 70 mm and is ca. 120 mm between every second consecutive sensors (which share 60° FOV). Considering an average distance from the object along the spiral staircase of approximately 800 mm, the hypothesis of center of projection coincidence is far from being realistic and using stitched spherical images would imply strong image coordinate residuals.
The camera offers various shooting modes, enabling the capture of 360° still images, videos, and timelapses, making it suitable for various applications, including dynamic scene documentation. Equirectangular images can be stabilized using a 9-axis gyroscope to ensure consistent orientation, and the camera comes equipped with a built-in GNSS module. Users can adjust acquisition parameters such as ISO, shutter speed, and white balance.
2.2.2. MG1 Spherical Camera
The MG1 spherical camera is a hardware component of the backpack mounted mobile mapping system Heron MS Twin Color, developed by Gexcel S.r.l. [44]. It is adapted from the commercial camera Labpano Pilot Insight. It is equipped with four 1/2.3" Sony IMX577 CMOS sensors placed in a square configuration with a maximum baseline between opposing cameras of around 6 cm (Figure 3b and Table 2). Each sensor boast a native resolution of 3032x4048 pixels, reduced to 2530x4048 via software. The sensors’ detector pitch is 1.55 µm. Each camera is equipped with a 2.2 mm fisheye optic with a maximum field of view coverage of 185°. The MG1 camera is normally integrated in the Heron mobile mapping system and therefore does not feature an interface for stand-alone use. The specific model used in this investigation is a test model that can be operated by means of a web UI (User Interface) through an ethernet cable connecting the camera to a tablet device. The web UI allows for both video and single shots capture. For the single shots capture mode, at each triggering event, two files are automatically generated, a stitched equirectangular panorama shot and a mosaic of the four raw images placed side by side. Individual raw images are retrieved by segmenting the mosaic raw image (see Figure 5b). The web UI allows adjusting ISO, shutter speed and white balance. However, during this investigation, automatic mode was used with the camera rigidly mounted on a photographic tripod.
2.2.3. ANT 3D Multi-Camera Rig
The Ant3D multi-camera system is engineered for dynamic acquisitions, offering handheld operation to capture sequences of synchronized images. Comprising five global shutter cameras, each boasting a resolution of 2448x2048 pixels and equipped with fisheye lenses featuring a focal length of 2.7mm, the device is optimized for versatility and adaptability in various environments. The arrangement of the cameras is designed to be ideal in narrow space acquisition scenarios, prioritizing factors such as agility, transportation efficiency, maneuverability, FOV, and the baseline length between cameras [32].
The multi-camera is operated hand-held on the movement by an operator walking through the environment to be scanned. Positioned roughly on a plane and directed outward along a shared symmetry axis (Figure 4 and Table 3), the cameras collectively offer an expansive FOV covering the entire frontal hemisphere. Notably, the system is engineered to omit imaging of the rear hemisphere to avoid inadvertently capturing the operator in the frame.
The multi-camera setup incorporates three illuminators, facilitating the acquisition of imagery in low-light or dark environments. The device is tethered to a backpack, housing a dedicated control computer unit and a rechargeable battery pack, ensuring extended operational endurance and autonomy during field deployments [39].
The user interface is placed on the hand-held device itself together with the cameras and the illuminators. Through the touchscreen the operator can control capture parameters such as shutter speed, gain and capture interval. At each capture event, the five cameras acquire simultaneously, triggered by a hardware synchronization connection and individual fisheye images are saved (Figure 5c).
Figure 5.
Fisheye images acquired by the three camera systems: (a) INSTA 360; (b) MG1; (c) ANT3D.
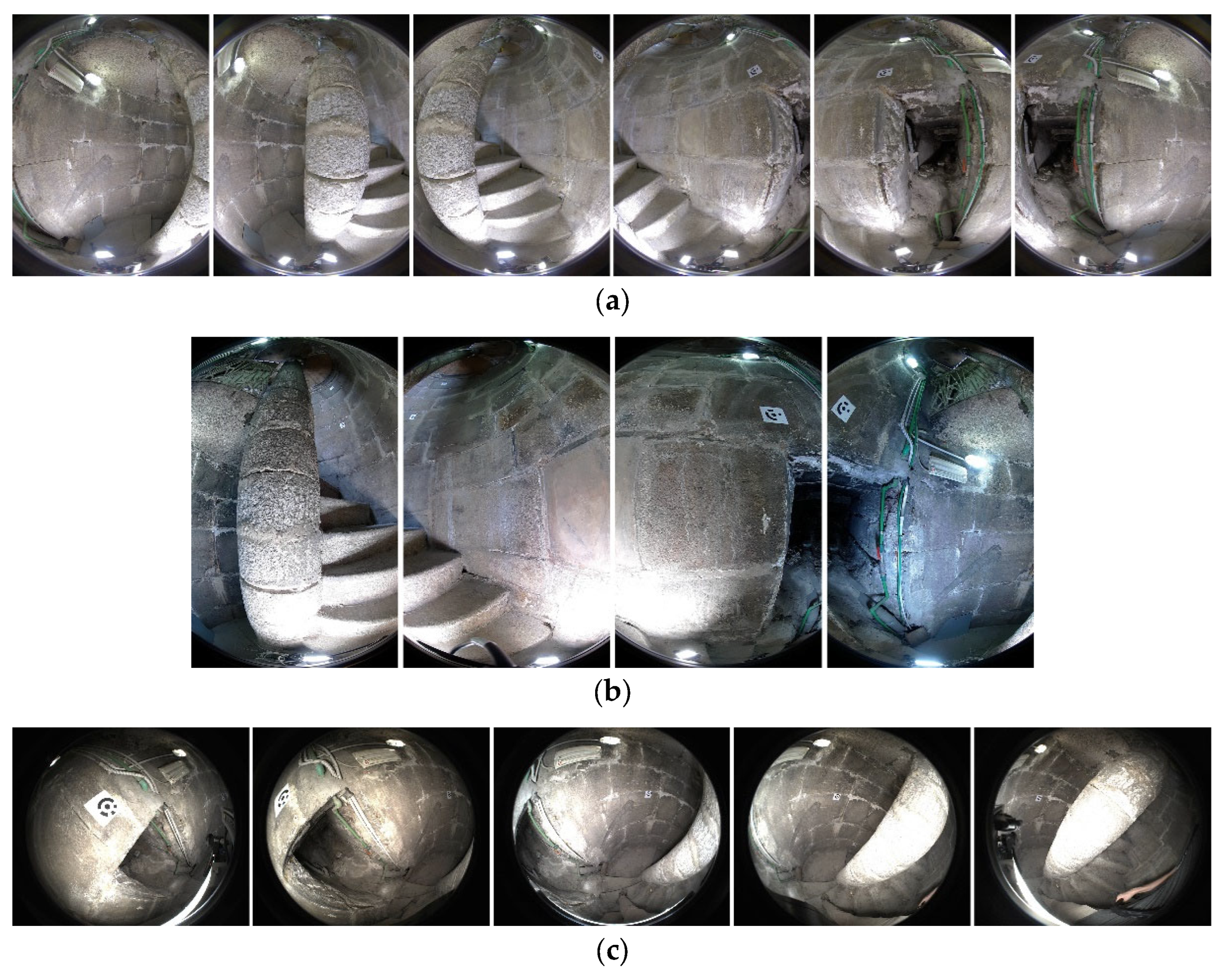
Table 4.
Summary of the technical characteristics of the three cameras.
| Camera system | # sensors | H FOV | Sensor FOV | Image resolution |
|---|---|---|---|---|
| INSTA 360 Pro 2 | 6 | 360° | 200° | 4000x3000 |
| MG1 | 4 | 360° | 185° | 2530x4048 |
| ANT3D | 5 | 270° | 190° | 2448x2048 |
2.3. Camera Calibration
Camera calibration is critical in multi-camera systems based on fisheye lenses. While the wide FOV of fisheye lenses introduces significant distortion that need to be accurately corrected, it is also crucial to accurately estimate the spatial relationships (including relative shifts and angles) between the individual sensors in the system. This estimation helps better constrain the geometry of the camera network and reduces the degrees of freedom in the photogrammetric block.
In this study all the cameras were initially pre-calibrated to derive the IO and distortion parameters that characterize each camera and the relative shifts and angles between the cameras RO.
To assess how much the final accuracy of the photogrammetric block is influenced by the calibration procedures, two different calibration sets were examined. These sets were obtained in two distinct environments, primarily differing in dimensions, both of which are representative of indoor settings where the use of spherical cameras is particularly suitable. The first environment (hereinafter Calibration Room 1 – CR1, Figure 6) is a small, indoor room comparable in size to the Minguzzi staircase (1.8 x 0.8 x 2 m). Conversely, the second environment (hereinafter Calibration Room 2 – CR2, Figure 7) is a larger (8 x 8 x 4 m) outdoor area enclosed on all four perimeter sides.
The choice to use environments of diverse dimensions stems from the intention of evaluate if the distance of objects from the shooting point affects the accurate estimation of calibration parameters. Although the Minguzzi staircase is a narrow environment with consistent dimensions throughout its length, the surveyed path for this study encompasses areas adjacent to both the upper and lower accesses of the staircase. Thus, the path can be divided into three portions: a brief section touching the lower level of the Cathedral's roofs, a longer stretch along the staircase itself, and a portion of the Cathedral's nave. These segments exhibit considerable variability in size, with the staircase portion averaging about 70 cm in width, the nave section reaching heights of 20 m, and the roof section forming an almost square-shaped area of 8 x 8 m with no ceiling.
Additionally, in multi-camera systems, particularly those with spherical configurations, the issue of object distance variability from the camera is significantly amplified. The wide FOV (up to 360°) means that each shot captures elements both nearby and far away simultaneously, resulting in significant fluctuations in image scale unless operating within highly confined spaces.
2.3.1. Calibration Images’ Acquisition
Both calibration environments are situated within the Milan Cathedral and are constructed from blocks of pink marble, providing a distinct and well-defined texture. In addition, photogrammetric circular coded targets were used to mark GCPs and Check Points (CPs). In CR1, the targets were strategically placed on all walls, the floor, and the ceiling, while in CR2, they were placed solely on the side walls. The target coordinates were fully surveyed using a total station in CR2, while, in CR1, due to spatial constraints that inhibited comprehensive topographic surveying, some targets were measured with a total station, while the coordinates of the others were estimated with an accuracy of 0.5 mm through a redundant photogrammetric acquisition performed using a DSLR Nikon D810 equipped with 24 mm lenses.
Very redundant photogrammetric blocks were acquired with all three multi-cameras. Due to differences in instrument configurations and acquisition characteristics, it was not possible to follow the same capture scheme and ensure the same number of images. ANT 3D, for example, is designed to continuously acquire data while handheld and requires a round trip. In contrast, INSTA Pro2 and MG1 can be tripod-mounted for static acquisitions and, with their 360° coverage, do not require a return acquisition. Nevertheless, a uniform acquisition schema was maintained throughout. In CR1, images were captured along parallel strips at varying elevations relative to the ground, whereas in CR2, they were acquired following a predominantly regular checkerboard pattern.
To improve parameter decoupling, each camera was rotated in different poses for every shooting position. The following table provides a summary of the acquired images. The following table (Table 5) summarizes details of the different calibration acquisitions.
2.3.2. Image Processing (Calibration)
Image processing was performed on raw fisheye images using Agisoft Metashape v2.1 [45]. Each dataset underwent processing through two distinct pipelines.
In the first calibration pipeline (P1), the images captured by individual sensors were treated as standalone images, devoiding of any relative constraints with respect to the other sensors. Conversely, the second pipeline calibration (P2) imposed constraints on the images, treating them as components of a multi-camera system and establishing relative positions and rotations between the sensors.
Structure from motion was initiated after automatic target detection, with initialization of IO and RO parameters based on technical sheet specifications. In P1, the focal length underwent precalibration, while in P2, precalibration encompassed both the focal length and the relative orientation among sensors. The initial estimate of the slave sensors' RO was defined with a weight corresponding to pseudo-observations of 5 mm for translations and 1 degree for rotations.
The targets' reference coordinates were imported and treated as GCPs to enhance orientation robustness. Subsequently, tie points were subject to two rounds of filtering, resulting in the elimination of tie points with high collinearity residuals. Approximately 10% of all tie points were discarded at each filtering stage, after which a new bundle adjustment was computed.
Finally, the computed IO parameters and, in P2 only, the adjusted RO parameters, were exported. Figure 8 summarizes the calibration process, which outputs 4 calibration sets for each camera: CR1-P1, CR1-P2, CR2-P1 and CR2-P2.
2.4. Image Acquisition
Images were acquired with all three cameras following the same acquisition schema. The acquisition started from the top of the staircase, including an outdoor portion of the Cathedral's lower-level roofs, continued along the entire development of the staircase, and ended in the first bay of the Cathedral's nave. For each instrument, three different acquisitions were performed to assess process repeatability. The cameras' setup remained consistent throughout the entire path, with slight variations between the instruments based on their specific characteristics.
As for the calibration, INSTA 360 Pro2 and MG1 were employed in single-shot mode and mounted on a tripod to prevent capturing the operator in the frame and to avoid motion blur due to significantly reduced lighting conditions. To guarantee sufficient illumination, three light sources were fixed to the tripod legs and dimmed to achieve the ideal exposure, striking a balance between the necessity for optimal illumination and the potential for overexposure due to the proximity of the illuminators to the staircase walls. The exposure settings of the INSTA varied across the acquisitions. During the first acquisition, the auto exposure mode was employed, allowing the camera to automatically adjust to the prevailing environmental conditions . In the subsequent two acquisitions, instead, the ISO speed was prioritized, by setting it to a fix value of 100 ISO, with the objective of achieving the highest image quality. The use of a tripod was instrumental in these processes, enabling long exposure times without the risk of motion blur.
The MG1 acquisition was instead performed always with automatic settings.
Images were taken at each step of the staircase, maintaining an average base length of 30 cm between subsequent shots. Given the 360° FOV of the two cameras, the entire imaging procedure was conducted in a single direction, descending the staircase, and was completed in about one hour.
The acquisition using ANT 3D was instead performed on the move, handholding the instrument. The imaging process was conducted in both downward and upward directions, since the instrument does not acquire backwards. Illumination was supplied by three lights integrated directly in the device. The images were captured at a frame rate of 1 frame per second, resulting in a base-length between consecutive images averaging between 15-20 cm. The entire acquisition process was finished in approximately 20 minutes.
Table 6 summarizes the number of images acquired for each camera and information regarding the shooting points and acquisition time.
Figure 9.
Structure from motion processing result and picture of the camera system during data acquisition: (a) INSTA 360; (b) MG1; (c) ANT3D.
Figure 9.
Structure from motion processing result and picture of the camera system during data acquisition: (a) INSTA 360; (b) MG1; (c) ANT3D.

2.5. Image Processing and Evaluation Methodology
To evaluate the behavior of the three multi-camera systems and optimize the processing strategies, different pipelines were tested, considering different bundle adjustment setup changing the relative constraints between the sensors (RO) and interior orientation parameters calibration strategy. It should be noted that although the INSTA 360 Pro 2 and the MG1 cameras can output equirectangular images by stitching the fisheye images captured by individual sensors, stitched images were not considered in this study. Previous research [29] has shown a significant reduction in the accuracy of models derived from equirectangular images. Further investigations into optimizing the stitching process would be required but are beyond the scope of this article. Therefore, all processing was conducted directly on the fisheye images captured by individual sensors, utilizing a fisheye camera model and following the processing strategies detailed below.
- Free images – IO not fixed: in this pipeline, each image was processed without any relative constraints with the other images acquired from the same position. In other words, all the images were considered to be independent from each other, as they were not acquired using a multi-camera system. As for the IO parameters, they were adjusted on the job while only the focal length was initialized according to its value from technical specification.
- Free images – IO pre-calibrated and fixed: similar to the previous pipeline, the relative constraints between images captured from the same position were not considered. The IO parameters were, instead, set to the values obtained from pre-calibrations. All the IO parameters estimated in the various calibration sets, described in Section 2.3.2 (CR1-P1, CR1-P2, CR2-P1 and CR2-P2), were employed in the subsequent analysis. Contrary to what could be expected, in this pipeline, not only the IO parameters obtained from independent sensor calibration (P1) were considered, but also those derived from the multi-camera constrained calibration (P2). This approach was taken because the IO and RO parameters are correlated. The aim was to assess how constraining or freeing the RO parameters influences the estimation of the IO parameters.
- Multi-camera – IO and RO not fixed: the third pipeline involved the processing of images, applying a multi-camera constraint (RO) between images acquired from the same position. In other words, this means that the relative orientation parameters between the cameras, once estimated, remain constant across all shooting positions. The Structure from Motion (SfM) was initialized by setting the focal length according to the technical specifications. All other IO parameters and the RO among sensors were adjusted during the Bundle Block Adjustment (BBA).
-
Multi-camera – fixed: finally, in this pipeline, the multi-camera constraint was imposed on images acquired from the same position, and both IO and RO were fixed according to different configurations:
- IO parameters were fixed to values estimated in the precalibrations, while RO were adjusted during the BBA;
- Both IO and RO parameters were kept fixed;
- RO parameters were pre-calibrated, while IO parameters were estimated in the BBA.
For all the configurations, the pre-calibrated values of the parameters refer to those estimated in calibration sets CR1-P2 and CR2-P2.
All the tests were conducted using an equidistant fisheye camera model combined with the Brown distortion model (f, cx, cy, k1, k2, k3, p1, p2). Image orientation was initially performed without GCPs in the SfM process. Then, a BBA was carried out, treating control points as tie points. Finally, the reference system was established by inputting the ground coordinates of the points and setting up GCPs and CPs according to two different constraint scenarios (Figure 10):
- A.
- 6 GCPs were used, 2 placed at the top of the staircase and 4 at the base, to constrain the block at both the start and end of the path, in order to assess the performance of the cameras under a stable ground control solution.
- A.
- B. To assess, instead, the global drift of the photogrammetric block along the staircase in the worst-case scenario, only the 4 GCPs placed at the base of the staircase were used, while the rest of the path was left unconstrained.
Both GCPs and CPs were identified on easily recognizable architectural features, with their coordinates derived from a previous photogrammetric survey [23]. It is worth noting that the accuracy of GCPs and CPs is approximately 1 cm. Typically, it is recommended to use a ground truth dataset obtained with instruments that are three to four times more precise [46] than those being assessed. In this particular case, however, it is quite challenging to provide a ground truth with such characteristics, since all current surveying techniques exhibit the same weakness in terms of drift-errors. Therefore, the target accuracy will be considered achieved when the residuals Root Mean Squared Error (RMSE) on the CPs are close to 1 cm, without considering fluctuations below 0.5 cm as significant. Moreover, the repeatability test conducted on the three datasets will serve as the main output to assess the precision of the three cameras.
3. Results
3.1. INSTA 360 Pro 2
Table 7 shows the residuals on CPs across different pipelines and ground control solutions using INSTA 360 Pro2.
Analyzing ground control solution A, which involves 6 GCPs (4 at the base and 2 at the top of the staircase) and is the recommended minimal control solution, it can be observed that the camera achieves excellent accuracy. The RMSE on the CPs is approximately 1 cm, which aligns with the target accuracy.
Using on-the-job calibration (pipelines 1 and 3) yields the best accuracy results, with RMSE ranging between 0.8 cm and 1.2 cm. The only exception is D1 in pipeline 1, which shows an RMSE of 4.4 cm. This discrepancy may be related to the different exposure settings used for the camera in this specific acquisition. Here, auto exposure mode was used, resulting in ISO speed values varying between 100 and 400, with most images at ISO 400. In contrast, datasets D2 and D3 were acquired with a fixed ISO value of 100. This, along with slight variations in the capture geometry in the nave at the base of the staircase, may have resulted in less stability in the block. This instability is not compensated for, when processing images without relative position constraints between sensors (pipeline 1). However, the multi-camera constraint (pipeline 3) seems to better manage the (likely) weakness of D1, resulting in identical outcomes for all three datasets.
Using pre-calibrated IO parameters (Pipeline 2) slightly degrades the results, with RMSE ranging from 0.9 cm to 1.3 cm for datasets D2 and D3. As already pointed out, D1 shows discrepancies compared to the other two datasets. D1 shows RMSE values of 5.2 cm and 5.7 cm when using pre-calibrated parameters in RC1, while using the parameters estimated in RC2 yields better results, with RMSE values of 1.6 cm and 1.9 cm.
In consideration of processing pipeline 4, the results suggest that using pre-calibrated parameters is not recommended when coupled with the multi-camera constraint. More specifically, pre-calibrating only the IO parameters (pipeline 4a) results in a slight deterioration in performance compared to pipeline 3, with RMSE values ranging from 1.2 to 1.5 cm. However, pre-calibrating the RO parameters results in considerable inaccuracy in the estimation of camera orientations, with RMSE values reaching up to 7.8 cm.
In ground control solution B (only 4 GCPs at the base of the staircase), high drift errors are evident at the top, as expected. The observed drift can be primarily attributed to the inaccurate estimation of the base lengths along the trajectory in the absence of ground constraints, which exhibits a progressive increase from the base to the summit of the staircase, with a predominant influence in the Z direction. This issue also appears to be dataset-specific. As previously observed, datasets D2 and D3 generally outperform D1 and demonstrate more consistent behavior. Overall, the multi-camera constraint (pipelines 2 and 4) provides greater stability to the block in comparison to the use of images without relative constraints, effectively mitigating the occurrence of drift errors in D1. Moreover, the pre-calibration of the IO parameters represents an effective method for enhancing the results (pipeline 4a).
3.2. MG1
Table 8 reports the results obtained with the MG1 camera. Both solution A and B exhibit the same residuals patterns across the various tests, with solution B resulting in residuals averaging in the order of a tens of centimetres and solution A averaging in the order of few centimetres and reaching the 1 cm target accuracy. Concentrating on solution A, we can notice as the multi-camera approach results in more stable and predicting outcomes: comparing pipeline 1 with pipeline 3, the latter (multi-camera approach) not only produced lower RMSE but also significantly reduced the variability across the three datasets. Pipeline 1 resulted in CPs RMSE ranging from 2.5 cm up to 6.6 cm, while with pipeline 3 all three datasets aligned on almost identical results with a CPs RMSE of 1.4 cm. Pipeline 2, where different pre-calibrated IO were considered, does not significantly and consistently improve the results compared to the un-constrained solution (pipeline 1). For dataset D1 pre-calicabrated IO resulted in better results RMSE ranging between 1.1 cm and 4.7 cm compared to the 6.6 cm RMSE of pipeline 1. However, for datasets D2 and D3 the opposite is true, with pipeline 1 producing almost consistently the better results than pipeline 2. Ultimately, using pre-calibrated IO had the effect of reducing the high variability observed with pipeline 1, but on average also resulted in a slight worsening of the results. On the other hand, when pre-calibrated IO are used within the multi-camera approach (pipeline 4a), nearly identical results to the unconstrained pipeline 3 throughout all datasets can be observed. No significant difference can be observed between the CR1 and CR2 tests suggesting that the variations between the two calibrations are compensated by the estimated RO constraint. From the fully constrained pipeline (pipeline 4b), we can observe an average worsening of the RMSE and an increase in the variance of the results across the three datasets. Moreover, a significant difference can be observed between the CR1 and CR2 calibrations, with the latter performing better on average and the D2 dataset specifically producing the best results of all MG1 tests (0.9 cm RMSE and 1.7 cm max error). However, it is the authors opinion that the increased variance observed with pipeline 4b including the best performing result, testify for the fully constrained approach being very sensitive to the specific dataset characteristics rather than being effective in forcing an ideal solution. From pipeline 4c we observe a rather small variance between the three datasets, however, with respect to the un-constrained multi-camera approach (pipeline 3), the results are constantly slightly worse averaging in 2.2 cm RMSE. Ultimately, the multi-camera approach resulted in better and more consistent result than the single camera approach. The most consistent results are produced by pipeline 3 and pipeline 4a among which pipeline 3 should be preferred since it does not require the pre-calibration and cannot be negatively affected by incorrect or outdated precalibration.
3.3. ANT 3D
Table 9 reports the CPs results of all ANT3D tests. Across the tests, especially focusing on solution B, one can notice the worse performance of D3 with respect to the other two datasets that almost constantly perform significantly worse. Considering that all three datasets were acquired in the same fashion, the significant outlier could be appointed to a difference in the capturing parameters, particularly the ISO, due to a different dimmer setting of the illuminators.
Focusing on solution A, it is observed that both pipeline 1 and pipeline 3 produced good results both in the low RMSE and in the low variance between datasets. Pipeline 3 performed slightly better with a CPs RMSE of 1.2 cm for D1 and D2, improving from an average RMSE of 2 cm for the same datasets in pipeline 1. Comparing pipeline 2 with pipeline 1 results, it can be noticed that the IO pre-calibration never led to an improvement of the RMSE. Rather, it resulted in worsening the performance of D1 and D2, specifically from an average of 2 cm in pipeline 1 to an average of 4.4 cm in pipeline 2, with no significant difference observable between CR1 and CR2 calibration. A different behavior can be observed comparing pipeline 4a to pipeline 3. In this case no significant change can be detected by implementing IO pre-calibration. Looking at pipelines 4b and 4c, a difference emerges between the performance of CR1 and CR2 favoring the latter, which resulted from a calibration dataset more similar to the staircase environment. Both pipelines 4b-CR1 and 4c-CR1 produced good results, averaging 2 cm and 1.6 cm respectively (considering D1 and D2 only) even if slightly worse than the un-constrained pipeline 3, averaging 1.2 cm. These approaches, however, have the advantages of providing reconstruction scaling from the RO constraints. Finally, it is worth noting solution B performance of pipeline 4b-CR2, discarding again the faulty D3 dataset, the average RMSE is 3.9 cm, which is to be considered very positively considering the weak GCPs constrain of solution B. These latter results suggest that pipeline 4b is favorable in those scenarios where good GCPs distribution is inhibited. The significant difference between CR1 and CR2 in this case: 3.9 cm against 10.9 cm, and similarly in all others pipeline 4 tests, also suggests that the small room calibration (CR1) yields the more effective values. In ideal scenarios, i.e. with proper GCPs, pipeline 3 yields the best results and pre-calibration worsens the outcomes. On the other hand, in challenging scenarios (open-handed unconstrained path), pre-calibration of both IO and RO significantly improves the results over the un-constrained approach (pipeline 3).
4. Discussion
The results presented in Section 3 reveal variable behavior across different cameras and datasets. This variability highlights the complexity of the phenomena under investigation. However, cross-cutting conclusions can be drawn that are broadly applicable. These insights are intended to serve as operational guidelines to facilitate a more consistent approach for the effective utilization of these systems. With this aim, in addition to the absolute RMSE, the discussions will heavily consider the reliability of results concerning their repeatability.
Table 10 and the scatter plots in Figure 11 show the level of accuracy achieved by the different systems using ground control solution A. The results are organized by processing pipeline, Table 10 aggregates the results from all datasets (D1, D2, D3) and from both calibration parameters (CR1 and CR2), while Figure 11 depicts all individual results therefore highlighting consistency and variability across the different processing pipelines. In Figure 11, the colored horizontal marks depict the RMSE values obtained for each dataset. The scatter plot is used to illustrate the variability of results across each processing pipeline. Meanwhile, the black lines represent the average RMSE values for each pipeline and for the two different calibrations.
The graphs indicate that pipeline 3, which applies a multi-camera constraint between sensors while estimating IO and RO parameters during the BBA, provides the lowest average RMSE values and ensures the greatest stability in the results. The ANT3D data should be interpreted excluding dataset D3, since, as described in Section 3.3, this dataset behaves differently from the others and results in significantly lower accuracy (30 mm for D3 compared to 12 mm for D1 and D2). Consequently, it influences the behavior of the aggregated data.
Implementing a multi-camera constraint between sensors enhances the consistency of results and mitigates dataset-dependent behaviors, which may occur in pipeline 1 where each image is processed independently. While pipeline 1 can occasionally deliver excellent results, such as 8 mm for D2 with the INSTA 360 Pro 2, it does not consistently achieve this performance across all datasets. The multi-camera constraint adds stability to the block orientation and helps prevent potential drift effects.
In terms of interior orientation, fixing the IO parameters without the multi-camera constraint (pipeline 2) typically does not yield significant improvements compared to pipeline 1. For the INSTA 360 Pro2, both the average and minimum RMSE values remain fairly consistent, although the variability of the results increases. In the case of MG1, significant improvements are observed in specific cases (e.g., D1), yet the variability remains notably high, with RMSE values reaching up to 49 mm. For both the two spherical cameras, this behavior seems to be affected by the two different calibration sets. Analyzing the distinct average values for each calibration reveals that they display differing behaviors, with better performance achieved using the parameters derived from CR2.
In contrast, for ANT3D, the behavior is the opposite: fixing the IO parameters results in a substantial reduction in accuracy and the performance of the two calibration sets is the same.
When considering pipelines 4, which apply the multi-camera constraint among the sensors, fixing the IO parameters (pipeline 4a) can be beneficial. Overall, it is observed that for all cameras, the results remain closely aligned with those achieved using pipeline 3, and the variability is kept to a minimum. In some instances, especially with MG1, even higher accuracy can be attained compared to those possible with pipeline 3. It is worth noting that this pipeline seems to be largely unaffected by the use of different calibration sets (CR1 or CR2), thereby maintaining robustness without necessitating perfect estimates of the IO parameters.
Different considerations need to be made when addressing the pre-calibration of RO parameters. When only the pre-calibrated RO parameters are fixed (pipeline 4c), the performance varies across instruments. For the INSTA, the behavior generally remains fairly consistent among the datasets, while a slight deviation is observable varying the calibration sets, with higher accuracy provided by CR1. Nevertheless, this pipeline produces the worst overall results. For MG1, pipeline 4c results in slightly lower accuracy than pipeline 3, but performs better than pipelines 1 and 2, with consistent results among datasets and calibration sets. With ANT 3D, the behavior is significantly affected by the calibration parameters. While CR1 generates results that align closely with those obtained from pipelines 1, 3, and 4a, CR2 delivers the poorest outcomes overall.
Finally, when both the IO parameters and the RO parameters are fixed (pipeline 4b), the results are found to be heavily influenced by the calibration set. This is not surprising, as constraining all parameters limits the degrees of freedom in the orientation solution. The correctness of the parameter estimation is then crucial, since any inaccuracies impact directly the object point coordinates. For both the INSTA and ANT 3D cameras, CR1 produces the best results, which are generally consistent with those from the top-performing pipelines (3 and 4a). The RMSE values obtained with CR2 are, on average, 104% higher for ANT3D and as much as 307% higher for the INSTA. This raises the consideration that the size of the calibration environment may play a role, suggesting that instruments should be calibrated in environments of comparable size to the most part of the object being surveyed, such as the R1 room. Further analysis should be conducted on this specific point focusing on the variability of the estimated calibration parameter values. However, this lies beyond the scope of the current work.
Conversely, for the MG1, the behavior appears to be the opposite, with CR2 outperforming CR1. However, this camera shows the highest variability in results with this pipeline, preventing any reliable conclusions from being drawn.
Looking at the aggregated results in Table 10, pipeline 3 clearly stands out for all camera systems as the processing approach that overall resulted in the best and most consistent results with pipeline 4a performing similarly, only slightly worse on average. The other approaches were able to produce some of the best results in specific datasets, as indicated by the minimum RMSE, however, they also produces the worst results, as indicated by the maximum RMSE.
Some final remarks will follow about reliability in particularly challenging scenarios where a proper ground constraint cannot be guaranteed (i.e., ground solution B) will follow. In these challenging environments, such systems have proven to be capable of achieving accuracies worse than 10 cm. In the absence of external constraints provided by GCPs, it is necessary to leverage the rigidity of the multi-camera system as a constraint. Therefore, applying a processing pipeline that incorporates the multi-camera constraint among the sensors (pipelines 3 and 4) is crucial for fixing relative baselines and mitigating drift. Additionally, using pre-calibrated IO parameters (pipeline 4a) significantly enhances the stability of the block and allows for achieving accuracies equal to 5 cm. For the MG1, even the constraint of only RO parameters (pipeline 4c) is beneficial, with an RMSE of 5 cm.
5. Conclusions
The paper described the results of a test designed to evaluate accuracy and precision among three different multi-camera systems: the INSTA 360 Pro2, MG1, and ANT3D, specifically for surveying narrow and complex spaces. The tests were conducted by processing the raw fisheye images captured by these three instruments, employing various strategies for processing the photogrammetric block. The processing pipelines considered different relative constraints between the sensors (including no constraints and multi-camera constraints), as well as varying calibrations of IO and RO parameters and ground control solutions.
The test demonstrated the reliability of these instruments for surveying environments with particularly challenging and even prohibitive characteristics for other established surveying techniques. With proper ground support, i.e. GCPs at both the beginning and end of the path, all instruments achieved the target accuracy of 1 cm. However, when ground support is provided only at the beginning of the path, the accuracy drops to values between 5 and 10 cm.
Regarding the various processing pipelines, the results were quite variable depending on the instrument and the dataset. Nevertheless, from an operational standpoint, it can be concluded that it is better to apply a multi-camera constraint but estimate both the IO and RO parameters during the BBA (pipeline 3). On the other hand, in scenarios with less redundant block geometry, not stable ground control, or if challenges arise in orienting specific images, it might be preferable to lock only the IO parameters.
6. Patents
The ANT3D multi-camera involved in this study resulted in the patent proposal n° 102021000000812. The patent was licensed on 24 January 2023.
Author Contributions
Conceptualization, L.P., N.B., and R.R.; methodology, L.P., N.B., and R.R.; formal analysis, L.P., and N.B.; investigation, L.P., and N.B.; writing—original draft preparation, L.P., N.B., and R.R.; writing—review and editing, L.P., N.B., and R.R.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the project "HUMANITA - Human-Nature Interactions and Impacts of Tourist Activities on Protected Areas", supported by the Interreg CENTRAL EUROPE Programme 2021-2027 with co-financing from the European Regional Development Fund.
Data Availability Statement
Data supporting the findings of this study is available from the authors on request.
Acknowledgments
The authors would like to thank professor Francesco Fassi from Politecnico di Milano and professor Giorgio Vassena from Università degli Studi di Brescia for providing parts of the resources for carrying out this investigation; Veneranda Fabbrica del Duomo di Milano for allowing the test to take place in the Milan’s Cathedral; and M.Sc. Antonio Mainardi, professor Francesco Fassi and professor Cristiana Achille for the assistance provided during the data collection.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Antipov, I.T.; Kivaev, A.I. Panoramic Photographs in Close Range Photogrammetry. International Archives of Photogrammtery and Remote Sensing 1984, 25. [Google Scholar]
- Andrew, A.M. Multiple View Geometry in Computer Vision. Kybernetes 2001, 30, 1333–1341. [Google Scholar] [CrossRef]
- Zhang, Z.; Deriche, R.; Faugeras, O.; Luong, Q.T. A Robust Technique for Matching Two Uncalibrated Images through the Recovery of the Unknown Epipolar Geometry. Artif Intell 1995, 78, 87–119. [Google Scholar] [CrossRef]
- Akihiko, T.; Atsushi, I.; Ohnishi, N. Two-and Three-View Geometry for Spherical Cameras. In Proceedings of the Proc. of the Sixth Workshop on Omnidirectional Vision, Camera Networks and Non- classical Cameras; 2005; Vol. 105, pp. 29–34.
- Pagani, A.; Stricker, D. Structure from Motion Using Full Spherical Panoramic Cameras. In Proceedings of the Proceedings of the IEEE International Conference on Computer Vision; 2011; pp. 375–382.
- Luhmann, T.; Tecklenburg, W. 3-D Object Reconstruction From Multiple-Station Panorama Imagery. Institute for Applied Photogrammetry and Geoinformatics 2004, 1–8. [Google Scholar]
- Lato, M.J.; Bevan, G.; Fergusson, M. Gigapixel Imaging and Photogrammetry: Development of a New Long Range Remote Imaging Technique. Remote Sensing 2012, Vol. 4, Pages 3006-3021 2012, 4, 3006–3021. [Google Scholar] [CrossRef]
- Haggrén, H.; Hyyppa, H.; Jokinena, O.; Kukko, A.; Nuikka, M.; Pitkänen, T.; Pöntinen, P.; Rönnholma, P. Photogrammetric Application of Spherical Imaging. Panoramic Photogrammetry Workshop 2004, 10. [Google Scholar]
- Fangi, G.; Nardinocchi, C. Photogrammetric Processing of Spherical Panoramas. Photogrammetric Record 2013, 28, 293–311. [Google Scholar] [CrossRef]
- Kwiatek, K.; Tokarczyk, R. Photogrammetric Applications of Immersive Video Cameras. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences; 2014; Vol. 2, pp. 211–218.
- Perfetti, L.; Teruggi, S.; Achille, C.; Fassi, F. Rapid and low-cost photogrammetric survey of hazardous sites, from measurements to vr dissemination. [CrossRef]
- Barazzetti, L.; Previtali, M.; Roncoroni, F. Can We Use Low-Cost 360 Degree Cameras to Create Accurate 3D Models? In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; 2018; Vol. 42, pp. 69–75.
- Neale, W.T.; Terpstra, T.; McKelvey, N.; Owens, T. Visualization of Driver and Pedestrian Visibility in Virtual Reality Environments. SAE Technical Papers 2021. [Google Scholar] [CrossRef]
- Insta360 Insta360 ONE X2. Available online: https://www.insta360.com/product/insta360-onex2/ (accessed on 29 July 2024).
- Previtali, M.; Cantini, L.; Barazzetti, L. Combined 360° video and uav reconstruction of small-town historic city centers. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2023, XLVIII-M-2–2023, 1233–1240. [CrossRef]
- Ricoh The RICOH THETA 360-Degree Camera Has a Solid Track Record for Capturing Vehicle Interiors. Available online: https://theta360.com/en/contents/lb_carsales/ (accessed on 26 July 2024).
- Pepe, M.; Alfio, V.S.; Costantino, D.; Herban, S. Rapid and Accurate Production of 3D Point Cloud via Latest-Generation Sensors in the Field of Cultural Heritage: A Comparison between SLAM and Spherical Videogrammetry. Heritage 2022, Vol. 5, Pages 1910-1928 2022, 5, 1910–1928. [Google Scholar] [CrossRef]
- iSTAR ISTAR Fusion - NCTech 360o Panoramic Camera. Available online: https://www.shop.nctechimaging.com/shop/istar-fusion/ (accessed on 26 July 2024).
- Pérez Ramos, A.; Robleda Prieto, G. Only image based for the 3d metric survey of gothic structures by using frame cameras and panoramic cameras. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2016, XLI-B5, 363–370. [CrossRef]
- Insta360 Insta360 Titan – Professional 360 VR 3D Camera | 11K Capture. Available online: https://www.insta360.com/product/insta360-titan/ (accessed on 26 July 2024).
- Panono Panono 360 Camera 16K | Panono. Available online: https://www.panono.com/ (accessed on 26 July 2024).
- Fangi, G.; Pierdicca, R.; Sturari, M.; Malinverni, E.S. Improving Spherical Photogrammetry Using 360°OMNI-Cameras: Use Cases and New Applications. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; Copernicus GmbH, May 30 2018; Vol. 42, pp. 331–337.
- Perfetti, L.; Polari, C.; Fassi, F. Fisheye photogrammetry: tests and methodologies for the survey of narrow spaces. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; February 23 2017; Vol. XLII-2/W3, pp. 573–580.
- Janiszewski, M.; Torkan, M.; Uotinen, L.; Rinne, M. Rapid Photogrammetry with a 360-Degree Camera for Tunnel Mapping. Remote Sensing 2022, Vol. 14, Page 5494 2022, 14, 5494. [Google Scholar] [CrossRef]
- Rezaei, S.; Maier, A.; Arefi, H. Quality Analysis of 3D Point Cloud Using Low-Cost Spherical Camera for Underpass Mapping. Sensors 2024, Vol. 24, Page 3534 2024, 24, 3534. [Google Scholar] [CrossRef] [PubMed]
- Barazzetti, L.; Previtali, M.; Roncoroni, F. 3D Modelling with the Samsung Gear 360. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; 2017; Vol. 42, pp. 85–90.
- Perfetti, L.; Polari, C.; Fassi, F. Fisheye Multi-Camera System Calibration for Surveying Narrow and Complex Architectures. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives 2018, 42, 877–883. [CrossRef]
- Losè, L.T.; Chiabrando, F.; Tonolo, F.G. Documentation of Complex Environments Using 360° Cameras. The Santa Marta Belltower in Montanaro. Remote Sensing 2021, Vol. 13, Page 3633 2021, 13, 3633. [Google Scholar] [CrossRef]
- Bruno, N.; Perfetti, L.; Fassi, F.; Roncella, R. Photogrammetric Survey of Narrow Spaces in Cultural Heritage: Comparison of Two Multi-Camera Approaches. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; Copernicus GmbH, February 14 2024; Vol. 48, pp. 87–94.
- Koehl, M.; Delacourt, T.; Boutry, C. Image capture with synchronized multiple-cameras for extraction of accurate geometries. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2016, XLI-B1, 653–660. [CrossRef]
- Holdener, D.; Nebiker, S.; Blaser, S. Design and implementation of a novel portable 360° stereo camera with low-cost action cameras. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2017, XLII-2-W8, 105–110. [CrossRef]
- Ortiz-Coder, P.; Sánchez-Ríos, A. A Self-Assembly Portable Mobile Mapping System for Archeological Reconstruction Based on VSLAM-Photogrammetric Algorithm. Sensors 2019, Vol. 19, Page 3952 2019, 19, 3952. [Google Scholar] [CrossRef] [PubMed]
- Perfetti, L.; Fassi, F.; Vassena, G. Ant3D—A Fisheye Multi-Camera System to Survey Narrow Spaces. Sensors 2024, Vol. 24, Page 4177 2024, 24, 4177. [Google Scholar] [CrossRef] [PubMed]
- Perfetti, L.; Fassi, F.; Vassena, G. Ant3D—A Fisheye Multi-Camera System to Survey Narrow Spaces. Sensors 2024, 24. [Google Scholar] [CrossRef] [PubMed]
- Teppati Losè, L.; Chiabrando, F.; Spanò, A. Preliminary evaluation of a commercial 360 multi-camera rig for photogrammetric purposes. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2018, XLII–2, 1113–1120. [CrossRef]
- Meyer, D.E.; Lo, E.; Klingspon, J.; Netchaev, A.; Ellison, C.; Kuester, F.; Lo, E.; Klingspon, J.; Netchaev, A.; Ellison, C.; et al. TunnelCAM- A HDR Spherical Camera Array for Structural Integrity Assessments of Dam Interiors. Electronic Imaging 2020, 32, 1–8. [Google Scholar] [CrossRef]
- Panella, F.; Roecklinger, N.; Vojnovic, L.; Loo, Y.; Boehm, J. Cost-benefit analysis of rail tunnel inspection for photogrammetry and laser scanning. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2020, XLIII-B2-2020, 1137–1144. [CrossRef]
- Nocerino, E.; Nawaf, M.M.; Saccone, M.; Ellefi, M.B.; Pasquet, J.; Royer, J.P.; Drap, P. Multi-camera system calibration of a low-cost remotely operated vehicle for underwater cave exploration. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2018, XLII–1, 329–337. [CrossRef]
- Perfetti, L.; Fassi, F. Handheld fisheye multicamera system: surveying meandering architectonic spaces in open-loop mode - accuracy assessment. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives 2022, 46, 435–442. [CrossRef]
- Barazzetti, L.; Previtali, M.; Roncoroni, F. 3D MODELING WITH 5K 360° VIDEOS. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; 2022; Vol. 46, pp. 65–71.
- Teruggi, S.; Fassi, F. HOLOLENS 2 SPATIAL MAPPING CAPABILITIES IN VAST MONUMENTAL HERITAGE ENVIRONMENTS. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; 2022; Vol. 46, pp. 489–496.
- Photo Stitching Software 360 Degree Panorama Image Software - PTGui Stitching Software. Available online: https://ptgui.com/ (accessed on 8 October 2024).
- Autopano - Download. Available online: https://autopano.it.softonic.com/ (accessed on 8 October 2024).
- HERON - Gexcel HERON. Available online: https://heron.gexcel.it/it/soluzioni-gexcel-per-il-rilevamento-3d/heron-sistemi-portatili-di-rilevamento-3d/ (accessed on 4 October 2024).
- Agisoft Metashape. Agisoft 2021, 7–9.
- Höhle, J.; Potuckova, M. Assessment of the Quality of Digital Terrain Medels. Official Publication - EuroSDR 2011.
Figure 1.
(a) An internal view of the Minguzzi spiral staircase; (b) the location of the Minguzzi staircase inside the Milan Cathedral.
Figure 1.
(a) An internal view of the Minguzzi spiral staircase; (b) the location of the Minguzzi staircase inside the Milan Cathedral.

Figure 2.
(a) the INSTA 360 Pro2 camera; (b) Schematics of the INSTA 360 Pro2 camera system.
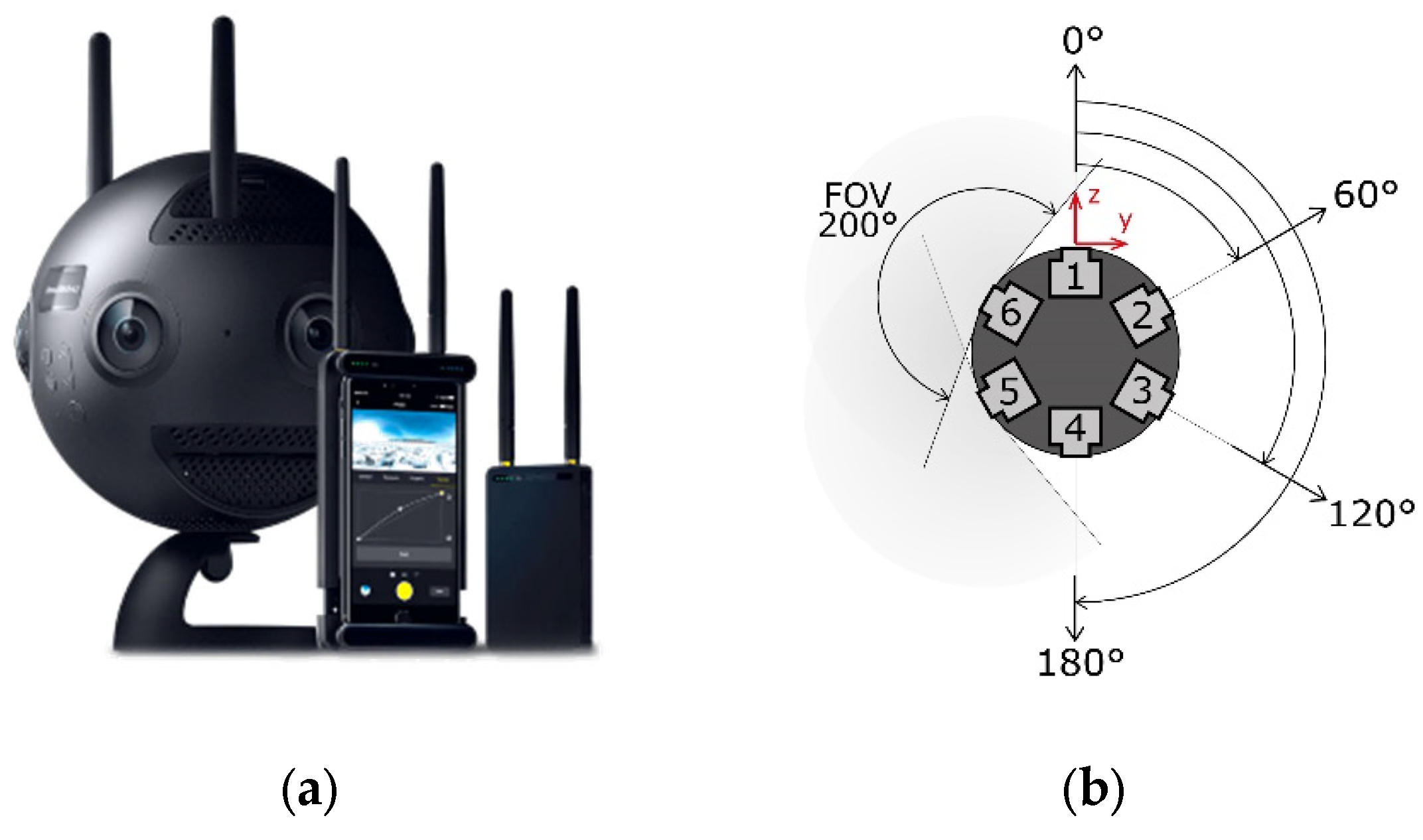
Figure 3.
(a) the MG1 camera; (b) Schematics of the MG1 camera system.
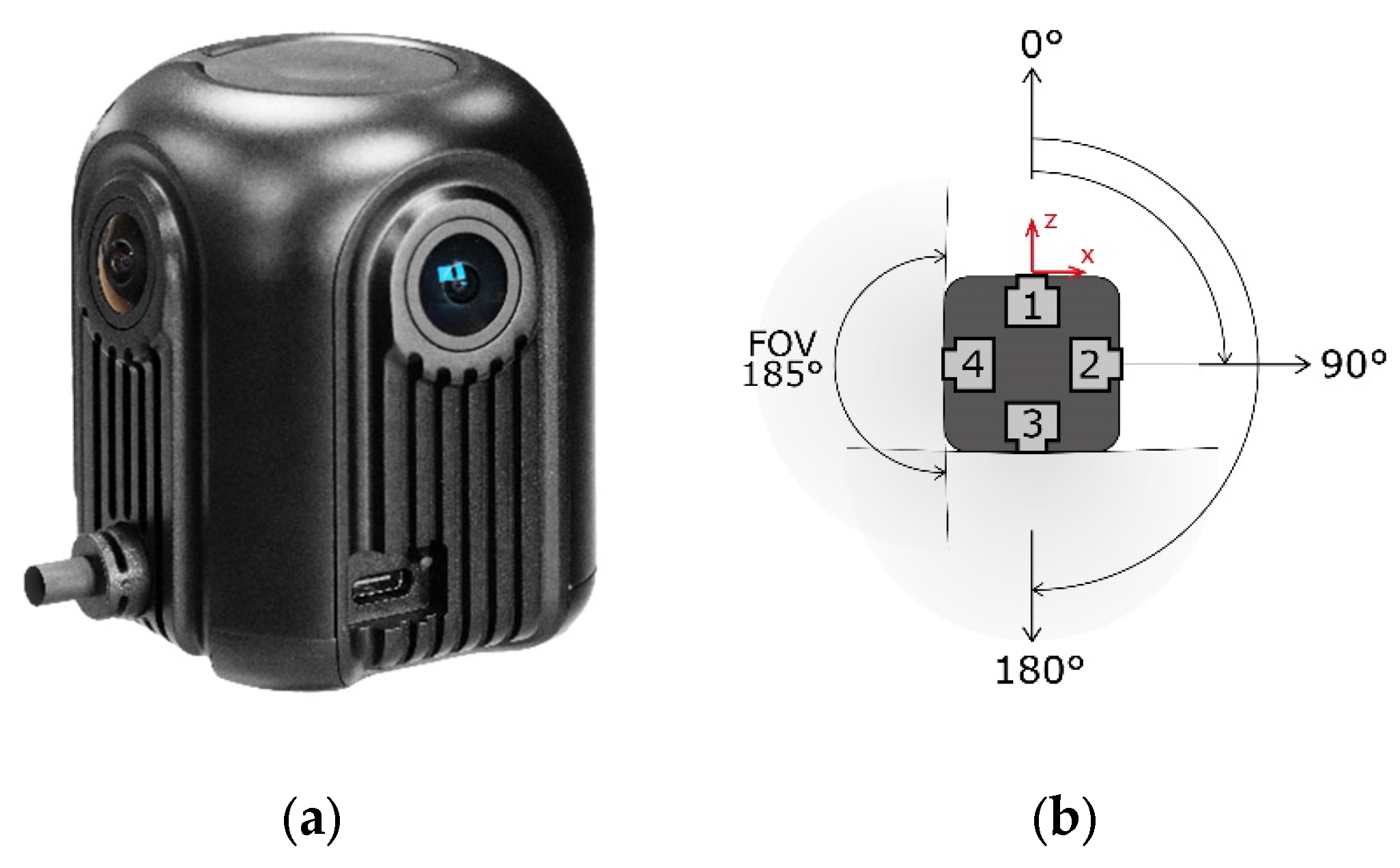
Figure 4.
(a) the ANT3D multi-camera; (b) Schematics of the ANT3D multi-camera.
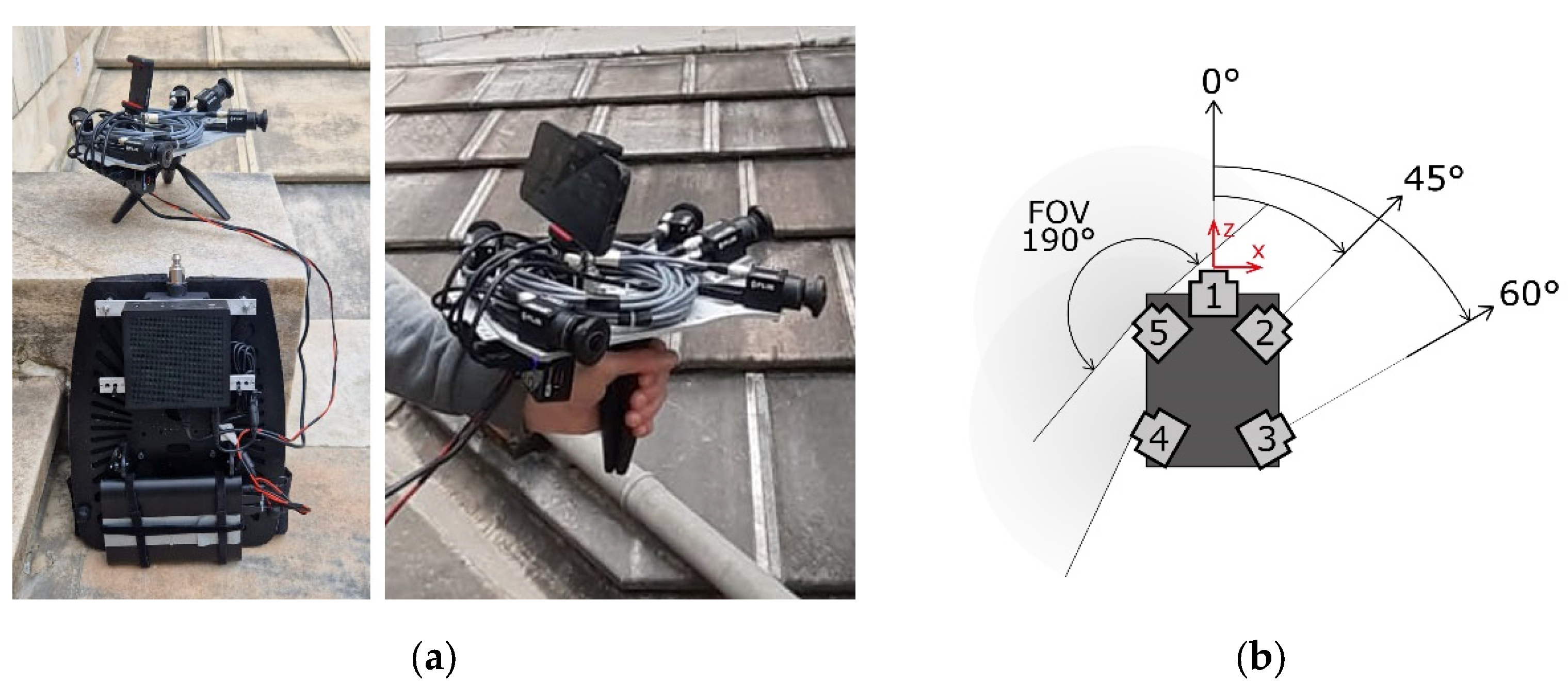
Figure 6.
(a) Calibration room 1; (b) INSTA 360 during calibration; (c) MG1 during calibration.

Figure 7.
(a) Calibration room 2; (b) INSTA 360 during calibration; (c) ANT3D during calibration.
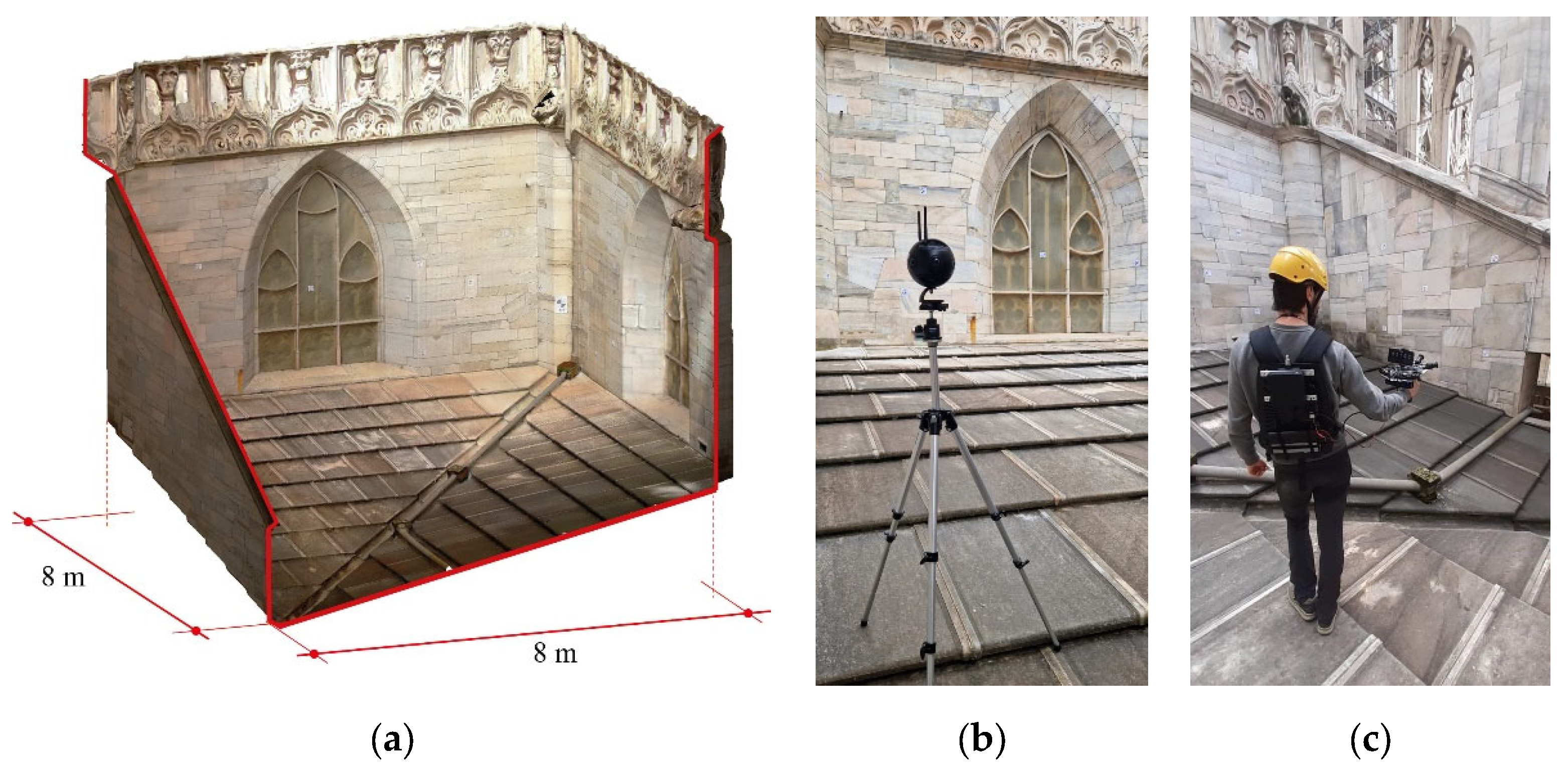
Figure 8.
Calibration pipelines.
Figure 10.
Scheme of the reference points distribution and of the two ground control solutions. CPs in yellow and GCPs in red.
Figure 10.
Scheme of the reference points distribution and of the two ground control solutions. CPs in yellow and GCPs in red.
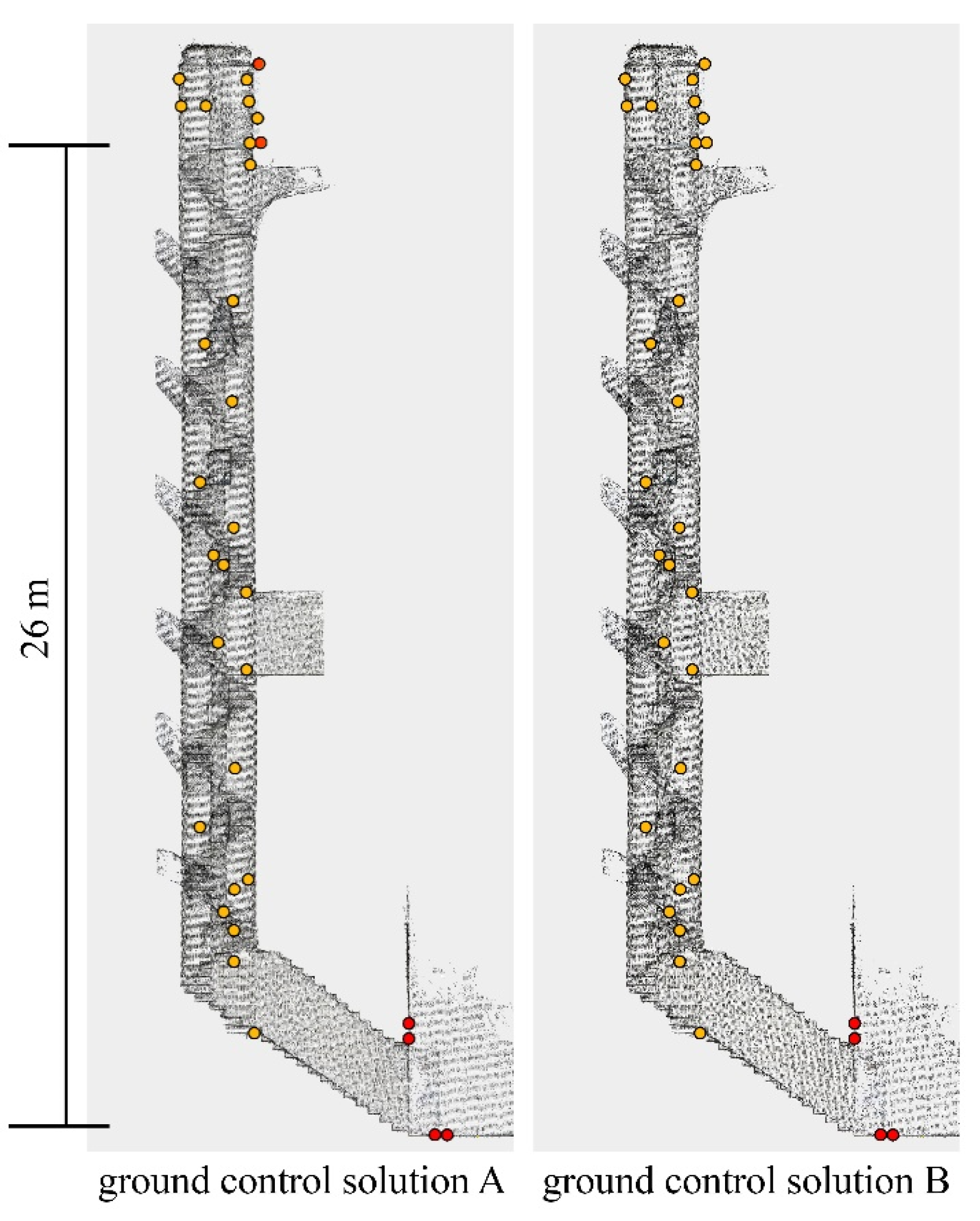
Figure 11.
Scatter plots showing the RMSE distribution for each dataset and processing pipeline in solution A. The black lines represent the average RMSE values for each pipeline and for the two different calibration sets (CR1 and CR2).
Figure 11.
Scatter plots showing the RMSE distribution for each dataset and processing pipeline in solution A. The black lines represent the average RMSE values for each pipeline and for the two different calibration sets (CR1 and CR2).
Table 1.
Nominal relative positions of the cameras’ centers of projection in the INSTA Pro2.
| Camera | X [mm] | Y [mm] | Z [mm] |
|---|---|---|---|
| Sensor 1 | 0 | 0 | 0 |
| Sensor 2 | 0 | 60 | -35 |
| Sensor 3 | 0 | 60 | -104 |
| Sensor 4 | 0 | 0 | -138 |
| Sensor 5 | 0 | -60 | -104 |
| Sensor 6 | 0 | -60 | -35 |
Table 2.
Nominal relative positions of the cameras’ centers of projection in the MG1.
| Camera | X [mm] | Y [mm] | Z [mm] |
|---|---|---|---|
| Sensor 1 | 0 | 0 | 0 |
| Sensor 2 | 33 | -5 | -33 |
| Sensor 3 | 0 | -10 | -66 |
| Sensor 4 | -33 | -5 | -33 |
Table 3.
Nominal relative positions of the cameras’ centers of projection in the ANT3D.
| Camera | X [mm] | Y [mm] | Z [mm] |
|---|---|---|---|
| Sensor 1 | 0 | 0 | 0 |
| Sensor 2 | 103 | 23 | -22 |
| Sensor 3 | 113 | -48 | -218 |
| Sensor 4 | -113 | -48 | -218 |
| Sensor 5 | -103 | 23 | -22 |
Table 5.
Summary of the number of images acquired for each camera and calibration room, along with information regarding the shooting points and acquisition time.
Table 5.
Summary of the number of images acquired for each camera and calibration room, along with information regarding the shooting points and acquisition time.
| Camera | Dataset | N Img. | N shooting Points |
Time |
|---|---|---|---|---|
| ANT 3D | CR1 | 1865 | 373 | 6’ |
| CR2 | 2555 | 511 | 9’ | |
| INSTA 360 | CR1 | 552 | 92 | 55’ |
| CR2 | 948 | 158 | 95’ | |
| MG1 | CR1 | 332 | 83 | 15’ |
| CR2 | 204 | 51 | 10’ |
Table 6.
Summary of image acquisition information for each camera in the Minguzzi staircase.
| Camera | Dataset | N Img. | N shooting Points |
Time | Avg. base-length [cm] |
Multiplicity* |
|---|---|---|---|---|---|---|
| ANT | D1 | 4125 | 825 | 14’ | 20 | 4.06 |
| D2 | 6025 | 1205 | 20’ | 15 | 5.33 | |
| D3 | 6965 | 1393 | 23’ | 18 | 5.63 | |
| INSTA | D1 | 978 | 163 | 75’ | 30 | 2.98 |
| D2 | 1038 | 173 | 60’ | 33 | 3.38 | |
| D3 | 984 | 164 | 65’ | 33 | 3.17 | |
| MG1 | D1 | 764 | 191 | 34’ | 28 | 2.89 |
| D2 | 696 | 174 | 47’ | 28 | 2.67 | |
| D3 | 764 | 191 | 35’ | 30 | 2.79 |
* Obtained as the ratio between the total number of projections and the number of valid tie-points used for matching.
Table 7.
Stats of RMSE on CPs in all the processing configurations for INSTA 360 Pro2.
| Processing Pipeline and calibration set |
Dataset | Tie points | CPs RMSE [mm] Ground control solution A |
CPs RMSE [mm] Ground control solution B |
|||
|---|---|---|---|---|---|---|---|
| XYZ | Max XYZ | XYZ | Max XYZ | ||||
| 1 | On the job calibr. | D1 | 879633 | 44 | 69 | 336 | 499 |
| D2 | 813157 | 8 | 13 | 71 | 96 | ||
| D3 | 818508 | 11 | 18 | 77 | 105 | ||
| 2 | CR1–P1 | D1 | 893652 | 52 | 82 | 349 | 521 |
| D2 | 818762 | 13 | 24 | 67 | 94 | ||
| D3 | 824431 | 13 | 27 | 44 | 62 | ||
| CR2-P1 | D1 | 892653 | 19 | 30 | 162 | 236 | |
| D2 | 817454 | 9 | 14 | 38 | 56 | ||
| D3 | 822887 | 10 | 20 | 35 | 59 | ||
| CR1–P2 | D1 | 891499 | 57 | 89 | 356 | 533 | |
| D2 | 817716 | 13 | 23 | 78 | 107 | ||
| D3 | 822333 | 13 | 23 | 70 | 93 | ||
| CR2-P2 | D1 | 891890 | 16 | 27 | 150 | 218 | |
| D2 | 816158 | 9 | 14 | 34 | 51 | ||
| D3 | 821924 | 10 | 19 | 33 | 55 | ||
| 3 | On the job calibr. | D1 | 879464 | 12 | 20 | 150 | 199 |
| D2 | 812502 | 9 | 17 | 104 | 139 | ||
| D3 | 817664 | 12 | 22 | 67 | 91 | ||
| 4a | CR1–P2 | D1 | 892815 | 12 | 21 | 39 | 59 |
| D2 | 817528 | 15 | 26 | 87 | 120 | ||
| D3 | 822653 | 13 | 26 | 66 | 88 | ||
| CR2-P2 | D1 | 891965 | 13 | 22 | 62 | 87 | |
| D2 | 811383 | 12 | 21 | 61 | 84 | ||
| D3 | 820830 | 14 | 27 | 84 | 114 | ||
| 4b | CR1–P2 | D1 | 905495 | 14 | 20 | 40 | 61 |
| D2 | 820668 | 9 | 18 | 61 | 83 | ||
| D3 | 828802 | 13 | 21 | 41 | 59 | ||
| CR2-P2 | D1 | 885943 | 49 | 68 | 84 | 112 | |
| D2 | 809392 | 53 | 74 | 104 | 140 | ||
| D3 | 819930 | 47 | 64 | 93 | 123 | ||
| 4c | CR1–P2 | D1 | 877463 | 67 | 101 | 134 | 186 |
| D2 | 811230 | 52 | 78 | 108 | 148 | ||
| D3 | 817036 | 50 | 75 | 101 | 139 | ||
| CR2-P2 | D1 | 876400 | 55 | 82 | 111 | 155 | |
| D2 | 810635 | 78 | 114 | 149 | 205 | ||
| D3 | 816889 | 75 | 111 | 146 | 199 | ||
Table 8.
Stats of RMSE on CPs in all the processing configurations for MG1.
| Processing Pipeline and calibration set |
Dataset | Tie points | CPs RMSE [mm] Ground control solution A |
CPs RMSE [mm] Ground control solution B |
|||
|---|---|---|---|---|---|---|---|
| XYZ | Max XYZ | XYZ | Max XYZ | ||||
| 1 | On the job calibr. | D1 | 619258 | 66 | 107 | 293 | 452 |
| D2 | 702890 | 25 | 42 | 69 | 91 | ||
| D3 | 687807 | 31 | 54 | 95 | 155 | ||
| 2 | CR1–P1 | D1 | 619386 | 47 | 78 | 149 | 232 |
| D2 | 710869 | 31 | 54 | 235 | 334 | ||
| D3 | 690609 | 47 | 78 | 342 | 494 | ||
| CR2-P1 | D1 | 616305 | 15 | 26 | 140 | 190 | |
| D2 | 706245 | 32 | 54 | 208 | 303 | ||
| D3 | 687467 | 42 | 71 | 288 | 416 | ||
| CR1–P2 | D1 | 618706 | 37 | 59 | 152 | 235 | |
| D2 | 713849 | 33 | 57 | 244 | 347 | ||
| D3 | 691981 | 49 | 82 | 344 | 499 | ||
| CR2-P2 | D1 | 616239 | 11 | 19 | 115 | 153 | |
| D2 | 707600 | 14 | 25 | 118 | 165 | ||
| D3 | 688606 | 36 | 62 | 249 | 358 | ||
| 3 | On the job calibr. | D1 | 612744 | 14 | 24 | 42 | 62 |
| D2 | 695731 | 14 | 21 | 47 | 75 | ||
| D3 | 677700 | 13 | 23 | 62 | 84 | ||
| 4a | CR1–P2 | D1 | 621133 | 20 | 29 | 74 | 99 |
| D2 | 706307 | 11 | 18 | 53 | 72 | ||
| D3 | 681742 | 13 | 22 | 78 | 108 | ||
| CR2-P2 | D1 | 618363 | 13 | 20 | 48 | 72 | |
| D2 | 699732 | 11 | 21 | 69 | 96 | ||
| D3 | 679098 | 16 | 27 | 65 | 93 | ||
| 4b | CR1–P2 | D1 | 608574 | 59 | 91 | 155 | 223 |
| D2 | 717572 | 40 | 64 | 116 | 161 | ||
| D3 | 694560 | 29 | 50 | 51 | 74 | ||
| CR2-P2 | D1 | 616949 | 18 | 31 | 39 | 57 | |
| D2 | 701885 | 9 | 17 | 15 | 20 | ||
| D3 | 676474 | 52 | 77 | 29 | 184 | ||
| 4c | CR1–P2 | D1 | 613096 | 25 | 36 | 72 | 106 |
| D2 | 696110 | 24 | 31 | 64 | 89 | ||
| D3 | 677904 | 17 | 24 | 49 | 65 | ||
| CR2-P2 | D1 | 613054 | 22 | 27 | 61 | 85 | |
| D2 | 693585 | 20 | 26 | 49 | 73 | ||
| D3 | 678032 | 23 | 30 | 56 | 78 | ||
Table 9.
Stats of RMSE on CPs in all the processing configurations for ANT3D.
| Processing Pipeline and calibration set |
Dataset | Tie points | CPs RMSE [mm] Ground control solution A |
CPs RMSE [mm] Ground control solution B |
|||
|---|---|---|---|---|---|---|---|
| XYZ | Max XYZ | XYZ | Max XYZ | ||||
| 1 | On the job calibr. | D1 | 1739473 | 13 | 23 | 85 | 131 |
| D2 | 2106220 | 26 | 44 | 119 | 174 | ||
| D3 | 2694585 | 26 | 46 | 179 | 256 | ||
| 2 | CR1–P1 | D1 | 1747416 | 47 | 77 | 273 | 434 |
| D2 | 2112804 | 37 | 63 | 186 | 272 | ||
| D3 | 2695973 | 26 | 46 | 175 | 250 | ||
| CR2-P1 | D1 | - | - | - | - | - | |
| D2 | 2120274 | 48 | 78 | 206 | 304 | ||
| D3 | 2695412 | 27 | 47 | 179 | 256 | ||
| CR1–P2 | D1 | 1746528 | 50 | 79 | 276 | 441 | |
| D2 | 2109952 | 38 | 64 | 174 | 255 | ||
| D3 | 2695820 | 26 | 46 | 176 | 251 | ||
| CR2-P2 | D1 | - | - | - | - | - | |
| D2 | 2121102 | 44 | 70 | 186 | 274 | ||
| D3 | 2694728 | 27 | 48 | 181 | 259 | ||
| 3 | On the job calibr. | D1 | 1710564 | 12 | 22 | 44 | 67 |
| D2 | 2042197 | 12 | 24 | 71 | 98 | ||
| D3 | 2366771 | 30 | 46 | 227 | 307 | ||
| 4a | CR1–P2 | D1 | 1710258 | 13 | 26 | 42 | 63 |
| D2 | 2046646 | 17 | 31 | 73 | 106 | ||
| D3 | 2371298 | 31 | 46 | 211 | 285 | ||
| CR2-P2 | D1 | - | - | - | - | - | |
| D2 | 2061375 | 15 | 27 | 87 | 125 | ||
| D3 | 2380192 | 29 | 49 | 107 | 146 | ||
| 4b | CR1–P2 | D1 | 1709358 | 14 | 27 | 39 | 59 |
| D2 | 2064097 | 26 | 40 | 39 | 63 | ||
| D3 | 2378591 | 39 | 54 | 299 | 401 | ||
| CR2-P2 | D1 | - | - | - | - | - | |
| D2 | 2009176 | 53 | 81 | 109 | 156 | ||
| D3 | 2311030 | 60 | 71 | 139 | 190 | ||
| 4c | CR1–P2 | D1 | 1680383 | 16 | 22 | 45 | 70 |
| D2 | 1869994 | 16 | 26 | 59 | 87 | ||
| D3 | 2366071 | 32 | 46 | 221 | 298 | ||
| CR2-P2 | D1 | - | - | - | - | - | |
| D2 | 1836873 | 61 | 101 | 130 | 194 | ||
| D3 | 2336029 | 64 | 83 | 109 | 149 | ||
Table 10.
Summary of results obtained with ground control solution A. For each pipeline and camera, the average, the minimum and the maximum values of RMSE are reported.
Table 10.
Summary of results obtained with ground control solution A. For each pipeline and camera, the average, the minimum and the maximum values of RMSE are reported.
| Ground control solution A - RMSE [mm] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| INSTA | MG1 | ANT 3D | |||||||
| Pipeline | Avg. | Min. | Max. | Avg. | Min. | Max. | Avg. | Min. | Max. |
| 1 | 21 | 8 | 44 | 41 | 25 | 66 | 21 | 13 | 26 |
| 2 | 19 | 9 | 57 | 33 | 11 | 49 | 37 | 26 | 50 |
| 3 | 11 | 9 | 12 | 14 | 13 | 14 | 18 | 12 | 30 |
| 4a | 13 | 12 | 15 | 14 | 11 | 20 | 21 | 13 | 31 |
| 4b | 31 | 9 | 53 | 35 | 9 | 59 | 38 | 14 | 60 |
| 4c | 63 | 50 | 78 | 22 | 17 | 25 | 38 | 16 | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








