1. Introduction
Wildfires are a recurring and increasingly severe threat to ecosystems, human infrastructure, and water resources. Accurate burn severity mapping (BSM) is essential for effective disaster response [
1], ecological restoration [
2], and long-term water quality management [
3]. Machine learning (ML) combined with satellite remote sensing data, particularly those leveraging optical satellites, has become a critical tool in wildfire severity assessment [
4].
Reflectance changes are a key indicator used in BSM to distinguish between burnt and unburnt areas. When a wildfire occurs, the vegetation and soil undergo physical and chemical changes, which alter how they reflect light across different parts of the electromagnetic spectrum [
5]. Burnt vegetation absorbs more visible light and reflects less in the near-infrared (NIR) spectrum than healthy, unburned vegetation [
6]. These changes in reflectance can be captured by optical satellite sensors and are used to identify and map burnt areas. Indices like the Normalized Burn Ratio (NBR) utilize these reflectance differences to assess the severity of the burn [
7] and help monitor ecosystem recovery following a wildfire [
8].
Implementing ML techniques has revolutionized remote sensing and environmental monitoring. ML models can handle vast volumes of data and identify complex patterns that traditional empirical methods might overlook. For instance, these models have enhanced satellite-based precipitation estimation and correction, leading to more accurate rainfall data — essential for weather forecasting and climate studies [
9,
10,
11,
12]. Furthermore, ML has significantly improved streamflow predictions, resulting in more reliable water flow forecasts, crucial for flood management, water resource planning, and reservoir operations [
13,
14,
15,
16]. In BSM studies, ML applications have demonstrated superior accuracy [
17,
18,
19,
20,
21,
22].
Vegetation indices, commonly calculated from combinations of spectral bands, are crucial predictors in assessing the extent and intensity of wildfire damage. Incorporating more indices typically improves the classification of burn severity levels. However, when too many indices derived from the same spectral bands are included in ML models, multicollinearity—a condition where predictors are highly correlated—can arise. This leads to redundant information and a subsequent reduction in classification accuracy. To address this issue, techniques such as feature reduction (FR), which involves selecting a subset of the original variables, and feature extraction (FE), which transforms data into a lower-dimensional space while preserving essential characteristics, are commonly employed. Van et al. (2024) introduced a novel FR approach to BSM using mono-temporal Sentinel-2 satellite data within an eXplainable AI (XAI) framework [
23]. Their methodology incorporates qualitative and quantitative feature selection, a crucial step in the broader feature extraction process, to improve the accuracy and interpretability of ML models. By applying a Random Forest (RF) algorithm optimized through SHapley Additive exPlanation (SHAP) and forward stepwise selection, the study narrowed down 235 potential predictors to the 12 most critical. While effective, Van et al. (2024) face a key limitation: the high computational complexity and resource demands of the XAI techniques. These constraints may restrict the approach's accessibility to research teams without advanced computational resources, making it challenging for broader adoption.
Principal component analysis (PCA) is one of the most widely used FE methods due to its ability to transform large sets of correlated variables into smaller, uncorrelated components. By reducing dimensionality, PCA enhances the performance of ML classifiers and other predictive models. Numerous studies have demonstrated its effectiveness, particularly in improving the accuracy of models used in burn severity assessments, where datasets often contain complex, interrelated features [
24,
25,
26]. For instance, Koutsias et al. (2009) applied PCA to enhance the visibility of burned areas in Landsat-7 imagery [
27]. By transforming the multivariate data, they demonstrated that PCA effectively distinguishes burnt surfaces by reducing the dimensionality of the dataset, which in turn highlights the most significant changes pertinent to identifying burned areas. Chen et al. (2015) employed PCA to streamline the handling of extensive spectral data from high spectral resolution MASTER airborne images by reducing the number of spectral bands from 50 to a smaller number of principal components, reducing the computational load and enhancing the efficiency of the analysis process [
28]. Similarly, in the recent study by Kulinan et al. (2024), PCA was used as a critical step to enhance classification efficiency [
20]. PCA was applied after extracting textural features from Sentinel-2 imagery to identify the most relevant features for burned area classification. In many of these studies, PCA has demonstrated its usefulness in reducing noise and improving computational efficiency and model accuracy, particularly when working with high-dimensional satellite data.
Despite the widespread use of principal component analysis (PCA) as a dimensionality reduction technique in BSM, very few studies have critically evaluated its performance relative to other FE methods. Most research has defaulted to PCA due to its simplicity and well-established status in the field. However, this narrow focus overlooks the potential benefits that alternative methods could offer. As advances in ML and remote sensing continue to evolve, techniques such as t-distributed stochastic neighbor embedding (t-SNE) [
29], uniform manifold approximation and projection (UMAP) [
30], and linear discriminant analysis (LDA) [
31] have shown promise in other areas of environmental modeling but remain underexplored in the context of wildfire mapping. The lack of comparative studies examining a broader array of FE techniques suggests a gap in the literature.
This study seeks to enhance the accuracy of ML classifiers in BSM by evaluating FE techniques that mitigate multicollinearity in vegetation indices. Using composite burn index (CBI) data from the 2014 Carlton Complex fire in the United States as a case study, we used 112 vegetation indices from seven Landsat-8 bands. We then applied and compared 13 different FE techniques, including linear and nonlinear methods such as PCA, t-SNE, LDA, Isomap, UMAP, Factor analysis (FA), Independent component analysis (ICA), Multidimensional scaling (MDS), Truncated singular value decomposition (TSVD), Non-negative matrix factorization (NMF), Locally linear embedding (LLE), Spectral embedding (SE), and Neighborhood components analysis (NCA). The performance of these techniques was benchmarked against six ML classifiers.
In the following sections, we will provide a detailed description of our methodology, present the results of our comparative analysis, and discuss the implications of our findings for future BSM and management practices.
2. Methodology
2.1. Feature Extraction Methods
2.1.1. Principal Component Analysis (PCA)
PCA is a linear dimensionality reduction technique that transforms the original data into a set of linearly uncorrelated components called principal components [
32]. These components maximize the variance in the data. The transformation is defined as:
where X is the data matrix of shape n×p, with n samples (CBI data) and p features (vegetation indices), and W is the matrix of eigenvectors corresponding to the k largest eigenvalues of the covariance matrix of X.
2.1.2. Linear Discriminant Analysis (LDA)
LDA is a supervised linear method that maximizes the ratio of between-class variance to within-class variance, providing optimal class separability [
33]. It projects the data into a lower-dimensional space using the following criterion:
|
(2) |
where is the between-class scatter matrix, and is the within-class scatter matrix. represents the projection matrix.
2.1.3. t-DISTRIBUTED STOCHASTIC NEIGHBOR EMBEDDING (t-SNE)
t-SNE is a nonlinear technique that embeds high-dimensional data into a lower-dimensional space by minimizing the divergence between probability distributions of pairwise point distances in high- and low-dimensional spaces [
34]. Given the pairwise similarities
Pij in high-dimensional space and
Qij in the lower-dimensional space, t-SNE minimizes:
|
(3) |
2.1.4. Isomap
Isomap is a nonlinear extension of classical Multidimensional Scaling (MDS) that seeks to preserve the geodesic distances between points on a manifold [
35]. The geodesic distance
is computed as the shortest path between points in the neighborhood graph. The final embedding is found by applying classical MDS to the geodesic distance matrix.
2.1.5. Uniform Manifold Approximation and Projection (UMAP)
UMAP is a manifold learning technique that optimizes a fuzzy set representation of the local neighborhood in high-dimensional space and attempts to preserve local and global data structures [
36]. UMAP seeks to minimize the cross-entropy between the fuzzy simplicial sets in high- and low-dimensional spaces:
|
(4) |
where are the high- and low-dimensional fuzzy simplicial sets, respectively.
2.1.6. Independent Component Analysis (ICA)
ICA is a linear method that separates a multivariate signal into additive, independent components [
37]. Unlike PCA, which focuses on variance, ICA assumes that the source components are non-Gaussian and statistically independent. The mixing model is defined as:
where A is the mixing matrix, and S is the source matrix of independent components.
2.1.7. Factor Analysis (FA)
FA is a statistical method that assumes the observed data are generated by fewer unobserved latent variables (factors) plus some noise [
38]. The model is represented as:
where L is the loading matrix, F is the latent factors, and ϵ is the noise.
2.1.8. Multidimensional Scaling (MDS)
MDS aims to preserve pairwise Euclidean distances in the low-dimensional embedding [
39]. It minimizes the stress function:
|
(7) |
where is the distance between points i and j in the lower-dimensional space, and is the distance in the original space.
2.1.9. Spectral Embedding (SE)
SE, or Laplacian Eigenmaps, is a nonlinear method that uses the eigenvectors of the graph Laplacian to embed the data in a lower-dimensional space [
40]. The graph Laplacian L is constructed from the adjacency matrix of the nearest-neighbor graph and the embedding is derived by solving the generalized eigenvalue problem:
where D is the degree matrix, L=D−A is the graph Laplacian, and y are the embedding coordinates.
2.1.10. Locally Linear Embedding (LLE)
LLE is a nonlinear dimensionality reduction technique that preserves the local structure of the data [
41]. It computes weights
Wij that best reconstruct each data point from its neighbors, and then minimizes the reconstruction error in the lower-dimensional space:
|
(9) |
where is the i-th data point, and are the reconstruction weights.
2.1.11. Non-Negative Matrix Factorization (NMF)
NMF is a linear method that decomposes the data matrix
X into two non-negative matrices
W and
H, such that:
where W represents the basis vectors and H the coefficients. This method is useful when the data components, such as spectral indices, are expected to be non-negative.
2.1.12. Truncated Singular Value Decomposition (TSVD)
TSVD is a variant of PCA where only the top
k singular values and corresponding vectors are retained [
42]. The data matrix X is decomposed as:
where U and V are orthogonal matrices, and Σ is the diagonal matrix of singular values. Only the top k singular values are used to reconstruct the data.
2.1.13. Neighborhood Components Analysis (NCA)
NCA is a supervised, nonlinear method that learns a linear transformation that maximizes the accuracy of nearest neighbor classification [
43]. The transformation matrix
A is learned by minimizing the stochastic loss function:
|
(12) |
where xi and xj are data points, and A is the learned transformation.
2.2. Satellite Data Acquisition and Preprocessing
Landsat-8 is a satellite in the Landsat program that captures Earth observation data, specifically designed for monitoring changes in the environment and land use. Launched in 2013, it carries two key instruments: the Operational Land Imager (OLI) and the Thermal Infrared Sensor (TIRS). OLI captures images in nine spectral bands, including visible, NIR, and SWIR, allowing for detailed analysis of vegetation, water bodies, and urban areas. TIRS measures thermal radiation in two bands, particularly useful for monitoring surface temperatures, heat patterns, and water stress. Landsat-8’s data, with a spatial resolution of 30 meters for most bands and 100 meters for thermal bands, offers high-quality imagery used in various applications such as disaster monitoring, agriculture, forestry, and climate change research. With a revisit time of 16 days, Landsat-8 provides consistent, repeatable coverage of Earth's surface, making it an essential tool for long-term environmental monitoring.
We used Google Earth Engine to acquire and pre-process Landsat-8 data due to its comprehensive tools and datasets [
44]. To mitigate seasonal variations and accurately represent post-wildfire conditions, we utilized a mono-temporal approach, selecting images from one month before and one month after the field survey date. We chose atmospherically corrected surface reflectance products for their precision in measuring ground reflectance, unaffected by atmospheric distortions such as scattering and absorption [
45]. We only considered images with a maximum cloud coverage of 25%, resulting in five viable scenes. Finally, to generate a composite image that incorporates seven high-resolution bands (Ultra blue, Red, Green, Blue, NIR, SWIR1, and SWIR2), we systematically applied the median filter and band selection functions across the entire dataset.
2.3. Data Structuring
We organized our input data into a numerical matrix format for pixel-based classification. In this structure, each column represents a different feature, such as an optical index, while the rows correspond to labeled data.
2.3.1. Optical Index Generation
The selection of optical indices was based on the premise that the distinctive characteristics of burned areas differ from those of unburned sites. We selected nine commonly used indices from BSM research (
Table 1). Additionally, we generated synthetic optical indices through custom calculations that combined various spectral bands to emphasize wildfire-related features, such as vegetation loss, soil exposure, and burned areas. These formulations included normalized difference (a-b)/(a+b) and ratio-based a/b calculations, where a and b represent any two of the seven Landsat-8 bands. As a result, 118 indices, including the seven original bands, were used in this study.
2.3.2. Data Labeling: Composite burn Index (CBI)
The CBI method, developed by Key and Benson (2006), is a widely used technique to assess the severity of wildfires across different vegetation strata [
47]. The method evaluates fire effects in five distinct layers: substrate (soil and ground cover), herbaceous vegetation, shrubs, intermediate tree layers, and canopy trees. For each layer, a trained observer assigns a burn severity rating based on criteria, such as vegetation mortality, scorch height, and changes in surface fuels. CBI is typically applied within predefined plots, allowing for calculating an overall burn severity score by averaging the ratings across strata. This method provides a standardized and comprehensive approach to quantify fire impacts, aiding in ecological recovery assessments and landscape-level fire management strategies.
In our study, we used the dataset titled ‘Composite Burn Index (CBI) Data for the Conterminous US, Burned Areas Boundaries, Collected Between 1994 and 2018’ because it provides a comprehensive and standardized assessment of wildfire burn severity across a wide geographical and temporal range. The dataset is published by the U.S. Geological Survey, labeling might involve categorizing various burn severity levels across different regions of the U.S. using satellite imagery and ground measurements. This dataset spans over two decades and provides valuable information on the extent of burned areas, aiding in analyzing fire impact on ecosystems. The 2014 Carlton Complex Fire was selected for this study because it is the largest wildfire in Washington State's history, burning approximately 256,108 acres. Its scale presents a unique opportunity to study various burn severities across diverse vegetation types and landscapes, making it an ideal case for advancing BSM techniques. Additionally, the fire contains the highest number of CBI measurements—a total of 328 plots—offering a rich and comprehensive dataset for ML modeling (
Table 2) [
55].
2.4. Machine Learning
Six different ML models were selected to ensure the robustness and generalization of data classification. Each model has unique strengths and weaknesses, enhancing our ability to test our methodology comprehensively. Additionally, employing multiple models facilitates the validation of results, with consistent findings across different models improving the reliability of the research. This section briefly outlines three ML models chosen for their prominence in literature and practical BSM applications.
2.4.1. Random Forest (RF)
RF is an ensemble learning method that constructs multiple decision trees during training and outputs the mode of the classes from individual trees [
57]. Each tree is trained on a bootstrap sample from the dataset, and at each node, only a random subset of features is considered for splitting, reducing overfitting. Given a set of decision trees T
1, T
2, …, T
M, the final predicted class
ŷ for an input
x is determined by majority voting:
|
(13) |
The individual decision trees are built by recursively splitting the data based on feature values to maximize a certain criterion, such as Gini impurity or information gain.
2.4.2. Support Vector Machine (SVM)
SVM is a supervised learning model that aims to find the hyperplane that best separates classes in the feature space [
58]. For linearly separable data, the hyperplane is defined by:
where
w is the weight vector,
x is the input vector, and
b is the bias term. SVM seeks to maximize the margin
γ, the distance between the hyperplane and the closest data points (support vectors). This is achieved by solving the optimization problem:
|
(15) |
where represents the class labels and the feature vectors. For non-linearly separable data, SVM can apply kernel functions K(xi, xj) to transform the input space into a higher-dimensional feature space, allowing for a more flexible decision boundary.
2.4.3. K-Nearest Neighbors (KNN)
KNN is a simple, non-parametric classifier that assigns a class to an input
x based on the majority class of its
k-nearest neighbors in the feature space [
59]. The distance metric, typically Euclidean distance, is used to find the
k closest data points to
x. The predicted class
ŷ is:
|
(16) |
where presents the set of the k-nearest neighbors of x in the training data and is the label of neighbor i. The number of neighbors k is a hyperparameter that controls the classifier's behavior, balancing local sensitivity (low k) and global generalization (high k).
2.4.4. Logistic Regression (LR)
Logistic Regression is a linear classifier used for binary or multiclass classification problems [
60]. It models the probability of a sample belonging to a particular class using the logistic sigmoid function. For binary classification, the probability
is given by:
|
(17) |
where
w is the weight vector, and
x is the input feature vector. The decision rule for classification is:
|
(18) |
The model parameters
w are estimated by maximizing the log-likelihood function:
|
(19) |
2.4.5. Multi-Layer Perceptron (MLP)
MLP is an artificial neural network (ANN) consisting of layers of multiple neurons (nodes) [
61]. Each neuron in a layer receives input from the previous layer, applies a weighted sum followed by a nonlinear activation function, and passes the result to the next layer. For a single hidden layer MLP, the output of the network is:
|
(20) |
where and are weight matrices, and are bias vectors, and f is the activation function, commonly the sigmoid function or rectified linear unit (ReLU). The MLP is trained using backpropagation to minimize a loss function, such as cross-entropy, for classification tasks.
2.4.6. Adaptive Boosting (AB)
AB is an ensemble method that combines weak classifiers to create a strong classifier [
62]. AdaBoost trains a series of weak learners (e.g., decision stumps) iteratively, giving more weight to misclassified samples at each step. The final prediction is a weighted sum of the weak classifiers' predictions:
|
(21) |
where is the t-th weak classifier, and is its corresponding weight based on its accuracy. The weights are updated at each iteration according to the classification error of . Samples misclassified by receive higher weights in the next iteration, forcing the subsequent classifier to focus on difficult examples.
2.4.7. Particle Swarm Optimization (PSO)
PSO, a hyper-parameter optimization technique inspired by the social behavior of birds flocking, is used in this study (
Table 3). In PSO, a group of particles (candidate solutions) explore the search space, where each particle adjusts its position based on its own experience (personal best) and the experience of the entire swarm (global best) [
63]. The velocity of each particle is updated using a combination of inertia, cognitive influence (how close the particle is to its own best solution), and social influence (how close it is to the swarm's best solution). Mathematically, the velocity update is given by:
|
(22) |
where w is the inertia, and are the cognitive and social coefficients, and , are random factors. The particle's position is then updated based on the new velocity. The process repeats iteratively until a stopping criterion is met, to converge on an optimal solution by exploiting the shared knowledge of the swarm.
2.5. Validation Metrics
This study evaluates model accuracy using a set of comprehensive metrics, including Overall accuracy (OA), Precision, Recall, and F1-score (
Table 4). OA generally measures how well the model correctly classifies instances across all categories. Precision focuses on the model's ability to correctly identify positive instances without misclassifying negative ones, while Recall assesses how well the model captures all relevant positive instances in the dataset. The F1-score, a harmonic mean of Precision and Recall, offers a balanced assessment of the model's performance by considering both false positives and false negatives, making it especially useful in cases of an imbalance between classes. These metrics together provide a robust evaluation of the model’s effectiveness in the study.
2.6. Case Study
The Carlton Complex Fire (
Figure 1), which ignited in July 2014 due to lightning strikes amidst severe drought conditions, became the largest and one of the most destructive wildfires in Washington State's history [
64]. Located in north-central Washington's Okanogan County, the fire began as four blazes—the Stokes, Gold Hikes, French Creek, and Cougar Flat fires—merged into a massive inferno fueled by high temperatures and strong winds. Over its duration, the fire scorched approximately 256,108 acres of land, destroyed over 300 homes and numerous other structures, and caused an estimated
$98 million in damages. Thousands of residents were forced to evacuate as the fire damaged infrastructure, including power lines and communication networks. Despite the efforts of over 3,000 firefighters from various agencies, the fire was not fully contained until late August 2014. The Carlton Complex Fire left lasting scars on the landscape, leading to environmental issues like soil erosion and habitat loss, and profoundly impacted local communities, underscoring the challenges of wildfire management and the need for improved preparedness in the face of changing climate conditions.
3. Results
We benchmark 13 feature extraction methods using six ML models to evaluate their performance comprehensively. The evaluation process is outlined as follows.
• Step 1: We automatically select 54 training points of each fire severity level (Table
2), ensuring a robust balance sample size [
55].
• Step 2: We subsequently employ a 70/30 split ratio to divide the training and testing datasets—a standard practice that optimally balances training and validation needs.
• Step 3: To enhance our results' reliability and statistical robustness, steps 1 and 2 are repeated 1000 times, mitigating any anomalies that might influence the outcomes due to variability in data splits.
3.1. Comparative Performance Analysis of Feature Extraction Methods
This analysis compares 13 feature extraction (FE) methods to determine which performs best across multiple classifiers. The primary goal is identifying the methods that help classifiers maintain high burn severity mapping (BSM) performance, as measured by Overall accuracy (OA), Precision, Recall, and F1-Score. Each FE method is evaluated using three components to ensure a fair and comprehensive comparison. This choice is driven by the limitations of certain methods like t-SNE and LDA, which constrain the maximum number of components to the number of classes minus one. That limit is three, in this case, ensuring all methods are evaluated on equal terms.
Figure 2 presents 3D scatter plots showing the results of FE methods applied to our BSM dataset with four burn severity levels: no burn, low, moderate, and high severity. Each scatter plot represents the first three components derived from a given feature reduction method, and the goal is to visually assess how well the methods separate the burn severity classes.
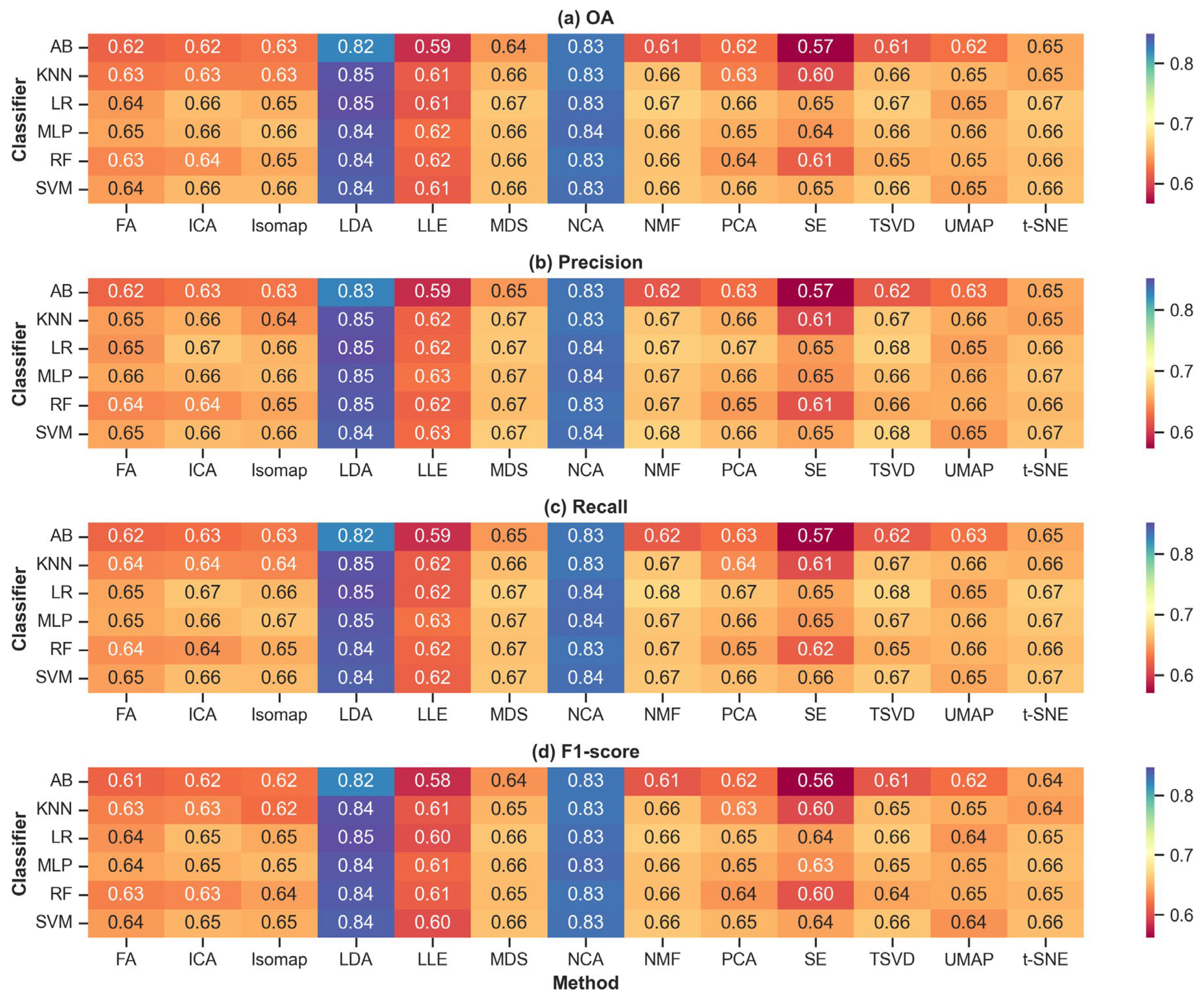
Figure 3 presents the classification results by different ML models when applied to various RF methods. Overall, LDA consistently emerges as the top-performing RF method across various classifiers and performance metrics. When evaluating the OA, LDA achieves superior results with high values across all classifiers, reaching 0.84 with SVM, RF, and MLP; and 0.82 for AB. Notably, even for the weaker classifiers like KNN and LR, LDA still delivers a relatively strong accuracy of 0.85, outperforming most other methods. Regarding Precision, LDA also excels, showing a high precision value of 0.84 with SVM and 0.85 with RF, MLP, LR, and KNN, indicating its ability to effectively minimize false positives. LDA’s Recall performance follows a similar trend, maintaining consistently high recall values, such as 0.84 with SVM and RF, and 0.85 with MLP, RF, and KNN, showcasing its ability to capture relevant instances effectively. The F1-score heatmap further cements LDA's dominance, with high F1-scores across classifiers, including 0.84 for KNN and 0.85 for LR, reflecting its balanced strength between precision and recall.
While LDA leads overall, NCA closely follows, occasionally surpassing LDA in specific cases, especially with the AB model. For instance, when using AB, NCA achieves a slightly higher F1-score of 0.83 compared to LDA’s 0.82 and achieves the same 0.83 for OA, Precision, and Recall. This demonstrates NCA's ability to enhance performance slightly with this classifier, even though it tends to be less effective than LDA in most other scenarios. In other cases, such as with SVM, MLP, and LR, NCA performs closely to LDA but doesn’t surpass it, typically trailing by only a small margin, such as achieving 0.84 in F1-score for SVM, just slightly lower than LDA’s value. These small differences highlight that, while NCA is a robust dimensionality reduction method, particularly for AB, LDA remains the most reliable and high-performing method across different classifiers, making it the optimal choice for dimensionality reduction in this context.
3.2. Impact of Feature Extraction Components on Classifier Performance
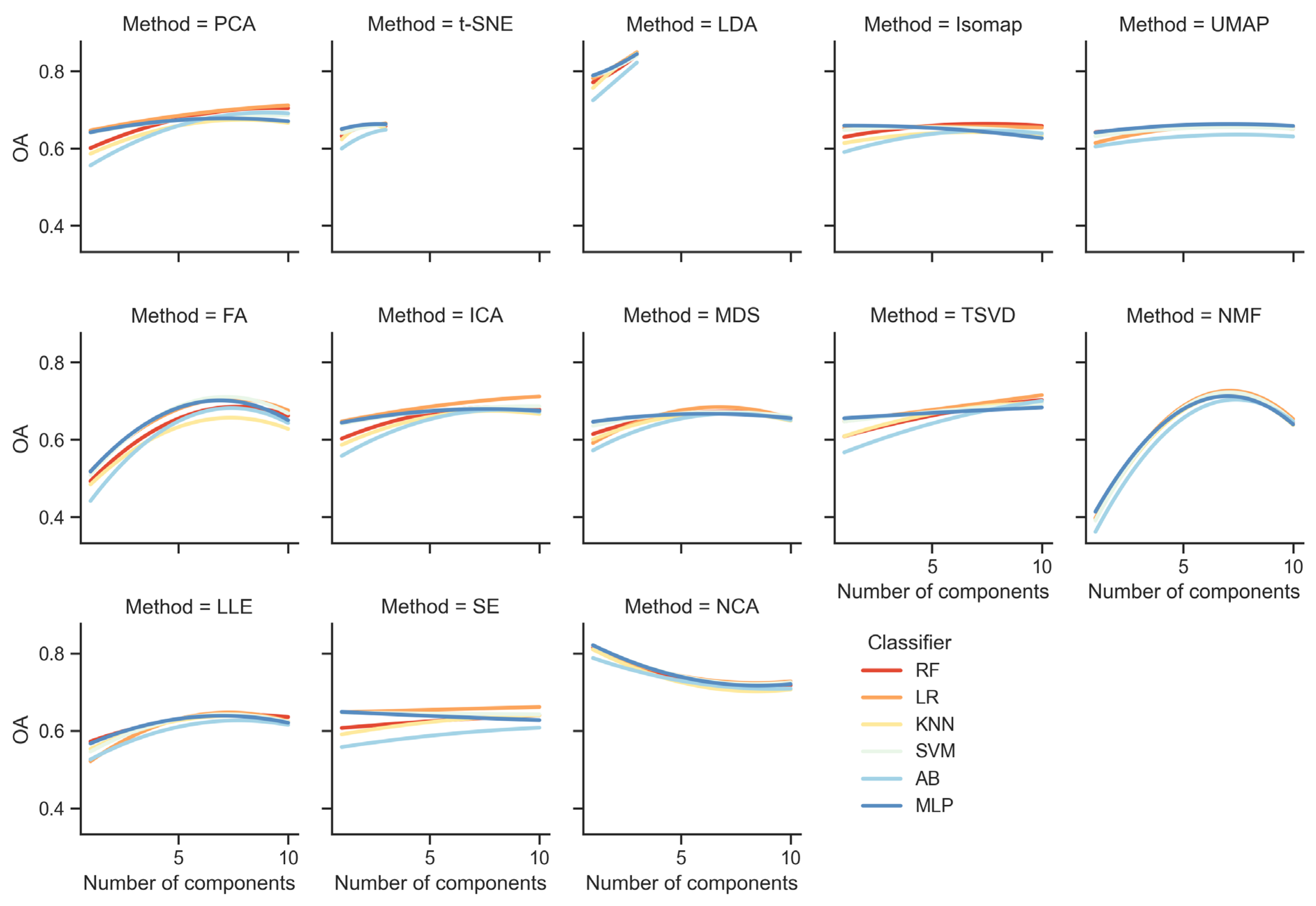
This analysis explores the relationship between the number of components used in various FE methods and their impact on OA (
Figure 4). To approach this analysis more effectively, we group the FE methods based on their behavior as the number of components increases and then analyze each group. This allows for a more structured and insightful analysis by focusing on methods that share similar patterns in performance. The methods can be grouped into three main groups based on their behavior. Understanding these groupings allows for more informed decisions when selecting the number of components for each feature reduction method, maximizing classification performance across models.
Group 1 (G1) consists of methods that exhibit a steady increase in performance as the number of components increases. PCA, t-SNE, LDA, ICA, and TSVD into this category. PCA shows a clear improvement as components increase, with the OA rising from approximately 0.6 at one component to nearly 0.7 or more by 10 components. This behavior suggests that more components allow PCA to retain more variance and preserve critical information, which improves classification performance. For example, classifiers like RF, LR, and MLP perform consistently better with 10 components, reaching accuracy levels close to 0.7. Similarly, t-SNE and LDA demonstrate a gradual increase in accuracy as the number of components increases. From around 0.75 at one component, LDA reaches approximately 0.85 at three components, indicating that more components help capture more independent features that improve classification accuracy. ICA and TSVD also follow this trend, with accuracy increasing steadily from 0.6 at one component to over 0.65 at 10 components for classifiers like SVM and LR. This suggests that those methods benefit from additional components as more of the original feature space is retained, helping to maintain or improve classifier performance.
G2 includes methods that reach peak performance at a certain number of components and then either plateau or show a decline in accuracy with further increases in components. NMF, FA, MDS, and LLE exhibit this behavior. NMF shows a significant increase in accuracy up to around seven components, reaching 0.70 for most classifiers, but beyond this point, accuracy starts to decline, dropping back to around 0.63 at 10 components. This indicates that NMF performs best with seven components, and increasing beyond this introduces unnecessary complexity, leading to decreased performance. This pattern highlights the risk of overfitting with too many components. FA also peaks around seven components, where accuracy reaches approximately 0.68 across classifiers, and then plateaus or slightly declines with further increases. MDS and LLE behave similarly, with accuracy gradually improving to about eight components, reaching 0.65, but then plateaus or slightly declines as the number of components increases. For methods in this group, selecting an optimal number of components (around seven) is advisable, as adding more components beyond this point does not yield significant performance improvements and may even degrade accuracy.
The final group, G3, consists of methods that show little to no sensitivity to the number of components, meaning their performance remains stable, improves minimally, or decreases as components increase. Isomap, UMAP, SE, and NCA fall into this category. Isomap and UMAP show stable performance across most classifiers, with accuracy hovering between 0.60 and 0.62 regardless of the number of components. This suggests that those models capture most of the important structures with very few components, and adding more components does not significantly impact classification performance. SE shows a small increase in accuracy as the number of components increases, but the improvement is minimal, with accuracy hovering around 0.60 to 0.63. This suggests that MDS captures the relevant information with a few components and does not benefit significantly from increasing the dimensionality. In contrast to the other methods, NCA shows a slight decline in performance as the number of components increases. Accuracy starts around 0.8 with one component but drops to around 0.75 as the number of components increases. This indicates that NCA performs best with fewer components, and adding more introduces noise or irrelevant features, reducing classifier performance. In conclusion, for methods in this group, there is little benefit to increasing the number of components beyond three, as performance remains relatively stable. In the case of NCA, limiting the number of components is crucial to avoid performance degradation.
4. Discussion
This study aimed to evaluate the effectiveness of various FE techniques in improving the accuracy of ML classifiers for BSM. Our results indicate that LDA consistently outperforms other FE methods across various classifiers and performance metrics (Figure 3). LDA achieved the highest OA, reaching 0.84 with SVM, RF, and MLP classifiers and 0.82 with AB. Even with less robust classifiers like KNN and LR, LDA maintained strong accuracies of 0.85, surpassing other methods. Regarding precision, LDA demonstrated high values (0.84–0.85), effectively minimizing false positives. Similarly, LDA's recall values remained consistently high (0.84–0.85), indicating its proficiency in correctly identifying burnt areas. The F1-scores underscore LDA's balanced performance between precision and recall, with values up to 0.85 across different classifiers. NCA emerged as a close second to LDA, occasionally surpassing it in specific instances, particularly with the AB classifier. For example, NCA achieved a slightly higher F1-score of 0.83 compared to LDA's 0.82 with AB, and matched LDA's OA, precision, and recall at 0.83.
However, an intriguing observation emerged when using NCA with the AB classifier and when the number of components was limited to one (Figure 4). Under these specific conditions, NCA slightly outperformed LDA. For instance, with the AB classifier, NCA achieved a marginally higher F1-score of 0.83 compared to LDA's 0.82 and matched or exceeded LDA in OA, precision, and recall. Additionally, when reducing the dimensionality to a single component, NCA yielded better results than LDA. The superior performance of NCA under these specific conditions suggests that certain classifier-FE method combinations can yield better results in BSM when tailored appropriately. NCA is a supervised, nonlinear FE technique that learns a linear transformation of the input data to improve the accuracy of nearest neighbor classification. Its ability to directly optimize classification performance may offer advantages when the feature space is constrained to a single dimension.
These findings align with prior research emphasizing the effectiveness of LDA in dimensionality reduction and classification tasks, such as groundwater [
65,
66], storm deposits [
67], Natura 2000 habitats [
68], forest-tree species [
69] and fruit-tree crop classification [
70]. Unlike unsupervised methods like PCA, LDA is a supervised technique that considers class labels to maximize class separability, which is crucial in BSM, where distinguishing between different burn severity levels is essential. Previous studies have predominantly utilized PCA due to its simplicity and widespread adoption [
20,
24,
25,
26,
27,
28], but our results suggest that LDA may offer superior performance in BSM contexts where class discrimination is critical. The performance of NCA, while notable, has been less explored in BSM applications. NCA focuses on learning a distance metric that improves the performance of nearest neighbor classifiers, which may explain its occasional superiority with the AB classifier. However, its slightly lower performance compared to LDA indicates that it may not consistently capture the most discriminative features necessary for optimal classification in BSM.
The implications of this study extend beyond the immediate context of BSM. Improved burn severity classification can inform better post-disaster management strategies, from prioritizing reforestation areas to assessing water quality risks. Furthermore, this research underscores the potential of ML and advanced dimensionality reduction techniques to address complex environmental monitoring problems, potentially improving decision-making in other areas, such as flood mapping or biodiversity assessments. Despite the promising results, several limitations should be acknowledged. First, the study focused on a single fire event (the 2014 Carlton Complex fire), limiting the generalizability of the findings to other fire events or regions. Additionally, the vegetation indices generated were based solely on Landsat-8 data, which, while widely used, might not capture the full spectral information necessary for optimal classifier performance. Other data sources like Sentinel-2 or hyperspectral sensors may offer additional insights.
Future research could address these limitations by testing the effectiveness of LDA and other dimensionality reduction techniques across a broader range of fire events and regions. Furthermore, integrating additional satellite data could improve classifier accuracy even further. Another avenue of investigation could involve ensemble methods that combine multiple feature extraction techniques to handle multicollinearity and non-linear relationships simultaneously. Finally, expanding this research to include real-time monitoring applications could significantly enhance the utility of BSM for on-the-ground disaster management efforts.
5. Conclusions
This study evaluated various feature extraction (FE) techniques to enhance machine learning (ML) classifiers for burn severity mapping (BSM) by mitigating multicollinearity among vegetation indices. Using data from the 2014 Carlton Complex fire and 118 vegetation indices from Landsat-8, we found that Linear discriminant analysis (LDA) consistently outperformed other FE methods across multiple classifiers, making it a reliable choice for dimensionality reduction in BSM. Notably, Neighborhood components analysis (NCA) occasionally surpassed LDA under specific conditions—particularly with the Adaptive boosting (AB) classifier and when using only one component—highlighting the importance of tailoring FE methods to the classifier and data characteristics. The number of components significantly impacted classifier performance, with different FE methods exhibiting varying behaviors as components increased. These findings underscore the need for careful selection and tuning of FE methods and the number of components to optimize BSM models, ultimately contributing to more accurate and efficient wildfire management strategies.
Author Contributions
Conceptualization, L.N.V., G.L.; methodology, L.N.V.; formal analysis, L.N.V., G.L.; writing—original draft preparation, L.N.V.; visualization, L.N.V.; data curation, L.N.V.; writing—review and editing, G.L.; supervision, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Disaster-Safety Platform Technology Development Program of the National Research Foundation of Korea (NRF), funded by the Ministry of Science and ICT (No. 2022M3D7A1090338).
Data Availability Statement
The data presented in this study are available on request from the authors.
Conflicts of Interest
All authors declare no conflict of interest.
References
- Burnett, J.T.; Edgeley, C.M. Factors Influencing Flood Risk Mitigation after Wildfire: Insights for Individual and Collective Action after the 2010 Schultz Fire. International Journal of Disaster Risk Reduction 2023, 94, 103791. [Google Scholar] [CrossRef]
- Souza-Alonso, P.; Saiz, G.; García, R.A.; Pauchard, A.; Ferreira, A.; Merino, A. Post-Fire Ecological Restoration in Latin American Forest Ecosystems: Insights and Lessons from the Last Two Decades. Forest Ecology and Management 2022, 509, 120083. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Sanches Fernandes, L.F. Hydrology and Stream Water Quality of Fire-Prone Watersheds. Current Opinion in Environmental Science & Health 2021, 21, 100243. [Google Scholar] [CrossRef]
- Chuvieco, E.; Mouillot, F.; van der Werf, G.R.; San Miguel, J.; Tanase, M.; Koutsias, N.; García, M.; Yebra, M.; Padilla, M.; Gitas, I.; et al. Historical Background and Current Developments for Mapping Burned Area from Satellite Earth Observation. Remote Sensing of Environment 2019, 225, 45–64. [Google Scholar] [CrossRef]
- Koutsias, N.; Karteris, M. Burned Area Mapping Using Logistic Regression Modeling of a Single Post-Fire Landsat-5 Thematic Mapper Image. International Journal of Remote Sensing 2000, 21, 673–687. [Google Scholar] [CrossRef]
- van Wagtendonk, J.W.; Root, R.R.; Key, C.H. Comparison of AVIRIS and Landsat ETM+ Detection Capabilities for Burn Severity. Remote Sensing of Environment 2004, 92, 397–408. [Google Scholar] [CrossRef]
- Boucher, J.; Beaudoin, A.; Hébert, C.; Guindon, L.; Bauce, E. Assessing the Potential of the Differenced Normalized Burn Ratio (dNBR) for Estimating Burn Severity in Eastern Canadian Boreal Forests. International Journal of Wildland Fire 2017, 26, 32–45. [Google Scholar] [CrossRef]
- Zahura, F.T.; Bisht, G.; Li, Z.; McKnight, S.; Chen, X. Impact of Topography and Climate on Post-Fire Vegetation Recovery across Different Burn Severity and Land Cover Types through Random Forest. Ecological Informatics 2024, 82, 102757. [Google Scholar] [CrossRef]
- Le, X.-H.; Nguyen Van, L.; Hai Nguyen, D.; Nguyen, G.V.; Jung, S.; Lee, G. Comparison of Bias-Corrected Multisatellite Precipitation Products by Deep Learning Framework. International Journal of Applied Earth Observation and Geoinformation 2023, 116, 103177. [Google Scholar] [CrossRef]
- Nguyen, G.V.; Le, X.H.; Nguyen Van, L.; Do, T.T.M.; Jung, S.; Lee, G. Machine Learning Approaches for Reconstructing Gridded Precipitation Based on Multiple Source Products. Journal of Hydrology: Regional Studies. [CrossRef]
- Nguyen, G.V.; Le, X.-H.; Van, L.N.; Jung, S.; Yeon, M.; Lee, G. Application of Random Forest Algorithm for Merging Multiple Satellite Precipitation Products across South Korea. Remote Sensing 2021, 13, 4033. [Google Scholar] [CrossRef]
- Nguyen, G.V.; Le, X.-H.; Van, L.N.; Jung, S.; Choi, C.; Lee, G. Evaluating the Performance of Light Gradient Boosting Machine in Merging Multiple Satellite Precipitation Products Over South Korea. In Proceedings of the Proceedings of the 4th International Conference on Sustainability in Civil Engineering; Springer, Singapore, 2024; pp. 513–522.
- Le, X.-H.; Van, L.N.; Nguyen, G.V.; Nguyen, D.H.; Jung, S.; Lee, G. Towards an Efficient Streamflow Forecasting Method for Event-Scales in Ca River Basin, Vietnam. Journal of Hydrology: Regional Studies 2023, 46, 101328. [Google Scholar] [CrossRef]
- Tran, V.; Ivanov, V.; Kim, J. Data Reformation – A Novel Data Processing Technique Enhancing Machine Learning Applicability for Predicting Streamflow Extremes. Advances in Water Resources 2023, 182, 104569. [Google Scholar] [CrossRef]
- Tran, V.N.; Ivanov, V.Y.; Xu, D.; Kim, J. Closing in on Hydrologic Predictive Accuracy: Combining the Strengths of High-Fidelity and Physics-Agnostic Models. Geophysical Research Letters 2023, 50, e2023GL104464. [Google Scholar] [CrossRef]
- Nguyen, G.V.; Nguyen Van, L.; Jung, S.; Hyunuk, A.; Lee, G. Exploring the Power of Physics-Informed Neural Networks for Accurate and Efficient Solutions to 1D Shallow Water Equations. Journal of Korean Water Resources Association 2023, 56, 939–953. [Google Scholar]
- Collins, L.; Griffioen, P.; Newell, G.; Mellor, A. The Utility of Random Forests for Wildfire Severity Mapping. Remote Sensing of Environment 2018, 216, 374–384. [Google Scholar] [CrossRef]
- Holden, Z.A.; Morgan, P.; Evans, J.S. A Predictive Model of Burn Severity Based on 20-Year Satellite-Inferred Burn Severity Data in a Large Southwestern US Wilderness Area. Forest Ecology and Management 2009, 258, 2399–2406. [Google Scholar] [CrossRef]
- Van, L.N.; Tran, V.N.; Nguyen, G.V.; Yeon, M.; Do, M.T.-T.; Lee, G. Enhancing Wildfire Mapping Accuracy Using Mono-Temporal Sentinel-2 Data: A Novel Approach through Qualitative and Quantitative Feature Selection with Explainable AI. Ecological Informatics 2024, 81, 102601. [Google Scholar] [CrossRef]
- Kulinan, A.S.; Cho, Y.; Park, M.; Park, S. Rapid Wildfire Damage Estimation Using Integrated Object-Based Classification with Auto-Generated Training Samples from Sentinel-2 Imagery on Google Earth Engine. International Journal of Applied Earth Observation and Geoinformation 2024, 126, 103628. [Google Scholar] [CrossRef]
- Badola, A.; Panda, S.K.; Roberts, D.A.; Waigl, C.F.; Jandt, R.R.; Bhatt, U.S. A Novel Method to Simulate AVIRIS-NG Hyperspectral Image from Sentinel-2 Image for Improved Vegetation/Wildfire Fuel Mapping, Boreal Alaska. International Journal of Applied Earth Observation and Geoinformation 2022, 112, 102891. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M.; Chanussot, J. Burnt-Net: Wildfire Burned Area Mapping with Single Post-Fire Sentinel-2 Data and Deep Learning Morphological Neural Network. Ecological Indicators 2022, 140, 108999. [Google Scholar] [CrossRef]
- Van, L.N.; Tran, V.N.; Nguyen, G.V.; Yeon, M.; Do, M.T.-T.; Lee, G. Enhancing Wildfire Mapping Accuracy Using Mono-Temporal Sentinel-2 Data: A Novel Approach through Qualitative and Quantitative Feature Selection with Explainable AI. Ecological Informatics 2024, 81, 102601. [Google Scholar] [CrossRef]
- Richards, J.A. Thematic Mapping from Multitemporal Image Data Using the Principal Components Transformation. Remote Sensing of Environment 1984, 16, 35–46. [Google Scholar] [CrossRef]
- Siegert, F.; Ruecker, G. Use of Multitemporal ERS-2 SAR Images for Identification of Burned Scars in South-East Asian Tropical Rainforest. International Journal of Remote Sensing 2000, 21, 831–837. [Google Scholar] [CrossRef]
- Nielsen, T.T.; Mbow, C.; Kane, R. A Statistical Methodology for Burned Area Estimation Using Multitemporal AVHRR Data. International Journal of Remote Sensing 2002, 23, 1181–1196. [Google Scholar] [CrossRef]
- Koutsias, N.; Mallinis, G.; Karteris, M. A Forward/Backward Principal Component Analysis of Landsat-7 ETM+ Data to Enhance the Spectral Signal of Burnt Surfaces. ISPRS Journal of Photogrammetry and Remote Sensing 2009, 64, 37–46. [Google Scholar] [CrossRef]
- Chen, G.; Metz, M.R.; Rizzo, D.M.; Dillon, W.W.; Meentemeyer, R.K. Object-Based Assessment of Burn Severity in Diseased Forests Using High-Spatial and High-Spectral Resolution MASTER Airborne Imagery. ISPRS Journal of Photogrammetry and Remote Sensing 2015, 102, 38–47. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J.; Ye, M.; James, S.C.; Tang, Z.; Dong, J.; Xing, T. Using t-Distributed Stochastic Neighbor Embedding (t-SNE) for Cluster Analysis and Spatial Zone Delineation of Groundwater Geochemistry Data. Journal of Hydrology 2021, 597, 126146. [Google Scholar] [CrossRef]
- Yu, T.-T.; Chen, C.-Y.; Wu, T.-H.; Chang, Y.-C. Application of High-Dimensional Uniform Manifold Approximation and Projection (UMAP) to Cluster Existing Landfills on the Basis of Geographical and Environmental Features. Science of The Total Environment 2023, 904, 167013. [Google Scholar] [CrossRef]
- M, G.J. Secure Water Quality Prediction System Using Machine Learning and Blockchain Technologies. Journal of Environmental Management 2024, 350, 119357. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal Components Analysis (PCA). Computers & Geosciences 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Martinez, A.M.; Kak, A.C. PCA versus LDA. IEEE Transactions on Pattern Analysis and Machine Intelligence 2001, 23, 228–233. [Google Scholar] [CrossRef]
- Balamurali, M.; Silversides, K.L.; Melkumyan, A. A Comparison of T-SNE, SOM and SPADE for Identifying Material Type Domains in Geological Data. Computers & Geosciences 2019, 125, 78–89. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; Silva, V. de; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction 2020.
- Comon, P. Independent Component Analysis, A New Concept? Signal Processing 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Jöreskog, K.G. Factor Analysis as an Errors-in-Variables Model. In Principals of Modern Psychological Measurement; Routledge, 1983 ISBN 978-0-203-05665-3.
- Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Generalized Multidimensional Scaling: A Framework for Isometry-Invariant Partial Surface Matching. Proc Natl Acad Sci U S A 2006, 103, 1168–1172. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized Cuts and Image Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 2000, 22, 888–905. [Google Scholar] [CrossRef]
- Belkina, A.C.; Ciccolella, C.O.; Anno, R.; Halpert, R.; Spidlen, J.; Snyder-Cappione, J.E. Automated Optimized Parameters for T-Distributed Stochastic Neighbor Embedding Improve Visualization and Analysis of Large Datasets. Nat Commun 2019, 10, 1–12. [Google Scholar] [CrossRef]
- Vu, T.; Chunikhina, E.; Raich, R. Perturbation Expansions and Error Bounds for the Truncated Singular Value Decomposition. Linear Algebra and its Applications 2021, 627, 94–139. [Google Scholar] [CrossRef]
- Goldberger, J.; Hinton, G.E.; Roweis, S.; Salakhutdinov, R.R. Neighbourhood Components Analysis. In Proceedings of the Advances in Neural Information Processing Systems; MIT Press, 2004; Vol. 17. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sensing of Environment 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary Analysis of the Performance of the Landsat 8/OLI Land Surface Reflectance Product. Remote Sensing of Environment 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Chuvieco, E.; Martín, M.P.; Palacios, A. Assessment of Different Spectral Indices in the Red-near-Infrared Spectral Domain for Burned Land Discrimination. International Journal of Remote Sensing 2002, 23, 5103–5110. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape Assessment (LA). 2006.
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sensing of Environment 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sensing of Environment 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Pinty, B.; Verstraete, M.M. GEMI: A Non-Linear Index to Monitor Global Vegetation from Satellites. Vegetatio 1992, 101, 15–20. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy Near-Infrared Reflectance and Terrestrial Photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef] [PubMed]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sensing of Environment 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and Soil Lines in Visible Spectral Space: A Concept and Technique for Remote Estimation of Vegetation Fraction. International Journal of Remote Sensing 2002, 23, 2537–2562. [Google Scholar] [CrossRef]
- Smith, A.M.S.; Wooster, M.J.; Drake, N.A.; Dipotso, F.M.; Falkowski, M.J.; Hudak, A.T. Testing the Potential of Multi-Spectral Remote Sensing for Retrospectively Estimating Fire Severity in African Savannahs. Remote Sensing of Environment 2005, 97, 92–115. [Google Scholar] [CrossRef]
- Collins, L.; McCarthy, G.; Mellor, A.; Newell, G.; Smith, L. Training Data Requirements for Fire Severity Mapping Using Landsat Imagery and Random Forest. Remote Sensing of Environment 2020, 245, 111839. [Google Scholar] [CrossRef]
- Miller, J.D.; Knapp, E.E.; Key, C.H.; Skinner, C.N.; Isbell, C.J.; Creasy, R.M.; Sherlock, J.W. Calibration and Validation of the Relative Differenced Normalized Burn Ratio (RdNBR) to Three Measures of Fire Severity in the Sierra Nevada and Klamath Mountains, California, USA. Remote Sensing of Environment 2009, 113, 645–656. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support Vector Machines. IEEE Intelligent Systems and their Applications 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest Neighbor Pattern Classification. IEEE Transactions on Information Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Hosmer, T.; Le Cessie, S.; Lemeshow, S. A Comparison of Goodness-of-Fit Tests for the Logistic Regression Model. Statistics in Medicine 1997, 16, 965–980. [Google Scholar] [CrossRef]
- Kelley, H.J. Gradient Theory of Optimal Flight Paths. ARS Journal 1960, 30, 947–954. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive Logistic Regression: A Statistical View of Boosting (With Discussion and a Rejoinder by the Authors). The Annals of Statistics 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evolutionary Computation 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Halofsky, J.E.; Peterson, D.L.; Harvey, B.J. Changing Wildfire, Changing Forests: The Effects of Climate Change on Fire Regimes and Vegetation in the Pacific Northwest, USA. Fire Ecology 2020, 16, 4. [Google Scholar] [CrossRef]
- Amiri, V.; Nakagawa, K. Using a Linear Discriminant Analysis (LDA)-Based Nomenclature System and Self-Organizing Maps (SOM) for Spatiotemporal Assessment of Groundwater Quality in a Coastal Aquifer. Journal of Hydrology 2021, 603, 127082. [Google Scholar] [CrossRef]
- Wilson, S.R.; Close, M.E.; Abraham, P. Applying Linear Discriminant Analysis to Predict Groundwater Redox Conditions Conducive to Denitrification. Journal of Hydrology 2018, 556, 611–624. [Google Scholar] [CrossRef]
- Leszczyńska, K.; Moskalewicz, D.; Stattegger, K. Statistical Approach to Identify Storm Deposits and Cryptic Event Layers from Grain-Size Data, Mechelinki, Poland, Baltic Sea. CATENA 2024, 242, 108130. [Google Scholar] [CrossRef]
- Jarocińska, A.; Kopeć, D.; Kycko, M.; Piórkowski, H.; Błońska, A. Hyperspectral vs. Multispectral Data: Comparison of the Spectral Differentiation Capabilities of Natura 2000 Non-Forest Habitats. ISPRS Journal of Photogrammetry and Remote Sensing 2022, 184, 148–164. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral Discrimination of Tropical Rain Forest Tree Species at Leaf to Crown Scales. Remote Sensing of Environment 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Peña, M.A.; Liao, R.; Brenning, A. Using Spectrotemporal Indices to Improve the Fruit-Tree Crop Classification Accuracy. ISPRS Journal of Photogrammetry and Remote Sensing 2017, 128, 158–169. [Google Scholar] [CrossRef]
Figure 1.
Location of the 2014 Carlton Complex wildfire used in this study.
Figure 1.
Location of the 2014 Carlton Complex wildfire used in this study.
Figure 2.
Visualization of dimensionality reduction techniques. Each plot represents a 3D data projection using three main components.
Figure 2.
Visualization of dimensionality reduction techniques. Each plot represents a 3D data projection using three main components.
Figure 3.
Heatmaps representing the performance of 13 feature extraction (FE) methods on four different metrics: (a) Overall accuracy (OA), (b) Precision, (c) Recall, and (d) F1-score, across six machine learning classifiers. The x-axis of each heatmap lists the FR methods, while the y-axis lists the classifiers. The color intensity in each heatmap indicates the mean performance score of 1,000 simulations.
Figure 3.
Heatmaps representing the performance of 13 feature extraction (FE) methods on four different metrics: (a) Overall accuracy (OA), (b) Precision, (c) Recall, and (d) F1-score, across six machine learning classifiers. The x-axis of each heatmap lists the FR methods, while the y-axis lists the classifiers. The color intensity in each heatmap indicates the mean performance score of 1,000 simulations.
Figure 4.
Relationship between the number of components used in 13 feature reduction methods and the performance (Overall accuracy, OA) of six classifiers—RF, LR, KNN, SVM, AB, and MLP. The x-axis in each plot shows the number of components, while the y-axis represents the OA. Each line corresponds to one of the classifiers fitted by quadratic polynomial regression models.
Figure 4.
Relationship between the number of components used in 13 feature reduction methods and the performance (Overall accuracy, OA) of six classifiers—RF, LR, KNN, SVM, AB, and MLP. The x-axis in each plot shows the number of components, while the y-axis represents the OA. Each line corresponds to one of the classifiers fitted by quadratic polynomial regression models.
Table 1.
Lists of nine established indices were used in this study. Acronyms: BAI —Burn Area Index, SAVI—Soil-Adjusted Vegetation Index, EVI—Enhanced Vegetation Index, GEMI—Global Environment Monitoring Index, NIRv—Near-Infrared Reflectance of Vegetation, VARI—Visible Atmospherically Resistant Index, NDVI—Normalized Difference Vegetation Index, and CSI—Char Soil Index.
Table 1.
Lists of nine established indices were used in this study. Acronyms: BAI —Burn Area Index, SAVI—Soil-Adjusted Vegetation Index, EVI—Enhanced Vegetation Index, GEMI—Global Environment Monitoring Index, NIRv—Near-Infrared Reflectance of Vegetation, VARI—Visible Atmospherically Resistant Index, NDVI—Normalized Difference Vegetation Index, and CSI—Char Soil Index.
| No. |
Index |
Formula |
References |
| 1 |
BAI |
|
[46] |
| 2 |
NBR |
|
[47] |
| 3 |
SAVI |
|
[48] |
| 4 |
EVI |
|
[49] |
| 5 |
GEMI |
, where
|
[50] |
| 6 |
NIRv |
|
[51] |
| 7 |
NDVI |
|
[52] |
| 8 |
VARI |
|
[53] |
| 9 |
CSI |
|
[54] |
Table 2.
Burn severity category definition used in this study, proposed by Miller & Thode (2009) [
56].
Table 2.
Burn severity category definition used in this study, proposed by Miller & Thode (2009) [
56].
| Severity category |
CBI values |
Number of data |
| No burn |
0.00−0.1 |
110 |
| Low |
0.1−1.24 |
105 |
| Moderate |
1.25−2.24 |
54 |
| High |
2.25−3.00 |
59 |
Table 3.
Optimal values of hyperparameters of six ML models using the PSO method.
Table 3.
Optimal values of hyperparameters of six ML models using the PSO method.
| Models |
Hyper-parameters |
Optimal values |
|
| SVM |
C |
1.261 |
|
| kernel |
‘poly’ |
|
| gamma |
‘scale’ |
|
| degree |
2 |
|
| coef0 |
5.846 |
|
| RF |
n_estimators |
199 |
|
| max_depth |
25 |
|
| min_samples_split |
12 |
|
| min_samples_leaf |
2 |
|
| max_features |
‘sqrt’ |
|
| criterion |
‘log_loss’ |
|
| MLP |
hidden_layer_sizes |
(100, 100) |
|
| activation |
‘tanh’ |
|
| solver |
‘adam’ |
|
| alpha |
0.00342 |
|
| learning_rate |
‘constant’ |
|
| AB |
max_depth |
8 |
|
| min_samples_split |
10 |
|
| min_samples_leaf |
2 |
|
| n_estimators |
168 |
|
| learning_rate |
0.623 |
|
| algorithm |
‘SAMME’ |
|
| LR |
C |
2.437 |
|
| solver |
lbfgs |
|
| |
n_neighbors |
12 |
|
| KNN |
weights |
‘uniform’ |
|
| |
algorithm |
‘auto’ |
|
Table 4.
Statistical metrics used in this study. Acronyms: TP—True positives, TN—True negatives, FP—False positives, and FN—False negatives.
Table 4.
Statistical metrics used in this study. Acronyms: TP—True positives, TN—True negatives, FP—False positives, and FN—False negatives.
| Metrics |
Formula |
Range |
Optimal value |
| OA |
|
0.0‒1.0 |
1.0 |
| Precision |
|
0.0‒1.0 |
1.0 |
| Recall |
|
0.0‒1.0 |
1.0 |
| F1-score |
|
0.0‒1.0 |
1.0 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).