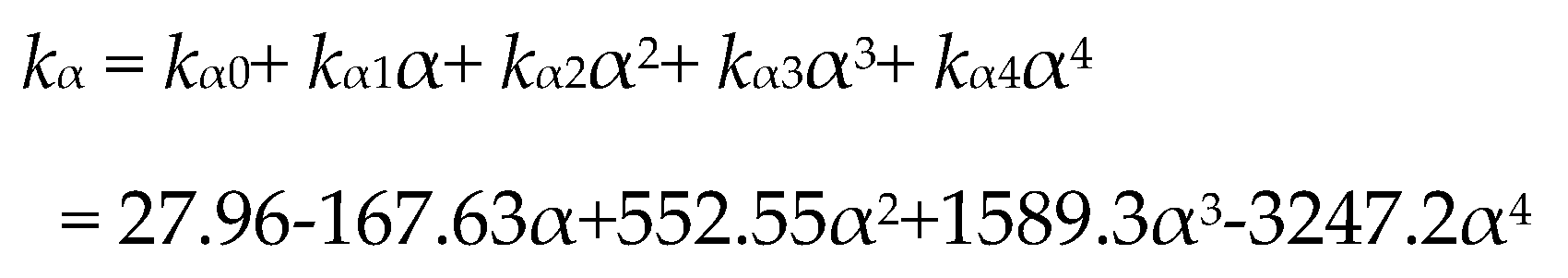1. Introduction
Nonlinear aeroelastic phenomena, such as limit cycle oscillation [
1] and free-play flutter [
2], not only threaten the aircraft structure, but can even result in loss of control. This challenge attracts many researchers to develop aeroelastic control for flutter suppression and avoidance of LCO [
3].Usually passive flutter control has been widely used for wing flutter suppression in practical engineering, such as mass balance, local stiffness enhancement, etc., however, this method requires extra mass and makes the airplane heavier [
4]. Therefore, active flutter control has been proposed and the objectives are to suppress flutter and to make the airplane flight exceed its flutter speed.
Active flutter control is a hot topic to suppress wing flutter by using modern control theories. Many researchers proposed useful schemes for active flutter suppression. Ouyang
et al. studied the influence of flap camber on the wing flutter bounds, and proposed a Linear Quadratic Guassian (LQG) based control to actively suppress the aeroelastic response by the flap deflection, and the flutter speed and frequency of the wing will be changed by the orders of the reduced order model of the morphing flap camber [
5]. Na et. al. proposed a LQG control method with sliding mode control (SMC) observer to active control of composite thin-walled beam structures in compressible flow, the dynamic aeroelastic responses of the beam structures subject to sharp-edged gust, blast loads and sonic-boom are investigated by this method [
6]. Compared with linear aeroelasticity, nonlinear aeroelastic issue is more attractive, which includes freeplay, time delay and cubic nonlinearities in aeroelastic systems. Neil
et al. studied structure nonlinear effect, analyzed and experimented by a rigid wing supported by a nonlinear spring [
7]. Lee
et al. presented the effect of a cubic structure restoring force on the flutter of a two dimensional airfoil placed in an incompressible flow, and the results showed the dependence of the divergence flutter boundary on initial conditions for a soft spring, while the independence of the divergence flutter boundary on initial conditions for the hard spring [
8]. To stabilize a nonlinear aeroelastic system, Singh
et al. proposed an adaptive backstepping output feedback control scheme, and trajectory control of the pitch angle is achieved by this method [
9]. To deal with model uncertainties of aeroelastic systems, Lin
et al. suggested a decoupled fuzzy sliding mode control (DFSMC), and the DFSMC system was designed to control the plunge and pitch motions simultaneously [
10].Chen et. al. proposed a terminal SMC (TSMC)for aeroelastic systems, the LCO suffered in the aeroelastic system is removed by the TSMC [
11]. Mukhopadhyay introduced historical perspective on analysis and control of aeroelasticity over the century, and showed some experiments of aeroelastic control for different aircrafts [
12]. Bouma
et al. investigated structural and aerodynamic nonlinearities effects for three degrees of freedom (DOF) aeroelastic systems, and stall effects were introduced using quasi-steady and unsteady aerodynamic representations [
13]. Vishal
et al. studied the synchronization characteristics of a pitch–plunge aeroelastic system, possessing discontinuous nonlinearities in both structural and aerodynamic fronts. Meanwhile, a multi-physics fluid–structure interaction problem possessing coupled non-smooth nonlinearities can be alleviated by the use of synchronization theory [
14]. Livne gave a survey on aircraft active flutter suppression (AFS) through state of the art, and AFS wind tunnel test and flight-test programs were illustrated [
15].
Flutter suppression theory has also been developed by the researchers. Considering delayed control problem, a single time delay was determined according to both the critical stability condition and the stability margins, Zou
et al. proposed a delayed proportional–differential (PD) controller for robust suppression the body-freedom flutter (BFF) of a flying-wing drone [
16].Trapani and Guo proposed a rudderless aeroelastic fin for a flexible blended-wing-body UAV to improve divergence and flutter margin [
17]. Although these methods are useful for the linear time-invariant systems, they cannot guarantee the closed-loop performances of the nonlinear and time-varying aeroelastic system. For the structural nonlinearities and unsteady flow, Zhang and Behal proposed a continuous robust controller to realize aeroelastic vibration control of a two dimensional airfoil [
18]. Lee and Singh proposed an
L1 adaptive control for the aeroelastic system with unsteady aerodynamics and gust load [
19].For the nonlinear aeroelastic system, Platanitis and Strganac proposed a feedback linearization combined with model reference, and it can adaptively suppress LCO of a typical wing section with LE and TE control surfaces [
20]. Prime set up a linear parameter varying (LPV) model for the three DOF Nonlinear Aeroelastic Test Apparatus (NATA), and developed a
H2 robust control by linear matrix inequalities [
21]. Li
et al. proposed a state-dependent Riccati equation based method to control an airfoil section with control surface nonlinearities, but it depended on the accurate model [
22]. To reduce dependence on the model, Tang et al. proposed a neural network based active flutter suppression under control input constraints [
23], but neural networks need extensive calculations. Recently Gao introduced sliding mode control into an aeroelastic system and presented a finite-time fault-tolerant control for wing flutter suppression [
24].Chen
et al. proposed a free-model deep reinforcement learning algorithm for the active flutter suppression through aeroelsatic wind tunnel testing, thus the jet flow intensity can be intelligently selected according to the real-time state of the flexible wing [
25].
Since the aircrafts fly in a varying environment, the influence of model uncertainties and external disturbances on aeroelastic systems have also been considered by the researchers. Pettit briefly described aerodynamic and structure uncertainties and applications of uncertainty with design optimization [
26]. For the nonlinear perturbations, Hao
et al. analyzed stochastic nonlinear flutter behaviors of 3-DOF wing model by the stochastic p-bifurcation analysis method [
27].Lee and Singh proposed a robust higher-order super-twisting control to deal with aeroelastic system with unsteady aerodynamics [
28]. To estimate unknown parameters, Prabhu and Srinivas proposed an intelligent observer and then robust control of a three degrees of freedom aeroelastic model [
29], but the neural network based observer has a heavy computational load. To improve the convergence speed of the aeroelastic system, Chen
et al. proposed a terminal sliding mode control to reach the target within a finite time frame [
30], and Yuan
et al. proposed a sliding mode observer control for a two dimensional aeroelastic system with gusts [
31]. Xu
et al. also applied Backstepping Sliding Mode Control (BSMC) design to suppress the LCO with uncertainties and external disturbances [
32]. All these methods can suppress or attenuate external disturbances and achieve the desired robust performances, however an alternative approach is available, the so-called disturbance observer based control (DOBC). The DOBC lumps all internal uncertainties and external disturbances acting on the aeroelastic system into a single term and then identifies them by the DO. The DO can provide fast, excellent control performances and smooth control actions without using large feedback gains [
33]. Liu and Whidborne have proposed a nonlinear disturbance observer to deal with bounded unknown disturbances [
34], but this observer does not cope well with variable disturbances, and the output tracking responses by this DO-BSMC cannot be guaranteed to converge within finite time.
Motivated by Xu’s [
32] and Chen’s work [
33], this paper considers trajectory tracking control for the two-dimensional airfoil-flap aeroelastic system. The major contributions of this work are as follows:
Considering quasi-steady and unsteady aerodynamic loads, nonlinear dynamic models are set up for an aeroelastic two-dimensional airfoil with both trailing-edge and leading-edge control surfaces.
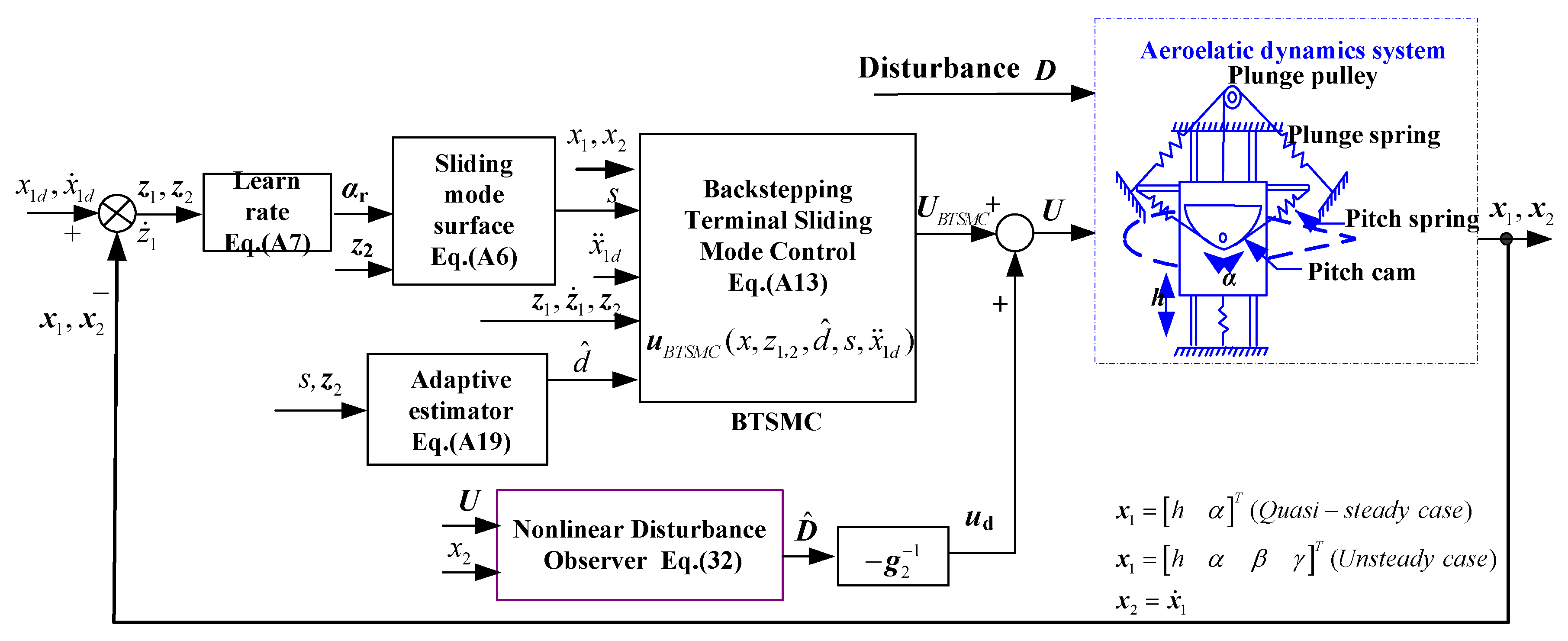
To suppress flutter, a backstepping terminal sliding-mode control is proposed for the two-dimensional airfoil-flap aeroelastic system. The benefits of this approach have TSMC merits of high robustness, fast transient response and finite time convergence, as well as backstepping control in terms of globally asymptotic stability.
To overcome the limitation of the BTSMC being dependent on prior knowledge, a nonlinear disturbance observer is designed for coping with model uncertainties and variable external bounded gust disturbances, which is different from Backstepping SMC for flutter suppression [
32].
To adjust the speed where the aeroelastic response converges to zero, a learning rate is incorporated into the BTSMC design.
Simulation results show the proposed DO-BTSMC method is effective and has advantages in LCO suppression and flutter control for a two-dimensional wing with LE and TE control surfaces.
This paper is organized as follows.
Section 2 establishes the nonlinear aeroelastic dynamics model of the two-dimensional airfoil-flap system.
Section 3 proposes a DO-BTSMC design, and stability is analyzed for the closed-loop control system. Simulations and analysis are in
Section 4. Some conclusions are given in
Section 5.
2. Aeroelastic System Dynamic Model
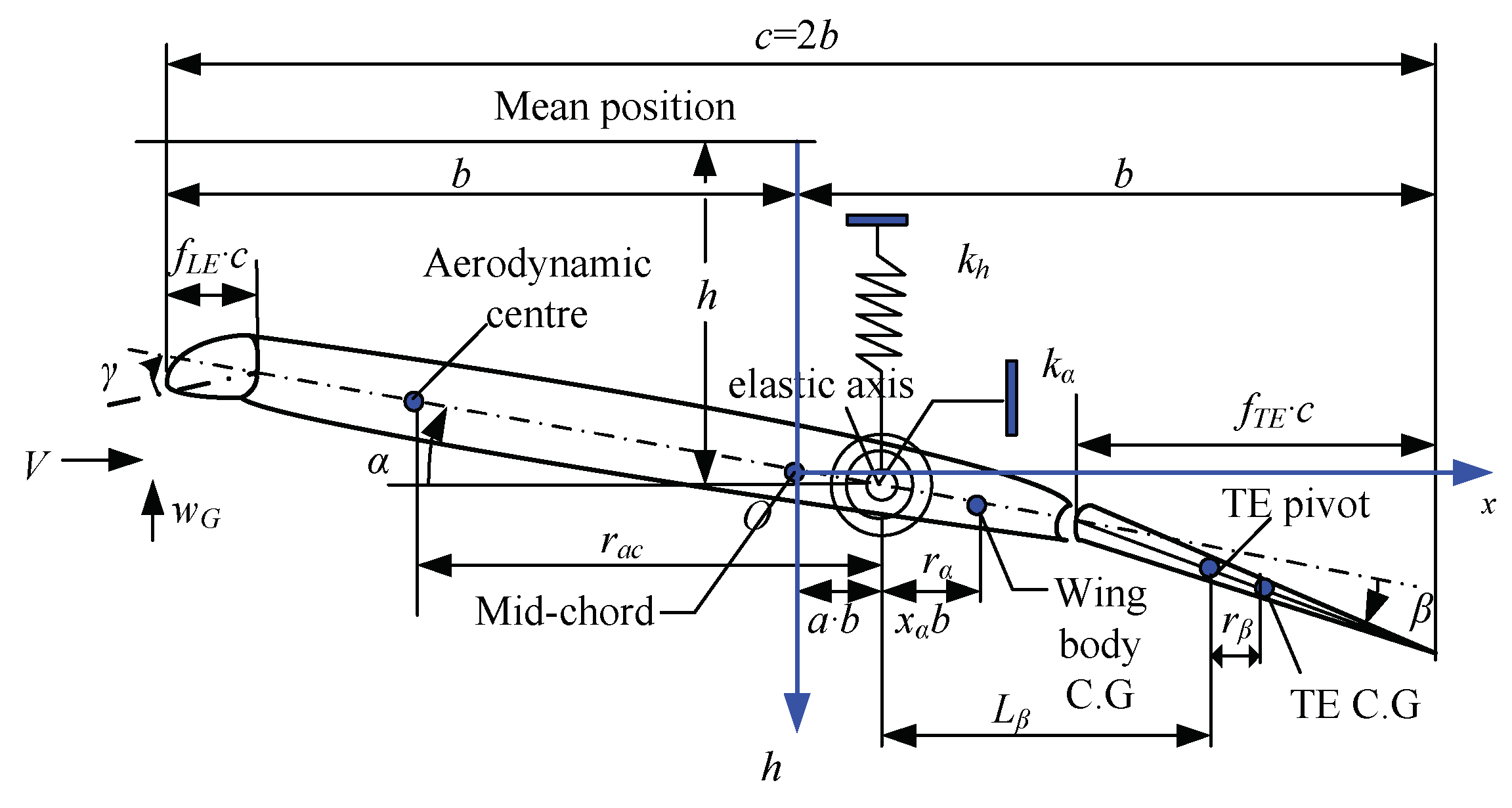
The studied model is a two-DOF pitch-plunge wing section with both LE and TE control surfaces and is shown in
Figure 1, both control surfaces are used as control inputs.
The physical parameters of the wing are listed as follows, a is nondimensional distance from midchord to elastic axis position, b and c denote semichord and full chord length of wing section respectively.
The aeroelastic governing models are established as follows [
20]
where
C
mα, eff , C
mβ, eff , and C
mγ, eff are the effective dynamic and control moment derivatives due to angle of attack and trailing- and leading-edge control surface deflection, respectively, about the elastic axis and are defined as follows
mT denote total mass of pitch–plunge system, cα and ch denote damping of pitch and plunge respectively, kα and kh denote pitch and plunge stiffness respectively, sp is wing section span, Iα denotes total pitch moment of inertia about elastic axis,ρ denotes air density, h is plunge displacement, V is freestream velocity, α is angle of attack (AOA),β and γ trailing- and leading-edge control surface deflection respectively, CL, CLα, CLβ, CLγ denote wing section lift coefficients and Cm, Cmα, Cmβ, Cmγ denote wing section pitch moment coefficients at quarter-chord.
Denote the state variable vector is
and uncertain functions of plunge and AOA motions are
The servo motor dynamics for the TE and LE can be modeled as a second-order system of the form
where
and
are the damping of the TE and LE respectively,
and
are stiffness of the TE and LE respectively, and
and
denote the desired positions of the servo motors for the TE and LE respectively.
and
denote the rotational wingbody of mass and inertia respectively,
,
and
are the moments of inertia of the TE and LE about its pivot respectively ,
,
,
and
are the rotational TE and LE section of mass and inertia respectively. Let
,
denotes a translational body of mass.
When the aerodynamic performance of the airfoil is unsteady, the equations of motion for the entire system can be set up by Lagrangian energy theory,
where
denotes Lagrangian function. The expanded form of (10) is
wherea * denotes symmetric matrix element,
The aerodynamic force and moment in (8) can be calculated by Theodorsen method [
35,
36]
where
Ti (i =1,2,…,14) are the Theodorsen constants, see Appendix B [
37].
is derived from those by Throdorsen [
35,
36,
37].
The aerodynamic force and moments in (13)-(15) are dependent on Theodorsen function C(k), where k is the non-dimensional reduced frequency of harmonic oscillation, C(k) can be approximated by Jones method,
where c
1=0.0075, c
2=0.10055, c
3=0.0455, c
4=0.3. C(s) can be presented as a state-space model as follows
where
The aerodynamic force and moments can be described as the sum of non-circulatory and circulatory loads,
where
Fnc and
Fc are non-circulatory load and circulatory load respectively. Denote
, x
a = [x
a1, x
a2]
T, then we get
where
xα is nondimensional distance from elastic axis to centre of mass, and meeting
xα=
rcg /
b,
rcg is distance from elastic axis to centre of mass.
and
are the Theodorsen constants for the TE and LE respectively. Substitute (17) , (13) - (15) into (11), then yields
where(3)
Denote the full state vector
, the overall state-space model is
where the
A and B matrix are as follows
where
Since there exists wind disturbance for the aeroelastic system, then the external disturbance
D is considered and added into the system of (6) and (25) as
where
and
denote external disturbances and bound by
,
DU is a real value meeting
DU≥0. Denote
,
. The aerodynamic loads due to the wind disturbances are defined as [
38]
where
denotes the disturbance velocity,
τ is a dimensionless time variable defined as
, so
.Suppose that the above disturbance can be generated by a linear exogenous system [
33],
where
,
Wd,
Vd are coefficient matrices with corresponding dimensions.
Airfoil aeroelastic vibration Control Problem: The control objective is to suppress the aeroelastic vibrations, so the desired smooth trajectory xd can be chosen to be zero for all time. Alternatively the desired trajectory xd along with the actual pitching and plunging variables is driven toward the origin.
Figure 1.
Model of the two-dimensional flexible wing.
Figure 1.
Model of the two-dimensional flexible wing.
Figure 2.
Block diagram of the proposed DO-BTSMC controller.
Figure 2.
Block diagram of the proposed DO-BTSMC controller.
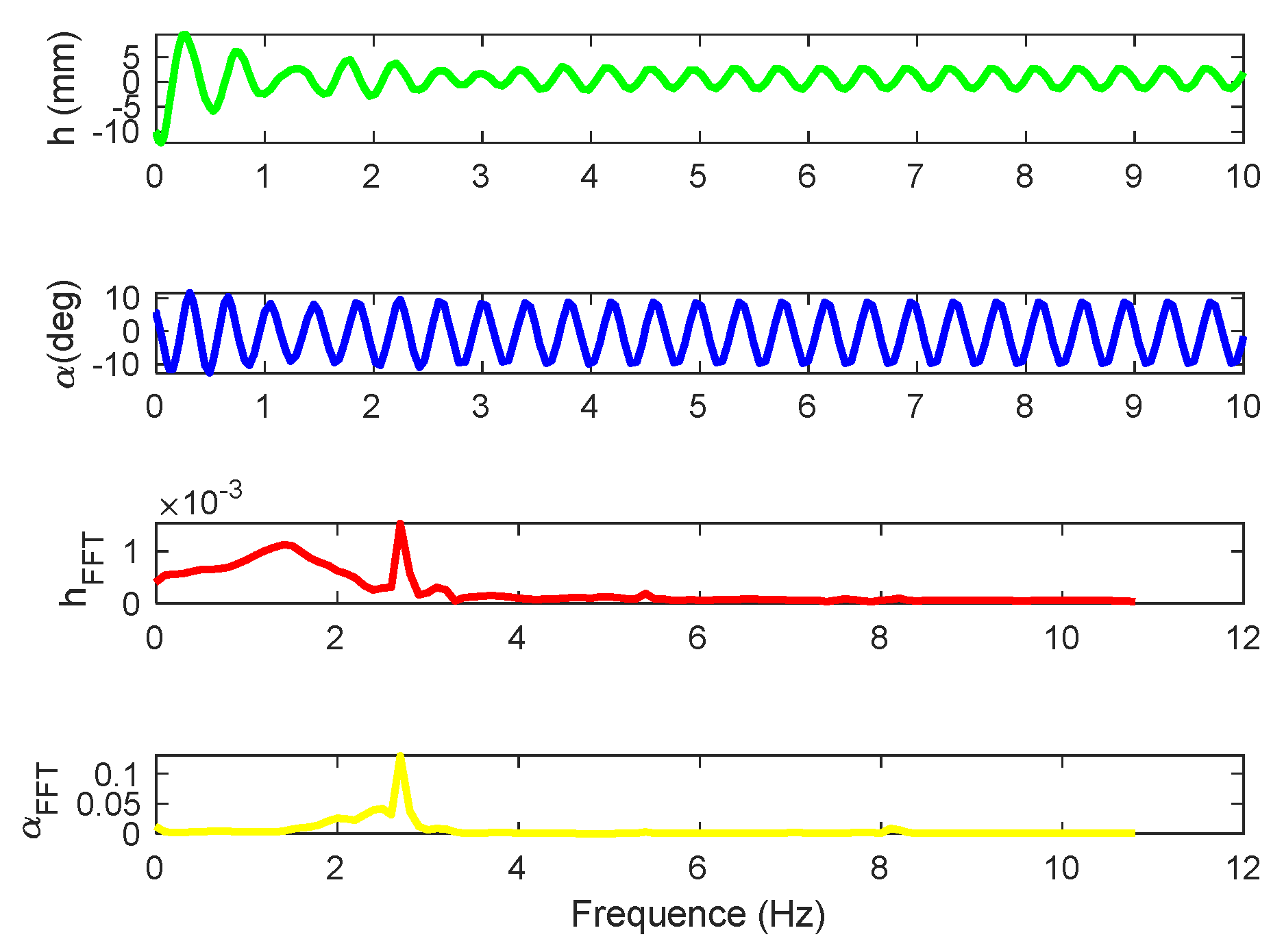
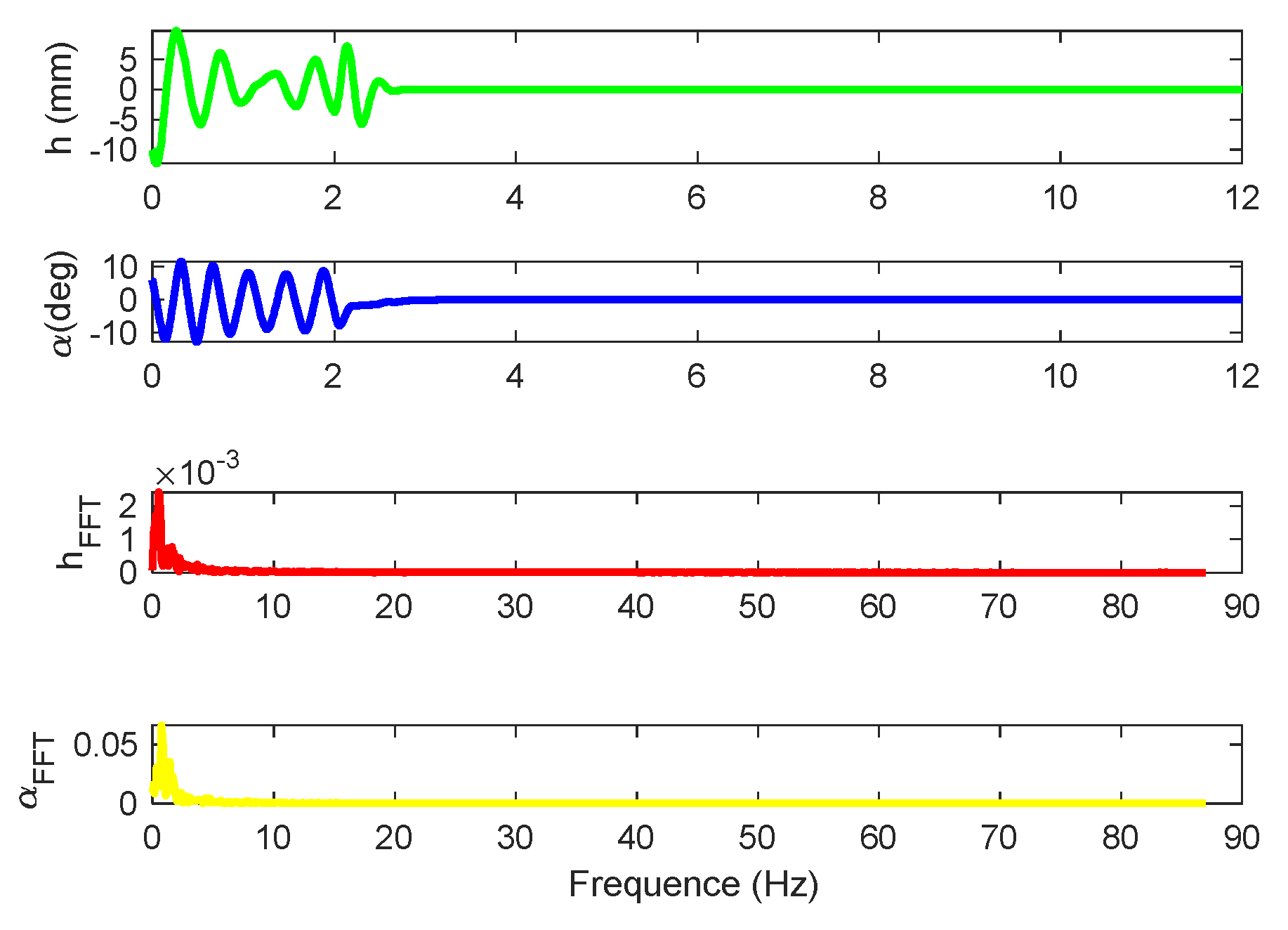
Figure 3.
Responses of the open-loop system at the airspeed of V = 11.4m/s.
Figure 3.
Responses of the open-loop system at the airspeed of V = 11.4m/s.
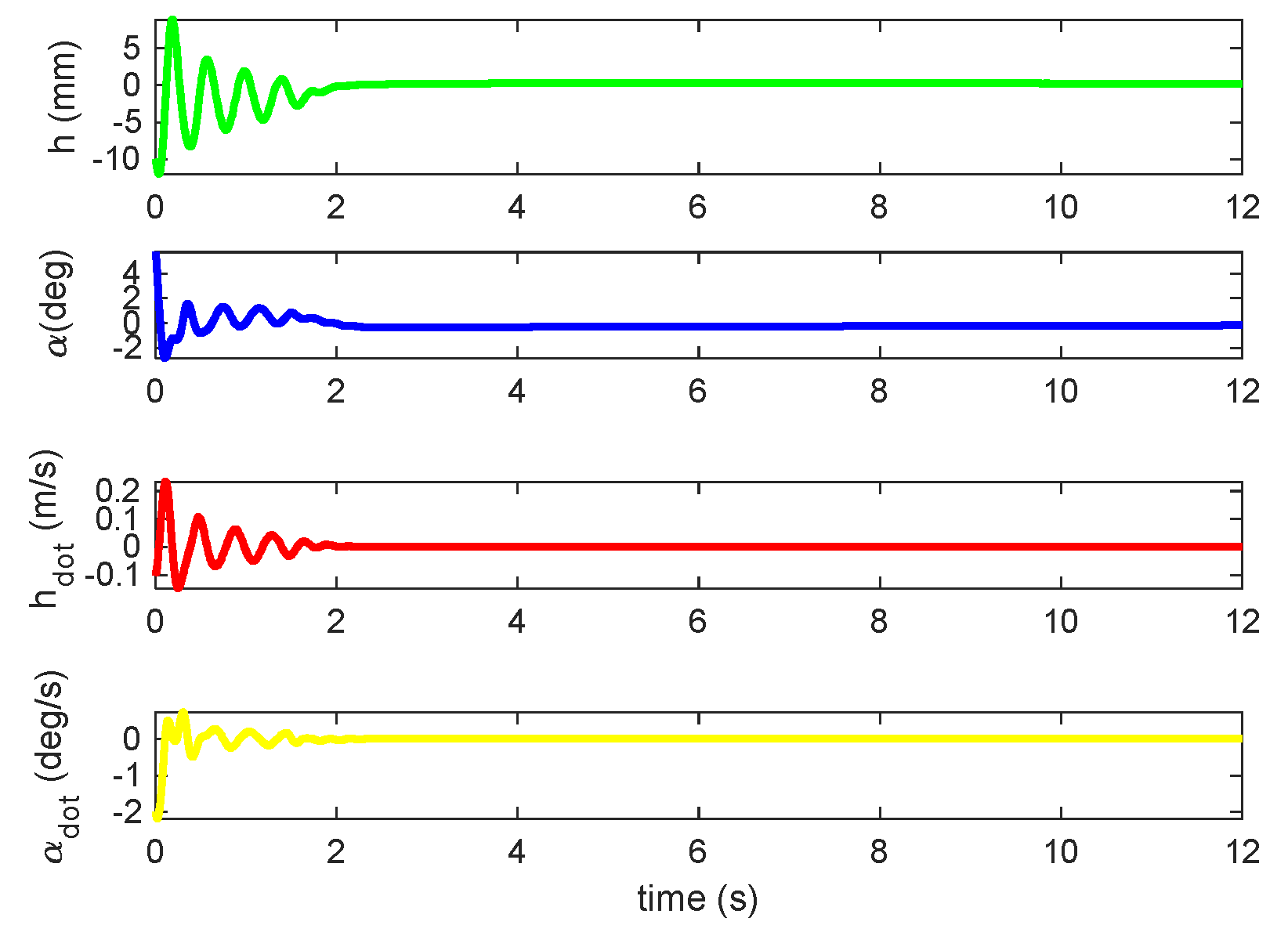
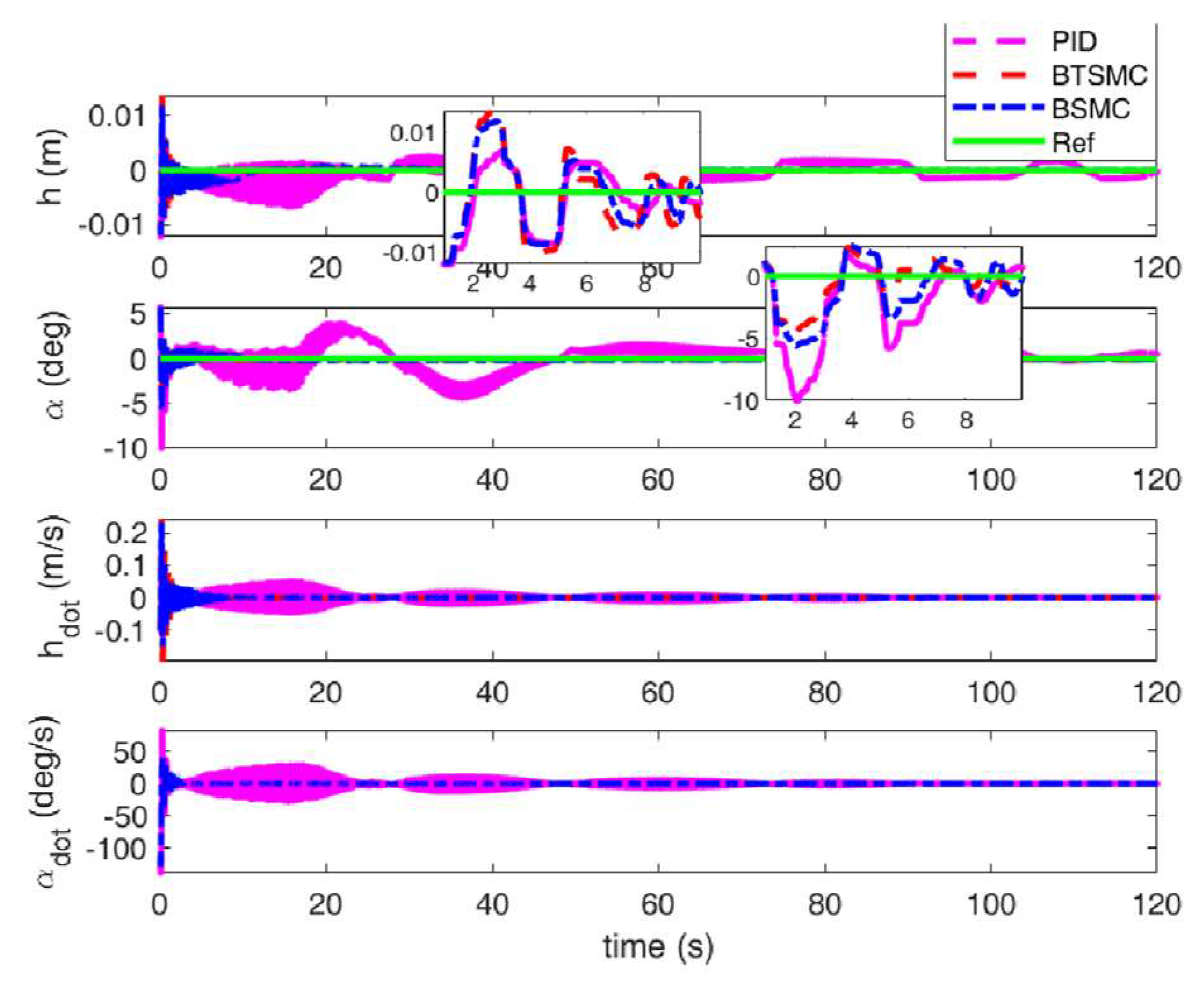
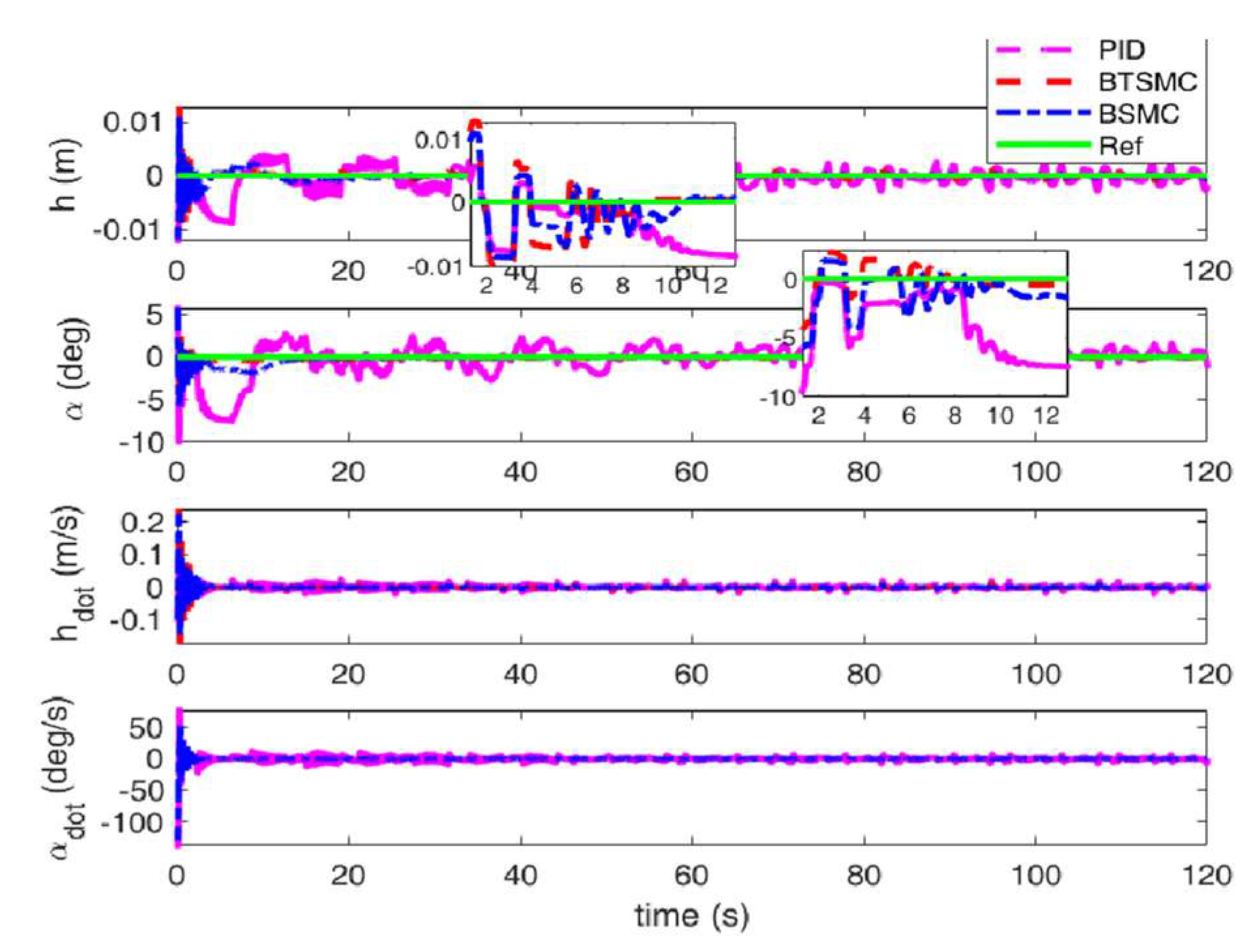
Figure 4.
Output responses of plunge and pitch motions.
Figure 4.
Output responses of plunge and pitch motions.
Figure 5.
Output responses of plunge and pitch motions without control (high stiffness).
Figure 5.
Output responses of plunge and pitch motions without control (high stiffness).
Figure 6.
Output responses of plunge and pitch motions with control inputs (high stiffness).
Figure 6.
Output responses of plunge and pitch motions with control inputs (high stiffness).
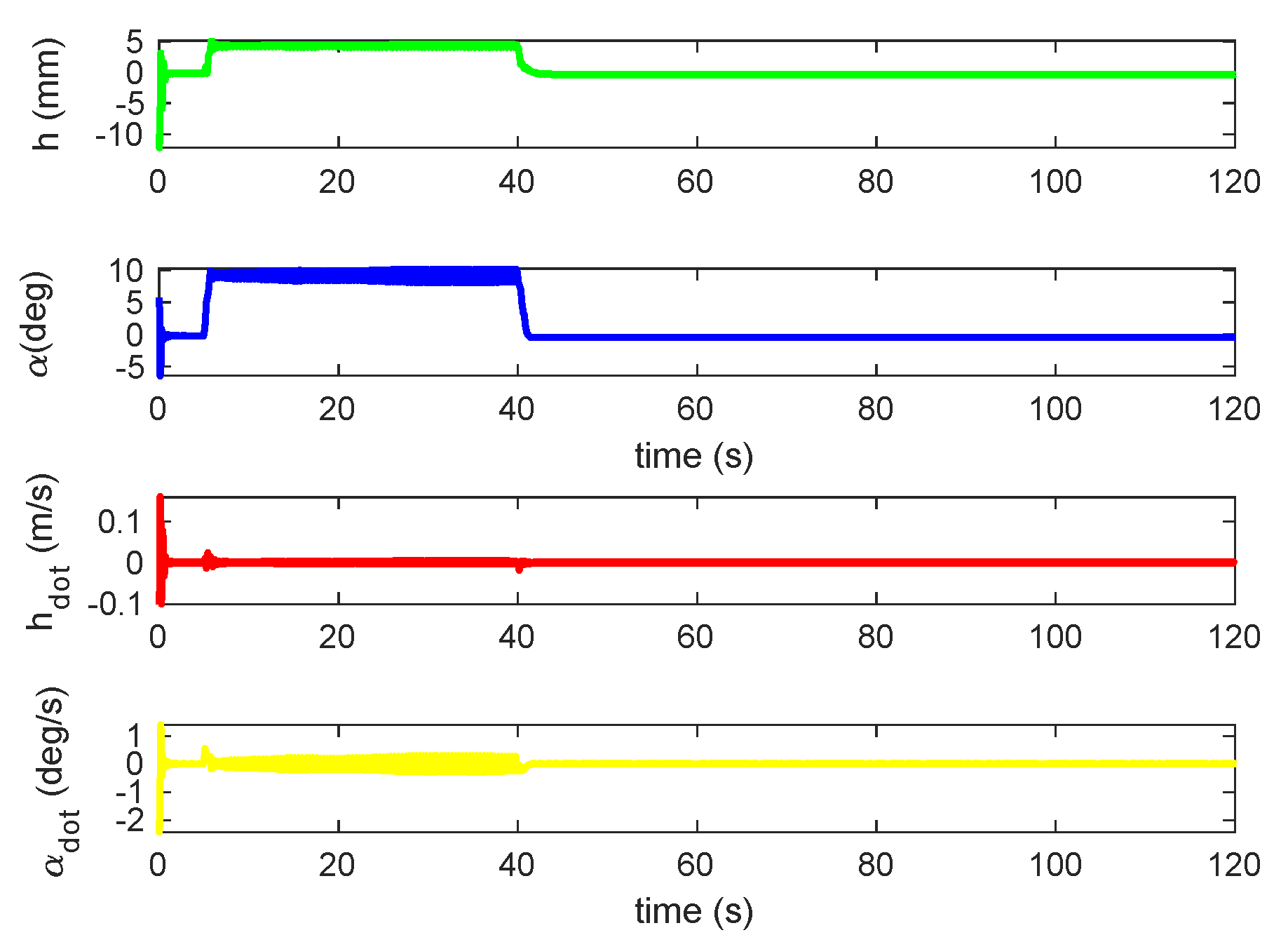
Figure 7.
Output responses of plunge and pitch motions under 10deg AOA command.
Figure 7.
Output responses of plunge and pitch motions under 10deg AOA command.
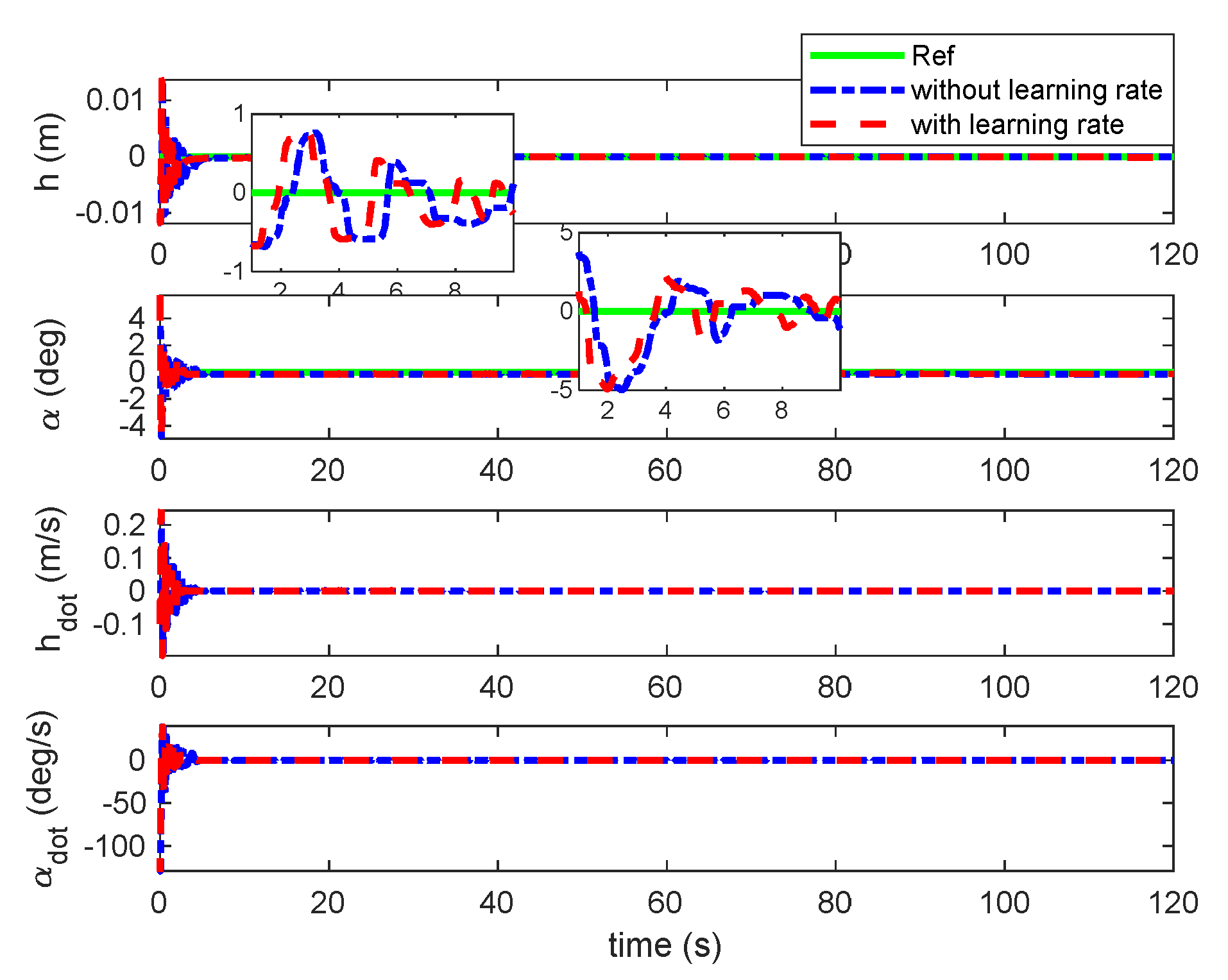
Figure 8.
Responses of plunge and pitch under triangular gust with quasi-steady aerodynamic loads.
Figure 8.
Responses of plunge and pitch under triangular gust with quasi-steady aerodynamic loads.
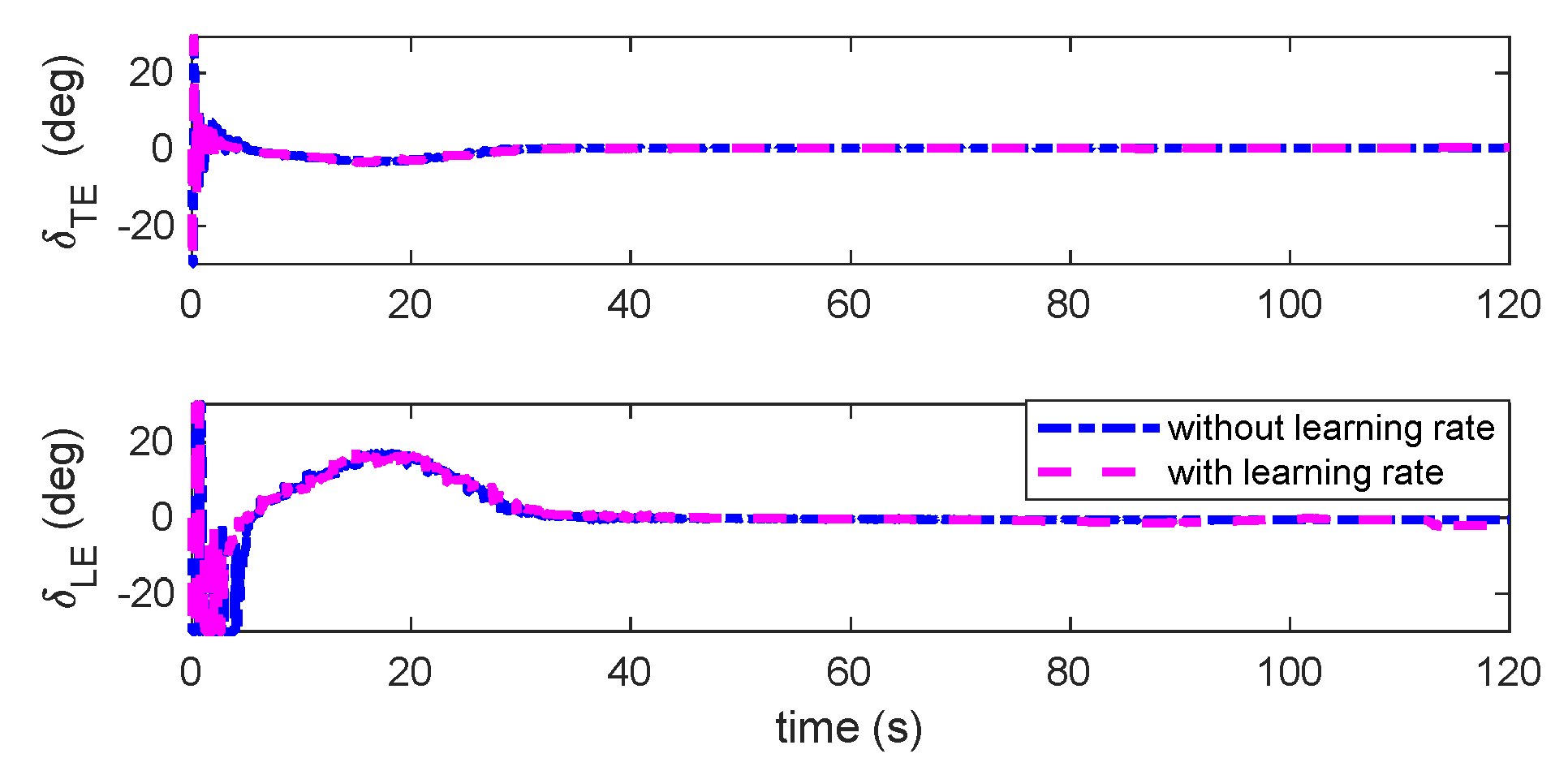
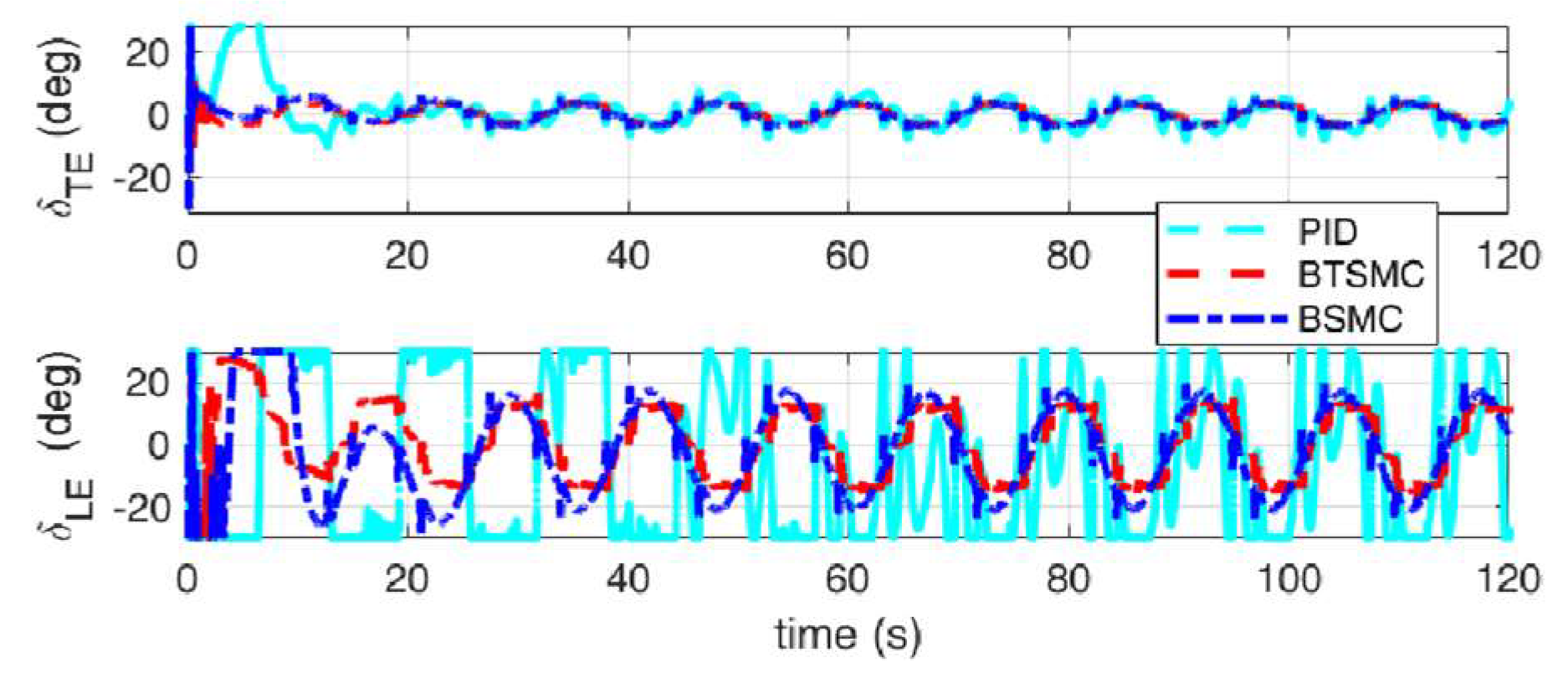
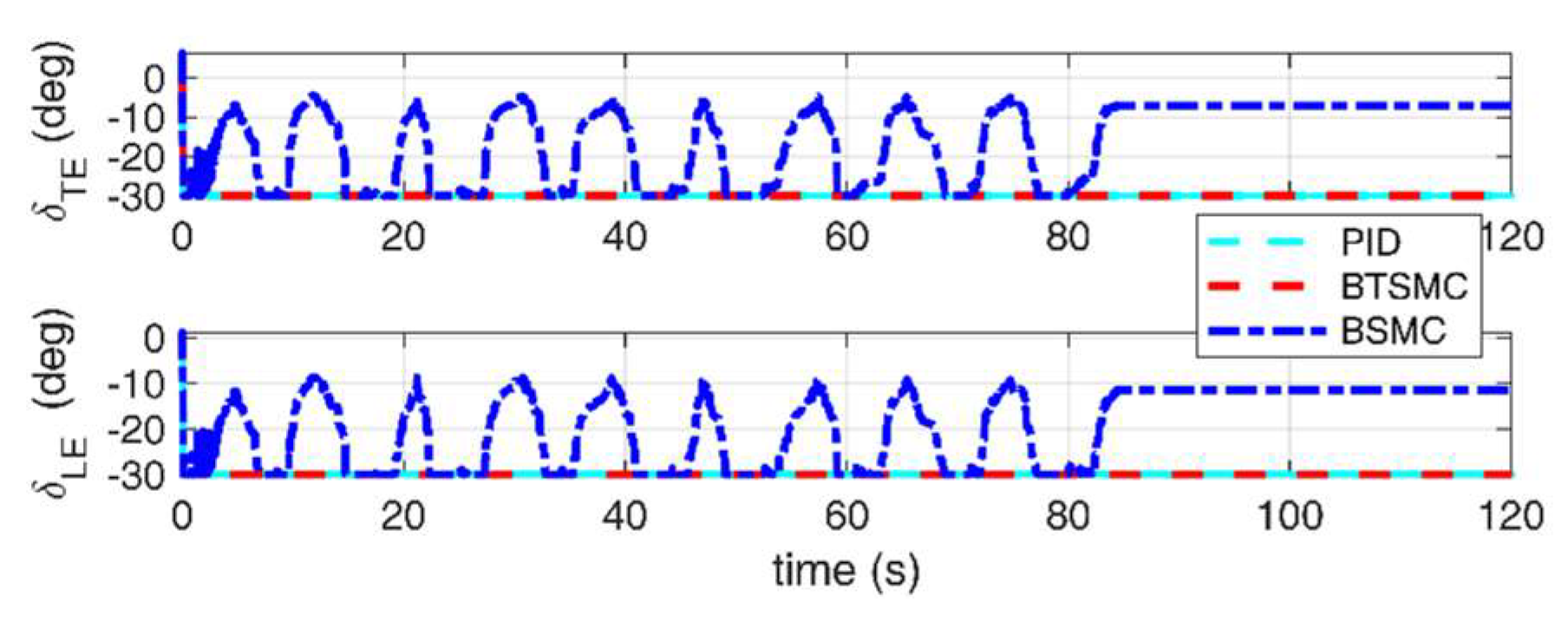
Figure 9.
Deflection of TE and LE control under triangular gust with quasi-steady aerodynamic loads.
Figure 9.
Deflection of TE and LE control under triangular gust with quasi-steady aerodynamic loads.
Figure 10.
Output responses of plunge and pitch under sine gust with quasi-steady aerodynamic loads.
Figure 10.
Output responses of plunge and pitch under sine gust with quasi-steady aerodynamic loads.
Figure 11.
Deflection of TE and LE control under sine gust with quasi-steady aerodynamic loads.
Figure 11.
Deflection of TE and LE control under sine gust with quasi-steady aerodynamic loads.
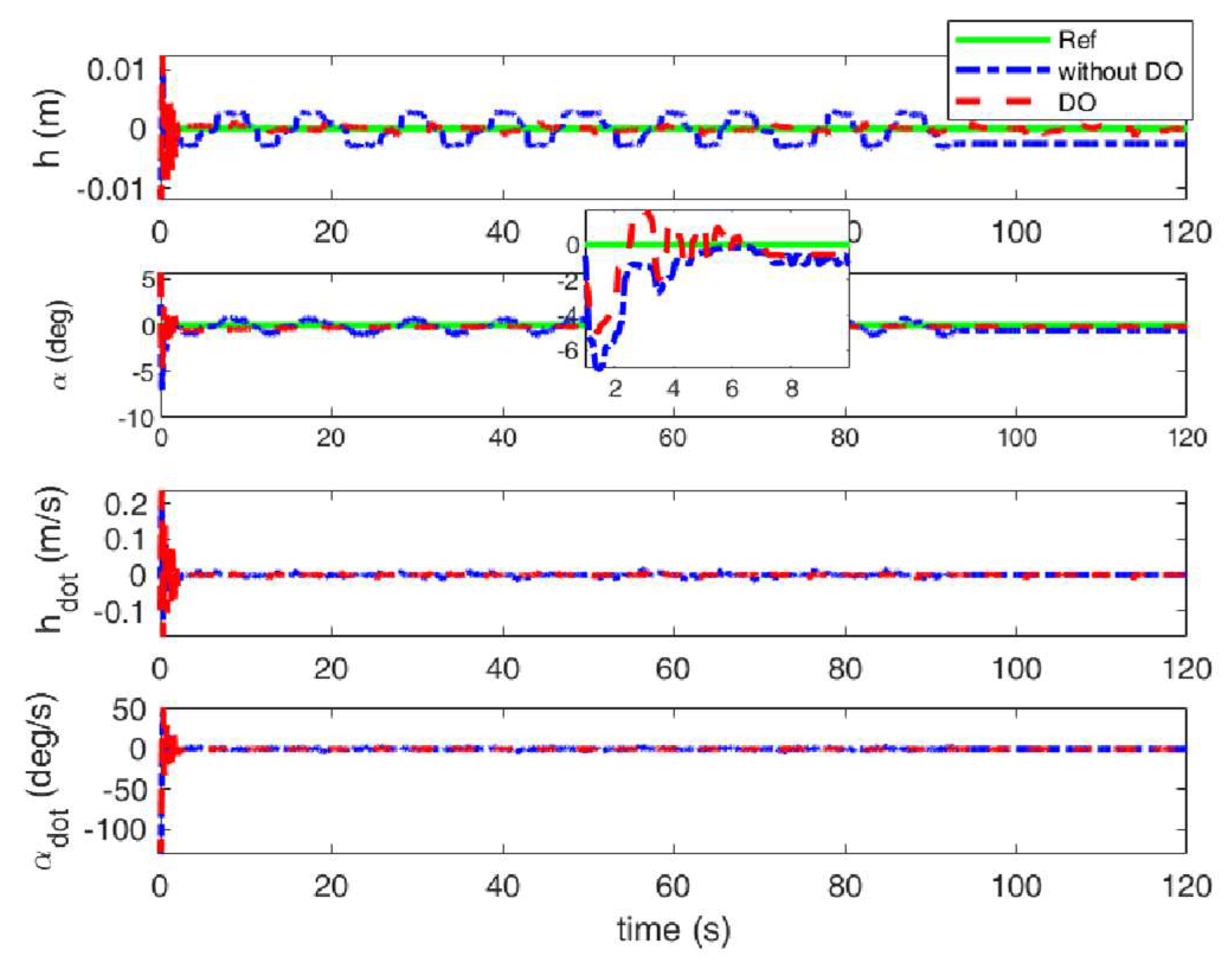
Figure 12.
Responses of plunge and pitch under triangular gust with quasi-steady aerodynamic loads.
Figure 12.
Responses of plunge and pitch under triangular gust with quasi-steady aerodynamic loads.
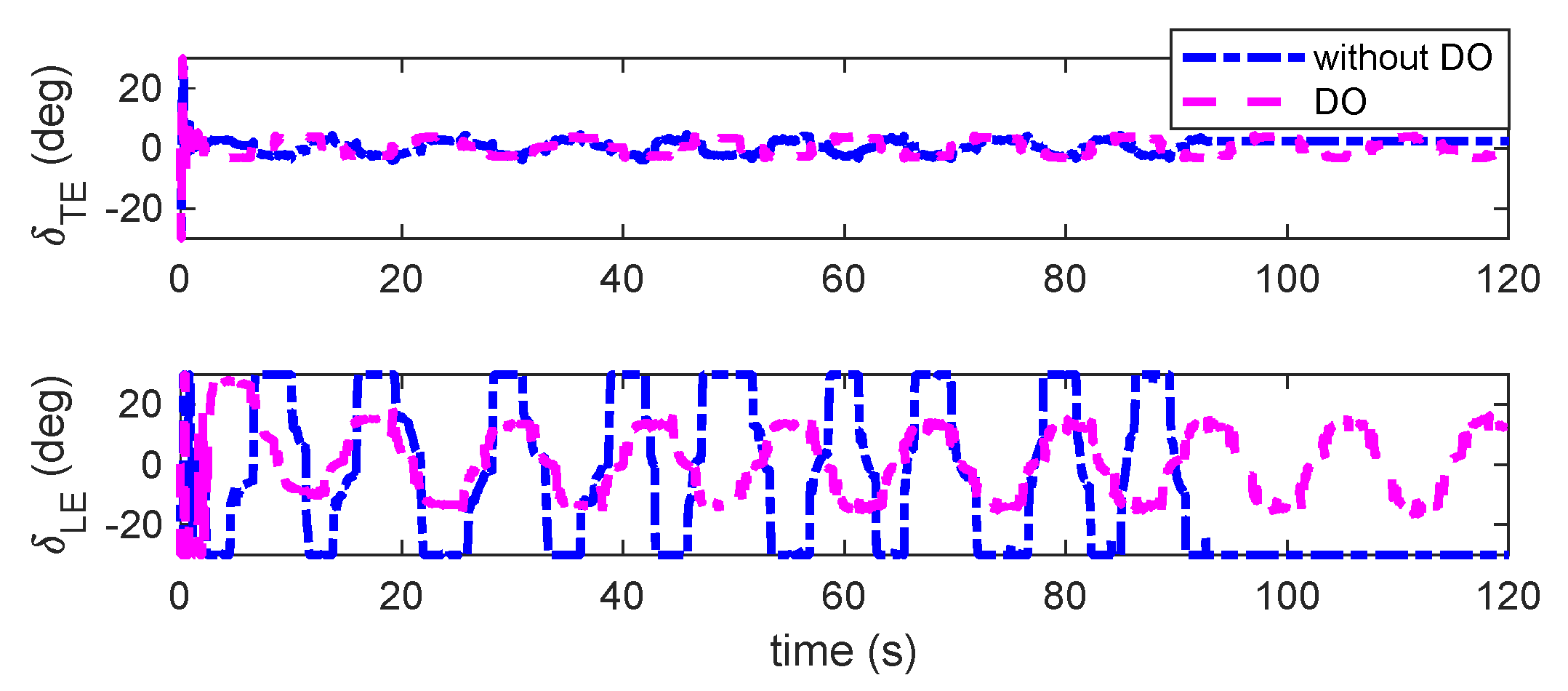
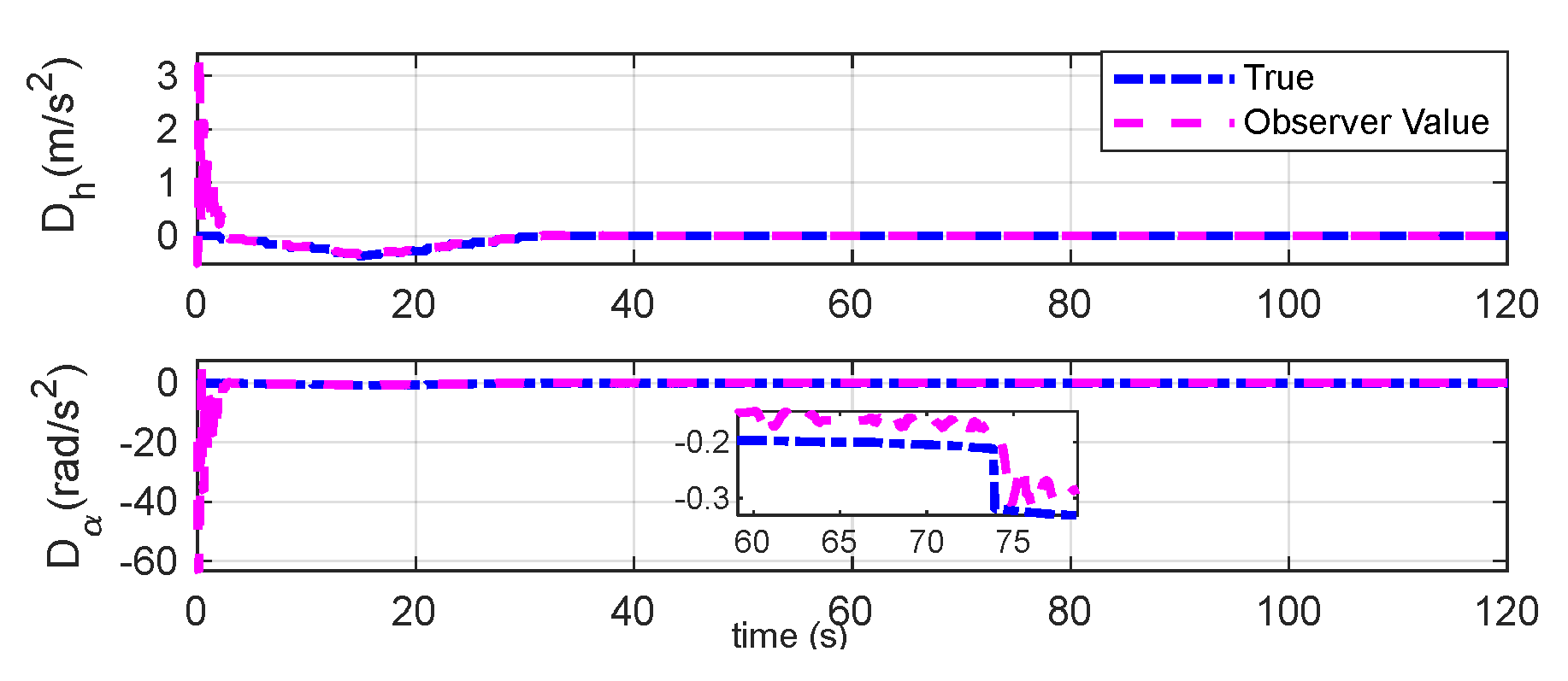
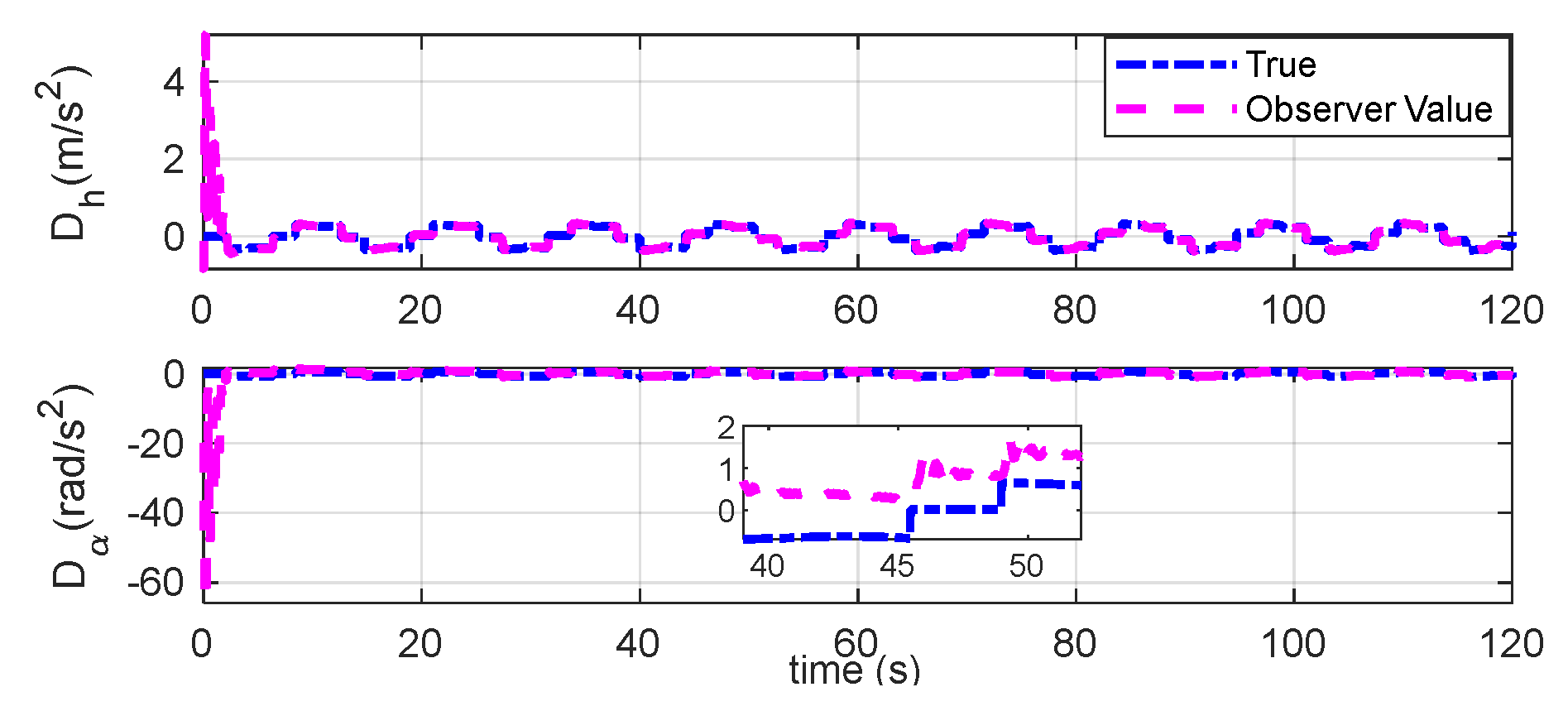
Figure 13.
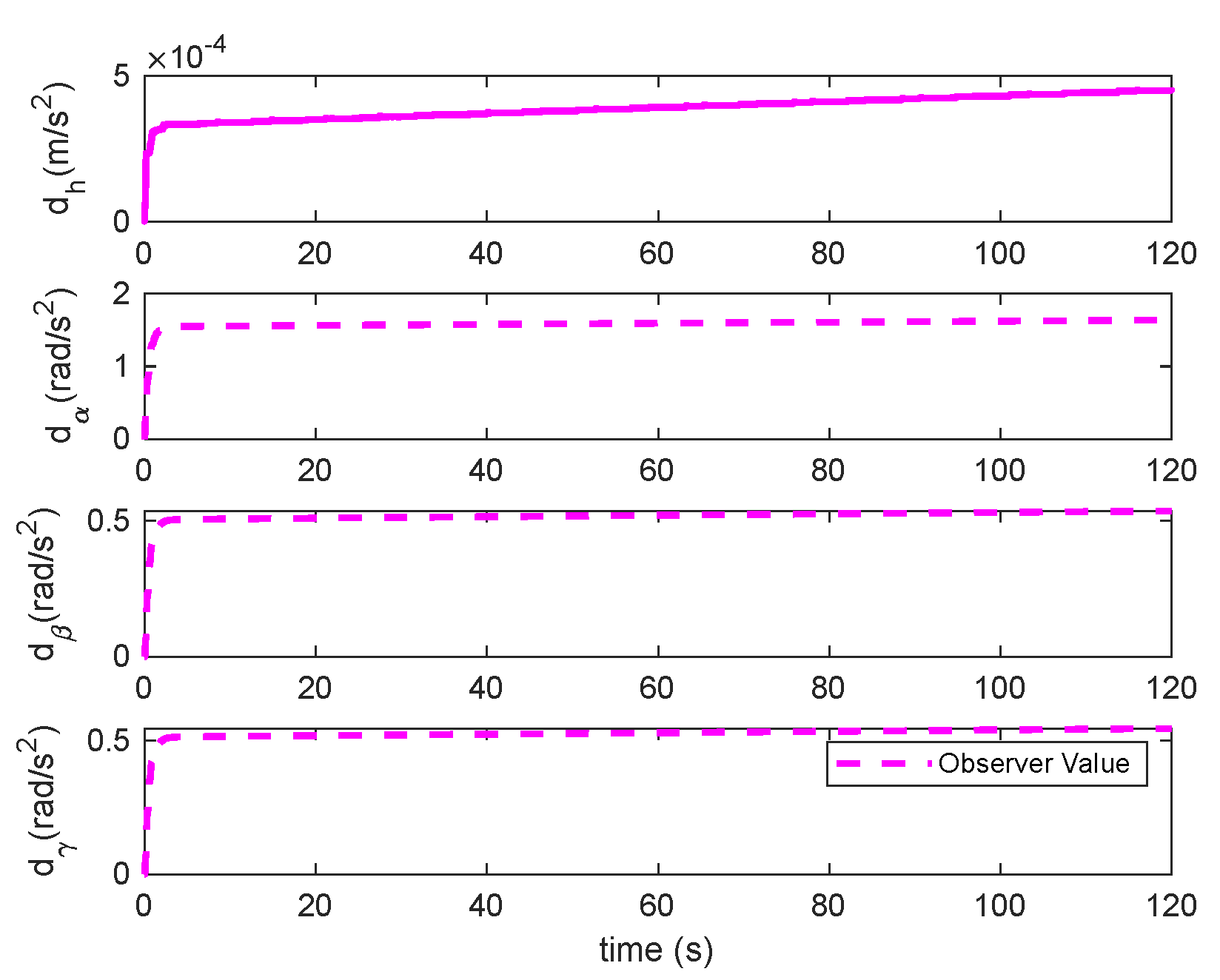
Observable disturbances estimation under triangular gust.
Figure 13.
Observable disturbances estimation under triangular gust.
Figure 14.
Unobservable disturbances estimation under triangular gust.
Figure 14.
Unobservable disturbances estimation under triangular gust.
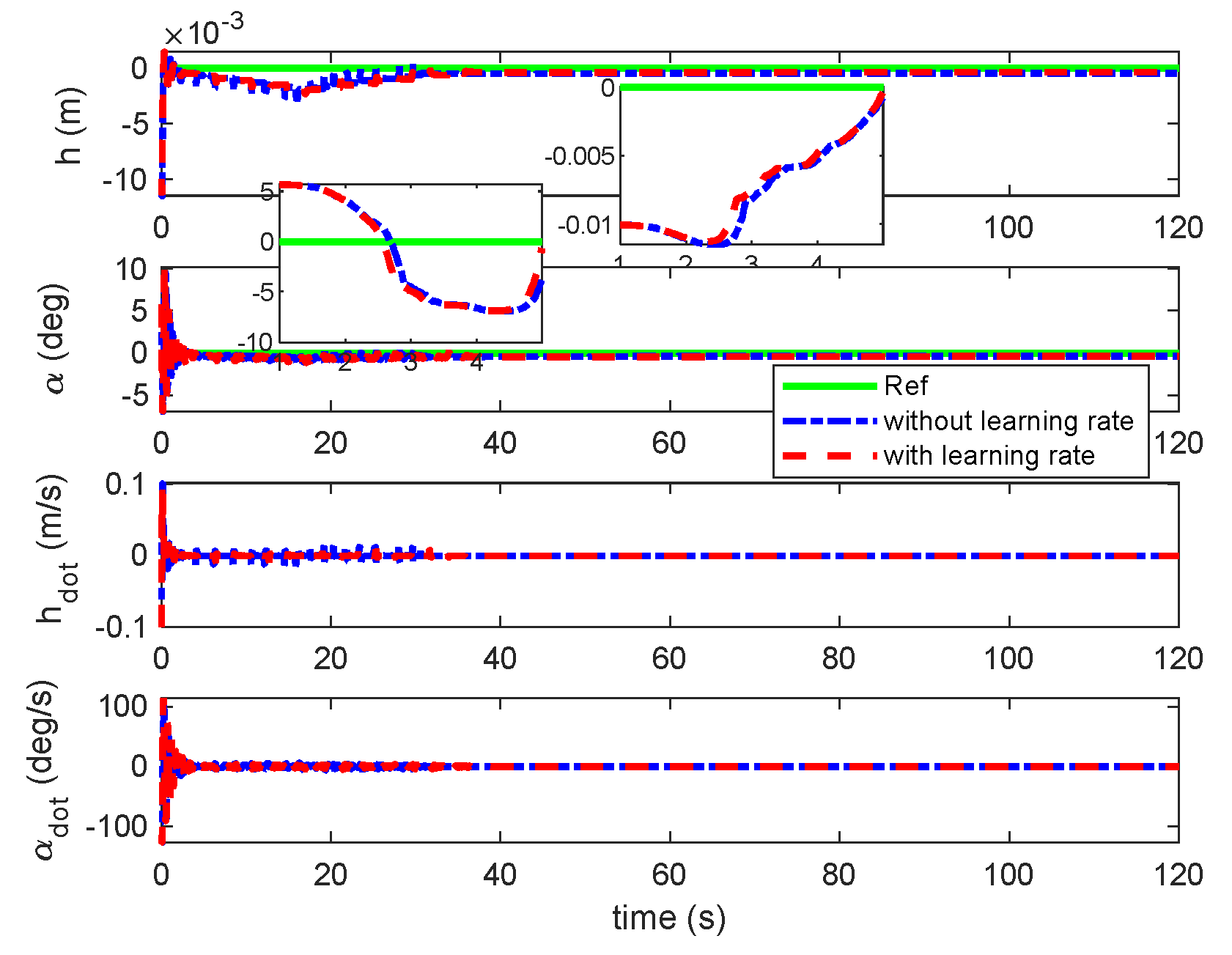
Figure 15.
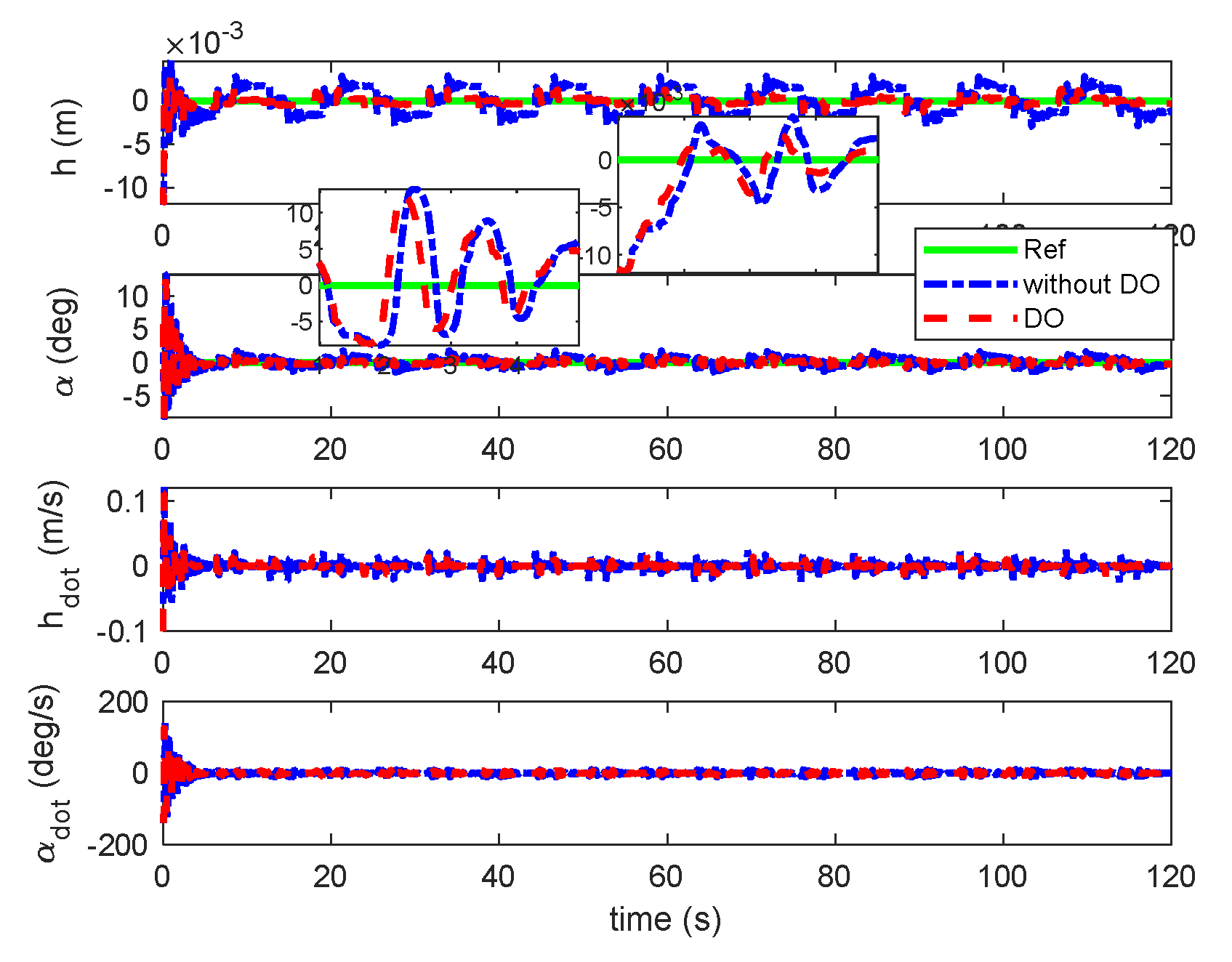
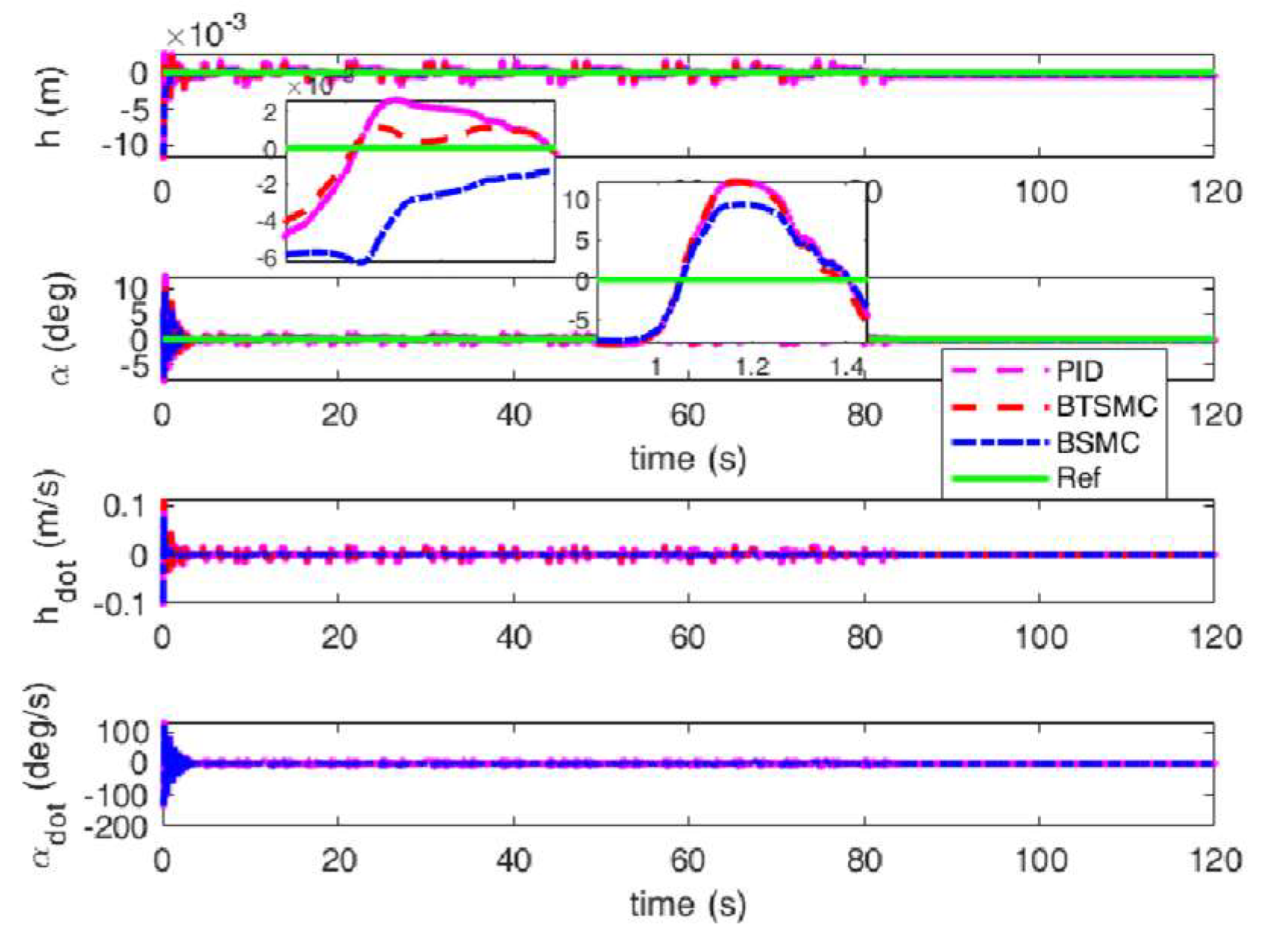
Responses of plunge and pitch under triangular gust with unsteady aerodynamic loads.
Figure 15.
Responses of plunge and pitch under triangular gust with unsteady aerodynamic loads.
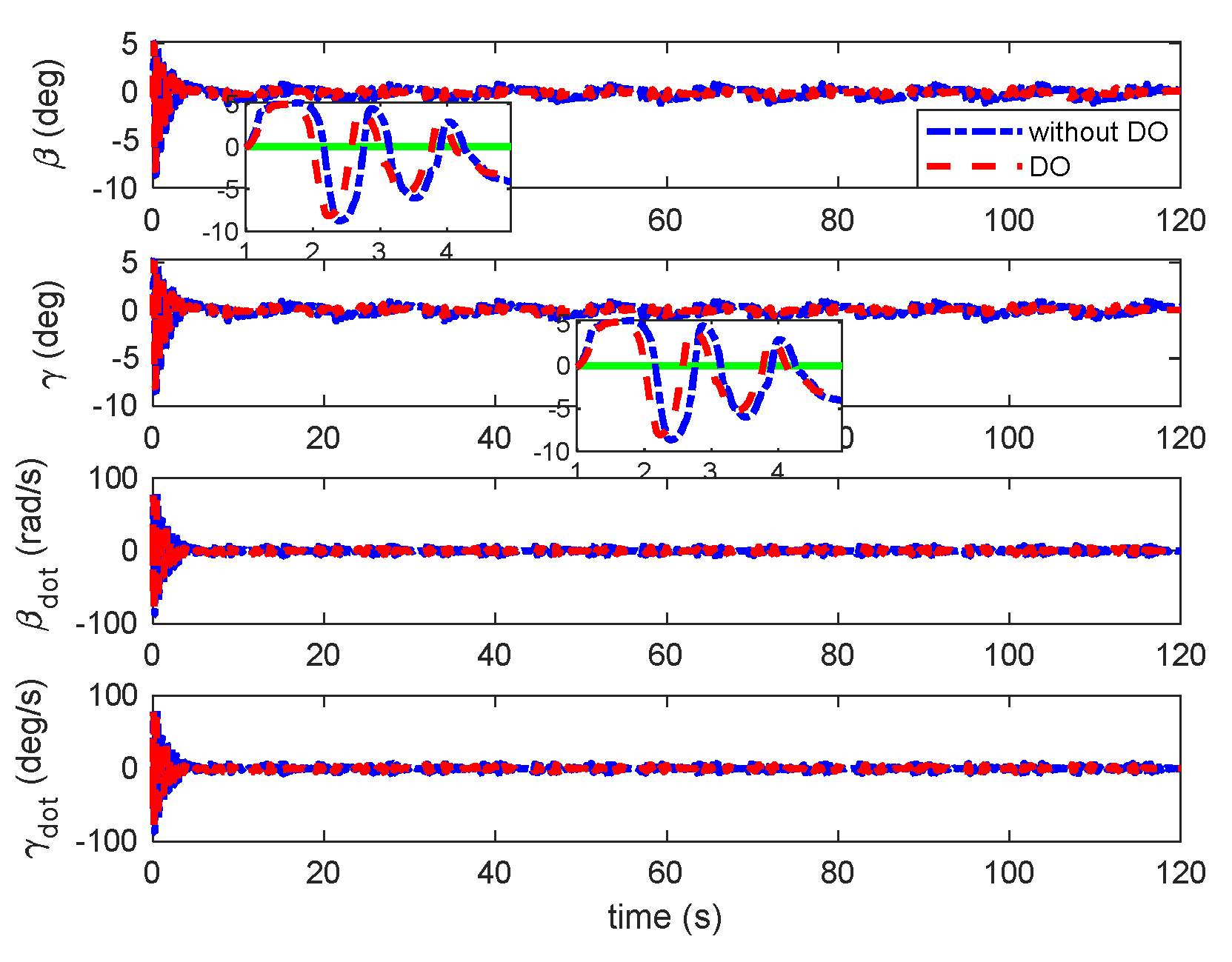
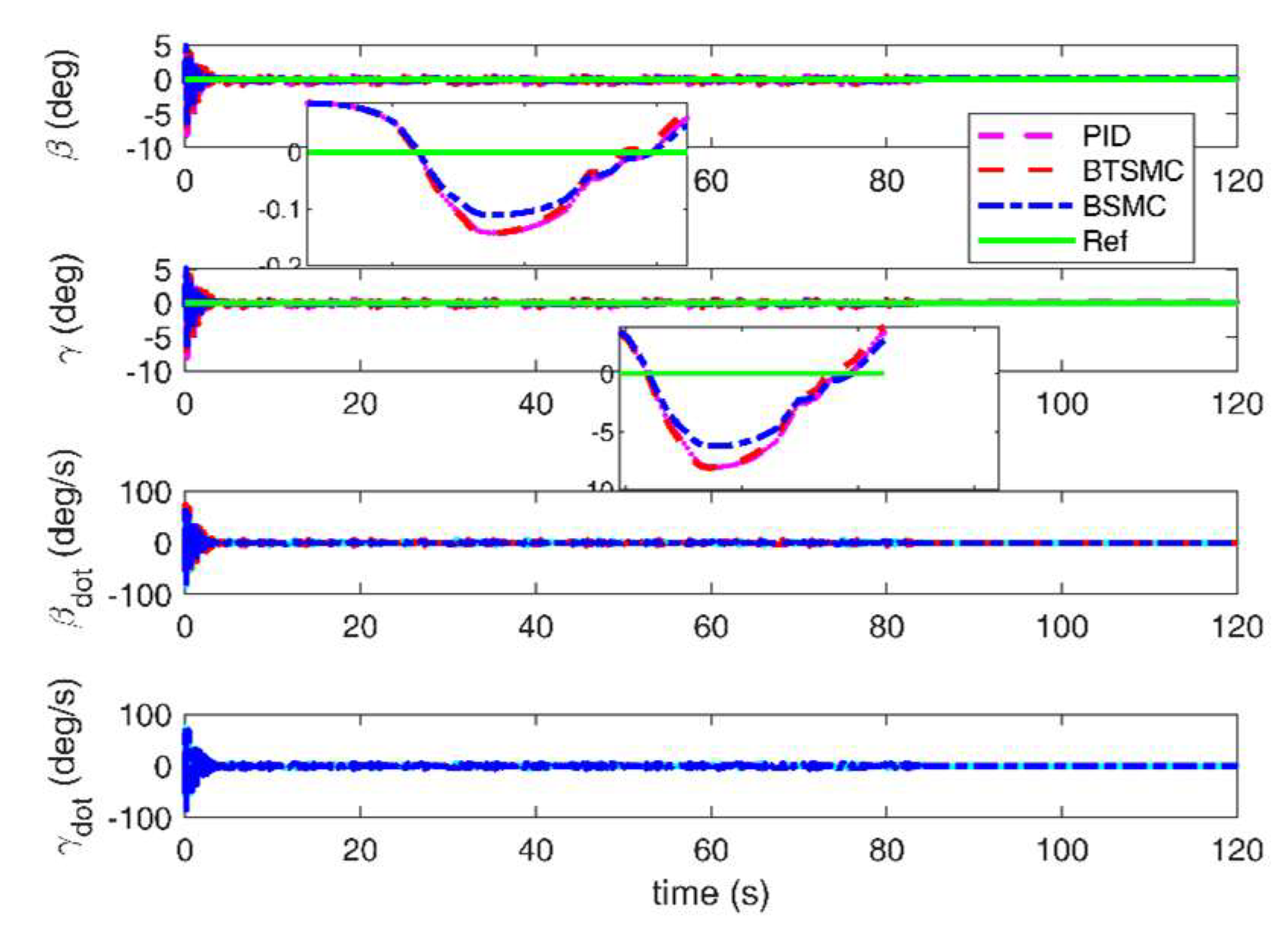
Figure 16.
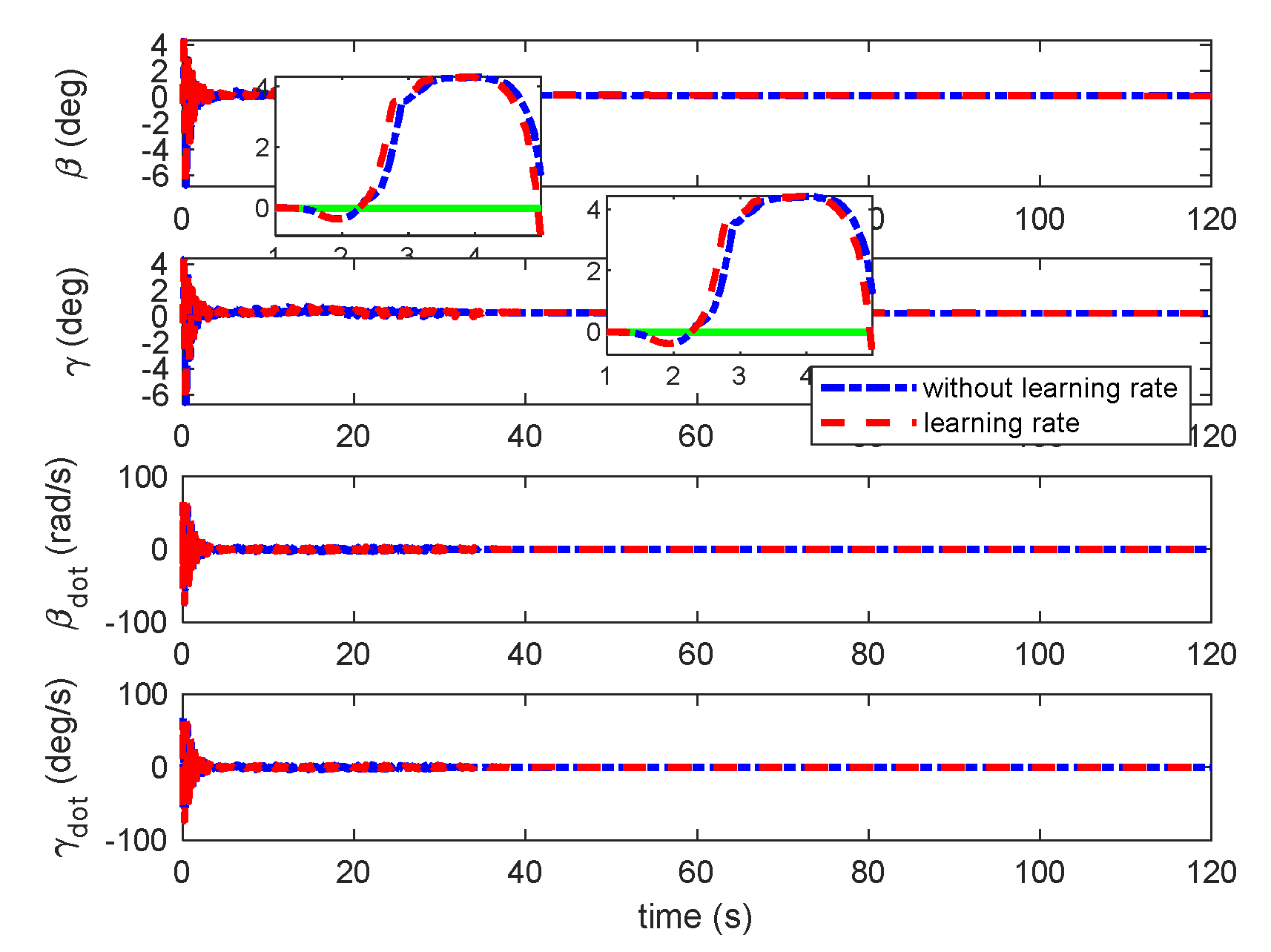
Responses of β and γ under triangular gust with unsteady aerodynamic loads.
Figure 16.
Responses of β and γ under triangular gust with unsteady aerodynamic loads.
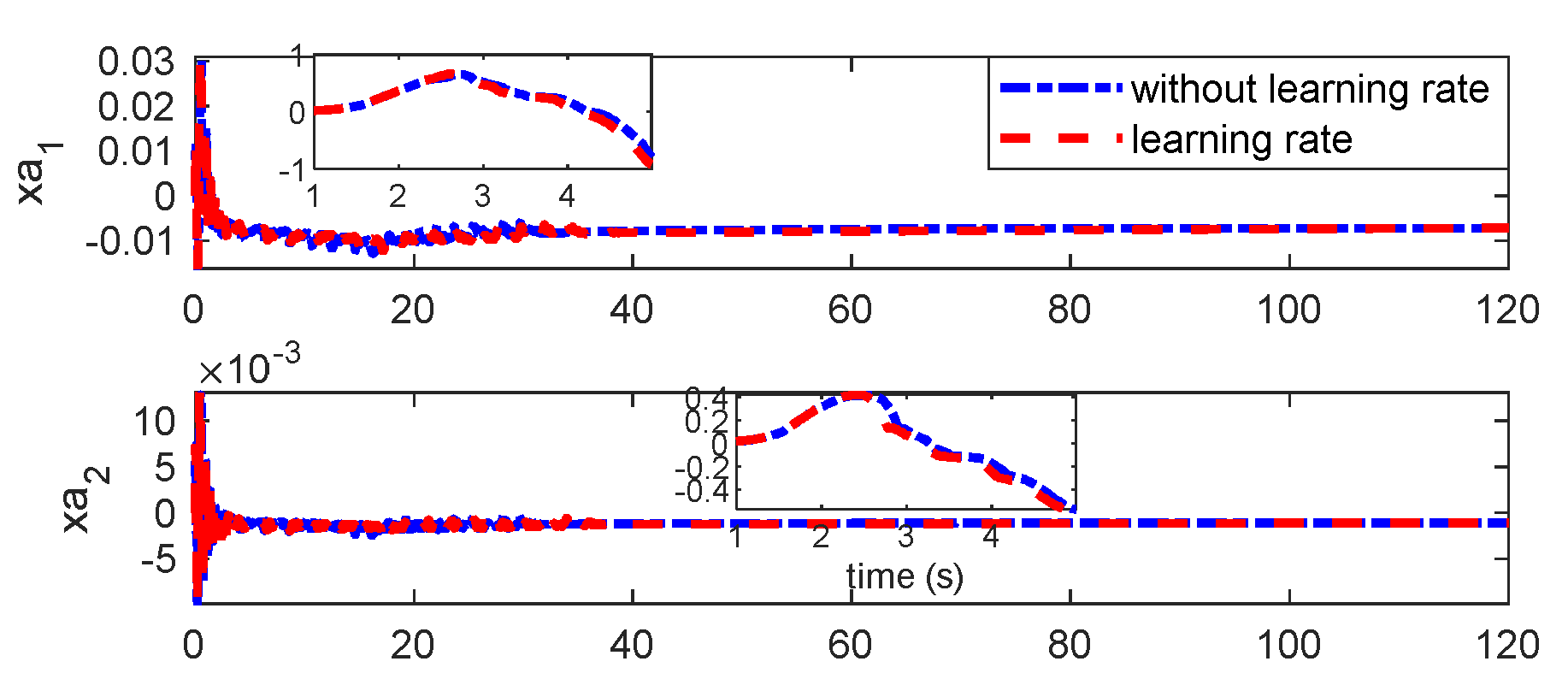
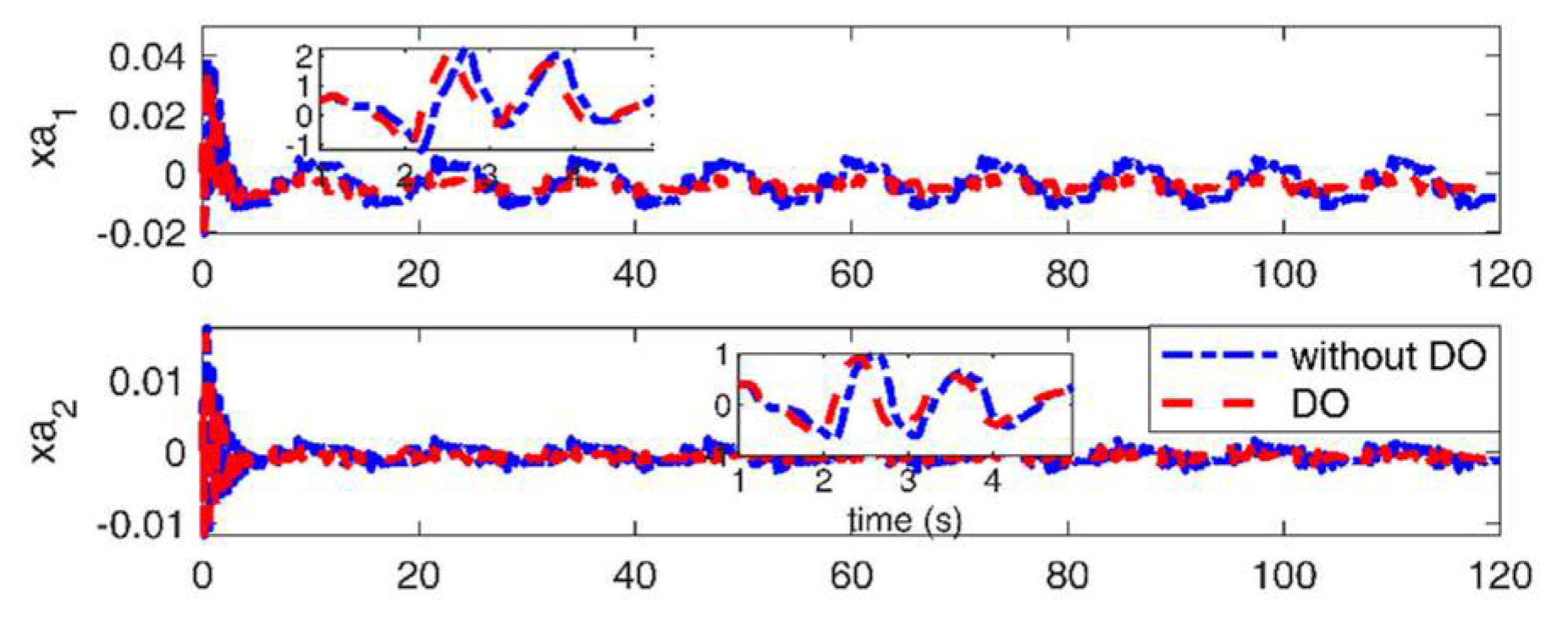
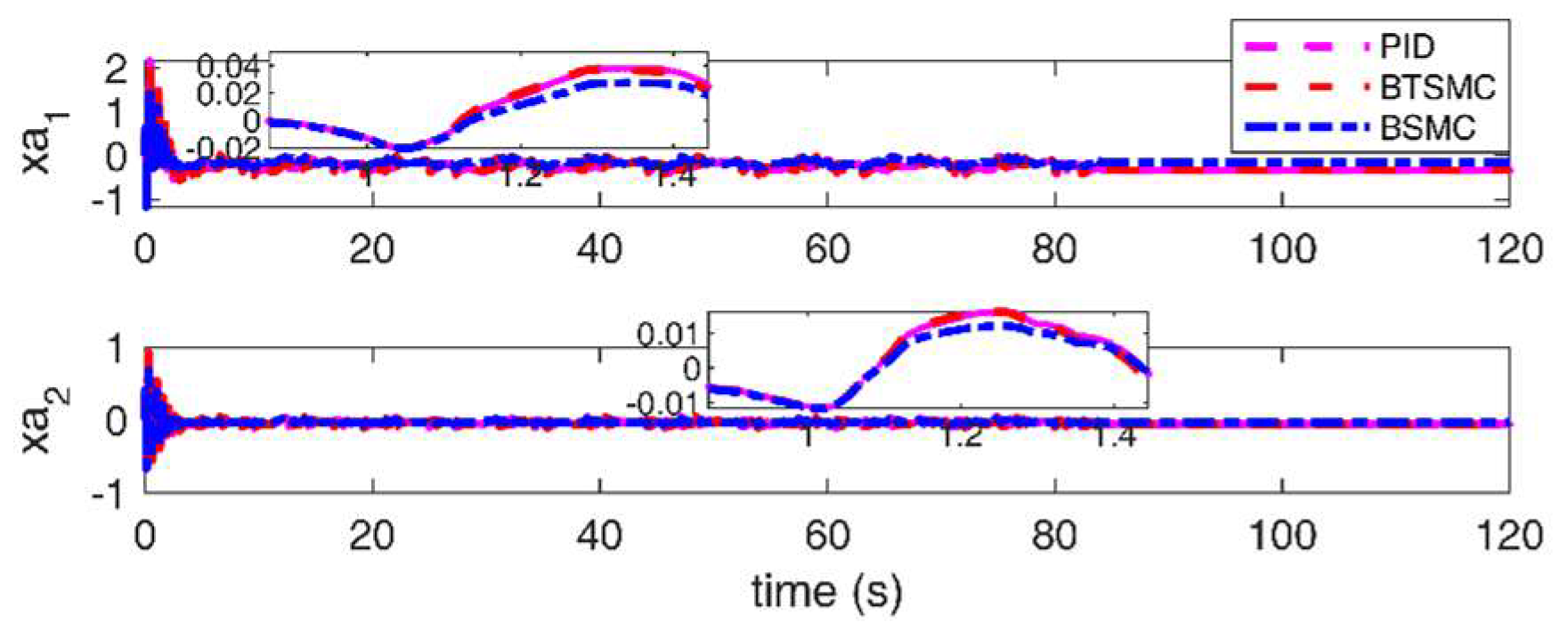
Figure 17.
Responses of aerodynamic states under triangular gust with unsteady aerodynamic loads.
Figure 17.
Responses of aerodynamic states under triangular gust with unsteady aerodynamic loads.
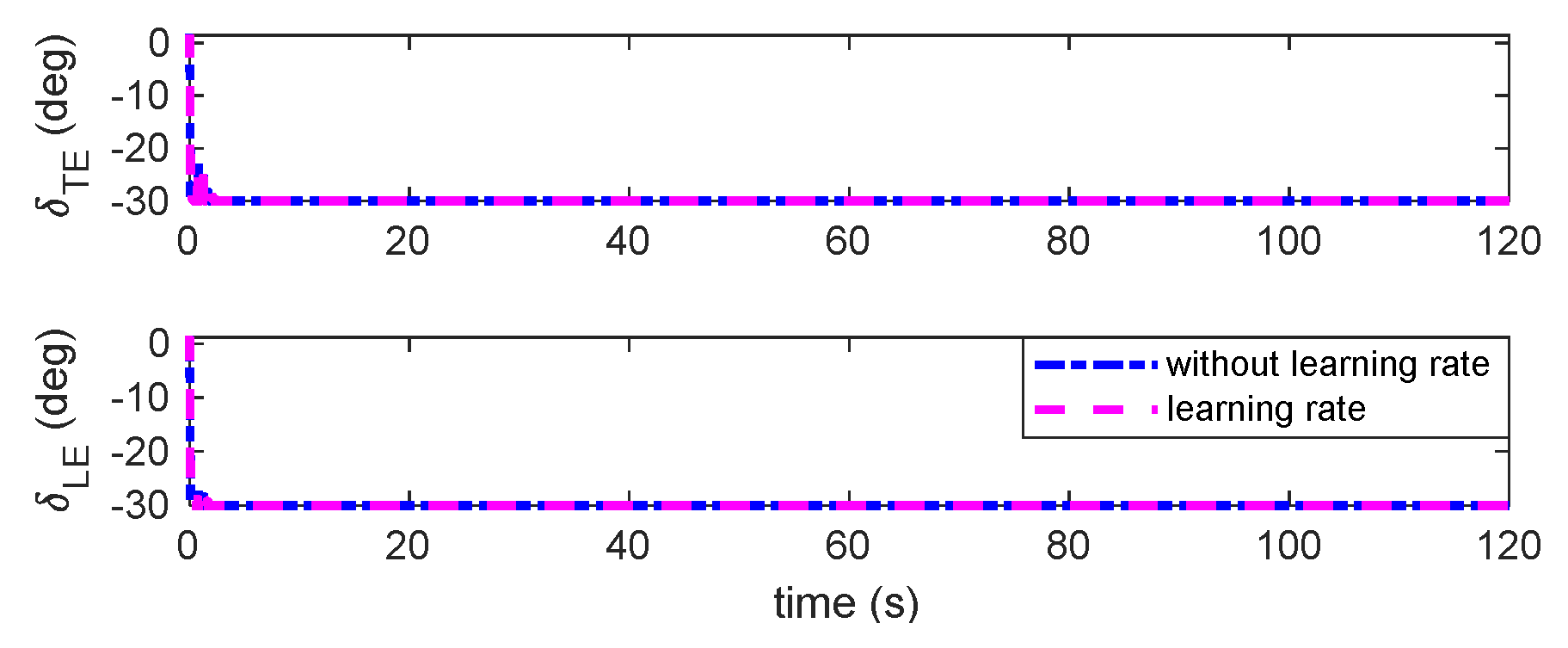
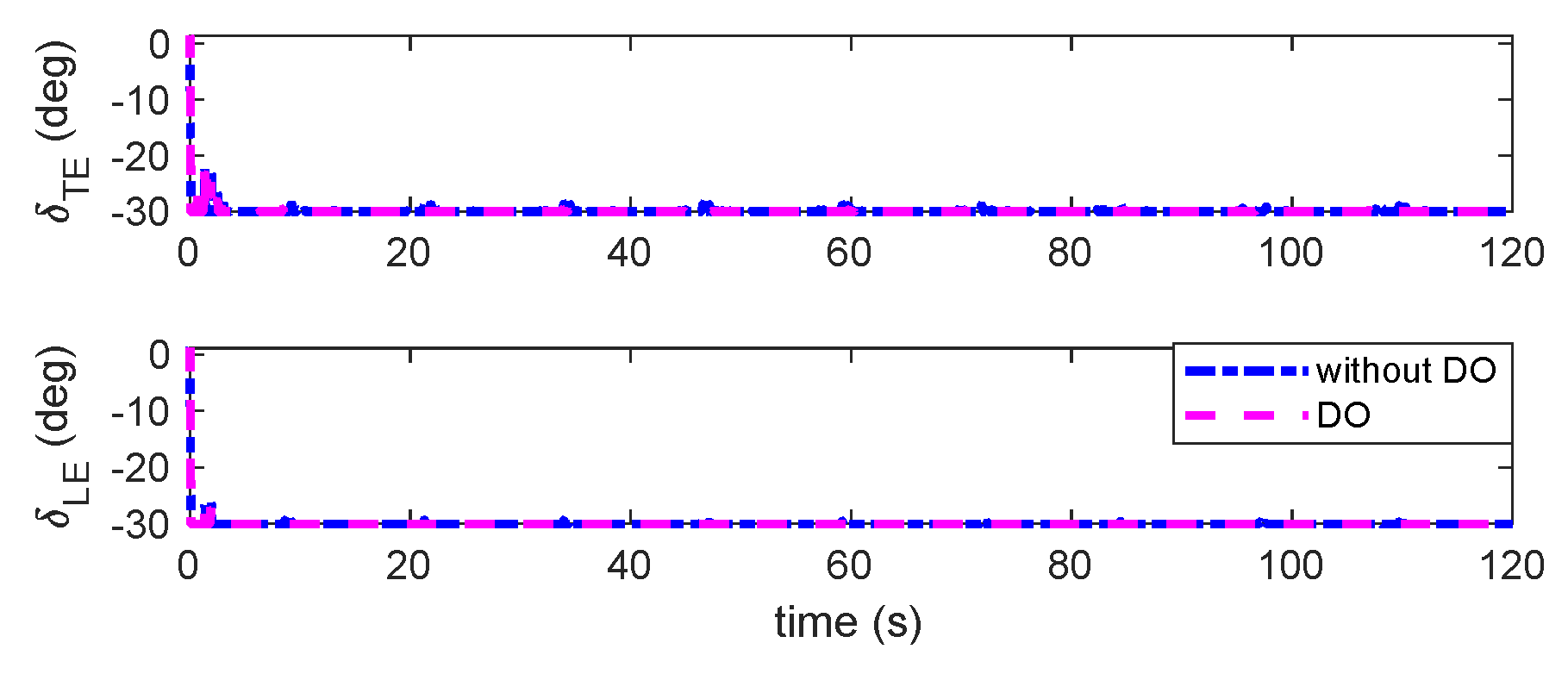
Figure 18.
Deflection of TE and LE control under triangular gust with unsteady aerodynamic loads.
Figure 18.
Deflection of TE and LE control under triangular gust with unsteady aerodynamic loads.
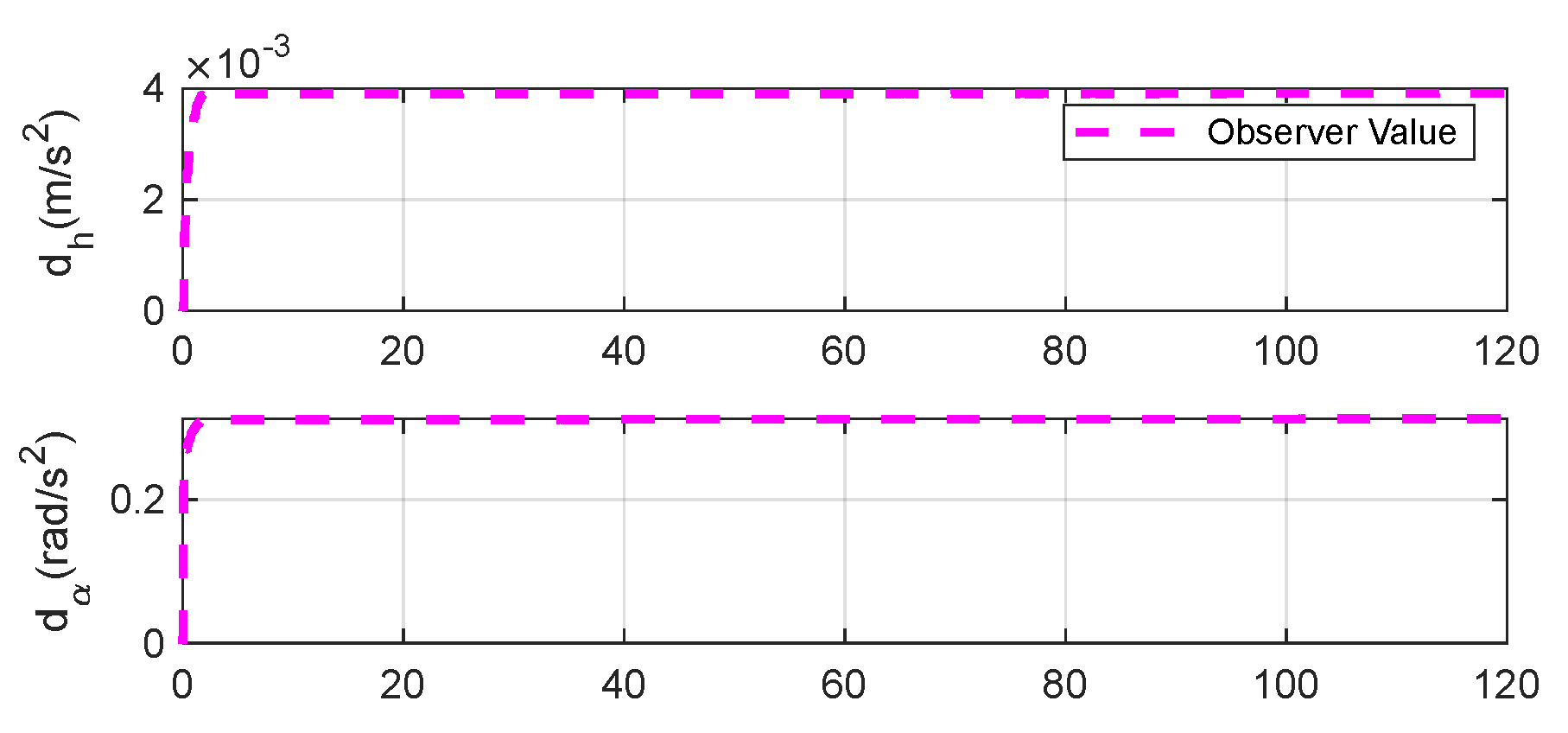
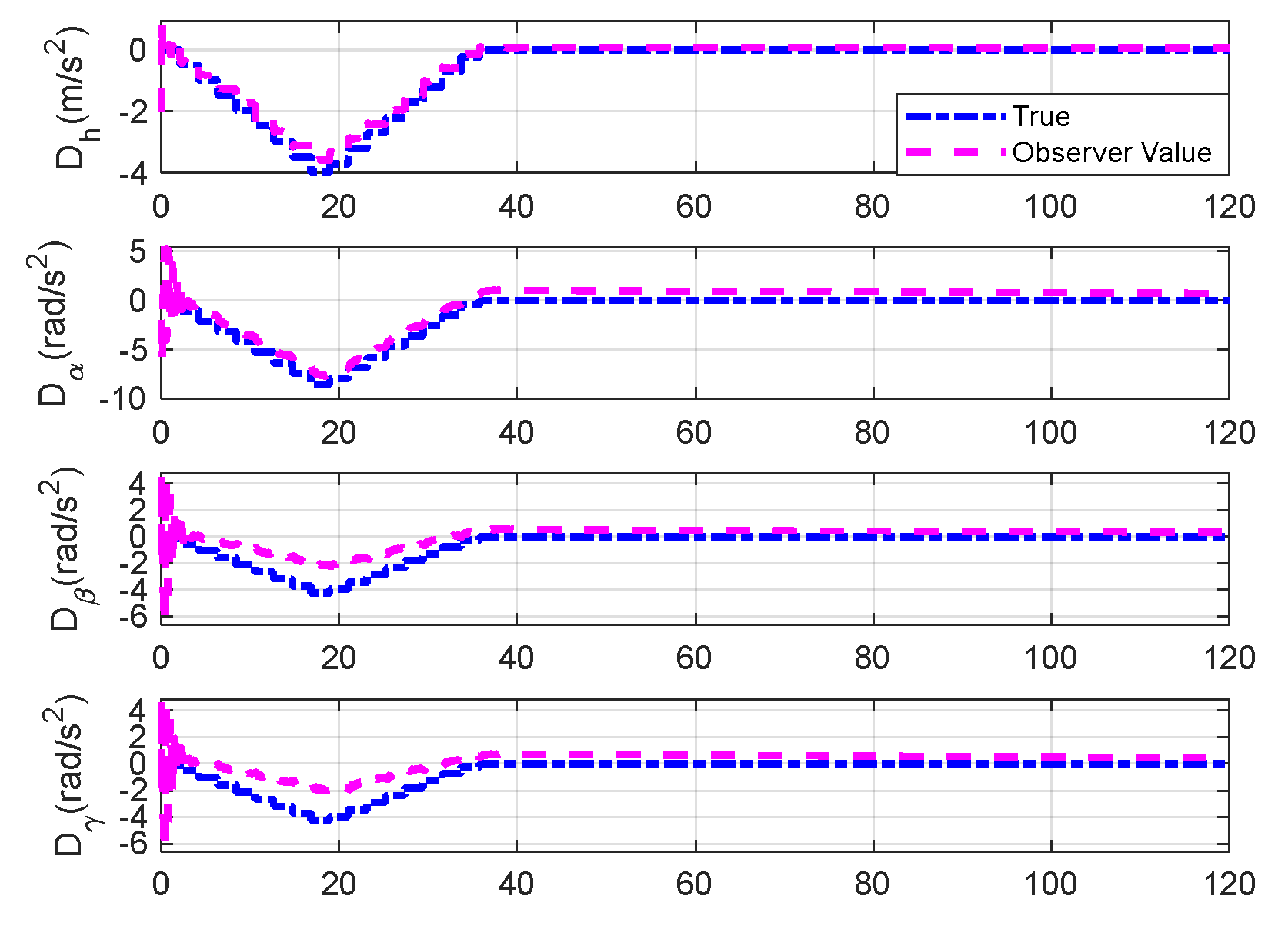
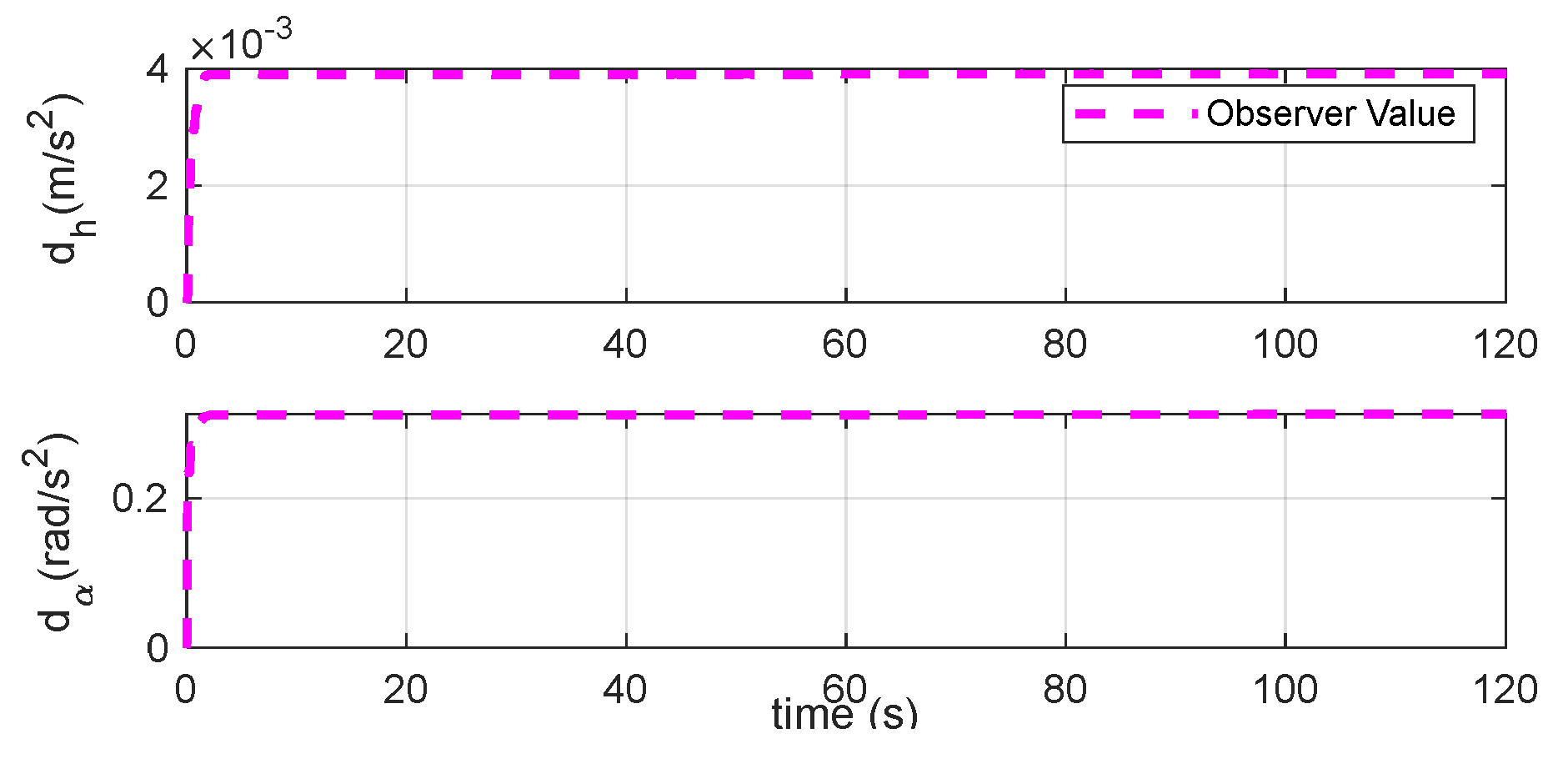
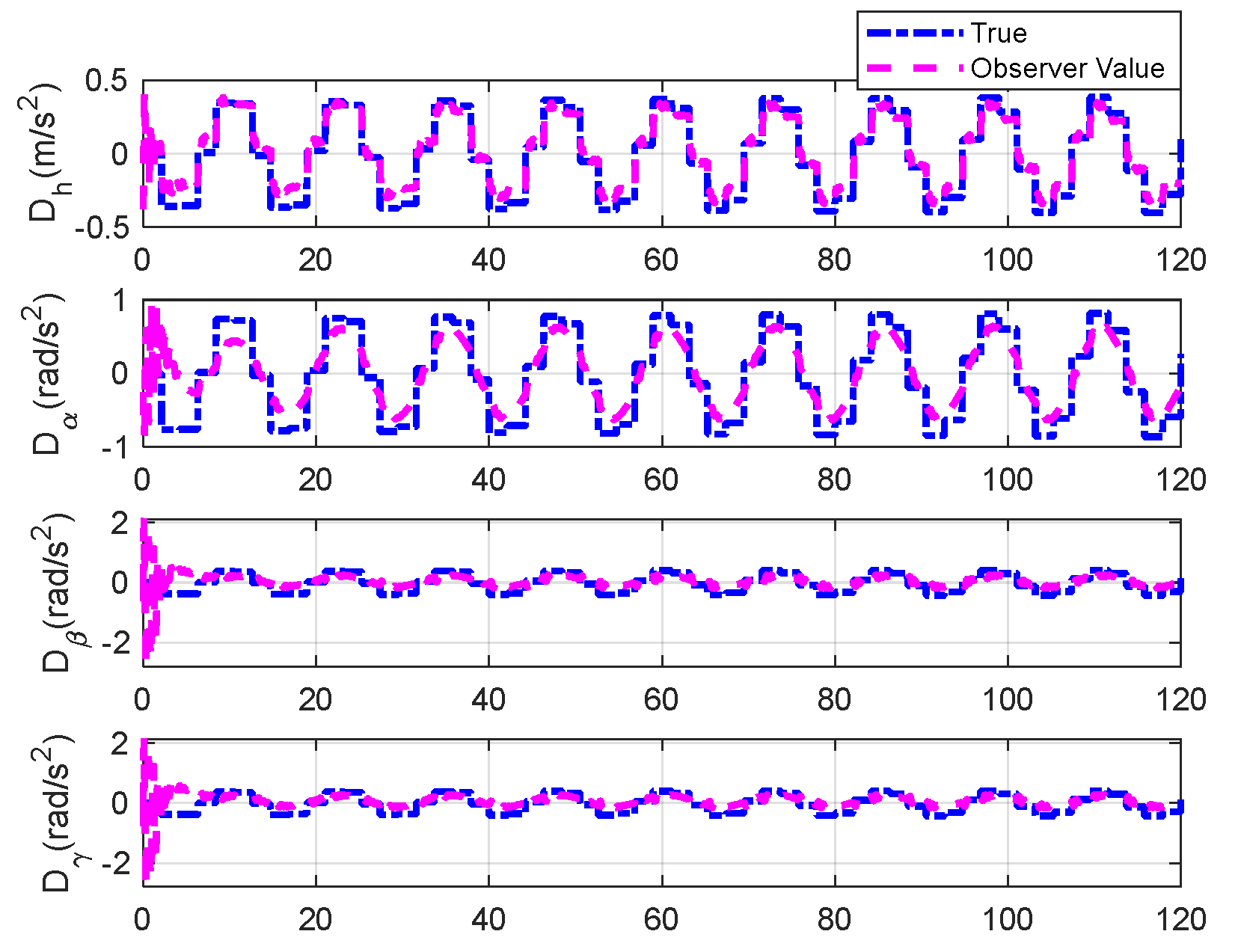
Figure 19.
Disturbances estimation under triangular gust by DO.
Figure 19.
Disturbances estimation under triangular gust by DO.
Figure 20.
Output responses of plunge and pitch under sine gust with unsteady aerodynamic loads.
Figure 20.
Output responses of plunge and pitch under sine gust with unsteady aerodynamic loads.
Figure 21.
Responses of β and γ under sine gust with unsteady aerodynamic loads.
Figure 21.
Responses of β and γ under sine gust with unsteady aerodynamic loads.
Figure 22.
Responses of aerodynamic states under sine gust with unsteady aerodynamic loads.
Figure 22.
Responses of aerodynamic states under sine gust with unsteady aerodynamic loads.
Figure 23.
Deflection of TE and LE control under sine gust with unsteady loads.
Figure 23.
Deflection of TE and LE control under sine gust with unsteady loads.
Figure 24.
Responses of plunge and pitch under sine gust with quasi-steady aerodynamic loads.
Figure 24.
Responses of plunge and pitch under sine gust with quasi-steady aerodynamic loads.
Figure 25.
Observable disturbances estimation under sine gust with quasi-steady aerodynamic loads.
Figure 25.
Observable disturbances estimation under sine gust with quasi-steady aerodynamic loads.
Figure 26.
Unobservable disturbances estimation under sine gust with quasi-steady aerodynamic loads.
Figure 26.
Unobservable disturbances estimation under sine gust with quasi-steady aerodynamic loads.
Figure 27.
Deflection of TE and LE control under sine gust with quasi-steady aerodynamic loads.
Figure 27.
Deflection of TE and LE control under sine gust with quasi-steady aerodynamic loads.
Figure 28.
Responses of plunge and pitch under sine gust with unsteady aerodynamic loads.
Figure 28.
Responses of plunge and pitch under sine gust with unsteady aerodynamic loads.
Figure 29.
Responses of β and γ under under sine gust with unsteady aerodynamic loads.
Figure 29.
Responses of β and γ under under sine gust with unsteady aerodynamic loads.
Figure 30.
Responses of aerodynamic states under sine gust with unsteady aerodynamic loads.
Figure 30.
Responses of aerodynamic states under sine gust with unsteady aerodynamic loads.
Figure 31.
Observable disturbances estimation under sine gust with unsteady aerodynamic loads.
Figure 31.
Observable disturbances estimation under sine gust with unsteady aerodynamic loads.
Figure 32.
Unobservable disturbances estimation under sine gust with unsteady aerodynamic loads.
Figure 32.
Unobservable disturbances estimation under sine gust with unsteady aerodynamic loads.
Figure 33.
Deflection of TE and LE control under sine gust with unsteady aerodynamic loads.
Figure 33.
Deflection of TE and LE control under sine gust with unsteady aerodynamic loads.
Table 1.
Parameters of the two-dimensional wing.
Table 1.
Parameters of the two-dimensional wing.
| Quasisteady aerodynamic model |
Unsteady aerodynamic model |
| Parameter |
Value |
Parameter |
Value |
|
mwing
|
4.34 kg |
mh
|
6.815kg |
|
mW(total)
|
5.23 kg |
mα |
5.715kg |
|
mT
|
15.57 kg |
mβ |
0.537kg |
| sp |
0.5945m |
mγ |
0.5kg |
| b |
0.1905m |
Iα |
0.119kg.m2
|
| a |
−0.6719 |
Iβ |
1e-5 kg.m2
|
| c |
0.381m |
Iγ |
1e-5 kg.m2
|
|
ICG.wing
|
0.04342 kg⸱m2
|
rα |
0.040m |
|
Icam
|
0.04697 kg⸱m2
|
rβ |
0 |
| ch
|
27.43 kg/s |
rγ |
0 |
| cα
|
0.0360kg⸱m2/s |
rac |
-0.033m |
| ρ |
1.225kg/m3
|
r3/4c |
0.233m |
|
rcg
|
−b(0.0998+a) |
Lβ |
0.233m |
| CLα |
6.757 |
Lγ |
-0.01m |
| CLβ |
3.774 |
kβs |
766.08 Iβ
|
| Cmα |
0 |
cβs |
41.82 Iβ
|
| Cmβ |
−0.6719 |
kγs |
530.24 Iγ
|
| CLγ |
−0.1566 |
cγs |
44.27 Iγ
|
| Cmγ |
−0.1005 |
cα
|
0.205Nm.s/rad |
| kh
|
2844N/m |
ch |
27.43 Nm.s/rad |
| xα
|
rcg/b m |
ωnβs
|
27.68 rad/s |
| fLE
|
0.15 |
ζβs
|
0.7555 |
| fTE
|
0.2 |
ωnγs
|
23.03 rad/s |
|
Iα
|
Icam +ICG.wing +mwing(rcg)2 kg⸱m2
|
ζγskh
|
0.9612844N/m |
| kα
|
12.77+53.47α+1003α2Nm/rad |
kα
|
27.96-167.63α+552.55α2+1589.3α3-3247.2α4
|
Table 2.
Selected parameters of the controller (Quasi-steady case).
Table 2.
Selected parameters of the controller (Quasi-steady case).
| Controller |
parameters |
Value |
| PID |
kp,z1, ki,z1, kp,z2, ki,z2
|
diag(0.1,0.1), diag(0.1,0.1), diag(1,1),diag(0.4,0.4) |
| BTSMC |
|
The same as Section4.1 |
| BSMC |
K1, λ1
|
diag(0.4,0.2),diag(0.5,0.5) |
| |
hs, ς
|
diag(0.5,0.5), diag(50, 30) |
| |
φs, βs
|
0.4, 1 |
Table 3.
Performance comparative data under triangular and sine gusts.
Table 3.
Performance comparative data under triangular and sine gusts.
| Gust input |
Controller |
Data |
Rising time(s) |
Over-shoots |
RMSE |
| Triangular gust(Case I, Example 1) |
No LR (with DO) |
h |
0.1770 |
0.0134 |
0.0023 |
| α |
- |
- |
0.0129 |
| LR (with DO) |
h |
0.1187 |
0.0136 |
0.0022 |
| α |
- |
- |
0.0120 |
| Sine gust(Case I, Example 2) |
No DO (No LR) |
h |
0.1084 |
0.0104 |
0.0027 |
| α |
- |
- |
0.0160 |
| DO (No LR) |
h |
0.1205 |
0.0124 |
0.0018 |
| |
α |
- |
- |
0.0110 |
Table 4.
Performance comparative data under triangular gust (Quasi-steady aerodynamic loads).
Table 4.
Performance comparative data under triangular gust (Quasi-steady aerodynamic loads).
| Controller |
Data |
Rising time(s) |
Over-shoots |
RMSE |
| DO-PID |
h |
0.1467 |
0.0067 |
0.0026 |
| |
α |
- |
- |
0.0345 |
| DO-BTSMC |
h |
0.1187 |
0.0136 |
0.0021 |
| α |
- |
- |
0.0120 |
| DO-BSMC |
h |
0.1215 |
0.0118 |
0.0022 |
| α |
- |
- |
0.0153 |
Table 5.
Selected parameters of the controller (Unsteady case).
Table 5.
Selected parameters of the controller (Unsteady case).
| Controller |
parameters |
Value |
| PID |
kp,z1, ki,z1, kp,z2, ki,z2
|
diag(0.1,0.1,0.1,0.1), diag(0.1,0.1,0.1,0.1), diag(1,1,1,1),diag(0.4,0.4, 0.4, 0.4) |
| BTSMC |
K1, λ1
|
K1=diag(0.2,0.1,0.1,0.1), λ=1.8*diag(1,1,1,1). |
| p, q |
5, 3 |
|
β, α0, β1
|
β=diag(1,1,1,1), α0=10, β1=3,
|
|
hs, ς
|
hs=diag(0.5,0.5,0.5,0.5), ς=diag(30,50, 30, 30),
|
|
φs, βs
|
φs=0.4,βs=1
|
| BSMC |
K1, λ1
|
diag(0.2,0.1,0.1,0.1),diag(0.5,0.5,0.5,0.5) |
|
hs, ς
|
diag(0.5,0.5,0.5,0.5), diag(30,50, 30, 30) |
|
φs, βs
|
0.4, 1 |
Table 6.
Performance comparative data under triangular and sine gusts with unsteady aerodynamic loads.
Table 6.
Performance comparative data under triangular and sine gusts with unsteady aerodynamic loads.
| Gust input |
Controller |
Data |
Rising time(s) |
Over-shoots |
RMSE |
| Triangular gust(Case II, Example 3) |
No LR (with DO) |
h |
0.2438 |
0.0010 |
0.0022 |
| α |
- |
0.1758 |
0.0285 |
| LR (with DO) |
h |
0.2278 |
0.0015 |
0.0020 |
| α |
- |
0.1782 |
0.0281 |
| Sine gust(Case II, Example 4) |
No DO (No LR) |
h |
0.1704 |
0.0045 |
0.0019 |
| α |
- |
0.2312 |
0.0267 |
| DO (No LR) |
h |
0.1447 |
0.0025 |
0.0013 |
| |
α |
- |
0.2144 |
0.0218 |
Table 7.
Performance comparative data under parameter uncertainty and sine gust (Quasi-steady Case).
Table 7.
Performance comparative data under parameter uncertainty and sine gust (Quasi-steady Case).
| Controller |
Data |
Rising time(s) |
Over-shoots |
RMSE |
| DO-PID |
h |
0.1481 |
0.0077 |
0.0025 |
| |
α |
- |
- |
0.0447 |
| DO-BTSMC |
h |
0.1205 |
0.0124 |
0.0018 |
| α |
- |
- |
0.0110 |
| DO-BSMC |
h |
0.1275 |
0.0045 |
0.0014 |
| α |
- |
- |
0.0173 |
Table 8.
Performance comparative data under parameter uncertainty and sine gust (Unsteady Case).
Table 8.
Performance comparative data under parameter uncertainty and sine gust (Unsteady Case).
| Controller |
Data |
Rising time(s) |
Over-shoots |
RMSE |
| DO-PID |
h |
0.1916 |
0.0024 |
0.0017 |
| |
α |
- |
0.2137 |
0.0199 |
| DO-BTSMC |
h |
0.1415 |
0.0025 |
0.0010 |
| α |
- |
0.2147 |
0.0183 |
| DO-BSMC |
h |
1.3885 |
0.0004 |
0.0010 |
| α |
- |
0.1645 |
0.0151 |