Prerpints.org logo
Preprint
Article

A Simulation-Assisted Field Investigation on Control System Upgrade for a Heat-Pump Heating Project

Altmetrics

Downloads

122

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 October 2024

Posted:

15 October 2024

You are already at the latest version

Alerts
Abstract
Heat pump-based renewable energy and waste heat recycling has become the mainstay of the Clean Heating Plan. Still, configuring a fit control system for that remains a worthwhile research topic. In order to address the problems that arose in the previous heating period, this study configures a Smith-predictor-based PID cascade control system with an advanced fireworks algorithm that adaptively tunes the structural parameters of controllers. Simulation and live measures demonstrate that the upgraded control scheme counters the adverse effects of time lag, reduces overshoot, and shortens the settling time. Further, benefiting from a delicate balance between heating demand and supply, the heating system with upgraded management increases the average exergetic efficiency by 11.4% and decreases the complaint rate by 76.5%. Note that the advanced fireworks algorithm mitigates the adverse effect of capacity lag and simultaneously accelerates the optimizing and converging processes, exhibiting its comprehensive competitiveness among this study’s three intelligent optimization algorithms. Nonetheless, the forecast and regulation of the return water temperature of the heating system are independent of each other in this research. Configuring an integral predictive control structure for the return water temperature of heating systems is worthwhile in the future.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Since the “Winter Clean Heating Plan” [1] was implemented in northern China, the heating energy consumption in most cities has been effectively restrained [2,3]. In the meantime, heating efficiency is enhanced, leading to a noticeable improvement in the ecological environment [4,5]. In this process, national industrial and energy structures are continuously optimized, with various types of waste heat and renewable energy gradually replacing coal-fired boilers as the preferred clean heat sources [6,7,8]. Heat pumps directly enhance the quality of heat within these clean heat sources, improving the availability of clean energy [9,10]. Figure 1 shows the schematic diagram of a water/ground-source heat pump heating system.
Compared with traditional district heating systems, the characteristics of heat pump heating are as follows [11,12]: 1) Stable and efficient operation of heat pump units requires a stable energy output from low-temperature heat sources; 2) To ensure safe and reliable operation of equipment, the load rate of heat pump units should not remain at excessively high (>95%) or low (<50%) levels for a long time; 3) To meet the universality of compressors and refrigerants, the temperature difference between supply and return water in the condenser is usually limited to within 10 °C; 4) To limit the energy consumption for heating water distribution, heat pump units are often arranged near heating users such as heat exchange stations or building equipment floors; 5) Cascade utilization of energy asks that the supply water temperature for heating (usually around 40~45 °C) should match the indoor temperature level of users. The restrictions above profoundly change the production, distribution, and consumption patterns of heating [13]. Hence, practitioners need to adjust system design and operational details promptly based on information about heat source conditions, performance characteristics of heat pumps and networks, and the behavior of heating users. Still, such adjustment is not always straightforward [14,15].
The practice in clean heating projects shows that upgrading physical equipment is an essential precondition, with subsequent control system upgrades and adaptations often determining the ultimate success of a project [16,17]. The effect of control system upgrades and adaptations is shown through improved control performance, such as timely response, fast stability, precise regulation, and supply-demand matching. In order to achieve such an effect, the following efforts should be made: 1) master the response characteristics of the controlled object to match controllers; 2) design an adaptive tuning methodology for optimizing the structural parameters of controllers in time [18,19].
Heat transfer processes, being the core of a heating system, are always the main controlled objects. Mastering the response characteristics of each heat transfer process is essential to ensure the control quality of heating systems. Based on time-domain identification methods, Khodadadi and Dehghani determined the characteristics of indoor heating processes that are first-order inertia-lag processes [20,21]. It was the same as the characteristics of heat transfer processes in shell-and-tube heat exchangers and industrial steam condensers [22,23]. In addition, Gao et al. investigated the temperature control process for an air-source heat pump water unit. They also provided object characteristics as a product of two first-order inertia-lag processes [24].
Nevertheless, Wang et al. discovered that non-integer order objects are closer to the actual heat transfer process in furnaces because this process is susceptible to other processes in the furnace [25], even though a first-order inertia-lag object can approximate the non-integer order object. Compared with fractional-order objects, the time constant of integer-order objects decreases by an order of magnitude, while the time delay increases by three orders of magnitude. Thus, heat transfer processes in a clean heating system should be considered a fractional order object with time delay.
According to the response characteristics of each heat transfer process in heating systems, fitting a control law is significant to matching controllers. Ultimately, the dynamic characteristics of controllers decide the quality of control. Even though PID control remains the most widely used control law in the HVAC (heating, ventilation, and air conditioning) field for its simplicity and intelligibility, the traditional integer order PID control cannot fulfill the regulation function for sophisticated systems. In modern heating systems where waste heat and renewable energy sources are utilized extensively, the controlled object is impacted by corresponding processes. Thus, any disturbance will alter the response characteristics of each controlled process in the heating system [26,27]. Owing to a finite number of structural parameters of controllers and unsuitable tuning methods that cannot modify these structural parameters in time, the conventional integer order PID controller is almost unable to adapt to the alterations in response characteristics. Consequently, increasing the degree of freedom of controllers’ structural parameters and optimizing the tuning methodology have become the dominant measures to improve control performance.
Wang et al. used a PID controller with fuzzy rules to increase the degree of freedom of controllers’ structural parameters and improve the adaptive tuning capacity, effectively controlling the secondary network supply water temperature of the district heating networks [28]. Further, by integrating fuzzy rules with a fractional-order PID controller, Al-Dhaifallah improved the disturbance rejection capability and tracking ability of dynamic set-points for the working fluid temperature in a heat transfer process [29]. The two studies above show that the fuzzy rule-based controller parameter tuning method improves overshoot, steady-state error, and settling time of system response. In addition, Lu et al. applied neural networks to identify and optimize a heat pump system control [30]. By combining online model identification with self-tuning control principles, the optimal control law for heating systems was derived. They found that the proposed control system possesses good tracking performance and anti-interference ability. Then Abdullah et al. achieved self-tuning of structural parameters for PID controllers in nonlinear heat exchangers, shortening tuning time and reducing overshoot [31].
Meanwhile, some researchers employ the fractional-order PID control law to increase the degree of freedom of controllers’ structural parameters and apply intelligent enhancement techniques to tune that adaptively. Liu et al. tuned the structural parameters of a fractional-order PID controller with an adaptive particle swarm optimization algorithm [32]. This algorithm primarily uses an adaptive dynamic weighting and asynchronous learning factor adjustment strategy, which balances the algorithm’s global and local search performance, thereby achieving enhanced convergence towards global optimality. They found that the proposed algorithm exhibits superior optimization performance compared to differential evolution algorithms and standard particle swarm optimization algorithms. More importantly, the intelligent optimization algorithm tuned fractional-order PID control shows a shorter response and settling time than the neural networks-based adaptive control. Then, what kind of intelligent optimization algorithm should be employed to tune the structural parameters of a fractional-order PID controller?
In 2010, Tan et al. proposed the Fireworks Algorithm, which combines the strengths of swarm intelligence algorithms with narrow-sense evolutionary algorithms [33]. The fireworks algorithm adopts a unique framework for cooperative and competitive mechanisms and an innovative search strategy called ‘explosion’. Its distinctive design and high efficiency have attracted increasing research interest. Xue et al. proposed an improved firework algorithm based on the adaptive principle and bimodal Gaussian function for tuning the structural parameters of PID controllers [34]. The enhanced algorithm is proven more effective and accessible to implement than three other typical algorithms by comparing the parameter tuning process and results. Yin et al. introduced an individual gene mutation into the adaptive firework algorithm to increase the diversity of mutation sparks, considerably overcoming local optimal traps [35]. This algorithm has higher search efficiency than the adaptive fireworks algorithm and genetic algorithm and exhibits significant advantages in optimizing control performance. Moreover, enhanced fireworks algorithms, such as improving operators, introducing elite strategies, enhancing interaction mechanisms among individuals, and using fireworks-based combined intelligent algorithms, are proposed for competitiveness enhancement [36]. Yet, few studies or practices use fireworks algorithms to improve control performance in modern heating systems.
The paper is based on an actual clean heating renovation project and completes the upgrade of the control system within the framework of heat pump heating. An advanced fireworks algorithm is used to tune the structural parameters of controllers. The following introduces the approach and methods for upgrading the control system. After that, the performance of the advanced control system is tested by MATLAB Simulink. Hence, the control program is refreshed onsite in the project to test its effectiveness in management. Finally, we compare and analyze the effect of control system upgrade on heating efficiency and energy consumption of heating systems before and after.

2. Methods

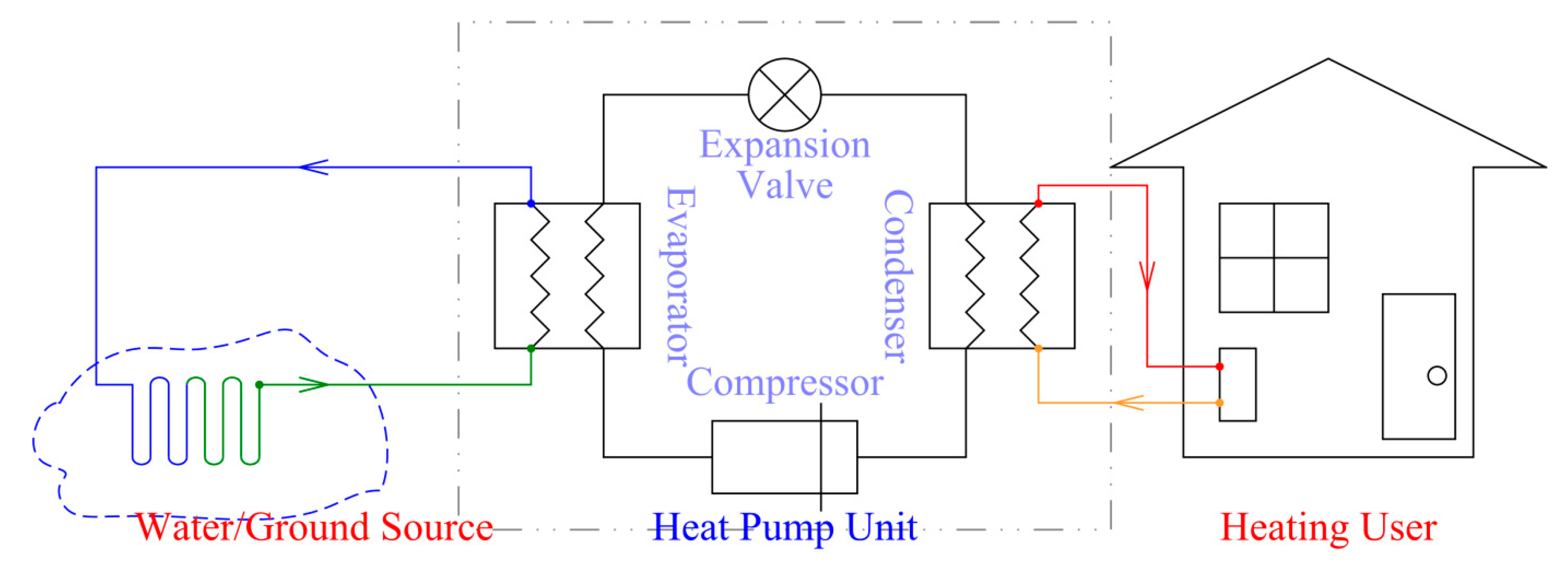
2.1. Live Laboratory Description

A field operating-based study is conducted to test the effect of a control system upgrade through a heat-pump heating retrofit project in Shanxi, China (Figure 2).
The project features are as follows:
1) Situated in a cold climate zone with a heating period of four months (from around November 15th to around March 15th of the following year);
2) Heating area of 23,000 m2, serving residential users;
3) Transitioning from a district boiler heating system to a water-source heat pump heating system utilizing a low-temperature heat source (20 °C), which is the cooling water from nearby factories; Figure 1 shows the schematic diagram of water-source heat pumps;
4) Completed renovations on the heat source, distribution network, and building insulation, and installed transmitters for temperature, pressure, flow rate measurements and balancing valves or/and regulating valves for the distribution network and end-users;
5) Identified the response characteristics of specific key equipment/components approximated by the first-order inertia-lag objects as follows:
The heat pump compressor:
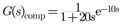
Preprints 121029 i001
The heat pump condenser:
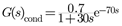
Preprints 121029 i002
The heat load:
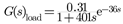
Preprints 121029 i003
where s and G(s) are the complex variable and first-order inertia-lag object, respectively. Note that the heat pump condenser possesses the most prolonged time delay, while the heat load owes the most significant time constant.
6) A single-loop PID controller was employed with the control variable of the condenser outlet water temperature. Figure 3 shows the structure of this control system. As seen from Figure 3, the set value of condenser outlet water temperature (TS.SET) minus the measurement (I1) of that is the deviation (e1) of the controlled variable, which is sent to the PID controller. Through calculations, the PID controller sends the adjustment signals (U1) to the electric motor of the compressor, regulating the refrigerant flow rate (mR) to manage the heat exchange capacity of the condenser for changing its output water temperature (TS).
During the first heating period after the physical equipment was upgraded, some problems arose, such as unsatisfactory thermal comfort among users, delayed regulation response time, low energy efficiency of the heat pump units, and high energy consumption of circulating water pumps. The operational data and the user complaints imply that the cause is multifaceted:
1) As Figure 3 shows, the control law neglects the effect of heat transfer processes in indoor heating on the supply-demand balance and users’ thermal comfort. The return water temperature instead of the supply water temperature of heating systems directly reflects the change in heat demand. When the program sets a supply water temperature for heating by outdoor meteorological conditions [37,38], the return water temperature of heating systems tends to rise with the heat load declines and reduces with the heat load increases. Thus, the supply water temperature, being the controlled variable, must consider the significant effect of capacity delay in the indoor heat transfer processes.
2) The integer-order PID controller is not good at managing non-integral order objects nor adapts to addressing objects with a long time delay.
3) The integer-order PID controller with three structural parameters is insufficient to subtly balance the effects of integral, differential, and proportion because the optimal solutions are limited to the right half of the complex plane.
4) The tuning method of ZN can scarcely adapt to the alterations in response characteristics of controlled objects.
5) A narrow difference between supply and return water temperatures (about 5 °C) is employed in the heating system to ensure hydraulic equilibrium among users, leading to remarkable energy consumption for the heating water distribution. Meanwhile, to protect the thermal comfort of distant users, a high level of supply temperature results in significant energy consumption for the heat pump units.

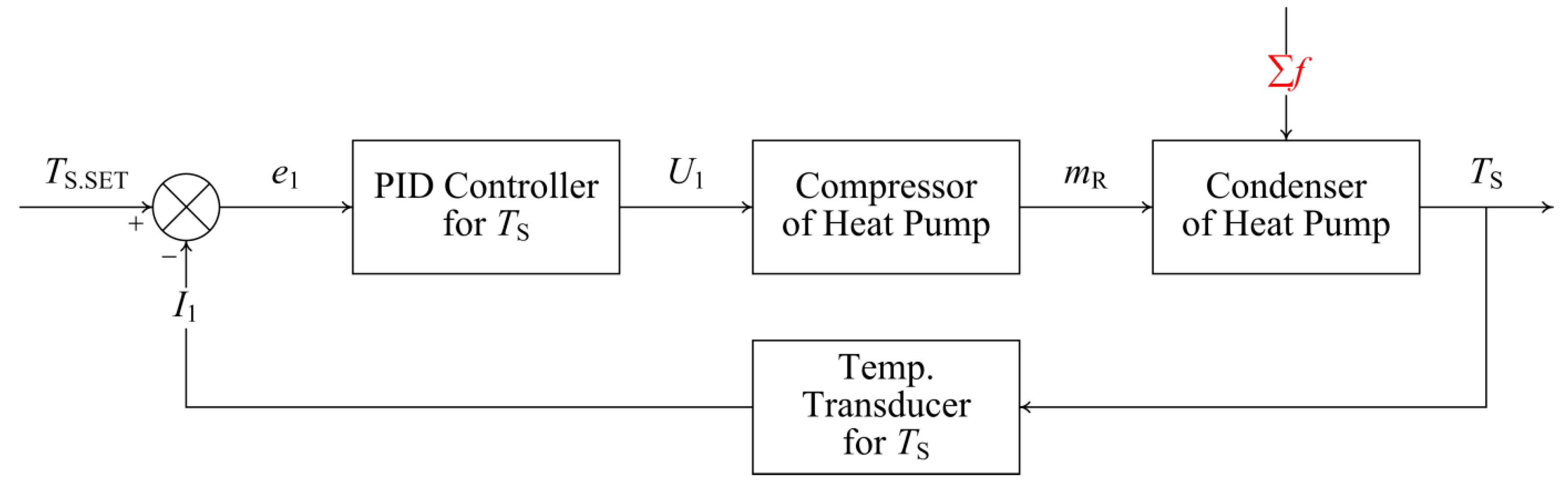
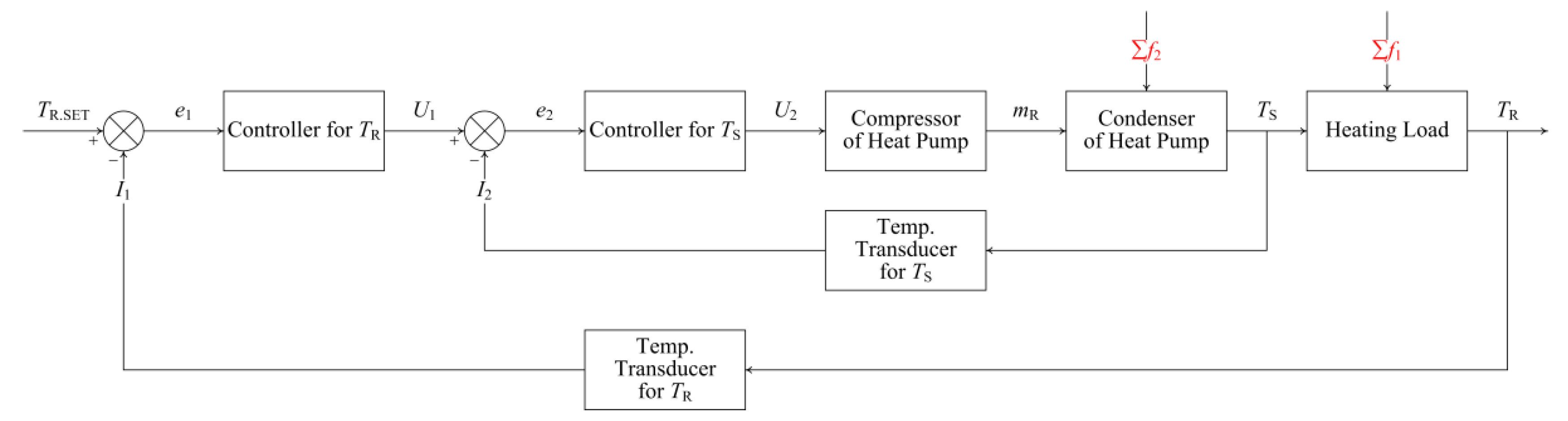
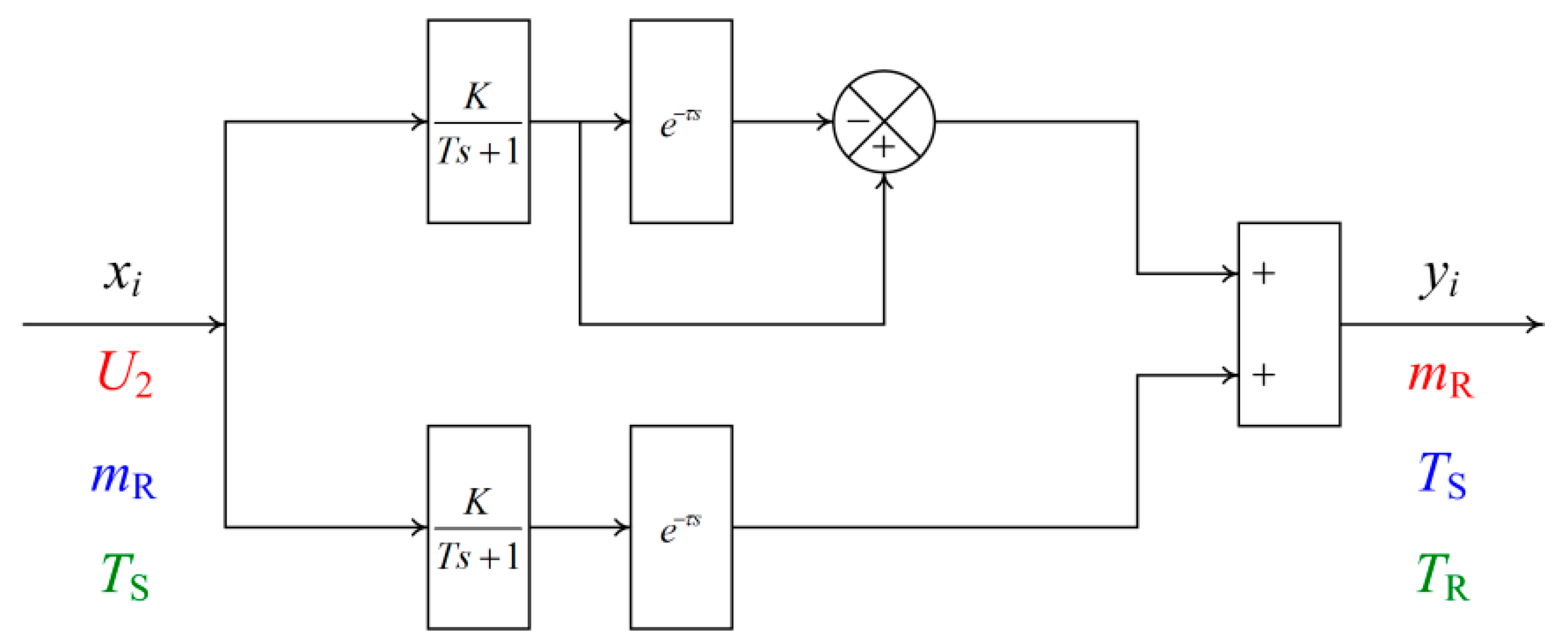
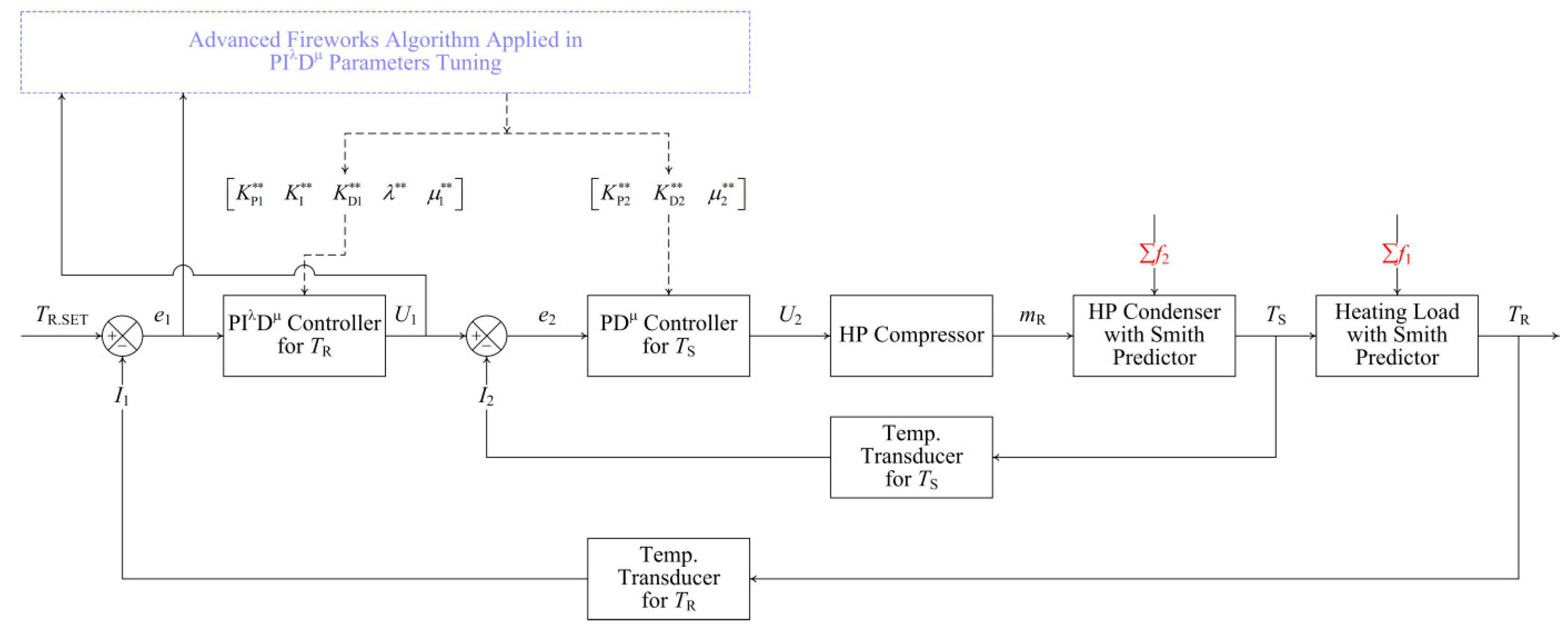
2.2. Advanced Control Strategy and Controller Design

According to the analysis above, some efforts aimed at upgrading the control system have been conducted as follows:
1) The return water temperature and the supply one, the principal and auxiliary controlled variables, respectively, replace the single-loop structure with a cascade control structure, directly responding to the heat load variation.
The primary and secondary controllers have different tasks in a cascade control system. The task of the secondary controller is to quickly overcome disturbances in the secondary loop without requiring perfect control of the secondary parameter, while the task of the central controller is to ensure that the main controlled parameter meets the high requirements specified by process regulations. In this study, the ultimate goal of the heating system is to provide the users with thermal comfort and simultaneously reduce energy consumption for heating. Thus, the return water temperature needs precise regulation to adapt to the variation of heat demand. In contrast, the supply water temperature requires immediate response rather than accurate management, which profited from the positive impact of building envelope thermal inertia [39]. Figure 4 shows the upgraded cascade control structure.
As Figure 4 shows, the set value of return water temperature (TR.SET) minus the measurement (I1) of that is the deviation (e1) of the controlled variable, which is sent to the controller for TR. Through calculations, the controller for TR outputs the signal U1, then the signal U1 minus the measurement (I2) of condenser outlet water temperature is the deviation (e2) of the secondary controlled variable, which is sent to the controller for TS. Through calculations, the controller for TS sends the adjustment signals (U2) to the electric motor of the compressor, regulating the refrigerant flow rate (mR) to manage the heat exchange capacity of the condenser for changing its output water temperature (TS). Ultimately, heating users respond to TS and output the return water temperature (TR).
2) Incorporate controlled objects with the Smith predictor [40], countering the adverse effects of time lag on regulation, as Figure 5 shows.
3) Configure fractional-order controllers for the fractional-order objects. Specifically, a PDμ controller is adopted to adjust the supply water temperature quickly. In contrast, a PIλDμ controller precisely manages the return water temperature. Compared to integral-order PID controllers, fractional-order PID controllers offer more flexibility in parameter tuning due to adding two adjustable parameters: integral operator order λ and derivative operator order μ [41]. Thus, fractional-order PID controllers are suitable for controlling nonlinear systems [42,43].
4) Tune the structural parameters of fractional-order PID controllers with an advanced fireworks algorithm to adapt to the alterations in the response characteristics of controlled objects. Section 2.3 introduces the advanced fireworks algorithm and its application in this study.
5) Increase the supply-return water temperature difference of the heat pump units from 5 °C to 10 °C to reduce distribution losses in the heating system. In the meantime, the set value of the return water temperature determined by the actual heat load ensures that the output power of heat pump units fits the heat demand. Therefore, the supply water temperature as the secondary controlled variable adapts to the change in the heat load, decreasing the energy consumption of the heat pump units. In particular, this study uses the forecast method of return water temperatures in a heating system provided by Wang et al. [44]. Hebei Hongrui Intelligent Engineering Technology Co., LTD implements this forecast method in the live laboratory.
6) Adjust the opening of balance valves installed in each building/unit by calculating deviations between return water temperatures of the building/unit and heating system, ensuring hydraulic and thermal equilibrium among buildings/units. After that, since the valve authority of flow regulating valves at users’ terminals has been improved, hydraulic and thermal equilibrium among users is available, that is, ‘on-demand heating’.

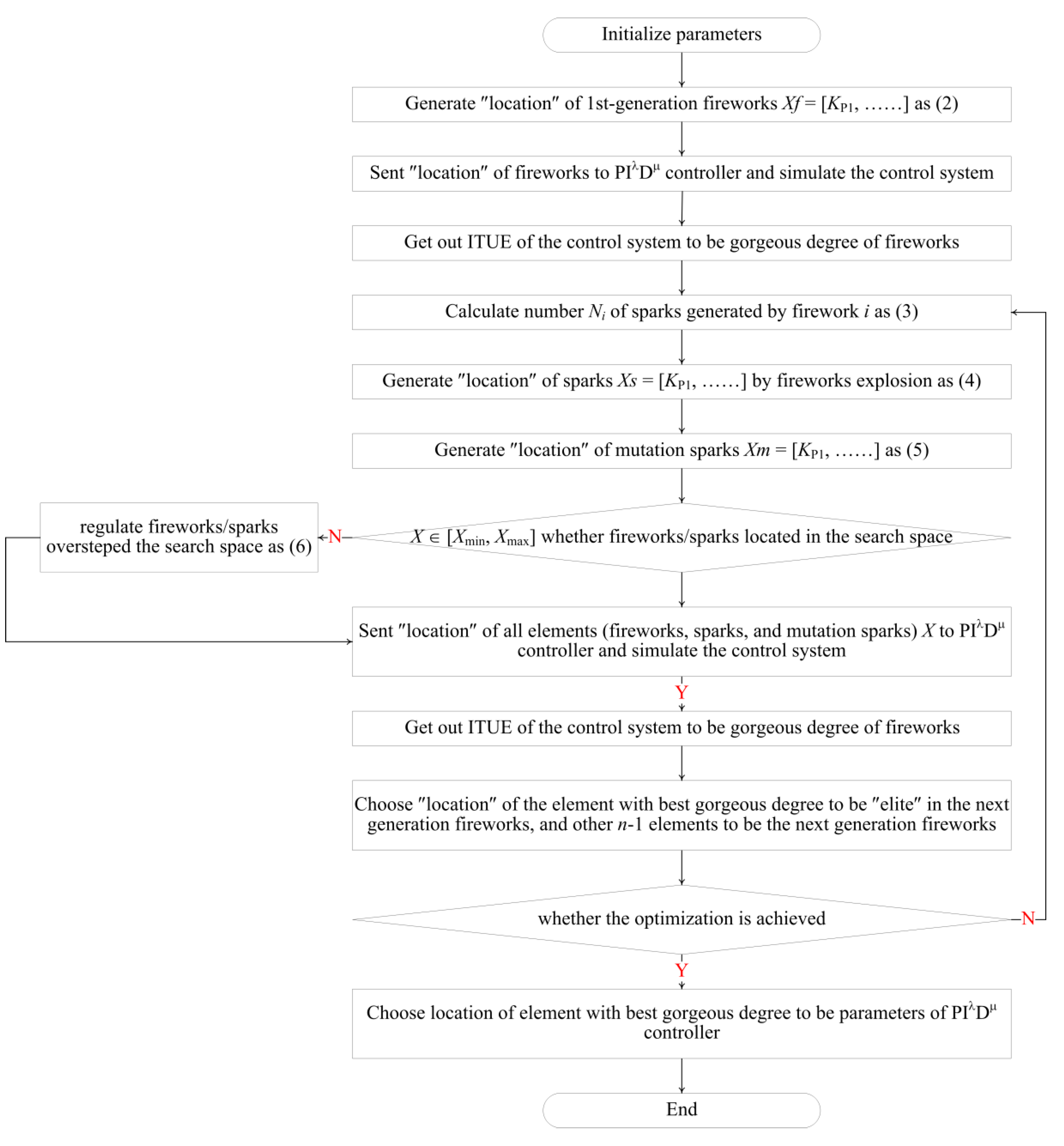
2.3. Advanced Adaptive Tuning Algorithm

The cascade control system has eight structural parameters, namely KP2, KD2, μ2, KP1, KI, KD1, λ, and μ1. Tuning these parameters increases the computational load. Thus, an advanced fireworks algorithm is employed to search for optimal solutions for the structural parameters. Additionally, a multi-objective optimization approach is adopted to comprehensively evaluate the control system’s performance as much as possible. A comprehensive evaluation index called ITUE has been designed using the linear weighting summation method, as shown in Eq. (1), the fitness function for optimization [34].
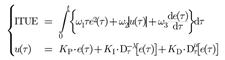
Preprints 121029 i004
where ω1, ω2, and ω3 are the three weight values of ITUE, controller output, and system error rate, respectively. ω2 is applied to avoid exporting a control value that is too large to be beyond the amplitude of the controller in engineering, and ω3 is used to prevent an excessive rate of error, which may cause sensor delay in engineering.
The fireworks algorithm utilizes random factors and selection strategies to form a parallel explosive search method. It is characterized by fast solution speed, implicit parallelism, and a balance between cooperation (global optimization) and competition (local optimization). It is a global probabilistic search method that can find optimal solutions for complex optimization problems. Since its initial development in 2010, various variants have been developed with continuously improving performance, achieving significant application effects in multiple fields [36]. In this study, the following improvements are made to the standard fireworks algorithm [45]:
1) Adopt the Cauchy mutation strategy instead of the Gaussian mutation strategy to enhance perturbation ability and broaden the range of variation, making it easier to escape local optima.
2) With an adaptive explosion radius, during the initial iterations, a larger explosion radius is used to strengthen global exploration capability. Later iterations employ a smaller explosion radius to enhance local search capability, accelerating algorithm convergence and balancing solution accuracy with convergence speed.
3) The elite-random selection strategy selects the best individual from a candidate set composed of fireworks, exploding sparks, and Cauchy sparks as the ‘elite’ for the next generation of fireworks. The rest are randomly selected (with possible repetitions) from the candidate set. This approach ensures both retaining optimal individuals’ absolute advantage in the fireworks population and maintaining population diversity while reducing computational complexity.
Based on the advanced fireworks algorithm, the steps for tuning the controller’s structural parameters are as follows:
Step 1: Initialize the parameters of the fireworks algorithm, including the number of fireworks (n), maximum iteration count (Nmax), and number of mutation sparks.
Step 2: Initialize a set of controller’s structural parameters (KP2, KD2, μ2, KP1, KI, KD1, λ, μ1) by randomly selecting positions for each firework as described in Eq. (2).
Step 3: Ignite fireworks to generate sparks by generating a new generation of structural parameter sets from the initial set using Eq. (3), where Eq. (4) determines their positions.
Step 4: Generate mutation sparks through explosive mutations by applying mutation behavior to create a new generation of the controller’s structural parameter sets according to Eq. (5). Eq. (6) describes measures taken when encountering out-of-range fireworks/sparks.
Step 5: Compare all fireworks, explosion sparks, and Cauchy sparks by simulating control systems with each set of controller’s structural parameters to obtain corresponding fitness function values ITUE.
Step 6: Select the best individual from the candidate pool composed of fireworks, explosion sparks, and Cauchy sparks as an ‘elite’ for the next generation of fireworks; randomly select others from this pool (with possible repetitions); collectively form the next generation and conduct simulations.
Step 7: If system performance meets requirements or the maximum iteration count is reached during the search process, select the firework with the highest fitness function value as the optimal solution for the problem; otherwise, repeat Step 3.
The random selection of firework positions is described by Eq. (2).
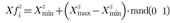
Preprints 121029 i005
The number of sparks generated from fireworks during detonation is given by Eq. (3).
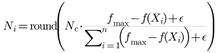
Preprints 121029 i006
The locations where explosion sparks appear are determined by Eq. (4).
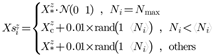
Preprints 121029 i007
The positions where mutation sparks occur are defined by Eq. (5).
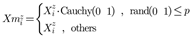
Preprints 121029 i008
Measures to handle out-of-bounds fireworks/sparks are specified in Eq. (6).
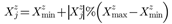
Preprints 121029 i009
where Xzmin and Xzmax are the lower and upper boundary of searching space in dimension z and rand (0 1) is the displacement parameter generated from a standard uniform distribution on the open interval (0, 1). Nc is the total sparks number constant, fmax is the maximum value of the objective function among the n fireworks, and ε is the machine epsilon. Due to the limitation of the manufacturing process, the number of sparks generated by fireworks should be no more than Nmax and no less than Nmin: that is, Nmax should replace Ni if Ni is bigger than Nmax, and Nmin should replace Ni if Ni is smaller than Nmin. Xzc is the historical location information of Cauchy sparks; Xz∗ is the location information of the current best fireworks, i.e., the optimal fireworks; Ni is the number of explosive sparks generated by the i-th fireworks; <Ni> is the average number of explosive sparks of the population; N(0 1) is a Gaussian distribution function with mean 0 and variance 1. Cauchy(0 1) is the standard Cauchy distribution function, and p is the probability of random variation. Xzj represents the position of the j-th individual beyond the boundary in the z dimension; Xzmax and Xzmin are the upper and lower boundaries of the z-th dimension, respectively. % is the symbol of modular operation.
Figure 6 shows the flowchart for tuning the controller parameters based on the advanced fireworks algorithm. Figure 7 depicts the complete framework of a heat-pump heating control system.

2.4. Tuning Algorithm Tests

Based on Figure 7 and the response characteristics of each process in the cascade control system, a corresponding Simulink configuration model in the MATLAB platform is established. The initial return water temperature and set value are 40.0 °C and 35.0 °C, respectively. Eight structural parameters of the controllers range as follows: KP1 ∈ [28, 37]; KI ∈ [6, 11]; KD1 ∈ [45, 55]; λ ∈ [0.6, 0.9]; μ1 ∈ [0.5, 0.7]; KP2 ∈ [1, 4]; KD2 ∈ [55, 63]; μ2 ∈ [0.6, 0.9]. By observing the tuning process combined with a series of indicators such as controlling time tc, steady-state error ESS, overshoot, and decay ratio, tuning algorithms’ optimizing and convergent performance can be measured.
Further, to verify the tracking performance of the upgraded control system, the initial return water temperature and its set value are configured by 40.0 °C and 36.5 °C, respectively. Then, the set value of the return water temperature is reset to 35.0 °C at 298 s in the test. After that, to verify the anti-interference performance of the upgraded control system, the initial return water temperature and its set value are configured by 38.5 °C and 35.0 °C, respectively. When the system’s running time is 228.9 s, insert a transient interference signal of 36.0 °C.
The simulation tests above support live measures of the upgraded control system. In the live measure, the set value of the return water temperature is configured by the thermal load prediction algorithm integrating singular spectrum analysis and neural network [44]. The performance of the old version control system and the upgraded one will be contrasted through individual short- and long-term observations. The short-term tests aim to verify the response characteristics of controlled variables and the behavior of the central apparatus in the heating system. Meanwhile, long-term tests propose to observe the heating performance in a complete heating period. The heating performance that the study is concerned with includes supply-demand balance, the energy consumption of heat pump units and circulating water pumps separately, and users’ complaints about excess or shortage of heating.

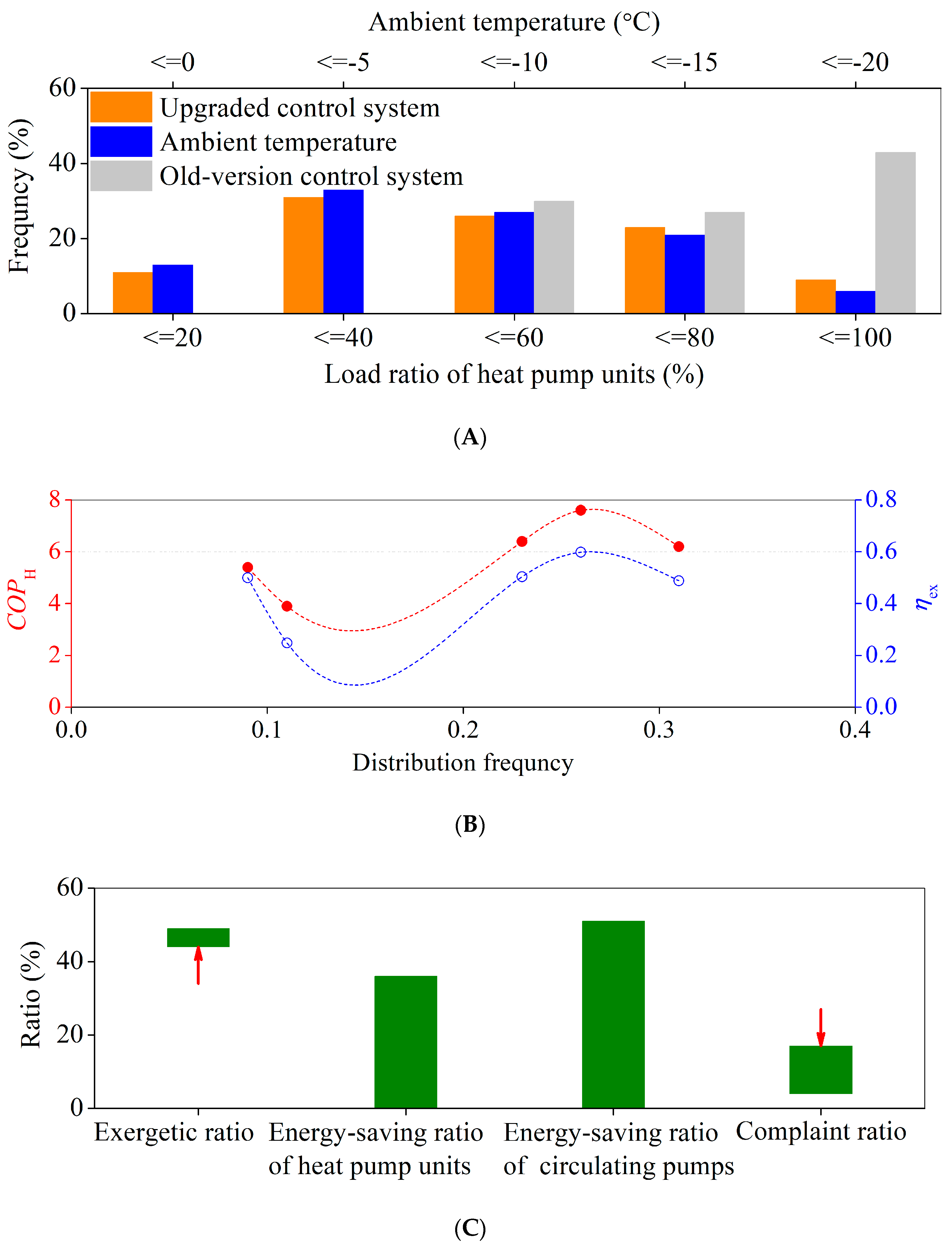
3. Results and Discussion

3.1. Simulation Test Results

Figure 8 presents the tuning process of eight structural parameters for the PIλDμ controller and PDμ controller and shows the convergence details of the objective function ITUE during this process. As shown in Figure 8, eight parameters converge to global optimal values after the seventh iteration, overwhelming local optima while balancing accuracy and diversity. Meanwhile, function ITUE approaches the optimal value and tends to stabilize after seven iterations. Table 1 summarizes the tuning results of eight structural parameters and exhibits several performance indicators. As seen from Table 1, the overshoot and decay ratio indicators are within appropriate ranges, and the adjustment time and ITUE are ideal with minimal steady-state error. Hence, the upgraded control system performs well, and the adaptive tuning approach is feasible and efficient.
Figure 9 displays the unit-step response test results of different control schemes for managing the heating temperatures. As shown in Figure 9, the old-version control system (with the supply water temperature as the controlled variable) possesses a time lag of more than 80 s, with a significant overshoot of 22.2% and a long settling time of 1320 s. In contrast, three Smith-predicted PIλDμ cascade control systems (with the return water temperature as the controlled variable) reduce capacity lag by 37.5% ~ 100%, weaken overshoot by 61.3% ~ 100%, and shorten settling time by 54.5% ~ 84.8%. Among three Smith-predicted PIλDμ cascade control systems [25,46], the system employing the advanced fireworks algorithm exhibits apparent advantages, especially regarding response time. Note that although the particle swarm algorithm combined with fuzzy rules [25] achieves zero overshoot, the advanced fireworks algorithm outperforms it in the capacity lag (reduced by 65 s) and adjustment time (shortened by 50 s) restraint.
Based on the identical controlled variable and control structure, three kinds of adaptive tuning algorithms present diverse response characteristics with the uniform input of the unit step. Compared with other algorithms, the fireworks algorithm displays the best comprehensive performance. The explosive search mechanism within the fireworks algorithm accelerates the optimizing and converging processes simultaneously. Even though the fuzzy rules exhibit an excellent smooth response, concerned with a relatively loose requirement for overshoot in control processes, the fireworks algorithm remains preferred with its timely response and rapid stability.
Figure 10 exhibits the response curves of the return water temperature and its deviation, as well as the supply water temperature and compressor speed, during the adjustment of heating water temperatures. As seen from Figure 10, after the adjustment starts, the deviation of the return water temperature peaks at 48 s and stabilizes at around 100 s; the return water temperature reaches its minimum value at 50 s and stabilizes at around 100 s. The compressor speed reaches its peak within 0.9 s after receiving the downward adjustment command, reaches its minimum value at 50 s, and stabilizes at around 100 s, while the supply water temperature reaches its minimum value within 9.7 s after receiving the downward command and tends to stabilize at around 100 s. Although there is resistance and hysteresis in each stage of the regulation process, the upgraded control system effectively compensates for such adverse impacts.
Figure 11 presents the return water temperature response curve in tracking and anti-interference performance tests. As shown in Figure 11, after the regulation starts, the return water temperature reaches the minimum value at 48 s and stabilizes at 100 s. When a disturbance of 1 °C temperature rise is applied at 228.9 s, the return water temperature reaches the minimum value at 278.8 s and stabilizes at 309.3 s. Such results verify that the upgraded control system can track and resist interference for the return water temperature.

3.2. Live Measure

Figure 12 presents the short-term field records of the heating system supply/return water temperature, indoor air temperature, heating circulating pump frequency, and user-side regulating valve opening before and after the adjustment of heating water temperatures. As seen from Figure 12, at time zero, the measured indoor air temperature for a nearby user is 19.6 °C, while there are many cases where the indoor air temperature of distant users is below 18.0 °C. Under multiple constraints, such as a high limit of 50.0 °C for the supply water temperature, an upper limit of 5.5 °C for the supply-return water temperature difference, and a maximum operating frequency of 50 Hz for the heating circulating pump, traditional control schemes can only meet the indoor air temperature requirements by increasing the supply water temperature and adjusting the users’ regulating valves. Therefore, at 24 s, the nearby user’s regulating valve opening is increased from 16.7% to 20.6%. At the same time, the distant users’ regulating valve opening is adjusted to fully open (100%) when their indoor air temperatures are below 18.0 °C. At 89 s, raise the supply water temperature from 46.3 °C to 49.6 °C. At 105 s, the indoor air temperature of this nearby user exceeds 20.1 °C and reaches 23.0 °C at 220 s. After that, it fluctuates between 22.5 °C and 23.0 °C.
At 171 s, the proximal user’s regulating valve opening has been reduced to 19.5%, but it still failed to eliminate its overheating state. Conversely, the indoor air temperatures for distal users have improved, reaching above 19.0 °C. In order to ensure the indoor air temperature requirements for distal users, the initial control scheme has no choice but to increase the supply water temperature, enhance the heating flow rate towards them, and restrict the proximal users’ regulating valve opening. Such measures conflict with each other and even contradict one another. Hence, the system operates under unfavorable conditions characterized by a high flow rate, slight temperature difference, high parameters, and low load, meaning energy waste and a failure of hydraulic and thermal equilibrium within the secondary network. Given that, the upgraded control scheme is implemented at 579 s.
At 579 s, the compressor load is first reduced, followed by a decrease in the operating frequency of the heating circulating water pump. Meanwhile, the regulating valve openings for the nearby users have increased. From 579 s, there are four stages of decreasing the operating frequency of the heating circulating water pump; by 639 s, it decreases from 48.9 Hz to 30.1 Hz. Meanwhile, there are four stages of increasing the proximal users’ regulating valve opening from 19.5% to 47.1%. As seen in Figure 12, the indoor air temperature of the nearby user starts to decrease from 22.9 °C and stabilizes around 688 s at approximately 20.0 °C with slight fluctuations, successfully eliminating overheating issues. The heating system’s supply and return water temperatures reach stability around 950 s, at 45.3 °C and 35.1 °C, respectively. A pleasing result is that despite lowering both heating water temperature and flow rate, the indoor air temperature level for far-end users does not drop but instead remains around 20.0 °C.
In a long-term observation of the heating performance derived from diverse control schemes, a sharp contrast is exhibited in Figure 13. As shown in Figure 13A, with the upgrade of the control system, the load rate of heat pump units and the ambient temperature display an identical distribution, implying a delicate balance in heating supply and demand. In contrast, by the management of the initial control system, the load rate distribution of heat pump units and the ambient temperature distribution show a significant difference, meaning a bad fit between heating supply and demand. Specifically, the heat pump units have to operate under excess heating conditions to avoid complaints about heating shortages from most users.
Moreover, Figure 13B plots the distribution characteristics of the heating coefficient of performance (COPH) and exergetic ratio (ηex) in a complete heating period with the management of the upgraded control system. As seen from Figure 13B, both the heating coefficient of performance and exergetic ratio reach higher levels in the 23–31% frequency range, meaning that the upgraded heating system performs efficiently for most of the heating period.
Figure 13C concludes the energy efficiency benefits from the supply-demand match and high performance. As seen from Figure 13C, with the control system upgrade, the average exergetic efficiency increases by 11.4%, from 44% to 49%. The complaint rate decreases by 76.5%, from 17% to 4%. Note that the complaints include complaints about excess or shortage of heating. Moreover, the accumulated energy consumption of heat pump units and circulating water pumps and valves drops by 36% and 51%, respectively. The corresponding operating costs decline individually by 37% and 53%.
In conclusion, the upgraded control system exhibits remarkable performance in practical application. It ensures thermal comfort for users while reducing unnecessary energy consumption and improves operating efficiency as well as quality of management for heat pump units and heating systems.

4. Conclusions

Upgrading corresponding control systems is essential to achieve the considerable benefits of the Clean Heating Plan. Based on an actual clean heating renovation project in Shanxi Province, China, this study upgrades the control system for water-source heat pump heating. We configure a Smith-predictor-based PIλDμ cascade control system with an advanced fireworks algorithm that adaptively tunes the structural parameters of controllers to solve the problems that arose in the last heating period. Simulation and live measure results demonstrate that the upgraded control scheme counters the adverse effects of time lag, reduces overshoot, and shortens the settling time. Further, benefiting from a delicate balance between heating demand and supply, the heating system with the upgraded management achieves an increase of 11.4% in the average exergetic efficiency and a decrease of 76.5% in the complaint rate. Note that the advanced fireworks algorithm mitigates the adverse effect of capacity lag and simultaneously accelerates the optimizing and converging processes, exhibiting its comprehensive competitiveness among this study’s three intelligent optimization algorithms. Nevertheless, the forecast and regulation of the return water temperature of the heating system are independent of each other. Configuring an integral predictive control structure for heat pump heating systems will be worthwhile in the future.

Author Contributions

D.Q. Conceptualization; Methodology; Validation; Formal Analysis; Investigation; Data Curation; Writing & Review & Editing. J.W.: Review & Editing. L.W. Writing & Review & Editing. Y.Y.: Review. R.K.: Technical seminar. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The data supporting this study’s findings are available from the corresponding author upon reasonable request.

Acknowledgments

This work is financially supported by the National Key R&D Program of China (Grant No. 2021YFE0116100). A valuable contribution towards live application by Hebei Hongrui Intelligent Engineering Technology Co., LTD, Shijiazhuang, China, is expressed in sincere gratitude.

Conflicts of Interest

Declaration of competing interest. The authors have no conflicts of interest to disclose.

References

  1. National Development and Reform Commission, National Energy Administration, Ministry of Finance et al. Clean Heating Planning in winter in northern China (2017-2021). 2017. (In Chinese) https://www.gov.cn/xinwen/2017-12/20/content_5248855.htm/.
  2. Wu, J.; Song, L.; Wang, Z.; Sun, Y.; Wang, J. Implementation evaluation of clean heating pilot city in Northern China during the 13th Five-Year Plan period. Environmental Protection Science, 2023, 49: 48-55. (In Chinese). [CrossRef]
  3. Wang, Y.; Liu, W. Evaluating the effect of Clean Heating Policy Pilot on air quality improvement: A quasi-experimental study based on three batches of pilot cities in China. China Environmental Science, 2024, 44: 581-592. (In Chinese). [CrossRef]
  4. Zhai, Y.; Li, S. Summary research and prospect of clean heating renovation in northern rural areas of China. China Energy and Environmental Protection, 2023, 45: 194-200. (In Chinese). [CrossRef]
  5. Hou, L.; Ding, H.; Wang, S. Impact assessment of clean heating on carbon emission in rural residential building field. Building Science, 2022, 38: 260-265. (In Chinese). [CrossRef]
  6. Wen, Y.; Cao, Y.; Zhao, X.; Gao, W.; Lv, H. CiteSpace-based clean heating policy and technology development process and trend analysis. HV&AC, 2023, 53: 171-176. (In Chinese). [CrossRef]
  7. Song, L.; Wu, J.; Sun, Y.; Zhang, W. Research on the Renovation Technology and Subsidy Policy of Rural Clean Heating in the 14th Five-year Plan Period. Environmental Protection, 2022, 50: 15-20. (In Chinese). [CrossRef]
  8. Fu, B. Pay attention to building energy-saving renovation with the aim of promoting the sustainable development of clean heating in rural areas. Energy of China, 2023, 45: 82-90. (In Chinese) https://kns.cnki.net/kcms2/article/abstract?v=UeijT_GnegCbocwAfR1jEP_vTXXfG6cUXwuWe9bULk5Usf7TBNp8i_3i4-LF8hxMBN258GBLVOjHGnicqKI7WzyIU0f0LtJfmcj35gVbXdX70DEUDVCeJy6hSxo6PLh9h5r0CM1UwF0=&uniplatform=NZKPT&language=CHS/.
  9. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Standard for Nearly Zero Energy Buildings (GB/T 51350-2019). 2019. (In Chinese) www.mohurd.gov.cn/.
  10. Chinese Society for Urban Studies. Evaluation Standard for Ultra-Low Energy Buildings (T/CSUS 15-2021). 2021. (In Chinese) http://www.chinasus.org/.
  11. Capone, M.; Guelpa, E.; Verda, V. Optimal installation of heat pumps in large district heating networks. Energies, 2023, 16: 1448. [CrossRef]
  12. Gong Y, Ma G, Jiang Y; et al. Research progress on the fifth-generation district heating system based on heat pump technology. Journal of Building Engineering, 2023, 71: 106533. [CrossRef]
  13. Pesola, A. Cost-optimization model to design and operate hybrid heating systems ? Case study of district heating system with decentralized heat pumps in Finland. Energy, 2023, 281: 128241. [CrossRef]
  14. Sayegh, M.A.; Jadwiszczak, P.; Axcell, B.P. Heat pump placement, connection and operational modes in European district heating. Energy & Buildings, 2018, 166: 122-144. [CrossRef]
  15. Kontu, K.; Rinne, S.; Junnila, S. Introducing modern heat pumps to existing district heating systems ? Global lessons from viable decarbonizing of district heating in Finland. Energy, 2019, 166: 862-870. [CrossRef]
  16. Dongellini, M.; Naldi, C.; Morini, G.L. Influence of sizing strategy and control rules on the energy saving potential of heat pump hybrid systems in a residential building. Energy Conversion and Management, 2021, 235: 114022. [CrossRef]
  17. Wei, Z.; Ren, F.; Yue, B. Data-driven application on the optimization of a heat pump system for district heating load supply: A validation based on onsite test. Energy Conversion and Management, 2022, 266: 115851. [CrossRef]
  18. Lashkari B, Chen Y, Musílek M; et al. Intelligent scheduling of heat pumps to minimize the cost of electricity. 2020 21st International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 2020, 1-6. [CrossRef]
  19. Yüce A, Deniz F N, Tan N; et al. Obtaining the time response of control systems with fractional order PID from frequency responses. 2015 9th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 2015, 832-836. [CrossRef]
  20. Khodadadi, H.; Dehghani, A. Fuzzy logic self-tuning PID controller design based on Smith predictor for the heating system. 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Korea (South), 2016, 161-166. [CrossRef]
  21. Dehghani, A.; Khodadadi, H. Designing a neuro-fuzzy PID controller based on Smith predictor for heating system. 2017 17th International Conference on Control, Automation and Systems (ICCAS), Jeju, Korea (South), 2017, 15-20. [CrossRef]
  22. Al-Dhaifallah, M. Heat Exchanger Control Using Fuzzy Fractional-Order PID. 2019 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 2019, 73-77. [CrossRef]
  23. Yang, X.; Liu, T.; Sun, A. Auto-control of Water Condenser Based on PID Controller. AMR 2011, 225-226: 186-189. https://api.semanticscholar.org/CorpusID:111166572.
  24. Gao, L.; Yang, Y.; Ren, X.; Gu, H.; Han, Q.; Yu, J. Qingqing and Y. Jingya, Research on temperature control system based on IPSO optimized fuzzy PID. 2020 39th Chinese Control Conference (CCC), Shenyang, China, 2020, 2014-2019. [CrossRef]
  25. Wang, Y.; Liu, Y.; Zhu, R.; Zhang, Y. Fractional-order PID controller of a heating-furnace system. Advanced Materials Research, 2012, 490-495: 1145-1149. https://api.semanticscholar.org/CorpusID:122576625.
  26. Jiang A, Zhang Q, Wang H; et al. An improved dynamic real-time optimization strategy for heat pump heating system. CIESC Journal, 2019, 70: 1494-1504. (In Chinese). [CrossRef]
  27. Jiang P, Xu B, Li Q; et al. Buildings heat pump heating systems for demand response. District Heating, 2023: 100-111. (In Chinese). [CrossRef]
  28. Wang, C.; Liu, R. Modeling and simulation of a fuzzy PID controller for heat exchanger systems in district heating. Proceedings of the 2nd International Conference on Electronics, Network and Computer Engineering (ICENCE 2016), 699-703. [CrossRef]
  29. Al-Dhaifallah, M. Heat exchanger control using fuzzy fractional-order PID. 2019 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 2019, 73-77. [CrossRef]
  30. Lu, Y.; Yang, Y.; Gu, H.; Zhang, Y. Identification and self-tuning control of heat pump system based on neural network. 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 2016, 6687-6691. [CrossRef]
  31. Abdullah, Z.; Othman, M.; Taip, F. Neural network based adaptive PID controller of nonlinear heat exchanger. 2019 IEEE 9th International Conference on System Engineering and Technology (ICSET), Shah Alam, Malaysia, 2019, 453-458. [CrossRef]
  32. Liu, X. Optimization design on fractional order PID controller based on adaptive particle swarm optimization algorithm. Nonlinear Dyn, 2016, 84: 379-386. [CrossRef]
  33. Tan, Y.; Zhu, Y. Fireworks Algorithm for Optimization. In: Tan Y, Shi Y, Tan K. (EDS) Advances in Swarm Intelligence. ICSI 2010. Lecture Notes in Computer Science, 6145. Springer, Berlin, Heidelberg. [CrossRef]
  34. Xue, J.; Wang, Y.; Li, H.; Meng, X.; Xiao, J. Advanced fireworks algorithm and its application research in PID parameters tuning. Mathematical Problems in Engineering, 2016, 2016, 2534632: 1-9. [CrossRef]
  35. Yin X, Li X, Liu L, Wang L, Improved fireworks algorithm and its application in PID parameters tuning. 2017 36th Chinese Control Conference (CCC), Dalian, China, 2017, 9841-9846. [CrossRef]
  36. Li, J.; Tan, Y. A comprehensive review of the fireworks algorithm. ACM Computing Surveys, 2019, 52: 1-28. [CrossRef]
  37. Zhang, G.; Li, F.; Geng, Y. Design of temperature control system for air heat pump water supply machine based on incremental PID control. Computer & Digital Engineering, 2021, 49: 268-271+321. (In Chinese). [CrossRef]
  38. Wei, Q. Design and research of the PID temperature controlling system based on air-source heat pump water supply unit. University of Chinese Academy of Sciences, 2017. (In Chinese) https://kns.cnki.net/kcms2/article/abstract?v=aKxFI3wG76hThvB4DmBe8HG0SNtTzn2s3MhayKfaKce0w4dGMrZTb1NcZCEXXCSvt_D7qHQpLz7xRHUuMwz8omJqLI25wtQRQouI8TQheA2fNPryZOUDmODt4Dp5y8U-GAgKZN6YSJSL08Ifh5KBKXlGbEQHhpJ-5Lgs5Uv-yhCRy98_atEEHVh-XITgBME-pUa0rUxNi4A=&uniplatform=NZKPT&language=CHS.
  39. Dongellini M, Valdiserri P, Naldi C; et al. The role of emitters, heat pump size, and building massive envelope elements on the seasonal energy performance of heat pump-based heating systems. Energies, 2020, 13: 5098. [CrossRef]
  40. Huang, H.; Zhang, S.; Yang, Z.; Tian, Y.; Zhao, X.; Yuan, Z.; Hao, S.; Leng, J.; Wei, Y. Modified Smith fuzzy PID temperature control in an oil-replenishing device for deep-sea hydraulic system. Ocean Engineering, 2018, 149, 14–22. [CrossRef]
  41. Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Transactions on Automatic Control, 1999, 44: 208-214. https://api.semanticscholar.org/CorpusID:125597477.
  42. Wang, C. Study on fractional order PID controller parameter tuning methods and design. Changchun, Jilin University, 2013. https://kns.cnki.net/kcms2/article/abstract?v=UeijT_GnegAq2hSWOd876zUVESEjjmjbxe87f_gKEMeKGeIwjJcNJYW0LzK-l9hm4RbQTiLVBGuqf1FeoEsTLYRDDRzaMt_n3n480COkl_m2Uo_HZb4aofnoamR2U3jU&uniplatform=NZKPT&language=CHS/.
  43. Jamil, A.; Tu, W.; Ali, S.; Terriche, Y.; Guerrero, J. Fractional-order PID controllers for temperature control: A review. Energies, 2022, 15, 3800. [CrossRef]
  44. Wang Y, Song Z, You S; et al. Thermal load prediction algorithm integrating singular spectrum analysis and neural network. Journal of Tianjin University (Science and Technology), 2023, 56: 573-578. (In Chinese). [CrossRef]
  45. Zeng, M.; Zhao, Z.; Li, Z. Self-learning improved fireworks algorithm with Cauchy mutation. Journal of Chinese Computer Systems, 2020, 41: 264-270. (In Chinese) https://kns.cnki.net/kcms2/article/abstract?v=UeijT_GnegC6DKCMRCVy92HIUamWeyI8DbSsHxjYXzddlCadFvDTGCftwMfZaUH48T9Cy3aeMfY-36NWpkSxV_QI5R_kCR5d-i08YBwBEUv6MpTN83Ad2abTBgK5TYXvF_09a9L714g=&uniplatform=NZKPT&language=CHS/.
  46. Wei, M.; Li, S.; Zhou, J.; Wang, C.; Yang, R. Cascade control mode of indoor temperature PIλDµ and supply air temperature PDµ for multi-evaporator air-conditioning system. Control Theory & Applications: 1-10 [2024-03-02]. (In Chinese) http://kns.cnki.net/kcms/detail/44.1240.TP.20230928.0818.024.html.
Preprints 121029 g001
Figure 1. The schematic diagram of a water/ground-source heat pump heating system.
Figure 1. The schematic diagram of a water/ground-source heat pump heating system.
Preprints 121029 g001
Preprints 121029 g002
Figure 2. The heat-pump heating retrofit project located in Shanxi, China.
Figure 2. The heat-pump heating retrofit project located in Shanxi, China.
Preprints 121029 g002
Preprints 121029 g003
Figure 3. The structure of the single-loop PID control system.
Figure 3. The structure of the single-loop PID control system.
Preprints 121029 g003
Preprints 121029 g004
Figure 4. The structure of the proposed control system.
Figure 4. The structure of the proposed control system.
Preprints 121029 g004
Preprints 121029 g005
Figure 5. The controlled objects with Smith predictor.
Figure 5. The controlled objects with Smith predictor.
Preprints 121029 g005
Preprints 121029 g006
Figure 6. Controller parameters tuning model based on the advanced fireworks algorithm.
Figure 6. Controller parameters tuning model based on the advanced fireworks algorithm.
Preprints 121029 g006
Preprints 121029 g007
Figure 7. The complete framework of the heat-pump heating control system.
Figure 7. The complete framework of the heat-pump heating control system.
Preprints 121029 g007
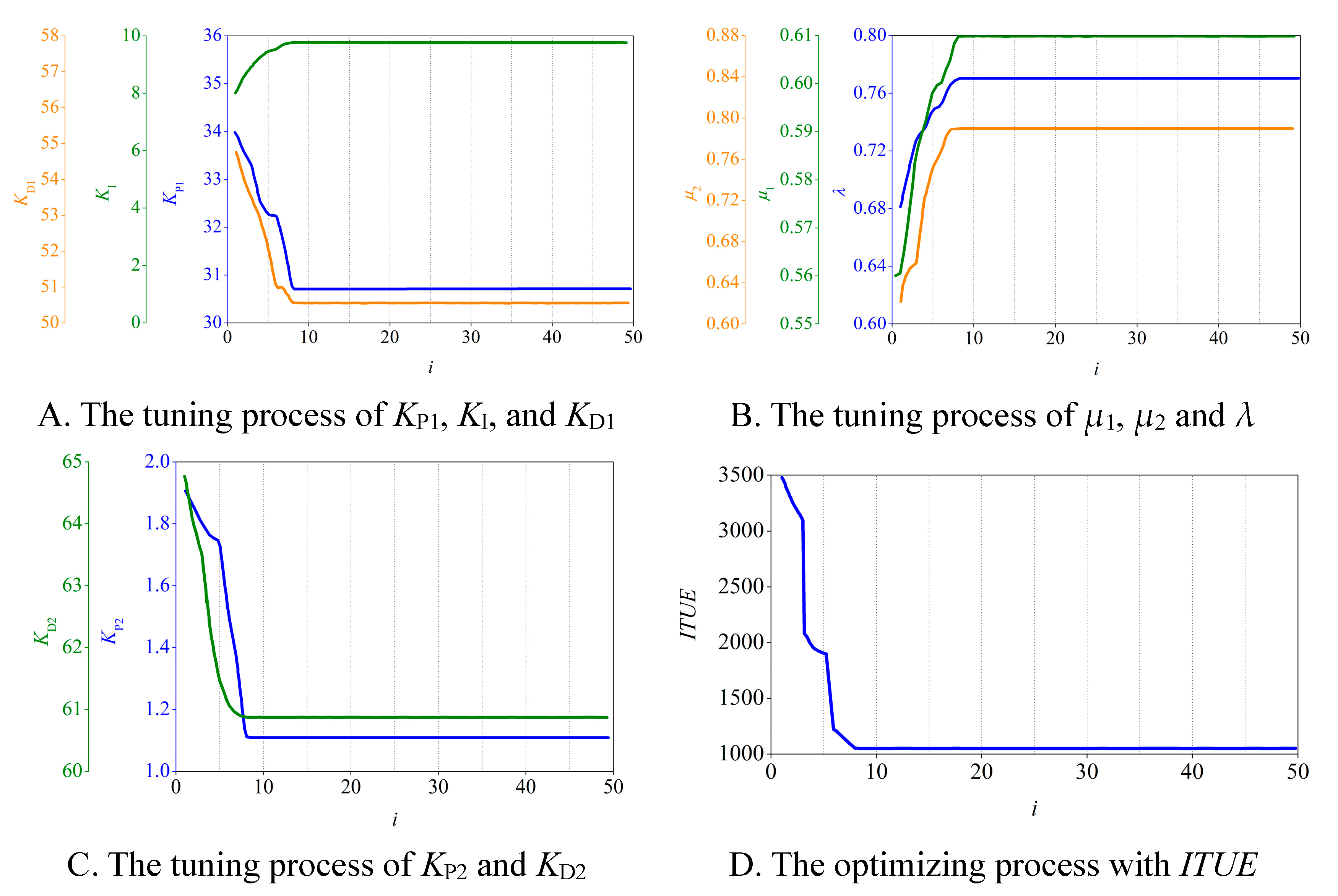
Preprints 121029 g008
Figure 8. The tuning process of eight controller structural parameters.
Figure 8. The tuning process of eight controller structural parameters.
Preprints 121029 g008
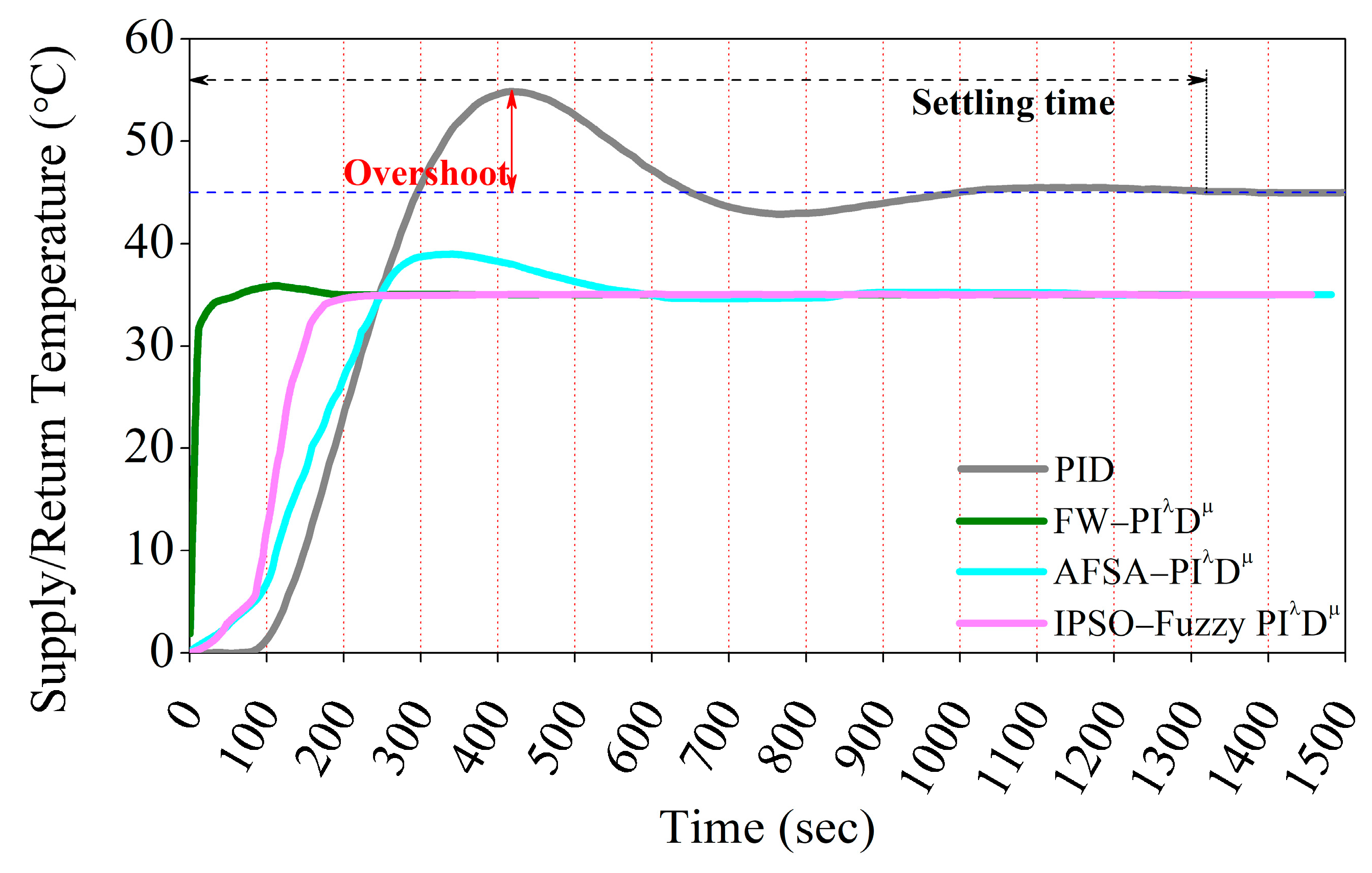
Preprints 121029 g009
Figure 9. The unit-step response test results of different control schemes/algorithms.
Figure 9. The unit-step response test results of different control schemes/algorithms.
Preprints 121029 g009
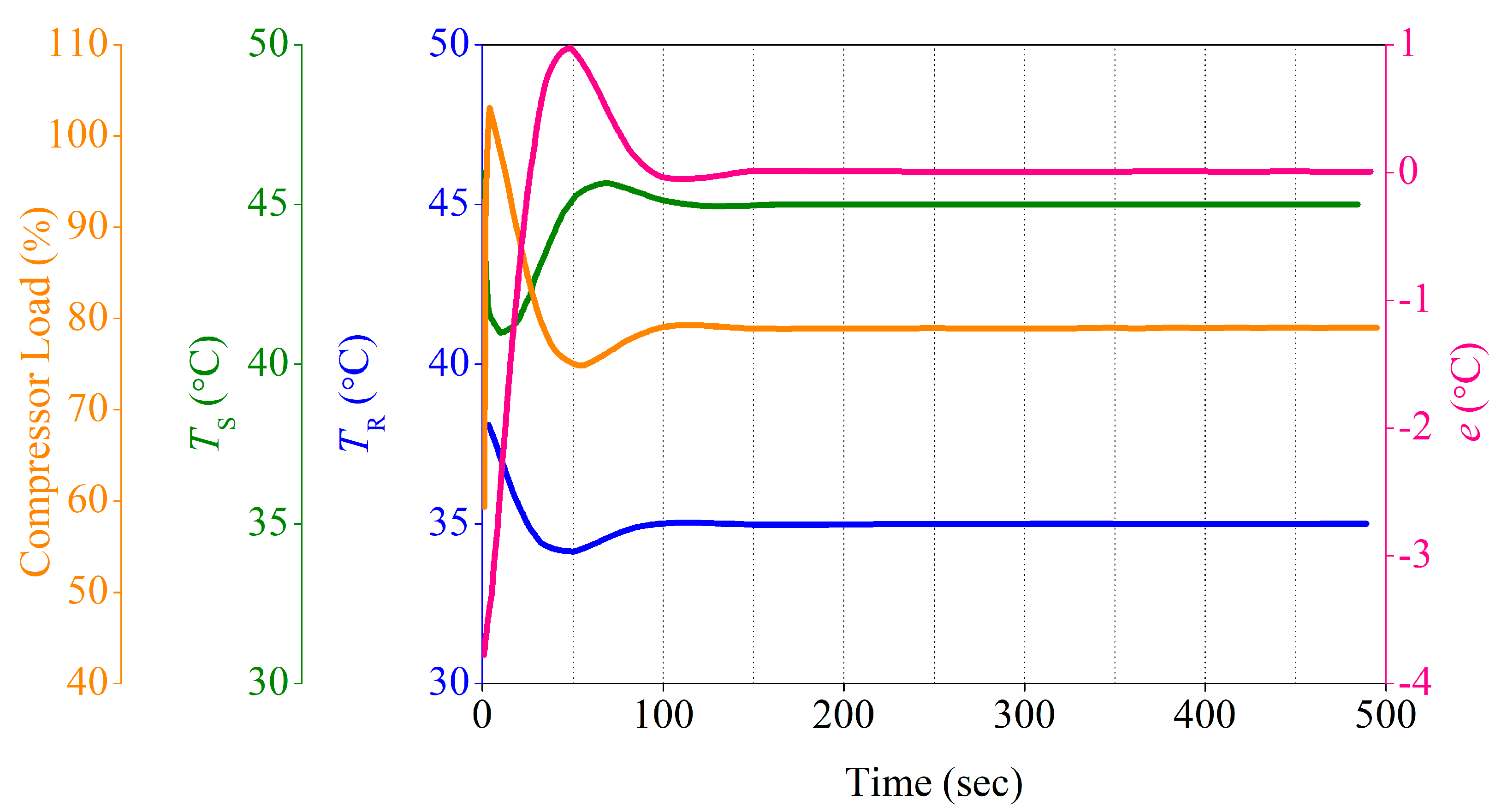
Preprints 121029 g010
Figure 10. The response curves during the simulation adjustment of heating water temperature.
Figure 10. The response curves during the simulation adjustment of heating water temperature.
Preprints 121029 g010
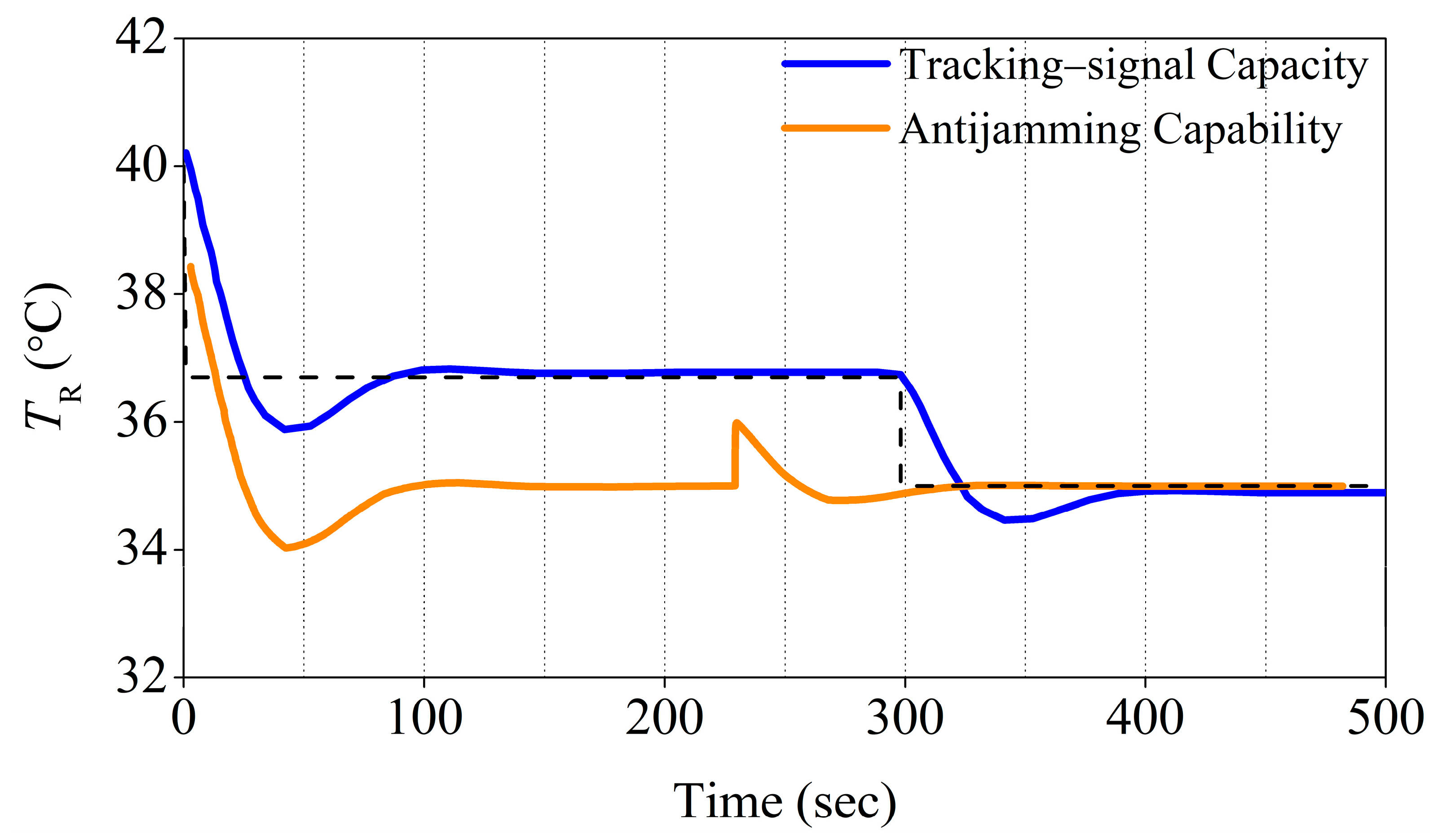
Preprints 121029 g011
Figure 11. The response curve of the return water temperature in tracking and anti-interference performance test.
Figure 11. The response curve of the return water temperature in tracking and anti-interference performance test.
Preprints 121029 g011
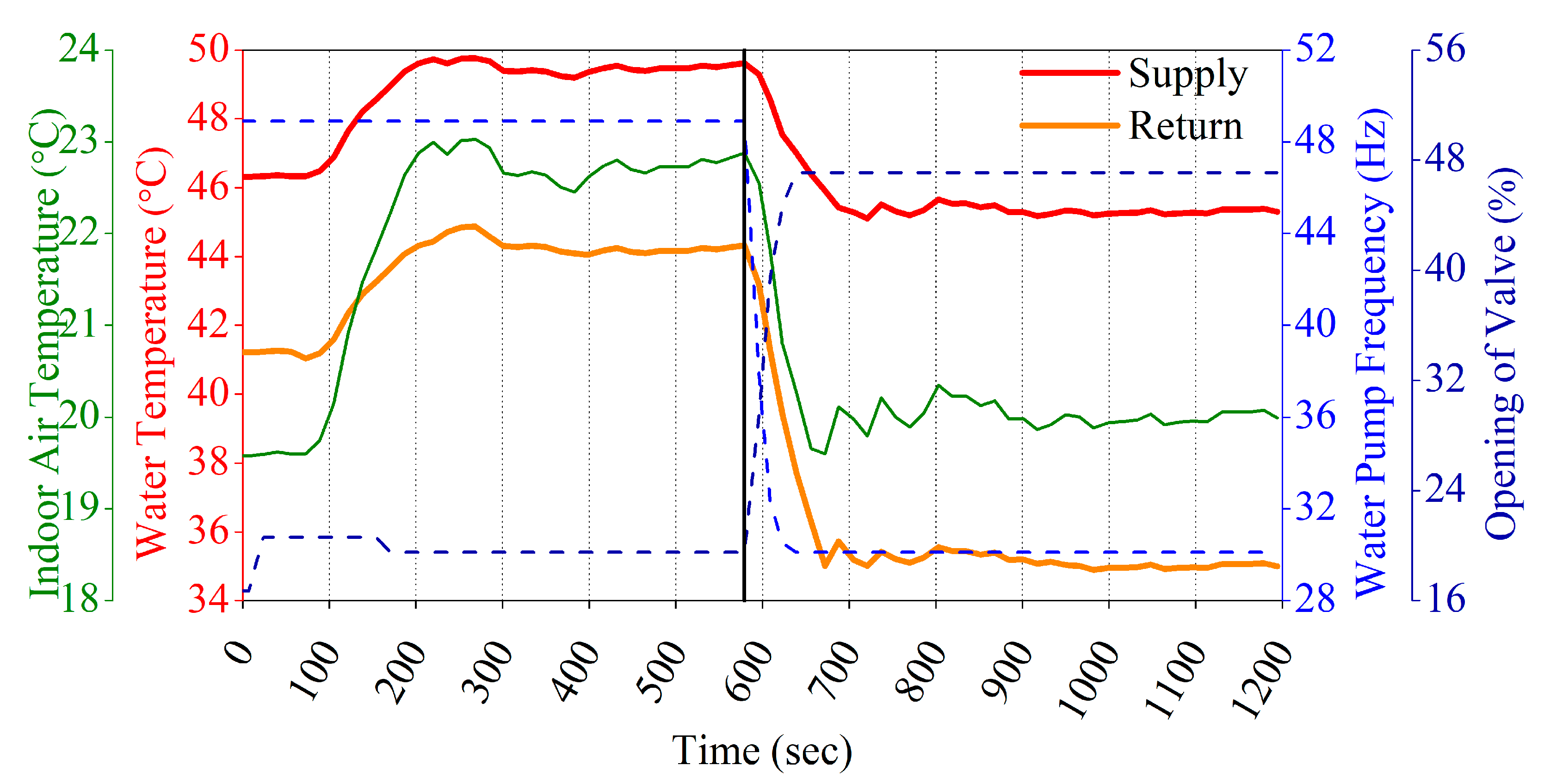
Preprints 121029 g012
Figure 12. The field records before and after the adjustment of heating water temperature.
Figure 12. The field records before and after the adjustment of heating water temperature.
Preprints 121029 g012
Preprints 121029 g013
Figure 13. The heating performance improvement in a complete heating period. (A). The distribution of heat pump load rate and ambient temperature. (B). The distribution characteristics of the heating coefficient of performance and exergetic ratio. (C). The energy efficiency benefits from the supply-demand match and high performance
Figure 13. The heating performance improvement in a complete heating period. (A). The distribution of heat pump load rate and ambient temperature. (B). The distribution characteristics of the heating coefficient of performance and exergetic ratio. (C). The energy efficiency benefits from the supply-demand match and high performance
Preprints 121029 g013
Table 1. The tuning results and several performance indicators.
Table 1. The tuning results and several performance indicators.
KP1 KI KD1 λ μ1 KP2 KD2 μ2 ITUE
30.71 9.76 50.56 0.77 0.61 1.11 60.88 0.79 1051
tc Ess Overshoot n:1
99.31 sec 5.87E-05 2.51% 8:1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Hardware in the Loop Real-Time Simulation for Heating Systems: Model Validation and Dynamics Analysis

Wessam El-Baz

et al.

,

2018

Systematic Development of application-oriented Operating Strategies at the Example of an Industrial Heating Supply System

Lukas Theisinger

et al.

,

2024

A Distributed Optimization Method for Energy Saving of Parallel-Connected Pumps in HVAC System

Xuetao Wang

et al.

,

2020

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated