Preprint

Article

One Way Equations in the Classical Mechanics. Conservation Laws

Altmetrics

Downloads

Views

Comments

Bojidar Djrdjev^*

This version is not peer-reviewed

Submitted:

13 October 2024

Posted:

15 October 2024

You are already at the latest version

Alerts

Abstract

The paper provides analysis that the generation of the gyroscopic torque described by the vector multiplication is one-way inertial phenomenon. Respectively, vector multiplication is one-way equation from the type: If B times C is equal A, A is not equal B times C. Presumably, it affects the Conservation Laws.

Keywords:

Subject: Physical Sciences - Applied Physics

1. Introduction

One definition states that the object of the Mathematics is to equalize qualities and quantities. In this paper we will deal with inertial categories as angular speed, inertial momentum, quantity of motion, torque. Although this, the Author will keep within the more abstract mathematical terms “qualities and quantities” in this paper.

The fundamental ideas for equation, the meaning of the equality, is that the quantities and qualities from both sides of the equation are equal each other reversibly. Therefore we connect both sides of the equations by the two ways equality (parity) marc “=”. Practically it means precisely that the quantities and qualities from one side of the equation can be converted physically into the qualities and quantities at the other side of the equation, and vice versa, reversibly. The reversible physical conversion of the quantities and qualities is the absolute condition for their Conservation.

Lt’s illustrate it by simple example: Let’s have three stacks per five apples as initial state of quantities and qualities. If we follow the succession of the conversion we record the initial state on the left side of the equation, simply because we record and read it from left to right. Then we convert physically the initial state into the state of fifteen apples, recording it on the right side. Reversibly, it must be possible to convert the state of fifteen apples in one stack into the previous state of three stacks per five apples. In short, if three times five is equal fifteen, fifteen must be also equal tree times five. No quality or quantity must be changed.

All math operations same as all maths and trigonometric functions from the math hierarchy are also reversible, or possess reversible anti-function: sine and reversible arcsine, tangent and reversible arctangent…, graduation and rooting, logarithm and antilogarithm, integrating and differencing, and so on and so forth.

The architecture of the Math has been created primary to serve the needs of the Mechanics (Physics), reflecting real physical phenomena. Therefore, the fundamental property of the Math to equalize reversibly converted quantities and qualities is no accident. It is identical (theoretical mirror shape) with the fundamental property of the Nature to equalize reversibly converted physical quantities and qualities.

Clearly, the essence of the Newtonian and Classical Mechanics is the two-ways parity of the converted inertial qualities and quantities. Examples: If a force/torque is applied to a mass it accelerates the mass, but in the same time the accelerated mass reacts with a force. The force (torque) creates acceleration, and the acceleration creates force (torque) reversibly. Every applied force creates equal and opposite reaction. Every vector in the space can be projected on the axes X, Y and Z, and reversibly: The vector sum of the projections is equal the vector. And so on and so forth.

2. Problem Formulation

The gyroscope is well known and its inertial effects are widely used. Most likely, thousands of papers and books about gyroscope are published all around the World. The majority of them are focused on the inertial navigation. We will analyze the physical performance of the gyroscope, as it is described by the Vector Multiplication in the light of the “Prior Art” state from the Introduction.

2.1. The Gyroscope

Let’s have a flywheel in rotation about the axis of rotation X and in turning about the axis of turning Y (Figure 1). The result is that the flywheel generates the famous gyroscopic torque about Z, perpendicular to the first two. The red arrows show the geometrical directions of the converted from X and Y to Z quantities and qualities. The Vector Multiplication (1) from the textbooks (we don’t need to cite textbooks) formulates that the magnitude of the gyroscopic torque is equal the quantity of motion about X times the angular speed about Y.

{\vec{τ}}_{z} = J_{x} {\vec{ω}}_{x} \times {\vec{ω}}_{y}

(1)

J_{x} {\overset{⇀}{ω}}_{x} \times {\vec{ω}}_{y} = {\vec{τ}}_{z}

(2)

If we arrange the succession of the appearing of the participating quantities and qualities, on the way we record and read the equation (from left to right), we must record the incoming quantities and qualities (the quantity of motion about X and the angular speed of turning about Y) on the left, then the resulted gyroscopic torque on the right (2). But for the moment it is not so important, because the two ways equality mark predicts that the vector multiplication is satisfied in both directions: from left to right and from right to left as well. The remark just can help us to understand the situation.

2.2. The Problem Formulation

Independently how we record the vector multiplication, both sides are connected by the two-ways equality mark “=”. Therefore having in mind the example with the apples from the Introduction we expect that if the angular speeds in X and Y create the gyroscopic torque in Z, the reversible conversion is natural and must be physically possible. Physically, the reversibility means that if we apply a torque to the flywheel about Z, the torque must be converted reversibly into an angular speed about X and another one about Y. Factually we expect that the red arrows (Figure 1) of the geometrical “forward” conversion must be completed oppositely, from Z to X and from Z to Y.

The question is critically important because: If the reversibility is not satisfied, the quantities and qualities will not be recovered, and disproportions will be collected. So, let’s say it again: The property of the reversible equalization of converted quantities and qualities means that: If we apply on the flywheel the exact torque about Y, we received during the “forward” conversion, we must make the flywheel to rotate about X, and also about Y with the exactly same angular speeds as before, because the two ways equality mark “=” promises it.

2.3. The Physical Experiment

Let’s have the same flywheel from Figure 1, but in peace (see Figure 2). Then let’s apply a torque about Z equal the generated one in the Figure 1. The great question is what will happen? Will we receive reversibly the angular speeds in X and in Y as the two-ways equality mark predicts?

The great answer is: Not at all! Instead of the predicted result, we receive angular acceleration of the flywheel about Z, reversibly proportional to the inertial moment of the flywheel about Z, according to the Second Newtonian Law. Physically and experimentally we receive at the right side of the equation (1) qualities and quantities different then the ones predicted by the two ways equality mark.

2.4. On the Possibilities to Recover Reversibly the Initial State in X and Y

The Newtonian Mechanics is not capable to recover the quantities and qualities in X and Y at the right side of (1) using the ones from the left side, because it doesn’t possess spatial properties (properties to transfer quantities and qualities from one to other degree of freedom). The Gyroscope is capable to transfer and convert the quantities and qualities from one to other degree of freedom i.e. from the right to the left side of the equation (1). But the Gyroscope fails to recover reversibly the quantities and qualities at the right side of the same equation (1) using the ones from the left side, because, as is seems, it possesses one way spatial properties. It looks that the only way to recover the quantities and qualities at the right side of (1) using the ones from the left side is to apply the gyroscope again, but somehow oppositely. Detailed analysis (not provided here) points that even if we apply the gyroscopic phenomenon differently by all possible ways, and as many times as we wish, we can’t recover the initial inertial state in full scale.

Recovering the initial state in full scale is not possible even if we take in account that, the specific of the generation of the gyroscopic torque is that only the axis Y is fixed (let’s say, to some vehicle). The axes X and Z are in turning about Y, and respectively the vectors of the angular speed about X and the gyroscopic torque about Z are in turning about Y constantly.

The influence of the turning axes X and Z can be avoided if we use the improved SDD (Sector-rated in Diametrical Direction) Flywheel, combined with appropriate motion about X and Y (Figure 3). It is explained in details in [1,2], and [3]. We receive the inertial machine from Figure 3 capable to perform one way transfer of quantities and qualities between fixed axes irreversibly and permanently. Taking in account the above capability, we can build our discussion on the idea that the irreversible transfer and conversion of inertial qualities and quantities is between three fixed to the Space, Earth or vehicle axes/degrees of freedom.

2.5. A Brief Survey

-There are one way equations in the Chemistry.

-Important role in the Quantum Mechanics play unidirectional equations from the type: If A is equal B, B is not equal A.

-There is one way transfer of heat from high temperature to low temperature bodies. It creates disproportion between the constantly decreasing high temperature heat and the constantly increasing low temperature heat (Entropy).

-One way conversions are widely used in the cryptography.

-In some aspects the math inequalities can be accepted as one way.

2.6. One Way Equality Mark

As it seams the concept for one way conversions/equations is not so strange for the Physics, although that (probably) it is news for the Classical Mechanics. To mark the one way conversions between both sides of the equation (Figure 4 a), a small arrow is used. The Author considers this not so appropriate because it doesn’t show that the quantities and qualities are equal, even unidirectional, instead to be for example unequal. Therefore the Author uses in his analyses compilation of the common two way equality mark with added arrow above (Figure 4 b). The simplified one way equality mark consists of one dash (the half of “=”) and arrow above (Figure 4 c).

We consider that the correct way to record the vector multiplication is to use one way equality mark. We record the vector multiplication following the succession of the appearance of the physical quantities and qualities. We direct the one way equality mark from left to right (Figure 4 d). If we follow the succession from the textbooks (Figure 4 e), we direct it from right to left. The one raw simplified version is shown on Figure 4 g.

Let’s record the full scale of the possible inertial conversions (Figure 4 f), including the Spatial and the Newtonian ones. We record the vector multiplication following the succession of the appearance of the physical quantities and qualities. The applied in Z torque doesn’t recover reversibly the quantities and qualities in X and Y on the left of the vector multiplication. Instead of this it crates angular acceleration of the flywheel about Z, according to the Second Newtonian Law. Since the Newtonian Mechanics is reversible, we connect both sides of the Newtonian Second Law by the common two way equality mark. The red arrows underline the directions of the physical conversions.

Factually the transferred and converted from X and Y into Z quantities and quantities remain in Z. We don’t forget that behind the records from Figure 4 exist real physical (inertial) phenomena.

3. Problem Solution

The actual state of the affairs is that we face a Natural Spatial Inertial Phenomenon. The Author’s vision is described in [4], same as in [1,2] and [3], in particular. The Spatial Inertial Phenomenon is irreversible. The irreversibility affects the Conservation of the quantities and qualities by one or other way, unavoidably.

Because of this we can’t suggest problem solution here. The Author even is not sure: If the irreversibility in the Mechanics is problem or opportunity?

Certainly the only reasonable problem solution we can suggest here is to apply the Scientific Method on the subject matter of the Spatial Inertia persistently, independently of the result.

4. Conclusion

The Vector Multiplication in the Classical Mechanics is one way equation. Respectively the generation of the gyroscopic torque is one way inertial phenomenon.

There aren’t contributing authors.

No funding was received for conducting this study.

The author has no conflict of interest to declare that are relevant to the content of this article.

References

Bojidar Djordjev, Free (Reactionless) Torque Generation Fiction or Reality, 4^th WSEAS/IASME International Conference on Dynamical Systems and Control pages 139-144, 2008.
Bojidar Djordjev, Forces Generative Method, US Patent Application Number 12/312,724.
Bojidar Djordjev, Free (Reactionless) Torque generation or Free Propulsion Concept, SPESIF 2010 AIP Conference Proceeding Volume 1208 (1) pp 324-338.
Bojidar Djordjev, Reactionless Motion explained by the Laws of the Nonlinear Dynamics leading to e mew method to explain and calculate the gyroscopic torque and its possible relation to the spin of electron, WSEAS Transactions on Applied and Theoretical Mechanics, Vol.9, E-ISSN 2224-3429, pp. 252-263.

Figure 1. Geometrical diagram of the generation of the gyroscopic torque.

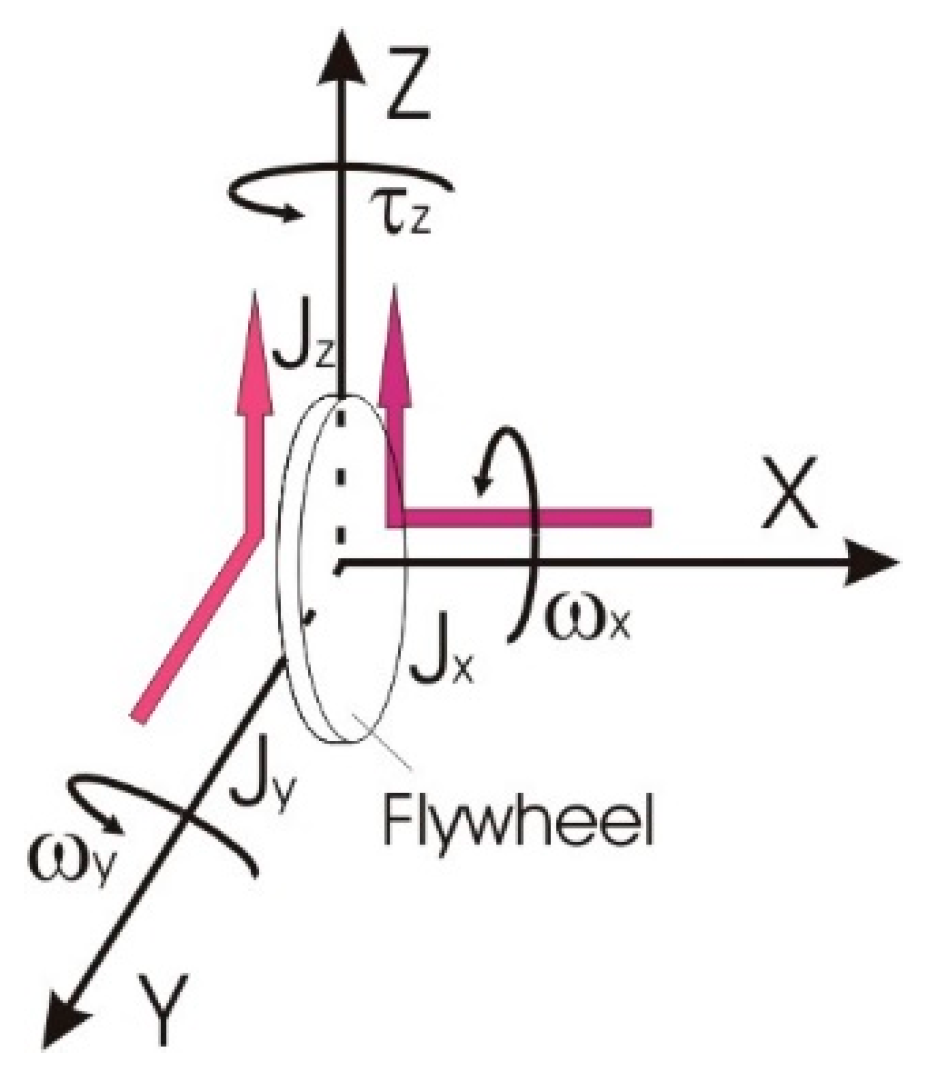
Figure 2. The result of the reversible experiment.

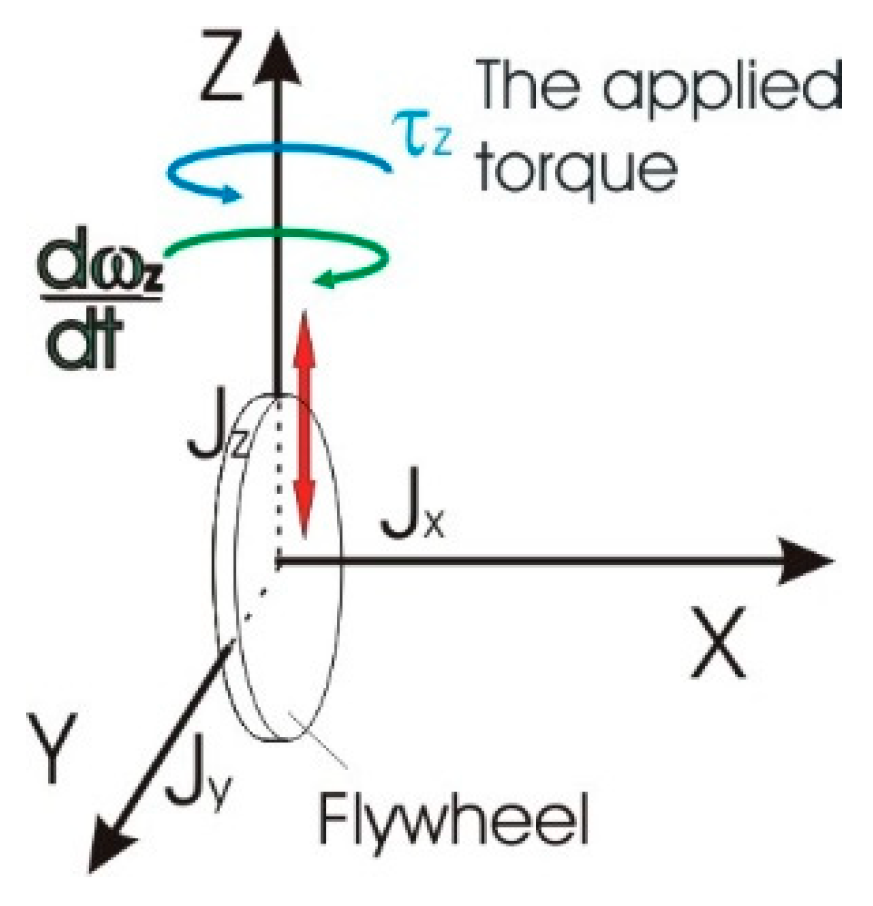
Figure 3. The First Spatial Inertial Machine capable of one way transfer and conversion of quantities and qualities between fixed to the vehicle axes irreversibly and permanently, 2004.

Figure 4. The one way equality mark and its application.

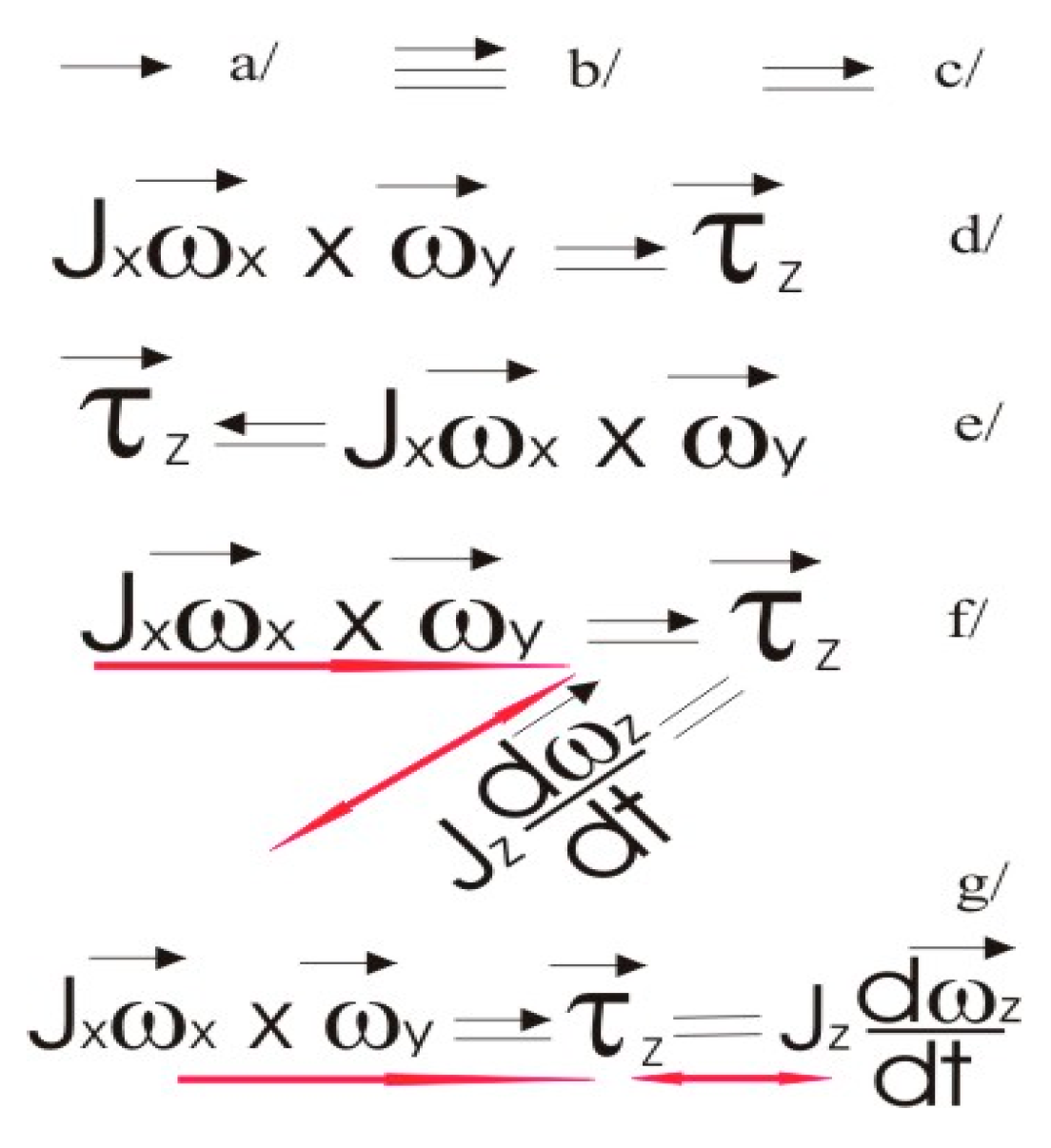
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.