Preprint

Article

Simplified Gravity Load Collapse Dynamic Analysis of Old-Type Reinforced Concrete Frames

Altmetrics

Downloads

Views

200

Comments

A peer-reviewed article of this preprint also exists.

Konstantinos G. Megalooikonomou^*

This version is not peer-reviewed

Submitted:

04 November 2024

Posted:

05 November 2024

You are already at the latest version

Alerts

Abstract

The results of shaking table tests from previous studies on a one-story, two-bay reinforced concrete frame—exhibiting both shear and axial failures—were compared with nonlinear dynamic analyses using simplified models intended to evaluate the collapse potential of older reinforced concrete structures. To replicate the nonlinear behavior of columns, whether shear-critical or primarily flexure-dominant, a one-component beam model was applied. This model features a linear elastic element connected in series to a rigid-plastic, linearly hardening spring at each end, representing a concentrated plasticity component. To account for strength degradation through path-dependent plasticity, a negative slope model as degradation was implemented, linking points at both shear and axial failure. The shear failure points were determined through pushover analysis of shear-critical columns using the Phaethon software. Although the simplified model provided a reasonable approximation of the overall frame response and lateral strength degradation especially in terms of drift, its reduced computational demands led to some discrepancies between the calculated and measured shear forces and drifts during certain segments of the time-history response.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Reinforced concrete buildings constructed before the implementation of modern seismic design standards present a major global risk for earthquake safety. These older structures are highly vulnerable to severe damage or even collapse during strong earthquakes, which has historically resulted in considerable loss of life. Many fatalities in past earthquakes are directly linked to the collapse of such buildings. Since the introduction of the capacity design concept in seismic codes in the 1980s, the safety disparity between earthquake-resistant buildings and those built before 1980 has widened, heightening concerns worldwide. Earthquakes such as those in Athens (1999), Turkey (1999), L’Aquila (2009)—which the author personally witnessed while residing there—and the 2023 Turkey-Syria earthquakes underscore the critical need for improved assessment and retrofitting of older reinforced concrete structures. Over the past 20 years, extensive research and code advancements have targeted this issue, as the detailing in these older buildings often falls significantly short of current standards for earthquake-resistant design.

Reinforced concrete (RC) columns are crucial to a building’s overall performance, as their failure can lead to extensive, disproportionate damage throughout the structure. The behavior of RC columns under the combined effects of axial load, shear, and flexure has been widely studied. For columns primarily exhibiting flexural behavior, sectional analysis or a fiber model in a one-dimensional stress field can reasonably estimate both ultimate strength and yielding deformation. However, when a column’s behavior is driven by shear or shear and flexure, sectional analysis alone falls short, as shear forces generate stress fields that extend through the member to its supports [1,2].

Recently, researchers have shown increased interest in the lateral load behavior of columns, particularly regarding axial failure that can lead to building collapse [3,4]. Before specific design requirements were introduced in the 1970s, reinforced concrete building frames in high-seismicity areas were built with detailing and proportions similar to those designed mainly for gravity loads. In these structures, columns were not typically designed to be stronger than beams, so column failure mechanisms are common in buildings from that period, especially in areas without infill walls, such as soft-story structures like the Imperial County Hospital or buildings with window-framing columns, as seen in the Van Nuys Holiday Inn [5,6]. Columns often featured widely spaced transverse reinforcement, which contributed to failure modes involving shear or combined flexure-shear failure. As shear failure advances, the degradation of the concrete core can reduce the column's capacity to carry axial loads. When this capacity declines, gravity loads must be redistributed to adjacent structural elements. A sudden loss of axial capacity can trigger a rapid, dynamic redistribution of internal forces within the frame, potentially leading to progressive collapse. This type of structural response has been observed in numerous strong earthquakes worldwide, including the Perachora Earthquake in Greece (1982), the L’Aquila Earthquake in Italy (2009), and others [7].

One example of a member-based approach to modeling shear effects is the strut-and-tie mechanism, which is used in the D-regions of beams and columns. Here, a 45° diagonal strut extends through the concrete member, covering a distance at least equal to the member's depth. Despite this, many design codes treat shear strength as a cross-sectional property [8], though alternative approaches like strut-and-tie models [8,9,10,11] are available, albeit less commonly used and often unfamiliar to many practitioners.

More advanced approaches, such as variable-angle strut-and-tie models, adjust the angle of the strut based on the level of transverse reinforcement. For instance, Eurocode 2 (2004) [13] permits a strut angle between 22.5° and 45°, with the specific angle varying according to the required transverse reinforcement. A more detailed approach, as outlined in AASHTO 2013 [10] and Model Code 2010 [9], is based on the Modified Compression Field Theory (MCFT), developed by Vecchio & Collins (1986) [14], which is widely regarded as the most comprehensive framework for understanding the shear behavior of reinforced concrete members.

The most advanced seismic design and assessment techniques available today still rely on some form of nonlinear analysis, whether static or dynamic. These analyses are typically carried out using frame elements with differing degrees of approximation. The two primary approaches used are lumped-plasticity models and distributed-inelasticity models.

Distributed-inelasticity elements allow for the direct integration of section response [15,16]. In this approach, fiber beam elements are especially effective for studying the behavior of RC structures under reversed cyclic loading, as they accurately capture moment-axial force (M-N) coupling and the interaction between concrete and steel within the section. While many fiber beam-column elements have been developed to reliably represent axial force and flexural effects, the interaction between normal and shear forces is more complex, and only a limited number of modeling strategies have been fully implemented to address this [17].

In contrast, lumped-plasticity elements require parameter calibration based on the response of an actual or ideal frame element under simplified loading conditions. This calibration is crucial because the behavior of concentrated plasticity elements depends on the moment–rotation relationship of their components. For an actual frame element, the end moment–rotation relationship is determined by integrating the section response, similar to the process used in a fiber beam element [19].

To model the behavior of prismatic members, where normal stresses and strains vary across a cross-section depth in response to flexural moment demands (maintaining plane sections), Vecchio and Collins (1988) [18] introduced the MCFT within a layered analysis framework, commonly known as a fiber model [19]. In this method, kinematic assumptions for flexure and shear (represented by sectional curvature and shear strain) drive the algorithm, while principal stress and strain orientations are calculated at multiple layers across the member’s depth. Nonlinear constitutive material laws, defining uniaxial stress-strain behavior in the principal directions, are used to determine the stress state and ensure equilibrium of the stress resultants. Here, concrete fibers are treated as biaxially stressed elements within the cross-section, with their in-plane stresses analyzed through MCFT. This approach was later refined to enhance the accuracy of shear stress distribution across the section. These advanced formulations were implemented in Response 2000 [20], a nonlinear analysis program for structural members.

When applying the MCFT to seismic assessments, several modifications are required to address the unique demands of cyclic loading. One challenge is that most experimental data supporting the MCFT is based on tests with monotonic loading, offering limited understanding of the model's behavior under cyclic displacement reversals and related degradation mechanisms. Additionally, the method assumes uniformly distributed reinforcement, which does not adequately represent older structures with sparse reinforcement. Another limitation is the absence of explicit modeling for bond-slip degradation effects on the shear behavior of RC members.

This limitation, along with the distinctive behavior of lightly reinforced concrete columns where shear and flexure interact, was recently investigated by developing a fiber beam model grounded in the MCFT [21]. This theory was applied using an exact Timoshenko fiber element that also accounts for the substantial effect of tensile reinforcement pullout due to anchorage or short lap splices on the column’s overall lateral drift. These capabilities were incorporated into a standalone Windows program named "Phaethon" [21], with a user interface developed in C++. The program aids engineers in analyzing substandard reinforced concrete columns with both rectangular and circular cross-sections.

Utilizing the moment-rotation envelope results from a cantilever shear-critical column analyzed using Phaethon software, one can model an inelastic frame structure subjected to shear, axial, or pull-out failures by placing a rigid plastic spring at the expected shear failure location. This approach also accounts for the impact of anchorage or lap-splice pullout slip on total drift and incorporates a negative degradation slope effect. The slope of the degradation links the moment-rotation envelope point where shear failure occurs to the axial failure point, beyond which the column cannot sustain its gravity loads. The section of the member between the two rigid plastic springs remains perfectly elastic. Giberson [22,23] generalized the original one-component model. A significant benefit of this method is that inelastic deformation at the ends of the member is determined solely by the moment applied there, allowing for any moment-rotation hysteretic model to be assigned to the spring. While this straightforward model has received some reasonable criticism, it is anticipated to perform effectively for relatively low-rise frame structures, particularly where the inflection point of a reinforced concrete column is situated near mid-height.

The main objective of Performance-Based Earthquake Engineering is to determine an "acceptable" probability of collapse. Collapse should be assessed as accurately as possible using nonlinear dynamic analysis. A thorough set of guidelines will provide a framework for tackling the complexities associated with nonlinear softening responses during significant displacements and deformations, thereby facilitating the acceptance of nonlinear response analyses in professional practice [24,25,26,27,28,29,30,31]. The introduction of straightforward yet effective column models, such as those presented in this study, which incorporate localized effects like shear and anchorage or lap splice slip within a coherent element formulation, will help mitigate issues of non-convergence and reduce computational time.

This paper contributes to the field of seismic assessment of older RC frames through nonlinear dynamic analyses in the following ways as also Figure 1 depicts:

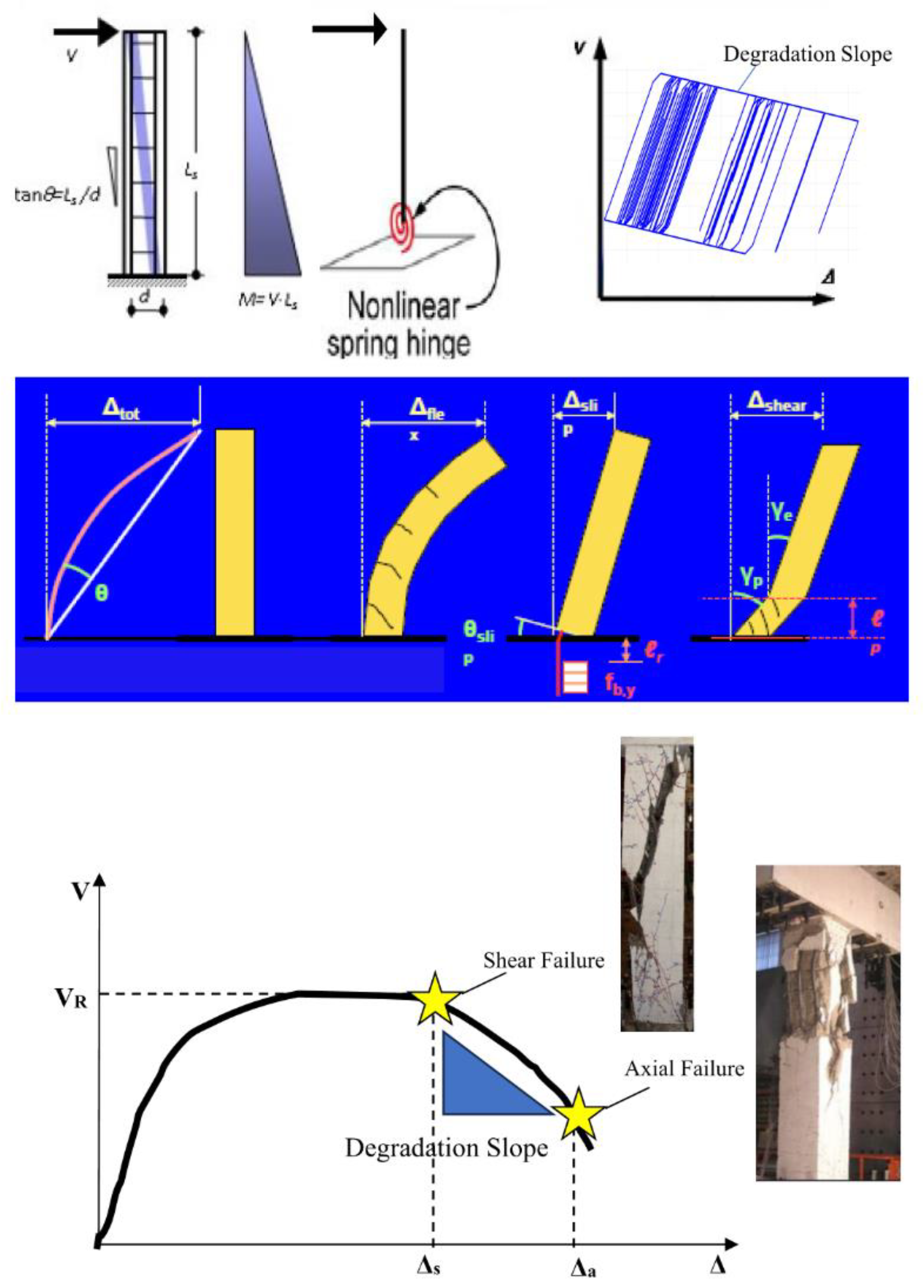
The formulation of path-dependent one-component element response with strength degradation due to shear and axial failures is described in detail.
A self-developed MATLAB [32] code is created in order to run a nonlinear dynamic analysis on one-story, two-bay reinforced concrete frame experiencing both shear and axial failures and was simulated with the above formulated beam element.
The proposed analytical model can also address the stress state of a column under full cyclic load reversals, accounting for both flexure- and shear-dominated response conditions in RC columns, while also considering the contribution of anchorage or lap-splice pullout slip to the total drift.
A reduced computational model for prediction of dynamic response of old reinforced concrete structures under seismic loads is developed based on the moment-rotation envelope results from cantilever shear-critical columns analyzed by Phaethon Windows software.
Inelastic frame structure experiencing shear, axial or pull-out failures are modeled in this study by placing a rigid plastic spring at the location where shear failure is predicted considering the contribution of anchorage and pullout slip in the total drift and applying a degradation slope. The negative slope connects the point on the moment-rotation envelope where shear failure occurs to the point of axial failure.
The proposed approach advantage is the inelastic deformation at the member ends depends solely on the moment applied at the end, allowing any moment-rotation hysteretic model to be assigned to the spring hence simplifying the analytical and numerical modeling.

This study is organized as follows: Following the introduction, which outlines the objectives of this research paper, Section 2 details the formulation of a path-dependent, one-component element response with strength degradation. Section 3 provides a comprehensive comparison of the proposed analytical model with experimental results found in the literature. Lastly, Section 4 discusses the output results, while Section 5 presents the conclusions and suggestions for future work.

2. Materials and Methods

It is valuable to examine one-component beam model formulation in greater detail, as it exemplifies a category of elements that rely on assumptions about internal force distribution. These elements are crucial in contemporary earthquake engineering analysis, as they accurately represent the force distribution within a member and lead to a reliable numerical implementation.

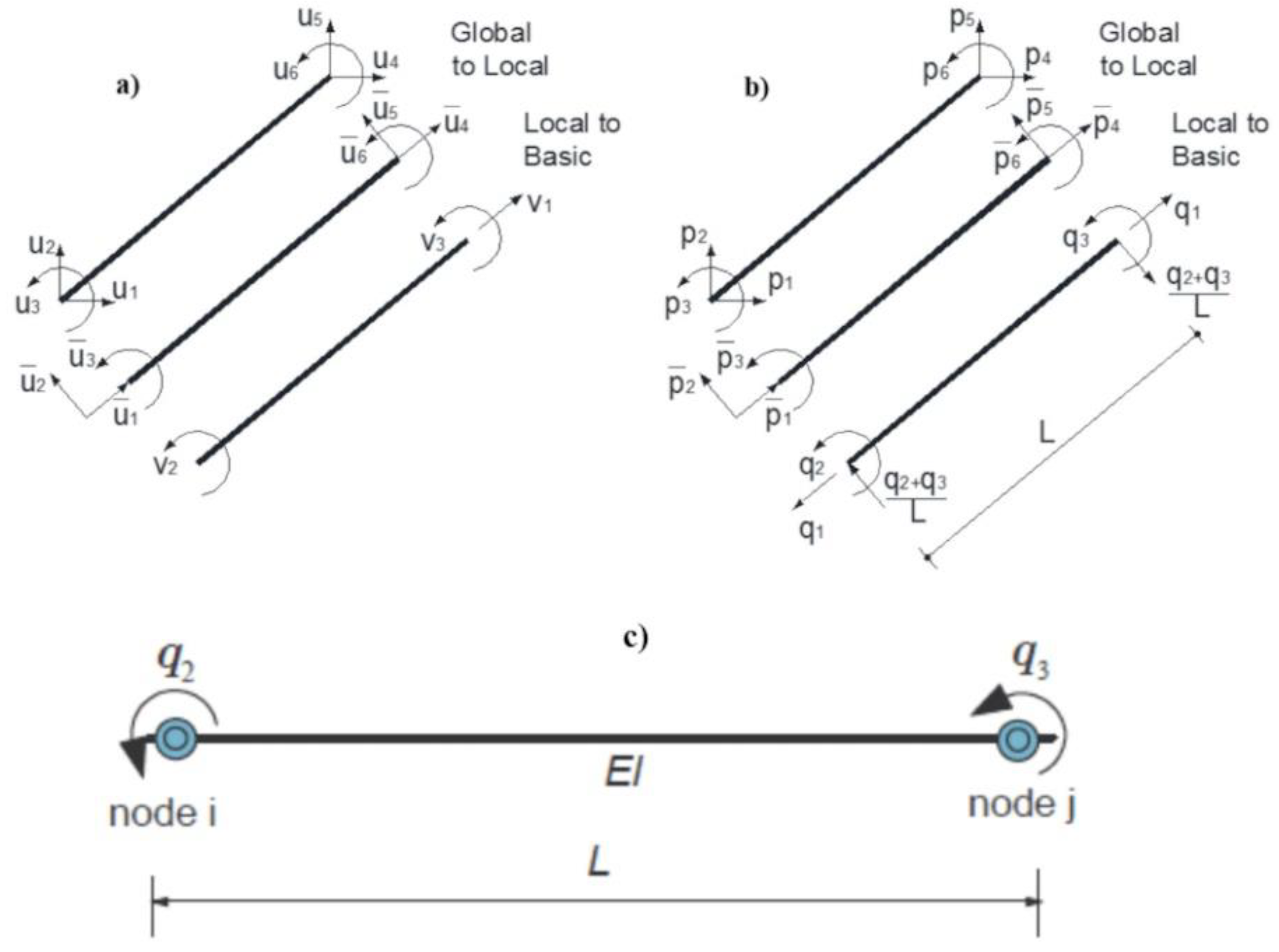
2.1. Path-Dependent Element Response with Strength Degradation

For a linear elastic, perfectly plastic beam with non-smooth multi-surface plasticity, the equilibrium, compatibility, and constitutive relations of the elastic component, along with the yield function, are provided in the following equations as illustrated in Figure 2 (p denotes plastic and e denotes elastic, M_p is the plastic moment and k is the stiffness) [15,33,34,35]:

Equilibrium : q = q_{e} = q_{p}

(1)

Compatibility : v = v_{e} + v_{p} with v_{p} = (\begin{matrix} 0 \\ v_{p 2} \\ v_{p 3} \end{matrix})

(2)

Constitutive relation of elastic component : q = k_{e} \cdot v_{e} = k_{e} \cdot (v - v_{p})

(3)

Yield function : f_{1} (q_{2}, q_{3}) = |q_{2}| - M_{p i} \leq 0 for node i

(4)

Yield function : f_{2} (q_{2}, q_{3}) = |q_{3}| - M_{p j} \leq 0 for node j

(5)

There are now two independent yield surfaces, one for node i and one for node j. These can be expressed more concisely by using the relationship |x| = sign(x)x:

f_{1} (q_{2}, q_{3}) = s i g n (q_{2}) (q_{2}) - M_{p i} \leq 0

(6)

f_{2} (q_{2}, q_{3}) = s i g n (q_{3}) (q_{3}) - M_{p j} \leq 0

(7)

Introducing the derivative:

\frac{\partial f_{1}}{\partial q} = (\begin{matrix} 0 \\ s i g n (q_{2}) \\ 0 \end{matrix}) = n_{2}

(8)

\frac{\partial f_{2}}{\partial q} = (\begin{matrix} 0 \\ 0 \\ s i g n (q_{3}) \end{matrix}) = n_{3}

(9)

Using the definition

n = [\begin{matrix} n_{2} & n_{3} \end{matrix}]

and

\frac{\partial f}{\partial q} = n^{T}

the yield conditions can be reformulated:

f (q_{2}, q_{3}) = n^{T} q - q_{p l} \leq 0 with q_{p l} = (\begin{matrix} 0 \\ M_{p i} \\ M_{p j} \end{matrix})

(10)

The flow rule for non-smooth plasticity is provided below:

Flow rule : {\dot{v}}_{p} = n_{2} β_{2} + n_{3} β_{3} = n β iff f (q_{2}, q_{3}) = n^{T} q - q_{p l} = 0

(11)

Kuhn - Tucker conditions : β_{k} \geq 0 and f_{k} \leq 0 and β_{k} f_{k} = 0 for k = 2, 3

(12)

Consistency condition : β_{k} \dot{f_{k}} = 0 for k = 2, 3

(13)

The plastic flow

β_{k}

can be defined from the consistency condition

β_{k} \dot{f_{k}} = 0

for k=2,3

\dot{f} = n \cdot \dot{q = n \cdot k_{e} (\dot{v} - \dot{v_{p}})}

(14)

Substituting the flow rule with

\dot{v_{p}} = n β

\dot{f} = \dot{n \cdot k_{e} (\dot{v} - n β)}

(15)

According to the consistency condition

β_{k} > 0

only if

\dot{f_{k}} = 0

for k=2,3 (α stands for active node, i.e., for a node with

\dot{f_{a}} = 0

β_{a} = \frac{(n_{a}^{T} k_{e} \dot{v})}{(n_{a}^{T} k_{e} n_{a})}

(16)

The tangent modulus during plastic flow is expressed as:

k = k_{e} - \frac{k_{e} n_{a} n_{a}^{T} k_{e}}{(n_{a}^{T} k_{e} n_{a})}

(17)

The summary of multi-surface plasticity for a linear elastic, perfectly plastic beam is presented below (cyclic rules similar to bilinear model):

Additive deformation decomposition $v = v_{e} + v_{p}$
Force-deformation relation $q = k_{e} \cdot v_{e} = k_{e} \cdot (v - v_{p})$
Yield condition $f (q_{2}, q_{3}) = n^{T} q - q_{p l} \leq 0$ with $n = [\begin{matrix} n_{2} & n_{3} \end{matrix}]$
Flow rule ${\dot{v}}_{p} = n_{2} β_{2} + n_{3} β_{3} = n β$ iff $f (q_{2}, q_{3}) = n^{T} q - q_{p l} = 0$
Kuhn – Tucker conditions $β_{k} \geq 0$ and $f_{k} \leq 0$ and $β_{k} f_{k} = 0$ for k=2,3
Consistency condition $β_{k} \dot{f_{k}} = 0$ for k=2,3

In order for the kinematic hardening H_k to be included, the Equations 16 and 17 are rewritten as follows:

β_{a} = \frac{(n_{a}^{T} k_{e} \dot{v})}{(n_{a}^{T} (k_{e} + H_{k}) n_{a})}

(18)

k = k_{e} - \frac{k_{e} n_{a} n_{a}^{T} k_{e}}{n_{a}^{T} (k_{e} + H_{k}) n_{a}}

(19)

The degradation slope H_k equals to the negative slope connecting the point of the response at shear failure to the point at axial failure of a shear-critical RC column. For flexure-dominant elements the kinematic hardening can have a positive value or could be omitted.

To identify the shear failure point of a shear-critical column, a pushover analysis of a single cantilever column is conducted using Phaethon software. For this analysis, the sectional model in Phaethon, which can be either rectangular or circular based on the MCFT, is employed alongside the footing anchorage model developed by Tastani and Pantazopoulou (2013) [36] or the lap-splice model proposed by Megalooikonomou (2024) [21], all integrated within Phaethon Windows software. A lateral point load that increases progressively is applied at the tip of the cantilever. The entire height of the cantilever column is represented by a single exact Timoshenko force-based fiber element, which accounts for shear effects in adjusting the principal directions throughout the fiber section depth, with the number of Gauss-Lobatto integration points determined by the user. Additionally, the user specifies the analysis step size for the lateral load and the total number of steps leading up to the maximum load, which indicates shear failure. Since the fiber approach utilizing MCFT [20] does not accurately depict the descending behavior of shear-critical columns, Phaethon implements a load-controlled procedure that maintains a constant load-step size while updating only the stiffness. The shear failure point is indicated by the last converged step of the incremental algorithm. It is important to recognize that, in practice, the response of a shear-critical column exhibits a descending branch after reaching peak strength, indicating brittle behavior. However, the embedded algorithm simulates only up to the strength attainment and shear failure point. Beyond the maximum load, the descending part of the capacity curve is illustrated by a line connecting the peak load point (shear failure) to the point of axial failure, which is defined in terms of drift according to Elwood and Moehle (2005) [4], with 20% of the peak load regarded as the residual load at axial failure. This also establishes the negative degradation slope, H_k, of the moment-rotation envelope for the shear-critical column, which will be utilized in the subsequent section of the nonlinear time-history analysis.

The following section of the results of this study will present a comparison between the results of shaking table tests conducted on a one-story reinforced concrete frame (height: 1628 mm) with two bays (each bay measuring 1830 mm), which experienced both shear and axial failures [37,38], and nonlinear dynamic analyses performed with simplified models aimed at evaluating the collapse of older reinforced concrete structures. To replicate the nonlinear behavior of the columns—both those susceptible to shear failure and those more prone to flexural failure—the one-component beam model discussed in this section will be employed. Before however present the correlation with the experimental results a short description of the experimental setup from the literature is necessary.

2.2. Experimental Test Setup

Shake table tests were conducted [37,38] to examine the dynamics of shear and axial load failures in reinforced concrete columns when an alternative load path is available for redistributing loads. The test setup included three columns fixed at their bases and connected by a beam at the top. The central column, which had a square cross-section and widely spaced transverse reinforcement, was prone to shear failure, leading to subsequent axial load failure during the tests. As the central column failed, shear and axial loads were redistributed to the adjacent ductile circular columns. Two test specimens were built and assessed. The first specimen supported a mass that induced axial load stresses in the column comparable to those expected in a seven-story building. In the second specimen, hydraulic jacks were used to increase the axial load on the central column, thereby increasing the demand for axial load redistribution as the column began to fail. Both specimens were subjected to one horizontal component of a scaled ground motion recorded during the 1985 earthquake in Chile. A comparison of the results from both specimens indicated that the behavior of the frame was influenced by the initial axial stress of the center column. The specimen with the lower axial load experienced shear failure while retaining most of its initial axial load. Conversely, the specimen with the higher axial load showed shear failure of the central column at lower drift levels and earlier in the ground motion record, resulting in axial failure of the central column. Displacement data recorded just after the onset of axial failure indicate two mechanisms contributing to the shortening of the center column during axial failure: first, large pulses that cause a sudden increase in vertical displacement after reaching a critical drift, and second, smaller oscillations that appear to "grind down" the shear failure plane. Additionally, dynamic amplification of axial loads transferred from the center column to the outer columns was observed during the axial failure of the central column.

A total mass of 31.000 kg at each planar-frame specimen was supported at the top by a beam that was 1.5 meters wide. The columns were based on footings connected to multi-axis load cells (Figure 3 (a)). The center column was constructed with minimal transverse reinforcement (A_sh/bs = 0.18%, where A_sh is the area of transverse reinforcement parallel to the applied shear, b is the width of the column—230 mm by 230 mm—with 4 #4 corner bars and 4 #5 center bars with a yield strength of 479.18 MPa, and s is the spacing of the transverse reinforcement, which consisted of W2.9 wire spaced at 152 mm with a tensile strength of 717 MPa, featuring 90° hooks). The outer columns had a circular cross-section with a diameter of 255 mm and were reinforced with closely spaced spirals (#3 spirals at 50 mm). The acceleration values recorded on the shake table during testing will be utilized in the numerical simulation in the following section. The only distinction between the two specimens was the initial axial load applied to the center column. For Specimen 1, the axial load on the center column was 0.10A_gf_c, whereas for Specimen 2, it was 0.24A_gf_c (where A_g represents the gross cross-sectional area and f_c is the measured concrete strength, which was 24.27 MPa). The axial load in Specimen 2 was increased to investigate the effect of axial load on shear and axial failures. This higher load was achieved by post-tensioning the specimen to the shaking table with pneumatic jacks, which helped prevent undesired changes in the vibration period due to the added reactive mass.

During testing, the center column of Specimen 1 exhibited a decrease in lateral-load capacity, likely due to shear failure, but did not experience axial failure. In contrast, Specimen 2's center column underwent both shear and axial-load failures. Consequently, Specimen 2 will be used in the numerical simulation to correlate with the experimental results. For more information about the specimens, test setup, and experimental outcomes, please refer to [37,38].

3. Results

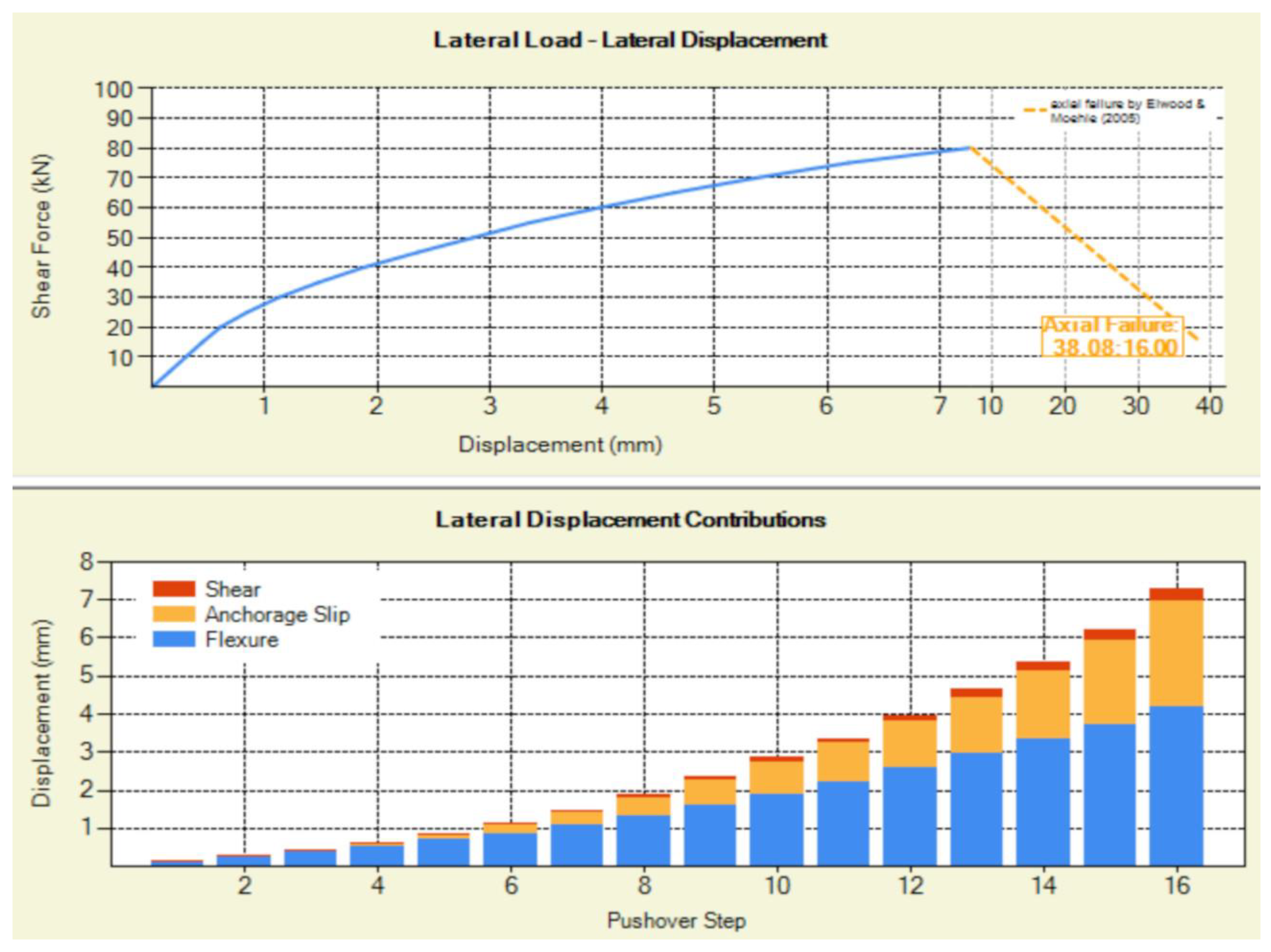
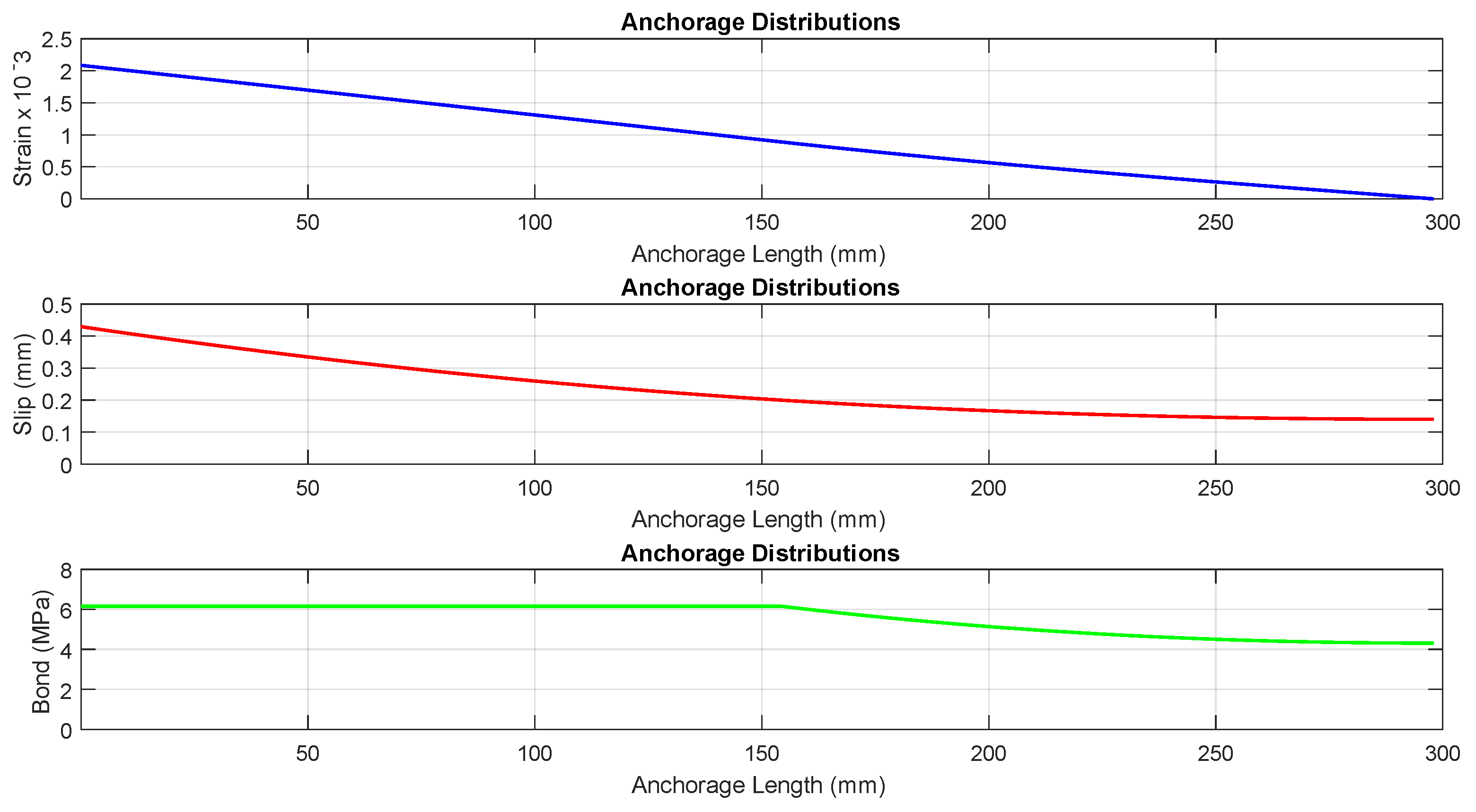
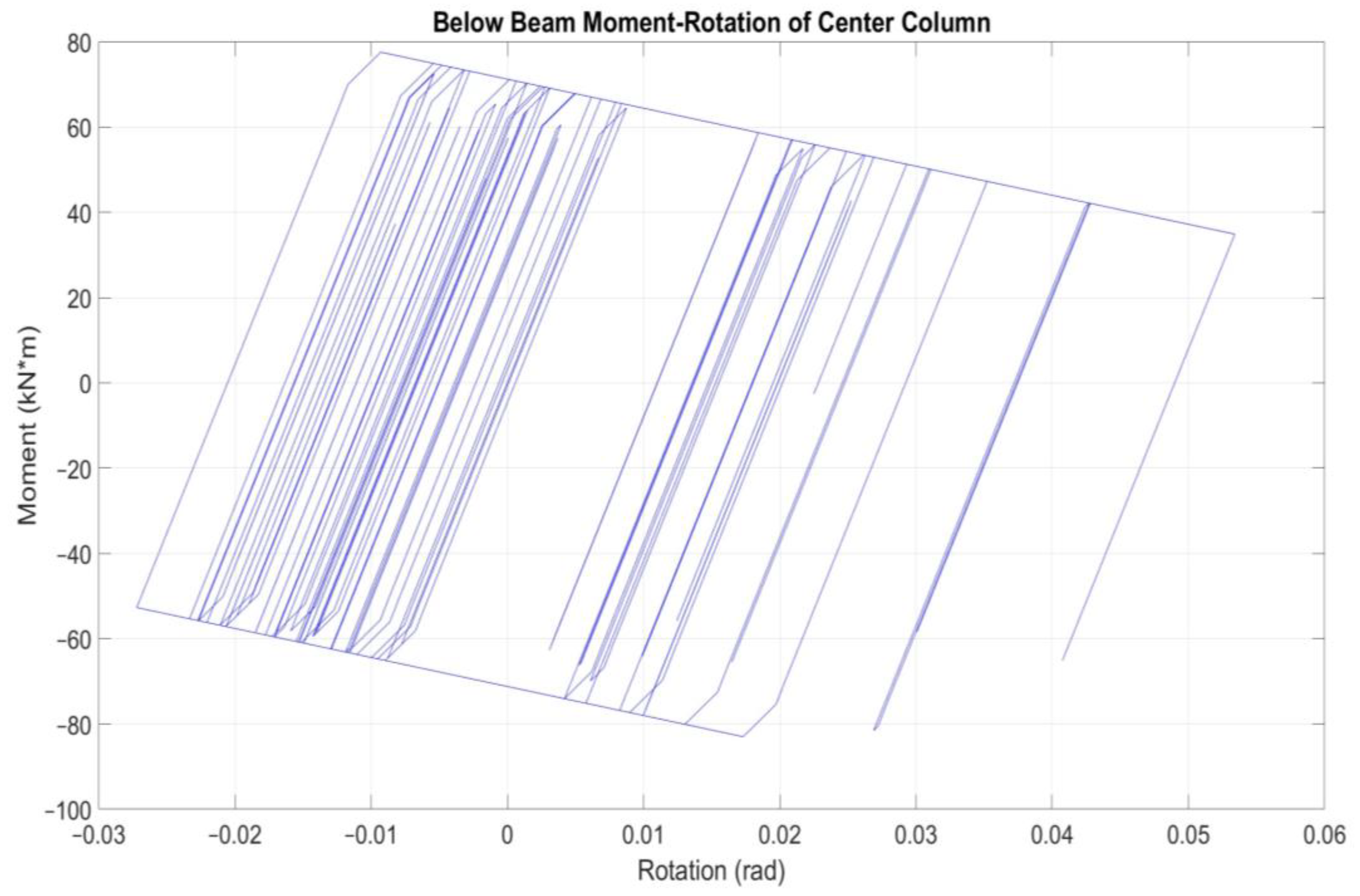
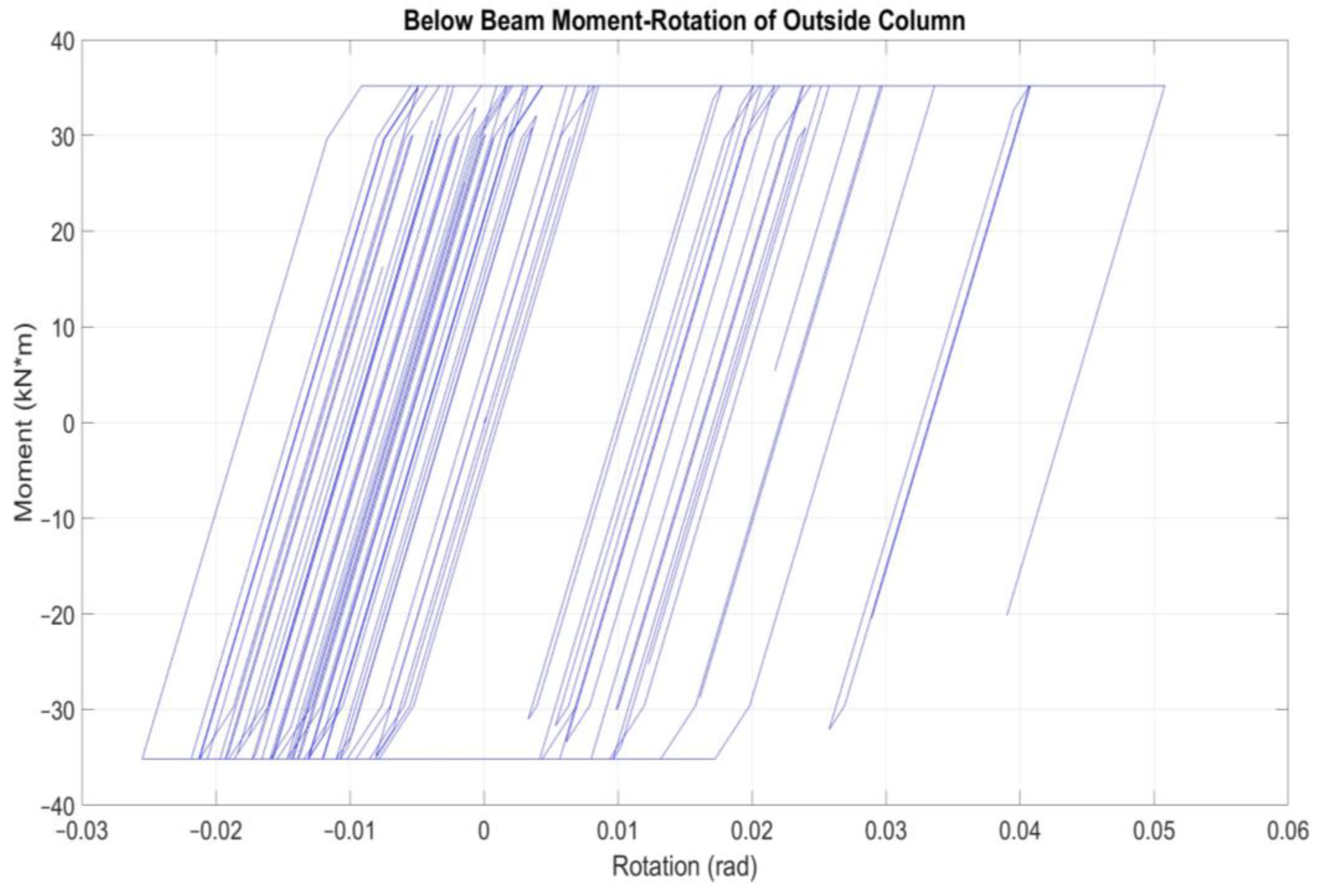
3.1. Pushover Analysis of Center Shear-Critical RC Cantilever Column.

In this section, the center column of Specimen 2 from the previously described shake table test will be analyzed using pushover analysis with Phaethon software [21]. Table 1 provides detailed information about the properties of the column under investigation.

For each point load applied at the tip of the cantilever, the corresponding shear force at specified sections of the column (integration points) aligns with the applied load, creating a constant shear force diagram. The flexural moment at the base of the column, along with the moment distribution, is derived from the lateral load, resulting in a steady shear force. The concentric axial load (whether tensile or compressive) applied at the tip of the cantilever remains constant throughout the pushover analysis and along the length of the cantilever, ensuring that every section of the column experiences the same axial force as that at the tip.

By employing this method, the resisting section forces should converge to the previously determined section forces based on the moment, shear, and axial load diagrams of the cantilever column under a constant axial load and progressively increasing lateral point loads at the tip. Once the section forces converge (using the Newton-Raphson iteration algorithm) along the cantilever column to match the correct values from the force diagrams resulting from the applied horizontal and axial loads at the tip, the axial deformation, curvature, and shear strain for each section can be calculated.

By integrating the curvatures along the shear span of the cantilever column, the rotation due to flexure is determined, which can be easily converted into lateral displacement due to flexure by multiplying it by the shear span length. Similarly, integrating the shear strains across multiple sections (with positions determined using Gauss-Lobatto integration scheme) along the cantilever column’s length (integration points) provides the lateral displacement caused by the shear distortion mechanism of the column. Finally, the rotation and displacement resulting from the pull-out of the tensile reinforcement are determined using the theoretical framework outlined in [36]. These contributions from flexure, shear, and anchorage are then combined to determine the total lateral displacement, of the cantilever column at each lateral load increment. This process continues until reaching the maximum lateral load (point of shear failure), establishing the column's capacity curve. As already described, beyond the maximum load, the descending part of the capacity curve is depicted by a line connecting the peak load point (corresponding to shear failure) to the point of axial failure, as described by Elwood and Moehle (2005) [4]. At this point, 20% of the peak load is considered as the residual load during axial failure. This also defines the negative degradation slope behavior of the moment-rotation envelope for the shear-critical column, which will be used in the next section for nonlinear time-history analysis. Figure 4 and Figure 5 present the results of the shear-critical center column of Figure 3 under study. According to Figure 4 the point of shear failure defined by Phaethon software for the cantilever center shear-critical column of Specimen 2 is V_sh = 80 kN and Δ_sh = 7.27 mm. The axial failure event is depicted also in the same Figure. Thus, the negative degradation slope in terms of moment-rotation can be defined.

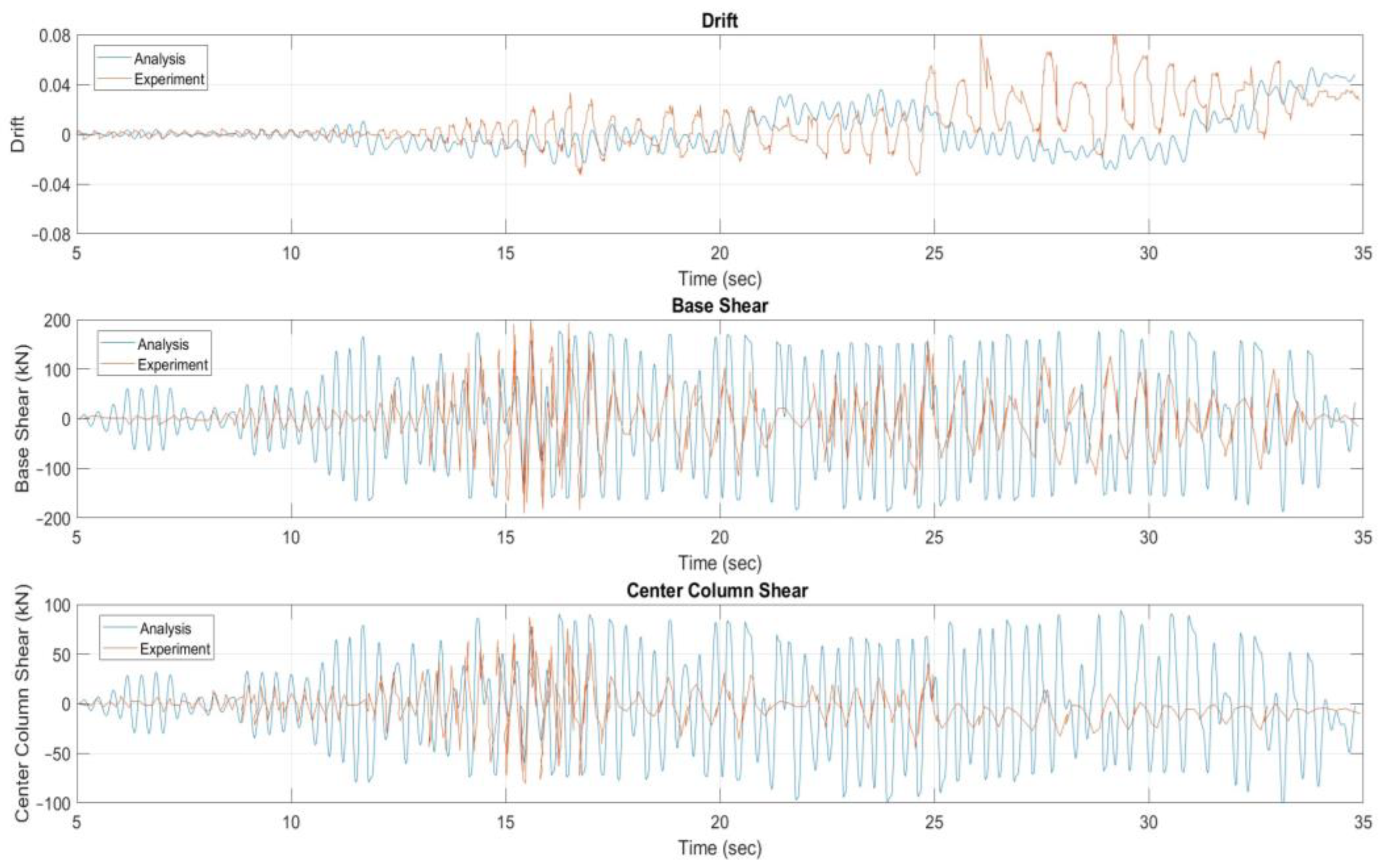
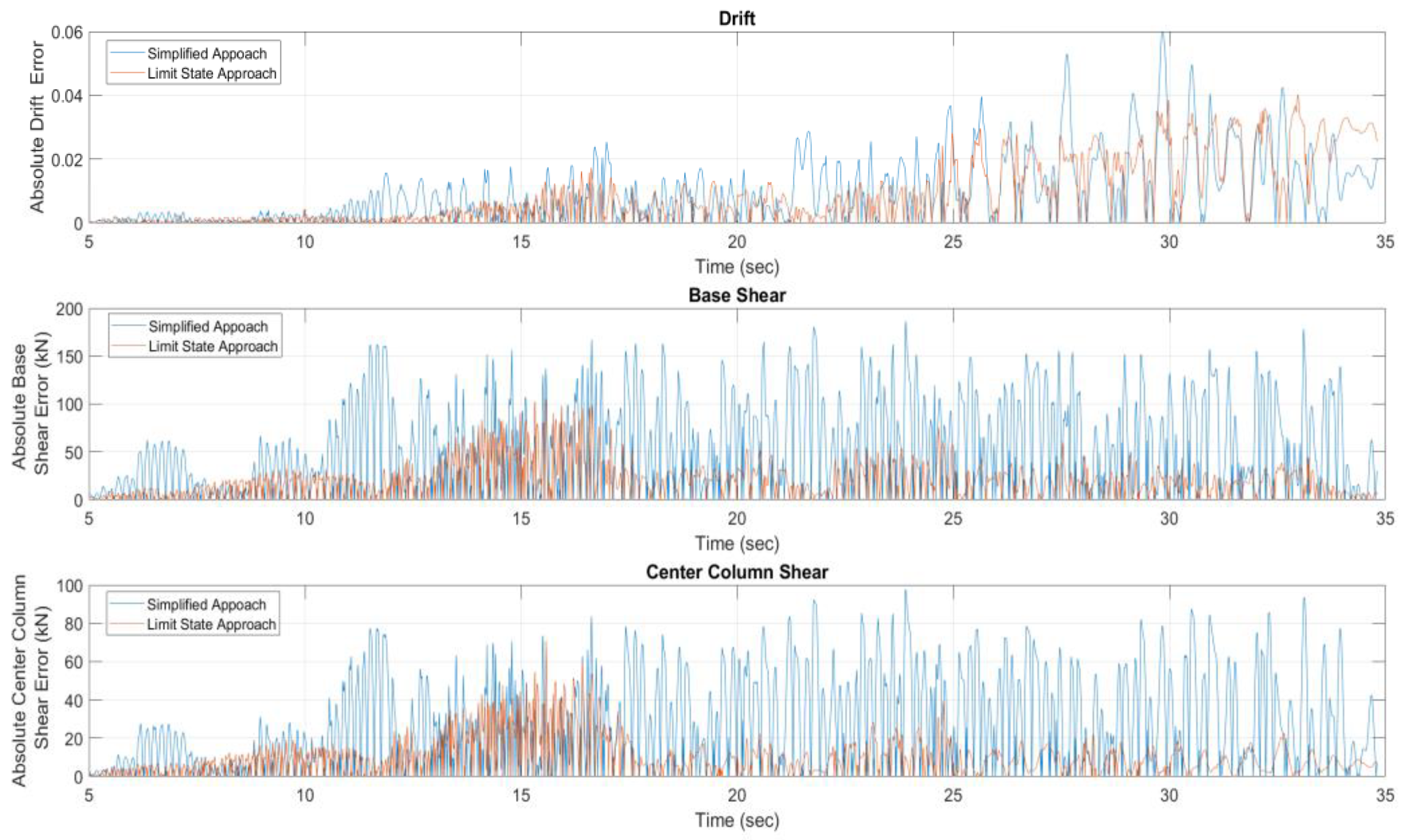
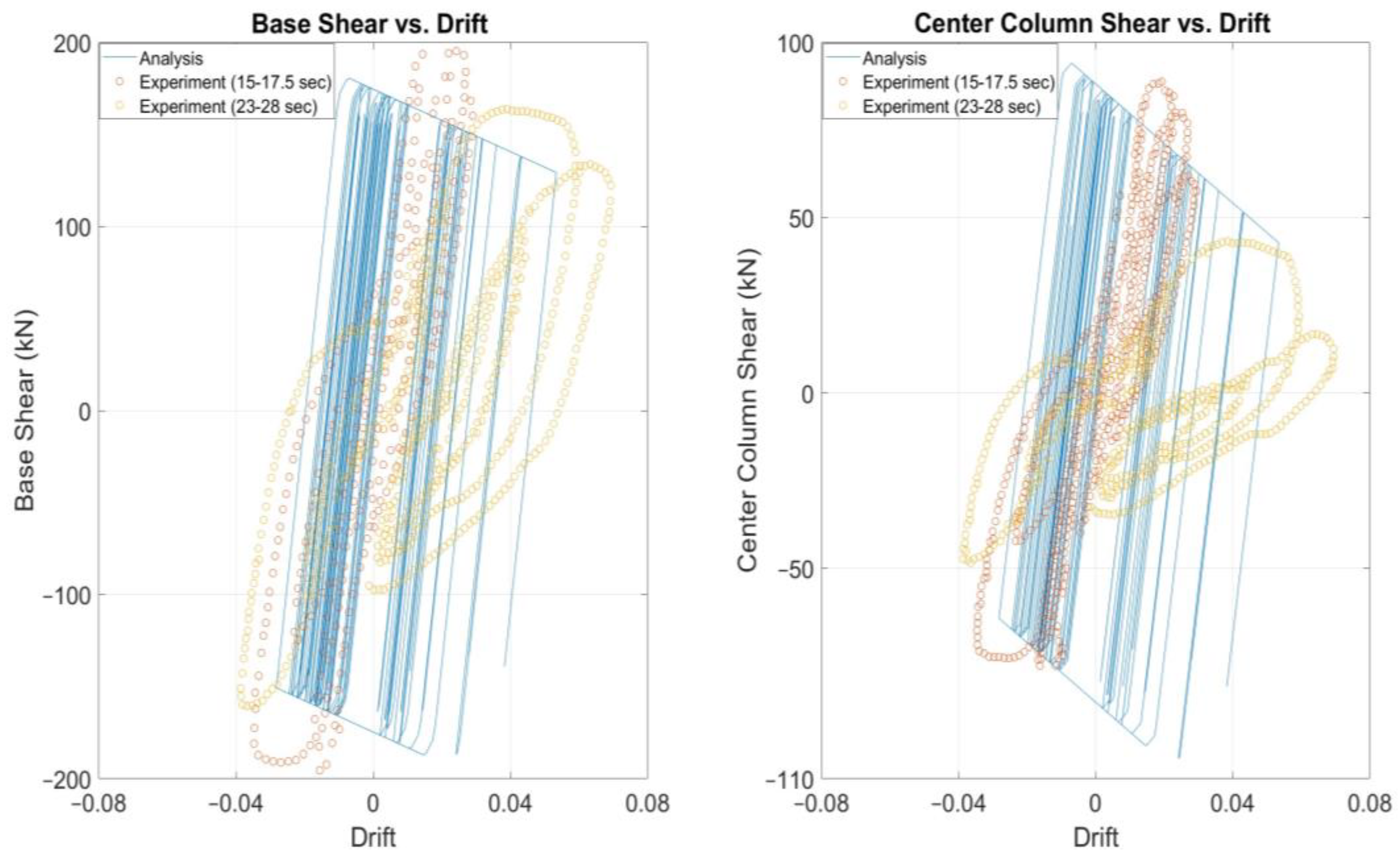
3.2. Nonlinear Time-History Analysis of Specimen 2

A MATLAB code [32] was developed for the nonlinear time-history analysis of the already introduced Specimen 2 by Elwood and Moehle [37, 38]. The model of the 2D shear-critical RC frame fixed at the base can be seen in Figure 3b. All columns were modeled by employing the one-component beam model of Section 2. To the center column was applied, as already described, the negative degradation slope defined in the previous Section along with its secant stiffness’ elastic properties until the point of shear failure. To the side columns the experimental reported yielding moment was employed along with its elastic stiffness. Since the side columns sustain fluctuating axial load during testing a mean yielding moment value was introduced. The horizontal beams (Figure 3b) were modeled as 2D linear elastic beam elements with elastic properties.

In the case of earthquake excitation, the support degrees of freedom (DOFs) are assumed to move together following a specified ground acceleration history in the global coordinate system. The key step is to express the total acceleration relative to a fixed reference frame as the sum of the acceleration of the support DOFs and the additional acceleration of the free DOFs relative to the supports [39].

Central difference time integration method algorithm is used to solve the equations of motion. The advantage of the central difference method is that the stiffness matrix does not rely on the static stiffness matrix, which may change at each time step under nonlinear material behavior, requiring re-assembly and re-triangularization. In contrast, with the central difference method, the effective stiffness remains constant, provided the damping stiffness matrix is constant, as is commonly assumed with Rayleigh damping adopted also in this study (mass and stiffness proportional damping) [39]. Additionally, this method does not require iterations within each time step, unlike the implicit time integration method. However, the central difference method is only conditionally stable, meaning it requires a small-time step for accurate integration. The introduced ground motion is the recorded acceleration values on the shake table during testing of Specimen 2. The equivalent viscous damping was set at 2% of critical damping for the fundamental mode of the shear-critical RC frame. The masses were lumped equally at the horizontal beams’ nodes and an additional vertical load was applied at the top node of the center column [0.24A_gf_c (where A_g (230x230 mm²) is the gross cross-sectional area and f_c is the measured concrete strength (24.27 MPa)].

Figure 6 depicts the numerical and experimental nonlinear time-history response. It can be seen that there are similar value-ranges in the response however the reduced computational cost of the modeling approach led to some deviations between the calculated and measured shear forces and drifts during portions of the time-history response. Regarding drift, the permanent damage drift at 35s-time history has almost the same value. Base shear and center column shear forces are comparable but once the rigid plastic hardening springs of one-component model are triggered then there is no fluctuation in the sustained envelope shear forces apart from the negative degradation slope response as it would happen by employing distributed inelasticity beam elements.

In order to clarify the level of accuracy of this simplified approach, the absolute error of the model’s response compared to the experimental for Specimen 2 was defined in Figure 7 and also the same error definition was included for the detailed and more advanced numerical modeling with limit state models combined with distributed inelasticity beam models by Elwood and Moehle [38]. The absolute error is defined as the subtraction from the absolute value of the numerical response, of the absolute value of the experimental response, since for the overall practical seismic assessment purposes monotonic conditions’ rules are usually applied. It can be seen that albeit the reduced computational effort the simplified approach in terms of drifts is comparable and especially for the permanent drift damage (which is of special interest) better than the detailed approach. In terms of shear forces the detailed approach is better since as it is already mentioned once the rigid plastic hardening springs of one-component model are triggered then there is no fluctuation in the sustained envelope shear forces apart from the degradation slope response as it would happen by employing distributed inelasticity beam elements. Moreover, the fluctuation of the axial load and its interaction with moment at the side circular columns is not taken into account as it happens with the detailed approach.

The above remarks are confirmed also by Figure 8. The corresponding time responses between numerical model and experimental test do not coincide at every time step. The effective stiffness and strength degradation in the central shear-critical column is well captured. Moreover, it can be seen that this simplified numerical model cannot represent the degradation of loading and unloading stiffnesses with increasing displacement amplitude reversals. The employed moment-rotation envelopes below horizontal beams of the columns of Specimen 2 both shear-critical but also flexure-dominant can be seen in Figure 9 and Figure 10. Considering the brittle specimen response and the low computational cost for this simplified model approach for collapse modeling, the results are acceptable.

4. Discussion

During an earthquake, columns can experience a wide range of loading histories, which may include a single large pulse or several smaller-amplitude cycles. These cycles can sometimes result in shear failure or even collapse, where the column loses its ability to support gravity loads. Previous research [1,2] has shown that such collapse cannot be explained by a simple combination of shear force and axial load. Instead, it is governed by an interaction envelope that depends on both the loading history and the peak deformation exerted on the column (maximum drift demand).

To understand how the loading history affects a column's response, it is important to note that structural members undergoing lateral displacement reversals tend to lengthen due to the accumulation of permanent tensile strains in the longitudinal reinforcement crossing diagonal shear cracks. As displacement cycles increase in amplitude, the cracks widen. This is depicted in the axial stress-strain diagram of the reinforcement after yielding, where permanent strains are biased in tension due to the neutral axis shifting towards the compression side of the member's cross-section after cracking. Axial load plays a key role in this process, as it helps keep the cracks partially closed, thereby delaying the elongation and ratcheting of the column.

Additionally, research [1,2] shows that increasing the number of cycles beyond the yield displacement can reduce a column’s drift capacity at shear failure. One of the goals of this research is to better understand these effects and develop simplified tools to identify the failure characteristics at the loss of axial load-bearing capacity, as well as the impact of drift demand on the column’s deformation capacity.

As already mentioned, collapse should be quantified as accurately as possible through nonlinear dynamic analysis. A comprehensive set of guidelines will serve as a foundation for addressing the complexities of nonlinear softening responses under large displacements and deformations, helping to promote the acceptance of nonlinear response analyses in professional practice. The introduction of simple but effective column models, like those presented in this study, which account for localized effects such as shear and anchorage or lap splice slip within a consistent element formulation, will reduce non-convergence issues and computational time. The correlation of the proposed model with the experimental results produces acceptable results especially in terms of drifts and permanent damage and the model succeeds in reducing the computational effort.

Finally, it should be noted that the goal of this study is to simplify the assessment of collapse of RC frame structures so the presented methodology could be used in large-area-scale seismic assessment. It is not intended to substitute the introduced in the literature review advanced methods and, in a way, as for example with MCFT it is based also on its estimates through Phaethon Windows software. The intended improvement lies upon its simplifications without losing reasonability in its results.

5. Conclusions

One-component beam model formulation exemplifies a category of elements that rely on assumptions about internal force distribution. These elements are crucial in contemporary earthquake engineering analysis, as they accurately represent the force distribution within a member and lead to a reliable numerical implementation. Using the moment-rotation envelope results from cantilever shear-critical columns analyzed by Phaethon software, an inelastic frame structure experiencing shear, axial or pull-out failures can be modeled by placing a rigid plastic spring at the location where shear failure is anticipated considering also the contribution of anchorage or lap-splice pullout slip in the total drift and applying a negative degradation slope. The slope of the degradation connects the point on the moment-rotation envelope where shear failure occurs to the point of axial failure, beyond which the column can no longer support its gravity loads. The part of the member between the two rigid plastic springs remains perfectly elastic. A key advantage of this approach is that inelastic deformation at the member ends depends solely on the moment applied at the end, allowing any moment-rotation hysteretic model to be assigned to the spring. The results of shaking table tests on a one-story, two-bay reinforced concrete frame experiencing both shear and axial failures were compared after creating a self-developed MATLAB code [32] running nonlinear dynamic analyses and implementing this one-component beam model for columns prone to shear failure but also including those with more flexure-dominant behavior under cyclic reversals. While the simplified model yielded reasonable predictions of the overall frame response and lateral strength degradation, the reduced computational cost of the modeling approach led to some deviations between the calculated and measured shear forces and drifts during portions of the time-history response. It can be seen that albeit the reduced computational effort the simplified approach in terms of drifts is comparable to a more detailed approach from the literature and especially for the permanent drift damage (which is of special interest) better than the detailed approach. In terms of shear forces the detailed approach is better since once the rigid plastic hardening springs of one-component model are triggered then there is no fluctuation in the sustained envelope shear forces apart from the degradation slope response as it would happen by employing distributed inelasticity beam elements. Moreover, the fluctuation of the axial load and its interaction with moment at the side circular columns is not taken into account as it happens with this detailed approach. Based on the research included in this paper, a future goal is to implement the proposed element into a commercial software for larger scale nonlinear dynamic analyses of real RC structures. To this direction possible improvements are inclusion of the aspects of smooth and/or corroded steel bars for seismic assessment of old-type RC frames. Finally, a further validation of the proposed model with larger shake table experiments would confirm its acceptance and robustness.

Data Availability Statement

All included data in this study is available upon request from the corresponding author.

Conflicts of Interest

The author declares no conflict of interest.

References

Megalooikonomou K.G. Modeling the behavior of shear-critical reinforced concrete columns under lateral loads. Ph.D. Thesis, Department of Civil and Environmental Engineering, Faculty of Engineering, University of Cyprus, Nicosia, Cyprus, December 2019. [CrossRef]
Megalooikonomou, K.G. Seismic Assessment and Retrofit of Reinforced Concrete Columns, 1st ed.; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, ISBN (10): 1-5275-2785-9, ISBN (13): 978-1-5275-2785-0, 2019; p. 387. [Google Scholar]
Elwood, K.J.; Moehle, J.P. Drift capacity of reinforced concrete columns with light transverse reinforcement. Earthquake Spectra 2005, 21, 71–89. [Google Scholar] [CrossRef]
Elwood, K.J.; Moehle, J.P. Axial Capacity Model for Shear-Damaged Columns. ACI Structural Journal 2005, 102, 578–587. [Google Scholar]
Asteris, P.G.; Antoniou, S.T.; Sophianopoulos, D.S.; Chrysostomou, C.Z. Mathematical Macromodeling of Infilled Frames: State of the Art". Journal of Structural Engineering ASCE 2011, 137, 1508–1517. [Google Scholar] [CrossRef]
Gicev V., Trifunac M.D., Non-linear earthquake waves in seven-storey reinforced concrete hotel, Report CE 06-03, 2006, Dept. of Civil Eng. Univ. of Southern California, Los Angeles, California.
Palomo, I.R.I.; Frappa, G.; de Almeida, L.C.; Trautwein, L.M.; Pauletta, M. Analytical and numerical models to determine the strength of RC exterior beam–column joints retrofitted with UHPFRC. Engineering Structures 2024, 312, 118244. [Google Scholar] [CrossRef]
ACI Committee 318 Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary, American Concrete Institute, Farmington Hills, MI. USA, 2014.
Fib Model Code Chapter 6: Interface Characteristics, Ernst & Sohn Publications, Berlin, Germany, 2010.434.
AASHTO LRFD Bridge Design Specifications and Commentary, 3rd Edition, American Association of State Highway Transportation Officials, Washington, D.C, 2013 1264.
Morsch, E. Der Eisenbetonbau-Seine Theorie und Anwendung, 5th Edition, Vol. 1, Part 1, 1922, Wittwer, Stuttgart, Germany.
Ritter, W. Die Bauweise Hennebique. Schweizerische Bauzeitung 1899, 33, 59–61. [Google Scholar]
EN 1992-1-1: Eurocode 2: Design of concrete structures – Part 1-1: General rules and rules for buildings, European Committee for Standardization (CEN), Brussels, 2004.
Vecchio, F.J.; Collins, M.P. The modified compression field theory for reinforced concrete elements subjected to shear. ACI Journal Proceedings, 1986, 83, 219–231. [Google Scholar]
Filippou, F. C. , and Fenves, G. L. Methods of analysis for earthquake-resistant structures. In: Bozorgnia Y, Bertero VV (eds) Earthquake engineering: From engineering seismology to performance-based engineering. CRC Press, Boca Raton, 2004.
Mergos, P.E.; Kappos, A.J. A distributed shear and flexural flexibility model with shear–flexure interaction for R/C members subjected to seismic loading. Earthquake Engng. Struct. Dyn. 2008, 37, 1349–1370. [Google Scholar] [CrossRef]
Ceresa, P.; Petrini, L.; Pinho, R. Flexure-shear fiber beam-column elements for modeling frame structures under seismic loading-state of the art. J. Earthq. Eng. 2007, 11, 46–88. [Google Scholar] [CrossRef]
Vecchio, F.J.; Collins, M.P. Predicting the Response of Reinforced Concrete Beams Subjected to Shear Using Modified Compression Field Theory. ACI Struct. J. 1988, 85, 258–268. [Google Scholar]
Zeris, C.A. Three-Dimensional Nonlinear Response of Reinforced Concrete Buildings. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of California, Berkeley, California, USA, 1986. [Google Scholar]
Bentz, E.C. Sectional Analysis of Reinforced Concrete Members. PhD Thesis, Department of Civil Engineering, University of Toronto, Toronto, Canada, 2000. [Google Scholar]
Megalooikonomou, K.G. Monotonic and Cyclic Seismic Analyses of Old-Type RC Columns with Short Lap Splices. Constr. Mater. 2024, 4, 329–341. [Google Scholar] [CrossRef]
Giberson, M. F. The response of nonlinear multi-story structures subjected to earthquake excitation, Earthquake Engineering Research Laboratory, California Institute of Technology, Pasadena, CA, EERL Report, 1967.
Giberson, M.F. Two Nonlinear Beams with Definition of Ductility, Journal of Structural Division, ASCE, 1969 95(ST2),137 - 157.
Zimos, D.K.; Mergos, P.E.; Kappos, A.J. Modelling of R/C members accounting for shear failure localisation: finite element model and verification. Earthq. Eng. Struct. Dyn. 2018, 47, 1631–1650. [Google Scholar] [CrossRef]
Zou, X.; Gong, M.; Zuo, Z.; Liu, Q. An efficient framework for structural seismic collapse capacity assessment based on an equivalent SDOF system. Eng. Struct. 2024, 300, 117213. [Google Scholar] [CrossRef]
Zou, X.; Gong, M.; Zuo, Z. An efficient method based on shear models for structural seismic response prediction considering hysteretic characteristics. Bull Earthquake Eng 2024. [Google Scholar] [CrossRef]
Hwang, H.; Oh, K.; Choi, I.; Kang, J.; Shin, J. Rapid Estimation Method of Allowable Axial Load for Existing RC Building Structures to Improve Sustainability Performance. Sustainability 2024, 16, 6578. [Google Scholar] [CrossRef]
Lapiro, I.; Eid, R.; Kovler, K. Degradation of RC Columns under Combined Exposure to Axial Loading, Stray Currents, and Chloride Ingress. Materials 2024, 17, 1295. [Google Scholar] [CrossRef] [PubMed]
Yang, Y.; Yang, H.; Fan, Z.; Mu, Z. Crack Propagation Law of Reinforced Concrete Beams. Applied Sciences 2024, 14, 409. [Google Scholar] [CrossRef]
LeBorgne, M.R.; Ghannoum, W.M. Analytical element for simulating lateral-strength degradation in reinforced concrete columns and other frame members. J. Struct. Eng. 2014, 140, 04014038. [Google Scholar] [CrossRef]
Baradaran Shoraka, M.; Elwood, K.J. Mechanical model for non-ductile reinforced concrete columns. J. Earthq. Eng. 2013, 17, 937–957. [Google Scholar] [CrossRef]
Mathworks. (2024). MATLAB: User's Guide (R2024b).
Megalooikonomou, K.G. KADET-based One-component Beam Model for the Simulation of Cyclic Lateral Response of URM walls. In Proceedings of the 18th World Conference on Earthquake Engineering (18WCEE), Milan, Italy, 1–5 July 2024. [Google Scholar]
Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Dover Publications, 2000.
Tastani, S.P.; Pantazopoulou, S.J. Reinforcement and concrete bond: State determination along the development length. J. Struct. Eng. ASCE 2013, 139, 1567–1581. [Google Scholar] [CrossRef]
Elwood, K. Shake Table Tests and Analytical Studies on the Gravity Load Collapse of Reinforced Concrete Frames. PhD Thesis, University of California, Berkeley, Berkeley, USA, 2002. [Google Scholar]
Elwood, K.J.; Moehle, J.P. Dynamic collapse analysis for a reinforced concrete frame sustaining shear and axial failures. Earthq. Eng. Struct. Dyn. 2008, 37, 991–1012. [Google Scholar] [CrossRef]
Chopra, A.K. Dynamics of structures. Pearson Education India, 2007.

Figure 1. Graphical research framework of this study (Δ_shear cantilever lateral displacement due to shear mechanism, Δ_slip cantilever lateral displacement due to pull-out slip of anchorage or lap-splice, Δ_flex cantilever lateral displacement due to flexure, Δ_tot total lateral displacement, l_r yield penetration length in the anchorage, f_by local bond strength of the anchorage, l_p plastic hinge length, γ_e elastic shear strain, γ_p plastic shear strain. θ cantilever lateral rotation, θ_slip cantilever lateral rotation due to pull-out slip, V_R shear strength, L_s shear span, d column section effective depth, V seismic shear force, Δ lateral displacement, Δ_s lateral displacement at shear failure, Δ_a lateral displacement at axial failure) .

Figure 2. Beam (a) displacements and (b) forces in global, local and basic reference systems and c) one-component beam model.

Figure 3. (a) Specimen 2 of shake table test [37,38] (b) Simplified numerical model implemented in MATLAB 2024b.

Figure 4. Capacity curve of center shear-critical column of Specimen 2 and lateral displacement contributions for each step of the pushover analysis (16 total pushover steps of 5 kN)[This is a screenshot from Phaethon Windows software user’s interface].

Figure 5. Strain, Slip and Bond distributions along the straight anchorage length of center shear-critical column of Specimen 2 for pushover step 15 of Phaethon Windows software. See also Figure 1 and 4.

Figure 6. Time-history responses in terms of drift, base shear, and center column shear of Specimen 2.

Figure 7. Absolute Error Time-history responses in terms of drift, base shear, and center column shear of Specimen 2.

Figure 8. Shear hysteretic response of Specimen 2.

Figure 9. Below beam moment-rotation hysteretic response of center column of Specimen 2.

Figure 10. Below beam moment-rotation hysteretic response of outside column of Specimen 2.

Table 1. Details of central shear-critical RC columns of Specimen 2 (units: mm, MPa, kN).

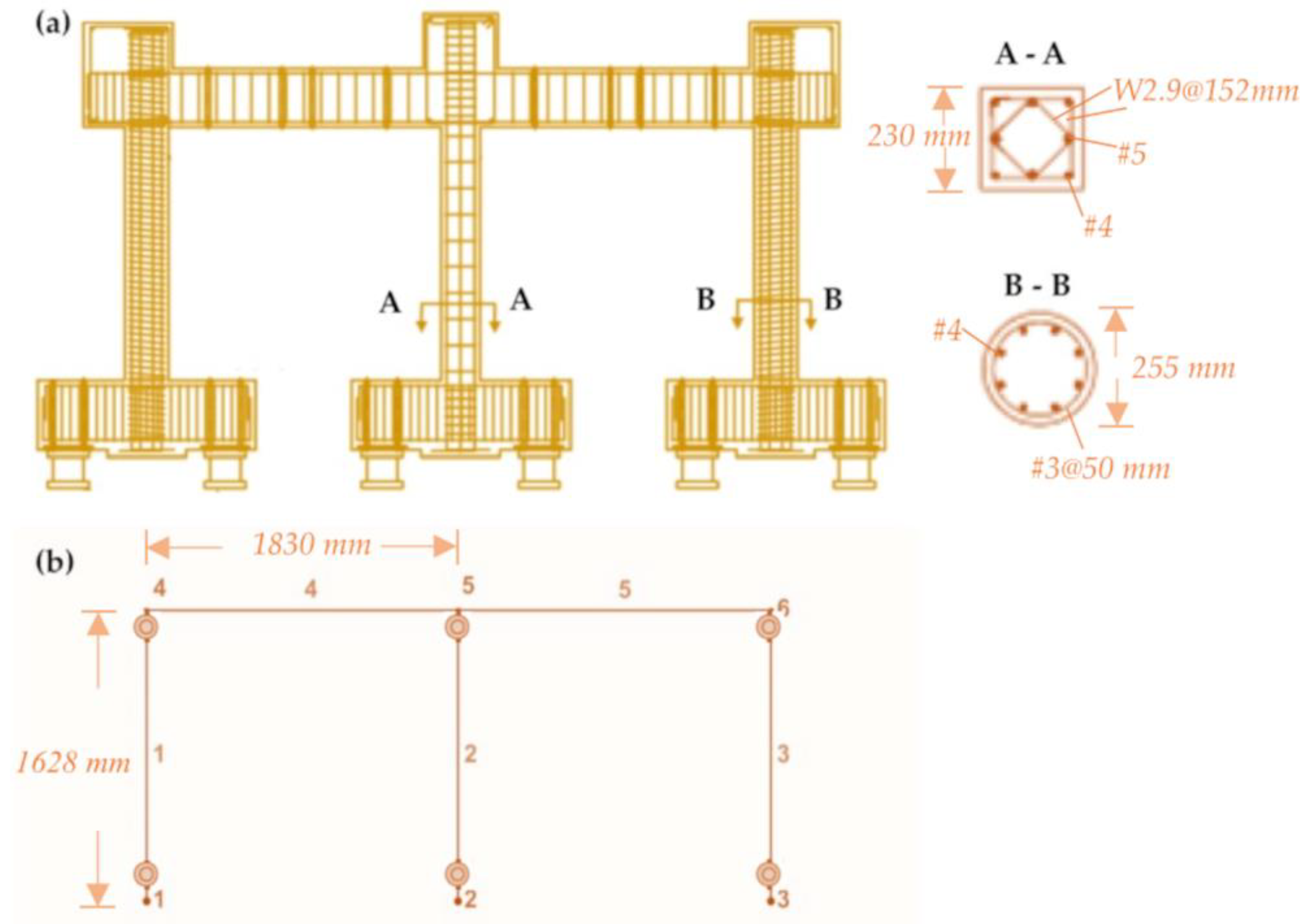
Case	Axial Load (kN)	Width (mm) – Depth (mm)	Shear Span (mm) – StraightAnchorage Length (mm)	Clear Cover (mm)	Concrete Strength (MPa)	Number - Diameter (mm) – Reinforcing ratio of Longitudinal Bars	Yielding Strength of Long. Bars (MPa)	Ultimate Strength (MPa) – Spacing (mm) – Diameter (mm) –Ratio of Transv. Reinf.
Elwood and Moehle [37,38] – (Spec. 2 – Center Column)	308.132	230 230	814 298	25.4	24.27	4 and 4 12.7 and 15.875 0.0245	479.18	717 152 4.9 0.00236

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.