Prerpints.org logo
Preprint
Article

Functional Nano-Metallic Coatings for Solar Cells

Altmetrics

Downloads

56

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 October 2024

Posted:

14 October 2024

You are already at the latest version

Alerts
Abstract
We have collected theoretical arguments supporting the functional role of nano-metallic coatings of solar cells, which enhance their efficiency via by plasmon strengthening of absorption of sun-light photons and reduction of binding energy of photo-excitons. The quantum character of plasmonic effect related with the absorption of photons (called as optical plasmonic effect) is described in terms of Fermi golden rule for quantum transitions of semiconductor band electrons induced by plasmons from a nano-metallic coating. The plasmonic effect related with the lowering of exciton binding energy (called as electrical plasmonic effect) is also quantumly characterized with particular significance for metalized perovskite solar cells. Quantum coupling between plasmons in nanoparticles from a coating with band electrons in a semiconductor substrate significantly modifies material properties (dielectric functions) both of particles and of a semiconductor, beyond the ability of a classical electrodynamics description.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

The most important feature of any solar cell is its efficiency, which gives an information what part of the solar energy of irradiating photons is converted into a usable electric energy in the cell. For p-n junction solar cells this efficiency is ranged by so-called Shockley–Queisser limit [1,2]. An assessment of this limit had taken into account the matching of the semiconductor band structure (in particular of the forbidden band) to sun-light spectrum and losses due to recombination of electrons and holes and radiative thermal losses—all in the idealized p-n junction cell assuming that photo-excitons are created mostly in the region of the junction. As the result the simplified function of the efficiency with respect to the forbidden gap width E g is identified, which has a maximum of ca. 33.7% at E g ≃ 1.34 eV. This theoretical limit is not achieved in practice because of the negligence of various parasitic factors not included in the derivation of the idealized limit and it is not easy to accommodate the forbidden gap in utilized materials to the optimal one. For Si p-n junction solar cells with E g ∼ 1.14 eV, the achievable efficiency is ca 27 %. Other popular solar cells like CIGS or thin film solar cells utilized GaAs, CdTe and others, have usually lower efficiency (at the simplest architecture) [3]. Chemical or hybrid solar cells without any p-n junction (as popular now perovskite cells) do not belong to the class of cells embraced by the Shockley–Queisser limit, though their efficiency is also lower than the fixed limit—for chemical cells the efficiency is lower than ca. 10 %, whereas for perovskite cells it reaches ca. 26 % [4].
There are, however, various routes to surpass the Shockley–Queisser limit by tandem architecture of cells to better accommodate absorption ability to the solar spectrum, quantum dot admixtures or metallic nano-component coverings with appropriately tailored their absorption spectra to mediate in an optimal harvesting of the sun-light incident radiation. The easiest but very effective is the latter method as plasmonics of metallic nanoparticles allows for easy strengthening of solar radiation absorption utilising small amount of material and by low cost methods of particle deposition. In the case of p-n junction solar cells the nano-metallic coating must be located at the distance of ca. 1 μ m from the p-n junction region to gain a maximum of photon absorption strengthening [5,6,7,8,9,10,11]. In the case of chemical and hybrid solar cells (including perovskite cells) the plasmonic photovoltaic effect is different, but of also high efficiency via internal electrical plasmonic channel in the cell related with the reduction by plasmons of the binding energy of photo-excitons resulting in acceleration of the exciton dissociation at the interface with the electron or hole transport layers, originally described in [12] and experimentally confirmed [13,14,15,16,17].
In the present paper the role and mechanism of operation of nano-metallic functional coatings both for p-n junction and perovskite cells will be described in detail and the theoretical background for the photovoltaic plasmonic effects will be presented. In the following paragraph the arguments are collected behind the scale of confinement for usable metallic particles (nanometer scale and various shape, material and structure of most efficient particles in coatings). Next the role of plasmons in strengthening of absorption of photons (optical type photovoltaic plasmonic effect) in p-n junction cells will be presented with emphasizing its quantum character beyond the ability of conventional numerical simulators for photovoltaic devices (illustrated on examples). The discussion of the range of plasmonic effect from nano-metallic coatings will be supported by the experimental verification, which is important for a proper localization of active nano-metallic coating in the multilayer device to gain maximum effect. Next the idea of a different role of plasmons in perovskite cells will be described and some examples of nano-metallic coatings in these cells will be listed. Some more extensive calculations and details are shifted to Appendix.

2. Why the Nano-Scale of Metallic Particles for Plasmonic Coatings?

The most convenient size of metallic plasmonic components is defined by the optimal transfer of energy via plasmon oscillations in these particles, which sharply depends on the particle size. In other words, particles must exhibit extreme emission and absorption of energy (which are dual according to the general scheme of quantum transitions). The emission of energy by plasmons can be estimated by the radiative damping of plasmonic oscillations. Conventionally surface plasmons are studied by the solution of the Maxwell-Fresnel problem for electromagnetic field passing trough and reflecting on the boundary between a metal and its dielectric surroundings [18]. For such an approach a metal is characterized by its bulk properties, i.e., by assumption as the prerequisite of the bulk plasmon frequency [18] ω p = n e 2 ε 0 m , where e and m are the charge and the mass of the electron, respectively, n is the free electron concentration in a metal (different in various metals) and ε 0 is the dielectric constant ( ε 0 = 1 36 π 10 − 9 C2/Nm2). Bulk plasmon frequency has been introduced by Drude and Lorentz upon a penomenological approach to the response of a metal to the electrognatic field assuming independent oscillatory model for all free electrons in a metal, which in synchrony take part in collective iscillations called plasmons. Only in 1952 the microscopic quantum (random phase approximation) approach by Pines and Bohm [19,20] clarified that the synchronised electomagnetic response of all electrons is conditioned by the Coulomb repulsion of electrons and the formula for ω p in bulk metal has been formally derived formally. This opened the way to analyze plasmonic oscillations in confined geometry of a metal, in particular, for metallic nanospheres, revealing [21,22] various modes of plasmons in metallic nanoparticles—the infinite family of surface plasmon modes (in the case of regular spherical geometry numbered by angular momentum quantum numbers, l = 21 , ⋯ , ∞ and m = − l , ⋯ , l for each l), and also the infinite family of volume plasmon modes numbered by l, m and by an index of zeros of spherical Bessel function for particular l[22]—as listed in Appendix A. Surface plasmons are related with oscillations of all electron in a sample of a translational type—thus, non-balanced (by uniform positive jellium) electron density fluctuations occur only on the sample surface. In the case of volume plasmons in a nanosphere a local charge fluctuations occur also along the radius of the particle. The latter are not possible to be accounted for by the boundary Maxwell-Fresnel problem. We have noticed [22], that volume plasmons in a nanosphere have larger frequency than bulk plasmons ω p , whereas surface plasmon modes have lower frequencies than ω p .
The most pronounced surface plasmon mode is a dipole mode with l = 1 and m = − 1 , 0 , + 1 possible to be represented as the oscillating dipole D ( t ) pinned to the sphere center (cf. Appendix B)—its frequency is named as the Mie frequency as is also obtainable by Maxwell-Fresnel problem solution [18]. The microscopic quantum approach to plasmons by Pines and Bohm allows, however, for the consideration of also plasmon damping, which in the case of the phenomenological approach upon the Drude-Lorentz model (in Maxwell-Fresnel problem) was limited only to electron scattering of Ohmic type. For plasmons in a nanometer scale of confinement the more important is, however, another channel of plasmon damping, not manifesting itself in a bulk metal. This channel of plasmon damping is related with radiation of oscillating charges taking away energy and hampering oscillations—called as the Lorentz friction [23,24]. Related losses can be described as an effective electric field E L = 2 3 c 3 ∂ 3 D ( t ) ∂ t 3 , which slows down electron velocity and reduces oscillations of the dipole D ( t ) . For a single electron the Lorentz friction is negligibly small but for many electrons oscillating in synchrony, it can achieve large value. To assess this value and to determine the offset of the domination of Lorentz friction channel over plasmon damping, we must solve the dynamical equation for dipole type plasmons in a metallic nanosphere [22] Chapter 5 (note in addition that at the resonance frequency of e-m wave with plasmons in a nanosphere, its wavelength highly exceeds the nanoparticle radius a and the dipole approximation holds, i.e., only the dipole mode of plasmons is excited by such a e-m wave, as the electric field of the resonant e-m wave is almost homogeneous along entire nanoparticle). The dynamical equation for dipole mode of surface plasmons in a nanosphere is as follows (cf. Appendix B),
∂ 2 ∂ t 2 + 2 τ 0 ∂ ∂ t + ω 1 2 D ( t ) = ω 1 2 a 3 E L ( t ) ,
where the right hand side of the equation expresses the Lorentz friction acting on dipole D ( t ) and the left hand side of the equation resolves to the harmonic oscillator equation for the dipole D ( t ) with self frequency ω 1 and damping rate 1 τ 0 . The Lorentz friction force is as follows [23,24],
E L ( t ) = 2 3 c 3 ∂ 3 D ( t ) ∂ t 3 .
Equation (1) is the third order differential equation, which breaks essentially the harmonicity of its solution. The Lorentz friction term (unharmonic one) is of damping type as of the odd order for the time derivative.
To compare contributions of various terms to the oscillation damping it is convenient to change to dimensionless time variable t → t ′ = ω 1 t , where ω 1 is the frequency of dipole plasmon self-oscillations if its damping is neglected (Mie frequency, which is size-independent and for a sphere ω 1 = ω p 3 [18]). Then Equation (1) attains the form,
∂ 2 D ( t ′ ) ∂ t ′ 2 + 2 τ 0 ω 1 ∂ D ( t ′ ) ∂ t ′ + D ( t ′ ) = 2 3 ω 1 a c 3 ∂ 3 D ( t ′ ) ∂ t ′ 3 ,
where
1 τ 0 = v F 2 λ b + C v F 2 a ,
describes Ohmic type losses due to electron scattering on other electrons, crystal imperfections, admixtures, phonons and nanoparticle boundaries ( λ b is the mean free path of electrons in bulk metal, v F is the Fermi velocity of electrons, C is a constant of order of unity describing the type of electron reflection from the nanoparticle border, a is the radius of a nanosphere). For D ( t ′ ) ∼ e − i Ω t ′ (Fourier picture) Equation (3) gains the form,
− Ω 2 − i Ω 2 τ 0 ω 1 + 1 = i 2 3 Ω 3 ( ω 1 a / c ) 3 ,
which admits an exact solution as follows,
Ω 1 = − i 3 g − i 2 1 / 3 ( 1 + 6 g u ) 3 g 2 + 27 g 2 + 18 g u + 4 ( − 1 − 6 g u ) 3 + ( 2 + 27 g 2 + 18 g u ) 2 1 / 3 − i 2 + 27 g 2 + 18 g u + 4 ( − 1 − 6 g u ) 3 + ( 2 + 27 g 2 + 18 g u ) 2 1 / 3 3 × 2 1 / 3 g = i α , Ω 2 = − i 3 g + i ( 1 + i 3 ) ( 1 + 6 g u ) 3 × 2 2 / 3 g 2 + 27 g 2 + 18 g u + 4 ( − 1 − 6 g u ) 3 + ( 2 + 27 g 2 + 18 g u ) 2 1 / 3 + i ( 1 − i 3 ) 2 + 27 g 2 + 18 g u + 4 ( − 1 − 6 g u ) 3 + ( 2 + 27 g 2 + 18 g u ) 2 1 / 3 6 × 2 1 / 3 g = ω + i 1 τ , Ω 3 = − i 3 g + i ( 1 − i 3 ) ( 1 + 6 g u ) 3 × 2 2 / 3 g 2 + 27 g 2 + 18 g u + 4 ( − 1 − 6 g u ) 3 + ( 2 + 27 g 2 + 18 g u ) 2 1 / 3 + i ( 1 + i 3 ) 2 + 27 g 2 + 18 g u + 4 ( − 1 − 6 g u ) 3 + ( 2 + 27 g 2 + 18 g u ) 2 1 / 3 6 × 2 1 / 3 g = − ω + i 1 τ ,
where u = 1 τ 0 ω 1 and g = 2 / 3 a ω 1 c 3 . Ω 1 is purely imaginary—this solution is unstable and must be discarded. This is the well known artifact in Maxwell electrodynamics of the self-acceleration of a charge due to its own Lorentz friction force, i.e., the divergent solution of the dynamic equation with third order derivative, m d 2 r d t 2 = c o n s t . d 3 r d t 3 (cf. paragraph 75 in [23]), which is associated with a formal renormalization of the field-mass of the charge: infinite for a point-like charge and canceled in an artificial manner by an arbitrarily assumed negative infinite non-field mass, resulting in the ordinary mass of e.g., an electron, although not defined in a properly mathematical way. Ω 2 and Ω 3 (equivalent due to the complex conjugation) display the frequency ω and the damping rate 1 τ of oscillations. 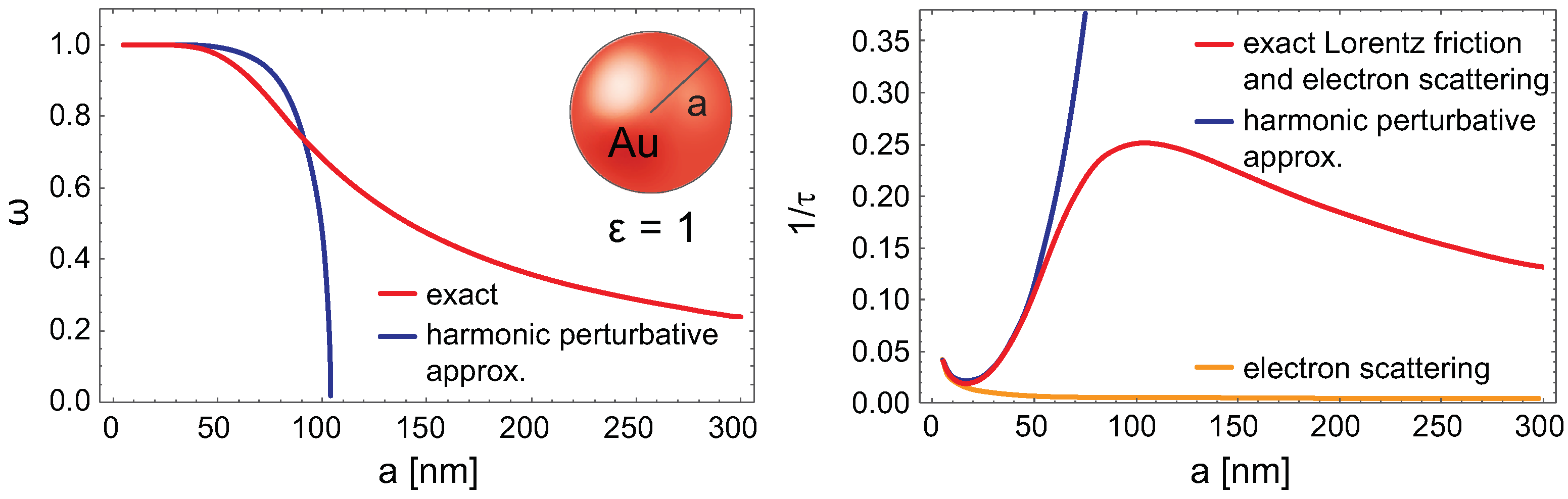Here, ω and 1 τ are not mutually linked as for an ordinary harmonic damped oscillator, for which ω = ω 1 2 − 1 τ 2 , because the Lorentz friction causes an essential unharmonic change as illustrated in Figure 1. Both ω and 1 τ depend on the size of a nanosphere a and on the frequency ω 1 . As illustrated in Figure 1, the Lorentz friction causes plasmon damping ca. 100 times larger than that due to electron scattering 1 τ 0 at ca. a ∼ 50 − 150 nm radius of Au nanoparticle in vacuum, though the Lorentz friction is much smaller for a < 10 nm (negligible for a < 3 nm) due to too low number of electrons in small nanoparticles, or for a > 500 nm and in the bulk limit—in bulk the Lorentz friction of plasmons does not contribute to their damping, as e-m wave cannot propagate inside a metal. As is visible in Figure 1, exact accounting for of the Lorentz friction qualitatively differs from the harmonic oscillator behavior. The harmonic oscillations terminate in overdamped regime when the 1 ω 1 2 τ 2 ≥ 1 (thinner lines in the figure represent a perturbative solution of Equation (1) in the harmonic regime, when the right hand side of Equation (1) is considered as the perturbation). The Lorentz friction term is proportional to a 3 , then if it is treated as the perturbation, then it grows rapidly with the size of a particle a and 1 ω 1 2 τ 2 quickly achieves 1, which stops oscillations. This is incorrect picture as the perturbation is too high and the perturbative solution cannot be applied [22]. The exact inclusion of the Lorentz friction reveals a different behavior—oscillations never stop and the relation ω = ω 1 2 − 1 τ 2 does not hold. Though the Lorentz friction term is still proportional to a 3 , the related damping 1 τ attains some maximum at certain a and next drops again for larger a—as is shown in Figure 1 on the example of Au nanoparticles. This clarifies why medium size metallic nanoparticles can serve for the efficient transfer of the e-m energy—they intensively radiate dipole surface plasmon energy and mirror-like absorb e-m energy of photons to high amplitude dipole mode of surface plasmons.

3. Nano-Metallic Coating on Absorbing Substrate

When a metallic nanoparticle is deposited on or embedded in an absorbing substrate, as in the case of metallic nano-coatings of a semiconductor surface (as e.g., in Figure 2), then the additional channel of energy transfer from plasmons to semiconductor band electrons opens. This causes additional damping of plasmons besides 1 τ 0 and of Lorentz friction described in the previous paragraph. This new channel is pure quantum and can be assessed by application of the Fermi golden rule describing quantum transitions of electrons in the substrate semiconductor between its valence and conduction bands induced by the radiation of surface plasmon in closely located metallic nanoparticles. The dipole oscillating mode of surface plasmons D ( t ) induces in its surroundings the electric and magnetic field according to the following formulae [23,24],
E ( r + R , t ) = 1 ε − ∂ 2 v 2 ∂ t 2 1 R − ∂ v ∂ t 1 R 2 − 1 R 3 D ( r , t − R / v ) + 1 ε ∂ 2 v 2 ∂ t 2 1 R + ∂ v ∂ t 3 R 2 + 3 R 3 n ( n · D ( r , t − R / v ) ) ,
and
B ( r + R , t ) = − 1 ε ∂ 2 v 2 ∂ t 2 1 R + ∂ v ∂ t 1 R 2 ( n × D ( r , t − R / v ) ) ,
for the electric and magnetic field radiated by the dipole oscillating in point r , D ( r , t ) in any other point r + R . The vector R is arbitrary, with the versor n = R R , where R is the length of R . The electric E and magnetic B fields in the point r + R at the time instant t had to be induced by the dipole D at r at the earlier time instant t − R / v , as the electromagnetic signal propagation is limited by the light velocity in the medium v = c ε , where ε is the dielectric permittivity of the medium and c = 3 × 10 8 m/s is the light speed in vacuum. The signs · and × represent scalar and vector products, respectively.
In the above equations the terms with denominators of R 3 , R 2 , and R are named as near-field, medium-field, and far-field zone components of the dipole radiation, respectively [23,24], because terms with the denominator R 3 are largest at small distances from the point r , whereas terms with R denominator prevail at greater distances. The radiated magnetic field (in Equation (8)) has no near-field zone component. When the dipole D ( t ) = D 0 e i ω t represents the surface plasmon mode oscillating with ω frequency in a nanoparticle, then its interaction with the surrounding (or substrate) semiconductor is defined mostly by the near-field electric radiation (due to proximity). This field acts onto band electrons in the substrate and a related interaction term in the Hamiltonian of electrons is as follows (by virtue of Equation (7)), V ( R , t ) = e ε R 2 n · D 0 s i n ( ω t + α ) = w + e i ω t + w − e − i ω t , where w + = ( w − ) * = e ε R 2 e i α i R 2 n · D 0 .
One can verify that − ∇ R V ( R , t ) of this scalar potential gives the electric force e E ω with E ω = 1 ε R 3 [ n ( n · D 0 ) − D 0 ] , which is the ω -Fourier component of the near-field zone electric field (7) in the point R (neglecting the time retardation for small R, moreover in near-field zone B ω = 0 ).
The Fermi golden rule formula for the probability per time unit of the transition of an electron between the valence band state Ψ k 1 = 1 ( 2 π ) 3 / 2 e i k 1 · R − i E p ( k 1 ) t / ℏ with E p ( k 1 ) = − ℏ 2 k 1 2 2 m p * − E g and the conduction band state Ψ k 2 = 1 ( 2 π ) 3 / 2 e i k 2 · R − i E n ( k 2 ) t / ℏ with E n ( k 2 ) = ℏ 2 k 2 2 2 m n * (where the indices n and p refer to electrons from the conduction and valence bands, respectively, and E g is the forbidden gap) and induced by plasmon radiation is given as follows [22],
w ( k 1 , k 2 ) = 2 π ℏ < k 1 | w + | k 2 > 2 δ ( E p ( k 1 ) − E n ( k 2 ) + ℏ ω ) ,
where ω is the frequency of plasmons and the matrix element
〈 k 1 | w + | k 2 〉 = 1 ( 2 π ) 3 ∫ d 3 R e ε 2 i e i α n ^ · D 0 1 R 2 e − i ( k 1 − k 2 ) · R .
The integral in this matrix element can be calculated analytically, with the result,
< k 1 | w + | k 2 > = − 1 ( 2 π ) 3 e e i α ε D 0 c o s Θ ( 2 π ) ∫ a ∞ d R 1 q d d R s i n q R q R = 1 ( 2 π ) 2 e e i α ε D 0 · q q 2 s i n q a q a → a → 0 1 ( 2 π ) 2 e e i α ε D 0 · q q 2 .
To estimate the absorption probability, the summation over all initial and final states in both bands must be next performed taking into account the occupation of both bands,
δ w = ∫ d 3 k 1 ∫ d 3 k 2 f 1 ( 1 − f 2 ) w ( k 1 , k 2 ) − f 2 ( 1 − f 1 ) w ( k 2 , k 1 ) ,
where f 1 and f 2 are Fermi-Dirac distribution functions of electrons in the initial and final states, respectively. For the room temperature f 2 ≃ 0 and f 1 ≃ 1 , which gives,
δ w = ∫ d 3 k 1 ∫ d 3 k 2 · w ( k 1 , k 2 ) .
After the integration we arrive at the expression
δ w = 4 3 μ 2 ( m n * + m p * ) 2 ( ℏ ω − E g ) e 2 D 0 2 m n * m p * 2 π ℏ 5 ε 2 ∫ 0 1 d x s i n 2 ( x a ξ ) ( x a ξ ) 2 1 − x 2 = 4 3 μ 2 m n * m p * e 2 D 0 2 2 π ℏ 3 ε 2 ξ 2 ∫ 0 1 d x s i n 2 ( x a ξ ) ( x a ξ ) 2 1 − x 2 .
In limiting cases, we ultimately obtain,
δ w = 4 3 μ m n * m p * ( ℏ ω − E g ) e 2 D 0 2 ℏ 5 ε 2 , for a ξ ≪ 1 , 4 3 μ 3 / 2 2 ℏ ω − E g e 2 D 0 2 a ℏ 4 ε 2 , for a ξ ≫ 1 ,
where the parameter ξ = 2 ( ℏ ω − E g ) ( m n * + m p * ) ℏ is expressed in terms of effective masses of carriers in both bands, forbidden gap, and plasmon frequency. The formula (15) displays the semiconductor photo-effect mediated by plasmons in a nano-metallic coating. One can compare it with the ordinary photo-effect, when incident photons with energy ℏ ω directly excite photo-excitons in a semiconductor with the probability (per time unit) [25],
δ w 0 = 4 2 3 μ 5 / 2 e 2 m p * 2 ω ε ℏ 3 ε E 0 2 V 8 π ℏ ω ( ℏ ω − E g ) 3 / 2 .
Taking into account that the number of ℏ ω photons in the volume V is equal to ε E 0 2 V 8 π ℏ ω , the probability of single-photon absorption by the semiconductor per time unit takes the following form in the ordinary photo-effect,
q 0 = δ w 0 ε E 0 2 V 8 π ℏ ω − 1 = 4 2 3 μ 5 / 2 e 2 m p * 2 ω ε ℏ 3 ( ℏ ω − E g ) 3 / 2 .
In the same way one can find the probability of absorption mediated by plasmons per one incident photon using Equation (15), i.e.,
q m = β N m δ w ε E 0 2 V 8 π ℏ ω − 1 ,
where N m is the number of metallic nanospheres in a coating, β is a factor accounting for all effects not directly included (type of deposition, surface effects, collective effects in the coating). To calculate this expression explicitly one must express the amplitude of dipole surface plasmon D 0 by E 0 —the amplitude of incident light e-m wave. This can be achieved in the scheme of forced and damped oscillator of plasmons, for which,
D 0 = e 2 n e 4 π a 3 3 m E 0 ( ω 1 2 − ω 2 ) 2 + 4 ω 2 / τ ′ 2 ,
where damping of plasmons
1 τ ′ ω 1 = 4 β μ m n * m p * ( ℏ ω 1 − E g ) e 2 a 3 3 ℏ 4 ε , for a ξ ≪ 1 , 4 β μ 3 / 2 2 ℏ ω 1 − E g e 2 a 2 3 ℏ 3 ε , for a ξ ≫ 1 .
The above formula has been derived in [22] upon the assumption that the transfer of energy described by δ w ℏ ω highly exceeds losses due to electron scattering at plasmon oscillations. The Lorentz friction is here screened by the absorbing medium, in which a metallic nanoparticle is embedded. This damping rate has been estimated by assessment of exponential lowering of plasmon initial energy without it pumping by photons but excited initially by a rapid switching on of an electric field at t = 0 [21]. The total energy transferred in this case to the semiconductor with probability of interband transitions in the semiconductor given by Equation (15) and exponentially expiring plasmon oscillations with the rate 1 τ ′ , equals to,
A = β ∫ 0 ∞ δ w ℏ ω d t = β ℏ ω δ w τ ′ / 2 .
This energy is equal the initial energy of the plasmon (not supported next by photons), thus A can be also estimated by the electric field amplitude of the excitation signal at t = 0 , cf. [21]. Comparing A calculated in two different manners, one can extract the formula (20) for plasmon damping rate in the nano-metallic coating due to the coupling with band electrons in a semiconductor substrate.
For the probability of absorption of a single photon mediated by plasmons in a metallic coating q m (at the different scenario, when sun-light photons continuously irradiate the system and the photon energy income is balanced by its transfer to band electrons via plasmons), we find finally,
q m = β C 0 128 9 π 2 a 3 μ m n * m p * m 2 ( ℏ ω − E g ) e 6 n e 2 ω ℏ 4 ε 3 f 2 ( ω ) , for a ξ ≪ 1 , β C 0 128 9 2 π 2 a 2 μ 3 / 2 m 2 ℏ ω − E g e 6 n e 2 ω ℏ 3 ε 3 f 2 ( ω ) , for a ξ ≫ 1 ,
where C 0 = N m 4 / 3 π a 3 V , V is the volume of the semiconductor, N m is the number of metallic nanospheres in a metallic coating and f ( ω ) = 1 ( ω 1 2 − ω 2 ) 2 + 4 ω 2 / τ ′ 2 (here ω 1 is the self-frequency of dipole surface plasmon mode in a metallic nanoparticle and ω is a frequency of incident photons—the forcing field for the forced and damped oscillator of the plasmon dipoles in metallic coating; upon the scheme of forced and damped oscillations a frequency of plasmons equals to the frequency of incident photons—the forcing field). The equation system (22) with (20) formulate fully analytic description of by plasmon mediated photo-effect, which in the case of the presence of the nano-metallic coating of the semiconductor substrate substitutes the conventional direct photo-effect formula (17). Note that to calculate q m (by Equation (22)), the knowledge of τ ′ (given by Equation (20)) is required.
To compare the efficiency of photon absorption via plasmons in nano-metallic coating with direct absorption of photons in a semiconductor, one must calculate,
q m q 0 = 8 π 2 a 3 β C 0 m n * ( m p * ) 5 / 2 e 4 n e 2 ω 2 f 2 ( ω ) 3 2 μ 3 / 2 m 2 ℏ ω − E g ℏ 3 ε 2 , for a ξ ≪ 1 , 8 π 2 a 2 β C 0 ( m p * ) 2 e 4 n e 2 ω 2 f 2 ( ω ) 3 μ m 2 ( ℏ ω − E g ) ℏ 2 ε 2 , for a ξ ≫ 1 .
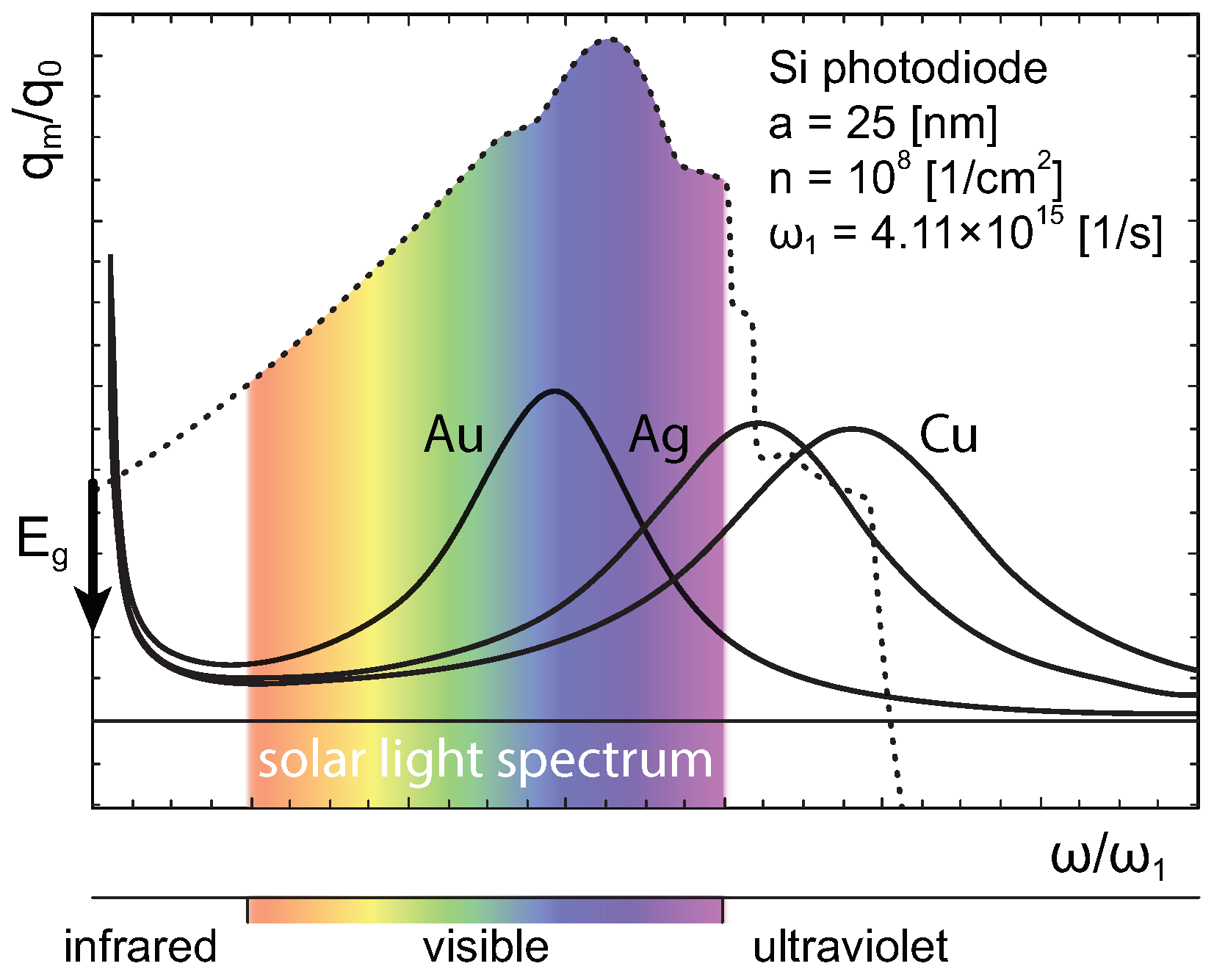
The above formula is sufficient to esimate in a fully quantum manner the plasmonic enhancement of photon absorption in a semiconductor substrate when this absorption is mediated by plasmons in a nano-metallic coating. This leads directly to the estimation (in an analytic form) of the efficiency gain of solar cells due to application of plasmonics components strengthening absorption of sun-light photons. The derived formula describes the plasmon mediated photo-effect in dependence on semiconductor band parameters (effective masses in valence and conduction bands and forbidden gap) and on nano-metallic coating parameters (self-frequency of the dipole mode of surface plasmons in a single metallic nanoparticle, its radius and the concentration of nanoparticles in a coating). The function q m / q 0 gives the ω spectrum of the absorption gain over the direct photo-effect and translates immediately into the measure of the solar cell efficiency increase due to a nano-metallic coating, because the photo-current in a photo-diode with plasmonic additions is given by I ′ = | e | N ( q 0 + q m ) A , where N is the number of incident photons; q 0 and q m are the probabilities of single-photon absorption in the ordinary photo-effect [25] and of single-photon absorption mediated by the presence of metallic nanospheres, respectively; and A = τ f n t n + τ f p t p is the amplification factor (where τ f n ( p ) are the recombination times of carriers of both signs and t n ( p ) are the drive times, i.e., the times required to traverse the distance between electrodes, for the carriers). From the above formulae, it follows that (here, I = I ′ ( q m = 0 ) , i.e., the photocurrent without metallic modifications)
I ′ I = 1 + q m q 0 ,
where the ratio q m / q 0 is given by Equation (23). The examples of (24) are plotted for several photovoltaic structures in Figure 3.

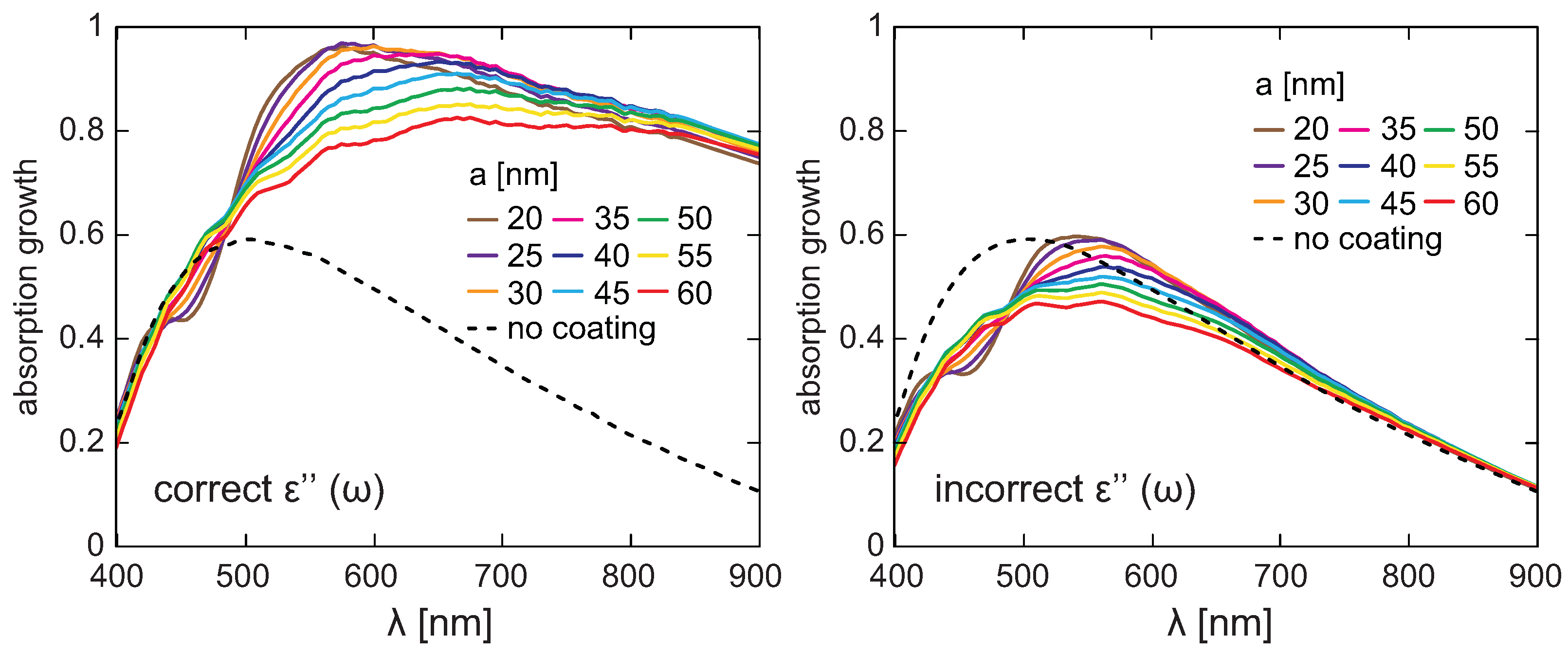
4. Inaccuracy of Photovoltaic Plasmonic Effect Numerical Simulations Without Quantum Corrections

The estimation of the efficiency of photovoltaic plasmonic effect described above, i.e., of the strengthening of photon absorption in the semiconductor mediated by surface dipole plasmons in nano-metallic coating requires an application of the quantum Fermi golden rule. The damping rate of plasmons due to coupling of plasmons to band electrons in the substrate semiconductor (as given by Equation (20)) occurs size and material dependent and highly exceeds scattering losses of plasmons. Hence, the dielectric function for metallic nanoparticles in the Drude-Lorentz form as for bulk metal with only small damping due to scattering (4) is strongly underestimated. The metallic nanoparticle coupled with surrounding absorbing medium (semiconductor) is in fact different system (with different material characteristics) than the same metallic nanoparticle in vacuum or in a dielectric surroundings. The difference concerns its dielectric function, which is not longer that of the bulk metal. If one uses the bulk metal dielectric function as the prerequisite for the solution of Maxwell-Fresnel problem numerically (e.g., by finite element method by Comsol packet) to simulate e-m wave absorption (and reflection), the true energy transfer by described above quantum transitions induced by plasmons is not accounted for. A Comsol-type simulation can only determine the concentration of local electric field of incident light e-m wave close to the curvature of the metallic nanoparticle and related strengthening of the ordinary photo-effect. However, by plasmons mediated photo-effect is essentially different quantum phenomenon and not only classical strengthening of the ordinary photo-effect. To include these both channels—classical and quantum ones, the Comsol-type simulation must be performed with the modified dielectric functions of metallic nanocomponents (with correction of plasmon damping given by Equation (20) besides Equation (4)) and also modified material characteristics of substrate semiconductors (in particular its absorption rate—the same as damping rate of plasmons due commonly shared quantum coupling). The correction is large as for nanometer scale of metallic nanoparticles the quantum effect is ca. ten times more efficient than the classical one—cf. Figure 4 for illustration.
This is an exceptional situation when due to quantum coupling in the near-field zone of plasmons in the nano-metallic coating with surrounding semiconductor, the presence of this absorbing medium modifies plasmon oscillations—their frequency and damping. For light sources separated by macroscopic distance from receivers such an effect is not present. For example, the shining of the Sun is not modified by the presence of the Earth or of other planets, but shining of plasmons is strongly modified by the presence in their near-field zone of the semiconductor absorber. This is a strong quantum effect manifesting itself in functioning of nano-metallic coatings of semiconductors. Note that the dielectric function of a metallic nano-particle in the coating is defined both by the size of the particle, metal type and band characteristics of the coupled semiconductor and is strongly different than the dielectric function of the same metallic nano-particle in vacuum. The same with regard to the semiconductor substrate decorated with metallic components. Its dielectric function is also modified—due to the quantum channel of energy transfer from plasmons to band electrons, the absorption rate in the semiconductor is equal to the emission rate of plasmons.
This concerns also other systems of plasmonic antenna-receiver type frequently studied numerically for applications for catalysts, sensors, detectors or spectrometers improved by plasmonic metallic nano-antenna. A quantum subsystem of the receiver must be considered subjected to the influence of plasmons from nanoparticle antenna upon the Fermi golden rule, which can modify the overall system behavior in comparison to only classical assessment of plasmon impact via numerical solution of Maxwell-Fresnel boundary problem (an assessment of only classical strengthening of local electric field near the curvature of the plasmonic antenna is insufficient here).

5. What Is the Range of Plasmon Influence in the Absorbing Substrate of the Nano-Metallic Coating?

The plasmon effect caused by a nano-metallic coating of a semiconductor substrate is the phenomenon of the proximity class, both with regard to its quantum and classical components. The focusing of the electric field of the incident light e-m wave (the classical effect) is ranged to the close vicinity of a metallic nanoparticle and is especially large near local curvature of the particle—as has been demonstrated for various shape metallic nanoparticles [22]. The same with the range of the quantum coupling along the scheme of the Fermi golden rule—the interaction entering the Hamiltonian of the substrate quickly diminishes with the growth of a separation of the nano-metallic coating and substrate semiconductor regions.
We have demonstrated that this range is, however, not lower that one micrometer scale. This has been evidences [5,22] by the comparison of the efficiency gain in a Si photo-diode covered directly with silver nanoparticles and covered with the same Ag nanoparticles, but separated from the Si substrate with one nanometer thick spacer layer of ZnO nanorods (cf. Figure 5). The photo-response of Si photo-diode exhibited the same strengthening by plasmonic coating regardless the one micrometer separation. This has evidences that the range of the plasmonic photovoltaic effect is not lower than the one micrometer. Therefore in the case of thin film solar cells one can expect a particular effectiveness of nano-metallic coatings (e.g., in perovskite cells with ultra-thin absorber layer of ca. 300 nm, the whole photo-active semiconductor material (perovskite) is within the range of plasmonic effect regardless the positioning of metallic nanoparticles). However, in more thick solar cells, like Si cell, the positioning of the metallic coating with respect to the p-n junction region cannot exceed micrometer scale, as is also demonstrated in variety of experiments [7,8,9,10,11,26,27,28,29,30] cf. Table 8.3 in [22].

6. Non-Optical Function of Nano-Metallic Coatings of Perovskite Solar Cells

Operation rules of perovskite cells differ from conventional p-n junction cells in a manner of the dissociation of photoexcitons. In p-n junction cells the liberation of electrons and holes from their coupled pairs (excitons) takes place in the junction region due to the junction voltage. For instance, in Si p-n junction cell, the juction voltage is of order of 1 V, thus excitons with typical binding energy of ca. 100 meV are almost instantly dissociated if are exposed to the action of the junction voltage. Separated positive and negative carries are next pushed in opposite directions by the same voltage and flow toward opposite electrodes. In perovskite cells photoexcitons randomly flow toward electron or hole transport layers and there, on the interface between two materials with different energies of the conduction and valence bad edges, pairs of electrons and holes are decoupled in local contact voltage. One sign components of excitons, electrons or holes at the interface with electron or hole transport layer, respectively, are captured by the local potential gradient oppositely oriented for electrons and holes, whereas the opposite sign carriers liberated at such exciton dissociation are pushed toward the opposite electrode. These gradients of potential are comparable to exciton binding energy and decouple electron-hole pairs the more efficiently the lower is the exciton binding energy. Here is the role of plasmonic admixtures—the mediation of plasmons in creation of excitons causes not only an increase of photon absorption but also lowers the binding energy of photoexcitons within the near-field zone of oscillating dipoles of surface plasmons in metallic nanoparticles, most intensively for photon energies close to plasmonic resonances in these nanoparticles. By the appropriately tailoring these plasmonic resonances in metallic nano-components (always very keen to absorb photons—as shown in pragraph Section 2) to optimally cover the sun-light spectrum and increase the related population of photoexcitons, is thus possible to enhance the ratio of excitons with lower binding energy. This translates into a significant strengthening of the photocurrent in a perovskite cell, even though the plasmonic strengthening of the absorption of photons is week in perovskites due to their inconvenient band parameters [31]. This scenario has been supported by experiments with variety of shape, size, material and structure of used metallic nanoparticles to create nano-metallic coatings of the perovskite layer in a cell [15,16,17].
The electrical plasmonic photovoltaic effect can be quantified in a similar manner as the optical one presented in paragraph Section 3. From the Equation (10) we notice that matrix element 〈 k 1 | w + | k 2 〉 is not diagonal in vectors k . It means that to interband transitions induced by plasmons contribute also nonvertical ones with different k 1 and k 2 . This is different in comparison to the ordinary photo-effect where by direct excitation by photons only vertical interband transitions are allowed, what follows from the different perburbation of electron band Hamiltonian by interaction with photons than with plasmons. Photons are described by the e-m wave which enter the Hamiltonian via a vector potential A ( R , t ) = A 0 e i ( q · R − ω t ) (at gauge that scalar potential vanishes and d i v A = 0 ) [25]. Hence, in the direct photo-effect the matrix element similar to (10) is proportional to Dirac delta δ ( k 2 − k 1 − q ) expressing the momentum conservation for photons ω = c q (where ω is the frequency of the photon—that one which enters the energy Dirac delta in the Fermi golden rule for ordinary direct photo-effect [25], and c is the light velocity in vacuum). Because ℏ ω must be equal to E n ( k 2 ) − E p ( k 1 ) ∼ E g (due to the energy Dirac delta in Fermi golden rule expressing energy conservation at transitions) then the length of photon momentum q = ω / c is negligible small in comparison to electron momenta—thus, we deal here with only vertical interband transitions k 2 = k 1 . The contribution of non-vertical transitions in by plasmons mediated excitations (as the matrix element (10) is not diagonal) is the reason why by plasmon created excitons are more probable than those created directly by photons. However, by plasmon created excitons differ from those created by phonons in the arbitrary q —the difference of electron and hole momenta in the exciton (for directly by photons created excitons q = 0 ). The excitons with nonzero q have lower binding energy as both carries in a pair have not balanced momenta in any reference frame. It means that for q ≠ 0 electron and hole tend to separate one from another, which reduces the pair binding energy by Δ E ( q ) = ℏ 2 q 2 2 μ . 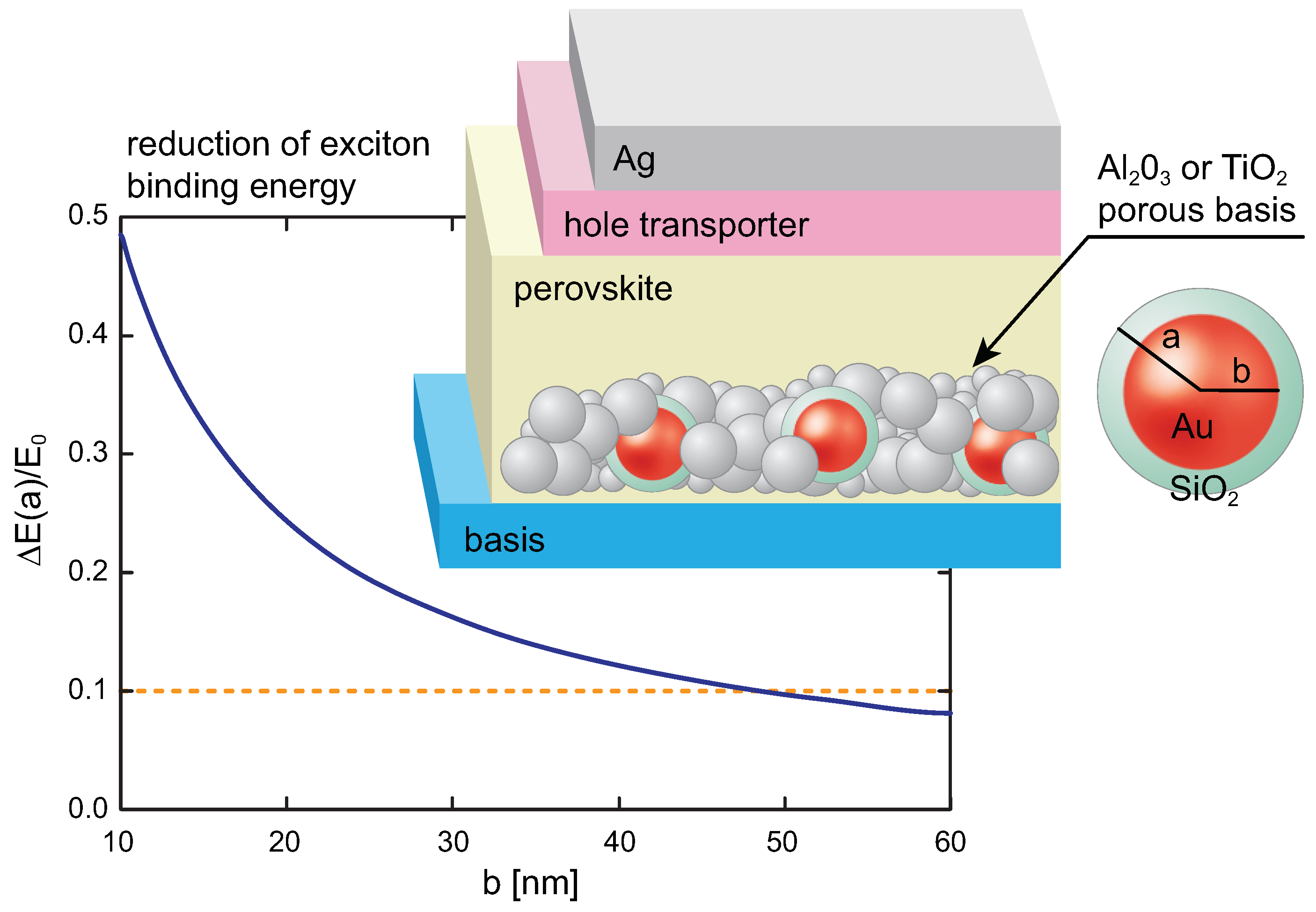Averaging over all initial and final band states and using the formula (10), one can calculate the mean value of exciton binding energy reduction,
Δ E ( a ) = ∫ d 3 k 1 ∫ d 3 k 2 ℏ 2 q 2 2 μ w ( k 1 , k 2 ) ∫ d 3 k 1 ∫ d 3 k 2 w ( k 1 , k 2 ) = ℏ 2 2 μ ∫ 0 1 d x s i n 2 ( x a ξ ) a 2 1 − x 2 ∫ 0 1 d x s i n 2 ( x a ξ ) ( x a ξ ) 2 1 − x 2 ,
where μ = m n * m p * m n * + m p * is the reduced mass of the electron-hole pair, ξ = 2 ( ℏ ω − E g ) ( m n * + m p * ) ℏ and a is the radius of metallic nanosphere in the coating (in the case of core-shell plasmonic components a should be substituted by b = a + δ , where δ is the thickness of the outer insulating shell). The function Δ E ( a ) is plotted in Figure 6. This is a core of the electrical plasmonic effect, as the reduction of the binding energy via plasmon created excitons accelerates their dissociation at the interface with the electron or hole transport layer in a perovskite cell. This acceleration translates onto the the increase of the photocurrent in the cell. Note that the by plasmon strengthen absorption rate induces an increase of the voltage in the cell. Hence, it is possible to distinguish between two plasmonic effect via comparison of experimental I − V characteristics of the metallized cell compared to this characteristics without plasmonic additions—cf. e.g., [10,15,16,17]—cf. 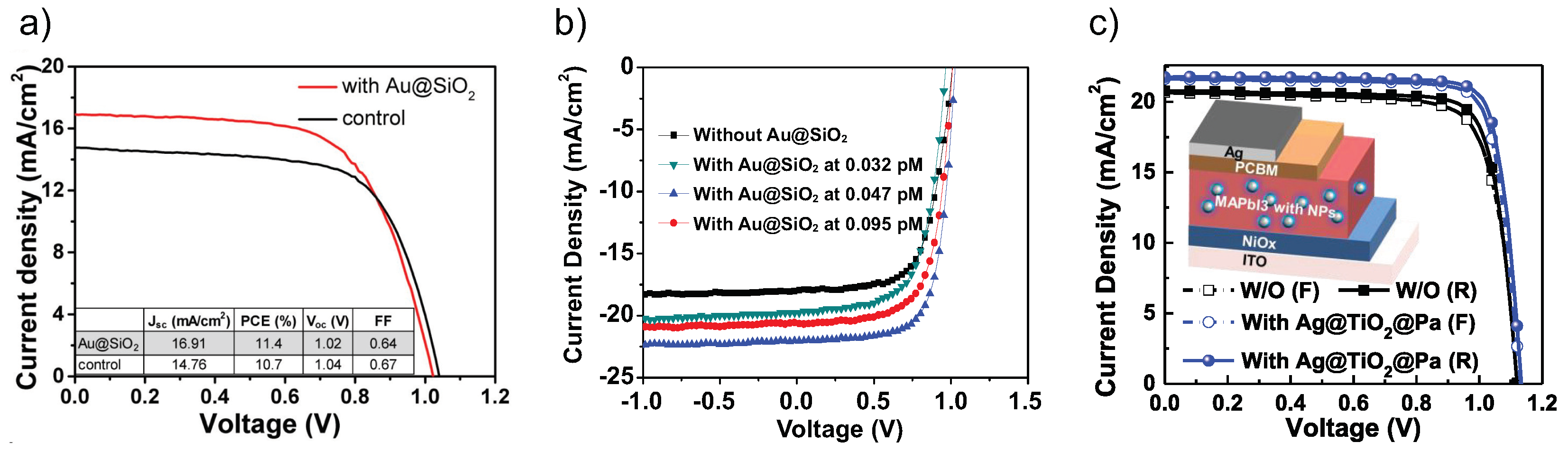Figure 7 and Figure 8.
In perovskite cells the electrical effect dominates, though is unimportant in p-n junction cells in favor of the optical plasmonic effect. To compare with the experiment for pervskite cells, one can estimate Δ E for a perovskite CH3NH3 PbI 3 − α Clα cell with the crystal lattice cell axes, a 1 = a 2 ≃ 0.85 nm, a 3 ≃ 0.45 nm, and the refraction index 2.5 − 3 . The estimation of the exciton binding energy gives thus ca. 100 meV (at μ m ε 2 ∼ 8 × 10 − 3 ), as reported in [17]. For the averaged q ∼ 0.075 × 2 π / l (where l ∼ 0.5 nm is taken to estimate the size of the Brillouin zone, and 0.075 taken as the averaged size of q on the Brillouin zone scale), the reducing of the exciton binding energy by plasmonic additions (at μ = 0.5 m , as in perovskite and gold particles used in the experiment [17]) is as large as Δ E ∼ 70 meV, perfectly fitting to the independently measured by photoluminescence methods in the metalized perovskite cell with the increased efficiency [17].
In perovskite cells an important drawback is related with low durability of the multilayer structure, which translates onto efficiency losses during the operation. In particular, the addition to perovskite layer metallic electrodes by high temperature evaporation perturbs interface morphology resulting in component escape, defect density rebound, carrier extraction barrier and film stability deterioration. To protect against such parasitic effects a variety of buffer coatings have been designed—recently, by engineering a bilayer structure composed of graphene oxide and graphite flakes to eliminate the unwanted film inconsistencies. The resulting perovskite photovoltaic device with the efficiency of 25.5 % was obtained, which demonstrated negligible photovoltaic performance loss after operating for 2000 hours [32]. Similar problems occur at additions of nano-metallic coatings to a perovskite layer close to the interface with electron or hole transport layer, which perturbs local morphology resulting in the increase of parasitic defects lowering the operation efficiency. To reduce losses the core-shell nanoparticles are applied to separate a metal surface from the surroundings, which are designed appropriately to minimize perturbations, by e.g., SiO2 outer shell for Au nanoparticles [17] or even more complicated bi-shell-core metallic components Ag@TiO2@organic shell(benzonic acid fellerene C60) [16] (cf. Figure 7).

7. Conclusions

We argue that the utilization of specially designed nano-metallic coatings with low concentration on nanoparticles can significantly increase the efficiency of photovoltaic devices, both of conventional p-n junction cells as well as of hybrid chemical cells like perovskite ones. The plasmonic mediation in photon harvesting from the incident sun-light occurs very efficient due to the exceptional ability of surface plasmons in metallic nanoparticls (in particular in Au, Ag or Cu to fit to sun-light spectrum) to transfer energy from photons to semiconductor substrate increasing overall photon absorption rate of a cell (optical plasmonic effect) and reducing the binding energy of excitons (electrical plasmonic effect). Both effects are sensitive to band parameters of the semiconductor substrate and require an optimal accommodation of plasmon resonances in metallic nanoparticles. This opens a way to a special engineering of these nano-metallic components including multi-shell-core their structures (protecting against morphology perturbation in a local environment) or varying nanoparticle shape (to appropriately tailor plasmonic resonances). For instance, an application of nanorods doubles the plasmonic resonance in a tunable manner via changing the aspect ratio of rods and can better fit to used perovskite material—it has been demonstrated that the application of Au@SiO2 nanorods increased the efficiency of PEDOT:PSS/perovskite/PCBM photovoltaic cell by 40 % [15]. Important is also the location of the nano-metallic active layer. As we have demonstrated that the range of the plasmonic effect exceeds one micrometer scale, thus in the case of a perovskite layer with optimal thickness of ca. 300 nm, the whole material is inside the near-field zone of plasmon radiation at any distribution of metallic components and the positioning of metallic nanoparticles can be arbitrary but chosen to minimize local morphology perturbations. As the nano-metalization is cheap (due to small amount of metal expenditure) and easy to deposit by various techniques, but very efficient in strengthening both the voltage (optical plasmonic effect) and the photo-current (electrical plasmonic effect), such a method of surpassing the Shockley–Queisser-type efficiency limit seems to be promising and universal in p-n junction as well as in perovskite cells including not explored yet application of nano-metalization in various tandem cell architectures [31,33,34,35].
In conclusions we emphasize that functional nano-metallic coatings must be always considered as the subsystems of the whole systems coating-substrate (in the general scheme of coupled plasmonic antenna-receiver), as a quantum coupling of plasmons with quantum degrees of freedom in a substrate significantly changes properties and characteristics of both coupled metallic particles and semiconductor. Coupled subsystems are not the same as identical but separated ones.

Conflicts of Interest

No conflicts of interest is declared.

Appendix A. Structure of Plasmons in a Nanosphere

The microscopic description of plasmon oscillations in bulk metal by quantum random phase approximation (RPA) [19,20] can be developed onto confined pieces of a metal like metallic nanospheres [22]. The scheme of the RPA approach resolves itself to the dermination of the dynamic equation for local electron density fluctuations on the background of a uniform jellium of positive ions in a metal. This dynamic equation can be found by Heisenberg equation for time derivative of an operator. The Hamiltonian of interacting electrons H = ∑ i = 1 N p i 2 2 m + 1 2 ∑ i , j = 1 , i ≠ j N e 2 | r i − r j | can be rewritten as follows,
H = ∑ i p i 2 2 m + ∑ k ′ V k 2 ρ k + ρ k − N ,
where V k = 4 π e 2 k 2 is the Fourier transform of the Coulomb potential and ρ k = ∑ i e − i k · r i is the Fourier component of local density of electrons in a point r , ρ ( r ) = ∑ i δ ( r − r i ) = ∑ k ρ k e i k · r . The prim mark at the sum (in Equation (A1)) indicates that the component with k = 0 is omitted here, which corresponds to the inclusion of the uniform jellium ideally canceling the uniform electron distribution with k = 0 , i.e., ρ 0 . The above Hamiltonian representation allows us to write out the dynamic equation by twice application of the Heisenberg equation ρ ˙ k = 1 i ℏ [ ρ k , H ] − (for details cf. [19]),
ρ ¨ k = − ∑ i e − i k · r i − k · p i m + ℏ k 2 2 m 2 − ∑ q ′ 4 π e 2 m q 2 k · q ρ k − q ρ q .
The first term on the right hand side of the equation represents a contribution caused by the kinetic energy of particles, whereas the second one is linked with the particle interaction. Let us rewrite the equation and shift the last its term taken for k = q to the left-hand side of the equation (for k = q in this term it occurs the large factor ρ 0 = N ), which gives the formula [19,20],
ρ ¨ k + ω p 2 ρ k = − ∑ i e − i k · r i − k · p i m + ℏ k 2 2 m 2 − ∑ q ≠ k ′ 4 π e 2 m q 2 q · k ρ k − q ρ q ,
where ω p = 4 π n e 2 m 1 / 2 is called as the plasmon frequency of free electrons in a bulk metal (here in Gauss units, but if one changes to SI, ω p = n e 2 ε 0 m 1 / 2 ).
From Equation (A3) we notice that the second term in the right hand side of the equation is small (as ρ k is small for all k ≠ 0 ) and can be neglected—this is the sense of RPA. The first term in the right hand side is caused by kinetic energy and also can be tentatively omitted (it gives the dispersion of plasmons, but we look for the gap of these excitations), hence we arrive with pure harmonic oscillations for any ρ k with the plasmon frequency ω p (the gap of these excitations). Note that plasmon oscillations are conditioned by the mutual repulsion of electrons. Thus, in an electron gas no plasmon exist (this fundamental fact is not noticeable in macroscopic approach to plasmons upon phenomenological Drude-Lorentz model [18]).
This derivation of plasmons can be extended onto the case of a metallic nanosphere with radius a, as it has been done in [22]. The first difference is a finite spherical jellium, n ( r ) = n Θ ( a − r ) (where n is the equilibrium positive charge density and Θ is the Heaviside step function), which explicitly enter the Hamiltonian of electrons in a nanosphere. Twice application of the Heisenberg formula for the operator time derivative leads to the similar equation as (A3), but due to presence of the Θ function in Hamiltonian, the terms with the Dirac delta occur now (as the gradient of Θ function is the Dirac delta). The Dirac delta on the rim of the nanosphere distinguishes surface plasmons in this particle, whereas other terms (without multiplication by the Dirac delta) describe volume plasmon oscillations. Omitting here a tedious formal derivation (cf. [22]) we list here only final results for particular plasmon mode frequencies.
For surface plasmons we have obtained self-oscillations with frequencies equal to ω 0 l = ω p l 2 l + 1 , corresponding to various multipole modes (numbered with l, which is the angular momentum number of the spherical function). For volume modes the frequencies are as follows, ω n l = ω p 1 + x n l 2 k T 2 a 2 , where l is again the angular momentum number of the spherical function Y l m ( Ω ) (all plasmon modes are degenerated versus the magnetic number m of the spherical function) and x n l are consecutive nodes (n=1,2,3,...) of the l-th Bessel function displaying fluctuations of the electron density along the nanosphere radius (for surface plasmons no such fluctuations are present, i.e., the density of electrons is homogeneous along the sphere radius and non-zero fluctuations are only on the sphere surface), k T = 6 π n e 2 / v F is the reciprocal of the Thomas-Fermi radius. We see that frequencies of surface plasmons are always lower than ω p (volume plasmon in bulk), whereas volume plasmons in a nanosphere have frequencies greater than ω p . For details and the derivation cf. [22] Chapter 4.

Appendix B. Dipole Mode of Surface Plasmon Oscillations in a Nanosphere

The plamon resonance frequencies for a metallic nanosphere have the corresponding e-m wave wavelength λ = 2 π c / ω much larger than a—thus the electric field of this resonant e-m wave is almost homogeneous over whole volume of the nanoparticle. The uniform electric field can excite only the dipole type mode of surface plasmons with l = 1 and m = − 1 , 0 , 1 . Electron response to the driving field E ( t ) (which is homogeneous over the nanosphere, corresponding to the dipole approximation for nanospheres) resolves itself to a single dipole type mode, effectively described by the three-component function denoted here as Q 1 m ( t ) ( l = 1 and m = − 1 , 0 , 1 ). The dynamical equation of RPA type reduces in this case to the following one,
∂ 2 Q 1 m ( t ) ∂ t 2 + 2 τ 0 ∂ Q 1 m ( t ) ∂ t + ω 1 2 Q 1 m ( t ) = 4 π 3 e n e m E z ( t ) δ m , 0 + 2 E x ( t ) δ m , 1 + E y ( t ) δ m , − 1 ,
where ω 1 = ω p 3 ε is the dipole surface plasmon frequency (including a dielectric surroundings with the permittivity ε ). The electron density fluctuations described by Equation (A4) are following,
δ ρ ( r , t ) = 0 , r < a , ∑ m = − 1 1 Q 1 m ( t ) Y 1 m ( Ω ) , r ≥ a , r → a + ,
where Y 1 m ( Ω ) are the spherical functions for l = 1 and Ω is the solid angle collecting spherical coordinates on the sphere surface. The notation r → a + describes the limit to the sphere surface from above needed to properly define the Dirac delta on the surface (because the Dirac delta as the distribution must be defined for an inner point of some open set [22]). For dipole-type plasmonic oscillations as presented by Equation (A5), the dipole of electron system D ( t ) can be written as follows,
D ( t ) = e ∫ d 3 r r δ ρ ( r , t ) = 2 π 3 e a 3 Q 1 , 1 ( t ) , Q 1 , − 1 ( t ) , 2 Q 1 , 0 ( t )
and the dipole D ( t ) satisfies following equation (obtained via rewriting Equation (A4)),
∂ 2 ∂ t 2 + 2 τ 0 ∂ ∂ t + ω 1 2 D ( t ) = a 3 4 π e 2 n e 3 m E ( t ) = ε a 3 ω 1 2 E ( t ) .
According to Equation (A6) we notice that the dipole of plasmon oscillations scales with the nano-sphere radius as a 3 , which indicates that all electrons in the sphere contribute to the surface plasmon excitations. This can be referred to the fact that the surface plasmon modes correspond to uniform translation-type oscillations of the whole electron liquid. Inside the sphere the uniformly shifted charge of electrons is still exactly compensated by static and also uniform positive jellium, while a not balanced charge density fluctuations occur only on the surface. One can note that in the case of the volume plasmons the non-compensated charge density fluctuations are present inside the sphere, because the volume plasmon modes are related to compressional modes resulting in volume charge fluctuations not balanced by the jellium along the radius inside the nanosphere.
The damping term 1 τ 0 accounts for the dissipation of the energy of plasmons due to the scattering of electrons similar as for the Ohmic losses. This channel of the energy dissipation includes all types of scattering phenomena: electron-electron, electron-phonon, electron-admixture collisions as usually for Ohmic losses and additionally the contribution related to scattering of electrons on the nanoparticle boundary [36]. All these scattering processes causes the attenuation of plasmons and their energy is dissipated irreversibly and finally converted into heat. If we include additionally the radiation losses in the form of the Lorentz friction, we arrive at the Equation (1).

References

  1. Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. Journal of Appl. Phys. 1961, 32, 510. [Google Scholar] [CrossRef]
  2. Rúhle, S. Tabulated values of the Shockley–Queisser limit for single junction solar cells. Solar Energy 2016, 130, 139. [Google Scholar] [CrossRef]
  3. Fraunhofer Institute for Solar Energy Systems. Photovoltaics Report 2021.
  4. Bi, C.; Wang, Q.; Shao, Y.; Yuan, Y.; Xiao, Z.; Huang, J. Non-wetting Surface Driven High Aspect Ratio Crystalline Grain Growth for Efficient Hybrid Perovskite Solar Cells. Nat. Commun. 2015, 6, 7747. [Google Scholar] [CrossRef] [PubMed]
  5. Jacak, W.; Popko, E.; Henrykowski, A.; Zielony, E.; Luka, G.; Pietruszka, R.; Witkowski, B.; Wachnicki, L.; Godlewski, M.; Chang, L.B.; et al. On the size dependence and the spatial range for the plasmon effect in photovoltaic efficiency enhancement. Sol. Energy Mater. Sol. Cells 2016, 147, 1. [Google Scholar] [CrossRef]
  6. Pillai, S.; Catchpole, K.; Trupke, T.; Green, M. Surface plasmon enhanced silicon solar cells. Journal of Applied Physics 2007, 101, 093105. [Google Scholar] [CrossRef]
  7. Stuart, H.R.; Hall, D.G. Island size effects in nanoparticle-enhanced photodetectors. Appl. Phys. Lett. 1998, 73, 3815. [Google Scholar] [CrossRef]
  8. Luo, L.; Xie, C.; Wang, X.; Yu, Y.; Wu, C.; Hu, H.; Zhou, K.; Zhang, X.; Jie, J. Surface plasmon resonance enhanced highly efficient planar silicon solar cell. Nano Energy 2014, 9, 112–120. [Google Scholar] [CrossRef]
  9. Losurdo, M.; Giangregorio, M.M.; Bianco, G.V.; Sacchetti, A.; Capezzuto, P.; Bruno, G. Enhanced absorption in Au nanoparticles/a-Si:H/c-Si heterojunction solar cells exploiting Au surface plasmon resonance. Solar En. Mat. and Solar Cells 2009, 93, 1749. [Google Scholar] [CrossRef]
  10. Jeng, M.; Chen, Z.; Xiao, Y.; Chang, L.; Ao, J.; Sun, Y.; Popko, E.; Jacak, W.; Chow, L. Improving Efficiency of Multicrystalline Silicon and CIGS Solar Cells by Incorporating Metal Nanoparticles. Materials 2015, 8, 6761–6771. [Google Scholar] [CrossRef]
  11. Schaadt, D.M.; Feng, B.; Yu, E.T. Enhanced semiconductor optical absorption via surface plasmon excitation in metal nanoparticles. Appl. Phys. Lett. 2005, 86, 063106. [Google Scholar] [CrossRef]
  12. Jacak, W.A.; Jacak, J.E. New Channel of Plasmon Photovoltaic Effect in Metalized Perovskite Solar Cells. J. Phys. Chem. C 2019, 123, 30633. [Google Scholar] [CrossRef]
  13. Li, S.; Zhu, X.; Wang, B.; Qiao, Y.; Liu, W.; Yang, H.; Liu, N.; Chen, M.; Lu, H.; Yang, Y. Influence of Ag Nanoparticles with Different Sizes and Concentrations Embedded in a TiO2 Compact Layer on the Conversion Efficiency of Perovskite Solar Cells. Nanoscale Research Letters 2018, 13, 210. [Google Scholar] [CrossRef]
  14. Xia, Z.; Zhang, C.; Feng, Z.; Wu, Z.; Wang, Z.; Chen, X.; Huang, S. Synergetic Effect of Plasmonic Gold Nanorods and MgO for Perovskite Solar Cells. Nanomaterials 2020, 10, 1830. [Google Scholar] [CrossRef]
  15. Wu, R.; Yang, B.; Zhang, C.; Huang, Y.; Cui, Y.; Liu, P.; Zhou, C.; Hao, Y.; Gao, Y.; Yang, J. Prominent Efficiency Enhancement in Perovskite Solar Cells Employing Silica-Coated Gold Nanorods. J. of Phys. Chem. C 2016, 120, 6996. [Google Scholar] [CrossRef]
  16. Yao, K.; Zhong, H.; Liu, Z.; Xiong, M.; Leng, S.; Zhang, J.; Xu, Y.; Wang, W.; Zhou, L.; Huang, H.; et al. Plasmonic Metal Nanoparticles with Core-Bishell Structure for High-Performance Organic and Perovskite Solar Cells. ACS Nano 2019, 13, 5397. [Google Scholar] [CrossRef]
  17. Zhang, W.; Saliba, M.; Stranks, S.; Sun, Y.; Shi, X.; Wiesner, U.; Snaith, H. Enhancement of perovskite-based solar cells employing core-shell metal nanoparticles. Nano Lett. 2013, 13, 4505. [Google Scholar] [CrossRef]
  18. Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, 1983. [Google Scholar]
  19. Pines, D. Elementary Excitations in Solids; ABP Perseus Books: Massachusetts, 1999. [Google Scholar]
  20. Pines, D.; Bohm, D. A Collective Description of Electron Interactions: II. Collective vs Individual Particle Aspects of the Interactions. Phys. Rev. 1952, 85, 338. [Google Scholar] [CrossRef]
  21. Jacak, J.; Krasnyj, J.; Jacak, W.; Gonczarek, R.; Chepok, A.; Jacak, L. Surface and volume plasmons in metallic nanospheres in semiclassical RPA-type approach; near-field coupling of surface plasmons with semiconductor substrate. Phys. Rev. B 2010, 82, 035418. [Google Scholar] [CrossRef]
  22. Jacak, W. Quantum Nano-plasmonics; Cambridge UP: Cambridge, 2020. ISBN 978110847 8397.
  23. Landau, L.D.; Lifshitz, E.M. Field Theory; Nauka: Moscow, 1973. [Google Scholar]
  24. Jackson, J.D. Classical Electrodynamics; John Willey and Sons Inc.: New York, 1998. [Google Scholar]
  25. Kiriejew, P.S. Physics of Semiconductors; PWN: Warsaw, 1969. [Google Scholar]
  26. Matheu, P.; Lim, S.; Derkacs, D.; McPheeters, C.; Yu, E. Metal and dielectric nanoparticle scattering for improved optical absorption in photovoltaic devices. Applied Physics Letters 2008, 93, 113108. [Google Scholar] [CrossRef]
  27. Lim, S.; Mar, W.; Matheu, P.; Derkacs, D.; Yu, E. Photocurrent spectroscopy of optical absorption enhancement in silicon photodiodes via scattering from surface plasmon polaritons in gold nanoparticles. Journal of Applied Physics 2007, 101, 104309. [Google Scholar] [CrossRef]
  28. Pillai, S.; Catchpole, K.R.; Trupke, T.; Zhang, G.; Zhao, J.; M. A, G. Enhancement emission from Si-based light-emitting diodes using surface plasmons. Appl. Phys. Lett. 2006, 88, 161102. [Google Scholar] [CrossRef]
  29. Ho, W.; Hu, C.; Yeh, C.; Lee, Y. External quantum efficiency and photovoltaic performance of silicon cells deposited with aluminum, indium, and silver nanoparticles. Japanese Journal of Applied Physics 2016, 55, 08RG03. [Google Scholar] [CrossRef]
  30. Temple, T.; Mahanama, G.; Reehal, H.; Bagnall, D. Influence of localized surface plasmon excitation in silver nanoparticles on the performance of silicon solar cells. Solar Energy Materials and Solar Cells 2009, 93, 1978–1985. [Google Scholar] [CrossRef]
  31. Laska, M.; Krzemińska, Z.; Kluczyk-Korch, K.; Schaadt, D.; Popko, E.; Jacak, W.A.; Jacak, J.E. Metallization of solar cells, exciton channel of plasmon photovoltaic effect in perovskite cells. Nano Energy 2020, 75, 104751. [Google Scholar] [CrossRef]
  32. Luo, C.; Gao, F.; Wang, X.; Zhan, C.; Zhang, X.; Zheng, G.; Zhang, X.; Gao, X.; He, Z.; Zhao, Q. Eliminating performance loss from perovskite films to solar cells. Science Advances 2024, 10, 0790. [Google Scholar] [CrossRef]
  33. Li, Z.; Zhu, K. Ultra-High Efficiency Perovskite-Perovskite Tandem Solar Cells. Material Matters 2018, 13, 1. https://www.sigmaaldrich.com/PL/pl/technical-documents/technical-article/materials-science-and- engineering/photovoltaics-and-solar-cells/ultra-high-efficiency-perovskite-perovskite-tandem-solar- cells.
  34. Rajagopal, A.; Yang, Z.; Jo, S.; Braly, I.L.; Liang, P.; Hillhouse, H.W. Highly Efficient Perovskite–Perovskite Tandem Solar Cells Reaching 80% of the Theoretical Limit in Photovoltage. Advanced Materials 2017, 29, 1702140. [Google Scholar] [CrossRef]
  35. Heo, J.H.; Im, S.H. CH3NH3PbBr3-CH3NH3PbI3 Perovskite–Perovskite Tandem Solar Cells with Exceeding 2.2 V Open Circuit Voltage. Advanced Matterials 2016, 28, 5121, https://www.onlinelibrary.wiley.com/doi/full/10.1002/adma.201501629. [Google Scholar] [CrossRef]
  36. Brongersma, M.L.; Hartman, J.W.; Atwater, H.A. Phys  . Rev. B 2000, 62, R16356. [Google Scholar] [CrossRef]
Preprints 121209 g001
Figure 1. Exact solution of Equation (3) (as given analytically by the second equation in (6)) for parameters of Au nanoparticle in vacuum, for the comparative demonstration of the role of Lorentz friction for damping of plasmon oscillations. Ca. 100-times larger losses due to radiative Lorentz friction compared to the scattering losses (caused by metal imperfections, phonons and particle boundary) is visible at radius of a particle ∼ 50 − 150 nm, though the role of Lorentz friction strongly diminishes for smaller and much lager particles. A strong deviation from the harmonic damped oscillations (marked by blue lines) is noticeable—in particular, for the damping including Lorentz friction any overdamped regime does not exist, in contrary to harmonic damped oscillations.
Figure 1. Exact solution of Equation (3) (as given analytically by the second equation in (6)) for parameters of Au nanoparticle in vacuum, for the comparative demonstration of the role of Lorentz friction for damping of plasmon oscillations. Ca. 100-times larger losses due to radiative Lorentz friction compared to the scattering losses (caused by metal imperfections, phonons and particle boundary) is visible at radius of a particle ∼ 50 − 150 nm, though the role of Lorentz friction strongly diminishes for smaller and much lager particles. A strong deviation from the harmonic damped oscillations (marked by blue lines) is noticeable—in particular, for the damping including Lorentz friction any overdamped regime does not exist, in contrary to harmonic damped oscillations.
Preprints 121209 g001
Preprints 121209 g002
Figure 2. The electron microscope images of four examples of metallic (Au) nanoparticle coatings of cSi solar cell with growing (a)–(d) concentration and used in the experiment [10]. The optimal concentration occurred a medium one (c), but in all (a)–(d) samples a very rare distribution of particles is visible, which translates into small material expenditure.
Figure 2. The electron microscope images of four examples of metallic (Au) nanoparticle coatings of cSi solar cell with growing (a)–(d) concentration and used in the experiment [10]. The optimal concentration occurred a medium one (c), but in all (a)–(d) samples a very rare distribution of particles is visible, which translates into small material expenditure.
Preprints 121209 g002
Preprints 121209 g003
Figure 3. Function q m q 0 with respect to the frequency of incident photons calculated according to Equation (23) for Si photodiode covered with Au, Ag or Cu nanoparticles with radius a = 25 nm and surface coating concentration n = 10 8 1/cm2 on the background of sun-light spectrum. The typical shape of forced and damped oscillations is noticeable for different resonant frequencies in various metals, which demonstrates usability of coatings to strengthen light absorption from different parts of sun-light spectrum.
Figure 3. Function q m q 0 with respect to the frequency of incident photons calculated according to Equation (23) for Si photodiode covered with Au, Ag or Cu nanoparticles with radius a = 25 nm and surface coating concentration n = 10 8 1/cm2 on the background of sun-light spectrum. The typical shape of forced and damped oscillations is noticeable for different resonant frequencies in various metals, which demonstrates usability of coatings to strengthen light absorption from different parts of sun-light spectrum.
Preprints 121209 g003
Preprints 121209 g004
Figure 4. Absorption enhancement in Si substrate by coatings with Au nanoparticles with varying particle radius a = 20 , 25 , 30 , 35 , 40 , 45 , 50 , 55 , 60 nm and particle separation 4 a in Comsol simulation of periodic distribution of particles in the coating. Left panel—with the inclusion of the quantum coupling between plasmons in nanoparticles to band electrons in Si substrate for varying wavelength (frequency) of incident light e-m wave, compared to bare Si surface without any coating—dashed line. Right panel—without inclusion of quantum corrections to material dielectric functions of metallic nanoparticles and semiconductor substrate. The giant error due to the negligence of quantum corrections is visible.
Figure 4. Absorption enhancement in Si substrate by coatings with Au nanoparticles with varying particle radius a = 20 , 25 , 30 , 35 , 40 , 45 , 50 , 55 , 60 nm and particle separation 4 a in Comsol simulation of periodic distribution of particles in the coating. Left panel—with the inclusion of the quantum coupling between plasmons in nanoparticles to band electrons in Si substrate for varying wavelength (frequency) of incident light e-m wave, compared to bare Si surface without any coating—dashed line. Right panel—without inclusion of quantum corrections to material dielectric functions of metallic nanoparticles and semiconductor substrate. The giant error due to the negligence of quantum corrections is visible.
Preprints 121209 g004
Preprints 121209 g005
Figure 5. The idea of the experimental verification of the range of plasmonic effect. The Si photodiode with Ag particle coating is compared with the same photodiode with additionally deposited on its surface ZnO vertical nanorods with a lenght 1 μ m and diameter ∼ 300 nm (a), next covered from above with Ag nanoparticles (b). The strengthening of the absorption of photons measured via the photocurrent increase in Si photodiode occurred comparable at the absence and at the presence of the nanorod buffer [5].
Figure 5. The idea of the experimental verification of the range of plasmonic effect. The Si photodiode with Ag particle coating is compared with the same photodiode with additionally deposited on its surface ZnO vertical nanorods with a lenght 1 μ m and diameter ∼ 300 nm (a), next covered from above with Ag nanoparticles (b). The strengthening of the absorption of photons measured via the photocurrent increase in Si photodiode occurred comparable at the absence and at the presence of the nanorod buffer [5].
Preprints 121209 g005
Preprints 121209 g006
Figure 6. Averaged reduction of the exciton binding energy induced by the interaction with surface dipole plasmon in metallic nanoparticle (with radius a) embedded in the perovskite layer. The binding energy shift is renormalized by the energy on the border of the Brillouin zone, E 0 = ℏ 2 p 0 2 2 μ , where p 0 = π / l and l ≃ 5 nm is the averaged linear size of the elementary cell of the perovskite ( E 0 ∼ 200 meV for μ ∼ 0.35 m , cf. [17]).
Figure 6. Averaged reduction of the exciton binding energy induced by the interaction with surface dipole plasmon in metallic nanoparticle (with radius a) embedded in the perovskite layer. The binding energy shift is renormalized by the energy on the border of the Brillouin zone, E 0 = ℏ 2 p 0 2 2 μ , where p 0 = π / l and l ≃ 5 nm is the averaged linear size of the elementary cell of the perovskite ( E 0 ∼ 200 meV for μ ∼ 0.35 m , cf. [17]).
Preprints 121209 g006
Preprints 121209 g007
Figure 7. Three examples of nano-metallic coatings of perovskite solar cells. (a) coating of Au@SiO2 core-shell particles ( a ∼ 40 nm b ∼ 48 nm) embedded in the perovskite close to the interface with electron transport layer in the experiment [17]. (b) Au@Si02 nanorods embedded at the interface of the perovskite with PEDOT:PSS layer in multilayered perovskite cell in the experiment [15]. (c) coating of bi-shell-core metallic components Ag@TiO2@organic shell with fullerene C60 embedded in a PIDTT-DFBT:PC71BM transport layer (outer shell of benzoic acid fullerene C60 prohibits the agregation of nanoparticles in the PIDTT layer of the perovskite cell) in the experiment [16].
Figure 7. Three examples of nano-metallic coatings of perovskite solar cells. (a) coating of Au@SiO2 core-shell particles ( a ∼ 40 nm b ∼ 48 nm) embedded in the perovskite close to the interface with electron transport layer in the experiment [17]. (b) Au@Si02 nanorods embedded at the interface of the perovskite with PEDOT:PSS layer in multilayered perovskite cell in the experiment [15]. (c) coating of bi-shell-core metallic components Ag@TiO2@organic shell with fullerene C60 embedded in a PIDTT-DFBT:PC71BM transport layer (outer shell of benzoic acid fullerene C60 prohibits the agregation of nanoparticles in the PIDTT layer of the perovskite cell) in the experiment [16].
Preprints 121209 g007
Preprints 121209 g008
Figure 8. The enhancement of the perovskite cell efficiency for three examples of nano-metallic coatings (a), (b) and (c) shown in Figure 7, respectively. In each case a significant increase of the photo-current is revealed but not of the voltage, which evidences the prominent role of the electric plasmonic effect in metallized perovskite cells.
Figure 8. The enhancement of the perovskite cell efficiency for three examples of nano-metallic coatings (a), (b) and (c) shown in Figure 7, respectively. In each case a significant increase of the photo-current is revealed but not of the voltage, which evidences the prominent role of the electric plasmonic effect in metallized perovskite cells.
Preprints 121209 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated