The study provides a comprehensive examination of the theory and applications of mathematical operators, aligning with the content areas of Mathematics, Engineering, Physics, and Computer Science. The investigation of the convergence properties of Chlodovsky type Bernstein operators using the Korovkin-type theorem is directly part of mathematical analysis and approximation theory. Such studies yield significant results applicable to fields like mathematical modeling and optimization. Furthermore, the optimization of convergence rates of operators through system control contributes to the more efficient and stable management of systems within control engineering. Lastly, visual illustrations created using Maple demonstrate the convergence rates of operators on specific functions, contributing to modeling and simulation techniques used in computer science. In this context, our work offers a valuable addition to the scope of the journal Symmetry.

Approximation theory is rapidly emerging as an essential tool, extending its influence beyond classical domains to other mathematical areas such as differential equations, orthogonal polynomials, and geometric design. Following the introduction of Korovkin’s renowned theorem in 1950, the topic of approximating functions using linear positive operators has become an increasingly significant focus within approximation theory. A wealth of literature has been produced on this subject [1,2,10,12,14,15,23,24,31,32].

In recent years, particularly over the last twenty years, the role of q-calculus in approximation theory has been thoroughly investigated. The initial work on Bernstein polynomials derived from q-integers was conducted by Lupaş [6]. His findings indicated that q-Bernstein polynomials can provide superior approximations compared to classical methods when an appropriate choice of q is made. This discovery has encouraged numerous researchers to develop q-generalizations of various operators and to explore their approximation properties further. Numerous studies have contributed to this field [3,7,8,13].

Lately, Mursaleen et al. have concentrated on utilizing $(p,q)-$calculus for approximations through linear positive operators, introducing the $(p,q)-$analogues of Bernstein operators [20,21]. They analyzed the uniform convergence of these operators and determined their rates of convergence. For additional recent studies related to $(p,q)-$operators, readers can refer to [17,18,19,26,27].

The main motivation behind this study is that, to the authors’ knowledge, there have been no investigations into approximating two-variable operators using $(p,q)-$ calculus thus far. In this context, we introduce two dimensional Chlodovsky type Bernstein operators based on $(p,q)-$integers. We investigate the approximation properties of our newly defined operators with the aid of the Korovkin-type theorem. Furthermore, we delve into the local approximation characteristics and determine the rates of convergence through the modulus of continuity and a Lipschitz type maximal function. A Voronovskaja type theorem relevant to these operators is also presented. Another significant aim of this research is to examine the weighted approximation properties of our operators in the first quadrant of ${\mathbb{R}}_{+}^2$, specifically within the range of $[0,\infty )\times [0,\infty )$. To achieve these results, we intend to apply a weighted Korovkin-type theorem. We will begin by revisiting some definitions and notations pertinent to the concept of (p, q)-calculus. The (p, q)-integer associated with a given number n is defined as The $(p,q)-$factorial ${\left[n\right]}_{p,q}!$ and the $(p,q)-$binomial coefficients are defined as: and

Further, the $(p,q)-$binomial expansions are given as and

Further information related to $(p,q)-$calculus can be found in [25,28].

Recently, Ansari and Karaisa [16] have defined and studied $(p,q)-$analogue of Chlodovsky operators as follows: where

For $0<q_1,q_2<p_1,p_2\le 1$, we define Chlodovsky type two dimensional Bernstein operator based on $(p,q)-$integers as follows: for all $n,m\in N$, $f\in C\left(I_{{\alpha }_n{\beta }_m}\right)$ with $I_{{\alpha }_n{\beta }_m}=\{(x,y):0\le {\alpha }_n\le x,0\le {\beta }_m\le y\}$ and $C\left(I_{{\alpha }_n{\beta }_m}\right)=\{f:I_{{\alpha }_n{\beta }_m}⟶R\mathrm{is}\mathrm{continuous}\}$. Here $\left({\alpha }_n\right)$ and $\left({\beta }_m\right)$ be increasing unbounded sequences of positive real numbers such that

Also, the basis elements are

We require the following lemmas to establish our main results.

From Lemma 1, we have following:

Using Lemma 2 and by linearity of $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$, we have

In this section, we analyze the convergence rates of the operators $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ to the function $f(x,y)$ using the modulus of continuity. Furthermore, we will present a summary of the relevant notations and definitions concerning the modulus of continuity and Peetre’s K-functional for bivariate real-valued functions.

For a function $f\in C\left(I_{ab}\right)$, the complete modulus of continuity in the bivariate context is defined as follows: for every $(t,s),(x,y)\in I_{ab}$. Additionally, the partial moduli of continuity concerning x and y are defined as follows:

It is evident that they fulfill the properties of the standard modulus of continuity [11].

For $\delta >0$, the Peetre-K functional [22] is defined as follows: where $C^2\left(I_{ab}\right)$ is the space of functions of f such that f, ${\displaystyle \frac{{\partial }^{j}f}{\partial x^j}}$ and ${\displaystyle \frac{{\partial }^{j}f}{\partial y^j}}$$(j=1,2)$ in $C\left(I_{ab}\right)$. The norm $\parallel .\parallel$ on the space $C^2\left(I_{ab}\right)$ is defined by

We now provide an estimate for the rate of convergence of the operators $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$.

For ${\widehat{\alpha }}_1,{\widehat{\alpha }}_2\in (0,1]$ and $(s,t),(x,y)\in I_{ab}$, we define the Lipschitz class $LipM({\widehat{\alpha }}_1,{\widehat{\alpha }}_2)$ for the bivariate case as follows:

Below, we obtained three-dimensional graphs illustrating the convergence rates of operators to specific functions using the Maple [30] software.

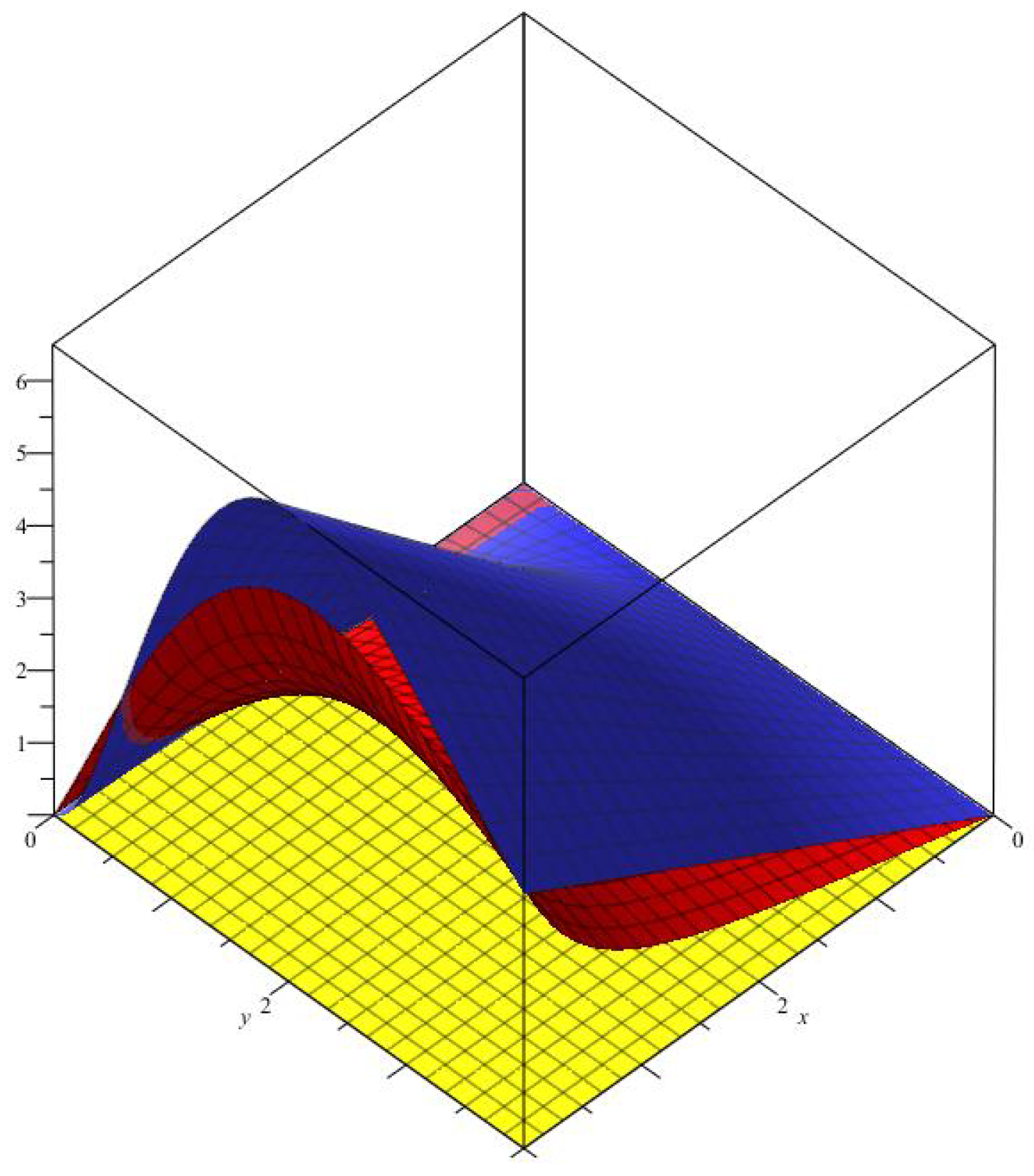
Example 1. Figure 1 shows the optimal approximation of operators

$C_{20,20}^{(0.999,0.9),(0.999,0.9)}(f;x,y)$(red), $C_{20,20}^{(0.90,0.86),(0.996,0.89)}(f;x,y)$(yellow)

with ${\alpha }_n=ln\left(n\right)$, ${\beta }_m=\sqrt{m}$ to function $f(x,y)=3x{y}^2{e}^{-y}$(blue).

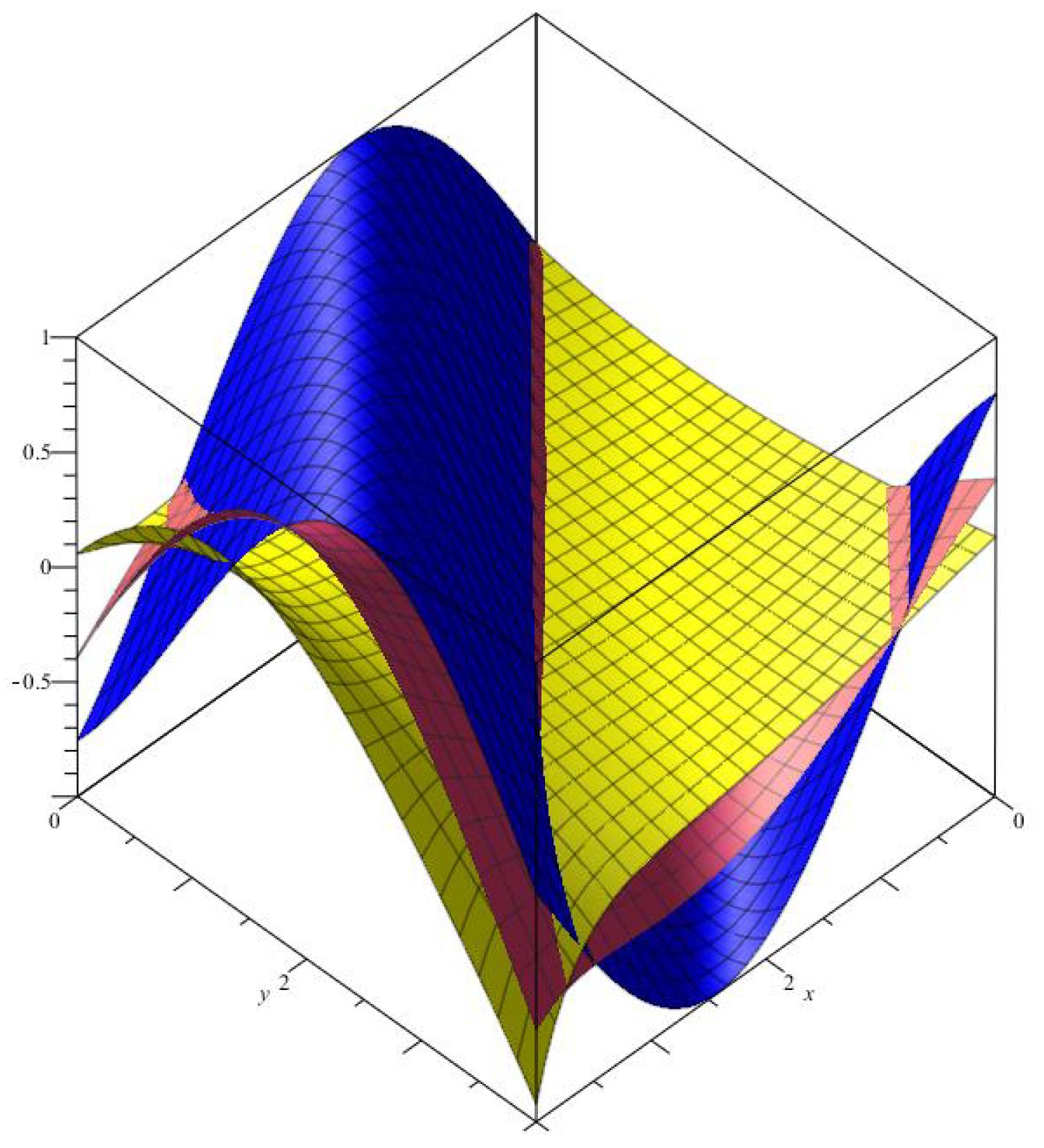
Example 2. Figure 2 shows the optimal approximation of operators $C_{20,20}^{(0.999,0.9),(0.99,0.9)}(f;x,y)$(red), $C_{20,20}^{(0.990,0.86),(0.996,0.89)}(f;x,y)$(yellow)

with ${\alpha }_n=ln\left(n\right)$, ${\beta }_m=\sqrt{m}$ to function $f(x,y)=sin(x-y)$(blue).

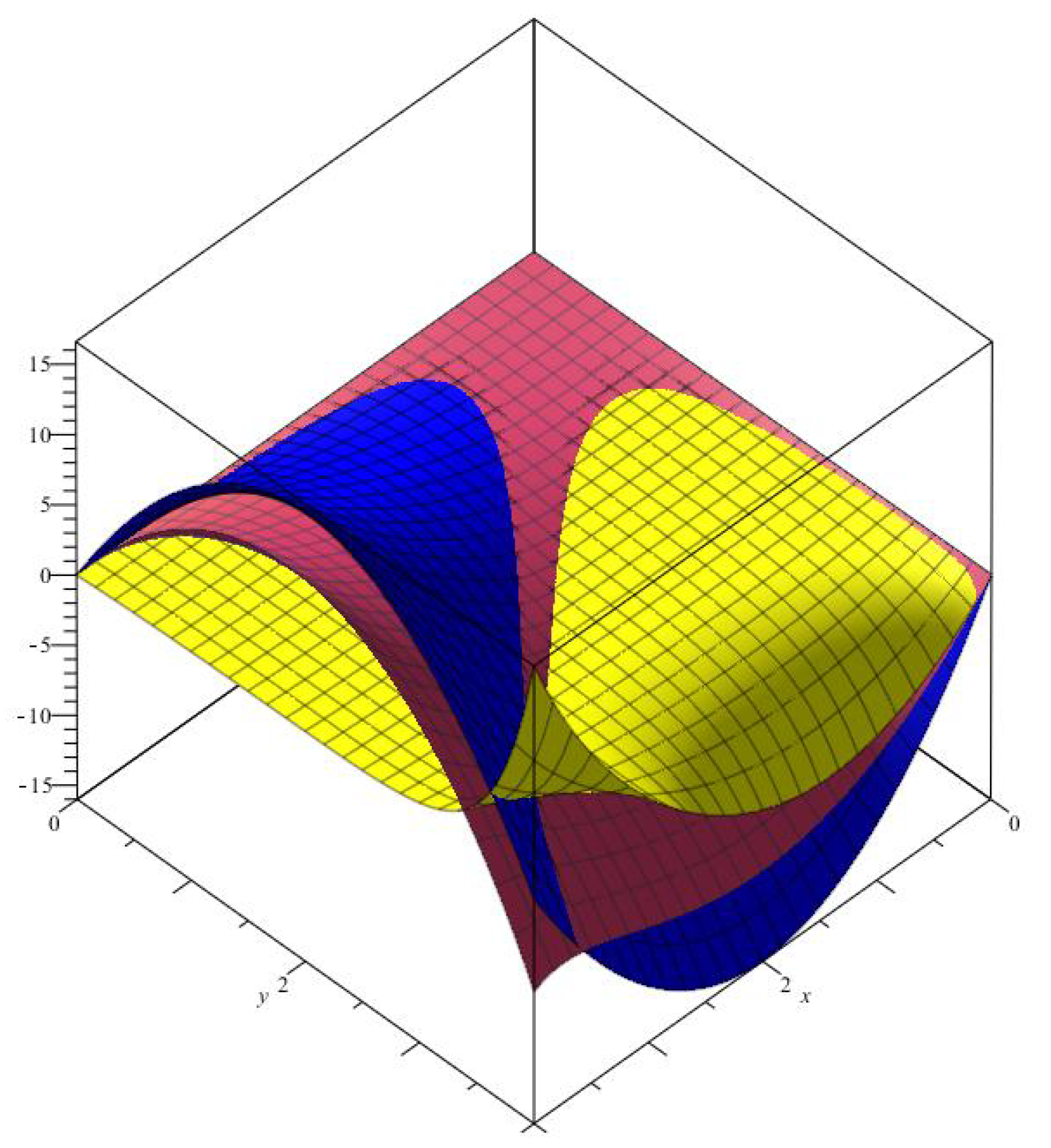
Example 3. Figure 3 shows the optimal approximation of operators

$C_{20,20}^{(0.99,0.9),(0.999,0.96)}(f;x,y)$(red), $C_{20,20}^{(0.99,0.9),(0.990,0.90)}(f;x,y)$(yellow)

with ${\alpha }_n=ln\left(n\right)$, ${\beta }_m=ln\left(m\right)$ to function $f(x,y)=x^{2}y-x{y}^2)$(blue).