Prerpints.org logo
Preprint
Article

Generative Simplex Mapping: Non-Linear Endmember Extraction and Spectral Unmixing for Hyperspectral Imagery

This version is not peer-reviewed.

Submitted:

14 October 2024

Posted:

15 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
We introduce a new model for non-linear endmember extraction and spectral unmixing of hyperspectral imagery called Generative Simplex Mapping (GSM). The model represents endmember mixing using a latent space with points sampled within a (n−1)-simplex corresponding to the abundance of n unique sources. Points in this latent space are non-linearly mapped to reflectance spectra via a flexible function combining linear and non-linear mixing. Due to the probabilistic formulation of the GSM, spectral variability is also estimated by a precision parameter describing the distribution of observed spectra. Model parameters are determined using a generalized expectation-maximization algorithm. In the event of purely linear mixing, non-linear contributions are naturally driven to zero. The GSM outperforms three varieties of non-negative matrix factorization for both endmember extraction accuracy and abundance estimation on a synthetic data set of linearly mixed spectra from the USGS spectral library. In a second experiment, the GSM is applied to real hyperspectral imagery captured over a pond in North Texas. The model is able to accurately identify spectral signatures corresponding to near-shore algae, water, and rhodmaine tracer dye introduced into the pond to simulate water contamination by a localized source. Abundance maps generated using the GSM accurately track evolution of the dye plume as it mixes into the surrounding water.
Keywords: 
Subject: 
Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Hyperspectral imaging has emerged as a keystone technology in remote sensing, where the ability to discern variations between high-resolution spectra supports a plethora of critical applications such as environmental monitoring, biodiversity conservation, sustainable agriculture, and more. In recent years, many remote sensing platforms have been deployed with hyperspectral imaging payloads such as the Italian PRISMA mission launched in 2019, the German EnMAP launched in 2022, and recently NASA’s PACE satellite launched in 2024 [1,2,3]. Many future missions also plan to incorporate hyperspectral imaging capabilities such as the European Space Agency’s CHIME which will include over 200 bands spanning visible, near-infrared (NIR), and short-wave infrared (SWIR) wavelengths [4]. The continued development of hyperspectral imaging technology has also led to a considerable reduction in size that enables its inclusion in the payloads of small unmanned aerial vehicles (UAVs) [5,6]. Despite the proliferation of hyperspectral imaging data sources, the considerable increase in data volume associated with hyperspectral images (HSI) poses significant challenges to real-time analysis at scale.
Many approaches have been developed to make sense of the HSI data. For example, spectral indices such as the popular normalized difference vegetation index (NDVI) can be computed by taking ratios of spectral bands tailored to track specific reflectance characteristics [7,8]. These indices have the advantage of being easy to compute, but suffer from significant variability between instruments while ignoring most of the information captured in HSI spectra [9]. An alternative approach is to pair HSI data with in situ measurements to enable supervised models that map spectra directly to parameters of interest. However, this approach relies on serendipitous satellite overpasses above sensing sites to generate sufficient quantities of aligned data for model training and evaluation. For example, Aurin et al. combined data from over 30 years of oceanographic field campaigns with paired satellite imagery to develop robust models for the inversion of key water quality indicators such as colored dissolved organic matter [10]. This approach can be accelerated by combining UAV-based hyperspectral imaging with rapid in situ data collection using autonomous boats [11,12]. However, these supervised methods rely on a priori knowledge of expected sources to identify appropriate reference sensors for data collection. In light of these limitations, unsupervised methods are needed which can reliably extract source signatures from high-dimensional HSI.
The spatial resolution of hyperspectral imagers generally results in pixels with mixed signals from multiple sources called endmembers. The task of unsupervised source identification using HSI data therefore involves two steps: endmember extraction and abundance estimation. Techniques such as vertex component analysis (VCA), the pixel purity index (PPI), and N-FINDR solve this first task by identifying HSI endmember spectra assuming the presence of some pure (unmixed) pixels [13,14,15]. By further assuming a linear mixing model (LMM) in which observed spectra are described by a linear combination of endmembers with non-negative abundances, HSI can be unmixed using a variety of techniques such as constrained least squares [16,17]. Among these methods, Nonnegative Matrix Factorization (NMF) is a widely used approach which extracts endmember spectra and unmixes abundances simultaneously via matrix factorization [18,19,20]. The update equations for NMF can be formulated as multiplicative updates which guarantee the non-negativity of endmember spectra and their associated abundances [21]. For this reason, the continued development of new NMF varieties remains an active area of research.
In realistic scenes, multiple scattering and surface variability can easily challenge the assumption of linear mixing [22]. Water-based HSI specifically are prone to non-linear mixing effects due to absorption features of dissolved and suspended substances, fluorescence of organic matter, and particulate scattering in turbid waters [23,24,25]. With the growing popularity of deep learning approaches in remote sensing, a variety of models based on autoencoder architectures have been introduced for unmixing HSI data [26,27,28,29]. However, the complexity introduced by these models significantly impacts training time and decreases the interpretability of the resulting model. An ideal approach should enable both endmember extraction and non-linear unmixing while accounting for spectral variability.
The self-organizing map (SOM) is an unsupervised machine learning method that maps high-dimensional data to a low-dimensional grid while preserving the topological relationships between data points [30]. This low-dimensional representation provides a convenient way to visualize HSI data while the weight vectors for each SOM node can be interpreted as representative spectra [31,32,33]. If labelled reference spectra are available, the SOM can be used to enable semi-supervised labeling of HSI pixels [34]. The SOM has also been shown to be effective for the compression of HSIs acquired by a CubeSat [35]. Despite these capabilities, the SOM does not offer a probabilistic interpretation and relies on a heuristic training procedure with hyperparameters that can be challenging to tune. To address these shortcomings, Bishop et al. introduced the Generative Topographic Mapping (GTM), a probabilistic latent-variable model inspired by the SOM [36]. When choosing a two-dimensional latent space, the GTM can be used to visualize the distribution of HSI spectra while mapping the latent space nodes to the HSI data space provides endmembers [37]. Unfortunately, the rectangular latent space grid employed by the GTM does not directly translate into endmember abundances, and the expectation-maximization (EM) algorithm used to train the GTM does not guarantee non-negativity of GTM node spectra.
In this paper, we introduce a new variant of the GTM dubbed Generative Simplex Mapping (GSM), which can extract endmember spectra and unmix non-linear mixtures. By replacing the rectangular latent space of the GTM with a gridded ( n − 1 ) -simplex, the vertices of the GSM can be immediately interpreted as endmembers corresponding to n unique spectral signatures. The mapping from the latent space to the HSI data space models signal mixing while barycentric coordinates for the latent space simplex represent relative endmember abundances. Additionally, by taking inspiration from the multiplicative updates of NMF, the GSM algorithm maintains the non-negativity of resulting endmember spectra. If only linear mixing is present, the GSM algorithm drives non-linear contributions to 0. Prior distributions included for GSM model weights yield hyperparameters which can be tuned to control the smoothness of the resulting spectra and the degree of non-linear mixing applied.
The remainder of the paper is structured as follows. Section 2 describes the proposed method. Section 3 and Section 4 describe experiments using simulated and real HSI data to evaluate the GSM model. Section 5 discusses additional applications and extensions of the GSM to be explored in future work. Finally, Section 6 finishes the paper with some closing remarks.

2. Generative Simplex Mapping

In the original GTM formulation, the data vectors x (reflectance spectra) are described by latent variables z mapped into the data space by a non-linear function ψ . The data space distribution is taken to be normal with the precision parameter β to account for measurement noise and spectral variability. The GSM uses same structure, that is
p ( x ∣ z , W , β ) = β 2 π D / 2 exp − β 2 ∥ ψ ( z ; W ) − x ∥ 2
where W are model weights which parameterize the mapping ψ .
Assuming data are uniformly sampled from an embedded manifold in the data space, the GTM models the latent space using a rectangular grid with K-many nodes of equal prior probability. To adapt the GTM to describe endmember mixing, the GSM makes two key changes. The first is to replace the rectangular GTM grid with a gridded simplex with N v vertices. The barycentric coordinates for each node then describe the relative abundance of each endmember with each vertex corresponding to a pure endmember. The second change is to replace equal prior probabilities with adaptive mixing coefficients π k to allow the GSM to model HSI with nonuniform mixing distributions. Together, this leads to a latent space prior distribution given by
p ( z ) = ∑ k K π k δ ( z − z k ) where ∑ k K π k = 1 .
For a data set containing N-many records, these definitions yield a log likelihood function given by
L = ∑ n N ln ∑ k K π k p ( x n ∣ z k , W , β )
which can be maximized to obtain optimal values for model weights W , mixing coefficients π k , and precision β . Rather than optimizing Equation (3) directly, we instead choose a particular form for ψ to allow fitting the GSM via an EM algorithm.
In the standard LMM model, the mapping ψ is given by ψ ( z ; W ) = W z where the columns of W correspond to endmember spectra. To model non-linear mixing, z is replaced by the output of M-many activation functions such that ψ ( z ; W ) = W ϕ ( z ) . The activations applied to each GSM node can then be collected to form a matrix with elements Φ k m = ϕ m ( z k ) . For m ≤ N v , we take Φ k m = [ z k ] m to model linear mixing. The remaining M − N v activations are computed using radial basis functions (RBF) with centers μ m distributed throughout the simplex (but not at the vertices) with
Φ k m = s − ∥ z k − μ m ∥ s ; ∥ z k − μ m ∥ ≤ s 0 ; ∥ z k − μ m ∥ > s
where s is the spacing between RBF centers. In this form, the first N v columns of W correspond to endmember spectra, while the remaining columns account for additional non-linear effects. For linear mixing, the GSM training algorithm should therefore drive W d m to 0 for m ≥ N v . A visualization of the GSM model is shown in Figure 1.
To further constrain the model, we introduce prior distributions on the weights W . For m ≤ N v we take W d m ∼ N ( 0 , λ e − 1 ) corresponding to a zero-mean Gaussian with variance λ e − 1 . For m > N v we use a zero-mean Laplace distribution, W d m ∼ λ w 2 exp ( − λ w | W d m | ) , with scale parameter λ w − 1 . Under these choices λ e corresponds to L 2 regularization on endmember spectra while λ w corresponds to L 1 regularization on the non-linear activations. In other words, λ e governs the smoothness of the resulting endmembers while λ w encourages sparsity for the non-linear contributions.
An EM algorithm for the GSM model can now be formulated as follows. Suppose that we have current estimates for the model weights W , mixing coefficients π k , and precision parameter β . During the expectation step we compute the posterior probabilities, that is, the responsibility of each GSM node for each spectrum in the data set:
R k n = p ( z k ∣ x n , W , β ) = π k p ( x n ∣ z k , W , β ) ∑ k ′ K π k ′ p ( x n ∣ z k ′ , W , β ) .
For the maximization step, we consider the expectation of the penalized complete-data log likelihood given by
Q = ∑ n N ∑ k K R k n ln π k + D 2 ln β 2 π − β 2 ∑ d D ∑ m M W d m Φ k m − X n d 2 + N v D 2 ln λ e 2 π − λ 2 ∑ d D ∑ m = 1 N v W d m 2 + ( M − N v ) D ln λ w 2 − λ w ∑ d D ∑ m = N v + 1 M W d m
where X n d is the d-th component of the n-th spectrum in the data set. Equation (6) is then maximized with respect to π k , β , and W to obtain new parameter values. For a detailed overview of the EM procedure, the reader is directed to ref. [38].
For π k , optimization can be performed using Lagrange multipliers to maintain the condition that ∑ k π k = 1 . Doing so yields
π k new = 1 N ∑ n R k n
Optimization of Equation (6) with respect to W leads to a linear system which can be solved using standard numerical methods. However, in this form, we cannot guarantee the non-negativity of W required to describe reflectance spectra. Therefore, we take inspiration from the multiplicative updates for NMF introduced by Lee and Seung [18]. A standard gradient-based update for W would normally take the form
W new = W + η ∂ Q ∂ W
for some learning rate η . Therefore, we differentiate to obtain
∂ Q ∂ W = − β W Φ T G Φ − Λ + β X T R T Φ
where G is a diagonal matrix with G k k = ∑ n R k n and Λ is given by
Λ d m = λ e W d m ; m ≤ N v λ w ; m > N v
If we allow individual learning rates η d m for each element of W , then choosing
η d m = W d m β W Φ T G Φ d m + Λ d m
results in a multiplicative update rule given by
W d m n e w = W d m · β X T R T Φ d m β W Φ T G Φ d m + Λ d m
From Equation (12), it is clear that we are multiplying W d m by strictly non-negative values, and therefore, non-negative W d m will remain so during each update. This update can also be repeated multiple times during each M-step to accelerate convergence.
Optimizing Equation (6) with respect to β yields the final update equation:
1 β new = 1 N D ∑ n N ∑ k K R k n ∥ ψ ( z k ; W ) − x n ∥ 2 .
To train a GSM model, weights W are randomly initialized to positive values. The mixing coefficients are initially set to π k = 1 / K . Finally, the precision parameter β is initialized to the variance of the ( N v + 1 ) -th principal component. After initialization, the expectation and maximization steps are repeated in turn until Q converges to a predetermined tolerance level. For large N v we note that generating a regular grid within the simplex becomes cumbersome as the number of grid nodes scales as k + N v − 2 N v − 1 for k nodes per edge. An alternative approach is to randomly sample points within the simplex to obtain a total of K nodes. A Dirichlet distribution
p ( z ) = Γ ( ∑ i N v α i ) ∏ i N v Γ ( α i ) ∏ i N v [ z ] i α i − 1
with all α i = 1 can be used to uniformly sample within the simplex. Since the mixing coefficients π k are adaptive, variability in node separation should not significantly impact the resulting GSM.
The probabilistic form of the GSM means that a variety of information criteria can be used to evaluate the model fits. In this paper we consider two metrics, the Bayesian Information Criterion (BIC),
BIC = P ln ( N ) − 2 L ,
and the Akaike Information Criterion (AIC),
AIC = 2 P − 2 L
where P is the total number of model parameters and L is the log likelihood from Equation (3).
The map ψ provides the representation of each node z k in the data space. Importantly, applying ψ to each vertex extracts endmember spectra from the GSM. Slices R : , n of the matrix R define the responsibility of each latent node z k for the n-th spectrum x n in the data set. Therefore once the GSM has been trained, R can be used to unmix endmember abundances by representing each record in the latent space via the mean:
z ^ n = ∑ k K R k n z k .
A freely available implementation of the GSM is provided at [39]. The code is written in the Julia programming language and follows the Machine Learning in Julia (MLJ) common interface [40,41].

3. Experiments

3.1. Linear Mixing: Comparison to NMF

To illustrate the effectiveness of the GSM, we first demonstrate its ability to model simple linear mixing by driving non-linear weights to zero during the fitting process. To this end, a synthetic data set comprising linear mixtures of three sample spectra from the U.S. Geological Survey digital spectral library was generated by sampling 1000 abundance vectors from a Dirichlet distribution with α 1 = α 2 = α 3 = 1 / 3 [42]. These source spectra and abundances are visualized in Figure 2.
Zero-mean Gaussian noise was added to the data to yield 9 data sets with signal-to-noise ratios (SNR) ranging from 0 to ∞ to examine the impact of random noise on GSM performance. For each of these data sets, a GSM was trained using 25 nodes per edge with λ e set to the default value of 0.01 and λ w fixed to 100. The large value of λ w was chosen to encourage the GSM to prefer models with limited non-linear mixing.
For comparison, NMF models were also trained on each data set as this method is both highly popular and does not include the pure-pixel assumption common to other technqieus like VCA and PPI. Countless variations on the original NMF method have been introduced into the literature with one review identifying more than 100 distinct NMF variations [19]. For the purpose of evaluating the GSM, we considered the standard ℓ 2 and KL-divergence formulations introduced by Lee and Seung [21]. We also included the robust ℓ 2 , 1 NMF as described by Kong et al [43].
Four metrics were used to compare model performance. For endmember extraction the mean spectral angle and mean RMSE between true endmembers ρ i and extracted endmembers ρ ^ i were computed where the spectral angle for the i-th endmember is defined as
θ ( ρ i , ρ ^ i ) = arccos 〈 ρ i , ρ ^ i 〉 ∥ ρ i ∥ · ∥ ρ ^ i ∥
and the RMSE for the i-th endmember is
RMSE ( ρ i , ρ ^ i ) = 1 D − 1 ∑ d D ρ i ( λ d ) − ρ ^ i ( λ d ) 2 .
Abundance estimation was similarly evaluated using the Mean RMSE between true abundance and estimated abundance values for each endmember. Finally, the reconstruction RMSE, that is, the RMSE computed between the original data set and the data set reconstructed via the extracted endmembers and their associated abundances was computed. This provides a model-agnostic criterion to guarantee that each model sufficiently converged during training.

3.2. Non-Linear Mixing: Water Contaminant Identification

To assess the ability of the GSM to unmix realistic scenes likely to involve non-linear mixing effects, we consider a data set of real HSI collected in Montague, North Texas on 9 December 2020. A Freefly Alta-X autonomous quadcopter was used as a UAV platform and equipped with a Resonon Pika XC2 visible+near-infrared (VNIR) hyperspectral imager to acquire multiple HSI. Each HSI pixel included 462 wavelength bins ranging from 391 to 1011 nm. To evaluate the ability of GSM to identify potential contaminant sources, rhodamine dye, a commonly used tracer in hydrological studies, was released into a pond. Two UAV flights spaced 15 minutes apart were used to capture the evolution of the plume as it dispersed into the surrounding water.
The hyperspectral imager is in a pushbroom configuration so that HSI was captured one scan line at a time. Data from an embedded GPS/INS unit enable direct georectification of captured imagery using the method described in [44]. Additionally, an upward-facing Ocean Optics UV-Vis NIR spectrometer with a cosine corrector was included on the top of the UAV to measure incident solar irradiance. The configuration of the UAV together with a sample HSI are shown in Figure 3. For a more detailed description of the system, the reader is directed to ref. [11,12].
Raw HSI were converted to reflectance using the downwelling irradiance spectrum captured simultaneously with each HSI. Given the UAV flies with the imager oriented to nadir, the reflectance is then given by
ρ ( λ ) = π L ( λ ) / E d ( λ )
where L is the spectral radiance, E d is the downwelling irradiance, and a factor of π is included resulting from the assumption of diffuse upwelling radiance [45]. The UAV flights were performed near solar noon to maximize the amount of sunlight illuminating the water. For this pond in North Texas, this corresponded to an average solar zenith angle of 56 . 7 ∘ resulting in HSI with negligible sunglint effects.
From the collected HSI, a water-only pixel mask was generated by identifying all pixel spectra with a normalized difference water index (NDWI) greater than 0.25 as defined in ref. [46]. Of these water pixels, a combined data set of 15 , 000 spectra was sampled for GSM training. As a final processing step, reflectance spectra were limited to λ ≤ 900 nm as wavelengths above this threshold showed significant noise.
In order to justify values for the appropriate number of endmembers, the final data set was decomposed using principal component analysis (PCA). A plot of the explained variance organized for each PCA component is shown in Figure 4
The PCA decomposition of the data suggests that at least 3 endmembers should be used for a mixing model and beyond 6 there is little added benefit. Based on these observations, multiple GSM models were trained with N v ranging from 3 to 6, λ e ranging from 0.001 to 1.0 , and λ w ranging from 1 to 1000 in order to explore the GSM parameter space. From these, a final model was identified using the BIC, AIC, and reconstruction RMSE. The resulting GSM was then explored to examine extracted endmembers and map the evolution of the rhodamaine plume by using the abundances given by the latent space representation of each pixel in the HSI.

4. Results

4.1. Linear Mixing

The results of GSM training on the synthetic linear mixing data set described in Section 3 are illustrated in Figure 5. Three versions of NMF were trained corresponding to Euclidean ( ℓ 2 ), KL-Divergence, and ℓ 2 , 1 cost functions. GSM models using both a regular simplex grid and a grid of points sampled using a uniform Dirichlet distribution (referred to as a big GSM model) were trained to compare performance in linear mixing tasks.
The quality of endmember extraction is measured by the mean spectral angle and the mean endmember RMSE. As Figure 5 indicates, both versions of the GSM outperformed their NMF counterparts. Additionally, we note that for all GSM models, even including SNR = 0 , all model weights W d m for m > N v corresponding to non-linear mixing were driven identically to 0.0 . This confirms that, for data sets with purely linear mixing and random noise, the GSM correctly fits a mixing model without introducing unnecessary complexity.
The quality of the unmixing, that is, the estimation of the abundance, performed by each model was evaluated using the mean abundance RMSE. Here we again see that both versions of the GSM outperformed NMF. To justify that all models were fairly trained to convergence, the RMSE data reconstruction was also computed. This metric uses the trained mixing model to compute the error between the original data set and the reconstructed spectra generated using the extracted endmembers and their abundances. For all GSM and NMF models, the RMSE data reconstruction converged to the level of random noise introduced into the data. These results reflect a fair comparison between the NMF and GSM models.
In Figure 6, we plot the endmembers extracted for the GSM model trained on the synthetic data set with SNR = 20 .
The extracted endmembers clearly fit the original source spectra while capturing local reflectance features. Furthermore, the GSM precision parameter β which is tuned during model training, provides an assessment of spectral variability due to random noise. In Figure 6 this is indicated by the colored band centered around each extracted spectrum with a width of 2 β − 1 corresponding to 2 standard deviations. The SNR of 20 added to this example corresponds to zero-mean Gaussian noise with a standard deviation of σ = 0.0493 . After training, the GSM found β − 1 = 0.0495 that accurately captures the introduced noise. This ability to assess the spectral variability of extracted endmembers is a key advantage of the GSM.

4.2. Non-Linear Mixing: Rhodamine Dye Plume

For the data set of real HSI spectra described in Section 3, 80 GSM models were trained to explore the GSM hyperparameter space. The performance of the model was compared using the BIC, AIC and RMSE reconstruction with the results of the top 10 performing models shown in Table 1.
As the table indicates, a non-linear GSM with N v = 3 , λ e = 0.01 , and λ w = 1.0 achieved minimum BIC, AIC, and reconstruction RMSE values. The lower value of λ w identified from these models reflects the presence of non-linear mixing effects in the HSI data. Although the values of model weights W d m for m > N v corresponding to non-linear mixing were 0 for the synthetic data set, here these weights obtained a small but non-negligible median value of 0.0012 .
Reflectance spectra generated by the trained GSM corresponding to the maximum abundance values for each endmember are plotted in Figure 7. Based on their signatures, these endmembers are identified with water, vegetation (including near shore, filamentous blue-green algae) and the rhodmaine dye plume.
By assigning a unique color to each endmember, the spatial distribution of HSI spectra can be visualized by using estimated abundances to smoothly interpolate between endmember colors as shown in panel b of Figure 7. In other words, this method provides a fuzzy semantic segmentation of HSI pixels. Alternatively, each HSI pixel could be assigned a single class corresponding to the endmember with maximal abundance. In this way, the GSM can be used to visualize high-dimensional HSI spectra.
To showcase the ability of the GSM to identify spatially localized contaminant sources, abundance maps were generated for each individual end member using the trained GTM to unmix all water pixels in the HSI. In Figure 8 these abundance maps are compared for each endmember. The abundance map for the water endmember covers a majority of the center of the pond and decreases near the edge of the rhodamine plume where the dye and water mix. The vegetation in shallow water near the shore and the rhodamine dye plume in the western half of the pond are also clearly identified by their abundance maps. Given an HSI pixel resolution of 0.1 × 0.1 m 2 , the spatial extent of vegetation is estimated to be 378.6 m 2 while the plume initially extends across 255.7 m 2 .
Applying the trained GSM to unmix HSI from UAV flights provides an efficient way to map the dispersion and transport of contaminant. Figure 9 demonstrates this by mapping the growing extent of rhodamine dye between successive UAV flights. In just 15 minutes, the plume expands from an initial area of 255.7 m 2 to over 571.8 m 2 as the dye mixes with the surrounding water.

5. Discussion

The proliferation of hyperspectral imaging technologies in the remote sensing and environmental monitoring communities underscores the need for efficient algorithms that can make sense of high-dimensional HSI. Of particular interest are unsupervised algorithms which utilize all available wavelength bins to identify unique source profiles that present realistic scenes. The GSM introduced in this paper is a novel method that simultaneously performs endmember extraction and spectral unmixing. Unlike popular endmember extraction algorithms, such as VCA, PPI, and N-FINDR, GSM does not assume the presence of pure pixels in HSI. Furthermore, the flexible structure of the mapping from the GSM latent space to the spectral data space allows the GSM to model non-linear mixing effects, distinguishing it from other widely used linear models such as NMF. Being a probabilistic model also enables the GSM to quantify the spectral variability through the precision parameter β as indicated in Figure 6. This additional capability is critical for analysis of realistic HSI where sensor noise, viewing geometry, and scene illumination all introduce uncertainty into extracted endmembers.
The growing popularity of deep learning methods has led many to explore applications of deep learning to the spectral unmixing problem. Variations in auto-encoder architectures are a popular choice for both endmember extraction and unmixing. For example, Borsoi et al. used a variational autoencoder to more accurately identify the spectral variability in a LMM [28]. Similarly, Palson et al. introduced an autoencoder with convolution layers to extend the LMM by incorporating spatial context from neighboring HSI pixels [29]. However, the increased complexity of deep neural network approaches makes interpreting the latent space learned by encoder layers challenging and can dramatically increase training time and data volume requirements. In contrast, the latent space of the GSM is immediately interpretable due to the imposed simplex geometry, while the form of ψ leaves room to explore a variety of non-linear mixing models. In this paper, ψ was constructed to add non-linear effects as additions or perturbations to an underlying linear mixing model with the λ w hyperparameter provided to control the degree of non-linearity considered. In the original GTM formulation that inspired the GSM, the mapping ψ strictly uses non-linear features generated by Gaussian RBFs. Alternatively, one could easily construct ψ for specific non-linear models such as bilinear mixing by introducing features which depend on higher-order combinations of the latent space (abundance) coordinates. However, it is important to note that the EM algorithm formulated for GSM training is made possible due to the linear combination of activations ϕ ( z ) with model weights W . For mixing models which instead depend non-linearly on weights W , an EM algorithm may require iterative non-linear solves during each M step.
The main limitation of the GSM is the curse of dimensionality encountered when generating a grid on the ( N v − 1 ) -simplex for large numbers of endmembers, N v . This can be mitigated by instead randomly sampling points within the interior of the simplex using a uniform Dirichlet distribution to obtain a pre-determined number of nodes across the latent space. As the mixing coefficients π k are adapted during training, the variability in the spacing of the internodes should not significantly affect the performance of the model. In fact, this was confirmed for the simulated data set as summarized in Figure 5. For considerably large data sets, the size of the responsibility matrix R can also lead to extended training times. This can be addressed by augmenting the EM procedure to updated using mini-batches of training samples during each E-step as described by Bishop et al. for the GTM in ref. [47]. Rather than updating the full responsibility matrix, a subset of R corresponding to a single batch of training data can be evaluated with all other entries kept constant. The GSM may also be extended in other ways, for example, by replacing the precision parameter β with a covariance matrix to model wavelength-dependent spectral variability common to many hyperspectral imaging platforms.
Based on the results of applying the GSM to real HSI as illustrated in Figure 8 and Figure 9, one clear application of the GSM is to contaminant identification and water quality assessment. Modern UAV platforms make it possible to rapidly image bodies of water where direct access for in-situ data collection is restricted. By equipping UAVs with hyperspectral imagers, the GSM can be used to identify abnormal spectral signatures corresponding to localized contaminant sources. Generating semantic segmentations of collected HSI as in panel b of Figure 7 makes it easy to compare multiple HSI without resorting to pseudocolor images generated from a limited number of wavelength bands. Since the GSM models the distribution of all HSI spectra rather than individual parameters, it may also aid in-situ data collection by suggesting sampling points which maximize the area traversed in the GSM latent space rather than uniformly sampling across a wide spatial extent. Similar approaches have been developed to guide autonomous data collection vehicles by casting route planning as a prize collecting travelling salesman problem subject to resource constraints [48,49].
As a final consideration, we note that the problem of endmember extraction and spectral unmixing for HSI is identical to source apportionment in the context of air quality. Here, the goal is to identify measurement profiles associated with sources of ambient air pollution based on measurements at a receptor site. A popular model for source apportionment studies is Positive Matrix Factorization (PMF) introduced by Paatero and Tapper [50,51]. Just like NMF, PMF decomposes measurements into a convex combination of source profiles and relative abundances subject to non-negativity constraints. These linear receptor models assume that the sources are not transformed during transport to the receptor, ignoring changes due to chemical reactions. Non-linear mixing models such as the GSM introduced here may, therefore, prove beneficial in this additional domain.

6. Conclusions

In this paper, we introduced the GSM as a novel method for unsupervised endmember extraction and spectral unmixing. The model was compared to three varieties of NMF on a synthetic data set of linearly mixed spectra from the USGS spectral database. Across all noise levels, the GSM outperformed NMF for both endmember accuracy and abundance estimation. When applied to real HSI collected over a north Texas pond, the GSM accurately models spectral mixing including non-linear effects. Rhodamine dye was released into the pond to simulate a localized contaminant source. Endmember abundances estimated by the GSM corresponding to the dye accurately tracked the evolution of the plume as it mixed into the surrounding water. These examples illustrate the power of combining non-linear mixing models together with UAV-based hyperspectral imaging for environmental monitoring and water quality analysis. Future work will further develop the GSM to incorporate wavelength dependent spectral variability. Additionally the GSM may prove useful for air quality studies as a non-linear source apportionment model.

7. Patents

A provisional US patent application for this work has been filed on 2024-10-10 entitled: Generative Simplex Mapping: Non-Linear Endmember Extraction And Spectral Unmixing For Hyperspectral Imagery, application number 63/705,854.

Author Contributions

Methodology, J.W.; conceptualization, J.W.; software, J.W.; validation, J.W.; formal analysis, J.W.; investigation J.W.; resources, D.J.L.; writing—original draft preparation, J.W.; writing—review and editing, J.W. and D.J.L.; visualization, J.W.; supervision, D.J.L.; project administration, D.J.L.; funding acquisition, D.J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the following grants: the Texas National Security Network Excellence Fund award for Environmental Sensing Security Sentinels; the SOFWERX award for Machine Learning for Robotic Teams and NSF Award OAC-2115094; support from the University of Texas at Dallas Office of Sponsored Programs, Dean of Natural Sciences and Mathematics, and Chair of the Physics Department is gratefully acknowledged; TRECIS CC* Cyberteam (NSF #2019135); NSF OAC-2115094 Award; and EPA P3 grant number 84057001-0.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The hyperspectral images supporting the conclusions of this article will be made available by the authors on request. An implementation of the GSM model in the Julia programming language is available at https://github.com/john-waczak/GenerativeTopographicMapping.jl, accessed on 21 August 2024.

Acknowledgments

David Shaefer is gratefully acknowledged for his help coordinating UAV flights during HSI collection. We thank Adam Aker, Lakitha Wijeratne, Shawhin Talebi, Ashen Fernando, Prabuddha Dewage, Mazhar Iqbal, Matthew Lary, and Gokul Balagopal for their help deploying the UAV. Don MacLaughlin, Scotty MacLaughlin, and the city of Plano, TX, are gratefully acknowledged for allowing us to deploy the UAV on their property. Christopher Simmons is gratefully acknowledged for his computational support.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
PRISMA Hyperspectral Precuror of the Application Mission
EnMAP Environmental Mapping and Analysis Program
PACE Plankton, Aerosol, Cloud, ocean Ecosystem
CHIME Copernicus Hyperspectral Imaging Mission for the Environment
NIR Near Infrared
SWIR Short-wave Infrared
UAV Unmanned Aerial Vehicle
HSI Hyperspectral Image
NDVI Normalized Difference Vegetation Index
VCA Vertex Component Analysis
PPI Pixel Purity Index
LMM Linear Mixing Model
NMF Non-negative Matrix Factorization
SOM Self-Organizing Map
GTM Generative Topographic Mapping
EM Expectation-Maximization
GSM Generative Simplex Mapping
RBF Radial Basis Function
RMSE Root Mean Square Error
PCA Principal Component Analysis
PMF Positive Matrix Factorization

References

  1. Loizzo, R.; Guarini, R.; Longo, F.; Scopa, T.; Formaro, R.; Facchinetti, C.; Varacalli, G. Prisma: The Italian Hyperspectral Mission. IGARSS 2018 - 2018 IEEE International Geoscience and Remote Sensing Symposium, 2018, p. nil. [CrossRef]
  2. Storch, T.; Honold, H.P.; Chabrillat, S.; Habermeyer, M.; Tucker, P.; Brell, M.; Ohndorf, A.; Wirth, K.; Betz, M.; Kuchler, M.; Mühle, H.; Carmona, E.; Baur, S.; Mücke, M.; Löw, S.; Schulze, D.; Zimmermann, S.; Lenzen, C.; Wiesner, S.; Aida, S.; Kahle, R.; Willburger, P.; Hartung, S.; Dietrich, D.; Plesia, N.; Tegler, M.; Schork, K.; Alonso, K.; Marshall, D.; Gerasch, B.; Schwind, P.; Pato, M.; Schneider, M.; de los Reyes, R.; Langheinrich, M.; Wenzel, J.; Bachmann, M.; Holzwarth, S.; Pinnel, N.; Guanter, L.; Segl, K.; Scheffler, D.; Foerster, S.; Bohn, N.; Bracher, A.; Soppa, M.A.; Gascon, F.; Green, R.; Kokaly, R.; Moreno, J.; Ong, C.; Sornig, M.; Wernitz, R.; Bagschik, K.; Reintsema, D.; Porta, L.L.; Schickling, A.; Fischer, S. The Enmap Imaging Spectroscopy Mission Towards Operations. Remote Sensing of Environment 2023, 294, 113632. [Google Scholar] [CrossRef]
  3. Gorman, E.; Kubalak, D.A.; Deepak, P.; Dress, A.; Mott, D.B.; Meister, G.; Werdell, J. The NASA Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission: an emerging era of global, hyperspectral Earth system remote sensing. Sensors, Systems, and Next-Generation Satellites XXIII, 2019, p. nil. [CrossRef]
  4. Rast, M.; Nieke, J.; Adams, J.; Isola, C.; Gascon, F. Copernicus Hyperspectral Imaging Mission for the Environment (Chime). 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, 2021, p. nil. [CrossRef]
  5. Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J. Hyperspectral Imaging: a Review on Uav-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sensing 2017, 9, 1110. [Google Scholar] [CrossRef]
  6. Arroyo-Mora, J.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.; Ifimov, G.; Elmer, K.; Leblanc, G. Implementation of a Uav-Hyperspectral Pushbroom Imager for Ecological Monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef]
  7. Thenkabail, P.S.; Smith, R.B.; Pauw, E.D. Hyperspectral Vegetation Indices and Their Relationships With Agricultural Crop Characteristics. Remote Sensing of Environment 2000, 71, 158–182. [Google Scholar] [CrossRef]
  8. Thenkabail, P.S.; Lyon, J.G.; Huete, A. Hyperspectral indices and image classifications for agriculture and vegetation; CRC press, 2018.
  9. van Leeuwen, W.J.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-Sensor Ndvi Data Continuity: Uncertainties and Implications for Vegetation Monitoring Applications. Remote Sensing of Environment 2006, 100, 67–81. [Google Scholar] [CrossRef]
  10. Aurin, D.; Mannino, A.; Lary, D.J. Remote Sensing of Cdom, Cdom Spectral Slope, and Dissolved Organic Carbon in the Global Ocean. Applied Sciences 2018, 8, 2687. [Google Scholar] [CrossRef]
  11. Lary, D.J.; Schaefer, D.; Waczak, J.; Aker, A.; Barbosa, A.; Wijeratne, L.O.H.; Talebi, S.; Fernando, B.; Sadler, J.; Lary, T.; Lary, M.D. Autonomous Learning of New Environments With a Robotic Team Employing Hyper-Spectral Remote Sensing, Comprehensive In-Situ Sensing and Machine Learning. Sensors 2021, 21, 2240. [Google Scholar] [CrossRef]
  12. Waczak, J.; Aker, A.; Wijeratne, L.O.H.; Talebi, S.; Fernando, A.; Dewage, P.M.H.; Iqbal, M.; Lary, M.; Schaefer, D.; Lary, D.J. Characterizing Water Composition With an Autonomous Robotic Team Employing Comprehensive in Situ Sensing, Hyperspectral Imaging, Machine Learning, and Conformal Prediction. Remote Sensing 2024, 16, 996. [Google Scholar] [CrossRef]
  13. Nascimento, J.; Dias, J. Vertex Component Analysis: a Fast Algorithm To Unmix Hyperspectral Data. IEEE Transactions on Geoscience and Remote Sensing 2005, 43, 898–910. [Google Scholar] [CrossRef]
  14. Boardman, J.W.; Kruse, F.A.; Green, R.O. Mapping target signatures via partial unmixing of AVIRIS data. Summaries of the fifth annual JPL airborne earth science workshop. Volume 1: AVIRIS workshop, 1995.
  15. Winter, M.E. N-FINDR: an algorithm for fast autonomous spectral end-member determination in hyperspectral data. SPIE Proceedings, 1999. [CrossRef]
  16. Keshava, N.; Mustard, J. Spectral Unmixing. IEEE Signal Processing Magazine 2002, 19, 44–57. [Google Scholar] [CrossRef]
  17. Heinz, D.; Chang, C.I.; Althouse, M. Fully constrained least-squares based linear unmixing [hyperspectral image classification]. IEEE 1999 International Geoscience and Remote Sensing Symposium. IGARSS’99 (Cat. No.99CH36293), 1999, Vol. 2, pp. 1401–1403 vol.2. [CrossRef]
  18. Lee, D.D.; Seung, H.S. Learning the Parts of Objects By Non-Negative Matrix Factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
  19. Feng, X.R.; Li, H.C.; Wang, R.; Du, Q.; Jia, X.; Plaza, A. Hyperspectral Unmixing Based on Nonnegative Matrix Factorization: a Comprehensive Review. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 4414–4436. [Google Scholar] [CrossRef]
  20. Feng, X.R.; Li, H.C.; Wang, R.; Du, Q.; Jia, X.; Plaza, A. Hyperspectral Unmixing Based on Nonnegative Matrix Factorization: a Comprehensive Review. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 4414–4436. [Google Scholar] [CrossRef]
  21. Lee, D.; Seung, H.S. Algorithms for Non-negative Matrix Factorization. Advances in Neural Information Processing Systems; Leen, T.; Dietterich, T.; Tresp, V., Eds. MIT Press, 2000, Vol. 13.
  22. Heylen, R.; Parente, M.; Gader, P. A Review of Nonlinear Hyperspectral Unmixing Methods. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
  23. Nima, C.; Frette. ; Hamre, B.; Stamnes, J.J.; Chen, Y.C.; Sørensen, K.; Norli, M.; Lu, D.; Xing, Q.; Muyimbwa, D.; Ssenyonga, T.; Stamnes, K.H.; Erga, S.R. Cdom Absorption Properties of Natural Water Bodies Along Extreme Environmental Gradients. Water 2019, 11, 1988. [Google Scholar] [CrossRef]
  24. Gilerson, A.; Zhou, J.; Hlaing, S.; Ioannou, I.; Schalles, J.; Gross, B.; Moshary, F.; Ahmed, S. Fluorescence Component in the Reflectance Spectra From Coastal Waters. Dependence on Water Composition. Optics Express 2007, 15, 15702. [Google Scholar] [CrossRef]
  25. Witte, W.G.; Whitlock, C.H.; Harriss, R.C.; Usry, J.W.; Poole, L.R.; Houghton, W.M.; Morris, W.D.; Gurganus, E.A. Influence of Dissolved Organic Materials on Turbid Water Optical Properties and Remote-sensing Reflectance. Journal of Geophysical Research: Oceans 1982, 87, 441–446. [Google Scholar] [CrossRef]
  26. Su, Y.; Marinoni, A.; Li, J.; Plaza, A.; Gamba, P. Nonnegative sparse autoencoder for robust endmember extraction from remotely sensed hyperspectral images. 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), 2017. [CrossRef]
  27. Su, Y.; Li, J.; Plaza, A.; Marinoni, A.; Gamba, P.; Chakravortty, S. Daen: Deep Autoencoder Networks for Hyperspectral Unmixing. IEEE Transactions on Geoscience and Remote Sensing 2019, 57, 4309–4321. [Google Scholar] [CrossRef]
  28. Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M. Deep Generative Endmember Modeling: an Application To Unsupervised Spectral Unmixing. IEEE Transactions on Computational Imaging 2020, 6, 374–384. [Google Scholar] [CrossRef]
  29. Palsson, B.; Ulfarsson, M.O.; Sveinsson, J.R. Convolutional Autoencoder for Spectral-Spatial Hyperspectral Unmixing. IEEE Transactions on Geoscience and Remote Sensing 2021, 59, 535–549. [Google Scholar] [CrossRef]
  30. Kohonen, T. The Self-Organizing Map. Proceedings of the IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
  31. Cantero, M.C.; Perez, R.M.; Martinez, P.J.; Aguilar, P.L.; Plaza, J.; Plaza, A. Analysis of the behavior of a neural network model in the identification and quantification of hyperspectral signatures applied to the determination of water quality. SPIE Proceedings, 2004, p. nil. [CrossRef]
  32. Duran, O.; Petrou, M. A Time-Efficient Method for Anomaly Detection in Hyperspectral Images. IEEE Transactions on Geoscience and Remote Sensing 2007, 45, 3894–3904. [Google Scholar] [CrossRef]
  33. Ceylan, O.; Taskin, G. Feature Selection Using Self Organizing Map Oriented Evolutionary Approach. 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, 2021. [CrossRef]
  34. Riese, F.M.; Keller, S.; Hinz, S. Supervised and Semi-Supervised Self-Organizing Maps for Regression and Classification Focusing on Hyperspectral Data. Remote Sensing 2019, 12, 7. [Google Scholar] [CrossRef]
  35. Richardson, A.; Risien, C.; Shillington, F. Using Self-Organizing Maps To Identify Patterns in Satellite Imagery. Progress in Oceanography 2003, 59, 223–239. [Google Scholar] [CrossRef]
  36. Bishop, C.M.; Svensén, M.; Williams, C.K.I. Gtm: the Generative Topographic Mapping. Neural Computation 1998, 10, 215–234. [Google Scholar] [CrossRef]
  37. Waczak, J.; Aker, A.; Wijeratne, L.O.H.; Talebi, S.; Fernando, A.; Dewage, P.M.H.; Iqbal, M.; Lary, M.; Schaefer, D.; Balagopal, G.; Lary, D.J. Unsupervised Characterization of Water Composition With Uav-Based Hyperspectral Imaging and Generative Topographic Mapping. Remote Sensing 2024, 16, 2430. [Google Scholar] [CrossRef]
  38. Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer-Verlag: Berlin, Heidelberg, 2006; pp. 435–455. [Google Scholar]
  39. Waczak, J. GenerativeTopographicMapping.jl, 2024. [CrossRef]
  40. Bezanson, J.; Karpinski, S.; Shah, V.B.; Edelman, A. Julia: a Fast Dynamic Language for Technical Computing. nil 2012, nil, nil. [Google Scholar] [CrossRef]
  41. Blaom, A.D.; Kiraly, F.; Lienart, T.; Simillides, Y.; Arenas, D.; Vollmer, S.J. Mlj: a Julia Package for Composable Machine Learning. arXiv 2020, nil, nil. [Google Scholar] [CrossRef]
  42. Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.; Lowers, H.A.; Driscoll, R.L. ; others. USGS spectral library version 7. Technical report, US Geological Survey, 2017. [CrossRef]
  43. Kong, D.; Ding, C.; Huang, H. Robust nonnegative matrix factorization using L21-norm. Proceedings of the 20th ACM international conference on Information and knowledge management, 2011. [CrossRef]
  44. Muller, R.; Lehner, M.; Muller, R.; Reinartz, P.; Schroeder, M.; Vollmer, B. A program for direct georeferencing of airborne and spaceborne line scanner images. International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences 2002, 34, 148–153. [Google Scholar]
  45. Ruddick, K.G.; Voss, K.; Banks, A.C.; Boss, E.; Castagna, A.; Frouin, R.; Hieronymi, M.; Jamet, C.; Johnson, B.C.; Kuusk, J.; Lee, Z.; Ondrusek, M.; Vabson, V.; Vendt, R. A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data Over Water. Remote Sensing 2019, 11, 1742. [Google Scholar] [CrossRef]
  46. McFEETERS, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. International Journal of Remote Sensing 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
  47. Bishop, C.M.; Svensén, M.; Williams, C.K. Developments of the Generative Topographic Mapping. Neurocomputing 1998, 21, 203–224. [Google Scholar] [CrossRef]
  48. Balas, E. The prize collecting traveling salesman problem and its applications. In The traveling salesman problem and its variations; Springer, 2007; pp. 663–695.
  49. Suryan, V.; Tokekar, P. Learning a Spatial Field in Minimum Time With a Team of Robots. IEEE Transactions on Robotics 2020, 36, 1562–1576. [Google Scholar] [CrossRef]
  50. Paatero, P.; Tapper, U. Positive Matrix Factorization: a Non-negative Factor Model With Optimal Utilization of Error Estimates of Data Values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
  51. Ulbrich, I.M.; Canagaratna, M.R.; Zhang, Q.; Worsnop, D.R.; Jimenez, J.L. Interpretation of Organic Components From Positive Matrix Factorization of Aerosol Mass Spectrometric Data. Atmospheric Chemistry and Physics 2009, 9, 2891–2918. [Google Scholar] [CrossRef]
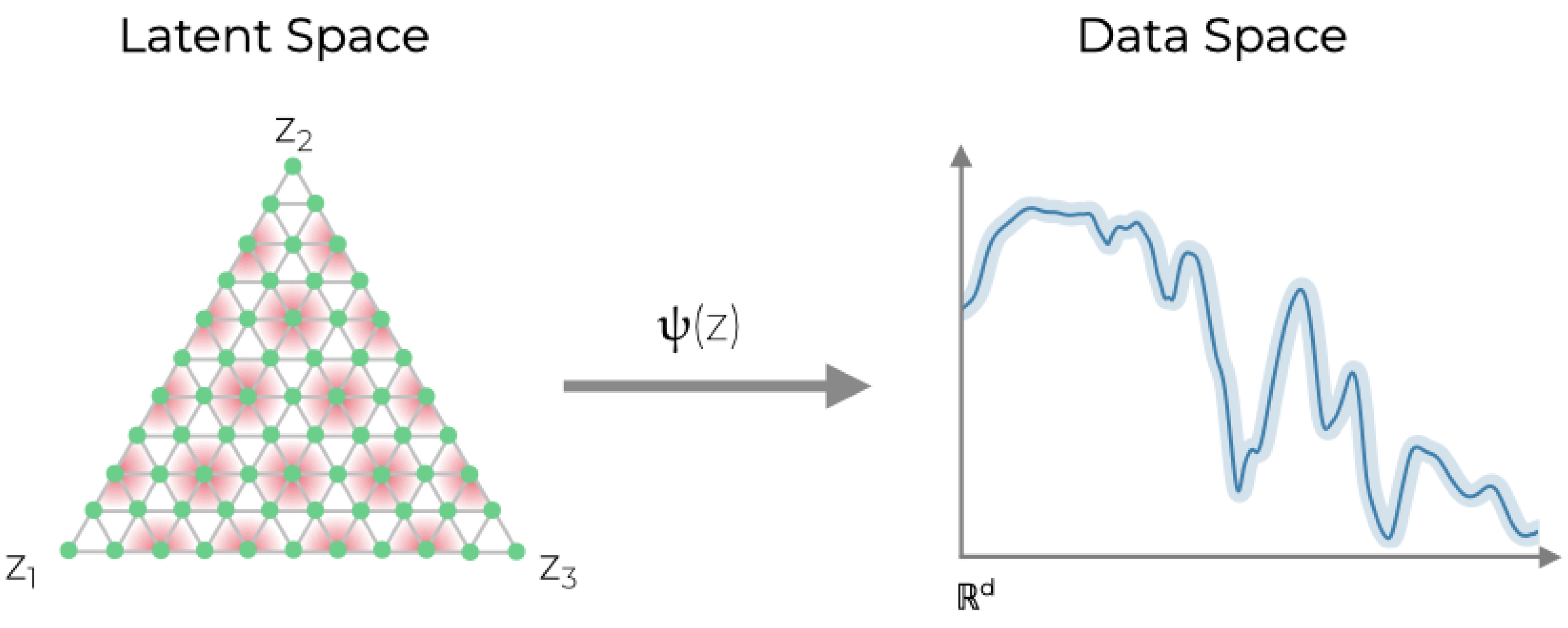
Preprints 121250 g001
Figure 1. Illustration of the GSM. The latent space consists of a grid of K-many points (green dots) distributed throughout a simplex with N v vertices. Barycentric coordinates of each node in the simplex correspond to the relative abundance of N v -many unique sources. Here, N v = 3 has been chosen for illustrative purposes. Nodes are mapped into the data space via the map ψ ( z ) utilizing M-many radially symmetric basis functions (red). Spectral variability is estimated via the precision parameter β shown here in the data space as a light blue band around the spectrum given by ψ ( z ) .
Figure 1. Illustration of the GSM. The latent space consists of a grid of K-many points (green dots) distributed throughout a simplex with N v vertices. Barycentric coordinates of each node in the simplex correspond to the relative abundance of N v -many unique sources. Here, N v = 3 has been chosen for illustrative purposes. Nodes are mapped into the data space via the map ψ ( z ) utilizing M-many radially symmetric basis functions (red). Spectral variability is estimated via the precision parameter β shown here in the data space as a light blue band around the spectrum given by ψ ( z ) .
Preprints 121250 g001
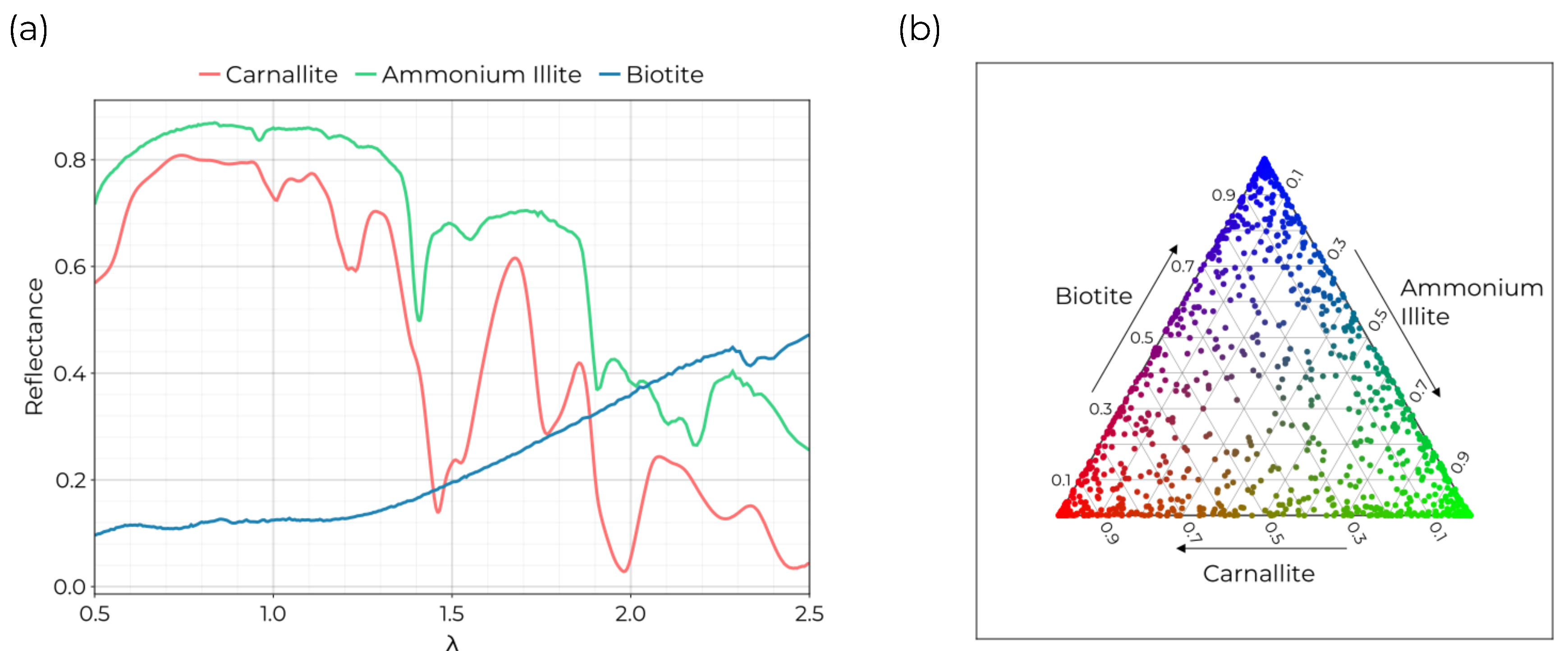
Preprints 121250 g002
Figure 2. Synthetic data set formed from USGS spectra. (a) Spectra from the USGS spectral database used as the ground truth endmembers. These spectra were selected following the example in ref. [13]. (b) The abundance distribution sampled for in the data set. Samples were generated from a Dirichlet distribution with α 1 = α 2 = α 3 = 1 / 3 .
Figure 2. Synthetic data set formed from USGS spectra. (a) Spectra from the USGS spectral database used as the ground truth endmembers. These spectra were selected following the example in ref. [13]. (b) The abundance distribution sampled for in the data set. Samples were generated from a Dirichlet distribution with α 1 = α 2 = α 3 = 1 / 3 .
Preprints 121250 g002
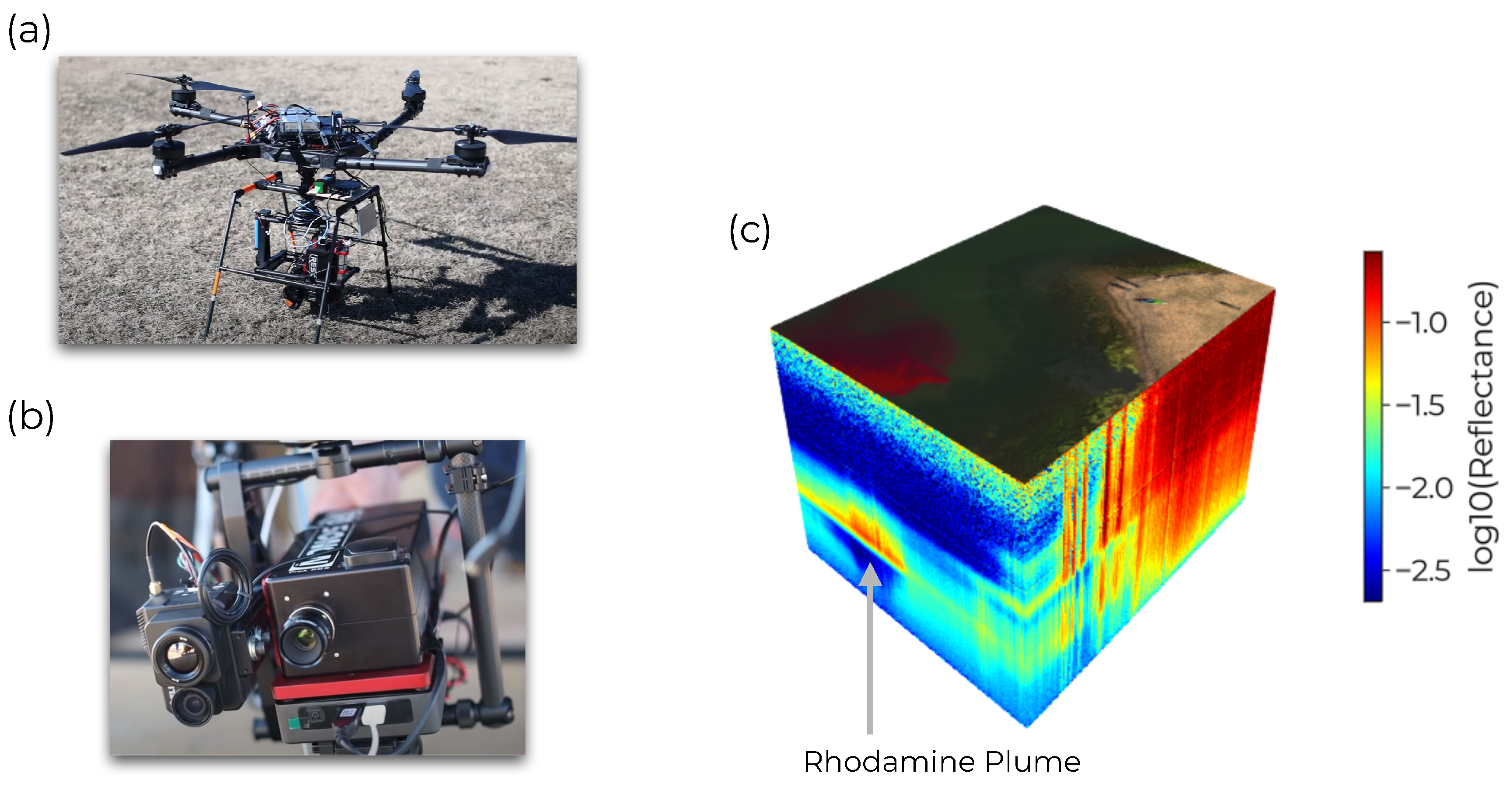
Preprints 121250 g003
Figure 3. Real HSI Data set. (a) the UAV used to collect hyperspectral images. (b) The Resonon Pika XC2 hyperspectral imager used to acquire HSI. (c) A sample hyperspectral data cube. Spectra a plotted using at their geographic position with the log10-reflectance colored along the z axis and a pseudocolor image on top. The signature of the rhodamine dye plume is clearly identifiable in the water.
Figure 3. Real HSI Data set. (a) the UAV used to collect hyperspectral images. (b) The Resonon Pika XC2 hyperspectral imager used to acquire HSI. (c) A sample hyperspectral data cube. Spectra a plotted using at their geographic position with the log10-reflectance colored along the z axis and a pseudocolor image on top. The signature of the rhodamine dye plume is clearly identifiable in the water.
Preprints 121250 g003
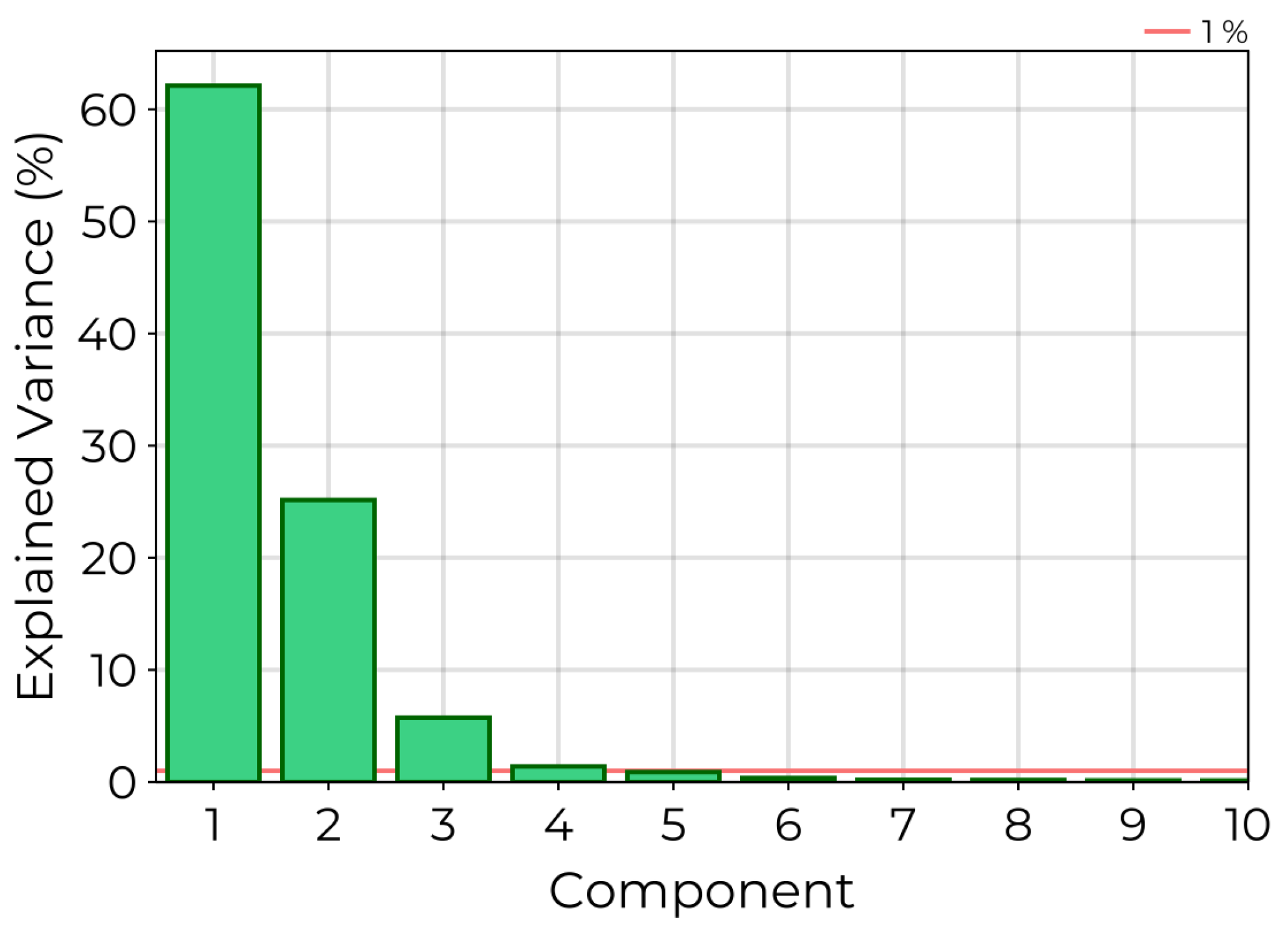
Preprints 121250 g004
Figure 4. Explained variance of PCA components for the real HSI data set. A red horizontal line is superimposed on the graph, marking an explained variance of 1 % . All components past the fourth explain less than 1 % of the observed variance.
Figure 4. Explained variance of PCA components for the real HSI data set. A red horizontal line is superimposed on the graph, marking an explained variance of 1 % . All components past the fourth explain less than 1 % of the observed variance.
Preprints 121250 g004
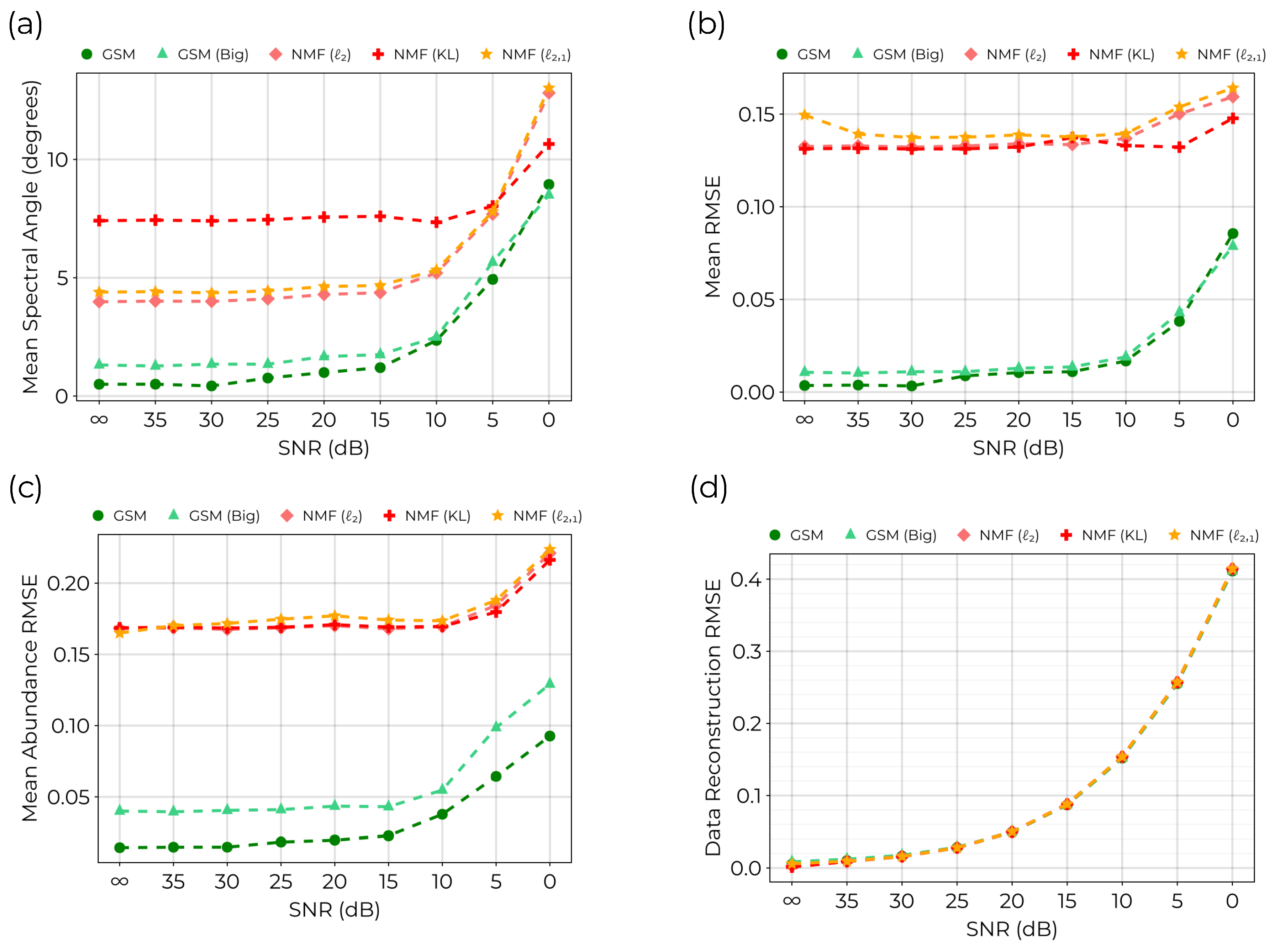
Preprints 121250 g005
Figure 5. Comparison of GSM against NMF on simulated linear mixing data set using USGS spectra. (a) The mean spectral angle computed between extracted endmembers and original endmembers. (b) the mean RMSE computed between extracted endmembers and original endmembers. (c) The mean abundance RMSE computed between original abundance data for each endmember and extracted abundances. (d) The reconstruction RMSE which evaluates the quality of fit. All models realized similar values reflecting convergence of the models to the level of random noise introduced into the data.
Figure 5. Comparison of GSM against NMF on simulated linear mixing data set using USGS spectra. (a) The mean spectral angle computed between extracted endmembers and original endmembers. (b) the mean RMSE computed between extracted endmembers and original endmembers. (c) The mean abundance RMSE computed between original abundance data for each endmember and extracted abundances. (d) The reconstruction RMSE which evaluates the quality of fit. All models realized similar values reflecting convergence of the models to the level of random noise introduced into the data.
Preprints 121250 g005
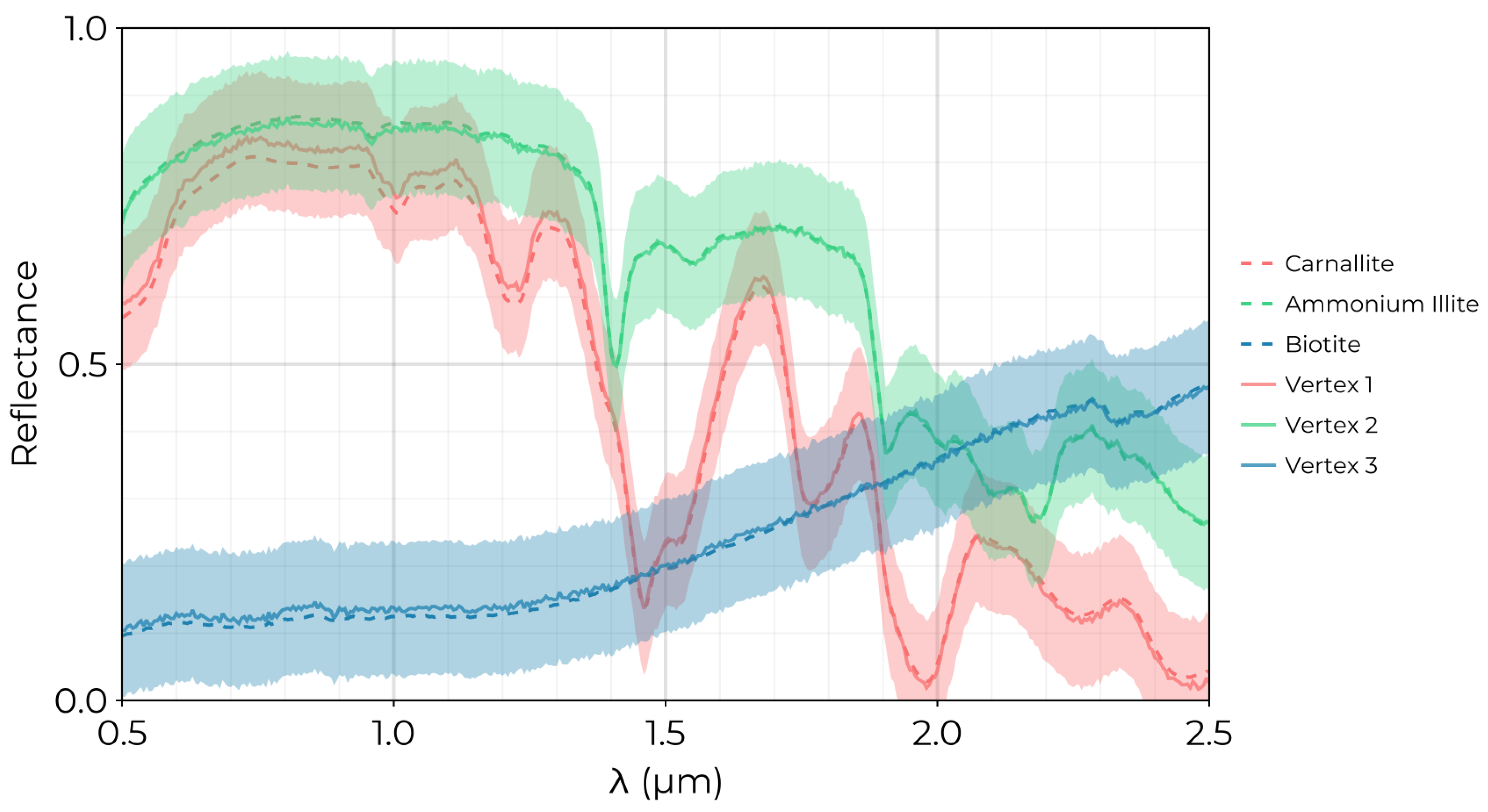
Preprints 121250 g006
Figure 6. Endmembers extracted by the GSM for the simulated linear mixing data set with SNR = 20 . The dashed lines correspond to original endmember spectra from the USGS spectral database. Solid lines superimposed on the plot indicate the extracted endmember spectra. Colored bands are included around each spectrum corresponding to the spectral variability estimated by the GSM precision parameter β where the band width is 2 β − 1 corresponding to 2 standard deviations.
Figure 6. Endmembers extracted by the GSM for the simulated linear mixing data set with SNR = 20 . The dashed lines correspond to original endmember spectra from the USGS spectral database. Solid lines superimposed on the plot indicate the extracted endmember spectra. Colored bands are included around each spectrum corresponding to the spectral variability estimated by the GSM precision parameter β where the band width is 2 β − 1 corresponding to 2 standard deviations.
Preprints 121250 g006
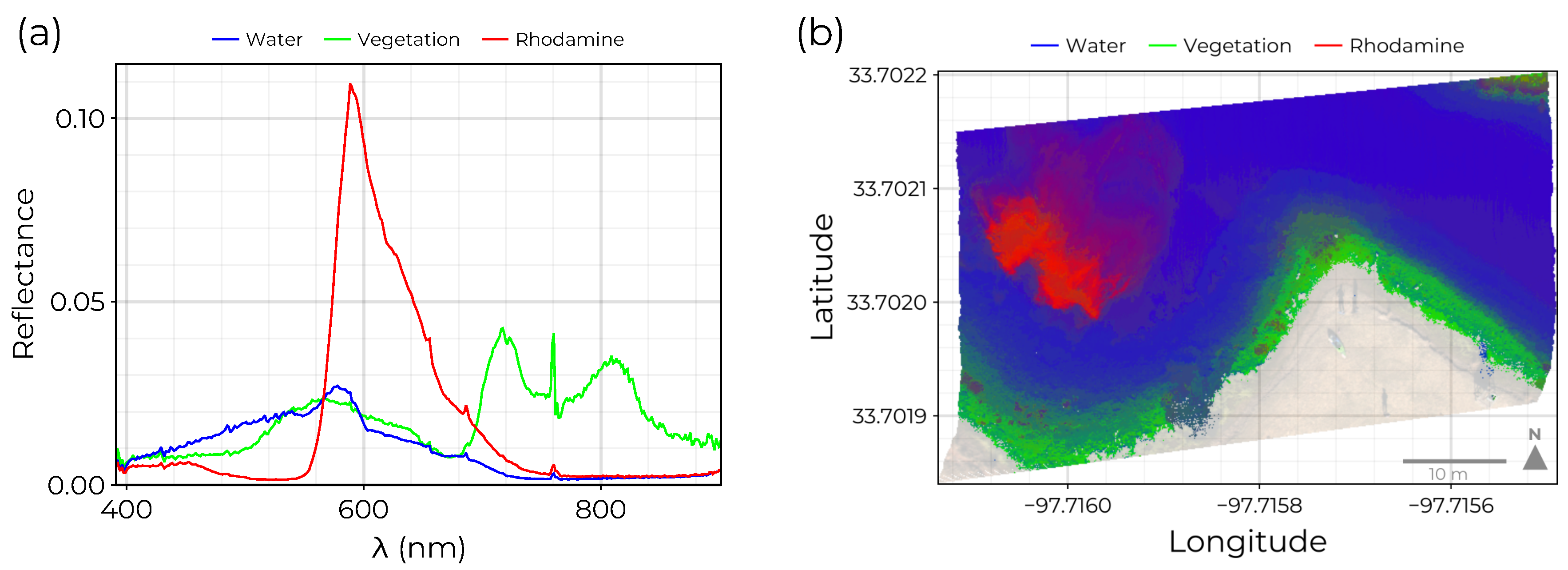
Preprints 121250 g007
Figure 7. GSM applied to water spectra from real HSI data set: (a) Spectra generated by the trained GSM for samples with maximum abundance for each endmember. Based on these spectral profiles, endmembers are identified with water, near-shore vegetation, and rhodamine dye. (b) A HSI segmented according to the relative abundance of each endmember. Each water pixel is colored by smoothing interpolating between red, green, and blue colors using the relative abundance estimated for rhodamine, vegetation, and water spectra. The rhodamine plume is clearly identifiable in the western portion of the HSI.
Figure 7. GSM applied to water spectra from real HSI data set: (a) Spectra generated by the trained GSM for samples with maximum abundance for each endmember. Based on these spectral profiles, endmembers are identified with water, near-shore vegetation, and rhodamine dye. (b) A HSI segmented according to the relative abundance of each endmember. Each water pixel is colored by smoothing interpolating between red, green, and blue colors using the relative abundance estimated for rhodamine, vegetation, and water spectra. The rhodamine plume is clearly identifiable in the western portion of the HSI.
Preprints 121250 g007
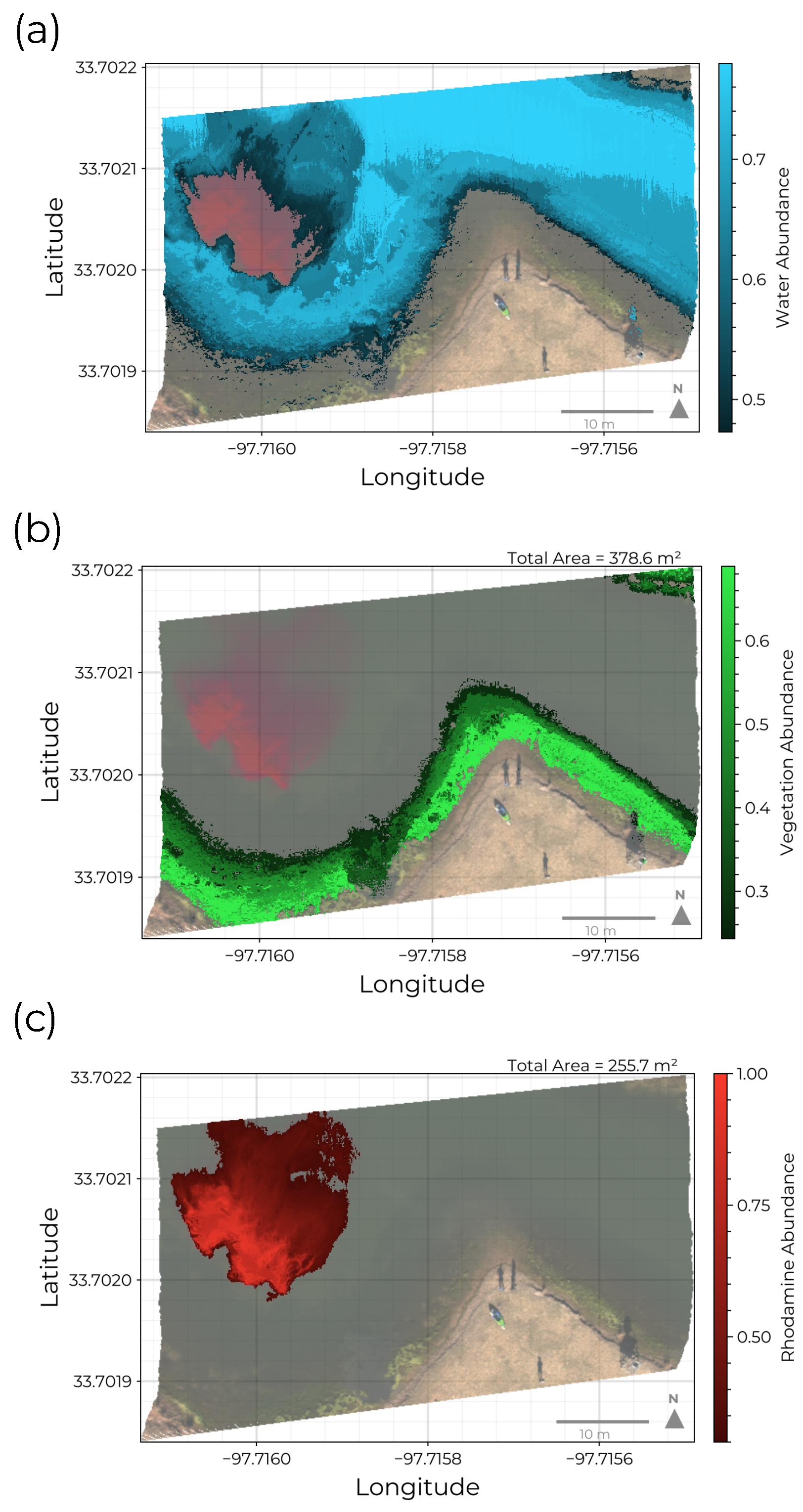
Preprints 121250 g008
Figure 8. Endmember abundance distributions: (a) The spatial distribution of abundance for the water class. This source dominates in the center of the pond and decreases towards the shore where vegetation begins to dominate the reflectance signal. The water endmember abundance is also observed to decreases near the edge of the rhodamine plume reflecting dye mixing and diffusion. (b) The spatial distribution of vegetation. This endmember includes filamentous blue-green algae observed to accumulate in shallow waters near the shore. (c) The rhodamine dye plume extent segmented from the HSI. The total area for near-shore vegetation and rhodamine are estimated to be 378.6 m 2 and 255.7 m 2 , respectively.
Figure 8. Endmember abundance distributions: (a) The spatial distribution of abundance for the water class. This source dominates in the center of the pond and decreases towards the shore where vegetation begins to dominate the reflectance signal. The water endmember abundance is also observed to decreases near the edge of the rhodamine plume reflecting dye mixing and diffusion. (b) The spatial distribution of vegetation. This endmember includes filamentous blue-green algae observed to accumulate in shallow waters near the shore. (c) The rhodamine dye plume extent segmented from the HSI. The total area for near-shore vegetation and rhodamine are estimated to be 378.6 m 2 and 255.7 m 2 , respectively.
Preprints 121250 g008
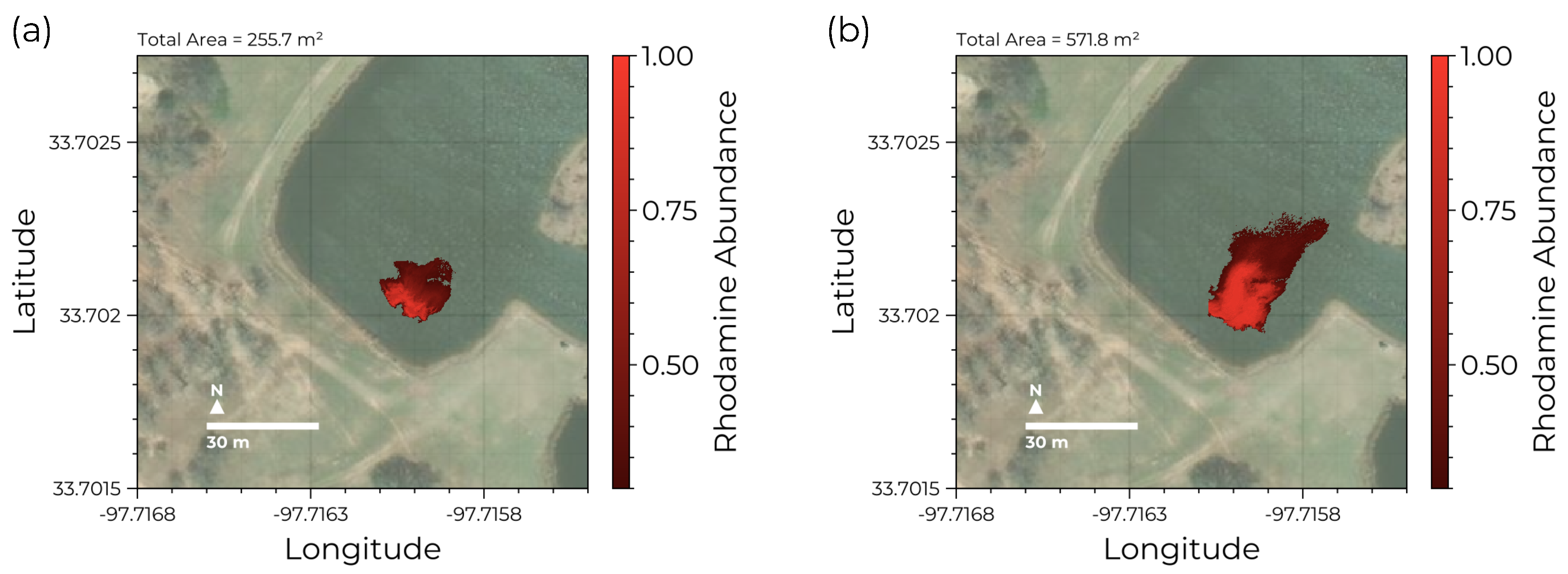
Preprints 121250 g009
Figure 9. Rhodamine plume evolution: Using the trained GSM we can track the dispersion of the rhodamine dye plume between successive drone flights. (a) The initial plume distribution after release. Here the dye subsumes an area of 255.7 m 2 . (b) The same plume imaged 15 minutes later now extends across an area of 571.8 m 2
Figure 9. Rhodamine plume evolution: Using the trained GSM we can track the dispersion of the rhodamine dye plume between successive drone flights. (a) The initial plume distribution after release. Here the dye subsumes an area of 255.7 m 2 . (b) The same plume imaged 15 minutes later now extends across an area of 571.8 m 2
Preprints 121250 g009
Table 1. GSM hyperparameter optimization for the real HSI data set: Multiple GSM models were trained to explore the impact of model hyperparameters. N v values from 3 to 6 were explored as suggested by the PCA decomposition of the data set. λ e was varied from 0.001 to 1.0 and λ w ranged from 1 to 1000. Here we report the top 10 models ranked by increasing BIC. The AIC and reconstruction RMSE are also included for comparison.
Table 1. GSM hyperparameter optimization for the real HSI data set: Multiple GSM models were trained to explore the impact of model hyperparameters. N v values from 3 to 6 were explored as suggested by the PCA decomposition of the data set. λ e was varied from 0.001 to 1.0 and λ w ranged from 1 to 1000. Here we report the top 10 models ranked by increasing BIC. The AIC and reconstruction RMSE are also included for comparison.
N v λ e λ w BIC AIC Reconstruction RMSE
3 0.01 1.0 − 6.195 × 10 7 − 6.269 × 10 7 0.000989
3 0.001 1.0 − 6.194 × 10 7 − 6.268 × 10 7 0.000989
3 0.1 1.0 − 6.192 × 10 7 − 6.265 × 10 7 0.000991
3 1.0 1.0 − 6.186 × 10 7 − 6.260 × 10 7 0.001190
4 1.0 1.0 − 6.181 × 10 7 − 6.255 × 10 7 0.001002
4 0.1 1.0 − 6.175 × 10 7 − 6.249 × 10 7 0.001008
4 0.01 1.0 − 6.173 × 10 7 − 6.247 × 10 7 0.001009
4 0.001 1.0 − 6.173 × 10 7 − 6.247 × 10 7 0.001009
4 0.1 10.0 − 6.171 × 10 7 − 6.245 × 10 7 0.001011
3 1.0 10.0 − 6.166 × 10 7 − 6.239 × 10 7 0.001014
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated