Prerpints.org logo
Preprint
Article

Vertical Jump Height Estimation using Low-Sampling IMU in Countermovement Jumps: A Feasible Alternative to Motion Capture and Force Platforms

This version is not peer-reviewed.

Submitted:

14 October 2024

Posted:

15 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Vertical jump height is a reliable measure of lower limb functionality for countermovement jumps. Motion capture systems and force platforms are considered gold standards to assess athletes’ performance during these motions, however their use in ecological settings is limited by high costs and lack of portability. This study aimed to evaluate the feasibility of low-sampling rate Inertial Measurement Units as an alternative to gold standard systems. The validity of three computational methods for IMU-based data—Numerical Double Integration, Take-Off Velocity and Flight Time—was assessed using data from 18 healthy subjects who performed five bilateral and ten unilateral countermovement jumps. Data were simultaneously collected from an IMU positioned at the L5 level, a motion capture system, and two force platforms. Comparisons revealed that the Numerical Double Integration method exhibited the highest correlation (0.87), the lowest bias (2.5 cm) compared to gold standards, and excellent reliability (0.88). Although the Take-Off Velocity and Flight Time methods demonstrated comparable performance for bilateral jumps, their accuracy in unilateral jumps was reduced. Overall, low-sampling rate IMU with Numerical Double Integration method proves to be a reliable and portable alternative for field-based CMJs assessment, warranting future investigation across diverse populations and jump modalities.
Keywords: 
Subject: 
Engineering  -   Bioengineering

1. Introduction

Vertical jumps (VJs) are a commonly assessed motor task in sport and clinical settings, providing valuable insights into lower limb function [1]. As a reliable benchmark for performance assessment, VJs are widely used during training to assess athletic ability [2], identify injury risks and guide rehabilitation programs [3]. Among the various types of VJs, countermovement jumps (CMJs) are particularly widespread due to their widely proven reliability and validity in estimating explosive power of the lower limbs [4,5]. The simplicity of the testing protocols, repeatability, and the higher ecological validity have made CMJs an ideal tool for the assessment and comparison of lower limbs performance across different sports [6,7,8,9,10], age groups [11,12,13,14] and sexes [15]. Furthermore, inter-limb asymmetries in CMJ metrics have been shown to correlate with injury rates, increasing research interest in this assessment as a valuable tool for injury prevention [16].
CMJs are characterized by an unloading downward phase, a breaking phase, a propulsive upward phase, a flight phase and a final landing phase [5]. Although several metrics can be calculated for each jump phase, it has been proven that the performance variables (e.g., jump height, modified reactive strength index) are the ones showing the highest reliability [5]. In particular, the most effective and investigated measure of CMJ performance is vertical jump height (VJH) [5,17,18].
Force platforms (FP) and motion capture systems (MCap) are considered gold standard tools for estimating VJH from CMJ [19,20,21]. However, these systems are typically expensive and require a laboratory setup, limiting their portability and use in real-world, ecological settings. As a result, several alternative devices have been developed for use in non-laboratory environments, including linear transducers, contact mats, photoelectric cells, camera-based smartphone applications and, more recently, Inertial Measurement Units (IMUs) [21,22,23].
IMUs have gained widespread use with the development of Micro-Electro-Mechanical Systems (MEMS) technology, which integrates accelerometers, gyroscopes and a magnetometer to measure raw accelerations and angular velocities [24,25]. When combined with sensor fusion algorithms, IMUs can provide kinematic and temporal data to track three-dimensional body movements [26]. Additionally, their relatively low costs, power consumption and compact size make IMUs ideal for in-field CMJ assessment [23,25]. However, ensuring the accuracy and precision of these devices is essential to provide practitioners with accurate and reliable information [27]. High-sampling rate IMUs (> 100 Hz) have been validated for VJH estimation by comparing them with gold standard reference systems [27]. However, in practical applications, low-sampling rate IMUs are preferred because of their reduced power consumption, which extends battery life and allows data recording over longer periods [28]. Moreover, the low-sampling rate also reduces the amount of data collected, simplifying data processing and storage, which can be critical in field-based applications or when multiple sensors are used simultaneously. Despite these practical advantages, lower sampling rates may reduce the accuracy of calculated metrics, such as VJH, due to potential undersampling of the jump’s dynamic phases [28]. Therefore, it is crucial to evaluate whether low-sampling rate IMUs can still provide accurate and reliable estimates of VJH compared to high-sampling rate devices and gold standard systems.
Several studies that have shown that the choice of the appropriate calculation method according to the VJH definition chosen is crucial when validating technological tools [18]. In the present study, VJH is defined as the difference between the maximum height reached by the center of mass (COM) during the jump (Hmax) and the standing height (H0) [18]. Therefore, VJH calculated from the MCap system consists of tracking the vertical displacement of the COM, approximated from the positions of the markers placed on the subject’s body [29,30,31]. In contrast, FP do not directly provide vertical displacement, necessitating the use of specific calculation methods to estimate VJH from three-dimensional force data. The numerical double integration (NDI) method has been proven to be the one of the most reliable and accurate approaches to quantify VJH when calculated as the difference between Hmax and H0 with a dual FP setup [18,32,33]. In addition, it has been proven that NDI method provides VJH estimates with the most negligible difference compared to MCap [18,32,33].
While numerous studies have evaluated the validity of IMU sensors against gold standard systems, there is still a lack of standardized method for calculating VJH from IMU-derived data [27]. When using IMU data, VJH can be computed using three main calculation methods: (a) numerical double integration (NDI), (b) take-off velocity (TOV) method and (c) flight time (FT) method [34]. The NDI method involves double integration of vertical acceleration, assuming zero initial acceleration and calculating VJH as the maximum vertical displacement. The TOV method assumes the subject is only influenced by gravity during the jump, treating the body as a particle under constant acceleration (g), with take-off velocity determined by integrating filtered acceleration data before take-off (TO). The FT method relates VJH to FT, defined as the interval between TO and landing (LA) [35].
Several studies have validated these methods for calculating VJH with high-sampling rate IMU sensors. However, to date, no studies have investigated the feasibility of low-sampling rate IMUs for this purpose [18,27]. In this study, we hypothesized that low-sampling rate IMUs could serve as a feasible, portable, and compact alternative to gold standard systems for estimating VJH in CMJs. This hypothesis was tested by using a single low-sampling frequency IMU to calculate VJH via NDI, TOV and FT methods. Additionally, we sought to identify the most accurate method for estimating VJH from IMU data. Finally, a test-retest paradigm was implemented to determine the reliability of such.

2. Materials and Methods

The study was conducted at the “Luigi Divieti” Posture and Movement Analysis Laboratory (Department of Electronics, Information and Bioengineering (DEIB), Politecnico di Milano, Milano, Italy) in accordance with the postulates of the Declaration of Helsinki and with the approval of the Ethics Committee of the Politecnico di Milano (Protoc. No. 22/2021, 14 June 2021).

2.1. Participants

Eighteen healthy subjects (12 females and 6 males, age: 24.6 ± 1.9 years, height: 169.4 ± 7.5 cm, and body mass: 56.2 ± 10.4 kg) voluntarily participated in the study and provided their written Informed Consent for the use of their data. Subjects were included according to the following criteria: (i) age over 18 years; (ii) BMI between 18.5 kg/m² and 24.9 kg/m²; (iii) absence of neurological or musculoskeletal impairments and (iv) absence of injury or surgery within the previous six months.

2.2. Equipment

Data were collected simultaneously from the three following systems:
  • A MCap system composed of eight infrared cameras (SMART DX 100, BTS-Bioengineering, Milan, Italy) with an accuracy of < 0.2 mm over a 2x2x2 m volume and a sampling frequency of 100 Hz.
  • Two FPs (AMTI, USA Inc. Watertown, MA) measuring 464 x 508 x 82.5 mm with an accuracy of ± 0.1% of the applied load and a sampling frequency of 200 Hz.
  • An IMU (XSens DOT, Xsens Technologies B.V, Enschede, The Netherlands) with Bluetooth Low Energy (BLE) wireless connectivity and 60 Hz sampling frequency. It provides triaxial accelerations ([m/s2], ±16g full scale), triaxial angular velocities ([◦/s], ±2000◦/s full scale) and magnetic field measurements within the sensor’s fixed frame.
To synchronize data across all the systems, signals were resampled to the lowest common sampling rate (i.e., IMU sampling frequency at 60 Hz).

2.3. Procedure

Participants were informed of the purpose of the study and their height and body mass were recorded prior to testing. Before the experimental session, subjects completed a standard warm-up consisting of 4 minutes of jogging on a treadmill at self-selected pace, followed by 3 minutes of submaximal vertical jumps to familiarize themselves with the testing environment.
Subsequently, subjects were instrumented with three passive spherical markers placed on the sacrum and bilaterally over the anterior superior iliac spine. The IMU was mounted at the level of L5, identified by palpation as the midpoint between the posterior superior iliac spines. To minimize the effects of skin motion artifacts during jumps, the IMU was secured with a non-invasive elastic band. Participants were briefed on the proper execution of the CMJ, which involved an initial downward movement followed by a rapid upward jump without arm swing, ensuring minimal posture change to reduce potential effects on VJH. The depth of the countermovement was not controlled. Participants were then instructed to place each foot on a FP and 5-second static data were recorded from the three systems prior to CMJ execution.
Each participant performed double-leg CMJs (DL-CMJ), right-leg CMJs (R-CMJ) and left-leg CMJs (L-CMJ), with at least 30 seconds of rest between each jump and 3 minutes of rest between each jump category, until 5 correct jumps were performed for each task. Therefore, motion data for a total of 90 jumps from MCap, IMU and FP for each jump modality were collected.

2.4. Data Processing

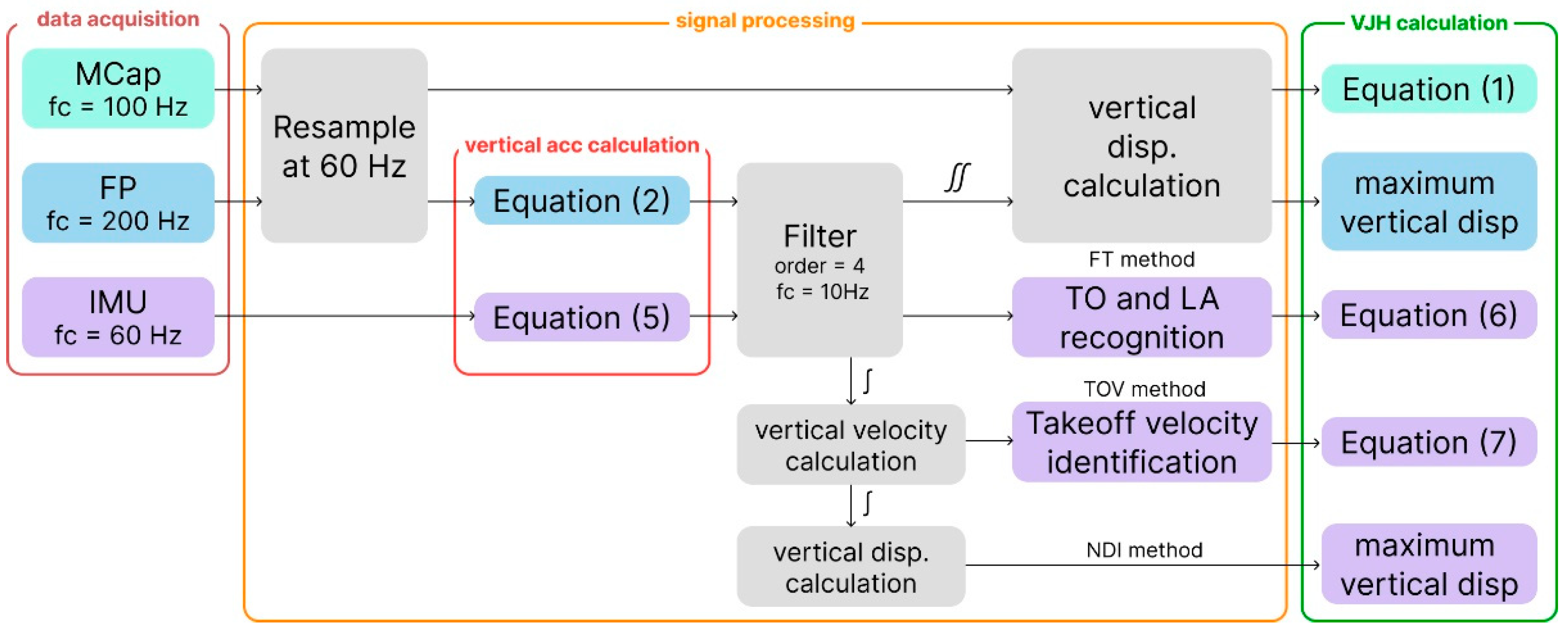
Motion data were analyzed in MATLAB (v.2023a, MathWorks, Natick, MA, USA) through customized algorithms. The VJH was computed for each system through a different calculation method.

2.4.1. MCap Data

The vertical trajectories of the three passive markers were averaged to approximate the vertical displacement of the pelvis COM [31]. The VJH was calculated using the following equation:
VJHMCap = Hmax – H0,
where Hmax is maximum height reached by the pelvis COM, calculated as the absolute maximum of the vertical trajectory, and H0 is the height of the COM in the resting position obtained by during the 5-second static recording.

2.4.2. FP Data

Vertical acceleration ( a v e r t F P , [m/s2]) was calculated by dividing the vertical force signal (Fz, [N]) by the subject’s mass, according to Newton’s second law of motion, and subtracting the contribution of gravitational acceleration (g, [m/s2]), as in (2). The Fz signal was obtained as the average of the Fz signal from both platforms. The subject’s mass was derived by dividing the vertical force during the 5-second static recording (F0z, [N]) by g. This process is summarized by the following equation:
a v e r t F P = F z F 0 z g − g   ,
A low-pass Butterworth filter (order = 4, cut-off frequency = 10 Hz) was applied to the a v e r t F P signal, and then double-integrated via the trapezoidal rule from the onset of movement until landing to obtain the vertical displacement signal, according to the NDI method [18,33]. The VJHFP was determined as the maximum value of the vertical displacement.

2.4.3. IMU Data

Vertical acceleration was transformed from the IMU’s local reference frame (S) to a fixed global reference frame (G) using quaternion-based rotation to account for potential misalignment during manual sensor placement on the participant’s trunk [36]. This transformation ensured that the acceleration data could be analyzed in a consistent global context, unaffected by variations in sensor placement or body orientation. In S, the x-axis was aligned with gravity pointing upwards, the z-axis was aligned with the forward direction relative to the participant’s sagittal plane and y-axis orthogonal to the resulting XZ plane. In G, the z-axis was aligned with gravity, the x-axis laid within the global horizontal plane, corresponding to the participant’s forward direction when standing upright, and the y-axis was orthogonal to the ZX plane, completing the right-handed coordinate system.
To describe the transformation required to rotate the acceleration vector from S to G, quaternion data – obtained as output from the IMU sensor as in (3) – were used to derive a rotation matrix ( R G S ) for each time sample, defined as in (4):
q = [ q w , q x , q y , q z ] ,
R G S = 1 − 2 ( q y 2 + q z 2 ) 2 ( q x q y − q z q w ) 2 ( q x q z + q y q w 2 ( q x q y + q z q w 1 − 2 ( q x 2 + q z 2 ) 2 ( q y q z − q x q w ) 2 ( q x q z − q y q w ) 2 ( q y q z + q x q w ) 1 − 2 ( q x 2 + q y 2 ) ,
The three-dimensional global acceleration vector was obtained by multiplying the acceleration vector in the local reference frame (aS) by R G S . The absolute vertical acceleration a v e r t I M U was extracted as the third component (z-axis) of the global acceleration vector and subtracting the contribution of g, as in (5):
a v e r t I M U = R G S × ( a S ) T z T − g ,
The absolute vertical acceleration a v e r t I M U was then filtered with a low-pass Butterworth filter (order = 4, cut-off frequency = 10 Hz) and used to calculate the VJH through the FT, TOV and NDI methods, as described below:
  • The FT method is based on the identification of TO and LA events from the a v e r t I M U . TO is defined as the instant when a v e r t I M U crosses the zero-acceleration threshold, while LA is identified as the last observation of a v e r t I M U less than 0. V J H I M U F T is then obtained as in (6) [35]:
    V J H I M U F T = L A − T O 2 × g 8  
  • The TOV considers the subject as only affected by gravity during the jump and neglecting the air resistance. V J H I M U T O V is calculated from (7), where TOV is takeoff velocity determined by integration of a v e r t I M U measured before the TO instant defined as in the FT method [37]:
    V J H I M U T O V = T O V 2 2 g  
  • The NDI consists in the double-integration of the a v e r t I M U via the trapezoidal rule to obtain the vertical displacement [37]. The V J H I M U N D I was calculated as the maximum value of the vertical displacement [37].
The main steps applied to the signals obtained from the different systems are summarized in Figure 1.

2.5. Statistical Analysis

The statistical analysis was performed using JASP (JASP Team 2023, Version 0.17.3) and MATLAB (v.2023a, MathWorks, Natick, MA, USA).
The normality of the VJH estimates from the different systems and IMU-based calculation methods was assessed using the Shapiro-Wilk test. The test indicated a non-normal distribution (p < 0.05), leading to the use of non-parametric statistical methods [38]. Descriptive statistics for each calculation method are presented as median and Interquartile Range (IQR).
The agreement between the two gold standard systems (MCap and FP) was evaluated using Spearman’s rank correlation coefficients (⍴s). The strength of the correlation was classified as follows: |⍴s| ≤ 0.4, weak; 0.4 < |⍴s| ≤ 0.6, moderate; 0.6 < |⍴s| ≤ 0.8, strong; and |⍴s| > 0.8, very strong [39]. Additionally, the Bland-Altman analysis was performed to calculate the systematic bias and the limits of agreement (LoA, systematic bias ± 1.96 standard deviations of the differences) for each jumping modality [40]. A single gold standard value (VJHGSV) was computed by averaging the estimates from the two gold standard systems, due to the high level of agreement observed.
The Friedman test was applied to identify significant differences between the VJHGSV and the three IMU-based methods across the different jump modalities (DL-CMJ, R-CMJ, and L-CMJ). The effect size estimation was based on Kendall’s W coefficient of concordance [41]. Post-hoc pairwise comparisons were conducted using the Conover test with Bonferroni correction to control for multiple comparisons. Bland-Altman analysis was also used to quantify the systematic bias and LoA between the VJHGSV and each IMU method, as well as among the IMU methods themselves.
The test-retest reliability of the VJH estimates for each method was evaluated using the Intraclass Correlation Coefficient with a two-way mixed-effects model (ICC(2,1)), which assesses both the consistency and absolute agreement of repeated measurements [42]. ICC values were interpreted as: < 0.5 poor reliability; 0.5 ≤ ICC < 0.75 moderate reliability; 0.75 ≤ ICC < 0.9 good reliability; and ICC ≥ 0.9 excellent reliability.
All statistical tests were performed with a significance level set at α= 0.05.

3. Results

3.1. Agreement between Gold Standard Systems

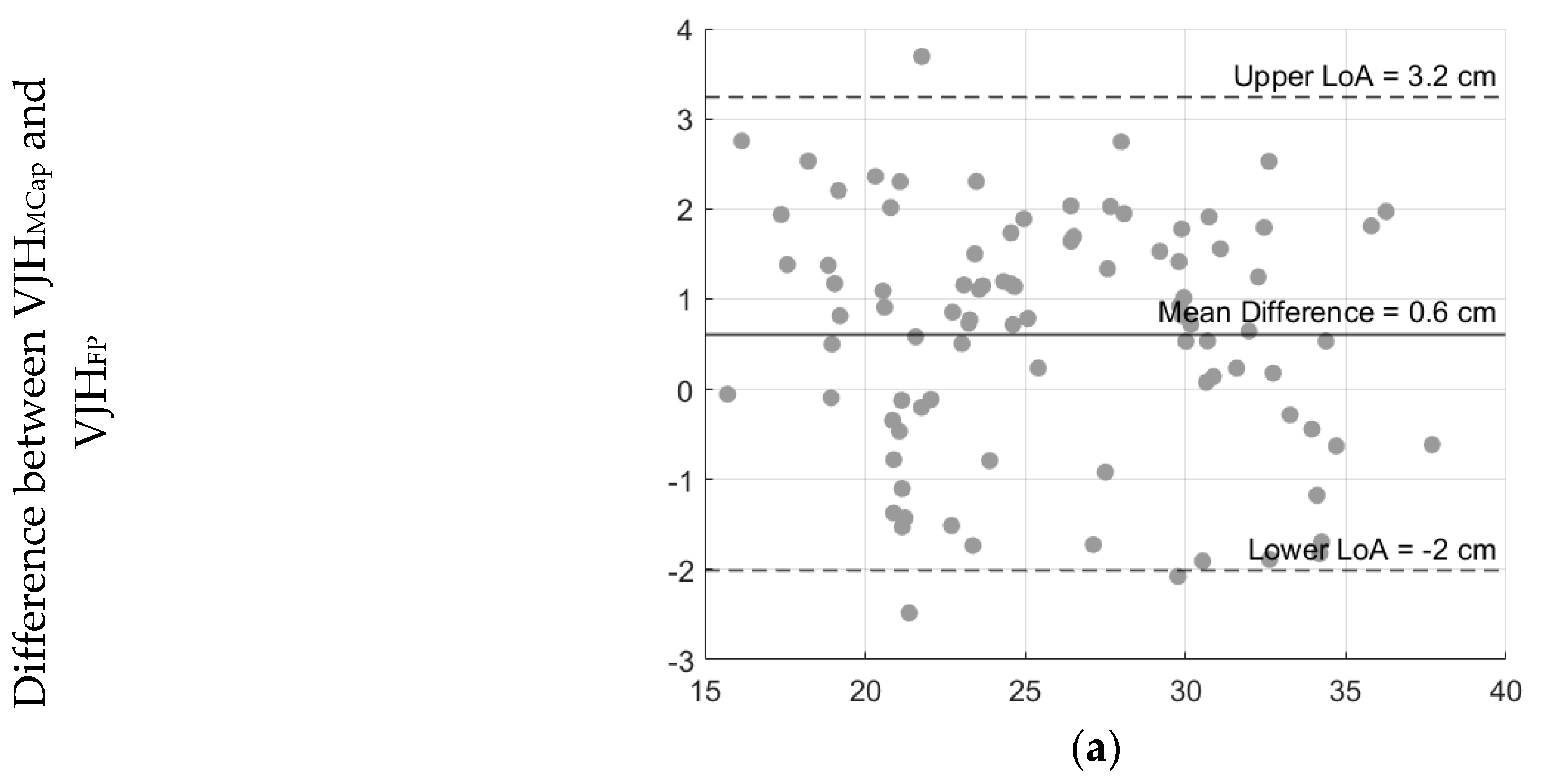
Table 1 reports the Spearman’s correlation coefficients revealing significant and strong correlations between the two gold standard systems across all modalities (⍴s ranging from 0.88 to 0.9, p < 0.001), indicating a high level of agreement. Bland-Altman analysis (Table 1 and Figure 2) showed a systematic bias close to zero for the DL-CMJ and relatively narrow LoA range (-2.9 to 4.4 cm). However, R-CMJ and L-CMJ showed larger biases (-1.7 cm and -2.5 cm, respectively) and wider upper and lower LoA range for the SL-CMJ (8.5 cm and 11.1 cm for R-CMJ and L-CMJ, respectively), indicating greater variability in the estimates for these modalities.
Due to the high agreement and the relatively low systematic bias between the MCap and FP, a single reference value was computed by averaging the estimates from MCap and FP and used for further comparisons with the IMU (gold standard value, VJHGSV).

3.2. Agreement between VJHGSV and IMU Calculation Methods

For all jumping modalities, the IMU-based methods systematically underestimated VJH compared to the VJHGSV (Table 2). In particular,   V J H I M U N D I showed closer agreement with VJHGSV across all modalities with respect to FT and TOV methods, while V J H I M U F T and V J H I M U T O V exhibited larger deviations especially in the R- and L-CMJ conditions. Nevertheless, the results from the Friedman test revealed significant differences among the methods for all the jumping conditions (p-values < 0.001).
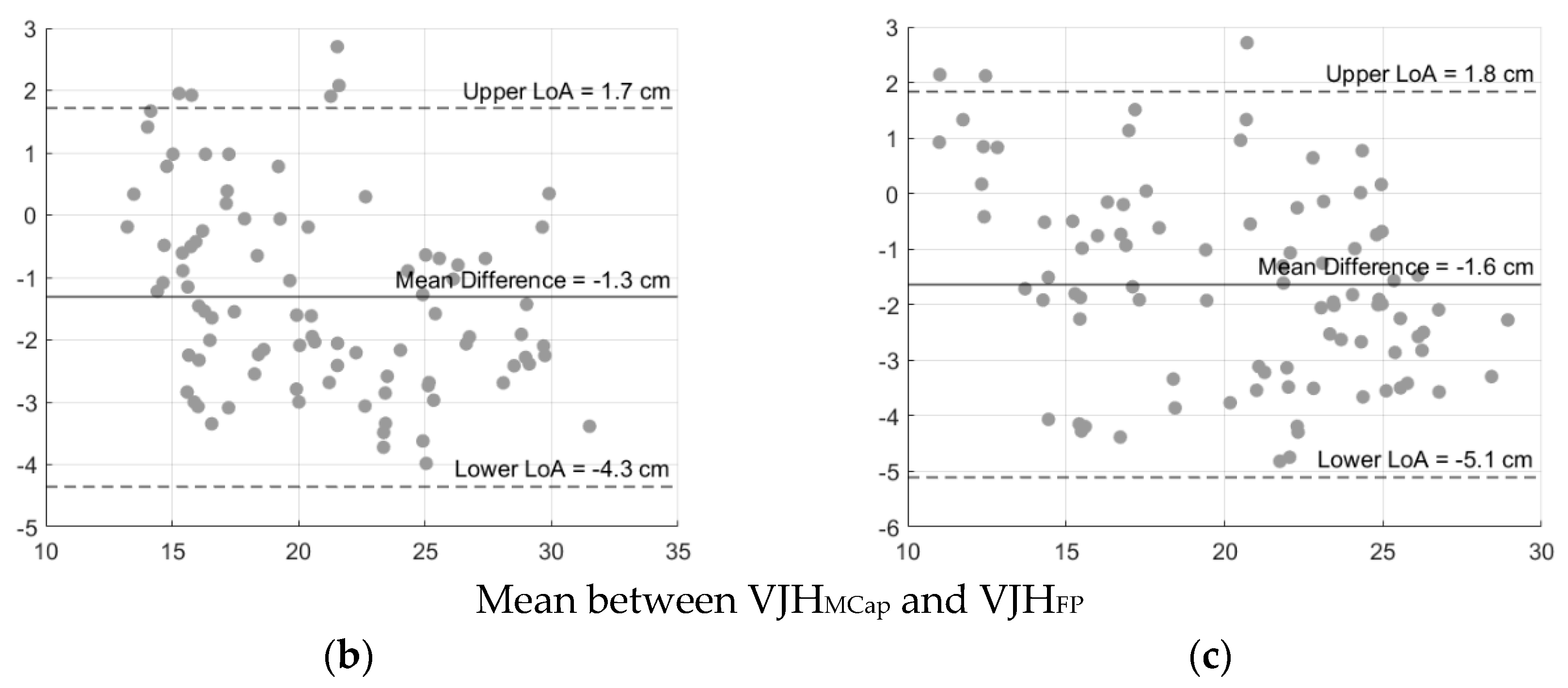
The Bland-Altman analysis (Table 3) performed on all the computation methods revealed a systematic bias within 4 cm for DL-CMJ across the different IMU-based calculation methods. However, the R-CMJ and L-CMJ conditions demonstrated larger systematic biases and wider LoA with respect to DL-CMJ, particularly for the V J H I M U F T and V J H I M U T O V methods, indicating reduced agreement with the VJHGSV. This suggests that IMU-based methods may offer reasonable accuracy for DL-CMJ, but their performance declines in SL-CMJ.
The Conover post-hoc test performed on DL-CMJ revealed that both the NDI and the TOV methods significantly underestimated VJH compared to the VJHGSV (p < 0.001 after Bonferroni correction), while the FT method exhibited a non-significant difference (p = 0.080). Comparisons among the IMU methods showed no significant differences, with the FT and TOV methods yielding particularly similar results (p = 1.000) in all jump modalities. In case of SL-CMJ, the NDI method showed no significant difference compared to the VJHGSV for both the R-CMJ (p = 1.000) and L-CMJ (p = 0.151), while FT and TOV methods exhibited significant differences in both R-CMJ and L-CMJ (p < 0.001).
Spearman’s rank correlation coefficients between the VJHGSV and the IMU-based methods were calculated to evaluate their association in the different jump modalities.
The Spearman’s coefficients indicated a strong correlation between the VJHGSV and the IMU-based methods (Table 4), with all correlations being significant (p < 0.05). Notably, the NDI method showed the highest correlation with the VJHGSV (⍴s ≥ 0.85 for all the jump modalities). Very strong correlations (⍴s ≥ 0.89) are shown between all the IMU-based methods and VJHGSV in the DL-CMJ condition. However, the correlations were slightly lower for R-CMJ and L-CMJ, particularly for the FT (⍴s = 0.74 and ⍴s = 0.83) and TOV methods (⍴s = 0.80 and ⍴s = 0.80), suggesting variability in the consistency of these methods across different jump modalities.
The results obtained indicate that, although all IMU-based methods tend to underestimate VJH relative to the VJHGSV, the NDI seems to demonstrate the most consistent performance among the three IMU-based methods across the different jump modalities.

3.3. Test-Retest Reliability

The test-retest reliability of the VJHGSV and of the three IMU-based calculation methods was assessed using the Intraclass Correlation Coefficient (ICC) with a two-way mixed-effects model (ICC (2,1)). Table 5 provides the ICC values for each method across the three different jump modalities.
The VJHGSV showed excellent reliability across all modalities, with ICC values above 0.89 (Table 5), indicating high consistency in VJH measurements between trials. Among the IMU-based methods, the NDI demonstrated the highest average ICC (0.87), suggesting strong reliability across all jump modalities. Specifically, the NDI method showed an excellent reliability in DL-CMJ (ICC = 0.92), and good reliability in R-CMJ and L-CMJ (ICC = 0.85 and 0.86, respectively). The FT method exhibited moderate to high reliability depending on the jumping modality, with an average ICC of 0.83. The TOV method showed the lowest reliability among the IMU methods, with an average ICC of 0.79. Although it demonstrated good reliability in DL-CMJ (ICC = 0.92), its reliability was substantially lower for R-CMJ (ICC = 0.72) and L-CMJ (ICC = 0.73) with respect to other methods.
Excellent reliability was observed for DL-CMJ across all calculation methods, whereas SL-CMJ generally showed lower reliability, possibly due to increased variability in single-leg jumps.

4. Discussion

VJH is recognized as a reliable metric for assessing CMJ performance [5,17,18]. MCap systems and FP are recognized as the gold standards for VJH assessment, but their substantial cost and lack of portability limit their use, particularly in ecological environments [19,20,21]. This study investigated whether a low sampling rate IMU could serve as a portable and compact alternative to gold standard systems for estimating VJH in CMJs. The accuracy and reliability of three computational methods (NDI, TOV, and FT) for calculating VJH from a low-sampling rate IMU was evaluated against MCap and FP systems.
The results demonstrated that the MCap and FP systems showed strong agreement and minimal systematic bias, confirming their reliability as gold standards. These results are consistent with previous studies that have demonstrated the reliability of MCap and FP for VJH measurements [23,27,30,34,36]. Furthermore, the present study confirmed that the NDI method is a robust approach to calculating VJH using dual FP systems, with minimal differences compared to MCap systems [18,32,33]. Among the IMU-based methods, NDI method yielded the highest accuracy, exhibiting the strongest correlation with the gold standards and the lowest systematic bias. This is consistent with earlier studies suggesting that NDI is the most accurate method for estimating VJH from IMUs [34]. However, the present study extends these findings by demonstrating that even at a low sampling rate, NDI retains strong performance, which is notable given the typical reliance on high-frequency data in previous research [18,27].
A systematic bias of approximately 4.0 cm was observed when comparing the NDI method to the gold standard systems for DL-CMJs. This bias could be attributed to the different approximation of the COM in different systems. The IMU, positioned at the L5 vertebra, estimated the COM based on a single point [36], whereas the MCap system used multiple markers on the pelvis, potentially introducing discrepancies, as identified in the Bland-Altman analysis (Table 3). For single-leg CMJs (SL-CMJs), the bias was more pronounced due to the increased difficulty of estimating the COM in a unilateral stance. This could be improved by directly placing a marker on the IMU sensor, as suggested by [36]. Despite these challenges, the NDI method demonstrated a high level of agreement and reliability with the gold standards, corroborating findings from prior research [34,36]. Nevertheless, the results should be interpreted with caution due to the small sample size of this study.
In DL-CMJs, the FT and TOV methods performed comparably to the NDI method, exhibiting similar systematic bias and correlation coefficients relative to the gold standards. However, their performance declined significantly in SL-CMJs, likely due to the increased difficulty in maintaining consistent posture at take-off and landing, which is a critical assumption for the FT method [34,36]. Additionally, the identification of these events is even more critical when considering the relatively low sampling frequency of the IMU compared to FP and MCap systems, as well as that of the IMUs used in other similar studies [18]. Lastly, the identification of these events is particularly sensitive to sensor noise and soft tissue artifact which can introduce errors, as reported in previous studies [43]. While the NDI method is also affected by these issues, its sensitivity to such disturbances is generally lower [34]. Similar limitations have been noted in studies using higher-sampling rate IMUs, but our study suggests that even at reduced sampling rates, these effects can still influence performance, warranting further research [18,27]. Nevertheless, future research should investigate strategies to reduce these fluctuations, potentially improving the precision of IMU-based methods for estimating VJH.
An important implication of the present study is having obtained reliable and accurate VJH estimates using a low-sampling rate IMU, advantageous for applications requiring low power consumption, portability, and fast data processing, such as in-field performance testing, rehabilitation monitoring, and sports analytics. This is particularly relevant for industries exploring the integration of IMUs with TinyML (machine learning on microcontrollers) and edge computing, where real-time analysis and long duration batteries are crucial. Our findings suggest that the NDI method could be integrated into these platforms to provide reliable VJH estimates during sport practice, offering a feasible alternative to traditional systems that are less adaptable to real-world, ecological environments.
Future research should focus on further optimizing the NDI method for low-power applications by improving algorithms to handle sensor noise and soft tissue artifacts. In addition, strategies should be developed to improve the detection of take-off and landing events, particularly for SL-CMJs. Moreover, expanding this analysis to other jump types, such as squat jumps or drop jumps, could broaden the applicability of low-sampling rate IMUs. This would enable their use in a wide range of sports, including volleyball, basketball, and football, where vertical jump performance is a key indicator of athletic ability.

5. Conclusions

This study demonstrates that the NDI method provides the highest accuracy and agreement with gold standard systems for estimating VJH from low-sampling frequency IMUs. The TOV and FT methods, while adequate for DL-CMJ, showed reduced accuracy in SL-CMJ, likely due to challenges in measuring take-off velocity and flight time precisely. These findings support the use of IMU sensors with the NDI method as a viable alternative for field-based assessments, particularly where portability and ease of use are crucial.
Despite the promising results, some limitations must be acknowledged. The sample size, though sufficient for statistical power analysis, was relatively small and homogeneous. Future studies should include a broader range of participants, encompassing athletes from various sports and performance levels, to enhance the generalizability of these findings. Additionally, different jump modalities and conditions may impact the performance of IMU-based methods, necessitating further investigation. Future research should focus on validating the robustness and reliability of the NDI method across diverse populations and CMJ variations to solidify its application in both clinical and sport settings.

Author Contributions

Conceptualization, G.V. and V.C.; methodology, G.V.; software, A.B. and G.V.; validation, G.V. and A.B.; formal analysis, G.V.; investigation, G.V.; data curation, G.V.; writing—original draft preparation, G.V.; writing—review and editing, M.G. and V.C.; visualization, G.V. and V.C.; supervision, M.G. and V.C.; project administration, M.G. and V.C.. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of Politecnico di Milano (protocol code 10/2023, 8 March 2023).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors upon request.

Acknowledgments

The authors would like to acknowledge Margherita Cittadini and Valeria De Benedetto for their valuable contribution to the project.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Liebermann, D.G.; Katz, L. On the Assessment of Lower-Limb Muscular Power Capability. Isokinetics and Exercise Science 2003, 11, 87–94. [Google Scholar] [CrossRef]
  2. Karatrantou, K.; Gerodimos, V.; Voutselas, V.; Manouras, N.; Famisis, K.; Ioakimidis, P. Can Sport-Specific Training Affect Vertical Jumping Ability during Puberty? Biol Sport 2019, 36, 217–224. [Google Scholar] [CrossRef]
  3. Manske, R.; Reiman, M. Functional Performance Testing for Power and Return to Sports. Sports Health 2013, 5, 244–250. [Google Scholar] [CrossRef]
  4. Markovic, G.; Dizdar, D.; Jukic, I.; Cardinale, M. Reliability and Factorial Validity of Squat and Countermovement Jump Tests. J Strength Cond Res 2004, 18, 551–555. [Google Scholar] [CrossRef] [PubMed]
  5. Anicic, Z.; Janicijevic, D.; Knezevic, O.M.; Garcia-Ramos, A.; Petrovic, M.R.; Cabarkapa, D.; Mirkov, D.M. Assessment of Countermovement Jump: What Should We Report? Life 2023, 13, 190. [Google Scholar] [CrossRef] [PubMed]
  6. Taylor, K.-L.; Chapman, D.W.; Cronin, J.B.; Newton, M.J.; Gill, N. Fatigue Monitoring in High Performance Sport: A Survey of Current Trends. 2012, 20.
  7. Freitas, V.H.; Nakamura, F.Y.; Miloski, B.; Samulski, D.; Bara-Filho, M.G. Sensitivity of Physiological and Psychological Markers to Training Load Intensification in Volleyball Players. J Sports Sci Med 2014, 13, 571–579. [Google Scholar] [PubMed]
  8. McLean, B.D.; Coutts, A.J.; Kelly, V.; McGuigan, M.R.; Cormack, S.J. McLean, B.D.; Coutts, A.J.; Kelly, V.; McGuigan, M.R.; Cormack, S.J. Neuromuscular, Endocrine, and Perceptual Fatigue Responses During Different Length Between-Match Microcycles in Professional Rugby League Players. 2010. [CrossRef]
  9. Mooney, M.G.; Cormack, S.; O’Brien, B.J.; Morgan, W.M.; McGuigan, M. Impact of Neuromuscular Fatigue on Match Exercise Intensity and Performance in Elite Australian Football. The Journal of Strength & Conditioning Research 2013, 27, 166. [Google Scholar] [CrossRef]
  10. Oliver, J.; Armstrong, N.; Williams, C. Changes in Jump Performance and Muscle Activity Following Soccer-Specific Exercise. Journal of Sports Sciences 2008, 26, 141–148. [Google Scholar] [CrossRef]
  11. Nikolaidis, P. Age-Related Differences in Countermovement Vertical Jump in Soccer Players 8-31 Years Old: The Role of Fat-Free Mass. American Journal of Sports Science and Medicine 2014, 2, 60–64. [Google Scholar] [CrossRef]
  12. Orhan, Ö.; Çimen Polat, S.; Yarim, I. Relationship Between Jump Performance and Sport Ages in U16 Basketball Players. Journal of Education and Learning 2019, 8, 207. [Google Scholar] [CrossRef]
  13. Kitamura, K.; Pereira, L.A.; Kobal, R.; Cal Abad, C.C.; Finotti, R.; Nakamura, F.Y.; Loturco, I. Loaded and Unloaded Jump Performance of Top-Level Volleyball Players from Different Age Categories. Biol Sport 2017, 34, 273–278. [Google Scholar] [CrossRef] [PubMed]
  14. Palazzi, D.; Williams, B.; Glynn, J.; Graham-Smith, P. Absolute and Relative CMJ Performance across Different Age Groups and Sports in Young Male Athletes; 2015.
  15. McMahon, J.J.; Rej, S.J.E.; Comfort, P. Sex Differences in Countermovement Jump Phase Characteristics. Sports (Basel) 2017, 5, 8. [Google Scholar] [CrossRef]
  16. Guan, Y.; Bredin, S.S.D.; Taunton, J.; Jiang, Q.; Wu, N.; Warburton, D.E.R. Predicting the Risk of Injuries Through Assessments of Asymmetric Lower Limb Functional Performance: A Prospective Study of 415 Youth Taekwondo Athletes. Orthopaedic Journal of Sports Medicine 2023, 11, 23259671231185586. [Google Scholar] [CrossRef]
  17. Philpott, L.K.; Forrester, S.E.; van Lopik, K.A.; Hayward, S.; Conway, P.P.; West, A.A. Countermovement Jump Performance in Elite Male and Female Sprinters and High Jumpers. Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology 2021, 235, 131–138. [Google Scholar] [CrossRef]
  18. Xu, J.; Turner, A.; Comfort, P.; Harry, J.R.; McMahon, J.J.; Chavda, S.; Bishop, C. A Systematic Review of the Different Calculation Methods for Measuring Jump Height During the Countermovement and Drop Jump Tests. Sports Med 2023, 53, 1055–1072. [Google Scholar] [CrossRef] [PubMed]
  19. Leard, J.S.; Cirillo, M.A.; Katsnelson, E.; Kimiatek, D.A.; Miller, T.W.; Trebincevic, K.; Garbalosa, J.C. Validity of Two Alternative Systems for Measuring Vertical Jump Height. J Strength Cond Res 2007, 21, 1296–1299. [Google Scholar] [CrossRef] [PubMed]
  20. Eagles, A.; Sayers, M. Motion Capture System versus Common Force Platform Methodologies for Vertical Jump Analysis. International Journal of Physical Medicine & Rehabilitation 2016, 4. [Google Scholar] [CrossRef]
  21. Montalvo, S.; Gonzalez, M.; Dietze-Hermosa, M.; Eggleston, J.; Dorgo, S. Common Vertical Jump and Reactive Strength Index Measuring Devices: A Validity and Reliability Analysis. Journal of strength and conditioning research Publish Ahead of Print. 2021. [Google Scholar] [CrossRef]
  22. Buckthorpe, M.; Morris, J.; Folland, J.P. Validity of Vertical Jump Measurement Devices. Journal of Sports Sciences 2012, 30, 63–69. [Google Scholar] [CrossRef]
  23. Marković, S.; Dopsaj, M.; Tomažič, S.; Kos, A.; Nedeljković, A.; Umek, A. Can IMU Provide an Accurate Vertical Jump Height Estimate? Applied Sciences 2021, 11, 12025. [Google Scholar] [CrossRef]
  24. Arlotti, J.S.; Carroll, W.O.; Afifi, Y.; Talegaonkar, P.; Albuquerque, L.; Ball, J.E.; Chander, H.; Petway, A. Benefits of IMU-Based Wearables in Sports Medicine: Narrative Review. IJKSS 2022, 10, 36–43. [Google Scholar] [CrossRef]
  25. Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
  26. Marković, S.; Dopsaj, M.; Tomažič, S.; Umek, A. Potential of IMU-Based Systems in Measuring Single Rapid Movement Variables in Females with Different Training Backgrounds and Specialization. Applied Bionics and Biomechanics 2020, 2020, 7919514. [Google Scholar] [CrossRef] [PubMed]
  27. Clemente, F.; Badicu, G.; Hasan, U.; Akyildiz, Z.; Pino Ortega, J.; Silva, R.; Rico-González, M. Validity and Reliability of Inertial Measurement Units (IMUs) for Jump Height Estimations: A Systematic Review. Human Movement 2021, 23, 1–20. [Google Scholar] [CrossRef]
  28. Liu, T.; Chen, C.; King, M.; Qian, G.; Fu, J. Balancing Power Consumption and Data Analysis Accuracy Through Adjusting Sampling Rates: Seeking for the Optimal Configuration of Inertial Sensors for Power Wheelchair Users; Duffy, V.G., Ed.; Springer International Publishing: Cham, 2015; Volume 9185, pp. 184–192. [Google Scholar]
  29. Rago, V.; Brito, J.; Figueiredo, P.; Carvalho, T.; Fernandes, T.; Fonseca, P.; Rebelo, A. Countermovement Jump Analysis Using Different Portable Devices: Implications for Field Testing. Sports (Basel) 2018, 6, 91. [Google Scholar] [CrossRef]
  30. Camuncoli, F.; Barni, L.; Nutarelli, S.; Rocchi, J.E.; Barcillesi, M.; Di Dio, I.; Sambruni, A.; Galli, M. Validity of the Baiobit Inertial Measurements Unit for the Assessment of Vertical Double- and Single-Leg Countermovement Jumps in Athletes. IJERPH 2022, 19, 14720. [Google Scholar] [CrossRef] [PubMed]
  31. Wade, L.; Lichtwark, G.A.; Farris, D.J. Comparisons of Laboratory-Based Methods to Calculate Jump Height and Improvements to the Field-Based Flight-Time Method. Scandinavian Journal of Medicine & Science in Sports 2020, 30, 31–37. [Google Scholar] [CrossRef]
  32. Wank, V.; Coenning, C. On the Estimation of Centre of Gravity Height in Vertical Jumping. Ger J Exerc Sport Res 2019, 49, 454–462. [Google Scholar] [CrossRef]
  33. Conceição, F.; Lewis, M.; Lopes, H.; Fonseca, E.M.M. An Evaluation of the Accuracy and Precision of Jump Height Measurements Using Different Technologies and Analytical Methods. Applied Sciences 2022, 12, 511. [Google Scholar] [CrossRef]
  34. Toft Nielsen, E.; Jørgensen, P.B.; Mechlenburg, I.; Sørensen, H. Validation of an Inertial Measurement Unit to Determine Countermovement Jump Height. Asia-Pacific Journal of Sports Medicine, Arthroscopy, Rehabilitation and Technology 2019, 16, 8–13. [Google Scholar] [CrossRef]
  35. Bosco, C.; Luhtanen, P.; Komi, P.V. A Simple Method for Measurement of Mechanical Power in Jumping. Europ. J. Appl. Physiol. 1983, 50, 273–282. [Google Scholar] [CrossRef] [PubMed]
  36. Picerno, P.; Camomilla, V.; Capranica, L. Countermovement Jump Performance Assessment Using a Wearable 3D Inertial Measurement Unit. Journal of Sports Sciences 2011, 29, 139–146. [Google Scholar] [CrossRef] [PubMed]
  37. Petersen, E.; Jørgensen, P.; Mechlenburg, I.; Sørensen, H. Validation of an Inertial Measurement Unit to Determine Countermovement Jump Height. Asia-Pacific Journal of Sports Medicine, Arthroscopy, Rehabilitation and Technology 2018, 16. [Google Scholar] [CrossRef]
  38. Mishra, P.; Pandey, C.M.; Singh, U.; Gupta, A.; Sahu, C.; Keshri, A. Descriptive Statistics and Normality Tests for Statistical Data. Ann Card Anaesth 2019, 22, 67–72. [Google Scholar] [CrossRef]
  39. Akoglu, H. User’s Guide to Correlation Coefficients. Turk J Emerg Med 2018, 18, 91–93. [Google Scholar] [CrossRef]
  40. Bland, J.M.; Altman, D.G. Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
  41. Tomczak, M.; Tomczak, E. The Need to Report Effect Size Estimates Revisited. An Overview of Some Recommended Measures of Effect Size. 2014, 1. [Google Scholar]
  42. Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J Chiropr Med 2016, 15, 155–163. [Google Scholar] [CrossRef]
  43. Forner-Cordero, A.; Mateu-Arce, M.; Forner-Cordero, I.; Alcántara, E.; Moreno, J.; Pons, J. Study of the Motion Artefacts of Skin-Mounted Inertial Sensors under Different Attachment Conditions. Physiological measurement 2008, 29, N21–N31. [Google Scholar] [CrossRef]
Preprints 121195 g001
Figure 1. Main steps to obtain VJH from raw data of the three systems.
Figure 1. Main steps to obtain VJH from raw data of the three systems.
Preprints 121195 g001
Preprints 121195 g002aPreprints 121195 g002b
Figure 2. Bland–Altman Plots for VJHMCap and VJHFP. (a) DL-CMJ; (b) R-CMJ; (c) L-CMJ. The centre lines represent the systematic bias between systems and the Upper and Lower LoA [n = 90].
Figure 2. Bland–Altman Plots for VJHMCap and VJHFP. (a) DL-CMJ; (b) R-CMJ; (c) L-CMJ. The centre lines represent the systematic bias between systems and the Upper and Lower LoA [n = 90].
Preprints 121195 g002aPreprints 121195 g002b
Table 1. Median (IQR), Spearman’s coefficients (⍴s) and systematic bias with LoA from gold standard methods.
Table 1. Median (IQR), Spearman’s coefficients (⍴s) and systematic bias with LoA from gold standard methods.
Modality VJHMCap (cm) VJHFP (cm) ⍴s Systematic bias (LoA) (cm)
DL-CMJ 26.2 (5.4) 25.6 (5.5) 0.97* 0.6 (-2.0 to 3.2)
R-CMJ 20.2 (4.7) 21.5 (5.2) 0.94* -1.3 (-4.3 to 1.7)
L-CMJ 19.5 (4.4) 21.1 (5.0) 0.93* -1.6 (-5.1 to 1.8)
* Significant correlation (p < 0.001). DL-CMJ = double-leg countermovement jump; R- = right; L- = left; VJH = Vertical Jump Height; MCap = Motion Capture systems; FP = Force Platform; ⍴s = Spearman’s rank correlation coefficient; LoA = Level of Agreement.
Table 2. Median (IQR) for the VJHGSV and the three IMU-based VJH computations: NDI, FT and TOV and different jumping modalities. The two columns on the right-hand side displayed the Friedman test results in terms of χ² and Kendall’s W.
Table 2. Median (IQR) for the VJHGSV and the three IMU-based VJH computations: NDI, FT and TOV and different jumping modalities. The two columns on the right-hand side displayed the Friedman test results in terms of χ² and Kendall’s W.
Modality VJHGSV (cm) V J H I M U N D I (cm) V J H I M U F T (cm) V J H I M U T O V (cm) χ²(3) W
DL-CMJ 24.6 (9.0) 21.1 (6.8) 21.1 (9.0) 21.2 (9.1) 23.87* 0.44
R-CMJ 20.0 (8.6) 19.1 (7.5) 13.3 (5.9) 13.3 (6.7) 44.53* 0.83
L-CMJ 21.6 (7.6) 19.0 (7.8) 13.8 (5.6) 13.9 (8.1) 49.20* 0.91
* Significant p-values (p < 0.05); DL-CMJ = double-leg countermovement jump; R- = right; L- = left; VJH = Vertical Jump Height; GSV = gold standard values; IMU = Inertial Measurement Unit; NDI = Numerical Double Integration; FT = Flight Time; TOV = Take-off Velocity.
Table 3. Systematic bias, LoA and p-values after Bonferroni correction obtained from the Bland-Altman analysis and Conover test.
Table 3. Systematic bias, LoA and p-values after Bonferroni correction obtained from the Bland-Altman analysis and Conover test.
Comparison Modality Systematic bias (LoA) (cm) pbonf
VJHGSV – V J H I M U N D I DL-CMJ 4.0 (-0.9 to 8.8) < 0.001*
R-CMJ 1.5 (-3.9 to 6.9) 1.000
L-CMJ 1.9 (-3.2 to 7.1) 0.151
VJHGSV – V J H I M U F T DL-CMJ 3.0 (-0.3 to 6.4) 0.080
R-CMJ 7.8 (-0.3 to 15.9) < 0.001*
L-CMJ 7.1 (0.4 to 13.8) < 0.001*
VJHGSV – V J H I M U T O V DL-CMJ 3.4 (-3.7 to 10.4) 0.004*
R-CMJ 7.7 (1.2 to 14.1) < 0.001*
L-CMJ 7.1 (0.5 to 13.7) < 0.001*
V J H I M U N D I – V J H I M U F T DL-CMJ -0.9 (-3.9 to 2.1) 0.273
R-CMJ 6.3 (-2.6 to 15.2) 0.002*
L-CMJ 5.1 -2.8 to 13.1) 0.020*
V J H I M U N D I – V J H I M U T O V DL-CMJ -0.6 (-9.2 to 8.1) 1.000
R-CMJ 6.2 (-0.1 to 12.4) < 0.001*
L-CMJ 5.2 (-0.9 to 11.2) 0.002*
V J H I M U F T – V J H I M U T O V DL-CMJ 0.4 (-6.8 to 7.5) 1.000
R-CMJ -0.1 (-9.3 to 9.1) 1.000
L-CMJ 0.1 (-8.5 to 8.6) 1.000
* Significant p-values (p < 0.05). DL-CMJ = double-leg countermovement jump; R- = right; L- = left; VJH = Vertical Jump Height; GSV = gold standard values; IMU = Inertial Measurement Unit; NDI = Numerical Double Integration; FP = Force Platform; TOV = Take-off Velocity.
Table 4. Spearman’s rank correlation coefficients between VJHGSV and IMU-based methods.
Table 4. Spearman’s rank correlation coefficients between VJHGSV and IMU-based methods.
Method Modality VJHGSV V J H I M U N D I V J H I M U F T V J H I M U T O V
VJHGSV DL-CMJ -
R-CMJ -
L-CMJ -
V J H I M U N D I DL-CMJ 0.90* -
R-CMJ 0.85* -
L-CMJ 0.85* -
V J H I M U F T DL-CMJ 0.93* 0.95* -
R-CMJ 0.74* 0.63* -
L-CMJ 0.83* 0.68* -
V J H I M U T O V DL-CMJ 0.89* 0.83* 0.89* -
R-CMJ 0.80* 0.77* 0.61* -
L-CMJ 0.80* 0.84* 0.67* -
* Significant correlation (p < 0.001). DL-CMJ = double-leg countermovement jump; R- = right; L- = left; VJH = Vertical Jump Height; GSV = gold standard values; IMU = Inertial Measurement Unit; NDI = Numerical Double Integration; FP = Force Platform; TOV = Take-off Velocity.
Table 5. Intraclass correlation coefficients of the calculation methods.
Table 5. Intraclass correlation coefficients of the calculation methods.
Modality VJHGSV V J H I M U N D I V J H I M U F T V J H I M U T O V
ICC (2,1) DL-CMJ 0.97 0.92 0.94 0.92
R-CMJ 0.89 0.85 0.74 0.72
L-CMJ 0.94 0.86 0.81 0.73
Average 0.93 0.88 0.83 0.79
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated