Prerpints.org logo
Preprint
Article

The Discharge-Induced Polarity-Dependent Propagation Characteristics of a Strong Shock Wave

This version is not peer-reviewed.

Submitted:

15 October 2024

Posted:

15 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
The specifics of a shock wave propagation down a positive column of a dc discharge in molecular chemically inert gases has been investigated. It was shown that axial gradients caused by the imbalance in the charged particle momentum transfer to the gas molecules can be a reason for the shock velocity dependence on the electric field direction. In the pure nitrogen gas, the calculated shock velocity difference up to 13.5% is in good agreement with 12% value obtained in the experiment. A returning gas flow organizing in the discharge as a possible mechanism for an extended shock structure, and a number of kinetical factors capable of affecting the shock motion are discussed.
Keywords: 
Subject: 
Physical Sciences  -   Fluids and Plasmas Physics

I. Introduction

The motion characteristics and the structure of a shock wave are inherently determined by the properties of the medium through which it propagates. For example, a shock encountering a glow discharge experiences an acceleration, its intensity visibly decreases, and the front undergoes continuous distortions [1]. In case of significant heating or due to the fast-evolving processes in the presence of radiation or fast expansion, non-equilibrium states established in the flow past the shock wave promote an extended shock structure. It forms as a result of a relative delay between different terms contributing to the energy content of the gas [2]. The presence of substantially strong transverse thermal gradients in the gas and the wall friction have been in discussion as other causes affecting the shock’s propagation mode. In experiments, the discharge effects on the shock structure are observed in the form of deflection signal weakening and widening that, upon the exit from the area of perturbation can be reversed. The electric double layer set at the shock front due to presence of electric charges in the afterglow of a dc discharge is among other effects on the shock structure [3].
Another remarkable feature that did not receive much attention yet is the electrode polarity dependence of the shock velocity when it propagates through a positive column of a dc discharge. In the experiments [1,4] carried out in pure nitrogen, in certain interval of discharge currents, the measurements showed an around 12% effect of electric field orientation on the average shock propagation velocity. In the experiment, the shocks were always produced at the same end of the discharge tube, while the electrode polarity was switched for each pair of measurements. It was found that when the electric field was aligned in the direction of the shock propagation, the shock slowed down, and when the electric field was in the opposite direction – the shock accelerated. In the report, an additional effect of local minimum of the average shock velocity observed near the cathode, with no such minimum near the anode, was explained with electrostatic interaction between the shock and the cathode-adjacent sheath, or due to local temperature gradients. It was also reported that, for the discharge currents of 10 mA, 30 mA, and 50 mA, the recovery length for the shock front was noticeably longer when the electric field was in the direction of the shock propagation. In an attempt to explain the shock velocity difference, it was admitted that the data cannot be totally attributed to a heavy particle single collision energy transfer process or described by a modified van der Waal’s equation of state. An interaction between the shock induced double layer and the electric field in the positive column [2] was mentioned as one of possible mechanisms.
In further search for feasible mechanisms of the shock acceleration, the ability of discharges to modify the state of the gas is one to explore. The effects of discharges on the gas have been known at least back to 1895, and an extensive review of the studies of pioneer researchers of that time was done in [5]. The main observation of the researchers was that a passage of a discharge through a pure gas results in a pressure difference between the two electrode regions. In air and nitrogen at low pressures below 0.1 Torr, the pressure at the cathode was found greater than that at the anode. Using the techniques accounting for gas absorption at electrodes and walls, the phenomena was explained by a drift of ions to the cathode where they are neutralized and build up a gas pressure.
At higher pressures of p > 0.1 Torr and current densities j ≈ 1 A/cm2, in Ar, Ne, He, N2, and H2, the effect was found much larger in magnitude and in the opposite direction, namely with the pressure being considerably larger at the anode. In narrow, capillary tubes the effect was much stronger reaching up to 30% of the total pressure. The effect increased with the total current, and it was stronger in gases of larger molecular weight. In wider tubes (0,45 to 2 cm2) an empirical formula for pressure difference was introduced by Ruttenauer [5]. Later experiments [6] with noble gases at pressures less than 10 Torr in capillary tubes with radius of 1.25 to 6 mm, report pressure differentials on the level of 10−4 to 10−2 Torr at currents less than 1 Amp, and they were in the interval 10−1- 1 Torr at larger currents of 1 to 6 Amp. At later times, with the invention of chemical lasers, those processes were found detrimental to laser’s operation and forced the use of bypasses equalizing pressure between the ends of the tube. Significant pressure difference on the level of Δp = 0.25-1.2 torr was also measured in the 30-cm length and 1.25 mm radius positive column [7]. Experimenting with various discharge parameters, it was determined that Δ p ∼ i p 0 / T g and Δ p ∼ i / p 0 R 4 , where i, p0, T0, and R are the discharge current, gas pressure, temperature, and the tube radius accordingly.
In reference [8], the effect was explained with diffusion of electrons to the tube walls. It was assumed that the axial motion of gas particles is due to the force on the neutral component from the charged particles, often termed in the literature as Langmuir and Dryvesteyn force,
F w → = e n i − n e E
For uniformly ionized gas, when the number of charged particles of both signs is equal, the net force is zero, because the momentum attained by the charged particles in electric field of the discharge and transferred to the neutral component is equal in both axial directions. The balance between the number of charged particles in the positive column becomes broken if there is a sink mechanism to which the charges of one sign are lost. For example, in the presence of electron diffusion to the walls, the ionized gas looses those charges from its volume. The wall becoming negatively charged will repeal most of the electrons and attract the ions. Because of slowdown for electrons in the electric field of walls, the momentum transfer to the walls from the ions will prevail over that from electrons. This causes the imbalance in the axial momentum transfer, when a portion of the momentum that could be passed to the neutrals by the ions is lost at the walls, while the contribution from the electrons is almost unchanged. Broken balance in the momentum transfer results in the net force on the neutral component pointing in the anode direction [5].
The key role of the wall effects on the neutral flow has been cited in other related fields of research. Among them, the Dielectric Barrier Discharge (DBD) experiments for flow generation, where the charges of a certain sign are collected on a dielectric surface separating two electrodes to which RF electric field is applied. In Electro Hydro Dynamics (EHD) research, the gas flow induced by a DBD applied in the gas across the dielectric take place in a close proximity to the wall. Historically, the phenomena of flow generation was first observed in a corona discharge and was termed at that time as an electric wind. The importance of a surface charge deposited on the dielectric in DBD discharges for effective force production on the neutral component by electric space charge, was also pointed out in [9], and the leading role of charging the dielectric surface in DBD for the neutral gas acceleration was also stressed in [10]. Although the type of discharge (RF) used in this research is periodic, some of the insights on the role of the processes that occur during one-half period of alternating polarity can be still found useful to borrow, provided that there is enough time for the system to come to a steady state. Similarly to what occurs at the walls in a dc discharge tube, the particles of one sign in the gas volume attach to the dielectric. Because of the imbalance in the force exerted on neutral gas due to particles of both signs, the neutrals are pushed along the dielectric surface. Within one of the two phases (forward and backward strokes during one alternating electric field period), in case the under-dielectric electrode is negative, a cloud of excessive negative charge, electrons or negative ions, forms in the gas volume above the dielectric. The net momentum imbalance, with the lack of momentum transfer from the positive charges, results a non-zero net force on the neutral component of the gas toward the anode, creating the “electric wind” flow. It is the distinct feature of the DBD that the force is always pointing in the same direction during both the forward and backward strokes of the discharge. The plasma based method in aerodynamic flow control [11] employs the ion drift induced by RF electric fields imparting momentum transfer to near-surface fluid and thus generating a wall jet. Similar flow producing mechanism was found to be dominant in the generation of plasma jets used in EHD thrusters in [12], and in DBD actuators for propulsion and boundary layer control [13]. Magneto Hydro Dynamics (MHD) methods is another branch used for flow control by removal of electrons from plasma volume to the wall surface, resulting in body forces exerted by electric or magnetic fields on charged particles that are coupled to the neutral component of the gas. The main advantage of the techniques is the absence of moving parts, and thus it is found useful in aerospace applications for controlling near-surface flow within laminar or turbulent boundary layers, thus affecting the flow separation, the drag, and the shock-boundary layer interaction.
The achieved upper values of the induced gas flow velocities in the EHD applications employing the DBD are typically on the order of several meters per second, and the numbers are strongly dependent on the experimental arrangements. In numerical calculations [14] carried in the air at atmospheric pressure and ambient temperature, the ONERA in-house Navier-Stokes solver CEDRE has been used to compute averaged over one period flow created by the DBD discharge. The discharge-induced neutral gas flow in very close proximity to the dielectric wall (0.2 cm) was determined up to 6 m/s near the anode tip for the parallel velocity component, and the perpendicular component a little over the exposed electrode reached about 1.8 m/s. It was found that the effect of the actuator quickly fades as the distance from the dielectric increases.
Qualitatively the phenomenon of gas pumping was first described by Langmuir in [8], and Dryvesteyn in [5]. An empirical formula was derived there for the case when the free paths of electrons and ions are much less than the discharge tube radius. The unbalanced force component due to the wall effect pushes the neutral component toward the anode mainly in the wall region. Near the axis, the gas was found moving back, toward the cathode. The net transport of gas as positive ions was still toward the cathode, because the number of ions ni was slightly greater than that for electrons ne. The empirical relation for the pressure difference derived for various gases in wider tubes of 0.45 to 2 cm2 cross section, and 40 to 150 cm long, obtained in [5] has the following form
Δ p = 2.4 ⋅ 10 − 6 p i E M l R 2
where p – gas pressure in Torrs, R - radius of discharge tube in cm, l - length of the discharge positive column in cm, i - discharge current in Amps, M – molecular weight in mass units, E - electric field in V/cm.
The mechanisms underlying the gas pumping can be found described in detail in [15]. In addition to the force (1) on the gas due to wall effects, the volume force Fv pointing in the opposite direction was introduced there, making the total force
F = e n e − n i E − F v
The volume force component arises due to ambipolar diffusion and consequently it is maximal at the center and minimal near the wall. The volume force absolute value was found to be much larger than that for the wall-effect component, and thus stronger gas pumping and induced flow velocities are expected. An expression for the volume force associated with the charged particle density gradients in the radial electric field was derived in [16] by applying the laws of mass and momentum conservation for electrons, ions, and neutrals. The total force on neutral component (termed there as the charged-particle momentum transfer diversion force)
F v → = − m e v d e − m i v d i Ω
where vde and vdi are the drift velocities and Ω is the total rate of charged particle production in ionization and recombination processes, Ω = Ω i − Ω r . Assuming that disappearance of electrons and ions from the volume is determined by the ambipolar diffusion to the wall, taking into account that m e v d e ≪ m i v d i , Te >>Ti,, that the electron temperature and the drift velocities vde and vdi are independent of the axial and radial coordinates, and expressing the rate as Ω = n e D a / Λ 2 , the axial component of the force was obtained as follows
F v → = − m i n e D a Λ 2 v d i ,
Here, Λ is the characteristic diffusion length in the discharge tube corresponding to fundamental diffusion mode, and Da is ambipolar diffusion coefficient. For the electron density distribution given by the fundamental diffusion mode, the force (5) has maximum at the center of the tube and minimum at the wall. In case the discharge is confined by a solid wall at which the electrons and ions recombine and dissipate their momenta, the force profile has a parabolic shape with the force direction toward the anode and the zero value at the wall. 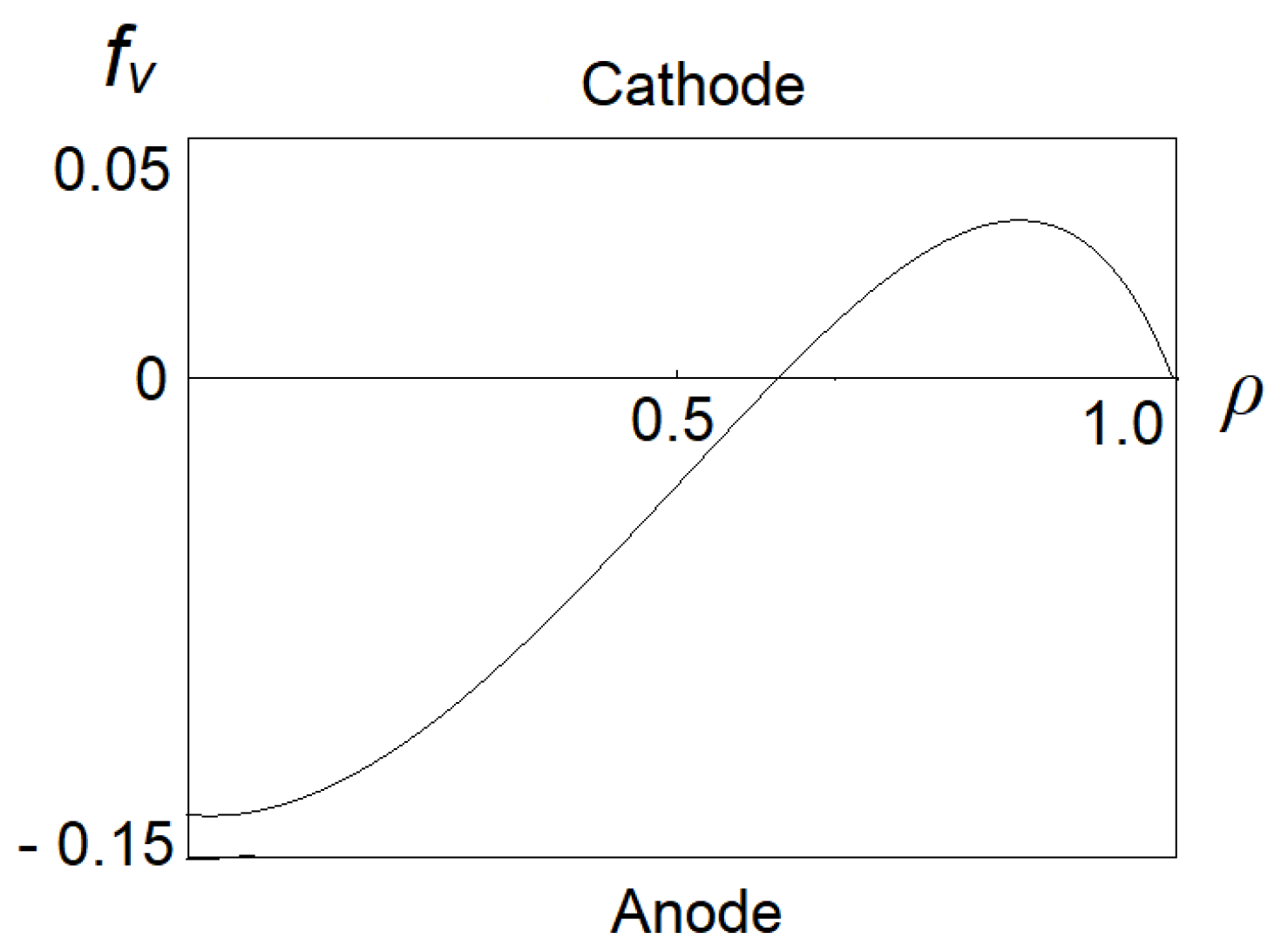However, when the wall is at some distance from the active discharge region, the force vanishes at the location where the total rate of charged particle production Ω is zero. As it goes further toward the wall, the force reverses its sign as recombination outside of the active region prevails over ionization, so the total rate turns negative. The force still vanishes at the wall as no charged particle can reach it. Thus the gas flow in the center of the tube will move toward the anode, and the flow will be in the opposite direction in the region closer to the wall, as shown in the schematic diagram of Figure 1. Thus the presence of the walls is not actually required for generation of the volume force, and the direction of this force is opposite to the Langmuir and Dryvesteyn force.
Since the volume force is in addition to the wall force (1), the total force obtained by integration over the plasma volume should include both components. With that said, it can be then supposed that a competing balance between the wall and ambipolar diffusion effects described with the two force components in the expression (4), could probably explain the mentioned above “contradicting” pressure differences of opposite signs found by the pioneer experimenters.
A number of other fine physical mechanisms participating in the gas pumping were discussed in [17]. In this approach, special attention to the momentum transfer to neutral particles during the ion motion in the radial field set in the discharge was given. The resulting corrections to the volume force (1) were based on the fact that, in an elastic collision with a neutral particle at rest, it is only on the average all the momentum an ion gained in the electric filed is transferred to the gas molecule. Actually, an ion exiting the collision will still possess some axial momentum, then gains more during its free motion in the field and looses about half its total axial momentum upon next collision with a gas molecule. Then, assuming no charge-exchange processes, the difference in the momentum exchange with neutrals for the following two types of ions was considered. The so called “old” ions begin with some momentum and then gain more before their next collision, while the “new” ones just born in an ionization begin with zero momentum and later gain some more energy. Then the old ions arriving at a specific radial location r after a previous collision will possess a larger amount of momentum compared to that of a “newly” created ion and arriving at the same location. Therefore the “new” ions give much less momentum to the gas on the average than the “old” ions do. This reduces the contribution to the force due to new ions by an additional factor. In the high pressure approximation, when the thermal velocity v t h = 2 k T i / m i determines the time between collisions and the free path length, i.e. when the drift velocity vdr << vth, the correction factor was found to be 1/6, yielding for the force due to the new ions,
F n e w = 1 6 e E Δ n i
while in the low pressure approximation, vdr >> vth, the correction factor to the force is predictably less significant,
F n e w = 3 2 3 e E Δ n i
The expression for the axial neutral particle flow velocity induced by the forces and the velocity radial distribution were determined in [15] from the solution of the mass and momentum conservation equations applied to a cylindrical positive column of a dc discharge. Particularly, considering the problem in a cross section of a closed (no by-pass) discharge tube as a function of the radial coordinate r, and assuming quasi-neutral positive column where the loss of electrons and ions is governed by ambipolar diffusion toward the walls, the force was obtained as follows
F v → = − m i v d i Ω = − k J 0 j 0,1 ρ
Here the dimensionless coordinate ρ = r/R, J 0 j 0,1 ρ is the zeroth-order Bessel function distribution of electron density and j 0,1 is its first root, k = m i n e 0,0 v d i D a Λ 2 , and the characteristic diffusion length is given by Λ = R / j 0,1 . The expression for the axial component of the flow velocity
V N ρ = m i n e 0,0 v d i D a η f v ρ ,   where   f v ρ = 4 J 1 j 0,1 j 0,1 1 − ρ 2 − J 0 j 0,1 ρ
was obtained assuming that: the volume force Fv (r) is independent of the axial coordinate z, i.e. when the electric properties of the discharge are independent of z, ∂ p ∂ z ≪ p L ; the flow is laminar, i.e. when the Reynolds number Re < 2000, or the flow Mach number MN << 1; and the neutral particle flow velocity is much less then the axial ion drift velocity, V N ≪ v d i . The radial profile of flow velocity determined by the function fv (ρ) in (9) is shown in the schematic diagram of Figure 1.
The diagram demonstrates that the induced gas flow moves toward the anode at the tube center, and its motion reverses in the area near the wall.
In summarizing the above research and applying it to the problem of shock propagation, it can be concluded that the two effects of discharges on the gas, namely the induced neutral particle flow and the axial gas parameter gradients, are among the factors capable of influencing the shock motion. It is still a question whether the effects are strong enough to affect the shock velocity on the levels observed in experiments. The first factor associated with the neutral gas flow in the axial direction will cause the shock to propagate locally either with the flow or against it, that, in the laboratory reference frame, will either add to or subtract from the shock velocity. However, taking into account that the flow velocities, being typically between few cm/s to a few m/s, are incomparably smaller then that for the shock, they cannot attribute to the shock acceleration to the observed levels. As to the second factor, in the presence of gas pumping in a discharge the shock will propagate under nonuniform gas conditions, the condition known of strongly affecting the shock motion. In the next section, this factor will be tested to see to what degree it is capable of causing the shock acceleration.
All relations for the shock propagation velocities in the discharge will be derived for the specific conditions of the experiment [1], further referred to as “the experiment”. Based on the relations, numerical estimations will be done for the purpose of matching the results with the measurements. In the experiment, a shock wave was generated in a spark gap, always at one end of a 3 cm diameter pyrex tube (next to the cathode) filled with pure nitrogen gas at up to 30 Torr pressure. The reported values of the stored pulse energy in a HV capacitor between 7 and 144 J will be utilized to estimate the explosion energy used for the shock production, assuming that a significant portion of it was invested in the shock. A longitudinal plasma column was created in a dc discharge with a pair of cylindrical electrodes separated by 20 cm. The measurements of local shock velocity moving through the discharge was done using the laser beam deflection technique. It was arranged with two laser stations placed at x1 = 5.3 cm (pos.1) and x2 = 15.8 cm (pos.2) mean positions from the cathodic electrode, with lasers in each pair of the stations being separated by 2.59 cm. Thus a portion of the positive column was used to determine the average shock velocity at two locations separated by the base distance Δx = 10.5 cm. Simultaneously, the discharge-current dependent gas temperatures were spectroscopically measured at both locations. At 20 Torr gas pressure and 50 mA discharge current, the temperature values were determined as T1 = 542.8 K at pos.1 (cathode side) and T2 = 772.3 K at pos.2 (anode side). The shock velocity was measured twice, second time with the polarity of the electrodes switched, and then the measurements were compared. It was found that when the shock was moving from cathode to anode, its final velocity V+ was higher compared to the value V- at the start of motion. At 20 Torr gas pressure and the discharge current I = 50 mA, the shock accelerated from V- = 590 m/s to V+ = 630 m/s, thus gaining the velocity difference V+ - V- = 40 m/s, that is 6.5% increase. When the polarity of the electrodes was switched, the effect was opposite: the shock’s starting velocity at pos.1 was higher than its final value at pos.2. The corresponding shock deceleration by approximately V- - V+ = 550‒520 = 30 m/s was recorded (decrease by 5.5%), thus yielding the total two-way velocity difference of 12%.

II. The Effect of Axial Gas Parameter Gradients

In this section, the shock velocity will be determined at two positions inside the positive column assuming the presence of an axial gas parameter gradient. The calculations will be done treating the gas as radially uniform, and the effects of radial gradients will be discussed later in the conclusion section of this article. In trying to reconstruct the state of the gas that could be established in the experiment, the difference in the gas temperature measurements at the two ends of the testing section will be used. Since the temperature was higher at the anode side, the local heating typically observed near the cathode can be ruled out, and therefore the presence of volume distribution will be supposed. A number of specific parameter gradients will be tested for their ability to affect the shock motion to the levels close to those observed in experiments.
Using the relation (2) at the conditions of the experiment, the obtained gas pumping value of Δp = 2.8·10−3 Torr can be found rather negligible. The reason for this could be that the empirical formula (2) was deduced for tubes of relatively smaller diameters of up to 2 cm3, while that in the experiment is well outside of the interval. The tube dimensions of a larger ratio R/L appear advantageous in equalizing the pressure along the tube thus making the pressure difference insignificant. Then, considering the value of gas pressure p fixed throughout the positive column and taking different gas temperatures at the two locations, T1 = 542.8 K at pos.1 and T2 = 772.3 K at pos.2, in the ideal gas approximation the densities at the cathode and anode sides are
ρ 01 = p / R T 1 and   ρ 02 = p / R T 2
accordingly. At the above temperatures and p = 20 Torr, the density values are ρ01 = 1.656·10−2 kg/m3 and ρ02 = 1.160·10−2 kg/m3. Thus the density is higher at the cathode side, and it continuously decreases in the direction toward the anode. Therefore, depending on the electrode polarity, the shock propagates in the gas of either increasing or decreasing density. In the experiment, the measured shock velocity was found increasing when it moved from cathode to anode, and it was reversed in the opposite direction. Therefore the shock was observed accelerating when moving through the gas of decreasing density and slowing down in the opposite direction at the 5-6% levels in each direction, the facts to be verified in this section below.
The problem of a shock wave propagating through the media of varying density has been studied before, particularly for the exponential [2,18] and the power law [19,20] density distributions, the latter also including the linear type of it. Since the distribution established in the discharge was not specified in the experiments, all the three types will be considered.
For a shock wave propagating through a gas with density changing exponentially, a solution for its coordinate as a function of time was obtained in [2,18]. It was supposed that the shock was produced in an explosion with the energy E at a point located in a medium of changing density.
First, consider a shock moving in the direction of decreasing density
ρ = ρ 0 e x p − x / z 0
where z0 is the scale of the density gradient and ρ0 is the density at the start of the shock’s travel. The parameter z0 can be estimated using the experimental data for the temperatures T1 at pos.1 and T2 at pos.2, with the separation between the positions Δx. In case of equal pressures at the two positions,
z 0 = Δ x l n T 2 / T 1
that, for the gap width Δx = 10.5 cm yields z0 = 28 cm. This value is comparable to Δx and therefore a noticeable influence of the gradient on the shock propagation should be expected.
The first part of the solution applicable to the initial times immediately after the explosion was obtained in an analytical form. In accordance to this solution, during the time interval t0 < 5τ, where τ = z 0 5 ρ 0 / E , the dimensionless flow velocity U r t τ is a sharply decreasing function of time. For the times t > t0, the solution was obtained in a numerical form that shows continuous acceleration of the shock. Among the reasons for the transitional behavior of the solution, one can expect the influence of a rarefaction wave that quickly ceases as the shock moves further from the explosion point. Given that in the experiment the shock produced under the explosion-like conditions (arc discharge) develops in an environment closely limited with the tube walls, and that prior to entering the testing section it propagated significant distance through the gas, the effects at the initial times after the shock production can be disregarded and the solution for times t > t0 will be utilized. At this stage of motion, the solution for the flow velocity
U r t τ = u r t τ z 0
obtained in a numerical form, can be approximated with the exponential function
U r t τ = U 0 e x p a t τ
where a is the numerical factor determined from the data. Taking into account the scaling factor in (13), the solution (14) transforms to the following form for the dimensionless flow velocity
u r t = u 0 e x p a u p t
where the parameters u0 = 0.0475(z0/τ) and aup = ln(8)/(15τ) are determined from the fit to the data (13). In the strong shock approximation, the velocities for the shock and the flow behind it are related as
V s w = γ + 1 2 u r
from which we obtain the velocity function for the shock propagating through the decreasing density gradient
V s w u p = ε 1 e x p ε 2 t + t λ
Here, γ is the specific heat ratio,
ε 1 = 0.0474 1 + γ z 0 τ ,   and   ε 2 = 0.1386 / τ
The parameter tλ in relation (17) is introduced to match the function to the specific value of the shock velocity at the beginning of its motion through the testing gap. For this, the boundary condition {t = 0, V(up)sw = V1}is used together with the eq. (17), from which
t λ = 7.2150 τ l n V 1 u p τ 0.04738 γ + 1 z 0
Here V(up)1 is the experimental value of the shock velocity V1 = 590 m/s at the beginning of its travel (at pos. 1).
The shock travel time through the discharge over the base distance Δx can be determined by integrating eq. (17) over time for x, that gives
x = ε 1 ε 2 e x p ε 2 t + t λ − x 0
From the boundary condition {t = 0, x = 0}, the integration constant in (20)
x 0 = ε 1 ε 2 e x p ε 2 t λ
Then the travel time tp is determined by applying the boundary condition {t = tp, x = Δx} to eq. (20), from which
t p = − t λ + 1 ε 2 l n ε 2 ε 1 Δ x + x 0
Finally, using (17), the shock velocity V 2 u p t = t p at its final location (pos.2),
V 2 u p = ε 1 e x p ε 2 t p + t λ
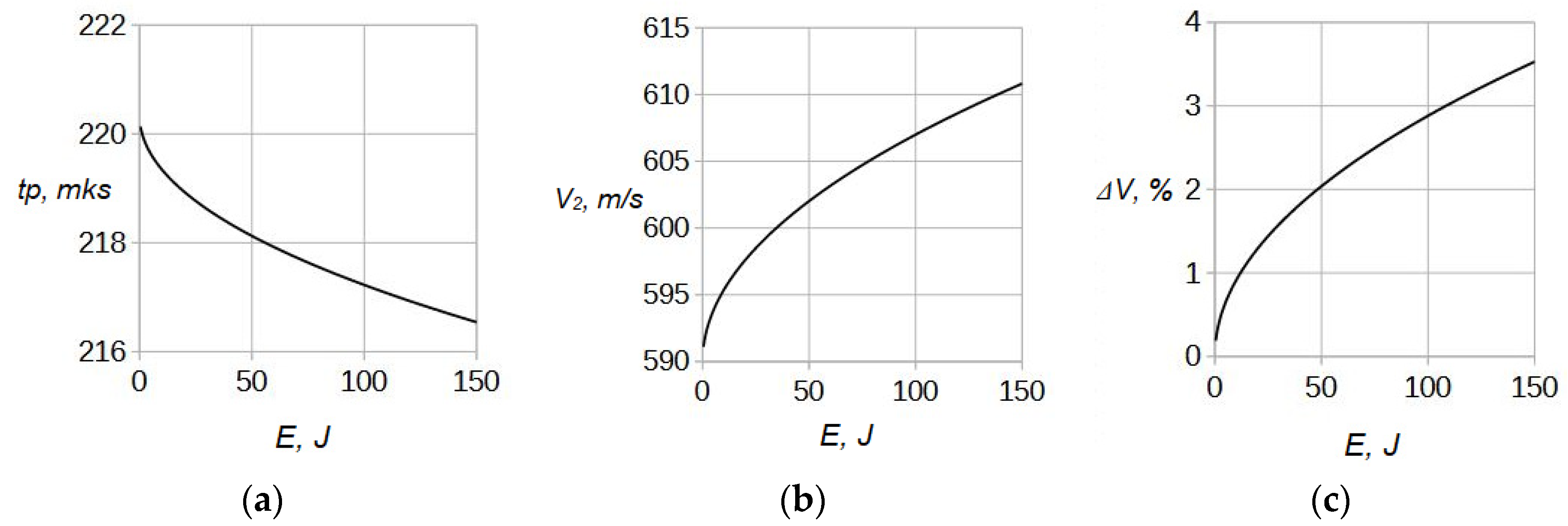
The graph in Figure 2a presents numerical values of the shock travel time tp from (22) vs. the explosion energy E, between locations at pos.1 and pos.2, i.e. over the testing distance Δx =10.5 cm. The corresponding shock velocities (23) are shown in the graph in Figure 2b. Since the exact value of the explosion energy at which the data was obtained in the experiment was not reported, the calculations were performed in the whole interval of energies, up to E = 150 J.
The graph in the Figure 2(b) shows that the shock starts its motion down the decreasing density path with the velocity V(up)1 = 590 m/s (as measured at pos.1), and accelerates up to V(up)2 = 611 m/s when reaching pos.2 (at the maximum value of the explosion energy, E = 150 J). The relative increase in the velocity Δ V u p = V 2 u p − V 1 u p / V 1 u p acquired by the shock between pos.1 and pos.2 is demonstrated in the Figure 2c. It is non-linearly dependent on the shock strength and increases with its value reaching 3.5% at the maximum energy of 150 J. The corresponding experimental value for the shock propagating in this direction is 6.5%.
In case the shock propagates in the opposite direction, i.e. down the increasing density path
ρ = ρ 0 e x p x / z 0
the corresponding numerical solution for the flow velocity obtained in [2,18] is the decreasing function of time. As in the previous case, we approximate it with an exponential function for the flow velocity Ur (t/τ)
U r t τ = U 0 d e x p − a d t τ
where the parameters U0d = 0.7478 and ad = 0.4024 are obtained from the fit to the data, and the scale of the density gradient is determined by the same relation (12). Using the scaling factor for the velocity
U r t τ = u r τ z 0
and relation (16) between the flow and shock velocities, we obtain for the shock
V s w d = δ 1 e x p − δ 2 t + t η
where
δ 1 = γ + 1 2 z 0 τ U 0 ,   δ 2 = a d τ
The parameter tη in (27) is similarly introduced to match the function to the particular value of the velocity V(d)1 measured at the beginning of the shock’s motion through the testing gap. For this, the boundary condition {t = 0, Vsw = V(d)1} is used together with the eq. (27), where V(d)1 is the measured velocity with which the shock starts its travel through the testing gap at pos.1. From this condition, we obtain
t η = − 1 δ 2 l n V 1 d δ 1
The shock travel time in the discharge can be determined by integrating the eq. (27) over time for x, from which we obtain
x d = − δ 1 δ 2 e x p − δ 2 t + t η + x 0 d
The integration constant in (30) is obtained from the second boundary condition, {t = 0, xd = 0},
x 0 d = δ 1 δ 2 e x p − δ 2 t η
Then the shock travel time over the base length Δx is determined by applying the third boundary condition {t = tp, xd = Δx} to eq. (30), from which
t p d = − t η d − 1 δ 2 l n − δ 2 δ 1 Δ x − x 0 d
Finally, in accordance to eq. (27), the shock velocity at the end of the testing gap
V 2 d t = t p = δ 1 e x p − δ 2 t p d + t η d
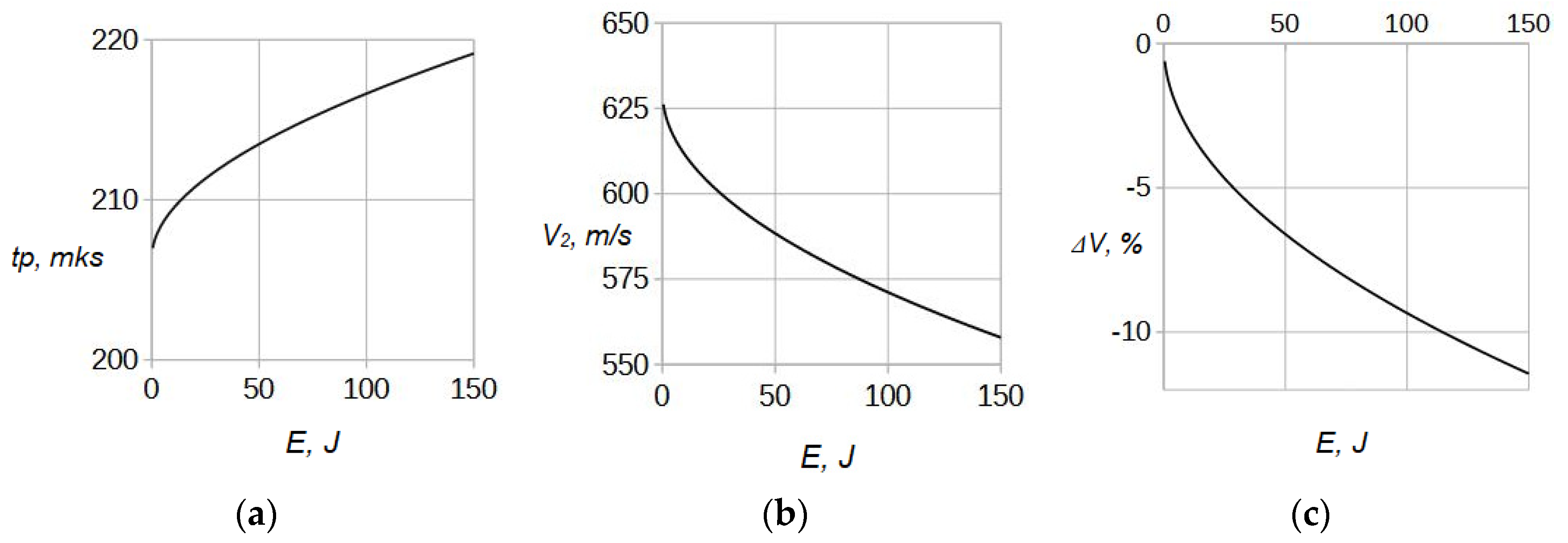
Numerical results for the travel times tp over the propagation distance Δx =10.5 cm are obtained from (32) and plotted in Figure 3a as a function of the explosion energy E. In the graph, the slowing down action of the increasing density gradient is demonstrated with longer travel times. The corresponding shock velocities (33) acquired for the times tp are plotted in the graph of Figure 3b. It shows that the shock starts its motion at pos.1 with the velocity V(d)1 = 630 m/s, as measured in the experiment, and decelerates non-linearly to V(d)2 = 550 m/s (at E = 150 J) when reaching the location at pos.2. The relative change of the velocity Δ V d = V 2 d − V 1 d / V 1 d over the testing gap length Δx = 10.5 cm is shown in Figure 3c. It is is non-linearly dependent on the shock strength and reaches 12% at the maximum energy E. In the experiment, the corresponding measured value of the velocity difference is 6.5%. Combing the results into two-way effect, i.e. for the shock velocity difference when the electrode polarity is switched, the value ΔV(up) = 3.5% in case of decreasing density is added to ΔV(d)= 12% for the case of increasing density, yielding the total maximum velocity difference ΔV = 15.5% (at E = 150 J). The result is higher than the corresponding experimental value of 12%. However in comparing the values, it should be noted that the maximum equivalent of the explosion energy used in the experiment was 120 J. At this energy, the calculated value taken from the graphs is ΔV = 13.5%. Also, there are always unavoidable losses causing only a portion of the spark energy to be invested in the shock wave. This requires the calculated velocity change to be taken at some lower energy E < 120 J, thus bringing it further down, closer to the experimental measurements.
The problem of a shock propagating through a medium with the density increasing in accordance to the power law
ρ x = ξ x α
was considered in 1950s by a number of authors in [19,20,21]. The solution for the shock velocity v as a function of travel distance x was obtained in the form of numerical exponents β
v = ζ x − β
The solution covers linear distribution at α = 1, quadratic at α = 2, and parabolic at α = ½. The numerical parameters β obtained for each distribution case are presented in the first column of the Table I.
Applying the solution to the conditions of the experiment, we use the boundary conditions at pos.1,{x = x1, ρ = ρ1, v = v1}, and at pos.2 {x = x2, ρ = ρ2, v = v2}, from which
x 2 x 1 = ρ 2 ρ 1 1 α
and
v 2 v 1 = ρ 2 ρ 1 − β α
Then the velocity decrease Δv = v2 – v1 associated with the density increase by Δρ = ρ2 - ρ1 over the distance Δx = x2 -x1
Δ v v 1 = 1 − Δ ρ ρ 1 − β α − 1
Using the values of β from the Table I, we obtain the final forms of the expression (38) for each distribution type,
Δ v v 1 = 1 − Δ ρ ρ 1 − 0.21779 − 1 , α = 2
Δ v v 1 = 1 − Δ ρ ρ 1 − 0.22335 − 1 , α = 1
Δ v v 1 = 1 − Δ ρ ρ 1 − 0.22820 − 1 , α = ½
In the pure nitrogen gas, for particular value of the density change Δ ρ ρ 1 = 0.2977 corresponding to the temperatures T1 and T2 measured at the two ends of the testing gap, the relative velocity difference
Δ v v 1 = 0.08005 , α = 2
Δ v v 1 = 0.08213 , α = 1
Δ v v 1 = 0.08399 , α = ½
The results (42-44), also summarized in Table I, show that the velocity difference is on the level of 8.0-8.4%, while the corresponding experimental value for this direction of the electric field is 5.5%.
The solution (38) does not give a dependence on the shock intensity and thus does not allow analyzing the discrepancy on this factor. In discussing how close matching between the calculated and experimental values can be expected, the following two major facts should be noted. First, in the experiment the exact value of the stored capacitor energy used here as the explosion energy equivalent, was not specified for the data on the velocity difference. Therefore, the calculation results should rather be treated as obtained in the whole interval of energies, and, in comparison with the data, the estimate of the ultimate precision is in limbo. And second, the shock velocity was measured as averaged with laser separation of 2.5 cm in each station. This value is comparable to the base measurement distance Δx = 10.5 cm, and therefore this should add to the experimental uncertainty. With this, and accounting that the calculated values were obtained slightly above the experimental ones and the actual shock strength in the experiment could be only lower than that assumed in the calculations, the estimated values can still be considered quite closely falling within the measurement error of the experiment. Therefore, it can be concluded that the density gradients induced by the discharge are fully capable of accelerating the shock to the levels observed in the experiments.

III. Conclusion and Discussion

The reasons causing a shock wave acceleration or deceleration in a positive column of a dc discharge depending on orientation of electric field have been explored. Analyzing the existing research on the gas state established by a discharge passing through it, two main properties phenomenologically capable of affecting the shock motion were identified. At the conditions of the experiment, the neutral gas flow induced by the discharge was found too weak to cause the observed effect. However, the axial gas density gradients caused by the imbalance in the momentum transfer to the neutral component in the discharge, have been shown fully capable of causing the shock acceleration. Numerical calculations showed that the linear, exponential, and power law distributions can affect the shock motion at the levels observed in experiments. The gradient strengths were estimated based on the difference in the gas temperature measured at the two ends of the testing section in the positive column. The assumption of the gradient presence in the gas volume was justified with the fact that the gas temperature near the anode was measured higher than that by the cathode, and consequently the effects of local gas heating typically present in the cathode region could be ruled out.
Applying the existing solutions for a shock wave propagating through a non-uniform medium, the expressions for the shock velocities up and down the gradients were derived for the specific settings of the experiment. Numerical calculations done for the base distance of 10.5 cm showed that, for a two-way motion of the shock relative to the electric field direction, i.e. up and down the exponentially decreasing density, the combined relative difference in the shock propagation velocities amounts to up to 13.5% (at the explosion energy of 120 J). If unavoidable losses of the energy of the spark generating the shock wave are taken into account, this value goes down bringing the result closer to the corresponding experimental value of 12%. In case of density increasing with the power law over the same base distance, the shock slows down by 8.0%, 8.2%, and 8.4% for the exponential index α equal to 2, 1, and ½ accordingly. The result is still not far from the experimental value of 5.5% and, accounting for the measurement technique uncertainty, it falls closely within the measurement accuracy. Thus it can be concluded that, with a good accuracy, the gas gradients induced by a dc discharge are capable of shock acceleration or deceleration observed in the experiments.
Simultaneously with the shock acceleration, the changes in the shock structure such as small bending and widening of the shock front are among other characteristics of the discharge effects. Since positive columns of dc discharges are characterized by uniformity to a high degree, the absence of strong local non-uniformities make such mechanisms as shock refraction or transverse density gradients out of consideration. In trying to explain the phenomena, a returning gas flow organizing in the discharge tube can be evoked. Induction of the flow is the consequence of the charged particle radial distribution set in the positive column, in which the axial flow velocity component features the two-way motion profile as in Figure 1. In the laboratory reference frame, when the flow velocity is added to the shock velocity in one region and subtracted in another, those portions of the shock front will be pulled in the two opposite directions. This results in the front’s continuously increasing deformation as the shock progresses through the discharge. The effect is obviously very weak because the flow velocities uup and ud are very small compared to that of the shock Vsw. However, noting that the total widening ΔS of the front
Δ S = u u p + u d t p ,   t p = L / V s w − u u p − u d
is time- (or the propagation length L) dependent, the deformation will accumulate. Similar considerations apply when the shock is moving toward the cathode, in which case the signs of the velocities Vsw, uup, and ud in (45) reverse to opposite, however the resulting shock profile will be oriented same way as in the first case. In applying this to the experiment [1] however, where the ring type of electrodes was used, the returning flow distribution is unlikely. In this case, the shock front distortion should be expected of a parabolic shape, following the flow velocity distribution with ud = 0. Assuming the flow velocity of 1 m/s and at the conditions of the experiment, the estimated shock front widening is on the order of 0.2 mm over the testing gap length of 10 cm, the value that is observable in experiments.
Next, interesting and relevant to this research effect to discuss is the electrode-polarity dependent shock front recovery. The phenomenon takes place at the exit of the discharge, where PAD signals first widened during the shock’s propagation through the positive column, return to its pre-entrance delta-function shape. In the experiment, the recovery length was defined as the distance from the edge of the ring electrode at the end of the glow discharge to the axial location at the end of the tube where the PAD signals recovered. At discharge currents of 10 mA, 30 mA, and 50 mA, the recovery length increased accordingly when the electric field was in the direction of the shock propagation. In explaining the effect, it should be noted that, in the experiment, the shock exiting the electrode area was entering a neutral, cooler, quiescent gas, thus making the plasma effects irrelevant. In this case, thermal gradients in the vicinity of ring electrodes featuring sufficiently strong temperature steps at both ends of the positive column, could cause the front recovery difference. In this case, the shock transitioning from a heated plasma of the positive column into a cooler neutral gas behind the ring electrodes (supposedly of the same temperature at both tube ends), experiences different temperature steps at the crossings: a larger one at the anode, where the plasma temperature is higher, and a smaller one behind the cathode, where it is lower. Assuming the recovery proceeds via the shock refraction mechanism, i.e. largely due to the acoustic impedance change in the two media, the weaker temperature step in the cathode area results in a slower deformation of the front back to its originally planar shape. Similarly, when the shock moves in the opposite direction, starting at the cathode, upon reaching the anode it experiences a stronger temperature jump that supports a faster front restoration, with a shorter recovery distance [22]. While the presence of sharp interfaces at the end of a positive column may not be common, the interfaces of widths extended to some degree are shown to refract the shocks as well [23].
Although the presence of axial gradients in the gas have been shown here as one of feasible reasons for the shock acceleration, other mechanisms also capable of contributing to the phenomenon to some degree should be mentioned. One of them is the electrostatic force taking place in the presence of ionization and externally applied electric fields [24]. The fields of the magnitude on the order of kV/cm present in the sheath region of the cathode can influence the charge separation layer across the shock front that can affect the front structure and its recovery. The evidence and the possibility of mitigating the strength of propagating detonation shocks by application of electric fields was first suggested by J. J. Thomson as early as 1910 [25]. The electrostatic forces acting on the double layer caused by charge separation across the shock front were also cited as a reason for the propagating shock structure alteration in the Direct Simulation Monte Carlo (DSMC) analysis [26].
In the next step aiming at possible applications of the findings, a number of key factors that can be used to manipulate the effect strength may be derived from other research with overlapping interests. DBD environment is one them, provided that major distinctions are kept in mind: a short, nano- to microsecond pulse duration may result in nonequilibrium processes and thus timing in kinetical processes is important; significant electric field component pointing toward the wall that, in contrast to volume forces in dc discharge, keeps the effect localized in the immediate vicinity of the wall; in DBD, no matter what the electrode polarity is, the gas will always be pushed to the same direction along the wall [10].
Contrary to mostly pure gas environments used in the studies on the gas pumping in dc discharges, the DBD research typically conducted in the air adds useful insights on contribution of kinetical processes. Oxygen component abundant in the air, unlike the nitrogen, carries highly electronegative properties thus allowing production of negative ions in the discharge. For air plasma at atmospheric pressure and ambient temperature, three-body attachment of electrons to oxygen
e + 2O2 → O2- +O2
is a potent electron loss mechanism [27]. The reaction (46) is dependent on the square of O2 concentration and proceeds in two stages via the Bloch-Bradbury mechanism: first vibrationally excited ions O2-* are formed that later stabilized in a collision with another O2 molecule. Thus the main mechanism of negative ions is the 3-body two-stage electron attachment to the electronically excited molecule, in which O2(a1Δg) molecule is extremely stable to deactivation by collision with other molecules or walls. The attachment rates in a discharge are dependent on the E/N factor, and as the electric field increases, the three-body electron attachment to oxygen rate increases, thus decreasing the electron density number. With further increase in E/N, such processes as electron detachment from O2- due to collision with N2 or with the exited state O2(a1Δg) molecules result in an increase in the electron density as the attachment rates decrease. The dominant role of negative ions, O2- in the actuation has been discussed in [28], and three-body electron attachment was also shown to be one of more important processes for removal of low-energy electrons from the upper atmosphere [29], and in the weakly ionized gas in DBD [30]. A number of interesting facts were found in the studies [27] showing that water vapor may absorb electron energy thus reducing its energy in the flow. Among the reactions found contributing to the balance are the increase of reaction rate for 3-body electron attachment to oxygen with electric field strength, and detachment of electrons from negative ions that may occur due to acceleration of negative ions by electric field with a subsequent detaching collision with N2, O2, or O2(a1Δg) molecules. Accounting that the gas pumping force is dependent of the charged particle number and the momentum transfer imbalances, introducing the kinetic factor is one of the keys to control it.
Among other factors that might affect the imbalance in the momentum transfer to the neutral component and consequently the gas pumping effect, are gas mixes and dosed addition of other gases. Electrophoresis, the process of separation of heavy and lighter gases, is one of the obvious ways of establishing desired density gradients if an appropriate mix is chosen. The gas addition effect was studied in [31], using an asymmetrical DBD flow actuation. In the pure nitrogen gas, the positive ions born during the first phase (forward stroke) of the RF-cycle drift toward the under-dielectric electrode, producing strong ion wind suction through momentum exchange collisions with neutrals. A lesser flow was induced during the reverse voltage swing, however it was significantly enhanced by adding oxygen to the gas. The increase of total ion numbers, compared to pure nitrogen, was attributed to lower ionization potential of O2 [32]. Similar effects were also recorded in experiments with EHD thruster using plasma jets at low pressure of 10 Torr in oxygen, argon, and nitrogen [12]. An EHD thruster uses externally applied electric field that generates plasma inducing the flow of charged particles. It transfers its momentum to neutral component of the plasma, thus generating the flow stream jetting out of the thruster. The experiments showed that using oxygen as propellants resulted in much more efficient thrust and thrust-to-power ratio yielding the axial flow velocity about 15 cm/s, while in the two other gases it was limited with 5 cm/s. With relatively short duration of electric field pulses, the inertia of a heavy negative ion in gaining energy in the electric field was associated with the delay in gaining the drift velocity Vi- until it is equal to that for a positive ion Vi+. The evidence for this was also described in [33], where the effect of momentum transfer from ions to gas molecules was negligibly small due to the short duration of the nanosecond pulses used to generate plasma driving the helium jet. The effect of the delay can be accumulated thus creating a disbalance in the force on the neutral gas relative to virtually instant energy gain by electrons.
Considering the presence of reaction (46) in dc discharges, the possibility of affecting the shock motion is dependent on ability of the negative ions to change the momentum transfer balance. First considering the force component on the charged particles due to wall effects, F = e(ne+ni++ni--)E, the production of negative ions does not appear influencing the force via the change in the number of charges of one sign or momentum transfer rate. One of the reasons is that an increase in negative ion number is compensated by the loss in the number of electrons. As to the momentum transfer, slower and less frequently colliding negative ions should still transfer the same energy to the neutral particles as the lost electrons did. If the ion drift velocity is much higher then that for the gas flow, the gas molecules can be considered at rest and, on the average, all momentum of a charged particle in a collision is given up to a neutral molecule. In an elastic collision, the momentum transfer Δeg from an electron to a neutral gas molecule
Δ e g = ν e g m e V e
and that from a negative ion to a molecule
Δ i g = ν i g m i V i
where νeg and νig are the momentum transfer collision frequencies, and Ve and Vi are the electron and the ion drift velocities accordingly. Using the definition of drift velocity V d = μ E and for the particle mobility μ = e / ν m , we obtain
Δ e a / Δ i a = 1
It follows then that, assuming that in the three-body collision (46) between two oxygen molecules and an energetic electron the newly created negative ions have time to gain energy in the electric field, the contributions from the two components to the wall force component are equal and occur in the same axial direction. The disbalance due to non-equilibrium state that may be present in short pulse discharge plasmas will cease in the static settings of a dc discharge positive column and thus will not contribute.
The above situation changes in the presence of charge transfer reactions, when fast ions hitting neutral molecules exchange the charge but do not share kinetic energy, the reaction that results in a slow ion and a fast neutral molecule. A fast ion becomes a fast neutral, and a slow neutral molecule becomes a slow ion. Considering this reaction in an elastic collision, assume that on the average a moving ion transfers all its energy to a gas molecule. In terms of momentum transfer, the reaction is equivalent to elastic momentum transfer in a regular ion-molecule collision, and thus does not introduce a change in the net force on the gas. However, if to take into account the fact that actually, at random, an ion can still retain about a half of its momentum after an elastic collision with a neutral molecule, the charge transfer reaction allows twice a net momentum transfer to the gas compared to that in a regular elastic ion-molecule collision [17]. The reverse process occurs when a fast neutral molecule picks up a charge from a slow ion and the pair become a fast ion and slow molecule. Consequently, the momentum is transferred back from the neutral component to the ion resulting in the momentum loss for this component. In a steady state attainable in dc discharges, and accounting for the rates of the reactions in the presence of negative ions in the mix of gases, a desirable change in the net force on the neutral component and consequently the induced gradients and the gas flow can be expected.
The results obtained in this work can be found useful in the fields of research studying shock waves interacting with discharge environments, particularly for manipulating of hypersonic flows. Among them are the aerospace applications for flap-less flight control, wave drag and sonic boom attenuation, or anywhere else where shock waves encounter areas of active discharges.

References

  1. Bletzinger, P.; Ganguly, B.N. Local acoustic shock velocity and shock structure recovery measurements in glow discharges. Phys. Letters A 1999, 258, 342–249. [Google Scholar] [CrossRef]
  2. Zel’dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High Temperature Hydrodynamic Phenomena II; Academic: New York, 1966; p. 525. [Google Scholar]
  3. Avramenko, R.F.; Rukhadze, A.A.; Teselkin, S.F. Structure of a shock wave in a weakly ionized non-isothermal plasma. JETP Lett. 1985, 34, 85–87. [Google Scholar]
  4. White, A.; Aithal, S.; Subramaniam, V.V. Experimental studies of spark generated shock waves, Conference Paper AIAA-99–3670. In Proceedings of the 30th Plasmadynamics and Lasers Conference, Norfolk, VA, 28 June–1 July 1999. [Google Scholar]
  5. Enciclopedia of physics, V. XXII, Gas Discharges II, Edited by S. Flugge, Springer Verlag, Berlin-Gettingen-Heidelberg, 1956, pg.199.
  6. M. N. Hirsh, H. J. Oskam, Electrical Discharges, V.1, Gaseous Electronics, Academic Press (1978).
  7. Chester, A. Experimental measurements of gas pumping in an Argon discharge. Phys. Rev. 1968, 169, 169. [Google Scholar] [CrossRef]
  8. Langmuir, I. The pressure effect and other phenomena in gaseous discharges. J. of the Franklin Inst. 1923, 196, 751–762. [Google Scholar] [CrossRef]
  9. Opatis, D.; Schneider, M.; Miles, R.; Likhanskii, A.; Machetert, S. Surface charge in dielectric barrier discharge plasma actuators. Phys. Plasmas 2008, 15, 073505. [Google Scholar] [CrossRef]
  10. Likhanskii, A.; Schneider, M.; Machetert, S.; Miles, R. Modeling of interaction between weakly ionized near-surface plasmas and gas flow, 44th AIAA Aerospace Science Meeting and exhibit, 2006, Reno, NV.
  11. Kim, W.; Do, H.; Mungal, M.; Cappelli, M. On the role of oxygen in dielectric barrier discharge actuation of aerodynamic flows. Appl. Phys. Lett. 2007, 91, 181501. [Google Scholar] [CrossRef]
  12. Granados, V.; Pinheiro, M.; Sa, P. ,Study of the design and efficiency of single stage EHD thrusters at the sub-atmospheric pressure of 1. 3 kPa. Physics of Plasmas 2017, 24, 123513. [Google Scholar] [CrossRef]
  13. Thomas, F.; Corke, T.; Iqbal, M.O.; Kozlov, A.; Schatzman, D. Optimization of Dielectric Barrier Discharge Plasma Actuators for Active Aerodynamic Flow Control. AIAA Journal 2009, 47, 2169–2178. [Google Scholar] [CrossRef]
  14. Dufour, G.; Rogier, F. Numerical Modeling of Dielectric Barrier Discharge Based Plasma Actuators for Flow Control: the COPAIER/CEDRE Example. J. Aerospace Lab, Plasmas for High Speed Flow Control 2015, (10). [Google Scholar]
  15. Oskam, H.J. Axial Pressure Gradient in Direct-Current Discharges. Phys. Fluids 1969, 12, 2449–2451. [Google Scholar] [CrossRef]
  16. Leiby, C.; Oskam, H. Volume forces in plasmas. Phys. Fluids 1967, 10, 9. [Google Scholar] [CrossRef]
  17. Chester, A. Gas pumping in discharge tubes. Phys. Rev. 1968, 169, 172–184. [Google Scholar] [CrossRef]
  18. Andriankin, E.I.; Kogan, A.M.; Kompaneets, A.S.; Krainov, V.P. Propagation of a strong explosion in an inhomogeneous atmosphere. PMTF 1962, 6, 3–7. [Google Scholar]
  19. Gandel’man, G.M.; Frank-Kamenetskii, D.A. Shock wave emergence at a stellar surface. Soviet Physics Doklady 1956, 1, 223–226. [Google Scholar]
  20. Sakurai, A. On the problem of a shock wave arriving at the edge of gas. Commune. Pure Apl. Math. 1960, 13, 353–370. [Google Scholar] [CrossRef]
  21. Johnson, C.W. On gas flow in one dimension following a normal shock of variable strength. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 1954, 221, 257–267. [Google Scholar] [CrossRef]
  22. Markhotok, A. Non-Symmetry in the Shock Refraction at a Closed Interface as a Recovery Mechanism. Dynamics 2024, 4, 57–80. [Google Scholar] [CrossRef]
  23. Markhotok, A.; Popovic, S. Shock wave refraction enhancing conditions on an extended interface. Phys. Plasmas 2013, 20. [Google Scholar] [CrossRef]
  24. White, A.R.; Aithal, S.M.; Subramaniam, V.V. On the characteristics of spark generated shock wave. Phys. Fluids 2000, 12, 924–934. [Google Scholar]
  25. Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer; McGraw-Hill: New York, NY, USA, 1984; p. 515. [Google Scholar]
  26. Garner, W.E.; Saunders, S.W. Ionization in gas explosions. Faraday Soc. Trans. 1926, 22, 281. [Google Scholar] [CrossRef]
  27. Vidmar, R.; Stalder, K. Air chemistry and power to generate and sustain plasma: plasma lifetime calculations. AIAA 41st Aerospace Sciences Meeting and Exhibit, 2003, Reno, NV.
  28. Alexandrov, N. Three-body electron attachment to O2(a1Δg). Chem. Phys. Lett. 1993, 212, 409–412. [Google Scholar] [CrossRef]
  29. McEwan, M.; Philips, L. Chemistry of the atmosphere; Arnold: Paris, 1975. [Google Scholar]
  30. Raizer, Y.P. Gas Discharge Physics; Springer-Verlag: New York, 1991. [Google Scholar] [CrossRef]
  31. Enloe, C.; McLaughlin, T.; Font, G.; Baughn, J. 43rd Aerospace Science Meeting and Exhibit, Reno NV (2205), Paper N 2005-0564.
  32. Font, G.; Morgan, W. Recent Progress in Dielectric Barrier Discharges for Aerodynamic Flow Control. Contrib. Plas. Phys. 2007, 47, 103. [Google Scholar] [CrossRef]
  33. Logothetis, D.; Papadopolous, P.K.; Svarnas, P.; Vafeas, P.; Vafeas, P. Comparison of two electro-hydrodynamic force models for the interaction between helium jet flow and an atmospheric-pressure “plasma jet”, 12th international conference of computational methods in sciences and engineering, March 2016. [CrossRef]
Preprints 121278 g001
Figure 1. Schematic diagram for the function fv vs. the dimensionless radial coordinate ρ obtained in [15].Vn fv ρ.
Figure 1. Schematic diagram for the function fv vs. the dimensionless radial coordinate ρ obtained in [15].Vn fv ρ.
Preprints 121278 g001
Preprints 121278 g002
Figure 2. (a) Shock travel times tp over the testing distance Δx vs. the explosion energy E. (b) Shock velocity V2 = V(up)2 at the end of testing gap. (c) Relative difference in the shock velocities ΔV in percents. The shock moves in the direction of exponentially decreasing density.
Figure 2. (a) Shock travel times tp over the testing distance Δx vs. the explosion energy E. (b) Shock velocity V2 = V(up)2 at the end of testing gap. (c) Relative difference in the shock velocities ΔV in percents. The shock moves in the direction of exponentially decreasing density.
Preprints 121278 g002
Preprints 121278 g003
Figure 3. Shock parameters acquired over the testing distance Δx. (a) Shock’s travel time tp vs. the explosion energy E. (b) Shock velocity V2 = V(d)2(tp) at the end of the testing gap. (c) Relative difference in the shock velocities ΔV in percents. The shock moves in the direction of exponentially increasing density.
Figure 3. Shock parameters acquired over the testing distance Δx. (a) Shock’s travel time tp vs. the explosion energy E. (b) Shock velocity V2 = V(d)2(tp) at the end of the testing gap. (c) Relative difference in the shock velocities ΔV in percents. The shock moves in the direction of exponentially increasing density.
Preprints 121278 g003
Table I. Summary for solutions obtained for the shock propagation velocity in references [19,20,21] in the form of exponents β vs. the exponent α, and the relative shock velocity difference Δv/v obtained in this work.
Table I. Summary for solutions obtained for the shock propagation velocity in references [19,20,21] in the form of exponents β vs. the exponent α, and the relative shock velocity difference Δv/v obtained in this work.
β α Δv/v, %
0.44 2 8.01
0.22 1 8.21
0.11 ½ 8.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated