Prerpints.org logo
Preprint
Article

Analysis of Transient Characteristics and Fault Ride-through Control of Hybrid Grid-tied Converters with Grid-following and Grid-forming

Altmetrics

Downloads

66

Views

27

Comments

0

Submitted:

14 October 2024

Posted:

15 October 2024

You are already at the latest version

Alerts
Abstract
When grid-following (GFL) and grid-forming (GFM) converters are interconnected with the grid, they are mutually coupled through the grid impedance. During grid faults, the transient behavior of these converters becomes intricate due to the presence of coupling terms. Instabilities in one converter can propagate to the other, posing challenges to fault ride-through capability. Firstly, a mathematical model was presented for a hybrid grid-tied system comprising two converters, investigated the conditions for equilibrium points, and employed phase-plane analysis to elucidate the mutual influence mechanism during faults. Then, a method to adjust the power angle of GFM according to the voltage drop was proposed and used in GFL to improve its phase-locked loop. At the same time, considering the influence of GFL current injection, the fault current of GFM was limited, so as to realize the hybrid fault ride-through control. The proposed approach ensures that GFM converters contribute reactive current support to the grid during faults, while GFL converters adhere to grid guidelines for current injection, thereby preventing overcurrent and phase angle instability in both converters. Finally, simulation results validated the correctness and effectiveness of the proposed control strategy.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the implementation of carbon peaking and carbon neutrality policies, renewable energy sources such as wind and photovoltaic power are rapidly developing. The proportion of non-synchronous generators in the power system is increasing significantly [1,2,3]. A high proportion of new energy and power electronic equipment has become a notable characteristic of power systems. However, using grid-following converters as the main grid-connected devices does not provide sufficient inertia and damping for the system, resulting in a further decrease in system inertia, which jeopardizes the safe operation of the power system. Grid-forming converters, which possess the characteristics of a synchronous generator, have garnered widespread attention. Compared to grid-following converters, they can effectively function as a voltage source, allowing them to regulate system voltage and frequency and provide necessary inertia and damping support. Nevertheless, grid-following converters still have advantages that grid-forming converters cannot replace. On the other hand, the current new energy power stations are equipped with grid-following converters, making it impractical to replace them all with grid-forming converters. Therefore, a feasible alternative is to modify some of the already installed converters to grid-forming control. This implies that in future power systems, both grid-following and grid-forming converters will coexist [4,5,6].
In the event of a grid fault, a synchronous generator can inject 6 to 8 times its rated current (pu) to support the grid [7]. However, the overcurrent tolerance of converters is relatively low. Without proper control, this could lead to disconnection of renewable energy generation equipment from the grid or damage to the converters. To address this, IEEE standard 2800-2022 provides detailed technical requirements for renewable energy generation equipment regarding fault ride-through capabilities [8]. Currently, research mainly focuses on the transient processes of single grid-following (GFL) or single grid-forming (GFM) converters during fault ride-through, with an emphasis on the control of fault current and power angle. For GFL (grid-following converters), reference [9] adjusts the active current injection during faults through the feedback of the phase-locked loop (PLL) frequency, but the steady-state operating point and stability are difficult to predict. Reference [10] proposes locking the PLL during faults to maintain the output of the previous moment; however, this approach is challenging to meet the grid code requirements. Reference [11] suggests locking only the integral part of the PLL during faults, but this method fails when there is no equilibrium point after the fault. Reference [12] proposes setting the ratio of active and reactive currents based on the grid impedance after a fault. While this ensures the existence of an equilibrium point, it still cannot fully comply with grid codes. For GFM (grid-forming converters), reference [13] switches the grid-forming control to grid-following control during faults. However, this process requires a backup PLL and may face stability issues in weak grid environments. References [14,15,16] adopt a current limiting method in the current loop of the converter’s double closed-loop control to limit fault currents. However, this approach turns the voltage source into a current source, making power control difficult, reducing stability, and potentially causing instability. Reference [17] proposes a strategy using voltage limiting to control fault current, locking the reactive voltage droop, and calculating the reference voltage based on the maximum allowable current. References [18,19] respectively analyze the transient characteristics of parallel grid-following and grid-forming converters and explore the issue of transient synchronization stability in islanded AC microgrids, considering the dynamic interactions between grid-forming and grid-following converters. However, there is relatively little research on fault ride-through issues under hybrid grid conditions. In fact, during faults, the cooperation between converters with different control strategies can provide better service to the grid.
To overcome the aforementioned limitations, this study introduces a hybrid fault ride-through control strategy aimed at improving the issue of fault ride-through during symmetrical voltage dips when low voltage faults occur in the grid. The main contributions of this strategy are as follows:
  • Parallel System Construction: A coupled effect is generated by the parallel connection of Grid Forming (GFM) and Grid Following (GFL) systems, allowing for the analysis of fault ride-through issues and transient stability under these conditions.
  • Power Stability: A mechanical power adjustment loop is introduced in GFM, and a grid-structured improved phase-locked loop is employed in GFL to determine the balance point between GFM and GFL.
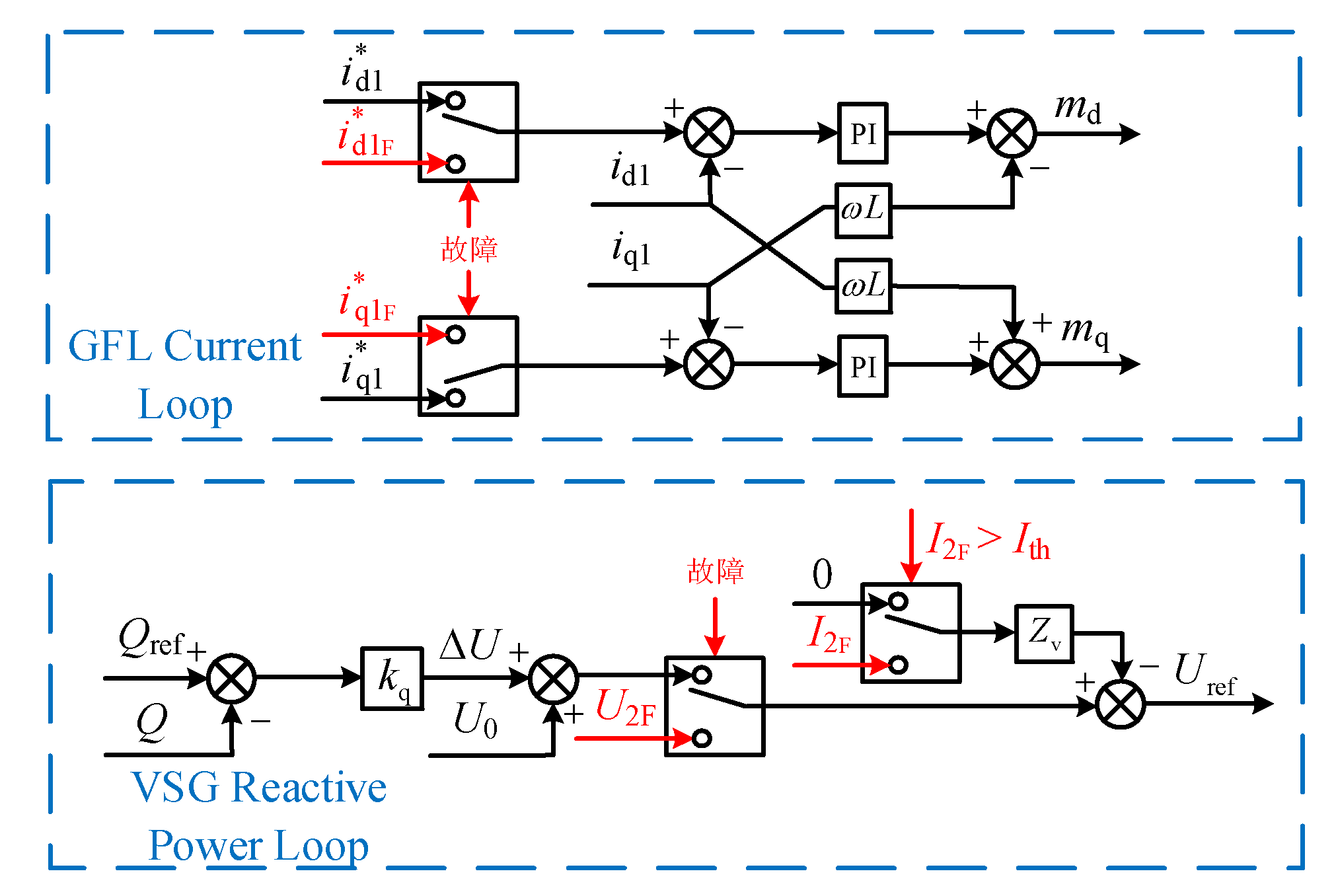
  • Reactive Power Locking: The reactive power output that complies with grid guidelines is supported by replacing the reactive power output with the calculated GFM output voltage U2F to support the grid containing GFL.
  • Transient Fault Current Control: Transient virtual impedance is utilized to suppress transient overcurrent, preventing excessive short-circuit current from damaging power electronic devices in GFM.
The structure of this paper is organized as follows: Section 2 constructs the basic model of the grid-following/grid-forming converter hybrid grid-connected system (HGS). Section 3 analyzes the interaction mechanism between GFL and GFM when a low-voltage fault occurs in the power grid. Section 4 proposes a GFM power angle control considering the influence of GFL current injection and a hybrid fault ride-through control strategy based on an improved grid-forming phase-locked loop. During the fault period, this strategy can not only ensure the power angle stability and limited fault current of the GFM but also enable the GFL to inject current in accordance with the grid guidelines. Section 5 verifies the correctness and effectiveness of the proposed control strategy through simulation.

2. Parallel System of Grid-Following and Grid-Forming Converters

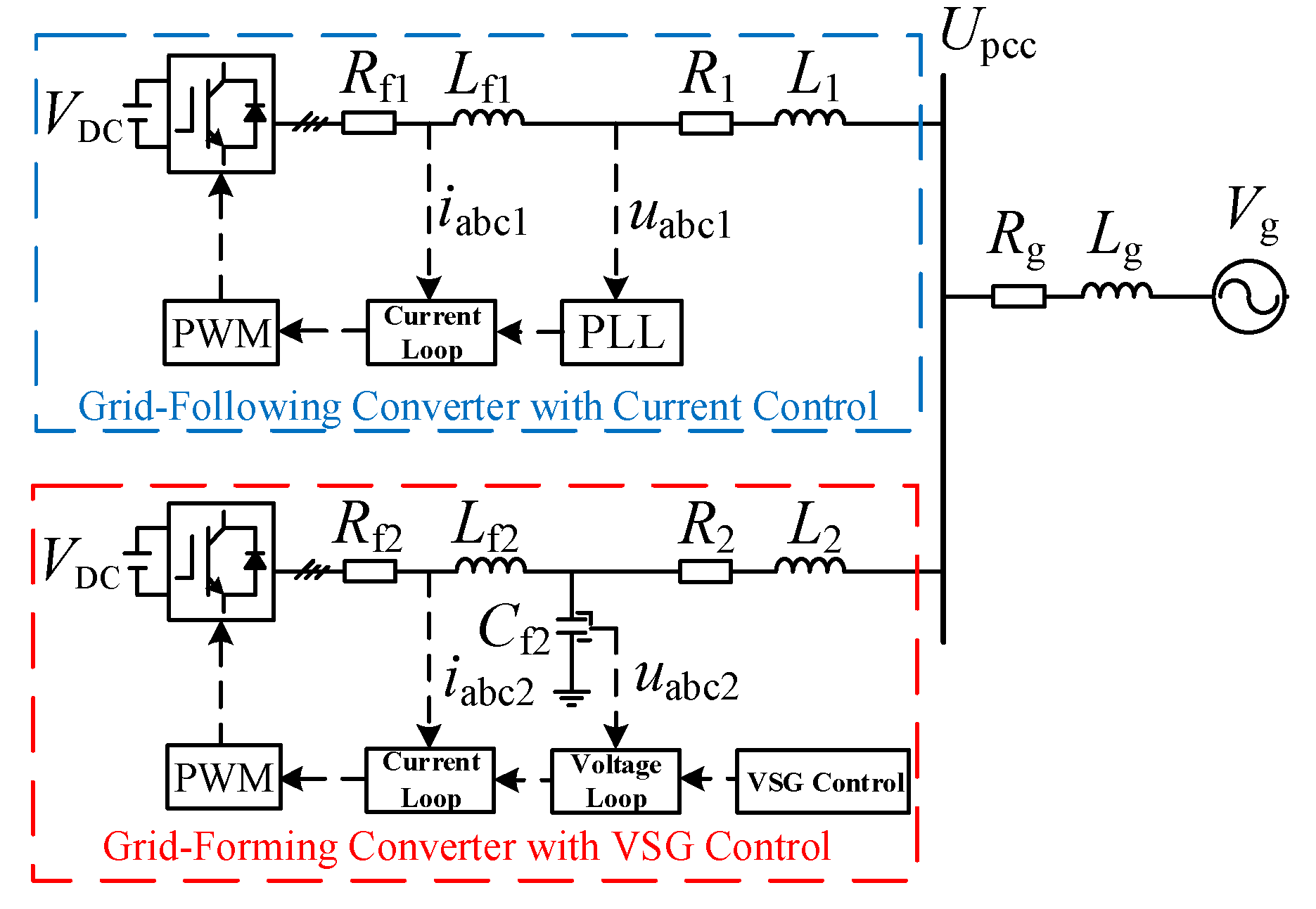
2.1. Main Circuit System Topology

The topology of the studied Hybrid Grid System (HGS) is shown in Figure 1. The grid-following converter uses Phase Locked Loop (PLL) control. There are various control methods for the grid-forming converter, such as Virtual Synchronous Generator (VSG) control, droop control, power synchronization control, and virtual oscillation control. This paper focuses on the more mature Virtual Synchronous Generator control as an example for discussion. Both converters are connected to the main grid through a Point of Common Coupling (PCC).
In this figure, VDC is a constant DC voltage; Rf1, Lf1, Rf2, and Lf2 are the filter resistances and filter inductances for the Grid-Following (GFL) and Grid-Forming (GFM) converters, respectively; Cf2 is the filter capacitor for the GFM converter; R1, L1, R2, and L2 are the line resistances and line inductances for the GFL and GFM converters, respectively; Rg and Lg represent the line resistance and inductance between the Point of Common Coupling (PCC) and the grid; Upcc is the voltage at the Point of Common Coupling; iabc1 and iabc2 are the converter-side currents for the GFL and GFM converters, respectively; uabc1 and uabc2 are the output voltages for the GFL and GFM converters, respectively; Vg is the grid voltage.

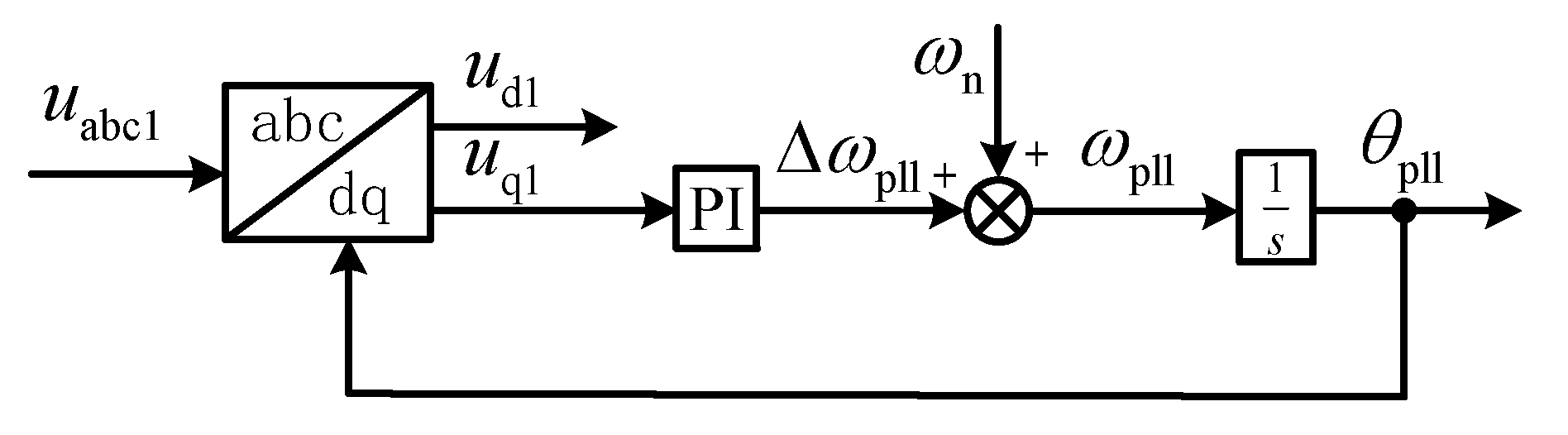
2.2. Grid-Following Converter Based on Current Control

The control part of a current-controlled voltage source converter (CCS) includes a phase-locked loop (PLL), power control loop, current control loop, and PWM signal modulation, among others. The core of the control is the PLL, which achieves synchronization of the CCS with the grid by estimating and tracking the phase of the grid-connected point voltage uabc1. The schematic diagram of the phase-locked loop is shown in Figure 2.
Its mathematical model can be expressed as:
d θ p l l d t = ω p l l d ω p l l d t = k i u q 1 + k p d u q 1 d t
In the equations: θpll is the output phase angle of the phase-locked loop; ωpll is the output angular frequency of the phase-locked loop; ud1 and uq1 are the d-axis and q-axis voltages of the grid-connected point, respectively; ki and kp are the proportional and integral gains of the PI controller. θpll is used as the angle for the Park transformation, achieving decoupled control of active and reactive power by aligning uabc1 with the d-axis, ensuring that uq1 = 0.

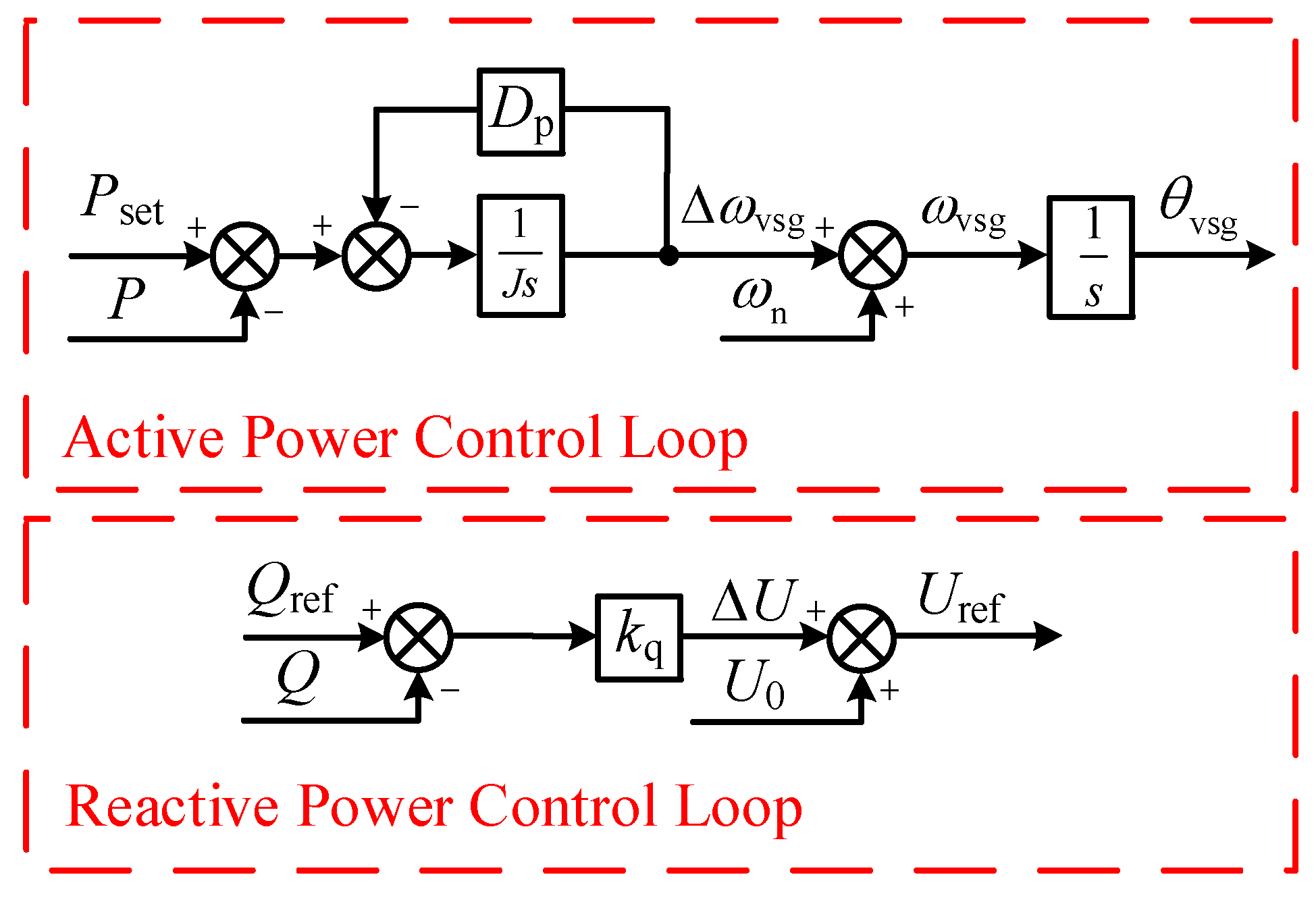
2.3. Grid-Forming Converter Based on VSG Control

The control part of a Virtual Synchronous Generator (VSG) includes an active power loop, a reactive power loop, dual voltage-current control loops, and PWM signal modulation. The core of the control is the active and reactive power loops. VSG achieves synchronization with the grid by mimicking the rotor characteristic equations of a synchronous generator. Consequently, a grid-forming converter based on virtual synchronous generator control possesses the external characteristics of a synchronous generator. The schematic diagram is shown in Figure 3.
The mathematical model of the active power loop can be expressed as:
d θ p l l d t = ω p l l d ω p l l d t = k i u q 1 + k p d u q 1 d t
In the equations: θvsg is the output phase angle of the VSG; ωvsg is the derivative of θvsg; Pset is the input mechanical power; P is the output active power of the VSG; ωn is the nominal angular frequency; J is the moment of inertia; and Dp is the damping coefficient.
The active power loop adjusts θvsg to regulate the output active power P of the VSG, ultimately ensuring that P = Pset.
The mathematical model of the reactive power loop can be expressed as:
U r e f = U 0 + k q Q r e f − Q
In the equations: Uref is the output voltage of the VSG; U0 is the set value of the output voltage; kq is the droop coefficient of the reactive power loop; Qref is the reactive power reference value; and Q is the output reactive power of the VSG.
The reactive power loop adjusts the output voltage reference value based on the output reactive power.

3. Mathematical Model and Transient Characteristics of Parallel System

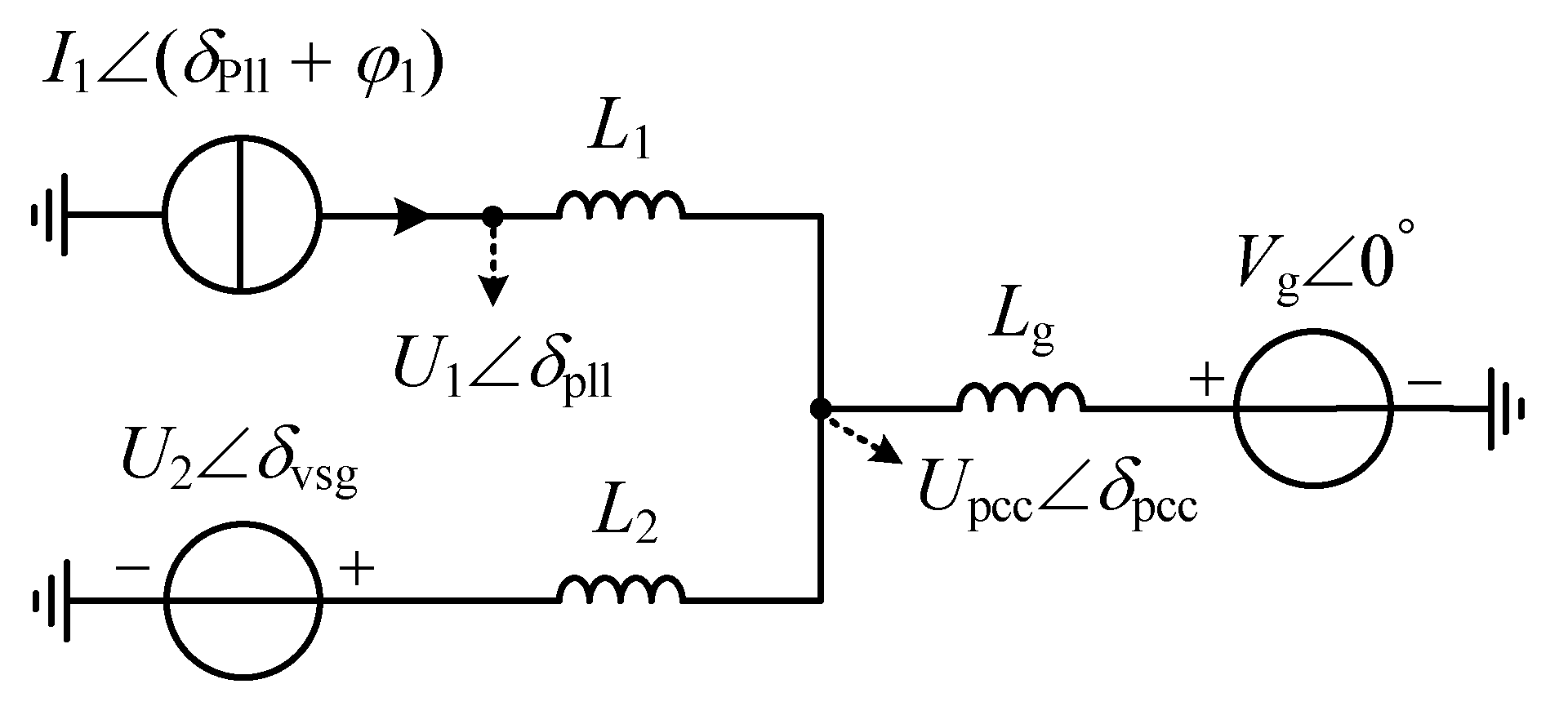
3.1. Mathematical Modeling of HGS.

The bandwidth of the current loop in the grid-following converter (GFL) is significantly larger than the bandwidth of the phase-locked loop (PLL). By ignoring the dynamic process of the current loop, the GFL can be approximated as a current source. Similarly, in the grid-forming converter (GFM), the adjustment speed of the inner voltage and current loops is much faster than that of the active and reactive power loops. By neglecting the dynamic process of the inner voltage and current loops, the GFM can be approximated as a voltage source. Circuit impedance is considered negligible, and the phase angle of the grid voltage is taken as the reference angle. The equivalent circuit diagram of Figure 1 is shown in Figure 4.
In this figure,I1 is the RMS value of the output current of the current-controlled converter; U1 is the RMS value of the output voltage of the GFL;θpll is the phase angle difference between the PLL and the grid, corresponding to the power angle of a synchronous generator, and for convenience, it will be referred to as the power angle hereafter; φ1 is the phase angle difference between voltage U1 and current I1; U2 is the RMS value of the output voltage of the GFM; δvsg is the power angle of the GFM; Vg is the RMS value of the grid voltage.
According to the superposition theorem, the PCC voltage Upcc∠δpcc in Figure 4 can be expressed in the stationary reference frame as:
U p c c ∠ δ p c c = j k 1 I 1 ∠ δ p c c + φ 1 + k 2 U 2 ∠ δ v s g + k 3 V g ∠ 0 °
In the equation: k 1 = ω pll L 2 L g L 2 + L g ; k 2 = L g L 2 + L g ; k 3 = L 2 L 2 + L g .
The point where the phase-locked loop (PLL) measures the voltage is U1∠δpll, which can be expressed as:
U 1 ∠ δ p l l = j k 4 I 1 ∠ δ p l l + φ 1 + k 2 U 2 ∠ δ v s g + k 3 V g ∠ 0 °
In the equation: k 4 = ω p l l L 1 + ω p l l L 2 L g L 2 + L g .
Transforming equation(5) to the dq rotating reference frame based on the phase-locked loop (PLL), the q-axis voltage of U1 can be obtained as:
u q 1 = k 4 i d 1 + k 2 U 2 s i n δ v s g − δ p l l − k 3 V g s i n δ p l l
In equation (6): typically,δvsg,δpll∈[0,π/2].
Comparing equation (6) with the case of a single grid-following converter (GFL) connected to the grid, it can be observed that the q-axis voltage uq1 of the GFL has an additional impedance drop coupling term. The magnitude of this coupling term is related to k2, U2, δvsg, and δpll, indicating that the power angle of the phase-locked loop (PLL) is also influenced by the GFM power angle δvsg.
From Figure 4, the single-phase output complex power of the GFM can be expressed as:
S ˙ 2 = U 2 ∠ δ v s g U 2 ∠ δ v s g − U p c c ∠ δ p c c j X 2 *
In the equation, X2 = ωn L2, where ωn is the nominal angular frequency.
Substituting equation (4) into equation (7), we obtain:
P 2 = k 3 U 2 V g X 2 s i n δ v s g − k 1 U 2 I 1 X 2 c o s δ v s g − δ p l l − φ 1
Q 2 = U 2 2 − k 2 U 2 2 X 2 − k 3 U 2 V g X 2 c o s δ v s g − k 1 U 2 I 1 X 2 s i n δ v s g − δ p l l − φ 1
From equations (8) and (9), it can be seen that the GFL affects both the active power loop and the reactive power loop of the GFM. Compared to the single machine case, an additional active power coupling term and a reactive power coupling term are introduced. The magnitude of this impact is related to k1、U2、I1、X2、δvsg, δpll, and φ1. The power angle of the GFM is also influenced by the output current I1 of the GFL. By calculating the three-phase active power using equation (8) and substituting it into equation (2), it can be obtained that the GFM in steady state satisfies equation (10).
P s e t − 3 k 3 U 2 V g X 2 s i n δ v s g + 3 k 1 U 2 I 2 X 2 c o s δ v s g − δ p l l − φ 1 = 0
In summary, the transient analysis model of the HGS can be obtained, as shown in Figure 5. It can be seen that the integration of the GFL adds a power coupling term to the GFM; similarly, the GFM adds an impedance drop coupling term to the GFL.

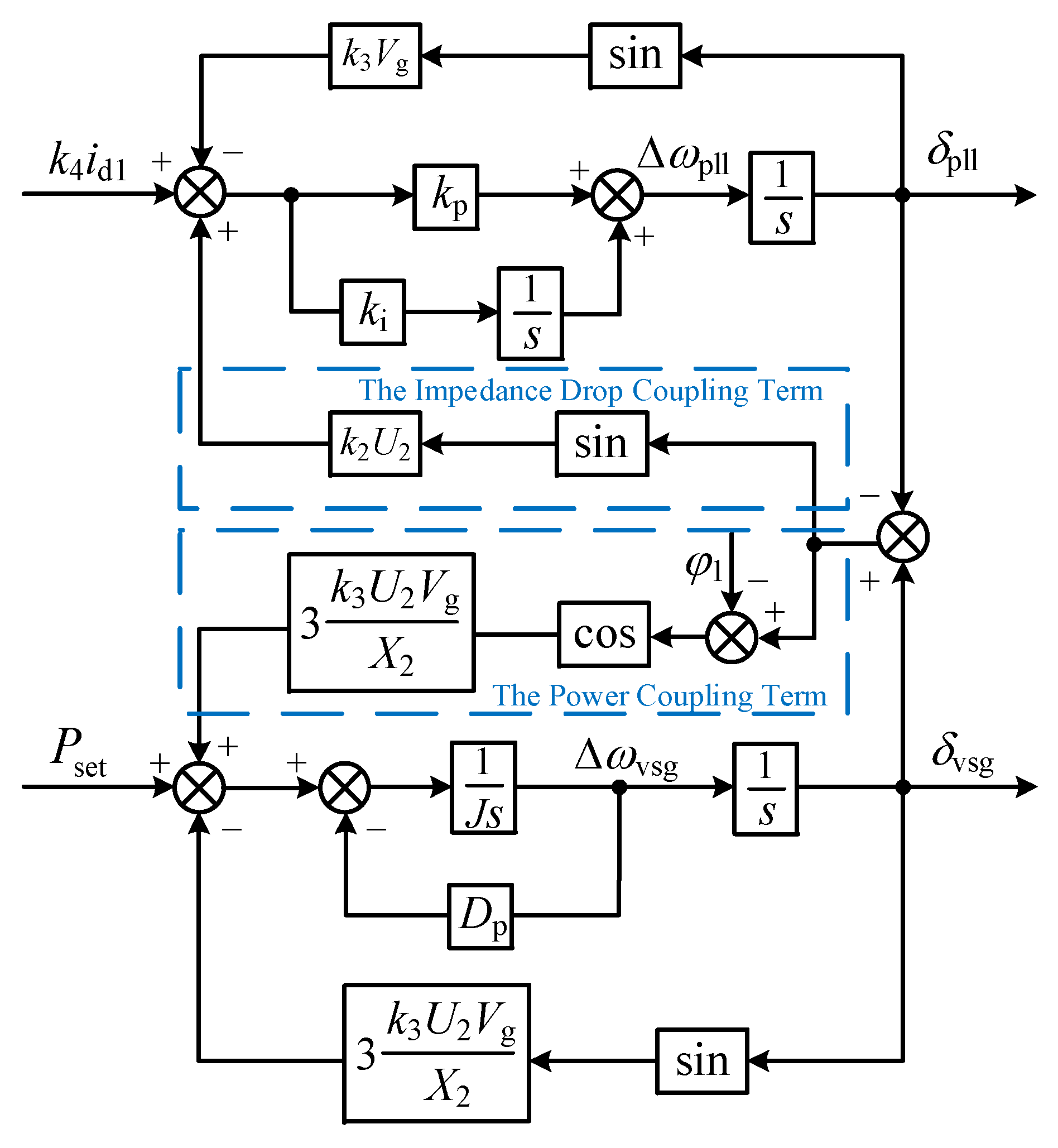
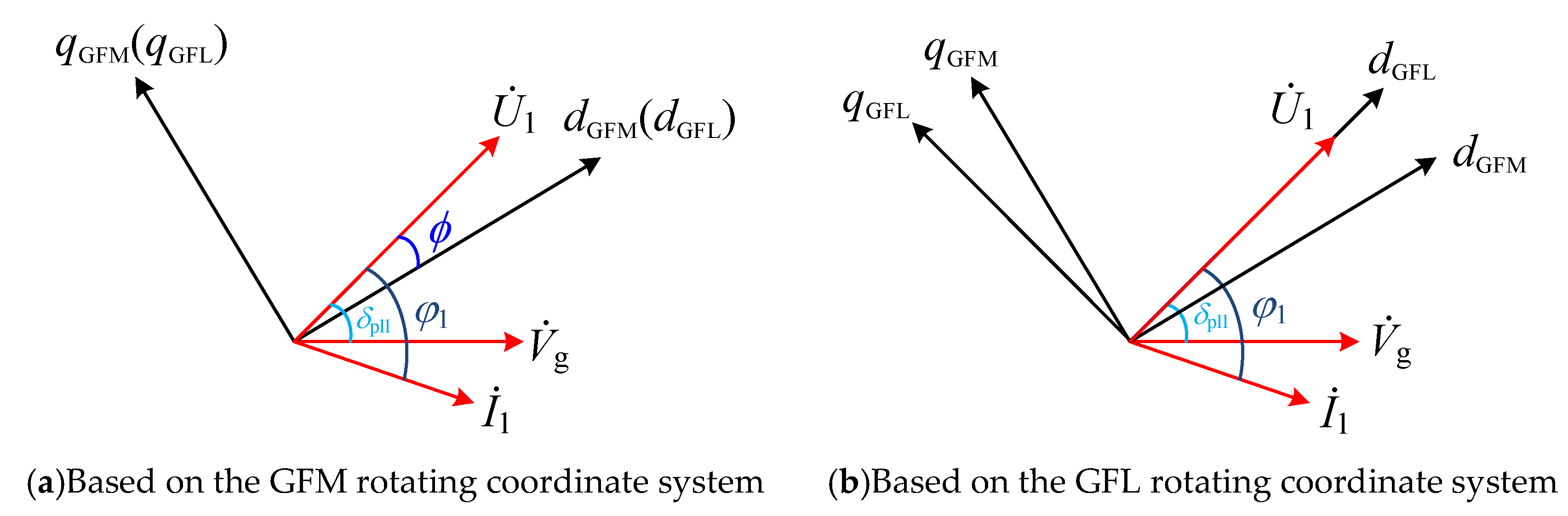
3.2. Transient Stability Analysis Considering Coupling Effects

Setting equation (6) to zero, the condition for the PLL to have an equilibrium point can be obtained as:
k 2 U 2 k 4 2 + k 3 V g k 4 2 + 2 k 2 k 3 U 2 V g k 4 2 c o s δ v s g ≥ i d 1
When the GFM operates stably,δvsg ∈[0, π/2].If i d 1 > k 2 U 2 + k 3 V g k 4 ,then equation (11) cannot be satisfied, and there is no equilibrium point for the PLL. If i d 1 ≤ k 2 U 2 + k 3 V g k 4 , then equation (11) can be satisfied, and an equilibrium point exists for the PLL.
From equation (10), it can be seen that the presence of I1 increases δvsg, reducing the stability margin of the GFM. The magnitude of δvsg is directly proportional to k1, U2, and I1, and inversely proportional to X2. If I1 is too large, it may cause the initially stable GFM to lose power angle stability. If the GFM loses power angle stability due to a fault or other reasons, its output angle δvsg increases indefinitely. As indicated by equation (11), when δvsg=2kπ+π, k∈Z, the impact on the PLL is maximized, leading to two possible situations: ① If equation (11) is not satisfied, the GFL becomes unstable.② If equation (11) is satisfied, since δvsg increases indefinitely, equation (6) remains in a state of adjustment and cannot stabilize or converge to 0, indicating that the GFL becomes unstable.
Therefore, transient instability in the GFM will trigger a chain reaction, causing transient instability in the GFL.
From equation (10), the GFM has a steady-state point when the following condition is satisfied:
9 k 3 U 2 V g X 2 2 + 9 k 1 U 2 I 1 X 2 2 − 18 k 1 k 3 U 2 2 V g I 1 X 2 2 s i n δ p l l + φ 1 ≥ P s e t
When the GFL operates stably,δpll ∈ [0, π/2] and φ1 ∈ [-π/2, 0].If P s e t > 3 k 3 U 2 V g + k 1 U 2 I 1 X 2 , equation (12) cannot be satisfied, and there is no equilibrium point for the GFM.If P s e t ≤ 3 k 3 U 2 V g + k 1 U 2 I 1 X 2 , then equation (12) can be satisfied, and an equilibrium point exists for the GFM.
From equation (6), it can be seen that when δvsg > δ pll, δ pll increases, and the stability margin of the GFL decreases. When δvsg < δpll, δpll decreases, and the stability margin of the GFL increases. When δvsg = δpll, the coupling term is zero, and δpll is not affected by the GFM. If the GFL loses synchronization stability due to a fault or other reasons, the PLL will have no equilibrium point, causing the power angle δpll to increase indefinitely, thereby affecting the GFM. There are two possible scenarios:① If equation (12) is not satisfied, the GFM becomes unstable. ② If equation (12) is satisfied, due to δpll increasing indefinitely, equation (10) remains in a state of adjustment and cannot converge to zero, indicating that the GFM becomes unstable.
Therefore, when the GFL experiences transient instability, the increase in its output phase also causes the GFM to experience transient instability.
In summary, it is essential to ensure the simultaneous stability of both converters; instability in either one will affect the stability of the other.
Additionally, during grid voltage sag, the GFM, being a voltage source type, can experience transient overcurrent and steady-state overcurrent. Under fault conditions, the circuit satisfies:
9 k 3 U 2 V g X 2 2 + 9 k 1 U 2 I 1 X 2 2 − 18 k 1 k 3 U 2 2 V g I 1 X 2 2 s i n δ p l l + φ 1 ≥ P s e t
In the equation:i2F is the instantaneous value of the GFM output current during a fault;u2F is the instantaneous value of the GFM output voltage during a fault;vgF is the instantaneous value of the grid voltage during a fault;i1 is the instantaneous value of the output current of the current-controlled converter.
From equation (13), it can be seen that the presence of the GFL can reduce the fault current of the GFM.
During a fault, reducing the GFL output current id1 not only ensures the existence of the PLL equilibrium point, but also, as seen from equation (6), the reduction of id1 can slow down the acceleration process of the GFL output ωpll during the fault, thereby reducing the deviation of ωpll. Since the inertia of the GFM is much larger than the equivalent inertia of the GFL, the increase rate of δvsg is slower than that of δpll during a fault. Additionally, because the fault duration is short, during the fault, (δvsg − δpll) ∈ [-π/2, 0] [18]. For purely active power output, φ1 = 0, and the reduction in id1 is much greater than the change in the cosine function, so the effect of the cosine function can be ignored. Therefore, when id1 is reduced, the power coupling term in equation (8) is also reduced. From equation (2), it can be seen that this also helps to slow down the acceleration of the GFM output ωvsg during the fault, reducing the deviation of ωvsg. The phase plane diagram of the HGS under different id1 conditions during a fault is shown in Figure 6.
From Figure 6, it can be observed that reducing the active current of the GFL can slow down the acceleration process of both the GFL and GFM during a fault, thereby improving the synchronization stability of the two converters. Moreover, the smaller the id1, the better the synchronization stability of the two converters; conversely, the larger the id1, the worse the synchronization stability of the two converters.
During a fault, reducing the input mechanical power Pset of the GFM not only ensures the existence of the GFM’s equilibrium point but, as shown in equation (2), also slows down the acceleration process of the GFM’s output ωvsg during the fault, reducing the deviation of ωvsg. A decrease in Pset during a fault causes the δvsg of the GFM, which has inertia, to increase more slowly than δpll. The smaller the Pset, the slower the increase of δvsg, the larger the | δvsg − δpll |, and the smaller the impedance drop coupling term in equation (6), resulting in a smaller deviation of the GFL’s output ωpll. The phase plane diagram of the HGS under different Pset conditions during a fault is shown in Figure 7.
From Figure 7, it can also be seen that reducing the input mechanical power Pset of the GFM can similarly slow down the acceleration process of both the GFM and GFL during a fault, thereby enhancing the synchronization stability of the two converters. Moreover, the smaller the Pset, the better the synchronization stability of the two converters; conversely, the larger the Pset, the worse the synchronization stability of the two converters.

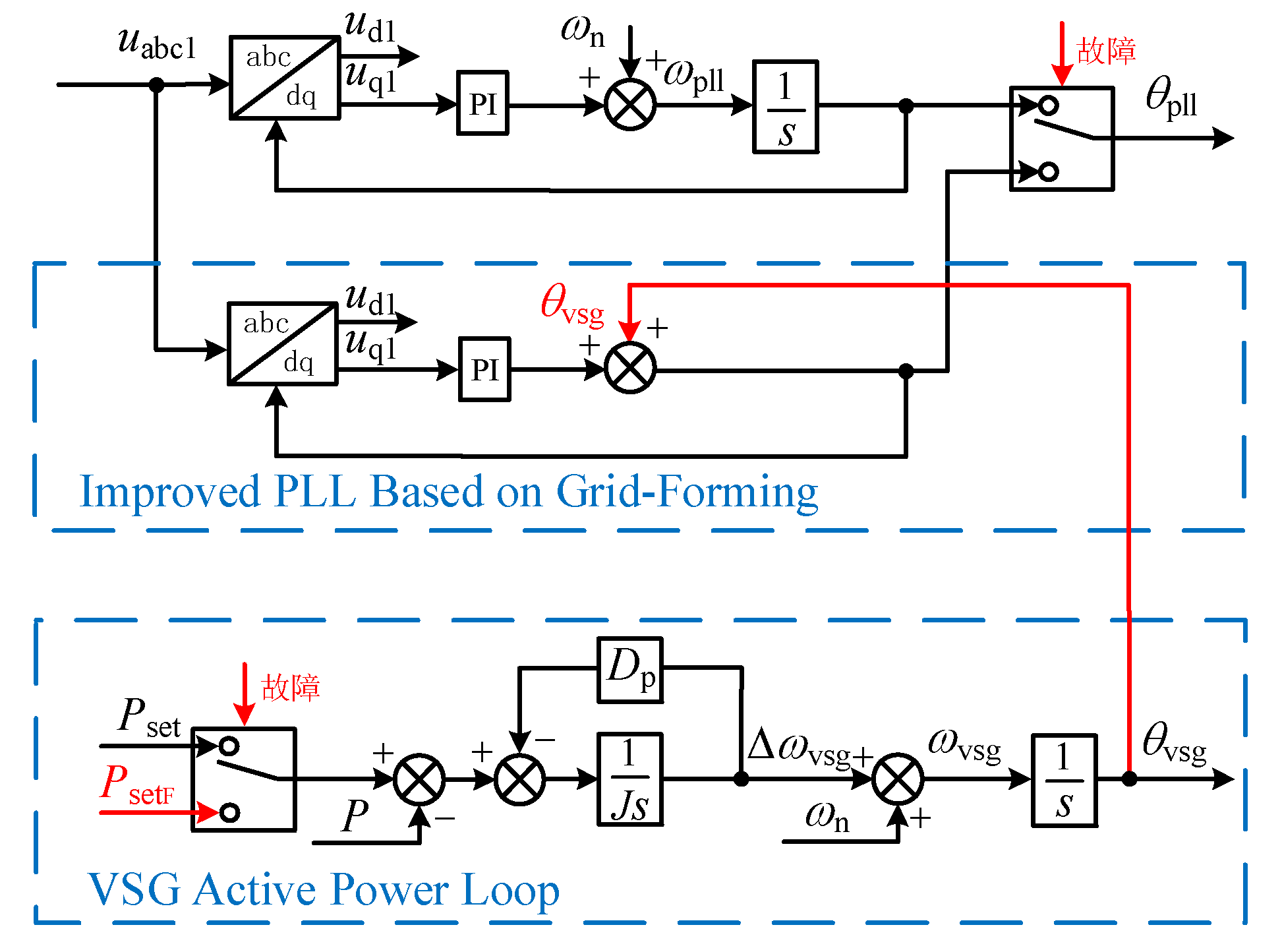
4. Fault Ride-through Control of the HGS

During a low voltage sag fault in the grid, the HGS faces three issues: power angle instability caused by the power imbalance between the GFM and GFL; outputting reactive current in compliance with grid codes to support the grid; and the risk of overcurrent due to the large short-circuit current of the GFM, which threatens power electronic equipment.
From the previous analysis, it is known that reducing id1 and Pset during a grid fault helps ensure the existence of the equilibrium points of the GFL and GFM, and simultaneously enhances the transient stability of both converters. However, the conditions for the existence of the equilibrium points of both converters are coupled through the GFL power angle δpll, the GFL output current I1, the GFM power angle δvsg, and the GFM output voltage U2. Directly controlling the power angles by adjusting id1 and Pset is quite challenging. Therefore, this paper first determines the values of the GFM power angle δvsgF, the fault currents I1F and I2F during the fault, and then calculates the required VSG output voltage U2F and mechanical power PsetF based on the power angles.

4.1. Transient Power Angle Control

During a grid fault, while maintaining power angle stability, the GFM power angle δvsgF is adjusted based on the extent of the grid voltage sag to modify the reactive component of the output current during the fault, thereby supporting the grid. The adjustment rules are as follows:
δ v s g F = V g F V g δ 2 0 , 0.2 < V g F V g < 0.9               0 , V g F V g ≤ 0.2
In the equation, δ 0 2 is the power angle of the GFM before the fault;VgF is the RMS value of the grid phase voltage after the fault. During the fault, by adjusting Pset, we can control the power angle of the GFM, making it reach δvsgF under the corresponding VgF.
According to equation (11), the equilibrium point of the PLL is not only related to the output current id1 but also affected by the inductances L1, L2, and Lg. Therefore, by adjusting only the current, especially in a weak grid environment, it is impossible to ensure the existence of the equilibrium point. Hence, the output phase angle θvsg of the GFM is transmitted to the PLL. However, under this circumstance, the PLL becomes an open-loop system with a steady-state error, making it impossible to precisely align U ( 。 ) 1 with the d-axis.
From Figure 8(a), it can be seen that there is a fixed angular differenceφ between U ( 。 ) 1 and the d-axis dGFL of the GFL. Therefore, the angle of the GFL needs to be adjusted by adding a fixed angleφon the basis of θvsg. This can be obtained by measuring the deviation of uq1 and applying PI control.
θ p l l = θ v s g + ϕ ϕ = k p u q 1 + k i ∫ u q 1
Using equation (15), an improved PLL based on the grid-forming model can be obtained, which can also precisely align U1 with the d-axis of the two-phase rotating coordinate system of the GFL, as shown in Figure 8(b). At this point, the active power and reactive power of the GFL are decoupled.
The PsetF during the fault can be obtained as:
P s e t F = 3 k 3 U 2 V g F X 2 s i n δ v s g F − 3 k 1 U 2 I 1 X 2 c o s ϕ + φ 1
After introducing the input mechanical power adjustment loop in the GFM and adopting the improved PLL based on the grid-forming model in the GFL, the control block diagrams of the GFM and GFL are shown in Figure 9. In this case, as long as the GFM remains stable, the stability of the GFL can be ensured.

4.2. Fault Current Control

4.2.1. Steady-State Current Control

Although the GFM is stabilized by adjusting the input mechanical power, this does not effectively suppress the overcurrent phenomenon. Even though the presence of the GFL can reduce the fault current of the GFM, the GFM may still generate a significant fault current when there is a substantial drop in grid voltage. Therefore, when the fault current I2F exceeds 1.5 times the rated current, the control of the GFM fault current I2F is as follows:
I 2 F = 1.5 I 2 n
In equation (17): I2n is the rated value of the GFM output current.
Since the GFL is a current source type, it will not generate steady-state overcurrent during a fault. However, to support the grid, it needs to output reactive current. The adjustment rules for the output current of the grid-following type are as follows:
I q 1 F = 0 ,   V g F V g ≥ 0.9 − 1.5 0.9 − V g F V g I 1 n ,   0.2 ≤ V g F V g < 0.9 − 1.05 I 1 n ,   V g F V g < 0.2
I d 1 F = I 1 n 2 − I q 1 F 2   , V g F V g ≥ 0.2                     0                   , V g F V g < 0.2
In the equation:I1n is the rated value of the GFL output current;Id1F is the d-axis output current of the GFL during a fault;Iq1F is the q-axis output current of the GFL during a fault.
Based on equations (14), (18), and (19), the values of δvsgF, Iq1F, and Id1F are obtained, respectively. From equations (4), (6), (8), and (17), the following system of equations can be derived:
A − k 3 V g 2 + B 2 − 2 1.5 X 2 I 2 n 2 = 0 k 4 i d 1 F − k 2 U 2 F s i n ϕ − k 3 V g s i n δ v s g F + ϕ = 0 P s e f F = C s i n δ v s g F − D c o s ϕ + φ l F
In equation (20):
In equation (20): φ 1 F = a r c t a n I q 1 F I d 1 F ; I 1 F = I d 1 F 2 + I q 1 F 2 ;
A = U 2 F c o s δ v s g F + k 1 I 1 F s i n δ v s g F + ϕ + φ 1 F − k 2 U 2 F c o s δ v s g F ; B = U 2 F s i n δ v s g F − k 1 I 1 F c o s δ v s g F + ϕ + φ 1 F − k 2 U 2 F s i n δ v s g F ; C = 3 k 3 U 2 F V g X 2 .
Equation (20) can be solved using numerical methods to obtain the output voltage U2F of the GFM and the input mechanical power PsetF during a fault. Since the reactive power loop adjusts the output voltage command, this may lead to inaccurate fault current control. Therefore, during a fault, the reactive power loop is locked, and the calculated U2F is used to replace the output of the reactive power loop.

4.2.2. Steady-State Current Control

The transient current of the GFL is small and has a minimal impact on the system, so it can be neglected. However, the transient current of the GFM is relatively large, and adjusting the reference voltage of the reactive power loop alone is not effective. If left unchecked, it can damage transistors.
Therefore, transient virtual impedance [20] is used to suppress transient overcurrent. The threshold current Ith for the virtual impedance is set slightly above 1.5 times I2n. When the detected fault current exceeds Ith, the virtual impedance is activated; otherwise, the virtual impedance remains inactive. By combining the virtual impedance with the adjustment of the reactive power loop, the output voltage of the GFM can be expressed as:
U r e f = U 2 F − I 2 F Z v
In equation (21): Zv is the virtual impedance.
The overall current control block diagram is shown in Figure 10:

5. Case Study

To verify the theoretical analysis and the proposed fault ride-through control strategy, a hybrid grid-connected model of grid-following and grid-forming converters, as shown in Figure 1, was built in Matlab/Simulink. The system parameters are listed in Table 1.

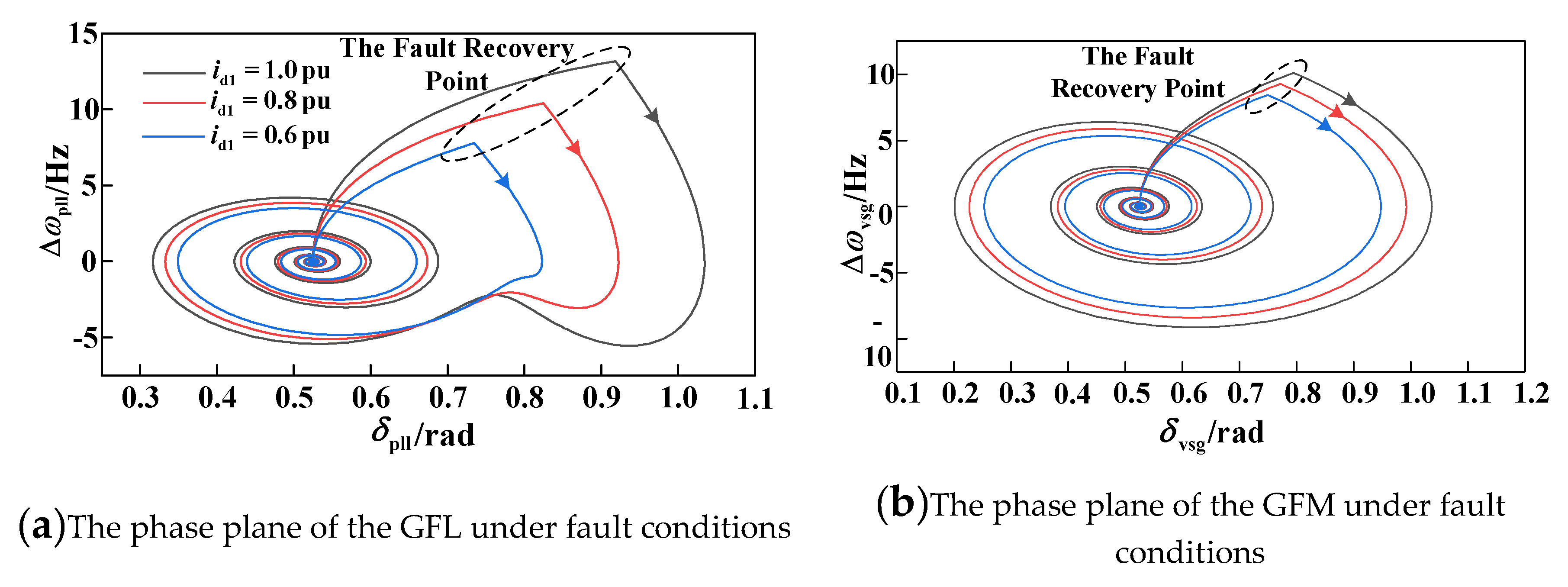
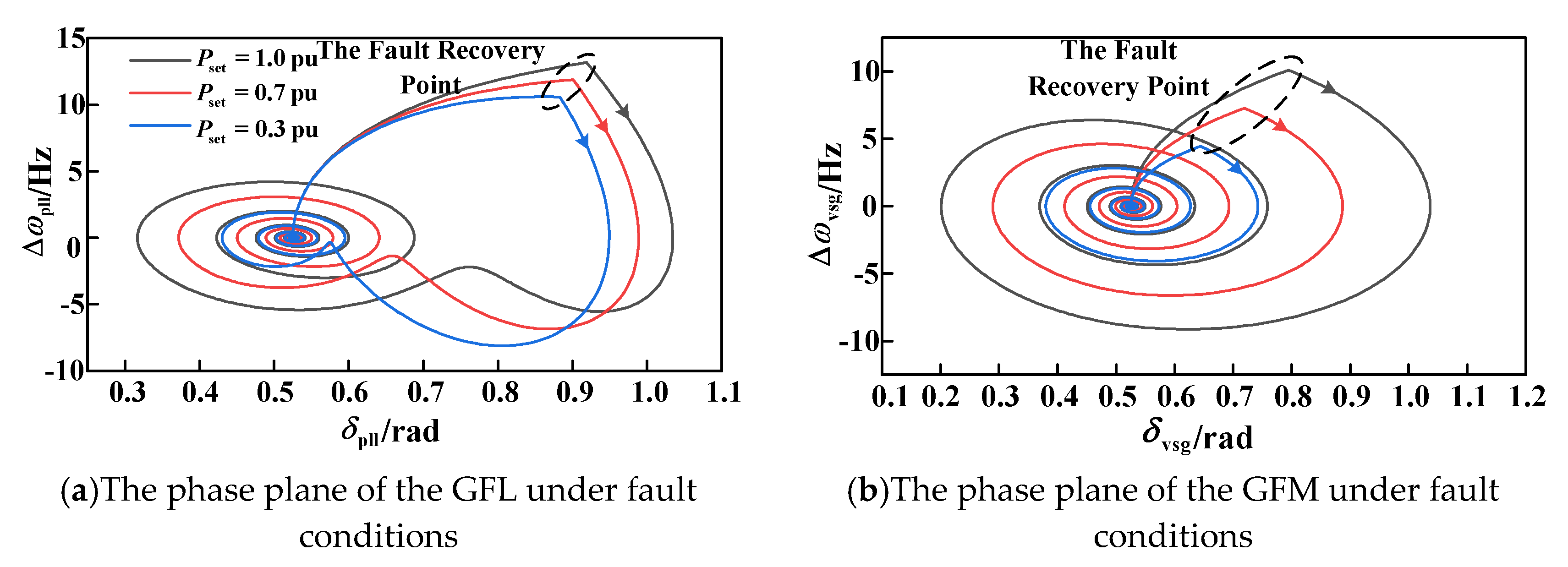
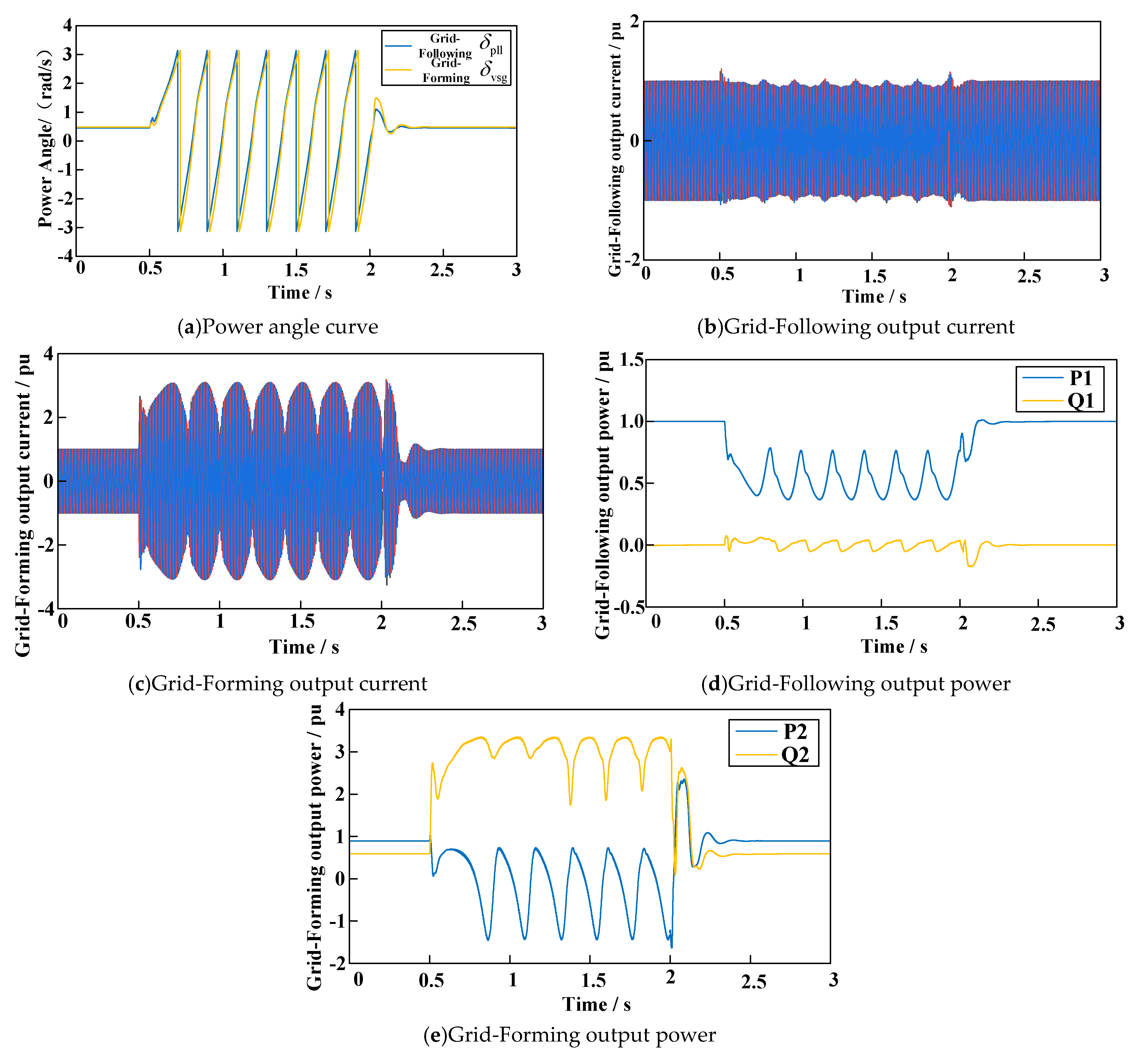
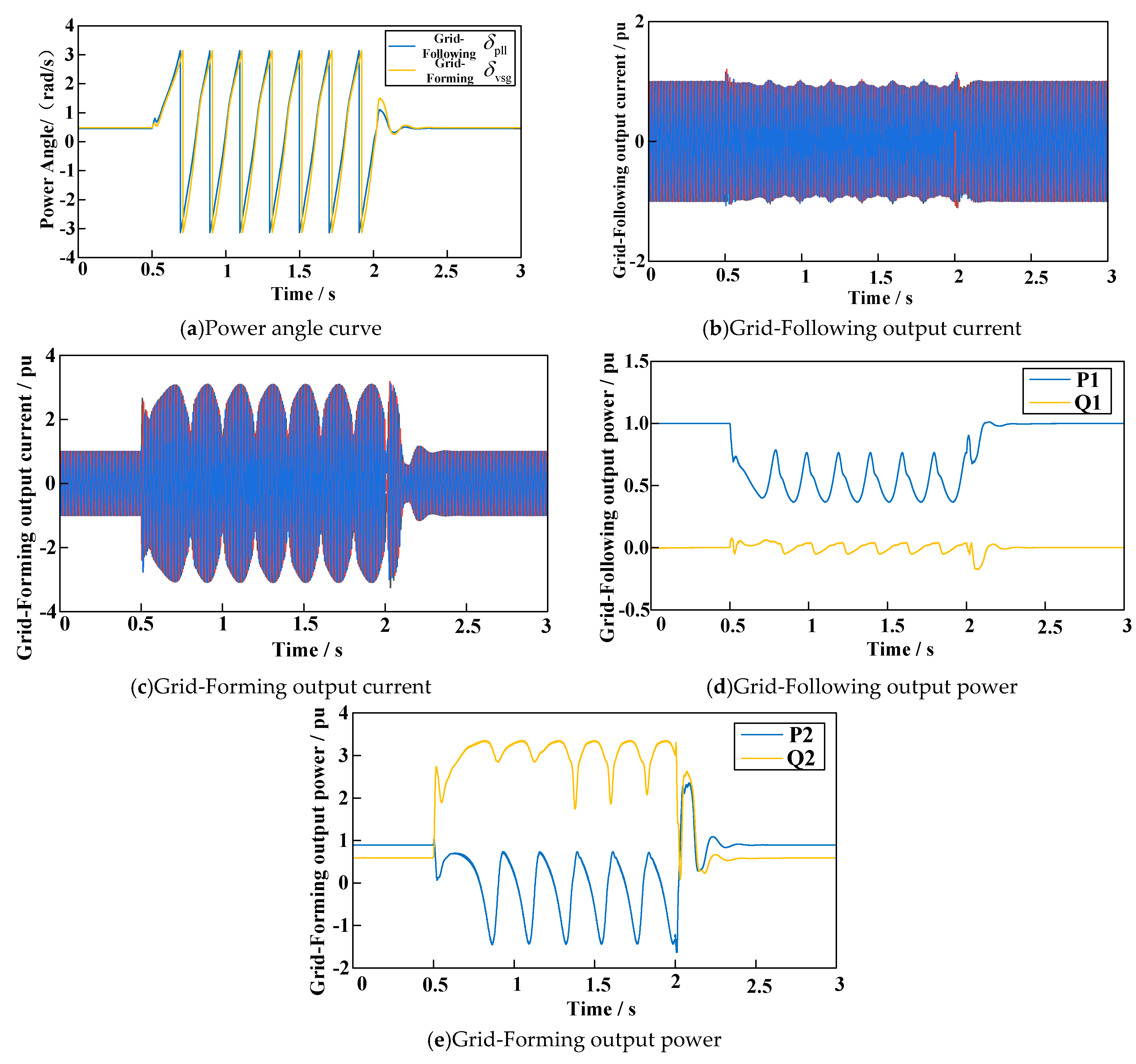
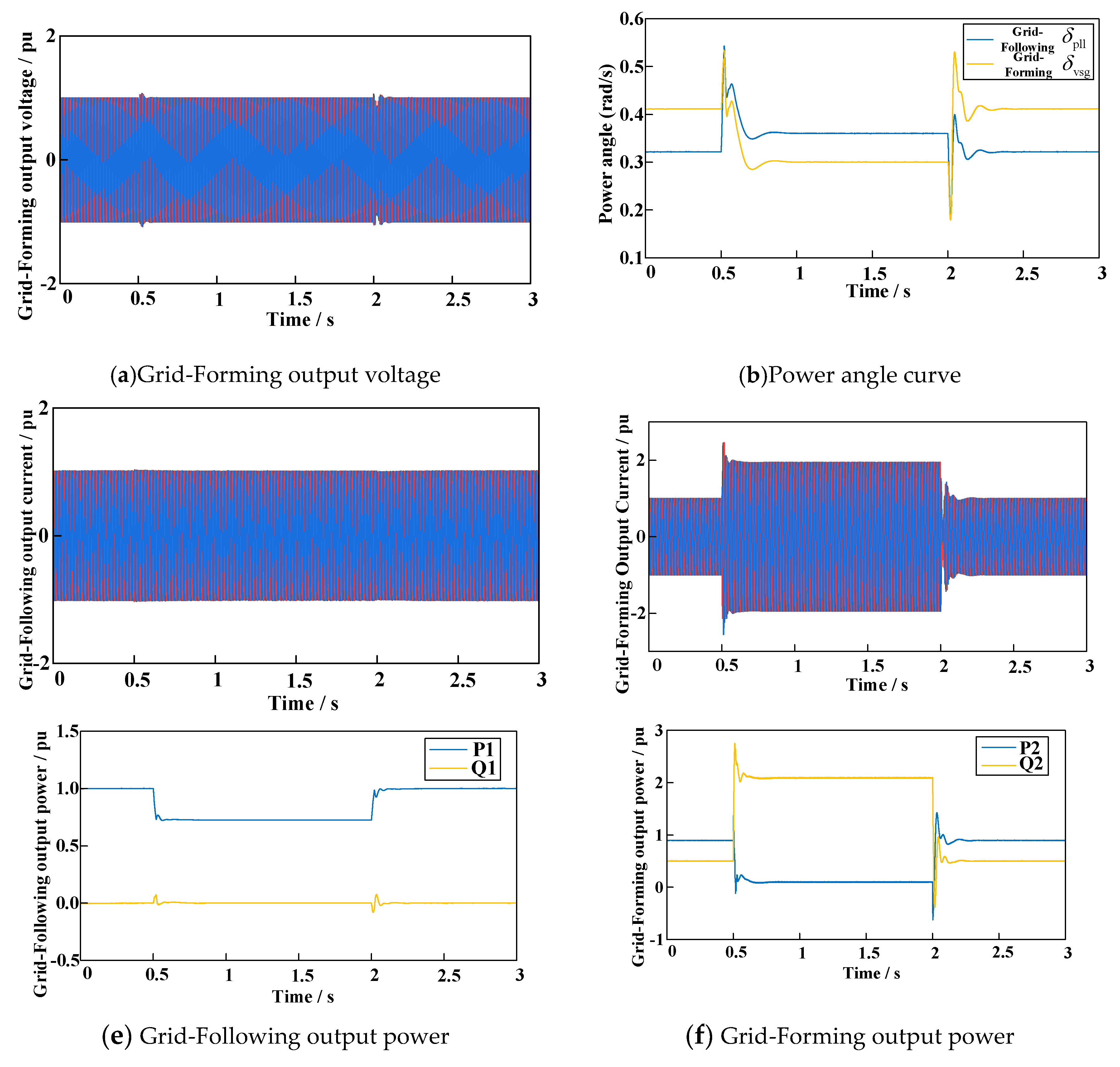
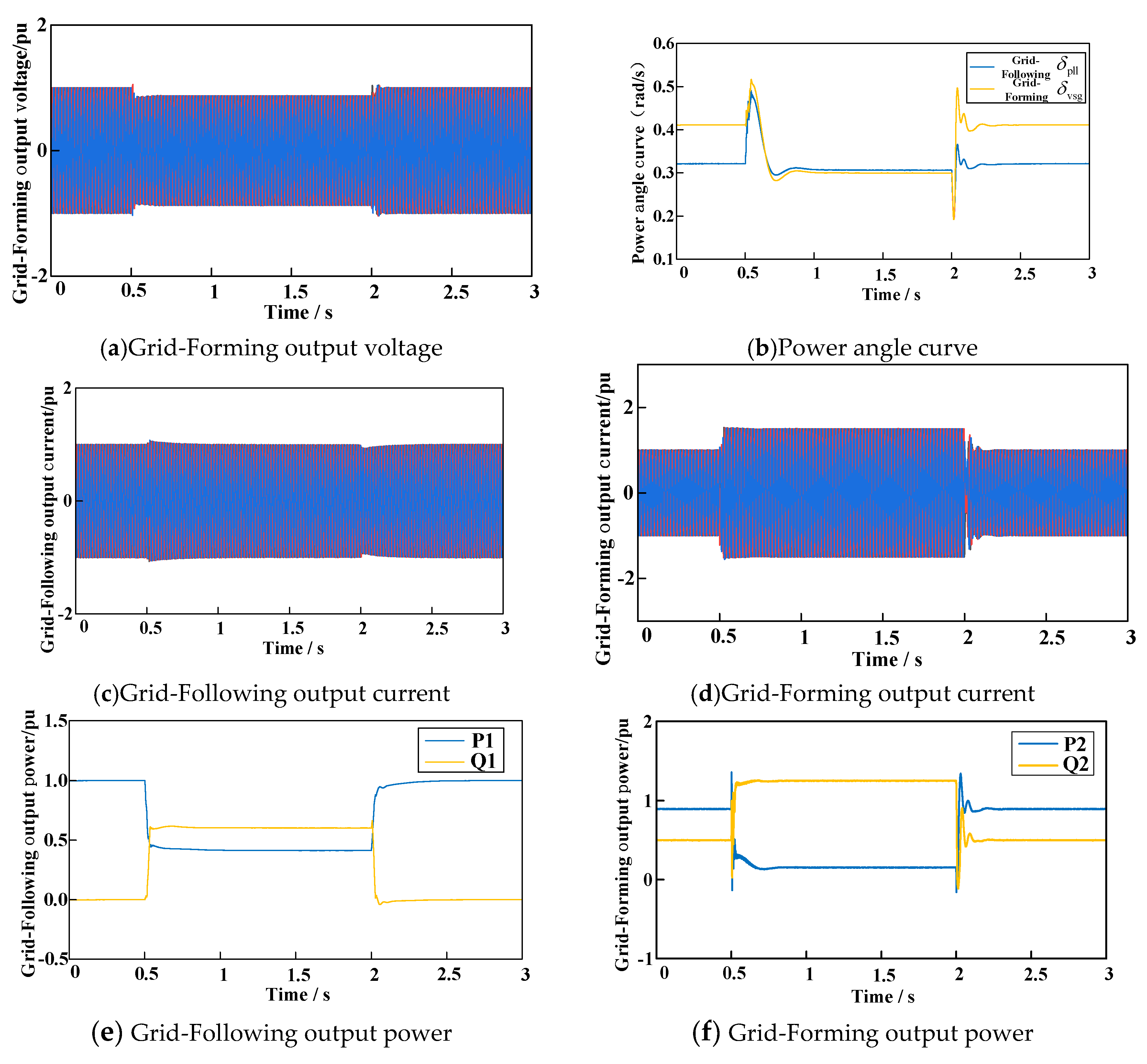
5.1. Output Characteristics of GFM and GFL during Fault Conditions

When the three-phase grid voltage drops to 0.5, the output currents and power angles of the GFM and GFL are shown in Figure 11. The simulation duration is set to 3 seconds, with a fault occurring at 0.5 seconds and clearing at 2 seconds. As seen in Figure 11, during the fault, the power angles of both the GFM and GFL increase indefinitely. The output currents of the two converters are affected by the power angles, resulting in oscillations. Since the GFM is a voltage source type, its maximum current amplitude reaches three times its rated operating value. The output active and reactive power of both converters also experience oscillations.
Figure 12. a) shows the power angle curves of both converters when the d-axis current reference value I * d1 of the grid-following converter is changed from 1 pu to 2.5 pu at 0.5 s and restored to 1 pu at 2 s. Figure 12(b) shows the power angle curves of both converters when the input mechanical power Pset of the grid-forming converter is changed from 1 pu to 3 pu at 0.5 s and restored to 1 pu at 2 s. Based on the output power angles, it can be seen that the occurrence of power angle instability in the GFL immediately causes power angle instability in the GFM. Similarly, the occurrence of power angle instability in the GFM immediately causes power angle instability in the GFL. This verifies the analysis of the mutual influence between the two converters mentioned earlier.

5.2. Verification of the Proposed Fault Ride-through Control Strategy

Figure 13 shows the output waveforms when the grid voltage symmetrically drops to 0.4 pu at 0.5 seconds and rises back to 1 pu at 2 seconds. During the fault, transient power angle control is applied to the HGS, and both the GFL and GFM remain stable after a brief transient process. As seen in Figure 13(b), during the fault, by adjusting the input mechanical power Pset of the GFM and using the improved PLL based on the grid-forming model for the GFL, the power angles of both converters can be kept stable. However, as shown in Figure 13(d), the transient current output by the GFM is too large, and the steady-state current also exceeds 1.5 pu, approaching 2 pu. From Figure 13(f), it can be seen that this is due to the excessive reactive current output by the GFM. Although reactive current can support the grid, there is still a risk of damaging transistors. Therefore, it is necessary to suppress transient and steady-state overcurrents through fault current control.
Figure 14 shows the waveforms of the HGS when transient power angle and fault current control are implemented as the grid voltage symmetrically drops to 0.4 pu. Similarly, the GFL and GFM remain stable after a brief transient process. As shown in Figure 14(d), during the fault, by reducing the output voltage of the GFM, the GFM’s output current is precisely controlled to 1.5 pu. Thanks to the virtual impedance, the transient current is also effectively suppressed. As depicted in Figure 14(e), the GFL, while remaining stable, is able to provide reactive current in accordance with grid codes, supporting the grid. After the fault is cleared, both converters can return to their pre-fault operating state after a brief transient process.

6. Conclusion

Focusing on the parallel hybrid grid connection of GFL and GFM converters, a mathematical model is established to study the challenges of achieving fault ride-through during symmetric grid voltage sags. The following conclusions are drawn.
1) Due to the coupling effect, the instability of one converter will cause the instability of the other converter. During a fault, reducing the id1 of the GFL or the Pset of the GFM can simultaneously improve the transient stability of both converters.
2) During a fault, the GFM adjusts the power angle according to the extent of the grid voltage sag and modifies the output voltage while considering the impact of the current injected by the GFL when limiting current. This approach can effectively suppress short-circuit overcurrent and maintain power angle stability. The GFL uses an improved PLL based on grid-forming control, which can effectively prevent GFL instability and inject current into the grid in accordance with grid codes.
3) The study preliminarily explores the mutual influence mechanism and fault ride-through control of GFL and GFM parallel grid connection under symmetrical faults. The transient process and fault control of both converters under asymmetrical faults are more complex. The next step will be to study control strategies under asymmetrical faults.

Author Contributions

Conceptualization, Baoyu Zhai and Shuchao Liang; methodology, Baoyu Zhai; software, Zhi Xu.; validation, Shuchao Liang, Fengyi Deng and Haiyang Wu; formal analysis, Haiyang Wu; investigation, Haiyang Wu.; resources, Junru Chen; data curation, Fengyi Deng; writing—original draft preparation, Baoyu Zhai; writing—review and editing, Fengyi Deng; visualization, Haiyang Wu; supervision, Junru Chen; project administration, Junru Chen; funding acquisition, Junru Chen. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Science and Technology Department of Xinjiang under grant No. 2022A01004.

Data Availability Statement

The data used to support the findings of this study are included in the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Y. Wang, S. Lou, Y. Wu and S. Wang, “Flexible Operation of Retrofitted Coal-Fired Power Plants to Reduce Wind Curtailment Considering Thermal Energy Storage,” IEEE Transactions on Power Systems, vol. 35, no. 2, pp. 1178-1187, March 2020.
  2. B. Zhou et al., “Optimal Scheduling of Biogas–Solar–Wind Renewable Portfolio for Multicarrier Energy Supplies,” IEEE Transactions on Power Systems, vol. 33, no. 6, pp. 6229-6239, Nov. 2018.
  3. T. Ding, R. Bo, H. Sun, F. Li and Q. Guo, “A Robust Two-Level Coordinated Static Voltage Security Region for Centrally Integrated Wind Farms,” IEEE Transactions on Smart Grid, vol. 7, no. 1, pp. 460-470, Jan. 2016.
  4. Rosso R, Engelken S, Liserre M, “Robust Stability Investigation of the Interactions Among Grid-Forming and Grid-Following Converters,” IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8: 991-1003.
  5. Yang C, Huang L, Xin H, et al., “Placing Grid-Forming Converters to Enhance Small Signal Stability of PLL-Integrated Power Systems, “ IEEE Transactions on Power Systems, 2020. 36: 991-1003.
  6. Zhao X, Flynn D, “Stability enhancement strategies for a 100% grid-forming and grid-following converter-based Irish power system, “ IET Renewable Power Generation, 2022, 16: 125-138.
  7. Taul M G, Wang X F, Davari P, et al. “Current Limiting Control With Enhanced Dynamics of Grid-Forming Converters During Fault Conditions, “ IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8: 1062-1073.
  8. “Ieee standard for interconnection and interoperability of inverter-based resources (ibrs) interconnecting with associated transmission electric power systems, “ IEEE Std 2800-2022, pp. 1–180, 2022.
  9. Göksu Ö, Teodorescu R, Bak C L, et al. “Instability of Wind Turbine Converters During Current Injection to Low Voltage Grid Faults and PLL Frequency Based Stability Solution,” IEEE Transactions on Power Systems, 2014, 29: 1683-1691.
  10. Weise B. “Impact of K-factor and active current reduction during fault-ride-through of generating units connected via voltage-sourced converters on power system stability, “ IET Renewable Power Generation, 2015, 9: 25-36.
  11. He X Q, Geng H, Xi J B, et al. “Resynchronization analysis and improvement of grid-connected VSCs during grid faults, “ IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9: 438-450.
  12. Ma S, Geng H, Liu L, et al. “Grid-synchronization stability improvement of large scale wind farm during severe grid fault, “ IEEE Transactions on Power Systems, 2018, 33: 216-226.
  13. Shi K, Song W, Xu P F, et al. “Low-voltage ride-through control strategy for a virtual synchronous generator based on smooth switching,” IEEE Access, 2017, 6:2703–2711.
  14. J. Xi, J. Wang, J. Zhang, Y. Zhang, C. Su and C. Liu, “Current Limiting Strategy of Grid-forming Converter Based on Additional Current Loop,” 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 2022, pp. 328-332.
  15. Shuai Z K, Shen C, Xuan Liu, et al. “Transient angle stability of virtual synchronous generators using Lyapunov’s direct method,” IEEE Transactions on Smart Grid, 2019, 10: 4648-4661.
  16. Y. Zheng, T. Wang, S. He, Y. Wu, Y. Kang and D. Liu, “Analytical Expression of Short Circuit Current for Virtual Synchronous Generator with Improved Low Voltage Ride Through Control Strategy,” 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 2023, pp. 1-5.
  17. Chen J, Prystupczuk F, O’ Donnell T. “Use of voltage limits for current limitations in grid-forming converters,” CSEE Journal of Power and Energy Systems, 2020, 6: 259-269.
  18. H. Cheng, Z. Shuai, C. Shen, X. Liu, Z. Li and Z. J. Shen, “Transient Angle Stability of Paralleled Synchronous and Virtual Synchronous Generators in Islanded Microgrids,” IEEE Transactions on Power Electronics, vol. 35, no. 8, pp. 8751-8765, Aug. 2020.
  19. Z. Tian et al., “Transient Synchronization Stability of an Islanded AC Microgrid Considering Interactions Between Grid-Forming and Grid-Following Converters,” IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 11, no. 4, pp. 4463-4476, Aug. 2023.
  20. Paquette A D, Divan D M. “Virtual impedance current limiting for inverters in microgrids with synchronous generators,” IEEE Transactions on Industry Applications, 2015, 51: 1630-1638.
Preprints 121156 g001
Figure 1. Parallel topology of grid-connected converters with grid-following and grid-forming.
Figure 1. Parallel topology of grid-connected converters with grid-following and grid-forming.
Preprints 121156 g001
Preprints 121156 g002
Figure 2. Schematic diagram of phase locked loop.
Figure 2. Schematic diagram of phase locked loop.
Preprints 121156 g002
Preprints 121156 g003
Figure 3. Virtual synchronous machine control schematic diagram.
Figure 3. Virtual synchronous machine control schematic diagram.
Preprints 121156 g003
Preprints 121156 g004
Figure 4. HGS equivalent circuit diagram.
Figure 4. HGS equivalent circuit diagram.
Preprints 121156 g004
Preprints 121156 g005
Figure 5. Transient analysis model of HGS.
Figure 5. Transient analysis model of HGS.
Preprints 121156 g005
Preprints 121156 g006
Figure 6. Phase portrait of different id1 of GFL.
Figure 6. Phase portrait of different id1 of GFL.
Preprints 121156 g006
Preprints 121156 g007
Figure 7. Phase portrait of different Pset of GFM.
Figure 7. Phase portrait of different Pset of GFM.
Preprints 121156 g007
Preprints 121156 g008
Figure 8. Voltage vector diagram.
Figure 8. Voltage vector diagram.
Preprints 121156 g008
Preprints 121156 g009
Figure 9. HGS transient power angle control.
Figure 9. HGS transient power angle control.
Preprints 121156 g009
Preprints 121156 g010
Figure 10. HGS fault current control.
Figure 10. HGS fault current control.
Preprints 121156 g010
Preprints 121156 g011
Figure 11. Output waveform under symmetrical fault of grid
Figure 11. Output waveform under symmetrical fault of grid
Preprints 121156 g011
Preprints 121156 g012
Figure 12. Change the reference value of the inverter.
Figure 12. Change the reference value of the inverter.
Preprints 121156 g012
Preprints 121156 g013
Figure 13. Output waveform under transient power Angle fault ride-through control only.
Figure 13. Output waveform under transient power Angle fault ride-through control only.
Preprints 121156 g013
Preprints 121156 g014
Figure 14. Output waveform under transient power Angle and current fault ride-through control.
Figure 14. Output waveform under transient power Angle and current fault ride-through control.
Preprints 121156 g014
Table 1. Parameters of HGS.
Table 1. Parameters of HGS.
Parameter Value
DC bus voltage (VDC/V) 800
Grid voltage amplitude (Vg/V) 311
Grid angular frequency (ωg/(rad/s)) 314
GFL line inductance (L1/mH) 3.2
GFM line inductance(L2/ mH) 3.2
Grid inductance(Lg/ mH) 4
GFM moment of inertia (J/(kg/m2)) 5
GFM active power damping coefficient (Dp) 130
GFM reactive power droop coefficient(kq) 0.01
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated