Overview of Technologies for Solar Refrigeration Systems and Heat Storage: The Use of Computational Fluid Dynamics for the Analysis of Their Energy Efficiency

The article reviews selected solar systems that utilize solar energy for cooling production. Particular attention is given to research on individual components of these systems, aimed at improving their efficiency and performance. The article focuses on the analysis of literature concerning the design of thermal storage units, with an emphasis on the use of computational fluid dynamics (CFD) as a research tool. Conclusions from scientists’ research regarding the impact of tank shape, thermal insulation, flow parameters, and the use of stratification partitions on heat storage efficiency have been presented. The literature review indicates that thermal storage units play a key role in the efficiency of solar systems, and thermal stratification within them can significantly improve their performance.

Keywords:

Subject:

Engineering - Energy and Fuel Technology

1. Introduction

Renewable energy sources (RES) and thermal storage systems are playing an increasingly important role in the context of global energy management challenges. Solar systems, which utilize solar energy to produce heat, operate on the principle of converting solar radiation into thermal energy, making them an environmentally friendly alternative to traditional energy sources. The application of such technologies in cooling, especially in regions with high solar exposure, is becoming increasingly popular, and many studies confirm their efficiency [1,2,3].

In this context, absorption cooling technology is gaining importance as an innovative and eco-friendly solution. These systems, based on key components such as a generator, condenser, evaporator and absorber (Figure 1), most commonly use lithium bromide solutions with water or ammonia with appropriate absorbents. They operate by utilizing thermal energy to produce cooling and are particularly effective in sunny climates where the availability of solar energy matches the demand for cooling.

To improve the efficiency and performance of solar cooling systems, a variety of research efforts are being conducted. One of the techniques used for this purpose is computational fluid dynamics [5], which finds broad application in various fields, including the analysis of solar cooling system performance [6,7,8]. By employing appropriate turbulence models [9,10], computational fluid dynamics allows for detailed modeling and optimization of thermodynamic processes, which is crucial for analyzing heat flows and energy efficiency. In the context of solar cooling systems, numerical techniques can be an important tool for enhancing absorption cooling systems, which are an eco-friendly alternative to traditional compressor-based systems.

In addition to research on performance optimization using numerical techniques, new design solutions are also being developed. In article [11], a proposal for a solar cooling system with an additional economizer is presented. This system consists of a solar collector, condenser, evaporator, and, in this case, a dephlegmator and economizer (Figure 2). At the center of the system is a generator/absorber, separated by a throttling valve, which serves two functions: during the day, it acts as a generator, and at night, as an absorber.

The increasing popularity of solar cooling systems is supported by numerous studies and implementation of solar-powered absorption chillers. From an economic perspective, the use of thermal storage units is particularly beneficial, as they allow for the accumulation of excess thermal energy during the day and its utilization during periods of low sunlight, such as at night. Numerical simulations play a crucial role here, enabling the optimization of thermal storage, minimizing energy losses, and maximizing the efficiency of the entire cooling system.

The aim of this article is to present the technologies used in solar cooling systems, with a particular emphasis on computational fluid dynamics (CFD) as a key analysis method. The article analyzes both the designs of solar cooling systems and thermal storage units, including the materials used in their construction and the efficiency of thermal energy storage.

2. Solar Cooling Systems

Solar-powered cooling systems present a promising alternative to traditional methods, offering a more sustainable solution. One of the most commonly used solutions is absorption chillers, which can vary in design and performance depending on the working fluid used. The main advantage of these systems is their ability to efficiently utilize heat while minimizing electricity consumption. There are various configurations of such systems, depending on the working fluids used, which affect their efficiency and optimization potential.

In publication [4], the authors discuss various absorption chiller solutions, focusing on the simplest and most common single-effect absorption system. There are two configurations of this system, depending on the working fluid used. When a water and lithium bromide solution is used, the system operates by using the heat supplied to the generator to evaporate the refrigerant, and the solution is heated to the temperature of the absorber. This process is characterized by a certain irreversibility due to the high temperature of the generator. To reduce losses associated with irreversibility, heat exchangers are installed in the systems, which improve process efficiency by raising the temperature of the solution before it reaches the generator. Experiments show that the use of a heat exchanger can increase the Coefficient of Performance (COP) by as much as 60%.

If a water-ammonia solution is used, the system requires an additional component – a rectifier, which purifies the refrigerant before it enters the condenser. The absence of a rectifier would result in liquid accumulation in the evaporator, negatively affecting the system’s efficiency.

The authors suggest that future research should focus on integrating cooling systems with various technological innovations, such as hydrogen production, solid oxide fuel cells, thermal storage, or units with variable COP. They also highlight the need for further experiments with new refrigerants and research aimed at improving the efficiency of cooling systems, both numerical and experimental, particularly in the context of enhancing COP values.

2.1. Types of Thermal Energy Storage

In addition to the proper selection of system components, effective thermal energy storage is crucial for the efficient operation of a solar cooling system. There are several types of thermal energy storage, as categorized by the authors of publication [12] (Figure 3).

The basic division includes two main categories: thermal and chemical energy storage. Thermal storage is further divided into sensible heat storage, which can occur in liquids and solids, and latent heat storage, which occurs during phase changes such as liquid-gas, solid-liquid, and solid-solid. Chemical storage, on the other hand, involves the use of chemical reactions (heat of reaction), heat pumps, and technologies based on heat pipes, which can transfer heat in the form of steam or other heating media, thereby supporting chemical or energy processes.

Based on the analysis of the above diagram and publication [13], a classification of energy storage systems has been proposed, taking into account the advantages and disadvantages of each type (Figure 4).

The most developed and widely available technology is sensible heat storage, which involves raising or lowering the temperature of materials that store heat as internal energy. The materials used can be in a liquid or solid state. Water is one of the most popular materials due to its low cost and high specific heat, but its use is limited to temperatures below 100°C. Alternatively, liquid salts offer excellent thermal properties, higher stability, and the ability to store heat at higher temperatures. Unfortunately, their use is more complex and expensive, particularly due to safety issues, especially with oils or liquid sodium. Additionally, it has the lowest energy storage capacity, which significantly increases the size of the system. Latent heat storage, on the other hand, provides a higher storage capacity through phase change materials (PCMs), which store and release heat during phase transitions, such as solid to liquid, liquid to gas, or from one solid phase to another. The high phase change enthalpy makes the heat storage density in this technology much greater than in sensible heat storage. However, without proper improvements in heat transfer, the efficiency of latent storage may be limited due to poor heat transfer. The final type, chemical heat storage, offers the highest capacity among thermal energy storage technologies, as it is based on energy released or absorbed during chemical reactions. It uses organic or inorganic materials that can store large amounts of heat. Despite high efficiency, this technology is limited by the complexity of chemical reactors, the need to control reactions, reversibility issues, and the chemical stability of materials, which hinders its widespread application.

Figure 5 presents a comparison of the three types of heat storage technologies – sensible, latent, and thermochemical – in terms of the volume of storage needed to store the same amount of energy [14]. The focus is on their energy efficiency, measured in megajoules per cubic meter (MJ/m³), illustrating the significant difference in energy density stored across the different technologies.

A very important aspect of describing heat storage is also considering the size of the storage systems. To store the same amount of sensible heat equal to 6480 MJ, a storage volume approximately seven times larger is required compared to thermochemical technology. Such a difference in storage sizes impacts the choice of technology depending on the available space and the requirements of the energy system.

Scientists from the Mineral and Energy Economy Research Institute of the Polish Academy of Sciences presented a comparison in their work [15] in the form of a table (Table 1) of a different thermal energy storage technologies in terms of capacity, power, efficiency, storage duration, and costs.

Sensible heat storage systems are the cheapest option but offer low capacity and efficiency. Phase change storage systems provide higher efficiency and greater flexibility in storage duration, but they are more expensive. Thermochemical storage systems, on the other hand, have the highest capacity and efficiency, but their costs are the highest, making the most suitable for shorter energy storage periods.

2.2. Heat Storage Materials and Methods for Improving Their Thermal Conductivity

A key factor for effective energy management in energy systems is the type of materials used for heat storage and innovative methods to improve their thermal conductivity, which enables more effective use of available energy sources.

In the publication by PhD Jerzy Chodura [16], concerning modern methods of solar energy storage and utilization, the author addresses the issue of mismatch between the current availability of solar energy and the actual needs of the user. He points out numerous limitations of traditional systems, such as their large sizes, the limited thermal capacity of water as a storage medium, and the lack of ability to effectively utilize energy when the storage tanks are full while solar energy is still available.

Due to the limited capacity of water to store energy (about 60 kWh/m³), research has begun on materials with higher storage efficiency and new methods of heat storage. One of the solutions is phase change materials (PCMs), which can store a large amount of energy at significantly lower temperatures than water. The energy stored during a phase change, such as the melting of ice, is much greater than the energy needed to heat water to 80°C.

Phase change materials offer the ability to store heat over a wide temperature range, from below 0°C to over 800°C, making them useful in both heating and cooling systems. Due to this property, they can be used to store both heat and cold. In Figure 6, included in publication [17], the relationship between temperature and melting energy for various heat storage materials is presented. Groups of phase change materials are illustrated in the context of their thermal properties, further highlighting their diversity and application in effective energy management.

With such knowledge, it is possible to assess the potential applications of these materials in heat storage systems depending on the required temperature and energy parameters.

A key aspect of reducing the charging and discharging time of thermal energy storage systems is optimizing the thermal conductivity of the materials used in these systems. Higher thermal conductivity of materials allows for more efficient heat flow, which directly affects the speed of charging and discharging the energy storage systems. To enhance this process, the authors of the text [18] decided to use materials with high thermal conductivity. In their research, they utilized elements such as plates, spheres, and metal powders. These inserts aimed to increase the efficiency of heat exchange in the storage systems. Although their application yielded positive results, the increase in thermal conductivity proved to be limited, ranging from 60% to 150%.

Although these materials contributed to improving the efficiency of the systems, the authors decided to explore other solutions in search of materials with even higher conductivity parameters. In this context carbon materials were highlighted, which can achieve thermal conductivity levels of up to 470 W/(m·K). Due to their exceptional properties, these materials were tested for their application in thermal energy storage systems. The research showed that the use of carbon materials yielded significant results, leading to a twofold increase in heat transfer efficiency in energy storage tanks. Thanks to such innovations, it is possible to significantly accelerate the charging and discharging processes of the systems, improving their overall performance.

3. CFD

Numerical simulations, including CFD methods, play a key role in the analysis of many issues, such as solving mining aerology problems [19,20] or optimizing ventilation processes in large-scale halls [21]. The technique is also widely used in improving the performance of refrigeration systems and thermal storage, enabling accurate modeling of complex thermodynamic processes. Thanks to advanced computational algorithms, it is possible to optimize the parameters of the systems, leading to increased energy efficiency and reduced operating costs. Theoretical research also allows the identification of innovative solutions that can significantly improve the use of renewable energy under different climatic conditions.

One example of using numerical simulations to determine the theoretical performance of a system is published [11]. Researchers from the Department of Mechanical Engineering at a public university in Saudi Arabia used numerical simulations to evaluate the performance of a solar absorption cooling system in a desert climate where the cooling sector consumes more than 60% of electricity. Their research focused on improving the efficiency of the system by adding an economizer, which recovers excess heat from the absorber. The economizer, acting as a heat exchanger, reduces the overall energy demand of the system by storing heat and using it to heat the solution in the generator.

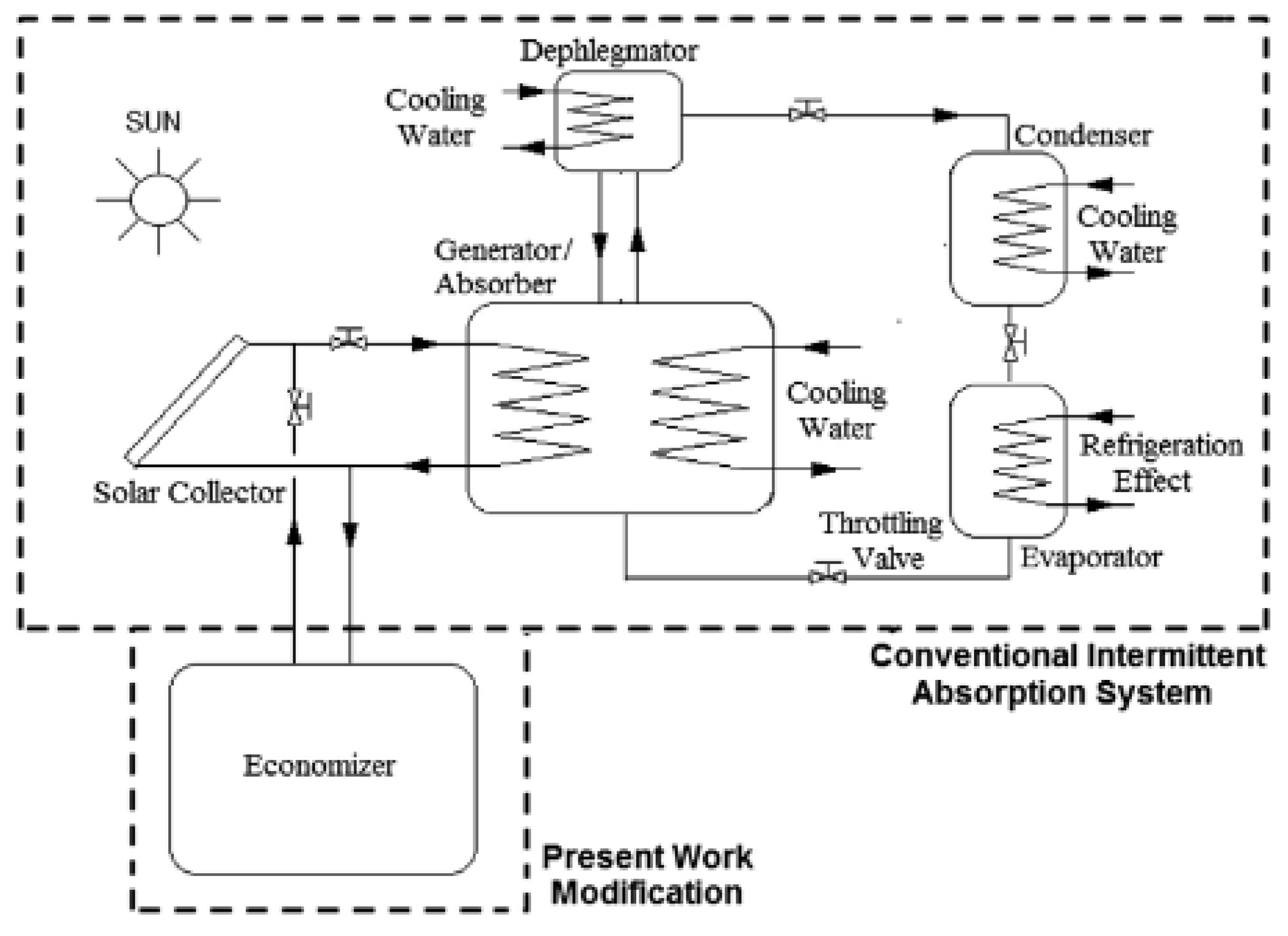
Simulations were carried out using Engineering Equation Solver (EES) software, which enables advanced numerical calculations and optimization. The analysis showed that the economizer significantly increased the efficiency of the system, reducing the need for energy for pressurization and cooling production, and enabling a reduction in the area of the solar collector. Simulation results showed a 20% increase in the coefficient of performance of the system with the economizer.

The authors of the text [22] created a numerical model of a solar-assisted heating, ventilation and air-conditioning system for an educational building in a desert climate. The goal of this project was to predict the performance of the system, optimize control parameters and achieve savings compared to the installation of photovoltaic panels. Simulations focused on analyzing thermodynamic changes in the system over time.

The designed system is shown in Figure 7. Its mode of operation varied according to the time of day and year, using solar energy to heat water and power an absorption chiller during the day and summer. At night and in winter, the system used stored heat or cooling, adjusting operation to meet the building’s current heating and cooling needs.

TRNSYS software was used to develop the model, which allows the time-series simulation of thermodynamic interactions in various energy systems, including those based on solar energy [23]. The model aimed to find the optimal control strategy that maximizes the use of solar energy for heating and cooling the building.

Simulations showed that the cooling system operated more efficiently at lower heating medium temperatures, which is beneficial for longer absorption chiller operation cycles. Supporting cooling with solar energy was able to reduce the total cooling energy demand by 33% to 43%. In addition, better results were obtained at lower operating temperatures for the solar panels. During the heating season, the solar system was able to cover more than 90% of the heating demand, provided appropriate energy-saving strategies were used. The solar collectors operated efficiently at the lowest possible discharge temperature, and during the transitional season the building could operate without an external energy source, using excess heat to produce chilled water, which was stored for later.

Figure 8 shows a model of the tank that illustrates the linear temperature profile along its height.

The tank model did not allow any node to have a temperature higher than the node above it, as this could result in disruption of thermal stratification. In the event of such a situation, adiabatic mixing of the two nodes and equalization of temperatures occurred. The changing temperatures of the heating medium significantly affect the efficiency of the system and the absorption processes, which is crucial for optimizing the operation of thermal energy storage.

3.1. Using CFD to Simulate Thermal Stratification in Thermal Energy Storage Facilities

The growing interest in thermal energy storage technologies, especially in the context of Concentrated Solar Power (CSP) systems, underscores the importance of effective management and optimization of these systems. This technology is gaining popularity due to its ability to integrate with thermal energy storage (TES - Thermal Energy Storage) systems, which significantly improve the reliability and flexibility of energy supply.

According to the authors of the review [24], thermal storage is a key component in solar energy systems. Such thermal stores create layers of working fluid due to temperature differences, where the warmest particles rise to the top and cooler particles sink to the bottom. Such an arrangement lowers the return temperature of the medium to the solar collector, which increases the efficiency of the system. Research indicates that thermal stratification in thermal storage contributes to better utilization of stored energy and facilitates its further storage. The stratification reduces the rate at which liquids are mixed, which reduces the time it takes to charge the storage compared to storages that lack distinct layers of liquids at different temperatures. A key factor affecting the effectiveness of stratification is the proportionality factor. According to Al-Marafi’s research, increasing the height-to-diameter ratio of a storage tank beyond a value of 4 brings no further benefit. Thermal stratification can also be improved by adding obstacles to the inside of the storage, reducing the flow rate of the medium, and moving the inlet and outlet to the edge of the tank [25,26]. 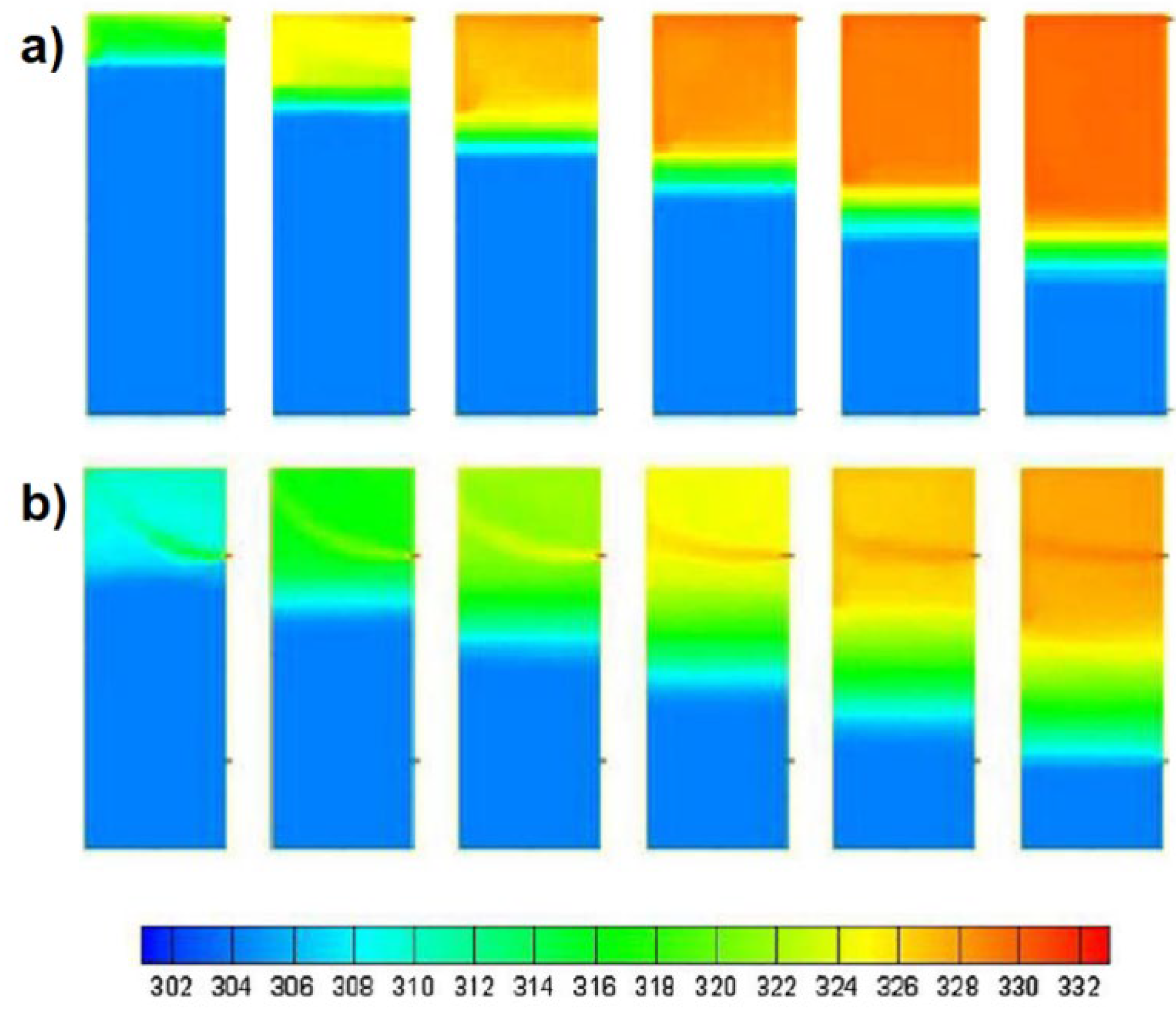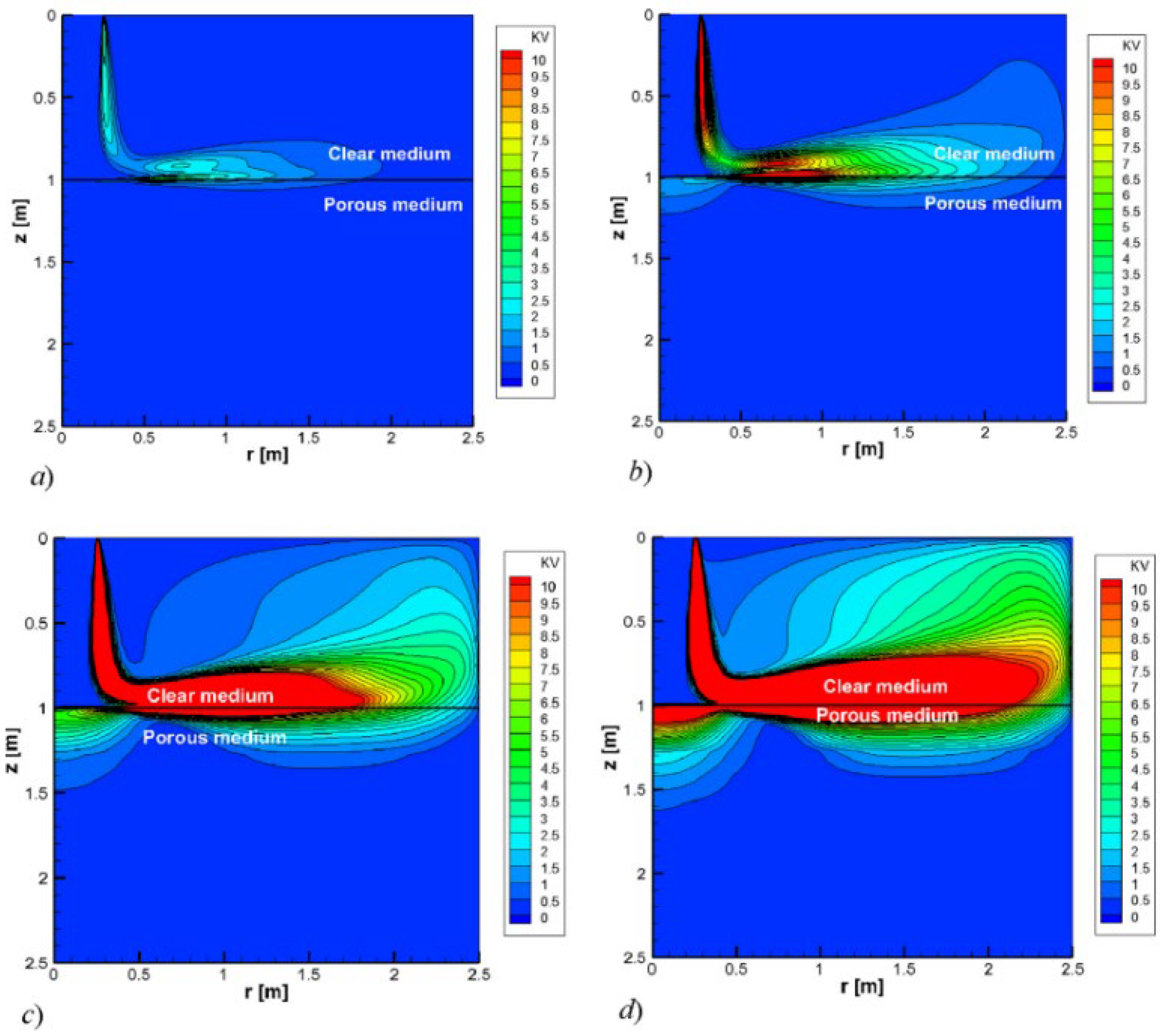Confirmation of one of the above statements can be found in Figure 9, showing the temperature distribution in the thermal storage for two variants of the location of the inlet and outlet of the working medium.

From the figure above, it can be seen that there is more pronounced thermal stratification when the spigots are closer to the horizontal surfaces of the tank. In this case, layers with different temperatures are better separated, indicating less mixing of heat between layers. As the distance increases, the temperature gradient is more blurred, suggesting more intense mixing and thus greater thermal stratification, which can lead to less efficient use of energy in storage.

In the context of the thermal stratification in question, low-cost thermal stores that use thermocline technology are an interesting alternative. A thermocline is a thin layer that separates liquids of different temperatures, thus preserving thermal stratification - a process in which temperature differences in different layers of liquids are maintained, without excessive mixing of hot and cold water. However, poorly designed systems can lead to intense mixing of hot and cold liquids, which adversely affects temperature stratification and ultimately reduces the thermal performance of the storage facility. The thickness of the thermocline determines the level of mixing of liquids of different temperatures - a thin and stable thermocline reduces heat transfer between hot and cold water during tank loading and unloading, improving stratification.

Factors negatively affecting stratification in TES systems [27] primarily include natural convection with the environment, mixing due to the kinetic force of the fluid entering the tank, thermal diffusion and thermal conductivity in the water, and the interaction of walls, pipes and other internal components. The shape factor of the tank (Aspect Ratio) also plays an important role. To improve the performance of thermal storage, special attention is paid to the type of heat transfer fluid (HTF - Heat Transfer Fluid) and the stratification process. Physical and geometrical parameters such as inlet velocity, supply temperature, tank aspect ratio and the presence of stratification baffles that optimize temperature distribution and minimize mixing of layers with different temperatures are also important factors. CFD simulations provide a better understanding and optimization of thermal stratification processes, which increases the efficiency and reliability of TES systems in CSP technology.

In response to the growing demand for efficient heat storage materials, the authors of the text [28] presented a novel approach. They used air as the working medium and used a porous bed as the charge inside the tank. CFD simulations using the k-ε model investigated the effect of heat conduction coefficient and Capacity Ratio on the charging efficiency of the thermal storage. Various values of Reynolds number between 8300 and 50000, heat conduction coefficient (3.5-1062) and heat capacity of the cartridge (1483-7415) were analyzed. Two simulation scenarios included air turbulence in the porous structure and the thermal behavior of the system.

Figure 10 shows the distribution of turbulent kinetic energy in the inlet region of the tank. Hot air injection generates turbulent flow, especially in the zone where the medium contacts the porous material. Analysis of the turbulence kinetic energy (KV) for different values of the Reynolds number shows that the KV rate increases significantly as it increases, penetrating deeper into the porous medium. The highest KV values occur near the air inlet (r = 0 to r = 0.25 m), and as the Re number increases, the area of clear flow is filled with high KV values.

The results showed that lower thermal conductivity values reduced heat loss, resulting in higher temperatures inside the tank after longer charging times. Heat capacity had a significant effect on transition moments, and higher Reynolds numbers, which imply stronger turbulence in the flow, reduced the benefit of using materials with low thermal conductivity. To compensate for this, it was necessary to increase the thermal conductivity of the materials.

A paper [29] described a two-dimensional numerical model for analyzing the process of energy storage and release in a thermocline of molten salt in a porous medium. The model of a cylindrical tank, considered the process of heat storage by introducing high-temperature molten salt into the tank through an upper valve while removing lower-temperature salt through a valve at the bottom. The process of recovering the stored heat was reversed: cold molten salt flowed into the bottom of the tank, while hot salt flowed out the top.

Simulations showed that during storage charging, the thermocline layer stabilizes and grows over time, although the rate of growth decreases. The authors noted that although stable thermocline layers are formed in a tank with porous material, its heat storage efficiency is lower compared to tanks with pure molten salt. Ultimately, choosing materials with high heat capacity and optimizing the structure of porous fillers can improve the performance and cost-effectiveness of the storage.

Another important case described in the article [30], was the study of simultaneous charging and energy extraction from the thermal storage. The authors developed a model of a thermocline reservoir using molten salt as a medium and various filling materials: quartzite rock, slag stones and alumina ceramics. The effects of charging and discharging intensities on the thickness of the thermocline layer and stored power were analyzed. The tank was subjected to stable charging or intermittent charging while discharging continuously. At Figure 6 shows the simulation results in the form of temperature distribution in tanks with different media and the process of thermocline formation.

Simulations showed that a tank filled with pure molten salt provided better thermal stratification compared to tanks with additional materials. The thickness of the thermocline layer increased with increasing flow rate, and the use of filler promoted uniform layer distribution along the radius of the tank. The greatest thickness of the thermocline was achieved with alumina ceramics. For the same flow rate, the temperature gradient was smaller for slagstone than for quartzite rock, suggesting that slagstone performs better as a heat storage material. In addition, continuous charging proved to be more efficient than intermittent charging at higher flow rates.

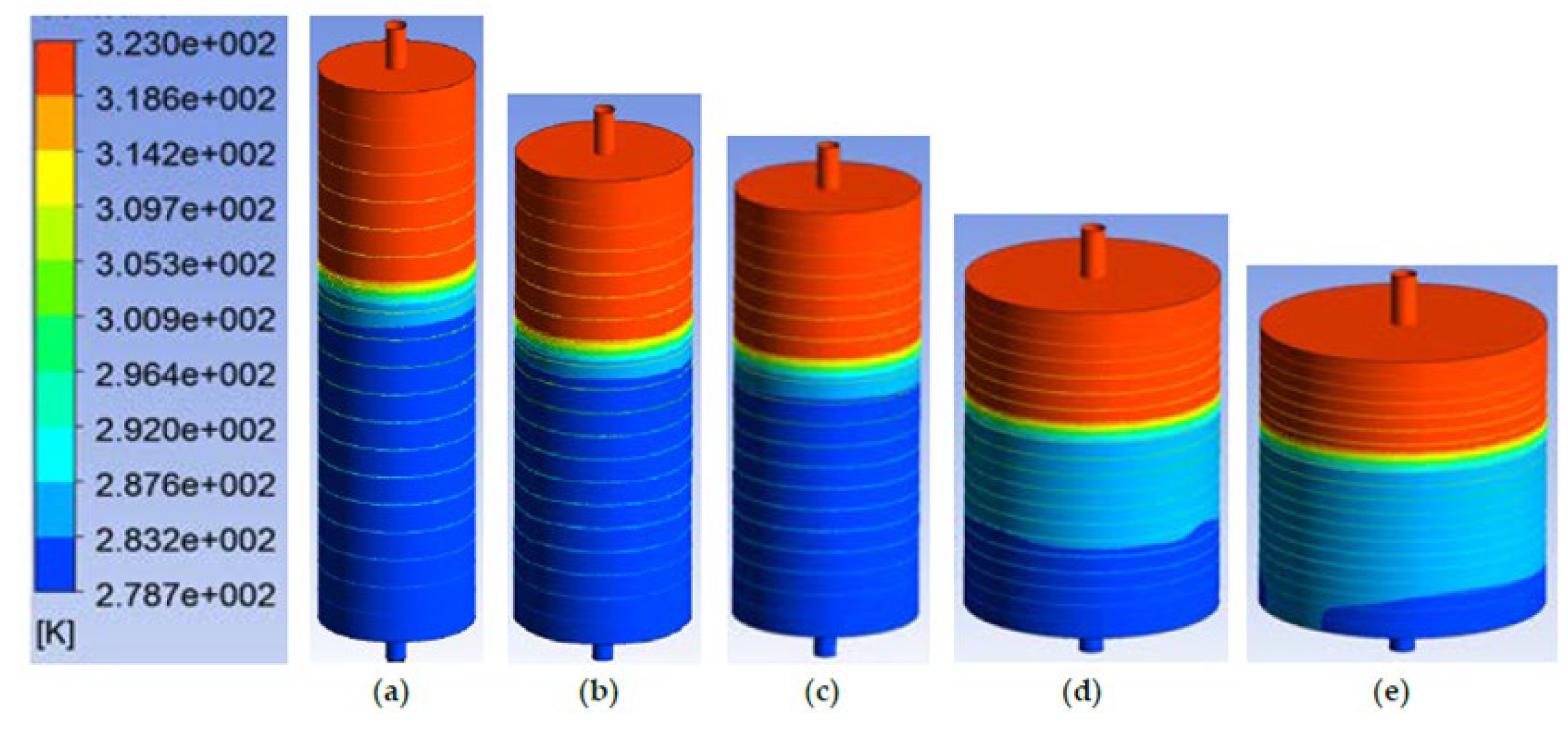
Much research has focused on the thermal processes occurring inside heat storage tanks. Researchers from the Department of Science and Engineering at Queensland University of Technology in Australia [31] analyzed the theoretical performance of such tanks to identify key factors affecting their thermal efficiency in heating and cooling applications. Using CFD simulations, they studied five different fully insulated storage tank geometries with water as the heat transfer medium. The goal was to determine how the inlet velocity of the water, the ratio of tank dimensions and the temperature difference between the tank water and the charging water affect water mixing and thermocline layer formation. The tanks differed in their aspect ratio, that is, the ratio of height to diameter (TES 1: AR=3.8, TES 2: AR=2.75, TES 3: AR=2.38, TES 4: AR=1.33, TES 5: AR=1).

Figure 11 clearly shows the favorable effect of a high aspect ratio on the process of thermocline formation. In addition, it was noted that thermal stratification improved significantly as the temperature difference between the inlet medium and the initial temperature in the tank increased, along with lower inlet velocities. Observations showed that reducing the temperature difference between tank water and inlet water from 80°C to 10°C led to an increase in mixing by as much as 303%. Reducing the dimension ratio from 3.8 to 1.0 increased mixing by 143%. A similar trend was also observed when the inlet water velocity was increased. It is interesting to note that in the tank with the highest AR ratio (TES-1), it was possible to increase the inlet velocity without a clear effect on the shape of the thermocline after it was formed.

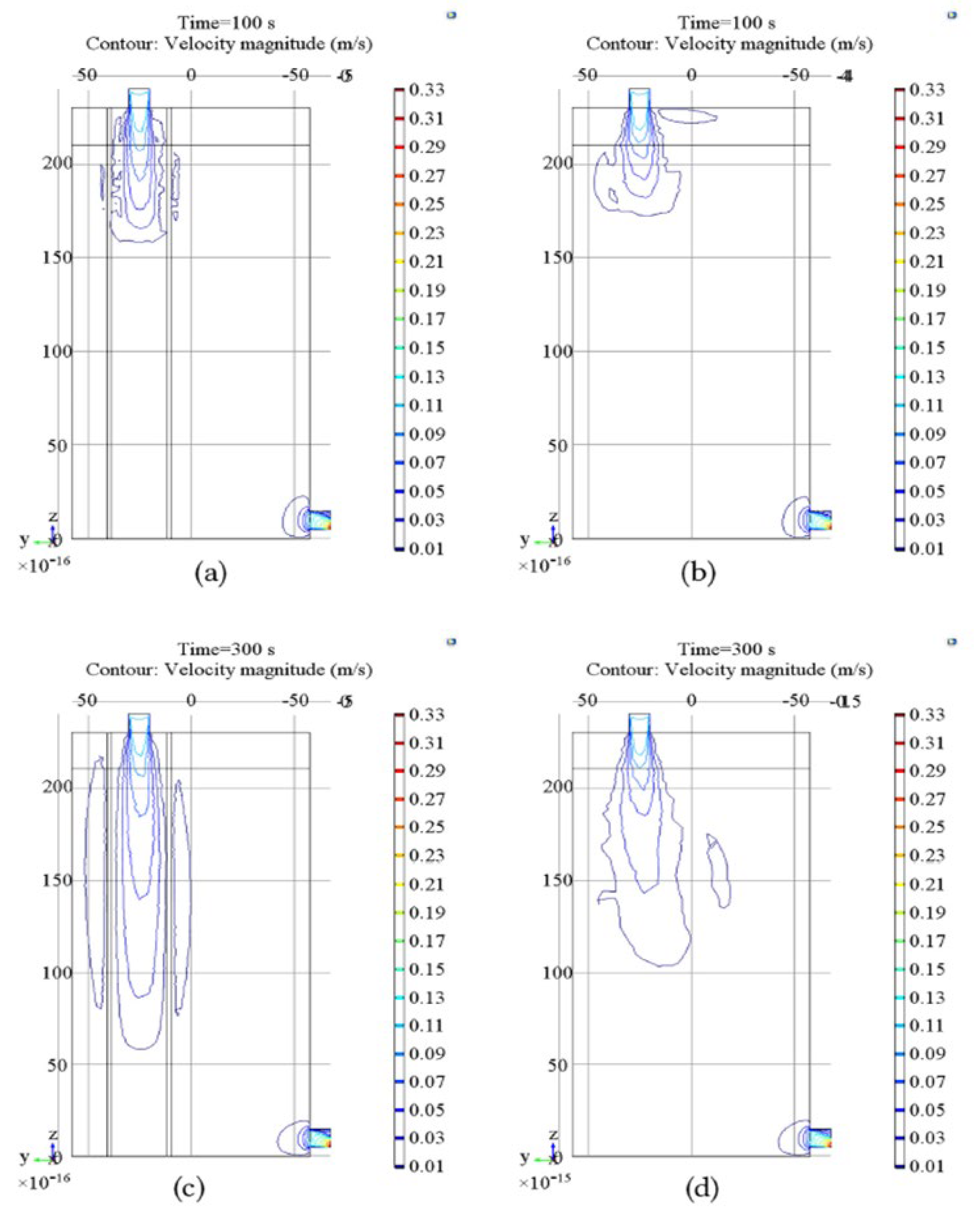
In an article [32], a research team from the University of Nantes in France studied the problem of uneven flow distribution in a single-tank solar salt heat storage system. Their proposal to solve this problem was to use stratification baffles with openings to improve the uniformity of temperature distribution in the tank. Using CFD, they conducted 2D simulations of the temperature distribution and fluid velocity during storage loading and unloading.

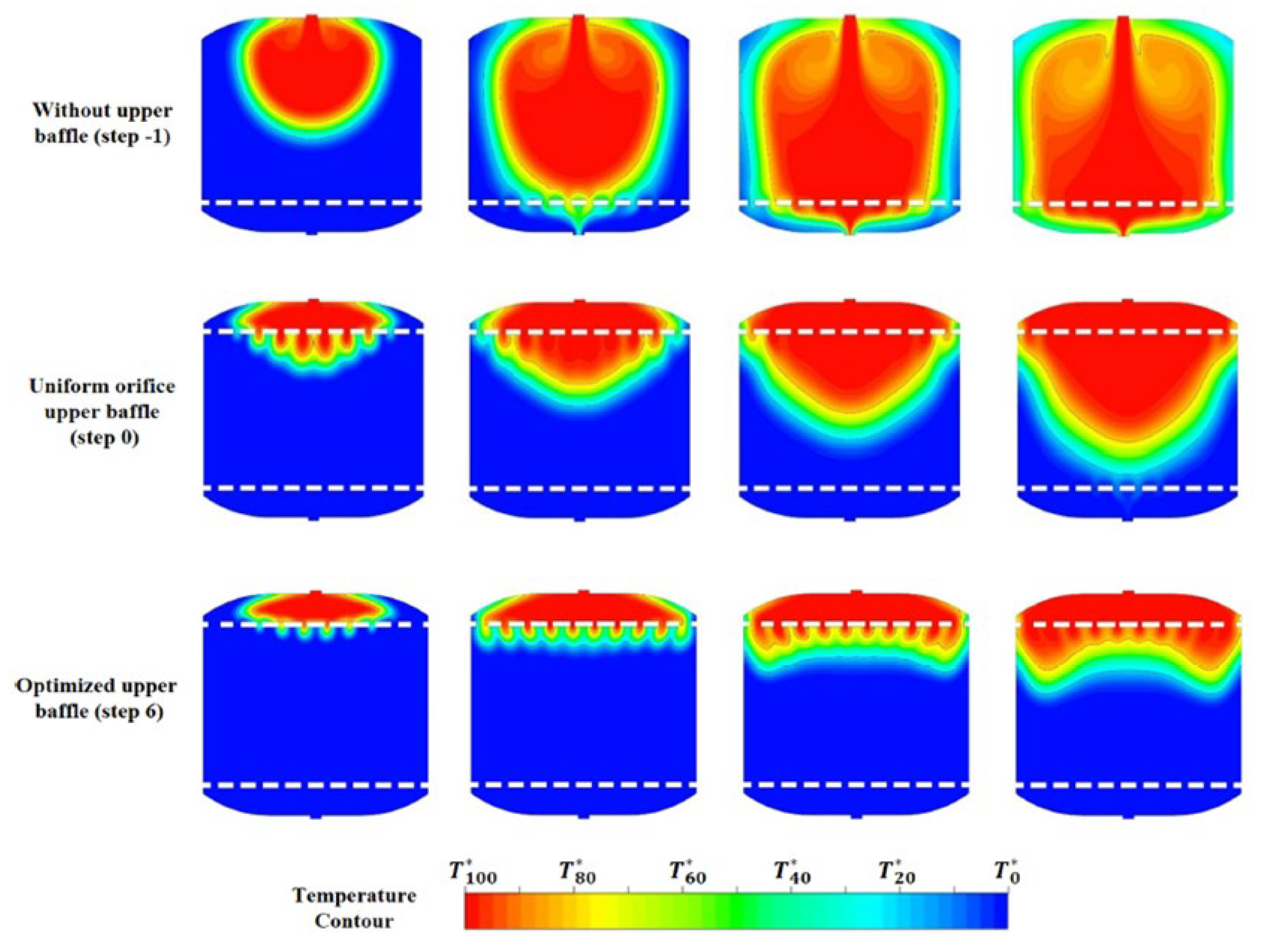
At the beginning of the study, they focused on the charging process and conducted three key CFD simulations for different configurations of tank geometry. The first simulation involved a tank without a top baffle (step -1), the second with two uniform baffles with openings (step 0), and the third involved an optimized baffle geometry whose distances and widths were adjusted based on an iterative optimization process (Figure 12). The optimization algorithm in MATLAB, implemented in six iterations (step 6), analyzed the data from the first two simulations and calculated changes in geometric parameters, which were then used to run new simulations in Ansys FLUENT. This yielded an optimized baffle configuration that provided the highest heat storage efficiency.

When analyzing the cyclic operation of the storage, including both loading and unloading, it was found that the geometry of the lower baffle has a significant impact on the efficiency of the unloading process. Therefore, using the optimized upper baffle from previous studies, an additional optimization of the lower baffle was carried out. The results showed that the optimized lower baffle improves the efficiency of both charging and discharging, leading to better flow management and less heat loss in the tank.

Various design parameters such as Reynolds number, aspect ratio, cone angle, number of holes in the baffle and baffle porosity were also analyzed. It was found that optimizing the two baffles significantly improves the efficiency of heat charging and discharging in thermal reservoirs, and their appropriate combination yields the best results. A higher Reynolds number negatively affected temperature stratification, suggesting the need to control the fluid flow velocity at the inlet. In addition, a positive cone angle (θ=+15°) improved control of warm liquid flow compared to a negative angle (θ=-15°). The larger number of holes, higher aspect ratio and lower porosity of the baffles improved stratification, leading to more efficient heat storage.

Another example of the use of computational fluid dynamics in studying the degree of thermal stratification of thermal storage tanks is published [33]. A team of researchers from Shandong University in China developed three models of three-dimensional cylindrical storage tanks that differ in the number of stratification surfaces with an opening. Numerical simulations were used to study the effects of the number of obstructions and fluid inlet velocity on thermal stratification (Figure 13).

It turned out that increasing the number of obstacles significantly improved stratification in the tank. Specifically, at an initial velocity of 0.3 m/s, the tank with two obstacles was more effective in reducing the mixing of hot and cold water compared to the others. Thermocline thickness measurements were 0.87 m, 0.23 m and 0.29 m for one, two and three baffles, respectively. As the inlet velocity increased, mixing increased, especially in tanks with one barrier. Tank number 3 showed the least sensitivity to changes in velocity, and the thinnest thermocline layer was observed at 0.20-0.25 m/s.

A study by a team of researchers from the CanmetENERGY institute in Canada [34] aimed to investigate the effects of design and operational parameters during charging on the flow, thermal stratification and performance of the heat tank in solar energy systems. Two key design parameters were considered in the analysis: the aspect ratio (the ratio of the tank’s height to its diameter) and the position of the inlet and outlet ports. The operating parameters were mass flow rate, hot water temperature at the inlet, and initial water temperature. The study used CFD simulations of a three-dimensional insulated cylindrical tank with water as the medium.

The results showed that a high aspect ratio (AR = 3.5) provided the best thermal stratification. The higher the coefficient, the greater the temperature gradient between layers, which promoted better stratification. Decreasing the coefficient (AR = 2) led to worse stratification and lower temperatures. Changing the height of the tank at a constant diameter had no significant effect on stratification.

The location of the inlet/outlet port proved equally crucial. The best results were obtained with the inlet located near the top of the tank, where the thermal layer developed the fastest (Figure 14).

Ports placed lower promoted more complex water mixing. The high hot water flow rate affected more intensive mixing, but stable thermal stratification was maintained. The optimal flow rate was 0.15 kg/s.

In the context of the inlet temperature, regardless of the difference between the initial temperature and the inlet water temperature, thermal stratification was stable and water mixing was minimal.

An article by researchers from the Department of Engineering and Energy in India [35] analyzed the performance of single-phase tank heat storage systems using different inlet configurations and working materials. They analyzed water and solar salt (a mixture of NaNO3 and KNO3) in different tank variants - both with and without a distributor. The study was based on CFD simulations, taking into account the location of the hot medium inlet and the presence of the distributor (Figure 15). The distributor in a heat storage system is designed to evenly distribute the hot medium in the tank, which translates into improved thermal stratification and increases the thermal efficiency of the system.

The results showed that the use of a distributor significantly improved thermal efficiency regardless of the working material. In the case of water, the distributor significantly reduced the thickness of the thermocline layer, which promoted better thermal stratification. In contrast, solar salt showed lower efficiency compared to water under the same conditions. The article emphasizes that the distributor improves thermal efficiency, especially in systems with water, while for systems with solar salt, further research is needed to improve the results.

Other researchers at the same institute in India investigated a thermal energy storage system using molten salts as the heat transfer medium and quartzite stones as the filler. In a paper [36], they analyzed the effect of stone size on the performance of the thermal storage (TES) charging and discharging process using a three-dimensional model under laminar and turbulent flow conditions, verified by experimental results. The study included analysis of thermodynamic and geometric parameters, and the CFD-Taguchi method was used to optimize the system.

The results showed that charging and discharging efficiency decreased with time, and the optimal Reynolds number range (100-300) allowed better thermal stratification in the tank. Turbulent flow reduced system efficiency by 17.14% compared to laminar flow. Inlet temperature mainly affected heat loss through the outer walls, while smaller quartzite stones improved storage efficiency, although stones that were too fine or too large reduced porosity, which negatively affected charging and discharging processes.

The most significant parameters affecting performance were porosity and aspect ratio. The optimal settings, determined by the CFD-Taguchi method, were an aspect ratio of 0.25, Reynolds number of 10, porosity of 0.8 and fill size of 0.01 m.

3.2. Using CFD to Simulate Heat Loss in Thermal Energy Storage Systems

One of the main challenges in thermal energy storage systems negatively affecting their performance is heat loss. In order to reduce these losses and better understand the thermal processes occurring in thermal storage, computational fluid dynamics methods are also widely used.

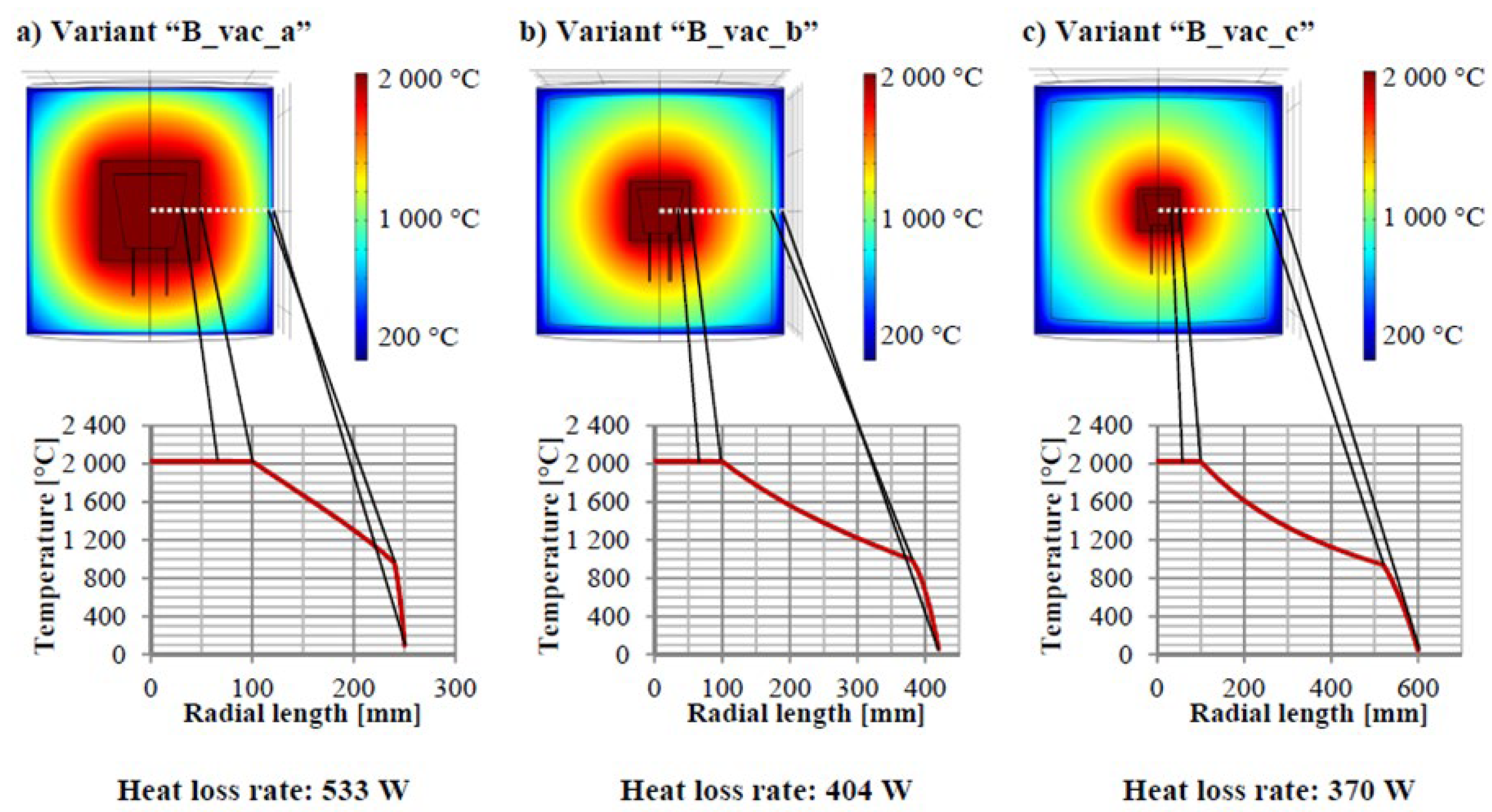
Researchers at the University of Stuttgart have focused their research on insulating materials for thermal energy stores operating at high temperatures of up to 2000°C [37]. Their research focuses on multilayer insulation, in which materials with better temperature stability are placed closer to the heat source.

Numerous simulations have been carried out to study heat loss and temperature propagation as a function of insulation materials, insulation layer thickness and gaseous atmosphere. The thermal storage (TES) was modeled as a truncated cone with a height of 150 mm and diameters of 100 mm and 150 mm, maintaining a constant temperature of 2300 K.

The authors of the publication found that increasing insulation thickness can lead to an increase in heat loss. As a result, they suggest that the use of vacuum in insulation can significantly reduce thermal conductivity, which can almost halve the heat loss rate with less insulation thickness. They expressed the need for further research into vacuum materials and the costs associated with maintaining the vacuum, as well as alternative insulation techniques such as multilayer foil insulation.

Analysis of all tested variants (air, argon and vacuum layer between insulation layers) showed that the heat loss coefficient decreases with increasing total insulation thickness (Figure 16). However, increasing the thickness of the insulation leads to a decrease in effectiveness in reducing heat loss. This is due to the increasing external heat-transfer surface area with greater total insulation thickness. Heat loss reduction efficiency refers to how effectively an insulation reduces heat loss compared to its thickness. When insulation thickness increases, the amount of heat lost initially decreases noticeably. However, after a certain point, further increases in insulation thickness bring less and less benefit in reducing heat loss.

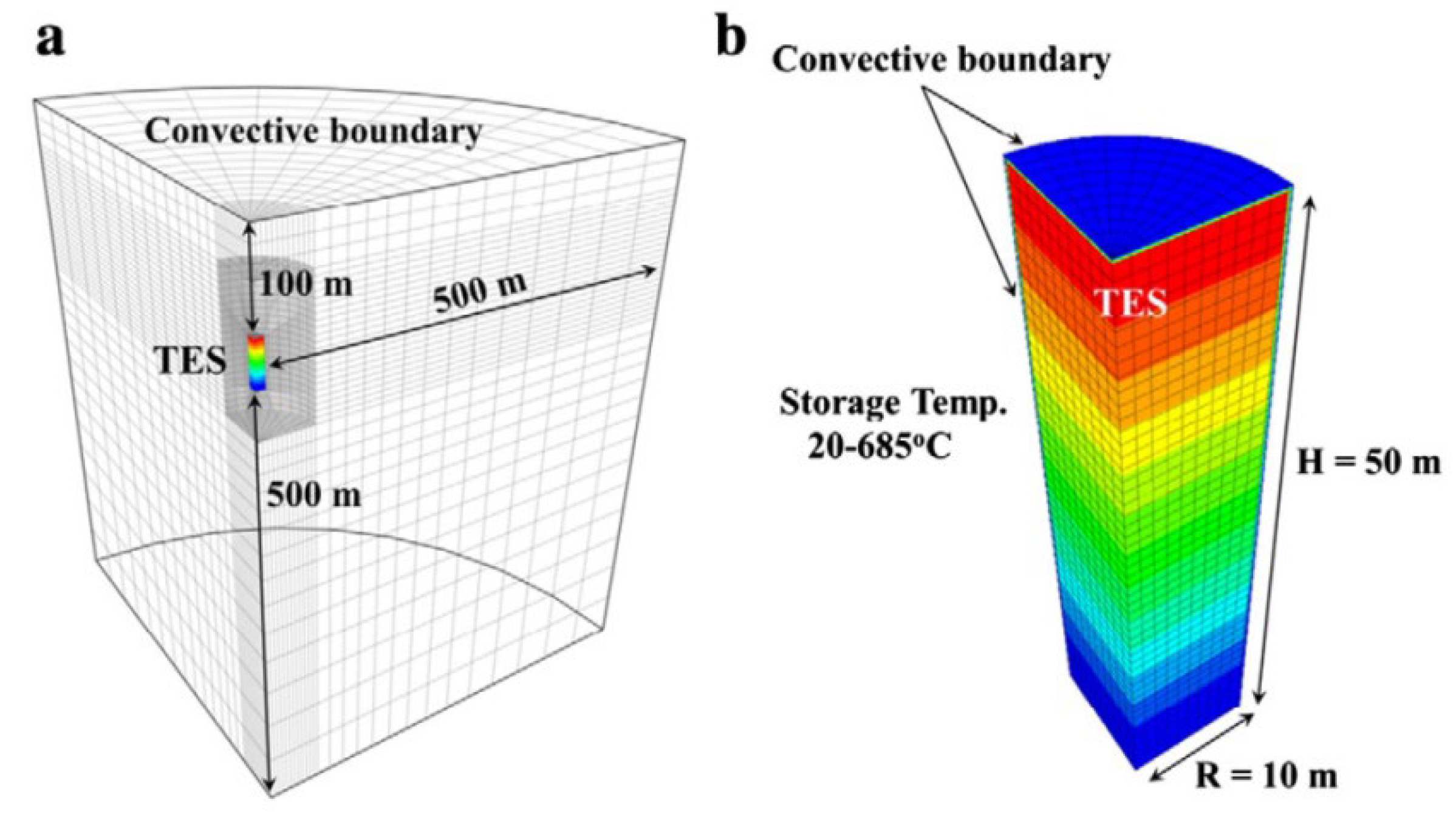
The article [38] presents research on thermal energy storage systems in the context of insulation efficiency and heat loss in two different types of systems: rock cavern and above-ground (Figure 17), which focused on comparing heat loss and heat transfer efficiency in these two systems.

The study used a TES storage model using loosely stacked stones that stores heat up to 685°C. Numerical simulations were carried out, which included analysis of heat transfer in the stone packs and evaluation of ambient heat loss. The simulations were carried out over 10 years to determine the effects of various parameters on heat storage efficiency.

The results showed that cave TES systems have lower heat loss (69.2% lower) and better long-term stability compared to above-ground systems. In the first five days, there was no significant difference in the rate of heat loss between the two technologies (185.2-243.5 kW for cave TES and 188.0-241.3 kW for aboveground TES). However, in the last five days, the rate of heat loss in the cave system was significantly lower (162.48-110.23 kW) than in the aboveground system (190.3-242.0 kW).

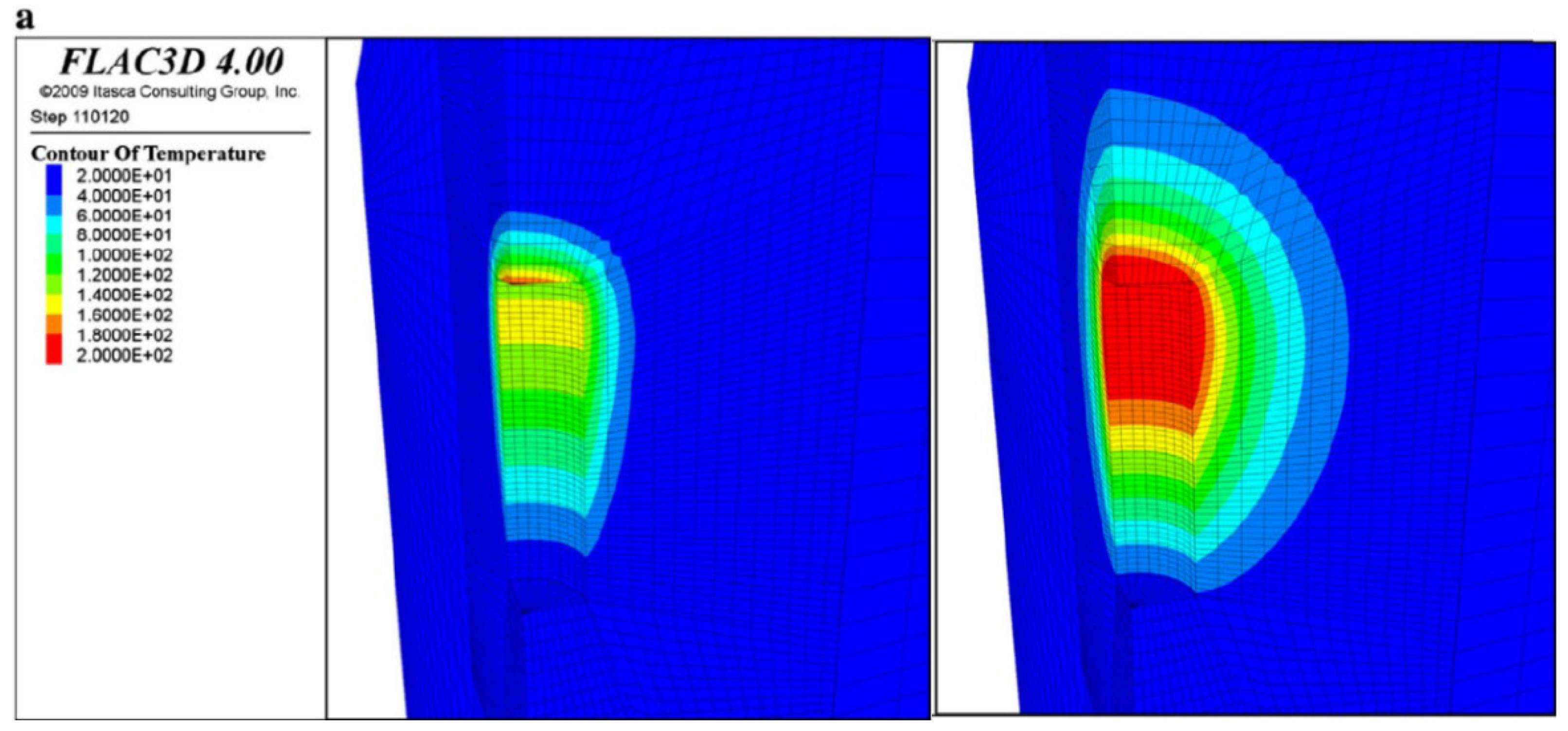
Interestingly, the authors simulated the predicted temperature distribution on the rocks surrounding the cave storage after one year and 10 years of operation (Figure 18).

Cave systems have shown less sensitivity to changes in insulation performance in long-term use, making them a more efficient solution compared to above-ground systems.

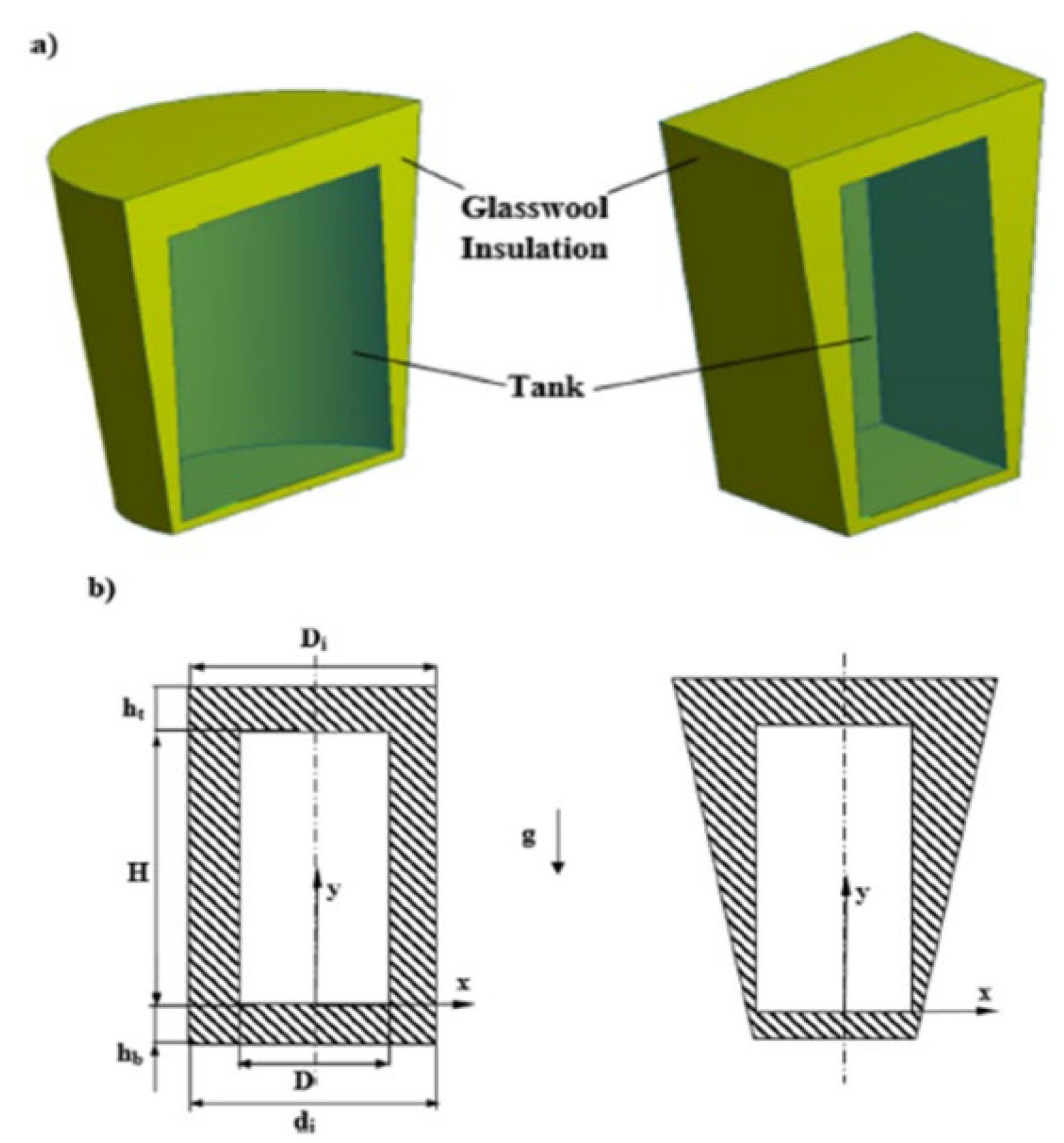
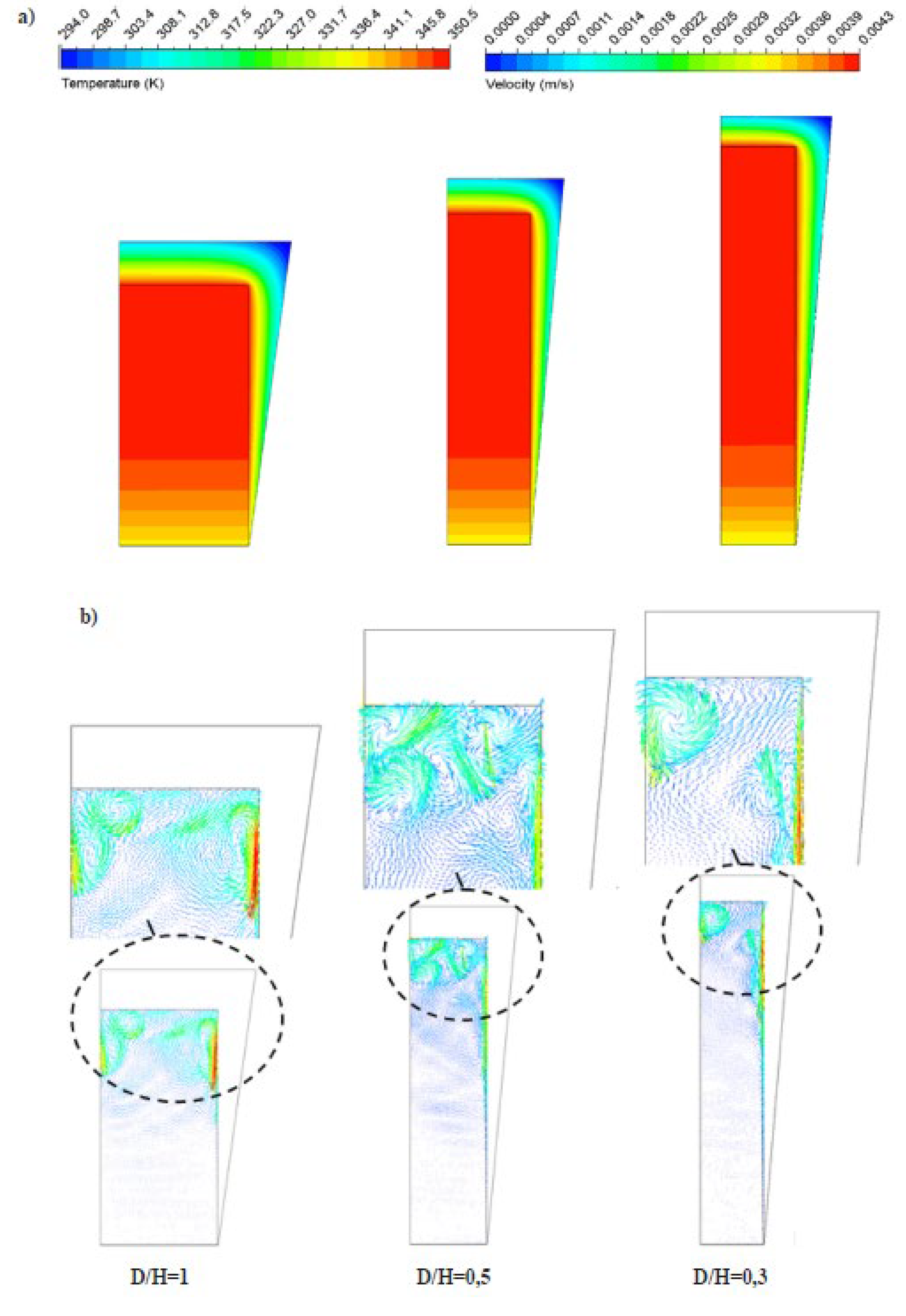
A Turkish scientist from Amasya University [39] studied the effect of using glass wool insulation for a cylindrical tank (truncated cone insulation) and a rectangular tank (pyramid-shaped insulation) (Figure 19) on improving thermal stratification in hot water tanks. The results of the temperature distribution and velocity of the medium in the tank, obtained by simulation, are shown in Figure 20.

The effects of three parameters were analyzed: tank size ratio, diameter ratio, and thickness of bottom and top insulation. According to the study, the highest loss of exergy efficiency was only 0.034% for truncated cone insulation and 0.02% for truncated pyramid insulation, indicating minimal loss of exergy when using these geometries. In addition, the results showed that lowering the ratios of tank dimensions, bottom and top insulation diameters, and insulation thickness significantly improves thermal stratification, leading to a significant increase in the temperature difference between the bottom and top of the tank. The maximum increase in thermal stratification was recorded at certain values of these parameters, confirming the effectiveness of truncated cone and pyramid-shaped insulation in improving the efficiency of hot water tanks.

Computational fluid dynamics (CFD) methods are commonly used to analyze heat loss in thermal energy storage (TES) systems. These simulations allow detailed modeling of heat transfer processes, taking into account the influence of various parameters such as tank geometry, insulation materials and ambient conditions. With CFD, it is possible to evaluate insulation efficiency, predict temperature distribution and optimize thermal storage designs, minimizing energy losses. This allows better design of TES systems with higher efficiency and long-term thermal stability.

4. Conclusions

This article discusses technologies related to renewable energy sources, with a particular focus on solar cooling systems and thermal storage units. It presents a literature review on solar energy-based cooling systems, including the use of absorption chillers and thermal storage units, which enable the optimization of these systems. The research conducted by the authors of the publication demonstrates that the appropriate use of thermal storage increases the efficiency of the systems, allowing for the accumulation of excess energy and its subsequent utilization.

The second part of the article focuses on the analysis of thermal processes occurring in thermal storage units, using computational fluid dynamics. CFD simulations allow for modeling the charging and discharging processes of the storage units and analyzing the flow of the working medium. A key element in improving the efficiency of these systems is thermal stratification, which limits the mixing of heat and cold in the storage unit, thereby increasing its performance.

The above review of articles provides valuable insight into the application of CFD methods in the analysis of thermal storage, highlighting their significant role in improving such systems. Most studies indicate the critical importance of optimizing tank geometry and flow parameters (such as the Reynolds number) in enhancing thermal storage efficiency. Stable thermocline layers can be achieved through the appropriate selection of filling materials (e.g., quartzite stones), which support the improvement of thermal energy storage (TES) system performance. Furthermore, various thermal storage technologies are presented, emphasizing the advantages and limitations of each. CFD analysis enables the refinement of tank geometry and the reduction of heat losses, which is crucial for increasing the efficiency of solar cooling systems.

Research indicates the need for further development of thermal storage technologies and the materials used in them, which will enable the future estimation of potential costs for building actual cooling systems that utilize solar energy. The use of numerical simulations for these purposes will contribute to better energy management in the context of global climate-related challenges.

Author Contributions

Conceptualization, J.J., M.F. and H.J.; methodology, M.F. and H.J.; analysis, M.F. and H.J.; investigation, M.F. and H.J.; resources, J.J., M.F., H.J, M.W. and K.S.; data curation, J.J., M.F., H.J. and K.S.; writing—original draft preparation, M.F. and H.J; writing—review and editing, J.J., M.W. and K.S.; visualization, M.F. and H.J.; supervision, J.J. and K.S.; project administration, J.J..; funding acquisition, J.J.. All authors have read and agreed to the published version of the manuscript.

Funding

This paper is financed from the statutory funds of the Strata Mechanics Research Institute of the Polish Sciences Academy.

Data Availability Statement

Not applicable.

Acknowledgments

This paper is financed from the statutory funds of the Strata Mechanics Research Institute of the Polish Sciences Academy.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Bujok, T.; Sowa, M.; Boruta, P.; Mika, Ł.; Sztekler, K.; Chaja, P.R. Possibilities of Integrating Adsorption Chiller with Solar Collectors for Polish Climate Zone. Energies 2022, 15, 6233. [Google Scholar] [CrossRef]
Tsoutsos, T.; Aloumpi, E.; Gkouskos, Z.; Karagiorgas, M. Design of a solar absorption cooling system in a Greek hospital. Energy and Buildings 2010, 42(2), 265–272. [Google Scholar] [CrossRef]
Figaj, R.; Szubel, M.; Przenzak, E.; Filipowicz, M. Feasibility of a small-scale hybrid dish/flat-plate solar collector system as a heat source for an absorption cooling unit. Applied Thermal Engineering 2019, 163, 114399. [Google Scholar] [CrossRef]
Srikhirin, P.; Aphornratana, S.; Chungpaibulpatana, S. A review of absorption refrigeration technologies. Renewable and Sustainable Energy Reviews 2001, 5, 343–372. [Google Scholar] [CrossRef]
de Souza, A., Ed. How to – Understand Computational Fluid Dynamics Jargon; NAFEMS Ltd.: 2005.
Kong, L.; Yuan, W.; Zhu, N. CFD simulations of thermal stratification heat storage water tank with an inside cylinder with openings. Procedia Engineering 2016, 146, 394–399. [Google Scholar] [CrossRef]
Gao, L.; Lu, H.; Sun, B.; Che, D.; Dong, L. Numerical and experimental investigation on thermal stratification characteristics affected by the baffle plate in thermal storage tank. Journal of Energy Storage 2021, 34, 102117. [Google Scholar] [CrossRef]
Hosseinnia, S.M.; Akbari, H.; Sorin, M. Numerical analysis of thermocline evolution during charging phase in a stratified thermal energy storage tank. Journal of Energy Storage 2021, 40, 102682. [Google Scholar] [CrossRef]
Menter, F. Turbulence Modeling for Engineering Flows. ANSYS 2012 Inc. ( 2012. [Google Scholar]
Menter, F. Best Practice - Scale-Resolving Simulations in ANSYS CFD - Application Brief Version 2.0 (2015).
Said, S.A.M.; El-Shaarawi, M.A.I.; Siddiqui, M.U. Intermittent absorption refrigeration system equipped with an economizer. Energy 2013, 61, 332–344. [Google Scholar] [CrossRef]
Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renewable and Sustainable Energy Review 2009, 13, 318–345. [Google Scholar] [CrossRef]
Tian, Y.; Zhao, C.Y. A review of solar collectors and thermal energy storage in solar thermal applications. Applied Energy 2013, 104, 538–553. [Google Scholar] [CrossRef]
Shamshirgaran, S.R.; Khalaji Assadi, M.; Viswanatha Sharma, K. Application of nanomaterials in solar thermal energy storage. Heat Mass Transfer 2017, 54, 1555–1577. [Google Scholar] [CrossRef]
Jastrzębski, P.; Saługa, P.W. Innowacyjne metody magazynowania ciepła. Zeszyty Naukowe Instytutu Gospodarki Surowcami Mineralnymi i Energią Polskiej Akademii Nauk 2018, 105, 225–232. [Google Scholar] [CrossRef]
Nowoczesne metody magazynowania i wykorzystywania energii słonecznej. Available online: https://www.rynekinstalacyjny.pl/artykul/kolektory-sloneczne/10958,nowoczesne-metody-magazynowania-i-wykorzystywania-energii-slonecznej (accessed on 18 September 2024).
Quant, L. Study of a Urea-based Phase Change Material for Thermal Energy Storage. Doctoral Thesis, University of the Basque Country UPV/EHU, University of Pau et des Pays de l’Adour, 2020. [Google Scholar]
Nakaso, K.; Teshima, H.; Yoshimura, A.; Nogami, S.; Hamada, Y.; Fukai, J. Extension of heat transfer area using carbon fiber cloths in latent heat thermal energy storage tanks. Chemical Engineering and Processing 2008, 47, 879–885. [Google Scholar] [CrossRef]
Branny, M.; Jaszczur, M.; Wodziak, W.; Szmyd, J. Experimental and numerical analysis of air flow in a dead-end channel. Journal of Physics: Conference Series 2016, 745, 032045. [Google Scholar] [CrossRef]
Ren, T.; Wang, Z. Computational fluid dynamics modelling of respirable dust and gas behaviour on a longwall face. In Proceedings of the Australian Mine Ventilation Conference, Adelaide, SA, Australia, 1–3 July 2013; Australasian Institute of Mining and Metallurgy: Australia, 2013; pp. 191–200. [Google Scholar]
Seduikyte, L.; Stasiulienė, L.; Prasauskas, T.; Martuzevičius, D.; Černeckienė, J.; Ždankus, T.; Dobravalskis, M.; Fokaides, P. Field Measurements and Numerical Simulation for the Definition of the Thermal Stratification and Ventilation Performance in a Mechanically Ventilated Sports Hall. Energies 2019, 12, 2243. [Google Scholar] [CrossRef]
Ortiz, M.; Barsun, H.; He, H.; Vorobieff, P.; Mammoli, A. Modeling of a solar-assisted HVAC system with thermal storage. Energy and Buildings 2010, 42(4), 500–509. [Google Scholar] [CrossRef]
Sornek, K.; Filipowicz, M. Symulacje dynamiczne systemów OZE z wykorzystaniem oprogramowania TRNSYS. Czasopismo Inżynierii Lądowej, Środowiska i Architektury 2017, 64(4/II), 387–394. [Google Scholar]
Chidambaram, L.A.; Ramana, A.S.; Kamaraj, G.; Velraj, R. Review of solar cooling methods and thermal storage options. Renewable and Sustainable Energy Reviews 2011, 15(6), 3220–3228. [Google Scholar] [CrossRef]
Al-Marafie, A.; Moustafa, S.M.; Al-Kandarie, A. Factors Affecting Static Stratification of Thermal Water Storage. Energy Sources 1989, 11(3), 183–199. [Google Scholar] [CrossRef]
Ievers, S.; Lin, W. Numerical simulation of three-dimensional flow dynamics in a hot water storage tank. Applied Energy 2009, 86(12), 2604–2614. [Google Scholar] [CrossRef]
Haller, M.Y.; Cruickshank, C.A.; Streicher, W.; Harrison, S.J.; Andersen, E.; Furbo, S. Methods to determine stratification efficiency of thermal energy storage processes – Review and theoretical comparison. Solar Energy 2009, 83, 1847–1860. [Google Scholar] [CrossRef]
Rodrigues, F.A.; de Lemos, M.J.S. Effect of porous material properties on thermal efficiencies of a thermocline storage tank. Applied Thermal Engineering 2020, 115194. [Google Scholar] [CrossRef]
Yin, H.; Ding, J.; Jiang, R.; Yang, X. Thermocline characteristics of molten-salt thermal energy storage in porous packed-bed tank. Applied Thermal Engineering 2017, 110, 855–863. [Google Scholar] [CrossRef]
ELSihy, E.S.; Wang, X.; Xu, C.; Du, X. Numerical investigation on simultaneous charging and discharging process of molten-salt packed-bed thermocline storage tank employing in CSP plants. Renewable Energy 2020. [Google Scholar] [CrossRef]
Karim, A.; Burnett, A.; Fawzia, S. Investigation of Stratified Thermal Storage Tank Performance for Heating and Cooling Applications. Energies 2018, 11(5), 1049. [Google Scholar] [CrossRef]
Lou, W.; Fan, Y.; Luo, L. Single-tank thermal energy storage systems for concentrated solar power: Flow distribution optimization for thermocline evolution management. Journal of Energy Storage 2020, 32, 101749. [Google Scholar] [CrossRef]
Feng, H.; Li, H.; He, S.; Qi, J.; Han, K.; Gao, M. Numerical simulation on thermal stratification performance in thermocline water storage tank with multi-stage middle perforated obstacles. Thermal Science and Engineering Progress 2022, 35, 101473. [Google Scholar] [CrossRef]
Yaïci, W.; Ghorab, M.; Entchev, E.; Hayden, S. Three-dimensional unsteady CFD simulations of a thermal storage tank performance for optimum design. Applied Thermal Engineering 2013, 60(1-2), 152–163. [Google Scholar] [CrossRef]
Shaikh, W.; Wadegaonkar, A.; Kedare, S.B.; Bose, M. Numerical simulation of single media thermocline based storage system. Solar Energy 2018, 174, 207–217. [Google Scholar] [CrossRef]
Nandi, B.R.; Bandyopadhyay, S.; Banerjee, R. Numerical modeling and analysis of dual medium thermocline thermal energy storage. Journal of Energy Storage 2018, 16, 218–230. [Google Scholar] [CrossRef]
Lang, S.; Bestenlehner, D.; Marx, R.; Drück, H. Thermal insulation of an ultra-high temperature thermal energy store for concentrated solar power. In Proceedings of the SolarPACES 2017: International Conference on Concentrating Solar Power and Chemical Energy Systems, Santiago, Chile, 26–29 September 2017. [Google Scholar] [CrossRef]
Park, J.-W.; Park, D.; Ryu, D.-W.; Choi, B.-H.; Park, E.-S. Analysis on heat transfer and heat loss characteristics of rock cavern thermal energy storage. Engineering Geology 2014, 181, 142–156. [Google Scholar] [CrossRef]
Kurşun, B. Thermal stratification enhancement in cylindrical and rectangular hot water tanks with truncated cone and pyramid shaped insulation geometry. Solar Energy 2018, 169, 512–525. [Google Scholar] [CrossRef]

Figure 1. A single-stage absorption cooling system with LiBr-water as the working fluid and a thermal storage unit in the form of a heat exchanger [4].

Figure 2. Cooling system diagram [11].

Figure 3. Types of energy thermal storage [12].

Figure 4. Types of energy storage.

Figure 5. Comparison of the demand for heat storage volume of 6480 MJ for the analyzed storage technologies [14].

Figure 6. Types of phase change materials and their properties [17].

Figure 7. Block diagram showing solar collectors (FPA and VTA), hot water storage tanks (HWT) and cold water storage tanks (CWT), absorption chiller, heating and cooling coils, and layout of auxiliary equipment [22].

Figure 8. Tank temperature profiles for each node [23].

Figure 9. Temperature distribution in the thermal storage when the inlet and outlet are located at a) 20 mm, b) 300 mm from the horizontal surfaces of the tank [26].

Figure 10. Turbulence kinetic energy field in the tank inlet zone: (a) Re 8.3 × 10³, (b) Re 1.7 × 10⁴, (c) Re 3.3 × 10⁴, (d) Re 5 × 10⁴. [28].

Figure 11. Simulation results of different TES systems after 1600 s: (a) TES-1; (b) TES-2; (c) TES-3; (d) TES-4; (e) TES-5 [31].

Figure 12. Comparison of the evolution of temperature profiles in the tank during the charging process (step -1: lower baffle only, step 0: upper and lower baffle, step 6: lower baffle and optimized upper baffle) [32].

Figure 13. Effect of different number of obstacles on temperature distribution in tanks at initial (t1=0.1) and final (t2=1) times [33].

Figure 14. Effect of inlet and outlet location on temperature distribution after 1000 s. [34].

Figure 15. Contours of water velocity in tanks: (a) with distributor, t=100s; (b) without distributor, t=100s; (c) with distributor, t=300s; (d) without distributor, t=300s [35].

Figure 16. Thermographic images of a planar cross-section through the center of the thermal energy storage (TES) for the B_vacuum variant, along with plots of temperature as a function of radial length from the center to the outer surface of the insulation and the heat loss coefficient [37].

Figure 17. Grids with quarter symmetry for (a) the cave TES model and (b) the above-ground TES model [38].

Figure 18. Temperature distributions of the surrounding rock estimated at (a) 1 year and (b) 10 years after the start of mining [38].

Figure 19. Geometry and dimensions of the storage tank: (a) 3D section view, (b) 2D section view [39].

Figure 20. Temperature and velocity distributions for a rectangular hot water tank with pyramid-shaped insulation geometry: (a) temperature distribution, (b) velocity vectors [39].

Table 1. Comparison of heat storage parameters [15].

Storage Technology	Capacity [kWh/t]	Power [MW]	Efficiency [%]	Storage Period	Cost [euro/kWh]
Sensible heat storage	10-50	0.001-10	50-90	Days/months	0.1-10
Storages based on phase change materials	50-150	0.001-1	75-90	Hours/months	10-50
Storages using thermochemical reactions	120-250	0.01-1	75-100	Hours/months	8-100

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer