1. Introduction
Traditional power generation primarily relies on fossil fuels, which release large amounts of greenhouse gases when burned, exacerbating the issue of global warming. At the same time, the depletion of fossil fuels has led to a steady increase in prices [
1]. Utilizing renewable energy for distributed generation offers significant economic and environmental benefits, making it a highly viable solution [
2]. Wind energy, as an emerging renewable resource with relatively mature technology, has become a promising method of renewable energy generation and plays a key role in promoting the sustainable development of global energy [
3].
With the widespread adoption of wind power globally, its penetration into the grid continues to increase, posing significant threats to the stability and security of the power grid due to its randomness, volatility, and intermittency [
4,
5,
6]. To address this challenge, HESS offers a solution by smoothing complex wind power fluctuations to enhance the stability of grid integration [
7,
8]. Due to the varying functions of energy storage devices, battery storage, which is energy-based, offers high energy density and shorter cycle life, making it suitable for low-frequency power fluctuations. In contrast, supercapacitor storage, which is power-based, features high power density and longer cycle life, with strong environmental benefits. It can suppress high-frequency power fluctuations and reduce batteries’ charge and discharge cycles, thereby extending their lifespan [
9,
10,
11]. The application of hybrid energy storage systems in microgrids achieves complementary advantages, leading to energy management issues among different storage units. It is essential to allocate real-time power effectively to utilize each storage unit’s unique functional characteristics, representing both a future direction and a challenge.
Energy storage in microgrids is shifting from traditional centralized systems to more flexible and efficient distributed storage. Distributed energy storage is scattered across various renewable energy generation sources and critical loads, enabling units with similar functions to achieve collective autonomy and coordinated management. This is significant for enhancing the overall performance of microgrids. A key issue in this context is how to ensure that the SOC of each storage unit remains consistent. Otherwise, the imbalance of the SOC among storage units may cause some units to enter protection mode due to the risk of overcharging or discharging, increasing the burden on other units and hindering the efficient operation of the energy storage group. From the perspective of the control structure of distributed hybrid energy storage energy management systems, they can be classified into centralized control, decentralized control, and distributed control [
12,
13,
14,
15,
16]. Centralized control consists of a central controller and local controllers. As the number of distributed power sources increases, there is a greater demand for the central controller to have strong computational capabilities. This reliance on the central controller can lead to issues such as a single point of failure and a curse of dimensionality in the system [
13,
14]. In a decentralized control system, each control unit operates independently and makes decisions based on local information, with no direct communication or collaboration between units. Since each unit optimizes only based on local data, this can lead to globally suboptimal solutions and lower overall system efficiency [
15]. Distributed control only requires ’neighbor communication’ to obtain global information. Through cooperation among intelligent agents, tasks are accomplished, enhancing system efficiency and reliability while reducing communication costs and delays. Multi-agent distributed control offers advantages such as autonomous decision-making and coordinated control. Compared to traditional centralized control, it significantly lowers communication costs and improves system efficiency, making it increasingly applicable in microgrids [
16].
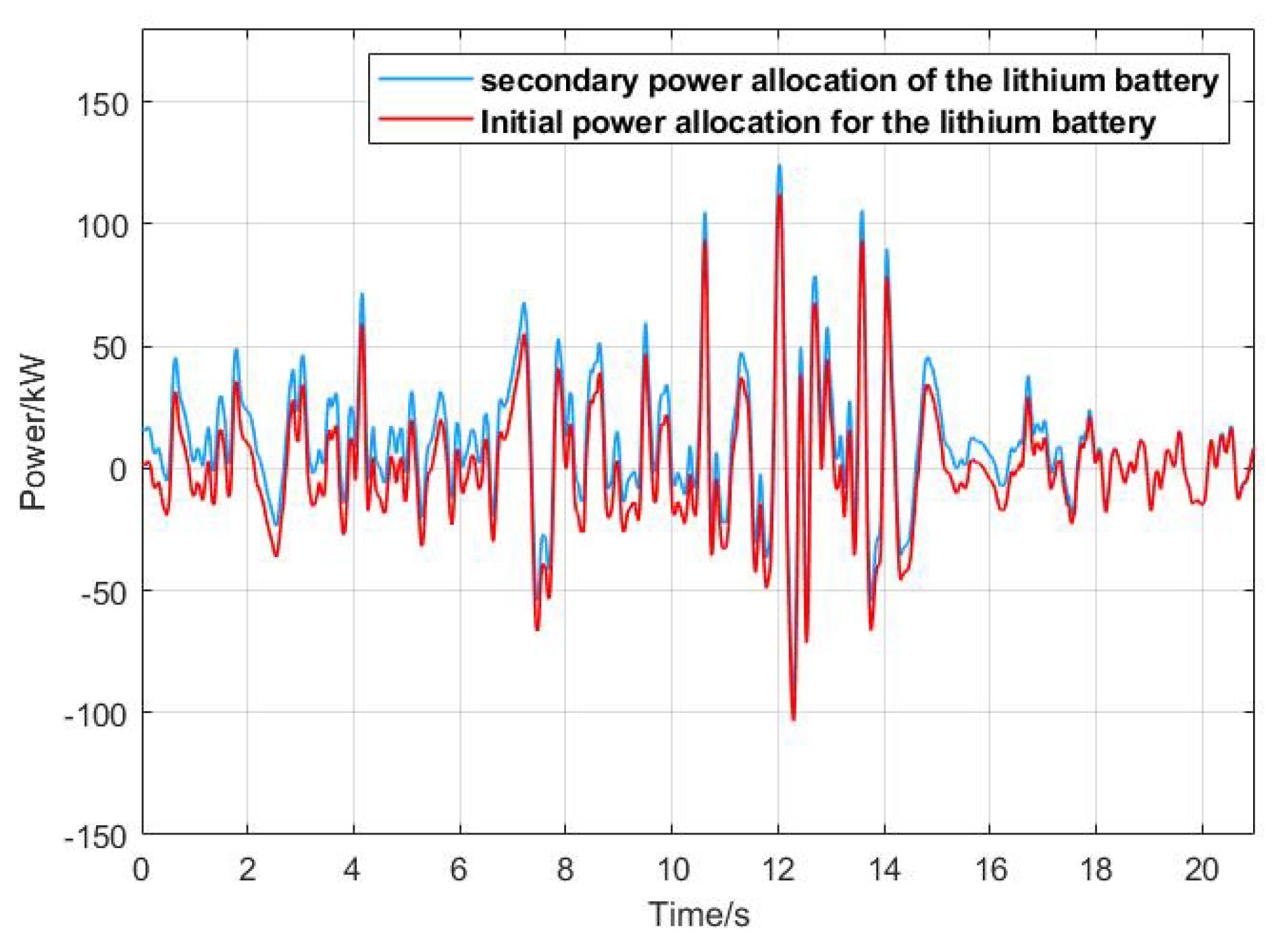
The application of hybrid energy storage systems in microgrids achieves complementary advantages but also creates energy management challenges among different storage units. Therefore, it is necessary to allocate smoothing power based on the characteristics of each storage component to suit the features of hybrid storage. This approach maximizes their effectiveness while extending their lifespan, which is essential for the initial power allocation in hybrid storage systems. Due to variations in factors such as the initial SOC of the storage units, the precision of manufacturing processes, and the degree of aging, the imbalance in SOC among different storage units can lead to some units entering protection mode due to the risk of overcharging or discharging. This increases the burden on other units and hinders the efficient operation of the energy storage group. Therefore, it is necessary to adjust the reference power for hybrid storage to prevent overutilization and underutilization of the storage devices. This adjustment process constitutes the secondary allocation in hybrid energy storage [
17]. Reference [
18] uses a Low-Pass Filter (LPF) for the initial power allocation of HESS and employs an adaptive time constant based on the LPF to optimize the utilization of supercapacitors and the operating time of batteries, thereby enhancing their lifespan. Reference [
19] employs traditional Extended Droop Control (EDC) for initial power allocation and introduces a SOC reference value to design a controller that adjusts the droop coefficient in real time, thereby achieving SOC balancing for hybrid energy storage. Reference [
20] designs an LPF for initial power allocation and implements a fuzzy control system to adaptively adjust the parameters of the LPF, ensuring the adaptive regulation of the SOC in hybrid energy storage and preventing overcharging and discharging. Reference [
21] employs a virtual capacitance and resistance descent method for the initial power allocation of hybrid energy storage and introduces an adaptive capacitance droop controller for supercapacitors to improve their SOC curve. Reference [
22] proposes a Weighted Moving Average (WMA) filter to achieve the initial allocation of HESS. It then uses a Model Predictive Control (MPC) method to quickly adjust the SOC of HESS during the wind power smoothing process, thereby reducing battery lifespan deterioration. Since Huang introduced empirical mode decomposition, reference [
23] has proposed a fully non-recursive variational mode decomposition model that reduces mode mixing and demonstrates greater robustness to noise. Although it is influenced by the number of modes K and the penalty parameter
, it offers significant advantages in power allocation.Reference [
24] proposes a method for smoothing photovoltaic power fluctuations in HESS based on VMD, achieving initial power allocation. VMD can adaptively determine the grid-connected power and the smoothing power of HESS, facilitating secondary allocation and extending the lifespan of the batteries. Reference [
25] proposes the use of the Artificial Hummingbird Algorithm (AHA) for parameter optimization of VMD, thereby enabling effective initial power allocation for hybrid energy storage. A fuzzy controller is employed to further optimize the initially allocated power, ensuring that the SOC of the hybrid storage remains stable within a fixed range. Reference [
26] introduces SVMD based on VMD. This method eliminates the influence of the mode K parameter, requiring only the setting of a maximum parameter
to sequentially extract modes. Moreover, the computational complexity of SVMD is significantly lower than that of VMD, and it exhibits greater robustness to the initial values of the mode center frequencies. Reference [
27] employs SVMD to decompose wind power and performs piecewise reconstruction of the mode functions for the initial allocation of hybrid energy storage power. "Then, an energy storage power model is established, and the target model is solved while considering the constraints of charging and discharging power and the state of charge, resulting in the optimal configuration of the hybrid energy storage system. Currently, the application of successive SVMD and VMD combined with fuzzy control in the power allocation of HESS is relatively limited. However, leveraging the advantages of both control methods may yield superior energy management outcomes when applied together in distributed hybrid energy storage systems. Furthermore, most existing studies utilize a single fuzzy controller; however, a single controller often fails to adapt to the varying power adjustment needs of hybrid energy storage systems across different periods. This limitation may result in uneven power distribution, potentially leading to issues such as overcharging and over-discharging.
In summary, to ensure the long-term power smoothing effectiveness of the wind-storage hybrid system and the reliability of battery functions, it is crucial to optimize the SOC of the HESS from an operational control perspective. This optimization involves reducing the depth of charging and discharging cycles while minimizing unnecessary charging and discharging events. Furthermore, from the perspective of maximum charging and discharging power, the energy storage units can be operated within a reasonable power range based on their parameters, enabling the distribution of wind power that meets the requirements for power smoothing. Therefore, building on existing research, this paper proposes a method that considers the goal of SOC equilibrium control by combining power modal decomposition algorithms with the optimized snake-ladybird algorithm, designing a multi-fuzzy rule-based approach for controlling the target power of energy storage. The main technical contributions of this study are as follows:
A method is proposed to prevent the overuse or underutilization of any specific energy storage device within the HESS, as well as to manage prioritization or gradual charging.
The grid-connected power optimization selection method based on SBOA-VMD effectively enhances the stability and output reliability of the grid power, ensuring the smooth operation of the power system. Utilizing the decomposition characteristics of SBOA-SVMD allows for a more precise selection of smoothing power according to the specific characteristics of each energy storage unit, thereby reducing fluctuations in grid power and improving system stability and response speed.
A multi-fuzzy controller is designed in partitions based on the deviation between the SOC of energy storage units and the global average SOC. This strengthens the SOC balance among storage units, preventing individual or group units from exiting operation due to overcharging or over-discharging, thereby enhancing the overall system reliability.
The structure of this paper is as follows:
Section 2 introduces the system network structure model;
Section 3 presents the optimization algorithm, modal decomposition algorithm, and power allocation strategy;
Section 4 provides the simulation analysis; and finally, the conclusions are presented.
3. Hybrid Energy Storage Power Allocation Strategy
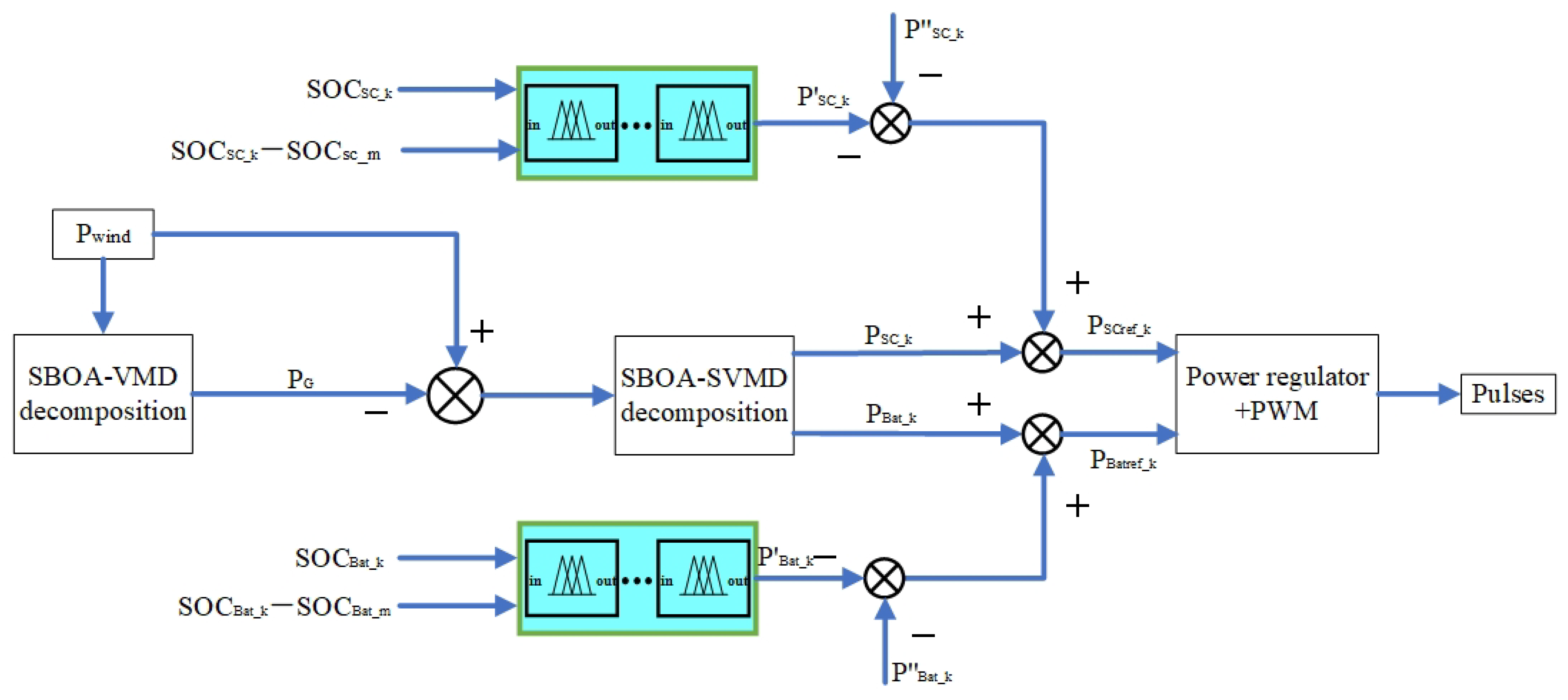
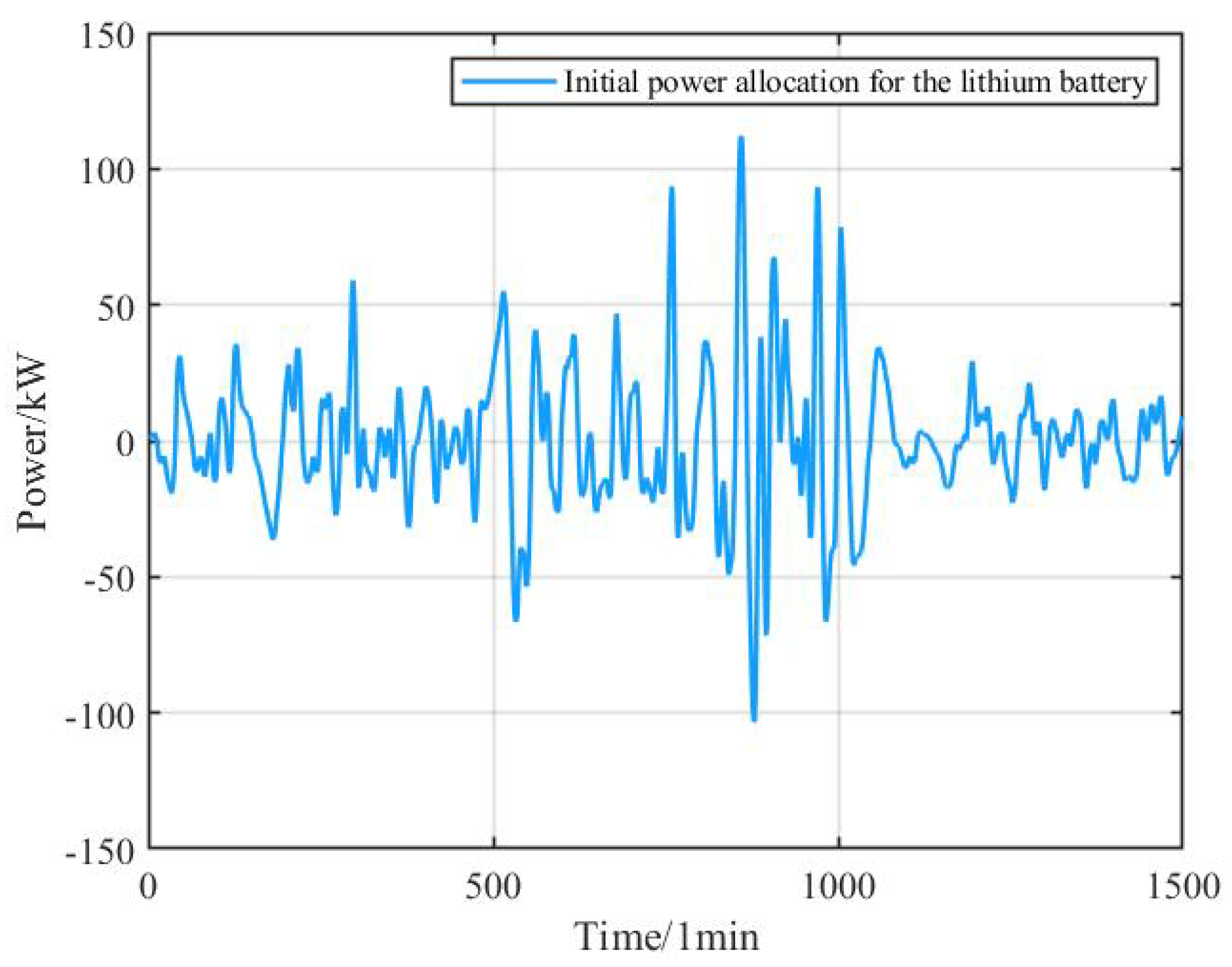
In the initial power allocation, successive variational mode decomposition (SVMD) extracts one modal component at a time, which can effectively reduce mode mixing and result in more independent modes, while having lower computational complexity compared to VMD. SVMD does not require prior knowledge of the number of modes; it adaptively extracts modes from the signal one by one, reducing dependence on parameter selection, and is only influenced by the maximum parameter . variational mode decomposition (VMD) is a technique that simultaneously decomposes a signal into multiple modes. The number of modes K and the penalty parameter significantly affect the decomposition results of VMD. When the value of K is too large, it can lead to over-decomposition, whereas if it is too small, under-decomposition occurs. Similarly, if the value of is too high, it may result in the loss of frequency band information, while a lower value can lead to redundant information. Therefore, this paper introduces the Secretary Bird Optimization Algorithm(SBOA) to optimize the parameters of SVMD and VMD, selecting the mean envelope entropy as the fitness function. This approach determines the maximum for SVMD and the optimal parameter pair for VMD, thereby obtaining the grid-connected power and hybrid energy storage power.
3.1. Successive Variational Modal Decomposition
The superior decomposition modes of successive variational mode decomposition (SVMD) and the algorithm’s low complexity, when applied to hybrid energy storage systems, enable better allocation of power between batteries and supercapacitors, thereby extending the lifespan of the storage units.
The wind power
during the mth decomposition of SVMD is divided into two parts: the mth mode
and the residual signal
, where
includes the undecomposed part of SVMD
and the sum of modes from the 1st to the
th. The formula is as follows:
During the SVMD decomposition process, each mode should remain compact around its central frequency, while minimizing mode aliasing between
and
. The constraint conditions to meet this requirement are as follows:
The establishment of the Lagrange function ensures the algorithm’s robustness against interference and the fidelity of signal decomposition, which includes a combination of the quadratic penalty term
and the Lagrange multiplier
. The formulation is as follows:
SVMD transforms an m-dimensional problem into m-one-dimensional optimization problems, thereby reducing the number of iterations and saving time.
3.2. Variational Modal Decomposition
Although the successive variational mode decomposition (SVMD) achieves better decomposition results, each modal power frequency range is relatively wide, which does not meet the requirements for grid connection power. In contrast, the variational mode decomposition (VMD) generates modal combinations with frequencies below
, from which modes that satisfy grid connection standards are selected for integration into the grid into the grid.
where k represents the number of decomposition modes;
denotes the sum of all mode functions;
represents the set of their center frequencies; denotes the derivative concerning time;
is the dirichlet distribution function; * is the convolution operator;
denotes the squared gradient norm;
is the original signal to be decomposed.
By introducing a secondary penalty factor
and a lagrange multiplier
Equation (
17) is transformed into an equivalent unconstrained variational problem, which is then solved using the alternating direction method of multipliers to obtain the optimal solution. The expression is as follows:
where n represents the number of iterations;
represents the frequency domain of the kth modal component after updating;
denotes the updated frequency of the kth modal component;
is the step size, with
.
3.3. Principles of the Secretary Bird Optimization Algorithm
The Secretary Bird Optimization Algorithm (SBOA), introduced in 2024, is a novel swarm optimization technique that models the hunting and escaping behaviors of secretary birds in two distinct stages. During these stages, each member of the secretary bird group is updated accordingly. The hunting behavior is generally divided into three processes: searching for prey, attacking prey, and consuming prey. Meanwhile, escaping behavior is classified into two types: environmental camouflage and rapid movement, such as flying or running swiftly.
The first stage involves the secretary bird’s hunting strategy (exploration phase), where the hunting process is divided into three equal time intervals. This approach enhances the algorithm’s diversity and global search ability. The position update formula for this first stage is provided below:
where j represents the dimension of the variable; X denotes the positions of the secretary bird group;
indicates the position of the ith secretary bird;
represents the value of a variable for the ith secretary bird in the jth dimension;
denotes the new position of the ith secretary bird in the jth dimension during the first stage;
and
are random candidate solutions during the iteration;
is the best historical position of the secretary bird;
represents an array with dimensions
randomly generated in the interval [0,1];
represents the objective function value obtained by the ith secretary bird, and
represents the new objective function value obtained by the ith secretary bird; t and T represent the current iteration count and the maximum iteration count, respectively; RB is a
dimensional array randomly generated from the standard normal distribution; RL indicates the Levy flight strategy, where
and
;
and
are random numbers within the interval [0,1];
denotes the gamma function.
The second stage is the secretary bird’s escaping strategy (exploitation phase), where both escaping strategies can be represented by Equation (
25). The position update formula for the second stage is shown below:
where
represents the new position of the ith secretary bird in the jth dimension during the second stage;
represents the new objective function value obtained by the ith secretary bird during the second stage;
denotes an array of dimension
randomly generated from a normal distribution;
represents the random candidate solution for the current iteration; K denotes a random value of either 1 or 2;
is a random number generated between 0 and 1.
3.3.1. SBOA-Optimized VMD and SVMD Algorithm
When the SBOA algorithm searches for the optimal parameters for SVMD and VMD decomposition, it is necessary to define a fitness function to evaluate whether the selected parameters are optimal. The quality of the chosen fitness function significantly impacts the effectiveness of the SBOA in parameter selection. The average envelope entropy can effectively evaluate the quality of decomposition, filter useful modes, and capture the nonlinear characteristics of the signal, thereby helping to improve the decomposition performance of the wind power signal. The calculation method for average envelope entropy is as follows:
where
and
represent the optimal combination;
is the envelope entropy of each modal component after Hilbert demodulation; i denotes the number of sampling points;
is the normalized form of
;
represents the envelope signal.
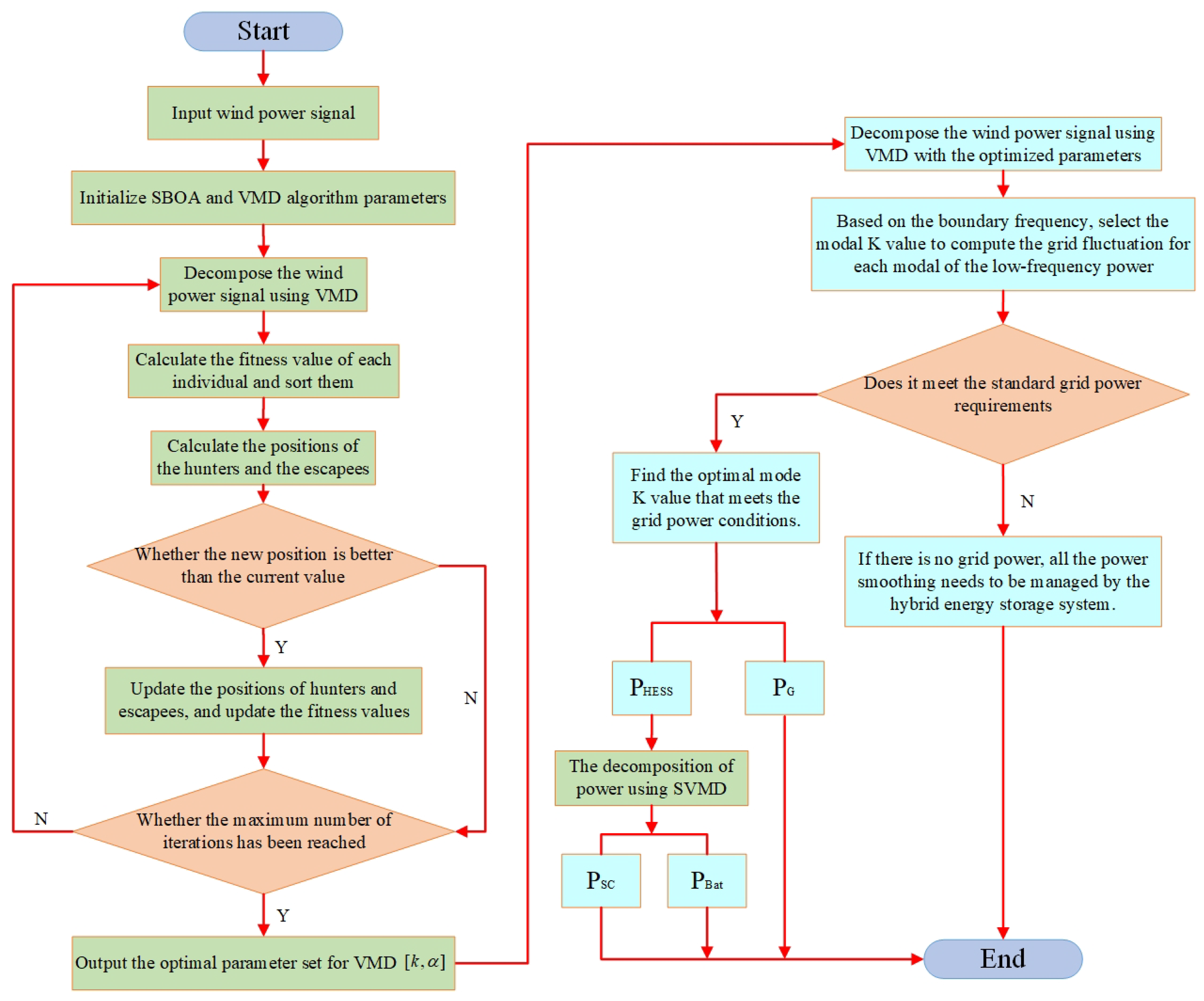
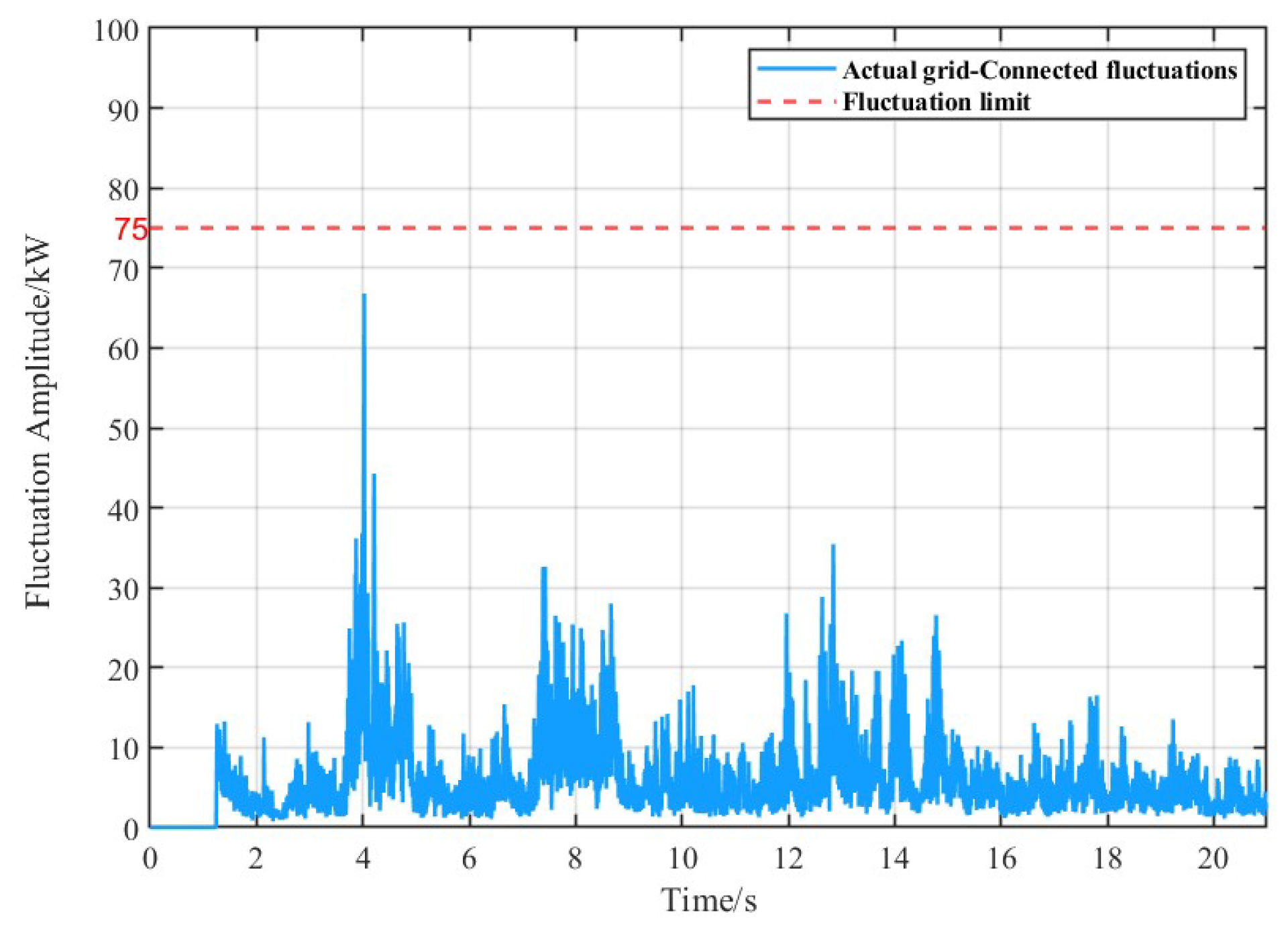
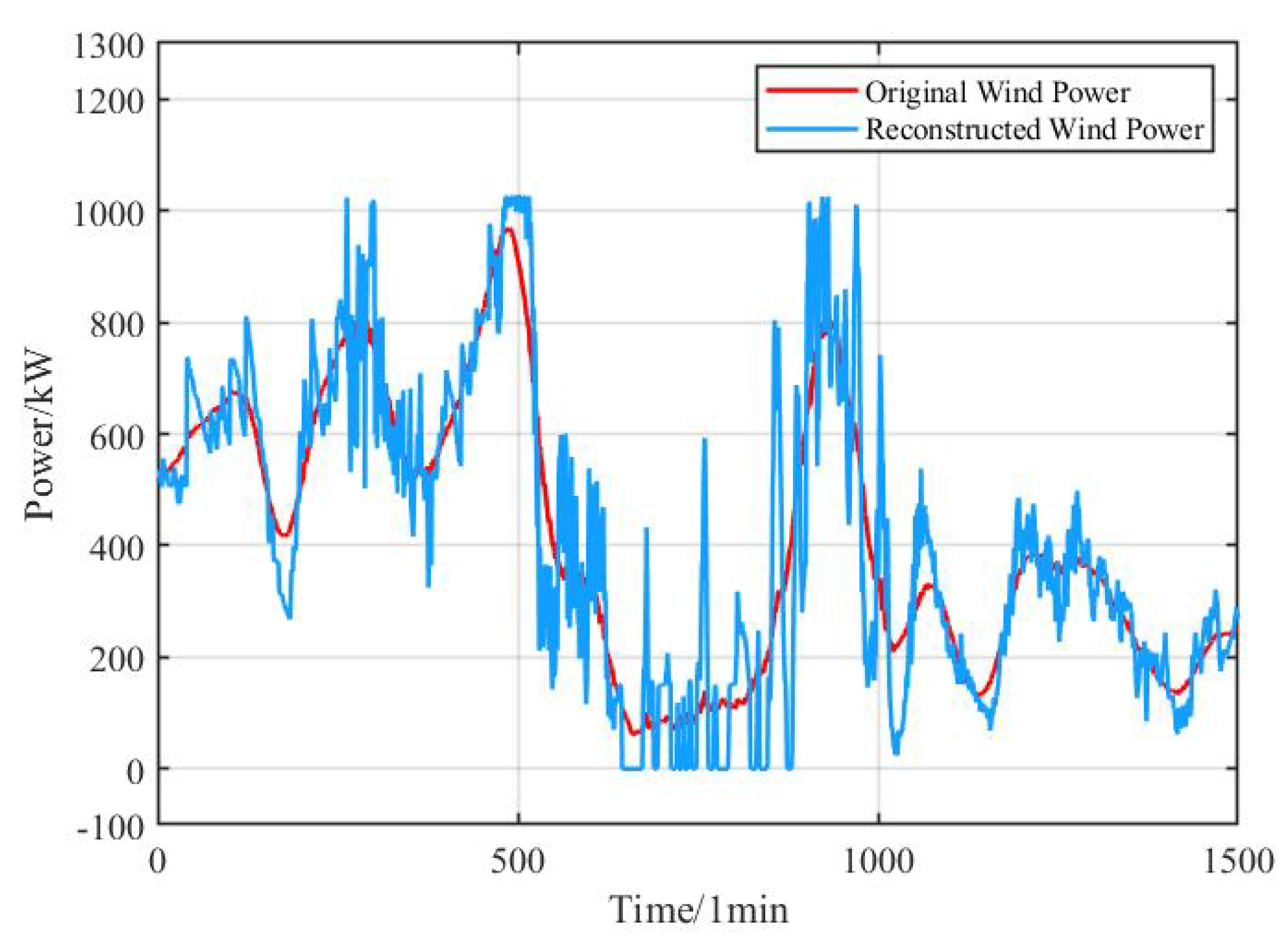
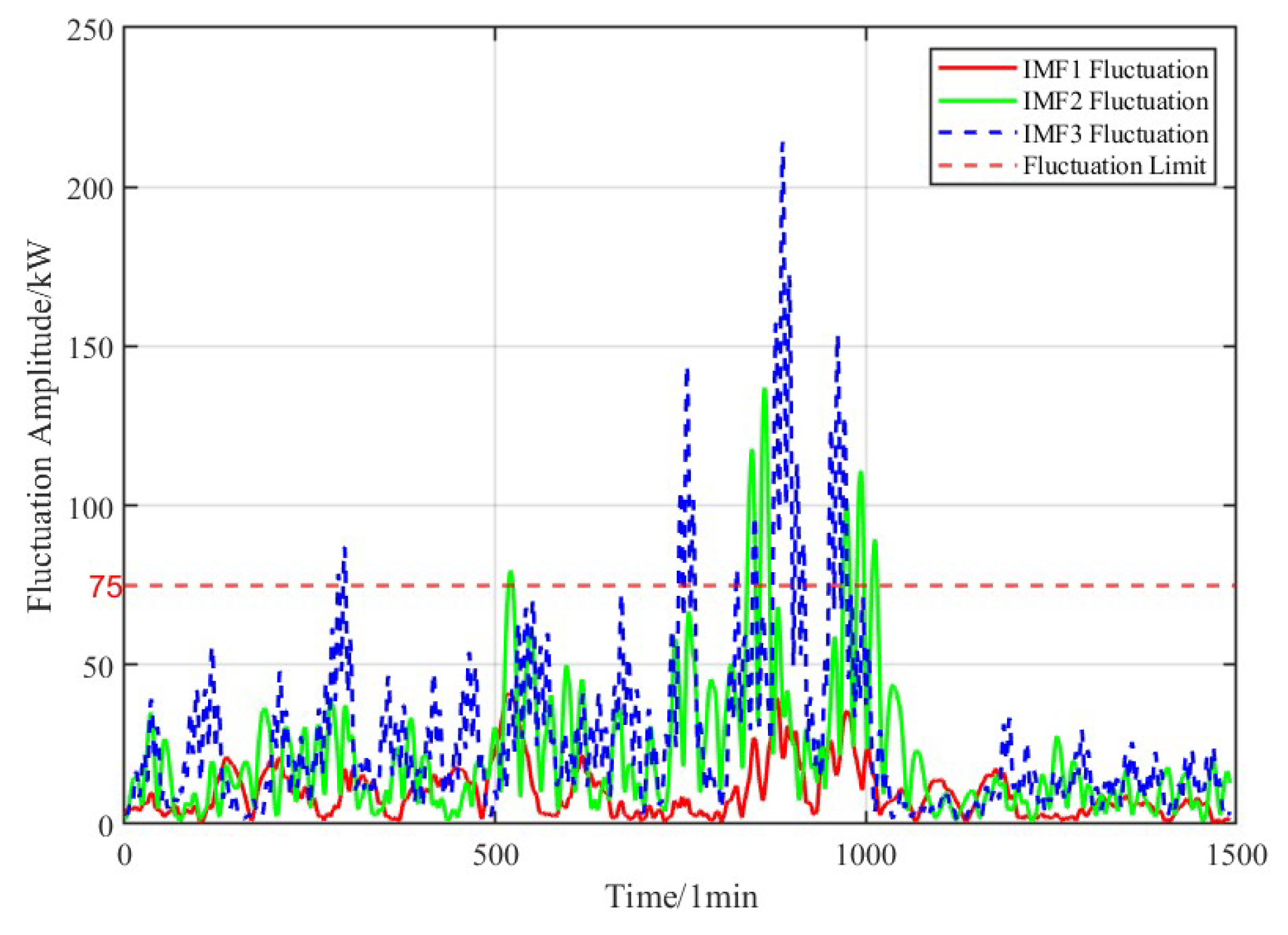
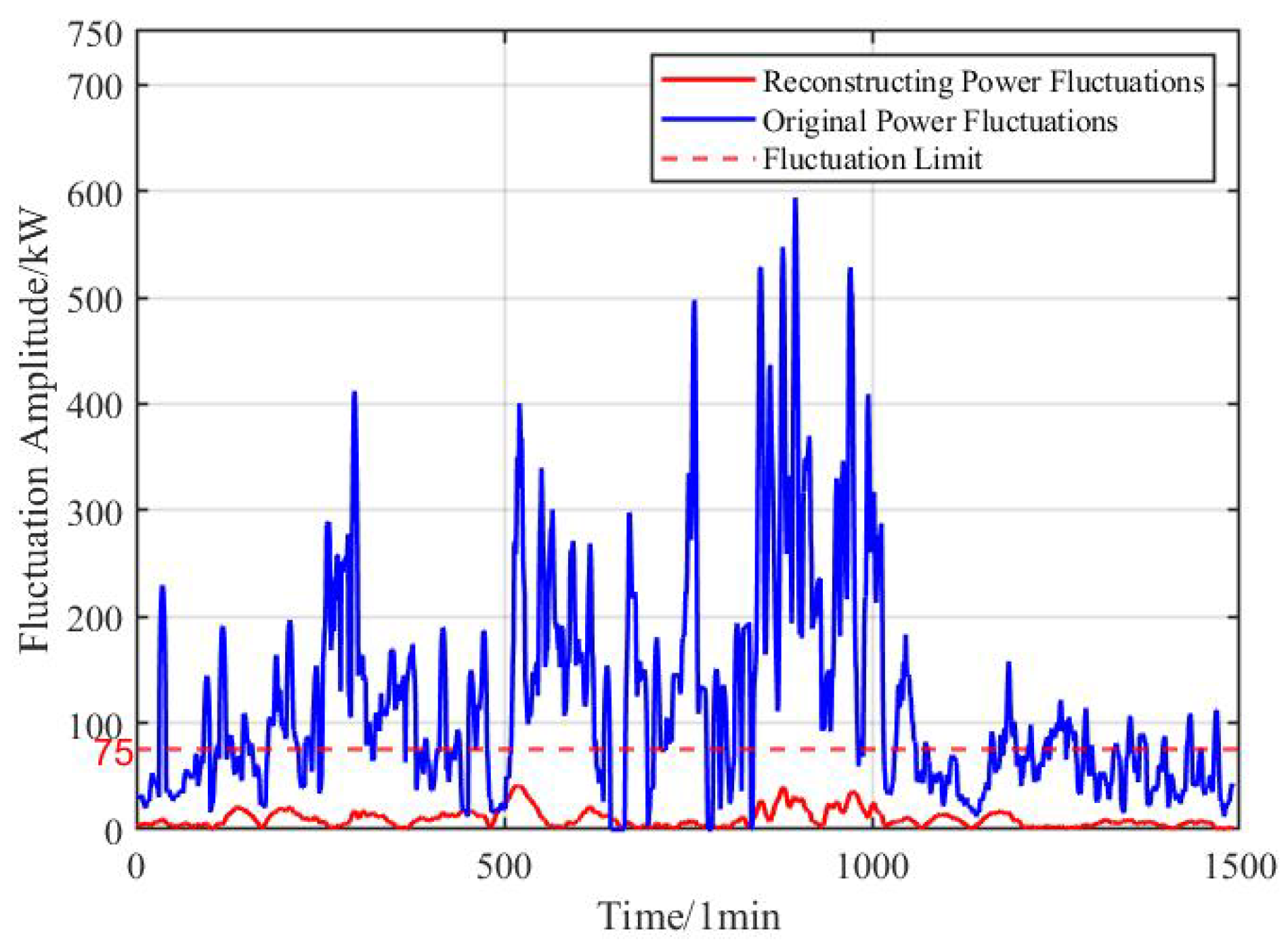
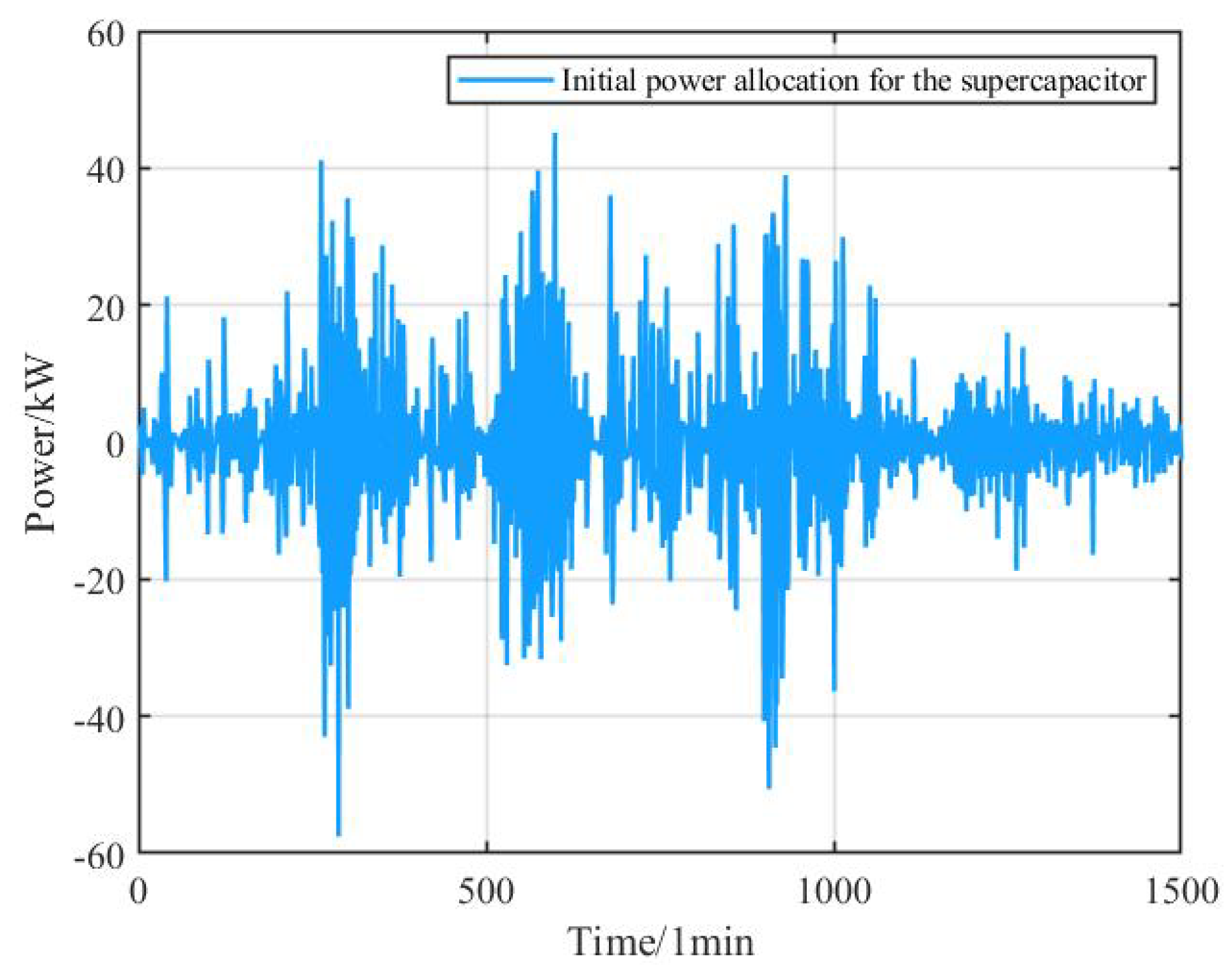
This study selects the average envelope entropy as the fitness function, with the minimum value of the average envelope entropy as the optimization objective. This approach results in obtaining the optimal parameters for as well as the maximum parameter . Based on the optimal parameters, the original signal is decomposed, with the boundary frequency for the energy storage units set at . This meets the requirement that the 10-minute grid-connected fluctuation amount is typically to of the installed wind power capacity. The flowchart for the initial power distribution strategy of wind power is shown in the figure below:
Figure 2.
Flowchart of the initial power allocation using VMD and SVMD.
Figure 2.
Flowchart of the initial power allocation using VMD and SVMD.
3.4. Hybrid Energy Storage Multi-Fuzzy Control Power Secondary Distribution Strategy
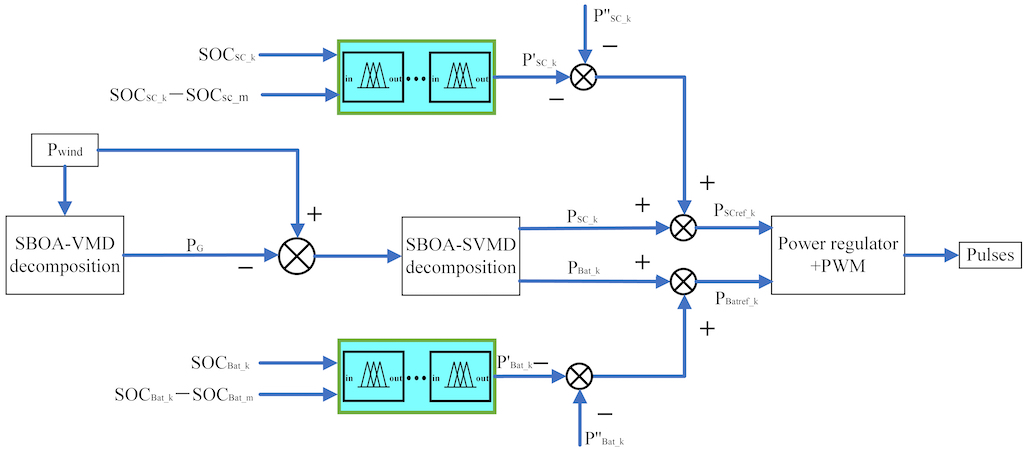
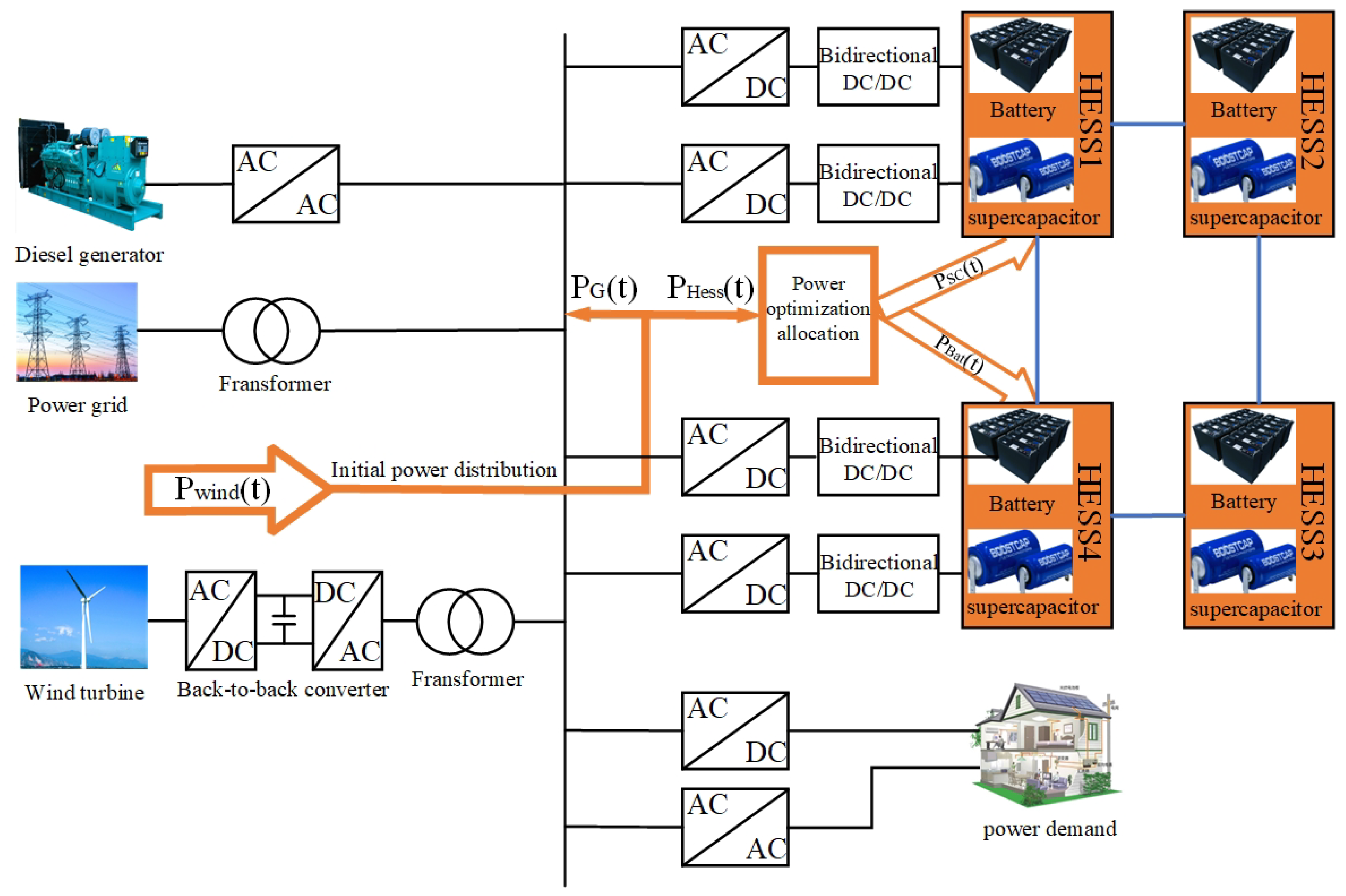
Due to differences in installed capacity, aging progress, and manufacturing processes, the initial state of charge (SOC) and capacity of hybrid energy storage systems (HESS) often vary from one another. If the discharge rate of the hybrid energy storage system (HESS) varies during the discharge process, HESS units with lower states of charge (SOC) will complete their discharge first. This inconsistency can reduce the capacity utilization and lifespan of the HESS. Therefore, balancing the state of charge (SOC) of a non-isolated hybrid energy storage system (HESS) is crucial. In the secondary power distribution process, HESS units with higher SOC will output more power or absorb less, while those with lower SOC will absorb more power or output less. This approach ensures that the HESS operates within its normal working range. The control structure diagram is shown in
Figure 3.
Figure 4,
represents the wind power signal;
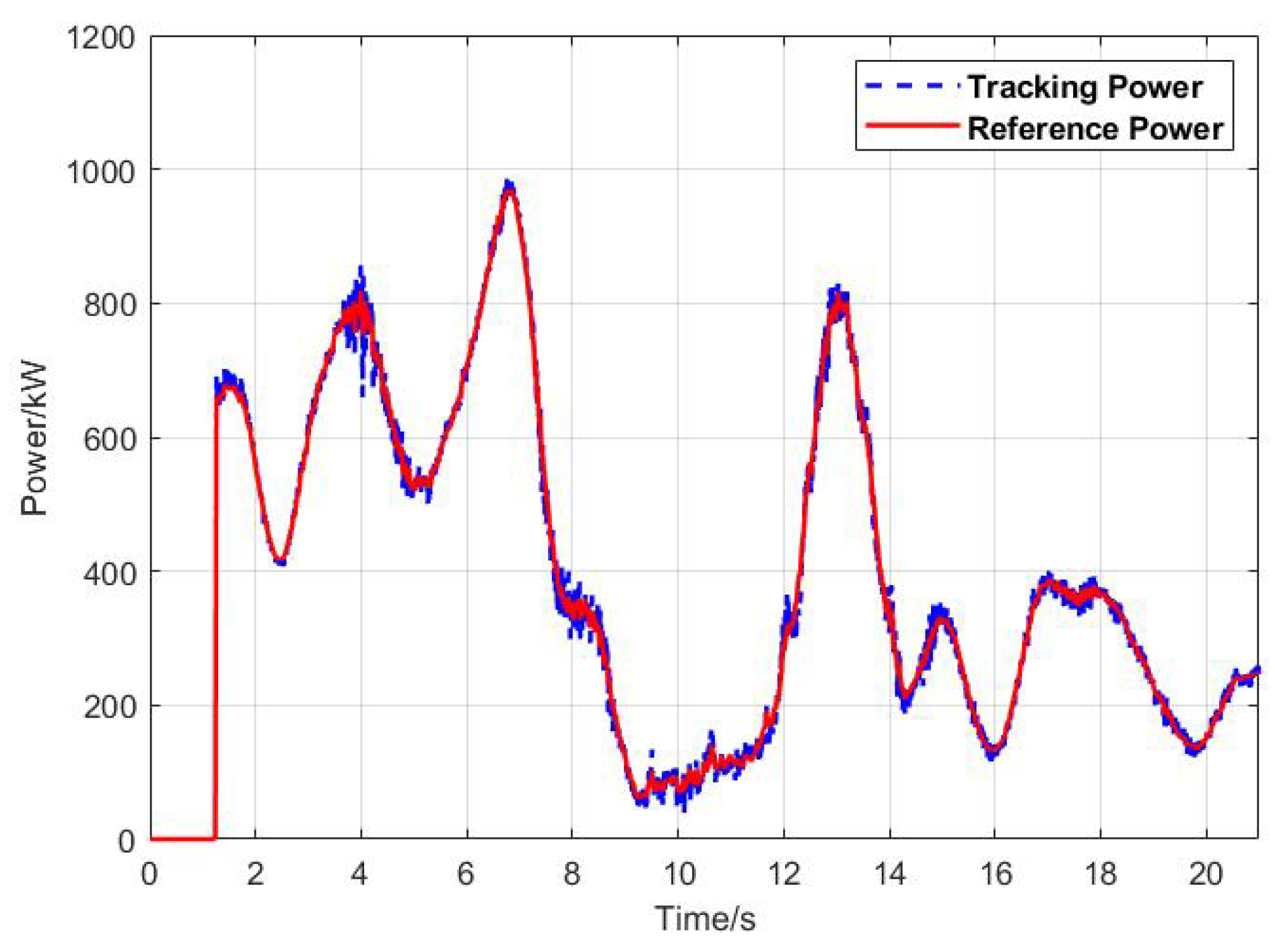
denotes the grid-connected power;
and
indicate the SOC states of the kth supercapacitor and battery, respectively;
and
represent the average SOC of the supercapacitor and battery group;
and
denote the smoothing power of the kth supercapacitor and battery;
and
illustrate the power adjustment by the fuzzy control for the supercapacitor and its actual power;
and
depict the power adjustment by the fuzzy control for the battery and its actual power;
and
represent the reference power of the kth supercapacitor and battery, respectively. The power regulator and PWM controller generate pulse signals to control the three-phase inverter, which regulates the power output of the energy storage units. Each energy storage unit is analogous to an individual agent, which communicates through equations (32) and (33) to obtain the global average state of charge (SOC).
where k represents the number of iterations;
denotes the initial state of charge (SOC) for the ith agent, with
and
;
refers to the ith energy storage unit agent; and
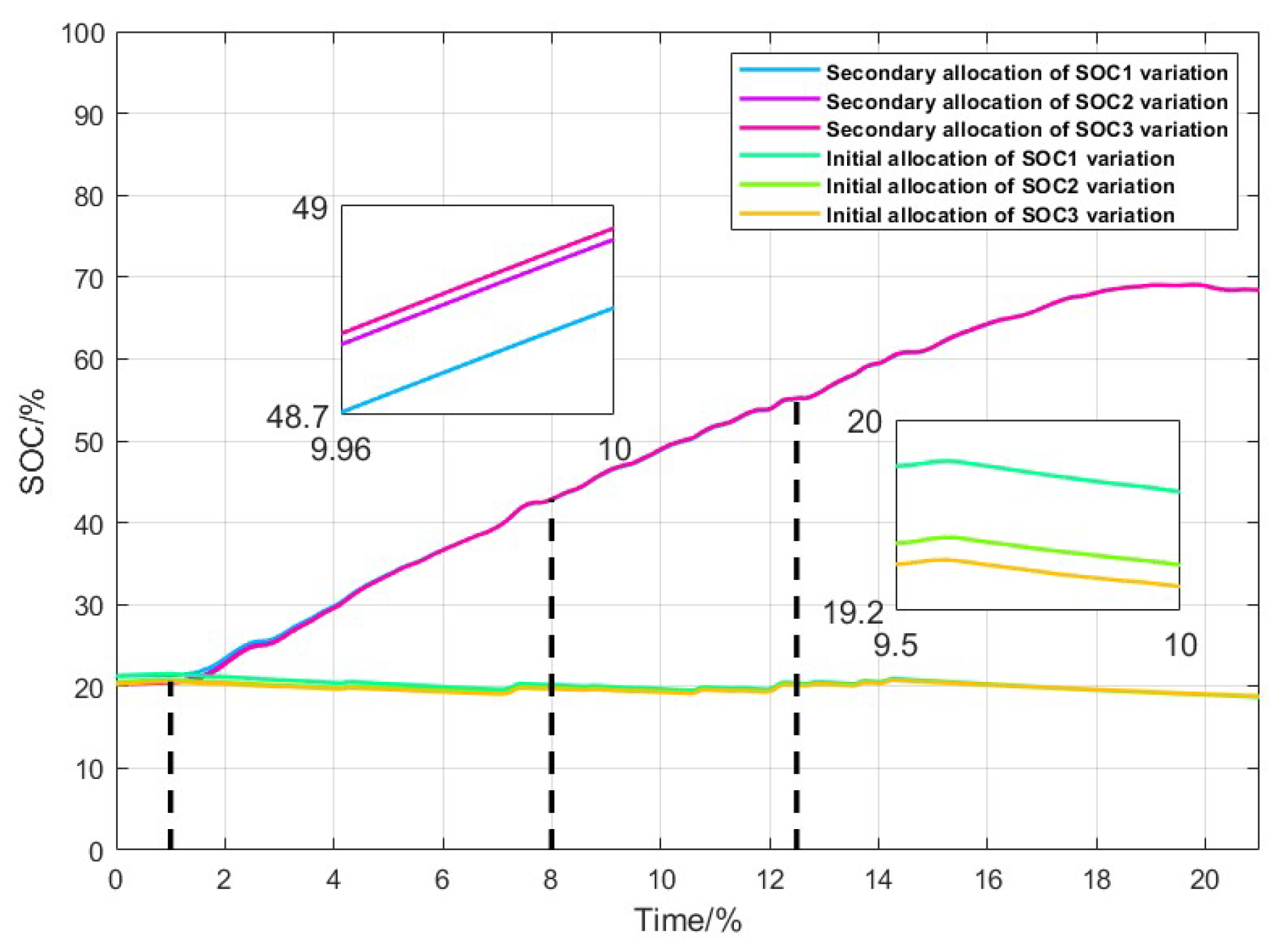
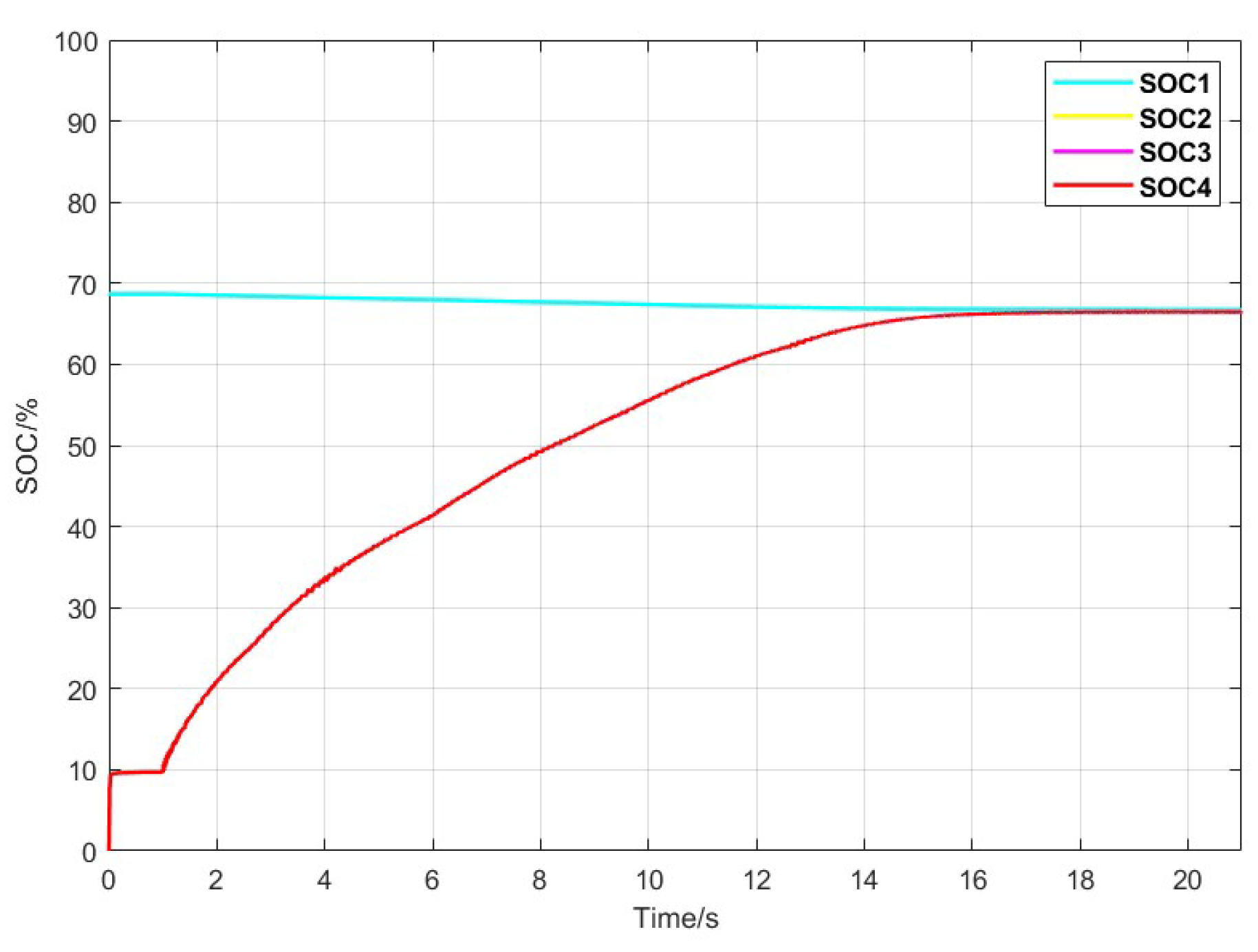
indicates the cumulative variable between the ith agent and the jth agent. If an energy storage unit leaves the system or if the communication within the storage units changes, the new system will still converge to the average value of the current number of energy storage units. This algorithm distributes the leader’s role evenly among all energy storage units, ensuring that the algorithm does not fail due to the loss of a single energy storage unit. Ultimately, the energy storage system achieves the collective average state of charge (SOC) of the storage units.
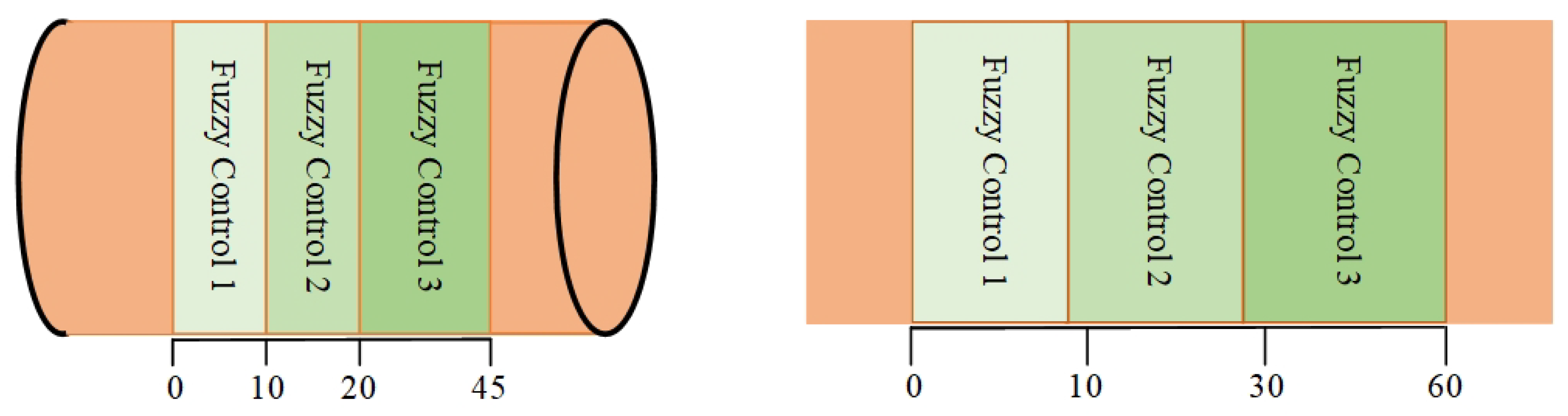
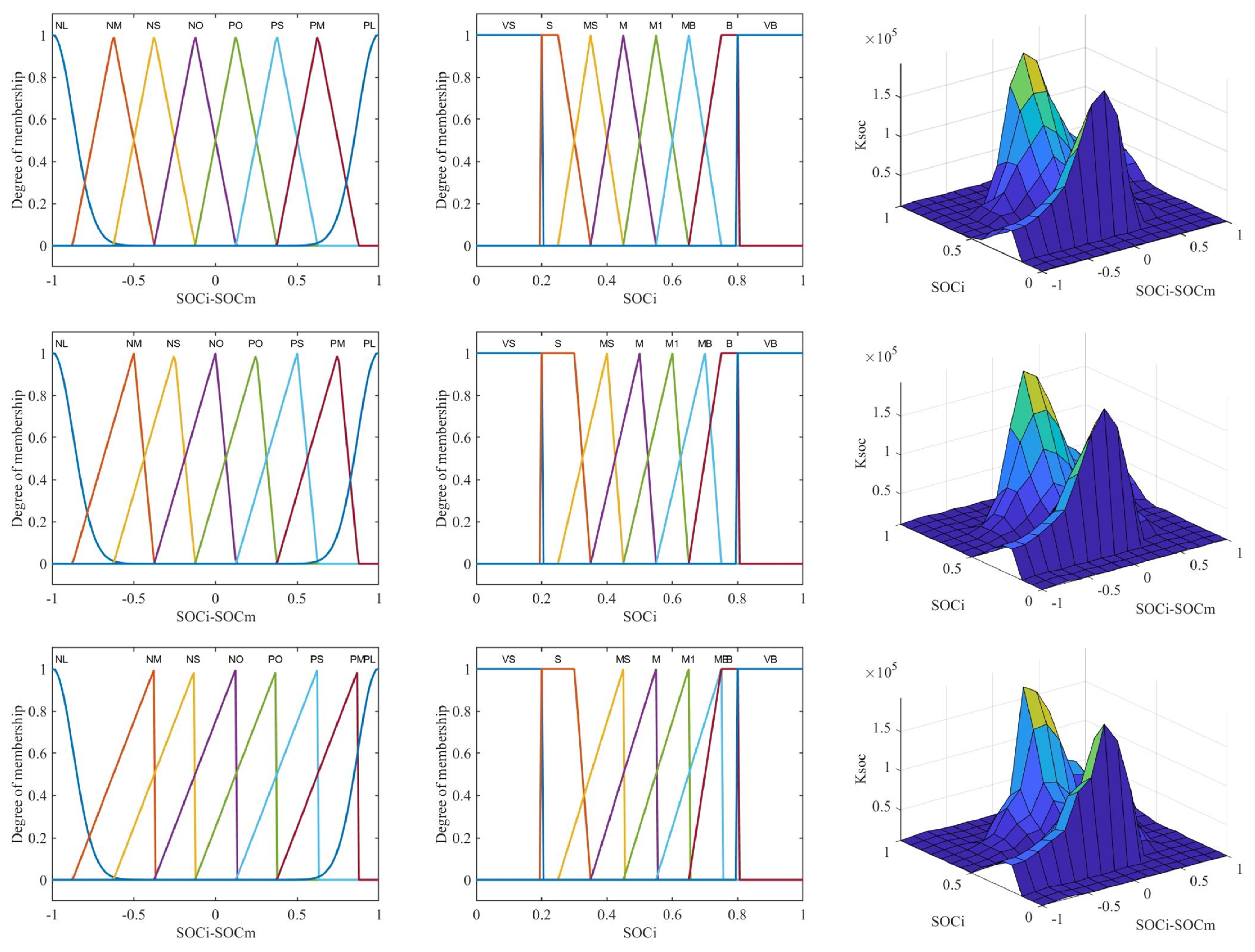
Figure 3 shows multi-fuzzy controllers in the secondary distribution of the power, which include three fuzzy controllers with three dual input single outputs. Due to SOC deviations, it is necessary to design a fuzzy control system for the hybrid energy storage system. The inputs for the fuzzy controller are
and
, where the basic domain of
is
, The fuzzy control set is
, representing Very Small, Small, Moderately Small, Medium, Medium 1, Moderately Big, Big, Very Big; The deviation range of
is
, and after multiplying by a certain scaling factor, the basic domain becomes
; The fuzzy set is
, representing Negative Large, Negative Medium, Negative Small, Negative Zero, Positive Zero, Positive Small, Positive Medium, Positive Large. The output includes power correction coefficients
and
. When the deviation
is very small, the correction coefficient needs to be sufficiently large to be effective. Therefore, after multiplying by a scaling factor, the basic domain is
, and the fuzzy set is
. Each controller follows the same set of fuzzy control rules, as shown in
Table 1.
To illustrate,
Figure 5 shows the three-dimensional surface plots of the input membership functions and the relationships between inputs and outputs for the three fuzzy controllers, using the multi-fuzzy control optimization of batteries as an example.
In the design of multi-fuzzy controllers, appropriate fuzzy controllers are selected for each interval based on the deviation, achieving dynamic partition control of the SOC for the hybrid energy storage system. When the slope of the membership function in the fuzzy controller is set higher, the system will make adjustments in response to slight changes in the input variables. When the slope of the membership function in the fuzzy controller is set to be more gradual, the system will adjust in response to a wider range of changes in the input variables.
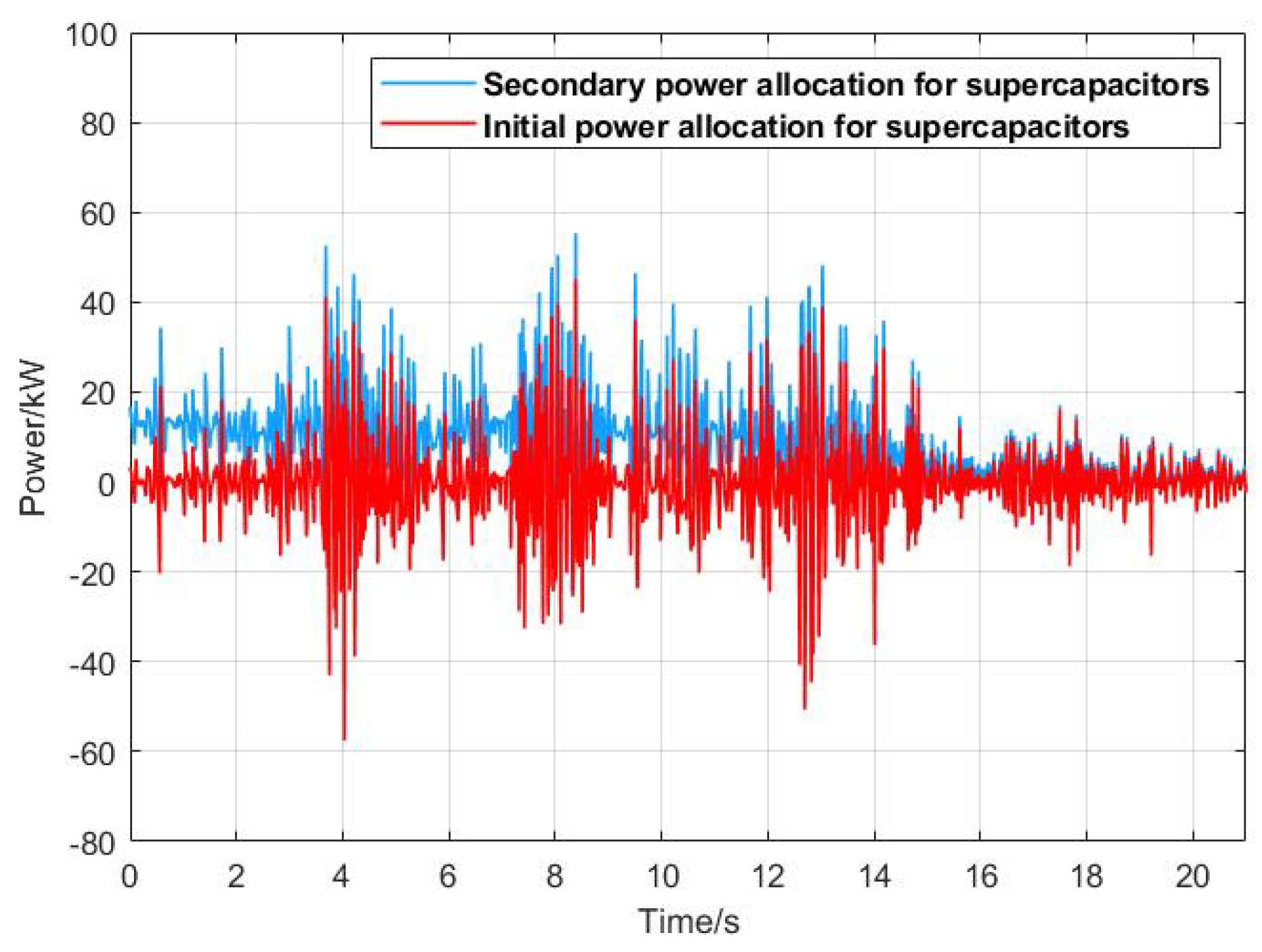
The initial wind power allocation strategy only considers frequency characteristics and does not take into account the state of charge (SOC) of supercapacitors and batteries, nor the impact of changes in their SOC on power distribution. Considering that the difference
includes the impact of changes in the state of charge (SOC), a global variable
is introduced. his approach ensures that all energy storage units are treated equally in the control strategy, reducing the influence of a single leader’s SOC and aligning them with the global variable
. Ultimately, this leads to a convergence towards the average SOC of all units. By taking these effects into account, the power of the hybrid energy storage system is adjusted using multi-fuzzy control. Partitioning is conducted based on the
deviation to adjust the power of the hybrid energy storage system. The specific correction principles are as follows: When the battery and supercapacitor operate within their normal SOC ranges, inaccuracies in the initial power allocation cause deviations between each battery and supercapacitor’s SOC and their average SOC. The deviation range is
. When the deviation is within the range
, it indicates a significant SOC difference between them. To quickly align with the average SOC, the rules of Fuzzy Controller 3 are executed. When the deviation is within the range
, it indicates a smaller SOC difference between them, suggesting that the system has moved out of the SOC danger zone. To follow the average SOC faster, the rules of Fuzzy Controller 2 are executed. When the deviation is in the range
, it indicates that the SOC deviation between energy storage units is minimal, and the SOC of the storage units is nearly balanced while being out of the danger zone. In this case, the rules of Fuzzy Control 1 are applied. This approach ensures that the energy storage system continuously tracks the average SOC, minimizes the depth of charging/discharging, and reduces unnecessary charging/discharging events. It prevents any single battery from excessive charging or discharging, which could disrupt system stability and reduce the battery’s lifespan. The goal is to prevent state-of-charge (SOC) from exceeding its limits while dynamically adjusting it to keep it within a reasonable range.In
Figure 5,
and
represent the actual power consumption of the supercapacitor and battery, respectively, while the corrected powers are denoted by
and
.
Figure 5.
Partition control diagram of battery and supercapacitor SOC deviations from the average SOC
Figure 5.
Partition control diagram of battery and supercapacitor SOC deviations from the average SOC
Author Contributions
Conceptualization, R.H. and Jq.L.; methodology, R.H. and Jq.L.; software, R.H. and Jq.L.; validation, R.H., J.Z., Jq.L., Jh.L. and W.C.; formal analysis, Jq.L., Jh.L. and W.C.; investigation, R.H. and J.Z.; resources, R.H. and J.Z.; writing—original draft preparation, R.H., Jq.L.; writing—review and editing, R.H., J.Z. and Jq.L.; visualization, Jq.L., Jh.L. and W.C.; supervision, R.H. and J.Z.; project administration, R.H.; funding acquisition, R.H. and J.Z.. All authors have read and agreed to the published version of the manuscript.